Turbulence radiation interaction in channel flow with various optical depths

Abstract

The present work consists of an investigation of the turbulence radiation interaction (TRI) in a radiative turbulent channel flow of grey gas bounded by isothermal hot and cold walls. The optical thickness $\unicode[STIX]{x1D70F}$ of the channel is varied from 0.1 to 10 to observe different regimes of TRI. A high-resolution finite volume method for radiative heat transfer is employed and coupled with the direct numerical simulation (DNS) of the flow. The resulting effects of TRI on temperature statistics are strongly dependent on the considered optical depth. In particular, the contrasting role of emission and absorption is highlighted. For a low optical thickness the effect of radiative fluctuations on temperature statistics is low and causes the reduction of temperature variance through the dissipating action of emission. On the other hand, while increasing optical thickness to relatively high levels, the dissipation of temperature variance is balanced, at low wavenumbers in the turbulence spectrum, through the preferential action of absorption, which increases the large-scale temperature fluctuations. A significant rise in the effect of radiation on the temperature variance can be observed as a consequence of the reduction of radiative heat transfer length scales.

1 Introduction

When dealing with high-temperature applications, thermal radiation plays an important role in the heat transfer process. For this reason, great attention must be paid to participating media that are able to emit and absorb radiation. Many theoretical analyses and experimental investigations have shown the occurrence of interactions between radiation quantities and turbulence, mainly due to the nonlinearity between radiative heat transfer and temperature (Coelho 2012). These interactions can be of interest in a wide range of applications that include radiative and convective heat transfer, from turbulent combustion and flames (Viskanta & Mengüç 1987), to harvesting solar energy for solar thermal power applications (Pourasani & Mani 2017). Turbulence radiation interaction (TRI) can be classified into two main phenomena, namely: (1) the appearance of a fluctuating radiative field produced by turbulent motion and (2) the modification of turbulence structures due to the action of radiative heat transfer.

When regarding the first effect, a large amount of open literature is available, mainly because of its importance in combustion science. In particular Coelho, Teerling & Roekaerts (2003), Tesse, Dupoirieux & Taine (2004), Coelho (2007), Deshmukh, Modest & Haworth (2008), Gupta, Modest & Haworth (2009) and Roger, Coelho & da Silva (2011), have studied the influence of turbulence on thermal radiation for non-reactive and reactive flows in different conditions. The common conclusion is that the influence of fluctuations of the radiative field on the mean radiative power are mainly negligible for non-reactive flows, whereas they largely affect reactive flows, in which the high-temperature gradients produce large temperature fluctuations. This results in a highly fluctuating radiative field that can increase the medium transmissivity and the heat losses by up to $30\,\%$ .

On the other hand, the effect of radiative heat transfer on the modification of the turbulence field has received much less attention. The first theoretical studies have been performed in the field of atmospheric science, since infrared radiation plays a large role in heating and cooling the atmosphere, due to the presence of highly absorbing H $_{2}$ O and CO $_{2}$ . Townsend (1958), in his pioneering work, observed the influence of TRI on the temperature variance in a turbulent flow. He identified the role of radiation in the destruction of temperature fluctuations and derived an expression for the radiative dissipation. Coantic & Simonin (1984) investigated the impact of radiative cooling on the planetary boundary layer. They noticed that the radiative dissipation is proportional to the ratio of the Planck absorption coefficient $\unicode[STIX]{x1D6FD}_{P}$ to the Kolmogorov wavenumber $k_{D}$ . Thus, it decreases for highly turbulent flows and increases for highly absorbing flows. The impact of radiation on turbulent atmospheres was further analysed by Schertzer & Simonin (1982) using the assumption of homogeneous isotropic turbulence. They focused on the spectral budget of the temperature variance and defined the relative spectral damping rate, which is spectral counterpart of the radiative dissipation introduced by Townsend (1958). They observed that for weak radiative effects, radiative cooling has only a slight perturbation on the turbulent temperature spectra, while for large radiative effects the turbulent temperature spectrum is strongly modified. The theory developed in the field of atmospheric science has been extended by Soufiani (1991) to high-temperature radiating gases in homogeneous isotropic turbulence. Investigating the spectral radiative dissipation term in H $_{2}$ O and CO $_{2}$ , he concluded that, at high temperatures, radiation modifies the turbulent temperature spectrum mainly in the high-frequency region.

Figure 1. Geometry for channel flow, wall bounded in the $y$ direction and periodic in the homogeneous directions.

More recently, detailed numerical studies to investigate the effect of the TRI on turbulence have been performed with the aid of large-eddy simulation (LES) and direct numerical simulation (DNS). Sakurai et al. (2010) investigated the effect of TRI on buoyant turbulent motions in a horizontal plane channel flow using the optically thin approximation. The results showed that radiation causes a breakup of the organized large-scale vortices, resulting in a reduction of the turbulent heat flux with the increase of the optical thickness. They explained this decrease with the modification of mean gradients rather than through the direct dissipative action of radiation. Zhang et al. (2013) performed a DNS of a channel flow with a low-Mach-number approximation. They studied the role of gas-to-gas and gas-to-wall radiative heat transfer in the modification of the mean temperature profile with an optimized emission-based reciprocity Monte Carlo method. Vicquelin et al. (2014) calculated the radiative term in the enthalpy variance and the turbulent heat flux transport equation. Based on their results they proposed a ‘radiation scaling’ to scale all radiation-affected quantities. LES of a supersonic channel and pipe flow in conjunction with the discrete ordinates method (DOM) for radiative transport was performed (Ghosh et al. 2011; Ghosh, Friedrich & Stemmer 2014) to study the influence of TRI in supersonic flows. TRI, in this case, acted mainly on the mean temperature and density, modifying the work done by the mean flow and pressure distribution. The effect of radiative dissipation was not observed. Finally, Ghosh & Friedrich (2015) investigated the influence of radiative heat transfer in inert and reactive mixing layers with coupled LES and DOM. Again, the direct influence of radiation on the temperature variance was found to be negligible when compared to the other budgets of temperature variance.

While some effort has been spent in the theoretical analysis of the variation of TRI with optical depth, all the numerical investigations have been performed with low to intermediate values of $\unicode[STIX]{x1D70F}$ . Furthermore, theoretical investigations included only homogeneous turbulence. Therefore, a clear identification of the effect of TRI within inhomogeneous turbulence for different optical depths is still lacking. We therefore investigate TRI in a fully developed channel flow for different optical thicknesses (which can be interpreted as the ratio of geometric length scales, characteristic of the large eddies, to radiative length scales). A particular emphasis will be given to high optical thickness. We will use the incompressible assumption to isolate the effect of radiation on temperature variance. We will analyse the results and substantiate the findings by comparison with the theory produced in the field of atmospheric science. In particular, the effect of radiation on the turbulent temperature spectra will be examined. In doing so, the contrasting effects of radiative emission and absorption will be independently treated to provide a meaningful analysis.

2 Numerical details

Turbulence radiation interactions are studied by means of a fully coupled DNS and radiation finite volume method (FVM) in a fully developed turbulent channel flow. The domain is periodic in the streamwise and spanwise directions and bounded by isothermal parallel planes in the wall-normal direction. $x$ , $y$ and $z$ represent streamwise, wall-normal and spanwise direction components, with corresponding velocity components $u$ , $v$ and $w$ . A representation of the geometry is shown in figure 1.

In order to clearly distinguish the effect of a varying optical thickness, the flow has been considered non-scattering and grey (absorption coefficient independent of wavelength). Therefore, only total quantities (integrated in wavelength) need to be discussed. In addition, only one-way coupling between energy and momentum has been considered, to simplify the analysis (i.e. no influence of temperature in the momentum equation). The scaled governing equations for an absorbing–emitting incompressible flow read

(2.1) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{i}}=0, & \displaystyle\end{eqnarray}$$

(2.2) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}t}+u_{j}\frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}=-\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}x_{i}}+\frac{1}{Re}\frac{\unicode[STIX]{x2202}^{2}u_{i}}{\unicode[STIX]{x2202}{x_{j}}^{2}}, & \displaystyle\end{eqnarray}$$

(2.3) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}{\unicode[STIX]{x2202}t}+u_{j}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}{\unicode[STIX]{x2202}x_{j}}=\frac{1}{RePr}\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D703}}{\unicode[STIX]{x2202}{x_{j}}^{2}}-\frac{Q_{r}}{RePrPl}, & \displaystyle\end{eqnarray}$$

(2.4) $$\begin{eqnarray}\displaystyle & \displaystyle s_{j}\frac{\unicode[STIX]{x2202}I}{\unicode[STIX]{x2202}x_{j}}=\unicode[STIX]{x1D70F}(I_{b}-I). & \displaystyle\end{eqnarray}$$

The coupling between energy equation and the absorbing–emitting radiative transfer equation (RTE) (2.4), is via the non-dimensional divergence of the radiative heat flux $Q_{r}=\unicode[STIX]{x2202}q_{rj}/\unicode[STIX]{x2202}x_{j}$ calculated as

(2.5) $$\begin{eqnarray}Q_{r}=\frac{\unicode[STIX]{x2202}q_{rj}}{\unicode[STIX]{x2202}x_{j}}=\unicode[STIX]{x1D70F}\left(\underbrace{4I_{b}}_{E_{m}}-\underbrace{\frac{1}{\unicode[STIX]{x03C0}}\int _{4\unicode[STIX]{x03C0}}I\,\text{d}\unicode[STIX]{x1D6FA}}_{G}\right).\end{eqnarray}$$

$E_{m}$ is the radiative emission and $G$ is the incident radiation. Non-dimensional variables $\boldsymbol{x},t,\boldsymbol{s},\boldsymbol{u},p,\unicode[STIX]{x1D703},I_{b},I,\boldsymbol{q}_{r}$ are spatial coordinate vector, time, propagation direction vector, velocity vector, pressure, temperature, black-body intensity, intensity and radiative heat flux vector, defined as follows:

(2.6) $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \boldsymbol{x}=\frac{\boldsymbol{x}^{\ast }}{\unicode[STIX]{x1D6FF}^{\ast }},\quad t=t^{\ast }\frac{U_{b}^{\ast }}{\unicode[STIX]{x1D6FF}^{\ast }},\quad \boldsymbol{u}=\frac{\boldsymbol{u}^{\ast }}{U_{b}^{\ast }},\quad p=\frac{p^{\ast }}{\unicode[STIX]{x1D70C}{U_{b}^{\ast }}^{2}},\quad \unicode[STIX]{x1D703}=\frac{T^{\ast }-T_{c}^{\ast }}{T_{h}^{\ast }-T_{c}^{\ast }},\\ \displaystyle I_{b}=\left(\frac{\unicode[STIX]{x1D703}}{T_{0}}+1\right)^{4},\quad I=\unicode[STIX]{x03C0}\frac{I^{\ast }}{\unicode[STIX]{x1D70E}{T_{c}^{\ast }}^{4}},\quad \boldsymbol{q}_{r}=\frac{1}{\unicode[STIX]{x03C0}}\int _{4\unicode[STIX]{x03C0}}I\boldsymbol{s}\,\text{d}\unicode[STIX]{x1D6FA},\end{array}\right\}\end{eqnarray}$$

where $U_{b}^{\ast }$ is the bulk velocity, $\unicode[STIX]{x1D6FF}^{\ast }$ is the half-channel height, while $T^{\ast }$ is the dimensional temperature and $T_{h}^{\ast }$ and $T_{c}^{\ast }$ are the temperature of the hot and cold wall, respectively. The non-dimensional parameters are:

1. (i) Reynolds number $Re=U_{b}^{\ast }\unicode[STIX]{x1D6FF}^{\ast }\unicode[STIX]{x1D70C}^{\ast }/\unicode[STIX]{x1D707}^{\ast }$ ,

2. (ii) Prandtl number $Pr=\unicode[STIX]{x1D707}^{\ast }c_{p}^{\ast }/\unicode[STIX]{x1D706}^{\ast }$ ,

3. (iii) Planck number $Pl=(\unicode[STIX]{x1D706}^{\ast }\unicode[STIX]{x0394}T^{\ast })/(\unicode[STIX]{x1D70E}^{\ast }{T_{c}^{\ast }}^{4}\unicode[STIX]{x1D6FF}^{\ast })$ ,

4. (iv) optical thickness $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D705}^{\ast }\unicode[STIX]{x1D6FF}^{\ast }$ ,

5. (v) temperature ratio $T_{0}=T_{c}^{\ast }/\unicode[STIX]{x0394}T^{\ast }$ ,

where $\unicode[STIX]{x1D70C}^{\ast },\unicode[STIX]{x1D707}^{\ast },c_{p}^{\ast },\unicode[STIX]{x1D706}^{\ast },\unicode[STIX]{x1D70E}^{\ast }$ , $\unicode[STIX]{x1D705}^{\ast }$ and $\unicode[STIX]{x0394}T^{\ast }$ are density, dynamic viscosity, specific heat capacity, thermal conductivity, Stefan–Boltzmann constant, absorption coefficient and temperature difference between hot and cold wall, respectively. The asterisk $^{\ast }$ represents the corresponding dimensional variables, while $\text{d}\unicode[STIX]{x1D6FA}$ is the infinitesimal solid angle. The asterisk will be dropped in the rest of the report as all the results will be presented in terms of non-dimensional variables.

A pressure gradient in the streamwise direction is applied in order to maintain a constant Reynolds number based on bulk velocity. Spectral differentiation with Fourier expansion and periodic boundary conditions is used in the homogeneous directions ( $x$ and $z$ ) with a skew-symmetric formulation of the advection term, while a sixth-order staggered compact finite difference (Lele 1992; Boersma 2011) is used to discretize spatial derivatives in the wall-normal direction. A pressure correction scheme is applied based on the projection method. For the validation of the DNS code, the reader is referred to Patel et al. (2015). The RTE is solved using the finite volume method (FVM) of Chai, Lee & Patankar (1994). A high-resolution bounded scheme for a non-uniform mesh (CLAM scheme) as described in Coelho (2002) is employed for the spatial discretization of the RTE using the deferred correction implementation. Reynolds number, Prandtl number and $T_{0}$ are constant for all the simulations with values of $2900$ , $1$ and $1.5$ , respectively. The Planck number is kept low, with a value of $0.03$ , to ensure a high relevance of radiative heat transfer. The walls are considered to be a black surface with emissivity $\unicode[STIX]{x1D716}_{w}=1$ . The optical thickness varies by two orders of magnitude, being 0.1, 1 and 10. The size of the computational domain in the streamwise and spanwise directions is $4\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FF}$ and $3\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FF}/2$ , respectively. The computational grid is composed of $192\times 168\times 168$ cells in the streamwise, spanwise and wall-normal directions for all cases. The grid resolution is $\unicode[STIX]{x0394}x^{+}=12.1$ , $\unicode[STIX]{x0394}z^{+}=5.2$ and $\unicode[STIX]{x0394}y^{+}=0.85$ and $2.92$ at the wall and in the centre, respectively. This grid is considered fine enough to resolve the velocity field at the current Reynolds number (Kim, Moin & Moser 1987), while temperature spectra that prove the grid adequacy for temperature scales are shown in § 4. The directional dependency of intensity is discretized with the use of an angular grid of $8\times 12$ elements in the polar and azimuthal directions on a unit sphere, respectively, resulting in a set of $96$ independent directions. The results will be analysed by means of Reynolds averaging, where a generic variable $X$ can be decomposed in a sum of a mean component $\overline{X}$ and a fluctuating component $X^{\prime }$ .

3 Mean flow statistics

Before starting the quantitative analysis of the investigated cases, a qualitative view is given by means of instantaneous temperature fluctuation contours. Velocity is not shown, since temperature does not influence the momentum equation. For a detailed description of velocity statistics at the considered Reynolds number, the reader is referred to Kim & Moin (1987) and Kim et al. (1987). Wall-normal planes at $z/\unicode[STIX]{x1D6FF}=3/4\unicode[STIX]{x03C0}$ are shown in figure 2, while figure 3 shows wall-parallel planes at $y/\unicode[STIX]{x1D6FF}=1.4$ . From top to bottom the contours show: no radiation, $\unicode[STIX]{x1D70F}=0.1$ , $\unicode[STIX]{x1D70F}=1$ and $\unicode[STIX]{x1D70F}=10$ . The snapshot contours clearly show the reduction of temperature fluctuations when moving from non-radiative to radiative cases. For a high optical thickness ( $\unicode[STIX]{x1D70F}=10$ ) small-scale temperature fluctuations reduce in comparison with large-scale fluctuations, and a large dissipation of temperature fluctuations near the walls occurs. These features of radiative flows will be explained in more detail in the next sections.

Figure 2. Snapshots of $\unicode[STIX]{x1D703}^{\prime }$ on the wall-normal plane at $z/\unicode[STIX]{x1D6FF}=3/4\unicode[STIX]{x03C0}$ . From (a) to (d): no radiation, $\unicode[STIX]{x1D70F}=0.1$ , $\unicode[STIX]{x1D70F}=1$ , $\unicode[STIX]{x1D70F}=10$ . The red line highlights the position $y/\unicode[STIX]{x1D6FF}=1.4$ .

Figure 3. Snapshots of $\unicode[STIX]{x1D703}^{\prime }$ on the wall-parallel plane at $y/\unicode[STIX]{x1D6FF}=1.4$ . From (a) to (d): no radiation, $\unicode[STIX]{x1D70F}=0.1$ , $\unicode[STIX]{x1D70F}=1$ , $\unicode[STIX]{x1D70F}=10$ .

3.1 Mean profiles

Figure 4(a–d) shows the average profiles of non-dimensional temperature $\overline{\unicode[STIX]{x1D703}}$ , divergence of radiative heat flux $\overline{Q}_{r}$ (the inlay shows a zoom on the $y$ -axis), incident radiation $\overline{G}$ and radiative emission $\overline{E}_{m}$ , respectively. Note that $\overline{Q}_{r}$ represents the combined effect of an emission sink, $\unicode[STIX]{x1D70F}\overline{E}_{m}$ , and an absorption source, $\unicode[STIX]{x1D70F}\overline{G}$ , of energy. Radiative heat transfer has a strong influence on temperature profiles in all three cases. Boundary emissions remain constant as the temperature at the boundary is fixed and $\unicode[STIX]{x1D716}_{w}=1$ (i.e. no reflection and transmission take place).

Figure 4. Averaged profiles, grey solid line: no radiation, dashed line: $\unicode[STIX]{x1D70F}=0.1$ , dashed-dotted line: $\unicode[STIX]{x1D70F}=1$ , black solid line: $\unicode[STIX]{x1D70F}=10$ . (a) Mean temperature; (b) mean radiative heat source (the inlay shows a zoom on the $y$ -axis around $\overline{Q}_{r}=0$ ); (c) mean incident radiation; (d) mean emission.

For a low optical thickness ( $\unicode[STIX]{x1D70F}=0.1$ ), radiative heat transfer causes an increase in bulk temperature and a flattening of the temperature profile in the core of the channel. These results are caused by the long range of radiative heat transfer, which enables a direct heat exchange between the hot and the cold side. Due to the low absorption coefficient, the available energy source, $\unicode[STIX]{x1D70F}\overline{G}$ , as seen in figure 4(c), is fairly homogeneous throughout the channel. On the hot side, as well as in the core of the channel, the temperature gradient reduces due to the increased bulk temperature, while it grows significantly on the cold side for the same reason.

Upon increasing the optical thickness ( $\unicode[STIX]{x1D70F}=1$ ), the length scales of radiative heat transfer reduce due to larger absorption (i.e. intensity beams travel a shorter distance before being absorbed), shifting the radiative energy source, $\unicode[STIX]{x1D70F}\overline{G}$ , towards the hot side of the channel. This shift can be observed in figure 4(c) as the slope of the incident radiation profile steepens. The temperature gradient increases in the channel core, while the gradients near the walls are reduced. A further increase of the optical thickness ( $\unicode[STIX]{x1D70F}=10$ ) causes an additional steepening of the slope of the incident radiation profile, which results in a drastic decrease of the temperature gradient near both walls. The result is an almost linear temperature profile. For $\unicode[STIX]{x1D70F}=0.1$ , $\overline{Q}_{r}$ undergoes a monotonic transition from positive to negative values, resulting in a sink of energy on the hot side and a source on the cold side. Upon increasing the optical thickness, a local minimum and maximum appear close to the hot and cold walls, respectively, due to the shortening of radiative heat transfer length scales. Near the hot wall, due to incoming radiation from the boundary, absorption levels are higher than emission. The opposite occurs near the cold wall. The result is then the presence of a local source/sink of energy and a subsequent reduction in temperature gradients near the walls at a high enough $\unicode[STIX]{x1D70F}$ .

3.2 Heat fluxes

Reynolds averaging equation (2.3) for a fully developed channel flow results in:

(3.1) $$\begin{eqnarray}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}y}\left(\frac{1}{RePr}\frac{\unicode[STIX]{x2202}\overline{\unicode[STIX]{x1D703}}}{\unicode[STIX]{x2202}y}-\overline{v^{\prime }\unicode[STIX]{x1D703}^{\prime }}\right)-\frac{\overline{Q}_{r}}{RePrPl}=0.\end{eqnarray}$$

Integrating (3.1) in wall-normal direction yields:

(3.2) $$\begin{eqnarray}\frac{1}{RePr}\frac{\unicode[STIX]{x2202}\overline{\unicode[STIX]{x1D703}}}{\unicode[STIX]{x2202}y}-\overline{v^{\prime }\unicode[STIX]{x1D703}^{\prime }}-\int _{0}^{y}\frac{\overline{Q}_{r}}{RePrPl}\,\text{d}y=C_{1},\end{eqnarray}$$

where $C_{1}=\overline{q}_{w}-\overline{q}_{R,hw}$ , with $\overline{q}_{w}$ the total heat flux and $\overline{q}_{R,hw}$ the radiative heat flux at the hot wall. The flow is statistically homogeneous in the spanwise and streamwise directions, hence it follows that:

(3.3) $$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\overline{q}_{rx}}{\unicode[STIX]{x2202}x}=\frac{\unicode[STIX]{x2202}\overline{q}_{rz}}{\unicode[STIX]{x2202}z}=0.\end{eqnarray}$$

This allows one to state that:

(3.4) $$\begin{eqnarray}\int _{0}^{y}\overline{Q}_{r}\,\text{d}y=\overline{q}_{ry}+C_{2},\end{eqnarray}$$

where $C_{2}=\overline{q}_{R,hw}RePrPl$ . Using (3.4) in (3.2) it is possible to define the three heat transfer mechanisms (conductive ${\mathcal{D}}$ , convective ${\mathcal{U}}$ and radiative $\overline{q}_{R}$ ) as:

(3.5) $$\begin{eqnarray}\overline{q}_{w}=\underbrace{-\frac{1}{RePr}\frac{\unicode[STIX]{x2202}\overline{\unicode[STIX]{x1D703}}}{\unicode[STIX]{x2202}y}}_{{\mathcal{D}}}\underbrace{+\overline{v^{\prime }\unicode[STIX]{x1D703}^{\prime }}}_{{\mathcal{U}}}\underbrace{+\frac{\overline{q}_{ry}}{RePrPl}}_{\overline{q}_{R}}.\end{eqnarray}$$

Figure 5(a) shows the overall heat transfer in the channel ${\mathcal{D}}+{\mathcal{U}}+\overline{q}_{R}$ , while the individual heat fluxes for $\unicode[STIX]{x1D70F}=0.1,1,10$ are shown in figure 5(b–d). In figure 5(b) the radiative flux on the cold wall $\overline{q}_{R,cw}$ is subtracted from the radiative heat flux to improve the visibility and to highlight its gradient.

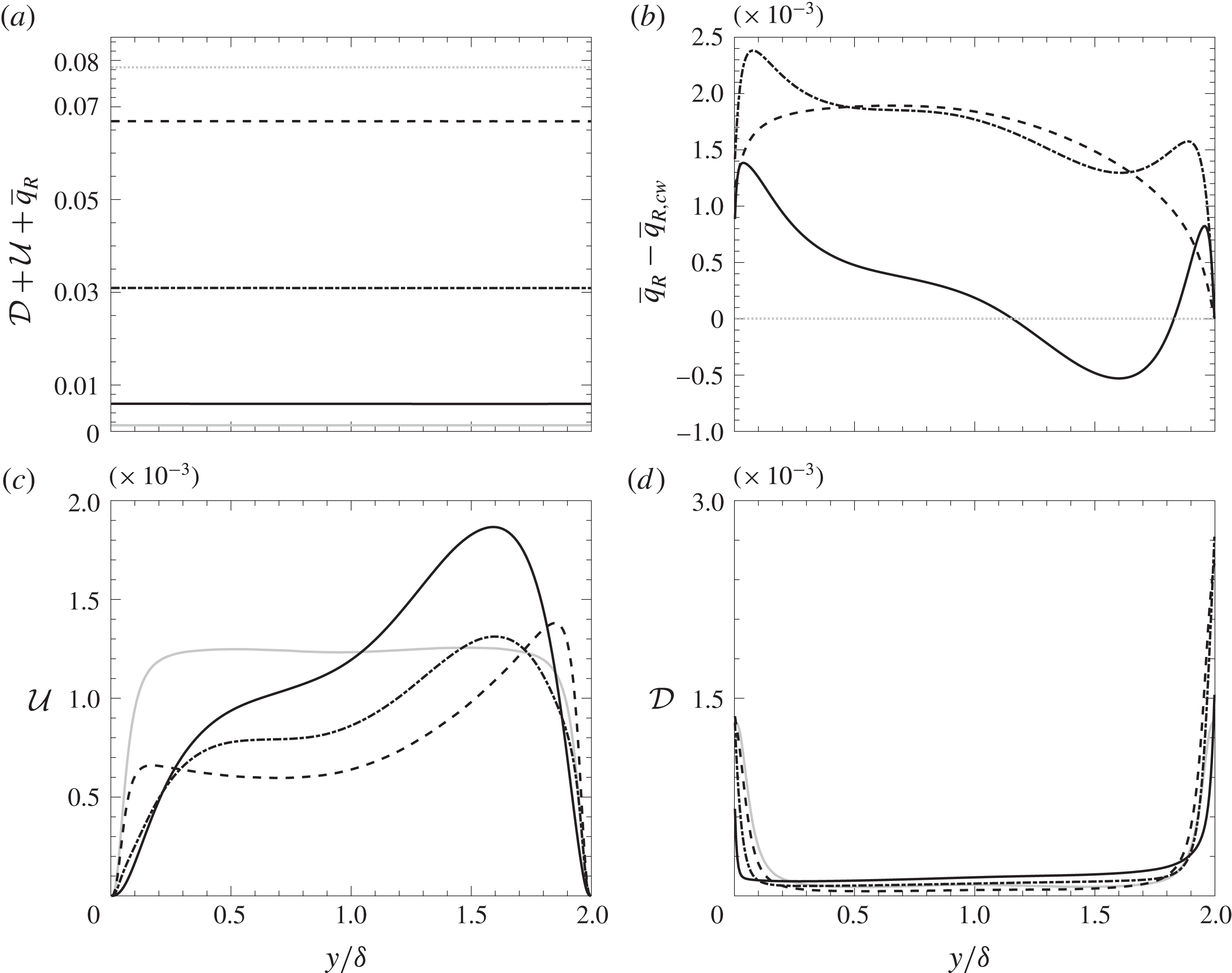
Figure 5. Contribution to heat flux by different heat transfer mechanisms, grey solid line: no radiation, grey dotted line: $\unicode[STIX]{x1D70F}=0$ , dashed line: $\unicode[STIX]{x1D70F}=0.1$ , dashed-dotted line: $\unicode[STIX]{x1D70F}=1$ , black solid line: $\unicode[STIX]{x1D70F}=10$ . (a) Total heat flux; (b) mean radiative heat flux minus wall radiative flux on the cold side; (c) mean wall-normal turbulent heat flux; (d) mean conductive heat flux.

By inspecting figure 5(a) a drastic increase in the overall heat flux between non-radiating and radiating cases is noticeable. Since the magnitudes of the turbulent and convective heat flux remain the same (figure 5 c,d), the increment of the total heat flux shown is caused by radiative heat transfer. Furthermore, the heat flux tends to reduce significantly when the optical thickness is increased. Nevertheless, the rapid reduction in $\overline{q}_{R}$ with an increase of $\unicode[STIX]{x1D70F}$ does not readily translate into a decrease of the contribution of radiation in the overall heat transfer to the fluid. A distinction must be made between wall–wall, fluid–wall and fluid–fluid radiative heat flux. As explained by Zhang et al. (2013), the wall–wall contribution refers to the constant flux between the walls; this contribution does not affect the fluid temperature. The fluid–wall flux includes both the heat flux that, emanating from the hot wall, is absorbed by the flow, and the heat flux generated by emission from the flow that reaches the cold wall. The former contribution increases the temperature of the fluid, while the latter decreases it. The fluid–fluid contribution refers to the heat flux originating within the fluid due to emission, and reabsorbed before reaching the cold wall. This contribution is responsible for shaping the temperature profile and does not modify the mean temperature within the channel. The correct magnitude of these three contributions cannot be estimated by inspection of the total $\overline{q}_{R}$ , but a qualitative explanation can be inferred by considering the simple Beer–Lambert law. To show the extent of wall–wall radiative heat flux, a case with a transparent medium and a radiative wall has been added to figure 5(a,b) (grey dotted line). For this case, the radiative heat flux, entirely composed of the wall–wall contribution, reaches the maximum possible value since it is not obstructed by the fluid. For $\unicode[STIX]{x1D70F}=0.1$ , the thermal radiative waves can still travel relatively undisturbed from the hot to the cold wall since the transmissivity of the channel, $\text{e}^{-2\unicode[STIX]{x1D70F}}$ , is high ( $0.819$ ). Therefore, wall–wall radiative heat flux comprises the major share of $\overline{q}_{R}$ . The consequence is a high heat transfer between the hot and cold wall, but a relatively small share of thermal radiation that is effectively exchanged with the fluid. When the optical thickness increases, the radiative heat flux diminishes, but the wall–wall contribution decreases more rapidly, since the transmissivities for $\unicode[STIX]{x1D70F}=1$ and $\unicode[STIX]{x1D70F}=10$ are $0.135$ and $2.1\times 10^{-9}$ , respectively. In other words, a higher share of thermal radiation travelling from the hot to the cold side is absorbed and redistributed within the media.

The shape of the radiative heat flux in figure 5(b) is determined by the action of emission and absorption. The increase of $\overline{q}_{R}$ near the hot wall is due to the effect of emission augmentation; while moving towards the cold boundary, thermal radiation is absorbed, resulting in a reduction of $\overline{q}_{R}$ . The peaks observed for $\unicode[STIX]{x1D70F}=1$ and $10$ are related to the local near-wall sink/source noticed in figure 4(b).

Figure 5(c) presents profiles of turbulent heat flux. In a non-radiating case, the turbulent heat flux is symmetric and constant in the channel core. The symmetry of $\overline{v^{\prime }\unicode[STIX]{x1D703}^{\prime }}$ is lost for radiative cases, where a peak originates on the cold side. For a low optical thickness ( $\unicode[STIX]{x1D70F}=0.1$ ) turbulent heat flux is suppressed near the hot wall, as well as in the rest of the channel due to the decrease in temperature gradient and a lower fluctuating thermal field. By increasing the optical thickness to $\unicode[STIX]{x1D70F}=1$ the peak at the cold side is reduced and shifted towards the core. In the centre of the channel, turbulent heat transfer is enhanced by the increase of optical thickness. For a high-optical-thickness case ( $\unicode[STIX]{x1D70F}=10$ ), turbulent heat flux is strongly intensified on the cold side and the peak is further shifted to the centre.

3.2.1 Scaling of turbulent heat flux in radiative flows

Vicquelin et al. (2014) analysed radiative flows to find a radiative scaling for turbulent heat transfer. This radiative-based scaling factor ( $\unicode[STIX]{x1D6FE}$ ) would ensure that

(3.6) $$\begin{eqnarray}\frac{\overline{v^{\prime }\unicode[STIX]{x1D703}^{\prime }}_{R}}{\unicode[STIX]{x1D6FE}_{R}}\approx \frac{\overline{v^{\prime }\unicode[STIX]{x1D703}^{\prime }}_{0}}{\unicode[STIX]{x1D6FE}_{0}},\end{eqnarray}$$

where the subscripts $R$ and $0$ denote quantities for radiative and non-radiative cases, respectively. If (3.6) holds, it is possible to obtain an expression for the turbulent heat diffusivity using the turbulent heat flux in a non-radiative case as:

(3.7) $$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{t}=\frac{1}{\unicode[STIX]{x1D70C}c_{p}}\frac{\overline{v^{\prime }\unicode[STIX]{x1D703}^{\prime }}_{R}}{(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x1D703}}/\unicode[STIX]{x2202}y)_{R}}=\frac{1}{\unicode[STIX]{x1D70C}c_{p}}\frac{\unicode[STIX]{x1D6FE}_{R}}{(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x1D703}}/\unicode[STIX]{x2202}y)_{R}}\frac{\overline{v^{\prime }\unicode[STIX]{x1D703}^{\prime }}_{0}}{\unicode[STIX]{x1D6FE}_{0}}.\end{eqnarray}$$

This allows the calculation of the turbulent Prandtl number in a radiative turbulent flow by comparison with a non-radiative flow, where models for $Pr_{t}$ are well established. The resulting relation, see Vicquelin et al. (2014), is

(3.8) $$\begin{eqnarray}{Pr_{t}}_{R}=\frac{1}{RePr}\frac{(\unicode[STIX]{x2202}\overline{\unicode[STIX]{x1D703}}/\unicode[STIX]{x2202}y)_{R}}{\unicode[STIX]{x1D6FE}_{R}}({Pr_{t}}_{0}+{\unicode[STIX]{x1D708}_{t}}_{0}RePr),\end{eqnarray}$$

with the proposed scaling factor $\unicode[STIX]{x1D6FE}_{R}(y)=\overline{q}_{w}-\overline{q}_{R}(y)$ , where $\overline{q}_{w}$ is the wall heat flux while $\overline{q}_{R}(y)$ is the radiative heat flux within the channel. When no radiative heat transfer is involved, the scaling factor reduces to the conductive heat flux at the wall, $\unicode[STIX]{x1D6FE}_{0}=\overline{q}_{w,0}$ .

Given equation (3.2), it is true that:

(3.9) $$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{R}=\overline{q}_{w}-\overline{q}_{R}={\mathcal{U}}+{\mathcal{D}}.\end{eqnarray}$$

Using (3.9), equation (3.6) can be reformulated as:

(3.10) $$\begin{eqnarray}\frac{{\mathcal{U}}_{R}}{{\mathcal{U}}_{R}+{\mathcal{D}}_{R}}\approx \frac{{\mathcal{U}}_{0}}{{\mathcal{U}}_{0}+{\mathcal{D}}_{0}},\end{eqnarray}$$

and further rewritten as:

(3.11) $$\begin{eqnarray}\frac{{\mathcal{D}}_{R}}{{\mathcal{U}}_{R}}\approx \frac{{\mathcal{D}}_{0}}{{\mathcal{U}}_{0}},\end{eqnarray}$$

i.e. the relative importance of turbulent heat transfer over conduction remains constant as radiation is introduced and the optical thickness is increased.

The resulting profiles of radiation-scaled ${\mathcal{U}}$ are shown in figure 6(a), while the modelled and the calculated turbulent Prandtl numbers from (3.8) are shown in figure 6(b). The value of the non-radiative turbulent Prandtl number calculated from DNS is used in (3.8).

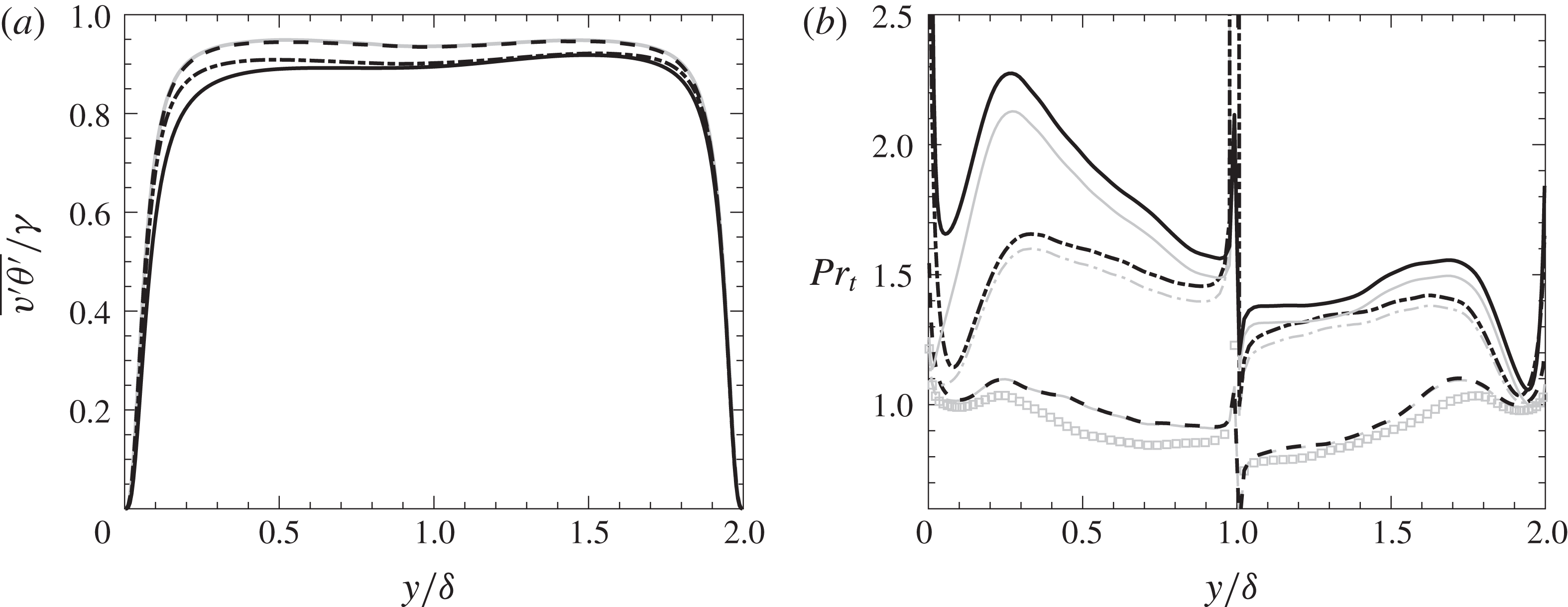
Figure 6. (a) Scaled turbulent heat transfer. Grey solid line: no radiation, dashed line: $\unicode[STIX]{x1D70F}=0.1$ , dashed-dotted line: $\unicode[STIX]{x1D70F}=1$ , black solid line: $\unicode[STIX]{x1D70F}=10$ . (b) Turbulent Prandtl number calculated from DNS and modelled. Symbols: ${Pr_{t}}_{0}$ ; black lines: DNS results; grey lines: modelled $Pr_{t}$ . Dashed line: $\unicode[STIX]{x1D70F}=0.1$ , dashed-dotted line: $\unicode[STIX]{x1D70F}=1$ , solid line: $\unicode[STIX]{x1D70F}=10$ .

The turbulent Prandtl number increases significantly when increasing the optical thickness, depicting the decrease in convective effects on mean temperature. The model developed by Vicquelin et al. (2014) performs exceptionally well with low optical thickness, being able to exactly reproduce ${Pr_{t}}_{R}$ . For intermediate values of optical thickness the model seems to deviate slightly from the calculated values, while showing a relevant deviation for higher values of optical thickness ( $\unicode[STIX]{x1D70F}=10$ ).

In a constant property flow, condition (3.11) can be met identically only if $Pr_{t}$ is independent of $\unicode[STIX]{x1D70F}$ , since turbulent Prandtl number is defined as:

(3.12) $$\begin{eqnarray}Pr_{t}=-\frac{{\mathcal{D}}}{{\mathcal{U}}}\unicode[STIX]{x1D708}_{t}RePr,\end{eqnarray}$$

where $\unicode[STIX]{x1D708}_{t}$ is the turbulent viscosity, which is constant with $\unicode[STIX]{x1D70F}$ in an incompressible flow.

In order to better understand the disagreement between the model and DNS, it is necessary to point out the interplay between the energy equation, equation (3.5), and the transport equation of turbulent heat flux ${\mathcal{U}}$ that, in an incompressible, absorbing–emitting, turbulent flow reads:

(3.13) $$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \underbrace{-\overline{{v^{\prime }}^{2}}\frac{\unicode[STIX]{x2202}\overline{\unicode[STIX]{x1D703}}}{\unicode[STIX]{x2202}y}}_{{\mathcal{P}}_{{\mathcal{U}}}}\underbrace{+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}y}\left(\frac{1}{RePr}\overline{v^{\prime }\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}^{\prime }}{\unicode[STIX]{x2202}y}}+\frac{1}{Re}\overline{\unicode[STIX]{x1D703}^{\prime }\frac{\unicode[STIX]{x2202}v^{\prime }}{\unicode[STIX]{x2202}y}}-\frac{1}{Re}\overline{{v^{\prime }}^{2}\unicode[STIX]{x1D703}^{\prime }}\right)}_{\unicode[STIX]{x1D719}_{{\mathcal{U}}}+{\mathcal{T}}_{{\mathcal{U}}}}\nonumber\\ \displaystyle & & \displaystyle +\,\underbrace{-\overline{\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}^{\prime }}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}v^{\prime }}{\unicode[STIX]{x2202}x_{j}}}\frac{Pr+1}{RePr}}_{\unicode[STIX]{x1D716}_{{\mathcal{U}}}}\underbrace{-\overline{\unicode[STIX]{x1D703}^{\prime }\frac{\unicode[STIX]{x2202}p^{\prime }}{\unicode[STIX]{x2202}y}}}_{\unicode[STIX]{x1D6F1}_{{\mathcal{U}}}}\underbrace{-\frac{1}{RePrPl}\overline{Q_{r}^{\prime }v^{\prime }}}_{{\mathcal{R}}_{{\mathcal{U}}}}.\end{eqnarray}$$

${\mathcal{P}}_{{\mathcal{U}}}$ is turbulent production, $\unicode[STIX]{x1D719}_{{\mathcal{U}}}$ is molecular and viscous diffusion, ${\mathcal{T}}_{{\mathcal{U}}}$ is turbulent transport, $\unicode[STIX]{x1D716}_{{\mathcal{U}}}$ is the molecular and viscous dissipation, $\unicode[STIX]{x1D6F1}_{{\mathcal{U}}}$ is the pressure term (sum of pressure diffusion and pressure strain) and ${\mathcal{R}}_{{\mathcal{U}}}$ is the radiative term (sum of emissive and absorptive term). Figure 7(a) shows the production term for ${\mathcal{U}}$ , while figure 7(b) presents the profiles of the radiation term. For $\unicode[STIX]{x1D70F}=0.1$ , the introduction of the average radiative heat flux in (3.5) causes the turbulent heat flux ${\mathcal{U}}$ to reduce in the channel core (figure 5 c). As apparent, for a low optical thickness, the decrease of ${\mathcal{U}}$ is balanced by the decrease in temperature gradient, resulting in the validity of condition (3.11). This occurs since the direct effect of TRI on ${\mathcal{U}}$ (namely term $\overline{Q_{r}^{\prime }v^{\prime }}$ in (3.13)) has a negligible contribution. Therefore, a change in mean temperature gradient would readily reflect in a modification of ${\mathcal{U}}$ through the reduction of the turbulent production ${\mathcal{P}}_{{\mathcal{U}}}$ , keeping the ${\mathcal{D}}/{\mathcal{U}}$ ratio constant. In other words, only mean radiative effects (i.e.  $\overline{q}_{R}$ in (3.5)) play a role. Since direct radiative effects are negligible, equation (3.13) keeps the balance between ${\mathcal{U}}$ and ${\mathcal{D}}$ . Consequently, the modelled turbulent Prandtl number for a low optical thickness agrees with the value calculated from DNS. However, condition (3.11) is not a suitable approximation when increasing the optical thickness, since the direct effect of TRI becomes relevant. It should be noted that ${\mathcal{P}}_{{\mathcal{U}}}$ is representative of ${\mathcal{D}}$ , since the term $\overline{{v^{2}}^{\prime }}$ is not affected by temperature in the present case. Therefore, the increase in temperature gradient with the increase of $\unicode[STIX]{x1D70F}$ is directly related to the rise in ${\mathcal{R}}_{{\mathcal{U}}}$ , which represents the direct effect of radiative fluctuations on $\unicode[STIX]{x1D703}^{\prime }$ . This increase is not reflected in the same fashion on the turbulent heat transfer ${\mathcal{U}}$ . Namely, with the increase of radiative effects in the centre of the channel (as it will be explained in detail in the next sections), ${\mathcal{P}}_{{\mathcal{U}}}$ adapts to an increased ${\mathcal{R}}_{{\mathcal{U}}}$ , leading to an increased ${\mathcal{D}}/{\mathcal{U}}$ ratio. This increase causes ${\mathcal{U}}_{R}/\unicode[STIX]{x1D6FE}_{R}<{\mathcal{U}}_{0}/\unicode[STIX]{x1D6FE}_{0}$ , resulting in a deviation of the modelled turbulent Prandtl number. The deviation is larger on the hot side, since the model does not account for radiative field fluctuations (indeed, to consider a constant ${\mathcal{D}}/{\mathcal{U}}$ ratio implies that radiative fluctuations have no effect on $\unicode[STIX]{x1D703}^{\prime }$ ). As will be shown in §§ 3.3 and 4, the direct effect of radiation on thermal turbulence is directly proportional to the cube of the mean temperature, causing a larger deviation on the hot side.

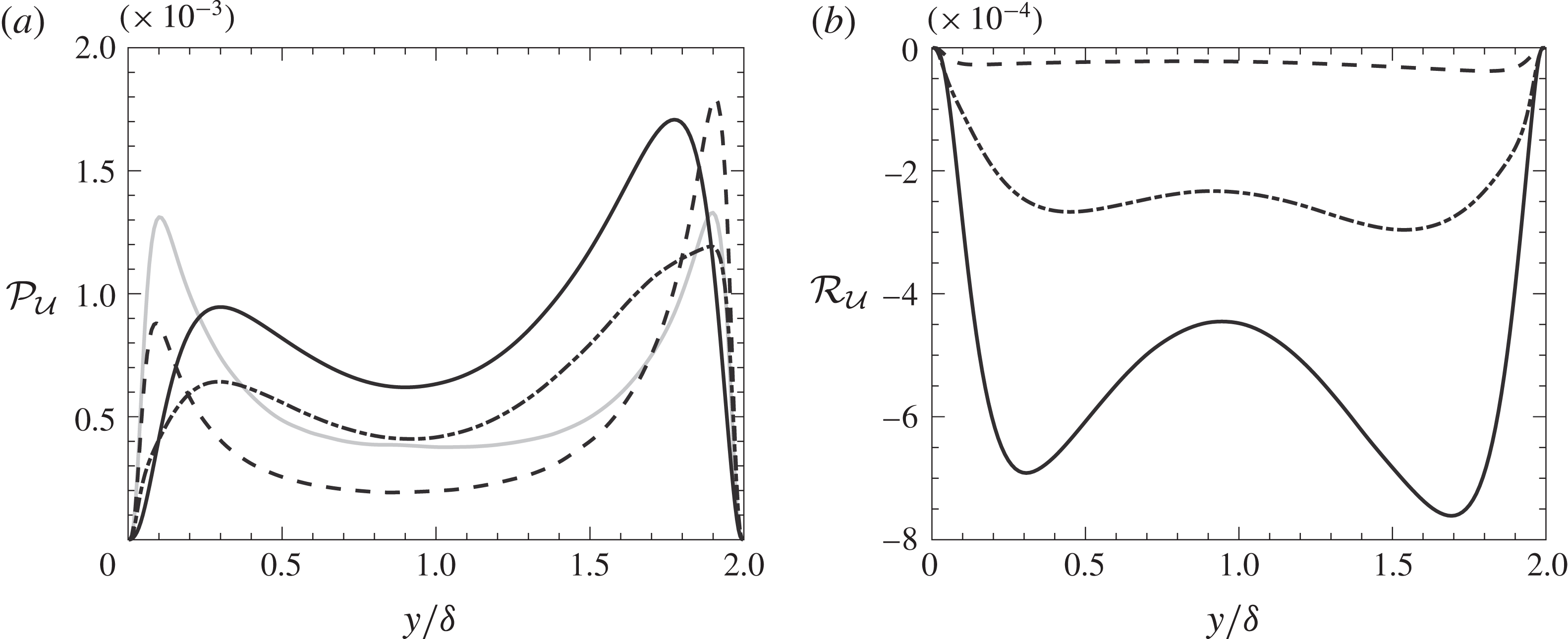
Figure 7. (a) Turbulent production of ${\mathcal{U}}$ . (b) Radiative term. Grey solid line: no radiation, dashed line: $\unicode[STIX]{x1D70F}=0.1$ , dashed-dotted line: $\unicode[STIX]{x1D70F}=1$ , black solid line: $\unicode[STIX]{x1D70F}=10$ .

3.3 Temperature variance and fluctuations of radiative quantities

Figure 8 shows temperature root mean square profiles for all cases. For the non-radiating case the temperature root mean square profile is symmetric, with peaks near the walls and a maximum in the centre of the channel. The peaks near the walls are caused by a high correlation of temperature fluctuations with the streamwise velocity fluctuations (Kim & Moin 1987). The local maximum located in the channel core is generated by pockets of cold and hot fluid transported from the boundaries towards the centre.

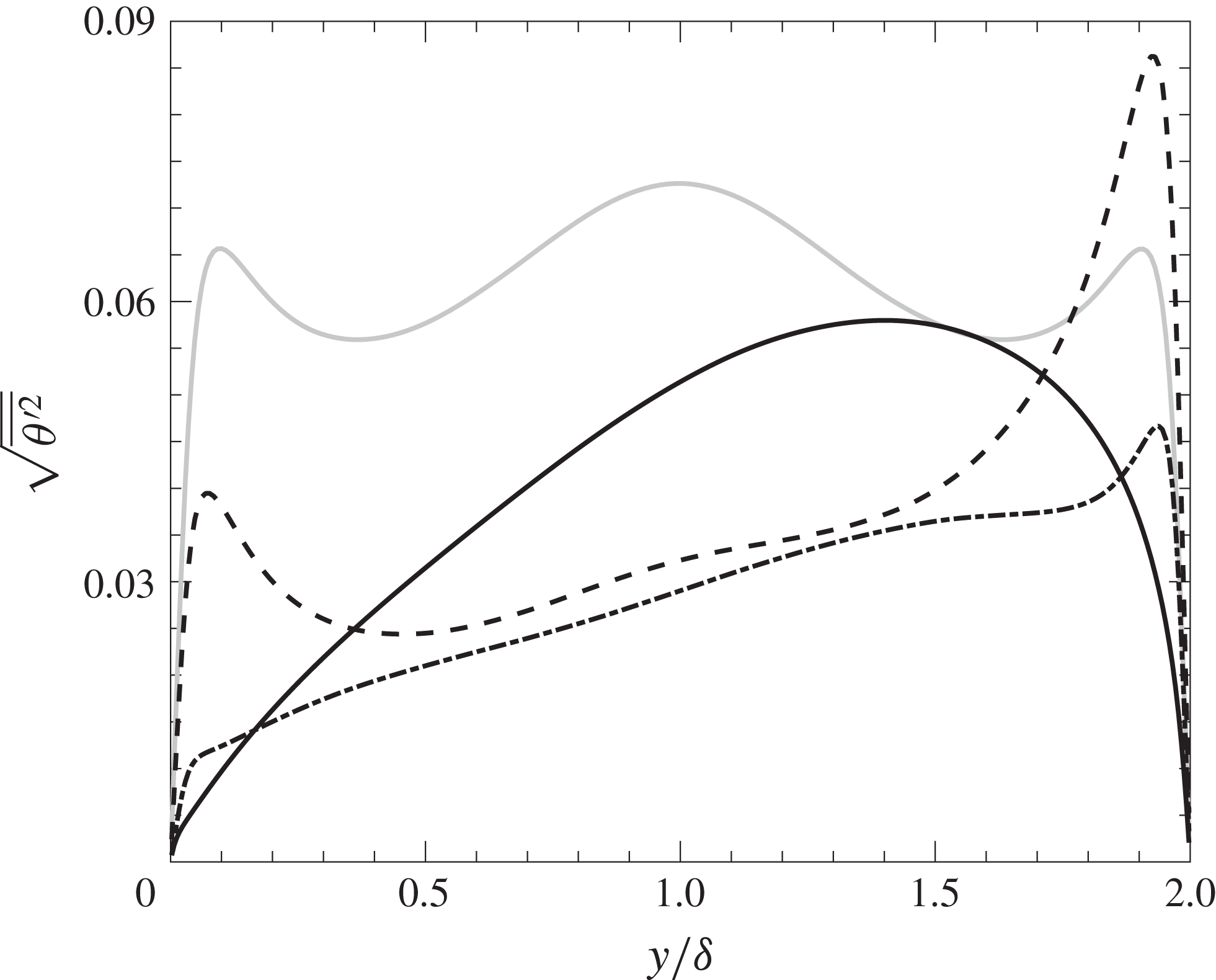
Figure 8. Turbulent intensity of temperature fluctuation, grey solid line: no radiation, dashed line: $\unicode[STIX]{x1D70F}=0.1$ , dashed-dotted line: $\unicode[STIX]{x1D70F}=1$ , black solid line: $\unicode[STIX]{x1D70F}=10$ .

The influence of radiation on the turbulent temperature field can be analysed by means of the evolution equation for temperature fluctuations (which results from the subtraction of the Reynolds averaged to the instantaneous energy equation):

(3.14) $$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}^{\prime }}{\unicode[STIX]{x2202}t}+\overline{u_{j}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}^{\prime }}{\unicode[STIX]{x2202}x_{j}}+v^{\prime }\frac{\unicode[STIX]{x2202}\overline{\unicode[STIX]{x1D703}}}{\unicode[STIX]{x2202}y}+\frac{\unicode[STIX]{x2202}u_{j}^{\prime }\unicode[STIX]{x1D703}^{\prime }}{\unicode[STIX]{x2202}x_{j}}-\frac{\unicode[STIX]{x2202}\overline{v^{\prime }\unicode[STIX]{x1D703}^{\prime }}}{\unicode[STIX]{x2202}y}=\frac{1}{RePr}\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D703}^{\prime }}{\unicode[STIX]{x2202}x_{j}^{2}}-\unicode[STIX]{x1D70F}\frac{E_{m}^{\prime }}{RePrPl}+\unicode[STIX]{x1D70F}\frac{G^{\prime }}{RePrPl}.\end{eqnarray}$$

$G^{\prime }$ is a source of temperature fluctuation, while $E_{m}^{\prime }$ acts as a sink. Note that $E_{m}^{\prime }$ is always positively correlated to $\unicode[STIX]{x1D703}^{\prime }$ , since

(3.15) $$\begin{eqnarray}E_{m}^{\prime }=4[(\unicode[STIX]{x1D703}/T_{0}+1)^{4}]^{\prime }\propto \overline{\unicode[STIX]{x1D703}}^{3}\unicode[STIX]{x1D703}^{\prime }.\end{eqnarray}$$

As a positive $\unicode[STIX]{x1D703}^{\prime }$ fluctuation occurs a positive $E_{m}^{\prime }$ fluctuation follows, which increases emission and subsequently reduces temperature. The opposite is observed for negative  $\unicode[STIX]{x1D703}^{\prime }$ . Therefore, $E_{m}^{\prime }$ acts as a stabilization phenomenon towards the temperature field, reducing temperature fluctuations. In addition, emission fluctuations are proportional to the cube of the mean temperature, hence, in general, a higher temperature ensures higher levels of $E_{m}^{\prime }$ . On the other hand, $G^{\prime }$ counteracts the effects of $E_{m}^{\prime }$ , and where fluctuations of $G$ are high, the stabilizing effect of emission is weaker, allowing for higher $\unicode[STIX]{x1D703}^{\prime }$ values. Also the effect of $G^{\prime }$ is enhanced with a larger $\overline{\unicode[STIX]{x1D703}}$ , as will be explained in § 4.

The near-wall peak locations of $\overline{{\unicode[STIX]{x1D703}^{\prime }}^{2}}$ are retained for the low-optical-thickness case ( $\unicode[STIX]{x1D70F}=0.1$ ). The radiative power fluctuations are dominated by the emission fluctuations $E_{m}^{\prime }$ (figure 9 a) and, in conjunction with a lower temperature gradient, cause a mitigation of the temperature variance peak on the hot side. Indeed, $G^{\prime }$ (figure 9 b) shows a negligible contribution to (3.14). On the other hand, the high-temperature gradient occurring on the cold side increases the temperature variance near the cold wall beyond the non-radiative case. This rise in fluctuation levels is not a direct effect of radiation, rather an effect of the increased production due to a higher temperature gradient (see the discussion on temperature variance budgets in § 3.4). The turbulent transport of hot and cold pockets towards the centre of the channel is reduced, since turbulent structures, directed to the core, emit radiation, causing the temperature to stabilize before the centre is reached. As a result, the temperature variance in the channel core is strongly damped.

For an intermediate optical depth ( $\unicode[STIX]{x1D70F}=1$ ), fluctuation levels are largely reduced both on the hot and cold side due to the direct action of radiative emission, which provides a means of stabilization to temperature fluctuations. The turbulent transport of hot and cold temperature pockets is further decreased through emission of thermal radiation, which causes a reduction in temperature variance. In the core of the channel, near $y/\unicode[STIX]{x1D6FF}=1.5$ , incident radiation fluctuations $G^{\prime }$ grow larger and slightly counteract the sink produced by $E_{m}^{\prime }$ (see § 3.4).

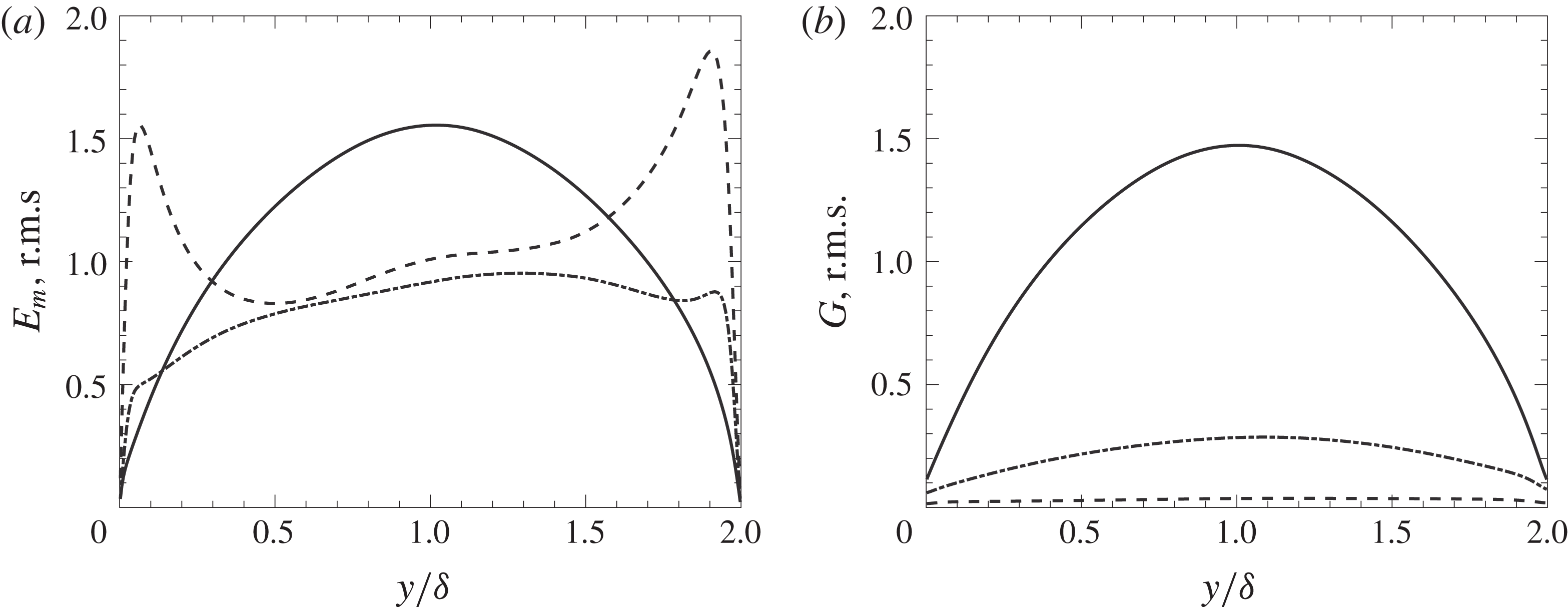
Figure 9. Root mean square profiles of emission (a) and incident radiation (b), dashed line: $\unicode[STIX]{x1D70F}=0.1$ , dashed-dotted line: $\unicode[STIX]{x1D70F}=1$ , black solid line: $\unicode[STIX]{x1D70F}=10$ .

Interestingly, we noticed that further increasing the optical thickness to $\unicode[STIX]{x1D70F}=10$ produces a higher level of temperature fluctuations than the previous radiative cases, since temperature variance partly recovers in the core of the channel. The small peak of $\overline{{\unicode[STIX]{x1D703}^{\prime }}^{2}}$ at $y/\unicode[STIX]{x1D6FF}\approx 1.5$ , noticed for $\unicode[STIX]{x1D70F}=1$ , grows for $\unicode[STIX]{x1D70F}=10$ and shifts towards the centre (at $y/\unicode[STIX]{x1D6FF}=1.4$ ). Near-wall fluctuations are largely reduced both on the hot and cold side. This increase in temperature variance is caused by $G^{\prime }$ that reaches a magnitude comparable to $E_{m}^{\prime }$ .

In figure 9(b) it is possible to notice the drastic increase in incident radiation fluctuations upon increasing the optical thickness. This rise is caused by the reduction of radiative transfer length scales; incident radiation at a high optical thickness can be regarded mostly as a short-range phenomenon, hence being heavily influenced by local temperature fluctuations. We noticed that the peak of incident radiation fluctuations is always located around the centre of the channel. As will be explained in § 4, incident radiation is mostly influenced by large temperature scales, while small thin structures mostly behave as a transparent media. For this reason $G$ fluctuations are mostly concentrated near the channel centre, where temperature fluctuations are usually associated with larger and more isotropic scales of motion, while they decrease towards the walls, where vortices are characterized by thin streaky structures.

3.4 Budgets of the temperature variance

Budgets of the temperature variance are shown, to investigate the influence of radiation on the turbulent temperature field. The transport equation for temperature variance in the presence of radiative heat transfer reads:

(3.16) $$\begin{eqnarray}0=\underbrace{-2\overline{v^{\prime }\unicode[STIX]{x1D703}^{\prime }}\frac{\unicode[STIX]{x2202}\overline{\unicode[STIX]{x1D703}}}{\unicode[STIX]{x2202}y}}_{{\mathcal{P}}_{\unicode[STIX]{x1D703}}}\underbrace{+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}y}\left(\frac{1}{RePr}\frac{\unicode[STIX]{x2202}\overline{{\unicode[STIX]{x1D703}^{\prime }}^{2}}}{\unicode[STIX]{x2202}y}-\overline{v^{\prime }{\unicode[STIX]{x1D703}^{\prime }}^{2}}\right)}_{\unicode[STIX]{x1D719}_{m}+{\mathcal{T}}_{\unicode[STIX]{x1D703}}}\underbrace{-\frac{2}{RePr}\overline{\left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}^{\prime }}{\unicode[STIX]{x2202}x_{j}}\right)^{2}}}_{\unicode[STIX]{x1D716}_{m}}\underbrace{-\frac{2}{RePrPl}\overline{Q_{r}^{\prime }\unicode[STIX]{x1D703}^{\prime }}}_{{\mathcal{R}}},\end{eqnarray}$$

where ${\mathcal{P}}_{\unicode[STIX]{x1D703}}$ is the turbulent production, $\unicode[STIX]{x1D719}_{m}$ is the molecular diffusion, ${\mathcal{T}}_{\unicode[STIX]{x1D703}}$ is the turbulent transport, $\unicode[STIX]{x1D716}_{m}$ is the molecular dissipation and ${\mathcal{R}}$ is the radiation term. The radiation term, in analogy with the molecular terms ( $\unicode[STIX]{x1D719}_{m}$ , $\unicode[STIX]{x1D716}_{m}$ ), can be decomposed into a diffusion and a dissipation term with (2.5):

(3.17) $$\begin{eqnarray}{\mathcal{R}}=\underbrace{-\frac{2}{RePrPl}\frac{\unicode[STIX]{x2202}\overline{{q_{r}}_{y}^{\prime }\unicode[STIX]{x1D703}^{\prime }}}{\unicode[STIX]{x2202}y}}_{\unicode[STIX]{x1D719}_{r}}\underbrace{+\frac{2}{RePrPl}\overline{\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}^{\prime }}{\unicode[STIX]{x2202}x_{j}}{q_{r}}_{j}^{\prime }}}_{\unicode[STIX]{x1D716}_{r}},\end{eqnarray}$$

with $\unicode[STIX]{x1D719}_{r}$ the radiative diffusion and $\unicode[STIX]{x1D716}_{r}$ the radiative dissipation.

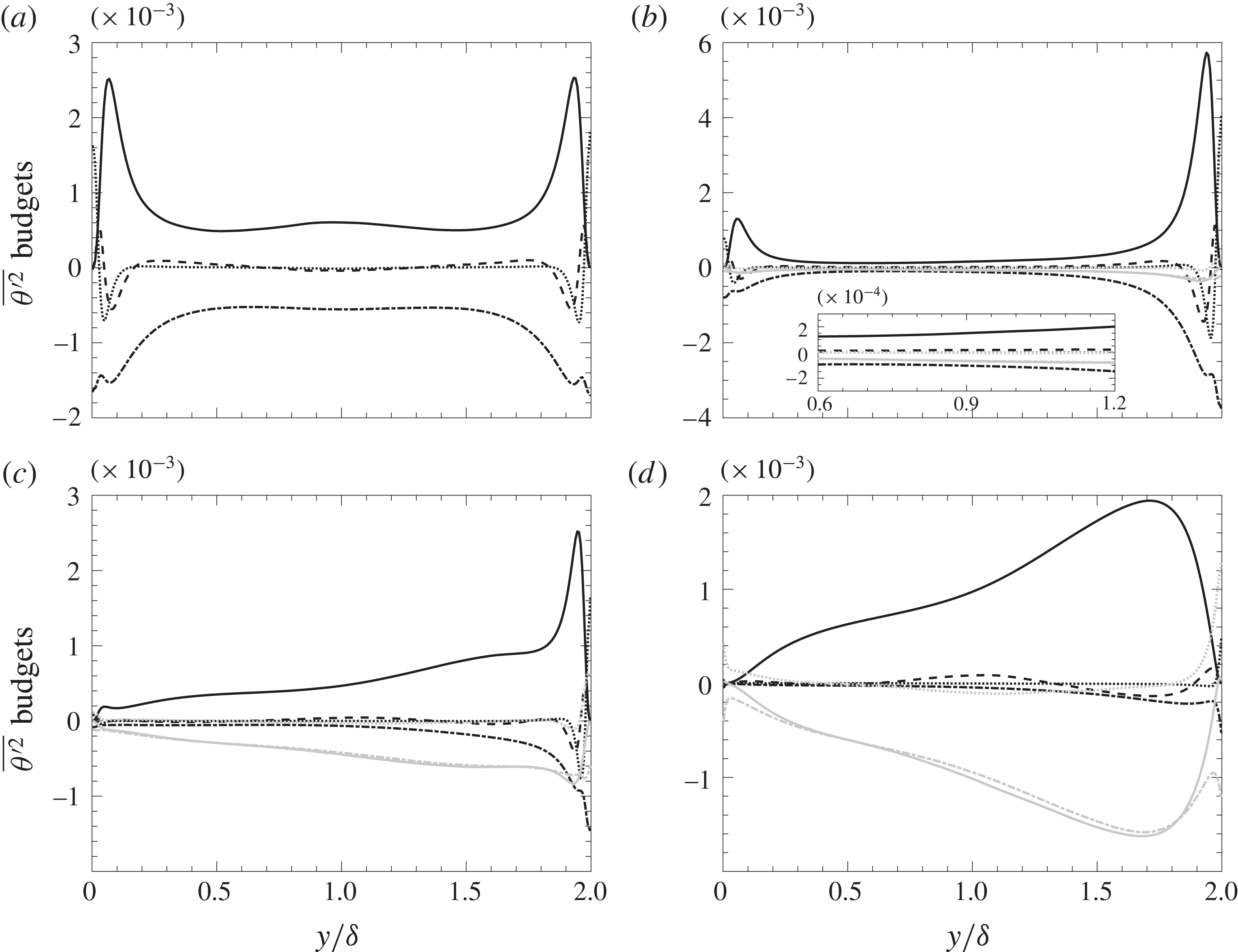
Figure 10. Budgets of temperature variance, (a): non-radiative channel flow, (b):  $\unicode[STIX]{x1D70F}=0.1$ , inclusion highlights the core zone ( $x/\unicode[STIX]{x1D6FF}=0.4{-}1.2$ ), (c):  $\unicode[STIX]{x1D70F}=1$ , (d):  $\unicode[STIX]{x1D70F}=10$ . Black solid line: turbulent production ${\mathcal{P}}_{\unicode[STIX]{x1D703}}$ , dashed line: turbulent transport ${\mathcal{T}}_{\unicode[STIX]{x1D703}}$ , black dotted line: molecular diffusion $\unicode[STIX]{x1D719}_{m}$ , black dashed-dotted line: molecular dissipation $\unicode[STIX]{x1D716}_{m}$ , grey dotted line: radiative diffusion $\unicode[STIX]{x1D719}_{r}$ , grey dashed-dotted line: radiative dissipation $\unicode[STIX]{x1D716}_{r}$ , grey solid line: radiative term ${\mathcal{R}}$ .

The budgets of temperature variance of the non-radiative and the radiative channel flows are presented in figure 10(a–d), where figure 10(a) corresponds to no radiation, 10(b) to $\unicode[STIX]{x1D70F}=0.1$ , 10(c) to $\unicode[STIX]{x1D70F}=1$ and 10(d) to $\unicode[STIX]{x1D70F}=10$ . Contrary to the profiles in figure 10(a), the budgets of temperature variance for the radiative flows in the figures are non-symmetrical.

For the low-optical-thickness case, a noticeable rise in the production can be observed near the cold wall, due to the increase of the temperature gradient. In order to balance the larger production rate, molecular dissipation, molecular diffusion and turbulent transport increase when compared to a non-radiative case. The opposite effect is experienced in the rest of the channel, where the lower temperature gradient causes an overall reduction in the magnitude of the budgets. The radiation terms ( ${\mathcal{R}}$ , $\unicode[STIX]{x1D719}_{r}$ and $\unicode[STIX]{x1D716}_{r}$ ) show a negligible contribution near the boundaries. A direct effect of radiation can be noticed in the core of the channel, where radiative dissipation $\unicode[STIX]{x1D716}_{r}$ aids molecular dissipation in balancing production (inlay in figure 10 b). Indeed, at a low optical thickness, radiation acts mainly through the modification of mean profiles, as noticed by several previous studies (Sakurai et al. 2010; Ghosh et al. 2011; Ghosh & Friedrich 2015), but in the centre of the channel we noticed a non-negligible direct effect of radiative dissipation.

For an intermediate optical depth, figure 10(c), adjacent to the hot wall, the budgets reduce drastically, due to the lower turbulent production and the large effect of emission that results in lower $\unicode[STIX]{x1D703}^{\prime }$ . On the cold side the same effect is observed, with an overall reduction in budgets of temperature variance. In contrast, in the channel core, production rate increases. The combination of an increase in turbulent production, caused by the rise in the temperature gradient, and the rise of $G^{\prime }$ , is balanced by the strong growth of radiation dissipation. Molecular diffusion and dissipation experience a further reduction, being relevant on the cold side only. It will be shown that the appearance of a mildly fluctuating absorption field shifts the temperature variance towards the core, where larger structures are present (see the discussion on temperature length scales in radiative flows in § 4).

By further increasing the optical thickness, figure 10(d), an enhancement of the effects already noticed for $\unicode[STIX]{x1D70F}=1$ occurs. In the whole core of the channel, an overall increase in the magnitude of the budgets is noticed. The molecular terms fall off, showing the complete dominance of radiative terms. On the hot side, production is minimized due to the lower mean temperature gradient and the large effect of emission that reduces $\unicode[STIX]{x1D703}^{\prime }$ . All the budgets near the hot wall reduce significantly, except for the radiative terms $\unicode[STIX]{x1D719}_{r}$ and $\unicode[STIX]{x1D716}_{r}$ , which increase and balance each other. Indeed, by reducing the radiation length scales, radiative terms reduce to local quantities acting akin to molecular terms, as already noticed by Townsend (1958). The production is located further away from the wall, consistently with the shift of $\unicode[STIX]{x1D703}_{rms}$ towards the centre of the channel, observed in § 3.3. Turbulent transport slightly grows in the core of the channel in order to redistribute fluctuations produced in the new peak location ( $y/\unicode[STIX]{x1D6FF}\approx 1.7$ ). Therefore, with increasing optical thickness, the relevance of molecular terms is reduced in favour of the radiative terms; the radiative dissipation and diffusion substitute the role of the molecular dissipation and diffusion in balancing the production. Hence, for a high enough optical thickness, the effect of radiation is not restricted to the modification of mean quantities, but acts directly on temperature statistics. The evidence collected from the analysis of the temperature variance budgets suggests that a further increase in the optical thickness would result in a further alignment of the production with the $\overline{{G^{\prime }}^{2}}$ peak (figure 9 b). Furthermore, the temperature fluctuations would recover and the radiative terms ( $\unicode[STIX]{x1D719}_{r}$ and $\unicode[STIX]{x1D716}_{r}$ ) would behave qualitatively similar to the molecular terms ( $\unicode[STIX]{x1D719}_{m}$ and $\unicode[STIX]{x1D716}_{m}$ ) in a non-radiative channel flow.

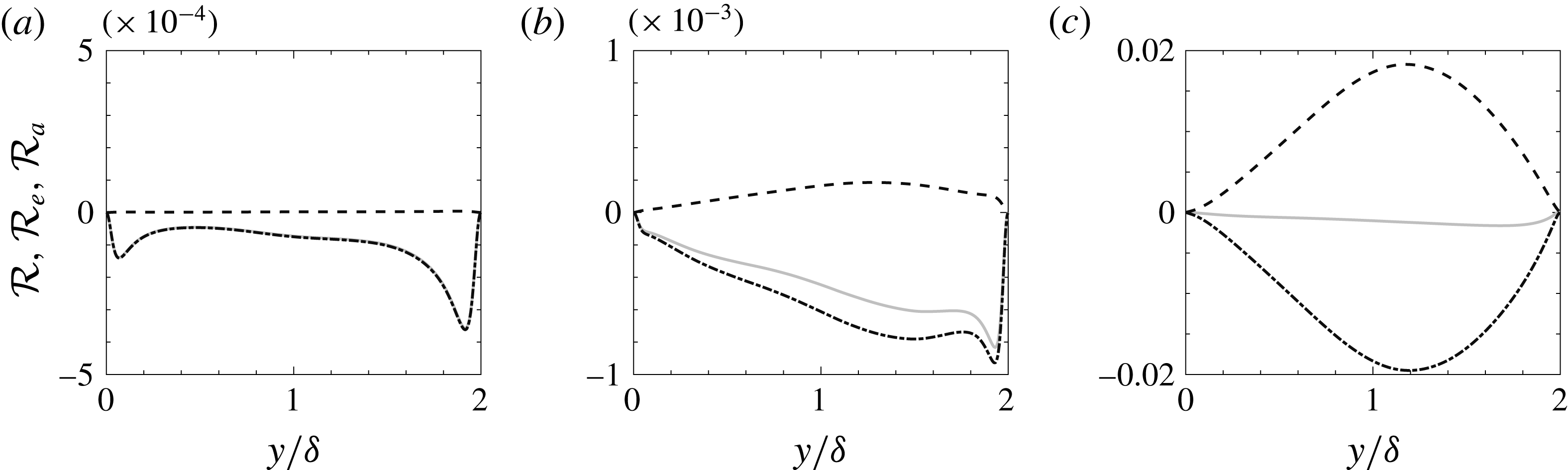
Figure 11. Radiation term ${\mathcal{R}}$ decomposed in absorption ${\mathcal{R}}_{a}$ and emission term ${\mathcal{R}}_{e}$ . Grey solid lines: ${\mathcal{R}}$ , dashed-dotted lines: ${\mathcal{R}}_{e}$ , dashed lines: ${\mathcal{R}}_{a}$ . (a) $\unicode[STIX]{x1D70F}=0.1$ , (b) $\unicode[STIX]{x1D70F}=1$ , (c) $\unicode[STIX]{x1D70F}=10$ .

To highlight the effects of absorption and emission fluctuations, that act as a production and dissipation term for $\overline{{\unicode[STIX]{x1D703}^{2}}^{\prime }}$ , the radiative term ${\mathcal{R}}$ can also be decomposed as

(3.18) $$\begin{eqnarray}{\mathcal{R}}={\mathcal{R}}_{e}+{\mathcal{R}}_{a},\end{eqnarray}$$

where

(3.19a,b ) $$\begin{eqnarray}{\mathcal{R}}_{e}=-\frac{2\unicode[STIX]{x1D70F}}{RePrPl}\overline{E_{m}^{\prime }\unicode[STIX]{x1D703}^{\prime }},\quad {\mathcal{R}}_{a}=\frac{2\unicode[STIX]{x1D70F}}{RePrPl}\overline{G^{\prime }\unicode[STIX]{x1D703}^{\prime }}.\end{eqnarray}$$

Figure 11 shows the profiles of ${\mathcal{R}}$ , ${\mathcal{R}}_{e}$ and ${\mathcal{R}}_{a}$ . As the optical thickness increases, the effect of the absorption production term grows drastically. Indeed $G^{\prime }$ is the cause of a modification of the thermal turbulence field, while emission fluctuations act as a dissipation of thermal fluctuations. It can also be noticed that ${\mathcal{R}}$ , ${\mathcal{R}}_{a}$ and ${\mathcal{R}}_{e}$ increase substantially in magnitude upon increasing the optical thickness. The reason why ${\mathcal{R}}_{a}$ peaks always in the centre of the channel, is elucidated in the next section.

4 Spectral analysis of TRI

4.1 Mathematical description of TRI in isotropic turbulence

Before proceeding towards discussing the results obtained for turbulent channel flow it is useful to analytically investigate the effect of radiation on the turbulent temperature scales in homogeneous isotropic turbulence. A mathematical derivation of the scale dependence of emission and absorption for a simple grey absorbing–emitting gas is outlined below (Coantic & Simonin 1984; Soufiani 1991).

A three-dimensional Fourier transformation of the fluctuating RTE, obtained by subtracting the instantaneous and averaged form of (2.4), presented in § 2, yields

(4.1) $$\begin{eqnarray}\widehat{I^{\prime }}(\boldsymbol{k})=\left(\frac{\unicode[STIX]{x1D70F}^{2}}{\unicode[STIX]{x1D70F}^{2}+(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{s})^{2}}-\text{i}\frac{\unicode[STIX]{x1D70F}(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{s})}{\unicode[STIX]{x1D70F}^{2}+(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{s})^{2}}\right)\widehat{I_{b}^{\prime }}(\boldsymbol{k}),\end{eqnarray}$$

where $\boldsymbol{k}$ is the non-dimensional wavenumber vector $(k_{x},k_{y},k_{z})$ . Since

(4.2) $$\begin{eqnarray}\widehat{G^{\prime }}(\boldsymbol{k})=\frac{1}{\unicode[STIX]{x03C0}}\int _{4\unicode[STIX]{x03C0}}\widehat{I^{\prime }}(\boldsymbol{k})\,\text{d}\unicode[STIX]{x1D6FA},\end{eqnarray}$$

and $\widehat{I_{b}^{\prime }}(\boldsymbol{k})\neq f(\unicode[STIX]{x1D6FA})$ (isotropic emission), then

(4.3) $$\begin{eqnarray}\widehat{G^{\prime }}(\boldsymbol{k})=\frac{\widehat{I_{b}^{\prime }}(\boldsymbol{k})}{\unicode[STIX]{x03C0}}\int _{4\unicode[STIX]{x03C0}}\left(\frac{\unicode[STIX]{x1D70F}^{2}}{\unicode[STIX]{x1D70F}^{2}+(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{s})^{2}}-\text{i}\frac{\unicode[STIX]{x1D70F}(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{s})}{\unicode[STIX]{x1D70F}^{2}+(\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{s})^{2}}\right)\,\text{d}\unicode[STIX]{x1D6FA}.\end{eqnarray}$$

An analytical solution to (4.3) exists, leading to the formulation of the Fourier transform of emission and absorption in homogeneous isotropic turbulence,

(4.4) $$\begin{eqnarray}\displaystyle & \displaystyle \widehat{E_{m}^{\prime }}(\boldsymbol{k})=4\widehat{I_{b}^{\prime }}(\boldsymbol{k})\propto \overline{\unicode[STIX]{x1D703}}^{3}\widehat{\unicode[STIX]{x1D703}^{\prime }}(\boldsymbol{k}), & \displaystyle\end{eqnarray}$$

(4.5) $$\begin{eqnarray}\displaystyle & \displaystyle \widehat{G^{\prime }}(\boldsymbol{k})=4\widehat{I_{b}^{\prime }}(\boldsymbol{k})\frac{\unicode[STIX]{x1D70F}}{k}\text{atan}\left(\frac{k}{\unicode[STIX]{x1D70F}}\right)=4\widehat{E_{m}^{\prime }}\,f(k,\unicode[STIX]{x1D70F})\propto \overline{\unicode[STIX]{x1D703}}^{3}\widehat{\unicode[STIX]{x1D703}^{\prime }}(\boldsymbol{k})f(k,\unicode[STIX]{x1D705}). & \displaystyle\end{eqnarray}$$

Absorption is spectrally related to emission in a periodic domain by the function $f(k,\unicode[STIX]{x1D70F})$ where $k=\Vert \boldsymbol{k}\Vert$ . It is important to remember that, in grey gases, emission fluctuations always lead to a sink of temperature variance, while absorption fluctuations cause a source of temperature variance. This is not strictly true for non-grey gases, where $\unicode[STIX]{x1D705}^{\prime }$ can modify the roles of emission and absorption. Since $0<f(k,\unicode[STIX]{x1D70F})<1$ , the sink is always predominant and, in homogeneous isotropic turbulence, the spectral effect of radiation always leads to a dissipation of the temperature spectrum. On the other hand, since $\widehat{G^{\prime }}(\boldsymbol{k})\propto f(k,\unicode[STIX]{x1D70F})$ , this dissipation is heavily affected by both the wavenumber and the optical thickness. Emission scales are proportional to temperature scales at every $k$ since, from a Fourier transformation of $E_{m}^{\prime }\propto \overline{\unicode[STIX]{x1D703}}^{3}\unicode[STIX]{x1D703}^{\prime }$ (proportionality relation (3.15)), it follows that $\widehat{{E_{m}}^{\prime }}(\boldsymbol{k})\propto \widehat{\unicode[STIX]{x1D703}^{\prime }}(\boldsymbol{k})$ . Therefore, emission leads to a sink on the temperature spectra that is proportional to the spectral energy at every wavenumber. On the other hand, $\widehat{G^{\prime }}(\boldsymbol{k})$ heavily modifies the spectra, since absorption scales depend on the wavenumber as $f(k,\unicode[STIX]{x1D70F})$ (figure 12). In addition, radiative effects on the turbulent temperature spectrum, both of emission and absorption, increase with temperature since $\widehat{{I_{b}}^{\prime }}(\boldsymbol{k})\propto \overline{\unicode[STIX]{x1D703}}^{3}$ , as anticipated in § 3.3.

Figure 12. Modification function $f(k,\unicode[STIX]{x1D70F})$ over wavenumber for different optical depths.

The shape of $f(k,\unicode[STIX]{x1D70F})$ highlights the different behaviour of absorption when different temperature length scales are involved in the radiative heat transfer. If a turbulent temperature structure is large enough (i.e.  $k$ is small enough), it can be considered ‘opaque’, since it is able to capture the incoming radiation. Even though small scales are able to emit radiation, they are too thin to absorb, and thus can be considered transparent to incoming radiation. This behaviour of temperature scales is dictated by the magnitude of the optical thickness. For a larger $\unicode[STIX]{x1D70F}$ , the ability to absorb a greater quantity of incoming thermal radiation is extended to smaller scales. Therefore, increasing the optical thickness causes the ‘opaque wavenumber’ threshold to increase and the $f(k,\unicode[STIX]{x1D70F})$ slope to diminish (figure 12). Additionally, the effects of absorption and emission are amplified by the optical thickness $\unicode[STIX]{x1D70F}$ , since $\widehat{Q_{r}^{\prime }}=\unicode[STIX]{x1D70F}(\widehat{E_{m}^{\prime }}-\widehat{G^{\prime }})$ .

From this analysis we conclude the following. (1) The absorption reduces $\widehat{Q_{r}^{\prime }}(\boldsymbol{k})$ , resulting in a source of temperature variance, while emission increases $\widehat{Q_{r}^{\prime }}(\boldsymbol{k})$ , causing a dissipation of temperature fluctuations. (2) At a low optical thickness, a non-negligible effect of $G$ is observed only on the larger scales, while the higher-frequency fluctuations are still dominated by the effect of emission. (3) Upon increasing the optical thickness, absorption length scales are reduced, and are hence more correlated with temperature scales. Therefore, absorption is able to contrast emission effects up to larger wavenumbers. When the optically thick limit is reached $\widehat{G^{\prime }}(\boldsymbol{k})=\widehat{E_{m}^{\prime }}(\boldsymbol{k})$ over all significant wavenumbers. (4) The combined effect of emission and absorption, for a $\unicode[STIX]{x1D705}$ large enough, results in a withdrawal of energy at a constant rate throughout the scales due to emission, and a preferential accumulation of energy on the larger scales due to the effect of absorption. The temperature spectrum’s slope steepens as a result. (5) Modifying the significative wavenumbers of temperature in the system (i.e. increasing $Re$ or $Pr$ ) results in a modification of the radiation effects over the turbulent temperature spectra due to the wavenumber dependency of $f(k,\unicode[STIX]{x1D70F})$ . (6) A higher mean temperature results in an enhancement of both emission and absorption effects on the turbulent temperature spectrum.

4.2 Temperature spectra in turbulent radiative channel flows

In inhomogeneous anisotropic turbulence the turbulent temperature spectra will be different based on the location and the direction considered. In particular, in a turbulent channel flow with isothermal hot and cold walls, turbulent temperature structures are thin and streaky near the walls and somewhat larger and isotropic in the core (i.e. are characterized by a spectrum with energy concentrated at relatively small $\Vert \boldsymbol{k}\Vert$ while exhibiting the same trend in $k_{z}$ and $k_{x}$ ).

Since temperature structures are not homogeneous, different radiative effects will apply in different zones. In particular, where large and more isotropic structures are present, absorption will be more effective, retaining the emitted thermal energy, while where structures are thin and streaky (near the walls), emission will dominate, redistributing energy towards/from the walls and the centre of the channel.

Figure 13. Pre-multiplied, normalized turbulent temperature spectra contours $kE_{\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}}(k)/\overline{{\unicode[STIX]{x1D703}^{\prime }}^{2}}$ . (a,c,e) Spanwise spectra. (b,d,f) Streamwise spectra. Lines correspond to non-radiative case, while background contours correspond to (a) $\unicode[STIX]{x1D70F}=0.1$ ; (b) $\unicode[STIX]{x1D70F}=0.1$ ; (c) $\unicode[STIX]{x1D70F}=1$ ; (d) $\unicode[STIX]{x1D70F}=1$ ; (e) $\unicode[STIX]{x1D70F}=10$ ; (f) $\unicode[STIX]{x1D70F}=10$ .

Figure 13 shows the comparison of the normalized pre-multiplied temperature spectra, in the spanwise and streamwise directions, between radiative cases (background contours) and the non-radiative case (line contours). When $\unicode[STIX]{x1D70F}=0.1$ , figure 13(a,b), the whole channel is optically thin; therefore, emission dominates over absorption and no significant change in energy redistribution can be noticed. For $\unicode[STIX]{x1D70F}=1$ , figure 13(c,d), a slight steepening of the spectra can be noticed in the core of the channel. Indeed, when increasing optical thickness to $\unicode[STIX]{x1D70F}=10$ , figure 13(e,f), large structures located in the centre of the channel become opaque. This causes the emitted radiation to be reabsorbed within the large scales. We therefore observe that, in the core of the channel, the large, isotropic temperature scales grow in size and intensity, due to the action of radiative absorption.

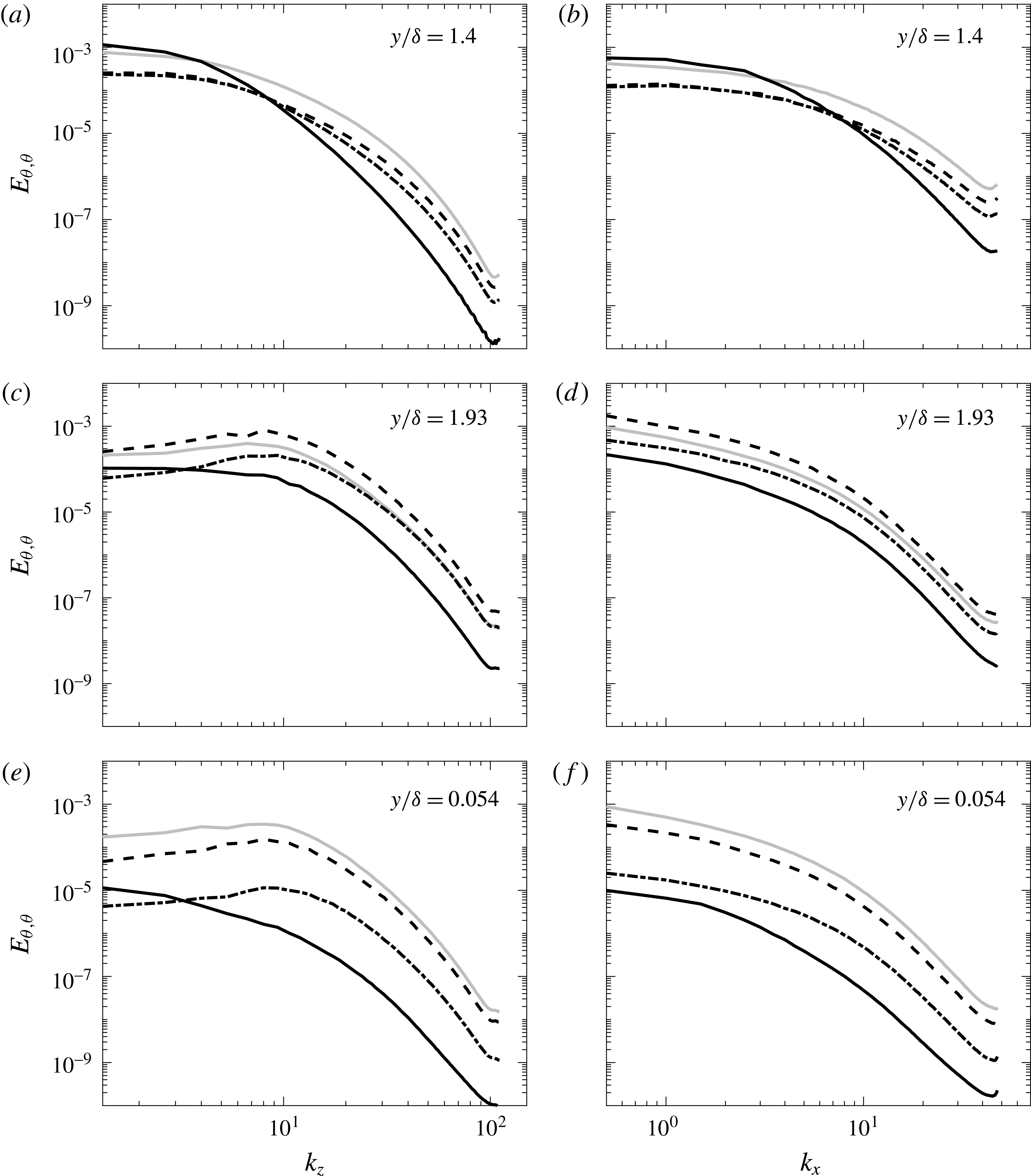
Figure 14. Turbulent temperature spectra $E_{\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}}$ for different locations. (a,c,e) Spanwise spectra. (b,d,f) Streamwise spectra. Grey solid line: no radiation, dashed line: $\unicode[STIX]{x1D70F}=0.1$ , dashed-dotted line: $\unicode[STIX]{x1D70F}=1$ , black solid line: $\unicode[STIX]{x1D70F}=10$ .

Spanwise turbulent temperature spectra at the locations $y/\unicode[STIX]{x1D6FF}=1.4$ , $y/\unicode[STIX]{x1D6FF}=1.93$ and $y/\unicode[STIX]{x1D6FF}=0.054$ (location of temperature variance peaks) are shown in figures 14(a), 14(c), 14(e), respectively, while figure 14(b,d,f) show streamwise turbulent temperature spectra at the same locations. By analysing figure 14(a,b), it is possible to notice that for a low optical thickness, case $\unicode[STIX]{x1D70F}=0.1$ , the thermal fluctuations are reduced proportionally throughout the whole spectrum and the slope is not significantly affected. This emphasizes that absorption does not play a significant role and that radiation affects the temperature spectrum through the emission TRI. A further decrease in overall thermal fluctuation intensity can be observed for $\unicode[STIX]{x1D70F}=1$ , with a larger fluctuation reduction concentrated at large wavenumbers (i.e. within the small scales). The modification of the turbulent temperature spectrum for $\unicode[STIX]{x1D70F}=1$ proves that the increase of $\overline{{G^{\prime }}^{2}}$ mostly affects large scales, while at small wavelength the stabilizing action of emission remains unaffected by absorption. Upon increasing the optical thickness ( $\unicode[STIX]{x1D70F}=10$ ) the temperature fluctuations located in the low-wavenumber region grow beyond the level of a non-radiative case. We conclude that, due to the emission–absorption process, radiation energy emitted at small scales is absorbed by the low-wavenumber range. The reduction of fluctuation due to emission is further amplified at high wavenumbers, confirming the previous observation of optically thin behaviour at the small scales.

Figure 15. Schematic diagram of TRI in anisotropic turbulence. The solid lines show a qualitative representation of temperature structures (assuming positive temperature fluctuation for simplicity), while the dashed circles show the characteristic length scale of radiation. Radiative emission is isotropic (i.e. emission occurs similarly in every direction). The influence of dimension and anisotropy of temperature structures is highlighted. The more isotropic the structure (near the centreline), the more efficient it is in absorbing the radiation emitted within itself, whereas anisotropic structures (near the walls) will dissipate their energy towards the lower temperature surroundings. A larger $\unicode[STIX]{x1D70F}$ would reduce the dimensions of the dashed circle, which would eventually fit in smaller anisotropic scales.

Figure 14(c,d) depicts turbulent temperature spectra for all cases at $y/\unicode[STIX]{x1D6FF}=1.93$ . In the streamwise direction (figure 14 d), due to the low level of incident radiation fluctuations, we observe a constant rate dissipation throughout the whole spectrum, except for $\unicode[STIX]{x1D70F}=0.1$ where the higher temperature gradient produces higher $\unicode[STIX]{x1D703}^{\prime }$ (see § 3.4). In the spanwise direction, the same behaviour as for the streamwise direction is noticed, with the exception of $\unicode[STIX]{x1D70F}=10$ , where, in the low-wavenumber range, absorption partly contrasts the dissipation effects of emission.

Finally, figure 14(e,f) shows the spanwise and streamwise spectra at $y/\unicode[STIX]{x1D6FF}=0.0545$ , respectively. Qualitatively the slopes of the spectra are much similar to what is observed for $y/\unicode[STIX]{x1D6FF}=1.93$ , but all effects are enhanced by the higher mean temperature, which increases radiative effects (as discussed in § 4.1). It is crucially important to point out that the results analysed in this section must be related to the observation of the impact of TRI discussed in § 3.4. There it is shown that the direct effect of radiation grows dramatically with an increase in $\unicode[STIX]{x1D70F}$ , and therefore the impact of radiation on temperature at a low optical thickness ( $\unicode[STIX]{x1D70F}=0.1$ ) is not only connected to direct effects, since also the modification of the mean temperature profile plays a large role.

Therefore, we summarize as follows. (1) For a low optical thickness the TRI effect mainly translates into a dissipation of thermal turbulence throughout the whole spectrum. For a higher optical thickness, besides dissipating fluctuations, TRI produces a withdrawal of energy from the small scales by the action of emission, which is then deposited within the large scales through absorption. A steepening of the turbulent temperature spectrum thus occurs as a consequence of the accumulation of energy in the low-frequency range. (2) Since radiative emission is isotropic, high anisotropy of temperature structures reduces absorption effects. (3) The accumulation of energy in large thermal eddies is noticed only in the core of the channel, where large and isotropic structures are present. In the near-wall region, where the growth of $G^{\prime }$ is inhibited by the presence of thin and highly anisotropic structures, a localized reduction of temperature fluctuation is observed for higher optical thicknesses, similarly to low optical thickness. (4) The higher mean temperature near the hot wall results in an enhancement of the radiative effects.

A clear visualization of the features described above is obtained with instantaneous contours of temperature fluctuations shown in figures 2 and 3, and is summarized in the schematic diagram in figure 15.

A simple diagram summarizing the effects of TRI on temperature fluctuations is shown in figure 16. Both mean and fluctuating radiative quantities have an effect on temperature statistics. While mean radiation indirectly affects $\unicode[STIX]{x1D703}^{\prime }$ through the modification of $\overline{\unicode[STIX]{x1D703}}$ , fluctuations of $E_{m}$ and $G$ have a direct effect on $\unicode[STIX]{x1D703}^{\prime }$ .

Figure 16. Schematic diagram of TRI in constant property flow. These relations will retain their validity in compressible turbulent flows. We did not investigate the effect of turbulence on radiation ( $\unicode[STIX]{x1D703}^{\prime }\rightarrow \overline{E}_{m},\overline{G}$ , shown as dashed) since it is reported to be negligible for non-reactive flows (Roger et al. 2011; Coelho 2012; Vicquelin et al. 2014; Ghosh & Friedrich 2015). While $E_{m}^{\prime }$ is directly connected to $\overline{\unicode[STIX]{x1D703}}$ and $\unicode[STIX]{x1D703}^{\prime }$ , the connection between $\overline{\unicode[STIX]{x1D703}}$ , $\unicode[STIX]{x1D703}^{\prime }$ and $G^{\prime }$ occurs in a spectral domain, since $G$ is a long-range variable, dependent on the whole temperature field.

5 Summary and concluding remarks

In the present work, a comprehensive study of TRI in a radiative turbulent channel flow has been performed. The modification of the temperature field upon varying the optical thickness has been extensively investigated with the aid of temperature variance budgets and turbulent temperature spectra. The results show different magnitudes and qualitative behaviours of TRI when different optical depths are considered, and highlight particularly the contrasting effects of radiative absorption and emission on TRI.

For a low optical thickness ( $\unicode[STIX]{x1D70F}=0.1$ ) the role of absorption is limited to the modification of mean profiles since incident radiation ( $G$ ) is not influenced by local thermal fluctuations. On the other hand, emission affects the whole temperature spectrum, stabilizing temperature and reducing thermal fluctuations mainly in the channel core. The direct effect of radiation on temperature variance is thus linked only to emission, and has a relatively small impact due to the low absorption coefficient. For an intermediate case ( $\unicode[STIX]{x1D70F}=1$ ) the effects are amplified and a strong depletion of the thermal fluctuation field is noticed because of emission. When increasing the optical depth to moderately optically thick levels ( $\unicode[STIX]{x1D70F}=10$ ), temperature variance shows a large influence on absorption due to a stronger local coupling between temperature and incident radiation. When $\unicode[STIX]{x1D70F}=10$ , energy is withdrawn from the whole spectrum due to a tight coupling of emission and temperature fluctuations, and it is accumulated on the large scales that are more sensitive to absorption fluctuations. The effect of a larger absorption fluctuation field is then translated into a modification of TRI. Radiative fluctuations are not only restricted to dissipating temperature fluctuation, but also cause a redistribution of fluctuations over the temperature scales.

The effect of anisotropic turbulence results in a reduction of the aforementioned TRI transition near the boundaries, where the thin streaky structures are not able to retain the emitted thermal radiation. In the centre of the channel, on the other hand, the larger isotropic structures can absorb and contain the redistributed energy.

Furthermore, a study of the budgets of temperature variance shows that with an increase in the optical thickness, the direct effect of radiation on temperature statistics grows drastically, replacing the role of molecular terms in dissipating and redistributing temperature variance. The radiative term ( ${\mathcal{R}}$ ) has been investigated, in analogy with molecular terms, by decomposition into two quantities, namely radiative diffusion $\unicode[STIX]{x1D719}_{r}$ and radiative dissipation $\unicode[STIX]{x1D716}_{r}$ . As the optical thickness is increased, we observed a similarity between the behaviour of radiative and molecular terms.

The results obtained provide a general and comprehensive study on the effect of TRI for various optical depths. The study has been realized by employing the grey gas assumption; therefore, additional simulations have to be performed to observe the effect of a real gas spectrum in the modification of TRI. Indeed, non-grey gases could show interesting effects and, therefore, a spectral simulation will be object of future work, with the utilization of an improved radiation model that can handle accurate spectral intensities and absorption coefficients. Nonetheless, the description outlined is considered to provide a valuable baseline for the analysis of more complicated cases.