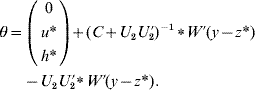1. Introduction
The aim of breeding values is to describe the genetic superiority of individuals and hence the capability of individuals to transmit favourable alleles to their progenies. Today the standard approach in animal breeding is to predict breeding values using the mixed model methodology of Best Linear Unbiased Prediction (BLUP) (Henderson, Reference Henderson1984). When applying BLUP, first genetic parameters (variances) are usually estimated by using restricted maximum likelihood (REML) (Patterson & Thompson, Reference Patterson and Thompson1971). In plant breeding, the prediction of breeding values was considered almost exclusively in research studies (for a review, see Piepho et al., Reference Piepho, Möhring, Melchinger and Büchse2008). Recently, breeding values have been predicted in self-pollinating crops by accounting for the inbreeding among lines (Bauer et al., Reference Bauer, Reetz and Léon2006; Oakey et al., Reference Oakey, Verbyla, Pitchford, Cullis and Kuchel2006; Bauer & Léon, Reference Bauer and Léon2008). Selecting by breeding values outperforms commonly used selection strategies, especially if datasets are unbalanced, contain large pedigrees or heritability of the regarded trait is low.
Breeding values are predicted either by a frequentist BLUP approach or by applying Bayesian Gibbs sampling. In general, a frequentist approach provides only the point estimates for breeding values, but separate accuracy estimates based on prediction error variance can be derived afterwards. In a Bayesian framework, by contrast, the whole posterior distribution of the breeding values is estimated conditionally on the data and by considering prior information. The Gibbs sampling algorithm, developed by Geman & Geman (Reference Geman and Geman1984), led to an increased use of Bayesian methods in quantitative genetics (e.g. Thomas, Reference Thomas1992; Wang et al., Reference Wang, Rutledge and Gianola1993; Sorensen et al., Reference Sorensen, Wang, Jensen and Gianola1994). By computing breeding values via Gibbs sampling, accuracy/interval estimates can be obtained since the full marginal posterior distribution of all the parameters of interest is sampled.
In crops, the use of Bayesian Gibbs sampling to predict breeding values is rare. Soria et al. (Reference Soria, Basurco, Toval, Silio, Rodriguez and Toro1998) considered Gibbs sampling in a tree-breeding program of Tasmanian bluegum (Eucalyptus globulus Labill.) to get inferences about breeding values and genetic parameters. Inferences about major genes and polygenic effects (general and specific combining ability) in a progeny population of Loblolly pine (Pinus taeda L.) were obtained by using a parent blocking Gibbs sampler (Zeng et al., Reference Zeng, Ghosh and Li2004). In Scots pine (Pinus sylvestris L.), Waldmann & Ericsson (Reference Waldmann and Ericsson2006) computed a multi-trait individual tree model for a diallele progeny dataset. In a following study, Waldmann et al. (Reference Waldmann, Hallander, Hoti and Sillanpää2008) developed a fast hybrid Gibbs sampler, which accounted for additive and dominance variances in a mixed model using the same Scots pine dataset as above. Gwaze & Woolliams (Reference Gwaze and Woolliams2001) estimated a quadrivariate tree model to obtain covariance components for height across two sites and two ages for the Loblolly pine (P. taeda L.). In this study, the two sites and two ages were treated as different traits.
Of all the previous quantitative genetics research studies of plant science, Bayesian Gibbs sampling has mainly been applied in forest tree breeding. It seems that the Gibbs sampler has not yet been applied to predicting breeding values in annual crops, especially if they are self-pollinated. Additionally, there is no Gibbs sampling algorithm available for statistical models where genotype-by-environment interactions are included. Genotype-by-environment interactions occur if lines react differently to changing environmental conditions resulting often in a different rank order of the lines in each environment (Weber & Wricke, Reference Weber, Wricke and Kang1990). Therefore, plant breeders are forced to evaluate the lines in several locations and years for estimating the genetic performance. The genotype-by-environment interactions can be analysed for example in a stability analysis (Becker & Léon, Reference Becker and Léon1988) or by an Additive Main Effects Multiplicative Interaction (AMMI) model (Gauch, Reference Gauch1988). Note that the genotype-by-environment interactions being commonly observed in breeding plants and, to a lower extent in animals, are different to the so-called genotype-by-environment correlations that occur mainly in animal breeding. Genotype-by-environment correlations can arise when elite animals are kept in a more favourable environment than weaker animals. In this case, the genotype and the corresponding environmental conditions are correlated among each other (Falconer & Mackay, Reference Falconer and Mackay1996). In plant breeding, usually genotype-by-environment correlation is avoided by adequate experimental field designs due to randomization of environments. As in plant breeding the genotype-by-environment interactions have much more importance, this interaction effect should be accounted for in the Bayesian model to predict breeding values. Up to now, considering interaction effects in Bayesian Gibbs sampling is scarce.
Thus, the objective of our research is to predict Bayesian breeding values of spring barley (Hordeum vulgare L.) lines and of a ‘virtual’ parental population of self-pollinating crops generated by computer simulation. A Gibbs sampling algorithm was developed that (i) is adapted to the high degree of inbreeding in a parental population of self-pollinating crops and (ii) accounts for genotype-by-environment interactions. In addition, standard REML estimates from a frequentist approach were also calculated for comparison.
2. Material and methods
(i) Simulation
Following Bauer & Léon (Reference Bauer and Léon2008), a ‘virtual’ population of 100 parental inbred lines was generated by Monte Carlo simulation using the Interactive Matrix Language (IML) of SAS software (SAS Institute, 2004). As the Bayesian prediction of breeding values was computationally demanding, a multi-environmental field trial for one year was generated. All lines were cultivated at three locations with three blocks and two replications each. The phenotypic value of a line consisted of a genotypic value, and of random location, genotype-by-location interaction, block and residual effects. The genotypic value of a line was obtained by first generating random additive-genetic effects for each of the 150 loci from a standard normal distribution following the one-locus model and then summing these additive-genetic effects over all 150 loci. In addition, for 10% of the parental lines a random measurement error was computed as systematic noise to make the data simulation more realistic. This heterogeneity leads to an increase of the residual for some genotypes. All simulated effects, except of genotype-by-location interaction and residual effects, were normally distributed with a mean of zero and a standard deviation of one [N(0, 1)].
The genotype-by-location interaction effect was simulated by assigning in a first step a normally distributed random number [N(0, 0·5)] to each possible combination of location and allele (B or b) at a locus as related lines are assumed to have a similar genotype-by-location interaction. Then, for all lines the interaction effects are added over all loci at each location separately. Thus, the more alleles that two lines have in common, the more similar their genotype-by-environment interactions will appear.
In the simulation, all parental lines were measured for a high and a low heritable trait. To obtain traits with a different heritability, the residual effects were generated from a normal distribution with a mean of zero but a varying standard deviation. The high (low) heritable trait was computed from a residual effect with a standard deviation of 17 (56).
The population of parental lines was divided into a base and a progeny population. The base population comprised 30 lines that were randomly crossed with each other to produce 70 progeny lines. The progeny lines were self-pollinated until they reached homozygosity. Hence, all lines in the population were assumed to be homozygous with an inbreeding coefficient of 0·99. For the whole population, pedigree information was available.
The simulation procedure of the parental population was repeated 100 times. The SEEDGEN macro, written by Fan et al. (Reference Fan, Felsövályi, Sivo and Keenan2002), was used to avoid overlapping streams in the generation of random numbers.
(ii) Field data
Field data of 82 spring barley (H. vulgare L.) lines originating from the German North Rhine–Westphalia core collection (Bauer et al., Reference Bauer, Reetz and Léon2006, Reference Bauer, Reetz and Léon2008) were used. The lines were cultivated in a randomized complete-block design at the Research Station ‘Dikopshof’ of University of Bonn near to Cologne (Germany) in two different years (2002 and 2003) with three replications each. The lines were measured for the trait ‘thousand kernel mass’. Pedigree information was available for all lines.
(iii) Data analysis
Breeding values were predicted by a frequentist approach using the software package ASReml 2.0 (Gilmour et al., Reference Gilmour, Gogel, Cullis and Thompson2005) as well as by the Bayesian blocked Gibbs sampling algorithm of García-Cortés & Sorensen (Reference García-Cortés and Sorensen1996), which was implemented in Matlab 7 (2007). Both approaches were computed for 100 simulation replicates of the ‘virtual’ population of parental lines and for the spring barley lines.
Pedigree information was accounted for in the genetic relationship matrix A, which considers the additive-genetic variances and covariances among the lines. Henderson (Reference Henderson1976) and Quaas (Reference Quaas1976) developed a recursive algorithm to calculate this matrix efficiently. There, the authors assumed that the base population is not inbred. Considering self-pollinating crops, however, usually the base population is highly inbred. Ignoring this degree of inbreeding in the base population would lead to biased breeding values of these lines. Thus, following Bauer & Léon (Reference Bauer and Léon2008) the coefficient of inbreeding of the lines was accounted for not only for the progenies but also for their parents in the base population by obtaining all diagonal elements of the A-matrix from 1+Fi (where Fi equals the coefficient of inbreeding). This is in contrast to Henderson (Reference Henderson1976), who did not consider the coefficient of inbreeding in computing the diagonal elements of parental individuals.
(a) Frequentist approach
In a frequentist approach, all effects were assumed to be random, so that the X matrix includes only the overall population mean. Therefore, the corresponding linear model of the ‘virtual’ parental population can be written in matrix notation as
where y is the vector of phenotypic observations; β is the vector of the fixed effect; u is the vector of the random genotypic effect of the lines; s is the vector of the random location effect; t is the vector of the random block effect; h is the vector of the random genotype-by-location interaction effect; and e is the vector of residual effect. X, Z, P, Q and F represent the corresponding design matrices.
Similarly, the statistical model of the spring barley lines follows from:
where l is the vector of the random year effect; h is the vector of the random genotype-by-year interaction effect; V and F are design matrices.
For simplification, in the following, the genotype-by-location interaction in the ‘virtual’ population and the genotype-by-year interaction of the spring barley lines will be summarized as genotype-by-environment interaction.
The resulting covariance structures of the estimated effects are: Var(u)=Aσg 2, Var(s)=Iσs 2, Var(t)=Iσt 2, Var(l)=Iσl 2, Var(h)=Iσh 2, Var(e)=Iσe 2=R (with A=genetic relationship matrix; R=matrix of variances and covariances of residual effects; I=identity matrix; σg 2=variance of genotypic effects; σs 2=variance of location effects; σt 2=variance of block effects; σl 2=variance of year effects; σh 2=variance of genotype-by-environment interaction effects; σe 2=residual variance).
The corresponding Mixed Model Equations (MME) to the statistical model of the ‘virtual’ population, which are obtained in a frequentist approach, are:

where α1=σe 2/σg 2, α2=σe 2/σs 2, α3=σe 2/σt 2 and α4=σe 2/σh 2.
(b) Bayesian block Gibbs sampling
In a Bayesian framework, all unknown parameters are sampled from distributions and are therefore treated as random. In this study, the overall mean and the effects for location, block (‘virtual’ population) and year (field data) were considered in the X-matrix. Thus, the statistical model is displayed as
To compute a Bayesian analysis, prior distributions are assigned to β, u, h, σg 2, σh 2 and σe 2. For β, we assumed an improper prior distribution with p(β)∝constant. The prior distributions of u and h were equal to u|σg 2~N(0, Aσg 2) and h|σh 2~N(0, Iσh 2), respectively. For genotype-by-environment and residual variance, uninformative priors were used. The prior specifications for the variance components were supposed to be scaled inverted chi-square distributions (Gianola & Sorensen, Reference Gianola and Sorensen2002):

where σi2 is the variance component of factor i, vi is the degree of belief parameter and S i2 is the prior value.
In the Bayesian analysis, two approaches were applied that differ in the way the genotype-by-environment interaction is modelled. In the first approach, the variance of the genotype-by-environment interaction was considered similarly to the frequentist approach (REML), where the variance of the genotype-by-environment interaction σh2 is assumed to be independently and identically normally distributed as h|σh 2~N(0, Iσh 2). This strategy is referred to as Bayes_ID. In a second approach, we replaced the identity matrix I with an extended relationship matrix A ext (=A⊗I) as related lines often show a similar genotype-by-environment interaction (Bayes_Aext).
In the Gibbs sampler, the unknown parameters can be updated and drawn either elementwise (single-site Gibbs sampler) or blockwise (blocked Gibbs sampler). Using the single-site Gibbs sampler, parameters are updated element by element (see e.g. Thomas, Reference Thomas1992; Lin, Reference Lin1999; Gianola & Sorensen, Reference Gianola and Sorensen2002). As convergence can be very slow, the blocked Gibbs sampler (García-Cortés & Sorensen, Reference García-Cortés and Sorensen1996) was applied in this study, which drew all parameters as a single block. The disadvantage of this grouped Gibbs sampling is that each iteration needs the inverse of the coefficient matrix C, which can slow down the algorithm.
The coefficient matrix C of the MME equals

The vector of the right-hand side of the MME is W′y, with W=(X Z F). All unknown parameters are summarized in the vector θ. Then according to Gianola & Sorensen (Reference Gianola and Sorensen2002) θ can be obtained from

where z is a random vector of pseudo-observations with [z|μ, u, h, σe 2]~N(Xμ+Zu+Fh, Iσe 2). Original idea in the García-Cortés & Sorensen (Reference García-Cortés and Sorensen1996) algorithm was to calculate the inverse of the large C matrix using iterative methods. However, in the present study, due to relatively small size of C, the inverse of C was calculated using direct methods. The inverse of C is not defined if the C-matrix is characterized by rank deficiencies, which occurs if the number of linearly independent rows or columns is smaller than the total number of rows and columns of this matrix. In this case, we calculated the pseudoinverse of C using the nullspace U 2 of the C-matrix, because this procedure is computationally more efficient than computing simply the pseudoinverse (see Appendix for the derivation). Therefore, θ is calculated from

The variance components are sampled from

with ![]() ,
, ![]() and
and ![]() degrees of freedom of a scaled inverted chi-square distribution (n=number of lines; q=number of genotype-by-environment interaction levels; N=number of observations; vu, vh, ve=degree of belief parameter),
degrees of freedom of a scaled inverted chi-square distribution (n=number of lines; q=number of genotype-by-environment interaction levels; N=number of observations; vu, vh, ve=degree of belief parameter), ![]() ,
, ![]() and
and ![]() . To obtain flat priors, vu, vh, ve were chosen to be −2, and Su 2, Sh 2, Se 2 being equal to 0.
. To obtain flat priors, vu, vh, ve were chosen to be −2, and Su 2, Sh 2, Se 2 being equal to 0.
The algorithm of the blocked Gibbs sampler is as follows:
1. Initialize the parameters α1, α4, σg 2, σh 2 and σe 2. In this study, the starting value for all parameters was equal to 1.
2. Generate u* from N(0, Aσg 2).
3. Generate h* from N(0, Iσh 2).
4. Generate z* from N(Zu*+Fh*, Iσe 2).
5. Compute W′ (y−z*).
6. Calculate θ as
 if C has full rank. Otherwise, if a rank deficiency of C occurs, calculate θ as
if C has full rank. Otherwise, if a rank deficiency of C occurs, calculate θ as

7. Calculate
 ,
,  and
and  .
.8. Sample
 from
from  , where i=u, h, e.
, where i=u, h, e.9. Compute the variance components from
 with i=u, h, e.
with i=u, h, e.10. Calculate the variance ratios
 and
and  .
.11. Update the coefficient matrix C.
12. Repeat steps 1 to 11 until the MCMC chain converges.
As related lines are supposed to have a similar genotype-by-environment interaction, we modified the Gibbs sampler by including an extended genetic relationship matrix A ext in a second run. The extended A ext-matrix was obtained by calculating the Kronecker product of the genetic relationship matrix A with an identity matrix with a size depending on the number of locations (cf. Smith et al., Reference Smith, Cullis and Gilmour2001). This extended A ext-matrix then has a block structure. Here, the dataset has to be sorted by location, because it would not otherwise be possible to invert A ext.
Using the extended relationship matrix A ext, instead of the identity matrix, to account for the genotype-by-environment interaction in Gibbs sampling, the coefficient matrix C in the MME is obtained from

The prior distribution of h equals h|σh 2~N(0, A extσh 2). So, in the Gibbs sampling, h* is generated from N(0, A ext σh 2). The variance component for genotype-by-environment interaction is sampled from ![]() , where
, where ![]() .
.
Accounting for relationship information in the REML variance component estimation of genotype-by-environment interaction variance by using the matrix A ext was not possible due to singularities in the Average Information matrix that is considered in the ASReml program. In Bayesian Gibbs sampling, the problem of singularities in a matrix was solved by accounting for the nullspace of this matrix in the computation of the pseudoinverse.
The Gibbs sampler was run for 50 000 iterations with a ‘burn-in’ period of 20 000 iterations, although, to save storage capacity, only every 10th sample was considered. The computing time on a Pentium 2·66 GHz dual core processor was a couple of minutes for the frequentist approach and one week for the Bayesian analyses of all simulation replicates.
(iv) Evaluating results from frequentist approach and Bayesian analyses
For each simulation replicate and for the spring barley lines, in the Bayesian analyses, point (mean, median and mode) and interval (95% highest posterior density region) estimates of posterior distribution of variance components were calculated using Matlab 7 (2007). Following Hoti et al. (Reference Hoti, Sillanpää and Holmström2002), a kernel smoothing approach was used to summarize the posterior distribution for mode estimation. Also, the standard deviations of the posterior variance component distributions were derived.
To obtain Bayesian breeding values, point estimates (mean, median and kernel-density-based mode) of the posterior distributions of the estimated genetic line effects were computed. Then, for each analysis (frequentist approach, Bayes_ID and Bayes_Aext) of the ‘virtual’ population, Spearman's rank correlation coefficient, between estimated breeding values and true genotypic values of the lines, was calculated using the software package SAS 9.1 (SAS Institute, 2004). Spearman's correlation coefficient is derived by first ranking the data and then using the ranks in the formula of Pearson's correlation coefficient. In addition, prediction error variance was derived by computing the variance of the difference between estimated breeding values and true genotypic values.
To summarize the results of the ‘virtual’ population, the arithmetic means and standard deviations of the REML estimated variance components, Bayesian point and interval estimates, standard deviations of posterior distributions and true (simulated) variance components were computed over all simulation replicates.
The heritability h 2 was calculated for all traits based on true (simulated) variance components (in the ‘virtual’ population) and on estimated values of variance components given by the frequentist approach, Bayes_ID and Bayes_Aext analyses. To compute the heritability of traits measured in plant breeding trials, one has to account for the fact that in contrast to animals where the heritability usually is based on the individual itself as reference unit, the same (homozygous) plant genotype can be cultivated in replicated field plots in several environments. In the milk production of cows at different days in lactation, a related situation can occur where multiple observations on the same animal were obtained, which give rise to permanent environmental variance. To choose the plant genotype as reference unit for computing the heritability, the fraction of the phenotypic variance being transmitted to the progenies has to be considered. Thus, in the present case, the variances of genotype-by-environment and residual have to be divided by the number of locations, blocks and replications as follows (Hanson, Reference Hanson, Hanson and Robinson1963):
where σg 2 is the variance of genotypic effects; σh 2 is the variance of genotype-by-environment interaction effects; σe 2 is the residual variance; j is the number of locations; k is the number of blocks; and l is the number of replications within each block and location.
For the Bayesian analyses, first based on the estimated variance components the posterior distributions of heritabilities were computed. Then, the posterior mean, median, mode, standard deviation and 95% highest posterior density interval of the heritabilities were obtained.
3. Results
In this study, genetic effects were predicted by a frequentist approach and two variants of Bayesian methods (Bayes_ID and Bayes_Aext). In Bayesian analyses, the mean, median and mode were calculated as point estimates of the posterior distributions. For comparison, in the ‘virtual’ population true (simulated) values were also given. The results of the variance component and breeding value estimation of the ‘virtual’ population and of the spring barley lines will be presented below.
(i) ‘Virtual’ parental population
In general, with increasing heritability, the estimated variance components correspond to the true values to a greater extent, the standard deviation of posterior distributions is smaller and the posterior distribution is less skewed (Table 1, Fig. 1). In addition, for the genotype-by-environment interaction variance (a small variance component), the posterior distribution is more skewed than for the residual variance (a large variance component) (Fig. 1). In comparing the Bayesian point estimates, except for the case of the Bayes_ID analysis of a low heritable trait, the mean, median and mode were estimated close together and located within the 95% highest posterior density region. If the Bayes_ID method is used for a trait with low heritability, the mean is the only estimate that gives reasonable results (Table 1).

Fig. 1. Frequency distribution of the posterior variance components obtained by Bayes_ID and Bayes_Aext for two traits in the ‘virtual’ population. Additionally, point estimates and the 95% highest posterior density regions are given (straight line=posterior mean; dashed line=posterior median; dotted line=posterior mode). In this figure, the results of one simulation replicate are displayed. (a) Additive genetic variance of a low heritable trait. (b) Additive genetic variance of a high heritable trait. (c) Genotype-by-environment interaction variance of a low heritable trait. (d) Genotype-by-environment interaction variance of a high heritable trait. (e) Residual variance of a low heritable trait. (f) Residual variance of a high heritable trait.
Table 1. Posterior mean, median, mode, standard deviation (std) and 95% highest posterior density (HPD) obtained from Bayes_ID and Bayes_Aext methods, estimates from the frequentist approach (REML) and true (simulated) values of variance components for two traits of the ‘virtual’ population (with additive genetic variance σg2, genotype-by-environment interaction variance σh2, residual variance σe2). In addition, heritability (h2) estimates are displayed. All estimates were averaged over the 100 simulation replicates

For both traits, the additive-genetic variance is overestimated by the Bayes_Aext method, whereas the Bayes_ID values correspond well to the REML and true (simulated) values. If the heritability of the regarded trait is high, the genotype-by-environment interaction variance is underestimated when the Bayes_Aext analysis is performed, but is estimated accurately with the Bayes_ID and frequentist approaches. With low heritability, erroneous interaction variance components were obtained using the Bayes_ID method. Using the Bayes_Aext or frequentist approaches, however, an estimation of the genotype-by-environment interaction was possible, resulting in overestimated variance components. The estimation of residual variance components yielded slightly overestimated values for Bayesian analyses for both traits (Table 1, Fig. 1). Independently, if the Bayes_ID or Bayes_Aext method is computed, the differences between the estimated and true variance components are higher for additive and genotype-by-environment interaction variances than for the residual variance components.
Heritability was estimated from variance components obtained from REML, Bayes_ID and Bayes_Aext. Similar heritability estimates were found for Bayes_ID and REML, which correspond to the true (simulated) heritability. In contrast, when using Bayes_Aext, slightly overestimated heritability estimates were observed.
To determine how accurate the breeding values were predicted by the frequentist, Bayes_ID and Bayes_Aext approaches, Spearman's rank correlation coefficient between estimated breeding value and true (simulated) genotypic value of the lines and the prediction error variance were calculated for each analysis (Tables 2 and 3). In general, the rank correlation coefficient is higher and the prediction error variance is lower for a high heritable trait than for a trait with low heritability. If we consider a high heritable trait, similar rank correlation coefficients and prediction error variances are obtained for all analyses. By contrast for a low heritable trait, the rank correlation coefficient is maximized and the prediction error variance is minimized for the frequentist approach and the Bayes_Aext analysis. The lowest rank correlation and the largest prediction error variance were obtained with the Bayes_ID method.
Table 2. Spearman's rank correlation coefficient between true genotypic values and point estimates of breeding values obtained by a frequentist approach and Bayesian analyses of a high and a low heritable trait in the ‘virtual’ population. The rank correlation coefficients were averaged over all simulation replicates

Table 3. Prediction error variance of breeding values obtained by a frequentist approach and Bayesian point estimates of a high and a low heritable trait in the ‘virtual’ population. The prediction error variances were averaged over all simulation replicates

Considering the standard deviation over the 100 simulation replicates in the ‘virtual’ population, the standard deviation of the variance components of genotype-by-environment interaction is similar to that of the true genotype-by-environment interaction variance if the Bayes_Aext method was used (Table 4). In contrast, the standard deviation of the variance components of genotype-by-environment interaction obtained by Bayes_ID or a frequentist approach is increased greatly over the simulation replicates for both traits. For a low heritable trait, the Bayes_Aext method and a frequentist approach result in lower standard deviations of Spearman's rank correlation coefficient and prediction error variance over all simulation replicates than Bayes_ID analysis.
Table 4. Standard deviation over simulation replicates of posterior mean, median, mode, standard deviation (post. std) and 95% highest posterior density (HPD) obtained from Bayes_ID and Bayes_Aext methods, and estimates from the frequentist approach (REML) for variance component estimates, Spearman's rank correlation coefficient and prediction error variance of two traits having a high and a low heritability h2 in the ‘virtual’ population (with additive genetic variance σg2, genotype-by-environment interaction variance σh2, residual variance σe2)

(ii) Spring barley lines
The genetic parameters of the spring barley lines were predicted by Bayes_ID, Bayes_Aext and a frequentist approach. For all analyses, similar variance components were observed (Table 5). In addition, the trait heritability, the highest posterior density regions and the standard deviation of the posterior distributions of all variance components are in the same range for the Bayes_ID and the Bayes_Aext method. By comparing the point estimates of the posterior distributions, as in the ‘virtual’ parental population, the mode estimate is smaller than the median that is smaller than the mean (Table 5, Fig. 2).

Fig. 2. Frequency distribution of the posterior variance components obtained by Bayes_ID and Bayes_Aext for the trait ‘thousand kernel mass’ of the spring barley lines. Additionally, point estimates and the 95% highest posterior density regions are given (straight line=posterior mean; dashed line=posterior median; dotted line=posterior mode). (a) Additive genetic variance. (b) Genotype-by-environment interaction variance. (c) Residual variance.
Table 5. Posterior mean, median, mode, standard deviation and 95% highest posterior density (HPD) obtained from Bayes_ID and Bayes_Aext methods, and estimates from the frequentist approach (REML) for the trait ‘thousand kernel mass’ of the spring barley lines (with additive genetic variance σg2, genotype-by-environment interaction variance σh2, residual variance σe2). In addition, heritability (h2) estimates are displayed

4. Discussion and conclusions
In this study, a Bayesian model was used to account for genotype-by-environment interaction in two different ways. In the first Bayesian analysis (Bayes_ID), the interaction effect was modelled and treated exactly as in the frequentist approach. However, as related lines are assumed to have a similar genotype-by-environment interaction, we modified the model by including an extended genetic relationship matrix A ext, in a second Bayesian analysis (Bayes_Aext). The objective of the current study was to determine if Bayes_Aext leads to more accurate breeding values than Bayes_ID. For comparison, breeding values were also predicted using a frequentist approach. To estimate the genetic parameters, multi-environmental data of a ‘virtual’ parental population were considered. To verify the results obtained by Bayesian analyses and a frequentist approach in the ‘virtual’ population, additionally field data of spring barley lines were used.
In the frequentist approach using ASReml software (Gilmour et al., Reference Gilmour, Gogel, Cullis and Thompson2005), the estimation is divided into two steps. First, the variance components are estimated by REML (Patterson & Thompson, Reference Patterson and Thompson1971), by applying the Average Information algorithm of Gilmour et al. (Reference Gilmour, Thompson and Cullis1995). Next, the estimated REML variance components are used in the MME to predict breeding values. The disadvantage of this strategy is that the uncertainty of the estimated variance components is underestimated because it is not incorporated in the BLUP estimates. By contrast in the Bayesian analyses, it is possible to estimate the variance components and breeding values simultaneously by Gibbs sampling. Thus, the uncertainty of estimated variance components can be accounted for. Getting accurate estimates of the variance components is important because biased estimates can lead to increased prediction errors of breeding values (van Tassell et al., Reference Van Tassell, Casella and Pollak1995). Due to the mentioned differences between a Bayesian and a frequentist framework, one should have in mind that the methods are not fully comparable, although in this study the general model is the same in Bayesian and frequentist approaches.
In our study, in the ‘virtual’ parental population, with increasing heritability of the trait, the differences between the estimated variance components and true (simulated) values decreased, and the standard deviation of posterior distribution was lowered. Phenotypic observations of a high heritable trait are mainly influenced by genetic effects, rather than environmental effects, which leads to an increased prediction accuracy. For additive-genetic and genotype-by-environment interaction variance components, slightly skewed posterior distributions were obtained (Figs 1 and 2). This skewness occurs especially for small variance components (van Tassell et al., Reference Van Tassell, Casella and Pollak1995), which could be due to the fact that variance components are allowed to only take positive values (Hazelton & Gurrin, Reference Hazelton and Gurrin2003). Skewed posterior distributions can result in biased point estimates, such as the mean, median and mode (Zeger & Karim, Reference Zeger and Karim1991; Burton et al., Reference Burton, Tiller, Gurrin, Cookson, Musk and Palmer1999), which differ highly among each other (Hazelton & Gurrin, Reference Hazelton and Gurrin2003). In our study, the differences between the estimated variance components and true (simulated) values were higher for additive-genetic and genotype-by-environment interactions than for residual variance (Table 1, Fig. 1). This is because of the skewed additive-genetic and genotype-by-environment interaction posterior distributions, whereas the residual posterior variance was closer to a normal distribution. Waldmann & Ericsson (Reference Waldmann and Ericsson2006) and Waldmann et al. (Reference Waldmann, Hallander, Hoti and Sillanpää2008) also stated that the Scots pine (P. sylvestris L.) estimates of genetic variance components were more biased due to the posterior distributions being more skewed than the residual variance. In our field data example of spring barley lines, similar variance components were obtained by all prediction strategies (Table 5). For all variance components, we found similar values for the mean, median and mode (Tables 1 and 5). Van Tassell et al. (Reference Van Tassell, Casella and Pollak1995) stated that the mean is more appropriate for estimating the variance components than the mode. Additionally, with decreasing heritability of the regarded traits, the differences between the estimates increased, which is also in accordance with Waldmann & Ericsson (Reference Waldmann and Ericsson2006).
For estimating the mode of a posterior distribution, the mode is usually computed based on a histogram of the MCMC samples. However, this approach depends on the bin width and the sideway shift of the bin grids of the histogram leading to biased mode estimates. Hoti et al. (Reference Hoti, Sillanpää and Holmström2002) introduced a kernel density estimation to smooth the shape of the posterior distribution. The use of kernel smoothing can improve the localization of the mode estimate significantly.
Heritability estimates provided by REML and Bayes_ID in the ‘virtual’ population were found to be quite similar to heritability estimates from simulated data (Table 1). In contrast, heritability estimates of the Bayes_Aext variance components were slightly overestimated, since, in this analysis, the additive-genetic variance was positively biased. This could be due to the fact that the genetic relationship matrix was accounted for twice in the Bayes_Aext model. Gwaze & Woolliams (Reference Gwaze and Woolliams2001) also found a larger heritability when computed with a Bayesian analysis, rather than a REML analysis. In contrast, in the spring barley population Bayes_ID method resulted in a larger heritability estimate than REML, but the lowest heritability estimate was found using Bayes_Aext analysis.
In self-pollinated crops, breeding values are estimates of the true genotypic value of the lines. To predict breeding values having BLUP characteristics, a frequentist approach or a Bayesian method can be used. All strategies should maximize the correlation between true and estimated breeding values and minimize the prediction error variance. Thus, in this study for each analysis, Spearman's rank correlation coefficient between breeding value and true genotypic value (Table 2) and the prediction error variance of estimated breeding values (Table 3) were computed. The higher the rank correlation and the lower the prediction error variance, the more accurate the corresponding prediction method. In general, with decreasing heritability the rank correlation between estimated breeding value and true genotypic value will be lower because of the larger environmental influence on the phenotype, and hence the prediction error variance will be higher. Especially for a low heritable trait, the prediction strategy Bayes_Aext is superior to Bayes_ID (Tables 2 and 3). Predicting breeding values by using the Bayes_Aext method or a frequentist approach, the estimated breeding values correspond to the true genotypic value to a greater extent than using the Bayes_ID method. Thus, it seems to be important to account for the relationship information between lines not only in predicting the genetic line effect but also in computing genotype-by-environment interactions (Bayes_Aext), if a Bayesian prediction strategy is applied considering genotype-by-environment interactions in the statistical model. In contrast, in a frequentist approach (REML), the integration of relationship information in the calculation of genotype-by-environment interaction variance resulted in singularities in the Average Information matrix. In animal breeding, Schenkel et al. (Reference Schenkel, Schaeffer and Boettcher2002) did not find any differences between the rank correlations of a Bayesian or a frequentist approach to simulated breeding values. Also, Robinson (Reference Robinson1991) and Harville & Carriquirry (Reference Harville and Carriquirry1992) stated that the differences between breeding values predicted by a frequentist or a Bayesian approach are minimal. The superiority of Bayes_Aext analysis for a low heritable trait is supported by considering the standard deviations of estimated genotype-by-environment interaction variances, Spearman's rank correlation coefficients and prediction error variances over all simulation replicates (Table 4). Especially for a low heritable trait, a lower standard deviation over the simulation replicates was obtained by the Bayes_Aext method being similar to that of true (simulated) values than with Bayes_ID analysis.
If genotype and environment are correlated among each other as it often occurs in animal breeding, heterogeneity of the residual variance can be found. In such situations, for each environment an own residual could be considered in the model (Fernando et al., Reference Fernando, Knights and Gianola1984) to avoid occurrence of erroneous genotype-by-environment interaction variance due to heterogeneity of variances. In plant breeding, however, due to the fact that the lines are completely homozygous (pure inbred lines), it is possible to cultivate the same genotype on several locations in different years. Thus, by choosing an appropriate field design, the heterogeneity of the residual variance can be greatly reduced. Therefore, in this study, the heterogeneity of the residual variance is not accounted for in the statistical models.
A further increase in prediction accuracy is expected by taking information of molecular markers in the estimation of breeding values into account. One option would be to include genetic similarities calculated based on molecular marker data in the prediction instead of the commonly used genetic relationship matrix (Bauer et al., Reference Bauer, Reetz and Léon2006, Reference Bauer, Reetz and Léon2008). This approach is advantageous if pedigree information among the lines is missing or unavailable. Another strategy is to predict genome-wide breeding values considering the marker scans of the whole genome (Meuwissen et al., Reference Meuwissen, Hayes and Goddard2001).
In self-pollinating populations, the parental lines are characterized by a high degree of inbreeding. In computing the genetic relationship matrix A, Henderson (Reference Henderson1976) assumed that the parental base population is not inbred and unrelated. If Henderson's recursive algorithm is also used for parental inbred lines, the resulting breeding values will be underestimated. Hence, in this study the degree of inbreeding of parental lines was taken into account by calculating all diagonal elements of A-matrix by 1+Fi (where Fi=coefficient of inbreeding).
A Bayesian approach can be advantageous if the population size is large or the model structure is complex, because it may be easier to compute the sampling of the marginal posterior distributions (Blasco, Reference Blasco2001; Duangjinda et al., Reference Duangjinda, Misztal, Bertrand and Tsuruta2001) than the frequentist analysis with its two-stage approach. The disadvantage of the Bayesian prediction of breeding value is its high computing costs. Therefore, it is important to sample the marginal posterior distribution efficiently. In general, the Gibbs sampler developed by Geman & Geman (Reference Geman and Geman1984) is used. The single-site Gibbs sampler (Gianola & Sorensen, Reference Gianola and Sorensen2002) updates each parameter consecutively, yielding a random sample of the marginal posterior distribution. To obtain a faster convergence rate, García-Cortés & Sorensen (Reference García-Cortés and Sorensen1996) developed a blocked Gibbs sampling algorithm, which we also have used in our study. In this algorithm, the conditional distribution of all parameters is updated in a blockwise manner. However, in a population with large pedigree size the blocked sampler can be slow as solutions to the huge equation systems of the MME are still required. Thus, it could be more efficient to use a hybrid Gibbs sampler, such as that developed by Waldmann et al. (Reference Waldmann, Hallander, Hoti and Sillanpää2008). In the hybrid sampler, the fast but slow mixing single-site sampler is combined with the slow but fast mixing block updating. Another approach to speed up the blocked Gibbs sampler is to account for rank deficiencies of the coefficient matrix C during matrix inversion. If the C-matrix does not have full rank, a pseudoinverse has to be calculated, which is also computationally demanding. Thus, by considering the nullspace of the C-matrix in the calculation of the pseudoinverse of C, the computing time of sampling the posterior distribution can be shortened, because the nullspace does not change during the MCMC sampling and must therefore be computed only once.
In conclusion, considering the degree of inbreeding in Bayesian analysis was possible without any problems. If genotype-by-environment interactions occur in the data, standard Bayesian Gibbs sampling and a frequentist approach resulted in similar estimates if the trait has a high heritability. For such traits, Bayesian as well as frequentist methods can be recommended although a Bayesian approach could be more appropriate if the statistical model is more complicated. For low heritable traits, however, the standard Gibbs sampling approach is not a suitable strategy to account for genotype-by-environment interactions. Therefore, as related lines are supposed to show similar interactions, an extended genetic relationship matrix was included in the term of genotype-by-environment interaction in the model used to estimate breeding values. This strategy was found to be superior to the commonly used Bayesian model.
We gratefully thank Patrik Waldmann (University of Umeå, Sweden) for a Gibbs sampling Matlab code that provided a basis for our developing work and Boby Mathew (University of Bonn, Germany) for helpful discussions about the manuscript. We also thank Shizhong Xu (University of California, USA) and an anonymous reviewer for valuable comments and suggestions on the manuscript.
Appendix
Assume a symmetric n×n matrix C having full rank r. In this case, the calculation of C −1, the inverse of C-matrix can be represented by an eigenvalue decomposition of C as
where D denotes a diagonal matrix with the eigenvalues λi as diagonal coefficients and U symbolizes an orthonormal matrix with U′=U −1 and U′U=I (with identity matrix I). The columns of U, denoted by u (i ), represent the eigenvectors corresponding to the eigenvalues λi. Accounting for the orthogonality of the matrix U the inverse matrix C −1 is obtained from:
However, sometimes the number of independent rows or columns of C can be smaller than the total number of rows and columns, which means that a rank deficiency d of the C-matrix has occurred. The rank deficiency can be calculated from d=n−r, where r gives the rank of the C-matrix. Assuming d>0, the spectral decomposition of C-matrix is as follows:

where U 1 and U 2 are orthogonal subspaces of U.
Then, the inverse of the C-matrix can be substituted by the pseudoinverse, which is a special kind of a generalized inverse (Ben-Israel & Greville, Reference Ben-Israel and Greville2003). The pseudoinverse of C, denoted as C+, can be derived from:
To speed up the computation, the orthogonal nullspace U 2 of the C-matrix can be used in the calculation of the pseudoinverse C + (Koch, Reference Koch2007). For that, the orthogonal subspace U 2 is added to the matrix C resulting in a regular matrix spanning the full space and existing inverse. After the inversion, the subspace U 2 is subtracted. Therefore, the pseudoinverse C + can now be represented by
or equivalently with
Proof.

In conclusion, using the orthogonal nullspace U 2 of C-matrix in the calculation of the pseudoinverse C + speeds up the inversion of C because in our application the subspace U 2 has to be computed only once and does not change during the MCMC sampling.


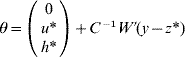 if C has full rank. Otherwise, if a rank deficiency of C occurs, calculate θ as
if C has full rank. Otherwise, if a rank deficiency of C occurs, calculate θ as