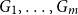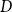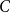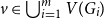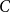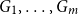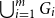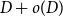1. Introduction
A proper colouring of a graph
![]() $G$
is an assignment of colours to the vertices of
$G$
is an assignment of colours to the vertices of
![]() $G$
such that no two vertices assigned the same colour are adjacent, and the chromatic number of
$G$
such that no two vertices assigned the same colour are adjacent, and the chromatic number of
![]() $G$
, denoted
$G$
, denoted
![]() $\chi (G)$
, is the minimal number of colours needed to properly colour
$\chi (G)$
, is the minimal number of colours needed to properly colour
![]() $G$
. A list assignment for a graph
$G$
. A list assignment for a graph
![]() $G$
is a map
$G$
is a map
![]() $L$
whose domain is the vertex set
$L$
whose domain is the vertex set
![]() $V(G)$
of
$V(G)$
of
![]() $G$
where
$G$
where
![]() $L(v)$
is a finite set called the ‘list of available colours for
$L(v)$
is a finite set called the ‘list of available colours for
![]() $v$
’, and an
$v$
’, and an
![]() $L$
-colouring of
$L$
-colouring of
![]() $G$
is a proper colouring
$G$
is a proper colouring
![]() $\phi$
of
$\phi$
of
![]() $G$
such that
$G$
such that
![]() $\phi (v) \in L(v)$
for every
$\phi (v) \in L(v)$
for every
![]() $v\in V(G)$
. If
$v\in V(G)$
. If
![]() $G$
has an
$G$
has an
![]() $L$
-colouring, then
$L$
-colouring, then
![]() $G$
is
$G$
is
![]() $L$
-colourable. The list chromatic number of
$L$
-colourable. The list chromatic number of
![]() $G$
, denoted
$G$
, denoted
![]() $\chi _\ell (G)$
, is the minimum
$\chi _\ell (G)$
, is the minimum
![]() $k \in{\mathbb{N}}$
such that
$k \in{\mathbb{N}}$
such that
![]() $G$
is
$G$
is
![]() $L$
-colourable for every list assignment
$L$
-colourable for every list assignment
![]() $L$
satisfying
$L$
satisfying
![]() $|L(v)| \geq k$
for all
$|L(v)| \geq k$
for all
![]() $v \in V(G)$
.
$v \in V(G)$
.
We say graphs
![]() $G_1, \dots, G_m$
are nearly disjoint if
$G_1, \dots, G_m$
are nearly disjoint if
![]() $|V(G_i) \cap V(G_j)| \leq 1$
for all distinct
$|V(G_i) \cap V(G_j)| \leq 1$
for all distinct
![]() $i, j \in [m]$
. In this paper, we prove an asymptotically optimal bound on the (list) chromatic number of a union of nearly disjoint graphs of bounded maximum degree (see Theorem 1.1), which confirms a special case of a conjecture of Vu (see Conjecture 1.2) and generalizes several well-known results on hypergraph edge-colouring. We derive our bound from a more general result (see Theorem 1.3) concerning
$i, j \in [m]$
. In this paper, we prove an asymptotically optimal bound on the (list) chromatic number of a union of nearly disjoint graphs of bounded maximum degree (see Theorem 1.1), which confirms a special case of a conjecture of Vu (see Conjecture 1.2) and generalizes several well-known results on hypergraph edge-colouring. We derive our bound from a more general result (see Theorem 1.3) concerning
![]() $L$
-colourings when
$L$
-colourings when
![]() $L$
is a list assignment for a union of nearly disjoint graphs such that
$L$
is a list assignment for a union of nearly disjoint graphs such that
![]() $L$
has bounded maximum colour degree. This result also implies a result of Reed and Sudakov [Reference Reed and Sudakov25]. We also prove a bound on the chromatic number of a union of nearly disjoint graphs of bounded chromatic number (see Theorem 1.4).
$L$
has bounded maximum colour degree. This result also implies a result of Reed and Sudakov [Reference Reed and Sudakov25]. We also prove a bound on the chromatic number of a union of nearly disjoint graphs of bounded chromatic number (see Theorem 1.4).
1.1 Line graphs of linear hypergraphs and nearly disjoint graph unions
A hypergraph
![]() $\mathcal H$
is a pair
$\mathcal H$
is a pair
![]() ${\mathcal H} = (V, E)$
where
${\mathcal H} = (V, E)$
where
![]() $V$
is a set whose elements are called vertices and
$V$
is a set whose elements are called vertices and
![]() $E \subseteq 2^V$
is a set of subsets of
$E \subseteq 2^V$
is a set of subsets of
![]() $V$
whose elements are called edges. A proper edge-colouring of a hypergraph
$V$
whose elements are called edges. A proper edge-colouring of a hypergraph
![]() $\mathcal H$
is an assignment of colours to the edges of
$\mathcal H$
is an assignment of colours to the edges of
![]() $\mathcal H$
such that no two edges of the same colour share a vertex, and the chromatic index of
$\mathcal H$
such that no two edges of the same colour share a vertex, and the chromatic index of
![]() $\mathcal H$
, denoted
$\mathcal H$
, denoted
![]() $\chi^{\prime}({\mathcal H})$
, is the minimum number of colours used by a proper edge-colouring of
$\chi^{\prime}({\mathcal H})$
, is the minimum number of colours used by a proper edge-colouring of
![]() $\mathcal H$
. The line graph of a hypergraph
$\mathcal H$
. The line graph of a hypergraph
![]() $\mathcal H$
is the graph
$\mathcal H$
is the graph
![]() $G$
where
$G$
where
![]() $V(G)$
is the edge set of
$V(G)$
is the edge set of
![]() $\mathcal H$
, and
$\mathcal H$
, and
![]() $e, f \in V(G)$
are adjacent in
$e, f \in V(G)$
are adjacent in
![]() $G$
if
$G$
if
![]() $e \cap f \neq \emptyset$
. Note that the chromatic index of a hypergraph is the chromatic number of its line graph. The list chromatic index of a hypergraph
$e \cap f \neq \emptyset$
. Note that the chromatic index of a hypergraph is the chromatic number of its line graph. The list chromatic index of a hypergraph
![]() $\mathcal H$
, denoted
$\mathcal H$
, denoted
![]() $\chi^{\prime}_\ell ({\mathcal H})$
, is the list chromatic number of its line graph.
$\chi^{\prime}_\ell ({\mathcal H})$
, is the list chromatic number of its line graph.
A hypergraph
![]() $\mathcal H$
is linear if every two distinct edges of
$\mathcal H$
is linear if every two distinct edges of
![]() $\mathcal H$
intersect in at most one vertex and
$\mathcal H$
intersect in at most one vertex and
![]() $k$
-bounded if every edge of
$k$
-bounded if every edge of
![]() $\mathcal H$
has size at most
$\mathcal H$
has size at most
![]() $k$
. A celebrated result of Pippenger and Spencer [Reference Pippenger and Spencer22] implies that
$k$
. A celebrated result of Pippenger and Spencer [Reference Pippenger and Spencer22] implies that
![]() $k$
-bounded linear hypergraphs of maximum degree at most
$k$
-bounded linear hypergraphs of maximum degree at most
![]() $D$
have chromatic index at most
$D$
have chromatic index at most
![]() $D + o(D)$
for fixed
$D + o(D)$
for fixed
![]() $k$
as
$k$
as
![]() $D\rightarrow \infty$
, and a similarly influential result of Kahn [Reference Kahn14] generalizes the Pippenger–Spencer theorem to list colouring. (Both of these results apply more generally to hypergraphs of small codegree, and not only to linear hypergraphs.) An intermediate result of Kahn [Reference Kahn13, Theorem 3] was also crucial to proving the Erdős–Faber–Lovász conjecture asymptotically. This conjecture states that a nearly disjoint union of
$D\rightarrow \infty$
, and a similarly influential result of Kahn [Reference Kahn14] generalizes the Pippenger–Spencer theorem to list colouring. (Both of these results apply more generally to hypergraphs of small codegree, and not only to linear hypergraphs.) An intermediate result of Kahn [Reference Kahn13, Theorem 3] was also crucial to proving the Erdős–Faber–Lovász conjecture asymptotically. This conjecture states that a nearly disjoint union of
![]() $n$
complete graphs, each on at most
$n$
complete graphs, each on at most
![]() $n$
vertices, has chromatic number at most
$n$
vertices, has chromatic number at most
![]() $n$
, and it was recently confirmed for all large
$n$
, and it was recently confirmed for all large
![]() $n$
by Kang, Methuku, and the authors [Reference Kang17]. Note that the line graph of a
$n$
by Kang, Methuku, and the authors [Reference Kang17]. Note that the line graph of a
![]() $k$
-bounded linear hypergraph is a union of nearly disjoint complete graphs, such that at most
$k$
-bounded linear hypergraph is a union of nearly disjoint complete graphs, such that at most
![]() $k$
of them contain any given vertex. Thus, the following result strengthens both the Pippenger–Spencer theorem and Kahn’s list edge-colouring theorem for the case of linear hypergraphs.
$k$
of them contain any given vertex. Thus, the following result strengthens both the Pippenger–Spencer theorem and Kahn’s list edge-colouring theorem for the case of linear hypergraphs.
Theorem 1.1.
For every
![]() $C,{\varepsilon } \gt 0$
, the following holds for all sufficiently large
$C,{\varepsilon } \gt 0$
, the following holds for all sufficiently large
![]() $D$
. If
$D$
. If
![]() $G_1, \dots, G_m$
are nearly disjoint graphs of maximum degree at most
$G_1, \dots, G_m$
are nearly disjoint graphs of maximum degree at most
![]() $D$
, such that each vertex
$D$
, such that each vertex
![]() $v \in \bigcup _{i=1}^m V(G_i)$
is contained in at most
$v \in \bigcup _{i=1}^m V(G_i)$
is contained in at most
![]() $C$
of them, then
$C$
of them, then
![]() $\chi _\ell \left(\bigcup _{i=1}^m G_i\right) \leq (1 +{\varepsilon })D$
.
$\chi _\ell \left(\bigcup _{i=1}^m G_i\right) \leq (1 +{\varepsilon })D$
.
Theorem 1.1 also confirms a special case of the following conjecture of Vu [Reference Vu27], and (as our discussion shows) it recovers several of its significant consequences.
Conjecture 1.2 (Vu [Reference Vu27]). For every
![]() $\zeta,{\varepsilon } \gt 0$
, the following holds for all sufficiently large
$\zeta,{\varepsilon } \gt 0$
, the following holds for all sufficiently large
![]() $D$
. If
$D$
. If
![]() $G$
is a graph of maximum degree at most
$G$
is a graph of maximum degree at most
![]() $D$
and every two distinct vertices have at most
$D$
and every two distinct vertices have at most
![]() $\zeta D$
common neighbours in
$\zeta D$
common neighbours in
![]() $G$
, then
$G$
, then
![]() $\chi _\ell (G) \leq (\zeta +{\varepsilon }) D$
.
$\chi _\ell (G) \leq (\zeta +{\varepsilon }) D$
.
Indeed, Conjecture 1.2, if true, implies Theorem 1.1 with
![]() $1/ C$
and
$1/ C$
and
![]() $C(D + C^2)$
playing the roles of
$C(D + C^2)$
playing the roles of
![]() $\zeta$
and
$\zeta$
and
![]() $D$
, respectively. If
$D$
, respectively. If
![]() $G_1, \dots, G_m$
are nearly disjoint graphs of maximum degree at most
$G_1, \dots, G_m$
are nearly disjoint graphs of maximum degree at most
![]() $D$
, such that each vertex
$D$
, such that each vertex
![]() $v \in \bigcup _{i=1}^m V(G_i)$
is contained in at most
$v \in \bigcup _{i=1}^m V(G_i)$
is contained in at most
![]() $C$
of them, then every two distinct vertices in
$C$
of them, then every two distinct vertices in
![]() $G\,:\!=\, \bigcup _{i=1}^m G_i$
have at most
$G\,:\!=\, \bigcup _{i=1}^m G_i$
have at most
![]() $D + C^2$
common neighbours, and
$D + C^2$
common neighbours, and
![]() $G$
has maximum degree at most
$G$
has maximum degree at most
![]() $CD$
. Vu [Reference Vu27] initially observed that a similar argument shows that Conjecture 1.2 implies Kahn’s [Reference Kahn14] bound on the list chromatic index of linear hypergraphs of bounded maximum degree, and this was a major motivation for the conjecture: ‘The bound in [Conjecture 1.2], if valid, would be an amazing result. For instance, it would immediately imply a deep theorem of Kahn on the list chromatic index of [linear] hypergraphs.’ [Reference Vu27, p. 109]. The only other nontrivial result towards Vu’s conjecture so far was recently obtained by Hurley et al. [Reference Hurley, de Joannis de Verclos and Kang12], who proved a bound on the chromatic number of graphs as in Conjecture 1.2. Their result confirms the weaker version of the conjecture that considers the chromatic number rather than the list chromatic number, in the case when
$CD$
. Vu [Reference Vu27] initially observed that a similar argument shows that Conjecture 1.2 implies Kahn’s [Reference Kahn14] bound on the list chromatic index of linear hypergraphs of bounded maximum degree, and this was a major motivation for the conjecture: ‘The bound in [Conjecture 1.2], if valid, would be an amazing result. For instance, it would immediately imply a deep theorem of Kahn on the list chromatic index of [linear] hypergraphs.’ [Reference Vu27, p. 109]. The only other nontrivial result towards Vu’s conjecture so far was recently obtained by Hurley et al. [Reference Hurley, de Joannis de Verclos and Kang12], who proved a bound on the chromatic number of graphs as in Conjecture 1.2. Their result confirms the weaker version of the conjecture that considers the chromatic number rather than the list chromatic number, in the case when
![]() $\zeta \gt 1 - o({\varepsilon }^{2/3})$
. We remark that even finding an independent set of the required size is still an open problem (which was already raised by Vu [Reference Vu27]).
$\zeta \gt 1 - o({\varepsilon }^{2/3})$
. We remark that even finding an independent set of the required size is still an open problem (which was already raised by Vu [Reference Vu27]).
1.2 colour degrees
Our main result in this paper is actually a generalization of Theorem 1.1 that also implies a result of Reed and Sudakov [Reference Reed and Sudakov25]. For a graph
![]() $G$
with list assignment
$G$
with list assignment
![]() $L$
, we define the colour degree of each
$L$
, we define the colour degree of each
![]() $v\in V(G)$
and
$v\in V(G)$
and
![]() $c \in L(v)$
to be
$c \in L(v)$
to be
![]() $d_{G, L}(v, c) \,:\!=\, |\{u \in N_G(v) \,:\, c\in L(u)\}|$
and the maximum colour degree of
$d_{G, L}(v, c) \,:\!=\, |\{u \in N_G(v) \,:\, c\in L(u)\}|$
and the maximum colour degree of
![]() $G$
and
$G$
and
![]() $L$
to be
$L$
to be
![]() $\Delta (G, L) \,:\!=\, \max _{v\in V(G)}\max _{c\in L(v)}d_{G, L}(v, c)$
. Note that
$\Delta (G, L) \,:\!=\, \max _{v\in V(G)}\max _{c\in L(v)}d_{G, L}(v, c)$
. Note that
![]() $\Delta (G, L) \leq \Delta (G)$
. The following is our main result.
$\Delta (G, L) \leq \Delta (G)$
. The following is our main result.
Theorem 1.3.
For every
![]() $C,{\varepsilon } \gt 0$
, the following holds for all sufficiently large
$C,{\varepsilon } \gt 0$
, the following holds for all sufficiently large
![]() $D$
. Let
$D$
. Let
![]() $G_1, \dots, G_m$
be graphs that
$G_1, \dots, G_m$
be graphs that
-
(i) are nearly disjoint and
-
(ii) satisfy
 $|\{i \in [m] \,:\, v \in V(G_i)\}| \leq C$
for every
$|\{i \in [m] \,:\, v \in V(G_i)\}| \leq C$
for every
 $v \in \bigcup _{i=1}^m V(G_i)$
.
$v \in \bigcup _{i=1}^m V(G_i)$
.
If
![]() $L$
is a list assignment for
$L$
is a list assignment for
![]() $G \,:\!=\, \bigcup _{i=1}^m G_i$
satisfying
$G \,:\!=\, \bigcup _{i=1}^m G_i$
satisfying
-
(iii)
 $\Delta (G_i, L|_{V(G_i)}) \leq D$
for every
$\Delta (G_i, L|_{V(G_i)}) \leq D$
for every
 $i \in [m]$
and
$i \in [m]$
and
-
(iv)
 $|L(v)| \geq (1 +{\varepsilon })D$
for every
$|L(v)| \geq (1 +{\varepsilon })D$
for every
 $v\in V(G)$
,
$v\in V(G)$
,
then
![]() $G$
is
$G$
is
![]() $L$
-colourable.
$L$
-colourable.
Note that Theorem 1.1 immediately follows from Theorem 1.3.
Theorem 1.3 actually holds more generally for correspondence colouring, also known as DP-colouring (see Theorem 5.2), and this result also implies the recent result of Molloy and Postle [Reference Molloy and Postle19], that
![]() $k$
-bounded linear hypergraphs of maximum degree at most
$k$
-bounded linear hypergraphs of maximum degree at most
![]() $D$
have correspondence chromatic index at most
$D$
have correspondence chromatic index at most
![]() $D + o(D)$
. A proof of Theorem 5.2 can be obtained with only minor modifications to our argument used to prove Theorem 1.3. Thus, for the sake of presentation, we choose to first provide a complete proof of Theorem 1.3 for list colouring. Then, in Section 5, we describe the modifications necessary to prove Theorem 5.2, its correspondence colouring generalization.
$D + o(D)$
. A proof of Theorem 5.2 can be obtained with only minor modifications to our argument used to prove Theorem 1.3. Thus, for the sake of presentation, we choose to first provide a complete proof of Theorem 1.3 for list colouring. Then, in Section 5, we describe the modifications necessary to prove Theorem 5.2, its correspondence colouring generalization.
The case
![]() $m = 1$
(or equivalently,
$m = 1$
(or equivalently,
![]() $C = 1$
) in Theorem 1.3 is a result of Reed and Sudakov [Reference Reed and Sudakov25]. For every
$C = 1$
) in Theorem 1.3 is a result of Reed and Sudakov [Reference Reed and Sudakov25]. For every
![]() $C \in{\mathbb{N}}$
, let
$C \in{\mathbb{N}}$
, let
![]() $f_C(D)$
denote the smallest integer for which the following holds: If
$f_C(D)$
denote the smallest integer for which the following holds: If
![]() $G_1, \dots, G_m$
are graphs satisfying (i) and (ii), and if
$G_1, \dots, G_m$
are graphs satisfying (i) and (ii), and if
![]() $L$
is a list assignment for
$L$
is a list assignment for
![]() $G \,:\!=\, \bigcup _{i=1}^m G_i$
satisfying (iii) such that
$G \,:\!=\, \bigcup _{i=1}^m G_i$
satisfying (iii) such that
![]() $|L(v)| \geq D + f_C(D)$
for every
$|L(v)| \geq D + f_C(D)$
for every
![]() $v \in V(G)$
, then
$v \in V(G)$
, then
![]() $G$
is
$G$
is
![]() $L$
-colourable. Clearly,
$L$
-colourable. Clearly,
![]() $f_C(D) \geq 1$
. Theorem 1.3 implies that
$f_C(D) \geq 1$
. Theorem 1.3 implies that
![]() $f_C(D) = o(D)$
, but it would be interesting to prove better asymptotics. A bound of
$f_C(D) = o(D)$
, but it would be interesting to prove better asymptotics. A bound of
![]() $f_C(D) \leq D^{1 - 1/C}$
for
$f_C(D) \leq D^{1 - 1/C}$
for
![]() $C \geq 2$
would match the best known bound on the list chromatic index of linear hypergraphs due to Molloy and Reed [Reference Molloy and Reed20]. Reed [Reference Reed24] conjectured that
$C \geq 2$
would match the best known bound on the list chromatic index of linear hypergraphs due to Molloy and Reed [Reference Molloy and Reed20]. Reed [Reference Reed24] conjectured that
![]() $f_1(D) = 1$
for every
$f_1(D) = 1$
for every
![]() $D \in{\mathbb{N}}$
. Bohman and Holzman [Reference Bohman and Holzman4] disproved this conjecture, and Reed and Sudakov [Reference Reed and Sudakov25] asked whether
$D \in{\mathbb{N}}$
. Bohman and Holzman [Reference Bohman and Holzman4] disproved this conjecture, and Reed and Sudakov [Reference Reed and Sudakov25] asked whether
![]() $f_1(D) = O(1)$
. Another interesting direction would be to generalize Theorem 1.3 so as to also imply the generalization of the Reed–Sudakov result in which the maximum colour degree condition is replaced with an average one, proved by Glock and Sudakov [Reference Glock and Sudakov10] and Kang and Kelly [Reference Kang and Kelly18]. For other related results and open problems involving list colouring and colour degrees, see for example [Reference Alon and Assadi1–Reference Anderson, Bernshteyn and Dhawan3, Reference Cambie and Kang6]. More generally, for a recent survey on colouring results and open problems obtained via nibble methods, see [Reference Kang16].
$f_1(D) = O(1)$
. Another interesting direction would be to generalize Theorem 1.3 so as to also imply the generalization of the Reed–Sudakov result in which the maximum colour degree condition is replaced with an average one, proved by Glock and Sudakov [Reference Glock and Sudakov10] and Kang and Kelly [Reference Kang and Kelly18]. For other related results and open problems involving list colouring and colour degrees, see for example [Reference Alon and Assadi1–Reference Anderson, Bernshteyn and Dhawan3, Reference Cambie and Kang6]. More generally, for a recent survey on colouring results and open problems obtained via nibble methods, see [Reference Kang16].
1.3 colouring nearly disjoint graphs of bounded chromatic number
Erdős proposed several variations of the Erdős–Faber–Lovász conjecture. For example, relaxing the condition of nearly disjointness, Erdős [Reference Erdős8, Problem 9] asked for the largest possible chromatic number of a union of
![]() $n$
complete graphs, each on at most
$n$
complete graphs, each on at most
![]() $n$
vertices, that pairwise intersect in at most
$n$
vertices, that pairwise intersect in at most
![]() $t$
vertices. Building on the methods of [Reference Kang17], this problem was recently solved by Kang, Methuku, and the authors [Reference Kang, Kelly, Kühn, Methuku and Osthus15]. Here we discuss a problem related to a question of Erdős [Reference Erdős9, p. 26] on bounds on the chromatic number of a union of nearly disjoint graphs
$t$
vertices. Building on the methods of [Reference Kang17], this problem was recently solved by Kang, Methuku, and the authors [Reference Kang, Kelly, Kühn, Methuku and Osthus15]. Here we discuss a problem related to a question of Erdős [Reference Erdős9, p. 26] on bounds on the chromatic number of a union of nearly disjoint graphs
![]() $G_i$
if we know their chromatic number (rather than their maximum degree as in Section 1.1).
$G_i$
if we know their chromatic number (rather than their maximum degree as in Section 1.1).
Accordingly, for a family
![]() $\mathcal G$
of graphs and
$\mathcal G$
of graphs and
![]() $m \in{\mathbb{N}}$
, let
$m \in{\mathbb{N}}$
, let
![]() $f(m,{\mathcal G})$
be the largest possible chromatic number of the union of at most
$f(m,{\mathcal G})$
be the largest possible chromatic number of the union of at most
![]() $m$
nearly disjoint graphs in
$m$
nearly disjoint graphs in
![]() $\mathcal G$
. Recall that the Erdős–Faber–Lovász conjecture states that a nearly disjoint union of
$\mathcal G$
. Recall that the Erdős–Faber–Lovász conjecture states that a nearly disjoint union of
![]() $n$
complete graphs, each on at most
$n$
complete graphs, each on at most
![]() $n$
vertices, has chromatic number at most
$n$
vertices, has chromatic number at most
![]() $n$
. Thus, the Erdős–Faber–Lovász conjecture can be expressed as follows: For all
$n$
. Thus, the Erdős–Faber–Lovász conjecture can be expressed as follows: For all
![]() $n \in{\mathbb{N}}$
, we have
$n \in{\mathbb{N}}$
, we have
![]() $f(n, \{K_1, \dots, K_n\}) \leq n$
, where
$f(n, \{K_1, \dots, K_n\}) \leq n$
, where
![]() $K_t$
denotes the complete graph on
$K_t$
denotes the complete graph on
![]() $t$
vertices. However, it is straightforward to show that
$t$
vertices. However, it is straightforward to show that
![]() $f(n, \{K_1, \dots, K_n\}) \leq \max \{n, f(n, \{K_{n-1}\})\}$
, and it is well-known that
$f(n, \{K_1, \dots, K_n\}) \leq \max \{n, f(n, \{K_{n-1}\})\}$
, and it is well-known that
![]() $f(n, \{K_{n-1}\}) \geq n$
for
$f(n, \{K_{n-1}\}) \geq n$
for
![]() $n \geq 3$
. Hence, the Erdős–Faber–Lovász conjecture can be reduced to the seemingly weaker statement that
$n \geq 3$
. Hence, the Erdős–Faber–Lovász conjecture can be reduced to the seemingly weaker statement that
![]() $f(n, \{K_{n-1}\}) \leq n$
for every
$f(n, \{K_{n-1}\}) \leq n$
for every
![]() $n \in{\mathbb{N}}$
.
$n \in{\mathbb{N}}$
.
Erdős [Reference Erdős9, p. 26] proposed the following variation of the Erdős–Faber–Lovász conjecture: ‘Let
![]() $G_1, \dots, G_m$
be
$G_1, \dots, G_m$
be
![]() $m$
graphs each of chromatic number
$m$
graphs each of chromatic number
![]() $n$
. Assume that no two
$n$
. Assume that no two
![]() $G$
’s have an edge in common. What is the smallest
$G$
’s have an edge in common. What is the smallest
![]() $m$
for which
$m$
for which
![]() $\bigcup _{i=1}^m G_i$
has chromatic number greater than
$\bigcup _{i=1}^m G_i$
has chromatic number greater than
![]() $n$
? Perhaps one can further demand that any two
$n$
? Perhaps one can further demand that any two
![]() $G$
’s have at most one vertex in common.’ It turns out the answers to these two questions are ‘two’ and ‘three’ respectively. (For the former, observe that a complete graph on
$G$
’s have at most one vertex in common.’ It turns out the answers to these two questions are ‘two’ and ‘three’ respectively. (For the former, observe that a complete graph on
![]() $n + 1$
vertices can be expressed as the union of a complete graph on
$n + 1$
vertices can be expressed as the union of a complete graph on
![]() $n$
vertices and a star with no edges in common; for the latter, see Theorem 1.4(ii) below.) The latter question can also be expressed as follows: What is the smallest
$n$
vertices and a star with no edges in common; for the latter, see Theorem 1.4(ii) below.) The latter question can also be expressed as follows: What is the smallest
![]() $m$
for which
$m$
for which
![]() $f(m,{\mathcal G}^\chi _n) \gt n$
, where
$f(m,{\mathcal G}^\chi _n) \gt n$
, where
![]() ${\mathcal G}^\chi _n$
is the set of graphs of chromatic number at most
${\mathcal G}^\chi _n$
is the set of graphs of chromatic number at most
![]() $n$
? Although this question is straightforward to answer, we believe that further analysis of the function
$n$
? Although this question is straightforward to answer, we believe that further analysis of the function
![]() $f(m,{\mathcal G}^\chi _n)$
itself is warranted (which was probably the original intention of the above question of Erdős). In this direction, we prove the following.
$f(m,{\mathcal G}^\chi _n)$
itself is warranted (which was probably the original intention of the above question of Erdős). In this direction, we prove the following.
Theorem 1.4.
-
(i) The following holds for all
 $m, n \in{\mathbb{N}}$
with
$m, n \in{\mathbb{N}}$
with
 $m + n$
sufficiently large: If
$m + n$
sufficiently large: If
 $G_1, \dots, G_m$
are nearly disjoint graphs, each of chromatic number at most
$G_1, \dots, G_m$
are nearly disjoint graphs, each of chromatic number at most
 $n$
, then
$n$
, then
 $\chi \left(\bigcup _{i=1}^m G_i\right) \leq m + n - 2$
.
$\chi \left(\bigcup _{i=1}^m G_i\right) \leq m + n - 2$
. -
(ii) For every
 $n \geq 2$
, there exist nearly disjoint graphs
$n \geq 2$
, there exist nearly disjoint graphs
 $G_1, G_2, G_3$
, each of chromatic number at most
$G_1, G_2, G_3$
, each of chromatic number at most
 $n$
, such that
$n$
, such that
 $\chi (G_1\cup G_2 \cup G_3) \geq n + 1$
.
$\chi (G_1\cup G_2 \cup G_3) \geq n + 1$
.
Theorem 1.4(i) implies that
![]() $f(m,{\mathcal G}^\chi _n) \leq m + n - 2$
when
$f(m,{\mathcal G}^\chi _n) \leq m + n - 2$
when
![]() $m + n$
is sufficiently large, and Theorem 1.4(ii) implies that this bound is tight for
$m + n$
is sufficiently large, and Theorem 1.4(ii) implies that this bound is tight for
![]() $m = 3$
. However, this bound can likely be improved for larger
$m = 3$
. However, this bound can likely be improved for larger
![]() $m$
. In particular, it is tempting to conjecture that
$m$
. In particular, it is tempting to conjecture that
![]() $f\left(n,{\mathcal G}^\chi _{n-1}\right) \leq n$
, which by the discussion above, would imply the Erdős–Faber–Lovász conjecture if true; however, this was disproved by Postle [Reference Postle23], as follows.
$f\left(n,{\mathcal G}^\chi _{n-1}\right) \leq n$
, which by the discussion above, would imply the Erdős–Faber–Lovász conjecture if true; however, this was disproved by Postle [Reference Postle23], as follows.
Theorem 1.5 (Postle [Reference Postle23]). For every
![]() $m \in{\mathbb{N}}$
divisible by three and
$m \in{\mathbb{N}}$
divisible by three and
![]() $n \geq m - 1$
, there exist nearly disjoint graphs
$n \geq m - 1$
, there exist nearly disjoint graphs
![]() $G_1, \dots, G_m$
, each of chromatic number at most
$G_1, \dots, G_m$
, each of chromatic number at most
![]() $n$
, such that
$n$
, such that
![]() $\chi \left(\bigcup _{i=1}^m G_i\right) \geq n + m/ 6$
.
$\chi \left(\bigcup _{i=1}^m G_i\right) \geq n + m/ 6$
.
Because of the connection to the Erdős–Faber–Lovász conjecture, we find it most interesting to study the function
![]() $f\left(n,{\mathcal G}^\chi _{n-1}\right)$
. Theorems 1.4(i) and 1.5 imply that for large
$f\left(n,{\mathcal G}^\chi _{n-1}\right)$
. Theorems 1.4(i) and 1.5 imply that for large
![]() $n$
we have
$n$
we have
We think it would be interesting to determine
![]() $\lim _{n\rightarrow \infty }f\left(n,{\mathcal G}^\chi _{n-1}\right)/ n$
, assuming the limit exists. By (1), it would be in the range
$\lim _{n\rightarrow \infty }f\left(n,{\mathcal G}^\chi _{n-1}\right)/ n$
, assuming the limit exists. By (1), it would be in the range
![]() $[7/6, 2]$
.
$[7/6, 2]$
.
Considering Theorem 1.1, it is natural to also ask for
![]() $f\left(n,{\mathcal G}^\Delta _{n - 1}\right)$
$f\left(n,{\mathcal G}^\Delta _{n - 1}\right)$
![]() $\left(\textrm{or}\ f\left(n,{\mathcal G}^\Delta _{n - 2}\right)\right)$
, where
$\left(\textrm{or}\ f\left(n,{\mathcal G}^\Delta _{n - 2}\right)\right)$
, where
![]() ${\mathcal G}^\Delta _{n}$
is the set of graphs of maximum degree at most
${\mathcal G}^\Delta _{n}$
is the set of graphs of maximum degree at most
![]() $n$
. However, it is straightforward to show that
$n$
. However, it is straightforward to show that
![]() $f\left(n,{\mathcal G}^\Delta _{n - 1}\right) = f(n, \{K_n\}) = f(n, \{K_{n - 1}\}) = f\left(n,{\mathcal G}^\Delta _{n - 2}\right)$
for every
$f\left(n,{\mathcal G}^\Delta _{n - 1}\right) = f(n, \{K_n\}) = f(n, \{K_{n - 1}\}) = f\left(n,{\mathcal G}^\Delta _{n - 2}\right)$
for every
![]() $n \geq 3$
.
$n \geq 3$
.
1.4 Outline of the paper
Sections 2–4 are devoted to the proof of Theorem 1.3. We prove Theorem 1.3 using a semi-random colouring procedure (also referred to as the ‘nibble method’). Each step of this procedure is obtained by an application of Lemma 2.1, which is proved in Section 4. Section 3 provides some probabilistic tools needed in the proof of Lemma 2.1. In Section 2, we prove Theorem 1.3 (assuming Lemma 2.1). As mentioned, Theorem 1.3 holds more generally for correspondence colouring. In Section 5, we formally state this generalization and describe how to modify the proof of Theorem 1.3 to prove it. In Section 6, we prove Theorems 1.4 and 1.5.
2. Proof of Theorem 1.3
In this section we prove Theorem 1.3, assuming the following lemma. Given
![]() $k \in{\mathbb{Z}}$
, we write
$k \in{\mathbb{Z}}$
, we write
![]() $\log ^k D \,:\!=\, (\log D)^k$
, where the logarithm is base
$\log ^k D \,:\!=\, (\log D)^k$
, where the logarithm is base
![]() $e$
. Given
$e$
. Given
![]() $\Lambda, D, C, p \in{\mathbb{R}}$
, we also define
$\Lambda, D, C, p \in{\mathbb{R}}$
, we also define
 \begin{align*}{\Lambda _{\mathbb{E}}}(\Lambda, D, C, p) &\,:\!=\, \left (1 - \frac{p}{\Lambda }\right )^{DC}\Lambda && \mathrm{and}\\{D_{{\mathbb{E}}}}(\Lambda, D, C, p) &\,:\!=\, \left ((1 - p)\left (1 - \frac{p}{\Lambda }\right )^{D(C-1)} + p\left (1 - \left (1 - \frac{p}{\Lambda }\right )^{DC}\right )\right ) D. \end{align*}
\begin{align*}{\Lambda _{\mathbb{E}}}(\Lambda, D, C, p) &\,:\!=\, \left (1 - \frac{p}{\Lambda }\right )^{DC}\Lambda && \mathrm{and}\\{D_{{\mathbb{E}}}}(\Lambda, D, C, p) &\,:\!=\, \left ((1 - p)\left (1 - \frac{p}{\Lambda }\right )^{D(C-1)} + p\left (1 - \left (1 - \frac{p}{\Lambda }\right )^{DC}\right )\right ) D. \end{align*}
Lemma 2.1.
For every
![]() $C,{\varepsilon } \gt 0$
, there exists
$C,{\varepsilon } \gt 0$
, there exists
![]() $D_{5.3}$
such that the following holds for every
$D_{5.3}$
such that the following holds for every
![]() $D \geq D_{(5.3)}$
. Let
$D \geq D_{(5.3)}$
. Let
![]() $G_1, \dots, G_m$
be graphs, and let
$G_1, \dots, G_m$
be graphs, and let
![]() $L$
be a list assignment for
$L$
be a list assignment for
![]() $G \,:\!=\, \bigcup _{i=1}^m G_i$
satisfying (i)–(iv) (of Theorem 1.3
). If
$G \,:\!=\, \bigcup _{i=1}^m G_i$
satisfying (i)–(iv) (of Theorem 1.3
). If
![]() $|L(v)| = \lceil \Lambda \rceil$
for every
$|L(v)| = \lceil \Lambda \rceil$
for every
![]() $v\in V(G)$
, where
$v\in V(G)$
, where
![]() $(1 +{\varepsilon })D \le \Lambda \le 10CD$
, and if
$(1 +{\varepsilon })D \le \Lambda \le 10CD$
, and if
![]() $\log ^{-1} D \geq p \geq \log ^{-2}D$
, then there exist
$\log ^{-1} D \geq p \geq \log ^{-2}D$
, then there exist
![]() $X\subseteq V(G)$
, an
$X\subseteq V(G)$
, an
![]() $L|_X$
-colouring
$L|_X$
-colouring
![]() $\phi$
of
$\phi$
of
![]() $G[X]$
, and a list assignment
$G[X]$
, and a list assignment
![]() $L^{\prime}$
for
$L^{\prime}$
for
![]() $G - X$
satisfying
$G - X$
satisfying
![]() $L^{\prime}(v) \subseteq L(v) \setminus \{\phi (u) \,:\, u \in N_G(v)\cap X\}$
for every
$L^{\prime}(v) \subseteq L(v) \setminus \{\phi (u) \,:\, u \in N_G(v)\cap X\}$
for every
![]() $v\in V(G)\setminus X$
, such that
$v\in V(G)\setminus X$
, such that
-
(2.1.1)
 $|L^{\prime}(v)| = \left \lceil{\Lambda _{\mathbb{E}}}(\Lambda, D, C, p) - \Lambda ^{4/5}\right \rceil$
for every
$|L^{\prime}(v)| = \left \lceil{\Lambda _{\mathbb{E}}}(\Lambda, D, C, p) - \Lambda ^{4/5}\right \rceil$
for every
 $v\in V(G)\setminus X$
and
$v\in V(G)\setminus X$
and
-
(2.1.2)
 $\Delta (G_i - X, L^{\prime}|_{V(G_i - X)}) \leq{D_{{\mathbb{E}}}}(\Lambda, D, C, p) + D^{4/5}$
for every
$\Delta (G_i - X, L^{\prime}|_{V(G_i - X)}) \leq{D_{{\mathbb{E}}}}(\Lambda, D, C, p) + D^{4/5}$
for every
 $i \in [m]$
.
$i \in [m]$
.
We prove Lemma 2.1 in Section 4 by analysing a random colouring procedure, but we already explain some of the ideas involved in the proof now. In our random colouring procedure, we randomly assign each vertex
![]() $v \in V(G)$
a colour
$v \in V(G)$
a colour
![]() $\psi (v) \in L(v)$
uniformly at random from its list, and we ‘activate’ vertices independently at random with probability
$\psi (v) \in L(v)$
uniformly at random from its list, and we ‘activate’ vertices independently at random with probability
![]() $p$
. (We really only need to assign colours to activated vertices, but for technical reasons it is convenient to define the procedure this way.) For each vertex, we remove any colour from its list assigned to an activated neighbour, and we let
$p$
. (We really only need to assign colours to activated vertices, but for technical reasons it is convenient to define the procedure this way.) For each vertex, we remove any colour from its list assigned to an activated neighbour, and we let
![]() $X$
be the set of activated vertices whose colour was not assigned to any of its activated neighbours. We obtain
$X$
be the set of activated vertices whose colour was not assigned to any of its activated neighbours. We obtain
![]() $L^{\prime}$
by further truncating each vertex’s list to have the desired size, and we show that with nonzero probability,
$L^{\prime}$
by further truncating each vertex’s list to have the desired size, and we show that with nonzero probability,
![]() $X$
,
$X$
,
![]() $L^{\prime}$
, and
$L^{\prime}$
, and
![]() $\phi \,:\!=\, \psi |_X$
satisfy (2.1.1) and (2.1.2).
$\phi \,:\!=\, \psi |_X$
satisfy (2.1.1) and (2.1.2).
To that end, assuming without loss of generality that
![]() $d_{G_i, L}(v, c) = D$
for every
$d_{G_i, L}(v, c) = D$
for every
![]() $i \in [m]$
and
$i \in [m]$
and
![]() $v \in V(G_i)$
with
$v \in V(G_i)$
with
![]() $c \in L(v)$
(see Proposition 4.1), it is straightforward to show that a vertex ‘keeps’ a given colour in its list with probability
$c \in L(v)$
(see Proposition 4.1), it is straightforward to show that a vertex ‘keeps’ a given colour in its list with probability
![]() $(1 - p/ \Lambda )^{DC}$
(see Proposition 4.2). Thus, after applying this procedure,
$(1 - p/ \Lambda )^{DC}$
(see Proposition 4.2). Thus, after applying this procedure,
![]() ${\Lambda _{\mathbb{E}}}(\Lambda, D, C, p)$
is the expected number of remaining available colours for each vertex, and
${\Lambda _{\mathbb{E}}}(\Lambda, D, C, p)$
is the expected number of remaining available colours for each vertex, and
![]() ${D_{{\mathbb{E}}}}(\Lambda, D, C, p)$
is an upper bound on the expected colour degree of each pair of vertex and colour from its list (see (4) and Lemma 4.3). We show that with very high probability (at least
${D_{{\mathbb{E}}}}(\Lambda, D, C, p)$
is an upper bound on the expected colour degree of each pair of vertex and colour from its list (see (4) and Lemma 4.3). We show that with very high probability (at least
![]() $1 - \exp \left (-D^{1/4}\right )$
– see Lemma 4.5), the number of remaining colours available for a given vertex, and the colour degree in
$1 - \exp \left (-D^{1/4}\right )$
– see Lemma 4.5), the number of remaining colours available for a given vertex, and the colour degree in
![]() $G - X$
of a given pair of vertex and colour, are not significantly larger than
$G - X$
of a given pair of vertex and colour, are not significantly larger than
![]() ${\Lambda _{\mathbb{E}}}(\Lambda, D, C, p)$
and
${\Lambda _{\mathbb{E}}}(\Lambda, D, C, p)$
and
![]() ${D_{{\mathbb{E}}}}(\Lambda, D, C, p)$
, respectively. We complete the proof by applying the Lovász Local Lemma.
${D_{{\mathbb{E}}}}(\Lambda, D, C, p)$
, respectively. We complete the proof by applying the Lovász Local Lemma.
To prove Theorem 1.3, we iteratively apply Lemma 2.1
![]() $O(C{\varepsilon }^{-1}\log D)$
times, each time reapplying the lemma with
$O(C{\varepsilon }^{-1}\log D)$
times, each time reapplying the lemma with
![]() $p = \log ^{-1}D$
and with
$p = \log ^{-1}D$
and with
![]() $G_1 - X, \dots, G_m - X$
and
$G_1 - X, \dots, G_m - X$
and
![]() $L^{\prime}$
playing the roles of
$L^{\prime}$
playing the roles of
![]() $G_1, \dots, G_m$
and
$G_1, \dots, G_m$
and
![]() $L$
, respectively, before completing the colouring with Lemma 2.3 below. The requirement
$L$
, respectively, before completing the colouring with Lemma 2.3 below. The requirement
![]() $L^{\prime}(v) \subseteq L(v) \setminus \{\phi (u) \,:\, u \in N_G(v) \cap X\}$
ensures that adjacent vertices are not assigned the same colour in different iterations, so each iteration extends a proper partial colouring of
$L^{\prime}(v) \subseteq L(v) \setminus \{\phi (u) \,:\, u \in N_G(v) \cap X\}$
ensures that adjacent vertices are not assigned the same colour in different iterations, so each iteration extends a proper partial colouring of
![]() $G$
.
$G$
.
This approach – known as the ‘nibble method’ or the ‘semi-random method’ – has led to numerous important developments in graph colouring (see [Reference Kang16, Reference Molloy and Reed21]). Our random colouring procedure was in fact already used by Reed and Sudakov [Reference Reed and Sudakov25] to prove the special case of Theorem 1.3 when
![]() $C = 1$
; however, our analysis of the procedure is different even in this special case, drawing ideas from a recent proof of Kang and Kelly [Reference Kang and Kelly18], and we need new ideas to analyse the procedure for
$C = 1$
; however, our analysis of the procedure is different even in this special case, drawing ideas from a recent proof of Kang and Kelly [Reference Kang and Kelly18], and we need new ideas to analyse the procedure for
![]() $C \gt 1$
. Recall that Theorem 1.3 also implies Kahn’s [Reference Kahn14] bound on the chromatic index of linear uniform hypergraphs and that Theorem 5.2 implies Molloy and Postle’s [Reference Molloy and Postle19] generalization of Kahn’s result to correspondence colouring. These edge-colouring results are also proved with a semi-random approach, but the random colouring procedures used in these proofs are slightly different from ours. Since vertices may lose colours unnecessarily in our procedure – it would suffice to only remove colours from a vertex’s list that were assigned to a neighbour in
$C \gt 1$
. Recall that Theorem 1.3 also implies Kahn’s [Reference Kahn14] bound on the chromatic index of linear uniform hypergraphs and that Theorem 5.2 implies Molloy and Postle’s [Reference Molloy and Postle19] generalization of Kahn’s result to correspondence colouring. These edge-colouring results are also proved with a semi-random approach, but the random colouring procedures used in these proofs are slightly different from ours. Since vertices may lose colours unnecessarily in our procedure – it would suffice to only remove colours from a vertex’s list that were assigned to a neighbour in
![]() $X$
, but this version of the procedure would be more challenging to analyse – Reed and Sudakov [Reference Reed and Sudakov25] called the procedure ‘wasteful’ (see also [Reference Molloy and Reed21, Chapter 12]). Nevertheless, this wastefulness is negligible because our activation probability
$X$
, but this version of the procedure would be more challenging to analyse – Reed and Sudakov [Reference Reed and Sudakov25] called the procedure ‘wasteful’ (see also [Reference Molloy and Reed21, Chapter 12]). Nevertheless, this wastefulness is negligible because our activation probability
![]() $p$
is small. However, Kahn [Reference Kahn14] did not consider activation probabilities and consequently could not afford to use a wasteful variant of his procedure. Molloy and Postle’s [Reference Molloy and Postle19] proof does consider activation probabilities but is still different from ours, even in the special case of edge-colouring; in particular, vertices (of the line graph) may be assigned multiple colours in their colouring procedure.
$p$
is small. However, Kahn [Reference Kahn14] did not consider activation probabilities and consequently could not afford to use a wasteful variant of his procedure. Molloy and Postle’s [Reference Molloy and Postle19] proof does consider activation probabilities but is still different from ours, even in the special case of edge-colouring; in particular, vertices (of the line graph) may be assigned multiple colours in their colouring procedure.
Let us now explain how we use Lemma 2.1 to prove Theorem 1.3. Crucially, (2.1.1) and (2.1.2) together imply that after each iteration of Lemma 2.1, the ratio of the number of remaining available colours for each vertex to the maximum remaining colour degree in each
![]() $G_i$
, while initially only
$G_i$
, while initially only
![]() $1 +{\varepsilon }$
, improves by a factor of at least
$1 +{\varepsilon }$
, improves by a factor of at least
![]() $1 +{\varepsilon } p/ 4$
. Moreover, the number of available colours does not decrease too much in each iteration. The following proposition makes this calculation precise.
$1 +{\varepsilon } p/ 4$
. Moreover, the number of available colours does not decrease too much in each iteration. The following proposition makes this calculation precise.
Proposition 2.2.
For every
![]() $C\geq 1$
and
$C\geq 1$
and
![]() $0 \lt{\varepsilon } \lt 1$
there exists
$0 \lt{\varepsilon } \lt 1$
there exists
![]() $D_{2.2}$
such that the following holds for every
$D_{2.2}$
such that the following holds for every
![]() $D \geq D_{2.2}$
. If
$D \geq D_{2.2}$
. If
![]() $\log ^{-1}D \geq p \geq \log ^{-2}D$
and
$\log ^{-1}D \geq p \geq \log ^{-2}D$
and
![]() $10CD \geq \Lambda \geq (1 +{\varepsilon })D$
, then
$10CD \geq \Lambda \geq (1 +{\varepsilon })D$
, then
and
Proof. First we prove (3). Clearly,
and (3) follows immediately, since
![]() $p\left (1 - \left (1 - p/ \Lambda \right )^{DC}\right ) \gt 0$
.
$p\left (1 - \left (1 - p/ \Lambda \right )^{DC}\right ) \gt 0$
.
Now we prove (2). By (3), since
![]() $\Lambda \leq 10CD$
and
$\Lambda \leq 10CD$
and
![]() $\log ^{-1} D \geq p \geq \log ^{-2}D$
,
$\log ^{-1} D \geq p \geq \log ^{-2}D$
,
Let
and note that
Since
![]() $1 + x \leq (1 + x/ n)^n$
for
$1 + x \leq (1 + x/ n)^n$
for
![]() $x \leq |n|$
and
$x \leq |n|$
and
![]() $\Lambda \geq (1 +{\varepsilon })D$
, we have
$\Lambda \geq (1 +{\varepsilon })D$
, we have
 \begin{align*} W & \leq \frac {1 - p}{1 - p/(1 + {\varepsilon })} + p\left (\frac {1}{1 - pC/(1 + {\varepsilon })} - 1\right ) + \frac {D^{-1/5}}{1 - pC/(1 + {\varepsilon })} \leq 1 - p + \frac {p}{1 + {\varepsilon }} +O(p^2)\\& \leq 1 - \frac {p{\varepsilon }}{3}. \end{align*}
\begin{align*} W & \leq \frac {1 - p}{1 - p/(1 + {\varepsilon })} + p\left (\frac {1}{1 - pC/(1 + {\varepsilon })} - 1\right ) + \frac {D^{-1/5}}{1 - pC/(1 + {\varepsilon })} \leq 1 - p + \frac {p}{1 + {\varepsilon }} +O(p^2)\\& \leq 1 - \frac {p{\varepsilon }}{3}. \end{align*}
Since
![]() $(1 - p{\varepsilon }/ 3)^{-1} \geq 1 + p{\varepsilon }/ 3$
, by combining the inequalities above, we have that the left side of (2) is at least
$(1 - p{\varepsilon }/ 3)^{-1} \geq 1 + p{\varepsilon }/ 3$
, by combining the inequalities above, we have that the left side of (2) is at least
as desired.
We apply Lemma 2.1 iteratively until the ratio of the number of remaining available colours to the maximum remaining colour degree reaches
![]() $8CD$
: (2) will imply that this ratio improves by a factor of at least
$8CD$
: (2) will imply that this ratio improves by a factor of at least
![]() $1 +{\varepsilon }/ (4\log D)$
, so that we only need at most
$1 +{\varepsilon }/ (4\log D)$
, so that we only need at most
![]() $33C{\varepsilon }^{-1} \log D$
iterations, and (3) will ensure that carrying out this many iterations is indeed possible. After this process, we can finish with the following result of Reed [Reference Reed24] (which is proved via a simple application of the Lovász Local Lemma).
$33C{\varepsilon }^{-1} \log D$
iterations, and (3) will ensure that carrying out this many iterations is indeed possible. After this process, we can finish with the following result of Reed [Reference Reed24] (which is proved via a simple application of the Lovász Local Lemma).
Lemma 2.3 (Reed [Reference Reed24]). Let
![]() $G$
be a graph with list assignment
$G$
be a graph with list assignment
![]() $L$
. If
$L$
. If
![]() $|L(v)| \geq 8D$
for every
$|L(v)| \geq 8D$
for every
![]() $v \in V(G)$
and
$v \in V(G)$
and
![]() $\Delta (G, L) \leq D$
, then
$\Delta (G, L) \leq D$
, then
![]() $G$
is
$G$
is
![]() $L$
-colourable.
$L$
-colourable.
Now we prove Theorem 1.3.
Proof of Theorem
1.3
. Without loss of generality, we may assume that
![]() ${\varepsilon } \lt 1$
. Let
${\varepsilon } \lt 1$
. Let
![]() $p \,:\!=\, \log ^{-1} D$
,
$p \,:\!=\, \log ^{-1} D$
,
![]() $D_0 \,:\!=\, D$
and
$D_0 \,:\!=\, D$
and
![]() $\Lambda _0 \,:\!=\, (1 +{\varepsilon })D_0$
, and for each integer
$\Lambda _0 \,:\!=\, (1 +{\varepsilon })D_0$
, and for each integer
![]() $0\le i \le 33C/({\varepsilon } p)$
, let
$0\le i \le 33C/({\varepsilon } p)$
, let
 \begin{align*} \Lambda _{i + 1} &\,:\!=\,{\Lambda _{\mathbb{E}}}(\Lambda _i, D_i, C, p) - \Lambda _i^{4/5} && \mathrm{and}\\ D_{i + 1} &\,:\!=\,{D_{{\mathbb{E}}}}(\Lambda _i, D_i, C, p) + D_i^{4/5}. \end{align*}
\begin{align*} \Lambda _{i + 1} &\,:\!=\,{\Lambda _{\mathbb{E}}}(\Lambda _i, D_i, C, p) - \Lambda _i^{4/5} && \mathrm{and}\\ D_{i + 1} &\,:\!=\,{D_{{\mathbb{E}}}}(\Lambda _i, D_i, C, p) + D_i^{4/5}. \end{align*}
Applying Proposition 2.2 inductively, for every integer
![]() $0\le i \le 33C/({\varepsilon } p)$
, by (3) we have
$0\le i \le 33C/({\varepsilon } p)$
, by (3) we have
where the second inequality uses that
![]() $(1 + x/ n)^n \geq e^x(1 - x^2/ n)$
for
$(1 + x/ n)^n \geq e^x(1 - x^2/ n)$
for
![]() $|x| \leq n$
. By (2),
$|x| \leq n$
. By (2),
Moreover, we have
In particular, there exists an integer
![]() $0 \lt i^* \leq 33C/ ({\varepsilon } p)$
such that
$0 \lt i^* \leq 33C/ ({\varepsilon } p)$
such that
![]() $\lceil \Lambda _{i^*}\rceil/ D_{i^*} \geq 8C$
and
$\lceil \Lambda _{i^*}\rceil/ D_{i^*} \geq 8C$
and
![]() $\lceil \Lambda _{i^* - 1}\rceil/ D_{i^* - 1} \lt 8C$
. We may assume
$\lceil \Lambda _{i^* - 1}\rceil/ D_{i^* - 1} \lt 8C$
. We may assume
![]() $D$
is sufficiently large so that
$D$
is sufficiently large so that
![]() $D_{i^*} \geq D_{2.1}$
.
$D_{i^*} \geq D_{2.1}$
.
By (iv), we may assume without loss of generality that
![]() $|L(v)| = \lceil \Lambda _0\rceil$
for every
$|L(v)| = \lceil \Lambda _0\rceil$
for every
![]() $v \in V(G)$
, since we can truncate each list until equality holds. Now let
$v \in V(G)$
, since we can truncate each list until equality holds. Now let
![]() $G_{j,0} \,:\!=\, G_j$
for each
$G_{j,0} \,:\!=\, G_j$
for each
![]() $j \in [m]$
, let
$j \in [m]$
, let
![]() $H_0 \,:\!=\, G$
, and let
$H_0 \,:\!=\, G$
, and let
![]() $L_0 \,:\!=\, L$
. Due to the above calculations, inductively by Lemma 2.1, for each integer
$L_0 \,:\!=\, L$
. Due to the above calculations, inductively by Lemma 2.1, for each integer
![]() $0\le i \lt i^*$
, there is a set
$0\le i \lt i^*$
, there is a set
![]() $X_i \subseteq V(H_i)$
and an
$X_i \subseteq V(H_i)$
and an
![]() $L_i|_{X_i}$
-colouring
$L_i|_{X_i}$
-colouring
![]() $\phi _i$
of
$\phi _i$
of
![]() $H_i[X_i]$
and a list assignment
$H_i[X_i]$
and a list assignment
![]() $L_{i+1}$
for
$L_{i+1}$
for
![]() $H_{i+1}\,:\!=\, H_i - X_i$
satisfying
$H_{i+1}\,:\!=\, H_i - X_i$
satisfying
![]() $L_{i+1}(v) \subseteq L_i(v) \setminus \{\phi _i(u) \,:\, u \in N_{H_i}(v) \cap X_i\}$
such that
$L_{i+1}(v) \subseteq L_i(v) \setminus \{\phi _i(u) \,:\, u \in N_{H_i}(v) \cap X_i\}$
such that
-
 $\Delta \left(G_{j, i + 1}, L_{i + 1}|_{V(G_{j, i+1})}\right) \leq D_{i + 1}$
for each
$\Delta \left(G_{j, i + 1}, L_{i + 1}|_{V(G_{j, i+1})}\right) \leq D_{i + 1}$
for each
 $j \in [m]$
and
$j \in [m]$
and -
 $|L_{i + 1}(v)| = \lceil \Lambda _{i + 1}\rceil \ge (1+{\varepsilon }) D_{i+1}$
,
$|L_{i + 1}(v)| = \lceil \Lambda _{i + 1}\rceil \ge (1+{\varepsilon }) D_{i+1}$
,
where
![]() $G_{j, i + 1} \,:\!=\, G_{j, i} - X_i$
.
$G_{j, i + 1} \,:\!=\, G_{j, i} - X_i$
.
Let
![]() $X \,:\!=\, \bigcup _{i=1}^{i^*-1} X_i$
, let
$X \,:\!=\, \bigcup _{i=1}^{i^*-1} X_i$
, let
![]() $\phi (v) \,:\!=\, \phi _i(v)$
if
$\phi (v) \,:\!=\, \phi _i(v)$
if
![]() $v \in X_i$
for some integer
$v \in X_i$
for some integer
![]() $0\le i \lt i^*$
, let
$0\le i \lt i^*$
, let
![]() $G^{\prime} \,:\!=\, H_{i^*}$
, and let
$G^{\prime} \,:\!=\, H_{i^*}$
, and let
![]() $L^{\prime} \,:\!=\, L_{i^*}$
. By construction,
$L^{\prime} \,:\!=\, L_{i^*}$
. By construction,
![]() $\phi$
is an
$\phi$
is an
![]() $L|_X$
-colouring of
$L|_X$
-colouring of
![]() $G[X]$
, and by the choice of
$G[X]$
, and by the choice of
![]() $i^*$
, we have
$i^*$
, we have
-
 $|L^{\prime}(v)| \geq 8C D_{i^*}$
and
$|L^{\prime}(v)| \geq 8C D_{i^*}$
and -
 $\Delta (G^{\prime}, L^{\prime}) \leq C\max \{\Delta \left(G_{j, i^*}, L_{i^*}|_{V\left(G_{j,i^*}\right)}\right) :{j \in [m]}\} \leq CD_{i^*}$
.
$\Delta (G^{\prime}, L^{\prime}) \leq C\max \{\Delta \left(G_{j, i^*}, L_{i^*}|_{V\left(G_{j,i^*}\right)}\right) :{j \in [m]}\} \leq CD_{i^*}$
.
Therefore by Lemma 2.3,
![]() $G^{\prime}$
has an
$G^{\prime}$
has an
![]() $L^{\prime}$
-colouring
$L^{\prime}$
-colouring
![]() $\phi^{\prime}$
, and we can combine
$\phi^{\prime}$
, and we can combine
![]() $\phi$
and
$\phi$
and
![]() $\phi^{\prime}$
to obtain an
$\phi^{\prime}$
to obtain an
![]() $L$
-colouring of
$L$
-colouring of
![]() $G$
, as desired.
$G$
, as desired.
3. Probabilistic tools
In this section we provide some probabilistic tools used in the proof of Lemma 2.1 in Section 4. The first such tool is the Lovász Local Lemma.
Lemma 3.1 (Lovász Local Lemma [Reference Erdős and Lovász7]). Let
![]() $p\in [0,1)$
and
$p\in [0,1)$
and
![]() $\mathcal A$
a finite set of events such that for every
$\mathcal A$
a finite set of events such that for every
![]() $A\in \mathcal A$
,
$A\in \mathcal A$
,
-
 ${{\mathbb{P}}\left [A\right ] } \leq p$
, and
${{\mathbb{P}}\left [A\right ] } \leq p$
, and
-
 $A$
is mutually independent of a set of all but at most
$A$
is mutually independent of a set of all but at most
 $d$
other events in
$d$
other events in
 $\mathcal A$
.
$\mathcal A$
.
If
![]() $4pd\leq 1$
, then the probability that none of the events in
$4pd\leq 1$
, then the probability that none of the events in
![]() $\mathcal A$
occur is strictly positive.
$\mathcal A$
occur is strictly positive.
Next we need a concentration inequality of Bruhn and Joos [Reference Bruhn and Joos5], derived from Talagrand’s inequality [Reference Talagrand26]. To that end, we introduce the following definition.
Definition 3.2. Let
![]() $(( \boldsymbol{\Omega} _i, \boldsymbol{\Sigma} _i,{\mathbb{P}}_i))$
be probability spaces, and let
$(( \boldsymbol{\Omega} _i, \boldsymbol{\Sigma} _i,{\mathbb{P}}_i))$
be probability spaces, and let
![]() $( \boldsymbol{\Omega}, \boldsymbol{\Sigma},{\mathbb{P}})$
be their product space. We say a random variable
$( \boldsymbol{\Omega}, \boldsymbol{\Sigma},{\mathbb{P}})$
be their product space. We say a random variable
![]() ${\textbf X} \,:\, \boldsymbol{\Omega} \rightarrow{\mathbb{R}}$
has upward
${\textbf X} \,:\, \boldsymbol{\Omega} \rightarrow{\mathbb{R}}$
has upward
![]() $(s, \delta )$
-certificates with respect to a set of exceptional outcomes
$(s, \delta )$
-certificates with respect to a set of exceptional outcomes
![]() $ \boldsymbol{\Omega} ^* \subseteq \boldsymbol{\Omega}$
if for every
$ \boldsymbol{\Omega} ^* \subseteq \boldsymbol{\Omega}$
if for every
![]() $\omega \in \boldsymbol{\Omega} \setminus \boldsymbol{\Omega} ^*$
and every
$\omega \in \boldsymbol{\Omega} \setminus \boldsymbol{\Omega} ^*$
and every
![]() $t \gt 0$
, there exists an index set
$t \gt 0$
, there exists an index set
![]() $I$
of size at most
$I$
of size at most
![]() $s$
so that
$s$
so that
![]() ${\textbf X}(\omega^{\prime}) \geq{\textbf X}(\omega ) - t$
for every
${\textbf X}(\omega^{\prime}) \geq{\textbf X}(\omega ) - t$
for every
![]() $\omega^{\prime} \in \boldsymbol{\Omega} \setminus \boldsymbol{\Omega} ^*$
for which the restrictions
$\omega^{\prime} \in \boldsymbol{\Omega} \setminus \boldsymbol{\Omega} ^*$
for which the restrictions
![]() $\omega |_I$
and
$\omega |_I$
and
![]() $\omega^{\prime}|_I$
differ in at most
$\omega^{\prime}|_I$
differ in at most
![]() $t/ \delta$
coordinates.
$t/ \delta$
coordinates.
Theorem 3.3 (Bruhn and Joos [Reference Bruhn and Joos5]). Let
![]() $(( \boldsymbol{\Omega} _i, \boldsymbol{\Sigma} _i,{\mathbb{P}}_i))$
be probability spaces, let
$(( \boldsymbol{\Omega} _i, \boldsymbol{\Sigma} _i,{\mathbb{P}}_i))$
be probability spaces, let
![]() $( \boldsymbol{\Omega}, \boldsymbol{\Sigma},{\mathbb{P}})$
be their product space, and let
$( \boldsymbol{\Omega}, \boldsymbol{\Sigma},{\mathbb{P}})$
be their product space, and let
![]() $ \boldsymbol{\Omega} ^*\in \boldsymbol{\Sigma}$
be a set of exceptional outcomes. Let
$ \boldsymbol{\Omega} ^*\in \boldsymbol{\Sigma}$
be a set of exceptional outcomes. Let
![]() ${\textbf X} \,:\, \boldsymbol{\Omega} \rightarrow{\mathbb{R}}$
be a non-negative random variable, let
${\textbf X} \,:\, \boldsymbol{\Omega} \rightarrow{\mathbb{R}}$
be a non-negative random variable, let
![]() $M \,:\!=\, \max \{\sup{\textbf X}, 1\}$
, and let
$M \,:\!=\, \max \{\sup{\textbf X}, 1\}$
, and let
![]() $ \delta \geq 1$
. If
$ \delta \geq 1$
. If
![]() ${{\mathbb{P}}\left [ \boldsymbol{\Omega} ^*\right ] } \leq M^{-2}$
and
${{\mathbb{P}}\left [ \boldsymbol{\Omega} ^*\right ] } \leq M^{-2}$
and
![]() $\textbf X$
has upward
$\textbf X$
has upward
![]() $(s, \delta )$
-certificates, then for
$(s, \delta )$
-certificates, then for
![]() $t \gt 50 \delta \sqrt s$
,
$t \gt 50 \delta \sqrt s$
,
4. Proof of Lemma 2.1
This section is devoted to the proof of Lemma 2.1. It will be convenient to assume that equality holds in (ii) and (iii) of Theorem 1.3 and that moreover
![]() $d_{G_i, L}(v, c) = D$
for every
$d_{G_i, L}(v, c) = D$
for every
![]() $v \in V(G)$
and
$v \in V(G)$
and
![]() $c \in L(v)$
, so we first prove the following proposition which enables us to consider an embedding of
$c \in L(v)$
, so we first prove the following proposition which enables us to consider an embedding of
![]() $G$
for which these properties hold.
$G$
for which these properties hold.
Proposition 4.1.
Let
![]() $C, \Lambda, D \in{\mathbb{N}}$
, let
$C, \Lambda, D \in{\mathbb{N}}$
, let
![]() $G_1, \dots, G_m$
be nearly disjoint graphs, and let
$G_1, \dots, G_m$
be nearly disjoint graphs, and let
![]() $L$
be a list assignment for
$L$
be a list assignment for
![]() $G \,:\!=\, \bigcup _{i=1}^m G_i$
. If
$G \,:\!=\, \bigcup _{i=1}^m G_i$
. If
![]() $|\{i \in [m] \,:\, v \in V(G_i)\}| \leq C$
and
$|\{i \in [m] \,:\, v \in V(G_i)\}| \leq C$
and
![]() $|L(v)| = \Lambda$
for every
$|L(v)| = \Lambda$
for every
![]() $v \in V(G)$
and
$v \in V(G)$
and
![]() $\Delta (G_i, L|_{V(G_i)}) \leq D$
for every
$\Delta (G_i, L|_{V(G_i)}) \leq D$
for every
![]() $i \in [m]$
, then there exist nearly disjoint graphs
$i \in [m]$
, then there exist nearly disjoint graphs
![]() $G^{\prime}_1, \dots, G^{\prime}_{m^{\prime}}$
for some
$G^{\prime}_1, \dots, G^{\prime}_{m^{\prime}}$
for some
![]() $m^{\prime} \geq m$
and a list assignment
$m^{\prime} \geq m$
and a list assignment
![]() $L^{\prime}$
for
$L^{\prime}$
for
![]() $G^{\prime} \,:\!=\, \bigcup _{i=1}^{m^{\prime}}G^{\prime}_i$
such that
$G^{\prime} \,:\!=\, \bigcup _{i=1}^{m^{\prime}}G^{\prime}_i$
such that
-
(4.1.1)
 $G_i \subseteq G^{\prime}_i$
for every
$G_i \subseteq G^{\prime}_i$
for every
 $i \in [m]$
,
$i \in [m]$
, -
(4.1.2)
 $L^{\prime}(v) = L(v)$
for every
$L^{\prime}(v) = L(v)$
for every
 $v \in V(G)$
,
$v \in V(G)$
, -
(4.1.3)
 $|\{i \in [m^{\prime}] \,:\, v \in V(G^{\prime}_i)\}| = C$
for every
$|\{i \in [m^{\prime}] \,:\, v \in V(G^{\prime}_i)\}| = C$
for every
 $v \in V(G^{\prime})$
,
$v \in V(G^{\prime})$
, -
(4.1.4)
 $|L^{\prime}(v)| = \Lambda$
for every
$|L^{\prime}(v)| = \Lambda$
for every
 $v \in V(G^{\prime})$
, and
$v \in V(G^{\prime})$
, and
-
(4.1.5)
 $d_{G^{\prime}_i, L^{\prime}}(v, c) = D$
for every
$d_{G^{\prime}_i, L^{\prime}}(v, c) = D$
for every
 $i \in [m^{\prime}]$
and
$i \in [m^{\prime}]$
and
 $v \in V(G^{\prime}_i)$
with
$v \in V(G^{\prime}_i)$
with
 $c \in L^{\prime}(v)$
.
$c \in L^{\prime}(v)$
.
The proof of Proposition 4.1 can be found in the appendix. For the remainder of this section, we let
![]() $C,{\varepsilon } \gt 0$
, and we let
$C,{\varepsilon } \gt 0$
, and we let
![]() $D$
be sufficiently large, we let
$D$
be sufficiently large, we let
![]() $p$
satisfy
$p$
satisfy
![]() $\log ^{-1} D \geq p \geq \log ^{-2}D$
, and we let
$\log ^{-1} D \geq p \geq \log ^{-2}D$
, and we let
![]() $G\,:\!=\, \bigcup _{i=1}^mG_i$
with list assignment
$G\,:\!=\, \bigcup _{i=1}^mG_i$
with list assignment
![]() $L$
satisfying the hypotheses of Lemma 2.1. For convenience, we assume
$L$
satisfying the hypotheses of Lemma 2.1. For convenience, we assume
![]() $\Lambda$
and
$\Lambda$
and
![]() $D$
are integers where it does not affect the argument. By Proposition 4.1, we may assume without loss of generality that
$D$
are integers where it does not affect the argument. By Proposition 4.1, we may assume without loss of generality that
![]() $|\{i \in [m] \,:\, v \in V(G_i)\}| = C$
for every
$|\{i \in [m] \,:\, v \in V(G_i)\}| = C$
for every
![]() $v\in V(G)$
and that
$v\in V(G)$
and that
![]() $d_{G_i, L}(v, c) = D$
for every
$d_{G_i, L}(v, c) = D$
for every
![]() $i \in [m]$
and
$i \in [m]$
and
![]() $v \in V(G)$
with
$v \in V(G)$
with
![]() $c \in L(v)$
.
$c \in L(v)$
.
For every pair
![]() $(A, \psi )$
satisfying
$(A, \psi )$
satisfying
![]() $A \subseteq V(G)$
and
$A \subseteq V(G)$
and
![]() $\psi (v) \in L(v)$
for each
$\psi (v) \in L(v)$
for each
![]() $v\in V(G)$
,
$v\in V(G)$
,
-
let
 $L_{A, \psi }(v) \,:\!=\, L(v) \setminus \{\psi (u) \,:\, u \in N_G(v)\cap A\}$
for every
$L_{A, \psi }(v) \,:\!=\, L(v) \setminus \{\psi (u) \,:\, u \in N_G(v)\cap A\}$
for every
 $v \in V(G)$
, and
$v \in V(G)$
, and -
let
 $X_{A, \psi } \,:\!=\, \{v \in A \,:\, \psi (v) \in L_{A, \psi }(v)\}$
.
$X_{A, \psi } \,:\!=\, \{v \in A \,:\, \psi (v) \in L_{A, \psi }(v)\}$
.
Note that
![]() $X_{A, \psi } = A \setminus \bigcup _{v \in A}\{u \in N_G(v) \,:\, \psi (u) = \psi (v)\}$
.
$X_{A, \psi } = A \setminus \bigcup _{v \in A}\{u \in N_G(v) \,:\, \psi (u) = \psi (v)\}$
.
We will consider the probability space
![]() $( \boldsymbol{\Omega}, \boldsymbol{\Sigma},{\mathbb{P}})$
of such pairs
$( \boldsymbol{\Omega}, \boldsymbol{\Sigma},{\mathbb{P}})$
of such pairs
![]() $(A, \psi )$
where
$(A, \psi )$
where
-
each vertex in
 $G$
is in
$G$
is in
 $A$
independently and uniformly at random with probability
$A$
independently and uniformly at random with probability
 $p$
and
$p$
and -
 $\psi (v) \in L(v)$
is chosen independently and uniformly at random for each
$\psi (v) \in L(v)$
is chosen independently and uniformly at random for each
 $v \in V(G)$
.
$v \in V(G)$
.
Note that
![]() $\left( \boldsymbol{\Omega}, \boldsymbol{\Sigma},{\mathbb{P}}\right)$
is the product space of
$\left( \boldsymbol{\Omega}, \boldsymbol{\Sigma},{\mathbb{P}}\right)$
is the product space of
![]() $\left( \boldsymbol{\Omega} ^{\mathrm{act}}_{v}, \boldsymbol{\Sigma} ^{\mathrm{act}}_{v},{\mathbb{P}}^{\mathrm{act}}_{v}\right)$
and
$\left( \boldsymbol{\Omega} ^{\mathrm{act}}_{v}, \boldsymbol{\Sigma} ^{\mathrm{act}}_{v},{\mathbb{P}}^{\mathrm{act}}_{v}\right)$
and
![]() $\left( \boldsymbol{\Omega} ^{\mathrm{col}}_{v}, \boldsymbol{\Sigma} ^{\mathrm{col}}_{v},{\mathbb{P}}^{\mathrm{col}}_{v}\right)$
taken over all
$\left( \boldsymbol{\Omega} ^{\mathrm{col}}_{v}, \boldsymbol{\Sigma} ^{\mathrm{col}}_{v},{\mathbb{P}}^{\mathrm{col}}_{v}\right)$
taken over all
![]() $v \in V(G)$
, where
$v \in V(G)$
, where
![]() $\left( \boldsymbol{\Omega} ^{\mathrm{act}}_{v}, \boldsymbol{\Sigma} ^{\mathrm{act}}_{v},{\mathbb{P}}^{\mathrm{act}}_{v}\right)$
models whether
$\left( \boldsymbol{\Omega} ^{\mathrm{act}}_{v}, \boldsymbol{\Sigma} ^{\mathrm{act}}_{v},{\mathbb{P}}^{\mathrm{act}}_{v}\right)$
models whether
![]() $v \in A$
and
$v \in A$
and
![]() $\left( \boldsymbol{\Omega} ^{\mathrm{col}}_{v}, \boldsymbol{\Sigma} ^{\mathrm{col}}_{v},{\mathbb{P}}^{\mathrm{col}}_{v}\right)$
models the choice of
$\left( \boldsymbol{\Omega} ^{\mathrm{col}}_{v}, \boldsymbol{\Sigma} ^{\mathrm{col}}_{v},{\mathbb{P}}^{\mathrm{col}}_{v}\right)$
models the choice of
![]() $\psi (v)$
. We will use this fact to apply Theorem 3.3.
$\psi (v)$
. We will use this fact to apply Theorem 3.3.
We will use the Lovász Local Lemma to show that with nonzero probability,
![]() $X = X_{A, \psi }$
and
$X = X_{A, \psi }$
and
![]() $L^{\prime} = L_{A, \psi }|_{V(G)\setminus X}$
(with lists possibly truncated) satisfy the lemma with
$L^{\prime} = L_{A, \psi }|_{V(G)\setminus X}$
(with lists possibly truncated) satisfy the lemma with
![]() $\phi = \psi |_X$
. To that end, we define the following random variables for each vertex
$\phi = \psi |_X$
. To that end, we define the following random variables for each vertex
![]() $v\in V(G)$
and
$v\in V(G)$
and
![]() $c\in L(v)$
and
$c\in L(v)$
and
![]() $i \in [m]$
:
$i \in [m]$
:
-
 $ \boldsymbol{\Lambda}_v(A, \psi ) \,:\!=\, \left |L_{A,\psi }(v)\right |$
,
$ \boldsymbol{\Lambda}_v(A, \psi ) \,:\!=\, \left |L_{A,\psi }(v)\right |$
, -
 $ \textbf{D}_{v, c, i}(A, \psi ) \,:\!=\, \left |\left \{u \in N_{G_i}(v) \,:\, c \in L_{A, \psi }(u)\right \} \setminus X_{A, \psi }\right |$
,
$ \textbf{D}_{v, c, i}(A, \psi ) \,:\!=\, \left |\left \{u \in N_{G_i}(v) \,:\, c \in L_{A, \psi }(u)\right \} \setminus X_{A, \psi }\right |$
, -
 $ \textbf{Y}_{v, c, i}(A, \psi ) \,:\!=\, \left |\left \{u \in N_{G_i}(v) \cap A \,:\, c \in L(u)\right \} \setminus X_{A, \psi }\right |$
,
$ \textbf{Y}_{v, c, i}(A, \psi ) \,:\!=\, \left |\left \{u \in N_{G_i}(v) \cap A \,:\, c \in L(u)\right \} \setminus X_{A, \psi }\right |$
, -
 $ \textbf{R}_{v, c, i}(A, \psi ) \,:\!=\, \left |\left \{u \in N_{G_i}(v) \setminus A \,:\, c \in L(u)\right \} \setminus \bigcup _{u \in A\setminus V(G_i) \,:\, \psi (u) = c}N_G(u)\right |$
.
$ \textbf{R}_{v, c, i}(A, \psi ) \,:\!=\, \left |\left \{u \in N_{G_i}(v) \setminus A \,:\, c \in L(u)\right \} \setminus \bigcup _{u \in A\setminus V(G_i) \,:\, \psi (u) = c}N_G(u)\right |$
.
Note that
 \begin{align} \textbf{D}_{v, c, i}(A, \psi ) & = \textbf{Y}_{v, c, i}(A, \psi ) - |\{u \in (N_{G_i}(v) \cap A)\setminus X_{A, \psi } \,:\, c \in L(u)\} \setminus \bigcup _{u \in A \,:\, \psi (u) = c}N_G(u)\}| \nonumber\\& \quad + |\{u \in N_{G_i}(v) \setminus A \,:\, c \in L(u)\} \setminus \bigcup _{u \in A \,:\, \psi (u) = c}N_G(u)\}| \leq \textbf{Y}_{v, c, i}(A, \psi ) + \textbf{R}_{v, c, i}(A, \psi ). \end{align}
\begin{align} \textbf{D}_{v, c, i}(A, \psi ) & = \textbf{Y}_{v, c, i}(A, \psi ) - |\{u \in (N_{G_i}(v) \cap A)\setminus X_{A, \psi } \,:\, c \in L(u)\} \setminus \bigcup _{u \in A \,:\, \psi (u) = c}N_G(u)\}| \nonumber\\& \quad + |\{u \in N_{G_i}(v) \setminus A \,:\, c \in L(u)\} \setminus \bigcup _{u \in A \,:\, \psi (u) = c}N_G(u)\}| \leq \textbf{Y}_{v, c, i}(A, \psi ) + \textbf{R}_{v, c, i}(A, \psi ). \end{align}
To apply the Lovász Local Lemma, we first show that for each
![]() $v \in V(G)$
, we have that
$v \in V(G)$
, we have that
![]() $ \boldsymbol{\Lambda}_v$
is at least the quantity in (2.1.1) with high probability, and for each
$ \boldsymbol{\Lambda}_v$
is at least the quantity in (2.1.1) with high probability, and for each
![]() $c \in L(v)$
and
$c \in L(v)$
and
![]() $i \in [m]$
such that
$i \in [m]$
such that
![]() $v \in V(G_i)$
, we have that
$v \in V(G_i)$
, we have that
![]() $ \textbf{D}_{v, c, i}$
is at most the quantity in (2.1.2) with high probability. To that end, we first compute the expectation of these random variables and then apply Theorem 3.3. However, it is not possible to apply Theorem 3.3 to
$ \textbf{D}_{v, c, i}$
is at most the quantity in (2.1.2) with high probability. To that end, we first compute the expectation of these random variables and then apply Theorem 3.3. However, it is not possible to apply Theorem 3.3 to
![]() $ \textbf{D}_{v, c, i}$
directly to obtain any meaningful bound. (Consider the case
$ \textbf{D}_{v, c, i}$
directly to obtain any meaningful bound. (Consider the case
![]() $C = m = 1$
when
$C = m = 1$
when
![]() $G_1$
is complete. Either no vertex in
$G_1$
is complete. Either no vertex in
![]() $A$
is assigned
$A$
is assigned
![]() $c$
, in which case
$c$
, in which case
![]() $c \in L_{A, \psi }(u)$
for every vertex
$c \in L_{A, \psi }(u)$
for every vertex
![]() $u$
, or some vertex in
$u$
, or some vertex in
![]() $A$
is assigned
$A$
is assigned
![]() $c$
, in which case
$c$
, in which case
![]() $c \notin L_{A, \psi }(u)$
for all
$c \notin L_{A, \psi }(u)$
for all
![]() $u \in V(G)$
.) Nevertheless, we can apply Theorem 3.3 to both
$u \in V(G)$
.) Nevertheless, we can apply Theorem 3.3 to both
![]() $ \textbf{Y}_{v, c, i}$
and
$ \textbf{Y}_{v, c, i}$
and
![]() $ \textbf{R}_{v, c, i}$
and moreover show that
$ \textbf{R}_{v, c, i}$
and moreover show that
![]() $ \textbf{Y}_{v, c, i} + \textbf{R}_{v, c, i}$
is at most the quantity in (2.1.2) with high probability. Hence, (4) implies the required bound for
$ \textbf{Y}_{v, c, i} + \textbf{R}_{v, c, i}$
is at most the quantity in (2.1.2) with high probability. Hence, (4) implies the required bound for
![]() $ \textbf{D}_{v, c, i}$
as well.
$ \textbf{D}_{v, c, i}$
as well.
In order to compute the expected values of
![]() $ \boldsymbol{\Lambda}_v$
,
$ \boldsymbol{\Lambda}_v$
,
![]() $ \textbf{Y}_{v, c, i}$
, and
$ \textbf{Y}_{v, c, i}$
, and
![]() $ \textbf{R}_{v, c, i}$
, we need the following simple proposition.
$ \textbf{R}_{v, c, i}$
, we need the following simple proposition.
Proposition 4.2.
For every
![]() $i \in [m]$
,
$i \in [m]$
,
![]() $v\in V(G_i)$
, and
$v\in V(G_i)$
, and
![]() $c \in L(v)$
,
$c \in L(v)$
,
Moreover, for every
![]() $v\in V(G)$
and
$v\in V(G)$
and
![]() $c\in L(v)$
,
$c\in L(v)$
,
Proof. First we prove (5). For each
![]() $u \in N_{G_i}(v)$
with
$u \in N_{G_i}(v)$
with
![]() $c \in L(u)$
, we have
$c \in L(u)$
, we have
![]() ${{\mathbb{P}}\left [u \in A\right ] } = p$
and
${{\mathbb{P}}\left [u \in A\right ] } = p$
and
![]() ${{\mathbb{P}}\left [\psi (u) = c\right ] } = 1/ \Lambda$
, and the events that
${{\mathbb{P}}\left [\psi (u) = c\right ] } = 1/ \Lambda$
, and the events that
![]() $u \in A$
and that
$u \in A$
and that
![]() $\psi (u) = c$
are independent. Moreover, these events are mutually independent for all such
$\psi (u) = c$
are independent. Moreover, these events are mutually independent for all such
![]() $u$
, so
$u$
, so
 \begin{equation*} {{\mathbb {P}}\left [\not \exists u \in N_{G_i}(v) \cap A \text { s.t. }\psi (u) = c\right ] } = \prod _{u \in N_{G_i}(v) \,:\, c \in L(u)}\left (1 - {{\mathbb {P}}\left [u \in A\right ] }\cdot {{\mathbb {P}}\left [\psi (u) = c\right ] }\right ) = \left (1 - \frac {p}{\Lambda }\right )^D, \end{equation*}
\begin{equation*} {{\mathbb {P}}\left [\not \exists u \in N_{G_i}(v) \cap A \text { s.t. }\psi (u) = c\right ] } = \prod _{u \in N_{G_i}(v) \,:\, c \in L(u)}\left (1 - {{\mathbb {P}}\left [u \in A\right ] }\cdot {{\mathbb {P}}\left [\psi (u) = c\right ] }\right ) = \left (1 - \frac {p}{\Lambda }\right )^D, \end{equation*}
as desired.
Now we prove (6). For every
![]() $v\in V(G)$
and
$v\in V(G)$
and
![]() $c \in L(v)$
, we have
$c \in L(v)$
, we have
![]() $c \in L_{A, \psi }(v)$
if and only if there is no
$c \in L_{A, \psi }(v)$
if and only if there is no
![]() $u \in N_{G_i}(v) \cap A$
with
$u \in N_{G_i}(v) \cap A$
with
![]() $\psi (u) = c$
for every
$\psi (u) = c$
for every
![]() $i$
for which
$i$
for which
![]() $v \in V(G_i)$
. By (i), these events are mutually independent for all such
$v \in V(G_i)$
. By (i), these events are mutually independent for all such
![]() $i$
(of which there are
$i$
(of which there are
![]() $C$
by (ii)), so by (5),
$C$
by (ii)), so by (5),
as desired.
Now we compute the expectations of our random variables.
Lemma 4.3.
Every vertex
![]() $v\in V(G)$
satisfies
$v\in V(G)$
satisfies
Moreover, for every
![]() $i \in [m]$
,
$i \in [m]$
,
![]() $v \in V(G_i)$
, and
$v \in V(G_i)$
, and
![]() $c \in L(v)$
,
$c \in L(v)$
,
Proof. By the linearity of expectation, we have
![]() ${{\mathbb{E}}\left [ \boldsymbol{\Lambda}_v\right ] } = \sum _{c\in L(v)}{{\mathbb{P}}\left [c \in L_{A, \psi }(v)\right ] }$
, so (7) follows from (6).
${{\mathbb{E}}\left [ \boldsymbol{\Lambda}_v\right ] } = \sum _{c\in L(v)}{{\mathbb{P}}\left [c \in L_{A, \psi }(v)\right ] }$
, so (7) follows from (6).
Again by the linearity of expectation, we have
Note that
![]() ${{\mathbb{P}}\left [u \in A \text{ and } u \notin X_{A, \psi }\right ] } ={{\mathbb{P}}\left [u \in A \text{ and } \psi (u) \notin L_{A, \psi }(u)\right ] }$
, and the events that
${{\mathbb{P}}\left [u \in A \text{ and } u \notin X_{A, \psi }\right ] } ={{\mathbb{P}}\left [u \in A \text{ and } \psi (u) \notin L_{A, \psi }(u)\right ] }$
, and the events that
![]() $u \in A$
and that
$u \in A$
and that
![]() $\psi (u) \notin L_{A, \psi }(u)$
are independent. We have
$\psi (u) \notin L_{A, \psi }(u)$
are independent. We have
![]() ${{\mathbb{P}}\left [u \in A\right ] } = p$
and
${{\mathbb{P}}\left [u \in A\right ] } = p$
and
![]() ${{\mathbb{P}}\left [\psi (u) \notin L_{A, \psi }(u)\right ] } = 1 - \left (1 - p/ \Lambda \right )^{DC}$
by (6), so (8) follows from the equation above.
${{\mathbb{P}}\left [\psi (u) \notin L_{A, \psi }(u)\right ] } = 1 - \left (1 - p/ \Lambda \right )^{DC}$
by (6), so (8) follows from the equation above.
By the linearity of expectation, we have
By (5),
![]() ${{\mathbb{P}}\left [\psi (w) \neq c \forall w \in N_{G_j}(u) \cap A, j\in [m]\setminus \{i\}\right ] } = \left (1 - p/ \Lambda \right )^{D(C - 1)}$
. Since the events that
${{\mathbb{P}}\left [\psi (w) \neq c \forall w \in N_{G_j}(u) \cap A, j\in [m]\setminus \{i\}\right ] } = \left (1 - p/ \Lambda \right )^{D(C - 1)}$
. Since the events that
![]() $u \notin A$
and
$u \notin A$
and
![]() $\psi (w) \neq c \forall w \in N_{G_j}(u)\cap A, j\in [m]\setminus \{i\}$
are independent, (9) follows from the equation above.
$\psi (w) \neq c \forall w \in N_{G_j}(u)\cap A, j\in [m]\setminus \{i\}$
are independent, (9) follows from the equation above.
Now we need to show that the random variables in Lemma 4.3 are close to their expectation with high probability. We use Theorem 3.3, the ‘exceptional outcomes’ version of Talagrand’s Inequality. To that end, we define an exceptional outcome for each vertex and show that it is unlikely. First, for each vertex
![]() $v\in V(G)$
and
$v\in V(G)$
and
![]() $c\in L(v)$
and
$c\in L(v)$
and
![]() $i \in [m]$
, we define the random variable
$i \in [m]$
, we define the random variable
-
 $ \textbf{F}_{v, c, i}(A, \psi ) \,:\!=\, \left |\left \{u \in N_{G_i}(v) \,:\, \psi (u) = c\right \}\right |$
.
$ \textbf{F}_{v, c, i}(A, \psi ) \,:\!=\, \left |\left \{u \in N_{G_i}(v) \,:\, \psi (u) = c\right \}\right |$
.
Then, for each vertex
![]() $v\in V(G)$
and
$v\in V(G)$
and
![]() $i \in [m]$
, we define
$i \in [m]$
, we define
-
 $ \boldsymbol{\Omega} ^*_{v, i} = \{(A, \psi ) \,:\, \exists u \in \{v\} \cup N_{G_i}(v) \cup N^2_{G_i}(v), \exists c\in L(u), \textbf{F}_{u, c, i}(A, \psi ) \geq \log D \}$
,
$ \boldsymbol{\Omega} ^*_{v, i} = \{(A, \psi ) \,:\, \exists u \in \{v\} \cup N_{G_i}(v) \cup N^2_{G_i}(v), \exists c\in L(u), \textbf{F}_{u, c, i}(A, \psi ) \geq \log D \}$
,
where
![]() $N^2_{G_i}(v)$
is the set of vertices at distance two from
$N^2_{G_i}(v)$
is the set of vertices at distance two from
![]() $v$
in
$v$
in
![]() $G_i$
. To apply Theorem 3.3 to
$G_i$
. To apply Theorem 3.3 to
![]() $ \textbf{Y}_{v, c, i}$
, we will show that
$ \textbf{Y}_{v, c, i}$
, we will show that
![]() $ \textbf{Y}_{v, c, i}$
has upward
$ \textbf{Y}_{v, c, i}$
has upward
![]() $(s, \delta )$
-certificates with respect to exceptional outcomes
$(s, \delta )$
-certificates with respect to exceptional outcomes
![]() $ \boldsymbol{\Omega} ^*_{v, i}$
with
$ \boldsymbol{\Omega} ^*_{v, i}$
with
![]() $s = 4D$
and
$s = 4D$
and
![]() $\delta = \log D$
. It turns out that we need to consider these exceptional outcomes because, for example, if there is a set of more than
$\delta = \log D$
. It turns out that we need to consider these exceptional outcomes because, for example, if there is a set of more than
![]() $\log D$
vertices in
$\log D$
vertices in
![]() $N_{G_i}(v) \cap A$
that are all assigned the same colour, then changing the outcome of a single trial (in particular the trial determining either
$N_{G_i}(v) \cap A$
that are all assigned the same colour, then changing the outcome of a single trial (in particular the trial determining either
![]() $\psi (u)$
or whether
$\psi (u)$
or whether
![]() $u \in A$
for some
$u \in A$
for some
![]() $u \in \{v\} \cup N_{G_i}(v) \cup N^2_{G_i}(v)$
for which
$u \in \{v\} \cup N_{G_i}(v) \cup N^2_{G_i}(v)$
for which
![]() $ \textbf{F}_{u, c, i}(A, \psi ) \geq \log D$
for some
$ \textbf{F}_{u, c, i}(A, \psi ) \geq \log D$
for some
![]() $c\in L(u)$
) can affect the value of
$c\in L(u)$
) can affect the value of
![]() $ \textbf{Y}_{v, c, i}$
by more than
$ \textbf{Y}_{v, c, i}$
by more than
![]() $\log D$
(see the final part of the proof of Lemma 4.5 for more details). We remark that the event
$\log D$
(see the final part of the proof of Lemma 4.5 for more details). We remark that the event
![]() $ \boldsymbol{\Omega} ^*_{v, i}$
contains more outcomes than is necessary; it is simply more convenient to consider
$ \boldsymbol{\Omega} ^*_{v, i}$
contains more outcomes than is necessary; it is simply more convenient to consider
![]() $ \boldsymbol{\Omega} ^*_{v, i}$
, and the argument adapts more easily for correspondence colouring in Section 5.
$ \boldsymbol{\Omega} ^*_{v, i}$
, and the argument adapts more easily for correspondence colouring in Section 5.
Now we bound the probability of these exceptional events. For this, we assume without loss of generality that
![]() $uv \in E(G)$
only if
$uv \in E(G)$
only if
![]() $L(u) \cap L(v) \neq \emptyset$
, so each
$L(u) \cap L(v) \neq \emptyset$
, so each
![]() $G_i$
has maximum degree at most
$G_i$
has maximum degree at most
![]() $\Lambda D$
.
$\Lambda D$
.
Proposition 4.4.
Every vertex
![]() $v\in V(G)$
and
$v\in V(G)$
and
![]() $i \in [m]$
satisfies
$i \in [m]$
satisfies
Proof. First we bound the probability that
![]() $ \textbf{F}_{u, c, i}$
is too large for each
$ \textbf{F}_{u, c, i}$
is too large for each
![]() $u \in V(G)$
and
$u \in V(G)$
and
![]() $c\in L(u)$
, as follows:
$c\in L(u)$
, as follows:
 \begin{equation*} {{\mathbb {P}}\left [ \textbf {F}_{u, c, i} \geq \log D\right ] } \leq \sum _{i = \lceil \log D\rceil }^{D}\binom {D}{i}\left (\frac {1}{\Lambda }\right )^i \leq \sum _{i=\lceil \log D\rceil }^{D}\left (\frac {eD}{i\Lambda }\right )^i \leq \sum _{i=\lceil \log D\rceil }^{D}\left (\frac {e}{i}\right )^i. \end{equation*}
\begin{equation*} {{\mathbb {P}}\left [ \textbf {F}_{u, c, i} \geq \log D\right ] } \leq \sum _{i = \lceil \log D\rceil }^{D}\binom {D}{i}\left (\frac {1}{\Lambda }\right )^i \leq \sum _{i=\lceil \log D\rceil }^{D}\left (\frac {eD}{i\Lambda }\right )^i \leq \sum _{i=\lceil \log D\rceil }^{D}\left (\frac {e}{i}\right )^i. \end{equation*}
Since each term in the sum is at most
![]() $(e/\log D)^{\log D}$
and there are at most
$(e/\log D)^{\log D}$
and there are at most
![]() $D$
terms, it follows that
$D$
terms, it follows that
Thus, combining the above inequality with the Union Bound, we have
![]() ${{\mathbb{P}}\left [ \boldsymbol{\Omega} ^*_{v,i}\right ] } \leq \Lambda (1 + \Lambda D + \Lambda ^2D^2)\left (\log D\right )^{- \log D} \leq 11^3 C^3D^5\left (\log D\right )^{- \log D}$
, as desired.
${{\mathbb{P}}\left [ \boldsymbol{\Omega} ^*_{v,i}\right ] } \leq \Lambda (1 + \Lambda D + \Lambda ^2D^2)\left (\log D\right )^{- \log D} \leq 11^3 C^3D^5\left (\log D\right )^{- \log D}$
, as desired.
Combining Theorem 3.3 and Proposition 4.4, we show that
![]() $ \boldsymbol{\Lambda}_v$
,
$ \boldsymbol{\Lambda}_v$
,
![]() $ \textbf{Y}_{v, c, i}$
, and
$ \textbf{Y}_{v, c, i}$
, and
![]() $ \textbf{R}_{v, c, i}$
are close to their expectation with high probability in the following lemma.
$ \textbf{R}_{v, c, i}$
are close to their expectation with high probability in the following lemma.
Lemma 4.5.
Every vertex
![]() $v\in V(G)$
satisfies
$v\in V(G)$
satisfies
Moreover, if
![]() $v \in V(G_i)$
and
$v \in V(G_i)$
and
![]() $c \in L(v)$
, then
$c \in L(v)$
, then
Proof. First we prove (10). We apply Theorem 3.3 with exceptional outcomes
![]() $ \boldsymbol{\Omega} ^* = \emptyset$
. To that end, we show that
$ \boldsymbol{\Omega} ^* = \emptyset$
. To that end, we show that
![]() $\Lambda - \boldsymbol{\Lambda}_v$
has upward
$\Lambda - \boldsymbol{\Lambda}_v$
has upward
![]() $(s, \delta )$
-certificates with respect to
$(s, \delta )$
-certificates with respect to
![]() $ \boldsymbol{\Omega} ^*$
, where
$ \boldsymbol{\Omega} ^*$
, where
![]() $s = 2\Lambda$
and
$s = 2\Lambda$
and
![]() $\delta = 1$
. Let
$\delta = 1$
. Let
![]() $(A, \psi ) \in \boldsymbol{\Omega}$
. For every
$(A, \psi ) \in \boldsymbol{\Omega}$
. For every
![]() $c \in L(v) \setminus L_{A, \psi }(v)$
, there is at least one neighbour
$c \in L(v) \setminus L_{A, \psi }(v)$
, there is at least one neighbour
![]() $u \in N_{G}(v)$
of
$u \in N_{G}(v)$
of
![]() $v$
such that
$v$
such that
![]() $u \in A$
and
$u \in A$
and
![]() $\psi (u) = c$
. Choose one such neighbour, and denote it by
$\psi (u) = c$
. Choose one such neighbour, and denote it by
![]() $u_c$
. Let
$u_c$
. Let
![]() $I_{A, \psi }$
index the trials determining whether
$I_{A, \psi }$
index the trials determining whether
![]() $u_c \in A$
and
$u_c \in A$
and
![]() $\psi (u_c) = c$
for each
$\psi (u_c) = c$
for each
![]() $c \in L(v)\setminus L_{A, \psi }(v)$
. Now if
$c \in L(v)\setminus L_{A, \psi }(v)$
. Now if
![]() $(A^{\prime}, \psi^{\prime}) \in \boldsymbol{\Omega}$
differs from
$(A^{\prime}, \psi^{\prime}) \in \boldsymbol{\Omega}$
differs from
![]() $(A, \psi )$
in at most
$(A, \psi )$
in at most
![]() $t$
of the trials indexed by
$t$
of the trials indexed by
![]() $I_{A, \psi }$
(and differs arbitrarily for trials not indexed by
$I_{A, \psi }$
(and differs arbitrarily for trials not indexed by
![]() $I_{A, \psi }$
), then all but at most
$I_{A, \psi }$
), then all but at most
![]() $t$
colours in
$t$
colours in
![]() $L(v) \setminus L_{A, \psi }(v)$
are also in
$L(v) \setminus L_{A, \psi }(v)$
are also in
![]() $L(v) \setminus L_{A^{\prime}, \psi^{\prime}}(v)$
. Hence,
$L(v) \setminus L_{A^{\prime}, \psi^{\prime}}(v)$
. Hence,
![]() $\Lambda - \boldsymbol{\Lambda}_v(A^{\prime}, \psi^{\prime}) \geq \Lambda - \boldsymbol{\Lambda}_v(A, \psi ) - t$
, and since
$\Lambda - \boldsymbol{\Lambda}_v(A^{\prime}, \psi^{\prime}) \geq \Lambda - \boldsymbol{\Lambda}_v(A, \psi ) - t$
, and since
![]() $I_{A, \psi } \leq 2\Lambda = s$
, it follows that
$I_{A, \psi } \leq 2\Lambda = s$
, it follows that
![]() $\Lambda - \boldsymbol{\Lambda}_v$
has upward
$\Lambda - \boldsymbol{\Lambda}_v$
has upward
![]() $(s, \delta )$
-certificates, as desired. Therefore by Theorem 3.3 with
$(s, \delta )$
-certificates, as desired. Therefore by Theorem 3.3 with
![]() $t = D^{2/3}$
,
$t = D^{2/3}$
,
as desired.
Now we prove (12). We apply Theorem 3.3 with exceptional outcomes
![]() $ \boldsymbol{\Omega} ^* = \emptyset$
. To that end, we show that
$ \boldsymbol{\Omega} ^* = \emptyset$
. To that end, we show that
![]() $D - \textbf{R}_{v, c, i}$
has upward
$D - \textbf{R}_{v, c, i}$
has upward
![]() $(s, \delta )$
-certificates with respect to
$(s, \delta )$
-certificates with respect to
![]() $ \boldsymbol{\Omega} ^*$
, where
$ \boldsymbol{\Omega} ^*$
, where
![]() $s = 3D$
and
$s = 3D$
and
![]() $\delta = 1$
. Let
$\delta = 1$
. Let
![]() $(A, \psi ) \in \boldsymbol{\Omega}$
, and note that
$(A, \psi ) \in \boldsymbol{\Omega}$
, and note that
For every
![]() $u \in \{x \in N_{G_i}(v) \,:\, c \in L(x)\} \cap \bigcup _{w \in A\setminus V(G_i) \,:\, \psi (w) = c}N_G(w)$
, there is at least one neighbour
$u \in \{x \in N_{G_i}(v) \,:\, c \in L(x)\} \cap \bigcup _{w \in A\setminus V(G_i) \,:\, \psi (w) = c}N_G(w)$
, there is at least one neighbour
![]() $w \in N_{G_j}(u)$
of
$w \in N_{G_j}(u)$
of
![]() $u$
where
$u$
where
![]() $j \in [m]\setminus \{i\}$
such that
$j \in [m]\setminus \{i\}$
such that
![]() $w \in A$
and
$w \in A$
and
![]() $\psi (w) = c$
. Choose one such neighbour, and denote it by
$\psi (w) = c$
. Choose one such neighbour, and denote it by
![]() $w_u$
. By (i), the vertices
$w_u$
. By (i), the vertices
![]() $w_u$
are distinct for different choices of
$w_u$
are distinct for different choices of
![]() $u$
. Let
$u$
. Let
![]() $I_{A, \psi }$
index the trials determining whether
$I_{A, \psi }$
index the trials determining whether
![]() $u \in A$
for each
$u \in A$
for each
![]() $u \in \{x \in N_{G_i}(v) \,:\, c \in L(x)\}$
and whether
$u \in \{x \in N_{G_i}(v) \,:\, c \in L(x)\}$
and whether
![]() $w_u \in A$
and
$w_u \in A$
and
![]() $\psi (w_u) = c$
for each
$\psi (w_u) = c$
for each
![]() $u \in \{x \in N_{G_i}(v) \,:\, c \in L(x)\} \cap \bigcup _{w \in A\setminus V(G_i) \,:\, \psi (w) = c}N_G(w)$
. Now if
$u \in \{x \in N_{G_i}(v) \,:\, c \in L(x)\} \cap \bigcup _{w \in A\setminus V(G_i) \,:\, \psi (w) = c}N_G(w)$
. Now if
![]() $(A^{\prime}, \psi^{\prime}) \in \boldsymbol{\Omega}$
differs from
$(A^{\prime}, \psi^{\prime}) \in \boldsymbol{\Omega}$
differs from
![]() $(A, \psi )$
in at most
$(A, \psi )$
in at most
![]() $t$
of the trials indexed by
$t$
of the trials indexed by
![]() $I_{A, \psi }$
(and differs arbitrarily for trials not indexed by
$I_{A, \psi }$
(and differs arbitrarily for trials not indexed by
![]() $I_{A, \psi }$
), all but at most
$I_{A, \psi }$
), all but at most
![]() $t$
vertices in
$t$
vertices in
![]() $\{x \in N_{G_i}(v) \,:\, c \in L(x)\} \cap (A \cup \bigcup _{w \in A\setminus V(G_i) \,:\, \psi (w) = c}N_G(w))$
are in
$\{x \in N_{G_i}(v) \,:\, c \in L(x)\} \cap (A \cup \bigcup _{w \in A\setminus V(G_i) \,:\, \psi (w) = c}N_G(w))$
are in
![]() $\{x \in N_{G_i}(v) \,:\, c \in L(x)\} \cap (A^{\prime} \cup \bigcup _{w \in A^{\prime}\setminus V(G_i) \,:\, \psi^{\prime}(w) = c}N_G(w))$
. Hence,
$\{x \in N_{G_i}(v) \,:\, c \in L(x)\} \cap (A^{\prime} \cup \bigcup _{w \in A^{\prime}\setminus V(G_i) \,:\, \psi^{\prime}(w) = c}N_G(w))$
. Hence,
![]() $D - \textbf{R}_{v, c, i}(A^{\prime}, \psi^{\prime}) \geq D - \textbf{R}_{v, c, i}(A, \psi ) - t$
, and since
$D - \textbf{R}_{v, c, i}(A^{\prime}, \psi^{\prime}) \geq D - \textbf{R}_{v, c, i}(A, \psi ) - t$
, and since
![]() $I_{A, \psi } \leq 3D = s$
, it follows that
$I_{A, \psi } \leq 3D = s$
, it follows that
![]() $ \textbf{R}_{v, c, i}$
has upward
$ \textbf{R}_{v, c, i}$
has upward
![]() $(s, \delta )$
-certificates, as desired. Therefore by Theorem 3.3 with
$(s, \delta )$
-certificates, as desired. Therefore by Theorem 3.3 with
![]() $t = D^{2/3}$
,
$t = D^{2/3}$
,
as desired.
Finally, we prove (11). We apply Theorem 3.3 with exceptional outcomes
![]() $\boldsymbol{\Omega} ^* = \boldsymbol{\Omega} ^*_{v, i}$
. To that end, we show that
$\boldsymbol{\Omega} ^* = \boldsymbol{\Omega} ^*_{v, i}$
. To that end, we show that
![]() $ \textbf{Y}_{v, c, i}$
has upward
$ \textbf{Y}_{v, c, i}$
has upward
![]() $(s, \delta )$
-certificates with respect to
$(s, \delta )$
-certificates with respect to
![]() $ \boldsymbol{\Omega} ^*$
, where
$ \boldsymbol{\Omega} ^*$
, where
![]() $s = 4D$
and
$s = 4D$
and
![]() $\delta = \log D$
. Let
$\delta = \log D$
. Let
![]() $(A, \psi ) \in \boldsymbol{\Omega} \setminus \boldsymbol{\Omega} ^*$
. For every
$(A, \psi ) \in \boldsymbol{\Omega} \setminus \boldsymbol{\Omega} ^*$
. For every
![]() $u \in \{x \in N_{G_i}(v) \cap A \,:\, c \in L(x)\} \setminus X_{A, \psi }$
, there is at least one neighbour
$u \in \{x \in N_{G_i}(v) \cap A \,:\, c \in L(x)\} \setminus X_{A, \psi }$
, there is at least one neighbour
![]() $w \in N_{G}(u)$
of
$w \in N_{G}(u)$
of
![]() $u$
such that
$u$
such that
![]() $w \in A$
and
$w \in A$
and
![]() $\psi (w) = \psi (u)$
. Choose one such neighbour, and denote it by
$\psi (w) = \psi (u)$
. Choose one such neighbour, and denote it by
![]() $w_u$
. Let
$w_u$
. Let
![]() $I_{A, \psi }$
index the trials determining whether
$I_{A, \psi }$
index the trials determining whether
![]() $u \in A$
, whether
$u \in A$
, whether
![]() $w_u \in A$
, and the assignment of
$w_u \in A$
, and the assignment of
![]() $\psi (u)$
and
$\psi (u)$
and
![]() $\psi (w_u)$
for each
$\psi (w_u)$
for each
![]() $u \in \{x \in N_{G_i}(v) \cap A \,:\, c \in L(x)\}$
. Since
$u \in \{x \in N_{G_i}(v) \cap A \,:\, c \in L(x)\}$
. Since
![]() $(A, \psi )\notin \boldsymbol{\Omega} ^*_v$
, the multi-set
$(A, \psi )\notin \boldsymbol{\Omega} ^*_v$
, the multi-set
![]() $\{w_u \,:\, u \in (N_{G_i}(v) \cap A) \setminus X_{A, \psi },\ c \in L(u)\}$
has maximum multiplicity at most
$\{w_u \,:\, u \in (N_{G_i}(v) \cap A) \setminus X_{A, \psi },\ c \in L(u)\}$
has maximum multiplicity at most
![]() $\log D$
(as otherwise, if
$\log D$
(as otherwise, if
![]() $w$
appears more than
$w$
appears more than
![]() $\log D$
times in this multi-set, then
$\log D$
times in this multi-set, then
![]() $ \textbf{F}_{w, \psi (w), i}(A, \psi ) \gt \log D$
). Hence, if
$ \textbf{F}_{w, \psi (w), i}(A, \psi ) \gt \log D$
). Hence, if
![]() $(A^{\prime}, \psi^{\prime}) \in \boldsymbol{\Omega}$
differs from
$(A^{\prime}, \psi^{\prime}) \in \boldsymbol{\Omega}$
differs from
![]() $(A, \psi )$
in at most
$(A, \psi )$
in at most
![]() $t/ \log D$
of the trials indexed by
$t/ \log D$
of the trials indexed by
![]() $I_{A, \psi }$
(and differs arbitrarily for trials not indexed by
$I_{A, \psi }$
(and differs arbitrarily for trials not indexed by
![]() $I_{A, \psi }$
), then all but at most
$I_{A, \psi }$
), then all but at most
![]() $t$
vertices in
$t$
vertices in
![]() $\{x \in N_{G_i}(v) \cap A \,:\, c \in L(x)\} \setminus X_{A, \psi }$
are in
$\{x \in N_{G_i}(v) \cap A \,:\, c \in L(x)\} \setminus X_{A, \psi }$
are in
![]() $\{x \in N_{G_i}(v) \cap A^{\prime} \,:\, c \in L(x)\} \setminus X_{A^{\prime}, \psi^{\prime}}$
. Hence,
$\{x \in N_{G_i}(v) \cap A^{\prime} \,:\, c \in L(x)\} \setminus X_{A^{\prime}, \psi^{\prime}}$
. Hence,
![]() $ \textbf{Y}_{v, c, i}(A^{\prime}, \psi^{\prime}) \geq \textbf{Y}_{v, c, i}(A, \psi ) - t$
, and since
$ \textbf{Y}_{v, c, i}(A^{\prime}, \psi^{\prime}) \geq \textbf{Y}_{v, c, i}(A, \psi ) - t$
, and since
![]() $I_{A, \psi } \leq 4D = s$
, it follows that
$I_{A, \psi } \leq 4D = s$
, it follows that
![]() $ \textbf{Y}_{v, c, i}$
has upward
$ \textbf{Y}_{v, c, i}$
has upward
![]() $(s, \delta )$
-certificates, as desired. Therefore by Theorem 3.3 with
$(s, \delta )$
-certificates, as desired. Therefore by Theorem 3.3 with
![]() $t = D^{2/3}$
and Proposition 4.4,
$t = D^{2/3}$
and Proposition 4.4,
as desired.
Finally we can prove Lemma 2.1, using Lemmas 4.3 and 4.5.
Proof of Lemma
2.1
. First, rather than showing (2.1.1), it suffices to show that
![]() $|L^{\prime}(v)| \geq \left (1 - p/\Lambda \right )^{DC}\Lambda - \Lambda ^{4/5}$
for every
$|L^{\prime}(v)| \geq \left (1 - p/\Lambda \right )^{DC}\Lambda - \Lambda ^{4/5}$
for every
![]() $v \in V(G)\setminus X$
, since we can truncate each list until equality holds.
$v \in V(G)\setminus X$
, since we can truncate each list until equality holds.
We consider
![]() $(A, \psi )$
chosen randomly as described earlier, and we define the following set of bad events for each vertex
$(A, \psi )$
chosen randomly as described earlier, and we define the following set of bad events for each vertex
![]() $v\in V(G)$
and
$v\in V(G)$
and
![]() $c\in L(v)$
and
$c\in L(v)$
and
![]() $i \in [m]$
:
$i \in [m]$
:
 \begin{align*} \mathcal A_v &= \left \{ (A, \psi ) \,:\, \boldsymbol{\Lambda}_v(A, \psi ) \lt{{\mathbb{E}}\left [ \boldsymbol{\Lambda}_v\right ] } - \Lambda ^{4/5}\right \},\\ \mathcal A_{v, c, i} &= \left \{ (A, \psi ) \,:\, \textbf{Y}_{v, c, i} \gt{{\mathbb{E}}\left [ \textbf{Y}_{v, c, i}\right ] } + D^{4/5}/2 \right \}, \text{ and}\\ \mathcal A^{\prime}_{v, c, i} &= \left \{(A, \psi ) \,:\, \textbf{R}_{v,c,i}(A, \psi ) \gt{{\mathbb{E}}\left [ \textbf{R}_{v, c, i}\right ] } + D^{4/5}/2\right \}. \end{align*}
\begin{align*} \mathcal A_v &= \left \{ (A, \psi ) \,:\, \boldsymbol{\Lambda}_v(A, \psi ) \lt{{\mathbb{E}}\left [ \boldsymbol{\Lambda}_v\right ] } - \Lambda ^{4/5}\right \},\\ \mathcal A_{v, c, i} &= \left \{ (A, \psi ) \,:\, \textbf{Y}_{v, c, i} \gt{{\mathbb{E}}\left [ \textbf{Y}_{v, c, i}\right ] } + D^{4/5}/2 \right \}, \text{ and}\\ \mathcal A^{\prime}_{v, c, i} &= \left \{(A, \psi ) \,:\, \textbf{R}_{v,c,i}(A, \psi ) \gt{{\mathbb{E}}\left [ \textbf{R}_{v, c, i}\right ] } + D^{4/5}/2\right \}. \end{align*}
Letting
![]() $\mathcal A$
be the union of all such bad events, note that each event in
$\mathcal A$
be the union of all such bad events, note that each event in
![]() $\mathcal A$
is mutually independent of all but at most
$\mathcal A$
is mutually independent of all but at most
![]() $(\lceil \Lambda \rceil CD)^4 \leq (11C^2D^2)^4$
other events in
$(\lceil \Lambda \rceil CD)^4 \leq (11C^2D^2)^4$
other events in
![]() $\mathcal A$
. By Lemma 4.5, every event in
$\mathcal A$
. By Lemma 4.5, every event in
![]() $\mathcal A$
occurs with probability at most
$\mathcal A$
occurs with probability at most
![]() $\exp \left (-D^{1/4}\right )$
. Therefore by the Lovász Local Lemma, there exists
$\exp \left (-D^{1/4}\right )$
. Therefore by the Lovász Local Lemma, there exists
![]() $(A, \psi )\notin \mathcal A$
.
$(A, \psi )\notin \mathcal A$
.
Now we show that
![]() $X \,:\!=\, X_{A, \psi }$
and
$X \,:\!=\, X_{A, \psi }$
and
![]() $L^{\prime} \,:\!=\, L_{A, \psi }|_{V(G)\setminus X}$
satisfy the lemma with
$L^{\prime} \,:\!=\, L_{A, \psi }|_{V(G)\setminus X}$
satisfy the lemma with
![]() $\phi \,:\!=\, \psi |_X$
. Indeed,
$\phi \,:\!=\, \psi |_X$
. Indeed,
![]() $\phi$
is an
$\phi$
is an
![]() $L|_X$
-colouring of
$L|_X$
-colouring of
![]() $G[X]$
and since
$G[X]$
and since
![]() $X \subseteq A$
, we have
$X \subseteq A$
, we have
![]() $L^{\prime}(v) \subseteq L(v)\setminus \{\phi (u) \,:\, u \in N_G(v) \cap X\}$
, as required. Moreover, for every
$L^{\prime}(v) \subseteq L(v)\setminus \{\phi (u) \,:\, u \in N_G(v) \cap X\}$
, as required. Moreover, for every
![]() $v\in V(G)$
, since
$v\in V(G)$
, since
![]() $(A, \psi ) \notin \mathcal A_v$
, by (7), we have
$(A, \psi ) \notin \mathcal A_v$
, by (7), we have
![]() $|L^{\prime}(v)| \geq \left (1 - p/\Lambda \right )^{DC}\Lambda - \Lambda ^{4/5}$
, as desired, and if
$|L^{\prime}(v)| \geq \left (1 - p/\Lambda \right )^{DC}\Lambda - \Lambda ^{4/5}$
, as desired, and if
![]() $v \in V(G_i)$
and
$v \in V(G_i)$
and
![]() $c\in L(v)$
, then since
$c\in L(v)$
, then since
![]() $(A, \psi ) \notin \mathcal A_{v, c, i} \cup \mathcal A^{\prime}_{v, c, i}$
, by (4), (8), and (9), we have (2.1.2), as desired.
$(A, \psi ) \notin \mathcal A_{v, c, i} \cup \mathcal A^{\prime}_{v, c, i}$
, by (4), (8), and (9), we have (2.1.2), as desired.
5. Correspondence colouring
In this section we introduce correspondence colouring and describe how to generalize Theorem 1.3 to this setting.
Definition 5.1. Let
![]() $G$
be a graph with list assignment
$G$
be a graph with list assignment
![]() $L$
.
$L$
.
-
If
 $M$
is a map with domain
$M$
is a map with domain
 $E(G)$
where for each
$E(G)$
where for each
 $e=uv\in E(G)$
,
$e=uv\in E(G)$
,
 $M(e)$
is a matching of
$M(e)$
is a matching of
 $\{u\}\times L(u)$
and
$\{u\}\times L(u)$
and
 $\{v\}\times L(v)$
, we say
$\{v\}\times L(v)$
, we say
 $(L, M)$
is a correspondence assignment for
$(L, M)$
is a correspondence assignment for
 $G$
.
$G$
. -
An
 $(L, M)$
-colouring of
$(L, M)$
-colouring of
 $G$
is a map
$G$
is a map
 $\phi$
with domain
$\phi$
with domain
 $V(G)$
such that
$V(G)$
such that
 $\phi (u)\in L(u)$
for every
$\phi (u)\in L(u)$
for every
 $u\in V(G)$
, and every
$u\in V(G)$
, and every
 $e=uv\in E(G)$
satisfies
$e=uv\in E(G)$
satisfies
 $(u, \phi (u))(v, \phi (v))\notin M(e)$
. If
$(u, \phi (u))(v, \phi (v))\notin M(e)$
. If
 $G$
has an
$G$
has an
 $(L, M)$
-colouring, then we say
$(L, M)$
-colouring, then we say
 $G$
is
$G$
is
 $(L, M)$
-colourable.
$(L, M)$
-colourable. -
The correspondence chromatic number of
 $G$
, also called the
$G$
, also called the
 $DP$
-chromatic number, denoted
$DP$
-chromatic number, denoted
 $\chi _{DP}(G)$
, is the minimum
$\chi _{DP}(G)$
, is the minimum
 $k$
such that
$k$
such that
 $G$
is
$G$
is
 $(L, M)$
-colourable for every correspondence assignment
$(L, M)$
-colourable for every correspondence assignment
 $(L, M)$
satisfying
$(L, M)$
satisfying
 $|L(v)| \geq k$
for all
$|L(v)| \geq k$
for all
 $v\in V(G)$
.
$v\in V(G)$
.
For convenience, if
![]() $uv\in E(G)$
,
$uv\in E(G)$
,
![]() $c_1\in L(u)$
,
$c_1\in L(u)$
,
![]() $c_2\in L(v)$
, and
$c_2\in L(v)$
, and
![]() $(u, c_1)(v, c_2)\in M(uv)$
, we will just write
$(u, c_1)(v, c_2)\in M(uv)$
, we will just write
![]() $c_1c_2\in M(uv)$
. For each
$c_1c_2\in M(uv)$
. For each
![]() $v \in V(G)$
and
$v \in V(G)$
and
![]() $c \in L(v)$
, we will let
$c \in L(v)$
, we will let
![]() $N_{G, (L, M)}(v, c) \,:\!=\, \{(u, c^{\prime}) \,:\, uv \in E(G), cc^{\prime} \in M(uv)\}$
, and we omit the subscript in
$N_{G, (L, M)}(v, c) \,:\!=\, \{(u, c^{\prime}) \,:\, uv \in E(G), cc^{\prime} \in M(uv)\}$
, and we omit the subscript in
![]() $N_{G, (L, M)}(v, c)$
when it is clear from the context. Note that if for each
$N_{G, (L, M)}(v, c)$
when it is clear from the context. Note that if for each
![]() $e=uv\in E(G)$
and
$e=uv\in E(G)$
and
![]() $c\in L(u)\cap L(v)$
, we have
$c\in L(u)\cap L(v)$
, we have
![]() $cc\in M(uv)$
, then an
$cc\in M(uv)$
, then an
![]() $(L, M)$
-colouring is an
$(L, M)$
-colouring is an
![]() $L$
-colouring. Hence, every graph
$L$
-colouring. Hence, every graph
![]() $G$
satisfies
$G$
satisfies
![]() $\chi _\ell (G)\leq \chi _{DP}(G)$
.
$\chi _\ell (G)\leq \chi _{DP}(G)$
.
For a graph
![]() $G$
with correspondence assignment
$G$
with correspondence assignment
![]() $(L, M)$
, we define the colour degree of each
$(L, M)$
, we define the colour degree of each
![]() $v\in V(G)$
and
$v\in V(G)$
and
![]() $c \in L(v)$
to be
$c \in L(v)$
to be
![]() $d_{G, (L, M)}(v, c) \,:\!=\, |N_{G, (L, M)}(v, c)|$
and the maximum colour degree to be
$d_{G, (L, M)}(v, c) \,:\!=\, |N_{G, (L, M)}(v, c)|$
and the maximum colour degree to be
![]() $\Delta (G, (L, M)) \,:\!=\, \max _{v\in V(G)}\max _{c \in L(v)}d_{G, (L, M)}(v, c)$
. With only minor modifications to the argument used to prove Theorem 1.3, which we describe below, we can strengthen Theorem 1.3 to the setting of correspondence colouring, as follows.
$\Delta (G, (L, M)) \,:\!=\, \max _{v\in V(G)}\max _{c \in L(v)}d_{G, (L, M)}(v, c)$
. With only minor modifications to the argument used to prove Theorem 1.3, which we describe below, we can strengthen Theorem 1.3 to the setting of correspondence colouring, as follows.
Theorem 5.2.
For every
![]() $C,{\varepsilon } \gt 0$
, the following holds for all sufficiently large
$C,{\varepsilon } \gt 0$
, the following holds for all sufficiently large
![]() $D$
. Let
$D$
. Let
![]() $G_1, \dots, G_m$
be graphs that
$G_1, \dots, G_m$
be graphs that
-
(i) are nearly disjoint and
-
(ii) satisfy
 $|\{i \in [m] \,:\, v \in V(G_i)\}| \leq C$
for every
$|\{i \in [m] \,:\, v \in V(G_i)\}| \leq C$
for every
 $v \in \bigcup _{i=1}^m V(G_i)$
.
$v \in \bigcup _{i=1}^m V(G_i)$
.
If
![]() $(L, M)$
is a correspondence assignment for
$(L, M)$
is a correspondence assignment for
![]() $G \,:\!=\, \bigcup _{i=1}^m G_i$
satisfying
$G \,:\!=\, \bigcup _{i=1}^m G_i$
satisfying
-
(iii)
 $\Delta (G_i, (L|_{V(G_i)}, M|_{E(G_i)}) \leq D$
for every
$\Delta (G_i, (L|_{V(G_i)}, M|_{E(G_i)}) \leq D$
for every
 $i \in [m]$
and
$i \in [m]$
and
-
(iv)
 $|L(v)| \geq (1 +{\varepsilon })D$
for every
$|L(v)| \geq (1 +{\varepsilon })D$
for every
 $v\in V(G)$
,
$v\in V(G)$
,
then
![]() $G$
is
$G$
is
![]() $(L, M)$
-colourable.
$(L, M)$
-colourable.
As mentioned, Theorem 5.2 implies that Corollary 1.1 actually holds for the correspondence chromatic number, which in turn implies the main result of [Reference Molloy and Postle19], that linear and uniform hypergraphs of maximum degree at most
![]() $D$
have correspondence chromatic index at most
$D$
have correspondence chromatic index at most
![]() $D + o(D)$
.
$D + o(D)$
.
To prove Theorem 5.2, we use the argument presented in Section 2, but with Lemmas 2.1 and 2.3 replaced with the following lemmas, respectively.
Lemma 5.3.
For every
![]() $C,{\varepsilon } \gt 0$
, there exists
$C,{\varepsilon } \gt 0$
, there exists
![]() $D_{5.3}$
such that the following holds for every
$D_{5.3}$
such that the following holds for every
![]() $D \geq D_{5.3}$
. Let
$D \geq D_{5.3}$
. Let
![]() $G_1, \dots, G_m$
be graphs, and let
$G_1, \dots, G_m$
be graphs, and let
![]() $(L, M)$
be a correspondence assignment for
$(L, M)$
be a correspondence assignment for
![]() $G \,:\!=\, \bigcup _{i=1}^m G_i$
satisfying (i)–(iv) (of Theorem
5.2
). If
$G \,:\!=\, \bigcup _{i=1}^m G_i$
satisfying (i)–(iv) (of Theorem
5.2
). If
![]() $|L(v)| = \lceil \Lambda \rceil$
for every
$|L(v)| = \lceil \Lambda \rceil$
for every
![]() $v\in V(G)$
, where
$v\in V(G)$
, where
![]() $(1 +{\varepsilon })D \le \Lambda \le 10CD$
, and if
$(1 +{\varepsilon })D \le \Lambda \le 10CD$
, and if
![]() $\log ^{-1} D \geq p \geq \log ^{-2}D$
, then there exist
$\log ^{-1} D \geq p \geq \log ^{-2}D$
, then there exist
![]() $X\subseteq V(G)$
, an
$X\subseteq V(G)$
, an
![]() $(L|_X, M|_{E(G[X])})$
-colouring
$(L|_X, M|_{E(G[X])})$
-colouring
![]() $\phi$
of
$\phi$
of
![]() $G[X]$
, and a correspondence assignment
$G[X]$
, and a correspondence assignment
![]() $L^{\prime}$
for
$L^{\prime}$
for
![]() $G - X$
satisfying
$G - X$
satisfying
![]() $L^{\prime}(v) \subseteq \{c \in L(v)\,:\, (v, c) \in (\{v\}\times L(v)) \setminus \bigcup _{u \in X}N(u, \phi (u))\}$
for every
$L^{\prime}(v) \subseteq \{c \in L(v)\,:\, (v, c) \in (\{v\}\times L(v)) \setminus \bigcup _{u \in X}N(u, \phi (u))\}$
for every
![]() $v\in V(G)$
, such that
$v\in V(G)$
, such that
-
(5.3.1)
 $|L^{\prime}(v)| = \left \lceil{\Lambda _{\mathbb{E}}}(\Lambda, D, C, p) - \Lambda ^{4/5}\right \rceil$
for every
$|L^{\prime}(v)| = \left \lceil{\Lambda _{\mathbb{E}}}(\Lambda, D, C, p) - \Lambda ^{4/5}\right \rceil$
for every
 $v\in V(G)\setminus X$
and
$v\in V(G)\setminus X$
and
-
(5.3.2)
 $\Delta (G_i - X, (L^{\prime}|_{V(G_i - X)}, M|_{E(G_i - X)})) \leq{D_{{\mathbb{E}}}}(\Lambda, D, C, p) + D^{4/5}$
for every
$\Delta (G_i - X, (L^{\prime}|_{V(G_i - X)}, M|_{E(G_i - X)})) \leq{D_{{\mathbb{E}}}}(\Lambda, D, C, p) + D^{4/5}$
for every
 $i \in [m]$
.
$i \in [m]$
.
Lemma 5.4.
Let
![]() $G$
be a graph with correspondence assignment
$G$
be a graph with correspondence assignment
![]() $L$
. If
$L$
. If
![]() $|L(v)| \geq 8D$
for every
$|L(v)| \geq 8D$
for every
![]() $v \in V(G)$
and
$v \in V(G)$
and
![]() $\Delta (G, (L, M)) \leq D$
, then
$\Delta (G, (L, M)) \leq D$
, then
![]() $G$
is
$G$
is
![]() $(L, M)$
-colourable.
$(L, M)$
-colourable.
Lemma 5.4, like Lemma 2.3, can be proved with a straightforward application of the Lovász Local Lemma. A stronger result (with ‘
![]() $|L(v)| \geq 8D$
’ replaced by ‘
$|L(v)| \geq 8D$
’ replaced by ‘
![]() $|L(v)| \geq 2D$
’) also follows easily from a well-known result of Haxell [Reference Haxell11] on independent transversals.
$|L(v)| \geq 2D$
’) also follows easily from a well-known result of Haxell [Reference Haxell11] on independent transversals.
Therefore it remains to describe how the argument presented in Section 4 to prove Lemma 2.1 can be modified to obtain Lemma 5.3. We consider the same probability space
![]() $( \boldsymbol{\Omega}, \boldsymbol{\Sigma},{\mathbb{P}})$
of pairs
$( \boldsymbol{\Omega}, \boldsymbol{\Sigma},{\mathbb{P}})$
of pairs
![]() $(A, \psi )$
, but we instead define
$(A, \psi )$
, but we instead define
![]() $L_{A, \psi }(v) \,:\!=\, \{c \in L(v) \,:\, (v, c) \in \left (\{v\}\times L(v)\right ) \setminus \bigcup _{u\in A}N(u, \psi (u))\}$
. The definition of
$L_{A, \psi }(v) \,:\!=\, \{c \in L(v) \,:\, (v, c) \in \left (\{v\}\times L(v)\right ) \setminus \bigcup _{u\in A}N(u, \psi (u))\}$
. The definition of
![]() $X_{A, \psi }$
and of
$X_{A, \psi }$
and of
![]() $ \boldsymbol{\Lambda}_v(A, \psi )$
remains the same, but we replace the definitions of
$ \boldsymbol{\Lambda}_v(A, \psi )$
remains the same, but we replace the definitions of
![]() $ \textbf{D}_{v, c, i}(A, \psi )$
,
$ \textbf{D}_{v, c, i}(A, \psi )$
,
![]() $ \textbf{Y}_{v, c, i}(A, \psi )$
, and
$ \textbf{Y}_{v, c, i}(A, \psi )$
, and
![]() $ \textbf{R}_{v, c, i}(A, \psi )$
with the following:
$ \textbf{R}_{v, c, i}(A, \psi )$
with the following:
-
•
 $ \textbf{D}_{v, c, i}(A, \psi ) \,:\!=\, \left |\left \{ (u, c^{\prime}) \in N_{G_i, (L|_{V(G_i)}, M|_{E(G_i)})}(v, c) \,:\, u \notin X_{A, \psi }, c^{\prime} \in L_{A, \psi }(u)\right \}\right |$
,
$ \textbf{D}_{v, c, i}(A, \psi ) \,:\!=\, \left |\left \{ (u, c^{\prime}) \in N_{G_i, (L|_{V(G_i)}, M|_{E(G_i)})}(v, c) \,:\, u \notin X_{A, \psi }, c^{\prime} \in L_{A, \psi }(u)\right \}\right |$
, -
•
 $ \textbf{Y}_{v, c, i}(A, \psi ) \,:\!=\, \left |\left \{ (u, c^{\prime}) \in N_{G_i, (L|_{V(G_i)}, M|_{E(G_i)})}(v, c) \,:\, u \in A \setminus X_{A, \psi }\right \}\right |$
, and
$ \textbf{Y}_{v, c, i}(A, \psi ) \,:\!=\, \left |\left \{ (u, c^{\prime}) \in N_{G_i, (L|_{V(G_i)}, M|_{E(G_i)})}(v, c) \,:\, u \in A \setminus X_{A, \psi }\right \}\right |$
, and -
•
 $ \textbf{R}_{v, c, i}(A, \psi ) \,:\!=\, \left |\left \{ (u, c^{\prime}) \in N_{G_i, (L|_{V(G_i)}, M|_{E(G_i)})}(v, c) \,:\, u \notin A\right \} \setminus \bigcup _{u \in A\setminus V(G_i)}N_{G, (L, M)}(u, \psi (u))\right |$
.
$ \textbf{R}_{v, c, i}(A, \psi ) \,:\!=\, \left |\left \{ (u, c^{\prime}) \in N_{G_i, (L|_{V(G_i)}, M|_{E(G_i)})}(v, c) \,:\, u \notin A\right \} \setminus \bigcup _{u \in A\setminus V(G_i)}N_{G, (L, M)}(u, \psi (u))\right |$
.
The definition of
![]() $ \boldsymbol{\Omega} ^*_{v, i}$
remains the same, but we replace the definition of
$ \boldsymbol{\Omega} ^*_{v, i}$
remains the same, but we replace the definition of
![]() $ \textbf{F}_{v, c, i}(A, \psi )$
with the following:
$ \textbf{F}_{v, c, i}(A, \psi )$
with the following:
-
•
 $ \textbf{F}_{v, c, i}(A, \psi ) \,:\!=\, \left |\left \{(u, c^{\prime}) \in N_{G_i, (L_{V(G_i)}, M_{E(G_i)})}(v, c) \,:\, \psi (u) = c^{\prime}\right \}\right |$
.
$ \textbf{F}_{v, c, i}(A, \psi ) \,:\!=\, \left |\left \{(u, c^{\prime}) \in N_{G_i, (L_{V(G_i)}, M_{E(G_i)})}(v, c) \,:\, \psi (u) = c^{\prime}\right \}\right |$
.
The remainder of the proof can be obtained via straightforward modifications, so we omit the details. This completes the proof of Lemma 5.3 and in turn implies Theorem 5.2.
6. Proof of Theorems 1.4 and 1.5
In this section, we prove Theorems 1.4 and 1.5. Recall that
![]() $f(m,{\mathcal G})$
is the largest possible chromatic number of the union of at most
$f(m,{\mathcal G})$
is the largest possible chromatic number of the union of at most
![]() $m$
nearly disjoint graphs in
$m$
nearly disjoint graphs in
![]() $\mathcal G$
, and
$\mathcal G$
, and
![]() ${\mathcal G}^\chi _n$
is the set of graphs of chromatic number at most
${\mathcal G}^\chi _n$
is the set of graphs of chromatic number at most
![]() $n$
. We begin by providing the construction that certifies that
$n$
. We begin by providing the construction that certifies that
![]() $f(3,{\mathcal G}^\chi _n) \geq n + 1$
.
$f(3,{\mathcal G}^\chi _n) \geq n + 1$
.
Proof of Theorem
1.4(ii). Let
![]() $H_1$
and
$H_1$
and
![]() $H_2$
be complete graphs on
$H_2$
be complete graphs on
![]() $n + 1$
vertices such that
$n + 1$
vertices such that
![]() $V(H_1) \cap V(H_2) = \{v\}$
for some vertex
$V(H_1) \cap V(H_2) = \{v\}$
for some vertex
![]() $v$
, let
$v$
, let
![]() $u \in V(H_1) \setminus \{v\}$
, let
$u \in V(H_1) \setminus \{v\}$
, let
![]() $w \in V(H_2) \setminus \{v\}$
, let
$w \in V(H_2) \setminus \{v\}$
, let
![]() $G_1 \,:\!=\, H_1 - uv$
, let
$G_1 \,:\!=\, H_1 - uv$
, let
![]() $G_2 \,:\!=\, H_2 - wv$
, and let
$G_2 \,:\!=\, H_2 - wv$
, and let
![]() $G_3$
be the graph consisting of the single edge
$G_3$
be the graph consisting of the single edge
![]() $uw$
. It is straightforward to check that
$uw$
. It is straightforward to check that
-
•
 $G_1$
,
$G_1$
,
 $G_2$
, and
$G_2$
, and
 $G_3$
are nearly disjoint,
$G_3$
are nearly disjoint, -
•
 $\chi (G_i) \leq n$
for every
$\chi (G_i) \leq n$
for every
 $i \in [3]$
, and
$i \in [3]$
, and -
•
 $\chi (G_1 \cup G_2 \cup G_3) = n + 1$
,
$\chi (G_1 \cup G_2 \cup G_3) = n + 1$
,
as desired.
To prove Theorem 1.4, it remains to prove the bound
![]() $f(m,{\mathcal G}^\chi _n) \leq m + n - 2$
when
$f(m,{\mathcal G}^\chi _n) \leq m + n - 2$
when
![]() $m + n$
is sufficiently large. First we note the following immediate consequence of the main result in [Reference Kang17] (namely that the Erdős–Faber–Lovász conjecture holds for all sufficiently large
$m + n$
is sufficiently large. First we note the following immediate consequence of the main result in [Reference Kang17] (namely that the Erdős–Faber–Lovász conjecture holds for all sufficiently large
![]() $n$
).
$n$
).
Theorem 6.1 ([Reference Kang17]). The following holds for all sufficiently large
![]() $C$
: If
$C$
: If
![]() $G_1, \dots, G_m$
are nearly disjoint graphs satisfying
$G_1, \dots, G_m$
are nearly disjoint graphs satisfying
![]() $\max \left \{m, |V(G_1)|, \dots, |V(G_m)|\right \} \leq C$
, then
$\max \left \{m, |V(G_1)|, \dots, |V(G_m)|\right \} \leq C$
, then
![]() $\chi \left (\bigcup _{i=1}^m G_i\right ) \leq C$
.
$\chi \left (\bigcup _{i=1}^m G_i\right ) \leq C$
.
Proof of Theorem
1.4(i). Suppose to the contrary, and let
![]() $G_1, \dots, G_m$
be nearly disjoint graphs, each of chromatic number at most
$G_1, \dots, G_m$
be nearly disjoint graphs, each of chromatic number at most
![]() $n$
, such that
$n$
, such that
![]() $\chi \left(\bigcup _{i=1}^m G_i\right) \gt m + n - 2$
and
$\chi \left(\bigcup _{i=1}^m G_i\right) \gt m + n - 2$
and
![]() $|V\left(\bigcup _{i=1}^m G_i\right)|$
is minimum. Note that
$|V\left(\bigcup _{i=1}^m G_i\right)|$
is minimum. Note that
![]() $n \geq 2$
as otherwise
$n \geq 2$
as otherwise
![]() $\chi \left(\bigcup _{i=1}^m G_i\right) = 1$
. By Theorem 6.1 with
$\chi \left(\bigcup _{i=1}^m G_i\right) = 1$
. By Theorem 6.1 with
![]() $n + m - 2$
playing the role of
$n + m - 2$
playing the role of
![]() $C$
, there exists
$C$
, there exists
![]() $i \in [m]$
such that
$i \in [m]$
such that
![]() $|V(G_i)| \gt m + n - 2$
, and we may assume without loss of generality that
$|V(G_i)| \gt m + n - 2$
, and we may assume without loss of generality that
![]() $i = 1$
. Let
$i = 1$
. Let
![]() $X \,:\!=\, V(G_1) \setminus \bigcup _{i=2}^m V(G_i)$
. Since
$X \,:\!=\, V(G_1) \setminus \bigcup _{i=2}^m V(G_i)$
. Since
![]() $G_1, \dots, G_m$
are nearly disjoint,
$G_1, \dots, G_m$
are nearly disjoint,
Since
![]() $\chi (G_1) \leq n$
, there is a partition
$\chi (G_1) \leq n$
, there is a partition
![]() $I_1, \dots, I_n$
of
$I_1, \dots, I_n$
of
![]() $V(G_1)$
into independent sets. By (13) and the pigeonhole principle, there exists some
$V(G_1)$
into independent sets. By (13) and the pigeonhole principle, there exists some
![]() $j\in [n]$
such that either
$j\in [n]$
such that either
![]() $|I_j \cap X| \gt 1$
or both
$|I_j \cap X| \gt 1$
or both
![]() $I_j \cap X$
and
$I_j \cap X$
and
![]() $I_j \setminus X$
are nonempty. We may assume without loss of generality that
$I_j \setminus X$
are nonempty. We may assume without loss of generality that
![]() $j = 1$
, so there exist distinct vertices
$j = 1$
, so there exist distinct vertices
![]() $u, v\in I_1$
such that
$u, v\in I_1$
such that
![]() $u \in X$
. Let
$u \in X$
. Let
![]() $G^{\prime}_1$
be the graph obtained from
$G^{\prime}_1$
be the graph obtained from
![]() $G_1$
by identifying
$G_1$
by identifying
![]() $u$
and
$u$
and
![]() $v$
into a single new vertex. Crucially,
$v$
into a single new vertex. Crucially,
![]() $G^{\prime}_1, G_2, \dots, G_m$
are nearly disjoint,
$G^{\prime}_1, G_2, \dots, G_m$
are nearly disjoint,
![]() $\chi (G^{\prime}_1) \leq n$
, and
$\chi (G^{\prime}_1) \leq n$
, and
![]() $\chi (G^{\prime}_1 \cup \bigcup _{i=2}^m G_i) \geq \chi \left(\bigcup _{i=1}^m G_i\right)$
, contradicting the choice of
$\chi (G^{\prime}_1 \cup \bigcup _{i=2}^m G_i) \geq \chi \left(\bigcup _{i=1}^m G_i\right)$
, contradicting the choice of
![]() $G_1, \dots, G_m$
to have
$G_1, \dots, G_m$
to have
![]() $|V\left(\bigcup _{i=1}^m G_i\right)|$
minimum.
$|V\left(\bigcup _{i=1}^m G_i\right)|$
minimum.
Now we prove Theorem 1.5. In this proof, we use a Latin square to construct a graph of large chromatic number. An order-
![]() $n$
Latin square is an
$n$
Latin square is an
![]() $n\times n$
array of
$n\times n$
array of
![]() $n$
symbols where each row and column contains each symbol exactly once. That is, for an order-
$n$
symbols where each row and column contains each symbol exactly once. That is, for an order-
![]() $n$
Latin square
$n$
Latin square
![]() $L$
, with rows, columns, and symbols indexed by
$L$
, with rows, columns, and symbols indexed by
![]() $A$
,
$A$
,
![]() $B$
, and
$B$
, and
![]() $C$
, respectively, we have
$C$
, respectively, we have
![]() $\{L(a, b) \,:\, b \in{B}\} ={C}$
for every
$\{L(a, b) \,:\, b \in{B}\} ={C}$
for every
![]() $a \in{A}$
and
$a \in{A}$
and
![]() $\{L(a, b) \,:\, a \in{A}\} ={C}$
for every
$\{L(a, b) \,:\, a \in{A}\} ={C}$
for every
![]() $b \in{B}$
.
$b \in{B}$
.
Proof of Theorem
1.5
. First, let
![]() $G \cong K_{m}$
, and since
$G \cong K_{m}$
, and since
![]() $3 \mid m$
, there exist sets
$3 \mid m$
, there exist sets
![]() ${A},{B},{C} \subseteq V(G)$
of size
${A},{B},{C} \subseteq V(G)$
of size
![]() $m/ 3$
that partition
$m/ 3$
that partition
![]() $V(G)$
. Since
$V(G)$
. Since
![]() $n \geq m - 1$
, we can let
$n \geq m - 1$
, we can let
![]() $G^{\prime}$
be the multigraph obtained from
$G^{\prime}$
be the multigraph obtained from
![]() $G$
by adding
$G$
by adding
![]() $n - (m - 1) + m/ 3$
loops to each vertex in
$n - (m - 1) + m/ 3$
loops to each vertex in
![]() ${A} \cup{B}$
and
${A} \cup{B}$
and
![]() $n - (m - 1)$
loops to each vertex in
$n - (m - 1)$
loops to each vertex in
![]() $C$
, and we let
$C$
, and we let
![]() $H$
be the line graph of
$H$
be the line graph of
![]() $G^{\prime}$
. Let
$G^{\prime}$
. Let
![]() $L$
be an order-
$L$
be an order-
![]() $(m/ 3)$
Latin square with rows, columns, and symbols indexed by
$(m/ 3)$
Latin square with rows, columns, and symbols indexed by
![]() $A$
,
$A$
,
![]() $B$
, and
$B$
, and
![]() $C$
, respectively, and for each
$C$
, respectively, and for each
![]() $a \in{A}$
and
$a \in{A}$
and
![]() $b \in{B}$
, let
$b \in{B}$
, let
![]() $e^{ab}_1$
denote the edge in
$e^{ab}_1$
denote the edge in
![]() $H$
with ends
$H$
with ends
![]() $ab$
and
$ab$
and
![]() $ac$
, and let
$ac$
, and let
![]() $e^{ab}_2$
denote the edge in
$e^{ab}_2$
denote the edge in
![]() $H$
with ends
$H$
with ends
![]() $ab$
and
$ab$
and
![]() $bc$
, where
$bc$
, where
![]() $c = L(a, b)$
. Let
$c = L(a, b)$
. Let
We prove that
![]() $H^{\prime}$
has chromatic number at least
$H^{\prime}$
has chromatic number at least
![]() $n + m/ 6$
and is a nearly disjoint union of
$n + m/ 6$
and is a nearly disjoint union of
![]() $m$
graphs of chromatic number
$m$
graphs of chromatic number
![]() $n$
, as desired.
$n$
, as desired.
To that end, for each
![]() $v \in V(G)$
, let
$v \in V(G)$
, let
![]() $G_v\,:\!=\, H^{\prime}[\{e \in E(G^{\prime}) \,:\, e \ni v\}]$
. By construction, the graphs in
$G_v\,:\!=\, H^{\prime}[\{e \in E(G^{\prime}) \,:\, e \ni v\}]$
. By construction, the graphs in
![]() $\{G_v \,:\, v \in V(G)\}$
are nearly disjoint, and
$\{G_v \,:\, v \in V(G)\}$
are nearly disjoint, and
![]() $H^{\prime} = \bigcup _{v \in V(G)} G_v$
. Moreover,
$H^{\prime} = \bigcup _{v \in V(G)} G_v$
. Moreover,
![]() $G_v$
is isomorphic to
$G_v$
is isomorphic to
![]() $K_{n + m/3}$
with a matching of size
$K_{n + m/3}$
with a matching of size
![]() $m/3$
removed for every
$m/3$
removed for every
![]() $v \in{A} \cup{B}$
and is isomorphic to
$v \in{A} \cup{B}$
and is isomorphic to
![]() $K_{n}$
for every
$K_{n}$
for every
![]() $v \in{C}$
, so
$v \in{C}$
, so
![]() $\chi (G_v) = n$
for every
$\chi (G_v) = n$
for every
![]() $v \in V(G)$
, as required.
$v \in V(G)$
, as required.
To prove that
![]() $\chi (H^{\prime}) \geq n + m/ 6$
, we let
$\chi (H^{\prime}) \geq n + m/ 6$
, we let
![]() $\phi$
be a proper colouring of
$\phi$
be a proper colouring of
![]() $H^{\prime}$
using at most
$H^{\prime}$
using at most
![]() $k$
colours, and we show that
$k$
colours, and we show that
![]() $k \geq n + m/6$
, as follows. First, let
$k \geq n + m/6$
, as follows. First, let
We claim that the following holds:
-
(a)
 $|{B}_a| \geq n + m/ 3 - k$
for every
$|{B}_a| \geq n + m/ 3 - k$
for every
 $a \in{A}$
,
$a \in{A}$
, -
(b)
 $|{A}_b| \geq n + m/ 3 - k$
for every
$|{A}_b| \geq n + m/ 3 - k$
for every
 $b \in{B}$
, and
$b \in{B}$
, and -
(c)
 $\sum _{a\in{A}}|{B}_a| + \sum _{b \in{B}}|{A}_b| \leq \frac{m^2}{9}$
.
$\sum _{a\in{A}}|{B}_a| + \sum _{b \in{B}}|{A}_b| \leq \frac{m^2}{9}$
.
Altogether, a)–(c) imply that
![]() $(2m/ 3)(n + m/ 3 - k) \leq m^2/ 9$
. Rearranging terms in this inequality, we have
$(2m/ 3)(n + m/ 3 - k) \leq m^2/ 9$
. Rearranging terms in this inequality, we have
![]() $k \geq n + m/ 6$
, as desired. Thus, it remains to prove (c)–(c).
$k \geq n + m/ 6$
, as desired. Thus, it remains to prove (c)–(c).
To prove (a), fix some
![]() $a \in{A}$
. Since
$a \in{A}$
. Since
![]() $\phi$
is a proper colouring, the colours assigned to
$\phi$
is a proper colouring, the colours assigned to
![]() $\{ab \,:\, b \in{B}_a\}$
and the colours assigned to vertices of
$\{ab \,:\, b \in{B}_a\}$
and the colours assigned to vertices of
![]() $G_a$
not incident to an edge of
$G_a$
not incident to an edge of
![]() $\left\{e^{ab}_1 \,:\, b \in{B}_a\right\}$
are distinct. Thus, since at most
$\left\{e^{ab}_1 \,:\, b \in{B}_a\right\}$
are distinct. Thus, since at most
![]() $k$
colours are used in total,
$k$
colours are used in total,
![]() $|{B}_a| + n + m/ 3 - 2|{B}_a| \leq k$
. Rearranging terms in this inequality, we have
$|{B}_a| + n + m/ 3 - 2|{B}_a| \leq k$
. Rearranging terms in this inequality, we have
![]() $|{B}_a| \geq n + m/ 3 - k$
, as desired. The proof of (b) is essentially the same, so we omit the details.
$|{B}_a| \geq n + m/ 3 - k$
, as desired. The proof of (b) is essentially the same, so we omit the details.
To prove (c), suppose to the contrary that
![]() $\sum _{a\in A}|{B}_a| + \sum _{b\in B}|{A}_b| \gt m^2/ 9$
. In this case, there is a pair
$\sum _{a\in A}|{B}_a| + \sum _{b\in B}|{A}_b| \gt m^2/ 9$
. In this case, there is a pair
![]() $(a, b) \in{A} \times{B}$
such that
$(a, b) \in{A} \times{B}$
such that
![]() $a \in{A}_b$
and
$a \in{A}_b$
and
![]() $b \in{B}_a$
. Letting
$b \in{B}_a$
. Letting
![]() $c = L(a, b)$
, since
$c = L(a, b)$
, since
![]() $a \in{A}_b$
, we have
$a \in{A}_b$
, we have
![]() $\phi (ab) = \phi (bc)$
, and since
$\phi (ab) = \phi (bc)$
, and since
![]() $b \in{A}_a$
, we have
$b \in{A}_a$
, we have
![]() $\phi (ab) = \phi (ac)$
. However, since
$\phi (ab) = \phi (ac)$
. However, since
![]() $\phi$
is a proper colouring,
$\phi$
is a proper colouring,
![]() $\phi (bc) \neq \phi (ac)$
, a contradiction.
$\phi (bc) \neq \phi (ac)$
, a contradiction.
Acknowledgements
We thank Luke Postle for allowing us to include the proof of Theorem 1.5.
Financial support
This project has received partial funding from the European Research Council under the European Union’s Horizon 2020 research and innovation programme (grant agreement no. 786198, T. Kelly, D. Kühn and D. Osthus). The research leading to these results was also partially supported by the EPSRC, grant nos. EP/N019504/1 (T. Kelly and D. Kühn) and EP/S00100X/1 (D. Osthus).