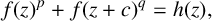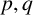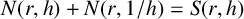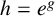NOTES ON FERMAT-TYPE DIFFERENCE EQUATIONS

Abstract

We consider the existence problem of meromorphic solutions of the Fermat-type difference equation

$$ \begin{align*} f(z)^p+f(z+c)^q=h(z), \end{align*} $$

where $p,q$ are positive integers, and h has few zeros and poles in the sense that $N(r,h) + N(r,1/h) = S(r,h)$. As a particular case, we consider $h=e^g$, where g is an entire function. Additionally, we briefly discuss the case where h is small with respect to f in the standard sense $T(r,h)=S(r,f)$.

1. Introduction and motivation

Throughout this note, we assume familiarity with standard notation and key results from Nevanlinna theory [7]. In particular, a meromorphic function $\varphi $ is termed a small function of f if the Nevanlinna characteristic $T(r, \varphi )$ satisfies $T(r, \varphi ) = S(r, f)$ . Here, $S(r, f)$ denotes any quantity such that $S(r, f) = o(T(r, f))$ as $r \rightarrow \infty $ , potentially outside an exceptional set of finite linear or logarithmic measure. For brevity, we denote the set of all meromorphic functions that are small with respect to f by $\mathcal {S}(f)$ . The order and hyper-order of a meromorphic function f are defined respectively by

$$ \begin{align*} \rho(f):=\limsup _{r \rightarrow \infty} \frac{\log T(r, f)}{\log r} \quad \text{and}\quad \rho_2(f):=\limsup _{r \rightarrow \infty} \frac{\log \log T(r, f)}{\log r}. \end{align*} $$

In 1970, Yang [16] applied Nevanlinna’s value distribution theory to investigate the Fermat functional equation

(1.1) $$ \begin{align} a(z)f(z)^p+b(z)g(z)^q=1, \end{align} $$

where $p, q \geq 3$ are integers, f and g denote nonconstant meromorphic functions, and $a, b$ are meromorphic functions that are respectively small compared with f and g. Yang [16, Theorem 1] showed that (1.1) cannot hold unless $p=q=3$ . However, if f and g are entire, then (1.1) cannot hold even if $p=q=3$ . Indeed, upon careful inspection of the proof of [16, Theorem 1], one can express Yang’s result in terms of

$$ \begin{align*} \Theta(a, f):=1-\limsup _{r \rightarrow \infty} \frac{\overline{N}(r, {1}/{(f-a)})}{T(r, f)} \end{align*} $$

as follows.

Theorem 1.1. Let p and q be positive integers satisfying ${1}/{p} + {1}/{q} < {2}/{3}$ . Then, (1.1) has no nonconstant meromorphic solutions f and g. Moreover, if ${1}/{p} + {1}/{q} < 1$ , there exists no nonconstant meromorphic solution of (1.1) such that $\Theta (\infty , f) = \Theta (\infty , g) = 1$ .

Motivated by this and the development of difference analogues of Nevanlinna’s theory (see, for example, [3, 6, 12]), there are many explorations of the Fermat-type difference equation

(1.2) $$ \begin{align} f(z)^p+f(z+c)^q=h(z), \end{align} $$

where c is a nonzero constant and h is a given meromorphic function. For instance, it has been shown in [8, 14] that if h is a nonzero constant and $p=q=3$ , then (1.2) does not admit nonconstant meromorphic solutions with $\rho _{2}(f)<1$ . Later, Lü and Guo [13] extended this conclusion to the case when $h = e^{\alpha z+\beta }$ , under the conditions $p \geq 3$ and $q \geq 2$ or $p \geq 2$ and $q \geq 3$ , excluding the exceptional case of trivial solutions, which applies when $p=q$ and

$$ \begin{align*} f(z)=\mu e^{(\alpha z+\beta) / p} \quad \text {with}\quad \mu^p(1+e^{\alpha c})=1. \end{align*} $$

For the case $h = e^{g}$ , where g is a nonconstant polynomial, Bi and Lü [2] employed properties of elliptic functions to establish the nonexistence of nontrivial meromorphic solutions with $\rho _{2}(f)<1$ for (1.2) when $p=q=3$ . Additionally, they proved the same result [2, Theorem 2] when $h\in \mathcal {S}(f)$ and has $0$ and $\infty $ as Borel exceptional values. More recently, Guo and Liu [5] investigated the case $h = e^{g}$ in (1.2), with g being a nonconstant entire function.

Motivated by these results, we explore the existence problem of meromorphic solutions to (1.2) when h belongs to some specific classes. In Section 2, we investigate the case where h has few zeros and poles, in the sense that

(1.3) $$ \begin{align} N(r,h)+N\bigg( r,\frac{1}{h}\bigg) =S(r,h). \end{align} $$

We will refer to the class of functions that satisfy (1.3) as $\mathcal {A}$ . In particular, we will consider the case $h=e^g$ , where g is a nonconstant entire function. In Section 3, we discuss the case when h is small with respect to the solution f in the standard sense of $T(r,h)=S(r,f)$ . Indeed, we show that a large class of meromorphic functions cannot satisfy the equation

(1.4) $$ \begin{align} f(z)^{p}+f(z+c)^{p}=h(z), \end{align} $$

where $p\geq 3$ and h has two Borel exceptional values.

2. The case $h\in \mathcal {A}$

In this section, we consider (1.2) where p and q are distinct positive integers and h belongs to the class $\mathcal {A}$ . Note that all functions in $\mathcal {A}$ must be transcendental meromorphic functions. Then, we will examine the case $h=e^P$ , with P a nonconstant entire function.

Before we proceed to state our main results, we require the following elementary lemma.

Lemma 2.1. Let $p,q$ be distinct positive integers and let h be a meromorphic function. If f is a meromorphic function with $\rho _{2}(f)<1$ that satisfies (1.2), then

$$ \begin{align*} N(r,f)\asymp N(r,h) \quad \text{and} \quad T(r,f)\asymp T(r,h), \end{align*} $$

outside an exceptional set of finite logarithmic measure. In particular, $\rho _{2}(h)=\rho _{2}(f)$ .

Proof. Without loss of generality, we assume that $p>q$ . From [12, Lemma 1.2.10],

$$ \begin{align*} (p-q-o(1))T(r,f)\leq T(r,h)\leq (p+q+o(1))T(r,f) \end{align*} $$

and

$$ \begin{align*} (p-q-o(1))N(r,f)\leq N(r,h)\leq (p+q+o(1))N(r,f), \end{align*} $$

outside an exceptional set of finite logarithmic measure. By a standard argument, see [4, Lemma 5], we may remove the exceptional set to obtain $\rho _{2}(h)=\rho _{2}(f)$ .

Now, we are ready to state our first result.

Theorem 2.2. Let $h \in \mathcal {A}$ and let $p>q$ be positive integers. Then, (1.2) has no meromorphic solutions with $\rho _{2}(f) < 1$ except when $p=2$ and $q=1$ . In this case, either:

1. (1) $f(z)=e^{\alpha z+\beta }-1$ , where $\alpha , \beta \in \mathbb {C}$ satisfy $e^{\alpha c}=2$ ; or

2. (2) $T(r,f)= \overline {N}( r,1/f') +S(r,f).$

Remark 2.3. (a) According to [5, Remark 1.7], we observe that conclusion (1) of Theorem 2.2 might hold. In fact, an example such as $f(z) = e^{\alpha z} - 1$ solves the equation

$$ \begin{align*}f(z)^{2}+f(z+c)=e^{2\alpha z},\end{align*} $$

where $\alpha $ is a nonzero constant satisfying $e^{\alpha c} = 2$ .

(b) Theorem 2.2 includes the result given in [5, Theorem 1.6(iii)]. Indeed, it was shown there that the equation

$$ \begin{align*} f(z)^2+f(z+c)=e^{g(z)}, \end{align*} $$

where g is a nonconstant entire function, has no meromorphic solutions with $\rho _2(f) < 1$ satisfying $N(r,1/f') = S(r,f)$ except functions f of the type

(2.1) $$ \begin{align} f(z)=\bigg(\int \frac{a}{2} e^{-g(z) / 2} \,dz+b\bigg) e^{g(z) / 2},\quad a,b \in\mathbb{C}. \end{align} $$

However, according to Theorem 2.2(2), $N(r,1/f') = S(r,f)$ implies $T(r,f)=S(r,f)$ , which is impossible. Hence, (2.1) reduces to Theorem 2.2(1).

(c) To find a concrete example for the conclusion of Theorem 2.2(2) remains open at present. Note that if conclusion (2) holds, then for any $a\in \mathbb {C}$ , we have $\delta (a,f)=0$ . This can be deduced from the estimate

$$ \begin{align*} m\bigg( r,\frac{1}{f-a}\bigg) &\leq m\bigg( r,\frac{1}{f'}\bigg) +S(r,f)\nonumber\\ &=T(r,f')-N\bigg( r,\frac{1}{f'}\bigg)+S(r,f) \nonumber\\ &\leq T(r,f)-N\bigg( r,\frac{1}{f'}\bigg)+S(r,f)=S(r,f).\nonumber \end{align*} $$

Proof of Theorem 2.2.

Clearly, from Lemma 2.1, f must be a transcendental meromorphic function with $N(r,f)=S(r,f)$ . Differentiating (1.2) gives

(2.2) $$ \begin{align} f(z)^{p-1}\bigg( pf'(z)-\frac{h'(z)}{h(z)}f(z)\bigg) =- f(z+c)^{q-1}\bigg( qf'(z+c)-\frac{h'(z)}{h(z)}f(z+c)\bigg). \end{align} $$

Denote

(2.3) $$ \begin{align} \varphi(z):=pf'(z)-\frac{h'(z)}{h(z)}f(z). \end{align} $$

Note that

$$ \begin{align*} T\bigg( r,\frac{h'}{h}\bigg) =\overline{N}(r,h)+\overline{N}\bigg( r,\frac{1}{h}\bigg)+S(r,h)=S(r,h). \end{align*} $$

This, along with $N(r,f)=S(r,f)$ , leads to $N(r,\varphi )=S(r,f)$ .

Since $p\geq q+1$ , we may recall the delay-difference variant of the Clunie lemma (see [10] and [12, page 20]) to obtain $m(r,\varphi )=S(r,f)$ and hence $T(r,\varphi )=S(r,f)$ .

Suppose first that $\varphi \equiv 0$ . Then, by simple integration,

(2.4) $$ \begin{align} f(z)^p=Ah(z) \end{align} $$

for some constant A. However, from (2.2),

$$ \begin{align*} qf'(z+c)-\frac{h'(z)}{h(z)}f(z+c)\equiv 0, \end{align*} $$

which in turn implies that

(2.5) $$ \begin{align} f(z+c)^q=Bh(z), \end{align} $$

where B is a constant. Recalling again [12, Lemma 1.2.10], and combining (2.4) and (2.5),

$$ \begin{align*} (p-q)T(r,f)=S(r,f), \end{align*} $$

which is a contradiction. Thus, we may now assume that $\varphi \not \equiv 0$ and (2.3) can be rewritten as

(2.6) $$ \begin{align} \frac{1}{f(z)}=\frac{1}{\varphi(z)}\bigg( p\frac{f'(z)}{f(z)}-\frac{h'(z)}{h(z)}\bigg). \end{align} $$

This implies

$$ \begin{align*} T(r,f)=N\bigg(r,\frac{1}{f}\bigg) +S(r,f). \end{align*} $$

Note that if $z_0$ is a multiple zero of f that is not a zero or pole of h, then $z_0$ is a zero of $\varphi $ . Hence, the contribution of $N_{2)}(r,1/f)$ is $S(r,f)$ , and so

(2.7) $$ \begin{align} T(r,f)=N_{1)}\bigg(r,\frac{1}{f}\bigg) +S(r,f). \end{align} $$

If $p\geq q+2$ , then we may write (2.2) as

$$ \begin{align*} f(z)^{p-2}(f(z)\varphi(z))=- f(z+c)^{q-1}\bigg( qf'(z+c)-\frac{h'(z)}{h(z)}f(z+c)\bigg). \end{align*} $$

Applying again the delay-difference Clunie lemma to conclude that

$$ \begin{align*}m(r,f\varphi )=T(r,f\varphi )=S(r,f),\end{align*} $$

we obtain

$$ \begin{align*}T(r,f)=m\bigg( r,\frac{f\varphi}{\varphi} \bigg) \leq m(r,f\varphi )+T(r,\varphi )+O(1)=S(r,f),\end{align*} $$

which is a contradiction.

So, we must have $p=q+1$ . Since $h\in \mathcal {A}$ , we can write $h=\pi e^{g}$ , where g is an entire function and $\pi $ is a small function of h. Consequently, $T(r,\pi )=S(r,f)$ . Therefore, (1.2) can be rewritten as

(2.8) $$ \begin{align} F(z)^p+G(z) ^{p-1}=\pi(z), \end{align} $$

where $F:=f/e^{g/p}$ and $G:=f_c/e^{g/(p-1)},$ where $f_c:=f(z+c)$ . To apply Theorem 1.1 to (2.8), we have to show that $\pi $ is a small function of F and G. Indeed, from (2.7), we have $ N(r,1/f) =~(1-~o(1))~T(r,f) $ outside of an exceptional set E of finite linear measure. Therefore, provided $r\not \in E$ ,

$$ \begin{align*} \frac{T(r,\pi)}{T(r,f/\exp (g/p))}&=\frac{T(r,\pi)}{T(r,\exp (g/p)/f)+O(1)} =(1+o(1))\frac{T(r,\pi)}{T(r,\exp (g/p)/f)}\\ &\leq (1+o(1))\frac{T(r,\pi)}{N(r,\exp (g/p)/f)} =(1+o(1))\frac{T(r,\pi)}{N(r,1/f)}\\ &=\frac{1+o(1)}{1-o(1)}\frac{T(r,\pi)}{T(r,f)}=o(1). \end{align*} $$

Recalling that $T(r,f_c)=T(r,f)+S(r,f)$ , we may use a similar reasoning to conclude that $\pi $ is a small function of $f_c/e^{g/(p-1)}$ as well.

In the remainder of the proof, we discuss cases according to the values of p.

Case 1. If $p\geq 4$ , then according to Theorem 1.1, (2.8) admits only constant solutions. Therefore,

(2.9) $$ \begin{align} f(z)=\alpha e^{g(z)/p}, \quad f(z+c)=\beta e^{g(z)/(p-1)}, \end{align} $$

where $\alpha $ , $\beta $ are constants that satisfy $\alpha ^p+\beta ^{p-1}=\pi $ . Now,

$$ \begin{align*} f(z+c)=\alpha e^{g(z+c)/p}=\beta e^{g(z)/(p-1)}, \end{align*} $$

which means that $(p-1)g_c-pg$ is a constant. If g is a polynomial, then it must be a constant, which contradicts the fact that $h=\pi e^g$ is transcendental. If g is not a polynomial, then it satisfies the equation

$$ \begin{align*} \frac{g'(z+c)}{g'(z)}=\frac{p}{p-1}, \end{align*} $$

and by using [1, Lemma 3.3], we deduce that $\rho (g)\geq 1$ . Therefore, $\rho _{2}(f)=\rho _{2}(h)\geq 1,$ which is again a contradiction.

Case 2. If $p=3$ , then by recalling that $N(r,F)=N(r,G)=N(r,f)=S(r,f)$ , we can infer that

$$ \begin{align*} \Theta(\infty,F)=\Theta(\infty,G)=\Theta(\infty,f)=1. \end{align*} $$

Hence, by applying Theorem 1.1 again, we conclude that (1.2) has solutions only in the form of (2.9) with $\alpha ^3+\beta ^2=\pi $ . Similar reasoning as in the case $p\geq 4$ leads to a contradictory conclusion $\rho _{2}(f)\geq 1$ .

Case 3. Assume now that $p=2$ (implying that we also have $q=1$ ). Recall that the auxiliary function $\varphi \not \equiv 0$ takes the form

(2.10) $$ \begin{align} \varphi(z):=2f'(z)-\frac{h'(z)}{h(z)}f(z). \end{align} $$

Taking the first derivative of $\varphi $ yields

$$ \begin{align*} \varphi'(z)=2f"(z)-\frac{h'(z)}{h(z)}f'(z)-\bigg( \frac{h'(z)}{h(z)}\bigg) 'f(z)=\frac{\varphi'(z)}{\varphi(z)}\bigg(2f'(z)-\frac{h'(z)}{h(z)}f(z) \bigg), \end{align*} $$

which can be expressed as

$$ \begin{align*} A(z)f'(z)+B(z) f(z)=0, \end{align*} $$

where

$$ \begin{align*} A(z):=2\frac{f"(z)}{f'(z)}-\frac{h'(z)}{h(z)}-2\frac{\varphi'(z)}{\varphi(z)} \quad \text{and}\quad B(z):=\frac{\varphi'(z)}{\varphi(z)}\frac{h'(z)}{h(z)}-\bigg( \frac{h'(z)}{h(z)}\bigg)'. \end{align*} $$

Since f mainly has simple zeros, assume that $z_0$ is a simple zero of f that is neither a zero nor a pole of h. Consequently, $z_0$ is not a zero of $\varphi $ and so not a pole of B. Thus, $z_0$ is a zero of A. Now, define the function

$$ \begin{align*} \psi(z):=\frac{A(z)}{f(z)}. \end{align*} $$

Based on the preceding discussion, we can deduce that $N(r, \psi ) = \overline {N}(r,1/f') + S(r, f)$ . Combining this with the fact that $m(r,1/f) = S(r,f)$ (see (2.6)), we conclude that

$$ \begin{align*}T(r,\psi)=\overline{N}\bigg( r,\frac{1}{f'}\bigg) +S(r,f).\end{align*} $$

Note that, according to [17, Theorem 1.24],

$$ \begin{align*} N\bigg(r, \frac{1}{f'}\bigg) \leq N\bigg(r, \frac{1}{f}\bigg)+ \overline{N}(r, f)+S(r, f)= N_{1)}\bigg( r,\frac{1}{f}\bigg) +S(r, f). \end{align*} $$

Assume first that $\psi \not \equiv 0$ . Then,

$$ \begin{align*} T(r,f)=m(r,f)+S(r,f)&=m\bigg( r,\frac{A}{\psi}\bigg)+S(r,f)\nonumber\\ &\leq T\bigg( r,\frac{1}{\psi}\bigg) -N\bigg( r,\frac{1}{\psi}\bigg) +S(r,f)\nonumber\\ &=\overline{N}\bigg( r,\frac{1}{f'}\bigg) -N\bigg( r,\frac{1}{\psi}\bigg) +S(r,f)\nonumber\\ &\leq N_{1)}\bigg( r,\frac{1}{f}\bigg) -N\bigg( r,\frac{1}{\psi}\bigg) +S(r,f).\nonumber \end{align*} $$

Combining this with (2.7) yields $N(r,1/\psi )=S(r,f)$ , that is,

$$ \begin{align*} T(r,f)= \overline{N}\bigg( r,\frac{1}{f'}\bigg) +S(r,f). \end{align*} $$

Consider now the case $\psi \equiv 0$ . This implies that both $A \equiv 0$ and $B \equiv 0$ . To proceed, we distinguish two possible sub-cases.

Subcase (i). If $\varphi $ is not constant, then straightforward integration of the equations $A \equiv 0$ and $B \equiv 0$ yields

(2.11) $$ \begin{align} (f'(z))^2=C_1\varphi(z)^2h(z) \end{align} $$

and

(2.12) $$ \begin{align} \varphi(z)=C_2\frac{h'(z)}{h(z)}, \end{align} $$

where $C_1$ and $C_2$ are nonzero constants. Substituting (2.12) into (2.10) and integrating the result yields

(2.13) $$ \begin{align} (f(z)+C_2)^2=C_3h(z), \end{align} $$

where $C_3$ is a nonzero constant. Combining (2.11), (2.12) and (2.13) results in

$$ \begin{align*} \frac{ f'(z)}{f(z)+C_2}=C_4\frac{h'(z)}{h(z)}, \end{align*} $$

where $C_4$ is a nonzero constant. By simple integration,

$$ \begin{align*} f(z)+C_2=C_5h(z). \end{align*} $$

This, together with (2.13) results in a contradiction.

Now assume that $\varphi $ is a nonzero constant. Keeping in mind that $A\equiv 0$ and $B\equiv 0$ , we find $h'/h$ is a constant, say $h'/h\equiv 2\alpha $ . This results in $h\equiv C_{h}e^{2\alpha z},$ with $C_{h}$ being a constant. Since $2{f"}/{f'}\equiv {h'}/{h}$ , by elementary integration,

$$ \begin{align*}(f'(z))^{2}=C_{6}h(z)=C_{6}C_{h}e^{2\alpha z}.\end{align*} $$

This means that $f'\equiv C_{7}e^{\alpha z}$ and so, by integration, f must be of the form $e^{\alpha z+\beta }+\gamma ,$ with constants $\beta , \gamma $ . Substituting this into (1.2),

$$ \begin{align*}e^{2\alpha z+2\beta}+2\gamma e^{\alpha z+\beta}+\gamma^{2}+e^{\alpha c}e^{\alpha z+\beta}+\gamma =C_{h}e^{2\alpha z}.\end{align*} $$

Clearly, the constant term $\gamma ^{2}+\gamma $ must vanish; thus, $\gamma = 0$ or $\gamma = -1$ . However, $\gamma \neq 0$ , as it would contradict (2.7). Therefore, the only possibility is $\gamma = -1$ , leading to

$$ \begin{align*}(e^{2\beta}-C_{h})e^{2\alpha z}+(e^{\alpha c}-2)e^{\alpha z+\beta}=0.\end{align*} $$

This may happen if $e^{\alpha c}=2$ and $C_{h}=e^{2\beta }$ , thereby completing the proof.

We close this section by considering the equation

(2.14) $$ \begin{align} f(z)^p+f(z+c)^q=e^{g(z)}, \end{align} $$

where g is a nonconstant entire function and $p, q$ are positive integers that are not necessarily distinct. The following corollary improves [5, Theorem 1.6(iv)].

Corollary 2.4. Let g be a nonconstant entire function and let $p,q\geq 3$ be integers. Then:

1. (1) if $p\neq q$ , (2.14) has no meromorphic solutions with $\rho _{2}(f) < 1$ ;

2. (2) if $p=q\geq 3$ , (2.14) has no nontrivial meromorphic solutions with $\rho _{2}(f) < 1$ .

Proof. Assertion (1) immediately follows from Theorem 2.2.

As for assertion (2), if $p=q\geq 4$ , we may write (2.14) as

$$ \begin{align*} \bigg(\frac{f(z)}{e^{g(z)/p}}\bigg)^p + \bigg(\frac{f(z+c)}{e^{g(z)/p}}\bigg)^p = 1. \end{align*} $$

By applying Theorem 1.1, we obtain $ f(z) = \alpha e^{g(z)/p}$ and $f(z+c) = \beta e^{g(z)/p}$ , where ${\alpha ^p + \beta ^p = 1}$ . A reasoning similar to Case 1 in the proof of Theorem 2.2 leads to the conclusion that f takes the form

$$ \begin{align*}f(z)=\alpha \exp\bigg( \frac{az+b}{p}\bigg),\end{align*} $$

where $\alpha $ is a nonzero constant satisfying the condition $\alpha ^p(1 + e^{ac}) = 1$ . This representation corresponds to a trivial solution.

Finally, we assume that $p=q=3$ . Then (2.14) can be written as follows:

$$ \begin{align*} F(z)^3+\beta(z)F(z+c)^3 =1, \end{align*} $$

where

$$ \begin{align*}F(z)=\frac{f(z)}{e^{g(z) / 3}} \quad \text{and}\quad \beta(z)=e^{g(z+c)-g(z)}.\end{align*} $$

By making use of [12, Lemma 1.2.10],

$$ \begin{align*} T(r,e^g)\leq (3+o(1))T(r,f) \end{align*} $$

possibly outside an exceptional set of finite logarithmic measure $E_1$ and, moreover, $\rho _{2}(e^g)=\delta <1$ . Note that [6, Theorem 5.1] yields

$$ \begin{align*} T(r,\beta)=m\bigg( r,\frac{e^{g(z+c)}}{e^{g(z)}}\bigg) =o\bigg( \frac{T(r,e^g)}{r^{1-\delta-\varepsilon}}\bigg) \end{align*} $$

for all r outside an exceptional set of finite logarithmic measure $E_2$ . Combining these inequalities yields, for all $r\not \in E_1 \cup E_2$ ,

$$ \begin{align*} \frac{T(r,\beta)}{T(r,f)} \leq (3+o(1))\frac{T(r,\beta)}{T(r,e^g)}=o\bigg( \frac{1}{r^{1-\delta-\varepsilon}}\bigg), \end{align*} $$

implying $T(r,\beta )=S(r,f)$ . Consequently, following the same proof as in Case (iv) of [5, Theorem 1.6], we conclude that $\beta $ is a constant and $f = Ae^{g/3}$ with $A^3 = 1$ , constituting a trivial solution.

3. The case $h\in \mathcal {S}(f)$

In this section, we discuss the existence of solutions to (1.2), where h is a small meromorphic function in the standard sense of $T(r,h)=S(r,f)$ . For clarity, we first present the following proposition which discusses the existence of nonconstant meromorphic solutions to (1.2) when p and q are distinct integers.

Proposition 3.1. Let f be a meromorphic function and let $h\in \mathcal {S}(f)$ .

1. (1) If $p> q \geq 3$ , then (1.2) has no nonconstant meromorphic solutions.

2. (2) If $p> q \geq 2$ , then (1.2) has no nonconstant entire solutions.

3. (3) If $p> q \geq 1$ and $\rho _{2}(f) < 1$ , then (1.2) has no nonconstant meromorphic solutions.

Proof. The cases (1) and (2) can be deduced easily from Theorem 1.1. Suppose now that $p>q\geq 1$ and f is a solution to (1.2) with $\rho _{2}(f)<1$ . We may write (1.2) in the form

$$ \begin{align*}f(z)^{p}+\bigg(\frac{f(z+c)}{f(z)}\bigg)^{q}f(z)^{q}=h (z). \end{align*} $$

By [6, Theorem 5.1] (see also [12, Lemma 1.2.8]), we conclude that

$$ \begin{align*}p m(r,f)\leq q m(r,f)+S(r,f),\end{align*} $$

and so $m(r,f)=S(r,f)$ . However, we can apply [6, Lemma 8.3] (see also [12, Lemma 1.2.10]) to (1.2). This yields

$$ \begin{align*}pN(r,f)\leq qN(r,f)+S(r,f),\end{align*} $$

thus implying $N(r,f) = S(r,f)$ . Consequently, $T(r,f) = S(r,f)$ , which is a contradiction.

Next, we consider the case where $p=q\geq 3$ in (1.2). In fact, referring to Theorem 1.1, it becomes evident that no nonconstant meromorphic solutions exist to (1.2) when $p=q>3$ . By combining this result with [2, Theorem 2], we can immediately deduce the following corollary.

Corollary 3.2. Let f be a meromorphic function of hyper-order $\rho _{2}(f)<1$ , and let $h\in \mathcal {S}(f)$ with two Borel exceptional values $0$ and $\infty .$ Then f does not satisfy (1.4) provided $p\geq 3$ .

Motivated by this, it is natural to ask whether this phenomenon remains valid when considering $h \in \mathcal {S}(f)$ with two Borel exceptional values $d \neq 0$ and $\infty $ .

Unfortunately, we could not give a positive answer to this question. However, the following proposition illustrates that such an assumption prevents the existence of a large class of meromorphic functions. In particular, it shows that any meromorphic solution to (1.4) must be periodic and cannot possess any Borel exceptional value.

Proposition 3.3. Let f be a meromorphic function of hyper-order $\rho _{2}(f)<1$ , and let $h\in \mathcal {S}(f)$ with two Borel exceptional values $d\in \mathbb {C}$ and $\infty $ . If f satisfies (1.4), then $p=3$ and the following assertions hold:

1. (1) $h=e^{az+b}+d$ , where $a,b$ are constants with $e^{ac}=1$ and $d\neq 0$ ;

2. (2) f is periodic and satisfies the equation

   $$ \begin{align*} f(z)^3=\pi(z)\exp\bigg( \frac{\log(-1)}{c}z\bigg) +\frac{1}{2}( e^{az+b}+d) , \end{align*} $$
   where $\pi $ is a c-periodic meromorphic function such that
   $$ \begin{align*}\lim\limits_{\substack{r\to \infty\\ r\not\in E}}\frac{T(r,\pi)}{r}=\infty,\end{align*} $$
   where E is an exceptional set of finite linear measure;

3. (3) $T(r,f)=\overline {N}(r,f)+S(r,f)$ ;

4. (4) $T(r,f)=\overline {N}(r,1/f)+S(r,f)$ . In addition, for any $\alpha \in \mathcal {S}(f)$ that does not satisfy (1.4),

   $$ \begin{align*} T(r,f)=N\bigg( r,\frac{1}{f-\alpha}\bigg) +S(r,f). \end{align*} $$

Proof of Proposition 3.3.

Assuming the existence of a meromorphic function f that satisfies (1.4), we infer from Theorem 1.1 and [2, Theorem 2] that $p=3$ and $d\neq 0$ .

Following the reasoning in the beginning of the proof of [2, Theorem 2] (see [2, page 6]), we conclude that h is periodic with period c and, consequently, $f^3$ is periodic with period $2c$ . Now, recall that h has two Borel exceptional values $d\neq 0$ and $\infty $ . Then we have the representation

$$ \begin{align*}h(z)=\pi(z)e^{P(z)}+d,\end{align*} $$

where P is an entire function, $\pi $ a meromorphic function of finite order and

$$ \begin{align*}\rho_{2}(h)=\rho_2(e^P)=\rho(P)<1.\end{align*} $$

Making use of the periodicity of h and [18, Proposition 3.1], we see that P must be a polynomial. If $\deg P\geq 2$ , then by [18, Proposition 3.1], we have $\rho (\pi )\geq \deg P$ . However,

$$ \begin{align*} \rho(\pi)=\lambda(h-d)<\rho(h)=\deg P, \end{align*} $$

which is a contradiction. Hence, $\deg P=1$ and $\pi $ has an order less than one. Using [18, Remark 3.1], we observe that $\pi $ is a constant. Therefore, $h\equiv e^{az+b}+d,$ where $a,b$ are constants with $e^{ac}=1$ . This proves assertion (1).

Now, noting that $\tfrac 12h$ is a particular solution to the difference equation

(3.1) $$ \begin{align} g(z)+g(z+c)=h(z) \end{align} $$

and making use of the theory of difference equations in the complex domain [15, Ch. 7], we deduce that the general solution to (3.1) takes the form

$$ \begin{align*} g(z)=\pi(z)\exp\bigg( \frac{\log(-1)}{c}z\bigg) +\frac{1}{2}h(z), \end{align*} $$

where $\pi $ is a c-periodic meromorphic function. Therefore, assertion (2) follows by considering $g=f^3$ and $h\equiv e^{az+b}+d$ .

Next, since $h\in \mathcal {S}(f)$ , according to [11, Lemma 1], we derive assertion (3). Additionally, by employing Nevanlinna’s second main theorem,

$$ \begin{align*} T(r,f^3)&\leq \overline{N}(r,f^3)+\overline{N}\bigg( r,\frac{1}{f^3}\bigg) + \overline{N}\bigg( r,\frac{1}{f^3-h}\bigg) +S(r,f)\nonumber\\ &\leq 2T(r,f)+\overline{N}\bigg( r,\frac{1}{f_c^3}\bigg)+S(r,f).\nonumber \end{align*} $$

From this and [12, Lemma 1.2.10], we conclude the first part of assertion (4). The last part of assertion (4) is a direct consequence of [9, Lemma 2.2].