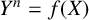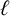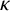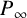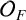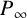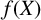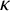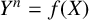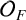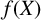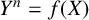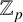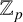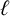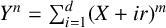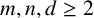1 Introduction
Let
![]() $n\geq 2$
be an integer and
$n\geq 2$
be an integer and
![]() $\kappa $
be a finite field of characteristic
$\kappa $
be a finite field of characteristic
![]() $\ell>0$
. Let F be a global function field with field of constants
$\ell>0$
. Let F be a global function field with field of constants
![]() $\kappa $
and assume that there exists a prime
$\kappa $
and assume that there exists a prime
![]() $P_\infty $
of F of degree
$P_\infty $
of F of degree
![]() $1$
. In other words, we assume that there is a prime
$1$
. In other words, we assume that there is a prime
![]() $P_\infty $
which is totally inert in the composite
$P_\infty $
which is totally inert in the composite
![]() $\bar {\kappa }\cdot F$
. The ring of integers
$\bar {\kappa }\cdot F$
. The ring of integers
![]() $\mathcal {O}_F$
consists of all functions
$\mathcal {O}_F$
consists of all functions
![]() $f\in F$
with no poles away from
$f\in F$
with no poles away from
![]() $P_\infty $
. Given a polynomial
$P_\infty $
. Given a polynomial
![]() $f(X)$
with coefficients in
$f(X)$
with coefficients in
![]() $\kappa $
, we study solutions to the superelliptic Diophantine equation
$\kappa $
, we study solutions to the superelliptic Diophantine equation
![]() $Y^n=f(X)$
for which both X and Y lie in
$Y^n=f(X)$
for which both X and Y lie in
![]() $\mathcal {O}_F$
. Superelliptic equations over function fields form an important part of the modern theory of Diophantine equations. There has been significant interest in proving finiteness results, as well as in obtaining effective bounds for the number of solutions. Over algebraic number fields, the equation
$\mathcal {O}_F$
. Superelliptic equations over function fields form an important part of the modern theory of Diophantine equations. There has been significant interest in proving finiteness results, as well as in obtaining effective bounds for the number of solutions. Over algebraic number fields, the equation
![]() $Y^n=f(X)$
was shown by LeVeque in 1964 to have finitely many solutions, provided certain additional conditions are met (see [Reference LeVeque10, Theorem 1]). Brindza [Reference Brindza6] later obtained an effective bound on the number of solutions to such superelliptic equations. For further details, we refer the reader to [Reference Shorey and Tijdeman16, Ch. 8]. In the function field case, effective bounds on the number of solutions were obtained by Mason and Brindza [Reference Mason and Brindza11, page 168]. In greater detail, given a solution
$Y^n=f(X)$
was shown by LeVeque in 1964 to have finitely many solutions, provided certain additional conditions are met (see [Reference LeVeque10, Theorem 1]). Brindza [Reference Brindza6] later obtained an effective bound on the number of solutions to such superelliptic equations. For further details, we refer the reader to [Reference Shorey and Tijdeman16, Ch. 8]. In the function field case, effective bounds on the number of solutions were obtained by Mason and Brindza [Reference Mason and Brindza11, page 168]. In greater detail, given a solution
![]() $(X,Y)$
to
$(X,Y)$
to
![]() $Y^n=f(X)$
, this result provides an effective upper bound on the height of X in terms of the genus of the function field F [Reference Mason and Brindza11, page 166, l.21].
$Y^n=f(X)$
, this result provides an effective upper bound on the height of X in terms of the genus of the function field F [Reference Mason and Brindza11, page 166, l.21].
We consider the class of superelliptic Diophantine equations
![]() $Y^n=f(X)$
, for which the coefficients of
$Y^n=f(X)$
, for which the coefficients of
![]() $f(X)$
lie in the field of constants. We derive conditions for there to be no nonconstant solutions. Given a natural number N, denote by
$f(X)$
lie in the field of constants. We derive conditions for there to be no nonconstant solutions. Given a natural number N, denote by
![]() $h_F[N]$
the cardinality of the N-torsion in the class group of F. The understanding here is that
$h_F[N]$
the cardinality of the N-torsion in the class group of F. The understanding here is that
![]() $h_F[1]=1$
.
$h_F[1]=1$
.
Theorem 1.1 (Theorem 2.4).
Let
![]() $\ell $
be a prime number and F be a global function field of characteristic
$\ell $
be a prime number and F be a global function field of characteristic
![]() $\ell $
. Let
$\ell $
. Let
![]() $\mathcal {O}_F$
be the ring of integers of F. Denote by
$\mathcal {O}_F$
be the ring of integers of F. Denote by
![]() $\kappa $
the field of constants of F. Let
$\kappa $
the field of constants of F. Let
![]() $f(X)$
be a polynomial with coefficients in
$f(X)$
be a polynomial with coefficients in
![]() $\kappa $
. Let
$\kappa $
. Let
![]() $q\neq \ell $
be a prime number and let
$q\neq \ell $
be a prime number and let
![]() $k>0$
be the least integer such that
$k>0$
be the least integer such that
![]() $h_F[q^k]=h_F[q^{k-1}]$
. Assume that the following conditions are satisfied:
$h_F[q^k]=h_F[q^{k-1}]$
. Assume that the following conditions are satisfied:
-
(1)
 $f(X)$
factorises into
$f(X)$
factorises into
 $f(X)=a_0(X-a_1)^{n_1}\cdots (X-a_t)^{n_t}$
, where
$f(X)=a_0(X-a_1)^{n_1}\cdots (X-a_t)^{n_t}$
, where
 $a_0\in \kappa $
,
$a_0\in \kappa $
,
 $a_1,\ldots , a_t$
are distinct elements in
$a_1,\ldots , a_t$
are distinct elements in
 $\kappa $
,
$\kappa $
,
 $n_1,\ldots , n_t$
are positive integers and
$n_1,\ldots , n_t$
are positive integers and
 $t\geq 2$
;
$t\geq 2$
; -
(2) at least two of the exponents
 $n_i$
are not divisible by q.
$n_i$
are not divisible by q.
Then any solution
![]() $(X,Y)$
to
$(X,Y)$
to
for which
![]() $X,Y\in \mathcal {O}_F$
is constant, that is, X and Y are both in
$X,Y\in \mathcal {O}_F$
is constant, that is, X and Y are both in
![]() $\kappa $
.
$\kappa $
.
We shall apply our analysis to study a class of Diophantine equations which involve perfect powers in arithmetic progressions. Let
![]() $m, n, d\geq 2$
be integers and let
$m, n, d\geq 2$
be integers and let
![]() $r\geq 1$
. There has been significant interest in the classification of integral solutions to the Diophantine equation
$r\geq 1$
. There has been significant interest in the classification of integral solutions to the Diophantine equation
(see [Reference Argáez-García and Patel1–Reference Bérczes, Pink, Savaş and Soydan5, Reference Hajdu7, Reference Koutsianas and Patel8, Reference Patel13]).
We also explore themes motivated by the Iwasawa theory of function fields. Mazur [Reference Mazur12] initiated the Iwasawa theory of elliptic curves over number fields, which had applications to the growth of Mordell–Weil ranks of elliptic curves in certain infinite towers of number fields. One hopes to extend such lines of investigation to curves of higher genus (see [Reference Ray14]) and, more generally, to study the stability and growth of solutions to any Diophantine equation in an infinite tower of global fields. We study certain function field analogues of such questions. However, instead of elliptic curves, we consider the class of superelliptic equations of the form
![]() $Y^n=f(X)$
, where
$Y^n=f(X)$
, where
![]() $f(X)$
has constant coefficients. Let us explain our results in greater detail. Given any integer n, there is a unique extension
$f(X)$
has constant coefficients. Let us explain our results in greater detail. Given any integer n, there is a unique extension
![]() $\kappa _n/\kappa $
such that
$\kappa _n/\kappa $
such that
![]() $\operatorname {Gal}(\kappa _n/\kappa )$
is isomorphic to
$\operatorname {Gal}(\kappa _n/\kappa )$
is isomorphic to
![]() $\mathbb {Z}/n\mathbb {Z}$
. Given a prime p, set
$\mathbb {Z}/n\mathbb {Z}$
. Given a prime p, set
![]() $\kappa _n^{(p)}$
to denote
$\kappa _n^{(p)}$
to denote
![]() $\kappa _{p^n}$
and set
$\kappa _{p^n}$
and set
![]() $F_n^{(p)}$
to denote the composite
$F_n^{(p)}$
to denote the composite
![]() $F\cdot \kappa _n^{(p)}$
. This gives rise to a tower of function field extensions
$F\cdot \kappa _n^{(p)}$
. This gives rise to a tower of function field extensions
Let
![]() $\mathbb {Z}_p$
denote the ring of p-adic integers, that is, the valuation ring of
$\mathbb {Z}_p$
denote the ring of p-adic integers, that is, the valuation ring of
![]() $\mathbb {Q}_p$
. The constant
$\mathbb {Q}_p$
. The constant
![]() $\mathbb {Z}_p$
-extension of F is the infinite union
$\mathbb {Z}_p$
-extension of F is the infinite union
It is easy to see that the Galois group
![]() $\operatorname {Gal}(F_\infty ^{(p)}/F)$
is isomorphic to
$\operatorname {Gal}(F_\infty ^{(p)}/F)$
is isomorphic to
![]() $\mathbb {Z}_{p}$
. Let
$\mathbb {Z}_{p}$
. Let
![]() $h_F$
denote the class number of F (see [Reference Rosen15, Ch. 5]). Note that since
$h_F$
denote the class number of F (see [Reference Rosen15, Ch. 5]). Note that since
![]() $P_\infty $
is assumed to have degree
$P_\infty $
is assumed to have degree
![]() $1$
, it remains inert in
$1$
, it remains inert in
![]() $F_n^{(p)}$
for all p. Let
$F_n^{(p)}$
for all p. Let
![]() $\mathcal {O}_{\infty }^{(p)}$
and
$\mathcal {O}_{\infty }^{(p)}$
and
![]() $\mathcal {O}_{n}^{(p)}$
respectively be the rings of integers of
$\mathcal {O}_{n}^{(p)}$
respectively be the rings of integers of
![]() $F_\infty ^{(p)}$
and
$F_\infty ^{(p)}$
and
![]() $F_n^{(p)}$
, that is, the functions
$F_n^{(p)}$
, that is, the functions
![]() $f\in F_\infty $
with no poles away from
$f\in F_\infty $
with no poles away from
![]() $P_\infty $
. We now state our main result.
$P_\infty $
. We now state our main result.
Theorem 1.2 (Theorem 3.2).
Let
![]() $\ell $
be a prime number and F be a global function field of characteristic
$\ell $
be a prime number and F be a global function field of characteristic
![]() $\ell $
. Let
$\ell $
. Let
![]() $\kappa $
be the field of constants of F and let p and q be prime numbers that are not necessarily distinct. Assume that
$\kappa $
be the field of constants of F and let p and q be prime numbers that are not necessarily distinct. Assume that
![]() $q\neq \ell $
. Let
$q\neq \ell $
. Let
![]() $f(X)$
be a polynomial with coefficients in
$f(X)$
be a polynomial with coefficients in
![]() $\kappa $
satisfying the following conditions:
$\kappa $
satisfying the following conditions:
-
(1) the polynomial
 $f(X)$
factorises into
$f(X)$
factorises into
 $f(X)=a_0(X-a_1)^{n_1}\cdots (X-a_t)^{n_t}$
, where
$f(X)=a_0(X-a_1)^{n_1}\cdots (X-a_t)^{n_t}$
, where
 $a_0\in \kappa $
,
$a_0\in \kappa $
,
 $a_1,\ldots , a_t$
are distinct elements in
$a_1,\ldots , a_t$
are distinct elements in
 $\kappa $
,
$\kappa $
,
 $n_1,\ldots , n_t$
are positive integers and
$n_1,\ldots , n_t$
are positive integers and
 $t\geq 2$
;
$t\geq 2$
; -
(2) at least two of the exponents
 $n_i$
are not divisible by q.
$n_i$
are not divisible by q.
Then the following assertions hold.
-
(i) Suppose that p and q are distinct. Then, for all sufficiently large numbers
 $k>0$
, the only solutions
$k>0$
, the only solutions
 $(X,Y)$
to
$(X,Y)$
to
 $Y^{q^k}=f(X)$
that are contained in
$Y^{q^k}=f(X)$
that are contained in
 $\mathcal {O}_\infty ^{(p)}$
are constant.
$\mathcal {O}_\infty ^{(p)}$
are constant. -
(ii) Suppose that
 $p\nmid h_F$
. Then the only solutions
$p\nmid h_F$
. Then the only solutions
 $(X,Y)$
to
$(X,Y)$
to
 $Y^p=f(X)$
that are contained in
$Y^p=f(X)$
that are contained in
 $\mathcal {O}_\infty ^{(p)}$
are constant.
$\mathcal {O}_\infty ^{(p)}$
are constant.
As a consequence of this result, for any prime p, there are only finitely many numbers n, that are not powers of
![]() $\ell $
, for which
$\ell $
, for which
![]() $Y^n=f(X)$
has solutions in
$Y^n=f(X)$
has solutions in
![]() $F_\infty ^{(p)}$
. The methods used in proving the theorem are applied to another question of independent interest. Let K be a field of positive characteristic
$F_\infty ^{(p)}$
. The methods used in proving the theorem are applied to another question of independent interest. Let K be a field of positive characteristic
![]() $\ell $
and A be the polynomial ring
$\ell $
and A be the polynomial ring
![]() $K[T_1, \ldots , T_n]$
.
$K[T_1, \ldots , T_n]$
.
Theorem 1.3 (Theorem 4.1).
With the notation as above, let
![]() $f(X)$
be a polynomial with all of its coefficients and roots in K. Let
$f(X)$
be a polynomial with all of its coefficients and roots in K. Let
![]() $q\neq \ell $
be a prime number and assume that the following conditions are satisfied:
$q\neq \ell $
be a prime number and assume that the following conditions are satisfied:
-
(1)
 $f(X)$
factorises into
$f(X)$
factorises into
 $f(X)=a_0(X-a_1)^{n_1}\cdots (X-a_t)^{n_t}$
, where
$f(X)=a_0(X-a_1)^{n_1}\cdots (X-a_t)^{n_t}$
, where
 $a_0\in K$
,
$a_0\in K$
,
 $a_1,\ldots , a_t$
are distinct elements in K,
$a_1,\ldots , a_t$
are distinct elements in K,
 $n_1,\ldots , n_t$
are positive integers and
$n_1,\ldots , n_t$
are positive integers and
 $t\geq 2$
;
$t\geq 2$
; -
(2) at least two of the exponents
 $n_i$
are not divisible by q.
$n_i$
are not divisible by q.
Then any solution
![]() $(X,Y)\in A^2$
to
$(X,Y)\in A^2$
to
is constant, that is, X and Y are both in K.
It follows from this result that if
![]() $n>1$
is not a power of
$n>1$
is not a power of
![]() $\ell $
, then
$\ell $
, then
![]() $X^n=f(X)$
does not have nonconstant solutions in A.
$X^n=f(X)$
does not have nonconstant solutions in A.
Organisation
In Section 2 we prove criteria for the constancy of solutions to
![]() $Y^n=f(X)$
in global function fields F. The main result in Section 2 is Theorem 2.4. In Section 3 we extend the results in Section 2 to prove the constancy of solutions to the above equation in
$Y^n=f(X)$
in global function fields F. The main result in Section 2 is Theorem 2.4. In Section 3 we extend the results in Section 2 to prove the constancy of solutions to the above equation in
![]() $\mathbb {Z}_p$
-extensions of F. It is in this section that we prove the main result of the paper, that is, Theorem 3.2. In Section 4 we prove similar results for the polynomial rings over a field. Finally, in Section 5 we study the specific case where
$\mathbb {Z}_p$
-extensions of F. It is in this section that we prove the main result of the paper, that is, Theorem 3.2. In Section 4 we prove similar results for the polynomial rings over a field. Finally, in Section 5 we study the specific case where
![]() $f(X)=\sum _{i=1}^k (X+ir)^m$
.
$f(X)=\sum _{i=1}^k (X+ir)^m$
.
2 Constancy of solutions to
 $Y^n=f(X)$
in a global function field
$Y^n=f(X)$
in a global function field
In this section we introduce basic notions and prove results about the solutions to certain Diophantine equations over global function fields. Throughout this section,
![]() $\ell $
is a prime number and A is an integral domain of characteristic
$\ell $
is a prime number and A is an integral domain of characteristic
![]() $\ell $
with field of constants
$\ell $
with field of constants
![]() $\kappa $
. We introduce the notion of a discrete valuation on A.
$\kappa $
. We introduce the notion of a discrete valuation on A.
Definition 2.1. A function
![]() $d:A\rightarrow \mathbb {Z}$
is said to be a discrete valuation if the following conditions are satisfied:
$d:A\rightarrow \mathbb {Z}$
is said to be a discrete valuation if the following conditions are satisfied:
-
(1) the values taken by d are nonnegative;
-
(2) if
 $\mathbf {1}$
is the identity element of A, then
$\mathbf {1}$
is the identity element of A, then
 $d(\mathbf {1})=0$
;
$d(\mathbf {1})=0$
; -
(3) if
 $f,g\in A$
are nonzero elements, then
$f,g\in A$
are nonzero elements, then
 $d(fg)=d(f)+d(g)$
;
$d(fg)=d(f)+d(g)$
; -
(4)
 $d(f+g)\leq \operatorname \max \{d(f),d(g)\}$
,
$d(f+g)\leq \operatorname \max \{d(f),d(g)\}$
, -
(5) if
 $d(f)<d(g)$
, then
$d(f)<d(g)$
, then
 $d(f+g)=d(f)$
.
$d(f+g)=d(f)$
.
Let
![]() $A_0$
be the subring of A consisting of all elements
$A_0$
be the subring of A consisting of all elements
![]() $a\in A$
for which
$a\in A$
for which
![]() $d(a)\leq 0$
. Given
$d(a)\leq 0$
. Given
![]() $f,g\in A$
, we say that f divides g if
$f,g\in A$
, we say that f divides g if
![]() $fh=g$
for some
$fh=g$
for some
![]() $h\in A$
. It is clear that if f divides g then
$h\in A$
. It is clear that if f divides g then
![]() $d(f)\leq d(g)$
.
$d(f)\leq d(g)$
.
Lemma 2.2. Let q be a prime number such that
![]() $q\neq \ell $
, and A be an integral domain of characteristic
$q\neq \ell $
, and A be an integral domain of characteristic
![]() $\ell $
equipped with a function d satisfying conditions (1)–(5) of Definition 2.1. Let
$\ell $
equipped with a function d satisfying conditions (1)–(5) of Definition 2.1. Let
![]() $f,g,c\in A$
satisfy the equation
$f,g,c\in A$
satisfy the equation
Then
![]() $d(f), d(g)\leq d(c)$
. In particular, f and g are contained in
$d(f), d(g)\leq d(c)$
. In particular, f and g are contained in
![]() $A_0$
if c is contained in
$A_0$
if c is contained in
![]() $A_0$
.
$A_0$
.
Proof. Suppose by way of contradiction that
![]() $d(f)>d(c)$
or
$d(f)>d(c)$
or
![]() $d(g)>d(c)$
. Assume first that
$d(g)>d(c)$
. Assume first that
![]() $d(f)>d(c)$
. Set
$d(f)>d(c)$
. Set
![]() $e:=(g-f)$
. From (2.1), we find that e divides c. As a result,
$e:=(g-f)$
. From (2.1), we find that e divides c. As a result,
![]() $d(e)\leq d(c)< d(f)$
. Hence by property (5) in Definition 2.1,
$d(e)\leq d(c)< d(f)$
. Hence by property (5) in Definition 2.1,
Therefore, we have deduced that
![]() $d(g)>d(c)$
. Rewrite (2.1) as
$d(g)>d(c)$
. Rewrite (2.1) as
and expand the left-hand side of this equation via the binomial expansion to give
 $$ \begin{align*}qeg^{q-1}+{q\choose 2} e^2 g^{q-2}+\cdots +e^q=c.\end{align*} $$
$$ \begin{align*}qeg^{q-1}+{q\choose 2} e^2 g^{q-2}+\cdots +e^q=c.\end{align*} $$
Note that since
![]() $d(e)<d(g)$
, we find that, for all i such that
$d(e)<d(g)$
, we find that, for all i such that
![]() $2\leq i\leq q$
,
$2\leq i\leq q$
,
 $$ \begin{align*}d\left({q\choose i}e^i g^{q-i}\right)< d(qeg^{q-1})\end{align*} $$
$$ \begin{align*}d\left({q\choose i}e^i g^{q-i}\right)< d(qeg^{q-1})\end{align*} $$
and therefore,
This implies that
![]() $d(g)\leq d(c)$
, a contradiction. On the other hand, if we assume that
$d(g)\leq d(c)$
, a contradiction. On the other hand, if we assume that
![]() $d(g)>d(c)$
(instead of assuming that
$d(g)>d(c)$
(instead of assuming that
![]() $d(f)>d(c)$
), the same argument applies.
$d(f)>d(c)$
), the same argument applies.
We shall illustrate this result in various cases of interest. In this section we study Diophantine equations over global function fields F. Let
![]() $\ell $
be a prime number and denote by
$\ell $
be a prime number and denote by
![]() $\mathbb {F}_\ell $
the finite field with
$\mathbb {F}_\ell $
the finite field with
![]() $\ell $
elements (that is,
$\ell $
elements (that is,
![]() $\mathbb {Z}/\ell \mathbb {Z}$
). Fix an algebraic closure
$\mathbb {Z}/\ell \mathbb {Z}$
). Fix an algebraic closure
![]() $\bar {F}$
of F. Let
$\bar {F}$
of F. Let
![]() $\kappa $
be the algebraic closure of
$\kappa $
be the algebraic closure of
![]() $\mathbb {F}_\ell $
in F and let
$\mathbb {F}_\ell $
in F and let
![]() $\bar {\kappa }$
be the algebraic closure of
$\bar {\kappa }$
be the algebraic closure of
![]() $\kappa $
in
$\kappa $
in
![]() $\bar {F}$
. Set
$\bar {F}$
. Set
![]() $F'$
to denote the composite of F with
$F'$
to denote the composite of F with
![]() $\bar {\kappa }$
.
$\bar {\kappa }$
.
Following [Reference Rosen15, Ch. 5], a prime v of F is by definition the maximal ideal of a discrete valuation ring
![]() $\mathcal {O}_v\subset F$
with fraction field equal to F. A divisor of F is a finite linear combination
$\mathcal {O}_v\subset F$
with fraction field equal to F. A divisor of F is a finite linear combination
![]() $D=\sum _v n_v v$
of primes v. In this sum, the
$D=\sum _v n_v v$
of primes v. In this sum, the
![]() $n_v$
are all integers and the set of primes v for which
$n_v$
are all integers and the set of primes v for which
![]() $n_v\neq 0$
is referred to as the support of D. Given a function
$n_v\neq 0$
is referred to as the support of D. Given a function
![]() $g\in F$
, denote by
$g\in F$
, denote by
![]() $\operatorname {div}(g)$
the associated principal divisor. Note that any principal divisor has degree
$\operatorname {div}(g)$
the associated principal divisor. Note that any principal divisor has degree
![]() $0$
. Two divisors are considered equivalent if they differ by a principal divisor. The class group of F is the group of divisor classes of degree
$0$
. Two divisors are considered equivalent if they differ by a principal divisor. The class group of F is the group of divisor classes of degree
![]() $0$
and has finite cardinality (see [Reference Rosen15, Lemma 5.6]). Denote by
$0$
and has finite cardinality (see [Reference Rosen15, Lemma 5.6]). Denote by
![]() $h_F$
the class number, that is, the number of elements in the class group. Given a natural number N, denote by
$h_F$
the class number, that is, the number of elements in the class group. Given a natural number N, denote by
![]() $h_F[N]$
the cardinality of the N-torsion in the class group.
$h_F[N]$
the cardinality of the N-torsion in the class group.
The field
![]() $F'$
is identified with the field of fractions of a projective algebraic curve
$F'$
is identified with the field of fractions of a projective algebraic curve
![]() $\mathfrak {X}$
over
$\mathfrak {X}$
over
![]() $\bar {\kappa }$
. A point
$\bar {\kappa }$
. A point
![]() $w\in \mathfrak {X}(\bar {\kappa })$
is also referred to as a prime of
$w\in \mathfrak {X}(\bar {\kappa })$
is also referred to as a prime of
![]() $F'$
, since it corresponds to a valuation ring
$F'$
, since it corresponds to a valuation ring
![]() $\mathcal {O}_w\subset F'$
with fraction field
$\mathcal {O}_w\subset F'$
with fraction field
![]() $F'$
. Given a prime w of
$F'$
. Given a prime w of
![]() $F'$
and a prime v of F, we say that w lies above (or divides) v if the natural inclusion of fields
$F'$
and a prime v of F, we say that w lies above (or divides) v if the natural inclusion of fields
![]() $F\hookrightarrow F'$
induces an inclusion of valuation rings
$F\hookrightarrow F'$
induces an inclusion of valuation rings
![]() $\mathcal {O}_v\hookrightarrow \mathcal {O}_w$
. Given a function
$\mathcal {O}_v\hookrightarrow \mathcal {O}_w$
. Given a function
![]() $g\in F$
or
$g\in F$
or
![]() $g\in F'$
, denote by
$g\in F'$
, denote by
![]() $\operatorname {ord}_v(g)$
or
$\operatorname {ord}_v(g)$
or
![]() $\operatorname {ord}_w(g)$
) respectively the order of vanishing of g at v or w. We refer to
$\operatorname {ord}_w(g)$
) respectively the order of vanishing of g at v or w. We refer to
![]() $d_v(g):=-\operatorname {ord}_v(g)$
and
$d_v(g):=-\operatorname {ord}_v(g)$
and
![]() $d_w(g):=-\operatorname {ord}_w(g)$
as the order of the pole of g at v and w, respectively. Given a finite and nonempty set of primes S of F, the ring of S-integers
$d_w(g):=-\operatorname {ord}_w(g)$
as the order of the pole of g at v and w, respectively. Given a finite and nonempty set of primes S of F, the ring of S-integers
![]() $\mathcal {O}_S$
consists of all functions
$\mathcal {O}_S$
consists of all functions
![]() $g\in F$
such that
$g\in F$
such that
![]() $d_v(g)\leq 0$
for all primes
$d_v(g)\leq 0$
for all primes
![]() $v\notin S$
. Let
$v\notin S$
. Let
![]() $\bar {S}$
be the set of primes of
$\bar {S}$
be the set of primes of
![]() $F'$
that lie above S. Let A denote the composite
$F'$
that lie above S. Let A denote the composite
![]() $\mathcal {O}_S\cdot \bar {\kappa }$
. A function
$\mathcal {O}_S\cdot \bar {\kappa }$
. A function
![]() $g\in A$
has the property that
$g\in A$
has the property that
![]() $d_w(g)\leq 0$
for all
$d_w(g)\leq 0$
for all
![]() $w\notin \bar {S}$
. According to our conventions,
$w\notin \bar {S}$
. According to our conventions,
![]() $\mathcal {O}_F$
is the ring of S integers where
$\mathcal {O}_F$
is the ring of S integers where
![]() $S:=\{P_\infty \}$
. Since
$S:=\{P_\infty \}$
. Since
![]() $P_\infty $
is a prime of degree
$P_\infty $
is a prime of degree
![]() $1$
, it is totally inert in
$1$
, it is totally inert in
![]() $F'$
. By abuse of notation, the single prime in
$F'$
. By abuse of notation, the single prime in
![]() $\bar {S}$
is also denoted by
$\bar {S}$
is also denoted by
![]() $P_\infty $
.
$P_\infty $
.
We list some basic properties of the function
![]() $d_w$
on A. The following result applies for any ring of
$d_w$
on A. The following result applies for any ring of
![]() $\bar {S}$
-integers.
$\bar {S}$
-integers.
Lemma 2.3. Let f and g be a functions in A and w be a point in
![]() $\mathfrak {X}(\bar {\kappa })$
. Then the following assertions hold:
$\mathfrak {X}(\bar {\kappa })$
. Then the following assertions hold:
-
(1) if
 $d_w(g)\leq 0$
for all
$d_w(g)\leq 0$
for all
 $w\in \bar {S}$
, then g is a constant function;
$w\in \bar {S}$
, then g is a constant function; -
(2)
 $d_w(fg)=d_w(f)+d_w(g)$
;
$d_w(fg)=d_w(f)+d_w(g)$
; -
(3) if
 $d_w(f)>d_w(g)$
, then
$d_w(f)>d_w(g)$
, then
 $d_w(f+g)=d_w(f)$
.
$d_w(f+g)=d_w(f)$
.
Proof. Note that since g is contained in A,
![]() $d_w(g)\leq 0$
for all points
$d_w(g)\leq 0$
for all points
![]() $w\notin \bar {S}$
. Therefore, the assumption that
$w\notin \bar {S}$
. Therefore, the assumption that
![]() $d_w(g)\leq 0$
implies that g has no poles and thus must be a constant function. This proves part (1).
$d_w(g)\leq 0$
implies that g has no poles and thus must be a constant function. This proves part (1).
Part (2) clearly follows from the relation
![]() $\operatorname {ord}_w(fg)=\operatorname {ord}_w(f)+\operatorname {ord}_w(g)$
.
$\operatorname {ord}_w(fg)=\operatorname {ord}_w(f)+\operatorname {ord}_w(g)$
.
For part (3), we note that
![]() $f+g=f(1+g/f)$
. Since it is assumed that
$f+g=f(1+g/f)$
. Since it is assumed that
![]() $d_w(f)>d_w(g)$
, it follows that
$d_w(f)>d_w(g)$
, it follows that
![]() $g/f$
vanishes at w. As a result,
$g/f$
vanishes at w. As a result,
![]() $d_w(1+g/f)=0$
and thus
$d_w(1+g/f)=0$
and thus
which proves the result.
Recall that
![]() $P_\infty $
is a prime of degree
$P_\infty $
is a prime of degree
![]() $1$
and
$1$
and
![]() $\mathcal {O}_F$
is the associated ring of integers in F.
$\mathcal {O}_F$
is the associated ring of integers in F.
Theorem 2.4. Let
![]() $\ell $
be a prime number and F be a global function field of characteristic
$\ell $
be a prime number and F be a global function field of characteristic
![]() $\ell $
. Let
$\ell $
. Let
![]() $\mathcal {O}_F$
be the ring of integers of F. Denote by
$\mathcal {O}_F$
be the ring of integers of F. Denote by
![]() $\kappa $
the field of constants of F. Let
$\kappa $
the field of constants of F. Let
![]() $f(X)$
be a polynomial with coefficients in
$f(X)$
be a polynomial with coefficients in
![]() $\kappa $
. Let
$\kappa $
. Let
![]() $q\neq \ell $
be a prime number and let
$q\neq \ell $
be a prime number and let
![]() $k>0$
be the least integer such that
$k>0$
be the least integer such that
![]() $h_F[q^k]=h_F[q^{k-1}]$
. Assume that the following conditions are satisfied:
$h_F[q^k]=h_F[q^{k-1}]$
. Assume that the following conditions are satisfied:
-
(1)
 $f(X)$
factorises into
$f(X)$
factorises into
 $f(X)=a_0(X-a_1)^{n_1}\ldots (X-a_t)^{n_t},$
where
$f(X)=a_0(X-a_1)^{n_1}\ldots (X-a_t)^{n_t},$
where
 $a_0\in \kappa $
,
$a_0\in \kappa $
,
 $a_1,\ldots , a_t$
are distinct elements in
$a_1,\ldots , a_t$
are distinct elements in
 $\kappa $
,
$\kappa $
,
 $n_1,\ldots , n_t$
are positive integers and
$n_1,\ldots , n_t$
are positive integers and
 $t\geq 2$
;
$t\geq 2$
; -
(2) at least two of the exponents
 $n_i$
are not divisible by q.
$n_i$
are not divisible by q.
Then any solution
![]() $(X,Y)$
to
$(X,Y)$
to
for which
![]() $X,Y\in \mathcal {O}_F$
is constant, that is, X and Y are both in
$X,Y\in \mathcal {O}_F$
is constant, that is, X and Y are both in
![]() $\kappa $
.
$\kappa $
.
Proof. Since the elements
![]() $a_1,\ldots , a_t$
are distinct elements of
$a_1,\ldots , a_t$
are distinct elements of
![]() $\kappa $
, we find that for all
$\kappa $
, we find that for all
![]() $i, j$
such that
$i, j$
such that
![]() $i\neq j$
,
$i\neq j$
,
![]() $(X-a_i)-(X-a_j)=a_j-a_i$
is a nonzero element of
$(X-a_i)-(X-a_j)=a_j-a_i$
is a nonzero element of
![]() $\kappa $
. Therefore, for
$\kappa $
. Therefore, for
![]() $i\neq j$
, the divisors
$i\neq j$
, the divisors
![]() $\operatorname {div}(X-a_i)$
and
$\operatorname {div}(X-a_i)$
and
![]() $\operatorname {div}(X-a_j)$
have disjoint supports.
$\operatorname {div}(X-a_j)$
have disjoint supports.
From equation (2.2),
 $$ \begin{align*} q^k \operatorname{div}(Y)=\sum_{i=1}^t n_i \operatorname{div}(X-a_i).\end{align*} $$
$$ \begin{align*} q^k \operatorname{div}(Y)=\sum_{i=1}^t n_i \operatorname{div}(X-a_i).\end{align*} $$
Since the divisors
![]() $\operatorname {div}(X-a_i)$
have disjoint supports for all i, there are divisors
$\operatorname {div}(X-a_i)$
have disjoint supports for all i, there are divisors
![]() $D_i'$
such that
$D_i'$
such that
![]() $q^k D_i'=n_i\operatorname {div}(X-a_i)$
. Recall that it is assumed that there are two distinct indices i and j such that
$q^k D_i'=n_i\operatorname {div}(X-a_i)$
. Recall that it is assumed that there are two distinct indices i and j such that
![]() $q\nmid n_i$
and
$q\nmid n_i$
and
![]() $q\nmid n_j$
. Without loss of generality, assume that
$q\nmid n_j$
. Without loss of generality, assume that
![]() $q\nmid n_1$
and
$q\nmid n_1$
and
![]() $q\nmid n_2$
. Therefore, there exist divisors
$q\nmid n_2$
. Therefore, there exist divisors
![]() $D_1$
and
$D_1$
and
![]() $D_2$
such that
$D_2$
such that
![]() $q^k D_i=\operatorname {div}(X-a_i)$
for
$q^k D_i=\operatorname {div}(X-a_i)$
for
![]() $i=1,2$
. The divisor classes
$i=1,2$
. The divisor classes
![]() $[D_1]$
and
$[D_1]$
and
![]() $[D_2]$
in the class group are in the
$[D_2]$
in the class group are in the
![]() $q^k$
-torsion subgroup of the class group. Since
$q^k$
-torsion subgroup of the class group. Since
![]() $h_F[q^k]=h_F[q^{k-1}]$
, we find that
$h_F[q^k]=h_F[q^{k-1}]$
, we find that
![]() $q^{k-1}D_i$
is principal for
$q^{k-1}D_i$
is principal for
![]() $i=1,2$
. Let f and g be functions in F such that
$i=1,2$
. Let f and g be functions in F such that
Thus
![]() $u_1f^q=(X-a_1)$
and
$u_1f^q=(X-a_1)$
and
![]() $u_2 g^q=(X-a_2)$
, where
$u_2 g^q=(X-a_2)$
, where
![]() $u_1$
and
$u_1$
and
![]() $u_2$
are contained in
$u_2$
are contained in
![]() $\kappa $
. Note that since
$\kappa $
. Note that since
![]() $(X-a_i)$
has no poles away from
$(X-a_i)$
has no poles away from
![]() $\{P_\infty \}$
, the same is true for f and g, hence,
$\{P_\infty \}$
, the same is true for f and g, hence,
![]() $f,g\in \mathcal {O}_F$
. Setting
$f,g\in \mathcal {O}_F$
. Setting
![]() $A:=\mathcal {O}_F\cdot \bar {\kappa }$
, we may replace f by
$A:=\mathcal {O}_F\cdot \bar {\kappa }$
, we may replace f by
![]() $u_1^{1/q} f$
and g by
$u_1^{1/q} f$
and g by
![]() $u_2^{1/q} g$
, and thus assume that
$u_2^{1/q} g$
, and thus assume that
![]() $f^q=(X-a_1)$
and
$f^q=(X-a_1)$
and
![]() $g^q=(X-a_2)$
for some elements
$g^q=(X-a_2)$
for some elements
![]() $f,g\in A$
. We find that
$f,g\in A$
. We find that
![]() $f^q-g^q=a_2-a_1$
is a nonzero element of
$f^q-g^q=a_2-a_1$
is a nonzero element of
![]() $\kappa $
. The pair
$\kappa $
. The pair
![]() $(A,d_{P_\infty })$
satisfies properties (1)–(5) and therefore
$(A,d_{P_\infty })$
satisfies properties (1)–(5) and therefore
![]() $d_{P_\infty }(f)=d_{P_\infty }(g)=0$
by Lemma 2.2. Therefore, by Lemma 2.3(1), f and g are both in
$d_{P_\infty }(f)=d_{P_\infty }(g)=0$
by Lemma 2.2. Therefore, by Lemma 2.3(1), f and g are both in
![]() $\kappa $
. Hence,
$\kappa $
. Hence,
![]() $X=f^q+a_1$
is in
$X=f^q+a_1$
is in
![]() $\kappa $
and thus so is Y.
$\kappa $
and thus so is Y.
Remark 2.5. We make the following observations.
-
• Theorem 2.4 implies that
 $k=1$
if
$k=1$
if
 $q\nmid h_F$
.
$q\nmid h_F$
. -
• If the roots
 $a_i$
are not contained in F, we may base-change F by an extension
$a_i$
are not contained in F, we may base-change F by an extension
 $\kappa '$
of
$\kappa '$
of
 $\kappa $
which is generated by the roots
$\kappa $
which is generated by the roots
 $a_i$
.
$a_i$
. -
• Suppose that
 $f(X)$
satisfies the conditions of Theorem 2.4. Since
$f(X)$
satisfies the conditions of Theorem 2.4. Since
 $q\nmid h_F$
for all but finitely many primes q, it follows that
$q\nmid h_F$
for all but finitely many primes q, it follows that
 $Y^q=f(X)$
has no nonconstant solutions in F for all but finitely many primes q. In fact, it is easy to see that Theorem 2.4 implies that
$Y^q=f(X)$
has no nonconstant solutions in F for all but finitely many primes q. In fact, it is easy to see that Theorem 2.4 implies that
 $Y^n=f(X)$
has no nonconstant solutions for all but finitely many natural numbers n.
$Y^n=f(X)$
has no nonconstant solutions for all but finitely many natural numbers n.
3 Constancy of solutions to
 $Y^n=f(X)$
in the constant
$Y^n=f(X)$
in the constant
 $\mathbb {Z}_p$
-extension of a function field
$\mathbb {Z}_p$
-extension of a function field
In this section we apply Theorem 2.4 to study questions motivated by Iwasawa theory. Given primes p and q (not necessarily distinct), let
![]() $h_n(p,q)$
denote
$h_n(p,q)$
denote
![]() $\# \operatorname {Cl}(F_n^{(p)})[q^\infty ]$
, the cardinality of the
$\# \operatorname {Cl}(F_n^{(p)})[q^\infty ]$
, the cardinality of the
![]() $q^\infty $
-torsion in the class group of
$q^\infty $
-torsion in the class group of
![]() $F_n^{(p)}$
.
$F_n^{(p)}$
.
Theorem 3.1 (Leitzel, Rosen).
Let p and q be (not necessarily distinct) prime numbers and F be a function field of characteristic
![]() $\ell $
. The following assertions hold:
$\ell $
. The following assertions hold:
-
(1) if p and q are distinct, then, as n goes to infinity, the quantity
 $h_n(p,q)$
is bounded;
$h_n(p,q)$
is bounded; -
(2) if p does not divide
 $h_F$
, then
$h_F$
, then
 $h_n(p,p)=1$
for all n.
$h_n(p,p)=1$
for all n.
Proof. Part (1) follows from [Reference Rosen15, Theorem 11.6]. For function fields of genus
![]() $1$
, the result was proved by Leitzel [Reference Leitzel9]. For part (2), see [Reference Rosen15, Proposition 11.3].
$1$
, the result was proved by Leitzel [Reference Leitzel9]. For part (2), see [Reference Rosen15, Proposition 11.3].
Recall notation from the introduction. The prime
![]() $P_\infty $
is totally inert in
$P_\infty $
is totally inert in
![]() $F_\infty ^{(p)}$
for any prime p. We set
$F_\infty ^{(p)}$
for any prime p. We set
![]() $\mathcal {O}_\infty ^{(p)}$
to denote the ring of integers of
$\mathcal {O}_\infty ^{(p)}$
to denote the ring of integers of
![]() $F_\infty ^{(p)}$
, that is, the functions with no poles outside
$F_\infty ^{(p)}$
, that is, the functions with no poles outside
![]() $\{P_\infty \}$
. The following is the main result of this paper.
$\{P_\infty \}$
. The following is the main result of this paper.
Theorem 3.2. Let
![]() $\ell $
be a prime number and F be a global function field with field of constants
$\ell $
be a prime number and F be a global function field with field of constants
![]() $\kappa $
. Let p and q be prime numbers that are not necessarily distinct, and assume that
$\kappa $
. Let p and q be prime numbers that are not necessarily distinct, and assume that
![]() $q\neq \ell $
. Let
$q\neq \ell $
. Let
![]() $f(X)$
be a polynomial with coefficients in
$f(X)$
be a polynomial with coefficients in
![]() $\kappa $
satisfying the conditions of Theorem 2.4. Then the following assertions hold.
$\kappa $
satisfying the conditions of Theorem 2.4. Then the following assertions hold.
-
(1) If p and q are distinct, then, for all sufficiently large numbers
 $k>0$
, the only solutions
$k>0$
, the only solutions
 $(X,Y)$
to
$(X,Y)$
to
 $Y^{q^k}=f(X)$
in
$Y^{q^k}=f(X)$
in
 $\mathcal {O}_\infty ^{(p)}$
are constant.
$\mathcal {O}_\infty ^{(p)}$
are constant. -
(2) If
 $p\nmid h_F$
, then the only solutions
$p\nmid h_F$
, then the only solutions
 $(X,Y)$
to
$(X,Y)$
to
 $Y^p=f(X)$
in
$Y^p=f(X)$
in
 $\mathcal {O}_\infty ^{(p)}$
are constant.
$\mathcal {O}_\infty ^{(p)}$
are constant.
Proof. First, we consider the case where
![]() $p\ne q$
. From Theorem 3.1(1),
$p\ne q$
. From Theorem 3.1(1),
![]() $h_{n}(p,q)$
is bounded as n goes to infinity. Choose
$h_{n}(p,q)$
is bounded as n goes to infinity. Choose
![]() $k>0$
such that
$k>0$
such that
![]() $q^k$
is larger than
$q^k$
is larger than
![]() $\operatorname \max h_n(p,q)$
. From Theorem 2.4,
$\operatorname \max h_n(p,q)$
. From Theorem 2.4,
![]() $Y^{q^k}=f(X)$
has no nonconstant solutions in
$Y^{q^k}=f(X)$
has no nonconstant solutions in
![]() $\mathcal {O}_n^{(p)}$
for all n, and therefore, no nonconstant solutions in
$\mathcal {O}_n^{(p)}$
for all n, and therefore, no nonconstant solutions in
![]() $\mathcal {O}_\infty ^{(p)}$
. Hence, there are no nonconstant solutions in
$\mathcal {O}_\infty ^{(p)}$
. Hence, there are no nonconstant solutions in
![]() $F_\infty $
.
$F_\infty $
.
Next, we consider the case where
![]() $p=q$
and
$p=q$
and
![]() $p\nmid h_F$
. Note that if
$p\nmid h_F$
. Note that if
![]() $p\nmid h_F$
, then by Theorem 3.1(2),
$p\nmid h_F$
, then by Theorem 3.1(2),
![]() $ h_n(p,p)=1$
for all n. It follows from Theorem 2.4 that
$ h_n(p,p)=1$
for all n. It follows from Theorem 2.4 that
![]() $Y^p=f(X)$
has no nonconstant solutions in
$Y^p=f(X)$
has no nonconstant solutions in
![]() $\mathcal {O}_n^{(p)}$
for all n, and therefore no nonconstant solutions in
$\mathcal {O}_n^{(p)}$
for all n, and therefore no nonconstant solutions in
![]() $\mathcal {O}_\infty ^{(p)}$
.
$\mathcal {O}_\infty ^{(p)}$
.
4 Constancy of solutions to
 $Y^n=f(X)$
in a polynomial ring in r-variables
$Y^n=f(X)$
in a polynomial ring in r-variables
In this section we study solutions to equations of the form
![]() $Y^n=f(X)$
in polynomial rings over a field. Let K be any field of characteristic
$Y^n=f(X)$
in polynomial rings over a field. Let K be any field of characteristic
![]() $\ell>0$
and A be the polynomial ring
$\ell>0$
and A be the polynomial ring
![]() $K[T_1, \ldots , T_r]$
. Given a polynomial g, let
$K[T_1, \ldots , T_r]$
. Given a polynomial g, let
![]() $d_i(g)$
be the degree of g viewed as a polynomial in
$d_i(g)$
be the degree of g viewed as a polynomial in
![]() $T_i$
over the subring
$T_i$
over the subring
![]() $K[T_1, \ldots , T_{i-1}, T_{i+1}, \ldots , T_r]$
. The pair
$K[T_1, \ldots , T_{i-1}, T_{i+1}, \ldots , T_r]$
. The pair
![]() $(A,d_i)$
satisfies conditions (1)–(5) of Definition 2.1. The class group
$(A,d_i)$
satisfies conditions (1)–(5) of Definition 2.1. The class group
![]() $\operatorname {Cl}(A)$
denotes the group of equivalence classes of Weil divisors. Since A is a unique factorisation domain, we have that
$\operatorname {Cl}(A)$
denotes the group of equivalence classes of Weil divisors. Since A is a unique factorisation domain, we have that
![]() $\operatorname {Cl}(A)=0$
.
$\operatorname {Cl}(A)=0$
.
Theorem 4.1. With the notation above, let
![]() $f(X)$
be a polynomial with all of its coefficients in K. Let
$f(X)$
be a polynomial with all of its coefficients in K. Let
![]() $q\neq \ell $
be a prime number and assume that the following conditions are satisfied:
$q\neq \ell $
be a prime number and assume that the following conditions are satisfied:
-
(1)
 $f(X)$
factorises into
$f(X)$
factorises into
 $f(X)=a_0(X-a_1)^{n_1}\ldots (X-a_t)^{n_t},$
where
$f(X)=a_0(X-a_1)^{n_1}\ldots (X-a_t)^{n_t},$
where
 $a_0\in K$
,
$a_0\in K$
,
 $a_1,\ldots , a_t$
are distinct elements in K,
$a_1,\ldots , a_t$
are distinct elements in K,
 $n_1,\ldots , n_t$
are positive integers and
$n_1,\ldots , n_t$
are positive integers and
 $t\geq 2$
;
$t\geq 2$
; -
(2) at least two of the exponents
 $n_i$
are not divisible by q.
$n_i$
are not divisible by q.
Then any solution
![]() $(X,Y)\in A^2$
to
$(X,Y)\in A^2$
to
is constant, that is, X and Y are both in K.
Proof. Note that the algebraic closure of K in A is equal to K. We may as well replace K by its algebraic closure and assume without loss of generality that K is algebraically closed and that
![]() $q\nmid n_1$
and
$q\nmid n_1$
and
![]() $q\nmid n_2$
. Since the class group of A is trivial, the same argument as in the proof of Theorem 2.4 shows that
$q\nmid n_2$
. Since the class group of A is trivial, the same argument as in the proof of Theorem 2.4 shows that
![]() $(X-a_1)=f^q$
and
$(X-a_1)=f^q$
and
![]() $(X-a_2)=g^q$
for
$(X-a_2)=g^q$
for
![]() $f,g\in A$
. Therefore,
$f,g\in A$
. Therefore,
![]() $f^q-g^q=a_2-a_1$
, an element of K. Lemma 2.2 then implies that
$f^q-g^q=a_2-a_1$
, an element of K. Lemma 2.2 then implies that
![]() $d_i(f)=d_i(g)=0$
for all i, hence
$d_i(f)=d_i(g)=0$
for all i, hence
![]() $f,g$
are both in K. The result follows.
$f,g$
are both in K. The result follows.
5 Perfect powers that are sums of powers in arithmetic progressions
In this section we apply the results from previous sections to study the solutions of a Diophantine equation involving perfect powers in arithmetic progression:
Here,
![]() $m, n, r, d$
are integers such that
$m, n, r, d$
are integers such that
![]() $m, n, d\geq 2$
and
$m, n, d\geq 2$
and
![]() $r\geq 1$
. Let
$r\geq 1$
. Let
![]() $\Delta $
denote the discriminant of
$\Delta $
denote the discriminant of
![]() $f(X)$
viewed as a polynomial with integral coefficients.
$f(X)$
viewed as a polynomial with integral coefficients.
Theorem 5.1. Let F be a function field with characteristic
![]() $\ell \geq 5$
and field of functions
$\ell \geq 5$
and field of functions
![]() $\kappa $
. Let
$\kappa $
. Let
![]() $q\neq \ell $
be a prime. Assume that the following conditions are satisfied.
$q\neq \ell $
be a prime. Assume that the following conditions are satisfied.
-
(1) All roots of
 $f(X)$
are contained in
$f(X)$
are contained in
 $\kappa $
.
$\kappa $
. -
(2)
 $\ell \nmid r$
.
$\ell \nmid r$
. -
(3) At least one of the following conditions are satisfied:
-
(a)
 $\ell \nmid \Delta $
;
$\ell \nmid \Delta $
; -
(b)
 $q>m$
and
$q>m$
and
 $d\not \equiv 0,\pm 1\,\mod {\ell }$
.
$d\not \equiv 0,\pm 1\,\mod {\ell }$
.
-
Let k be the minimal value such that
![]() $h_F[q^k]=h_F[q^{k-1}]$
. Then there are no nonconstant solutions
$h_F[q^k]=h_F[q^{k-1}]$
. Then there are no nonconstant solutions
![]() $(X,Y)$
to
$(X,Y)$
to
 $$ \begin{align*}Y^{q^k}=f(X)=\sum_{i=1}^d (X+ir)^m\end{align*} $$
$$ \begin{align*}Y^{q^k}=f(X)=\sum_{i=1}^d (X+ir)^m\end{align*} $$
in
![]() $\mathcal {O}_F^2$
.
$\mathcal {O}_F^2$
.
Proof. With the notation from the statement of Theorem 2.4, we write
 $$ \begin{align*}f(X)=a_0\prod_{j=1}^t (X-a_i)^{n_i},\end{align*} $$
$$ \begin{align*}f(X)=a_0\prod_{j=1}^t (X-a_i)^{n_i},\end{align*} $$
where
![]() $a_1,\ldots , a_t$
are distinct elements of
$a_1,\ldots , a_t$
are distinct elements of
![]() $\kappa $
. The result follows from Theorem 2.4 provided that:
$\kappa $
. The result follows from Theorem 2.4 provided that:
-
(1)
 $t\geq 2$
;
$t\geq 2$
; -
(2) at least two of the exponents
 $n_i$
are not divisible by q.
$n_i$
are not divisible by q.
Note that if
![]() $\ell \nmid \Delta $
, then all roots of
$\ell \nmid \Delta $
, then all roots of
![]() $f(X)$
are distinct in
$f(X)$
are distinct in
![]() $\kappa $
. Hence,
$\kappa $
. Hence,
![]() $n_i=1$
for all i and
$n_i=1$
for all i and
![]() $t=d\geq 2$
. In particular, both of the above conditions are satisfied.
$t=d\geq 2$
. In particular, both of the above conditions are satisfied.
On the other hand, assume that
![]() $q>m$
. Clearly, all values
$q>m$
. Clearly, all values
![]() $n_i$
are less than or equal to
$n_i$
are less than or equal to
![]() $\operatorname {deg} f(X)\leq m$
, and since
$\operatorname {deg} f(X)\leq m$
, and since
![]() $q>m$
, it follows that
$q>m$
, it follows that
![]() $q\nmid n_i$
for all i. It suffices to check that
$q\nmid n_i$
for all i. It suffices to check that
![]() $t\geq 2$
if
$t\geq 2$
if
![]() $d\not \equiv 0,\pm 1 \,\mod {\ell }$
. Suppose not, then
$d\not \equiv 0,\pm 1 \,\mod {\ell }$
. Suppose not, then
![]() $f(X)$
is of the form
$f(X)$
is of the form
![]() $d(X+a)^m$
, for some
$d(X+a)^m$
, for some
![]() $a\in \kappa $
. Expanding
$a\in \kappa $
. Expanding
![]() $f(X)=\sum _{i=1}^d (X+ir)^m$
,
$f(X)=\sum _{i=1}^d (X+ir)^m$
,
 $$ \begin{align*}\begin{split} \sum_{i=1}^d (X+ir)^m &= \sum_{i=1}^d \sum_{j=0}^m {m\choose j} i^{j} r^{j} X^{m-j}\\ &= \sum_{j=0}^m {m\choose j}r^{j}\bigg( \sum_{i=1}^d i^{j}\bigg)X^{m-j}\\ &=d X^m+mr\bigg(\frac{d(d+1)}{2}\bigg)X^{m-1}+{m\choose 2}r^2\bigg(\frac{d(d+1)(2d+1)}{6}\bigg)X^{m-2}+\cdots. \end{split}\end{align*} $$
$$ \begin{align*}\begin{split} \sum_{i=1}^d (X+ir)^m &= \sum_{i=1}^d \sum_{j=0}^m {m\choose j} i^{j} r^{j} X^{m-j}\\ &= \sum_{j=0}^m {m\choose j}r^{j}\bigg( \sum_{i=1}^d i^{j}\bigg)X^{m-j}\\ &=d X^m+mr\bigg(\frac{d(d+1)}{2}\bigg)X^{m-1}+{m\choose 2}r^2\bigg(\frac{d(d+1)(2d+1)}{6}\bigg)X^{m-2}+\cdots. \end{split}\end{align*} $$
Since
![]() $f(X)=d(X+a)^m$
and
$f(X)=d(X+a)^m$
and
![]() $\ell \nmid d$
, we find that
$\ell \nmid d$
, we find that
 $$ \begin{align*}a^j=r^j \bigg( \frac{1}{d}\sum_{i=1}^d i^{\,j}\bigg)\end{align*} $$
$$ \begin{align*}a^j=r^j \bigg( \frac{1}{d}\sum_{i=1}^d i^{\,j}\bigg)\end{align*} $$
for all values of j. In particular,
We thus arrive at the relation
The relation holds in
![]() $\mathbb {Z}/\ell \mathbb {Z}$
. Since
$\mathbb {Z}/\ell \mathbb {Z}$
. Since
![]() $\ell \nmid r$
and
$\ell \nmid r$
and
![]() $d\not \equiv -1\,\mod {\ell }$
by assumption, relation (5.1) gives
$d\not \equiv -1\,\mod {\ell }$
by assumption, relation (5.1) gives
This is not possible since it is assumed that
![]() $d\not \equiv 1\,\mod {\ell }$
. Thus, Theorem 2.4 applies to give the result.
$d\not \equiv 1\,\mod {\ell }$
. Thus, Theorem 2.4 applies to give the result.
Theorem 5.2. Let F be a function field with characteristic
![]() $\ell \geq 5$
and field of functions
$\ell \geq 5$
and field of functions
![]() $\kappa $
. Let
$\kappa $
. Let
![]() $q\neq \ell $
be a prime. Assume that the following conditions are satisfied.
$q\neq \ell $
be a prime. Assume that the following conditions are satisfied.
-
(1) All roots of
 $f(X)$
are contained in
$f(X)$
are contained in
 $\kappa $
.
$\kappa $
. -
(2)
 $\ell \nmid r$
.
$\ell \nmid r$
. -
(3) At least one of the following conditions are satisfied:
-
(a)
 $\ell \nmid \Delta $
;
$\ell \nmid \Delta $
; -
(b)
 $q>m$
and
$q>m$
and
 $d\not \equiv 0,\pm 1\,\mod {\ell }$
.
$d\not \equiv 0,\pm 1\,\mod {\ell }$
.
-
Let p be any prime number. Then the following assertions hold.
-
(i) If
 $p\neq q$
, then for all large enough values of
$p\neq q$
, then for all large enough values of
 $k>0$
, there are no nonconstant solutions to
$k>0$
, there are no nonconstant solutions to
 $Y^{q^k}=f(X)$
in
$Y^{q^k}=f(X)$
in
 $\mathcal {O}_\infty ^{(p)}$
.
$\mathcal {O}_\infty ^{(p)}$
. -
(ii) If
 $p=q$
and
$p=q$
and
 $p\nmid h_F$
, then there are no nonconstant solutions to
$p\nmid h_F$
, then there are no nonconstant solutions to
 $Y^p=f(X)$
in
$Y^p=f(X)$
in
 $\mathcal {O}_\infty ^{(p)}$
.
$\mathcal {O}_\infty ^{(p)}$
.
Proof. It follows from the proof of Theorem 5.1 that the conditions of Theorem 3.2 are satisfied, and thus the result follows.
Theorem 5.3. Let K be a field of characteristic
![]() $\ell \geq 5$
and let A be the polynomial ring
$\ell \geq 5$
and let A be the polynomial ring
![]() $K[T_1, \ldots , T_r]$
. Let
$K[T_1, \ldots , T_r]$
. Let
![]() $q\neq \ell $
be a prime. Assume that the following conditions are satisfied.
$q\neq \ell $
be a prime. Assume that the following conditions are satisfied.
-
(1) All roots of
 $f(X)$
are contained in K.
$f(X)$
are contained in K. -
(2)
 $\ell \nmid r$
.
$\ell \nmid r$
. -
(3) At least one of the following conditions are satisfied:
-
(a)
 $\ell \nmid \Delta $
;
$\ell \nmid \Delta $
; -
(b)
 $q>m$
and
$q>m$
and
 $d\not \equiv 0,\pm 1\,\mod {\ell }$
.
$d\not \equiv 0,\pm 1\,\mod {\ell }$
.
-
Then any solution
![]() $(X,Y)\in A^2$
to
$(X,Y)\in A^2$
to
is constant, that is, X and Y are both in K.