Hostname: page-component-669899f699-g7b4s Total loading time: 0 Render date: 2025-04-26T18:33:33.168Z Has data issue: false hasContentIssue false
  • English
  • Français

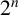A PROOF OF HIRSCHHORN’S CONJECTURE ON $2^n$-DISSECTION OF EULER’S PRODUCT

Part of: Sequences and sets Combinatorics

Published online by Cambridge University Press:  08 October 2024

BIPUL KUMAR SARMAH Open the ORCID record for BIPUL KUMAR SARMAH [Opens in a new window]  and
SATYAJIT GAYAN Open the ORCID record for SATYAJIT GAYAN [Opens in a new window]
BIPUL KUMAR SARMAH*
Affiliation:
Department of Mathematical Sciences, Tezpur University, Napaam 784028, Sonitpur, Assam, India
SATYAJIT GAYAN
Affiliation:
Department of Mathematical Sciences, Tezpur University, Napaam 784028, Sonitpur, Assam, India e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Using properties of Ramanujan’s theta functions, we give an elementary proof of Hirschhorn’s conjecture on 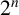$2^n$-dissection of Euler’s product 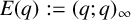$E(q):=(q;q)_\infty $.

Keywords

Euler’s productdissectionRamanujan’s theta functions

MSC classification

Primary: 05A30: $q$-calculus and related topics
Secondary: 11B65: Binomial coefficients; factorials; $q$-identities
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 111 , Issue 2 , April 2025 , pp. 186 - 196
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Berndt, B. C., Ramanujan’s Notebooks, Part III (Springer-Verlag, New York, 1991).CrossRefGoogle Scholar
Berndt, B. C., Number Theory in the Spirit of Ramanujan (American Mathematical Society, Providence, RI, 2006).CrossRefGoogle Scholar
Cao, Z., ‘Integer matrix exact covering systems and product identities for theta functions’, Int. Math. Res. Not. IMRN 2011 (2011), 4471–4514.Google Scholar
Evans, R. J., ‘Theta function identities’, J. Math. Anal. Appl. 147(1) (1990), 97–121.CrossRefGoogle Scholar
Hirschhorn, M. D., The Power of $q$ , Developments in Mathematics, 49 (Springer, Cham, 2017).Google Scholar
McLaughlin, J., ‘ $m$ -Dissections of some infinite products and related identities’, Ramanujan J. 59 (2022), 313–350.CrossRefGoogle Scholar
Ramanathan, K. G., ‘Generalisations of some theorems of Ramanujan’, J. Number Theory 29(2) (1988), 118–137.CrossRefGoogle Scholar