I. INTRODUCTION
State-of-the-art lossless image compression algorithms, such as, JPEG-LS [Reference Weinberger, Seroussi and Sapiro1], CALIC [Reference Wu and Memon2], and EDP [Reference Li and Orchard3], have been proposed in the context-adaptive predictive coding framework. The essential components of the framework are prediction followed by entropy coding of the resulting residuals. In the framework, an image is encoded in a predefined order, such as, the raster scan order. It relies on the observation that the intensity value of a pixel is highly correlated with its previously encoded neighboring pixels and thus they can be used to make an effective prediction for the current pixel. The beneficial effect of prediction is that the zero-order entropy of the residual is significantly lower than that of the original image. Therefore, encoding of the residuals, instead of the original images, using entropy coding, such as Huffman codes and arithmetic codes, yields better compression in practice.
Entropy coding of the residuals requires knowledge of their probability distribution. It can be observed that the distribution of residuals depends on the image's activity level, e.g., edginess and smoothness, around the pixel to be coded. Therefore, in the context-based adaptive coding framework, instead of using the same distribution throughout the entire image, probability distributions are chosen adaptively based on image activity around the pixels. The pixels which are used to determine the level of activity of the image in the vicinity of the current pixel form the causal neighborhood template for context modeling. The template for prediction and context modeling need not be the same.
Let I be an image of size M×N and the elements of I take values from the set
![]() $A = \{0, 1, \ldots, \alpha-1\}$
, i.e.,
$A = \{0, 1, \ldots, \alpha-1\}$
, i.e.,
where v i, j ∈A. Let a context modeling scheme yield K different contexts. A lower empirical entropy can be achieved with a large value of K. However, the saving in entropy comes with an associated model cost, which is proportional to K. More specifically, in coding the n=M×N pixels, the per-symbol asymptotic model cost is lower bounded by the followingFootnote 1 [Reference Rissanen4],
To efficiently exploit the spatial correlation, an effective context modeling scheme needs to include a sufficient number of neighboring pixels in the template. However, when the alphabet size is large such as that in eight-bit grayscale images, straightforward use of the pixel intensities or gradients in the template to label a context leads to the context dilution problem [Reference Rissanen4–Reference Rissanen6]. Context dilution refers to the fact that the count statistics are spread out among too many contexts, which affects the accuracy of probability estimates. Thus, the saving in the entropy term is outweighed by the associated model cost if too many contexts are used to closely model the image statistics. For example, let us consider a simple model for context determination where the values of four neighboring pixels determine the context of a pixel. For eight-bit grayscale images, then the total number of possible contexts is 2564. Apart from the prohibitive storage requirement, images do not contain sufficient number of pixels to reliably estimate the probability distribution of pixel intensities in all those contexts.
To address this problem of context dilution, the schemes proposed in the literature rely on quantization to reduce the number of contexts. These schemes essentially determine the context of a pixel based on quantized gradients computed from the causal neighborhood template. For example, context determination in JPEG-LS involves separate non-linear quantization of three local gradients followed by merging of contexts of opposite signs which results in 365 different contexts. On the other hand, CALIC relies on an error energy term, which is the weighted sum of the absolute values of seven local gradients. To compute the context of a pixel, CALIC non-linearly quantizes the error energy term which yields eight different contexts. In the absence of a systematic approach, the context models proposed in the literature have been designed using ad-hoc techniques based on extensive experimentation.
Quantization of local gradients only reduces the number of contexts K. However, the alphabet size α can still significantly contribute to the overall model cost, especially when α is large. For a b-bit image, we need to estimate the probabilities of 2 b different values in each context. Thus, even for eight-bit images, the alphabet size is considered very large. Therefore, JPEG-LS takes a parametric approach, while CALIC resorts to a tail truncation technique, to address the issue of large alphabet size. JPEG-LS uses a parametric distribution to approximate the probability distribution of the residuals. More specifically, it uses the two-sided geometric distribution (TSGD) [Reference Merhav, Seroussi and Weinberger7], which can be specified by only two parameters, to model the distribution of residuals. Thus, instead of estimating the probabilities of all possible values of the residuals, it needs to estimate the values of only two parameters to completely specify a particular TSGD. In contrast, CALIC directly encodes the value of a residual if it is within a pre-specified range, otherwise it encodes an escape symbol followed by the original value.
It follows from the above discussion that context models proposed in the literature have been designed mostly in an ad-hoc fashion. In contrast, we take an alternative approach where we fix a simple context model and then rely on a systematic technique to exploit more complex correlations to achieve efficient compression. The essential idea is to reduce the alphabet size to the minimum, i.e., to binary. Clearly this requires efficient binary representation of the image as bitmaps that preserve the spatial correlation. The proposed scheme then relies on a simpler template for context determination which includes only the unit vectors from the three-dimensional (3D) volume of bitmaps resulting from the binarization step. Although, the minimal context is very efficient in exploiting the correlation in smooth regions, it is less effective in capturing more complex correlations. Therefore, we propose a recursive scheme to efficiently exploit more complex correlations. The idea is to partition a bitmap into two rectangular smaller blocks such that the context-conditioned entropy of the resulting blocks are less than the context-conditioned entropy of the original bitmap. The resulting rectangular blocks are then recursively partitioned until further partitioning of a block does not decrease the context-conditioned entropy.
The idea of efficient binarization that translates an image's spatial correlation into spatial homogeneity and inter bit plane correlation in the resulting bitmaps was initially proposed in [Reference Ali, Murshed, Shahriyar and Paul8]. In this paper, we extend the idea as follows. Firstly, we demonstrate that the use of average value of the residuals, instead of the mid value of the alphabet, in inducing the hierarchical decomposition (HD) of the residual alphabet provides a more effective binarization of the residual images. Secondly, as opposed to the complex context used in [Reference Ali, Murshed, Shahriyar and Paul8], we argue that a simple context model is effective in exploiting the spatial homogeneity and inter bit plane correlation in the bitmaps resulting from the binarization step. Thirdly, we refine the idea of the bitmap encoding algorithm originally proposed in [Reference Ali, Murshed, Shahriyar and Paul8]. More specifically, instead of using the suboptimal polarization heuristic, we propose using Rissanen lower bound to decide on the partition boundaries in isolating blocks within which statistical correlation remains stationary. Finally, we present extensive experimental results to analyze the performances of different variants of the proposed scheme. Some preliminary results of this research were published in [Reference Ali, Murshed, Shahriyar and Paul8].
The organization of rest of the paper is as follows. In Section II, we compare and contrast two binarization schemes. We present a bitmap encoding scheme that can efficiently exploit the spatial correlation present in a binary image in Section III. In Section IV, we present the experimental results to demonstrate the efficacy of the proposed scheme. Finally, we conclude the paper in Section V.
II. BINARIZATION
The main motivation for maximal reduction of the alphabet size to binary comes from the expectation that it would greatly simplify the subsequent context modeling and entropy coding stages. However, to effectively address the context dilution problem, a binarization scheme is required to exhibit two important characteristics. Firstly, a binarization scheme should not incur any loss of information. Secondly, the spatial correlation that exists among non-binary symbols in an image should be captured as the correlation among few bit positions in the bitmaps. The first characteristic is, indeed, satisfied by any binarization scheme that maps each of the non-binary symbols from the alphabet to a unique binary codeword. For a one-to-one mapping, the probabilities of non-binary symbols can be computed from their binary representations according to the total probability theorem [Reference Papoulis and Pillai9,Reference Marpe, Schwarz and Wiegand10]. However, the second requirement warrants more explanation. In the rest of this section, we discuss two different approaches to binarization to highlight the importance of the second requirement in addressing the problem of context dilution.
A) Bit plane decomposition (BPD)
Let I be an image as defined (1). Let
![]() $v_{i,j,k} \in \{ 0, 1\}$
be the kth significant bit in the b-bit binary representation of v
i, j
. Then, the BPD of I results in b bitmaps
$v_{i,j,k} \in \{ 0, 1\}$
be the kth significant bit in the b-bit binary representation of v
i, j
. Then, the BPD of I results in b bitmaps
![]() $I_{0}, I_{1}, \ldots, I_{b-1}$
. Clearly, the kth bit plane,
$I_{0}, I_{1}, \ldots, I_{b-1}$
. Clearly, the kth bit plane,
![]() $k = 0, \ldots, b - 1$
, is defined as
$k = 0, \ldots, b - 1$
, is defined as
Now, encoding of I requires us to encode the bit planes
![]() $I_{0}, I_{1}, \ldots, I_{b - 1}$
in a particular order. Although this representation is simple, the spatial correlations among the pixels are not translated into correlations among the adjacent bit planes. Thus, effective exploitation of the spatial correlation requires that encoding of a bit plane be conditioned on all previously encoded bit planes. This, in turn, requires that the template for context determination should include neighboring bits from multiple bit planes. However, the number of context K increases exponentially with the size of the template. Therefore, the straightforward BPD scheme can lead to the context dilution problem. On the other hand, if a simple context model includes only few neighboring bits from adjacent bit planes then it exploits the spatial correlation only partially.
$I_{0}, I_{1}, \ldots, I_{b - 1}$
in a particular order. Although this representation is simple, the spatial correlations among the pixels are not translated into correlations among the adjacent bit planes. Thus, effective exploitation of the spatial correlation requires that encoding of a bit plane be conditioned on all previously encoded bit planes. This, in turn, requires that the template for context determination should include neighboring bits from multiple bit planes. However, the number of context K increases exponentially with the size of the template. Therefore, the straightforward BPD scheme can lead to the context dilution problem. On the other hand, if a simple context model includes only few neighboring bits from adjacent bit planes then it exploits the spatial correlation only partially.
Gray codes: An alternative to binary representation of non-negative integers is Gray codes. Gray codes, which ensure that the binary representation of consecutive non-negative integers do not differ in more than one bit positions, are expected to enhance the correlations among adjacent bit planes as compared with simple binary representation. However, prediction is an integral part of state-of-the-art lossless image compression framework. It is well known that the distributions of the prediction residuals in images are highly peaked at 0 that can be closely modeled with Laplace distributions [Reference Howard and Vitter11]. When the residuals are mapped to non-negative integers using Rice mapping or signed-magnitude representation, the resulting non-negative integers mostly follow geometric distribution [Reference Weinberger, Seroussi and Sapiro1]. According to geometric distribution, probabilities of smaller non-negative integers are much higher than those of larger non-negative integers. Now, in binary representation of smaller non-negative integers, 1’s appear only in lower bit positions. On the other hand, in Gray codes, 1’s can appear in higher bit positions even for smaller non-negative integers. Thus, the bit planes, resulting from the binary representation of the residuals, exhibit more spatial homogeneity than those resulting from Gray codes. Therefore, Gray codes, which enhances the inter bit plane correlation, effectively achieve negligible compression gain in practice when compared against straightforward BPD as demonstrated in Section IV.
Although the above BPD schemes do not satisfy the second requirement, they enable us to use binary arithmetic coding (BAC) for entropy encoding. Implementation of BAC is computationally much simpler as compared with general α-ary arithmetic coding. Encoding of a symbol in an adaptive α-ary arithmetic codec requires at least two multiplications, in addition to several computationally complex operations to update the estimates of probabilities. In contrast, there are several fast multiplication-free implementations for BAC [Reference Marpe, Schwarz and Wiegand10].
B) Hierarchical decomposition
The essential idea of HD is to recursively divide the alphabet of an image [Reference Pinho and António12]. The recursive division process naturally induces a binary tree where the value associated with a node represents the division boundary. During the process of division a bitmap can also be associated with the corresponding node. The bits in a bitmap represents whether the intensities of the corresponding pixels in the image are larger than the value associated with the node. Then, the binary tree and the bitmaps associated its the nodes provide a binary decomposition of the original image.
Let I be an image as defined in (1). Now, the alphabet A of I can be decomposed using a binary tree as follows. Let us associate with each node of the tree a set of integers
![]() $S = \{s_{0}, \ldots, s_{\beta-1} \} \subseteq A$
. Initially S=A is associated with the root of the binary tree. Let us divide S into two sets [s
0, t] and
$S = \{s_{0}, \ldots, s_{\beta-1} \} \subseteq A$
. Initially S=A is associated with the root of the binary tree. Let us divide S into two sets [s
0, t] and
![]() $[t+1, s_{\beta}-1]$
. Then, the division boundary t is associated with the node. Let us also associate with the node a bitmap B,
$[t+1, s_{\beta}-1]$
. Then, the division boundary t is associated with the node. Let us also associate with the node a bitmap B,
where b
i, j
=0, if
![]() $x_{i,j} \in [s_{0},t]$
and b
i, j
=1, if
$x_{i,j} \in [s_{0},t]$
and b
i, j
=1, if
![]() $x_{i,j} \in [t+1, s_{\beta}-1]$
. In the next step, the node is expanded into two child nodes. The set of integers S associated with the node is then divided into two subsets
$x_{i,j} \in [t+1, s_{\beta}-1]$
. In the next step, the node is expanded into two child nodes. The set of integers S associated with the node is then divided into two subsets
![]() $S_{l} = \{s_{0}, \ldots, t\}$
and
$S_{l} = \{s_{0}, \ldots, t\}$
and
![]() $S_{r} = \{t + 1, \ldots, s_{\beta-1}\}$
and are assigned to the left and right child nodes, respectively. The procedure is repeated at the child nodes until the cardinality of the set of non-negative integers associated with a node becomes less than 3. These leaf nodes are not expanded as the values of the pixels, corresponding to these nodes, can be uniquely determined from the associated bitmaps.
$S_{r} = \{t + 1, \ldots, s_{\beta-1}\}$
and are assigned to the left and right child nodes, respectively. The procedure is repeated at the child nodes until the cardinality of the set of non-negative integers associated with a node becomes less than 3. These leaf nodes are not expanded as the values of the pixels, corresponding to these nodes, can be uniquely determined from the associated bitmaps.
Encoding order for the bitmaps and “don't care”: Now, for lossless coding of an image, both the binary tree and the bitmaps associated with its nodes must be coded in a predefined order. If the tree and the associated bitmaps are encoded in pre-order, i.e., root-left–right order, then we do not need to encode all the bits from the bitmaps associated with the child nodes. Let
![]() $B_{\rm root}$
be the bitmap associated with the root node. Now,
$B_{\rm root}$
be the bitmap associated with the root node. Now,
![]() $B_{\rm root}$
represents information about all the elements in I. More specifically, if at the root node, the alphabet A is split at t, then 0’s in
$B_{\rm root}$
represents information about all the elements in I. More specifically, if at the root node, the alphabet A is split at t, then 0’s in
![]() $B_{\rm root}$
denotes that the value of the elements at corresponding positions in I are less than or equal to t and 1’s indicate that they are larger than t. In pre-order traversal of the tree, the value and the bitmap associated with the root node must be encoded first followed by pre-order encoding of the left and right sub-trees, respectively. Let
$B_{\rm root}$
denotes that the value of the elements at corresponding positions in I are less than or equal to t and 1’s indicate that they are larger than t. In pre-order traversal of the tree, the value and the bitmap associated with the root node must be encoded first followed by pre-order encoding of the left and right sub-trees, respectively. Let
![]() $B_{\rm left}$
and
$B_{\rm left}$
and
![]() $B_{\rm right}$
be the bitmaps associated with the left and right child nodes of the root node, respectively. Since during the encoding of the bitmap
$B_{\rm right}$
be the bitmaps associated with the left and right child nodes of the root node, respectively. Since during the encoding of the bitmap
![]() $B_{\rm left}$
, the bitmap
$B_{\rm left}$
, the bitmap
![]() $B_{\rm root}$
is already encoded, we need to consider only the positions of 0’s in
$B_{\rm root}$
is already encoded, we need to consider only the positions of 0’s in
![]() $B_{\rm root}$
. The rest of the positions in
$B_{\rm root}$
. The rest of the positions in
![]() $B_{\rm root}$
can thus be considered as “don't care”. Similarly, only the positions of 1’s in
$B_{\rm root}$
can thus be considered as “don't care”. Similarly, only the positions of 1’s in
![]() $B_{\rm root}$
should be considered during the encoding of
$B_{\rm root}$
should be considered during the encoding of
![]() $B_{\rm right}$
.
$B_{\rm right}$
.
Encoding of residual: Although the binarization schemes, discussed above, can directly operate on the original images, our experimental results demonstrated that encoding of the prediction residuals is more efficient than that of the original images. This is due to the fact that, for natural images, the zero-order entropy of the residual is usually significantly lower than that of the original image. Besides, prediction significantly enhances the spatial homogeneity in the residual images, which can be efficiently exploited by the bitmap coding algorithm presented in Section III.
Example: Figure 1 shows the bitmaps resulting from the binarization of Image 6 from the Kodak test set [13] using the above two schemes. For prediction, we used the median edge detector (MED) predictor from JPEG-LS. The binarization step requires that the residual be mapped to non-negative integers. In the figure, we have used the signed-magnitude representation of the residuals. It follows from the figure that spatial homogeneity in the magnitude image is significantly higher than that in the original image. BPD of residual magnitudes results in seven bit planes. Spatial correlation within the bit planes gradually decreases from the most significant bit plane to the least significant bit plane. To binarize the residual magnitude image using the HD technique, we used the average magnitude as the division boundary. Figure 1(d) shows the resulting binary tree and the bitmaps associated with the nodes up to depth 2. In the bitmaps, the “don't care” positions are shown in red.

Fig. 1. Binarization of grayscale version of Image 6 from the Kodak test set [13]: (a) the original image; (b) signed-magnitude representation of the residuals where the MED predictor from JPEG-LS [1] was used for prediction; (c) binarization of the residual magnitudes using BPD; and (d) binarization of the residual magnitudes using the HD technique. While binarization using BPD yields seven bit planes, HD results in a binary tree. Associated with each node of the tree is a value and a bitmap. The 0’s (black pixels) in the bitmap denote that residual magnitudes at corresponding positions are less than or equal to the value associated with the node, while 1’s (white pixels) denote that they are larger than that. In the bitmaps, the red pixels denote “don't care” positions.
It may appear that with HD we need to encode many more bits than with BPD. However, it follows from Fig. 1(d) that in the bitmaps associated with the nodes, other than the root node, most of the positions are “don't care”. Indeed, if the tree is completely balanced, the number of bits encoded with HD is the same as that encoded with BPD. However, HD has the advantage that if there exists significant spatial correlation among the neighboring pixels, then the bitmaps are expected to exhibit a strong clustering tendency. Besides, if the value associated with a node is chosen judiciously, the spatial correlation among the neighboring pixels is expected to be captured as the correlation between the bitmaps associated with the parent node and the child node. Thus, a simpler context model, that includes only adjacent bits from the same bitmap and from that associated with the parent node, is expected to efficiently exploit the spatial correlation that exists in the original image.
III. BITMAP CODING WITH RECURSIVE PARTITIONING (BCRP)
For lossless compression of an image, all the bitmaps resulting from the binarization stage must be encoded. For a given context model, each of the bitmaps can be encoded independently using the context adaptive binary arithmetic coding (CABAC) [Reference Marpe, Schwarz and Wiegand10]. However, it is well known that the statistical properties do not remain the same throughout an entire image. Although an effective template for context determination can model the higher-order dependency among the neighboring pixels, the pattern of correlation usually varies over a natural image. To account for this non-stationarity of image statistics, the schemes proposed in the literature usually give larger weight to immediate past than the remote past. For example, both JPEG-LS and CALIC periodically reset the values of the variables used for statistical learning, instead of continuously updating them. When the number of samples in a context attains a predetermined threshold, they halve the values of the variables associated with that context. In contrast to this approach, we proposed a bitmap encoding algorithm that recursively partitions a bitmap into rectangular blocks, which are then encoded using CABAC. The motivation for partitioning is to explicitly identify the blocks within which the statistical correlations remain stationary.
Let U and V be correlated bitmaps of dimension M×N,
Let U be the bitmap to be encoded and V be the bitmap available both at the encoder and the decoder. The objective is to efficiently encode U, by exploiting its spatial correlation and the correlation that exists between U and V.
To keep the model cost to a minimum, we choose the simplest model that includes only three bits, one bit from each of the dimensions X, Y, and Z (see Fig. 1(c)), in the template for context determination. More specifically, the context of a bit u
i, j
is determined using previously encoded three neighboring bits u
i, j−1, u
i−1, j
and v
i, j
. However, instead of encoding the whole bitmap based on this context, we recursively partition U into rectangular blocks and encode each block independently based on this context using CABAC. We denote this scheme by BCRP–CABAC in this paper. The partitioning information, which also needs to be encoded, can be represented efficiently with a binary tree. Let Δ be the current block of dimension h×w encompassing a rectangular block of pixels from U. Initially Δ=U. The block Δ of size
![]() $\eta = h \times w$
can be split in h−1, and w−1 ways along the Y- and X-axes, respectively. Let a split s form two sub-blocks Δ1 and Δ2 with η1 and η2 elements, respectively. Now, this partition can lead to a saving in bits if the total number of bits required to independently encode Δ1 and Δ2, along with the overhead of encoding the partitioning information, is less than that required to encode Δ.
$\eta = h \times w$
can be split in h−1, and w−1 ways along the Y- and X-axes, respectively. Let a split s form two sub-blocks Δ1 and Δ2 with η1 and η2 elements, respectively. Now, this partition can lead to a saving in bits if the total number of bits required to independently encode Δ1 and Δ2, along with the overhead of encoding the partitioning information, is less than that required to encode Δ.
Instead of explicitly encoding and then computing the bits required to encode a block, which is computationally intensive, we rely on a heuristic. The tree that induces the partitioning is thus constructed by a simple recursive algorithm with a greedy optimization heuristic. In [Reference Ali, Murshed, Shahriyar and Paul8], we proposed the polarization heuristic for partitioning decisions. Let ℓ, ℓ1, and ℓ2 be the number of 0’s in Δ, Δ1, and Δ2, respectively. Then, polarization of 0−1 elements by the split s is defined as
Then, the optimization objective was to find the split s* that maximize the 0−1 polarization. The motivation for the polarization heuristic was to isolate homogeneous blocks of 0’s (Type I) or 1’s (Type II). Since these nodes can be completely decoded from its type, no further information is required to be encoded. Although, this heuristic accurately measures the number of bits required to encode a completely homogeneous block, it cannot reliably estimate the number of bits required to encode a non-homogeneous block. Thus, in this paper, we propose to use the Rissanen lower bound [Reference Rissanen4] as the heuristic, which includes both the context-conditioned entropy and the model cost. Let C U be the context map of U,
where c
i, j
is the context label of u
i, j
computed according to the template
![]() $[u_{i,j-1}, u_{i-1,j}, v_{i,j}]$
. Then according to the Rissanen lower bound, the expected number of bits to encode Δ is bounded by the following:
$[u_{i,j-1}, u_{i-1,j}, v_{i,j}]$
. Then according to the Rissanen lower bound, the expected number of bits to encode Δ is bounded by the following:
where
![]() $H(\Delta \vert C_{\Delta})$
is the context-conditioned entropy of Δ and K is the total number of possible context labels. For our simple context model, specified by the template
$H(\Delta \vert C_{\Delta})$
is the context-conditioned entropy of Δ and K is the total number of possible context labels. For our simple context model, specified by the template
![]() $[u_{i,j-1}, u_{i-1,j}, v_{i,j}]$
, we have K=8. In our proposed technique, we use (9) with equality as the heuristic, i.e.,
$[u_{i,j-1}, u_{i-1,j}, v_{i,j}]$
, we have K=8. In our proposed technique, we use (9) with equality as the heuristic, i.e.,
Given that H Δ is a reliable estimate for the total number of bits required to encode Δ, the bit saving achieved by the split s can be measured as
Then, our objective is to find the split s* that maximize the bit savings,
If
![]() $\gamma_{s^*} \lt 0$
, it is expected that the bits required to independently encode the sub-blocks is greater than that required to encode the current block. This, in turn, suggests terminating further partitioning of Δ. In that case, the block is classified as a Type III leaf node. On the other hand,
$\gamma_{s^*} \lt 0$
, it is expected that the bits required to independently encode the sub-blocks is greater than that required to encode the current block. This, in turn, suggests terminating further partitioning of Δ. In that case, the block is classified as a Type III leaf node. On the other hand,
![]() $\gamma_{s^{\ast}} \gt 0$
indicates that the split is expected to yield better compression. Thus, if
$\gamma_{s^{\ast}} \gt 0$
indicates that the split is expected to yield better compression. Thus, if
![]() $\gamma_{s^{\ast}} \gt 0$
, the partition decision is retained and the resulting blocks Δ1 and Δ2 are then recursively partitioned. A split (non-leaf) node is classified into either Type Y or Type X depending on whether the optimal split is found along Y- or X-axes, respectively.
$\gamma_{s^{\ast}} \gt 0$
, the partition decision is retained and the resulting blocks Δ1 and Δ2 are then recursively partitioned. A split (non-leaf) node is classified into either Type Y or Type X depending on whether the optimal split is found along Y- or X-axes, respectively.
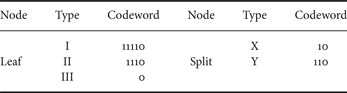
Encoding of the syntax elements: The entire tree is encoded in the pre-order depth-first traversal sequence where the root of the tree is encoded first, then recursively the left sub-tree, and finally, recursively the right sub-tree. During encoding of the tree, the type of each node is encoded using the Huffman codes shown in Table 1 that were found by analyzing the probability of each type in the test set. For nodes of Types Y and X, we need to encode the split position as well. In the proposed scheme, the split positions are first encoded using fixed-length codes. If the optimal split is found at position
![]() $l \in \{1,\ldots,P - 1\}$
, where P is the range of the block's dimension along the optimal axis, l is encoded using
$l \in \{1,\ldots,P - 1\}$
, where P is the range of the block's dimension along the optimal axis, l is encoded using
![]() $\lfloor \log_{2}(P-1) \rfloor +1$
bits.
$\lfloor \log_{2}(P-1) \rfloor +1$
bits.
Table 1. Huffman codes for the syntax elements.
Example: Figure 2 presents the partitions achieved by the proposed algorithm on the bitmap associated with the left node of the root node in Fig. 1(d). It follows from the figure that the statistical properties within the blocks do not change significantly, while that between the adjacent blocks are significantly different. This demonstrates the ability of the proposed scheme in separating the blocks according to the stationarity of the correlation statistics. It also follows from the figure the important role that the “don't care” positions play in the partitioning and encoding algorithm. “Don't care” positions greatly facilitate the isolation of Type I (all 0’s) and Type II (all 1’s) blocks.

Fig. 2. Partitioning of the bitmap, associated with the left node of the root node in Fig. 1(d), achieved by the proposed bitmap encoding algorithm.
The overall scheme: The overall scheme, based on the idea of binarization and recursive bitmap partitioning, is depicted in Fig. 3. The scheme consists of three stages: prediction, binarization, and bitmap encoding. In the prediction stage, each of the pixels is predicted, in raster scan order, from previously encoded neighborhood pixels. Then the residual is represented in signed-magnitude form. The magnitude map is then binarized using either BPD or HD schemes presented in Section II. Finally, the sign bitmap and bitmaps are encoded using the BCRP–CABAC algorithm presented above.

Fig. 3. Conceptual block diagram of the proposed scheme. The scheme essentially consists of three stages: prediction, binarization, and bitmap coding. The stages are decoupled in the sense that one is free to choose the specific techniques to be used in those stages. For example, we can choose to use JPEG-LS predictor, HD binarization scheme, and BCRP–CABAC algorithm in prediction, binarization, and bitmap coding stages, respectively.
IV. EXPERIMENTAL RESULTS
We evaluated the performance of the proposed coding scheme on the 24 eight-bit grayscale version of Kodak images [13]. The images are of sizes
![]() $768 \times 512$
or
$768 \times 512$
or
![]() $512 \times 768$
. In the prediction stage of our scheme, we used the MED predictor from JPEG-LS. Therefore, we compare our performance against JPEG-LS, to demonstrate the efficiency of the proposed scheme.
$512 \times 768$
. In the prediction stage of our scheme, we used the MED predictor from JPEG-LS. Therefore, we compare our performance against JPEG-LS, to demonstrate the efficiency of the proposed scheme.
After prediction, the binarization step requires mapping the residuals to non-negative integers. In the proposed scheme, we relied on the signed-magnitude representation of the residuals. The 0’s and 1’s in the sign bitmap denote that the corresponding residuals are non-negative (≥0) and negative (<0), respectively. Thus, the spatial homogeneity in the magnitude image can be slightly improved by decreasing the magnitudes of the negative residuals by one. After decoding of the sign bitmap, the actual magnitudes of the negative residuals can be recovered by increasing their values by one. The magnitude images were then binarized into a set of bitmaps. We experimented with both BPD and HD schemes for binarization. After binarization, the bitmaps were encoded using the BCRP–CABAC algorithm presented in Section III. For both of the binarization schemes, encoding of sign bitmaps followed the encoding of the bitmaps resulting from the binarization of residual magnitudes.
A) BPD binarization
Let R be a magnitude image. Let
![]() $R_{0}, R_{1}, \ldots, R_{L}$
be the bit planes resulting from the binarization of R using either simple binary representation or Gray codes. For b-bit grayscale images, we can reduce a residual, modulo 2
b
, to a value in the range
$R_{0}, R_{1}, \ldots, R_{L}$
be the bit planes resulting from the binarization of R using either simple binary representation or Gray codes. For b-bit grayscale images, we can reduce a residual, modulo 2
b
, to a value in the range
![]() $[-2^{b-1}, 2^{b-1}-1]$
[Reference Weinberger, Seroussi and Sapiro1]. Since, the images in the test set are eight-bit grayscale images, clearly we have L=6. For a BPD-based binarization, the bit planes are encoded in order from most significant bit plane to least significant bit plane. Now, let H(R
k
|Y, X) denotes the context-conditioned entropy of the bit plane R
k
, where the context of the bit r
i, j, k
is determined using two previously encoded adjacent bits along Y and X axes, i.e.,
$[-2^{b-1}, 2^{b-1}-1]$
[Reference Weinberger, Seroussi and Sapiro1]. Since, the images in the test set are eight-bit grayscale images, clearly we have L=6. For a BPD-based binarization, the bit planes are encoded in order from most significant bit plane to least significant bit plane. Now, let H(R
k
|Y, X) denotes the context-conditioned entropy of the bit plane R
k
, where the context of the bit r
i, j, k
is determined using two previously encoded adjacent bits along Y and X axes, i.e.,
![]() $[r_{i-1,j,k}, r_{i,j-1,k}]$
. Similarly, let H(R
k
|Z) and
$[r_{i-1,j,k}, r_{i,j-1,k}]$
. Similarly, let H(R
k
|Z) and
![]() $H(R_{k}\vert Z,Y,X)$
denote the context-conditioned entropies of R
k
, where [r
i, j, k+1] and
$H(R_{k}\vert Z,Y,X)$
denote the context-conditioned entropies of R
k
, where [r
i, j, k+1] and
![]() $[r_{i,j,k-1}, r_{i-1,j,k}, r_{i,j-1,k}]$
are used for context determination, respectively.
$[r_{i,j,k-1}, r_{i-1,j,k}, r_{i,j-1,k}]$
are used for context determination, respectively.
In Fig. 4, we show the average context-conditioned entropies of the bit planes for different context models. In the figure, we compare the performance of simple binary representation against two variants of Gray codes: 128-PAM and 128-QAM [Reference Agrell, Lassing, Ström and Ottosson14]. It follows from Fig. 4(a) that, the first-order entropies of the bit planes resulting from simple binary representation is less than those resulting from both variants of Gray codes. Usage of the context models [Y, X] and [Z] lowered the entropies of the bit planes for all the three BPD schemes. We argued in Section II-A that while Gray codes slightly enhance the inter bit plane correlation, they affect the spatial correlation within the bit planes. Therefore, when the context model [Y, X] was used, the BPD scheme based on simple binary representation performed better than those based on 128-PAM and 128-QAM. In contrast, 128-QAM-based BPD performed best when the context model [Z] was used. Finally, in case of the context model [Z, Y, X], 128-QAM outperformed both binary representation and 128-PAM only marginally. In the rest of the paper, we only consider the context model [Z, Y, X] for any BPD-based scheme. Between the two variants of Gray codes, we used 128-QAM due to its superior performance against 128-PAM.

Fig. 4. Context conditioned entropies of different bit planes achieved by different BPD schemes using the context models: (a) First-order entropy; (b) [X, Y]=[r
i−1, j, k
, r
i, j−1, k
]; (c) [Z]=[r
i, j, k−1]; and (d)
![]() $[X,Y,Z] = [r_{i,j,k-11,r_{i-1,j,k}, r_{i,j-1,k}}]$
.
$[X,Y,Z] = [r_{i,j,k-11,r_{i-1,j,k}, r_{i,j-1,k}}]$
.
In Table 2, we show the compression rates achieved with the proposed BCRP–CABAC scheme where the BPD method was used in the binarization stage. To demonstrate the beneficial effect of BCRP–CABAC over CABAC, in Table 2, we compare the compression rates achieved by BPD–CABAC and BPD–BCRP–CABAC. While BPD–CABAC encodes the bit planes as a whole using CABAC, in BPD–BCRP–CABAC, bit planes are encoded using BCRP–CABAC. It follows from the table that BPD–BCRP–CABAC is consistently superior to BPD–CABAC achieving a bit-rate saving of 4.6%.
Table 2. Compression rates (bits/pixel) achieved by different schemes on the Kodak grayscale images [13]. BPD–CABAC refers to the scheme where the bit planes resulting from BPD are encoded using CABAC, while BPD–BCRP–CABAC denotes the scheme where those bit planes are encoded using BCRP-CABAC. BPDG–CABAC and BPDG–BCRP–CABAC are variants of BPD–CABAC and BPD–BCRP–CABAC where Gray codes are used for binarization of the residuals.

In Table 2, we also show the performance improvement achieved by both BPD–CABAC and BPD–BCRP–CABAC due to the use of Gray codes for binarization of the residuals. The variants of BPD–CABAC and BPD–BCRP–CABAC with Gray codes are denoted in the table as BPDG–CABAC and BPDG–BCRP–CABAC, respectively. BPDG–CABAC and BPDG–BCRP–CABAC, on average, resulted in negligible bit-rate savings of about 0.02 and 0.01 bits/pixel over BPD–CABAC and BPD–BCRP–CABAC, respectively.
B) HD binarization
An important parameter in HD is the choice of a division boundary t at the non-leaf nodes. While the use of mid-intensity value for binarization of original images was suggested in [Reference Pinho and António12], our experimental results demonstrated that the average intensity is a good choice for residual images.
In Table 3, we show the performance of the proposed scheme where the HD method was used for binarization. We experimented with both the options (mid magnitude and average magnitude) of selecting the division boundary. Both HDMid–CABAC and HDMid–BCRP–CABAC schemes used the mid value of the residual magnitudes as the division boundary. However, while HDMid–CABAC used CABAC, HDMid–BCRP–CABAC relied on BCRP–CABAC to encode the resulting bitmaps. HDAvg–CABAC and HDAvg–BCRP–CABAC are variants of HDMid–CABAC and HDMid–BCRP–CABAC, where the average residual magnitude was used as the division boundary. It follows from the table that encoding using BCRP–CABAC performed better than that using CABAC for both the choices of division boundary. The table also shows that the HD method using average value yielded better compression than that using the mid value for both CABAC-based and BCRP–CABAC-based encoding.
Table 3. Compression rates (bits/pixel) achieved by different schemes based on HD binarization. HDMid-CABAC refers to the scheme where the bitmaps, resulting from HD binarization using mid magnitude as the division boundary, are encoded using CABAC, while HDMid-BCRP-CABAC denotes the scheme where those bitmaps are encoded using BCRP-CABAC. HDAvg-CABAC and HDAvg-BCRP-CABAC are variants of HDMid-CABAC and HDMid-BCRP-CABAC where average magnitude is used in the HD binarization stage, instead of mid magnitude, as the division boundary.

In Table 4, we present the performance of the proposed scheme (HDAvg–BCRP–CABAC) compared against JPEG-LS. In our experiment, we used HP Labs’ software implementation of JPEG-LS [Reference Weinberger, Seroussi and Sapiro15]. It follows from the table that the proposed scheme performed better than JPEG-LS in compressing 23 out of 24 test images. The savings in bit-rate achieved by the proposed scheme against JPEG-LS was more than 1.56%, on average. Our experimental results also demonstrated that the compression efficiency of JPEG-LS significantly depends on the orientation of the image. For example, the size of the images 4, 9–10, and 17–19 is 768×512, while the rest of the images are of size 512×768. The direct compression of images 4, 9–10, and 17–19 using JPEG-LS required 5.155 bits/pixels, on average. However, when these images were rotated, JPEG-LS required only 4.306 bits/pixels, on average. In Table 4, we have used the improved results for fair comparison, since JPEG-LS can be modified to rotate the portrait images before compression. In contrast, the performance of proposed scheme is almost invariant to the orientation of the images.
Table 4. Compression efficiency (bits/pixel) of the proposed scheme against JPEG-LS. Since the proposed scheme also used the same predictor as JPEG-LS, the results demonstrate the efficacy of the proposed scheme in exploiting the spatial homogeneity.

The proposed HDAvg–BCRP–CABAC scheme requires encoding some side information which include the binary tree resulting from the HD step. Besides, in the BCRP–CABAC step, it needs to encode the types of the blocks using the Huffman codes presented in Table 1. It follows from Table 4 that the syntax overhead of the proposed scheme is only about 0.1%.
V. CONCLUSION
In this paper, we have proposed a lossless image compression scheme by taking a minimalistic approach to context modeling. The scheme, which operates in the residual domain, relies on binarization of the residuals for maximum reduction of the alphabet size. We have argued that straightforward binarization alone cannot handle the context dilution problem without compromising the compression efficiency. Therefore, we have proposed to use the HD method for binarization, which is able to capture the spatial correlation in the residual image as the correlation between the bitmaps associated with the child and parent nodes.
Instead of compressing the bitmaps using CABAC, the most widely used entropy coding scheme, we proposed a bitmap coding scheme using recursive partitioning. It is well known that signals in natural images are highly non-stationary. Therefore, while the pattern of correlation changes within the same image, a context template can model the higher-order dependency among the neighboring pixels only locally. Thus, the proposed BCRP–CABAC scheme recursively partitions an image aiming at explicitly identifying the blocks within which the statistical correlation remains the same. The proposed scheme, using JPEG-LS predictor, HD-based binarization, and BCRP–CABAC entropy coding, achieved a bit-rate saving of 1.56% over JPEG-LS in compressing the images from the Kodak test set.
ACKNOWLEDGEMENTS
The authors would like to thank Shane Moore for his editorial support during the writing of the paper. This research is supported by the Australian Research Council (ARC) under the Discovery Project DP130103670. Some preliminary results of the research were presented in PCS 2015.
Mortuza Ali received the B.Sc. Engg. (Hons) degree in Computer Science and Engineering from Bangladesh University of Engineering and Technology (BUET), Dhaka, Bangladesh, in 2001 and obtained his Ph.D. degree in Information Technology from Monash University, Australia, in 2009. He was a Lecturer in the Department of Computer Science and Engineering, Bangladesh University of Engineering and Technology, Bangladesh, from 2001 to 2004. After the completion of his Ph.D., he worked as a Research Fellow in the Department of Electrical and Electronic Engineering, the University of Melbourne (2009–2011) and Gippsland School of Information Technology, Monash University (2012–2013), Australia. Since 2014, he is with the School of Engineering and Information Technology, Federation University Australia. His major research interests are in the area of distributed source coding, lossless compression, and video coding.
Manzur Murshed received a B.Sc. Engg. (Hons) degree in Computer Science and Engineering from Bangladesh University of Engineering and Technology, Dhaka in 1994 and a Ph.D. degree in Computer Science from the Australian National University, Canberra in 1999. Currently, he is a Robert HT Smith Professor and Personal Chair in the Faculty of Science and Technology and the Research Director the Centre for Multimedia Computing, Communications, and Artificial Intelligence Research at Federation University Australia. Previously, he served Monash University as the Head of Gippsland School of Information Technology from 2007 to 2013. His research interests include video technology, information theory, wireless communications, Cloud computing, and security & privacy. He has published 200+ refereed research papers and received $ 1.7M competitive research funding, including three Australian Research Council Discovery Projects grants, and successfully supervised 22 Ph.D.s. He served as an Associate Editor of IEEE Transactions on Circuits and Systems for Video Technology in 2012.
Shampa Shahriyar has completed her B.Sc. Engg. degree from the Department of Computer Science and Engineering of Bangladesh University of Engineering and Technology (BUET) in 2011. She also served as a lecturer in the same department before joining Monash University Australia for her Ph.D. program in 2013. Shampa is the recipient of Monash Postgraduate scholarship (MGS) for pursuing her Ph.D. Moreover, she has achieved some mentionable awards during her candidature, like Facebook's 2014 Grace Hopper Scholarship, Monash Faculty of IT Champion of Three Minute Thesis (3MT) competition 2014 and Champion of FIT Innovation Showcase HDR Poster Competition 2014. Her research interest is multi-view video coding; especially depth coding. In particular, she works on efficient depth coding to support 3D and multiple view video transmission. She has published in several high ranked conferences of image and video processing and data compression (DCC 2015, ICME 2014, 2016) as a first author.
Manoranjan Paul received Ph.D. degree from Monash University, Australia in 2005. Currently, he is a Senior Lecturer and E-Health Research Leader in CM3 Machine Learning Research Unit at Charles Sturt University (CSU), Australia. His major research interests are in the fields of video coding, hyperspectral imaging and medical signal analysis. He has published more than 100 refereed publications. He is an invited Keynote Speaker on Video Coding in IEEE WoWMoM Video Everywhere Workshop 2014, IEEE DICTA 2013 and IEEE ICCIT 2010. Dr. Paul is a Senior Member of the IEEE and ACS. Currently Dr. Paul is an Associate Editor of EURASIP Journal on Advances in Signal Processing. Dr. Paul received Research Supervision Excellence Award 2015 and Research Excellence Award 2013 in the Faculty of Business at CSU. Dr. Paul received more than $ 1M funding including an Australian Research Council Discovery Project. More detailed can be found in http://csusap.csu.edu.au/rpaul/










