No CrossRef data available.
Published online by Cambridge University Press: 19 March 2024
In large-scale galaxy surveys, particularly deep ground-based photometric studies, galaxy blending was inevitable. Such blending posed a potential primary systematic uncertainty for upcoming surveys. Current deblenders predominantly depended on analytical modelling of galaxy profiles, facing limitations due to inflexible and imprecise models. We presented a novel approach, using a U-net structured transformer-based network for deblending astronomical images, which we term the CAT-deblender. It was trained using both RGB and the grz-band images, spanning two distinct data formats present in the Dark Energy Camera Legacy Survey (DECaLS) database, including galaxies with diverse morphologies in the training dataset. Our method necessitated only the approximate central coordinates of each target galaxy, sourced from galaxy detection, bypassing assumptions on neighbouring source counts. Post-deblending, our RGB images retained a high signal-to-noise peak, consistently showing superior structural similarity against ground truth. For multi-band images, the ellipticity of central galaxies and median reconstruction error for r-band consistently lie within 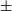 $\pm$0.025 to
$\pm$0.025 to 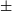 $\pm$0.25, revealing minimal pixel residuals. In our comparison of deblending capabilities focused on flux recovery, our model showed a mere 1% error in magnitude recovery for quadruply blended galaxies, significantly outperforming SExtractor’s higher error rate of 4.8%. Furthermore, by cross-matching with the publicly accessible overlapping galaxy catalogs from the DECaLS database, we successfully deblended 433 overlapping galaxies. Moreover, we have demonstrated effective deblending of 63 733 blended galaxy images, randomly chosen from the DECaLS database.
$\pm$0.25, revealing minimal pixel residuals. In our comparison of deblending capabilities focused on flux recovery, our model showed a mere 1% error in magnitude recovery for quadruply blended galaxies, significantly outperforming SExtractor’s higher error rate of 4.8%. Furthermore, by cross-matching with the publicly accessible overlapping galaxy catalogs from the DECaLS database, we successfully deblended 433 overlapping galaxies. Moreover, we have demonstrated effective deblending of 63 733 blended galaxy images, randomly chosen from the DECaLS database.