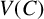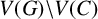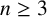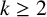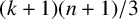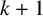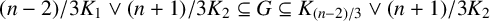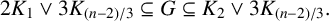1 Introduction
All terminology and notation not defined in this paper are the same as those in [Reference Bondy and Murty2]. All graphs considered in this paper are simple and undirected. Let
![]() $G=(V(G), E(G))$
be a graph. Let H be a subgraph of G and
$G=(V(G), E(G))$
be a graph. Let H be a subgraph of G and
![]() $v\in V(G)$
. We use
$v\in V(G)$
. We use
![]() $N_H(v)$
to denote the neighbours of v in H and
$N_H(v)$
to denote the neighbours of v in H and
![]() $d_H(v)=|N_H(v)|$
. If
$d_H(v)=|N_H(v)|$
. If
![]() $H=G$
, we write
$H=G$
, we write
![]() $N(v)=N_G(v)$
and
$N(v)=N_G(v)$
and
![]() $d(v)=|N(v)|$
. If
$d(v)=|N(v)|$
. If
![]() $S\subseteq V(G)$
, then
$S\subseteq V(G)$
, then
![]() $N_H(S)=(\bigcup _{v\in S}N_H(v))\backslash S$
,
$N_H(S)=(\bigcup _{v\in S}N_H(v))\backslash S$
,
![]() $G[S]$
denotes the subgraph induced by S and
$G[S]$
denotes the subgraph induced by S and
![]() $G-S=G[V(G)-S]$
. For two disjoint sets
$G-S=G[V(G)-S]$
. For two disjoint sets
![]() $X,Y\subseteq V(G)$
,
$X,Y\subseteq V(G)$
,
![]() $E(X,Y)$
denotes the set of edges between X and Y. For any
$E(X,Y)$
denotes the set of edges between X and Y. For any
![]() $x,y\in V(G)$
, an
$x,y\in V(G)$
, an
![]() $(x,y)$
-path denotes a path starting at x and ending at y.
$(x,y)$
-path denotes a path starting at x and ending at y.
The independence number and connectivity of G are denoted by
![]() $\alpha (G)$
and
$\alpha (G)$
and
![]() $\kappa (G)$
, respectively. Denote by
$\kappa (G)$
, respectively. Denote by
![]() $K_n$
a complete graph of order n. Let
$K_n$
a complete graph of order n. Let
![]() $c(G)$
and
$c(G)$
and
![]() $p(G)$
denote the order of a longest cycle and path in a graph G, respectively.
$p(G)$
denote the order of a longest cycle and path in a graph G, respectively.
Let C be a cycle. We denote by
![]() $\overrightarrow {C}$
the cycle C with a given orientation and by
$\overrightarrow {C}$
the cycle C with a given orientation and by
![]() $\overleftarrow {C}$
the cycle C with the reverse orientation. If
$\overleftarrow {C}$
the cycle C with the reverse orientation. If
![]() $u,v\in V(C)$
, then
$u,v\in V(C)$
, then
![]() $u\overrightarrow {C}v$
denotes the consecutive vertices of C from u to v in the direction specified by
$u\overrightarrow {C}v$
denotes the consecutive vertices of C from u to v in the direction specified by
![]() $\overrightarrow {C}$
. The same vertices, in reverse order, are given by
$\overrightarrow {C}$
. The same vertices, in reverse order, are given by
![]() $v\overleftarrow {C}u$
. If
$v\overleftarrow {C}u$
. If
![]() $u=v$
, then
$u=v$
, then
![]() $u\overrightarrow {C}v=\{u\}$
. We will consider both
$u\overrightarrow {C}v=\{u\}$
. We will consider both
![]() $u\overrightarrow {C}v$
and
$u\overrightarrow {C}v$
and
![]() $v\overleftarrow {C}u$
as paths and vertex sets. We use
$v\overleftarrow {C}u$
as paths and vertex sets. We use
![]() $u^{+i}$
and
$u^{+i}$
and
![]() $u^{-i}$
to denote the ith successor and predecessor of u, respectively. In particular,
$u^{-i}$
to denote the ith successor and predecessor of u, respectively. In particular,
![]() $u^+=u^{+1}$
and
$u^+=u^{+1}$
and
![]() $u^-=u^{-1}$
. If
$u^-=u^{-1}$
. If
![]() $A\subset V(C)$
, we write
$A\subset V(C)$
, we write
![]() $A^{+i}=\{a^{+i}~|~ a\in A \}$
and
$A^{+i}=\{a^{+i}~|~ a\in A \}$
and
![]() $A^{-i}=\{a^{-i}~|~ a\in A \}$
. In particular,
$A^{-i}=\{a^{-i}~|~ a\in A \}$
. In particular,
![]() $A^+=A^{+1}$
and
$A^+=A^{+1}$
and
![]() $A^-=A^{-1}$
. Similar notation is used for paths.
$A^-=A^{-1}$
. Similar notation is used for paths.
Let G be a simple connected graph. For an integer
![]() $k\geq 2$
, define
$k\geq 2$
, define
 $$ \begin{align*}\sigma_{k}(G)=\min\bigg\{\sum_{i=1}^{k} d(x_i)~|~\{x_1,\ldots,x_{k}\}~ \text{is an independent set of}~ G\bigg\}\end{align*} $$
$$ \begin{align*}\sigma_{k}(G)=\min\bigg\{\sum_{i=1}^{k} d(x_i)~|~\{x_1,\ldots,x_{k}\}~ \text{is an independent set of}~ G\bigg\}\end{align*} $$
if
![]() $\alpha (G)\geq k$
and otherwise,
$\alpha (G)\geq k$
and otherwise,
![]() $\sigma _k(G)=\infty $
.
$\sigma _k(G)=\infty $
.
A cycle C of a graph G is dominating if
![]() $V(C)$
is a dominating set and
$V(C)$
is a dominating set and
![]() $V(G)\backslash V(C)$
is an independent set. The problem of existence of cycles is a classic and widely studied topic, of which the existence of dominating cycles is an interesting extension. In 1980, Bondy [Reference Bondy1] first gave a degree sum condition on 2-connected graphs such that every longest cycle is dominating. In 2005, Lu et al. [Reference Lu, Liu and Tian4] studied the same problem to 3-connected graphs. In 2021, we extended these two results as follows.
$V(G)\backslash V(C)$
is an independent set. The problem of existence of cycles is a classic and widely studied topic, of which the existence of dominating cycles is an interesting extension. In 1980, Bondy [Reference Bondy1] first gave a degree sum condition on 2-connected graphs such that every longest cycle is dominating. In 2005, Lu et al. [Reference Lu, Liu and Tian4] studied the same problem to 3-connected graphs. In 2021, we extended these two results as follows.
Theorem 1.1 (Wu et al. [Reference Wu, Chen and Cheng5]).
Let G be a k-connected graph on n vertices with
![]() $k\geq 2$
. If
$k\geq 2$
. If
![]() $\sigma _{k+1}(G)>(k+1)(n+1)/3$
, then every longest cycle is dominating.
$\sigma _{k+1}(G)>(k+1)(n+1)/3$
, then every longest cycle is dominating.
In [Reference Bondy1, Reference Lu, Liu and Tian4, Reference Wu, Chen and Cheng5], the authors gave two examples
![]() $G_1$
and
$G_1$
and
![]() $G_2$
to show that the bounds of their results are sharp:
$G_2$
to show that the bounds of their results are sharp:
![]() $G_1=k K_1\vee (k+1)K_2$
and
$G_1=k K_1\vee (k+1)K_2$
and
![]() $G_2=K_k\vee (k+1)K_2$
. Let
$G_2=K_k\vee (k+1)K_2$
. Let
![]() ${G_1\subseteq G \subseteq G_2}$
and
${G_1\subseteq G \subseteq G_2}$
and
![]() $S=V(G)\backslash V((k+1)K_2)$
. Clearly,
$S=V(G)\backslash V((k+1)K_2)$
. Clearly,
![]() $n=|G|=3k+2$
,
$n=|G|=3k+2$
,
![]() $k=(n-2)/3$
,
$k=(n-2)/3$
,
![]() $d(u)=(n+1)/3$
for
$d(u)=(n+1)/3$
for
![]() $u\in V(G)\backslash S$
and
$u\in V(G)\backslash S$
and
![]() $d(u)\geq (2n+2)/3$
for
$d(u)\geq (2n+2)/3$
for
![]() $u\in S$
. Since G contains
$u\in S$
. Since G contains
![]() $K_{k,2k+2}$
as its spanning subgraph and
$K_{k,2k+2}$
as its spanning subgraph and
![]() $K_{k,2k+2}$
is k-connected, G is k-connected. Any independent set of G with cardinality
$K_{k,2k+2}$
is k-connected, G is k-connected. Any independent set of G with cardinality
![]() $k+1$
contains no vertex of S. Moreover, each component of
$k+1$
contains no vertex of S. Moreover, each component of
![]() $G-S=(k+1)K_2$
contributes only one vertex to any independent set of cardinality
$G-S=(k+1)K_2$
contributes only one vertex to any independent set of cardinality
![]() $k+1$
. Hence,
$k+1$
. Hence,
![]() $\sigma _{k+1}(G)=(k+1)(n+1)/3$
. Since S is a vertex cut of G and
$\sigma _{k+1}(G)=(k+1)(n+1)/3$
. Since S is a vertex cut of G and
![]() $G-S=(k+1)K_2$
, any longest cycle uses at most k vertices of S and k components of
$G-S=(k+1)K_2$
, any longest cycle uses at most k vertices of S and k components of
![]() $G-S$
. Therefore, G has no dominating cycle. Moreover, if
$G-S$
. Therefore, G has no dominating cycle. Moreover, if
![]() $k=2$
and
$k=2$
and
![]() $2K_1\vee 3K_{(n-2)/3}\subseteq G\subseteq K_2\vee 3K_{(n-2)/3}$
, then
$2K_1\vee 3K_{(n-2)/3}\subseteq G\subseteq K_2\vee 3K_{(n-2)/3}$
, then
![]() $\sigma _3(G)=n+1$
, G is 2-connected and G has no dominating cycle. From this, we guess that these graphs are the extremal graphs.
$\sigma _3(G)=n+1$
, G is 2-connected and G has no dominating cycle. From this, we guess that these graphs are the extremal graphs.
In this paper, we characterise the extremal graphs when the equality of the bound of Theorem 1.1 holds. Our main result is the following.
Theorem 1.2. Let G be a k-connected graph on n vertices with
![]() $k\geq 2$
. If
$k\geq 2$
. If
![]() $\sigma _{k+1} (G)\geq (k+1)(n+1)/3$
, then every longest cycle is dominating or
$\sigma _{k+1} (G)\geq (k+1)(n+1)/3$
, then every longest cycle is dominating or
![]() $(n-2)/3K_1\vee (n+1)/ 3K_2\subseteq G \subseteq K_{(n-2)/3}\vee (n+1)/3K_2$
or
$(n-2)/3K_1\vee (n+1)/ 3K_2\subseteq G \subseteq K_{(n-2)/3}\vee (n+1)/3K_2$
or
![]() $2K_1\vee 3K_{(n-2)/3}\subseteq G \subseteq K_2\vee 3K_{(n-2)/3}.$
$2K_1\vee 3K_{(n-2)/3}\subseteq G \subseteq K_2\vee 3K_{(n-2)/3}.$
2 Proof of Theorem 1.2
Before proving Theorem 1.2, we shall give some notation and lemmas which were introduced in [Reference Fournier and Fraisse3, Reference Wu, Chen and Cheng5, Reference Zhang6].
Lemma 2.1 (Fournier and Fraisse [Reference Fournier and Fraisse3]).
Let G be a k-connected graph on n vertices with
![]() $k\geq 2$
. If
$k\geq 2$
. If
![]() $\sigma _{k+1}(G)\geq c$
, then
$\sigma _{k+1}(G)\geq c$
, then
![]() $c(G)\geq \min \{n,2c/(k+1)\}$
.
$c(G)\geq \min \{n,2c/(k+1)\}$
.
Let G be a k-connected graph on n vertices with
![]() $k\geq 2$
and C a longest cycle of G with a given orientation. If C is not dominating, then we let H be a component of
$k\geq 2$
and C a longest cycle of G with a given orientation. If C is not dominating, then we let H be a component of
![]() $G-V(C)$
with
$G-V(C)$
with
![]() $|H|\geq 2$
and
$|H|\geq 2$
and
![]() $N_C(H)=\{x_1,x_2,\ldots ,x_t\}$
, where the subscripts agree with the orientation of C. Let
$N_C(H)=\{x_1,x_2,\ldots ,x_t\}$
, where the subscripts agree with the orientation of C. Let
![]() $a_i$
be the first noninsertible vertex occurring on
$a_i$
be the first noninsertible vertex occurring on
![]() $x_i^+\overrightarrow {C}x_{i+1}^-$
,
$x_i^+\overrightarrow {C}x_{i+1}^-$
,
![]() $A=\{a_1,a_2,\ldots ,a_t\}$
and
$A=\{a_1,a_2,\ldots ,a_t\}$
and
![]() $A_h=\{a_i \mid x_i\in N(h)\}$
for
$A_h=\{a_i \mid x_i\in N(h)\}$
for
![]() $h\in V(H)$
.
$h\in V(H)$
.
Lemma 2.2 (Wu et al. [Reference Wu, Chen and Cheng5]).
![]() $A\cup \{h\}$
is an independent set for
$A\cup \{h\}$
is an independent set for
![]() $h\in V(H)$
.
$h\in V(H)$
.
Lemma 2.3 (Wu et al. [Reference Wu, Chen and Cheng5]).
Suppose
![]() $h_1,h_2\in V(H)$
with
$h_1,h_2\in V(H)$
with
![]() $h_1\neq h_2$
and
$h_1\neq h_2$
and
![]() $a_i,a_j\in A_{h_1}$
with
$a_i,a_j\in A_{h_1}$
with
![]() $i\neq j$
. Then
$i\neq j$
. Then
![]() $d(h_2)+d(a_i)+d(a_j)\leq n+1$
.
$d(h_2)+d(a_i)+d(a_j)\leq n+1$
.
Lemma 2.4 (Wu et al. [Reference Wu, Chen and Cheng5]).
Suppose
![]() $h_1,h_2\in V(H)$
with
$h_1,h_2\in V(H)$
with
![]() $h_1\neq h_2$
and
$h_1\neq h_2$
and
![]() $a_i\in A_{h_1}, a_j\in A_{h_2}$
with
$a_i\in A_{h_1}, a_j\in A_{h_2}$
with
![]() $i\neq j$
. Then
$i\neq j$
. Then
![]() $d(h_1)+d(a_i)+d(a_j)\leq n+1$
.
$d(h_1)+d(a_i)+d(a_j)\leq n+1$
.
Lemma 2.5 (Wu et al. [Reference Wu, Chen and Cheng5]).
Suppose
![]() $h_1,h_2,h_3$
are three distinct vertices of
$h_1,h_2,h_3$
are three distinct vertices of
![]() $V(H)$
and
$V(H)$
and
![]() $a_i,a_j,a_\ell $
are three distinct vertices of A with
$a_i,a_j,a_\ell $
are three distinct vertices of A with
![]() $a_i\in A_{h_1},a_j\in A_{h_2},a_\ell \in A_{h_3}$
. Then
$a_i\in A_{h_1},a_j\in A_{h_2},a_\ell \in A_{h_3}$
. Then
![]() $d(a_i)+d(a_j)+d(a_\ell )\leq n$
.
$d(a_i)+d(a_j)+d(a_\ell )\leq n$
.
Lemma 2.6 (Wu et al. [Reference Wu, Chen and Cheng5]).
Suppose
![]() $h_1,h_2\in V(H)$
with
$h_1,h_2\in V(H)$
with
![]() $h_1\neq h_2$
and
$h_1\neq h_2$
and
![]() $a_i,a_j,a_\ell $
are three distinct vertices of A with
$a_i,a_j,a_\ell $
are three distinct vertices of A with
![]() $a_i\in A_{h_1},a_j,a_\ell \in A_{h_2}$
. Then
$a_i\in A_{h_1},a_j,a_\ell \in A_{h_2}$
. Then
![]() $d(a_i)+d(a_j)+d(a_\ell )\leq n+1$
.
$d(a_i)+d(a_j)+d(a_\ell )\leq n+1$
.
Proof of Theorem 1.2.
Let C be a longest cycle of G. Suppose C is not a dominating cycle. Then
![]() $|C|\leq n-2$
and
$|C|\leq n-2$
and
![]() $G-V(C)$
has a component H with
$G-V(C)$
has a component H with
![]() ${|H|\geq 2}$
. Give C an orientation
${|H|\geq 2}$
. Give C an orientation
![]() $\overrightarrow {C}$
. Let
$\overrightarrow {C}$
. Let
![]() $N_C(H)=\{x_1,x_2,\ldots ,x_t\}$
where the appearance of
$N_C(H)=\{x_1,x_2,\ldots ,x_t\}$
where the appearance of
![]() $\{x_1,x_2,\ldots ,x_t\}$
agrees with the orientation of
$\{x_1,x_2,\ldots ,x_t\}$
agrees with the orientation of
![]() $\overrightarrow {C}$
. Since G is k-connected, we have
$\overrightarrow {C}$
. Since G is k-connected, we have
![]() $t\geq k\geq 2$
. Define
$t\geq k\geq 2$
. Define
![]() $a_i, A, A_h$
as at the beginning of this section. By Lemma 2.2,
$a_i, A, A_h$
as at the beginning of this section. By Lemma 2.2,
![]() $A\cup \{h\}$
is an independent set with at least
$A\cup \{h\}$
is an independent set with at least
![]() $k+1$
vertices for any
$k+1$
vertices for any
![]() $h\in V(H)$
. Let
$h\in V(H)$
. Let
![]() ${S=\{v\in V(G)~|~ d(v)\leq (n+1)/3\}}$
and
${S=\{v\in V(G)~|~ d(v)\leq (n+1)/3\}}$
and
![]() $L=\{v\in V(G)~|~ d(v)> (n+1)/3\}$
.
$L=\{v\in V(G)~|~ d(v)> (n+1)/3\}$
.
Claim 1.
![]() $d(u)=(n+1)/3$
for each
$d(u)=(n+1)/3$
for each
![]() $u\in A\cup N_H(C)$
.
$u\in A\cup N_H(C)$
.
Proof. If
![]() $A\cup N_H(C)\subseteq S$
, then since
$A\cup N_H(C)\subseteq S$
, then since
![]() $\sigma _{k+1}(G)\geq (k+1)(n+1)/3$
and
$\sigma _{k+1}(G)\geq (k+1)(n+1)/3$
and
![]() $A\cup \{h\}$
is an independent set with at least
$A\cup \{h\}$
is an independent set with at least
![]() $k+1$
vertices for any
$k+1$
vertices for any
![]() $h\in N_H(C)$
, we can deduce that
$h\in N_H(C)$
, we can deduce that
![]() $d(u)=(n+1)/3$
for each
$d(u)=(n+1)/3$
for each
![]() $u\in A\cup N_H(C)$
. So it suffices to show that
$u\in A\cup N_H(C)$
. So it suffices to show that
![]() $A\cup N_H(C)\subseteq S$
.
$A\cup N_H(C)\subseteq S$
.
Suppose there exists a vertex
![]() $a_i$
of A such that
$a_i$
of A such that
![]() $a_i\in L$
where
$a_i\in L$
where
![]() $1\leq i\leq t$
. Assume
$1\leq i\leq t$
. Assume
![]() ${a_i\in A_h}$
for some
${a_i\in A_h}$
for some
![]() $h\in V(H)$
. Since G is k-connected and
$h\in V(H)$
. Since G is k-connected and
![]() $|H|\geq 2$
, we have
$|H|\geq 2$
, we have
![]() ${|N_C(V(H)\backslash \{h\}))|\geq k-1}$
. Take a subset X of
${|N_C(V(H)\backslash \{h\}))|\geq k-1}$
. Take a subset X of
![]() $N_C(V(H)\backslash \{h\})\backslash \{x_i\}$
with
$N_C(V(H)\backslash \{h\})\backslash \{x_i\}$
with
![]() $k-2$
vertices and let
$k-2$
vertices and let
![]() $A_X=\{a_j \mid x_j\in X\}$
. We take a vertex
$A_X=\{a_j \mid x_j\in X\}$
. We take a vertex
![]() $x_\ell \in N_C(V(H)\setminus\{h\}) - X-\{x_i\}$
if possible or
$x_\ell \in N_C(V(H)\setminus\{h\}) - X-\{x_i\}$
if possible or
![]() $x_\ell \in N_C(h)-X-\{x_i\}$
otherwise. By Lemma 2.2,
$x_\ell \in N_C(h)-X-\{x_i\}$
otherwise. By Lemma 2.2,
![]() $\{a_i,a_\ell,h\}\cup A_X$
is an independent set with
$\{a_i,a_\ell,h\}\cup A_X$
is an independent set with
![]() $ k+1$
vertices. Since
$ k+1$
vertices. Since
![]() $X\subseteq (N_C(V(H-h))\backslash \{x_i\})$
, each vertex
$X\subseteq (N_C(V(H-h))\backslash \{x_i\})$
, each vertex
![]() $x_j$
of X has a neighbour in H different from h. Therefore, by Lemma 2.4, we have
$x_j$
of X has a neighbour in H different from h. Therefore, by Lemma 2.4, we have
![]() $d(h)+d(a_i)+d(a_\ell)\leq n+1$
, and by Lemmas 2.5 and 2.6, we have
$d(h)+d(a_i)+d(a_\ell)\leq n+1$
, and by Lemmas 2.5 and 2.6, we have
![]() $d(a_i)+d(a_p)+d(a_q)\leq n+1$
for
$d(a_i)+d(a_p)+d(a_q)\leq n+1$
for
![]() $a_p,a_q\in A_X$
. Since
$a_p,a_q\in A_X$
. Since
![]() $a_i\in L$
, we have
$a_i\in L$
, we have
![]() $d(a_p)+d(a_q)<2(n+1)/3$
for
$d(a_p)+d(a_q)<2(n+1)/3$
for
![]() $a_p,a_q\in A_X$
. Thus,
$a_p,a_q\in A_X$
. Thus,
 $$ \begin{align*} \sigma_{k+1}(G)&\leq[d(h)+d(a_i)+d(a_\ell)]+\sum_{a_p\in A_X}d(a_p)\\[5pt] &<(n+1)+(k-2)(n+1)/3 =(k+1)(n+1)/3, \end{align*} $$
$$ \begin{align*} \sigma_{k+1}(G)&\leq[d(h)+d(a_i)+d(a_\ell)]+\sum_{a_p\in A_X}d(a_p)\\[5pt] &<(n+1)+(k-2)(n+1)/3 =(k+1)(n+1)/3, \end{align*} $$
which is a contradiction. Hence,
![]() $A\subseteq S$
.
$A\subseteq S$
.
Suppose there is a vertex
![]() $h^*$
of
$h^*$
of
![]() $N_H(C)$
such that
$N_H(C)$
such that
![]() $h^*\in L$
. If
$h^*\in L$
. If
![]() $t=2$
, then by Lemma 2.1,
$t=2$
, then by Lemma 2.1,
![]() $|C|\geq 2(n+1)/3$
and as
$|C|\geq 2(n+1)/3$
and as
![]() $h^*\in L$
,
$h^*\in L$
,
![]() $n=|G|\geq |C|+|H|\geq 2(n+1)/ 3+d(h^*)-d_C(h^*)+1>2(n+1)/3+(n+1)/3-2+1=n$
, which is a contradiction. Thus,
$n=|G|\geq |C|+|H|\geq 2(n+1)/ 3+d(h^*)-d_C(h^*)+1>2(n+1)/3+(n+1)/3-2+1=n$
, which is a contradiction. Thus,
![]() $t\geq 3$
. Take
$t\geq 3$
. Take
![]() $x_j\in N_C(h^*)$
. Since
$x_j\in N_C(h^*)$
. Since
![]() $|N_C(V(H)\backslash \{h^*\}))|\geq k-1$
, we may assume that
$|N_C(V(H)\backslash \{h^*\}))|\geq k-1$
, we may assume that
![]() $hx_\ell \in E(G)$
where
$hx_\ell \in E(G)$
where
![]() $h\in V(H)\backslash \{h^*\}$
and
$h\in V(H)\backslash \{h^*\}$
and
![]() $\ell \neq j$
. By Lemma 2.4, we have
$\ell \neq j$
. By Lemma 2.4, we have
![]() $d(h^*)+d(a_j)+d(a_\ell )\leq n+1$
. Since
$d(h^*)+d(a_j)+d(a_\ell )\leq n+1$
. Since
![]() $h^*\in L$
, we have
$h^*\in L$
, we have
![]() $d(a_j)+d(a_\ell )<2(n+1)/3$
. If
$d(a_j)+d(a_\ell )<2(n+1)/3$
. If
![]() $t\geq k+1$
, then we take a subset B of
$t\geq k+1$
, then we take a subset B of
![]() $A\backslash \{a_j,a_\ell \}$
with
$A\backslash \{a_j,a_\ell \}$
with
![]() $k-1$
vertices, and hence
$k-1$
vertices, and hence
![]() $\sigma _{k+1}(G)\leq d(a_j)+d(a_\ell )+\sum _{a_p\in B\backslash \{a_j,a_\ell \}}d(a_p)<(k+1)(n+1)/3$
, which is a contradiction. Hence,
$\sigma _{k+1}(G)\leq d(a_j)+d(a_\ell )+\sum _{a_p\in B\backslash \{a_j,a_\ell \}}d(a_p)<(k+1)(n+1)/3$
, which is a contradiction. Hence,
![]() $t\leq k$
. Since
$t\leq k$
. Since
![]() $t\geq k$
, we have
$t\geq k$
, we have
![]() $t=k$
. Therefore,
$t=k$
. Therefore,
![]() $A\cup \{h^*\}$
is an independent set with
$A\cup \{h^*\}$
is an independent set with
![]() $k+1$
vertices. Since
$k+1$
vertices. Since
![]() $A\subseteq S$
and
$A\subseteq S$
and
![]() $d(h^*)+d(a_j)+d(a_\ell )\leq n+1$
,
$d(h^*)+d(a_j)+d(a_\ell )\leq n+1$
,
 $$ \begin{align*} \sigma_{k+1}(G)\leq[d(h^*)+d(a_j)+d(a_\ell)]+\sum_{a_p\in A\backslash\{a_j,a_\ell\}}d(a_p) \leq(k+1)(n+1)/3. \end{align*} $$
$$ \begin{align*} \sigma_{k+1}(G)\leq[d(h^*)+d(a_j)+d(a_\ell)]+\sum_{a_p\in A\backslash\{a_j,a_\ell\}}d(a_p) \leq(k+1)(n+1)/3. \end{align*} $$
As
![]() $\sigma _{k+1}(G)\geq (k+1)(n+1)/3$
, we have
$\sigma _{k+1}(G)\geq (k+1)(n+1)/3$
, we have
![]() $\sigma _{k+1}(G)=(k+1)(n+1)/3$
. Therefore,
$\sigma _{k+1}(G)=(k+1)(n+1)/3$
. Therefore,
![]() $d(h^*)+d(a_j)+d(a_\ell )=n+1$
and
$d(h^*)+d(a_j)+d(a_\ell )=n+1$
and
![]() $d(a_p)=(n+1)/3$
for
$d(a_p)=(n+1)/3$
for
![]() $a_p\in A\backslash \{a_j,a_\ell \}$
. Since
$a_p\in A\backslash \{a_j,a_\ell \}$
. Since
![]() ${h^*\in L}$
, we have
${h^*\in L}$
, we have
![]() $d(a_j)+d(a_\ell )<2(n+1)/3$
. Hence,
$d(a_j)+d(a_\ell )<2(n+1)/3$
. Hence,
![]() $\min \{d(a_j),d(a_\ell )\}<(n+1)/3$
. If
$\min \{d(a_j),d(a_\ell )\}<(n+1)/3$
. If
![]() $\max \{d(a_j),d(a_\ell )\}<(n+1)/3$
, then as
$\max \{d(a_j),d(a_\ell )\}<(n+1)/3$
, then as
![]() $t\geq 3$
and
$t\geq 3$
and
![]() $d(a_p)=(n+1)/3$
for
$d(a_p)=(n+1)/3$
for
![]() $a_p\in A\backslash \{a_j,a_\ell \}$
, we have
$a_p\in A\backslash \{a_j,a_\ell \}$
, we have
![]() $d(h^*)+d(a_j)+d(a_p)>n+1$
for
$d(h^*)+d(a_j)+d(a_p)>n+1$
for
![]() $a_p\notin A_{h^*}$
or
$a_p\notin A_{h^*}$
or
![]() $d(h^*)+d(a_\ell )+d(a_p)>n+1$
, for otherwise, we have a contradiction to Lemma 2.4. Thus,
$d(h^*)+d(a_\ell )+d(a_p)>n+1$
, for otherwise, we have a contradiction to Lemma 2.4. Thus,
![]() $\max \{d(a_j),d(a_\ell )\}=(n+1)/3$
as
$\max \{d(a_j),d(a_\ell )\}=(n+1)/3$
as
![]() $A\subseteq S$
. Moreover,
$A\subseteq S$
. Moreover,
![]() $A\backslash \{a_\ell \}=A_{h^*}$
if
$A\backslash \{a_\ell \}=A_{h^*}$
if
![]() $d(a_\ell )<(n+1)/3$
and
$d(a_\ell )<(n+1)/3$
and
![]() $A_{h^*}=\{a_j\}$
if
$A_{h^*}=\{a_j\}$
if
![]() $d(a_j)<(n+1)/3$
. Since
$d(a_j)<(n+1)/3$
. Since
![]() $t\geq 3$
, we take
$t\geq 3$
, we take
![]() $a_q\in A\backslash \{a_j,a_\ell \}$
. If
$a_q\in A\backslash \{a_j,a_\ell \}$
. If
![]() $d(a_j)<(n+1)/3$
, then
$d(a_j)<(n+1)/3$
, then
![]() $d(a_\ell )=(n+1)/3$
and
$d(a_\ell )=(n+1)/3$
and
![]() $A_h^*=\{a_j\}$
. Hence,
$A_h^*=\{a_j\}$
. Hence,
![]() $a_q\notin A_{h^*}$
. If
$a_q\notin A_{h^*}$
. If
![]() $a_q\in A_h$
, then
$a_q\in A_h$
, then
![]() $d(h^*)+d(a_\ell )+d(a_q)> n+1$
, which is in contradiction to Lemma 2.3. Thus,
$d(h^*)+d(a_\ell )+d(a_q)> n+1$
, which is in contradiction to Lemma 2.3. Thus,
![]() $a_q\notin A_h$
. By Lemma 2.4,
$a_q\notin A_h$
. By Lemma 2.4,
![]() $d(h)+d(a_\ell )+d(a_q)\leq n+1$
. Since
$d(h)+d(a_\ell )+d(a_q)\leq n+1$
. Since
![]() $d(a_p)=(n+1)/3$
for
$d(a_p)=(n+1)/3$
for
![]() $a_p\in A\backslash \{a_j,a_\ell \}$
,
$a_p\in A\backslash \{a_j,a_\ell \}$
,
 $$ \begin{align*}\sigma_{k+1}(G)\leq d(h)+d(a_\ell)+d(a_q)+d(a_j)+\sum_{a_p\in A\backslash\{a_j,a_\ell,a_q\}}d(a_p)<(k+1)(n+1)/3,\end{align*} $$
$$ \begin{align*}\sigma_{k+1}(G)\leq d(h)+d(a_\ell)+d(a_q)+d(a_j)+\sum_{a_p\in A\backslash\{a_j,a_\ell,a_q\}}d(a_p)<(k+1)(n+1)/3,\end{align*} $$
which is a contradiction. Thus,
![]() $d(a_j)=(n+1)/3$
and so
$d(a_j)=(n+1)/3$
and so
![]() $d(a_\ell )<(n+1)/3$
and
$d(a_\ell )<(n+1)/3$
and
![]() ${A\backslash \{a_\ell \}=A_{h^*}}$
. Thus,
${A\backslash \{a_\ell \}=A_{h^*}}$
. Thus,
![]() $a_q\in A_{h^*}$
and
$a_q\in A_{h^*}$
and
![]() $d(h)+d(a_q)+d(a_j)\leq n+1$
by Lemma 2.3. Since
$d(h)+d(a_q)+d(a_j)\leq n+1$
by Lemma 2.3. Since
![]() $d(a_p)= (n+1)/3$
for
$d(a_p)= (n+1)/3$
for
![]() $a_p\in A\backslash \{a_j,a_\ell \}$
,
$a_p\in A\backslash \{a_j,a_\ell \}$
,
 $$ \begin{align*}\sigma_{k+1}(G)\leq d(h)+d(a_q)+d(a_j)+d(a_\ell)+\sum_{a_p\in A\backslash\{a_j,a_\ell,a_q\}}d(a_p)<(k+1)(n+1)/3,\end{align*} $$
$$ \begin{align*}\sigma_{k+1}(G)\leq d(h)+d(a_q)+d(a_j)+d(a_\ell)+\sum_{a_p\in A\backslash\{a_j,a_\ell,a_q\}}d(a_p)<(k+1)(n+1)/3,\end{align*} $$
which is a contradiction. Thus,
![]() $N_H(C)\subseteq S$
.
$N_H(C)\subseteq S$
.
Claim 2.
![]() $d_C(h)\geq 2$
for each
$d_C(h)\geq 2$
for each
![]() $h\in V(H)$
.
$h\in V(H)$
.
Proof. By Lemma 2.2,
![]() $\{h,a_1,\ldots ,a_k\}$
is an independent set with
$\{h,a_1,\ldots ,a_k\}$
is an independent set with
![]() $k+1$
vertices for each
$k+1$
vertices for each
![]() $h\in V(H)$
. By Claim 1,
$h\in V(H)$
. By Claim 1,
![]() $A\subseteq S$
and hence
$A\subseteq S$
and hence
 $$ \begin{align*} (k+1)(n+1)/3\leq\sigma_{k+1}(G)\leq d(h)+\sum_{\ell=1}^{k}d(a_\ell)=d(h)+k(n+1)/3. \end{align*} $$
$$ \begin{align*} (k+1)(n+1)/3\leq\sigma_{k+1}(G)\leq d(h)+\sum_{\ell=1}^{k}d(a_\ell)=d(h)+k(n+1)/3. \end{align*} $$
Thus,
![]() $d(h)\geq (n+1)/3$
. If
$d(h)\geq (n+1)/3$
. If
![]() $d_C(h)\leq 1$
, then by Lemma 2.1,
$d_C(h)\leq 1$
, then by Lemma 2.1,
which is a contradiction. Hence,
![]() $d_C(h)\geq 2$
.
$d_C(h)\geq 2$
.
By Claim 2,
![]() $N_H(C)=V(H)$
, and hence by Claim 1,
$N_H(C)=V(H)$
, and hence by Claim 1,
For convenience, we assume
![]() $V(H)=\{h_1,h_2,\ldots ,h_{|H|}\}$
in what follows.
$V(H)=\{h_1,h_2,\ldots ,h_{|H|}\}$
in what follows.
Claim 3.
![]() $|H|=2$
or
$|H|=2$
or
![]() $|N_C(H)|=2$
.
$|N_C(H)|=2$
.
Proof. If there exists a matching M with three independent edges between
![]() $V(H)$
and
$V(H)$
and
![]() $V(C)$
, we write
$V(C)$
, we write
![]() $M=\{x_ih_i,x_jh_j,x_\ell h_k\}$
where
$M=\{x_ih_i,x_jh_j,x_\ell h_k\}$
where
![]() $h_i,h_j,h_k\in V(H)$
. By Claim 1,
$h_i,h_j,h_k\in V(H)$
. By Claim 1,
![]() ${d(a_i)+d(a_j)+d(a_\ell )=n+1}$
, which is in contradiction to Lemma 2.5. Therefore, the maximum matching number between
${d(a_i)+d(a_j)+d(a_\ell )=n+1}$
, which is in contradiction to Lemma 2.5. Therefore, the maximum matching number between
![]() $V(H)$
and
$V(H)$
and
![]() $V(C)$
is no more than 2. If
$V(C)$
is no more than 2. If
![]() $|H|=2$
, then the result holds. So we may assume that
$|H|=2$
, then the result holds. So we may assume that
![]() $|H|\geq 3$
. If
$|H|\geq 3$
. If
![]() $k\geq 3$
, then as G is k-connected and
$k\geq 3$
, then as G is k-connected and
![]() $|H|\geq 3$
, there exist three independent edges between
$|H|\geq 3$
, there exist three independent edges between
![]() $V(H)$
and
$V(H)$
and
![]() $V(C)$
, which is a contradiction. Hence,
$V(C)$
, which is a contradiction. Hence,
![]() $k=2$
. Since
$k=2$
. Since
![]() $k=2$
and
$k=2$
and
![]() $|H|\geq 3$
, there exist two independent edges between between
$|H|\geq 3$
, there exist two independent edges between between
![]() $V(H)$
and
$V(H)$
and
![]() $V(C)$
. Suppose
$V(C)$
. Suppose
![]() $x_ph_p,x_qh_q\in E(G)$
where
$x_ph_p,x_qh_q\in E(G)$
where
![]() $h_p,h_q\in V(H)$
. Since the maximum matching number between
$h_p,h_q\in V(H)$
. Since the maximum matching number between
![]() $V(H)$
and
$V(H)$
and
![]() $V(C)$
is no more than 2, we have
$V(C)$
is no more than 2, we have
![]() $N_C(V(H)\backslash \{h_p,h_q\})\subseteq \{x_p,x_q\}$
, and hence by Claim 2,
$N_C(V(H)\backslash \{h_p,h_q\})\subseteq \{x_p,x_q\}$
, and hence by Claim 2,
![]() $N_C(V(H))=\{x_p,x_q\}$
. That is,
$N_C(V(H))=\{x_p,x_q\}$
. That is,
![]() $|N_C(H)|=2$
.
$|N_C(H)|=2$
.
Claim 4. We have:
-
(1)
 $N_C(h_i)=N_C(H)$
for
$N_C(h_i)=N_C(H)$
for
 $1\leq i\leq |H|$
;
$1\leq i\leq |H|$
; -
(2) H is complete;
-
(3)
 $|H|=2$
,
$|H|=2$
,
 $|C|=n-2$
and
$|C|=n-2$
and
 $t=(n-2)/3$
, or
$t=(n-2)/3$
, or
 $|H|=(n-2)/3$
,
$|H|=(n-2)/3$
,
 $|C|=(2n+2)/3$
and
$|C|=(2n+2)/3$
and
 $t=2$
;
$t=2$
; -
(4)
 $|x_i^+\overrightarrow {C}x_{i+1}^-|=|H|$
for
$|x_i^+\overrightarrow {C}x_{i+1}^-|=|H|$
for
 $1\leq i\leq t$
(where
$1\leq i\leq t$
(where
 $i+1$
is taken modulo
$i+1$
is taken modulo
 $t)$
.
$t)$
.
Proof. First we consider the case
![]() $|H|=2$
. Clearly,
$|H|=2$
. Clearly,
![]() $H\cong K_2$
. Since
$H\cong K_2$
. Since
![]() ${d(h_i)= (n+1)/3}$
for
${d(h_i)= (n+1)/3}$
for
![]() $1\leq i\leq 2$
and
$1\leq i\leq 2$
and
![]() $H\cong K_2$
, we have
$H\cong K_2$
, we have
![]() $d_C(h_i)=d(h_i)-d_H(h_i)=(n-2)/3$
. Suppose
$d_C(h_i)=d(h_i)-d_H(h_i)=(n-2)/3$
. Suppose
![]() $|N_C(h_1)\cap N_C(h_2)|=r$
. Since
$|N_C(h_1)\cap N_C(h_2)|=r$
. Since
![]() $H\cong K_2$
and by the maximality of C, we have
$H\cong K_2$
and by the maximality of C, we have
![]() ${|x_i^+\overrightarrow {C}x_{i+1}^-|\geq 2}$
for
${|x_i^+\overrightarrow {C}x_{i+1}^-|\geq 2}$
for
![]() $x_i\in N_C(h_1)\cap N_C(h_2)$
and
$x_i\in N_C(h_1)\cap N_C(h_2)$
and
![]() $|x_i^+\overrightarrow {C}x_{i+1}^-|\geq 1$
otherwise. Therefore,
$|x_i^+\overrightarrow {C}x_{i+1}^-|\geq 1$
otherwise. Therefore,
![]() $n-2\geq |C|\geq 3r+2[(n-2)/3-r]+2[(n-2)/3-r]=(4n-8)/3-r$
and hence
$n-2\geq |C|\geq 3r+2[(n-2)/3-r]+2[(n-2)/3-r]=(4n-8)/3-r$
and hence
![]() ${r\geq (n-2)/3}$
. Since
${r\geq (n-2)/3}$
. Since
![]() $r\leq d_C(h_i)=(n-2)/3$
for
$r\leq d_C(h_i)=(n-2)/3$
for
![]() $i=1,2$
, we have
$i=1,2$
, we have
![]() $r=d_C(h_i)= (n-2)/3$
for
$r=d_C(h_i)= (n-2)/3$
for
![]() $i=1,2$
, and hence
$i=1,2$
, and hence
![]() $N_C(H)=N_C(h_1)=N_C(h_2)$
and
$N_C(H)=N_C(h_1)=N_C(h_2)$
and
![]() $t=(n-2)/3$
. Finally, since
$t=(n-2)/3$
. Finally, since
![]() $r=(n-2)/3$
, we have
$r=(n-2)/3$
, we have
![]() $n-2\geq |C|\geq (4n-8)/3-r=n-2$
and hence
$n-2\geq |C|\geq (4n-8)/3-r=n-2$
and hence
![]() $|C|=n-2$
. Moreover,
$|C|=n-2$
. Moreover,
![]() $|x_i^+\overrightarrow {C}x_{i+1}^-|=2$
for each
$|x_i^+\overrightarrow {C}x_{i+1}^-|=2$
for each
![]() $1\leq i\leq t$
.
$1\leq i\leq t$
.
Now we consider the case
![]() $|H|\geq 3$
. Since
$|H|\geq 3$
. Since
![]() $|H|\geq 3$
and by Claim 3,
$|H|\geq 3$
and by Claim 3,
![]() $|N_C(H)|=2$
, and hence by Claim 2,
$|N_C(H)|=2$
, and hence by Claim 2,
![]() $N_C(h_i)\hspace{-1pt}=\hspace{-1pt}N_C(H)\hspace{-1pt}=\hspace{-1pt}\{x_1,x_2\}$
for
$N_C(h_i)\hspace{-1pt}=\hspace{-1pt}N_C(H)\hspace{-1pt}=\hspace{-1pt}\{x_1,x_2\}$
for
![]() $1\hspace{-1pt}\leq\hspace{-1pt} i\hspace{-1pt}\leq\hspace{-1pt} |H|$
. Since
$1\hspace{-1pt}\leq\hspace{-1pt} i\hspace{-1pt}\leq\hspace{-1pt} |H|$
. Since
![]() $d(h_i)\hspace{-1pt}=\hspace{-1pt}(n\hspace{-1pt}+\hspace{-1pt}1)/3$
and
$d(h_i)\hspace{-1pt}=\hspace{-1pt}(n\hspace{-1pt}+\hspace{-1pt}1)/3$
and
![]() $d_C(h_i)=2$
, we have
$d_C(h_i)=2$
, we have
![]() $d_H(h_i)=(n-5)/3$
for
$d_H(h_i)=(n-5)/3$
for
![]() $1\leq i\leq |H|$
, and hence by Lemma 2.1,
$1\leq i\leq |H|$
, and hence by Lemma 2.1,
![]() $n\geq |H|+|C|\geq 1+d_H(h_i)+2(n+1)/3=n$
. Therefore,
$n\geq |H|+|C|\geq 1+d_H(h_i)+2(n+1)/3=n$
. Therefore,
![]() $|C|=2(n+1)/3$
and
$|C|=2(n+1)/3$
and
![]() $|H|=(n-2)/3$
. Since
$|H|=(n-2)/3$
. Since
![]() $d_H(h_i)=(n-5)/3$
for
$d_H(h_i)=(n-5)/3$
for
![]() $1\leq i\leq |H|$
and
$1\leq i\leq |H|$
and
![]() $|H|=(n-2)/3$
, H is complete and so there exists a Hamiltonian path Q connecting
$|H|=(n-2)/3$
, H is complete and so there exists a Hamiltonian path Q connecting
![]() $h_1$
and
$h_1$
and
![]() $h_2$
in H. Since
$h_2$
in H. Since
![]() $N_C(h_i)=\{x_1,x_2\}$
for
$N_C(h_i)=\{x_1,x_2\}$
for
![]() $1\leq i\leq |H|$
, we have
$1\leq i\leq |H|$
, we have
![]() $x_1h_1,x_2h_2\in E(G)$
, and hence,
$x_1h_1,x_2h_2\in E(G)$
, and hence,
![]() $x_1h_1Qh_2x_2\overrightarrow {C}x_1$
is a cycle. By the maximality of C,
$x_1h_1Qh_2x_2\overrightarrow {C}x_1$
is a cycle. By the maximality of C,
![]() $|x_1^+\overrightarrow {C}x_2^-|\geq |Q|=|H|=(n-2)/3$
. Likewise,
$|x_1^+\overrightarrow {C}x_2^-|\geq |Q|=|H|=(n-2)/3$
. Likewise,
![]() $|x_2^+\overrightarrow {C}x_1^-|\geq (n-2)/3$
. Hence,
$|x_2^+\overrightarrow {C}x_1^-|\geq (n-2)/3$
. Hence,
![]() $(2n+2)/3=|C|= |x_1^+\overrightarrow {C}x_2^-|+|x_2^+\overrightarrow {C}x_1^-|+|\{x_1,x_2\}|\geq (2n+2)/3$
. Thus,
$(2n+2)/3=|C|= |x_1^+\overrightarrow {C}x_2^-|+|x_2^+\overrightarrow {C}x_1^-|+|\{x_1,x_2\}|\geq (2n+2)/3$
. Thus,
![]() $|x_i^+\overrightarrow {C}x_{i+1}^-|= |H|$
for
$|x_i^+\overrightarrow {C}x_{i+1}^-|= |H|$
for
![]() $1\leq i\leq 2$
.
$1\leq i\leq 2$
.
By Claim 4(1),
![]() $x_ih_1,x_{i+1}h_2\in E(G)$
where i is taken modulo t. By Claim 4(2), H is complete. Let Q be a Hamiltonian path connecting
$x_ih_1,x_{i+1}h_2\in E(G)$
where i is taken modulo t. By Claim 4(2), H is complete. Let Q be a Hamiltonian path connecting
![]() $h_1$
and
$h_1$
and
![]() $h_2$
in H. Let
$h_2$
in H. Let
![]() ${\mathcal {C}=x_ih_1Qh_2x_{i+1}\overrightarrow {C}x_i}$
. Clearly,
${\mathcal {C}=x_ih_1Qh_2x_{i+1}\overrightarrow {C}x_i}$
. Clearly,
![]() $\mathcal {C}$
is a cycle of G. By Claim 4(4),
$\mathcal {C}$
is a cycle of G. By Claim 4(4),
![]() $|x_i^+\overrightarrow {C}x_{i+1}^-|=|H|=|Q|$
and hence
$|x_i^+\overrightarrow {C}x_{i+1}^-|=|H|=|Q|$
and hence
![]() $|\mathcal {C}|=|C|$
. By the maximality of C,
$|\mathcal {C}|=|C|$
. By the maximality of C,
![]() $\mathcal {C}$
is a longest cycle. Let
$\mathcal {C}$
is a longest cycle. Let
![]() $\mathcal {H}$
be a component of
$\mathcal {H}$
be a component of
![]() $G-V(\mathcal {C})$
. Observing that
$G-V(\mathcal {C})$
. Observing that
![]() $x_i^+\overrightarrow {C}x_{i+1}^-$
is a path of some component of
$x_i^+\overrightarrow {C}x_{i+1}^-$
is a path of some component of
![]() $G-\mathcal {C}$
with
$G-\mathcal {C}$
with
![]() $|x_i^+\overrightarrow {C}x_{i+1}^-|=|H|=n-|C|=n-|\mathcal {C}|$
, it follows that
$|x_i^+\overrightarrow {C}x_{i+1}^-|=|H|=n-|C|=n-|\mathcal {C}|$
, it follows that
![]() $x_i^+\overrightarrow {C}x_{i+1}^-$
is a Hamiltonian path of
$x_i^+\overrightarrow {C}x_{i+1}^-$
is a Hamiltonian path of
![]() $\mathcal {H}$
. Hence,
$\mathcal {H}$
. Hence,
![]() $|\mathcal {H}|=|H|$
. It is clear that (2.1) and Claim 4 hold for
$|\mathcal {H}|=|H|$
. It is clear that (2.1) and Claim 4 hold for
![]() $(\mathcal {C},\mathcal {H})$
with respect to
$(\mathcal {C},\mathcal {H})$
with respect to
![]() $(C,H)$
.
$(C,H)$
.
If
![]() $|H|=(n-2)/3$
, then
$|H|=(n-2)/3$
, then
![]() $|\mathcal {H}|=|H|=(n-2)/3$
. By Claim 4(3),
$|\mathcal {H}|=|H|=(n-2)/3$
. By Claim 4(3),
![]() $|N_{\mathcal {C}}(\mathcal {H})|=2$
, and since
$|N_{\mathcal {C}}(\mathcal {H})|=2$
, and since
![]() $x_i^+x_i,x_{i+1}^-x_{i+1}\in E(G)$
,
$x_i^+x_i,x_{i+1}^-x_{i+1}\in E(G)$
,
![]() $x_i^+,x_{i+1}^-\in V(\mathcal {H})$
and
$x_i^+,x_{i+1}^-\in V(\mathcal {H})$
and
![]() $x_i,x_{i+1}\in V(\mathcal {C})$
, we have
$x_i,x_{i+1}\in V(\mathcal {C})$
, we have
![]() ${N_{\mathcal {C}}(\mathcal {H})=\{x_1,x_2\}}$
. By Claim 4(1),
${N_{\mathcal {C}}(\mathcal {H})=\{x_1,x_2\}}$
. By Claim 4(1),
![]() $N_{\mathcal {C}}(u)=\{x_1,x_2\}$
for
$N_{\mathcal {C}}(u)=\{x_1,x_2\}$
for
![]() $u\in V(\mathcal {H})$
. Additionally,
$u\in V(\mathcal {H})$
. Additionally,
![]() $|\mathcal {H}|=(n-2)/3$
and by Claim 4(2),
$|\mathcal {H}|=(n-2)/3$
and by Claim 4(2),
![]() $\mathcal {H}\cong K_{(n-2)/3}$
. Therefore, by the choice of i,
$\mathcal {H}\cong K_{(n-2)/3}$
. Therefore, by the choice of i,
![]() $G[x_1^+\overrightarrow {C}x_2^-]\cong K_{(n-2)/3}$
,
$G[x_1^+\overrightarrow {C}x_2^-]\cong K_{(n-2)/3}$
,
![]() $G[x_2^+\overrightarrow {C}x_1^-]\cong K_{(n-2)/3}$
and
$G[x_2^+\overrightarrow {C}x_1^-]\cong K_{(n-2)/3}$
and
![]() $N(u)=\{x_1,x_2\}$
for
$N(u)=\{x_1,x_2\}$
for
![]() $u\in V(C)\backslash \{x_1,x_2\}$
. By Claim 4(2) and (1),
$u\in V(C)\backslash \{x_1,x_2\}$
. By Claim 4(2) and (1),
![]() $H\cong K_{(n-2)/3}$
and
$H\cong K_{(n-2)/3}$
and
![]() $N(h)=\{x_1,x_2\}$
for any
$N(h)=\{x_1,x_2\}$
for any
![]() $h\in V(H)$
. It follows that
$h\in V(H)$
. It follows that
![]() $G\cong 2K_1\vee 3K_{(n-2)/3}$
or
$G\cong 2K_1\vee 3K_{(n-2)/3}$
or
![]() $G\cong K_2\vee 3K_{(n-2)/3}$
.
$G\cong K_2\vee 3K_{(n-2)/3}$
.
If
![]() $|H|=2$
, then
$|H|=2$
, then
![]() $|\mathcal {H}|=|H|=2$
and hence
$|\mathcal {H}|=|H|=2$
and hence
![]() $H\cong K_2$
. By Claim 4(3),
$H\cong K_2$
. By Claim 4(3),
![]() $|N_{\mathcal {C}}(\mathcal {H})|=(n-2)/3$
. Since (2.1) holds for
$|N_{\mathcal {C}}(\mathcal {H})|=(n-2)/3$
. Since (2.1) holds for
![]() $\mathcal {H}$
and
$\mathcal {H}$
and
![]() $\mathcal {H}\cong K_2$
, we have
$\mathcal {H}\cong K_2$
, we have
![]() $d_{\mathcal {C}}(x_i^+)=(n-2)/3$
. Since
$d_{\mathcal {C}}(x_i^+)=(n-2)/3$
. Since
![]() $x_i^+x_i\in E(G)$
where
$x_i^+x_i\in E(G)$
where
![]() $x_i^+\in V(\mathcal {H})$
and
$x_i^+\in V(\mathcal {H})$
and
![]() $x_i\in V(\mathcal {C})$
, we have
$x_i\in V(\mathcal {C})$
, we have
![]() $x_i\in N_{\mathcal {C}}(x_i^+)$
. Since
$x_i\in N_{\mathcal {C}}(x_i^+)$
. Since
![]() $d_{\mathcal {C}}(x_i^+)=(n-2)/3$
,
$d_{\mathcal {C}}(x_i^+)=(n-2)/3$
,
![]() $H\cong K_2$
and by Claim 4(1) and the maximality of
$H\cong K_2$
and by Claim 4(1) and the maximality of
![]() $\mathcal {C}$
, we have
$\mathcal {C}$
, we have
![]() $N_{\mathcal {C}}(x_i^+)=\{x_1,x_2,\ldots ,x_{(n-2)/3}\}$
. By Claim 4(1),
$N_{\mathcal {C}}(x_i^+)=\{x_1,x_2,\ldots ,x_{(n-2)/3}\}$
. By Claim 4(1),
![]() $N_{\mathcal {C}}(u)=\{x_1,x_2,\ldots ,x_{(n-2)/3}\}$
for
$N_{\mathcal {C}}(u)=\{x_1,x_2,\ldots ,x_{(n-2)/3}\}$
for
![]() $u\in V(\mathcal {H})$
. Thus, by the choice of i,
$u\in V(\mathcal {H})$
. Thus, by the choice of i,
![]() $G[x_i^+\overrightarrow {C}x_{i+1}^-]\cong K_2$
and
$G[x_i^+\overrightarrow {C}x_{i+1}^-]\cong K_2$
and
![]() $N_{\mathcal {C}}(u)=\{x_1,x_2,\ldots ,x_{(n-2)/3}\}$
for
$N_{\mathcal {C}}(u)=\{x_1,x_2,\ldots ,x_{(n-2)/3}\}$
for
![]() $u\in x_i^+\overrightarrow {C}x_{i+1}^-$
for any
$u\in x_i^+\overrightarrow {C}x_{i+1}^-$
for any
![]() $1\leq i\leq (n-2)/3$
. Therefore, together with Claim 4, we deduce that
$1\leq i\leq (n-2)/3$
. Therefore, together with Claim 4, we deduce that
![]() ${(n-2)/3K_1\vee (n+1)/3K_2\subseteq G \subseteq K_{(n-2)/3}\vee (n+1)/3K_2}$
.
${(n-2)/3K_1\vee (n+1)/3K_2\subseteq G \subseteq K_{(n-2)/3}\vee (n+1)/3K_2}$
.
This completes the proof.
Acknowledgement
We are grateful to the anonymous referees for their very careful comments which helped us improve an earlier version of this paper.