INTRODUCTION
Dengue is a flaviviral infection transmitted by Aedes mosquitoes. The dengue viruses are among the most widespread geographically of the arboviruses and are found in tropical and subtropical areas where 2·5–3 billion people are at risk of infection [Reference Gubler1]. The past two decades have seen an unprecedented geographical expansion of dengue, the reasons of which are complex and include increasing urbanization, lack of effective vector control, climate change and international travel [Reference Wilder-Smith and Gubler2].
Many of the dengue endemic countries are popular tourist destinations and dengue has emerged as a frequent problem in international travellers [Reference Wilder-Smith and Schwartz3]. GeoSentinel is a global network of travel medicine providers [Reference Freedman4] and dengue accounts for up to 2% of all illness in returned travellers who visit GeoSentinel clinics [Reference Schwartz5]. The GeoSentinel surveillance network has shown that over the past decade dengue has become a more frequent diagnosis than malaria in ill returned travellers from all tropical regions outside of Africa [Reference Freedman6]. Risk factors for acquiring dengue depend on duration of travel, season and destination [Reference Schwartz5, Reference Cobelens7].
Most of dengue virus infections in travellers are acquired in Asia, followed by the Americas and only a small proportion in Africa [Reference Freedman6–Reference Jelinek8]. Within Asia, Thailand is one of the countries with the highest risk of travellers acquiring dengue [Reference Schwartz5]. However, these data are based on a surveillance system that depend on returning travellers who seek healthcare (during or post-travel) at GeoSentinel sites and therefore the true incidence of dengue in travellers cannot be determined due to the lack of a denominator.
Risk estimates can be calculated for dengue-endemic countries provided that local data on the force of infection and variations over time are available. We used mathematical models to estimate the risk of non-immune persons acquiring dengue when travelling to Thailand.
METHODS
We obtained data on national epidemiology of dengue in Thailand from 1990 until 2007 which are freely available on the website of the South East Asia Regional Office of the World Health Organization (SEARO) (http://www.searo.who.int/LinkFiles/Dengue_dengue_Thailand.pdf).
We calculated the average risk for a non-immune traveller who arrives in Thailand in four different moments of time, i.e. in the dry season (winter months), spring (spring months), the wet season (summer) and autumn. We used an adaptation of the model developed by Massad et al. [Reference Massad9] to describe the dynamics of dengue. The model estimates the force of infection, which means the incidence density rate (per capita number of new cases per year) for the period [Reference Burattini10]. The force of infection is defined as the per capita number of new cases per time unit as
where N H is the total human population, I M(t) is the number of infected mosquitoes, a is the mosquito biting rate and b is the probability that an infectious mosquito will infect a human susceptible.
We calculated the probability of an individual acquiring dengue, πtravellers, after arriving in Thailand, depending upon the length of stay (for ω days) and also depending on the time of arrival (at day Ω), using the following equation:
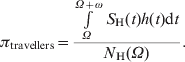 $$\pi _{{\rm travellers}} \equals {{\int \limits_{\Omega }^{\Omega \plus \omega } {S_{\rm H} \lpar t\rpar h\lpar t\rpar {\rm d}t} } \over {N_{\rm H} \lpar \Omega \rpar }}.\hskip89.5pt$$
$$\pi _{{\rm travellers}} \equals {{\int \limits_{\Omega }^{\Omega \plus \omega } {S_{\rm H} \lpar t\rpar h\lpar t\rpar {\rm d}t} } \over {N_{\rm H} \lpar \Omega \rpar }}.\hskip89.5pt$$In the interval between Ω and Ω + ω, a total of ![]() $\int _{\Omega }^{\Omega \plus \omega } $S H(t)h(t)dt new infections occur. This quantity divided by the total number of individuals in the population at time Ω gives the probability πtravellers above.
$\int _{\Omega }^{\Omega \plus \omega } $S H(t)h(t)dt new infections occur. This quantity divided by the total number of individuals in the population at time Ω gives the probability πtravellers above.
The model is deterministic with stochastic parameters and assumes a Poisson distribution for the mosquito biting rate, a, and a Gamma distribution for the probability of acquiring dengue from an infected mosquito, b. We used stochastic methods since the relatively small number of travellers is associated with random fluctuations of the biting rate and therefore fluctuations in the probability of infection should be considered. The models and the variables for the models are described in the Appendix. The parameters applied for the numerical simulations are shown in Table 1.
Table 1. Model parameters, biological meaning, values and sources

From the force of infection we calculated the risk of acquiring dengue for travellers to Thailand arriving in a typical year (averaged over a 17-year period).
RESULTS
Figure 1 shows how the model fits into the actual data (averaged over a 17-years period) of the national epidemiology of Thailand. In Figure 2 we show the model's simulation for non-infected and infected mosquitoes along with the definition of ‘seasons’: winter is the dry season, summer is the rainy reason, spring and autumn are the interim seasons approximately corresponding with the calendar months of the Northern hemisphere.

Fig. 1. The model's fit to the actual national epidemiology of dengue in Thailand averaged over 17 years, from 1990 to 2007. Symbols (•) represent actual data [data from the national epidemiology of Thailand as obtained from the South East Asia Regional Office of the World Health Organization (http://www.searo.who.int/LinkFiles/Dengue_dengue_Thailand.pdf)]. The continuous line (––) represents data obtained from our mathematical model.

Fig. 2. The model's simulation for non-infected (thick line) and infected (thin line) mosquitoes along with the definition of ‘seasons’: winter is the dry season, summer is the rainy reason, spring and autumn are the interim seasons approximately corresponding with the calendar months of the Northern hemisphere.
Our modelling showed that a traveller arriving in the season of highest transmission (designated ‘autumn’ and representing the period of the year between the wet and the dry season) who has a stay of 1 week has a risk of acquiring dengue of 0·2% (95% CI 0·16–0·23), whereas the risk for travel of 2 and 4 weeks' duration is 0·43% (95% CI 0·41–0·50) and 0·81% (95% CI 0·76–0·87), respectively (Table 2). Table 1 also shows the risk for the rainy and dry season for 1, 2, 3 and 4 weeks of travel duration.
Table 2. Risk of acquiring dengue in travellers to Thailand depending on season and duration of travel average risk of dengue in percentage

All values given are percentages.
Figure 3 presents the result of risk estimation for travellers arriving in each of the four seasons in a logarithmic scale depending on length of stay in Thailand.

Fig. 3. Continuous lines represents the average of 1000 stochastic simulations of the model. Dotted lines represent the 95% confidence intervals.
DISCUSSION
Previous studies have attempted to determine the cumulative risk of acquiring dengue in travellers [Reference Cobelens7, Reference Potasman, Srugo and Schwartz11], but such studies do not take into account the seasonality and year to year oscillation of dengue, nor the duration of travel. Most reports are limited to passive surveillance or sentinel surveillance and may therefore underestimate the true risk. First of all, dengue is a disease of short duration and travellers may therefore not seek healthcare in their countries of origin. Second, dengue is not a legally notifiable disease in most countries where travellers originate from. Last, passive surveillance only takes into account symptomatic disease. However, asymptomatic dengue infections are also important in travellers as repeat travel may expose a previously infected traveller to more severe disease [Reference Wilder-Smith and Schwartz3].
Our data highlight that the risk of non-immune travellers acquiring dengue in Thailand is substantial and varies with season and duration of travel. The difference in incidence between the low and peak season is more than 100-fold. The increase in incidence is proportional with the length of stay. During the high season for a 4-week stay in Thailand, we estimated a risk of 0·81% in non-immune travellers. Such an incidence is substantial. During the dry season, the typical travel season, the incidence is 0·0003%. The incidence of 0·81% after 1 month's travel during the high-risk reason is very similar to that found in two prospective seroconversion studies in Israeli and Dutch travellers [Reference Cobelens7, Reference Potasman, Srugo and Schwartz11]. During a mean of 6 months' stay in Israeli travellers in Thailand the seroconversion rate was 6·7% – and these data were from 1998, a high epidemic year [Reference Potasman, Srugo and Schwartz11]. Probable dengue infection was found in 13/447 Dutch travellers to all dengue-endemic countries (incidence rate 30/1000 person-months) [Reference Cobelens7]. The fact that our study results based on mathematical models is in keeping with prospective seroconversion studies underlines that our model reflects actual data and can therefore also be applied to other dengue-endemic countries. However, mathematical models in contrast to seroconversion studies, offer additional information taking into account various travel scenarios such as seasonality and duration of travel.
The Dutch study showed an asymptomatic/symptomatic ratio of 3·3/1 [Reference Cobelens7]. Our study considered all dengue infections (symptomatic and asymptomatic) in a non-immune population. The incidence of symptomatic dengue is therefore about three times lower than the actual numbers calculated in our models, but it should be taken into account that the ratio of asymptomatic to symptomatic dengue may vary between 1 and 10 dependent on age, host factors and geography [Reference Guzman and Kouri12].
Using similar mathematical models we found that the risk of acquiring dengue for travellers to Thailand is far higher compared to travellers to Singapore [Reference Massad and Wilder-Smith13]. This finding is consistent with the fact that dengue is more frequent in Thailand than in Singapore [Reference Wilder-Smith14].
Quantifying the risk of dengue in travellers is an important piece of information to the travel medicine provider and traveller alike. Risk estimates based on mathematical modelling will help the travel medicine provider give better evidence-based advice to travellers to dengue-endemic countries.
APPENDIX
Equations for the model
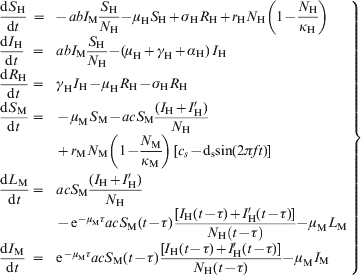 $$\scale89%\left{\matrix{ {{\displaystyle{{{\rm d}S_ {\rm H} } \over {{\rm d}t}}}} \hfill \tab \hskip-12pt \equals \hskip-7pt \tab \hskip-1.5pt {\minus abI_{\rm M} {\displaystyle{{S_ {\rm H} } \over {N_{\rm H} }}} \minus \mu _{\rm H} S_{\rm H} \plus \sigma _{\rm H} R_{\rm H} \plus r_{\rm H} N_{\rm H} \left( {1 \minus {\displaystyle{{N_ {\rm H} } \over {\kappa _{\rm H} }}}} \right)} \hfill \vskip8pt \cr {{\displaystyle{{{\rm d}I_{\rm H} } \over {{\rm d}t}}}} \hfill \tab \hskip-8pt \equals \hskip-8pt \hfill \tab {abI_{\rm M} {\displaystyle{{S_{\rm H} } \over {N_{\rm H} }}} \minus \lpar \mu _{\rm H} \plus \gamma _{\rm H} \plus \alpha _{\rm H} \rpar \,I_{\rm H} } \hfill \vskip8pt \cr {{\displaystyle{{{\rm d}R_{\rm H} } \over {{\rm d}t}}}} \hfill \tab \hskip-8pt \equals \hskip-8pt \hfill \tab {\gamma _{\rm H} I_{\rm H} \minus \mu _{\rm H} R_{\rm H} \minus \sigma _{\rm H} R_{\rm H} } \hfill \vskip8pt \cr {{\displaystyle{{{\rm d}S_{\rm M} } \over {{\rm d}t}}}} \hfill \tab \hskip-8pt \equals \hskip-8pt \hfill \tab { \minus \mu _{\rm M} S_{\rm M} \minus acS_{\rm M} {\displaystyle{{\lpar I_{\rm H} \plus I'_{\rm H} \rpar } \over {N_{\rm H} }}}} \hfill \vskip8pt \cr {} \hfill \tab {} \hfill \tab { \plus r_{\rm M} N_{\rm M} \left( {1 \minus {\displaystyle{{N_{\rm M} } \over {\kappa _{\rm M} }}}} \right)\,\lsqb c_{s} \minus {\rm d}_{\rm s} {\rm sin}\lpar 2\pi ft\rpar \rsqb } \hfill \vskip12pt \cr {{\displaystyle{{{\rm d}L_{\rm M} } \over {{\rm d}t}}}} \hfill \tab \hskip-8pt \equals \hskip-8pt \hfill \tab {acS_{\rm M} {\displaystyle{{\lpar I_{\rm H} \plus I'_{\rm H} \rpar } \over {N_{\rm H} }}}} \hfill \vskip8pt \cr {} \hfill \tab {} \hfill \tab { \minus {\rm e}^{ \minus \mu _{{\rm M}} \tau } acS_{\rm M} \lpar t \minus \tau \rpar \,{\displaystyle{{\lsqb I_{\rm H} \lpar t \minus \tau \rpar \plus I'_{\rm H} \lpar t \minus \tau \rpar \rsqb } \over {N_{\rm H} \left( {t \minus \tau } \right)}}} \minus \mu _{\rm M} L_{\rm M} } \hfill \vskip8pt \cr {{\displaystyle{{{\rm d}I_{\rm M} } \over {{\rm d}t}}}} \hfill \tab \hskip-8pt \equals \hskip-8pt \hfill \tab {{\rm e}^{ \minus \mu _{{\rm M}} \tau } acS_{\rm M} \lpar t \minus \tau \rpar \,{\displaystyle{{\lsqb I_{\rm H} \lpar t \minus \tau \rpar \plus I'_{\rm H} \lpar t \minus \tau \rpar \rsqb } \over {N_{\rm H} \lpar t \minus \tau \rpar }}} \minus \mu _{\rm M} I_{\rm M} } \hfill \cr} } \right\}}$$
$$\scale89%\left{\matrix{ {{\displaystyle{{{\rm d}S_ {\rm H} } \over {{\rm d}t}}}} \hfill \tab \hskip-12pt \equals \hskip-7pt \tab \hskip-1.5pt {\minus abI_{\rm M} {\displaystyle{{S_ {\rm H} } \over {N_{\rm H} }}} \minus \mu _{\rm H} S_{\rm H} \plus \sigma _{\rm H} R_{\rm H} \plus r_{\rm H} N_{\rm H} \left( {1 \minus {\displaystyle{{N_ {\rm H} } \over {\kappa _{\rm H} }}}} \right)} \hfill \vskip8pt \cr {{\displaystyle{{{\rm d}I_{\rm H} } \over {{\rm d}t}}}} \hfill \tab \hskip-8pt \equals \hskip-8pt \hfill \tab {abI_{\rm M} {\displaystyle{{S_{\rm H} } \over {N_{\rm H} }}} \minus \lpar \mu _{\rm H} \plus \gamma _{\rm H} \plus \alpha _{\rm H} \rpar \,I_{\rm H} } \hfill \vskip8pt \cr {{\displaystyle{{{\rm d}R_{\rm H} } \over {{\rm d}t}}}} \hfill \tab \hskip-8pt \equals \hskip-8pt \hfill \tab {\gamma _{\rm H} I_{\rm H} \minus \mu _{\rm H} R_{\rm H} \minus \sigma _{\rm H} R_{\rm H} } \hfill \vskip8pt \cr {{\displaystyle{{{\rm d}S_{\rm M} } \over {{\rm d}t}}}} \hfill \tab \hskip-8pt \equals \hskip-8pt \hfill \tab { \minus \mu _{\rm M} S_{\rm M} \minus acS_{\rm M} {\displaystyle{{\lpar I_{\rm H} \plus I'_{\rm H} \rpar } \over {N_{\rm H} }}}} \hfill \vskip8pt \cr {} \hfill \tab {} \hfill \tab { \plus r_{\rm M} N_{\rm M} \left( {1 \minus {\displaystyle{{N_{\rm M} } \over {\kappa _{\rm M} }}}} \right)\,\lsqb c_{s} \minus {\rm d}_{\rm s} {\rm sin}\lpar 2\pi ft\rpar \rsqb } \hfill \vskip12pt \cr {{\displaystyle{{{\rm d}L_{\rm M} } \over {{\rm d}t}}}} \hfill \tab \hskip-8pt \equals \hskip-8pt \hfill \tab {acS_{\rm M} {\displaystyle{{\lpar I_{\rm H} \plus I'_{\rm H} \rpar } \over {N_{\rm H} }}}} \hfill \vskip8pt \cr {} \hfill \tab {} \hfill \tab { \minus {\rm e}^{ \minus \mu _{{\rm M}} \tau } acS_{\rm M} \lpar t \minus \tau \rpar \,{\displaystyle{{\lsqb I_{\rm H} \lpar t \minus \tau \rpar \plus I'_{\rm H} \lpar t \minus \tau \rpar \rsqb } \over {N_{\rm H} \left( {t \minus \tau } \right)}}} \minus \mu _{\rm M} L_{\rm M} } \hfill \vskip8pt \cr {{\displaystyle{{{\rm d}I_{\rm M} } \over {{\rm d}t}}}} \hfill \tab \hskip-8pt \equals \hskip-8pt \hfill \tab {{\rm e}^{ \minus \mu _{{\rm M}} \tau } acS_{\rm M} \lpar t \minus \tau \rpar \,{\displaystyle{{\lsqb I_{\rm H} \lpar t \minus \tau \rpar \plus I'_{\rm H} \lpar t \minus \tau \rpar \rsqb } \over {N_{\rm H} \lpar t \minus \tau \rpar }}} \minus \mu _{\rm M} I_{\rm M} } \hfill \cr} } \right\}}$$In addition, we separated a cohort (denoted by primes and called ‘probe’) that is followed through the entire outbreak and that is used to calculate the probability that an individual gets dengue infection, according to equation (2), described in the main text.
The evolution equations for the probe cohort are:
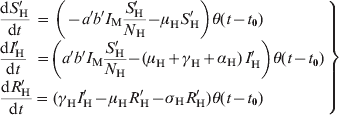 $$\left.\matrix{ {{\displaystyle{{{\rm d}S'_{\rm H} } \over {{\rm d}t}}\hskip2pt \equals\tab \hskip2pt \left( { \minus a'b'I_{\rm M} {\displaystyle{{S'_{\rm H} } \over {N_{\rm H} }}} \minus \mu _{\rm H} S'_{\rm H}} \right)}{{\theta \lpar t \minus t_{\setnum{0}} \rpar}}}\hfill \cr {\displaystyle{{{\rm d}I'_{\rm H} } \over {{\rm d}t}}\hskip4pt \equals\tab \left({a'b'I_{\rm M} {\displaystyle{{S'_{\rm H} } \over {N_{\rm H} }}} \minus \lpar \mu _{\rm H} \plus \gamma _{\rm H} \plus \alpha _{\rm H} \rpar \,I'_{\rm H}} \right) {\theta \lpar t \minus t_{\setnum{0}}} \rpar}\hfill \cr { \hskip-38pt{\displaystyle{{{\rm d}R'_{\rm H} } \over {{\rm d}t}} \equals \tab \hskip2pt{\lpar \gamma _{\rm H} I'_{\rm H} \minus \mu _{\rm H} R'_{\rm H} \minus \sigma _{\rm H} R'_{\rm H} \rpar \theta \lpar t \minus t_{\setnum{0}} \rpar }\hfill\cr}} }\right \}$$
$$\left.\matrix{ {{\displaystyle{{{\rm d}S'_{\rm H} } \over {{\rm d}t}}\hskip2pt \equals\tab \hskip2pt \left( { \minus a'b'I_{\rm M} {\displaystyle{{S'_{\rm H} } \over {N_{\rm H} }}} \minus \mu _{\rm H} S'_{\rm H}} \right)}{{\theta \lpar t \minus t_{\setnum{0}} \rpar}}}\hfill \cr {\displaystyle{{{\rm d}I'_{\rm H} } \over {{\rm d}t}}\hskip4pt \equals\tab \left({a'b'I_{\rm M} {\displaystyle{{S'_{\rm H} } \over {N_{\rm H} }}} \minus \lpar \mu _{\rm H} \plus \gamma _{\rm H} \plus \alpha _{\rm H} \rpar \,I'_{\rm H}} \right) {\theta \lpar t \minus t_{\setnum{0}}} \rpar}\hfill \cr { \hskip-38pt{\displaystyle{{{\rm d}R'_{\rm H} } \over {{\rm d}t}} \equals \tab \hskip2pt{\lpar \gamma _{\rm H} I'_{\rm H} \minus \mu _{\rm H} R'_{\rm H} \minus \sigma _{\rm H} R'_{\rm H} \rpar \theta \lpar t \minus t_{\setnum{0}} \rpar }\hfill\cr}} }\right \}$$for
- a′=
Poisson(0·164)
- b′=
Gamma(0·088, 0·0003),
 $$\left {\matrix{ {\hskip-1pt N_{\rm H} }\tab \hskip-8pt \equals \hskip-8pt \tab {S_{\rm H} \plus I_{\rm H} \plus R_{\rm H} } \hfill \cr {\hskip-1pt N_{\rm H} } \tab \hskip-8pt \equals \hskip-8pt \tab {N_{\rm H} \plus S_{\rm H} \plus I_{\rm H} \plus R_{\rm H} } \hfill \cr {N_{\rm M} } \tab \hskip-8pt \equals \hskip-8pt \tab {S_{\rm M} \plus L_{\rm M} \plus I_{\rm M} } \hfill \cr} } \right \}$$
$$\left {\matrix{ {\hskip-1pt N_{\rm H} }\tab \hskip-8pt \equals \hskip-8pt \tab {S_{\rm H} \plus I_{\rm H} \plus R_{\rm H} } \hfill \cr {\hskip-1pt N_{\rm H} } \tab \hskip-8pt \equals \hskip-8pt \tab {N_{\rm H} \plus S_{\rm H} \plus I_{\rm H} \plus R_{\rm H} } \hfill \cr {N_{\rm M} } \tab \hskip-8pt \equals \hskip-8pt \tab {S_{\rm M} \plus L_{\rm M} \plus I_{\rm M} } \hfill \cr} } \right \}$$and θ(t – t 0) is the Heaviside function.
The parameters' biological significance and the values used in the numerical simulation of the model are shown in Table 1.
We introduced the term [c s – d s sin(2πft)] in the susceptible mosquito population in order to simulate seasonality in the mosquito population. The parameters c s and d s (c s>d s) modulate the intensity of the seasonality, mimicking deep or light winters, depending on the difference between those parameters' values.
ACKNOWLEDGEMENTS
This research was undertaken by partners from the ‘DengueTools’ consortium [Reference Wilder-Smith15]. DengueTools is funded under the Health theme of the Seventh Framework Programme of the European Community, Grant Agreement Number: 282589.
DECLARATION OF INTEREST
None.







