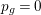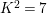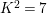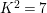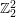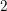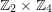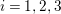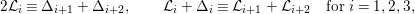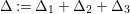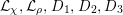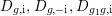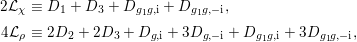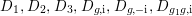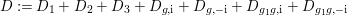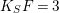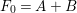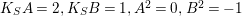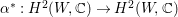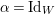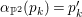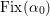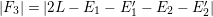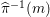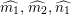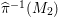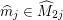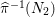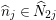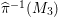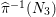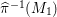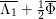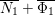1 Introduction
The birational automorphism groups of projective varieties are extensively studied. Nowadays we know that, for a projective variety of general type
![]() $X$
over an algebraically closed field of characteristic zero, the number of birational automorphisms of
$X$
over an algebraically closed field of characteristic zero, the number of birational automorphisms of
![]() $X$
is bounded by
$X$
is bounded by
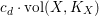 $c_{d}\cdot \text{vol}(X,K_{X})$
, where
$c_{d}\cdot \text{vol}(X,K_{X})$
, where
![]() $c_{d}$
is a constant which only depends on the dimension
$c_{d}$
is a constant which only depends on the dimension
![]() $d$
of
$d$
of
![]() $X$
, and
$X$
, and
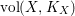 $\text{vol}(X,K_{X})$
is the volume of the canonical divisor
$\text{vol}(X,K_{X})$
is the volume of the canonical divisor
![]() $K_{X}$
(cf. [Reference Hacon, McKernan and Xu13]). Furthermore, we know that
$K_{X}$
(cf. [Reference Hacon, McKernan and Xu13]). Furthermore, we know that
![]() $c_{1}=42$
and
$c_{1}=42$
and
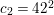 $c_{2}=42^{2}$
according to the classical Hurwitz theorem and to Xiao’s theorem (cf. [Reference Xiao25] and [Reference Xiao26]). However, even in low dimensions, it is usually nontrivial to calculate the automorphism groups of explicit varieties of general type (for example, see [Reference Keum15], [Reference Prasad and Yeung23], [Reference Cartwright and Steger8] and [Reference Maggiolo17]).
$c_{2}=42^{2}$
according to the classical Hurwitz theorem and to Xiao’s theorem (cf. [Reference Xiao25] and [Reference Xiao26]). However, even in low dimensions, it is usually nontrivial to calculate the automorphism groups of explicit varieties of general type (for example, see [Reference Keum15], [Reference Prasad and Yeung23], [Reference Cartwright and Steger8] and [Reference Maggiolo17]).
We focus on automorphisms of minimal smooth complex surfaces of general type with
![]() $p_{g}=0$
and
$p_{g}=0$
and
![]() $K^{2}=7$
. Involutions on such surfaces have been studied in [Reference Lee and Shin16] and [Reference Rito24]. All the possibilities of the quotient surfaces and the fixed loci of the involutions are listed. In order to find new examples, we have tried to classify such surfaces with commuting involutions in [Reference Chen10] and succeeded in constructing a new family of surfaces in [Reference Chen9]. We briefly recall the main results of [Reference Chen10]. Throughout the article,
$K^{2}=7$
. Involutions on such surfaces have been studied in [Reference Lee and Shin16] and [Reference Rito24]. All the possibilities of the quotient surfaces and the fixed loci of the involutions are listed. In order to find new examples, we have tried to classify such surfaces with commuting involutions in [Reference Chen10] and succeeded in constructing a new family of surfaces in [Reference Chen9]. We briefly recall the main results of [Reference Chen10]. Throughout the article,
![]() $S$
denotes a minimal smooth surface of general type with
$S$
denotes a minimal smooth surface of general type with
![]() $p_{g}=0$
and
$p_{g}=0$
and
![]() $K^{2}=7$
over
$K^{2}=7$
over
![]() $\mathbb{C}$
.
$\mathbb{C}$
.
Theorem 1.1. [Reference Chen10, Theorem 1.1]
Assume that the automorphism group
![]() $\text{Aut}(S)$
contains a subgroup
$\text{Aut}(S)$
contains a subgroup
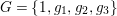 $G=\{1,g_{1},g_{2},g_{3}\}$
, which is isomorphic to
$G=\{1,g_{1},g_{2},g_{3}\}$
, which is isomorphic to
![]() $\mathbb{Z}_{2}^{2}$
. Let
$\mathbb{Z}_{2}^{2}$
. Let
![]() $R_{g_{i}}$
be the divisorial part of the fixed locus of the involution
$R_{g_{i}}$
be the divisorial part of the fixed locus of the involution
![]() $g_{i}$
for
$g_{i}$
for
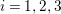 $i=1,2,3$
. Then the canonical divisor
$i=1,2,3$
. Then the canonical divisor
![]() $K_{S}$
is ample and
$K_{S}$
is ample and
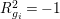 $R_{g_{i}}^{2}=-1$
for
$R_{g_{i}}^{2}=-1$
for
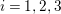 $i=1,2,3$
. Moreover, there are only three numerical possibilities for the intersection numbers
$i=1,2,3$
. Moreover, there are only three numerical possibilities for the intersection numbers
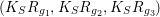 $(K_{S}R_{g_{1}},K_{S}R_{g_{2}},K_{S}R_{g_{3}})$
:
$(K_{S}R_{g_{1}},K_{S}R_{g_{2}},K_{S}R_{g_{3}})$
:
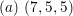 $(a)~(7,5,5)$
,
$(a)~(7,5,5)$
,
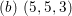 $(b)~(5,5,3)$
and
$(b)~(5,5,3)$
and
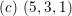 $(c)~(5,3,1)$
. The intersection numbers
$(c)~(5,3,1)$
. The intersection numbers
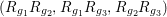 $(R_{g_{1}}R_{g_{2}},R_{g_{1}}R_{g_{3}},R_{g_{2}}R_{g_{3}})$
have the following values:
$(R_{g_{1}}R_{g_{2}},R_{g_{1}}R_{g_{3}},R_{g_{2}}R_{g_{3}})$
have the following values:
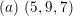 $(a)~(5,9,7)$
,
$(a)~(5,9,7)$
,
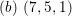 $(b)~(7,5,1)$
and
$(b)~(7,5,1)$
and
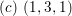 $(c)~(1,3,1)$
, respectively.
$(c)~(1,3,1)$
, respectively.
In the above theorem, we adopt the convention that
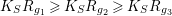 $K_{S}R_{g_{1}}\geqslant K_{S}R_{g_{2}}\geqslant K_{S}R_{g_{3}}$
,
$K_{S}R_{g_{1}}\geqslant K_{S}R_{g_{2}}\geqslant K_{S}R_{g_{3}}$
,
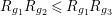 $R_{g_{1}}R_{g_{2}}\leqslant R_{g_{1}}R_{g_{3}}$
in case (a) and
$R_{g_{1}}R_{g_{2}}\leqslant R_{g_{1}}R_{g_{3}}$
in case (a) and
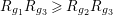 $R_{g_{1}}R_{g_{3}}\geqslant R_{g_{2}}R_{g_{3}}$
in case (b). Actually, we have completely classified the surfaces in case (a) and case (b) in [Reference Chen10]. But we do not know any example of the surfaces in case (c). One may ask whether there are noncommutative involutions on
$R_{g_{1}}R_{g_{3}}\geqslant R_{g_{2}}R_{g_{3}}$
in case (b). Actually, we have completely classified the surfaces in case (a) and case (b) in [Reference Chen10]. But we do not know any example of the surfaces in case (c). One may ask whether there are noncommutative involutions on
![]() $S$
. Here we give a negative answer.
$S$
. Here we give a negative answer.
Theorem 1.2. If
![]() ${\it\alpha}$
is an involution of
${\it\alpha}$
is an involution of
![]() $S$
, then
$S$
, then
![]() ${\it\alpha}$
is contained in the center of
${\it\alpha}$
is contained in the center of
![]() $\text{Aut}(S)$
.
$\text{Aut}(S)$
.
We prove the above theorem in Section 3. The key step is Theorem 3.1 which shows that any two involutions on
![]() $S$
commute. Theorem 3.1 also has the following corollary.
$S$
commute. Theorem 3.1 also has the following corollary.
Corollary 1.3. Assume that
![]() $(S,G)$
is a pair satisfying the assumption of Theorem 1.1. Then
$(S,G)$
is a pair satisfying the assumption of Theorem 1.1. Then
![]() $g_{1},g_{2}$
and
$g_{1},g_{2}$
and
![]() $g_{3}$
are exactly all the involutions of
$g_{3}$
are exactly all the involutions of
![]() $\text{Aut}(S)$
.
$\text{Aut}(S)$
.
The corollary immediately implies that if
![]() $\text{Aut}(S)$
contains a nontrivial subgroup which is isomorphic to
$\text{Aut}(S)$
contains a nontrivial subgroup which is isomorphic to
![]() $\mathbb{Z}_{2}^{r}$
, then
$\mathbb{Z}_{2}^{r}$
, then
![]() $r=1$
or
$r=1$
or
![]() $r=2$
. We remark that there are surfaces of general type with
$r=2$
. We remark that there are surfaces of general type with
![]() $p_{g}=0$
,
$p_{g}=0$
,
![]() $K^{2}=8$
and their automorphism groups contain subgroups which are isomorphic to
$K^{2}=8$
and their automorphism groups contain subgroups which are isomorphic to
![]() $\mathbb{Z}_{2}^{3}$
(cf. [Reference Mendes Lopes and Pardini19, Example 4.2–4.4]).
$\mathbb{Z}_{2}^{3}$
(cf. [Reference Mendes Lopes and Pardini19, Example 4.2–4.4]).
As an application, we calculate the automorphism groups of the surfaces in the case (a) of Theorem 1.1. These surfaces are those constructed by Inoue in [Reference Inoue14] who found the first examples of surfaces of general type with
![]() $p_{g}=0$
and
$p_{g}=0$
and
![]() $K^{2}=7$
. They can be described as finite Galois
$K^{2}=7$
. They can be described as finite Galois
![]() $\mathbb{Z}_{2}^{2}$
-covers of the
$\mathbb{Z}_{2}^{2}$
-covers of the
![]() $4$
-nodal cubic surface (see Example 4.1, which is from [Reference Mendes Lopes and Pardini19, Example 4.1]).
$4$
-nodal cubic surface (see Example 4.1, which is from [Reference Mendes Lopes and Pardini19, Example 4.1]).
Theorem 1.4. Let
![]() $S$
be an Inoue surface. Then
$S$
be an Inoue surface. Then
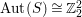 $\text{Aut}(S)\cong \mathbb{Z}_{2}^{2}$
or
$\text{Aut}(S)\cong \mathbb{Z}_{2}^{2}$
or
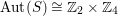 $\text{Aut}(S)\cong \mathbb{Z}_{2}\times \mathbb{Z}_{4}$
. If
$\text{Aut}(S)\cong \mathbb{Z}_{2}\times \mathbb{Z}_{4}$
. If
![]() $S$
is a general Inoue surface, then
$S$
is a general Inoue surface, then
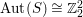 $\text{Aut}(S)\cong \mathbb{Z}_{2}^{2}$
.
$\text{Aut}(S)\cong \mathbb{Z}_{2}^{2}$
.
Inoue surfaces form a
![]() $4$
-dimensional irreducible connected component in the Gieseker moduli space of canonical models of surfaces of general type (cf. [Reference Bauer and Catanese3]). The proof of Theorem 1.4 actually shows that
$4$
-dimensional irreducible connected component in the Gieseker moduli space of canonical models of surfaces of general type (cf. [Reference Bauer and Catanese3]). The proof of Theorem 1.4 actually shows that
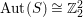 $\text{Aut}(S)\cong \mathbb{Z}_{2}^{2}$
for
$\text{Aut}(S)\cong \mathbb{Z}_{2}^{2}$
for
![]() $S$
outside a
$S$
outside a
![]() $2$
-dimensional irreducible closed subset of this connected component (see Remark 4.3). We also exhibit a
$2$
-dimensional irreducible closed subset of this connected component (see Remark 4.3). We also exhibit a
![]() $2$
-dimensional family of Inoue surfaces with
$2$
-dimensional family of Inoue surfaces with
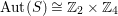 $\text{Aut}(S)\cong \mathbb{Z}_{2}\times \mathbb{Z}_{4}$
(see Section 5). They are finite Galois
$\text{Aut}(S)\cong \mathbb{Z}_{2}\times \mathbb{Z}_{4}$
(see Section 5). They are finite Galois
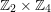 $\mathbb{Z}_{2}\times \mathbb{Z}_{4}$
-covers of a
$\mathbb{Z}_{2}\times \mathbb{Z}_{4}$
-covers of a
![]() $5$
-nodal weak Del Pezzo surface of degree two, which is the minimal resolution of one node of the
$5$
-nodal weak Del Pezzo surface of degree two, which is the minimal resolution of one node of the
![]() $6$
-nodal Del Pezzo surface of degree two.
$6$
-nodal Del Pezzo surface of degree two.
2 Preliminaries
2.1 Fixed point formulas and rational curves
Let
![]() $X$
be a smooth projective surface over the complex number field. We only consider surfaces with
$X$
be a smooth projective surface over the complex number field. We only consider surfaces with
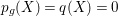 $p_{g}(X)=q(X)=0$
. In this case,
$p_{g}(X)=q(X)=0$
. In this case,
![]() $X$
has Picard number
$X$
has Picard number
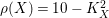 ${\it\rho}(X)=10-K_{X}^{2}$
by Noether’s formula and the Hodge decomposition. Also the expotential cohomology sequence gives
${\it\rho}(X)=10-K_{X}^{2}$
by Noether’s formula and the Hodge decomposition. Also the expotential cohomology sequence gives
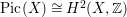 $\text{Pic}(X)\cong H^{2}(X,\mathbb{Z})$
. Poincaré duality implies that the intersection form on
$\text{Pic}(X)\cong H^{2}(X,\mathbb{Z})$
. Poincaré duality implies that the intersection form on
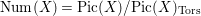 $\text{Num}(X)=\text{Pic}(X)/\text{Pic}(X)_{\text{Tors}}$
is unimodular.
$\text{Num}(X)=\text{Pic}(X)/\text{Pic}(X)_{\text{Tors}}$
is unimodular.
Assume that
![]() $X$
has a nontrivial automorphism
$X$
has a nontrivial automorphism
![]() ${\it\tau}$
. Denote by
${\it\tau}$
. Denote by
![]() $\text{Fix}({\it\tau})$
the fixed locus of
$\text{Fix}({\it\tau})$
the fixed locus of
![]() ${\it\tau}$
. Let
${\it\tau}$
. Let
![]() $k_{{\it\tau}}$
be the number of isolated fixed points of
$k_{{\it\tau}}$
be the number of isolated fixed points of
![]() ${\it\tau}$
and let
${\it\tau}$
and let
![]() $R_{{\it\tau}}$
be the divisorial part of
$R_{{\it\tau}}$
be the divisorial part of
![]() $\text{Fix}({\it\tau})$
. Then
$\text{Fix}({\it\tau})$
. Then
![]() $R_{{\it\tau}}$
is a disjoint union of irreducible smooth curves. We denote by
$R_{{\it\tau}}$
is a disjoint union of irreducible smooth curves. We denote by
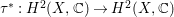 ${\it\tau}^{\ast }:H^{2}(X,\mathbb{C})\rightarrow H^{2}(X,\mathbb{C})$
the induced linear map on the second singular cohomology group (note that
${\it\tau}^{\ast }:H^{2}(X,\mathbb{C})\rightarrow H^{2}(X,\mathbb{C})$
the induced linear map on the second singular cohomology group (note that
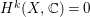 $H^{k}(X,\mathbb{C})=0$
for
$H^{k}(X,\mathbb{C})=0$
for
![]() $k=1,3$
). The following proposition follows directly from the topological and holomorphic Lefschetz fixed point formulas (cf. [Reference Atiyah and Singer1, p. 567]; see also [Reference Dolgachev, Mendes Lopes and Pardini11, Lemma 4.2]). The automorphism
$k=1,3$
). The following proposition follows directly from the topological and holomorphic Lefschetz fixed point formulas (cf. [Reference Atiyah and Singer1, p. 567]; see also [Reference Dolgachev, Mendes Lopes and Pardini11, Lemma 4.2]). The automorphism
![]() ${\it\tau}$
is called an involution if it is of order
${\it\tau}$
is called an involution if it is of order
![]() $2$
.
$2$
.
Proposition 2.1. If
![]() ${\it\tau}$
is an involution, then
${\it\tau}$
is an involution, then
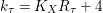 $k_{{\it\tau}}=K_{X}R_{{\it\tau}}+4$
and
$k_{{\it\tau}}=K_{X}R_{{\it\tau}}+4$
and
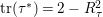 $\text{tr}({\it\tau}^{\ast })=2-R_{{\it\tau}}^{2}$
. If
$\text{tr}({\it\tau}^{\ast })=2-R_{{\it\tau}}^{2}$
. If
![]() ${\it\tau}$
is of order
${\it\tau}$
is of order
![]() $3$
, then
$3$
, then
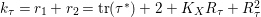 $k_{{\it\tau}}=r_{1}+r_{2}=\text{tr}({\it\tau}^{\ast })+2+K_{X}R_{{\it\tau}}+R_{{\it\tau}}^{2}$
and
$k_{{\it\tau}}=r_{1}+r_{2}=\text{tr}({\it\tau}^{\ast })+2+K_{X}R_{{\it\tau}}+R_{{\it\tau}}^{2}$
and
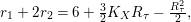 $r_{1}+2r_{2}=6+\frac{3}{2}K_{X}R_{{\it\tau}}-\frac{R_{{\it\tau}}^{2}}{2},$
where
$r_{1}+2r_{2}=6+\frac{3}{2}K_{X}R_{{\it\tau}}-\frac{R_{{\it\tau}}^{2}}{2},$
where
![]() $r_{j}$
is the number of isolated fixed points of
$r_{j}$
is the number of isolated fixed points of
![]() ${\it\tau}$
of type
${\it\tau}$
of type
![]() $\frac{1}{3}(1,j)$
for
$\frac{1}{3}(1,j)$
for
![]() $j=1,2$
.
$j=1,2$
.
Throughout this article, we denote by
![]() $S$
a smooth minimal complex surface of general type with
$S$
a smooth minimal complex surface of general type with
![]() $p_{g}=0$
and
$p_{g}=0$
and
![]() $K_{S}^{2}=7$
. Then
$K_{S}^{2}=7$
. Then
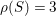 ${\it\rho}(S)=3$
and
${\it\rho}(S)=3$
and
![]() $S$
contains at most one
$S$
contains at most one
![]() $(-2)$
-curve (this follows from Poincaré duality; cf. [Reference Chen10, Lemma 2.5]). Here an
$(-2)$
-curve (this follows from Poincaré duality; cf. [Reference Chen10, Lemma 2.5]). Here an
![]() $m$
-curve (for
$m$
-curve (for
![]() $m\leqslant 0$
) on a smooth surface stands for an irreducible smooth rational curve with self-intersection number
$m\leqslant 0$
) on a smooth surface stands for an irreducible smooth rational curve with self-intersection number
![]() $m$
. We have a similar result for
$m$
. We have a similar result for
![]() $(-3)$
-curves.
$(-3)$
-curves.
Lemma 2.2. The surface
![]() $S$
contains at most one
$S$
contains at most one
![]() $(-3)$
-curve.
$(-3)$
-curve.
Proof. Assume by contradiction that
![]() $S$
contains two distinct
$S$
contains two distinct
![]() $(-3)$
-curves
$(-3)$
-curves
![]() $C_{1}$
and
$C_{1}$
and
![]() $C_{2}$
. Then the intersection matrix of
$C_{2}$
. Then the intersection matrix of
![]() $K_{S},C_{1}$
and
$K_{S},C_{1}$
and
![]() $C_{2}$
has determinant
$C_{2}$
has determinant
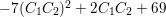 $-7(C_{1}C_{2})^{2}+2C_{1}C_{2}+69$
. Since
$-7(C_{1}C_{2})^{2}+2C_{1}C_{2}+69$
. Since
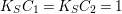 $K_{S}C_{1}=K_{S}C_{2}=1$
, the algebraic index theorem yields
$K_{S}C_{1}=K_{S}C_{2}=1$
, the algebraic index theorem yields
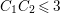 $C_{1}C_{2}\leqslant 3$
. Because the intersection form on
$C_{1}C_{2}\leqslant 3$
. Because the intersection form on
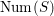 $\text{Num}(S)$
is unimodular and
$\text{Num}(S)$
is unimodular and
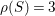 ${\it\rho}(S)=3$
,
${\it\rho}(S)=3$
,
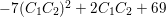 $-7(C_{1}C_{2})^{2}+2C_{1}C_{2}+69$
is a square number. Then we have
$-7(C_{1}C_{2})^{2}+2C_{1}C_{2}+69$
is a square number. Then we have
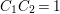 $C_{1}C_{2}=1$
since
$C_{1}C_{2}=1$
since
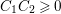 $C_{1}C_{2}\geqslant 0$
.
$C_{1}C_{2}\geqslant 0$
.
The divisor
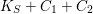 $K_{S}+C_{1}+C_{2}$
has Zariski decomposition (see [Reference Miyaoka21, Section 3])
$K_{S}+C_{1}+C_{2}$
has Zariski decomposition (see [Reference Miyaoka21, Section 3])
![]() $P+N$
with
$P+N$
with
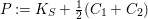 $P:=K_{S}+\frac{1}{2}(C_{1}+C_{2})$
the positive part and
$P:=K_{S}+\frac{1}{2}(C_{1}+C_{2})$
the positive part and
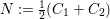 $N:=\frac{1}{2}(C_{1}+C_{2})$
the negative part. According to [Reference Miyaoka21, Theorem 1.1], we have
$N:=\frac{1}{2}(C_{1}+C_{2})$
the negative part. According to [Reference Miyaoka21, Theorem 1.1], we have
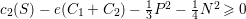 $c_{2}(S)-e(C_{1}+C_{2})-\frac{1}{3}P^{2}-\frac{1}{4}N^{2}\geqslant 0$
. Here
$c_{2}(S)-e(C_{1}+C_{2})-\frac{1}{3}P^{2}-\frac{1}{4}N^{2}\geqslant 0$
. Here
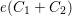 $e(C_{1}+C_{2})$
denotes the topological Euler number of
$e(C_{1}+C_{2})$
denotes the topological Euler number of
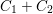 $C_{1}+C_{2}$
and
$C_{1}+C_{2}$
and
![]() $c_{2}(S)$
denotes the second Chern number of
$c_{2}(S)$
denotes the second Chern number of
![]() $S$
. It is clear that
$S$
. It is clear that
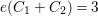 $e(C_{1}+C_{2})=3$
and the Noether formula gives
$e(C_{1}+C_{2})=3$
and the Noether formula gives
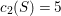 $c_{2}(S)=5$
. The inequality above yields
$c_{2}(S)=5$
. The inequality above yields
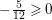 $-\frac{5}{12}\geqslant 0$
, a contradiction.◻
$-\frac{5}{12}\geqslant 0$
, a contradiction.◻
Lemma 2.3. (See also the table in [Reference Lee and Shin16])
Let
![]() ${\it\tau}$
be an involution on
${\it\tau}$
be an involution on
![]() $S$
. Then
$S$
. Then
 $K_{S}R_{{\it\tau}}\in \{1,3,5,7\}$
and
$K_{S}R_{{\it\tau}}\in \{1,3,5,7\}$
and
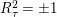 $R_{{\it\tau}}^{2}=\pm 1$
. If
$R_{{\it\tau}}^{2}=\pm 1$
. If
![]() $R_{{\it\tau}}^{2}=1$
, then
$R_{{\it\tau}}^{2}=1$
, then
![]() $K_{S}$
is ample and
$K_{S}$
is ample and
![]() $R_{{\it\tau}}$
is irreducible with
$R_{{\it\tau}}$
is irreducible with
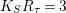 $K_{S}R_{{\it\tau}}=3$
.
$K_{S}R_{{\it\tau}}=3$
.
Proof. For
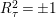 $R_{{\it\tau}}^{2}=\pm 1$
, see the proof of [Reference Bauer4, Proposition 3.6]. According to [Reference Calabri, Ciliberto and Mendes Lopes2, Lemma 3.2 and Proposition 3.3(v)],
$R_{{\it\tau}}^{2}=\pm 1$
, see the proof of [Reference Bauer4, Proposition 3.6]. According to [Reference Calabri, Ciliberto and Mendes Lopes2, Lemma 3.2 and Proposition 3.3(v)],
![]() $k_{{\it\tau}}$
is an odd integer and
$k_{{\it\tau}}$
is an odd integer and
![]() $k_{{\it\tau}}\leqslant 11$
. So
$k_{{\it\tau}}\leqslant 11$
. So
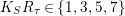 $K_{S}R_{{\it\tau}}\in \{1,3,5,7\}$
by Proposition 2.1.
$K_{S}R_{{\it\tau}}\in \{1,3,5,7\}$
by Proposition 2.1.
Assume that
![]() $R_{{\it\tau}}^{2}=1$
. If
$R_{{\it\tau}}^{2}=1$
. If
![]() $K_{S}$
is not ample, then
$K_{S}$
is not ample, then
![]() $S$
has a unique
$S$
has a unique
![]() $(-2)$
-curve
$(-2)$
-curve
![]() $C$
. The intersection number matrix of
$C$
. The intersection number matrix of
![]() $K_{S},R_{{\it\tau}}$
and
$K_{S},R_{{\it\tau}}$
and
![]() $C$
has determinant
$C$
has determinant
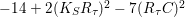 $-14+2(K_{S}R_{{\it\tau}})^{2}-7(R_{{\it\tau}}C)^{2}$
. The determinant equals
$-14+2(K_{S}R_{{\it\tau}})^{2}-7(R_{{\it\tau}}C)^{2}$
. The determinant equals
![]() $0$
, for, otherwise, the Chern classes of
$0$
, for, otherwise, the Chern classes of
![]() $K_{S},R_{{\it\tau}}$
and
$K_{S},R_{{\it\tau}}$
and
![]() $C$
form a basis of
$C$
form a basis of
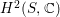 $H^{2}(S,\mathbb{C})$
and they are
$H^{2}(S,\mathbb{C})$
and they are
![]() ${\it\tau}^{\ast }$
-invariant, a contradiction to
${\it\tau}^{\ast }$
-invariant, a contradiction to
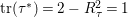 $\text{tr}({\it\tau}^{\ast })=2-R_{{\it\tau}}^{2}=1$
by Proposition 2.1. It follows that
$\text{tr}({\it\tau}^{\ast })=2-R_{{\it\tau}}^{2}=1$
by Proposition 2.1. It follows that
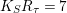 $K_{S}R_{{\it\tau}}=7$
and
$K_{S}R_{{\it\tau}}=7$
and
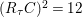 $(R_{{\it\tau}}C)^{2}=12$
. This is impossible. So
$(R_{{\it\tau}}C)^{2}=12$
. This is impossible. So
![]() $K_{S}$
is ample.
$K_{S}$
is ample.
The algebraic index theorem gives
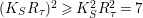 $(K_{S}R_{{\it\tau}})^{2}\geqslant K_{S}^{2}R_{{\it\tau}}^{2}=7$
and thus
$(K_{S}R_{{\it\tau}})^{2}\geqslant K_{S}^{2}R_{{\it\tau}}^{2}=7$
and thus
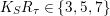 $K_{S}R_{{\it\tau}}\in \{3,5,7\}$
. Let
$K_{S}R_{{\it\tau}}\in \{3,5,7\}$
. Let
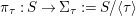 ${\it\pi}_{{\it\tau}}:S\rightarrow {\rm\Sigma}_{{\it\tau}}:=S/\langle {\it\tau}\rangle$
be the quotient morphism. We have
${\it\pi}_{{\it\tau}}:S\rightarrow {\rm\Sigma}_{{\it\tau}}:=S/\langle {\it\tau}\rangle$
be the quotient morphism. We have
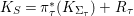 $K_{S}={\it\pi}_{{\it\tau}}^{\ast }(K_{{\rm\Sigma}_{{\it\tau}}})+R_{{\it\tau}}$
.
$K_{S}={\it\pi}_{{\it\tau}}^{\ast }(K_{{\rm\Sigma}_{{\it\tau}}})+R_{{\it\tau}}$
.
If
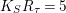 $K_{S}R_{{\it\tau}}=5$
, then
$K_{S}R_{{\it\tau}}=5$
, then
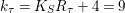 $k_{{\it\tau}}=K_{S}R_{{\it\tau}}+4=9$
and
$k_{{\it\tau}}=K_{S}R_{{\it\tau}}+4=9$
and
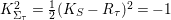 $K_{{\rm\Sigma}_{{\it\tau}}}^{2}=\frac{1}{2}(K_{S}-R_{{\it\tau}})^{2}=-1$
. So
$K_{{\rm\Sigma}_{{\it\tau}}}^{2}=\frac{1}{2}(K_{S}-R_{{\it\tau}})^{2}=-1$
. So
![]() ${\rm\Sigma}$
has
${\rm\Sigma}$
has
![]() $9$
nodes. The minimal resolution
$9$
nodes. The minimal resolution
![]() $W_{{\it\tau}}$
of
$W_{{\it\tau}}$
of
![]() ${\rm\Sigma}_{{\it\tau}}$
has Picard number
${\rm\Sigma}_{{\it\tau}}$
has Picard number
![]() $11$
and it contains
$11$
and it contains
![]() $9$
disjoint
$9$
disjoint
![]() $(-2)$
-curves. If
$(-2)$
-curves. If
![]() ${\rm\Sigma}_{{\it\tau}}$
has Kodaira dimension
${\rm\Sigma}_{{\it\tau}}$
has Kodaira dimension
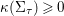 ${\it\kappa}({\rm\Sigma}_{{\it\tau}})\geqslant 0$
, by [Reference Dolgachev, Mendes Lopes and Pardini11, Proposition 4.1],
${\it\kappa}({\rm\Sigma}_{{\it\tau}})\geqslant 0$
, by [Reference Dolgachev, Mendes Lopes and Pardini11, Proposition 4.1],
![]() $W_{{\it\tau}}$
is minimal. This contradicts
$W_{{\it\tau}}$
is minimal. This contradicts
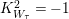 $K_{W_{{\it\tau}}}^{2}=-1$
. So
$K_{W_{{\it\tau}}}^{2}=-1$
. So
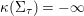 ${\it\kappa}({\rm\Sigma}_{{\it\tau}})=-\infty$
and
${\it\kappa}({\rm\Sigma}_{{\it\tau}})=-\infty$
and
![]() $W_{{\it\tau}}$
is a rational surface. This contradicts [Reference Dolgachev, Mendes Lopes and Pardini11, Theorem 3.3]. Hence
$W_{{\it\tau}}$
is a rational surface. This contradicts [Reference Dolgachev, Mendes Lopes and Pardini11, Theorem 3.3]. Hence
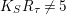 $K_{S}R_{{\it\tau}}\not =5$
.
$K_{S}R_{{\it\tau}}\not =5$
.
In the same manner we see that
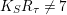 $K_{S}R_{{\it\tau}}\not =7$
(see also [Reference Mendes Lopes and Pardini20]). So
$K_{S}R_{{\it\tau}}\not =7$
(see also [Reference Mendes Lopes and Pardini20]). So
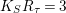 $K_{S}R_{{\it\tau}}=3$
. Because
$K_{S}R_{{\it\tau}}=3$
. Because
![]() $K_{S}$
is ample and
$K_{S}$
is ample and
![]() $R_{{\it\tau}}$
is a disjoint union of smooth irreducible curves, the algebraic index theorem shows that
$R_{{\it\tau}}$
is a disjoint union of smooth irreducible curves, the algebraic index theorem shows that
![]() $R_{{\it\tau}}$
is irreducible.◻
$R_{{\it\tau}}$
is irreducible.◻
2.2 Abelian covers
We briefly recall some facts from the theory of abelian covers from [Reference Pardini22]. Assume that
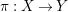 ${\it\pi}:X\rightarrow Y$
is a finite abelian cover between projective varieties with
${\it\pi}:X\rightarrow Y$
is a finite abelian cover between projective varieties with
![]() $X$
normal and
$X$
normal and
![]() $Y$
smooth. Let
$Y$
smooth. Let
![]() $\mathfrak{S}$
be the Galois group of
$\mathfrak{S}$
be the Galois group of
![]() ${\it\pi}$
and let
${\it\pi}$
and let
![]() $\mathfrak{S}^{\ast }$
be the group of characters of
$\mathfrak{S}^{\ast }$
be the group of characters of
![]() $\mathfrak{S}$
. Then the action of
$\mathfrak{S}$
. Then the action of
![]() $\mathfrak{S}$
induces a splitting:
$\mathfrak{S}$
induces a splitting:
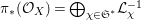 ${\it\pi}_{\ast }({\mathcal{O}}_{X})=\bigoplus _{{\it\chi}\in \mathfrak{S}^{\ast }}{\mathcal{L}}_{{\it\chi}}^{-1}$
, where
${\it\pi}_{\ast }({\mathcal{O}}_{X})=\bigoplus _{{\it\chi}\in \mathfrak{S}^{\ast }}{\mathcal{L}}_{{\it\chi}}^{-1}$
, where
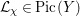 ${\mathcal{L}}_{{\it\chi}}\in \text{Pic}(Y)$
and
${\mathcal{L}}_{{\it\chi}}\in \text{Pic}(Y)$
and
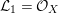 ${\mathcal{L}}_{1}={\mathcal{O}}_{X}$
. For each nontrivial cyclic subgroup
${\mathcal{L}}_{1}={\mathcal{O}}_{X}$
. For each nontrivial cyclic subgroup
![]() $\mathfrak{C}$
of
$\mathfrak{C}$
of
![]() $\mathfrak{S}$
and each generator
$\mathfrak{S}$
and each generator
![]() ${\it\psi}\in \mathfrak{C}^{\ast }$
, there is a unique effective divisor
${\it\psi}\in \mathfrak{C}^{\ast }$
, there is a unique effective divisor
![]() $D_{\mathfrak{C},{\it\psi}}$
of
$D_{\mathfrak{C},{\it\psi}}$
of
![]() $Y$
associated to the pair
$Y$
associated to the pair
![]() $(\mathfrak{C},{\it\psi})$
. The cover
$(\mathfrak{C},{\it\psi})$
. The cover
![]() ${\it\pi}$
is determined by
${\it\pi}$
is determined by
![]() ${\mathcal{L}}_{{\it\chi}}$
and
${\mathcal{L}}_{{\it\chi}}$
and
![]() $D_{\mathfrak{C},{\it\psi}}$
with some specified relations (cf. [Reference Pardini22, Theorem 2.1]). We mainly apply this theory when
$D_{\mathfrak{C},{\it\psi}}$
with some specified relations (cf. [Reference Pardini22, Theorem 2.1]). We mainly apply this theory when
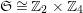 $\mathfrak{S}\cong \mathbb{Z}_{2}\times \mathbb{Z}_{4}$
or
$\mathfrak{S}\cong \mathbb{Z}_{2}\times \mathbb{Z}_{4}$
or
![]() $\mathfrak{S}\cong \mathbb{Z}_{2}^{2}$
.
$\mathfrak{S}\cong \mathbb{Z}_{2}^{2}$
.
We set up some notation and conventions. Denote by
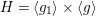 $H=\langle g_{1}\rangle \times \langle g\rangle$
a group isomorphic to
$H=\langle g_{1}\rangle \times \langle g\rangle$
a group isomorphic to
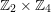 $\mathbb{Z}_{2}\times \mathbb{Z}_{4}$
, where
$\mathbb{Z}_{2}\times \mathbb{Z}_{4}$
, where
![]() $g_{1},g$
are generators of
$g_{1},g$
are generators of
![]() $H$
,
$H$
,
![]() $g_{1}$
is of order
$g_{1}$
is of order
![]() $2$
and
$2$
and
![]() $g$
is of order
$g$
is of order
![]() $4$
. Denote by
$4$
. Denote by
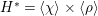 $H^{\ast }=\langle {\it\chi}\rangle \times \langle {\it\rho}\rangle$
the group of characters of
$H^{\ast }=\langle {\it\chi}\rangle \times \langle {\it\rho}\rangle$
the group of characters of
![]() $H$
, where
$H$
, where
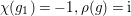 ${\it\chi}(g_{1})=-1,{\it\rho}(g)=\text{i}$
and
${\it\chi}(g_{1})=-1,{\it\rho}(g)=\text{i}$
and
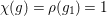 ${\it\chi}(g)={\it\rho}(g_{1})=1$
. The group
${\it\chi}(g)={\it\rho}(g_{1})=1$
. The group
![]() $H$
contains a unique subgroup
$H$
contains a unique subgroup
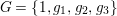 $G=\{1,g_{1},g_{2},g_{3}\}$
which is isomorphic to
$G=\{1,g_{1},g_{2},g_{3}\}$
which is isomorphic to
![]() $\mathbb{Z}_{2}^{2}$
, where
$\mathbb{Z}_{2}^{2}$
, where
![]() $g_{2}=g^{2}$
and
$g_{2}=g^{2}$
and
 $g_{3}=g_{1}g_{2}$
. Denote by
$g_{3}=g_{1}g_{2}$
. Denote by
![]() ${\it\chi}_{i}\in G^{\ast }$
the nontrivial character orthogonal to
${\it\chi}_{i}\in G^{\ast }$
the nontrivial character orthogonal to
![]() $g_{i}$
for
$g_{i}$
for
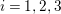 $i=1,2,3$
.
$i=1,2,3$
.
When
![]() $\mathfrak{S}=G$
, we simply set
$\mathfrak{S}=G$
, we simply set
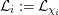 ${\mathcal{L}}_{i}:={\mathcal{L}}_{{\it\chi}_{i}}$
and
${\mathcal{L}}_{i}:={\mathcal{L}}_{{\it\chi}_{i}}$
and
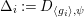 ${\rm\Delta}_{i}:=D_{\langle g_{i}\rangle ,{\it\psi}}$
, where
${\rm\Delta}_{i}:=D_{\langle g_{i}\rangle ,{\it\psi}}$
, where
![]() ${\it\psi}$
is the unique nontrivial character of
${\it\psi}$
is the unique nontrivial character of
![]() $\langle g_{i}\rangle$
. Similarly, when
$\langle g_{i}\rangle$
. Similarly, when
![]() $\mathfrak{S}=H$
, we set
$\mathfrak{S}=H$
, we set
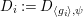 $D_{i}:=D_{\langle g_{i}\rangle ,{\it\psi}}$
for
$D_{i}:=D_{\langle g_{i}\rangle ,{\it\psi}}$
for
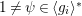 $1\not ={\it\psi}\in \langle g_{i}\rangle ^{\ast }$
. For the cyclic group
$1\not ={\it\psi}\in \langle g_{i}\rangle ^{\ast }$
. For the cyclic group
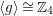 $\langle g\rangle \cong \mathbb{Z}_{4}$
, we set
$\langle g\rangle \cong \mathbb{Z}_{4}$
, we set
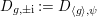 $D_{g,\pm \text{i}}:=D_{\langle g\rangle ,{\it\psi}}$
for
$D_{g,\pm \text{i}}:=D_{\langle g\rangle ,{\it\psi}}$
for
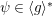 ${\it\psi}\in \langle g\rangle ^{\ast }$
with
${\it\psi}\in \langle g\rangle ^{\ast }$
with
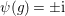 ${\it\psi}(g)=\pm \text{i}$
. We adopt a similar convention for the cyclic group
${\it\psi}(g)=\pm \text{i}$
. We adopt a similar convention for the cyclic group
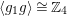 $\langle g_{1}g\rangle \cong \mathbb{Z}_{4}$
.
$\langle g_{1}g\rangle \cong \mathbb{Z}_{4}$
.
In what follows, the indices
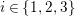 $i\in \{1,2,3\}$
should be understood as residue classes modulo
$i\in \{1,2,3\}$
should be understood as residue classes modulo
![]() $3$
. Also linear equivalence and numerical equivalence between divisors are denoted by
$3$
. Also linear equivalence and numerical equivalence between divisors are denoted by
![]() $\equiv$
and
$\equiv$
and
![]() $\stackrel{num}{{\sim}}$
, respectively.
$\stackrel{num}{{\sim}}$
, respectively.
Proposition 2.4. (cf. [Reference Catanese6], [Reference Pardini22, Theorem 2.1 and Corollary 3.1])
Let
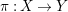 ${\it\pi}:X\rightarrow Y$
be a finite abelian cover between projective varieties. Assume that
${\it\pi}:X\rightarrow Y$
be a finite abelian cover between projective varieties. Assume that
![]() $X$
is normal and
$X$
is normal and
![]() $Y$
is smooth.
$Y$
is smooth.
-
(a) If the Galois group of
 ${\it\pi}$
is
${\it\pi}$
is
 $G$
, then
$G$
, then
 ${\it\pi}$
is determined by the following data: Divisors
${\it\pi}$
is determined by the following data: Divisors
 ${\rm\Delta}_{i}$
and
${\rm\Delta}_{i}$
and
 ${\mathcal{L}}_{i}$
(
${\mathcal{L}}_{i}$
(
 $i=1,2,3$
) such that (2.1)and moreover the divisors
$i=1,2,3$
) such that (2.1)and moreover the divisors $$\begin{eqnarray}\displaystyle 2{\mathcal{L}}_{i}\equiv {\rm\Delta}_{i+1}+{\rm\Delta}_{i+2},\qquad {\mathcal{L}}_{i}+{\rm\Delta}_{i}\equiv {\mathcal{L}}_{i+1}+{\mathcal{L}}_{i+2}\quad \text{for }i=1,2,3, & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 2{\mathcal{L}}_{i}\equiv {\rm\Delta}_{i+1}+{\rm\Delta}_{i+2},\qquad {\mathcal{L}}_{i}+{\rm\Delta}_{i}\equiv {\mathcal{L}}_{i+1}+{\mathcal{L}}_{i+2}\quad \text{for }i=1,2,3, & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
 ${\rm\Delta}_{i}$
are effective and
${\rm\Delta}_{i}$
are effective and
 ${\rm\Delta}:={\rm\Delta}_{1}+{\rm\Delta}_{2}+{\rm\Delta}_{3}$
is reduced.
${\rm\Delta}:={\rm\Delta}_{1}+{\rm\Delta}_{2}+{\rm\Delta}_{3}$
is reduced.
-
(b) If the Galois group of
 ${\it\pi}$
is
${\it\pi}$
is
 $H$
, then
$H$
, then
 ${\it\pi}$
is determined by the following reduced data (see [Reference Pardini22, Proposition 2.1]): Divisors
${\it\pi}$
is determined by the following reduced data (see [Reference Pardini22, Proposition 2.1]): Divisors
 ${\mathcal{L}}_{{\it\chi}},{\mathcal{L}}_{{\it\rho}},D_{1},D_{2},D_{3}$
,
${\mathcal{L}}_{{\it\chi}},{\mathcal{L}}_{{\it\rho}},D_{1},D_{2},D_{3}$
,
 $D_{g,\text{i}},D_{g,-\text{i}},D_{g_{1}g,\text{i}}$
and
$D_{g,\text{i}},D_{g,-\text{i}},D_{g_{1}g,\text{i}}$
and
 $D_{g_{1}g,-\text{i}}$
such that (2.2)and moreover the divisors
$D_{g_{1}g,-\text{i}}$
such that (2.2)and moreover the divisors $$\begin{eqnarray}\displaystyle 2{\mathcal{L}}_{{\it\chi}} & \equiv & \displaystyle D_{1}+D_{3}+D_{g_{1}g,\text{i}}+D_{g_{1}g,-\text{i}},\nonumber\\ \displaystyle 4{\mathcal{L}}_{{\it\rho}} & \equiv & \displaystyle 2D_{2}+2D_{3}+D_{g,\text{i}}+3D_{g,-\text{i}}+D_{g_{1}g,\text{i}}+3D_{g_{1}g,-\text{i}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 2{\mathcal{L}}_{{\it\chi}} & \equiv & \displaystyle D_{1}+D_{3}+D_{g_{1}g,\text{i}}+D_{g_{1}g,-\text{i}},\nonumber\\ \displaystyle 4{\mathcal{L}}_{{\it\rho}} & \equiv & \displaystyle 2D_{2}+2D_{3}+D_{g,\text{i}}+3D_{g,-\text{i}}+D_{g_{1}g,\text{i}}+3D_{g_{1}g,-\text{i}},\end{eqnarray}$$
 $D_{1},D_{2},D_{3},D_{g,\text{i}},D_{g,-\text{i}},D_{g_{1}g,\text{i}}$
and
$D_{1},D_{2},D_{3},D_{g,\text{i}},D_{g,-\text{i}},D_{g_{1}g,\text{i}}$
and
 $D_{g_{1}g,-\text{i}}$
are effective and is reduced.
$D_{g_{1}g,-\text{i}}$
are effective and is reduced. $$\begin{eqnarray}\displaystyle D:=D_{1}+D_{2}+D_{3}+D_{g,\text{i}}+D_{g,-\text{i}}+D_{g_{1}g,\text{i}}+D_{g_{1}g,-\text{i}} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D:=D_{1}+D_{2}+D_{3}+D_{g,\text{i}}+D_{g,-\text{i}}+D_{g_{1}g,\text{i}}+D_{g_{1}g,-\text{i}} & & \displaystyle \nonumber\end{eqnarray}$$
3 Two involutions commute
We first deduce Corollary 1.3 and Theorem 1.2 from the following theorem.
Theorem 3.1. Let
![]() $S$
be a smooth minimal surface of general type with
$S$
be a smooth minimal surface of general type with
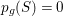 $p_{g}(S)=0$
and
$p_{g}(S)=0$
and
![]() $K_{S}^{2}=7$
. Assume that
$K_{S}^{2}=7$
. Assume that
![]() $\text{Aut}(S)$
contains two distinct involutions
$\text{Aut}(S)$
contains two distinct involutions
![]() ${\it\alpha}$
and
${\it\alpha}$
and
![]() ${\it\beta}$
. Then
${\it\beta}$
. Then
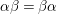 ${\it\alpha}{\it\beta}={\it\beta}{\it\alpha}$
.
${\it\alpha}{\it\beta}={\it\beta}{\it\alpha}$
.
Proof of Corollary 1.3.
On the contrary, suppose that
![]() ${\it\alpha}$
is an involution of
${\it\alpha}$
is an involution of
![]() $\text{Aut}(S)$
other than
$\text{Aut}(S)$
other than
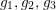 $g_{1},g_{2},g_{3}$
. Theorem 3.1 implies
$g_{1},g_{2},g_{3}$
. Theorem 3.1 implies
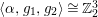 $\langle {\it\alpha},g_{1},g_{2}\rangle \cong \mathbb{Z}_{2}^{3}$
. Therefore, there are seven involutions
$\langle {\it\alpha},g_{1},g_{2}\rangle \cong \mathbb{Z}_{2}^{3}$
. Therefore, there are seven involutions
![]() ${\it\theta}$
in
${\it\theta}$
in
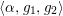 $\langle {\it\alpha},g_{1},g_{2}\rangle$
and seven numbers
$\langle {\it\alpha},g_{1},g_{2}\rangle$
and seven numbers
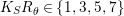 $K_{S}R_{{\it\theta}}\in \{1,3,5,7\}$
by Lemma 2.3. Since any two involutions generate a subgroup of type
$K_{S}R_{{\it\theta}}\in \{1,3,5,7\}$
by Lemma 2.3. Since any two involutions generate a subgroup of type
![]() $\mathbb{Z}_{2}^{2}$
, by Theorem 1.1, we conclude that each of the three numbers
$\mathbb{Z}_{2}^{2}$
, by Theorem 1.1, we conclude that each of the three numbers
![]() $1,3$
and
$1,3$
and
![]() $7$
occurs at most once. Furthermore, Theorem 1.1(a) also implies that if
$7$
occurs at most once. Furthermore, Theorem 1.1(a) also implies that if
![]() $7$
occurs, then the other six numbers are all equal to
$7$
occurs, then the other six numbers are all equal to
![]() $5$
. Hence there are at least five involutions
$5$
. Hence there are at least five involutions
![]() ${\it\theta}$
for which
${\it\theta}$
for which
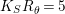 $K_{S}R_{{\it\theta}}=5$
. There must be a subgroup of type
$K_{S}R_{{\it\theta}}=5$
. There must be a subgroup of type
![]() $\mathbb{Z}_{2}^{2}$
containing three of these five, a contradiction to Theorem 1.1.◻
$\mathbb{Z}_{2}^{2}$
containing three of these five, a contradiction to Theorem 1.1.◻
Proof of Theorem 1.2.
We may assume that
![]() $\text{Aut}(S)$
contains at least two involutions. These two involutions generate a subgroup
$\text{Aut}(S)$
contains at least two involutions. These two involutions generate a subgroup
![]() $G\cong \mathbb{Z}_{2}^{2}$
by Theorem 3.1. We still denote by
$G\cong \mathbb{Z}_{2}^{2}$
by Theorem 3.1. We still denote by
![]() $g_{1},g_{2}$
and
$g_{1},g_{2}$
and
![]() $g_{3}$
the involutions of
$g_{3}$
the involutions of
![]() $G$
. Let
$G$
. Let
![]() ${\it\tau}$
be any automorphism of
${\it\tau}$
be any automorphism of
![]() $S$
. Corollary 1.3 gives
$S$
. Corollary 1.3 gives
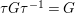 ${\it\tau}G{\it\tau}^{-1}=G$
. Since
${\it\tau}G{\it\tau}^{-1}=G$
. Since
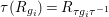 ${\it\tau}(R_{g_{i}})=R_{{\it\tau}g_{i}{\it\tau}^{-1}}$
, we have
${\it\tau}(R_{g_{i}})=R_{{\it\tau}g_{i}{\it\tau}^{-1}}$
, we have
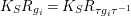 $K_{S}R_{g_{i}}=K_{S}R_{{\it\tau}g_{i}{\it\tau}^{-1}}$
and
$K_{S}R_{g_{i}}=K_{S}R_{{\it\tau}g_{i}{\it\tau}^{-1}}$
and
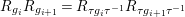 $R_{g_{i}}R_{g_{i+1}}=R_{{\it\tau}g_{i}{\it\tau}^{-1}}R_{{\it\tau}g_{i+1}{\it\tau}^{-1}}$
for
$R_{g_{i}}R_{g_{i+1}}=R_{{\it\tau}g_{i}{\it\tau}^{-1}}R_{{\it\tau}g_{i+1}{\it\tau}^{-1}}$
for
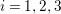 $i=1,2,3$
. From this observation and Theorem 1.1, we conclude that
$i=1,2,3$
. From this observation and Theorem 1.1, we conclude that
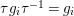 ${\it\tau}g_{i}{\it\tau}^{-1}=g_{i}$
for
${\it\tau}g_{i}{\it\tau}^{-1}=g_{i}$
for
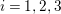 $i=1,2,3$
and complete the proof.◻
$i=1,2,3$
and complete the proof.◻
The remaining of this section is devoted to prove Theorem 3.1. We assume by contradiction that
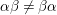 ${\it\alpha}{\it\beta}\not ={\it\beta}{\it\alpha}$
. We will deduce a contradiction through a sequence of lemmas and propositions. We use the same notation as Section 2. Recall that
${\it\alpha}{\it\beta}\not ={\it\beta}{\it\alpha}$
. We will deduce a contradiction through a sequence of lemmas and propositions. We use the same notation as Section 2. Recall that
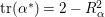 $\text{tr}({\it\alpha}^{\ast })=2-R_{{\it\alpha}}^{2}$
,
$\text{tr}({\it\alpha}^{\ast })=2-R_{{\it\alpha}}^{2}$
,
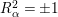 $R_{{\it\alpha}}^{2}=\pm 1$
and
$R_{{\it\alpha}}^{2}=\pm 1$
and
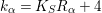 $k_{{\it\alpha}}=K_{S}R_{{\it\alpha}}+4$
(see Proposition 2.1 and Lemma 2.3).
$k_{{\it\alpha}}=K_{S}R_{{\it\alpha}}+4$
(see Proposition 2.1 and Lemma 2.3).
Lemma 3.2. The order of
![]() ${\it\alpha}{\it\beta}$
is an odd integer.
${\it\alpha}{\it\beta}$
is an odd integer.
Proof. Assume by contradiction that the order of
![]() ${\it\alpha}{\it\beta}$
is
${\it\alpha}{\it\beta}$
is
![]() $2k$
and
$2k$
and
![]() $k\geqslant 2$
. Let
$k\geqslant 2$
. Let
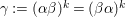 ${\it\gamma}:=({\it\alpha}{\it\beta})^{k}=({\it\beta}{\it\alpha})^{k}$
. Then
${\it\gamma}:=({\it\alpha}{\it\beta})^{k}=({\it\beta}{\it\alpha})^{k}$
. Then
![]() ${\it\gamma}$
is an involution and
${\it\gamma}$
is an involution and
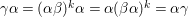 ${\it\gamma}{\it\alpha}=({\it\alpha}{\it\beta})^{k}{\it\alpha}={\it\alpha}({\it\beta}{\it\alpha})^{k}={\it\alpha}{\it\gamma}$
. Therefore,
${\it\gamma}{\it\alpha}=({\it\alpha}{\it\beta})^{k}{\it\alpha}={\it\alpha}({\it\beta}{\it\alpha})^{k}={\it\alpha}{\it\gamma}$
. Therefore,
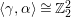 $\langle {\it\gamma},{\it\alpha}\rangle \cong \mathbb{Z}_{2}^{2}$
. Then
$\langle {\it\gamma},{\it\alpha}\rangle \cong \mathbb{Z}_{2}^{2}$
. Then
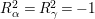 $R_{{\it\alpha}}^{2}=R_{{\it\gamma}}^{2}=-1$
by Theorem 1.1. Similarly,
$R_{{\it\alpha}}^{2}=R_{{\it\gamma}}^{2}=-1$
by Theorem 1.1. Similarly,
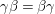 ${\it\gamma}{\it\beta}={\it\beta}{\it\gamma}$
and
${\it\gamma}{\it\beta}={\it\beta}{\it\gamma}$
and
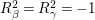 $R_{{\it\beta}}^{2}=R_{{\it\gamma}}^{2}=-1$
. So
$R_{{\it\beta}}^{2}=R_{{\it\gamma}}^{2}=-1$
. So
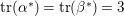 $\text{tr}({\it\alpha}^{\ast })=\text{tr}({\it\beta}^{\ast })=3$
.
$\text{tr}({\it\alpha}^{\ast })=\text{tr}({\it\beta}^{\ast })=3$
.
Let
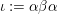 ${\it\iota}:={\it\alpha}{\it\beta}{\it\alpha}$
. Note that
${\it\iota}:={\it\alpha}{\it\beta}{\it\alpha}$
. Note that
![]() ${\it\alpha},{\it\beta}$
and
${\it\alpha},{\it\beta}$
and
![]() ${\it\iota}$
are three distinct involutions in
${\it\iota}$
are three distinct involutions in
![]() $\text{Aut}(S)$
and
$\text{Aut}(S)$
and
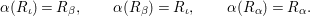 $$\begin{eqnarray}\displaystyle {\it\alpha}(R_{{\it\iota}})=R_{{\it\beta}},\qquad {\it\alpha}(R_{{\it\beta}})=R_{{\it\iota}},\qquad {\it\alpha}(R_{{\it\alpha}})=R_{{\it\alpha}}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\alpha}(R_{{\it\iota}})=R_{{\it\beta}},\qquad {\it\alpha}(R_{{\it\beta}})=R_{{\it\iota}},\qquad {\it\alpha}(R_{{\it\alpha}})=R_{{\it\alpha}}. & & \displaystyle\end{eqnarray}$$
Recall that
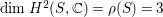 $\dim H^{2}(S,\mathbb{C})={\it\rho}(S)=3$
. Now
$\dim H^{2}(S,\mathbb{C})={\it\rho}(S)=3$
. Now
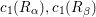 $c_{1}(R_{{\it\alpha}}),c_{1}(R_{{\it\beta}})$
and
$c_{1}(R_{{\it\alpha}}),c_{1}(R_{{\it\beta}})$
and
![]() $c_{1}(R_{{\it\iota}})$
are not a basis of
$c_{1}(R_{{\it\iota}})$
are not a basis of
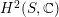 $H^{2}(S,\mathbb{C})$
, for otherwise, (3.1) implies
$H^{2}(S,\mathbb{C})$
, for otherwise, (3.1) implies
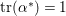 $\text{tr}({\it\alpha}^{\ast })=1$
, which is a contradiction to
$\text{tr}({\it\alpha}^{\ast })=1$
, which is a contradiction to
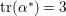 $\text{tr}({\it\alpha}^{\ast })=3$
.
$\text{tr}({\it\alpha}^{\ast })=3$
.
So the intersection number matrix of
![]() $R_{{\it\alpha}},R_{{\it\beta}}$
and
$R_{{\it\alpha}},R_{{\it\beta}}$
and
![]() $R_{{\it\iota}}$
has determinant zero. That is
$R_{{\it\iota}}$
has determinant zero. That is
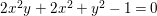 $2x^{2}y+2x^{2}+y^{2}-1=0$
, where
$2x^{2}y+2x^{2}+y^{2}-1=0$
, where
 $x:=R_{{\it\alpha}}R_{{\it\iota}}=R_{{\it\alpha}}R_{{\it\beta}}$
(see (3.1)) and
$x:=R_{{\it\alpha}}R_{{\it\iota}}=R_{{\it\alpha}}R_{{\it\beta}}$
(see (3.1)) and
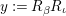 $y:=R_{{\it\beta}}R_{{\it\iota}}$
. Observe that
$y:=R_{{\it\beta}}R_{{\it\iota}}$
. Observe that
![]() $y\geqslant 0$
; otherwise,
$y\geqslant 0$
; otherwise,
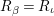 $R_{{\it\beta}}=R_{{\it\iota}}$
and
$R_{{\it\beta}}=R_{{\it\iota}}$
and
![]() ${\it\beta}={\it\iota}$
, a contradiction to
${\it\beta}={\it\iota}$
, a contradiction to
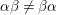 ${\it\alpha}{\it\beta}\not ={\it\beta}{\it\alpha}$
. It follows that
${\it\alpha}{\it\beta}\not ={\it\beta}{\it\alpha}$
. It follows that
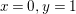 $x=0,y=1$
and the nontrivial linear relation among
$x=0,y=1$
and the nontrivial linear relation among
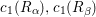 $c_{1}(R_{{\it\alpha}}),c_{1}(R_{{\it\beta}})$
and
$c_{1}(R_{{\it\alpha}}),c_{1}(R_{{\it\beta}})$
and
![]() $c_{1}(R_{{\it\iota}})$
is
$c_{1}(R_{{\it\iota}})$
is
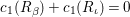 $c_{1}(R_{{\it\beta}})+c_{1}(R_{{\it\iota}})=0$
. This contradicts the fact that the divisor
$c_{1}(R_{{\it\beta}})+c_{1}(R_{{\it\iota}})=0$
. This contradicts the fact that the divisor
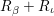 $R_{{\it\beta}}+R_{{\it\iota}}$
is strictly effective. Hence the order of
$R_{{\it\beta}}+R_{{\it\iota}}$
is strictly effective. Hence the order of
![]() ${\it\alpha}{\it\beta}$
is an odd integer.◻
${\it\alpha}{\it\beta}$
is an odd integer.◻
Recall that our aim is to deduce a contradiction from the assumption
 ${\it\alpha}{\it\beta}\not ={\it\beta}{\it\alpha}$
. According to the previous lemma, from now on, we may assume that the order
${\it\alpha}{\it\beta}\not ={\it\beta}{\it\alpha}$
. According to the previous lemma, from now on, we may assume that the order
![]() $r$
of
$r$
of
![]() ${\it\alpha}{\it\beta}$
is an odd prime. In fact, if
${\it\alpha}{\it\beta}$
is an odd prime. In fact, if
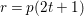 $r=p(2t+1)$
for some prime
$r=p(2t+1)$
for some prime
![]() $p\geqslant 3$
and some integer
$p\geqslant 3$
and some integer
![]() $t>0$
, then
$t>0$
, then
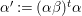 ${\it\alpha}^{\prime }:=({\it\alpha}{\it\beta})^{t}{\it\alpha}$
and
${\it\alpha}^{\prime }:=({\it\alpha}{\it\beta})^{t}{\it\alpha}$
and
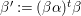 ${\it\beta}^{\prime }:=({\it\beta}{\it\alpha})^{t}{\it\beta}$
are involutions and the order of
${\it\beta}^{\prime }:=({\it\beta}{\it\alpha})^{t}{\it\beta}$
are involutions and the order of
![]() ${\it\alpha}^{\prime }{\it\beta}^{\prime }$
is
${\it\alpha}^{\prime }{\it\beta}^{\prime }$
is
![]() $p$
. In particular, we have
$p$
. In particular, we have
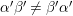 ${\it\alpha}^{\prime }{\it\beta}^{\prime }\not ={\it\beta}^{\prime }{\it\alpha}^{\prime }$
. We may replace
${\it\alpha}^{\prime }{\it\beta}^{\prime }\not ={\it\beta}^{\prime }{\it\alpha}^{\prime }$
. We may replace
![]() ${\it\alpha},{\it\beta}$
by
${\it\alpha},{\it\beta}$
by
![]() ${\it\alpha}^{\prime },{\it\beta}^{\prime }$
and continue our discussion.
${\it\alpha}^{\prime },{\it\beta}^{\prime }$
and continue our discussion.
The subgroup
![]() $\langle {\it\alpha},{\it\beta}\rangle$
of
$\langle {\it\alpha},{\it\beta}\rangle$
of
![]() $\text{Aut}(S)$
is isomorphic to the dihedral group of order
$\text{Aut}(S)$
is isomorphic to the dihedral group of order
![]() $2r$
. Let
$2r$
. Let
![]() $D_{r}$
denote this subgroup. Since
$D_{r}$
denote this subgroup. Since
![]() $r$
is a prime, all the involutions in
$r$
is a prime, all the involutions in
![]() $D_{r}$
are pairwise conjugate and
$D_{r}$
are pairwise conjugate and
![]() $D_{r}$
has exactly one nontrivial normal subgroup
$D_{r}$
has exactly one nontrivial normal subgroup
![]() $\langle {\it\alpha}{\it\beta}\rangle$
, which is the commutator subgroup. Any irreducible linear representation of
$\langle {\it\alpha}{\it\beta}\rangle$
, which is the commutator subgroup. Any irreducible linear representation of
![]() $D_{r}$
has dimension at most two, and any irreducible
$D_{r}$
has dimension at most two, and any irreducible
![]() $2$
-dimensional representation of
$2$
-dimensional representation of
![]() $D_{r}$
is isomorphic to the matrix representation given by
$D_{r}$
is isomorphic to the matrix representation given by
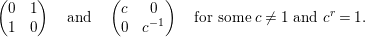 $$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}0 & 1\\ 1 & 0\end{array}\right)\quad \text{and}\quad \left(\begin{array}{@{}cc@{}}c & 0\\ 0 & c^{-1}\end{array}\right)\quad \text{for some}~c\not =1~\text{and}~c^{r}=1.\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}0 & 1\\ 1 & 0\end{array}\right)\quad \text{and}\quad \left(\begin{array}{@{}cc@{}}c & 0\\ 0 & c^{-1}\end{array}\right)\quad \text{for some}~c\not =1~\text{and}~c^{r}=1.\end{eqnarray}$$
Lemma 3.3. With the same assumption as above, we have
-
(a) the canonical
 $K_{S}$
is ample;
$K_{S}$
is ample; -
(b) the curves
 $R_{{\it\alpha}}$
and
$R_{{\it\alpha}}$
and
 $R_{{\it\beta}}$
generate a pencil
$R_{{\it\beta}}$
generate a pencil
 $|F|$
of curves with
$|F|$
of curves with
 $F^{2}=1$
and
$F^{2}=1$
and
 $K_{S}F=3$
, and
$K_{S}F=3$
, and
 $|F|$
has a simple base point
$|F|$
has a simple base point
 $p$
;
$p$
; -
(c) the group
 $D_{r}$
acts faithfully on
$D_{r}$
acts faithfully on
 $|F|$
.
$|F|$
.
Proof. Set
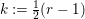 $k:=\frac{1}{2}(r-1)$
and set
$k:=\frac{1}{2}(r-1)$
and set
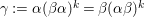 ${\it\gamma}:={\it\alpha}({\it\beta}{\it\alpha})^{k}={\it\beta}({\it\alpha}{\it\beta})^{k}$
. Then
${\it\gamma}:={\it\alpha}({\it\beta}{\it\alpha})^{k}={\it\beta}({\it\alpha}{\it\beta})^{k}$
. Then
![]() ${\it\alpha},{\it\beta}$
and
${\it\alpha},{\it\beta}$
and
![]() ${\it\gamma}$
are three distinct involutions and they are pairwise conjugate. Therefore,
${\it\gamma}$
are three distinct involutions and they are pairwise conjugate. Therefore,
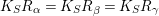 $K_{S}R_{{\it\alpha}}=K_{S}R_{{\it\beta}}=K_{S}R_{{\it\gamma}}$
and
$K_{S}R_{{\it\alpha}}=K_{S}R_{{\it\beta}}=K_{S}R_{{\it\gamma}}$
and
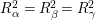 $R_{{\it\alpha}}^{2}=R_{{\it\beta}}^{2}=R_{{\it\gamma}}^{2}$
. Since
$R_{{\it\alpha}}^{2}=R_{{\it\beta}}^{2}=R_{{\it\gamma}}^{2}$
. Since
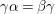 ${\it\gamma}{\it\alpha}={\it\beta}{\it\gamma}$
and
${\it\gamma}{\it\alpha}={\it\beta}{\it\gamma}$
and
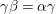 ${\it\gamma}{\it\beta}={\it\alpha}{\it\gamma}$
,
${\it\gamma}{\it\beta}={\it\alpha}{\it\gamma}$
,
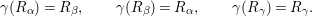 $$\begin{eqnarray}\displaystyle {\it\gamma}(R_{{\it\alpha}})=R_{{\it\beta}},\qquad {\it\gamma}(R_{{\it\beta}})=R_{{\it\alpha}},\qquad {\it\gamma}(R_{{\it\gamma}})=R_{{\it\gamma}}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\gamma}(R_{{\it\alpha}})=R_{{\it\beta}},\qquad {\it\gamma}(R_{{\it\beta}})=R_{{\it\alpha}},\qquad {\it\gamma}(R_{{\it\gamma}})=R_{{\it\gamma}}. & & \displaystyle\end{eqnarray}$$
We claim that
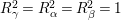 $R_{{\it\gamma}}^{2}=R_{{\it\alpha}}^{2}=R_{{\it\beta}}^{2}=1$
. Otherwise, as in the proof of Lemma 3.2, we could deduce a contradiction by calculating the determinant of the intersection number matrix of
$R_{{\it\gamma}}^{2}=R_{{\it\alpha}}^{2}=R_{{\it\beta}}^{2}=1$
. Otherwise, as in the proof of Lemma 3.2, we could deduce a contradiction by calculating the determinant of the intersection number matrix of
![]() $R_{{\it\alpha}},R_{{\it\beta}}$
and
$R_{{\it\alpha}},R_{{\it\beta}}$
and
![]() $R_{{\it\gamma}}$
and by calculating
$R_{{\it\gamma}}$
and by calculating
![]() $\text{tr}({\it\gamma}^{\ast })$
.
$\text{tr}({\it\gamma}^{\ast })$
.
Then (a) follows from Lemma 2.3. Lemma 2.3 also gives
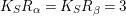 $K_{S}R_{{\it\alpha}}=K_{S}R_{{\it\beta}}=3$
. The algebraic index theorem implies
$K_{S}R_{{\it\alpha}}=K_{S}R_{{\it\beta}}=3$
. The algebraic index theorem implies
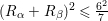 $(R_{{\it\alpha}}+R_{{\it\beta}})^{2}\leqslant \frac{6^{2}}{7}$
and thus
$(R_{{\it\alpha}}+R_{{\it\beta}})^{2}\leqslant \frac{6^{2}}{7}$
and thus
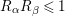 $R_{{\it\alpha}}R_{{\it\beta}}\leqslant 1$
. Since
$R_{{\it\alpha}}R_{{\it\beta}}\leqslant 1$
. Since
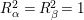 $R_{{\it\alpha}}^{2}=R_{{\it\beta}}^{2}=1$
, the equality holds and
$R_{{\it\alpha}}^{2}=R_{{\it\beta}}^{2}=1$
, the equality holds and
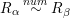 $R_{{\it\alpha}}\stackrel{num}{{\sim}}R_{{\it\beta}}$
. Similarly, we have
$R_{{\it\alpha}}\stackrel{num}{{\sim}}R_{{\it\beta}}$
. Similarly, we have
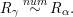 $R_{{\it\gamma}}\stackrel{num}{{\sim}}R_{{\it\alpha}}.$
$R_{{\it\gamma}}\stackrel{num}{{\sim}}R_{{\it\alpha}}.$
Let
![]() $p$
be the unique intersection point of
$p$
be the unique intersection point of
![]() $R_{{\it\alpha}}$
and
$R_{{\it\alpha}}$
and
![]() $R_{{\it\gamma}}$
. Then (3.2) implies that
$R_{{\it\gamma}}$
. Then (3.2) implies that
![]() $R_{{\it\alpha}},R_{{\it\beta}}$
and
$R_{{\it\alpha}},R_{{\it\beta}}$
and
![]() $R_{{\it\gamma}}$
pairwise intersect transversely at the point
$R_{{\it\gamma}}$
pairwise intersect transversely at the point
![]() $p$
. Recall that
$p$
. Recall that
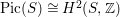 $\text{Pic}(S)\cong H^{2}(S,\mathbb{Z})$
and
$\text{Pic}(S)\cong H^{2}(S,\mathbb{Z})$
and
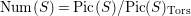 $\text{Num}(S)=\text{Pic}(S)/\text{Pic}(S)_{\text{Tors}}$
. Let
$\text{Num}(S)=\text{Pic}(S)/\text{Pic}(S)_{\text{Tors}}$
. Let
![]() $m$
be the smallest positive integer such that
$m$
be the smallest positive integer such that
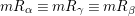 $mR_{{\it\alpha}}\equiv mR_{{\it\gamma}}\equiv mR_{{\it\beta}}$
. Let
$mR_{{\it\alpha}}\equiv mR_{{\it\gamma}}\equiv mR_{{\it\beta}}$
. Let
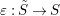 ${\it\varepsilon}:\tilde{S}\rightarrow S$
be the blowup at
${\it\varepsilon}:\tilde{S}\rightarrow S$
be the blowup at
![]() $p$
, let
$p$
, let
![]() $E$
be the exceptional curve and let
$E$
be the exceptional curve and let
![]() $\tilde{R_{{\it\alpha}}}$
be the strict transform of
$\tilde{R_{{\it\alpha}}}$
be the strict transform of
![]() $R_{{\it\alpha}}$
, and so forth. Then
$R_{{\it\alpha}}$
, and so forth. Then
![]() $|m\tilde{R_{{\it\alpha}}}|$
induces a fibration
$|m\tilde{R_{{\it\alpha}}}|$
induces a fibration
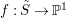 $f:\tilde{S}\rightarrow \mathbb{P}^{1}$
and
$f:\tilde{S}\rightarrow \mathbb{P}^{1}$
and
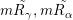 $m\tilde{R_{{\it\gamma}}},m\tilde{R_{{\it\alpha}}}$
and
$m\tilde{R_{{\it\gamma}}},m\tilde{R_{{\it\alpha}}}$
and
![]() $m\tilde{R_{{\it\beta}}}$
are fibers of
$m\tilde{R_{{\it\beta}}}$
are fibers of
![]() $f$
.
$f$
.
The fibration
![]() $f$
has
$f$
has
![]() $E$
as a
$E$
as a
![]() $m$
-section. If
$m$
-section. If
![]() $m\geqslant 2$
, we easily obtain a contradiction by applying the Hurwitz formula for
$m\geqslant 2$
, we easily obtain a contradiction by applying the Hurwitz formula for
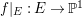 $f|_{E}:E\rightarrow \mathbb{P}^{1}$
. Therefore,
$f|_{E}:E\rightarrow \mathbb{P}^{1}$
. Therefore,
![]() $m=1$
,
$m=1$
,
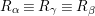 $R_{{\it\alpha}}\equiv R_{{\it\gamma}}\equiv R_{{\it\beta}}$
and
$R_{{\it\alpha}}\equiv R_{{\it\gamma}}\equiv R_{{\it\beta}}$
and
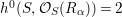 $h^{0}(S,{\mathcal{O}}_{S}(R_{{\it\alpha}}))=2$
. And (b) is proved.
$h^{0}(S,{\mathcal{O}}_{S}(R_{{\it\alpha}}))=2$
. And (b) is proved.
For (c), first note that
![]() $p$
is a fixed point of
$p$
is a fixed point of
![]() $D_{r}$
. So
$D_{r}$
. So
![]() $D_{r}$
acts faithfully on the tangent space
$D_{r}$
acts faithfully on the tangent space
![]() $\text{T}_{p}S$
of
$\text{T}_{p}S$
of
![]() $S$
to the point
$S$
to the point
![]() $p$
. According to the discussion before the lemma, this action is irreducible. Because
$p$
. According to the discussion before the lemma, this action is irreducible. Because
![]() $r$
is an odd number, the corresponding action of
$r$
is an odd number, the corresponding action of
![]() $D_{r}$
on
$D_{r}$
on
![]() $\mathbb{P}(\text{T}_{p}S)$
is faithful. Since
$\mathbb{P}(\text{T}_{p}S)$
is faithful. Since
![]() $F^{2}=1$
,
$F^{2}=1$
,
![]() $p$
is a smooth point of
$p$
is a smooth point of
![]() $F$
and thus
$F$
and thus
![]() $\text{T}_{p}F$
is a
$\text{T}_{p}F$
is a
![]() $1$
-dimensional linear subspace of
$1$
-dimensional linear subspace of
![]() $\text{T}_{p}S$
for any
$\text{T}_{p}S$
for any
![]() $F\in |F|$
. From this, we conclude that
$F\in |F|$
. From this, we conclude that
![]() $D_{r}$
acts faithfully on
$D_{r}$
acts faithfully on
![]() $|F|$
.◻
$|F|$
.◻
Because
![]() $D_{r}$
acts faithfully on
$D_{r}$
acts faithfully on
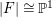 $|F|\cong \mathbb{P}^{1}$
, every automorphism has exactly two invariant curves in
$|F|\cong \mathbb{P}^{1}$
, every automorphism has exactly two invariant curves in
![]() $|F|$
. For every involution
$|F|$
. For every involution
![]() ${\it\theta}\in D_{r}$
, one of the two
${\it\theta}\in D_{r}$
, one of the two
![]() ${\it\theta}$
-invariant curves in
${\it\theta}$
-invariant curves in
![]() $|F|$
is
$|F|$
is
![]() $R_{{\it\theta}}$
. Denote the other one by
$R_{{\it\theta}}$
. Denote the other one by
![]() $F_{{\it\theta}}$
. Then
$F_{{\it\theta}}$
. Then
![]() $F_{{\it\theta}}$
contains the seven isolated fixed points of
$F_{{\it\theta}}$
contains the seven isolated fixed points of
![]() ${\it\theta}$
. Denote by
${\it\theta}$
. Denote by
![]() $F_{0}$
one of the two
$F_{0}$
one of the two
![]() ${\it\alpha}{\it\beta}$
-invariant curves in
${\it\alpha}{\it\beta}$
-invariant curves in
![]() $|F|$
. Then the other one is
$|F|$
. Then the other one is
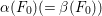 ${\it\alpha}(F_{0})(={\it\beta}(F_{0}))$
and
${\it\alpha}(F_{0})(={\it\beta}(F_{0}))$
and
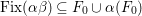 $\text{Fix}({\it\alpha}{\it\beta})\subseteq F_{0}\cup {\it\alpha}(F_{0})$
. We shall show that
$\text{Fix}({\it\alpha}{\it\beta})\subseteq F_{0}\cup {\it\alpha}(F_{0})$
. We shall show that
![]() $F_{0}$
is not
$F_{0}$
is not
![]() $2$
-connected. But first we need the following lemma about the action of
$2$
-connected. But first we need the following lemma about the action of
![]() $D_{r}$
on the singular cohomology group.
$D_{r}$
on the singular cohomology group.
Lemma 3.4. The automorphism
![]() ${\it\alpha}{\it\beta}$
acts trivially on
${\it\alpha}{\it\beta}$
acts trivially on
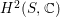 $H^{2}(S,\mathbb{C})$
. In particular, the quotient surface
$H^{2}(S,\mathbb{C})$
. In particular, the quotient surface
![]() $S/D_{r}$
has Picard number
$S/D_{r}$
has Picard number
![]() $2$
.
$2$
.
Proof. We have seen that
![]() ${\it\alpha},{\it\beta}$
and thus
${\it\alpha},{\it\beta}$
and thus
![]() $D_{r}$
act trivially on the
$D_{r}$
act trivially on the
![]() $2$
-dimensional linear subspace generated by
$2$
-dimensional linear subspace generated by
![]() $c_{1}(K_{S})$
and
$c_{1}(K_{S})$
and
![]() $c_{1}(F)$
. Because
$c_{1}(F)$
. Because
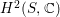 $H^{2}(S,\mathbb{C})$
is
$H^{2}(S,\mathbb{C})$
is
![]() $3$
-dimensional and
$3$
-dimensional and
![]() ${\it\alpha}{\it\beta}$
is contained in the kernel of any
${\it\alpha}{\it\beta}$
is contained in the kernel of any
![]() $1$
-dimensional representation of
$1$
-dimensional representation of
![]() $D_{r}$
,
$D_{r}$
,
![]() ${\it\alpha}{\it\beta}$
acts trivially on
${\it\alpha}{\it\beta}$
acts trivially on
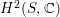 $H^{2}(S,\mathbb{C})$
. Hence the invariant subspace of
$H^{2}(S,\mathbb{C})$
. Hence the invariant subspace of
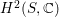 $H^{2}(S,\mathbb{C})$
for the
$H^{2}(S,\mathbb{C})$
for the
![]() $D_{r}$
-action is
$D_{r}$
-action is
![]() $2$
-dimensional and
$2$
-dimensional and
![]() $S/D_{r}$
has Picard number
$S/D_{r}$
has Picard number
![]() $2$
.◻
$2$
.◻
We analyze the members of the pencil
![]() $|F|$
which are not
$|F|$
which are not
![]() $2$
-connected. This will help us to determine the base locus of the linear system
$2$
-connected. This will help us to determine the base locus of the linear system
 $|K_{S}+F|$
in the proof of Proposition 3.6 and to find a basis of
$|K_{S}+F|$
in the proof of Proposition 3.6 and to find a basis of
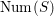 $\text{Num}(S)$
. We continue to use the fact that
$\text{Num}(S)$
. We continue to use the fact that
![]() $S$
has Picard number
$S$
has Picard number
![]() $3$
.
$3$
.
Lemma 3.5. Assume that
![]() $|F|$
contains a curve which is not
$|F|$
contains a curve which is not
![]() $2$
-connected. Then
$2$
-connected. Then
-
(a) the curves in
 $|F|$
which are not
$|F|$
which are not
 $2$
-connected are exactly the
$2$
-connected are exactly the
 ${\it\alpha}{\it\beta}$
-invariant curves
${\it\alpha}{\it\beta}$
-invariant curves
 $F_{0}$
and
$F_{0}$
and
 ${\it\alpha}(F_{0})$
;
${\it\alpha}(F_{0})$
; -
(b)
 $F_{0}=A+B$
, where
$F_{0}=A+B$
, where
 $A$
and
$A$
and
 $B$
are irreducible curves, and
$B$
are irreducible curves, and
 $K_{S}A=2,K_{S}B=1,A^{2}=0,B^{2}=-1$
and
$K_{S}A=2,K_{S}B=1,A^{2}=0,B^{2}=-1$
and
 $AB=1$
. Moreover,
$AB=1$
. Moreover,
 $A$
contains the base point
$A$
contains the base point
 $p$
of
$p$
of
 $|F|$
.
$|F|$
.
Proof. Assume that
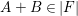 $A+B\in |F|$
,
$A+B\in |F|$
,
![]() $A>0$
,
$A>0$
,
![]() $B>0$
and
$B>0$
and
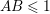 $AB\leqslant 1$
. Because
$AB\leqslant 1$
. Because
![]() $K_{S}$
is ample and
$K_{S}$
is ample and
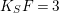 $K_{S}F=3$
, we may assume
$K_{S}F=3$
, we may assume
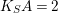 $K_{S}A=2$
and
$K_{S}A=2$
and
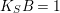 $K_{S}B=1$
. Then
$K_{S}B=1$
. Then
![]() $B$
is irreducible. The algebraic index theorem and the adjunction formula imply
$B$
is irreducible. The algebraic index theorem and the adjunction formula imply
![]() $A^{2}\leqslant 0$
and
$A^{2}\leqslant 0$
and
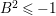 $B^{2}\leqslant -1$
. In particular, by Lemma 3.4,
$B^{2}\leqslant -1$
. In particular, by Lemma 3.4,
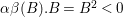 ${\it\alpha}{\it\beta}(B).B=B^{2}<0$
and thus
${\it\alpha}{\it\beta}(B).B=B^{2}<0$
and thus
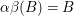 ${\it\alpha}{\it\beta}(B)=B$
. Hence
${\it\alpha}{\it\beta}(B)=B$
. Hence
![]() $A+B$
is one of the
$A+B$
is one of the
![]() ${\it\alpha}{\it\beta}$
-invariant curves
${\it\alpha}{\it\beta}$
-invariant curves
![]() $F_{0}$
and
$F_{0}$
and
![]() ${\it\alpha}(F_{0})$
.
${\it\alpha}(F_{0})$
.
Because
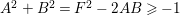 $A^{2}+B^{2}=F^{2}-2AB\geqslant -1$
, the argument above yields
$A^{2}+B^{2}=F^{2}-2AB\geqslant -1$
, the argument above yields
![]() $A^{2}=0$
,
$A^{2}=0$
,
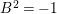 $B^{2}=-1$
and
$B^{2}=-1$
and
![]() $AB=1$
. Then
$AB=1$
. Then
![]() $FA=1$
and
$FA=1$
and
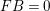 $FB=0$
. So the simple base point
$FB=0$
. So the simple base point
![]() $p$
of
$p$
of
![]() $|F|$
belongs to
$|F|$
belongs to
![]() $A$
. It remains to show that
$A$
. It remains to show that
![]() $A$
is irreducible.
$A$
is irreducible.
Assume
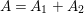 $A=A_{1}+A_{2}$
with
$A=A_{1}+A_{2}$
with
![]() $A_{1}>0$
and
$A_{1}>0$
and
![]() $A_{2}>0$
. Because
$A_{2}>0$
. Because
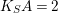 $K_{S}A=2$
and
$K_{S}A=2$
and
![]() $K_{S}$
is ample,
$K_{S}$
is ample,
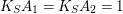 $K_{S}A_{1}=K_{S}A_{2}=1$
and both
$K_{S}A_{1}=K_{S}A_{2}=1$
and both
![]() $A_{1}$
and
$A_{1}$
and
![]() $A_{2}$
are irreducible. We now calculate the intersection numbers
$A_{2}$
are irreducible. We now calculate the intersection numbers
![]() $A_{1}^{2},A_{2}^{2}$
and
$A_{1}^{2},A_{2}^{2}$
and
![]() $A_{1}A_{2}$
. For
$A_{1}A_{2}$
. For
![]() $i=1,2$
, the algebraic index theorem and the adjunction formula imply
$i=1,2$
, the algebraic index theorem and the adjunction formula imply
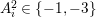 $A_{i}^{2}\in \{-1,-3\}$
. Note that
$A_{i}^{2}\in \{-1,-3\}$
. Note that
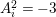 $A_{i}^{2}=-3$
if and only if
$A_{i}^{2}=-3$
if and only if
![]() $A_{i}$
is a
$A_{i}$
is a
![]() $(-3)$
-curve. Since
$(-3)$
-curve. Since
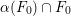 ${\it\alpha}(F_{0})\cap F_{0}$
consists of one point
${\it\alpha}(F_{0})\cap F_{0}$
consists of one point
![]() $p$
,
$p$
,
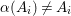 ${\it\alpha}(A_{i})\not =A_{i}$
for
${\it\alpha}(A_{i})\not =A_{i}$
for
![]() $i=1,2$
. We conclude that
$i=1,2$
. We conclude that
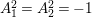 $A_{1}^{2}=A_{2}^{2}=-1$
by Lemma 2.2. Then
$A_{1}^{2}=A_{2}^{2}=-1$
by Lemma 2.2. Then
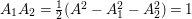 $A_{1}A_{2}=\frac{1}{2}(A^{2}-A_{1}^{2}-A_{2}^{2})=1$
.
$A_{1}A_{2}=\frac{1}{2}(A^{2}-A_{1}^{2}-A_{2}^{2})=1$
.
Because
![]() $FA=1$
, we may assume
$FA=1$
, we may assume
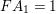 $FA_{1}=1$
and
$FA_{1}=1$
and
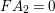 $FA_{2}=0$
. It follows that
$FA_{2}=0$
. It follows that
![]() $p\in A_{1}$
,
$p\in A_{1}$
,
![]() $p\not \in A_{2}$
and
$p\not \in A_{2}$
and
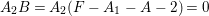 $A_{2}B=A_{2}(F-A_{1}-A-2)=0$
. Since
$A_{2}B=A_{2}(F-A_{1}-A-2)=0$
. Since
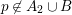 $p\not \in A_{2}\cup B$
,
$p\not \in A_{2}\cup B$
,
![]() $S$
contains four disjoint curves
$S$
contains four disjoint curves
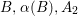 $B,{\it\alpha}(B),A_{2}$
and
$B,{\it\alpha}(B),A_{2}$
and
![]() ${\it\alpha}(A_{2})$
, all with self-intersection number
${\it\alpha}(A_{2})$
, all with self-intersection number
![]() $(-1)$
, a contradiction to
$(-1)$
, a contradiction to
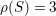 ${\it\rho}(S)=3$
. Therefore
${\it\rho}(S)=3$
. Therefore
![]() $A$
is irreducible.◻
$A$
is irreducible.◻
The following proposition determines the order of the automorphism
![]() ${\it\alpha}{\it\beta}$
.
${\it\alpha}{\it\beta}$
.
Proposition 3.6. The pencil
![]() $|F|$
contains a curve which is not
$|F|$
contains a curve which is not
![]() $2$
-connected and the automorphism
$2$
-connected and the automorphism
![]() ${\it\alpha}{\it\beta}$
is of order
${\it\alpha}{\it\beta}$
is of order
![]() $3$
.
$3$
.
Proof. Let
![]() $F$
be any curve in
$F$
be any curve in
![]() $|F|$
. The long exact sequence of cohomology groups associated to the exact sequence
$|F|$
. The long exact sequence of cohomology groups associated to the exact sequence
 $0\rightarrow {\mathcal{O}}_{S}(K_{S})\rightarrow {\mathcal{O}}_{S}(K_{S}+F)\rightarrow {\mathcal{O}}_{F}(K_{F})\rightarrow 0$
shows that
$0\rightarrow {\mathcal{O}}_{S}(K_{S})\rightarrow {\mathcal{O}}_{S}(K_{S}+F)\rightarrow {\mathcal{O}}_{F}(K_{F})\rightarrow 0$
shows that
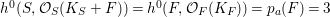 $h^{0}(S,{\mathcal{O}}_{S}(K_{S}+F))=h^{0}(F,{\mathcal{O}}_{F}(K_{F}))=p_{a}(F)=3$
and the trace of
$h^{0}(S,{\mathcal{O}}_{S}(K_{S}+F))=h^{0}(F,{\mathcal{O}}_{F}(K_{F}))=p_{a}(F)=3$
and the trace of
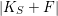 $|K_{S}+F|$
on
$|K_{S}+F|$
on
![]() $F$
is complete. Thus
$F$
is complete. Thus
 $|K_{S}+F|$
defines a rational map
$|K_{S}+F|$
defines a rational map
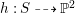 $h:S{\dashrightarrow}\mathbb{P}^{2}$
and
$h:S{\dashrightarrow}\mathbb{P}^{2}$
and
![]() $h$
is defined on
$h$
is defined on
![]() $F$
whenever
$F$
whenever
![]() $|K_{F}|$
is base point free. In particular,
$|K_{F}|$
is base point free. In particular,
![]() $h$
is defined on the smooth curve
$h$
is defined on the smooth curve
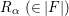 $R_{{\it\alpha}}~(\in |F|)$
and
$R_{{\it\alpha}}~(\in |F|)$
and
![]() $h(R_{{\it\alpha}})$
is the canonical image of
$h(R_{{\it\alpha}})$
is the canonical image of
![]() $R_{{\it\alpha}}$
. The same statement holds by replacing
$R_{{\it\alpha}}$
. The same statement holds by replacing
![]() ${\it\alpha}$
by
${\it\alpha}$
by
![]() ${\it\beta}$
.
${\it\beta}$
.
Because there is a
![]() $D_{r}$
-linearization on
$D_{r}$
-linearization on
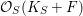 ${\mathcal{O}}_{S}(K_{S}+F)$
, the rational map
${\mathcal{O}}_{S}(K_{S}+F)$
, the rational map
![]() $h$
is
$h$
is
![]() $D_{r}$
-equivariant. Therefore,
$D_{r}$
-equivariant. Therefore,
![]() $h(R_{{\it\alpha}})$
is contained in the fixed locus of the action of
$h(R_{{\it\alpha}})$
is contained in the fixed locus of the action of
![]() ${\it\alpha}$
on
${\it\alpha}$
on
![]() $\mathbb{P}^{2}$
. Note that an involution on
$\mathbb{P}^{2}$
. Note that an involution on
![]() $\mathbb{P}^{2}$
has a line and a point as the fixed locus. It follows that
$\mathbb{P}^{2}$
has a line and a point as the fixed locus. It follows that
![]() ${\it\alpha}$
acts trivially on
${\it\alpha}$
acts trivially on
![]() $\mathbb{P}^{2}$
because
$\mathbb{P}^{2}$
because
![]() $h(R_{{\it\alpha}})$
is a conic curve or a quartic curve. Similarly,
$h(R_{{\it\alpha}})$
is a conic curve or a quartic curve. Similarly,
![]() ${\it\beta}$
and thus
${\it\beta}$
and thus
![]() $D_{r}$
act trivially on
$D_{r}$
act trivially on
![]() $\mathbb{P}^{2}$
. Therefore,
$\mathbb{P}^{2}$
. Therefore,
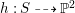 $h:S{\dashrightarrow}\mathbb{P}^{2}$
factors through the quotient morphism
$h:S{\dashrightarrow}\mathbb{P}^{2}$
factors through the quotient morphism
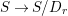 $S\rightarrow S/D_{r}$
.
$S\rightarrow S/D_{r}$
.
Note that
![]() $K_{S}$
is ample,
$K_{S}$
is ample,
![]() $F$
is nef and
$F$
is nef and
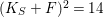 $(K_{S}+F)^{2}=14$
. First assume that
$(K_{S}+F)^{2}=14$
. First assume that
![]() $h$
is a morphism. Then it is finite and it has degree
$h$
is a morphism. Then it is finite and it has degree
![]() $14$
. We thus get
$14$
. We thus get
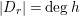 $|D_{r}|=\deg h$
and
$|D_{r}|=\deg h$
and
![]() $r=7$
. It follows that the induced morphism
$r=7$
. It follows that the induced morphism
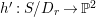 $h^{\prime }:S/D_{r}\rightarrow \mathbb{P}^{2}$
is an isomorphism. So the invariant linear subspace of
$h^{\prime }:S/D_{r}\rightarrow \mathbb{P}^{2}$
is an isomorphism. So the invariant linear subspace of
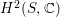 $H^{2}(S,\mathbb{C})$
for the
$H^{2}(S,\mathbb{C})$
for the
![]() $D_{r}$
-action is isomorphic to
$D_{r}$
-action is isomorphic to
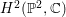 $H^{2}(\mathbb{P}^{2},\mathbb{C})$
, which is
$H^{2}(\mathbb{P}^{2},\mathbb{C})$
, which is
![]() $1$
-dimensional. This contradicts Lemma 3.4 and thus
$1$
-dimensional. This contradicts Lemma 3.4 and thus
![]() $h$
is not a morphism.
$h$
is not a morphism.
We now analyze the base locus of
![]() $h$
. If
$h$
. If
![]() $F$
is
$F$
is
![]() $2$
-connected,
$2$
-connected,
![]() $|K_{F}|$
is base point free by [Reference Catanese, Franciosi, Hulek and Reid5, Theorem 3.3] and
$|K_{F}|$
is base point free by [Reference Catanese, Franciosi, Hulek and Reid5, Theorem 3.3] and
![]() $h$
is defined on
$h$
is defined on
![]() $F$
. Hence the base locus of
$F$
. Hence the base locus of
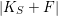 $|K_{S}+F|$
is contained in the curves of
$|K_{S}+F|$
is contained in the curves of
![]() $|F|$
, which are not
$|F|$
, which are not
![]() $2$
-connected. According to Lemma 3.5,
$2$
-connected. According to Lemma 3.5,
![]() $|F|$
contains exactly two such curves
$|F|$
contains exactly two such curves
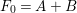 $F_{0}=A+B$
and
$F_{0}=A+B$
and
![]() ${\it\alpha}(F_{0})$
. Similar arguments as above show that the trace of
${\it\alpha}(F_{0})$
. Similar arguments as above show that the trace of
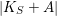 $|K_{S}+A|$
(respectively
$|K_{S}+A|$
(respectively
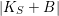 $|K_{S}+B|$
) on
$|K_{S}+B|$
) on
![]() $A$
(respectively
$A$
(respectively
![]() $B$
) is complete. Since
$B$
) is complete. Since
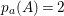 $p_{a}(A)=2$
and
$p_{a}(A)=2$
and
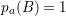 $p_{a}(B)=1$
,
$p_{a}(B)=1$
,
![]() $|K_{A}|$
and
$|K_{A}|$
and
![]() $|K_{B}|$
are base point free by [Reference Catanese, Franciosi, Hulek and Reid5, Theorem 3.3]. Because
$|K_{B}|$
are base point free by [Reference Catanese, Franciosi, Hulek and Reid5, Theorem 3.3]. Because
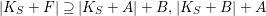 $|K_{S}+F|\supseteq |K_{S}+A|+B,|K_{S}+B|+A$
,
$|K_{S}+F|\supseteq |K_{S}+A|+B,|K_{S}+B|+A$
,
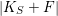 $|K_{S}+F|$
has exactly two base points
$|K_{S}+F|$
has exactly two base points
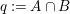 $q:=A\cap B$
and
$q:=A\cap B$
and
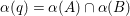 ${\it\alpha}(q)={\it\alpha}(A)\cap {\it\alpha}(B)$
.
${\it\alpha}(q)={\it\alpha}(A)\cap {\it\alpha}(B)$
.
Therefore,
![]() $h$
is a finite morphism outside the base locus and
$h$
is a finite morphism outside the base locus and
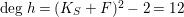 $\deg h=(K_{S}+F)^{2}-2=12$
. Since
$\deg h=(K_{S}+F)^{2}-2=12$
. Since
![]() $h$
factors through
$h$
factors through
![]() $S/D_{r}$
, we have
$S/D_{r}$
, we have
 $|D_{r}|=6$
and
$|D_{r}|=6$
and
![]() $r=3$
.◻
$r=3$
.◻
According to Lemma 3.5 and Proposition 3.6, the
![]() ${\it\alpha}{\it\beta}$
-invariant curve
${\it\alpha}{\it\beta}$
-invariant curve
![]() $F_{0}$
has
$F_{0}$
has
![]() $A$
and
$A$
and
![]() $B$
as irreducible components with
$B$
as irreducible components with
![]() $AB=1$
. It is easy to check that
$AB=1$
. It is easy to check that
![]() $F,A$
and
$F,A$
and
![]() ${\it\alpha}(A)$
generate
${\it\alpha}(A)$
generate
 $\text{Num}(S)$
and
$\text{Num}(S)$
and
 $K_{S}\stackrel{num}{{\sim}}F+A+{\it\alpha}(A)$
. We shall show that
$K_{S}\stackrel{num}{{\sim}}F+A+{\it\alpha}(A)$
. We shall show that
![]() $K_{S}$
is indeed linearly equivalent to
$K_{S}$
is indeed linearly equivalent to
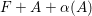 $F+A+{\it\alpha}(A)$
, hence contradict
$F+A+{\it\alpha}(A)$
, hence contradict
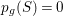 $p_{g}(S)=0$
and complete the proof of Theorem 3.1. For this purpose, we turn to the quotient surface
$p_{g}(S)=0$
and complete the proof of Theorem 3.1. For this purpose, we turn to the quotient surface
![]() $S/D_{3}$
and analyze
$S/D_{3}$
and analyze
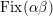 $\text{Fix}({\it\alpha}{\it\beta})$
.
$\text{Fix}({\it\alpha}{\it\beta})$
.
Proposition 3.7. The automorphism
![]() ${\it\alpha}{\it\beta}$
has
${\it\alpha}{\it\beta}$
has
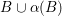 $B\cup {\it\alpha}(B)$
as the divisorial part of the fixed locus and it has five isolated fixed points
$B\cup {\it\alpha}(B)$
as the divisorial part of the fixed locus and it has five isolated fixed points
 $p,q_{1},q_{2},{\it\alpha}(q_{1})$
and
$p,q_{1},q_{2},{\it\alpha}(q_{1})$
and
![]() ${\it\alpha}(q_{2})$
, where
${\it\alpha}(q_{2})$
, where
![]() $q_{1}$
and
$q_{1}$
and
![]() $q_{2}$
are contained in
$q_{2}$
are contained in
![]() $A$
. Each isolated fixed point of
$A$
. Each isolated fixed point of
![]() ${\it\alpha}{\it\beta}$
is of type
${\it\alpha}{\it\beta}$
is of type
![]() $\frac{1}{3}(1,2)$
.
$\frac{1}{3}(1,2)$
.
Proof. We have seen that
![]() $F_{0}$
and
$F_{0}$
and
![]() ${\it\alpha}(F_{0})$
are
${\it\alpha}(F_{0})$
are
![]() ${\it\alpha}{\it\beta}$
-invariant and
${\it\alpha}{\it\beta}$
-invariant and
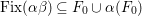 $\text{Fix}({\it\alpha}{\it\beta})\subseteq F_{0}\cup {\it\alpha}(F_{0})$
. Moreover, the curves
$\text{Fix}({\it\alpha}{\it\beta})\subseteq F_{0}\cup {\it\alpha}(F_{0})$
. Moreover, the curves
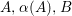 $A,{\it\alpha}(A),B$
and
$A,{\it\alpha}(A),B$
and
![]() ${\it\alpha}(B)$
are
${\it\alpha}(B)$
are
![]() ${\it\alpha}{\it\beta}$
-invariant. Also note that a point
${\it\alpha}{\it\beta}$
-invariant. Also note that a point
![]() $q$
is a fixed point (respectively an isolated fixed point) of
$q$
is a fixed point (respectively an isolated fixed point) of
![]() ${\it\alpha}{\it\beta}$
if and only if so is the point
${\it\alpha}{\it\beta}$
if and only if so is the point
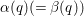 ${\it\alpha}(q)(={\it\beta}(q))$
.
${\it\alpha}(q)(={\it\beta}(q))$
.
We claim that neither
![]() $A$
nor
$A$
nor
![]() ${\it\alpha}(A)$
is contained in
${\it\alpha}(A)$
is contained in
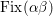 $\text{Fix}({\it\alpha}{\it\beta})$
. Otherwise, both
$\text{Fix}({\it\alpha}{\it\beta})$
. Otherwise, both
![]() $A$
and
$A$
and
![]() ${\it\alpha}(A)$
are contained in
${\it\alpha}(A)$
are contained in
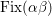 $\text{Fix}({\it\alpha}{\it\beta})$
. Since
$\text{Fix}({\it\alpha}{\it\beta})$
. Since
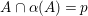 $A\cap {\it\alpha}(A)=p$
, this contradicts the fact that the divisorial part of
$A\cap {\it\alpha}(A)=p$
, this contradicts the fact that the divisorial part of
![]() ${\it\alpha}{\it\beta}$
is a disjoint union of smooth curves. The claim is proved.
${\it\alpha}{\it\beta}$
is a disjoint union of smooth curves. The claim is proved.
Now assume by contradiction that
![]() $B$
is not contained in
$B$
is not contained in
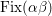 $\text{Fix}({\it\alpha}{\it\beta})$
. Then nor is
$\text{Fix}({\it\alpha}{\it\beta})$
. Then nor is
![]() ${\it\alpha}(B)$
and
${\it\alpha}(B)$
and
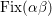 $\text{Fix}({\it\alpha}{\it\beta})$
consists of isolated fixed points. Then
$\text{Fix}({\it\alpha}{\it\beta})$
consists of isolated fixed points. Then
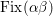 $\text{Fix}({\it\alpha}{\it\beta})$
has five fixed points by Proposition 2.1 and Lemma 3.4. Three of these points are
$\text{Fix}({\it\alpha}{\it\beta})$
has five fixed points by Proposition 2.1 and Lemma 3.4. Three of these points are
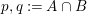 $p,q:=A\cap B$
and
$p,q:=A\cap B$
and
![]() ${\it\alpha}(q)$
. Denote the other two by
${\it\alpha}(q)$
. Denote the other two by
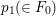 $p_{1}(\in F_{0})$
and by
$p_{1}(\in F_{0})$
and by
![]() ${\it\alpha}(p_{1})$
. We must have
${\it\alpha}(p_{1})$
. We must have
![]() $p_{1}\in B$
. Otherwise, the nontrivial automorphism
$p_{1}\in B$
. Otherwise, the nontrivial automorphism
![]() ${\it\alpha}{\it\beta}|_{B}$
has exactly one fixed point
${\it\alpha}{\it\beta}|_{B}$
has exactly one fixed point
![]() $q$
, which is a smooth point of
$q$
, which is a smooth point of
![]() $B$
since
$B$
since
![]() $AB=1$
. This is impossible because
$AB=1$
. This is impossible because
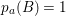 $p_{a}(B)=1$
. Therefore,
$p_{a}(B)=1$
. Therefore,
![]() $p_{1}\in B$
. It follows that
$p_{1}\in B$
. It follows that
![]() ${\it\alpha}{\it\beta}|_{A}$
has exactly two fixed points
${\it\alpha}{\it\beta}|_{A}$
has exactly two fixed points
![]() $p$
and
$p$
and
![]() $q$
, which are smooth points of
$q$
, which are smooth points of
![]() $A$
. Note that
$A$
. Note that
![]() $A$
has at most two singular points since
$A$
has at most two singular points since
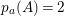 $p_{a}(A)=2$
. Because the singular locus of
$p_{a}(A)=2$
. Because the singular locus of
![]() $A$
is
$A$
is
![]() ${\it\alpha}{\it\beta}$
-invariant and
${\it\alpha}{\it\beta}$
-invariant and
![]() ${\it\alpha}{\it\beta}|_{A}$
has order
${\it\alpha}{\it\beta}|_{A}$
has order
![]() $3$
, we conclude that
$3$
, we conclude that
![]() $A$
is indeed smooth. However, the Hurwitz formula shows that
$A$
is indeed smooth. However, the Hurwitz formula shows that
![]() ${\it\alpha}{\it\beta}|_{A}$
has either one or four fixed points, a contradiction.
${\it\alpha}{\it\beta}|_{A}$
has either one or four fixed points, a contradiction.
So
![]() $B$
and
$B$
and
![]() ${\it\alpha}(B)$
are contained in
${\it\alpha}(B)$
are contained in
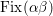 $\text{Fix}({\it\alpha}{\it\beta})$
. In particular,
$\text{Fix}({\it\alpha}{\it\beta})$
. In particular,
![]() $B$
and
$B$
and
![]() ${\it\alpha}(B)$
are smooth curves. Then
${\it\alpha}(B)$
are smooth curves. Then
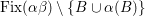 $\text{Fix}({\it\alpha}{\it\beta})\setminus \{B\cup {\it\alpha}(B)\}$
consists of five isolated fixed points and each fixed point is of type
$\text{Fix}({\it\alpha}{\it\beta})\setminus \{B\cup {\it\alpha}(B)\}$
consists of five isolated fixed points and each fixed point is of type
![]() $\frac{1}{3}(1,2)$
by Proposition 2.1 and Lemma 3.4. These points must be contained in
$\frac{1}{3}(1,2)$
by Proposition 2.1 and Lemma 3.4. These points must be contained in
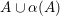 $A\cup {\it\alpha}(A)$
.◻
$A\cup {\it\alpha}(A)$
.◻
Now we are able to describe the quotient map
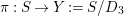 ${\it\pi}:S\rightarrow Y:=S/D_{3}$
, where
${\it\pi}:S\rightarrow Y:=S/D_{3}$
, where
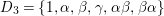 $D_{3}=\{1,{\it\alpha},{\it\beta},{\it\gamma},{\it\alpha}{\it\beta},{\it\beta}{\it\alpha}\}$
and
$D_{3}=\{1,{\it\alpha},{\it\beta},{\it\gamma},{\it\alpha}{\it\beta},{\it\beta}{\it\alpha}\}$
and
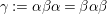 ${\it\gamma}:={\it\alpha}{\it\beta}{\it\alpha}={\it\beta}{\it\alpha}{\it\beta}$
. The divisorial parts and isolated fixed points of cyclic subgroups of
${\it\gamma}:={\it\alpha}{\it\beta}{\it\alpha}={\it\beta}{\it\alpha}{\it\beta}$
. The divisorial parts and isolated fixed points of cyclic subgroups of
![]() $D_{3}$
are as follows (see the discussion before Lemma 3.4 and Proposition 3.7):
$D_{3}$
are as follows (see the discussion before Lemma 3.4 and Proposition 3.7):
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}rrr@{}}\hspace{-1.3pt}\text{cyclic subgroups} & \text{divisorial part} & \text{isolated fixed points}\\ \hspace{-1.3pt}\langle {\it\alpha}\rangle ~(\text{resp.}~\langle {\it\beta}\rangle ,\langle {\it\gamma}\rangle )\cong \mathbb{Z}_{2} & R_{{\it\alpha}}~(\text{resp.}~R_{{\it\beta}},R_{{\it\gamma}}) & \text{7 points on}~F_{{\it\alpha}}~(\text{resp.}~F_{{\it\beta}},F_{{\it\gamma}})\\ \hspace{-1.3pt}\langle {\it\alpha}{\it\beta}\rangle \cong \mathbb{Z}_{3} & B,{\it\alpha}(B) & p,q_{1},q_{2},{\it\alpha}(q_{1}),{\it\alpha}(q_{2})\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}rrr@{}}\hspace{-1.3pt}\text{cyclic subgroups} & \text{divisorial part} & \text{isolated fixed points}\\ \hspace{-1.3pt}\langle {\it\alpha}\rangle ~(\text{resp.}~\langle {\it\beta}\rangle ,\langle {\it\gamma}\rangle )\cong \mathbb{Z}_{2} & R_{{\it\alpha}}~(\text{resp.}~R_{{\it\beta}},R_{{\it\gamma}}) & \text{7 points on}~F_{{\it\alpha}}~(\text{resp.}~F_{{\it\beta}},F_{{\it\gamma}})\\ \hspace{-1.3pt}\langle {\it\alpha}{\it\beta}\rangle \cong \mathbb{Z}_{3} & B,{\it\alpha}(B) & p,q_{1},q_{2},{\it\alpha}(q_{1}),{\it\alpha}(q_{2})\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
Note that
![]() $p$
is the unique point with the stabilizer
$p$
is the unique point with the stabilizer
![]() $D_{3}$
. From the action of
$D_{3}$
. From the action of
![]() $D_{3}$
on the tangent space
$D_{3}$
on the tangent space
![]() $\text{T}_{p}S$
(see the proof of Lemma 3.3(c)), it is easily seen that
$\text{T}_{p}S$
(see the proof of Lemma 3.3(c)), it is easily seen that
![]() ${\it\pi}(p)$
is a smooth point of
${\it\pi}(p)$
is a smooth point of
![]() $Y$
. We conclude that
$Y$
. We conclude that
![]() $Y$
has seven nodes and two
$Y$
has seven nodes and two
![]() $A_{2}$
-singularities
$A_{2}$
-singularities
![]() ${\it\pi}(q_{1})$
and
${\it\pi}(q_{1})$
and
![]() ${\it\pi}(q_{2})$
. In particular,
${\it\pi}(q_{2})$
. In particular,
![]() $Y$
is Gorenstein. The ramification formula gives
$Y$
is Gorenstein. The ramification formula gives
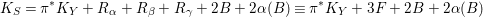 $$\begin{eqnarray}\displaystyle K_{S}={\it\pi}^{\ast }K_{Y}+R_{{\it\alpha}}+R_{{\it\beta}}+R_{{\it\gamma}}+2B+2{\it\alpha}(B)\equiv {\it\pi}^{\ast }K_{Y}+3F+2B+2{\it\alpha}(B) & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K_{S}={\it\pi}^{\ast }K_{Y}+R_{{\it\alpha}}+R_{{\it\beta}}+R_{{\it\gamma}}+2B+2{\it\alpha}(B)\equiv {\it\pi}^{\ast }K_{Y}+3F+2B+2{\it\alpha}(B) & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
and thus
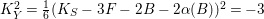 $K_{Y}^{2}=\frac{1}{6}(K_{S}-3F-2B-2{\it\alpha}(B))^{2}=-3$
.
$K_{Y}^{2}=\frac{1}{6}(K_{S}-3F-2B-2{\it\alpha}(B))^{2}=-3$
.
Let
 $B^{\prime }={\it\pi}(B)$
. Then
$B^{\prime }={\it\pi}(B)$
. Then
![]() $B^{\prime }$
is contained in the smooth locus of
$B^{\prime }$
is contained in the smooth locus of
![]() $Y$
. Note that
$Y$
. Note that
![]() $B^{\prime }$
is a smooth elliptic curve and
$B^{\prime }$
is a smooth elliptic curve and
 ${\it\pi}^{\ast }B^{\prime }=3B+3{\it\alpha}(B)$
. So
${\it\pi}^{\ast }B^{\prime }=3B+3{\it\alpha}(B)$
. So
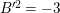 ${B^{\prime }}^{2}=-3$
and
${B^{\prime }}^{2}=-3$
and
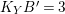 $K_{Y}B^{\prime }=3$
. Since
$K_{Y}B^{\prime }=3$
. Since
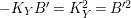 $-K_{Y}B^{\prime }=K_{Y}^{2}={B^{\prime }}^{2}$
,
$-K_{Y}B^{\prime }=K_{Y}^{2}={B^{\prime }}^{2}$
,
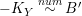 $-K_{Y}\stackrel{num}{{\sim}}B^{\prime }$
by Lemma 3.4. This implies that
$-K_{Y}\stackrel{num}{{\sim}}B^{\prime }$
by Lemma 3.4. This implies that
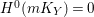 $H^{0}(mK_{Y})=0$
for
$H^{0}(mK_{Y})=0$
for
![]() $m\geqslant 1$
. As the quotient of
$m\geqslant 1$
. As the quotient of
![]() $S$
,
$S$
,
![]() $Y$
has irregularity
$Y$
has irregularity
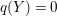 $q(Y)=0$
. Therefore,
$q(Y)=0$
. Therefore,
![]() $Y$
is a rational surface. Note that linear equivalence and numerical equivalence between divisors are the same on a smooth rational surface. Since
$Y$
is a rational surface. Note that linear equivalence and numerical equivalence between divisors are the same on a smooth rational surface. Since
![]() $Y$
contains only rational double points and
$Y$
contains only rational double points and
![]() $B^{\prime }$
is contained in the smooth locus of
$B^{\prime }$
is contained in the smooth locus of
![]() $Y$
, we have
$Y$
, we have
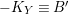 $-K_{Y}\equiv B^{\prime }$
indeed. Then by (3.3),
$-K_{Y}\equiv B^{\prime }$
indeed. Then by (3.3),
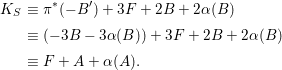 $$\begin{eqnarray}\displaystyle K_{S} & \equiv & \displaystyle {\it\pi}^{\ast }(-B^{\prime })+3F+2B+2{\it\alpha}(B)\nonumber\\ \displaystyle & \equiv & \displaystyle (-3B-3{\it\alpha}(B))+3F+2B+2{\it\alpha}(B)\nonumber\\ \displaystyle & \equiv & \displaystyle F+A+{\it\alpha}(A).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K_{S} & \equiv & \displaystyle {\it\pi}^{\ast }(-B^{\prime })+3F+2B+2{\it\alpha}(B)\nonumber\\ \displaystyle & \equiv & \displaystyle (-3B-3{\it\alpha}(B))+3F+2B+2{\it\alpha}(B)\nonumber\\ \displaystyle & \equiv & \displaystyle F+A+{\it\alpha}(A).\nonumber\end{eqnarray}$$
We obtain a contradiction to
 $p_{g}(S)=0$
and complete the proof of Theorem 3.1.
$p_{g}(S)=0$
and complete the proof of Theorem 3.1.
4 Inoue surfaces
As mentioned in the introduction, Inoue surfaces have been the first examples of surfaces of general type with
![]() $p_{g}=0$
and
$p_{g}=0$
and
![]() $K^{2}=7$
(cf. [Reference Inoue14]). Here we describe them as finite Galois
$K^{2}=7$
(cf. [Reference Inoue14]). Here we describe them as finite Galois
![]() $\mathbb{Z}_{2}^{2}$
-covers of the
$\mathbb{Z}_{2}^{2}$
-covers of the
![]() $4$
-nodal cubic surface, following [Reference Mendes Lopes and Pardini19, Example 4.1]. At the end of this section, we prove Theorem 1.4.
$4$
-nodal cubic surface, following [Reference Mendes Lopes and Pardini19, Example 4.1]. At the end of this section, we prove Theorem 1.4.
Example 4.1. Let
 ${\it\sigma}:W\rightarrow \mathbb{P}^{2}$
be the blowup of the six vertexes
${\it\sigma}:W\rightarrow \mathbb{P}^{2}$
be the blowup of the six vertexes
 $p_{1},p_{2},p_{3},p_{1}^{\prime },p_{2}^{\prime },p_{3}^{\prime }$
of a complete quadrilateral on
$p_{1},p_{2},p_{3},p_{1}^{\prime },p_{2}^{\prime },p_{3}^{\prime }$
of a complete quadrilateral on
![]() $\mathbb{P}^{2}$
(see Figure 1). Denote by
$\mathbb{P}^{2}$
(see Figure 1). Denote by
![]() $E_{i}$
(respectively
$E_{i}$
(respectively
![]() $E_{i}^{\prime }$
) the exceptional curve of
$E_{i}^{\prime }$
) the exceptional curve of
![]() $W$
over
$W$
over
![]() $p_{i}$
(respectively
$p_{i}$
(respectively
![]() $p_{i}^{\prime }$
) and denote by
$p_{i}^{\prime }$
) and denote by
![]() $L$
the pullback of a general line by
$L$
the pullback of a general line by
![]() ${\it\sigma}$
. Then
${\it\sigma}$
. Then
 $\text{Pic}(W)=\mathbb{Z}L\oplus \bigoplus _{i=1}^{3}(\mathbb{Z}E_{i}\oplus \mathbb{Z}E_{i}^{\prime })$
.
$\text{Pic}(W)=\mathbb{Z}L\oplus \bigoplus _{i=1}^{3}(\mathbb{Z}E_{i}\oplus \mathbb{Z}E_{i}^{\prime })$
.
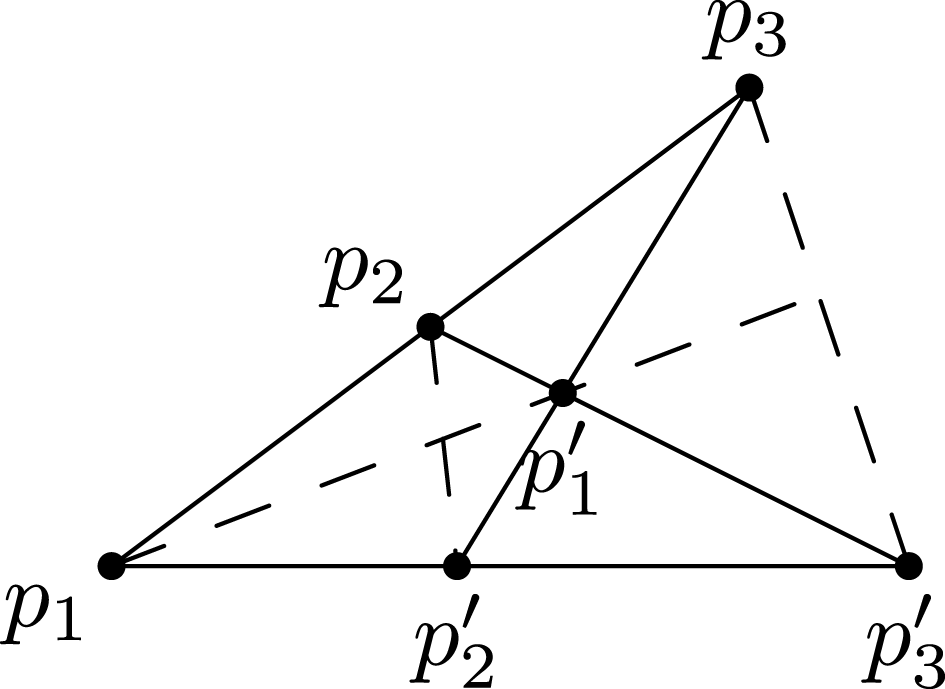
Figure 1. Configurations of the points
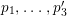 $p_{1},\ldots ,p_{3}^{\prime }$
.
$p_{1},\ldots ,p_{3}^{\prime }$
.
The surface
![]() $W$
has four disjoint
$W$
has four disjoint
![]() $(-2)$
-curves. They are the proper transforms of the four sides of the quadrilateral and their divisor classes are
$(-2)$
-curves. They are the proper transforms of the four sides of the quadrilateral and their divisor classes are
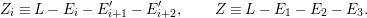 $$\begin{eqnarray}\displaystyle Z_{i}\equiv L-E_{i}-E_{i+1}^{\prime }-E_{i+2}^{\prime },\qquad Z\equiv L-E_{1}-E_{2}-E_{3}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Z_{i}\equiv L-E_{i}-E_{i+1}^{\prime }-E_{i+2}^{\prime },\qquad Z\equiv L-E_{1}-E_{2}-E_{3}. & & \displaystyle \nonumber\end{eqnarray}$$
Let
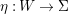 ${\it\eta}:W\rightarrow {\rm\Sigma}$
be the morphism contracting there curves. Then
${\it\eta}:W\rightarrow {\rm\Sigma}$
be the morphism contracting there curves. Then
![]() ${\rm\Sigma}$
is the
${\rm\Sigma}$
is the
![]() $4$
-nodal cubic surface.
$4$
-nodal cubic surface.
Let
![]() ${\rm\Gamma}_{1},{\rm\Gamma}_{2}$
and
${\rm\Gamma}_{1},{\rm\Gamma}_{2}$
and
![]() ${\rm\Gamma}_{3}$
be the proper transforms of the three diagonals of the quadrilateral, that is,
${\rm\Gamma}_{3}$
be the proper transforms of the three diagonals of the quadrilateral, that is,
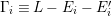 ${\rm\Gamma}_{i}\equiv L-E_{i}-E_{i}^{\prime }$
for
${\rm\Gamma}_{i}\equiv L-E_{i}-E_{i}^{\prime }$
for
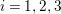 $i=1,2,3$
. Note that they are exactly the
$i=1,2,3$
. Note that they are exactly the
![]() $(-1)$
-curves which are disjoint from any
$(-1)$
-curves which are disjoint from any
![]() $(-2)$
-curve. For each
$(-2)$
-curve. For each
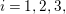 $i=1,2,3,$
$i=1,2,3,$
![]() $W$
has a pencil of rational curves
$W$
has a pencil of rational curves
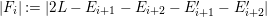 $|F_{i}|:=|2L-E_{i+1}-E_{i+2}-E_{i+1}^{\prime }-E_{i+2}^{\prime }|$
. Observe that
$|F_{i}|:=|2L-E_{i+1}-E_{i+2}-E_{i+1}^{\prime }-E_{i+2}^{\prime }|$
. Observe that
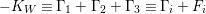 $-K_{W}\equiv {\rm\Gamma}_{1}+{\rm\Gamma}_{2}+{\rm\Gamma}_{3}\equiv {\rm\Gamma}_{i}+F_{i}$
for
$-K_{W}\equiv {\rm\Gamma}_{1}+{\rm\Gamma}_{2}+{\rm\Gamma}_{3}\equiv {\rm\Gamma}_{i}+F_{i}$
for
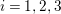 $i=1,2,3$
.
$i=1,2,3$
.
We define three effective divisors on
![]() $W$
$W$
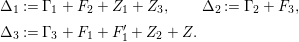 $$\begin{eqnarray}\displaystyle & & \displaystyle {\rm\Delta}_{1}:={\rm\Gamma}_{1}+F_{2}+Z_{1}+Z_{3},\qquad {\rm\Delta}_{2}:={\rm\Gamma}_{2}+F_{3},\nonumber\\ \displaystyle & & \displaystyle {\rm\Delta}_{3}:={\rm\Gamma}_{3}+F_{1}+F_{1}^{\prime }+Z_{2}+Z.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\rm\Delta}_{1}:={\rm\Gamma}_{1}+F_{2}+Z_{1}+Z_{3},\qquad {\rm\Delta}_{2}:={\rm\Gamma}_{2}+F_{3},\nonumber\\ \displaystyle & & \displaystyle {\rm\Delta}_{3}:={\rm\Gamma}_{3}+F_{1}+F_{1}^{\prime }+Z_{2}+Z.\end{eqnarray}$$
We require that
![]() $F_{i}$
(
$F_{i}$
(
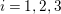 $i=1,2,3$
) and
$i=1,2,3$
) and
![]() $F_{1}^{\prime }$
are smooth
$F_{1}^{\prime }$
are smooth
![]() $0$
-curves such that the divisor
$0$
-curves such that the divisor
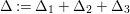 ${\rm\Delta}:={\rm\Delta}_{1}+{\rm\Delta}_{2}+{\rm\Delta}_{3}$
has only nodes. It is directly shown that there are divisors
${\rm\Delta}:={\rm\Delta}_{1}+{\rm\Delta}_{2}+{\rm\Delta}_{3}$
has only nodes. It is directly shown that there are divisors
![]() ${\mathcal{L}}_{1},{\mathcal{L}}_{2}$
and
${\mathcal{L}}_{1},{\mathcal{L}}_{2}$
and
![]() ${\mathcal{L}}_{3}$
satisfying (2.1) in Proposition 2.4. Then there is a smooth finite
${\mathcal{L}}_{3}$
satisfying (2.1) in Proposition 2.4. Then there is a smooth finite
![]() $G$
-cover
$G$
-cover
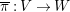 $\overline{{\it\pi}}:V\rightarrow W$
branched on the divisors
$\overline{{\it\pi}}:V\rightarrow W$
branched on the divisors
![]() ${\rm\Delta}_{1},{\rm\Delta}_{2}$
and
${\rm\Delta}_{1},{\rm\Delta}_{2}$
and
![]() ${\rm\Delta}_{3}$
. The (set theoretic) inverse image of a
${\rm\Delta}_{3}$
. The (set theoretic) inverse image of a
![]() $(-2)$
-curve under
$(-2)$
-curve under
![]() $\overline{{\it\pi}}$
is a disjoint union of two
$\overline{{\it\pi}}$
is a disjoint union of two
![]() $(-1)$
-curves. Let
$(-1)$
-curves. Let
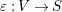 ${\it\varepsilon}:V\rightarrow S$
be the blowdown of these eight
${\it\varepsilon}:V\rightarrow S$
be the blowdown of these eight
![]() $(-1)$
-curves. Then there is a finite
$(-1)$
-curves. Then there is a finite
![]() $G$
-cover
$G$
-cover
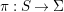 ${\it\pi}:S\rightarrow {\rm\Sigma}$
such that the following diagram (4.2) commutes.
${\it\pi}:S\rightarrow {\rm\Sigma}$
such that the following diagram (4.2) commutes.
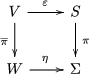
The surface
![]() $S$
is a smooth minimal surface of general type with
$S$
is a smooth minimal surface of general type with
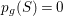 $p_{g}(S)=0$
and
$p_{g}(S)=0$
and
![]() $K_{S}^{2}=7$
. It is called an Inoue surface. When the curves
$K_{S}^{2}=7$
. It is called an Inoue surface. When the curves
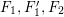 $F_{1},F_{1}^{\prime },F_{2}$
and
$F_{1},F_{1}^{\prime },F_{2}$
and
![]() $F_{3}$
vary, we obtain a
$F_{3}$
vary, we obtain a
![]() $4$
-dimensional family of Inoue surfaces.
$4$
-dimensional family of Inoue surfaces.
Lemma 4.2. Let
![]() $W$
be as in Example 4.1.
$W$
be as in Example 4.1.
-
(a) Let
 ${\it\alpha}$
be an automorphism on
${\it\alpha}$
be an automorphism on
 $W$
. If the induced map
$W$
. If the induced map
 ${\it\alpha}^{\ast }:H^{2}(W,\mathbb{C})\rightarrow H^{2}(W,\mathbb{C})$
is the identity, then
${\it\alpha}^{\ast }:H^{2}(W,\mathbb{C})\rightarrow H^{2}(W,\mathbb{C})$
is the identity, then
 ${\it\alpha}=\text{Id}_{W}$
.
${\it\alpha}=\text{Id}_{W}$
. -
(b) Let
 ${\it\alpha}_{\mathbb{P}^{2}}$
be the involution on
${\it\alpha}_{\mathbb{P}^{2}}$
be the involution on
 $\mathbb{P}^{2}$
such that
$\mathbb{P}^{2}$
such that
 ${\it\alpha}_{\mathbb{P}^{2}}(p_{k})=p_{k}^{\prime }$
for
${\it\alpha}_{\mathbb{P}^{2}}(p_{k})=p_{k}^{\prime }$
for
 $k=1,3$
. It induces an involution
$k=1,3$
. It induces an involution
 ${\it\alpha}_{0}$
on
${\it\alpha}_{0}$
on
 $W$
. Then
$W$
. Then
 $\text{Fix}({\it\alpha}_{0})$
consists of the
$\text{Fix}({\it\alpha}_{0})$
consists of the
 $(-1)$
-curve
$(-1)$
-curve
 ${\rm\Gamma}_{2}$
and three isolated fixed points
${\rm\Gamma}_{2}$
and three isolated fixed points
 ${\rm\Gamma}_{1}\cap {\rm\Gamma}_{3}$
,
${\rm\Gamma}_{1}\cap {\rm\Gamma}_{3}$
,
 $E_{2}\cap F_{3}^{\ast }$
and
$E_{2}\cap F_{3}^{\ast }$
and
 $E_{2}^{\prime }\cap F_{3}^{\ast }$
, where
$E_{2}^{\prime }\cap F_{3}^{\ast }$
, where
 $F_{3}^{\ast }$
is the unique smooth
$F_{3}^{\ast }$
is the unique smooth
 ${\it\alpha}_{0}$
-invariant curve in the pencil
${\it\alpha}_{0}$
-invariant curve in the pencil
 $|F_{3}|=|2L-E_{1}-E_{1}^{\prime }-E_{2}-E_{2}^{\prime }|$
.
$|F_{3}|=|2L-E_{1}-E_{1}^{\prime }-E_{2}-E_{2}^{\prime }|$
.
Proof. For (a), the assumption implies that the
![]() $(-1)$
-curves
$(-1)$
-curves
![]() $E_{i}$
and
$E_{i}$
and
![]() $E_{i}^{\prime }$
(
$E_{i}^{\prime }$
(
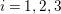 $i=1,2,3$
) are
$i=1,2,3$
) are
![]() ${\it\alpha}$
-invariant. So
${\it\alpha}$
-invariant. So
![]() ${\it\alpha}$
comes from an automorphism on
${\it\alpha}$
comes from an automorphism on
![]() $\mathbb{P}^{2}$
which has
$\mathbb{P}^{2}$
which has
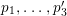 $p_{1},\ldots ,p_{3}^{\prime }$
as fixed points and thus it is the identity morphism.
$p_{1},\ldots ,p_{3}^{\prime }$
as fixed points and thus it is the identity morphism.
For (b), note that
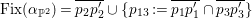 $\text{Fix}({\it\alpha}_{\mathbb{P}^{2}})=\overline{p_{2}p_{2}^{\prime }}\cup \{p_{13}:=\overline{p_{1}p_{1}^{\prime }}\cap \overline{p_{3}p_{3}^{\prime }}\}$
and
$\text{Fix}({\it\alpha}_{\mathbb{P}^{2}})=\overline{p_{2}p_{2}^{\prime }}\cup \{p_{13}:=\overline{p_{1}p_{1}^{\prime }}\cap \overline{p_{3}p_{3}^{\prime }}\}$
and
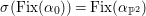 ${\it\sigma}(\text{Fix}({\it\alpha}_{0}))=\text{Fix}({\it\alpha}_{\mathbb{P}^{2}})$
. Because
${\it\sigma}(\text{Fix}({\it\alpha}_{0}))=\text{Fix}({\it\alpha}_{\mathbb{P}^{2}})$
. Because
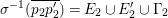 ${\it\sigma}^{-1}(\overline{p_{2}p_{2}^{\prime }})=E_{2}\cup E_{2}^{\prime }\cup {\rm\Gamma}_{2}$
and the divisorial part of
${\it\sigma}^{-1}(\overline{p_{2}p_{2}^{\prime }})=E_{2}\cup E_{2}^{\prime }\cup {\rm\Gamma}_{2}$
and the divisorial part of
![]() ${\it\alpha}_{0}$
is smooth,
${\it\alpha}_{0}$
is smooth,
![]() $\text{Fix}({\it\alpha}_{0})$
has
$\text{Fix}({\it\alpha}_{0})$
has
![]() ${\rm\Gamma}_{2}$
as the divisorial part. Then
${\rm\Gamma}_{2}$
as the divisorial part. Then
![]() ${\it\alpha}_{0}$
has three isolated fixed points by Proposition 2.1. The point
${\it\alpha}_{0}$
has three isolated fixed points by Proposition 2.1. The point
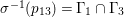 ${\it\sigma}^{-1}(p_{13})={\rm\Gamma}_{1}\cap {\rm\Gamma}_{3}$
is an isolated fixed point of
${\it\sigma}^{-1}(p_{13})={\rm\Gamma}_{1}\cap {\rm\Gamma}_{3}$
is an isolated fixed point of
![]() ${\it\alpha}_{0}$
. Note that
${\it\alpha}_{0}$
. Note that
![]() ${\it\alpha}_{0}$
induces a nontrivial action on the pencil
${\it\alpha}_{0}$
induces a nontrivial action on the pencil
![]() $|F_{3}|$
. So
$|F_{3}|$
. So
![]() $|F_{3}|$
contains exactly two
$|F_{3}|$
contains exactly two
![]() ${\it\alpha}_{0}$
-invariant curves
${\it\alpha}_{0}$
-invariant curves
 ${\rm\Gamma}_{1}+{\rm\Gamma}_{2}$
and
${\rm\Gamma}_{1}+{\rm\Gamma}_{2}$
and
![]() $F_{3}^{\ast }$
. Since
$F_{3}^{\ast }$
. Since
![]() $E_{2}$
and
$E_{2}$
and
![]() $E_{2}^{\prime }$
are also
$E_{2}^{\prime }$
are also
![]() ${\it\alpha}_{0}$
-invariant, the intersection points
${\it\alpha}_{0}$
-invariant, the intersection points
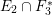 $E_{2}\cap F_{3}^{\ast }$
and
$E_{2}\cap F_{3}^{\ast }$
and
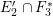 $E_{2}^{\prime }\cap F_{3}^{\ast }$
are isolated fixed points of
$E_{2}^{\prime }\cap F_{3}^{\ast }$
are isolated fixed points of
![]() ${\it\alpha}_{0}$
.◻
${\it\alpha}_{0}$
.◻
Proof of Theorem 1.4.
Let
 ${\it\tau}\in \text{Aut}(S)$
. By Theorem 1.2,
${\it\tau}\in \text{Aut}(S)$
. By Theorem 1.2,
![]() $\text{Fix}(g_{i})$
is
$\text{Fix}(g_{i})$
is
![]() ${\it\tau}$
-invariant for
${\it\tau}$
-invariant for
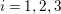 $i=1,2,3$
and
$i=1,2,3$
and
![]() ${\it\tau}$
induces an automorphism
${\it\tau}$
induces an automorphism
![]() ${\it\alpha}_{{\rm\Sigma}}$
on the quotient surface
${\it\alpha}_{{\rm\Sigma}}$
on the quotient surface
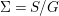 ${\rm\Sigma}=S/G$
. So the branch locus
${\rm\Sigma}=S/G$
. So the branch locus
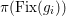 ${\it\pi}(\text{Fix}(g_{i}))$
(for
${\it\pi}(\text{Fix}(g_{i}))$
(for
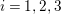 $i=1,2,3$
) of
$i=1,2,3$
) of
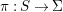 ${\it\pi}:S\rightarrow {\rm\Sigma}$
is
${\it\pi}:S\rightarrow {\rm\Sigma}$
is
![]() ${\it\alpha}_{{\rm\Sigma}}$
-invariant.
${\it\alpha}_{{\rm\Sigma}}$
-invariant.
Assume that
![]() ${\it\tau}\not \in G$
, that is,
${\it\tau}\not \in G$
, that is,
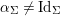 ${\it\alpha}_{{\rm\Sigma}}\not =\text{Id}_{{\rm\Sigma}}$
. The automorphism
${\it\alpha}_{{\rm\Sigma}}\not =\text{Id}_{{\rm\Sigma}}$
. The automorphism
![]() ${\it\alpha}_{{\rm\Sigma}}$
lifts to the minimal resolution
${\it\alpha}_{{\rm\Sigma}}$
lifts to the minimal resolution
![]() $W$
of
$W$
of
![]() ${\rm\Sigma}$
. Denote by
${\rm\Sigma}$
. Denote by
![]() ${\it\alpha}$
the induced automorphism on
${\it\alpha}$
the induced automorphism on
![]() $W$
. Then
$W$
. Then
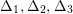 ${\rm\Delta}_{1},{\rm\Delta}_{2},{\rm\Delta}_{3}$
(see the diagram (4.2)) are
${\rm\Delta}_{1},{\rm\Delta}_{2},{\rm\Delta}_{3}$
(see the diagram (4.2)) are
![]() ${\it\alpha}$
-invariant because
${\it\alpha}$
-invariant because
![]() ${\rm\Delta}_{i}$
is the inverse image of
${\rm\Delta}_{i}$
is the inverse image of
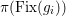 ${\it\pi}(\text{Fix}(g_{i}))$
under the morphism
${\it\pi}(\text{Fix}(g_{i}))$
under the morphism
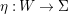 ${\it\eta}:W\rightarrow {\rm\Sigma}$
. These divisors are given by (4.1). It follows that the
${\it\eta}:W\rightarrow {\rm\Sigma}$
. These divisors are given by (4.1). It follows that the
![]() $(-1)$
-curves
$(-1)$
-curves
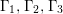 ${\rm\Gamma}_{1},{\rm\Gamma}_{2},{\rm\Gamma}_{3}$
, the
${\rm\Gamma}_{1},{\rm\Gamma}_{2},{\rm\Gamma}_{3}$
, the
![]() $0$
-curves
$0$
-curves
![]() $F_{2},F_{3}$
and the curves
$F_{2},F_{3}$
and the curves
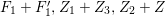 $F_{1}+F_{1}^{\prime },Z_{1}+Z_{3},Z_{2}+Z$
are
$F_{1}+F_{1}^{\prime },Z_{1}+Z_{3},Z_{2}+Z$
are
![]() ${\it\alpha}$
-invariant. Note that the Chern classes of
${\it\alpha}$
-invariant. Note that the Chern classes of
 ${\rm\Gamma}_{1},{\rm\Gamma}_{2},{\rm\Gamma}_{3}$
and the Chern classes of
${\rm\Gamma}_{1},{\rm\Gamma}_{2},{\rm\Gamma}_{3}$
and the Chern classes of
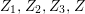 $Z_{1},Z_{2},Z_{3},Z$
generate
$Z_{1},Z_{2},Z_{3},Z$
generate
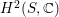 $H^{2}(S,\mathbb{C})$
. The argument above implies that
$H^{2}(S,\mathbb{C})$
. The argument above implies that
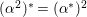 $({\it\alpha}^{2})^{\ast }=({\it\alpha}^{\ast })^{2}$
is the identity morphism. Then
$({\it\alpha}^{2})^{\ast }=({\it\alpha}^{\ast })^{2}$
is the identity morphism. Then
![]() ${\it\alpha}$
is an involution by Lemma 4.2.
${\it\alpha}$
is an involution by Lemma 4.2.
Since
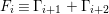 $F_{i}\equiv {\rm\Gamma}_{i+1}+{\rm\Gamma}_{i+2}$
, the fibration
$F_{i}\equiv {\rm\Gamma}_{i+1}+{\rm\Gamma}_{i+2}$
, the fibration
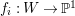 $f_{i}:W\rightarrow \mathbb{P}^{1}$
induced by
$f_{i}:W\rightarrow \mathbb{P}^{1}$
induced by
![]() $|F_{i}|$
is
$|F_{i}|$
is
![]() ${\it\alpha}$
-equivalent for
${\it\alpha}$
-equivalent for
 $i=1,2,3$
. Note that
$i=1,2,3$
. Note that
![]() $f_{2}$
has three singular fibers
$f_{2}$
has three singular fibers
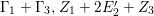 ${\rm\Gamma}_{1}+{\rm\Gamma}_{3},Z_{1}+2E_{2}^{\prime }+Z_{3}$
and
${\rm\Gamma}_{1}+{\rm\Gamma}_{3},Z_{1}+2E_{2}^{\prime }+Z_{3}$
and
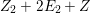 $Z_{2}+2E_{2}+Z$
. According to the discussion above, these three fibers are
$Z_{2}+2E_{2}+Z$
. According to the discussion above, these three fibers are
![]() ${\it\alpha}$
-invariant. Because any nontrivial automorphism on
${\it\alpha}$
-invariant. Because any nontrivial automorphism on
![]() $\mathbb{P}^{1}$
has at most two fixed points,
$\mathbb{P}^{1}$
has at most two fixed points,
![]() ${\it\alpha}$
respects the fibration
${\it\alpha}$
respects the fibration
![]() $f_{2}$
, that is,
$f_{2}$
, that is,
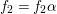 $f_{2}=f_{2}{\it\alpha}$
. In particular,
$f_{2}=f_{2}{\it\alpha}$
. In particular,
![]() $E_{2}$
and
$E_{2}$
and
![]() $E_{2}^{\prime }$
are
$E_{2}^{\prime }$
are
![]() ${\it\alpha}$
-invariant.
${\it\alpha}$
-invariant.
Note that
![]() $f_{1}$
has three singular fibers
$f_{1}$
has three singular fibers
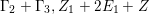 ${\rm\Gamma}_{2}+{\rm\Gamma}_{3},Z_{1}+2E_{1}+Z$
and
${\rm\Gamma}_{2}+{\rm\Gamma}_{3},Z_{1}+2E_{1}+Z$
and
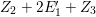 $Z_{2}+2E_{1}^{\prime }+Z_{3}$
. If
$Z_{2}+2E_{1}^{\prime }+Z_{3}$
. If
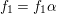 $f_{1}=f_{1}{\it\alpha}$
, then all the
$f_{1}=f_{1}{\it\alpha}$
, then all the
![]() $(-2)$
-curves
$(-2)$
-curves
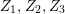 $Z_{1},Z_{2},Z_{3}$
and
$Z_{1},Z_{2},Z_{3}$
and
![]() $Z$
are
$Z$
are
![]() ${\it\alpha}$
-invariant since
${\it\alpha}$
-invariant since
![]() ${\it\alpha}$
also respects
${\it\alpha}$
also respects
![]() $f_{2}$
. Then
$f_{2}$
. Then
![]() ${\it\alpha}^{\ast }$
is the identity morphism and so is
${\it\alpha}^{\ast }$
is the identity morphism and so is
![]() ${\it\alpha}$
by Lemma 4.2, a contradiction to our assumption. So
${\it\alpha}$
by Lemma 4.2, a contradiction to our assumption. So
![]() ${\it\alpha}$
induces a nontrivial action on
${\it\alpha}$
induces a nontrivial action on
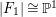 $|F_{1}|\cong \mathbb{P}^{1}$
. Since the singular
$|F_{1}|\cong \mathbb{P}^{1}$
. Since the singular
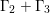 ${\rm\Gamma}_{2}+{\rm\Gamma}_{3}$
is
${\rm\Gamma}_{2}+{\rm\Gamma}_{3}$
is
![]() ${\it\alpha}$
-invariant,
${\it\alpha}$
-invariant,
![]() ${\it\alpha}$
must permute the other two singular fibers of
${\it\alpha}$
must permute the other two singular fibers of
![]() $f_{1}$
. Hence
$f_{1}$
. Hence
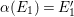 ${\it\alpha}(E_{1})=E_{1}^{\prime }$
and
${\it\alpha}(E_{1})=E_{1}^{\prime }$
and
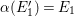 ${\it\alpha}(E_{1}^{\prime })=E_{1}$
. Similarly, by considering the action of
${\it\alpha}(E_{1}^{\prime })=E_{1}$
. Similarly, by considering the action of
![]() ${\it\alpha}$
on
${\it\alpha}$
on
![]() $|F_{3}|$
, we see that
$|F_{3}|$
, we see that
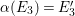 ${\it\alpha}(E_{3})=E_{3}^{\prime }$
and
${\it\alpha}(E_{3})=E_{3}^{\prime }$
and
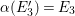 ${\it\alpha}(E_{3}^{\prime })=E_{3}$
.
${\it\alpha}(E_{3}^{\prime })=E_{3}$
.
We conclude that
![]() ${\it\alpha}$
is the involution
${\it\alpha}$
is the involution
![]() ${\it\alpha}_{0}$
in Lemma 4.2. We actually prove that if
${\it\alpha}_{0}$
in Lemma 4.2. We actually prove that if
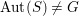 $\text{Aut}(S)\not =G$
, then
$\text{Aut}(S)\not =G$
, then
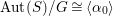 $\text{Aut}(S)/G\cong \langle {\it\alpha}_{0}\rangle$
, and in the Equation (4.1), the curve
$\text{Aut}(S)/G\cong \langle {\it\alpha}_{0}\rangle$
, and in the Equation (4.1), the curve
![]() $F_{3}$
in
$F_{3}$
in
![]() ${\rm\Delta}_{2}$
is indeed the curve
${\rm\Delta}_{2}$
is indeed the curve
![]() $F_{3}^{\ast }$
in Lemma 4.2(b) and
$F_{3}^{\ast }$
in Lemma 4.2(b) and
 $F_{1}^{\prime }={\it\alpha}_{0}(F_{1})$
in
$F_{1}^{\prime }={\it\alpha}_{0}(F_{1})$
in
![]() ${\rm\Delta}_{3}$
. Combining with Theorem 1.2 and Corollary 1.3, we complete the proof of Theorem 1.4.◻
${\rm\Delta}_{3}$
. Combining with Theorem 1.2 and Corollary 1.3, we complete the proof of Theorem 1.4.◻
Remark 4.3. When the curves
![]() $F_{1}$
and
$F_{1}$
and
![]() $F_{2}$
vary, the Inoue surfaces corresponding to the branch divisors (4.1) with
$F_{2}$
vary, the Inoue surfaces corresponding to the branch divisors (4.1) with
 $F_{3}=F_{3}^{\ast }$
and
$F_{3}=F_{3}^{\ast }$
and
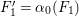 $F_{1}^{\prime }={\it\alpha}_{0}(F_{1})$
form a
$F_{1}^{\prime }={\it\alpha}_{0}(F_{1})$
form a
![]() $2$
-dimensional irreducible closed subset of the total
$2$
-dimensional irreducible closed subset of the total
![]() $4$
-dimensional family of Inoue surfaces. Also Lemma 4.2 shows that
$4$
-dimensional family of Inoue surfaces. Also Lemma 4.2 shows that
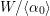 $W/\langle {\it\alpha}_{0}\rangle$
has three nodes. Moreover, it contains three
$W/\langle {\it\alpha}_{0}\rangle$
has three nodes. Moreover, it contains three
![]() $(-2)$
-curves in the smooth locus and these curves are the images of
$(-2)$
-curves in the smooth locus and these curves are the images of
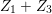 $Z_{1}+Z_{3}$
,
$Z_{1}+Z_{3}$
,
![]() $Z_{2}+Z$
and
$Z_{2}+Z$
and
![]() ${\rm\Gamma}_{2}$
under the quotient map from
${\rm\Gamma}_{2}$
under the quotient map from
![]() $W$
to
$W$
to
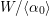 $W/\langle {\it\alpha}_{0}\rangle$
. This observation motivates us to construct some special Inoue surfaces in the next section.
$W/\langle {\it\alpha}_{0}\rangle$
. This observation motivates us to construct some special Inoue surfaces in the next section.
5 Special Inoue surfaces
We construct a
![]() $2$
-dimensional family of Inoue surfaces with automorphism groups isomorphic to
$2$
-dimensional family of Inoue surfaces with automorphism groups isomorphic to
 $\mathbb{Z}_{2}\times \mathbb{Z}_{4}$
. We use the notation in Section 2.2.
$\mathbb{Z}_{2}\times \mathbb{Z}_{4}$
. We use the notation in Section 2.2.
Let
 $q,q_{1},q_{2},q_{3},q_{1}^{\prime },q_{2}^{\prime }$
and
$q,q_{1},q_{2},q_{3},q_{1}^{\prime },q_{2}^{\prime }$
and
![]() $q_{3}^{\prime }$
be seven points on
$q_{3}^{\prime }$
be seven points on
![]() $\mathbb{P}^{2}$
with the configuration as in Figure 2.
$\mathbb{P}^{2}$
with the configuration as in Figure 2.
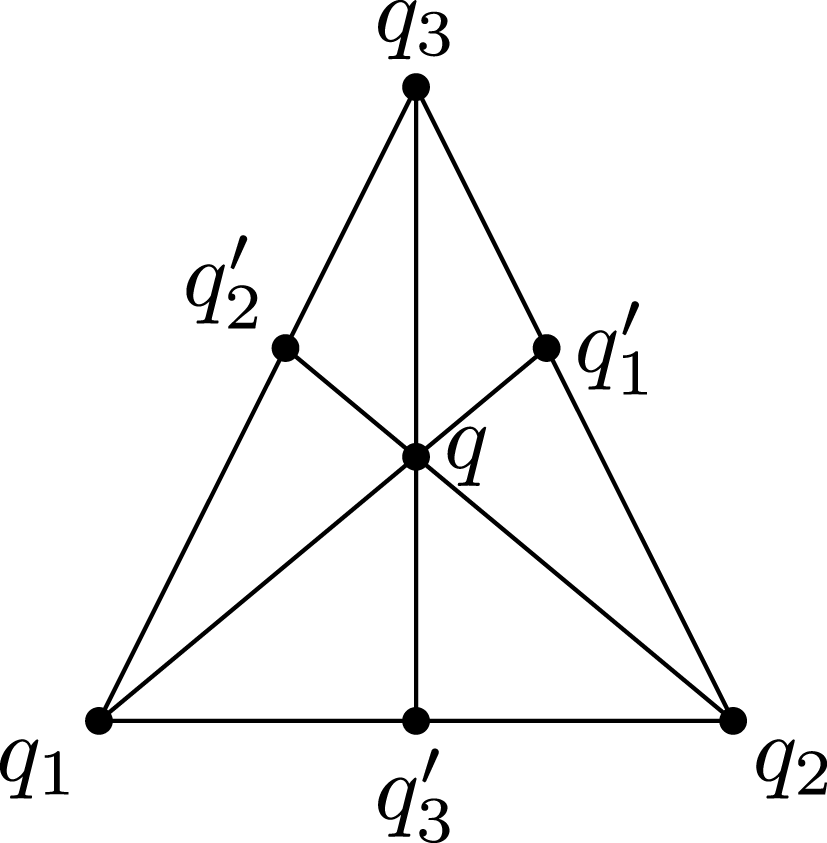
Figure 2. Configurations of the points
 $q,q_{1},\ldots ,q_{3}^{\prime }$
.
$q,q_{1},\ldots ,q_{3}^{\prime }$
.
Let
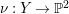 ${\it\nu}:Y\rightarrow \mathbb{P}^{2}$
be the blowup of these points. Denote by
${\it\nu}:Y\rightarrow \mathbb{P}^{2}$
be the blowup of these points. Denote by
![]() $Q_{i}$
(respectively
$Q_{i}$
(respectively
![]() $Q_{i}^{\prime }$
,
$Q_{i}^{\prime }$
,
![]() $Q$
) the exceptional curve of
$Q$
) the exceptional curve of
![]() $Y$
over
$Y$
over
![]() $q_{i}$
(respectively
$q_{i}$
(respectively
![]() $q_{i}^{\prime }$
,
$q_{i}^{\prime }$
,
![]() $q$
) and by
$q$
) and by
![]() $L$
the pullback of a general line by
$L$
the pullback of a general line by
![]() ${\it\nu}$
. Then
${\it\nu}$
. Then
 $\text{Pic}(W)=\mathbb{Z}L\oplus \mathbb{Z}Q\oplus (\bigoplus _{i=1}^{3}\mathbb{Z}Q_{i}\oplus \mathbb{Z}Q_{i}^{\prime })$
. The surface
$\text{Pic}(W)=\mathbb{Z}L\oplus \mathbb{Z}Q\oplus (\bigoplus _{i=1}^{3}\mathbb{Z}Q_{i}\oplus \mathbb{Z}Q_{i}^{\prime })$
. The surface
![]() $Y$
has six disjoint
$Y$
has six disjoint
![]() $(-2)$
-curves and their divisor classes are:
$(-2)$
-curves and their divisor classes are:
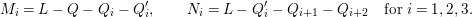 $$\begin{eqnarray}\displaystyle M_{i}=L-Q-Q_{i}-Q_{i}^{\prime },\qquad N_{i}=L-Q_{i}^{\prime }-Q_{i+1}-Q_{i+2}\quad \text{for }i=1,2,3. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{i}=L-Q-Q_{i}-Q_{i}^{\prime },\qquad N_{i}=L-Q_{i}^{\prime }-Q_{i+1}-Q_{i+2}\quad \text{for }i=1,2,3. & & \displaystyle \nonumber\end{eqnarray}$$
Let
![]() ${\rm\Lambda}_{i}$
be the proper transform of the line
${\rm\Lambda}_{i}$
be the proper transform of the line
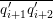 $\overline{q_{i+1}^{\prime }q_{i+2}^{\prime }}$
, that is,
$\overline{q_{i+1}^{\prime }q_{i+2}^{\prime }}$
, that is,
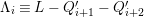 ${\rm\Lambda}_{i}\equiv L-Q_{i+1}^{\prime }-Q_{i+2}^{\prime }$
for
${\rm\Lambda}_{i}\equiv L-Q_{i+1}^{\prime }-Q_{i+2}^{\prime }$
for
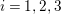 $i=1,2,3$
.
$i=1,2,3$
.
We describe four base-point-free pencils of rational curves on
![]() $Y$
. They are
$Y$
. They are
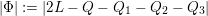 $|{\rm\Phi}|:=|2L-Q-Q_{1}-Q_{2}-Q_{3}|$
and
$|{\rm\Phi}|:=|2L-Q-Q_{1}-Q_{2}-Q_{3}|$
and
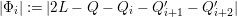 $|{\rm\Phi}_{i}|:=|2L-Q-Q_{i}-Q_{i+1}^{\prime }-Q_{i+2}^{\prime }|$
(
$|{\rm\Phi}_{i}|:=|2L-Q-Q_{i}-Q_{i+1}^{\prime }-Q_{i+2}^{\prime }|$
(
 $i=1,2,3$
). The singular members of
$i=1,2,3$
). The singular members of
![]() $|{\rm\Phi}|$
are
$|{\rm\Phi}|$
are
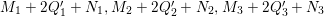 $M_{1}+2Q_{1}^{\prime }+N_{1},M_{2}+2Q_{2}^{\prime }+N_{2},M_{3}+2Q_{3}^{\prime }+N_{3}$
and those of
$M_{1}+2Q_{1}^{\prime }+N_{1},M_{2}+2Q_{2}^{\prime }+N_{2},M_{3}+2Q_{3}^{\prime }+N_{3}$
and those of
![]() $|{\rm\Phi}_{i}|$
(fixed
$|{\rm\Phi}_{i}|$
(fixed
![]() $i$
) are
$i$
) are
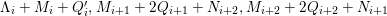 ${\rm\Lambda}_{i}+M_{i}+Q_{i}^{\prime },M_{i+1}+2Q_{i+1}+N_{i+2},M_{i+2}+2Q_{i+2}+N_{i+1}$
. Also note that
${\rm\Lambda}_{i}+M_{i}+Q_{i}^{\prime },M_{i+1}+2Q_{i+1}+N_{i+2},M_{i+2}+2Q_{i+2}+N_{i+1}$
. Also note that
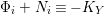 ${\rm\Phi}_{i}+N_{i}\equiv -K_{Y}$
for
${\rm\Phi}_{i}+N_{i}\equiv -K_{Y}$
for
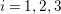 $i=1,2,3$
.
$i=1,2,3$
.
Let
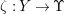 ${\it\zeta}:Y\rightarrow {\rm\Upsilon}$
be the morphism contracting the five
${\it\zeta}:Y\rightarrow {\rm\Upsilon}$
be the morphism contracting the five
![]() $(-2)$
-curves
$(-2)$
-curves
 $M_{1},M_{2},N_{2},M_{3}$
and
$M_{1},M_{2},N_{2},M_{3}$
and
![]() $N_{3}$
. Then
$N_{3}$
. Then
![]() ${\rm\Upsilon}$
has five nodes and contains a unique
${\rm\Upsilon}$
has five nodes and contains a unique
![]() $(-2)$
-curve
$(-2)$
-curve
![]() ${\it\zeta}(N_{1})$
in the smooth locus.
${\it\zeta}(N_{1})$
in the smooth locus.
Now we define the following effective divisors on
![]() $Y$
:
$Y$
:
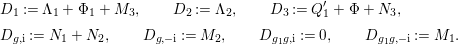 $$\begin{eqnarray}\displaystyle & & \displaystyle \quad \hspace{5.0pt}D_{1}:={\rm\Lambda}_{1}+{\rm\Phi}_{1}+M_{3},\qquad D_{2}:={\rm\Lambda}_{2},\qquad D_{3}:=Q_{1}^{\prime }+{\rm\Phi}+N_{3},\nonumber\\ \displaystyle & & \displaystyle \quad \hspace{5.0pt}D_{g,\text{i}}:=N_{1}+N_{2},\qquad D_{g,-\text{i}}:=M_{2},\qquad D_{g_{1}g,\text{i}}:=0,\qquad D_{g_{1}g,-\text{i}}:=M_{1}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \quad \hspace{5.0pt}D_{1}:={\rm\Lambda}_{1}+{\rm\Phi}_{1}+M_{3},\qquad D_{2}:={\rm\Lambda}_{2},\qquad D_{3}:=Q_{1}^{\prime }+{\rm\Phi}+N_{3},\nonumber\\ \displaystyle & & \displaystyle \quad \hspace{5.0pt}D_{g,\text{i}}:=N_{1}+N_{2},\qquad D_{g,-\text{i}}:=M_{2},\qquad D_{g_{1}g,\text{i}}:=0,\qquad D_{g_{1}g,-\text{i}}:=M_{1}.\end{eqnarray}$$
We also define the following divisors:
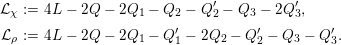 $$\begin{eqnarray}\displaystyle {\mathcal{L}}_{{\it\chi}} & := & \displaystyle 4L-2Q-2Q_{1}-Q_{2}-Q_{2}^{\prime }-Q_{3}-2Q_{3}^{\prime },\nonumber\\ \displaystyle {\mathcal{L}}_{{\it\rho}} & := & \displaystyle 4L-2Q-2Q_{1}-Q_{1}^{\prime }-2Q_{2}-Q_{2}^{\prime }-Q_{3}-Q_{3}^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{L}}_{{\it\chi}} & := & \displaystyle 4L-2Q-2Q_{1}-Q_{2}-Q_{2}^{\prime }-Q_{3}-2Q_{3}^{\prime },\nonumber\\ \displaystyle {\mathcal{L}}_{{\it\rho}} & := & \displaystyle 4L-2Q-2Q_{1}-Q_{1}^{\prime }-2Q_{2}-Q_{2}^{\prime }-Q_{3}-Q_{3}^{\prime }.\end{eqnarray}$$
We require that
![]() ${\rm\Phi}\in |{\rm\Phi}|$
and
${\rm\Phi}\in |{\rm\Phi}|$
and
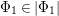 ${\rm\Phi}_{1}\in |{\rm\Phi}_{1}|$
are smooth curves such that the divisor
${\rm\Phi}_{1}\in |{\rm\Phi}_{1}|$
are smooth curves such that the divisor
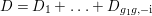 $D=D_{1}+\ldots +D_{g_{1}g,-\text{i}}$
has only nodes. These divisors satisfy (2.2) in Proposition 2.4. So there is a finite Galois
$D=D_{1}+\ldots +D_{g_{1}g,-\text{i}}$
has only nodes. These divisors satisfy (2.2) in Proposition 2.4. So there is a finite Galois
![]() $H$
-cover
$H$
-cover
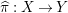 $\widehat{{\it\pi}}:X\rightarrow Y$
and
$\widehat{{\it\pi}}:X\rightarrow Y$
and
![]() $X$
is normal.
$X$
is normal.
We use [Reference Pardini22, Propositions 3.1 and 3.3] to analyze the singular locus of
![]() $X$
.
$X$
.
Lemma 5.1. Let
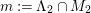 $m:={\rm\Lambda}_{2}\cap M_{2}$
and
$m:={\rm\Lambda}_{2}\cap M_{2}$
and
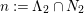 $n:={\rm\Lambda}_{2}\cap N_{2}$
.
$n:={\rm\Lambda}_{2}\cap N_{2}$
.
-
(a) The inverse image
 $\widehat{{\it\pi}}^{-1}(m)$
(resp.
$\widehat{{\it\pi}}^{-1}(m)$
(resp.
 $\widehat{{\it\pi}}^{-1}(n)$
) consists of two points
$\widehat{{\it\pi}}^{-1}(n)$
) consists of two points
 $\widehat{m_{1}}$
and
$\widehat{m_{1}}$
and
 $\widehat{m_{2}}$
(resp.
$\widehat{m_{2}}$
(resp.
 $\widehat{n_{1}}$
and
$\widehat{n_{1}}$
and
 $\widehat{n_{2}}$
), each of which has stabilizer
$\widehat{n_{2}}$
), each of which has stabilizer
 $\langle g\rangle$
.
$\langle g\rangle$
. -
(b) The points
 $\widehat{m_{1}},\widehat{m_{2}},\widehat{n_{1}}$
and
$\widehat{m_{1}},\widehat{m_{2}},\widehat{n_{1}}$
and
 $\widehat{n_{2}}$
are exactly the singularities of
$\widehat{n_{2}}$
are exactly the singularities of
 $X$
and they are nodes.
$X$
and they are nodes. -
(c) The curve
 $\widehat{{\it\pi}}^{-1}(M_{2})$
is a disjoint union of two irreducible smooth curves
$\widehat{{\it\pi}}^{-1}(M_{2})$
is a disjoint union of two irreducible smooth curves
 $\widehat{M}_{21}$
and
$\widehat{M}_{21}$
and
 $\widehat{M}_{22}$
, and
$\widehat{M}_{22}$
, and
 $\widehat{M}_{2j}$
has self-intersection number
$\widehat{M}_{2j}$
has self-intersection number
 $(-\frac{1}{2})$
and
$(-\frac{1}{2})$
and
 $\widehat{m}_{j}\in \widehat{M}_{2j}$
for
$\widehat{m}_{j}\in \widehat{M}_{2j}$
for
 $j=1,2$
. The curve
$j=1,2$
. The curve
 $\widehat{{\it\pi}}^{-1}(N_{2})$
consists of two irreducible smooth curves
$\widehat{{\it\pi}}^{-1}(N_{2})$
consists of two irreducible smooth curves
 $\widehat{N}_{21}$
and
$\widehat{N}_{21}$
and
 $\widehat{N}_{22}$
, and
$\widehat{N}_{22}$
, and
 $\widehat{N}_{2j}$
has self-intersection number
$\widehat{N}_{2j}$
has self-intersection number
 $(-\frac{1}{2})$
and
$(-\frac{1}{2})$
and
 $\widehat{n}_{j}\in \widehat{N}_{2j}$
for
$\widehat{n}_{j}\in \widehat{N}_{2j}$
for
 $j=1,2$
.
$j=1,2$
. -
(d) The curve
 $\widehat{{\it\pi}}^{-1}(M_{3})$
is a disjoint union four
$\widehat{{\it\pi}}^{-1}(M_{3})$
is a disjoint union four
 $(-1)$
-curves and so is
$(-1)$
-curves and so is
 $\widehat{{\it\pi}}^{-1}(N_{3})$
.
$\widehat{{\it\pi}}^{-1}(N_{3})$
. -
(e) The curve
 $\widehat{{\it\pi}}^{-1}(M_{1})$
is a
$\widehat{{\it\pi}}^{-1}(M_{1})$
is a
 $(-1)$
-curve.
$(-1)$
-curve.
Proof. [Reference Pardini22, Proposition 3.1] shows that
![]() $X$
is smooth outside
$X$
is smooth outside
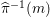 $\widehat{{\it\pi}}^{-1}(m)$
and
$\widehat{{\it\pi}}^{-1}(m)$
and
![]() $\widehat{{\it\pi}}^{-1}(n)$
. Note that
$\widehat{{\it\pi}}^{-1}(n)$
. Note that
![]() $M_{2}$
intersects only one irreducible component of
$M_{2}$
intersects only one irreducible component of
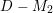 $D-M_{2}$
; that is
$D-M_{2}$
; that is
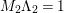 $M_{2}{\rm\Lambda}_{2}=1$
. Because
$M_{2}{\rm\Lambda}_{2}=1$
. Because
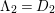 ${\rm\Lambda}_{2}=D_{2}$
,
${\rm\Lambda}_{2}=D_{2}$
,
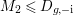 $M_{2}\leqslant D_{g,-\text{i}}$
and
$M_{2}\leqslant D_{g,-\text{i}}$
and
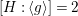 $[H:\langle g\rangle ]=2$
, we conclude that
$[H:\langle g\rangle ]=2$
, we conclude that
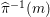 $\widehat{{\it\pi}}^{-1}(m)$
consists of two points, each of which has stabilizer
$\widehat{{\it\pi}}^{-1}(m)$
consists of two points, each of which has stabilizer
![]() $\langle g\rangle$
. These two points are nodes of
$\langle g\rangle$
. These two points are nodes of
![]() $X$
according to [Reference Pardini22, Proposition 3.3]. For the same reason, we have
$X$
according to [Reference Pardini22, Proposition 3.3]. For the same reason, we have
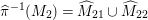 $\widehat{{\it\pi}}^{-1}(M_{2})=\widehat{M}_{21}\cup \widehat{M}_{22}$
with
$\widehat{{\it\pi}}^{-1}(M_{2})=\widehat{M}_{21}\cup \widehat{M}_{22}$
with
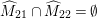 $\widehat{M}_{21}\cap \widehat{M}_{22}=\emptyset$
and
$\widehat{M}_{21}\cap \widehat{M}_{22}=\emptyset$
and
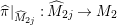 $\widehat{{\it\pi}}|_{\widehat{M}_{2j}}:\widehat{M}_{2j}\rightarrow M_{2}$
is an isomorphism. We also have
$\widehat{{\it\pi}}|_{\widehat{M}_{2j}}:\widehat{M}_{2j}\rightarrow M_{2}$
is an isomorphism. We also have
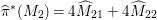 $\widehat{{\it\pi}}^{\ast }(M_{2})=4\widehat{M}_{21}+4\widehat{M}_{22}$
. Thus (a)–(c) follow from the discussion above. Similar arguments apply to (d) and (e). For (d), just note that
$\widehat{{\it\pi}}^{\ast }(M_{2})=4\widehat{M}_{21}+4\widehat{M}_{22}$
. Thus (a)–(c) follow from the discussion above. Similar arguments apply to (d) and (e). For (d), just note that
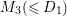 $M_{3}({\leqslant}D_{1})$
and
$M_{3}({\leqslant}D_{1})$
and
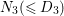 $N_{3}({\leqslant}D_{3})$
are connected irreducible components of
$N_{3}({\leqslant}D_{3})$
are connected irreducible components of
![]() $D$
. And (e) follows from the observation that
$D$
. And (e) follows from the observation that
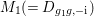 $M_{1}(=D_{g_{1}g,-\text{i}})$
intersects exactly two irreducible components of
$M_{1}(=D_{g_{1}g,-\text{i}})$
intersects exactly two irreducible components of
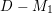 $D-M_{1}$
and
$D-M_{1}$
and
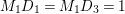 $M_{1}D_{1}=M_{1}D_{3}=1$
.◻
$M_{1}D_{1}=M_{1}D_{3}=1$
.◻
Now we explain how to obtain the smooth minimal model of
![]() $X$
. On the minimal resolution
$X$
. On the minimal resolution
![]() $\widetilde{X}$
of
$\widetilde{X}$
of
![]() $X$
, the strict transforms of
$X$
, the strict transforms of
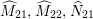 $\widehat{M}_{21},\widehat{M}_{22},\widehat{N}_{21}$
and
$\widehat{M}_{21},\widehat{M}_{22},\widehat{N}_{21}$
and
![]() $\widehat{N}_{22}$
are
$\widehat{N}_{22}$
are
![]() $(-1)$
-curves. Each of these
$(-1)$
-curves. Each of these
![]() $(-1)$
-curves intersects transversely at one point with exactly one of the four
$(-1)$
-curves intersects transversely at one point with exactly one of the four
![]() $(-2)$
-curves over the nodes of
$(-2)$
-curves over the nodes of
![]() $X$
. So we can contract the four curves
$X$
. So we can contract the four curves
 $\widehat{M}_{21},\widehat{M}_{22},\widehat{N}_{21}$
and
$\widehat{M}_{21},\widehat{M}_{22},\widehat{N}_{21}$
and
![]() $\widehat{N}_{22}$
of
$\widehat{N}_{22}$
of
![]() $X$
to smooth points on another surface.
$X$
to smooth points on another surface.
Let
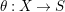 ${\it\theta}:X\rightarrow S$
be the morphism contracting the disjoint union of the nine
${\it\theta}:X\rightarrow S$
be the morphism contracting the disjoint union of the nine
![]() $(-1)$
-curves
$(-1)$
-curves
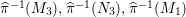 $\widehat{{\it\pi}}^{-1}(M_{3}),\widehat{{\it\pi}}^{-1}(N_{3}),\widehat{{\it\pi}}^{-1}(M_{1})$
and the four curves
$\widehat{{\it\pi}}^{-1}(M_{3}),\widehat{{\it\pi}}^{-1}(N_{3}),\widehat{{\it\pi}}^{-1}(M_{1})$
and the four curves
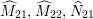 $\widehat{M}_{21},\widehat{M}_{22},\widehat{N}_{21}$
and
$\widehat{M}_{21},\widehat{M}_{22},\widehat{N}_{21}$
and
![]() $\widehat{N}_{22}$
. Then there is a smooth
$\widehat{N}_{22}$
. Then there is a smooth
![]() $H$
-cover
$H$
-cover
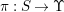 ${\it\pi}:S\rightarrow {\rm\Upsilon}$
such that the outer square of the following diagram (5.3) commutes.
${\it\pi}:S\rightarrow {\rm\Upsilon}$
such that the outer square of the following diagram (5.3) commutes.

We confirm that
![]() $S$
is the smooth minimal model of
$S$
is the smooth minimal model of
![]() $X$
by the following proposition.
$X$
by the following proposition.
Proposition 5.2. The surface
![]() $S$
is an Inoue surface.
$S$
is an Inoue surface.
Proof. From [Reference Pardini22, Theorem 2.1], we obtain
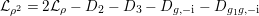 ${\mathcal{L}}_{{\it\rho}^{2}}=2{\mathcal{L}}_{{\it\rho}}-D_{2}-D_{3}-D_{g,-\text{i}}-D_{g_{1}g,-\text{i}}$
. Then
${\mathcal{L}}_{{\it\rho}^{2}}=2{\mathcal{L}}_{{\it\rho}}-D_{2}-D_{3}-D_{g,-\text{i}}-D_{g_{1}g,-\text{i}}$
. Then
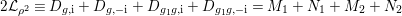 $2{\mathcal{L}}_{{\it\rho}^{2}}\equiv D_{g,\text{i}}+D_{g,-\text{i}}+D_{g_{1}g,\text{i}}+D_{g_{1}g,-\text{i}}=M_{1}+N_{1}+M_{2}+N_{2}$
by Proposition 2.4(b) and (5.2). Let
$2{\mathcal{L}}_{{\it\rho}^{2}}\equiv D_{g,\text{i}}+D_{g,-\text{i}}+D_{g_{1}g,\text{i}}+D_{g_{1}g,-\text{i}}=M_{1}+N_{1}+M_{2}+N_{2}$
by Proposition 2.4(b) and (5.2). Let
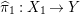 $\widehat{{\it\pi}}_{1}:X_{1}\rightarrow Y$
be the double cover branched along the four disjoint
$\widehat{{\it\pi}}_{1}:X_{1}\rightarrow Y$
be the double cover branched along the four disjoint
![]() $(-2)$
-curves
$(-2)$
-curves
 $M_{1},N_{1},M_{2}$
and
$M_{1},N_{1},M_{2}$
and
![]() $N_{2}$
. Note that
$N_{2}$
. Note that
![]() ${\it\rho}^{2}$
is the unique character of
${\it\rho}^{2}$
is the unique character of
![]() $H^{\ast }$
which is trivial on
$H^{\ast }$
which is trivial on
![]() $G$
. So the Galois group of
$G$
. So the Galois group of
![]() $\widehat{{\it\pi}}_{1}$
is
$\widehat{{\it\pi}}_{1}$
is
![]() $H/G$
and the cover
$H/G$
and the cover
![]() $\widehat{{\it\pi}}$
factors through a
$\widehat{{\it\pi}}$
factors through a
![]() $G$
-cover
$G$
-cover
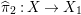 $\widehat{{\it\pi}}_{2}:X\rightarrow X_{1}$
.
$\widehat{{\it\pi}}_{2}:X\rightarrow X_{1}$
.
We have
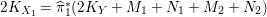 $2K_{X_{1}}=\widehat{{\it\pi}}_{1}^{\ast }(2K_{Y}+M_{1}+N_{1}+M_{2}+N_{2})$
and
$2K_{X_{1}}=\widehat{{\it\pi}}_{1}^{\ast }(2K_{Y}+M_{1}+N_{1}+M_{2}+N_{2})$
and
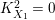 $K_{X_{1}}^{2}=0$
. The inverse images of
$K_{X_{1}}^{2}=0$
. The inverse images of
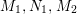 $M_{1},N_{1},M_{2}$
and
$M_{1},N_{1},M_{2}$
and
![]() $N_{2}$
under
$N_{2}$
under
![]() $\widehat{{\it\pi}}_{1}$
are
$\widehat{{\it\pi}}_{1}$
are
![]() $(-1)$
-curves. Also
$(-1)$
-curves. Also
 $\widehat{{\it\pi}}_{1}^{-1}(M_{3})$
is a disjoint union of two
$\widehat{{\it\pi}}_{1}^{-1}(M_{3})$
is a disjoint union of two
![]() $(-2)$
-curves and so is
$(-2)$
-curves and so is
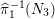 $\widehat{{\it\pi}}_{1}^{-1}(N_{3})$
. Let
$\widehat{{\it\pi}}_{1}^{-1}(N_{3})$
. Let
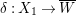 ${\it\delta}:X_{1}\rightarrow \overline{W}$
be the morphism contracting three
${\it\delta}:X_{1}\rightarrow \overline{W}$
be the morphism contracting three
![]() $(-1)$
-curves
$(-1)$
-curves
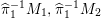 $\widehat{{\it\pi}}_{1}^{-1}M_{1},\widehat{{\it\pi}}_{1}^{-1}M_{2}$
and
$\widehat{{\it\pi}}_{1}^{-1}M_{1},\widehat{{\it\pi}}_{1}^{-1}M_{2}$
and
![]() $\widehat{{\it\pi}}_{1}^{-1}N_{2}$
. Then
$\widehat{{\it\pi}}_{1}^{-1}N_{2}$
. Then
![]() $\overline{W}$
is a weak Del Pezzo surface of degree three.
$\overline{W}$
is a weak Del Pezzo surface of degree three.
Let
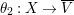 ${\it\theta}_{2}:X\rightarrow \overline{V}$
be the morphism contracting the curves
${\it\theta}_{2}:X\rightarrow \overline{V}$
be the morphism contracting the curves
 $\widehat{{\it\pi}}^{-1}(M_{1})$
,
$\widehat{{\it\pi}}^{-1}(M_{1})$
,
 $\widehat{{\it\pi}}^{-1}(M_{2})$
and
$\widehat{{\it\pi}}^{-1}(M_{2})$
and
 $\widehat{{\it\pi}}^{-1}(N_{2})$
. We obtain a smooth Galois finite
$\widehat{{\it\pi}}^{-1}(N_{2})$
. We obtain a smooth Galois finite
![]() $G$
-cover
$G$
-cover
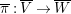 $\overline{{\it\pi}}:\overline{V}\rightarrow \overline{W}$
and a commutative diagram (5.3). The branch locus of
$\overline{{\it\pi}}:\overline{V}\rightarrow \overline{W}$
and a commutative diagram (5.3). The branch locus of
![]() $\overline{{\it\pi}}$
is
$\overline{{\it\pi}}$
is
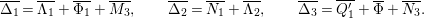 $$\begin{eqnarray}\displaystyle \qquad \overline{{\rm\Delta}_{1}}=\overline{{\rm\Lambda}_{1}}+\overline{{\rm\Phi}_{1}}+\overline{M_{3}},\qquad \overline{{\rm\Delta}_{2}}=\overline{N_{1}}+\overline{{\rm\Lambda}_{2}},\qquad \overline{{\rm\Delta}_{3}}=\overline{Q_{1}^{\prime }}+\overline{{\rm\Phi}}+\overline{N_{3}}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \qquad \overline{{\rm\Delta}_{1}}=\overline{{\rm\Lambda}_{1}}+\overline{{\rm\Phi}_{1}}+\overline{M_{3}},\qquad \overline{{\rm\Delta}_{2}}=\overline{N_{1}}+\overline{{\rm\Lambda}_{2}},\qquad \overline{{\rm\Delta}_{3}}=\overline{Q_{1}^{\prime }}+\overline{{\rm\Phi}}+\overline{N_{3}}. & & \displaystyle\end{eqnarray}$$
Here we denote by
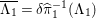 $\overline{{\rm\Lambda}_{1}}={\it\delta}\widehat{{\it\pi}}_{1}^{-1}({\rm\Lambda}_{1})$
, and so forth. We claim that
$\overline{{\rm\Lambda}_{1}}={\it\delta}\widehat{{\it\pi}}_{1}^{-1}({\rm\Lambda}_{1})$
, and so forth. We claim that
-
(i)
 $\overline{{\rm\Lambda}_{1}}$
,
$\overline{{\rm\Lambda}_{1}}$
,
 $\overline{N_{1}}$
and
$\overline{N_{1}}$
and
 $\overline{Q_{1}^{\prime }}$
are
$\overline{Q_{1}^{\prime }}$
are
 $(-1)$
-curves;
$(-1)$
-curves; -
(ii)
 $\overline{{\rm\Phi}_{1}}$
and
$\overline{{\rm\Phi}_{1}}$
and
 $\overline{{\rm\Lambda}_{2}}$
are
$\overline{{\rm\Lambda}_{2}}$
are
 $0$
-curves, and
$0$
-curves, and
 $\overline{{\rm\Phi}}$
is a disjoint union of two
$\overline{{\rm\Phi}}$
is a disjoint union of two
 $0$
-curves in the same linear system;
$0$
-curves in the same linear system; -
(iii)
 $\overline{M_{3}}$
(
$\overline{M_{3}}$
(
 $\overline{N_{3}}$
) is a disjoint union of two
$\overline{N_{3}}$
) is a disjoint union of two
 $(-2)$
-curves; these two
$(-2)$
-curves; these two
 $(-2)$
-curves are disjoint from the
$(-2)$
-curves are disjoint from the
 $(-1)$
-curves in (i);
$(-1)$
-curves in (i); -
(iv)
 $\overline{{\rm\Lambda}_{1}}+\frac{1}{2}\overline{{\rm\Phi}}$
,
$\overline{{\rm\Lambda}_{1}}+\frac{1}{2}\overline{{\rm\Phi}}$
,
 $\overline{N_{1}}+\overline{{\rm\Phi}_{1}}$
and
$\overline{N_{1}}+\overline{{\rm\Phi}_{1}}$
and
 $\overline{Q_{1}^{\prime }}+\overline{{\rm\Lambda}_{2}}$
and are linearly equivalent to
$\overline{Q_{1}^{\prime }}+\overline{{\rm\Lambda}_{2}}$
and are linearly equivalent to
 $-K_{\overline{W}}$
.
$-K_{\overline{W}}$
.
For example, because the general member of
![]() $|{\rm\Phi}|$
is disjoint from
$|{\rm\Phi}|$
is disjoint from
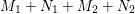 $M_{1}+N_{1}+M_{2}+N_{2}$
, the curve
$M_{1}+N_{1}+M_{2}+N_{2}$
, the curve
![]() $\widehat{{\it\pi}}_{1}^{-1}({\rm\Phi})$
is a disjoint union of two
$\widehat{{\it\pi}}_{1}^{-1}({\rm\Phi})$
is a disjoint union of two
![]() $0$
-curves in the same linear system and so is
$0$
-curves in the same linear system and so is
![]() $\overline{{\rm\Phi}}$
. In particular,
$\overline{{\rm\Phi}}$
. In particular,
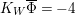 $K_{W}\overline{{\rm\Phi}}=-4$
and
$K_{W}\overline{{\rm\Phi}}=-4$
and
![]() $\frac{1}{2}\overline{{\rm\Phi}}$
is well defined in
$\frac{1}{2}\overline{{\rm\Phi}}$
is well defined in
![]() $\text{Pic}(\overline{W})$
. For the
$\text{Pic}(\overline{W})$
. For the
![]() $(-1)$
-curve
$(-1)$
-curve
![]() ${\rm\Lambda}_{1}$
on
${\rm\Lambda}_{1}$
on
![]() $Y$
, since
$Y$
, since
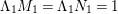 ${\rm\Lambda}_{1}M_{1}={\rm\Lambda}_{1}N_{1}=1$
and
${\rm\Lambda}_{1}M_{1}={\rm\Lambda}_{1}N_{1}=1$
and
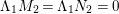 ${\rm\Lambda}_{1}M_{2}={\rm\Lambda}_{1}N_{2}=0$
, the curve
${\rm\Lambda}_{1}M_{2}={\rm\Lambda}_{1}N_{2}=0$
, the curve
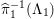 $\widehat{{\it\pi}}_{1}^{-1}({\rm\Lambda}_{1})$
is a
$\widehat{{\it\pi}}_{1}^{-1}({\rm\Lambda}_{1})$
is a
![]() $(-2)$
-curve, and it intersects with
$(-2)$
-curve, and it intersects with
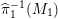 $\widehat{{\it\pi}}_{1}^{-1}(M_{1})$
transversely at one point and it is disjoint from
$\widehat{{\it\pi}}_{1}^{-1}(M_{1})$
transversely at one point and it is disjoint from
 $\widehat{{\it\pi}}_{1}^{-1}(M_{2})$
and
$\widehat{{\it\pi}}_{1}^{-1}(M_{2})$
and
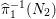 $\widehat{{\it\pi}}_{1}^{-1}(N_{2})$
. So
$\widehat{{\it\pi}}_{1}^{-1}(N_{2})$
. So
![]() $\overline{{\rm\Lambda}_{1}}$
is a
$\overline{{\rm\Lambda}_{1}}$
is a
![]() $(-1)$
-curve. Moreover, we have
$(-1)$
-curve. Moreover, we have
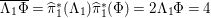 $\overline{{\rm\Lambda}_{1}}\overline{{\rm\Phi}}=\widehat{{\it\pi}}_{1}^{\ast }({\rm\Lambda}_{1})\widehat{{\it\pi}}_{1}^{\ast }({\rm\Phi})=2{\rm\Lambda}_{1}{\rm\Phi}=4$
. Finally, the algebraic index theorem yields
$\overline{{\rm\Lambda}_{1}}\overline{{\rm\Phi}}=\widehat{{\it\pi}}_{1}^{\ast }({\rm\Lambda}_{1})\widehat{{\it\pi}}_{1}^{\ast }({\rm\Phi})=2{\rm\Lambda}_{1}{\rm\Phi}=4$
. Finally, the algebraic index theorem yields
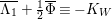 $\overline{{\rm\Lambda}_{1}}+\frac{1}{2}\overline{{\rm\Phi}}\equiv -K_{W}$
. Other statements can be proved in the same manner.
$\overline{{\rm\Lambda}_{1}}+\frac{1}{2}\overline{{\rm\Phi}}\equiv -K_{W}$
. Other statements can be proved in the same manner.
Comparing (5.4) to (4.1), we conclude that
![]() $S$
is an Inoue surface.◻
$S$
is an Inoue surface.◻
When
![]() ${\rm\Phi}$
and
${\rm\Phi}$
and
![]() ${\rm\Phi}_{1}$
vary, we obtain a
${\rm\Phi}_{1}$
vary, we obtain a
![]() $2$
-dimensional family of Inoue surfaces with automorphism groups isomorphic to
$2$
-dimensional family of Inoue surfaces with automorphism groups isomorphic to
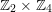 $\mathbb{Z}_{2}\times \mathbb{Z}_{4}$
.
$\mathbb{Z}_{2}\times \mathbb{Z}_{4}$
.
Remark 5.3. We may directly show that
![]() $K_{S}$
is ample,
$K_{S}$
is ample,
![]() $K_{S}^{2}=7$
and
$K_{S}^{2}=7$
and
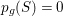 $p_{g}(S)=0$
for the surface
$p_{g}(S)=0$
for the surface
![]() $S$
in (5.3). According to the proof of [Reference Pardini22, Proposition 4.2], we have
$S$
in (5.3). According to the proof of [Reference Pardini22, Proposition 4.2], we have
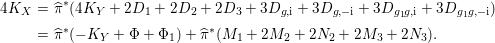 $$\begin{eqnarray}\displaystyle 4K_{X} & = & \displaystyle \widehat{{\it\pi}}^{\ast }(4K_{Y}+2D_{1}+2D_{2}+2D_{3}+3D_{g,\text{i}}+3D_{g,-\text{i}}+3D_{g_{1}g,\text{i}}+3D_{g_{1}g,-\text{i}})\nonumber\\ \displaystyle & = & \displaystyle \widehat{{\it\pi}}^{\ast }(-K_{Y}+{\rm\Phi}+{\rm\Phi}_{1})+\widehat{{\it\pi}}^{\ast }(M_{1}+2M_{2}+2N_{2}+2M_{3}+2N_{3}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 4K_{X} & = & \displaystyle \widehat{{\it\pi}}^{\ast }(4K_{Y}+2D_{1}+2D_{2}+2D_{3}+3D_{g,\text{i}}+3D_{g,-\text{i}}+3D_{g_{1}g,\text{i}}+3D_{g_{1}g,-\text{i}})\nonumber\\ \displaystyle & = & \displaystyle \widehat{{\it\pi}}^{\ast }(-K_{Y}+{\rm\Phi}+{\rm\Phi}_{1})+\widehat{{\it\pi}}^{\ast }(M_{1}+2M_{2}+2N_{2}+2M_{3}+2N_{3}).\nonumber\end{eqnarray}$$
It follows that
 $4K_{S}={\it\pi}^{\ast }(-K_{{\rm\Upsilon}}+{\it\phi}+{\it\phi}_{1})$
and
$4K_{S}={\it\pi}^{\ast }(-K_{{\rm\Upsilon}}+{\it\phi}+{\it\phi}_{1})$
and
![]() $K_{S}^{2}=7$
, where
$K_{S}^{2}=7$
, where
![]() $|{\it\phi}|$
and
$|{\it\phi}|$
and
![]() $|{\it\phi}_{1}|$
are base-point-free pencils on
$|{\it\phi}_{1}|$
are base-point-free pencils on
![]() ${\rm\Upsilon}$
induced by
${\rm\Upsilon}$
induced by
![]() $|{\rm\Phi}|$
and
$|{\rm\Phi}|$
and
![]() $|{\rm\Phi}_{1}|$
. The linear system
$|{\rm\Phi}_{1}|$
. The linear system
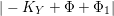 $|-K_{Y}+{\rm\Phi}+{\rm\Phi}_{1}|$
is base point free, and the corresponding morphism contracts exactly the nodal curves
$|-K_{Y}+{\rm\Phi}+{\rm\Phi}_{1}|$
is base point free, and the corresponding morphism contracts exactly the nodal curves
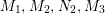 $M_{1},M_{2},N_{2},M_{3}$
and
$M_{1},M_{2},N_{2},M_{3}$
and
![]() $N_{3}$
. Hence
$N_{3}$
. Hence
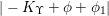 $|-K_{{\rm\Upsilon}}+{\it\phi}+{\it\phi}_{1}|$
is ample and so is
$|-K_{{\rm\Upsilon}}+{\it\phi}+{\it\phi}_{1}|$
is ample and so is
![]() $K_{S}$
. For each
$K_{S}$
. For each
![]() ${\it\psi}\in H^{\ast }$
, we can calculate
${\it\psi}\in H^{\ast }$
, we can calculate
![]() ${\mathcal{L}}_{{\it\psi}}$
by [Reference Pardini22, Theorem 2.1] and then easily show that
${\mathcal{L}}_{{\it\psi}}$
by [Reference Pardini22, Theorem 2.1] and then easily show that
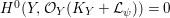 $H^{0}(Y,{\mathcal{O}}_{Y}(K_{Y}+{\mathcal{L}}_{{\it\psi}}))=0$
. It follows that
$H^{0}(Y,{\mathcal{O}}_{Y}(K_{Y}+{\mathcal{L}}_{{\it\psi}}))=0$
. It follows that
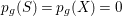 $p_{g}(S)=p_{g}(X)=0$
by [Reference Pardini22, Proposition 4.1].
$p_{g}(S)=p_{g}(X)=0$
by [Reference Pardini22, Proposition 4.1].
Remark 5.4. We remark that Theorem 1.4 contributes to the study of the moduli space of the Inoue surfaces. Let
![]() ${\mathcal{M}}_{1,7}^{\text{can}}$
be the Gieseker moduli space of canonical models of surfaces of general type with
${\mathcal{M}}_{1,7}^{\text{can}}$
be the Gieseker moduli space of canonical models of surfaces of general type with
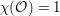 ${\it\chi}({\mathcal{O}})=1$
and
${\it\chi}({\mathcal{O}})=1$
and
![]() $K^{2}=7$
(cf. [Reference Gieseker12]). Let
$K^{2}=7$
(cf. [Reference Gieseker12]). Let
![]() $S$
be any Inoue surface. Denote by
$S$
be any Inoue surface. Denote by
![]() $[S]$
the corresponding point in
$[S]$
the corresponding point in
![]() ${\mathcal{M}}_{1,7}^{\text{can}}$
and by
${\mathcal{M}}_{1,7}^{\text{can}}$
and by
![]() $\text{B}(S)$
be the base of the Kuranishi family of deformations of
$\text{B}(S)$
be the base of the Kuranishi family of deformations of
![]() $S$
. Recall the facts that the tangent space of
$S$
. Recall the facts that the tangent space of
![]() $\text{B}(S)$
is
$\text{B}(S)$
is
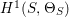 $H^{1}(S,{\rm\Theta}_{S})$
, where
$H^{1}(S,{\rm\Theta}_{S})$
, where
![]() ${\rm\Theta}_{S}$
is the tangent sheaf of
${\rm\Theta}_{S}$
is the tangent sheaf of
![]() $S$
, and that the germ
$S$
, and that the germ
 $({\mathcal{M}}_{1,7}^{\text{can}},[S])$
is analytically isomorphic to
$({\mathcal{M}}_{1,7}^{\text{can}},[S])$
is analytically isomorphic to
 $\text{B}(S)/\text{Aut}(S)$
. It has been shown in [Reference Bauer and Catanese3] that the group
$\text{B}(S)/\text{Aut}(S)$
. It has been shown in [Reference Bauer and Catanese3] that the group
![]() $G$
acts trivially on
$G$
acts trivially on
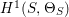 $H^{1}(S,{\rm\Theta}_{S})$
and
$H^{1}(S,{\rm\Theta}_{S})$
and
![]() $\text{B}(S)$
is smooth of dimension
$\text{B}(S)$
is smooth of dimension
![]() $4$
.
$4$
.
Now assume that
![]() $S$
is a special Inoue surface constructed here. We can use the same method as in the proof of [Reference Bauer and Catanese3, Theorem 5.1] to conclude that the invariant subspace of
$S$
is a special Inoue surface constructed here. We can use the same method as in the proof of [Reference Bauer and Catanese3, Theorem 5.1] to conclude that the invariant subspace of
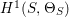 $H^{1}(S,{\rm\Theta}_{S})$
for the
$H^{1}(S,{\rm\Theta}_{S})$
for the
![]() $H$
-action has dimension
$H$
-action has dimension
![]() $2$
. Note that
$2$
. Note that
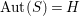 $\text{Aut}(S)=H$
and
$\text{Aut}(S)=H$
and
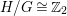 $H/G\cong \mathbb{Z}_{2}$
. Combining the result of [Reference Bauer and Catanese3], we see that
$H/G\cong \mathbb{Z}_{2}$
. Combining the result of [Reference Bauer and Catanese3], we see that
 $({\mathcal{M}}_{1,7}^{\text{can}},[S])$
is analytically isomorphic to
$({\mathcal{M}}_{1,7}^{\text{can}},[S])$
is analytically isomorphic to
 $(\mathbb{C}^{2}\times \text{Spec}\,\mathbb{C}[x,y,z]/(xz-y^{2}),0)$
.
$(\mathbb{C}^{2}\times \text{Spec}\,\mathbb{C}[x,y,z]/(xz-y^{2}),0)$
.
Acknowledgments
The author thanks Xiaotao Sun for all the support during the preparation of the article. The author is greatly indebted to Jinxing Cai for many discussions and helpful suggestions. The author also would like to express his appreciation to the anonymous referee for his/her valuable suggestions.