Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2025-01-02T16:12:39.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal mixing via tensorization for random independent sets on arbitrary trees

Part of: Markov processes

Published online by Cambridge University Press:  26 November 2024

Charilaos Efthymiou ,
Thomas P. Hayes ,
Daniel Štefankovič  and
Eric Vigoda
Charilaos Efthymiou*
Affiliation:
Department of Computer Science, University of Warwick, Coventry, UK
Thomas P. Hayes
Affiliation:
Department of Computer Science and Engineering, University at Buffalo, New York, USA
Daniel Štefankovič
Affiliation:
Department of Computer Science, University of Rochester, Rochester, USA
Eric Vigoda
Affiliation:
Department of Computer Science, University of California, Santa Barbara, USA
*
Corresponding author: Charilaos Efthymiou; Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the mixing time of the single-site update Markov chain, known as the Glauber dynamics, for generating a random independent set of a tree. Our focus is obtaining optimal convergence results for arbitrary trees. We consider the more general problem of sampling from the Gibbs distribution in the hard-core model where independent sets are weighted by a parameter 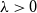$\lambda \gt 0$; the special case 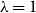$\lambda =1$ corresponds to the uniform distribution over all independent sets. Previous work of Martinelli, Sinclair and Weitz (2004) obtained optimal mixing time bounds for the complete 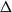$\Delta$-regular tree for all 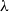$\lambda$. However, Restrepo, Stefankovic, Vera, Vigoda, and Yang (2014) showed that for sufficiently large 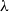$\lambda$ there are bounded-degree trees where optimal mixing does not hold. Recent work of Eppstein and Frishberg (2022) proved a polynomial mixing time bound for the Glauber dynamics for arbitrary trees, and more generally for graphs of bounded tree-width.

We establish an optimal bound on the relaxation time (i.e., inverse spectral gap) of 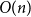$O(n)$ for the Glauber dynamics for unweighted independent sets on arbitrary trees. We stress that our results hold for arbitrary trees and there is no dependence on the maximum degree 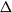$\Delta$. Interestingly, our results extend (far) beyond the uniqueness threshold which is on the order 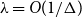$\lambda =O(1/\Delta )$. Our proof approach is inspired by recent work on spectral independence. In fact, we prove that spectral independence holds with a constant independent of the maximum degree for any tree, but this does not imply mixing for general trees as the optimal mixing results of Chen, Liu, and Vigoda (2021) only apply for bounded-degree graphs. We instead utilize the combinatorial nature of independent sets to directly prove approximate tensorization of variance via a non-trivial inductive proof.

Keywords

Markov Chain Monte Carlomixing timeindependent setshard-core modelapproximate counting algorithmssampling algorithms

MSC classification

Primary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)
Type
Paper
Information
Combinatorics, Probability and Computing , First View , pp. 1 - 17
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Charilaos Efthymiou: Research supported in part by EPSRC NIA, grant EP/V050842/1, and Centre of Discrete Mathematics and Applications (DIMAP). Daniel Stefankovic: Research supported in part by NSF grant CCF-1563757. Eric Vigoda: Research supported in part by NSF grant CCF-2147094.

References

Anari, N., Liu, K. and Gharan, S. O. (2020) Spectral independence in high-dimensional expanders and applications to the hardcore model. FOCS 2020: 1319–1330.CrossRefGoogle Scholar
Berger, N., Kenyon, C., Mossel, E. and Peres, Y. (2005) Glauber dynamics on trees and hyperbolic graphs. Probab. Theory Relat. Fields 131(3) 311–340.CrossRefGoogle Scholar
Bhatnagar, N., Sly, A. and Tetali, P. (2016) Decay of correlations for the hardcore model on the $d$ -regular random graph. Electron. J. Probab. 21 1–42.CrossRefGoogle Scholar
Blanca, A., Caputo, P., Chen, Z., Parisi, D., Štefankovič, D. and Vigoda, E. (2022) On Mixing of Markov Chains: Coupling, Spectral Independence, and Entropy Factorization. pp. 3670–3692, In Proceedings of the 33rd Annual ACM-SIAM Symposium on Discrete Algorithms (SODA). SIAM.CrossRefGoogle Scholar
Brightwell, G. and Winkler, P. (2004) A second threshold for the hard-core model on a Bethe lattice. Random Struct. Algor. 24(3) 303–314.CrossRefGoogle Scholar
Caputo, P. (2023) Lecture notes on Entropy and Markov Chains. Preprint, available from: http://www.mat.uniroma3.it/users/caputo/entropy.pdf.Google Scholar
Caputo, P., Menz, G. and Tetali, P. (2015) Approximate tensorization of entropy at high temperature. Annales de la Faculté des sciences de Toulouse. Mathématiques 24(4) 691–716.Google Scholar
Caputo, P. and Parisi, D. (2021) Block factorization of the relative entropy via spatial mixing. Commun. Math. Phys. 388(2) 793–818.CrossRefGoogle Scholar
Chen, X., Yang, X., Yin, Y., and Zhang, X.. Spectral independence beyond total influence on trees and related graphs. arXiv preprint arXiv:2404.04668, 2024.Google Scholar
Chen, Z. (2024) Combinatorial approach for factorization of variance and entropy in spin systems. pp. 4988–5012, In Proceedings of the 35th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA).CrossRefGoogle Scholar
Chen, Y. and Eldan, R. (2022) Localization schemes: A framework for proving mixing bounds for Markov chains. pp. 110–122, In Proceedings of the 63rd Annual IEEE Symposium on Foundations of Computer Science (FOCS).CrossRefGoogle Scholar
Chen, X., Feng, W., Yin, Y. and Zhang, X. (2022) Optimal mixing for two-state anti-ferromagnetic spin systems. pp. 588–599, In Proceedings of the 63rd Annual IEEE Symposium on Foundations of Computer Science (FOCS).CrossRefGoogle Scholar
Chen, X., Feng, W., Yin, Y. and Zhang, X. (2024) Rapid mixing of Glauber dynamics via spectral independence for all degrees. SIAM J. Comput. FOCS21-224–FOCS21-298.CrossRefGoogle Scholar
Chen, Z. and Gu, Y. (2024) Fast sampling of $b$ -matchings and $b$ -edge covers, pp. 4972–4987, In Proceedings of the 35th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA).CrossRefGoogle Scholar
Chen, Z., Liu, K., Mani, N. and Moitra, A. (2023) Strong spatial mixing for colorings on trees and its algorithmic applications. pp. 810–845, In Proceedings of the 64th Annual IEEE Symposium on Foundations of Computer Science (FOCS).CrossRefGoogle Scholar
Chen, Z., Liu, K. and Vigoda, E. (2021) Optimal mixing of Glauber dynamics: Entropy factorization via high-dimensional expansion. pp. 1537–1550, In Proceedings of the 53rd Annual ACM Symposium on Theory of Computing (STOC).CrossRefGoogle Scholar
Chen, Z., Liu, K. and Vigoda, E. (2022) Spectral independence via stability and applications to Holant-type problems. pp. 149–160, In Proceedings of the 63rd Annual IEEE Symposium on Foundations of Computer Science (FOCS).CrossRefGoogle Scholar
Delcourt, M., Heinrich, M. and Perarnau, G. (2020) The Glauber dynamics for edge-colorings of trees. Random Struct. Algor. 57(4) 1050–1076.CrossRefGoogle Scholar
Eppstein, D. and Frishberg, D. (2023) Rapid mixing of the hardcore Glauber dynamics and other Markov chains in bounded-treewidth graphs, pp. 30:1–30:13, In Proceedings of the 34th International Symposium on Algorithms and Computation (ISAAC), vol. 283. Schloss Dagstuhl - Leibniz-Zentrum fur Informatik.Google Scholar
Efthymiou, C., Hayes, T. P., Štefankovič, D. and Vigoda, E., (2023). Optimal mixing via tensorization for random independent sets on arbitrary trees. arXiv preprint arXiv:2307.07727, version 2.Google Scholar
Galanis, A., Štefankovič, D. and Vigoda, E. (2016) Inapproximability of the partition function for the antiferromagnetic Ising and hard-core models. Comb. Probab. Com. 25(4) 500–559.CrossRefGoogle Scholar
Hayes, T. P. and Sinclair, A. (2007) A general lower bound for mixing of single-site dynamics on graphs. Ann. Appl. Probab. 17(3) 931–952.CrossRefGoogle Scholar
Liu, K. (2021) From coupling to spectral independence and blackbox comparison with the down-up walk. In APPROX-RANDOM, pp. 32:1–32:21. Google Scholar
Lucier, B., Molloy, M. and Peres, Y. (2009) The Glauber dynamics for colourings of bounded degree trees. In Randomization and Approximation Techniques in Computer Science (RANDOM), pp. 631–645. Google Scholar
Martin, J. B. (2003) Reconstruction thresholds on regular trees. Discrete Random Walks, DIMACS Series in Discrete Mathematics and Theoretical Computer Science, pp.191–204. Google Scholar
Martinelli, F., Sinclair, A. and Weitz, D. (2003) The Ising model on trees: boundary conditions and mixing time. pp. 628–639, In Proceedings of the 44th Annual IEEE Symposium on Foundations of Computer Science (FOCS).CrossRefGoogle Scholar
Martinelli, F., Sinclair, A. and Weitz, D. (2004) Fast mixing for independent sets, colorings and other models on trees. pp. 456–465, In Proceedings of the 15th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA). SIAM.Google Scholar
Mossel, E. (2004) Survey: Information flow on trees. In Graphs, Morphisms and Statistical Physics, DIMACS Series in Discrete Mathematics and Theoretical Computer Science, pp. 155–170. CrossRefGoogle Scholar
Mossel, E., Weitz, D. and Wormald, N. C. (2007) On the hardness of sampling independent sets beyond the tree threshold. Probab. Theory Relat. Fields 143(3-4) 401–439.CrossRefGoogle Scholar
Restrepo, R., Štefankovič, D., Vera, J. C., Vigoda, E. and Yang, L. (2014) Phase transition for Glauber dynamics for independent sets on regular trees. SIAM J. Discrete Math. 28(2) 835–861.CrossRefGoogle Scholar
Sly, A. (2010) Computational transition at the uniqueness threshold. pp. 287–296, In Proceedings of the 51st Annual IEEE Symposium on Foundations of Computer Science (FOCS).CrossRefGoogle Scholar
Sly, A. and Sun, N. (2014) The computational hardness of counting in two-spin models on $d$ -regular graphs. Ann. Probab. 42(6) 2383–2416.CrossRefGoogle Scholar
Štefankovič, D., Vempala, S. and Vigoda, E. (2009) Adaptive simulated annealing: A near-optimal connection between sampling and counting. J. ACM 56(3) 1–36.CrossRefGoogle Scholar