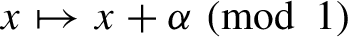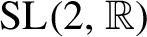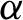Asymptotic scaling and universality for skew products with factors in SL(2,$\boldsymbol {\mathbb {R}}$)

Abstract

We consider skew-product maps over circle rotations $x\mapsto x+\alpha \;(\mod 1)$ with factors that take values in ${\textrm {SL}}(2,{\mathbb {R}})$ . In numerical experiments, with $\alpha $ the inverse golden mean, Fibonacci iterates of maps from the almost Mathieu family exhibit asymptotic scaling behavior that is reminiscent of critical phase transitions. In a restricted setup that is characterized by a symmetry, we prove that critical behavior indeed occurs and is universal in an open neighborhood of the almost Mathieu family. This behavior is governed by a periodic orbit of a renormalization transformation. An extension of this transformation is shown to have a second periodic orbit as well, and we present some evidence that this orbit attracts supercritical almost Mathieu maps.

1 Introduction

We consider the asymptotic behavior of skew products

(1.1) $$ \begin{align} A^{\ast q}(x)\mathrel{\mathop=^{\textrm{def}}} A(x+(q-1)\alpha)\cdots A(x+2\alpha)A(x+\alpha)A(x), \end{align} $$

as $q\to \infty $ along certain subsequences, where A is a real analytic function from the circle ${\Bbb T}=\mathbb {R}/\mathbb {Z}$ to the group ${\textrm {SL}}(2,\mathbb {R})$ . Here, $\alpha $ is a given irrational number and $x\mapsto x+\alpha $ is considered modulo $1$ . Our main results concern the inverse golden mean $\alpha =\sqrt {5}/2-1/2$ , but we expect analogous results to hold for arbitrary quadratic irrationals.

The products (1.1) arise when iterating a map G on ${\Bbb T}\times \mathbb {R}^2$ of the form

(1.2) $$ \begin{align} G(x,y)=(x+\alpha,A(x)y),\quad x\in{\Bbb T}, y\in\mathbb{R}^2. \end{align} $$

Such maps will be called skew-product maps. We will use the notation $G=(\alpha ,A)$ and refer to A as the factor of G. In this notation, the qth iterate of G is $G^q=(q\alpha ,A^{\ast q})$ , with $A^{\ast q}$ given by (1.1). We note that the map G is invertible, with inverse ${G^{-1}=(-\alpha ,A(.-\alpha )^{-1})}$ . The qth iterate of $G^{-1}$ will be denoted by $G^{-q}$ .

Two dynamical quantities associated with such a skew-product map G are its Lyapunov exponent $L(G)$ and its fibered rotation number $\varrho (G)$ . They are defined by

(1.3) $$ \begin{align} L(G)=\lim_{q\to\infty}\frac{1}{ q}\log\kern-2pt\|A^{\ast q}(x)\|,\quad \varrho(G)=\lim_{q\to\infty}\frac{1}{ 2\pi q}\arg\mathcal{G}^q(x,\vartheta), \end{align} $$

where $\arg (x,\vartheta )=\vartheta $ . Here, $\mathcal {G}$ denotes a lift of the map $(x,y)\mapsto (x+\alpha ,\|A(x)y\|^{-1} A(x)y)$ from ${\Bbb T}\times {\Bbb S}$ to ${\Bbb T}\times \mathbb {R}$ , where ${\Bbb S}$ denotes the unit circle $\|y\|=1$ in $\mathbb {R}^2$ . Assuming that $A:{\Bbb T}\to {\textrm {SL}}(2,\mathbb {R})$ is continuous, homotopic to the function $x\mapsto \textbf {1}$ , and that $\alpha $ irrational, the limit for $\varrho (G)$ does not depend on x or $\vartheta $ , and convergence is uniform. Furthermore, it is independent modulo $1$ of the choice of the lift $\mathcal {G}$ . Under the same assumptions, the limit for $L(G)$ exists and is constant almost everywhere in x. For proofs of these and related facts we refer to [9, 10, 25, 34].

A skew-product map G is said to be of Schrödinger type if its factor is of the form

(1.4) $$ \begin{align} A(x)=A((E,s),x)= \begin{bmatrix} {E-\unicode{x3bb} v(x)}&{-1}\\ {1}&{0} \end{bmatrix} ,\quad\unicode{x3bb}=e^s. \end{align} $$

A bi-infinite orbit $n\mapsto (x_n,y_n)$ for such a map G has the property that $y_n=[{u_n\atop u_{n-1}}]$ for some sequence $n\mapsto u_n$ of real numbers. If $x_0=0$ , then this sequence u is a solution of the equation $H^\alpha _\unicode{x3bb} u=Eu$ , where $H^\alpha _\unicode{x3bb} $ is the Schrödinger operator given by the equation

(1.5) $$ \begin{align} (H^\alpha_\unicode{x3bb} u)_n=u_{n+1}+u_{n-1}+\unicode{x3bb} v(n\alpha)u_n,\quad n\in\mathbb{Z}. \end{align} $$

The choice of potential $v(x)=2\cos (2\pi (x+\xi ))$ defines the family of operators $H^\alpha _\unicode{x3bb} $ that are knows as almost Mathieu (AM) operators. They describe the motion of an electron on $\mathbb {Z}^2$ under the influence of a magnetic flux $2\pi \alpha $ per unit cell, if one restricts to wave functions $\phi (n,m)=e^{-2\pi im\xi }u_n$ . The full Hamiltonian for this system is known as the Hofstadter Hamiltonian [27, 30]. These operators have been studied extensively over the past $20$ years. Three reviews can be found in [13, 33, 41].

Some of the most interesting phenomena in physics arise from the fact that asymptotic quantities can depend in a non-trivial way on model parameters. In the AM family, the main parameters (besides $\alpha $ ) are the coupling constant $\unicode{x3bb} $ and the energy E. The asymptotic quantities include the Lyapunov exponent L and the fibered rotation number $\varrho $ . We describe some of the many known properties in what follows [6, 8, 13, 26, 33, 41]. Here, we suppress the dependence on the parameter $\xi $ , since it is trivial, as was mentioned after (1.3).

Assume that $\alpha $ is irrational. Then the spectrum $\Sigma ^\alpha _\unicode{x3bb} $ of the operator $H^\alpha _\unicode{x3bb} $ on $\ell ^2(\mathbb {Z})$ is a Cantor set of measure $2-2\min \{\unicode{x3bb} ,1/\unicode{x3bb} \}$ . For all energies in the spectrum, the Lyapunov exponent of the corresponding AM map G is given by $L(G)=\max \{0,\log \unicode{x3bb} \}$ . The fibered rotation number $\varrho $ is a continuous decreasing function of the energy E, and it is constant on each spectral gap (a connected component of $\mathbb {R}\setminus \Sigma ^\alpha _\unicode{x3bb} $ ). As was described first in [34, 57], this resonance phenomenon has an interesting arithmetic aspect: each gap can be labeled canonically by an integer k, known as the Hall conductance. On the gap with index k, the fibered rotation number is constant and satisfies $1-2\varrho (G)\equiv k\alpha \;(\mod 1)$ . The left-hand side of this congruence can also be identified with the integrated density of states [9–11, 25] for the Hamiltonian $H^\alpha _\unicode{x3bb} $ .

Regions where asymptotic quantities depend analytically on model parameters are also called phases. By varying the parameters, it is possible to induce phase transitions. A common phenomenon observed in such transitions is universality: within a large class of systems, the type of singularity is independent of the system being considered, down to precise values of observable quantities. The theory of critical phenomena aims to explain situations where the singularities involve power laws. Power law behavior represents asymptotic scale invariance, and the quantities that describe such universal scaling are known as critical exponents.

Similar phenomena have been observed in comparatively simple systems. Some examples will be mentioned below. Based on numerical observations and partial results [37, 39], we conjecture that skew-product maps exhibit such universal scaling as well.

To be more specific, we consider the inverse golden mean $\alpha _\ast =\sqrt {5}/2-1/2$ . Denote by $p_k/q_k$ the kth continued fraction approximant for $\alpha _\ast $ . That is, $p_k$ is the kth Fibonacci number, and $q_k=p_{k+1}$ .

Conjecture 1.1. There exists a ‘large’ class $\mathcal {A}$ of real analytic functions $A:{\Bbb T}\to {\textrm {SL}}(2,\mathbb {R})$ , which includes the AM factors for $\xi =\alpha _\ast /2$ , for which the following holds. Let $\varrho $ be a rational number in $[0,\tfrac {1}{2}]$ . Then for every real analytic two-parameter family $\beta \mapsto A(\beta ,.)$ of functions in $\mathcal {A}$ that satisfies a certain transversality condition, there exists a parameter value $\beta _\ast $ where the map $(\alpha _\ast ,A(\beta _\ast ,.))$ has fibered rotation number $\varrho $ , as well as three matrices $L,C,M\in {\textrm {GL}}(2,\mathbb {R})$ , such that the limits

(1.6) $$ \begin{align} \begin{aligned} B_\ast(\beta,x) &=\lim_{n\to\infty}L^{-n}A^{\ast p_{\ell n}} (\beta_\ast+CM^{-n}\beta, \alpha_\ast^{\ell n}x)L^n,\\ A_\ast(\beta,x) &=\lim_{n\to\infty}L^{-n}A^{\ast q_{\ell n}} (\beta_\ast+CM^{-n}\beta,\,\alpha_\ast^{\ell n}x)L^n, \end{aligned} \end{align} $$

exist for all $x\in \mathbb {R}$ and are independent of the given family. Here $\ell $ is some positive integer that depends only on $\varrho $ . Furthermore, L is conjugate to some fixed matrix $L_\ell \in {\textrm {GL}}(2,\mathbb {R})$ , and M is conjugate to some fixed diagonal matrix $\mathop {\textrm {diag}}(\mu _1,\mu _2)$ .

This conjecture has motivated the work presented in this paper as well as our earlier work in [37–39]. The integers $\ell $ that appear in (1.6) can be obtained by considering the map on the torus ${\Bbb T}^2$ given by the matrix $[{1~1\atop 1~0}]$ . Every point $(0,\varrho )$ with $\varrho $ rational lies on a periodic orbit for this map. The number $\ell =\ell (\varrho )$ is the shortest such period. For a class $\mathcal {A}$ that includes the AM factors, one finds that $\ell $ must be a multiple of $3$ , due to a symmetry of this family. For more details we refer to [39].

We believe that Conjecture 1.1 holds for any irrational $\alpha _\ast $ that has a periodic continued fraction expansion. (For general quadratic irrationals, the same should apply after finitely many steps of the transformation $\mathfrak {R}$ defined below.) An extended version could include $\alpha $ as a parameter. Based on renormalization arguments, we expect a similar scaling in the difference $\alpha -\alpha _\ast $ . But we have not investigated this situation.

An important aspect of Conjecture 1.1 is universality: near its critical point $\beta _\ast $ , the behavior of a family can be described accurately in terms of just two parameters. The limits in (1.6), as well as the conjugacy class of the matrices L and M, are independent of the family. Universality of this type plays an important role in the description of critical phenomena in condensed matter physics, where it is impossible to know a system precisely.

The points $\beta _\ast $ represent phase transitions for the chosen family. In the AM family parametrized by $\beta =(E,s)$ , it is known that the system described by the Hamiltonian $H^\alpha _\unicode{x3bb} $ undergoes a transition from a conducting phase (absolutely continuous spectrum) for $\unicode{x3bb} =e^s<1$ to an insulation phase (pure point spectrum) for $\unicode{x3bb} =e^s>1$ . For proofs and references we refer to [32]. So in this case, we expect that $s_\ast =0$ at each critical point $\beta _\ast =(E_\ast ,s_\ast )$ . Furthermore, our numerical computations suggest that the scaling M is diagonal.

The ‘phase portrait’ for $\unicode{x3bb} =1$ , obtained by plotting the spectrum $H^\alpha _1$ as a set-valued function of $\alpha $ , is known as the Hofstadter butterfly [30]. A detailed topological description of the Hofstadter butterfly can be found in [46]. One of its striking features, aside from the gap labeling, is a local self-similarity property: successive magnifications about certain points seem to yield an asymptotic limit set [37, 39, 50–52].

Cases where the expected phase transitions have been studied from the point of view of critical phenomena cover the rotation numbers $\varrho =\tfrac {1}{2},\tfrac {3}{8},\tfrac {2}{6},\tfrac {1}{4},\tfrac {1}{6},\tfrac {1}{8},0$ . The values $\varrho =\tfrac {1}{2}$ and $\varrho =0$ correspond to the energies $E_\ast =\mp 2.5975\ldots $ at the bottom and top of the spectrum, respectively. The value $\varrho =\tfrac {1}{4}$ corresponds to $E_\ast =0$ , for symmetry reasons. These three cases have been considered in [37, 39]. In particular, rough numerical computations indicate that the Hofstadter butterfly is asymptotically invariant under a scaling about the point $(\alpha _\ast ,E_\ast )$ , and that the scaling factor in the energy direction is given by the constant $\mu _1$ .

A framework that has been extremely successful in describing critical phenomena is renormalization. In the area of dynamical systems, this includes period-doubling cascades for interval maps [12, 17, 18, 20, 42, 44, 54] or area-preserving maps [14, 16, 22], critical circle mappings [15, 40, 48, 59], and the breakup of invariant tori in area-preserving maps [3, 35, 36, 43], to name just a few.

In the problem at hand, we expect renormalization to work as follows. The functions $B_n$ and $A_n$ whose limits are being considered in (1.6) are the factors associated with two skew-product maps $F_n$ and $G_n$ that depend on a parameter $\beta $ . In the renormalization framework, the sequence of pairs $P_n=(F_n,G_n)$ lie on an orbit of a transformation $\mathfrak {R}$ that acts on a space of pairs. The accumulation property (1.6) describes convergence (modulo reparametrization) $P_n\to P_\ast $ to a fixed point $P_\ast $ of $\mathfrak {R}^\ell $ . The fixed point $P_\ast $ and the observed accumulation rates are universal, due to the fact that they reflect properties of the transformation $\mathfrak {R}$ . In particular, we expect $\mathfrak {R}^\ell $ to be hyperbolic at $P_\ast $ , with a two-dimensional local unstable manifold. This manifold is given by the family of pairs $\beta \mapsto \texttt{P}_\ast (\beta )$ whose factors are limit functions $B_\ast $ and $A_\ast $ in (1.6). The transversality condition mentioned in Conjecture 1.1 requires that the given family be transversal to the stable manifold of $\mathfrak {R}^\ell $ . And $\beta _\ast $ is the value of the parameter $\beta $ where a given family intersects the stable manifold.

Our goal here is to verify this renormalization picture in a setup that is restricted but includes most of the essential aspects. After finding an appropriate transformation $\mathfrak {R}$ , the first step in any renormalization group (RG) analysis is to prove the existence of a small invariant set, such as a periodic orbit. For the type of skew-product maps considered here, a fixed point of $\mathfrak {R}^3$ was obtained in [36] for $\varrho \in \{\tfrac {1}{2},0\}$ . A theorem concerning the existence of a fixed point of $\mathfrak {R}^6$ associated with $\varrho =\tfrac {1}{4}$ was announced in [39]. A proof of this theorem will be given in §4.

Constructing a fixed point $P_\ast $ for $\mathfrak {R}^\ell $ is a local analysis (near an approximate fixed point). By contrast, proving that the AM family and others are attracted to the unstable manifold of $\mathfrak {R}^\ell $ at $P_\ast $ is a global analysis and much harder. A simplified version of this problem was considered in [38], in a situation where the Hofstadter Hamiltonian reduces to skew-product maps with factors that take values in the circle $\mathbb {R}\cup \{\infty \}$ . Here we prove convergence (1.6) with ${\textrm {SL}}(2,\mathbb {R})$ factors, including the AM factors, but only in a restricted one-parameter setup.

Before describing our main results, we would like to mention a peculiarity of these skew-product maps. High-accuracy computations suggest [39] that the eigenvalue $\mu _1$ associated with $\varrho \in \{\tfrac {1}{2},0\}$ is a zero of the polynomial ${\mathcal {P}_6(z)=z^4-196z^3-58z^2-4z+1}$ . And the eigenvalue $\mu _1$ associated with $\varrho =\tfrac {1}{4}$ is a zero of $\mathcal {P}_3(z)=z^4-30z^3-24z^2- 10 z-1$ . In both cases, the product of the two real roots of $\mathcal {P}_\ell $ is $(-\alpha )^{-\ell }$ . Furthermore, the value of $\mu _2$ appears to be $\alpha ^{-\ell }$ . In fact, computations that were carried out in the context of the present paper suggest that the eigenvalues of $D\mathfrak {R}^\ell (P_\ast )$ can all be written down in algebraic form. It is unusual that universal constants associated with critical phenomena are algebraically related to basic system parameters, such as the flux parameter $\alpha $ here. Known exceptions are statistical mechanics models in two dimensions, where the large-scale asymptotic is governed by a conformal symmetry. The class of skew-product maps that includes the AM maps seems to be governed by symmetries as well, but it is not clear how the symmetries of the Hofstadter model [19, 28, 58] generate the algebraic eigenvalues that are observed here.

2 Main results

As is common in the renormalization of maps that include a circle rotation, we first generalize the notion of periodicity by considering commuting pairs of maps. Consider the map $F=(1,\textbf {1})$ on $\mathbb {R}\times \mathbb {R}^2$ , defined by $F(x,y)=(x+1,y)$ . A skew-product map $G=(\alpha ,A)$ with a factor $A:\mathbb {R}\to {\textrm {SL}}(2,\mathbb {R})$ represents a map on the cylinder ${\Bbb T}\times \mathbb {R}^2$ if and only if G commutes with F. A more general skew-product map $F=(1,B)$ on $\mathbb {R}\times \mathbb {R}^2$ can be viewed as defining a cylinder ${\Bbb T}_F\times \mathbb {R}^2$ embedded in $\mathbb {R}\times \mathbb {R}^2$ , by identifying points on the orbit of F. If G commutes with F, then G defines a map on this cylinder ${\Bbb T}_F\times \mathbb {R}^2$ .

Consider now pairs $(F,G)$ of maps $F=(1,B)$ and $G=(\alpha ,A)$ on $\mathbb {R}\times \mathbb {R}^2$ that commute. Here, $\alpha $ can be an arbitrary irrational number between $0$ and $1$ . Then the renormalized pair is defined by the equation

(2.1) $$ \begin{align} \mathfrak{R}((F,G))=(\check F,\check G),\quad \check F=\Lambda^{-1}G\Lambda,\quad \check G=\Lambda^{-1}FG^{-c}\Lambda, \end{align} $$

where c is the integer part of $\alpha ^{-1}$ , and where $\Lambda (x,y)=(\alpha x,L_1y)$ . Here, $L_1$ is a suitable non-singular $2\times 2$ matrix that can chosen to depend on the pair $(F,G)$ . By construction, the first component of $\check F$ is again $1$ , while the first component of $\check G$ is $\check \alpha =\alpha ^{-1}-c$ . We note that $\alpha \mapsto \check \alpha $ is the Gauss map that appears in the continued fraction expansion of $\alpha $ .

In what follows, $\alpha $ is assumed to be the inverse golden mean. Its continued fraction expansion is $\alpha =1/(1+1/(1+\cdots ))$ , so $\alpha $ is a fixed point of the Gauss map, and $c=1$ in equation (2.1). As mentioned earlier, we expect to find a period of $\mathfrak {R}$ that is a multiple of $3$ . This leads us to consider orbits of the third iterate of $\mathfrak {R}$ , which is of the form

(2.2) $$ \begin{align} \mathfrak{R}^3(P)=(\Lambda_3^{-1}G^2F^{-1}\Lambda_3, \Lambda_3 FG^{-1}FG^{-2}\Lambda_3),\quad P=(F,G), \end{align} $$

with $\Lambda _3(x,y)=(\alpha ^3 x,L_3y)$ for some suitable non-singular $2\times 2$ matrix $L_3$ .

What plays an important role in our analysis are symmetry properties. A $2\times 2$ matrix $\Sigma $ will be called a reflection if $\Sigma ^2=\textbf {1}$ and $\mathop {\textrm {det}}(\Sigma )=-1$ . An invertible map H on $\mathbb {R}\times \mathbb {R}^2$ is said to be reversible with respect to $\Sigma $ if

(2.3) $$ \begin{align} H^{-1}=\mathcal{S} H\mathcal{S},\quad\mathcal{S}(x,y)=(-x,\Sigma y). \end{align} $$

For a skew-product map $H=(\gamma ,C)$ , reversibility with respect to $\Sigma $ is equivalent to the property

(2.4) $$ \begin{align} C_\circ(x)^{-1}=\Sigma C_\circ(-x)\Sigma,\quad C_\circ(x)\mathrel{\mathop=^{\textrm{def}}} C\bigg(x-\frac{\gamma}{2}\bigg). \end{align} $$

The matrix-valued function $C_\circ $ defined by (2.4) will be referred to as the symmetric factor of H, even if H is not reversible. A pair $P=(F,G)$ will be called reversible if both F and G are reversible with respect to the same reflection $\Sigma $ . Since the matrix $\Sigma $ depends on a choice of coordinates, we will specify it only when necessary.

The following result was announced in [37]. A proof will be given in §4.3.

Theorem 2.1. Let $\alpha $ be the inverse golden mean. Then $\mathfrak {R}^6$ has a reversible fixed point $P_\star =(F_\star ,G_\star )$ with $F_\star =(1,B_\star )$ and $G_\star =(\alpha ,A_\star )$ commuting. The factors $B_\star $ and $A_\star $ are non-constant entire functions with values in ${\textrm {SL}}(2,\mathbb {R})$ . The scaling $L_6$ at $P_\star $ has real eigenvalues $\mathcal {V}$ and $\mathcal {V}^{-1}$ whose sum is $2\alpha ^{-3}$ , up to an error less that $10^{-429}$ .

To be more precise, the scaling matrix $L_6$ mentioned in this theorem is the product of the matrix $L_3(P_\star )$ appearing in the transformation $P_\star \mapsto P=\mathfrak {R}^3(P_\star )$ , and the matrix $L_3(P)$ appearing in the transformation $P\mapsto P_\star =\mathfrak {R}^3(P)$ . The exact form of $L_6$ depends on the chosen coordinates.

As a by-product of our (computer-assisted) proof of this theorem, we have accurate bounds on the various quantities involved, as well as other numerical data. These data include approximate values for the two expanding eigenvalues $\mu _1$ and $\mu _2$ of $D\mathfrak {R}^6(P_\star )$ .

As will be described in §4, the AM family for $\xi ={\alpha }/{2}$ is reversible, due to the fact that $x\mapsto E-\unicode{x3bb} \cos (2\pi x)$ is an even function. By choosing the y-scaling $L_3$ appropriately, reversibility (for a fixed $\Sigma $ ) is preserved under renormalization. So we expect Conjecture 1.1 to hold within a class of reversible pairs. The fixed point $P_\star $ described in Theorem 2.1 is associated with the fibered rotation number $\varrho =\tfrac {1}{4}$ . In the AM family, this corresponds to the energy $E_\ast =0$ .

Our main goal in this paper is to prove Conjecture 1.1 in a simplified setting where the analysis can be restricted to one-parameter families. This lead us to consider maps that are anti-reversible. To be more precise, define $-(\gamma ,C)=(\gamma ,-C)$ . Using the same notation as in (2.3), we say that H is anti-reversible with respect to $\Sigma $ if $H^{-1}=-\mathcal {S} H\mathcal {S}$ . A pair $(F,G)$ is said to be anti-reversible, if F is reversible and G anti-reversible with respect to the same reflection $\Sigma $ .

If we choose $\xi ={\alpha }/{2}-\tfrac {1}{4}$ , then the AM map G is anti-reversible, but only for $E~=~0$ , due to the fact that $x\mapsto E-\unicode{x3bb} \sin (2\pi x)$ is an odd function precisely when $E=0$ . So the idea is to restrict our analysis to anti-reversible pairs. By choosing the y-scaling $L_3$ appropriately, anti-reversibility (for a fixed $\Sigma $ ) is preserved under renormalization. So we expect Conjecture 1.1 to hold for one-parameter families in this restricted class, except that the RG transformation has only a single expanding direction.

Based on Theorem 2.1, we expect to find a fundamental period $6$ in this case. Somewhat unexpectedly, we find a period $3$ .

Theorem 2.2. Let $\alpha $ be the inverse golden mean. Then $\mathfrak {R}^3$ has an anti-reversible fixed point $P_\ast =(F_\ast ,G_\ast )$ with $F_\ast =(1,B_\ast )$ and $G_\ast =(\alpha ,A_\ast )$ commuting. The factors $B_\ast $ and $A_\ast $ are non-constant entire functions with values in ${\textrm {SL}}(2,\mathbb {R})$ . The scaling $L_3$ at $P_\ast $ is an orthogonal reflection in $\mathbb {R}^2$ about some line (that depends on the choice of coordinates). An extension of $\mathfrak {R}_3$ to pairs that need not commute is hyperbolic, with a single expanding direction with eigenvalue $\mu _2\ge \alpha ^{-3}$ .

A proof of this theorem will be given in §5.1.

Remark 1. In the anti-reversible case, our RG transformations $\mathfrak {R}^3$ and $\mathfrak {R}_3$ include an extra step $(B,A)\mapsto (-B,-A)$ . We will ignore this step here, for example by identifying pairs of factors up to a sign.

For the pair $P_\ast $ and the eigenvalue $\mu _2$ described in Theorem 2.2 we also have the following result. Here, and in the remaining part of this paper, $\alpha $ always denotes the inverse golden mean, unless specified otherwise.

Theorem 2.3. Consider the AM factors (1.4) with $\xi ={\alpha }/{2}-\tfrac {1}{4}$ and energy $E=0$ . Denote by $p_n$ the nth Fibonacci number and let $q_n=p_{n+1}$ . Then there exists an open disk $D\subset \mathbb {C}$ centered at the origin, such that the limits

(2.5) $$ \begin{align} \begin{aligned} B_\ast(s,x) &=\lim_{n\to\infty}L_3^{-n}A^{\ast p_{3n}}(\mu_2^{-3n}s,\alpha^{3n}x)L_3^n,\\ A_\ast(s,x) &=\lim_{n\to\infty}L_3^{-n}A^{\ast q_{3n}}(\mu_2^{-3n}s,\alpha^{3n}x)L_3^n, \end{aligned} \end{align} $$

exist for all $s\in D$ and all $x\in \mathbb {C}$ . Here, $L_3$ is some orthogonal reflection in the plane. The functions $(s,x)\mapsto A_\ast (s,x)$ and $(s,x)\mapsto B_\ast (s,x)$ are analytic on $D\times \mathbb {C}$ , and the convergence in (2.5) is uniform on compact subsets of this domain. The family of pairs $s\mapsto \texttt{P}_\ast (s)$ associated with the limit factors (2.5) is a parametrization of the local unstable manifold of $\mathfrak {R}_3$ at $P_\ast $ . Furthermore, the same holds for any real-analytic family $\texttt{P}$ in some open neighborhood (in a suitable topology) of the AM family, after an initial affine reparametrization $s\mapsto s_\ast +cs$ with $c\ne 0$ .

A proof of this theorem will be given in §5.2. To be more precise, our proof of Theorems 2.1, 2.2, and 2.3 is computer-assisted. This means that some estimates have been verified (rigorously) with the aid of a computer. The main steps and ideas are described in §8. For details we refer to the source code of our programs, see the Data Availability section.

The main part of our analysis is carried out in a space $\mathcal {F}_\rho $ of pairs of maps $F=(1,B)$ and $G=(\alpha ,A)$ whose symmetric factors $A_\circ $ and $B_\circ $ are analytic in a bounded domain $|x|<{\rho _{_{\textrm{F}}}}$ and $|x|<{\rho _{_{\textrm{G}}}}$ , respectively. The ‘suitable topology’ mentioned in Theorem 2.3 only compares factors on this bounded domain; so, in particular, the factors need not be periodic. Entire analyticity of $A_\ast $ and $B_\ast $ is obtained a posteriori from the fact that the transformation $\mathfrak {R}^3$ is analyticity-improving. (And it is not hard to see that these factors are of finite exponential type.)

To be more specific, we consider the fixed point problem for $\mathfrak {R}_3$ instead of $\mathfrak {R}^3$ , where

(2.6) $$ \begin{align} \mathfrak{R}_3(P)=(\Lambda_3^{-1}GF^{-1}G\Lambda_3, \Lambda_3 G^{-1}FG^{-1}FG^{-1}\Lambda_3). \end{align} $$

This makes no difference for commuting pairs. But for non-commuting pairs, which need to be included in our analysis, the transformation $\mathfrak {R}^3$ does not in general preserve (anti-)reversibility, while $\mathfrak {R}_3$ does. After constructing a fixed point $(F_\ast ,G_\ast )$ for the transformation $\mathfrak {R}_3$ , we can use (2.5) to conclude that $F_\ast $ and $G_\ast $ commute. Our extension of $\mathfrak {R}_3$ to nearly-commuting pairs also includes a ‘commutator correction’ which makes this transformation contracting in the direction of non-commuting perturbations.

Hyperbolicity of $\mathfrak {R}_3$ is proved via estimates on the derivative $D\mathfrak {R}_3$ on some cylinder $C_1'$ centered at $P_\ast $ . In order to prove Theorem 2.3, we show that some RG iterate of the anti-reversible AM family defines a curve that is properly aligned with a cylinder $C_0'\subset C_1'$ . This constitutes the global part of our analysis. What remains is again a purely local problem.

One of the claims in Theorem 2.3 is that the parameter value $s_\ast $ for which the AM pair is attracted to the fixed point $P_\ast $ is zero. This is specific to the AM family and has to be proved separately. Similarly, our guess that $\mu _2=\alpha ^{-3}$ is based on special properties of the AM family. A proof is again outside the scope of renormalization.

In our proof that $s_\ast =0$ , we use the fact that the Lyapunov exponent of the AM map G for a spectral energy is $L(G)=\max \{0,\log \unicode{x3bb} \}$ . The general idea is that $q\mapsto G^q$ tends to infinity if $L(G)$ is positive. An argument along these lines shows that $s_\ast \le 0$ . Proving that $s_\ast \ge 0$ turns out to be significantly harder.

A useful tool in our proof of Theorem 2.3 is a Lyapunov exponent for pairs $P=(F,G)$ . This exponent $L(P)$ is defined in such a way that it agrees with $L(G)$ , if $F=(1,\textbf {1})$ and $G=(\alpha ,A)$ , with $\alpha $ the inverse golden mean. It also has the property that

(2.7) $$ \begin{align} L(\mathfrak{R}(P))=\alpha^{-1}L(P). \end{align} $$

This shows, for example, that $L(P_\ast )=0$ . Equation (2.7) also suggests that $\mu _2=\alpha ^{-3}$ . Unfortunately, we can only prove that $\mu _2\ge \alpha ^{-3}$ .

The problem of proving $\mu _2\le \alpha ^{-3}$ is related to the question of whether L takes a positive value on the local unstable manifold of $\mathfrak {R}_3$ at $P_\ast $ . Our pursuit of this question has led to some interesting observations that we shall now describe.

Given that $L(P)$ is an asymptotic quantity, it is necessary to consider the unstable manifold $\mathcal {W}^u$ globally, at least on the side where we expect $L(P)$ to be positive. Based on numerical experiments, our conjecture is that $\mathcal {W}^u$ gets attracted to a ‘supercritical’ fixed point $P_\diamond $ . In fact, all AM pairs with $\unicode{x3bb}>1$ and $E=0$ appear to be get attracted to this fixed point.

To be more specific, we have to describe an extension of $\mathfrak {R}_3$ to pairs of skew-product maps whose factors need not have determinant $1$ . Let $H=(\gamma ,C)$ . If $\mathop {\textrm {det}}(C)$ is the constant function $x\mapsto 1$ , then the inverse $H^{-1}$ of H agrees with the quasi-inverse

(2.8) $$ \begin{align} H^\dagger=(-\alpha,C^\dagger(.-\alpha)) \quad\textrm{where } C^\dagger=\begin{bmatrix} {d}&{-b}\\ {-c}&{a} \end{bmatrix} \quad\textrm{if } C=\begin{bmatrix} {a}&{b}\\ {c}&{d} \end{bmatrix}. \end{align} $$

Thus, we can extend the domain of $\mathfrak {R}_3$ by replacing the inverse maps in our definition (2.6) by their quasi-inverses. But we assume that the determinants are non-negative. In our proof of Theorems 2.1 and 2.2, we use such an extension of $\mathfrak {R}_3$ for pairs whose factors have determinants close to $x\mapsto 1$ . The extended transformation $\mathfrak {R}_3$ includes (as its last step) a normalization that divides each factor by the square root of its determinant. So any fixed point of $\mathfrak {R}_3$ or $\mathfrak {R}_3^2$ has factors that take values in ${\textrm {SL}}(2,\mathbb {R})$ .

In what follows, we allow factors that (are non-zero but) can have arbitrary non-negative constant determinants. But our RG transformation now includes a normalization step that divides each factor by its norm. This is useful in cases where the norms would otherwise tend to infinity under iteration of $\mathfrak {R}_3$ . For such an extension we find the following result.

Theorem 2.4. There exists entire functions $b_\diamond $ and $a_\diamond $ of order $1$ , with $x\mapsto b_\diamond (x-\tfrac {1}{2})$ even and $x\mapsto a_\diamond (x-{\alpha }/{2})$ odd, such that the pair $P_\diamond =((1,B_\diamond ),(\alpha ,A_\diamond ))$ , with

(2.9) $$ \begin{align} B_\diamond(x)=b_\diamond(x) \begin{bmatrix} {0}&{0}\\ {0}&{1} \end{bmatrix},\quad A_\diamond(x)=a_\diamond(x)\begin{bmatrix} {1}&{0}\\ {0}&{0} \end{bmatrix}\!, \end{align} $$

is a fixed point of $\mathfrak {R}_3$ with $L_3=[{0~1\atop 1~0}]$ . The zeros of $b_\diamond $ are all simple and define a non-periodic bi-infinite sequence of real numbers whose gaps take exactly three distinct values: $\tfrac {1}{2}$ , $\alpha ^{-1}$ , and $\alpha ^{-1}+\tfrac {1}{2}$ . The zeros of $a_\diamond $ have an analogous property, except that the gaps only take two distinct values: $\tfrac {1}{2}$ and $\alpha ^{-1}-\tfrac {1}{2}$ .

Numerically, we find that $P_\diamond $ attracts supercritical AM pairs, as well as pairs $\texttt{P}(s)$ with $s>0$ on the unstable manifold of $P_\ast $ . Our computations covered several values of $\unicode{x3bb} $ between $1+2^{-32}$ and $2$ , both for $\xi ={\alpha }/{2}-\tfrac {1}{4}$ and $\xi ={\alpha }/{2}$ . To be more precise, the y-scaling has to include a rotation; otherwise the limit can be a rotated version of $P_\diamond $ . We would expect similar behavior for other energies in the spectrum of $H^\alpha _\unicode{x3bb} $ , as well as for other quadratic irrationals $\alpha $ that have a periodic continued fraction expansion.

For the inverse golden mean, it should be possible to prove that the (anti-)reversible AM pair with $\unicode{x3bb} $ sufficiently large is attracted to $P_\diamond $ under iteration of $\mathfrak {R}_3$ , but such an analysis would go beyond the scope of this paper. A strong-coupling fixed point for an approximate renormalization scheme has been constructed in [45].

What we will prove here is the following theorem.

Theorem 2.5. Let $P_0$ be an anti-reversible AM pair with coupling constant $\unicode{x3bb}>1$ . Consider the set of accumulation points of the sequence $n\mapsto \mathfrak {R}^{3n}(P_0)$ in the space $\mathcal {F}_\rho $ mentioned earlier. This set $K_\ast $ is compact and invariant under $\mathfrak {R}_3$ . Let $P=((1,B),(\alpha ,A))$ be any pair in $K_\ast $ . Then A and B extend to non-constant entire functions, with $b_\circ =\mathop {\mathrm {tr}}(B_\circ )$ even and $a_\circ =\mathop {\mathrm {tr}}(A_\circ )$ odd. Furthermore, $B(x)=0$ wherever $b_\diamond (x)=0$ , and $A(x)=0$ wherever $a_\diamond (x)=0$ .

A proof of Theorems 2.4 and 2.5 will be given in §7.

We have not investigated the asymptotic behavior of subcritical pairs, like the AM pairs for $\unicode{x3bb} <1$ . Results on almost-reducibility [7] suggest that such pairs converge to some $\mathfrak {R}$ -invariant set that consists of pairs whose factors are constant. (The y-scaling $L_1$ could be different from what we use here.) The action of $\mathfrak {R}$ on pairs with constant factors is trivial. In particular, it is easy to find periodic orbits for any rational fibered rotation number $\varrho $ . Whether or not AM pairs with non-small positive coupling constant $\unicode{x3bb} <1$ and rational fibered rotation number $\varrho $ converge to such a ‘subcritical’ fixed point (of $\mathfrak {R}^\ell $ for some $\ell $ ) is a global question and not easy to answer.

3 The RG transformation for anti-reversible pairs

The main goal in this section is to properly formulate the fixed point problem considered in Theorem 2.2. Our RG analysis of anti-reversible pairs will be continued in §5, after having covered the reversible case in §4.

3.1 Some basic facts and identities

Let $P=(F,G)$ be a pair of skew-product maps $F=(1,B)$ and $G=(\alpha ,A)$ whose factors B and A take values in ${\textrm {GL}}(2,\mathbb {R})$ and have positive determinants. Then the renormalized pair $\tilde P=\mathfrak {R}_3(P)$ is given by

(3.1) $$ \begin{align} \tilde P=(\tilde F,\tilde G),\quad \tilde F=\Lambda_3^{-1}\hat F\Lambda_3,\quad \tilde G=\Lambda_3^{-1}\hat G\Lambda_3, \end{align} $$

where

(3.2) $$ \begin{align} \hat F=GF^\dagger G,\quad \hat G=G^\dagger FG^\dagger FG^\dagger. \end{align} $$

Here, $F^\dagger $ and $G^\dagger $ denote the quasi-inverses of F and G, respectively, as defined in (2.8). The first component of $\hat F$ is $2\alpha -1=\alpha ^3$ . So after scaling by $\alpha ^3$ , the first component of $\tilde F$ is again $1$ . Similarly, the first component of $\hat G$ is $2-3\alpha =\alpha ^4$ . So after scaling by $\alpha ^3$ , the first component of $\tilde G$ is again $\alpha $ . The symmetric factor $\hat B$ of $\hat F$ is given by

(3.3) $$ \begin{align} \textstyle \hat B_\circ(x)=A_\circ\bigg(\dfrac{\alpha-1}{ 2}+x\bigg)B_\circ(x)^\dagger A_\circ\bigg(\dfrac{1-\alpha}{ 2}+x\bigg), \end{align} $$

and for the symmetric factor $\hat A$ of $\hat G$ we obtain

(3.4) $$ \begin{align} \textstyle \hat A_\circ(x)=A_\circ((1-\alpha)+x)^\dagger B_\circ\bigg(\dfrac{1-\alpha}{ 2}+x\bigg)A_\circ(x)^\dagger B_\circ\bigg(\dfrac{\alpha-1}{ 2}+x\bigg) A_\circ((\alpha-1)+x)^\dagger. \end{align} $$

The symmetric factors associated with $\tilde P=\mathfrak {R}_3(P)$ are now obtained via scaling:

(3.5) $$ \begin{align} \tilde B_\circ(x)=L_3^{-1}\hat B_\circ(\alpha^3 x)L_3,\quad \tilde A_\circ(x)=L_3^{-1}\hat A_\circ(\alpha^3 x)L_3. \end{align} $$

Notice that such a relation is obvious for the regular factors. But it holds for the symmetric factors as well, as a short computation shows. Our choice for the y-scaling matrices $L_3$ will be described in §3.2.

Next, let us consider some consequences of (anti-)reversibility. To this end, and for reference later on, define

(3.6) $$ \begin{align} J=\begin{bmatrix} {0}&{1}\\ {-1}&{0} \end{bmatrix},\quad S=\begin{bmatrix} {1}&{0}\\ {0}&{-1} \end{bmatrix},\quad M=2^{-1/2} \begin{bmatrix} {1}&{1}\\ {1}&{-1} \end{bmatrix}. \end{align} $$

With the exception of §4, (anti-)reversibility in this paper is defined with respect to the reflection $\Sigma =iJ$ . Notice that conjugacy by $iJ$ keeps real matrices real.

Assume now that $F=(1,B)$ is reversible and $G=(\alpha ,A)$ anti-reversible, both with respect to $\Sigma =iJ$ . A short computation shows that this condition is equivalent to

(3.7) $$ \begin{align} B_\circ(x)^\top=B_\circ(-x),\quad A_\circ(x)^\top=-A_\circ(-x). \end{align} $$

Here, $C^\top $ denotes the transpose of a matrix C.

What makes skew-products over irrational rotations difficult to deal with is that products $A^{\ast q}(x)$ with large q can vary vastly in size, as a function of x. If the Lyapunov exponent $L=L(G)$ is positive, then $A^{\ast q}(x)$ grows asymptotically like $e^{qL}$ for typical values of x. Particularly large factors can be obtained via the identity

(3.8) $$ \begin{align} (-1)^m A_\circ^{\ast 2m}(iy) =U(iy)^\ast U(iy), \end{align} $$

where $U(x)=A_\circ ((m-\tfrac {1}{2})\alpha +x) \cdots A_\circ ({\alpha }/{2}+x)$ , and where $U^\ast =\overline {U}^\top $ denotes the adjoint of U. So, in particular, $(-1)^m A_\circ ^{\ast 2m}(iy)$ is a positive matrix for $y\in \mathbb {R}$ . This fact will be used in several of our proofs.

On the other hand, products with many factors can be of order $1$ in size. Consider the case where $\mathop {\textrm {det}}(A)=1$ . Using that $A_\circ (-x)=-J^{-1}A_\circ (x)^{-1}J$ , we have

(3.9) $$ \begin{align} (-1)^m A^{\ast(2m+1)}_\circ(x) =V(x)A_\circ(x)J^{-1}V(-x)^{-1}J, \end{align} $$

where $V(x)=A_\circ (m\alpha +x)\cdots A_\circ (\alpha +x)$ . If $A_\circ (0)=-J$ , then this implies that

(3.10) $$ \begin{align} (-1)^m A_\circ^{\ast(2m+1)}(0)=-J. \end{align} $$

This applies, for example, to the AM map with $\xi ={\alpha }/{2}-\tfrac {1}{4}$ and $E=0$ . And it is independent of the value of $\unicode{x3bb} $ . So for $\unicode{x3bb}>1$ , sub-products that appear in $A^q$ that are of the form (3.10) are much smaller than sub-products of the form (3.8) for $y=0$ . This is the mechanism that produces the zeros described in Theorem 2.5.

In the remainder of this paper, we consider the AM maps with respect to the basis defined by the column vectors of the matrix M given in (3.6). In this representation, the symmetric factor of the anti-reversible AM map is given by

(3.11) $$ \begin{align} A_\circ= \begin{bmatrix} {t_\circ}&{t_\circ+1}\\ {t_\circ-1}&{t_\circ} \end{bmatrix},\quad t_\circ(x)=\unicode{x3bb}\sin(2\pi x). \end{align} $$

3.2 Scaling and normalization

As mentioned earlier, we choose $L_3$ to be a reflection matrix. In the coordinates considered here,

(3.12) $$ \begin{align} L_3=L(\vartheta)\mathrel{\mathop=^{\textrm{def}}} \begin{bmatrix} {\cos(\vartheta+\pi/4)}&{-\sin(\vartheta+\pi/4)}\\ {-\sin(\vartheta+\pi/4)}&{-\cos(\vartheta+\pi/4)} \end{bmatrix}\!. \end{align} $$

Notice that $L(\vartheta )=L(0)e^{-\vartheta J}$ , where $e^{-\vartheta J}$ is a rotation by $\vartheta $ . Notice also that $L_3^2=\textbf {1}$ . So $L_3$ drops out in a fixed point equation for $\mathfrak {R}_3^2$ . But if $P=(F,G)$ is a fixed point of $\mathfrak {R}_3^2$ , then a conjugacy by any rotation yields another fixed point.

The goal is to get uniqueness by choosing $\vartheta =\vartheta (P)$ in such a way that $\tilde P=\mathfrak {R}_3(P)$ satisfies a suitable normalization condition. With a y-scaling $L_3$ of the form (3.12), the symmetric factor of $\tilde F=\Lambda _3^{-1}\hat F\Lambda _3$ is given by

(3.13) $$ \begin{align} \tilde B_\circ(0) =e^{\vartheta J} \begin{bmatrix} {a}&{u}\\ {v}&{d} \end{bmatrix} e^{-\vartheta J},\quad \begin{bmatrix} {a}&{u}\\ {v}&{d} \end{bmatrix} \mathrel{\mathop=^{\textrm{def}}} -L(0)\hat B_\circ(0)L(0), \end{align} $$

where $\hat B_\circ $ is as described in (3.3). The negative sign on the right-hand side of this equation is due to the step $(B,A)\mapsto (-B,-A)$ mentioned in Remark 1. As a normalization condition, we impose that the two entries on the main diagonal of $\tilde B_\circ (0)$ agree. A straightforward computation shows that this determines $\mathfrak {c}=\cos (2\vartheta )$ and $\mathfrak {s}=\sin (2\vartheta )$ as follows:

(3.14) $$ \begin{align} \mathfrak{s}=\frac{a-d}{ q},\quad\mathfrak{c}=-\frac{u+v}{ q},\quad q=\sqrt{(u+v)^2+(a-d)^2}. \end{align} $$

As tedious as such computations may be, explicit expressions like (3.14) are needed in a computer-assisted proof that is by nature highly constructive. In order to get explicit expressions for the derivative $D\mathfrak {R}_3(P)\dot P$ , it is convenient to consider a family of pairs P that depend differentiably on a parameter. Then the quantities $a,u,v,d$ defined by (3.13) depend differentiably on the parameter as well. Using the ‘dot notation’ for derivatives with respect to the parameter, the derivatives of $\mathfrak {s}$ and $\mathfrak {c}$ are given by

(3.15) $$ \begin{align} \dot{\mathfrak{s}}=\frac{\mathfrak{c}}{ q} [\mathfrak{c}(\dot a-\dot d)+\mathfrak{s}(\dot u+\dot v)],\quad \dot{\mathfrak{c}}=-\frac{\mathfrak{s}}{ q} [\mathfrak{c}(\dot a-\dot d)+\mathfrak{s}(\dot u+\dot v)]. \end{align} $$

At this point we have defined the ‘basic’ version of our RG transformation $\mathfrak {R}_3$ for skew-product pairs $P=(F,G)$ . We are not assuming that $F=(1,B)$ and $G=(\alpha ,A)$ commute, nor that A and B have determinant $1$ . But the transformation does not behave as desired for non-commuting pairs or for factors that have determinants not equal to $1$ . Denote this basic version by $\mathcal {R}_3$ . Our extended version of $\mathfrak {R}_3$ is defined as

(3.16) $$ \begin{align} \mathfrak{R}_3=\mathfrak{N}\circ\mathcal{R}_3\circ\mathfrak{C}, \end{align} $$

where $\mathfrak {C}$ is a ‘commutator correction’ that will be defined later, and where $\mathfrak {N}$ performs a renormalization of determinants.

To normalize determinants, we simply choose

(3.17) $$ \begin{align} \mathfrak{N}((\gamma,C))=(\gamma,\mathcal{N}(C)),\quad \mathcal{N}(C)=[\mathop{\textrm{det}}(C)]^{-1/2}C. \end{align} $$

If the determinant of C is close to $1$ , then (3.17) is well defined and $\mathcal {N}(C)$ has determinant  $1$ . We note that, if $H=(\gamma ,C)$ is (anti-)reversible, then $\mathop {\textrm {det}}(C)$ is an even function, so $\mathfrak {N}(H)$ is still (anti-)reversible. For a pair $P=(F,G)$ we define $\mathfrak {N}$ componentwise.

For estimates of derivatives $D\mathfrak {R}_3(P)\dot P$ , we use that the derivative of $\mathcal {N}$ at $C=[{a~u\atop v~d}]$ is given by

(3.18) $$ \begin{align} D\mathcal{N}(C)\dot C= \mathop{\textrm{det}}(C)^{-1/2}\dot C -\tfrac{1}{2}\mathop{\textrm{det}}(C)^{-3/2}[a\dot d+d\dot a-u\dot v-v\dot u]C. \end{align} $$

3.3 Commutators

The linearization of the basic transformation $\mathcal {R}_3$ at the fixed point $P_\ast $ can have non-contracting directions that are associated with non-commuting perturbations of $P_\ast $ . Formally, one can see that $D\mathcal {R}_3(P_\ast )$ must have an eigenvalue $-1$ . And numerically, another eigenvalue is the number $\mathcal {V}=8.3524100320\ldots $ that appears in Theorem 2.1. The goal is to eliminate these two eigenvalues. This will be done in the next section.

First, we need some generalities. Consider the commutator $\Theta =FG(GF)^{-1}$ for a pair $P=(F,G)$ . A straightforward computation shows that the commutator for the renormalized pair $\tilde P=(\tilde F,\tilde G)$ is given by

(3.19) $$ \begin{align} \tilde{\Theta}=(G\Lambda_3)^{-1}\Theta^{-1}(G\Lambda_3). \end{align} $$

If we write $\Theta =(0,C)$ and $\tilde {\Theta }=(0,\tilde C)$ , then

(3.20) $$ \begin{align} \tilde C(x)=L(\vartheta)^{-1} A(\alpha^3x)^{-1}C(\alpha^3x+\alpha)^{-1} A(\alpha^3x)L(\vartheta). \end{align} $$

Consider the change of variables $x=({1+\alpha })/{ 2}+z$ and define

(3.21) $$ \begin{align} \mathcal{C}(P,z)=\textstyle C\bigg(\dfrac{1+\alpha}{ 2}+z\bigg),\quad \mathcal{A}(P,z)=A_0\bigg(\dfrac{1}{2}+\alpha^3z\bigg)L(\vartheta_P). \end{align} $$

Then equation (3.20) becomes

(3.22) $$ \begin{align} \mathcal{C}(\tilde P,z) =\mathcal{A}(P,z)^{-1}\mathcal{C}(P,\alpha^3 z)^{-1}\mathcal{A}(P,z). \end{align} $$

From this equation one can see that the eigenvalues of $\Theta \mapsto \tilde {\Theta }$ at $\Theta ={\textrm {I}}$ are determined by the behavior of $\mathcal {C}(P,z)$ near $z=0$ .

Thus, consider $\mathcal {C}(P)=\mathcal {C}(P,0)=C(({1+\alpha })/{ 2})$ . An explicit computation shows that

(3.23) $$ \begin{align} \textstyle \mathcal{C}(P) =XY^{-1},\quad X=B_0\bigg(\dfrac{\alpha}{ 2}\bigg) A_0\bigg(-\dfrac{1}{ 2}\bigg),\quad Y=A_0\bigg(\dfrac{1}{ 2}\bigg)B_0\bigg(-\dfrac{\alpha}{ 2}\bigg). \end{align} $$

Assume now that G is anti-reversible with respect to $\Sigma =iJ$ . Then $JXJ=Y^{-1}$ . So X, Y, and $XY^{-1}$ are of the form

(3.24) $$ \begin{align} X=\begin{bmatrix} {a}&{b}\\ {c}&{d} \end{bmatrix},\quad Y=-\begin{bmatrix} {a}&{c}\\ {b}&{d} \end{bmatrix},\quad XY^{-1}=\begin{bmatrix} {-1+b(b-c)}&{-a(b-c)}\\ {d(b-c)}&{-1-c(b-c)} \end{bmatrix}, \end{align} $$

with $ad-bc=1$ . If $XY^{-1}$ is the identity matrix, then $X=Y=J$ . So in our applications, the matrix elements a and d are close to zero.

3.4 Commutator corrections

The commutator correction map $\mathfrak {C}$ is the first step in our RG transformation (3.16). The goal is for $P'=\mathfrak {C}(P)$ to satisfy $\mathcal {C}(P')=\textbf {1}$ . We define $\mathfrak {C}$ as a composition of three maps. To simplify notation, each of these maps will be denoted by $P\mapsto P'$ .

Step 1. Here we replace the symmetric factor $A_\circ $ of G by

(3.25) $$ \begin{align} A_\circ'=RA_\circ R,\quad R=\begin{bmatrix} {\rho}&{r}\\ {r}&{\rho} \end{bmatrix},\quad \rho^2=1+r^2, \end{align} $$

while keeping $B_\circ '=B_\circ $ . The goal is to choose r in such a way that $\mathop {\textrm {tr}}(X')=0$ . Notice that R is reversible, in the sense that $J^{-1}RJ=R^{-1}$ . Since G is anti-reversible, this guarantees that the map $G'$ is anti-reversible as well. Write

(3.26) $$ \begin{align} A_\circ\bigg(-\frac{1}{2}\bigg) =\begin{bmatrix} {t_A+s_A}&{u_A}\\ {v_A}&{t_A-s_A} \end{bmatrix} ,\quad B_\circ\bigg(\frac{\alpha}{2}\bigg) =\begin{bmatrix} {t_B+s_B}&{u_B}\\ {v_B}&{t_B-s_B} \end{bmatrix}, \end{align} $$

and define

(3.27) $$ \begin{align} \begin{aligned} \varepsilon&=\mathop{\textrm{tr}}(X_\circ),\\ \tau&=4t_A t_B+(u_A+v_A)(u_B+v_B),\\ \sigma&=(u_A+v_A)2t_B+2t_A(u_B+v_B). \end{aligned} \end{align} $$

A tedious but trivial computation shows that $\mathop {\textrm {tr}}(X')=0$ if we choose

(3.28) $$ \begin{align} r=\frac{-\varepsilon}{ \sqrt{ \tfrac12 (\sigma^2-2\varepsilon\tau) +\tfrac12 \sqrt{(\sigma^2-2\varepsilon\tau)^2-4(\tau^2-\sigma^2)\varepsilon^2}}}. \end{align} $$

And for the derivative with respect to a parameter, we obtain

(3.29) $$ \begin{align} \dot r=-\frac{\dot{\varepsilon}+r(\rho\dot{\sigma}+r\dot{\tau})}{\varphi},\quad \varphi=\sigma\rho+r(2\tau+r\sigma\rho^{-1}). \end{align} $$

Step 2. Assume now that $\mathop {\textrm {tr}}(X)=0$ . The second correction $P\mapsto P'$ is defined via a transformation

(3.30) $$ \begin{align} A_\circ'=\mathcal{K} A_\circ\mathcal{K},\quad B_\circ'=\mathcal{K}^{-1} B_\circ\mathcal{K}^{-1},\quad \mathcal{K}= \begin{bmatrix}{\kappa^{1/2}}&{0}\\ {0}&{\kappa^{-1/2}} \end{bmatrix}, \end{align} $$

and the goal is to have

(3.31) $$ \begin{align} X'=\begin{bmatrix} {s}&{w}\\ {-w}&{-s} \end{bmatrix} \quad\textrm{if } X=\begin{bmatrix} {s}&{b}\\ {c}&{-s} \end{bmatrix}. \end{align} $$

Recall that $X\approx J$ in our applications, so that $s\approx 0$ , $b\approx 1$ , and $c\approx -1$ . Clearly $X'=\mathcal {K}^{-1}X\mathcal {K}$ is of the desired form if we choose

(3.32) $$ \begin{align} \kappa=\sqrt{-b/c}. \end{align} $$

Then $w=\sqrt {-bc}$ . The derivative with respect to a parameter is trivial, so we will not give it here.

Step 3. Assume now that $X=[{\phantom {-} s~\phantom {-} w\atop -w~-s}]$ . The third correction $P\mapsto P'$ is of the form

(3.33) $$ \begin{align} A_\circ'=RA_\circ R,\quad B_\circ'=R^{-1}B_\circ R^{-1}, \quad R=\begin{bmatrix} {\rho}&{r}\\ {r}&{\rho} \end{bmatrix}, \end{align} $$

with $\rho ^2=1+r^2$ . The goal is to determine r in such a way that $X'=R^{-1}XR$ is equal to J. An explicit computation shows that this is achieved with

(3.34) $$ \begin{align} r=\frac{-s}{\sqrt{2(w^2-s^2)+2w\sqrt{w^2-s^2}}}. \end{align} $$

For the derivative with respect to a parameter, we find that

(3.35) $$ \begin{align} \dot r=-\frac{\tfrac12 \dot s+r(\dot w\rho+\dot sr)}{\psi},\quad \psi=w\rho+r(2s+w\rho^{-1}r). \end{align} $$

3.5 The fixed point problem

Consider now the transformation $\mathfrak {R}_3$ defined by (3.16). Our first goal is to prove that $\mathfrak {R}_3$ has a fixed point $P_\ast $ that has potentially the properties described in Theorem 2.2. As is common in many computer-assisted proofs, we associate with the given transformation $\mathfrak {R}_3$ a quasi-Newton map $\mathfrak {M}$ that we hope to be a contraction near some approximate fixed point $\bar P$ . Picking an approximate inverse ${\textrm {I}}-M$ of ${\textrm {I}}-D\mathfrak {R}_3(\bar P)$ , we define

(3.36) $$ \begin{align} \mathfrak{M}(p)=\mathfrak{R}_3(\bar P+({\textrm{I}}-M)p)-\bar P+Mp. \end{align} $$

Here, the sum of map-pairs is defined componentwise, and $c_1(\gamma ,C_1)+c_2(\gamma ,C_2)$ is defined as $(\gamma ,c_1C_1+c_2C_2)$ . Notice that, if p is a fixed point of $\mathfrak {M}$ , then $P=\bar P+ ({\textrm {I}}-M)p$ is a fixed point of $\mathfrak {R}_3$ .

The following function spaces have already been used in [36]. Given $\rho>0$ , denote by $\mathcal {G}_\rho $ the space of all real analytic functions g on $(-\rho ,\rho )$ that have a finite norm

(3.37) $$ \begin{align} \|g\|_\rho=\sum_{n=0}^\infty|g_n|\rho^n,\quad g(x)=\sum_{n=0}^\infty g_n x^n. \end{align} $$

Notice that every function $g\in \mathcal {G}_\rho $ extends analytically to the complex disk $|x|<\rho $ . Furthermore, $\mathcal {G}_\rho $ is a Banach algebra under the pointwise product of functions.

The space of matrix functions

(3.38) $$ \begin{align} C_\circ= \begin{bmatrix} {t_\circ+s_\circ}&{u_\circ}\\ {v_\circ}&{t_\circ-s_\circ} \end{bmatrix} , \end{align} $$

with $t_\circ $ , $u_\circ $ , $v_\circ $ , and $s_\circ $ belonging to $\mathcal {G}_\rho $ , will be denoted by $\mathcal {G}_\rho ^4$ . The norm of $C_\circ \in \mathcal {G}_\rho ^4$ is defined as $\|C_\circ \|_\rho =\|t_\circ \|_\rho +\|u_\circ \|_\rho +\|v_\circ \|_\rho +\|s_\circ \|_\rho $ .

Given a pair $\rho =(\rho _{\text {F}},\rho _{\text {G}})$ of positive real numbers, we define $\mathcal {F}_\rho $ to be the vector space of all pairs $\mathcal {P}=(B_\circ ,A_\circ )$ in $\mathcal {G}_{\rho _{\text {F}}}^4\times \mathcal {G}_{\rho _{\text {G}}}^4$ , equipped with the norm $\|\mathcal {P}\|_\rho =\|B_\circ \|_{\rho _{\text {F}}}+\|A_\circ \|_{\rho _{\text {G}}}$ . The subspace of pairs $\mathcal {P}\in \mathcal {F}_\rho $ that satisfy the (anti-)reversibility conditions (3.7) will be denoted by $\mathcal {F}_\rho ^{\hskip 2.3pt r}$ .

For simplicity, and when no confusion can arise, we will identify a skew-product map $H=(\gamma ,C)$ with its symmetric factor $C_\circ $ . Referring to the representation (3.38), we note that H is reversible with respect to $iJ$ if and only if the functions $t_\circ $ and $s_\circ $ are even, while $v_\circ (-x)=u_\circ (x)$ . Or $C_\circ $ is anti-reversible precisely if $t_\circ $ and $s_\circ $ are odd, while $v_\circ (x)=-u_\circ (-x)$ .

In our applications, we always choose $\varrho _{\mathrm F}\le \varrho _{\mathrm G}$ . Under these conditions, (3.3) and (3.4) show that $\mathfrak {R}_3$ is well defined on $\mathcal {F}_\rho $ if

(3.39) $$ \begin{align} \tfrac{1}{2}<\rho_{\text{G}}\le \rho_{\text{F}}<\alpha^{-3}\rho_{\text{G}}-\tfrac{1}{2}\alpha^{-1}. \end{align} $$

To be more precise, the conditions needed in the normalization step $\mathfrak {N}$ and for the commutator correction $\mathfrak {C}$ (all of which represent ad hoc choices) also require some mild non-degeneracy properties. We note that the domain conditions for the transformation $\mathfrak {R}$ are more restrictive than the conditions (3.39) for $\mathfrak {R}_3$ . But both are satisfied with comfortable margins in the case $\rho _{\kern0.7pt\textrm{F}}=2$ and $\rho _{\kern0.7pt\textrm{G}}={11}/{8}$ considered below.

For reference later on, we note that the transformation $\mathfrak {R}_3$ is compact, due to the analyticity-improving property of $\mathfrak {R}_3$ . To be more precise, the transformation $(B_\circ ,A_\circ )\mapsto (\tilde B_\circ ,\tilde A_\circ )$ defined by equations (3.3), (3.4), and (3.5) maps bounded sets in $\mathcal {F}_\rho $ to bounded sets in $\mathcal {F}_{\rho '}$ , for some choice of $\rho _{\kern0.7pt\textrm{F}}'>\rho _{\kern0.7pt\textrm{F}}$ and $\rho _{\kern0.7pt\textrm{G}}'>\rho _{\kern0.7pt\textrm{G}}$ . And the inclusion map from $\mathcal {F}_{\rho '}$ into $\mathcal {F}_\rho $ is compact.

Lemma 3.1. Let $\rho =(2,{11}/{8})$ . Then there exist a pair $\bar P$ in $\mathcal {F}_\rho ^{\hskip2.3pt r}$ , a bounded linear operator M on $\mathcal {F}_\rho ^{\hskip 2.3pt r}$ , and positive constants $\varepsilon ,K,\delta $ satisfying $\varepsilon +K\delta <\delta $ , such that the transformation $\mathfrak {M}$ defined by (3.36) is analytic in $B_\delta $ and satisfies

(3.40) $$ \begin{align} \|\mathfrak{M}(0)\|_\rho\le\varepsilon,\quad \|D\mathfrak{M}(p)\|_\rho\le K,\quad p\in B_\delta, \end{align} $$

where $B_\delta $ denotes the open ball of radius $\delta $ in $\mathcal {F}_\rho ^{\hskip 2.3pt r}$ , centered at the origin. Every pair $p\in B_\delta $ has the following properties. The matrix components of $P=\bar P+({\textrm {I}}-M)p$ are non-constant and satisfy the bound $\|P-\bar P\|_\rho <10^{-450}$ . Furthermore, the angle $\vartheta =\vartheta (P)$ satisfies $\sin (2\vartheta )=-0.01760801\ldots .$

Our proof of this lemma is computer-assisted, as described in §8. These estimates will be used in §5.1 to give a proof of Theorem 2.2.

Remark 2. The angle $\vartheta $ mentioned in Lemma 3.1 depends on the choice of coordinates. So it seems to say something about the AM model, but it is not clear what. In this context, we note that the change of coordinates M which yields AM factors of the form (3.11) achieves nothing useful in the case $\xi ={\alpha }/{2}-\tfrac {1}{4}$ considered here. It was chosen since it diagonalizes the y-scaling in the reversible case $\xi ={\alpha }/{2}$ .

4 The RG transformation for reversible pairs

The goal here is to reduce the proof of Theorem 2.1 to technical estimates similar to those in Lemma 3.1. An extra step is necessary to prove that the pair $P_\star $ commutes.

4.1 Scaling and normalization

We work in a basis where the AM factor $A_\circ $ for $\xi ={\alpha }/{2}$ and $E=0$ takes the form (3.11), with the sine replaced by a cosine. The corresponding AM map G is reversible with respect to $\Sigma =S$ , with S as defined in (3.6). So throughout this section, we restrict to pairs that are reversible with respect to $\Sigma =S$ . Referring to (3.38), reversibility of $H=(\gamma ,C)$ is equivalent to the functions $t_\circ ,u_\circ ,v_\circ $ being even and $s_\circ $ odd.

The matrix $L_3$ that enters the definition $\Lambda _3(x,y)=(\alpha ^3x,L_3 y)$ of the scaling used for $\mathfrak {R}^3$ and $\mathfrak {R}_3$ is taken to be of the form

(4.1) $$ \begin{align} L_3=Se^{\sigma_3 S}= \begin{bmatrix}{e^{\sigma_3}}&{0}\\ {0}&{-e^{-\sigma_3}} \end{bmatrix}, \end{align} $$

with $\sigma _3=\sigma _3(P)$ depending on the pair P being renormalized. Notice that $L_3$ commutes with S, so conjugacy by $\Lambda_3$ preserves reversibility.

Instead of $\mathfrak {R}^6$ , we first consider the transformation

(4.2) $$ \begin{align} \mathfrak{R}_6=\mathfrak{R}_3^2\circ\mathfrak{C},\quad \mathfrak{R}_3=\mathfrak{N}\circ\mathcal{R}_3, \end{align} $$

where $\mathcal {R}_3$ is the ‘basic’ RG transformation $P\mapsto \tilde P$ defined by equations (3.1) and (3.2). The transformation $\mathfrak {N}$ renormalizes determinants, as described after (3.17). The transformation $\mathfrak {C}$ is a commutator correction that will be described below.

With a y-scaling $L_3$ of the form (4.1), the symmetric factor of $\tilde F=\Lambda _3^{-1}\hat F\Lambda _3$ is given by

(4.3) $$ \begin{align} \tilde B_\circ(0)=\Lambda_3^{-1}\hat B_\circ(0)\Lambda_3 =\begin{bmatrix} {a}&{-e^{-2\sigma_3}u}\\ {-e^{2\sigma_3}v}&{d} \end{bmatrix},\quad \begin{bmatrix} {a}&{u}\\ {v}&{d} \end{bmatrix} \mathrel{\mathop=^{\textrm{def}}}\hat B_\circ(0), \end{align} $$

where $\hat B_\circ $ is as described in (3.3). We determine $\sigma _3=\sigma _3(P)$ is such a way that the off-diagonal elements of $\tilde B_\circ (0)$ are equal in modulus. In other words, $e^{-2\sigma _3}|u|=e^{2\sigma _3}|v|$ . Unless $uv=0$ , which does not occur in the cases considered, this trivially determines the scaling exponent $\sigma _3(P)$ .

4.2 Commutator correction

Unlike in the anti-reversible case, the largest eigenvalue of $\mathfrak {R}_3^2(P_\star )$ in the non-commuting direction appears to be $1$ . Our goal here is to eliminate this eigenvalue. One reason is that an eigenvalue of $1$ makes a quasi-Newton map ill-defined. Another reason is that the correction will be needed to prove that the pair $P_\star $ is in fact commuting.

The commutator for $P=(F,G)$ at $x=({1+\alpha })/{ 2}$ is again given by equation (3.23). By reversibility, we have $SXS=Y^{-1}$ . So X, Y, and $XY^{-1}$ are of the form

(4.4) $$ \begin{align} X=\begin{bmatrix} {a}&{b}\\ {c}&{d} \end{bmatrix},\quad Y=\begin{bmatrix} {d}&{b}\\ {c}&{a} \end{bmatrix},\quad XY^{-1}=\textbf{1}+(a-d)\begin{bmatrix} {a}&{-b}\\ {c}&{-d} \end{bmatrix}, \end{align} $$

with $ad-bc=1$ . In particular, $\mathop {\textrm {tr}}(XY^{-1})=1+(a-d)^2$ . So reversibility implies that the trace of the commutator does not change to first order. This motivates what follows. Consider a commutator correction $\mathfrak {C}:P\mapsto P'$ of the form

(4.5) $$ \begin{align} A_\circ'=RA_\circ R,\quad B_\circ'=R^{-1}B_0R^{-1},\quad R=\begin{bmatrix} {\rho}&{r}\\ {r}&{\rho} \end{bmatrix}, \end{align} $$

with $\rho ^2=1+r^2$ . Then $\mathfrak {C}(P')=X'{Y'}^{-1}$ , with $X'=R^{-1}XR$ and $Y'=RYR^{-1}$ . Ideally, we can find r in such away that $X'=Y'$ , or equivalently, that

(4.6) $$ \begin{align} Y=R^{-2}XR^2. \end{align} $$

As it turns out, this can be achieved not only to first order, but exactly, by choosing

(4.7) $$ \begin{align} r=\frac{q}{ 2}\bigg(\frac{2}{(1-q^2)^{1/2}+1-q^2}\bigg)^{1/2}, \quad q=-\frac{a-d}{ c-b}. \end{align} $$

This completes the definition (4.2) of the transformation $\mathfrak {R}_6$ . For estimates of the derivative $D\mathfrak {R}_6(P)\dot P$ we use that

(4.8) $$ \begin{align} \dot r=\frac{\dot q}{ 2}\cdot\frac{\rho}{ 1-q^2},\quad \dot q=\frac{(\dot a-\dot d)-q(\dot c-\dot b)}{ c-b}. \end{align} $$

4.3 Proof of Theorem 2.1

In this subsection we give a proof of Theorem 2.1 based on estimates that have been verified with the aid of a computer. We start by solving the fixed point equation for $\mathfrak {R}_6$ . To this end, we use again a quasi-Newton map of the type (3.36), namely

(4.9) $$ \begin{align} \mathfrak{M}(p)=\mathfrak{R}_6(\bar P+({\textrm{I}}-M)p)-\bar P+Mp, \end{align} $$

where $\bar P$ is an approximate fixed point of $\mathfrak {R}_6$ , and where ${\textrm {I}}-M$ is an approximation for the inverse of ${\textrm {I}}-D\mathfrak {R}_3(\bar P)$ . The relevant functions spaces are the spaces $\mathcal {G}_\rho $ and $\mathcal {F}_\rho $ defined in §3.5. But $\mathcal {F}_\rho ^{\hskip 2.3pt r}$ now denotes the subspace of $\mathcal {F}_\rho $ of pairs that are reversible with respect to S.

Lemma 4.1. Let $\rho =(3,2)$ . Then there exist a pair $\bar P$ in $\mathcal {F}_\rho ^{\hskip2.3pt r}$ , a bounded linear operator M on $\mathcal {F}_\rho ^{\hskip 2.3pt r}$ , and positive constants $\varepsilon ,K,\delta $ satisfying $\varepsilon +K\delta <\delta $ , such that the transformation $\mathfrak {M}$ defined by (4.9) is analytic in $B_\delta $ and satisfies

(4.10) $$ \begin{align} \|\mathfrak{M}(0)\|_\rho\le\varepsilon,\quad \|D\mathfrak{M}(p)\|_\rho\le K,\quad p\in B_\delta, \end{align} $$

where $B_\delta $ denotes the open ball of radius $\delta $ in $\mathcal {F}_\rho ^{\hskip 2.3pt r}$ , centered at the origin. Every pair $p\in B_\delta $ has the following properties. The matrix components of $P=\bar P+({\textrm {I}}-M)p$ are non-constant and satisfy the bound $\|P-\bar P\|_\rho <10^{-439}$ . Furthermore, the six-step scaling factor $\mathcal {V}=e^{\sigma _6(P)}$ satisfies the bound described in Theorem 2.1.

Our proof of this lemma is computer-assisted, as described in §8.

By the contraction mapping theorem, Lemma 4.1 guarantees the existence of a fixed point $p_\star \in B_\delta $ for $\mathfrak {M}$ and thus a fixed point $P_\star =\bar P+({\textrm {I}}-M)p_\star $ for $\mathfrak {R}_6$ . The symmetric factors for $F_\star $ and $G_\star $ are analytic in the disks $|x|<\rho _F$ and $|x|<\rho _G$ , respectively. A trivial computation, using the expressions (3.3) and (3.4) for the symmetric factors of $\hat F=GF^\dagger G$ and $\hat G=G^\dagger FG^\dagger FG^\dagger $ , respectively, shows that radii of the domains of analyticity increase with each iteration of $\mathfrak {R}_3$ by a factor larger than $1$ . The factor approaches $\alpha ^{-3}$ as the number of iterations increases. This shows that $B_\star $ and $A_\star $ extend to entire functions.

What remains to be proved is that the components $F_\star $ and $G_\star $ of the pair $P_\star $ commute. To this end, consider the commutator factor $\mathcal {C}(P,z)$ defined by (3.21). It admits a representation (3.22), with

(4.11) $$ \begin{align} \mathcal{A}(P,z)=A_0\big(\tfrac{1}{2}+\alpha^3z\big)Se^{\sigma_3(P)S}. \end{align} $$

Let $P_3=\mathfrak {R}_3(P)$ and $P_6=\mathfrak {R}_3(P_3)$ . Applying the identity (3.22) twice, we obtain

(4.12) $$ \begin{align} \mathcal{C}(P_6,z)=\mathcal{A}_2(P,z)^{-1} \mathcal{C}(P,\alpha^6 z)\mathcal{A}_2(P,z), \end{align} $$

where

(4.13) $$ \begin{align} \mathcal{A}_2(P,z)=\mathcal{A}(P,\alpha^3z)\mathcal{A}(P_3,z). \end{align} $$

Let $\mathcal {C}(P)=\mathcal {C}(P,0)$ .

Consider now the pair $P=\mathfrak {C}(P_\star )$ . Then $\mathcal {C}(P)$ is the identity matrix. This follows from our definition of the commutator correction $\mathfrak {C}$ . Given that $P_\star $ is a fixed point of $\mathfrak {R}_6=\mathfrak {R}_3^2\circ \mathfrak {C}$ and thus $P_6=P_\star $ , we see from (4.12) that $\mathcal {C}(P_\star )$ is the identity matrix as well. This implies, in particular, that $P=P_\star $ , so that $P_\star $ is a fixed point of $\mathfrak {R}_3^2$ .

In the case $P=P_\star $ , equation (4.12) is a linear fixed point equation for the function $z\mapsto \mathcal {C}(P_\star ,z)$ . We already know that $\mathcal {C}(P_\star ,z)$ is the identity matrix for $z=0$ . Whether or not the same holds for $z\ne 0$ depends on the eigenvalues of the matrix $\mathcal {A}_2(P_\star )=\mathcal {A}_2(P_\star ,0)$ .

Lemma 4.2. The eigenvalues of $\mathcal {A}_2(P_\star )$ are $\nu =2.8900536382\ldots $ and $\nu ^{-1}$ .

Our proof of this lemma is computer-assisted, as described in §8. It also verifies that the origin $z=0$ belongs to the domain of analyticity of the function that appears in (4.12). But this could easily be checked by hand as well.

We note that $\nu $ appears to satisfy the equation $\nu +\nu ^{-1}=2\alpha ^{-1}$ . If this is the case, and if the scaling factor $\mathcal {V}$ in Theorem 2.1 satisfies $\mathcal {V}+\mathcal {V}^{-1}=2\alpha ^{-3}$ , then $\nu ^2=\mathcal {V}$ .

In some open neighborhood of the origin in $\mathbb {C}$ , we have either $\mathfrak {C}(P_\star ,z)=\textbf {1}$ for all z, or else

(4.14) $$ \begin{align} \mathcal{C}(P_\star,z)=\textbf{1}+z^n[\mathcal{C}_n+\mathcal{O}(1)] \end{align} $$

for some non-zero matrix $\mathcal {C}_n$ and some integer $n\ge 1$ . Substituting this expression for $\mathcal {C}(P_\star ,z)$ into (4.12) yields the identity

(4.15) $$ \begin{align} \mathcal{C}_n=\alpha^{6n}\mathcal{A}_2(P_\star)^{-1}\mathcal{C}_n\mathcal{A}_2(P_\star). \end{align} $$

The eigenvalues of $\mathcal {C}_n\mapsto \alpha ^{6n}\mathcal {A}_2(P_\star )^{-1}\mathcal {C}_n\mathcal { A}_2(P_\star )$ are $\alpha ^{6n}$ and $\alpha ^{6n}\nu ^{\pm 2}$ . They are all less than $1$ , so equation (4.15) cannot have a solution $\mathcal {C}_n\ne 0$ . This shows that the commutator of $F_\star $ and $G_\star $ is constant and equal to the identity in some open neighborhood of $x=({1+\alpha })/{ 2}$ . Given that $B_\star $ and $A_\star $ are entire analytic, this implies that $F_\star $ and $G_\star $ commute.

At this point, the proof of Theorem 2.1 is reduced to the task of verifying the bounds in Lemmas 4.1 and 4.2.

5 Hyperbolicity

Here we consider again the anti-reversible case and the AM maps (3.11).

5.1 Proof of Theorem 2.2

Our goal here is to prove Theorem 2.2, with the exception of the inequality $\mu _2\ge \alpha ^{-3}$ , based on estimates that can be (and have been) verified with the aid of a computer. The inequality $\mu _2\ge \alpha ^{-3}$ will be proved in §6.

By the contraction mapping theorem, Lemma 3.1 guarantees the existence of a fixed point $p_\ast \in B_\delta $ for $\mathfrak {M}$ and thus a fixed point $P_\ast =\bar P+({\textrm {I}}-M)p_\ast $ for $\mathfrak {R}_3$ . For the same reasons as in the reversible case, the factors $B_\ast $ and $A_\ast $ associated with $P_\ast $ extend to entire functions.

In order to prove hyperbolicity and related properties, we consider the transformation $\mathfrak {T}$ defined by

(5.1) $$ \begin{align} \mathfrak{T}(p)=\mathcal{L}^{-1}[\mathfrak{R}_3^2(P_\ast+\mathcal{L} p)-P_\ast], \end{align} $$

where $\mathcal {L}$ is a suitable linear isomorphism of $\mathcal {F}_\rho ^{\hskip 2.3pt r}$ . Clearly $p_\ast =0$ is a fixed point of $\mathfrak {T}$ . We expect the derivative $D\mathfrak {T}(0)$ to have an eigenvalue $\alpha ^{-6}$ and no other spectrum outside the open unit disk. Thus, we consider a decomposition $\mathcal {F}_\rho ^{\hskip 2.3pt r}=\mathcal {U}\oplus \mathcal {W}$ , where $\mathcal {U}$ is a convenient one-dimensional subspace of $\mathcal {F}_\rho ^{\hskip 2.3pt r}$ . We will refer to $\mathcal {U}$ and $\mathcal {W}$ as the vertical and horizontal subspaces, respectively. Now the isomorphism $\mathcal {L}$ is chosen in such a way that the expected expanding direction of $D\mathfrak {T}(0)$ is roughly vertical. Writing an element $q\in \mathcal {F}_\rho ^{\hskip 2.3pt r}$ as $q=[{u\atop w}]$ , with $u\in \mathcal {U}$ and $w\in \mathcal {W}$ , we obtain a representation

(5.2) $$ \begin{align} D\mathfrak{T}(p)q= \begin{bmatrix} {M_{uu}(p)}&{M_{uw}(p)}\\ {M_{wu}(p)}&{M_{ww}(p)} \end{bmatrix} \begin{bmatrix}{u}\\ {w} \end{bmatrix},\quad q=\begin{bmatrix} {u}\\{w} \end{bmatrix}. \end{align} $$

By choosing $\mathcal {L}$ properly, the operators $M_{uw}(p):\mathcal {W}\to \mathcal {U}$ and $M_{wu}(p):\mathcal {U}\to \mathcal {W}$ can be made small for all p near $p_\ast =0$ . And $M_{uu}(p)$ should be close to $\alpha ^{-6}\simeq 18$ . In order to simplify notation, we identify $\mathcal {U}$ with $\mathbb {R}$ by choosing a unit vector $u_0\in \mathcal {U}$ and identifying the vector $tu_0$ with the coefficient t.

Specific estimates are obtained in terms of an enclosure

(5.3) $$ \begin{align} N_{uu}^{-}\le M_{uu}(p)\le N_{uu}^{+} \end{align} $$

and upper bounds

(5.4) $$ \begin{align} \|M_{uw}(p)\|\le N_{uw},\quad \|M_{wu}(p)\|\le N_{wu},\quad \|M_{ww}(p)\|\le N_{ww} \end{align} $$

that hold for all pairs p in a suitable cylinder $C_1$ . Here, and in what follows, $\|.\|$ denotes the norm in $\mathcal {F}_\rho $ . To be more precise, we determine two cylinders $C_0$ and $C_1$ such that

(5.5) $$ \begin{align} C_0\subset C_1,\quad C_j=[-h_j,h_j]\times\{w\in\mathcal{W}: \|w\|<r\}, \end{align} $$

with $0<r<h_0<h_1$ . Notice that both cylinders are centered at $p_\ast =0$ . The goal is to show that $\mathfrak {T}$ maps $C_0$ into $C_1$ and $C_1\setminus C_0$ into the complement of $C_0$ . To this end, it suffices to prove that

(5.6) $$ \begin{align} \begin{aligned} N_{uu}^{+}h_0+N_{uw}r&<h_1,\quad N_{wu}h_0+N_{ww}r<r,\\ N_{uu}^{-}h_0-N_{uw}r&>h_0. \end{aligned} \end{align} $$

Here, we have used that $\mathfrak {T}(p+q)-\mathfrak {T}(p)=\int _0^1 D\mathfrak {T}(p+sq)q\,ds$ whenever p and $p+q$ both belong to $C_1$ .

Lemma 5.1. There exists a linear isomorphism $\mathcal {L}$ of $\mathcal {F}_\rho ^{\hskip 2.3pt r}$ , as well as positive real numbers $r<h_0<h_1,N_{uu}^{-}<N_{uu}^{+},N_{uw},N_{wu},N_{ww}$ that satisfy (5.6), such that the derivative of the transformation $\mathfrak {T}$ defined by (5.1) satisfies the bounds (5.3) and (5.4) for every $p\in C_1$ . So $\mathfrak {T}$ maps $C_0$ into $C_1$ and $C_1\setminus C_0$ to the complement of $C_0$ , with room to spare for taking interiors and/or closures. Let

(5.7) $$ \begin{align} a_{\pm}=N_{uu}^{\pm}\pm N_{uw},\quad b=N_{wu}+N_{ww},\quad c=N_{uu}^{-}-N_{uw}-N_{wu}-N_{ww}. \end{align} $$

Then $a_{+}<19$ , $b<\tfrac {1}{4}$ , and $c>17$ .

Our proof of this lemma is computer-assisted, as described in §8.

One of the consequences of the ‘uniform hyperbolicity’ described in Lemma 5.1 is the following corollary.

Corollary 5.2. Let $p\in C_0$ . Then either $\mathfrak {T}^n(p)$ belongs to $C_1\setminus C_0$ for some $n>0$ , or else $\mathfrak {T}^n(p)\to 0$ as $n\to \infty $ .

Proof. Let $p\in C_0$ . Since the orbit of p can exit $C_0$ only via the set $C_1\setminus C_0$ , it suffices to consider the case where $p_n=\mathfrak {R}^n(p)$ belongs to $C_0$ for all $n\ge 0$ .

Write $p_n=[{u_n\atop w_n}]$ with $u_n\in \mathcal {U}$ and $w_n\in \mathcal {W}$ . From (5.3) and (5.4) we see that

(5.8) $$ \begin{align} |u_{n+1}|\ge N_{uu}^{-}|u_n|-N^{uw}\|w_n\|,\quad \|w_{n+1}\|\le N_{wu}|u_n|+N_{ww}\|w_n\|, \end{align} $$

for all $n\ge 0$ . Assume for contradiction that $|u_m|-\|w_m\|>0$ for some $m\ge 0$ . Then

(5.9) $$ \begin{align} |u_{m+1}|-\|w_{m+1}\| \ge N_{uu}^{-}|u_m|-N_{uw}\|w_m\|-N_{wu}|u_m|-N_{ww}\|w_m\|>c\|w_m\|, \end{align} $$

with $c>0$ as defined in (5.7). So we have $|u_n|-\|w_n\|>0$ for all $n\ge m$ . Combining this with the first inequality in (5.8), we find that

(5.10) $$ \begin{align} |u_{n+1}|>a|u_n|, \end{align} $$

for all $n\ge m$ , with $a=a_{-}$ as defined in (5.7). Given that $a>1$ , this leads to a contradiction. So we must have $|u_n|\le \|w_n\|$ for all $n\ge 0$ . By the second inequality in (5.8), this implies that

(5.11) $$ \begin{align} \|w_{n+1}\|\le N_{wu}|u_n|+N_{ww}\|w_n\|\le b\|w_n\|, \end{align} $$

for all $n\ge 0$ , with b as defined in (5.7). Given that $b<1$ , we find that $w_n\to 0$ as $n\to \infty $ . But $|u_n|\le \|w_n\|$ for all $n\ge 0$ , so $u_n\to \infty $ as well. Thus, $p_n\to 0$ as claimed.

The bounds $a_{-}>17$ and $b<\tfrac {1}{4}$ from Lemma 5.1 yield information about the spectrum of $D\mathfrak {T}(0)$ , using the theorem below, for example. We note that the operator $D\mathfrak {T}(0)$ is compact, for the reasons described before Lemma 3.1.

Theorem 5.3. [2]

Let A be a compact linear operator on a real Banach space $\mathbb {R}\times W$ . For $u\in \mathbb {R}$ and $w\in W$ , write $A(u+w)=u'+w'$ with $u'\in \mathbb {R}$ and $w'\in W$ . Assume that there exist positive real numbers $b<a$ such that $\|w'\|\le b\max \{|u|,\|w\|\}$ , and such that $|u'|\ge a|u|$ whenever $|u|\ge \|w\|$ . Then A has a simple eigenvalue of modulus at least a and no other eigenvalue of modulus greater than b.

Here, in the real setting, a non-real number $\xi +i\eta $ is said to be an eigenvalue of A if there exist non-zero vectors x and y such that $Ax=\xi x-\eta y$ and $Ay=\xi y+\eta x$ .

As a consequence of Lemma 5.1 and Theorem 5.3 we have the following corollary.

Corollary 5.4. The derivative $D\mathfrak {T}(p_\ast )$ at $p_\ast =0$ has a real eigenvalue $\unicode{x3bb} \ge a_{-}$ and no other spectrum outside the disk $|z|\le b$ . The local unstable manifold of $\mathfrak {T}$ at the fixed point $p_\ast =0$ is the graph of a real analytic function $\texttt{P}_\ast $ from an open neighborhood of the origin in $\mathcal {U}$ to $\mathcal {W}$ . Furthermore, $\texttt{P}_\ast $ extends to a real analytic function on an open neighborhood of $[-h_0,h_0]$ , taking values in $\{w\in \mathcal {W}: \|w\|<r\}$ .

The existence and real analyticity of the local unstable manifold near $p_\ast =0$ follows from standard theorems on invariant manifolds. Its extension is obtained by iterating $\mathfrak {T}$ and using Corollary 5.2.

Clearly Corollary 5.4 translates trivially to an analogous result for the transformation $\mathfrak {R}_3^2$ . In fact, an analogous result holds for $\mathfrak {R}_3$ as well, since $P_\ast $ is a fixed point of $\mathfrak {R}_3$ . Our reason for considering the second iterate of $\mathfrak {R}_3$ in this section is that it was easier to find a good isomorphism $\mathcal {L}$ in this case.

5.2 Proof of Theorem 2.3, Part I

Our goal here is to prove Theorem 2.3, based on estimates that can be (and have been) verified with the aid of a computer. A transversality condition that is needed, and the claim that $s_\ast =0$ , will be proved in §6.

Here we consider the unstable manifold of $\mathfrak {R}_3$ at $P_\ast $ to be a curve in the cylinder $C_0'=P_\ast +\mathcal {L} C_0$ rather than a graph. A possible parametrization of this curve is given by $\texttt{P}_\ast (t)=P_\ast +\mathcal {L}(tu_0+\texttt{P}_\ast (t))$ , with t ranging in $[-h_0,h_0]$ . Here $u_0\in \mathcal {U}$ is the unit vector mentioned earlier. The projection of $\texttt{P}_\ast $ onto $\mathcal {L}\mathcal {U}$ is a strictly increasing function; and as t increases from $-h_0$ to $h_0$ , the curve $\texttt{P}$ connects the bottom of $C_0'$ to the top.

Given a real number $c>0$ , consider the extension of $\mathfrak {R}_3$ to one-parameter families of pairs $s\mapsto \texttt{P}(s)$ , defined by the equation

(5.12) $$ \begin{align} \mathfrak{F}_c(\texttt{P})(s)=\mathfrak{R}_3(\texttt{P}(cs)). \end{align} $$

Lemma 5.5. Consider the AM family $\texttt{P}$ for $\unicode{x3bb} =e^s$ . Then there exist real numbers $\sigma ,\varepsilon>0$ and an integer $m>0$ , such that the following statement holds. Consider the curve $\texttt{P}_0=\mathfrak {F}_{\alpha ^3}^{2m}(\texttt{P})$ . Then $\texttt{P}_0(s)$ lies in the interior of $C_0'$ for $-\sigma <s<\sigma $ . As s is increased from $-\sigma -\varepsilon $ to $\sigma +\varepsilon $ , the curve $\texttt{P}_0$ enters the cylinder $C_0'$ through the bottom (corresponding to $u=-h_0$ for $C_0$ ) at $s=-\sigma $ and leaves it through the top (corresponding to $u=-h_0$ for $C_0$ ), at $s=\sigma $ . An analogous statement holds if $\texttt{P}$ is replaced by $\mathfrak {F}_{\alpha ^3}(\texttt{P})$ .

Our (computer-assisted) proof of this lemma implements the transformation $\mathfrak {F}_{\alpha ^3}$ on a space of curves $s\mapsto \texttt{P}(s)$ in $\mathcal {F}_\rho $ that are analytic in a disk $|s|<\delta $ of radius $\delta =2^{-96}$ . In this space, we determine bounds on the curve $\texttt{P}_0=\mathfrak {F}_{\alpha ^3}^{2m}(\texttt{P})$ for $m=66$ that imply the claims of Theorem 2.3 via strict inequalities. For further details we refer to §8.

Some immediate consequences of Lemma 5.5 are as follows. There exist an increasing sequence $n\mapsto s_n^{-}$ and a decreasing sequence $n\mapsto s_n^{+}$ , with $s_n^{-}<s_n^{+}$ for all n, such that the curve $\texttt{P}_n=\mathfrak {F}_1^{2n}(\texttt{P}_0)$ enters the bottom of the cylinder $C_0'$ at the parameter value $s_n^{-}$ and leaves the top of the cylinder for the first time at a parameter value $s_n^{+}$ .

Pick a parameter value $s_\infty $ that belongs to $[s_n^{-},s_n^{+}]$ for every n. Then the orbit $n\mapsto \mathfrak {R}_3^{2n}(\texttt{P}_0(s_\infty ))$ converges to $P_\ast $ by Corollary 5.2. If n is sufficiently large, then the pair $\texttt{P}_n(s_\infty )$ is close enough to $P_\ast $ for perturbative arguments to apply. In particular, if $\texttt{P}_n$ intersects the local stable manifold transversally, then we can use the graph transform [29] to characterize convergence.

The graph transform $\mathfrak {F}$ associated with $\mathfrak {R}_3^2$ takes the form $\mathfrak {F}(\texttt{P})=\mathfrak {R}_3^2\circ \texttt{P}\circ R$ . Here, $R=R(\texttt{P})$ is a real analytic function defined near $s_\infty $ . Its dependence on $\texttt{P}$ is real analytic and can be chosen in such a way that $\mathfrak {F}$ has an attracting fixed point. By construction, this fixed point is the (canonically parametrized) local unstable manifold of $\mathfrak {R}_3$ at $P_\ast $ . If $\texttt{P}$ is any curve in the domain of $\mathfrak {F}$ , then the sequence $k\mapsto \mathfrak {F}^k(\texttt{P})$ converges to the fixed point of $\mathfrak {F}$ , and $k\mapsto R(\mathfrak {F}^k(\texttt{P}))$ converges to the function $s\mapsto \mu _2^{-1}s$ . In fact, R can be chosen affine, at the expense of possibly weakening the rate of convergence.

Assume now that $s_\infty $ must have the value $0$ , and that the curves $\texttt{P}_n$ , for n sufficiently large, are transversal to the local stable manifold of $\mathfrak {R}_3$ at $P_\ast $ . These properties will be proved in §6.

In this case, the reparametrization function R can be chosen linear. Since convergence of $k\mapsto R(\mathfrak {F}^k(\texttt{P}_n))$ to the function $s\mapsto \mu _2^{-2}s$ is exponential, we can in fact choose the fixed reparametrization $s\mapsto \mu _2^{-2}s$ at each step. This show that if $\texttt{P}$ is the AM family with parameter $\unicode{x3bb} =e^s$ , then the sequence $n\mapsto \mathfrak {F}_{\mu _2^{-2}}^n(\texttt{P}_0)$ converges to $\texttt{P}_\ast $ , modulo a one-time linear reparametrization. Here we assume that the local unstable manifold $\texttt{P}_\ast $ has been parametrized in such a way that it is a fixed point of $\mathfrak {F}_{\mu _2^{-2}}$ .

The same holds if $\texttt{P}$ is replaced by $\mathfrak {F}_{\alpha ^3}(\texttt{P})$ . So the above arguments can be repeated for the graph transform associated with $\mathfrak {R}_3$ . We note that the pairs $\texttt{P}_\ast (t)$ are limits of renormalized AM pairs, so they are commuting.

Since transversality to the local stable manifold is stable under small perturbations, we can repeat the same arguments for a sufficiently small perturbation of the AM curve. The only difference is that a one-time affine reparametrization is needed.

6 The Lyapunov exponent

The Lyapunov exponent will be used to establish a connection between observable quantities and local properties of $\mathfrak {R}_3$ near the fixed point $P_\ast $ .

6.1 The critical coupling

Let $G=(\alpha ,A)$ be the anti-reversible AM map with coupling constant $\unicode{x3bb} =e^s$ . Let $\unicode{x3bb} _\ast $ be a value of the parameter $\unicode{x3bb} $ for which the pair $P=(F,G)$ with $F=(1,\textbf {1})$ gets attracted to $P_\ast $ under the iteration of $\mathfrak {R}_3^2$ . The goal here is to show that $\unicode{x3bb} _\ast =1$ .

First, we claim that $\unicode{x3bb} _\ast \le 1$ . To see why, consider $\unicode{x3bb}>1$ . Then the Lyapunov exponent $L(G)=\log \unicode{x3bb} $ is positive. Thus, by Proposition 6.4 in §6.2, the sequence of functions $n\mapsto \|A^{\ast q_n}(\alpha ^n.)\|$ cannot stay bounded on $[-1,1]$ as $n\to \infty $ . So we cannot have $\mathfrak {R}^n(P)\to P_\ast $ as $n\to \infty $ along multiples of $3$ .

Our next goal is to exclude the possibility $\unicode{x3bb} _\ast <1$ . The following result is Theorem 3.4 in [4]. It applies to the AM map $G=(\alpha ,A)$ , for any irrational $\alpha $ whose continued fraction denominators $q_n$ satisfy $\lim _n q_n^{-1}\log q_{n+1}=0$ .

Theorem 6.1. [4]

Let $0<\unicode{x3bb} <1$ and assume that E belongs to the spectrum of $H_\unicode{x3bb} ^\alpha $ . There exist constants $a,b,c>0$ such that for all $q>0$ ,

(6.1) $$ \begin{align} \|A^{\ast q}(z)\|\le bq^a,\quad |\mathrm{Im}\, z|\le c. \end{align} $$

An analogous result for Diophantine $\alpha $ was probably proved earlier. Corollary 4.5 in [7] comes close, but it considers only the real domain.

In what follows, if $G=(\alpha ,A)$ is an arbitrary skew-product map, we will write $A^{\alpha \ast q}$ instead of $A^{\ast q}$ for the product (1.1), in order to emphasize the dependence on $\alpha $ .

Let G be an anti-reversible AM map for energy zero and $\alpha $ the inverse golden mean. Consider the corresponding pair $P=(F,G)$ with $F=(1,\textbf {1})$ , and its RG iterates $P_n=\mathfrak {R}_3^{2n}$ . We choose here even powers of $\mathfrak {R}_3$ , so that the reflections $L(0)$ that are part of the scaling $L_3=L(0)e^{-\vartheta J}$ cancel. And for the fixed point $P_\ast $ , the rotations cancel as well, since $L(0)e^{-\vartheta J}L(0)=e^{-\vartheta J}$ . Thus, in order to simplify notation, consider $\mathfrak {R}_3$ with ${L_3=\textbf {1}}$ . Then we can perform an initial rotation $A\mapsto e^{\vartheta J}Ae^{-\vartheta J}$ in such a way that $P_n\to P_\ast $ with $L_3=\textbf {1}$ fixed. Then $P_n=(F_n,G_n)$ with $F_n=(1,B_n)$ and $G_n=(\alpha ,A_n)$ , where

(6.2) $$ \begin{align} A_n(x)=A^{\alpha\ast q_{6n}}(\alpha^{6n}x),\quad B_n(x)=A^{\alpha\ast q_{6n-1}}(\alpha^{6n}x). \end{align} $$

As described earlier, the factors $A_\ast $ and $B_\ast $ of the fixed point $P_\ast $ are entire, due to the analyticity-improving property of $\mathfrak {R}_3$ . For the same reason, we have convergence $A_n\to A_\ast $ and $B_n\to B_\ast $ , uniformly on compact subsets of $\mathbb {C}$ .

Now let u and v be fixed but arbitrary non-negative integers, not both zero. Then

(6.3) $$ \begin{align} A_n^{\alpha\ast u}(.+v)B_n^{1\ast v} \to A_\ast^{\alpha\ast u}(.+v)B_\ast^{1\ast v}, \end{align} $$

uniformly on compact subsets of $\mathbb {C}$ .

Proposition 6.2. Assume that $\unicode{x3bb} _\ast <1$ . Then $x\mapsto A_\infty ^{\alpha \ast u}(x+v)B_\infty ^{1\ast v}(x)$ is a polynomial whose degree cannot be larger than the constant a in Theorem 6.1.

Proof. Let M be some fixed $2\times 2$ matrix and define

(6.4) $$ \begin{align} f_n=\mathop{\textrm{tr}}(M A_n^{\alpha\ast u}(.+v)B_n^{1\ast v}),\quad f_\ast=\mathop{\textrm{tr}}(M A_\ast^{\alpha\ast u}(.+v)B_\ast^{1\ast v}). \end{align} $$

By Theorem 6.1 we have a bound

(6.5) $$ \begin{align} |f_n(z)|\le 2b(uq_{6n-1}+vq_{6n})^a \le C(\alpha u+v)^a\alpha^{-6na},\quad |\textrm{Im}\, z|\le c\alpha^{-6n}, \end{align} $$

for some fixed constant $C>0$ . Now restrict to a disk $|z|\le r$ of radius $r>0$ . If n is sufficiently large, then

(6.6) $$ \begin{align} \partial_z^k f_n(z)=\frac{k!}{ 2\pi i}\int_{\Gamma_n} \frac{f_n(\zeta)}{(\zeta-z)^{k+1}}\,d\zeta, \end{align} $$

where $\Gamma _n$ is the path along the two circles in $\mathbb {C}/(\alpha ^{-6n}\mathbb {Z})$ at $\mathop {\textrm {Im}}\zeta =\pm c\alpha ^{-6n}$ . Using the bound (6.5) and the fact that $|\Gamma _n|=2\alpha ^{-6n}$ , we have

(6.7) $$ \begin{align} \begin{aligned} |\partial_z^k f_n(z)| &\le\frac{k!}{ 2\pi}2\alpha^{-6n}(c\alpha^{-6n}-r)^{-k-1} C(\alpha u+v)^a\alpha^{-6na}\\[3pt] &\le C_k(\alpha u+v)^a\alpha^{6n(k-a)}, \end{aligned} \end{align} $$

for some constant $C_k>0$ . Thus, if $k>a$ , then the derivative $\partial _z^k f_\ast (z)=\lim _n\partial _z^k f_n(z)$ vanishes on the disk $|z|<r$ .

This shows that $f_\ast $ is a polynomial of degree $\lfloor a\rfloor $ or less. Since M was arbitrary, we conclude that $x\mapsto A_\infty ^{\alpha \ast u}(x+v)B_\infty ^{1\ast v}(x)$ is a polynomial of degree $\lfloor a\rfloor $ or less.

Theorem 6.3. $\unicode{x3bb} _\ast =1$ .

Proof. We have already established that $\unicode{x3bb} _\ast \le 1$ . Assume for contradiction that $\unicode{x3bb} _\ast <1$ . In what follows, x and y denote real numbers. Given any $m>0$ , denote by $d_m$ the polynomial degree of $A_\ast ^{\ast m}$ , meaning the maximal degree of any of the components of $A_\ast ^{\ast m}$ . Clearly, $x\mapsto A_\ast ^{\alpha \ast m}(\omega x+z)$ has degree $d_m$ as well, for any complex numbers $\omega \ne 0$ and z.

Consider now the identity (3.8), which holds whenever $(\alpha ,A)$ is anti-reversible. By taking the trace of $(-1)^m A_\circ ^{\ast 2m}(iy)$ , we obtain the square of the Hilbert–Schmidt norm of $U(iy)=A_\circ ((m-\tfrac {1}{2})\alpha +iy)\cdots A_\circ ({\alpha }/{2}+iy)$ . Applying this to $A=A_\ast $ , we see that the function $y\mapsto A^{\ast 2m}_\ast (iy)$ must have degree $2d_m$ . Iterating this argument shows that $A_\ast ^{\ast 2^j}$ has degree $2^jd_1$ . But the degree of $A_\ast ^{\ast 2^j m}$ cannot exceed a, by Proposition 6.2. Thus, we must have $d_1=0$ .

An analogous argument shows that $B_\ast $ has degree $0$ as well. But we know that neither $A_\ast $ nor $B_\ast $ is constant. So $\unicode{x3bb} _\ast =1$ .

6.2 A Lyapunov exponent for pairs

Let $\alpha $ be an irrational number between $0$ and $1$ . To a pair $P=(F,G)$ , with $F=(1,B)$ and $G=(\alpha ,A)$ , we associate a renormalized pair as in (2.1) by setting

(6.8) $$ \begin{align} \mathfrak{R}(P)=(\Lambda^{-1}G\Lambda,\Lambda^{-1}FG^{-c}\Lambda). \end{align} $$

For simplicity, we restrict here to the trivial scaling $\Lambda =\Lambda (P)$ , given by $\Lambda (x,y)=(\alpha x,y)$ . Consider now the iterates $P_n=\mathfrak {R}^n(P)$ . The components of $P_n$ are of the form $F_n=(1,B_n)$ and $G_n=(\alpha _n,A_n)$ . After choosing a suitable norm for the factors $A_n$ , a Lyapunov-type exponent for pairs can be defined by setting

(6.9) $$ \begin{align} \ell(P)=\limsup_{n\to\infty}q_n^{-1}\log\kern-2pt\|A_n\|, \end{align} $$

where $q_n$ is the nth continued fraction denominator for $\alpha $ .

Consider first the case where $F=(1,\textbf {1})$ . Then the functions $A_n$ are scaled versions of $A^{q_n}$ . To be more precise, $A_n(x)=A^{\ast q_n}(\bar \alpha _n x)$ , where $\bar \alpha _n=\alpha _0\alpha _1\ldots \alpha _{n-1}$ . Taking the sup norm in (6.9) on a domain $|x|<\varepsilon $ , we have $\ell (P)=\ell _\varepsilon (G)$ , where

(6.10) $$ \begin{align} \ell_\epsilon(G)=\limsup_{n\to\infty} q_n^{-1}\log\sup_{|x|\le\epsilon}\|A^{\ast q_n}(\bar\alpha_n x)\|. \end{align} $$

Here, and in what follows, we assume that A is a continuous $1$ -periodic function on $\mathbb {R}$ , taking values in ${\textrm {SL}}(2,\mathbb {R})$ .

Proposition 6.4. Let $\alpha \in \mathbb {R}\setminus \mathbb {Q}$ be of finite type, in the sense that the sequence $n\mapsto \alpha _n$ is bounded away from zero. Then the $\limsup $ in (6.10) exists as a limit, and $\ell _\epsilon (G)$ agrees with the Lyapunov exponent $L(G)$ .

Proof. We may assume that $L(G)>0$ . Then, by Oseledets’s theorem [47], we have

(6.11) $$ \begin{align} \lim_q\frac{1}{ q}\log\frac{\|A^{\ast q}(x_0)v_0\|}{\|v_0\|}=L(G), \end{align} $$

for almost every $x_0\in \mathbb {R}$ , and for all vectors $v_0$ outside some one-dimensional subspace of $\mathbb {R}^2$ that can depend on $x_0$ . Now fix such an $x_0$ and $v_0$ .

Using the three-gap theorem [53, 55, 56], we can find an integer $k>0$ and sequences $n\mapsto t_n$ and $n\mapsto s_n$ of positive integers, such that

(6.12) $$ \begin{align} q_n\le t_n\le q_{n+k},\quad |x_0+t_n\alpha-s_n|\le\epsilon\bar\alpha_n. \end{align} $$

Setting $x_n=x_0+t_n\alpha -s_n$ and $v_n=A^{\ast t_n}(x_0)v_0$ , we have

(6.13) $$ \begin{align} \frac{1}{ q_n}\log\frac{\|A^{\ast q_n}(x_n)v_n\|}{\|v_n\|} &=\bigg(1+\frac{t_n}{ q_n}\bigg)\frac{1}{ q_n+t_n}\log\frac{\|A^{\ast(q_n+t_n)}(x_0)v_0\|}{\|v_0\|}\nonumber\\[3pt] &\quad-\frac{t_n}{ q_n}\;\frac{1}{ t_n}\log\frac{\|A^{\ast t_n}(x_0)v_0\|}{\|v_0\|}. \end{align} $$

Notice that $1\le t_n/q_n\le C$ for some fixed constant C. Thus, the right-hand side of (6.13) converges to $L(G)$ as $n\to \infty $ . This yields a lower bound $\ell _\epsilon (G)\ge L(G)$ . The upper bound $\ell _\epsilon (G)\le L(G)$ follows from Furman’s theorem [21].

In what follows, we assume that $\alpha $ is the inverse golden mean. Then $c=1$ in equation (6.8), and $\alpha _n=\alpha $ for all n. In addition, we restrict to pairs in the set $\mathcal {F}_\rho \kern-2pt'$ defined below, where $\rho =(\rho _{\kern0.7pt\textrm{F}},\rho _{\kern0.7pt\textrm{G}})$ is assumed to satisfy

(6.14) $$ \begin{align} \tfrac{1}{2}\alpha^{-2}<{\rho_{_{\textrm{G}}}},\quad \tfrac{1}{2}\alpha+\alpha{\rho_{_{\textrm{G}}}}\le{\rho_{_{\textrm{F}}}}\le\alpha^{-1}{\rho_{_{\textrm{G}}}}. \end{align} $$

Definition 6.5. Define $\mathcal {F}_\rho \kern-2pt'$ to be the set of pairs $P=(F,G)$ in $\mathcal {F}_\rho ^{\hskip 2.3pt r}$ with the property that the maps F and G commute, and that their factors have determinant $1$ .

Condition (6.14) guarantees that $\mathfrak {R}$ defines a dynamical system on $\mathcal {F}_\rho \kern-2pt'$ . This condition is satisfied, for example, for the values $\rho =(2,{11}/{8})$ and $\rho =(3,2)$ that are used in Lemma 3.1 and Lemma 4.1, respectively.

Using that $q_n^{-1}=(1+\alpha ^2)\alpha ^n+\mathcal {O}(\alpha ^{3n})$ , we can rewrite (6.9) as

(6.15) $$ \begin{align} \ell(P)=\limsup_{n\to\infty}L_n(P), \end{align} $$

where

(6.16) $$ \begin{align} L_n(P)=(1+\alpha^2)\alpha^n\log\kern-2pt\|A_{n,\circ}\|_{\rho_{_{\textrm{G}}}},\quad A_{n,\circ}(x)=A^{\ast q_n}_\circ(\alpha^n x). \end{align} $$

Here, we have used that scaling and ‘symmetrizing’ commute, as mentioned after (3.5).

Remark 3. If we restrict n in (6.16) to multiples of $3$ and replace $\mathfrak {R}^3$ by $\mathfrak {R}_3$ , then the weaker domain condition (3.39) is sufficient. In addition, the restriction to commuting pairs can be omitted in this case. We will not do this here, simply to avoid complicating the notation.

Our main reason for considering a Lyapunov exponent based on the functionals $L_n$ is that it transforms conveniently under renormalization:

(6.17) $$ \begin{align} L_n(\mathfrak{R}(P))=\alpha^{-1}L_{n-1}(P),\quad n=1,2,\ldots. \end{align} $$

So we have $\ell (\mathfrak {R}(P))=\alpha ^{-1}\ell (P)$ . Clearly, $\ell $ vanishes on any periodic orbit of $\mathfrak {R}$ .

Proposition 6.6. Let $G=(\alpha ,A)$ be an anti-reversible AM map with $\alpha $ the inverse golden mean. Then the limit $\lim _{n\to \infty }L_n(P)$ exists and is equal to $L(G)$ .

Proof. Let $r=\rho _G$ . Consider the sup norm in (6.10) for small $\epsilon>0$ . Since the evaluation map $g\mapsto g(x)$ is continuous on $\mathcal {G}_r$ for $|x|\le r$ , this norm is bounded from above by $C\|A_{n,\circ }\|_r$ for some fixed constant $C>0$ . So we have $\liminf _{n\to \infty }L_n(P)\ge L(G)$ .

Next, consider the AM map $G_\delta $ with factor $A_\delta (x)=A(x+i\delta )$ . Using the (well-known) fact that $\log\kern-2pt \|A^{\ast q}(x+i\delta )\|$ is a convex function of $\delta $ , we have

(6.18) $$ \begin{align} L(P)\le \limsup_{n\to\infty}q_n^{-1} \sup_{|x|\le\epsilon}\log\kern-2pt\|A^{\ast q_n}_\circ(\alpha^n x\pm i\delta)\| \le\ell_\epsilon(G_\delta)=L(G_\delta), \end{align} $$

for $\epsilon>0$ sufficiently large (depending only on r) and every $\delta>0$ . The ‘ $\pm $ ’ in equation (6.18) includes a maximum over the two signs. But by anti-reversibility, the supremum over $|x|\le \epsilon $ does not depend on the sign.

Now we can use the fact [5] that $L(G_\delta )=\max \{0,\log \unicode{x3bb} +2\pi \delta \,\}$ . Thus, taking $\delta \to 0$ in (6.18) yields $\limsup _{n\to \infty }L_n(P)\le L(G)$ . This proves the claim in Proposition 6.6.

For more general pairs in $\mathcal {F}_\rho \kern-2pt'$ , the $\limsup $ in (6.15) may not be a limit. An easy way to cure this problem is to define a slightly different Lyapunov-type exponent as follows:

(6.19) $$ \begin{align} L(P)=\limsup_{n\to\infty}\frac{1}{ 1+\alpha^2} [L_n(P)+\alpha^2 L_{n-1}(P)]. \end{align} $$

Theorem 6.7. Assume that $P\in \mathcal {F}_\rho \kern-2pt'$ for some choice of $\rho =({\rho _{_{\mathrm{F}}}},{\rho _{_{\mathrm{G}}}})$ that satisfies (6.14). Then the sequence $n\mapsto L_n(P)+\alpha ^2 L_{n-1}(P)$ is decreasing. As a consequence, the $\limsup $ in (6.19) is achieved as a limit, and L is upper semicontinuous on $\mathcal {F}_{\rho}{\kern-1.9pt'}$ . Furthermore, the value of $L(P)$ does not depend on the choice of $\rho $ .

Proof. For $n\ge 0$ define

(6.20) $$ \begin{align} b_n=b_n(\rho)=\log\kern-2pt\|B_{n,\circ}\|_{\rho_{_{\textrm{F}}}},\quad a_n=a_n(\rho)=\log\kern-2pt\|A_{n,\circ}\|_{\rho_{_{\textrm{G}}}}. \end{align} $$

Assume now that $n\ge 1$ . Then the domain conditions (6.14) guarantee that

(6.21) $$ \begin{align} b_n\le a_{n-1},\quad a_n\le b_{n-1}+a_{n-1}. \end{align} $$

Using that $1+\alpha =\alpha ^{-1}$ , this yields the bound

(6.22) $$ \begin{align} L_n(P)+\alpha^2L_{n-1}(P) &=(1+\alpha^2) [\alpha^n a_n+\alpha^{n+1}a_{n-1}]\nonumber\\[3pt] &\le(1+\alpha^2) [\alpha^n b_{n-1}+\alpha^n a_{n-1}+\alpha^{n+1}a_{n-1}]\nonumber\\[3pt] &\le(1+\alpha^2) [\alpha^n a_{n-2}+\alpha^n(1+\alpha)a_{n-1}]\nonumber\\[3pt] &=\alpha^2L_{n-2}(P)+L_{n-1}(P), \end{align} $$

for $n\ge 2$ . This shows that the sequence $n\mapsto L_n(P)+\alpha ^2L_{n-1}(P)$ is decreasing and thus has a limit. Since each $L_k$ is continuous, the limit is upper semicontinuous.

Next consider another domain parameter $\varrho $ satisfying (6.14). Let us write $L_n(\varrho )$ instead of $L_n(P)$ when the domain parameter is $\varrho $ , and $L_n(\rho )$ when the domain parameter is $\rho $ . Using that $\mathfrak {R}$ is analyticity-improving, there exist $k>0$ and a constant $c_k>0$ such that

(6.23) $$ \begin{align} \|B_{n+k}\|_{\varrho_{_{\textrm{F}}}}\le e^{c_k}\|B_n\|_{\rho_{_{\textrm{F}}}}^{q_{n-2}}\|A_n\|_{\rho_{_{\textrm{G}}}}^{q_{n-1}},\quad \|A_{n+k}\|_{\varrho_{_{\textrm{F}}}}\le e^{c_k}\|B_n\|_{\rho_{_{\textrm{F}}}}^{q_{n-1}}\|A_n\|_{\rho_{_{\textrm{G}}}}^{q_n}, \end{align} $$

for every $n\ge 0$ . Taking logarithms and using the identity

(6.24) $$ \begin{align} \begin{bmatrix} {q_{k-2}}&{q_{k-1}}\\ {q_{k-1}}&{q_k} \end{bmatrix} \begin{bmatrix}{\alpha}\\ {1} \end{bmatrix} = \begin{bmatrix} {0}&{1}\\ {1}&{1} \end{bmatrix}^k \begin{bmatrix} {\alpha}\\ {1} \end{bmatrix} =\alpha^{-k} \begin{bmatrix} {\alpha}\\ {1} \end{bmatrix}, \end{align} $$

we find that

(6.25) $$ \begin{align} \alpha^2L_{n+k-1}(\varrho)+L_{n+k}(\varrho) \le C_k\alpha^n+\alpha^2L_{n-1}(\rho)+L_n(\rho), \end{align} $$

with $C_k=(1+\alpha ^2)^2\alpha ^kc_k$ . An analogous inequality holds if $\varrho $ and $\rho $ are exchanged. This shows that $L(P)$ is independent of the choice of $\rho $ .

Using upper semicontinuity and (6.17), together with the fact that the pair $P_\ast $ commutes, we immediately obtain the following corollary.

Corollary 6.8. Consider a pair $P\in \mathcal {F}_\rho \kern-2pt'$ . Then $L(\mathfrak {R}(P))=\alpha ^{-1}L(P)$ . So, in particular, $L(P_\ast )=0$ . Furthermore, if $\mathfrak {R}^{3n}(P)\to P_\ast $ as $n\to \infty $ , then $L(P)=0$ .

6.3 Transversal intersection

At this point we can complete the proof of Theorem 2.3. We already know from §6.1 that $s_\ast =1$ . What remains to be proved is that some RG iterate of the AM family intersects the local stable manifold $\mathcal {W}^s$ of $\mathfrak {R}_3$ transversally, and that $\mu _2\ge \alpha ^{-3}$ .

To this end, consider the splitting $\mathcal {F}_\rho =W^u\oplus W^s$ , where $W^u$ is the unstable subspace for the operator $D\mathfrak {R}_3(P_\ast )$ and $W^s$ the stable subspace. Then $P_\ast +W^s$ is tangent to $\mathcal {W}^s$ at $P_\ast $ . And $\mathcal {W}^s$ is the graph of a real analytic function from $W^s$ to $P_\ast +W^u$ . To be more precise, this holds locally, near $P_\ast $ . So we restrict our analysis to a suitable open ball B in $\mathcal {F}_\rho $ that is centered at $P_\ast $ . Using that $\mathcal {W}^s$ is a graph, we can define the height of a pair $P\in B$ relative to $\mathcal {W}^s$ in the direction of $W^u$ .

Consider the AM family $s\mapsto \texttt{P}(s)$ associated with the factor (3.11) for $\unicode{x3bb} =e^s$ . Define $\texttt{P}_n=\mathfrak {F}_1^n(\texttt{P})$ , where $\mathfrak {F}_1$ denotes the pointwise version of $\mathfrak {R}_3$ defined by (5.12). Notice that $\mathfrak {R}_3$ may be replaced by $\mathfrak {R}^3$ , since the AM pairs commute. Recall that Lyapunov exponent of $\texttt{P}(s)$ is $\max \{0,s\}$ . So by (2.7), the Lyapunov exponent of $\texttt{P}_n(s)$ is $\alpha ^{-3n}s$ . And recall from §6.1 that $0$ is the unique value of s for which $\texttt{P}(s)$ is attracted to $P_\ast $ under the iteration of $\mathfrak {R}_3$ . If n is sufficiently large, so that the pair $\texttt{P}_n(0)$ lies on $\mathcal {W}^s$ in B, then the pairs $\texttt{P}_n(s)$ for $s>0$ cannot lie on $\mathcal {W}^s$ . Here, we have Corollary 6.8. In what follows, k denotes some (large) value of n for which this holds.

Now choose $t>0$ such that $\texttt{P}_\ast (t)$ belongs to B. Let $\Sigma _0$ be a codimension- $1$ subspace of $\mathcal {F}_\rho $ that passes through $\texttt{P}_\ast (t)$ and is transversal to the unstable manifold $\texttt{P}_\ast $ . We may assume also that $\Sigma _0$ does not intersect $\mathcal {W}^s$ . For $n=1,2,\ldots ,$ define $\Sigma _n$ to be the inverse image of $\Sigma _{n-1}$ under $\mathfrak {R}_3$ , restricted to B. If B has been chosen sufficiently small, then the $\unicode{x3bb} $ -lemma [49] guarantees that the following statements hold. The sets $\Sigma _n$ are real analytic manifolds. Furthermore, the sequence $n\mapsto \Sigma _n$ accumulates at the stable manifold $\mathcal {W}^s$ of $\mathfrak {R}_3$ at $P_\ast $ asymptotically like $\mu _2^{-n}$ . To be more precise, if $\texttt {Q}$ is any (real analytic) curve in B that crosses $\mathcal {W}^s$ transversally at the point $\texttt {Q}(0)$ , then near this point, and for sufficiently large k, the curve $\texttt {Q}$ intersects $\Sigma _n$ for a unique parameter value $s_n$ . Furthermore, the sequence $n\mapsto \mu _2^ns_n$ converges to a non-zero constant.

Consider now the curve $\texttt {Q}=\texttt{P}_k$ . Denote by $h(s)$ the height of $\texttt {Q}(s)$ above $\mathcal {W}^s$ in the direction of $W^u$ . By analyticity, we have $h(s)=as^m+\mathcal {O}(s^{m+1})$ for some $m\ge 1$ , with ${a\ne 0}$ . Thus, for sufficiently large n, the curve $\texttt {Q}$ intersects $\Sigma _n$ at some parameter value $s_n>0$ . We may choose the smallest such value. By construction, the point $\mathfrak {R}^{3n}(\texttt {Q}(s_n))$ lies on $\Sigma _0$ . So we must have $\mu _2^n s_n^m\ge b$ for sufficiently large n, where b is some positive constant. Using that the Lyapunov exponent is bounded on B, and that $\mathfrak {R}^{3n}(\texttt {Q}(s_n))$ has Lyapunov exponent $\alpha ^{-3(n+k)}s_n$ , we also have $\alpha ^{-3n}s_n\le c$ for some $c>0$ . Thus, $\mu _2\ge \alpha ^{-3m}$ . We know from Lemma 5.1 that $\mu _2\le \sqrt {19}$ . And if $m\ge 2$ , then $\alpha ^{-3m}>17$ . So we must have $m=1$ . This implies that $\texttt {Q}=\mathfrak {F}_1^k(\texttt{P})$ intersects $\mathcal {W}^s$ transversally, and that $\mu _2\ge \alpha ^{-3}$ . This completes the proof of Theorem 2.3.

Remark 4. The parameter values $s_n$ depend on the value of k defining the curve $\texttt {Q}=\texttt{P}_k$ . Writing $s_n=s_{k,n}$ we obtain $\mathfrak {R}^{3(k+n)}(\texttt{P}(s_{k,n}))\to \texttt{P}_\ast (t)$ in the limit $k\to \infty $ . If we assume that $\mu _2=\alpha ^{-3}$ , then this implies that $\texttt{P}_\ast (t)$ has a positive Lyapunov exponent.

7 Supercritical maps

The main goal in this section is to prove Theorems 2.4 and 2.5.

7.1 Limiting zeros

Here we consider the factor normalization that was mentioned before Theorem 2.4. Recall from (3.16) that $\mathfrak {R}_3=\mathfrak {N}\circ \mathcal {R}_3\circ \mathfrak {C}$ , where $\mathfrak {C}$ is a commutator correction, and where $\mathfrak {N}$ normalizes determinants to $1$ . The factor normalization of a pair $P=((1,B),(\alpha ,A))$ is componentwise, $\mathfrak {N}(P)=((1,\mathcal {M}(B),(\alpha ,\mathcal {N}(A))$ , with $\mathcal {M}$ and $\mathcal {N}$ of the form

(7.1) $$ \begin{align} \mathcal{M}(B)=M(B)^{-1}B,\quad\mathcal{N}(A)=N(A)^{-1}A. \end{align} $$

Up to now we have used $M(B)=\mathop {\textrm {det}}(B)^{1/2}$ and $N(A)=\mathop {\textrm {det}}(A)^{1/2}$ .

Here, we are interested only in pairs that commute and whose factors have constant non-negative determinants. So we omit the commutator correction $\mathfrak {C}$ and choose for M and N the norms in $\mathcal {F}_\rho $ . Other choices would work equally well, as long as they guarantee that the orbits of $\mathfrak {R}_3$ remain bounded without tending to zero. In order to simplify the description, we also choose a trivial y-scaling $L_3=\textbf {1}$ .

Let $K_0$ be a set of pairs $P\in \mathcal {F}_\rho $ whose norm is bounded by some fixed constant, and that satisfy $L(P)\ge \varepsilon $ for some fixed $\varepsilon>0$ . Recall that the transformation $\mathfrak {R}^3$ is compact, as described before Lemma 3.1. Here, and in what follows, we assume that the domain parameter $\rho $ satisfies condition (3.39). Consequently, the sets $K_n=\mathfrak {R}^{3n}(K_0)$ for $n>0$ all have compact closures. Denote by $K_\ast $ the set of all accumulation points from the sequence $n\mapsto K_n$ . This set is compact and invariant under $\mathfrak {R}_3$ . By taking $K_0$ invariant under conjugacies by a rotation, the limit set $K_\ast $ has the same property. Notice that the pairs in $K_\ast $ belong to $\mathcal {F}_\rho $ , so their factors are analytic.

Let $P\in K_0$ and define $P_n=\mathfrak {R}_3^n(P)$ for $n\ge 0$ . By (3.3), (3.4), and (3.5), the symmetric factors associated with the pairs $P_n$ are related via

(7.2) $$ \begin{align} \begin{aligned} N_n B_{n,\circ}(x) =A_{n-1,\circ}\bigg(\alpha^3\bigg(x-\dfrac{\alpha^{-1}}{2}\bigg)\bigg) B_{n-1,\circ}(\alpha^3x)^\dagger A_{n-1,\circ}\bigg(\alpha^3\bigg(x+\dfrac{\alpha^{-1}}{2}\bigg)\bigg) \end{aligned} \end{align} $$

and

(7.3) $$ \begin{align} M_n A_{n,\circ}(x) &= A_{n-1,\circ}(\alpha^3(x+\alpha^{-1}))^\dagger B_{n-1,\circ}\bigg(\alpha^3\bigg(x+\dfrac{\alpha^{-1}}{2}\bigg)\bigg)\nonumber\\ &\quad\times A_{n-1,\circ}(\alpha^3x)^\dagger B_{n-1,\circ}\bigg(\alpha^3\bigg(x-\dfrac{\alpha^{-1}}{2}\bigg)\bigg) A_{n-1,\circ}(\alpha^3(x-\alpha^{-1}))^\dagger. \end{align} $$

Here, $M_n$ and $N_n$ are the normalization factors that appear in the definition of $P_n=\mathfrak {R}_3(P_{n-1})$ . Assume now that $K_0$ is a set of pairs $P=(F,G)$ with $F=(1,\textbf {1})$ and $G=(\alpha ,A)$ , and with the property that $A_\circ (0)=-J$ . The latter condition is satisfied, for example, for the anti-reversible AM family. In this case, (3.10) implies that

(7.4) $$ \begin{align} A_{n,\circ}(0)=\pm\varepsilon_n J,\quad\varepsilon_n=\mathcal{O}(\alpha^{-3n}). \end{align} $$

Here, $\varepsilon _n$ is a product of n factors $N_m^{-1}$ or $M_m^{-1}$ for $m=1,2,\ldots ,n$ . The given estimate on $\varepsilon _n$ uses the fact that, under the iteration of $\mathcal {R}_3$ , the norms grow at least as quickly as the Lyapunov exponents. Thus, as $n\to \infty $ , the values at $x=0$ of the factors $A_{n,\circ }$ tend to zero, uniformly in our sequence $n\mapsto K_n$ .

There are many other values of x where $A_{n,\circ }(x)$ tends to zero. An example is $x=\alpha ^{-1}$ . At this value of x, the last factor in (7.3) is of size $\mathcal {O}(\alpha ^{-3n})$ for large n. Thus, as $n\to \infty $ , the values at $x=\alpha ^{-1}$ of the factors $A_{n,\circ }$ tend to zero as well. The search for such zeros can be made more systematic as follows.

Let $P=((1,B),(\alpha ,A))$ be a pair in $K_\ast $ , and let $\tilde P=((1,\tilde B),(\alpha ,\tilde A))$ be the image of P under the transformation $\mathfrak {R}_3$ . Denote by $\mathcal {A}$ and $\mathcal {B}$ be the set of zeros of $A_\circ $ and $B_\circ $ , respectively. Then (7.2) shows that the set of zeros of $\tilde B_\circ $ includes the set

(7.5) $$ \begin{align} \tilde{\mathcal{B}}=\bigg[\alpha^{-3}\mathcal{B} \bigcup_{m=\pm1}\bigg(\alpha^{-3}\mathcal{A}+\dfrac{m}{2}\alpha^{-1}\bigg)\bigg], \end{align} $$

and (7.3) shows that the set of zeros of $\tilde A_\circ $ includes

(7.6) $$ \begin{align} \tilde{\mathcal{A}}=\bigg[\bigcup_{m=\pm1}\bigg(\alpha^{-3}\mathcal{B}+\dfrac{m}{2}\alpha^{-1}\bigg) \bigcup_{m=0,\pm1}(\alpha^{-3}\mathcal{A}+m\alpha^{-1})\bigg]. \end{align} $$

This defines a transformation that maps a pair of sets of complex numbers $\mathcal {P}=(\mathcal {B},\mathcal {A})$ to a pair $\tilde {\mathcal {P}}=(\tilde {\mathcal {B}},\tilde {\mathcal {A}})$ . Consider iterates $\mathcal {P}_1,\mathcal {P}_2,\ldots $ under this transformation $\mathcal {P}\mapsto \tilde {\mathcal {P}}$ , starting with a pair $\mathcal {P}_0=(\mathcal {B}_0,\mathcal {A}_0)$ .

Notice that the imaginary parts of non-real points in $\mathcal {B}_0$ or $\mathcal {A}_0$ expand by a factor $\alpha ^{-3}$ under the transformation $\mathcal {P}\mapsto \tilde {\mathcal {P}}$ . Thus, the limit sets ( $\limsup $ or $\liminf $ ) $\mathcal {B}_\ast $ and $\mathcal {A}_\ast $ are always subsets of $\mathbb {R}$ .

In the case at hand, $\mathcal {A}_0$ includes $0$ , since $A_\circ (0)=0$ for all pairs in K. So consider and $\mathcal {A}_0=\{0\}$ . Then $\mathcal {A}_1$ includes $0$ as well, due to the map $x\mapsto \alpha ^{-3}x$ that appears in (7.6) for $m=0$ . So it is clear that $\mathcal {B}_{n+1}\supset \mathcal {B}_n$ and $\mathcal {A}_{n+1}\supset \mathcal {A}_n$ for all n. Thus, $\mathcal {B}_n\nearrow \mathcal {B}_\infty $ and $\mathcal {A}_n\nearrow \mathcal {A}_\infty $ for a pair of sets $\mathcal {P}_\infty =(\mathcal {B}_\infty ,\mathcal {A}_\infty )$ .

A zero that appears for the AM family but that is not included in the above set $\mathcal {A}_\infty $ is $x=\tfrac {1}{2}$ . And $x=-\tfrac {1}{2}$ appears as well, due to anti-reversibility. To see how these zeros occur, denote by $C_n(x)$ the product of the last two factors in (7.3). An explicit computation shows that

(7.7) $$ \begin{align} C_n(x) =A^{\ast q_{3n-2}}_0\bigg(\alpha^{3n}x+\dfrac{q_{3n-1}}{2}\alpha\bigg). \end{align} $$

Using that $q_k\alpha -q_{k-1}=(-1)^k\alpha ^{k+1}$ , one finds that $C_n({\sigma }/{2})=J$ for $\sigma =(-1)^{3n-1}$ . This implies that the factor $A_\circ $ for an anti-reversible AM pair $P\in K_\ast $ has a zero at $x=\pm \tfrac {1}{2}$ . The same holds for other anti-reversible pairs $P=((1,\textbf {1}),(\alpha ,A))$ with A of Schrödinger type (1.4).

To see how the zeros at $\pm \tfrac {1}{2}$ propagate under iteration of $\mathcal {P}\mapsto \tilde {\mathcal {P}}$ , consider and $\mathcal {A}_0=\{-\tfrac {1}{2},\tfrac {1}{2}\}$ . Then $\mathcal {A}_1$ includes $\pm \tfrac {1}{2}$ as well, since $\pm \tfrac {1}{2}$ is a fixed point of the map $x\mapsto \alpha ^{-3}x\mp \alpha ^{-1}$ that appears in (7.6). Again we have $\mathcal {B}_n\nearrow \mathcal {B}_\infty $ and $\mathcal {A}_n\nearrow \mathcal {A}_\infty $ for a pair of sets $\mathcal {P}_\infty =(\mathcal {B}_\infty ,\mathcal {A}_\infty )$ .

7.2 The supercritical fixed point

The recursion relations (7.5) and (7.6) can be obtained more easily from pairs of commuting skew-product maps with factors that take values in ${\textrm {GL}}(1,\mathbb {R})$ instead of ${\textrm {GL}}(2,\mathbb {R})$ . A map $g:(x,y)\mapsto (x+\alpha ,a(x)y)$ of this type will again be written as $g=(\alpha ,a)$ . Given a pair $p=(f,g)$ of such maps $f=(-1,b)$ and $g=(\alpha ,a)$ , the renormalized pair $\mathcal {R}(p)$ is given by

(7.8) $$ \begin{align} \mathcal{R}(p)=(\unicode{x3bb}^{-1}g\unicode{x3bb}, \unicode{x3bb}^{-1}fg^c\unicode{x3bb}),\quad \unicode{x3bb}(x,y)=(-\alpha x,y), \end{align} $$

with the same positive integer c as in (2.1). The analogue of anti-reversibility here is the requirement that $b_\circ $ be even and $a_\circ $ odd. The analogue of a Schrödinger pair is a pair $p=(f,g)$ with components $f=(-1,1)$ and $g=(\alpha ,a)$ , where a is periodic with period $1$ .

Let us restrict now to the case where $\alpha $ is the inverse golden mean. Then $c=1$ at every RG step. If p is anti-reversible, then the relation between the zeros for $p=(f,g)$ and the zeros for $\tilde p=\mathcal {R}^3(p)$ is trivially given by (7.5) and (7.6).

Consider again skew product maps with factors in ${\textrm {GL}}(2,\mathbb {R})$ . Let $P_0$ be an anti-reversible AM pair with $\unicode{x3bb}>1$ . Consider the pairs $P_n=\mathfrak {R}_3^n(P_0)$ for $n\ge 1$ and the associated symmetric factors $B_{n,\circ }$ and $A_{n,\circ }$ . These factors can be obtained iteratively via (7.2) and (7.3). We give some numerical observations.

Observation 5. As n increases, the factors $B_{n,\circ }$ and $A_{n,\circ }$ approach symmetric matrices with constant null spaces.

In other words, if we start with $K_0=\{P\}$ , then the limit set $K_\ast $ appears to consist of pairs whose symmetric factors are of the form

(7.9) $$ \begin{align} B_\circ(x)=b_\circ(x)WW^\top,\quad A_\circ(x)=a_\circ(x)VV^\top, \end{align} $$

where W and V are constant unit vectors in $\mathbb {R}^2$ . Notice that $b_\circ =\mathop {\textrm {tr}}(B_\circ )$ has to be even and $a_\circ =\mathop {\textrm {tr}}(A_\circ )$ odd. This follows from the (anti-)reversibility property (7.9). The part of Observation 5 that we cannot prove is that $A_\circ $ is symmetric, and that V and W are constant. It is possible to give some formal arguments, but we will not do this here. If V and W are assumed to be constant, then the fact that F has to commute with both G and $G^\dagger $ implies that $W=V^\dagger $ .

Observation 6. The sequence of pairs $n\mapsto P_n$ converges to a fixed point of $\mathfrak {R}_3$ .

To be more precise, if we use the trivial y-scaling $L_2=\textbf {1}$ , as we have done so far in this section, then convergence is to a period $2$ of $\mathfrak {R}_3$ . The traces $b_\circ $ and $a_\circ $ reproduce after one step of $\mathfrak {R}_3$ , but the directions V and $W=V^\dagger $ only repeat after two steps. Using instead $L_3=L(\vartheta )$ of the form (3.12), with $\vartheta =\vartheta (P)$ chosen appropriately, the sequence $n\mapsto P_n$ converges numerically to a fixed point of $\mathfrak {R}_3$ , with the properties described in Theorem 2.4.

Proof of Theorem 2.4

We give only a sketch here, since the proof follows closely the steps used in [38].

First, notice that the fixed point equation for a pair of the form described in Theorem 2.4 reduces to a fixed point equation for the functions $b_\diamond $ and $a_\diamond $ . This is essentially the fixed point equation for the third power $\mathcal {R}^3$ of the operator $\mathcal {R}$ defined by (7.8), with $c=1$ , except for a constant renormalization of the factors b and a.

For simplicity, let us redefine $b_\diamond $ and $a_\diamond $ to be the symmetric factors of the desired fixed point. Then we have a good guess as to where their zeros are: starting with and $\mathcal {A}_0=\{-\tfrac {1}{2},0,\tfrac {1}{2}\}$ , an iteration of the map $\mathcal {P}\mapsto \tilde {\mathcal {P}}$ yields a limit pair $\mathcal {P}_\infty =(\mathcal {B}_\infty ,\mathcal {A}_\infty )$ that should be the set of zeros associated with the symmetric factors of the fixed point.

For the actual construction, it is more convenient to start with and $\mathcal {A}_0=\tfrac {1}{2}\mathbb {Z}$ . This corresponds to starting with the pair P whose symmetric factors are

(7.10) $$ \begin{align} B_\circ(x)=\begin{bmatrix} 0&0\\ 0&1 \end{bmatrix},\quad A_\circ(x)=2\sin(2\pi x)\begin{bmatrix} 1&0\\ 0&0 \end{bmatrix}, \end{align} $$

and then iterating $\mathfrak {R}^3$ with $L_3=[{0~1\atop 1~0}]$ . Notice that the symmetric factor $A_\circ $ in this equation is the limit as $\unicode{x3bb} \to \infty $ of the anti-symmetric AM factor (in its standard form), after dividing it by $\unicode{x3bb} $ .

The symmetric factors that are being generated by iterating the map $(B_\circ ,A_\circ )\mapsto (\hat B_\circ ,\hat A_\circ )$ defined by (3.3) and (3.4) have their zeros modulo $\tfrac {1}{2}$ on the orbit of the point $x=0$ under the translation $x\mapsto x+\alpha $ on the circle ${\Bbb T}/2=\mathbb {R}/(2\mathbb {Z})$ . Thus, by the three-gap theorem [53, 55, 56], the gaps between adjacent zeros on ${\Bbb T}/2$ take at most three distinct values. To be more specific, there are exactly three distinct gaps, except when the orbit has length $q_{3n}$ , at which point the largest gap gets closed. So after n iterations, the resulting factor $\hat B_\circ $ has $q_{3n-1}$ zeros on ${\Bbb T}/2$ with three distinct gaps, while the factor $\hat A_\circ $ has $q_{3n}$ zeros on ${\Bbb T}/2$ with two distinct gaps.

The same applies to the iteration $(B_\circ ,A_\circ )\mapsto (\tilde B_\circ ,\tilde A_\circ )$ , except that the circle gets enlarged by a factor $\alpha ^{-3}$ at each step. Furthermore, the zeros that lie within some fixed positive angle of the origin reproduce after each step [38]. This yields the limiting sequences of zeros described in Theorem 2.4.

The symmetric factors that are being generated during this iteration have a Weierstrass representation as products, determined (up to a constant factor) by their zeros. Here, we use the fact that $b_\circ $ is even and $a_\circ $ odd, so it is possible to work with products of order $\tfrac {1}{2}$ . By controlling the zero sets $\mathcal {B}_n$ and $\mathcal {A}_n$ , one finds uniform convergence on compact sets to a pair of limit functions $b_\diamond $ and $a_\diamond $ . For details we refer to [38], where RG fixed points have been constructed for skew-products with meromorphic factors.

The gap sizes listed in (2.9) were obtained by iterating the map $\mathcal {P}\mapsto \tilde {\mathcal {P}}$ a few times, starting with the sets and $\mathcal {A}_0=\{-\tfrac {1}{2},0,\tfrac {1}{2}\}$ .

The following will be used in the proof of Theorem 2.5 below.

Proposition 7.1. Let . Let $X=\{0\}$ or $X=\{-\tfrac {1}{2},\tfrac {1}{2}\}$ or $X=\{-\tfrac {1}{2},0,\tfrac {1}{2}\}$ . Assume that $X\subset \mathcal {A}_1$ whenever $X\subset \mathcal {A}_0$ . Then $\mathcal {A}_0=X$ leads to the same limit pair $\mathcal {P}_\infty $ as $\mathcal {A}_0=X+\mathbb {Z}$ .

Proof. For $n\ge 0$ define ${\Bbb T}_n=\mathbb {R}/(\alpha ^{3n}\mathbb {Z})$ . Consider first the case $\mathcal {A}_0=X+\mathbb {Z}$ . By construction, the points in $\mathcal {B}_n$ constitute $|X|$ orbits of length $q_{3n-1}$ for the translation $x\mapsto x+\alpha ^{3n+1}$ on the circle ${\Bbb T}_n$ , and the points in $\mathcal {A}_n$ constitute $|X|$ orbits of length $q_{3n}$ . Furthermore, the orbits are symmetric with respect to $x\mapsto -x$ .

Consider now $\mathcal {A}_0=X$ instead of $\mathcal {A}_0=X+\mathbb {Z}$ . Then we must get the same orbits on ${\Bbb T}_n$ , simply by counting points. For $m>0$ , denote by $a(n,m)$ and $b(n,m)$ the number of points in $\mathcal {A}_n$ and $\mathcal {B}_n$ , respectively, that lie within a distance m from the origin in ${\Bbb T}_n$ .

Next, construct $\mathcal {B}_n$ and $\mathcal {A}_n$ as subsets of $\mathbb {R}$ instead of ${\Bbb T}_n$ . Now the number of points in $\mathcal {B}_n$ or $\mathcal {A}_n$ that lie within a distance m of the origin can be smaller than $b(n,m)$ or $a(n,m)$ , respectively. However, this does not happen if n is sufficiently large. The reason is that map $\mathcal {P}\mapsto \tilde {\mathcal {P}}$ is ‘expanding’ by a factor $\alpha ^{-3}$ . To be more precise, let $c>\alpha ^3$ . Then, for m larger than some constant that only depends on c, the points in $\tilde {\mathcal {B}}_n\cap [-m,m]$ and $\tilde {\mathcal {A}}_n\cap [-m,m]$ are determined via $\mathcal {P}\mapsto \tilde {\mathcal {P}}$ from the points in $\mathcal {B}_n\cap [-cm,cm]$ and $\mathcal {A}_n\cap [-cm,cm]$ , if n is sufficiently large. This shows that $\mathcal {A}_0=X$ leads to the same limit pair $\mathcal {P}_\infty $ as $\mathcal {A}_0=X+\mathbb {Z}$ .

Notice that $\liminf _n\mathcal {B}_n=\limsup _n\mathcal {B}_n$ and $\liminf _n\mathcal {A}_n=\limsup _n\mathcal { A}_n$ in the above.

Proof of Theorem 2.5

Consider the choice $M(B)=\|B_\circ \|$ and $N(A)=\|A_\circ \|$ in the definition (7.1) of our factor normalization. Let $P\in K_\ast $ . Given that P belongs to $\mathcal {F}_\rho $ and lies in the range of $\mathfrak {R}_3^n$ for every n, the factors B and A extend analytically to all of $\mathbb {C}$ . Furthermore, $b_\circ =\mathop {\textrm {tr}}(B_\circ )$ is even and $a_\circ =\mathop {\textrm {tr}}(A_\circ )$ odd, due to the anti-reversibility property (7.9).

By construction, the symmetric factors $B_\circ $ and $A_\circ $ have norm $1$ and determinant $0$ .

The claim in Theorem 2.5 concerning the zeros of B and A follows from our discussion in the previous subsection, together with the characterization of the set of zeros for the functions $b_\diamond $ and $a_\diamond $ given in the proof of Theorem 2.4, as well as Proposition 7.1.

Remark 7. If one assumes that some point P on the unstable manifold of $\mathfrak {R}_3$ at $P_\ast $ converges to $P_\diamond $ under iteration of $\mathfrak {R}_3$ , then it is possible to show that $\mu _2=\alpha ^{-3}$ . The reason is that the asymptotic behavior under renormalization becomes trivial in this case.

8 Computer estimates

What remains to be done is to verify the estimates in Lemmas 3.1, 4.1, 4.2, 5.1, and 5.5. This is carried out with the aid of a computer. This part of the proof is written in the programming language Ada [1] (see the Data Availability section). The following is meant to be a rough guide for the reader who wishes to check the correctness of our programs.

8.1 Enclosures and data types

Bounds on a vector x in a space $\mathcal {X}$ , also referred to as enclosures for x, are given here by sets $X\subset \mathcal {X}$ that include x and are representable as data on a computer. Data of type Ball are pairs $\texttt {B}=(\texttt {B.C},\texttt {B.R})$ , where B.C and B.R are representable numbers, with $\texttt {B.R}\ge 0$ . In a Banach algebra $\mathcal {X}$ with unit $\textbf {1}$ , the enclosure associated with a Ball B is the ball $\texttt {B}_{\mathcal {X}}=\{x\in \mathcal {X}:\|x-(\texttt {B.C})\textbf {1}\|\le \texttt {B.R}\}$ . Our other enclosures are closed convex subsets of $\mathcal {X}$ that admit a canonical decomposition

(8.1) $$ \begin{align} S=\sum_n x_n\texttt{B(n)}_{\mathcal{X}}, \end{align} $$

where each $x_n$ is a representable element in $\mathcal {X}$ , and where each B(n) is a Ball with center $\textbf {0}$ or $\textbf {1}$ . Notice that a Ball can have radius zero.

Consider now a disk $D=\{z\in \mathbb {C}:|z|<\rho \}$ with representable radius $\rho>0$ . An analytic function $g:D\to \mathcal {X}$ admits a Taylor series representation $g(z)=\sum _{n=0}^\infty g_nz^n$ with coefficients $g_n\in \mathcal {X}$ . Denote by $\mathcal {G}$ the space of all such functions that have a finite norm $\|g\|=\sum _{n=0}^\infty \|g_n\|\rho ^n$ . Assume that $\mathcal {X}$ carries a type of enclosures named Scalar. To each such enclosure $\texttt {S}_{\mathcal {X}}\subset \mathcal {X}$ we can associate a set $\texttt {S}_{\mathcal {G}}\subset \mathcal {G}$ by replacing each ball $\texttt {B(n)}_{\mathcal {X}}$ in the decomposition (8.1) of $S=\texttt {S}_{\mathcal {X}}$ by the ball $\texttt {B(n)}_{\mathcal {G}}$ .

Given an integer $D>0$ , our enclosures for functions in $\mathcal {G}$ are specified by data of type Taylor1. A Taylor1 is in essence a pair P=(P.F,P.C), where $\texttt {P.F}\le D$ is a non-negative integer, and where P.C is an array(0 .. D) of Scalar. The corresponding enclosure is the set

(8.2) $$ \begin{align} \texttt{P}_{\mathcal{G}}=\sum_{n=0}^{m-1}\texttt{P.C(n)}_{\mathcal{X}}\mathcal{P}_n +\sum_{n=m}^D\texttt{P.C(n)}_{\mathcal{G}}\mathcal{P}_n,\quad\mathcal{P}_n(z)=z^n, \end{align} $$

where $m=\texttt {P.F}$ . Notice that the first sum in (8.2) is a polynomial, while each term in the second sum is in general a non-polynomial. This allows for efficient estimates in the problem considered here. For precise definitions we refer to the Ada package Taylors1.

Quadruples of Taylor1 define a type TMat2 that is used for enclosures of $2\times 2$ matrices A with entries in $\mathcal {G}$ . By including another component $\alpha \in \mathbb {Z}[\tfrac {1}{2}\sqrt {5}-\tfrac {1}{2}]$ we obtain enclosures for skew-product maps $G=(\alpha ,A)$ . The corresponding data type is named Skew. Enclosures on pairs $P=(F,G)$ are described by data of type Skew2. For details we refer to the child package Taylors1.Skews2.

In most of our packages, the type Scalar is generic, meaning unspecified, except for a list of available operations. When instantiated with Scalar => Ball, the packages Taylors1 and Taylors1.Skews2 define enclosures for the spaces $\mathcal {G}_\rho $ , $\mathcal {G}_\rho ^4$ , and $\mathcal {F}_\rho $ described in §3.5.

A particular instantiation of Taylors1, with Scalar => Ball, is named S_T in the package FamRG. The resulting type Taylor1 is named TScalar. A second instantiation of Taylors1, with Scalar => TScalar, is named T_T. The type of Taylor1 defined by T_T describes analytic functions from a disk $|s|<\delta $ to $\mathcal {G}_\rho $ . Now it suffices to instantiate the child package T_T.Skews2, to obtain Skew2-type enclosures on analytic curves in the space $\mathcal {F}_\rho $ . This covers all major data types used in our programs.

8.2 Bounds and procedures

After having defined enclosures for (elements in) the various spaces that are needed in our analysis, we need to implement bounds on maps between these spaces. In this context, a bound on a map $f:\mathcal {X}\to \mathcal {Y}$ is a function F that assigns to a set $X\subset \mathcal {X}$ of a given type (Xtype) a set $Y\subset \mathcal {Y}$ of a given type (Ytype), in such a way that $y=f(x)$ belongs to Y whenever $x\in X$ . In Ada, such a bound F can be implemented by defining an appropriate procedure F(X: in Xtype; Y: out Ytype). In practice, the domain of F is restricted. If X does not belong to the domain of F, the F raises an Exception which causes the program to abort.

Our type Ball is defined in the package MPFR.Floats.Balls, using centers B.C of type MPFloat and radii B.R of type LLFloat. Data of type MPFloat are high-precision floating-point numbers, and the elementary operations for this type are implemented by using the open-source MPFR library [24]. Data of type LLFloat are standard extended floating-point numbers [31] of the type commonly supported by hardware. Both types support controlled rounding. Bounds on the basic operations for this type Ball are defined and implemented in MPFR.Floats.Balls.

Using the definition (8.2) of a Taylor1-type enclosure, it is clearly possible to implement a bound Prod on the map $(f,g)\mapsto f*g$ from $\mathcal {G}\times \mathcal {G}$ to $\mathcal {G}$ . This and other basic bounds that include the type Taylor1 are defined in package Taylors1. Basic bounds that involve the types Skew and Skew2 are defined in the package Taylors1.Skew2. This includes a bound Normalize on the map $\mathfrak {N}$ defined by (3.17). It also includes a bound Inv on the map $G\mapsto G^\dagger $ and a bound Prod_GFG on the product $(F,G)\mapsto GFG$ . Combining the two yields bounds on the products that appear in the definition of the operator $\mathfrak {R}_3$ .

Bounds on problem-specific maps such as $\mathfrak {R}_3$ are mostly defined in child packages of Taylors1.Skew2. Among the exceptions are the bounds named Equalize on the normalization transformations defined in §§3.2 and 4.1. The package Taylors1.Skew2.RG3r implements bounds on operations such as $\mathfrak {R}_6$ that are used only for reversible pairs, while Taylors1.Skew2.RG3a implements bounds that are specific to anti-reversible pairs. This includes procedures named Commutize that provide bounds on the commutator-correction map $\mathfrak {C}$ . A bound on the derivative of $\mathfrak {C}$ is named DCommmutize. The same naming convention is used for other derivative bounds.

Up to this level, the same bounds can be used for pairs and for families of pairs. To choose one or the other, is suffices to instantiate the package Taylors1 and its children with the desired type of Scalar. But for derivative bounds on maps such as $\mathfrak {M}$ , we need to be able to enumerate the degrees of freedom, so it matters whether Scalar encloses a number or a Taylor series.

8.3 Linear operators and modes

In the packages MapR, FamRG, and their children, degrees of freedom are associated with a type Mode. To simplify the discussion, consider first the space $\mathcal {G}_\rho $ . In this case, a ‘coefficient mode’ $c_n$ represents a monomial $\mathcal {P}_n$ of degree n, and an ‘error mode’ $e_n$ represents the unit ball in the subspace of all functions $g=e\mathcal {P}_n$ with $e\in \mathcal {G}_\rho $ . So Taylor1-type enclosure (8.2) in $\mathcal {G}_\rho $ is a finite linear combination of modes for $\mathcal {G}_\rho $ . A proper collection of normalized modes $\{h_1,h_2,\ldots ,h_m\}$ defines an analogue of a finite basis for $\mathcal {G}_\rho $ . Due to our choice of norm in $\mathcal {G}_\rho $ , the operator norm of a bounded linear $T:\mathcal {G}_\rho \to \mathcal {G}_\rho $ is simply $\|T\|=\max _n\|Th_n\|$ . Given that each mode $h_n$ admits a representation of type Taylor1, a bound on $\|T\|$ is easily obtained from a bound on T.

This generalizes readily to the space $\mathcal {F}_\rho ^{\hskip 2.3pt r}$ . The corresponding type CMode is defined in the package MapRG. For a ‘basis’ of such modes we use the type CModes. In MapRG we also instantiate two generic packages Linear and Linear.Contr that implement bounds on a quasi-Newton map (and its derivative) of the type (3.36) in terms of bounds on the given map (and its derivative). Using these facilities, the child package MapRG.RG3a implements a bound DContrNorm on the norm of $D\mathfrak {M}$ , where $\mathfrak {M}$ is the transformation defined by (3.36). This procedure is used to verify the bound on the operator norm of $D\mathfrak {M}(p)$ in Lemma 3.1.

The operator M that enters the definition (3.36) is a ‘matrix’ on a subspace spanned by finitely many coefficient modes, and on the complementary subspace it is the zero operator. This matrix is included as a data file Contr3aMat.132 (see the Data Availability section). The matrix M that is used in the definition (4.9) is included in as a file Contr3rMat.134. The operator $\mathcal {L}$ that enters the definition (5.1) is a ‘matrix’ L on a subspace spanned by finitely many coefficient modes, and on the complementary subspace it is the identity operator. This matrix L is included in the file Iso.132.28. A bound on its inverse is obtained and saved by running the program Invert_Iso.

The child package MapRG.RG3r is an analogue of MapRG.RG3a, but for reversible pairs.

The package FamRG and its children define an analogue of the MapRG hierarchy, but for analytic curves $s\mapsto \texttt{P}(s)$ . The modes for this space are named DModes. However, these modes are not needed in our current proof. (An earlier version implemented the graph transform method that is described in §5.2.) The child package FamRG.RG3a implements the bounds that are used in our proof of Lemma 5.5. This includes a bound Plain_FamRG3 on the transformation $\mathfrak {F}_c$ defined in (5.12), for the special value $c=\alpha ^3\kern-1pt$ .

8.4 Organizing the bounds

Our proof of Lemma 5.5 is organized in the main program Iter_AM_Fam_Sin6. Starting with an enclosure for the anti-reversible AM family for $\unicode{x3bb} $ near $1$ , it does little more than iterating the above-mentioned bound Plain_FamRG3. The bounds are in essence numerical computations, but, as should be clear by now, they include rigorous estimates of truncation errors and rounding errors.

The same is true for our proof of the remaining lemmas. The approximate solutions $\bar P$ referred to in Lemmas 3.1 and 4.1 have been computed numerically beforehand. First we used a numerical versions of Iter_AM_Fam_Sin6 (or Iter_AM_Fam_Cos6 in the reversible case) to obtain rough approximate fixed points for $\mathfrak {R}_3^2$ . Then the approximations were improved via the procedures IterContr in the packages MapRG.RG3a and MapRG.RG3r, respectively. (Numerical versions of our programs are obtained simply by using for Scalar the type Rep instead of Ball.) The results are in the data files approx-Fix3a.trunc and approx-Fix6r.trunc (see the Data Availability section).

The main programs that are used to verify the estimates in Lemmas 3.1, 4.1, and 5.1 are Check_RG3a_Fixpt, Check_RG6r_Fixpt, and CheckNorms_DRGN3. They do little more than instantiating the required packages with the appropriate parameters, reading data files if needed, and then handing the task over to the proper procedure(s) in the instantiated packages.

Our programs were run successfully on a standard desktop machine, using a public version of the gcc/gnat compiler [23]. Instructions on how to compile and run these programs can be found in the README file that is included with the source code (see the Data Availability section).