Introduction
Ice Stream B is changing over time. The mouth of the ice stream is known to be slowing and widening (Reference Stephenson and BindschadlerStephenson and Bindschadler, 1988; Reference Bindschadler and VornbergerBindschadler and Vornberger, 1998). A similar reduction in speed and widening of the ice stream has been observed for the upper portion of tributary B2 (Reference Hulbe and WhillansHulbe and Whillans, 1997; Reference Hamilton, Whillans and MorganHamilton and others, 1998; Reference Harrison, Echelmeyer and LarsenHarrison and others, 1998). Neither the cause nor the future course of these changes is known with confidence. As a contribution to describing changes along the ice stream, we report on changes at the head of one of the tributaries to Ice Stream B (Fig 1).

Fig. 1. Location of the study region. The small box outlines the study area (Fig 2). Shaded regions are ice-stream shear margin boundaries from Reference Shabtaie and BentleyShabtaie and Bentley (1987). The black arrow indicates the mean flow direction.
This study focuses on a special group of crevasses informally called the “chromosomes”. It was discovered by Reference Vornberger and WhillansVornberger and Whillans (1986) and described in detail by Reference Merry and WhillansMerry and Whillans (1993). The name refers to the unusual crevasse shapes, which bear resemblance to pairs of separating chromosomes (Fig. 2). The group ofcrevasses is located at the upstream end of the northernmost (glacier-right) shear margin to the B1b tributary of Ice Stream B. The manifestation of a heavily crevassed margin suggests that the area is very near the onset of ice-stream flow. Force-budget calculations indicate that ice speed and lateral drag increase in the along-flow direction while driving stress and basal drag decrease (Appendix and Fig. 8, shown later; see also Reference Whillans and van der VeenWhillans and Van der Veen, 1997). Similar combinations of flow characteristics have been used to define ice-stream flow vs inland-style flow (Reference BentleyBentley, 1987; Reference Bindschadler, Chen and VornbergerBindschadler and others, 2000). Ice thickness and surface elevation at this site have been measured by radio-echo sounding (Reference Retzlaff, Lord and BentleyRetzlaff and others, 1993). Surface velocity measurements are obtained here by tracking of persistent features in repeat satellite imagery Our objective is to describe the strain-rate and stress pattern in the region, model crevasse development and evolution, and explain the observed patterns of crevasses.

Fig. 2. SPOT HRV image of the study area. The white arrows are feature displacements over ∼4 year time period. Crosses mark feature matches of near zero displacement outboard of the shear margin (the southern edge of the Unicorn). Roman numerals label the groups of crevasses discussed in the text. The dashed line marks the approximate beginning of the chaotic zone that develops downstream into the “heffalump” shear margin (image ID: 10905699312131619481P, © SPOT Image Corporation).
Crevasse Groups
Crevasses within the chromosomes form distinct groups, as shown in Figure 3. The simplest examples are in group I. Crevasses forming chromosomes intersect with one another at a “node” (Fig. 2). Groups II and III contain crevasses similar to those in group I, but the curvature of the crevasses evolves from convex upstream to convex downstream. Faint sets of crevasses are also observed within the more developed crevasses of groups I and II. Relatively short sets of chromosomes, truncated by longer crevasses, are observed within group III.

Fig. 3. Tracing of crevasses in Figure 2.1–III refer to three distinct groups of chromosomes (white traces). Faint crevasses are observed in group land between groups land II (black traces). Connecting crevasses and truncated chromosome packets are observed downstream of group II and within group III (black traces). The dashed white line marks the boundary between the ice stream and the interstream ridge (approximately connecting the zero-flow crossess in Fig 2). The black arrow indicates the mean flow direction.
The boundary between the ice stream and the interstream ridge includes nodes and, closer to the ridge, crevasses diagonal to ice-stream motion. Downstream these evolve into a chaotic zone and outboard arcuate crevasses, respectively. The outboard arcuate crevasses are like those at other ice-stream margins and those modeled by Reference Vornberger and WhillansVornberger and Whillans (1990). The chaotic zone (rough-textured ice due to densely intersecting crevasses and drift mounds) that develops downstream of group III continues on to become the “heffalump” shear margin described by Reference Merry and WhillansMerry and Whillans (1993).
Motion Determination
Common surface features (i.e. crevasses and drift mounds) in a pair of spatially overlapping, temporally separated Système probatoire pour l’observation de la terre (SPOT) high resolution visible (HRV) images are tracked over a time interval of approximately 4 years (images acquired on 14 December 1989 and 13 December 1993). The method is similar to that developed by Reference Bindschadler and ScambosBindschadler and Scambos (1991) and applied in other studies (Reference Lucchitta, Mullins, Allison and FerrignoLucchitta and others, 1993,Reference Lucchitta, Mullins, Smith and Ferrigno1994,Reference Lucchitta, Rosanova and Mullins1995; Reference Bindschadler, Fahnestock, Skvarca and ScambosBindschadler and others, 1994, Reference Bindschadler, Vornberger, Blankenship, Scambos and Jacobel1996; Reference Whillans and TsengWhillans and Tseng, 1995; Reference Frezzotti, Capra and VittuariFrezotti and others, 1998). Details on the feature-matching algorithm, a test of matching-derived velocities against independent measurements, and the quality assessment of matches can be found in Reference Whillans and TsengWhillans and Tseng (1995).
Uncertainties in the geolocation of images result in false, systematic displacements, and require a more precise image co-registration. There are no rock outcrops in the region to use for this purpose. However, surface-based measurements of ice motion in part of the region (the “unicorn”, shown in Figs 1 and 3) are known to be <3 m a−1 (Reference Whillans and van der VeenWhillans and Van der Veen, 1993). Over the time interval between the two images this estimated ice motion is less than a single 10 m × 10 m pixel. Thus, this ice is nearly stagnant and features there can be used for image co-registration. Thirty-five common features were used to approximately co-register the two images. Thirty of these features are among the outboard crevasses shown in Figure 2, and five more are in a corresponding outboard position for the “dragon” (a shear margin farther north). No rotation correction was required to the orientations provided by SPOT image in order to achieve an accurate co-registration. The mean displacement of the 35 co-registration points is subtracted from feature-tracking displacements to remove most of the geolocation bias.
The residual co-registration bias leads to uncertainties in the measured components of velocity. The root-mean-square variation among the 35 co-registration points is 25 m. This leads to an uncertainty in components of absolute velocity of 6.3 m a−1. Relative velocities are more precise, being ultimately limited by the image pixel dimensions (10 m) and the time interval between images (3.998 a). The root-mean-square uncertainty in relative velocity components is (102 m2 + 102 m2)1/2/3.998 a = 3.5 m a−1.
Speeds into the head of tributary B1b are about 60 m a−1 and increase to 80 m a−1 5 km downstream. Such speeds are typical for the heads of the ice streams (Reference Whillans and van der VeenWhillans and Van der Veen, 1993; Reference Price and WhillansPrice and Whillans, 1998; Reference JoughinJoughin and others, 1999). Ice flow in the chromosomes region is likely dominated by motion at the glacier bed (Reference PricePrice, 1998).
Modeling Crevasse Shape
Following conventional views on crevasse formation, crevasses are taken to form perpendicular to the principal extending strain rate, where that strain rate is sufficiently large (Reference NyeNye, 1959; Reference Meier, Kamb, Allen and SharpMeier and others, 1974; Reference Raymond and ColbeckRaymond, 1980; Reference Vornberger and WhillansVornberger and Whillans, 1990; Reference VaughanVaughan, 1993). In this region, crevasses are observed to begin opening where displacement determinations find the principal extending strain rate to be about 0.003 a−1 Over time, a crevasse may rotate according to differential velocity along its length. These two principles have been combined to successfully model other crevasse shapes on Ice Stream B (Reference Vornberger and WhillansVornberger and Whillans, 1990).
Reference Merry and WhillansMerry and Whillans (1993) advanced a conceptual model to explain the nodes observed in the chromosomes region (see Reference Merry and WhillansMerry and Whillans, 1993, fig. 3). Relatively newer crevasses intersect relatively older, more deformed crevasses at a common point of intersection, forming a node. For any chromosome-shaped set of crevasses, the oldest crevasse on the interstream ridge is that farthest upstream. Its temporal counterpart within the ice stream is the farthest downstream. While the nodes appear to be weak sites within the ice that encourage crevasse formation, their origin is unknown. As such, they are not included in the formulation of the present model.
We model the velocity field using polynomial expressions fit to the measured components of velocity shown in Figure 2. For each group of crevasses (I–III), the extent of velocity measurements defines the two-dimensional model domain. The x and y axes are aligned along- and across-flow, respectively, and the origin is at the point of zero horizontal motion, where the crevasse trace intersects with the interstream ridge. A good representation of the measured velocity profiles is achieved with a first-order polynomial in the along-flow direction and a fourth-order polynomial in the across-flow direction. A fourth-order polynomial provides good approximations to across-flow velocity profiles elsewhere on Ice Stream B (Reference Whillans, Bolzan and ShabtaieWhillans and others, 1987). Those authors found that the along-flow component of velocity varied across-flow as a constant, times the distance from the ice-stream center line raised to the fourth power. In the present case, the position of the center line is not well known, so a polynomial containing all terms is used. A fourth-order relation also describes lateral drag resisting a significant fraction of the ice-stream motion. Approximately 60% of the resistance to motion in the chromosomes region is due to lateral drag (see Appendix), so the use of a fourth-order relation is valid. Figure 4 shows the measured velocities and the polynomial fits to those velocities. The polynomial representations of the velocities agree with discrete measurements to within the range of measurement uncertainties (see below) and are not expected to introduce any further uncertainties.

Fig. 4. Along-flow component of velocity measured within crevasse groups I–III (filled circles), plotted with distance from the ice-stream margin (white line in Fig 3). Fourth-order polynomial fits to the velocities (solid curves and axes) and shear strain rates derived from them (dashed curves and axes) are also shown. The R2 values for all fits are ≥0.99.
The strain-rate field for each crevasse group is calculated from the first derivative of the along- and across-flow polynomials (Fig. 4). The modeled crevasses are assumed to form where the principal extending strain rate is ≥0.003 a−1 and to grow instantaneously along their length, perpendicular to the principal extending strain rate. Crevasses are allowed to grow to the limits of the model domain. Because the model does not include the role of nodes, modeled crevasses intersect with the interstream ridge instead of slightly inboard of the ridge. A modeled crevasse trace for group III is shown in Figure 5.

Fig. 5. Modeled crevasse shapes for group III at 10 year time intervals. Ice flow is in the x direction. The black dashed line is equivalent to the white dashed line in Figure 3.
The main features of the modeled crevasse are that the trace of the crevasse evolves from convex upstream to convex downstream. The change in shape is most pronounced in the region within about 3 km from the interstream-ridge/ice-stream boundary. The modeled evolution of crevasse shape closely resembles crevasse shapes observed in the imagery (Fig.2).
Matching Model to Observation
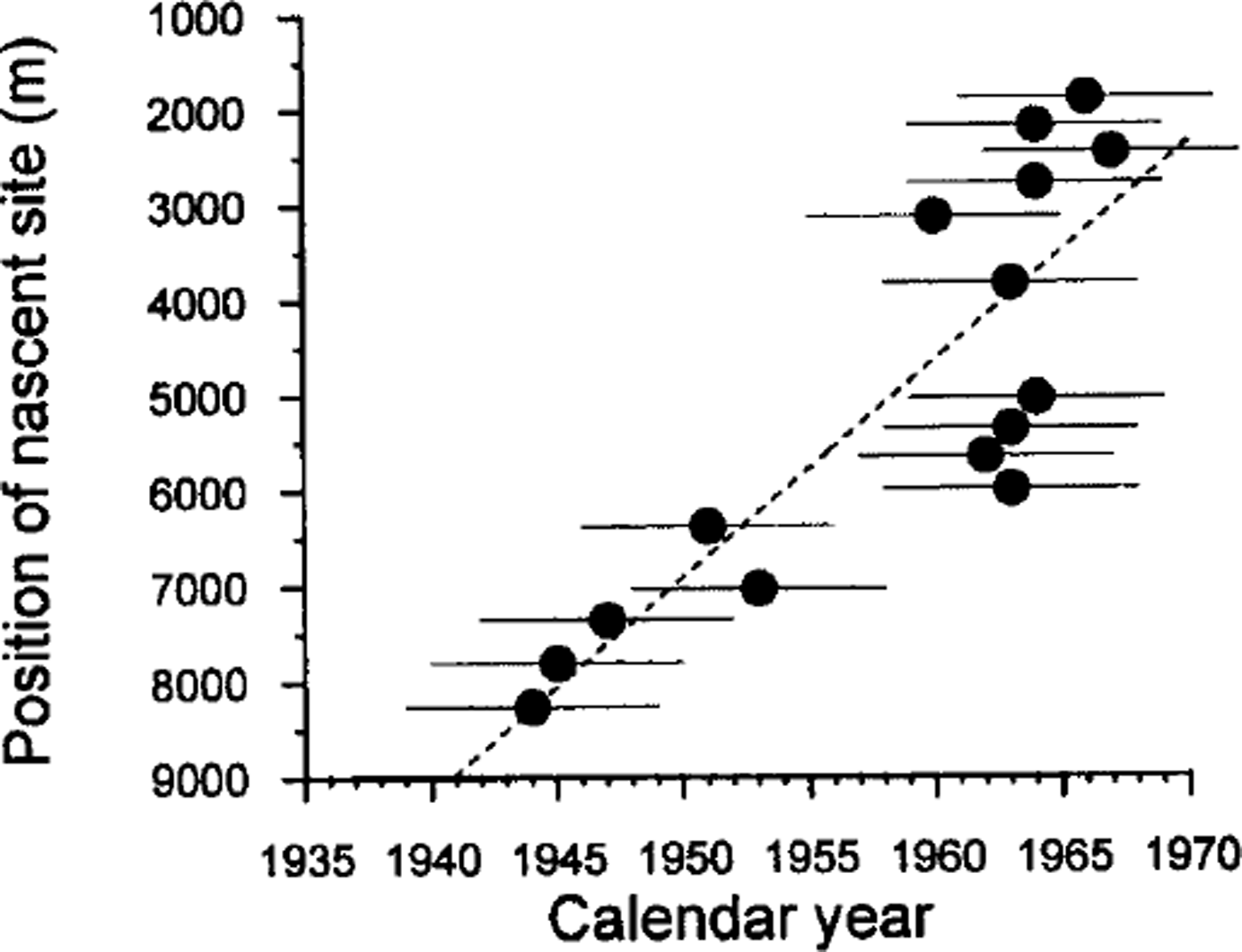
The match between modeled and observed crevasses is used to assign dates and positions of formation to select crevasses in groups I–III. Crevasse age and nascent shape are mapped in Figure 6. Age vs nascent position along the transect A–A′ in Figure 6 is shown in Figure 7. Progressively younger crevasses have formed farther upstream over time. This means that the sites of crevasse formation have migrated upstream over time. The solid line in Figure 7 is a linear fit to these values. It indicates a mean migration rate of 230 m a−1.

Fig. 6. Modeled age, nascent shape and nascent position of select crevasses within crevasse groups I–III. The black dashed line is equivalent to the white dashed line in Figure 3.
Uncertainties in crevasse age and nascent site
Uncertainties in the estimated age of the crevasses are due to uncertainties in the measured strain rates and to the possibility that strain rates have changed over time. Based on propagation of measurement uncertainties, the uncertainty in shear strain rates calculated from neighboring feature matches is ≤0.003 a−1. The uncertainty in along-flow stretching rates is ∼0.001 a−1. The small difference derives from the fact that the along-flow stretching rate is less variable in the across-flow direction than is the across-flow shearing rate. The primary region of interest for crevasse modeling is within 3 km of the interstream ridge, where the deformation is concentrated. Within this zone, the uncertainty in strain rates results in an age uncertainty of (≤5 years for the modeled crevasses. Propagating these uncertainties leads to an uncertainty of 16 m a−1 in the mean migration rate of nascent sites.
The sites of crevasse initiation appear to have migrated upstream over time, implying that stretching rates and ice speed in the region have increased over time. For any fixed geographic location, the mean velocity over time would then be slightly less than the present-day velocities used in the modeling. This effect would lead to a slight increase in the ages of crevasses presented here. The calculated migration rate would be relatively unaffected.
Cause of Changes in Onset Location
The site of tension large enough to form crevasses appears to have migrated upstream over time. This implies an upstream migration of the ice-stream onset. Thus, stretching rates and glacier speed at a geographically fixed site have increased. The most likely explanation for these changes is an increase over time in the rate of basal slip near the onset site.
The fast speed of ice streams is enabled by basal lubrication that favors rapid motion at the bed. By extension, the beginning of ice-stream flow must be associated with an along-flow increase in lubrication. The amount of lubrication is linked with some combination of water production rate, water collection at the bed and bed roughness. Perhaps one or more of these quantities has changed over time at the onset, resulting in faster ice speeds and a subsequent upstream migration of the ice-stream onset.
The rate of meltwater production is linked to the rate of work done by the moving ice stream, expressed as the product of speed and driving stress. The driving stress is about twice as large among group II and III crevasses as elsewhere (Fig. 8). Ice velocity has been measured 12 km downstream of the chromosomes (station 13 of Reference Whillans and van der VeenWhillans and Van der Veen (1993)), within the chromosomes, and is estimated for upstream sites according to the along-flow velocity gradient measured here. The product of driving stress and speed (which may be discerned from the curves in Figure 8) has a maximum near groups II and III. A small change in speed or driving stress could lead to a positive feedback in heat production, which could further alter ice speed. A feedback between basal melting and ice speed could be responsible for the current location of the onset and for changes in the onset site over time.

Fig. 8. Surface speed (upper dashed line), surface elevation (upper solid line), driving stress averaged over ∼10 km (long-dashed line, middle), hydraulic potential (short-dashed line, middle) and basal elevation (lower solid line) along a downstream transect that includes the chromosomes region. The locations of crevasse groups I–III are indicated by long, vertical dashes. Flow is from left to right. The triangles in the uppermost plot are velocity measurements within and downstream of the study area. The dashed black line is a linear fit to those data. The most downstream measurement (rightmost) is station 13 from Reference Whillans and van der VeenWhillans and Van der Veen (1993).
Changes in the volume of subglacial water are a second possible cause for the implied time changes at the crevasse initiation site. The amount of subglacial water depends on water production and on the subglacial hydrologic potential gradient: the smaller the gradient, the more probable subglacial ponding. The gradient is calculated from measurements of ice thickness and surface elevation (Reference Retzlaff, Lord and BentleyRetzlaff and others, 1993), neglecting spatial variations in effective pressure. Water-flow trajectories from upstream converge towards the head of Ice Stream B1b (x = y = −4.5 in fig. 1 of Reference Alley, Anandakrishnan, Bentley and LordAlley and others (1994)). Furthermore, there is a reverse basal gradient (x ≈ 15–25 km in Fig. 8) that is an order of magnitude larger than the surface slope, making a favorable setting for a subglacial lake (and the elimination of subglacial friction). Small changes in the surface elevation profile in the vicinity of the lake would cause changes in lake area. An increase in the lake area would lubricate more of the bed and result in a speed increase in the chromosomes region. The increase in speed would stretch and thin the ice upstream, thereby reducing the surface slope and providing a positive feedback on lake size. Time-changes in the area of the proposed lake could be the reason for the observed ice-flow changes in the chromosomes region.
If a subglacial lake exists, it might be identified by geophysical studies. Reference Bentley, Lord and LiuBentley and others (1998) used airborne radio-echo sounding to produce maps of basal-reflection strength beneath the downstream portions of Ice Streams B and C. The reflection strength is used to delimit areas of the bed that are wet vs areas that are frozen. Similar analysis of the radio-echo sounding data from Reference Retzlaff, Lord and BentleyRetzlaff and others (1993) could be used to look for evidence of the proposed lake upstream from the chromosomes. Unfortunately, thick ice and signal scattering from surface and buried crevasses limits the sensitivity of the basal-reflection strength in these areas. Subglacial lakes on the scale of ≤10 km would not likely be observed through a similar analysis (personal communication from N. Lord, 1999).
A third possibility for the migration of the ice-stream onset is an along-flow change in bed roughness. The roughness change could be between igneous and sedimentary rock (e.g. Reference Anandakrishnan, Blankenship, Alley and StoffaAnandakrishnan and others, 1998; Reference BellBell and others, 1998), between different types of sedimentary rocks, or could involve the presence or absence of a soft, moldable, basal till. However, it seems unlikely that bed roughness could change over the short time-scales being considered (tens of years). This hypothesis is thus discarded.
Development of Crevasse Patterns
There is a simple progression of crevasse types along-flow in the region. The presence of the nodes would seem to indicate that these are nucleation sites; from the nodes, crevasses grow toward the interstream ridge to make the outboard “hook-shaped” crevasses and also grow toward the ice stream, where their growth directions become more transverse to flow. Initially, all crevasses are convex upstream. Over time, shear strain rotates the crevasses out of alignment with the causative stress field and they become progressively more convex downstream. Our observations (Figs 2 and 3) indicate that after rotation of about 10°, new crevasses can form at the original, convex-upstream orientations.
Minor sets of chromosomes, truncated by longer crevasses, are observed in group III, close to the interstream ridge (Fig. 3). After the long crevasses are rotated downstream, short, connecting crevasses appear to form between them. Over time, these connecting crevasses are also rotated downstream, and new crevasses open up at the old orientations. The minor, truncated sets of chromosomes form in a manner similar to the longer chromosome sets but within a more limited area.
A “chaotic zone”, like the one observed near the bottom of the image in Figure 2, is the product of continued development of the region most densely populated with crevasses. At this point, crevasses have undergone a net rotation of approximately 90° and have been subjected to a shear strain rate of 0.010–0.015 a for approximately 50 years. A chaotic zone is then a suite of crevasses similar to the ones modeled here, but with so many superposed generations that specific crevasse histories are difficult to unravel.
The faint crevasses within groups I and II appear to be buried (Figs 2 and 3). This interpretation would suggest that they are older than more prominent crevasses nearby and possibly inactive. However, the faint crevasses are forming near the nascent sites for crevasse groups I and II, and their shape is similar to that modeled for very young crevasses (Fig. 5). These crevasses are likely the youngest observed in the imagery. Possibly they lack wide, sagging bridges, making them appear faint in the imagery. Our model predicts that the faint crevasses formed between approximately 1979 and 1989. Aerial photographs from 1983 show the same sets of faint crevasses, so they must have formed closer to 1979 in order to be wide enough for detection in the photos.
A 1995 SPOT image shows no crevasses in addition to those seen in the 1983 aerial photos. If new crevasses have formed in the region they are not wide enough to be visible in the most recent SPOT image. Alternatively, there may have been a hiatus in crevasse formation between the time of the photos and the time of the recent images. A hiatus of similar length is observed to have taken place between the 1950s and the 1960s (Fig. 7).
Conclusions
Inland migration of the ice-stream onsets has been predicted or inferred in previous work, but never measured directly. Reference Alley and WhillansAlley and Whillans (1991) and Reference BindschadlerBindschadler (1997) derived headward migration rates on the order of 500 m a−1. That is comparable to our measured rate of 230 ma−1. Interestingly, the retreat rate of the grounding line over the past 7500 years is of a similar scale (120 m a−1; Reference Conway, Hall, Denton, Gades and WaddingtonConway and others, 1999). If the migration rate measured here persists, the onset to tributary B1b would reach the inland West Antarctic ice-sheet divide in approximately 1400 years.
The discovery of inland migration at an onset to Ice Stream B, together with the overall negative mass balance of Ice Stream B’s catchment (Reference Whillans and BindschadlerWhillans and Bindschadler, 1988), indicates that changes in the West Antarctic ice streams occur at their most inland reaches. Changes on the ice streams are not limited to the grounding zone, but also involve the central portion of grounded ice, thereby having relevance to the long-term behavior of the ice sheet and global sea level.
The cause for the migration is not known, but it likely involves changes in the rate of production, or more likely the storage of subglacial water near the ice-stream onset. Subglacial water storage is related to the combination of reverse-sloping-bed topography and, more importantly, shallow surface slope. It is beyond the scope of the present work to speculate on the initial cause for the shallow surface slopes near the ice-stream onset (e.g. regional mass-balance changes, long-term ice-sheet thinning). However, it is noted that this geometry, once established, may lead to a positive feedback between subglacial water storage, inland onset migration and further shallowing of surface slopes upstream.
The present analysis of crevasse evolution suggests a kinematic model for the formation of an ice-stream chaotic zone within a developing shear margin. Crevasses form in a zone of shear, but rotation of crevasses out of alignment with the stress field leads to the formation of new crevasses. Over time, this process creates a region of densely intersecting crevasses that ultimately becomes the chaotic zone. The “heffalump” chaotic zone at the northern margin to B1b takes approximately 50 years to form over a distance of 3 km. Once formed, it is maintained for the full length of the ice-stream tributary (∼180 km; Reference Merry and WhillansMerry and Whillans, 1993).
Acknowledgements
Suggestions from D. Dahl-Jensen and an anonymous reviewer helped to improve the manuscript. The authors also wish to thank C. Hulbe and R. Bindschadler for many helpful comments. Research was supported by the U.S. National Science Foundation (grant No. 0PP-9316509). This is Byrd Polar Research Center contribution No. 1190.
Appendix
Force balance at the head of Ice Stream B1b
The role of lateral shear stress in resisting the ice motion can be estimated according to the large-scale balance of forces, following the method of Whillans and Van der Veen (1997). The balance of forces acting on a block of ice with length L, width W and mean thickness H is

in a Cartesian coordinate system. The x and y axes are in the horizontal plane and are oriented along- and across-flow, respectively. L is parallel to the ice-flow direction and W is equal to the half-width of the ice stream. Dividing Equation (A1) by the area, LW, gives the balance equation in terms of stresses,

The first term on the left in Equation (A2) is the driving stress, given by the familiar relation τ dx = ρgH sin α, where ρ is the density of ice, g is the acceleration due to gravity and α is the ice-sheet surface slope. Driving stress is balanced by basal drag (second term on the left in Equation (A2)), lateral drag (third term on the left in Equation (A2)), and longitudinal stresses pulling upstream and downstream (fourth and fifth terms on the left in Equation (A2), respectively). Rxy and Rxx are the depth-averaged shear and longitudinal resistive stresses, respectively. Longitudinal stresses are negligible when considering averages over long distances (e.g. Whillans and Van der Veen, 1993, 1997), as is done here. Neglecting the longitudinal terms leaves:
Driving stress is balanced by drag at the glacier bed and by lateral shear stress.
Shear stress is computed using a simplification of the inverse flow law for glacier ice,

where ux is the component of velocity parallel to ice flow. The last term on the right is the shear strain rate, in which gradients in the across-flow component of velocity are ignored because they are negligible in the study area. The shear strain rate is at least an order of magnitude larger than other strain rates in the region, and so is assumed to be approximately equal to the effective strain rate in Equation (A4) (term in square brackets). B is the temperature-dependent rate factor (Reference HookeHooke, 1998).
Lateral drag at the chromosomes site is calculated using data from several sources. Shear strain rates are taken from the feature-tracking displacements presented here. The rate factor is a depth-averaged value, calculated according to a temperature profile measured near the Upstream Bravo (UpB) camp on tributary B2 (Reference Engelhardt, Humphrey, Kamb and FahnestockEngelhardt and others, 1990). The half-width of tributary B1b (W) is estimated from satellite imagery, and the mean thickness (H) is taken from maps of Reference Retzlaff, Lord and BentleyRetzlaff and others (1993). The mean driving stress, lateral drag and basal drag are 39, 23 and 16 kPa, respectively, so lateral drag accounts for 60% of the resistance to flow. Between 10 and 20 km downstream of the chromosomes, the mean driving stress, lateral drag and basal drag are 12, 12 and 0 kPa, respectively, so lateral drag accounts for 100% of the resistance to flow (Whillans and Van der Veen, 1997, table 1). The measurements indicate that within the chromosomes region, lateral drag is progressively replacing basal drag as the dominant control on ice motion.