1 INTRODUCTION
Low-frequency radio astronomy is once again on the scientific frontier, driven in large part by the goal of measuring the radio emission from high-redshift neutral hydrogen during the Epoch of Reionisation (EoR), predicted to lie in the 50–200 MHz part of the radio spectrum (e.g. Furlanetto, Oh, & Briggs, Reference Furlanetto, Oh and Briggs2006; Morales & Wyithe, Reference Morales and Wyithe2010). In addition to established telescopes working at these frequencies, such as the Giant Metrewave Radio Telescope (‘GMRT’, Swarup et al., Reference Swarup, Ananthakrishnan, Kapahi, Rao, Subrahmanya and Kulkarni1991), the Mauritius Radio Telescope (Golap et al., Reference Golap, Shankar, Sachdev, Dodson and Sastry1998), and the Jansky Very Large Array (‘JVLA’, Clarke et al., Reference Clarke2015), several new telescopes are now operating in this frequency range including the Low Frequency Array (‘LOFAR’, van Haarlem et al., Reference van Haarlem2013), the Precision Array for Probing the EoR (‘PAPER’, Parsons et al., Reference Parsons2010), the Long Wavelength Array (‘LWA’, Ellingson et al., Reference Ellingson2013), and the Murchison Widefield Array (‘MWA’, Lonsdale et al., Reference Lonsdale2009; Tingay et al., Reference Tingay2013). All of these instruments have performed, or are undertaking, large-area sky surveys (Cohen et al., Reference Cohen, Lane, Cotton, Kassim, Lazio, Perley, Condon and Erickson2007; Heald et al., Reference Heald2015; Lane et al., Reference Lane, Cotton, van Velzen, Clarke, Kassim, Helmboldt, Lazio and Cohen2014)Footnote 1. The survey properties, including limiting flux density, resolution, surface brightness sensitivity, and sky coverage vary considerably between instruments and survey programs.
We present the details of the GaLactic Extragalactic All-sky MWA (GLEAM) survey, which is surveying the sky south of declination + 25° with the MWA. GLEAM was conceived to provide data for many science goals including studies of : radio galaxies and active galactic nuclei; galaxy clusters; the Magellanic clouds; diffuse galactic emission and the Galactic magnetic field; galactic and extragalactic spectral lines; supernova remnants; Galactic H ii regions; pulsars and pulsar wind nebulae; and cosmic rays. GLEAM is intended to leave a significant legacy dataset from the MWA that can be utilised for its capabilities in the time, frequency, polarisation, and field-of-view domains. GLEAM’s two-year observing program began in August 2013.
The myriad MWA science opportunities enabled by large sky area surveys, including in the time domain, are detailed in Bowman et al. (Reference Bowman2013).
In Section 2, we describe the survey goals and observation strategy of GLEAM. In Section 3, we describe the image features and data processing issues associated with GLEAM. In Section 4, we calculate the thermal- noise sensitivity of GLEAM mosaiced images for different observing frequencies, image weighting schemes, and pointings. In Section 5, we discuss outputs from GLEAM and compare to other radio surveys covering a large fraction of the southern hemisphere.
2 SURVEY STRATEGY
An advantage for the survey speed of low-frequency radio telescopes is a large field-of-view. For the MWA, whose main antenna ‘tiles’ have an effective width of approximately 4 m, this is especially true. In addition, the 128 tiles of the MWA provide excellent snapshot u, v-coverage, which is essential for both the imaging and calibration fidelity of such wide-field data. The combination of huge instantaneous field-of-view and excellent snapshot u, v-coverage makes the MWA well suited to surveying large volumes of the universe in a short time. As has been previously demonstrated (Bernardi et al., Reference Bernardi2013; Hurley-Walker et al., Reference Hurley-Walker2014), meridian drift scans are an effective surveying technique for the MWA and we re-used the basic strategy for GLEAM.
The sky was divided into seven strips in declination and five frequency ranges, as summarised in Table 1. The declinations were chosen such that the peak in the primary beam response for a given setting corresponds approximately to the half power point of the neighbouring beam along the meridian at 150 MHz, which also makes the beams overlap at the half power points at 216 MHz. Examples of the primary beam patterns for the various frequencies and declinations are shown in Figure 1.

Figure 1. Examples of the MWA’s primary beams used in the survey overlaid on the sky at LST 18 h as seen from the MWA site. The contours show the half-power levels relative to the peak in the beam for that declination where the solid (red) lines are for the ‘X’ (east-west oriented) dipoles and the dashed black lines are for the ‘Y’ (north-south oriented) dipoles. The additional smaller ellipses at the extreme north and south for the higher frequency images are due to the chromatic grating lobes of the MWA primary beam exceeding the half power level of the main lobe.
Table 1. GLEAM survey observing parameters.

The instantaneous frequency coverage of the MWA is 30.72 MHz, so the frequency range between 72 and 231 MHz was divided into five bands that provide near contiguous coverage but avoid the band around 137 MHz that is contaminated by satellite interference. The central frequencies of the bands are listed in Table 1.
While GLEAM is designed to cover the entire sky south of δ + 25°, some sky north of δ + 25° will be accessible with reduced sensitivity in the mid and lower parts of the GLEAM frequency range due to the larger primary beam size at those frequencies.
The region around the south celestial pole (SCP) is a special case for GLEAM due to its low elevation from the MWA site. At the lower frequencies, the SCP region is included in the − 72° declination observations. For the two highest frequency ranges, extra observations pointed at the SCP are used to cover this region.
GLEAM observing was executed as a series of week-long campaigns where a single declination setting was observed in a night, covering a strip between approximately 8 and 10 h in length, depending on the time of year. Radio emission from the Sun can overwhelm other radio sources at MWA frequencies, so observations were only performed at night. Within a night, the observing was broken into a series of 120 s scans for each frequency, cycling through all five frequency settings over 10 min. Within a scan, typically 108 s of usable data were collected. Every two hours throughout the night, a calibration field containing a bright, compact source was observed over all five frequency settings, again as a set of 120 s scans totalling 10 min.
During the first year of GLEAM observations, visibility data were recorded with the default MWA time and frequency resolution of 0.5 s and 40 kHz respectively. This covered the entire sky as originally planned for GLEAM. In the second year of GLEAM, enhancements to the MWA correlator (Ord et al., Reference Ord2015) allowed data to be recorded in 10-kHz mode, hence the second year of GLEAM was recorded with 2 s time resolution and 10-kHz frequency resolution, increasing the usefulness of the dataset for spectral line and polarisation science. In addition, for the second year of GLEAM, the antennas were pointed off-meridian by + 1 or − 1 h in alternating observing campaigns to increase the overall hour angle coverage over the entire sky.
GLEAM observations were also used commensally as part of the MWA Transients Survey (‘MWATS’, Bell et al., in preparation), which is a time-domain survey combining GLEAM data with separate observations to regularly monitor the radio sky. The aim of MWATS is to revisit three of the GLEAM declination strips (+ 1.6°, − 26.7°, and − 55°) on timescales of seconds, hours, and months using data centred at 154 MHz only. The motivations for this survey are as follows: (i) To obtain temporal data on an extremely large and robust sample of low-frequency sources to explore and quantify both intrinsic and extrinsic variability; (ii) To search and find new classes of low-frequency radio transients that previously remained undetected and obscured from multi-wavelength discovery; (iii) To place rigorous limits on the occurrence of both transients and variables prior to the SKA era.
3 DATA PROCESSING AND MOSAICING
Here we briefly review the main features of the MWA and refer the reader to Tingay et al. (Reference Tingay2013) for details.
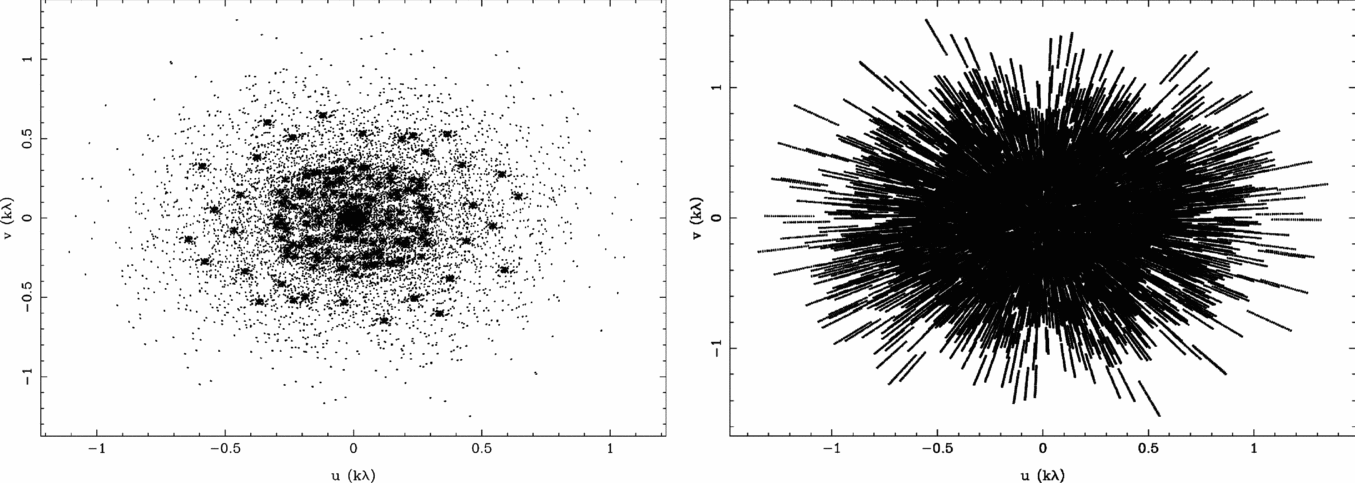
The MWA’s 128 antenna tiles are distributed over an area approximately 2.5 km in diameter. The array has a central core of approximately 40% of the tiles with the remainder distributed for u, v-coverage. An example of u, v-coverage for a 154-MHz zenith-pointed snapshot is shown in Figure 2. The excellent instantaneous u, v-coverage of the MWA is advantageous for both calibration and imaging.

Figure 2. MWA monochromatic (left) and 30-MHz multi-frequency synthesis (right) u, v-coverage for a 2-min zenith-pointed snapshot centred on 154 MHz.
As discussed in Ord et al. (Reference Ord2010), MWA snapshot images follow the well-defined slant orthographic projection which is supported by most current astronomy software. The simplest approach for mosaicing GLEAM images is image-based weighted addition, after regridding to a common coordinate frame. This approach was used in Hurley-Walker et al. (Reference Hurley-Walker2014) and we adopt the same approach here to calculate sensitivity (see Section 4).
Data are typically pre-processed through the Cotter pipeline (Offringa et al., Reference Offringa2015) which flags radio-frequency interference (RFI) and optionally reformats the data into standard radio astronomy data formats.
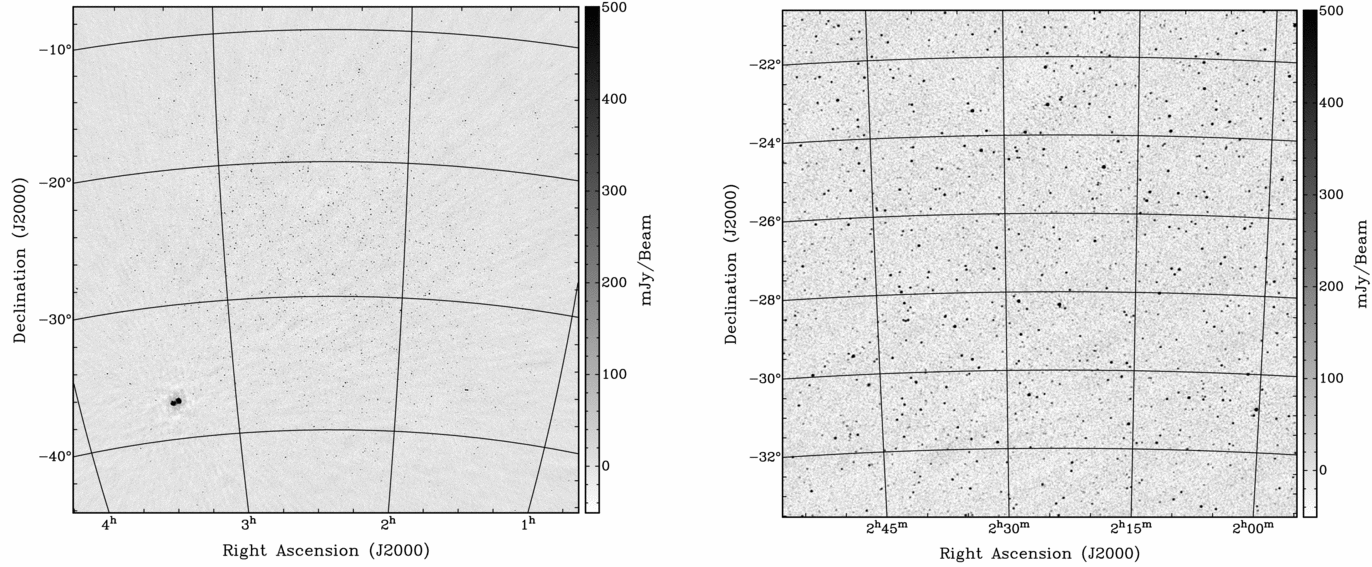
Figure 3 shows example snapshot images from GLEAM at high Galactic latitude. Images containing almost the entire main lobe of the primary beam can be generated with standard (~ ×3) oversampling of the synthesised beam in image space and 4096 × 4096 image pixels. The beam size in Figure 3 is 2.46 × 2.24 arcmin and the pixels are 34 arcsec across at the image centre. In this example, the giant radio galaxy Fornax A can be seen in the lower left of the image, however the vast majority of extragalactic radio sources are unresolved in GLEAM.

Figure 3. An example of a high Galactic latitude zenith-pointed 2-min snapshot for a single (YY) polarisation centred at 154 MHz using full-bandwidth multi-frequency synthesis with robust parameter = −1. The left panel shows the full 4096 × 4096 image (not primary beam corrected), which extends almost to the first beam null. The right image is zoomed to the field centre. The beam size in these images is 2.46 × 2.24 arcmin.
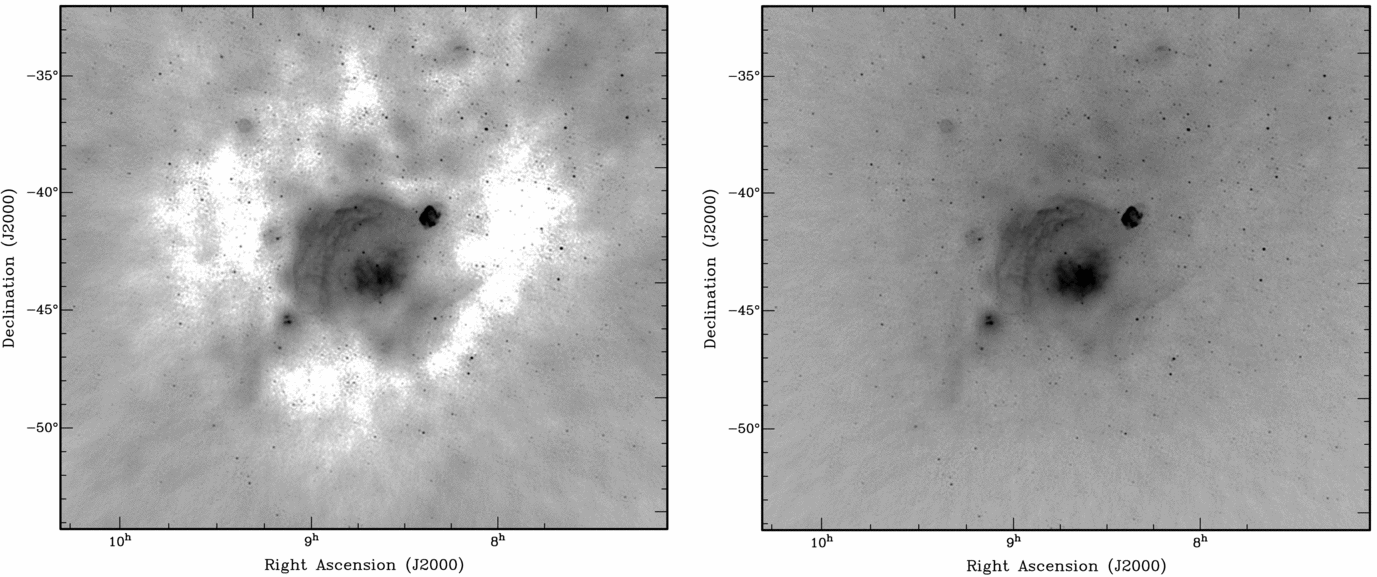
Figure 4 shows example snapshot images from GLEAM on the Galactic plane region containing the Gum Nebula from the declination − 40° drift scan. The left image is the restored image just using MWA data and shows a negative bowl on the largest scales around the region due to missing zero-spacing flux. The right image shows the same region with the addition of zero-spacing information using miriad’s ‘immerge’ task (Sault, Teuben, & Wright, Reference Sault, Teuben and Wright1995) using a scaled, regridded, and primary beam weighted image from 408-MHz data (Haslam et al., Reference Haslam, Salter, Stoffel and Wilson1982). The 408-MHz data were scaled by a constant spectral index of − 0.6, however since Figure 4 is only meant for illustrative purposes, we allowed ‘immerge’ to adjust the flux scales of the datasets in an overlap region for baseline lengths between 10 and 45 m, hence the overall flux scale is only approximate. These images demonstrate the MWA’s excellent surface brightness sensitivity.

Figure 4. An example of the Gum Nebula region of the Galactic plane including the Vela and Puppis A supernova remnants from a 2-min snapshot in the declination − 40° drift scan centred on 154 MHz. Images were made with full bandwidth synthesis over 30.72 MHz and robust = 0.5 weighting. The left image shows a restored image after deconvolution with no additional zero-spacing information. The right image shows the result after using miriad’s ‘immerge’ task to include zero-spacing information based on 408-MHz data (Haslam et al., Reference Haslam, Salter, Stoffel and Wilson1982). The beam size in these images is 4.22 × 3.97 arcmin. The colour bar has been omitted because the absolute flux scale is not yet correct, but the two images have the same intensity scaling.
3.1 Calibration
The GLEAM observation strategy includes a calibration scan on a bright compact source every two hours. The MWA is phase stable over many hours and phase calibration solutions are readily transferred between pointings, after which self-calibration can reduce residual phase and amplitude calibration errors. Calibration sources used for GLEAM include 3C444, Pictor A, Taurus A, Hydra A, Virgo A, and Hercules A, most of which have well-determined flux densities over the GLEAM frequency range. These scans are useful for diagnostic purposes and are used to apply an initial amplitude and phase calibration solution onto the survey data.
Since the absolute response of the MWA’s primary beam changes depending on pointing, the flux scale of snapshots made via calibration transfer must be scaled by the ratio of the absolute primary beam response on the target field to the absolute primary beam response on the calibration field. This procedure was used to set the flux scale of the example snapshot images used in this paper but is limited by how accurately the model primary beam represents the true primary beam.
The full survey, however, has the advantage that many thousands of sources sample the primary beam response as they drift through it during the night and that the primary beam response is constant throughout the night. This provides a mechanism to build an accurate empirical model of the primary beam and simultaneously bootstrap the absolute flux scale using a large sample of sources. The overlapping declination ranges of GLEAM also provide a way to ensure both the primary beam correction and overall flux scale is consistent over the entire sky.
Some complications do arise in processing GLEAM snapshots into mosaics, in particular: effects of the ionosphere; strong sources in the primary beam sidelobes; and instrumental polarisation.
Concerning the ionosphere, the MWA is located at the Murchison Radio-astronomy Observatory (MRO), the location of which was chosen in part due to its favourable ionospheric characteristicsFootnote 2 in the mid-latitude southern hemisphere. For GLEAM purposes, the ionosphere over the MRO is typically stable (Herne et al., Reference Herne, Kennewell, Lynch and Carrano2014) with slowly varying changes in Total Electron Content (TEC) causing arcmin-scale shifts in source positions over timescales of hours (Hurley-Walker et al., Reference Hurley-Walker2014; Arora et al., Reference Arora2015), which is of order the size of the MWA synthesised beam. Under typical conditions, these shifts can be described as a single bulk position offset for all sources in the field, an effect which can be corrected for in an image simply by adjusting the reference coordinates in the image metadata. Unusual ionospheric, tropospheric, and solar wind conditions do occasionally occur and are the subject of specific detailed studies (Loi et al., Reference Loi2015). Nights that showed detrimental ionospheric behaviour were re-observed.
Powerful radio sources (Cygnus A, Centaurus A, Virgo A, Taurus A, etc) in the MWA’s sidelobes can cause artefacts in multi-frequency synthesis images that cannot be deconvolved. These artefacts are due to chromatic effects and the nature of the MWA’s primary beams where, after calibration of the main lobe of the beam, differences between antenna tiles manifest themselves as differences in the sidelobes of the primary beam. These bright sources can be modelled and subtracted, in principle, via advanced interferometric techniques such as ‘peeling’ and ‘A-projection’ (van der Tol, Jeffs, & van der Veen, Reference van der Tol, Jeffs and van der Veen2007; Mitchell et al., Reference Mitchell, Greenhill, Wayth, Sault, Lonsdale, Cappallo, Morales and Ord2008; Bhatnagar et al., Reference Bhatnagar, Cornwell, Golap and Uson2008; Tasse et al., Reference Tasse, van der Tol, van Zwieten, van Diepen and Bhatnagar2013), but are a problem for conventional deconvolution where all primary beams are assumed to be identical. For GLEAM, such sources are a problem in a fraction of data (~ 25%).
3.2 Polarisation
Since the MWA’s antenna tiles are fixed on the ground, the MWA’s primary beam is subject to many significant instrumental polarisation effects. Full polarisation data products in instrumental coordinates (XX,YY,XY, and YX) are stored by default from the MWA correlator (Ord et al., Reference Ord2015). The two main issues for polarisation are instrumental cross polarisation, due mostly to geometric effects, and a difference in the magnitude of the co-polarisation (XX and YY) response within a tile. The cross polarisation is an inevitable projection effect which causes an unpolarised source to generate correlated signal in the cross-polarisation correlator outputs (XY and YX) independent of any electronic leakage. The difference in co-polar response (XX and YY) is expected partly due to simple geometric effects (i.e. a dipole’s effective length shortens as a source moves closer to its long axis) and array mutual coupling effects. Both of these effects are considered in the tile model detailed in Sutinjo et al. (Reference Sutinjo, O’Sullivan, Lenc, Wayth, Padhi, Hall and Tingay2015), and this model has been adopted as the standard for all MWA data processing.
Processing with appropriate calibration and imaging techniques (e.g. Mitchell et al., Reference Mitchell, Greenhill, Wayth, Sault, Lonsdale, Cappallo, Morales and Ord2008; Offringa et al., Reference Offringa2014), to account for direction-dependent and time-dependent effects, allows both linear (Stokes Q, U) and circular polarisation (Stokes V) images to be produced. As the polarised source counts are significantly lower than in total intensity (Stokes I), linear and circular polarisation images are in principle far less affected by source confusion and can achieve sensitivity levels that approach thermal noise.
Circular polarisation can easily be processed in a similar manner to that used for total intensity (Stokes I) imaging, that is, by treating the entire frequency band in a continuum-like mode. However, care must be taken when imaging the two linear polarisation (Stokes Q and U) as even small degrees of Faraday rotation can significantly rotate the polarisation angle of the radiation across the observing bandwidth, resulting in significant bandwidth depolarisation. To reduce the effect of bandwidth depolarisation, it is necessary to image Q and U in a spectral-like mode using the fine (10 or 40 kHz) channels available in the GLEAM data. Rotation measure (RM) synthesis (Brentjens & de Bruyn, Reference Brentjens and de Bruyn2005) may then be used to recover the linear polarisation maps from the resulting RM cube at selected Faraday depths (ϕ), as was previously demonstrated by Bernardi et al. (Reference Bernardi2013).
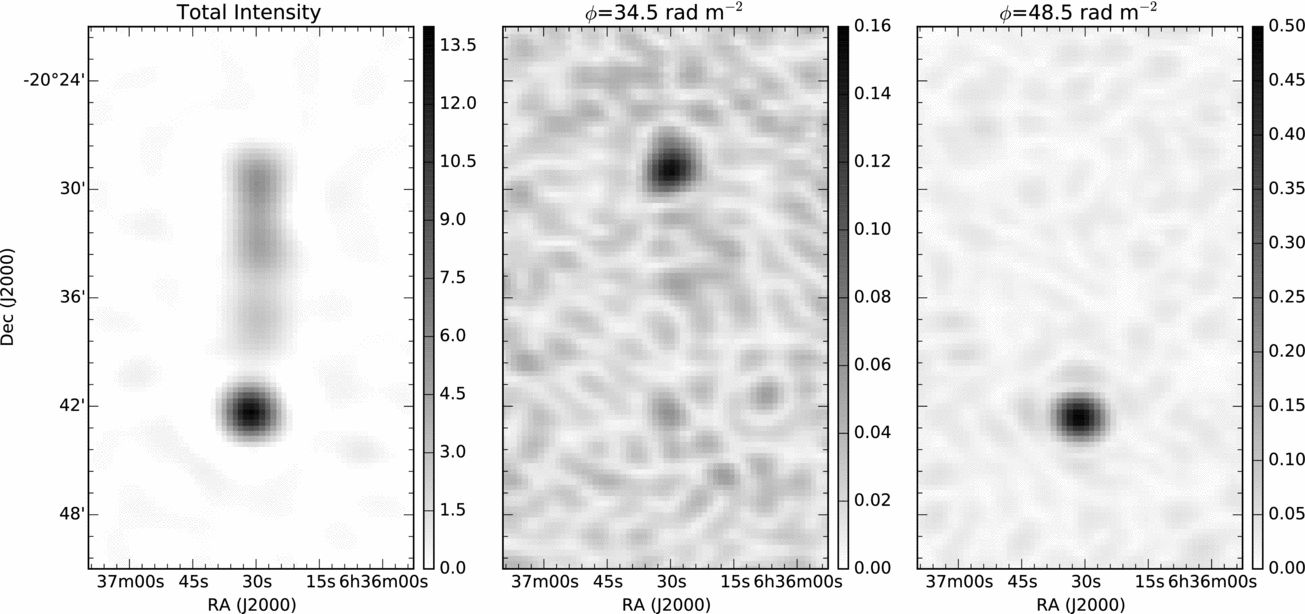
Figure 5 presents an example polarised source, PMN J0636-2041, detected with early GLEAM data. The total intensity image was processed using continuum-mode imaging and shows a source with an extended morphology. The linear polarisations were processed using spectral mode imaging at 40-kHz spectral resolution and RM synthesis. The polarised intensity images, selected from the resulting RM cube, show that the northern and southern components of this source exhibit peaks at two different Faraday depths (ϕ = 34.5 ± 0.1 rad m− 2 and ϕ = 48.5 ± 0.05 rad m− 2 respectively.) These are both consistent with VLA observations of this source at 1.4 GHz (Taylor, Stil, & Sunstrum, Reference Taylor, Stil and Sunstrum2009).

Figure 5. Total intensity map of PMN J0636-2041 and the associated polarised intensity maps of the source taken at two different Faraday depths (ϕ=34.5 rad m− 2 and 48.5 rad m− 2). All images were processed using uniform visibility weighting in the 138.88–169.60 MHz band. Units are Jy beam− 1 for total intensity and Jy beam− 1 RMSF− 1 for polarised intensity.
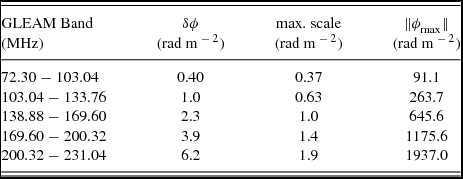
The resolution (δϕ), maximum scale size sensitivity (max. scale) and Faraday depth range (![]() $\Vert \phi _{\text{max}}\Vert$) available when using the RM synthesis technique is a function of the channel width, the bandwidth, and the highest frequency channel available (Brentjens & de Bruyn, Reference Brentjens and de Bruyn2005). This has been summarised in Table 2 for each of the GLEAM observing bands. Note that maximum scale size is always smaller than the resolution in ϕ space. Essentially, this means that the MWA cannot resolve Faraday thick clouds in ϕ space in any single band. Where sensitivity to wider structures in Faraday space is required, lower frequency bands can be combined with the upper frequency band. In this instance, the maximum scale size is set by the upper band (1.9 rad m− 2) but the resolution is increased by the separation of the bands.
$\Vert \phi _{\text{max}}\Vert$) available when using the RM synthesis technique is a function of the channel width, the bandwidth, and the highest frequency channel available (Brentjens & de Bruyn, Reference Brentjens and de Bruyn2005). This has been summarised in Table 2 for each of the GLEAM observing bands. Note that maximum scale size is always smaller than the resolution in ϕ space. Essentially, this means that the MWA cannot resolve Faraday thick clouds in ϕ space in any single band. Where sensitivity to wider structures in Faraday space is required, lower frequency bands can be combined with the upper frequency band. In this instance, the maximum scale size is set by the upper band (1.9 rad m− 2) but the resolution is increased by the separation of the bands.
Table 2. Polarisation parameters for GLEAM observing bands with 40-kHz frequency resolution.
While high precision is achievable in Faraday space, it should be noted that the true Faraday depth measured will be affected by the ionosphere. The magnitude of the ionospheric degradation can be reduced by observing at night and at zenith. However, applications that require high-accuracy measurements of Faraday depth will need to correct for the ionospheric component. Observations with the 32-tile commissioning array confirmed that codes that predict the ionospheric Faraday rotation, e.g. ionFR (Sotomayor-Beltran et al., Reference Sotomayor-Beltran2013) and ALBUSFootnote 3, are consistent with the observed effect on linearly polarised sources. During the course of a GLEAM observation, the ionospheric component of the Faraday rotation does not vary significantly; typical variations are of order ~ 0.3 rad m− 2. However, the overall ionospheric Faraday rotation component can vary significantly from epoch to epoch, often by several rad m− 2, and should be corrected for.
All polarisation observations are affected by some level of polarisation leakage from one Stokes parameter to another. For dipole instruments such as the MWA, polarisation leakage is a frequency-dependent and position-dependent effect resulting from errors in the primary beam model used for calibration. The effect results in a proportion of the Stokes I signal ‘leaking’ into Stokes Q, U, and V. In Faraday space, this results in an increased flux density at ϕ = 0 rad m− 2. The magnitude of leakage increases with frequency and with angular distance from zenith. In the 139–170 MHz band, the leakage is of order 1 − 2% within 10° of zenith but can increase to ~ 5% at the survey extremities (Sutinjo et al., Reference Sutinjo, O’Sullivan, Lenc, Wayth, Padhi, Hall and Tingay2015).
The GLEAM observations provide an outstanding data set for exploring diffuse polarised emission from the Milky Way. Even on a per-snapshot basis, the densely sampled core of the full 128-tile MWA array has excellent sensitivity to large-scale structures that may be expected from diffuse galactic polarised emission. Bernardi et al. (Reference Bernardi2013) observed such emission with the 32-tile MWA prototype and found the total polarisation surface brightness peaking at ~ 200 mJy beam− 1. By employing a natural weighting scheme to improve sensitivity to large-scale structures, the MWA array can image such features with a signal to noise ratio of ~ 70 in a single 2-min snapshot. This level of sensitivity may indeed be sufficient to observe variations in the ionosphere by observing variations in Faraday rotation in the diffuse Galactic background.
3.3 Comparison of the GLEAM and ATLAS images in the CDFS
The third data release from the Australia Telescope Large Area Survey (ATLAS DR3; Franzen et al., Reference Franzen2015) covers an area of 3.6 deg2 coincident with the Chandra Deep Field South (CDFS; α = 03h30m16.3s; δ = −28o05′12.4′′ J2000) to a typical sensitivity of 14~μJy beam− 1 at 1.4 GHz. We have compared the ATLAS image of the CDFS with the declination − 27° GLEAM mosaic at 147–154 MHz, which is closely matched in declination to the CDFS. Given the much higher sensitivity of ATLAS, we expect all GLEAM sources to be detected in ATLAS. We compared source positions in the two images but not source flux densities since the absolute flux density scale for GLEAM is only approximately correct.
The resolution of the GLEAM mosaic is 130 arcsec and that of the ATLAS image is 16.3 × 6.8 arcsec. We convolved the ATLAS image to the same resolution as the GLEAM mosaic. We then ran the source finder aegean (Hancock et al., Reference Hancock, Murphy, Gaensler, Hopkins and Curran2012) on both images using a 5σ detection threshold; 133 sources were detected in the ATLAS image and 36 in the corresponding region of the GLEAM image. Figure 6 shows the GLEAM mosaic of the CDFS, overlayed with the positions of the ATLAS and GLEAM sources.

Figure 6. Section of a 147 − 154 MHz declination − 27° XX mosaic coincident with the CDFS. The greyscale is linear and runs from − 20 to + 50 mJy (the overall flux scale is only approximately correct). GLEAM detections above 5σ are shown as red crosses of the same shapes as their fitted Gaussian parameters. Detections above 5σ in the 1.4-GHz ATLAS image of the field, convolved to the same resolution as the GLEAM image, are shown as blue ellipses of the same shapes as their fitted Gaussian parameters. The solid black contour indicates the boundary of the ATLAS CDFS mosaic.
All 36 GLEAM sources have a counterpart in ATLAS within 90 arcsec. While the largest offset between ATLAS and GLEAM positions is 90 arcsec, the second largest offset is only 31 arcsec; the median offset is 9 arcsec. Examination of the original ATLAS image shows that the largest offset is caused by two sources being blended in the low-resolution ATLAS and GLEAM images: the ATLAS position lies closer to the western source because it is brighter at 1.4 GHz and the GLEAM position lies closer to the eastern source because it is brighter at 150 MHz.
For many of the ATLAS sources with no counterpart in GLEAM, examination of the GLEAM image shows a weak source at the ATLAS position detected at the ~ 3σ level. Since all GLEAM sources above 5σ are detected in ATLAS, we conclude that away from the Galaxy and other extremely bright sources, sources can be reliably detected close to a 5σ detection limit in our GLEAM mosaics.
4 SENSITIVITY
The MWA is designed for its system temperature to be sky noise dominated over the frequency ranges covered by GLEAM (Tingay et al., Reference Tingay2013). As such, the expected thermal noise in a snapshot image depends on the region of sky being observed and, to a lesser extent, the beam pointing used during the observation.
Using image-based linear mosaicing, the thermal noise in the final mosaic is reduced by the weighted contribution of images contributing to the final mosaic. In the ideal case, the noise is reduced as ![]() $\sqrt{N}$ for N images contributing to a given region of the mosaic. In general, the images contributing to the mosaic are variance weighted by the primary beam (Holdaway, Reference Holdaway1999). For GLEAM, this means that the contribution to the final mosaic from a particular region of sky varies as it drifts through the primary beam.
$\sqrt{N}$ for N images contributing to a given region of the mosaic. In general, the images contributing to the mosaic are variance weighted by the primary beam (Holdaway, Reference Holdaway1999). For GLEAM, this means that the contribution to the final mosaic from a particular region of sky varies as it drifts through the primary beam.
We calculated the expected thermal noise properties of GLEAM mosaics based on noise-only simulations that match the GLEAM observing strategy. We used a single fiducial system temperature (Tf = 200 K) for two image weighting scenarios, as parametrised by the ‘robust’ parameter. More naturally weighted snapshots (robust = 1), which are likely to be used for imaging diffuse emission, have better theoretical sensitivity than more uniformly weighted ones (robust = − 1), which are more likely to be used for imaging compact sources at the highest resolution.
To calculate the thermal noise in a mosaic, we simulate 2 h of noise-only GLEAM observations for each frequency and declination using miriad’s ‘uvgen’ task using Tf as the system temperature and matching the duration, duty cycle, bandwidth (including the reduction in usable bandwidth due to commonly flagged channels), and frequency setup of GLEAM. Each 2-min snapshot is imaged with full bandwidth synthesis and weighted according to the primary beam model (Sutinjo et al., Reference Sutinjo, O’Sullivan, Lenc, Wayth, Padhi, Hall and Tingay2015) for the frequency and declination and accumulated into the mosaic using the ‘regrid’ task. Likewise, the primary beam ‘weights’ are accumulated into a weight mosaic for each snapshot. After accumulating all snapshots, the mosaic image is divided by the accumulated weight image.
The noise in the mosaic was measured in approximately 5° × 5° of the inner part of the mosaic using the ‘imstat’ task, and the results for all frequencies and declinations are shown in Table 3 for both robust parameters.
Table 3. GLEAM expected thermal noise sensitivity (mJy beam− 1) from a 2-h mosaic, assuming fiducial system temperature Tf = 200 K. Columns are the frequency in MHz, rows are the declination in degrees.(a) Robust − 1
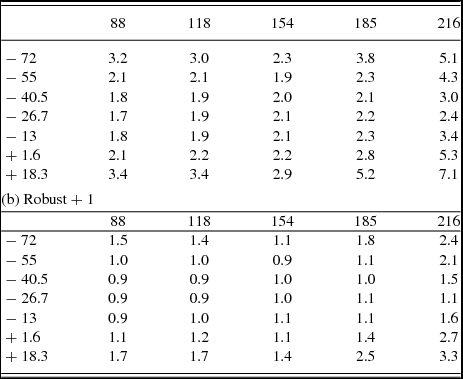
Clearly, the fiducial system temperature Tf is not applicable for most GLEAM frequencies and pointings, hence the values in Table 3 must be scaled by the appropriate system temperature for region of sky and frequency.
To enable this scaling, we calculated the expected beam-weighted average sky temperature over the range of frequencies, pointings, and LSTs relevant to GLEAM (Figure 7). The correct theoretical thermal noise in an image can then be derived by calculating the correct T sys for that image by scaling by the ratio of the average sky temperature (T true) for that frequency/LST/pointing, plus receiver noise (TR ≈ 50 K), to the fiducial value, i.e. by T true + TR)/Tf. For example, at 154 MHz the ‘cold’ extragalactic sky will generate a system temperature of approximately 300 K (Figure 7) hence the theoretical thermal noise for a uniformly weighted mosaic of that region of the sky will be (300/200) × 2.1 mJy = 3.2 mJy beam− 1 (near the zenith).

Figure 7. Beam-weighted sky average temperature for the seven declinations used by GLEAM depending on LST. Panels show the five central frequencies used by GLEAM: 88, 118, 154, 185, and 216 MHz.
4.1 Confusion and excess image noise in Stokes I
The MWA’s synthesised beam is large enough that classical confusion should become a limiting factor in wide- bandwidth mosaics or long duration synthesis images, compared to thermal noise. It is difficult to precisely estimate the classical confusion because the differential source counts at low frequencies between 1 and 100 mJy are currently not well known. To estimate the classical confusion, we model the differential source counts in this flux density range as n(S) = kS γ. Based on Wieringa (Reference Wieringa1991), who measured the 327 MHz counts down to ~ 1 mJy using the Westerbork Synthesis Radio Telescope (WSRT), we estimate k = 4 000 and γ = −1.6 at 327 MHz. Assuming the spectral index of sources is − 0.7, k can be scaled to frequency ν MHz by the factor (ν/327)− 0.7(1 + γ). Using this differential source count model scaled to 154 MHz and following Condon (Reference Condon1974) using a signal-to-noise threshold of 6, the 1σ classical confusion for an image with synthesised beam size 2.4 arcmin (i.e. a uniformly weighted image made at 154 MHz) is approximately 2 mJy. There is substantial uncertainty in this estimate because the overall scaling is uncertain at the ~ 25% level and because the slope of the source count function is known to change at mJy flux densities at higher frequencies (e.g. Windhorst, Mathis, & Neuschaefer, Reference Windhorst, Mathis and Neuschaefer1990). For example, a small change in γ from − 1.6 to − 1.8 around mJy flux densities will triple the estimated classical confusion. GLEAM and other contemporary low-frequency surveys will make a substantial contribution to better understand the low-frequency source counts.
Full synthesis 2-min Stokes I snapshot images have a theoretical thermal noise of 5 mJy for T sys = 200 K using robust − 1. Despite this, such images typically contain ~ 20 − 30 mJy background noise and the background between instrumental polarisation (XX and YY) images tends to be correlated. The reason for the excess background is still under investigation, but is most likely due to a combination of classical and sidelobe confusion (sidelobe confusion is the extra background variance due to the combined sidelobes of all the faint unsubtracted sources within the primary beam). Sidelobe confusion is more pronounced for the MWA than for radio telescopes with larger antennas due to the MWA’s huge field-of-view. A detailed analysis of the impact of sidelobe confusion to MWA snapshot and long-duration synthesis images is underway (Wayth et al., in preparation). For the time being, the excess background, which is only found in Stokes I, is treated simply as excess noise which integrates down with time and bandwidth.
5 GLEAM OUTPUTS
We plan to process GLEAM data and release data products in stages. The expected data products from GLEAM include: an extragalactic Stokes I compact source catalogue; a full polarisation compact source catalogue; maps of diffuse extragalactic polarised foreground; and maps of the diffuse emission (both Stokes I and polarised) in the Galactic plane. Most sources will have at least five independent continuum flux density measurements made over GLEAM’s frequency range and further subdivision of the frequency range is possible.
5.1 Extragalactic sources
GLEAM covers 7.5 sr of extragalactic (|b| > 10) sky. Assuming a 6σ source detection threshold of 120 mJy in the 180-MHz frequency band, we again model the differential source counts, n(S), between 0.1 and 1.0 Jy as a power-law based on the general properties of source counts at similar frequencies (e.g. Wieringa, Reference Wieringa1991; Williams, Intema, & Röttgering, Reference Williams, Intema and Röttgering2013). UsingFootnote 4n(S) = 3 600S − 1.78 and a detection threshold of 120 mJy, we estimate GLEAM will detect approximately 19 500 sources sr− 1 or 150 000 sources in the extragalactic sky visible to the MWA. Bright residual structure extending far from the Galactic plane and regions around bright compact sources may have higher than typical background noise, which will affect source detection locally. By comparison, the MWA Commissioning Survey (‘MWACS’, Hurley-Walker et al., Reference Hurley-Walker2014) found 7 540 sources sr− 1 with a detection threshold of 200 mJy or greater, depending on the local noise properties of the mosaic.
5.2 Comparison to other southern hemisphere surveys
There have been relatively few sky surveys in the southern hemisphere compared to the northern, especially at low frequencies. Surveys below 1 GHz that cover a substantial fraction of the southern hemisphere are listed in Table 4. We also note the Culgoora array observed selected sources at 80 and 160 MHz (Slee, Reference Slee1995), but did not perform a blind survey.
Table 4. Summary of radio surveys below 1 GHz substantially covering the southern hemisphere.

a Assuming 150λ is the shortest effective baseline for the VLA B array at 74 MHz.
b At 154 MHz.
c Large et al. (Reference Large, Mills, Little, Crawford and Sutton1981).
d Bock, Large, & Sadler (Reference Bock, Large and Sadler1999); Mauch et al. (Reference Mauch, Murphy, Buttery, Curran, Hunstead, Piestrzynski, Robertson and Sadler2003). See also MGPS-2 (Murphy et al., Reference Murphy, Mauch, Green, Hunstead, Piestrzynska, Kels and Sztajer2007) for sources with |b| < 10.
e Cohen et al. (Reference Cohen, Lane, Cotton, Kassim, Lazio, Perley, Condon and Erickson2007); Lane et al. (Reference Lane, Cotton, van Velzen, Clarke, Kassim, Helmboldt, Lazio and Cohen2014).
g Jacobs et al. (Reference Jacobs2011).
h Mills, Slee, & Hill (Reference Mills, Slee and Hill1958, Reference Mills, Slee and Hill1960, Reference Mills, Slee and Hill1961).
Table 4 shows that GLEAM is comparable in angular resolution and sky coverage to the all extragalactic sky Molonglo Reference Catalogue (MRC), but will be an order of magnitude more sensitive with full polarisation and sensitivity to very large structures. GLEAM will complement The GMRT Sky Survey (TGSS) and VLA Low-Frequency Sky Survey (VLSS) with similar sensitivity, but slightly poorer resolution, filling in the entire sky south of δ = +25. GLEAM will also form an excellent complementary dataset to the LOFAR MSSS (Heald et al., Reference Heald2015), which will have similar sensitivity and angular resolution in the northern hemisphere. GLEAM will be unparalleled in its ability to image large, low surface brightness structures, both Galactic and extragalactic, in full polarisation. The strengths of MWA’s surface brightness sensitivity have already been made evident by the serendipitous discovery of a relic radio galaxy in early MWA data (Hurley-Walker et al., Reference Hurley-Walker2015).
6 CONCLUSION
We have presented the observing strategy, data processing strategy, and theoretical sensitivity of the MWA GLEAM survey.
GLEAM covers the entire radio sky south of declination + 25° between 72 and 231 MHz. GLEAM aims to leave a significant legacy dataset for the MWA and GLEAM data are being used for many Galactic, extragalactic, and time domain science programs. Data products will include a compact source catalogue and maps of the diffuse Galactic and extragalactic sky, both in Stokes I and in polarisation. The Stokes I compact source catalogue, in particular, will have an order of magnitude improvement in sensitivity compared to the MRC. Looking towards the SKA era, GLEAM will provide a foundation sky model that can be used in preparation for SKA-low key science programs.
GLEAM data are unparalleled in areas where the MWA’s strengths lie, including very wide field-of-view, full polarisation, high surface brightness sensitivity at large angular scales, and broad frequency coverage. The broad frequency coverage and fine frequency resolution of GLEAM provide a large lever arm for both polarisation studies using RM synthesis and to measure spectral indices.
We showed example snapshot images from GLEAM and discussed practical issues associated with forming mosaics from GLEAM including calibration, ionospheric and primary beam polarisation effects, as well as the effect of strong sources in the primary beam sidelobes. We discussed how confusion impacts the background noise level in Stokes I images, which is a consequence the MWA’s very large field-of-view.
Finally, we calculated the theoretical thermal noise sensitivity for GLEAM mosaics and showed how the expected thermal noise depends on the region of the sky being imaged, the observing frequency and the image weighting scheme.
ACKNOWLEDGEMENTS
This scientific work makes use of the Murchison Radio-astronomy Observatory, operated by CSIRO. We acknowledge the Wajarri Yamatji people as the traditional owners of the Observatory site. Support for the MWA comes from the US National Science Foundation (grants AST-0457585, PHY-0835713, CAREER-0847753, and AST-0908884), the Australian Research Council (LIEF grants LE0775621 and LE0882938), the US Air Force Office of Scientific Research (grant FA9550-0510247), and the Centre for All-sky Astrophysics (an Australian Research Council Centre of Excellence funded by grant CE110001020). Support is also provided by the Smithsonian Astrophysical Observatory, the MIT School of Science, the Raman Research Institute, the Australian National University, and the Victoria University of Wellington (via grant MED-E1799 from the New Zealand Ministry of Economic Development and an IBM Shared University Research Grant). The Australian Federal government provides additional support via the Commonwealth Scientific and Industrial Research Organisation (CSIRO), National Collaborative Research Infrastructure Strategy, Education Investment Fund, and the Australia India Strategic Research Fund, and Astronomy Australia Limited, under contract to Curtin University. This work was supported by resources provided by the Pawsey Supercomputing Centre with funding from the Australian Government and the Government of Western Australia. We acknowledge the iVEC Petabyte Data Store, the Initiative in Innovative Computing, and the CUDA Center for Excellence sponsored by NVIDIA at Harvard University, and the International Centre for Radio Astronomy Research (ICRAR), a Joint Venture of Curtin University, and The University of Western Australia, funded by the Western Australian State government.