Article contents
Notes on hyperelliptic mapping class groups
Published online by Cambridge University Press: 31 October 2023
Abstract
Hyperelliptic mapping class groups are defined either as the centralizers of hyperelliptic involutions inside mapping class groups of oriented surfaces of finite type or as the inverse images of these centralizers by the natural epimorphisms between mapping class groups of surfaces with marked points. We study these groups in a systematic way. An application of this theory is a counterexample to the genus 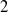 $2$ case of a conjecture by Putman and Wieland on virtual linear representations of mapping class groups. In the last section, we study profinite completions of hyperelliptic mapping class groups: we extend the congruence subgroup property to the general class of hyperelliptic mapping class groups introduced above and then determine the centralizers of multitwists and of open subgroups in their profinite completions.
$2$ case of a conjecture by Putman and Wieland on virtual linear representations of mapping class groups. In the last section, we study profinite completions of hyperelliptic mapping class groups: we extend the congruence subgroup property to the general class of hyperelliptic mapping class groups introduced above and then determine the centralizers of multitwists and of open subgroups in their profinite completions.
Keywords
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust
References
- 1
- Cited by



