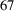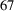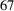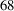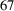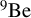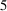1 Introduction
Particle acceleration using lasers[
Reference Tajima and Dawson
1
] has been studied for about four decades and, after the development of chirped pulse amplification[
Reference Strickland and Mourou
2
], laser intensity has increased up to 10
![]() ${}^{23}$
W/cm
${}^{23}$
W/cm
![]() ${}^2$
[
Reference Mourou, Tajima and Bulanov
3
,
Reference Tanaka, Spohr, Balabanski, Balascuta, Capponi, Cernaianu, Cuciuc, Cucoanes, Dancus, Dhal, Diaconescu, Doria, Ghenuche, Ghita, Kisyov, Nastasa, Ong, Rotaru, Sangwan, Söderström, Stutman, Suliman, Tesileanu, Tudor, Tsoneva, Ur, Ursescu and Zamfir
4
]. At present various particles of photons, electrons, ions and neutrons are generated by laser facilities. Ions have been accelerated by the electrostatic field generated by the electron pressure gradient, so-called target normal sheath acceleration (TNSA)[
Reference Snavely, Key, Hatchett, Cowan, Roth, Phillips, Stoyer, Henry, Sangster, Singh, Wilks, MacKinnon, Offenberger, Pennington, Yasuike, Langdon, Lasinski, Johnson, Perry and Campbell
5
–
Reference Wilks, Langdon, Cowan, Roth, Singh, Hatchett, Key, Pennington, MacKinnon and Snavely
8
]. Neutrons are generated by photodisintegration reactions with
${}^2$
[
Reference Mourou, Tajima and Bulanov
3
,
Reference Tanaka, Spohr, Balabanski, Balascuta, Capponi, Cernaianu, Cuciuc, Cucoanes, Dancus, Dhal, Diaconescu, Doria, Ghenuche, Ghita, Kisyov, Nastasa, Ong, Rotaru, Sangwan, Söderström, Stutman, Suliman, Tesileanu, Tudor, Tsoneva, Ur, Ursescu and Zamfir
4
]. At present various particles of photons, electrons, ions and neutrons are generated by laser facilities. Ions have been accelerated by the electrostatic field generated by the electron pressure gradient, so-called target normal sheath acceleration (TNSA)[
Reference Snavely, Key, Hatchett, Cowan, Roth, Phillips, Stoyer, Henry, Sangster, Singh, Wilks, MacKinnon, Offenberger, Pennington, Yasuike, Langdon, Lasinski, Johnson, Perry and Campbell
5
–
Reference Wilks, Langdon, Cowan, Roth, Singh, Hatchett, Key, Pennington, MacKinnon and Snavely
8
]. Neutrons are generated by photodisintegration reactions with
![]() $\gamma$
-rays generated by laser–plasma interactions[
Reference Arikawa, Utsugi, Alessio, Nagai, Abe, Kojima, Sakata, Inoue, Fujioka, Zhang, Chen, Park, Williams, Morita, Sakawa, Nakata, Kawanaka, Jitsuno, Sarukura, Miyanaga, Nakai, Shiraga, Nishimura and Azechi
9
], laser fusion reactions such as
$\gamma$
-rays generated by laser–plasma interactions[
Reference Arikawa, Utsugi, Alessio, Nagai, Abe, Kojima, Sakata, Inoue, Fujioka, Zhang, Chen, Park, Williams, Morita, Sakawa, Nakata, Kawanaka, Jitsuno, Sarukura, Miyanaga, Nakai, Shiraga, Nishimura and Azechi
9
], laser fusion reactions such as
![]() $\mathrm{d}\left(\mathrm{p},\mathrm{np}\right)\mathrm{p}$
and
$\mathrm{d}\left(\mathrm{p},\mathrm{np}\right)\mathrm{p}$
and
![]() $\mathrm{d}{\left(\mathrm{d},\mathrm{n}\right)}^3$
He reactions[
Reference Kar, Green, Ahmed, Alejo, Robinson, Cerchez, Clarke, Doria, Dorkings, Fernandez, Mirfayzi, McKenna, Naughton, Neely, Norreys, Peth, Powell, Ruiz, Swain, Willi and Borghesi
10
] or nuclear reactions by placing a secondary target behind the first target for ion acceleration[
Reference Mirfayzi, Alejo, Ahmed, Raspino, Ansell, Wilson, Armstrong, Butler, Clarke, Higginson, Kelleher, Murphy, Notley, Rusby, Schooneveld, Borghesi, McKenna, Rhodes, Neely, Brenner and Kar
11
–
Reference Mori, Yogo, Hayakawa, Mirfayzi, Lan, Abe, Arikawa, Golovin, Wei, Honoki, Nakai, Mima, Nishimura, Fujioka and Kodama
14
]. The energies of ions accelerated by laser reach several tens of MeV, thus making it possible to generate neutrons through nuclear reactions, such as
$\mathrm{d}{\left(\mathrm{d},\mathrm{n}\right)}^3$
He reactions[
Reference Kar, Green, Ahmed, Alejo, Robinson, Cerchez, Clarke, Doria, Dorkings, Fernandez, Mirfayzi, McKenna, Naughton, Neely, Norreys, Peth, Powell, Ruiz, Swain, Willi and Borghesi
10
] or nuclear reactions by placing a secondary target behind the first target for ion acceleration[
Reference Mirfayzi, Alejo, Ahmed, Raspino, Ansell, Wilson, Armstrong, Butler, Clarke, Higginson, Kelleher, Murphy, Notley, Rusby, Schooneveld, Borghesi, McKenna, Rhodes, Neely, Brenner and Kar
11
–
Reference Mori, Yogo, Hayakawa, Mirfayzi, Lan, Abe, Arikawa, Golovin, Wei, Honoki, Nakai, Mima, Nishimura, Fujioka and Kodama
14
]. The energies of ions accelerated by laser reach several tens of MeV, thus making it possible to generate neutrons through nuclear reactions, such as
![]() ${}^7$
Li
${}^7$
Li
![]() ${\left(\mathrm{p},\mathrm{n}\right)}^7$
Be[
Reference Mirfayzi, Alejo, Ahmed, Raspino, Ansell, Wilson, Armstrong, Butler, Clarke, Higginson, Kelleher, Murphy, Notley, Rusby, Schooneveld, Borghesi, McKenna, Rhodes, Neely, Brenner and Kar
11
],
${\left(\mathrm{p},\mathrm{n}\right)}^7$
Be[
Reference Mirfayzi, Alejo, Ahmed, Raspino, Ansell, Wilson, Armstrong, Butler, Clarke, Higginson, Kelleher, Murphy, Notley, Rusby, Schooneveld, Borghesi, McKenna, Rhodes, Neely, Brenner and Kar
11
],
![]() ${}^9$
Be
${}^9$
Be
![]() $\left(\mathrm{d},\mathrm{xn}\right)$
and
$\left(\mathrm{d},\mathrm{xn}\right)$
and
![]() ${}^9$
Be
${}^9$
Be
![]() $\left(\mathrm{p},\mathrm{n}\right)$
[
Reference Kleinschmid, Bagnoud, Deppert, Favalli, Frydrych, Hornung, Jahn, Schaumann, Tebartz, Wagner, Wurden, Zielbauer and Roth
12
–
Reference Mori, Yogo, Hayakawa, Mirfayzi, Lan, Abe, Arikawa, Golovin, Wei, Honoki, Nakai, Mima, Nishimura, Fujioka and Kodama
14
]. The flux of the laser-driven neutron sources (LDNSs) has been increased up to approximately 10
$\left(\mathrm{p},\mathrm{n}\right)$
[
Reference Kleinschmid, Bagnoud, Deppert, Favalli, Frydrych, Hornung, Jahn, Schaumann, Tebartz, Wagner, Wurden, Zielbauer and Roth
12
–
Reference Mori, Yogo, Hayakawa, Mirfayzi, Lan, Abe, Arikawa, Golovin, Wei, Honoki, Nakai, Mima, Nishimura, Fujioka and Kodama
14
]. The flux of the laser-driven neutron sources (LDNSs) has been increased up to approximately 10
![]() ${}^{11}$
neutrons/sr[
Reference Kleinschmid, Bagnoud, Deppert, Favalli, Frydrych, Hornung, Jahn, Schaumann, Tebartz, Wagner, Wurden, Zielbauer and Roth
12
–
Reference Mori, Yogo, Hayakawa, Mirfayzi, Lan, Abe, Arikawa, Golovin, Wei, Honoki, Nakai, Mima, Nishimura, Fujioka and Kodama
14
]. Although neutrons in the MeV energy region are primarily produced by LDNSs, low-energy neutrons in thermal and epi-thermal regions can also be generated using moderators[
Reference Mirfayzi, Alejo, Ahmed, Raspino, Ansell, Wilson, Armstrong, Butler, Clarke, Higginson, Kelleher, Murphy, Notley, Rusby, Schooneveld, Borghesi, McKenna, Rhodes, Neely, Brenner and Kar
11
,
Reference Mirfayzi, Yogo, Lan, Ishimoto, Iwamoto, Nagata, Nakai, Arikawa, Abe, Golovin, Honoki, Mori, Okamoto, Shokita, Neely, Fujioka, Mima, Nishimura, Kar and Kodama
15
]. LDNSs have the characteristics of high brightness and short pulses, and are expected to be useful for various applications. Several experiments have demonstrated imaging using fast neutrons provided from an LDNS[
Reference Roth, Jung, Falk, Guler, Deppert, Devlin, Favalli, Fernandez, Gautier, Geissel, Haight, Hamilton, Hegelich, Johnson, Merrill, Schaumann, Schoenberg, Schollmeier, Shimada, Taddeucci, Tybo, Wagner, Wender, Wilde and Wurden
16
–
Reference Mima, Yogo, Mirfayzi, Lan, Arikawa, Abe and Nishimura
19
]. LDNSs are also expected to be used for single-shot radiography to non-destructive inspections with the combination of thermal neutrons and X-rays[
Reference Yogo, Mirfayzi, Arikawa, Abe, Wei, Mori, Lan, Hoonoki, Golovin, Koga, Suzuki, Kanasaki, Fujioka, Nakai, Hayakawa, Mima, Nishimura, Kar and Kodama
20
,
Reference Wei, Yogo, Hayakawa, Arikawa, Abe, Nakanishi, Mirfayzi, Lan, Mori, Mima, Fujioka, Murakami, Nakai, Nishimura, Kar and Kodama
21
]. Furthermore, elemental analysis using nuclear resonance absorption with low-energy neutrons from an LDNS has been demonstrated[
Reference Yogo, Mirfayzi, Arikawa, Abe, Wei, Mori, Lan, Hoonoki, Golovin, Koga, Suzuki, Kanasaki, Fujioka, Nakai, Hayakawa, Mima, Nishimura, Kar and Kodama
20
].
${}^{11}$
neutrons/sr[
Reference Kleinschmid, Bagnoud, Deppert, Favalli, Frydrych, Hornung, Jahn, Schaumann, Tebartz, Wagner, Wurden, Zielbauer and Roth
12
–
Reference Mori, Yogo, Hayakawa, Mirfayzi, Lan, Abe, Arikawa, Golovin, Wei, Honoki, Nakai, Mima, Nishimura, Fujioka and Kodama
14
]. Although neutrons in the MeV energy region are primarily produced by LDNSs, low-energy neutrons in thermal and epi-thermal regions can also be generated using moderators[
Reference Mirfayzi, Alejo, Ahmed, Raspino, Ansell, Wilson, Armstrong, Butler, Clarke, Higginson, Kelleher, Murphy, Notley, Rusby, Schooneveld, Borghesi, McKenna, Rhodes, Neely, Brenner and Kar
11
,
Reference Mirfayzi, Yogo, Lan, Ishimoto, Iwamoto, Nagata, Nakai, Arikawa, Abe, Golovin, Honoki, Mori, Okamoto, Shokita, Neely, Fujioka, Mima, Nishimura, Kar and Kodama
15
]. LDNSs have the characteristics of high brightness and short pulses, and are expected to be useful for various applications. Several experiments have demonstrated imaging using fast neutrons provided from an LDNS[
Reference Roth, Jung, Falk, Guler, Deppert, Devlin, Favalli, Fernandez, Gautier, Geissel, Haight, Hamilton, Hegelich, Johnson, Merrill, Schaumann, Schoenberg, Schollmeier, Shimada, Taddeucci, Tybo, Wagner, Wender, Wilde and Wurden
16
–
Reference Mima, Yogo, Mirfayzi, Lan, Arikawa, Abe and Nishimura
19
]. LDNSs are also expected to be used for single-shot radiography to non-destructive inspections with the combination of thermal neutrons and X-rays[
Reference Yogo, Mirfayzi, Arikawa, Abe, Wei, Mori, Lan, Hoonoki, Golovin, Koga, Suzuki, Kanasaki, Fujioka, Nakai, Hayakawa, Mima, Nishimura, Kar and Kodama
20
,
Reference Wei, Yogo, Hayakawa, Arikawa, Abe, Nakanishi, Mirfayzi, Lan, Mori, Mima, Fujioka, Murakami, Nakai, Nishimura, Kar and Kodama
21
]. Furthermore, elemental analysis using nuclear resonance absorption with low-energy neutrons from an LDNS has been demonstrated[
Reference Yogo, Mirfayzi, Arikawa, Abe, Wei, Mori, Lan, Hoonoki, Golovin, Koga, Suzuki, Kanasaki, Fujioka, Nakai, Hayakawa, Mima, Nishimura, Kar and Kodama
20
].
One of the expected applications using LDNSs is the production of medical radioisotopes by a compact laser system inside of hospitals. Radioisotopes, which may radiate a
![]() $\gamma$
-ray with an energy of a few hundred keV, such as
$\gamma$
-ray with an energy of a few hundred keV, such as
![]() ${}^{99\mathrm{m}}$
Tc (half-life 6.02 h), are used for single-photon emission computed tomography (SPECT) in medical diagnostic scans. At present, most medical radioisotopes have been provided from nuclear reactors and accelerators, and they have been distributed to hospitals. A positron emitter
${}^{99\mathrm{m}}$
Tc (half-life 6.02 h), are used for single-photon emission computed tomography (SPECT) in medical diagnostic scans. At present, most medical radioisotopes have been provided from nuclear reactors and accelerators, and they have been distributed to hospitals. A positron emitter
![]() ${}^{18}$
F with a half-life of 1.8 h, which is used for positron emission tomography (PET), is produced by compact cyclotron accelerators located inside of hospitals. In addition to medical diagnostic scans, radioisotopes with half-lives of several days have been used for cancer therapy. The radioisotope
${}^{18}$
F with a half-life of 1.8 h, which is used for positron emission tomography (PET), is produced by compact cyclotron accelerators located inside of hospitals. In addition to medical diagnostic scans, radioisotopes with half-lives of several days have been used for cancer therapy. The radioisotope
![]() ${}^{67}$
Cu with a half-life of 2.58 d is a good candidate for a radiopharmaceutical for cancer therapy because of its appropriate nuclear and chemical properties[
Reference Novak-Hofer and Schubiger
22
–
Reference Smith, Bowers and Ehst
24
].
${}^{67}$
Cu with a half-life of 2.58 d is a good candidate for a radiopharmaceutical for cancer therapy because of its appropriate nuclear and chemical properties[
Reference Novak-Hofer and Schubiger
22
–
Reference Smith, Bowers and Ehst
24
].
![]() ${}^{67}$
Cu decays to an excited state or the ground state of the daughter nucleus
${}^{67}$
Cu decays to an excited state or the ground state of the daughter nucleus
![]() ${}^{67}$
Zn through the emission of a
${}^{67}$
Zn through the emission of a
![]() $\beta$
-ray with a maximum energy of 392, 484 or 577 keV. When an excited state is generated, it subsequently decays to the ground state of
$\beta$
-ray with a maximum energy of 392, 484 or 577 keV. When an excited state is generated, it subsequently decays to the ground state of
![]() ${}^{67}$
Zn with emission of
${}^{67}$
Zn with emission of
![]() $\gamma$
-rays with energies of 91, 93 and 185 keV. During therapy, a radiopharmaceutical including
$\gamma$
-rays with energies of 91, 93 and 185 keV. During therapy, a radiopharmaceutical including
![]() ${}^{67}$
Cu is accumulated inside of a tumor in a human body, therefore making the
${}^{67}$
Cu is accumulated inside of a tumor in a human body, therefore making the
![]() $\beta$
-rays radiated from
$\beta$
-rays radiated from
![]() ${}^{67}$
Cu appropriate to effectively kill the cancer cells with a lethal dose. In addition, the
${}^{67}$
Cu appropriate to effectively kill the cancer cells with a lethal dose. In addition, the
![]() $\gamma$
-rays radiated from the
$\gamma$
-rays radiated from the
![]() ${}^{67}$
Cu-radiopharmaceutical accumulated in the cancer are suitable for SPECT imaging. Therefore,
${}^{67}$
Cu-radiopharmaceutical accumulated in the cancer are suitable for SPECT imaging. Therefore,
![]() ${}^{67}$
Cu is expected to be used for radioimmunotheranostics[
Reference Ting, Chang, Wang and Lee
25
], and various production methods of
${}^{67}$
Cu is expected to be used for radioimmunotheranostics[
Reference Ting, Chang, Wang and Lee
25
], and various production methods of
![]() ${}^{67}$
Cu have been studied for future operation.
${}^{67}$
Cu have been studied for future operation.
![]() ${}^{67}$
Cu production with protons and deuterons using accelerators has been studied, where
${}^{67}$
Cu production with protons and deuterons using accelerators has been studied, where
![]() ${}^{67}$
Cu is produced via
${}^{67}$
Cu is produced via
![]() ${}^{68}$
Zn(p, 2p)
${}^{68}$
Zn(p, 2p)
![]() ${}^{67}$
Cu[
Reference Dasgupta, Mausner and Srivastava
26
,
Reference Katabuchi, Watanabe, Ishioka, Iida, Hanaoka, Endo and Matsuhashi
27
],
${}^{67}$
Cu[
Reference Dasgupta, Mausner and Srivastava
26
,
Reference Katabuchi, Watanabe, Ishioka, Iida, Hanaoka, Endo and Matsuhashi
27
],
![]() ${}^{70}$
Zn(p,
${}^{70}$
Zn(p,
![]() $\alpha$
)
$\alpha$
)
![]() ${}^{67}$
Cu[
Reference Mirzadeh, Mausner and Srivastava
23
] and
${}^{67}$
Cu[
Reference Mirzadeh, Mausner and Srivastava
23
] and
![]() ${}^{70}$
Zn(d,
${}^{70}$
Zn(d,
![]() $\alpha \mathrm{n}$
)
$\alpha \mathrm{n}$
)
![]() ${}^{67}$
Cu reactions[
Reference Kozempel, Abbas, Simonelli, Bulgheroni, Holzwarth and Gibson
28
]. One of the feasible production methods is photodisintegration reactions;
${}^{67}$
Cu reactions[
Reference Kozempel, Abbas, Simonelli, Bulgheroni, Holzwarth and Gibson
28
]. One of the feasible production methods is photodisintegration reactions;
![]() ${}^{67}$
Cu can be produced by the
${}^{67}$
Cu can be produced by the
![]() ${}^{68}$
Zn(
${}^{68}$
Zn(
![]() $\gamma$
, p)
$\gamma$
, p)
![]() ${}^{67}$
Cu reaction[
Reference Yagi and Kondo
29
–
Reference Hovhannisyan, Bakhshiyan and Dallakyanc
31
] with
${}^{67}$
Cu reaction[
Reference Yagi and Kondo
29
–
Reference Hovhannisyan, Bakhshiyan and Dallakyanc
31
] with
![]() $\gamma$
-rays provided from electron accelerators. Production by neutron-induced reactions was also studied (Figure 1).
$\gamma$
-rays provided from electron accelerators. Production by neutron-induced reactions was also studied (Figure 1).
![]() ${}^{67}$
Cu can be produced by the
${}^{67}$
Cu can be produced by the
![]() ${}^{67}$
Zn(n, p)
${}^{67}$
Zn(n, p)
![]() ${}^{67}$
Cu[
Reference Mausner, Kolsky, Joshi and Srivastava
32
–
Reference Kawabata, Motoishi, Ota, Motomura, Saeki, Tsukada, Hashimoto, Iwamoto, Nagai and Hashimoto
35
] and
${}^{67}$
Cu[
Reference Mausner, Kolsky, Joshi and Srivastava
32
–
Reference Kawabata, Motoishi, Ota, Motomura, Saeki, Tsukada, Hashimoto, Iwamoto, Nagai and Hashimoto
35
] and
![]() ${}^{68}$
Zn(n, np)
${}^{68}$
Zn(n, np)
![]() ${}^{67}$
Cu[
Reference Kin, Nagai, Iwamoto, Minato, Iwamoto, Hatsukawa, Segawa, Harada, Konno, Ochiai and Takakura
34
–
Reference Sato, Tsukada, Watanabe, Ishioka, Kawabata, Saeki, Nagai, Kin, Minato, Iwamoto and Iwamoto
36
] reactions.
${}^{67}$
Cu[
Reference Kin, Nagai, Iwamoto, Minato, Iwamoto, Hatsukawa, Segawa, Harada, Konno, Ochiai and Takakura
34
–
Reference Sato, Tsukada, Watanabe, Ishioka, Kawabata, Saeki, Nagai, Kin, Minato, Iwamoto and Iwamoto
36
] reactions.

Figure 1 Partial nuclear chart around Zn and nuclear reactions with neutrons on a natural Zn target.
![]() ${}^{64}$
Cu,
${}^{64}$
Cu,
![]() ${}^{66}$
Cu and
${}^{66}$
Cu and
![]() ${}^{68}$
Cu are produced by (n, p) reactions with high-energy neutrons on
${}^{68}$
Cu are produced by (n, p) reactions with high-energy neutrons on
![]() ${}^{64}$
Zn,
${}^{64}$
Zn,
![]() ${}^{66}$
Zn and
${}^{66}$
Zn and
![]() ${}^{68}$
Zn, respectively.
${}^{68}$
Zn, respectively.
![]() ${}^{63}$
Cu,
${}^{63}$
Cu,
![]() ${}^{65}$
Cu and
${}^{65}$
Cu and
![]() ${}^{69}$
Cu
${}^{69}$
Cu
![]() ${}^m$
are produced by (n, 2n) reactions on
${}^m$
are produced by (n, 2n) reactions on
![]() ${}^{64}$
Zn,
${}^{64}$
Zn,
![]() ${}^{66}$
Zn and
${}^{66}$
Zn and
![]() ${}^{70}$
Zn, respectively.
${}^{70}$
Zn, respectively.
![]() ${}^{66}$
Cu and
${}^{66}$
Cu and
![]() ${}^{67}$
Cu
${}^{67}$
Cu
![]() ${}^m$
are generated by (n, pn) reactions from
${}^m$
are generated by (n, pn) reactions from
![]() ${}^{67}$
Zn and
${}^{67}$
Zn and
![]() ${}^{86}$
Zn, respectively. High-energy neutrons could produce
${}^{86}$
Zn, respectively. High-energy neutrons could produce
![]() ${}^{65}$
Ni by the
${}^{65}$
Ni by the
![]() ${}^{68}$
Zn(n,
${}^{68}$
Zn(n,
![]() $\alpha$
)
$\alpha$
)
![]() ${}^{65}$
Ni reaction. Neutron capture also occurs.
${}^{65}$
Ni reaction. Neutron capture also occurs.
LDNSs provide primary fast neutrons in the energy range of 1
![]() $-$
20 MeV, making them suitable for production of
$-$
20 MeV, making them suitable for production of
![]() ${}^{67}$
Cu via neutron-induced reactions, as presented here. In the present study, we explore the possibility of
${}^{67}$
Cu via neutron-induced reactions, as presented here. In the present study, we explore the possibility of
![]() ${}^{67}$
Cu production by LDNSs with a high-power laser. The activation method is one of the tools used to evaluate precisely the number of unstable isotopes. In our previous studies, the numbers of fast neutrons with energies of 8
${}^{67}$
Cu production by LDNSs with a high-power laser. The activation method is one of the tools used to evaluate precisely the number of unstable isotopes. In our previous studies, the numbers of fast neutrons with energies of 8
![]() $-$
20 MeV and thermal neutrons were quantitatively evaluated using activation methods[
Reference Mori, Yogo, Hayakawa, Mirfayzi, Lan, Abe, Arikawa, Golovin, Wei, Honoki, Nakai, Mima, Nishimura, Fujioka and Kodama
14
,
Reference Mori, Yogo, Hayakawa, Mirfayzi, Lan, Wei, Abe, Arikawa, Nakai, Mima, Nishimura, Fujioka and Kodama
37
]. Here, we demonstrated
$-$
20 MeV and thermal neutrons were quantitatively evaluated using activation methods[
Reference Mori, Yogo, Hayakawa, Mirfayzi, Lan, Abe, Arikawa, Golovin, Wei, Honoki, Nakai, Mima, Nishimura, Fujioka and Kodama
14
,
Reference Mori, Yogo, Hayakawa, Mirfayzi, Lan, Wei, Abe, Arikawa, Nakai, Mima, Nishimura, Fujioka and Kodama
37
]. Here, we demonstrated
![]() ${}^{67}$
Cu production with an irradiation of laser-driven neutrons on a natural Zn metal target and measured the radioactivities of the unstable isotopes and isomer generated in the Zn target. The evaluation of the produced radioisotopes was carried out by
${}^{67}$
Cu production with an irradiation of laser-driven neutrons on a natural Zn metal target and measured the radioactivities of the unstable isotopes and isomer generated in the Zn target. The evaluation of the produced radioisotopes was carried out by
![]() $\gamma$
-ray measurement with a high-purity germanium (HPGe) detector and we reveal the activities of
$\gamma$
-ray measurement with a high-purity germanium (HPGe) detector and we reveal the activities of
![]() ${}^{67}$
Cu and the unstable isotopes of Zn, Cu and Ni.
${}^{67}$
Cu and the unstable isotopes of Zn, Cu and Ni.
2 Experimental methods
The neutron irradiation experiment was carried out using the petawatt laser for fast ignition experiments (LFEX) laser system at the Institute of Laser Engineering (ILE) at Osaka University[
Reference Kawanaka, Miyanaga, Azechi, Kanabe, Jitsuno, Kondo, Fujimoto, Morio, Matsuo, Kawakami, Mizoguchi, Tauchi, Yano, Kudo and Ogura
38
]. To generate and accelerate ions we focused four laser pulses provided from LFEX on a target with an intensity of approximately 1.5
![]() $\times$
10
$\times$
10
![]() ${}^{19}$
W/cm
${}^{19}$
W/cm
![]() ${}^2$
and with a duration of 1.5 ps in full width at half maximum (FWHM). Figure 2 shows the experimental setup of the target installed in the vacuum chamber. The angle between the laser axis and the normal vector of the target foil was 42
${}^2$
and with a duration of 1.5 ps in full width at half maximum (FWHM). Figure 2 shows the experimental setup of the target installed in the vacuum chamber. The angle between the laser axis and the normal vector of the target foil was 42
![]() ${}^{\circ }$
. As the target, a deuterated carbon [(C
${}^{\circ }$
. As the target, a deuterated carbon [(C
![]() ${}_8$
D
${}_8$
D
![]() ${}_8$
)
${}_8$
)
![]() ${}_n$
, henceforth referred to as CD] foil with a thickness of 5 μm was used. A plasma was induced by the laser and, subsequently, ions of protons and deuterons were accelerated from the plasma via TNSA[
Reference Fuchs, Antici, d’Humières, Lefebvre, Borghesi, Brambrink, Cecchetti, Kaluza, Malka, Manclossi, Meyroneinc, Mora, Schreiber, Toncian, Pépin and Audebert
39
–
Reference Yogo, Mima, Iwata, Tosaki, Morace, Arikawa, Fujioka, Johzaki, Sentoku, Nishimura, Sagisaka, Matsuo, Kamitsukasa, Kojima, Nagatomo, Nakai, Shiraga, Murakami, Tokita, Kawanaka, Miyanaga, Yamanoi, Norimatsu, Sakagami, Bulanov, Kondo and Azechi
41
]. In the TNSA, a target foil is irradiated by a laser with an intensity higher than or equal to 10
${}_n$
, henceforth referred to as CD] foil with a thickness of 5 μm was used. A plasma was induced by the laser and, subsequently, ions of protons and deuterons were accelerated from the plasma via TNSA[
Reference Fuchs, Antici, d’Humières, Lefebvre, Borghesi, Brambrink, Cecchetti, Kaluza, Malka, Manclossi, Meyroneinc, Mora, Schreiber, Toncian, Pépin and Audebert
39
–
Reference Yogo, Mima, Iwata, Tosaki, Morace, Arikawa, Fujioka, Johzaki, Sentoku, Nishimura, Sagisaka, Matsuo, Kamitsukasa, Kojima, Nagatomo, Nakai, Shiraga, Murakami, Tokita, Kawanaka, Miyanaga, Yamanoi, Norimatsu, Sakagami, Bulanov, Kondo and Azechi
41
]. In the TNSA, a target foil is irradiated by a laser with an intensity higher than or equal to 10
![]() ${}^{18}$
W/cm
${}^{18}$
W/cm
![]() ${}^2$
to make a plasma. The generated plasma is extended into a vacuum for the opposite side (rear side) to the laser irradiation side to generate a charge separation field, by which ions on the rear surface of the target could be accelerated up to several tens of MeV. The accelerated protons and deuterons have continuous energies, of which the spectral density decreases with increasing energies. The maximum energies of the protons and deuterons using LFEX are typically 30 and 20 MeV, respectively[
Reference Golovin, Mirfayzi, Shokita, Abe, Lan, Arikawa, Morace, Pikuz and Yogo
42
]. A Be block with a size of
${}^2$
to make a plasma. The generated plasma is extended into a vacuum for the opposite side (rear side) to the laser irradiation side to generate a charge separation field, by which ions on the rear surface of the target could be accelerated up to several tens of MeV. The accelerated protons and deuterons have continuous energies, of which the spectral density decreases with increasing energies. The maximum energies of the protons and deuterons using LFEX are typically 30 and 20 MeV, respectively[
Reference Golovin, Mirfayzi, Shokita, Abe, Lan, Arikawa, Morace, Pikuz and Yogo
42
]. A Be block with a size of
![]() $\phi$
10 mm
$\phi$
10 mm
![]() $\times$
5 mm was installed 4 mm downstream from the CD foil. The accelerated ions generated neutrons by p+
$\times$
5 mm was installed 4 mm downstream from the CD foil. The accelerated ions generated neutrons by p+
![]() ${}^9$
Be and d+
${}^9$
Be and d+
![]() ${}^9$
Be reactions[
Reference Kleinschmid, Bagnoud, Deppert, Favalli, Frydrych, Hornung, Jahn, Schaumann, Tebartz, Wagner, Wurden, Zielbauer and Roth
12
–
Reference Mori, Yogo, Hayakawa, Mirfayzi, Lan, Abe, Arikawa, Golovin, Wei, Honoki, Nakai, Mima, Nishimura, Fujioka and Kodama
14
]. High-energy neutrons are predominantly generated by the
${}^9$
Be reactions[
Reference Kleinschmid, Bagnoud, Deppert, Favalli, Frydrych, Hornung, Jahn, Schaumann, Tebartz, Wagner, Wurden, Zielbauer and Roth
12
–
Reference Mori, Yogo, Hayakawa, Mirfayzi, Lan, Abe, Arikawa, Golovin, Wei, Honoki, Nakai, Mima, Nishimura, Fujioka and Kodama
14
]. High-energy neutrons are predominantly generated by the
![]() ${}^9$
Be(p, n)
${}^9$
Be(p, n)
![]() ${}^9$
B reaction with high-energy protons. Around the Be block, a semi-cylindrical polyethylene moderator with a volume of 157 cm
${}^9$
B reaction with high-energy protons. Around the Be block, a semi-cylindrical polyethylene moderator with a volume of 157 cm
![]() ${}^3$
in a stainless-steel case was located. The thicknesses of the top and side were 5 mm and the thickness of the bottom was 2 mm (see Figure 2). To produce
${}^3$
in a stainless-steel case was located. The thicknesses of the top and side were 5 mm and the thickness of the bottom was 2 mm (see Figure 2). To produce
![]() ${}^{67}$
Cu, a natural Zn target with a size of
${}^{67}$
Cu, a natural Zn target with a size of
![]() $\phi$
10 mm
$\phi$
10 mm
![]() $\times$
5 mm and a weight of 2.86 g was placed behind the Be target. The neutron energy spectrum was measured by the time of flight (TOF) method. A benzophenon-doped BBQ liquid scintillation detector with a size of
$\times$
5 mm and a weight of 2.86 g was placed behind the Be target. The neutron energy spectrum was measured by the time of flight (TOF) method. A benzophenon-doped BBQ liquid scintillation detector with a size of
![]() $\phi$
60 mm
$\phi$
60 mm
![]() $\times$
60 mm with a photomultiplier tube (PMT; Thron EMI, 9902KBT)[
Reference Abe, Hosoda, Arikawa, Nagai, Kojima, Sakata, Inoue, Iwasa, Iwano, Yamanoi, Fujioka, Nakai, Sarukura, Shiraga, Norimatsu and Azechi
43
] was located 8.3 m downstream from the center of the target chamber, and the angle between the laser axis and the TOF beam line was approximately 15
$\times$
60 mm with a photomultiplier tube (PMT; Thron EMI, 9902KBT)[
Reference Abe, Hosoda, Arikawa, Nagai, Kojima, Sakata, Inoue, Iwasa, Iwano, Yamanoi, Fujioka, Nakai, Sarukura, Shiraga, Norimatsu and Azechi
43
] was located 8.3 m downstream from the center of the target chamber, and the angle between the laser axis and the TOF beam line was approximately 15
![]() ${}^{\circ }$
, corresponding to 57
${}^{\circ }$
, corresponding to 57
![]() ${}^{\circ }$
away from the normal vector of the Be target. The output signal from the PMT was recorded by an oscilloscope shot by shot and the neutron energy spectrum for each laser shot was obtained from each signal[
Reference Mirfayzi, Kar, Ahmed, Krygier, Green, Alejo, Clarke, Freeman, Fuchs, Jung, Kleinschmidt, Morrison, Najmudin, Nakamura, Norreys, Oliver, Roth, Vassura, Zepf and Borghesi
44
].
${}^{\circ }$
away from the normal vector of the Be target. The output signal from the PMT was recorded by an oscilloscope shot by shot and the neutron energy spectrum for each laser shot was obtained from each signal[
Reference Mirfayzi, Kar, Ahmed, Krygier, Green, Alejo, Clarke, Freeman, Fuchs, Jung, Kleinschmidt, Morrison, Najmudin, Nakamura, Norreys, Oliver, Roth, Vassura, Zepf and Borghesi
44
].
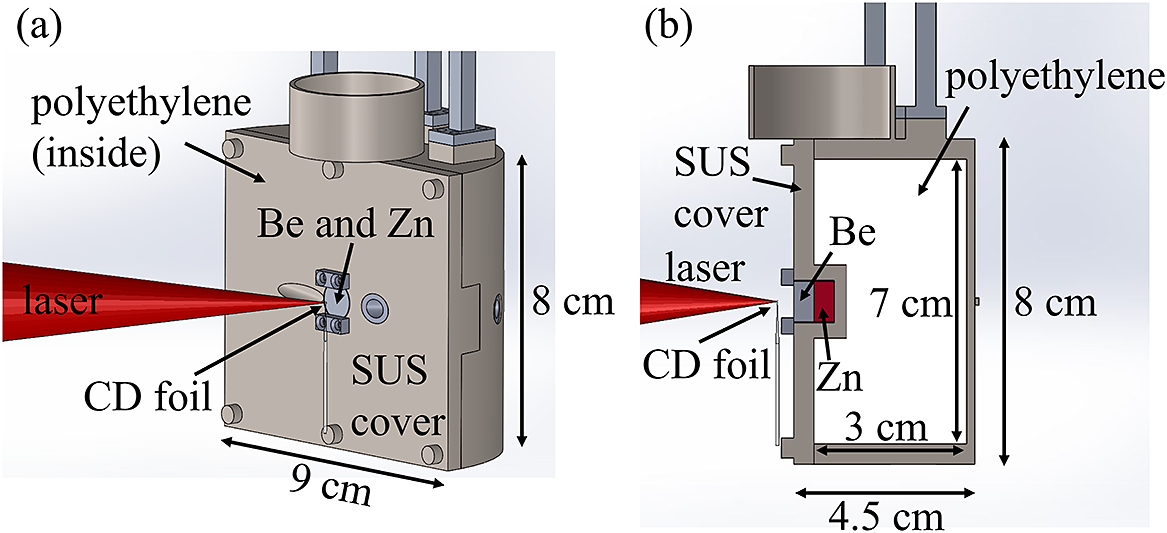
Figure 2 Experimental setup for the laser shot to generate neutrons. The laser is focused on the CD foil target. The Be neutron converter is placed 4 mm downstream of the CD foil. Behind the Be target, the Zn target was set in the hole at the center of the front surface.
Unstable isotopes and isomers were produced via nuclear reactions of the neutrons and stable isotopes of Zn. Eleven minutes after the laser shot, the Zn target was moved from the target chamber to obtain the
![]() $\gamma$
-ray signals. The
$\gamma$
-ray signals. The
![]() $\gamma$
-rays emitted from the produced nuclides were measured with an HPGe detector. The efficiency of the HPGe detector relative to a
$\gamma$
-rays emitted from the produced nuclides were measured with an HPGe detector. The efficiency of the HPGe detector relative to a
![]() $\phi$
3 inch
$\phi$
3 inch
![]() $\times$
3 inch NaI(Tl) scintillation detector was approximately 70%. A multichannel analyzer (TechnoAP, APG7400A) was used to acquire the pulse height of the amplifier, and the dead time was less than 0.07%. Copper plates with a thickness of 5 mm and lead blocks with a thickness of 10 cm were used for background radiation shielding. Standard
$\times$
3 inch NaI(Tl) scintillation detector was approximately 70%. A multichannel analyzer (TechnoAP, APG7400A) was used to acquire the pulse height of the amplifier, and the dead time was less than 0.07%. Copper plates with a thickness of 5 mm and lead blocks with a thickness of 10 cm were used for background radiation shielding. Standard
![]() $\gamma$
-ray sources of
$\gamma$
-ray sources of
![]() ${}^{152}$
Eu and
${}^{152}$
Eu and
![]() ${}^{133}$
Ba were used for calibration of the detection efficiency and energy of the HPGe detector. The
${}^{133}$
Ba were used for calibration of the detection efficiency and energy of the HPGe detector. The
![]() $\gamma$
-ray measurements of the laser-neutron irradiated Zn sample and background with a non-irradiated Zn target were conducted for 120 and 99 h, respectively, with the same background shield.
$\gamma$
-ray measurements of the laser-neutron irradiated Zn sample and background with a non-irradiated Zn target were conducted for 120 and 99 h, respectively, with the same background shield.
Table 1 Produced nuclides and their half-lives,
![]() $\gamma$
-ray energies, emission probabilities of the
$\gamma$
-ray energies, emission probabilities of the
![]() $\gamma$
-rays, nuclear reactions, numbers and activities.
$\gamma$
-rays, nuclear reactions, numbers and activities.

3 Experimental results
Figure 3 shows the energy spectrum of the generated neutrons, which was measured using the TOF method with the scintillation detector located 57
![]() ${}^{\circ }$
from the normal vector of the Be block. The maximum energy is approximately 17 MeV, and the number of neutrons decreases with increasing energy. The neutron yield was 8
${}^{\circ }$
from the normal vector of the Be block. The maximum energy is approximately 17 MeV, and the number of neutrons decreases with increasing energy. The neutron yield was 8
![]() $\times$
10
$\times$
10
![]() ${}^9$
neutrons/sr in the energy range from 1 MeV to the maximum energy. The maximum energy is high enough to induce the
${}^9$
neutrons/sr in the energy range from 1 MeV to the maximum energy. The maximum energy is high enough to induce the
![]() ${}^{67}$
Zn(n, p)
${}^{67}$
Zn(n, p)
![]() ${}^{67}$
Cu and
${}^{67}$
Cu and
![]() ${}^{68}$
Zn(n, np)
${}^{68}$
Zn(n, np)
![]() ${}^{67}$
Cu reactions. Note that the total number and the maximum energy are expected to be lower than those of the neutrons emitted forward, respectively.
${}^{67}$
Cu reactions. Note that the total number and the maximum energy are expected to be lower than those of the neutrons emitted forward, respectively.

Figure 3 Fast neutron spectrum obtained from the TOF measurement. The neutron energies reached 17 MeV.
The produced radioisotopes and isomers were identified using the analysis of
![]() $\gamma$
-rays radiated following
$\gamma$
-rays radiated following
![]() $\beta$
decay or internal decay of the isomers. For some nuclear species, the decay curves of
$\beta$
decay or internal decay of the isomers. For some nuclear species, the decay curves of
![]() $\gamma$
-rays were also used for identification. The number of a produced nuclide was evaluated from the peak area in the energy spectrum. Figures 4(a)–4(c) show the
$\gamma$
-rays were also used for identification. The number of a produced nuclide was evaluated from the peak area in the energy spectrum. Figures 4(a)–4(c) show the
![]() $\gamma$
-ray spectra from the neutron-irradiated Zn sample, the background and their subtraction in the three different energy ranges. In these spectra, the
$\gamma$
-ray spectra from the neutron-irradiated Zn sample, the background and their subtraction in the three different energy ranges. In these spectra, the
![]() $\gamma$
-rays of
$\gamma$
-rays of
![]() ${}^{63}$
Zn,
${}^{63}$
Zn,
![]() ${}^{65}$
Zn,
${}^{65}$
Zn,
![]() ${}^{69}$
Znm,
${}^{69}$
Znm,
![]() ${}^{64}$
Cu,
${}^{64}$
Cu,
![]() ${}^{66}$
Cu and
${}^{66}$
Cu and
![]() ${}^{67}$
Cu are observed. Because the peaks of the 93 and 185-keV
${}^{67}$
Cu are observed. Because the peaks of the 93 and 185-keV
![]() $\gamma$
-rays radiated from
$\gamma$
-rays radiated from
![]() ${}^{67}$
Cu in the energy spectrum were overlapped with the
${}^{67}$
Cu in the energy spectrum were overlapped with the
![]() $\gamma$
-rays from
$\gamma$
-rays from
![]() ${}^{234}$
Th and
${}^{234}$
Th and
![]() ${}^{235}$
U in the background, the background spectrum was subtracted from the Zn sample spectrum. Figures 4(d)–4(f) show the
${}^{235}$
U in the background, the background spectrum was subtracted from the Zn sample spectrum. Figures 4(d)–4(f) show the
![]() $\gamma$
-ray spectra measured for 8.1 h, 5.1 h and 8 min, respectively. In Figures 4(d) and 4(e),
$\gamma$
-ray spectra measured for 8.1 h, 5.1 h and 8 min, respectively. In Figures 4(d) and 4(e),
![]() $\gamma$
-rays radiated from
$\gamma$
-rays radiated from
![]() ${}^{71}$
Zn
m
(T
${}^{71}$
Zn
m
(T
![]() ${}_{1/2}$
= 4.0 h) and
${}_{1/2}$
= 4.0 h) and
![]() ${}^{65}$
Ni (T
${}^{65}$
Ni (T
![]() ${}_{1/2}$
= 2.5 h) are observed, respectively. In contrast, when the measuring time is as short as 8 min, the
${}_{1/2}$
= 2.5 h) are observed, respectively. In contrast, when the measuring time is as short as 8 min, the
![]() $\gamma$
-ray peak of
$\gamma$
-ray peak of
![]() ${}^{68}$
Cu
m
with a half-life of 3.8 min appears [see Figure 4(f)]. From the energy spectra and decay curves,
${}^{68}$
Cu
m
with a half-life of 3.8 min appears [see Figure 4(f)]. From the energy spectra and decay curves,
![]() ${}^{63}$
Zn,
${}^{63}$
Zn,
![]() ${}^{65}$
Zn,
${}^{65}$
Zn,
![]() ${}^{69}$
Zn
m
,
${}^{69}$
Zn
m
,
![]() ${}^{71}$
Zn
m
,
${}^{71}$
Zn
m
,
![]() ${}^{64}$
Cu,
${}^{64}$
Cu,
![]() ${}^{66}$
Cu,
${}^{66}$
Cu,
![]() ${}^{67}$
Cu,
${}^{67}$
Cu,
![]() ${}^{68}$
Cu
m
and
${}^{68}$
Cu
m
and
![]() ${}^{65}$
Ni were identified. Table 1 shows the properties and measured activities of the radioisotopes. Note that the only upper limit of the radioactivity of
${}^{65}$
Ni were identified. Table 1 shows the properties and measured activities of the radioisotopes. Note that the only upper limit of the radioactivity of
![]() ${}^{71}$
Zn was obtained by taking the square root of background around 910.27 keV. Although the 511.56-keV
${}^{71}$
Zn was obtained by taking the square root of background around 910.27 keV. Although the 511.56-keV
![]() $\gamma$
-ray with a highest emission probability of 32% is radiated from
$\gamma$
-ray with a highest emission probability of 32% is radiated from
![]() ${}^{71}$
Zn, it is difficult to use it for the estimation of radioactivity because its energy is nearly equal to 511 keV, which is one of the strongest background
${}^{71}$
Zn, it is difficult to use it for the estimation of radioactivity because its energy is nearly equal to 511 keV, which is one of the strongest background
![]() $\gamma$
-rays.
$\gamma$
-rays.

Figure 4
![]() $\gamma$
-ray spectra measured for 120 h, 8.1 h, 5.1 h and 8 min. (a)–(c) The
$\gamma$
-ray spectra measured for 120 h, 8.1 h, 5.1 h and 8 min. (a)–(c) The
![]() $\gamma$
-ray spectra integrated for 120 h. The background signal measured for 99 h was normalized to the target measurement of 120 h. (d) The
$\gamma$
-ray spectra integrated for 120 h. The background signal measured for 99 h was normalized to the target measurement of 120 h. (d) The
![]() $\gamma$
-ray spectrum measured for 8.1 h, where peaks corresponding to
$\gamma$
-ray spectrum measured for 8.1 h, where peaks corresponding to
![]() ${}^{71}$
Zn
m
are observed. (e) The
${}^{71}$
Zn
m
are observed. (e) The
![]() $\gamma$
-ray spectrum for 5.1 h, where peaks for
$\gamma$
-ray spectrum for 5.1 h, where peaks for
![]() ${}^{65}$
Ni are observed. (f) The
${}^{65}$
Ni are observed. (f) The
![]() $\gamma$
-ray spectrum for 8 min, which shows the
$\gamma$
-ray spectrum for 8 min, which shows the
![]() ${}^{68}$
Cu
m
peak at 526 keV.
${}^{68}$
Cu
m
peak at 526 keV.
4 Discussion
In the present study, we revealed that the radioisotope
![]() ${}^{67}$
Cu was generated by nuclear reactions on the natural Zn target with laser-driven neutrons, and obtained (3.3
${}^{67}$
Cu was generated by nuclear reactions on the natural Zn target with laser-driven neutrons, and obtained (3.3
![]() $\pm$
0.5)
$\pm$
0.5)
![]() $\times$
10
$\times$
10
![]() ${}^5$
atoms of
${}^5$
atoms of
![]() ${}^{67}$
Cu corresponding to the radioactivity of 1.0
${}^{67}$
Cu corresponding to the radioactivity of 1.0
![]() $\pm$
0.2 Bq for
$\pm$
0.2 Bq for
![]() ${}^{67}$
Cu using only a single laser shot. We evaluated the expected radioactivity of
${}^{67}$
Cu using only a single laser shot. We evaluated the expected radioactivity of
![]() ${}^{67}$
Cu and the other isotopes measured in the present experiment using the PHITS version 3.08 Monte Carlo simulation code[
Reference Sato, Iwamoto, Hashimoto, Ogawa, Furuta, Abe, Kai, Tsai, Matsuda, Iwase, Shigyo, Sihver and Niita
45
]. The cross-sections of the nuclear reactions were taken from the JENDL–4.0 nuclear data library[
Reference Shibata, Iwamoto, Nakagawa, Iwamoto, Ichihara, Kunieda, Chiba, Furutaka, Otuka, Ohsawa, Murata, Matsunobu, Zukeran, Kamada and Katakura
46
], as shown in Figure 5. Note that although the cross-sections at energies higher than 20 MeV are not included in the database, this upper limit is higher than the maximum energy of the neutrons assumed in the calculation. We calculated the radioactivities for the present experimental setup, and the measured neutron spectrum, as shown in Figure 4, was used as input data. The results are also presented in Table 2. There is disagreement between the experimental and calculated values. As listed in Table 2, the calculated radioactivities are lower than the measured values by a factor of 2.8
${}^{67}$
Cu and the other isotopes measured in the present experiment using the PHITS version 3.08 Monte Carlo simulation code[
Reference Sato, Iwamoto, Hashimoto, Ogawa, Furuta, Abe, Kai, Tsai, Matsuda, Iwase, Shigyo, Sihver and Niita
45
]. The cross-sections of the nuclear reactions were taken from the JENDL–4.0 nuclear data library[
Reference Shibata, Iwamoto, Nakagawa, Iwamoto, Ichihara, Kunieda, Chiba, Furutaka, Otuka, Ohsawa, Murata, Matsunobu, Zukeran, Kamada and Katakura
46
], as shown in Figure 5. Note that although the cross-sections at energies higher than 20 MeV are not included in the database, this upper limit is higher than the maximum energy of the neutrons assumed in the calculation. We calculated the radioactivities for the present experimental setup, and the measured neutron spectrum, as shown in Figure 4, was used as input data. The results are also presented in Table 2. There is disagreement between the experimental and calculated values. As listed in Table 2, the calculated radioactivities are lower than the measured values by a factor of 2.8
![]() $-$
200. The measured radioactivity of
$-$
200. The measured radioactivity of
![]() ${}^{67}$
Cu is 50 times larger than the calculated one. This discrepancy suggests that the number of the high-energy neutrons irradiating on the Zn target is more than the value assumed in the present calculation. This probably comes from the fact that the neutron energy spectrum used as the input was measured at 57
${}^{67}$
Cu is 50 times larger than the calculated one. This discrepancy suggests that the number of the high-energy neutrons irradiating on the Zn target is more than the value assumed in the present calculation. This probably comes from the fact that the neutron energy spectrum used as the input was measured at 57
![]() ${}^{\circ }$
. Because the neutron density is, in general, the largest at the forward angle, the assumed neutron flux and the maximum energy are considered to be lower than the actual values. Thus, we multiply the calculated yield of
${}^{\circ }$
. Because the neutron density is, in general, the largest at the forward angle, the assumed neutron flux and the maximum energy are considered to be lower than the actual values. Thus, we multiply the calculated yield of
![]() ${}^{67}$
Cu by the scaling factor of 50 in the following discussion.
${}^{67}$
Cu by the scaling factor of 50 in the following discussion.

Figure 5 Cross sections used in the simulation calculation, which are taken from the JENDL-4.0 nuclear data library.
Table 2 Experimental activities, calculated activities and their ratio of the obtained activities in the present experiment. The calculated activities were obtained using the PHITS simulation code with the measured neutron energy spectrum.

Radioisotopic impurity is one of the key parameters for the realization of a radiopharmaceutical. To evaluate the radioisotopic impurity, we also evaluated the radioactivities of other isotopes, as listed in Table 2. The radioactivities of
![]() ${}^{63}$
Zn,
${}^{63}$
Zn,
![]() ${}^{69}$
Znm,
${}^{69}$
Znm,
![]() ${}^{64}$
Cu,
${}^{64}$
Cu,
![]() ${}^{66}$
Cu,
${}^{66}$
Cu,
![]() ${}^{68}$
Cum and
${}^{68}$
Cum and
![]() ${}^{65}$
Ni are stronger than that of
${}^{65}$
Ni are stronger than that of
![]() ${}^{67}$
Cu by one to three orders of magnitude. In general, the Zn and Ni isotopes could be separated from the Cu isotopes with chemical processes[
Reference Watanabe, Iida, Suzui, Katabuchi, Ishii, Kawachi, Hanaoka, Matsuhashi, Endo and Ishioka
47
]. Among the Cu isotopes, because the half-lives of
${}^{67}$
Cu by one to three orders of magnitude. In general, the Zn and Ni isotopes could be separated from the Cu isotopes with chemical processes[
Reference Watanabe, Iida, Suzui, Katabuchi, Ishii, Kawachi, Hanaoka, Matsuhashi, Endo and Ishioka
47
]. Among the Cu isotopes, because the half-lives of
![]() ${}^{66}$
Cu and
${}^{66}$
Cu and
![]() ${}^{68}$
Cu
m
are shorter than 6 min, after the cooling time of 12 h their activities decrease lower than 10
${}^{68}$
Cu
m
are shorter than 6 min, after the cooling time of 12 h their activities decrease lower than 10
![]() ${}^{-40}$
Bq (see Table 1). Even if we use chemical separation and cooling processes, the unstable isotope
${}^{-40}$
Bq (see Table 1). Even if we use chemical separation and cooling processes, the unstable isotope
![]() ${}^{64}$
Cu still remains.
${}^{64}$
Cu still remains.
![]() ${}^{64}$
Cu is predominantly produced by the
${}^{64}$
Cu is predominantly produced by the
![]() ${}^{64}$
Zn(n, p)
${}^{64}$
Zn(n, p)
![]() ${}^{64}$
Cu reaction on the stable isotope
${}^{64}$
Cu reaction on the stable isotope
![]() ${}^{64}$
Zn with an isotopic fraction of 48.6%. To decrease the impurity of
${}^{64}$
Zn with an isotopic fraction of 48.6%. To decrease the impurity of
![]() ${}^{64}$
Cu, when we use the isotope enriched target of
${}^{64}$
Cu, when we use the isotope enriched target of
![]() ${}^{67}$
Zn or
${}^{67}$
Zn or
![]() ${}^{68}$
Zn, in which the isotopic fraction of
${}^{68}$
Zn, in which the isotopic fraction of
![]() ${}^{64}$
Zn is lower than 0.0486%, it is possible to decrease the
${}^{64}$
Zn is lower than 0.0486%, it is possible to decrease the
![]() ${}^{64}$
Cu radioactivity lower than 0.47 Bq. The experiment/simulation ratio for
${}^{64}$
Cu radioactivity lower than 0.47 Bq. The experiment/simulation ratio for
![]() ${}^{64}$
Cu is 23.9, as listed in Table 2, which is lower than that for
${}^{64}$
Cu is 23.9, as listed in Table 2, which is lower than that for
![]() ${}^{67}$
Cu. This is because
${}^{67}$
Cu. This is because
![]() ${}^{67}$
Cu is produced by the
${}^{67}$
Cu is produced by the
![]() ${}^{68}$
Zn(n, np)
${}^{68}$
Zn(n, np)
![]() ${}^{67}$
Cu reaction with relatively high-energy neutrons, but
${}^{67}$
Cu reaction with relatively high-energy neutrons, but
![]() ${}^{64}$
Cu cannot be produced by the
${}^{64}$
Cu cannot be produced by the
![]() ${}^{65}$
Zn(n, np)
${}^{65}$
Zn(n, np)
![]() ${}^{64}$
Cu reaction on the unstable isotope
${}^{64}$
Cu reaction on the unstable isotope
![]() ${}^{65}$
Zn. Thus, when we use relatively high-energy neutrons, the radioactivity of
${}^{65}$
Zn. Thus, when we use relatively high-energy neutrons, the radioactivity of
![]() ${}^{64}$
Cu decreases.
${}^{64}$
Cu decreases.
To estimate the activity of
![]() ${}^{67}$
Cu that can be produced in hospitals, we calculate a possible yield of
${}^{67}$
Cu that can be produced in hospitals, we calculate a possible yield of
![]() ${}^{67}$
Cu using a laser for an optimized target system, as shown in Figure 6. We assume an enriched
${}^{67}$
Cu using a laser for an optimized target system, as shown in Figure 6. We assume an enriched
![]() ${}^{67}$
Zn target for neutron irradiation. A well-type Zn target has a
${}^{67}$
Zn target for neutron irradiation. A well-type Zn target has a
![]() $\phi$
30 cm
$\phi$
30 cm
![]() $\times$
3 cm size with a hole of
$\times$
3 cm size with a hole of
![]() $\phi$
5 cm
$\phi$
5 cm
![]() $\times$
15 cm. The volume of the Zn target is approximately 2.1
$\times$
15 cm. The volume of the Zn target is approximately 2.1
![]() $\times$
10
$\times$
10
![]() ${}^4$
cm
${}^4$
cm
![]() ${}^3$
. In the bottom of the hole, the Be neutron generation target is located. The unstable isotope
${}^3$
. In the bottom of the hole, the Be neutron generation target is located. The unstable isotope
![]() ${}^{67}$
Cu is predominantly produced via the
${}^{67}$
Cu is predominantly produced via the
![]() ${}^{67}$
Zn(n, p)
${}^{67}$
Zn(n, p)
![]() ${}^{67}$
Cu reaction with neutrons with energies up to 17 MeV. We finally obtain the expected radioactivity of approximately 54 Bq for a single laser shot without the scaling factor of 50. Although we used a low-frequency high-power laser for the present demonstration, a high-frequency laser will be most efficient for the laser system placed inside hospitals because of its compactness and ability to provide laser intensity higher than 10
${}^{67}$
Cu reaction with neutrons with energies up to 17 MeV. We finally obtain the expected radioactivity of approximately 54 Bq for a single laser shot without the scaling factor of 50. Although we used a low-frequency high-power laser for the present demonstration, a high-frequency laser will be most efficient for the laser system placed inside hospitals because of its compactness and ability to provide laser intensity higher than 10
![]() ${}^{20}$
W/cm
${}^{20}$
W/cm
![]() ${}^2$
, leading to effective neutron generation. If we irradiate the laser-driven neutrons in the condition as assumed above for 10,000 s with a frequency of 10 Hz, we can obtain approximately 270 MBq of
${}^2$
, leading to effective neutron generation. If we irradiate the laser-driven neutrons in the condition as assumed above for 10,000 s with a frequency of 10 Hz, we can obtain approximately 270 MBq of
![]() ${}^{67}$
Cu with the scaling factor. This result suggests the possibility of production of medical radioisotopes using LDNSs in hospitals, although further studies are required for more realistic estimation.
${}^{67}$
Cu with the scaling factor. This result suggests the possibility of production of medical radioisotopes using LDNSs in hospitals, although further studies are required for more realistic estimation.

Figure 6 Geometry of the calculation of the yield of
![]() ${}^{67}$
Cu using a laser for an optimized target system. (a) Cross-sectional view of the Be and
${}^{67}$
Cu using a laser for an optimized target system. (a) Cross-sectional view of the Be and
![]() ${}^{67}$
Zn target. (b) 3D image of the target.
${}^{67}$
Zn target. (b) 3D image of the target.
5 Summary
In this study, we have demonstrated production of a medical radioisotope,
![]() ${}^{67}$
Cu, using LFEX at Osaka University. Neutrons with energies of up to 17 MeV have been generated using
${}^{67}$
Cu, using LFEX at Osaka University. Neutrons with energies of up to 17 MeV have been generated using
![]() $\mathrm{p}$
+
$\mathrm{p}$
+
![]() ${}^9$
Be and
${}^9$
Be and
![]() $\mathrm{d}$
+
$\mathrm{d}$
+
![]() ${}^9$
Be reactions on the secondary target located behind the ion acceleration target. The neutron energy spectrum at 57
${}^9$
Be reactions on the secondary target located behind the ion acceleration target. The neutron energy spectrum at 57
![]() ${}^{\circ }$
is obtained from the TOF method. The radioactivities of the generated unstable isotopes and isomers were evaluated from
${}^{\circ }$
is obtained from the TOF method. The radioactivities of the generated unstable isotopes and isomers were evaluated from
![]() $\gamma$
-ray energy spectra measured with an HPGe detector. The
$\gamma$
-ray energy spectra measured with an HPGe detector. The
![]() ${}^{67}$
Cu radioactivity of 1.0
${}^{67}$
Cu radioactivity of 1.0
![]() $\pm$
0.2 Bq was obtained, which is about 50 times higher than the value calculated using the PHITS simulation code. This may originate from the fact that the neutron energy spectrum was measured at 57
$\pm$
0.2 Bq was obtained, which is about 50 times higher than the value calculated using the PHITS simulation code. This may originate from the fact that the neutron energy spectrum was measured at 57
![]() ${}^{\circ }$
and, thus, the maximum energy and total number are lower than those of the neutrons irradiating on the Zn target. We estimated radioactivity of
${}^{\circ }$
and, thus, the maximum energy and total number are lower than those of the neutrons irradiating on the Zn target. We estimated radioactivity of
![]() ${}^{67}$
Cu using a future laser system and the PHITS code, obtaining the result that it is possible to produce 270 MBq of
${}^{67}$
Cu using a future laser system and the PHITS code, obtaining the result that it is possible to produce 270 MBq of
![]() ${}^{67}$
Cu using a high-frequency laser for 10,000 s irradiation. This suggests that the medical radioisotope may be produced in a compact laser system inside of a hospital in the future.
${}^{67}$
Cu using a high-frequency laser for 10,000 s irradiation. This suggests that the medical radioisotope may be produced in a compact laser system inside of a hospital in the future.
Acknowledgements
This work was supported by the JSPS Bilateral Program (Grant No. JSPSBP120209922) and JSPS KAKENHI (Grant Nos. JP22H02007 and JP22H01239).