Hostname: page-component-f554764f5-246sw Total loading time: 0 Render date: 2025-04-23T00:15:33.088Z Has data issue: false hasContentIssue false
  • English
  • Français

The minimal flow unit and origin of two-dimensional elasto-inertial turbulence

Published online by Cambridge University Press:  20 November 2024

Hongna Zhang Open the ORCID record for Hongna Zhang [Opens in a new window] ,
Haotian Cheng ,
Suming Wang ,
Wenhua Zhang ,
Xiaobin Li  and
Fengchen Li
Hongna Zhang
Affiliation:
State Key Laboratory of Engine, Tianjin University, Tianjin 300350, PR China
Haotian Cheng
Affiliation:
State Key Laboratory of Engine, Tianjin University, Tianjin 300350, PR China
Suming Wang
Affiliation:
State Key Laboratory of Engine, Tianjin University, Tianjin 300350, PR China
Wenhua Zhang*
Affiliation:
State Key Laboratory of Engine, Tianjin University, Tianjin 300350, PR China
Xiaobin Li
Affiliation:
State Key Laboratory of Engine, Tianjin University, Tianjin 300350, PR China
Fengchen Li
Affiliation:
State Key Laboratory of Engine, Tianjin University, Tianjin 300350, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

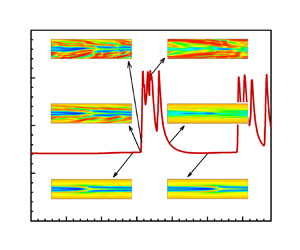
The research on elasto-inertial turbulence (EIT), a new type of turbulent flow, has reached the stage of identifying the minimal flow unit (MFU). On this issue, direct numerical simulations of FENE-P fluid flow in two-dimensional channels with variable sizes are conducted in this study. We demonstrate with the increase of channel length that the simulated flow experiences several different flow patterns, and there exists an MFU for EIT to be self-sustained. At Weissenberg number ($Wi$) higher than the one required to excite EIT, when the channel length is relatively small, a steady arrowhead regime (SAR) flow structure and a laminar-like friction coefficient is achieved. However, as the channel length increases, the flow can fully develop into EIT characterized with high flow drag. Close to the size of the MFU, the simulated flow behaves intermittently between the SAR state with low drag and EIT state with high drag. The flow falling back to ‘laminar flow’ is caused by the insufficient channel size below the MFU. Furthermore, we give the relationship between the value of the MFU and the effective $Wi$, and explain its physical reasons. Moreover, the intermittent flow regime obtained based on the MFU gives us an opportunity to look into the origin and exciting process of EIT. Through capturing the onset process of EIT, we observed that EIT originates from the sheet-like extension structure located near the wall, which is maybe related to the wall mode rather than the centre mode. The fracture and regeneration of this sheet-like structure is the key mechanism for the self-sustaining of EIT.

JFM classification

Non-Newtonian Flows: Viscoelasticity Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulence theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 999 , 25 November 2024 , A82
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alves, M.A., Oliveira, P.J. & Pinho, F.T. 2021 Numerical methods for viscoelastic fluid flows. Annu. Rev. Fluid Mech. 53, 509–541.CrossRefGoogle Scholar
Beneitez, M., Page, J., Dubief, Y. & Kerswell, R.R. 2024 Multistability of elasto-inertial two-dimensional channel flow. J. Fluid Mech. 981, A30.CrossRefGoogle Scholar
Beneitez, M., Page, J. & Kerswell, R.R. 2023 Polymer diffusive instability leading to elastic turbulence in plane Couette flow. Phys. Rev. Fluids 8, L101901.CrossRefGoogle Scholar
Choueiri, G.H., Lopez, J.M. & Hof, B. 2018 Exceeding the asymptotic limit of polymer drag reduction. Phys. Rev. Lett. 120, 124501.CrossRefGoogle ScholarPubMed
Choueiri, G.H., Lopez, J.M., Varshney, A., Sankar, S. & Hof, B. 2021 Experimental observation of the origin and structure of elastoinertial turbulence. Proc. Natl Acad. Sci. USA 118 (45), e2102350118.CrossRefGoogle ScholarPubMed
Couchman, M.M.P., Beneitez, M., Page, J. & Kerswell, R.R. 2024 Inertial enhancement of the polymer diffusive instability. J. Fluid Mech. 981, A2.CrossRefGoogle Scholar
Dubief, Y., Page, J., Kerswell, R.R., Terrapon, V.E. & Steinberg, V. 2022 First coherent structure in elasto-inertial turbulence. Phys. Rev. Fluids 7, 073301.CrossRefGoogle Scholar
Dubief, Y., Terrapon, V.E. & Hof, B. 2023 Elasto-inertial turbulence. Annu. Rev. Fluid Mech. 55, 675–705.CrossRefGoogle Scholar
Dubief, Y., Terrapon, V.E. & Julio, S. 2013 On the mechanism of elasto-inertial turbulence. Phys. Fluids 25, 110817.CrossRefGoogle ScholarPubMed
Garg, P., Chaudhary, I., Khalid, M., Shankar, V. & Subramanian, G. 2018 Viscoelastic pipe flow is linearly unstable. Phys. Rev. Lett. 121, 024502.CrossRefGoogle ScholarPubMed
Graham, M.D. 2014 Drag reduction and the dynamics of turbulence in simple and complex fluids. Phys. Fluids 26 (10), 101301.CrossRefGoogle Scholar
Groisman, A. & Steinberg, V. 2000 Elastic turbulence in a polymer solution flow. Nature 405 (6782), 53–55.CrossRefGoogle Scholar
Groisman, A. & Steinberg, V. 2004 Elastic turbulence in curvilinear flows of polymer solutions. New J. Phys. 6 (1), 29.CrossRefGoogle Scholar
Jiménez, J. & Moin, P. 1991 The minimal flow unit in near-wall turbulence. J. Fluid Mech. 225, 213–240.CrossRefGoogle Scholar
Khalid, M., Chaudhary, I., Garg, P., Shankar, V. & Subramanian, G. 2021 The centre-mode instability of viscoelastic plane Poiseuille flow. J. Fluid Mech. 915, A43.CrossRefGoogle Scholar
Li, F.C., Yu, B., Wei, J.J. & Kawaguchi, Y. 2012 Turbulent Drag Reduction by Surfactant Additives. John Wiley & Sons.Google Scholar
Page, J., Dubief, Y. & Kerswell, R.R. 2020 Exact travelling wave solutions in viscoelastic channel flow. Phys. Rev. Lett. 125, 154501.CrossRefGoogle ScholarPubMed
Samanta, D., Dubief, Y., Holzner, M., Schafer, C., Morozov, A.N., Wagner, C. & Hof, B. 2013 Elasto-inertial turbulence. Proc. Natl Acad. Sci. USA 110, 10557.CrossRefGoogle ScholarPubMed
Sánchez, H.A.C., Jovanović, M.R., Kumar, S., Morozov, A., Shankar, V., Subramanian, G. & Wilson, H.J. 2022 Understanding viscoelastic flow instabilities: Oldroyd-B and beyond. J. Non-Newtonian Fluid Mech. 302, 104742.CrossRefGoogle Scholar
Shekar, A., McMullen, R., McKeon, B. & Graham, M. 2020 Self-sustained elastoinertial Tollmien–Schlichting waves. J. Fluid Mech. 897, A3.CrossRefGoogle Scholar
Shekar, A., McMullen, R.M., McKeon, B.J. & Graham, M.D. 2021 Tollmien–Schlichting route to elastoinertial turbulence in channel flow. Rev. Fluids 6, 093301.CrossRefGoogle Scholar
Shekar, A., McMullen, R.M., Wang, S.N., McKeon, B.J. & Graham, M.D. 2019 Critical-layer structures and mechanisms in elastoinertial turbulence. Phys. Rev. Lett. 122, 124503.CrossRefGoogle ScholarPubMed
Shu, C. 1998 Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws. In Advanced Numerical Approximation of Nonlinear Hyperbolic Equations (ed. Quarteroni, A.), pp. 325–432. Springer.CrossRefGoogle Scholar
Sid, S., Terrapon, V.E. & Dubief, Y. 2018 Two-dimensional dynamics of elasto-inertial turbulence and its role in polymer drag reduction. Phys. Rev. Fluids 3, 011301.CrossRefGoogle Scholar
Steinberg, V. 2021 Elastic turbulence: an experimental view on inertialess random flow. Annu. Rev. Fluid Mech. 53, 27–58.CrossRefGoogle Scholar
Toms, B.A. 1949 Some observations on the flow of linear polymer solutions through straight tubes at large Reynolds numbers. In Proc. 1st International Congress on Rheology, vol. 2, pp. 135–141. North-Holland.Google Scholar
Wan, D.D., Sun, G.R. & Zhang, M.Q. 2021 Subcritical and supercritical bifurcations in axisymmetric viscoelastic pipe flows. J. Fluid Mech. 929, A16.CrossRefGoogle Scholar
Wang, S.M., Zhang, W.H., Wang, X.Y., Li, X.B., Zhang, H.N. & Li, F.C. 2021 Maximum drag reduction state of viscoelastic turbulent channel flow: marginal inertial turbulence or elasto-inertial turbulence. J. Fluid Mech 960, A12.CrossRefGoogle Scholar
White, C.M. & Mungal, M.G. 2008 Mechanics and prediction of turbulent drag reduction with polymer additives. Annu. Rev. Fluid Mech. 40, 235–256.CrossRefGoogle Scholar
Xi, L. & Bai, X. 2016 Marginal turbulent state of viscoelastic fluids: a polymer drag reduction perspective. Phys. Rev. E 93, 043118.CrossRefGoogle ScholarPubMed
Xi, L. & Graham, M.D. 2010 Turbulent drag reduction and multistage transitions in viscoelastic minimal flow units. J. Fluid Mech. 647, 421–452.CrossRefGoogle Scholar
Xi, L. & Graham, M.D. 2011 Active and hibernating turbulence in minimal channel flow of Newtonian and polymeric fluids. Phys. Rev. Lett. 104, 218301.Google Scholar
Yin, G., Huang, W.X. & Xu, C.X. 2018 Prediction of near-wall turbulence using minimal flow unit. J. Fluid Mech. 841, 654–673.CrossRefGoogle Scholar
Zhang, H.N., Zhang, W.H., Wang, X.Y., Li, Y.S., Ma, Y., Li, X.B. & Li, F.C. 2023 On the role of tensor interpolation in solving high-Wi viscoelastic fluid flow. Phys. Fluids 35, 031708.CrossRefGoogle Scholar
Zhang, W.H., Zhang, H.N., Wang, Z.M., Li, Y.K., Yu, B. & Li, F.C. 2022 Repicturing viscoelastic drag-reducing turbulence by introducing dynamics of elasto-inertial turbulence. J. Fluid Mech. 940, A31.CrossRefGoogle Scholar
Zhu, L. & Xi, L. 2021 Nonasymptotic elastoinertial turbulence for asymptotic drag reduction. Phys. Rev. Fluids 6, 014601.CrossRefGoogle Scholar
Supplementary material: File

Zhang et al. supplementary movie 1

Statistical and structural evolutions for Case A: SX = 5, Wi = 40, Re = 2000, L2 = 10000 and β = 0.9.
Download Zhang et al. supplementary movie 1(File)
File 1.9 MB
Supplementary material: File

Zhang et al. supplementary movie 2

Statistical and structural evolutions for Case B: SX = 8, Wi = 100, Re = 2000, L2 = 10000 and β = 0.9.
Download Zhang et al. supplementary movie 2(File)
File 2.2 MB