Article contents
Connecting the time evolution of the turbulence interface to coherent structures
Published online by Cambridge University Press: 24 June 2020
Abstract
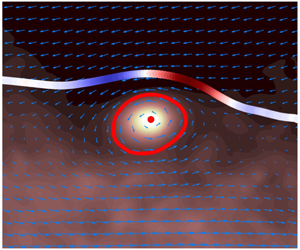
The surface area of turbulent/non-turbulent interfaces (TNTIs) is continuously produced and destroyed via stretching and curvature/propagation effects. Here, the mechanisms responsible for TNTI area growth and destruction are investigated in a turbulent flow with and without stable stratification through the time evolution equation of the TNTI area. We show that both terms have broad distributions and may locally contribute to either production or destruction. On average, however, the area growth is driven by stretching, which is approximately balanced by destruction by the curvature/propagation term. To investigate the contribution of different length scales to these processes, we apply spatial filtering to the data. In doing so, we find that the averages of the stretching and the curvature/propagation terms balance out across spatial scales of TNTI wrinkles and this scale-by-scale balance is consistent with an observed scale invariance of the nearby coherent vortices. Through a conditional analysis, we demonstrate that the TNTI area production (destruction) is localized at the front (lee) edge of the vortical structures in the interface proximity. Finally, we show that while basic mechanisms remain the same, increasing stratification reduces the rates at which TNTI surface area is produced as well as destroyed. We provide evidence that this reduction is largely connected to a change in the multiscale geometry of the interface, which tends to flatten in the wall-normal direction at all active length scales of the TNTI.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
Footnotes
This original version of this article was published with some incorrect author information. A notice detailing this has been published and the error rectified in the online PDF and HTML copies.
References
A correction has been issued for this article:
- 24
- Cited by
Linked content
Please note a has been issued for this article.


