Hostname: page-component-669899f699-b58lm Total loading time: 0 Render date: 2025-04-24T10:51:02.580Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of iteration operators on self-maps of locally compact Hausdorff spaces

Part of: Smooth dynamical systems: general theory Nonlinear operators and their properties

Published online by Cambridge University Press:  03 May 2023

CHAITANYA GOPALAKRISHNA ,
MURUGAN VEERAPAZHAM  and
WEINIAN ZHANG
CHAITANYA GOPALAKRISHNA
Affiliation:
Statistics and Mathematics Unit, Indian Statistical Institute, R.V. College Post, Bengaluru-560059, India (e-mail: [email protected])
MURUGAN VEERAPAZHAM
Affiliation:
Department of Mathematical and Computational Sciences, National Institute of Technology Karnataka, Surathkal, Mangalore-575 025, India (e-mail: [email protected])
WEINIAN ZHANG*
Affiliation:
School of Mathematics, Sichuan University, Chengdu, Sichuan 610064, P. R. China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we prove the continuity of iteration operators 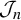$\mathcal {J}_n$ on the space of all continuous self-maps of a locally compact Hausdorff space X and generally discuss dynamical behaviors of them. We characterize their fixed points and periodic points for 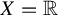$X=\mathbb {R}$ and the unit circle 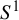$S^1$. Then we indicate that all orbits of 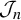$\mathcal {J}_n$ are bounded; however, we prove that for 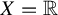$X=\mathbb {R}$ and 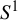$S^1$, every fixed point of $\mathcal {J}_n$ which is non-constant and equals the identity on its range is not Lyapunov stable. The boundedness and the instability exhibit the complexity of the system, but we show that the complicated behavior is not Devaney chaotic. We give a sufficient condition to classify the systems generated by iteration operators up to topological conjugacy.

Keywords

Iteration operatorperiodic pointschaosBabbage equationtopological conjugacy

MSC classification

Primary: 37C25: Fixed points, periodic points, fixed-point index theory
Secondary: 39B12: Iteration theory, iterative and composite equations 47H30: Particular nonlinear operators (superposition, Hammerstein, Nemytskiĭ, Uryson, etc.)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 44 , Issue 3 , March 2024 , pp. 749 - 768
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Arens, R. F.. A topology for spaces of transformations. Ann. of Math. (2) 47(3) (1946), 480–495.Google Scholar
Babbage, C.. An essay towards the calculus of functions. Philos. Trans. Roy. Soc. London 105 (1815), 389–423.Google Scholar
Bessaga, C. and Pełczyński, A.. Selected Topics in Infinite-Dimensional Topology (Mathematical Monographs, 58). PWN–Polish Scientific Publishers, Warsaw, 1975.Google Scholar
Block, L. S. and Coppel, W. A.. Dynamics in One Dimension (Lecture Notes in Mathematics, 1513). Springer, Berlin, 1992.Google Scholar
Blokh, A. M.. The set of all iterates is nowhere dense in $C([0,1],[0,1])$ . Trans. Amer. Math. Soc. 333(2) (1992), 787–798.Google Scholar
Bödewadt, U. T.. Zur iteration reeller functionen. Math. Z. 49 (1944), 497–516.Google Scholar
Conway, J. B.. Functions of One Complex Variable (Graduate Texts in Mathematics, 11), 2nd edn. Springer, New York, 1978.Google Scholar
Devaney, R. L.. An Introduction to Chaotic Dynamical Systems. Westview Press, New York, 1991.Google Scholar
Fort, M. K.. The embedding of homeomorphisms in flows. Proc. Amer. Math. Soc. 6(6) (1955), 960–967.Google Scholar
Holmgren, R. A.. A First Course in Discrete Dynamical Systems. Springer, New York, 1991.Google Scholar
Jarczyk, W.. On an equation of linear iteration. Aequationes Math. 51(3) (1996), 303–310.Google Scholar
Jarczyk, W.. Babbage equation on the circle. Publ. Math. 63(3) (2003), 389–400.Google Scholar
Kuczma, M.. On monotonic solutions of a functional equation I. Ann. Polon. Math. 9 (1960), 295–297.Google Scholar
Kuczma, M.. Functional Equations in a Single Variable. Polish Scientific Publishers, Warsaw, 1968.Google Scholar
Kundu, S. and Garg, P.. The compact-open topology: a new perspective. Topology Appl. 156(4) (2009), 686–696.Google Scholar
Li, T.-Y. and Yorke, J. A.. Period three implies chaos. Amer. Math. Monthly 82(10) (1975), 985–992.Google Scholar
McCoy, R. A. and Ntantu, I.. Topological Properties of Spaces of Continuous Functions (Lecture Notes in Mathematics, 1315). Springer, Berlin, 1988.Google Scholar
McShane, N.. On the periodicity of homomorphisms of the real line. Amer. Math. Monthly 68(6) (1961), 562–563.Google Scholar
Milnor, J.. Dynamics in One Complex Variable, 3rd edn. Princeton University Press, Princeton, NJ, 2006.Google Scholar
Milnor, J. and Thurston, W.. On Iterated Maps of the Interval. Dynamical Systems (Lecture Notes in Mathematics, 1342). Ed. Alexander, J. C.. Springer, New York, 1988, pp. 465–563.Google Scholar
Munkres, J. R.. Topology, 2nd edn. Prentice Hall, Inc., Upper Saddle River, NJ, 2000.Google Scholar
Narici, L. and Beckenstein, E.. Topological Vector Spaces (Pure and Applied Mathematics, 296), 2nd edn. CRC Press, Boca Raton, FL, 2011.Google Scholar
Veerapazham, M., Gopalakrishna, C. and Zhang, W.. Dynamics of the iteration operator on the space of continuous self-maps. Proc. Amer. Math. Soc. 149(1) (2021), 217–229.Google Scholar
Vincze, E.. Über die Charakterisierung der assoziativen Funktionen von mehreren Veränderlichen. Publ. Math. Debrecen 6 (1959), 241–253.Google Scholar
Wall, C. T. C.. A Geometric Introduction to Topology. Dover Publications, New York, 1993.Google Scholar
Willard, S.. General Topology. Dover Publications, Inc., Mineola, NY, 2004.Google Scholar
Zhang, W.. PM functions, their characteristic intervals and iterative roots. Ann. Polon. Math. 65(2) (1997), 119–128.Google Scholar
Zhang, W. M. and Zhang, W.. Continuity of iteration and approximation of iterative roots. J. Comput. Appl. Math. 235(5) (2011), 1232–1244.Google Scholar