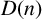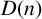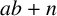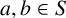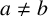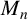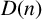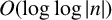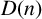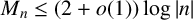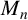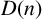1 Introduction
A set
![]() $\{a_{1},a_{2},\ldots , a_{m}\}$
of distinct positive integers is a Diophantine m-tuple if the product of any two distinct elements in the set is one less than a square. A famous example of a Diophantine quadruple is
$\{a_{1},a_{2},\ldots , a_{m}\}$
of distinct positive integers is a Diophantine m-tuple if the product of any two distinct elements in the set is one less than a square. A famous example of a Diophantine quadruple is
![]() $\{1,3,8,120\}$
, due to Fermat. Such a construction is optimal in the sense that there is no Diophantine
$\{1,3,8,120\}$
, due to Fermat. Such a construction is optimal in the sense that there is no Diophantine
![]() $5$
-tuple, recently confirmed by He et al. [Reference He, Togbé and Ziegler8]. There are many generalisations and variants of Diophantine tuples. We refer to the recent book of Dujella [Reference Dujella6] for a comprehensive overview.
$5$
-tuple, recently confirmed by He et al. [Reference He, Togbé and Ziegler8]. There are many generalisations and variants of Diophantine tuples. We refer to the recent book of Dujella [Reference Dujella6] for a comprehensive overview.
In this paper, we focus on one natural generalisation that has been studied extensively. Let n be a nonzero integer. A set S of positive integers is a Diophantine tuple with the property
![]() $D(n)$
if
$D(n)$
if
![]() $ab+n$
is a perfect square for each
$ab+n$
is a perfect square for each
![]() $a,b \in S$
with
$a,b \in S$
with
![]() $a \neq b$
. It is of special interest to estimate the quantity
$a \neq b$
. It is of special interest to estimate the quantity
![]() $M_n$
, the maximum size of a Diophantine tuple with the property
$M_n$
, the maximum size of a Diophantine tuple with the property
![]() $D(n)$
. We have mentioned that
$D(n)$
. We have mentioned that
![]() $M_1=4$
[Reference He, Togbé and Ziegler8]. Analogously, Bliznac Trebješanin and Filipin [Reference Bliznac Trebješanin and Filipin2] proved that
$M_1=4$
[Reference He, Togbé and Ziegler8]. Analogously, Bliznac Trebješanin and Filipin [Reference Bliznac Trebješanin and Filipin2] proved that
![]() $M_4=4$
. More recently, Bonciocat et al. [Reference Bonciocat, Cipu and Mignotte3] proved that
$M_4=4$
. More recently, Bonciocat et al. [Reference Bonciocat, Cipu and Mignotte3] proved that
![]() $M_{-1}=M_{-4}=3$
.
$M_{-1}=M_{-4}=3$
.
It is widely believed that
![]() $M_n$
is uniformly bounded (for example, this follows from the uniformity conjecture) [Reference Becker and Murty1, Reference Dujella4]. Using elementary congruence considerations, it is easy to show that
$M_n$
is uniformly bounded (for example, this follows from the uniformity conjecture) [Reference Becker and Murty1, Reference Dujella4]. Using elementary congruence considerations, it is easy to show that
![]() $M_n=3$
when
$M_n=3$
when
![]() $n \equiv 2 \pmod {4}$
(see [Reference Dujella6, Section 5.4.1] for more discussions). In a remarkable paper [Reference Dujella and Luca7], Dujella and Luca showed that if p is a prime, then
$n \equiv 2 \pmod {4}$
(see [Reference Dujella6, Section 5.4.1] for more discussions). In a remarkable paper [Reference Dujella and Luca7], Dujella and Luca showed that if p is a prime, then
![]() $M_p$
and
$M_p$
and
![]() $M_{-p}$
are both bounded by
$M_{-p}$
are both bounded by
![]() $3 \cdot 2^{168}$
. However, for a generic n, the best-known upper bound on
$3 \cdot 2^{168}$
. However, for a generic n, the best-known upper bound on
![]() $M_n$
is of the form
$M_n$
is of the form
![]() $O(\log |n|)$
.
$O(\log |n|)$
.
Following [Reference Becker and Murty1, Reference Dujella4, Reference Dujella5], for Diophantine tuples with the property
![]() $D(n)$
, we separate the contribution of large, intermediate and small elements as follows:
$D(n)$
, we separate the contribution of large, intermediate and small elements as follows:
 $$ \begin{align*} & A_n=\sup \{|S \cap[|n|^3,+\infty)|: S \text { has the property } D(n)\}, \\ & B_n=\sup \{|S \cap(n^2,|n|^3)|: S \text { has the property } D(n)\}, \\ & C_n=\sup \{|S \cap[1, n^2]|: S \text { has the property } D(n)\}. \end{align*} $$
$$ \begin{align*} & A_n=\sup \{|S \cap[|n|^3,+\infty)|: S \text { has the property } D(n)\}, \\ & B_n=\sup \{|S \cap(n^2,|n|^3)|: S \text { has the property } D(n)\}, \\ & C_n=\sup \{|S \cap[1, n^2]|: S \text { has the property } D(n)\}. \end{align*} $$
In [Reference Dujella4], Dujella showed that
![]() $A_n \leq 31$
. The best known upper bound on
$A_n \leq 31$
. The best known upper bound on
![]() $B_n$
is
$B_n$
is
![]() $B_n \leq 0.6071 \log |n|+O(1)$
, due to Dujella [Reference Dujella5]. As for
$B_n \leq 0.6071 \log |n|+O(1)$
, due to Dujella [Reference Dujella5]. As for
![]() $C_n$
, the best result,
$C_n$
, the best result,
 $$ \begin{align} C_n\leq 2\log |n|+O\bigg(\frac{\log |n|}{(\log \log |n|)^2}\bigg), \end{align} $$
$$ \begin{align} C_n\leq 2\log |n|+O\bigg(\frac{\log |n|}{(\log \log |n|)^2}\bigg), \end{align} $$
is due to Becker and Murty [Reference Becker and Murty1]. Summing the bounds on
![]() $A_n, B_n$
and
$A_n, B_n$
and
![]() $C_n$
yields
$C_n$
yields
![]() $M_n\leq (2.6071+o(1))\log |n|$
, the best known upper bound on
$M_n\leq (2.6071+o(1))\log |n|$
, the best known upper bound on
![]() $M_n$
[Reference Becker and Murty1].
$M_n$
[Reference Becker and Murty1].
Our main result is the following improved upper bounds for
![]() $B_n$
and
$B_n$
and
![]() $M_n$
.
$M_n$
.
Theorem 1.1. We have
 $$ \begin{align*}B_n=O(\log \log |n|), \quad M_n\leq 2\log |n|+O\bigg(\frac{\log |n|}{(\log \log |n|)^2}\bigg).\end{align*} $$
$$ \begin{align*}B_n=O(\log \log |n|), \quad M_n\leq 2\log |n|+O\bigg(\frac{\log |n|}{(\log \log |n|)^2}\bigg).\end{align*} $$
The key observation of our improvement is that the contribution of intermediate elements can be bounded more efficiently. To achieve that, we separate the contribution of large and intermediate elements differently. For each
![]() $\epsilon>0$
, let
$\epsilon>0$
, let
 $$ \begin{align*} & A_n^{(\epsilon)}=\sup \{|S \cap(|n|^{2+\epsilon},+\infty)|: S \text { has the property } D(n)\},\\ & B_n^{(\epsilon)}=\sup \{|S \cap(n^2, |n|^{2+\epsilon}]|: S \text { has the property } D(n)\}. \end{align*} $$
$$ \begin{align*} & A_n^{(\epsilon)}=\sup \{|S \cap(|n|^{2+\epsilon},+\infty)|: S \text { has the property } D(n)\},\\ & B_n^{(\epsilon)}=\sup \{|S \cap(n^2, |n|^{2+\epsilon}]|: S \text { has the property } D(n)\}. \end{align*} $$
We give the following estimates on
![]() $A_n^{(\epsilon )}$
and
$A_n^{(\epsilon )}$
and
![]() $B_n^{(\epsilon )}$
.
$B_n^{(\epsilon )}$
.
Theorem 1.2. The following estimates hold uniformly for all
![]() $\epsilon \in (0,1)$
and all nonzero integers n:
$\epsilon \in (0,1)$
and all nonzero integers n:
To estimate
![]() $B_n$
and
$B_n$
and
![]() $M_n$
, note that
$M_n$
, note that
By setting
 $$ \begin{align*}\epsilon=\frac{\log \log |n|}{\log |n|},\end{align*} $$
$$ \begin{align*}\epsilon=\frac{\log \log |n|}{\log |n|},\end{align*} $$
we see that Theorem 1.1 follows from Theorem 1.2 and (1.1) immediately.
2 Proofs
Our proofs are inspired by several arguments used in [Reference Dujella4, Reference Dujella5, Reference Yip9]. We first recall three useful lemmas from [Reference Dujella4].
Lemma 2.1 [Reference Dujella4, Lemma 2].
Let n be a nonzero integer. Let
![]() $\{a, b, c, d \}$
be a Diophantine quadruple with the property
$\{a, b, c, d \}$
be a Diophantine quadruple with the property
![]() $D(n)$
and
$D(n)$
and
![]() $a<b<c<d$
. If
$a<b<c<d$
. If
![]() $c>b^{11}|n|^{11}$
, then
$c>b^{11}|n|^{11}$
, then
![]() $d\leq c^{131}$
.
$d\leq c^{131}$
.
Lemma 2.2 [Reference Dujella4, Lemma 3].
Let n be a nonzero integer. If
![]() $\{a, b, c\}$
is a Diophantine triple with the property
$\{a, b, c\}$
is a Diophantine triple with the property
![]() $D(n)$
and
$D(n)$
and
![]() $ab+n=r^2, ac+n=s^2, bc+n=t^2$
, then there exist integers
$ab+n=r^2, ac+n=s^2, bc+n=t^2$
, then there exist integers
![]() $e, x, y, z$
such that
$e, x, y, z$
such that
and
Lemma 2.3 [Reference Dujella4, Lemma 5].
Let n be an integer with
![]() $|n|\geq 2$
. Let
$|n|\geq 2$
. Let
![]() $\{a, b, c, d \}$
be a Diophantine quadruple with the property
$\{a, b, c, d \}$
be a Diophantine quadruple with the property
![]() $D(n)$
. If
$D(n)$
. If
![]() $n^2< a<b<c<d$
, then
$n^2< a<b<c<d$
, then
![]() $c>3.88a$
and
$c>3.88a$
and
![]() $d>4.89c$
.
$d>4.89c$
.
Next, we deduce a gap principle from the above two lemmas.
Corollary 2.4. Let n be an integer with
![]() $|n|\geq 2$
. Let
$|n|\geq 2$
. Let
![]() $\{a, b, c, d \}$
be a Diophantine quadruple with the property
$\{a, b, c, d \}$
be a Diophantine quadruple with the property
![]() $D(n)$
. If
$D(n)$
. If
![]() $n^2< a<b<c<d$
, then
$n^2< a<b<c<d$
, then
Proof. We apply Lemma 2.2 to the Diophantine triple
![]() $\{b,c,d\}$
. Since
$\{b,c,d\}$
. Since
![]() $b>n^2$
and
$b>n^2$
and
![]() $be+n^2 \geq 0$
, it follows that
$be+n^2 \geq 0$
, it follows that
![]() $e \geq 0$
. If
$e \geq 0$
. If
![]() $e=0$
, then Lemma 2.2 implies that
$e=0$
, then Lemma 2.2 implies that
which is impossible in view of Lemma 2.3. Thus,
![]() $e\geq 1$
and Lemma 2.2 implies that
$e\geq 1$
and Lemma 2.2 implies that
Now we are ready to prove Theorem 1.2.
Proof of Theorem 1.2.
Let
![]() $\epsilon \in (0,1)$
and n be a nonzero integer.
$\epsilon \in (0,1)$
and n be a nonzero integer.
We first bound
![]() $B_n^{(\epsilon )}$
. Let S be a Diophantine tuple with the property
$B_n^{(\epsilon )}$
. Let S be a Diophantine tuple with the property
![]() $D(n)$
, such that all elements in S are in
$D(n)$
, such that all elements in S are in
![]() $[n^2, |n|^{2+\epsilon }]$
. By Lemma 2.3, the elements in S grow exponentially. More precisely,
$[n^2, |n|^{2+\epsilon }]$
. By Lemma 2.3, the elements in S grow exponentially. More precisely,
The bound on
![]() $B_n^{(\epsilon )}$
follows.
$B_n^{(\epsilon )}$
follows.
Next we estimate
![]() $A_n^{(\epsilon )}$
. Let S be a Diophantine tuple with the property
$A_n^{(\epsilon )}$
. Let S be a Diophantine tuple with the property
![]() $D(n)$
, such that all elements in S are at least
$D(n)$
, such that all elements in S are at least
![]() $|n|^{2+\epsilon }$
. Label the elements in S in increasing order as
$|n|^{2+\epsilon }$
. Label the elements in S in increasing order as
![]() $a_1<a_2<\cdots $
. By Corollary 2.4,
$a_1<a_2<\cdots $
. By Corollary 2.4,
holds for each
![]() $i \geq 2$
. For each
$i \geq 2$
. For each
![]() $i \geq 2$
, let
$i \geq 2$
, let
![]() $b_i=a_i/n^2$
. Then we have
$b_i=a_i/n^2$
. Then we have
![]() $b_{i+2}>b_ib_{i+1}$
. Note that
$b_{i+2}>b_ib_{i+1}$
. Note that
![]() $b_2=a_2/n^2$
and
$b_2=a_2/n^2$
and
![]() $b_3>b_2=a_2/n^2$
. Define the sequence
$b_3>b_2=a_2/n^2$
. Define the sequence
![]() $\{\beta _i\}_{i=2}^{\infty }$
recursively by
$\{\beta _i\}_{i=2}^{\infty }$
recursively by
By induction, we have
![]() $b_i>(a_2/n^2)^{\beta _i}$
. It follows that
$b_i>(a_2/n^2)^{\beta _i}$
. It follows that
 $$ \begin{align} a_i>\frac{a_2^{\beta_i}}{|n|^{2\beta_i-2}}. \end{align} $$
$$ \begin{align} a_i>\frac{a_2^{\beta_i}}{|n|^{2\beta_i-2}}. \end{align} $$
Since
![]() $\beta _i \to \infty $
, we can choose k sufficiently large such that
$\beta _i \to \infty $
, we can choose k sufficiently large such that
let
![]() $k=k(\epsilon )$
be the smallest such k. If
$k=k(\epsilon )$
be the smallest such k. If
![]() $|S|<k$
, we are done. Otherwise, (2.1) implies that
$|S|<k$
, we are done. Otherwise, (2.1) implies that
 $$ \begin{align*} a_k>\frac{a_2^{\beta_k}}{|n|^{2\beta_k-2}}=a_2^{11}|n|^{11} \cdot \frac{a_2^{\beta_k-11}}{|n|^{2\beta_k+9}}> a_2^{11}|n|^{11} |n|^{(\beta_k-11)(2+\epsilon)-(2\beta_k+9)}> a_2^{11}|n|^{11}. \end{align*} $$
$$ \begin{align*} a_k>\frac{a_2^{\beta_k}}{|n|^{2\beta_k-2}}=a_2^{11}|n|^{11} \cdot \frac{a_2^{\beta_k-11}}{|n|^{2\beta_k+9}}> a_2^{11}|n|^{11} |n|^{(\beta_k-11)(2+\epsilon)-(2\beta_k+9)}> a_2^{11}|n|^{11}. \end{align*} $$
Now Lemma 2.1 implies that the largest element in S is at most
![]() $a_k^{131}$
. By a similar argument as above, for each
$a_k^{131}$
. By a similar argument as above, for each
![]() $i \geq 2$
, we have
$i \geq 2$
, we have
 $$ \begin{align} a_{k+i}> \frac{a_k^{\beta_i}}{|n|^{2\beta_i-2}}. \end{align} $$
$$ \begin{align} a_{k+i}> \frac{a_k^{\beta_i}}{|n|^{2\beta_i-2}}. \end{align} $$
Since
![]() $\beta _i \to \infty $
, we can choose
$\beta _i \to \infty $
, we can choose
![]() $\ell $
sufficiently large such that
$\ell $
sufficiently large such that
let
![]() $\ell =\ell (\epsilon )$
be the smallest such
$\ell =\ell (\epsilon )$
be the smallest such
![]() $\ell $
. Note that both k and
$\ell $
. Note that both k and
![]() $\ell $
are explicitly computable constants depending only on
$\ell $
are explicitly computable constants depending only on
![]() $\epsilon $
. Since the sequence
$\epsilon $
. Since the sequence
![]() $(\beta _i)$
grows exponentially, it follows that
$(\beta _i)$
grows exponentially, it follows that
![]() $k(\epsilon )$
and
$k(\epsilon )$
and
![]() $\ell (\epsilon )$
are of the order
$\ell (\epsilon )$
are of the order
![]() $\log ({1}/{\epsilon })$
.
$\log ({1}/{\epsilon })$
.
If
![]() $|S|\geq k+\ell $
, then (2.2) implies that
$|S|\geq k+\ell $
, then (2.2) implies that
 $$ \begin{align*} a_{k+\ell}> \frac{a_k^{\beta_{\ell}}}{|n|^{2\beta_{\ell}-2}}=a_k^{131} \cdot \frac{a_k^{\beta_{\ell}-131}}{|n|^{2\beta_{\ell}-2}}>a_k^{131} |n|^{(\beta_{\ell}-131)(2+\epsilon)-(2\beta_{\ell}-2)}>a_k^{131}, \end{align*} $$
$$ \begin{align*} a_{k+\ell}> \frac{a_k^{\beta_{\ell}}}{|n|^{2\beta_{\ell}-2}}=a_k^{131} \cdot \frac{a_k^{\beta_{\ell}-131}}{|n|^{2\beta_{\ell}-2}}>a_k^{131} |n|^{(\beta_{\ell}-131)(2+\epsilon)-(2\beta_{\ell}-2)}>a_k^{131}, \end{align*} $$
which is a contradiction. Therefore,
![]() $|S|< k+\ell $
. Thus,
$|S|< k+\ell $
. Thus,
![]() $A_n^{(\epsilon )}\leq k(\epsilon )+\ell (\epsilon )\ll \log ({1}/{\epsilon })$
, where the implicit constant is absolute.
$A_n^{(\epsilon )}\leq k(\epsilon )+\ell (\epsilon )\ll \log ({1}/{\epsilon })$
, where the implicit constant is absolute.
Acknowledgement
The author thanks the anonymous referees for their valuable comments and suggestions.