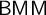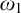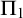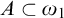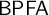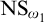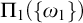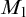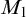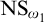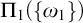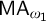1 Introduction
This article deals with the possibility of a (boldface)
![]() $\mathbf {\Delta _1}$
-definition (over
$\mathbf {\Delta _1}$
-definition (over
![]() $H(\omega _2)$
) of the nonstationary ideal on
$H(\omega _2)$
) of the nonstationary ideal on
![]() $\omega _1$
in the presence of various forcing axioms. As we shall see, stronger assumptions rule out the existence of such
$\omega _1$
in the presence of various forcing axioms. As we shall see, stronger assumptions rule out the existence of such
![]() $\mathbf {\Delta }_1$
-definitions, whereas weaker assumptions are consistent with such
$\mathbf {\Delta }_1$
-definitions, whereas weaker assumptions are consistent with such
![]() $\mathbf {\Delta }_1$
-definitions, even in the presence of
$\mathbf {\Delta }_1$
-definitions, even in the presence of
![]() $\text {NS}_{\omega _1}$
being saturated.
$\text {NS}_{\omega _1}$
being saturated.
The main results are as follows.
Theorem 1.1. Assume
![]() $\mathsf {BMM}^{}$
and that there exists a Woodin cardinal. Then for no
$\mathsf {BMM}^{}$
and that there exists a Woodin cardinal. Then for no
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\varphi (v_0,v_1)$
and no parameter
$\varphi (v_0,v_1)$
and no parameter
![]() $A \subset \omega _1$
does it hold that
$A \subset \omega _1$
does it hold that
Theorem 1.2. Assume that Woodin’s axiom
![]() $(\ast )$
holds. Then for no
$(\ast )$
holds. Then for no
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\varphi (v_0,v_1)$
and no parameter
$\varphi (v_0,v_1)$
and no parameter
![]() $A \subset \omega _1$
does it hold that
$A \subset \omega _1$
does it hold that
In contrast to these two impossibility results we also obtain two theorems which show that under weaker assumptions,
![]() $\Pi _1$
definitions of
$\Pi _1$
definitions of
![]() $\text {NS}_{\omega _1}$
are possible.
$\text {NS}_{\omega _1}$
are possible.
Theorem 1.3. There is a universe in which
![]() $\mathsf {BPFA}$
holds and
$\mathsf {BPFA}$
holds and
![]() $\text {NS}_{\omega _1}$
is
$\text {NS}_{\omega _1}$
is
![]() $\Pi _1(\{\omega _1\})$
-definable.
$\Pi _1(\{\omega _1\})$
-definable.
Theorem 1.4. Assume that the canonical inner model with one Woodin cardinal
![]() $M_1$
exists. Then there is a generic extension of
$M_1$
exists. Then there is a generic extension of
![]() $M_1$
where
$M_1$
where
![]() $\text {NS}_{\omega _1}$
is saturated and
$\text {NS}_{\omega _1}$
is saturated and
![]() $\Pi _1(\{\omega _1\})$
-definable and
$\Pi _1(\{\omega _1\})$
-definable and
![]() $\mathsf {MA_{\omega _1}}$
holds.
$\mathsf {MA_{\omega _1}}$
holds.
The paper is organized as follows. We will prove the theorems in the order stated above, thus we start with the two impossibility results, then follow up with the two possibility results. The methods and techniques which are used in this article are quite varied and we will provide only very few preliminary definitions, instead assuming the reader knows the basics of the stationary tower forcing (see [Reference Larson9] for an extensive account) and
![]() $\mathbb {P}_{\text {max}}$
(see [Reference Larson, Foreman and Kanamori10] or [Reference Woodin19]), as well as the coding technique of Caicedo and Velickovic [Reference Caicedo and Velickovic2].
$\mathbb {P}_{\text {max}}$
(see [Reference Larson, Foreman and Kanamori10] or [Reference Woodin19]), as well as the coding technique of Caicedo and Velickovic [Reference Caicedo and Velickovic2].
2 Impossibility results
This section collects two results which show that strong assumptions entail the impossibility of a boldface
![]() $\Sigma _1$
-definition of
$\Sigma _1$
-definition of
![]() $\text {NS}_{\omega _1}$
. We assume that the reader is familiar with Woodin’s stationary tower and with
$\text {NS}_{\omega _1}$
. We assume that the reader is familiar with Woodin’s stationary tower and with
![]() $\mathbb {P}_{\text {max}}$
-forcing.
$\mathbb {P}_{\text {max}}$
-forcing.
2.1 Impossibility under
 $\mathsf {BMM}$
plus the existence of a Woodin Cardinal
$\mathsf {BMM}$
plus the existence of a Woodin Cardinal
The goal of this section is to prove that under
![]() $\mathsf {BMM}^{} +$
“there exists a Woodin cardinal,
$\mathsf {BMM}^{} +$
“there exists a Woodin cardinal,
![]() $"$
no
$"$
no
![]() $\Sigma _1$
formula (boldface) can define stationary subsets of
$\Sigma _1$
formula (boldface) can define stationary subsets of
![]() $\omega _1$
correctly. We use Bagaria’s theorem [Reference Bagaria1] saying that
$\omega _1$
correctly. We use Bagaria’s theorem [Reference Bagaria1] saying that
![]() $\mathsf {BMM}$
is equivalent to the statement that
$\mathsf {BMM}$
is equivalent to the statement that
![]() $H(\aleph _{2})$
is
$H(\aleph _{2})$
is
![]() $\Sigma _{1}$
-elementary in the
$\Sigma _{1}$
-elementary in the
![]() $H(\aleph _{2})$
of any forcing extension in which every stationary subset of
$H(\aleph _{2})$
of any forcing extension in which every stationary subset of
![]() $\omega _{1}$
from the ground model remains stationary.
$\omega _{1}$
from the ground model remains stationary.
Theorem 2.1. Assume
![]() $\mathsf {BMM}$
and the existence of a Woodin cardinal
$\mathsf {BMM}$
and the existence of a Woodin cardinal
![]() $\delta $
. Then for no parameter
$\delta $
. Then for no parameter
![]() $A \subset \omega _1$
and for no
$A \subset \omega _1$
and for no
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\varphi (v_0,v_1)$
in the language of set theory, does
$\varphi (v_0,v_1)$
in the language of set theory, does
![]() $\varphi $
define the stationary subsets of
$\varphi $
define the stationary subsets of
![]() $\omega _1$
, i.e., we do not have that
$\omega _1$
, i.e., we do not have that
Proof Assume for a contradiction that there is a
![]() $\Sigma _1$
- formula
$\Sigma _1$
- formula
![]() $\varphi $
and a set
$\varphi $
and a set
![]() $A \subset \omega _1$
such that
$A \subset \omega _1$
such that
![]() $\forall T \in P(\omega _1) (T$
is stationary iff
$\forall T \in P(\omega _1) (T$
is stationary iff
![]() $\varphi (T,A)$
). Let
$\varphi (T,A)$
). Let
![]() $\delta $
be our Woodin cardinal.
$\delta $
be our Woodin cardinal.
Let
and let g be
![]() $\mathbb {P}_{<\delta }$
-generic over V where
$\mathbb {P}_{<\delta }$
-generic over V where
![]() $\mathbb {P}_{<\delta }$
is the associated full stationary tower. Assume that g contains
$\mathbb {P}_{<\delta }$
is the associated full stationary tower. Assume that g contains
![]() $S_0$
, which is possible by the stationarity of
$S_0$
, which is possible by the stationarity of
![]() $S_0$
. As usual we can form the generic elementary embedding in the universe
$S_0$
. As usual we can form the generic elementary embedding in the universe
![]() $V[g]$
:
$V[g]$
:
for a transitive inner model M of
![]() $V[g]$
. Membership in the generic filter g for the stationary tower forcing can be characterized using j, namely we have that
$V[g]$
. Membership in the generic filter g for the stationary tower forcing can be characterized using j, namely we have that
Thus
![]() $S_0 \in g$
yields
$S_0 \in g$
yields
![]() $j" H(\omega _2)^V \in j(S_0)$
. In particular
$j" H(\omega _2)^V \in j(S_0)$
. In particular
![]() $j"H(\omega _2)^V$
is transitive, and as
$j"H(\omega _2)^V$
is transitive, and as
![]() $H(\omega _2)^V$
is the transitive collapse of
$H(\omega _2)^V$
is the transitive collapse of
![]() $j"H(\omega _2)^V$
, we obtain that
$j"H(\omega _2)^V$
, we obtain that
![]() $j"H(\omega _2)^V=H(\omega _2)^V$
and that the critical point
$j"H(\omega _2)^V=H(\omega _2)^V$
and that the critical point
![]() $crit(j)$
of the elementary embedding j must be
$crit(j)$
of the elementary embedding j must be
![]() $\ge \omega _2^V$
. As
$\ge \omega _2^V$
. As
![]() $H(\omega _2)^V \in j(S_0)$
,
$H(\omega _2)^V \in j(S_0)$
,
![]() $|H(\omega _2)^V|=\aleph _1$
in M, so
$|H(\omega _2)^V|=\aleph _1$
in M, so
![]() $crit(j)=\omega _2^V$
. We have
$crit(j)=\omega _2^V$
. We have
![]() $P(\omega _1) \cap V \in M$
, as
$P(\omega _1) \cap V \in M$
, as
![]() $H(\omega _2)^V \in j(S_0) \subset M$
.
$H(\omega _2)^V \in j(S_0) \subset M$
.
It is a theorem of Taylor (see [Reference Taylor16]) that
![]() $\mathsf {MA_{\omega _1}}$
implies that
$\mathsf {MA_{\omega _1}}$
implies that
![]() $\text {NS}_{\omega _1}$
is not
$\text {NS}_{\omega _1}$
is not
![]() $\omega _1$
-dense. As
$\omega _1$
-dense. As
![]() $P(\omega _1) \cap V$
has size
$P(\omega _1) \cap V$
has size
![]() $|\omega _2^V|=\aleph _1$
in M, there is a stationary set
$|\omega _2^V|=\aleph _1$
in M, there is a stationary set
![]() $D \subset \omega _1$
in M such that
$D \subset \omega _1$
in M such that
![]() $T \backslash D$
is stationary for every stationary
$T \backslash D$
is stationary for every stationary
![]() $T \in P(\omega _1) \cap V$
. By Theorem 2.5.8 of [Reference Larson9],
$T \in P(\omega _1) \cap V$
. By Theorem 2.5.8 of [Reference Larson9],
![]() $V[g] \models M^{<\delta } \cap V[g] \subset M$
. Since
$V[g] \models M^{<\delta } \cap V[g] \subset M$
. Since
![]() $\delta $
remains strongly inaccessible in
$\delta $
remains strongly inaccessible in
![]() $V[g]$
, this implies that
$V[g]$
, this implies that
![]() $V[g]$
is a stationary set preserving extension of V. Further it is still true in
$V[g]$
is a stationary set preserving extension of V. Further it is still true in
![]() $V[g]$
that D is stationary and
$V[g]$
that D is stationary and
![]() $T \backslash D$
is stationary for all
$T \backslash D$
is stationary for all
![]() $T \notin \text {NS}_{\omega _1}^{V}$
.
$T \notin \text {NS}_{\omega _1}^{V}$
.
In the next step we use the ordinary club shooting forcing
![]() $\mathbb {P}_{\omega _1 \backslash D}$
over
$\mathbb {P}_{\omega _1 \backslash D}$
over
![]() $V[g]$
to shoot a club through the complement of D. The forcing will not destroy any stationary subsets from
$V[g]$
to shoot a club through the complement of D. The forcing will not destroy any stationary subsets from
![]() $V \cap P(\omega _1)$
:
$V \cap P(\omega _1)$
:
Fact 2.2. If h denotes a generic filter for
![]() $\mathbb {P}_{\omega _1 \backslash D}$
over
$\mathbb {P}_{\omega _1 \backslash D}$
over
![]() $V[g]$
, then if
$V[g]$
, then if
![]() $T \in P(\omega _1) \cap V$
is stationary in V then it will remain stationary in
$T \in P(\omega _1) \cap V$
is stationary in V then it will remain stationary in
![]() $V[g,h]$
.
$V[g,h]$
.
Proof Fix a stationary (in V)
![]() $T \in P(\omega _1) \cap V$
and let
$T \in P(\omega _1) \cap V$
and let
![]() $p \in \mathbb {P}_{\omega _1 \backslash D}$
be a condition and
$p \in \mathbb {P}_{\omega _1 \backslash D}$
be a condition and
![]() $\tau $
be a name in
$\tau $
be a name in
![]() $V[g]^{\mathbb {P}_{\omega _1 \backslash D}}$
such that
$V[g]^{\mathbb {P}_{\omega _1 \backslash D}}$
such that
![]() $p \Vdash \tau $
is a club in
$p \Vdash \tau $
is a club in
![]() $\omega _1$
. We shall find a
$\omega _1$
. We shall find a
![]() $q' < p$
such that
$q' < p$
such that
![]() $q' \Vdash \tau \cap T \ne \emptyset $
.
$q' \Vdash \tau \cap T \ne \emptyset $
.
As
![]() $T\backslash D$
is stationary in
$T\backslash D$
is stationary in
![]() $V[g]$
, we fix a sufficiently large regular
$V[g]$
, we fix a sufficiently large regular
![]() $\theta $
and pick a countable
$\theta $
and pick a countable
![]() $X \prec H(\theta )^{V[g]}$
such that
$X \prec H(\theta )^{V[g]}$
such that
![]() $p,\mathbb {P}_{\omega _1 \backslash D}$
and
$p,\mathbb {P}_{\omega _1 \backslash D}$
and
![]() $\tau $
are elements of X and which satisfies
$\tau $
are elements of X and which satisfies
![]() $\alpha = X \cap \omega _1 \in T \backslash D$
. It is straightforward to construct an infinite, descending sequence of conditions q in X with domain
$\alpha = X \cap \omega _1 \in T \backslash D$
. It is straightforward to construct an infinite, descending sequence of conditions q in X with domain
![]() $\alpha $
such that for every dense
$\alpha $
such that for every dense
![]() $D \subset \mathbb {P}_{\omega _1 \backslash D}$
,
$D \subset \mathbb {P}_{\omega _1 \backslash D}$
,
![]() $D \in X$
there is a
$D \in X$
there is a
![]() $\xi < \alpha $
such that
$\xi < \alpha $
such that
![]() $q \upharpoonright \xi \in D \cap X$
. Finally
$q \upharpoonright \xi \in D \cap X$
. Finally
![]() $q':=q \cup \{ (\alpha , \alpha )\}$
is a condition in the forcing as desired.
$q':=q \cup \{ (\alpha , \alpha )\}$
is a condition in the forcing as desired.
So
![]() $V[g,h]$
is a stationary set preserving extension of V. But now by our hypothesis and by elementarity of
$V[g,h]$
is a stationary set preserving extension of V. But now by our hypothesis and by elementarity of
![]() $j:V \rightarrow M$
we get that
$j:V \rightarrow M$
we get that
and hence
as
![]() $\varphi $
is
$\varphi $
is
![]() $\Sigma _1$
, and consequentially
$\Sigma _1$
, and consequentially
In
![]() $V[g,h]$
the set D is nonstationary; thus
$V[g,h]$
the set D is nonstationary; thus
This statement is
![]() $\Sigma _1$
with parameter
$\Sigma _1$
with parameter
![]() $A \subset \omega _1$
in the language of set theory, and as
$A \subset \omega _1$
in the language of set theory, and as
![]() $\mathsf {BMM}$
is assumed to hold true in V we conclude that
$\mathsf {BMM}$
is assumed to hold true in V we conclude that
which is a contradiction.
2.2 Impossibility under
 $(\ast )$
$(\ast )$
Our next goal is to derive the same conclusion from Woodin’s
![]() $(\ast )$
-principle. Recall that the
$(\ast )$
-principle. Recall that the
![]() $(\ast )$
-principle states that:
$(\ast )$
-principle states that:
-
–
 $AD$
holds in
$AD$
holds in
 $L(\mathbb {R})$
and
$L(\mathbb {R})$
and -
–
 $L(P(\omega _1))$
is a
$L(P(\omega _1))$
is a
 $\mathbb {P}_{\text {max}}$
-generic extension of
$\mathbb {P}_{\text {max}}$
-generic extension of
 $L(\mathbb {R})$
.
$L(\mathbb {R})$
.
It has been shown very recently by the third author and D. Aspero that
![]() $\mathsf {MM^{++}}$
implies
$\mathsf {MM^{++}}$
implies
![]() $(\ast )$
, solving a long-standing open question. Their proof paved the way for a third impossibility result, namely that under
$(\ast )$
, solving a long-standing open question. Their proof paved the way for a third impossibility result, namely that under
![]() $\mathsf {MM}$
, there is no
$\mathsf {MM}$
, there is no
![]() $A \subset \omega _1$
and no
$A \subset \omega _1$
and no
![]() $\Sigma _1$
-formula which defines stationarity. The proof is due to the third author and Xiuyuan Sun and will appear soon (see [Reference Schindler and Sun14]).
$\Sigma _1$
-formula which defines stationarity. The proof is due to the third author and Xiuyuan Sun and will appear soon (see [Reference Schindler and Sun14]).
Theorem 2.3. Assume that
![]() $(\ast )$
holds. Then there do not exist an
$(\ast )$
holds. Then there do not exist an
![]() $A \subset \omega _1$
and a
$A \subset \omega _1$
and a
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\varphi (v_0,v_1)$
in the language of set theory such that
$\varphi (v_0,v_1)$
in the language of set theory such that
Proof Let
![]() $V=L(\mathbb {R})[g]$
, where g is
$V=L(\mathbb {R})[g]$
, where g is
![]() $\mathbb {P}_{\text {max}}$
-generic over
$\mathbb {P}_{\text {max}}$
-generic over
![]() $L(\mathbb {R})$
. Suppose toward a contradiction that
$L(\mathbb {R})$
. Suppose toward a contradiction that
![]() $A \subseteq \omega _{1}$
and
$A \subseteq \omega _{1}$
and
![]() $\varphi $
witness that the conclusion of the theorem fails. Since
$\varphi $
witness that the conclusion of the theorem fails. Since
![]() $P(\omega _{1}) = P(\omega _{1})_{G}$
, there exist a condition
$P(\omega _{1}) = P(\omega _{1})_{G}$
, there exist a condition
![]() $p = \langle (M,I), b \rangle \in g$
and a set
$p = \langle (M,I), b \rangle \in g$
and a set
![]() $a \in P(\omega _{1})^{M}$
such that
$a \in P(\omega _{1})^{M}$
such that
![]() $A = j_{p,g}(a)$
, where
$A = j_{p,g}(a)$
, where
![]() $j_{p,g}$
is the unique iteration of
$j_{p,g}$
is the unique iteration of
![]() $(M,I)$
sending b to
$(M,I)$
sending b to
![]() $A_{g} = \bigcup \{ c : \langle (N,J), c \rangle \in g\}$
. By the genericity of g, it suffices to find a condition
$A_{g} = \bigcup \{ c : \langle (N,J), c \rangle \in g\}$
. By the genericity of g, it suffices to find a condition
![]() $r = \langle (P,K), c\rangle < p$
and a set
$r = \langle (P,K), c\rangle < p$
and a set
![]() $e \in K$
such that
$e \in K$
such that
![]() $H(\aleph _{2})^{P} \models \varphi (e, j_{p,r}(a))$
, where
$H(\aleph _{2})^{P} \models \varphi (e, j_{p,r}(a))$
, where
![]() $j_{p,r}$
is the iteration of
$j_{p,r}$
is the iteration of
![]() $(M,I)$
sending b to c.
$(M,I)$
sending b to c.
First, let
![]() $q = \langle (N,J), d \rangle $
any condition below p, as witnessed by the iteration
$q = \langle (N,J), d \rangle $
any condition below p, as witnessed by the iteration
![]() $j_{p,q} \colon (M,I) \to (M^{*}, I^{*})$
. Then
$j_{p,q} \colon (M,I) \to (M^{*}, I^{*})$
. Then
![]() $|M^{*}| = \aleph _{1}$
in N, and
$|M^{*}| = \aleph _{1}$
in N, and
![]() $N \models \mathsf {MA_{\omega _1}}$
. Hence by the result of Taylor cited above, there is no
$N \models \mathsf {MA_{\omega _1}}$
. Hence by the result of Taylor cited above, there is no
![]() $\omega _1$
-dense, normal ideal in N. In particular, there must be a
$\omega _1$
-dense, normal ideal in N. In particular, there must be a
![]() $T \in (J^{+})^N$
such that
$T \in (J^{+})^N$
such that
![]() $S \backslash T$
is an element of
$S \backslash T$
is an element of
![]() $(J^{+})^N$
for all
$(J^{+})^N$
for all
![]() $S \in P(\omega _{1})^{M^{*}} \setminus I^{*}$
.
$S \in P(\omega _{1})^{M^{*}} \setminus I^{*}$
.
Again by the genericity of g, there is a condition
![]() $r_{0} = \langle (P_{0}, K_{0}), c \rangle $
below q, as witnessed by the
$r_{0} = \langle (P_{0}, K_{0}), c \rangle $
below q, as witnessed by the
![]() $j_{q,r_{0}} \colon (N,J) \to (N^{*}, J^{*})$
, such that the formula
$j_{q,r_{0}} \colon (N,J) \to (N^{*}, J^{*})$
, such that the formula
![]() $\varphi (j_{q,r_{0}}(T), j_{q,r_{0}}(j_{p,q}(a)))$
holds in
$\varphi (j_{q,r_{0}}(T), j_{q,r_{0}}(j_{p,q}(a)))$
holds in
![]() $H(\aleph _{2})^{P_{0}}$
. Since
$H(\aleph _{2})^{P_{0}}$
. Since
![]() $L(\mathbb {R}) \models \mathsf {AD}$
, we may also assume that there exists a Woodin cardinal in
$L(\mathbb {R}) \models \mathsf {AD}$
, we may also assume that there exists a Woodin cardinal in
![]() $P_{0}$
, and that
$P_{0}$
, and that
![]() $K_{0}$
is
$K_{0}$
is
![]() $\text {NS}_{\omega _1}^{P_{0}}$
(this follows, for instance, from Theorem 5.36 of [Reference Woodin19] with
$\text {NS}_{\omega _1}^{P_{0}}$
(this follows, for instance, from Theorem 5.36 of [Reference Woodin19] with
![]() $n=2$
, and the fact that the partial order
$n=2$
, and the fact that the partial order
![]() $\textrm {Col}(\omega _{1}, \mathord {<}\delta )$
forces
$\textrm {Col}(\omega _{1}, \mathord {<}\delta )$
forces
![]() $\text {NS}_{\omega _1}$
to be presaturated whenever
$\text {NS}_{\omega _1}$
to be presaturated whenever
![]() $\delta $
is a Woodin cardinal).
$\delta $
is a Woodin cardinal).
Now,
![]() $j_{q, r_{0}}(j_{p,q})$
is an iteration of
$j_{q, r_{0}}(j_{p,q})$
is an iteration of
![]() $(M,I)$
to
$(M,I)$
to
![]() $(j_{q, r_{0}}(M^{*}), j_{q, r_{0}}(I^{*}))$
sending b to c. By the definition of the order on
$(j_{q, r_{0}}(M^{*}), j_{q, r_{0}}(I^{*}))$
sending b to c. By the definition of the order on
![]() $\mathbb {P}_{\mathrm {max}}$
conditions,
$\mathbb {P}_{\mathrm {max}}$
conditions,
![]() $J^{*} = N^{*} \cap K_{0}$
, from which it follows that
$J^{*} = N^{*} \cap K_{0}$
, from which it follows that
![]() $S \backslash j_{q,r_{0}}(T)$
is stationary in
$S \backslash j_{q,r_{0}}(T)$
is stationary in
![]() $P_{0}$
, for all S in
$P_{0}$
, for all S in
Applying Fact 2.2, force over
![]() $P_{0}$
to make
$P_{0}$
to make
![]() $j_{q,r_{0}}(T)$
nonstationary, while preserving the stationarity of each member of
$j_{q,r_{0}}(T)$
nonstationary, while preserving the stationarity of each member of
![]() $j_{q,r_{0}}(P(\omega _{1})^{M^{*}} \setminus I^{*})$
. Call this extension
$j_{q,r_{0}}(P(\omega _{1})^{M^{*}} \setminus I^{*})$
. Call this extension
![]() $P_{0}'$
.
$P_{0}'$
.
The rest of the argument consists of the standard machinery for building
![]() $\mathbb {P}_{\mathrm {max}}$
conditions. Let P be the result of forcing over
$\mathbb {P}_{\mathrm {max}}$
conditions. Let P be the result of forcing over
![]() $P^{\prime }_{0}$
with
$P^{\prime }_{0}$
with
![]() $\textrm {Col}(\omega _{1},\mathord {<}\delta )^{P^{\prime }_{0}}$
followed by some c.c.c. forcing making
$\textrm {Col}(\omega _{1},\mathord {<}\delta )^{P^{\prime }_{0}}$
followed by some c.c.c. forcing making
![]() $\mathsf {MA_{\omega _1}}$
hold. Let P be this forcing extension, and let K be
$\mathsf {MA_{\omega _1}}$
hold. Let P be this forcing extension, and let K be
![]() $\text {NS}_{\omega _1}^{P}$
. Then
$\text {NS}_{\omega _1}^{P}$
. Then
![]() $r = \langle (P,K), c\rangle $
and
$r = \langle (P,K), c\rangle $
and
![]() $e = j_{q,r_{0}}(T)$
are as desired.
$e = j_{q,r_{0}}(T)$
are as desired.
3 Possibility results
3.1
 $\mathsf {BPFA}$
and the
$\mathsf {BPFA}$
and the
 $\Pi _1$
-definability of
$\Pi _1$
-definability of
 $\text {NS}_{\omega _1}$
$\text {NS}_{\omega _1}$
The goal of this section is to show that
![]() $\mathsf {BPFA}$
is consistent with a
$\mathsf {BPFA}$
is consistent with a
![]() $\Sigma _1$
-definition of
$\Sigma _1$
-definition of
![]() $\text {NS}_{\omega _1}^+$
. The proof of this section relies on a new coding technique which exploits mutually stationary sets.
$\text {NS}_{\omega _1}^+$
. The proof of this section relies on a new coding technique which exploits mutually stationary sets.
3.1.1 Mutually stationary preserving forcing
Definition 3.1. Let K be a collection of regular cardinals with bounded supremum below
![]() $\kappa $
, and suppose that we have
$\kappa $
, and suppose that we have
![]() $S_\eta \subseteq \eta $
for each
$S_\eta \subseteq \eta $
for each
![]() $\eta \in K$
. Then the collection of sets
$\eta \in K$
. Then the collection of sets
![]() $\{ S_\eta \mid \eta \in K \}$
is mutually stationary if and only if for all algebras
$\{ S_\eta \mid \eta \in K \}$
is mutually stationary if and only if for all algebras
![]() $\mathcal {A}$
on
$\mathcal {A}$
on
![]() $\kappa $
, there is an
$\kappa $
, there is an
![]() $N\prec \mathcal {A}$
such that
$N\prec \mathcal {A}$
such that
Foreman and Magidor [Reference Foreman and Magidor3] show that every sequence
![]() $\vec S$
of stationary sets with
$\vec S$
of stationary sets with
![]() $S_\eta \subset \eta \cap \operatorname {Cof}(\omega )$
is mutually stationary. Let
$S_\eta \subset \eta \cap \operatorname {Cof}(\omega )$
is mutually stationary. Let
![]() $\mathcal {T}_{\vec {S}}$
be the collection of all countable N such that for all
$\mathcal {T}_{\vec {S}}$
be the collection of all countable N such that for all
![]() $\eta _i\in N$
,
$\eta _i\in N$
,
![]() $\sup (N\cap \eta _i)\in S_i.$
$\sup (N\cap \eta _i)\in S_i.$
Theorem 3.2 (Foreman–Magidor).
Let
![]() $\langle \eta _i \mid i<j \rangle $
be an increasing sequence of regular cardinals. Let
$\langle \eta _i \mid i<j \rangle $
be an increasing sequence of regular cardinals. Let
![]() $\vec S=\langle S_i \mid i<j \rangle $
be a sequence of stationary sets such that
$\vec S=\langle S_i \mid i<j \rangle $
be a sequence of stationary sets such that
![]() $S_i\subseteq \eta _i \cap \textrm {Cof}(\omega )$
. If
$S_i\subseteq \eta _i \cap \textrm {Cof}(\omega )$
. If
![]() $\theta $
is a regular cardinal greater than all
$\theta $
is a regular cardinal greater than all
![]() $\eta _i$
and
$\eta _i$
and
![]() $\mathcal {A}$
is an algebra on
$\mathcal {A}$
is an algebra on
![]() $\theta $
, then there is an
$\theta $
, then there is an
![]() $N\prec \mathcal {A}$
which belongs to the class
$N\prec \mathcal {A}$
which belongs to the class
![]() $\mathcal {T}_{\vec {S}}$
. Hence
$\mathcal {T}_{\vec {S}}$
. Hence
![]() $\vec S$
is mutually stationary.
$\vec S$
is mutually stationary.
From now on, we assume all stationary subsets of ordinals discussed in this section are concentrated on countable cofinality. The corresponding notion for being club in this context is that of an unbounded set which is closed under
![]() $\omega $
-sequences.
$\omega $
-sequences.
Definition 3.3. Suppose
![]() $\vec S=\{ S_\eta \mid \eta \in K\}$
is mutually stationary and that for every
$\vec S=\{ S_\eta \mid \eta \in K\}$
is mutually stationary and that for every
![]() $\eta \in K$
,
$\eta \in K$
,
![]() $S_{\eta }$
is stationary, co-stationary in
$S_{\eta }$
is stationary, co-stationary in
![]() $\eta \cap $
Cof
$\eta \cap $
Cof
![]() $ ({\omega })$
. We say a forcing poset
$ ({\omega })$
. We say a forcing poset
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\vec S$
-preserving if the following holds
$\vec S$
-preserving if the following holds
![]() $:$
Suppose
$:$
Suppose
![]() $\theta> 2^{ \vert \mathbb {P}^+\vert }$
is regular. Suppose M is a countable elementary submodel of
$\theta> 2^{ \vert \mathbb {P}^+\vert }$
is regular. Suppose M is a countable elementary submodel of
![]() $H(\theta )$
with
$H(\theta )$
with
![]() $\{\mathbb {P},\vec S\}\subset M$
and
$\{\mathbb {P},\vec S\}\subset M$
and
![]() $M\in \mathcal {T}_{\vec {S}}$
. Suppose
$M\in \mathcal {T}_{\vec {S}}$
. Suppose
![]() $p\in \mathbb {P}\cap M$
. Then there exists an
$p\in \mathbb {P}\cap M$
. Then there exists an
![]() $(M,\mathbb {P} )$
-generic condition q extending p.
$(M,\mathbb {P} )$
-generic condition q extending p.
Remark
-
1. Any proper forcing is
 $\vec S$
-preserving.
$\vec S$
-preserving. -
2. When
 $K=\{ \omega _1\}$
and
$K=\{ \omega _1\}$
and
 $\vec {S}=S \subset \omega _1$
, the definition of
$\vec {S}=S \subset \omega _1$
, the definition of
 $\vec S$
-preserving is identical to the usual definition of S-proper forcing.
$\vec S$
-preserving is identical to the usual definition of S-proper forcing. -
3. Let
 $\vec {S}$
be such that each
$\vec {S}$
be such that each
 $S_{\eta } \in \vec S$
is stationary, co-stationary in
$S_{\eta } \in \vec S$
is stationary, co-stationary in
 $\eta \cap Cof(\omega )$
. Then an example of a non-proper,
$\eta \cap Cof(\omega )$
. Then an example of a non-proper,
 $\vec S$
preserving forcing is the forcing poset
$\vec S$
preserving forcing is the forcing poset
 $Club(S_\eta )$
for a fixed
$Club(S_\eta )$
for a fixed
 $\eta $
, i.e., the forcing which adds an unbounded subset to
$\eta $
, i.e., the forcing which adds an unbounded subset to
 $S_\eta $
which is closed under
$S_\eta $
which is closed under
 $\omega $
-sequences, via countable approximations.
$\omega $
-sequences, via countable approximations.
The preservation theorems for countable support iterations of proper forcings can be generalized to
![]() $\vec S$
-preserving forcings.
$\vec S$
-preserving forcings.
Lemma 3.4. If
![]() $\langle P_i, \dot {Q}_i \mid i< \alpha \rangle $
is a countable support iteration of forcing notions and for each
$\langle P_i, \dot {Q}_i \mid i< \alpha \rangle $
is a countable support iteration of forcing notions and for each
![]() $i<\alpha $
,
$i<\alpha $
,
![]() $\Vdash _{P_i}$
“
$\Vdash _{P_i}$
“
![]() $\dot {Q}_i$
is
$\dot {Q}_i$
is
![]() $\vec S$
-preserving” then
$\vec S$
-preserving” then
![]() $P_\alpha $
is
$P_\alpha $
is
![]() $\vec S$
-preserving.
$\vec S$
-preserving.
Proof (Sketch, following the proof of [Reference Jech8, Theorem 31.15], in particular Lemma 31.17) We will only need to show by induction on
![]() $j\le \alpha $
that for any
$j\le \alpha $
that for any
![]() $N\in \mathcal T_{\vec {S}}$
, if
$N\in \mathcal T_{\vec {S}}$
, if
![]() $j, \langle P_i, \dot {Q}_i \mid i< \alpha \rangle \in N$
, then:
$j, \langle P_i, \dot {Q}_i \mid i< \alpha \rangle \in N$
, then:
-
(*) N For every
 $q_0\in N\cap P_j$
that is
$q_0\in N\cap P_j$
that is
 $(N,P_j)$
-generic and every
$(N,P_j)$
-generic and every
 $\dot {p} \in V^{P_j}$
such that
$\dot {p} \in V^{P_j}$
such that  $$\begin{align*}q_0 \Vdash_j \dot{p} \in (P_{\alpha} \cap N) \land \dot{p} \upharpoonright j \in \dot{G}_j \end{align*}$$
$$\begin{align*}q_0 \Vdash_j \dot{p} \in (P_{\alpha} \cap N) \land \dot{p} \upharpoonright j \in \dot{G}_j \end{align*}$$
there is an
 $(N,P_{\alpha })$
generic condition
$(N,P_{\alpha })$
generic condition
 $q \in P_{\alpha }$
extending
$q \in P_{\alpha }$
extending
 $q_0$
, that is
$q_0$
, that is
 $q \upharpoonright j = q_0$
and
$q \upharpoonright j = q_0$
and
 $q \Vdash _{\alpha } \dot {p} \in \dot {G}_{\alpha }$
.
$q \Vdash _{\alpha } \dot {p} \in \dot {G}_{\alpha }$
.
The statement
![]() $(\ast )_N$
is identical to Lemma 31.17 in [Reference Jech8]. It can be checked that the original proof also works here, which gives the iteration theorem exactly as in the proof of Theorem 31.15.
$(\ast )_N$
is identical to Lemma 31.17 in [Reference Jech8]. It can be checked that the original proof also works here, which gives the iteration theorem exactly as in the proof of Theorem 31.15.
In our proof of the main theorem of this section, we will use forcings which have a specific form, so they get a name.
Definition 3.5. Let
![]() $\kappa $
be an inaccessible cardinal. Let
$\kappa $
be an inaccessible cardinal. Let
![]() $\vec S= \langle S_{i} \mid i< \kappa \rangle $
be mutually stationary. We say a forcing poset
$\vec S= \langle S_{i} \mid i< \kappa \rangle $
be mutually stationary. We say a forcing poset
![]() $\mathbb {P}$
is an
$\mathbb {P}$
is an
![]() $ \vec S$
-coding if
$ \vec S$
-coding if
![]() $\delta \le \kappa $
and
$\delta \le \kappa $
and
![]() $\mathbb {P}= \langle \mathbb {P}_\alpha , \dot {\mathbb {Q}}_\alpha \mid \alpha <\delta \rangle $
satisfies the following
$\mathbb {P}= \langle \mathbb {P}_\alpha , \dot {\mathbb {Q}}_\alpha \mid \alpha <\delta \rangle $
satisfies the following
![]() $:$
$:$
-
–
 $\mathbb {P}$
is a countable support iteration.
$\mathbb {P}$
is a countable support iteration. -
– For any
 $\alpha <\delta $
, one of the followings holds
$\alpha <\delta $
, one of the followings holds
 $:$
$:$
-
1. Assume that
 $\alpha $
is inaccessible and
$\alpha $
is inaccessible and
 $\mathbb {P}_\alpha $
is forcing equivalent to a forcing of size less than or equal to
$\mathbb {P}_\alpha $
is forcing equivalent to a forcing of size less than or equal to
 $\alpha $
.Footnote
1
Assume that in
$\alpha $
.Footnote
1
Assume that in
 $V^{\mathbb {P}_\alpha }$
,
$V^{\mathbb {P}_\alpha }$
,
 $\langle B_\beta \mid \beta <2^\alpha \rangle $
is an enumeration of
$\langle B_\beta \mid \beta <2^\alpha \rangle $
is an enumeration of
 $P( {\alpha } )$
. Then
$P( {\alpha } )$
. Then
 $\dot {\mathbb {Q}}_\alpha $
is allowed to be the countably supported product
$\dot {\mathbb {Q}}_\alpha $
is allowed to be the countably supported product
 $\prod _{\beta < 2^{\alpha }} \dot {\mathbb {R}}_{\beta }$
, where each
$\prod _{\beta < 2^{\alpha }} \dot {\mathbb {R}}_{\beta }$
, where each
 $\dot {\mathbb {R}}_{\beta }$
is itself defined to be using countable support.
$\dot {\mathbb {R}}_{\beta }$
is itself defined to be using countable support. $$ \begin{align*}\prod_{j\in B_\beta}Club(S_{\alpha\cdot(\beta+1)+2j}) \times \prod_{j\notin B_\beta}Club(S_{\alpha\cdot(\beta+1)+2j+1})\end{align*} $$
$$ \begin{align*}\prod_{j\in B_\beta}Club(S_{\alpha\cdot(\beta+1)+2j}) \times \prod_{j\notin B_\beta}Club(S_{\alpha\cdot(\beta+1)+2j+1})\end{align*} $$
-
2. In all other cases, we have that
 $\Vdash _{\mathbb {P}_\alpha }\dot {\mathbb {Q}}_\alpha $
is proper.
$\Vdash _{\mathbb {P}_\alpha }\dot {\mathbb {Q}}_\alpha $
is proper.
-
Let
![]() $\eta $
be an regular cardinal, and we say
$\eta $
be an regular cardinal, and we say
![]() $\mathbb {P}$
is an
$\mathbb {P}$
is an
![]() $\eta $
-
$\eta $
-
![]() $\vec S$
coding if
$\vec S$
coding if
![]() $(1)$
is replaced by
$(1)$
is replaced by
-
(1′)
 $\alpha \ge \eta $
is inaccessible and
$\alpha \ge \eta $
is inaccessible and
 $\mathbb {P}_\alpha $
is forcing equivalent to a forcing of size less than or equal to
$\mathbb {P}_\alpha $
is forcing equivalent to a forcing of size less than or equal to
 $\alpha $
. In
$\alpha $
. In
 $V^{\mathbb {P}_\alpha }$
,
$V^{\mathbb {P}_\alpha }$
,
 $\langle B_\beta \mid \beta <2^\alpha \rangle $
is an enumeration of
$\langle B_\beta \mid \beta <2^\alpha \rangle $
is an enumeration of
 $P(\alpha )$
. Then
$P(\alpha )$
. Then
 $\dot {\mathbb {Q}}_{\alpha }$
is allowed to be the countably supported product
$\dot {\mathbb {Q}}_{\alpha }$
is allowed to be the countably supported product
 $\prod _{\beta < 2^{\alpha }} \dot {\mathbb {R}}_{\beta }$
where each
$\prod _{\beta < 2^{\alpha }} \dot {\mathbb {R}}_{\beta }$
where each
 $\dot {\mathbb {R}}_{\beta }$
is itself
$\dot {\mathbb {R}}_{\beta }$
is itself  $$ \begin{align*}\prod_{j\in B_\beta}Club(S_{\alpha\cdot(\beta+1)+2j}) \times \prod_{j\notin B_\beta}Club(S_{\alpha\cdot(\beta+1)+2j+1}).\end{align*} $$
$$ \begin{align*}\prod_{j\in B_\beta}Club(S_{\alpha\cdot(\beta+1)+2j}) \times \prod_{j\notin B_\beta}Club(S_{\alpha\cdot(\beta+1)+2j+1}).\end{align*} $$
By Lemma 3.4, once we can show that every factor of an
![]() $\vec {S}$
-coding is
$\vec {S}$
-coding is
![]() $\vec {S}$
-preserving, and we can deduce that if
$\vec {S}$
-preserving, and we can deduce that if
![]() $\mathbb {P}$
is an
$\mathbb {P}$
is an
![]() $\vec S$
-coding forcing, then
$\vec S$
-coding forcing, then
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\vec S$
-preserving. This assertion follows from the proof of the next lemma which says that we will not accidentally code unwanted information whenever we use an
$\vec S$
-preserving. This assertion follows from the proof of the next lemma which says that we will not accidentally code unwanted information whenever we use an
![]() $\vec {S}$
-coding forcing.
$\vec {S}$
-coding forcing.
Lemma 3.6. Suppose that
![]() $\vec S$
is stationary, co-stationary. Suppose
$\vec S$
is stationary, co-stationary. Suppose
![]() $\mathbb {P}$
is an
$\mathbb {P}$
is an
![]() $\vec S$
-coding forcing. Then for any
$\vec S$
-coding forcing. Then for any
![]() $i \in \kappa $
, the followings are equivalent
$i \in \kappa $
, the followings are equivalent
![]() $:$
$:$
-
(a)
 $\Vdash _{\mathbb {P}} S_{i}$
contains an
$\Vdash _{\mathbb {P}} S_{i}$
contains an
 $\omega $
-club.
$\omega $
-club. -
(b) There are
 $\beta ,\alpha ,j$
, and a set
$\beta ,\alpha ,j$
, and a set
 $B_{\beta } \subset V_{\alpha }$
such that
$B_{\beta } \subset V_{\alpha }$
such that
 $j \in B_{\beta }$
if
$j \in B_{\beta }$
if
 $\beta \cdot (\alpha +1)+2j=i$
and i is even and
$\beta \cdot (\alpha +1)+2j=i$
and i is even and
 $j \notin B_{\beta }$
if
$j \notin B_{\beta }$
if
 $\beta \cdot (\alpha +1)+2j+1=i$
and i is odd.
$\beta \cdot (\alpha +1)+2j+1=i$
and i is odd.
Proof ((b)
![]() $\rightarrow $
(a)) Follow from the definition of the forcing.
$\rightarrow $
(a)) Follow from the definition of the forcing.
((a)
![]() $\rightarrow $
(b)) Fix an i and assume without loss of generality that i is even. Write
$\rightarrow $
(b)) Fix an i and assume without loss of generality that i is even. Write
![]() $i= \beta \cdot ({\alpha +1}) +2j$
and suppose for a contradiction that j is not an element of
$i= \beta \cdot ({\alpha +1}) +2j$
and suppose for a contradiction that j is not an element of
![]() $B_{\beta }$
. By the definition of
$B_{\beta }$
. By the definition of
![]() $\vec S$
coding forcing, we must have added a club through
$\vec S$
coding forcing, we must have added a club through
![]() $S_{\beta (\alpha +1)+2j+1}$
instead. Let
$S_{\beta (\alpha +1)+2j+1}$
instead. Let
![]() $\vec T$
be the sequence
$\vec T$
be the sequence
![]() $\langle T_k \mid k<\kappa \rangle $
, where
$\langle T_k \mid k<\kappa \rangle $
, where
![]() $T_k=S_{k}$
if
$T_k=S_{k}$
if
![]() $k\neq i$
and
$k\neq i$
and
![]() $T_i=\eta _i\setminus S_{i}$
. It follows from Theorem 3.2 again that
$T_i=\eta _i\setminus S_{i}$
. It follows from Theorem 3.2 again that
![]() $\vec T$
is mutually stationary. We will prove that
$\vec T$
is mutually stationary. We will prove that
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\vec T$
-preserving to derive a contradiction. Indeed, we shall see that
$\vec T$
-preserving to derive a contradiction. Indeed, we shall see that
![]() $\vec T$
-preservation implies that
$\vec T$
-preservation implies that
![]() $\eta _i \setminus S_i$
must remain stationary after forcing with
$\eta _i \setminus S_i$
must remain stationary after forcing with
![]() $\mathbb {P}$
, yet
$\mathbb {P}$
, yet
![]() $\mathbb {P} \Vdash " S_i$
contains an
$\mathbb {P} \Vdash " S_i$
contains an
![]() $\omega $
-club
$\omega $
-club
![]() $"$
which is impossible.
$"$
which is impossible.
To see that
![]() $\vec {T}$
preserving forcings preserve the stationarity of every
$\vec {T}$
preserving forcings preserve the stationarity of every
![]() $S_{\eta _i} \in \vec {T}$
, we only need to note that for any name
$S_{\eta _i} \in \vec {T}$
, we only need to note that for any name
![]() $\dot C$
of a subset of
$\dot C$
of a subset of
![]() $\eta _i$
which is unbounded and
$\eta _i$
which is unbounded and
![]() $\omega $
-closed, and any countable elementary substructure N which contains
$\omega $
-closed, and any countable elementary substructure N which contains
![]() $\dot C$
and for which
$\dot C$
and for which
![]() $\sup (N\cap \eta _i)\in S_{\eta _i}$
, any
$\sup (N\cap \eta _i)\in S_{\eta _i}$
, any
![]() $(N,\mathbb {P})$
-generic condition q forces
$(N,\mathbb {P})$
-generic condition q forces
![]() $\dot C\cap ( S_{\eta _i})\neq \emptyset $
.
$\dot C\cap ( S_{\eta _i})\neq \emptyset $
.
Next we show by induction that each
![]() $\dot {Q}_{\beta }$
is forced to be
$\dot {Q}_{\beta }$
is forced to be
![]() $\vec T$
-preserving. Work in
$\vec T$
-preserving. Work in
![]() $V[G_\beta ]$
. If
$V[G_\beta ]$
. If
![]() $\dot Q_{\beta }/G_\beta $
is proper, then it is also
$\dot Q_{\beta }/G_\beta $
is proper, then it is also
![]() $\vec T$
-preserving. Otherwise, (1) holds. Now
$\vec T$
-preserving. Otherwise, (1) holds. Now
![]() $\dot {Q}_\beta /G_{\beta }$
is a countable support product of club adding forcings. Fix any
$\dot {Q}_\beta /G_{\beta }$
is a countable support product of club adding forcings. Fix any
![]() $N\in \mathcal T_{\vec {T}}$
which is a countable substructure of
$N\in \mathcal T_{\vec {T}}$
which is a countable substructure of
![]() $H(\theta )^{V[G_\beta ]}$
. For any
$H(\theta )^{V[G_\beta ]}$
. For any
![]() $p\in N\cap \dot Q_{\beta }$
, we can construct a countable decreasing sequence of conditions
$p\in N\cap \dot Q_{\beta }$
, we can construct a countable decreasing sequence of conditions
![]() $\langle p_n \mid n<\omega \rangle $
meeting all dense set in N. Define q coordinatewise by setting
$\langle p_n \mid n<\omega \rangle $
meeting all dense set in N. Define q coordinatewise by setting
![]() $q(j)$
to be the closure of
$q(j)$
to be the closure of
![]() $\bigcup _{n<\omega } p_n(j)$
if
$\bigcup _{n<\omega } p_n(j)$
if
![]() $i\in N$
and trivial otherwise. Note that any non-trivial
$i\in N$
and trivial otherwise. Note that any non-trivial
![]() $q(j)$
is equal to
$q(j)$
is equal to
![]() $\bigcup _{n<\omega } p_n(j)\cup \{\sup (N\cap \eta _j)\}$
, where
$\bigcup _{n<\omega } p_n(j)\cup \{\sup (N\cap \eta _j)\}$
, where
![]() $\eta _j=\sup (S_j)$
is a regular cardinal. As
$\eta _j=\sup (S_j)$
is a regular cardinal. As
![]() $N\in \mathcal T_{\vec {T}}$
we have
$N\in \mathcal T_{\vec {T}}$
we have
![]() $\sup (N\cap \eta _{j})\in S_j$
, whenever
$\sup (N\cap \eta _{j})\in S_j$
, whenever
![]() $q(j)$
is non-trivial. Hence
$q(j)$
is non-trivial. Hence
![]() $q<p$
is a condition witnessing that each factor of the iteration is
$q<p$
is a condition witnessing that each factor of the iteration is
![]() $\vec T$
-preserving, so the iteration
$\vec T$
-preserving, so the iteration
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\vec T$
-preserving as well. But now
$\vec T$
-preserving as well. But now
![]() $S_i$
must remain stationary after we forced with
$S_i$
must remain stationary after we forced with
![]() $\mathbb {P}$
, which is a contradiction to
$\mathbb {P}$
, which is a contradiction to
![]() $(a)$
.
$(a)$
.
The proof also shows that
![]() $\vec S$
-coding preserves stationary subset of
$\vec S$
-coding preserves stationary subset of
![]() $\omega _1$
if
$\omega _1$
if
![]() $ {\sup (S_0)>\omega _1}$
. As a Corollary of Lemma 3.6 and the definition of
$ {\sup (S_0)>\omega _1}$
. As a Corollary of Lemma 3.6 and the definition of
![]() $\vec S$
-coding, in any generic extension by
$\vec S$
-coding, in any generic extension by
![]() $\vec S$
-coding and any even i, at most one of
$\vec S$
-coding and any even i, at most one of
![]() $S_{i}$
and
$S_{i}$
and
![]() $S_{i+1}$
contains a club.
$S_{i+1}$
contains a club.
The next lemma follows immediately from the definitions, so we skip its proof.
Lemma 3.7. Suppose
![]() $\mathbb {P}= \langle P_\alpha , \dot {Q}_\alpha \mid \alpha <\delta \rangle $
is a countable support iteration. Suppose for any
$\mathbb {P}= \langle P_\alpha , \dot {Q}_\alpha \mid \alpha <\delta \rangle $
is a countable support iteration. Suppose for any
![]() $\alpha>0$
,
$\alpha>0$
,
![]() $\dot {Q}_\alpha $
is forced to be
$\dot {Q}_\alpha $
is forced to be
![]() $\eta _\alpha $
-
$\eta _\alpha $
-
![]() $\vec S$
coding of length
$\vec S$
coding of length
![]() $l(\alpha )$
, where
$l(\alpha )$
, where
![]() $\eta _ \alpha =\max \{\vert \mathbb {P}_\alpha \vert ^+, \Sigma _{\beta <\alpha }l(\beta ) \}$
. Also let
$\eta _ \alpha =\max \{\vert \mathbb {P}_\alpha \vert ^+, \Sigma _{\beta <\alpha }l(\beta ) \}$
. Also let
![]() $\eta _0$
be regular. Then
$\eta _0$
be regular. Then
![]() $\mathbb {P}$
is forcing equivalent to an
$\mathbb {P}$
is forcing equivalent to an
![]() $\eta _0$
-
$\eta _0$
-
![]() $\vec S$
coding.
$\vec S$
coding.
We are mainly interested in performing
![]() $\vec S $
-coding forcing over L. Now we can define the coding machinery to be used in the later section.
$\vec S $
-coding forcing over L. Now we can define the coding machinery to be used in the later section.
Definition 3.8. Suppose
![]() $\alpha $
is in inaccessible in L and
$\alpha $
is in inaccessible in L and
![]() $X\subseteq P(\alpha )$
. We say
$X\subseteq P(\alpha )$
. We say
![]() $\vec S$
codes X if
$\vec S$
codes X if
![]() $:$
$:$
-
1. For any even
 $i\in [\alpha , (\alpha ^+)^L)$
, one of
$i\in [\alpha , (\alpha ^+)^L)$
, one of
 $S_{i}$
and
$S_{i}$
and
 $S_{i+1}$
contains a club.
$S_{i+1}$
contains a club. -
2. For any
 $x \in X$
, there is a
$x \in X$
, there is a
 $\beta < (\alpha ^+)^L$
such that for every
$\beta < (\alpha ^+)^L$
such that for every
 $j < \alpha $
,
$j < \alpha $
,  $$ \begin{align*}j\in x\text{ if and only if }S_{\alpha\cdot(\beta+1)+2i}\text{ contains a club}\end{align*} $$
$$ \begin{align*}j\in x\text{ if and only if }S_{\alpha\cdot(\beta+1)+2i}\text{ contains a club}\end{align*} $$
and
 $$ \begin{align*}j\notin x\text{ if and only if }S_{\alpha\cdot(\beta+1)+2i+1}\text{ contains a club.}\end{align*} $$
$$ \begin{align*}j\notin x\text{ if and only if }S_{\alpha\cdot(\beta+1)+2i+1}\text{ contains a club.}\end{align*} $$
Let
![]() $\vec C=\langle C_i \mid i\in [\alpha , (\alpha ^+)^L) \rangle $
be a club sequence which witnesses (2). Then we say that
$\vec C=\langle C_i \mid i\in [\alpha , (\alpha ^+)^L) \rangle $
be a club sequence which witnesses (2). Then we say that
![]() $\vec C$
is an
$\vec C$
is an
![]() $\vec S$
code for X.
$\vec S$
code for X.
A useful fact is the upward absoluteness of the coding between certain pairs of models.
Lemma 3.9. Suppose
![]() $N\subset M$
are two ZFC
$N\subset M$
are two ZFC
![]() $^-$
transitive models,
$^-$
transitive models,
![]() $N\models \vec C$
is a
$N\models \vec C$
is a
![]() $\vec S$
code for
$\vec S$
code for
![]() $X \subset \alpha $
,
$X \subset \alpha $
,
![]() $\alpha $
is inaccessible in
$\alpha $
is inaccessible in
![]() $L^M$
, and
$L^M$
, and
![]() $((\alpha ^+)^L)^M= ((\alpha ^+)^L)^N$
. Suppose in M for any even
$((\alpha ^+)^L)^M= ((\alpha ^+)^L)^N$
. Suppose in M for any even
![]() $i\in [\alpha , (\alpha ^+)^L)$
, at most one of
$i\in [\alpha , (\alpha ^+)^L)$
, at most one of
![]() $S_{i}$
and
$S_{i}$
and
![]() $S_{i+1}$
contains a club. Then
$S_{i+1}$
contains a club. Then
![]() $M\models "\vec C$
is a
$M\models "\vec C$
is a
![]() $\vec S$
code for
$\vec S$
code for
![]() $X."$
$X."$
Proof This follows from the definition. Note that being a club is an absolute property between transitive models.
Lemma 3.10. Suppose
![]() $\mathbb {P}$
is an
$\mathbb {P}$
is an
![]() $\vec S$
-coding over L,
$\vec S$
-coding over L,
![]() $\alpha $
is inaccessible,
$\alpha $
is inaccessible,
![]() $X\subseteq P(\alpha )$
, and
$X\subseteq P(\alpha )$
, and
![]() $\vec S \upharpoonright (\alpha ^+)^L$
codes X. Then
$\vec S \upharpoonright (\alpha ^+)^L$
codes X. Then
![]() $X=P(\alpha )^{L[G_\alpha ]}$
.
$X=P(\alpha )^{L[G_\alpha ]}$
.
Proof By Lemma 3.6, for any i,
![]() $S_i$
contains a club if there is some stage
$S_i$
contains a club if there is some stage
![]() $\beta $
such that
$\beta $
such that
![]() $\dot {Q}_\beta $
satisfies (1) in the definition. But
$\dot {Q}_\beta $
satisfies (1) in the definition. But
![]() $\dot {Q}_\alpha $
forces
$\dot {Q}_\alpha $
forces
![]() $\vec S \upharpoonright (\alpha ^+)^L$
to code
$\vec S \upharpoonright (\alpha ^+)^L$
to code
![]() $P(\alpha )^{L[G_\alpha ]}$
. Hence by Lemma 3.9,
$P(\alpha )^{L[G_\alpha ]}$
. Hence by Lemma 3.9,
![]() $\vec S \upharpoonright (\alpha ^+)^L$
codes
$\vec S \upharpoonright (\alpha ^+)^L$
codes
![]() $P(\alpha )^{L[G_\alpha ]}$
in
$P(\alpha )^{L[G_\alpha ]}$
in
![]() $L[G]$
and since
$L[G]$
and since
![]() $\vec S \upharpoonright (\alpha ^+)^L$
codes X,
$\vec S \upharpoonright (\alpha ^+)^L$
codes X,
![]() $X = P(\alpha )^{L[G_\alpha ]}$
.
$X = P(\alpha )^{L[G_\alpha ]}$
.
3.1.2 A model of BPFA and
 $\Delta _1$
-definability of
$\Delta _1$
-definability of
 $\text {NS}_{\omega _1}$
$\text {NS}_{\omega _1}$
Theorem 3.11. Suppose that
![]() $V=L$
and
$V=L$
and
![]() $\delta $
is a reflecting cardinal. Then there is a forcing poset P such that in
$\delta $
is a reflecting cardinal. Then there is a forcing poset P such that in
![]() $L^{P}$
, the following statements hold
$L^{P}$
, the following statements hold
![]() $:$
$:$
-
1. BPFA.
-
2.
 $\omega _1=\omega _1^L$
and
$\omega _1=\omega _1^L$
and
 $\omega _2=\delta $
.
$\omega _2=\delta $
. -
3. The nonstationary ideal on
 $\omega _1$
is
$\omega _1$
is
 $\Sigma _1(\{\omega _1\})$
-definable over
$\Sigma _1(\{\omega _1\})$
-definable over
 $\langle H(\omega _2), \in \rangle $
.
$\langle H(\omega _2), \in \rangle $
.
Proof We first choose a sequence
![]() $\langle S_ \alpha \mid \alpha \in \mathop {\textrm {Lim}}(\delta )\rangle $
uniformly in
$\langle S_ \alpha \mid \alpha \in \mathop {\textrm {Lim}}(\delta )\rangle $
uniformly in
![]() $\alpha < \delta $
satisfying:
$\alpha < \delta $
satisfying:
-
–
 $S_\alpha \subset \alpha $
.
$S_\alpha \subset \alpha $
. -
– If
 $\alpha $
is a regular cardinal, then
$\alpha $
is a regular cardinal, then
 $S_\alpha $
is stationary co-stationary in
$S_\alpha $
is stationary co-stationary in
 $\alpha \cap \textrm {Cof}(\omega )$
.
$\alpha \cap \textrm {Cof}(\omega )$
.
The existence of such a sequence
![]() $\langle S_ \alpha \mid \alpha \in \mathop {\textrm {Lim}}(\delta )\rangle $
follows from the fact that we do have a
$\langle S_ \alpha \mid \alpha \in \mathop {\textrm {Lim}}(\delta )\rangle $
follows from the fact that we do have a
![]() $\Sigma _1$
-definable global well-order of L,
$\Sigma _1$
-definable global well-order of L,
![]() $<_L$
, and we just pick recursively at each stage the
$<_L$
, and we just pick recursively at each stage the
![]() $<_L$
-least such
$<_L$
-least such
![]() $S_{\alpha }$
.
$S_{\alpha }$
.
Now we define the forcing poset P. The forcing
![]() $P=\langle P_\alpha , \dot {Q}_\alpha \mid \alpha <\delta \rangle $
will be a countable support iteration of length
$P=\langle P_\alpha , \dot {Q}_\alpha \mid \alpha <\delta \rangle $
will be a countable support iteration of length
![]() $\delta $
. We require the size of each iterand to be smaller than
$\delta $
. We require the size of each iterand to be smaller than
![]() $\delta $
. As a consequence P satisfies
$\delta $
. As a consequence P satisfies
![]() $\delta $
-cc. We demand that
$\delta $
-cc. We demand that
![]() $\dot {Q}_\alpha $
is trivial unless
$\dot {Q}_\alpha $
is trivial unless
![]() $\alpha $
is an inaccessible cardinal and
$\alpha $
is an inaccessible cardinal and
![]() $P_\alpha \subset L_\alpha $
. We split into two cases if
$P_\alpha \subset L_\alpha $
. We split into two cases if
![]() $\alpha $
is inaccessible.
$\alpha $
is inaccessible.
-
– (
 $\alpha $
is an inaccessible limit of inaccessibles) We follow an idea from Goldstern and Shelah [Reference Goldstern and Shelah4]. Pick
$\alpha $
is an inaccessible limit of inaccessibles) We follow an idea from Goldstern and Shelah [Reference Goldstern and Shelah4]. Pick
 $A\subset \omega _1$
and a
$A\subset \omega _1$
and a
 $\Sigma _1$
formula
$\Sigma _1$
formula
 $\exists x\psi (x,A)$
. A and
$\exists x\psi (x,A)$
. A and
 $\exists x \psi $
are chosen in a bookkeeping way so that during the whole iteration, each pair
$\exists x \psi $
are chosen in a bookkeeping way so that during the whole iteration, each pair
 $(A,\exists x\psi )$
will be dealt with unboundedly many times. Since
$(A,\exists x\psi )$
will be dealt with unboundedly many times. Since
 $\delta $
is reflecting, we can reflect the statement “there is a strong limit cardinal
$\delta $
is reflecting, we can reflect the statement “there is a strong limit cardinal
 $\lambda> \alpha $
and a
$\lambda> \alpha $
and a
 $\mathbb {P}_{\alpha }$
-name
$\mathbb {P}_{\alpha }$
-name
 $\dot {\mathbb {Q}} \in L_{\lambda }$
for an
$\dot {\mathbb {Q}} \in L_{\lambda }$
for an
 $(\alpha $
-
$(\alpha $
-
 $\vec S)^{L_{\lambda }}$
-coding forcing Q which forces a witness to
$\vec S)^{L_{\lambda }}$
-coding forcing Q which forces a witness to
 $\exists x\psi (x,{A})."$
$\exists x\psi (x,{A})."$
Hence there is such a
 $\lambda $
already below
$\lambda $
already below
 $\delta $
and the forcing
$\delta $
and the forcing
 $\dot {\mathbb {Q}}^{G_{\alpha }} \in L_{\lambda } [G_{\alpha }]$
, which is an
$\dot {\mathbb {Q}}^{G_{\alpha }} \in L_{\lambda } [G_{\alpha }]$
, which is an
 $\alpha $
-
$\alpha $
-
 $\vec S$
-coding forcing of length
$\vec S$
-coding forcing of length
 $\lambda < \delta $
and uses
$\lambda < \delta $
and uses
 $\vec {S}^{L_{\lambda }}$
above
$\vec {S}^{L_{\lambda }}$
above
 $\alpha $
as the sequence to code with, which of course is the same as
$\alpha $
as the sequence to code with, which of course is the same as
 $\vec {S} \upharpoonright \lambda $
above
$\vec {S} \upharpoonright \lambda $
above
 $\alpha $
. In this situation we use the forcing
$\alpha $
. In this situation we use the forcing
 $\dot {\mathbb {Q}}^{G_{\alpha }}$
at stage
$\dot {\mathbb {Q}}^{G_{\alpha }}$
at stage
 $\alpha $
.If there is no such Q, we set
$\alpha $
.If there is no such Q, we set
 $\dot {Q}_\alpha $
to be trivial forcing.
$\dot {Q}_\alpha $
to be trivial forcing. -
– (
 $\alpha $
is inaccessible but not as in the first item)
$\alpha $
is inaccessible but not as in the first item)
 $\dot {Q}_\alpha $
is trivial unless
$\dot {Q}_\alpha $
is trivial unless
 $\vert P_\alpha \vert \le \alpha $
. Work in
$\vert P_\alpha \vert \le \alpha $
. Work in
 $L[G_\alpha ]$
, where
$L[G_\alpha ]$
, where
 $G_\alpha $
is a
$G_\alpha $
is a
 $P_\alpha $
generic filter over L. Assume that
$P_\alpha $
generic filter over L. Assume that
 $\vert P_\alpha \vert = \alpha $
is inaccessible. Then we choose
$\vert P_\alpha \vert = \alpha $
is inaccessible. Then we choose
 $\langle B_\beta \mid \beta <2^\alpha \rangle $
to be an enumeration of
$\langle B_\beta \mid \beta <2^\alpha \rangle $
to be an enumeration of
 $P(\alpha )^{V[G_\alpha ]}$
. Let Q be the forcing using countable support, where each factor
$P(\alpha )^{V[G_\alpha ]}$
. Let Q be the forcing using countable support, where each factor $$\begin{align*}Q= \prod_{\beta < 2^{\alpha}} {\mathbb{R}}_{\beta}, \end{align*}$$
$$\begin{align*}Q= \prod_{\beta < 2^{\alpha}} {\mathbb{R}}_{\beta}, \end{align*}$$
 ${\mathbb {R}}_{\beta }$
is defined to be again with countable support. Then we force with Q at stage
${\mathbb {R}}_{\beta }$
is defined to be again with countable support. Then we force with Q at stage $$ \begin{align*}\prod_{i\in B_\beta}Club(S_{\alpha\cdot(\beta+1)+2i}) \times \prod_{i\notin B_\beta}Club(S_{\alpha\cdot(\beta+1)+2i+1})\end{align*} $$
$$ \begin{align*}\prod_{i\in B_\beta}Club(S_{\alpha\cdot(\beta+1)+2i}) \times \prod_{i\notin B_\beta}Club(S_{\alpha\cdot(\beta+1)+2i+1})\end{align*} $$
 $\alpha $
.
$\alpha $
.
It follows from the definition of P that for any
![]() $\alpha <\delta $
, the forcing
$\alpha <\delta $
, the forcing
![]() $\dot {Q}_{\alpha }$
is forced to be an
$\dot {Q}_{\alpha }$
is forced to be an
![]() $\alpha $
-
$\alpha $
-
![]() $\vec S$
coding forcing. Applying Lemma 3.7, we know that P is an
$\vec S$
coding forcing. Applying Lemma 3.7, we know that P is an
![]() $\vec {S}$
-coding forcing. Moreover, for any
$\vec {S}$
-coding forcing. Moreover, for any
![]() $\alpha $
inaccessible, the tail
$\alpha $
inaccessible, the tail
![]() $P /P_\alpha $
is an
$P /P_\alpha $
is an
![]() $\alpha $
-
$\alpha $
-
![]() $\vec S_{}$
coding.
$\vec S_{}$
coding.
Now as P is
![]() $\vec S$
-preserving, P preserves
$\vec S$
-preserving, P preserves
![]() $\omega _1$
. On the other hand, P is
$\omega _1$
. On the other hand, P is
![]() $\delta $
-c.c and P preserves
$\delta $
-c.c and P preserves
![]() $\delta $
and all cardinals above
$\delta $
and all cardinals above
![]() $\delta $
. By the definition of the forcing in the second case, all cardinals below
$\delta $
. By the definition of the forcing in the second case, all cardinals below
![]() $\delta $
are collapsed to
$\delta $
are collapsed to
![]() $\omega _1$
. In summary,
$\omega _1$
. In summary,
![]() $\omega _1^{L^P}=\omega _1^L$
and
$\omega _1^{L^P}=\omega _1^L$
and
![]() $\omega _2^{L^P}=\delta $
.
$\omega _2^{L^P}=\delta $
.
Lemma 3.12.
![]() $P \Vdash \mathsf {BPFA}$
.
$P \Vdash \mathsf {BPFA}$
.
Proof Work in
![]() $L[G]$
. Let
$L[G]$
. Let
![]() $A\subset \omega _1$
and
$A\subset \omega _1$
and
![]() $Q \in L[G]$
be a proper forcing which adds a witness to the
$Q \in L[G]$
be a proper forcing which adds a witness to the
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\exists x\psi (x,A)$
. Now let
$\exists x\psi (x,A)$
. Now let
![]() $\alpha $
be a stage such that
$\alpha $
be a stage such that
![]() $A\in L[G_\alpha ]$
,
$A\in L[G_\alpha ]$
,
![]() $\alpha $
is an inaccessible limit of inaccessibles, and
$\alpha $
is an inaccessible limit of inaccessibles, and
![]() $( A,\exists x \psi )$
is to be dealt with at stage
$( A,\exists x \psi )$
is to be dealt with at stage
![]() $\alpha $
. In
$\alpha $
. In
![]() $L[G]$
, the forcing
$L[G]$
, the forcing
![]() $P/(P_\alpha *\dot {Q})$
is an
$P/(P_\alpha *\dot {Q})$
is an
![]() $\alpha $
-
$\alpha $
-
![]() $\vec S$
coding forcing adding a witness to
$\vec S$
coding forcing adding a witness to
![]() $\exists x \psi (x,A)$
. Hence, we must be in the first case of the definition of our iteration at stage
$\exists x \psi (x,A)$
. Hence, we must be in the first case of the definition of our iteration at stage
![]() $\alpha $
and
$\alpha $
and
![]() $Q_\alpha $
is an
$Q_\alpha $
is an
![]() $\alpha $
-
$\alpha $
-
![]() $\vec S$
coding forcing which adds a witness to
$\vec S$
coding forcing which adds a witness to
![]() $\exists x \psi (x,A)$
. Thus
$\exists x \psi (x,A)$
. Thus
![]() $H(\omega _2)^{L[G_{\alpha +1}]}\models \exists x\psi (x, A)$
. By upward absoluteness,
$H(\omega _2)^{L[G_{\alpha +1}]}\models \exists x\psi (x, A)$
. By upward absoluteness,
![]() $H(\omega _2)^{L[G]}\models \exists x\psi (x, A)$
.
$H(\omega _2)^{L[G]}\models \exists x\psi (x, A)$
.
Lemma 3.13. Work in
![]() $L[G]$
. Let S be a subset of
$L[G]$
. Let S be a subset of
![]() $\omega _1$
. Then the following are equivalent
$\omega _1$
. Then the following are equivalent
![]() $:$
$:$
-
(a) S is stationary.
-
(b) There is an
 $\alpha $
, inaccessible in L, with
$\alpha $
, inaccessible in L, with
 $P_\alpha \subseteq L_\alpha $
and S is stationary in
$P_\alpha \subseteq L_\alpha $
and S is stationary in
 $L[G_\alpha ]$
.
$L[G_\alpha ]$
. -
(c) There is an
 $\alpha $
, inaccessible in L, there is
$\alpha $
, inaccessible in L, there is
 $\vec {C} \in L[G_{\alpha +1}]$
which is an
$\vec {C} \in L[G_{\alpha +1}]$
which is an
 $\vec S$
code for
$\vec S$
code for
 $P(\alpha )^{L[G_\alpha ]}$
, and there is a transitive model M of
$P(\alpha )^{L[G_\alpha ]}$
, and there is a transitive model M of
 $\mathsf {ZF}^-$
such that
$\mathsf {ZF}^-$
such that
 $\vec {C} \in M$
and M thinks that
$\vec {C} \in M$
and M thinks that
 $S \in P(\alpha )^{L[G_{\alpha }]}$
is stationary.
$S \in P(\alpha )^{L[G_{\alpha }]}$
is stationary.
Proof ((a)
![]() $\rightarrow $
(c)) Let
$\rightarrow $
(c)) Let
![]() $\alpha $
be inaccessible but not a limit of inaccessibles and consider stage
$\alpha $
be inaccessible but not a limit of inaccessibles and consider stage
![]() $\alpha $
of the iteration which we can assume to be such that
$\alpha $
of the iteration which we can assume to be such that
![]() $S\in L[G_\alpha ]$
and
$S\in L[G_\alpha ]$
and
![]() $\vert P_\alpha \vert \le \alpha $
. Now
$\vert P_\alpha \vert \le \alpha $
. Now
![]() $Q_\alpha $
forces the existence of a
$Q_\alpha $
forces the existence of a
![]() $\vec {C}$
-sequence which is an
$\vec {C}$
-sequence which is an
![]() $\vec S$
code for
$\vec S$
code for
![]() $P(\alpha )^{L[G_\alpha ]}$
. Any transitive M which contains
$P(\alpha )^{L[G_\alpha ]}$
. Any transitive M which contains
![]() $\vec {C}$
is as desired in (c); moreover M will automatically think that S is stationary if S is stationary in
$\vec {C}$
is as desired in (c); moreover M will automatically think that S is stationary if S is stationary in
![]() $L[G]$
.
$L[G]$
.
((b)
![]() $\rightarrow $
(a)) The tail of forcing
$\rightarrow $
(a)) The tail of forcing
![]() $P/P_\alpha $
is
$P/P_\alpha $
is
![]() $\alpha $
-
$\alpha $
-
![]() $\vec S$
coding. Now the proof of Lemma 3.6 shows
$\vec S$
coding. Now the proof of Lemma 3.6 shows
![]() $P/P_\alpha $
preserves stationarity of S.
$P/P_\alpha $
preserves stationarity of S.
((c)
![]() $\rightarrow $
(b)) If M is as in the assumption,
$\rightarrow $
(b)) If M is as in the assumption,
![]() $P(\alpha )^{L[G_{\alpha }]}$
is a subset of M. Therefore, if M thinks
$P(\alpha )^{L[G_{\alpha }]}$
is a subset of M. Therefore, if M thinks
![]() $S \subseteq \alpha $
is stationary, then so must
$S \subseteq \alpha $
is stationary, then so must
![]() $L[G_{\alpha }]$
.
$L[G_{\alpha }]$
.
We now present the
![]() $\Sigma _1$
definition of stationary subsets of
$\Sigma _1$
definition of stationary subsets of
![]() $\omega _1$
over the structure
$\omega _1$
over the structure
![]() $(H(\omega _2), \in , \{\omega _1\})$
. Let
$(H(\omega _2), \in , \{\omega _1\})$
. Let
![]() $\psi (x)$
describe the following statement: there are objects A and M such that:
$\psi (x)$
describe the following statement: there are objects A and M such that:
-
(i)
 $A= \langle C_i \mid i \in [\alpha , \beta ) \rangle $
is a sequence with
$A= \langle C_i \mid i \in [\alpha , \beta ) \rangle $
is a sequence with
 $C_i$
an
$C_i$
an
 $\omega $
-club in the ordinal
$\omega $
-club in the ordinal
 $\sup (C_i \cap Ord)=\eta _i$
.
$\sup (C_i \cap Ord)=\eta _i$
. -
(ii) All
 $\eta _i$
are regular cardinals in L and
$\eta _i$
are regular cardinals in L and
 $\eta _\alpha =\alpha $
is inaccessible in L.
$\eta _\alpha =\alpha $
is inaccessible in L. -
(iii) M is a transitive ZFC
 $^-$
model with
$^-$
model with
 $\omega _1=\omega _1^M$
,
$\omega _1=\omega _1^M$
,
 $((\alpha ^+)^L)^M= (\alpha ^+)^L$
, and
$((\alpha ^+)^L)^M= (\alpha ^+)^L$
, and
 $x\in M$
.
$x\in M$
. -
(iv) M thinks that
 $\exists M_0 (M_0 \models \mathsf {ZF}^- \land M_0$
is transitive and
$\exists M_0 (M_0 \models \mathsf {ZF}^- \land M_0$
is transitive and
 $x \in P(\omega _1)^{M_0} \land M_0 \models " x$
is stationary
$x \in P(\omega _1)^{M_0} \land M_0 \models " x$
is stationary
 $"$
) and additionally
$"$
) and additionally -
(v) M thinks that A is an
 $\vec S \upharpoonright (\alpha ^+)^L$
code for
$\vec S \upharpoonright (\alpha ^+)^L$
code for
 $P^{M_0}(\alpha )$
and
$P^{M_0}(\alpha )$
and
 $x \in P^{M_0}(\alpha )$
.
$x \in P^{M_0}(\alpha )$
.
It is routine to check (i), (iv), and (v) are all
![]() $\Sigma _1$
over
$\Sigma _1$
over
![]() $\langle H(\omega _2),\in , \{\omega _1\} \rangle $
. For (ii) and the penultimate assertion of (iii), as
$\langle H(\omega _2),\in , \{\omega _1\} \rangle $
. For (ii) and the penultimate assertion of (iii), as
![]() $L[G]\models \mathsf {BPFA}$
, we can apply a trick of Todorcevic (cf. [Reference Todorcevic17, Proof of Lemma 4]) to get
$L[G]\models \mathsf {BPFA}$
, we can apply a trick of Todorcevic (cf. [Reference Todorcevic17, Proof of Lemma 4]) to get
![]() $\Sigma _1$
formulas
$\Sigma _1$
formulas
![]() $\psi _0 (x)$
and
$\psi _0 (x)$
and
![]() $\psi _1 (x)$
such that
$\psi _1 (x)$
such that
![]() $H(\omega _2)\models \psi _0(\beta )$
if and only if
$H(\omega _2)\models \psi _0(\beta )$
if and only if
![]() $\beta $
is a regular cardinal in L and
$\beta $
is a regular cardinal in L and
![]() $H(\omega _2)\models \psi _1(\beta )$
if and only if
$H(\omega _2)\models \psi _1(\beta )$
if and only if
![]() $\beta $
is an inaccessible cardinal in L.
$\beta $
is an inaccessible cardinal in L.
Here
![]() $\psi _0(x)$
is the formula describing the existence of a specialization function of the tree
$\psi _0(x)$
is the formula describing the existence of a specialization function of the tree
![]() $T_x$
, where
$T_x$
, where
![]() $T_x$
is derived from the canonical global square sequence in L. It is a consequence of
$T_x$
is derived from the canonical global square sequence in L. It is a consequence of
![]() $\mathsf {BPFA}$
that x is uncountable regular in L if and only if such a specialization function exists. Now
$\mathsf {BPFA}$
that x is uncountable regular in L if and only if such a specialization function exists. Now
![]() $\psi _1(x)$
is a formula saying that
$\psi _1(x)$
is a formula saying that
![]() $\alpha $
is regular and a limit of regular cardinals in L.
$\alpha $
is regular and a limit of regular cardinals in L.
It is now clear that
![]() $\psi (x)$
is
$\psi (x)$
is
![]() $\Sigma _1$
over
$\Sigma _1$
over
![]() $\langle H(\omega _2),\in , \{\omega _1\} \rangle .$
What is left is to show that
$\langle H(\omega _2),\in , \{\omega _1\} \rangle .$
What is left is to show that
![]() $\psi (x)$
indeed characterizes stationarity.
$\psi (x)$
indeed characterizes stationarity.
Lemma 3.14. In
![]() $L[G]$
, for any
$L[G]$
, for any
![]() $x\subseteq \omega _1$
,
$x\subseteq \omega _1$
,
![]() $H(\omega _2)\models \psi (x)$
if and only if x is stationary.
$H(\omega _2)\models \psi (x)$
if and only if x is stationary.
Proof If
![]() $x\subset \omega _1$
is stationary, then, by Lemma 3.13(c), we do immediately get a witness
$x\subset \omega _1$
is stationary, then, by Lemma 3.13(c), we do immediately get a witness
![]() $M_0 \in H(\omega _2)$
and an A, so finding a transitive model M which contains
$M_0 \in H(\omega _2)$
and an A, so finding a transitive model M which contains
![]() $M_0$
immediately witnesses that
$M_0$
immediately witnesses that
![]() $\psi (x)$
holds.
$\psi (x)$
holds.
Conversely, let x, A, M, and
![]() $M_0$
be as given by the definition of
$M_0$
be as given by the definition of
![]() $\psi (x)$
, and we shall show that x is stationary. But if
$\psi (x)$
, and we shall show that x is stationary. But if
![]() $\psi (x)$
holds, then
$\psi (x)$
holds, then
![]() $M_0$
thinks that A is an
$M_0$
thinks that A is an
![]() $\vec {S} \upharpoonright (\alpha ^+)^L$
-code for
$\vec {S} \upharpoonright (\alpha ^+)^L$
-code for
![]() $P^{M_0}(\alpha )$
. By item
$P^{M_0}(\alpha )$
. By item
![]() $(ii)$
of
$(ii)$
of
![]() $\psi $
, this also means that A is an
$\psi $
, this also means that A is an
![]() $\vec {S}$
-code for
$\vec {S}$
-code for
![]() $P(\alpha )^{L[G_{\alpha }] }$
and by (c) of Lemma 3.13 it is true that x is indeed stationary.
$P(\alpha )^{L[G_{\alpha }] }$
and by (c) of Lemma 3.13 it is true that x is indeed stationary.
3.2 A model for
 $\mathsf {MA_{\omega _1}}$
,
$\mathsf {MA_{\omega _1}}$
,
 $\text {NS}_{\omega _1}$
being saturated and
$\text {NS}_{\omega _1}$
being saturated and
 $\Delta _1(\{\omega _1\})$
-definable
$\Delta _1(\{\omega _1\})$
-definable
In this section we improve an earlier result of [Reference Hoffelner6]; we show that given a Woodin cardinal, there is a model such that
![]() $\text {NS}_{\omega _1}$
is saturated,
$\text {NS}_{\omega _1}$
is saturated,
![]() $\Delta _1$
-definable over
$\Delta _1$
-definable over
![]() $H(\omega _2)$
from parameters while Martin’s Axiom also holds true. If one forces over the canonical inner model with one Woodin cardinal
$H(\omega _2)$
from parameters while Martin’s Axiom also holds true. If one forces over the canonical inner model with one Woodin cardinal
![]() $M_1$
, then the construction yields a model where additionally
$M_1$
, then the construction yields a model where additionally
![]() $\text {NS}_{\omega _1}$
is definable with
$\text {NS}_{\omega _1}$
is definable with
![]() $\omega _1$
as the only parameter.
$\omega _1$
as the only parameter.
3.2.1 Short summary of the main features of the model
 $W_1$
$W_1$
The proof relies heavily on the coding machinery introduced in [Reference Hoffelner6], where it is shown that, given a Woodin cardinal
![]() $\delta $
, then there is a universe in which
$\delta $
, then there is a universe in which
![]() $\text {NS}_{\omega _1}$
is saturated and
$\text {NS}_{\omega _1}$
is saturated and
![]() $\Delta _1(\vec {C}, \vec {T}^0)$
-definable, where
$\Delta _1(\vec {C}, \vec {T}^0)$
-definable, where
![]() $\vec {C}$
is an arbitrary ladder system on
$\vec {C}$
is an arbitrary ladder system on
![]() $\omega _1$
and
$\omega _1$
and
![]() $\vec {T}^0$
is an independent sequence (independence will be defined in a moment below) of Suslin trees of length
$\vec {T}^0$
is an independent sequence (independence will be defined in a moment below) of Suslin trees of length
![]() $\omega $
. As this coding is rather convoluted, we will not define it here in detail but instead only highlight the most important notions and features of it. Our notation will be exactly as in [Reference Hoffelner6].
$\omega $
. As this coding is rather convoluted, we will not define it here in detail but instead only highlight the most important notions and features of it. Our notation will be exactly as in [Reference Hoffelner6].
We shall use Suslin trees on
![]() $\omega _1$
for creating a
$\omega _1$
for creating a
![]() $\mathbf {\Sigma _1}$
-definition of stationarity. To facilitate things, the trees should satisfy a certain property:
$\mathbf {\Sigma _1}$
-definition of stationarity. To facilitate things, the trees should satisfy a certain property:
Definition 3.15. Let
![]() $\vec {T} = (T_{\alpha } \, : \, \alpha < \kappa )$
be a sequence of Suslin trees. We say that the sequence is an independent family of Suslin trees if for every finite set
$\vec {T} = (T_{\alpha } \, : \, \alpha < \kappa )$
be a sequence of Suslin trees. We say that the sequence is an independent family of Suslin trees if for every finite set
![]() $e= \{e_0, e_1,\ldots ,e_n\} \subset \kappa $
the product
$e= \{e_0, e_1,\ldots ,e_n\} \subset \kappa $
the product
![]() $T_{e_0} \times T_{e_1} \times \cdot \cdot \cdot \times T_{e_n}$
is again a Suslin tree.
$T_{e_0} \times T_{e_1} \times \cdot \cdot \cdot \times T_{e_n}$
is again a Suslin tree.
Independent sequences of Suslin trees can be used to code arbitrary information using the two well-known and mutually exclusive ways to destroy a Suslin tree, namely either shooting a branch through the tree or specializing it. More precisely, given a set
![]() $X \subset \omega _1$
and an independent sequence of Suslin trees
$X \subset \omega _1$
and an independent sequence of Suslin trees
![]() $\vec {T}=(T_i \, : \, i < \omega _1)$
, we can code the characteristic function of X into
$\vec {T}=(T_i \, : \, i < \omega _1)$
, we can code the characteristic function of X into
![]() $\vec {T}$
via forcing with the finitely supported product of
$\vec {T}$
via forcing with the finitely supported product of
 $$ \begin{align*} \mathbb{P}_i= \begin{cases} T_i, & \text{ if } i \in X, \\ Sp(T_i), & \text{ if } i \notin X, \end{cases} \end{align*} $$
$$ \begin{align*} \mathbb{P}_i= \begin{cases} T_i, & \text{ if } i \in X, \\ Sp(T_i), & \text{ if } i \notin X, \end{cases} \end{align*} $$
where
![]() $T_i$
just denotes the forcing one obtains when forcing with the Suslin tree
$T_i$
just denotes the forcing one obtains when forcing with the Suslin tree
![]() $T_i$
(which adds a cofinal branch to
$T_i$
(which adds a cofinal branch to
![]() $T_i$
) and
$T_i$
) and
![]() $Sp(T_i)$
denotes the forcing which specializes the tree
$Sp(T_i)$
denotes the forcing which specializes the tree
![]() $T_i$
. Note that the independence of
$T_i$
. Note that the independence of
![]() $\vec {T}$
buys us that the finitely supported product has the ccc as well. We will eventually use this mechanism to create a generic extension of V with a
$\vec {T}$
buys us that the finitely supported product has the ccc as well. We will eventually use this mechanism to create a generic extension of V with a
![]() $\Sigma _1(\vec {C},\vec {T}^0)$
-definition of being stationary on
$\Sigma _1(\vec {C},\vec {T}^0)$
-definition of being stationary on
![]() $\omega _1$
.
$\omega _1$
.
The construction of such a universe shall be sketched now. We start with a universe V with one Woodin cardinal
![]() $\delta $
with
$\delta $
with
![]() $\diamondsuit $
. We fix a ladder system
$\diamondsuit $
. We fix a ladder system
![]() $\vec {C}$
and an
$\vec {C}$
and an
![]() $\omega $
-sequence of independent Suslin trees
$\omega $
-sequence of independent Suslin trees
![]() $\vec {T}^0$
and start a first, nicely supported iteration (using Miyamoto’s nice iterations; see [Reference Miyamoto12]) of length
$\vec {T}^0$
and start a first, nicely supported iteration (using Miyamoto’s nice iterations; see [Reference Miyamoto12]) of length
![]() $\delta $
over V which combines Shelah’s proof of the saturation of
$\delta $
over V which combines Shelah’s proof of the saturation of
![]() $\text {NS}_{\omega _1}$
from a Woodin cardinal with the forcings invented by Caicedo and Velickovic (see [Reference Caicedo and Velickovic2]) and other forcings whose purpose is to create a model
$\text {NS}_{\omega _1}$
from a Woodin cardinal with the forcings invented by Caicedo and Velickovic (see [Reference Caicedo and Velickovic2]) and other forcings whose purpose is to create a model
![]() $W_0$
which will have several features listed below which will turn out to be useful.
$W_0$
which will have several features listed below which will turn out to be useful.
In a next step we force over
![]() $W_0$
with a variant of almost disjoint coding which is due to Harrington (see [Reference Harrington5]), which is used to ensure that over the resulting generic extension of
$W_0$
with a variant of almost disjoint coding which is due to Harrington (see [Reference Harrington5]), which is used to ensure that over the resulting generic extension of
![]() $W_0$
, denoted by
$W_0$
, denoted by
![]() $W_1$
, there is a
$W_1$
, there is a
![]() ${\Sigma _1}(\vec {C},\vec {T}^0)$
-definable
${\Sigma _1}(\vec {C},\vec {T}^0)$
-definable
![]() $\omega _2$
-sequence of
$\omega _2$
-sequence of
![]() $\aleph _1$
-sized, transitive models which are sufficiently smart to determine whether a member is a stationary subset of
$\aleph _1$
-sized, transitive models which are sufficiently smart to determine whether a member is a stationary subset of
![]() $\omega _1$
of
$\omega _1$
of
![]() $W_0$
or a Suslin tree in
$W_0$
or a Suslin tree in
![]() $W_0$
. These sufficiently smart models are called suitable. The point of suitable models is that they can correctly compute a fixed, independent sequence
$W_0$
. These sufficiently smart models are called suitable. The point of suitable models is that they can correctly compute a fixed, independent sequence
![]() $\vec {T}=(T_{\alpha } \, : \, \alpha < \omega _2)$
of Suslin trees. Due to this correctness, we can identify, in a
$\vec {T}=(T_{\alpha } \, : \, \alpha < \omega _2)$
of Suslin trees. Due to this correctness, we can identify, in a
![]() $\Sigma _1(\vec {C},\vec {T}^0)$
-way, whether a given
$\Sigma _1(\vec {C},\vec {T}^0)$
-way, whether a given
![]() $\omega _1$
-block of trees is in
$\omega _1$
-block of trees is in
![]() $\vec {T}$
. The sequence
$\vec {T}$
. The sequence
![]() $\vec {T}$
will be used later to code up being stationary in a
$\vec {T}$
will be used later to code up being stationary in a
![]() $\Sigma _1(\vec {T}^0, \vec {C})$
-way.
$\Sigma _1(\vec {T}^0, \vec {C})$
-way.
To summarize the above, starting from an arbitrary V which contains a Woodin cardinal
![]() $\delta $
with
$\delta $
with
![]() $\diamondsuit $
, and fixing a ladder system on
$\diamondsuit $
, and fixing a ladder system on
![]() $\omega _1 \vec {C}$
and an
$\omega _1 \vec {C}$
and an
![]() $\omega $
-sequence of independent Suslin trees
$\omega $
-sequence of independent Suslin trees
![]() $\vec {T}^0$
, we create first a generic extension
$\vec {T}^0$
, we create first a generic extension
![]() $W_0$
and then a further generic extension
$W_0$
and then a further generic extension
![]() $W_1$
such that in
$W_1$
such that in
![]() $W_1$
the following holds:
$W_1$
the following holds:
-
1.
 $\delta =\aleph _2$
.
$\delta =\aleph _2$
. -
2. In
 $W_1$
, the nonstationary ideal is saturated and its saturation is ccc-indestructible.
$W_1$
, the nonstationary ideal is saturated and its saturation is ccc-indestructible. -
3. Every real in
 $W_0$
is coded by a triple of limit ordinals
$W_0$
is coded by a triple of limit ordinals
 $(\alpha , \beta , \gamma )$
below
$(\alpha , \beta , \gamma )$
below
 $\omega _2$
relative to the ladder system
$\omega _2$
relative to the ladder system
 $\vec {C}$
(in the sense of Caicedo–Velickovic; see [Reference Hoffelner6, Theorem 18(‡)]).
$\vec {C}$
(in the sense of Caicedo–Velickovic; see [Reference Hoffelner6, Theorem 18(‡)]). -
4. Every subset
 $X \subseteq \omega _1$
,
$X \subseteq \omega _1$
,
 $X \in W_0$
is coded by a real
$X \in W_0$
is coded by a real
 $r_X \in W_0$
relative to the fixed almost disjoint family of reals F we recursively obtain from our ladder system
$r_X \in W_0$
relative to the fixed almost disjoint family of reals F we recursively obtain from our ladder system
 $\vec {C}$
.
$\vec {C}$
. -
5. There is an
 $\omega _2$
-sequence of independent Suslin trees
$\omega _2$
-sequence of independent Suslin trees
 $\vec {T} = (T_i \, : \, \omega < i < \omega _2) \in W_1$
whose initial segments are uniformly and correctly definable in suitable models. The set of suitable models is itself
$\vec {T} = (T_i \, : \, \omega < i < \omega _2) \in W_1$
whose initial segments are uniformly and correctly definable in suitable models. The set of suitable models is itself
 $\Sigma _1(\vec {C}, \vec {T}^0)$
-definable in
$\Sigma _1(\vec {C}, \vec {T}^0)$
-definable in
 $W_1$
using as parameters the ladder system
$W_1$
using as parameters the ladder system
 $\vec {C}$
, and one
$\vec {C}$
, and one
 $\omega $
-block of independent Suslin tree
$\omega $
-block of independent Suslin tree
 $\vec {T}^0=(T_n \, : \, n \in \omega )$
. As a consequence,
$\vec {T}^0=(T_n \, : \, n \in \omega )$
. As a consequence,
 $\vec {T}$
is
$\vec {T}$
is
 $\Sigma _1(\vec {C},\vec {T}^0)$
-definable over
$\Sigma _1(\vec {C},\vec {T}^0)$
-definable over
 $W_1$
.
$W_1$
. -
6. The definition of
 $\vec {T}$
remains the same in all generic extensions of
$\vec {T}$
remains the same in all generic extensions of
 $W_1$
by forcings with the countable chain condition. So
$W_1$
by forcings with the countable chain condition. So
 $W_1$
is a reasonable candidate for a ground model using coding forcings which have the ccc.
$W_1$
is a reasonable candidate for a ground model using coding forcings which have the ccc.
In a second iteration, using
![]() $W_1$
as the ground model, we force with coding forcings using Suslin trees that are applied to make
$W_1$
as the ground model, we force with coding forcings using Suslin trees that are applied to make
![]() $\text {NS}_{\omega _1} \Sigma _1(\vec {C},\vec {T}^0)$
-definable. We force with a finitely supported iteration of ccc forcings over
$\text {NS}_{\omega _1} \Sigma _1(\vec {C},\vec {T}^0)$
-definable. We force with a finitely supported iteration of ccc forcings over
![]() $W_1$
. As a consequence we preserve the saturation of the nonstationary ideal and the sequence
$W_1$
. As a consequence we preserve the saturation of the nonstationary ideal and the sequence
![]() $\vec {T}$
is still
$\vec {T}$
is still
![]() $\Sigma _1(\vec {C}, \vec {T}^0)$
-definable in the extension. The only forcings which are used in this second iteration are the Suslin trees from our independent sequence
$\Sigma _1(\vec {C}, \vec {T}^0)$
-definable in the extension. The only forcings which are used in this second iteration are the Suslin trees from our independent sequence
![]() $\vec {T}^{>0}=(T_i \, : \, i > \omega )$
, which we either specialize or destroy via the addition of an
$\vec {T}^{>0}=(T_i \, : \, i > \omega )$
, which we either specialize or destroy via the addition of an
![]() $\omega _1$
-branch. We will use a bookkeeping function and start to write characteristic functions of every stationary subset of
$\omega _1$
-branch. We will use a bookkeeping function and start to write characteristic functions of every stationary subset of
![]() $\omega _1$
into
$\omega _1$
into
![]() $\omega _1$
-blocks of
$\omega _1$
-blocks of
![]() $\vec {T}^{>0}$
using either the specialization forcing or shooting a branch through elements of
$\vec {T}^{>0}$
using either the specialization forcing or shooting a branch through elements of
![]() $\vec {T}^{>0}$
.
$\vec {T}^{>0}$
.
This will eventually yield a universe
![]() $W_{\omega _2}$
where the nonstationary ideal remains saturated and where stationary subsets of
$W_{\omega _2}$
where the nonstationary ideal remains saturated and where stationary subsets of
![]() $\omega _1$
can be characterized as follows:
$\omega _1$
can be characterized as follows:
Fact 3.16. There are
![]() $\Sigma _1(\vec {C}, \vec {T}^0)$
-formulas
$\Sigma _1(\vec {C}, \vec {T}^0)$
-formulas
![]() $\Phi (r)$
and
$\Phi (r)$
and
![]() $\Psi (S)$
where the formula
$\Psi (S)$
where the formula
![]() $\Phi (r)$
defines a set of reals such that every member is an almost disjoint code for some
$\Phi (r)$
defines a set of reals such that every member is an almost disjoint code for some
![]() $\aleph _1$
-sized, transitive model which can be used to compute the sequence
$\aleph _1$
-sized, transitive model which can be used to compute the sequence
![]() $\vec {T}^{>0}$
of Suslin trees correctly
$\vec {T}^{>0}$
of Suslin trees correctly
![]() $($
these models are the suitable models mentioned earlier
$($
these models are the suitable models mentioned earlier
![]() $)$
. The formula
$)$
. The formula
![]() $\Psi (S)$
then defines stationary subsets of
$\Psi (S)$
then defines stationary subsets of
![]() $\omega _1$
in
$\omega _1$
in
![]() $W_{\omega _2}$
in the following way
$W_{\omega _2}$
in the following way
![]() $:$
$:$
-
Ψ(S) if and only if there is an
 $\aleph _1$
-sized, transitive model N which contains
$\aleph _1$
-sized, transitive model N which contains
 $\vec {C}$
and
$\vec {C}$
and
 $\vec {T}^0$
such that N models that
$\vec {T}^0$
such that N models that
 $:$
$:$
-
– There exists a real x such that
 $\Phi (x)$
holds, i.e., x is a code for a suitable model M.
$\Phi (x)$
holds, i.e., x is a code for a suitable model M. -
– There exists an ordinal
 $\alpha $
in the suitable model M such that
$\alpha $
in the suitable model M such that
 $\vec {T}'$
is the
$\vec {T}'$
is the
 $\alpha $
-th
$\alpha $
-th
 $\omega _1$
block of the definable sequence of independent Suslin trees as computed in M and N sees a full pattern on
$\omega _1$
block of the definable sequence of independent Suslin trees as computed in M and N sees a full pattern on
 $\vec {T}'$
.
$\vec {T}'$
. -
–
 $\forall \beta < \omega _1 ( \beta \in S$
if and only if
$\forall \beta < \omega _1 ( \beta \in S$
if and only if
 $\vec {T}' (\beta )$
has a branch
$\vec {T}' (\beta )$
has a branch
 $)$
.
$)$
. -
–
 $\forall \beta < \omega _1 (\beta \notin S$
if and only if
$\forall \beta < \omega _1 (\beta \notin S$
if and only if
 $\vec {T}' (\beta )$
is special
$\vec {T}' (\beta )$
is special
 $)$
.
$)$
.
-
Note that
![]() $\Psi (S)$
is of the form
$\Psi (S)$
is of the form
![]() $\exists N (N \models \cdots );$
thus
$\exists N (N \models \cdots );$
thus
![]() $\Psi $
is a
$\Psi $
is a
![]() $\Sigma _1$
-formula.
$\Sigma _1$
-formula.
3.2.2 Forcing over
 $W_1$
$W_1$
We shall show how to modify the construction just sketched to obtain a model where additionally
![]() $\mathsf {MA_{\omega _1}}$
holds. As before we will construct the model
$\mathsf {MA_{\omega _1}}$
holds. As before we will construct the model
![]() $W_1$
. We will proceed, however, not coding up stationary subsets of
$W_1$
. We will proceed, however, not coding up stationary subsets of
![]() $\omega _1$
as we do in [Reference Hoffelner6] but instead coding up a second
$\omega _1$
as we do in [Reference Hoffelner6] but instead coding up a second
![]() $\omega _2$
-block of generically added Suslin trees first.
$\omega _2$
-block of generically added Suslin trees first.
In an
![]() $\omega _2$
-length iteration we first use Tennenbaum’s forcing over
$\omega _2$
-length iteration we first use Tennenbaum’s forcing over
![]() $W_1$
to add an independent sequence of Suslin trees of length
$W_1$
to add an independent sequence of Suslin trees of length
![]() $\omega _2$
and use our definable independent sequence
$\omega _2$
and use our definable independent sequence
![]() $\vec {T}$
to code up the added Suslin trees. First let us briefly recall the definition of Tennenbaum’s forcing.
$\vec {T}$
to code up the added Suslin trees. First let us briefly recall the definition of Tennenbaum’s forcing.
Definition 3.17. Tennenbaum’s forcing
![]() $\mathbb {P}_T$
consists of conditions which are finite trees
$\mathbb {P}_T$
consists of conditions which are finite trees
![]() $(T,<_T)$
,
$(T,<_T)$
,
![]() $T \subset \omega _1$
, such that
$T \subset \omega _1$
, such that
![]() $\alpha < \beta $
if
$\alpha < \beta $
if
![]() $\alpha <_T \beta $
, and
$\alpha <_T \beta $
, and
![]() $(T_1, <_{T_1}) < (T_2,<_{T_2})$
holds if
$(T_1, <_{T_1}) < (T_2,<_{T_2})$
holds if
![]() $T_2 \subset T_1$
and
$T_2 \subset T_1$
and
![]() $<_{T_2} = <_{T_1} \cap (T_2 \times T_2)$
.
$<_{T_2} = <_{T_1} \cap (T_2 \times T_2)$
.
It is well-known that
![]() $\mathbb {P}_T$
is Knaster and adds generically a Suslin tree to the ground model.
$\mathbb {P}_T$
is Knaster and adds generically a Suslin tree to the ground model.
So we start with the model
![]() $W_1$
as our ground model. Let
$W_1$
as our ground model. Let
![]() $\vec {C}$
be our fixed ladder system on
$\vec {C}$
be our fixed ladder system on
![]() $\omega _1$
and let
$\omega _1$
and let
![]() $\vec {T}^0$
be a fixed independent sequence of Suslin trees of length
$\vec {T}^0$
be a fixed independent sequence of Suslin trees of length
![]() $\omega $
. In
$\omega $
. In
![]() $W_1$
there is a
$W_1$
there is a
![]() $\Sigma _1(\vec {C}, \vec {T}^0)$
-definable
$\Sigma _1(\vec {C}, \vec {T}^0)$
-definable
![]() $\omega _2$
-sequence of
$\omega _2$
-sequence of
![]() $\omega _1$
-blocks of independent Suslin trees
$\omega _1$
-blocks of independent Suslin trees
![]() $\vec {T}=(\vec {T}^{\alpha } \, : \, \alpha < \omega _2)$
, where for every
$\vec {T}=(\vec {T}^{\alpha } \, : \, \alpha < \omega _2)$
, where for every
![]() $0 \ne \alpha < \omega _2$
,
$0 \ne \alpha < \omega _2$
,
![]() $\vec {T}^{\alpha }=(T_{\eta }^{\alpha } \, : \, \eta < \omega _1)$
, and
$\vec {T}^{\alpha }=(T_{\eta }^{\alpha } \, : \, \eta < \omega _1)$
, and
![]() $\vec {T}$
forms an independent sequence of Suslin trees.
$\vec {T}$
forms an independent sequence of Suslin trees.
Over
![]() $W_1$
we start a finitely supported iteration
$W_1$
we start a finitely supported iteration
![]() $\mathbb {Q}= ((\mathbb {Q}_{\alpha },\dot {\mathbb {R}}_{\alpha }) \, : \, \alpha < \omega _2)$
and let
$\mathbb {Q}= ((\mathbb {Q}_{\alpha },\dot {\mathbb {R}}_{\alpha }) \, : \, \alpha < \omega _2)$
and let
![]() $H_{\alpha }$
denote the generic filter for
$H_{\alpha }$
denote the generic filter for
![]() $\mathbb {Q}_{\alpha }$
. For every
$\mathbb {Q}_{\alpha }$
. For every
![]() $\alpha < \omega _2$
, using
$\alpha < \omega _2$
, using
![]() $W_1[G_{\alpha }]$
as the ground model,
$W_1[G_{\alpha }]$
as the ground model,
![]() $\dot {\mathbb {R}}^{G_{\alpha }}_{\alpha }$
is defined to be
$\dot {\mathbb {R}}^{G_{\alpha }}_{\alpha }$
is defined to be
![]() $\mathbb {Q}^1_{\alpha } \ast \mathbb {Q}^2_{\alpha }$
, where
$\mathbb {Q}^1_{\alpha } \ast \mathbb {Q}^2_{\alpha }$
, where
![]() $\mathbb {Q}^1_{\alpha }$
is Tennenbaum’s
$\mathbb {Q}^1_{\alpha }$
is Tennenbaum’s
![]() $\mathbb {P}_T$
and
$\mathbb {P}_T$
and
![]() $\mathbb {Q}_{\alpha }^2$
codes up the tree generically added by
$\mathbb {Q}_{\alpha }^2$
codes up the tree generically added by
![]() $\mathbb {Q}_{\alpha }^1$
, called
$\mathbb {Q}_{\alpha }^1$
, called
![]() $h_{\alpha } \subset \omega _1$
in the following way. The partial order
$h_{\alpha } \subset \omega _1$
in the following way. The partial order
![]() $\mathbb {Q}_{\alpha }^2$
is defined to be a finitely supported product of the factors:
$\mathbb {Q}_{\alpha }^2$
is defined to be a finitely supported product of the factors:
 $$ \begin{align*} \mathbb{Q}_{\alpha}^2 = \begin{cases} T^{\alpha}_{\eta}, & \text{ if } \eta \in h_{\alpha}, \\ Sp(T^{\alpha}_{\eta}), & \text{ if } \eta \notin h_{\alpha}. \end{cases} \end{align*} $$
$$ \begin{align*} \mathbb{Q}_{\alpha}^2 = \begin{cases} T^{\alpha}_{\eta}, & \text{ if } \eta \in h_{\alpha}, \\ Sp(T^{\alpha}_{\eta}), & \text{ if } \eta \notin h_{\alpha}. \end{cases} \end{align*} $$
It is immediate to see that the resulting universe
![]() $W_2= W_1[H_{\omega _2}]$
is a ccc extension of
$W_2= W_1[H_{\omega _2}]$
is a ccc extension of
![]() $W_1$
, and thus
$W_1$
, and thus
![]() $\text {NS}_{\omega _1}$
remains saturated and as in [Reference Hoffelner6] one can show that the generically added sequence of Suslin trees
$\text {NS}_{\omega _1}$
remains saturated and as in [Reference Hoffelner6] one can show that the generically added sequence of Suslin trees
![]() $(h_{\alpha } \, : \, \alpha < \omega _2)$
is an independent,
$(h_{\alpha } \, : \, \alpha < \omega _2)$
is an independent,
![]() $\Sigma _1(\vec {C}, \vec {T}^0)$
-definable sequence of Suslin trees via the formula in the following fact:
$\Sigma _1(\vec {C}, \vec {T}^0)$
-definable sequence of Suslin trees via the formula in the following fact:
Fact 3.18. There is a
![]() $\Sigma _1(\vec {C}, \vec {T}^0)$
-formula
$\Sigma _1(\vec {C}, \vec {T}^0)$
-formula
![]() $\Psi (h)$
which defines the generically added Suslin trees
$\Psi (h)$
which defines the generically added Suslin trees
![]() $(h_{\alpha } \, : \, \alpha < \omega _2)$
of
$(h_{\alpha } \, : \, \alpha < \omega _2)$
of
![]() $W_2:$
$W_2:$
-
Ψ(h) if and only if there is an
 $\aleph _1$
-sized, transitive model N which contains
$\aleph _1$
-sized, transitive model N which contains
 $\vec {C}$
and
$\vec {C}$
and
 $\vec {T}^0$
such that N models that
$\vec {T}^0$
such that N models that
 $:$
$:$
-
– There exists a real x such that
 $\Phi (x)$
holds, i.e., x is a code for a suitable model M.
$\Phi (x)$
holds, i.e., x is a code for a suitable model M. -
– There exists an ordinal
 $\alpha $
in the suitable model M such that
$\alpha $
in the suitable model M such that
 $\vec {T}'$
is the
$\vec {T}'$
is the
 $\alpha $
-th
$\alpha $
-th
 $\omega _1$
block of the definable sequence of independent Suslin trees as computed in M and N sees a full pattern on
$\omega _1$
block of the definable sequence of independent Suslin trees as computed in M and N sees a full pattern on
 $\vec {T}'$
.
$\vec {T}'$
. -
–
 $\forall \beta < \omega _1 ( \beta \in h$
if and only if
$\forall \beta < \omega _1 ( \beta \in h$
if and only if
 $\vec {T}' (\beta )$
has a branch
$\vec {T}' (\beta )$
has a branch
 $)$
.
$)$
. -
–
 $\forall \beta < \omega _1 (\beta \notin h$
if and only if
$\forall \beta < \omega _1 (\beta \notin h$
if and only if
 $\vec {T}' (\beta )$
is special
$\vec {T}' (\beta )$
is special
 $)$
.
$)$
.
-
In a second step, we use
![]() $W_2$
as our ground model and force in an
$W_2$
as our ground model and force in an
![]() $\omega _2$
-length, finitely supported iteration
$\omega _2$
-length, finitely supported iteration
![]() $\mathsf {MA_{\omega _1}}$
while simultaneously coding up stationary subsets of
$\mathsf {MA_{\omega _1}}$
while simultaneously coding up stationary subsets of
![]() $\omega _1$
using the boldface
$\omega _1$
using the boldface
![]() $\Sigma _1$
-definable sequence of trees
$\Sigma _1$
-definable sequence of trees
![]() $(h_{\alpha } \, : \, \alpha < \omega _2)$
. We write
$(h_{\alpha } \, : \, \alpha < \omega _2)$
. We write
![]() $\vec {h}^{\alpha }$
for the
$\vec {h}^{\alpha }$
for the
![]() $\alpha $
-th
$\alpha $
-th
![]() $\omega _1$
-block of elements of the sequence
$\omega _1$
-block of elements of the sequence
![]() $(h_{\beta } \, : \, \beta < \omega _2)$
and let
$(h_{\beta } \, : \, \beta < \omega _2)$
and let
![]() $h^{\alpha }_{\beta }$
denote the
$h^{\alpha }_{\beta }$
denote the
![]() $\beta $
-th element of the
$\beta $
-th element of the
![]() $\alpha $
-th
$\alpha $
-th
![]() $\omega _1$
-block.
$\omega _1$
-block.
We do the usual forcing to code characteristic functions of stationary subsets of
![]() $\omega _1$
into
$\omega _1$
into
![]() $\vec {h}^{\alpha }$
, but additionally we feed in forcings of size
$\vec {h}^{\alpha }$
, but additionally we feed in forcings of size
![]() $\aleph _1$
with the countable chain condition to produce a model of
$\aleph _1$
with the countable chain condition to produce a model of
![]() $\mathsf {MA_{\omega _1}}$
. Note that all the forcings we use have the ccc and thus we will preserve the saturation of
$\mathsf {MA_{\omega _1}}$
. Note that all the forcings we use have the ccc and thus we will preserve the saturation of
![]() $\text {NS}_{\omega _1}$
.
$\text {NS}_{\omega _1}$
.
In order to prevent the forcings we use to get
![]() $\mathsf {MA_{\omega _1}}$
from adding branches or specializing functions to the Suslin trees we want to use for coding, we will force
$\mathsf {MA_{\omega _1}}$
from adding branches or specializing functions to the Suslin trees we want to use for coding, we will force
![]() $\mathsf {MA_{\omega _1}}$
in a “diagonal way.
$\mathsf {MA_{\omega _1}}$
in a “diagonal way.
![]() $"$
We define a finitely supported iteration
$"$
We define a finitely supported iteration
![]() $((\mathbb {R}_{\alpha }, \dot {\mathbb {S}}_{\alpha } ) \, : \, \alpha < \omega _2)$
of ccc forcing over
$((\mathbb {R}_{\alpha }, \dot {\mathbb {S}}_{\alpha } ) \, : \, \alpha < \omega _2)$
of ccc forcing over
![]() $W_2$
inductively using a bookkeeping function F. We let
$W_2$
inductively using a bookkeeping function F. We let
![]() $F \in W_2$
,
$F \in W_2$
,
![]() $F: \omega _2 \rightarrow \omega _2 \times \omega _2 \times 2$
such that for every
$F: \omega _2 \rightarrow \omega _2 \times \omega _2 \times 2$
such that for every
![]() $(\alpha , \beta , i) \in \omega _2 \times \omega _2 \times 2$
,
$(\alpha , \beta , i) \in \omega _2 \times \omega _2 \times 2$
,
![]() $F^{-1} (\alpha , \beta , i)$
is an unbounded subset in
$F^{-1} (\alpha , \beta , i)$
is an unbounded subset in
![]() $\omega _2$
. Assume we are at stage
$\omega _2$
. Assume we are at stage
![]() $\alpha < \omega _2$
and we have already defined the iteration
$\alpha < \omega _2$
and we have already defined the iteration
![]() $\mathbb {R}_{\alpha }$
up to
$\mathbb {R}_{\alpha }$
up to
![]() $\alpha < \omega _2$
. We let
$\alpha < \omega _2$
. We let
![]() $I_{\alpha }$
denote the generic filter for
$I_{\alpha }$
denote the generic filter for
![]() $\mathbb {R}_{\alpha }$
. We also assume by induction that each one of the first
$\mathbb {R}_{\alpha }$
. We also assume by induction that each one of the first
![]() $\alpha $
-many
$\alpha $
-many
![]() $\omega _1$
-blocks of trees
$\omega _1$
-blocks of trees
![]() $\vec {h}^{\beta }$
,
$\vec {h}^{\beta }$
,
![]() $\beta < \alpha $
has already been used for coding, but the elements of the sequences
$\beta < \alpha $
has already been used for coding, but the elements of the sequences
![]() $(\vec {h}^{\eta } \, : \eta \ge \alpha )$
still form an independent sequence of Suslin trees in
$(\vec {h}^{\eta } \, : \eta \ge \alpha )$
still form an independent sequence of Suslin trees in
![]() $W_2[I_{\alpha }]$
. The forcing we have to use next is determined by the value of
$W_2[I_{\alpha }]$
. The forcing we have to use next is determined by the value of
![]() $F(\alpha )$
.
$F(\alpha )$
.
-
1. If
 $F(\alpha )=(\beta , \gamma , 0)$
, then we look at the
$F(\alpha )=(\beta , \gamma , 0)$
, then we look at the
 $\beta $
-th stationary subset S of
$\beta $
-th stationary subset S of
 $\omega _1$
in
$\omega _1$
in
 $W_2[I_{\gamma }]$
and use the
$W_2[I_{\gamma }]$
and use the
 $\alpha $
-th
$\alpha $
-th
 $\omega _1$
-block of
$\omega _1$
-block of
 $\vec {h}$
,
$\vec {h}$
,
 $\vec {h}^{\alpha }=(h^{\alpha }_{\eta } \, : \, \eta < \omega _1)$
to code up S, i.e., we will force with
$\vec {h}^{\alpha }=(h^{\alpha }_{\eta } \, : \, \eta < \omega _1)$
to code up S, i.e., we will force with
 $\dot {\mathbb {S}}^{I_{\alpha }}_{\alpha } := \prod _{i < \omega _1} \mathbb {P}_i$
with finite support, where
$\dot {\mathbb {S}}^{I_{\alpha }}_{\alpha } := \prod _{i < \omega _1} \mathbb {P}_i$
with finite support, where  $$ \begin{align*} \mathbb{P}_i = \begin{cases} h^{\alpha}_{\eta}, & \text{ if } \eta \in S, \\ Sp(h^{\alpha}_{\eta}), & \text{ if } \eta \notin S, \end{cases} \end{align*} $$
$$ \begin{align*} \mathbb{P}_i = \begin{cases} h^{\alpha}_{\eta}, & \text{ if } \eta \in S, \\ Sp(h^{\alpha}_{\eta}), & \text{ if } \eta \notin S, \end{cases} \end{align*} $$
where
 $h^{\alpha }_{\eta }$
here is considered as a forcing notion when forcing with the tree and
$h^{\alpha }_{\eta }$
here is considered as a forcing notion when forcing with the tree and
 $Sp(h^{\alpha }_{\eta })$
denotes the specialization forcing for the tree
$Sp(h^{\alpha }_{\eta })$
denotes the specialization forcing for the tree
 $h^{\alpha }_{\eta }$
.
$h^{\alpha }_{\eta }$
. -
2. If
 $F(\alpha )=(\beta , \gamma , 1)$
, then we look at the
$F(\alpha )=(\beta , \gamma , 1)$
, then we look at the
 $\beta $
-th forcing
$\beta $
-th forcing
 $\mathbb {B}$
of size
$\mathbb {B}$
of size
 $\aleph _1$
in
$\aleph _1$
in
 $W_2[I_{\gamma }]$
which has the countable chain condition as seen in the universe
$W_2[I_{\gamma }]$
which has the countable chain condition as seen in the universe
 $W_2[I_{\alpha }]$
. We can consider the iteration
$W_2[I_{\alpha }]$
. We can consider the iteration
 $((\mathbb {R}_{\zeta } \, : \, \zeta < \alpha ) \ast \mathbb {B})$
which has a dense subforcing of size
$((\mathbb {R}_{\zeta } \, : \, \zeta < \alpha ) \ast \mathbb {B})$
which has a dense subforcing of size
 $\aleph _1$
(the dense set is just the set of conditions in
$\aleph _1$
(the dense set is just the set of conditions in
 $\mathbb {R}_{\alpha } \ast \mathbb {B}$
which are fully decided), ccc forcing in
$\mathbb {R}_{\alpha } \ast \mathbb {B}$
which are fully decided), ccc forcing in
 $W_2$
and can thus be seen as a subset of
$W_2$
and can thus be seen as a subset of
 $\omega _1$
in
$\omega _1$
in
 $W_2$
. As
$W_2$
. As
 $W_2=W_1[H_{\omega _2}]$
, there is a stage
$W_2=W_1[H_{\omega _2}]$
, there is a stage
 $\nu < \omega _2$
such that (a forcing equivalent to)
$\nu < \omega _2$
such that (a forcing equivalent to)
 $((\mathbb {R}_{\zeta } \, : \, \zeta < \alpha ) \ast \mathbb {B})$
is in
$((\mathbb {R}_{\zeta } \, : \, \zeta < \alpha ) \ast \mathbb {B})$
is in
 $W_1[H_{\nu }]$
. Now if
$W_1[H_{\nu }]$
. Now if
 $\nu \le \alpha $
we let
$\nu \le \alpha $
we let
 $\dot {\mathbb {S}}^{I_{\alpha }}_{\alpha }$
be
$\dot {\mathbb {S}}^{I_{\alpha }}_{\alpha }$
be
 $\mathbb {B}$
. Otherwise we force with the trivial forcing.
$\mathbb {B}$
. Otherwise we force with the trivial forcing.
In the first case of the definition we will write codes in the sequence
![]() $(\vec {h}^{\alpha } \, : \, \alpha < \omega _2)$
of blocks of Suslin trees. The definition of the second case ensures that we will not accidentally write an unwanted pattern when forcing for
$(\vec {h}^{\alpha } \, : \, \alpha < \omega _2)$
of blocks of Suslin trees. The definition of the second case ensures that we will not accidentally write an unwanted pattern when forcing for
![]() $\mathsf {MA_{\omega _1}}$
.
$\mathsf {MA_{\omega _1}}$
.
Lemma 3.19. Assume we are at stage
![]() $\alpha $
of our iteration and we are in the nontrivial part of case 2 of the definition, and thus we force with an
$\alpha $
of our iteration and we are in the nontrivial part of case 2 of the definition, and thus we force with an
![]() $\aleph _1$
-sized
$\aleph _1$
-sized
![]() $\dot {\mathbb {S}}^{I_{\alpha }}_{\alpha }=\mathbb {B}$
. Then, if
$\dot {\mathbb {S}}^{I_{\alpha }}_{\alpha }=\mathbb {B}$
. Then, if
![]() $I_{\alpha +1}$
is
$I_{\alpha +1}$
is
![]() $\mathbb {R}_{\alpha +1}=\mathbb {R}_{\alpha } \ast \dot {\mathbb {S}}_{\alpha }$
-generic over
$\mathbb {R}_{\alpha +1}=\mathbb {R}_{\alpha } \ast \dot {\mathbb {S}}_{\alpha }$
-generic over
![]() $W[H_{\omega _2}]$
, all the Suslin trees in
$W[H_{\omega _2}]$
, all the Suslin trees in
![]() $\vec {h}_{\zeta }$
,
$\vec {h}_{\zeta }$
,
![]() $\zeta \ge \alpha $
remain Suslin trees in
$\zeta \ge \alpha $
remain Suslin trees in
![]() $W[H_{\omega _2}][ I_{\alpha +1}]$
.
$W[H_{\omega _2}][ I_{\alpha +1}]$
.
Proof Assume that we are at stage
![]() $\alpha $
, and thus the model we have produced so far is
$\alpha $
, and thus the model we have produced so far is
![]() $W_1[H_{\omega _2}][ I_{\alpha }]$
and we force with
$W_1[H_{\omega _2}][ I_{\alpha }]$
and we force with
![]() $\dot {\mathbb {S}}_{\alpha }$
which is a ccc forcing of size
$\dot {\mathbb {S}}_{\alpha }$
which is a ccc forcing of size
![]() $\aleph _1$
in
$\aleph _1$
in
![]() $W_1[H_{\nu }][I_{\alpha }]$
for
$W_1[H_{\nu }][I_{\alpha }]$
for
![]() $\nu \le \alpha $
. Consider some block
$\nu \le \alpha $
. Consider some block
![]() $\vec {h}^{\zeta }$
,
$\vec {h}^{\zeta }$
,
![]() $\zeta \ge \alpha $
in the universe
$\zeta \ge \alpha $
in the universe
![]() $W_1[H_{\omega _2}][\mathbb {R}_{\alpha } \ast \dot {\mathbb {S}}_{\alpha }]$
. The latter universe is obtained via the iteration
$W_1[H_{\omega _2}][\mathbb {R}_{\alpha } \ast \dot {\mathbb {S}}_{\alpha }]$
. The latter universe is obtained via the iteration
and the right-hand side can be rewritten as
As we can switch the order in products, the latter can be written as
and consequentially the
![]() $W_1[H_{\nu }]$
-generic filter
$W_1[H_{\nu }]$
-generic filter
![]() $H_{\nu , \omega _2}$
for the tail
$H_{\nu , \omega _2}$
for the tail
![]() $(\mathbb {Q}_{\zeta } / \mathbb {Q}_{\nu } \, : \, \zeta> \nu , \zeta < \omega _2)$
remains generic over the model
$(\mathbb {Q}_{\zeta } / \mathbb {Q}_{\nu } \, : \, \zeta> \nu , \zeta < \omega _2)$
remains generic over the model
![]() $W_1[(\mathbb {Q}_{\zeta } \, : \, \zeta \le \nu ) \ast (\mathbb {R}_{\alpha } \ast \dot {\mathbb {S}}_{\alpha })]$
. This means in particular that the generically added Suslin trees
$W_1[(\mathbb {Q}_{\zeta } \, : \, \zeta \le \nu ) \ast (\mathbb {R}_{\alpha } \ast \dot {\mathbb {S}}_{\alpha })]$
. This means in particular that the generically added Suslin trees
![]() $\vec {h}^{\zeta }, \zeta> \nu $
for Tennenbaum’s forcing for adding a Suslin tree which are elements in
$\vec {h}^{\zeta }, \zeta> \nu $
for Tennenbaum’s forcing for adding a Suslin tree which are elements in
![]() $H_{\nu , \omega _2}$
remain generic even over the ground model
$H_{\nu , \omega _2}$
remain generic even over the ground model
![]() $W_1[H_{\nu } \ast I_{\alpha +1}]$
. Now Tennenbaum’s forcing is computed in an absolute way in every universe with the same
$W_1[H_{\nu } \ast I_{\alpha +1}]$
. Now Tennenbaum’s forcing is computed in an absolute way in every universe with the same
![]() $\omega _1$
, and trivially, every generic filter for it is a Suslin tree. Hence we obtain that every
$\omega _1$
, and trivially, every generic filter for it is a Suslin tree. Hence we obtain that every
![]() $h^{\zeta }_{\eta }$
,
$h^{\zeta }_{\eta }$
,
![]() $\zeta> \nu , \eta < \omega _1$
is a Suslin tree in
$\zeta> \nu , \eta < \omega _1$
is a Suslin tree in
![]() $W_1[H_{\nu } \ast I_{\alpha +1} ]$
, and thus every
$W_1[H_{\nu } \ast I_{\alpha +1} ]$
, and thus every
![]() $h^{\zeta }_{\eta }$
,
$h^{\zeta }_{\eta }$
,
![]() $\zeta \ge \alpha \ge \nu $
is a Suslin tree in
$\zeta \ge \alpha \ge \nu $
is a Suslin tree in
![]() $W_1[H_{\omega _2} \ast I_{\alpha +1}]$
as claimed.
$W_1[H_{\omega _2} \ast I_{\alpha +1}]$
as claimed.
After
![]() $\omega _2$
-many steps we arrive at
$\omega _2$
-many steps we arrive at
![]() $W_2[I_{\omega _2}]$
which has the desired properties. The first thing to note is that we are in full control of the codes which are written into the sequences of blocks of Suslin trees
$W_2[I_{\omega _2}]$
which has the desired properties. The first thing to note is that we are in full control of the codes which are written into the sequences of blocks of Suslin trees
![]() $(\vec {h}^{\alpha } \, : \, \alpha < \omega _2)$
.
$(\vec {h}^{\alpha } \, : \, \alpha < \omega _2)$
.
Lemma 3.20. In
![]() $W_2[I_{\omega _2}]$
, a set
$W_2[I_{\omega _2}]$
, a set
![]() $S \subset \omega _1$
is stationary if and only if there is an
$S \subset \omega _1$
is stationary if and only if there is an
![]() $\alpha < \omega _2$
such that
$\alpha < \omega _2$
such that
-
 $\forall \beta < \omega _1 (( \beta \in S \leftrightarrow h^{\alpha }_{\beta }$
has a branch
$\forall \beta < \omega _1 (( \beta \in S \leftrightarrow h^{\alpha }_{\beta }$
has a branch
 $)$
and
$)$
and
 $(\beta \notin S \leftrightarrow h^{\alpha }_{\beta }$
is special
$(\beta \notin S \leftrightarrow h^{\alpha }_{\beta }$
is special
 $))$
.
$))$
.
Proof If S is stationary then the rules of the iteration guarantee that there is such an
![]() $\alpha < \omega _2$
with the desired properties. On the other hand if there is an
$\alpha < \omega _2$
with the desired properties. On the other hand if there is an
![]() $\alpha < \omega _2$
such that the
$\alpha < \omega _2$
such that the
![]() $\alpha $
-th block
$\alpha $
-th block
![]() $\vec {h}^{\alpha }$
sees a certain 0,1-pattern then by the last lemma, this pattern must come from the first case in the definition of our iteration. Hence S has to be stationary.
$\vec {h}^{\alpha }$
sees a certain 0,1-pattern then by the last lemma, this pattern must come from the first case in the definition of our iteration. Hence S has to be stationary.
Theorem 3.21. In
![]() $W_2[I_{\omega _2}]$
,
$W_2[I_{\omega _2}]$
,
![]() $\mathsf {MA_{\omega _1}}$
holds and
$\mathsf {MA_{\omega _1}}$
holds and
![]() $\text {NS}_{\omega _1}$
is saturated and
$\text {NS}_{\omega _1}$
is saturated and
![]() $\Delta _1(\vec {C}, \vec {T}^0)$
-definable over
$\Delta _1(\vec {C}, \vec {T}^0)$
-definable over
![]() $H(\omega _2)$
.
$H(\omega _2)$
.
Proof That
![]() $\text {NS}_{\omega _1}$
is saturated is clear as
$\text {NS}_{\omega _1}$
is saturated is clear as
![]() $W_2[I_{\omega _2}]$
is a ccc extension of
$W_2[I_{\omega _2}]$
is a ccc extension of
![]() $W_0$
and
$W_0$
and
![]() $\text {NS}_{\omega _1}$
is saturated in
$\text {NS}_{\omega _1}$
is saturated in
![]() $W_0$
and ccc indestructible. The proof that
$W_0$
and ccc indestructible. The proof that
![]() $\mathsf {MA_{\omega _1}}$
holds in
$\mathsf {MA_{\omega _1}}$
holds in
![]() $W_2[I_{\omega _2}]$
is also clear as a standard computation yields that the continuum is
$W_2[I_{\omega _2}]$
is also clear as a standard computation yields that the continuum is
![]() $\aleph _2$
in
$\aleph _2$
in
![]() $W_2[I_{\omega _2}]$
. It is sufficient to show that
$W_2[I_{\omega _2}]$
. It is sufficient to show that
![]() $\mathsf {MA_{\omega _1}}$
holds for ccc posets of size
$\mathsf {MA_{\omega _1}}$
holds for ccc posets of size
![]() $\aleph _1$
. Let
$\aleph _1$
. Let
![]() $\mathbb {P} \in W_2[I_{\omega _2}]$
be such a poset. Then there is a stage
$\mathbb {P} \in W_2[I_{\omega _2}]$
be such a poset. Then there is a stage
![]() $\nu < \omega _2$
such that
$\nu < \omega _2$
such that
![]() $\mathbb {P} \in W_2[I_{\nu }]$
. The rules of the iteration yield that we will consider
$\mathbb {P} \in W_2[I_{\nu }]$
. The rules of the iteration yield that we will consider
![]() $\mathbb {P}$
unboundedly often after stage
$\mathbb {P}$
unboundedly often after stage
![]() $\nu $
. Thus there will be a stage
$\nu $
. Thus there will be a stage
![]() $\alpha < \omega _2$
such that
$\alpha < \omega _2$
such that
![]() $\mathbb {P}$
is considered by the bookkeeping F and
$\mathbb {P}$
is considered by the bookkeeping F and
![]() $\mathbb {R}_{\alpha } \ast \mathbb {P}$
is an element of
$\mathbb {R}_{\alpha } \ast \mathbb {P}$
is an element of
![]() $W_1[H_{\nu }]$
for
$W_1[H_{\nu }]$
for
![]() $\nu \le \alpha $
, and hence we used
$\nu \le \alpha $
, and hence we used
![]() $\mathbb {P}$
in the iteration
$\mathbb {P}$
in the iteration
![]() $(\mathbb {R}_{\eta } \, : \, \eta < \omega _2)$
, so
$(\mathbb {R}_{\eta } \, : \, \eta < \omega _2)$
, so
![]() $\mathsf {MA_{\omega _1}}$
holds.
$\mathsf {MA_{\omega _1}}$
holds.
In order to see that, in
![]() $W_2[I_{\omega _2}]$
, being a stationary subset of
$W_2[I_{\omega _2}]$
, being a stationary subset of
![]() $\omega _1$
has a
$\omega _1$
has a
![]() $\Sigma _1(\vec {C}, \vec {T}^0)$
-definition we exploit the fact that the trees
$\Sigma _1(\vec {C}, \vec {T}^0)$
-definition we exploit the fact that the trees
![]() $(h_{\alpha } \, : \, \alpha < \omega _2)$
are
$(h_{\alpha } \, : \, \alpha < \omega _2)$
are
![]() $\Sigma _1(\vec {C}, \vec {T}^0)$
-definable in
$\Sigma _1(\vec {C}, \vec {T}^0)$
-definable in
![]() $W_1[I_{\omega _2}]$
. We claim that the following
$W_1[I_{\omega _2}]$
. We claim that the following
![]() $\Sigma _1(\vec {C}, \vec {T}^0)$
-formula
$\Sigma _1(\vec {C}, \vec {T}^0)$
-formula
![]() $\varphi (S)$
defines being stationary in
$\varphi (S)$
defines being stationary in
![]() $W_2[I_{\omega _2}]$
:
$W_2[I_{\omega _2}]$
:
-
 $\varphi (S)$
if and only if there exists a triple of
$\varphi (S)$
if and only if there exists a triple of
 $(M_1, M_2, M_3)$
of transitive models of size
$(M_1, M_2, M_3)$
of transitive models of size
 $\aleph _1$
such that
$\aleph _1$
such that
 $M_1 \subset M_2 \subset M_3$
,
$M_1 \subset M_2 \subset M_3$
,
 $M_1$
is a suitable model and
$M_1$
is a suitable model and
 $M_2$
sees a full pattern on the trees in some
$M_2$
sees a full pattern on the trees in some
 $\omega _1$
-block
$\omega _1$
-block
 $\vec {T}^{\alpha }$
. This pattern itself yields an
$\vec {T}^{\alpha }$
. This pattern itself yields an
 $\omega _1$
-block of trees
$\omega _1$
-block of trees
 $\vec {h}^{\beta }$
and
$\vec {h}^{\beta }$
and
 $M_3$
sees a full pattern on
$M_3$
sees a full pattern on
 $\vec {h}^{\beta }$
and this pattern is the characteristic function for S.
$\vec {h}^{\beta }$
and this pattern is the characteristic function for S.
Note that the formula
![]() $\varphi (S)$
is of the form
$\varphi (S)$
is of the form
![]() $\exists M_1,M_2,M_3 \,\sigma (M_1,M_2,M_3,S)$
and
$\exists M_1,M_2,M_3 \,\sigma (M_1,M_2,M_3,S)$
and
![]() $\sigma $
is
$\sigma $
is
![]() $\Delta _1$
as all the statements in
$\Delta _1$
as all the statements in
![]() $\sigma $
are of the form
$\sigma $
are of the form
![]() $M_i \models \cdots $
which is a
$M_i \models \cdots $
which is a
![]() $\Delta _1$
-formula.
$\Delta _1$
-formula.
By absoluteness and the way we defined our iteration, it is clear that if
![]() $S \subset \omega _1$
is stationary in
$S \subset \omega _1$
is stationary in
![]() $W_2[I_{\omega _2}]$
, then
$W_2[I_{\omega _2}]$
, then
![]() $\varphi (S)$
holds.
$\varphi (S)$
holds.
On the other hand, if
![]() $\varphi (S)$
is true and
$\varphi (S)$
is true and
![]() $M_1,M_2$
, and
$M_1,M_2$
, and
![]() $M_3$
are witnesses to the truth of
$M_3$
are witnesses to the truth of
![]() $\varphi (S)$
, then, as they see full patterns, their local patterns must coincide with the patterns in the real world
$\varphi (S)$
, then, as they see full patterns, their local patterns must coincide with the patterns in the real world
![]() $W_2[I_{\omega _2}]$
. But the last lemma ensures that the patterns of
$W_2[I_{\omega _2}]$
. But the last lemma ensures that the patterns of
![]() $W_2[I_{\omega _2}]$
characterize stationarity, so the proof is finished.
$W_2[I_{\omega _2}]$
characterize stationarity, so the proof is finished.
As in [Reference Hoffelner6], instead of working in an arbitrary V with a Woodin cardinal, we can work over the canonical inner model with one Woodin cardinal
![]() $M_1$
. This has the advantage that we can replace the two parameters
$M_1$
. This has the advantage that we can replace the two parameters
![]() $\vec {C}$
and
$\vec {C}$
and
![]() $\vec {T}^0$
by just
$\vec {T}^0$
by just
![]() $\{ \omega _1 \}$
. We will not go into any details and just claim that the above proof can be applied over
$\{ \omega _1 \}$
. We will not go into any details and just claim that the above proof can be applied over
![]() $M_1$
, with all the modifications exactly as in [Reference Hoffelner6]. We therefore obtain the last theorem of this article.
$M_1$
, with all the modifications exactly as in [Reference Hoffelner6]. We therefore obtain the last theorem of this article.
Theorem 3.22. Let
![]() $M_1$
be the canonical inner model with one Woodin cardinal. Then there is a generic extension of
$M_1$
be the canonical inner model with one Woodin cardinal. Then there is a generic extension of
![]() $M_1$
, in which
$M_1$
, in which
![]() $\text {NS}_{\omega _1}$
is saturated and
$\text {NS}_{\omega _1}$
is saturated and
![]() $\Pi _1(\{\omega _1\})$
-definable over
$\Pi _1(\{\omega _1\})$
-definable over
![]() $H(\omega _2)$
and in which
$H(\omega _2)$
and in which
![]() $\mathsf {MA_{\omega _1}}$
holds.
$\mathsf {MA_{\omega _1}}$
holds.
3.2.3 Open questions
We end with a couple of natural problems which remain open.
Question 1. Assume the existence of a Woodin cardinal. Is there a universe in which
![]() $\mathsf {BPFA}$
holds,
$\mathsf {BPFA}$
holds,
![]() $\text {NS}_{\omega _1}$
is
$\text {NS}_{\omega _1}$
is
![]() $\mathbf {\Delta _1}$
-definable over
$\mathbf {\Delta _1}$
-definable over
![]() $H(\omega _2)$
and
$H(\omega _2)$
and
![]() $\text {NS}_{\omega _1}$
is saturated?
$\text {NS}_{\omega _1}$
is saturated?
Question 2. Assume the existence of a reflecting cardinal. Is
![]() $\mathsf {BPFA}$
consistent with the non-existence of a
$\mathsf {BPFA}$
consistent with the non-existence of a
![]() $\Pi _1(\{\omega _1\})$
-definition of
$\Pi _1(\{\omega _1\})$
-definition of
![]() $\text {NS}_{\omega _1}$
?
$\text {NS}_{\omega _1}$
?
On a final note, the natural follow-up question to Theorem 3.11, namely
Problem 1. Is it consistent with
![]() $\mathsf {PFA}$
that there is a
$\mathsf {PFA}$
that there is a
![]() $\Sigma _1$
-formula and a set
$\Sigma _1$
-formula and a set
![]() $A \subset \omega _1$
such that
$A \subset \omega _1$
such that
has been solved positively very recently by the authors of this article (see the upcoming [Reference Hoffelner, Larson, Schindler and Wu7]).
Funding
The first and third authors were supported by the Deutsche Forschungsgemeinschaft (DFG German Research Foundation) under Germanys Excellence Strategy EXC 2044 390685587, Mathematics Münster: Dynamics-Geometry-Structure. The second author was supported in part by NSF research grants DMS-1201494 and DMS-1764320.