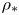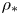1. Introduction
Tokamaks and stellarators are fusion reactor concepts that use magnetic fields to reduce the rate of loss of particles, momentum and energy from the reactor's toroidal confinement volume. In general, the confining magnetic fields are produced both by magnets that surround the toroidal confinement region, and by currents flowing through the confined plasma. To a great extent, the detailed spatial patterns of magnetic fields determine whether the operating conditions of a tokamak or stellarator permit sustained thermonuclear fusion reactions. Consequently, a key step in the design of any tokamak or stellarator reactor is the evaluation of reactor performance as a function of magnetic geometry.
Turbulent transport is one major factor that limits reactor performance. Turbulence in the fuel column is driven by the steep gradients of density, velocity and temperature that exist between the hot, sometimes rapidly flowing, dense fuel core and the relatively cold, diffuse environment. Under optimal conditions, the turbulent fluctuations are small-amplitude perturbations of the steady-state plasma density, temperature, etc. but these fluctuations nonetheless enhance losses, reduce insulation (by rapidly mixing cold plasma from the outer region with hot plasma in the reactor core) and generally limit reactor performance (Abel et al. Reference Abel, Barnes, Cowley, Dorland and Schekochihin2008). Decades of meticulous experiments and direct observations of plasma fluctuations in many tokamaks and stellarators have established a good understanding of when and where the turbulence arises, how intense it is, its dominant wavelengths and frequencies, and so on. The evaluation of the expected performance of any proposed tokamak or stellarator reactor design therefore essentially requires some way to estimate properties of the plasma turbulence that will arise as a result of the details of the proposed magnetic field geometry.
More than two decades of extensive validation campaigns have established that gyrokinetic theory quantitatively describes this turbulence. Many gyrokinetic simulation codes (Parker, Lee & Santoro Reference Parker, Lee and Santoro1993; Kotschenreuther, Rewoldt & Tang Reference Kotschenreuther, Rewoldt and Tang1995; Dorland et al. Reference Dorland, Jenko, Kotschenreuther and Rogers2000; Jenko Reference Jenko2000; Lin et al. Reference Lin, Hahm, Lee, Tang and White2000; Jost et al. Reference Jost, Tran, Cooper, Villard and Appert2001; Candy & Waltz Reference Candy and Waltz2003; Idomura, Tokuda & Kishimoto Reference Idomura, Tokuda and Kishimoto2003; Watanabe & Sugama Reference Watanabe and Sugama2005; Wang et al. Reference Wang, Lin, Tang, Lee, Ethier, Lewandowski, Rewoldt, Nahm and Manickam2006; Jolliet et al. Reference Jolliet, Bottino, Angelino, Hatzky, Tran, Mcmillan, Sauter, Appert, Idomura and Villard2007; Idomura et al. Reference Idomura, Ida, Kano, Aiba and Tokuda2008; Peeters et al. Reference Peeters, Camenen, Casson, Hornsby, Snodin, Strintzi and Szepesi2009; Candy, Belli & Bravenec Reference Candy, Belli and Bravenec2016; Barnes, Parra & Landreman Reference Barnes, Parra and Landreman2019; Lanti et al. Reference Lanti, Ohana, Tronko, Hayward-Schneider, Bottino, McMillan, Mishchenko, Scheinberg, Biancalani, Angelino and Brunner2020) have been used to study, test and ultimately validate our understanding of how plasma turbulence depends on the magnetic geometry (see e.g. Belli, Hammett & Dorland (Reference Belli, Hammett and Dorland2008), Marinoni et al. (Reference Marinoni, Brunner, Camenen, Coda, Graves, Lapillonne, Pochelon, Sauter and Villard2009), Mynick, Xanthopoulos & Boozer (Reference Mynick, Xanthopoulos and Boozer2009) and White (Reference White2019)). Because there are many algorithmic trade-offs to consider when setting up a turbulence simulation code, no single gyrokinetic code is ‘best’ for these purposes. In this paper we present GX, a fast gyrokinetic solver where our primary motivations and targets are fusion reactor design, optimization and wide-ranging physics exploration at reactor scales.
What does this mean in practice? It means primarily that we have prioritized time to solution (together with quantitative uncertainty estimates) over comprehensiveness and full realism, and that we aim to provide simple runtime control parameters to shift smoothly from very fast but relatively less accurate calculations such as are of most value in ‘outer loops’ of a design activity, to more comprehensive, ‘standard’ results that are (much) more expensive to evaluate. Moreover, instead of retrofitting an existing CPU-based code, we started from scratch, with every algorithmic design decision made to target graphics processors (GPUs), which are among the fastest computational platforms available today, with NVIDIA or AMD GPUs providing most of the computer power for seven of the top 10 fastest supercomputers in the world (Strohmaier et al. Reference Strohmaier, Dongarra, Simon and Meuer2022). Finally, since we are interested in reactors specifically, we focused on the reactor limit of small $\rho _* \equiv \rho _i/R$![]() , where $\rho _i$
, where $\rho _i$![]() is the typical radius of gyration of an ion in the plasma, and $R$
is the typical radius of gyration of an ion in the plasma, and $R$![]() is the major radius of the device. In the small $\rho _*$
is the major radius of the device. In the small $\rho _*$![]() limit, there are major simplifications to be had, corresponding physically to the opening of a wide ‘gap’ between typical radial correlation lengths $\lambda _{\rm corr}\sim \rho _i$
limit, there are major simplifications to be had, corresponding physically to the opening of a wide ‘gap’ between typical radial correlation lengths $\lambda _{\rm corr}\sim \rho _i$![]() of the turbulence and the radial gradient scale lengths $L\sim R$
of the turbulence and the radial gradient scale lengths $L\sim R$![]() . In contrast, present-day devices are not in the small $\rho _*$
. In contrast, present-day devices are not in the small $\rho _*$![]() limit, so turbulent eddies can be large enough to sample variations in the driving gradients and other relevant plasma properties. Additionally, because stellarators are non-axisymmetric, they have irreducible geometric variation within a given flux surface that makes the small $\rho _*$
limit, so turbulent eddies can be large enough to sample variations in the driving gradients and other relevant plasma properties. Additionally, because stellarators are non-axisymmetric, they have irreducible geometric variation within a given flux surface that makes the small $\rho _*$![]() limit more challenging. The turbulent correlation length $\lambda _{\rm corr}$
limit more challenging. The turbulent correlation length $\lambda _{\rm corr}$![]() must also be small compared with the distance that geometric differences within the flux surface change significantly. This limit exists for small enough $\rho _*$
must also be small compared with the distance that geometric differences within the flux surface change significantly. This limit exists for small enough $\rho _*$![]() , but it is roughly more challenging by a factor of the aspect ratio $R/a$
, but it is roughly more challenging by a factor of the aspect ratio $R/a$![]() , where $a$
, where $a$![]() is the minor radius of the torus. To account for the ‘mesoscale’ phenomena that may result and to complete the many quantitative validation studies that have been undertaken, many teams chose algorithms that handle radially non-local physics (often called ‘global’ codes). Codes that take advantage of the simpler, radially local, small $\rho _*$
is the minor radius of the torus. To account for the ‘mesoscale’ phenomena that may result and to complete the many quantitative validation studies that have been undertaken, many teams chose algorithms that handle radially non-local physics (often called ‘global’ codes). Codes that take advantage of the simpler, radially local, small $\rho _*$![]() limit are known as ‘flux-tube’ codes, and our new code GX is in this category. Several flux-tube turbulence calculations can then be coupled together with a transport solver to obtain transport time scale profile evolution on the device scale (Barnes et al. Reference Barnes, Abel, Dorland, Ernst, Hammett, Ricci, Rogers, Schekochihin and Tatsuno2009) or steady-state profiles (Candy et al. Reference Candy, Holland, Waltz, Fahey and Belli2009). This multiscale approach is asymptotically valid in the limit of vanishing $\rho _*$
limit are known as ‘flux-tube’ codes, and our new code GX is in this category. Several flux-tube turbulence calculations can then be coupled together with a transport solver to obtain transport time scale profile evolution on the device scale (Barnes et al. Reference Barnes, Abel, Dorland, Ernst, Hammett, Ricci, Rogers, Schekochihin and Tatsuno2009) or steady-state profiles (Candy et al. Reference Candy, Holland, Waltz, Fahey and Belli2009). This multiscale approach is asymptotically valid in the limit of vanishing $\rho _*$![]() (Abel et al. Reference Abel, Plunk, Wang, Barnes, Cowley, Dorland and Schekochihin2013). Recent work has also shown a novel approach to include radially global effects within the flux-tube formulation (Parra & Barnes Reference Parra and Barnes2015; St-Onge, Barnes & Parra Reference St-Onge, Barnes and Parra2022).
(Abel et al. Reference Abel, Plunk, Wang, Barnes, Cowley, Dorland and Schekochihin2013). Recent work has also shown a novel approach to include radially global effects within the flux-tube formulation (Parra & Barnes Reference Parra and Barnes2015; St-Onge, Barnes & Parra Reference St-Onge, Barnes and Parra2022).
To verify that GX correctly simulates gyrokinetic turbulence in the small $\rho _*$![]() limit, we present several tokamak and stellarator benchmarks of GX with established flux-tube gyrokinetic simulation codes. Note that while numerical verification (benchmarking) is code-specific, the extensive history of experimental validation of the gyrokinetic model is inherited by any verified gyrokinetic code and need not be repeated. GX is open-source scientific softwareFootnote 1 that is therefore ready for immediate design studies. Below, we show that GX can produce useful turbulence simulations in minutes using one (or a few) GPUs and higher fidelity results in a few hours using several GPUs.
limit, we present several tokamak and stellarator benchmarks of GX with established flux-tube gyrokinetic simulation codes. Note that while numerical verification (benchmarking) is code-specific, the extensive history of experimental validation of the gyrokinetic model is inherited by any verified gyrokinetic code and need not be repeated. GX is open-source scientific softwareFootnote 1 that is therefore ready for immediate design studies. Below, we show that GX can produce useful turbulence simulations in minutes using one (or a few) GPUs and higher fidelity results in a few hours using several GPUs.
Our algorithmic approach to solving the gyrokinetic system is based in pseudospectral methods. There is a long history of the use of Fourier pseudospectral methods in turbulence simulations to discretize the configuration space, especially in flux-tube gyrokinetic codes like GS2 (Kotschenreuther et al. Reference Kotschenreuther, Rewoldt and Tang1995; Dorland et al. Reference Dorland, Jenko, Kotschenreuther and Rogers2000), (non-global) GENE (Jenko & Dorland Reference Jenko and Dorland2001), CGYRO (Candy et al. Reference Candy, Belli and Bravenec2016) and stella (Barnes et al. Reference Barnes, Parra and Landreman2019). These methods have the advantage of spectrally accurate evaluation of derivatives. Building on this, we have developed a pseudospectral formulation for discretizing the velocity space in the gyrokinetic system using a Laguerre–Hermite spectral basis (Mandell, Dorland & Landreman Reference Mandell, Dorland and Landreman2018). Projecting the (perturbed) gyrokinetic distribution function onto this basis produces spectral modes that correspond to (gyro)fluid moment quantities (like density, parallel momentum, etc.), so that projection of the gyrokinetic equation corresponds to a gyrofluid system with arbitrarily many moments. In the lowest-resolution limit the model retains critical conservation laws (density, momentum, energy and free energy) and corresponds precisely to the well-established gyrofluid models of Dorland & Hammett (Reference Dorland and Hammett1993), Beer & Hammett (Reference Beer and Hammett1996) and Snyder & Hammett (Reference Snyder and Hammett2001) when their Landau-fluid closures are employed (Hammett & Perkins Reference Hammett and Perkins1990; Beer & Hammett Reference Beer and Hammett1996). At moderate velocity-space resolution, one can extend the Landau-fluid closure approach to accommodate more moments (Smith Reference Smith1997) or use ‘hypercollisions’ to close the moment hierarchy. At high velocity-space resolution, the model can retain a similar number of degrees of freedom as typically used in conventional gyrokinetic Eulerian models. A key advantage of our approach is therefore the flexibility to interpolate between these limits, depending on the desired balance of accuracy and speed for a particular calculation. Additionally, our Fourier–Laguerre–Hermite pseudospectral algorithm is a good fit for modern GPU computing: the algorithm relies heavily on fast transform methods that are well-optimized on GPUs, and the memory requirements of spectral algorithms are low enough to fit a problem onto one or a few GPUs. Several gyrokinetic codes have been ported to GPUs in recent years to target modern heterogeneous computing platforms (Madduri et al. Reference Madduri, Ibrahim, Williams, Im, Ethier, Shalf and Oliker2011; D'Azevedo et al. Reference D'Azevedo, Abbott, Koskela, Worley, Ku, Ethier, Yoon, Shephard, Hager, Lang, Choi, Podhorszki, Klasky, Parashar and Chang2018; Sfiligoi, Candy & Kostuk Reference Sfiligoi, Candy and Kostuk2018; Germaschewski et al. Reference Germaschewski, Allen, Dannert, Hrywniak, Donaghy, Merlo, Ethier, D'Azevedo, Jenko and Bhattacharjee2021; Ohana et al. Reference Ohana, Gheller, Lanti, Jocksch, Brunner and Villard2021; Belli et al. Reference Belli, Candy, Sfiligoi and Würthwein2022).
Similar works on Laguerre–Hermite spectral methods for drift kinetics (Jorge, Ricci & Loureiro Reference Jorge, Ricci and Loureiro2017) and gyrokinetics (Jorge, Frei & Ricci Reference Jorge, Frei and Ricci2019; Frei, Jorge & Ricci Reference Frei, Jorge and Ricci2020; Frei et al. Reference Frei, Ball, Hoffmann, Jorge, Ricci and Stenger2021; Frei, Ernst & Ricci Reference Frei, Ernst and Ricci2022a; Frei, Hoffmann & Ricci Reference Frei, Hoffmann and Ricci2022b; Hoffmann, Frei & Ricci Reference Hoffmann, Frei and Ricci2023a,Reference Hoffmann, Frei and Riccib) have shown promising results and can be viewed as complementary to our work. In particular, extensive linear benchmarks and convergence studies have been performed (Frei et al. Reference Frei, Hoffmann and Ricci2022b, Reference Frei, Hoffmann, Ricci, Brunner and Tecchioll2023), showing that the Laguerre–Hermite approach can be used successfully to model ion temperature gradient (ITG), trapped electron, kinetic ballooning and microtearing modes. Jorge et al. (Reference Jorge, Frei and Ricci2019), Frei et al. (Reference Frei, Ball, Hoffmann, Jorge, Ricci and Stenger2021, Reference Frei, Ernst and Ricci2022a,Reference Frei, Hoffmann and Riccib) develop, implement and study advanced gyrokinetic collision operators by leveraging the Laguerre–Hermite spectral approach. Nonlinear studies in Z-pinch (Hoffmann et al. Reference Hoffmann, Frei and Ricci2023b) and full toroidal (Hoffmann et al. Reference Hoffmann, Frei and Ricci2023a) geometry have also now been performed, showing that accurate nonlinear results, including the Dimits shift (Dimits et al. Reference Dimits, Bateman, Beer, Cohen, Dorland, Hammett, Kim, Kinsey, Kotschenreuther, Kritz, Lao, Mandrekas, Nevins, Parker, Redd, Shumaker, Sydora and Weiland2000), can be obtained with fewer basis functions than typically necessary for convergence of linear instabilities. Additionally, Frei et al. (Reference Frei, Jorge and Ricci2020) developed a Laguerre–Hermite projection of the full-$f$![]() gyrokinetic system to target the periphery of tokamaks, and Frei, Mencke & Ricci (Reference Frei, Mencke and Ricci2024) implemented the full-$f$
gyrokinetic system to target the periphery of tokamaks, and Frei, Mencke & Ricci (Reference Frei, Mencke and Ricci2024) implemented the full-$f$![]() system in slab geometry for modelling linear devices.
system in slab geometry for modelling linear devices.
The remainder of this paper is organized as follows. In § 2 we describe the gyrokinetic model. We describe the Fourier–Laguerre–Hermite pseudospectral formulation of the gyrokinetic system in § 4. Section 3 describes the magnetic geometry and coordinates used for tokamaks and stellarators. The time discretization scheme is described in § 5. In § 6, several benchmarks are presented comparing GX with established flux-tube gyrokinetic codes (GS2, GENE and stella) for linear and nonlinear cases in tokamak and stellarator geometries. Section 7 details the convergence properties of the Laguerre–Hermite basis for nonlinear calculations, along with details about GPU performance and multi-GPU scaling. Finally, we present the conclusions and future work in § 8.
2. Gyrokinetic model equations
In GX we solve the $\delta f$![]() gyrokinetic system. The literature of gyrokinetic theory is vast; our notation and philosophy follow four particular references: Antonsen & Lane (Reference Antonsen and Lane1980), Frieman & Chen (Reference Frieman and Chen1982), Barnes et al. (Reference Barnes, Abel, Dorland, Görler, Hammett and Jenko2010) and Abel et al. (Reference Abel, Plunk, Wang, Barnes, Cowley, Dorland and Schekochihin2013). The velocity space in gyrokinetic theory is two-dimensional because the particles gyrate very rapidly around their guiding centre position, averaging over any field variations that are encountered in one gyration period so that we can ignore the instantaneous position of the particle around its gyro-orbit. We choose to write the gyrokinetic equation in $(v_\parallel,\mu )$
gyrokinetic system. The literature of gyrokinetic theory is vast; our notation and philosophy follow four particular references: Antonsen & Lane (Reference Antonsen and Lane1980), Frieman & Chen (Reference Frieman and Chen1982), Barnes et al. (Reference Barnes, Abel, Dorland, Görler, Hammett and Jenko2010) and Abel et al. (Reference Abel, Plunk, Wang, Barnes, Cowley, Dorland and Schekochihin2013). The velocity space in gyrokinetic theory is two-dimensional because the particles gyrate very rapidly around their guiding centre position, averaging over any field variations that are encountered in one gyration period so that we can ignore the instantaneous position of the particle around its gyro-orbit. We choose to write the gyrokinetic equation in $(v_\parallel,\mu )$![]() coordinates, where $v_\parallel$
coordinates, where $v_\parallel$![]() is the speed in the direction of the magnetic field and $\mu \equiv v_\perp ^2/2B$
is the speed in the direction of the magnetic field and $\mu \equiv v_\perp ^2/2B$![]() is the magnetic moment, where $v_\perp$
is the magnetic moment, where $v_\perp$![]() is the speed perpendicular to the magnetic field and $B$
is the speed perpendicular to the magnetic field and $B$![]() is the local magnetic field strength. Using $\mu$
is the local magnetic field strength. Using $\mu$![]() as a coordinate takes advantage of the fact that $\mu$
as a coordinate takes advantage of the fact that $\mu$![]() is a gyrokinetic adiabatic invariant. These coordinates are not optimal for resolving the boundary layers in velocity that occur in linear gyrokinetic theory where particle orbits are ‘trapped’ in magnetic wells on one side of the boundary layer and ‘passing’ (untrapped) on the other. To resolve the sharp boundary layers it is better to use energy and pitch angle as one's velocity space coordinates (as is done in the GS2 code, for example, which optimizes its velocity space grid to enhance resolution near the trapped–passing boundary), but this leads to a considerably more complicated code implementation, particularly for stellarator applications, because of the need to carefully handle turning points in each magnetic well. However, in a sufficiently turbulent plasma, these boundary layers will be broadened, reducing the need for coordinates optimized for a sharp boundary. Thus, we have selected the coordinates that lead to simpler, more efficient code because we are particularly interested in calculating nonlinear turbulence properties (as opposed to linear stability conditions). These coordinates are also used in GENE and stella.
is a gyrokinetic adiabatic invariant. These coordinates are not optimal for resolving the boundary layers in velocity that occur in linear gyrokinetic theory where particle orbits are ‘trapped’ in magnetic wells on one side of the boundary layer and ‘passing’ (untrapped) on the other. To resolve the sharp boundary layers it is better to use energy and pitch angle as one's velocity space coordinates (as is done in the GS2 code, for example, which optimizes its velocity space grid to enhance resolution near the trapped–passing boundary), but this leads to a considerably more complicated code implementation, particularly for stellarator applications, because of the need to carefully handle turning points in each magnetic well. However, in a sufficiently turbulent plasma, these boundary layers will be broadened, reducing the need for coordinates optimized for a sharp boundary. Thus, we have selected the coordinates that lead to simpler, more efficient code because we are particularly interested in calculating nonlinear turbulence properties (as opposed to linear stability conditions). These coordinates are also used in GENE and stella.
Following (144) of Abel et al. (Reference Abel, Plunk, Wang, Barnes, Cowley, Dorland and Schekochihin2013), but expressing the equations in $(v_\parallel,\mu )$![]() velocity coordinates, neglecting strong equilibrium flows and normalizing all quantities to non-dimensional form (see appendix A), we have
velocity coordinates, neglecting strong equilibrium flows and normalizing all quantities to non-dimensional form (see appendix A), we have

Here, we have split the total distribution function as $F_s = F_{0s} + \delta f_s = F_{Ms}(1-Z_s\varPhi /\tau _s)+h_s$![]() , with $(Z_s/\tau _s) F_{Ms} \varPhi ({\boldsymbol r},t)$
, with $(Z_s/\tau _s) F_{Ms} \varPhi ({\boldsymbol r},t)$![]() and $h_s({\boldsymbol R},v_\parallel,\mu,t)$
and $h_s({\boldsymbol R},v_\parallel,\mu,t)$![]() the Boltzmann and non-Boltzmann parts of the $\delta f_s$
the Boltzmann and non-Boltzmann parts of the $\delta f_s$![]() perturbation, respectively. The equilibrium distribution function is a Maxwellian in energy $E$
perturbation, respectively. The equilibrium distribution function is a Maxwellian in energy $E$![]() (which we take to have no flows),
(which we take to have no flows),
and the fluctuating gyroaveraged distribution function satisfies $h_s\ll F_{Ms}$![]() . Note that in (2.1), the gradient of $F_M$
. Note that in (2.1), the gradient of $F_M$![]() at constant energy is denoted $\boldsymbol {\nabla }|_E F_M$
at constant energy is denoted $\boldsymbol {\nabla }|_E F_M$![]() . We also have the following dimensionless species parameters: equilibrium density $n_s$
. We also have the following dimensionless species parameters: equilibrium density $n_s$![]() ; equilibrium temperature $\tau _s$
; equilibrium temperature $\tau _s$![]() ; mass $m_s$
; mass $m_s$![]() , charge $Z_s$
, charge $Z_s$![]() ; thermal velocity $v_{ts}=\sqrt {\tau _s/m_s}$
; thermal velocity $v_{ts}=\sqrt {\tau _s/m_s}$![]() .
.
The distribution function describes the probability of finding a particle of species $s$![]() with gyrocentre position ${\boldsymbol R}$
with gyrocentre position ${\boldsymbol R}$![]() , velocity parallel to the magnetic field $v_\parallel$
, velocity parallel to the magnetic field $v_\parallel$![]() and magnetic moment $\mu =v_\perp ^2/2B$
and magnetic moment $\mu =v_\perp ^2/2B$![]() , where $v_\perp$
, where $v_\perp$![]() is the speed in the plane perpendicular to the magnetic field. The equilibrium magnetic field ${\boldsymbol B}$
is the speed in the plane perpendicular to the magnetic field. The equilibrium magnetic field ${\boldsymbol B}$![]() has magnitude $B=B({\boldsymbol r})$
has magnitude $B=B({\boldsymbol r})$![]() and direction $\hat {\boldsymbol b} = {\boldsymbol B}/B$
and direction $\hat {\boldsymbol b} = {\boldsymbol B}/B$![]() , and magnetic fluctuations are given by $\delta {\boldsymbol B} = \delta {\boldsymbol B}_\perp + \delta B_\parallel {\boldsymbol {\hat {b}}}$
, and magnetic fluctuations are given by $\delta {\boldsymbol B} = \delta {\boldsymbol B}_\perp + \delta B_\parallel {\boldsymbol {\hat {b}}}$![]() , where the perpendicular and parallel components can be expressed in terms of the vector potential ${\boldsymbol A} = {\boldsymbol A}_\perp + A_\parallel {\boldsymbol {\hat {b}}}$
, where the perpendicular and parallel components can be expressed in terms of the vector potential ${\boldsymbol A} = {\boldsymbol A}_\perp + A_\parallel {\boldsymbol {\hat {b}}}$![]() via $\delta {\boldsymbol B}_\perp = {[\boldsymbol {\nabla } \times {\boldsymbol A}]_\perp \simeq } \boldsymbol {\nabla } A_\parallel \times {\boldsymbol {\hat {b}}}$
via $\delta {\boldsymbol B}_\perp = {[\boldsymbol {\nabla } \times {\boldsymbol A}]_\perp \simeq } \boldsymbol {\nabla } A_\parallel \times {\boldsymbol {\hat {b}}}$![]() and $\delta B_\parallel = {\boldsymbol {\hat {b}}}\boldsymbol {\cdot }(\boldsymbol {\nabla } \times {\boldsymbol A}_\perp )$
and $\delta B_\parallel = {\boldsymbol {\hat {b}}}\boldsymbol {\cdot }(\boldsymbol {\nabla } \times {\boldsymbol A}_\perp )$![]() , respectively. The gyrokinetic potential $\chi ({\boldsymbol r},t)$
, respectively. The gyrokinetic potential $\chi ({\boldsymbol r},t)$![]() is composed of the electrostatic potential $\varPhi ({\boldsymbol r}, t)$
is composed of the electrostatic potential $\varPhi ({\boldsymbol r}, t)$![]() and the vector potential ${\boldsymbol A}({\boldsymbol r}, t)$
and the vector potential ${\boldsymbol A}({\boldsymbol r}, t)$![]() ,
,
and is a function of particle position $\boldsymbol r$![]() , where ${\boldsymbol r}= {\boldsymbol R} + \boldsymbol {\rho }$
, where ${\boldsymbol r}= {\boldsymbol R} + \boldsymbol {\rho }$![]() so that $\boldsymbol {\rho }$
so that $\boldsymbol {\rho }$![]() is the gyroradius vector that rotates at the gyrofrequency $\varOmega$
is the gyroradius vector that rotates at the gyrofrequency $\varOmega$![]() and points from the gyrocentre (at $\boldsymbol R$
and points from the gyrocentre (at $\boldsymbol R$![]() ) to the particle (at $\boldsymbol r$
) to the particle (at $\boldsymbol r$![]() ). In (2.1) gyroangle dependence is eliminated by gyroaveraging the potentials at fixed gyrocentre position ${\boldsymbol R}$
). In (2.1) gyroangle dependence is eliminated by gyroaveraging the potentials at fixed gyrocentre position ${\boldsymbol R}$![]() , denoted by
, denoted by
along with the corresponding gyroaveraged fluctuating velocity $\langle { {\boldsymbol v}_{\chi } \rangle }_{\boldsymbol R} = {\boldsymbol {\hat {b}}}\times \boldsymbol {\nabla } \langle { \chi \rangle }_{\boldsymbol R}$![]() . For most applications, the plasma $\beta$
. For most applications, the plasma $\beta$![]() is low and the magnetic drift velocity is ${\boldsymbol v}_d ={\hat {\boldsymbol b}}\times (v_\parallel ^2 {\hat {\boldsymbol b}}\boldsymbol {\cdot }\boldsymbol {\nabla }{\hat {\boldsymbol b}} + \mu \boldsymbol {\nabla } B)/B$
is low and the magnetic drift velocity is ${\boldsymbol v}_d ={\hat {\boldsymbol b}}\times (v_\parallel ^2 {\hat {\boldsymbol b}}\boldsymbol {\cdot }\boldsymbol {\nabla }{\hat {\boldsymbol b}} + \mu \boldsymbol {\nabla } B)/B$![]() . GX normally uses this low-$\beta$
. GX normally uses this low-$\beta$![]() approximation, but the full expression for the magnetic drifts can be selected at runtime.
approximation, but the full expression for the magnetic drifts can be selected at runtime.
The collision operator is denoted by $C(h)$![]() . Here we will follow Mandell et al. (Reference Mandell, Dorland and Landreman2018) and take the Dougherty model collision operator (Dougherty Reference Dougherty1964). Expressed in Fourier space, the like-species Dougherty collision operator is given by
. Here we will follow Mandell et al. (Reference Mandell, Dorland and Landreman2018) and take the Dougherty model collision operator (Dougherty Reference Dougherty1964). Expressed in Fourier space, the like-species Dougherty collision operator is given by

with the field-particle terms given by
Here we have the Bessel functions $J_{0 s}=J_{0}(\alpha _s)$![]() and $J_{1 s}=J_{1}(\alpha _s)$
and $J_{1 s}=J_{1}(\alpha _s)$![]() that result from the Fourier transform of gyroaverage operators, with $\alpha _s = \sqrt {2\mu B b_s}$
that result from the Fourier transform of gyroaverage operators, with $\alpha _s = \sqrt {2\mu B b_s}$![]() , $b_s = k_\perp ^2 \rho _s^2$
, $b_s = k_\perp ^2 \rho _s^2$![]() and $\rho _s = m_s v_{ts}/(Z_s B)$
and $\rho _s = m_s v_{ts}/(Z_s B)$![]() is the normalized gyroradius for species $s$
is the normalized gyroradius for species $s$![]() .
.
The Dougherty collision operator is a good physical model of like-particle collisions, which are important to gyrokinetic dynamics. It captures the physics of the collision operator presented in Abel et al. (Reference Abel, Barnes, Cowley, Dorland and Schekochihin2008), except that our collision frequency does not have velocity dependence, and there is no difference between the rates of pitch-angle scattering and slowing down. It is also attractive because its Laguerre–Hermite transform is sparse. More realistic collision operators could be included in our model in the future, such as those in Frei et al. (Reference Frei, Ball, Hoffmann, Jorge, Ricci and Stenger2021, Reference Frei, Ernst and Ricci2022a), which employs a similar Laguerre–Hermite spectral velocity approach as ours. The Dougherty model operator can also be extended to multiple species (Francisquez et al. Reference Francisquez, Juno, Hakim, Hammett and Ernst2022).
The electromagnetic potentials are determined by the gyrokinetic equivalent of Maxwell's equations. The electrostatic potential is determined by the quasineutrality equation,

where note that here the gyroaverage on the right-hand side is taken at constant particle position ${\boldsymbol r}$![]() . The parallel magnetic vector potential is determined by the parallel component of Ampère's law,
. The parallel magnetic vector potential is determined by the parallel component of Ampère's law,
with $\beta _\mathrm {ref} = 8{\rm \pi} n_\mathrm {ref} T_\mathrm {ref}/B_{\mathrm {N}}^2$![]() the plasma beta of the reference species. The perpendicular component of Ampère's law determines the perpendicular component of the vector potential, but is more conveniently expressed in terms of the parallel magnetic fluctuation, $\delta B_\parallel$
the plasma beta of the reference species. The perpendicular component of Ampère's law determines the perpendicular component of the vector potential, but is more conveniently expressed in terms of the parallel magnetic fluctuation, $\delta B_\parallel$![]() ,
,
where the double dot product is defined as $A : B = \sum _{ij} A_{ij} B_{ij}$![]() .
.
Finally, note that we can define an auxiliary distribution function
which eliminates the time derivative on the right-hand side of (2.1), resulting in
This is the form of the gyrokinetic equation that we will solve numerically.
3. Magnetic geometry and choice of coordinates
The geometric structure of a tokamak's magnetic field is axisymmetric, meaning there are no geometric variations that distinguish points at different toroidal angles. Most (but not all) gyrokinetic studies have focused on the axisymmetric limit. Stellarator magnetic fields are not axisymmetric. We have selected coordinates that are convenient for either case. Our spatial coordinates are aligned with the local background magnetic field so that we are able to efficiently resolve perturbations whose parallel wavelengths $\lambda _\parallel$![]() are $O(\rho _*^{-1})$
are $O(\rho _*^{-1})$![]() longer than the wavelengths $\lambda _\perp$
longer than the wavelengths $\lambda _\perp$![]() , perpendicular to the local magnetic field; these field-line-following coordinates reduce the number of grid points required to resolve the turbulence by a factor of $\rho _*$
, perpendicular to the local magnetic field; these field-line-following coordinates reduce the number of grid points required to resolve the turbulence by a factor of $\rho _*$![]() . In the case of stellarators, the lack of axisymmetry implies that even when one can describe the turbulence successfully as radially local, it might happen that the geometric variations in the binormal direction (within the magnetic surface) are not numerically well-separated from $\lambda _\perp$
. In the case of stellarators, the lack of axisymmetry implies that even when one can describe the turbulence successfully as radially local, it might happen that the geometric variations in the binormal direction (within the magnetic surface) are not numerically well-separated from $\lambda _\perp$![]() , even for reactor-relevant values of $\rho _*$
, even for reactor-relevant values of $\rho _*$![]() . We have chosen not to address this possibility; we assume that $\rho _*$
. We have chosen not to address this possibility; we assume that $\rho _*$![]() is small enough that the turbulence within each flux tube in a given flux surface is not affected by turbulence occurring in a different flux tube within the same surface.
is small enough that the turbulence within each flux tube in a given flux surface is not affected by turbulence occurring in a different flux tube within the same surface.
In this section, we will start with the general form of a divergence-free magnetic field, define key important quantities, various coordinate systems and briefly explain how they are used to obtain the geometry-dependent coefficients in the gyrokinetic model. Please refer to appendix E for specific mathematical details.
3.1. Axisymmetric configurations (tokamaks)
We start from the Clebsch form (D'haeseleer et al. Reference D'haeseleer, Hitchon, Callen and Shohet1991) for the equilibrium magnetic field:
We restrict our attention to solutions whose magnetic field lines lie on closed nested toroidal surfaces, known as flux surfaces. Here, flux surfaces are labelled by $\psi$![]() , a radial-like coordinate. On each surface, the binormal coordinate $\alpha$
, a radial-like coordinate. On each surface, the binormal coordinate $\alpha$![]() is a field-line label such that a line of constant $\alpha$
is a field-line label such that a line of constant $\alpha$![]() gives the path of a magnetic field line.
gives the path of a magnetic field line.
For tokamaks, we choose to define the coordinate $\psi$![]() to be the enclosed poloidal flux divided by $2{\rm \pi}$
to be the enclosed poloidal flux divided by $2{\rm \pi}$![]() ,
,
and the binormal coordinate $\alpha$![]() is chosen to be
is chosen to be
where $\phi$![]() and $\theta$
and $\theta$![]() are ‘straight-field-line’ toroidal and poloidal angles, respectively, and
are ‘straight-field-line’ toroidal and poloidal angles, respectively, and
is the safety factor.
3.2. Non-axisymmetric configurations (stellarators)
For stellarators, we find it more convenient to write the magnetic field in Clebsch form as
with the toroidal flux chosen as the radial-like coordinate,
and the binormal coordinate chosen to be
Here, $\iota (\psi ) = 1/q(\psi )$![]() is the rotational transform, and once again $\phi$
is the rotational transform, and once again $\phi$![]() and $\theta$
and $\theta$![]() are ‘straight-field-line’ toroidal and poloidal angles, respectively.
are ‘straight-field-line’ toroidal and poloidal angles, respectively.
3.3. Field-aligned coordinate system
Since GX is a local flux-tube code, it is advantageous to use a field-aligned coordinate system. Therefore, we introduce the field-aligned, flux-tube coordinates $(x, y, z)$![]() used by Beer, Cowley & Hammett (Reference Beer, Cowley and Hammett1995). Here, $x = x(\psi )$
used by Beer, Cowley & Hammett (Reference Beer, Cowley and Hammett1995). Here, $x = x(\psi )$![]() is a radial coordinate, $y= y(\alpha )$
is a radial coordinate, $y= y(\alpha )$![]() is a binormal coordinate, and $z=z(\theta )$
is a binormal coordinate, and $z=z(\theta )$![]() is a field-line-following coordinate that parametrizes distance along the equilibrium magnetic field using the poloidal angle $\theta$
is a field-line-following coordinate that parametrizes distance along the equilibrium magnetic field using the poloidal angle $\theta$![]() . The coordinates $x$
. The coordinates $x$![]() and $y$
and $y$![]() are normalized forms of $\psi$
are normalized forms of $\psi$![]() and $\alpha$
and $\alpha$![]() such that
such that
where $\psi _0$![]() and $\alpha _0$
and $\alpha _0$![]() are the values of equilibrium $\psi$
are the values of equilibrium $\psi$![]() and $\alpha$
and $\alpha$![]() at the centre of the flux tube. The coordinates $(x, y, z)$
at the centre of the flux tube. The coordinates $(x, y, z)$![]() have units of length. In the local flux-tube, $x$
have units of length. In the local flux-tube, $x$![]() and $y$
and $y$![]() vary on the length scale of the gyroradius whereas $z$
vary on the length scale of the gyroradius whereas $z$![]() varies on the length scale of the machine size. We require an equispaced coordinate $z$
varies on the length scale of the machine size. We require an equispaced coordinate $z$![]() along the field line, which is needed to utilize the Fourier spectral treatment of the parallel derivative terms in the gyrokinetic equation. The procedure for obtaining an equispaced, equal-arc $z$
along the field line, which is needed to utilize the Fourier spectral treatment of the parallel derivative terms in the gyrokinetic equation. The procedure for obtaining an equispaced, equal-arc $z$![]() coordinate is provided in appendix E.
coordinate is provided in appendix E.
Upon defining the field-aligned coordinate system, we can calculate the geometric coefficients required to compute the various terms in the gyrokinetic equation, as described briefly in appendix E. For a three-dimensional equilibrium, GX can read the output data generated by the VMEC code (Hirshman & Whitson Reference Hirshman and Whitson1983). For a two-dimensional axisymmetric equilibrium, GX can use a local equilibrium defined using a Miller parametrization (Miller et al. Reference Miller, Chu, Greene, Lin-Liu and Waltz1998). The user also has the option to work with simpler geometries like a slab or a cylindrical Z-pinch. Besides these native geometry options, GX can also read geometry data generated by the geometry module in the GS2 code; for example, this enables the capability to use experimentally relevant geometry derived from an EFIT equilibrium reconstruction.
4. Fourier–Laguerre–Hermite pseudospectral formulation
Here we present the Fourier–Laguerre–Hermite formulation of the electromagnetic $\delta f$![]() gyrokinetic system. Following Mandell et al. (Reference Mandell, Dorland and Landreman2018), and extending to include electromagnetic fluctuations, we solve the gyrokinetic equation by taking a Fourier transform in the perpendicular directions (which we will call $x$
gyrokinetic system. Following Mandell et al. (Reference Mandell, Dorland and Landreman2018), and extending to include electromagnetic fluctuations, we solve the gyrokinetic equation by taking a Fourier transform in the perpendicular directions (which we will call $x$![]() and $y$
and $y$![]() ; the parallel direction will be $z$
; the parallel direction will be $z$![]() ), a Laguerre transform in $\mu B$
), a Laguerre transform in $\mu B$![]() , and a Hermite transform in $v_\parallel$
, and a Hermite transform in $v_\parallel$![]() . Note that there are no major disadvantages to the choice of $\mu B$
. Note that there are no major disadvantages to the choice of $\mu B$![]() versus $\mu$
versus $\mu$![]() as a coordinate, and our choice to use $\mu B$
as a coordinate, and our choice to use $\mu B$![]() is natural because the Laguerre weight function becomes $\exp (-\mu B)$
is natural because the Laguerre weight function becomes $\exp (-\mu B)$![]() just like in the Maxwellian distribution.
just like in the Maxwellian distribution.
We define the Fourier–Laguerre–Hermite transform of the distribution function $h_{s}$![]() for species $s$
for species $s$![]() as
as

where ${\boldsymbol k_\perp } =k_x\boldsymbol {\nabla } x + k_y \boldsymbol {\nabla } y$![]() is the perpendicular wavenumber vector, $\psi _\ell (\mu B) = (-1)^\ell {\rm L}_{\ell }(\mu B)$
is the perpendicular wavenumber vector, $\psi _\ell (\mu B) = (-1)^\ell {\rm L}_{\ell }(\mu B)$![]() with
with
the Laguerre polynomials, and $\phi _m (v_\parallel ) = {{\rm He}_{m}({v}_\parallel )}/{\sqrt {m!}}$![]() with
with
the probabilists’ Hermite polynomials. In Fourier space, gyroaveraging operations (whether at constant $\boldsymbol R$![]() or constant $\boldsymbol r$
or constant $\boldsymbol r$![]() ) simply become multiplications by Bessel functions, so that the Fourier transform of the gyroaveraged potential is
) simply become multiplications by Bessel functions, so that the Fourier transform of the gyroaveraged potential is
Weighting the gyroaveraged potential by a Maxwellian and Laguerre–Hermite transforming results in
with

and $\mathcal {J}_\ell ^s\equiv 0$![]() when $\ell <0$
when $\ell <0$![]() or when $\ell \geq N_\ell$
or when $\ell \geq N_\ell$![]() , with $N_\ell$
, with $N_\ell$![]() the number of evolved Laguerre moments. The Fourier–Laguerre–Hermite transform of the auxiliary distribution function $g$
the number of evolved Laguerre moments. The Fourier–Laguerre–Hermite transform of the auxiliary distribution function $g$![]() is then
is then
The Fourier–Laguerre–Hermite transform of (2.13) then gives

Parallel convection, including bounce motion induced by magnetic trapping in the equilibrium magnetic field, is described by the terms proportional to $\boldsymbol {\nabla }_\parallel \equiv {\hat {\boldsymbol b}} \boldsymbol {\cdot } \boldsymbol {\nabla } = ({\hat {\boldsymbol b}}\boldsymbol {\cdot }\boldsymbol {\nabla } z) \partial /\partial z$![]() . The $\boldsymbol {\nabla }_\parallel H{^s_{\ell,m}}$
. The $\boldsymbol {\nabla }_\parallel H{^s_{\ell,m}}$![]() terms are evaluated spectrally by Fourier transforming in $z$
terms are evaluated spectrally by Fourier transforming in $z$![]() ,
,
with
Note that a spectral evaluation of this term requires an equispaced grid in $z$![]() , and we also require the $z$
, and we also require the $z$![]() coordinate to be an equal-arclength coordinate so that $({\hat {\boldsymbol b}}\boldsymbol {\cdot }\boldsymbol {\nabla } z)$
coordinate to be an equal-arclength coordinate so that $({\hat {\boldsymbol b}}\boldsymbol {\cdot }\boldsymbol {\nabla } z)$![]() is a constant (see § E.1) to avoid a convolution in (4.10). Additional details about this operation related to boundary conditions are given in § 4.2. Toroidicity gives rise to the terms proportional to the curvature drift operator ${\rm i} \omega _d^{\kappa } = (1/B){\hat {\boldsymbol b}}\times ({\hat {\boldsymbol b}}\boldsymbol {\cdot }\boldsymbol {\nabla }{\hat {\boldsymbol b}})\boldsymbol {\cdot } {{\rm i}\boldsymbol k_\perp }$
is a constant (see § E.1) to avoid a convolution in (4.10). Additional details about this operation related to boundary conditions are given in § 4.2. Toroidicity gives rise to the terms proportional to the curvature drift operator ${\rm i} \omega _d^{\kappa } = (1/B){\hat {\boldsymbol b}}\times ({\hat {\boldsymbol b}}\boldsymbol {\cdot }\boldsymbol {\nabla }{\hat {\boldsymbol b}})\boldsymbol {\cdot } {{\rm i}\boldsymbol k_\perp }$![]() and the $\boldsymbol {\nabla } B$
and the $\boldsymbol {\nabla } B$![]() drift operator ${\rm i} \omega _d^{\boldsymbol {\nabla } B} = (1/B^2){\hat {\boldsymbol b}}\times \boldsymbol {\nabla } B\boldsymbol {\cdot } {{\rm i}\boldsymbol k_\perp }$
drift operator ${\rm i} \omega _d^{\boldsymbol {\nabla } B} = (1/B^2){\hat {\boldsymbol b}}\times \boldsymbol {\nabla } B\boldsymbol {\cdot } {{\rm i}\boldsymbol k_\perp }$![]() is the $\boldsymbol {\nabla } B$
is the $\boldsymbol {\nabla } B$![]() . Drive terms from equilibrium gradients, denoted by $\mathcal {D}_{\ell,m}$
. Drive terms from equilibrium gradients, denoted by $\mathcal {D}_{\ell,m}$![]() , are given by
, are given by

where ${\rm i} \omega _*\equiv -\boldsymbol {\nabla } x \boldsymbol {\cdot } {\hat {\boldsymbol b}}\times {\rm i}{\boldsymbol k_\perp }={\rm i} k_y$![]() , and $L_{ns}$
, and $L_{ns}$![]() and $L_{Ts}$
and $L_{Ts}$![]() are the normalized density and temperature gradient scale lengths, respectively.
are the normalized density and temperature gradient scale lengths, respectively.
The like-species collision terms are given by

with the field-particle terms given by




The nonlinear terms are evaluated pseudospectrally in $(x,y,z,\mu B, m)$![]() space to avoid convolutions in both Fourier and Laguerre coefficients as (Mandell et al. Reference Mandell, Dorland and Landreman2018)
space to avoid convolutions in both Fourier and Laguerre coefficients as (Mandell et al. Reference Mandell, Dorland and Landreman2018)
where the complete pseudospectral expression for this term is given in appendix D.
Taking the Fourier–Laguerre–Hermite transform of the field equations, the quasineutrality equation, (2.9), becomes

the parallel component of Ampère's law, (2.10), becomes

and the perpendicular component of Ampère's law, (2.11), becomes

To solve these field equations numerically, it is more convenient to express them in terms of $G$![]() rather than $H$
rather than $H$![]() , which results in
, which results in



Note that while the sum $\sum (\mathcal {J}_\ell ^s)^2$![]() could be computed analytically in the $N_\ell \rightarrow \infty$
could be computed analytically in the $N_\ell \rightarrow \infty$![]() limit as $\varGamma _0(b) = I_0(b) \,{\rm e}^{-b}$
limit as $\varGamma _0(b) = I_0(b) \,{\rm e}^{-b}$![]() , with $I_0$
, with $I_0$![]() the modified Bessel function of the first kind, doing so breaks the energetic consistency of the equations (Mandell et al. Reference Mandell, Dorland and Landreman2018); thus these terms should be evaluated as truncated sums.
the modified Bessel function of the first kind, doing so breaks the energetic consistency of the equations (Mandell et al. Reference Mandell, Dorland and Landreman2018); thus these terms should be evaluated as truncated sums.
4.1. Hyperdissipation and closure
Grid-scale dissipation terms are used to ensure numerical stability and robustness. For dissipation in configuration space, we employ a hyperviscosity term of the standard form

where $k_{\perp,\mathrm {max}}$![]() is the largest dealiased perpendicular wavenumber in the simulation, and typical values of the variable parameters for nonlinear simulations are $D=0.05$
is the largest dealiased perpendicular wavenumber in the simulation, and typical values of the variable parameters for nonlinear simulations are $D=0.05$![]() and $n=2$
and $n=2$![]() . This provides a sink at the shortest wavelengths in the domain, which can be useful in nonlinear simulations to avoid spectral pileup. Unlike in other Eulerian gyrokinetic codes which include dissipation along the parallel direction via upwinding, (Kotschenreuther et al. Reference Kotschenreuther, Rewoldt and Tang1995; Jenko & Dorland Reference Jenko and Dorland2001; Candy et al. Reference Candy, Belli and Bravenec2016; Barnes et al. Reference Barnes, Parra and Landreman2019), the spectral discretization scheme used for the parallel direction in GX does not itself introduce dissipation in the parallel direction. The hypercollision operator and the parallel boundary conditions discussed below introduce some parallel dissipation. A standard parallel hyperdissipation operator of the form $k_\parallel ^{2n}$
. This provides a sink at the shortest wavelengths in the domain, which can be useful in nonlinear simulations to avoid spectral pileup. Unlike in other Eulerian gyrokinetic codes which include dissipation along the parallel direction via upwinding, (Kotschenreuther et al. Reference Kotschenreuther, Rewoldt and Tang1995; Jenko & Dorland Reference Jenko and Dorland2001; Candy et al. Reference Candy, Belli and Bravenec2016; Barnes et al. Reference Barnes, Parra and Landreman2019), the spectral discretization scheme used for the parallel direction in GX does not itself introduce dissipation in the parallel direction. The hypercollision operator and the parallel boundary conditions discussed below introduce some parallel dissipation. A standard parallel hyperdissipation operator of the form $k_\parallel ^{2n}$![]() could also be included, but we find that this is not necessary for the linear and nonlinear cases that we consider.
could also be included, but we find that this is not necessary for the linear and nonlinear cases that we consider.
Fine-scale structure in velocity space must also be regulated. The Dougherty collision operator fulfils this purpose by acting increasingly strongly on higher Laguerre and Hermite moments, limiting their amplitude. Thus, for a given collisionality, there is a physical cutoff at some ${\ell _\mathrm {cut}}$![]() and ${m_\mathrm {cut}}$
and ${m_\mathrm {cut}}$![]() beyond which fine scales in velocity space are completely wiped out by collisions. At this point, closure of the Laguerre–Hermite moment series by simple truncation (setting $G_{\ell,m}=0$
beyond which fine scales in velocity space are completely wiped out by collisions. At this point, closure of the Laguerre–Hermite moment series by simple truncation (setting $G_{\ell,m}=0$![]() for $\ell \geq {\ell _\mathrm {cut}}$
for $\ell \geq {\ell _\mathrm {cut}}$![]() or $m\geq {m_\mathrm {cut}}$
or $m\geq {m_\mathrm {cut}}$![]() ) is justified. This is the simplest high-resolution closure, but not the only option. One can also obtain an asymptotically correct collisional closure by assuming the collision term becomes dominant in the unresolved moment equations (Zocco, Helander & Connor Reference Zocco, Helander and Connor2015; Loureiro et al. Reference Loureiro, Dorland, Fazendeiro, Kanekar, Mallet, Vilelas and Zocco2016; Jorge et al. Reference Jorge, Ricci and Loureiro2017; Frei et al. Reference Frei, Hoffmann and Ricci2022b).
) is justified. This is the simplest high-resolution closure, but not the only option. One can also obtain an asymptotically correct collisional closure by assuming the collision term becomes dominant in the unresolved moment equations (Zocco, Helander & Connor Reference Zocco, Helander and Connor2015; Loureiro et al. Reference Loureiro, Dorland, Fazendeiro, Kanekar, Mallet, Vilelas and Zocco2016; Jorge et al. Reference Jorge, Ricci and Loureiro2017; Frei et al. Reference Frei, Hoffmann and Ricci2022b).
In the limit of low collisionality or lower Laguerre–Hermite resolution, however, the closure situation is more complicated. Unresolved moments are not expected to be negligible at collisionalities of interest, so closure by truncation will generally give poor results. One possible approach is to follow the collisionless closure approach pioneered by Hammett & Perkins (Reference Hammett and Perkins1990), which was used and extended in the gyrofluid models of Dorland & Hammett (Reference Dorland and Hammett1993), Beer & Hammett (Reference Beer and Hammett1996), Snyder & Hammett (Reference Snyder and Hammett2001) and Smith (Reference Smith1997) to model parallel, toroidal and nonlinear finite-Larmor-radius (FLR) phase mixing. However, the development of generalized closures in toroidal geometry for a system with an arbitrary number of moments is complicated and beyond the scope of the current work. Instead, we have found that employing a hypercollision operator that provides a sink at large $m$![]() allows well-behaved results even with simple closure by truncation at relatively low resolution. The operator takes the generic form
allows well-behaved results even with simple closure by truncation at relatively low resolution. The operator takes the generic form
We ensure that the operator conserves density, momentum and energy by only operating on moments with $m>2$![]() . Similar hypercollision operators (in Hermite space only) have been used in other contexts (Parker Reference Parker2015; Parker & Dellar Reference Parker and Dellar2015; Loureiro et al. Reference Loureiro, Dorland, Fazendeiro, Kanekar, Mallet, Vilelas and Zocco2016), and Parker (Reference Parker2015) also develops theory of a ‘hypercollisional plateau’ where the behaviour of the operator is insensitive to the choice of the variable parameters. In our operator, the coefficient $\nu _\mathrm {hyp}$
. Similar hypercollision operators (in Hermite space only) have been used in other contexts (Parker Reference Parker2015; Parker & Dellar Reference Parker and Dellar2015; Loureiro et al. Reference Loureiro, Dorland, Fazendeiro, Kanekar, Mallet, Vilelas and Zocco2016), and Parker (Reference Parker2015) also develops theory of a ‘hypercollisional plateau’ where the behaviour of the operator is insensitive to the choice of the variable parameters. In our operator, the coefficient $\nu _\mathrm {hyp}$![]() is chosen to approximately remove the same amount of fluctuation energy from the largest $m$
is chosen to approximately remove the same amount of fluctuation energy from the largest $m$![]() s as would be removed by parallel phase mixing. The details are provided in § B, and the result is
s as would be removed by parallel phase mixing. The details are provided in § B, and the result is
where $f_\mathrm {hyp}$![]() is an adjustable coefficient that is typically set to unity. The $|k_\parallel |$
is an adjustable coefficient that is typically set to unity. The $|k_\parallel |$![]() operator is evaluated spectrally by Fourier transforming in $z$
operator is evaluated spectrally by Fourier transforming in $z$![]() . The exponent $p$
. The exponent $p$![]() is chosen to be $p=N_m/2$
is chosen to be $p=N_m/2$![]() , which ensures that only the highest several Hermite modes are strongly damped, roughly independent of $N_m$
, which ensures that only the highest several Hermite modes are strongly damped, roughly independent of $N_m$![]() . While one could consider a similar hyperdissipation mechanism for large $\ell$
. While one could consider a similar hyperdissipation mechanism for large $\ell$![]() , we find that Laguerre hypercollisions are unnecessary even when using relatively low Laguerre resolution ($N_\ell \sim 4$
, we find that Laguerre hypercollisions are unnecessary even when using relatively low Laguerre resolution ($N_\ell \sim 4$![]() ) for problems of interest because phase mixing in $v_\parallel$
) for problems of interest because phase mixing in $v_\parallel$![]() dominates.
dominates.
4.2. Boundary conditions
In the flux tube approach we assume statistical periodicity in the perpendicular $(x,y)$![]() plane. In the parallel direction, we use the ‘twist-and-shift’ boundary condition (Beer et al. Reference Beer, Cowley and Hammett1995), which in the spectral representation can be accomplished by linking modes with different $k_x$
plane. In the parallel direction, we use the ‘twist-and-shift’ boundary condition (Beer et al. Reference Beer, Cowley and Hammett1995), which in the spectral representation can be accomplished by linking modes with different $k_x$![]() values into an extended $z$
values into an extended $z$![]() domain, such that
domain, such that
with $\delta k = 2{\rm \pi} k_y \hat {s}$![]() . We can then perform a Fourier transform on each extended $z$
. We can then perform a Fourier transform on each extended $z$![]() domain to evaluate the parallel streaming terms as given by (4.10).
domain to evaluate the parallel streaming terms as given by (4.10).
A Fourier representation naturally enforces a periodic boundary condition on $h$![]() at the ends of each extended domain, but this is not the physically correct boundary condition for non-zonal modes, which should have a zero incoming boundary condition in the infinite ballooning limit. Following Kotschenreuther et al. (Reference Kotschenreuther, Rewoldt and Tang1995), we would like to approximate this by enforcing a zero incoming boundary condition on $h$
at the ends of each extended domain, but this is not the physically correct boundary condition for non-zonal modes, which should have a zero incoming boundary condition in the infinite ballooning limit. Following Kotschenreuther et al. (Reference Kotschenreuther, Rewoldt and Tang1995), we would like to approximate this by enforcing a zero incoming boundary condition on $h$![]() at the ends of the extended domain, but this boundary condition cannot be enforced directly in Hermite space. Instead, we use a wave-absorbing layer (see e.g. Durran (Reference Durran2010), and references within) near the ends of each extended $z$
at the ends of the extended domain, but this boundary condition cannot be enforced directly in Hermite space. Instead, we use a wave-absorbing layer (see e.g. Durran (Reference Durran2010), and references within) near the ends of each extended $z$![]() domain for the non-zonal components of $h$
domain for the non-zonal components of $h$![]() to damp out perturbations leaving and re-entering the domain due to the natural periodicity of the Fourier representation. Following Beer (Reference Beer1995), we use a damping filter that is zero in most of the domain and ramps up smoothly near the ends of the extended domain as $d(\hat {z}) = A[1-2\hat {z}^2/(1+\hat {z}^4)]$
to damp out perturbations leaving and re-entering the domain due to the natural periodicity of the Fourier representation. Following Beer (Reference Beer1995), we use a damping filter that is zero in most of the domain and ramps up smoothly near the ends of the extended domain as $d(\hat {z}) = A[1-2\hat {z}^2/(1+\hat {z}^4)]$![]() , where $\hat {z} = (z-z_\mathrm {end})/z_\mathrm {width}$
, where $\hat {z} = (z-z_\mathrm {end})/z_\mathrm {width}$![]() is a normalized distance from the ends $z_\mathrm {end}$
is a normalized distance from the ends $z_\mathrm {end}$![]() . The width $z_\mathrm {width}$
. The width $z_\mathrm {width}$![]() and the scaling factor $A$
and the scaling factor $A$![]() are adjustable parameters; in appendix C we have performed a convergence study and found $z_\mathrm {width} = L_z/8$
are adjustable parameters; in appendix C we have performed a convergence study and found $z_\mathrm {width} = L_z/8$![]() and $A = 0.1/\Delta t$
and $A = 0.1/\Delta t$![]() to work well, where $L_z$
to work well, where $L_z$![]() the total length of the extended domain. The wave-absorbing damping operation can then be expressed as
the total length of the extended domain. The wave-absorbing damping operation can then be expressed as
The zonal modes $(k_y=0)$![]() are not filtered because these modes should be physically periodic, so the natural periodic boundary condition from the Fourier representation is the correct one. We have found this wave-absorbing layer to be particularly necessary for simulations with kinetic electrons.
are not filtered because these modes should be physically periodic, so the natural periodic boundary condition from the Fourier representation is the correct one. We have found this wave-absorbing layer to be particularly necessary for simulations with kinetic electrons.
The standard twist-and-shift boundary condition can be ill-suited for low magnetic shear regions, particularly in stellarators. Martin et al. (Reference Martin, Landreman, Xanthopoulos, Mandell and Dorland2018) have developed a generalization of the twist-and-shift boundary condition that alleviates some of these issues by using the integrated local shear (rather than global shear) in the ‘twist’. This generalized twist-and-shift boundary condition can be used in GX for stellarator geometries with stellarator symmetry. Investigation of a non-twisting flux-tube boundary condition (Ball & Brunner Reference Ball and Brunner2021) using GX is also in progress.
Martin et al. (Reference Martin, Landreman, Xanthopoulos, Mandell and Dorland2018) prescribe methods to choose the parallel domain length to enforce exact periodicity or continuous magnetic drifts at the ends of the flux tube. In addition to these options, we adopt an additional criterion for choosing the parallel domain length: to enforce a desired aspect ratio for the perpendicular computational domain. When using the standard twist-and-shift boundary condition, the aspect ratio is quantized as $L_x/L_y = J/(2{\rm \pi} |\hat {s}|)$![]() , with $J$
, with $J$![]() a non-zero integer. This results in $L_x \propto L_y/\hat {s}$
a non-zero integer. This results in $L_x \propto L_y/\hat {s}$![]() , which makes resolution requirements challenging for $\hat {s}\ll 1$
, which makes resolution requirements challenging for $\hat {s}\ll 1$![]() . In the generalized twist-and-shift boundary condition of Martin et al. (Reference Martin, Landreman, Xanthopoulos, Mandell and Dorland2018), the perpendicular aspect ratio of the flux tube is given by
. In the generalized twist-and-shift boundary condition of Martin et al. (Reference Martin, Landreman, Xanthopoulos, Mandell and Dorland2018), the perpendicular aspect ratio of the flux tube is given by
where $z_\mathrm {end}$![]() is the end of the flux tube and $J$
is the end of the flux tube and $J$![]() is again a non-zero integer. In a stellarator, this quantity varies as a function of the parallel domain length (see figure 7 of Martin et al. (Reference Martin, Landreman, Xanthopoulos, Mandell and Dorland2018)). The generalized twist-and-shift boundary condition thus provides the freedom to choose $z_\mathrm {end}$
is again a non-zero integer. In a stellarator, this quantity varies as a function of the parallel domain length (see figure 7 of Martin et al. (Reference Martin, Landreman, Xanthopoulos, Mandell and Dorland2018)). The generalized twist-and-shift boundary condition thus provides the freedom to choose $z_\mathrm {end}$![]() to obtain the desired aspect ratio (for some integer $J$
to obtain the desired aspect ratio (for some integer $J$![]() ). Using this prescription to enforce an aspect ratio of order unity can then alleviate the resolution requirements for geometries with small magnetic shear.
). Using this prescription to enforce an aspect ratio of order unity can then alleviate the resolution requirements for geometries with small magnetic shear.
5. Timestepping schemes
GX uses explicit time integration methods to advance the system. Along with several standard Runge–Kutta (RK) and strong stability-preserving RK (SSP RK) schemes (Gottlieb, Shu & Tadmor Reference Gottlieb, Shu and Tadmor2001), we also provide an option for the SSP 10-stage fourth-order method of Ketcheson (Reference Ketcheson2008) (a low-storage method ideal for the memory constraints of GPU computing). Additionally, the sparse banded structure of the linear system of (4.9) and the fact that the field equations only involve the lowest-order moments (instead of requiring integration over all velocity space) could allow the development of efficient implicit–explicit (IMEX) schemes for electron dynamics that avoid the timestep restriction of the fast electron motion; this will be a topic for future work. We have used the standard RK3 (third-order) scheme for all of the benchmark calculations presented in § 6.
In all of our timestepping schemes the timestep size $\Delta t$![]() is constrained by the stability region of the scheme. While in principle the linear eigenvalues of the system could be computed exactly and used to constrain the timestep to ensure that all eigenvalues lie within the stability region, we instead estimate the maximum (linear and nonlinear) frequencies on the grid in each of the $(x,y,z)$
is constrained by the stability region of the scheme. While in principle the linear eigenvalues of the system could be computed exactly and used to constrain the timestep to ensure that all eigenvalues lie within the stability region, we instead estimate the maximum (linear and nonlinear) frequencies on the grid in each of the $(x,y,z)$![]() directions via
directions via
with

the maximum shear Alfvén frequency on the grid. In the electrostatic limit ($\beta _\mathrm {ref} = 0$![]() ) this reduces to the high-frequency $\omega _H$
) this reduces to the high-frequency $\omega _H$![]() mode (Lee Reference Lee1987). Here, $k_{z,\mathrm {max}}$
mode (Lee Reference Lee1987). Here, $k_{z,\mathrm {max}}$![]() is the largest parallel wavenumber in the simulation and $k_{\perp,\mathrm {min}}$
is the largest parallel wavenumber in the simulation and $k_{\perp,\mathrm {min}}$![]() is the smallest perpendicular wavenumber. To evaluate $v_{\parallel,\mathrm {max}}$
is the smallest perpendicular wavenumber. To evaluate $v_{\parallel,\mathrm {max}}$![]() and $(\mu B)_\mathrm {max}$
and $(\mu B)_\mathrm {max}$![]() we use the maximum value of the Gauss–Hermite and Gauss–Laguerre collocation grids, respectively, which depend on the number of spectral modes used in the calculation, $N_m$
we use the maximum value of the Gauss–Hermite and Gauss–Laguerre collocation grids, respectively, which depend on the number of spectral modes used in the calculation, $N_m$![]() and $N_\ell$
and $N_\ell$![]() .
.
The constraint on the maximum stable timestep is then approximately given by
where $s$![]() is dependent on the stability region for the particular timestepping scheme (for example, $s=1.73$
is dependent on the stability region for the particular timestepping scheme (for example, $s=1.73$![]() for RK3, and $s=2.82$
for RK3, and $s=2.82$![]() for RK4), and $0< C\leq 1$
for RK4), and $0< C\leq 1$![]() is a user-defined scaling factor. Formally, the stability constraint with $C=1$
is a user-defined scaling factor. Formally, the stability constraint with $C=1$![]() is only valid for linear modes that do not grow or decay; thus we typically use $C\sim 0.5$
is only valid for linear modes that do not grow or decay; thus we typically use $C\sim 0.5$![]() –0.9 to ensure stability in the full nonlinear system with a spectrum of growing and damped modes.
–0.9 to ensure stability in the full nonlinear system with a spectrum of growing and damped modes.
6. Numerical benchmarks
In this section we show a variety of linear and nonlinear benchmarks of GX by comparing results with widely benchmarked gyrokinetic codes (GS2, stella, GENE) in both tokamak and stellarator geometry. In all cases, both linear and nonlinear, an initial value problem is solved. The numerical resolution and associated parameters used in each case are given in appendix G.
6.1. Tokamak benchmarks: Cyclone base case
For benchmarks in tokamak geometry, we choose a configuration based on the ‘Cyclone base case’ (CBC), a widely used benchmark case with concentric circular flux surfaces (Dimits et al. Reference Dimits, Bateman, Beer, Cohen, Dorland, Hammett, Kim, Kinsey, Kotschenreuther, Kritz, Lao, Mandrekas, Nevins, Parker, Redd, Shumaker, Sydora and Weiland2000). For this we use a Miller local equilibrium (Miller et al. Reference Miller, Chu, Greene, Lin-Liu and Waltz1998) with $R_0/a=2.78$![]() , $r/a=0.5$
, $r/a=0.5$![]() , $q=1.4$
, $q=1.4$![]() , $\hat {s}=0.8$
, $\hat {s}=0.8$![]() , $\kappa =1.0$
, $\kappa =1.0$![]() , $\delta =0.0$
, $\delta =0.0$![]() . Unless otherwise noted, the normalized gradient scale lengths are taken to be $a/L_{ni} = a/L_{ne} = 0.8$
. Unless otherwise noted, the normalized gradient scale lengths are taken to be $a/L_{ni} = a/L_{ne} = 0.8$![]() , $a/L_{Ti} = a/L_{Te}= 2.49$
, $a/L_{Ti} = a/L_{Te}= 2.49$![]() , and we also take $T_i = T_e$
, and we also take $T_i = T_e$![]() . In cases with kinetic electrons we take $m_i/m_e = 3670$
. In cases with kinetic electrons we take $m_i/m_e = 3670$![]() (deuterium ions). This series of benchmarks is inspired by the set of tokamak benchmarks chosen for stella by Barnes et al. (Reference Barnes, Parra and Landreman2019).
(deuterium ions). This series of benchmarks is inspired by the set of tokamak benchmarks chosen for stella by Barnes et al. (Reference Barnes, Parra and Landreman2019).
6.1.1. Linear results
We first make a linear comparison taking a Boltzmann (adiabatic) electron response, so that the quasineutrality equation (2.9) reduces to

where $\langle \langle \varPhi \rangle \rangle$![]() denotes the flux-surface average of $\varPhi$
denotes the flux-surface average of $\varPhi$![]() . In figure 1 we show normalized growth rates (figure 1a) and real frequencies (figure 1b) as a function of the normalized binormal wavenumber $k_y \rho _i$
. In figure 1 we show normalized growth rates (figure 1a) and real frequencies (figure 1b) as a function of the normalized binormal wavenumber $k_y \rho _i$![]() . GX results are shown with open blue circles connected by dashed lines, while results from GS2 are shown with yellow squares. The agreement between the two codes is very good across the range of unstable $k_y$
. GX results are shown with open blue circles connected by dashed lines, while results from GS2 are shown with yellow squares. The agreement between the two codes is very good across the range of unstable $k_y$![]() values. Here we included a small number of collisions in both codes to provide velocity-space regularization, taking the normalized ion collision frequency to be $\nu _{\rm ii} = 10^{-2} v_{\rm ti}/a$
values. Here we included a small number of collisions in both codes to provide velocity-space regularization, taking the normalized ion collision frequency to be $\nu _{\rm ii} = 10^{-2} v_{\rm ti}/a$![]() . Hypercollisions are not used in GX in this case. We next make linear comparisons using kinetic electrons between GX, GS2 and stella. Figure 2(a) shows normalized growth rates and real frequencies as a function of $k_y \rho _i$
. Hypercollisions are not used in GX in this case. We next make linear comparisons using kinetic electrons between GX, GS2 and stella. Figure 2(a) shows normalized growth rates and real frequencies as a function of $k_y \rho _i$![]() at ion scales in the electrostatic limit, with $\beta _\mathrm {ref}=10^{-5}$
at ion scales in the electrostatic limit, with $\beta _\mathrm {ref}=10^{-5}$![]() (we retain electromagnetic fluctuations even at low $\beta$
(we retain electromagnetic fluctuations even at low $\beta$![]() to alleviate the timestep restriction from the electrostatic $\omega _H$
to alleviate the timestep restriction from the electrostatic $\omega _H$![]() mode (Lee Reference Lee1987)). In this case we take $\nu _{\rm ee} = 10^{-2} v_{\rm ti}/a$
mode (Lee Reference Lee1987)). In this case we take $\nu _{\rm ee} = 10^{-2} v_{\rm ti}/a$![]() and $\nu _{\rm ii} = 1.65\times 10^{-4} v_{\rm ti}/a$
and $\nu _{\rm ii} = 1.65\times 10^{-4} v_{\rm ti}/a$![]() ; for best comparison with GX, we use the stella's Dougherty collision model option, even though stella also includes a more accurate Fokker–Planck collision operator (which produces results that agree even more closely with GS2 in this case). Hypercollisions were again not used in GX. We observe excellent agreement between GX and stella for the ITG branch $(\omega >0)$
; for best comparison with GX, we use the stella's Dougherty collision model option, even though stella also includes a more accurate Fokker–Planck collision operator (which produces results that agree even more closely with GS2 in this case). Hypercollisions were again not used in GX. We observe excellent agreement between GX and stella for the ITG branch $(\omega >0)$![]() , but the agreement is not as good for the trapped electron mode (TEM) branch $(\omega <0)$
, but the agreement is not as good for the trapped electron mode (TEM) branch $(\omega <0)$![]() . If there is a weakness in our scheme it is accurately capturing linear TEM instability, which requires resolving sharp trapped–passing boundaries in velocity space (which is not optimal in $v_\parallel,\mu$
. If there is a weakness in our scheme it is accurately capturing linear TEM instability, which requires resolving sharp trapped–passing boundaries in velocity space (which is not optimal in $v_\parallel,\mu$![]() coordinates) and is sensitive to the details of the collision operator (our Dougherty model collision operator is not as accurate as the collision operators in other standard gyrokinetic codes like GS2). Indeed, even getting this level of agreement required 128 Hermite modes in GX (for more resolution details, see appendix G). A more detailed study of TEM modes is left to future work, where we will explore more accurate collision operators and methods to enhance convergence. Note that Frei et al. (Reference Frei, Ball, Hoffmann, Jorge, Ricci and Stenger2021, Reference Frei, Ernst and Ricci2022a) have demonstrated the success of the Laguerre–Hermite method in resolving TEM modes with a more accurate collision operator. We also show growth rates and frequencies as a function of $k_y \rho _i$
coordinates) and is sensitive to the details of the collision operator (our Dougherty model collision operator is not as accurate as the collision operators in other standard gyrokinetic codes like GS2). Indeed, even getting this level of agreement required 128 Hermite modes in GX (for more resolution details, see appendix G). A more detailed study of TEM modes is left to future work, where we will explore more accurate collision operators and methods to enhance convergence. Note that Frei et al. (Reference Frei, Ball, Hoffmann, Jorge, Ricci and Stenger2021, Reference Frei, Ernst and Ricci2022a) have demonstrated the success of the Laguerre–Hermite method in resolving TEM modes with a more accurate collision operator. We also show growth rates and frequencies as a function of $k_y \rho _i$![]() at electron scales in figure 2(b), again in the electrostatic limit. There is once again strong agreement between GX and GS2 for these electron-temperature-gradient (ETG) modes.
at electron scales in figure 2(b), again in the electrostatic limit. There is once again strong agreement between GX and GS2 for these electron-temperature-gradient (ETG) modes.

Figure 1. Normalized growth rates (a) and real frequencies (b) as a function of the normalized binormal wavenumber $k_y{\rho _i}$![]() from GX (blue circles and dotted lines) and GS2 (yellow squares) for ‘Cyclone base case’ (CBC) parameters using a Boltzmann electron response.
from GX (blue circles and dotted lines) and GS2 (yellow squares) for ‘Cyclone base case’ (CBC) parameters using a Boltzmann electron response.

Figure 2. Normalized growth rates (i) and real frequencies (ii) as a function of the normalized binormal wavenumber $k_y{\rho _i}$![]() from GX (blue circles and dotted lines), GS2 (yellow squares) and stella (green inverted triangles) for CBC parameters using a kinetic electron response in the electrostatic limit ($\beta _\mathrm {ref} = 10^{-5}$
from GX (blue circles and dotted lines), GS2 (yellow squares) and stella (green inverted triangles) for CBC parameters using a kinetic electron response in the electrostatic limit ($\beta _\mathrm {ref} = 10^{-5}$![]() ). Ion scales (ITG and TEM) are shown in (a) and electron scales (ETG) are shown in (b).
). Ion scales (ITG and TEM) are shown in (a) and electron scales (ETG) are shown in (b).
We finally perform an electromagnetic linear benchmark of the transition from ITG instability to kinetic ballooning mode (KBM) instability. In this benchmark we include perpendicular magnetic fluctuations via finite $A_\parallel$![]() but we neglect parallel magnetic fluctuations ($\delta B_\parallel =0$
but we neglect parallel magnetic fluctuations ($\delta B_\parallel =0$![]() ). Taking $k_y\rho _i=0.3$
). Taking $k_y\rho _i=0.3$![]() , figure 3 shows normalized growth rates and real frequencies as a function of $\beta _\mathrm {ref}$
, figure 3 shows normalized growth rates and real frequencies as a function of $\beta _\mathrm {ref}$![]() , the reference beta. As $\beta _\mathrm {ref}$
, the reference beta. As $\beta _\mathrm {ref}$![]() increases, both GX and GS2 agree well and show moderate stabilization of the ITG mode until the transition to KBM around $\beta _\mathrm {ref} = 1.3\,\%$
increases, both GX and GS2 agree well and show moderate stabilization of the ITG mode until the transition to KBM around $\beta _\mathrm {ref} = 1.3\,\%$![]() . Additional work studying reactor-relevant electromagnetic instabilities (e.g. microtearing and toroidal Alfvén eigenmodes) with GX will be reported in future publications; successful modelling of collisionless microtearing with a Laguerre–Hermite formulation has been shown by Frei et al. (Reference Frei, Hoffmann, Ricci, Brunner and Tecchioll2023).
. Additional work studying reactor-relevant electromagnetic instabilities (e.g. microtearing and toroidal Alfvén eigenmodes) with GX will be reported in future publications; successful modelling of collisionless microtearing with a Laguerre–Hermite formulation has been shown by Frei et al. (Reference Frei, Hoffmann, Ricci, Brunner and Tecchioll2023).

Figure 3. Normalized growth rates (a) and real frequencies (b) as a function of the reference beta $\beta _\mathrm {ref}$![]() from GX (blue circles and dotted lines) and GS2 (yellow squares) for CBC parameters using a kinetic electron response, taking $k_y \rho _i = 0.3$
from GX (blue circles and dotted lines) and GS2 (yellow squares) for CBC parameters using a kinetic electron response, taking $k_y \rho _i = 0.3$![]() . Both codes show the transition from ITG instability at low $\beta _\mathrm {ref}$
. Both codes show the transition from ITG instability at low $\beta _\mathrm {ref}$![]() to kinetic ballooning mode (KBM) instability at high $\beta _\mathrm {ref}$
to kinetic ballooning mode (KBM) instability at high $\beta _\mathrm {ref}$![]() .
.
6.1.2. Nonlinear results
We first perform nonlinear CBC calculations using a Boltzmann electron response. Figure 4(a) shows time traces of the ion heat flux in gyro-Bohm units (computed using the expressions in appendix F), showing very good agreement in the time-averaged heat flux amongst GX and GS2. For GX, we show a case with moderate velocity resolution, $( N_\ell, N_m)=(8,16)$![]() , along with a coarse resolution case with $( N_\ell, N_m)=(4,8)$
, along with a coarse resolution case with $( N_\ell, N_m)=(4,8)$![]() . Additional details about velocity-space convergence for this case are given in § 7. We also show in figure 4(b) a scan of the ITG parameter, $a/L_{Ti}$
. Additional details about velocity-space convergence for this case are given in § 7. We also show in figure 4(b) a scan of the ITG parameter, $a/L_{Ti}$![]() , which again shows excellent agreement between GX and GS2 for all cases at both resolutions. The agreement at $a/L_T=1.5$
, which again shows excellent agreement between GX and GS2 for all cases at both resolutions. The agreement at $a/L_T=1.5$![]() is particularly notable because this is in the Dimits shift regime, where the system is linearly unstable to ITG but turbulence is suppressed by zonal flow dynamics. This regime was especially troublesome for the Beer gyrofluid model (Beer & Hammett Reference Beer and Hammett1996; Dimits et al. Reference Dimits, Bateman, Beer, Cohen, Dorland, Hammett, Kim, Kinsey, Kotschenreuther, Kritz, Lao, Mandrekas, Nevins, Parker, Redd, Shumaker, Sydora and Weiland2000), but we see that by extending that model to more moments (and neglecting the collisionless closure schemes) via our Laguerre–Hermite approach we can recover the Dimits shift with $(N_\ell,N_m)=(4,8)$
is particularly notable because this is in the Dimits shift regime, where the system is linearly unstable to ITG but turbulence is suppressed by zonal flow dynamics. This regime was especially troublesome for the Beer gyrofluid model (Beer & Hammett Reference Beer and Hammett1996; Dimits et al. Reference Dimits, Bateman, Beer, Cohen, Dorland, Hammett, Kim, Kinsey, Kotschenreuther, Kritz, Lao, Mandrekas, Nevins, Parker, Redd, Shumaker, Sydora and Weiland2000), but we see that by extending that model to more moments (and neglecting the collisionless closure schemes) via our Laguerre–Hermite approach we can recover the Dimits shift with $(N_\ell,N_m)=(4,8)$![]() . Hoffmann et al. (Reference Hoffmann, Frei and Ricci2023a) have studied the convergence of the Laguerre–Hermite basis for this case and also found that $(N_\ell,N_m)\geq (4,8)$
. Hoffmann et al. (Reference Hoffmann, Frei and Ricci2023a) have studied the convergence of the Laguerre–Hermite basis for this case and also found that $(N_\ell,N_m)\geq (4,8)$![]() is required to accurately capture the Dimits shift. Further from marginality, Hoffmann et al. (Reference Hoffmann, Frei and Ricci2023a) have found that even lower velocity resolution can be used with reasonable accuracy, which is consistent with the convergence study in § 7. Here, both GX and GS2 included a small number of collisions, taking the normalized ion collision frequency to be $\nu _{\rm ii} = 10^{-2} \, v_{\rm ti}/a$
is required to accurately capture the Dimits shift. Further from marginality, Hoffmann et al. (Reference Hoffmann, Frei and Ricci2023a) have found that even lower velocity resolution can be used with reasonable accuracy, which is consistent with the convergence study in § 7. Here, both GX and GS2 included a small number of collisions, taking the normalized ion collision frequency to be $\nu _{\rm ii} = 10^{-2} \, v_{\rm ti}/a$![]() . Hypercollisions were included in the GX calculations, with details given in § G.3.
. Hypercollisions were included in the GX calculations, with details given in § G.3.

Figure 4. (a) Time traces of ion heat flux $Q_i$![]() , normalized to gyro-Bohm units, $Q_{\rm GB}= n_i T_i v_{\rm ti}\rho _i^2/a^2$
, normalized to gyro-Bohm units, $Q_{\rm GB}= n_i T_i v_{\rm ti}\rho _i^2/a^2$![]() , for the CBC with a Boltzmann electron response from GX with moderate (blue) and coarse (green) velocity resolution, and GS2 (yellow). (b) Time-averaged gyro-Bohm-normalized ion heat flux, $Q_i/Q_{\rm GB}$
, for the CBC with a Boltzmann electron response from GX with moderate (blue) and coarse (green) velocity resolution, and GS2 (yellow). (b) Time-averaged gyro-Bohm-normalized ion heat flux, $Q_i/Q_{\rm GB}$![]() , as a function of the normalized inverse ITG scale length, $a/L_{Ti}$
, as a function of the normalized inverse ITG scale length, $a/L_{Ti}$![]() .
.
Nonlinear calculations with kinetic electrons are presented in figure 5, which shows excellent agreement amongst GX and GS2 for the time average of the heat flux in both the ion and electron channels. For GX, we show a case with moderate velocity resolution, $( N_\ell, N_m)=(4,16)$![]() , along with a higher resolution case with $( N_\ell, N_m)=(16,32)$
, along with a higher resolution case with $( N_\ell, N_m)=(16,32)$![]() . Additional details about velocity-space convergence for this case are given in § 7. Here we took $\beta _\mathrm {ref} = 10^{-3}$
. Additional details about velocity-space convergence for this case are given in § 7. Here we took $\beta _\mathrm {ref} = 10^{-3}$![]() along with $\nu _{\rm ee} = 10^{-2} v_{\rm ti}/a$
along with $\nu _{\rm ee} = 10^{-2} v_{\rm ti}/a$![]() and $\nu _{\rm ii} = 1.65\times 10^{-4} v_{\rm ti}/a$
and $\nu _{\rm ii} = 1.65\times 10^{-4} v_{\rm ti}/a$![]() for collisions in all codes, and hypercollisions were again used in GX (see § G.4).
for collisions in all codes, and hypercollisions were again used in GX (see § G.4).

Figure 5. Time traces of ion (solid) and electron (dashed) heat flux, normalized to ion gyro-Bohm units, for the CBC with kinetic electrons from GX with high velocity resolution (blue) and moderate velocity resolution (green) and GS2 (yellow).
6.2. Stellarator benchmarks: W7-X
For benchmarks in stellarator geometry, we choose a magnetic configuration from W7-X that has recently been used by González-Jerez et al. (Reference González-Jerez, Xanthopoulos, García-Regaña, Calvo, Alcusón, Bañón Navarro, Barnes, Parra and Geiger2022) to benchmark stella and GENE. The numerical equilibrium is obtained from VMEC (Hirshman & Whitson Reference Hirshman and Whitson1983), and we choose the so-called bean flux tube with $\alpha _0=0$![]() . To study ITG-driven instabilities and turbulence we take $a/L_{Ti}=3$
. To study ITG-driven instabilities and turbulence we take $a/L_{Ti}=3$![]() and $a/L_n=1$
and $a/L_n=1$![]() . The generalized twist-and-shift boundary condition of Martin et al. (Reference Martin, Landreman, Xanthopoulos, Mandell and Dorland2018) is used.
. The generalized twist-and-shift boundary condition of Martin et al. (Reference Martin, Landreman, Xanthopoulos, Mandell and Dorland2018) is used.
6.2.1. Linear results
We first make a linear comparison between GX and stella, taking a Boltzmann electron response. Figure 6 shows the normalized growth rates (figure 6a) and real frequencies (figure 6b) for a range of $k_y$![]() modes, with strong agreement between the two codes. Both codes use Dougherty model collisions with $\nu _{\rm ii} = 0.01\,v_{\rm ti}/a$
modes, with strong agreement between the two codes. Both codes use Dougherty model collisions with $\nu _{\rm ii} = 0.01\,v_{\rm ti}/a$![]() . This test corresponds to figure 5 of González-Jerez et al. (Reference González-Jerez, Xanthopoulos, García-Regaña, Calvo, Alcusón, Bañón Navarro, Barnes, Parra and Geiger2022). As observed in González-Jerez et al. (Reference González-Jerez, Xanthopoulos, García-Regaña, Calvo, Alcusón, Bañón Navarro, Barnes, Parra and Geiger2022), the discontinuity in the frequency is due to a change in mode structure for two branches of ITG. Both branches have very similar growth rates at $k_y \rho _i = 1.0$
. This test corresponds to figure 5 of González-Jerez et al. (Reference González-Jerez, Xanthopoulos, García-Regaña, Calvo, Alcusón, Bañón Navarro, Barnes, Parra and Geiger2022). As observed in González-Jerez et al. (Reference González-Jerez, Xanthopoulos, García-Regaña, Calvo, Alcusón, Bañón Navarro, Barnes, Parra and Geiger2022), the discontinuity in the frequency is due to a change in mode structure for two branches of ITG. Both branches have very similar growth rates at $k_y \rho _i = 1.0$![]() , resulting in a small but likely inconsequential disagreement between the codes in the frequency of the fastest-growing mode.
, resulting in a small but likely inconsequential disagreement between the codes in the frequency of the fastest-growing mode.

Figure 6. Normalized growth rates (a) and real frequencies (b) as a function of the normalized binormal wavenumber $k_y$![]() from GX (blue circles and dotted lines) and stella (yellow squares) for W7-X bean flux-tube geometry and ITG parameters using a Boltzmann electron response.
from GX (blue circles and dotted lines) and stella (yellow squares) for W7-X bean flux-tube geometry and ITG parameters using a Boltzmann electron response.
6.2.2. Nonlinear results
Moving on to the nonlinear version of this test case, figure 7 shows time traces of ion heat flux from GX along with the time traces from stella and GENE, which were taken directly from the supplementary data made available by González-Jerez et al. (Reference González-Jerez, Xanthopoulos, García-Regaña, Calvo, Alcusón, Bañón Navarro, Barnes, Parra and Geiger2022) (and corresponding to figure 12 in that work; however, note the factor of $\sqrt {2}$![]() difference in the definition of $v_{\rm ti}$
difference in the definition of $v_{\rm ti}$![]() , and hence a factor of $2\sqrt {2}$
, and hence a factor of $2\sqrt {2}$![]() difference in $Q_{\rm GB}$
difference in $Q_{\rm GB}$![]() , in GX relative to the definitions used in stella and GENE). Both stella and GENE used rather high velocity resolution for this case, with $N_{v_\parallel }=60$
, in GX relative to the definitions used in stella and GENE). Both stella and GENE used rather high velocity resolution for this case, with $N_{v_\parallel }=60$![]() , $N_\mu =24$
, $N_\mu =24$![]() . For GX we show a case with moderate velocity-space resolution, $( N_\ell, N_m)=(8,16)$
. For GX we show a case with moderate velocity-space resolution, $( N_\ell, N_m)=(8,16)$![]() , and a coarse resolution case with $( N_\ell, N_m)=(4,8)$
, and a coarse resolution case with $( N_\ell, N_m)=(4,8)$![]() . Both of these agree well with the higher-resolution cases from both stella and GENE, which indicates that the promising Laguerre–Hermite convergence observed in the tokamak benchmarks carries over to stellarators. Additionally, the wallclock time for the GX cases was 90 min (on four GPUs) in the moderate resolution case and 28 min (on one GPU) in the coarse case.
. Both of these agree well with the higher-resolution cases from both stella and GENE, which indicates that the promising Laguerre–Hermite convergence observed in the tokamak benchmarks carries over to stellarators. Additionally, the wallclock time for the GX cases was 90 min (on four GPUs) in the moderate resolution case and 28 min (on one GPU) in the coarse case.

Figure 7. Time traces of ion heat flux $Q_i$![]() , normalized to gyro-Bohm units, $Q_{\rm GB}= n_i T_i v_{\rm ti}\rho _i^2/a^2$
, normalized to gyro-Bohm units, $Q_{\rm GB}= n_i T_i v_{\rm ti}\rho _i^2/a^2$![]() , for the W7-X bean flux-tube geometry with a Boltzmann electron response. Results are shown from GX with moderate (blue) and coarse (red) velocity resolution, stella (yellow) and GENE (green).
, for the W7-X bean flux-tube geometry with a Boltzmann electron response. Results are shown from GX with moderate (blue) and coarse (red) velocity resolution, stella (yellow) and GENE (green).
7. Velocity-space convergence and GPU performance
Part of the motivation for the Laguerre–Hermite pseudospectral approach is the ability to successfully run at low velocity-space resolution without uncontrolled approximations, since in the lowest-resolution limit the system corresponds to established gyrofluid models like the one of Beer & Hammett (Reference Beer and Hammett1996), albeit without Beer & Hammett's collisionless closure schemes. Another motivation for the pseudospectral approach is its fit for GPU computing, since the spectral algorithm relies heavily on fast transform methods that are well-optimized on GPUs, and the memory requirements of the algorithm are low enough to fit a problem onto one or a few GPUs. We also make exclusive use of single-precision arithmetic, which is often sufficient for turbulence calculations (Maurer et al. Reference Maurer, Bañón Navarro, Dannert, Restelli, Hindenlang, Görler, Told, Jarema, Merlo and Jenko2020); there are no matrix inversions in our algorithm that would require higher precision, and we do not presently target simulations spanning both ion and electron scales that may stress the limits of single precision. The success of the benchmarks presented in the previous section is an additional indication that single-precision arithmetic is sufficient for a wide range of linear and nonlinear calculations.
In this section we examine the velocity-space convergence for the nonlinear CBC calculations with GX along with the performance of the calculations on one or several GPUs. Convergence and performance are complementary factors towards enabling first-principles transport calculations that are fast enough to be used for fusion reactor design along with wide-ranging parameter scans for physics discovery. In this section we will present results detailing convergence and performance for the nonlinear CBC benchmark cases from § 6.1.2.
Starting with the case with Boltzmann electrons, table 1 shows the results of several GX calculations, with coarsening velocity resolution as we progress down the table. For this problem the convergence of the Laguerre–Hermite basis is quite remarkable, allowing accurate results with resolution as coarse as $( N_\ell, N_m) = (4,6)$![]() . This is still a factor of four more moments than used in the Beer & Hammett (Reference Beer and Hammett1996) six-moment gyrofluid model, but it is quite coarse relative to typical gyrokinetic calculations with $O(10$
. This is still a factor of four more moments than used in the Beer & Hammett (Reference Beer and Hammett1996) six-moment gyrofluid model, but it is quite coarse relative to typical gyrokinetic calculations with $O(10$![]() –$100)$
–$100)$![]() velocity grid points. Thus, the flexibility of the Laguerre–Hermite representation to smoothly interpolate between gyrofluid and gyrokinetic resolution enables the full nonlinear CBC calculation to be run accurately in less than 4 min on a single GPU, a remarkable result.
velocity grid points. Thus, the flexibility of the Laguerre–Hermite representation to smoothly interpolate between gyrofluid and gyrokinetic resolution enables the full nonlinear CBC calculation to be run accurately in less than 4 min on a single GPU, a remarkable result.
Table 1. Velocity-space convergence and performance for the nonlinear CBC with Boltzmann electrons. Here $N_m$![]() is the number of Hermite modes and $N_\ell$
is the number of Hermite modes and $N_\ell$![]() is the number of Laguerre modes. Other resolution parameters were $N_x=192,\ N_y=64,\ N_z=24$
is the number of Laguerre modes. Other resolution parameters were $N_x=192,\ N_y=64,\ N_z=24$![]() . Accurate ion heat flux calculations can be obtained with resolution as coarse as $( N_\ell, N_m)\geq (4,6)$
. Accurate ion heat flux calculations can be obtained with resolution as coarse as $( N_\ell, N_m)\geq (4,6)$![]() (above the double bar). Each simulation was run to $t = 1000 a/v_{\rm ti}$
(above the double bar). Each simulation was run to $t = 1000 a/v_{\rm ti}$![]() , and we report the total wallclock time in minutes, the time per timestep in seconds, and the average timestep size $\langle \Delta t\rangle$
, and we report the total wallclock time in minutes, the time per timestep in seconds, and the average timestep size $\langle \Delta t\rangle$![]() (normalized to $a/v_{\rm ti}$
(normalized to $a/v_{\rm ti}$![]() ), which changes with $N_\ell$
), which changes with $N_\ell$![]() and $N_m$
and $N_m$![]() due to linear stability constraints. The number of NVIDIA A100 GPUs used for each calculation is listed in the final column. The resolutions shown in figure 4 are marked with a $\star$
due to linear stability constraints. The number of NVIDIA A100 GPUs used for each calculation is listed in the final column. The resolutions shown in figure 4 are marked with a $\star$![]() .
.

When we look at the Laguerre and Hermite spectra for these cases shown in figure 8, where $W_{g,s}(\ell,m) = \int |G_{\ell,m}^s|^2\, {{\rm d} x}\, {{\rm d} y}\, {\rm d}z$![]() is the free energy in each moment, and $W_{g,s}(\ell ) = \sum _m W_{g,s}(\ell, m)$
is the free energy in each moment, and $W_{g,s}(\ell ) = \sum _m W_{g,s}(\ell, m)$![]() and $W_{g,s}(m) = \sum _\ell W_{g,s}(\ell, m)$
and $W_{g,s}(m) = \sum _\ell W_{g,s}(\ell, m)$![]() , we can see why the convergence is very good: even for the coarsest resolution, the spectra at the scales that contribute dominantly to the heat flux (small $\ell$
, we can see why the convergence is very good: even for the coarsest resolution, the spectra at the scales that contribute dominantly to the heat flux (small $\ell$![]() and $m$
and $m$![]() ) are nearly identical. Note that hypercollisions are being used in these calculations, and this is helping to enhance convergence. Without hypercollisions (not shown), the results are only accurate with $( N_\ell, N_m) \geq (6,12)$
) are nearly identical. Note that hypercollisions are being used in these calculations, and this is helping to enhance convergence. Without hypercollisions (not shown), the results are only accurate with $( N_\ell, N_m) \geq (6,12)$![]() . This means that hypercollisions enable a five-fold reduction in simulation (wallclock) time for this case.
. This means that hypercollisions enable a five-fold reduction in simulation (wallclock) time for this case.

Figure 8. Laguerre (a) and Hermite (b) free energy spectra, $W_g$![]() , for the nonlinear CBC with a Boltzmann electron response with varying velocity-space resolution. All the spectra are nearly identical at the scales that contribute dominantly to the heat flux (small $\ell$
, for the nonlinear CBC with a Boltzmann electron response with varying velocity-space resolution. All the spectra are nearly identical at the scales that contribute dominantly to the heat flux (small $\ell$![]() and $m$
and $m$![]() ), which is consistent with the excellent convergence observed in table 1.
), which is consistent with the excellent convergence observed in table 1.
We perform a similar convergence study for the CBC with kinetic electrons, as shown in table 2. As above, $N_\ell =4$![]() is sufficient for accurate heat flux predictions in both ion and electron channels. However, Hermite convergence is not as strong here, with reasonable accuracy (within 15 % of the highest resolution case) requiring $N_m\gtrsim 16$
is sufficient for accurate heat flux predictions in both ion and electron channels. However, Hermite convergence is not as strong here, with reasonable accuracy (within 15 % of the highest resolution case) requiring $N_m\gtrsim 16$![]() . Examining the Laguerre and Hermite free energy spectra for these cases in figure 9, we see more structure in the Hermite spectra, especially for the electrons. The oscillatory nature of the electron spectrum, with higher amplitudes in even Hermite modes than odd, could be an indication that the toroidal drifts (which couple every other Hermite mode) are playing a strong role in the dynamics. This is consistent with the results of analytical and numerical convergence studies of the Laguerre–Hermite basis associated with toroidal drifts by Frei et al. (Reference Frei, Ernst and Ricci2022a, Reference Frei, Hoffmann, Ricci, Brunner and Tecchioll2023). Despite this structure, reasonably accurate results can be achieved in 159 min on four GPUs using $( N_\ell, N_m)=(4,16)$
. Examining the Laguerre and Hermite free energy spectra for these cases in figure 9, we see more structure in the Hermite spectra, especially for the electrons. The oscillatory nature of the electron spectrum, with higher amplitudes in even Hermite modes than odd, could be an indication that the toroidal drifts (which couple every other Hermite mode) are playing a strong role in the dynamics. This is consistent with the results of analytical and numerical convergence studies of the Laguerre–Hermite basis associated with toroidal drifts by Frei et al. (Reference Frei, Ernst and Ricci2022a, Reference Frei, Hoffmann, Ricci, Brunner and Tecchioll2023). Despite this structure, reasonably accurate results can be achieved in 159 min on four GPUs using $( N_\ell, N_m)=(4,16)$![]() . This is quite good for a nonlinear, electromagnetic gyrokinetic ITG simulation with real-mass-ratio kinetic electrons. Additional details about multi-GPU scaling are presented in § 7.1.
. This is quite good for a nonlinear, electromagnetic gyrokinetic ITG simulation with real-mass-ratio kinetic electrons. Additional details about multi-GPU scaling are presented in § 7.1.
Table 2. Velocity-space convergence and performance for the nonlinear CBC with kinetic electrons. Here $N_m$![]() is the number of Hermite modes and $N_\ell$
is the number of Hermite modes and $N_\ell$![]() is the number of Laguerre modes. Other resolution parameters were $N_x=192,\ N_y=64,\ N_z=24$
is the number of Laguerre modes. Other resolution parameters were $N_x=192,\ N_y=64,\ N_z=24$![]() . Reasonably accurate heat flux calculations (within 15 % of the highest resolution case) can be obtained with resolution as coarse as$( N_\ell, N_m)\geq (4,16)$
. Reasonably accurate heat flux calculations (within 15 % of the highest resolution case) can be obtained with resolution as coarse as$( N_\ell, N_m)\geq (4,16)$![]() (above the double bar). Each simulation was run to $t = 600 a/v_{\rm ti}$
(above the double bar). Each simulation was run to $t = 600 a/v_{\rm ti}$![]() , and we report the total wallclock time in minutes, the time per timestep in seconds, and the average timestep size $\langle \Delta t\rangle$
, and we report the total wallclock time in minutes, the time per timestep in seconds, and the average timestep size $\langle \Delta t\rangle$![]() (normalized to $a/v_{\rm ti}$
(normalized to $a/v_{\rm ti}$![]() ). The number of NVIDIA A100 GPUs used for each calculation is also shown. The resolutions used for the GX calculations shown in figure 5 are marked with a $\star$
). The number of NVIDIA A100 GPUs used for each calculation is also shown. The resolutions used for the GX calculations shown in figure 5 are marked with a $\star$![]() .
.


Figure 9. Laguerre (i) and Hermite (ii) spectra for ions (a) and electrons (b) for the nonlinear CBC with kinetic electrons with varying velocity-space resolution.
Note that using more Hermite modes not only adds to the size of the problem, but also makes the Courant–Friedrichs–Levy (CFL) constraint on the timestep more restrictive because the maximum parallel velocity $v_{\parallel \mathrm {max}}$![]() on the Hermite collocation grid increases with the number of Hermite modes. In future work we will try to alleviate this issue by constraining the maximum velocity on the collocation grid. However, a commonly used method of scaling the argument of the Hermite polynomials to reduce the extents of the collocation grid is ill-suited to our problem, since the resulting projection of a Maxwellian onto the scaled basis often diverges (Fok, Guo & Tang Reference Fok, Guo and Tang2001). Instead, an approach similar to that used by Candy et al. (Reference Candy, Belli and Bravenec2016) to bound the energy grid in CGYRO could be used here.
on the Hermite collocation grid increases with the number of Hermite modes. In future work we will try to alleviate this issue by constraining the maximum velocity on the collocation grid. However, a commonly used method of scaling the argument of the Hermite polynomials to reduce the extents of the collocation grid is ill-suited to our problem, since the resulting projection of a Maxwellian onto the scaled basis often diverges (Fok, Guo & Tang Reference Fok, Guo and Tang2001). Instead, an approach similar to that used by Candy et al. (Reference Candy, Belli and Bravenec2016) to bound the energy grid in CGYRO could be used here.
7.1. GPU scaling studies
For single-GPU calculations, the GPU threading architecture effectively enables dynamic parallelism over the entire phase space. In figure 10, we show that for a nonlinear CBC calculation with Boltzmann electrons, the algorithm scales roughly linearly with the number of radial grid points, $N_x$![]() . This is better than the $O(N\log N)$
. This is better than the $O(N\log N)$![]() cost that would be expected when the fast Fourier transform (FFT) in the pseudospectral algorithm dominates the cost. This is also better scaling than other gyrokinetic algorithms that require $O(N^2)$
cost that would be expected when the fast Fourier transform (FFT) in the pseudospectral algorithm dominates the cost. This is also better scaling than other gyrokinetic algorithms that require $O(N^2)$![]() operations due to matrix inversion.
operations due to matrix inversion.

Figure 10. Scaling of time per timestep (in seconds) versus the number of radial grid points, $N_x$![]() , for nonlinear CBC with Boltzmann electrons on a single GPU. Ideal linear scaling is shown with the dashed line, while the dot–dashed line shows $N_x \log N_x$
, for nonlinear CBC with Boltzmann electrons on a single GPU. Ideal linear scaling is shown with the dashed line, while the dot–dashed line shows $N_x \log N_x$![]() scaling (the expected scaling when FFTs dominate the algorithm).
scaling (the expected scaling when FFTs dominate the algorithm).
When considering multi-GPU parallelization, the cost of inter-GPU memory transfers can be quite large compared with floating point operations. Thus, it is important to design the scheme to minimize memory transfers and take advantage of the capability of modern GPUs to overlap communication with computation. Thus, in GX we have chosen a targeted multi-GPU parallelization scheme that currently parallelizes only species and Hermite modes across GPUs. In this scheme, communication is required to compute the total charge density and currents in the field equations, which takes the form of an all-reduce operation on a configuration-space-sized ($N_{k_x}\times N_{k_y}\times N_z$![]() ) object. Additionally, since the equation for the Hermite mode $m$
) object. Additionally, since the equation for the Hermite mode $m$![]() couples to modes $m-2$
couples to modes $m-2$![]() , $m-1$
, $m-1$![]() , $m+1$
, $m+1$![]() and $m+2$
and $m+2$![]() , we use ‘halo’ (or ‘ghost’) modes on each GPU, similar to standard parallelization schemes for finite differencing. Halo exchange is thus the other dominant form of communication, requiring inter-GPU transfers of objects of size $N_{k_x}\times N_{k_y}\times N_z\times N_\ell \times 2$
, we use ‘halo’ (or ‘ghost’) modes on each GPU, similar to standard parallelization schemes for finite differencing. Halo exchange is thus the other dominant form of communication, requiring inter-GPU transfers of objects of size $N_{k_x}\times N_{k_y}\times N_z\times N_\ell \times 2$![]() . We overlap the halo exchange with computation of most of the nonlinear terms (halo modes are only required for the nonlinear terms involving $A_\parallel$
. We overlap the halo exchange with computation of most of the nonlinear terms (halo modes are only required for the nonlinear terms involving $A_\parallel$![]() , and even for these the terms on the interior modes can be computed before the halo transfers have been completed).
, and even for these the terms on the interior modes can be computed before the halo transfers have been completed).
In figure 11 we show a strong scaling study for nonlinear CBC cases with two kinetic species. In each case we fix resolution (shown in the legend) and plot the time per timestep (figure 11a) and scaling efficiency (figure 11b) as we increase the number of GPUs used for the calculation. These calculations have been performed on Perlmutter at NERSC, where each node contains four A100 GPUs. The three cases have the same configuration space resolution and number of kinetic species as the cases in table 2. For reference, the (16,64) case running on a single GPU consumes approximately 90 % of the available GPU memory on a 40GB A100 GPU. In each case, the scaling efficiency is above 75 % parallelizing across four GPUs. The efficiency also improves as the problem size increases, which is expected because there is more computing time relative to communication time.

Figure 11. Strong scaling study for the nonlinear CBC with kinetic electrons showing the time per timestep (a) and the scaling efficiency (b) as a function of number of GPUs used, with fixed resolution for each curve. In each case the ideal scaling is shown with a dashed black line. The Laguerre–Hermite resolution parameters are listed in the legend as $(N_\ell, N_m)$![]() . The other resolution parameters are $N_x=192,\ N_y=64, N_z=24,\ N_\mathrm {species}=2$
. The other resolution parameters are $N_x=192,\ N_y=64, N_z=24,\ N_\mathrm {species}=2$![]() .
.
We also show in figure 12 weak scaling studies for the nonlinear CBC with two kinetic species and the same configuration space resolution as the cases in table 2. Here, we increase the number of Hermite modes proportionally to the number of GPUs used, so that $N_m=8 N_\mathrm {gpu}$![]() in each case. After parallelizing first over the two kinetic species, this results in 16 Hermite modes per GPU in all the calculations shown. We show the weak scaling for both $N_\ell =4$
in each case. After parallelizing first over the two kinetic species, this results in 16 Hermite modes per GPU in all the calculations shown. We show the weak scaling for both $N_\ell =4$![]() (blue) and $N_\ell =8$
(blue) and $N_\ell =8$![]() (yellow). The weak scaling efficiency, shown in (figure 12b), is ideal in both cases up to 32 GPUs ($N_m = 256$
(yellow). The weak scaling efficiency, shown in (figure 12b), is ideal in both cases up to 32 GPUs ($N_m = 256$![]() ), despite the fact that using more than four GPUs requires multiple nodes on Perlmutter, and communication between nodes can be slower than communication within a node due to the details of the interconnect hardware.
), despite the fact that using more than four GPUs requires multiple nodes on Perlmutter, and communication between nodes can be slower than communication within a node due to the details of the interconnect hardware.

Figure 12. Weak scaling study for the nonlinear CBC with kinetic electrons showing the time per timestep (a) and the scaling efficiency (b) as a function of number of GPUs used, with the number of Hermite modes $N_m$![]() scaling with the number of GPUs as $N_m=8N_\mathrm {gpu}$
scaling with the number of GPUs as $N_m=8N_\mathrm {gpu}$![]() . We show results for both $N_\ell =4$
. We show results for both $N_\ell =4$![]() (blue) and $N_\ell =8$
(blue) and $N_\ell =8$![]() (yellow). The ideal scaling is shown with dashed lines. The other resolution parameters are $N_x=192,\ N_y=64,\ N_z={24}, N_\mathrm {species}=2$
(yellow). The ideal scaling is shown with dashed lines. The other resolution parameters are $N_x=192,\ N_y=64,\ N_z={24}, N_\mathrm {species}=2$![]() .
.
8. Conclusion and future opportunities
In this work we have presented GX, a GPU-native gyrokinetic code focused on tokamak and stellarator design at reactor scales. We have described the numerical algorithms that we use to solve the electromagnetic $\delta f$![]() gyrokinetic system, in particular the discretization scheme that is pseudospectral in the entire five-dimensional phase space, leveraging the Laguerre–Hermite velocity-space formulation developed by Mandell et al. (Reference Mandell, Dorland and Landreman2018). We have shown several linear and nonlinear benchmarks against established flux-tube gyrokinetic codes in both tokamak and stellarator geometry, verifying that GX correctly simulates gyrokinetic turbulence in the small $\rho _*$
gyrokinetic system, in particular the discretization scheme that is pseudospectral in the entire five-dimensional phase space, leveraging the Laguerre–Hermite velocity-space formulation developed by Mandell et al. (Reference Mandell, Dorland and Landreman2018). We have shown several linear and nonlinear benchmarks against established flux-tube gyrokinetic codes in both tokamak and stellarator geometry, verifying that GX correctly simulates gyrokinetic turbulence in the small $\rho _*$![]() limit. The combination of GPU acceleration and favourable convergence properties of the Laguerre–Hermite velocity-space basis for nonlinear problems enables useful turbulence simulations in minutes.
limit. The combination of GPU acceleration and favourable convergence properties of the Laguerre–Hermite velocity-space basis for nonlinear problems enables useful turbulence simulations in minutes.
Additional work will also focus on improving the efficiency of simulations that include kinetic electrons. At present, the need to resolve the fast parallel electron motion results in an increase in simulation cost by a factor of roughly $2\sqrt {m_i/m_e}\approx 120$![]() compared with simulations with Boltzmann electrons (the factor of 2 is from the additional kinetic species, and the square root of the mass ratio comes from $v_{\rm te}/v_{\rm ti}$
compared with simulations with Boltzmann electrons (the factor of 2 is from the additional kinetic species, and the square root of the mass ratio comes from $v_{\rm te}/v_{\rm ti}$![]() ). We have also shown that kinetic electron cases may require more Hermite resolution, especially if resolving the trapped–passing boundary is essential. Exploration of different choices of velocity-space coordinates for the electrons or improvements to the basis functions used (for example, a method to bound the Hermite collocation points to constrain $v_{\parallel \mathrm {max}}$
). We have also shown that kinetic electron cases may require more Hermite resolution, especially if resolving the trapped–passing boundary is essential. Exploration of different choices of velocity-space coordinates for the electrons or improvements to the basis functions used (for example, a method to bound the Hermite collocation points to constrain $v_{\parallel \mathrm {max}}$![]() , as in Candy et al. (Reference Candy, Belli and Bravenec2016), which could alleviate the CFL timestep restriction) could increase efficiency. In addition, the reduced electron models of Beer & Hammett (Reference Beer and Hammett1996), Snyder & Hammett (Reference Snyder and Hammett2001) and Abel & Cowley (Reference Abel and Cowley2013) provide insight into how to eliminate the fast time scales associated with parallel electron motion. A combination of these approaches with implicit timestepping schemes could enable kinetic electron simulations with nearly the same efficiency as the Boltzmann electron simulations we have presented. Additionally, we are investigating machine-learning methods for subgrid models and closures (Barbour et al. Reference Barbour, Dorland, Barbour and Dorland2021, Reference Barbour, Dorland, Mandell, Gaur, McGrae-Menge, Pierce, Almanza, Chou, Alves, Fiuza and Loureiro2022), as well as methods for dynamically adapting the number of modes in the system.
, as in Candy et al. (Reference Candy, Belli and Bravenec2016), which could alleviate the CFL timestep restriction) could increase efficiency. In addition, the reduced electron models of Beer & Hammett (Reference Beer and Hammett1996), Snyder & Hammett (Reference Snyder and Hammett2001) and Abel & Cowley (Reference Abel and Cowley2013) provide insight into how to eliminate the fast time scales associated with parallel electron motion. A combination of these approaches with implicit timestepping schemes could enable kinetic electron simulations with nearly the same efficiency as the Boltzmann electron simulations we have presented. Additionally, we are investigating machine-learning methods for subgrid models and closures (Barbour et al. Reference Barbour, Dorland, Barbour and Dorland2021, Reference Barbour, Dorland, Mandell, Gaur, McGrae-Menge, Pierce, Almanza, Chou, Alves, Fiuza and Loureiro2022), as well as methods for dynamically adapting the number of modes in the system.
An essential target for GX is transport time scale macroscale profile evolution via coupling to a transport solver like Trinity (Barnes et al. Reference Barnes, Abel, Dorland, Ernst, Hammett, Ricci, Rogers, Schekochihin and Tatsuno2009; Qian et al. Reference Qian, Buck, Gaur, Mandell, Kim and Dorland2022) or a steady-state profile prediction solver like TGYRO (Candy et al. Reference Candy, Holland, Waltz, Fahey and Belli2009) or PORTALS (Rodriguez-Fernandez, Howard & Candy Reference Rodriguez-Fernandez, Howard and Candy2022). This will be described in a forthcoming paper. In this case, several GX flux-tube calculations are run in parallel at various radii, and the resulting turbulent fluxes are used to advance the transport equations for the equilibrium profiles on transport time scales. The efficiency of GX makes these simulations quite tractable in comparison with previous efforts. Further, since transport in a fusion reactor is usually quite stiff, small changes in profile gradients result in large changes in transport fluxes; conversely, this means that errors of order 10 % are quite tolerable since they will result in relatively negligible differences in the final equilibrium profiles. Thus, we can also leverage the flexibility of GX to run at quite low velocity resolution with only 10 %–20 % errors in the turbulent fluxes, as shown in the convergence studies.
Finally, since GX is specialized for reactor design, using GX as a turbulence model in the inner loop of optimization frameworks is of great interest. Kim et al. (Reference Kim, Buller, Conlin, Dorland, Dudt, Gaur, Jorge, Kolemen, Landreman, Mandell and Panici2024) have leveraged the DESC (Dudt et al. Reference Dudt, Conlin, Panici and Kolemen2022) optimization framework to demonstrate that stellarators can be optimized for turbulence using nonlinear GX calculations in the optimization loop. Additionally, coupling of GX to the SIMSOPT stellarator optimization framework (Landreman et al. Reference Landreman, Medasani, Wechsung, Giuliani, Jorge and Zhu2021) is in progress. Following the work of Highcock et al. (Reference Highcock, Mandell, Barnes and Dorland2018), optimization of core equilibrium profiles (and hence fusion power) is also tractable with a fast multiscale transport model composed of GX coupled to a transport solver.
Acknowledgements
The authors thank G. Hammett, M. Landreman, M. Zarnstorff, B. Buck, N. Barbour, J. Parisi, M. Barnes and F. Parra for helpful discussions and encouragement. Editor P. Ricci thanks the referees for their advice in evaluating this article.
Declaration of interest
The authors report no conflict of interest.
Funding
Research support came from the US Department of Energy (DOE) and the US National Science Foundation (NSF): N.R.M. was supported by the DOE Fusion Energy Sciences Postdoctoral Research Program administered by the Oak Ridge Institute for Science and Education (ORISE) for the DOE via Oak Ridge Associated Universities (ORAU) under DOE contract number DE-SC0014664 and by the Laboratory Directed Research and Development Program of the Princeton Plasma Physics Laboratory under US Department of Energy contract number DE-AC02-09CH11466; W.D., R.G. and P.K. were supported by DOE via the Scientific Discovery Through Advanced Computing Program under award number DESC0018429; P.K. is also supported by the DOE CSGF Program under award number DE-SC0024386; T.Q. was supported by NSF GRFP grant no. DGE-2039656. Computations were performed on the Stellar cluster at Princeton University/PPPL and the Perlmutter cluster at NERSC. All opinions expressed in this paper are the authors’ and do not necessarily reflect the policies and views of DOE, NSF, ORAU or ORISE.
Appendix A. Normalization
We choose a set of normalizations, described in table 3, for the fundamental quantities.
Table 3. Fundamental normalizing quantities.
Note that the specific definition of the normalizing quantities is arbitrary; for example, the normalizing length could be chosen to be the minor radius ($a_N = a$![]() ), the major radius ($a_N = R$
), the major radius ($a_N = R$![]() ) or some other length. Using the fundamental normalizations, we can define the reference thermal speed $v_{\rm {th,\ ref}} = \sqrt {T_{\rm {ref}}/M_{\rm {ref}}}$
) or some other length. Using the fundamental normalizations, we can define the reference thermal speed $v_{\rm {th,\ ref}} = \sqrt {T_{\rm {ref}}/M_{\rm {ref}}}$![]() , the reference cyclotron frequency $\varOmega _{\rm {ref}} = q_{\rm {ref}} B_{\rm {N}}/M_{\rm {ref}}$
, the reference cyclotron frequency $\varOmega _{\rm {ref}} = q_{\rm {ref}} B_{\rm {N}}/M_{\rm {ref}}$![]() and the reference gyroradius $\rho _{\rm {ref}} \equiv v_{\rm {th,ref}}/\varOmega _{\rm ref}$
and the reference gyroradius $\rho _{\rm {ref}} \equiv v_{\rm {th,ref}}/\varOmega _{\rm ref}$![]() . The ratio of the reference gyroradius $\rho _{\rm {ref}}$
. The ratio of the reference gyroradius $\rho _{\rm {ref}}$![]() and the normalizing length $a_{\rm {N}}$
and the normalizing length $a_{\rm {N}}$![]() is defined as
is defined as
which is the fundamental small parameter in the gyrokinetic model. Using table 3, we can also normalize all the independent variables and operators as shown in table 4 and all the dependent variables as shown in table 5. Using the normalizations given in tables 4 and 5, we can normalize the gyrokinetic model. Note that the term $\rho _{*}$![]() cancels out of all the equations once they are normalized. We also define the following non-dimensional species-specific parameters that appear throughout the normalized equations: $\tau _s = T_s/T_\mathrm {ref}$
cancels out of all the equations once they are normalized. We also define the following non-dimensional species-specific parameters that appear throughout the normalized equations: $\tau _s = T_s/T_\mathrm {ref}$![]() , $m_s = M_s/M_\mathrm {ref}$
, $m_s = M_s/M_\mathrm {ref}$![]() , $v_{ts} = v_{\mathrm {th},s}/v_\mathrm {th,ref}$
, $v_{ts} = v_{\mathrm {th},s}/v_\mathrm {th,ref}$![]() , $Z_s = q_s/q_\mathrm {ref}$
, $Z_s = q_s/q_\mathrm {ref}$![]() and $\rho _s = (v_{\mathrm {th},s}/\varOmega _s)/\rho _\mathrm {ref}$
and $\rho _s = (v_{\mathrm {th},s}/\varOmega _s)/\rho _\mathrm {ref}$![]() .
.
Table 4. Normalizing the quantities for the independent variables.
Table 5. Normalizing quantities for dependent variables.
Appendix B. Derivation of hypercollision operator
Consider the simplified system where the distribution function $g$![]() evolves due to only parallel free streaming. Fourier transforming in the parallel direction, a mode with parallel wavenumber $k$
evolves due to only parallel free streaming. Fourier transforming in the parallel direction, a mode with parallel wavenumber $k$![]() evolves via
evolves via
The solution is
Free streaming thus causes energy transfer to smaller scales in velocity space; this is the parallel phase mixing behaviour that produces Landau damping, as is well known. In the Hermite representation results this results in transfer of energy to higher $m$![]() , which can be seen by taking Hermite moments of the solution, giving
, which can be seen by taking Hermite moments of the solution, giving
Thus, a pulse propagating in $m$![]() reaches $m(t) = k^2 v_t^2 t^2$
reaches $m(t) = k^2 v_t^2 t^2$![]() at time $t$
at time $t$![]() . By differentiating in time we can obtain the advection ‘velocity’ in $m$
. By differentiating in time we can obtain the advection ‘velocity’ in $m$![]() -space,
-space,
Now consider the advection equation for the mode energy, $E(m) = |g_m|^2/2$![]() ,
,
The source $S$![]() only acts at low $m$
only acts at low $m$![]() . For dissipation, we will assume a hypercollision operator of the form
. For dissipation, we will assume a hypercollision operator of the form
which results in
In steady state ($\partial /\partial t \rightarrow 0$![]() ) at large enough $m$
) at large enough $m$![]() to neglect the source, we have
to neglect the source, we have
Inserting the advection velocity from (B4), we obtain
The solution of this differential equation is of the form
Note that in the limit of no dissipation ($\nu _\mathrm {hyp}\rightarrow 0$![]() ), we should have a constant $m-$
), we should have a constant $m-$![]() flux $\varGamma$
flux $\varGamma$![]() , which restricts the constant of integration to $C=\varGamma /(2k v_t)$
, which restricts the constant of integration to $C=\varGamma /(2k v_t)$![]() and makes the full solution
and makes the full solution
Now we would like to choose $\nu _\mathrm {hyp}$![]() so that the energy is damped to some fraction $f$
so that the energy is damped to some fraction $f$![]() by the time the energy reaches the grid scale at $m=m_\mathrm {max}$
by the time the energy reaches the grid scale at $m=m_\mathrm {max}$![]() . From this we obtain
. From this we obtain
Taking $f=0.1$![]() results in the operator presented in § 4.1. Note that undamped energy will be reflected and damped again as it travels from high $m$
results in the operator presented in § 4.1. Note that undamped energy will be reflected and damped again as it travels from high $m$![]() to low $m$
to low $m$![]() , resulting in only $f^2=0.01$
, resulting in only $f^2=0.01$![]() of the initial energy returning to low $m$
of the initial energy returning to low $m$![]() .
.
Appendix C. Convergence study for parallel boundary damping filter
In § 4.2 we defined the parallel boundary damping filter using two adjustable parameters: the width of the damping region $z_\mathrm {width}$![]() , and the scaling factor $A$
, and the scaling factor $A$![]() . Here we perform convergence studies to verify that we have chosen reasonable values of these parameters. We will use the kinetic electron CBC for these studies.
. Here we perform convergence studies to verify that we have chosen reasonable values of these parameters. We will use the kinetic electron CBC for these studies.
We first perform a scan of the scaling factor $A$![]() . Figure 13 shows the ion and electron heat flux as a function of $A\Delta t$
. Figure 13 shows the ion and electron heat flux as a function of $A\Delta t$![]() , with $\Delta t$
, with $\Delta t$![]() the timestep size. For this scan we have used $z_\mathrm {width} = L_z/8$
the timestep size. For this scan we have used $z_\mathrm {width} = L_z/8$![]() . We can see that the heat fluxes are converged when $A\Delta t \gtrsim 0.05$
. We can see that the heat fluxes are converged when $A\Delta t \gtrsim 0.05$![]() . We next perform a scan of the damping region width $z_\mathrm {width}$
. We next perform a scan of the damping region width $z_\mathrm {width}$![]() , as shown in figure 14. For this scan we use $A\Delta t = 0.1$
, as shown in figure 14. For this scan we use $A\Delta t = 0.1$![]() . By varying $z_\mathrm {width}/L_z$
. By varying $z_\mathrm {width}/L_z$![]() for several values of $N_z$
for several values of $N_z$![]() , we find that $z_\mathrm {width} = L_z/8$
, we find that $z_\mathrm {width} = L_z/8$![]() produces accurate results for each choice of $N_z$
produces accurate results for each choice of $N_z$![]() .
.

Figure 13. Time-averaged gyro-Bohm-normalized ion (solid blue circles) and electron (dashed yellow squares) heat fluxes as a function of $A\Delta t$![]() , with $A$
, with $A$![]() the scaling factor for the damping filter and $\Delta t$
the scaling factor for the damping filter and $\Delta t$![]() the timestep size.
the timestep size.

Figure 14. Time-averaged gyro-Bohm-normalized ion (solid) and electron (dashed) heat fluxes as a function of $z_\mathrm {width}/L_z$![]() , with $z_\mathrm {width}$
, with $z_\mathrm {width}$![]() the width of the damping region and $L_z$
the width of the damping region and $L_z$![]() the parallel length of the flux tube. Colours indicate different values of parallel resolution $N_z$
the parallel length of the flux tube. Colours indicate different values of parallel resolution $N_z$![]() .
.
Appendix D. Pseudospectral evaluation of nonlinear terms
The nonlinear terms are evaluated pseudospectrally in $(x,y,z,\mu B, m)$![]() space to avoid convolutions in both Fourier and Laguerre coefficients as (Mandell et al. Reference Mandell, Dorland and Landreman2018)
space to avoid convolutions in both Fourier and Laguerre coefficients as (Mandell et al. Reference Mandell, Dorland and Landreman2018)

This requires zero-padding of the arrays in the perpendicular and Laguerre dimensions to avoid aliasing, as described in Appendix D of Mandell et al. (Reference Mandell, Dorland and Landreman2018). Fourier transforms are evaluated using the cuFFT library. The Laguerre transforms are expressed as matrix multiplications and implemented using the cuBLAS library.
Appendix E. Geometry details
In this appendix, we will describe how the geometry-related coefficients are calculated in the GX code. First, we define the different coordinate systems and relevant identities and briefly outline the process of calculating the geometry-related coefficients. Next, we list all the geometric quantities used by GX in the field-line following coordinate system. Finally, we describe the process of obtaining an equal-arc, equispaced coordinate from a general coordinate $z$![]() .
.
Consider a magnetic coordinate system $(\psi, \phi, \theta )$![]() , where $\psi$
, where $\psi$![]() is a flux surface label, $\phi$
is a flux surface label, $\phi$![]() is the cylindrical toroidal angle and $\theta$
is the cylindrical toroidal angle and $\theta$![]() is a generalized poloidal angle. A general three-dimensional equilibrium is a union of nested flux surfaces labelled with the flux surface label $\psi$
is a generalized poloidal angle. A general three-dimensional equilibrium is a union of nested flux surfaces labelled with the flux surface label $\psi$![]() , which is usually produced by an equilibrium code in the cylindrical coordinate $(R, \phi, Z)$
, which is usually produced by an equilibrium code in the cylindrical coordinate $(R, \phi, Z)$![]() . The first step is to calculate the Jacobian from the cylindrical to the curvilinear coordinates $(\psi, \phi, \theta )$
. The first step is to calculate the Jacobian from the cylindrical to the curvilinear coordinates $(\psi, \phi, \theta )$![]() ,
,
where the last equality in (E1) is a consequence of the duality relation (D'haeseleer et al. Reference D'haeseleer, Hitchon, Callen and Shohet1991); and
where $X_i$![]() and $X_{j}$
and $X_{j}$![]() are coordinates. Using the Jacobian and the duality relation we calculate the gradients $\boldsymbol {\boldsymbol {\nabla }} \psi, \boldsymbol {\boldsymbol {\nabla }} \phi, \boldsymbol {\boldsymbol {\nabla }} \theta$
are coordinates. Using the Jacobian and the duality relation we calculate the gradients $\boldsymbol {\boldsymbol {\nabla }} \psi, \boldsymbol {\boldsymbol {\nabla }} \phi, \boldsymbol {\boldsymbol {\nabla }} \theta$![]() from the gradients $\boldsymbol {\boldsymbol {\nabla }} R, \boldsymbol {\boldsymbol {\nabla }} \phi, \boldsymbol {\boldsymbol {\nabla }} Z$
from the gradients $\boldsymbol {\boldsymbol {\nabla }} R, \boldsymbol {\boldsymbol {\nabla }} \phi, \boldsymbol {\boldsymbol {\nabla }} Z$![]() . For example, we calculate $\boldsymbol {\boldsymbol {\nabla }} \psi$
. For example, we calculate $\boldsymbol {\boldsymbol {\nabla }} \psi$![]() using the following relation:
using the following relation:

where the vector $\boldsymbol {R}=(R, \phi, Z)$![]() is output from a typical equilibrium solver. Upon calculating the gradients of the coordinates $(\psi, \theta, \phi )$
is output from a typical equilibrium solver. Upon calculating the gradients of the coordinates $(\psi, \theta, \phi )$![]() , we can easily obtain the gradients of the field-line-following coordinate $(x, y, z)$
, we can easily obtain the gradients of the field-line-following coordinate $(x, y, z)$![]() . In addition to that, an equilibrium code also outputs scalar-valued physical quantities like the plasma pressure $p(\psi )$
. In addition to that, an equilibrium code also outputs scalar-valued physical quantities like the plasma pressure $p(\psi )$![]() , and the safety factor $q(\psi )$
, and the safety factor $q(\psi )$![]() and vector-valued physical quantities like $B$
and vector-valued physical quantities like $B$![]() , $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\boldsymbol {\nabla }}\theta$
, $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\boldsymbol {\nabla }}\theta$![]() , $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\boldsymbol {\nabla }}\phi$
, $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\boldsymbol {\nabla }}\phi$![]() . These quantities are then used to compute all the geometric coefficients defined below,
. These quantities are then used to compute all the geometric coefficients defined below,
In the local flux-tube limit we evaluate all of these quantities at $x=x_0$![]() , with $x_0$
, with $x_0$![]() denoting the flux surface of interest. In non-axisymmetric configurations the coefficients also in general depend on the field line label $y$
denoting the flux surface of interest. In non-axisymmetric configurations the coefficients also in general depend on the field line label $y$![]() , so we also evaluate the coefficients at $y=y_0$
, so we also evaluate the coefficients at $y=y_0$![]() to select a particular field line of interest. This ensures that the geometric coefficients are only functions of the parallel coordinate $z$
to select a particular field line of interest. This ensures that the geometric coefficients are only functions of the parallel coordinate $z$![]() . These quantities form a complete set of geometry-related coefficients needed for a GX simulation. These quantities also coincide with the geometry definitions in GS2.
. These quantities form a complete set of geometry-related coefficients needed for a GX simulation. These quantities also coincide with the geometry definitions in GS2.
E.1 Calculating an equispaced, equal-arc z
Generally speaking, ${gradpar}$![]() is a function of $z$
is a function of $z$![]() . However, it is often convenient to transform to a $z$
. However, it is often convenient to transform to a $z$![]() -grid where ${gradpar}$
-grid where ${gradpar}$![]() is a constant. This is strictly necessary in GX to allow Fourier spectral treatment of the parallel streaming term in the gyrokinetic equation. To do this, we seek a grid $\hat {z}$
is a constant. This is strictly necessary in GX to allow Fourier spectral treatment of the parallel streaming term in the gyrokinetic equation. To do this, we seek a grid $\hat {z}$![]() such that
such that
where $C$![]() is a constant. A differential element in the field-line following coordinates $(x, y, z)$
is a constant. A differential element in the field-line following coordinates $(x, y, z)$![]() can be written as
can be written as
On a given field line, ${{\rm d} x} = {{\rm d} y} = 0$![]() . Using the duality relation (E2), we can write
. Using the duality relation (E2), we can write
For a differential line element along the field line, we dot (E14) with the unit vector $\boldsymbol {b}$![]() to get
to get
Repeating the same process for the coordinate system $(x, y, \hat {z})$![]() and using (E15)
and using (E15)
Integrating (E16) first for one period in $z$![]() (or $\hat {z}$
(or $\hat {z}$![]() ) and using the fact that
) and using the fact that
we get

Using $C$![]() , we can now obtain $\hat {z}$
, we can now obtain $\hat {z}$![]() for each value of $z$
for each value of $z$![]() by integrating (E16)
by integrating (E16)
The resulting $\hat {z}$![]() coordinate is an equal-arc coordinate. Upon obtaining the equal-arc $\hat {z}$
coordinate is an equal-arc coordinate. Upon obtaining the equal-arc $\hat {z}$![]() , we interpolate all geometric coefficients onto an equispaced grid $\tilde {z}$
, we interpolate all geometric coefficients onto an equispaced grid $\tilde {z}$![]() . This makes $\tilde {z}$
. This makes $\tilde {z}$![]() an equispaced, equal-arc coordinate. Note that this procedure can be used for any field-line-following coordinate.
an equispaced, equal-arc coordinate. Note that this procedure can be used for any field-line-following coordinate.
Appendix F. Turbulent fluxes
Here we document expressions for turbulent fluxes in the Fourier–Laguerre–Hermite basis.
F.1 Heat flux
The normalized radial heat flux for species $s$![]() is defined as
is defined as

where $\{\cdots \}^*$![]() denotes a complex conjugate, and
denotes a complex conjugate, and



Note that since ${\boldsymbol v}_{\chi } \boldsymbol {\cdot } \boldsymbol {\nabla } \chi = 0$![]() , the convection of the integral of $h$
, the convection of the integral of $h$![]() at fixed ${\boldsymbol r}$
at fixed ${\boldsymbol r}$![]() is equal to the convection of the integral of $g$
is equal to the convection of the integral of $g$![]() at fixed ${\boldsymbol r}$
at fixed ${\boldsymbol r}$![]() . In physical units, the heat flux for species $s$
. In physical units, the heat flux for species $s$![]() is $Q_{{\rm phys}, s} = (n_0 v_{{\rm th}} T)_{\rm ref} \rho _*^2 Q_s\equiv Q_{GB,\mathrm {ref}} Q_s$
is $Q_{{\rm phys}, s} = (n_0 v_{{\rm th}} T)_{\rm ref} \rho _*^2 Q_s\equiv Q_{GB,\mathrm {ref}} Q_s$![]() .
.
F.2 Particle flux
Similarly, the normalized radial particle flux for species $s$![]() is defined as
is defined as

with



as defined in § 4. In physical units, the particle flux for species $s$![]() is $\varGamma _{{\rm phys}, s} = (n_0 v_{{\rm th}})_{\rm ref} \rho _*^2 \varGamma _s\equiv \varGamma _{GB,\mathrm {ref}}\varGamma _s$
is $\varGamma _{{\rm phys}, s} = (n_0 v_{{\rm th}})_{\rm ref} \rho _*^2 \varGamma _s\equiv \varGamma _{GB,\mathrm {ref}}\varGamma _s$![]() .
.
Appendix G. Numerical resolution for benchmark cases
Here we provide the numerical resolution and associated parameters used in each benchmark case from § 6. In all cases, normalizing quantities below follow the GX conventions above (as opposed to the normalization conventions of the various other codes).
G.1 Linear CBC, Boltzmann electrons (figure 1)
GX calculations used: three $2{\rm \pi}$![]() segments in an extended ballooning domain each with $N_z=24$
segments in an extended ballooning domain each with $N_z=24$![]() parallel grid points; $N_m=48$
parallel grid points; $N_m=48$![]() Hermite modes; $N_\ell =16$
Hermite modes; $N_\ell =16$![]() Laguerre modes.
Laguerre modes.
GS2 calculations used: three $2{\rm \pi}$![]() segments in an extended ballooning domain each with $N_z=25$
segments in an extended ballooning domain each with $N_z=25$![]() parallel grid points; 32 energy grid points; 33 pitch angles (20 in the untrapped region of velocity space and 13 in the trapped region).
parallel grid points; 32 energy grid points; 33 pitch angles (20 in the untrapped region of velocity space and 13 in the trapped region).
G.2 Linear CBC, kinetic electrons (figures 2 and 3)
GX calculations used: three $2{\rm \pi}$![]() segments in an extended ballooning domain each with $N_z=24$
segments in an extended ballooning domain each with $N_z=24$![]() parallel grid points; $N_m=128$
parallel grid points; $N_m=128$![]() Hermite modes; $N_\ell =16$
Hermite modes; $N_\ell =16$![]() Laguerre modes.
Laguerre modes.
GS2 calculations used: three $2{\rm \pi}$![]() segments in an extended ballooning domain each with $N_z=25$
segments in an extended ballooning domain each with $N_z=25$![]() parallel grid points; 32 energy grid points; 33 pitch angles (20 in the untrapped region of velocity space and 13 in the trapped region).
parallel grid points; 32 energy grid points; 33 pitch angles (20 in the untrapped region of velocity space and 13 in the trapped region).
The stella calculations used: three $2{\rm \pi}$![]() segments in an extended ballooning domain each with $N_z=25$
segments in an extended ballooning domain each with $N_z=25$![]() parallel grid points; 48 $v_\parallel$
parallel grid points; 48 $v_\parallel$![]() (evenly spaced) grid points with $v_{\parallel,\mathrm {max}}=3\sqrt {2} v_{\rm ti}$
(evenly spaced) grid points with $v_{\parallel,\mathrm {max}}=3\sqrt {2} v_{\rm ti}$![]() ; 16 $\mu$
; 16 $\mu$![]() grid points with $v_{\perp,\mathrm {max}} = 3\sqrt {2} v_{\rm ti}$
grid points with $v_{\perp,\mathrm {max}} = 3\sqrt {2} v_{\rm ti}$![]() .
.
G.3 Nonlinear CBC, Boltzmann electrons (figure 4 and table 1)
GX calculations used: one $2{\rm \pi}$![]() ballooning domain segment with $N_z=24$
ballooning domain segment with $N_z=24$![]() parallel grid points; $N_x=192$
parallel grid points; $N_x=192$![]() radial grid points (which corresponds to $N_{k_x}=127$
radial grid points (which corresponds to $N_{k_x}=127$![]() dealiased Fourier modes); $N_y=64$
dealiased Fourier modes); $N_y=64$![]() binormal grid points (which corresponds to $N_{k_y}=22$
binormal grid points (which corresponds to $N_{k_y}=22$![]() dealiased $k_y\geq 0$
dealiased $k_y\geq 0$![]() Fourier modes, with the $k_y<0$
Fourier modes, with the $k_y<0$![]() modes determined by the reality condition). The velocity-space resolution varied by case and is provided in the main text. The perpendicular box dimensions were approximately $190\rho _i\times 190\rho _i$
modes determined by the reality condition). The velocity-space resolution varied by case and is provided in the main text. The perpendicular box dimensions were approximately $190\rho _i\times 190\rho _i$![]() . The hyperdissipation parameters used were: hyperviscosity with $D=0.05$
. The hyperdissipation parameters used were: hyperviscosity with $D=0.05$![]() and $n=4$
and $n=4$![]() ; hypercollisions with $f_\mathrm {hyp}=1$
; hypercollisions with $f_\mathrm {hyp}=1$![]() ; $p=N_m/2$
; $p=N_m/2$![]() .
.
GS2 calculations used: one $2{\rm \pi}$![]() ballooning domain segment with $N_z=24$
ballooning domain segment with $N_z=24$![]() parallel grid points, $N_x=192$
parallel grid points, $N_x=192$![]() radial grid points ($N_{k_x}=127$
radial grid points ($N_{k_x}=127$![]() ); $N_y=64$
); $N_y=64$![]() binormal grid points ($N_{k_y}=22$
binormal grid points ($N_{k_y}=22$![]() ); 16 energy grid points; 33 pitch angles (20 in the untrapped region of velocity space and 13 in the trapped region). The perpendicular box dimensions were approximately $190\rho _i\times 190\rho _i$
); 16 energy grid points; 33 pitch angles (20 in the untrapped region of velocity space and 13 in the trapped region). The perpendicular box dimensions were approximately $190\rho _i\times 190\rho _i$![]() .
.
G.4 Nonlinear CBC, kinetic electrons (figure 5 and table 2)
GX calculations used: one $2{\rm \pi}$![]() ballooning domain segment with $N_z=24$
ballooning domain segment with $N_z=24$![]() parallel grid points; $N_x=192$
parallel grid points; $N_x=192$![]() radial grid points (which corresponds to $N_{k_x}=127$
radial grid points (which corresponds to $N_{k_x}=127$![]() dealiased Fourier modes); $N_y=64$
dealiased Fourier modes); $N_y=64$![]() binormal grid points (which corresponds to $N_{k_y}=22$
binormal grid points (which corresponds to $N_{k_y}=22$![]() dealiased Fourier modes). The velocity-space resolution varied by case and is provided in the main text. The perpendicular box dimensions were approximately $190\rho _i\times 190\rho _i$
dealiased Fourier modes). The velocity-space resolution varied by case and is provided in the main text. The perpendicular box dimensions were approximately $190\rho _i\times 190\rho _i$![]() . The hyperdissipation parameters used were: hyperviscosity with $D=0.05$
. The hyperdissipation parameters used were: hyperviscosity with $D=0.05$![]() and $n=4$
and $n=4$![]() ; hypercollisions with $f_\mathrm {hyp}=1$
; hypercollisions with $f_\mathrm {hyp}=1$![]() ; $p=N_m/2$
; $p=N_m/2$![]() .
.
GS2 calculations used: one $2{\rm \pi}$![]() ballooning domain segment with $N_z=32$
ballooning domain segment with $N_z=32$![]() parallel grid points, $N_x=192$
parallel grid points, $N_x=192$![]() radial grid points ($N_{k_x}=127$
radial grid points ($N_{k_x}=127$![]() ); $N_y=64$
); $N_y=64$![]() binormal grid points ($N_{k_y}=22$
binormal grid points ($N_{k_y}=22$![]() ); 16 energy grid points; 36 pitch angles (19 in the untrapped region of velocity space and 17 in the trapped region). The perpendicular box dimensions were approximately $190\rho _i\times 190\rho _i$
); 16 energy grid points; 36 pitch angles (19 in the untrapped region of velocity space and 17 in the trapped region). The perpendicular box dimensions were approximately $190\rho _i\times 190\rho _i$![]() .
.
G.5 Linear W7-X case (figure 6)
GX calculations used: six $2{\rm \pi}$![]() ballooning domain segments (corresponding to six poloidal turns) with $N_z=256$
ballooning domain segments (corresponding to six poloidal turns) with $N_z=256$![]() parallel grid points; $N_m=16$
parallel grid points; $N_m=16$![]() Hermite modes; $N_\ell =8$
Hermite modes; $N_\ell =8$![]() Laguerre modes.
Laguerre modes.
The stella calculations used: 33 field periods with $N_z=256$![]() parallel grid points; $N_{v_\parallel }=32$
parallel grid points; $N_{v_\parallel }=32$![]() ; $N_\mu =8$
; $N_\mu =8$![]() .
.
G.6 Nonlinear W7-X case (figure 7)
GX calculations used: one $2{\rm \pi}$![]() ballooning domain segment (corresponding to a single poloidal turn) with $N_z=128$
ballooning domain segment (corresponding to a single poloidal turn) with $N_z=128$![]() parallel grid points, $N_x=64$
parallel grid points, $N_x=64$![]() radial grid points (which corresponds to $N_{k_x}=43$
radial grid points (which corresponds to $N_{k_x}=43$![]() dealiased Fourier modes); $N_y=192$
dealiased Fourier modes); $N_y=192$![]() binormal grid points (which corresponds to $N_{k_y}=64$
binormal grid points (which corresponds to $N_{k_y}=64$![]() dealiased Fourier modes). The velocity-space resolution varied by case and is provided in the main text. The perpendicular box dimensions were approximately $132\rho _i\times 89\rho _i$
dealiased Fourier modes). The velocity-space resolution varied by case and is provided in the main text. The perpendicular box dimensions were approximately $132\rho _i\times 89\rho _i$![]() . The hyperdissipation parameters used were: hyperviscosity with $D=0.05$
. The hyperdissipation parameters used were: hyperviscosity with $D=0.05$![]() and $n=4$
and $n=4$![]() ; hypercollisions with $f_\mathrm {hyp}=1$
; hypercollisions with $f_\mathrm {hyp}=1$![]() and $p=N_m/2$
and $p=N_m/2$![]() .
.
For stella and GENE calculation details, refer to Tables 2 and 3 (test 5) of González-Jerez et al. (Reference González-Jerez, Xanthopoulos, García-Regaña, Calvo, Alcusón, Bañón Navarro, Barnes, Parra and Geiger2022).