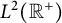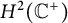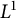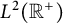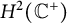1 Introduction
Let
![]() $1\leq p < \infty $
, and let H be a Hardy kernel of index p, that is, a mapping
$1\leq p < \infty $
, and let H be a Hardy kernel of index p, that is, a mapping
![]() $H: (0,\infty ) \times (0,\infty ) \to \mathbb C$
which is homogenous of degree
$H: (0,\infty ) \times (0,\infty ) \to \mathbb C$
which is homogenous of degree
![]() $-1$
and satisfies
$-1$
and satisfies
![]() $\int _0^\infty |H(1,s)|s^{-1/p} ds< \infty $
(see Definition 2.1). As a straightforward consequence of the celebrated Hardy’s inequality [Reference Hardy, Littlewood and Pólya9, Theorem 319], one obtains that H defines an operator
$\int _0^\infty |H(1,s)|s^{-1/p} ds< \infty $
(see Definition 2.1). As a straightforward consequence of the celebrated Hardy’s inequality [Reference Hardy, Littlewood and Pólya9, Theorem 319], one obtains that H defines an operator
![]() $A_H$
given by
$A_H$
given by
which is bounded on
![]() $L^p(\mathbb {R}^+)$
, where
$L^p(\mathbb {R}^+)$
, where
![]() $\mathbb R^+ := (0,\infty )$
. Hardy’s inequality also allows us to define a bounded operator
$\mathbb R^+ := (0,\infty )$
. Hardy’s inequality also allows us to define a bounded operator
![]() $D_H$
on the Hardy spaces on the half plane
$D_H$
on the Hardy spaces on the half plane
![]() $H^p(\mathbb C^+)$
, where
$H^p(\mathbb C^+)$
, where
![]() $\mathbb C^+:=\{z \in \mathbb C \, | \, \Re z> 0\}$
, by
$\mathbb C^+:=\{z \in \mathbb C \, | \, \Re z> 0\}$
, by
 $$ \begin{align} \begin{aligned} \qquad(D_H F) (z) &:= \int_0^\infty H(|z|,s) F^\theta(s) \, ds \\ &= \int_0^\infty H(1,s) F(sz)\, ds, \quad z = |z|e^{i\theta} \in \mathbb C^+, \: F \in H^p(\mathbb C^+), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \qquad(D_H F) (z) &:= \int_0^\infty H(|z|,s) F^\theta(s) \, ds \\ &= \int_0^\infty H(1,s) F(sz)\, ds, \quad z = |z|e^{i\theta} \in \mathbb C^+, \: F \in H^p(\mathbb C^+), \end{aligned} \end{align} $$
where
![]() $F^\theta (r):= F(re^{i\theta })$
, for
$F^\theta (r):= F(re^{i\theta })$
, for
![]() $r>0, \: \theta \in (-\pi /2,\pi /2)$
. Indeed, the last term in (1.2) shows that
$r>0, \: \theta \in (-\pi /2,\pi /2)$
. Indeed, the last term in (1.2) shows that
![]() $D_H F$
is holomorphic (see, for example, [Reference Hung, Ky and Quang11]), and the boundedness of
$D_H F$
is holomorphic (see, for example, [Reference Hung, Ky and Quang11]), and the boundedness of
![]() $D_H F$
follows by an application of Hardy’s inequality together with the realization of the norm of
$D_H F$
follows by an application of Hardy’s inequality together with the realization of the norm of
![]() $H^p(\mathbb C^+)$
given in [Reference Sedletskii19] by
$H^p(\mathbb C^+)$
given in [Reference Sedletskii19] by
 $$ \begin{align} \|F\|_{H^p} = \sup_{-\pi/2 < \theta < \pi/2} \left(\frac{1}{2\pi} \int_0^\infty |F^\theta(r)|^p \, dr\right)^{\frac{1}{p}}, \qquad F \in H^p(\mathbb C^+). \end{align} $$
$$ \begin{align} \|F\|_{H^p} = \sup_{-\pi/2 < \theta < \pi/2} \left(\frac{1}{2\pi} \int_0^\infty |F^\theta(r)|^p \, dr\right)^{\frac{1}{p}}, \qquad F \in H^p(\mathbb C^+). \end{align} $$
We will refer to these families of bounded operators on
![]() $L^p(\mathbb R^+)$
and
$L^p(\mathbb R^+)$
and
![]() $H^p(\mathbb C^+)$
as Hardy operators. These families have been actively studied, and are often labeled as Hausdorff operators due to its relation to the Hausdorff summability method through the function
$H^p(\mathbb C^+)$
as Hardy operators. These families have been actively studied, and are often labeled as Hausdorff operators due to its relation to the Hausdorff summability method through the function
![]() $\varphi (t) := H(t,1)$
for
$\varphi (t) := H(t,1)$
for
![]() $t>0$
(see the survey articles [Reference Chen, Fan and Wang4, Reference Liflyand15] for more details).
$t>0$
(see the survey articles [Reference Chen, Fan and Wang4, Reference Liflyand15] for more details).
On the other hand, recall that a Hilbert space X of complex-valued functions with domain
![]() $\Omega $
is said to be a reproducing kernel Hilbert space (RKHS) if and only if point evaluations
$\Omega $
is said to be a reproducing kernel Hilbert space (RKHS) if and only if point evaluations
![]() $L_x f:= f(x)$
are continuous functionals for all
$L_x f:= f(x)$
are continuous functionals for all
![]() $x \in \Omega $
. Then, by the Riesz representation theorem, for each
$x \in \Omega $
. Then, by the Riesz representation theorem, for each
![]() $x \in \Omega $
, there exists a unique
$x \in \Omega $
, there exists a unique
![]() $K_x \in X$
such that
$K_x \in X$
such that
![]() $f(x) = L_x f = (f\, | \, K_x)$
for all
$f(x) = L_x f = (f\, | \, K_x)$
for all
![]() $f \in X$
, where
$f \in X$
, where
![]() $(\cdot \, |\, \cdot )$
denotes the inner product in X. Then the reproducing kernel
$(\cdot \, |\, \cdot )$
denotes the inner product in X. Then the reproducing kernel
![]() $K: \Omega \times \Omega \to \mathbb C$
of X is defined by
$K: \Omega \times \Omega \to \mathbb C$
of X is defined by
The kernel K determines the space X. More precisely, X can be recovered from K as the completion of
![]() $\mbox {span}\{K_x\, | \, x\in \Omega \}$
under the norm given by scalar product
$\mbox {span}\{K_x\, | \, x\in \Omega \}$
under the norm given by scalar product
![]() $( K_y \,|\, K_x ) := K(x,y)$
(see the proof of the Moore–Aronszajn theorem [Reference Aronszajn1]).
$( K_y \,|\, K_x ) := K(x,y)$
(see the proof of the Moore–Aronszajn theorem [Reference Aronszajn1]).
In this paper, we focus on the range spaces of Hardy operators in the Hilbertian case, that is, for
![]() $p=2$
. We show that these spaces are RKHSs and obtain their reproducing kernels. Our work is partly motivated by papers [Reference Galé, Matache, Miana and Sánchez-Lajusticia7, Reference Galé, Miana and Sánchez-Lajusticia8], where the range spaces of generalized Cesàro operators
$p=2$
. We show that these spaces are RKHSs and obtain their reproducing kernels. Our work is partly motivated by papers [Reference Galé, Matache, Miana and Sánchez-Lajusticia7, Reference Galé, Miana and Sánchez-Lajusticia8], where the range spaces of generalized Cesàro operators
![]() $\mathcal {C}_\alpha $
on
$\mathcal {C}_\alpha $
on
![]() $L^2(\mathbb R^+)$
and
$L^2(\mathbb R^+)$
and
![]() $H^2(\mathbb C^+)$
are analyzed as RKHSs. In this context, it is more appropriate to deal with Hardy operators using Hardy kernels H rather than one-dimensional functions
$H^2(\mathbb C^+)$
are analyzed as RKHSs. In this context, it is more appropriate to deal with Hardy operators using Hardy kernels H rather than one-dimensional functions
![]() $\varphi $
associated with Hausdorff operators. Indeed, the set
$\varphi $
associated with Hausdorff operators. Indeed, the set
![]() $\mathfrak {H}_p$
of Hardy kernels of index p is naturally endowed with a structure of convolution (see [Reference Boyd2, Reference Fabes, Jodeit and Lewis6, Reference Leibowitz13]). More precisely,
$\mathfrak {H}_p$
of Hardy kernels of index p is naturally endowed with a structure of convolution (see [Reference Boyd2, Reference Fabes, Jodeit and Lewis6, Reference Leibowitz13]). More precisely,
![]() $\mathfrak {H}_p$
is a Banach algebra with multiplication
$\mathfrak {H}_p$
is a Banach algebra with multiplication
![]() $\bullet $
given by
$\bullet $
given by
(see Section 2).
In the setting of Hardy operators on
![]() $L^2(\mathbb R^+)$
, our main result is that, for a Hardy kernel H of index
$L^2(\mathbb R^+)$
, our main result is that, for a Hardy kernel H of index
![]() $2$
, the range space
$2$
, the range space
![]() $\mathcal A(H) = A_H (L^2(\mathbb R^+))$
becomes an RKHS (continuously included in
$\mathcal A(H) = A_H (L^2(\mathbb R^+))$
becomes an RKHS (continuously included in
![]() $L^2(\mathbb R^+)$
) if and only if H belongs to a certain ideal of
$L^2(\mathbb R^+)$
) if and only if H belongs to a certain ideal of
![]() $\mathfrak {H}_2$
(see Theorem 3.3). In this case, the reproducing kernel
$\mathfrak {H}_2$
(see Theorem 3.3). In this case, the reproducing kernel
![]() $K_H$
of
$K_H$
of
![]() $\mathcal A(H)$
is itself another Hardy kernel, given by
$\mathcal A(H)$
is itself another Hardy kernel, given by
where
![]() $H^\ast $
is the adjoint kernel of H (see Definition 2.2).
$H^\ast $
is the adjoint kernel of H (see Definition 2.2).
In the setting of Hardy spaces on the half plane, we prove in Theorem 4.3 that, for a given Hardy kernel H, the range space
![]() $\mathcal D(H)$
of a Hardy operator
$\mathcal D(H)$
of a Hardy operator
![]() $D_H$
is an RKHS, continuously included in
$D_H$
is an RKHS, continuously included in
![]() $H^2(\mathbb C^+)$
, with reproducing kernel given by
$H^2(\mathbb C^+)$
, with reproducing kernel given by
Here,
![]() $\mathcal {S}$
is the Stieltjes kernel and
$\mathcal {S}$
is the Stieltjes kernel and
![]() $(\cdot )^{hol}$
denotes the extension to
$(\cdot )^{hol}$
denotes the extension to
![]() $\mathbb C^+\times \mathbb C^+$
, which is holomorphic in the first variable and anti-holomorphic in the second one, whenever such an extension exists (Theorem 4.3).
$\mathbb C^+\times \mathbb C^+$
, which is holomorphic in the first variable and anti-holomorphic in the second one, whenever such an extension exists (Theorem 4.3).
Next, we establish Paley–Wiener-type results in Section 5. We show that the Laplace transform
![]() $\mathcal {L}$
provides an isometric isomorphism between
$\mathcal {L}$
provides an isometric isomorphism between
![]() $\mathcal A(H)$
and
$\mathcal A(H)$
and
![]() $\mathcal {D}(H^\top )$
(see Definition 2.2 for
$\mathcal {D}(H^\top )$
(see Definition 2.2 for
![]() $H^\top $
), and between
$H^\top $
), and between
![]() $\mathcal A(H)$
and
$\mathcal A(H)$
and
![]() $\mathcal {D}(H)$
under additional requirements on H.
$\mathcal {D}(H)$
under additional requirements on H.
In Section 6, we apply the results of preceding sections to several examples of range spaces of Hardy operators, such as generalized Cesàro and generalized Poisson operators. In particular, we retrieve results concerning generalized Cesàro operators in [Reference Galé, Miana and Sánchez-Lajusticia8], with simpler proofs.
2 Banach algebras of Hardy kernels
In this section, we are concerned with arbitrary
![]() $p \in [1,\infty )$
.
$p \in [1,\infty )$
.
Definition 2.1 Let
![]() $1\leq p <\infty $
, and let
$1\leq p <\infty $
, and let
![]() $H: \mathbb {R}^+\times \mathbb {R}^+ \rightarrow \mathbb {C}$
be a measurable map. H is said to be a Hardy kernel of index p if the following conditions hold.
$H: \mathbb {R}^+\times \mathbb {R}^+ \rightarrow \mathbb {C}$
be a measurable map. H is said to be a Hardy kernel of index p if the following conditions hold.
-
(i) H is homogeneous of degree
 $-1$
; that is, for all
$-1$
; that is, for all
 $\lambda>0$
,
$\lambda>0$
,
 $H(\lambda r, \lambda s) = \lambda ^{-1} H(r,s)$
for all
$H(\lambda r, \lambda s) = \lambda ^{-1} H(r,s)$
for all
 $ r,s> 0$
.
$ r,s> 0$
. -
(ii)
 $ \int _0^\infty |H(1,s)| s^{-1/p} ds < \infty $
, which is equivalent to
$ \int _0^\infty |H(1,s)| s^{-1/p} ds < \infty $
, which is equivalent to
 $\int _0^\infty |H(r,1)|r^{-1/p'} dr < \infty $
, where
$\int _0^\infty |H(r,1)|r^{-1/p'} dr < \infty $
, where
 $p'$
is such that
$p'$
is such that
 $1/p+1/p'=1$
(with
$1/p+1/p'=1$
(with
 $p'= \infty $
if
$p'= \infty $
if
 $p=1$
as usual).
$p=1$
as usual).
Hardy kernels are useful tools to construct bounded operators on the Lebesgue spaces
![]() $L^p(\mathbb {R}^+)$
through (1.1). This is a well-known result of Hardy, Littlewood, and Pólya (see [Reference Hardy, Littlewood and Pólya9, Theorem 319]), and it is part of folklore that such operators can be described as convolution operators by identifying a Hardy kernel H with the function
$L^p(\mathbb {R}^+)$
through (1.1). This is a well-known result of Hardy, Littlewood, and Pólya (see [Reference Hardy, Littlewood and Pólya9, Theorem 319]), and it is part of folklore that such operators can be described as convolution operators by identifying a Hardy kernel H with the function
![]() $g_H \in L^1(\mathbb R)$
given by
$g_H \in L^1(\mathbb R)$
given by
(see, for example, [Reference Boyd2, Reference Fabes, Jodeit and Lewis6]). If one wants
![]() $H \mapsto g_H$
to be a bijection, one must consider the following equivalence classes in the set of Hardy kernels of index p. We set that two Hardy kernels
$H \mapsto g_H$
to be a bijection, one must consider the following equivalence classes in the set of Hardy kernels of index p. We set that two Hardy kernels
![]() $H, G $
of index p are equivalent,
$H, G $
of index p are equivalent,
![]() $H \sim G$
, if and only if
$H \sim G$
, if and only if
![]() $H(r,1) = G(r,1)$
for a.e.
$H(r,1) = G(r,1)$
for a.e.
![]() $r>0$
. From now on,
$r>0$
. From now on,
![]() $\mathfrak {H}_p$
will denote this set of equivalence classes of Hardy kernels of index p, and we will refer to
$\mathfrak {H}_p$
will denote this set of equivalence classes of Hardy kernels of index p, and we will refer to
![]() $H \in \mathfrak {H}_p$
as a Hardy kernel rather than an equivalence class of Hardy kernels, so we identify an equivalence class by any of its elements.
$H \in \mathfrak {H}_p$
as a Hardy kernel rather than an equivalence class of Hardy kernels, so we identify an equivalence class by any of its elements.
As a consequence, the mapping
![]() $\Phi _p: \mathfrak {H}_p \rightarrow L^1(\mathbb R)$
defined by
$\Phi _p: \mathfrak {H}_p \rightarrow L^1(\mathbb R)$
defined by
![]() $\Phi _p(H) := g_H$
is a bijection, with inverse given by
$\Phi _p(H) := g_H$
is a bijection, with inverse given by
![]() $(\Phi _p^{-1} g) (r,s) = r^{-1/p} s^{-1/p'} g\left (\log \frac {r}{s}\right )$
, for a.e.
$(\Phi _p^{-1} g) (r,s) = r^{-1/p} s^{-1/p'} g\left (\log \frac {r}{s}\right )$
, for a.e.
![]() $r,s>0, \, g\in L^1(\mathbb {R})$
.
$r,s>0, \, g\in L^1(\mathbb {R})$
.
Next, we endow the linear space
![]() $\mathfrak {H}_p$
with the norm and product given, respectively, by
$\mathfrak {H}_p$
with the norm and product given, respectively, by
![]() $\|H\|_{\mathfrak {H}_p} := \|\Phi _p(H)\|_{L^1(\mathbb R)},\, H \bullet G := \Phi _p^{-1} ((\Phi _p H) \ast (\Phi _p G))$
for all
$\|H\|_{\mathfrak {H}_p} := \|\Phi _p(H)\|_{L^1(\mathbb R)},\, H \bullet G := \Phi _p^{-1} ((\Phi _p H) \ast (\Phi _p G))$
for all
![]() $H,G \in \mathfrak {H}_p$
, where
$H,G \in \mathfrak {H}_p$
, where
![]() $\ast $
stands for the usual convolution of two elements of
$\ast $
stands for the usual convolution of two elements of
![]() $L^1(\mathbb R)$
. We will denote the Banach algebra of bounded linear operators on a Banach space X by
$L^1(\mathbb R)$
. We will denote the Banach algebra of bounded linear operators on a Banach space X by
![]() $\mathcal {B}(X)$
.
$\mathcal {B}(X)$
.
Proposition 2.1 Let
![]() $1\leq p< \infty $
. The space
$1\leq p< \infty $
. The space
![]() $\mathfrak {H}_p$
is a commutative Banach algebra if provided with the norm and product
$\mathfrak {H}_p$
is a commutative Banach algebra if provided with the norm and product
 $$ \begin{align*} \|H\|_{\mathfrak{H}_p} &= \int_0^\infty |H(1,s)|s^{-1/p} \, ds, \\ (H \bullet G) (r,s) &= \int_0^\infty H(r,t) G(t,s) \, dt, \:\:\:\: r,s>0. \end{align*} $$
$$ \begin{align*} \|H\|_{\mathfrak{H}_p} &= \int_0^\infty |H(1,s)|s^{-1/p} \, ds, \\ (H \bullet G) (r,s) &= \int_0^\infty H(r,t) G(t,s) \, dt, \:\:\:\: r,s>0. \end{align*} $$
Moreover, the mappings
![]() $A_p: \mathfrak {H}_p \rightarrow \mathcal {B}(L^p(\mathbb {R}^+))$
,
$A_p: \mathfrak {H}_p \rightarrow \mathcal {B}(L^p(\mathbb {R}^+))$
,
![]() $D_p: \mathfrak {H}_p \rightarrow \mathcal {B}(H^p(\mathbb C^+))$
, given by
$D_p: \mathfrak {H}_p \rightarrow \mathcal {B}(H^p(\mathbb C^+))$
, given by
![]() $A_p (H) := A_H$
and
$A_p (H) := A_H$
and
![]() $D_p(H):=D_H$
, are bounded Banach algebra homomorphisms.
$D_p(H):=D_H$
, are bounded Banach algebra homomorphisms.
Proof It is readily seen that
![]() $\|H\|_{\mathfrak {H}_p} = \|g_H\|_{L^1(\mathbb R)} = \int _0^\infty |H(1,s)|s^{-1/p} \, ds$
. Let us prove the product identity. It follows that for
$\|H\|_{\mathfrak {H}_p} = \|g_H\|_{L^1(\mathbb R)} = \int _0^\infty |H(1,s)|s^{-1/p} \, ds$
. Let us prove the product identity. It follows that for
![]() $H,G \in \mathfrak {H}_p$
,
$H,G \in \mathfrak {H}_p$
,
 $$ \begin{align*} (H \bullet G) (r,s) &= \Phi_p^{-1} \left(\Phi_p(H) \ast \Phi_p(G)\right) (r,s) = r^{-1/p} s^{-1/p'} \left(g_H \ast g_G\right) \left(\log \frac{r}{s}\right) \\ &= r^{-1/p} s^{-1/p'}\int_{-\infty}^\infty G(1,e^{-t}) e^{-t/p'} H\left(1, e^{t-\log (r/s)}\right)e^{(t-\log (r/s))/p'}\, dt \\ &= \frac{1}{r} \int_0^\infty G(1,u^{-1}) H\left( 1,u\frac{s}{r}\right) \frac{du}{u} = \frac{1}{r} \int_0^\infty H\left(1, \frac{v}{r}\right) G\left(1, \frac{s}{v}\right) \frac{dv}{v} \\ &= \int_0^\infty H\left(r,v\right) G\left(v,s\right) \, dv, \qquad r,s>0. \end{align*} $$
$$ \begin{align*} (H \bullet G) (r,s) &= \Phi_p^{-1} \left(\Phi_p(H) \ast \Phi_p(G)\right) (r,s) = r^{-1/p} s^{-1/p'} \left(g_H \ast g_G\right) \left(\log \frac{r}{s}\right) \\ &= r^{-1/p} s^{-1/p'}\int_{-\infty}^\infty G(1,e^{-t}) e^{-t/p'} H\left(1, e^{t-\log (r/s)}\right)e^{(t-\log (r/s))/p'}\, dt \\ &= \frac{1}{r} \int_0^\infty G(1,u^{-1}) H\left( 1,u\frac{s}{r}\right) \frac{du}{u} = \frac{1}{r} \int_0^\infty H\left(1, \frac{v}{r}\right) G\left(1, \frac{s}{v}\right) \frac{dv}{v} \\ &= \int_0^\infty H\left(r,v\right) G\left(v,s\right) \, dv, \qquad r,s>0. \end{align*} $$
Next, it follows by Hardy’s inequality [Reference Hardy, Littlewood and Pólya9, Theorem 319] that
![]() $\|A_H\|_{\mathcal {B}(L^p)} \leq \|H\|_{\mathfrak {H}_p}$
. Moreover, one has that
$\|A_H\|_{\mathcal {B}(L^p)} \leq \|H\|_{\mathfrak {H}_p}$
. Moreover, one has that
 $$ \begin{align*} (A_{H\bullet G} f) (r) &= \int_0^\infty (H\bullet G)(r,s) f(s)\, ds = \int_0^\infty H(r,t) \int_0^\infty G(t,s) f(s) \,ds \, dt \\ &= (A_H A_G f)(r), \qquad f\in L^p(\mathbb R^+), \, \text{a.e. } r>0. \end{align*} $$
$$ \begin{align*} (A_{H\bullet G} f) (r) &= \int_0^\infty (H\bullet G)(r,s) f(s)\, ds = \int_0^\infty H(r,t) \int_0^\infty G(t,s) f(s) \,ds \, dt \\ &= (A_H A_G f)(r), \qquad f\in L^p(\mathbb R^+), \, \text{a.e. } r>0. \end{align*} $$
Note that
![]() $(D_H F)^\theta = A_H F^\theta $
. Thus, by (1.3) and what we have just proved,
$(D_H F)^\theta = A_H F^\theta $
. Thus, by (1.3) and what we have just proved,
 $$ \begin{align*} \|D_H F\|_{H^p} \leq \|A_H\|_{\mathcal{B}(L^p)} \sup_{-\pi/2 < \theta < \pi/2} \frac{1}{2\pi}\|F^\theta\|_{L^p} \leq \|H\|_{\mathfrak{H}_p} \|F\|_{H^p}, \quad F \in H^p(\mathbb C^+). \end{align*} $$
$$ \begin{align*} \|D_H F\|_{H^p} \leq \|A_H\|_{\mathcal{B}(L^p)} \sup_{-\pi/2 < \theta < \pi/2} \frac{1}{2\pi}\|F^\theta\|_{L^p} \leq \|H\|_{\mathfrak{H}_p} \|F\|_{H^p}, \quad F \in H^p(\mathbb C^+). \end{align*} $$
Similarly,
![]() $(D_{H\bullet G} F)^\theta = A_{H\bullet G} F^\theta = A_H A_G F^\theta = (D_H D_G F)^\theta $
for any
$(D_{H\bullet G} F)^\theta = A_{H\bullet G} F^\theta = A_H A_G F^\theta = (D_H D_G F)^\theta $
for any
![]() $F \in H^p(\mathbb C^+)$
and
$F \in H^p(\mathbb C^+)$
and
![]() $\theta \in \left (\frac {\pi }{2}, \frac {\pi }{2}\right )$
, and thus
$\theta \in \left (\frac {\pi }{2}, \frac {\pi }{2}\right )$
, and thus
![]() $D_{H \bullet G} = D_H D_G$
.
$D_{H \bullet G} = D_H D_G$
.
Next, we give a few definitions and properties regarding Hardy kernels that will be needed later. Let us denote by
![]() $\overline {z}$
the conjugate of
$\overline {z}$
the conjugate of
![]() $z\in \mathbb {C}$
.
$z\in \mathbb {C}$
.
Definition 2.2 Let
![]() $1<p<\infty $
, and let
$1<p<\infty $
, and let
![]() $H \in \mathfrak {H}_p$
. Set
$H \in \mathfrak {H}_p$
. Set
![]() $H^\top (r,s) := H(s,r)$
for all
$H^\top (r,s) := H(s,r)$
for all
![]() $r,s>0$
. Similarly, set
$r,s>0$
. Similarly, set
![]() $H^\ast (r,s) := \overline {H(s,r)}$
for all
$H^\ast (r,s) := \overline {H(s,r)}$
for all
![]() $r,s>0$
.
$r,s>0$
.
Remark 2.2 Let
![]() $1<p<\infty $
, and let
$1<p<\infty $
, and let
![]() $H,G \in \mathfrak {H}_p$
. One has that
$H,G \in \mathfrak {H}_p$
. One has that
![]() $H^\top , H^\ast \in \mathfrak {H}_{p'}$
, that
$H^\top , H^\ast \in \mathfrak {H}_{p'}$
, that
![]() $(H\bullet G)^\top = H^\top \bullet G^\top $
,
$(H\bullet G)^\top = H^\top \bullet G^\top $
,
![]() $(H \bullet G)^\ast = H^\ast \bullet G^\ast $
, and that
$(H \bullet G)^\ast = H^\ast \bullet G^\ast $
, and that
![]() $(H^\top )^\ast = (H^\ast )^\top $
.
$(H^\top )^\ast = (H^\ast )^\top $
.
Definition 2.3 Let
![]() $1 \leq p < \infty $
. We define
$1 \leq p < \infty $
. We define
![]() $\mathcal I_p \subset \mathfrak {H}_p$
as
$\mathcal I_p \subset \mathfrak {H}_p$
as
![]() $\mathcal I_p := \Phi _p^{-1}(L^1(\mathbb R)\cap L^{p'}(\mathbb R))$
.
$\mathcal I_p := \Phi _p^{-1}(L^1(\mathbb R)\cap L^{p'}(\mathbb R))$
.
Clearly,
![]() $\mathcal I_p$
is a dense ideal of
$\mathcal I_p$
is a dense ideal of
![]() $\mathfrak {H}_p$
since so is
$\mathfrak {H}_p$
since so is
![]() $L^1(\mathbb R)\cap L^{p'}(\mathbb R)$
in
$L^1(\mathbb R)\cap L^{p'}(\mathbb R)$
in
![]() $L^1(\mathbb R)$
. We characterize its elements in the lemma below. For
$L^1(\mathbb R)$
. We characterize its elements in the lemma below. For
![]() $H \in \mathfrak {H}_p$
, define the family
$H \in \mathfrak {H}_p$
, define the family
![]() $(H_s)_{s\in \mathbb {R}^+}$
of complex-valued functions defined a.e. in
$(H_s)_{s\in \mathbb {R}^+}$
of complex-valued functions defined a.e. in
![]() $\mathbb R^+$
, given by
$\mathbb R^+$
, given by
![]() $\{H_s := H(\cdot , s)\: | \: s \in \mathbb R^+\}$
. In particular,
$\{H_s := H(\cdot , s)\: | \: s \in \mathbb R^+\}$
. In particular,
![]() $H_r^\top = H(r,\cdot )$
for any
$H_r^\top = H(r,\cdot )$
for any
![]() $r>0$
.
$r>0$
.
Lemma 2.3 Let
![]() $1 \leq p < \infty $
, and let
$1 \leq p < \infty $
, and let
![]() $H\in \mathfrak {H}_p$
. The following are equivalent.
$H\in \mathfrak {H}_p$
. The following are equivalent.
-
(i)
 $H \in \mathcal I_p$
.
$H \in \mathcal I_p$
. -
(ii)
 $(H_r^\top )_{r>0} \subset L^{p'}(\mathbb {R}^+)$
.
$(H_r^\top )_{r>0} \subset L^{p'}(\mathbb {R}^+)$
. -
(iii)
 $H_1^\top \in L^{p'}(\mathbb {R}^+)$
.
$H_1^\top \in L^{p'}(\mathbb {R}^+)$
.
In any of the above cases, one has that
Proof All the statements of the equivalence are straightforward to obtain using the homogeneity of degree
![]() $-1$
of H and the definition of the function
$-1$
of H and the definition of the function
![]() $g_H$
. Let us show the equivalence
$g_H$
. Let us show the equivalence
![]() $(i)\iff (iii)$
. For
$(i)\iff (iii)$
. For
![]() $1<p<\infty $
,
$1<p<\infty $
,
 $$ \begin{align*} \|H_1^\top\|_{p'} &= \left(\int_0^\infty |H(1,s)|^{p'} \, ds \right)^{1/p'} = \left(\int_{-\infty}^\infty |H(1,e^{-t})|^{p'} e^{-t} \, dt \right)^{1/p'} = \|g_H\|_{p'}. \end{align*} $$
$$ \begin{align*} \|H_1^\top\|_{p'} &= \left(\int_0^\infty |H(1,s)|^{p'} \, ds \right)^{1/p'} = \left(\int_{-\infty}^\infty |H(1,e^{-t})|^{p'} e^{-t} \, dt \right)^{1/p'} = \|g_H\|_{p'}. \end{align*} $$
For
![]() $p=1$
, it is straightforward that
$p=1$
, it is straightforward that
![]() $\|H_1^\top \|_\infty = \|g_H\|_\infty $
since
$\|H_1^\top \|_\infty = \|g_H\|_\infty $
since
![]() $g_H (t) = H(1,e^{-t})$
for a.e.
$g_H (t) = H(1,e^{-t})$
for a.e.
![]() $t>0$
.
$t>0$
.
3 Hardy reproducing kernels on
 $\mathbb R^+ \times \mathbb R^+$
$\mathbb R^+ \times \mathbb R^+$
In this section, we analyze the range spaces of Hardy operators on
![]() $L^2(\mathbb R^+)$
, although some minor results are also valid for general p. Our main motivation is to characterize the conditions for which these range spaces are RKHSs (Proposition 3.2).
$L^2(\mathbb R^+)$
, although some minor results are also valid for general p. Our main motivation is to characterize the conditions for which these range spaces are RKHSs (Proposition 3.2).
Definition 3.1 Let
![]() $1\leq p < \infty $
, and let
$1\leq p < \infty $
, and let
![]() $H \in \mathfrak {H}_p$
. Let
$H \in \mathfrak {H}_p$
. Let
![]() $\mathcal A(H)$
be the range space
$\mathcal A(H)$
be the range space
We endow
![]() $\mathcal A(H)$
with a Banach (Hilbert if
$\mathcal A(H)$
with a Banach (Hilbert if
![]() $p=2$
) space structure through the canonical identification
$p=2$
) space structure through the canonical identification
![]() $\mathcal A(H) \cong L^p(\mathbb {R}^+)/\ker A_H$
.
$\mathcal A(H) \cong L^p(\mathbb {R}^+)/\ker A_H$
.
Let
![]() $C(\mathbb {R}^+)$
denote the space of continuous functions on
$C(\mathbb {R}^+)$
denote the space of continuous functions on
![]() $\mathbb R^+$
.
$\mathbb R^+$
.
Lemma 3.1 Let
![]() $1 \leq p < \infty $
, and let
$1 \leq p < \infty $
, and let
![]() $H \in \mathcal I_p \subset \mathfrak {H}_p$
. Then
$H \in \mathcal I_p \subset \mathfrak {H}_p$
. Then
![]() $\mathcal A(H) \subset C(\mathbb {R}^+)$
.
$\mathcal A(H) \subset C(\mathbb {R}^+)$
.
Proof Let
![]() $f \in L^p(\mathbb R^+)$
. We have that
$f \in L^p(\mathbb R^+)$
. We have that
where
![]() $(\tau _r f)(t):=f(rt)$
for
$(\tau _r f)(t):=f(rt)$
for
![]() $t>0$
,
$t>0$
,
![]() $\langle \cdot , \cdot \rangle $
denotes the dual product between
$\langle \cdot , \cdot \rangle $
denotes the dual product between
![]() $L^p(\mathbb {R}^+)$
and
$L^p(\mathbb {R}^+)$
and
![]() $L^{p'}(\mathbb {R}^+)$
, and
$L^{p'}(\mathbb {R}^+)$
, and
![]() $H_1^\top $
is defined before Lemma 2.3.
$H_1^\top $
is defined before Lemma 2.3.
Since the mapping
![]() $r\mapsto \tau _r f$
from
$r\mapsto \tau _r f$
from
![]() $\mathbb {R}^+$
into
$\mathbb {R}^+$
into
![]() $L^p(\mathbb {R}^+)$
is continuous for each
$L^p(\mathbb {R}^+)$
is continuous for each
![]() $f \in L^p(\mathbb {R}^+)$
, it follows that
$f \in L^p(\mathbb {R}^+)$
, it follows that
![]() $\langle \tau _r f, H_1^\top \rangle = (A_H f)(r)$
is also continuous in r; that is,
$\langle \tau _r f, H_1^\top \rangle = (A_H f)(r)$
is also continuous in r; that is,
![]() $A_H f \in C(\mathbb R^+)$
, as we wanted to show.
$A_H f \in C(\mathbb R^+)$
, as we wanted to show.
As a consequence of the lemma, point evaluations are well defined on
![]() $\mathcal A(H)$
whenever
$\mathcal A(H)$
whenever
![]() $H \in \mathcal I_p$
. Indeed, the proposition below adds a bit more information.
$H \in \mathcal I_p$
. Indeed, the proposition below adds a bit more information.
Proposition 3.2 Let
![]() $1 \leq p < \infty $
, and let
$1 \leq p < \infty $
, and let
![]() $H \in \mathfrak {H}_p$
. Then point evaluations are continuous functionals on
$H \in \mathfrak {H}_p$
. Then point evaluations are continuous functionals on
![]() $\mathcal A(H)$
if and only if
$\mathcal A(H)$
if and only if
![]() $H \in \mathcal I_p$
. In this case, for all
$H \in \mathcal I_p$
. In this case, for all
![]() $f\in \mathcal A(H)$
,
$f\in \mathcal A(H)$
,
Proof Let us assume first that point evaluations are well defined and continuous on
![]() $\mathcal A(H)$
, so for all
$\mathcal A(H)$
, so for all
![]() $r>0$
, the mapping
$r>0$
, the mapping
![]() $\Omega _r:L^p(\mathbb R^+) \rightarrow \mathbb C$
given by
$\Omega _r:L^p(\mathbb R^+) \rightarrow \mathbb C$
given by
![]() $\Omega _r f:= (A_H f)(r)$
is a well-defined continuous functional. Therefore, there exists
$\Omega _r f:= (A_H f)(r)$
is a well-defined continuous functional. Therefore, there exists
![]() $g_r \in L^{p'}(\mathbb R^+)$
such that
$g_r \in L^{p'}(\mathbb R^+)$
such that
![]() $(A_H f)(r) = \int _0^\infty g_r(s)f(s) ds$
for all
$(A_H f)(r) = \int _0^\infty g_r(s)f(s) ds$
for all
![]() $f \in L^p(\mathbb R^+)$
, which implies that
$f \in L^p(\mathbb R^+)$
, which implies that
![]() $H(r,s)=g_r(s)$
for a.e.
$H(r,s)=g_r(s)$
for a.e.
![]() $s>0$
. By Lemma 2.3, one gets that
$s>0$
. By Lemma 2.3, one gets that
![]() $H\in \mathcal I_p$
.
$H\in \mathcal I_p$
.
Now, let us assume that
![]() $H\in \mathcal I_p$
. By Lemma 3.1, it follows that point evaluations are well defined on
$H\in \mathcal I_p$
. By Lemma 3.1, it follows that point evaluations are well defined on
![]() $\mathcal A(H)$
. By Lemma 2.3, one has that
$\mathcal A(H)$
. By Lemma 2.3, one has that
![]() $(H_r^\top )_{r\in \mathbb {R}^+} \subset L^{p'}(\mathbb {R}^+)$
. Let
$(H_r^\top )_{r\in \mathbb {R}^+} \subset L^{p'}(\mathbb {R}^+)$
. Let
![]() $ f \in \mathcal A(H)$
,
$ f \in \mathcal A(H)$
,
![]() $g\in L^p(\mathbb {R}^+)$
be such that
$g\in L^p(\mathbb {R}^+)$
be such that
![]() $f = A_H g$
. Let
$f = A_H g$
. Let
![]() $[g+\ker A_H]$
be the quotient class of
$[g+\ker A_H]$
be the quotient class of
![]() $L^p(\mathbb {R}^+)/\ker A_H$
containing g. It follows that, for all
$L^p(\mathbb {R}^+)/\ker A_H$
containing g. It follows that, for all
![]() $\widetilde {g} \in [g+\ker A_H]$
,
$\widetilde {g} \in [g+\ker A_H]$
,
 $$ \begin{align*} |f(r)| &= |(A_H \widetilde{g})(r)| = \left|\int_0^\infty H(r,s) \widetilde{g}(s) \, ds \right| = \langle H_r^\top, \widetilde{g}\rangle \\ &\leq \inf_{\widetilde{g}\in [g+\ker A_H]} \|H_r^\top\|_{p'} \|\widetilde{g}\|_p = \|H_r^\top\|_{p'} \|[g+\ker A_H]\|_{L^p(\mathbb{R}^+) / \ker A_H} \\ &= r^{-1/p} \|H_1^\top\|_{p'} \|f\|_{\mathcal A(H)}, \qquad \forall r>0, \end{align*} $$
$$ \begin{align*} |f(r)| &= |(A_H \widetilde{g})(r)| = \left|\int_0^\infty H(r,s) \widetilde{g}(s) \, ds \right| = \langle H_r^\top, \widetilde{g}\rangle \\ &\leq \inf_{\widetilde{g}\in [g+\ker A_H]} \|H_r^\top\|_{p'} \|\widetilde{g}\|_p = \|H_r^\top\|_{p'} \|[g+\ker A_H]\|_{L^p(\mathbb{R}^+) / \ker A_H} \\ &= r^{-1/p} \|H_1^\top\|_{p'} \|f\|_{\mathcal A(H)}, \qquad \forall r>0, \end{align*} $$
where
![]() $\langle \cdot , \cdot \rangle $
denotes the dual product between
$\langle \cdot , \cdot \rangle $
denotes the dual product between
![]() $L^{p'}(\mathbb R^+)$
and
$L^{p'}(\mathbb R^+)$
and
![]() $L^p(\mathbb R^+)$
. Therefore, point evaluations are continuous on
$L^p(\mathbb R^+)$
. Therefore, point evaluations are continuous on
![]() $\mathcal A(H)$
.
$\mathcal A(H)$
.
The next theorem gives the reproducing kernel
![]() $K_H$
of
$K_H$
of
![]() $\mathcal A(H)$
for
$\mathcal A(H)$
for
![]() $H \in \mathcal I_2$
, which turns out to be a Hardy kernel as well.
$H \in \mathcal I_2$
, which turns out to be a Hardy kernel as well.
Theorem 3.3 Let
![]() $H \in \mathfrak {H}_2$
. Then
$H \in \mathfrak {H}_2$
. Then
![]() $\mathcal A(H)$
is an RKHS if and only if
$\mathcal A(H)$
is an RKHS if and only if
![]() $H \in \mathcal I_2$
, and in this case, its reproducing kernel
$H \in \mathcal I_2$
, and in this case, its reproducing kernel
![]() $K_H$
is continuous and given by
$K_H$
is continuous and given by
Then
![]() $K_H \in \mathfrak {H}_2$
, satisfying
$K_H \in \mathfrak {H}_2$
, satisfying
![]() $K_H = H \bullet H^\ast $
. As a consequence,
$K_H = H \bullet H^\ast $
. As a consequence,
![]() $K_{H^\ast } = K_H$
.
$K_{H^\ast } = K_H$
.
Proof By Proposition 3.2,
![]() $\mathcal A(H)$
is an RKHS if and only if
$\mathcal A(H)$
is an RKHS if and only if
![]() $H \in \mathcal I_2$
, and in this case,
$H \in \mathcal I_2$
, and in this case,
![]() $\mathcal A(H)$
is isometrically isomorphic to
$\mathcal A(H)$
is isometrically isomorphic to
![]() $L^2(\mathbb {R}^+) / \ker A_H \cong (\ker A_H)^\perp $
. Let us compute its reproducing kernel. Assume that
$L^2(\mathbb {R}^+) / \ker A_H \cong (\ker A_H)^\perp $
. Let us compute its reproducing kernel. Assume that
![]() $f \in \ker A_H$
, so it follows that
$f \in \ker A_H$
, so it follows that
for all
![]() $u>0$
, where
$u>0$
, where
![]() $H_u^\ast (v) = \overline {H(u,v)} = \overline {H_u^\top (v)}$
for a.e.
$H_u^\ast (v) = \overline {H(u,v)} = \overline {H_u^\top (v)}$
for a.e.
![]() $v>0$
. Therefore, one has that
$v>0$
. Therefore, one has that
![]() $H_u^\ast \in (\ker A_H)^\perp \subset L^2(\mathbb {R}^+)$
for all
$H_u^\ast \in (\ker A_H)^\perp \subset L^2(\mathbb {R}^+)$
for all
![]() $u>0$
.
$u>0$
.
Now, let
![]() $h_u = A_H H_u^\ast \in \mathcal A(H)$
, and let
$h_u = A_H H_u^\ast \in \mathcal A(H)$
, and let
![]() $f \in \mathcal A(H)$
, so that
$f \in \mathcal A(H)$
, so that
![]() $f = A_H g$
for a unique
$f = A_H g$
for a unique
![]() $g \in (\ker A_H)^\perp $
. Since
$g \in (\ker A_H)^\perp $
. Since
![]() $\mathcal A(H)\cong (\ker A_H)^\perp $
, it follows that, for all
$\mathcal A(H)\cong (\ker A_H)^\perp $
, it follows that, for all
![]() $u>0$
,
$u>0$
,
Hence,
![]() $K_H(v,u) = h_u(v) = (A_H H_u^\ast ) (v) = \int _0^\infty H(v,t) \overline {H(u,t)} \, dt$
for all
$K_H(v,u) = h_u(v) = (A_H H_u^\ast ) (v) = \int _0^\infty H(v,t) \overline {H(u,t)} \, dt$
for all
![]() $u,v>0$
, as we wanted to show.
$u,v>0$
, as we wanted to show.
Moreover,
![]() $K_H = H \bullet H^\ast = H^\ast \bullet H = K_{H^\ast }$
by Proposition 2.1 and Definition 2.2, and in particular
$K_H = H \bullet H^\ast = H^\ast \bullet H = K_{H^\ast }$
by Proposition 2.1 and Definition 2.2, and in particular
![]() $K_H$
turns out to be a Hardy kernel. The continuity of
$K_H$
turns out to be a Hardy kernel. The continuity of
![]() $K_H$
in each variable follows from the inclusion
$K_H$
in each variable follows from the inclusion
![]() $\mathcal A(H) \subset C(\mathbb {R}^+)$
(Lemma 3.1) and the fact that
$\mathcal A(H) \subset C(\mathbb {R}^+)$
(Lemma 3.1) and the fact that
![]() $K_H(r,s) = \overline {K_H(s,r)}, \: \text {for } r,s>0$
(see, for example, [Reference Neeb17, Lemma I.1.2]). But then,
$K_H(r,s) = \overline {K_H(s,r)}, \: \text {for } r,s>0$
(see, for example, [Reference Neeb17, Lemma I.1.2]). But then,
![]() $K_H : \mathbb R^+ \times \mathbb R^+ \to \mathbb C$
is continuous jointly on both variables since
$K_H : \mathbb R^+ \times \mathbb R^+ \to \mathbb C$
is continuous jointly on both variables since
![]() $K_H(r,s) = s^{-1} K_H(r/s,1)$
.
$K_H(r,s) = s^{-1} K_H(r/s,1)$
.
Let
![]() $\mathcal {H}_+$
be the one-sided Hilbert transform on
$\mathcal {H}_+$
be the one-sided Hilbert transform on
![]() $L^p(\mathbb R^+)$
defined by
$L^p(\mathbb R^+)$
defined by
The boundedness of
![]() $\mathcal {H}_+$
on
$\mathcal {H}_+$
on
![]() $L^p(\mathbb R^+)$
for
$L^p(\mathbb R^+)$
for
![]() $1<p<\infty $
immediately follows from the boundedness of the Hilbert transform on
$1<p<\infty $
immediately follows from the boundedness of the Hilbert transform on
![]() $L^p(\mathbb {R})$
(see, for example, [Reference Duoandikoetxea Zuazo5]). The following theorem has been inspired by [Reference Hung, Ky and Quang11, Reference Liflyand and Móricz14].
$L^p(\mathbb {R})$
(see, for example, [Reference Duoandikoetxea Zuazo5]). The following theorem has been inspired by [Reference Hung, Ky and Quang11, Reference Liflyand and Móricz14].
Theorem 3.4 Let
![]() $1 < p < \infty $
, and let
$1 < p < \infty $
, and let
![]() $H \in \mathfrak {H}_p$
. One has that
$H \in \mathfrak {H}_p$
. One has that
![]() $\mathcal {H}_+ A_H= A_H \mathcal {H}_+$
. Therefore,
$\mathcal {H}_+ A_H= A_H \mathcal {H}_+$
. Therefore,
![]() $\mathcal {H}_+$
defines a bounded operator on
$\mathcal {H}_+$
defines a bounded operator on
![]() $\mathcal A(H)$
.
$\mathcal A(H)$
.
Proof Let
![]() $f \in L^p(\mathbb {R}^+)$
. Then, for all
$f \in L^p(\mathbb {R}^+)$
. Then, for all
![]() $x>0$
,
$x>0$
,
 $$ \begin{align} \begin{aligned} (\mathcal{H}_+ (A_H f))(x) &=\lim_{\varepsilon \rightarrow 0^+}\frac{1}{\pi}\int_{(0,x-\varepsilon)\cup (x + \varepsilon, \infty)} \frac{1}{x-r} \int_0^\infty H(1,s) f(rs)\, ds \, dr \\ &= \lim_{\varepsilon \rightarrow 0^+} \int_0^\infty H(1,s) \frac{1}{\pi} \int_{(0,s(x-\varepsilon)) \cup (s(x + \varepsilon), \infty)} \frac{f(v)}{xs-v}\, dv \, ds. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} (\mathcal{H}_+ (A_H f))(x) &=\lim_{\varepsilon \rightarrow 0^+}\frac{1}{\pi}\int_{(0,x-\varepsilon)\cup (x + \varepsilon, \infty)} \frac{1}{x-r} \int_0^\infty H(1,s) f(rs)\, ds \, dr \\ &= \lim_{\varepsilon \rightarrow 0^+} \int_0^\infty H(1,s) \frac{1}{\pi} \int_{(0,s(x-\varepsilon)) \cup (s(x + \varepsilon), \infty)} \frac{f(v)}{xs-v}\, dv \, ds. \end{aligned} \end{align} $$
Here, we have applied Fubini to commute the integrals since
![]() $\int _0^\infty |H(1,s)f(\cdot s)|\, ds \in L^p(\mathbb R^+)$
and
$\int _0^\infty |H(1,s)f(\cdot s)|\, ds \in L^p(\mathbb R^+)$
and
![]() $\frac {1}{x-(\cdot )} \chi _{(0,x-\varepsilon ) \cap (x+\varepsilon , \infty )} (\cdot ) \in L^{p'}(\mathbb R^+)$
for all
$\frac {1}{x-(\cdot )} \chi _{(0,x-\varepsilon ) \cap (x+\varepsilon , \infty )} (\cdot ) \in L^{p'}(\mathbb R^+)$
for all
![]() $1<p< \infty $
.
$1<p< \infty $
.
Recall that the maximal operator
![]() $\mathcal {MH}_+$
defined as
$\mathcal {MH}_+$
defined as
![]() $(\mathcal {MH}_+ f)(x) :=$
$(\mathcal {MH}_+ f)(x) :=$
![]() $\sup _{\varepsilon>0} |(\mathcal {H}_{+,\varepsilon }f) (x)|, \text { for all } x>0$
, belongs to
$\sup _{\varepsilon>0} |(\mathcal {H}_{+,\varepsilon }f) (x)|, \text { for all } x>0$
, belongs to
![]() $\mathcal {B}(L^p(\mathbb {R}^+))$
, where
$\mathcal {B}(L^p(\mathbb {R}^+))$
, where
(see, for example, [Reference Duoandikoetxea Zuazo5, Corollary 3.13]). As a consequence, the bound
![]() $ |H (1,s) (\mathcal {H}_{+,s\varepsilon } f) (xs) | \leq |H(1,s)| (\mathcal {MH}_+ f)(xs)$
holds for every
$ |H (1,s) (\mathcal {H}_{+,s\varepsilon } f) (xs) | \leq |H(1,s)| (\mathcal {MH}_+ f)(xs)$
holds for every
![]() $\varepsilon>0$
, a.e.
$\varepsilon>0$
, a.e.
![]() $s>0$
. By Hardy’s inequality [Reference Hardy, Littlewood and Pólya9, Theorem 319],
$s>0$
. By Hardy’s inequality [Reference Hardy, Littlewood and Pólya9, Theorem 319],
![]() $|H(1,s)| (\mathcal {MH}_+ f)(xs)$
, as a function on
$|H(1,s)| (\mathcal {MH}_+ f)(xs)$
, as a function on
![]() $s>0$
, belongs to
$s>0$
, belongs to
![]() $L^1(\mathbb {R}^+)$
for a.e.
$L^1(\mathbb {R}^+)$
for a.e.
![]() $x>0$
. Thus, we apply the dominated convergence theorem to (3.1) to commute the limit and the integral
$x>0$
. Thus, we apply the dominated convergence theorem to (3.1) to commute the limit and the integral
![]() $\int _0^\infty $
. Hence,
$\int _0^\infty $
. Hence,
![]() $\mathcal A(H)$
is
$\mathcal A(H)$
is
![]() $\mathcal {H}_+$
invariant, and then the continuity of
$\mathcal {H}_+$
invariant, and then the continuity of
![]() $\mathcal {H}_+$
follows by the closed graph theorem.
$\mathcal {H}_+$
follows by the closed graph theorem.
4 Hardy reproducing kernels on
 $\mathbb C^+ \times \mathbb C^+$
$\mathbb C^+ \times \mathbb C^+$
Next, we proceed to analyze the range spaces of Hardy operators on the Hardy spaces of holomorphic functions on the right-hand half plane
![]() $H^2(\mathbb C^+)$
.
$H^2(\mathbb C^+)$
.
For
![]() $1 \leq p <\infty $
, recall that the Hardy space
$1 \leq p <\infty $
, recall that the Hardy space
![]() $H^p(\mathbb C^+)$
is formed by all holomorphic functions F on
$H^p(\mathbb C^+)$
is formed by all holomorphic functions F on
![]() $\mathbb C^+$
such that
$\mathbb C^+$
such that
 $$ \begin{align*}\|F\|_{H^p}:= \sup_{x>0} \left(\frac{1}{2\pi} \int_{-\infty}^\infty |F(x+iy)|^p \, dy\right)^{1/p}< \infty. \end{align*} $$
$$ \begin{align*}\|F\|_{H^p}:= \sup_{x>0} \left(\frac{1}{2\pi} \int_{-\infty}^\infty |F(x+iy)|^p \, dy\right)^{1/p}< \infty. \end{align*} $$
It is known that
![]() $H^2(\mathbb C^+)$
is an RKHS, with reproducing kernel
$H^2(\mathbb C^+)$
is an RKHS, with reproducing kernel
![]() $\mathcal {K}$
given by
$\mathcal {K}$
given by
(see [Reference Koosis12, Chapter VI]). Notice that the restriction of
![]() $\mathcal {K}$
to
$\mathcal {K}$
to
![]() $\mathbb R^+ \times \mathbb R^+$
defines the Stieltjes kernel
$\mathbb R^+ \times \mathbb R^+$
defines the Stieltjes kernel
![]() $\mathcal {S}(r,s) = \frac {1}{r+s}$
. One has that
$\mathcal {S}(r,s) = \frac {1}{r+s}$
. One has that
![]() $\mathcal {S} \in \mathfrak {H}_p$
for all
$\mathcal {S} \in \mathfrak {H}_p$
for all
![]() $1\leq p <\infty $
. Recall that
$1\leq p <\infty $
. Recall that
![]() $D_H$
is the Hardy operator on
$D_H$
is the Hardy operator on
![]() $H^p(\mathbb C^+)$
associated with
$H^p(\mathbb C^+)$
associated with
![]() $H \in \mathfrak {H}_p$
through (1.2).
$H \in \mathfrak {H}_p$
through (1.2).
Definition 4.1 Let
![]() $1\leq p < \infty $
, and let
$1\leq p < \infty $
, and let
![]() $H \in \mathfrak {H}_p$
. Endow
$H \in \mathfrak {H}_p$
. Endow
![]() $\mathcal D(H):= D_H (H^p(\mathbb C^+))$
with the structure of Banach space induced by the canonical isomorphism
$\mathcal D(H):= D_H (H^p(\mathbb C^+))$
with the structure of Banach space induced by the canonical isomorphism
![]() $\mathcal D(H) \cong H^p(\mathbb C^+) / \ker D_H$
.
$\mathcal D(H) \cong H^p(\mathbb C^+) / \ker D_H$
.
Remark 4.1 Let
![]() $H \in \mathfrak {H}_2$
. Using that
$H \in \mathfrak {H}_2$
. Using that
![]() $\displaystyle {D_H F = \int _0^\infty H(1,s) F(s \,\,\cdot ) \,ds}$
, it is simple to see that
$\displaystyle {D_H F = \int _0^\infty H(1,s) F(s \,\,\cdot ) \,ds}$
, it is simple to see that
![]() $(D_H F | G)_{H^2} = (F | D_{H^\ast } G)_{H^2}$
in the inner product in
$(D_H F | G)_{H^2} = (F | D_{H^\ast } G)_{H^2}$
in the inner product in
![]() $H^2(\mathbb C^+)$
. Since all Hardy operators commute between themselves (see Proposition 2.1),
$H^2(\mathbb C^+)$
. Since all Hardy operators commute between themselves (see Proposition 2.1),
![]() $D_H$
is a normal operator.
$D_H$
is a normal operator.
Next, we give the main theorem of this section, for which we will need the following lemma and definition. Set
![]() $\mathcal {K}_w := \mathcal {K}(\cdot ,w)$
for all
$\mathcal {K}_w := \mathcal {K}(\cdot ,w)$
for all
![]() $w\in \mathbb C^+$
, so
$w\in \mathbb C^+$
, so
![]() $\mathcal {K}_w \in H^2(\mathbb C^+)$
.
$\mathcal {K}_w \in H^2(\mathbb C^+)$
.
Lemma 4.2 Let
![]() $H \in \mathfrak {H}_2$
. For all
$H \in \mathfrak {H}_2$
. For all
![]() $z \in \mathbb C^+$
, one has that
$z \in \mathbb C^+$
, one has that
Proof Note that the vector-valued function
![]() $t \mapsto H(1,t) \mathcal {K}_{tz}$
is strong measurable, since
$t \mapsto H(1,t) \mathcal {K}_{tz}$
is strong measurable, since
![]() $t\mapsto H(1,t)$
is measurable, and
$t\mapsto H(1,t)$
is measurable, and
![]() $w \mapsto \mathcal {K}_w$
is continuous from
$w \mapsto \mathcal {K}_w$
is continuous from
![]() $\mathbb C^+$
to
$\mathbb C^+$
to
![]() $H^2(\mathbb C^2)$
. Then, for all
$H^2(\mathbb C^2)$
. Then, for all
![]() $z \in \mathbb C^+$
,
$z \in \mathbb C^+$
,
 $$ \begin{align*} \int_0^\infty\! | H(1,t)| \|\mathcal{K}_{tz} \|_{H^2}\, dt &= \!\int_0^\infty\! | H(1,t)| \sqrt{( \mathcal{K}_{tz}| \mathcal{K}_{tz})_{H^2}}\,dt = \!\int_0^\infty\! | H(1,t)| \sqrt{\mathcal{K}(tz, tz)} \, dt \\ &=\sqrt{\mathcal{K}(z,z)} \int_0^\infty | H(1,t)| t^{-1/2} \, dt= \sqrt{\mathcal{K}(z,z)} \|H\|_{\mathfrak{H}_2}< \infty.\\[-26pt] \end{align*} $$
$$ \begin{align*} \int_0^\infty\! | H(1,t)| \|\mathcal{K}_{tz} \|_{H^2}\, dt &= \!\int_0^\infty\! | H(1,t)| \sqrt{( \mathcal{K}_{tz}| \mathcal{K}_{tz})_{H^2}}\,dt = \!\int_0^\infty\! | H(1,t)| \sqrt{\mathcal{K}(tz, tz)} \, dt \\ &=\sqrt{\mathcal{K}(z,z)} \int_0^\infty | H(1,t)| t^{-1/2} \, dt= \sqrt{\mathcal{K}(z,z)} \|H\|_{\mathfrak{H}_2}< \infty.\\[-26pt] \end{align*} $$
Definition 4.2 We define
![]() ${\mathfrak {H}}_p^{hol}$
to be the subset of
${\mathfrak {H}}_p^{hol}$
to be the subset of
![]() $\mathfrak {H}_p$
consisting of those
$\mathfrak {H}_p$
consisting of those
![]() $H\in \mathfrak {H}_p$
with extension
$H\in \mathfrak {H}_p$
with extension
![]() $H^{hol}: \mathbb C^+ \times \mathbb C^+ \to \mathbb C$
such that:
$H^{hol}: \mathbb C^+ \times \mathbb C^+ \to \mathbb C$
such that:
-
•
 $H(r,s) = H^{hol}(r,s)$
for
$H(r,s) = H^{hol}(r,s)$
for
 $r,s>0$
,
$r,s>0$
, -
• the map
 $z \mapsto H^{hol}(z,w)$
is holomorphic on
$z \mapsto H^{hol}(z,w)$
is holomorphic on
 $\mathbb C^+$
for all
$\mathbb C^+$
for all
 $w \in \mathbb C^+$
, and
$w \in \mathbb C^+$
, and -
• the map
 $w \mapsto H^{hol}(z,\overline {w})$
is holomorphic on
$w \mapsto H^{hol}(z,\overline {w})$
is holomorphic on
 $\mathbb C^+$
for all
$\mathbb C^+$
for all
 $z \in \mathbb C^+$
.
$z \in \mathbb C^+$
.
Note that if
![]() $H \in \mathfrak {H}_p^{hol}$
, the extension
$H \in \mathfrak {H}_p^{hol}$
, the extension
![]() $H^{hol}$
is unique.
$H^{hol}$
is unique.
Notice that the Stieltjes kernel
![]() $\mathcal {S}$
satisfies that
$\mathcal {S}$
satisfies that
![]() $\mathcal {S} \in \mathfrak {H}_p^{hol}$
with
$\mathcal {S} \in \mathfrak {H}_p^{hol}$
with
![]() $\mathcal {S}^{hol} = \mathcal {K}$
.
$\mathcal {S}^{hol} = \mathcal {K}$
.
Theorem 4.3 Let
![]() $H \in \mathfrak {H}_2$
. One has that
$H \in \mathfrak {H}_2$
. One has that
![]() $H \bullet \mathcal {S} \bullet H^\ast \in \mathfrak {H}_2^{hol}$
, and that
$H \bullet \mathcal {S} \bullet H^\ast \in \mathfrak {H}_2^{hol}$
, and that
![]() $\mathcal D(H)$
is an RKHS with reproducing kernel
$\mathcal D(H)$
is an RKHS with reproducing kernel
![]() $\mathcal {K}_H$
given by
$\mathcal {K}_H$
given by
Proof Let G be in
![]() $(\ker D_H)^\perp $
such that
$(\ker D_H)^\perp $
such that
![]() $F = D_H(G) \in \mathcal D(H)$
.
$F = D_H(G) \in \mathcal D(H)$
.
Since
![]() $H^2(\mathbb C^+)$
is an RKHS, it follows from above that
$H^2(\mathbb C^+)$
is an RKHS, it follows from above that
![]() $\mathcal {D}(H)$
is an RKHS too. Let us compute its reproducing kernel
$\mathcal {D}(H)$
is an RKHS too. Let us compute its reproducing kernel
![]() $\mathcal {K}_H$
. As before, set
$\mathcal {K}_H$
. As before, set
![]() $\mathcal {K}_w (z) = \mathcal {K}(z,w)$
. For
$\mathcal {K}_w (z) = \mathcal {K}(z,w)$
. For
![]() $F =D_H G\in \mathcal D(H)$
,
$F =D_H G\in \mathcal D(H)$
,
![]() $z = |z|e^{i\theta } \in \mathbb C^+$
, and
$z = |z|e^{i\theta } \in \mathbb C^+$
, and
![]() $G \in (\ker D_H)^\perp $
, we have
$G \in (\ker D_H)^\perp $
, we have
 $$ \begin{align} \begin{aligned} F(z) &=\! \int_0^\infty\! \kern-1pt H(|z|,s) G^\theta(s) \,ds = \!\int_0^\infty\!\kern-1pt H(|z|,s) (G|\mathcal{K}_{se^{i\theta}})_{H^2} \, ds = \!\int_0^\infty\!\kern-1pt H(1,t) (G| \mathcal{K}_{tz})_{H^2} \, dt \\ &= \int_0^\infty (G|\overline { H(1,t)} \mathcal{K}_{tz})_{H^2} \, dt = \left(G\, \Big| \, \int_0^\infty \overline { H(1,t)} \mathcal{K}_{tz} \, dt\right)_{H^2}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} F(z) &=\! \int_0^\infty\! \kern-1pt H(|z|,s) G^\theta(s) \,ds = \!\int_0^\infty\!\kern-1pt H(|z|,s) (G|\mathcal{K}_{se^{i\theta}})_{H^2} \, ds = \!\int_0^\infty\!\kern-1pt H(1,t) (G| \mathcal{K}_{tz})_{H^2} \, dt \\ &= \int_0^\infty (G|\overline { H(1,t)} \mathcal{K}_{tz})_{H^2} \, dt = \left(G\, \Big| \, \int_0^\infty \overline { H(1,t)} \mathcal{K}_{tz} \, dt\right)_{H^2}, \end{aligned} \end{align} $$
where one can intertwine the integral sign with the inner product by Lemma 4.2.
Let
![]() $J \in \ker D_H$
. By substituting F by
$J \in \ker D_H$
. By substituting F by
![]() $D_H J = 0$
and G by J in (4.1), one concludes that
$D_H J = 0$
and G by J in (4.1), one concludes that
![]() $\int _0^\infty \overline { H(1,t)} \mathcal {K}_{tz} dt \in (\ker D_H)^\perp $
. Then, we have that
$\int _0^\infty \overline { H(1,t)} \mathcal {K}_{tz} dt \in (\ker D_H)^\perp $
. Then, we have that
Therefore, after rearranging some variables, one gets that the reproducing kernel
![]() $\mathcal {K}_H$
of
$\mathcal {K}_H$
of
![]() $\mathcal D(H)$
is given by
$\mathcal D(H)$
is given by
Now, let us see that the expression above coincides with the one given in the statement for all
![]() $z,w \in \mathbb R^+$
:
$z,w \in \mathbb R^+$
:
 $$ \begin{align*} &\left[D_H\left( \int_0^\infty \overline { H(1,t)}\mathcal{K}_{tw} dt \right)\right] (z) = \int_0^\infty H(z,s) \left( \int_0^\infty \overline { H(1,t)}\mathcal{K}_{tw} dt\right)(s) \, ds \\ =\: & \int_0^\infty H(z,s) \int_0^\infty \overline{H(1,t)} \mathcal{K}(s,tw) \, dt \, ds = \int_0^\infty H(z,s) \int_0^\infty \mathcal{S} (s,u) \overline{H(w,u)} \, du\, ds \\ =\: & \int_0^\infty H(z,s) \int_0^\infty \mathcal{S} (s,u) H^\ast(u,w) \, du \, ds =\int_0^\infty H(z,s) (\mathcal{S} \bullet H^\ast) (s,w) \,ds \\ =\: & \left(H \bullet \mathcal{S} \bullet H^\ast \right)(z,w). \end{align*} $$
$$ \begin{align*} &\left[D_H\left( \int_0^\infty \overline { H(1,t)}\mathcal{K}_{tw} dt \right)\right] (z) = \int_0^\infty H(z,s) \left( \int_0^\infty \overline { H(1,t)}\mathcal{K}_{tw} dt\right)(s) \, ds \\ =\: & \int_0^\infty H(z,s) \int_0^\infty \overline{H(1,t)} \mathcal{K}(s,tw) \, dt \, ds = \int_0^\infty H(z,s) \int_0^\infty \mathcal{S} (s,u) \overline{H(w,u)} \, du\, ds \\ =\: & \int_0^\infty H(z,s) \int_0^\infty \mathcal{S} (s,u) H^\ast(u,w) \, du \, ds =\int_0^\infty H(z,s) (\mathcal{S} \bullet H^\ast) (s,w) \,ds \\ =\: & \left(H \bullet \mathcal{S} \bullet H^\ast \right)(z,w). \end{align*} $$
Therefore,
![]() $\mathcal {K}_H(z,w) = \left (H \bullet \mathcal {S} \bullet H^\ast \right )(z,w)$
for all
$\mathcal {K}_H(z,w) = \left (H \bullet \mathcal {S} \bullet H^\ast \right )(z,w)$
for all
![]() $z,w \in \mathbb R^+$
.
$z,w \in \mathbb R^+$
.
Since all the elements in
![]() $\mathcal D(H) \subset H^2(\mathbb C^+)$
are holomorphic, we have that
$\mathcal D(H) \subset H^2(\mathbb C^+)$
are holomorphic, we have that
![]() $\mathcal {K}_H(z,w)$
is holomorphic in z, so it is determined for all
$\mathcal {K}_H(z,w)$
is holomorphic in z, so it is determined for all
![]() $(z,w) \in \mathbb C^+ \times \mathbb R^+$
by its restriction at
$(z,w) \in \mathbb C^+ \times \mathbb R^+$
by its restriction at
![]() $\mathbb R^+ \times \mathbb R^+$
. Moreover, since
$\mathbb R^+ \times \mathbb R^+$
. Moreover, since
![]() $\mathcal {K}_H$
is a reproducing kernel, we have that
$\mathcal {K}_H$
is a reproducing kernel, we have that
![]() $\mathcal {K}_H(z,w) = \overline {\mathcal {K}_H(w,z)}$
(see [Reference Neeb17, Lemma I.1.2]), and as a consequence,
$\mathcal {K}_H(z,w) = \overline {\mathcal {K}_H(w,z)}$
(see [Reference Neeb17, Lemma I.1.2]), and as a consequence,
![]() $\mathcal {K}_H(z,w)$
is anti-holomorphic in w, and by the same reasoning as before,
$\mathcal {K}_H(z,w)$
is anti-holomorphic in w, and by the same reasoning as before,
![]() $\mathcal {K}_H(z,w)$
is determined for all
$\mathcal {K}_H(z,w)$
is determined for all
![]() $z,w \in \mathbb C^+$
by its restriction to
$z,w \in \mathbb C^+$
by its restriction to
![]() $\mathbb C^+ \times \mathbb R^+$
. All these statements imply that
$\mathbb C^+ \times \mathbb R^+$
. All these statements imply that
![]() $H \bullet \mathcal {S} \bullet H^\ast \in \mathfrak {H}_2^{hol}$
and that its holomorphic extension is precisely
$H \bullet \mathcal {S} \bullet H^\ast \in \mathfrak {H}_2^{hol}$
and that its holomorphic extension is precisely
![]() $\mathcal {K}_H$
.
$\mathcal {K}_H$
.
5 Paley–Wiener theorems for range spaces
We wish to start this section with the following remark. Paley–Wiener’s theorem states that
![]() $\mathcal {L}: L^2(\mathbb R^+) \rightarrow H^2(\mathbb C^+)$
is an isometric isomorphism, where
$\mathcal {L}: L^2(\mathbb R^+) \rightarrow H^2(\mathbb C^+)$
is an isometric isomorphism, where
![]() $\mathcal {L}$
is the Laplace transform given by
$\mathcal {L}$
is the Laplace transform given by
(see [Reference Paley and Wiener18, Theorem V]).
This classical
![]() $L^2-H^2$
Paley–Wiener theorem can be used to prove that
$L^2-H^2$
Paley–Wiener theorem can be used to prove that
![]() $H^2(\mathbb C^+)$
is an RKHS with kernel
$H^2(\mathbb C^+)$
is an RKHS with kernel
![]() $\mathcal {K}(z,w) = \frac {1}{z+\overline {w}}$
[Reference Hilgert10, Proposition 1.8]. Conversely, one can reverse the implications of such a proof to obtain the
$\mathcal {K}(z,w) = \frac {1}{z+\overline {w}}$
[Reference Hilgert10, Proposition 1.8]. Conversely, one can reverse the implications of such a proof to obtain the
![]() $L^2-H^2$
Paley–Wiener theorem using RKHS theory (note that the kernel
$L^2-H^2$
Paley–Wiener theorem using RKHS theory (note that the kernel
![]() $\mathcal {K}$
of the space
$\mathcal {K}$
of the space
![]() $H^2(\mathbb C^+)$
can be obtained independently of Paley–Wiener’s theorem; see, for instance, [Reference Koosis12, Chapter VI]), as we show next.
$H^2(\mathbb C^+)$
can be obtained independently of Paley–Wiener’s theorem; see, for instance, [Reference Koosis12, Chapter VI]), as we show next.
Since the Laplace transform
![]() $\mathcal {L}$
acting on
$\mathcal {L}$
acting on
![]() $L^2(\mathbb R^+)$
is injective, one can endow the range space
$L^2(\mathbb R^+)$
is injective, one can endow the range space
![]() $\mathcal {L}(L^2(\mathbb R^+))$
with the structure of Hilbert space induced by the bijection
$\mathcal {L}(L^2(\mathbb R^+))$
with the structure of Hilbert space induced by the bijection
![]() $\mathcal {L}: L^2(\mathbb R^+) \to \mathcal {L}(L^2(\mathbb R^+))$
. For
$\mathcal {L}: L^2(\mathbb R^+) \to \mathcal {L}(L^2(\mathbb R^+))$
. For
![]() $F = \mathcal {L}f \in \mathcal {L}(L^2(\mathbb R^+))$
, one has
$F = \mathcal {L}f \in \mathcal {L}(L^2(\mathbb R^+))$
, one has
As a consequence,
![]() $\mathcal {L}(L^2(\mathbb R^+))$
is an RKHS with kernel
$\mathcal {L}(L^2(\mathbb R^+))$
is an RKHS with kernel
![]() $K_{\mathcal {L}}$
given by
$K_{\mathcal {L}}$
given by
That is, both
![]() $\mathcal {L}(L^2(\mathbb R^+))$
and
$\mathcal {L}(L^2(\mathbb R^+))$
and
![]() $H^2(\mathbb C^+)$
are RKHSs with the same kernel
$H^2(\mathbb C^+)$
are RKHSs with the same kernel
![]() $K_{\mathcal {L}} = \mathcal {K}$
, so
$K_{\mathcal {L}} = \mathcal {K}$
, so
![]() $\mathcal {L}(L^2(\mathbb R^+)) = H^2(\mathbb C^+)$
as Hilbert spaces (see, for instance, [Reference Neeb17, Lemma I.1.5]), and the claim follows.
$\mathcal {L}(L^2(\mathbb R^+)) = H^2(\mathbb C^+)$
as Hilbert spaces (see, for instance, [Reference Neeb17, Lemma I.1.5]), and the claim follows.
Now, we establish results of Paley–Wiener type for range spaces. We first show that
![]() $\mathcal {L}$
is an intertwining operator.
$\mathcal {L}$
is an intertwining operator.
Proposition 5.1
![]() $\mathcal {L} A_H = D_{H^\top } \mathcal {L}$
on
$\mathcal {L} A_H = D_{H^\top } \mathcal {L}$
on
![]() $L^2(\mathbb R^+)$
for all
$L^2(\mathbb R^+)$
for all
![]() $H\in \mathfrak {H}_2$
.
$H\in \mathfrak {H}_2$
.
Proof Let
![]() $z\in \mathbb C^+$
and
$z\in \mathbb C^+$
and
![]() $f \in L^2(\mathbb R^+)$
. One has
$f \in L^2(\mathbb R^+)$
. One has
 $$ \begin{align*} (\mathcal{L} A_H f)(z) &= \int_0^\infty e^{-rz} \int_0^\infty H(r,t)f(t)dt dr = \int_0^\infty e^{-rz} \int_0^\infty H(1,s)f(rs)ds dr \\ &= \int_0^\infty H(1,s) \int_0^\infty e^{-rz}f(rs) dr ds = \int_0^\infty H(1,s) (\mathcal{L}f)\left(\frac{z}{s}\right) \frac{ds}{s} \\ &= \int_0^\infty H(u,1) (\mathcal{L}f)\left(uz\right) du = (D_{H^\top} \mathcal{L}f)(z), \end{align*} $$
$$ \begin{align*} (\mathcal{L} A_H f)(z) &= \int_0^\infty e^{-rz} \int_0^\infty H(r,t)f(t)dt dr = \int_0^\infty e^{-rz} \int_0^\infty H(1,s)f(rs)ds dr \\ &= \int_0^\infty H(1,s) \int_0^\infty e^{-rz}f(rs) dr ds = \int_0^\infty H(1,s) (\mathcal{L}f)\left(\frac{z}{s}\right) \frac{ds}{s} \\ &= \int_0^\infty H(u,1) (\mathcal{L}f)\left(uz\right) du = (D_{H^\top} \mathcal{L}f)(z), \end{align*} $$
where we have applied Fubini’s theorem since both
![]() $r\mapsto \int _0^\infty |H(r,t) f(t)|\, dt$
and
$r\mapsto \int _0^\infty |H(r,t) f(t)|\, dt$
and
![]() $r\mapsto e^{-rz}$
are in
$r\mapsto e^{-rz}$
are in
![]() $L^2(\mathbb R^+)$
.
$L^2(\mathbb R^+)$
.
Theorem 5.2 Let
![]() $H \in \mathfrak {H}_2$
. The Laplace transform
$H \in \mathfrak {H}_2$
. The Laplace transform
![]() $\mathcal {L}$
restricted to
$\mathcal {L}$
restricted to
![]() $\mathcal A(H)$
is an isometric isomorphism onto
$\mathcal A(H)$
is an isometric isomorphism onto
![]() $\mathcal D(H^\top )$
,
$\mathcal D(H^\top )$
,
![]() $\mathcal {L}: \mathcal A(H) \rightarrow \mathcal D(H^\top )$
.
$\mathcal {L}: \mathcal A(H) \rightarrow \mathcal D(H^\top )$
.
Proof By the definition of
![]() $\mathcal A(H)$
and
$\mathcal A(H)$
and
![]() $\mathcal D(H^\top )$
, the restrictions
$\mathcal D(H^\top )$
, the restrictions
![]() $\widetilde {A_H}: (\ker A_H)^\perp \rightarrow \mathcal A(H)$
and
$\widetilde {A_H}: (\ker A_H)^\perp \rightarrow \mathcal A(H)$
and
![]() $\widetilde {D_{H^\top }}: (\ker D_{H^\top })^\perp \rightarrow \mathcal D(H^\top )$
are isometric isomorphisms. By the
$\widetilde {D_{H^\top }}: (\ker D_{H^\top })^\perp \rightarrow \mathcal D(H^\top )$
are isometric isomorphisms. By the
![]() $L^2-H^2$
Paley–Wiener theorem and Proposition 5.1, it follows that
$L^2-H^2$
Paley–Wiener theorem and Proposition 5.1, it follows that
![]() $(\ker D_{H^\top })^\perp = \mathcal {L} ((\ker A_H)^\perp )$
. Indeed, by Proposition 5.1, it easily follows that
$(\ker D_{H^\top })^\perp = \mathcal {L} ((\ker A_H)^\perp )$
. Indeed, by Proposition 5.1, it easily follows that
![]() $\mathcal {L}(\ker A_H) = \ker D_{H^\top }$
, and thus
$\mathcal {L}(\ker A_H) = \ker D_{H^\top }$
, and thus
![]() $( f\, | \, g )_{L^2} = 0$
for all
$( f\, | \, g )_{L^2} = 0$
for all
![]() $g \in \ker A_H$
if and only if
$g \in \ker A_H$
if and only if
![]() $(\mathcal {L}f\, | \, G )_{H^2} = 0$
for all
$(\mathcal {L}f\, | \, G )_{H^2} = 0$
for all
![]() $G \in \mathcal {L}(\ker A_H) = \ker D_{H^\top }$
.
$G \in \mathcal {L}(\ker A_H) = \ker D_{H^\top }$
.
Therefore, by Proposition 5.1 again, we obtain
![]() $\mathcal {L} f = \widetilde {D_{H^\top }} \mathcal {L} (\widetilde {A_H})^{-1} f$
for all
$\mathcal {L} f = \widetilde {D_{H^\top }} \mathcal {L} (\widetilde {A_H})^{-1} f$
for all
![]() $f \in \mathcal A(H)$
, where all the mappings
$f \in \mathcal A(H)$
, where all the mappings
![]() $\widetilde {D_{H^\top }}, \, \mathcal {L}$
(seen as an operator from the subspace
$\widetilde {D_{H^\top }}, \, \mathcal {L}$
(seen as an operator from the subspace
![]() $(\ker A_H)^\perp \subset L^2(\mathbb R^+)$
to the subspace
$(\ker A_H)^\perp \subset L^2(\mathbb R^+)$
to the subspace
![]() $(\ker D_{H^\top })^\perp \subset H^2(\mathbb C^+)$
), and
$(\ker D_{H^\top })^\perp \subset H^2(\mathbb C^+)$
), and
![]() $(\widetilde {A_H})^{-1}$
are in fact unitary operators. As a consequence,
$(\widetilde {A_H})^{-1}$
are in fact unitary operators. As a consequence,
![]() $\mathcal {L}: \mathcal A(H) \rightarrow \mathcal D(H^\top )$
defines an isometric isomorphism.
$\mathcal {L}: \mathcal A(H) \rightarrow \mathcal D(H^\top )$
defines an isometric isomorphism.
Corollary 5.3 Let
![]() $H \in \mathfrak {H}_2$
. The Laplace transform defines an isometric isomorphism
$H \in \mathfrak {H}_2$
. The Laplace transform defines an isometric isomorphism
![]() $\mathcal {L}: \mathcal A(H) \rightarrow \mathcal {D}(H)$
if and only if
$\mathcal {L}: \mathcal A(H) \rightarrow \mathcal {D}(H)$
if and only if
![]() $H \bullet H^\ast $
is a real-valued kernel.
$H \bullet H^\ast $
is a real-valued kernel.
Proof By the theorem above, we have that
![]() $\mathcal {L}: \mathcal A(H) \rightarrow \mathcal {D}(H)$
is an isometric isomorphism if and only if
$\mathcal {L}: \mathcal A(H) \rightarrow \mathcal {D}(H)$
is an isometric isomorphism if and only if
![]() $\mathcal {D}(H) = \mathcal {D}(H^\top )$
as Hilbert spaces, and this happens if and only if their reproducing kernels are the same,
$\mathcal {D}(H) = \mathcal {D}(H^\top )$
as Hilbert spaces, and this happens if and only if their reproducing kernels are the same,
![]() $\mathcal {K}_H = \mathcal {K}_{H^\top }$
. By Theorem 4.3, this is equivalent to
$\mathcal {K}_H = \mathcal {K}_{H^\top }$
. By Theorem 4.3, this is equivalent to
![]() $\mathcal {S} \bullet H \bullet H^\ast = \mathcal {S} \bullet H^\top \bullet (H^\top )^\ast $
. The injectivity of the Stieltjes transform
$\mathcal {S} \bullet H \bullet H^\ast = \mathcal {S} \bullet H^\top \bullet (H^\top )^\ast $
. The injectivity of the Stieltjes transform
![]() $A_{\mathcal {S}}$
(which can be proved via the Mellin transform; see, for example, [Reference Fabes, Jodeit and Lewis6]) implies that this holds if and only if
$A_{\mathcal {S}}$
(which can be proved via the Mellin transform; see, for example, [Reference Fabes, Jodeit and Lewis6]) implies that this holds if and only if
![]() $H \bullet H^\ast = H^\top \bullet (H^\top )^\ast = (H \bullet H^\ast )^\top $
. Then, the claim follows from the fact that
$H \bullet H^\ast = H^\top \bullet (H^\top )^\ast = (H \bullet H^\ast )^\top $
. Then, the claim follows from the fact that
![]() $(H\bullet H^\ast )^\top = \overline {H\bullet H^\ast }$
for all
$(H\bullet H^\ast )^\top = \overline {H\bullet H^\ast }$
for all
![]() $H \in \mathfrak {H}_2$
.
$H \in \mathfrak {H}_2$
.
Corollary 5.4 Let
![]() $H\in \mathfrak {H}_2$
. Either if H is symmetric, that is,
$H\in \mathfrak {H}_2$
. Either if H is symmetric, that is,
![]() $H=H^\top $
, or if H is real-valued, the Laplace transform
$H=H^\top $
, or if H is real-valued, the Laplace transform
![]() $\mathcal {L}$
restricts to an isometric isomorphism from
$\mathcal {L}$
restricts to an isometric isomorphism from
![]() $\mathcal A(H)$
onto
$\mathcal A(H)$
onto
![]() $\mathcal D(H)$
,
$\mathcal D(H)$
,
![]() $\mathcal {L}: \mathcal A(H)\rightarrow \mathcal D(H)$
.
$\mathcal {L}: \mathcal A(H)\rightarrow \mathcal D(H)$
.
We will see in Theorem 6.4 that, for any
![]() $H \in \mathfrak {H}_2$
, there exist isometric isomorphisms
$H \in \mathfrak {H}_2$
, there exist isometric isomorphisms
![]() $\mathscr {P}, \mathscr {Q}: \mathcal A(H) \to \mathcal D(H)$
related to the Poisson kernel.
$\mathscr {P}, \mathscr {Q}: \mathcal A(H) \to \mathcal D(H)$
related to the Poisson kernel.
6 Examples and applications
Here, we illustrate the theory given above with some examples and applications.
(1) Generalized Poisson operators. For
![]() $\alpha , \beta ,\mu $
real numbers, let
$\alpha , \beta ,\mu $
real numbers, let
![]() $P_{\alpha ,\beta ,\mu }(r,s) = r^{\alpha \mu - \beta } s^{\beta -1}(r^\alpha + s^\alpha )^{-\mu }$
for all
$P_{\alpha ,\beta ,\mu }(r,s) = r^{\alpha \mu - \beta } s^{\beta -1}(r^\alpha + s^\alpha )^{-\mu }$
for all
![]() $r,s>0$
. The spectral properties of its associated Hardy operator have been studied in [Reference Miana, Oliva-Maza, Aron, Gallardo-Gutiérrez, Martín, Ryabogin, Spitkovsky and Zvavitch16]. Regarding the properties considered in the present paper, we have that, for
$r,s>0$
. The spectral properties of its associated Hardy operator have been studied in [Reference Miana, Oliva-Maza, Aron, Gallardo-Gutiérrez, Martín, Ryabogin, Spitkovsky and Zvavitch16]. Regarding the properties considered in the present paper, we have that, for
![]() $p\in [1,\infty )$
and
$p\in [1,\infty )$
and
![]() $\alpha>0$
,
$\alpha>0$
,
![]() $P_{\alpha ,\beta ,\mu } \in \mathfrak {H}_p$
if and only if
$P_{\alpha ,\beta ,\mu } \in \mathfrak {H}_p$
if and only if
![]() $0<\beta - 1/p < \alpha \mu $
, and in this case,
$0<\beta - 1/p < \alpha \mu $
, and in this case,
![]() $P_{\alpha ,\beta ,\mu } \in \mathcal I_p$
. For
$P_{\alpha ,\beta ,\mu } \in \mathcal I_p$
. For
![]() $p=2$
, one has
$p=2$
, one has
where B is the Euler Beta function and
![]() $_2F_1$
is the hypergeometric Gaussian function. As particular cases, one has the following.
$_2F_1$
is the hypergeometric Gaussian function. As particular cases, one has the following.
Stieltjes kernel. For
![]() $\alpha = \beta = \mu =1$
, we obtain
$\alpha = \beta = \mu =1$
, we obtain
![]() $ P_{1,1,1}(r,s) = \mathcal {S}(r,s) =\displaystyle {\frac {1}{r+s}}$
for
$ P_{1,1,1}(r,s) = \mathcal {S}(r,s) =\displaystyle {\frac {1}{r+s}}$
for
![]() $r,s>0$
. By Theorem 3.3,
$r,s>0$
. By Theorem 3.3,
![]() $\mathcal A(\mathcal {S})$
is an RKHS with kernel
$\mathcal A(\mathcal {S})$
is an RKHS with kernel
 $$ \begin{align} K_{\mathcal{S}}(r,s) = \int_0^\infty \frac{1}{r+t}\frac{1}{t+s}\, dt = \begin{cases} \frac{1}{r-s}\log\frac{r}{s}, &\mbox{ if } r \neq s, \\ \frac{1}{r}, &\mbox{ if } r = s, \end{cases} \quad \mbox{for } r,s>0. \end{align} $$
$$ \begin{align} K_{\mathcal{S}}(r,s) = \int_0^\infty \frac{1}{r+t}\frac{1}{t+s}\, dt = \begin{cases} \frac{1}{r-s}\log\frac{r}{s}, &\mbox{ if } r \neq s, \\ \frac{1}{r}, &\mbox{ if } r = s, \end{cases} \quad \mbox{for } r,s>0. \end{align} $$
Poisson kernel and conjugate Poisson kernel. Recall that, for
![]() $x>0$
, the Poisson kernel
$x>0$
, the Poisson kernel
![]() $P^x$
and conjugate Poisson kernel
$P^x$
and conjugate Poisson kernel
![]() $Q^x$
on the half-right plane
$Q^x$
on the half-right plane
![]() $\mathbb C^+$
are given by
$\mathbb C^+$
are given by
These kernels give rise to Hardy kernels
![]() $P, Q$
as follows:
$P, Q$
as follows:
These kernels are related to the operators
![]() $\mathscr {P}, \mathscr {Q}: L^2(\mathbb R^+) \rightarrow H^2(\mathbb C^+)$
given by
$\mathscr {P}, \mathscr {Q}: L^2(\mathbb R^+) \rightarrow H^2(\mathbb C^+)$
given by
 $$ \begin{align*} (\mathscr{P} f)(z) := \sqrt{\frac{2}{\pi}} \int_0^\infty \frac{z}{z^2+s^2}f(s)\,ds, \qquad (\mathscr{Q} f)(z) := \sqrt{\frac{2}{\pi}} \int_0^\infty \frac{s}{z^2+s^2}f(s)\,ds, \end{align*} $$
$$ \begin{align*} (\mathscr{P} f)(z) := \sqrt{\frac{2}{\pi}} \int_0^\infty \frac{z}{z^2+s^2}f(s)\,ds, \qquad (\mathscr{Q} f)(z) := \sqrt{\frac{2}{\pi}} \int_0^\infty \frac{s}{z^2+s^2}f(s)\,ds, \end{align*} $$
for any
![]() $z\in \mathbb C^+$
,
$z\in \mathbb C^+$
,
![]() $f \in L^2(\mathbb R^+)$
. Indeed,
$f \in L^2(\mathbb R^+)$
. Indeed,
![]() $(\mathscr {P}f)(r) = \sqrt {2\pi } (A_P f)(r)$
and
$(\mathscr {P}f)(r) = \sqrt {2\pi } (A_P f)(r)$
and
![]() $(\mathscr {Q}f)(r) = \sqrt {2\pi } (A_Q f)(r)$
for
$(\mathscr {Q}f)(r) = \sqrt {2\pi } (A_Q f)(r)$
for
![]() $r>0$
,
$r>0$
,
![]() $f \in L^2(\mathbb R^+)$
. It is a matter of fact that
$f \in L^2(\mathbb R^+)$
. It is a matter of fact that
![]() $\mathscr {P}, \mathscr {Q}$
are isometric isomorphisms (see Remark 6.2). Here, we provide a proof of it based on results of this paper. Set
$\mathscr {P}, \mathscr {Q}$
are isometric isomorphisms (see Remark 6.2). Here, we provide a proof of it based on results of this paper. Set
Since any holomorphic function in
![]() $\mathbb C^+$
is determined by its restriction to
$\mathbb C^+$
is determined by its restriction to
![]() $\mathbb R^+$
, the space
$\mathbb R^+$
, the space
![]() $L^2_{hol}(\mathbb R^+)$
, regarded as a range space of
$L^2_{hol}(\mathbb R^+)$
, regarded as a range space of
![]() $H^2(\mathbb C^+)$
, is an RKHS isometrically isomorphic to
$H^2(\mathbb C^+)$
, is an RKHS isometrically isomorphic to
![]() $H^2(\mathbb C^+)$
with kernel
$H^2(\mathbb C^+)$
with kernel
![]() $\mathcal {S}(r,s) = \mathcal {K}(r,s) = \frac {1}{r+s}$
,
$\mathcal {S}(r,s) = \mathcal {K}(r,s) = \frac {1}{r+s}$
,
![]() $r,s>0$
. To see this, take
$r,s>0$
. To see this, take
![]() $F \in H^2(\mathbb C^+), \, f= F|_{\mathbb R^+}$
, and
$F \in H^2(\mathbb C^+), \, f= F|_{\mathbb R^+}$
, and
![]() $s>0$
. Then,
$s>0$
. Then,
as claimed.
Proposition 6.1 Both
![]() $\mathscr {P},\mathscr {Q}:L^2(\mathbb R^+) \to H^2(\mathbb C^+)$
are isometric isomorphisms.
$\mathscr {P},\mathscr {Q}:L^2(\mathbb R^+) \to H^2(\mathbb C^+)$
are isometric isomorphisms.
Proof Since
![]() $P = Q^\ast $
, Theorem 3.3 implies that
$P = Q^\ast $
, Theorem 3.3 implies that
![]() $\mathcal A(\sqrt {2\pi }P) = \mathcal A(\sqrt {2\pi }Q)$
is an RKHS on
$\mathcal A(\sqrt {2\pi }P) = \mathcal A(\sqrt {2\pi }Q)$
is an RKHS on
![]() $\mathbb R^+$
with kernel
$\mathbb R^+$
with kernel
![]() $K_{\sqrt {2\pi }P} = K_{\sqrt {2\pi }Q}$
given by
$K_{\sqrt {2\pi }P} = K_{\sqrt {2\pi }Q}$
given by
Therefore,
![]() $\mathcal A(\sqrt {2\pi }P) = \mathcal A(\sqrt {2\pi }Q) = L^2_{hol}(\mathbb R^+)$
as Hilbert spaces. Thus, all is left to prove is that
$\mathcal A(\sqrt {2\pi }P) = \mathcal A(\sqrt {2\pi }Q) = L^2_{hol}(\mathbb R^+)$
as Hilbert spaces. Thus, all is left to prove is that
![]() $\mathscr {P}f, \mathscr {Q}f$
are holomorphic on
$\mathscr {P}f, \mathscr {Q}f$
are holomorphic on
![]() $\mathbb C^+$
and that both
$\mathbb C^+$
and that both
![]() $\mathscr {P}, \mathscr {Q}$
are injective operators. First, claim which follows by an application of Morera’s theorem. For the second one, note that the Stieltjes transform
$\mathscr {P}, \mathscr {Q}$
are injective operators. First, claim which follows by an application of Morera’s theorem. For the second one, note that the Stieltjes transform
![]() $A_{\mathcal {S}}$
is an injective operator and that
$A_{\mathcal {S}}$
is an injective operator and that
![]() $A_{\mathcal {S}} = A_{P \bullet Q} = A_P A_Q = A_Q A_P$
. Thus, both
$A_{\mathcal {S}} = A_{P \bullet Q} = A_P A_Q = A_Q A_P$
. Thus, both
![]() $A_P, A_Q$
are injective, and so are
$A_P, A_Q$
are injective, and so are
![]() $\mathscr {P}, \mathscr {Q}$
.
$\mathscr {P}, \mathscr {Q}$
.
Remark 6.2 The proposition above is equivalent to Paley–Wiener’s theorem. To see this, set
![]() $L^2_{even}(\mathbb R) $
as the subset of even functions of
$L^2_{even}(\mathbb R) $
as the subset of even functions of
![]() $L^2(\mathbb R)$
, and note that the Fourier transform
$L^2(\mathbb R)$
, and note that the Fourier transform
![]() $\mathcal {F}$
restricts to an isometric mapping from
$\mathcal {F}$
restricts to an isometric mapping from
![]() $L^2_{even}(\mathbb R)$
onto itself. Set
$L^2_{even}(\mathbb R)$
onto itself. Set
![]() $\iota : L^2_{even}(\mathbb R) \rightarrow L^2(\mathbb R^+)$
by
$\iota : L^2_{even}(\mathbb R) \rightarrow L^2(\mathbb R^+)$
by
![]() $(\iota f)(r) := f(r)$
for a.e.
$(\iota f)(r) := f(r)$
for a.e.
![]() $r>0$
. Then
$r>0$
. Then
![]() $\iota \mathcal {F} \iota ^{-1}$
is a unitary operator on
$\iota \mathcal {F} \iota ^{-1}$
is a unitary operator on
![]() $L^2(\mathbb R^+)$
, and one easily obtains that
$L^2(\mathbb R^+)$
, and one easily obtains that
![]() $\mathscr {P} = \mathcal {L} \iota \mathcal {F} \iota ^{-1}$
. Hence,
$\mathscr {P} = \mathcal {L} \iota \mathcal {F} \iota ^{-1}$
. Hence,
![]() $\mathscr {P}$
is an isometric isomorphism if and only if
$\mathscr {P}$
is an isometric isomorphism if and only if
![]() $\mathcal {L}$
is an isometric isomorphism.
$\mathcal {L}$
is an isometric isomorphism.
By considering the subset of odd functions of
![]() $L^2(\mathbb R)$
, one obtains an analogous statement for
$L^2(\mathbb R)$
, one obtains an analogous statement for
![]() $\mathscr {Q}$
.
$\mathscr {Q}$
.
Some other consequences of results of this paper are the following.
Corollary 6.3 As a range space,
![]() $\mathcal {L}(H^2(\mathbb C^+))$
is an RKHS with kernel K given by
$\mathcal {L}(H^2(\mathbb C^+))$
is an RKHS with kernel K given by
 $$ \begin{align*} K(z,w) = \begin{cases} \frac{1}{z-\overline{w}}\log\frac{z}{\overline{w}}, \mbox{ if } z \neq \overline{w}, \\ \frac{1}{z}, \mbox{ if } z = \overline{w}, \end{cases} \quad \mbox{for } z,w\in \mathbb C^+. \end{align*} $$
$$ \begin{align*} K(z,w) = \begin{cases} \frac{1}{z-\overline{w}}\log\frac{z}{\overline{w}}, \mbox{ if } z \neq \overline{w}, \\ \frac{1}{z}, \mbox{ if } z = \overline{w}, \end{cases} \quad \mbox{for } z,w\in \mathbb C^+. \end{align*} $$
Here, we consider
![]() $\mathcal {L}:H^2(\mathbb C^+) \to H^2(\mathbb C^+)$
given by
$\mathcal {L}:H^2(\mathbb C^+) \to H^2(\mathbb C^+)$
given by
![]() $(\mathcal {L} F)(z) := \int _0^\infty e^{-zr}F(r)\, dr$
.
$(\mathcal {L} F)(z) := \int _0^\infty e^{-zr}F(r)\, dr$
.
Proof By Proposition 5.1, one has
![]() $\mathcal {L} \mathscr {Q} = \sqrt {2\pi } D_P \mathcal {L}$
. Thus,
$\mathcal {L} \mathscr {Q} = \sqrt {2\pi } D_P \mathcal {L}$
. Thus,
![]() $\mathcal {L}(H^2(\mathbb C^+)) = \mathcal {L} \mathscr {Q}(L^2(\mathbb R^+)) = \mathcal D(\sqrt {2\pi } P)$
regarded as Hilbert spaces, since all the operators considered in the equalities are isometric isomorphisms. Hence, by Theorems 3.3 4.3 and (6.2),
$\mathcal {L}(H^2(\mathbb C^+)) = \mathcal {L} \mathscr {Q}(L^2(\mathbb R^+)) = \mathcal D(\sqrt {2\pi } P)$
regarded as Hilbert spaces, since all the operators considered in the equalities are isometric isomorphisms. Hence, by Theorems 3.3 4.3 and (6.2),
and the claim follows by (6.1).
Next, we show that
![]() $\mathcal A(H)$
and
$\mathcal A(H)$
and
![]() $\mathcal D(H)$
are isometrically isomorphic for any
$\mathcal D(H)$
are isometrically isomorphic for any
![]() $H \in \mathfrak {H}_2$
.
$H \in \mathfrak {H}_2$
.
Corollary 6.4 Let
![]() $H\in \mathfrak {H}_2$
. Then
$H\in \mathfrak {H}_2$
. Then
![]() $\mathscr {P} A_H = D_H \mathscr {P}$
and
$\mathscr {P} A_H = D_H \mathscr {P}$
and
![]() $\mathscr {Q} A_H = D_H \mathscr {Q}$
. Hence, both
$\mathscr {Q} A_H = D_H \mathscr {Q}$
. Hence, both
![]() $\mathscr {P}, \mathscr {Q} :\mathcal A(H) \rightarrow \mathcal D(H)$
are isometric isomorphisms.
$\mathscr {P}, \mathscr {Q} :\mathcal A(H) \rightarrow \mathcal D(H)$
are isometric isomorphisms.
Proof Let us show the claim for
![]() $\mathscr {P}$
, since the proof for
$\mathscr {P}$
, since the proof for
![]() $\mathscr {Q}$
is completely analogous. Let
$\mathscr {Q}$
is completely analogous. Let
![]() $r>0$
and
$r>0$
and
![]() $f \in L^2(\mathbb R^+)$
. Then,
$f \in L^2(\mathbb R^+)$
. Then,
 $$ \begin{align*}(\mathscr{P} A_H f)(r) = \sqrt{\frac{2}{\pi}}(A_P A_H f)(r) = \sqrt{\frac{2}{\pi}} (A_H A_P f)(r) = (D_H \mathscr{P} f)(r), \end{align*} $$
$$ \begin{align*}(\mathscr{P} A_H f)(r) = \sqrt{\frac{2}{\pi}}(A_P A_H f)(r) = \sqrt{\frac{2}{\pi}} (A_H A_P f)(r) = (D_H \mathscr{P} f)(r), \end{align*} $$
where we have used that
![]() $A_P A_H = A_H A_P$
. It follows by analytic continuation that
$A_P A_H = A_H A_P$
. It follows by analytic continuation that
![]() $\mathscr {P} A_H = D_H \mathscr {P}$
(Proposition 2.1). Then, reasoning as in the proof of Theorem 5.2, we obtain
$\mathscr {P} A_H = D_H \mathscr {P}$
(Proposition 2.1). Then, reasoning as in the proof of Theorem 5.2, we obtain
![]() $\mathscr {P}: \mathcal A(H) \rightarrow \mathcal {D}(H)$
is a well-defined isometric isomorphism.
$\mathscr {P}: \mathcal A(H) \rightarrow \mathcal {D}(H)$
is a well-defined isometric isomorphism.
We define the one-sided Hilbert-like operator
![]() $\mathcal {H}_+^{\mathbb C^+}: H^2(\mathbb C^+) \to H^2(\mathbb C^+)$
by
$\mathcal {H}_+^{\mathbb C^+}: H^2(\mathbb C^+) \to H^2(\mathbb C^+)$
by
where
![]() $\gamma _z:(0,\infty )\rightarrow \mathbb C^+$
,
$\gamma _z:(0,\infty )\rightarrow \mathbb C^+$
,
![]() $\gamma _z(s) = sz$
.
$\gamma _z(s) = sz$
.
Corollary 6.5
![]() $\mathcal {H}_+^{\mathbb C^+}$
is a well-defined bounded operator on
$\mathcal {H}_+^{\mathbb C^+}$
is a well-defined bounded operator on
![]() $H^2(\mathbb C^+)$
and on
$H^2(\mathbb C^+)$
and on
![]() $\mathcal D(H)$
for any
$\mathcal D(H)$
for any
![]() $H \in \mathfrak {H}_2$
.
$H \in \mathfrak {H}_2$
.
Proof By Proposition 6.1, Corollary 6.4, and Theorem 3.4, the claim will follow once we prove that
![]() $\mathcal {H}_+^{\mathbb C^+} = \mathscr {P} \mathcal {H}_+ \mathscr {P}^{-1}$
. For
$\mathcal {H}_+^{\mathbb C^+} = \mathscr {P} \mathcal {H}_+ \mathscr {P}^{-1}$
. For
![]() $\theta \in \left (\frac {-\pi }{2}, \frac {\pi }{2}\right )$
, set
$\theta \in \left (\frac {-\pi }{2}, \frac {\pi }{2}\right )$
, set
![]() $P_\theta (r,s) := \frac {r e^{i\theta }}{r^2 e^{2i\theta } + s^2}$
for
$P_\theta (r,s) := \frac {r e^{i\theta }}{r^2 e^{2i\theta } + s^2}$
for
![]() $r,s>0$
. Then,
$r,s>0$
. Then,
![]() $P_\theta \in \mathfrak {H}_2$
, so
$P_\theta \in \mathfrak {H}_2$
, so
![]() $A_{P_\theta } \mathcal {H}_+ = \mathcal {H}_+ A_{P_\theta }$
on
$A_{P_\theta } \mathcal {H}_+ = \mathcal {H}_+ A_{P_\theta }$
on
![]() $L^2(\mathbb R^+)$
by Theorem 3.4, and it is readily seen that
$L^2(\mathbb R^+)$
by Theorem 3.4, and it is readily seen that
![]() $(\mathscr {P}f)^\theta = \sqrt {\frac {2}{\pi }} A_{P_\theta } f$
for any
$(\mathscr {P}f)^\theta = \sqrt {\frac {2}{\pi }} A_{P_\theta } f$
for any
![]() $f \in L^2(\mathbb R^+)$
. Furthermore, notice that
$f \in L^2(\mathbb R^+)$
. Furthermore, notice that
![]() $F^\theta \in L^2(\mathbb R^+)$
for any
$F^\theta \in L^2(\mathbb R^+)$
for any
![]() $F \in H^2(\mathbb C^+)$
by (1.3). Then,
$F \in H^2(\mathbb C^+)$
by (1.3). Then,
 $$ \begin{align*} (\mathscr{P} \mathcal{H}_+ \mathscr{P}^{-1} F)^\theta &= \sqrt{\frac{2}{\pi}} A_{P_\theta} \mathcal{H}_+ \mathscr{P}^{-1} F = \sqrt{\frac{2}{\pi}} \mathcal{H}_+ A_{P_\theta} \mathscr{P}^{-1} F = \mathcal{H}_+ (\mathscr{P} \mathscr{P}^{-1} F)^\theta \\ &= \mathcal{H}_+ F^\theta = (\mathcal{H}_+^{\mathbb C^+}F)^\theta, \qquad \theta \in \left(\frac{-\pi}{2}, \frac{\pi}{2}\right), \, F \in H^2(\mathbb C^+), \end{align*} $$
$$ \begin{align*} (\mathscr{P} \mathcal{H}_+ \mathscr{P}^{-1} F)^\theta &= \sqrt{\frac{2}{\pi}} A_{P_\theta} \mathcal{H}_+ \mathscr{P}^{-1} F = \sqrt{\frac{2}{\pi}} \mathcal{H}_+ A_{P_\theta} \mathscr{P}^{-1} F = \mathcal{H}_+ (\mathscr{P} \mathscr{P}^{-1} F)^\theta \\ &= \mathcal{H}_+ F^\theta = (\mathcal{H}_+^{\mathbb C^+}F)^\theta, \qquad \theta \in \left(\frac{-\pi}{2}, \frac{\pi}{2}\right), \, F \in H^2(\mathbb C^+), \end{align*} $$
and the claim follows. Analogously, one can prove that
![]() $\mathcal {H}_+^{\mathbb C^+} = \mathscr {Q} \mathcal {H}_+ \mathscr {Q}^{-1}$
.
$\mathcal {H}_+^{\mathbb C^+} = \mathscr {Q} \mathcal {H}_+ \mathscr {Q}^{-1}$
.
(2) Fractional kernels. Let
![]() $\alpha>0$
, and let
$\alpha>0$
, and let
![]() $(x)_+ =x$
, if
$(x)_+ =x$
, if
![]() $x \geq 0$
, and
$x \geq 0$
, and
![]() $(x)_+ =0$
otherwise. Set
$(x)_+ =0$
otherwise. Set
![]() $\mathcal {C}_\alpha (r,s) = \alpha (r-s)_+^{\alpha -1}r^{-\alpha }, \: r,s>0$
. These kernels are related to the Riemann–Liouville and Weyl fractional integrals of order
$\mathcal {C}_\alpha (r,s) = \alpha (r-s)_+^{\alpha -1}r^{-\alpha }, \: r,s>0$
. These kernels are related to the Riemann–Liouville and Weyl fractional integrals of order
![]() $\alpha $
. Their range spaces have been studied in [Reference Galé, Miana and Sánchez-Lajusticia8], where they are realized as spaces of Sobolev type of absolutely continuous functions of fractional order on
$\alpha $
. Their range spaces have been studied in [Reference Galé, Miana and Sánchez-Lajusticia8], where they are realized as spaces of Sobolev type of absolutely continuous functions of fractional order on
![]() $\mathbb {R}^+$
. Using the theory developed, we recover, with simpler proofs, some results given in [Reference Galé, Miana and Sánchez-Lajusticia8].
$\mathbb {R}^+$
. Using the theory developed, we recover, with simpler proofs, some results given in [Reference Galé, Miana and Sánchez-Lajusticia8].
Theorem 6.6 The range space
![]() $\mathcal A(\mathcal {C}_\alpha ) = \mathcal A(\mathcal {C}_\alpha ^\ast )$
is an RKHS if and only if
$\mathcal A(\mathcal {C}_\alpha ) = \mathcal A(\mathcal {C}_\alpha ^\ast )$
is an RKHS if and only if
![]() $\alpha>1/2$
. In this case, its kernel
$\alpha>1/2$
. In this case, its kernel
![]() $K_{\mathcal {C}_\alpha }$
is given by
$K_{\mathcal {C}_\alpha }$
is given by
 $$ \begin{align*} K_{\mathcal{C}_\alpha} (r,s) = \frac{\alpha}{\max(r,s) } \: _2F_1\left(1-\alpha, 1; \alpha+1; \frac{\min(r,s)}{\max(r,s)}\right), \quad \alpha> \frac{1}{2}, \:r \neq s>0, \end{align*} $$
$$ \begin{align*} K_{\mathcal{C}_\alpha} (r,s) = \frac{\alpha}{\max(r,s) } \: _2F_1\left(1-\alpha, 1; \alpha+1; \frac{\min(r,s)}{\max(r,s)}\right), \quad \alpha> \frac{1}{2}, \:r \neq s>0, \end{align*} $$
and
![]() $K_{\mathcal {C}_\alpha }(r,r) = \frac {\alpha ^2}{2\alpha -1}\frac {1}{r}, \: r>0$
. For
$K_{\mathcal {C}_\alpha }(r,r) = \frac {\alpha ^2}{2\alpha -1}\frac {1}{r}, \: r>0$
. For
![]() $\alpha>0$
, the range space
$\alpha>0$
, the range space
![]() $\mathcal D(\mathcal {C}_\alpha ) = \mathcal D(\mathcal {C}_\alpha ^\ast )$
is an RKHS with kernel
$\mathcal D(\mathcal {C}_\alpha ) = \mathcal D(\mathcal {C}_\alpha ^\ast )$
is an RKHS with kernel
![]() $\mathcal {K}_{\mathcal {C}_\alpha }$
given by
$\mathcal {K}_{\mathcal {C}_\alpha }$
given by
 $$ \begin{align*} \mathcal{K}_{\mathcal{C}_\alpha} (z,w) = \alpha^2 \int_0^1 \int_0^1 \frac{(1-x)^{\alpha-1} (1-y)^{\alpha-1}}{xz+y\overline{w}}dxdy, \quad z,w\in \mathbb C^+. \end{align*} $$
$$ \begin{align*} \mathcal{K}_{\mathcal{C}_\alpha} (z,w) = \alpha^2 \int_0^1 \int_0^1 \frac{(1-x)^{\alpha-1} (1-y)^{\alpha-1}}{xz+y\overline{w}}dxdy, \quad z,w\in \mathbb C^+. \end{align*} $$
In addition, the Laplace transform
![]() $\mathcal {L}$
defines an isometric isomorphism
$\mathcal {L}$
defines an isometric isomorphism
![]() $\mathcal {L}:\mathcal A(\mathcal {C}_\alpha ) \to \mathcal D(\mathcal {C}_\alpha )$
for any
$\mathcal {L}:\mathcal A(\mathcal {C}_\alpha ) \to \mathcal D(\mathcal {C}_\alpha )$
for any
![]() $\alpha>0$
.
$\alpha>0$
.
Proof It is readily seen that
![]() $\mathcal {C}_\alpha \in \mathcal I_p$
if and only if
$\mathcal {C}_\alpha \in \mathcal I_p$
if and only if
![]() $\alpha> 1/p$
. Hence, the claim is an immediate consequence of Theorems 3.3 4.3 and Corollary 5.4.
$\alpha> 1/p$
. Hence, the claim is an immediate consequence of Theorems 3.3 4.3 and Corollary 5.4.
Another kernel related to fractional theory, in particular with the Hadamard fractional integral (see [Reference Butzer, Kilbas and Trujillo3]), is
![]() $D_{\alpha ,c} := \frac {1}{\Gamma (\alpha )} \left (\frac {s}{r}\right )^{c} \left (\log \frac {r}{s}\right )^{\alpha - 1}\frac {1}{s}\chi _{(0,r)}(s)$
(
$D_{\alpha ,c} := \frac {1}{\Gamma (\alpha )} \left (\frac {s}{r}\right )^{c} \left (\log \frac {r}{s}\right )^{\alpha - 1}\frac {1}{s}\chi _{(0,r)}(s)$
(
![]() $r,s>0$
), for
$r,s>0$
), for
![]() $\alpha>0$
and
$\alpha>0$
and
![]() $c\in \mathbb R$
. It is readily seen that
$c\in \mathbb R$
. It is readily seen that
![]() $D_{\alpha ,c} \in \mathfrak {H}_p$
if and only if
$D_{\alpha ,c} \in \mathfrak {H}_p$
if and only if
![]() $c>1/p$
, and in this case,
$c>1/p$
, and in this case,
![]() $D_{\alpha ,c} \in \mathcal I_p$
if and only if
$D_{\alpha ,c} \in \mathcal I_p$
if and only if
![]() $\alpha> 1/p$
. In particular, if
$\alpha> 1/p$
. In particular, if
![]() $\alpha ,c>1/2$
, then
$\alpha ,c>1/2$
, then
 $$ \begin{align*}K_{D_{\alpha,c}}(r,s) = \frac{1}{\Gamma(\alpha)^2}\int_0^{\min\{r,s\}} \left(\frac{t^2}{rs}\right)^\mu \left(\log \frac{r}{t} \log\frac{s}{t}\right)^{\alpha-1}\frac{dt}{t^2}, \quad r,s>0, \end{align*} $$
$$ \begin{align*}K_{D_{\alpha,c}}(r,s) = \frac{1}{\Gamma(\alpha)^2}\int_0^{\min\{r,s\}} \left(\frac{t^2}{rs}\right)^\mu \left(\log \frac{r}{t} \log\frac{s}{t}\right)^{\alpha-1}\frac{dt}{t^2}, \quad r,s>0, \end{align*} $$
and
 $$ \begin{align*}\mathcal{K}_{D_{\alpha,c}}(z,w) = \frac{1}{\Gamma(\alpha)^2}\int_0^\infty \int_0^{\min\{1,x\}} \left(\frac{y^2}{x}\right)^\mu \left(\log \frac{1}{y} \log\frac{x}{y}\right)^{\alpha-1} \frac{1}{z+x\overline{w}}\, dy dx, \end{align*} $$
$$ \begin{align*}\mathcal{K}_{D_{\alpha,c}}(z,w) = \frac{1}{\Gamma(\alpha)^2}\int_0^\infty \int_0^{\min\{1,x\}} \left(\frac{y^2}{x}\right)^\mu \left(\log \frac{1}{y} \log\frac{x}{y}\right)^{\alpha-1} \frac{1}{z+x\overline{w}}\, dy dx, \end{align*} $$
for
![]() $z,w \in \mathbb C^+$
.
$z,w \in \mathbb C^+$
.
Acknowledgment
The author thanks J. E. Galé for several ideas, comments, and additional information, in particular for his helpful reviews. The author also thanks the referee for a meticulous review. Both of them have led to considerably improve the final version of the paper.