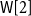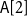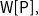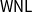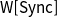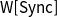1. Introduction
Černý’s conjecture is arguably the most famous open combinatorial problem concerning deterministic finite automata (DFA), somehow dating back to Černý (Reference Černý1964). Footnote 1 Recently, a particular Special Issue was dedicated to this conjecture being around for more than five decades; see Volkov (Reference Volkov2019). This Special Issue also contains an English translation of Černý’s paper, originally written in Slovak, see Černý (Reference Černý2019).
The key notion in Černý’s conjecture is that of a synchronizing word. A word x is called synchronizing for a DFA A, if there is a state
![]() $s_f$
, also called the synchronizing state of A, such that if A reads x starting in any state, it will end up in
$s_f$
, also called the synchronizing state of A, such that if A reads x starting in any state, it will end up in
![]() $s_f$
. The Černý conjecture given by Černý et al. (Reference Černý, Pirická and Rosenauerová1971) states that every n-state DFA can be synchronized by a word of length
$s_f$
. The Černý conjecture given by Černý et al. (Reference Černý, Pirická and Rosenauerová1971) states that every n-state DFA can be synchronized by a word of length
![]() $(n-1)^2$
if it can be synchronized at all. Although this bound was proven for several classes of finite-state automata, the general case is still widely open. The currently best upper bound is cubic, and only very little progress has been made; see Frankl (Reference Frankl1982), Pin (Reference Pin1983), Shitov (Reference Shitov2019), Szykuła (Reference Szykuła2018) in alphabetical, but incidentally also nearly in chronological order. Conversely, already Černý (Reference Černý1964) devised a family of DFAs that attain the mentioned quadratic bound. For instance, the 4-state automaton from Figure 3 has a smallest synchronizing word of length nine.
$(n-1)^2$
if it can be synchronized at all. Although this bound was proven for several classes of finite-state automata, the general case is still widely open. The currently best upper bound is cubic, and only very little progress has been made; see Frankl (Reference Frankl1982), Pin (Reference Pin1983), Shitov (Reference Shitov2019), Szykuła (Reference Szykuła2018) in alphabetical, but incidentally also nearly in chronological order. Conversely, already Černý (Reference Černý1964) devised a family of DFAs that attain the mentioned quadratic bound. For instance, the 4-state automaton from Figure 3 has a smallest synchronizing word of length nine.
The notion of a synchronizing word is not only important from a mathematical perspective, offering a nice combinatorial question, but it is quite important in a number of application areas, simply because synchronization is an important concept for many applied areas: parallel and distributed programming, system and protocol testing, information coding, robotics, etc. Therefore, it is also interesting to compute a shortest synchronizing word. Unfortunately, as it was shown by Rystsov (Reference Rystsov1980) and Eppstein (Reference Eppstein1990), the corresponding decision problem DFA-SW (defined in the following) is
![]() $\textsf{NP}$
-complete. Possible applications of this problem are explained in Kisielewicz et al. (Reference Kisielewicz, Kowalski and Szykuła2015). The problem has also been considered from the viewpoint of approximation by Berlinkov (Reference Berlinkov2014) and parameterized complexity by Bruchertseifer and Fernau (Reference Bruchertseifer and Fernau2021), Fernau et al. (Reference Fernau, Heggernes and Villanger2015), Fernau and Krebs (Reference Fernau and Krebs2017), Montoya and Nolasco (Reference Montoya and Nolasco2018).
$\textsf{NP}$
-complete. Possible applications of this problem are explained in Kisielewicz et al. (Reference Kisielewicz, Kowalski and Szykuła2015). The problem has also been considered from the viewpoint of approximation by Berlinkov (Reference Berlinkov2014) and parameterized complexity by Bruchertseifer and Fernau (Reference Bruchertseifer and Fernau2021), Fernau et al. (Reference Fernau, Heggernes and Villanger2015), Fernau and Krebs (Reference Fernau and Krebs2017), Montoya and Nolasco (Reference Montoya and Nolasco2018).

It is important to note at this point that we are working with complete DFAs in our definition; that is, a DFA can be specified as
![]() $A=(Q,\Sigma,\delta,q_0,F)$
, where Q is the finite-state alphabet,
$A=(Q,\Sigma,\delta,q_0,F)$
, where Q is the finite-state alphabet,
![]() $\Sigma$
is the finite input alphabet,
$\Sigma$
is the finite input alphabet,
![]() $\delta:Q\times\Sigma\to Q$
is the complete transition function, and
$\delta:Q\times\Sigma\to Q$
is the complete transition function, and
![]() $q_0\in Q$
and
$q_0\in Q$
and
![]() $F\subseteq Q$
specify the start state and the final state set that are actually inessential for the task of synchronization. While DFA-SW is
$F\subseteq Q$
specify the start state and the final state set that are actually inessential for the task of synchronization. While DFA-SW is
![]() $\textsf{NP}$
-complete, the complexity picture actually changes if we allow undefined transitions (i.e., if we move over to partial DFAs); the corresponding synchronization problem then becomes
$\textsf{NP}$
-complete, the complexity picture actually changes if we allow undefined transitions (i.e., if we move over to partial DFAs); the corresponding synchronization problem then becomes
![]() $\textsf{PSPACE}$
-complete; see Martyugin (Reference Martyugin2014). In fact, also based on the mentioned numerous applications of synchronizing automata, many variations have been studied. Here, we only mention some recent papers as Fernau et al. (Reference Fernau, Gusev, Hoffmann, Holzer, Volkov and Wolf2019, Reference Fernau, Wolf and Yamakami2020), Fernau and Wolf (Reference Fernau and Wolf2020), Wolf (Reference Wolf2020). However, we will mostly restrict our attention to the most classical variant of synchronizing automata in this paper.
$\textsf{PSPACE}$
-complete; see Martyugin (Reference Martyugin2014). In fact, also based on the mentioned numerous applications of synchronizing automata, many variations have been studied. Here, we only mention some recent papers as Fernau et al. (Reference Fernau, Gusev, Hoffmann, Holzer, Volkov and Wolf2019, Reference Fernau, Wolf and Yamakami2020), Fernau and Wolf (Reference Fernau and Wolf2020), Wolf (Reference Wolf2020). However, we will mostly restrict our attention to the most classical variant of synchronizing automata in this paper.
We will continue to study the problem (DFA-SW) from the point of parameterized complexity. The standard parameter for this problem is the length upper bound k. Also with future definitions of parameterized problems, we will follow the convention that k always denotes the parameter. As the synchronizability of DFAs can be checked in polynomial time (see Sandberg Reference Sandberg2005; Volkov Reference Volkov2008) and due to the polynomial upper bound on a shortest synchonizing word (if existent) as discussed above, we can assume that the parameter k is given in unary or binary, whatever is more convenient to us. It was shown in Bruchertseifer and Fernau (Reference Bruchertseifer and Fernau2021), Fernau et al. (Reference Fernau, Heggernes and Villanger2015), Montoya and Nolasco (Reference Montoya and Nolasco2018) that this problem is
![]() $\textsf{W}[2]$
-hard, even when restricted to quite particular (and restricted) forms of finite automata.
$\textsf{W}[2]$
-hard, even when restricted to quite particular (and restricted) forms of finite automata.
Also, other parameters have been studied, in particular, in Fernau et al. (Reference Fernau, Heggernes and Villanger2015), but they are of less interest to the present study where we focus on the standard parameter.
2. Organization of the Paper and Main Results
In Section 3, we introduce some basic notions of parameterized complexity. Observe that we pay special attention to some complexity classes like
![]() $\textsf{A}[2]$
or
$\textsf{A}[2]$
or
![]() $\textsf{WNL}$
that are less studied in the literature. Most problems that we look at are
$\textsf{WNL}$
that are less studied in the literature. Most problems that we look at are
![]() $\textsf{W}[2]$
-hard, but in our opinion, from a complexity theoretic viewpoint, an exact classification of parameterized problems should be at least attempted, beyond stating that they are
$\textsf{W}[2]$
-hard, but in our opinion, from a complexity theoretic viewpoint, an exact classification of parameterized problems should be at least attempted, beyond stating that they are
![]() $\textsf{W}[1]$
-hard and hence most likely outside
$\textsf{W}[1]$
-hard and hence most likely outside
![]() $\textsf{FPT}$
. In Section 4, we focus on studying (DFA-SW), a problem already defined in the introduction; here, our focus is on the length upper bound k as a parameter. As we can see in Section 5, there are several problems
$\textsf{FPT}$
. In Section 4, we focus on studying (DFA-SW), a problem already defined in the introduction; here, our focus is on the length upper bound k as a parameter. As we can see in Section 5, there are several problems
![]() $\textsf{FPT}$
-equivalent to (DFA-SW); this motivated us to introduce a new class of parameterized problems that we call
$\textsf{FPT}$
-equivalent to (DFA-SW); this motivated us to introduce a new class of parameterized problems that we call
![]() $\textsf{W}[\textsf{Sync}]$
. We prove that
$\textsf{W}[\textsf{Sync}]$
. We prove that
as a main result of Section 5. In particular, Monoid Factorization, Bounded Transformation Rank(r), and Bounded DFA-Intersection are complete for
![]() $\textsf{W}[\textsf{Sync}]$
. In Section 6, we describe problems that are both
$\textsf{W}[\textsf{Sync}]$
. In Section 6, we describe problems that are both
![]() $\textsf{W}[2]$
-hard and belong to
$\textsf{W}[2]$
-hard and belong to
![]() $\textsf{W}[\textsf{Sync}]$
. Conversely, in Section 7, we look into problems that are
$\textsf{W}[\textsf{Sync}]$
. Conversely, in Section 7, we look into problems that are
![]() $\textsf{W}[\textsf{Sync}]$
-hard and belong to some of the classes
$\textsf{W}[\textsf{Sync}]$
-hard and belong to some of the classes
![]() $\textsf{WNL}$
or
$\textsf{WNL}$
or
![]() $\textsf{W}[\textsf{P}]$
or
$\textsf{W}[\textsf{P}]$
or
![]() $\textsf{A}[2]$
. We also list problems (in Section 8) that behave similar to DFA-SW, being
$\textsf{A}[2]$
. We also list problems (in Section 8) that behave similar to DFA-SW, being
![]() $\textsf{W}[2]$
-hard and belonging to some of the classes
$\textsf{W}[2]$
-hard and belonging to some of the classes
![]() $\textsf{WNL}$
or
$\textsf{WNL}$
or
![]() $\textsf{W}[\textsf{P}]$
or
$\textsf{W}[\textsf{P}]$
or
![]() $\textsf{A}[2]$
, but where the exact relation to
$\textsf{A}[2]$
, but where the exact relation to
![]() $\textsf{W}[\textsf{Sync}]$
is unclear. In Section 9, we return to variations of Monoid Factorization that often present a completely different complexity behavior. In all sections, we highlight open problems in the hope that this paper can serve as an incentive for further research. More general questions and further thoughts are collected in the concluding Section 10.
$\textsf{W}[\textsf{Sync}]$
is unclear. In Section 9, we return to variations of Monoid Factorization that often present a completely different complexity behavior. In all sections, we highlight open problems in the hope that this paper can serve as an incentive for further research. More general questions and further thoughts are collected in the concluding Section 10.
A preliminary version of this paper appeared in Bruchertseifer and Fernau (Reference Bruchertseifer and Fernau2020).
3. A Primer in Parameterized Complexity
In this paper, we will encounter quite a number of notions in parameterized complexity. We will assume some familiarity with basic notions of that theory on side of the reader in the following. In particular, a parameterized reduction is a many-one reduction that consumes
![]() $\textsf{FPT}$
-time (in our cases, it mostly uses only polynomial time) and translates a parameter value k to a parameter value of f(k) (of the target problem), for some computable function f. One important property of this (as of all reasonable reduction notions) is transitivity: If there is a parameterized reduction from
$\textsf{FPT}$
-time (in our cases, it mostly uses only polynomial time) and translates a parameter value k to a parameter value of f(k) (of the target problem), for some computable function f. One important property of this (as of all reasonable reduction notions) is transitivity: If there is a parameterized reduction from
![]() $(\Pi_1,\kappa_1)$
to
$(\Pi_1,\kappa_1)$
to
![]() $(\Pi_2,\kappa_2)$
and from
$(\Pi_2,\kappa_2)$
and from
![]() $(\Pi_2,\kappa_2)$
to
$(\Pi_2,\kappa_2)$
to
![]() $(\Pi_3,\kappa_3)$
, then there is parameterized reduction from
$(\Pi_3,\kappa_3)$
, then there is parameterized reduction from
![]() $(\Pi_1,\kappa_1)$
to
$(\Pi_1,\kappa_1)$
to
![]() $(\Pi_3,\kappa_3)$
. Here,
$(\Pi_3,\kappa_3)$
. Here,
![]() $\kappa_i$
denotes the parameterization (function) for clarity. A parameterized complexity class can be characterized by one (complete) problem, assuming the class is closed under parameterized reductions. Examples comprise the following classes; for the typical problems, the parameter will be always called k:
$\kappa_i$
denotes the parameterization (function) for clarity. A parameterized complexity class can be characterized by one (complete) problem, assuming the class is closed under parameterized reductions. Examples comprise the following classes; for the typical problems, the parameter will be always called k:
-
 $\textsf{W}[1]$
Given a nondeterministic single-tape Turing machine and
$\textsf{W}[1]$
Given a nondeterministic single-tape Turing machine and
 $k\in\mathbb{N}$
, does it accept the empty word within at most k steps?
$k\in\mathbb{N}$
, does it accept the empty word within at most k steps? -
 $\textsf{W}[2]$
Given a nondeterministic multi-tape Turing machine and
$\textsf{W}[2]$
Given a nondeterministic multi-tape Turing machine and
 $k\in\mathbb{N}$
, does it accept the empty word within at most k steps?
$k\in\mathbb{N}$
, does it accept the empty word within at most k steps? -
 $\textsf{A}[2]$
Given an alternating single-tape Turing machine whose initial state is existential and that is allowed to switch only once into the set of universal states and
$\textsf{A}[2]$
Given an alternating single-tape Turing machine whose initial state is existential and that is allowed to switch only once into the set of universal states and
 $k\in\mathbb{N}$
, does it accept the empty word within at most k steps?
$k\in\mathbb{N}$
, does it accept the empty word within at most k steps? -
WNL Given a nondeterministic single-tape Turing machine and some integer
 $\ell\geq 0$
in unary and
$\ell\geq 0$
in unary and
 $k\in\mathbb{N}$
, does it accept the empty word within at most
$k\in\mathbb{N}$
, does it accept the empty word within at most
 $\ell$
steps, visiting at most k tape cells?
$\ell$
steps, visiting at most k tape cells? -
 $\textsf{W}[\textsf{P}]$
Given a nondeterministic single-tape Turing machine and some integer
$\textsf{W}[\textsf{P}]$
Given a nondeterministic single-tape Turing machine and some integer
 $\ell\geq 0$
in unary and
$\ell\geq 0$
in unary and
 $k\in\mathbb{N}$
, does it accept the empty word within at most
$k\in\mathbb{N}$
, does it accept the empty word within at most
 $\ell$
steps, thereby making at most
$\ell$
steps, thereby making at most
 $k\leq\ell$
nondeterministic steps?
$k\leq\ell$
nondeterministic steps?
More details can be found in textbooks like Downey and Fellows (Reference Downey and Fellows2013), Flum and Grohe (Reference Flum and Grohe2006). The Turing way to these complexity classes (i.e., using variants of Turing machines and defining parameterized problems on these machines) is described also in Cesati (Reference Cesati2003), Guillemot (Reference Guillemot2011). However, choosing a “typical” problem
![]() $\Pi$
and defining a (parameterized) complexity class as the set of all (parameterized) problems that are reducible (with a reasonable notion of reducibility) to
$\Pi$
and defining a (parameterized) complexity class as the set of all (parameterized) problems that are reducible (with a reasonable notion of reducibility) to
![]() $\Pi$
clearly also works for problems not related to Turing machines. In this paper, we actually suggest a new parameterized complexity class
$\Pi$
clearly also works for problems not related to Turing machines. In this paper, we actually suggest a new parameterized complexity class
![]() $\textsf{W}[\textsf{Sync}]$
as the class of parameterized problems that can be (parameterized) reduced to DFA-SW, a class that is situated as drawn in Figure 1, that is, somewhere between
$\textsf{W}[\textsf{Sync}]$
as the class of parameterized problems that can be (parameterized) reduced to DFA-SW, a class that is situated as drawn in Figure 1, that is, somewhere between
![]() $\textsf{W}[2]$
at its lower end and the intersection of
$\textsf{W}[2]$
at its lower end and the intersection of
![]() $\textsf{WNL}$
,
$\textsf{WNL}$
,
![]() $\textsf{A}[2]$
and
$\textsf{A}[2]$
and
![]() $\textsf{W}[\textsf{P}]$
at its upper end. Most of the remainder of this section and the following one is devoted to proving this relation of
$\textsf{W}[\textsf{P}]$
at its upper end. Most of the remainder of this section and the following one is devoted to proving this relation of
![]() $\textsf{W}[\textsf{Sync}]$
to
$\textsf{W}[\textsf{Sync}]$
to
![]() $\textsf{W}[2]$
,
$\textsf{W}[2]$
,
![]() $\textsf{WNL}$
,
$\textsf{WNL}$
,
![]() $\textsf{A}[2]$
and
$\textsf{A}[2]$
and
![]() $\textsf{W}[\textsf{P}]$
. Further interesting complexity classes (in our discussion) are as follows:
$\textsf{W}[\textsf{P}]$
. Further interesting complexity classes (in our discussion) are as follows:
![]() $\textsf{FPT}$
,
$\textsf{FPT}$
,
![]() $\textsf{W}[3]$
,
$\textsf{W}[3]$
,
![]() $\textsf{W}[\textsf{SAT}]$
,
$\textsf{W}[\textsf{SAT}]$
,
![]() $\textsf{A}[3]$
,
$\textsf{A}[3]$
,
![]() $\textsf{para-}\textsf{NP}$
and
$\textsf{para-}\textsf{NP}$
and
![]() $\textsf{XP}$
. Let us briefly introduce the complexity classes
$\textsf{XP}$
. Let us briefly introduce the complexity classes
![]() $\textsf{FPT}$
,
Footnote 2
$\textsf{FPT}$
,
Footnote 2
![]() $\textsf{XP}$
and
$\textsf{XP}$
and
![]() $\textsf{para-NP}$
, also see Flum and Grohe (Reference Flum and Grohe2006): If a parameterized problem
$\textsf{para-NP}$
, also see Flum and Grohe (Reference Flum and Grohe2006): If a parameterized problem
![]() $\Pi$
can be solved in time
$\Pi$
can be solved in time
![]() $\mathcal{O}^*(f(k))$
(for some function f) by a deterministic algorithm,
$\mathcal{O}^*(f(k))$
(for some function f) by a deterministic algorithm,
![]() $\Pi$
belongs to
$\Pi$
belongs to
![]() $\textsf{FPT}$
. If a parameterized problem
$\textsf{FPT}$
. If a parameterized problem
![]() $\Pi$
can be solved in time
$\Pi$
can be solved in time
![]() $n^{f(k)}$
for instances (x,k) of size n for some function f, then
$n^{f(k)}$
for instances (x,k) of size n for some function f, then
![]() $\Pi\in\textsf{XP}$
. If there is a nondeterministic algorithm running in time
$\Pi\in\textsf{XP}$
. If there is a nondeterministic algorithm running in time
![]() $\mathcal{O}^*(f(k))$
(for some function f), then
$\mathcal{O}^*(f(k))$
(for some function f), then
![]() $\Pi\in\textsf{para-}\textsf{NP}$
. For definitions of the other classes, we refer to the mentioned textbooks. From the literature, the following relations are known:
$\Pi\in\textsf{para-}\textsf{NP}$
. For definitions of the other classes, we refer to the mentioned textbooks. From the literature, the following relations are known:
 $\textsf{FPT}\subseteq \textsf{W}[1]\subseteq \textsf{W}[2]\subseteq \textsf{W}[3]\subseteq\cdots\subseteq \textsf{W}[\textsf{SAT}]\subseteq \textsf{W}[\textsf{P}]\subseteq (\textsf{para-}\textsf{NP} \cap \textsf{XP})$
;
$\textsf{FPT}\subseteq \textsf{W}[1]\subseteq \textsf{W}[2]\subseteq \textsf{W}[3]\subseteq\cdots\subseteq \textsf{W}[\textsf{SAT}]\subseteq \textsf{W}[\textsf{P}]\subseteq (\textsf{para-}\textsf{NP} \cap \textsf{XP})$
; $\textsf{FPT}\subseteq \textsf{W}[1]=\textsf{A}[1]\subseteq\textsf{W}[2]\subseteq\textsf{A}[2]\subseteq\textsf{A}[3]\subseteq \cdots\subseteq \textsf{AW}[\textsf{P}]\subseteq \textsf{XP}$
.
$\textsf{FPT}\subseteq \textsf{W}[1]=\textsf{A}[1]\subseteq\textsf{W}[2]\subseteq\textsf{A}[2]\subseteq\textsf{A}[3]\subseteq \cdots\subseteq \textsf{AW}[\textsf{P}]\subseteq \textsf{XP}$
.

Figure 1. Visualization of the complexity classes (“A
![]() $\rightarrow$
B” means “A is contained in B”).
$\rightarrow$
B” means “A is contained in B”).
Each of the inclusions that we have explicitly written is conjectured but not known to be strict. Also, no non-trivial inter-relations are known between the
![]() $\textsf{A}$
- and
$\textsf{A}$
- and
![]() $\textsf{W}$
-hierarchies, apart from
$\textsf{W}$
-hierarchies, apart from
![]() $\textsf{W}[t]\subseteq\textsf{A}[t]$
for each t.
$\textsf{W}[t]\subseteq\textsf{A}[t]$
for each t.
Guillemot defined
![]() $\textsf{WNL}$
in Guillemot (Reference Guillemot2011) in the same way as we described it above. Interesting formal language problems complete for
$\textsf{WNL}$
in Guillemot (Reference Guillemot2011) in the same way as we described it above. Interesting formal language problems complete for
![]() $\textsf{WNL}$
include Bounded DFA-Intersection, given k DFAs, with parameter k, plus the length of the word that should be accepted by all k automata, or Longest Common Subsequence, parameterized by the number of given strings. We will come back to these problems with different parameterizations below.
$\textsf{WNL}$
include Bounded DFA-Intersection, given k DFAs, with parameter k, plus the length of the word that should be accepted by all k automata, or Longest Common Subsequence, parameterized by the number of given strings. We will come back to these problems with different parameterizations below.
![]() $\textsf{WNL}$
is situated above all levels of the
$\textsf{WNL}$
is situated above all levels of the
![]() $\textsf{W}$
-hierarchy, because the last two mentioned problems are known to be hard for
$\textsf{W}$
-hierarchy, because the last two mentioned problems are known to be hard for
![]() $\textsf{W}[t]$
for any
$\textsf{W}[t]$
for any
![]() $t\geq 1$
, see Bodlaender et al. (Reference Bodlaender, Downey, Fellows and Wareham1995), Wareham (Reference Wareham2001). This proves the first part of the following theorem that we include also for the ease of reference.
$t\geq 1$
, see Bodlaender et al. (Reference Bodlaender, Downey, Fellows and Wareham1995), Wareham (Reference Wareham2001). This proves the first part of the following theorem that we include also for the ease of reference.
Theorem 1
![]() $\bigcup_{t\geq 1}\textsf{W}\mkern 2mu[t]\subseteq \textsf{WNL}\subseteq (\textsf{para-}\textsf{NP} \cap \textsf{XP})$
.
$\bigcup_{t\geq 1}\textsf{W}\mkern 2mu[t]\subseteq \textsf{WNL}\subseteq (\textsf{para-}\textsf{NP} \cap \textsf{XP})$
.
Proof. Clearly, by a standard product automaton construction, Bounded DFA-Intersection can be tested in time
![]() $\mathcal{O}(n^k)$
, where n is the maximum number of states of the input DFAs. Hence,
$\mathcal{O}(n^k)$
, where n is the maximum number of states of the input DFAs. Hence,
![]() $\textsf{WNL}$
is included in
$\textsf{WNL}$
is included in
![]() $\textsf{XP}$
.
$\textsf{XP}$
.
Recall that membership of Bounded DFA-Intersection (parameterized by the number of automata) in
![]() $\textsf{WNL}$
follows by guessing an input word letter-by-letter, keeping track of the DFAs by writing their k current states, plus a counter for the number of steps, on the tape of the Turing machine M. We can do so by using as many letters as there are states in the automata, plus q (which is given in unary). Alternatively, when counting the number of bits needed to write down the tape contents using the alphabet
$\textsf{WNL}$
follows by guessing an input word letter-by-letter, keeping track of the DFAs by writing their k current states, plus a counter for the number of steps, on the tape of the Turing machine M. We can do so by using as many letters as there are states in the automata, plus q (which is given in unary). Alternatively, when counting the number of bits needed to write down the tape contents using the alphabet
![]() $\{0,1\}$
, this amounts in
$\{0,1\}$
, this amounts in
![]() $\mathcal{O}(k\log\!(n))$
many bits, if n upper bounds the size (number of bits) of (an encoding) of a Bounded DFA-Intersection instance. Assuming that M has s many states, then there are obviously no more than
$\mathcal{O}(k\log\!(n))$
many bits, if n upper bounds the size (number of bits) of (an encoding) of a Bounded DFA-Intersection instance. Assuming that M has s many states, then there are obviously no more than
![]() $s\cdot 2^{\mathcal{O}(k\log n)}$
many configurations of M. With the help of an additional counter, using
$s\cdot 2^{\mathcal{O}(k\log n)}$
many configurations of M. With the help of an additional counter, using
![]() $\log\!(s\cdot 2^{\mathcal{O}(k\log n)})=\log\!(s)+\mathcal{O}(k\log n)$
many additional bits, we can ensure that such a nondeterministic Turing machine M’ (simulating M) would need no more time than
$\log\!(s\cdot 2^{\mathcal{O}(k\log n)})=\log\!(s)+\mathcal{O}(k\log n)$
many additional bits, we can ensure that such a nondeterministic Turing machine M’ (simulating M) would need no more time than
![]() $s\cdot 2^{\mathcal{O}(k\log n)}$
when moving through the configuration graph, avoiding visiting configurations twice. This proves the claimed membership in
$s\cdot 2^{\mathcal{O}(k\log n)}$
when moving through the configuration graph, avoiding visiting configurations twice. This proves the claimed membership in
![]() $\textsf{para-}\textsf{NP}$
. Hence,
$\textsf{para-}\textsf{NP}$
. Hence,
![]() $\textsf{WNL}$
is included in
$\textsf{WNL}$
is included in
![]() $\textsf{para-}\textsf{NP}$
.
$\textsf{para-}\textsf{NP}$
.
As a final remark concerning this detour to parameterized complexity, observe that
![]() $\textsf{WNL}$
is also closely linked to the class
$\textsf{WNL}$
is also closely linked to the class
![]() $\textsf{N}[f\, \textrm{poly},f\, \textrm{log}]$
of parameterized problems that can be solved nondeterministically (at the same time) obeying some time bound
$\textsf{N}[f\, \textrm{poly},f\, \textrm{log}]$
of parameterized problems that can be solved nondeterministically (at the same time) obeying some time bound
![]() $f(k)\cdot n^{c}$
for some constant c and some space bound
$f(k)\cdot n^{c}$
for some constant c and some space bound
![]() $f(k)\cdot \log\!(n)$
, where f is some (computable) function, k is the parameter (value), and n gives the instance size, as discussed in Elberfeld et al. (Reference Elberfeld, Stockhusen and Tantau2015). Our reasoning also shows that Bounded DFA-Intersection (parameterized by the number of automata) lies in
$f(k)\cdot \log\!(n)$
, where f is some (computable) function, k is the parameter (value), and n gives the instance size, as discussed in Elberfeld et al. (Reference Elberfeld, Stockhusen and Tantau2015). Our reasoning also shows that Bounded DFA-Intersection (parameterized by the number of automata) lies in
![]() $\textsf{N}[f\, \textrm{poly},f\, \textrm{log}]$
. Hence,
$\textsf{N}[f\, \textrm{poly},f\, \textrm{log}]$
. Hence,
![]() $\textsf{WNL}$
can be seen as the closure of
$\textsf{WNL}$
can be seen as the closure of
![]() $\textsf{N}[f\, \textrm{poly},f\, \textrm{log}]$
under parameterized reductions. So, although one can argue that
$\textsf{N}[f\, \textrm{poly},f\, \textrm{log}]$
under parameterized reductions. So, although one can argue that
![]() $\textsf{N}[f\, \textrm{poly},f\, \textrm{log}]$
(and also some other classes introduced by Elberfeld et al. Reference Elberfeld, Stockhusen and Tantau2015) is a better model of parameterized space complexity,
$\textsf{N}[f\, \textrm{poly},f\, \textrm{log}]$
(and also some other classes introduced by Elberfeld et al. Reference Elberfeld, Stockhusen and Tantau2015) is a better model of parameterized space complexity,
![]() $\textsf{WNL}$
fits better into the landscape of the
$\textsf{WNL}$
fits better into the landscape of the
![]() $\textsf{W}$
-hierarchy also depicted in Figure 1, being closed under parameterized reductions by its definition. Recall that parameterized reductions speak about time bounds and are hence not that well related to space complexities. Therefore, Elberfeld, Stockhusen, and Tantau considered other types of reductions in Elberfeld et al. (Reference Elberfeld, Stockhusen and Tantau2015).
$\textsf{W}$
-hierarchy also depicted in Figure 1, being closed under parameterized reductions by its definition. Recall that parameterized reductions speak about time bounds and are hence not that well related to space complexities. Therefore, Elberfeld, Stockhusen, and Tantau considered other types of reductions in Elberfeld et al. (Reference Elberfeld, Stockhusen and Tantau2015).
Because
![]() $\textsf{WNL}$
is a less known class that is still quite central to our current discussion, let us mention a variation of DFA-SW in the following. For a subset of states
$\textsf{WNL}$
is a less known class that is still quite central to our current discussion, let us mention a variation of DFA-SW in the following. For a subset of states
![]() $P\subseteq Q$
of a DFA
$P\subseteq Q$
of a DFA
![]() $A=(Q,\Sigma,\delta,q_0,F)$
, we say that
$A=(Q,\Sigma,\delta,q_0,F)$
, we say that
![]() $w\in\Sigma^*$
is P-synchronizing if, for all
$w\in\Sigma^*$
is P-synchronizing if, for all
![]() $p\in P$
,
$p\in P$
,
![]() $\delta^*(p,w)=s$
for some
$\delta^*(p,w)=s$
for some
![]() $s\in Q$
. In other words, a word is synchronizing for A if it is Q-synchronizing.
$s\in Q$
. In other words, a word is synchronizing for A if it is Q-synchronizing.

Notice that if m is given in binary and the restriction
![]() $|P|=k$
is missing, then this problem is even
$|P|=k$
is missing, then this problem is even
![]() $\textsf{PSPACE}$
-complete, because subset synchronization in itself (without the length bound) is already
$\textsf{PSPACE}$
-complete, because subset synchronization in itself (without the length bound) is already
![]() $\textsf{PSPACE}$
-complete; see Fernau et al. (Reference Fernau, Gusev, Hoffmann, Holzer, Volkov and Wolf2019) and Rystsov (Reference Rystsov1983) for more discussions. However, if m is presented in unary, as implicit in the problem definition, because the input DFA comes with a list of its states and this list contains more elements than k, then the problem is “only”
$\textsf{PSPACE}$
-complete; see Fernau et al. (Reference Fernau, Gusev, Hoffmann, Holzer, Volkov and Wolf2019) and Rystsov (Reference Rystsov1983) for more discussions. However, if m is presented in unary, as implicit in the problem definition, because the input DFA comes with a list of its states and this list contains more elements than k, then the problem is “only”
![]() $\textsf{NP}$
-complete, as it also follows from Montoya and Nolasco (Reference Montoya and Nolasco2018), but this also follows when considering
$\textsf{NP}$
-complete, as it also follows from Montoya and Nolasco (Reference Montoya and Nolasco2018), but this also follows when considering
![]() $P=Q$
. However, Montoya and Nolasco focused on the parameterized complexity of DFA-SW-from-Subset-sb and could prove the following result.
$P=Q$
. However, Montoya and Nolasco focused on the parameterized complexity of DFA-SW-from-Subset-sb and could prove the following result.
Theorem 2.
DFA-SW-from-Subset-sb, parameterized with the set size parameter k, is complete for the class
![]() $\textsf{WNL}$
, even when restricted to planar automata graph instances.
$\textsf{WNL}$
, even when restricted to planar automata graph instances.
4. Finding a Home for DFA-SW
As mentioned above, DFA-SW is known to be
![]() $\textsf{W}[2]$
-hard. However, no complexity class was hitherto suggested to which DFA-SW belongs. In this section, we will describe three different memberships.
$\textsf{W}[2]$
-hard. However, no complexity class was hitherto suggested to which DFA-SW belongs. In this section, we will describe three different memberships.
Theorem 3.
DFA-SW, parameterized with the length parameter k, is contained in the class
![]() $\textsf{WNL}$
.
$\textsf{WNL}$
.
Notice that membership in
![]() $\textsf{WNL}$
does not follow with the arguments presented by Montoya and Nolasco (Reference Montoya and Nolasco2018) for a different parameterization of the related problem DFA-Subset-sbSW, because that argument makes explicit use of the fact that the given set P of states contains k elements.
$\textsf{WNL}$
does not follow with the arguments presented by Montoya and Nolasco (Reference Montoya and Nolasco2018) for a different parameterization of the related problem DFA-Subset-sbSW, because that argument makes explicit use of the fact that the given set P of states contains k elements.
Proof. We now describe a nondeterministic Turing machine that visits at most f(k) many cells (ever), providing the required reduction. Given a DFA A with state set Q and input alphabet
![]() $\Sigma$
, where, w.l.o.g.,
$\Sigma$
, where, w.l.o.g.,
![]() $Q\cap\Sigma=\emptyset$
, together with a bound k on the length of a synchronizing word, a Turing machine M is constructed that works as follows:
$Q\cap\Sigma=\emptyset$
, together with a bound k on the length of a synchronizing word, a Turing machine M is constructed that works as follows:
-
(1). M writes a word of length at most k over the alphabet
 $\Sigma$
on its tape, followed by some letter from the alphabet Q; this means that M starts with making (at most)
$\Sigma$
on its tape, followed by some letter from the alphabet Q; this means that M starts with making (at most)
 $k+1$
nondeterministic guesses.
$k+1$
nondeterministic guesses. -
(2). For each
 $q\in Q$
(this information can be hard-coded in the finite-state memory of M), M first moves its head to the left end of its tape and then starts reading the tape content from left to right. Each time a symbol
$q\in Q$
(this information can be hard-coded in the finite-state memory of M), M first moves its head to the left end of its tape and then starts reading the tape content from left to right. Each time a symbol
 $a\in\Sigma$
is read, M updates the current state it stores according to the transition function of A. Finally, M will read a symbol from Q, and it will only continue working if this symbol equals the current state stored in the finite memory of M. Notice that (2) works deterministically.
$a\in\Sigma$
is read, M updates the current state it stores according to the transition function of A. Finally, M will read a symbol from Q, and it will only continue working if this symbol equals the current state stored in the finite memory of M. Notice that (2) works deterministically. -
(3). Only if M has completely processed the loop described in (2) (without abort), M will accept. This verifies that the guessed word over
 $\Sigma$
is indeed synchronizing, always leading into the state that was also previously guessed. Hence, M will accept the empty word if and only if there is a possibility to guess a synchronizing word of length at most k. It is also clear that the Turing machine makes at most
$\Sigma$
is indeed synchronizing, always leading into the state that was also previously guessed. Hence, M will accept the empty word if and only if there is a possibility to guess a synchronizing word of length at most k. It is also clear that the Turing machine makes at most
 $(|Q|+1)(2k+1)$
many steps.
Footnote 3
$(|Q|+1)(2k+1)$
many steps.
Footnote 3
Unfortunately, we do not know if our problem is
![]() $\textsf{WNL}$
-hard. Let us also remark that our reasoning in the previous result also proves that DFA-SW, parameterized with the length parameter k, is contained in
$\textsf{WNL}$
-hard. Let us also remark that our reasoning in the previous result also proves that DFA-SW, parameterized with the length parameter k, is contained in
![]() $\textsf{N}[f\, \textrm{poly},f\, \textrm{log}]$
, a class introduced in Elberfeld et al. (Reference Elberfeld, Stockhusen and Tantau2015) and also discussed above. We could also re-interpret the arguments of the previous proof to show that DFA-SW belongs to
$\textsf{N}[f\, \textrm{poly},f\, \textrm{log}]$
, a class introduced in Elberfeld et al. (Reference Elberfeld, Stockhusen and Tantau2015) and also discussed above. We could also re-interpret the arguments of the previous proof to show that DFA-SW belongs to
![]() $\textsf{W}[\textsf{P}]$
, based on the Turing machine characterization of
$\textsf{W}[\textsf{P}]$
, based on the Turing machine characterization of
![]() $\textsf{W}[\textsf{P}]$
.
$\textsf{W}[\textsf{P}]$
.
We failed when trying to put DFA-SW into
![]() $\textsf{W}[\textsf{SAT}]$
. In order to understand the difficulties, let us discuss a different strategy how to put DFA-SW into
$\textsf{W}[\textsf{SAT}]$
. In order to understand the difficulties, let us discuss a different strategy how to put DFA-SW into
![]() $\textsf{W}[\textsf{P}]$
. Recall the following relationships:
$\textsf{W}[\textsf{P}]$
. Recall the following relationships:
![]() $\textsf{W}[\textsf{SAT}]$
is characterized (via parameterized reductions) by the following problem. Given an arbitrary Boolean formula
$\textsf{W}[\textsf{SAT}]$
is characterized (via parameterized reductions) by the following problem. Given an arbitrary Boolean formula
![]() $\varphi$
, with X being its set of variables, does there exist an assignment
$\varphi$
, with X being its set of variables, does there exist an assignment
![]() $\alpha:X\to\{0,1\}$
that satisfies
$\alpha:X\to\{0,1\}$
that satisfies
![]() $\varphi$
, such that at most k variables are set to true (i.e., to 1)? Here, k is the parameter, also called the weight of the assignment. Similarly,
$\varphi$
, such that at most k variables are set to true (i.e., to 1)? Here, k is the parameter, also called the weight of the assignment. Similarly,
![]() $\textsf{W}[\textsf{P}]$
is characterized by the following problem. Given a Boolean circuit C, with X being its set of Boolean input variables, does there exist an assignment
$\textsf{W}[\textsf{P}]$
is characterized by the following problem. Given a Boolean circuit C, with X being its set of Boolean input variables, does there exist an assignment
![]() $\alpha:X\to\{0,1\}$
of weight at most k that satisfies C? Apart from the fact that circuits (graph-theoretically speaking, directed acyclic graphs) can represent Boolean functions more succinctly than formulas, another difference comes from the (related) fact that circuits can contain implicit variables (associated to inner logical gates) that might have to be made explicit in Boolean formulas, which means in particular that the weight of an assignment can change when moving from a Boolean circuit to an equivalent Boolean formula. This is the reason why we can prove in the following that DFA-SW, parameterized with the length parameter k, is contained in
$\alpha:X\to\{0,1\}$
of weight at most k that satisfies C? Apart from the fact that circuits (graph-theoretically speaking, directed acyclic graphs) can represent Boolean functions more succinctly than formulas, another difference comes from the (related) fact that circuits can contain implicit variables (associated to inner logical gates) that might have to be made explicit in Boolean formulas, which means in particular that the weight of an assignment can change when moving from a Boolean circuit to an equivalent Boolean formula. This is the reason why we can prove in the following that DFA-SW, parameterized with the length parameter k, is contained in
![]() $\textsf{W}[\textsf{P}]$
, but we do not know if we can adapt this proof toward showing membership in
$\textsf{W}[\textsf{P}]$
, but we do not know if we can adapt this proof toward showing membership in
![]() $\textsf{W}[\textsf{SAT}]$
. As mentioned above, we cannot tell what the relations between
$\textsf{W}[\textsf{SAT}]$
. As mentioned above, we cannot tell what the relations between
![]() $\textsf{WNL}$
and
$\textsf{WNL}$
and
![]() $\textsf{W}[\textsf{SAT}]$
or
$\textsf{W}[\textsf{SAT}]$
or
![]() $\textsf{W}[\textsf{P}]$
are, but assuming that
$\textsf{W}[\textsf{P}]$
are, but assuming that
![]() $\textsf{WNL}\neq \textsf{W}[\textsf{P}]$
holds, the following construction also shows that DFA-SW, parameterized with the length parameter k, is neither
$\textsf{WNL}\neq \textsf{W}[\textsf{P}]$
holds, the following construction also shows that DFA-SW, parameterized with the length parameter k, is neither
![]() $\textsf{WNL}$
-hard nor
$\textsf{WNL}$
-hard nor
![]() $\textsf{W}[\textsf{P}]$
-hard.
$\textsf{W}[\textsf{P}]$
-hard.
Theorem 4.
DFA-SW, parameterized with the length parameter k, is contained in the class
![]() $\textsf{W}\mkern 2mu[\textsf{P}\mkern 2mu]$
.
$\textsf{W}\mkern 2mu[\textsf{P}\mkern 2mu]$
.
Proof. We only give a sketch of the construction of a Boolean circuit that allows an assignment of weight k that outputs true if and only if the given DFA
![]() $A=(Q,\Sigma,\delta,q_0,F)$
has a synchronizing word of length at most k.
$A=(Q,\Sigma,\delta,q_0,F)$
has a synchronizing word of length at most k.
We introduce an input gate
 $I_{a,i}$
for each
$I_{a,i}$
for each
 $a\in\Sigma$
and
$a\in\Sigma$
and
 $1\leq i\leq k$
. The meaning should be the following: Symbol a is at position i in the synchronizing word that is guessed via an assignment to these input gates. Hence, we check with a small auxiliary logical sub-circuit if (exactly) one of the inputs from
$1\leq i\leq k$
. The meaning should be the following: Symbol a is at position i in the synchronizing word that is guessed via an assignment to these input gates. Hence, we check with a small auxiliary logical sub-circuit if (exactly) one of the inputs from
 $\{I_{a,i}\mid a\in \Sigma\}$
is set to one. In the following description, let w denote the word of length k that is meant by a satisfying assignment.
$\{I_{a,i}\mid a\in \Sigma\}$
is set to one. In the following description, let w denote the word of length k that is meant by a satisfying assignment.Moreover, there are (internal) gates
 $S_{q,i,p}$
for
$S_{q,i,p}$
for
 $q,p\in Q$
and
$q,p\in Q$
and
 $0\leq i\leq k$
, meaning that each of these gates outputs true if A, when started to digest the input w within state q, will reach state p after i steps. In particular, we can initialize
$0\leq i\leq k$
, meaning that each of these gates outputs true if A, when started to digest the input w within state q, will reach state p after i steps. In particular, we can initialize
 $S_{q,0,p}$
to output one (true) if and only if
$S_{q,0,p}$
to output one (true) if and only if
 $q=p$
. For
$q=p$
. For
 $i>0$
, the gate
$i>0$
, the gate
 $S_{q,i,p}$
outputs true if and only if both
$S_{q,i,p}$
outputs true if and only if both
 $I_{a,i}$
and
$I_{a,i}$
and
 $S_{q,i-1,r}$
output true and
$S_{q,i-1,r}$
output true and
 $\delta(r,a)=p$
.
$\delta(r,a)=p$
.Finally, the output gate O collects the information of all gates
 $S_{q,k,p}$
; it outputs true if and only if there is one
$S_{q,k,p}$
; it outputs true if and only if there is one
 $p\in Q$
such that for all
$p\in Q$
such that for all
 $q\in Q$
,
$q\in Q$
,
 $S_{q,k,p}$
outputs true.
$S_{q,k,p}$
outputs true.
It should be clear that the circuit that we described can be constructed in polynomial time if k is given in unary (and in
![]() $\textsf{FPT}$
-time otherwise, which is good enough for our purpose).
$\textsf{FPT}$
-time otherwise, which is good enough for our purpose).
A reader who knows about the definition of the
![]() $\textsf{W}$
-hierarchy in terms of weft will also recognize that this construction does not prove membership within any fixed level of that hierarchy, because the number of so-called large gates on paths from input gates to the output gate grows with k.
$\textsf{W}$
-hierarchy in terms of weft will also recognize that this construction does not prove membership within any fixed level of that hierarchy, because the number of so-called large gates on paths from input gates to the output gate grows with k.
We are now going to prove membership in yet another parameterized complexity class, namely
![]() $\textsf{A}[2]$
. Besides the mentioned
$\textsf{A}[2]$
. Besides the mentioned
![]() $\textsf{W}$
-hierarchy, there is another hierarchy of hard parameterized problems, which is the
$\textsf{W}$
-hierarchy, there is another hierarchy of hard parameterized problems, which is the
![]() $\textsf{A}$
-hierarchy. The best explanation of this hierarchy can be found in the textbook of Flum and Grohe (Reference Flum and Grohe2006). It is known that
$\textsf{A}$
-hierarchy. The best explanation of this hierarchy can be found in the textbook of Flum and Grohe (Reference Flum and Grohe2006). It is known that
![]() $\textsf{W}[t]\subseteq\textsf{A}[t]$
for each level t of the hierarchies. In particular,
$\textsf{W}[t]\subseteq\textsf{A}[t]$
for each level t of the hierarchies. In particular,
![]() $\textsf{W}[1]=\textsf{A}[1]$
, but no other equality is known. Moreover, it is unknown if
$\textsf{W}[1]=\textsf{A}[1]$
, but no other equality is known. Moreover, it is unknown if
![]() $\textsf{A}[2]$
is a subset of
$\textsf{A}[2]$
is a subset of
![]() $\textsf{W}[\textsf{P}]$
, so that the following membership of DFA-SW, parameterized with the length parameter k, can be seen as an indication that our problem is not complete for
$\textsf{W}[\textsf{P}]$
, so that the following membership of DFA-SW, parameterized with the length parameter k, can be seen as an indication that our problem is not complete for
![]() $\textsf{A}[2]$
.
$\textsf{A}[2]$
.
ecall that also
![]() $\textsf{A}[2]$
possesses a characterization in terms of Turing machines. Now, we are facing an alternating single-tape Turing machine whose initial state is existential and that is allowed to switch only once into the set of universal states when trying to accept the empty word in at most k steps, where k is the parameter. By observing that the switch between phases (1) and (2) of the description of the Turing machine M in the proof of Theorem 3 can be also viewed as switching between existentially and universally quantified states, M can be also re-interpreted to show:
$\textsf{A}[2]$
possesses a characterization in terms of Turing machines. Now, we are facing an alternating single-tape Turing machine whose initial state is existential and that is allowed to switch only once into the set of universal states when trying to accept the empty word in at most k steps, where k is the parameter. By observing that the switch between phases (1) and (2) of the description of the Turing machine M in the proof of Theorem 3 can be also viewed as switching between existentially and universally quantified states, M can be also re-interpreted to show:
Theorem 5.
DFA-SW, parameterized with the length parameter k, is contained in the class
![]() $\textsf{A}[2]$
.
$\textsf{A}[2]$
.
The latter result also follows when combining the reductions of Lemmas 14 and 15 below, because parameterized reductions are transitive as a relation between parameterized problems.
Let us now state the position of
![]() $\textsf{W}[\textsf{Sync}]$
within the better known parameterized complexity classes more formally.
$\textsf{W}[\textsf{Sync}]$
within the better known parameterized complexity classes more formally.
Corollary 1.
![]() $\textsf{W}\mkern 2mu[2]\subseteq \textsf{W}\mkern 2mu[\textsf{Sync}]\subseteq\textsf{A}[2]\cap\textsf{WNL}\cap\textsf{W}\mkern 2mu[\textsf{P}]\mkern 2mu$
.
$\textsf{W}\mkern 2mu[2]\subseteq \textsf{W}\mkern 2mu[\textsf{Sync}]\subseteq\textsf{A}[2]\cap\textsf{WNL}\cap\textsf{W}\mkern 2mu[\textsf{P}]\mkern 2mu$
.
5. Further Problems Complete for
 $\textsf{W}[\textsf{Sync}]$
$\textsf{W}[\textsf{Sync}]$
In the following problem statements, k is always the parameter that we are analyzing with respect to parameterized complexity. In each case, we prove a completeness result for
![]() $\textsf{W}[\textsf{Sync}]$
.
$\textsf{W}[\textsf{Sync}]$
.
5.1 DFAs with a sink state
Our first example is an easy modification of our basic problem DFA-SW. Recall that a state s of a DFA is a sink state if for all input letters a, we have
![]() $\delta(s,a)=s$
. Observe that if a DFA A possesses a sink state s, then A is synchronizable if and only if s is reachable from each (other) state of A; moreover, s is then the unique possible synchronizing state.
$\delta(s,a)=s$
. Observe that if a DFA A possesses a sink state s, then A is synchronizable if and only if s is reachable from each (other) state of A; moreover, s is then the unique possible synchronizing state.

Lemma 2. There is a polynomial time computable parameterized reduction that produces, given some DFA A and some integer k as an instance of DFA-SW, an equivalent instance (A’,k’) of DFA-SW such that A’ possesses a sink state.
Proof. Consider the DFA
![]() $A=(Q,\Sigma,\delta,q_0,F)$
. Without loss of generality, assume
$A=(Q,\Sigma,\delta,q_0,F)$
. Without loss of generality, assume
![]() $\Sigma\cap Q=\emptyset$
and
$\Sigma\cap Q=\emptyset$
and
![]() $\sigma\notin \Sigma\cup Q$
. Let
$\sigma\notin \Sigma\cup Q$
. Let
![]() $\Sigma'=\Sigma\cup Q\cup\{\sigma\}$
be the input alphabet of the DFA A’ that we are going to construct. An example for this construction can be found below. Let
$\Sigma'=\Sigma\cup Q\cup\{\sigma\}$
be the input alphabet of the DFA A’ that we are going to construct. An example for this construction can be found below. Let
![]() $s_0,\dots,s_k,f\notin Q$
be fresh states. Let
$s_0,\dots,s_k,f\notin Q$
be fresh states. Let
![]() $Q'=Q\cup \{s_0,\dots,s_k,f\}$
be the states of A’. Define the transition function
$Q'=Q\cup \{s_0,\dots,s_k,f\}$
be the states of A’. Define the transition function
![]() $\delta'$
as described in Figure 2. This describes the interesting aspects of the automaton A’. We claim that, letting
$\delta'$
as described in Figure 2. This describes the interesting aspects of the automaton A’. We claim that, letting
![]() $k'=k+1$
, then A has a synchronizing word of length at most k if and only if A’ has a synchronizing word of length (at most and exactly) k’.
$k'=k+1$
, then A has a synchronizing word of length at most k if and only if A’ has a synchronizing word of length (at most and exactly) k’.

Figure 2. How to define a transition function
![]() $\delta'$
of a DFA with a sink state f.
$\delta'$
of a DFA with a sink state f.

Figure 3. Černý’s 4-state automaton from Černý (Reference Černý1964).
Let
![]() $w\in\Sigma^*$
be a synchronizing word, leading A into state
$w\in\Sigma^*$
be a synchronizing word, leading A into state
![]() $q_f\in Q$
, with
$q_f\in Q$
, with
![]() $|w|\leq k$
. Then, it is easy to observe that the word
$|w|\leq k$
. Then, it is easy to observe that the word
![]() $w'=\sigma^{k-|w|}wq_f$
leads A’ into the sink state f, wherever A’ starts. Hence, w’ is a synchronizing word of length k’ as claimed. Notice that due to the sequence of states
$w'=\sigma^{k-|w|}wq_f$
leads A’ into the sink state f, wherever A’ starts. Hence, w’ is a synchronizing word of length k’ as claimed. Notice that due to the sequence of states
![]() $s_0,\dots,s_k,f$
, there cannot be any shorter synchronizing word in A’.
$s_0,\dots,s_k,f$
, there cannot be any shorter synchronizing word in A’.
Conversely, let w’ be a synchronizing word of length at most k’ for A’. As f is a sink state, it must be the synchronizing state. Since in particular
![]() $\delta^{\prime *}(s_0,w')=f$
,
$\delta^{\prime *}(s_0,w')=f$
,
![]() $|w'|=k'=k+1$
, and for the same reason,
$|w'|=k'=k+1$
, and for the same reason,
![]() $w'=w''q$
for some
$w'=w''q$
for some
![]() $w''\in (\Sigma\cup\{\sigma\})^k$
and
$w''\in (\Sigma\cup\{\sigma\})^k$
and
![]() $q\in Q$
. Observe that the special letter
$q\in Q$
. Observe that the special letter
![]() $\sigma$
either loops (on
$\sigma$
either loops (on
![]() $Q\cup \{f\}$
) or advances as any other letter from
$Q\cup \{f\}$
) or advances as any other letter from
![]() $\Sigma$
(on
$\Sigma$
(on
![]() $Q'\setminus Q$
). Therefore, if w’ is synchronizing for A’, then so is
$Q'\setminus Q$
). Therefore, if w’ is synchronizing for A’, then so is
![]() $\sigma^{k-|w|}wq$
, where w is obtained from w” by deleting all occurrences of
$\sigma^{k-|w|}wq$
, where w is obtained from w” by deleting all occurrences of
![]() $\sigma$
, that is,
$\sigma$
, that is,
![]() $w\in\Sigma^*$
. As
$w\in\Sigma^*$
. As
![]() $\sigma$
acts as the identity on Q, and because the final letter q indicates that, upon starting in some state from Q, the automaton must have reached state q (as w’ is leading to the sink state f), we can see that w is indeed a synchronizing word for A; moreover,
$\sigma$
acts as the identity on Q, and because the final letter q indicates that, upon starting in some state from Q, the automaton must have reached state q (as w’ is leading to the sink state f), we can see that w is indeed a synchronizing word for A; moreover,
![]() $|w|\leq k$
. This proves the correctness of the transformation.
$|w|\leq k$
. This proves the correctness of the transformation.
We will give an example for this proof in the following. As an example automaton, we chose the famous 4-state DFA designed by Černý (drawn in Figure 3) to illustrate that shortest synchronizing words could be surprisingly long, in this case, of length nine. More precisely,
![]() $w=baaabaaab$
leads all four states to
$w=baaabaaab$
leads all four states to
![]() $q_1$
, so that
$q_1$
, so that
![]() $wq_1$
synchronizes the resulting automaton (in our construction) if
$wq_1$
synchronizes the resulting automaton (in our construction) if
![]() $k\leq 9$
. The resulting automaton can be found in Figure 4.
$k\leq 9$
. The resulting automaton can be found in Figure 4.

Figure 4. Černý’s 4-state automaton would yield this
![]() $(k+6)$
-state automaton in our construction from Lemma 2.
$(k+6)$
-state automaton in our construction from Lemma 2.
Remark 1. Let us mention one more formal language fact about synchronizing words: there is a synchronizing word of length exactly k for a DFA A if and only if there is a synchronizing word of length at most k for A. This comes from the fact that if w is a synchronizing word, then also wu is synchronizing for any word u. Therefore, we can also employ the problem variation asking about the existence of a synchronizing word of length exactly k if it is more convenient.
5.2 Synchronizing subsets
As mentioned above, the question if a given subset of states can be synchronized poses even a
![]() $\textsf{PSPACE}$
-complete problem. When enriched with a length bound on the length of a subset-synchronizing word, we are back to an NP-complete problem, assuming that the length bound is given in a unary encoding. Motivated by these considerations, we consider the following parameterized problem.
$\textsf{PSPACE}$
-complete problem. When enriched with a length bound on the length of a subset-synchronizing word, we are back to an NP-complete problem, assuming that the length bound is given in a unary encoding. Motivated by these considerations, we consider the following parameterized problem.

Recall that we previously discussed this problem with the parameter
![]() $|P|$
, calling it DFA-SW-from-Subset-sb for clarity.
$|P|$
, calling it DFA-SW-from-Subset-sb for clarity.
Theorem 6.
DFA-SW-from-Subset, parameterized by an upper bound k on the length of a subset-synchronizing word, is complete for
![]() $\textsf{W}\mkern 2mu[\textsf{Sync}]$
.
$\textsf{W}\mkern 2mu[\textsf{Sync}]$
.
Notice that our discussions from Remark 1 translate verbatim also to this problem variation.
Proof. As a Q-synchronizing word is just another name for a synchronizing word, it is clear that DFA-SW-from-subset is
![]() $\textsf{W}[\textsf{Sync}]$
-hard. We prove membership in
$\textsf{W}[\textsf{Sync}]$
-hard. We prove membership in
![]() $\textsf{W}[\textsf{Sync}]$
in the following.
$\textsf{W}[\textsf{Sync}]$
in the following.
Consider a DFA
![]() $A=(Q,\Sigma,\delta,q_0,F)$
, together with a state subset P and an integer k. We define a new DFA
$A=(Q,\Sigma,\delta,q_0,F)$
, together with a state subset P and an integer k. We define a new DFA
![]() $A'=(Q',\Sigma',\delta',q_0,F)$
and an integer
$A'=(Q',\Sigma',\delta',q_0,F)$
and an integer
![]() $k'=k+1$
such that A possesses a P-synchronizing word of length k if and only if A’ has a synchronizing word of length k’.
$k'=k+1$
such that A possesses a P-synchronizing word of length k if and only if A’ has a synchronizing word of length k’.
Let
![]() $\bar P=\{\bar p\mid p\in P\}$
consists of (barred) copies of the states in P and let
$\bar P=\{\bar p\mid p\in P\}$
consists of (barred) copies of the states in P and let
![]() $Q'=Q\cup \bar P$
. Let
$Q'=Q\cup \bar P$
. Let
![]() $c\notin\Sigma$
be a fresh letter. Let
$c\notin\Sigma$
be a fresh letter. Let
![]() $\Sigma'=\Sigma\cup\{c\}$
. The transition function
$\Sigma'=\Sigma\cup\{c\}$
. The transition function
![]() $\delta'$
equals
$\delta'$
equals
![]() $\delta$
when restricted to
$\delta$
when restricted to
![]() $Q\times \Sigma$
. Now, fix some
$Q\times \Sigma$
. Now, fix some
![]() $p_{\text{fix}}\in P$
. Furthermore, define
$p_{\text{fix}}\in P$
. Furthermore, define
![]() $\delta'(q,c)=p_{\text{fix}}$
for
$\delta'(q,c)=p_{\text{fix}}$
for
![]() $q\in Q\setminus P$
and
$q\in Q\setminus P$
and
![]() $\delta'(\bar p,c)=\delta'(p,c)=p$
as well as
$\delta'(\bar p,c)=\delta'(p,c)=p$
as well as
![]() $\delta'(\bar p,a)=\bar p$
for any
$\delta'(\bar p,a)=\bar p$
for any
![]() $p\in P$
and
$p\in P$
and
![]() $a\in\Sigma$
.
$a\in\Sigma$
.
Now, if w is a P-synchronizing word for A, then (by construction) cw is a synchronizing word for A’. Conversely, if v is a synchronizing word for A’, then it must contain at least one occurrence of c, because otherwise there is no way to synchronize the states from
![]() $\bar P$
, as by construction, the states in
$\bar P$
, as by construction, the states in
![]() $\bar P$
cannot be synchronizing states. Assuming that v is of minimum length, we can deduce that v contains exactly one occurrence of c and this occurrence is at the very beginning of c. Now, after reading c and starting out from Q’, the DFA A’ will be in any of the states of P, which means that if we write
$\bar P$
cannot be synchronizing states. Assuming that v is of minimum length, we can deduce that v contains exactly one occurrence of c and this occurrence is at the very beginning of c. Now, after reading c and starting out from Q’, the DFA A’ will be in any of the states of P, which means that if we write
![]() $v=cw$
, then w is a P-synchronizing word for A.
$v=cw$
, then w is a P-synchronizing word for A.
5.3 Factoring monoids
We now present a problem originally introduced by Cai et al. (Reference Cai, Chen, Downey and Fellows1997) in the context of parameterized complexity. As also discussed in Section 9, it is crucial that the monoid in question is implicitly given in this type of generator problem.

We can speak of k as (an upper bound on) the generation length of
![]() $f_0$
. This problem (without the generation length bound k) was introduced as GEN in the seminal work of Kozen (Reference Kozen1977) and proven to be PSPACE-complete; it appeared as MS5 under the quite fitting name Finite Function Generation in Garey and Johnson (Reference Garey and Johnson1979, p. 280). With the generation length bound, Monoid Factorization, restricted to collections of bijections (i.e., permutations), was proven to be NP-complete in Even and Goldreich (Reference Even and Goldreich1981); this restricted problem was termed Minimum Generator Sequence by Even and Goldreich. We will discuss further variations of Monoid Factorization concerning aspects of parameterized complexity in Section 9.
$f_0$
. This problem (without the generation length bound k) was introduced as GEN in the seminal work of Kozen (Reference Kozen1977) and proven to be PSPACE-complete; it appeared as MS5 under the quite fitting name Finite Function Generation in Garey and Johnson (Reference Garey and Johnson1979, p. 280). With the generation length bound, Monoid Factorization, restricted to collections of bijections (i.e., permutations), was proven to be NP-complete in Even and Goldreich (Reference Even and Goldreich1981); this restricted problem was termed Minimum Generator Sequence by Even and Goldreich. We will discuss further variations of Monoid Factorization concerning aspects of parameterized complexity in Section 9.
With some background knowledge on transition monoids, it is clear that by interpreting a given DFA
![]() $A=(Q,\Sigma,\delta,q_0,F)$
as a collection
$A=(Q,\Sigma,\delta,q_0,F)$
as a collection
![]() $F_A$
of
$F_A$
of
![]() $|\Sigma|$
many mappings
$|\Sigma|$
many mappings
![]() $f_a:Q\to Q$
, by setting
$f_a:Q\to Q$
, by setting
![]() $f_a(q)=\delta(q,a)$
, we can solve a DFA synchronization problem given by (A,k) by solving
$f_a(q)=\delta(q,a)$
, we can solve a DFA synchronization problem given by (A,k) by solving
![]() $|Q|$
many instances
$|Q|$
many instances
![]() $(F_q,k)$
of Monoid Factorization, where
$(F_q,k)$
of Monoid Factorization, where
![]() $F_q=\{f_0=q\}\cup F_A$
and the aim is to represent the constant target map
$F_q=\{f_0=q\}\cup F_A$
and the aim is to represent the constant target map
![]() $f_0=q$
. The synchronization problem (A,k) is a YES-instance if some of the instances
$f_0=q$
. The synchronization problem (A,k) is a YES-instance if some of the instances
![]() $(F_q,k)$
are YES-instances. This shows that DFA-SW, parameterized with the length upper bound k, can be solved by a Turing reduction to Monoid Factorization, parameterized with the generation length upper bound k. Below, we will strengthen this toward presenting a many-one reduction.
$(F_q,k)$
are YES-instances. This shows that DFA-SW, parameterized with the length upper bound k, can be solved by a Turing reduction to Monoid Factorization, parameterized with the generation length upper bound k. Below, we will strengthen this toward presenting a many-one reduction.
Having a closer look at the proof of
![]() $\textsf{W}[2]$
-hardness of DFA-SW, parameterized with the length upper bound k (also discussed below in more details), which was presented in Fernau et al. (Reference Fernau, Heggernes and Villanger2015), we see that the resulting automaton has one sink state, and hence, this is the only possible synchronizing state. This means that the Turing reduction suggested in the previous paragraph can be indeed viewed as a many-one (Karp) reduction, as the constant target function is uniquely defined. Hence, this reasoning shows that Monoid Factorization, parameterized with the generation length upper bound k, is indeed
$\textsf{W}[2]$
-hardness of DFA-SW, parameterized with the length upper bound k (also discussed below in more details), which was presented in Fernau et al. (Reference Fernau, Heggernes and Villanger2015), we see that the resulting automaton has one sink state, and hence, this is the only possible synchronizing state. This means that the Turing reduction suggested in the previous paragraph can be indeed viewed as a many-one (Karp) reduction, as the constant target function is uniquely defined. Hence, this reasoning shows that Monoid Factorization, parameterized with the generation length upper bound k, is indeed
![]() $\textsf{W}[2]$
-hard. This result has been shown already in Cai et al. (Reference Cai, Chen, Downey and Fellows1997) by a different reduction from Dominating Set.
$\textsf{W}[2]$
-hard. This result has been shown already in Cai et al. (Reference Cai, Chen, Downey and Fellows1997) by a different reduction from Dominating Set.
Lemma 3. There is a polynomial time computable parameterized many-one reduction from Monoid Factorization, parameterized with some generation length upper bound, to DFA-SW, parameterized with some length upper bound.
Proof. Let
![]() $F=\{f_0,f_1,\dots,f_m\}$
be a collection of mappings
$F=\{f_0,f_1,\dots,f_m\}$
be a collection of mappings
![]() $f_i:Q\to Q$
and
$f_i:Q\to Q$
and
![]() $k\in\mathbb{N}$
. Define
$k\in\mathbb{N}$
. Define
![]() $\hat Q=Q\times Q\cup \{s_0,\dots,s_k,s_{k+1},f\}$
. Let
$\hat Q=Q\times Q\cup \{s_0,\dots,s_k,s_{k+1},f\}$
. Let
![]() $\Sigma=\{a_1,\dots,a_m,\sigma,\tau\}$
and define the transition function
$\Sigma=\{a_1,\dots,a_m,\sigma,\tau\}$
and define the transition function
![]() $\delta:\hat Q\times \Sigma\to \hat Q$
as defined in Figure 5. This describes the interesting aspects of the automaton
$\delta:\hat Q\times \Sigma\to \hat Q$
as defined in Figure 5. This describes the interesting aspects of the automaton
![]() $A_F$
. An illustrative example will be discussed below. We claim that (F,k) is a YES-instance of Monoid Factorization if and only if
$A_F$
. An illustrative example will be discussed below. We claim that (F,k) is a YES-instance of Monoid Factorization if and only if
![]() $(A_F,k+2)$
is a YES-instance of DFA-SW. Namely, if (F,k) is a YES-instance of Monoid Factorization, then there exists a selection of at most k mappings
$(A_F,k+2)$
is a YES-instance of DFA-SW. Namely, if (F,k) is a YES-instance of Monoid Factorization, then there exists a selection of at most k mappings
![]() $f_{i_1},\dots,f_{i_{k'}}$
,
$f_{i_1},\dots,f_{i_{k'}}$
,
![]() $k'\leq k$
, with
$k'\leq k$
, with
![]() $i_j\in \{1,\dots,m\}$
for
$i_j\in \{1,\dots,m\}$
for
![]() $j=1,\dots, k'$
, such that
$j=1,\dots, k'$
, such that
![]() $f_0=f_{i_1}\circ f_{i_2}\circ \cdots \circ f_{i_{k'}}$
. Then,
$f_0=f_{i_1}\circ f_{i_2}\circ \cdots \circ f_{i_{k'}}$
. Then,
![]() $w=\sigma^{k-k'+1}a_{i_1}\cdot a_{i_2}\cdots a_{i_{k'}}\tau $
synchronizes the DFA
$w=\sigma^{k-k'+1}a_{i_1}\cdot a_{i_2}\cdots a_{i_{k'}}\tau $
synchronizes the DFA
![]() $A_F$
. Clearly, w begins with
$A_F$
. Clearly, w begins with
![]() $\sigma^{k-k'+1}$
. When started in some
$\sigma^{k-k'+1}$
. When started in some
![]() $(q_1,q_2)$
,
$(q_1,q_2)$
,
![]() $A_F$
will be in state
$A_F$
will be in state
![]() $(q_1,q_1)$
after digesting
$(q_1,q_1)$
after digesting
![]() $\sigma^{k-k'+1}$
. The word
$\sigma^{k-k'+1}$
. The word
![]() $a_{i_1}\cdot a_{i_2}\cdots a_{i_{k'}}$
will then drive
$a_{i_1}\cdot a_{i_2}\cdots a_{i_{k'}}$
will then drive
![]() $A_F$
into some state
$A_F$
into some state
![]() $(q_1,q_2')$
. Now, upon reading
$(q_1,q_2')$
. Now, upon reading
![]() $\tau$
,
$\tau$
,
![]() $A_F$
could only enter (the only) synchronizing state f if
$A_F$
could only enter (the only) synchronizing state f if
![]() $q_2'=f_0(q_1)$
was true. If
$q_2'=f_0(q_1)$
was true. If
![]() $A_F$
starts reading w in any of the states
$A_F$
starts reading w in any of the states
![]() $ \{s_0,\dots,s_k,s_{k+1},f\}$
, it is straightforward to check that
$ \{s_0,\dots,s_k,s_{k+1},f\}$
, it is straightforward to check that
![]() $A_F$
will be in state f thereafter.
$A_F$
will be in state f thereafter.

Figure 5. Transition function
![]() $\delta$
of the constructed
$\delta$
of the constructed
![]() $\textsf{DFA-SW}$
instance.
$\textsf{DFA-SW}$
instance.
Conversely, if w is any word of length at most
![]() $k+2$
that is synchronizing for
$k+2$
that is synchronizing for
![]() $A_F$
, then it must be of length exactly
$A_F$
, then it must be of length exactly
![]() $k+2$
, as this is the shortest path length from
$k+2$
, as this is the shortest path length from
![]() $s_0$
down to f, which is a sink state and must hence be the synchronizing state. This also enforces w to start with
$s_0$
down to f, which is a sink state and must hence be the synchronizing state. This also enforces w to start with
![]() $\sigma$
and to end with
$\sigma$
and to end with
![]() $\tau$
. Also, w cannot contain another occurrence of
$\tau$
. Also, w cannot contain another occurrence of
![]() $\tau$
, as this would lead to
$\tau$
, as this would lead to
![]() $s_0$
again (from any of the states
$s_0$
again (from any of the states
![]() $s_i$
) and thereby prevent w from entering f, because the states
$s_i$
) and thereby prevent w from entering f, because the states
![]() $s_i$
should be walked through one-by-one, hence counting up to
$s_i$
should be walked through one-by-one, hence counting up to
![]() $k+2$
. Let us study the longest suffix
$k+2$
. Let us study the longest suffix
![]() $v\tau$
of w that satisfies
$v\tau$
of w that satisfies
![]() $v\in \{a_1,\dots,a_m\}^*$
. By the structure of w that we analyzed before, we must have
$v\in \{a_1,\dots,a_m\}^*$
. By the structure of w that we analyzed before, we must have
![]() $w=u\sigma v\tau $
, for some possibly empty word u such that
$w=u\sigma v\tau $
, for some possibly empty word u such that
![]() $u\sigma$
starts with
$u\sigma$
starts with
![]() $\sigma$
. In particular,
$\sigma$
. In particular,
![]() $|v|\leq k$
, as
$|v|\leq k$
, as
![]() $|u|+|v|=k$
. Hence, after reading the symbol
$|u|+|v|=k$
. Hence, after reading the symbol
![]() $\sigma$
preceding v,
$\sigma$
preceding v,
![]() $A_F$
will be in one of the states (q,q) or
$A_F$
will be in one of the states (q,q) or
![]() $s_i$
(for some
$s_i$
(for some
![]() $|u|+1\leq i\leq k+1$
) or f. Now, digesting v leads us into one of the states
$|u|+1\leq i\leq k+1$
) or f. Now, digesting v leads us into one of the states
![]() $s_{k+1}$
or f or (q,p), with
$s_{k+1}$
or f or (q,p), with
![]() $p= (f_{i_1}\circ f_{i_2}\circ \cdots \circ f_{i_{k'}})(q)$
, from which we can enter f only (after reading
$p= (f_{i_1}\circ f_{i_2}\circ \cdots \circ f_{i_{k'}})(q)$
, from which we can enter f only (after reading
![]() $\tau$
) if
$\tau$
) if
![]() $f_0(q)=p$
. This shows that, if
$f_0(q)=p$
. This shows that, if
![]() $u=a_{i_1}\cdot a_{i_2}\cdots a_{i_{k'}}$
, then
$u=a_{i_1}\cdot a_{i_2}\cdots a_{i_{k'}}$
, then
![]() $f_0=f_{i_1}\circ f_{i_2}\circ \cdots \circ f_{i_{k'}}$
.
$f_0=f_{i_1}\circ f_{i_2}\circ \cdots \circ f_{i_{k'}}$
.
Let us give an illustrative example for the construction used above in Lemma 3. We are considering the following three mappings
![]() $f_i:Q\to Q$
, with
$f_i:Q\to Q$
, with
![]() $Q=\{1,2,3,4\}$
.
$Q=\{1,2,3,4\}$
.
 \begin{equation*}\begin{array}{c|cccc} f_i & 1 & 2 & 3 & 4\\\hline f_0 & 1 & 1 & 1 & 1\\ f_1 & 2 & 3 & 4 & 1\\ f_2 & 1 & 2 & 3 & 1\end{array}\end{equation*}
\begin{equation*}\begin{array}{c|cccc} f_i & 1 & 2 & 3 & 4\\\hline f_0 & 1 & 1 & 1 & 1\\ f_1 & 2 & 3 & 4 & 1\\ f_2 & 1 & 2 & 3 & 1\end{array}\end{equation*}
This describes, together with some integer
![]() $k\geq 0$
, our instance of Monoid Factorization. In the equivalent instance of DFA-SW, the mappings
$k\geq 0$
, our instance of Monoid Factorization. In the equivalent instance of DFA-SW, the mappings
![]() $f_1$
and
$f_1$
and
![]() $f_2$
are modeled as the action of letters, leading to a two-letter input alphabet, say,
$f_2$
are modeled as the action of letters, leading to a two-letter input alphabet, say,
![]() $\Sigma'=\{a,b\}$
, which is enriched by two more symbols,
$\Sigma'=\{a,b\}$
, which is enriched by two more symbols,
![]() $\sigma,\tau$
. In particular,
$\sigma,\tau$
. In particular,
![]() $\sigma$
and
$\sigma$
and
![]() $\tau$
together model the target mapping
$\tau$
together model the target mapping
![]() $f_0$
(which is constant in our case), so that this construction, which can be found in Figure 6, results in another DFA capable of simulating the mentioned 4-state DFA designed by Černý (depicted in Figure 3) by an automaton with a sink state, yielding a somewhat more complicated construction (to this end) than the aforementioned one from Lemma 2 (see Figure 4).
$f_0$
(which is constant in our case), so that this construction, which can be found in Figure 6, results in another DFA capable of simulating the mentioned 4-state DFA designed by Černý (depicted in Figure 3) by an automaton with a sink state, yielding a somewhat more complicated construction (to this end) than the aforementioned one from Lemma 2 (see Figure 4).

Figure 6. An example for our construction from Lemma 3. Notice the similarities of the mappings to the actions of letters in Černý automaton (Figure 3). For arcs without labeling, the following holds: Arcs carried out with a or b, respectively, in the Černý automaton (i.e., the mappings
![]() $f_1$
and
$f_1$
and
![]() $f_2$
, respectively) are solid or dashed, respectively. Arcs resulting from transitions with
$f_2$
, respectively) are solid or dashed, respectively. Arcs resulting from transitions with
![]() $\sigma$
or
$\sigma$
or
![]() $\tau$
, respectively, are dotted, or dotted and dashed, respectively. Note that the arcs labeled
$\tau$
, respectively, are dotted, or dotted and dashed, respectively. Note that the arcs labeled
![]() $\tau$
are omitted in all vertices (i,j) for the sake of readability. They would lead from (i,i) to f and from (i,j) to (i,1) when
$\tau$
are omitted in all vertices (i,j) for the sake of readability. They would lead from (i,i) to f and from (i,j) to (i,1) when
![]() $j \neq i$
.
$j \neq i$
.
Theorem 7.
DFA-SW-sink, parameterized by an upper bound k on the length of a synchronizing word, is complete for
![]() $\textsf{W}\mkern 2mu[\textsf{Sync}]$
.
$\textsf{W}\mkern 2mu[\textsf{Sync}]$
.
Proof. As each DFA-SW-sink is trivially an instance of DFA-SW, the previous lemma shows the result.
We like to mention that there is another algebraic problem studied in the literature that looks quite similar to Monoid Factorization and that we define next:

With the idea of transformation monoids in mind, it is rather straightforward to see that this problem can be viewed just as an algebraic reformulation of DFA-SW; this was also observed in Volkov (Reference Volkov2008). We therefore only state the consequence that is interesting for our context.
Corollary 4.
Bounded Transformation Rank(1), parameterized by an upper bound k on the generation length, is complete for
![]() $\textsf{W}\mkern 2mu[\textsf{Sync}]$
.
$\textsf{W}\mkern 2mu[\textsf{Sync}]$
.
Goralčík and Koubek (Reference Goralčík and Koubek1995) also considered the problem Bounded Transformation Rank(r) for any
![]() $r\geq 1$
.
Footnote 4
This means that the condition
$r\geq 1$
.
Footnote 4
This means that the condition
![]() $|f_0(Q)|=1$
is replaced by
$|f_0(Q)|=1$
is replaced by
![]() $|f_0(Q)|=r$
in the problem definition above. By adding further elements to Q on which the mappings all act as identities, one easily obtains the next result.
$|f_0(Q)|=r$
in the problem definition above. By adding further elements to Q on which the mappings all act as identities, one easily obtains the next result.
Corollary 5. For any
![]() $r\geq 1$
, Bounded Transformation Rank(r), parameterized by an upper bound k on the generation length, is hard for
$r\geq 1$
, Bounded Transformation Rank(r), parameterized by an upper bound k on the generation length, is hard for
![]() $\textsf{W}\mkern 2mu[\textsf{Sync}]$
.
$\textsf{W}\mkern 2mu[\textsf{Sync}]$
.
As r is part of the problem definition (and hence fixed), we can strengthen the previous two statements as follows:
Theorem 8. For any
![]() $r\geq 1$
, Bounded Transformation Rank(r), parameterized by an upper bound k on the generation length, is complete for
$r\geq 1$
, Bounded Transformation Rank(r), parameterized by an upper bound k on the generation length, is complete for
![]() $\textsf{W}\mkern 2mu[\textsf{Sync}]$
.
$\textsf{W}\mkern 2mu[\textsf{Sync}]$
.
Proof. We will show how to reduce Bounded Transformation Rank(r) to Bounded Transformation Rank(1), which completes the argument.
Given a set
![]() $Q=\{q_1,\dots,q_n\}$
, a collection
$Q=\{q_1,\dots,q_n\}$
, a collection
![]() $F=\{f_1,\dots,f_m\}$
of mappings
$F=\{f_1,\dots,f_m\}$
of mappings
![]() $f_i:Q\to Q$
and
$f_i:Q\to Q$
and
![]() $k\in\mathbb{N}$
as an instance of Bounded Transformation Rank(r), we construct an instance
$k\in\mathbb{N}$
as an instance of Bounded Transformation Rank(r), we construct an instance
![]() $(\hat Q,\hat F,\hat k)$
of Bounded Transformation Rank(1) as follows. Let
$(\hat Q,\hat F,\hat k)$
of Bounded Transformation Rank(1) as follows. Let
![]() $\hat Q=Q\cup \{s\}\cup [k]\cup\{c_1,\dots,c_r\}$
, with pairwise disjoint unions, and
$\hat Q=Q\cup \{s\}\cup [k]\cup\{c_1,\dots,c_r\}$
, with pairwise disjoint unions, and
![]() $[k]=\{1,\dots,k\}$
. We interpret
$[k]=\{1,\dots,k\}$
. We interpret
![]() $f_i$
as acting on
$f_i$
as acting on
![]() $\hat Q$
by setting
$\hat Q$
by setting
![]() $f_i(s)=s$
,
$f_i(s)=s$
,
![]() $f_i(k)=c_1$
and
$f_i(k)=c_1$
and
![]() $f_i(j)=j+1$
for
$f_i(j)=j+1$
for
![]() $j\in [k-1]$
, as well as
$j\in [k-1]$
, as well as
![]() $f_i(x)=1$
if
$f_i(x)=1$
if
![]() $x\in \{c_1,\dots,c_r\}$
. We are now defining a collection
$x\in \{c_1,\dots,c_r\}$
. We are now defining a collection
![]() $\hat F$
of mappings from
$\hat F$
of mappings from
![]() $\hat Q$
to
$\hat Q$
to
![]() $\hat Q$
that contains F in this sense. We add
$\hat Q$
that contains F in this sense. We add
![]() $r\cdot \mathcal{O}(|Q|^r)$
many mappings
$r\cdot \mathcal{O}(|Q|^r)$
many mappings
![]() $g_{A,j}:\hat Q\to \hat Q$
into
$g_{A,j}:\hat Q\to \hat Q$
into
![]() $\hat F$
. Here,
$\hat F$
. Here,
![]() $A\subseteq Q$
,
$A\subseteq Q$
,
![]() $|A|=r$
,
$|A|=r$
,
![]() $j\in[r]=\{1,\dots,r\}$
. More precisely,
$j\in[r]=\{1,\dots,r\}$
. More precisely,
![]() $A=\{q_{\ell_1},\dots,q_{\ell_r}\}$
with
$A=\{q_{\ell_1},\dots,q_{\ell_r}\}$
with
![]() $\ell_j<\ell_{j+1}$
for
$\ell_j<\ell_{j+1}$
for
![]() $j\in [r-1]$
. For
$j\in [r-1]$
. For
![]() $j\in [r-1]$
, let
$j\in [r-1]$
, let
![]() $g_{A,j}(q_{\ell_j})=g_{A,j}(c_{j})=c_{j+1}$
, but
$g_{A,j}(q_{\ell_j})=g_{A,j}(c_{j})=c_{j+1}$
, but
![]() $g_{A,j}(c_{i})=c_1$
for
$g_{A,j}(c_{i})=c_1$
for
![]() $i\in [r]\setminus \{j\}$
. The case
$i\in [r]\setminus \{j\}$
. The case
![]() $j=r$
is covered by
$j=r$
is covered by
![]() $g_{A,r}(q_{\ell_r})=g_{A,r}(c_{r})=s$
. Moreover,
$g_{A,r}(q_{\ell_r})=g_{A,r}(c_{r})=s$
. Moreover,
![]() $g_{A,j}(x)=g_{A,j}(i)=1$
for any
$g_{A,j}(x)=g_{A,j}(i)=1$
for any
![]() $j\in [r]$
,
$j\in [r]$
,
![]() $i\in [k]$
,
$i\in [k]$
,
![]() $x\in Q\setminus A$
. In all other cases,
$x\in Q\setminus A$
. In all other cases,
![]() $g_{A,j}(x)=x$
. Furthermore, we add
$g_{A,j}(x)=x$
. Furthermore, we add
![]() $k-1$
increment mappings
$k-1$
increment mappings
![]() $\iota_j$
with
$\iota_j$
with
![]() $\iota_j(j)=j+1$
if
$\iota_j(j)=j+1$
if
![]() $j\in [k-1]$
that act as the identity on all other elements of
$j\in [k-1]$
that act as the identity on all other elements of
![]() $\hat Q$
. Finally, let
$\hat Q$
. Finally, let
![]() $\hat k=k+r$
to complete our description of
$\hat k=k+r$
to complete our description of
![]() $(\hat Q, \hat F, \hat k)$
constructed from (Q,F,k). Observe that the transformation is polynomial, because r is a constant. In particular,
$(\hat Q, \hat F, \hat k)$
constructed from (Q,F,k). Observe that the transformation is polynomial, because r is a constant. In particular,
If
![]() $f_{i_1},\dots,f_{i_{k'}}$
,
$f_{i_1},\dots,f_{i_{k'}}$
,
![]() $k'\leq k$
, exist with
$k'\leq k$
, exist with
![]() $i_j\in \{1,\dots,m\}$
for
$i_j\in \{1,\dots,m\}$
for
![]() $j=1,\dots, k'$
, such that
$j=1,\dots, k'$
, such that
![]() $f_0:=f_{i_1}\circ \cdots \circ f_{i_{k'}}$
satisfies
$f_0:=f_{i_1}\circ \cdots \circ f_{i_{k'}}$
satisfies
![]() $|f_0(Q)|=r$
, then there is some set
$|f_0(Q)|=r$
, then there is some set
![]() $A\subseteq Q$
,
$A\subseteq Q$
,
![]() $|A|=r$
, such that
$|A|=r$
, such that
![]() $f_0(Q)=A$
. Let
$f_0(Q)=A$
. Let
![]() $A=\{q_{\ell_1},\dots,q_{\ell_r}\}$
with
$A=\{q_{\ell_1},\dots,q_{\ell_r}\}$
with
![]() $\ell_j<\ell_{j+1}$
for
$\ell_j<\ell_{j+1}$
for
![]() $j\in [r-1]$
. Let
$j\in [r-1]$
. Let
![]() $k_\delta=k-k'$
. Composing first
$k_\delta=k-k'$
. Composing first
![]() $\iota_1\circ \cdots\circ \iota_{k_\delta}$
with
$\iota_1\circ \cdots\circ \iota_{k_\delta}$
with
![]() $f_0$
and then with
$f_0$
and then with
![]() $g_{A,1},\dots,g_{A,r}$
gives a mapping
$g_{A,1},\dots,g_{A,r}$
gives a mapping
![]() $\hat f_0$
with
$\hat f_0$
with
![]() $\hat f_0(\hat Q)=\{s\}$
. As described,
$\hat f_0(\hat Q)=\{s\}$
. As described,
![]() $\hat f_0$
can be expressed by composing
$\hat f_0$
can be expressed by composing
![]() $k+r=\hat k$
many mappings from
$k+r=\hat k$
many mappings from
![]() $\hat F$
. If
$\hat F$
. If
![]() $h_{1},\dots,h_{{k'}}$
,
$h_{1},\dots,h_{{k'}}$
,
![]() $k'\leq \hat k$
, exist with
$k'\leq \hat k$
, exist with
![]() $h_{j}\in \hat F$
for
$h_{j}\in \hat F$
for
![]() $j=1,\dots, k'$
, such that
$j=1,\dots, k'$
, such that
![]() $h_0:=h_{1}\circ h_{2}\circ \cdots \circ h_{{k'}}$
satisfies
$h_0:=h_{1}\circ h_{2}\circ \cdots \circ h_{{k'}}$
satisfies
![]() $|h_0(\hat Q)|=1$
, then by the structure of the mappings in
$|h_0(\hat Q)|=1$
, then by the structure of the mappings in
![]() $\hat F$
,
$\hat F$
,
![]() $h_0(\hat Q)=\{s\}$
. Moreover, as executing mappings from F after executing some
$h_0(\hat Q)=\{s\}$
. Moreover, as executing mappings from F after executing some
![]() $g_{A,j}$
has no further effects but possibly deferring the overall procedure, we can assume that this is not case here. Assuming that the mapping composition yields
$g_{A,j}$
has no further effects but possibly deferring the overall procedure, we can assume that this is not case here. Assuming that the mapping composition yields
![]() $h_0$
, it is clear that the last mapping executed equals some
$h_0$
, it is clear that the last mapping executed equals some
![]() $g_{A,r}$
. As in particular
$g_{A,r}$
. As in particular
![]() $h_0(1)=s$
, at least k other mappings must be from F or some increment mappings
$h_0(1)=s$
, at least k other mappings must be from F or some increment mappings
![]() $\iota_j$
. As
$\iota_j$
. As
![]() $h_0(c_1)=s$
, we must have used one mapping from
$h_0(c_1)=s$
, we must have used one mapping from
![]() $\{g_{A,j}\mid A\subseteq Q\}$
for each
$\{g_{A,j}\mid A\subseteq Q\}$
for each
![]() $j\in[r]$
. Due to the length bound
$j\in[r]$
. Due to the length bound
![]() $\hat k=k+r$
that is exactly met due to counting through
$\hat k=k+r$
that is exactly met due to counting through
![]() $1,\dots,k$
and through
$1,\dots,k$
and through
![]() $c_1,\dots,c_r$
, it is clear that the maps from
$c_1,\dots,c_r$
, it is clear that the maps from
![]() $\{g_{A,j}\mid A\subseteq Q\}$
were selected in order, starting with
$\{g_{A,j}\mid A\subseteq Q\}$
were selected in order, starting with
![]() $g_{A_1,1}$
, through
$g_{A_1,1}$
, through
![]() $g_{A_r,r}$
. Moreover, as “wrong selections” are sent to 1 (which is unaffordable by the length bound
$g_{A_r,r}$
. Moreover, as “wrong selections” are sent to 1 (which is unaffordable by the length bound
![]() $\hat k$
),
$\hat k$
),
![]() $A_1\setminus \{q_{\ell_1}\}\subseteq A_2$
, with
$A_1\setminus \{q_{\ell_1}\}\subseteq A_2$
, with
![]() $q_{\ell_1}$
being the first element of
$q_{\ell_1}$
being the first element of
![]() $A_1$
,
$A_1$
,
![]() $A_2\setminus \{q_{\ell_2}\}\subseteq A_3$
, with
$A_2\setminus \{q_{\ell_2}\}\subseteq A_3$
, with
![]() $q_{\ell_2}$
being the second element of
$q_{\ell_2}$
being the second element of
![]() $A_2$
, etc. means that finally a set
$A_2$
, etc. means that finally a set
![]() $A=\{q_{\ell_1},q_{\ell_2},\dots\}$
is selected with
$A=\{q_{\ell_1},q_{\ell_2},\dots\}$
is selected with
![]() $|A|=r$
, a set with which we could have started alternatively. Therefore, we can assume
$|A|=r$
, a set with which we could have started alternatively. Therefore, we can assume
![]() $A=A_1=A_2=\cdots=A_r$
. Hence, we can assume that
$A=A_1=A_2=\cdots=A_r$
. Hence, we can assume that
![]() $h_0$
is composed as
$h_0$
is composed as
![]() $h_0=f\circ g$
, where
$h_0=f\circ g$
, where
![]() $f=h_1\circ\cdots\circ h_k$
, such that
$f=h_1\circ\cdots\circ h_k$
, such that
![]() $h_1,\dots, h_{k_\delta}$
are increments,
$h_1,\dots, h_{k_\delta}$
are increments,
![]() $h_{k_\delta+1},\dots,h_k\in F$
and
$h_{k_\delta+1},\dots,h_k\in F$
and
![]() $g=h_{k+1}\circ \cdots \circ h_{ k+r}$
with
$g=h_{k+1}\circ \cdots \circ h_{ k+r}$
with
![]() $h_{k+j}=g_{A,j}$
for some
$h_{k+j}=g_{A,j}$
for some
![]() $A\subseteq Q$
. Now, leaving out all mappings
$A\subseteq Q$
. Now, leaving out all mappings
![]() $g_{A,j}$
and all possibly contained increment mappings, we are left with a sequence of
$g_{A,j}$
and all possibly contained increment mappings, we are left with a sequence of
![]() $k'\leq k$
many mappings from F that can be re-interpreted as acting on Q. As their composition
$k'\leq k$
many mappings from F that can be re-interpreted as acting on Q. As their composition
![]() $f_0$
, applied to Q, equals A, with
$f_0$
, applied to Q, equals A, with
![]() $|A|=r$
, the reverse implication is shown.
$|A|=r$
, the reverse implication is shown.
Finally, notice that due to the tight connections to automata theory, the previous proof can be also interpreted as a
![]() $\textsf{W}[\textsf{Sync}]$
-completeness result for the following family of problems Rank(r) DFA-Synchronizing Word (with
$\textsf{W}[\textsf{Sync}]$
-completeness result for the following family of problems Rank(r) DFA-Synchronizing Word (with
![]() $r\geq 1$
): Given a DFA
$r\geq 1$
): Given a DFA
![]() $A=(Q,\Sigma,\delta)$
and a number k, does there exist a word
$A=(Q,\Sigma,\delta)$
and a number k, does there exist a word
![]() $w\in\Sigma^{\leq k}$
such that
$w\in\Sigma^{\leq k}$
such that
![]() $|\delta(Q,w)|=r$
? This is also true for the problem variation where we ask whether
$|\delta(Q,w)|=r$
? This is also true for the problem variation where we ask whether
![]() $|\delta(Q,w)|\leq r$
instead. Looking back at the previous proof, this would mean that it is not that important to really count through all elements of up to r to ensure the exact cardinality of the chosen set; smaller sets would suffice.
$|\delta(Q,w)|\leq r$
instead. Looking back at the previous proof, this would mean that it is not that important to really count through all elements of up to r to ensure the exact cardinality of the chosen set; smaller sets would suffice.
5.4 Intersecting regular languages

Here, we took over the definition from Wareham (Reference Wareham2001), but as we can also see from the discussion in Remark 1, in our case it is not that important if we ask for a word exactly or at most k.
Theorem 9.
Bounded DFA-Intersection, parameterized by an upper bound on the length of the commonly accepted string, is complete for
![]() $\textsf{W}\mkern 2mu[\textsf{Sync}]$
.
$\textsf{W}\mkern 2mu[\textsf{Sync}]$
.
Previously, Wareham (Reference Wareham2001) only proved
![]() $\textsf{W}[2]$
-hardness for this parameterized problem.
$\textsf{W}[2]$
-hardness for this parameterized problem.
Proof. By Lemma 2, we need to consider only an instance
![]() $A=(Q,\Sigma,\delta,q_0,F)$
of DFA-SW with a sink state
$A=(Q,\Sigma,\delta,q_0,F)$
of DFA-SW with a sink state
![]() $s_f$
. Observe that A has a synchronizing word of length at most k if and only if A has a synchronizing word of length exactly k, because wu is a synchronizing word if w is. Define
$s_f$
. Observe that A has a synchronizing word of length at most k if and only if A has a synchronizing word of length exactly k, because wu is a synchronizing word if w is. Define
![]() $A_q=(Q,\Sigma,\delta,q,\{s_f\})$
and consider the DFA collection
$A_q=(Q,\Sigma,\delta,q,\{s_f\})$
and consider the DFA collection
![]() $\mathcal{A}=\{A_q\mid q\in Q\}$
. Observe that
$\mathcal{A}=\{A_q\mid q\in Q\}$
. Observe that
![]() $\bigcap_{q\in Q}L(A_q)$
contains some word
$\bigcap_{q\in Q}L(A_q)$
contains some word
![]() $w\in \Sigma^k$
if and only if A has a synchronizing word of length exactly k.
Footnote 5
$w\in \Sigma^k$
if and only if A has a synchronizing word of length exactly k.
Footnote 5
Conversely, if
![]() $\mathcal{A}=\{A_i\mid 1\leq i\leq \ell\}$
is a collection of DFAs
$\mathcal{A}=\{A_i\mid 1\leq i\leq \ell\}$
is a collection of DFAs
![]() $A_i=(Q_i,\Sigma,\delta_i,q_{0,i},F_i)$
, then construct an equivalent instance of DFA-SW as follows. First, assume that the state sets
$A_i=(Q_i,\Sigma,\delta_i,q_{0,i},F_i)$
, then construct an equivalent instance of DFA-SW as follows. First, assume that the state sets
![]() $Q_i$
are pairwise disjoint. Then, take two new letters a,b to form
$Q_i$
are pairwise disjoint. Then, take two new letters a,b to form
![]() $\Sigma'=\Sigma\cup\{\sigma,\tau\}$
. Let
$\Sigma'=\Sigma\cup\{\sigma,\tau\}$
. Let
![]() $Q'=\left(\bigcup_{i=1}^\ell Q_i\right)\cup \{s_0,\dots,s_k,s_{k+1},f\}$
be the state set of the DFA A that we construct. Define the transition function
$Q'=\left(\bigcup_{i=1}^\ell Q_i\right)\cup \{s_0,\dots,s_k,s_{k+1},f\}$
be the state set of the DFA A that we construct. Define the transition function
![]() $\delta$
as in Figure 7.
$\delta$
as in Figure 7.

Figure 7. Transition function
![]() $\delta$
of the constructed
$\delta$
of the constructed
![]() $\textsf{DFA-SW}$
instance.
$\textsf{DFA-SW}$
instance.
This describes the interesting aspects of the automaton A. We claim that, letting
![]() $k'=k+2$
, then
$k'=k+2$
, then
![]() $\bigcap_{i=1}^\ell L(A_i)$
contains some word
$\bigcap_{i=1}^\ell L(A_i)$
contains some word
![]() $w\in \Sigma^k$
if and only if A has a synchronizing word of length (at most and exactly) k’, namely
$w\in \Sigma^k$
if and only if A has a synchronizing word of length (at most and exactly) k’, namely
![]() $w'=\sigma w\tau$
. More precisely, similar to the construction from Lemma 3, the states
$w'=\sigma w\tau$
. More precisely, similar to the construction from Lemma 3, the states
![]() $s_i$
force to consider a word from
$s_i$
force to consider a word from
![]() $\{\sigma\}\Sigma^k\{\tau\}$
if there should be a synchronizing word of length k’ for A at all. One could move only from the part
$\{\sigma\}\Sigma^k\{\tau\}$
if there should be a synchronizing word of length k’ for A at all. One could move only from the part
![]() $A_i$
of A to f when reading
$A_i$
of A to f when reading
![]() $\tau$
, which also forces to have been in the set of final states
$\tau$
, which also forces to have been in the set of final states
![]() $F_i$
before. Digesting
$F_i$
before. Digesting
![]() $\sigma$
as the first letter lets
$\sigma$
as the first letter lets
![]() $A_i$
start in the initial state
$A_i$
start in the initial state
![]() $q_{0,i}$
.
$q_{0,i}$
.
We could also discuss the variant when we ask for a word of length at most k to be accepted by all automata in
![]() $\mathcal{A}$
. However, from the discussions of Remark 1, it immediately follows that also this variant is complete for
$\mathcal{A}$
. However, from the discussions of Remark 1, it immediately follows that also this variant is complete for
![]() $\textsf{W}[\textsf{Sync}]$
. Other variations show up when we switch to nondeterministic finite automata or to regular expressions for representing regular languages in these intersection problems. In these cases (and without defining the problems formally), we can only state the following observations.
$\textsf{W}[\textsf{Sync}]$
. Other variations show up when we switch to nondeterministic finite automata or to regular expressions for representing regular languages in these intersection problems. In these cases (and without defining the problems formally), we can only state the following observations.
Corollary 6.
Bounded NFA-Intersection, parameterized by an upper bound on the length of the commonly accepted string, is hard for
![]() $\textsf{W}\mkern 2mu[\textsf{Sync}]$
.
$\textsf{W}\mkern 2mu[\textsf{Sync}]$
.
Conversely, it would be interesting to discuss subregular language families for this type of problem, with the question in mind if we (still) obtain
![]() $\textsf{W}[\textsf{Sync}]$
-complete problems or not. Notice that (for instance) in the
$\textsf{W}[\textsf{Sync}]$
-complete problems or not. Notice that (for instance) in the
![]() $\textsf{W}[2]$
-hardness proof of Wareham (Reference Wareham2001, Lemma 6) concerning Bounded DFA-Intersection, only very simplistic automata have been used. This also means that the corresponding regular languages can be easily expressed by simple regular expressions, leading to the following result.
$\textsf{W}[2]$
-hardness proof of Wareham (Reference Wareham2001, Lemma 6) concerning Bounded DFA-Intersection, only very simplistic automata have been used. This also means that the corresponding regular languages can be easily expressed by simple regular expressions, leading to the following result.
Corollary 7.
Bounded Regular-Expression-Intersection, parameterized by the length of the commonly accepted string, is hard for
![]() $\textsf{W}\mkern 2mu[2]$
.
$\textsf{W}\mkern 2mu[2]$
.
The exact position of Bounded NFA-Intersection and of Bounded Regular-Expression-Intersection, in particular with respect to
![]() $\textsf{W}[\textsf{Sync}]$
, poses open questions. It would be also interesting to discuss further restrictions, leading to subclasses of NFA or of regular expressions, where it might be easier to prove membership in
$\textsf{W}[\textsf{Sync}]$
, poses open questions. It would be also interesting to discuss further restrictions, leading to subclasses of NFA or of regular expressions, where it might be easier to prove membership in
![]() $\textsf{W}[\textsf{Sync}]$
. It might be also an idea to quantify the degree of nondeterminism in these studies; we refer to Goldstine et al. (Reference Goldstine, Leung and Wotschke1992). In a sense, the preceding discussions are continued in the next sections, where we discuss other problems between
$\textsf{W}[\textsf{Sync}]$
. It might be also an idea to quantify the degree of nondeterminism in these studies; we refer to Goldstine et al. (Reference Goldstine, Leung and Wotschke1992). In a sense, the preceding discussions are continued in the next sections, where we discuss other problems between
![]() $\textsf{W}[2]$
and
$\textsf{W}[2]$
and
![]() $\textsf{W}[\textsf{Sync}]$
or hard for
$\textsf{W}[\textsf{Sync}]$
or hard for
![]() $\textsf{W}[\textsf{Sync}]$
, where again the precise parameterized complexity status in unknown.
$\textsf{W}[\textsf{Sync}]$
, where again the precise parameterized complexity status in unknown.
6. Problems between
 $\textsf{W}[2]$
and
$\textsf{W}[2]$
and
 $\textsf{W}[\textsf{Sync}]$
$\textsf{W}[\textsf{Sync}]$
One natural way to get problems below
![]() $\textsf{W}[\textsf{Sync}]$
is to consider only restricted variants of automata as admissible instances of DFA-SW. For instance, above we considered DFA-SW-sink. However, it is not always clear that we arrive at problem variants that are complete for
$\textsf{W}[\textsf{Sync}]$
is to consider only restricted variants of automata as admissible instances of DFA-SW. For instance, above we considered DFA-SW-sink. However, it is not always clear that we arrive at problem variants that are complete for
![]() $\textsf{W}[\textsf{Sync}]$
. For instance, Bruchertseifer and Fernau (Reference Bruchertseifer and Fernau2021) showed that the further restriction to so-called TTSPL automata (where the automaton multi-graphs can be described as two-terminal series-parallel multi-graphs with loops) results in a variation of DFA-SW that is still
$\textsf{W}[\textsf{Sync}]$
. For instance, Bruchertseifer and Fernau (Reference Bruchertseifer and Fernau2021) showed that the further restriction to so-called TTSPL automata (where the automaton multi-graphs can be described as two-terminal series-parallel multi-graphs with loops) results in a variation of DFA-SW that is still
![]() $\textsf{W}[2]$
-hard, which we were able to concretize in the long version to the effect that it is “only” contained in
$\textsf{W}[2]$
-hard, which we were able to concretize in the long version to the effect that it is “only” contained in
![]() $\textsf{W}[\textsf{Sync}]$
. In actual fact, it is an open problem if this problem variant is contained in
$\textsf{W}[\textsf{Sync}]$
. In actual fact, it is an open problem if this problem variant is contained in
![]() $\textsf{W}[2]$
or
$\textsf{W}[2]$
or
![]() $\textsf{W}[\textsf{Sync}]$
-hard, or really something “in-between.” As shown by Möhring (Reference Möhring1989), there are quite close connections between TTSP(L) graphs and so-called series-parallel partial orders. Without going into any details here, observe that the mappings
$\textsf{W}[\textsf{Sync}]$
-hard, or really something “in-between.” As shown by Möhring (Reference Möhring1989), there are quite close connections between TTSP(L) graphs and so-called series-parallel partial orders. Without going into any details here, observe that the mappings
![]() $Q\to Q$
that can be associated to input letters are monotone with respect to the series-parallel partial order corresponding to the TTSPL automaton graph. Our earlier constructions show:
$Q\to Q$
that can be associated to input letters are monotone with respect to the series-parallel partial order corresponding to the TTSPL automaton graph. Our earlier constructions show:
Corollary 8. DFA-SW, restricted to DFAs with TTSPL automata graphs, is polynomial time equivalent to Monoid Factorization, restricted to collections of mappings F that are monotone with respect to a given series-parallel partial order on the finite ground set Q.
This might indicate that we have found yet another class of parameterized problems living inside the by now classical parameterized complexity classes. However, this is just another open problem. As surveyed in Martyugin (Reference Martyugin2009), there are quite a number of subregular families of DFAs whose length-bounded synchronization problem stays NP-complete. A concise study of the corresponding parameterized complexities is still lacking. These are good further candidates of problems that are possibly complete for
![]() $\textsf{W}[\textsf{Sync}]$
, yielding lots of open problems.
$\textsf{W}[\textsf{Sync}]$
, yielding lots of open problems.
But, there are further problems lying between
![]() $\textsf{W}[2]$
and
$\textsf{W}[2]$
and
![]() $\textsf{W}[\textsf{Sync}]$
, as we will see next.
$\textsf{W}[\textsf{Sync}]$
, as we will see next.
6.1 Satisfying constraint satisfaction formulae
We consider constraint satisfaction formulae in conjunctive normal form, or CSP CNF for short, in the following. A CSP CNF formula
![]() $\varphi$
on k variables
$\varphi$
on k variables
![]() $x_1,\dots,x_k$
is given by a finite universe A, atomic sentences
$x_1,\dots,x_k$
is given by a finite universe A, atomic sentences
![]() $x_i=a$
for
$x_i=a$
for
![]() $1\leq i\leq k$
and
$1\leq i\leq k$
and
![]() $a\in A$
and a CNF built from these atomic sentences. Hence, for
$a\in A$
and a CNF built from these atomic sentences. Hence, for
![]() $A=\{0,1\}$
, this is equivalent to a classical Boolean CNF formula.
$A=\{0,1\}$
, this is equivalent to a classical Boolean CNF formula.

The Rystsov-Eppstein proof for
![]() $\textsf{NP}$
-hardness of DFA Synchronization given by Rystsov (Reference Rystsov1980) and Eppstein (Reference Eppstein1990) can be generalized to cope with CSP CNF formulae, preserving the parameter. This observation already proves:
$\textsf{NP}$
-hardness of DFA Synchronization given by Rystsov (Reference Rystsov1980) and Eppstein (Reference Eppstein1990) can be generalized to cope with CSP CNF formulae, preserving the parameter. This observation already proves:
Lemma 9.
![]() ${\rm CSP\ CNF\ S{\small ATISFIABILITY}}\in\textsf{W}\mkern 2mu[\textsf{Sync}]$
.
${\rm CSP\ CNF\ S{\small ATISFIABILITY}}\in\textsf{W}\mkern 2mu[\textsf{Sync}]$
.
What about the converse? We do not know, but we can prove instead the following hardness result.
Lemma 10.
![]() ${\rm CSP\ CNF\ S{\small ATISFIABILITY}}$
is
${\rm CSP\ CNF\ S{\small ATISFIABILITY}}$
is
![]() $\textsf{W}\mkern 2mu[2]$
-hard.
$\textsf{W}\mkern 2mu[2]$
-hard.
Proof. We reduce from Hitting Set, a standard
![]() $\textsf{W}[2]$
-complete problem. Let U be a universe and let
$\textsf{W}[2]$
-complete problem. Let U be a universe and let
![]() $\mathcal{S}$
be a set system over U. Moreover, k is the parameter. The task is to choose k elements
$\mathcal{S}$
be a set system over U. Moreover, k is the parameter. The task is to choose k elements
![]() $u_1,\dots,u_k\in U$
such that for each
$u_1,\dots,u_k\in U$
such that for each
![]() $S\in \mathcal{S}$
,
$S\in \mathcal{S}$
,
![]() $u_i\in S$
for some
$u_i\in S$
for some
![]() $1\leq i\leq k$
. To express this task as a CSP CNF formula with variables
$1\leq i\leq k$
. To express this task as a CSP CNF formula with variables
![]() $x_1,\dots,x_k$
, we simply add the clauses
$x_1,\dots,x_k$
, we simply add the clauses
 \begin{equation*}\bigvee_{i=1}^k\bigvee_{s\in S}x_i=s \end{equation*}
\begin{equation*}\bigvee_{i=1}^k\bigvee_{s\in S}x_i=s \end{equation*}
for each
![]() $S\in\mathcal{S}$
. Now, it should be clear that we can choose at most k different elements
$S\in\mathcal{S}$
. Now, it should be clear that we can choose at most k different elements
![]() $u_1,\dots,u_k\in U$
to cover all sets in the set system
$u_1,\dots,u_k\in U$
to cover all sets in the set system
![]() $\mathcal{S}$
if and only if the resulting CSP CNF formula (over the universe U) is satisfiable.
$\mathcal{S}$
if and only if the resulting CSP CNF formula (over the universe U) is satisfiable.
6.2 Long subsequences
We now discuss the well-known Longest Common Subsequence problem.

As explained in Wareham (Reference Wareham2001), by building an automaton
![]() $A_i$
for each
$A_i$
for each
![]() $x_i$
that accepts all subsequences of
$x_i$
that accepts all subsequences of
![]() $x_i$
, it is not hard to solve a Longest Common Subsequence instance by a Bounded DFA-Intersection instance, preserving our parameter. Hence:
$x_i$
, it is not hard to solve a Longest Common Subsequence instance by a Bounded DFA-Intersection instance, preserving our parameter. Hence:
Proposition 11.
![]() $\rm{L{\small ONGEST\ } C{\small OMMON\ } S{\small UBSEQUENCE}}\in\textsf{W}\mkern 2mu[\textsf{Sync}]$
.
$\rm{L{\small ONGEST\ } C{\small OMMON\ } S{\small UBSEQUENCE}}\in\textsf{W}\mkern 2mu[\textsf{Sync}]$
.
Observe that we can also use the previous proposition to prove Lemma 9, because one can modify the proof of Theorem 3 in Bodlaender et al. (Reference Bodlaender, Downey, Fellows and Wareham1995) to show the reduction
![]() ${\rm CSP\ CNF\ S{\small ATISFIABILITY}}\leq_{\textsf{FPT}}\rm{L{\small ONGEST\ } C{\small OMMON\ } S{\small UBSEQUENCE}}$
. Unfortunately, we do not know if Longest Common Subsequence is also hard for
${\rm CSP\ CNF\ S{\small ATISFIABILITY}}\leq_{\textsf{FPT}}\rm{L{\small ONGEST\ } C{\small OMMON\ } S{\small UBSEQUENCE}}$
. Unfortunately, we do not know if Longest Common Subsequence is also hard for
![]() $\textsf{W}[\textsf{Sync}]$
. We only know
$\textsf{W}[\textsf{Sync}]$
. We only know
![]() $\textsf{W}[2]$
-hardness from Bodlaender et al. (Reference Bodlaender, Downey, Fellows and Wareham1995); further membership results were unknown hitherto, so the previous proposition remedies this situation a bit.
$\textsf{W}[2]$
-hardness from Bodlaender et al. (Reference Bodlaender, Downey, Fellows and Wareham1995); further membership results were unknown hitherto, so the previous proposition remedies this situation a bit.
6.3 Discussions
One could also think of many ways to restrict the inputs of Bounded DFA-Intersection. For instance, observe that the automata constructed in the argument of Proposition 11 are all accepting finite languages. Is there a converse reduction from such a Bounded DFA-Intersection instance to some Longest Common Subsequence instance? Might this open question lead to another interesting complexity class between
![]() $\textsf{W}[2]$
and
$\textsf{W}[2]$
and
![]() $\textsf{W}[\textsf{Sync}]$
?
$\textsf{W}[\textsf{Sync}]$
?
Let us also mention that Guillemot (Reference Guillemot2011) has shown that Longest Common Subsequence, parameterized by the number of strings
![]() $\ell$
, is complete for
$\ell$
, is complete for
![]() $\textsf{WNL}$
. Likewise, Bounded DFA-Intersection, parameterized by the number of automata, is complete for
$\textsf{WNL}$
. Likewise, Bounded DFA-Intersection, parameterized by the number of automata, is complete for
![]() $\textsf{WNL}$
. Hence, whether or not two problems are
$\textsf{WNL}$
. Hence, whether or not two problems are
![]() $\textsf{FPT}$
-equivalent clearly depends on the chosen parameterization.
$\textsf{FPT}$
-equivalent clearly depends on the chosen parameterization.
Of course, having found two concrete problems between
![]() $\textsf{W}[2]$
and
$\textsf{W}[2]$
and
![]() $\textsf{W}[\textsf{Sync}]$
leads to the natural open question if they are mutually reducible. As mentioned above, we only know that
$\textsf{W}[\textsf{Sync}]$
leads to the natural open question if they are mutually reducible. As mentioned above, we only know that
![]() ${\rm CSP\ CNF\ S{\small ATISFIABILITY}}\leq_{\textsf{FPT}}\rm{L{\small ONGEST\ } C{\small OMMON\ } S{\small UBSEQUENCE}}$
. Further examples of problems below
${\rm CSP\ CNF\ S{\small ATISFIABILITY}}\leq_{\textsf{FPT}}\rm{L{\small ONGEST\ } C{\small OMMON\ } S{\small UBSEQUENCE}}$
. Further examples of problems below
![]() $\textsf{W}[\textsf{Sync}]$
can be obtained by restricting Bounded DFA-Intersection to subclasses of DFA. Notice that also for several such restricted classes of DFA, the basic problem is still NP-hard; see Arrighi et al. (Reference Arrighi, Fernau, Hoffmann, Holzer, Jecker, de Oliveira Oliveira and Wolf2021) for a recent study.
$\textsf{W}[\textsf{Sync}]$
can be obtained by restricting Bounded DFA-Intersection to subclasses of DFA. Notice that also for several such restricted classes of DFA, the basic problem is still NP-hard; see Arrighi et al. (Reference Arrighi, Fernau, Hoffmann, Holzer, Jecker, de Oliveira Oliveira and Wolf2021) for a recent study.
7. Problems Hard for
 $\textsf{W}[\textsf{Sync}]$
$\textsf{W}[\textsf{Sync}]$
In the following problem statements, k is always the parameter that we are analyzing with respect to parameterized complexity. In each case, we prove a hardness result for
![]() $\textsf{W}[\textsf{Sync}]$
. We remind the reader about the unknown status of Bounded NFA-Intersection. We also discuss memberships in
$\textsf{W}[\textsf{Sync}]$
. We remind the reader about the unknown status of Bounded NFA-Intersection. We also discuss memberships in
![]() $\textsf{WNL}$
,
$\textsf{WNL}$
,
![]() $\textsf{A}[2]$
,
$\textsf{A}[2]$
,
![]() $\textsf{A}[3],$
and
$\textsf{A}[3],$
and
![]() $\textsf{W}[\textsf{P}]$
.
$\textsf{W}[\textsf{P}]$
.
7.1 Intersecting regular languages again
Lemma 12.
Bounded NFA-Intersection, parameterized by the length of the commonly accepted string, is contained in
![]() $\textsf{WNL}$
.
$\textsf{WNL}$
.
Proof. We only sketch this proof, as it parallels previous ones. Let
![]() $\mathcal{A}$
be a collection of NFAs and
$\mathcal{A}$
be a collection of NFAs and
![]() $k\in\mathbb{N}$
. We can design a nondeterministic one-tape Turing machine M (starting on the empty input) that first guesses a string w of length k and then verifies, for each automaton
$k\in\mathbb{N}$
. We can design a nondeterministic one-tape Turing machine M (starting on the empty input) that first guesses a string w of length k and then verifies, for each automaton
![]() $A\in\mathcal{A}$
, that A accepts w. Only if all these simulations succeed, M will accept. As required, M needs only space k.
$A\in\mathcal{A}$
, that A accepts w. Only if all these simulations succeed, M will accept. As required, M needs only space k.
However, it is not clear to us how we could limit the number of guessing steps in the simulation of the previous proof; that is, it is an open question if Bounded NFA-Intersection belongs to
![]() $\textsf{W}[\textsf{P}]$
. Likewise, it is an open question if Bounded NFA-Intersection belongs to
$\textsf{W}[\textsf{P}]$
. Likewise, it is an open question if Bounded NFA-Intersection belongs to
![]() $\textsf{A}[2]$
, because it is not clear how to make this simulation work with only one switch from existential to universal states. Without going into details here, let us mention that with one further switch from universal to existential states, an alternating Turing machine could be designed that simulates a given Bounded NFA-Intersection instance in time f(k), which gives (see Flum and Grohe Reference Flum and Grohe2006 for details) the following result.
$\textsf{A}[2]$
, because it is not clear how to make this simulation work with only one switch from existential to universal states. Without going into details here, let us mention that with one further switch from universal to existential states, an alternating Turing machine could be designed that simulates a given Bounded NFA-Intersection instance in time f(k), which gives (see Flum and Grohe Reference Flum and Grohe2006 for details) the following result.
Lemma 13.
Bounded NFA-Intersection, parameterized by the length of the commonly accepted string, is contained in
![]() $\textsf{A}[3]$
.
$\textsf{A}[3]$
.
7.2 Extensions and orderings of words
Extension variants of Synchronizing Word have been studied before, as in Fernau and Hoffmann (Reference Fernau and Hoffmann2019). The underlying problem, which depends on the choice of a partial order
![]() $\prec$
on the set of all words, is defined as follows:
$\prec$
on the set of all words, is defined as follows:

Please note that the complexity varies fundamentally with the choice of the partial order. In the following, we will concentrate on the length-lexicographical ordering
![]() $\leq_{ll}$
as the partial order, where
$\leq_{ll}$
as the partial order, where
![]() $v\leq_{ll} w$
means that either
$v\leq_{ll} w$
means that either
![]() $|v|< |w|$
or that
$|v|< |w|$
or that
![]() $|v|=|w|$
and
$|v|=|w|$
and
![]() $v\leq_{lex} w$
, where
$v\leq_{lex} w$
, where
![]() $v\leq_{lex} w$
refers to a lexicographical (total) order induced by a given total order on the alphabet. In Fernau and Hoffmann (Reference Fernau and Hoffmann2019) and in Bruchertseifer and Fernau (Reference Bruchertseifer and Fernau2021), we are also discussing other (natural) partial orders. It should be noted that in some cases, the extension variants are solvable in polynomial time, while other cases lead to
$v\leq_{lex} w$
refers to a lexicographical (total) order induced by a given total order on the alphabet. In Fernau and Hoffmann (Reference Fernau and Hoffmann2019) and in Bruchertseifer and Fernau (Reference Bruchertseifer and Fernau2021), we are also discussing other (natural) partial orders. It should be noted that in some cases, the extension variants are solvable in polynomial time, while other cases lead to
![]() $\textsf{NP}$
- or
$\textsf{NP}$
- or
![]() $\textsf{co-}\textsf{NP}$
-hard problems. In particular, there is a
$\textsf{co-}\textsf{NP}$
-hard problems. In particular, there is a
![]() $\textsf{co-}\textsf{NP}$
-hardness of Ext DFA-SW-
$\textsf{co-}\textsf{NP}$
-hardness of Ext DFA-SW-
![]() $\leq_{ll}$
. To avoid clumsy formulations, we will therefore consider the
$\leq_{ll}$
. To avoid clumsy formulations, we will therefore consider the
![]() $\textsf{NP}$
-hard problem Co Ext DFA-SW-
$\textsf{NP}$
-hard problem Co Ext DFA-SW-
![]() $\leq_{ll}$
instead that reverses YES with NO answers compared to Ext DFA-SW-
$\leq_{ll}$
instead that reverses YES with NO answers compared to Ext DFA-SW-
![]() $\leq_{ll}$
.
$\leq_{ll}$
.
Theorem 10.
Co Ext DFA-SW-
![]() $\leq_{ll}$
, parameterized by
$\leq_{ll}$
, parameterized by
![]() $|u|$
, is contained in
$|u|$
, is contained in
![]() $\textsf{WNL}\cap \textsf{W}\mkern 2mu[\textsf{P}]\cap\textsf{A}[2]$
, but one can reduce DFA-SW, parameterized by a length upper bound k, to Co Ext DFA-SW-
$\textsf{WNL}\cap \textsf{W}\mkern 2mu[\textsf{P}]\cap\textsf{A}[2]$
, but one can reduce DFA-SW, parameterized by a length upper bound k, to Co Ext DFA-SW-
![]() $\leq_{ll}$
, parameterized by
$\leq_{ll}$
, parameterized by
![]() $|u|$
.
$|u|$
.
Proof. For membership
![]() ${\rm{C{\small O\ } E{\small XT\ }} \text{DFA-SW}}-{\leq_{ll}}\in \textsf{WNL}\cap\textsf{W}[\textsf{P}]\cap\textsf{A}[2]$
, we can modify the according proofs of Theorems 3, 4, or 5, constructing a nondeterministic Turing machine M as follows, given A and u. As in the previous construction, the machine can first guess a possible word
${\rm{C{\small O\ } E{\small XT\ }} \text{DFA-SW}}-{\leq_{ll}}\in \textsf{WNL}\cap\textsf{W}[\textsf{P}]\cap\textsf{A}[2]$
, we can modify the according proofs of Theorems 3, 4, or 5, constructing a nondeterministic Turing machine M as follows, given A and u. As in the previous construction, the machine can first guess a possible word
![]() $w\leq_{ll}u$
and verify if it is synchronizing. If such a word is found, then (A,u) is a NO-instance. The reduction itself checks if A is synchronizable at all, which can be done in polynomial time according to Sandberg (Reference Sandberg2005) and Volkov (Reference Volkov2008). We also have that if M does not find a synchronizing word
$w\leq_{ll}u$
and verify if it is synchronizing. If such a word is found, then (A,u) is a NO-instance. The reduction itself checks if A is synchronizable at all, which can be done in polynomial time according to Sandberg (Reference Sandberg2005) and Volkov (Reference Volkov2008). We also have that if M does not find a synchronizing word
![]() $w\leq_{ll}u$
, then (A,u) is a YES-instance, because as A is synchronizable, there must be a synchronizing word v. Remind that according to the previous tests,
$w\leq_{ll}u$
, then (A,u) is a YES-instance, because as A is synchronizable, there must be a synchronizing word v. Remind that according to the previous tests,
![]() $u\leq_{ll}v$
must hold.
$u\leq_{ll}v$
must hold.
We are now turning to the second claim. Consider a DFA A on the input alphabet
![]() $\Sigma$
, together with a number k, as an instance of DFA-SW. We can first check in polynomial time if A is synchronizable at all. If A is not synchronizable, then (A,k) (clearly) is a NO-instance of DFA-SW, so our reduction will produce some fixed NO-instance of Co Ext DFA-SW-
$\Sigma$
, together with a number k, as an instance of DFA-SW. We can first check in polynomial time if A is synchronizable at all. If A is not synchronizable, then (A,k) (clearly) is a NO-instance of DFA-SW, so our reduction will produce some fixed NO-instance of Co Ext DFA-SW-
![]() $\leq_{ll}$
. Hence, we now assume that A is synchronizable. Let
$\leq_{ll}$
. Hence, we now assume that A is synchronizable. Let
![]() $c\notin\Sigma$
be a fresh letter. Consider an arbitrary ordering
$c\notin\Sigma$
be a fresh letter. Consider an arbitrary ordering
![]() $<$
on
$<$
on
![]() $\Sigma$
, extended by
$\Sigma$
, extended by
![]() $c<x$
for all
$c<x$
for all
![]() $x\in\Sigma$
toward an ordering on
$x\in\Sigma$
toward an ordering on
![]() $\hat \Sigma=\Sigma\cup\{c\}$
. We are going to define the DFA
$\hat \Sigma=\Sigma\cup\{c\}$
. We are going to define the DFA
![]() $\hat A$
as an extension of A, working on the same state set Q. Let c simply act as the identity on Q. Hence, no word from
$\hat A$
as an extension of A, working on the same state set Q. Let c simply act as the identity on Q. Hence, no word from
![]() $c^*$
is synchronizing for
$c^*$
is synchronizing for
![]() $\hat A$
. As A is synchronizable,
$\hat A$
. As A is synchronizable,
![]() $\hat A$
is also synchronizable. Consider
$\hat A$
is also synchronizable. Consider
![]() $\hat A$
together with
$\hat A$
together with
![]() $u=c^{k+1}$
as an instance of Co Ext DFA-SW-
$u=c^{k+1}$
as an instance of Co Ext DFA-SW-
![]() $\leq_{ll}$
. If
$\leq_{ll}$
. If
![]() $\hat A$
has a synchronizing word w of length at most k, then clearly u is not extendible, as
$\hat A$
has a synchronizing word w of length at most k, then clearly u is not extendible, as
![]() $|w|<|u|$
. Otherwise, as
$|w|<|u|$
. Otherwise, as
![]() $\hat A$
is synchronizable,
$\hat A$
is synchronizable,
![]() $\hat A$
must have some synchronizing word w with
$\hat A$
must have some synchronizing word w with
![]() $|w|\geq |u|$
, and any synchronizing word of
$|w|\geq |u|$
, and any synchronizing word of
![]() $\hat A$
is of length at least
$\hat A$
is of length at least
![]() $|u|$
. As u is the smallest of all words in
$|u|$
. As u is the smallest of all words in
![]() $\hat\Sigma^*$
of length at least
$\hat\Sigma^*$
of length at least
![]() $|u|$
, any synchronizing word will hence extend u. Hence, if
$|u|$
, any synchronizing word will hence extend u. Hence, if
![]() $\hat A$
has no synchronizing word of length at most k, then u is extendible.
$\hat A$
has no synchronizing word of length at most k, then u is extendible.
The natural open question is if Co Ext DFA-SW-
![]() $\leq_{ll}$
is in
$\leq_{ll}$
is in
![]() $\textsf{W}[\textsf{Sync}]$
.
$\textsf{W}[\textsf{Sync}]$
.
In Bruchertseifer and Fernau (Reference Bruchertseifer and Fernau2021), we also showed that Ext DFA-SW-
![]() $\leq_{|}$
is
$\leq_{|}$
is
![]() $\textsf{W}[3]$
-hard, where
$\textsf{W}[3]$
-hard, where
![]() $|$
refers to the (scattered) subsequence ordering. But it is an open question if this extension problem belongs to
$|$
refers to the (scattered) subsequence ordering. But it is an open question if this extension problem belongs to
![]() $\textsf{W}[3]$
. Notice that there are few natural parameterized problems higher up in the
$\textsf{W}[3]$
. Notice that there are few natural parameterized problems higher up in the
![]() $\textsf{W}$
-hierarchy; see Chen and Zhang (Reference Chen and Zhang2006). However, the very idea of extension problems (not only applicable to formal language problems) seems to lead to such problems; we also refer to Bläsius et al. (Reference Bläsius, Friedrich, Lischeid, Meeks and Schirneck2019), Casel et al. (Reference Casel, Fernau, Ghadikolaei, Monnot and Sikora2018).
$\textsf{W}$
-hierarchy; see Chen and Zhang (Reference Chen and Zhang2006). However, the very idea of extension problems (not only applicable to formal language problems) seems to lead to such problems; we also refer to Bläsius et al. (Reference Bläsius, Friedrich, Lischeid, Meeks and Schirneck2019), Casel et al. (Reference Casel, Fernau, Ghadikolaei, Monnot and Sikora2018).
7.3 Non-universality questions for NFAs

Lemma 14.
Bounded NFA Non-Universality is
![]() $\textsf{W}\mkern 2mu[\textsf{Sync}]$
-hard.
$\textsf{W}\mkern 2mu[\textsf{Sync}]$
-hard.
Proof. We reduce from Bounded DFA-Intersection. Let
![]() $\mathcal{A}$
be a set of deterministic finite automata with the same input alphabet
$\mathcal{A}$
be a set of deterministic finite automata with the same input alphabet
![]() $\Sigma$
. To be more precise, let
$\Sigma$
. To be more precise, let
![]() $\mathcal{A}=\{A_1,\dots,A_n\}$
with
$\mathcal{A}=\{A_1,\dots,A_n\}$
with
![]() $A_i=(Q_i,\Sigma,\delta_i,q_{i,0},F_i)$
for
$A_i=(Q_i,\Sigma,\delta_i,q_{i,0},F_i)$
for
![]() $1\leq i\leq n$
. Without loss of generality, let
$1\leq i\leq n$
. Without loss of generality, let
![]() $Q_i\cap Q_j\neq\emptyset$
imply that
$Q_i\cap Q_j\neq\emptyset$
imply that
![]() $i=j$
. Define
$i=j$
. Define
![]() $Q=\bigcup_{i=1}^nQ_i$
. Let
$Q=\bigcup_{i=1}^nQ_i$
. Let
![]() $A=(Q,\Sigma,\delta,Q_0,F)$
be an NFA that is defined as follows. The set of initial states
$A=(Q,\Sigma,\delta,Q_0,F)$
be an NFA that is defined as follows. The set of initial states
![]() $Q_0$
equals
$Q_0$
equals
![]() $\{q_{i,0}\mid 1\leq i\leq n\}$
. The final states are
$\{q_{i,0}\mid 1\leq i\leq n\}$
. The final states are
![]() $F=\bigcup_{i=1}^n\left(Q_i\setminus F_i\right)$
. Interpreting the function
$F=\bigcup_{i=1}^n\left(Q_i\setminus F_i\right)$
. Interpreting the function
![]() $\delta_i$
as a set of triples
$\delta_i$
as a set of triples
![]() $(q_i,a,p_i)$
, with
$(q_i,a,p_i)$
, with
![]() $q_i,p_i\in Q_i$
and
$q_i,p_i\in Q_i$
and
![]() $a\in\Sigma$
, we can define the relation
$a\in\Sigma$
, we can define the relation
![]() $\delta$
as
$\delta$
as
![]() $\delta=\bigcup_{i=1}^n\delta_i$
. Now,
$\delta=\bigcup_{i=1}^n\delta_i$
. Now,
![]() $w\in\Sigma^*$
is accepted by all DFAs
$w\in\Sigma^*$
is accepted by all DFAs
![]() $A_i$
if and only if w is not accepted by A, because the state sets
$A_i$
if and only if w is not accepted by A, because the state sets
![]() $Q_i$
are pairwise disjoint.
$Q_i$
are pairwise disjoint.
Observe that the NFA A constructed in the preceding proof is very special, as its transition relation is actually a mapping. The only source of nondeterminism comes from the fact that A has n initial states. Alternatively, we could create a new single initial state
![]() $q_0$
and add transitions
$q_0$
and add transitions
![]() $(q_0,a,p_{i})$
whenever there is a transition
$(q_0,a,p_{i})$
whenever there is a transition
![]() $(q_{i,0},q,p_i)\in\delta_i$
. This way, we can get an NFA A’ with the property that for any
$(q_{i,0},q,p_i)\in\delta_i$
. This way, we can get an NFA A’ with the property that for any
![]() $w\in \Sigma^+$
, w is accepted by all
$w\in \Sigma^+$
, w is accepted by all
![]() $A_i$
if and only if w is not accepted by A’. Notice that now there is only one state (namely
$A_i$
if and only if w is not accepted by A’. Notice that now there is only one state (namely
![]() $q_0$
) that can be seen as the source of nondeterminism of A’. In particular, this proves that the number of “nondeterministic states” is not a useful (additional) parameter. Moreover, if an NFA with a single initial state and no “nondeterministic state,” that is, a DFA, is given, the question of the existence of a word of length k that is not accepted by this automaton becomes easy (solvable in polynomial time) by a product automaton construction, reducing it to the question of testing a single DFA for non-emptiness.
$q_0$
) that can be seen as the source of nondeterminism of A’. In particular, this proves that the number of “nondeterministic states” is not a useful (additional) parameter. Moreover, if an NFA with a single initial state and no “nondeterministic state,” that is, a DFA, is given, the question of the existence of a word of length k that is not accepted by this automaton becomes easy (solvable in polynomial time) by a product automaton construction, reducing it to the question of testing a single DFA for non-emptiness.
Lemma 15.
Bounded NFA Non-Universality belongs to
![]() $\textsf{A}[2]$
.
$\textsf{A}[2]$
.
Proof. We describe the work of an alternating single-tape Turing machine M that can be produced from a given NFA
![]() $A=(Q,\Sigma,\delta,Q_0,F)$
and
$A=(Q,\Sigma,\delta,Q_0,F)$
and
![]() $k\in\mathbb{N}$
in polynomial time, such that M accepts the empty word in 2k steps if and only if there is a word
$k\in\mathbb{N}$
in polynomial time, such that M accepts the empty word in 2k steps if and only if there is a word
![]() $w\in\Sigma^k$
that is not accepted by A. In the following, we describe how M works, and this way we also give sufficient details on how to construct M. The state set of M consists of
$w\in\Sigma^k$
that is not accepted by A. In the following, we describe how M works, and this way we also give sufficient details on how to construct M. The state set of M consists of
![]() $P=\{p_0,\dots,p_k\}$
and Q (the state set of the given NFA), where
$P=\{p_0,\dots,p_k\}$
and Q (the state set of the given NFA), where
![]() $P\setminus\{p_k\}$
are existential states and
$P\setminus\{p_k\}$
are existential states and
![]() $Q\cup\{p_k\}$
are universal states. The state
$Q\cup\{p_k\}$
are universal states. The state
![]() $p_0$
is the initial state of M. The set of final states of M is
$p_0$
is the initial state of M. The set of final states of M is
![]() $ Q\setminus F$
.
$ Q\setminus F$
.
-
First, M writes k letters from
 $\Sigma$
on its tape, moving its head from left to right. In this phase, M traverses the states
$\Sigma$
on its tape, moving its head from left to right. In this phase, M traverses the states
 $p_0,\dots,p_k$
in order. It ignores the tape contents (which should be empty anyways in the beginning).
$p_0,\dots,p_k$
in order. It ignores the tape contents (which should be empty anyways in the beginning). -
After entering
 $p_k$
, M reads the tape contents backwards, until it reaches the left end of the tape (again). More precisely, when being in state
$p_k$
, M reads the tape contents backwards, until it reaches the left end of the tape (again). More precisely, when being in state
 $p_k$
, M ignores its tape contents, and stays where it is, but moves from state
$p_k$
, M ignores its tape contents, and stays where it is, but moves from state
 $p_k$
(universally) to any of the states of
$p_k$
(universally) to any of the states of
 $Q_0$
.
$Q_0$
. -
When being in a state q from Q, M does the following:
-
It reads a tape symbol a.
-
If
 $(q,a,p)\in\delta$
, M moves to state p.
$(q,a,p)\in\delta$
, M moves to state p. -
The tape head moves one step to the left.
-
-
When M detects the right border of the tape, it stops working and accepts if it is in a state from
 $Q\setminus F$
.
$Q\setminus F$
.
As the states of
![]() $Q\cup\{p_k\}$
are universal, all possible computation paths of A are checked if they do not accept the guessed word
$Q\cup\{p_k\}$
are universal, all possible computation paths of A are checked if they do not accept the guessed word
![]() $w\in\Sigma^k$
. Therefore, the described reduction works.
$w\in\Sigma^k$
. Therefore, the described reduction works.
Notice that there are several aspects of the reduction described in the previous proof that might need small adaptations if we use a different concrete model of an alternating Turing machine. For instance, we (implicitly) assumed a Turing machine model where the tape is only (potentially) infinite to the right, but bounded to the left, and the left border could be detected. If we assume a tape that is (potentially) infinite to both sides, then we might need two more steps (of the Turing machine) to implement a left border by first printing a special border symbol and reading it in the end. But these details are inessential for our complexity result.
It is unclear to us (and hence an open question) if Bounded NFA Non-Universality belongs to
![]() $\textsf{WNL}$
or to
$\textsf{WNL}$
or to
![]() $\textsf{W}[\textsf{P}]$
, because in both cases, we face a model of nondeterministic Turing machine (if we follow the Turing way paved by Cesati Reference Cesati2003) that cannot cope with checking all possible nondeterministic ramifications of the given NFA, in particular, because the step bounds are given in unary. This leads to the intuition that Bounded NFA Non-Universality is indeed “harder” than DFA-SW. However, we do not see either why Bounded NFA Non-Universality should be hard for
$\textsf{W}[\textsf{P}]$
, because in both cases, we face a model of nondeterministic Turing machine (if we follow the Turing way paved by Cesati Reference Cesati2003) that cannot cope with checking all possible nondeterministic ramifications of the given NFA, in particular, because the step bounds are given in unary. This leads to the intuition that Bounded NFA Non-Universality is indeed “harder” than DFA-SW. However, we do not see either why Bounded NFA Non-Universality should be hard for
![]() $\textsf{WNL}$
or for
$\textsf{WNL}$
or for
![]() $\textsf{W}[\textsf{P}]$
. For instance, in order to prove
$\textsf{W}[\textsf{P}]$
. For instance, in order to prove
![]() $\textsf{WNL}$
-hardness, one could start with a Bounded DFA-Intersection instance
$\textsf{WNL}$
-hardness, one could start with a Bounded DFA-Intersection instance
![]() $(\mathcal{A},k)$
, now parameterized by
$(\mathcal{A},k)$
, now parameterized by
![]() $|\mathcal{A}|$
. However, in any classical construction linking Bounded DFA-Intersection to Bounded NFA Non-Universality, there is no obvious connection between
$|\mathcal{A}|$
. However, in any classical construction linking Bounded DFA-Intersection to Bounded NFA Non-Universality, there is no obvious connection between
![]() $|\mathcal{A}|$
and the string length parameter of Bounded NFA Non-Universality.
$|\mathcal{A}|$
and the string length parameter of Bounded NFA Non-Universality.
8. Problems that Feel Similar to Synchronizing DFAs
In this section, we like to collect problems that are
![]() $\textsf{W}[2]$
-hard and belong at least to some of the classes
$\textsf{W}[2]$
-hard and belong at least to some of the classes
![]() $\textsf{A}[2]$
,
$\textsf{A}[2]$
,
![]() $\textsf{W}\mkern 2mu[\textsf{P}]\mkern 2mu$
, or
$\textsf{W}\mkern 2mu[\textsf{P}]\mkern 2mu$
, or
![]() $\textsf{WNL}$
, but where the relation to
$\textsf{WNL}$
, but where the relation to
![]() $\textsf{W}[\textsf{Sync}]$
is unknown. Alas, we can present only one concrete problem, again related to synchronization.
$\textsf{W}[\textsf{Sync}]$
is unknown. Alas, we can present only one concrete problem, again related to synchronization.
Türker and Yenigün (Reference Türker and Yenigün2015) asked to extract a synchronizable sub-automaton that is as small as possible, obtained by deleting letters from its specification. This notion of a sub-automaton is of particular interest to us, as we are dealing with completely specified deterministic automata, and DFAs are not closed under most other notions of sub-automaton one might come up with, because they tend to produce incomplete automata. Türker and Yenegün formalized this idea as a weighted minimization problem. For our purposes, it is sufficient to consider the following unweighted variant:

Interestingly, Türker and Yenegün used nearly the same reduction as Fernau, Heggernes, and Villanger in Fernau et al. (Reference Fernau, Heggernes and Villanger2015) for a different purpose to prove the following result.
Theorem 11.
DFA-MSS is
![]() $\textsf{NP}$
-complete.
$\textsf{NP}$
-complete.
From that reduction, we can observe the following.
Corollary 16.
DFA-MSS, parameterized by the upper bound k on the size of the selected alphabet, is
![]() $\textsf{W}\mkern 2mu[2]$
-hard.
$\textsf{W}\mkern 2mu[2]$
-hard.
As with the other
![]() $\textsf{W}[2]$
-hard problems considered in this paper, membership in
$\textsf{W}[2]$
-hard problems considered in this paper, membership in
![]() $\textsf{W}[2]$
is open. Also in this case, we can prove membership in
$\textsf{W}[2]$
is open. Also in this case, we can prove membership in
![]() $\textsf{WNL}$
, although this is not completely trivial this time.
$\textsf{WNL}$
, although this is not completely trivial this time.
Theorem 12.
DFA-MSS is contained in
![]() $\textsf{WNL}\cap \textsf{W}\mkern 2mu[\textsf{P}]$
.
$\textsf{WNL}\cap \textsf{W}\mkern 2mu[\textsf{P}]$
.
Proof. Let (A,k) be an instance of DFA-MSS. Notice that in a first preprocessing step, we can eliminate letters a’ that act the same on the state set Q as another letter a that we decide to keep. Such a rule can be implemented to run in polynomial time, as we simply loop over all pairs of letters, so that we can now assume to face an automaton A with input alphabet
![]() $\Sigma$
and state set Q such that
$\Sigma$
and state set Q such that
![]() $|\Sigma|\leq |Q|^{|Q|}$
. Moreover, we can assume that
$|\Sigma|\leq |Q|^{|Q|}$
. Moreover, we can assume that
![]() $\Sigma$
contains more than
$\Sigma$
contains more than
![]() $\log\!(|Q|)$
many symbols, as otherwise we can test all subsets of
$\log\!(|Q|)$
many symbols, as otherwise we can test all subsets of
![]() $\Sigma$
(for synchronizability) in polynomial time. Finally, we can test in polynomial time if A itself is synchronizable at all, as proven in Sandberg (Reference Sandberg2005) and Volkov (Reference Volkov2008). Recall that the algorithm checking synchronizability tests if any pair of states can be synchronized within at most
$\Sigma$
(for synchronizability) in polynomial time. Finally, we can test in polynomial time if A itself is synchronizable at all, as proven in Sandberg (Reference Sandberg2005) and Volkov (Reference Volkov2008). Recall that the algorithm checking synchronizability tests if any pair of states can be synchronized within at most
![]() $|Q|$
steps. We adapt this strategy in the following.
$|Q|$
steps. We adapt this strategy in the following.
Now, we hard-wire the DFA into a Turing machine M as described in the following. In particular, this means that this Turing machine can keep track of pairs of states, say, (q,p) and update this information toward (q’,p’) in its finite memory (alternatively, on the tape, using state letters) upon reading a symbol
![]() $a\in\Sigma$
, such that q’ is reached from q (in the given DFA) and p’ is reached from p upon reading a. We also assume a fixed linear ordering
$a\in\Sigma$
, such that q’ is reached from q (in the given DFA) and p’ is reached from p upon reading a. We also assume a fixed linear ordering
![]() $<$
on the state set Q, and moreover, we assume that
$<$
on the state set Q, and moreover, we assume that
![]() $Q\cap \Sigma=\emptyset$
. Let
$Q\cap \Sigma=\emptyset$
. Let
![]() $q_a$
and
$q_a$
and
![]() $q_b$
be the smallest and second-to-smallest states in Q.
$q_b$
be the smallest and second-to-smallest states in Q.
The Turing machine M first guesses a sub-alphabet
![]() $\Sigma'$
by writing the corresponding k input letters on its tape. Moreover, it writes down
$\Sigma'$
by writing the corresponding k input letters on its tape. Moreover, it writes down
![]() $q_a$
next to
$q_a$
next to
![]() $q_b$
. After reading (and memorizing) the current state pair (q,p), initially
$q_b$
. After reading (and memorizing) the current state pair (q,p), initially
![]() $(q,p)=(q_a,q_b)$
, the machine (nondeterministically) reads one of the k guessed input letters on its tape and transfers to (q’,p’) in its internal memory. It continues doing so until it reaches a pair (r,r) for some
$(q,p)=(q_a,q_b)$
, the machine (nondeterministically) reads one of the k guessed input letters on its tape and transfers to (q’,p’) in its internal memory. It continues doing so until it reaches a pair (r,r) for some
![]() $r\in Q$
. If it reaches such a pair, it is verified that the pair (q,p) written on the tape can be synchronized. It continues by incrementing p on the tape (according to the linear order
$r\in Q$
. If it reaches such a pair, it is verified that the pair (q,p) written on the tape can be synchronized. It continues by incrementing p on the tape (according to the linear order
![]() $<$
) and then testing the synchronizability of the new pair of states on the tape with respect to the guessed sub-alphabet. M loops until the largest element of Q (with respect to
$<$
) and then testing the synchronizability of the new pair of states on the tape with respect to the guessed sub-alphabet. M loops until the largest element of Q (with respect to
![]() $<$
) is reached. Then, it would increment the first component q of the pair and set the second component of the pair of states to the smallest state larger than the first component’s state; then, again the inner loop is entered. Finally, when reaching the largest state in the first component, the procedure terminates, this way verifying that the automaton is indeed synchronizable when restricted to the guessed alphabet.
$<$
) is reached. Then, it would increment the first component q of the pair and set the second component of the pair of states to the smallest state larger than the first component’s state; then, again the inner loop is entered. Finally, when reaching the largest state in the first component, the procedure terminates, this way verifying that the automaton is indeed synchronizable when restricted to the guessed alphabet.
Obviously, the machine M uses only
![]() $k+c$
space for some constant c, depending upon details of the implementation. This proves that DFA-MSS belongs to
$k+c$
space for some constant c, depending upon details of the implementation. This proves that DFA-MSS belongs to
![]() $\textsf{WNL}$
.
$\textsf{WNL}$
.
Toward proving membership in
![]() $\textsf{W}[\textsf{P}]$
, recall that two states (q,q’) are synchronizable if and only if there is a path in the following directed auxiliary graph from (q,q’) to the target vertex t:
$\textsf{W}[\textsf{P}]$
, recall that two states (q,q’) are synchronizable if and only if there is a path in the following directed auxiliary graph from (q,q’) to the target vertex t:
![]() $V=Q\times Q\cup\{t\}$
is the set of vertices. There is an arc from (q,q’) to (p,p’) if there is some letter a such that the given DFA makes transitions from q to p and from q’ to p’ upon reading the letter a. Moreover, there are arcs from any vertex (q,q) to t. In our case, after having guessed the sub-alphabet, this information can be used to construct a sub-graph of the graph just described and write its description down on the tape (in polynomial time). Now, we can use, for example, Dijkstra’s algorithm to decide if there is such a path in this sub-graph, deterministically looping through all pairs of states. This describes a Turing machine M’ that first makes k guesses and then works deterministically a polynomial number of steps and hence proves membership in
$V=Q\times Q\cup\{t\}$
is the set of vertices. There is an arc from (q,q’) to (p,p’) if there is some letter a such that the given DFA makes transitions from q to p and from q’ to p’ upon reading the letter a. Moreover, there are arcs from any vertex (q,q) to t. In our case, after having guessed the sub-alphabet, this information can be used to construct a sub-graph of the graph just described and write its description down on the tape (in polynomial time). Now, we can use, for example, Dijkstra’s algorithm to decide if there is such a path in this sub-graph, deterministically looping through all pairs of states. This describes a Turing machine M’ that first makes k guesses and then works deterministically a polynomial number of steps and hence proves membership in
![]() $\textsf{W}[\textsf{P}]$
.
$\textsf{W}[\textsf{P}]$
.
The reader might have expected in the previous proof that logarithmic space would be needed by a Turing machine that (basically) verifies reachability in a graph with
![]() $|Q|^2$
many vertices. Notice that this is implicit in the model, because the Turing machine writes down letters of an arbitrary alphabet on its tape, not just bits. Breaking down to the bit level, one observes that indeed
$|Q|^2$
many vertices. Notice that this is implicit in the model, because the Turing machine writes down letters of an arbitrary alphabet on its tape, not just bits. Breaking down to the bit level, one observes that indeed
![]() $2\log_2\!(\lceil|Q|\rceil)+k\log_2\!(\lceil|\Sigma|\rceil)$
many bits are necessary to write down the letters used by the Turing machine in the previous construction.
$2\log_2\!(\lceil|Q|\rceil)+k\log_2\!(\lceil|\Sigma|\rceil)$
many bits are necessary to write down the letters used by the Turing machine in the previous construction.
Although we found similar parameterized complexity results for DFA-MSS as for DFA-SW, we are not aware of further close links between both problems. In particular, it remains an open question how to solve one problem with the help of the other (respecting our choice of parameters). In particular, the first Turing machine constructed in the previous proof (or straightforward re-interpretations) does not show membership in
![]() $\textsf{W}[\textsf{P}]$
, because the number of nondeterministic (guess) steps is not bounded in k (so that we had to design a second Turing machine that worked in a different way), nor in
$\textsf{W}[\textsf{P}]$
, because the number of nondeterministic (guess) steps is not bounded in k (so that we had to design a second Turing machine that worked in a different way), nor in
![]() $\textsf{A}[2]$
, since after guessing k letters, it would enter a universal state (to ensure that all pairs of states are tested for synchronizability), but then the synchronizing word should be guessed again, that is, now this machine would enter again some existential states. Even then, the number of steps is not bounded by a function in k, so that this does not prove membership in
$\textsf{A}[2]$
, since after guessing k letters, it would enter a universal state (to ensure that all pairs of states are tested for synchronizability), but then the synchronizing word should be guessed again, that is, now this machine would enter again some existential states. Even then, the number of steps is not bounded by a function in k, so that this does not prove membership in
![]() $\textsf{A}[3]$
.
Footnote 6
Furthering this question, we do not know of any fixed level of the
$\textsf{A}[3]$
.
Footnote 6
Furthering this question, we do not know of any fixed level of the
![]() $\textsf{A}$
-hierarchy to which this problem belongs.
$\textsf{A}$
-hierarchy to which this problem belongs.
9. Further Comments and Discussions on Monoid Factorization
Observe that it is important that the monoid used in Monoid Factorization is only implicitly given, not by a multiplication table. A variation could be:

However, an explicit representation of the multiplication table of
![]() $(Q^Q,\circ)$
(where
$(Q^Q,\circ)$
(where
![]() $Q^Q$
is the set of all mappings from Q to Q) would already take
$Q^Q$
is the set of all mappings from Q to Q) would already take
![]() $\mathcal{O}^*(|Q|^{2|Q|})$
space and hence allow to construct an arc-labeled directed graph with a vertex for each mapping
$\mathcal{O}^*(|Q|^{2|Q|})$
space and hence allow to construct an arc-labeled directed graph with a vertex for each mapping
![]() $Q\to Q$
and an arc-labeled
$Q\to Q$
and an arc-labeled
![]() $f_i$
from f to g if
$f_i$
from f to g if
![]() $f\circ f_i=g$
, where
$f\circ f_i=g$
, where
![]() $f_i$
is from the explicit set of generators
$f_i$
is from the explicit set of generators
![]() $F'=\{f_1,\dots,f_m\}$
. Now, the representability of
$F'=\{f_1,\dots,f_m\}$
. Now, the representability of
![]() $f_0$
with at most k mappings from F’ can be solved by looking for a path of length at most k in the directed graph we just described, leading from the identity mapping
$f_0$
with at most k mappings from F’ can be solved by looking for a path of length at most k in the directed graph we just described, leading from the identity mapping
![]() $\Delta_Q$
to
$\Delta_Q$
to
![]() $f_0$
. Hence, when the monoid is given in an explicit form, then the factorization problem can be solved in polynomial time (even in
$f_0$
. Hence, when the monoid is given in an explicit form, then the factorization problem can be solved in polynomial time (even in
![]() $\textsf{NL}$
, see the discussion in Barrington et al. Reference Barrington, Kadau, Lange and McKenzie2001). It might be interesting to study other implicitly given monoids with respect to the factorization question. Let us mention one more example. Assume that our implicitly given monoid operation is set union. Then, the corresponding factorization problem would take subsets
$\textsf{NL}$
, see the discussion in Barrington et al. Reference Barrington, Kadau, Lange and McKenzie2001). It might be interesting to study other implicitly given monoids with respect to the factorization question. Let us mention one more example. Assume that our implicitly given monoid operation is set union. Then, the corresponding factorization problem would take subsets
![]() $\{X_0,X_1,\dots,X_m\}$
of a given finite set S as an input, and the question is to pick at most k sets from
$\{X_0,X_1,\dots,X_m\}$
of a given finite set S as an input, and the question is to pick at most k sets from
![]() $\{X_1,\dots,X_m\}$
, say,
$\{X_1,\dots,X_m\}$
, say,
![]() $X_{i_1},\dots,X_{i_{k'}}$
, where
$X_{i_1},\dots,X_{i_{k'}}$
, where
![]() $k'\leq k$
, such that
$k'\leq k$
, such that
![]() $X_0=\bigcup_{j=1}^{k'}X_{i_j}$
. Obviously, this corresponds to Set Cover, which hence gives an example of a monoid factorization problem which, when parameterized by k, is complete for
$X_0=\bigcup_{j=1}^{k'}X_{i_j}$
. Obviously, this corresponds to Set Cover, which hence gives an example of a monoid factorization problem which, when parameterized by k, is complete for
![]() $\textsf{W}[2]$
. It might be interesting to investigate further implicitly given monoids from this parameterized perspective. We only mention as a last example from the literature Permutation Group Factorization, which is known to be
$\textsf{W}[2]$
. It might be interesting to investigate further implicitly given monoids from this parameterized perspective. We only mention as a last example from the literature Permutation Group Factorization, which is known to be
![]() $\textsf{W}[1]$
-hard but is lacking a precise classification; see Bodlaender et al. (Reference Bodlaender, Downey, Fellows and Wareham1995), Downey and Fellows (Reference Downey and Fellows2013). In the classical complexity context, we refer to Even and Goldreich (Reference Even and Goldreich1981) (where the problem has the name Minimum Generator Sequence) and Jerrum (Reference Jerrum1985).
$\textsf{W}[1]$
-hard but is lacking a precise classification; see Bodlaender et al. (Reference Bodlaender, Downey, Fellows and Wareham1995), Downey and Fellows (Reference Downey and Fellows2013). In the classical complexity context, we refer to Even and Goldreich (Reference Even and Goldreich1981) (where the problem has the name Minimum Generator Sequence) and Jerrum (Reference Jerrum1985).
Let us also mention that from the 1980s onwards, Martin Beaudry and his colleagues led a whole research agenda, looking at what they called the Membership Problem, which meant to look at special cases of Monoid Factorization; in many cases, they still obtain NP-hardness. We only mention here monoids with threshold (at least) two and point to Beaudry (1988,Reference Beaudry1994).
Footnote 7
It should be noted that the question whether or not an upper bound on the length of the factorization is given makes a difference for various special cases if it comes to classical complexity. None of these monoid classes has been studied from the angle of parameterized complexity. Further problems of this type are discussed in Böhler et al. (Reference Böhler, Glaßer, Schwarz and Wagner2005). To the best of our knowledge, none of these has been examined from the viewpoint of parameterized complexity and hence give a number of open questions. To mention one concrete problem of this type: Let
![]() $\{c_1,\dots,c_m\}$
be a collection of clauses, with variables
$\{c_1,\dots,c_m\}$
be a collection of clauses, with variables
![]() $\{x_1,\dots,x_n\}$
, and let
$\{x_1,\dots,x_n\}$
, and let
![]() $k\in\mathbb{N}$
. The question is if the empty clause can be derived within the resolution proof system within k resolution steps.
$k\in\mathbb{N}$
. The question is if the empty clause can be derived within the resolution proof system within k resolution steps.
Let us finally remark that the discussion of implicit or explicit representations also extends to finite automata. Namely, it is well-known that the question if a given DFA accepts a word of length k is easy to check, while DFA-SW is
![]() $\textsf{NP}$
-complete. Yet, we can build a DFA A’ from a DFA A with the classical power automaton construction, see Sandberg (Reference Sandberg2005), such that A’ accepts a word of length k if and only if A possesses a synchronizing word of length k. In other words, L(A’) can be viewed as an implicitly presented regular language. This type of presentation tends to make problems harder.
$\textsf{NP}$
-complete. Yet, we can build a DFA A’ from a DFA A with the classical power automaton construction, see Sandberg (Reference Sandberg2005), such that A’ accepts a word of length k if and only if A possesses a synchronizing word of length k. In other words, L(A’) can be viewed as an implicitly presented regular language. This type of presentation tends to make problems harder.
10. Open Questions and Concluding Thoughts
Throughout the paper, we already highlighted several concrete open questions. Let us now draw the reader’s attention to three more general questions.
Are there any relationships between
 $\textsf{W}[\textsf{SAT}]$
and
$\textsf{W}[\textsf{SAT}]$
and
 $\textsf{W}[\textsf{Sync}]$
?
$\textsf{W}[\textsf{Sync}]$
?Are there further problems in or hard for
 $\textsf{W}[\textsf{Sync}]$
? We explicitly mention the intersection problems from Sections 5.4 and 7 again here.
$\textsf{W}[\textsf{Sync}]$
? We explicitly mention the intersection problems from Sections 5.4 and 7 again here.Is there any relation between the class
 $\textsf{WNL}$
and the
$\textsf{WNL}$
and the
 $\textsf{A}$
-hierarchy?
$\textsf{A}$
-hierarchy?
There is some evidence that
![]() $\textsf{W}[\textsf{Sync}]$
is different from
$\textsf{W}[\textsf{Sync}]$
is different from
![]() $\textsf{A}[2]$
. Namely, if
$\textsf{A}[2]$
. Namely, if
![]() $\textsf{W}[\textsf{Sync}]=\textsf{A}[2]$
, then
$\textsf{W}[\textsf{Sync}]=\textsf{A}[2]$
, then
![]() $\textsf{A}[2]\subseteq \text{para-}\textsf{NP}$
, because
$\textsf{A}[2]\subseteq \text{para-}\textsf{NP}$
, because
![]() $\textsf{W}[\textsf{Sync}]\subseteq \text{para-}\textsf{NP}$
. As shown by Haan (2016), then all
$\textsf{W}[\textsf{Sync}]\subseteq \text{para-}\textsf{NP}$
. As shown by Haan (2016), then all
![]() $\Sigma_2^p$
-problems would be as “easy” as SAT from an algorithmic point of view, something which contradicts at least the practical experience with this type of problems.
$\Sigma_2^p$
-problems would be as “easy” as SAT from an algorithmic point of view, something which contradicts at least the practical experience with this type of problems.
It is also interesting to observe that most of our problems come from the area of formal languages, in most cases, from automata theory. This area has been a bit neglected from the perspective of parameterized complexity, see Fernau (Reference Fernau2019) for discussing further questions in this regard. Also, the class
![]() $\textsf{WNL}$
mostly hosts formal language problems, as already exhibited by Guillemot (Reference Guillemot2011). It would be interesting to see further problems situated in
$\textsf{WNL}$
mostly hosts formal language problems, as already exhibited by Guillemot (Reference Guillemot2011). It would be interesting to see further problems situated in
![]() $\textsf{WNL}$
or in
$\textsf{WNL}$
or in
![]() $\textsf{W}[\textsf{Sync}]$
coming from other areas. As problems related to string problems can be found in computational biology and also in computational social choice, we expect these to be good candidate areas to look into in the future.
$\textsf{W}[\textsf{Sync}]$
coming from other areas. As problems related to string problems can be found in computational biology and also in computational social choice, we expect these to be good candidate areas to look into in the future.
Acknowledgements
We are grateful for discussions on the topic of this paper with several colleagues. Further developments concerning the parameterized complexity of automata problems can be found in Fernau et al. (Reference Fernau, Hoffmann and Wehar2021).