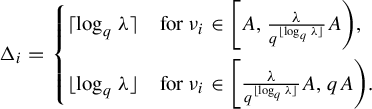Strongly aperiodic subshifts of finite type on hyperbolic groups

Abstract

We prove that a hyperbolic group admits a strongly aperiodic subshift of finite type if and only if it has at most one end.

1 Introduction

This paper is devoted to proving the following theorem.

Theorem. A hyperbolic group admits a strongly aperiodic subshift of finite type (SFT) if and only if it has at most one end.

Many groups are known to admit strongly aperiodic SFTs. One-ended hyperbolic groups (defined in §3.2) include all fundamental groups of closed hyperbolic n-manifolds, and indeed, the fundamental groups of all closed n-manifolds with negative sectional curvature. This generalizes surface groups [CGS17], which were the only hyperbolic groups known to admit such structure until the current work. Thus, we obtain the following result.

Corollary. The fundamental group of a closed n-manifold with negative sectional curvature admits a strongly aperiodic SFT.

In [Moz97], Mozes showed that uniform lattices in simple Lie groups of ranks at least $2$ admit strongly aperiodic SFTs; because rank-1 simple Lie groups are hyperbolic, we obtain the following corollary that complements Mozes’ result. (The symmetric space obtained by quotienting a rank-1 simple Lie group by its maximal compact subgroup is negatively curved. Because the Lie group (as well as any uniform lattice in it) are quasi-isometric to the symmetric space, they are $\delta $ -hyperbolic spaces (see, for example, [BH99]) and, therefore, the uniform lattice is a hyperbolic group.)

Corollary. A uniform lattice in a rank-1 simple Lie group admits a strongly aperiodic SFT.

We introduce the subject in this section and give an informal outline in §2. In §3, we formally define our terms and set up the proof, which is a combination of the results of §§3–9 as follows.

Proof of the Theorem Propositions 8.5, 8.12, and 9.5 show that any one-ended hyperbolic group G admits a non-empty SFT in which no configuration admits a non-torsion element in its stabilizer. By Proposition 3.3, G admits an SFT in which no configuration admits a torsion element in its stabilizer. Proposition 3.4 shows that the product of these subshifts is a strongly aperiodic SFT on G.

By Proposition 3.3, every zero-ended group (that is, every finite group) admits a strongly aperiodic SFT, and Cohen [Coh17] shows no group with two or more ends admits such a subshift.

Let G be a finitely generated group endowed with the word metric. Because G acts on itself transitively there are no invariants that distinguish elements of G. We seek such an invariant: a coloring of G, using finitely many colors, so that the coloring can be checked locally (an SFT), and so that any two group elements have distinct neighborhoods (strong aperiodicity). In other words, a strongly aperiodic SFT on a group G is given by a finite set of local rules for decorating G, so that all global symmetry arising from the group acting upon itself is destroyed.

In many settings, such as on ${\mathbb Z}^2\subset {\mathbb R}^2$ , SFTs are essentially the same phenomena as matching rule tiling spaces, which are each determined by a given finite set of marked-up tiles, such as the Penrose tiles. (Any SFT on $\mathbb {Z}^{2}$ can be interpreted as a matching rule tiling space on $\mathbb {R}^{2}$ . The converse does not hold [Rad94].) The two areas arose in different ways but soon became linked.

Wang [Wan60] interpreted remaining cases of Hilbert’s Entscheidungsproblem in the foundations of logic as being about how square tiles with marked edges might fit together in ${\mathbb Z}^2$ . This led Wang to ask whether one can algorithmically decide the ‘tiling problem’ (also known as the domino problem): Can a given finite set of tiles be used to form a tiling?

Wang pointed out that if the tiling problem in $\mathbb {Z}^{2}$ (or in another similar setting) were in fact undecidable, then there must exist aperiodic sets of tiles. (If there were not an aperiodic set of tiles, every set of tiles would either not tile the plane (and so have some maximum sized disk that can be tiled) or would admit a periodic tiling (and so have some finite fundamental domain). By enumerating finite configurations, one eventually determines which, deciding the problem. Note that the undecidability of the tiling problem in fact implies weak aperiodicity (defined below), but as it happens, there is no distinction between weak and strong aperiodicity in the Euclidean plane.) Soon after, Berger proved that the tiling problem is undecidable in ${\mathbb Z}^2$ and gave the first examples of an aperiodic sets of tiles [Ber66].

The ‘existence problem’ for SFTs on a group G asks whether a given set of local rules determine a non-empty subshift, that is, whether there exists a decoration of G satisfying the local rules. Berger’s result shows that this problem is undecidable when $G={\mathbb Z}^2$ . The recent survey [ABJ18] defines a natural ‘domino problem’ on SFTs on groups, and shows it is equivalent to the existence problem.

1.1 Subshifts

Given a finite set ${\mathcal A}$ , the set ${\mathcal A}^G$ consists of functions G to ${\mathcal A}$ (see §3.1 for more details). Equipped with the product topology and the G-action given in Definition 3.2, ${\mathcal A}^G$ is known as the full shift on G and its closed G-invariant subsets are known as subshifts. Subshifts are an essential tool in the study of dynamical systems; for example, every $0$ -dimensional expansive system on G is a subshift (see, for example, Proposition 2.8 of [CP93]), every expansive system is a factor of a subshift (e.g. Proposition 2.6 of [CP93]), and if G is non-amenable, a theorem of Seward [Sew14b, Theorem 1.2] shows that every topological dynamical system over G is a factor of a subshift.

1.2 SFTs

A pattern is a function $p:F{\rightarrow }{\mathcal A}$ from some finite $F\subseteq G$ . We say that a pattern $p:F{\rightarrow }{\mathcal A}$ appears in $\omega :G{\rightarrow }{\mathcal A}$ if there is some $g\in G$ such that $\omega (gf)=p(f)$ for all $f\in F$ . An SFT is a subset of ${\mathcal A}^G$ consisting of all $\omega \in {\mathcal A}^G$ in which no $p\in \mathcal {F}$ appears, for some finite collection $\mathcal {F}$ of forbidden patterns. For example, if ${\mathcal A}=\{0,1\}$ and $G={\mathbb Z}$ , the set of all $\omega \in {\mathcal A}^{\mathbb Z}$ such that $(\omega (n),\omega (n+1))$ is never equal to $(1,1)$ forms an SFT. It is well-known (and easy to see) that SFTs are subshifts. We refer to elements of an SFT as configurations.

Weak aperiodicity was not recognized until after Mozes’ definition of strong aperiodicity in [Moz97], in which he gives examples of both kinds. An SFT on an infinite group G is weakly aperiodic if it is non-empty and the G-orbit of every configuration is infinite, that is, a subgroup of G is allowed to fix a configuration, provided it has infinite index.

Similarly, a set of tiles is weakly aperiodic if it is possible to form a tiling with congruent copies of them, but never a tiling with a compact fundamental domain. (We note, however, that the stabilizer of such tiling may admit an infinite cyclic subgroup, as suggested in the figure in Remark 2.1.)

Block and Weinberger constructed a weakly aperiodic tile set for any non-amenable cover of a compact Riemannian manifold [BW92]. In the setting of infinite hyperbolic groups, weakly aperiodic SFTs were constructed by Gromov [Gro87, §§7.5, 7.6, 8.4] and Coornaert and Papadopoulos [CP93]; these SFTs exist on any hyperbolic group but are never strongly aperiodic.

Mozes [Moz97] gave weakly aperiodic sets of tiles on rank-1 symmetric spaces, by decorating tiles shaped like the fundamental domain of one lattice with information about how it may interact with the tiling by fundamental domains of another, incompatible lattice, and applying Mostow rigidity to prove weak aperiodicity.

1.3 Strong aperiodicity

A set of tiles is strongly aperiodic if it does admit a tiling, but does not admit any tiling with translational symmetry. Similarly an SFT is strongly aperiodic if it is non-empty and the G-action upon it is free, meaning that the stabilizer of any configuration is trivial. (Strongly aperiodic sets of tiles might allow tilings with a rotational symmetry—this is the case with both the Penrose and Robinson tiles. By analogy, some authors, such as [Jea15a], allow strongly aperiodic SFTs to include configurations with finite stabilizers.)

Wang himself conjectured that aperiodicity (of any kind) was absurd, but the first strongly aperiodic sets of tiles soon appeared in ${\mathbb Z}^2$ [Ber66, Rob71] and many others have been found since, mostly based on Berger’s initial use of hierarchically arranged structures [FO10, GS98, Moz89], or the theory of quasicrystals stemming from De Bruijn’s higher-dimensional analogue of Sturmian sequences [DB81a, DB81b]. Kari gave a third model [Kar96], which was adapted to give the first strongly aperiodic sets of tiles in hyperbolic n-space, ${\mathbb H}^n$ [GS05]; Kari extended this further to prove that the tiling problem is undecidable in ${\mathbb H}^2$ [Kar07]. Recently Jeandel and Rao gave a new construction on ${\mathbb Z}^2$ with a provably minimal set of aperiodic ‘Wang tiles’ [JR21]. We will give a list of groups known to have strongly aperiodic SFTs momentarily, but first we survey groups known not to have such subshifts.

1.4 Obstructions to the existence of a strongly aperiodic SFT

To see that ${\mathbb Z}$ has no strongly aperiodic SFT, let $\Omega \subset {\mathcal A}^{\mathbb Z}$ be a non-empty SFT, and consider any $\omega \in \Omega $ . Because there are only finitely many possible words of a given length in ${\mathcal A}$ , we see that $\omega $ contains a subword of the form $uvu$ for some words u and v which are longer than all of the forbidden patterns used to define $\Omega $ . However, then it is easy to check that $\ldots uvuvuv\ldots $ defines a periodic configuration in $\Omega $ . This was extended to all free groups by [Pia08].

The above argument was generalized by Cohen [Coh17], who showed that no group G with at least two ends admits a strongly aperiodic SFT. In addition, Jeandel [Jea15a] has shown that no finitely presented group with undecidable word problem admits a strongly aperiodic SFT. These are the only known obstructions and we naturally ask the following.

Question. Does there exist a one-ended finitely presented group with decidable word problem that does not admit a strongly aperiodic SFT?

1.5 Groups known to have a strongly aperiodic SFT

Whether or not a group admits a strongly aperiodic SFT is a quasi-isometry invariant under mild conditions [Coh17], and a commensurability invariant [CP15].

1. (i) As mentioned previously, Berger [Ber66] showed that ${\mathbb Z}^2$ itself admits a strongly aperiodic SFT. More generally, Jeandel [Jea15b] has shown that polycyclic groups admit strongly aperiodic SFTs.

2. (ii) The work of Barbieri and Sablik [BS19] shows that any group of the form ${\mathbb Z}^2 \rtimes H$ , where H is finitely generated and has decidable word problem, admits a strongly aperiodic SFT. This is a very broad collection of groups because it includes ${\mathbb Z}^2\times H$ for any H with decidable word problem, as well as the group $\text {Sol}\cong {\mathbb Z}^2\rtimes {\mathbb Z}$ .

3. (iii) The work of Mozes implies that uniform lattices in simple Lie groups of rank at least 2 admit strongly aperiodic SFTs [Moz97].

4. (iv) The work of Jeandel shows that, ${\mathbb Z}\times T$ admits a strongly aperiodic SFT, where T denotes Thompson’s group T. (In fact, Jeandel shows that ${\mathbb Z}\times H$ admits a strongly aperiodic SFT whenever H acts on the circle in a way which satisfies certain dynamical conditions [Jea15a].)

5. (v) The work of the first two authors [CGS17] shows that the fundamental group of any closed hyperbolic surface admits a strongly aperiodic SFT.

6. (vi) Barbieri shows that the direct product of any three infinite finitely generated groups with decidable word problem admits a strongly aperiodic SFT [Bar19].

7. (vii) For every counting number n, the Baumslag–Solitar groups $B(1,n)$ and $B(n,n)$ each admit a strongly aperiodic SFT [AS20, EM20].

Note that, with the exception of surface groups and the $B(1,n)$ Baumslag–Solitar groups, all other known examples of strongly aperiodic SFTs are on groups which have a direct product of infinite groups as a subgroup (though in ${\mathbb H}^n$ there are constructions of strongly aperiodic sets of tiles, these do not give rise to SFTs on lattices). There remain many naturally occurring groups, including mapping class groups, ${{\text {Out}(F_n)}}$ , some Coxeter groups, and non-uniform lattices in higher -rank Lie groups (such as $SL(n;{\mathbb Z})$ in $SL(n;{\mathbb R})$ ), for which it is unknown whether strongly aperiodic SFTs exist. In this paper, we address the case of hyperbolic groups.

1.6 Hyperbolic groups

Hyperbolic groups, introduced by Gromov [Gro87], are groups whose Cayley graphs satisfy a geometric ‘slim triangles’ condition which holds in hyperbolic space. (See §3.2 for definitions and [BH99] as a comprehensive reference.) These groups are quite well-behaved—for example, they are always finitely presented and have decidable word problem. The class of hyperbolic groups includes fundamental groups of closed hyperbolic manifolds, free groups, so-called ‘random groups’ (with high probability), groups satisfying certain geometric small cancellation conditions, and many Coxeter groups.

Groups acting discretely on hyperbolic space have been studied for over a century. Dehn [Deh87] showed that the word problem for surface groups is decidable by producing, for any such group, a rewriting system that shortens a given word monotonically, ending with the empty word exactly when the given word represents the identity of the group. Another classic property of surface groups is that their growth rate is exponential. This was slowly generalized: In 1968, Milnor [Mil68] showed that under certain negativity assumptions on the curvature of a closed manifold, the growth rate of its fundamental group is exponential. Cannon studied geometric and algorithmic properties of discrete subgroups of hyperbolic isometries [Can84, Can91], laying the groundwork for shortlex automata soon implicit in the work of Gromov [Gro87] and taking center stage in the work of Epstein et al [ECH+92]. Finally Gromov [Gro87] defined hyperbolic groups, which include fundamental groups of closed negatively curved manifolds, showing that they have exponential growth and are the only groups in which Dehn’s algorithm can be applied.

Our main theorem gives a strongly aperiodic subshift on any one-ended hyperbolic group, resolving the question of existence of these for all hyperbolic groups.

2 Outline of the proof

In this section, we give an informal overview to facilitate reading the paper. In §3 we define our terms more precisely.

Suppose that G is a one-ended hyperbolic group. It is not hard to show (Proposition 3.3) that G admits an SFT where no finite-order element fixes a configuration. Our main goal is, thus, to find an SFT where no infinite-order element fixes a configuration, because by Proposition 3.4 we could then take a product of these subshifts and obtain a strongly aperiodic SFT on G. This goal will be fulfilled by the populated shellings defined in §8 or, more precisely, by the set of all local data associated with populated shellings. Roughly speaking, this attack combines two key ideas from the literature.

1. (i) Shortlex shellings, defined in §5, are inspired by the SFTs used in [CP93, Gro87] to ‘code’ the boundary of a hyperbolic group. The set of local data of shortlex shellings forms a non-empty SFT for which the stabilizer of every configuration is virtually cyclic.

2. (ii) Incommensurability was introduced in [Kar96, Moz97] as a tool to construct strongly aperiodic SFTs and tilings. We apply incommensurability of growth rates, which is the key tool used in [CGS17] to ‘kill’ infinite cyclic periods on certain subshifts on surface groups (by decorating these subshifts with extra data).

2.1 Incommensurability

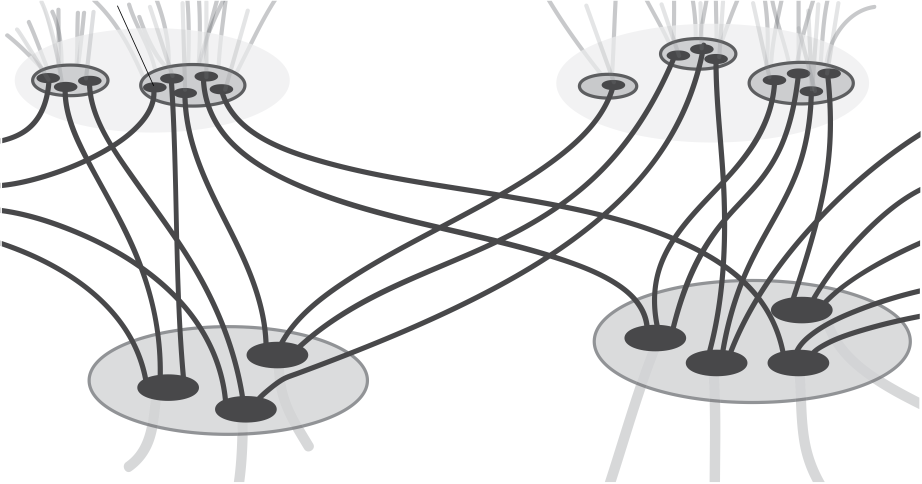
Fundamentally, as in [CGS17, GS05], our construction rests on the incommensurability of two distinct exponential growth rates (one arising as the growth of G, the other arbitrarily taken to be two or three). The illustration below demonstrates a similar phenomenon in the hyperbolic plane (drawn in the ‘horocyclic model’: vertical distances are accurate and horizontal ones scale exponentially with height; horizontal lines are horocycles).

Two patterns of ‘rectangles’ are shown, each rectangle having some predecessor above and some successors below. In the pattern drawn with dark lines, the number of rectangles doubles from row to row. In the gray pattern, light rectangles (which are all congruent) have one light and one dark rectangle as successors, and dark rectangles (which are all congruent) have one light and two dark successors. This system, asymptotically, has growth rate of $\phi ^2=((1+\sqrt {5})/2)^2$ ( $\phi $ is the golden ratio). The ratio of the spacing from row to row in either system is precisely fixed in relation to the other: $\log 2/\log \phi ^2$ . As this is not rational, the exact pattern of overlaps can never quite repeat from row to row.

By [CGS17, Main Technical Lemma] one may produce a strongly aperiodic tileset by decorating the gray tiles with the possible combinatorial data describing how they intersect the other tiling, such as how many dark lines intersect each edge of a gray tile, and requiring these decorations to match from tile to tile. More specifically, the sequence $(\Delta _i)$ consisting of the number of horizontal dark lines meeting the ith row of gray tiles could not be a periodic sequence, precisely because ${\log 2}/{\log (\phi ^2)}$ is irrational. (Note that in this case the elements of $(\Delta _{i})$ take only the values $1$ or $2$ .)

We will exploit this idea in our construction. Roughly speaking, we will be using ‘shortlex shellings’ to provide the underlying weakly aperiodic scaffolding (analogous to the gray tiling), on which we will place a second structure with incommensurate growth rate, ‘populated shellings’.

2.2 Shortlex shellings

In §5, we construct SFTs, much in the style of Gromov [Gro87] and Coornaert and Papadopoulos [CP93], which parameterize objects we call shortlex shellings (Definition 5.4). A shortlex shelling assigns some data to each element of G. These data impose simultaneously two compatible structures on G: a decomposition into horospherical layers (that is, layers which are locally modeled on spheres in G) and a spanning forest locally modeled on the tree of shortlex geodesics. We informally describe this here.

Given an arbitrary finitely generated group, with an ordered finite generating set, every group element g is represented by a unique word that is, first, a shortest representative of g (that is, a geodesic) and, second, earliest in the lexicographic ordering among all such geodesics (that is, a shortlex geodesic). In hyperbolic groups, the shortlex geodesics form a regular language, accepted by a shortlex finite-state automaton (FSA).

We define a model shelling, $X_0$ : to each group element $g\in G$ we associate the integer $h_0(g)=\operatorname {\mathrm {d}}(g,1_G)$ , the state $\operatorname{\textsf{state}}_0(g)$ of g in the shortlex FSA, and, for $g\neq 1_G$ , $P_0(g)$ , the unique element of G that precedes g on its shortlex geodesic from $1_G$ . A shortlex shelling is a function $X=(h,\operatorname{\textsf{state}},P)$ modeled on $(h_{0},\operatorname{\textsf{state}}_{0},P_{0})$ away from the identity (up to an additive constant for h). This means that on every finite subset $F\subset G$ , the restriction of X to F is identical to the restriction of $X_0$ to some translate of F which does not contain the identity, up to adding some constant integer, depending on F, to h.

A shortlex shelling $X=(h,\operatorname{\textsf{state}},P)$ is encoded by ‘local data’

, a function from G to a fixed finite set, where (for $g \in G$ and $a \in \mathcal S$ , a finite generating set for G)

is the derivative of h, defined as

and

is defined by taking

to be the generator a that takes us from g to $P(g)$ , that is, $P(g) = ga$ . We refer to level sets of h as horospheres (of X).

We construct local rules that are satisfied exactly by the local data of shortlex shellings, showing that the set forms a non-empty SFT (Proposition 5.5). This SFT factors onto $\partial G$ , the Gromov boundary of G, as do the subshifts suggested by Gromov [Gro87] and those constructed by Coornaert and Papadopoulos [CP93].

Because points of $\partial {G}$ have virtually cyclic stabilizers, it follows that these subshifts are all weakly aperiodic, more specifically, the stabilizer of any configuration in any of these subshifts is virtually cyclic and, hence, has infinite index (recall that G is one-ended). However, for any hyperbolic group, each of these subshifts has a configuration with infinite cyclic stabilizer and is not strongly aperiodic.

To that end, we construct populated shellings.

2.3 Populated shellings

In §8, we begin by fixing $q\in \{2,3\}$ such that no power of q is a power of the growth rate $\lambda $ of our shortlex machine; we say that q and $\lambda $ are incommensurable. We are going to define ‘populated shellings’, which decorate shortlex shellings with some extra data to kill any infinite cyclic periods, obtaining strong aperiodicity. In particular, a populated shelling of G consists of the following data:

1. (i) a shortlex shelling $X=(h,\operatorname{\textsf{state}},P)$ ;

2. (ii) a ‘population’ function ${\wp }:G{\rightarrow } \{0,\ldots ,n\}$ , for fixed population bound $ n \in {\mathbb N}$ ;

3. (iii) a ‘population growth’ function $\Delta $ constant on horospheres of X; and

4. (iv) a ‘parent–child matching’ function m

We further require that this data satisfies the following local rules. We think of elements of G as being villages, some of which are inhabited by people— ${\wp }(g)$ tells us the number of people living in g. Each person has some children who live nearby (at a bounded distance) in the next horosphere of X, and m describes this relationship, matching each child to its parent. Each person has exactly one parent, and a person living at some $g\in G$ has $q^{\Delta (g)}$ children.

We suggest this in the following diagram, with each parent living in a village in the lower horosphere having three children nearby in the next successive horosphere.

For a populated shelling Y, all of this information may be encoded by a function , called the ‘local data’ of the populated shelling, from G to a fixed finite set. By Proposition 8.5, the set of local data of populated shellings forms an SFT.

To prove our theorem, we show:

1. (i) that populated shellings exist for population bound n sufficiently large (Proposition 8.12); and

2. (ii) that their local data cannot have infinite-order periods (Proposition 9.5).

2.3.1 Infinite-order periods

We use the values of $\Delta $ to show that no populated shelling admits an infinite-order period. Recall that $\Delta $ was defined on group elements and required to be constant along on horospheres. As the horospheres naturally form a sequence, the values of $\Delta $ inherit a structure of a sequence $(\Delta _i)$ . We show that this sequence is not periodic, and that this implies that there are no infinite-order periods (this idea dates back to [Kar96]). In §9, we show that for certain finite sets S, the cardinality of $P^{-n}(S)$ must grow as $\lambda ^n$ . On the other hand, using the fact that quasi-geodesics stay close to geodesics in a hyperbolic group, Lemma 9.2 will show that:

1. (i) a sufficiently large finite set S, contained in a single horosphere, contains a person all of whose descendants live in $P^{-n}(S)$ ; therefore, the population of $P^{-n}(S)$ grows at least as fast as $q^{\sum \Delta }$ (the number of descendants of that person) (by $\sum \Delta $ we mean the sum of the values of $(\Delta _i)$ along n consecutive horospheres starting with the horosphere containing S);

2. (ii) all descendants of people in S live in $P^{-n}(S')$ for some finite set $S' \supset S$ , which will imply that the population of $P^{-n}(S)$ grows at most as fast as $K q^{\sum \Delta }$ (the number of descendants of the population of $S'$ , where $K>0$ is the total population of $S'$ ).

From this, it easily follows that $({1}/{n})\sum \Delta \log (q){\rightarrow }\log (\lambda )$ , which implies that the sequence $(\Delta _i)$ cannot be periodic by our incommensurability hypothesis. Lemma 9.1 implies that $(\Delta _i)$ would be periodic if the populated shelling Y had a period of infinite order, so we conclude (Proposition 9.5) that Y has no infinite-order period.

2.3.2 Existence

In §8.2, we show that populated shellings exist (Proposition 8.12), using the following strategy.

1. (i) We construct a sequence $(\nu _i,\Delta _i)$ such that each $\nu _i\in [A,qA]$ for an arbitrary fixed A, and each $\Delta _i \in \{\lfloor {\log _q\lambda }\rfloor , \lceil {\log _q\lambda }\rceil \}$ , satisfy $ q^{\Delta _i} \nu _i =\lambda \nu _{i+1} $ . In the figure in the section on Incommensurability, this $\Delta _i$ is analogous to the number of dark horizontal lines meeting the ith row of the gray tiling, whereas $\nu _i$ is analogous to the average frequency of dark-outlined tiles meeting each gray tile in the ith row of the gray tiling.

2. (ii) We show that, given such a sequence $\nu _i$ , it is possible to populate horospheres so that the ith horosphere has population density $\nu _i$ . In particular, the sum of ${\wp }$ over any finite set in a horosphere is equal to $\nu _i \times \mu (S)$ up to error bounded by $2\mu (\partial S)$ ( $\mu $ will be defined momentarily).

3. (iii) We use the Hall marriage theorem trick to show that when a density sequence is realized by a population function in this way, one may find a suitable parent–child matching.

2.4 Technical tools

Let $X=(h,\operatorname{\textsf{state}},P)$ be a shortlex shelling.

2.4.1 Measure

To regularize the growth of sets under $P^{-1}$ we describe a non-negative function $\mu $ defined on states of the shortlex machine with the following properties:

1. (i) the $\mu $ of a state $a \times \lambda $ is equal to the sum of $\mu (b)$ over the states b which may follow a in the shortlex machine, so that for any $w\in G$ we have

   $$ \begin{align*}\sum_{P(v)=w} \mu\circ\operatorname{\textsf{state}}(v) =\lambda ( \mu\circ\operatorname{\textsf{state}}(w)); \end{align*} $$

2. (ii) the set of vertices on which $\mu \circ \operatorname{\textsf{state}}$ is positive is dense.

In §3.3, similarly to [DFW19], we produce a left eigenvector of the transition matrix of the shortlex machine, with eigenvalue $\lambda $ , whose support consists of states with ‘maximal growth’—that is, states whose number of nth successors grows at the same rate as the group itself. In §6, we confirm that such states are dense in every shortlex shelling.

Remark 2.1. In the following diagram, we see a similar phenomenon for a tiling in the hyperbolic plane (using the horocyclic model): there are three types of ‘rectangular’ tiles, representing three states of an FSA, say $\texttt {a}, \texttt {b}$ , and $\texttt {c}$ ; these states correspond to the light, medium, and dark tiles, respectively. The ways these tiles may fit together one above some others, represent the FSA transitions $\texttt {a}\mapsto \texttt {a}, \texttt {c}, \texttt {b}$ ; $\texttt {b}\mapsto \texttt {a}, \texttt {b}$ ; $\texttt {c}\mapsto \texttt {c}, \texttt {b}$ . The widths of the rectangles are precisely in the proportions of the left eigenvector of the corresponding transition matrix. The bold vertical line marks a possible infinite cyclic symmetry, shifting by one row.

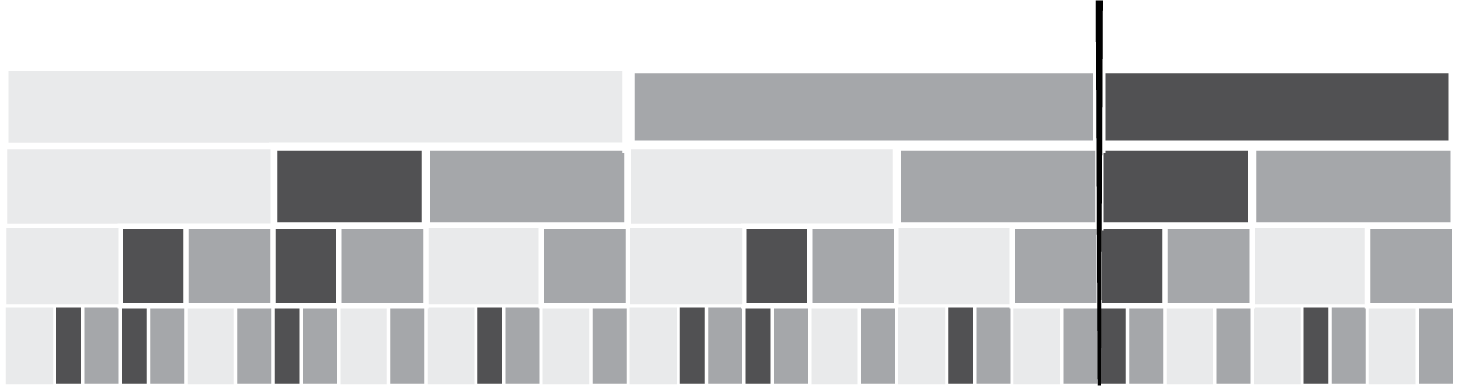
2.4.2 Divergence graphs

In §7, we define the ‘divergence graph’, a graph structure on each horosphere $H=h^{-1}(n)$ whose vertices are points $v\in H$ such that $\mu \circ \operatorname{\textsf{state}}(v)$ is positive, and two such vertices $v,w$ are connected by an edge exactly when their successor sets $P^{-n}\{v\},P^{-n}\{w\}$ remain at a bounded distance as $n{\rightarrow }\infty $ . These divergence graphs have two advantages.

First, they behave nicely under the successor map $P^{-1}$ : any pair of vertices connected by an edge will have some pair of successors that are also connected by an edge. In other words, every edge has one or more successor edges. Moreover, every edge has either a vertex or an edge as its predecessor, as indicated in the following diagram, with a larger, paler predecessor divergence graph in the background on one horosphere, and a smaller, darker successor on the next horosphere.

Second, exactly when a hyperbolic group is one-ended, its divergence graphs are connected (Lemma 7.4), as we show using the cutpoint conjecture (proved in [Swa96]). This is necessary in our construction to ensure that there are local rules which force the growth rate $\Delta $ to be constant on each particular horosphere.

2.4.3 Translation-like actions

To distribute the density of villagers about a horosphere, we shall use a translation-like action of ${\mathbb Z}$ on the divergence graph—that is, we cover the vertices of the divergence graph with disjoint ‘paths’ or injected images of ${\mathbb Z}$ .

A theorem of Seward shows that this may be done on any one- or two-ended connected graph with bounded degree, and in §4, we generalize this to any locally finite, countably infinite and connected graph.

3 Set-up

In this section, we establish our conventions and notation, and give foundational material for our construction. Section 3.1 recalls the definition of an SFT and explains why, in proving our main theorem, it is enough to give an SFT without infinite-order periods. Section 3.2 gives the definition of hyperbolic groups and their boundaries, as well as several lemmas describing their geometry which will be used throughout the following. Section 3.3 defines the shortlex automaton for a hyperbolic group and proves the important Proposition 3.17, which says that we may weigh each state of the shortlex FSA so that states of maximal growth have positive weight and the sum of the weights of the successors of any state a is equal to the growth rate of the group times the weight of a. Section 3.4 defines the derivative of a $1$ -Lipschitz function on a finitely generated group, and describes what we mean by ‘horofunction’.

We take ${\mathbb N}:=\{1,2,3,\ldots \}$ . We denote the number of elements of a finite set A by $\#A$ . We denote sequences as $(a_{n})_{n \in {\mathbb N}}$ (we sometimes write $(a_{n})$ ). The notation $[a..b]$ denotes the interval between a and b in ${\mathbb Z}$ , that is,

$$ \begin{align*}[a..b] := \{n \in {\mathbb Z}\ |\ a \leq n \leq b\}. \end{align*} $$

For infinite intervals, we write ${\mathbb Z}_{\geq a}$ , or ${\mathbb Z}_{\leq b}$ , or ${\mathbb Z}$ . For sums of values of some function f over some set R, we write $f_R := \sum _{x\in R} f(x)$ . We also write $f_{m..n}:=\sum _{k=m}^n f(k)$ .

We work exclusively in the discrete setting. A graph $\Gamma $ is a pair $(V(\Gamma ),E(\Gamma ))$ . The edges induce a metric on the vertices of a connected graph by setting $\operatorname {\mathrm {d}}(u,v) = 1$ whenever $u \neq v$ are vertices connected by an edge. A geodesic is a (globally) metric preserving map $\gamma :I \to X$ , where I is an interval in ${\mathbb Z}$ and $(X,\operatorname {\mathrm {d}})$ is a metric space; that is, for any $t_{1},t_{2} \in I$ we have $\operatorname {\mathrm {d}}(\gamma (t_{1}),\gamma (t_{2})) = |t_{1} - t_{2}|$ .

This paper is concerned with a fixed finitely generated group G with identity $1_G$ and a fixed finite generating set $\mathcal S = \mathcal S^{-1}$ .

As is customary we denote the set of finite words in letters of $\mathcal S$ by $\mathcal S^{*}$ (this includes the empty word), and identify a word w in $\mathcal S^{*}$ with the corresponding product $g \in G$ and say that w represents g. Because $\mathcal S$ generates G, this defines a map from $\mathcal S^{*}$ onto G. We denote the length of a word $w \in \mathcal S^{*}$ by $l(w)$ and for $g \in G$ we set

$$ \begin{align*} |g| := \min \{l(w) \ |\ w \in \mathcal S^{*}, w \text{ represents } g\}. \end{align*} $$

This induces a distance function on G called the word metric by setting

$$ \begin{align*} \operatorname{\mathrm{d}}(g_{1},g_{2}) = |g_{1}^{-1} g_{2}|. \end{align*} $$

It is well known, and easy to see, that d is indeed a metric turning G into a geodesic space—that is, for any $g_{1},g_{2} \in G$ there exist a geodesic $\gamma :[0..\operatorname {\mathrm {d}}(g_{1},g_{2})] \to G$ with $\gamma (0) = g_{1}$ and $\gamma (\operatorname {\mathrm {d}}(g_{1},g_{2})) = g_{2}$ . We denote balls as $B(r,g):=\{h\in G\ \mid \ \operatorname {\mathrm {d}}(h,g)\leq r\}$ .

Multiplication on the left defines an action of the group on itself by isometries:

$$ \begin{align*} \operatorname{\mathrm{d}}(g g_{1},g g_{2}) = |(g g_{1})^{-1} g g_{2}| = |g_{1}^{-1} g_{2}| = \operatorname{\mathrm{d}}(g_{1},g_{2}). \end{align*} $$

We say that $A \subset G$ is connected if there exists a path connecting any $g_{1},g_{2} \in A$ , by which we mean that there exists $\gamma :[a..b] \to A$ (for some $a,b \in {\mathbb Z}$ ) so that for any $t \in [a..b-1]$ we have that $\operatorname {\mathrm {d}}(\gamma (t),\gamma (t+1)) = 1$ .

Lemma 3.1. (Discrete Arzelà–Ascoli)

Let I be a possibly unbounded interval in ${\mathbb Z}$ . Let $(\gamma _n:I\to G)_{n\in {\mathbb N}}$ be a sequence of geodesics. If for each $t\in I$ , $(\gamma _n(t))_{n\in {\mathbb N}}$ takes finitely many values, then $(\gamma _{n})$ subconverges pointwise to some geodesic $\gamma $ .

Proof Convergence is obvious. For any interval $[a..b]\subset I$ , there is some $\gamma _{n}$ such that $\gamma |_{[a..b]}$ agrees with $\gamma _{n}|_{[a..b]}$ . Consequently, $b-a=\operatorname {\mathrm {d}}(\gamma (a),\gamma (b))$ . It follows that $\gamma $ is a geodesic.

3.1 SFTs

We give several standard definitions as follows.

Definition 3.2. Let G be a group and A some finite set equipped with the discrete topology. The full shift on G is $A^G:=\{\omega :G{\rightarrow } A\}$ with the product topology and the right G action given by $(\omega \cdot g)(h):=\omega (gh)$ . We call elements of $A^G$ configurations. By Tychonoff’s Theorem, $A^G$ is compact.

A cylinder set in ${\mathcal A}^G$ is a set of the form $ \prod _{g\in G} U_g$ , with each $U_g\subseteq {\mathcal A}$ and for all but finitely many $g\in G$ , $U_g={\mathcal A}$ . A clopen set is the finite union of cylinder sets.

A subset $\Omega $ of $A^G$ is said to be a subshift if it is closed and invariant under the right G action. A subshift $\Omega $ is called an SFT if there exists clopen $Z_1,\ldots ,Z_n$ such that $\Omega =\bigcap _{g\in G;i=1,\ldots ,n}Z_i\cdot g$ . We think of the $Z_i$ that define $\Omega $ as giving us ‘local rules’ which determine membership in $\Omega $ : to determine whether $\omega \in A^G$ is a configuration in $\Omega $ , we must see whether $\omega \cdot g$ is in $Z_i$ for all $g\in G$ and $i=1,\ldots ,n$ . In other words, we must check that $\omega $ takes on a prescribed form near every point in G.

We say that an SFT $\Omega $ is strongly aperiodic if it is non-empty and for any configuration $\omega \in \Omega $ we have that $\text {Stab}_G\omega =\{1_G\}$ , where $\text {Stab}_G\omega $ is the stabilizer of $\omega $ .

In the next proposition, we observe that any group with only finitely many conjugacy classes of torsion elements admits an SFT with no torsion elements in the stabilizer of any configuration. It is well-known that hyperbolic groups satisfy this condition (see, for example, [BH99, Theorem III. $\varGamma$ .3.2]).

That finite groups admit strongly aperiodic SFTs is trivial, but we include this within the following proposition for efficiency.

Proposition 3.3. Any finitely generated group with finitely many conjugacy classes of torsion elements admits a non-empty SFT $\Omega $ such that for all $\omega \in \Omega $ , $\text {Stab}_G\omega $ has no torsion elements.

It follows that any finite group admits a strongly aperiodic SFT.

Proof Let $g_1,\ldots , g_n$ be representatives of the conjugacy classes of the torsion elements in G. Let $N := \max |g_i|$ and $B:=B(N,1_G)$ . We define our SFT $\Omega \subset B^G$ as

$$ \begin{align*}\Omega:=\{\omega\in B^G\ | \ \text{ for any } g,g' \in G, \text{ if } \operatorname{\mathrm{d}}(g,g') \leq N \text{ then } \omega(g) \neq \omega(g')\}.\end{align*} $$

We show that $\Omega $ is non-empty: suppose we have assigned elements of B to some subset H of G. Let $g\in G\setminus H$ . This g is within N of at most $\#B-1$ elements of H, and so can be assigned some element of B distinct from any of those assigned to elements of H. This process defines an element $\omega \in \Omega $ , showing that $\Omega $ is not empty.

Let h be a torsion element of G, with $h=cg_i c^{-1}$ for some c and representative torsion element $g_i$ . Then $\operatorname {\mathrm {d}}(c,hc)= \operatorname {\mathrm {d}}(c,cg_ic^{-1}c)=\operatorname {\mathrm {d}}(c,cg_i)=\operatorname {\mathrm {d}}(1_G,g_i)=|g_i|\leq N$ .

Thus, for $\omega \in \Omega $ , $\omega (c)\neq \omega (hc)$ and so $\omega \cdot h \neq \omega $ . The proposition follows.

Our main result would give an SFT in which no configuration is stabilized by an element of infinite order. The next proposition shows that we can combine it with an SFT as constructed above to obtain a strongly aperiodic SFT as follows.

Proposition 3.4. If group G admits a non-empty SFT $\Omega _1$ such that for all $\omega _1\in \Omega _1$ , $\text {Stab}_G\omega _1$ has no torsion elements, and G admits a non-empty SFT $\Omega _2$ such that for all $\omega _2\in \Omega _2$ , $\text {Stab}_G\omega _2$ has no infinite-order elements, then G admits a strongly aperiodic SFT.

Proof Consider $\Omega = \Omega _1 \times \Omega _2$ with the diagonal G action. Suppose $\omega =(\omega _1,\omega _2) \in \Omega $ is invariant under $g \in G$ . Then both $\omega _1$ and $\omega _2$ are invariant under $g \in G$ , showing that g is neither torsion nor has infinite order, hence g is trivial.

3.2 Hyperbolic groups

Let G be a group generated by a finite set $\mathcal S$ , endowed with the word metric with respect to $\mathcal S$ .

Definition 3.5. Let $\delta>0$ . As suggested in the following diagram, a geodesic triangle in G is said to be $\delta $ -slim if every side is contained in the $\delta $ -neighborhood of the other two sides. We say that G is $\delta $ -hyperbolic if every geodesic triangle in G is $\delta $ -slim. If for some $\delta $ , G is $\delta $ -hyperbolic, we call G a hyperbolic group.

3.2.1 Properties of hyperbolic groups

A hyperbolic group is finitely presented [BH99, Corollary III. $\varGamma$ .3.26] and has, at most, finitely many conjugacy classes of finite-order elements [BH99, Theorem III. $\varGamma$ .3.2].

Definition 3.6. We say that G is one-ended if for all compact $K\subset H$ , $G\setminus K$ contains exactly one unbounded connected component.

Assumption. Henceforth, we assume that G is a one-ended hyperbolic group equipped with a fixed finite generating set $\mathcal S=\mathcal S^{-1}$ .

The following lemma introduces a technique which will be used frequently.

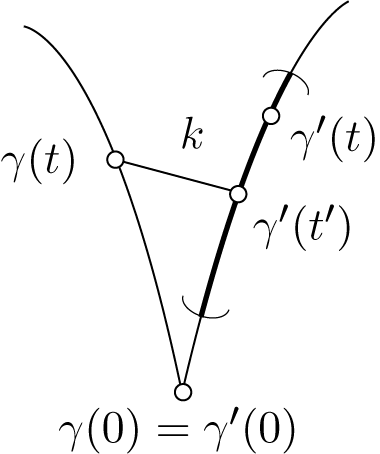
Lemma 3.7. (Repairing a ladder)

Let ${I},{I}'$ be intervals containing $0$ and let $\gamma :{I}{\rightarrow } G$ and $\gamma ':{I}'{\rightarrow } G$ be geodesics with $\gamma (0)=\gamma '(0)$ . If $\operatorname {\mathrm {d}}(\gamma (t),\gamma '(t'))\leq k$ for some $t\in {I},t'\in {I}'$ , then $\operatorname {\mathrm {d}}(\gamma (t),\gamma '(t))\leq 2k$ .

Proof Because $\gamma (0)=\gamma '(0)$ we have

$$ \begin{align*}t'=\operatorname{\mathrm{d}}(\gamma'(0),\gamma'(t')) \leq \operatorname{\mathrm{d}}(\gamma'(0),\gamma(t))+\operatorname{\mathrm{d}}(\gamma(t),\gamma(t')) \leq t+k,\end{align*} $$

and, by symmetry, $t\leq t'+k$ , so that

$$ \begin{align*}\operatorname{\mathrm{d}}(\gamma'(t'),\gamma'(t))=|t-t'|\leq k.\end{align*} $$

It follows that

$$ \begin{align*}\operatorname{\mathrm{d}}(\gamma(t),\gamma'(t)) \leq\operatorname{\mathrm{d}}(\gamma(t),\gamma'(t'))+\operatorname{\mathrm{d}}(\gamma'(t),\gamma'(t'))\leq 2k.\end{align*} $$

The next lemma gives some bounds on how long two geodesics from the same point will fellow travel.

Lemma 3.8. Let ${I}$ and be an interval containing $0$ , and let $\gamma :{I}\to G$ and $\gamma ':{I}{\rightarrow } G$ be geodesics with $\gamma (0)=\gamma '(0)$ . Suppose $t, T\in {I}$ are such that $t < T-\operatorname {\mathrm {d}}(\gamma (T),\gamma '(T))-2\delta ,$ then $\operatorname {\mathrm {d}}(\gamma (t),\gamma '(t))\leq 2\delta .$

Proof By slim triangles, $\gamma (t)$ is within $\delta $ of either $\gamma '$ or the geodesic ${\tilde {\gamma }}$ connecting $\gamma (T)$ to $\gamma '(T)$ . In the latter case, we have some $t'$ such that $\operatorname {\mathrm {d}}({\tilde {\gamma }}(t'),\gamma (t))\leq \delta $ and, thus,

$$ \begin{align*}\operatorname{\mathrm{d}}(\gamma(t),\gamma(T))\leq \operatorname{\mathrm{d}}(\gamma(t),{\tilde{\gamma}}(t'))+\operatorname{\mathrm{d}}({\tilde{\gamma}}(t'),\gamma(T))\leq \delta + \operatorname{\mathrm{d}}(\gamma(T),\gamma'(T)),\end{align*} $$

contradicting $\operatorname {\mathrm {d}}(\gamma (t),\gamma (T))=|T-t|>\operatorname {\mathrm {d}}(\gamma (T),\gamma '(T))+2\delta .$

Hence, $\gamma (t)$ is within $\delta $ of $\gamma '$ , so that there is some $t'$ such that $\operatorname {\mathrm {d}}(\gamma (t),\gamma '(t'))\leq \delta $ , and we may apply Lemma 3.7 to see that $\operatorname {\mathrm {d}}(\gamma (t),\gamma '(t))\leq 2\delta $ .

3.2.2 Slim quads

Consider a geodesic quad, that is, a union of geodesic segments of the form $\overline {AB},\overline {BC},\overline {CD},\overline {DA}$ . Because any diagonal of the quad is in the $\delta $ -neighborhood of each pair of sides it cuts off, it is clear that each side of the quad is within a $2\delta $ -neighborhood of the union of the other three. We now show how this implies bounds on the distance between corresponding points on two geodesic segments of equal length.

Lemma 3.9. Let $\gamma , \gamma ':[0..T]{\rightarrow } G$ be geodesics and let

$$ \begin{align*}k_0 = \operatorname{\mathrm{d}}(\gamma(0),\gamma'(0)),\quad k_T=\operatorname{\mathrm{d}}(\gamma(T),\gamma'(T)),\quad k=\max\{k_0,k_T\}.\end{align*} $$

For $0\leq t\leq T$ , we have

$$ \begin{align*}\operatorname{\mathrm{d}}(\gamma(t),\gamma'(t))\leq 3k+4\delta.\end{align*} $$

If $k_0+2\delta < t <T-k_T-2\delta $ , then $\operatorname {\mathrm {d}}(\gamma (t),\gamma '(t))\leq \min \{k_0,k_T\}+4\delta $ .

Proof Let ${\tilde {\gamma }}:\tilde {{I}}{\rightarrow } G$ be a geodesic connecting $\gamma (0)$ to ${\gamma '}(0)$ and ${\tilde {\gamma }}':\tilde {{I}}'{\rightarrow } G$ a geodesic connecting $\gamma (T)$ to ${\gamma '}(T)$ . Each side of the geodesic quad spanned by $\gamma ,{\tilde {\gamma }}',{\gamma '},{\tilde {\gamma }}$ is within the $2\delta $ neighborhood of the other three. In particular, $\gamma (t)$ must be within $2\delta $ of a point of ${\tilde {\gamma }}$ , ${\gamma '}$ , or ${\tilde {\gamma }}'$ .

Suppose first that there is some $t'\in \tilde {{I}}$ such that $\operatorname {\mathrm {d}}(\gamma (t),{\tilde {\gamma }}(t'))\leq 2\delta $ . By the triangle inequality, $t=\operatorname {\mathrm {d}}(\gamma (0),\gamma (t)) \leq \operatorname {\mathrm {d}}(\gamma (0),{\tilde {\gamma }}(t'))+\operatorname {\mathrm {d}}({\tilde {\gamma }}(t'),\gamma (t)) \leq k_0+2\delta $ . It follows that

$$ \begin{align*}\operatorname{\mathrm{d}}(\gamma(t),\gamma'(t)) &\leq\operatorname{\mathrm{d}}(\gamma(t),\gamma(0))+\operatorname{\mathrm{d}}(\gamma(0),{\gamma'}(0))+\operatorname{\mathrm{d}}({\gamma'}(0),{\gamma'}(t))\\ &= k_0+2\delta+k_0+k_0+2\delta\leq 3k_0+4\delta.\end{align*} $$

The case where $\gamma (t)$ is close to some ${\tilde {\gamma }}'(t')$ is similar, so we omit the proof.

Now suppose there is some $t'\in {I}$ such that $\operatorname {\mathrm {d}}(\gamma (t),{\gamma '}(t'))\leq 2\delta $ (note that we are always in this case if $k_0+2\delta <t<T-k_T-2\delta $ .) We have

$$ \begin{align*} T=&\operatorname{\mathrm{d}}({\gamma'}(0),{\gamma'}(T)) \\ & \leq\operatorname{\mathrm{d}}({\gamma'}(0),{\gamma'}(t'))+\operatorname{\mathrm{d}}({\gamma'}(t'),\gamma(t)) +\operatorname{\mathrm{d}}(\gamma(t),\gamma(T))+\operatorname{\mathrm{d}}(\gamma(T),{\gamma'}(T))\\ &\leq t'+2\delta+T-t+k_T, \end{align*} $$

so that $t'\geq t-k_T-2\delta $ . An entirely symmetric computation shows that $t\geq t'-k_T-2\delta $ and, hence,

$$ \begin{align*}|t-t'|\leq k_T+2\delta,\end{align*} $$

so that

$$ \begin{align*}\operatorname{\mathrm{d}}(\gamma(t),{\gamma'}(t)) \leq\operatorname{\mathrm{d}}(\gamma(t),{\gamma'}(t'))+\operatorname{\mathrm{d}}({\gamma'}(t'),{\gamma'}(t))\leq 2\delta+|t-t'| \leq k_T+4\delta. \end{align*} $$

Reversing $\gamma $ and ${\gamma '}$ , we also get the bound $\operatorname {\mathrm {d}}(\gamma (t),{\gamma '}(t))\leq k_0+4\delta $ . Hence, $\operatorname {\mathrm {d}}(\gamma (t), \gamma '(t)) \leq \min \{k_0,k_T\}+4\delta $ as desired.

3.2.3 Asymptotic geodesics stay close

We now show that the previous lemmas provide some constraints on the behavior of two geodesic rays which do not diverge from each other.

Definition 3.10. Two geodesic rays $\gamma ,\gamma ':{{\mathbb Z}_{\geq 0}}{\rightarrow } G$ are said to be asymptotic if $\operatorname {\mathrm {d}}(\gamma (t),\gamma '(t))$ is bounded—manifestly, this is an equivalence relation. We write $[\gamma ]$ for the equivalence class of $\gamma $ .

Lemma 3.11. Let $\gamma ,\gamma ':{{\mathbb Z}_{\geq 0}}{\rightarrow } G$ be asymptotic geodesic rays. For sufficiently large p, there exists q such that $\operatorname {\mathrm {d}}(\gamma (p),\gamma '(q))\leq 2\delta $ . Moreover, for all $t\in {{\mathbb Z}_{\geq 0}}$ ,

$$ \begin{align*}\operatorname{\mathrm{d}}(\gamma(t),\gamma'(t))\leq 3\operatorname{\mathrm{d}}(\gamma(0),{\gamma'}(0))+4\delta.\end{align*} $$

Finally, if $\gamma (0)={\gamma '}(0)$ , then $\operatorname {\mathrm {d}}(\gamma (t),{\gamma '}(t))\leq 2\delta $ for all $t\in {{\mathbb Z}_{\geq 0}}.$

Proof Choose $k>\sup _{t\in {{\mathbb Z}_{\geq 0}}}\operatorname {\mathrm {d}}(\gamma (t),{\gamma '}(t))$ .

For $p>k+2\delta $ , choose $T>p+k+2$ and consider a quad with sides $\gamma |_{[0..T]}$ and ${\gamma '}|_{[0..T]}$ together with geodesic segments ${\tilde {\gamma }}$ and $\hat {\gamma }$ connecting their endpoints. Because this quad is $2\delta $ -slim, we have that $\gamma (p)$ must be within $2\delta $ of one of the other three sides, and by the triangle inequality it cannot be close to ${\tilde {\gamma }}$ or $\hat {\gamma }$ . It follows that for some q, $\operatorname {\mathrm {d}}(\gamma (p),\gamma (q))\leq 2\delta $ .

Given t, choose $T>t+k+2\delta $ . If $t\leq \operatorname {\mathrm {d}}(\gamma (0),{\gamma '}(0))+2\delta $ , then we see directly that

$$ \begin{align*} \operatorname{\mathrm{d}}(\gamma(t),{\gamma'}(t)) &\leq\operatorname{\mathrm{d}}(\gamma(t),\gamma(0))+\operatorname{\mathrm{d}}(\gamma(0),{\gamma'}(0))+\operatorname{\mathrm{d}}({\gamma'}(0),{\gamma'}(t))\\ & \leq \operatorname{\mathrm{d}}(\gamma(0),{\gamma'}(0))+2\delta+\operatorname{\mathrm{d}}(\gamma(0),{\gamma'}(0))+\operatorname{\mathrm{d}}(\gamma(0),{\gamma'}(0))+2\delta\\ & =3\operatorname{\mathrm{d}}(\gamma(0),{\gamma'}(0))+4\delta \end{align*} $$

as desired. Otherwise, the last part of Lemma 3.9 yields the desired result.

The last part follows from Lemma 3.7 and the slim triangles condition or [BH99, Lemma III.H.3.3].

3.2.4 The boundary of a hyperbolic group

We now define a compact space, equipped with a G action, known as the boundary of G (see [BH99, §III.H.3] for details). Recall that $[\gamma ]$ is the equivalence class of all rays asymptotic to $\gamma $ .

Definition 3.12. Let $\partial G$ be the set of all equivalence classes $[\gamma ]$ as $\gamma $ ranges over geodesic rays in G. Here, G acts on $\partial G$ via left multiplication, so that $g\cdot [\gamma ]$ is given by the class of $t\mapsto g\gamma (t)$ .

To define a topology on $\partial G$ , fix some basepoint $p\in G$ . Given $\eta _n$ , a sequence of points of $\partial G$ and $\eta \in \partial G$ , we say that $\eta _n$ converges to $\eta $ if $\eta _n$ can be represented by a sequence of geodesics $\gamma _n$ with each $\gamma _n(0)=p$ and every subsequence of $\gamma _n$ subconverges pointwise to a geodesic ray representing $\eta $ . We topologize $\partial G$ so that a set K is closed if and only if K contains the limit of every convergent sequence of points of K.

The topology of $\partial G$ is independent of choice of basepoint [BH99, Proposition III.H.3.7]. We sometimes write $[\gamma ]$ for the element of $\partial G$ represented by a geodesic ray $\gamma $ .

Lemma 3.13. Let $(\gamma _n),(\gamma ^{\prime }_n)$ be sequences of geodesic rays such that $[\gamma _n]=[{\gamma '}_n]$ for all n and $\gamma _n$ converges pointwise to some geodesic ray $\gamma $ . If $\#\{\gamma ^{\prime }_n(0)\}<\infty $ , then $\gamma ^{\prime }_n$ subconverges pointwise to some $\gamma '$ asymptotic to $\gamma $ .

Proof By passing to a subsequence, we may assume without loss of generality that $\gamma _n(0)$ and ${\gamma '}_n(0)$ are constant sequences. Let $k=\operatorname {\mathrm {d}}(\gamma _n(0),{\gamma '}_n(0))$ . By Lemma 3.1, $\gamma ^{\prime }_n$ subconverges pointwise to some geodesic ray ${\gamma '}$ . By Lemma 3.11,

$$ \begin{align*}\operatorname{\mathrm{d}}(\gamma_n(t),{\gamma'}_n(t))\leq 3k+4\delta\end{align*} $$

for all n and t. It follows that $\operatorname {\mathrm {d}}(\gamma (t),{\gamma '}(t))\leq 3k+4\delta $ for all t and, hence, $[\gamma ]=[{\gamma '}]$ .

Three geodesics $\gamma _1$ , $\gamma _2$ , and $\gamma _3$ define an ideal triangle if and only if $\gamma _i(\infty ) = \gamma _{(i+1)}(-\infty )$ , the indices taken modulo 3.

Lemma 3.14. Any ideal triangle is $3\delta $ -slim.

Proof We first note that any (finite) hexagon is $3\delta $ -slim. Let p be a point on the hexagon, and divide the hexagon into two triangles and a quad as shown in the following. The result follows because quads are $2\delta $ -slim and triangles are $\delta $ -slim.

Let p be a point on an ideal triangle. Because the geodesics of the ideal triangle are pairwise asymptotic we may truncate the ideal triangle, forming a hexagon so that the new edges are more than $3\delta $ from p. This hexagon is $3\delta $ -slim, but p cannot be close to any point on the new edges. Hence, p is within $3\delta $ of some point on one of the other two geodesics in the ideal triangle.

3.3 Growth in a shortlex FSA

A remarkable fact about hyperbolic groups is that the language of shortlex geodesics is regular—we recall the relevant definitions here. For a detailed discussion, see, for example, [CF10, DFW19, ECH+92].

An FSA on alphabet $\mathcal S$ (where here $\mathcal S$ is an arbitrary finite set) is a directed graph whose edges are labeled by elements of $\mathcal S$ (for a formal definition, see, for example, [ECH+92]). The vertices of the FSA are called states. Sometimes we consider FSAs that have a special state called start; in that case, we only consider finite directed paths starting at that state, and we assume that the FSA had been pruned, that is, states that cannot be reached from the start state have been removed. Sometimes we consider FSAs without a start state, in which case we consider all finite directed paths in the FSA. The collection of all words obtained by reading the edge labels of finite directed paths in an FSA (with or without a start state) forms a subset of $\mathcal S^*$ (the collection of all finite words in $\mathcal S$ , including the empty word); a subset of this form is called a regular language.

3.3.1 Notation

Let $\Gamma $ be an FSA with states $V(\Gamma )$ . For a set of states $A\subset V(\Gamma )$ , we let $\Gamma (A)$ denote the subgraph spanned by A (itself an FSA). We let $[\Gamma ]$ denote the adjacency matrix (that is, if we number the states $\{a_1,\ldots ,a_n\}$ , $[\Gamma ]_{ij}$ denotes the number of transitions from $a_j$ to $a_i$ ). If a word $w\in S^*$ labels a valid path from a state a to a state b, we write $a{\buildrel w\over {\rightarrow }} b$ . If $a,b\in V(\Gamma )$ are such that $a{\buildrel w\over {\rightarrow }} b$ and $b{\buildrel w'\over {\rightarrow }} a$ (for some $w,w' \in S^*$ ), we say that $a\approx b$ . It is clear that $\approx $ is an equivalence relation (note that $a\approx a$ always holds, as the path may have length zero). The equivalence classes are called components. The Perron–Frobenius (PF) theorem asserts the following.

Lemma 3.15. If $A\subset V(\Gamma )$ is a component and $\#A\geq 2$ , then the largest modulus eigenvalue $\lambda _A$ of $[\Gamma (A)]$ is positive and has a positive left eigenvector.

3.3.2 The shortlex automaton

Recall our convention that $\mathcal S$ is a symmetric generating set for the one-ended hyperbolic group G. We say that $s_1\cdots s_{\ell }\in \mathcal S^*$ is a geodesic if $\ell $ is the minimal length of any word representing the same element of G as $s_1\cdots s_{\ell }$ . The collection of all geodesic words forms a regular language [ECH+92, Theorem 3.4.5]. Order the elements of $\mathcal S$ —this induces a lexicographic order on $\mathcal S^*$ . A word $s_1\cdots s_{\ell }$ is a shortlex geodesic if it is a geodesic and no geodesic representing the same group element precedes it in the lexicographic order. The set of all shortlex geodesics forms a regular language [ECH+92, Proposition 2.5.2], called the language of shortlex geodesics in G (and with generators $\mathcal S$ .)

Definition 3.16. Let $\lambda :=\lim _{i{\rightarrow }\infty }\#B(i,1_G)^{1/i}$ be the growth rate of G with respect to $\mathcal S$ (see, for example, [DFW19]). Let ${\mathcal M}$ denote a pruned FSA for the language of shortlex geodesics in G, and let ${\mathcal A}$ denote the vertex set of ${\mathcal M}$ .

We are going to show that $\lambda $ is an eigenvalue of the transition matrix $[{\mathcal M}]$ with a left eigenvector supported on a certain set of states (later we show that these states are dense in G). Write $\lambda _B$ for the PF eigenvalue of a component $B\subset {\mathcal A}$ . By [DFW19, Theorem 3.3, Corollary 3.7], $\lambda $ is equal to the maximum of the $\lambda _B$ . We say that a component B is big if $\lambda =\lambda _B$ .

Partition ${\mathcal A}$ into sets ${{\mathcal A}_{\text {max}}}\sqcup {{\mathcal A}_{\text {big}}}\sqcup {{\mathcal A}_{\text {min}}}$ where:

1. (i) ${{\mathcal A}_{\text {big}}}$ is the union of the big components;

2. (ii) ${{\mathcal A}_{\text {min}}}$ consists of all states that cannot lead to a big component;

3. (iii) ${{\mathcal A}_{\text {max}}}$ consists of everything else—that is, states which are not in a big component but may lead to a big component.

Proposition 3.17. There is a left eigenvector $\mu $ of $[{\mathcal M}]$ with eigenvalue $\lambda $ such that $\mu _i>0$ for $a_i\in {{\mathcal A}_{\text {max}}}\cup {{\mathcal A}_{\text {big}}}$ and $\mu _i=0$ for $a_i\in {{\mathcal A}_{\text {min}}}$ .

Proof We first construct a positive eigenvector ${\mu _{\text {big}}}$ of $[{\mathcal M}({{\mathcal A}_{\text {big}}})]$ with eigenvalue $\lambda $ , then a positive eigenvector $\mu _0$ of $[{\mathcal M}({{\mathcal A}_{\text {max}}}\sqcup {{\mathcal A}_{\text {big}}})]$ with eigenvalue $\lambda $ , then the desired eigenvector $\mu $ .

(1) From [Cal13, Lemma 3.4.2], there is no path from one big component to another (this is a moral equivalent of the fact, proved by Coornaert [Coo93], that the growth of G is precisely exponential, that is, $\#B(n,g)=\Theta (\lambda ^n)$ ). It follows that we may write $[{\mathcal M}({{\mathcal A}_{\text {big}}})]$ as a block diagonal matrix

$$ \begin{align*}[{\mathcal M}({{\mathcal A}_{\text{big}}})]=\begin{bmatrix}A_1& & \\ &\cdots & \\ & & A_n\end{bmatrix},\end{align*} $$

where each $A_i$ is $[{\mathcal M}(B)]$ for some big component B. Letting $\mu _i$ be the PF eigenvector for $A_i$ , we have that ${\mu _{\text {big}}}:=[\mu _1\:\cdots \:\mu _n]$ is a positive eigenvector for $[{\mathcal M}({{\mathcal A}_{\text {big}}})]$ with eigenvalue $\lambda $ .

(2) We may write

$$ \begin{align*}[{\mathcal M}({{\mathcal A}_{\text{max}}}\sqcup{{\mathcal A}_{\text{big}}})]=\begin{bmatrix}[{\mathcal M}({{\mathcal A}_{\text{max}}})]& 0 \\B &[{\mathcal M}({{\mathcal A}_{\text{big}}})]\end{bmatrix}\end{align*} $$

for some matrix B. Observe that $(\lambda {{\mathbb {I}}}-[{\mathcal M}({{\mathcal A}_{\text {max}}})])$ is invertible (where by ${{\mathbb {I}}}$ we mean the identity matrix), with inverse given by

$$ \begin{align*}(\lambda{{\mathbb{I}}}-[{\mathcal M}({{\mathcal A}_{\text{max}}})])^{-1}=\lambda({{\mathbb{I}}}+\lambda^{-1}[{\mathcal M}({{\mathcal A}_{\text{max}}})]+\lambda^{-2}[{\mathcal M}({{\mathcal A}_{\text{max}}})]^2+\cdots),\end{align*} $$

where the series (which is non-negative) converges because $\lambda $ is greater than any eigenvalue of $[{\mathcal M}({{\mathcal A}_{\text {max}}})]$ . We let $\mu _0$ be the row vector with first components those of ${\mu _{\text {big}}} B(\lambda {{\mathbb {I}}}-[{\mathcal M}({{\mathcal A}_{\text {max}}})])^{-1}$ , followed by the components of ${\mu _{\text {big}}}$ , or as a partitioned vector,

$$ \begin{align*}\mu_0:=[{\mu_{\text{big}}} B(\lambda{{\mathbb{I}}}-[{\mathcal M}({{\mathcal A}_{\text{max}}})])^{-1}\quad\ \ \ {\mu_{\text{big}}}].\end{align*} $$

We see that $\mu_0 $ is an eigenvector for $[{\mathcal M}({{\mathcal A}_{\text {max}}}\sqcup {{\mathcal A}_{\text {big}}})]$ by the following calculations. Write $\nu $ for ${\mu _{\text {big}}} B(\lambda {{\mathbb {I}}}-[{\mathcal M}({{\mathcal A}_{\text {max}}})])^{-1}$ , so

$$ \begin{align*}{\mu_{\text{big}}} B=\nu(\lambda{{\mathbb{I}}}-[{\mathcal M}({{\mathcal A}_{\text{max}}})]).\end{align*} $$

Hence,

$$ \begin{align*}\nu[{\mathcal M}({{\mathcal A}_{\text{max}}})]+{\mu_{\text{big}}} B=\lambda\nu,\end{align*} $$

which implies that $[\nu \quad {\mu _{\text {big}}}]$ is a non-negative left eigenvector of $[{\mathcal M}({{\mathcal A}_{\text {max}}}\sqcup {{\mathcal A}_{\text {big}}})]$ as desired, so we wish to show that it is positive.

Because each state of ${{\mathcal A}_{\text {max}}}$ may lead to a state of ${{\mathcal A}_{\text {big}}}$ , we see that for all $a_i\in {{\mathcal A}_{\text {max}}}$ , there is some $a_j\in {{\mathcal A}_{\text {big}}}$ and $k\geq 0$ such that $[B[{\mathcal M}({{\mathcal A}_{\text {max}}})]^k]_{ji}>0$ . By the geometric series formula for $(\lambda {{\mathbb {I}}}-[{\mathcal M}({{\mathcal A}_{\text {max}}})])^{-1}$ and the fact that every $[{\mu _{\text {big}}}]_j$ is positive, we thus see that every $[{\mu _{\text {big}}} B(\lambda {{\mathbb {I}}}-[{\mathcal M}({{\mathcal A}_{\text {max}}})])^{-1}]_i$ is positive and, hence, $\mu _0$ is positive.

(3) Finally, we may write

$$ \begin{align*} [{\mathcal M}]=\begin{bmatrix}[{\mathcal M}({{\mathcal A}_{\text{max}}}\cup{{\mathcal A}_{\text{big}}})]& 0 \\ \ast &[{\mathcal M}({{\mathcal A}_{\text{min}}})]\end{bmatrix}\end{align*} $$

and take $\mu :=[\mu _0\quad 0]$ as our desired eigenvector.

3.4 Horofunctions and their derivatives

Definition 3.18. Let $h:G{\rightarrow }{\mathbb Z}$ be a $1$ -Lipschitz function. The derivative

of h is the function

The following lemma says that two functions with the same derivative differ by a constant, as one might expect.

Lemma 3.19. Let $h_{1}, h_{2}:G \to \mathbb {Z}$ be $1$ -Lipschitz functions. If then $h_{1} - h_{2}$ is constant.

Proof [Coh17, Lemma 3.4] implies that, for a Lipschitz function h, $h(g)-h(g')$ may be recovered from , where p is a path connecting g to $g'$ . It follows that $h_1-h_2$ is constant.

There are multiple (essentially but not entirely equivalent) definitions of ‘horofunction’ in the literature. We will use the following definition.

Definition 3.20. An onto $1$ -Lipschitz function $h:G{\rightarrow } {\mathbb Z}$ is said to be a horofunction if the derivative is in the orbit closure of the derivative of the function

$$ \begin{align*}g\mapsto \operatorname{\mathrm{d}}(g,1_G).\end{align*} $$

Level sets of horofunctions will be referred to as horospheres.

For example, the horofunctions ${\mathbb Z}\to {\mathbb Z}$ , with the integers generated by $\pm 1$ , are given by $n\mapsto n+C$ and $n\mapsto -n+C$ as C ranges over ${\mathbb Z}$ .

Note that functions in the actual orbit of $g\mapsto \operatorname {\mathrm {d}}(g,1_G)$ are not onto ${\mathbb Z}$ , but only some ${\mathbb Z}_{\geq N}$ , and so only limit points of an unbounded orbit of such functions can possibly be horofunctions. The next lemma makes this precise.

Lemma 3.21. A function $h:G \to \mathbb {Z}$ is a horofunction if and only if there $g_{0} \in G$ and a sequence $(g_{n})_{n=1}^{\infty }$ of distinct elements of G such that h is the pointwise limit of the sequence $(f_{n})_{n=1}^{\infty }$ where

$$ \begin{align*}f_{n}(g):= \operatorname{\mathrm{d}}(g,g_n)-\operatorname{\mathrm{d}}(g_n,g_0).\end{align*} $$

Proof Let h be a horofunction. We produce the points $g_{n}$ . By definition, there exists a sequence of sets $S_{n} \subset G$ , $n \in {\mathbb N}$ satisfying:

1. (i) $S_{n} \subset S_{n+1}$ for all $n \in {\mathbb N}$ ;

2. (ii) $\bigcup S_{n} = G$ ;

3. (iii) for each $n\in {\mathbb N}$ , there exists $g_{n} \in G$ for which .

Note that these conditions imply that for any $m \geq n$ we have that . By restricting to subsets of $S_{n}$ we may assume that the graph spanned by $S_{n}$ is connected for each n.

Because h is onto $\mathbb {Z}$ , there exists $g_{0} \in G$ for which $h(g_{0}) = 0$ is satisfied. Moreover, for each $r>0$ , there is some N such that for all $n>N$ , the ball of radius r centered at $g_0$ is contained within $S_n$ .

Because each $f_n$ defined in the statement of the lemma differs from $\operatorname {\mathrm {d}}(g,g_{n})$ only by a constant, . By the conditions above we see that $f_{n}$ satisfies:

1. (i) ;

2. (ii) $f_n(g_{0}) = h(g_{0})$ .

As $S_{n}$ is connected, by Lemma 3.19, condition (1) above implies that $f_{n}|_{S_{n}} = h|_{S_{n}}$ . We see that

$$ \begin{align*} \lim_{n \to \infty}f_{n} = h. \end{align*} $$

It remains to show that the elements may be taken as distinct. Suppose not. Then after subsequencing if necessary we may assume that $(g_{n})_{n=1}^{\infty }$ is a constant sequence. In that case $h(g) = \operatorname {\mathrm {d}}(g,g_{n})+C$ for some constant $C\in {\mathbb Z}$ , contradicting the assumption that h is onto.

The converse follows from the definitions.

Lemma 3.22. Let h be a horofunction and $g_1,g_2 \in G$ . Suppose that $h(g_1) = h(g_2)$ . If, for some $x \in {\mathbb N}$ , we have that $\operatorname {\mathrm {d}}(g_1,g_2)> 2x + 2\delta $ , then for any geodesic $\gamma :[0..\operatorname {\mathrm {d}}(g_1,g_2)]\to G$ connecting $g_1$ and $g_2$ we have

$$ \begin{align*}h(\gamma(x)) \leq h(g_1) - (x - 2\delta).\end{align*} $$

Proof By reorienting $\gamma $ if necessary we may assume that $\gamma (0) = g_{1}$ . By Lemma 3.21, there exists $g_0 \in G$ and $C \in {\mathbb N}$ so that for all $t \in [0..\operatorname {\mathrm {d}}(g_1,g_2)]$ we have that $h(\gamma (t)) = \operatorname {\mathrm {d}}(g_0,\gamma (t)) - C$ . For $i=1,2$ , let $\gamma _{i}$ be a geodesic from $g_{i}$ to $g_{0}$ (so that $\gamma _{i}(0) = g_{i}$ ). By the slim triangle inequality, $\gamma (x)$ is within $\delta $ of some point of $\gamma _{1}$ or $\gamma _{2}$ , say p. We claim that $p \not \in \gamma _{2}$ ; assume that it is. Then $\operatorname {\mathrm {d}}(g_{1},p) \leq x+\delta $ . Again by the triangle inequality, $\operatorname {\mathrm {d}}(g_{0},p) \geq \operatorname {\mathrm {d}}(g_{0},g_{1})- (x+\delta )= \operatorname {\mathrm {d}}(g_{0},g_{2})- (x+\delta )$ , and so, as p is on a geodesic connecting $g_{0}$ and $g_{2}$ , we have that $\operatorname {\mathrm {d}}(p,g_{2}) \leq x+\delta $ . This shows that $\operatorname {\mathrm {d}}(g_{1},g_{2}) \leq 2x + 2\delta $ , contradicting our assumption.

Therefore, $p \in \gamma _{1}$ . By Lemma 3.7, we have that $\operatorname {\mathrm {d}}(\gamma (x),\gamma _{1}(x)) \leq 2 \operatorname {\mathrm {d}}(\gamma (x),p) \leq 2\delta $ and so

$$ \begin{align*} \operatorname{\mathrm{d}}(g_{0},\gamma(x)) \leq \operatorname{\mathrm{d}}(g_{0},\gamma_{1}(x)) + \operatorname{\mathrm{d}}(\gamma_{1}(x),\gamma(x)) \leq \operatorname{\mathrm{d}}(g_{0},g_{1}) - x + 2 \delta .\end{align*} $$

Thus,

$$ \begin{align*} h(\gamma(x)) = \operatorname{\mathrm{d}}(g_{0},\gamma(x)) - C \leq \operatorname{\mathrm{d}}(g_{0},g_{1}) - x + 2 \delta - C = h(g_{1}) - (x - 2\delta).\end{align*} $$

4 Translation-like $\mathbb {Z}$ actions

This section is independent of the rest of the paper (the result will be used in the proof of Lemma 8.7).

Throughout this section, let $\Gamma $ be a locally finite, countable graph. Let $\operatorname {\mathrm {d}}_{\Gamma }$ be the induced metric on the vertex set $V(\Gamma )$ (with the distance between vertices in distinct components being infinite). We now define the following.

Definition 4.1. (Translation-like $\mathbb {Z}$ action)

Let $\Gamma $ be a graph and L a positive integer. A translation-like $\mathbb {Z}$ action with defect L on $\Gamma $ is a bijection $f:V(\Gamma ) \to V(\Gamma )$ satisfying, for any $x \in V(\Gamma )$ :

1. (i) $\operatorname {\mathrm {d}}_{\Gamma }(x,f(x)) \leq L$ ;

2. (ii) $f^{i}(x) = x$ only for $i=0$ .

The orbit of x is $\{f^{i}(x)\}_{i \in \mathbb {Z}}$ .

In the definition above f is thought of as the generator of $\mathbb {Z}$ . In [Sew14a, Corollary 3.4] Seward showed that a connected graph of bounded degree admits a transitive translation-like $\mathbb {Z}$ action if and only if the graph has one or two ends. In Theorem 4.2, we generalize Seward’s work, removing the restriction on the number of ends and the degrees on the vertices, and obtaining a universal bound on the defect. However, the action we get is not transitive; this is necessarily the case because a graph with three or more ends does not admit a translation-like $\mathbb {Z}$ action.

The purpose of this section is to prove the following.

Theorem 4.2. A locally finite, countable graph admits a translation-like $\mathbb {Z}$ action if and only if all of its components are infinite; in that case, there is such an action with defect at most 3.

Proof of Theorem 4.2 Let $\Gamma $ be as in the statement of the theorem. Because a translation-like $\mathbb {Z}$ action restricts to a translation-like ${\mathbb Z}$ action on each component, we may assume that $\Gamma $ is connected. Clearly, every component of a graph admitting a translation-like $\mathbb {Z}$ action is infinite, and so we may further assume that $\Gamma $ is infinite.

Let $(X_{i})_{i}$ be a sequence of finite subsets of $V(\Gamma )$ satisfying:

1. (i) $X_{i} \subset X_{i+1}$ ;

2. (ii) $V(\Gamma ) = \bigcup _{i=1}^{\infty } X_{i}$ ;

3. (iii) the graph $\Gamma (X_{i})$ spanned by $X_{i}$ is connected.

We prove the following two simple lemmas.

Lemma 4.3. A sequence as above exists.

Proof Because $\Gamma $ is countably infinite and connected we may fix $v_{1},v_{2},\ldots ,$ an enumeration of $V(\Gamma )$ , so that for every $i>1$ there is $j<i$ so that $v_{j}$ and $v_{i}$ co-bound an edge. Set $X_{i}$ to be

$$ \begin{align*} X_{i} := \{v_{1},\ldots,v_{i}\} .\end{align*} $$

By construction and induction $(X_{i})_{i}$ satisfies conditions (i)–(iii) above.

For the next lemma, we need the following.

Definition 4.4. Given a graph H, let $H^{3}$ be the cube of H, defined by:

1. (i) $V(H^{3}) = V(H)$ ;

2. (ii) $u,v \in V(H^{3})$ co-bound an edge if and only if $\operatorname {\mathrm {d}}_{H}(u,v) \leq 3$ .

Lemma 4.5. If $H_{1}$ is a subgraph of $H_{2}$ then $H_{1}^{3}$ is a subgraph of $H_{2}^{3}$ .

Proof Clearly $V(H_{1}^{3}) \subset V(H_{2}^{3})$ . For any $u,v \in V(H_{1}^{3})$ we have

$$ \begin{align*} \operatorname{\mathrm{d}}_{H_{2}}(u,v) \leq \operatorname{\mathrm{d}}_{H_{1}}(u,v) .\end{align*} $$

If follows that any edge of $H_{1}^{3}$ is an edge of $H_{2}^{3}$ . The lemma follows.

In [Kar68], Karaganis proved that the cube of any finite connected graph with at least three vertices admits a Hamiltonian circuit. (In other words, the only finite connected graphs whose cube is not Hamiltonian is a single edge and, depending on one’s definition, a single vertex.) For each $i \geq 3$ , $\Gamma (X_{i})$ is such a graph; we apply Karaganis’ theorem and fix $H_{i}$ , a Hamiltonian circuit of $\Gamma (X_{i})^{3}$ .

We next construct a sequence denoted $(E_{i})_{i}$ satisfying the following five properties for each $i \geq 3$ :

1. (1) $E_{i}$ is a set of edges of $\Gamma ^{3}$ ;

2. (2) $E_{i}$ is finite;

3. (3) $E_{i} \subset E_{i+1}$ ;

4. (4) at every vertex $v_{j} \in X_{i}$ , we have that $E_{i}$ has exactly two edges adjacent to $v_{j}$ ;

5. (5) the edges of $E_{i}$ are contained in infinitely many of the $H_{k}$ .

Consider first $v_{1}$ . Because $v_{1}$ is covered by every $H_{k}$ and $\Gamma (X_{i})^{3}$ is locally finite, infinitely many of the $H_{k}$ traverse the same pair of edges, say $e_{1}$ and $e_{1}'$ , at $v_{1}$ . We subsequence $(H_{k})_{k}$ so that each $H_{k}$ in the subsequence traverses both $e_{1}$ and $e_{1}'$ (we do not rename the sequence). We set

$$ \begin{align*} E_{1} := \{e_{1},e_{1}'\} .\end{align*} $$

For each $i\ge 1$ , having constructed $E_{i}$ , we consider $v_{i+1}$ . Local finiteness implies that infinitely many of the (subsequenced) $H_{k}$ traverse the same edges at $v_{i+1}$ , say $e_{i+1}$ and $e_{i+1}'$ . We further subsequence $(H_{k})_{k}$ and so that each $H_{k}$ in the subsequence traverses both $e_{i+1}$ and $e_{i+1}'$ . We set

$$ \begin{align*} E_{i+1} := E_{i} \cup \{e_{i+1},e_{i+1}' \} \end{align*} $$

This completes the construction of the sequence $(E_i)$ satisfying the conditions above.

We set H to be the subgraph of $\Gamma ^{3}$ whose vertices are $V(\Gamma )$ , and whose edges are $\bigcup _{i} E_{i}$ .

Claim 4.6. We claim H is a union of disjointly embedded bi-infinite paths in $\Gamma ^{3}$ that cover $V(\Gamma )$ .

Proof By construction, the edges of H are among the edges of $\Gamma ^{3}$ and every vertex $V(\Gamma ^{3}) = V(\Gamma )$ is connected to exactly two edges of H. Therefore every component of H is a cycle or a bi-infinite path, and all we need to argue is that H has no cycles. Assume, for a contradiction, that $\Gamma '$ is such a cycle. Because $\Gamma '$ has only finitely many vertices, for sufficiently large k, $X_{k}$ contains every vertex of $\Gamma '$ and at least one more vertex. By condition (5) above we may assume that every edge of $\Gamma '$ is an edge of some $H_{k}$ . Because both $H_{k}$ and $\Gamma '$ are cycles, we see that $H_{k} = \Gamma '$ , an obvious contradiction.

We endow the paths H with an arbitrary orientation. Given a vertex $v \in V(\Gamma ^{3})$ , let $f(v)$ be the vertex that follows v in the appropriate path of H. By Claim 4.6 this defines a fixed-point free action of $\mathbb {Z}$ on $V(\Gamma ^{3}) = V(\Gamma )$ . Clearly, we have

$$ \begin{align*} \operatorname{\mathrm{d}}_{\Gamma}(v,f(v)) \leq 3\operatorname{\mathrm{d}}_{\Gamma^{3}}(v,f(v)) = 3 \end{align*} $$

Thus, f defines a translation-like $\mathbb {Z}$ action on $\Gamma $ , proving Theorem 4.2.

5 Shortlex shellings

Our goal in this section is to define shortlex shellings (Definition 5.4) and show that they are parameterized by an SFT (Proposition 5.5), much in the style of Coornaert and Papadopoulos [CP93, §3,4] or Gromov [Gro87, §§7.5, 7.6, 8.4]. A shortlex shelling assigns some data to each element of G. These data impose two simultaneous, compatible structures on G: a decomposition into horospherical layers (that is, layers which are locally modeled on spheres in G) and a spanning forest locally modeled on the tree of shortlex geodesics.

5.1 Notation

If $a,b\in {\mathcal A}$ and $w\in \mathcal S^*$ , we write $a{\buildrel w\over {\rightarrow }} b$ if the shortlex machine, starting in state a, ends up in state b after reading w. Given $P:G{\rightarrow } G$ and $S\subset G$ , let

$$ \begin{align*}P^{-n}S:=\{g\in G:P^n(g)\in S\}\end{align*} $$

(as expected) and denote

$$ \begin{align*}P^{-\ast}S:= \bigcup_{n=0}^{\infty} P^{-n}S,\end{align*} $$

which we will call the future cone of S with respect to P.

Given a function $\sigma :G{\rightarrow } A$ for any set A and $g\in G$ , let $\sigma \cdot g$ denote the function $G{\rightarrow } A$ given by $(\sigma \cdot g)(h)=\sigma (gh)$ . Given $S\subset G$ , the 1-interior of S consists of all $g\in G$ such that $B(1,g)\subset \mathcal S$ .

Definition 5.1. A preshelling is a triple $X=(h,\operatorname{\textsf{state}},P)$ , where $h:G{\rightarrow }{\mathbb Z}$ is a 1-Lipschitz function, $\operatorname{\textsf{state}}$ is a function $G{\rightarrow } {\mathcal A}$ and $P:G{\rightarrow } G$ satisfying, for all $g\in G$ , $d(g,P(g)){\leq 1}$ . Given such an X, define to be the triple , where .

Lemma 5.2. The set, in ${[-1..1]}^{\mathcal S}\times {\mathcal A} \times B(1,1_G)$ , of such that X is a preshelling is an SFT, which we denote $\Omega _0$ .

Proof Similar results appear in [CP93] for derivatives of horofunctions, and more generally as [Coh17, Theorem 3.2] for k-Lipschitz functions on finitely presented groups.

For any $\sigma \in ({[-1..1]}^{\mathcal S})^G$ , we may ‘integrate’ $\sigma $ along any path $\gamma $ by summing $\sigma (\gamma (n)):\mathcal S\to {[-1..1]}$ applied to $\gamma (n)^{-1}\gamma (n+1)$ .

If $\sigma $ integrates to $0$ around any translate of any relator in G, then $\sigma $ is the derivative of a $1$ -Lipschitz function which can be found by integrating from the identity.

The group G (being $\delta $ -hyperbolic) has a presentation with generators $\mathcal S$ and relators of length less than or equal to $8\delta +1$ (see the proof of Theorem III. $\varGamma $ .2.6 in [BH99]), which each fit within $B(4\delta +1,1_G)$ .

There are only finitely many distinct , which we take as our allowed cylinder sets defining a subshift $\Omega _0$ of finite type. By definition, each is within $\Omega _0$ . Moreover, if $\phi \in \Omega _0$ , then the first coordinate of $\phi $ integrates to $0$ around any relator and, hence, is the derivative of a $1$ -Lipschitz function $G\to {\mathbb Z}$ . There are no particular restrictions on the last two coordinates in a preshelling and so $\Omega _0$ is the set of all such that X is a preshelling.

Definition 5.3. Let $X_0=(h_0,\operatorname{\textsf{state}}_0,P_0)$ , where $h_0:G{\rightarrow }{\mathbb Z}$ , $\operatorname{\textsf{state}}_0:G{\rightarrow }{\mathcal A}$ and $P_0:G{\rightarrow } G$ are given as follows.

1. (i) For $g\in G$ , $h_0(g)=d(g,1_G)$ .

2. (ii) If $w\in \mathcal S^*$ is the shortlex minimal word representing $g\in G$ and $a_0$ is the initial state of the shortlex machine, then $\operatorname{\textsf{state}}_0(g)$ is the unique element of ${\mathcal A}$ such that $a_0{\buildrel w\over {\rightarrow }}\operatorname{\textsf{state}}_0(g)$ in the notation given at the start of this section.

3. (iii) Finally, $P_0(1_G)=1_G$ and for $g\neq 1_G$ , $P_0(g)$ is the vertex preceding g in the shortlex geodesic from $1_G$ to g. That is, $P_0(g)=h$ if and only if $(\operatorname{\textsf{state}} h)\stackrel {h^{-1}g}{\longrightarrow }(\operatorname{\textsf{state}} g)$ .

A shortlex shelling is a preshelling which is locally modeled by $X_0$ in the following sense.

Definition 5.4. A preshelling $X=(h,\operatorname{\textsf{state}},P)$ is said to be a shortlex shelling if, for every $g\in G$ and $R>0$ , there exists $g_0\in G$ such that we have the equality of restrictions

and, furthermore, $B(R,g_0)$ does not contain the identity $1_G$ .

For a preshelling X, if for some $F\subset G$ , we say that is modeled by on $gF$ . In other words, X being a shortlex shelling means that is modeled by on every finite subset of G. If $X=(h,\operatorname{\textsf{state}},P)$ is a shortlex shelling, then h is a horofunction (by definition of a horofunction).

We will show that the set of such that X is a shortlex shelling is formed by intersecting the preshelling SFT with further cylinder sets of radius $2\delta $ ; hence it is clear that it is an SFT. We will also show that is non-empty, and includes exactly the shortlex shellings.

Proposition 5.5. The collection of

such that X is a shortlex shelling forms a non-empty SFT. In particular, a preshelling X will be a shortlex shelling so long as, for every $g\in G$ , there exists $g_0\in G\setminus B(2\delta ,1_G)$ such that

Proof Let $X=(h,\operatorname{\textsf{state}},P)$ be a preshelling satisfying the given condition (that is modeled by on $2\delta $ balls not containing $1_G$ ). We wish to show that X is actually a shortlex shelling, that is, that on any $B(R,g)$ , is modeled by . We proceed by two steps. First, we show that is modeled by on the 1-interior of sets of the form $P^{-\ast }B(2\delta ,g)$ . Second, we show that every ball $B(R,g)$ is contained in the 1-interior of some cone. Finally we show the existence of a shortlex shelling X.

State determines future. Given $g\in G$ , because

is modeled on a ball away from $1_G$ , it is clear that

$$ \begin{align*}\{(g^{-1}g',\operatorname{\textsf{state}}(g')):P(g')=g\}=\{(s,b)\in\mathcal S\times{\mathcal A}:\operatorname{\textsf{state}}(g){\buildrel s\over{\rightarrow}}b\}.\end{align*} $$

Now, suppose that $\operatorname{\textsf{state}}(g)=\operatorname{\textsf{state}}_0(g_0)$ for some $g,g_0\in G$ . We observe by induction that $g'\in P^{-\ast }\{g\}$ if and only if, for the shortlex geodesic representative $w\in \mathcal S^*$ of $g^{-1}g'$ , $\operatorname{\textsf{state}}(g){\buildrel w\over {\rightarrow }}\operatorname{\textsf{state}}(g')$ . It follows that

$$ \begin{align*}g^{-1}P^{-*}\{g\}=g_0^{-1}P_0^{-*}\{g_0\}.\end{align*} $$

Furthermore, for $g'\in P^{-*}(g)$ , we have $\operatorname{\textsf{state}}(g')=\operatorname{\textsf{state}}_0(g_0g^{-1}g')$ and

, because the $\operatorname{\textsf{state}}(g)$ and $g^{-1}g'$ uniquely determine w as above. Equivalently, we have shown that

Finally, for $g'\in P^{-*}g$ , with w as above, we have

$$ \begin{align*}h(g')-h(g)=\ell(w)=h_0(g_0g^{-1}g')-h_0(g_0),\end{align*} $$

or, equivalently,

$$ \begin{align*}(h\cdot g)|_{g^{-1}P^{-*}\{g\}}= (h_0\cdot g_0)|_{g_0^{-1}P_0^{-*}\{g_0\}}+h(g)-h(g_0).\end{align*} $$

On the 1-interior of cones,

is modeled by

. Let $g,g_0\in G$ and suppose that

By the above considerations, we have that

$$ \begin{align*}g^{-1}P^{-*}B(2\delta,g)=g_0^{-1}P_0^{-*}B(2\delta,g_0),\end{align*} $$

and, furthermore,

and

$$ \begin{align*}h|_{g^{-1}P^{-*}B(2\delta,g)}= h_0|_{g_0^{-1}P_0^{-*}B(2\delta,g_0)}+h(g)-h_0(g_0).\end{align*} $$

Consequently, is modeled by on the 1-interior of $P^{-*}B(2\delta ,g)$ .

Every ball lies in the 1-interior of some cone. For every $R>0$ , $g\in G$ , $n\geq R+\delta +1$ , and $g'\in P_0^{-n}(g)$ , we claim that

$$ \begin{align*}P_0^{-*}B(\delta,g)\supset B(R,g').\end{align*} $$

To see this, for any $x\in B(R,g')$ , consider the geodesics along $\{P_0^i(g')\}$ and $\{P_0^i(x)\}$ from $g'$ and x to $1_G$ . Because g is in $\{P_0^i(g')\}$ , and $\operatorname {\mathrm {d}}(g,g')=n\geq R+\delta +1$ and $\operatorname {\mathrm {d}}(x,g')\leq \delta $ , by the triangle inequality, every point on any geodesic between x and $g'$ must be of distance greater than $\delta $ from g. By the $\delta $ -slim triangle condition, some point on the geodesic from x to $1_G$ is within $\delta $ of g, and so x is in $P_0^{-*}B(\delta ,g)$ .

It follows that for all $g\in G$ and $n\geq R+\delta +1$ ,

(*) $$ \begin{align} B(R,g)\subset P^{-*}B(\delta,P^n g). \end{align} $$

X is a shortlex shelling. If $n\geq R+\delta +2$ , we see from the above that is modeled by . It follows that X is a shortlex shelling.

There exists a shortlex shelling. Let $\{g_n\}$ be a sequence in G with $\operatorname {\mathrm {d}}(g_n,1_G)=n$ . By compactness has a subsequence that converges to a shortlex shelling.

Corollary 5.6. For any $g,g'\in G$ the geodesics $\gamma :n\mapsto P^n(g)$ and $\gamma ':n\mapsto P^n(g')$ are asymptotic.

Proof By (*), for all $n\ge \operatorname {\mathrm {d}}(g,g') +\delta + 2$ , the ball $B(\operatorname {\mathrm {d}}(g,g')+1,g)$ is contained in the cone $P^{-\ast } B(\delta , P^n(g))$ . Consequently $\gamma '$ must pass through $B(\delta , P^n(g))$ , and so for sufficiently large n, $P^n(g)$ is within $\delta $ of $\gamma '$ and the geodesics are asymptotic.

We now give a name to the SFT formed by local data of shortlex shellings.

Definition 5.7. Let $\Omega _S$ denote the set of all such that X is a shortlex shelling.

We note that this SFT always has configurations with infinite-order periods—for example take a horofunction with axis defined by a cycle in the shortlex FSA. The rest of the paper revolves around ‘populated shellings’, which are shortlex shellings decorated with some extra data that kills these periods.

6 The measure $\mu $

In this section, we prove Proposition 6.5, which shows that there is a ‘mass’ function $\mu :{\mathcal A}{\rightarrow }[0,\infty )$ such that for any shortlex shelling X, $\mu \circ \operatorname{\textsf{state}}$ is positive on a dense (in the sense of Definition 6.4) set of points, and the sum of $\mu \circ \operatorname{\textsf{state}}$ over the successors of $g\in G$ is equal to $\lambda \mu (\operatorname{\textsf{state}}(g))$ . This regularizes the growth of $P^{-1}$ —in particular, for a finite $S\subset G$ , we see that although $P^{-1}(S)$ may not have cardinality equal to $\lambda \# S$ , we still have that $\mu $ assigns exactly $\lambda $ times as much mass to $P^{-1}(S)$ as it does to S. This, in turn, will be crucial in showing that the populated shellings defined in §8 exist and have no infinite-order periods.

Recall that Proposition 3.17 gives a left eigenvector of $[{\mathcal M}]$ with eigenvalue $\lambda $ (where $\lambda $ is the growth rate of G with the generators $\mathcal S$ ), supported on states of maximal growth, that is, the states denoted by ${{\mathcal A}_{\text {big}}} \cup {{\mathcal A}_{\text {max}}}$ in Proposition 3.17.

Definition 6.1. Let $\mu :{\mathcal A}{\rightarrow }[0,\infty )$ be the function given $\mu (a_i)=\mu _i$ , where $\mu $ is the left eigenvector defined in Proposition 3.17, normalized so that the smallest non-zero value of $\mu $ is $1$ . Given a fixed shortlex shelling $X=(h,\operatorname{\textsf{state}},P)$ and $g\in G$ , $\mu (g)$ is understood to be $\mu (\operatorname{\textsf{state}}(g))$ .

Remark 6.2. Consequently, from the definitions of shortlex shelling and $\mu $ :

$$ \begin{align*}\sum_{P(b)=a} \mu(b) =\lambda\; \mu(a).\end{align*} $$

This is the key property of $\mu $ which will be exploited in the proof of Proposition 8.11, the existence of ‘populated shellings’.

Definition 6.3. For any shortlex shelling X, let $G^+$ consist of all $g\in G$ with $\mu (g)>0$ . For any horosphere H, let $H^+ := H\cap G^+$ .

Definition 6.4. (k-dense)

Let $(G,\operatorname {\mathrm {d}})$ be a metric space and $G'\subseteq G$ . We say that $G'$ is k-dense in G if for all $g\in G$ there exists $g'\in G'$ such that $\operatorname {\mathrm {d}}(g,g') \leq k$ .

Proposition 6.5. For any shortlex shelling X, the set $G^+$ is $2\delta $ -dense.

Proof In the proof of this proposition (which does not involve the SFT structure of $\Omega $ ), to be consistent with the left action of G on $\partial G$ , we define a left action of G on $\Omega _S$ given by

$$ \begin{align*} (g \cdot \omega)(g') := (\omega\cdot g^{-1})(g') = \omega (g^{-1} g'). \end{align*} $$

We proceed as follows. First, we describe a factor map $\pi :\Omega _S{\rightarrow }\partial G$ . We use this map, together with the fact the $\partial G$ is minimal as a G system, to show that every shortlex shelling includes states from ${{\mathcal A}_{\text {max}}}\cup {{\mathcal A}_{\text {big}}}$ . We then use a compactness argument to show that there exists a k such that ${{\mathcal A}_{\text {max}}}\cup {{\mathcal A}_{\text {big}}}$ states are k-dense in every shelling. Finally, we use the fact that the future of any $2\delta $ -ball contains a k-ball to conclude that such states are $2\delta $ -dense.

Coding the boundary. Given a shortlex shelling $X=(h,\operatorname{\textsf{state}},P)$ , consider

. The function $\gamma _X:n\mapsto P^n(1_G)$ satisfies $h \circ \gamma _{X}(n) = h(1_G)-n$ and defines a geodesic ray. This defines a map $\pi :\Omega _S \to \partial G$

We claim that $\pi $ is a factor map, that is, $\pi $ is continuous, equivariant, and surjective.

Continuity follows directly from the definitions. To see that $\pi $ is equivariant, fix $g \in G$ and let $g \cdot X := (h',\operatorname{\textsf{state}}',P')$ , so that

. We have that $\gamma _{g\cdot X}(n)=gP^n(g^{-1})$ because a simple induction shows that

$$ \begin{align*} P^{\prime n}(1_G)=gP^{n}(g^{-1}),\end{align*} $$

as $P^{\prime 0}(1_G)=gP^0(g^{-1})$ and the inductive hypothesis $P^{\prime n}(1_G)=gP^{n}(g^{-1})$ implies

By Corollary 5.6, we know that $\gamma :n\mapsto P^n(g^{-1})$ is asymptotic to $\gamma _X$ and, thus,

$$ \begin{align*}\pi(g\cdot X)=[\gamma_{g\cdot X}]=[g\cdot \gamma]=g\cdot\pi(X),\end{align*} $$

showing that $\pi $ is G-equivariant. Finally, by [Gro87], the action of G on its boundary is minimal, so the image of $\pi $ must be all of $\partial G$ , because it is a closed, non-empty subset of $\partial G$ preserved by G.

Every shortlex shelling includes a state of maximal growth. Let $\Omega _S'$ consist of all such that $X'=(h',\operatorname{\textsf{state}}',P')$ is a shortlex shelling with $\operatorname{\textsf{state}}'(G)\subseteq {{\mathcal A}_{\text {min}}}.$ We wish to show that $\Omega _S'$ is empty, so suppose otherwise. By minimality of $\partial G$ and the fact that $\pi $ is a factor map, we see that every point of $\partial G$ may be represented by an element $\pi (\Omega _S')$ .

Because $\operatorname{\textsf{state}}_0$ realizes values in ${{\mathcal A}_{\text {big}}}$ at infinitely many points, by compactness, there exists a shortlex shelling $X=(h,\operatorname{\textsf{state}},P)$ such that $\operatorname{\textsf{state}}(1_G)\in {{\mathcal A}_{\text {max}}}\cup {{\mathcal A}_{\text {big}}}$ . Let $X'=(h',\operatorname{\textsf{state}}',P')$ be a shortlex shelling such that and . For $g\in P^{-n}(1_G)$ , we may form asymptotic geodesics $\gamma ,\gamma '$ based at g via $\gamma (n)=P^n(g)$ and $\gamma '(n)=P^{\prime n}(g)$ and apply Lemma 3.11 to see that $P^{\prime n}(g)$ is within $2\delta $ of $1_G$ . Hence, $\#P^{\prime -n}B(2\delta ,1_G)\geq \#P^{-n}\{1_G\}.$ Because $\operatorname{\textsf{state}}(1_G)\in {{\mathcal A}_{\text {max}}}\cup {{\mathcal A}_{\text {big}}}$ , we know

$$ \begin{align*}\log(\#P^{-n}\{1_G\})/n{\rightarrow} \log(\lambda),\end{align*} $$

but because $\operatorname{\textsf{state}}'(B(2\delta ,1_G))\subset {{\mathcal A}_{\text {min}}}$ , we have

$$ \begin{align*}\limsup\log(\#P^{\prime -n}B(2\delta,1_G))/n<\log(\lambda),\end{align*} $$

giving us a contradiction. We conclude that $\Omega _S'$ must be empty.

Maximal growth states are k-dense for some k. Finally, suppose there is no k such that states of ${{\mathcal A}_{\text {max}}}\cup {{\mathcal A}_{\text {big}}}$ occur k-densely in every . Then there exist shortlex shellings $X_k=(h_k,\operatorname{\textsf{state}}_k,P_k)$ and $g_k\in G$ such that $\operatorname{\textsf{state}}_k(B(k,g_k))\subset {{\mathcal A}_{\text {min}}}$ . Then subconverges to some , but we must have , which we have seen is impossible.

Maximal growth states are $2\delta $ -dense. Suppose that $\operatorname{\textsf{state}}(B(2\delta ,g))\subseteq {{\mathcal A}_{\text {min}}}$ . We have seen in the proof of Proposition 5.5 that there exists some $g'\in P^{-*}(g)$ such that $B(k,g')\subseteq P^{-*}B(2\delta ,g)$ . Because ${{\mathcal A}_{\text {min}}}$ states, by definition, can only lead to ${{\mathcal A}_{\text {min}}}$ states, we have $\operatorname{\textsf{state}}(B(k,g'))\subseteq {{\mathcal A}_{\text {min}}}$ . Because $G^+$ is k-dense, we know that this cannot be the case, so we conclude that $G^+$ is in fact $2\delta $ -dense.

6.1 Finding dense states

We remark that, for any non-empty subshift $\Omega \subset A^G$ on any finitely generated group, there exists $B\subset A$ and $k\in {\mathbb N}$ such that $\Omega \cap B^G$ is non-empty and for all $b\in B$ and $\omega \in \Omega \cap B^G$ , we have that $\omega ^{-1}(b)$ is k-dense. To see this, simply take a minimal B such that $\Omega \cap B^G$ is non-empty—if, for all k, there were an $\omega _k\in \Omega \cap B^{G}$ such that the symbol $b\in B$ did not occur in $\omega _k|_{B(k,g_k)}$ , then $\omega _k\cdot g_k$ would subconverge to a configuration in $(B\setminus b)^G \cap \Omega $ . Furthermore, if $\Omega $ is an SFT, so is $\Omega \cap B^G$ . This construction may be used instead to enforce density.

7 The divergence graph on horospheres

For horospheres H of a shortlex shelling $X=(h,\operatorname{\textsf{state}},P)$ , we now construct a graph with vertices $H^+$ (as in Definition 6.3) which behaves nicely with respect to P in the sense that predecessors of neighboring vertices either coincide or are neighbors; and each pair of adjacent vertices admits a pair of adjacent successors. In other words, each edge has a predecessor (in the previous horosphere) that is an edge or a vertex, and each edge has at least one successor edge (in the next horosphere). We call this graph the divergence graph on H and show that its vertex set is dense in H (Lemma 7.1), that its edges have bounded length in the word metric (Lemma 7.3), and that it is connected (Lemma 7.4). When we define populated shellings in the next section, we require that a child of a person living at $v\in H^+$ must live in a village $u\in G$ whose predecessor $P(u)\in H^+$ lies close to v in the divergence graph on H. All of the facts noted here will be needed.

Lemma 7.1. For any horosphere H in a shortlex shelling X, $H^+$ is $4\delta $ -dense in H.

Proof Let v be a element of H and let B be the $2\delta $ ball in G around v. The future of B contains arbitrarily large balls and, in particular, must contain elements of $G^+$ . Thus, B contains an element of $G^+$ , say $v'$ . Now $v'$ must have either a predecessor or successor $v"$ in $H^+$ . We have that

$$ \begin{align*}\operatorname{\mathrm{d}}(v',v^{\prime\prime})=|h(v')-h(v^{\prime\prime})|\leq 2\delta\end{align*} $$

and, thus, $\operatorname {\mathrm {d}}(v",v)\leq 4\delta .$

Definition 7.2. The divergence graph on H has vertices $H^+$ and has an edge between $g_1$ and $g_2$ if and only if there exists C such that for all $n\in {\mathbb N}$ , $\operatorname {\mathrm {d}}(P^{-n}\{g_1\},P^{-n}\{g_2\})<C$ .

In Lemma 7.4 below, we show the divergence graph is connected. The following lemma shows that if the futures of two points in a horosphere remain a bounded distance apart, then the points and their futures are within $2\delta $ of one another and that valence in a divergence graph is bounded.

Lemma 7.3. Let $g_1,g_2$ be in some $H^+$ . If there exists $C>0$ such that for all $n\geq 0$ , $\operatorname {\mathrm {d}}(P^{-n}\{g_1\},P^{-n}\{g_2\})<C$ then for all $n\geq 0$ , $\operatorname {\mathrm {d}}(P^{-n}\{g_1\},P^{-n}\{g_2\})\leq 2\delta $ . In particular, if $g_1$ and $g_2$ are connected by an edge in a divergence graph then $\operatorname {\mathrm {d}}(g_1,g_2)\leq 2\delta $ , and so the valence of a vertex in a divergence graph is bounded by the size of $B(2\delta ,1_G)$ .

Proof Suppose for $g_1$ and $g_2$ in $H^+$ , there is some C with $\operatorname {\mathrm {d}}(P^{-n}\{g_1\},P^{-n}\{g_2\})<C$ for all n. Take some $n>C+2\delta $ . Let B be a ball containing $g_1,g_2,P^{-n}{g_1}$ , and $P^{-n}{g_2}$ . Because every ball lies in the 1-interior of some cone there exists some $g_0\in G$ and a constant $C'\in {\mathbb Z}$ such that for all $g'\in B$ , we have that $h(g')=\operatorname {\mathrm {d}}(g',g_0)-C'$ . Let $\gamma _i$ , $i=1,2$ , be a geodesic from $g_0$ to $g_i$ . Let $t=\operatorname {\mathrm {d}}(g_0,g_1)=\operatorname {\mathrm {d}}(g_0,g_2)$ . Then, by Lemma 3.8, $\operatorname {\mathrm {d}}(g_1,g_2)=\operatorname {\mathrm {d}}(\gamma _1(t),\gamma _2(t))\leq 2\delta $ .

Lemma 7.4. For any horosphere H, the divergence graph on $H^+$ is connected.

Proof Without loss of generality, set $H=h^{-1}(0)$ , and let $\xi $ denote the point of $\partial G$ represented by the geodesic ray $n\mapsto P^n(1_G)$ . A deep result of Swarup (building on work of Bowditch) asserts that $\partial G\setminus \xi $ is connected because G is one-ended [Swa96]. We use this to show that the divergence graph on $H^+$ is connected.

1. (i) By an X-geodesic, we mean a function $\gamma : {\mathbb Z} \to G^+$ satisfying ${\gamma (n) = P(\gamma (n+1))}$ . It follows that $\gamma $ is a geodesic and satisfies $h(\gamma (n+1)) = h(\gamma (n))+1$ . Therefore, $h \circ \gamma :{\mathbb Z} \to {\mathbb Z}$ is an order preserving bijection, and we reparameterize $\gamma $ so that $h(\gamma (n)) = n$ . By an X-ray we mean a function $\gamma :{\mathbb Z}_{\geq 0} \to G^+$ satisfying $\gamma (n) = P(\gamma (n+1))$ and $h(\gamma (0))=0$ .

2. (ii) It follows that there is a bijection between X-geodesics and X-rays: given an X-geodesic we obtain an X-ray by restricting its domain, and any X-ray $\gamma $ can be extended uniquely to an X-geodesic $\gamma '$ by setting $\gamma '(n) = \gamma (n)$ for $n \geq 0$ and $\gamma '(n) = P^{-n}(\gamma (0))$ for $n<0$ . By Corollary 5.6, the ends of $\gamma '$ are $\xi $ and $[\gamma ]$ .

3. (iii) If S is a subset of $H^+$ , let ${\Pi }(S)$ denote the subset of $\partial G$ consisting of all $[\gamma ]$ where $\gamma $ is an X-ray with $\gamma (0)\in S$ . We write ${\Pi }(g)$ for ${\Pi }(\{g\})$ .

Our strategy is as follows: starting with a component S of the divergence graph on $H^+$ , we show that ${\Pi }(S)$ and ${\Pi }(H^+ \setminus S)$ decompose $\partial G \setminus \{\xi \}$ as the disjoint union of closed sets, with ${\Pi }(S)$ non-empty. Therefore, ${\Pi }(H^+ \setminus S) = \emptyset $ , which will imply that S is the entire divergence graph.

To that end, we claim the following conditions are satisfied.

(1) For any $g\in H^+$ , ${\Pi }(g)\neq \emptyset $ . We define an X-ray from g recursively as follows: starting with $\gamma (0) = g$ , having defined $\gamma (n) \in H_n^+$ , choose $\gamma (n+1) \in P^{-1}(\gamma (n))\cap H^+_{(n+1)}$ , which is not empty because $\gamma (n) \in H_n^+$ . Then $[\gamma ] \in {\Pi }(g)$ , establishing the claim.

(2) ${\Pi }(H^+)=\partial {G}\setminus \xi $ . Let $\gamma $ be an X-ray defining $[\gamma ] \in {\Pi }(H^+)$ . Then $\gamma $ can be extended to an X-geodesic connecting $\xi $ to $[\gamma ]$ . Because no geodesic connects $\xi $ to itself, we have that $[\gamma ] \neq \xi $ . This shows that $\xi \notin {\Pi }(H^+)$ .

Let $\eta \in \partial {G}\setminus \xi $ . We must show that $\eta $ is represented by an X-geodesic. Let $\gamma $ be a bi-infinite geodesic connecting $\xi $ and $\eta $ , which exists by [BH99, Lemma III.H.3.2]. Now, for $n \in {\mathbb Z}$ we define a geodesic $\gamma _n$ as follows: pick $g_n \in B(2\delta ,\gamma (n))\cap G^+ $ (which is not empty by Proposition 6.5). Set $\gamma _n(t) := P^{n-t}(\gamma (n))$ . Similar to condition (1), set $\gamma _n(t+1)$ to be in $G^+ \cap P^{-1}(\gamma _n(t))$ for $t> n$ . By Lemma 3.11, we have that $\gamma _n(t) \in B(10\delta ,\gamma (t))$ for any $t \leq n$ . Therefore, for any $t \in {\mathbb Z}$ , $(\gamma _n(t))_{n\in {\mathbb N}}$ takes finitely many values. By Lemma 3.1 we have that $\gamma _n$ converges to a geodesic $\gamma '$ , and it is clear that (after reparametrizing) $\gamma '$ is an X-geodesic connecting $\xi $ at $-\infty $ to $\eta $ at $\infty $ . Thus $\eta \in {\Pi }(H^+)$ .

(3) ${\Pi }(S)\cap {\Pi }(H^+\setminus S) = \emptyset $ . By our definitions, any points $p, q\in H^+$ with ${\Pi }(p)\cap {\Pi }(q)\neq \emptyset $ share an edge in the divergence graph, and S is a component.

(4) For any $A \subset H$ we have that ${\Pi }(A)$ is closed in $\partial G \setminus \{\xi \}$ . Let $\eta ,\eta _{n} \in \partial G \setminus \{\xi \}$ satisfy:

1. (a) $\eta _{n} \to \eta $ ;

2. (b) $\eta _{n} \in {\Pi }(A)$ .

We will prove condition (4) by showing that $\eta \in {\Pi }(A)$ . Convergence on $\partial G$ is defined using the Gromov product, see Definitions [BH99, III.H.1.20, 3.15]. By Remark [BH99, III.H.3.17(6)] we have that $\eta _{n} \to \eta $ is equivalent to

$$ \begin{align*} \lim_{n \to \infty }(\eta_{n},\eta)_{p} = \infty \end{align*} $$

(where here $p \in G$ is an arbitrary basepoint) and, in particular, for any geodesic $\delta _{n}$ connecting $\eta _{n}$ to $\eta $ , we have that

$$ \begin{align*} \lim_{n \to \infty} \operatorname{\mathrm{d}}(p,\delta_{n}) = \infty .\end{align*} $$

We choose X-rays $\gamma ,\gamma _{n}$ so that:

1. (i) $[\gamma _{n}] = \eta _{n}$ and $\gamma _{n}(0) \in A$ ( $\gamma _{n}$ exists by assumption);

2. (ii) $[\gamma ] = \eta $ ( $\gamma $ exists by condition (2) above).

We will use $p := \gamma (0)$ as our basepoint. For sufficiently large n, we have that

$$ \begin{align*} \operatorname{\mathrm{d}}(\gamma(0),\delta_{n})> {3} \delta .\end{align*} $$

We now extend $\gamma $ and $\gamma _{n}$ to X-geodesics $\hat \gamma , \hat \gamma _{n}$ and consider the ideal triangle

$$ \begin{align*} \hat\gamma,\delta_{n}, \hat\gamma_{n} .\end{align*} $$

Because by Lemma 3.14 ideal geodesic triangles are ${3} \delta $ -slim, $\gamma (0) = \hat \gamma (0)$ is within ${3}\delta $ of $\hat \gamma _{n} \cup \delta _{n}$ , and we conclude that for some $t \in {\mathbb Z}$

$$ \begin{align*} \operatorname{\mathrm{d}}(\hat \gamma(0),\hat\gamma_{n}(t)) \leq {3}\delta .\end{align*} $$

Because $\hat \gamma , \hat \gamma _n$ are X-geodesics, we can conclude $t\le {3} \delta $ . Furthermore $\operatorname {\mathrm {d}}(\hat \gamma _n(t),\hat \gamma _n(0))=t$ and so we have that $ \operatorname {\mathrm {d}}(\gamma (0),\gamma _{n}(0)) = \operatorname {\mathrm {d}}(\hat \gamma (0),\hat \gamma _{n}(0)) \leq {6}\delta $ . Because this holds for every sufficiently large n, we conclude that $\{\gamma _{n}(0) \}$ is finite.

Therefore, $\gamma _n$ subconverges to some X-ray $\tilde \gamma $ with $\tilde \gamma (0)\in \{\gamma _n(0)\}\subset A$ . By Lemma 3.13, $[\gamma ]=[\tilde \gamma ]\in {\Pi }(A)$ . In particular, ${\Pi }(S)$ and ${\Pi }(H^+\setminus S)$ are closed in $\partial G\setminus \{\xi \}$ .

As noted above, [Swa96] shows that $\partial {G}\setminus \xi $ is connected. Consequently, by conditions (2), (3), and (4), one of ${\Pi }(H^+\setminus S)$ or ${\Pi }(S)$ is empty. By condition (1) we have that ${\Pi }(S)$ is not empty and, hence, ${\Pi }(H^+\setminus S)=\emptyset $ . Applying condition (1) again, we conclude that $H^+\setminus S$ is empty, completing the proof.

8 Populated shellings

In the remainder of the construction, we consider the divergence graphs (§7) on $H^+$ (Definition 6.3) for each horosphere H in each shortlex shelling X on G. Note that for each H, $G\setminus H$ has more than one infinite component; because G is one-ended, H, and therefore $H^+$ , must be infinite. By Lemma 7.4 the divergence graph is connected (because G is one-ended), and by Lemma 7.3 it is locally finite. Hence, by Theorem 4.2, the divergence graph admits a translation-like $\mathbb {Z}$ action (Definition 4.1), say given by $\psi :H^+ \to H^+$ , with defect $3$ . This translation-like $\mathbb Z$ action $\psi $ will be central to our proof in §8.2 of the existence of ‘populated shellings’, defined below.

For the following, for any $H^+$ , for any $R\subset H^+$ , we set ${\mathcal N} R $ to be the $3$ -neighborhood of R in the divergence graph on $H^+$ . Because, by Lemma 7.3, adjacent points in a divergence graph are at most $2\delta $ apart, we observe the following.

Lemma 8.1. For any $R\subset H^+$ , ${\mathcal N} R$ is contained within a $6\delta $ -neighborhood of R.

8.1 Populated shellings

Fix $q\in \{2,3\}$ such that $\log (q)\notin {\mathbb Q}\log (\lambda )$ .

Definition 8.2. A populated shelling of G (with population bound $N\in {\mathbb N}$ and growth by powers of q) is a shortlex shelling equipped with the following extra data:

1. (i) a ‘population’ function ${\wp }:G{\rightarrow } [0..N]$ ;

2. (ii) a ‘population growth’ function $\Delta :G{\rightarrow }\{\lfloor \log _q(\lambda )\rfloor ,\lceil \log _q(\lambda )\rceil \}$ ;

3. (iii) and a ‘parent–child matching’ function

   $$ \begin{align*}&{m}:\{(v,j,k)\ \mid \ v\in G, 1\leq j\leq{\wp}(v), 1\leq k\leq q^{\Delta(v)}\}\\ &\quad \to {\{(u,l)\ \mid\ u\in G, 1\leq l\leq {\wp}(u)\}}.\end{align*} $$

such that:

1. (a) denoting the coordinates of ${m}=({m}_G,{m}_{{\wp }})$ , for any triple $(v,j,k)$ in the domain, ${m}_G(v,j,k)\in P^{-1}{\mathcal N} \{v\}$ ;

2. (b) ${\wp }(v)=0\Leftrightarrow \mu (v)=0$ (so if $(v,j,k)$ is in the domain of m, then $v\in G^+$ );

3. (c) $\Delta $ is constant on horospheres; and

4. (d) ${m}$ is a bijection.

For a horosphere H, we refer to $\{(v,j):v\in H,j\in [1..{\wp }(v)]\}$ as the set of ‘people’ in H. We say that person $(v,j)$ ‘lives’ at a ‘village’ v. Each person $(v,j)$ has $q^{\Delta (v)}$ ‘children’ (which makes sense as $q^{\Delta (v)}\in {\mathbb N}$ ). For each $k\in [1.. q^{\Delta (v)}]$ , if ${m}(v,j,k)=(u,l)$ , then we say that $(u,l)$ is the kth ‘child’ of $(v,j)$ and, conversely, $(v,j)$ is the ‘parent’ of $(u,l)$ . Note that each person has exactly one parent.

Recall for the following that $\mathcal S$ is a fixed symmetric generating set for G (so $\mathcal S=\mathcal S^{-1}$ and $\mathcal S\cup \{1_G\}=B(1,1_G)$ ). Recall too that ${\mathcal A}$ is the set of states of the shortlex automaton ${\mathcal M}$ for G.

Definition 8.3. The local data associated with the populated shelling $X=(h,\operatorname{\textsf{state}},P,{\wp }, \Delta , {m})$ is the function

given by

where M is the finite set of functions with a (possibly empty) domain within $[1..{\wp }(v)]\times [1..q^{\delta (v)}]$ and range $B(6\delta {{+1}}, 1_G)\times [1..N]$ . We define

.

Remark 8.4. Because by Lemma 8.1, any point of ${\mathcal N} (v)$ lies within $6\delta $ of v, and because ${m}(v,j,k)\in P^{-1}{\mathcal N} (v)$ , then $\operatorname {\mathrm {d}}(v,{m}(v,j,k)) \le 6\delta + 1$ , and so the first coordinate of lies within $B(6\delta +1,1_G)$ . Moreover, is the empty function for $v\notin G^+$ . The first coordinate of gives the relative position of the village in which the kth child of the jth villager of v lives, and the second coordinate gives which villager that child is.

Proposition 8.5. The set of all such that X is a populated shelling forms an SFT, $\Omega _P$ .

We show that this SFT $\Omega _P$ is non-empty (for sufficiently large N) in Proposition 8.12 and that the stabilizer of any contains no infinite-order element (for appropriately chosen q) in Proposition 9.5.

Proof Recall Proposition 5.5 that $\Omega _S$ the set of , such that X is a shortlex shelling, is an SFT with cylinder sets of size $4\delta +1$ . We show that the set of , such that X is a populated shelling, is an SFT by taking cylinder sets of radius $6\delta +1\ge 4\delta +1$ , and show that these local rules are sufficient to enforce the conditions defining the functions ${\wp }, {m}$ , and $\Delta $ on a populated shelling.

Recall that by Lemma 7.1 the vertices of a divergence graph are $4\delta $ -dense in its horosphere and by Lemma 7.3 the distance between endpoints of a divergence edge is at most $2\delta $ . Because the group is one-ended, by Lemma 7.4, the divergence graph on each horosphere is connected. Consequently, to ensure that $\Delta $ is constant on horospheres it suffices to consider cylinder sets of size at least $4\delta $ . The conditions on ${\wp }$ and ${m}$ are defined within $(6\delta +1)$ -balls and so are ensured by cylinder sets of this size.

8.2 The existence of populated shellings

For each $i\in {\mathbb Z}$ , let $H=H_i$ be the level set $h^{-1}\{i\}$ . For convenience, when clear from context we will drop the subscript i. Recall, as discussed at the beginning of §8, that by Theorem 4.2 each divergence graph admits a translation-like $\mathbb {Z}$ action, $\psi :H^+ \to H^+$ , with defect 3.

For the remainder of this section, we fix some shortlex shelling $(h,\operatorname{\textsf{state}},P)$ , and on each $H^+$ a translation-like ${\mathbb Z}$ action $\psi $ . For any $R\subset H^+:=H\cap G^+$ , let $\partial R$ denote ${\mathcal N} R \setminus R$ , recalling that ${\mathcal N} R$ is the $3$ -neighborhood of R in $H^+$ with distance measured in the divergence graph.

Recall our conventions for summation: we write $f_R := \sum _{x\in R} f(x)$ for sums of values of some function f over some set R. We also write $f_{m..n}{:}=\sum _{k=m}^n f(k)$ .

Definition 8.6. Given $\nu , C {>} 0$ , we say that ${\wp }:H\to \{0,1,\ldots \}$ realizes density $\nu $ up to error C if the following conditions hold:

1. (i) ${\wp }(v)=0\Leftrightarrow \mu (v)=0$ ;

2. (ii) for any finite region $R\subset H$ , $ |{\wp }_{R} - \nu \ { \mu _{R}}|\leq C \mu _{\partial R}$ .

Recall from §6 that, by construction, the measure $\mu (v)\ge 1$ for all $v\in H^+$ . We prove the following.

Lemma 8.7. For any $\nu \ge 1$ there exists a function

$$ \begin{align*}{\wp}:H\to\{0\} \cup[\lfloor\nu\rfloor..\lceil\nu\max_{a\in{\mathcal A}}\mu(a)\rceil]\end{align*} $$

that realizes $\nu $ with error 2.

Proof Let $\Lambda \subset H^+$ be a set of orbit representatives for the translation-like ${\mathbb Z}$ action $\psi $ , and for each $\alpha \in \Lambda $ define $p_{\alpha }:{\mathbb Z}\to H^+$ as $p_{\alpha }(n)=\psi ^{n}(\alpha )$ . Of course, the images of these $p_{\alpha }$ are disjoint and cover $H^+$ .

Choosing arbitrary basepoint ${{\ast }}\in {\mathbb R}$ , we define ${\wp }$ on H as follows: On $H\setminus H^+$ , we define ${\wp }$ to be identically $0$ . Each $v\in H^+$ may be written uniquely as some $p_{\alpha }(n)$ . As in the following illustration, we define ${\wp }$ on $H^+$ , abbreviating ${\wp }(p_{\alpha }(n))$ , $\mu (p_{\alpha }(n))$ as ${\wp }_n$ and $\mu _n$ .

$$ \begin{align*} {\wp}(v)={\wp}(p_{\alpha}(n))={\wp}_n := \left\{\begin{array}{@{}ll} \lfloor {{\ast}}+\nu\,\mu_{0..n}\rfloor-\lfloor {{\ast}}+\nu\,\mu_{0..(n-1)}\rfloor, & n>0,\\ \\ \lfloor {{\ast}}+\nu\,\mu_{0}\rfloor-\lfloor {{\ast}} \rfloor, & n=0, \\ \\ \lfloor {{\ast}}\rfloor-\lfloor {{\ast}}-\nu\,\mu_{-1}\rfloor, & n = -1, \\ \\ \displaystyle \lfloor {{\ast}}-\nu\,\mu_{(n+1)..-1}\rfloor-\lfloor {{\ast}}-\nu\,\mu_{n..-1}\rfloor, & n<-1. \end{array}\right.\end{align*} $$

Note that for any $v\in G$ , ${\wp }(v)$ has the form

$$ \begin{align*}(\lfloor \nu\;\mu(v)+x\rfloor-\lfloor x\rfloor)\in\{0\} \cup[\lfloor\nu\rfloor..\lceil\nu\max_{a\in{\mathcal A}}\mu(a)\rceil]\end{align*} $$

for some $x\in {\mathbb R}$ . Recalling that $\nu \ge 1$ , and that if $\mu (v)\neq 0$ , then $\mu (v)\ge 1$ , we see that ${\wp }(v)= 0$ if and only if $\mu (v)=0$ .

By telescoping, along any finite interval of an orbit under $\psi $ ,

$$ \begin{align*} | {\wp}_{m..n} - \nu\ \mu_{m..n}| < 2. \end{align*} $$

We observe that $R\cap H^+$ is the disjoint union of maximal sets of the form $p_{\alpha }(a..b)$ . Because $\psi $ is $3$ -Lipshitz, between $p_{\alpha }(a)$ and $p_{\alpha }(a-1)$ the distance in the divergence graph is at most $3$ and so $p_{\alpha }(a-1)\in \partial R$ . (Recall that $\partial R := {\mathcal N} R \setminus R$ .)

Consequently, as indicated in the diagram above, there are at most $\#\partial R\cap H^+$ such maximal $p_{\alpha }(a..b)$ covering R, each contributing less than 2 to the error of ${\wp }$ . Because $\mu (v)\ge 1$ for any $v\in H^+$ , we have that $\#\partial R\cap H^+\leq \mu (\partial R)$ . Therefore,

$$ \begin{align*} |{\wp}_{R} - \nu\ { \mu_{R}}|\leq 2 \mu_{\partial R}\end{align*} $$

and ${\wp }$ realizes $\nu $ up to error 2.

Definition 8.8. Given a sequence $(\nu _i) {\in } {\mathbb R}^{{\mathbb Z}}$ , a function $f:G\to {\mathbb N}$ realizes $(\nu _i)$ up to error C if for any $i\in {\mathbb Z}$ , the restriction of ${\wp }$ to $H_i$ realizes $\nu _i$ up to error C.

We, thus, interpret Lemma 8.7 as the following.

Corollary 8.9. For any $A\geq 1$ , any sequence $(\nu _i)\in [A,qA]^{\mathbb Z}$ is realized up to error 2 by some function $\displaystyle {\wp }:G\to \{0\}\cup [\lfloor A \rfloor .. \lceil qA\max _{a\in {\mathcal A}}\mu (a)\rceil ]$ .

Definition 8.10. For any fixed $A\geq 1$ , we say that a sequence $(\nu _i, \Delta _i)_{i\in {\mathbb Z}}$ is balanced if for all $i\in {\mathbb Z}$ , it satisfies:

1. (i) $\nu _i\in ([A,qA)$ ;

2. (ii) $\Delta _i\in \{\lfloor \log _q\lambda \rfloor , \lceil \log _q\lambda \rceil \}$ ; and

3. (iii) $ \nu _{i+1}=({q^{\Delta _i}}/{\lambda })\nu _i$ where

   $$ \begin{align*}\Delta_i=\left\{\begin{array}{@{}ll} \lceil \log_q\lambda \rceil & \text{for } \nu_i\in \bigg[A,\frac{\lambda}{q^{\lfloor \log_q\lambda\rfloor} }A\bigg),\\[10pt] \lfloor \log_q\lambda \rfloor & \text{for } \nu_i\in \bigg[\frac{\lambda}{q^{\lfloor \log_q\lambda\rfloor} }A,qA\bigg). \end{array}\right.\end{align*} $$

For any $\nu _0\in [A,qA)$ , note there is a unique balanced sequence $(\nu _i, \Delta _i)_{i\in {\mathbb Z}}$ .

In any balanced sequence, we drop the subscript if the context is clear.

The following proposition ensures that local errors in the distribution of populations may be redistributed from horosphere to horosphere within bounded domains, constructing the ‘parent–child matching’ function ${m}$ of Definition 8.2.

Proposition 8.11. Suppose that $\displaystyle \lfloor A\rfloor>(2q+2)\max _{a\in {\mathcal A}}\mu (a)$ . For any balanced sequence $(\nu _i,\Delta _i)$ , and $\displaystyle {\wp }:G\to \{0\}\cup [\lfloor A \rfloor .. \lceil qA\max _{a\in {\mathcal A}}\mu (a)\rceil ]$ realizing $(\nu _i)\in [A,qA]^{\mathbb Z}$ up to error 2, there exists a bijection

$$ \begin{align*} {m}:\{(v,j,k):v\in H_i,\ j\in [1..{\wp}{(v)}],k\in [1..q^{\Delta_i}]\}\leftrightarrow \{(u,l):u\in H_{i+1}, l\in [1..{\wp}{(u)}]\} \end{align*} $$

such that if ${m}(v,j,k)=(u,l)$ , then $u\in P^{-1} {\mathcal N}\{v\}$ .

Proof We begin by describing a technique for producing bijections like the one we want. Let $\mathcal {G}$ be a locally finite bipartite graph with vertex partition ${{\mathscr C}}\sqcup {{\mathscr P}}$ . A perfect matching for $\mathcal {G}$ is a collection $\mathcal {E}$ of edges of $\mathcal {G}$ such that every vertex of $\mathcal {G}$ belongs to exactly one edge from $\mathcal {E}$ [CSC10, §H.2]. We say that $\mathcal {G}$ satisfies the Hall conditions [CSC10, Definition H.3.1] if the set of $\mathcal {G}$ -neighbors of any finite subset of ${{\mathscr C}}$ or ${{\mathscr P}}$ is at least as large as the subset itself. By [CSC10, Theorem H.3.6], $\mathcal {G}$ admits a perfect matching if and only if it satisfies the Hall conditions.

In our case, for a given i, we take ${{\mathscr P}}$ to be $\{(v,j,k):v\in H_i,\ j\in [1..{\wp }_v],k\in [1..q^{\Delta _i}]\}$ and ${{\mathscr C}}$ to be $\{(u,l):u\in H_{i+1}, l\in [1..{\wp }_u]\}$ , with an edge of $\mathcal {G}$ connecting $(v,j,k)$ and $(u,l)$ whenever $u\in P^{-1} {\mathcal N}\{v\}$ . If $\mathcal {E}$ were a perfect matching for $\mathcal {G}$ , then we could define the desired bijection ${m}$ by taking ${m}(v,j,k)=(u,l)$ , such that $(v,j,k)$ and $(u,l)$ span an edge of $\mathcal {E}$ . Therefore we only need to verify that $\mathcal {G}$ satisfies the Hall conditions.

Because any two villagers in the same village will have the same $\mathcal {G}$ -neighbors, without any loss of generality, we may take any finite subset X of ${{\mathscr P}}$ to be of the form $X= \{(v,j,k): v\in R,\ j\in [1..{\wp }(v)],k\in [1..q^{\Delta _i}]\}$ , for some finite subset R of $H_i$ . In $\mathcal G$ , X has ${\wp }_{P^{-1}{\mathcal N} R}$ neighbors. On the other hand, in the villages R, there are ${\wp }_R$ villagers, each of which is to be matched with $q^{\Delta _i}$ children. We therefore need to show that

$$ \begin{align*} q^{\Delta_i} \ {\wp}_R \leq {\wp}_{P^{-1}{\mathcal N} R}.\end{align*} $$

Similarly, without any loss of generality, we may take any finite subset of ${{\mathscr C}}$ to be of the form $X= \{(u,l): u\in R,\ l\in [1..{\wp }(u)]\}$ , for some finite subset R of $H_{i+1}$ . $\# X= {\wp }_R$ and X has $q^{\Delta _i} {\wp }_{{\mathcal N} P R}$ neighbors in $\mathcal {G}$ . Thus, we will also need to show that

$$ \begin{align*} q^{-\Delta_i}{\wp}_{R}\leq {\wp}_{{\mathcal N} PR}.\end{align*} $$

When the inequalities above are established, the proof of the proposition will be complete.

To show our desired inequalities, we need the following identities on any finite subsets $R,T$ of any horosphere H.

1. (1) ${\wp }_R{\leq }2\mu _{\partial R}+\nu \,\mu _R$ and (1 $'$ ) $\nu \,\mu _R{\leq }2\mu _{\partial R}+{\wp }_R$ . This follows from Corollary 8.9, because ${\wp }$ realizes $\nu \,\mu $ up to error 2.

2. (2) $\mu _T=({1}/{\lambda })\,\mu _{P^{-1}T}$ and (2 $'$ ) $\lambda \,\mu _{PT}\geq \mu _T$ : From the definition of $\mu $ and shortlex shelling, we have that

   $$ \begin{align*}\sum_{P(b)=a} \mu(b) = \lambda \mu(a)\end{align*} $$
   holds, giving (2) directly. For (2 $'$ ) observe that, in addition, $\mu _{P^{-1}PT}\geq \mu _T$ holds.

3. (3) $q^{\Delta }/ \lambda < q$ and (3 $'$ ) $\lambda q^{-\Delta }< q$ by the definition of each $\Delta $ in a balanced sequence.

4. (4) $\partial P^{-1}R\subset P^{-1}\partial R$ and, if R is ‘sibling-closed’, that is, if R satisfies $R=P^{-1}PR$ , then (4 $'$ ) $\partial P R\supset P\partial R$ .

By Definition 7.2, if $v,w$ are connected by an edge in the divergence graph, then $P(v), P(w)$ are identical or are connected by an edge in their divergence graph. It follows that ${\mathcal N} P^{-1} R\subset P^{-1} {\mathcal N} R$ and ${\mathcal N} PR\supset P {\mathcal N} R$ . The first inclusion implies (4). Under the assumption that R is sibling closed, the second inclusion implies (4 $'$ ).

1. (5) $(2q+2)\mu _T \leq {\wp }_T$ because for any $v\in H^+$ , ${\wp }(v)\geq \lfloor {\nu }\rfloor \geq A\geq (2q+2)\cdot \max _{{\mathcal A}}\mu (a)$ and ${\wp }(v)=0=\mu (v)$ otherwise.

We define $\nu ':=\nu _{i+1}$ , so that $\nu '={q^{\Delta }}/{\lambda }\nu $ and conversely $\nu ={\lambda }{q^{-\Delta }}\nu '$ .

For the $\rightarrow $ map, we need, for finite $R{\subset } H$ , that

$$ \begin{align*}q^{\Delta} \ {\wp}_{R} \leq {\wp}_{P^{-1}{\mathcal N} R}\end{align*} $$

$$ \begin{align*}\begin{array}{r@{}c@{}ll} q^{\Delta} {\wp}_R &\,\leq\,\, & q^{\Delta}(2\mu_{\partial R}+\nu\,\mu_R) & \text{by (1),} \\ & =\, & \displaystyle \frac{q^{\Delta}}{\lambda}(2\mu_{P^{-1}\partial R}+\nu\,\mu_{P^{-1}R}) & \text{by (2),} \\ & \leq\, & 2q \,\mu_{P^{-1}\partial R}+\nu'\,\mu_{P^{-1}R} & \text{by (3) and definition of } \nu', \\ & \leq\, & 2q\,\mu_{P^{-1}\partial R}+2\,\mu_{\partial P^{-1}R} +{\wp}_{P^{-1}R} & \text{by } (1') \\ & \leq\, & 2q\,\mu_{P^{-1}\partial R}+ 2\,\mu_{P^{-1}\partial R} +{\wp}_{P^{-1}R} & \text{by } (4), \\ & \leq\, & {\wp}_{P^{-1}\partial R}+{\wp}_{P^{-1}R} & \text{by } (5), \\ & =\, & {\wp}_{P^{-1}{\mathcal N} R} & \text{as desired.} \end{array}\end{align*} $$

To find an injection in the other direction, we need that for finite $R\subset H'$

$$ \begin{align*} q^{-\Delta} {\wp}_R\leq {\wp}_{{\mathcal N} P R}. \end{align*} $$

We replace R with its sibling closure $P^{-1}PR$ ; the left-hand side of the inequality cannot decrease and the right does not change, thus establishing the inequality for all R. We compute:

$$ \begin{align*}\begin{array}{r@{}c@{}ll} q^{-\Delta} {\wp}_R&\,\leq\,\, &q^{-\Delta}(2\,\mu_{\partial R}+\nu'\,\mu_R)& \text{by (1),} \\ &\leq& q^{-\Delta}(2\lambda\, \mu_{P\partial R}+\nu'\lambda\,\mu_{PR}) & \text{by } (2'), \\ &\leq& 2\lambda q^{-\Delta} \,\mu_{\partial PR}+\nu\,\mu_{PR} & \text{by } (4') \text{ and definition of } \nu, \\ &\leq&2q\mu_{\partial PR} + 2\,\mu_{\partial PR}+{\wp}_{PR}& \text{by } (3') \text{ and } (1'),\\ &\leq& {\wp}_{\partial PR}+{\wp}_{PR} & \text{by } (5),\\ &=& {\wp}_{{\mathcal N} P R} & \text{as desired.} \end{array}\end{align*} $$

This completes the proof of Proposition 8.11.

Proposition 8.12. For some N, there exists a populated shelling X with population bound N and growth by powers of q, and so the SFT $\Sigma $ is non-empty.

Proof Take $\displaystyle A>(2q+2)\max _{a\in {\mathcal A}}\mu (a)$ and $\displaystyle N>\lceil qA\max _{a\in {\mathcal A}}\mu (a)\rceil $ .

9 Aperiodicity

Any infinite hyperbolic group admits a shortlex shelling X such that is periodic—for example take a horofunction with axis defined by a cycle in the shortlex FSA. By contrast, Proposition 9.5 shall show that for a populated shelling X on a one-ended hyperbolic group, cannot have an infinite-order period, completing the proof of our main theorem. The idea is to show that any period of would induce a period of the ‘growth sequence’ $\Delta _i:=\Delta (h^{-1}(i))$ (this follows from Lemma 9.1), and then show that periods of the growth sequence cannot exist (Corollary 9.4).

We begin by showing that any infinite-order period, say for $\pi \in G$ , translates horospheres to horospheres and does not fix any horosphere as follows.

Lemma 9.1. Given a shortlex shelling $X=(h,\operatorname{\textsf{state}},P)$ , if is periodic under some infinite-order element $\pi \in G$ , then $h(\pi g)=h(g)+C_{\pi }$ for some non-zero constant $C_{\pi }\in {\mathbb Z}$ .

Proof Write $h\cdot \pi $ for $g\mapsto h(\pi g)$ , so that

By Lemma 3.19, h and $h\cdot \pi $ differ by a constant, that is, there is some $C_{\pi }\in {\mathbb Z}$ such that $h(\pi g)=h(g)+C_{\pi }$ .

We may see that $C_{\pi }\neq 0$ as follows. Without loss of generality, let $0=h(1_G)$ . If $C_{\pi }=0$ , then $\ldots ,\pi ^{-1},1_G,\pi ,\pi ^2,\ldots $ is a quasi geodesic lying in a horosphere [BH99, Corollary III. $\varGamma$ .3.10]. By [BH99, Corollary III.H.1.7] there is some N so that any geodesic from $1_G$ to any $\pi ^k$ remains within an N neighborhood of $(\pi ^k)$ . Any k with $\operatorname {\mathrm {d}}(1_G, \pi ^k)>2N+2\delta $ , contradicts Lemma 3.22.

Lemma 9.2. Let $X=(h,\operatorname{\textsf{state}},P,{\wp }, \Delta ,m)$ be a populated shelling. For any horosphere H and any $v\in H^+$ , there is some finite $S\subset H$ such that all the descendants of villagers in v lie in $P^{-*}S$ , the future of S. Furthermore, there is some finite $S'\subset H$ so that every villager living in $P^{-*}S$ is descended from a villager living in $S'$ .

Proof We write $\pi _G$ for the projection from $G\times {\mathbb N}\to G$ . Write $Q(u,l)=(v,j)$ where $(v,j,k)$ is the unique triple such that $m(v,j,k)=(u,l).$

We will show that there is a universal constant R so that for any villager $(u,l)$ and $n\in {\mathbb N}$ , we have $\operatorname {\mathrm {d}}(\pi _G(Q^{n}(u,l)), P^n(u))\leq 2R$ . The proposition will follow: For any v in any $H^+$ , take S to be the $2R$ -neighborhood of v and let $S'$ be the $2R$ -neighborhood of S.

Suppose that $(u,l)$ is a descendant of a villager at v, that is, that $\pi _G(Q^n(u,l))=v$ for some $n>0$ and $l\in [1..{\wp }(u)]$ . Let $v'=P^n(u)$ and take B to be a ball containing $\{P^{k}u\}_{k=0}^n \cup \{\pi _G Q^k(u,l)\}_{k=0}^n$ .

By the definition of a shortlex shelling, B is modeled in $X_0$ ; that is there exists $g\in G$ such that

Let $\gamma '$ be the geodesic given by $\gamma '(k)=vg^{-1}P_0^k(gv^{-1}u)$ , $k\in [0..(n+|g|)]$ .

Let $\gamma $ be the path defined by: for $k\in [0..n]$ , take $\gamma (k)=\pi _G Q^k(u,l)$ . For $k\in [n..(n+|g|)]$ , $\gamma (k)=vg^{-1}P_0^k(g)$ .

Observe that $h_0(gv^{-1}\gamma (k))=h_0(gv^{-1}u)-k$ and therefore $\operatorname {\mathrm {d}}(\gamma (i),\gamma (j)) \geq |i-j|$ .

We claim that $\operatorname {\mathrm {d}}(\gamma (k),\gamma (k+1))\leq 6\delta +1$ . For $k< n$ , edges of the divergence graph have length at most $2\delta $ (Lemma 7.3) and (by Definition 8.2 of a populated shelling) $m_G(v,j,k)$ lies in $P^{-1}$ of the $3$ -neighborhood of v in the divergence graph in the horosphere $h^{-1}(h(v))$ . For $k\geq n$ , $\operatorname {\mathrm {d}}(\gamma (k)$ , $\gamma (k+1))=1$ .

It follows that

$$ \begin{align*}|i-j|=|h(\gamma(i))-h(\gamma(j))| \leq \operatorname{\mathrm{d}}(\gamma(i),\gamma(j))\leq (6\delta +1)|i-j|\end{align*} $$

for $i,j\in [0..(n+|g|)]$ . Then $\gamma $ is a $(6\delta +1,0)$ -quasi geodesic, as defined in [BH99, Definition I.8.22].

We have that $\gamma (0)=\gamma '(0)=u$ and $\gamma (n+|g|)=\gamma '(n+|g|)=vg^{-1}$ . By Theorem III.H.1.7 of [BH99] every point of $\gamma $ is within a universal bound, which is denoted there by $R=R(\delta ,6\delta +1,0)$ , of some point of $\gamma $ . In particular, $v \in \gamma $ is within R of some point $v" \in \gamma '$ . Because $\operatorname {\mathrm {d}}(v',v") = |h(v')-h(v")| = |h(v)-h(v")| \leq \operatorname {\mathrm {d}}(v,v")\leq R$ , by the triangle inequality we conclude that $\operatorname {\mathrm {d}}(v,v') \leq 2R$ .

Recall that, if $X=(h,\operatorname{\textsf{state}},P,{\wp },\Delta ,{m})$ is a populated shelling, then $\Delta $ is constant on horospheres. Write $\Delta _i$ for the value achieved by $\Delta $ on $h^{-1}\{i\}$ . We will refer to $(\Delta _i)_{i\in {\mathbb Z}}$ as the growth sequence of X.

Corollary 9.3. In a populated shelling, there exists a non-empty finite set $S\subset H^+$ satisfying the following:

1. (1) $\log ( {\wp }_{P^{-n}S})=n\log (\lambda )+O(1)$ ;

2. (2) $\log ( {\wp }_{P^{-n}S})=\sum _{i=1}^n \Delta _i\log (q)+O(1)$ .

Proof Recall (Remark 6.2) that on any finite $S\subset H^+$ , $\mu _{P^{-n}S} = \lambda ^n\mu _S$ . The functions $\mu $ and ${\wp }$ have finite non-negative ranges, and have identical zero-sets (see Definition 8.2). Therefore, there are constants $c_1,c_2>0$ such that for any $v\in G$ , $c_1 {{\wp }(v)} \leq {\mu (v)}\leq c_2 {{\wp }(v)}$ . Consequently $ c_1 {{\wp }_{P^{-n}S}} \leq {\mu _{P^{-n}S}}\leq c_2 {{\wp }_{P^{-n}S}}$ and the first equality (1) follows.

Choose $v\in H^+$ . By Lemma 9.2 there exists some finite $S\subset H^+$ , such that all of the descendants of v lie in $P^{-*}S$ , the future of S and so ${\wp }_{P^{-n}S}\geq (q^{\sum _1^n{\Delta _i}}){\wp }_v$ , the number of such descendants.

Lemma 9.2 further shows there is some finite $S'\in H$ so that every villager living in $P^{-*}S$ is descended from a villager living in $S'$ , and so ${\wp }_{P^{-n}S}\leq q^{\sum _1^n{\Delta _i}}{\wp }_{P^{-n}S'}$ . Together these inequalities give (2).

Corollary 9.4. The growth sequence in a populated shelling is not periodic.

Proof Suppose the growth sequence $(\Delta _i)$ is periodic, with period $p\in {\mathbb N}$ . Let $\hat \Delta =\sum _{i=1}^{p} \Delta _i$ . For any $k\in {\mathbb N}$ , taking $n=pk$ , we have $pk\log (\lambda )+O(1)=\hat \Delta k\log (q)$ and, thus, $p\log (\lambda )+O(1/k)=\hat \Delta \log (q)$ . As $k\to \infty $ ,

$$ \begin{align*} \log(q)/\log(\lambda)=p/\hat\Delta\in{\mathbb Q} \end{align*} $$

a contradiction to our choice of q with respect to $\lambda $ .

Proposition 9.5. Let be the local data for a populated shelling $X=(h,\operatorname{\textsf{state}},P,{\wp }, \Delta ,{m})$ . Then the stabilizer of in G contains no infinite-order element.

Proof Suppose $\pi $ is in the stabilizer of , so that and $\pi $ has infinite order. By Lemma 9.1, there is a non-zero $C_{\pi }\in {\mathbb Z}$ such that $h(\pi g)=h(g)+C_{\pi }$ . Writing $(\Delta _i)$ for the growth sequence of X, it follows that $\Delta _{h(g)}=\Delta _{h(g)+C_{\pi }}$ for every $g\in G$ and, hence, $(\Delta _i)$ is $C_{\pi }$ -periodic, in contradiction to Lemma 9.4.