No CrossRef data available.
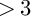 $>3$
$>3$Published online by Cambridge University Press: 28 February 2024
In this paper, we prove the nonvanishing and some special cases of the abundance for log canonical threefold pairs over an algebraically closed field k of characteristic 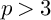 $p> 3$. More precisely, we prove that if
$p> 3$. More precisely, we prove that if 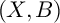 $(X,B)$ be a projective log canonical threefold pair over k and
$(X,B)$ be a projective log canonical threefold pair over k and 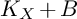 $K_{X}+B$ is pseudo-effective, then
$K_{X}+B$ is pseudo-effective, then 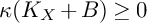 $\kappa (K_{X}+B)\geq 0$, and if
$\kappa (K_{X}+B)\geq 0$, and if 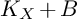 $K_{X}+B$ is nef and
$K_{X}+B$ is nef and 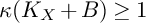 $\kappa (K_{X}+B)\geq 1$, then
$\kappa (K_{X}+B)\geq 1$, then 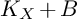 $K_{X}+B$ is semi-ample.
$K_{X}+B$ is semi-ample.
As applications, we show that the log canonical rings of projective log canonical threefold pairs over k are finitely generated and the abundance holds when the nef dimension 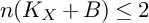 $n(K_{X}+B)\leq 2$ or when the Albanese map
$n(K_{X}+B)\leq 2$ or when the Albanese map 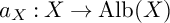 $a_{X}:X\to \mathrm {Alb}(X)$ is nontrivial. Moreover, we prove that the abundance for klt threefold pairs over k implies the abundance for log canonical threefold pairs over k.
$a_{X}:X\to \mathrm {Alb}(X)$ is nontrivial. Moreover, we prove that the abundance for klt threefold pairs over k implies the abundance for log canonical threefold pairs over k.