1. Introduction
Cold glaciers are defined as firn and ice bodies showing permanently sub-freezing temperatures over a minimum period of 1 year. Glaciers are temperate if their firn and ice is at pressure-melting point. Most of the existing ice bodies are neither cold nor temperate throughout. Such ice bodies are called polythermal (e.g. Reference PatersonPaterson, 1994).
In order to quantify firn temperatures, a mean annual firn temperature (MAFT) can be defined. Seasonal surface temperature fluctuations are reflected within the uppermost 1020 m of the firn body. Englacial temperatures measured to this depth shall be called near-surface firn temperatures, adapting the concept by Reference Hooke, Gould and BrzozowskiHooke and others (1983). The MAFT is found by extrapolating the seasonally undisturbed englacial temperature gradient to the surface. The above method is often inapplicable to sites with strong lateral firn and ice advection as well as to sites with important meltwater percolation. In these cases englacial temperature profiles below 15–20 m depth are often characterized by strong heat-flux anomalies, and hence do not reflect the actual in situ thermal conditions based on pure vertical heat-exchange processes. The MAFT can then be defined at a depth where the seasonal temperature fluctuations vanish, or, in practice, where they are within the accuracy range of the measurement.
The MAFT is the result of the energy and mass balance at the glacier surface. Important parameters determining the MAFT are the mean annual air temperature (MAAT), the radiation balance, the amount and seasonality of accumulation/ablation, the amount of penetrating and refreezing meltwater, the topographic location (hollow or ridge) and wind effects. Some of these parameters are closely linked to each other (e.g. the topography, wind effects and the amount of snow deposition). Other parameters which may influence the near-surface thermal regime are the glacier flow velocity, the extent and characteristics of the catchment basin, the intensity of friction at the glacier bed and of ice deformation, the ground heat flux and the occurrence of crevassed zones. The MAFT is generally higher than the MAAT because of the positive latent-heat flux within the snow and firn cover caused by percolating and refreezing meltwater.
Firn and ice temperatures in accumulation areas are of glacio-climatological relevance due to the fact that they
affect the viscosity of firn and ice (e.g. Reference PatersonPaterson, 1994);
assure the preservation of the glacio-chemical information in ice-core studies if they are deep enough (e.g. Reference Oeschger and LangwayOeschger and Langway, 1989);
can be used to detect atmospheric warming or cooling trends (Reference RobinRobin, 1983; Reference ZotikovZotikov, 1986; Reference HaeberliHaeberli, 1990; Reference Haeberli and FunkHaeberli and Funk, 1991; Reference MacAyeal, Firestone and WaddingtonMacAyeal and others, 1991; Reference Fischer, Wagenbach, Laternser and HaeberliFischer and others, 1995);
affect the stability of steep hanging glaciers (Reference AleanAlean, 1985; Reference Haeberli, Alean, Müller and FunkHaeberli and others, 1989a; Reference WagnerWagner, 1996; Reference Lüthi and FunkLüthi and Funk, 1997);
can influence the mass-balance evolution of a glacier (e.g. Reference Greuell and OerlemansGreuell and Oerlemans, 1986; Reference Konzelmann and BraithwaiteKonzelmann and Braithwaite, 1995).
For a long time it was assumed that glaciers in the Alps were generally temperate, although Reference VallotVallot (1913) already observed cold firn in the Mont Blanc massif in the late 19th century. The discussion about cold firn and ice in the Alps was restarted in the 1950s by investigations in the Monte Rosa massif (Reference FisherFisher, 1953, Reference Fisher1954, Reference Fisher1955, Reference Fisher1963) and in the Jungfrau area (Reference Haefeli and BrentaniHaefeli and Brentani, 1955, Reference Haefeli and Brentani1956). Today the existence of cold firn and ice in the Alps is uncontested. Reference HaeberliHaeberli (1976) and Reference Lliboutry, Briat, Creseveur and PourchetLliboutry and others (1976) first attempted to systematically assess the distribution of cold firn and ice in the Alps.
In the past extensive firn- and ice-temperature measurements took place predominantly at locations of practical or scientific interest in connection with construction work (e.g. Reference Haefeli and BrentaniHaefeli and Brentani, 1955, Reference Haefeli and Brentani1956; Reference Haeberli, Iken and SiegenthalerHaeberli and others, 1979) and high-Alpine core drillings (e.g. Reference Oeschger, Schotterer, Stauffer, Haeberli and RöthlisbergerOeschger and others, 1978; Reference Alean, Haeberli and SchädlerAlean and others, 1984; Reference Haeberli and FunkHaeberli and Funk, 1991; Reference Vincent, Vallon, Pinglot, Funk and ReynaudVincent and others, 1997). A scheme for the spatial distribution of cold firn and ice was outlined by Reference Hooke, Gould and BrzozowskiHooke and others (1983) including near-surface temperatures of Alpine and polar regions, and by Reference Haeberli and AleanHaeberli and Alean (1985) with firn and ice temperatures from the European Alps.
The present study focuses on firn and ice temperatures of high-altitude accumulation areas in the European Alps. It aims at a better understanding of the spatial distribution of cold firn and the climatic and topographic variables influencing its occurrence, by means of direct measurements and model calculations. The study views firn temperatures as an integral signal of various surface mass- and energy-exchange processes, rather than describing them within a physically based snow- and firn-cover model.
2. Description of the Field Sites
2.1. Jungfraufirn, Bernese Alps
The Jungfraufirn (46°32′ N, 7°59′30″ E) is situated in the central Bernese Alps (Fig. 1) and is part of Aletschgletscher, the longest (24 km) and largest (86 km3) glacier in the Alps (Fig. 2a). Earlier measurements on the upper Jungfraufirn clearly revealed temperate conditions (Reference Hughes and SeligmanHughes and Seligman, 1939; Reference PerutzPerutz, 1950). Rather different thermal conditions can be found on firn and ice ridges in the area. Distinct subzero temperatures (−1° to −3°C) were measured in the saddle area of the Jungfraujoch (Reference Haefeli and BrentaniHaefeli and Brentani, 1955, Reference Haefeli and Brentani1956) and on the adjacent Sphinx ridge, where a 10 m temperature of −6°C was found (VAW, unpublished).

Fig. 1. Location of the field sites in Switzerland.
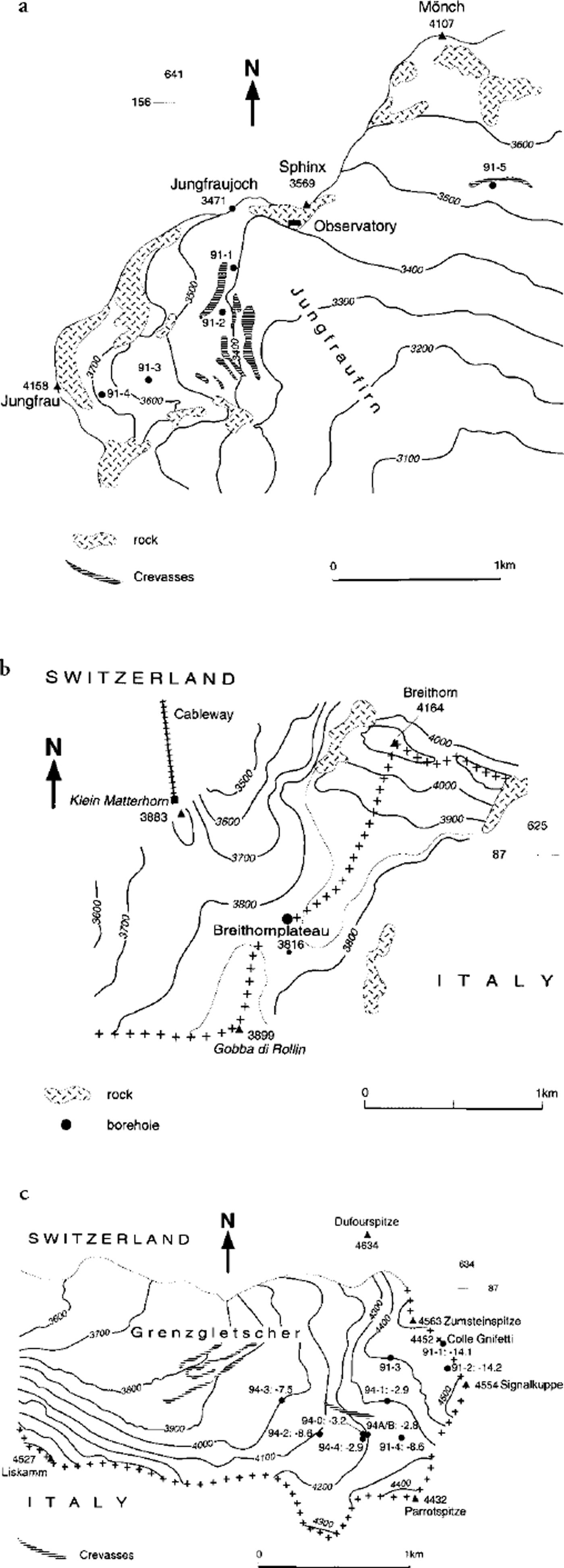
Fig. 2. Borehole locations. (a) The Jungfraufirn and the location of boreholes 91-1, 91-2, 91-3, 91-4 and 91-5 drilled in March 1991; (b) the Breithornplateau and the location of the borehole drilled in July 1991; and (c) the upper Grenzgletscher and the location of boreholes 91-1, 91-2, 91-3 and 91-4 drilled in 1991, and boreholes 94-0, 94-1, 94-2, 94-3, 94-4 and 94A/B drilled in 1994. In (c) the measured MAFT is given for each borehole.
In 1991 a total of five 20 m boreholes were drilled with a steam drill on the upper Jungfrau firn at 3410–3630 m a.s.l. (Fig. 2a). The measurements were designed to detect the boundary between cold and temperate firn and to investigate the influence of crevasses on the englacial temperature distribution.
2.2. Breithornplateau, Valais Alps
The Breithornplateau (45°55′50′′ N, 7°44′40′′ E) is a wide open glacier plateau south of Zermatt, Valais Alps, at the Swiss–Italian border (Fig. 1). It is situated between the mountain tops of the Breithorn (4164 m a.s.l.) to the north and the Gobba di Rollin (3899 m a.s.l.) to the southwest (Fig. 2b). Earlier temperature measurements were carried out on the neighbouring south slope of the Breithorn at approximately 4000 m a.s.l. in 1960 and 1961. The observed values measured in a 70 m long hand-dug(!) horizontal tunnel ranged between −5.5°C at the tunnel entrance and −0.5°C at the glacier bedrock. A water pocket was found in a second tunnel below the first one (Reference FisherFisher, 1963). Temperature measurements were carried out in 1991 and 1992 in a 30 m deep borehole 100 m north of the actual saddle point (3816 m a.s.l.) (Fig. 2b).
2.3. Upper Grenzgletscher, Valais Alps
The study area of the upper Grenzgletscher (45°55′30′′ N, 7°52′ E) is situated in the heart of the Monte Rosa massif, Valais Alps, close to the Swiss–Italian border (Fig. 1). It is surrounded by some of the highest peaks in the Alps (Fig. 2c). Grenzgletscher is part of Gornergletscher and is 14 km long, with an area of approximately 70 km2. The Grenzgletscher tongue is characterized by strikingly white, air-bubble-rich ice which indicates cold-firn metamorphosis in the accumulation area. Negative ice temperatures (−2° to −3°C) prevail at the glacier terminus (Reference HaeberliHaeberli, 1976).
The climate in the study area is characterized by highaltitude conditions, i.e. nearly persistent sub-zero air temperatures all year round, a high precipitation total and high to extreme wind speeds. The snow accumulation is strongly variable, ranging between 0.3 m w.e. a−1 at wind-exposed saddles and ridges and 2–3 m w.e. a−1 at wind-protected slopes and basins (Reference Gäggeler, von Gunten, Rössler, Oeschger and SchottererGäggeler and others, 1983; Reference Haeberli, Schotterer, Wagenbach, Schwitter and BortenschlagerHaeberli and others, 1983; Reference Alean, Haeberli and SchädlerAlean and others, 1984; Reference DoscherDöscher, 1996).
A series of firn- and ice-temperature measurements was carried out on the upper Grenzgletscher at 3900–4470 m a.s.l. in 1991, 1992 and 1994. During this time, temperatures were measured in a total of 10 boreholes at 14–120 m depth (Fig. 2c). These investigations took place in connection with different core-drilling projects by the Institute of Environmental Physics, Heidelberg, Germany, and the Laboratory of Radio and Environmental Chemistry, Villigen and Berne, Switzerland.
3. Discussion of the Firn- and Ice-Temperature Measurements
3.1. Methods and data analysis
Thermistor cables consisting of negative temperature coefficient (NTC) thermistors soldered onto a cable at different intervals (1–20 m) were lowered into steam- and coredrilled boreholes down to depths of 14–120 m. During the 1991 field investigation the thermistor cables were permanently installed in the boreholes, whereas in 1994 the cables were removed after each measurement in the open, air-filled boreholes. The boreholes were closed at the surface to avoid air circulation, and readings were taken after several hours until perfect thermal equilibrium was reached. The thermistors, which were previously calibrated in an ice-water bath at 0°C, measure the electrical resistance which has a functional relation to the temperature given by the Steinhart–Hart equation
where T (K) is the temperature, R (Ω) is the resistance and A, B and C are the calibration coefficients. In firn down to depths of about 30 m, steam drilling is a very efficient and easy way of drilling. It disturbs the temperature distribution in the close surroundings of the borehole, so a certain amount of time must elapse until the temperatures have adjusted to the previously undisturbed conditions. The time for complete adjustment within a measuring accuracy of 0.1°C is on the order of a few days up to about 2 weeks. Thus, extrapolation of a few continuous readings right after drilling is an easier way to obtain the final temperatures. Various extrapolation formulae were developed (Reference Carslaw and JaegerCarlslaw and Jaeger, 1959; Reference Lachenbruch and BrewerLachenbruch and Brewer, 1959). In a first approximation, the temperature T(t) plotted against 1/t(t = time since drilling, i. e. time which has elapsed since the drill tip reached the depth for the first time) tends to a linear relation. T(t) plotted vs 1/(t − s/2) or ln[t/(t − s)], where s is the duration of the thermal disturbance caused by the drilling process (period lasting from the time the drill tip reached the depth for the first time until the drilling hose is pulled out of the borehole), approaches a linear relation even faster. Care must be taken since the duration of the thermal disturbance can be largely prolonged by liquid water that remains in the borehole after the drilling process.
The extrapolation methods mentioned above were applied to all the measurements described below to yield first corrected firn-temperature values only a short time after drilling. At later field investigations the temperatures had perfectly adjusted to the prevailing conditions, and single readings could be taken to obtain accurate temperature values. The accuracy of the extrapolated temperatures is estimated to be better than ±0.2°C. The accuracy of the undisturbed measurements is on the order of ±0.1° to ±0.2°C (upper 10 m of the borehole) or better (below 10 m depth).
3.2. Jungfraufirn, Bernese Alps
The five investigated drill sites on the upper Jungfraufirn are located at 3410–3630 m a.s.l. (Fig. 2a). Boreholes 91-1 and 91-3 reflect temperate conditions, with a winter cold wave down to 15 m depth which completely disappears during the summer months (Fig. 3a). Boreholes 91-2 and 91-5 are situated close to crevasses. They may reflect special micro-climatic conditions of large crevasses. Seasonal temperature changes within the profiles can be observed down to 20 m depth. Whereas the firn cover at borehole 91-2 at 3410 m a.s.l. is warmed at the bottom of the profile in August (Fig. 3b), the lower thermistor in borehole 91-5 (3530 m a.s.l.) still indicates a cooling process during the same month (Fig. 3c). This phenomenon can be qualitatively explained by the fact that, in the first case, the crevasse acts as a preferred meltwater drainage channel where the meltwater is temporarily stored at the bottom of the crevasse, providing a large input of latent heat. In the latter case, the warming occurs mainly by heat conduction, as meltwater is sparse or the crevasse remains entirely meltwater-free, which causes the formation of slightly cold firn (−0.5° to −0.8°C) at 15–20 m depth. In this case, crevasses have a cooling effect on the surrounding firn body. Due to large snow deposition and avalanche activity, only one profile could be measured in borehole 91-4 in March 1991 (Fig. 2a). The very low near-surface temperature (−14°C at 5 m depth) and the value of −0.6°C found at 20 m depth suggest slightly cold conditions on the steep east slope of the Jungfrau. It seems that large winter accumulation could favour the formation of cold firn provided that the snow cover is not entirely warmed up by percolating melt-water during summer.

Fig. 3. Englacial temperature profiles on the Jungfraufirn measured in 1991. (a) Perfectly temperate conditions are depicted in borehole 91-3 (3540 m a.s.l). The thermal influence of a nearby crevasse is shown in (b) borehole 91-2 (3410 m a.s.l) and (c) borehole 91-5 (3530 m a.s. l.). Temperature fluctuations occur down to 20 m depth. In borehole 91-2, rapid warming can be observed in August, whereas cooling still goes on in the lower part of profile 91-5.
3.3. Breithornplateau, Valais Alps
Firn temperatures were measured in a 30 m deep steam-drilled borehole on four different occasions (Fig. 2b): 30 July–8 August 1991, 27 October 1991, 4 December 1991 and 10 April 1992. Except for the uppermost metres of the snow and firn cover, which of course cools down during the winter months, the measuring site seems to reflect temperate conditions. This rather surprising result has to be interpreted carefully, as no confirmation by additional measurements can be given. The tongue of Unterer Theodulgletscher, which is fed by ice from the south face of the Breithorn and the Breithornplateau, shows white, air-bubble-rich ice, a sign of cold-firn metamorphosis in the accumulation area. Due to recent warming trends it is, however, possible that the highly sensitive south slopes of the Breithorn, which were already close to temperate conditions in the 1960s (Reference FisherFisher, 1963), could have warmed, as may also be the case on the Breithornplateau itself.
3.4. Upper Grenzgletscher, Valais Alps
In 1991, firn temperatures were measured in four different 30 m deep steam-drilled boreholes between the saddle area of the Colle Gnifetti (4452 m a.s.l.) and the first large firn basin down-glacier at 4250 m a.s.l. (Fig. 2c). The measurements in the saddle area at 4452 (borehole 91-1) and 4470 (borehole 91-2) m a.s.l. confirmed the results described by Reference Oeschger, Schotterer, Stauffer, Haeberli and RöthlisbergerOeschger and others (1978) and by Reference Haeberli and FunkHaeberli and Funk (1991) and show that the measured profiles are close to steady-state conditions. Due to a heavy thunderstorm which completely destroyed the thermistor cable in borehole 91-1 and damaged the one in borehole 91-2, only a few readings could be taken. The corrected temperatures (cf. section 3.1) of borehole 91–1 are given in Figure 4a. Due to the saddle-point location (virtually no lateral advection), the englacial temperature gradient dT/dz can be extrapolated to the surface, which yields MAFTs of −14.1°C with dT/dz = 0.008°C m−1 (borehole 91-1) and −14.2°C with dT/dz = 0.025°C m−1 (borehole 91-2).

Fig. 4. Measured (thick lines) and calculated (thin lines) temperature profiles on the upper Grenzgletscher for boreholes (a) 91-1 (4452 m a.s.l.), (b) 94-1 (4300 m a.s.l) and (c) 94-2 (4100 m a.s.l).
Two temperature profiles per hole were registered in boreholes 91-3 and 91-4 between 4 and 9 August 1991 and on 26 October 1991. The temperatures of borehole 91-3 (4400 m a.s.l.) show a strong seasonal influence down to 20 m (cf. Fig. 3b and c). They indicate the thermal impact of an adjacent large crevasse and are not representative for the surrounding area. The temperature profiles measured at site 91-4 (4250 m a.s.l.) show a distinct seasonal variation down to 12 m depth. A 14 m temperature of −8.6°C and a temperature gradient of −0.12°C m at 14–24 m depth were observed. The negative gradient at depth may either be due to the advection of cold firn and ice from the saddle area or from the west face of the Signalkuppe or be a sign of recent warming. The uppermost 2 m of the profile became entirly temperate during summer.
In 1994, seven borehole temperature measurements were carried out. The 14 m holes 94-1, 94-2, 94-3 and 94-4 were drilled with a steam drill, whereas holes 94-0 (14 m), 94-A (120 m) and 94-B (28 m) resulted from electromechanical ice-core drilling (Fig. 2c). When looking at the three measured profiles of borehole 94-1 at 4300 m a.s.l., the most striking result is the unusually high 14 m temperature of about −3°C (Fig. 4b). Whereas the warming in May and June was mainly caused by heat conduction, latent-heat contribution from penetrating and refreezing meltwater determined the temperature distribution between June and September. The fact that the uppermost 4 m of the snow/firn cover became entirely temperate during the summer months can be explained by the high air temperatures in summer 1994. Compared to the 30 year mean from 1960 to 1990, a positive deviation of 1.7°C was observed at the high-Alpine research station at the Jungfraujoch (Fig. 2a) during June–August 1994. The reason for the generally high MAFT may, however, be the high net solar radiation total (cf. section 5).
At 4200 m a.s.l., readings were taken in four boreholes: 94-0, 94-4, 94-A and 94-B (Fig. 2c). The 14 m temperatures were all in the same range of approximately −3°C, which is equal to the value measured at 4300 m a.s.l. Although site 91-4 lies at nearly the same altitude as the sites around the 120 m hole 94-A and receives about the same radiation total, the 14 m value is considerably lower (−8.6°C). Meltwater effects in the vicinity of borehole 94-A might cause this difference.
In fact, firn and ice temperatures close to the melting point (−1° to −2°C) create a strong temperature anomaly with corresponding high heat fluxes at about 30 m depth in the electromechanically drilled deep hole 94-A (Fig. 5). This unusually warm ice can only be the result of a strong local heat source, i. e. both laterally inflowing ice formed under almost temperate conditions and percolating and refreezing meltwater. The meltwater could originate from an adjacent steep and cre-vassed south-facing slope and follow the firn–ice transition which can be expected at 30–40 m depth. Meltwater formation at the walls of these crevasses has, indeed, already been observed in spring. The shape of the profile at greater depth, however, clearly reveals the advection of cold ice from the upper reaches of Grenzgletscher, most probably from the Colle Gnifetti area. This section of the profile resembles the calculated englacial temperature profiles at the cold tongue of Gornergletscher (Reference Blatter and HaeberliBlatter and Haeberli, 1984).

Fig. 5. Temperature profile measured in the electromechanically drilled borehole 94A (4200 m a.s.l) on the upper Grenzgletscher, 31 October 1994, and calculated heat fluxes at 30 and 40 m depth using the measured temperature gradients and a temperature-dependent value for the thermal conductivity.
In contrast to the profiles measured at 4300 and 4200 m a.s.l., the adjacent northwest slope down-glacier is distinctly colder, with a 14 m temperature of −8.6°C at 4100 m a.s.l. (borehole 94-2; Fig. 4c) and of −7.5°C at 4000 m a.s.l. (borehole 94-3). The smaller radiation total due to topographic shading from the Liskamm and the evenly inclined slope (no lateral meltwater effects) may be responsible for the observed temperatures. Thus, the influence of latent heat is much weaker, although the warming of the uppermost metres is still considerable, indicating that the summer air temperatures of 1994 were strongly above the average.
The observed 14 m temperatures on the upper Grenzgletscher show a maximum seasonal variation of 0.05−0.18°C. Except for boreholes 91-4 and 94-2, the observed variations are all within the error range of the measurements. Thus, the 14 m temperatures equal MAFTs.
It can be summarized that the upper Grenzgletscher is cold throughout and that the observed MAFTs seem to be influenced by the aspect of the glacier (higher firn temperatures in aspects with high direct solar radiation input). Even at 4000 m a.s.l., clearly negative firn temperatures can still be observed due to the northwesterly course of the glacier, indicating that cold firn might reach far down-glacier.
4. Modelling Temperature Profiles for the Upper Grenzgletscher
Englacial temperature profiles are calculated for boreholes 91-1 (saddle point of Colle Gnifetti), 94-1 and 94-2 (upper Grenzgletscher) at 4450, 4300 and 4100 m a.s.l., respectively (Fig. 2c). These profiles are calculated to show the influence of heat-transfer mechanisms other than conduction. As a number of assumptions and simplifications are made (see below), they should be considered as an estimation rather than an accurate physical representation of the thermal state of the glacier.
The following assumptions and simplifications are made:
heat transfer is reduced to vertical heat conduction (vertical heat advection by surface accumulation, and corresponding downward motion of the snow and firn are neglected)
latent heat (refreezing meltwater); convective heat transport by the air and liquid water; sensible heat; radiation; frictional heat by ice deformation; lateral firn and ice advection; and the ground heat flux are neglected
the firn density is assumed to be constant with depth
the air temperature at the surface equals the snow surface temperature (being the result of the surface energy balance) and follows a sine curve with a period of 1 year
the monthly mean air temperatures are assigned to the 15th of each month.
With these assumptions and simplifications, a one-dimensional heat-conduction equation (Fourier equation) can be used for the calculations:
where T (°C) is the temperature, t (s) is the time, k (m2 s−1) is the thermal diffusivity and z(m) is the depth. The following two boundary conditions are taken to solve the equation:
-
1. A sinusoidal surface temperature variation
where T(0, t) (°C) is the surface temperature at time t, T 0 (°C) is the MAFT, ΔT 0 (°C) is the amplitude of the yearly variation of the air temperature, ω (s−1) is the angular frequency and φ is a constant phase shift.
-
2. A constant temperature gradient dT/dz at depth z,

The following solution results (cf., e.g., Reference PatersonPaterson, 1994):

with ω = 2π/P and k = K/ρc, where P(s) is the period, K (W m−1 K−1) is the thermal conductivity, ρ(kg m−3) is the density and c(J kg−1 K−1) is the heat capacity. φ is determined individually for each englacial temperature profile to shift the air-temperature maximum of the sine curve to the summer.
As the temperature gradient at infinite depth is not known for boreholes 94-1 and 94-2, the englacial temperature gradient dT/dz is assumed to be 0, which results in a constant temperature T 0 at infinite depth. For borehole 91–1 there is a constant temperature gradient dT/dz of 0.008°C m−1 at depth. The thermal conductivity K is determined as the mean of two empirical approaches (e.g. Reference PatersonPaterson, 1994, p. 205f., eq. 3 and 4):
and

where K i is the heat conductivity of ice (2.1 W m−1 K−1) and ρ i is the density of ice (900 kg m−3). K and the firn density p are assumed to be constant over the depth ranges considered. For ρ, measured values of 585 kg m−3 for borehole 91-1 (Reference Haeberli, Schmid and WagenbachHaeberli and others, 1988) and of 701.5 kg m−3 for boreholes 94-1 and 94-2 (Reference DoscherDoscher, 1996) are taken. A K value of 0.935 (borehole 91-1) and 1.264 Wm−1 K−1 (boreholes 94-1 and 94-2) results. Finally, the heat capacity c is set to 1998 J kg−1 K−1 (borehole 91-1) and 2027 J kg−1 K−1 (boreholes 94-1 and 94-2), which corresponds to a value at −14° and −10°C, respectively.
Air-temperature data from the high-Alpine research station at the Jungfraujoch (cf. Fig. 2a) are extrapolated to the relevant altitudes on Grenzgletscher using a mean temperature gradient of −0.65°C per 100 m altitude increase. To calculate mean surface temperature on Colle Gnifetti (borehole 91-1), the period 1976–90 with a MAAT of −13.5°C, a mean amplitude of 6.85°C and an air-temperature maximum in July is taken. This period corresponds roughly to the age of the firn at 13 m depth where the seasonal temperature fluctuations diminish. The 1990–93 MAAT is taken for boreholes 94-1 (MAAT of −11.8°C) and 94-2 (MAAT of −10.5°C), a mean amplitude of 6.85°C and an air-temperature maximum in August. This time-span reflects more or less the formation period of a 15 m firn layer as reflected in a measured density profile from borehole 94-A (Reference DoscherDoscher, 1996).
Different sources of error are possible for the calculation of the theoretical temperature profiles: A maximum error of 0. 3°C occurs due to the choice of a constant density with depth. The extrapolated air temperatures are considered to reflect the real conditions within an error range of ±0.5°C inferred from direct measurements made at Colle Gnifetti from 1986 to 1990. Another uncertainty results from the strongly density-dependent thermal conductivity. Varying it between 0.3 and 1.4 W m−1 K−1 leads to a maximum error of ± 0.8°C. Taking into account all these sources of error, the calculated profiles seem to reflect the “real heat conduction conditions” accurate to ±1.6°C.
For direct comparison, the results of the calculations are presented together with the measured temperatures in Figure 4. A satisfying result between calculated and measured temperature profiles is obtained for borehole 91-1 at Colle Gnifetti (Fig. 4a).The observed conditions at Colle Gnifetti differ from the modelled ones by 0.5°C. Nearly perfect coincidence results when the surface temperature is set to the measured MAFT of –14.1°C (Fig. 4a). Large discrepancies between measured and calculated temperature profiles for individual months can be observed at borehole 94-1 (Fig. 4b). This marked difference can be explained only by a strong influence of penetrating and refreezing meltwater. The modelled and the observed MAFT differ by almost 9°C. For borehole 94-2, calculated and observed profiles are very similar, presumably as a result of a much smaller radiation income and thus a small latent-heat contribution (Fig. 4c).The observed MAFT is only 1.8°C higher than the value one would expect with pure heat conduction. In the upper part of the profiles, the discrepancies between modelled and measured temperatures are, however, still considerable.
5. Statistical Analysis and Modelling the Firn-Temperature Distribution in the Alps
5.1. Linear regression
As stated in the introduction, the MAFT is mainly a result of various energy- and mass-exchange processes at the glacier surface. In the following, some of the major parameters and their relation to cold firn are statistically analyzed.
In a first step, altitude is linearly regressed against the MAFTs. Ice temperatures and MAFTs measured near crevasses are omitted in all regressions. All regression calculations are based on the assumption of independent observations and normally distributed residuals with uniform variances. Several statistical tests are carried out to check the correlative coherence, including the correlation coefficient r and the coefficient of determination r2. The significance is tested double-sided on a 5% level. A compilation of the firn temperatures is given in the Appendix; r and r 2 values are presented in Table 1. In Figure 6a all available MAFTs from the Alps are plotted against altitude. As almost all the MAFTs below 3900 m a.s.l. (triangles) are at 0°C, a regression calculation is made only for the values above 3900 m a.s.l. (circles), with r = −0.61 and r 2 = 0.37, which yields an altitude-dependent firn-temperature gradient of −1.2°C(100 m)−1. An even better correlation (r = −0.68, r 2 = 0.46) with a temperature gradient of −1.1°C (100 m)−1 results when looking at MAFTs in “cold topography” only, i. e. in northerly aspects (west–north–east (W-N-E)) and flat terrain (Fig. 6b). Flat firn saddles and mountain tops are usually “cold spots” (low accumulation rate, effective turbulent energy exchange in summer due to frequent air circulation and hence reduced meltwater infiltration). MAFTs in southerly aspects (east–south–west(E-S-W)) yield no obvious relation (Fig. 6c). The less clear situation in southerly aspects could be due to the limited dataset, with most of the values situated either in a limited elevation band or in the lower reaches of the firn areas, and thus close to the melting point. At 3900–4800 m a.s.l., tops and ridges show a smaller altitude-dependent firn-temperature gradient of −1.1 °C (100 m) than firn basins with −1.4°C (100 m) (see Table 1). Although the observed gradients are close to the dry-adiabatic lapse rate (−1°C (100 m)−1), the lapse rate found is believed to show the influence of latent-heat release rather than the effect of katabatic winds.

Fig. 6. Relation between measured MAFTs and altitude of (a) the whole sample (29 temperatures; cf. Appendix), (b) MAFTs in northerly aspects only and (c) MAFTs in southerly aspects only. In (a) and (b) a linear regression was calculated for MAFTs above 3900 m a.s.l. (circles), yielding a firn-temperature gradient of (a) −1.2°C (100 m)−1 and (b) −1.1°C (100 m)−1. No regression analysis was made for MAFTs below 3900 m a.s.l. (triangles) and for southerly aspects.
Table 1. Correlation coefficients (r) and coefficients of determination (r2) of the simple linear regression model between observed firn temperatures (MAFTs from the Alps) and altitude (cf text)

5.2. Multiple linear regression
In a second step, multiple linear regression is used to analyze the common effect of altitude and aspect, or altitude and calculated potential direct solar radiation, on the observed firn temperatures.
The potential direct solar radiation is an excellent approximation of the net radiation, which makes a major contribution to the surface energy balance and its spatial and temporal variation (Reference FunkFunk, 1985). The potential direct solar radiation is calculated using a grid-oriented computer program within the geographic information system ARC/INFO (Reference Funk and HoelzleFunk and Hoelzle, 1992), and digital elevation data of the upper Grenzgletscher. The program calculates the radiation total on a daily basis and considers topographic shading, as well as aspect and slope angle. Additionally, atmospheric scattering, reflection and absorption are taken into account. For practical reasons, the radiation input of a month is defined as the total of days 5, 10, 15, 20, 25 and 30. The total of these six values represents the individual month accurately enough as the mean of this total, and the total of 31 days differs by only 1–2%. For the regression calculations, a 1 year total was taken as the sum of the 12 individual months as calculated above.
The correlation coefficient r, the coefficient of determination r 2 and the p value (measure for the significance) are used to check the correlation between various parameters.
In the subsequent analysis, ice temperatures and firn temperatures which were influenced by crevasses are omitted. As the aspect does not represent numerical information, a coding system is used where north receives the smallest value (1) and south the highest (9). Aspects NW and NE (value 3), W and E (value 5) and SW and SE (value 7) are considered symmetrical. Thus, an aspect value of 1 represents the lowest, and a value of 9 the highest incoming radiation total. MAFTs in flat terrain are omitted in regressions against altitude and aspect, as a semi-quantitative value representing a certain radiation total cannot be clearly assigned.
Six models are calculated for different sets of MAFTs as a function of altitude and aspect. A compilation of all the MAFTs used for the regression can be found in the Appendix. The results of the calculated test quantities are presented in Table 2.
Table 2. Resulting test quantities of seven multiple linear regression models containing MAFTs from the Alps, as a function of altitude and aspect or radiation

No regression calculation is made for northerly aspects from the Monte Rosa area, because all the measurement sites are exposed to the NW, which resulted in a singular matrix. Models 1–4 yield good to very good test results. A large part of the variability (63–78%) can be explained by the parameters altitude and aspect. In the case of model 5, the dataset is too small or the values are not representative or both. Furthermore, one has to bear in mind that the MAFTs as used in models 1–4 were obtained over a period of up to 40 years, and could therefore be subject to climate changes. Models 1–4 and 6 were used within a distribution model for cold firn (cf. section 5.3).
A satisfactory result is obtained when regressing the nine MAFTs from the upper Grenzgletscher against altitude and calculated potential direct solar radiation (model 7): 74% of the variability can be explained by the two parameters, with a slightly significant p value of 0.0176 (Table 2).
The hypothesis that altitude and aspect are excellent proxy parameters for the occurrence of cold firn is thus confirmed by the statistical analysis.
5.3. The model FirnMap
Based on the results of the statistical analysis, a two-parameter model is presented which simulates the cold-firn distribution in the Alps. Altitude is used as a proxy parameter for the MAAT, and aspect as a proxy for the potential direct solar radiation.
The following model restrictions and assumptions are made:
validity for the European Alps only
more-or-less stable climate conditions over recent decades (the firn temperatures used were measured over the last 40 years)
restriction on accumulation areas (no validity for cold glacier ablation areas or for glaciers with extended superimposed-ice zones)
special local characteristics of the distribution of cold firn, such as air temperature, accumulation, meltwater infiltration, topography, the flow regime and crevassed zones, are disregarded.
Only a few direct measurements exist for steep ice walls. The mass and energy exchange might be quite different from more-or-less regular firn basins. Existing investigations (e.g.VAW, unpublished) show that these steep ice walls are at least as cold as corresponding firn areas in the same altitude range. Thus, the model can be applied to steep ice walls as well.
The multiple linear regression equations of models 1–4 and 6 presented in section 5.2 are considered. Due to bad test results, the outcome of model 5 is omitted. The MAFT is set to 0°C, and the equation solved to finally obtain the altitude and, as such, a lower boundary of the cold-firn distribution
where L bound is the lower boundary of the cold-firn distribution, A is the aspect code and a, b and c are coefficients. The coefficients b and c denote the gradients of the parameters altitude and aspect, respectively. The different lower boundaries for each aspect resulting from the five regression models are interpreted as natural fluctuations and represent an altitude band with a possible occurrence of cold firn. Therefore, this range is defined as a zone with a possible cold-firn occurrence, adapting a concept which was originally used in permafrost research (Reference HaeberliHaeberli, 1975).The occurrence of cold firn becomes statistically more probable for areas lying above the critical range. They can therefore be denoted probable.
5.4. Results
The results of the model calculations are given in Table 3.The lower boundary for a possible cold-firn occurrence in N aspects has been corrected to 3000 m a.s.l. (altitude of the mean firn line in N aspects), as the model boundary was lying below the mean firn line. The largest uncertainty range is found in NE, NW, E and W aspects. This is evident as the observed MAFTs vary most extensively in these aspects. The smallest fluctuation (400 m) results in slopes exposed to the north and to the southeast and southwest. Reference Lliboutry, Briat, Creseveur and PourchetLliboutry and others (1976) gave a minimum lower boundary of 3100–3200 m a.s.l. which agrees well with the calculated lower boundary of FirnMap in north-exposed slopes, whereas the general boundary between cold and temperate firn is estimated to be at 3800 m a.s.l. according to Lliboutry. Reference HaeberliHaeberli (1976) gives a mean lower boundary of 3600 m a.s.l., which corresponds well with the model. According to Reference Haeberli and AleanHaeberli and Alean (1985), an occurrence of cold firn and ice becomes possible above 3000 m a.s.l., again consistent with FirnMap.
Table 3. Lower boundaries of possible or probable cold-firn occurrence according to FirnMap (cf. text)

Glacier inventory data from the Alps (Reference Haeberli, Bösch, Scherler, Østrem and WallénHaeberli and others, 1989b) were used to determine cold-firn occurrences. The aspect of the accumulation area, the condition that the uppermost point of the glacier coincides with the lower boundary of a probable cold-firn distribution and a minimum glacier size of 1 km2 were the search conditions in the World Glacier Inventory database of the World Glacier Monitoring Service (Reference Hoelzle, Trindler, Haeberli, Hoelzle and SuterHoelzle and Trindler, 1998). The query yielded a surprisingly high number of 120 glaciers which probably or certainly (measurements) have cold-firn areas. Figure 7 gives an overview of mountain regions in the Alps with cold-firn areas based on FirnMap.

Fig. 7. Glacierized regions of the Alps with cold firn according to FirnMap.
Figure 8 shows the simulated distribution of cold-firn areas in the Monte Rosa area according to FirnMap. The calculations were made within the cell-based module GRID in ARC/INFO, a geo-relation tool for modelling and processing of spatial data. Two input datasets were needed: (1) a digital terrain model, and (2) area-based information on the present glacier extent.

Fig. 8. Cold-firn distribution in the Monte Rosa area, Switzerland, according to firn map.
6. Conclusions and Perspectives
Measurements in different mountain ranges in the European Alps confirm that the occurrence of cold-firn and -ice areas is a common phenomenon which can be found continuously on high-altitude glaciers and sporadically in lower reaches due to special microclimatological conditions.
Englacial temperature measurements using a steam drill and calibrated thermistor strings are a quick and cheap way to determine near-surface firn and ice temperatures down to about 30 m depth. Various extrapolation algorithms that correct for effects of thermal disturbance from drilling allow an immediate data analysis with good accuracy.
The large névé of the Jungfraufirn is predominantly temperate, with local “cold spots” in the vicinity of crevasses and at the foot of steep slopes with high snow accumulation. Whereas a large part of the flat Breithornplateau at 3800 m a.s.l. seems to be temperate, the upper reaches of the nearby Grenzgletscher are cold throughout. At 4200 m a.s.l. the glacier shows a striking anomaly (heat-flow inversion) in the temperature profile (Fig. 5) as a result of flow dynamics, with a cold maximum at about 100 m depth and increasing temperatures from there to the surface and to the bed.
Firn temperatures show a large spatial variability. Within limited altitude ranges of a few 100 m, they are mainly determined by the direct incoming solar radiation rather than the MAAT.
The statistical model FirnMap yields aspect-dependent lower limits for a possible or probable occurrence of cold firn. The lower limit for a probable occurrence varies between 3400 (N aspects) and 4150 (S aspects) m a.s.l.
According to the model and based on glacier inventory data, 120 glaciers in the Alps ( > 1 km2) probably or certainly have cold-firn areas.
With a potential future atmospheric warming, sensitive cold-firn areas in low-latitude mountain regions such as the Alps are likely to be subject to a warming on the order of the air-temperature increase. However, due to the fact that firn temperatures are very sensitive to meltwater input, which results in gradients of firn temperature (−1.2°C (100 m)−1) being considerably higher with respect to altitude than those of air temperature (−0.65°C (100 m)−1), firn warming might even clearly exceed atmospheric warming. In such a scenario, temperature changes within cold firn would not only constitute a strong climate-related signal (Reference CihlarCihlar and others, 1997), but they are also likely to affect other aspects of high mountain environments. As a consequence of rising firn temperatures, high-altitude ice cores for palaeoclimato-logical studies from the Alps could increasingly show melt-water-disturbed signals in the upper layers. Furthermore, glaciers with extended firn areas close to melting conditions could show an increase in ablation when becoming partly or entirely temperate. In order to improve current understanding of such phenomena and processes, further development of spatial as well as time-dependent firn-temperature modelling should be combined with systematic monitoring of firn temperatures at selected sites.
Acknowledgements
We gratefully acknowledge the assistance of many colleagues at the Laboratory of Hydraulics, Hydrology and Glaciology (VAW) at ETH Zürich and at the Department of Geography at the University of Zürich, for their technical support in the field, their help with data analysis and interpretation and for many critical and valuable comments. We are especially indebted to the Laboratory of Hydraulics, Hydrology and Glaciology (D. Vischer), the Department of Environmental Physics at the University of Heidelberg (D. Wagenbach) and the Laboratory of Radio and Environmental Chemistry at the University of Berne and at the Paul Scherrer Institute, Villigen, (H.W. Gäggeler) which provided important logistical and financial support for the field studies. R. L. Brown, U. H. Fischer and M. Funk made useful comments and helped to improve the manuscript. We would also like to thank C. S. Benson and an anonymous reviewer for carefully reviewing the present paper.
Appendix
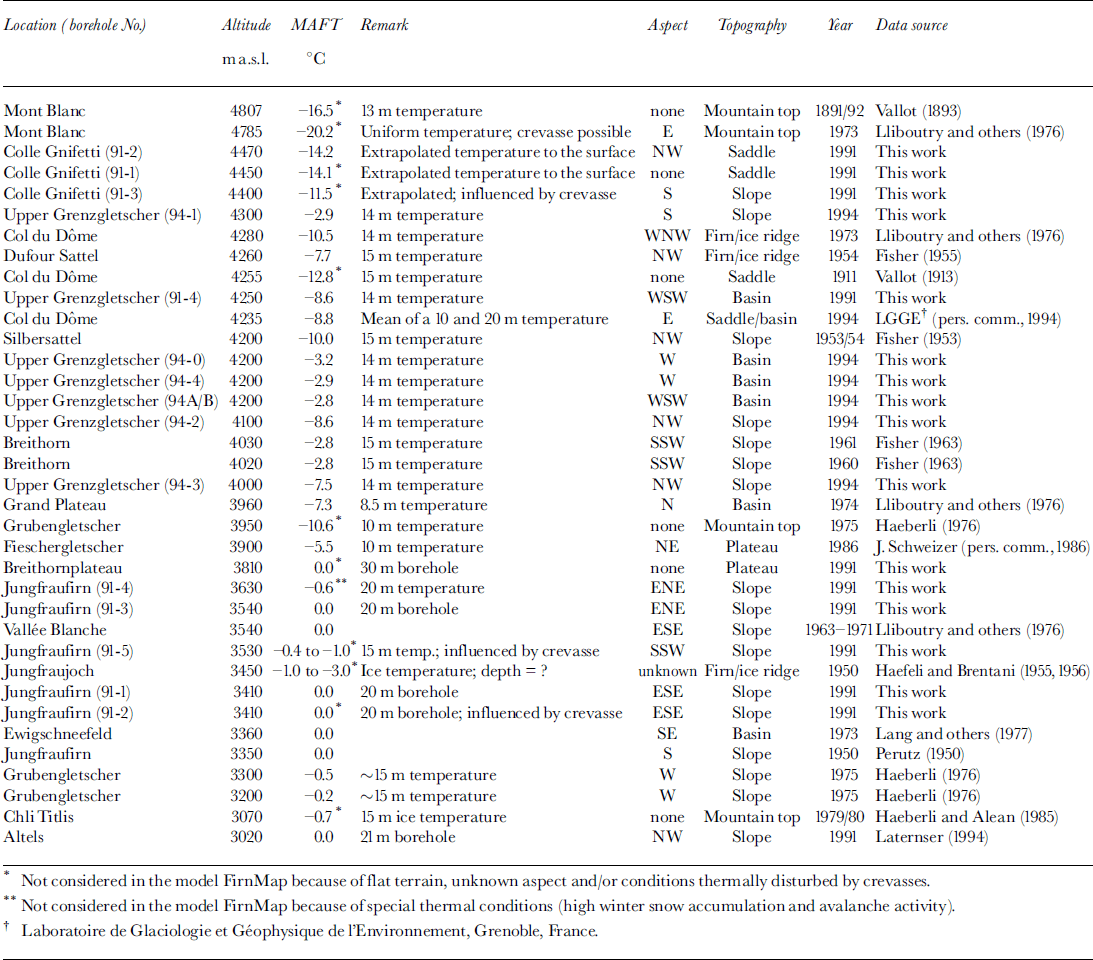
Compilation of firn temperatures from the Alps