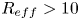Plasma flow suppression by the linear helical mirror system

Abstract

The paper presents experimental results from the SMOLA device that is the first facility with a helical mirror section of the magnetic system. This device was built in the Budker Institute of Nuclear Physics for the verification of the helical mirror confinement idea that is the technique of an active control of axial losses from a confinement zone. Theory predicts that, with rotating plasma, a helical mirror will provide suppression of the axial plasma flow and, simultaneously, density pinching to the axis. Experiments demonstrated the increase in plasma density in the entrance trap by a factor of 1.6 in the helical configuration. The integral axial flux from the transport section drops severalfold. The effective mirror ratio of the helical section was $R_{eff} > 10$. Particle flux returning by the helical mirror section towards the confinement zone was observed. At high corrugation ratios, the axial flux direction is different at the magnetic axis and in the periphery of the plasma in the helical section. All axial fluxes scale linearly with the plasma density, even if the ion mean free path is comparable to the total length of the helical section. Good agreement of the experimental results with theoretical predictions is found.

1. Introduction

Recent achievements of quasistationary high relative pressure and high performance regimes in open magnetic systems (Burdakov et al. 2007; Bagryansky et al. 2015; Gota et al. 2019) have boosted activities on the development of a next-step linear device with a fusion-grade plasma. This challenge is feasible if the device incorporates the best known and emerging physics and technologies (Bagryansky, Beklemishev & Postupaev 2019). The key challenge here is the need for a strong suppression of the particle and energy losses along the magnetic field from the confinement zone. The traditional approach to this problem is to add specialized sections of the magnetic system, thus creating either a tandem mirror or a multiple-mirror system (see the review papers of Dimov 1997; Burdakov & Postupaev 2018). The concept of the Gas-Dynamic Multiple-Mirror Trap (GDMT) next generation open trap includes the central gas-dynamic cell ($0.3\text {--}2 T$ at midplane, $12\text {--}20 T$ at the mirrors) and two attached classical multiple-mirror sections for improving the axial confinement (Beklemishev et al. 2013).

In this paper, we present an experimental demonstration of the efficiency of a helical mirror confinement system. The helical mirror confinement was suggested in Beklemishev (2013) for active control of an axial plasma flow through a multiple-mirror magnetic system with helical symmetry. Such a system resembles a straightened stellarator with one important difference. In closed magnetic surfaces of a stellarator, the radial electric field is maintained by plasma self-organization processes. In a helical mirror system, a required spatial profile of the radial electric field E can be set by proper biasing of endplates and limiters. This allows the direct control of the $E \times B$ plasma rotation, where B is the guiding magnetic field. The helical mirror proposal renewed an old idea of a plasma axial flow control by moving magnetic mirrors. Modulation of the guiding magnetic field travelling in the laboratory reference frame places limitations on the corrugation ratio and the possibility of utilizing superconducting coils, although such proposals exist (Be'ery, Gertsman & Seeman 2018). The idea of the helical mirror considers an axial flow of a rotating plasma through a static linear magnetic system with helical corrugation. Periodical variations of the magnetic field moving upstream in the plasma's reference frame transfer momentum to trapped particles and lead to plasma pumping towards the central trap. The multiple mirrors require the equal scales of the ion free path length and the corrugation period (Mirnov & Ryutov 1972) to provide momentum exchange between trapped and passing particles. At low density or high temperature this process requires turbulent scattering of the ions. The helical mirror should have two improvements over the classical multiple mirrors: the exponential law of confinement improvement with the system length and the radial pinch of the ions that can counteract the diffusive broadening of the plasma stream (Beklemishev 2016; Chernoshtanov & Ayupov 2021).

Concept exploration of the helical mirror SMOLA was put into operation at Budker Institute of Nuclear Physics at the end of 2017 (Postupaev et al. 2016; Sudnikov et al. 2017). Axial plasma flux suppression by the helical sections was demonstrated in the first experimental campaign, an integral suppression ratio of 2–2.5 was achieved (Sudnikov et al. 2019). An improvement of the suppression ratio with the increase of the magnetic field, corrugation ratio and plasma rotation velocity was demonstrated (Sudnikov et al. 2020). This paper presents the latest experimental results on the axial plasma flows in the helical mirror system in a broad range of the plasma densities at high rotation velocity and high corrugation ratio.

2. Experimental set-up and parameters

Layout of the SMOLA helical mirror is presented in figure 1. The device was built for studies of a low-temperature plasma flow through a 2.5-m-long transport section. Plasma was generated in the source with the magnetically insulated heated $LaB_6$ cathode (Ivanov et al. 2021). Then, the plasma was injected into a compact mirror trap in the entrance tank. In the discussed experiments the mirrors of this trap were asymmetric with mirror ratios $R \approx 8$ on the plasma source side and $R \approx 3$ on the helical mirror side. Axial plasma flows from the entrance tank to the transport section. This section has two independent magnetic systems, a solenoid for a straight field and a bispiral helical winding that forms helical magnetic mirrors. The spiral has $N = 12$ corrugation periods. The last part of the device is the exit expander that contains an exit limiter and a radially segmented plasma receiver endplates. The detailed description of the device can be found in Sudnikov et al. (2017).

Figure 1. Layout of the SMOLA helical mirror. Positions of the main diagnostics are indicated. Probe: double electrostatic probes, Emis.: emissive probe, D.Sp: Doppler spectroscopy, UV: photodiode detector of the vacuum ultraviolet radiation, Coils: 12-channel array of Mirnov coils, Mach: planar Mach probe.

The distribution of the guiding magnetic field is shown in figure 2. Later in this paper the magnetic configuration will be referred to by the guiding magnetic field in the transport section, all other magnetic fields vary proportionally. Another parameter is the mean corrugation ratio $R_{mean}$, which is the ratio of the maximal and the minimal magnetic field along the field line within the transport section averaged over the plasma cross-section. This parameter defines the fraction of locally trapped particles in the plasma. In the discussed experiments, the magnetic field was in the range $B_z = 40\text {--}100\,{\rm mT}$, and the mean corrugation ratio was in the range $R_{mean} = 1\text {--}1.7$, where $R_{mean} = 1$ stands for the straight field without the helical component. High corrugation ratios were achievable only at $B_z \leq 70\,{\rm mT}$ due to restrictions of the power system.

Figure 2. Guiding magnetic field profiles for different radii.

The plasma density between the mirrors in the entrance expander was in the range $n = (0.8\text {--}4)\times 10^{18}\,{\rm m}^{-3}$, temperatures were $T_i \approx 4\,{\rm eV}$ and $T_e \approx 30\,{\rm eV}$ (Ivanov et al. 2021). These values correspond to the mean free path of an ion in the entrance tank with respect to the Coulomb scattering $\lambda = 0.2\text {--}1\,{\rm m}$. The ion temperature measured in the exit expander was the same as in the entrance tank. The density in the transport section is by a factor 1.5–2 lower, thus giving the ratio of the mean free path to the period of the helical corrugation $\lambda /h \sim 1$ on the high density bound and $\lambda /h \sim N$ on the low density bound. The first case meets the criterion of multiple-mirror confinement with Coulomb scattering only, the second one requires anomalous scattering for flow suppression.

The helical mirror concept requires a fast rotation of the plasma due to $\boldsymbol{E}\times \boldsymbol{B}$ drift. The required radial electric field was created by biasing of the plasma source electrodes and of rings of the sectioned plasma receiver. Plasma rotation velocity in the discussed experiments was $\omega = (1-1.2)\times 10^6\,{\rm s}^{-1}$ in the entrance tank ($z = 1.15$ m) and $\omega = (0.4\text {--}0.8)\times 10^6\,{\rm s}^{-1}$ in the exit expander ($z = 4.34$ m). Here, we should note that, in the case of a constant potential along any field line, the factor $E/(r B)$ does not depend on the magnetic field. The difference in the angular velocity indicates the presence of the axial gradient of the electric field, and, therefore, non-zero axial current. Previously, it was shown that the observed angular velocity does not change significantly with the main plasma parameters, including the magnetic field (Inzhevatkina et al. 2021). The linear velocity of the plasma edge is presumably limited by the instabilities, which increase the effective transverse conductivity and decrease the electric field in the plasma. Strong helical field does not significantly reduce the angular velocity. The detailed explanation of the angular velocity dependencies requires a thorough investigation of the plasma motion and stability in a low magnetic field.

The main diagnostic for the plasma flux densities was a set of radially movable electrostatic probes distributed over the length of the device. This set includes one double probe measuring I–V characteristic ($z = 0.4$ m), four double probes in the ion saturation regime, one emissive probe and one Mach probe which has two planar double probes deposited on the opposite sides of a dielectric plate. The emissive probe was a self-emitting one (i.e. heated by the plasma) with thoriated tungsten wire. Reaching of the working temperature of the probe was verified by the black-body spectrum of the wire. The Mach probe was oriented normally to the guiding magnetic field, so the upstream side collects only ions with $v_z > 0$ and the downstream side collects only ions with $v_z < 0$. Two imaging Doppler spectrometers ($z = 1.15$ and $z = 4.34$ m) and the array of Mirnov coils ($z = 2.76$ m) were used to measure plasma rotation (Inzhevatkina et al. 2021). The spectrometers are also capable of measuring the Doppler broadening of the emission line of the charge-exchanged hydrogen, which depends on the ion temperature. Typical experimental waveforms are shown in figure 3. Time $t=$ 0 corresponds to the discharge initiation. The stable plasma discharge builds up during the first 40 ms. Stationary neutral gas distribution, which depends on the hydrogen flow rate in the plasma source, discharge current and configuration, is achieved in ${\sim }80\,{\rm ms}$. Average values on the flat top of the discharge ($t=90\text {--}150\,{\rm ms}$) are used to build up the radial profiles of the plasma parameters. The emissive probe reaches working temperature in $t\leq 40\,{\rm ms}$ at radial coordinates $r\leq 6\,{\rm cm}$. In the outer region ($r=6\text {--}8\,{\rm cm}$) the heating takes up to $t=90\,{\rm ms}$. The temperature rise time is consistent with the estimations of Hershkowitz et al. (1983). At $t=165\,{\rm ms}$ the plasma sources switches off to avoid damaging of the probes. Amplitude and velocity of the fluctuations of the experimental signals (see figure 3d,e) depend on the magnetic configuration and the plasma density. The fluctuation level rises in the helical configuration.

Figure 3. Typical waveforms of plasma parameters in discharges with straight ($R_{mean} = 1$, red curves) and helically corrugated ($R_{mean} = 1.52$, blue curves) magnetic configurations. From top to bottom: (a) the discharge current; (b) the voltage between the anode and the cathode of the plasma source; (c) the potential of the emissive probe at $z=0.4$ m; (d) the current of the double probe at $z=0.4$ m (I–V curve measurement); (e) the current of the upstream side of the Mach probe (ion saturation current measurement); (f) the neutral hydrogen pressure at $z=0.4$ m; (g) the neutral hydrogen pressure at $z=4.34$ m, (h) plasma rotation velocity at $z=1.15$ and $z=4.34$ m.

This experimental campaign was focused on the thorough investigation of the axial plasma fluxes in the transport section. For this reason, the detailed radial profiles of the plasma parameters were measured. In these experiments, we varied the guide magnetic field ($B_z = 40\text {--}100\,{\rm mT}$), the mean corrugation ratio ($R_{mean} = 1\text {--}1.7$) and the hydrogen flow rate from the gas feeding system into the plasma source. The last parameter determines the density of the generated plasma.

3. Profile fitting and model estimations

Typical radial profiles of the main plasma parameters in the entrance tank and in the transport section are shown in figure 4. The vertical error bars in these graphs correspond to the shot-to-shot reproducibility, the horizontal error bars correspond to the probe dimensions. The total particle flux through different cross-sections of the transport section can be compared in different magnetic configurations. The profiles were fitted by analytical functions. The following form returned the best fit for the entrance tank and for the beginning of the transport section:

(3.1)\begin{equation} f\left(r\right)=a_1 \exp \left(-\left(\frac{r-r_0}{r_1}\right)^4\right)+a_2 \exp\left(-\left(\frac{r-r_0}{r_2}\right)^2\right) .\end{equation}

Figure 4. Sample radial profiles. (a) Electron temperature; (b) plasma potential; (c) plasma density in the entrance tank; ion saturation flux density: (d) at the entrance of the transport section; (e) in the middle of the transport section on the upstream and downstream sides of the Mach probe; (f) near the exit of the transport section. Dots show experimental data, lines are fitting functions. Helical field corresponds to $R_{mean}=1.52$.

The sum of the shifted Gaussian functions provided a better fit in the other parts of the plasma stream

(3.2)\begin{equation} f\left(r\right)=a_1 \exp \left(-\left(\frac{r-r_0}{r_1}\right)^2\right)+a_2 \exp\left(-\left(\frac{r-r_0}{r_2}-\varDelta\right)^2\right). \end{equation}

In these equations, $r$ is the radial coordinate relative to the geometric axis of the vacuum chamber, $r_0$ is the position of the centre of the plasma stream, $r_1, r_2, a_1, a_2$ and $\varDelta$ are the fitting parameters. The radial shift $0 \leq r_0 \leq 1$ cm is determined by the radial component of the vacuum magnetic field and, therefore, by the mean corrugation depth.

We integrated these fitted functions over the cross-section in the assumption of azimuthal symmetry of the plasma parameters about the centre of the fitted function $r_0$. This method of integration makes it possible to estimate an error of the integral value.

Here, we should note important features of the observed profiles. Activation of the helical winding suppressed axial plasma flow through the transport section. Theory predicts (Beklemishev 2013) that the suppression factor should be higher at the plasma periphery, where the mirror ratio is larger, and close to unity at the magnetic axis where the field modulation from helical winding vanishes. In the experiment, we observed the simultaneous growth of the density in the entrance trap (figure 4c) and decrease of the density at the far end of the transport section (figure 4f). Moreover, two more predicted features were observed: plasma pinching to the axis and more intense axial flow of backscattered particles in the direction of the pressure gradient. These effects originate from the radial transport of the trapped ions towards the region of the most negative potential. Pinching is observed as the decrease of the plasma stream radius in the transport section (figure 4d–f) in the helical configuration. The flow of the backscattered ions is observed on the downstream side of the Mach probe. This flow rises near the axis with the activation of the helical field (figure 4e).

The flux density passing through the transport section can be estimated from the existing theory for further comparison with the experimental data. The particle fluxes in the helical field were predicted in Beklemishev (2016) with the assumption of the optimal conditions for the multiple-mirror scheme, i.e. the ratio of the mean free path to the period of the helical corrugation is $\lambda /h \sim 1$. As in Sudnikov et al. (2020), we take the characteristic length of the exponential decrease of the plasma density with the axial coordinate in the following form:

(3.3)\begin{equation} z_0=\frac{1}{\varLambda\kappa\zeta}\left(\frac{1+\kappa}{1+T_i/T_e} \frac{\partial \widetilde{E_r}}{\partial r}+\frac{\partial}{\partial r} \ln{\left(r\zeta n_{z=0}\right)}\right)^{{-}1}, \end{equation}

where $\kappa$ is the fraction of the trapped particles, $\varLambda$ is the ratio of the system length $L$ to the ion scattering mean free path $\lambda$, $n$ is the dimensionless density, $\zeta = c T_e/(e B_z \alpha a c_s)$, $B_z$ is guiding magnetic field, $\alpha$ is the average inclination of the magnetic field lines to the magnetic axis on the given flux surface, $a$ is the plasma radius, $c_s=\sqrt {T_e/m_i}$, m_i is the ion mass,  $\widetilde {E_r}$ is the radial electric field $E_r$ normalized by the electron temperature $T_e/e$ and plasma radius $a$. The temperatures ratio is about $T_i/T_e \approx 1/8$ for the particular experiments. For the given magnetic system the fraction of the trapped particles is estimated as $\kappa (r)\sim \cos {\theta _{lc}=\sqrt {1-{B_{min}(r)}/{B_{max}(r)}}}$, where $\theta _{lc}$ is the loss cone angle. Parameters $\zeta (r), \alpha (r)$ and $\kappa (r)$ depend only on the magnetic configuration, and therefore their dependencies on radius can be calculated for every experiment.

Earlier in Inzhevatkina et al. (2019) we demonstrated that the experimentally measured angular velocity of the plasma rotation did not depend on radius. This is consistent with the parabolic radial profile of the plasma potential (figure 4b). In this case, the derivative of the electric field $\partial E / \partial r$ is constant and proportional to the angular velocity of the plasma rotation. For these dependencies, the characteristic length depends on the experimental parameters as follows:

(3.4)\begin{equation} z_0=\frac{1}{\varLambda\kappa\zeta}\left(\frac{\omega eBca(1+\kappa)}{T_i+T_e}+ \frac{\partial}{\partial r}\ln{\left(n_{z=0}r\zeta\right)}\right)^{{-}1}. \end{equation}

The effects of the helical corrugation and the radial diffusion were calculated numerically in a way similar to Sudnikov et al. (2020). The transport section was split into 768 slices (64 slices in one period of the magnetic field variations). The radial density profile in any sequent slice was modified by the helical mirror

(3.5)\begin{equation} n_{i+1/2}(r)=n_{i}(r)\exp{\left(-\frac{{\rm d} z}{z_{0}(r)}\right)}, \end{equation}

where ${\rm d} z$ is the slice width and $z_{0}(r)$ is the characteristic length for the given field line. Then, the diffusive flux was calculated using the simple equation of axially symmetric diffusion,

(3.6)\begin{equation} n_{i+1}(r)=n_{i+1/2}(r)+D \frac{1}{r}\frac{{\rm d}}{{\rm d} r} \left( r \frac{{\rm d} n_{i+1/2}(r)}{{\rm d} r} \right). \end{equation}

The value of the diffusion coefficient $D$ was chosen to provide broadening by 10 % in straight configuration of the transport section observed in the experiment.

4. Experimental results

The radial profiles are significantly modified with the activation of the helical field. One can observe the increase of the density in the entrance trap, the growth of the maximal plasma flux density and the radial contraction of the plasma column in the helical configuration. The amplitude of the plasma flux and the width of the plasma stream at the exit from the transport section decreases significantly. One more notable effect is the significant rise of the particle flux density on the downstream side of the Mach probe. At a high corrugation ratio in the central region of the stream, the flux density returning back to the entrance tank becomes larger than the flux density going towards the exit expander. This change of the flux direction can be clearly seen at $r < 2$ cm on the sample radial profiles of the up- and downstream sides of the Mach probe (figure 4e). The width of the region with the reversed flow direction and the amplitude of the return flux depend on the magnetic configuration. The return flux appears in the region with the most negative potential. It stands in qualitative agreement with the model of radial transport (Beklemishev 2016), where the radial flux of the trapped ions is directed towards the axis in case of negative axis biasing, which induces plasma rotation in the direction opposite to the rotation in an ambipolar radial electric field.

One can integrate the fitted radial profiles of the flux density over the plasma cross-section. The dependencies of the integrated fluxes $F$ on the relative amplitude of the helical component of the magnetic field are shown in figure 5. Error bars correspond to uncertainties of the integral values calculated from the fitted profiles. The clearest evidence of the helical mirror effect is 1.6-fold rise in the number of the particles confined in the entrance tank between the simple mirror and the helical one (figure 5a) compared with the straight solenoidal configuration. It agrees well with the significant drop in the particle flux at the exit from the transport section (figure 5f). The particle flux decreases gradually with the increase of the corrugation ratio. At the high corrugation ratio ($R_{mean} = 1.7$) the integral flux from the transport section drops below the detectable level.

Figure 5. Dependencies of the particle number and integral flux on the mean corrugation ratio, $B_z=70\,{\rm mT}$. (a) Number of particles in the entrance tank; plasma fluxes: (b) at the entrance of the transport section; (c) in the middle of the transport section; (d) on the upstream and downstream sides of the Mach probe; (e) on both sides of the Mach probe (sum of the data from the previous panel); (f) at the exit of the transport section.

In contrast, the particle flux detected by the double probes in the entrance half of the transport section does not change significantly with the corrugation ratio (figure 5b,c). More detailed information on the particle flux was obtained by the Mach probe installed close to the centre of the transport section (figure 5d). The integral particle flux from the plasma source towards the exit from the transport section (i.e. the outcoming flux) gradually decreases, while the integral particle flux in the opposite direction (i.e. the return flux) increases by a factor of 1.5. At highest achievable corrugation ratio the difference between the outcoming and return fluxes becomes lower than the corresponding confidence interval. At the same time, the total flux to both sides of the Mach probe remains almost unchanged (figure 5e).

If the magnetic field is high enough to prevent diffusion, the dependence of the plasma parameters on the magnetic field becomes insignificant (see figure 6). In previous experiments (Sudnikov et al. 2020) the plasma stream degraded if the axial magnetic field was $B_z \leq 40\,{\rm mT}$. At higher fields the dependence of the flux suppression on $B_z$ in theory and in experiment was quite slow. Here, we also observe that the difference in fluxes and number of particles is insignificant in the region $B_z > 40\,{\rm mT}$.

Figure 6. Dependencies of the particle number and integral flux on the guiding magnetic field. (a) Number of particles in the entrance tank; (b) plasma flux at the exit of the transport section.

The dependence of the integral particle fluxes $F$ on density was measured at guide magnetic field $B_z = 70\,{\rm mT}$ and mean corrugation ratio $R_{mean} = 1.35$ (figure 7). All flux densities were normalized by the number of particles in the entrance tank in the straight configuration (see the right panels of figure 7) The difference between the normalized profiles in the straight and helical configurations is shown in figure 8. We should note that, at such a corrugation ratio, the effect of the helical confinement is not very pronounced (see figure 5). At the lower boundary of the gas feed intensity, the formally calculated classical ion free path length becomes larger than the device length; therefore, a transition from the collisional (gas-dynamic) confinement regime to the adiabatic (kinetic) one can be expected. Such transition can be responsible for the observed smaller normalized particle flux at the entrance of the transport at the low side of the gas flow rate. All fluxes, including the return flux on the downstream side of the Mach probe, scale linearly with the flux entering the transport section, at least at the densities in the entrance tank $n > 1.3 \times 10^{18}\,{\rm m}^{-3}$, which correspond to a mean free path with respect to Coulomb scattering in the transport section $\lambda \sim 5\,{h}$. No significant difference in the normalized local densities of the forward and return fluxes was observed (figure 8). The return flux was observed even at low classical collisionality (figure 8d).

Figure 7. Dependencies of the number of particles in the trap and flux densities at different coordinates on the gas feeding of the plasma source. Helical field corresponds to $R_{mean}=1.35$. Left: absolute values, right: normalized values. From top to bottom: (a) number of particles in the entrance tank; plasma fluxes (b) at the entrance of the transport section; (c) in the middle of the transport section; (d) on the upstream and downstream sides of the Mach probe.

Figure 8. Radial profiles (a) of the normalized density in the entrance tank in the helical configuration for different gas flow rates (labelled in ${\rm s}^{-1}$ units); (b–d) of the normalized local flux densities at different coordinates. Different shades of red and blue correspond to different gas feeds.

The electron temperature does not depend on the mean corrugation ratio and guiding magnetic field (figure 9a) and decreases slowly with the increase of the plasma density (figure 9c). At the same time, the potential drop between the centre and the periphery of the plasma decreases significantly with the increase of the corrugation ratio, increase of the plasma density and decrease of the guide magnetic field (figure 9b,d). The reduction of the potential drop is presumably caused by the increase of the radial electric conductivity due to the increase in the collision frequency or in the ion gyroradius.

Figure 9. Potentials and temperatures on the plasma axis at $z=0.40$ m. (a,c) Dependence of the electron temperature on the helical corrugation ratio and the average plasma density in the entrance tank, respectively; (b,d) the same for the plasma potential.

5. Particle balance and comparison with the model

As we have mentioned in the previous section, the classical ion free path length changes significantly in the studied density interval. If the density in the entrance trap exceeds $n\sim 10^{18}\,{\rm m}^{-3}$ the losses are gas dynamic and can be estimated as $F = n v_T S_m$ (Ryutov 1988), where $n$ and $v_T$ are the density and the thermal velocity of the ions in the entrance trap, $S_m$ is the cross-section of the plasma in the mirror. The losses are usually re-determined using the plasma cross-section in the minimal magnetic field $S_0 = R S_m$, where $R$ is the corresponding mirror ratio.

The losses are balanced with new ions from the plasma source and the return flux, which is generated by the transport section. The rate of plasma neutralization and neutral gas pumping matches the rate of plasma source feeding in steady state. The particle balance inside the confinement region can be described in the following form:

(5.1)\begin{equation} nvS_0\left(\frac{1}{R_1}+\frac{1}{R_2}\right)=F_{feed}+F_{return}, \end{equation}

where $R_1 = 8$ and $R_2 = 3$ are the simple mirror ratios of the minimal magnetic field to the plasma source field and to the guide magnetic field of the transport section, $F_{feed}$ is the flux from the plasma source and $F_{return}$ is the return flux from the transport section. Integration of the data obtained by the double probes provides the sum of the fluxes $nvS_0 + F_{return}$. This value can be compared with the theory, but it has practical meaning only outside of the transport section and at its end, where the return flux should be negligible. Their difference at the inlet of the transport section can be used to define the effective mirror ratio of the helical confinement system $R_{eff}$

(5.2)\begin{equation} F_{feed}=\frac{nvS_0}{R_1}+\left(\frac{nvS_0}{R_2}-F_{return}\right)=nvS_0 \left(\frac{1}{R_1}+\frac{1}{R_{eff}}\right). \end{equation}

Direct calculation of $R_{eff}$ from the experimental data is obstructed because the difference between $F_{feed}$ and gas dynamic losses towards the plasma source is close to zero. The lower estimate may be evaluated, giving $R_{eff} > 5$ at $R_{mean} = 1.35$, $R_{eff} > 8$ at $R_{mean} = 1.52$ and $R_{eff} > 10$ at $R_{mean} = 1.7$.

The axial flux towards the plasma source with the local density exceeding the density of the flux in the forward direction was observed directly. This flux is generated close to the plasma axis. Its occurrence takes place jointly with the reduction of the width of the forward flux. Both of these facts stand in qualitative agreement with the theoretical model. The return flux in the model consists of the trapped particles and therefore has an axial flow velocity comparable to the axial velocity of the multiple-mirror movement. Such flux by itself can be a source of the energy for the microinstabilities which lead to the anomalous scattering. This point is very important for the fusion reactor prospects of helical mirror systems. The weakest point of classical multiple mirrors is the requirement of equal scales of the ion free path length and the corrugation period (Mirnov & Ryutov 1972) that results in a prohibitively high plasma density at fusion temperatures. The presence of an anomalous scattering can improve the efficiency of multiple-mirror confinement in the ‘rare, hot’ part of the parameter space. We should note that an additional particle scattering was discussed earlier for experiments with classical passive multiple-mirror systems (Postupaev et al. 2017). Linear dependence of the experimentally measured particle fluxes on plasma density and a higher level of noise in the probe data in the helical configuration may be indirect evidence of this process, but the problem of the microinstability level requires further investigations.

The particle flux density at the exit from the transport section was compared with the model (see § 3). The guiding magnetic field and the mean corrugation ratio were taken from the magnetic configuration of the experiment. The angular velocity in the transport section was estimated as an average of the velocities in the entrance and exit tank. The experimental density profiles at the entrance of the transport section were taken as the input values. The same diffusion coefficient was used for all profiles. The most significant source of errors in the theoretical estimation is an uncertainty in the angular velocity, because the dependence of the flux suppression on the angular velocity is the steepest among other parameters. This value may depend on axial coordinate in general case, limiting the calculation accuracy. Taking into account this limitation, one can observe surprisingly good agreement of the experimental and calculated profiles (figure 10).

Figure 10. Experimental (dots) and calculated (lines) radial profiles of the plasma flux at the exit from the transport section at $z = 3.48$ m. Thin lines correspond to calculations without the diffusion.

6. Summary

The first systematic studies of the axial plasma flow through a linear helical mirror magnetic system in the SMOLA device successfully demonstrated the validity of the main theoretical predictions for a system of this kind. Comparing with our preliminary results (Sudnikov et al. 2020), minor improvements of the device parameters and operation regimes allowed clearer demonstration of the confinement improvement in the helical mirror system comparing with the simple solenoidal field in the transport section. High rotation velocity and high mean corrugation ratio resulted in an observable density increase in the entrance trap by a factor of 1.6 compared with the solenoidal field. The integral axial flux at the exit from the transport section decreases severalfold; this flux drops below the detectable level at corrugation ratio $R_{mean}=1.7$. The effective mirror ratio of the helical section was $R_{eff} > 10$.

Dependencies of the axial plasma flux on the mean corrugation ratio and plasma density were measured in different positions along the helical section. Increase in the corrugation ratio suppresses the flux from the entrance trap and increases the flux in the opposite direction. At high corrugation ratio, the flux direction is different near the axis and on the periphery of the plasma. Good agreement of the experimental results with theoretical expectations was found at high classical collisionality. At the same time, all axial fluxes scale linearly with density, even when the ion mean free path with respect to classical binary collisions is ${\sim }5$ times larger than the corrugation period. This observation surpasses expectations and piques interest in further investigations of the collisionless operation of helical mirrors.