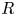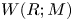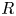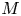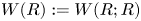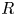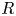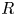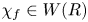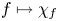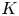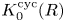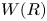Witt vectors with coefficients and characteristic polynomials over non-commutative rings

Abstract

For a not-necessarily commutative ring $R$ we define an abelian group $W(R;M)$ of Witt vectors with coefficients in an $R$-bimodule $M$. These groups generalize the usual big Witt vectors of commutative rings and we prove that they have analogous formal properties and structure. One main result is that $W(R) := W(R;R)$ is Morita invariant in $R$. For an $R$-linear endomorphism $f$ of a finitely generated projective $R$-module we define a characteristic element $\chi _f \in W(R)$. This element is a non-commutative analogue of the classical characteristic polynomial and we show that it has similar properties. The assignment $f \mapsto \chi _f$ induces an isomorphism between a suitable completion of cyclic $K$-theory $K_0^{\mathrm {cyc}}(R)$ and $W(R)$.

Introduction

In this paper, we define and study big Witt vectors with coefficients: concretely, for a not-necessarily commutative (but always unital and associative) ring $R$ and an $R$-bimodule $M$, we define an abelian group $W(R;M)$ called the group of big Witt vectors of $R$ with coefficients in $M$. We start by focusing on the case $M = R$ and set $W(R) := W(R;R)$.

• • If $R$ is a commutative ring, then our group $W(R)$ is the underlying group of the classical ring of big Witt vectors. The latter is a ‘global’ variant of the rings of $p$-typical Witt vectors.

• • If $R$ is non-commutative, then our group $W(R)$ agrees with the big non-commutative Witt vectors introduced by the second and third author in [KN18] as a global variant of Hesselholt's non-commutative $p$-typical Witt vectors [Hes97, Hes05]. We note that $W(R)$ is, in general, only an abelian group, but has an ‘external product’ $W(R) \otimes W(R) \to W(R \otimes R)$ generalizing the ring structure in the commutative case.

The abelian group $W(R)$ is defined as

(1)\begin{equation} W(R) := \frac{\big(1 + tR [\kern-0.15em[{t}]\kern-0.15em] \big)^{\mathrm{ab}}}{ 1 + rst \sim 1 +srt}, \end{equation}

where $1 + tR [\kern-0.15em[{t}]\kern-0.15em] $ is the multiplicative group of power series with constant term 1.¹ One of our main results is that $W(R)$ is invariant under Morita equivalence in $R$, and we show that our proof crucially uses the variant of Witt vectors with coefficients.

One of our motivations to study these groups is to define characteristic polynomials for endomorphisms over non-commutative rings. Recall that if $R$ is commutative and $A$ is an $(n\times n)$-matrix over $R$, then we have the (inverse) characteristic polynomial

(2)\begin{equation} \chi_A(t) = \det(\operatorname{id} - At), \end{equation}

which can be considered as an element in the abelian group $W(R) = 1 + tR [\kern-0.15em[{t}]\kern-0.15em] $. It has the following properties:

1. (i) it satisfies the trace property $\chi _{AB} = \chi _{BA}$; in particular, $\chi _{SAS^{-1}} = \chi _{A}$ so that it is independent of the choice of basis;

2. (ii) for a matrix of the form $A = \bigl (\begin {smallmatrix} A_1 & * \\ 0 & A_2 \end {smallmatrix}\bigr ),$ we have $\chi _{A} = \chi _{A_1} \cdot \chi _{A_2}$ and $\chi _{0_n} = 1$;

3. (iii) the negative of the logarithmic derivative is given by

   \[ -\frac{\chi'_A(t)}{\chi_A(t)} = \operatorname{tr}(A) + \operatorname{tr}(A^{2}) t + \operatorname{tr}(A^{3}) t^{2} + \cdots\ ; \]

4. (iv) the polynomial $\chi _A$ is natural in $R$.

In § 2.1 we generalize $\chi _A$ in two directions: we allow $R$ to be non-commutative and we replace the matrices $A$ by $R$-linear endomorphisms $f: P \to P$ of arbitrary finitely generated, projective $R$-modules $P$.²

Theorem A For every endomorphism $f: P \to P$ of a finitely generated, projective $R$-module $P$ there is an element $\chi _f \in W(R)$ generalizing the inverse characteristic polynomial (2) and which satisfies the analogues of properties (i)–(iv) above.

We define $\chi _f$ by an appropriate version of formula (2) using a non-commutative variant of the determinant (which we also construct). Before we explain this strategy in more detail, let us note that an immediate corollary of Theorem A is that the assignment $f \mapsto \chi _f$ defines a map

\[ K_0^{\mathrm{cyc}}(R) \to W(R) \]

where $K_0^{\mathrm {cyc}}(R)$ is the zeroth cyclic $K$-theory group of $R$ (see Definition 2.13). Such a map was previously constructed using homotopy theoretic methods, notably the cyclotomic trace, and our main motivation was to give a purely algebraic description of this map.

In order to prove Theorem A, that is, to define $\chi _f$, the Morita invariance of non-commutative Witt vectors is used in an essential way: the polynomial $(\operatorname {id} - ft )$ can naturally be considered as an element of $W(\operatorname {End}_R(P))$. By Morita invariance we have a canonical map

(3)\begin{equation} W(\operatorname{End}_R(P)) \to W(R) \end{equation}

so that we simply define $\chi _f$ as the image of $(\operatorname {id} - ft )$ under the map (3). The map (3), in turn, is a special case of the fact that for every additive functor $\operatorname {Proj}_S \to \operatorname {Proj}_R$ between categories of finitely generated, projective modules over rings $S$ and $R$, we obtain an induced map $W(S) \to W(R)$ on Witt vectors. Given the definition of $W(R)$ this is highly non-obvious: the idea is to first introduce groups $W(R; M)$ of Witt vectors with coefficients in a bimodule $M$ by replacing the power series ring in (1) by the completed tensor algebra of $M$ over $R$. Then the main result, which we prove in § 1.4, is that this construction satisfies the trace property (here we use terminology from Kaledin [Kal15] inspired by the work of Ponto [Pon10]).

Theorem B For an $S$-$R$-bimodule $M$ and an $R$-$S$-bimodule $N$ there is an isomorphism

\[ W(S; M \otimes_R N) \cong W(R; N \otimes_S M). \]

Using this result and the fact that every additive functor $\operatorname {Proj}_S \to \operatorname {Proj}_R$ is of the form $-\otimes _S M$ one formally obtains an induced map $W(S) \to W(R)$, see Corollary 1.36.

In addition to the trace property, we also generalize the structures present on classical Witt vectors of commutative rings, such as multiplication, Frobenius and Verschiebung maps, to the groups $W(R; M)$. The analogues of those structures in our setting are ‘external’, for example, the $p$th Frobenius $F_p$ is a map $W(R; M) \to W(R; M^{\otimes _R p})$ (see § 1.3). We also define a ghost component map which is essentially given by the logarithmic derivative (see Proposition 1.15) as well as $p$-typical and truncated Witt vectors with coefficients for non-commutative rings (see § 1.5).

We note that characteristic polynomials (and determinants) for non-commutative rings have been considered before by Ranicki [Ran98] and Sheiham [She01, She03]. We reformulate their approach and compare it with ours in § 2.3. Let us quickly summarize the situation: for commutative rings $R$ the characteristic polynomial $\chi _f$ is a polynomial rather than a power series in $W(R) = 1 + tR [\kern-0.15em[{t}]\kern-0.15em] $. The subgroup $W^{\operatorname {rat}}(R) \subseteq W(R)$ generated by polynomials is called the group of rational Witt vectors (and it is a subring). Then the fact that $\chi _f$ is a polynomial shows that the element $\chi _f$ as well as the image of $K_0^{\mathrm {cyc}}(R) \to W(R)$ lie in this subgroup. In the non-commutative situation this unfortunately turns out to be false: in general, $\chi _f \in W(R)$ cannot be represented by a polynomial.

However, we can still define a group $W^{\operatorname {rat}}(R)$ of rational Witt vectors for non-commutative rings (Definition 2.27) together with a not-necessarily injective homomorphism $W^{\operatorname {rat}}(R) \to W(R)$ and a lift $\chi _f^{\operatorname {rat}}$ of $\chi _f$. In fact, this map is a completion and the assignment $f \mapsto \chi ^{\operatorname {rat}}_f$ defines an isomorphism between the groups $K_0^{\mathrm {cyc}}(R)$ and $W^{\operatorname {rat}}(R)$ as shown by Sheiham, generalizing earlier work of Almkvist. Unfortunately, in order to establish the existence and the properties of the group $W^{\operatorname {rat}}(R)$ as well as the element $\chi ^{\operatorname {rat}}_f$ one crucially uses cyclic $K$-theory and a version of the Gauss algorithm. We have not been able to give a satisfactory, self-contained treatment of $W^{\operatorname {rat}}(R)$ and $\chi ^{\operatorname {rat}}_f$ similar to our treatment of $W(R)$ and $\chi _f$ (see Remark 2.40).

Relation to other work

As indicated previously, our definition of $W(R;M)$ was inspired by topological constructions. We will prove the precise connection in a forthcoming paper. More precisely, we show that there is a natural isomorphism

(4)\begin{equation} W(R;M) \cong \pi_0\operatorname{TR}(R;M). \end{equation}

Here the spectrum $\operatorname {TR}(R;M)$ was defined by Lindenstrauss and McCarthy in [LM12] using topological Hochschild homology $\operatorname {THH}(R;M)$ with its ‘external’ cyclotomic structure. For ${M = R}$ the spectrum $\operatorname {TR}(R;R)$ is the spectrum $\operatorname {TR}(R)$ studied by Hesselholt and Madsen, and in this case our isomorphism (4) recovers and generalizes their results [HM97, 3.3] as well as the non-commutative analogue of Hesselholt [Hes97, Hes05]. A special case of the isomorphism (4) lets us compute $\pi _0$ of the Hill–Hopkins–Ravenel norm [HHR16] for cyclic groups. For example, for any connective spectrum $X$ we obtain an isomorphism

\[ \pi^{C_{p^{n}}}_0\big( N_{e}^{C_{p^{n}}}X \big) \cong W_{p,n}(\mathbb{Z}; \pi_0 X), \]

where $W_{p,n}$ is the truncation of the Witt vectors defined in § 1.5.

Finally, Kaledin defines in [Kal18a] (see also [Kal18b]) abelian groups $\tilde {W}_n(V)$ of ‘polynomial Witt vectors’ for a vector space $V$ over a perfect field $k$ of characteristic $p$. In a forthcoming paper we will show that Kaledin's $\tilde {W}_n(V)$ is isomorphic to our group $W_{p,n}(k; V)$. In order to prove this we show the more general claim that if $R/p$ is a perfect $\operatorname {\mathbb {F}}_p$-algebra and $R$ and $M$ are sufficiently free, then $W_{p,n}(R/p,M/p)$ is isomorphic to the invariants of the cyclic tensor product of $p^{n}$ copies of $M$ modulo the image of the transfer map.

1. Big Witt vectors with coefficients

In this section, we define for any pair of a ring $R$ and a bimodule $M$ an abelian group $W(R;M)$ of Witt vectors of $R$ with coefficients of $M$. For a commutative ring $R$ and $M=R$ the group $W(R;R)$ recovers the usual additive group of (big) Witt vectors. For general $R$, $W(R;R)$ therefore forms a non-commutative analogue of Witt vectors, which was in the $p$-typical case first considered by Hesselholt [Hes97]. Like their commutative counterpart, our Witt vectors with coefficients carry additional structure, namely Verschiebung and Frobenius maps, which interact with coefficients in an interesting way, as well as an ‘external’ multiplication map. However, there is also additional structure which is not seen in the classical picture, namely a residual $C_n$-action if the coefficients are an $n$-fold tensor product $M\otimes _R\cdots \otimes _R M$ and, more generally, trace property isomorphisms $W(R;M\otimes _S N)\xrightarrow {\cong } W(S; N\otimes _R M)$. These imply that $W(R;R)$ is Morita invariant in $R$.

1.1 Preliminaries: the category of bimodules

We consider the category $\operatorname {biMod}$ of pairs $(R;M)$ where $R$ is a ring (unital, associative, but not necessarily commutative) and $M$ is an $R$-bimodule. A morphism $(R;M)\to (R';M')$ is a pair $(\alpha ;f)$ where $\alpha : R\to R'$ is a ring homomorphism and $f \colon M\to \alpha ^{*}M'$ is a map of $R$-bimodules, where $\alpha ^{*}$ is the restriction of scalars. We often denote a morphism only by $f$ and keep $\alpha$ implicit.

Given a bimodule $(R;M)$ and an integer $n\geq 1$, we define an $R$-bimodule $M^{\otimes _Rn}$ and an abelian group $M^{\circledcirc _Rn}$, respectively, by

\[ M^{\otimes_Rn}=\underbrace{M\otimes_R M\otimes_R\cdots\otimes_R M}_{n} \quad \mbox{and}\quad M^{\circledcirc_Rn}=M^{\otimes_Rn}/[R,M^{\otimes_Rn}] \]

where $[R,M^{\otimes _Rn}]$ is the abelian subgroup generated by the elements $rm-mr$ for $r\in R$ and $m\in M^{\otimes _Rn}$. We think of $M^{\circledcirc _Rn}$ as $n$ copies of $M$ tensored together around a circle, and these have a natural action of the cyclic group $C_{n}$ where a chosen generator $\sigma \in C_n$ acts by

\[ \sigma(m_1\otimes\cdots\,\otimes\, m_{n-1}\otimes m_n):=m_n\otimes m_1\otimes\cdots\otimes m_{n-1}. \]

Example 1.1 When $n=1$, we have that $M^{\circledcirc _R 1}=M/[R,M]$. When $M=R$, there is a canonical isomorphism $R^{\circledcirc _R n}\cong R/[R,R]$ with the quotient by the additive subgroup of commutators, for all $n\geq 1$. If $R$ is commutative and $M$ is an $R$-module considered as a bimodule, then $M^{\circledcirc _R n}\cong M^{\otimes _R n}$.

Definition 1.2 A bimodule $(R;M)$ is called free if $R$ is a free ring and $M$ is a free $R$-bimodule. A free resolution of $(R;M)$ is a reflexive coequalizer

in the category of bimodules, where $(R_0;M_0)$ and $(R_1;M_1)$ are free.

Remark 1.3 It turns out that reflexive coequalizers in $\operatorname {biMod}$ are computed on underlying sets. That is, $(R;M)$ is a reflexive coequalizer as in Definition 1.2 if and only if the underlying diagrams

are reflexive coequalizers of sets (or, equivalently, of abelian groups, or for the first one of rings). To see this, observe that the category $\operatorname {biMod}$ is equivalent to algebras of an operad with two colours (one for the ring, one for the bimodule) in abelian groups. Thus, sifted colimits are computed on underlying pairs of abelian groups. Finally, the forgetful functor from abelian groups to sets commutes with sifted colimits.

It follows that any object $(R;M)$ of $\operatorname {biMod}$ admits a free resolution, that can be constructed by taking $R_0=\operatorname {\mathbb {Z}}\{R\}$ and $R_1=\operatorname {\mathbb {Z}}\{\operatorname {\mathbb {Z}}\{R\}\}$ to be the free rings on the underlying sets of $R$ and $\operatorname {\mathbb {Z}}\{R\}$, respectively, $M_0$ the free $R_0$-bimodule on the underlying set of $M$, and $M_1$ the free $R_1$-bimodule on the underlying set of $M_0$. This is the canonical resolution associated to the adjoint pair

where $U$ sends $(R;M)$ to the pair of underlying sets $(R;M)$, and $F(X;Y)=(\operatorname {\mathbb {Z}}\{X\};\operatorname {\mathbb {Z}}\{X\}^{e}(Y))$. The associated diagram

exhibits $(R;M)$ as reflexive coequalizer, because this can be computed on underlying pairs in $\operatorname {Set}\times \operatorname {Set}$, where the diagram becomes split by the unit of the adjunction.

Lemma 1.4 For a free bimodule $(S;Q)$, the groups $(Q^{\circledcirc _{S}n})^{C_n}$ and $(Q^{\circledcirc _{S} n})_{C_n}$ are torsion free, and the transfer map $(Q^{\circledcirc _{S}n})_{C_n}\to (Q^{\circledcirc _{S} n})^{C_n}$ is injective. In particular, any bimodule $(R;M)$ can be resolved by $(S;Q)$ and $(S';Q')$ with torsion-free $(Q^{\circledcirc _{S} n})_{C_n}$, $(Q'^{\circledcirc _{S'} n})_{C_n}$, $(Q^{\circledcirc _{S} n})^{C_n}$ and $(Q'^{\circledcirc _{S'} n})^{C_n}$.

Proof. Say $S$ is a free ring on the set $X$ of generators, and $Q$ is the free $S$-bimodule on the set $Y$ of generators, i.e. $\bigoplus _{Y} S\otimes _{\operatorname {\mathbb {Z}}} S$. Then it is easily seen that $Q^{\circledcirc _{S}n}$ is a direct sum $\bigoplus _{Y^{\times n}} (S\otimes _{\operatorname {\mathbb {Z}}} S)^{\circledcirc _{S} n}$, where $C_n$ acts on the index set $Y^{\times n}$ by permuting the factors cyclically, and on the summands by the $C_n$ action on the cyclic tensor product. The cyclic tensor product $(S\otimes _{\operatorname {\mathbb {Z}}} S)^{\circledcirc _{S} n}$ is equivalent to $S^{\otimes _{\operatorname {\mathbb {Z}}} n}$ with $C_n$ acting by cyclic permutation.

As an abelian group $S$ is free on a set $T$, and $S^{\otimes _{\operatorname {\mathbb {Z}}} n}$ is free abelian on the set $T^{\times n}$, with $C_n$ acting by permutation. Thus, the whole $Q^{\circledcirc _{S}n}$ is a free abelian group on the set $Y^{\times n} \times T^{\times n}$, with $C_n$ acting by cyclic permutation on both factors. Thus, the $C_n$-invariants are torsion free, because they are a subgroup, and the coinvariants are the free abelian group on the set $(Y^{\times n} \times T^{\times n})/ C_n$, thus also torsion free.

The transfer map is injective because the composite $(Q^{\circledcirc _{S}n})_{C_n}\to (Q^{\circledcirc _{S} n})^{C_n}\to (Q^{\circledcirc _{S}n})_{C_n}$ of the transfer and the quotient map is multiplication by $n$, which is injective if $(Q^{\circledcirc _{S}n})_{C_n}$ is torsion free.

The category $\operatorname {biMod}$ has a monoidal structure, which is defined by the componentwise tensor product

\[ (R;M)\otimes (R';M'):=(R\otimes_{\operatorname{\mathbb{Z}}}R';M\otimes_{\operatorname{\mathbb{Z}}}M'), \]

where $M\otimes _{\operatorname {\mathbb {Z}}}M'$ has the obvious $R\otimes _{\operatorname {\mathbb {Z}}}R'$-bimodule structure.

Lemma 1.5 The category of monoids in $\operatorname {biMod}$ is isomorphic to the category of pairs $(R;M)$ where $R$ is a commutative ring and $M$ is a ring equipped with two ring homomorphisms $\eta _l : R\to M$ and $\eta _r : R\to M$ which are central (i.e. two different $R$-algebra structures on $M$). In particular, it contains the category of $R$-algebras $M$ over a commutative ring $R$ as a full subcategory.

Proof. A monoid structure on a bimodule $(R;M)$ is a morphism

\[ \mu=(\mu_R;\mu_M) : (R\otimes_{\operatorname{\mathbb{Z}}} R;M\otimes_{\operatorname{\mathbb{Z}}} M)\longrightarrow (R;M), \]

and a unit map $\eta =(\eta _R;\eta _M) : (\operatorname {\mathbb {Z}};\operatorname {\mathbb {Z}})\to (R;M)$, subject to the associativity and unitality axioms. The map $\mu _R$ and the unit $\eta _R$ then endow the ring $R$ with the structure of a monoid with respect to the tensor product of rings. By the Eckmann–Hilton argument [EH61, Theorem 4.17], $\mu _R$ is the multiplication of $R$ and $R$ must be a commutative ring. The map $\mu _M$ is a map of $R\otimes _{\operatorname {\mathbb {Z}}} R$-bimodules

\[ \mu_{M} : M\otimes_{\operatorname{\mathbb{Z}}} M\longrightarrow \mu^{*}_RM, \]

which endows $M$ with a ring structure $m\star n:=\mu _M(m\otimes n)$. The bimodule structure determines and is determined by the ring homomorphisms $\eta _l(a)=a\cdot 1$ and $\eta _r(b)=1\cdot b$ so that we have $a \cdot m = \eta _l(a) \star m$ and $m \cdot b = m \star \eta _r(b)$. As $\mu _M$ is a map of left $R\otimes _{\operatorname {\mathbb {Z}}} R$-modules we also have

\[ \eta_l(a) \star m=a \cdot m = (1 \cdot a)\cdot (m \star 1) = (1\cdot m) \star (a\cdot 1) = m \star \eta_l(a), \]

which shows that $\eta _l$ is central. Similarly, we see that $\eta _r$ is central.

Conversely, for arbitrary central ring morphisms

\[ \eta_l, \eta_r: R \to M \]

we equip $M$ with the bimodule structure $rms := \eta _l(r) \star m \star \eta _r(s)$ and one directly checks that then $\star$ is a map in $\operatorname {biMod}$.

The monoidal structure on $\operatorname {biMod}$ is, in fact, symmetric monoidal, where the symmetry isomorphism

\[ (R\otimes_{\operatorname{\mathbb{Z}}}R';M\otimes_{\operatorname{\mathbb{Z}}}M')\cong (R'\otimes_{\operatorname{\mathbb{Z}}}R;M'\otimes_{\operatorname{\mathbb{Z}}}M) \]

is defined by switching the factors componentwise. We immediately obtain the following.

Lemma 1.6 The category of commutative monoids in $\operatorname {biMod}$ is isomorphic to the category of pairs $(R;M)$ where $R$ is a commutative ring and $M$ is a commutative $R$-algebra in two different ways.

Note that, in general, a monoid $(R;M)$ is not an algebra over $(R;R)$. For this to happen, we need the two $R$-algebra structures on $M$ to agree.

1.2 Definition of big Witt vectors with coefficients

In this section, we give the definition of big Witt vectors with coefficients $W(R;M)$ for a (not-necessarily commutative) ring $R$ and an $R$-bimodule $M$, see Definition 1.8. This construction determines a functor from the category of bimodules to the category of abelian groups.

Definition 1.7 For a ring $R$ and a bimodule $M$, we define the completed tensor algebra

\[ \widehat{T}(R;M) = \prod_{n\geq 0} M^{\otimes_R n}. \]

We think of elements as representing formal power series of the form

\[ a_0 + a_1 \cdot t + a_2 \cdot t^{2} + a_3\cdot t^{3} + \cdots, \]

where $a_n\in M^{\otimes _R n}$. Note that the powers of $t$ are just notation indicating the grading, there is no element $t$. The ring structure is defined in the obvious way, and is continuous with respect to the product topology. We also define the topological subgroup of special units $\widehat {S}(R;M)$ to be the multiplicative subgroup of elements with constant term $a_0=1$.

The topology on the special units is explicitly given by filtering by degree. More precisely, we say that a special unit is in filtration $\geq n$ if it is of the form

\[ 1 + a_n t^{n} + a_{n+1} t^{n+1} + \cdots. \]

We denote the subgroup of filtration $\geq n$ special units by $\widehat S^{(n)}(R;M)$. Those form a neighbourhood basis of $1$. Observe that $\widehat S^{(n)}(R;M)/ \widehat S^{(n+1)}(R;M)$ is isomorphic to $M^{\otimes _R n}$, because modulo higher filtration, multiplication of special units of filtration $\geq n$ is just addition of the tensor length $n$ part.

Also observe that in the case $M=R$ the tensor algebra $\widehat {T}(R;M)$ is the power series ring $R [\kern-0.15em[{t}]\kern-0.15em] $, and the special units are just the elements of $R [\kern-0.15em[{t}]\kern-0.15em] $ with constant term $1$.

Definition 1.8 We define a ‘Teichmüller’ map of sets $\tau : M \to \widehat {S}(R;M)$ by sending $m\mapsto 1-mt$. We then define the abelian group of big Witt vectors as

\[ W(R;M) = \frac{ \widehat{S}(R;M)^{\mathrm{ab}}}{ \tau(rm) \sim \tau(mr)}, \]

where the relation runs over all possible $m\in M$ and $r\in R$, and we take the abelianisation and the quotient in Hausdorff topological groups, that is, divide by the closure of the normal subgroup generated by the relations we impose.

Remark 1.9 Throughout the paper, we treat $W(R;M)$ as a complete Hausdorff topological abelian group, see Proposition 1.14 and the constructions in § 1.3. Alternatively one can consistently treat $W(R;M)$ as a pro-object, or even just an inverse system, of the truncated Witt vectors discussed in detail in § 1.5. As discussed there, all the structure maps on $W(-;-)$ we discuss are compatible with truncation in the appropriate sense, and thus can be recovered in the untruncated setting from their truncated counterparts. The approach with pro-objects is the approach usually adopted when dealing with the de Rham–Witt complex.

Remark 1.10 When $R=M$ is commutative, we have that $W(R;R)$ is the multiplicative subgroup of power series with constant term one, which is the usual additive abelian group of Witt vectors $W(R)$.

Suppose more generally that $R$ is commutative and that $M$ is a solid commutative $R$-algebra, i.e. that the multiplication map $\mu : M\otimes _R M\to M$ is an isomorphism. In this case, the map of bimodules $(R;M)\to (M;M)$ induced by the algebra structure gives an isomorphism of abelian groups $W(R;M)\cong W(M;M)=W(M)$ with the usual Witt vectors of $M$ as follows immediately from the definitions. For example, $W(\operatorname {\mathbb {Z}};\operatorname {\mathbb {F}}_p)\cong W(\operatorname {\mathbb {F}}_p)$.

Remark 1.11 The (generally non-commutative) group $\widehat {S}(R;M)$ is written multiplicatively. However, we write the group structure on the abelian groups $W(R;M)$ additively. This should not lead to confusion, because we use the multiplicative notation precisely if we think about elements of $W(R;M)$ as representative power series in $\widehat {S}(R;M)$.

Lemma 1.12 The group $\widehat {S}(R;M)$ is topologically generated by elements of the form $(1 + x_0 \otimes \cdots \otimes x_{k-1} t^{k})$. More generally, given a generating set $G_k \subseteq M^{\otimes _R k}$ (as abelian groups) for every $k$, the group $\widehat {S}(R;M)$ is topologically generated by elements of the form $(1+ g_k t^{k})$ with $g_k\in G_k$.

Proof. Assume we have a special unit in filtration $\geq n$, that is, one of the form

\[ 1 + a_n t^{n} + a_{n+1} t^{n+1} + \cdots. \]

Then the coefficient $a_n$ can be written as a finite sum of elements in $G_n$, and we can split off corresponding factors of the form $(1 + g_n t^{n})$. This allows us to write any such special unit as a product of ones of the form $(1 + g_n t^{n})$ and a remainder term of higher filtration. Inductively, this proves that, up to a remainder term of arbitrarily high filtration, any element of $\widehat {S}(R;M)$ can be written as a product of terms of the form $(1 + g_k t^{k})$. This proves the claim.

Lemma 1.13 The filtration of $\widehat {S}(R;M)$ by $\widehat {S}^{(n)}(R;M)$ induces a filtration $W^{(n)}(R;M)$ on the quotient $W(R;M)$. This filtration is complete and Hausdorff.

Proof. The kernel of $\widehat {S}(R;M)\to W(R;M)$ is, by definition, closed and the group $\widehat {S}(R;M)$ is first countable, hence metrizable by the Birkhoff–Kakutani theorem. Moreover, the induced filtration generates the quotient topology. Thus, the claim follows from [Bou07, Chapitre IX, § 3, Proposition 4].

Proposition 1.14 As a functor from $\operatorname {biMod}$ to the category of Hausdorff topological groups, $\widehat {S}(-;-)$ and $W(-;-)$ commute with reflexive coequalizers.

Proof. We first check that $\widehat {S}(-;-)$ commutes with reflexive coequalizers. To see this, we need to check that if

is a reflexive coequalizer of bimodules, then $\widehat {S}(R;M)$ is obtained from $\widehat {S}(R_0;M_0)$ by quotienting by the closed normal subgroup $N$ generated by all $f(y)g(y)^{-1}$ for $y\in \widehat {S}(R_1;M_1)$. Surjectivity is clear, so we have to check that the kernel of $\widehat {S}(R_0;M_0)\to \widehat {S}(R;M)$ agrees with $N$. The subgroup $N$ is clearly contained in the kernel. Given an element $x$ in the kernel, it is of the form $(1+a_n t^{n} + \cdots )$, with $a_n$ in the kernel of the right map in the following diagram.

As reflexive coequalizers of abelian groups commute with tensor products, this diagram is also a reflexive coequalizer of abelian groups, so $a_n$ is of the form $f(b_n)-g(b_n)$. Thus, the original $x$ can up to a term of higher filtration (which is also in the kernel) be written as $x = f(1+b_n t^{n}) g(1+b_nt^{n})^{-1}$. Inductively, we can write any element in the kernel as a convergent product of elements of the form $f(y)g(y)^{-1}$, so the kernel is contained in $N$ as desired. We now want to show that $W(-;-)$ also commutes with reflexive coequalizers. To that end, let $N(R;M)$ denote the closed normal subgroup of $\widehat {S}(R;M)$ generated by commutators and elements of the form $(1+rmt)(1+mrt)^{-1}$, so that $W(R;M) = \widehat {S}(R;M)/N(R;M)$. As $\widehat {S}(-)$ commutes with reflexive coequalizers, we see that the coequalizer of $W(R_1;M_1)\rightrightarrows W(R_0;M_0)$ can be described as the quotient of $\widehat {S}(R;M)$ by the closure of the image of $N(R_0;M_0)$. Thus, we have to check that this closure agrees with $N(R;M)$. However, this is clear: $N(R;M)$ is topologically generated by commutators and elements of the form $(1+rmt)(1+mrt)^{-1}$, all of which are in the image.

We want to define a version with coefficients of the ghost map of the usual Witt vectors. We start by defining a map $\log : \widehat {S}(R;M)\to \operatorname {\mathbb {Q}}\widehat {\otimes }\,\widehat {T}(R;M)$, where $\widehat {\otimes }$ denotes the completed tensor product $\operatorname {\mathbb {Q}}\widehat {\otimes } \prod _{n\geq 0} M^{\otimes _R n} = \prod _{n\geq 0} \operatorname {\mathbb {Q}}\otimes M^{\otimes _R n}$, by

\[ \log(1 + f) = f - \tfrac{1}{2} f^{2} + \tfrac{1}{3} f^{3} - \cdots. \]

We also use $\log$ to refer to the map $\widehat {S}(R;M)\to \operatorname {\mathbb {Q}}\widehat {\otimes } \prod _{n\geq 1} M^{\circledcirc _R n}$ obtained by postcomposing with the quotient map $\widehat {T}(R;M) \to \prod _{n\geq 1} M^{\circledcirc _R n}$ to the cyclic tensor product of § 1.1.

A basic observation from algebra is that the derivative $ ({d}/{dt}) \log (1+f(t))$ over a commutative ring has integral coefficients, because it agrees with $f'\cdot (1+ f)^{-1}$. The key property of derivation is that the coefficient in front of $x^{n}$ is multiplied by $n$. In our setting with coefficients, it turns out that the correct analogue of multiplication with $n$ is the transfer (i.e. additive norm) with respect to the $C_n$ action on the abelian group $M^{\circledcirc _R n}$.

Define $\operatorname {tr}: \prod _{n\geq 1} (M^{\circledcirc _R n})_{C_n} \to \prod _{n\geq 1} (M^{\circledcirc _R n})^{C_n}$ to be the product of the transfers of the $C_n$ action on $M^{\circledcirc _R n}$. We define a map

\[ \operatorname{tlog}=-\operatorname{tr}\circ \log: \widehat{S}(R;M)\longrightarrow \operatorname{\mathbb{Q}}\widehat{\otimes} \prod_{n\geq 1} (M^{\circledcirc_R n})^{C_n}. \]

Note that for $R$ a commutative ring and $M=R$, $\operatorname {tlog}$ agrees with $-t\cdot \operatorname {dlog}$, the operator that sends a power series $1+f(t)$ to $-t$ times the derivative of $\log (1+f(t))$.³

Proposition 1.15 The map $\operatorname {tlog}:\widehat {S}(R;M)\to \operatorname {\mathbb {Q}}\widehat {\otimes } \prod _{n\geq 1} (M^{\circledcirc _R n})^{C_n}$ satisfies the following properties.

1. 1. It is a homomorphism with respect to the group structures given by multiplication in the domain, and addition in the codomain.

2. 2. It sends $1 - a_n t^{n}$ to the element

   \[ \operatorname{tlog}(1 - a_n t^{n})=\operatorname{tr}^{C_n}_e a_n t^{n} + \operatorname{tr}^{C_{2n}}_{C_2} a_n^{2} t^{2n} + \operatorname{tr}^{C_{3n}}_{C_3}a_n^{3} t^{3n} + \cdots, \]
   and, in particular, for $n=1$ we get that $\operatorname {tlog}(1 - a_1 t)= a_1 t + a_1^{2} t^{2} + a_1^{3} t^{3} + \cdots.$

3. 3. It satisfies

   \[ \operatorname{tlog}(1 - fg) = \operatorname{tlog}(1-gf) \]
   for any elements $f,g\in \widehat {T}(R;M)$, at least one of which has trivial constant term.

4. 4. It lifts uniquely along the rationalisation map to a natural homomorphism

   \[ \operatorname{tlog}: \quad \widehat{S}(R;M) \longrightarrow \prod_{n\geq 1} (M^{\circledcirc_R n})^{C_n}, \]
   which still has the above properties. Here, naturality is with respect to the category of bimodules $(R;M)$.

Proof. For the first claim, it suffices to show that $\log : \widehat {S}(R;M) \to \operatorname {\mathbb {Q}}\widehat {\otimes } \prod _{n\geq 1} (M^{\circledcirc _R n})_{C_n}$ is a homomorphism. We define an operator $\partial : \widehat {T}(R;M)\to \widehat {T}(R;M)$ that acts by multiplication with $n$ on the factor $M^{\otimes _R n}$. This satisfies $\partial (fg) = \partial f\cdot g + f\cdot \partial g$. In particular, we have

\[ \partial f^{n} = (\partial f) f^{n-1} + f (\partial f) f^{n-2} + \cdots + f^{n-1} (\partial f). \]

Now let us write $f \sim g$ when elements $f, g\in \operatorname {\mathbb {Q}}\widehat {\otimes } \widehat {T}(R;M)$ have the same image under the canonical map to $\operatorname {\mathbb {Q}}\widehat {\otimes } \prod _{n\geq 1} (M^{\circledcirc _R n})_{C_n}$. One easily sees by expanding that $fg \sim gf$ for any elements $f,g$. It follows that $\partial f^{n} \sim n (\partial f) f^{n-1}$, and for a special unit $u=1+f$:

\[ \partial \log u \sim (\partial f) - (\partial f)f + (\partial f)f^{2} - \cdots = (\partial f) \cdot (1 + f)^{-1} = (\partial u) \cdot u^{-1}. \]

Therefore, for any special units $u,v$, we see that

\begin{align*} \partial \log(uv) &\sim \partial(uv) \cdot (uv)^{-1} = ((\partial u) \cdot v + u\cdot (\partial v)) v^{-1} u^{-1} = (\partial u) \cdot u^{-1} + u \cdot (\partial v) \cdot v^{-1} \cdot u^{-1}\\ &= \partial \log u + u \cdot (\partial \log v) \cdot u^{-1}\sim \partial \log u + \partial \log v. \end{align*}

This shows that in the diagram

the lower composite from the leftmost node to the lower-right node is a homomorphism. However, because the rightmost vertical map is an isomorphism, the top horizontal composite is a homomorphism as well.

For the second claim, we calculate explicitly

\begin{align*} \operatorname{tlog}(1-a_nt^{n}) &= \operatorname{tr}_{e}^{C_{n}} a_n t^{n} + \operatorname{tr}_{e}^{C_{2n}} \frac{a_n^{2}}{2} t^{2n} + \operatorname{tr}^{C_{3n}}_{e}\frac{a_n^{3}}{3} t^{3n} + \cdots\\ &= \operatorname{tr}_{e}^{C_{n}} a_n t^{n} + \operatorname{tr}_{C_2}^{C_{2n}} \operatorname{tr}_{e}^{C_{2}} \frac{a_n^{2}}{2} t^{2n} + \operatorname{tr}^{C_{3n}}_{C_3} \operatorname{tr}^{C_{3}}_{e}\frac{a_n^{3}}{3} t^{3n} + \cdots\\ &= \operatorname{tr}^{C_n}_e a_n t^{n} + \operatorname{tr}^{C_{2n}}_{C_2} a_n^{2} t^{2n} + \operatorname{tr}^{C_{3n}}_{C_3}a_n^{3} t^{3n} + \cdots, \end{align*}

where the last equality comes from the fact that $a_n^{k}$ is already invariant under the action of the subgroup $C_k \subseteq C_{nk}$, so $\operatorname {tr}_{e}^{C_k}$ just acts by multiplication with $k$.

For the third claim, it suffices again to check this for the map $\log$. We have

\[ \log(1-fg) = -fg - \frac{fgfg}{2} - \cdots \sim -gf - \frac{gfgf}{2} - \cdots = \log(1-gf), \]

and, thus, they agree in $\operatorname {\mathbb {Q}}\widehat {\otimes }\prod _{n\geq 1} (M^{\circledcirc _R n})_{C_n}$.

For the last claim, we first observe that the image of $\operatorname {tlog}$ is integral, that is, contained in the image of the rationalisation $\prod _{n\geq 1} (M^{\circledcirc _R n})^{C_n}\to \operatorname {\mathbb {Q}}\widehat {\otimes }\prod _{n\geq 1} (M^{\circledcirc _R n})^{C_n}$. As $\widehat {S}(R;M)$ is topologically generated by elements of the form $(1+a_nt^{n})$, this follows immediately from the first two claims. For a pair $(R;M)$ where $(M^{\circledcirc _R n})^{C_n}$ is torsion free, the rationalisation is injective. Thus, on the full subcategory of those $(R;M)$ with torsion-free $(M^{\circledcirc _R n})^{C_n}$, $\operatorname {tlog}$ factors to a unique natural transformation as desired. As we are mapping to a Hausdorff topological group, $\widehat {S}(R;M)$ commutes with reflexive coequalizers in Hausdorff topological groups, and we can resolve every bimodule $(R;M)$ as a reflexive coequalizer of $(R_1;M_1)$ and $(R_0;M_0)$ with torsion-free $({M_i}^{\circledcirc _{R_i} n})^{C_n}$ (see Lemma 1.4), this natural transformation extends uniquely to all $(R;M)$.

We now want to show that $\operatorname {tlog}$ descends to the Witt vectors $W(R;M)$.

Lemma 1.16 Suppose $(R;M)$ is a bimodule with the property that the transfer maps $\operatorname {tr}: (M^{\circledcirc _R n})_{C_n} \to (M^{\circledcirc _R n})^{C_n}$ are injective for all $n$. Suppose further that $G\subseteq \widehat {S}(R;M)$ is a subgroup with the following properties:

1. 1. $G$ is closed;

2. 2. $G$ is contained in the kernel of $\operatorname {tlog}:\widehat {S}(R;M) \to \prod _{n\geq 1} (M^{\circledcirc _R n})^{C_n}$;

3. 3. for each $n$, each $i,j\geq 0$ with $i+j=n$, and each $x_i \in M^{\otimes _R i}$, $y_j\in M^{\otimes _R j}$, $G$ contains an element of the form $(1 - (x_i \otimes y_j - y_j\otimes x_i) t^{i+j} + \cdots )$.

Then $G$ agrees with the kernel of $\operatorname {tlog}: \widehat {S}(R;M) \to \operatorname {\mathbb {Q}}\widehat {\otimes }\prod _{n\geq 1} (M^{\circledcirc _R n})^{C_n}$.

Proof. We have to show that every element in the kernel of $\operatorname {tlog}$ can be written as a convergent product of elements in $G$. Suppose we have an element of the form $f_n=(1+a_nt^{n} + \cdots )$ in the kernel of $\operatorname {tlog}$, with $a_n\in M^{\otimes _R n}$. Then, because

\[ \operatorname{tlog}(1 + a_n t^{n} + \cdots) = - \operatorname{tr}_e^{C_n} a_n t^{n} + \cdots, \]

we have that $a_n$ is in the kernel of the composite $M^{\otimes _R n} \to (M^{\circledcirc _R n})_{C_n} \to (M^{\circledcirc _R n})^{C_n}$. As we assumed the latter map to be injective, $a_n$ is in the kernel of the quotient map $M^{\otimes _R n}\to (M^{\circledcirc _R n})_{C_n}$. This kernel is generated by differences of the form $x_i \otimes y_j - y_j \otimes x_i$ for $i+j=n$, with $x_i \in M^{\otimes _R i}$ and $y_j\in M^{\otimes _R j}$, so $a_n$ can be written as a sum of such elements. Now, by property 3, this implies that we can write $f_n$ as a product of elements in $G$ of filtration $\geq n$, and a remainder term of filtration $\geq n+1$, which by property 2 is also in the kernel of $\operatorname {tlog}$. Iterating this argument, property 1 implies that every element in the kernel of $\operatorname {tlog}$ is in $G$.

Lemma 1.17 We have the following description for the leading term of a commutator:

\[ [(1+a_n t^{n}+\cdots), (1+b_m t^{m}+\cdots)] = 1 + (a_nb_m - b_ma_n)\cdot t^{n+m} + \cdots. \]

Proof. We first compute the leading term for a commutator of $(1+a_n t^{n})$ and $(1+b_m t^{m})$. We have

\begin{align*} (1+a_n t^{n})(1+b_m t^{m}) &= (1 + a_n t^{n} + b_m t^{m} + a_n b_m t^{n+m})\\ &= (1 + a_n b_m t^{n+m} + \cdots) (1 + a_n t^{n} + b_m t^{m}). \end{align*}

Multiplying this with the inverse of $(1+b_m t^{m})(1+a_n t^{n})$, we obtain

\begin{align*} [(1+a_n t^{n}), (1+b_m t^{m})] &= (1 + a_n b_m t^{n+m} + \cdots) \cdot (1 + b_ma_n t^{n+m} + \cdots)^{-1}\\ &= 1 + (a_nb_m - b_ma_n)\cdot t^{n+m}+\cdots. \end{align*}

In particular, this shows that elements $(1+a_k t^{k})$ and $(1+b_l t^{l})$ commute up to terms of filtration $\geq k+l$. By continuity, we also obtain that arbitrary elements of filtration $\geq k$ and $\geq l$ commute up to terms of filtration $\geq k+l$. Thus, if we have

\begin{gather*} x = (1 + a_n t^{n} + \cdots) = (1+ a_n t^{n}) \cdot x',\\ y = (1+ b_m t^{m} + \cdots) = (1+b_m t^{m}) \cdot y', \end{gather*}

with $x'$ of filtration $>n$, and $y'$ of filtration $>m$, we see that, up to terms of filtration $>n+m$, $x'$ commutes with $(1+b_mt^{m})$, $y'$ commutes with $(1+a_nt^{n})$ and $x'$ commutes with $y'$. We thus obtain that $[x,y]$ and $[(1+a_n t^{n}), (1+b_mt^{m})]$ agree up to order $n+m$, from which the result follows.

This may suggest that the associated graded of the filtration $W^{(n)}(R;M)$ is given by $(M^{\circledcirc _R n})_{C_n}$ in degree $n$. However, it can be smaller than that. An example with $R=M$ can be found in [Hes05].

Proposition 1.18 The map $\operatorname {tlog}$ descends to a continuous group homomorphism

\[ \operatorname{tlog} : W(R;M) \longrightarrow \prod_{n\geq 1} (M^{\circledcirc_R n})^{C_n}, \]

which we call the ghost map. If all the transfer maps $(M^{\circledcirc _R n})_{C_n}\to (M^{\circledcirc _R n})^{C_n}$ are injective (for example, if $(M^{\circledcirc _R n})_{C_n}$ are torsion free; see Lemma 1.4), the ghost map is injective and, in fact, a homeomorphism onto its image.

Proof. The map clearly factors through the abelianisation, and by Proposition 1.15(3), we have $\operatorname {tlog}(1- rm \cdot t) = \operatorname {tlog}(1-mr\cdot t)$, so it factors through $W(R;M)$.

For injectivity, note that by Lemmas 1.16 and 1.17, the closed subgroup generated by commutators and elements of the form $(1-rm\cdot t)(1-mr\cdot t)^{-1}$ actually agrees with the kernel of $\operatorname {tlog}$ if the transfers are injective.

For the last part, it suffices to check the following stronger version of injectivity: if an element $f\in W(R;M)$ has the property that $\operatorname {tlog} f\in \prod _{n\geq 1} (M^{\circledcirc _R n})^{C_n}$ has filtration ${\geq}k$, then $f$ has filtration ${\geq}k$ as well. However, observe that this is exactly what the argument in the proof of Lemma 1.16 gives us.

Lemma 1.19 The group $W(R;M)$ agrees with the quotient of $\widehat {S}(R;M)$ by any of the following.

1. 1. The closed subgroup generated by commutators and all elements of the form $(1+rmt) (1+mrt)^{-1}$ for $r\in R$ and $m\in M$. (These are the relations that appear in our definition of $W(R;M)$, we recall them here for convenience.)

2. 2. The closed subgroup generated by commutators and all elements of the form

   \[ (1 - rf) \cdot (1 - fr)^{-1}, \]
   where $r\in R$ and $f\in \widehat {T}(R;M)$ with trivial constant term.

3. 3. The closed subgroup generated by all elements of the form

   \[ (1 - x_i y_j t^{i+j}) \cdot (1 - y_j x_i t^{i+j})^{-1}, \]
   with $i+j\geq 1$ and $x_i\in M^{\otimes _R i}$, $y_j\in M^{\otimes _R j}$. We allow $i=0$ or $j=0$, e.g. $x_0\in R$, so this relation includes the Teichmüller relations $\tau (rx)\tau (xr)^{-1}$.

4. 4. The closed subgroup generated by all elements of the form

   \[ (1 - fg) \cdot (1 - gf)^{-1} \]
   for elements $f,g\in \widehat {T}(R;M)$ with $f$ or $g$ having trivial constant term.

Proof. We have to show that all these subgroups of $\widehat {S}(R;M)$ agree. By resolving via reflexive coequalizers, we can reduce to the case where the transfers $\operatorname {tr}: (M^{\circledcirc _R n})_{C_n} \to (M^{\circledcirc _R n})^{C_n}$ are injective. In that case, we claim they all agree with the kernel of $\operatorname {tlog}: \widehat {S}(R;M) \to \prod _{n\geq 1} (M^{\circledcirc _R n})^{C_n}$. By Proposition 1.15, they are all contained in the kernel of $\operatorname {tlog}$, and using Lemma 1.17, we see that they also satisfy condition 3 of Lemma 1.16, which then implies the claim.

Lemma 1.20 The functor $W(-;-)$ commutes with finite products, that is, given pairs $(R; M)$ and $(S; N)$, the canonical map

\[ W(R\times S; M\times N) \to W(R;M)\times W(S;N) \]

is an isomorphism.

Proof. The map $\widehat {S}(R\times S;M\times N) \to \widehat {S}(R;M)\times \widehat {S}(S;N)$ is an isomorphism of topological groups. By Lemma 1.19, it suffices to check that it sends the closed subgroups generated by elements of the form $(1 - x_i y_j t^{i+j}) \cdot (1 - y_j x_i t^{i+j})^{-1}$ to each other. This follows from

\begin{align*} & (1 - (a_i,b_i) (a_j,b_j) t^{i+j}) \cdot (1 - (a_j,b_j) (a_i,b_i) t^{i+j})^{-1}\\ &\quad =(1- (a_i,0) (a_j,0) t^{i+j}) \cdot (1 - (a_j,0)(a_i,0) t^{i+j})^{-1}\\ &\qquad \cdot (1- (0,b_i) (0,b_j) t^{i+j}) \cdot (1 - (0,b_j)(0,b_i) t^{i+j})^{-1}. \end{align*}

1.3 The operators and the monoidal structure

We now construct additional structure on the big Witt vectors with coefficients: Verschiebung maps

\[ V_n : W(R; M^{\otimes_R n}) \to W(R; M), \]

Frobenius maps

\[ F_n : W(R; M)\to W(R; M^{\otimes_R n}), \]

a $C_n$-action on $W(R; M^{\otimes _R n})$ and a lax symmetric monoidal structure, that is, external products

\[ \star: W(R;M) \otimes\, W(S;N) \to W(R \otimes S; M \otimes N). \]

These satisfy the relations listed in Proposition 1.32. To do so, we first discuss a preferred set of generators of $W(R;M)$.

Definition 1.21 We let $\tau _n: M^{\times n} \to W(R;M)$ be the map

\[ \tau_n(m_1,\ldots, m_n) = (1 - m_1 \otimes \cdots \otimes m_n t^{n}). \]

Lemma 1.22 The images of $\tau _n$ generate $W(R;M)$ topologically. The maps $\tau _n$ are cyclically invariant, meaning that

\[ \tau_n(m_1,\ldots, m_n) = \tau_n(m_{\sigma(1)}, \ldots, m_{\sigma(n)}) \]

for any $\sigma \in C_n$, and they satisfy

\begin{align*} \tau_n(m_1,\ldots, m_i r, m_{i+1}, \ldots,m_n) &= \tau_n(m_1,\ldots, m_i, rm_{i+1}, \ldots,m_n),\\ \tau_n(rm_1, \ldots, m_n) &= \tau_n(m_1, \ldots, m_n r). \end{align*}

Proof. This follows immediately from Lemmas 1.12 and 1.19.

Remark 1.23 Note that $\tau _n$ arises by definition as the composition

\[ M^{\times n} \to M^{\otimes_R n} \to W(R;M), \]

where the second map sends an element $m \in M^{\otimes _R n}$ to $(1 - mt^{n})$. Using this we can (abusively) apply $\tau _n$ to an element of the tensor product which is not an elementary tensor. However, note that $\tau _n$ is not additive, so that the second map is not determined by $\tau _n$ and one has to be very careful here. For example, despite the identities of Lemma 1.22, the extension $M^{\otimes _R n} \to W(R;M)$ does not descend to the cyclic tensor power because it is not additive.

In order to identify the operators in ghost components, we make implicit use of the $C_k$-equivariant isomorphisms

\[ M^{\circledcirc_R nk}\cong (M^{\otimes_R n})^{\circledcirc_R k} \]

for all $n,k\geq 0$, where $C_k$ acts on the left-hand group as a subgroup of $C_{nk}$. The isomorphisms are induced by the canonical isomorphisms $M^{\otimes _R nk}\cong (M^{\otimes _R n})^{\otimes _R k}$ that send $m_1\otimes \cdots \otimes m_{nk}$ to $(m_1\otimes \cdots \otimes m_n)\otimes \cdots \otimes (m_{n(k-1)+1}\otimes \cdots \otimes m_{nk})$.

Proposition 1.24 There are continuous Verschiebung homomorphisms

\[ V_n: W(R; M^{\otimes_R n}) \to W(R; M) \]

for every $n\geq 1$, uniquely characterized by the commutativity of the following diagrams.

Under the ghost map, $V_n$ is compatible with the additive map

\[ \prod_{k\geq 1} (M^{\circledcirc_R nk})^{C_k} \longrightarrow \prod_{k\geq 1} (M^{\circledcirc_R k})^{C_k} \]

given on the factor $(M^{\circledcirc _R nk})^{C_k}$ by the transfer $\operatorname {tr}_{C_k}^{C_{nk}}$ to $(M^{\circledcirc _R nk})^{C_{nk}}$, that is,

\[ V_n\bigg(\sum_i w_{in} t^{i}\bigg) = \sum_i \operatorname{tr}_{C_i}^{C_{in}} w_{in} t^{in}. \]

They satisfy $V_n V_m = V_{nm}$ as maps $W(R; M^{\otimes _R nm}) \to W(R; M)$.

Proof. As the images of the maps $M^{\times n k}\to W(R; M^{\otimes _R n})$ topologically generate $W(R; M^{\otimes _R n})$, there is at most one $V_n$ with the desired properties.

For the existence, consider that the homomorphism $\widehat {S}(R;M^{\otimes _R n}) \to \widehat {S}(R;M)$ given by sending

\[ 1 + \sum_i a_i t^{i} \mapsto 1 + \sum_i a_i t^{ni} \]

preserves the relations given in Lemma 1.19, which were of the form

\[ (1 - x_i y_j t^{i+j}) \sim (1 - y_j x_i t^{i+j}). \]

Thus, this homomorphism factors to a homomorphism $V_n: W(R; M^{\otimes _R n}) \to W(R; M)$ as desired. Next, we compute that this $V_n$ is compatible with the given description on ghosts. However, it suffices to check this on generators. The ghost map sends

\begin{gather*} \operatorname{tlog}(1 - a_k t^{k}) = \operatorname{tr}_e^{C_k} a_k t^{k} + \operatorname{tr}_{C_2}^{C_{2k}} a_k^{2} t^{2k} + \cdots,\\ \operatorname{tlog} (V_n(1 - a_k t^{k})) = \operatorname{tlog}(1 - a_k t^{nk}) = \operatorname{tr}_e^{C_{nk}} a_k t^{nk} + \operatorname{tr}_{C_2}^{C_{2nk}} a_k^{2} t^{2nk} + \cdots. \end{gather*}

As $\operatorname {tr}_{C_{ik}}^{C_{nik}} \operatorname {tr}_{C_i}^{C_{ik}} = \operatorname {tr}_{C_i}^{C_{nik}}$, the described map on ghosts sends $\operatorname {tlog}(1 - a_k t^{k})$ to $\operatorname {tlog}(V_n(1-a_k t^{k}))$.

Finally, to check that $V_n V_m = V_{nm}$, it suffices that they agree on the image of $\tau _k$, which follows from the defining properties of $V_i$.

Note that this implies, in particular, that $\tau _k: M^{\times k} \to W(R;M)$ agrees with the composite

\[ \tau_k: M^{\times k} \to M^{\otimes_R k} \xrightarrow{\tau} W(R; M^{\otimes_R k}) \xrightarrow{V_k} W(R;M). \]

Proposition 1.25 There is a continuous homomorphism $\sigma : W(R; M^{\otimes _R n}) \to W(R;M^{\otimes _R n})$, uniquely characterized by the commutativity of the diagrams

where the left vertical map is given by $(m_1,\ldots, m_{nk-1}, m_{nk})\mapsto (m_{nk},m_1,\ldots,m_{nk-1})$. It has order $n$ and, thus, gives a $C_n$-action on $W(R; M^{\otimes n})$, which we refer to as Weyl action. This is compatible with the $C_n$-action on ghost components $\prod _{i\geq 1} (M^{\circledcirc ni})^{C_i}$ obtained degreewise as the residual action of $C_n \cong C_{ni}/C_i$.

Proof. Again, the images of the upper horizontal maps (jointly for all $k$) generate $W(R; M^{\otimes _R n})$ topologically, and so there is at most one homomorphism $\sigma$. To see one exists, it is sufficient to do so for $(R;M)$ with torsion-free $(M^{\circledcirc nk})_{C_k}$, because the target is Hausdorff and we can resolve any $(R;M)$ as a reflexive coequalizer of $(R_0;M_0)$ and $(R_1; M_1)$ with torsion-free $(M_i^{\circledcirc nk})_{C_k}$.

In the torsion-free case, we know by Proposition 1.18 that $\operatorname {tlog}$ is a homeomorphism onto its image. It is, therefore, sufficient to check that the described $C_n$-action on ghost components restricts to an action on the image of $\operatorname {tlog}$ or, more precisely, sends $\operatorname {tlog}(1 - m_1 \otimes \cdots \otimes m_{nk} t^{k})$ to $\operatorname {tlog}(1 - m_{nk} \otimes m_1\otimes \cdots \otimes m_{nk-1}t^{k})$.

The $ik$th coefficient of $\operatorname {tlog}(1 - m_1 \otimes \cdots \otimes m_{nk} t^{k})$ is given (Proposition 1.15) by

\[ \operatorname{tr}_{C_i}^{C_{ik}} (m_1 \otimes \cdots \otimes m_{nk})^{\otimes i}, \]

which is shifted by a generator of $C_{nik}$ (representing the residual action of a generator of $C_n = C_{nik}/C_{ik}$) to the element

\[ \operatorname{tr}_{C_i}^{C_{ik}} (m_{nk} \otimes m_1\otimes \cdots \otimes m_{nk-1})^{\otimes i}, \]

which is the $ik$th coefficient of $\operatorname {tlog}(1 -m_{nk} \otimes m_1\otimes \cdots \otimes m_{nk-1} t^{k})$.

The $n$th power of $\sigma$ acts as identity on ghost components, and because of naturality, this implies that $\sigma$ always has order $n$.

Proposition 1.26 There are continuous Frobenius homomorphisms

\[ F_n: W(R; M) \longrightarrow W(R; M^{\otimes_R n}) \]

for each $n\geq 1$, uniquely characterized by the following properties:

1. 1. $F_1=\operatorname {id}$ and $F_{nm} = F_n F_m$;

2. 2. for $n,m$ coprime, the squares

   
   commute;

3. 3. the diagrams

   
   commute;

4. 4. the diagrams

   
   commute.

Moreover, on the level of ghost components, $F_n$ is compatible with the map $\prod _{i\geq 1} (M^{\circledcirc _R i})^{C_i} \to \prod _{i\geq 1} (M^{\circledcirc _R in})^{C_i}$ that takes

\[ \sum_i w_i t^{i} \mapsto \sum_j w_{jn} t^{j}, \]

that is, projects away summands in degrees not divisible by $n$, and acts via the inclusion map

\[ (M^{\circledcirc_R jn})^{C_{jn}} \to (M^{\circledcirc_R jn})^{C_j} \]

on the remaining summands.

Proof. Because of the first property, it suffices to define $F_p$ for each prime $p$. Uniqueness then follows from the fact that $W(R;M)$ is generated by elements of the form $\tau _k(a_k) = V_k(\tau (a_k))$: if $k$ is prime to $p$, then the value of $F_pV_k(\tau (a_k))$ is determined by properties 2 and 4, as

\[ F_pV_k(\tau(a_k)) = V_kF_p(\tau(a_k)) = V_k(\tau(a_k^{p})). \]

If $k$ is divisible by $p$, say $k=p\cdot l$, then

\[ F_pV_k(\tau(a_k)) = F_pV_pV_l(\tau(a_k)) = \sum_{\sigma\in C_p} \sigma V_l(\tau(a_k)). \]

To show existence of $F_n$, it suffices to do this again in the case of injective $\operatorname {tlog}$, by resolving $(R,M)$ via reflexive coequalizers (Propositions 1.14 and 1.18). In this case, we define the map on ghost components by

\begin{align*} \prod_{i\geq 1} (M^{\circledcirc_R i})^{C_i} &\to \prod_{i\geq 1} (M^{\circledcirc_R in})^{C_i} \\ \sum_i w_i t^{i} &\mapsto \sum_j w_{jn} t^{j}. \end{align*}

This map is clearly continuous. By Proposition 1.18, we know that $\operatorname {tlog}$ exhibits $W(R; M)$ and $W(R; M^{\otimes _R n})$ as subspaces with the subspace topology. Thus, it suffices to show that this map sends the image of $\operatorname {tlog}$ to the image of $\operatorname {tlog}$. To see this it suffices to show (similarly to the argument for uniqueness of $F_p$ above) that this map on ghosts makes the ghost component analogues of the diagrams in properties 2, 3 and 4 commute.

Checking that the diagrams commute on ghosts is straightforward: for property 2, we have

where the condition that $n,m$ are coprime was used for evaluating the right vertical map: $im$ is divisible by $n$ if and only if $im$ is of the form $jnm$.

For properties 3 and 4, we similarly have the following.

The final piece of structure we want to discuss regards multiplicativity. The Witt vectors of a commutative ring admit a natural ring structure, which is not present in the general case of a possibly non-commutative ring and a possibly non-trivial coefficient bimodule. Rather, we show that $W(-;-)$ is lax symmetric monoidal as a functor of bimodules. For $R$ a commutative ring, this lax symmetric monoidal structure recovers the usual ring structure on $W(R)$ as follows: the multiplication is given as the composite map

\[ W(R)\otimes W(R) \to W(R\otimes R) \stackrel{\mu_*}{\longrightarrow} W(R), \]

which is well-defined because for a commutative ring the multiplication map $\mu : R\otimes R\to R$ is a ring homomorphism (see also Corollary 1.29).

We recall from § 1.1 that the tensor product of two bimodules $(R;M)$ and $(S;N)$ is $(R\otimes S;M\otimes N)$, where the tensor products are over $\mathbb {Z}$.

Proposition 1.27 The functor $W(-;-) : \operatorname {biMod}\to Ab$ admits a lax symmetric monoidal structure, where the maps

\[ W(R;M) \otimes W(S; N) \xrightarrow{*} W(R\otimes S; M\otimes N) \]

are induced from continuous bilinear maps

\[ W(R;M) \times W(S; N) \xrightarrow{*} W(R\otimes S; M\otimes N), \]

uniquely characterized by the following properties.

1. 1. (Frobenius reciprocity) The diagrams

   
   commute, as well as the flipped version (with roles of the two factors reversed). Here $s$ denotes the shuffle map, induced by the bimodule isomorphism which takes
   \[ (m_1\otimes \cdots \otimes m_k) \otimes (n_1 \otimes \cdots \otimes n_k) \mapsto (m_1\otimes n_1)\otimes\cdots (m_k\otimes n_k) \]

2. 2. The following diagram commutes.

   

Moreover, on ghosts, the map $*$ is given by

\[ \prod_{n\geq 1} (M^{\circledcirc_R n})^{C_n} \otimes \prod_{n\geq 1} (N^{\circledcirc_S n})^{C_n}\to \prod_{n\geq 1} ((M\otimes N)^{\circledcirc_{R\otimes S} n})^{C_n}, \]

which simply degreewise applies the shuffle map $(M^{\circledcirc _R n})^{C_n} \otimes (N^{\circledcirc _S n})^{C_n} \to ((M\otimes N)^{\circledcirc _{R\otimes S} n})^{C_n}$, in formulas

\[ \bigg(\sum_i a_i t^{i}\bigg) * \bigg(\sum_i b_i t^{i}\bigg) = \sum_i s(a_i\otimes b_i) t^{i}. \]

Proof. Uniqueness follows from the fact that elements of the form $\tau _k(a_k)=V_k\tau (a_k)$ form a set of topological generators. Indeed, the first and second conditions together show that

\[ V_k(\tau(a_k)) * \tau(b) = V_k(s(\tau(a_k) * F_k\tau(b))) = V_k(s(\tau(a_k) *\tau(b^{\otimes k}))) = V_k(\tau(s(a_k\otimes b^{\otimes k}))) \]

(where we have slightly overloaded the notation $s$ for the various shuffle isomorphisms), so by bilinearity and continuity, multiplication of arbitrary elements with elements of the form $\tau (b)$ is completely determined. The flipped version of the first condition now shows that

\[ f * V_k\tau(b_k) = V_k(s(F_k(f) * \tau(b_k))), \]

which is completely determined by the properties, following the first step.

As a reflexive coequalizer diagram in Hausdorff abelian groups is also an underlying reflexive coequalizer diagram in Hausdorff spaces, and reflexive coequalizers in Hausdorff abelian groups commute with finite products, if we choose resolutions of $(R;M)$ and $(S;N)$ by reflexive coequalizers, the diagram

is a reflexive coequalizer diagram in Hausdorff spaces. Thus, a continuous bilinear map $*$ as desired can be extended from the case of free rings and bimodules to all (and is then easily seen to be bilinear in general).

To construct $*$ in the free case, we proceed similarly to the proof of Proposition 1.26. We define the map on ghost components by the shuffle map as desired. This map is continuous if we restrict it to the product, analogously to the continuity of the map $*$ in question. Using Proposition 1.18 it therefore suffices to show that this map in ghost components sends the image of $\operatorname {tlog}$ to the image of $\operatorname {tlog}$, so that is gives rise to a well-defined map on Witt vectors which is continuous (in the appropriate sense). For this, it suffices to check that the described map on ghost components satisfies the ghost analogues of properties 1 and 2, because using both properties we can express $*$ again in terms of Verschiebung and Teichmüller maps.

On ghosts, we simply check

\begin{align*} &V_k\bigg(\sum_i a_{ik} t^{i}\bigg) * \bigg(\sum_i b_i t^{i}\bigg)\nonumber\\ &\quad =\bigg(\sum_i \operatorname{tr}_{C_i}^{C_{ik}} a_{ik} t^{ik}\bigg) * \bigg(\sum_i b_i t^{i}\bigg) =\sum_i s((\operatorname{tr}_{C_i}^{C_{ik}} a_{ik}) \otimes b_{ik}) t^{ik}\\ &\quad =\sum_i \operatorname{tr}_{C_i}^{C_{ik}} s(a_{ik} \otimes b_{ik}) t^{ik} =V_k\bigg(\sum_i s(a_{ik}\otimes b_{ik}) t^{i}\bigg)\\ &\quad=V_k\bigg(\bigg(\sum_i a_{ik} t^{i}\bigg) * \bigg(\sum_i b_{ik}t^{i}\bigg)\bigg) =V_k\bigg(\bigg(\sum_i a_{ik} t^{i}\bigg) * F_k \bigg(\sum_i b_i t^{i}\bigg)\bigg), \end{align*}

where the crucial equality is the third one, and uses that the transfer is linear with respect to multiplication with invariant elements (and $b_{ik}$ is, by assumption, $C_{ik}$-invariant).

The following are immediate consequences of the symmetric monoidal structure.

Corollary 1.28 Let $R$ be a commutative ring and $M$ an $R$-module (considered as an $R$-bimodule). The module structure $l_M : R\otimes M\to M$ and the multiplication $\mu _R$ of $R$ define a $W(R)$-module structure

\[ W(R;R)\otimes W(R;M)\stackrel{*}{\longrightarrow}W(R\otimes R;R\otimes M) \xrightarrow{(\mu_R,l_M)_\star}W(R;M). \]

Proof. One checks that the map $(\mu _R,l_M) : (R \otimes R;R \otimes M) \to (R;M)$ is a map in $\operatorname {biMod}$ which is straightforward.⁴ Then it follows that $(R;M)$ is a module in $\operatorname {biMod}$ over the commutative monoid $(R; R)$. Thus, the claim follows because $W(-;-)$ is lax symmetric monoidal.

Corollary 1.29 For every commutative ring $R$ and every $R$-algebra $R\to M$, the multiplication maps of $R$ and $M$ define a multiplication

\[ W(R;M)\otimes W(R;M)\stackrel{*}{\longrightarrow}W(R\otimes R;M\otimes M) \xrightarrow{(\mu_R,\mu_M)_\star}W(R;M) \]

making $W(R;M)$ into a $W(R)$-algebra. It is commutative if $M$ is commutative.

Remark 1.30 In the last corollary, we could have allowed two different $R$-algebra structures on $M$ (cf. Lemma 1.5) to obtain a ring structure on $W(R;M)$. However, in general, it would then not be a $W(R)$-algebra.

Corollary 1.31 Let $R$ be a commutative ring and $M$ an $R$-module with dual $M^{\vee }:=\hom _R(M,R)$. The evaluation map $\operatorname {ev} : M^{\vee }\otimes M\to R$ defines a $W(R)$-bilinear pairing

\[ \langle-,-\rangle : W(R;M^{\vee})\otimes W(R;M)\stackrel{*}{\longrightarrow}W (R\otimes R;M^{\vee}\otimes M)\xrightarrow{(\mu_R,\operatorname{ev})_\star}W(R). \]

Finally, we summarise the relations between the different structure maps on $W$ constructed previously. Most of these have already been established as part of the construction.

Proposition 1.32 The maps $V_n$, $F_n$, the $C_n$-action and the lax symmetric-monoidal structure satisfy the following properties:

1. 1. $V_nV_m = V_{nm}$;

2. 2. $F_nF_m = F_{nm}$;

3. 3. $V_n: W(R; M^{\otimes n}) \to W(R; M)$ is invariant under the $C_n$-action on $W(R; M^{\otimes n})$;

4. 4. $F_n: W(R; M)\to W(R; M^{\otimes n})$ is invariant under the $C_n$-action on $W(R; M^{\otimes n})$;

5. 5. $F_nV_n: W(R;M^{\otimes n}) \to W(R; M^{\otimes n})$ is the transfer $\sum _{\sigma \in C_n} \sigma$ and $F_nV_m = V_m F_n$ if $n,m$ are coprime;

6. 6. $F_n$ is a symmetric monoidal transformation;

7. 7. We have $V_n(x*F_n(y)) = V_n(x)*y$ for all $x\in W(R; M^{\otimes n})$ and $y\in W(S; N)$ (with the appropriate shuffle identifications suppressed, see Proposition 1.27).

Proof. Most of these formulas, namely properties 1, 2, 5 and 7, were proved in the construction of the Verschiebung, Frobenius and symmetric monoidal structure. The rest is easily checked explicitly on ghost components, by reducing to the case of injective $\operatorname {tlog}$. For example, properties 3 and 4 correspond to invariance of transfer and restriction maps.

Remark 1.33 An immediate consequence of the Frobenius reciprocity formula $V_n(F_n(y)*x) = y* V_n(x)$ is that for a module $M$ over a commutative ring $R$, the Frobenius and the Verschiebung operators are self-dual under the pairing of Corollary 1.31, in the sense that

\[ \langle \phi,V_n(x)\rangle=V_n\langle F_n(\phi),x\rangle \]

for all $\phi \in W(R;M^{\vee })$ and $x\in W(R;M^{\otimes _R n})$, where the $V_n$ on the right is the Verschiebung of $W(R)$.

1.4 The trace property and Morita invariance

We now show that $W(R;M)$ satisfies a certain trace invariance property in the sense of Kaledin [Kal15], inspired by work of Ponto [Pon10]. The Weyl action constructed in Proposition 1.25 admits a slight generalisation, where instead of considering the $n$-fold tensor power of a bimodule, we consider $n$ bimodules over possibly different rings. Concretely, consider rings $R_i$, and $R_i$-$R_{i+1}$-bimodules $M_{i, i+1}$. Here $i$ ranges over the numbers $0\leq i \leq n-1$ modulo $n$, that is, the last bimodule is an $R_{n-1}$-$R_0$-bimodule. In this situation, we can form $R_l$-$R_l$-bimodules

\[ M_{l,l+1} \otimes_{R_{l+1}} M_{l+1,l+2}\otimes_{R_{l+2}} \cdots \otimes_{R_{l-1}} M_{l-1,l}. \]

Proposition 1.34 (Trace property)

In the situation above, there is an isomorphism

\[ T : W(R_0; M_{0,1}\otimes_{R_1} \cdots \otimes_{R_{n-1}} M_{n-1,0}) \xrightarrow{\sim} W(R_{n-1}; M_{n-1,0}\otimes_{R_0} M_{0,1} \otimes_{R_1} \cdots \otimes_{R_{n-2}} M_{n-2,n-1}) \]

uniquely characterized by the commutative diagrams

where the left vertical map is the cyclic permutation of order $nk$. Under the ghost map, the isomorphism $T$ is compatible with the isomorphism

\[ \prod_{k\geq 1} ((M_{0,1}\otimes_{R_1} \cdots \otimes_{R_{n-1}} M_{n-1,0})^{\circledcirc_{R_0} k})^{C_k} \to \prod_{k\geq 1} ((M_{n-1,0}\otimes_{R_0} \cdots \otimes_{R_{n-2}} M_{n-2,n-1})^{\circledcirc_{R_{n-1}} k})^{C_k} \]

given on the $k$th factor by the cyclic permutation of order $nk$. The $n$-fold composition of $T$ defines an automorphism of $W(R_0; M_{0,1}\otimes _{R_1} \cdots \otimes _{R_{n-1}} M_{n-1,0})$, which is the identity.

Proof. Just as in the proof of Proposition 1.25, uniqueness follows immediately because the images of the $\tau _k$ form a system of generators. Existence is checked in the case of suitably free $R_i$, $M_{i,i+1}$, such that the $\operatorname {tlog}$ is injective, by computing that the claimed action on ghost components acts correctly on elements of the form $\operatorname {tlog}(\tau _k(a_k))$. Finally, the statement about the $n$-fold iterate of this isomorphism also follows by observing that the corresponding map on ghosts is the identity.

Remark 1.35 In the terminology of [PS13], Proposition 1.34 says, in particular, that $W$ is a shadow functor on the bicategory of bimodules.

For any ring $R$, we let $\operatorname {Proj}_R$ denote the category of finitely generated projective right $R$-modules.

Corollary 1.36 Every additive functor $A: \operatorname {Proj}_R \to \operatorname {Proj}_S$ induces a map of abelian groups $A_\ast \colon W(R) \to W(S)$ extending the functoriality of $W$ in ring homomorphisms. In particular, Morita equivalent rings $R$ and $S$ have isomorphic Witt vectors $W(R) \cong W(S)$.

Proof. Any additive functor $A : \operatorname {Proj}_R \to \operatorname {Proj}_S$ is of the form $A \cong (-) \otimes _R M$, where $M$ is the $R$-$S$-bimodule $M := A(R)$. Let $N$ be the $S$-$R$-bimodule $N := \operatorname {Hom}_S(M, S)$. There are bimodule maps

\[ \eta : R \to M \otimes_S N \quad \text{and} \quad \operatorname{ev} : N \otimes_R M \to S, \]

where the second map is the evaluation, whereas the first map corresponds under the isomorphism

(5)\begin{equation} M \otimes_S N \cong M \otimes_S \operatorname{Hom}_S(M, S) \cong \operatorname{Hom}_S(M,M) \end{equation}

to the map which sends $1 \in R$ to the identity. The isomorphism (5) uses the fact that $M$ is finitely generated projective over $S$. The desired map is defined as the composite

\[ W(R) = W(R;R) \stackrel{\eta_*}{\longrightarrow} W(R; M \otimes_S N) \cong W(S; N \otimes_R M) \stackrel{\operatorname{ev}_*}{\longrightarrow} W(S; S) = W(S), \]

where the middle isomorphism is from Proposition 1.34.

If $R$ and $S$ are Morita equivalent we can find an $R$-$S$-bimodule $M$ such that $\eta$ and $\operatorname {ev}$ are isomorphisms, and it follows that the map above is also an isomorphism.

Remark 1.37 In the $p$-typical case the Morita invariance of the Witt vectors has been shown by Hesselholt using a comparison to the topological invariant $\mathrm {TR}_0$. (See [Hes97], specifically (2.2.10) on page 130.) He also mentions that ‘One would like also to have an algebraic proof of this fact’ which is exactly what we have provided. It is remarkable that to prove this fact about Witt vectors of non-commutative rings one needs to introduce the more general notion of Witt vectors with coefficients. We consider this to be one of the main reasons to study this more general notion.

Remark 1.38 We finish this section by remarking that Corollary 1.36 implies additional functoriality for the construction $R\mapsto W(R)$.

1. 1. Every non-unital map of unital rings $f : R \to S$ gives rise to a functor

   \[ \operatorname{Proj}_R \to \operatorname{Proj}_S \qquad P \mapsto P \otimes_R (f(1) \cdot S) \]
   and, thus, to a map $W(R) \to W(S)$. One can, of course, see this directly, but Morita invariance gives a nice explanation for this additional functoriality.

2. 2. The functor $\oplus : \operatorname {Proj}_{R \times R} = \operatorname {Proj}_R \times \operatorname {Proj}_R \to \operatorname {Proj}_R$ induces a map $W(R \times R) = W(R) \oplus W(R) \to W(R)$, which coincides with the group structure by an Eckmann–Hilton argument.

3. 3. For every map $R \to S$ such that $S$ is finitely generated projective over $R$ there is a ‘transfer’ map $W(S) \to W(R)$ induced by the restriction functor $\operatorname {Proj}_S \to \operatorname {Proj}_R$. With some more work one can show that such a transfer map even exists if $S$ is a perfect complex over $R$.

1.5 Truncated Witt vectors with coefficients

We recall that a subset $S\subseteq \operatorname {\mathbb {N}}_{>0}$ is a truncation set if it has the property that $ab\in S$ implies $a\in S$ and $b\in S$.

Definition 1.39 For a truncation set $S$ we define $W_S(R;M)$ to be the quotient of $W(R;M)$ by the closed subgroup generated by the elements $\tau _n(x)$ for all $n\not \in S$.

For a prime $p$ the $p$-typical Witt vectors with coefficients are defined as

\[ W_p(R;M) := W_{\{1,p,p^{2},\ldots\}}(R;M) \]

and for $n \geq 1$ the truncated version by

\[ W_{p,n}(R;M) := W_{\{1,p,p^{2},\ldots ,p^{n-1}\}}(R;M). \]

For every inclusion $S'\subseteq S$, we have a natural reduction map

\[ R: W_S(R;M) \to W_{S'}(R;M). \]

Lemma 1.40 For $S =\bigcup _i S_i$ an increasing union of truncation sets $\cdots \subseteq S_i \subseteq S_{i+1} \subseteq \cdots$, the map

\[ W_S(R;M) \to \varprojlim W_{S_i}(R;M) \]

is an isomorphism.

Proof. Observe that the image filtration of the $\widehat {S}^{(n)}(R;M)$ on $W_S(R;M)$ is still Hausdorff and complete, by the same argument as in the proof of Lemma 1.13.

The map $W_S(R;M) \to W_{S_i}(R;M)$ is surjective, with kernel $K_i$ topologically generated by the elements of the form $\tau _n(x)$ with $n\not \in S_i$, and because elements of the form $\tau _n(x)$ with $n\not \in S$ are already zero in $W_S(R;M)$, $K_i$ is actually generated by those $\tau _n(x)$ with $n\in S\setminus S_i$. We let $d_i$ be the minimal element of $S\setminus S_i$. Thus, every element of $K_i$ has a representative of filtration $\geq d_i$. As $\bigcup S_i = S$, $d_i$ tends to $\infty$ with $i$ and, thus, the $K_i$ also form a Hausdorff and complete filtration of $W_S(R;M)$, which implies the claim.

For each truncation set $S$ we let $\pi _S$ be the projection map

\[ \prod _{n\geq 1} (M^{\circledcirc _R n})^{C_n} \to \prod _{n\in S} (M^{\circledcirc _R n})^{C_n}.\]

Lemma 1.41 There exists a unique map $\operatorname {tlog}_S$ making the diagram

commute. If the transfers $(M^{\circledcirc _R n})_{C_n}\to (M^{\circledcirc _R n})^{C_n}$ are injective for all $n\in S$, then $\operatorname {tlog}_S$ is also an embedding.

Proof. To check that $\operatorname {tlog}$ factors as claimed, it suffices to show that $\operatorname {tlog}(1-a_kt^{k})$ for $k\not \in S$ is sent to $0$ under the projection map $\prod _{n\geq 1} (M^{\circledcirc _R n})^{C_n} \to \prod _{n\in S} (M^{\circledcirc _R n})^{C_n}$. As

\[ \operatorname{tlog}(1-a_kt^{k}) = \sum_i \operatorname{tr}_{C_i}^{C_{ki}} a_k^{i} t^{ki}, \]

and $S$ contains no multiples of $ki$, this is clear.

Now assume that for each $n\in S$, the transfer $(M^{\circledcirc _R n})_{C_n}\to (M^{\circledcirc _R n})^{C_n}$ is injective. We want to show that $\operatorname {tlog}_S$ is injective. Let $x$ be an element in the kernel, say with a representative of the form $(1-a_kt^{k} + \cdots )$. If $k\not \in S$, we can factor this in the form $(1-a_kt^{k}) \cdot (1 - a_{k+1} t^{k+1} + \cdots )$, with the second factor still in the kernel of $\operatorname {tlog}_S$. If, on the other hand, $k\in S$, then we have

\[ \operatorname{tlog}(1-a_kt^{k} + \cdots) = \operatorname{tr}_e^{C_k}a_kt^{k} + \cdots, \]

so $a_k$ lies in the kernel of the transfer $M^{\circledcirc _R k} \to (M^{\circledcirc _R k})^{C_k}$. By assumption, this means that $a_k$ vanishes in $(M^{\circledcirc _R k})_{C_k}$. As in the proof of Lemma 1.16, this shows that we can multiply $(1-a_kt^{k} + \cdots )$ by a series with filtration $\geq k$ that vanishes in $W(R;M)$, in order to obtain a representative of the form $(1-a_{k+1}t^{k+1}+\cdots )$. This shows that any element which gets mapped by $\operatorname {tlog}_S$ to something of filtration $\geq k$ admits a representative of filtration $\geq k$. In particular, $\operatorname {tlog}_S$ is an embedding, because any element in the kernel equals a convergent product of elements trivial in $W_S(R;M)$ and, thus, vanishes.

For a truncation set $S$, we define $S/n := \{k\in \operatorname {\mathbb {N}}_{>0}\mid nk \in S\}$. This is again a truncation set.

Proposition 1.42 The Verschiebung and Frobenius maps descend to maps

\begin{align*} & V_n: W_{S/n}(R;M^{\otimes_R n}) \to W_S(R;M),\\ & F_n: W_{S}(R;M) \to W_{S/n}(R;M^{\otimes_R n}), \end{align*}

the Weyl action of $C_n$ on $W(R;M^{\otimes _R n})$ descends to a $C_n$ action on $W_S(R;M^{\otimes _R n})$, and the lax symmetric monoidal structure on $W(-;-)$ descends to one on $W_S(-;-)$. There are formulas for the ghost components of these maps analogous to the respective Propositions 1.24, 1.26, 1.25 and 1.27.

Proof. The formulas given on ghost components for the various structure maps are all seen to be compatible with the projections onto the respective index sets. Now note that if $\operatorname {tlog}_S$ is injective, the kernel of $W(R;M) \to W_S(R;M)$ is the same as the preimage of the kernel of the projection map $\prod _{n\geq 1} (M^{\circledcirc _R n})^{C_n} \to \prod _{n\in S} (M^{\circledcirc _R n})^{C_n}$ under $\operatorname {tlog}$. Thus, in the injective case, we see that the structure maps preserve these kernels and, thus, descend to structure maps on $W_S$. The statement for general pairs $(R;M)$ now follows by resolving by pairs where the relevant $\operatorname {tlog}$ are injective.

The following exact sequences are analogous to the sequences of [Kal18a, Lemma 3.2] for vector spaces over perfect fields of characteristic $p$.

Proposition 1.43 Let $M$ be an $R$-bimodule, let $S$ be a truncation set and let $k\geq 1$. We let $S'= S\setminus k\operatorname {\mathbb {N}}$. Then there is a natural exact sequence

\[ W_{S/k}(R;M^{\otimes_R k})_{C_k}\stackrel{V_k}{\longrightarrow} W_{S}(R;M)\stackrel{R}{\longrightarrow} W_{S'}(R;M)\to 0. \]

Proof. Recall that $W_{S'}(R;M)$ is, by definition, the quotient of $W(R;M)$ by the closed subgroup generated by all $\tau _d(a_d)$ for $a_d \in M^{\times d}$ and $d\not \in S'$. Equivalently, we can view this as the quotient of $W_S(R;M)$ by the image of that subgroup. As $\tau _d(a_d)$ for $d\in S$ is already zero in $W_S(R;M)$, we can obtain $W_{S'}(R;M)$ from $W_S(R;M)$ by quotienting just by all $\tau _d(a_d)$ for $d\in S\setminus S' = S\cap k\mathbb {N}$. We have to check that this coincides with the image of $V_k$. To see this, recall (Lemma 1.12) that $W_{S/k}(R;M^{\otimes _R k})$ is generated by elements of the form $\tau _l(a_{kl})$ with $a_{kl} \in M^{\times kl}$, and $l\in S/k$ or, equivalently, $kl\in S$. Now observe that

\[ V_k(\tau_l(a_{kl})) = \tau_{kl}(a_{kl}), \]

which proves the claim.

The Verschiebung is generally not injective. This is the case even for the usual non-commutative Witt vectors, that is, when $M=R$, by [Hes05]. The usual Witt vector Verschiebung is, however, injective if the ring has no torsion or if it is commutative.

Proposition 1.44 The Verschiebung $V_k : W_{S/k}(R;M^{\otimes _R k})_{C_k}\to W_{S}(R;M)$ is injective when the transfers $(M^{\circledcirc _R n})_{C_n} \to (M^{\circledcirc _R n})^{C_n}$ are injective for every $n\in S$ with $k\mid n$. This is satisfied, in particular, if $(M^{\circledcirc _R n})_{C_n}$ has no $n$-torsion for each such $n$.

Proof. Assume $x\in W_{S/k}(R;M^{\otimes _R k})_{C_k}$ is in the kernel. Assume $x$ is not $0$, so there exists a maximal $l$ such that $x$ has filtration $\geq l$. We write $x = \tau _{l}(a_{kl}) + x'$ with $x'$ of filtration $\geq l+1$. If $kl\not \in S$, then $\tau _{l}(a_{kl}) = 0$ in $W_{S/k}$, and so $x=x'$ and $x$ has filtration $\geq l+1$, contradicting the maximality of $l$. Thus, $kl \in S$.

The leading term of $\operatorname {tlog} V_k(x)$ agrees with that of $\operatorname {tlog} V_k(\tau _{l}(a_{kl})) = \operatorname {tlog} \tau _{kl}(a_{kl})$, which is given by $\operatorname {tr}_{e}^{C_{kl}}(a_{kl})$. As $kl\in S$, the vanishing of $V_k(x)$ therefore implies that $\operatorname {tr}_{e}^{C_{kl}}(a_{kl})=0$. As we assumed that the transfers $\operatorname {tr}: (M^{\circledcirc _R kl})_{C_{kl}} \to (M^{\circledcirc _R kl})^{C_{kl}}$ are injective, this implies that $a_{kl} = 0$ in $(M^{\circledcirc _R kl})_{C_{kl}}$. Similarly to the proof of Lemma 1.16, one can then write $(1+a_{kl}t^{l})$ in $\widehat {S}(R; M^{\otimes _R k})$ as a product of elements of the form $(1+x_i y_j t^{l})\cdot (1+y_j x_i t^{l})^{-1}$ with $x_i\in M^{\otimes _R i}$, $y_j\in M^{\otimes _R j}$, $i+j=kl$, and a remainder term of higher filtration. Observe that, from the definition of the $C_k$ action on $W(R; M^{\otimes k})$, the element $(1+x_i y_j t^{l})(1+y_j x_i t^{l})^{-1}$ represents $\tau _l(x_i y_j) - \sigma ^{j} \tau _l(x_i y_j)$. It follows that $x\in W_{S/k}(R;M^{\otimes _R k})_{C_k}$ has filtration bigger than $l$, contradicting the maximality of $l$. Thus, $x=0$.

2. Characteristic polynomials and cyclic $K$-theory

In this section, we define the characteristic polynomial for endomorphisms of finitely generated projective modules over non-commutative rings and compare it with Ranicki's and Sheiham's version of the Dieudonné determinant, see [She01]. We also discuss the group of rational Witt vectors and versions of the characteristic elements valued in this group.

2.1 Characteristic polynomials for non-commutative rings

We recall that for any ring $R$, not necessarily commutative, and any finitely generated projective right $R$-module $P$, the trace of Hattori [Hat65] and Stallings [Sta65] is the additive map

(6)\begin{equation} \operatorname{tr}_R \colon \operatorname{End}_R(P) \stackrel{\cong}{\longleftarrow} P\otimes_R P^{\vee} \xrightarrow{\operatorname{ev}} R/[R,R] . \end{equation}

Here $P^{\vee } = \operatorname {Hom}_R(P, R)$, and the evaluation $P\otimes _R P^{\vee } \xrightarrow {\operatorname {ev}} R/[R,R]$ is induced from the evaluation $P\otimes _{\mathbb {Z}} P^{\vee } \xrightarrow {\operatorname {ev}} R$. It is only well-defined in the quotient $R/[R,R]$ by the additive subgroup $[R,R]\subseteq R$ generated by the commutators. The trace satisfies $\operatorname {tr}(AB) = \operatorname {tr}(BA)$ and, thus, descends to a map $\operatorname {End}_R(P)/[\operatorname {End}_R(P), \operatorname {End}_R(P)] \longrightarrow R/[R,R]$ of abelian groups. The goal of this section is to give a (non-additive) refinement of the map (6) through the first ghost component map $W(R) \to R/ [R,R]$, that is, a map

\[ \chi: \operatorname{End}_R(P) \to W(R). \]

We first need an auxiliary construction. For every finitely generated projective $R$-module $P$ there is a fully faithful functor

(7)\begin{equation} (-)\otimes_{\operatorname{End}_R(P)}P: \operatorname{Proj}_{\operatorname{End}_R(P)}\to \operatorname{Proj}_{R} \end{equation}

and by Corollary 1.36 this induces an additive map

(8)\begin{equation} W(\operatorname{End}_R(P)) \longrightarrow W(R). \end{equation}

This map is not an isomorphism in general, but it is if the functor (7) is an equivalence of categories. By Morita theory this is the case if $P$ is free. We want to give a more general criterion for when this is the case.

Definition 2.1 Let $R$ be a ring (not necessarily commutative) and $P$ a finitely generated, projective $R$-module. We say that $P$ is supported everywhere if the functor $(-)\otimes _{\operatorname {End}_R(P)}P: \operatorname {Proj}_{\operatorname {End}_R(P)}\to \operatorname {Proj}_{R}$ is an equivalence of categories.

We note that the functor $\operatorname {Proj}_{\operatorname {End}_R(P)}\to \operatorname {Proj}_{R}$ is always fully faithful and its essential image is the full subcategory of $\operatorname {Proj}_{R}$ generated by $P$ under direct sums and retracts. Thus $P$ is supported everywhere precisely if $P$ generates $\operatorname {Proj}_{R}$ under direct sums and retracts.

Lemma 2.2 The module $P$ is supported everywhere precisely if the canonical evaluation map

\[ P^{\vee} \otimes_{\operatorname{End}_R(P)} P \to R \]

is an isomorphism. If $R$ is commutative, then this is also equivalent to the condition that $P$ has positive rank at every point of $\operatorname {Spec}(R)$.

In general, a sufficient condition for $P$ to have support everywhere is that $P$ contains $R$ as a summand.

Proof. The functor $(-)\otimes _{\operatorname {End}_R(P)}P: \operatorname {Proj}_{\operatorname {End}_R(P)}\to \operatorname {Proj}_{R}$ has a right adjoint given by $(-)\otimes _R P^{\vee }$ and the counit of the adjunction is given by the map $M \otimes _R P^{\vee } \otimes _{\operatorname {End}_R(P)} P \to M$, which implies the criterion. For the second condition we note that we can check the first condition Zariski-locally, and for free modules it is equivalent to being non-trivial.

Finally, to see that $P$ is supported everywhere, we have to show that $P$ is a generator of $\operatorname {Proj}_{R}$, which is immediate if $P$ contains a free summand.

Remark 2.3 A choice of summand inclusion of $P$ into a free $R$-module $R^{n}$ determines a relation between the maps (8) for $P$ and $R^{n}$. Namely, there is a commutative diagram

where the vertical map is induced by the non-unital ring homomorphism $\iota \colon \operatorname {End}_R(P)\to \operatorname {End}_R(R^{n})$ that extends an endomorphism by $0$ on the complement of $P$ (see Remark 1.38). The diagram commutes because for every $\operatorname {End}_R(P)$-module $M$ there is an isomorphism

\begin{align*} & M\otimes_{\operatorname{End}_R(P)}(\iota(1)\cdot \operatorname{End}_R(R^{n}))\otimes_{ \operatorname{End}_R(R^{n})}R^{n} \\ &\quad \cong M\otimes_{\operatorname{End}_R(P)}(\iota(1)\cdot \operatorname{End}_R(R^{n}))\otimes_{ \operatorname{End}_R(R^{n})}(\iota(1)\cdot R^{n})\\ &\quad \cong M\otimes_{\operatorname{End}_R(P)}P, \end{align*}

which is natural in $M$.

Proposition 2.4 We have the following properties.

1. 1. The map (8) is compatible with the product of traces on ghosts

   \[ \prod_{n\geq 1}\operatorname{tr}_R: \prod_{n\geq 1} \operatorname{End}_R(P)/[\operatorname{End}_R(P), \operatorname{End}_R(P)] \longrightarrow \prod_{n\geq 1} R/[R,R]. \]

2. 2. The map (8) is compatible with direct sums in the sense that the maps

   \[ W(\operatorname{End}_R P \times \operatorname{End}_R Q) \to W(\operatorname{End}_R(P \oplus Q)) \to W(R) \]
   and
   \[ W(\operatorname{End}_R P \times \operatorname{End}_R Q) \to W(\operatorname{End}_R P) \oplus W(\operatorname{End}_R Q) \to W(R) \oplus W(R) \xrightarrow{+} W(R) \]
   agree.

3. 3. For a map of the form $\varphi : P \xrightarrow {\psi } R \xrightarrow {x} P$ the element $\psi (x) \in R$ is a representative of the class $\operatorname {tr}(\varphi ) \in R/[R,R]$ and the map (8) sends $1 - \varphi t^{n}$ to $1 - \psi (x) t^{n}$.

Proof. We abbreviate $E := \operatorname {End}_R(P)$. By definition and the proof of Corollary 1.36, the map (8) is the composite of the top row of the diagram

where the composite of the bottom row is, by definition, the product of the traces. The description in ghost components follows from the commutativity of this diagram. The three upper squares commute by the naturality of the ghost map and by Proposition 1.34. The lower vertical isomorphisms in the first and third columns are from Example 1.1, where the $C_n$-actions on the cyclic powers are trivial. The lower middle isomorphism which makes the lower left square commute is defined by iterating the multiplication maps

\[ (P\otimes_RP^{\vee})\otimes_{E}(P\otimes_RP^{\vee}) \xrightarrow{P\otimes_R\operatorname{ev}\otimes_RP^{\vee}}P\otimes_RR\otimes_R P^{\vee}\cong P\otimes_RP^{\vee} \]

which correspond to the multiplication of $E$ under $\eta$. It is then easy to see that both composites in the lower right rectangle are

\[ (p_1\otimes_R\lambda_1)\otimes_E\cdots \otimes_E(p_n\otimes_R\lambda_n) \longmapsto \lambda_n(p_1)\lambda_1(p_2)\cdots \lambda_{n-1}(p_n). \]

For the second property, we note that both maps $W(\operatorname {End}_R P \times \operatorname {End}_R Q) \to W(R)$ are induced by functors

\[ \operatorname{Proj}_{\operatorname{End}_R P \times \operatorname{End}_R Q} \to \operatorname{\operatorname{Proj}_R} \]

which are easily seen to agree with the functor that sends $(M,N)$ to $(M \oplus N) \otimes _{(\operatorname {End}_R P \times \operatorname {End}_R Q)} (P \oplus Q)$.

For the third property, consider $\varphi = x \circ \psi \in \operatorname {End}_R{P}$. Using property 2, we can assume that $P$ admits $R$ as a direct summand, by replacing it with $P\oplus R$ if necessary (and replacing $\varphi$ correspondingly by the map $\varphi \oplus 0: P\oplus R \to P\oplus R$). Thus, we can choose $f: P\to R$ and $e: R\to P$ with $f\circ e=\operatorname {id}$. Now the element

\[ \varphi\in \operatorname{End}_R P\cong P\otimes_R P^{\vee} \otimes_{\operatorname{End}_R P} \cdots \otimes_R P^{\vee} \]

can be represented by the elementary tensor

\[ x\otimes_R f\otimes_{\operatorname{End}_R P} e \otimes_R \cdots \otimes_{\operatorname{End}_R P} e \otimes_R \psi. \]

By Proposition 1.34, the map (8) therefore sends $(1-\varphi t^{n})$ to $(1-\psi (x)f(e)\cdots f(e)t^{n})=(1-\psi (x)t^{n})$ as claimed.

Remark 2.5 Property 3 of Proposition 2.4 uniquely determines the map (8) in the sense that every other additive map $W(\operatorname {End}_R(P)) \longrightarrow W(R)$ with the same value on rank-one endomorphisms agrees with our map (8). This follows from Lemma 1.12 by observing that every element of $\operatorname {End}_R(P)$ splits as a sum of endomorphisms which factor through $R$: For free $P$, we see this by representing the endomorphism as a matrix, and writing the matrix as a sum of matrices with a single nonzero entry. For general projective $P$, we can write it as a retract of free $F$, that is, every endomorphism as composite

\[ P\to F \to F \to P, \]

and, thus, as sum of composites

\[ P\to F \to R \to F \to P. \]

Definition 2.6 Let $P$ be a finitely generated projective $R$-module and $f\in \operatorname {End}_R(P)$. We define the characteristic element $\chi _f \in W(R)$ to be the image of $f$ under the map

\[ \chi: \operatorname{End}_R(P)\stackrel{\tau}{\longrightarrow}W(\operatorname{End}_R(P)) \longrightarrow W(R), \]

where $\tau (f)=1 - f t$ as before and the second map is the map (8).

In the commutative case, where $W(R) = 1 + tR [\kern-0.15em[{t}]\kern-0.15em] $, we show in Proposition 2.9 that on free $R$-modules

\[ \chi_A = \det(1 - A t), \]

which agrees with the characteristic polynomial of $A$ up to a substitution. Thus, one can view $\chi _f$ as a non-commutative generalisation of the characteristic polynomial. Note that $W(R)$ is, in general, a quotient of the group of special units in the power series ring, so individual coefficients of $\chi _f$ are not well-defined. In addition, for a general $R$ and $P$, there does not need to be a polynomial representative for $\chi _f$.

We now prove that the characteristic element $\chi _f$ satisfies the usual properties of the characteristic polynomial.

Lemma 2.7 The characteristic element has the following properties.

1. 1. It is natural under basechange.

2. 2. For two endomorphisms $f,g: P\to P$ of a finitely generated projective $R$-module, we have $\chi _{fg} = \chi _{gf}$.

3. 3. For an endomorphism $f: P \to P$ the $n$th ghost component of $\chi _f$ is given by the trace $\operatorname {tr}_R(f^{n}) \in R/[R,R]$.

4. 4. (Additivity) For a short exact sequence of endomorphisms, that is, a commutative diagram in $\operatorname {Proj}_R$

   
   with exact rows, we have $\chi _{f_2} = \chi _{f_1}+\chi _{f_3}$ (cf. Remark 1.11).

Proof. The first statement is obvious from the definition. The second statement is an immediate consequence of the fact that $1 - fg t = 1 - gft$ in $W(\operatorname {End}_R(P))$ by definition. The third statement follows from Propositions 2.4(1) and 1.15. Indeed, the ghost components of $\tau (f)$ are given by

\[ \operatorname{tlog}(1-ft) = ft + f^{2} t^{2} + \cdots, \]

and so the ghost components of $\chi _f$ are given by

\[ \operatorname{tlog}(\chi_f) = \operatorname{tr}(f) t + \operatorname{tr}(f^{2}) t^{2} + \cdots. \]

For the fourth statement first consider the special case where the endomorphism splits, by which we mean that there exists a section $P_3 \to P_2$ such that, under the induced isomorphism $P_1\oplus P_3 \cong P_2$, $f_2$ corresponds to $f_1 \oplus f_3$. In other words, $1- f_2t$ is the image of $1- (f_1, f_3)t$ under the map $\oplus : W(\operatorname {End}_R(P_1) \times \operatorname {End}_R(P_3)) \to W(\operatorname {End}_R(P_2))$. Then the claim follows from property 2 of Proposition 2.4. For the general case, we choose a section $s: P_3\to P_2$, and under the isomorphism $P_2 \cong P_1\oplus P_3$ we write $f_2$ as a ‘block matrix’

\[ \bigg(\begin{array}{c|c} f_1 & \rho\\ \hline 0 & f_3 \end{array}\bigg), \]

where $f_i$ is an endomorphism of $P_i$, for $i=1,2$, and $\rho : P_3 \to P_1$ is $R$-linear. In $W(\operatorname {End}_R(P_1\oplus P_3))$ we see that

\[ \tau\bigg(\begin{array}{c|c} 0 & \rho\\ \hline 0 & 0 \end{array}\bigg) = \tau\bigg(\bigg(\begin{array}{c|c} 1 & 0\\ \hline 0 & 0 \end{array}\bigg)\bigg(\begin{array}{c|c} 0 & \rho\\ \hline 0 & 0 \end{array}\bigg)\bigg) = \tau \bigg(\bigg(\begin{array}{c|c} 0 & \rho\\ \hline 0 & 0 \end{array}\bigg)\bigg(\begin{array}{c|c} 1 & 0\\ \hline 0 & 0 \end{array}\bigg)\bigg) = \tau\bigg(\begin{array}{c|c} 0 & 0\\ \hline 0 & 0 \end{array}\bigg) = 1, \]

using the relation $\tau (ab) = \tau (ba)$ that holds in $W(-)$ by definition. Thus, the characteristic element of $\bigg (\begin {array}{c|c} 0 & \rho \\ \hline 0 & 0\end {array}\bigg )$ vanishes, and we further see that

\begin{gather*} \bigg(1 - \bigg(\begin{array}{c|c} f_1 & \rho\\ \hline 0 & f_3 \end{array}\bigg)t\bigg) = \bigg(1 - \bigg(\begin{array}{c|c} 0 & 0\\ \hline 0 & f_3 \end{array}\bigg)t\bigg)\bigg(1 - \bigg(\begin{array}{c|c} 0 & \rho\\ \hline 0 & 0 \end{array}\bigg)t\bigg)\bigg(1 - \bigg(\begin{array}{c|c} f_1 & 0\\ \hline 0 & 0 \end{array}\bigg)t\bigg),\\ \bigg(1 - \bigg(\begin{array}{c|c} 0 & 0\\ \hline 0 & f_3 \end{array}\bigg)t\bigg)\bigg(1 - \bigg(\begin{array}{c|c} f_1 & 0\\ \hline 0 & 0 \end{array}\bigg)t\bigg) = \bigg(1 - \bigg(\begin{array}{c|c} f_1 & 0\\ \hline 0 & f_3 \end{array}\bigg)t\bigg), \end{gather*}

which together imply that

\begin{align*} \tau\bigg(\begin{array}{c|c} f_1 & \rho\\ \hline 0 & f_3 \end{array}\bigg) &= \tau\bigg(\begin{array}{c|c} 0 & 0\\ \hline 0 & f_3 \end{array}\bigg)\tau\bigg(\begin{array}{c|c} 0 & \rho\\ \hline 0 & 0 \end{array}\bigg)\tau\bigg(\begin{array}{c|c} f_1 & 0\\ \hline 0 & 0 \end{array}\bigg)\\ &=\tau\bigg(\begin{array}{c|c} 0 & 0\\ \hline 0 & f_3 \end{array}\bigg)\tau\bigg(\begin{array}{c|c} f_1 & 0\\ \hline 0 & 0 \end{array}\bigg)=\tau\bigg(\begin{array}{c|c} f_1 & 0\\ \hline 0 & f_3 \end{array}\bigg)\end{align*}

Thus, the characteristic element of $f_2$ agrees with that of $f_1 \oplus f_3$, so by the previous case $\chi _{f_2} = \chi _{f_1} + \chi _{f_3}$.

Remark 2.8 An alternative construction of $\chi _f$ can be given using the axiomatic approach of Ponto and Shulman [PS13]. Using that $W(R;M)$ is a shadow functor (see Remark 1.35), the construction of [PS13, Definition 5.1] gives for any endomorphism $f \colon P \to P$ of a finitely generated projective $R$-module, a trace homomorphism of $f$

\[ W(\mathbb{Z}) \longrightarrow W(R). \]

The image of $1-t$ (the multiplicative unit) under this map then coincides with $\chi _f$. To see this one observes that there is a bimodule morphism

\[ (\mathbb{Z}; \mathbb{Z}) \longrightarrow (\operatorname{End}_R(P);\operatorname{End}_R(P)), \]

where the first map is the unit and the second map sends $1$ to $f$. This induces a homomorphism of abelian groups

\[ W(\mathbb{Z}) \longrightarrow W(\operatorname{End}_R(P)) \]

sending $1-t$ to $1-ft$. Chasing through the definitions it is easy to see that the composite

\[ W(\mathbb{Z}) \longrightarrow W(\operatorname{End}_R(P)) \longrightarrow W(R) \]

is the trace of Ponto and Shulman, and this sends $1-t$ to $\chi _f$. Properties 1 and 2 of Lemma 2.7 are, in fact, consequences of the formal properties of the trace (see [PS13, Corollary 7.3]), but the others require the explicit construction of $W(R;M)$.

Proposition 2.9 For $R$ a commutative ring, $P=R^{n}$ a free module of rank $n$, and $f\in \operatorname {End}_R(P)$ an endomorphism, the characteristic element $\chi _f \in W(R) = 1 + tR [\kern-0.15em[{t}]\kern-0.15em] $ is related to the classical characteristic polynomial $\chi _f^{\mathrm {cl}}$ by

\[ \chi_f(t) = \det(\operatorname{id} - tf) = t^{n} \det(t^{-1}\operatorname{id} - f) = t^{n} \chi_f^{\mathrm{cl}}(t^{-1}). \]

Proof. By naturality, it is sufficient to check the claim in the universal case, $R=\operatorname {\mathbb {Z}}[a_{ij}\,|\, 1\leq i\leq n, 1\leq j\leq n]$, with $f$ the endomorphism given by the matrix $(a_{ij})$. As $R$ is a domain, it embeds into an algebraically closed field $K$ of characteristic zero. As the map $W(R) \to W(K)$ is injective, it suffices to check that $\chi _f(t)$ and $t^{n} \chi _f^{\mathrm {cl}}(t^{-1})$ agree in $W(K)$. Over the algebraically closed $K$, however, $f$ can be brought into triangular form by a base change. This does not affect $\chi _f^{\mathrm {cl}}$ nor $\chi _f$, the latter because of property 2 of Lemma 2.7. For triangular $f$, with diagonal entries $\lambda _1, \ldots, \lambda _n$, property 3 of Lemma 2.7 implies $\chi _f = \prod (1-\lambda _i t)$, which agrees with $t^{n} \prod (t^{-1} - \lambda _i) = t^{n} \chi _f^{\mathrm {cl}}$.

Example 2.10 Even in the commutative case, the characteristic element is slightly more general than the usual inverse characteristic polynomial (by which we mean $\det (\operatorname {id}-tf)$): it makes sense for non-free projective modules. We note, however, that in the commutative case our polynomial is given by the formula

\[ \chi_f(t)=\sum_{i\geq 0}(-1)^{i} \operatorname{tr}(\Lambda^{i}f)t^{i}, \]

which makes sense for projective modules. This is well-known and already appears, for example, in Almkvist's work [Alm74] and can be used as a definition.

The usual (meaning: not inverse) characteristic polynomial can in the commutative situation also be extended to endomorphisms $f: P \to P$ of finitely generated projective modules over $R$. One simply defines it as before by the formula

\[ \chi_f^{\mathrm{cl}}(t) = \det(t \cdot \operatorname{id} - f), \]

where $t \cdot \operatorname {id} - f$ is considered as an endomorphism of the $R[t]$-module $P[t]$. For this definition, we use that the determinant makes sense for arbitrary endomorphisms $g: Q \to Q$ of finitely generated projective $S$-modules where $S$ is a commutative ring (here: $S = R[t]$ and $Q = P[t]$). One simply defines $\Lambda ^{\mathrm {rk}} Q$ to be the top exterior power of $Q$, where $\mathrm {rk}: \operatorname {Spec} (S) \to \mathbb {N}$ is the locally constant rank function for $Q$. Then $\Lambda ^{\mathrm {rk}} Q$ is a line bundle on $\mathrm {Spec}(S)$ and $\det (g) := \Lambda ^{\mathrm {rk}} g$ is an endomorphism of this line bundle, thus given by an element of $S$. Alternatively one finds a complement $Q'$ such that $Q \oplus Q'$ is free and defines the determinant of $g$ to be the determinant of the endomorphism $g \oplus \operatorname {id}_{Q'}$. We then have as in Proposition 2.9 the relation

\[ \chi_f(t) = t^{\mathrm{rk}} \chi_f^{\mathrm{cl}}(t^{-1}) \]

and the coefficients of $\chi _f^{\mathrm {cl}}$ are given by traces of the exterior powers $\Lambda ^{\mathrm {rk}-i}f$ similar to the formula above.

Example 2.11 We compute the characteristic element of the endomorphism

\[ A = \bigg(\begin{array}{cc} a & b\\c & d\end{array}\bigg) \in \operatorname{Mat}_{2\times 2}(R). \]

The fourth statement of Lemma 2.7 shows that elements of $W(\operatorname {Mat}_{n\times n}(R))$ of the form $1-Nt$, with $N$ strictly lower or upper triangular, vanish. More generally, elements of the form $1 - N t^{k} = V_k(1 - Nt)$ vanish. Thus, we can multiply an element of $W(\operatorname {Mat}_{n\times n}(R))$ with elementary matrices of the form $1-E_{ij}(t\lambda )$, $i\neq j$, $\lambda$ some power series, without changing it:

\begin{align*} \tau(A) &= \bigg(\begin{array}{cc} 1-at & -bt\\-ct & 1-dt\end{array}\bigg) \\ &= \bigg(\begin{array}{cc} 1-at & -bt\\0 & (1-dt)- c(1-at)^{-1}bt^{2}\end{array}\bigg)\\ &= \bigg(\begin{array}{cc} 1-at & 0\\0 & (1-dt)- c(1-at)^{-1}bt^{2}\end{array}\bigg). \end{align*}

From this, we see that

\begin{align*} \chi_A &= (1-at)(1-dt) - (1-at)c(1-at)^{-1}bt^{2}\\ &= 1-(a+d)t+(ad-cb)t^{2}-(ca-ac)bt^{3}-(ca^{2}-aca)bt^{4}-\cdots.\end{align*}

We observe that for commutative $R$, this simplifies to

\[ (1-at)(1-dt) - bc t^{2} = 1 - (a+d)t + (ad-bc)t^{2}, \]

which is, up to a substitution, the usual characteristic polynomial. However, as long as $a$ and $c$ do not commute, there is no reason to expect $\chi _A$ to have a polynomial representative.

Observe also that by a different row operation (killing the upper right entry), we could have obtained the representative

\[ \chi_A = (1-dt)(1-at) - (1-dt)b(1-dt)^{-1}ct^{2}, \]

which is not obviously equal to $(1-at)(1-dt) - (1-at)c(1-at)^{-1}bt^{2}$ under the relations we imposed on $W(R)$. It is interesting to see how the various symmetries of the characteristic polynomial arise in these non-commutative formulas.

Remark 2.12 Using the Gauss algorithm to compute the characteristic element as in the previous example also works for larger matrices. It can, in fact, be used to define the characteristic element $\chi _f$, in which case the well-definedness is the crucial property to establish. This strategy is employed by Ranicki and Sheiham (see [She03]) and we return to this viewpoint in Remark 2.20 and § 2.3.

Definition 2.13 The cyclic $K$-group $K_0^{\operatorname {cyc}}(R)$ is the quotient of the group completion of the abelian monoid of isomorphism classes $[P,f]$ of endomorphisms $f$ of finitely generated projective $R$-modules $P$, modulo the zero endomorphisms and the relation $[P_2,f_2]=[P_1,f_1]+[P_3,f_3]$ if $f_2$ is an extension of $f_1$ and $f_3$ as in Lemma 2.7.

The cyclic trace map $K_0^{\operatorname {cyc}}(R) \to W(R)$ is the natural group homomorphism that sends an element $[P,f]$ to $\chi _f\in W(R)$. This is well-defined by Lemma 2.7.

2.2 Determinants

We now give a quick discussion of non-commutative determinants and Dieudonné determinants over $R [\kern-0.15em[{t}]\kern-0.15em] $. We let $R$ be a possibly non-commutative ring and consider a finitely generated projective $R$-module $P$. This gives rise to a finitely generated projective module $P [\kern-0.15em[{t}]\kern-0.15em] $ over the power series ring $R [\kern-0.15em[{t}]\kern-0.15em] $. We have

\[ \operatorname{End}_{R [\kern-0.15em[{t}]\kern-0.15em] }(P [\kern-0.15em[{t}]\kern-0.15em] ) = \operatorname{End}_R(P) [\kern-0.15em[{t}]\kern-0.15em] . \]

We let $\operatorname {SEnd}_{R [\kern-0.15em[{t}]\kern-0.15em] }(P [\kern-0.15em[{t}]\kern-0.15em] )$ be the subset of $\operatorname {End}_{R [\kern-0.15em[{t}]\kern-0.15em] }(P [\kern-0.15em[{t}]\kern-0.15em] )$ consisting of those endomorphisms which reduce to the identity modulo $t$. Under the isomorphism to $\operatorname {End}_R(P) [\kern-0.15em[{t}]\kern-0.15em] $ these correspond to the power series whose first coefficient is the identity.

Definition 2.14 The (reduced) non-commutative determinant is the composite

\[ \det: \operatorname{SEnd}_{R [\kern-0.15em[{t}]\kern-0.15em] }(P [\kern-0.15em[{t}]\kern-0.15em] ) \to W(\operatorname{End}_R(P)) \to W(R), \]

where the first map sends the power series $\operatorname {id} - f t$ with $f \in \operatorname {End}_R(P) [\kern-0.15em[{t}]\kern-0.15em] $ to the represented element in $W(\operatorname {End}_R(P))$ and the second map is the map (8).

Remark 2.15 With this determinant we can write the characteristic element of an endomorphism $f: P \to P$ (see Definition 2.6) as

\[ \chi_f = \det(\operatorname{id} - ft), \]

where $\operatorname {id} - ft$ is considered as a special endomorphism of $P [\kern-0.15em[{t}]\kern-0.15em] $.

Lemma 2.16 The determinant is conjugation invariant, that is, for every $R [\kern-0.15em[{t}]\kern-0.15em] $-linear isomorphism $\alpha : P [\kern-0.15em[{t}]\kern-0.15em] \to Q [\kern-0.15em[{t}]\kern-0.15em] $ we have

\[ \det(\alpha f \alpha^{-1}) = \det(f) \]

for any special endomorphism $f$ of $P [\kern-0.15em[{t}]\kern-0.15em] $.

Proof. An isomorphism $P [\kern-0.15em[{t}]\kern-0.15em] \to Q [\kern-0.15em[{t}]\kern-0.15em] $ reduces to an isomorphism $P\to Q$. We can, thus, identify $P$ with $Q$ (note that the map (8) is clearly natural in isomorphisms of projective modules), and consider $\alpha$ as an automorphism of $P [\kern-0.15em[{t}]\kern-0.15em] $. Now the proof proceeds analogously to the proof of Lemma 2.7. Note that by Lemma 1.19, we have the relation

\[ (1+abt) = (1+bat) \]

in $W(\operatorname {End}_R(P))$ for arbitrary, not necessarily homogeneous elements $a,b\in \operatorname {End}_R(P) [\kern-0.15em[{t}]\kern-0.15em] $. Now, if we write $f=1+gt$, we see

\[ \alpha(1+gt) \alpha^{-1} = (1 + \alpha g\alpha^{-1}t) = (1 + gt) \]

in $W(\operatorname {End}_R(P))$.

We now define determinants for special endomorphisms of an arbitrary finitely generated projective module $Q$ over $R [\kern-0.15em[{t}]\kern-0.15em] $.

Lemma 2.17 Any finitely generated projective module $Q$ over $R [\kern-0.15em[{t}]\kern-0.15em] $ is up to isomorphism of the form $P [\kern-0.15em[{t}]\kern-0.15em] $ for $P$ a finitely generated, projective $R$-module.

Proof. We compare $Q$ with the module $P [\kern-0.15em[{t}]\kern-0.15em] $ with $P = Q/t$. Using the fact that $Q$ is projective one finds a lift

in the diagram which reduces to the identity modulo $t$. However, because $Q$ and $P [\kern-0.15em[{t}]\kern-0.15em] $ are both $t$-complete and $t$-torsion free (being finitely generated projective) this map has to be an isomorphism.

For a $R [\kern-0.15em[{t}]\kern-0.15em] $-module $Q$ we let $\operatorname {SEnd}_{R [\kern-0.15em[{t}]\kern-0.15em] }(Q)$ be the subset of $\operatorname {End}_{R [\kern-0.15em[{t}]\kern-0.15em] }(Q)$ consisting of all morphisms which reduce to the identity modulo $t$.

Definition 2.18 For $Q$ a finitely generated projective $R [\kern-0.15em[{t}]\kern-0.15em] $-module we define

\[ \det: \operatorname{SEnd}_{R [\kern-0.15em[{t}]\kern-0.15em] }(Q) \to W(R) \]

by choosing an isomorphism $Q \cong P [\kern-0.15em[{t}]\kern-0.15em] $ using Lemma 2.17 and forming the composite

\[ \operatorname{SEnd}_{R [\kern-0.15em[{t}]\kern-0.15em] }(Q) \cong \operatorname{SEnd}_{R [\kern-0.15em[{t}]\kern-0.15em] }(P [\kern-0.15em[{t}]\kern-0.15em] ) \to W(R) . \]

This does not depend on the choice of isomorphism by Lemma 2.16.

Lemma 2.19 The determinant is additive in the following sense: for a diagram

in which the vertical maps reduce to the identity modulo $t$ and the horizontal sequences agree and are exact, we have $\det (f_2) = \det (f_1) + \det (f_3)$.

Proof. By Lemma 2.17 the diagram is up to isomorphism of the form

where the horizontal sequences are given by inclusion and projection. Now the proof proceeds as the proof of Lemma 2.7, using that the relevant relations also hold for non-homogeneous elements.

Remark 2.20 There is a somewhat explicit form of this determinant, explained in [Ran98, Definition 14.3] where it lands in a slightly different group of which our $W(R)$ is a quotient. First, by adding the identity endomorphism on a complement to $f$ one can assume that $P = R^{n}$ is free so that $f$ is represented by a matrix $M \in \mathrm {Mat}_{n \times n}(R [\kern-0.15em[{t}]\kern-0.15em] )$. Modulo $t$ this matrix reduces to the identity. We can, thus, use Gaussian elimination to write $M$ as a product $M = LU$ with $L$ a lower triangular matrix with identity entries on the diagonal and $U = (u_{ij})$ an upper triangular matrix whose diagonal entries lie in $1 + t R [\kern-0.15em[{t}]\kern-0.15em] $. Then, by Lemma 2.19, the determinant $\det (f) \in W(R)$ is represented by the product $u_{11} \cdot \cdots \cdot u_{nn}$ of the diagonal entries of $U$.

Example 2.21 Let us spell out the algorithm given in the last remark for the case of $2 \times 2$ matrices. This works similar to Example 2.11 and is also explained in Ranicki's book [Ran98, Example 14.5]:

\[ \det \bigg(\begin{array}{cc} f_0 & f_1 \\ f_2 & f_3 \end{array}\bigg) = \det \bigg(\begin{array}{cc} f_0 & f_1 \\ 0 & f_3 - f_2 (f_0)^{-1} f_1 \end{array}\bigg) = f_0 ( f_3 - f_2 (f_0)^{-1} f_1) \in W(R). \]

Using different operations, we obtain similar formulas representing the same element in $W(R)$, e.g.

\[ \det \bigg(\begin{array}{cc} f_0 & f_1 \\ f_2 & f_3 \end{array}\bigg) = \det \bigg(\begin{array}{cc} f_0- f_2 (f_3)^{-1} f_1 & f_1 \\ 0 & f_3\end{array}\bigg) = (f_0- f_2 (f_3)^{-1} f_1) f_3. \]

Now we claim that the determinant induces a map $\tilde {K}_1(R [\kern-0.15em[{t}]\kern-0.15em] ) \to W(R)$ where $\tilde {K}_1(R [\kern-0.15em[{t}]\kern-0.15em] ) = \ker (K_1(R [\kern-0.15em[{t}]\kern-0.15em] ) \to K_1(R))$ is the reduced $K_1$-group of $R [\kern-0.15em[{t}]\kern-0.15em] $. Recall that $K_1(R [\kern-0.15em[{t}]\kern-0.15em] )$ can be realized as

\[ K_1(R [\kern-0.15em[{t}]\kern-0.15em] ) = \frac{\langle [f]: Q \xrightarrow{\cong} Q \mid Q \text{ f.g. projective} \rangle}{[fg] = [f] + [g]\quad [f \oplus g] = [f] + [g]} \]

where the generators are the isomorphism classes of automorphisms (f.g., finitely generated). By [She03, Lemma 4.1] the reduced group is isomorphic to

\[ \tilde{K}_1(R [\kern-0.15em[{t}]\kern-0.15em] ) = \frac{\langle [f]: Q \xrightarrow{\cong} Q \mid Q \text{ f.g. projective}, \varepsilon_*(f) = \operatorname{id} \rangle}{[fg] = [f] + [g],\quad [f \oplus g] = [f] + [g]}, \]

where $\varepsilon : R [\kern-0.15em[{t}]\kern-0.15em] \to R$ is the augmentation and the generators are again isomorphism classes, that is, $f: Q \to Q$ and $g: Q' \to Q'$ are identified if there exists a commutative square of the form

for an $R [\kern-0.15em[{t}]\kern-0.15em] $-linear isomorphism $\alpha$ (without any further condition on $\alpha$).⁵

Proposition 2.22 There is a well-defined group homomorphism

(9)\begin{equation} \det : \tilde{K}_1(R [\kern-0.15em[{t}]\kern-0.15em] ) \longrightarrow W(R), \end{equation}

which sends an element represented by $\alpha \in \operatorname {SEnd}_{R [\kern-0.15em[{t}]\kern-0.15em] }(Q)$ to $\det (\alpha )$ for any finitely generated projective $R [\kern-0.15em[{t}]\kern-0.15em] $-module $Q$.

Proof. We only have to check that the map is well-defined. The first relation follows because $\det$ is a group homomorphism by definition and the second follows from Lemma 2.19.

There is also a group homomorphism $1 + t R [\kern-0.15em[{t}]\kern-0.15em] \to \widetilde K_1(R [\kern-0.15em[{t}]\kern-0.15em] )$, and the composite

\[ 1 + t R [\kern-0.15em[{t}]\kern-0.15em] \to \widetilde K_1(R [\kern-0.15em[{t}]\kern-0.15em] ) \to W(R) \]

is the canonical quotient map. This shows that $W(R)$ is a quotient of $\tilde {K}_1(R [\kern-0.15em[{t}]\kern-0.15em] )$, and if $R$ is commutative the projection is even an isomorphism. However, in the non-commutative case this is not quite the case: the map $1 + t R [\kern-0.15em[{t}]\kern-0.15em] \to \widetilde K_1(R [\kern-0.15em[{t}]\kern-0.15em] )$ descends to an isomorphism

(10)\begin{equation} \frac{(1 + tR [\kern-0.15em[{t}]\kern-0.15em] )}{ 1+pqt \sim 1+qpt} \stackrel{\cong}{\longrightarrow}\tilde{K}_1(R [\kern-0.15em[{t}]\kern-0.15em] ), \end{equation}

where $p$ and $q$ are arbitrary power series over $R$, see [Paj95, PR00] and also [She03, Theorem B and Proposition 3.4]. The left-hand quotient looks similar to our Definition 1.8 but it is not: the quotient here is purely algebraic and in Definition 1.8 we close the subgroups by the topology. We see that the reason why the determinant map $\tilde {K}_1(R [\kern-0.15em[{t}]\kern-0.15em] ) \longrightarrow W(R)$ is not an isomorphism is that the algebraically defined $K$-theory group does not take the $t$-adic topology on the power series ring into consideration.

Remark 2.23 One can equip $\tilde {K}_1(R [\kern-0.15em[{t}]\kern-0.15em] )$ with the quotient topology induced from the topology on $1 + tR [\kern-0.15em[{t}]\kern-0.15em] $ induced by the filtration by powers of $t$. Then taking the completion with respect to this topology we get a completion $\tilde {K}_1(R [\kern-0.15em[{t}]\kern-0.15em] )^{\wedge }$ which is isomorphic to the Witt vectors $W(R)$. This follows from the isomorphism (10) above because taking the quotient in Hausdorff groups amounts to taking the quotient by the closure of the subgroup and because the Witt vectors are already complete by Lemma 1.13. Said differently: the completion map $\tilde {K}_1(R [\kern-0.15em[{t}]\kern-0.15em] ) \to \tilde {K}_1(R [\kern-0.15em[{t}]\kern-0.15em] )^{\wedge }$ is surjective, thus the non-completeness of $\tilde {K}_1(R [\kern-0.15em[{t}]\kern-0.15em] )$ lies entirely in the fact that it is, in general, not separated.

Applying the results of Sheiham [She03, Theorem B and Proposition 3.4] to $\widetilde K_1(R[t]/t^{n})$ one also gets an isomorphism

\[ \tilde{K}_1(R [\kern-0.15em[{t}]\kern-0.15em] )^{\wedge} \cong \underleftarrow{\lim}_n \widetilde K_1(R[t]/t^{n}) \]

induced by the canonical maps.

2.3 Rational Witt vectors

In this section, we construct a version of rational Witt vectors $W^{\operatorname {rat}}(R)$ mapping to $W(R)$ for a non-commutative ring $R$ and see that the characteristic polynomial actually takes values in $W^{\operatorname {rat}}(R)$. Most of the results are due to Sheiham [She01, She03] but we translate them into a language compatible with the current paper. Finally we discuss a generalisation of a theorem of Almkvist to the non-commutative setting.

The rough idea for rational Witt vectors is to replace the power series ring $R [\kern-0.15em[{t}]\kern-0.15em] $ in the definition of $W(R)$ by the polynomial ring $R[t]$. There are several differences between these two rings, the most important one for us is that in the power series ring, an element $p(t) \in R [\kern-0.15em[{t}]\kern-0.15em] $ is a unit precisely if the element $p(0) \in R$ is a unit. This of course fails for the polynomial ring and we have to force it universally in the process of defining the rational Witt vectors, that is, we consider a certain localisation $L_\varepsilon R[t]$. We first introduce this localisation abstractly.

Lemma 2.24 Let $\varepsilon : A \to R$ be a surjective map of not necessarily commutative rings. Then the following are equivalent:

1. 1. any endomorphism $f: Q \to Q$ of a finitely generated projective $A$-module $Q$, for which $\varepsilon _*(f)$ is an isomorphism of $R$-modules, is itself an isomorphism of $A$-modules;

2. 2. any element $a \in A$, for which $\varepsilon (a)$ is a unit in $R$, is itself a unit in $A$;

3. 3. any element $a \in A$, for which $\varepsilon (a) = 1$, is a unit in $A$;

4. 4. the kernel of $\varepsilon$ is contained in the Jacobson radical of $A$.

Proof. The implications $1 \Rightarrow 2 \Rightarrow 3 \Rightarrow 4$ are clear. For $4 \Rightarrow 1$, we want to use the following version of Nakayama's lemma for non-commutative rings:

If a two-sided ideal $I \subseteq A$ is contained in the Jacobson radical and a finitely generated $A$-module $M$ is zero modulo $I$, then $M$ is zero.

Now assume condition 4 holds and that $f: Q \to Q$ is a morphism as in condition 1. We let $M$ be the cokernel of $f$ which is finitely generated and vanishes modulo $\ker (\varepsilon )$. Thus, $M = 0$ and $f$ is surjective. As $Q$ is projective we can choose a section $s$ of $f$. Then $\varepsilon _*(s)$ is also an isomorphism and repeating the argument for $s$ gives that $s$ is also surjective, thus $f$ is an isomorphism.

Sheiham calls maps $A \to R$ as in Lemma 2.24 ‘local maps’. Note that the map ${R [\kern-0.15em[{t}]\kern-0.15em] \to R}$ satisfies the equivalent conditions but $R[t] \to R$ does not. We want to form the universal ‘localisation’ of $R[t]$ which does.

Lemma 2.25 For every surjective map of rings $\varepsilon : A \to R$, there is an initial factorisation $A \to L_\varepsilon A \to R$ such that $L_\varepsilon A \to R$ is surjective and satisfies the conditions of Lemma 2.24.

Proof. We set $A_0 :=A$ and let $S_0 \subseteq A_0$ be the set of elements $s \in A_0$ such that $\varepsilon (s) = 1$. Then we form the localisation $A_1 := A_0[S_0^{-1}]$ and obtain a factorisation

\[ A_0 \to A_1 \to R. \]

Now $A_1 \to R$ does not necessarily satisfy the condition of Lemma 2.24 because elements of the localisation $A_1$ might, in the absence of any Ore condition, be arbitrary sums of words in $A$ and $S_0^{-1}$. We can repeat the procedure inductively to define $A_{n+1} := A_{n}[S_n^{-1}]$ with $S_n = \varepsilon _n^{-1}(1)$. This gives a tower

\[ A_0 \to A_1 \to A_2 \to \cdots \]

of rings augmented over $R$ and we set $L_\varepsilon A := \operatorname {colim} A_i$. This ring has the desired properties by construction.

Remark 2.26 Ranicki and Sheiham use the Cohn localisation $\Sigma ^{-1}A$ to construct $L_\varepsilon A$ where $\Sigma$ denotes the set of matrices over $A$ which become invertible under basechange to $R$. Then $\Sigma ^{-1}A$ is the universal ring under $A$ over which the matrices in $\Sigma$ become isomorphisms. It turns out that, in contrast to our inductive procedure, a single iteration of this process is already enough to force the property that the morphism $\Sigma ^{-1}A \to R$ satisfies the equivalent conditions of Lemma 2.24, see [She01, § 3.1].

For a ring $R$ we let $R[t] \to L_\varepsilon R[t]$ be the localisation of the polynomial ring $R[t]$ with its augmentation $\varepsilon = \operatorname {ev}_0$ as in Lemma 2.25. Note that $t$ is still central in this ring and that for the map $\varepsilon : L_\varepsilon R[t] \to R$ the kernel is still generated by $t$ which follows from the fact that the short exact sequence

\[ 0\to R[t] \xrightarrow{t} R[t] \to R\to 0 \]

of $R[t]$-modules remains right exact after basechanging to $L_\varepsilon R[t]$ (and $R$ is, as an $R[t]$-module, already local, so $R\otimes _{R[t]} L_\varepsilon R[t]\cong R$).

Definition 2.27 We define the rational Witt vectors of $R$ as the abelian group

\[ W^{\operatorname{rat}}(R) = \frac{(1+ t L_\varepsilon R[t] )^{\mathrm{ab}} }{1 + r p t \sim 1+ prt} \]

where $1+ t L_\varepsilon R[t] \subseteq L_\varepsilon R[t]$ has the group structure given by multiplication, and the relations run over all $r \in R$ and $p \in L_\varepsilon R[t]$.

Remark 2.28 1. By the definition of Witt vectors (and Lemma 1.19(2)) there is a canonical map $W^{\operatorname {rat}}(R) \to W(R)$, which in the commutative case exhibits $W^{\operatorname {rat}}(R)$ as those power series in $R [\kern-0.15em[{t}]\kern-0.15em] $ that can be written as a quotient of polynomials with constant term $1$. In the non-commutative case, however, it turns out that the map $W^{\operatorname {rat}}(R) \to W(R)$ is not necessarily injective as shown by Sheiham in [She01]. In general, the map still exhibits $W(R)$ as the completion of $W^{\operatorname {rat}}(R)$ with respect to the $t$-adic filtration.

2. There are some slight variations of the relations that one can impose to obtain the same groups. For example, one has

\[ W^{\operatorname{rat}}(R) = \frac{(1+ t L_\varepsilon R[t] ) }{1 + pq t \sim 1+ qp t} \]

where $q$ and $p$ run through all elements in $L_\varepsilon R[t]$. Note that the commutators are contained in this subgroup (by [She03, Proposition 3.4]), so no abelianisation is needed. One also has

\[ W^{\operatorname{rat}}(R) = \frac{(1+ t L_\varepsilon R[t] ) }{1 + pq \sim 1+ qp } \]

where $p$ and $q$ run through all elements $L_\varepsilon R[t]$ such that $pq \in (t)$ and $qp \in (t)$. We have decided to give the definition that is closest to our Definition 1.8 of Witt vectors.

The fact that all these quotients agree can be seen as follows: by [She03, Proposition 3.4] the normal subgroup generated by $(1+pqt)(1+qpt)^{-1}$ for all $p,q\in L_\varepsilon R[t]$ agrees with the normal subgroup generated by all $(1+pq)(1+qp)^{-1}$ with $pq\in (t)$ and $qp\in (t)$. We show that the normal subgroup generated by all $(1+pqt)(1+qpt)^{-1}$ agrees with the relations in Definition 2.27. It contains commutators (by [She03, Proposition 3.4]) and the elements where $p$ is homogeneous of degree $0$, so we only need to show that all $(1+pqt)(1+qpt)^{-1}$ are contained in the subgroup generated by commutators and the elements where $p$ is homogeneous of degree $0$ or, equivalently, that in the abelianisation, the image of $(1+pqt)(1+qpt)^{-1}$ is contained in the subgroup generated by elements of the form $(1+p_0 q t)(1+q p_0 t)^{-1}$, with $p_0$ and $q_0$ homogeneous of degree $0$. To see this, observe that for $p$, $q$ with homogeneous degree $0$ components $p_0$, $q_0$:

\begin{align*} &(1+pqt)(1-p_0 qt) = (1 + (p-p_0 - pqp_0 t)q t),\\ &(1+qpt)(1-qp_0 t) = (1 + q(p-p_0 - pqp_0 t)t), \end{align*}

and by Proposition 3.4(3) for $\zeta =0$ in [She03], the right-hand sides agree in the abelianisation, so we have

\[ (1+pqt)(1+qpt)^{-1} = ((1-p_0 qt)(1-q p_0 t)^{-1})^{-1} \]

in the abelianisation.

The main reason to introduce rational Witt vectors here is that the characteristic element $\chi _f$ of an endomorphism $f: P \to P$, as defined in Definition 2.6, naturally lies in $W^{\operatorname {rat}}(R)$. More precisely, we have the following result.

Theorem 2.29 (Almkvist, Grayson, Ranicki, Sheiham)

For every ring $R$ we have group isomorphisms

where the first map sends a pair $[P,f]$ to the class of the automorphism $1 - ft: L_\varepsilon P[t] \to L_\varepsilon P[t]$ and the second map has the property that it sends the classes represented by elements in $1+ t L_\varepsilon R[t]$ (considered as an automorphism of the one-dimensional module $L_\varepsilon R[t]$) to the class this element represents in $W^{\operatorname {rat}}(R)$.

Proof. For $R$ commutative the equivalences are due to Almkvist [Alm74] and Grayson [Gra78]. In the non-commutative case they are shown in Ranicki [Ran98, §§ 10, 14] and Sheiham [She03].

Remark 2.30 We believe that there is a slightly incorrect definition in Ranicki's book: in Definitions 14.7 and 14.10 of [Ran98] the rational Witt vectors (of which our rational Witt vectors are a quotient) are defined as a subgroup of the Witt vectors. However, by [She01], the inclusion is neither injective nor are the rational Witt vectors the group completion of $1 + t R[t]$.

Finally Sheiham [She01] defines the characteristic element as the composite of the two maps of Theorem 2.29. This clearly maps to our characteristic element under the map $W^{\operatorname {rat}}(R) \to W(R)$. More generally, we can summarise the relation between the various characteristic polynomials and determinants defined in this paper and in [She01, She03] in the following commutative diagram.

Here the composition $K_0^{\operatorname {cyc}}(R) \to W(R)$ is the cyclic trace as defined in Definition 2.13. The horizontal surjective maps in the diagram are, in general, not injective, but one can describe the kernels using the results of this section as well as (10) and Remark 2.23. In particular note that the lower determinant is not an isomorphism, but rather a completion, as is the rightmost vertical map.

2.4 Characteristic polynomials with coefficients

In this section, we briefly explain how to generalize the constructions from §§ 2.1–2.3 to a setting with coefficients in an $R$-bimodule $M$. The results are analogous to the results of the previous sections and we present them in the same order.

First, we treat the characteristic element. Let $P$ be a finitely generated projective right $R$-module and $M$ an $R$-bimodule. Then $\operatorname {Hom}_R(P, P\otimes _R M)$ is an $\operatorname {End}_R(P)$-bimodule isomorphic to $P\otimes _R M\otimes _R P^{\vee }$. We thus obtain a map

where the second isomorphism is from Proposition 1.34. The composite map is an isomorphism if $P$ is supported everywhere, e.g. if it admits a free non-trivial summand, see Lemma 2.2.

Definition 2.31 The characteristic element of an $R$-module map $f: P\to P\otimes _R M$ is the image $\chi _f \in W(R;M)$ of $f$ under the map

\[ \chi : \operatorname{Hom}_R(P, P\otimes_R M)\stackrel{\tau}{\longrightarrow}W(\operatorname{End}_R(P); \operatorname{Hom}_R(P, P\otimes_R M)) \longrightarrow W(R;M). \]

For $M=R$, this clearly reduces to Definition 2.6.

The analogue of Lemma 2.7 also holds in this more general setting: let $R,S$ be rings, let $M$ be an $R$-$S$-bimodule, let $N$ be a $S$-$R$-bimodule, let $P$ be a finitely generated projective $R$-module and let $Q$ be a finitely generated projective $S$-module. Given morphisms $f: P \to Q \otimes _S N$ and $g: Q \to P \otimes _R M$, we write $gf$ for the composite $P\to Q \otimes _S N\to P \otimes _R M \otimes _S N$ of $f$ and $g\otimes _SN$.

Lemma 2.32 We have the following properties.

1. 1. In the situation above, the elements $\chi _{gf}$ and $\chi _{fg}$ correspond to each other under the trace isomorphism $W(R; M\otimes _SN) \cong W(S; N \otimes _R M)$ of Proposition 1.34.

2. 2. Given a commutative diagram

   (11)

   
   with exact rows, we have $\chi _{f_2} = \chi _{f_1}+\chi _{f_3}$.

3. 3. The $n$th ghost component of the characteristic polynomial of $f: P\to P\otimes _RM$ is given by

   \[ \operatorname{tr}(f^{n}) \in (M^{\circledcirc_R n})^{C_n}, \]
   where the trace of the morphism $f^{n}: P \to P \otimes _R M^{\otimes _R n}$ is defined as the image of $f^{n}$ under the map
   \[ \operatorname{tr}\colon \operatorname{Hom}_R(P, P \otimes_R M^{\otimes_R n}) \stackrel{\cong}{\longleftarrow} P\otimes_R M^{\otimes_R n} \otimes_R P^{\vee} \xrightarrow{\operatorname{ev}} M^{\otimes_R n} /[R,M^{\otimes_R n}] = M^{\circledcirc_R n}. \]

Proof. For the first statement, observe that a right $R$-module homomorphism $f: P\to Q\otimes _S N$ corresponds to an element of $Q\otimes _S N\otimes _R P^{\vee }$, which we also denote by $f$. Analogously, $g$ corresponds to an element of $P\otimes _R M \otimes _S Q^{\vee }$. The element represented by $\tau (g\otimes f)$ in

\[ W(\operatorname{End}_R(P); P\otimes_R M\otimes_S Q^{\vee}\otimes_{\operatorname{End}_S(Q)} Q\otimes_S N\otimes_R P^{\vee}) \]

maps to the image of $gf$ in $W(\operatorname {End}_R(P); P\otimes _R M\otimes _S N\otimes _R P^{\vee })$ and to the image of $fg$ in $W(\operatorname {End}_S(Q); Q\otimes _S N\otimes _R M \otimes _S Q^{\vee })$ under suitable evaluation maps and trace isomorphisms. We obtain $\chi (gf)$ and $\chi (fg)$ by further application of trace isomorphisms and evaluation maps, and one easily obtains the claim from naturality of the trace isomorphisms.

The second proof proceeds analogously to Lemma 2.7, and we also spell this out explicitly in the strictly more general situation of determinants, see Proposition 2.37 below.

The third statement follows from unwinding the definitions, using the description of the ghost map on Teichmüller elements.

Now we give the analogue for determinants with coefficients. We recall from Definition 1.7 that $\widehat {T}(R;M)$ denotes the completed tensor algebra of $M$ over $R$. We let $Q$ be a finitely generated, projective $\widehat {T}(R;M)$-module. The same argument as in Lemma 2.17, replacing all occurrences of ‘mod $t$ reduction’ by the basechange $(-)\otimes _{\widehat {T}(R;M)} R$, shows that $Q$ is up to (non-canonical) isomorphism of the form $P \otimes _R \widehat {T}(R;M)$ where $P$ is a finitely generated, projective $R$-module. More precisely $P$ is the basechange $\varepsilon _*Q$ along the augmentation map $\varepsilon : \widehat {T}(R;M) \to R$.

Definition 2.33 A $\widehat {T}(R;M)$-linear endomorphism $f: Q \to Q$ is called special if $\varepsilon _*(f) = \operatorname {id}$. We denote the subset of those by

\[ \operatorname{SEnd}_{\widehat{T}(R;M)}(Q) \subseteq \operatorname{End}_{\widehat{T}(R;M)}(Q). \]

Now for a given automorphism $f: Q \to Q$ we choose an isomorphism $Q \cong P\otimes _R \widehat {T}(R;M)$ and want to define the determinant of $f$ using this isomorphism. We then see that it is independent of the chosen isomorphism, similarly to the case without coefficients. We do this under the additional assumption that the module $P$ is supported everywhere, see Definition 2.1. This is not really a restriction as we can always replace $P$ by $P \oplus R$, which is supported everywhere by Lemma 2.2 and we show later that the determinant is a stable invariant.

Lemma 2.34 Let $P$ a finitely generated projective right $R$-module and let $M$ be a $R$-bimodule. If $P$ is supported everywhere, then we have canonical ring isomorphisms

\begin{gather*} \operatorname{End}_{\widehat{T}(R;M)}(P\otimes_R \widehat{T}(R;M)) \cong \widehat{T}(\operatorname{End}_R(P); P\otimes_R M\otimes_R P^{\vee}),\\ \operatorname{SEnd}_{\widehat{T}(R;M)}\big(P\otimes_R \widehat{T}(R;M)\big) \cong \widehat{S}(\operatorname{End}_R(P);P \otimes_R M \otimes_R P^{\vee}). \end{gather*}

Proof. For the first isomorphism, observe that

\[ \operatorname{End}_{\widehat{T}(R;M)}(P\otimes_R \widehat{T}(R;M)) \cong \operatorname{Hom}_R(P,P\otimes_R \widehat{T}(R;M)) \cong \prod_{n\geq 0} P\otimes_R M^{\otimes_R n} \otimes_R P^{\vee}, \]

as $\operatorname {End}_R(P)$-bimodules. As $P$ is supported everywhere, we can write $P\otimes _R M^{\otimes _R n}\otimes _R P^{\vee } \cong (P\otimes _R M\otimes _R P^{\vee })^{\otimes _{\operatorname {End}_R(P)} n}$, so we obtain

\[ \operatorname{End}_{\widehat{T}(R;M)}(P\otimes_R \widehat{T}(R;M)) \cong \widehat{T}(\operatorname{End}_R(P); P\otimes_R M\otimes_R P^{\vee}), \]

and one sees directly that this isomorphism maps $\operatorname {SEnd}$ on the left isomorphically to $\widehat {S}$ on the right.

Definition 2.35 For $P$ supported everywhere, we define the determinant as the composite

\begin{align*} \det: \operatorname{SEnd}_{\widehat{T}(R;M)}\big(P\otimes_R \widehat{T}(R;M)\big) &\cong{} \widehat{S}(\operatorname{End}_R(P);P \otimes_R M \otimes_R P^{\vee}) \\ &\to{} W(\operatorname{End}_R(P);P\otimes_R M\otimes_R P^{\vee}) \cong W(R; M), \end{align*}

where the last isomorphism is the trace property isomorphism from Proposition 1.34.

Lemma 2.36 The determinant is conjugation invariant, that is, for $P$ supported everywhere and any automorphism $\alpha : P\otimes _R \widehat {T}(R;M) \to P\otimes _R \widehat {T}(R;M)$ and any $f\in \operatorname {SEnd}_{\widehat {T}(R;M)}\big (P\otimes _R \widehat {T}(R;M)\big )$, we have $\det (\alpha f \alpha ^{-1})=\det (f)$.

Proof. We can consider $\alpha$ as an element of $\widehat {T}(\operatorname {End}_R(P);P\otimes _R M \otimes _R P^{\vee })$ and $f$ as an element of $\widehat {S}(\operatorname {End}_R(P); P\otimes _RM\otimes _R P^{\vee })$ by Lemma 2.34.

Now we proceed analogously to the proof of Lemma 2.16, writing $f=1+g$ with $g$ of positive filtration, and using the relation $(1 + \alpha g \alpha ^{-1}) = (1 + g)$.

Note that conjugation invariance allows us to obtain a well-defined notion of determinant for any special endomorphism $f: Q\to Q$ of a finitely generated projective $\widehat {T}(R;M)$-module $Q$, provided the basechange $Q\otimes _{\widehat {T}(R;M)} R$ is supported everywhere.

Proposition 2.37 Consider a short exact sequence of special endomorphisms of finitely generated, projective $\widehat {T}(R;M)$-modules

Assume that the basechanges $Q_i\otimes _{\widehat {T}(R;M)} R$ for $i=1,2,3$ are supported everywhere⁶, then we have that $\det (f_2) = \det (f_1) + \det (f_3)$.

Proof. First, we can choose isomorphisms $Q_1 \cong P_1\otimes _R \widehat {T}(R;M)$ and $Q_3 \cong P_3\otimes _R \widehat {T}(R;M)$ and split the exact sequence to reduce the situation to the following diagram.

(12)

We can now consider $f_2$ as element of $\widehat {S}(\operatorname {End}_R(P_1\oplus P_3); (P_1 \oplus P_3) \otimes _R M \otimes _R (P_1 \oplus P_3)^{\vee })$ using Lemma 2.34, i.e. as an element of

\[ \prod_{n\geq 1} (P_1 \oplus P_3) \otimes_R M^{\otimes_R n} \otimes_R (P_1 \oplus P_3)^{\vee}. \]

This splits additively into four factors of the form $\prod _{n\geq 1} P_i \otimes _R M^{\otimes _R n} \otimes _R P_j^{\vee }$, with $i,j\in \{1,3\}$, which one should regard as a block matrix decomposition of $f_2$ like in the proof of the additivity statement of Lemma 2.7. Commutativity of the diagram (12) translates to the fact that the coordinates of $f_2$ in $\prod _{n\geq 1} P_i \otimes _R M^{\otimes _R n} \otimes _R P_i^{\vee }$ are $f_i$ for $i=0,3$, and that the coordinate of $f_2$ in $\prod _{n\geq 1} P_3 \otimes _R M^{\otimes _R n} \otimes _R P_1^{\vee }$ vanishes, i.e. $f_2$ is ‘upper triangular’. Now we can use the same argument as in the proof of Lemma 2.7 to finish the proof, using the inhomogeneous relations from Lemma 1.19.

Remark 2.38 Proposition 2.37 shows, in particular, that the determinant of a special endomorphism $f$ of $Q$ does not change if we stabilize it by passing to $f\oplus \operatorname {id}: Q\oplus \widehat {T}(R;M)\to Q\oplus \widehat {T}(R;M)$. Thus, we can extend the definition to special endomorphisms of all finitely generated projective modules (without conditions on the support) preserving the properties from Lemma 2.36 and Proposition 2.37.

Finally, we want to discuss rational Witt vectors with coefficients. For an $R$-bimodule $M$ let

\[ T(R; M) := \bigoplus_{n \geq 0} M^{\otimes_R n} \]

be the tensor algebra. This admits an augmentation $\varepsilon : T(R;M) \to R$ and we let $L_\varepsilon T(R;M)$ be the localisation as in Lemma 2.25 which comes, by definition, with an augmentation $L_\varepsilon T(R;M) \to R$. We consider the subset

\[ S(R;M) \subseteq L_\varepsilon T(R;M) \]

given by those elements in $L_\varepsilon T(R;M)$ which lie over $1 \in R$.

Definition 2.39 The rational Witt vectors of $R$ with coefficients in $M$ are given by the abelian group

\[ W^{\operatorname{rat}}(R; M) := \frac{S(R;M)^{ab}}{1 + r p \sim 1+ pr}, \]

where $r \in R$ and $p \in \ker (L_\varepsilon T(R;M) \to R)$.

There is an obvious map $W^{\operatorname {rat}}(R;M) \to W(R;M)$ obtained from the map $S(R;M) \to \widehat {S}(R;M)$. The main result of [She03] is that there is an isomorphism

\[ \det: \tilde{K}_1(L_\varepsilon T(R;M) ) \xrightarrow{\cong} W^{\operatorname{rat}}(R;M) \]

induced by a determinant map. This map is defined by a similar strategy to that explained in Remark 2.20, that is, by bringing matrices into upper triangular form using Gauss elimination and then multiplying the diagonal entries. Part of the proof is to show that this is well-defined as an element of the rational Witt vectors.

There is also a version of the commutative diagram from the end of § 2.3 with coefficients, as follows.

Here $K_0^{\operatorname {cyc}}(R;M)$ refers to the group completion of the monoid of isomorphism classes of pairs $(P,f)$ with $P$ a finitely generated, projective $R$-module and $f$ an ‘endomorphism with coefficients’ $f : P\to P\otimes _R M$, modulo pairs of the form $(P,0)$ and the relation that $[P_2,f_2] = [P_1,f_1] + [P_3,f_3]$ whenever we have an extension as in Lemma 2.32. The vertical map to $\tilde {K}_1(L_\varepsilon T(R;M))$ is defined by sending $(P,f)$ to the automorphism $(1+f)$ of $P\otimes _R L_\varepsilon T(R;M)$, and the composite down to $W(R;M)$ can therefore be identified with the characteristic element $[P,f]\mapsto \chi _f$ (as in Definition 2.31).

Remark 2.40 It is a consequence of forthcoming work of the second and third author that the upper vertical map $K_0^{\operatorname {cyc}}(R;M) \to \tilde {K}_1(L_\varepsilon T(R;M))$ in the diagram is also an isomorphism and, thus, also the diagonal map $K_0^{\operatorname {cyc}}(R;M) \to W^{\operatorname {rat}}(R;M)$. Using this result one can deduce that $W^{\operatorname {rat}}(R; M)$ has the trace property, that is, that there are isomorphisms

(13)\begin{equation} W^{\operatorname{rat}}(R; M \otimes_S N) \cong W^{\operatorname{rat}}(S; N \otimes_R M) \end{equation}

similar to the trace property for Witt vectors as shown in Proposition 1.34. This follows from the fact that $K_0^{\operatorname {cyc}}(R;M)$ has the trace property, which can be seen by applying some basic localisation sequences. However, we have not been able to construct the isomorphism (13) directly from the definition of the rational Witt vectors.

If one assumes the trace property for rational Witt vectors then one can give more conceptual definitions of the determinant and the characteristic element valued in $W^{\operatorname {rat}}(R;M)$ similar to the constructions for non-rational Witt vectors described at the beginning of the section.