A simple model for simulating immunity rate dynamics in a tropical free-range poultry population after avian influenza vaccination

Summary

In developing countries, vaccination against highly pathogenic avian influenza subtype H5N1 (HPAI) in free-range poultry flocks is usually implemented as periodic campaigns and newborn chicks are generally not vaccinated by farmers between vaccination passes. The demographic population turnover leads to a continuous decrease in the population immunity rate (PIR) over time. We present a simple Leslie matrix model for estimating population turnover and PIR dynamics in a hypothetical small-size vaccinated free-range poultry population. Four different vaccination scenarios were identified assuming necessary procedures to achieve immunity. The results indicate that high levels of population immunity are difficult to sustain. Assuming an animal immunity response of 80% after vaccination and a constant population size, PIR 4 months after vaccination was ⩽30% in all the scenarios. Predictions averaged over time showed mean PIR between 36% and 48%, which is below the population immunity thresholds for eradication approximated from R₀ estimates.

INTRODUCTION

The current epizootic of highly pathogenic avian influenza subtype H5N1 (HPAI) in a number of African and Asian countries is an international concern [1]. Control measures emphasized for HPAI have centred on traditional stamping out procedures that entail the large-scale culling of infected flocks and contact flocks, and vaccination in order to reduce population susceptibility to infection and the amount of virus shed by infected birds [2]. In populations where HPAI has become well established, vaccination is recommended as a more appropriate control measure than stamping out [3].

In order to be effective, HPAI control strategies and in particular vaccination have to be adapted to local poultry production systems and socioeconomic contexts. In many developing countries, free-range or backyard flocks of indigenous chickens are a major if not the most important component of the poultry sector. For example, they represent >80% of the poultry flocks in Africa [4, 5] and are a significant contributory factor to the livelihood economics of most rural households in South-East Asia [6]. Free-range systems are characterized by limited to non-existent management interventions such as breeding, feeding, housing and health care. This lack of management activity can complicate the implementation of control strategies [7]. Population renewal is essentially determined by the balance between uncontrolled reproduction (births arise continuously during the year) and withdrawal of animals due to natural death and offtake (e.g. slaughtering, sales and gifts). Vaccination is usually implemented as periodic campaigns and newborn chicks are generally not vaccinated by farmers between vaccination passes [8–10]. In such situations, the demographic turnover is an epidemiologically important process that leads to a continuous decrease in the population immunity rate (PIR: proportion of immune birds in the population) over time.

The role of free-range poultry in the maintenance and propagation of virus is unclear and the epidemiological interactions with commercial production systems require further study. Where surveillance systems are sensitive in free-range systems and the density of free-range poultry is high, widespread disease with high prevalence and long chains of transmission is evident [11]. Nevertheless, free-range systems may not be the highest priority sector for disease control in many countries, as infection risk seems to increase according to the commercial practices and poultry population movements. Despite the practical difficulties of vaccinating free-range poultry, avian influenza has been controlled to a certain extent in countries such as Vietnam and China [9] in part by mass vaccination. Free-range poultry can be a key element in viral persistence due to the limited or non-existent management practices and environmental conditions [12]. Therefore, intervention packages that directly target free-range poultry are needed where evidence suggests that this sector is making important contributions to viral persistence. In that context, a better knowledge of PIR dynamics is required for prediction of the epidemiological impact of vaccination strategies on the circulation of virus and to support decision-making in the design of effective HPAI control measures. The objective of this paper is to estimate PIR dynamics in a hypothetical small-holder, free-range poultry population under different vaccination scenarios, using a simple model representing the population demographic turnover.

MATERIALS AND METHODS

Demographic model and PIR dynamics estimation

The method used was a Leslie matrix model [13]. Poultry population dynamics were simulated on 1-week time intervals by:

where x(t) and x(t+1) represent the vectors of the numbers of animals in the poultry population by sex and 1-week age group, at weeks t and t+1 respectively (see Appendix); and A represents the 1-week population projection matrix containing the fecundity and survival rates by sex and 1-week age group (see Appendix).

The method was based on the following main assumptions:

• • A round of vaccination in the population was able to be completed within 1 week in a pulsed manner, which was considered to be a realistic target for small farming communities (e.g. a village or a limited set of villages).

• • All the relevant immunocompetent animals living in the population were vaccinated during each vaccination round (no animal escaped).

• • Only a proportion (p _resp) of the vaccinated population was respondent and mounted a protective immune response (i.e. became protected) due to the vaccine.

• • Vaccinated respondent animals remained immune for a constant period of time (T) after the end of the vaccination protocol.

• • The population renewal depended on births and exits of animals due to natural death, slaughter, and external sales or gifts. No external animal entered the simulated population during the simulation period. This represented a situation where farmers could exchange animals within the community but could not receive them from external sources.

• • The population was considered to be in a demographic steady state, i.e. having constant growth rate and sex×age structure [13]:

where x(t) and x(t+1) are all proportional to w, the dominant right eigenvector of A (when standardized to sum to 1, w is the stable sex×age population structure); λ_week represents the 1-week population growth rate (e.g. λ_week=1·01 means that population increases by 1% per week) and is calculated by the dominant eigenvalue of A.

Based on these assumptions, post-vaccination PIR dynamics are decreasing functions of the population renewal rate and can be easily calculated from the components of the eigenvector w (see Appendix).

Application to a free-range chicken population

The method was applied to a hypothetical free-range chicken population. The PIR dynamics were estimated over a period of T=17 weeks, corresponding to the average duration of immunity in individual animals after avian influenza vaccination using commercial vaccines [14–16].

Four vaccination protocol scenarios were defined based on the number of vaccinations (doses of vaccine) needed for effective immunization, and the minimum age of immunocompetence, representing the minimum age for an animal to produce an immune response able to prevent disease. These scenarios were representative of the vaccination programmes currently in use in Asia with commercial HPAI inactivated vaccines (two administrations beginning at age 2 weeks) and/or recombinant vaccines (one administration, 1-day-old vaccination) [6, 8, 17, 18]. The scenarios were defined as follows:

• • One vaccination is needed to effectively immunize the animal and poultry aged ⩾1day are immunocompetent (1Shot-Age1).

• • One vaccination is needed to effectively immunize the animal and poultry aged ⩾14 days are immunocompetent (1Shot-Age14).

• • Two vaccinations are needed to effectively immunize the animal and poultry aged ⩾1 day are immunocompetent (2Shot-Age1).

• • Two vaccinations are needed to effectively immunize the animal and poultry aged ⩾14 days are immunocompetent (2Shot-Age14).

The 1Shot and 2Shot scenarios were assumed to be equally protective. In each scenario, the simulations of PIR dynamics started (time t=0) when the vaccination was considered to be effective, that is when animals were assumed to be protected against the infection. For Shot1 scenarios, vaccination was assumed to be effective immediately after vaccine administration. Delays in antibody production were not considered. For Shot2 scenarios, vaccination was assumed to be effective immediately after administration of the second dose of vaccine, 3 weeks after the first administration. No partial protection between the two shots was assumed.

In the demographic Leslie poultry model, eggs, chicks, growers and adults were the four age groups (each composed of successive 1-week age groups in matrix A and vector w) considered for defining the values of the parameters. Reference demographic parameters (Table 1) representing average values for tropical free-range poultry systems were defined from the literature [5, 19–28], except for the survival rate of hens which was adjusted to calibrate the model to represent a constant population size, i.e. to have λ_year=1. For ease of understanding, the population annual growth rate (λ_year) is used throughout the text instead of the weekly growth rate (λ_week). The λ_year is calculated as λ_week⁵² .

Table 1. Reference average demographic parameters used in the Leslie matrix model representing the hypothetical free-range poultry population in a demographic steady state with an annual population growth rate λ_year=1. (Using these parameters, hens and cocks represented 22·5% and 6·7% of the simulated population, respectively. The ratio of hens/cocks was 3·4.)

* Laying and incubation periods.

† Animals surviving until the end of the hens/cocks age group are removed by final culling.

‡ Survival rate=1 – natural mortality rate – offtake rate (offtake are slaughtering, sales, gifts, etc.). In the table rates correspond to survival over the complete age group for eggs, chicks and growers, and over 1 year for hens and cocks.

For each of the four vaccination scenarios the simulation process was completed in two steps. First, deterministic PIR dynamics were calculated for the reference demographic parameters (θ_ref). Second, Monte Carlo (MC) stochastic simulations were implemented for assessing sensitivity of PIR dynamics to λ_year. One MC simulation consisted of randomly generating the complete vector θ of the demographic parameters using a uniform probability distribution with minimum and maximum values equal to 0·75∗θ_ref and 1·25∗θ_ref, respectively. Each component of θ was simulated independently of the others. A total of 5000 MC simulations (this number of replications ensured the stability of the simulated results' probability distributions) of θ were implemented and λ_year and PIR dynamics were calculated for each simulation.

For simplicity in the text, results are only presented for p _resp=80%, a common value found for the herd immunity threshold, i.e. the minimum percentage of immune animals needed to protect the whole population [18, 29]. However, PIR corresponding to lower or higher p _resp can be calculated (in %) by (p _resp/80)∗PIR_80%. For example, all PIR presented in the present study must be multiplied by 1·25 if p _resp=100%, and by 0·625 if p _resp =50%. Results of the MC simulations were presented for t=17 weeks only.

RESULTS

Deterministic PIR dynamics corresponding to reference parameters (λ_year=1) are presented in Figure 1.

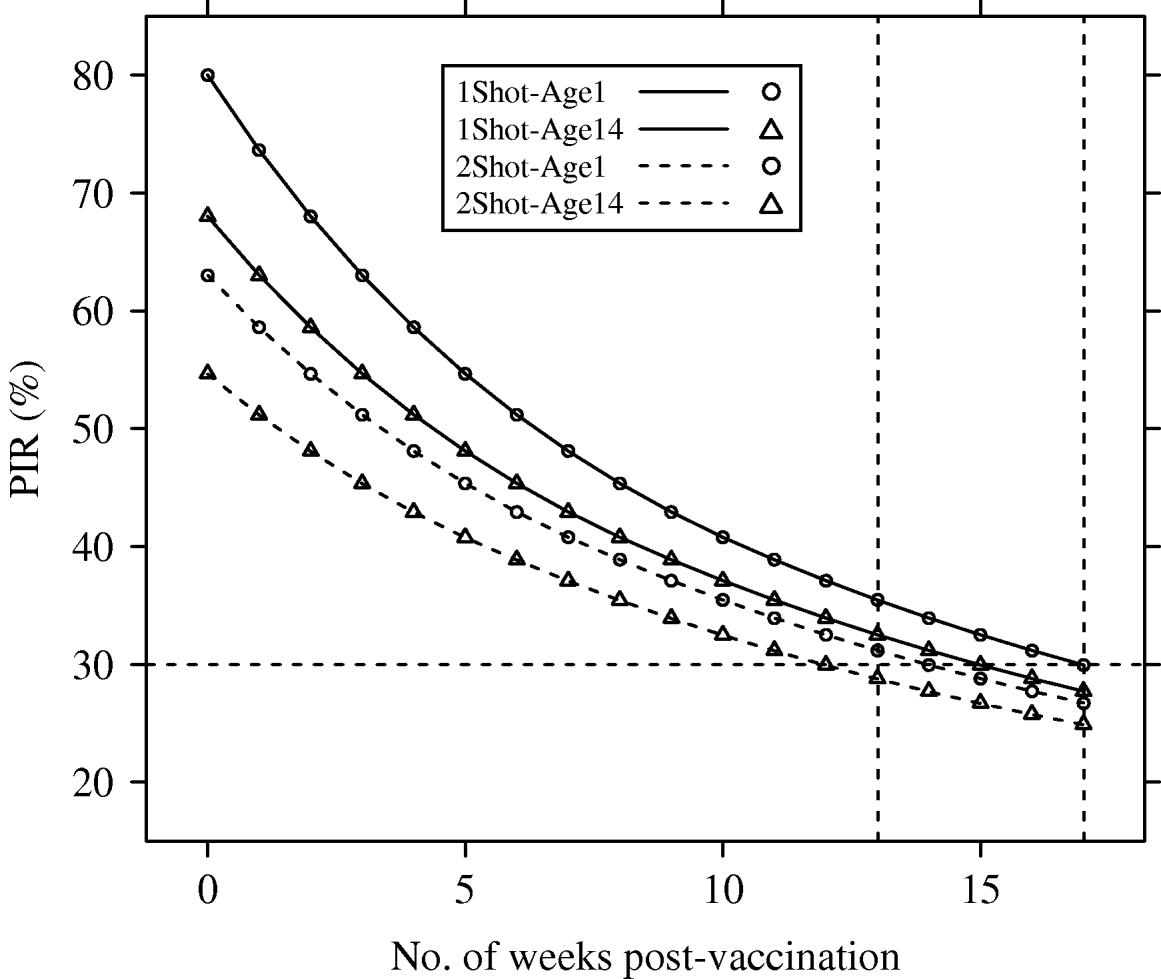
Fig. 1. Population immunity rates (PIR) for avian influenza in a hypothetical free-range and demographically steady-state (annual population growth rate λ_year=1), poultry population, estimated under four vaccination and age of immunocompetence scenarios (1Shot-Age1, 1Shot-Age14, 2Shot-Age1, 2Shot-Age14). For 1Shot scenarios, t=0 represented the time just after the first administration. For 2Shot scenarios, t=0 represented the time just after the second administration. Dotted vertical lines represent weeks 13 and 17.

The PIR at t=0 showed large differences between the scenarios. In the 1Shot-Age1 scenario, PIR(t=0) reached the maximal possible value (p _resp=80%) since all animals were vaccinated. In the 1Shot-Age14 scenario, only animals aged ⩾14 days (85% of the steady-state population) were vaccinated and the PIR(t=0) was 68%. In the 2Shot-Age1 scenario, animals born between the first administration and the booster (3-week delay) could not receive both administrations. Only animals aged ⩾21 days (79% of the steady-state population) received the complete protocol and the PIR(t=0) was 63%. In the 2Shot-Age14 scenario, due to the same booster delay, only animals aged ⩾35 days (68% of the steady-state population) received the complete protocol and the PIR(t=0) was 55%.

The PIR at t=17 weeks was between 25% (2Shot-Age14) and 30% (1Shot-Age1) for all four scenarios. Averaged over time between t=0 and t=17 weeks, PIRs for the four scenarios were 36% (2Shot-Age14), 40% (2Shot-Age1), 42% (1Shot-Age14) and 48% (1Shot-Age1).

In the MC simulations, all scenarios showed the same pattern. PIR decreased when λ_year increased. For example in the 1Shot-Age1 scenario, median PIR at week 17 decreased from 33% to 26% when λ_year increased from categories ‘<0·8’ to ‘⩾1·6’ (Fig. 2). The PIR showed variability in each of the λ_year categories (e.g. for 1Shot-Age1 and interval ‘0·8⩽λ_year<1·2’, 5% and 95% percentiles of PIR were 27% and 34%). This indicates that, within the λ_year categories, PIR was sensitive to the individual components (reproduction, mortality and offtake rates by sex and age group) of the demographic parameters vector θ.

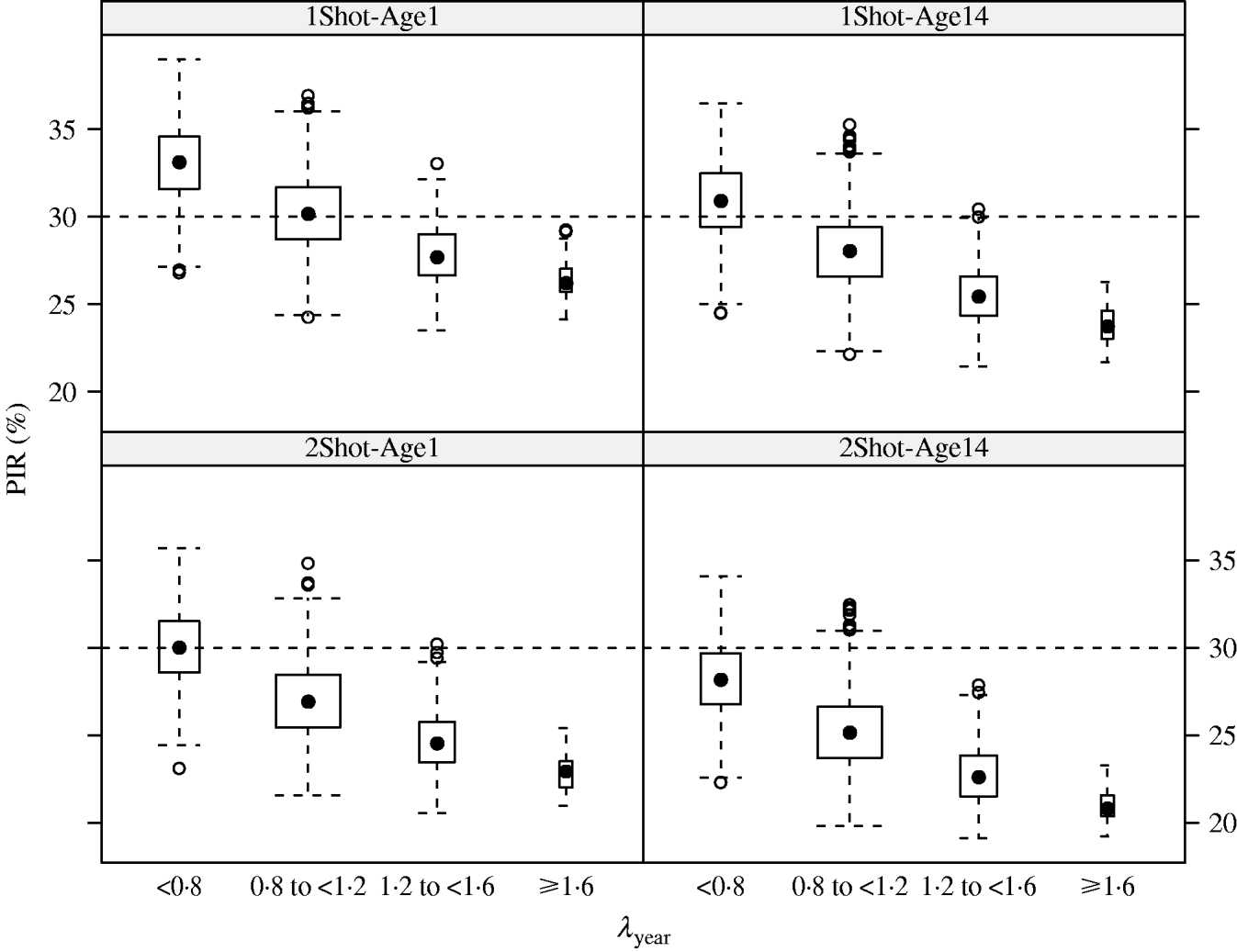
Fig. 2. Results (box-and-whiskers plots) of Monte Carlo simulations of population immunity rates (PIR) estimated for annual population growth rates (λ_year) between <0·8 and ⩾1·6 under four vaccination and age of immunocompetence scenarios (1Shot-Age1, 1Shot-Age14, 2Shot-Age1, 2Shot-Age14) at week 17 post-vaccination protocol.

DISCUSSION

Given the assumptions and the scenarios considered, the model showed that mass vaccination was unable to maintain high levels of population immunity at 4-month vaccination intervals. Assuming no escape of animals during the vaccination, immunity response p _resp=80% and constant population size, the highest average PIR at week 17 was only 30%. For p _resp=50% and 100%, PIR(t=17) become 19% and 38%, respectively. In case of escapes (with proportion p _escape), these results should be rescaled by (p _resp/80)∗(100 – p _escape)/100 instead of p _resp/80 only. The globally low immunity levels were due to the high natural flock turnover. This turnover resulted in a rapid increase in the proportion of susceptible animals in the flocks as farmers did not vaccinate newborn chicks systematically. It would have been even higher if the model relaxed the assumption of no external bird entries. The simulations showed a negative correlation between PIR and λ_year, which is coherent with the mathematical structure of the steady-state population vector w (see Appendix): an increase of λ_year generates an increase in the proportions of the youngest age groups in w and therefore of the turnover.

In evaluating vaccination programmes, it is essential that the objectives of the programme are clearly formulated and that the immunity targets required for meeting objectives are achievable. The majority of the estimates of the basic reproductive number (R ₀) for HPAI are in the range of 2–3 [30, 31]. The approximate critical population immunity threshold (PIR_cri) required to interrupt transmission can be back-calculated from R ₀ using the relationship [32]: PIR_cri=1–1/R ₀. If we accept the above estimates of R ₀ as accurate for within-flock transmission, a PIR_cri between 50% and 67% would be needed to interrupt virus circulation completely. Free-range poultry vaccination is very difficult to implement for economic and logistical reasons specifically related to the delivery of vaccinations [7, 9], particularly in booster protocols with two successive rounds. Despite these challenges, vaccination is considered as one of the main tools for the control of HPAI in endemic countries. To a certain extent it has proved efficient in controlling the infection [9]. In our model, the average PIR over the 17-week period for the four scenarios evaluated showed mean immunity levels between 36% (2Shot-Age14) and 48% (1Shot-Age1). These values are below the PIR thresholds to maintain population immunity approximated from the R ₀ estimates. Furthermore, immunity levels 17 weeks post-vaccination were ⩽30% in all scenarios. These findings suggest that vaccination cycles ⩾4 months might not be effective in controlling HPAI in backyard production systems and question the benefits of open-ended, untargeted mass vaccination strategies in free-range poultry. However, the impact of these moderate immunity levels should be further evaluated in transmission models and field research of the epidemiological impact of vaccination on disease incidence. Although vaccination is still advocated as a tool in endemic areas [33, 34], alternative vaccination approaches that harness producer incentives to reduce losses and that are based on risk targeting within free-range poultry are needed.

As expected, the model showed that if vaccination was assumed not to be possible before the age of 14 days, lower PIR are predicted for both single dose and booster regimens. This results from the presence of the unvaccinated component of the population that was aged <14 days at the time of vaccination. Based on current available vaccines, 14-day-old scenarios seem more realistic than 1-day-old scenarios. For example, preliminary results from vaccination trials with nationally produced H5N1 vaccines in Indonesia showed that vaccination before age 14 days did not result in solid, durable immunity [35]. Promising results have been shown for single-dose vaccination of 1-day-old chicks in commercial farms with the recombinant fowlpox-vectored vaccine in use in China, Mexico and Vietnam [36]. But fowlpox-vectored vaccines would not be efficient if the animals have been previously infected with fowlpox virus, which is likely for adult free-range chickens from developing countries. Moreover, fowlpox-vectored vaccines may not be effective in all species of interest, their efficacy is impaired in waterfowl as fowlpox virus does not replicate in such species [37].

At present, a common protocol used in both commercial and backyard systems in Asia is 2Shot-Age14 with inactivated vaccines or RGH5N1 [9, 18]. This scenario is less stringent in terms of targeted population as it might confer long-term immunity to a wide range of avian species (e.g. chickens, ducks, geese, turkeys) [18]. However, the model showed that when a booster regimen with two vaccinations was assumed to be required to reach the protective immunity, an important decrease in PIR occurred in comparison to the scenarios with a single dose, essentially in the first half of the simulation period. In particular, the low immunity levels predicted for 2Shot-Age14 resulted from the 14-day delay to first vaccination and also from the 3-week delay between doses. The chicks' first administration was at age 14 days, but these vaccinated chicks were only protected at the second administration, when they were aged 35 days. This negative impact of the hypothetic requirement of a booster is in agreement with post-vaccination surveillance data from Vietnam where a 2Shot-Age14 scenario is in place: <50% of the vaccinated poultry population seems to be protected after each campaign [8].

A major assumption when comparing scenarios in our model is that single-dose vaccination protocols conferred the same immunity as protocols with a booster. This is probably not true for conventional inactivated avian influenza vaccines. The preliminary results from vaccination trials with nationally produced H5N1 vaccines in Indonesia found that booster regimens resulted in higher peak titres and prolonged the duration of immunity significantly [35]. Moreover, results for booster scenarios rely on the assumption that the birds would not be protected between the two administrations which might not reflect the reality. Indeed, some birds might show partial protection between the two administrations depending on the vaccine type (inactivated or recombinant) [35, 38]. Hence, the actual initial PIR for 2Shot scenarios might be higher than that predicted in the model. Furthermore, results for single-dose scenarios from t=0 to t=2 weeks might have been overestimated as the model relies on the assumption that protection would be immediate (as for booster regimen) which in reality is not true as it would take around 2 weeks for the immune system to develop full protection. More biological knowledge is needed on the dynamics of the post-vaccination immune response at the animal level in order to refine the model assumptions and the vaccination scenarios to be compared with the model.

Besides the biological and immunological assumptions, the model is based on several other assumptions. The poultry population is assumed to be in a demographic steady state (stable sex×age structure and population growth rate). Additional simulations (not presented here) have shown that PIR dynamics can be affected if the population dynamics is in a transient regimen [13], for example during a herd restocking period just after a demographic shock, when the initial sex×age structure is far from the steady-state structure. In such a situation, the presented Leslie model can still be used to estimate PIR dynamics with the same formulae as in the Appendix, except that PIRs have to be calculated from population vectors x(t) simulated iteratively starting from the initial population vector x(0), instead of using the eigenvector w. However, in practice the difficulty of this approach is that dynamics in transient regimens depend not only on matrix A but also on the initial population structure (there are as many dynamics as initial structures). For example, initializing simulations with only juveniles or only adults in x(0) will give different transient regimens and then PIR patterns.

Another important point is that the model is only valid for populations with uncontrolled reproduction and a natural renewal. This is the case for free-range poultry but not for commercial chickens raised in flocks under all-in/all-out management. Other models are under development to assess the protective coverage within commercial production systems [10]. Finally, the model also assumed that the vaccination campaign was instantaneous and applied to a small farming community. However, there is no theoretical difficulty in extending the method to a region of N communities. One approach for calculating PIR would be to simulate independently, as presented in the present study, a set of N PIR dynamics and then average them for each week t after specifying a vaccination delay (possibly with spatial structure) between the N communities.

In the present study, demographic patterns and epidemiological scenarios were simplified. More elaborate models (e.g. individual-based dynamics models) [13, 39] can be used to study the impact of more complex and field-based vaccination scenarios, with a more holistic view of the epidemiology of the disease, interactions between different production sectors and economic impacts of the disease and its control, as well as the incentives driving actions. Nevertheless, our model is simple and suited to rapid implementation. Equations of Leslie models [13] can easily be transposed in a few days under any current programming language or spread-sheet. The model provides timely information to decision-makers for evaluating what can be expected to be achieved in small farming communities given a particular vaccination protocol, based on demographic data available from ad-hoc field surveys and the literature. Finally, the model can also be refined to evaluate PIR in other poultry species and especially free-range ducks which have been implicated as a major risk factor in the spread of disease in Asia [40], or in other livestock species (e.g. cattle, goats, sheep) extensively managed in traditional farming systems and submitted to vaccination campaigns.