The Chairman (Mr G. S. Mee, F.I.A.): Our paper is “A review of the Risk Margin – Solvency II and beyond” prepared by the Risk Margin Working Party. Our two speakers, Paul Fulcher and Andy Pelkiewicz, are from the working party. Following on, we will have Andrew (Chamberlain) to open the discussion for us.
Paul Fulcher is from Milliman and is a consulting actuary. He joined Milliman in 2018. Previously, he spent 20 years in the investment banking industry with Nomura, Royal Bank of Scotland and Union Bank of Switzerland, specialising in the area of asset liability management and capital market solutions for insurance companies across Europe. He also has experience in M&A Advisory in Japan, and actuarial consultancy in life office work. He is a member of the Life Board, and from 2015 to 2018, he was the Chair of the Life Research Committee.
Andy Pelkiewicz has spent most of his career at Sun Life and Axa Sun Life in the UK. In 2007, he joined HBOS European life business and was heavily involved in the development of Solvency II for companies in Germany, Luxembourg and the UK. In 2010, he moved to Germany in this role, and later he was the head of actuarial and investment at the Heidelberger Group. He retired in 2016.
Mr A. J. Pelkiewicz, F.I.A. (Introducing the paper): The working party was set up 2 years ago, following criticisms of the risk margin, in particular the Treasury Committee inquiry into EU insurance regulation.
Our brief was in two parts. The first part was to consider what “fixes” can be made either under Solvency II or post-Brexit, and the second part to carry out a more general examination of the purposes of risk margin and how that purpose can be fulfilled.
As well as preparing the paper, we have developed a simple model to illustrate the issues, and we have also carried out a survey of insurers. These are described in the paper, and the results of both are used to illustrate the points made in the paper.
I will be talking about the purpose and development of the risk margin and what the problems are. Paul (Fulcher) will describe the solutions that we have analysed and our conclusions.
I would like to start with a light-hearted imaginary description of the development of the risk margin. The paper gives a more formal description, but they are reasonably consistent. Let us imagine that we are the legislator trying to design a modern, international solvency system. Our first principle might be that the valuation methodology must be as prescriptive as possible, and we want to ensure that neither companies, nor their actuaries, use judgement more than absolutely necessary.
Market-consistent valuation follows that principle and is widely used. It is easy for assets but not straightforward for the liabilities. There is no deep and liquid market for insurance liabilities. You cannot phone up all of your competitors for a quotation every time you want to do a valuation. So, to be market consistent, we need to estimate the amount that a firm would have to pay in the market to transfer its liabilities. We calculate the best estimate. That is the expected value of the liabilities. But the transferee would want more than this. After all, he is taking on a risk. He is having to provide capital. In a market-consistent world, he wants to make a profit as well.
So, we need a proxy for the market cost to the transfer value in excess of the best estimate. There are a number of possible approaches to this. Paul (Fulcher) will be describing several of them later.
For our solution, as this imaginary legislator, we consider valuing the risks incurred and the cost of capital required. We consult with the industry and look at other solvency regimes, and decide to follow the wishes of the industry and copy the Swiss solution. We arrive at the proxy addition as the cost of capital in the transferee company over the full run-off period.
We need to define some assumptions about the transferee company. In the real world, business would probably to be transferred to a consolidator. It would be extremely difficult to define the characteristics of the consolidator in valuation regulations, as these require use of a lot of judgement.
One approach is similar to assuming that the transfer is to the original company; we assume that the transferee company is empty before the transfer and closed to new business, it de-risks assets, where possible, and adopts all practices and management actions of the original company and we will call it a reference undertaking. That is the risk margin.
The formula in Figure 1 is that in the Solvency II regulations for calculating the risk margin. It is based on the cost of future capital after a transfer to the reference undertaking. It is the capital in the reference undertaking, and it depends on a number of explicit assumptions. The cost of capital rate is fixed at 6% above risk-free. The discount rate is the normal risk-free rate. The reference undertaking is defined as I have described.
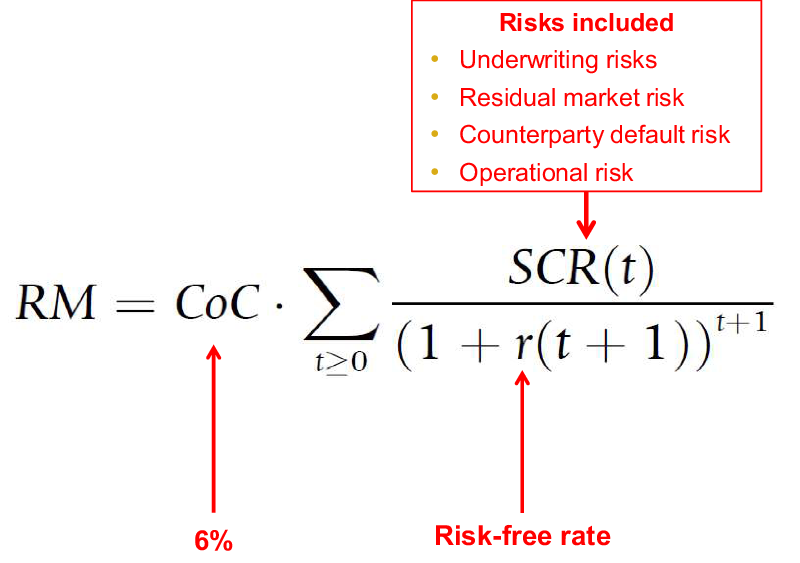
Figure 1. The Solvency II risk margin formula.
All these assumptions could be challenged. There is also an important implicit assumption. I have explained the risk margin as being part of market consistency. It could also be explained as being part of policyholder protection. The Solvency II capital requirement which is valued in the formula allows a firm to survive a 1-in-200-year event in the next year. The risk margin is the link to the future. You can see from the structure of the formula that it covers the cost of capital in each future year.
If the firm continues as planned, that capital will be required, so the formula in that situation is right. However, it also assumes the firm would be recapitalised after a 1-in-200-year event to full Solvency II standards confidently awaiting the next 1-in-200-year event, and the next.
The implicit assumption is that, following failure, Solvency II standards will continue to apply to liabilities. That is very desirable for customer protection but a high-risk margin adds to the cost to customers, and relaxing the assumed future solvency standard following failure could reduce the risk margin.
Balancing cost against policyholder protection is really a political issue, and indeed it was covered as such in the Treasury Committee though the politicians made it clear they looked for expert advice on such matters. But it does not seem to have been raised as a political question within the EU.
So what are the problems with the risk margin? Following the implementation of Solvency II, and the period shortly afterwards where long-term interest rates fell sharply, it became clear that the risk margin was not only large but extremely sensitive to interest rate movements, particularly for annuity business. Annuities are very important in the UK for the retirement provision system, both individual annuities and bulk purchase annuities (BPAs). They form a major product for the life insurance industry.
This means that the risk margin is very much a UK problem. The scale of the problem was demonstrated by a statement in 2017 from the Prudential Regulation Authority (PRA) that between December 2015 and September 2016, the overall risk margin of major UK life firms rose from £30 billion to £44 billion. The impact can also be seen in the results of our model. Our model is of a monoline annuity firm.
Figure 2 shows the monthly variation of the modelled risk margin as a percentage of the December 2015 value. It also shows the 12-year risk-free rate for comparison; it shows the extreme volatility with interest rates. It is difficult for firms to manage.

Figure 2. Variation of risk margin with risk-free rates.
I would also make the point that it is particularly volatile for annuity business and this is a monoline annuity firm. We have also modelled the risk margin as a percentage of best estimate liabilities. This is also volatile though obviously not as volatile as the value in pounds.
But it is still pretty volatile. 100% is December 2015, where the ratio was 7.7%. Of note here is that the risk margin was typically between 8% and 9% of best estimate. That is a significant burden. Our model uses the standard formula. Internal model firms would probably have an even higher ratio.
This is likely to be affecting the price of annuities with adverse consequences for retirement provision. However, the PRA claimed in its response to the Treasury Committee that there does not seem to have been a change in annuity prices relative to interest rates since Solvency II came in.
Another concern about the risk margin is that the size and volatility of the risk margin are encouraging firms to reinsure longevity risk outside the EU because it reduces and stabilises the risk margin. There may, of course, be sound business reasons for this, but to the extent that it is driven by regulatory arbitrage it may be undesirable.
Finally, the calculation of the risk margin is very complex. This problem has already been solved by firms through necessity. I would observe that it seems unsatisfactory that such a large item as the risk margin must normally be determined through approximate methods. We cover this complexity briefly in an appendix to the paper.
What has been happening as a result of the problems? I mentioned the Treasury Committee inquiry which took place in 2016 and 2017. The risk margin was a major theme. Andrew (Chamberlain) gave evidence on behalf of the IFoA and dealt with some very pertinent questions. I would recommend watching the video of it.
The Committee’s report concluded that a risk margin made contractual sense and should continue to form part of the UK regime. However, they recommended that the PRA should provide solutions to improve its calibration.
The initial PRA response was that it was actively looking at changes. A later statement in June last year was to the effect that no changes can be made pending further clarity on Brexit, and “pending further clarity on Brexit” remains the situation to this day.
European Insurance and Occupational Pensions Authority (EIOPA) also carried out a review of Solvency II regulations in 2017–2018. The working party contributed to the IFoA’s submission to the consultation.
In the case of the risk margin, we were disappointed to find that the scope of the review was limited to the 6% cost of capital rate. Our comments were much wider. EIOPA’s conclusion in the limited review was to the effect that the rate should probably be even higher than 6% but it would not recommend an increase at this point in time. Some of the assumptions used in reaching this conclusion could certainly be challenged.
The next review is next year and the European Commission has sent a formal request to EIOPA to carry this out. Disappointingly, the request limits the scope to retaining the cost of capital method. It requires consideration of factors other than the cost of capital.
Paul (Fulcher) will now describe our solutions to these problems.
Mr P. Fulcher, F.I.A. (introducing the paper): We came up with this list of 11 qualities that a desirable risk margin should possess.
The six in green on Figure 3 are ones that were originally looked at in 2006 when the risk margin was being designed. The other five yellow ones are ones which we have added based on discussions since then.

Figure 3. Qualities of a desirable risk margin.
It is interesting, given the ticks and crosses, which are our assessment of how the risk margin performs, it tends to be the ones that have been added are some of those that perform worse. In other words, the risk margin is now being judged by different standards.
So what are those qualities and how does the current risk margin shape up? Running through them quickly, policyholder protection is often forgotten. There is clearly a trade-off, as Andy (Pelkiewicz) said, between protection and cost. Have we gone too far?
Market consistency: our sound bite here would be the risk margin is constructed to be theoretically market consistent. Unfortunately, it does not seem to be very practically market consistent. In other words, the prices it throws out do not seem to bear much resemblance to the prices in the market. Interest rate sensitivity is one example. It is far more interest rate sensitive than reinsurance pricing.
Objectivity and consistency between firms: this is something the regulator would like but you might debate whether it is desirable.
Generally yes for the risk margin, but there are a couple of interesting points. It uses individual insurers’ capital requirements. If you have an internal model, it affects your risk margin. Given is a market-consistent price, I am not clear why it should. More importantly, the risk margin uses your level of diversification and that is one of our issues, as there is no reflection of the fact that if you are transferring it to the market, you would benefit from wider market diversification.
Applicability to different risks: there is fairly reasonable evidence that the risk margin is a little over penal on long-dated risk versus short-dated risk.
Is the calculation practical? It was not when people first had to do it but is reasonable now. That is why we have the two ticks there. If you have not solved the problems by now of calculating the risk margin, you have a bigger problem than the risk margin.
Avoiding procyclicality is one where the risk margin is clearly very sensitive to interest rates. But things are only procyclical if they exacerbate cycles, that is, the interest rate volatility in itself driving insurers to do excessive hedging which is making interest rates more volatile. There is some evidence of this but we are not totally convinced of that one, so the cross and question mark there.
Then international consistency: both International Financial Reporting Standard (IFRS) 17 and international capital standards, as well as Solvency II post-Brexit. Here the risk margin performs well, but there are other methods that you can use in some of those regimes.
Creating incentives: probably the biggest issue, hence our two crosses. Is the risk margin artificially incentivising people to reinsure longevity risk? Yes and no.
Many monoline insurers used to already reinsure their longevity risk offshore before Solvency II. And maybe, from a public policy point of view, it is not a bad thing that we reinsure our longevity risk to markets that have some diversification benefit. But there still does seem to be evidence of regulatory incentivised behaviour which never seems a great thing.
Theoretically sound: as noted, the risk margin theoretically makes sense.
So what are the options for change? We have divided these into two. The first are things that you could change within the directive and that firms lobbied about in the Solvency II process. These are all things that people put to EIOPA in the review Andy (Pelkiewicz) talked about.
The first one is to lower the cost of capital: halve the cost of capital and you halve the problem. That is pretty much the only thing EIOPA responded on, and they said “yes you are right, 6% is the wrong cost of capital. It should be somewhere between 6.7% and 7.8%”. That was not the answer that the industry hoped for.
Another one which was interesting, which had little debate by EIOPA is: should the cost of capital itself vary with interest rates? 6% is above risk-free; but as interest rates come down, do spreads come down? Think of different economic environment when risk-free rates are 15% or 1%, do you really expect the same level of compensation for risk? There is reasonable theoretical evidence we quote in the paper that that is not the case. The Chief Risk Officers forum did some work which said maybe a 100 basis point reduction in the risk-free rate might reduce your cost of capital, over and above risk-free, by 30 or 40 basis points.
Should you be able to use the matching adjustment or volatility adjustment? It is not always widely appreciated by those who have not done the calculations that in the risk margin calculation you throw that away. Your Solvency Capital Requirement is calculated with no matching adjustment or volatility adjustment. Similarly, your risk-free rate is the basic risk-free rate.
Possibly – although there is a quid pro quo of that – if you hold assets to earn the matching adjustment should you also hold capital against those assets? It is also an easy change to make and only requires the EIOPA guidelines to be tweaked.
Tapering of lifetime risks: if you keep projecting future Solvency Capital Requirements (SCRs), are you over counting the risks? The Association of British Insurers (ABI) came up with a pragmatic way of allowing for this, which we talk about in the paper. We have not discussed it in great detail. It essentially involves letting the SCR run-off.
Then the final one, probably the most interesting one in many respects, is should we just go for reinsurance pricing? If there is a market-consistent price for something, and it has a market, why are we not using the market price?
The recitals of Solvency II talk about that. They talk about the price you would have to pay to transfer the risk. And the original Solvency II distinguished between hedgeable risk and non-hedgeable risk. At some point that became financial risk and non-financial risk. You would have to unpick probably the level 2 delegated acts, but that could be an interesting option.
It is also worth saying that the ABI again had a solution here. It was debated at some length with the PRA. It involved management actions to achieve the same thing.
Just putting some numbers on that, reducing the cost of capital, putting some indicative reinsurance pricing on there, we think that for the block we looked at the implied cost of capital was about 3½% rather than 6%. That would get about the same level as reinsurance pricing. I should be interested if people have any views on that.
EIOPA indicated that the cost of capital should be 7.8%. So, a lot higher.
Using the matching adjustment, if you use a higher discount rate but then you allow for the SCR associated with the assets you get back where you started. That is a bit of a “be careful what you wish for” one for the industry. Then the tapering. We have just an illustration there of how that potentially reduces the risk margin.
Volatility: I have only put one option on Figure 4, which is the cost of capital sensitive to rates. The red bar is the result of making the cost of capital depending on rates. You can see that it is roughly about half the volatility. Interestingly, in international standards, they tested a more extreme view where the cost of capital literally goes down by 100 basis points for every 100 basis point reduction in rates. That makes the risk margin less risk sensitive. It will actually reduce if interest rates go down. That is probably over parameterised.

Figure 4. Comparing options – volatility.
Next we considered how these approaches measure up against our 11 objectives.
Referring to Figure 5 and just picking a few of these, the cost of capital method is very easy to implement. That is the easiest change to make.

Figure 5. Assessing the alternatives (1).
Cost of capital varying with rates: if you accept that there is excessive procyclicality, it definitely reduces the interest rate sensitivity. It seems to be close to market pricing as well.
Allowing for the matching adjustment and volatility adjustment: the tick and cross at the bottom for theoretically sound is because it is only sound if you then also allow for the risk associated with the assets. I will come onto how we think you could deal with that on the very last slide.
Then probably the one that caused the biggest debate in the working party and therefore has most double ticks and double crosses, is cost of reinsurance. It has some big advantages. It is market consistent by definition. By definition, it does not create false incentives because it is the same price at which you can transfer the risk.
How practical is it, really? It might solve longevity risk in the UK but it isn’t really an answer for, say, lapse risk. Andy (Pelkiewicz) made the point that, in the non-UK company for which he worked, lapse risk was what drove their risk margin. Lapse risk is not an easily tradeable market. That maybe does not work.
How do you do it? It is great if you are a person who frequently uses the reinsurance market and knows exactly where the pricing is. What about if you are a small insurer and do not? The more we thought it through, the more we felt that you would end up with the PRA telling you what the market price was. You are back to an artificial parameter.
So we quite like the use of market pricing but with some reservations.
Then more fundamental options for change. We tried not to reinvent the wheel here. We looked at what was being done internationally in this area. They fall into three broad categories. The first three are all variations on a theme. If I went back 10–20 years, no one had ever heard of the cost of capital method, and imagine if I had said to a room of actuaries “I have a risk and I want to be a bit prudent in the way that I allow for that risk what would you do?”
They would have answered: “Add a margin to the assumptions”. A provision for adverse deviation. A pad, a margin. Whatever you want to call it. You would add a bit for luck. Or a bit for risk.
There are various variations on that that we have seen used elsewhere. We have put the precedents on here.
As I said broadly there are three approaches. One is to say: do not use a best estimate, use a more prudent version. Solvency II originally tested this as an alternative: rather than use best estimate, or on top of best estimate, do a 75th percentile of your liabilities on a run-off basis. The difference between the two is the risk margin.
The second one is more, as I said, add margins. It is a traditional actuarial approach. Interestingly, it is used in the new risk-based regime in China, a rather large insurance market, where they add relatively arbitrary margins to each individual assumption.
The last one is the one that caused most debate in the working party. It seems a bit odd. But it is where international practice seems to be heading. It looks over 1 year like the SCR but has a much lower confidence level. Take something like the 75th percentile of non-hedgeable risk over 1 year. That method, almost by definition, ends up with a risk margin that is smaller than your SCR. It is only applied for some risks and is at a lower percentile. But it is, I would say, emerging as international best practice.
Finally, run-off. The precedent here is pension super funds consolidation vehicles. If you look at what the Department of Work & Pensions proposed, there was no reference to a 1-year Value at Risk (VaR) SCR. The focus was why do we not just run the whole thing off, forget the SCR and just do a 95th percentile overall? That is another approach.
The final one is why bother with risk margin at all? The insurer has already gone through a 1-in-200-year shock if they have lost their SCR: why should your customers think that they should have anything more than a 50–50 chance of getting their benefits at that point? If you do not like the answer, make the SCR a 1-in-500-year shock. In other words, just make the SCR bigger and forget the risk margin.
We would argue the battle against not having a risk margin seems to be lost. It is now in international standards; it is now in IFRS; the Treasury Select Committee did seem to push back on it.
Run-off capitalisation – theoretically, very interesting. Frankly, it involves changing Solvency II completely. Maybe we will let the pension superfunds play with that one and if it works we can copy it.
Where are we in our thinking? We quite like the VaR method because it is the international one that is emerging.
In terms of possible options for change, what would we do or what would we think about? We are quite sympathetic to allowing the cost of capital to change with interest rates. Maybe arguing to EIOPA that 6% was right when interest rates are much higher. But it is not appropriate nowadays in a zero interest rate or negative interest rate regime.
We are quite amenable using a liquidity premium in your SCR and discounting calculations, but one that can be earned in a risk-free way. So probably a lot lower than the matching adjustment. Probably something close to the volatility adjustment or something maybe in the 50 basis points range. You can argue it is a pure illiquidity premium associated with liabilities, and that earning does not involve credit risk.
We have some sympathy, if you can get round the practicalities, with treating longevity risk as hedgeable, where there is clearly a market price.
Then we have quite a lot of sympathy with the view that it if anything the international view has moved on from the cost of capital approach. Switzerland started with the cost of capital, we copied it; Bermuda sort-of copied us, if I could put it that way.
But looking at Asia: no one is using the cost of capital method. It has been put up there against this VaR method, and the cost of capital method has been forgotten about. If we want in a post-Brexit world to embrace the wider world, the VaR method seems to be winning out and exploring that approach could be interesting.
The Chairman: Our opener Andrew (Chamberlain) was chief actuary of Just, and a director of Just Retirement Limited and Partnership Life Assurance Company Limited until 1 December 2017.
He was the chair of the IFoA Life Board from July 2016 to June 2018 and has previously been both a member of Council and the chair of the Professional Regulation Executive Committee. He gave evidence on behalf of the IFoA to the Treasury Select Committee enquiry into the EU insurance regulation in January 2017.
Mr A. J. M. Chamberlain, F.I.A. (opening the discussion): This is one of the best papers I have read in recent years and I cannot find issues to challenge. So I shall focus or expand on some of the issues about the risk margin, stepping back a little bit more to fundamental principles which I tried to do with the Treasury Committee.
The points that have already been discussed by members of the working party include where does the risk margin come from? The whole Solvency II regime was a regime designed by regulators for regulators. That is one of the flaws in the whole thing.
Who pays for all this? It is not some hypothetical imaginary life assurance or general insurance industry but policyholders who end up paying for these regimes and we need to think about it from their perspective. For the purposes of our discussion, I am going to talk as if this issue of reassuring on a regulatory arbitrage driven basis was not happening.
In an ideal world you would not have any regimes that encourage regulatory arbitrage, but we do. If we assumed that this did not exist, I am pretty confident that the PRA figures would not be shown. In fact, the PRA themselves think that reassurance offshore has been a major cause of a lower change in annuity rates than might otherwise have occurred.
So, for the purposes of this discussion I am talking about the person who pays, the policyholder. Imagine the policyholder being asked to provide funding for his own contract.
We are going to have to hold an SCR against his contract, and charge for renting our capital to support the policy, which is to provide cover in case the half percentile probability occurs and we then have a problem.
After we have done that, we are then going to say that supposing this event happens, we are also going to have to hold some money just in case more events happen. We are going to have to get someone to set up another SCR to protect against more longevity crises, and so on.
So we are into the one in 40,000 event and should this also be costed.
At some point, you have to start thinking about what the role of the risk margin is. If you just had technical provisions, having a risk margin on top makes perfect sense. You do have to think about what it is supposed to achieve at the other end. However, you then get the idiotic situation where in some cases you will say to this hypothetical policyholder: I am going to have to set up this risk margin against having to set up another SCR.
The SCR that we are setting up on your policy, just for argument’s sake, is 100. Just in case we have this remote event, we have to set another one up. I need to set up another 120 because what I am going to do is assume whatever I need to set up, which should be less than 100, I am going to pay 6% rent to somebody over and above risk-free to do it. That can cost me more than the amount of money. I am going to charge for the setting up of £120 just in case I need to set up £100 later.
I do not think many people would buy a product where they were told if something happens you are going to have to borrow £100 and you have to make sure that you put £120 there to pay the cost of borrowing that £100.
If I have the £120, I will not borrow the £100, thank you. I only need £100.
To recap how we have got to where we are. Market consistency appears to be an ineffective system for working out how much should be held by an insurance company. What the insurance company needs to be able to do is to meet its liabilities as and when they fall due and we seem to have lost sight of that. That is what the policyholder expects. He pays an amount in to buy an annuity or to buy some policy – it does not matter what type it is. What does he ask for?
He wants to be paid what he is supposed to be paid when he is supposed to be paid it. He does not really care about what the balance sheet looks like and various other things in the intermediate period. He certainly does not want some sort of hypothetical nonsense that he has to pay for based on what somebody is trying to estimate what a non-existent market would charge for something or other.
What he is interested in is how much security he has, what events will run me out of my benefits. He may accept the one in 200 measure. But what he is then being asked for is insurance on the insurance.
How much is he really going to look at? This leads me to look at the issue as to what should be charged for? It is slightly muddled now in the UK particularly for annuities because of the way the Financial Services Compensation Scheme (FSCS) now pays 100% back. The policyholder, in a pure, economic sense, wants to pay nothing because he has a free insurance anyway from the FSCS. So we do have to look at the balance of fairness between the policyholder in the failing company and the rest of society, either other policyholders or, ultimately, taxpayers.
But what is that fairness? Where does it lie? To some extent that leads me on to thinking maybe these 100% guarantees are not a good idea. It does muddle the whole issue. Maybe the key is to have after this remote event has occurred something that is a little bit more run-off focused but does not necessarily provide for 100% of the liabilities to be met in that situation or the liabilities to be met in full with a very high probability.
There are many different ways that you could look at this. You could say that the probability of paying in full is 90%. Or you could say that there is a much higher probability of paying 95% or 90%. That would reduce the cost to the policyholder significantly.
The issue has already been raised about the contrast between the way insurance company regulations are being looked at and the pension superfunds.
I am not going to talk about the pension superfunds, as there are many practical issues that need to be considered.
This issue about the nature of the guarantees, the nature of the security, is a very important one. It is important just to go back. On page 18 of the working party’s report, they quote what the Treasury Committee said: “An additional margin which purports to represent the additional capital that a third party would need in order to run off the insurance firm in the case of an extreme event makes conceptual sense and should continue to form part of the UK solvency regime”.
The big challenge in that – and what they do not say – is what the additional capital a third party would need rather than what they were being told to have would be.
Mr J. G. Spain, F.I.A.: I have not worked in Life for about 40 years and know very little about it. My background is in Defined Benefit pensions. I have a few comments on what is an excellent paper. First of all, Paul (Fulcher) said cancer being cured only once: that is no longer the case in this country. People are being cured twice or more often.
Andy (Pelkiewicz) mentioned the reference undertaking of no assets and no liabilities, which reminded me of Philip Green’s sale of British Home Stores, which is not a good look.
He also stated right at the beginning that it is not a good idea for actuaries to exercise judgement. If judgement is not what we are offering, what is our expert role? Why are we charging very high fees to clients and ultimately to the policyholders? As Andrew (Chamberlain) forcefully said, they are the people who are paying for it.
In his contribution, Andrew (Chamberlain) mentioned looking at the liabilities that fall due with not having everything completely guaranteed. I agree with that. I realise that we are in a regulated world, but let us suppose that we could try to design regulations that would work well and then try to persuade the regulators that is what we really need. That is what the public duty ought to be via the IFoA and other institutions.
Instead of discounting, we should be using Asset and Liability Management. Then you have the option for proper judgement and advice being given to clients. You can let the undertakings decide what kind of contracts they want to market. They can tell their clients “if you come to us instead of to the competition, we will give you a 98% chance of achieving. But we are not going to guarantee it”.
Somebody else will say 97% for a slightly lower premium. Then we have got back to competition, which has to be a good thing.
If the working party had been able to think about going beyond the terms of reference, which is looking at what is there now, and considering how to tinker with it, “let us sweep it aside and try to put that forward”, that would have been interesting.
Mr M. G. White, F.I.A.: We talk about the sensitivity of the risk margin to the risk-free rate. But is this not really the same thing, the sensitivity of the SCR to the risk-free rate? Should not the discussion focus more on how the SCR is determined?
Looking at the question entirely differently, I have been more inclined to take the policyholder’s perspective exactly as Andrew (Chamberlain) set out in his opening remarks. I want to be really confident that in, say, 50 years’ time I will get the pension that has been promised. What sort of downside risk would I be prepared to accept? I would be prepared to accept some reduction in benefit but a very, very low chance of that happening. It is my pension and I am relying on it.
That captures one of the problems which I have with the entire SCR regime. Looking ahead just 1 year is not enough: if you look at the 1-year risk – and this is true for general insurance as well – and then you look at the 5-year risk, that 5-year risk is more than five times the 1-year risk.
My test would be: would the balance sheet be strong enough to provide that sort of confidence, however constructed? Maybe margins on each side with no specific risk margin, might be a way forward.
Mr R. A. Rae, F.I.A.: Congratulations on what is a very readable, informative and well-balanced paper. In terms of how you respond to this paper you need to define what the question is. Martin’s comments just now were interesting. They are raising the whole premise of Solvency II. I am a pragmatist and we start with where we are.
We have a regulatory regime that calculates technical provisions as the price at which you can transfer liabilities on an arm’s length basis. You have a year in which to do it. The capital that you need to hold is probably enough to withstand market shocks, demographic shocks or whatever shocks within that year while you find someone to transfer it to. That is a flawed basis.
If I accept that and then say, how do we improve it? It is clear there are a couple of things wrong with the risk margin. The first is that you cannot hedge its interest rate sensitivity. It would be great if that could be fixed. It is also not unreasonable to assume that somebody that was going to take on your block of liabilities would look to reinsure it. In which case treating longevity risk as a hedgeable risk is not an unreasonable assumption, given that there seems to be, at least at the moment, a reasonable market in transferring that risk.
3.3.1 of the paper notes how the price of transferring the risk goes up as the risk margin goes up. That rather suggests that a cost of capital is associated with such transfers and is therefore not an unreasonable approach to take. I agree with the Treasury Committee’s reflections on that.
Certainly, in the past, when I have looked at the transfers of business, we always used to take into account the cost of carrying capital. I am not aware that charging for the cost of locked up capital within companies has fallen away since I stopped looking at these things.
To me the measure of quality has to be coming up with technical provisions that represent the price at which you would transfer this block of liabilities to somebody else. It may be that the alternative 75th percentile approach achieves that.
I also like the idea of replicating some sort of reinsurance risk transfer as the pricing approach. Alternatively, other fixes could be explored if it is not replicating the transfer price. When working out the cost of capital, we used to discount not a risk-free rate, not a rate that included a Matching Adjustment or a Volatility Adjustment, but at an equity risk rate of return, which I believe takes much of the duration issue out of the risk margin.
So, concluding who can contribute to this debate? We could look to the IFoA to pass some comments on the way the pricing of annuity business is carried out.
I appreciate in all of these comments I am talking principally about the BPA markets. I am not talking about our continental friends that have all sorts of lapse risk within their liabilities. The PRA can obtain data in terms of what are the technical provisions of a block of business which has recently been bought within the BPA market. There is quite a decent market out there.
Mr Pelkiewicz (responding): For the avoidance of doubt, when I said actuaries should not exercise judgement; that was part of a light-hearted statement as to what a regulator might think. It was not my intention to state that as my view. Certainly, as an actuary, I have exercised judgement throughout my entire career.
Martin (White)’s comments are very interesting. Volatility of SCR: for annuity business, the risk margin is more volatile than the SCR. The volatility of the SCR itself is definitely a contributory factor. These things in theory should be looked at together. It is a very difficult question. I am not sure that there is an easy solution.
There was a comment about our scope as a working party: risk margin is perceived as a problem. Yes, you can look at the whole of how Solvency II looks at things but I feel as a working party that would have been too much for us. It was difficult enough to concentrate on the specific issues.
Mr Fulcher (responding): If you have a risk which can happen only once, which is, for example, everyone lives forever, then under the risk margin methodology, having a 6% cost of capital and low interest rates, you can almost end up holding more capital than anything that can possibly happen.
The ABI put together an example which seems to suggest you could almost have a risk margin that was higher than the cost of (on day one) capitalising your company as if someone would live forever. That was more the point. Maybe I should have said you cannot live forever twice and apologise for any unintended offence regarding cancer.
A couple of interesting points: Andrew (Chamberlain) and Dick (Rae) were considering different approaches which reflect the debate we have had in the working party. You can look at the risk margin in two ways. One is have a best estimate liability, a technical provision that seems a bit imprudent based on a market-consistent approach, any issues with market consistency notwithstanding. Then I need a bit on top of that which is the risk margin.
Having done that calculation, I need an SCR. The risk margin comes first. Then I have an SCR on top of that.
Andrew (Chamberlain) came at it from the point of view of starting with the SCR and debating if you really need a risk margin on top of that. The SCR is there to cover me for 1 in 200 years. And as I said, why would you want to have more than a 50–50 chance or less than a 50–50 chance of meeting your liabilities?
It is quite an open question whether the SCR and risk margin are really independent of each other in that regard. We had some disagreements in the working party about that.
It is interesting in that regard – again something else which caused debate in the working party (refer to 7.7.1 of the paper). In international capital standards, there is a lively debate at the moment about having set up your technical provisions, best estimate, and then having set-up risk margin on top of that, when you do your SCR calculation, should you assume that you can release some of the risk margin? In other words, is the risk margin, part of the available capital to absorb risks? That is, does the existence of the SCR means the risk margin is too prudent and I should allow myself to release that.
Again, as a working party, we came up with the conclusion that we were not that comfortable with that but it was definitely a debate among us. It is interesting. International Capital Standards is definitely exploring that route, particularly given that the Value at Risk (VaR) method that I talked about is almost double counting. You end up with a risk margin that is literally a subset of the SCR. Why would you want to have two of those?
That is currently a lively international debate. The American response to international standards is that this should be double counting, and you should be able to release the risk margin. The Chinese response is the same. The EU response – not surprisingly – is you definitely should not do that.
Finally, it is worth saying that the risk margin is more sensitive to interest rates than the SCR largely because of double discounting. It is projected SCRs that you then discount as well. Almost by definition, it is twice as sensitive. The calculation by construction ends up with a sensitive number.
Mr T. G. M. Stedman, F.I.A.: Following on from your comments about international capital standards and coming back to a question that you pose in the paper, what is the risk margin for? Solvency II has a very clear articulation of what a risk margin should represent even if it does not maybe calculate it correctly. Under IFRS 17, the risk adjustment is intended to represent something for the uncertainty and the best estimate liability.
Interestingly, currently international capital standards guidelines do not specify what it is for, and what the basis for preparation of the balance sheet is. That is partly what is driving the American view that it can be released in stress situations because there is no articulation of why I am holding this amount and what it represents.
Mr M. H. D. Kemp, F.I.A.: I have one comment and one question or a request for the committee. My comment picks up on Jon Spain’s issue about cancer being cured twice. An easier way of understanding the issue in question is to consider a different risk, namely lapse risk.
Suppose an insurer’s business is exposed to lapse risk, particularly mass lapse risk, and is also very long term with a very low expected lapse rate. It would need to set up an SCR contribution in respect of mass lapse risk. But if the business is long enough, the projected SCRs needed in the risk margin calculation effectively end up assuming that mass lapse occurs multiple times and the end result can contradict market-consistent principles.
Having informally raised this issue with EIOPA, their push back was that policies with these sorts of characteristics are comparatively rare in the EU. What the industry appears to be trying to focus on risks that are more relevant, like longevity risk, where a black and white case is harder to advance, but where some arguments can still be put forward suggesting that you are unlikely to get huge amounts of longevity improvement regularly every year going forwards.
Turning to my question or request for the committee, I note that we do not currently have a deep and liquid market for longevity risk. If we did have such a market and it was easy to demonstrate that longevity risk could be hedged, many of the arguments would become less relevant. Is there anything that the IFoA can do to regularise and make this market more transparent, more liquid, and therefore easier to demonstrate that the hedging arguments are sound and robust?
Mr Fulcher (responding): Your mass lapse illustration is extremely helpful. It is an argument where you end up holding capital for something that cannot occur twice. It does not make any sense at the end of the day. The cost of capital could not be 6% in that case. You can only lose your capital once, why would you want a return on that capital of more than the amount that you have got?
On the longevity market, I would say it is a deep market, a liquid market but not a transparent market. In other words, you can place £1 billion of longevity risk relatively easily so it is deep. If you do that without particularly moving the price, someone else could come along next Tuesday and maybe one reinsurer is taken out but there are five or six more – so it is deep and liquid. But what it is not is very transparent. You would have to go out there and get a quote if you want to know what the price is. It makes it hard to use objectively from a valuation point of view. There will be small firms which will struggle. What could the Institute and Faculty of Actuaries (IFoA) do about that?
If people were prepared to publish prices of longevity transactions that would help. Or if someone was prepared to have something – and one or two of the consultancies did go on this route – where you could feed your scheme in and get a price from people which was their best guess of what that price would be before you go into the detail of your scheme. That requires more an industry-wide initiative involving consultants, and related parties such as the actuarial and accounting professions.
Mr Chamberlain (responding): First, “cancer cannot be cured twice” was a loose term. What you could have said was that the number of deaths from cancer cannot reduce below zero.
On the reinsurance point, what we have to bear in mind is that unlike many other risks that are “hedged”, and it is not a term that one uses typically about reassurance, the risks are not always the same. Portfolios of pensions or annuities are not all identical. It is not as if you can pluck the price off from other transactions. The nature of what is being transacted will not be the same as other portfolios. The occupations may be different. The geographical spreads may be different; they may have been underwritten or not underwritten – all sorts of differences can result. It is never going to be easy to measure a price that could be transferred to another portfolio.
Mr Fulcher (responding): Also, data quality. People tell me things like do you have decent data and accurate figure percentage married can make a big difference to the prices.
Mr B. Bergman, F.I.A.: On the question of deep and liquid longevity prices, are we talking about “fair weather” prices? The risk margin is meant to be there to support the transfer of the liabilities after the SCR is lost. Just having a “fair weather” price is not really going to give you the answer that you need if the risk margin is to work in practice. After one company suffers stress, the price people will have to pay to transfer risk may go up, and certainly, if the industry suffers stress, then the market price of risk will definitely go up. The risk margin follows current market prices and hence does not pick up the inevitable spike in the price of risk following stress events.
Mr Fulcher (responding): We ended up with this in the paper. There ought to be a stressed through the cycle price. And there is also the lack of transparency. You can end up coming up with an arbitrary assumption. The counter-argument was that if people could evidence that price, then maybe they should be able to use it.
Mr Chamberlain (responding): It comes back to the basis of preparation. The requirement is to put market price at the date when the balance sheet is struck not the market price out of stress. You are not required to work out what the stress market price is. It is the balance sheet at the date when you strike the balance sheet.
Mr Pelkiewicz: Arguably, one can put that into the SCR.
Mr Chamberlain: I think arguably you have.
Mr Fulcher (responding): As a working party, we agreed you do not stress the risk margin in the SCR. The fact that you don’t stress it for rates gets a lot of attention, but one of our arguments on the cost of capital was probably a question mark around should we have a stressed cost of capital at least in the SCR calculation. Again, Andrew (Chamberlain)’s point, you could have margins on margins, if you are not careful. The ability to cope with something under stress twice.
Mr Chamberlain (responding): Then we also need to bear in mind we are typically dealing with long-term issues here. Unlike in a banking environment, where you get a crisis and everything has to be solved by tomorrow, you do not have to go out and resolve the transfer of the life insurance portfolio to somebody else within 24 hours. You could take several years over it.
The general insurance world has been dealing with run-offs, closures and eventual transfer to somebody else, a rump portfolio, or whatever, for decades and decades, if not a couple of centuries. There is not this urgency. That is one of the things that regulators have found it difficult to cope with. They want to tidy it all up instantly. That is not what you would do in practice. Nobody has ever done that in practice.
Mr Rae: I want to pick up a comment: there is an issue on the asset side because annuity portfolios are mostly backed by illiquid assets. How do you place a market value on an illiquid asset? It is exactly the same issue, just the other side of the coin.
Mr H. Ullah, F.I.A.: A great deal of time and money was spent on the Solvency II regulatory regime. Why was this not picked up earlier?
Mr Fulcher (responding): There was a sessional paper focusing on a Solvency II retrospective: I remember saying that there was very little in Solvency II that now the industry thinks is a disaster – I used “industry” in broad terms, that is, perhaps the actuarial profession thinks was a disaster – that we did not lobby for to start with, including using the cost of capital method.
The problem is the answer. Regarding the testing of Solvency II, if you look at the Quantitative Impact Studies, they were tested at a point in time. It is hard to think about what happens when interest rates are 0%. No one thought that would happen. We are supposed to be a long-term profession, so that is not a defence. But it does mean later events may be causing the decisions made in the past to look bad. If interest rates were still 5%–6%, we probably would not be having this discussion.
Mr Chamberlain: Although to be fair interest rates have not been below 3% ever in recorded history.
Mr Fulcher: Therefore, we have a problem that we did not test or think for. Similarly, Solvency II was not originally designed to cope with 2008 type credit crunches and other “unknown” things.
Mr Pelkiewicz: Fortunately, the 2008 financial crisis happened before Solvency II, so they came up with some solutions – the long-term guarantee package. The specific bad timing here is the collapse of interest rates followed immediately after the implementation of Solvency II. We as a profession perhaps should think more about these things but it would be extremely difficult to do so.
Mr White: I have two points. One is in response to questions on the drafting of Solvency II: I remember being very struck when reading the Solvency II drafting, and the discussion around it, it was inspired by the legal mindset. The legal mindset seemed to think that the more that they got actuaries to do lots of detailed hard work, the more you would remove uncertainty, which of course we cannot.
My question is: in your discussions, did you consider how the risk margin being a 6% flow on the projected SCR, in other words, a cash flow could possibly be invested in such a way as to be roughly resilient to movement in risk-free rates? In other words, you can invest that amount in a set of government bonds which would move as per the risk-free rate.
Mr Fulcher (responding): Yes, we did discuss that. I am probably on one side of the fence here so Andrew may have a different view about hedging the risk margin. I used to have a slide that I used in presentations about why firms did not hedge the risk margin. It was a combination that the calculation is a bit complicated and also that people think the risk margin is artificial so why would you want to hedge it, as it does not exist at the moment, for example, in your IFRS balance sheet.
Dick (Rae) made the point to me earlier that you are damned if you do and damned if you do not because if you hedge it because it is not stress tested you end up with an SCR exposure to rates up because in the SCR calculation you do not stress it. Then you have transitionals which make everything complicated.
The glib answer is that you could have hedged it. The real-world answer is there were many reasons not to do so. Therefore, people, by and large, did not. Therefore, we have the problems that we have now.
Mr Pelkiewicz (responding): I do not disagree. There is a short section in one of the appendices on hedging the risk margin. As I implied before, most companies did not realise what the problem was. Once interest rates dropped, you would probably have taken the view late in 2016 (which was the low point) that it cannot drop much lower and you would have taken a view not to hedge. But interest rates might have dropped further.
Mr Bergman: A slightly different point. The undercurrent is that the risk margin is too high, resulting perhaps in technical provisions that are too high. If you look at the market capitalisation of insurance companies and compare that to their Solvency II own funds less that which does not belong to shareholders, is it not the case that the market capitalisation is less than the Solvency II own funds? This suggests the investors are not overwhelmingly convinced that the technical provisions are necessarily too high or perhaps they are simply not convinced about strategy of the insurance company! Have you considered that at all?
Mr Fulcher (responding): If I speak to equity analysts, it seems to partly be the “not believe” part, in that they do not disagree but they do not believe because of the opacity of Market Consistent Embedded Value and Solvency II. They are not quite sure they believe the numbers anymore and surely “cash is cash”, which actually does not really make sense if you are an insurance company because if you cash accounted for an insurance company, annuities would look great. You would make a huge upfront profit and then you would have to pay out money.
There is also perception in markets around strategy and new business value, and other things as well.
When I have seen equity analysts trying to do an adjusted version of Solvency II balance sheets, they tend to throw away transitionals on the grounds that they are a bit of a nonsense. There might be a cost of capital saving to a transitional but it is not a real asset. They ignore things like the ultimate forward rate, and they tend to assume that the risk margins are a bit too high, in my experience, because of the 6% cost of capital.
There are a few published reports where people have tried to reconstruct Solvency II balance sheets and they show risk margin tends to be regarded as a bit high.
Mr Chamberlain: Also, there is the point that they are never quite sure what is going to hit the industry next. Ultimately, they are interested in what dividends can be paid, and so on. They are never quite sure what the regulatory regime is going to throw into the mix next so they discount values a bit.
Mr A. J. Scott, F.I.A.: You talked a little bit about the risk margin not being assumed to change in the SCR calculation, so where we got to was that would be margins on margins. That might be assuming that the risk margin would increase under an SCR stress. Considering this business that you can cure cancer only once, if my SCR event is that cancer has been cured, then would it not be reasonable in that scenario to release some of the risk margin because my projected SCRs would be lower? Therefore, allowing the risk margin to change in the SCR calculation might be a way of dealing with this point rather than the ABI’s tapering approach.
Mr Pelkiewicz (responding): A technical point on that: the regulations for the standard formula prohibit you from stressing the risk margin when you calculate SCR. In accordance with our model, if you did so it would slightly increase the SCR for the monoline annuity firm. It does not make a huge amount of difference.
Somebody mentioned previously the mass lapse stress. I have experience in this area. If your risk margin is dominated by the mass lapse stress, then if you were allowed to stress the risk margin when you calculated SCR, the SCR would fairly obviously reduce very significantly. It depends on the shape of your risk.
The Chairman (closing): I was reflecting on Andrew (Chamberlain)’s comments at the start that this was an excellent paper, and very balanced and hence maybe there would not be very much to disagree with. We have heard some quite extreme views and if I heard you correctly, Andrew, suggesting that we abolish market consistency.
The paper does not suggest that some of the current regulations around risk margin are as ridiculous as some commentators might say. Fixed-term cost of capital rate, for example, we heard is, if anything, too low. The simple addition of the matching adjustment may not be the magic bullet to solve some of these challenges.
We have had a good debate about some of the other areas that have been suggested within the paper that could be fixes.
There are challenges around prices of reinsurance. There is quite a lot of support from those here that perhaps it is not as bad as some others might suggest. In particular, it may be consistent with what we are already doing in the investment space, which is welcome.
It is to be hoped that the debate will continue. It remains for me to say thanks once again to the working party and to the speakers and we all agree that it is an excellent, balanced paper.







