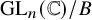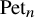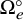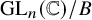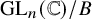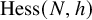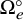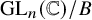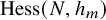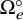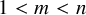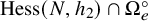1 Introduction
Hessenberg varieties are subvarieties of the full flag variety introduced by De Mari and Shayman and studied by De Mari, Procesi and Shayman [Reference De Mari, Procesi and Shayman11, Reference De Mari and Shayman12]. These varieties lie in a fruitful intersection of algebraic combinatorics and representation theory, such as hyperplane arrangements ([Reference Abe, Horiguchi, Masuda, Murai and Sato4, Reference Enokizono, Horiguchi, Nagaoka and Tsuchiya14, Reference Sommers and Tymoczko34]), Stanley’s chromatic symmetric functions ([Reference Brosnan and Chow9, Reference Guay-Paquet23, Reference Kiem and Lee27, Reference Shareshian and Wachs33]), Postnikov’s mixed Eulerian numbers ([Reference Berget, Spink and Tseng8, Reference Horiguchi24, Reference Nadeau and Tewari30]) and toric orbifolds associated with partitioned weight polytopes ([Reference Balibanu and Crooks7, Reference Horiguchi, Masuda, Shareshian and Song25]) in a recent development. In this paper, we generalize a result discovered by Dale Peterson to regular nilpotent Hessenberg varieties in type A via the explicit presentation of the quantum cohomology ring of flag varieties given by Ciocan–Fontanine and Givental–Kim.
Let n be a positive integer. The (full) flag variety
![]() $Fl({\mathbb {C}}^n)$
is the collection of nested sequences of linear subspaces
$Fl({\mathbb {C}}^n)$
is the collection of nested sequences of linear subspaces ![]() in
in
![]() ${\mathbb {C}}^n$
, where each
${\mathbb {C}}^n$
, where each
![]() $V_i$
denotes an i-dimensional subspace of
$V_i$
denotes an i-dimensional subspace of
![]() ${\mathbb {C}}^n$
. Let N be the regular nilpotent matrix in Jordan canonical form, that is, the nilpotent matrix in Jordan form with exactly one Jordan block. The Peterson variety
${\mathbb {C}}^n$
. Let N be the regular nilpotent matrix in Jordan canonical form, that is, the nilpotent matrix in Jordan form with exactly one Jordan block. The Peterson variety
![]() $\operatorname {\mathrm {Pet}}_n$
is defined to be the subvariety of the flag variety
$\operatorname {\mathrm {Pet}}_n$
is defined to be the subvariety of the flag variety
![]() $Fl({\mathbb {C}}^n)$
as follows:
$Fl({\mathbb {C}}^n)$
as follows:
Dale Peterson has discovered a surprising connection between a geometry of the Peterson variety
![]() $\operatorname {\mathrm {Pet}}_n$
and the quantum cohomologyFootnote
1
of the flag variety
$\operatorname {\mathrm {Pet}}_n$
and the quantum cohomologyFootnote
1
of the flag variety
![]() $Fl({\mathbb {C}}^n)$
, as explained below. Let
$Fl({\mathbb {C}}^n)$
, as explained below. Let
![]() $B^{-}$
be the set of lower triangular matrices in the general linear group
$B^{-}$
be the set of lower triangular matrices in the general linear group
![]() $\operatorname {\mathrm {GL}}_n({\mathbb {C}})$
. Let
$\operatorname {\mathrm {GL}}_n({\mathbb {C}})$
. Let
![]() $\Omega _e^\circ $
be the opposite Schubert cell associated with the identity element e, which is the
$\Omega _e^\circ $
be the opposite Schubert cell associated with the identity element e, which is the
![]() $B^{-}$
-orbit of the standard flag
$B^{-}$
-orbit of the standard flag
![]() $F_\bullet =(F_i)_{i}$
, where
$F_\bullet =(F_i)_{i}$
, where
![]() $F_i=\operatorname {\mathrm {span}}_{\mathbb {C}}\{e_1,\ldots ,e_i \}$
and
$F_i=\operatorname {\mathrm {span}}_{\mathbb {C}}\{e_1,\ldots ,e_i \}$
and
![]() $e_1,\ldots ,e_n$
are the standard basis of
$e_1,\ldots ,e_n$
are the standard basis of
![]() ${\mathbb {C}}^n$
. Note that
${\mathbb {C}}^n$
. Note that
![]() $\Omega _e^\circ $
is the open chart around the standard flag
$\Omega _e^\circ $
is the open chart around the standard flag
![]() $F_\bullet =(F_i)_{i}$
in
$F_\bullet =(F_i)_{i}$
in
![]() $Fl({\mathbb {C}}^n)$
. Due to Peterson’s statements in [Reference Peterson31], the coordinate ring of the intersection
$Fl({\mathbb {C}}^n)$
. Due to Peterson’s statements in [Reference Peterson31], the coordinate ring of the intersection
![]() ${\mathbb {C}}[\operatorname {\mathrm {Pet}}_n \cap \Omega _e^\circ ]$
is isomorphic to the quantum cohomology of the flag variety
${\mathbb {C}}[\operatorname {\mathrm {Pet}}_n \cap \Omega _e^\circ ]$
is isomorphic to the quantum cohomology of the flag variety
![]() $QH^*(Fl({\mathbb {C}}^n))$
as
$QH^*(Fl({\mathbb {C}}^n))$
as
![]() ${\mathbb {C}}$
-algebras:
${\mathbb {C}}$
-algebras:
This incredible result discovered by Peterson is unpublished, so we also refer the reader to [Reference Kostant29, Reference Rietsch32] for the result above. As
![]() ${\mathbb {C}}$
-vector spaces, the quantum cohomology
${\mathbb {C}}$
-vector spaces, the quantum cohomology
![]() $QH^*(Fl({\mathbb {C}}^n))$
is
$QH^*(Fl({\mathbb {C}}^n))$
is
![]() ${\mathbb {C}}1[q_1,\ldots ,q_{n-1}] \otimes _{\mathbb {C}} H^*(Fl({\mathbb {C}}^n))$
where we call
${\mathbb {C}}1[q_1,\ldots ,q_{n-1}] \otimes _{\mathbb {C}} H^*(Fl({\mathbb {C}}^n))$
where we call
![]() $q_1,\ldots ,q_{n-1}$
quantum parameters. The product structure on
$q_1,\ldots ,q_{n-1}$
quantum parameters. The product structure on
![]() $QH^*(Fl({\mathbb {C}}^n))$
is a certain deformation by quantum parameters of the ordinary cup product on
$QH^*(Fl({\mathbb {C}}^n))$
is a certain deformation by quantum parameters of the ordinary cup product on
![]() $H^*(Fl({\mathbb {C}}^n))$
. More explicitly, Ciocan–Fontanine and Givental–Kim gave in [Reference Ciocan-Fontanine16, Reference Givental and Kim22] an efficient presentation of the quantum cohomology ring
$H^*(Fl({\mathbb {C}}^n))$
. More explicitly, Ciocan–Fontanine and Givental–Kim gave in [Reference Ciocan-Fontanine16, Reference Givental and Kim22] an efficient presentation of the quantum cohomology ring
![]() $QH^*(Fl({\mathbb {C}}^n))$
in terms of generators and relations as follows. Let
$QH^*(Fl({\mathbb {C}}^n))$
in terms of generators and relations as follows. Let
![]() $\check M_n$
be the following matrix
$\check M_n$
be the following matrix

The quantized elementary symmetric polynomial
![]() $\check E_i^{(n)} \ (1 \leq i \leq n)$
in the polynomial ring
$\check E_i^{(n)} \ (1 \leq i \leq n)$
in the polynomial ring
![]() ${\mathbb {C}}[x_1,\ldots ,x_n,q_1,\ldots ,q_{n-1}]$
is defined by the coefficient of
${\mathbb {C}}[x_1,\ldots ,x_n,q_1,\ldots ,q_{n-1}]$
is defined by the coefficient of
![]() $\lambda ^{n-i}$
for the characteristic polynomial of
$\lambda ^{n-i}$
for the characteristic polynomial of
![]() $\check M_n$
multiplied by
$\check M_n$
multiplied by
![]() $(-1)^i$
, that is,
$(-1)^i$
, that is,
Note that by setting
![]() $q_s=0$
for all
$q_s=0$
for all
![]() $1 \leq s \leq n-1$
we have that
$1 \leq s \leq n-1$
we have that
![]() $\check E_i^{(n)}$
is the i-th elementary symmetric polynomial in the variables
$\check E_i^{(n)}$
is the i-th elementary symmetric polynomial in the variables
![]() $x_1,\ldots ,x_n$
. Then it is known from [Reference Ciocan-Fontanine16, Reference Givental and Kim22] that there is an isomorphism of
$x_1,\ldots ,x_n$
. Then it is known from [Reference Ciocan-Fontanine16, Reference Givental and Kim22] that there is an isomorphism of
![]() ${\mathbb {C}}$
-algebras
${\mathbb {C}}$
-algebras
Combining Peterson’s statement and the presentation above, we obtain the isomorphism
as
![]() ${\mathbb {C}}$
-algebras. In this paper, we generalize this isomorphism to regular nilpotent Hessenberg varieties by further quantizing the right-hand side above.
${\mathbb {C}}$
-algebras. In this paper, we generalize this isomorphism to regular nilpotent Hessenberg varieties by further quantizing the right-hand side above.
Consider a nondecreasing function
![]() $h: [n] \rightarrow [n]$
such that
$h: [n] \rightarrow [n]$
such that
![]() $h(j) \geq j$
for all
$h(j) \geq j$
for all
![]() $j=1,\ldots ,n$
where
$j=1,\ldots ,n$
where ![]() , which is called a Hessenberg function. We frequently write a Hessenberg function h as
, which is called a Hessenberg function. We frequently write a Hessenberg function h as
![]() $h = (h(1), h(2), \ldots , h(n))$
. The regular nilpotent Hessenberg variety
$h = (h(1), h(2), \ldots , h(n))$
. The regular nilpotent Hessenberg variety
![]() $\operatorname {\mathrm {Hess}}(N,h)$
associated with a Hessenberg function h is defined as
$\operatorname {\mathrm {Hess}}(N,h)$
associated with a Hessenberg function h is defined as
This object is a generalization of the Peterson variety
![]() $\operatorname {\mathrm {Pet}}_n$
since
$\operatorname {\mathrm {Pet}}_n$
since
![]() $\operatorname {\mathrm {Hess}}(N,h)$
is equal to
$\operatorname {\mathrm {Hess}}(N,h)$
is equal to
![]() $\operatorname {\mathrm {Pet}}_n$
whenever
$\operatorname {\mathrm {Pet}}_n$
whenever
![]() $h=(2,3,4,\ldots ,n,n)$
. We also note that if
$h=(2,3,4,\ldots ,n,n)$
. We also note that if
![]() $h=(n,n,\ldots ,n)$
, then
$h=(n,n,\ldots ,n)$
, then
![]() $\operatorname {\mathrm {Hess}}(N,h)=Fl({\mathbb {C}}^n)$
by definition. Recall that the flag variety
$\operatorname {\mathrm {Hess}}(N,h)=Fl({\mathbb {C}}^n)$
by definition. Recall that the flag variety
![]() $Fl({\mathbb {C}}^n)$
can be identified with
$Fl({\mathbb {C}}^n)$
can be identified with
![]() $\operatorname {\mathrm {GL}}_n({\mathbb {C}})/B$
where B is the set of upper triangular matrices in
$\operatorname {\mathrm {GL}}_n({\mathbb {C}})/B$
where B is the set of upper triangular matrices in
![]() $\operatorname {\mathrm {GL}}_n({\mathbb {C}})$
so that the first j column vectors of a matrix
$\operatorname {\mathrm {GL}}_n({\mathbb {C}})$
so that the first j column vectors of a matrix
![]() $g \in \operatorname {\mathrm {GL}}_n({\mathbb {C}})$
generate the j-th vector space
$g \in \operatorname {\mathrm {GL}}_n({\mathbb {C}})$
generate the j-th vector space
![]() $V_j$
for
$V_j$
for
![]() $j \in [n]$
. Under the identification
$j \in [n]$
. Under the identification
![]() $Fl({\mathbb {C}}^n) \cong \operatorname {\mathrm {GL}}_n({\mathbb {C}})/B$
, one can write
$Fl({\mathbb {C}}^n) \cong \operatorname {\mathrm {GL}}_n({\mathbb {C}})/B$
, one can write
where
![]() $H(h)$
is the set of matrices
$H(h)$
is the set of matrices
![]() $(a_{ij})_{i,j \in [n]}$
such that
$(a_{ij})_{i,j \in [n]}$
such that
![]() $a_{ij} = 0$
if
$a_{ij} = 0$
if
![]() $i> h(j)$
. (Note that a matrix
$i> h(j)$
. (Note that a matrix
![]() $(a_{ij})_{i,j \in [n]}$
in
$(a_{ij})_{i,j \in [n]}$
in
![]() $H(h)$
is not necessarily invertible.) Since
$H(h)$
is not necessarily invertible.) Since
![]() $\Omega _e^\circ $
is an affine open set in
$\Omega _e^\circ $
is an affine open set in
![]() $Fl({\mathbb {C}}^n)$
which is naturally identified with the set of lower triangular unipotent matrices, the intersection
$Fl({\mathbb {C}}^n)$
which is naturally identified with the set of lower triangular unipotent matrices, the intersection
![]() $\operatorname {\mathrm {Hess}}(N,h) \cap \Omega _e^\circ $
is described as
$\operatorname {\mathrm {Hess}}(N,h) \cap \Omega _e^\circ $
is described as
 $$ \begin{align} \operatorname{\mathrm{Hess}}(N,h) \cap \Omega_e^\circ = \left\{ g=\left( \begin{array}{@{\,}ccccc@{\,}} 1 & & & & \\ x_{21} & 1 & & & \\ x_{31} & x_{32} & 1 & & \\ \vdots& \vdots & \ddots & \ddots & \\ x_{n1} & x_{n2} & \cdots & x_{n \, n-1} & 1 \end{array} \right) \ \middle| (g^{-1}Ng)_{ij}=0 \ \text{for all} \atop \ j \in [n-1] \ \text{and} \ h(j) < i \leq n \right\}. \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Hess}}(N,h) \cap \Omega_e^\circ = \left\{ g=\left( \begin{array}{@{\,}ccccc@{\,}} 1 & & & & \\ x_{21} & 1 & & & \\ x_{31} & x_{32} & 1 & & \\ \vdots& \vdots & \ddots & \ddots & \\ x_{n1} & x_{n2} & \cdots & x_{n \, n-1} & 1 \end{array} \right) \ \middle| (g^{-1}Ng)_{ij}=0 \ \text{for all} \atop \ j \in [n-1] \ \text{and} \ h(j) < i \leq n \right\}. \end{align} $$
Motivated by this, we set
We remark that this scheme can be regarded as a zero scheme of some section of certain vector bundle over
![]() $\operatorname {\mathrm {GL}}_n({\mathbb {C}})/B$
, which is introduced in [Reference Abe, DeDieu, Galetto and Harada1]. See Section 3 for the details.
$\operatorname {\mathrm {GL}}_n({\mathbb {C}})/B$
, which is introduced in [Reference Abe, DeDieu, Galetto and Harada1]. See Section 3 for the details.
We now generalize the matrix
![]() $\check M_n$
in equation (1.1) to the following matrix
$\check M_n$
in equation (1.1) to the following matrix

Then we define the
![]() $q_{rs}$
-quantized elementary symmetric polynomial
$q_{rs}$
-quantized elementary symmetric polynomial
![]() $E_i^{(n)} \ (1 \leq i \leq n)$
in the polynomial ring
$E_i^{(n)} \ (1 \leq i \leq n)$
in the polynomial ring
![]() ${\mathbb {C}}[x_1,\ldots ,x_n,q_{rs} \mid 1 \leq r < s \leq n]$
by the coefficient of
${\mathbb {C}}[x_1,\ldots ,x_n,q_{rs} \mid 1 \leq r < s \leq n]$
by the coefficient of
![]() $\lambda ^{n-i}$
for the characteristic polynomial of
$\lambda ^{n-i}$
for the characteristic polynomial of
![]() $M_n$
multiplied by
$M_n$
multiplied by
![]() $(-1)^i$
, namely
$(-1)^i$
, namely
Note that by setting
![]() $q_{rs}=0$
for
$q_{rs}=0$
for
![]() $s-r>1$
and
$s-r>1$
and
![]() $q_{s \, s+1}=q_s$
, our polynomial
$q_{s \, s+1}=q_s$
, our polynomial
![]() $E_i^{(n)}$
is the (classical) quantized elementary symmetric polynomial
$E_i^{(n)}$
is the (classical) quantized elementary symmetric polynomial
![]() $\check E_i^{(n)}$
in
$\check E_i^{(n)}$
in
![]() ${\mathbb {C}}[x_1,\ldots ,x_n,q_1,\ldots ,q_{n-1}]$
. For a Hessenberg function
${\mathbb {C}}[x_1,\ldots ,x_n,q_1,\ldots ,q_{n-1}]$
. For a Hessenberg function
![]() $h: [n] \rightarrow [n]$
, we define
$h: [n] \rightarrow [n]$
, we define
![]() $^h E_i^{(n)}$
as the polynomial
$^h E_i^{(n)}$
as the polynomial
![]() $E_i^{(n)}$
by setting
$E_i^{(n)}$
by setting
![]() $q_{rs}=0$
for all
$q_{rs}=0$
for all
![]() $2 \leq s \leq n$
and
$2 \leq s \leq n$
and
![]() $1 \leq r \leq n-h(n+1-s)$
:
$1 \leq r \leq n-h(n+1-s)$
:
We will pictorially explain which variables
![]() $q_{rs}$
are set to
$q_{rs}$
are set to
![]() $0$
in the definition of
$0$
in the definition of
![]() $^h E_i^{(n)}$
in Example 4.11 and surrounding discussion. The main theorem of this paper is as follows:
$^h E_i^{(n)}$
in Example 4.11 and surrounding discussion. The main theorem of this paper is as follows:
Theorem 1.1. Let
![]() $h: [n] \rightarrow [n]$
be a Hessenberg function. Then there is an isomorphism of
$h: [n] \rightarrow [n]$
be a Hessenberg function. Then there is an isomorphism of
![]() ${\mathbb {C}}$
-algebras
${\mathbb {C}}$
-algebras
 $$ \begin{align} \Gamma(\mathcal{Z}(N,h)_e, \mathcal{O}_{\mathcal{Z}(N,h)_e}) \cong \frac{{\mathbb{C}}[x_1,\ldots,x_n, q_{rs} \mid 2 \leq s \leq n, n-h(n+1-s)<r<s]}{(^h E_1^{(n)}, \ldots, \, ^h E_n^{(n)})}, \end{align} $$
$$ \begin{align} \Gamma(\mathcal{Z}(N,h)_e, \mathcal{O}_{\mathcal{Z}(N,h)_e}) \cong \frac{{\mathbb{C}}[x_1,\ldots,x_n, q_{rs} \mid 2 \leq s \leq n, n-h(n+1-s)<r<s]}{(^h E_1^{(n)}, \ldots, \, ^h E_n^{(n)})}, \end{align} $$
where
![]() $\Gamma (\mathcal {Z}(N,h)_e, \mathcal {O}_{\mathcal {Z}(N,h)_e})$
is the set of global sections.
$\Gamma (\mathcal {Z}(N,h)_e, \mathcal {O}_{\mathcal {Z}(N,h)_e})$
is the set of global sections.
Note that we explicitly construct the isomorphism above. See Theorem 4.13 and Proposition 7.3 for the correspondence. In particular, we see that our quantum parameters
![]() $q_{rs}$
’s correspond to polynomials which define regular nilpotent Hessenberg varieties (up to signs). See Corollary 7.4.
$q_{rs}$
’s correspond to polynomials which define regular nilpotent Hessenberg varieties (up to signs). See Corollary 7.4.
As is well known, the cohomology ring
![]() $H^*(Fl({\mathbb {C}}^n))$
is isomorphic to the quotient of the polynomial ring
$H^*(Fl({\mathbb {C}}^n))$
is isomorphic to the quotient of the polynomial ring
![]() ${\mathbb {C}}[x_1,\ldots ,x_n]$
by the ideal generated by elementary symmetric polynomials, so the following is a consequence of Theorem 1.1.
${\mathbb {C}}[x_1,\ldots ,x_n]$
by the ideal generated by elementary symmetric polynomials, so the following is a consequence of Theorem 1.1.
Corollary 1.2. There is an isomorphism of
![]() ${\mathbb {C}}$
-algebras
${\mathbb {C}}$
-algebras
We say that a Hessenberg function
![]() $h: [n] \rightarrow [n]$
is indecomposable if it satisfies
$h: [n] \rightarrow [n]$
is indecomposable if it satisfies
![]() $h(j)>j$
for all
$h(j)>j$
for all
![]() $j \in [n-1]$
. It is known from [Reference Abe, DeDieu, Galetto and Harada1, Proposition 3.6] that if h is indecomposable, then the affine scheme
$j \in [n-1]$
. It is known from [Reference Abe, DeDieu, Galetto and Harada1, Proposition 3.6] that if h is indecomposable, then the affine scheme
![]() $\mathcal {Z}(N,h)_e$
is reduced. Therefore, we can conclude the following result from Theorem 1.1.
$\mathcal {Z}(N,h)_e$
is reduced. Therefore, we can conclude the following result from Theorem 1.1.
Corollary 1.3. If
![]() $h: [n] \rightarrow [n]$
is an indecomposable Hessenberg function, then there is an isomorphism of
$h: [n] \rightarrow [n]$
is an indecomposable Hessenberg function, then there is an isomorphism of
![]() ${\mathbb {C}}$
-algebras
${\mathbb {C}}$
-algebras
 $$ \begin{align*} {\mathbb{C}}[\operatorname{\mathrm{Hess}}(N,h) \cap \Omega_e^\circ] \cong \frac{{\mathbb{C}}[x_1,\ldots,x_n, q_{rs} \mid 2 \leq s \leq n, n-h(n+1-s)<r<s]}{(^h E_1^{(n)}, \ldots, \, ^h E_n^{(n)})}, \end{align*} $$
$$ \begin{align*} {\mathbb{C}}[\operatorname{\mathrm{Hess}}(N,h) \cap \Omega_e^\circ] \cong \frac{{\mathbb{C}}[x_1,\ldots,x_n, q_{rs} \mid 2 \leq s \leq n, n-h(n+1-s)<r<s]}{(^h E_1^{(n)}, \ldots, \, ^h E_n^{(n)})}, \end{align*} $$
where
![]() ${\mathbb {C}}[\operatorname {\mathrm {Hess}}(N,h) \cap \Omega _e^\circ ]$
is the coordinate ring of the open set
${\mathbb {C}}[\operatorname {\mathrm {Hess}}(N,h) \cap \Omega _e^\circ ]$
is the coordinate ring of the open set
![]() $\operatorname {\mathrm {Hess}}(N,h) \cap \Omega _e^\circ $
in
$\operatorname {\mathrm {Hess}}(N,h) \cap \Omega _e^\circ $
in
![]() $\operatorname {\mathrm {Hess}}(N,h)$
.
$\operatorname {\mathrm {Hess}}(N,h)$
.
The isomorphism in Corollary 1.3 is a natural generalization of equation (1.2) since the Hessenberg function
![]() $h=(2,3,4,\ldots ,n,n)$
which defines the Peterson variety
$h=(2,3,4,\ldots ,n,n)$
which defines the Peterson variety
![]() $\operatorname {\mathrm {Pet}}_n$
is indecomposable. In particular, our proof gives an elementary proof for Peterson’s statement via the presentation for the quantum cohomology
$\operatorname {\mathrm {Pet}}_n$
is indecomposable. In particular, our proof gives an elementary proof for Peterson’s statement via the presentation for the quantum cohomology
![]() $QH^*(Fl({\mathbb {C}}^n))$
given by [Reference Ciocan-Fontanine16, Reference Givental and Kim22].
$QH^*(Fl({\mathbb {C}}^n))$
given by [Reference Ciocan-Fontanine16, Reference Givental and Kim22].
We next apply Corollary 1.3 to the study of the singular locus of the open set
![]() $\operatorname {\mathrm {Hess}}(N,h) \cap \Omega _e^\circ $
in
$\operatorname {\mathrm {Hess}}(N,h) \cap \Omega _e^\circ $
in
![]() $\operatorname {\mathrm {Hess}}(N,h)$
for some Hessenberg functions h. There are partial results for studying singularities of Hessenberg varieties in [Reference Abe and Insko3, Reference Escobar, Precup and Shareshian15, Reference Insko and Yong26]. Indeed, an explicit presentation of the singular locus for the Peteson variety
$\operatorname {\mathrm {Hess}}(N,h)$
for some Hessenberg functions h. There are partial results for studying singularities of Hessenberg varieties in [Reference Abe and Insko3, Reference Escobar, Precup and Shareshian15, Reference Insko and Yong26]. Indeed, an explicit presentation of the singular locus for the Peteson variety
![]() $\operatorname {\mathrm {Pet}}_n$
is given by [Reference Insko and Yong26]. The singular locus for nilpotent Hessenberg varieties of codimension one in the flag variety
$\operatorname {\mathrm {Pet}}_n$
is given by [Reference Insko and Yong26]. The singular locus for nilpotent Hessenberg varieties of codimension one in the flag variety
![]() $Fl({\mathbb {C}}^n)$
is explicitly described in [Reference Escobar, Precup and Shareshian15]. Also, a recent paper [Reference Abe and Insko3] combinatorially determines which permutation flags in arbitrary regular nilpotent Hessenberg variety
$Fl({\mathbb {C}}^n)$
is explicitly described in [Reference Escobar, Precup and Shareshian15]. Also, a recent paper [Reference Abe and Insko3] combinatorially determines which permutation flags in arbitrary regular nilpotent Hessenberg variety
![]() $\operatorname {\mathrm {Hess}}(N,h)$
are singular points. We focus on the following Hessenberg function
$\operatorname {\mathrm {Hess}}(N,h)$
are singular points. We focus on the following Hessenberg function
We derive an explicit presentation of the singular locus of
![]() $\operatorname {\mathrm {Hess}}(N,h_m)$
from Corollary 1.3. For this purpose, we first study the singular locus of
$\operatorname {\mathrm {Hess}}(N,h_m)$
from Corollary 1.3. For this purpose, we first study the singular locus of
![]() $\operatorname {\mathrm {Hess}}(N,h_2)$
. More precisely, we show that the singularity of
$\operatorname {\mathrm {Hess}}(N,h_2)$
. More precisely, we show that the singularity of
![]() $\operatorname {\mathrm {Hess}}(N,h_2) \cap \Omega _e^\circ $
is related with a cyclic quotient singularity. We briefly explain the cyclic quotient singularity. Let
$\operatorname {\mathrm {Hess}}(N,h_2) \cap \Omega _e^\circ $
is related with a cyclic quotient singularity. We briefly explain the cyclic quotient singularity. Let
![]() $\mathfrak C_n$
be the cyclic group of order n generated by
$\mathfrak C_n$
be the cyclic group of order n generated by
![]() $\zeta $
, where
$\zeta $
, where
![]() $\zeta $
is a primitive n-th root of unity. Define the action of
$\zeta $
is a primitive n-th root of unity. Define the action of
![]() $\mathfrak C_n$
on
$\mathfrak C_n$
on
![]() ${\mathbb {C}}^2$
by
${\mathbb {C}}^2$
by
![]() $\zeta \cdot (x,y)=(\zeta x, \zeta ^{-1} y)$
for
$\zeta \cdot (x,y)=(\zeta x, \zeta ^{-1} y)$
for
![]() $\zeta \in \mathfrak C_n$
and
$\zeta \in \mathfrak C_n$
and
![]() $(x,y) \in {\mathbb {C}}^2$
. Then, the quotient space
$(x,y) \in {\mathbb {C}}^2$
. Then, the quotient space
![]() ${\mathbb {C}}^2/\mathfrak C_n$
is called the cyclic quotient singularity or the type
${\mathbb {C}}^2/\mathfrak C_n$
is called the cyclic quotient singularity or the type
![]() $A_{n-1}$
-singularity.
$A_{n-1}$
-singularity.
Theorem 1.4. There is an isomorphism
where
![]() $h_2=(2,n,\ldots ,n)$
.
$h_2=(2,n,\ldots ,n)$
.
Recall that
![]() $\operatorname {\mathrm {Hess}}(N,h_m) \cap \Omega _e^\circ $
is given in equation (1.3). As a corollary of Theorem 1.4, one can give the singular locus of
$\operatorname {\mathrm {Hess}}(N,h_m) \cap \Omega _e^\circ $
is given in equation (1.3). As a corollary of Theorem 1.4, one can give the singular locus of
![]() $\operatorname {\mathrm {Hess}}(N,h_2) \cap \Omega _e^\circ $
as the solution set of the equations
$\operatorname {\mathrm {Hess}}(N,h_2) \cap \Omega _e^\circ $
as the solution set of the equations
![]() $x_{i1}=0$
for
$x_{i1}=0$
for
![]() $2 \leq i \leq n$
and
$2 \leq i \leq n$
and
![]() $x_{n2}=0$
. Combining this description and Corollary 1.3, we can explicitly describe the singular locus of
$x_{n2}=0$
. Combining this description and Corollary 1.3, we can explicitly describe the singular locus of
![]() $\operatorname {\mathrm {Hess}}(N,h_m) \cap \Omega _e^\circ $
as follows.
$\operatorname {\mathrm {Hess}}(N,h_m) \cap \Omega _e^\circ $
as follows.
Theorem 1.5. Let
![]() $h_m$
be the Hessenberg function defined in equation (1.6) for
$h_m$
be the Hessenberg function defined in equation (1.6) for
![]() $2 \leq m \leq n-1$
. Then, the singular locus of
$2 \leq m \leq n-1$
. Then, the singular locus of
![]() $\operatorname {\mathrm {Hess}}(N,h_m) \cap \Omega _e^\circ $
is described as
$\operatorname {\mathrm {Hess}}(N,h_m) \cap \Omega _e^\circ $
is described as
 $$ \begin{align*} \left\{ g=\left( \begin{array}{@{\,}ccccc@{\,}} 1 & & & & \\ x_{21} & 1 & & & \\ x_{31} & x_{32} & 1 & & \\ \vdots& \vdots & \ddots & \ddots & \\ x_{n1} & x_{n2} & \cdots & x_{n \, n-1} & 1 \end{array} \right) \ \middle| x_{i1} = 0 \ \text{for all} \ 2 \leq i \leq n \atop \ \text{and} \ x_{nj} = 0 \ \text{for all} \ 2 \leq j \leq m \right\}. \end{align*} $$
$$ \begin{align*} \left\{ g=\left( \begin{array}{@{\,}ccccc@{\,}} 1 & & & & \\ x_{21} & 1 & & & \\ x_{31} & x_{32} & 1 & & \\ \vdots& \vdots & \ddots & \ddots & \\ x_{n1} & x_{n2} & \cdots & x_{n \, n-1} & 1 \end{array} \right) \ \middle| x_{i1} = 0 \ \text{for all} \ 2 \leq i \leq n \atop \ \text{and} \ x_{nj} = 0 \ \text{for all} \ 2 \leq j \leq m \right\}. \end{align*} $$
The explicit presentation in Theorem 1.5 is certain Schubert variety in the open set
![]() $\Omega _e^\circ $
, as explained below. Let
$\Omega _e^\circ $
, as explained below. Let
![]() $\mathfrak S_n$
be the permutation group on
$\mathfrak S_n$
be the permutation group on
![]() $[n]$
. For
$[n]$
. For
![]() $w \in \mathfrak S_n$
, the Schubert variety
$w \in \mathfrak S_n$
, the Schubert variety
![]() $X_w$
is defined by
$X_w$
is defined by
where
![]() $F_\bullet =(F_i)_{i}$
is the standard flag, that is,
$F_\bullet =(F_i)_{i}$
is the standard flag, that is,
![]() $F_i=\operatorname {\mathrm {span}}_{\mathbb {C}}\{e_1,\ldots ,e_i \}$
and
$F_i=\operatorname {\mathrm {span}}_{\mathbb {C}}\{e_1,\ldots ,e_i \}$
and
![]() $e_1,\ldots ,e_n$
are the standard basis of
$e_1,\ldots ,e_n$
are the standard basis of
![]() ${\mathbb {C}}^n$
. For
${\mathbb {C}}^n$
. For
![]() $2 \leq m \leq n-1$
, we define the permutation
$2 \leq m \leq n-1$
, we define the permutation
![]() $w_m \in \mathfrak S_n$
by
$w_m \in \mathfrak S_n$
by
in one-line notation. (See also equation (10.6).) Then one can see that
so we obtain the following result from Theorem 1.5.
Corollary 1.6. Let
![]() $2 \leq m \leq n-1$
. Then, the singular locus of
$2 \leq m \leq n-1$
. Then, the singular locus of
![]() $\operatorname {\mathrm {Hess}}(N,h_m) \cap \Omega _e^\circ $
is equal to
$\operatorname {\mathrm {Hess}}(N,h_m) \cap \Omega _e^\circ $
is equal to
The paper is organized as follows. After reviewing the definition of Hessenberg varieties and their defining equations in Section 2, we focus on regular nilpotent Hessenberg varieties in Section 3. Then we state the main theorem (Theorem 4.13) in Section 4. In Section 5, we show that the homomorphism (1.5) is well defined and surjective. In order to prove that it is in fact an isomorphism, we use the commutative algebra’s tool of Hilbert series and regular sequences. More specifically, we define certain degrees for the variables
![]() $\{x_{ij} \mid 1 \leq j < i \leq n \}$
appeared in equation (1.3) and
$\{x_{ij} \mid 1 \leq j < i \leq n \}$
appeared in equation (1.3) and
![]() $\{x_1,\ldots ,x_n, q_{rs} \mid 1 \leq r < s \leq n \}$
introduced in equation (1.4) so that the two sides of equation (1.5) are graded
$\{x_1,\ldots ,x_n, q_{rs} \mid 1 \leq r < s \leq n \}$
introduced in equation (1.4) so that the two sides of equation (1.5) are graded
![]() ${\mathbb {C}}$
-algebras in Section 6. We give a proof of our main theorem in Section 7. Next, turning our attention to the singular locus of
${\mathbb {C}}$
-algebras in Section 6. We give a proof of our main theorem in Section 7. Next, turning our attention to the singular locus of
![]() $\operatorname {\mathrm {Hess}}(N,h_m) \cap \Omega _e^\circ $
, where
$\operatorname {\mathrm {Hess}}(N,h_m) \cap \Omega _e^\circ $
, where
![]() $h_m$
is defined in equation (1.6), we give an explicit formula for partial derivatives
$h_m$
is defined in equation (1.6), we give an explicit formula for partial derivatives
![]() $\frac {\partial }{\partial x_s} \, ^h E_{i}^{(n)}$
and
$\frac {\partial }{\partial x_s} \, ^h E_{i}^{(n)}$
and
![]() $\frac {\partial }{\partial q_{rs}} \, ^h E_{i}^{(n)}$
in Section 8. Then we relate the singularity of
$\frac {\partial }{\partial q_{rs}} \, ^h E_{i}^{(n)}$
in Section 8. Then we relate the singularity of
![]() $\operatorname {\mathrm {Hess}}(N,h_2) \cap \Omega _e^\circ $
to the cyclic quotient singularity (Theorem 9.7) in Section 9. One can see that this fact yields an explicit description for the singular locus of
$\operatorname {\mathrm {Hess}}(N,h_2) \cap \Omega _e^\circ $
to the cyclic quotient singularity (Theorem 9.7) in Section 9. One can see that this fact yields an explicit description for the singular locus of
![]() $\operatorname {\mathrm {Hess}}(N,h_2) \cap \Omega _e^\circ $
(Corollary 9.9). In Section 10, we generalize this result to the singular locus of
$\operatorname {\mathrm {Hess}}(N,h_2) \cap \Omega _e^\circ $
(Corollary 9.9). In Section 10, we generalize this result to the singular locus of
![]() $\operatorname {\mathrm {Hess}}(N,h_m) \cap \Omega _e^\circ $
(Theorem 10.1) by using our main theorem together with the computations for partial derivatives
$\operatorname {\mathrm {Hess}}(N,h_m) \cap \Omega _e^\circ $
(Theorem 10.1) by using our main theorem together with the computations for partial derivatives
![]() $\frac {\partial }{\partial x_s} \, ^h E_{i}^{(n)}$
and
$\frac {\partial }{\partial x_s} \, ^h E_{i}^{(n)}$
and
![]() $\frac {\partial }{\partial q_{rs}} \, ^h E_{i}^{(n)}$
. We also see that the singular locus of
$\frac {\partial }{\partial q_{rs}} \, ^h E_{i}^{(n)}$
. We also see that the singular locus of
![]() $\operatorname {\mathrm {Hess}}(N,h_m) \cap \Omega _e^\circ $
is equal to the intersection of the Schubert variety
$\operatorname {\mathrm {Hess}}(N,h_m) \cap \Omega _e^\circ $
is equal to the intersection of the Schubert variety
![]() $X_{w_m}$
and
$X_{w_m}$
and
![]() $\Omega _e^\circ $
(Corollary 10.2).
$\Omega _e^\circ $
(Corollary 10.2).
2 Hessenberg varieties
In this section, we recall the definitions of Hessenberg varieties in type
![]() $A_{n-1}$
and their defining equations. We use the notation
$A_{n-1}$
and their defining equations. We use the notation ![]() throughout this paper.
throughout this paper.
Let n be a positive integer. A Hessenberg function is a function
![]() $h: [n] \to [n]$
satisfying the following two conditions
$h: [n] \to [n]$
satisfying the following two conditions
-
1.
 $h(1) \leq h(2) \leq \cdots \leq h(n)$
;
$h(1) \leq h(2) \leq \cdots \leq h(n)$
; -
2.
 $h(j) \geq j$
for all
$h(j) \geq j$
for all
 $j \in [n]$
.
$j \in [n]$
.
Note that
![]() $h(n)=n$
by definition. We frequently denote a Hessenberg function by listing its values in sequence, namely
$h(n)=n$
by definition. We frequently denote a Hessenberg function by listing its values in sequence, namely
![]() $h = (h(1), h(2), \ldots , h(n))$
. It is useful to see a Hessenberg function h pictorially by drawing a configuration of boxes on a square grid of size
$h = (h(1), h(2), \ldots , h(n))$
. It is useful to see a Hessenberg function h pictorially by drawing a configuration of boxes on a square grid of size
![]() $n \times n$
whose shaded boxes consist of boxes in the i-th row and the j-th column such that
$n \times n$
whose shaded boxes consist of boxes in the i-th row and the j-th column such that
![]() $i \leq h(j)$
for
$i \leq h(j)$
for
![]() $i, j \in [n]$
.
$i, j \in [n]$
.
Example 2.1. Let
![]() $n=5$
. Then,
$n=5$
. Then,
![]() $h=(3,3,4,5,5)$
is a Hessenberg function and the configuration of the shaded boxes is shown in Figure 1.
$h=(3,3,4,5,5)$
is a Hessenberg function and the configuration of the shaded boxes is shown in Figure 1.

Figure 1 The configuration corresponding to
![]() $h=(3,3,4,5,5)$
$h=(3,3,4,5,5)$
Let
![]() $\mathfrak {gl}_n({\mathbb {C}})$
be the set of
$\mathfrak {gl}_n({\mathbb {C}})$
be the set of
![]() $n \times n$
matrices. For a Hessenberg function h, we define
$n \times n$
matrices. For a Hessenberg function h, we define
which is called the Hessenberg space associated to h.
The (full) flag variety
![]() $Fl({\mathbb {C}}^n)$
is the set of nested complex linear subspaces of
$Fl({\mathbb {C}}^n)$
is the set of nested complex linear subspaces of
![]() ${\mathbb {C}}^n$
:
${\mathbb {C}}^n$
:
Let B be the set of upper triangular matrices in the general linear group
![]() $\operatorname {\mathrm {GL}}_n({\mathbb {C}})$
. As is well known, the flag variety
$\operatorname {\mathrm {GL}}_n({\mathbb {C}})$
. As is well known, the flag variety
![]() $Fl({\mathbb {C}}^n)$
can be identified with
$Fl({\mathbb {C}}^n)$
can be identified with
![]() $\operatorname {\mathrm {GL}}_n({\mathbb {C}})/B$
. Indeed, each flag
$\operatorname {\mathrm {GL}}_n({\mathbb {C}})/B$
. Indeed, each flag
![]() $V_\bullet \in Fl({\mathbb {C}}^n)$
is determined by a matrix g whose first j column vectors generate the j-th vector space
$V_\bullet \in Fl({\mathbb {C}}^n)$
is determined by a matrix g whose first j column vectors generate the j-th vector space
![]() $V_j$
for
$V_j$
for
![]() $j \in [n]$
. The correspondence
$j \in [n]$
. The correspondence
![]() $gB \mapsto V_{\bullet }$
above gives the identification
$gB \mapsto V_{\bullet }$
above gives the identification
![]() $Fl({\mathbb {C}}^n) \cong \operatorname {\mathrm {GL}}_n({\mathbb {C}})/B$
. For a linear operator
$Fl({\mathbb {C}}^n) \cong \operatorname {\mathrm {GL}}_n({\mathbb {C}})/B$
. For a linear operator
![]() $A: {\mathbb {C}}^n \rightarrow {\mathbb {C}}^n$
and a Hessenberg function
$A: {\mathbb {C}}^n \rightarrow {\mathbb {C}}^n$
and a Hessenberg function
![]() $h: [n] \to [n]$
, the Hessenberg variety
$h: [n] \to [n]$
, the Hessenberg variety
![]() $\operatorname {\mathrm {Hess}}(A,h)$
is defined to be the following subvariety of the flag variety
$\operatorname {\mathrm {Hess}}(A,h)$
is defined to be the following subvariety of the flag variety
![]() $Fl({\mathbb {C}}^n)$
:
$Fl({\mathbb {C}}^n)$
:
Hessenberg varieties are introduced in [Reference De Mari, Procesi and Shayman11, Reference De Mari and Shayman12]. Note that if
![]() $h=(n,n,\ldots ,n)$
, then
$h=(n,n,\ldots ,n)$
, then
![]() $\operatorname {\mathrm {Hess}}(A,h)=Fl({\mathbb {C}}^n)$
. By identifying
$\operatorname {\mathrm {Hess}}(A,h)=Fl({\mathbb {C}}^n)$
. By identifying
![]() $Fl({\mathbb {C}}^n)$
with
$Fl({\mathbb {C}}^n)$
with
![]() $\operatorname {\mathrm {GL}}_n({\mathbb {C}})/B$
, we can write the definition above as
$\operatorname {\mathrm {GL}}_n({\mathbb {C}})/B$
, we can write the definition above as
where
![]() $H(h)$
is the Hessenberg space defined in equation (2.1).
$H(h)$
is the Hessenberg space defined in equation (2.1).
Definition 2.2. Let
![]() $A \in \mathfrak {gl}_n({\mathbb {C}})$
and
$A \in \mathfrak {gl}_n({\mathbb {C}})$
and
![]() $i,j \in [n]$
. We define a polynomial
$i,j \in [n]$
. We define a polynomial
![]() $F_{i,j}^{A}$
on
$F_{i,j}^{A}$
on
![]() $\operatorname {\mathrm {GL}}_n({\mathbb {C}})$
by
$\operatorname {\mathrm {GL}}_n({\mathbb {C}})$
by
where
![]() $g=(v_1 \, \ldots \, v_n) \in \operatorname {\mathrm {GL}}_n({\mathbb {C}})$
is the decomposition into column vectors. In other words, the polynomial
$g=(v_1 \, \ldots \, v_n) \in \operatorname {\mathrm {GL}}_n({\mathbb {C}})$
is the decomposition into column vectors. In other words, the polynomial
![]() $F_{i,j}^{A}(g)$
is the determinant of the matrix obtained from g by replacing the i-th column vector of g to the j-th column vector of
$F_{i,j}^{A}(g)$
is the determinant of the matrix obtained from g by replacing the i-th column vector of g to the j-th column vector of
![]() $A g$
.
$A g$
.
Lemma 2.3. Let
![]() $A \in \mathfrak {gl}_n({\mathbb {C}})$
. For
$A \in \mathfrak {gl}_n({\mathbb {C}})$
. For
![]() $g \in \operatorname {\mathrm {GL}}_n({\mathbb {C}})$
and
$g \in \operatorname {\mathrm {GL}}_n({\mathbb {C}})$
and
![]() $i,j \in [n]$
, we have
$i,j \in [n]$
, we have
where
![]() $(g^{-1} A g)_{ij}$
denotes the
$(g^{-1} A g)_{ij}$
denotes the
![]() $(i,j)$
-th entry of the matrix
$(i,j)$
-th entry of the matrix
![]() $g^{-1} A g$
. In particular, we have
$g^{-1} A g$
. In particular, we have
Proof. Let
![]() $c_{ij}$
be the
$c_{ij}$
be the
![]() $(i,j)$
cofactor of g, namely
$(i,j)$
cofactor of g, namely
![]() $c_{ij}$
is obtained by multiplying the
$c_{ij}$
is obtained by multiplying the
![]() $(i,j)$
minor of g by
$(i,j)$
minor of g by
![]() $(-1)^{i+j}$
. Set
$(-1)^{i+j}$
. Set
![]() $\tilde g=(c_{ij})_{i,j \in [n]}^t=(c_{ji})_{i,j \in [n]}$
. Since
$\tilde g=(c_{ij})_{i,j \in [n]}^t=(c_{ji})_{i,j \in [n]}$
. Since
![]() $g^{-1}=\frac {1}{\det (g)} \, \tilde g$
, it suffices to show that
$g^{-1}=\frac {1}{\det (g)} \, \tilde g$
, it suffices to show that
We write
![]() $g=(v_1 \, \ldots \, v_n)$
and
$g=(v_1 \, \ldots \, v_n)$
and
![]() $A v_j=(b_{1j},\ldots ,b_{nj})^t$
. By the definition of
$A v_j=(b_{1j},\ldots ,b_{nj})^t$
. By the definition of
![]() $\tilde g$
, we have
$\tilde g$
, we have
 $$ \begin{align*} (\tilde g \cdot A g)_{ij} = \sum_{k=1}^n c_{ki} b_{kj} = \det (v_1 \, \ldots \, v_{i-1} \ A v_j \ v_{i+1} \,\ldots \, v_n), \end{align*} $$
$$ \begin{align*} (\tilde g \cdot A g)_{ij} = \sum_{k=1}^n c_{ki} b_{kj} = \det (v_1 \, \ldots \, v_{i-1} \ A v_j \ v_{i+1} \,\ldots \, v_n), \end{align*} $$
where we used the cofactor expansion along the i-th column for the last equality. This yields equation (2.4) as desired. The latter statement follows from the former statement and equation (2.3).
3 Regular nilpotent Hessenberg varieties
In this section, we review geometric properties for regular nilpotent Hessenberg varieties.
Let N be a regular nilpotent element in
![]() $\mathfrak {gl}_n({\mathbb {C}})$
, that is, a matrix whose Jordan canonical form consists of exactly one Jordan block with corresponding eigenvalue equal to
$\mathfrak {gl}_n({\mathbb {C}})$
, that is, a matrix whose Jordan canonical form consists of exactly one Jordan block with corresponding eigenvalue equal to
![]() $0$
. For a Hessenberg function h,
$0$
. For a Hessenberg function h,
![]() $\operatorname {\mathrm {Hess}}(N,h)$
is called the regular nilpotent Hessenberg variety. If
$\operatorname {\mathrm {Hess}}(N,h)$
is called the regular nilpotent Hessenberg variety. If
![]() $h=(2,3,4,\ldots ,n,n)$
, then
$h=(2,3,4,\ldots ,n,n)$
, then ![]() is called the Peterson variety, which is an object of an intense study by Dale Peterson [Reference Peterson31]. Surprisingly, the Peterson variety is related with the quantum cohomology of the flag variety ([Reference Kostant29, Reference Rietsch32]). We will explain the relation in Section 4. For any
is called the Peterson variety, which is an object of an intense study by Dale Peterson [Reference Peterson31]. Surprisingly, the Peterson variety is related with the quantum cohomology of the flag variety ([Reference Kostant29, Reference Rietsch32]). We will explain the relation in Section 4. For any
![]() $p \in \operatorname {\mathrm {GL}}_n({\mathbb {C}})$
, one can see that
$p \in \operatorname {\mathrm {GL}}_n({\mathbb {C}})$
, one can see that
![]() $\operatorname {\mathrm {Hess}}(N,h) \cong \operatorname {\mathrm {Hess}}(p^{-1}Np,h)$
which sends
$\operatorname {\mathrm {Hess}}(N,h) \cong \operatorname {\mathrm {Hess}}(p^{-1}Np,h)$
which sends
![]() $gB$
to
$gB$
to
![]() $p^{-1}gB$
. Thus, we may assume that N is in Jordan form:
$p^{-1}gB$
. Thus, we may assume that N is in Jordan form:
 $$ \begin{align} N = \begin{pmatrix} 0 & 1 & & \\ & \ddots & \ddots & \\ & & 0 & 1 \\ & & & 0 \\ \end{pmatrix}. \end{align} $$
$$ \begin{align} N = \begin{pmatrix} 0 & 1 & & \\ & \ddots & \ddots & \\ & & 0 & 1 \\ & & & 0 \\ \end{pmatrix}. \end{align} $$
We summarize geometric properties of
![]() $\operatorname {\mathrm {Hess}}(N,h)$
as follows.
$\operatorname {\mathrm {Hess}}(N,h)$
as follows.
Theorem 3.1 [Reference Anderson and Tymoczko5, Reference Insko and Yong26, Reference Kostant29, Reference Sommers and Tymoczko34].
Let
![]() $\operatorname {\mathrm {Pet}}_n$
be the Peterson variety. Let
$\operatorname {\mathrm {Pet}}_n$
be the Peterson variety. Let
![]() $\operatorname {\mathrm {Hess}}(N,h)$
be the regular nilpotent Hessenberg variety associated with a Hessenberg function h.
$\operatorname {\mathrm {Hess}}(N,h)$
be the regular nilpotent Hessenberg variety associated with a Hessenberg function h.
-
(i) The Peterson variety
 $\operatorname {\mathrm {Pet}}_n$
is singular for
$\operatorname {\mathrm {Pet}}_n$
is singular for
 $n \geq 3$
. Also,
$n \geq 3$
. Also,
 $\operatorname {\mathrm {Pet}}_n$
is normal if and only if
$\operatorname {\mathrm {Pet}}_n$
is normal if and only if
 $n \leq 3$
.
$n \leq 3$
. -
(ii) The complex dimension of
 $\operatorname {\mathrm {Hess}}(N,h)$
is given by
$\operatorname {\mathrm {Hess}}(N,h)$
is given by
 $\sum _{j=1}^n (h(j)-j)$
. In particular, we have
$\sum _{j=1}^n (h(j)-j)$
. In particular, we have
 ${\dim _{\mathbb {C}} \operatorname {\mathrm {Pet}}_n = n-1}$
.
${\dim _{\mathbb {C}} \operatorname {\mathrm {Pet}}_n = n-1}$
. -
(iii)
 $\operatorname {\mathrm {Hess}}(N,h)$
is irreducible.
$\operatorname {\mathrm {Hess}}(N,h)$
is irreducible.
As a property of regular nilpotent Hessenberg varieties, a special case of
![]() $\operatorname {\mathrm {Hess}}(N,h)$
can be decomposed into a product of smaller regular nilpotent Hessenberg varieties, as explained below. To explain this, we first recall the following terminology from [Reference Drellich13, Definition 4.4].
$\operatorname {\mathrm {Hess}}(N,h)$
can be decomposed into a product of smaller regular nilpotent Hessenberg varieties, as explained below. To explain this, we first recall the following terminology from [Reference Drellich13, Definition 4.4].
Definition 3.2. A Hessenberg function h is decomposable if
![]() $h(j)=j$
for some
$h(j)=j$
for some
![]() $j \in [n-1]$
. A Hessenberg function h is indecomposable if
$j \in [n-1]$
. A Hessenberg function h is indecomposable if
![]() $h(j)>j$
for all
$h(j)>j$
for all
![]() $j \in [n-1]$
. Note that an indecomposable Hessenberg function h satisfies
$j \in [n-1]$
. Note that an indecomposable Hessenberg function h satisfies
![]() $h(n-1)=h(n)=n$
.
$h(n-1)=h(n)=n$
.
If h is a decomposable Hessenberg function, that is,
![]() $h(j)=j$
for some
$h(j)=j$
for some
![]() $j \in [n-1]$
, then the Hessenberg function h can be decomposed into two smaller Hessenberg functions
$j \in [n-1]$
, then the Hessenberg function h can be decomposed into two smaller Hessenberg functions
![]() $h_1$
and
$h_1$
and
![]() $h_2$
defined by
$h_2$
defined by
![]() $h_1=(h(1),\ldots ,h(j))$
and
$h_1=(h(1),\ldots ,h(j))$
and
![]() $h_2=(h(j+1)-j,\ldots ,h(n)-j)$
as shown in Figure 2.
$h_2=(h(j+1)-j,\ldots ,h(n)-j)$
as shown in Figure 2.

Figure 2 The decomposition of
![]() $h=(2,3,3,5,5)$
into
$h=(2,3,3,5,5)$
into
![]() $h_1=(2,3,3)$
and
$h_1=(2,3,3)$
and
![]() $h_2=(2,2)$
$h_2=(2,2)$
Then, every
![]() $V_\bullet \in \operatorname {\mathrm {Hess}}(N,h)$
has
$V_\bullet \in \operatorname {\mathrm {Hess}}(N,h)$
has
![]() $V_j = \operatorname {\mathrm {span}}_{\mathbb {C}} \{e_1,\ldots ,e_j\}$
, where
$V_j = \operatorname {\mathrm {span}}_{\mathbb {C}} \{e_1,\ldots ,e_j\}$
, where
![]() $e_1,\ldots , e_n$
denote the standard basis of
$e_1,\ldots , e_n$
denote the standard basis of
![]() ${\mathbb {C}}^n$
and hence we have
${\mathbb {C}}^n$
and hence we have
where
![]() $N_1$
and
$N_1$
and
![]() $N_2$
are the regular nilpotent matrices in Jordan canonical form of size j and
$N_2$
are the regular nilpotent matrices in Jordan canonical form of size j and
![]() $n-j$
, respectively ([Reference Drellich13, Theorem 4.5]).
$n-j$
, respectively ([Reference Drellich13, Theorem 4.5]).
In a recent paper, Abe–Insko gave the condition that
![]() $\operatorname {\mathrm {Hess}}(N,h)$
is normal as follows.
$\operatorname {\mathrm {Hess}}(N,h)$
is normal as follows.
Theorem 3.3.
![]() $($
[Reference Abe and Insko3, Theorem 1.3]
$($
[Reference Abe and Insko3, Theorem 1.3]
![]() $)$
Let h be an indecomposable Hessenberg function. Then the regular nilpotent Hessenberg variety
$)$
Let h be an indecomposable Hessenberg function. Then the regular nilpotent Hessenberg variety
![]() $\operatorname {\mathrm {Hess}}(N,h)$
is normal if and only if h satisfies the condition that
$\operatorname {\mathrm {Hess}}(N,h)$
is normal if and only if h satisfies the condition that
![]() $h(i-1)> i$
or
$h(i-1)> i$
or
![]() $h(i)> i + 1$
for all
$h(i)> i + 1$
for all
![]() $1 < i < n-1$
.
$1 < i < n-1$
.
There is a natural partial order on Hessenberg functions. For two Hessenberg functions
![]() $h:[n] \rightarrow [n]$
and
$h:[n] \rightarrow [n]$
and
![]() $h':[n] \rightarrow [n]$
, we say
$h':[n] \rightarrow [n]$
, we say
![]() $h' \subset h$
if
$h' \subset h$
if
![]() $h'(j) \leq h(j)$
for all
$h'(j) \leq h(j)$
for all
![]() $j \in [n]$
. Note that if
$j \in [n]$
. Note that if
![]() $h' \subset h$
, then
$h' \subset h$
, then
![]() $\operatorname {\mathrm {Hess}}(N,h')$
is a closed subvariety of
$\operatorname {\mathrm {Hess}}(N,h')$
is a closed subvariety of
![]() $\operatorname {\mathrm {Hess}}(N,h)$
by the definition (2.2). Since
$\operatorname {\mathrm {Hess}}(N,h)$
by the definition (2.2). Since
![]() $h=(2,3,4,\ldots ,n,n)$
is the minimal Hessenberg function among indecomposable Hessenberg functions with respect to the partial order
$h=(2,3,4,\ldots ,n,n)$
is the minimal Hessenberg function among indecomposable Hessenberg functions with respect to the partial order
![]() $\subset $
, the Peterson variety
$\subset $
, the Peterson variety
![]() $\operatorname {\mathrm {Pet}}_n$
is the minimal Hessenberg variety among indecomposable regular nilpotent Hessenberg varieties with respect to the inclusion.
$\operatorname {\mathrm {Pet}}_n$
is the minimal Hessenberg variety among indecomposable regular nilpotent Hessenberg varieties with respect to the inclusion.
Let h be a Hessenberg function. One can see that the Hessenberg space
![]() $H(h)$
in equation (2.1) is stable under the adjoint action of B, so this induces a B-action on the quotient space
$H(h)$
in equation (2.1) is stable under the adjoint action of B, so this induces a B-action on the quotient space
![]() $\mathfrak {gl}_n({\mathbb {C}})/H(h)$
. We denote by
$\mathfrak {gl}_n({\mathbb {C}})/H(h)$
. We denote by
![]() $\overline {x}$
the image of
$\overline {x}$
the image of
![]() $x \in \mathfrak {gl}_n({\mathbb {C}})$
under the surjection
$x \in \mathfrak {gl}_n({\mathbb {C}})$
under the surjection
![]() $\mathfrak {gl}_n({\mathbb {C}}) \rightarrow \mathfrak {gl}_n({\mathbb {C}})/H(h)$
. In [Reference Abe, DeDieu, Galetto and Harada1], we consider the vector bundle
$\mathfrak {gl}_n({\mathbb {C}}) \rightarrow \mathfrak {gl}_n({\mathbb {C}})/H(h)$
. In [Reference Abe, DeDieu, Galetto and Harada1], we consider the vector bundle
![]() $\operatorname {\mathrm {GL}}_n({\mathbb {C}}) \times _B (\mathfrak {gl}_n({\mathbb {C}})/H(h))$
over the flag variety
$\operatorname {\mathrm {GL}}_n({\mathbb {C}}) \times _B (\mathfrak {gl}_n({\mathbb {C}})/H(h))$
over the flag variety
![]() $\operatorname {\mathrm {GL}}_n({\mathbb {C}})/B$
and its section
$\operatorname {\mathrm {GL}}_n({\mathbb {C}})/B$
and its section
![]() $s_A$
for
$s_A$
for
![]() $A \in \mathfrak {gl}_n({\mathbb {C}})$
defined by
$A \in \mathfrak {gl}_n({\mathbb {C}})$
defined by
where we denote by
![]() $[g,\overline {x}]$
the image of
$[g,\overline {x}]$
the image of
![]() $(g,\overline {x}) \in \operatorname {\mathrm {GL}}_n({\mathbb {C}}) \times (\mathfrak {gl}_n({\mathbb {C}})/H(h))$
under the surjection
$(g,\overline {x}) \in \operatorname {\mathrm {GL}}_n({\mathbb {C}}) \times (\mathfrak {gl}_n({\mathbb {C}})/H(h))$
under the surjection
![]() $\operatorname {\mathrm {GL}}_n({\mathbb {C}}) \times (\mathfrak {gl}_n({\mathbb {C}})/H(h)) \rightarrow \operatorname {\mathrm {GL}}_n({\mathbb {C}}) \times _B (\mathfrak {gl}_n({\mathbb {C}})/H(h))$
such that
$\operatorname {\mathrm {GL}}_n({\mathbb {C}}) \times (\mathfrak {gl}_n({\mathbb {C}})/H(h)) \rightarrow \operatorname {\mathrm {GL}}_n({\mathbb {C}}) \times _B (\mathfrak {gl}_n({\mathbb {C}})/H(h))$
such that
![]() $[g,\overline {x}]=[gb,\overline {b^{-1}xb}]$
for all
$[g,\overline {x}]=[gb,\overline {b^{-1}xb}]$
for all
![]() $b \in B$
. By the definition (2.3), one can see that the zero set of
$b \in B$
. By the definition (2.3), one can see that the zero set of
![]() $s_A$
is the Hessenberg variety
$s_A$
is the Hessenberg variety
![]() $\operatorname {\mathrm {Hess}}(A,h)$
.
$\operatorname {\mathrm {Hess}}(A,h)$
.
In general, let
![]() $\pi :E \rightarrow X$
be a vector bundle of rank r over a scheme X. If s is a section of E, then the zero scheme
$\pi :E \rightarrow X$
be a vector bundle of rank r over a scheme X. If s is a section of E, then the zero scheme
![]() $\mathcal {Z}(s)$
of s is defined as follows (cf. [Reference Fulton20]). Let
$\mathcal {Z}(s)$
of s is defined as follows (cf. [Reference Fulton20]). Let
![]() $(U_i, \varphi _i)_i$
be a local trivialization of E, that is, an open covering
$(U_i, \varphi _i)_i$
be a local trivialization of E, that is, an open covering
![]() $\{U_i\}_i$
of X and isomorphisms
$\{U_i\}_i$
of X and isomorphisms
![]() $\varphi _i$
of
$\varphi _i$
of
![]() $\pi ^{-1}(U_i)$
with
$\pi ^{-1}(U_i)$
with
![]() $U_i \times {\mathbb {C}}^r$
over
$U_i \times {\mathbb {C}}^r$
over
![]() $U_i$
such that the composites
$U_i$
such that the composites
![]() $\varphi _i \circ \varphi _j^{-1}$
are linear. Let
$\varphi _i \circ \varphi _j^{-1}$
are linear. Let
![]() $s_i: U_i \rightarrow {\mathbb {C}}^r$
determine the section s on
$s_i: U_i \rightarrow {\mathbb {C}}^r$
determine the section s on
![]() $U_i$
,
$U_i$
,
![]() $s_i=(s_{i_1},\ldots ,s_{i_r})$
,
$s_i=(s_{i_1},\ldots ,s_{i_r})$
,
![]() $s_{i_m}$
in the coordinate ring of
$s_{i_m}$
in the coordinate ring of
![]() $U_i$
; then
$U_i$
; then
![]() $\mathcal {Z}(s)$
is defined in
$\mathcal {Z}(s)$
is defined in
![]() $U_i$
by the ideal generated by
$U_i$
by the ideal generated by
![]() $s_{i_1},\ldots ,s_{i_r}$
.
$s_{i_1},\ldots ,s_{i_r}$
.
Motivated by the discussion above, we use the following definition introduced in [Reference Abe, DeDieu, Galetto and Harada1].
Definition 3.4.
![]() $($
[Reference Abe, DeDieu, Galetto and Harada1, Definition 3.1]
$($
[Reference Abe, DeDieu, Galetto and Harada1, Definition 3.1]
![]() $)$
Let
$)$
Let
![]() $N \in \mathfrak {gl}_n({\mathbb {C}})$
be the regular nilpotent element in equation (3.1). For a Hessenberg function h, let
$N \in \mathfrak {gl}_n({\mathbb {C}})$
be the regular nilpotent element in equation (3.1). For a Hessenberg function h, let
![]() $\mathcal {Z}(N,h)$
denote the zero scheme in
$\mathcal {Z}(N,h)$
denote the zero scheme in
![]() $\operatorname {\mathrm {GL}}_n({\mathbb {C}})/B$
of the section
$\operatorname {\mathrm {GL}}_n({\mathbb {C}})/B$
of the section
![]() $s_N$
.
$s_N$
.
Locally around
![]() $gB \in \operatorname {\mathrm {GL}}_n({\mathbb {C}})/B$
, the section
$gB \in \operatorname {\mathrm {GL}}_n({\mathbb {C}})/B$
, the section
![]() $s_N$
is represented by a collection of regular functions, and the scheme
$s_N$
is represented by a collection of regular functions, and the scheme
![]() $\mathcal {Z}(N, h)$
is locally the zero scheme of those functions. (See [Reference Abe, DeDieu, Galetto and Harada1, Lemma 3.4] for the detail.)
$\mathcal {Z}(N, h)$
is locally the zero scheme of those functions. (See [Reference Abe, DeDieu, Galetto and Harada1, Lemma 3.4] for the detail.)
Theorem 3.5.
![]() $($
[Reference Abe, DeDieu, Galetto and Harada1, Proposition 3.6]
$($
[Reference Abe, DeDieu, Galetto and Harada1, Proposition 3.6]
![]() $)$
If h is an indecomposable Hessenberg function, then the zero scheme
$)$
If h is an indecomposable Hessenberg function, then the zero scheme
![]() $\mathcal {Z}(N,h)$
of the section
$\mathcal {Z}(N,h)$
of the section
![]() $s_N$
is reduced.
$s_N$
is reduced.
We analyze the intersection of
![]() $\operatorname {\mathrm {Hess}}(N,h)$
and the opposite Schubert cell
$\operatorname {\mathrm {Hess}}(N,h)$
and the opposite Schubert cell
![]() $\Omega _e^\circ $
associated with the identity element e. Recall that
$\Omega _e^\circ $
associated with the identity element e. Recall that
![]() $\Omega _e^\circ $
is the
$\Omega _e^\circ $
is the
![]() $B^{-}$
-orbit of the identity flag
$B^{-}$
-orbit of the identity flag
![]() $eB/B$
in
$eB/B$
in
![]() $\operatorname {\mathrm {GL}}_n({\mathbb {C}})/B$
, where
$\operatorname {\mathrm {GL}}_n({\mathbb {C}})/B$
, where
![]() $B^{-}$
denotes the set of lower triangular matrices in
$B^{-}$
denotes the set of lower triangular matrices in
![]() $\operatorname {\mathrm {GL}}_n({\mathbb {C}})$
. In particular, each flag
$\operatorname {\mathrm {GL}}_n({\mathbb {C}})$
. In particular, each flag
![]() $V_\bullet \in \Omega _e^\circ $
has
$V_\bullet \in \Omega _e^\circ $
has
![]() $V_j$
spanned by the first j columns of a matrix with
$V_j$
spanned by the first j columns of a matrix with
![]() $1$
’s in the diagonal positions and
$1$
’s in the diagonal positions and
![]() $0$
’s to the right of these
$0$
’s to the right of these
![]() $1$
’s (cf. [Reference Fulton19, Section 10.2]). Thus, one can see that the opposite Schubert cell
$1$
’s (cf. [Reference Fulton19, Section 10.2]). Thus, one can see that the opposite Schubert cell
![]() $\Omega _e^\circ $
can be regarded as the following affine space:
$\Omega _e^\circ $
can be regarded as the following affine space:
 $$ \begin{align*} \Omega_e^\circ \cong \left\{ \left. \left( \begin{array}{@{\,}ccccc@{\,}} 1 & & & & \\ x_{21} & 1 & & & \\ x_{31} & x_{32} & 1 & & \\ \vdots& \vdots & \ddots & \ddots & \\ x_{n1} & x_{n2} & \cdots & x_{n \, n-1} & 1 \end{array} \right) \ \right| x_{ij} \in {\mathbb{C}} \ (1 \leq j < i \leq n) \right\} \cong {\mathbb{C}}^{\frac{1}{2}n(n-1)}. \end{align*} $$
$$ \begin{align*} \Omega_e^\circ \cong \left\{ \left. \left( \begin{array}{@{\,}ccccc@{\,}} 1 & & & & \\ x_{21} & 1 & & & \\ x_{31} & x_{32} & 1 & & \\ \vdots& \vdots & \ddots & \ddots & \\ x_{n1} & x_{n2} & \cdots & x_{n \, n-1} & 1 \end{array} \right) \ \right| x_{ij} \in {\mathbb{C}} \ (1 \leq j < i \leq n) \right\} \cong {\mathbb{C}}^{\frac{1}{2}n(n-1)}. \end{align*} $$
Note that
![]() $\Omega _e^\circ $
is an affine open set of the flag variety
$\Omega _e^\circ $
is an affine open set of the flag variety
![]() $\operatorname {\mathrm {GL}}_n({\mathbb {C}})/B$
and its coordinate ring is isomorphic to the polynomial ring
$\operatorname {\mathrm {GL}}_n({\mathbb {C}})/B$
and its coordinate ring is isomorphic to the polynomial ring
![]() ${\mathbb {C}}[x_{ij} \mid 1 \leq j < i \leq n]$
. Thus, we may identify
${\mathbb {C}}[x_{ij} \mid 1 \leq j < i \leq n]$
. Thus, we may identify
![]() $\Omega _e^\circ $
as
$\Omega _e^\circ $
as
![]() $\operatorname {\mathrm {Spec}} {\mathbb {C}}[x_{ij} \mid 1 \leq j < i \leq n]$
. From now on, we write
$\operatorname {\mathrm {Spec}} {\mathbb {C}}[x_{ij} \mid 1 \leq j < i \leq n]$
. From now on, we write

for simplicity. Since the first column vector of
![]() $Ng$
is
$Ng$
is
![]() $(x_{21},x_{31},x_{41},\ldots ,x_{n1},0)^t$
and the j-th column vector of
$(x_{21},x_{31},x_{41},\ldots ,x_{n1},0)^t$
and the j-th column vector of
![]() $Ng$
is
$Ng$
is
 $(\underbrace {0,\ldots ,0}_{j-2},\underbrace {1,x_{j+1 \, j},\ldots ,x_{nj},0}_{n-j+2})^t$
for
$(\underbrace {0,\ldots ,0}_{j-2},\underbrace {1,x_{j+1 \, j},\ldots ,x_{nj},0}_{n-j+2})^t$
for
![]() $j \geq 2$
, we can explicitly write
$j \geq 2$
, we can explicitly write
 $$ \begin{align} F_{i,1} &= \left| \begin{array}{@{\,}ccccc@{\,}} 1 & 0 & \cdots & 0 & x_{21} \\ x_{21} & 1 & \ddots & \vdots & x_{31} \\ \vdots & x_{32} & \ddots & 0 & \vdots \\ \vdots& \vdots & \ddots & 1 & \vdots \\ x_{i1} & x_{i2} & \cdots & x_{i \, i-1} & x_{i+1 \, 1} \end{array} \right| \ \ \ \text{for} \ j=1; \end{align} $$
$$ \begin{align} F_{i,1} &= \left| \begin{array}{@{\,}ccccc@{\,}} 1 & 0 & \cdots & 0 & x_{21} \\ x_{21} & 1 & \ddots & \vdots & x_{31} \\ \vdots & x_{32} & \ddots & 0 & \vdots \\ \vdots& \vdots & \ddots & 1 & \vdots \\ x_{i1} & x_{i2} & \cdots & x_{i \, i-1} & x_{i+1 \, 1} \end{array} \right| \ \ \ \text{for} \ j=1; \end{align} $$
 $$ \begin{align} F_{i,j} &= \left| \begin{array}{@{\,}ccccc@{\,}} 1 & 0 & \cdots & 0 & 1 \\ x_{j\,j-1} & 1 & \ddots & \vdots & x_{j+1\,j} \\ x_{j+1\,j-1} & x_{j+1\,j} & \ddots & 0 & \vdots \\ \vdots& \vdots & \ddots & 1 & \vdots \\ x_{i\,j-1} & x_{ij} & \cdots & x_{i \, i-1} & x_{i+1 \, j} \end{array} \right| \ \ \ \text{for} \ j \geq 2 \end{align} $$
$$ \begin{align} F_{i,j} &= \left| \begin{array}{@{\,}ccccc@{\,}} 1 & 0 & \cdots & 0 & 1 \\ x_{j\,j-1} & 1 & \ddots & \vdots & x_{j+1\,j} \\ x_{j+1\,j-1} & x_{j+1\,j} & \ddots & 0 & \vdots \\ \vdots& \vdots & \ddots & 1 & \vdots \\ x_{i\,j-1} & x_{ij} & \cdots & x_{i \, i-1} & x_{i+1 \, j} \end{array} \right| \ \ \ \text{for} \ j \geq 2 \end{align} $$
from Definition 2.2. Here, we take the convention that
![]() $x_{n+1\,j}=0$
. The determinant of
$x_{n+1\,j}=0$
. The determinant of
![]() $g \in \Omega _e^\circ $
is
$g \in \Omega _e^\circ $
is
![]() $1$
, so we have
$1$
, so we have
by Lemma 2.3. We set

By the discussion above, we have the following.
Proposition 3.6. Let h be a Hessenberg function. Then
In other words, the set of global sections
![]() $\Gamma (\mathcal {Z}(N,h)_e, \mathcal {O}_{\mathcal {Z}(N,h)_e})$
is given by
$\Gamma (\mathcal {Z}(N,h)_e, \mathcal {O}_{\mathcal {Z}(N,h)_e})$
is given by
In particular, if h is indecomposable, then the coordinate ring
![]() ${\mathbb {C}}[\operatorname {\mathrm {Hess}}(N,h) \cap \Omega _e^\circ ]$
of the open set
${\mathbb {C}}[\operatorname {\mathrm {Hess}}(N,h) \cap \Omega _e^\circ ]$
of the open set
![]() $\operatorname {\mathrm {Hess}}(N,h) \cap \Omega _e^\circ $
in
$\operatorname {\mathrm {Hess}}(N,h) \cap \Omega _e^\circ $
in
![]() $\operatorname {\mathrm {Hess}}(N,h)$
is
$\operatorname {\mathrm {Hess}}(N,h)$
is
by Theorem 3.5.
4 The main theorem
It can be extracted from Peterson’s statements in [Reference Peterson31] that the coordinate ring
![]() ${\mathbb {C}}[\operatorname {\mathrm {Pet}}_n \cap \Omega _e^\circ ]$
is isomorphic to the quantum cohomology ring of the flag variety
${\mathbb {C}}[\operatorname {\mathrm {Pet}}_n \cap \Omega _e^\circ ]$
is isomorphic to the quantum cohomology ring of the flag variety
![]() $QH^*(Fl({\mathbb {C}}^n))$
. This result is unpublished, so we also refer the reader to [Reference Kostant29, Reference Rietsch32] for the result. In this section, we first review an explicit presentation for the quantum cohomology ring
$QH^*(Fl({\mathbb {C}}^n))$
. This result is unpublished, so we also refer the reader to [Reference Kostant29, Reference Rietsch32] for the result. In this section, we first review an explicit presentation for the quantum cohomology ring
![]() $QH^*(Fl({\mathbb {C}}^n))$
given by [Reference Ciocan-Fontanine16, Reference Givental and Kim22]. Then we introduce a further quantization of the ring presentation for
$QH^*(Fl({\mathbb {C}}^n))$
given by [Reference Ciocan-Fontanine16, Reference Givental and Kim22]. Then we introduce a further quantization of the ring presentation for
![]() $QH^*(Fl({\mathbb {C}}^n))$
in natural way. Our main theorem relates
$QH^*(Fl({\mathbb {C}}^n))$
in natural way. Our main theorem relates
![]() $\Gamma (\mathcal {Z}(N,h)_e, \mathcal {O}_{\mathcal {Z}(N,h)_e})$
and our quantized ring presentation.
$\Gamma (\mathcal {Z}(N,h)_e, \mathcal {O}_{\mathcal {Z}(N,h)_e})$
and our quantized ring presentation.
The quantum cohomology ring of the flag variety
![]() $QH^*(Fl({\mathbb {C}}^n))$
is given by
$QH^*(Fl({\mathbb {C}}^n))$
is given by
as
![]() ${\mathbb {C}}$
-vector spaces. Here,
${\mathbb {C}}$
-vector spaces. Here,
![]() $q_1,\ldots ,q_{n-1}$
are called the quantum parameters. The product structure of
$q_1,\ldots ,q_{n-1}$
are called the quantum parameters. The product structure of
![]() $QH^*(Fl({\mathbb {C}}^n))$
is a certain deformation of the cup product in the ordinary cohomology
$QH^*(Fl({\mathbb {C}}^n))$
is a certain deformation of the cup product in the ordinary cohomology
![]() $H^*(Fl({\mathbb {C}}^n))$
. In order to describe an explicit presentation for
$H^*(Fl({\mathbb {C}}^n))$
. In order to describe an explicit presentation for
![]() $QH^*(Fl({\mathbb {C}}^n))$
, we need quantized elementary symmetric polynomials. Consider the matrix
$QH^*(Fl({\mathbb {C}}^n))$
, we need quantized elementary symmetric polynomials. Consider the matrix

and define quantized elementary symmetric polynomials
![]() $\check E_1^{(n)}, \ldots , \check E_n^{(n)}$
in the polynomial ring
$\check E_1^{(n)}, \ldots , \check E_n^{(n)}$
in the polynomial ring
![]() ${\mathbb {C}}[x_1,\ldots ,x_n,q_1,\ldots ,q_{n-1}]$
by the following equation
${\mathbb {C}}[x_1,\ldots ,x_n,q_1,\ldots ,q_{n-1}]$
by the following equation
where
![]() $I_n$
is the identity matrix of size n. By using the cofactor expansion along the s-th column for
$I_n$
is the identity matrix of size n. By using the cofactor expansion along the s-th column for
![]() $\det (\lambda I_s - \check M_s)$
, we have
$\det (\lambda I_s - \check M_s)$
, we have
This implies the following recursive formula
where we take the convention that
![]() $\check E_0^{(s-1)}=1, \check E_{-1}^{(s-2)}=0$
whenever
$\check E_0^{(s-1)}=1, \check E_{-1}^{(s-2)}=0$
whenever
![]() $r=1$
and
$r=1$
and
![]() $\check E_{s}^{(s-1)}=0$
whenever
$\check E_{s}^{(s-1)}=0$
whenever
![]() $r=s$
. By setting
$r=s$
. By setting
![]() $q_s = 0$
for all
$q_s = 0$
for all
![]() $s \in [n-1]$
,
$s \in [n-1]$
,
![]() $\check E_i^{(n)}$
is the (ordinary) i-th elementary symmetric polynomial in the variables
$\check E_i^{(n)}$
is the (ordinary) i-th elementary symmetric polynomial in the variables
![]() $x_1,\ldots ,x_n$
.
$x_1,\ldots ,x_n$
.
Theorem 4.1 [Reference Ciocan-Fontanine16, Reference Givental and Kim22].
There is an isomorphism of
![]() ${\mathbb {C}}$
-algebras
${\mathbb {C}}$
-algebras
Remark 4.2. The isomorphism above is stated in [Reference Givental and Kim22, Theorem 1] for integral coefficients. An explicit presentation of the quantum cohomology ring of partial flag varieties is given by [Reference Astashkevich and Sadov6, Reference Ciocan-Fontanine17, Reference Kim28].
Remark 4.3. By setting
![]() $q_s = 0$
for all
$q_s = 0$
for all
![]() $s \in [n-1]$
, the isomorphism (4.1) yields the well-known presentation for the (ordinary) cohomology ring of
$s \in [n-1]$
, the isomorphism (4.1) yields the well-known presentation for the (ordinary) cohomology ring of
![]() $Fl({\mathbb {C}}^n)$
. Note that
$Fl({\mathbb {C}}^n)$
. Note that
![]() $x_i$
is geometrically the first Chern class of the dual of the i-th tautological line bundle over
$x_i$
is geometrically the first Chern class of the dual of the i-th tautological line bundle over
![]() $Fl({\mathbb {C}}^n)$
. See, for example, [Reference Fulton19, Section 10.2, Proposition 3].
$Fl({\mathbb {C}}^n)$
. See, for example, [Reference Fulton19, Section 10.2, Proposition 3].
Theorem 4.4 (D. Peterson and [Reference Kostant29, Reference Rietsch32]).
There is an isomorphism of
![]() ${\mathbb {C}}$
-algebras
${\mathbb {C}}$
-algebras
Remark 4.5. Although we restricted the above discussion to the case of the full flag variety, the isomorphism above is in fact stated in [Reference Rietsch32, Theorem 4.2] for partial flag varieties. We also refer the reader to a recent paper [Reference Chow10] for general Lie types.
By Theorems 4.1 and 4.4, we obtain an isomorphism
as
![]() ${\mathbb {C}}$
-algebras. One can see from [Reference Rietsch32, Theorems 3.3 and 4.2] that the isomorphism above sends
${\mathbb {C}}$
-algebras. One can see from [Reference Rietsch32, Theorems 3.3 and 4.2] that the isomorphism above sends
![]() $x_{ij}$
to
$x_{ij}$
to
![]() $\check E_{i-j}^{(n-j)}$
under the presentation (3.8) for
$\check E_{i-j}^{(n-j)}$
under the presentation (3.8) for
![]() $h=(2,3,4,\ldots ,n,n)$
. We generalize equation (4.2) to arbitrary Hessenberg function h.
$h=(2,3,4,\ldots ,n,n)$
. We generalize equation (4.2) to arbitrary Hessenberg function h.
Definition 4.6. Consider the matrix

and define
![]() $q_{rs}$
-quantized elementary symmetric polynomials
$q_{rs}$
-quantized elementary symmetric polynomials
![]() $E_1^{(n)}, \ldots , E_n^{(n)}$
in the polynomial ring
$E_1^{(n)}, \ldots , E_n^{(n)}$
in the polynomial ring
![]() ${\mathbb {C}}[x_1,\ldots ,x_n,q_{rs} \mid 1 \leq r < s \leq n]$
by the following equation
${\mathbb {C}}[x_1,\ldots ,x_n,q_{rs} \mid 1 \leq r < s \leq n]$
by the following equation
In other words,
![]() $E_i^{(n)}$
is the coefficient of
$E_i^{(n)}$
is the coefficient of
![]() $\lambda ^{n-i}$
for
$\lambda ^{n-i}$
for
![]() $\det (\lambda I_n - M_n)$
multiplied by
$\det (\lambda I_n - M_n)$
multiplied by
![]() $(-1)^i$
.
$(-1)^i$
.
Remark 4.7. If
![]() $q_{rs}=0$
for
$q_{rs}=0$
for
![]() $s-r>1$
and
$s-r>1$
and
![]() $q_{s \, s+1}=q_s$
, then the polynomial
$q_{s \, s+1}=q_s$
, then the polynomial
![]() $E_i^{(n)}$
is equal to the (classical) quantized elementary symmetric polynomial
$E_i^{(n)}$
is equal to the (classical) quantized elementary symmetric polynomial
![]() $\check E_i^{(n)}$
in the polynomial ring
$\check E_i^{(n)}$
in the polynomial ring
![]() ${\mathbb {C}}[x_1,\ldots ,x_n,q_1,\ldots ,q_{n-1}]$
.
${\mathbb {C}}[x_1,\ldots ,x_n,q_1,\ldots ,q_{n-1}]$
.
Lemma 4.8. For
![]() $1 \leq r \leq s \leq n$
, we have
$1 \leq r \leq s \leq n$
, we have
 $$ \begin{align*} E_r^{(s)} = E_r^{(s-1)} + E_{r-1}^{(s-1)} x_s + \sum_{k=1}^{r-1} E_{r-1-k}^{(s-1-k)} q_{s-k \, s} \end{align*} $$
$$ \begin{align*} E_r^{(s)} = E_r^{(s-1)} + E_{r-1}^{(s-1)} x_s + \sum_{k=1}^{r-1} E_{r-1-k}^{(s-1-k)} q_{s-k \, s} \end{align*} $$
with the convention that
![]() $E_0^{(*)}=1$
for arbitrary
$E_0^{(*)}=1$
for arbitrary
![]() $*$
,
$*$
,
![]() $\sum _{k=1}^{r-1} E_{r-1-k}^{(s-1-k)} q_{s-k \, s}=0$
whenever
$\sum _{k=1}^{r-1} E_{r-1-k}^{(s-1-k)} q_{s-k \, s}=0$
whenever
![]() $r=1$
, and
$r=1$
, and
![]() $E_{s}^{(s-1)}=0$
whenever
$E_{s}^{(s-1)}=0$
whenever
![]() $r=s$
.
$r=s$
.
Proof. It follows from the cofactor expansion along the s-th column for
![]() $\det (\lambda I_s - M_s)$
that
$\det (\lambda I_s - M_s)$
that
![]() $\det (\lambda I_s - M_s)$
is equal to
$\det (\lambda I_s - M_s)$
is equal to
 $$ \begin{align} &(-1)^{s+2} q_{1s} + (-1)^{s+3} q_{2s} \det(\lambda I_1 - M_1) + \cdots + (-1)^{s+s} q_{s-1 \, s} \det(\lambda I_{s-2} - M_{s-2}) \\ & \hspace{20pt} + (-1)^{s+s} (\lambda - x_s) \det(\lambda I_{s-1} - M_{s-1}). \notag \end{align} $$
$$ \begin{align} &(-1)^{s+2} q_{1s} + (-1)^{s+3} q_{2s} \det(\lambda I_1 - M_1) + \cdots + (-1)^{s+s} q_{s-1 \, s} \det(\lambda I_{s-2} - M_{s-2}) \\ & \hspace{20pt} + (-1)^{s+s} (\lambda - x_s) \det(\lambda I_{s-1} - M_{s-1}). \notag \end{align} $$
Since we have
for each
![]() $1 \leq k \leq s-1$
by the definition, the coefficient of
$1 \leq k \leq s-1$
by the definition, the coefficient of
![]() $\lambda ^{s-r}$
for equation (4.3) is given by
$\lambda ^{s-r}$
for equation (4.3) is given by
 $$ \begin{align*} &(-1)^r q_{s-r+1 \, s} + (-1)^{r} q_{s-r+2 \, s} E_1^{(s-r+1)} + \cdots + (-1)^{r} q_{s-1 \, s} E_{r-2}^{(s-2)} \\ & \hspace{20pt} + (-x_s) (-1)^{r-1} E_{r-1}^{(s-1)} + (-1)^{r} E_r^{(s-1)}. \end{align*} $$
$$ \begin{align*} &(-1)^r q_{s-r+1 \, s} + (-1)^{r} q_{s-r+2 \, s} E_1^{(s-r+1)} + \cdots + (-1)^{r} q_{s-1 \, s} E_{r-2}^{(s-2)} \\ & \hspace{20pt} + (-x_s) (-1)^{r-1} E_{r-1}^{(s-1)} + (-1)^{r} E_r^{(s-1)}. \end{align*} $$
Namely, the coefficient of
![]() $\lambda ^{s-r}$
for
$\lambda ^{s-r}$
for
![]() $\det (\lambda I_s - M_s)$
is
$\det (\lambda I_s - M_s)$
is
as desired.
Example 4.9. Let
![]() $n=3$
. Then the
$n=3$
. Then the
![]() $E_r^{(s)}$
have the following form.
$E_r^{(s)}$
have the following form.
 $$ \begin{align*} &E_0^{(1)} = 1, \ \ \ E_1^{(1)} = E_0^{(0)}x_1 =x_1, \\ &E_0^{(2)} = 1, \ \ \ E_1^{(2)} = E_1^{(1)} + E_0^{(1)}x_2 = x_1+x_2, \ \ \ E_2^{(2)} = E_1^{(1)}x_2 + E_0^{(0)}q_{12} = x_1x_2+q_{12}, \\ &E_0^{(3)} = 1, \ \ \ E_1^{(3)} = E_1^{(2)} + E_0^{(2)}x_3 = x_1+x_2+x_3, \\ &E_2^{(3)} = E_2^{(2)} + E_{1}^{(2)}x_3 + E_0^{(1)}q_{23} = x_1x_2+x_1x_3+x_2x_3+q_{12}+q_{23}, \\ &E_3^{(3)} = E_{2}^{(2)}x_3 + E_1^{(1)}q_{23} + E_0^{(0)}q_{13}= x_1x_2x_3+x_1q_{23}+x_3q_{12}+q_{13}. \end{align*} $$
$$ \begin{align*} &E_0^{(1)} = 1, \ \ \ E_1^{(1)} = E_0^{(0)}x_1 =x_1, \\ &E_0^{(2)} = 1, \ \ \ E_1^{(2)} = E_1^{(1)} + E_0^{(1)}x_2 = x_1+x_2, \ \ \ E_2^{(2)} = E_1^{(1)}x_2 + E_0^{(0)}q_{12} = x_1x_2+q_{12}, \\ &E_0^{(3)} = 1, \ \ \ E_1^{(3)} = E_1^{(2)} + E_0^{(2)}x_3 = x_1+x_2+x_3, \\ &E_2^{(3)} = E_2^{(2)} + E_{1}^{(2)}x_3 + E_0^{(1)}q_{23} = x_1x_2+x_1x_3+x_2x_3+q_{12}+q_{23}, \\ &E_3^{(3)} = E_{2}^{(2)}x_3 + E_1^{(1)}q_{23} + E_0^{(0)}q_{13}= x_1x_2x_3+x_1q_{23}+x_3q_{12}+q_{13}. \end{align*} $$
Definition 4.10. Let
![]() $h: [n] \to [n]$
be a Hessenberg function. For each
$h: [n] \to [n]$
be a Hessenberg function. For each
![]() $1 \leq i \leq j \leq n$
, we define
$1 \leq i \leq j \leq n$
, we define
![]() $^h E_i^{(j)}$
as the polynomial
$^h E_i^{(j)}$
as the polynomial
![]() $E_i^{(j)}$
by setting
$E_i^{(j)}$
by setting
![]() $q_{rs}=0$
for all
$q_{rs}=0$
for all
![]() $2 \leq s \leq n$
and
$2 \leq s \leq n$
and
![]() $1 \leq r \leq n-h(n+1-s)$
:
$1 \leq r \leq n-h(n+1-s)$
:
The surviving variables in the polynomial
![]() $^h E_i^{(j)}$
are pictorially shown as follows. Let
$^h E_i^{(j)}$
are pictorially shown as follows. Let
![]() $w_0$
be the longest element of the symmetric group
$w_0$
be the longest element of the symmetric group
![]() $\mathfrak S_n$
on n letters
$\mathfrak S_n$
on n letters
![]() $[n]$
. Consider the matrix
$[n]$
. Consider the matrix
 $$ \begin{align} w_0 M_n w_0 = \left( \begin{array}{@{\,}ccccc@{\,}} x_n & -1 & 0 & \cdots & 0 \\ q_{n-1 \, n} & x_{n-1} & -1 & \ddots & \vdots \\ \vdots & \ddots & \ddots & \ddots & 0 \\ q_{2n} & \cdots & q_{23} & x_2 & -1 \\ q_{1n} & \cdots & q_{13} & q_{12} & x_1 \end{array} \right), \end{align} $$
$$ \begin{align} w_0 M_n w_0 = \left( \begin{array}{@{\,}ccccc@{\,}} x_n & -1 & 0 & \cdots & 0 \\ q_{n-1 \, n} & x_{n-1} & -1 & \ddots & \vdots \\ \vdots & \ddots & \ddots & \ddots & 0 \\ q_{2n} & \cdots & q_{23} & x_2 & -1 \\ q_{1n} & \cdots & q_{13} & q_{12} & x_1 \end{array} \right), \end{align} $$
where
![]() $w_0$
is regarded as the permutation matrix. Then
$w_0$
is regarded as the permutation matrix. Then
![]() $w_0 M_n w_0 \in H(h)$
if and only if
$w_0 M_n w_0 \in H(h)$
if and only if
![]() $q_{rs}=0$
for all
$q_{rs}=0$
for all
![]() $2 \leq s \leq n$
and
$2 \leq s \leq n$
and
![]() $1 \leq r \leq n-h(n+1-s)$
where
$1 \leq r \leq n-h(n+1-s)$
where
![]() $H(h)$
is the Hessenberg space defined in equation (2.1). In other words, the surviving variables in the polynomial
$H(h)$
is the Hessenberg space defined in equation (2.1). In other words, the surviving variables in the polynomial
![]() $^h E_i^{(j)}$
are pictorially the variables
$^h E_i^{(j)}$
are pictorially the variables
![]() $q_{rs}$
arranged in
$q_{rs}$
arranged in
![]() $w_0 M_n w_0$
such that
$w_0 M_n w_0$
such that
![]() $q_{rs}$
belongs to the configuration of the shaded boxes for the Hessenberg function h.
$q_{rs}$
belongs to the configuration of the shaded boxes for the Hessenberg function h.
Example 4.11. Let
![]() $n=5$
and
$n=5$
and
![]() $h=(3,3,4,5,5)$
, which is depicted in Example 2.1. Then
$h=(3,3,4,5,5)$
, which is depicted in Example 2.1. Then
![]() $^h E_i^{(j)}$
is a polynomial in the variables
$^h E_i^{(j)}$
is a polynomial in the variables
![]() $x_1,\ldots ,x_5,q_{12},q_{23},q_{34},q_{35},q_{45}$
for
$x_1,\ldots ,x_5,q_{12},q_{23},q_{34},q_{35},q_{45}$
for
![]() $1 \leq i \leq j \leq 5$
, as shown in Figure 3.
$1 \leq i \leq j \leq 5$
, as shown in Figure 3.

Figure 3 The polynomial
![]() $^h E_i^{(j)} \in {\mathbb {C}}[x_1,\ldots ,x_5,q_{12},q_{23},q_{34},q_{35},q_{45}]$
for
$^h E_i^{(j)} \in {\mathbb {C}}[x_1,\ldots ,x_5,q_{12},q_{23},q_{34},q_{35},q_{45}]$
for
![]() $h=(3,3,4,5,5)$
$h=(3,3,4,5,5)$
Remark 4.12. In our setting, the flag variety
![]() $Fl({\mathbb {C}}^n)$
is identified with
$Fl({\mathbb {C}}^n)$
is identified with
![]() $\operatorname {\mathrm {GL}}_n({\mathbb {C}})/B$
, while
$\operatorname {\mathrm {GL}}_n({\mathbb {C}})/B$
, while
![]() $Fl({\mathbb {C}}^n)$
is regarded as
$Fl({\mathbb {C}}^n)$
is regarded as
![]() $\operatorname {\mathrm {GL}}_n({\mathbb {C}})/B^{-}$
in [Reference Rietsch32]. Recall that the conjugation by
$\operatorname {\mathrm {GL}}_n({\mathbb {C}})/B^{-}$
in [Reference Rietsch32]. Recall that the conjugation by
![]() $w_0$
gives an isomorphism
$w_0$
gives an isomorphism
![]() $\operatorname {\mathrm {GL}}_n({\mathbb {C}})/B \cong \operatorname {\mathrm {GL}}_n({\mathbb {C}})/B^{-}$
since
$\operatorname {\mathrm {GL}}_n({\mathbb {C}})/B \cong \operatorname {\mathrm {GL}}_n({\mathbb {C}})/B^{-}$
since
![]() $B^{-}=w_0 B w_0$
. This relation might affect the reason why we take the conjugation by
$B^{-}=w_0 B w_0$
. This relation might affect the reason why we take the conjugation by
![]() $w_0$
in equation (4.4).
$w_0$
in equation (4.4).
We now state the main theorem of this paper.
Theorem 4.13. Let
![]() $h: [n] \to [n]$
be a Hessenberg function and
$h: [n] \to [n]$
be a Hessenberg function and
![]() $\mathcal {Z}(N,h)_e$
the intersection defined in equation (3.6). Then there is an isomorphism of
$\mathcal {Z}(N,h)_e$
the intersection defined in equation (3.6). Then there is an isomorphism of
![]() ${\mathbb {C}}$
-algebras
${\mathbb {C}}$
-algebras
 $$ \begin{align} \Gamma(\mathcal{Z}(N,h)_e, \mathcal{O}_{\mathcal{Z}(N,h)_e}) \cong \frac{{\mathbb{C}}[x_1,\ldots,x_n, q_{rs} \mid 2 \leq s \leq n, n-h(n+1-s)<r<s]}{(^h E_1^{(n)}, \ldots, \, ^h E_n^{(n)})}, \end{align} $$
$$ \begin{align} \Gamma(\mathcal{Z}(N,h)_e, \mathcal{O}_{\mathcal{Z}(N,h)_e}) \cong \frac{{\mathbb{C}}[x_1,\ldots,x_n, q_{rs} \mid 2 \leq s \leq n, n-h(n+1-s)<r<s]}{(^h E_1^{(n)}, \ldots, \, ^h E_n^{(n)})}, \end{align} $$
which sends
![]() $x_{ij}$
to
$x_{ij}$
to
![]() $^h E_{i-j}^{(n-j)}$
under the presentation (3.7). In particular, if h is indecomposable, then there is an isomorphism of
$^h E_{i-j}^{(n-j)}$
under the presentation (3.7). In particular, if h is indecomposable, then there is an isomorphism of
![]() ${\mathbb {C}}$
-algebras
${\mathbb {C}}$
-algebras
 $$ \begin{align} {\mathbb{C}}[\operatorname{\mathrm{Hess}}(N,h) \cap \Omega_e^\circ] \cong \frac{{\mathbb{C}}[x_1,\ldots,x_n, q_{rs} \mid 2 \leq s \leq n, n-h(n+1-s)<r<s]}{(^h E_1^{(n)}, \ldots, \, ^h E_n^{(n)})}, \end{align} $$
$$ \begin{align} {\mathbb{C}}[\operatorname{\mathrm{Hess}}(N,h) \cap \Omega_e^\circ] \cong \frac{{\mathbb{C}}[x_1,\ldots,x_n, q_{rs} \mid 2 \leq s \leq n, n-h(n+1-s)<r<s]}{(^h E_1^{(n)}, \ldots, \, ^h E_n^{(n)})}, \end{align} $$
which sends
![]() $x_{ij}$
to
$x_{ij}$
to
![]() $^h E_{i-j}^{(n-j)}$
under the presentation (3.8).
$^h E_{i-j}^{(n-j)}$
under the presentation (3.8).
We will prove Theorem 4.13 in Section 7. For this purpose, one first see that the homomorphism in equation (4.5) is well defined and surjective in the next section.
Remark 4.14. We will introduce certain degrees for the variables
![]() $\{x_{ij} \mid 1 \leq j < i \leq n \}$
and
$\{x_{ij} \mid 1 \leq j < i \leq n \}$
and
![]() $\{x_1,\ldots ,x_n, q_{rs} \mid 1 \leq r < s \leq n \}$
so that the two sides of equation (4.5) are graded
$\{x_1,\ldots ,x_n, q_{rs} \mid 1 \leq r < s \leq n \}$
so that the two sides of equation (4.5) are graded
![]() ${\mathbb {C}}$
-algebras (see Section 6 for the detail). We will prove that equation (4.5) is in fact an isomorphism as graded
${\mathbb {C}}$
-algebras (see Section 6 for the detail). We will prove that equation (4.5) is in fact an isomorphism as graded
![]() ${\mathbb {C}}$
-algebras in Section 7.
${\mathbb {C}}$
-algebras in Section 7.
5 Properties of
 $E_r^{(s)}$
$E_r^{(s)}$
In this section, we see relations between
![]() $x_s$
’s,
$x_s$
’s,
![]() $q_{rs}$
’s, and
$q_{rs}$
’s, and
![]() $E_r^{(s)}$
’s. Then we construct an explicit map from
$E_r^{(s)}$
’s. Then we construct an explicit map from
![]() $\Gamma (\mathcal {Z}(N,h)_e, \mathcal {O}_{\mathcal {Z}(N,h)_e})$
to our quotient ring
$\Gamma (\mathcal {Z}(N,h)_e, \mathcal {O}_{\mathcal {Z}(N,h)_e})$
to our quotient ring
![]() ${\mathbb {C}}[x_1,\ldots ,x_n, q_{rs} \mid 2 \leq s \leq n, n-h(n+1-s)<r<s]/(^h E_1^{(n)}, \ldots , \, ^h E_n^{(n)})$
.
${\mathbb {C}}[x_1,\ldots ,x_n, q_{rs} \mid 2 \leq s \leq n, n-h(n+1-s)<r<s]/(^h E_1^{(n)}, \ldots , \, ^h E_n^{(n)})$
.
Lemma 5.1. For
![]() $1 \leq r < s \leq n$
, we have
$1 \leq r < s \leq n$
, we have
 $$ \begin{align*} q_{rs} = \left| \begin{array}{@{\,}cccccc@{\,}} 1 & 0 & \cdots & \cdots & 0 & E_{1}^{(s)}-E_{1}^{(s-1)} \\ E_1^{(s-1)} & 1 & 0 & & \vdots & E_{2}^{(s)}-E_{2}^{(s-1)} \\ E_2^{(s-1)} & E_1^{(s-2)} & 1 & \ddots & \vdots & E_{3}^{(s)}-E_{3}^{(s-1)} \\ \vdots & \ddots & \ddots & \ddots & 0 & \vdots \\ \vdots & & \ddots & E_1^{(r+1)} & 1 & E_{s-r}^{(s)}-E_{s-r}^{(s-1)} \\ E_{s-r}^{(s-1)} & \cdots & \cdots & E_2^{(r+1)} & E_1^{(r)} & E_{s-r+1}^{(s)}-E_{s-r+1}^{(s-1)} \end{array} \right| \end{align*} $$
$$ \begin{align*} q_{rs} = \left| \begin{array}{@{\,}cccccc@{\,}} 1 & 0 & \cdots & \cdots & 0 & E_{1}^{(s)}-E_{1}^{(s-1)} \\ E_1^{(s-1)} & 1 & 0 & & \vdots & E_{2}^{(s)}-E_{2}^{(s-1)} \\ E_2^{(s-1)} & E_1^{(s-2)} & 1 & \ddots & \vdots & E_{3}^{(s)}-E_{3}^{(s-1)} \\ \vdots & \ddots & \ddots & \ddots & 0 & \vdots \\ \vdots & & \ddots & E_1^{(r+1)} & 1 & E_{s-r}^{(s)}-E_{s-r}^{(s-1)} \\ E_{s-r}^{(s-1)} & \cdots & \cdots & E_2^{(r+1)} & E_1^{(r)} & E_{s-r+1}^{(s)}-E_{s-r+1}^{(s-1)} \end{array} \right| \end{align*} $$
in the polynomial ring
![]() ${\mathbb {C}}[x_1,\ldots ,x_n,q_{rs} \mid 1 \leq r < s \leq n]$
.
${\mathbb {C}}[x_1,\ldots ,x_n,q_{rs} \mid 1 \leq r < s \leq n]$
.
Proof. For
![]() $1 \leq s \leq n$
, it follows from Lemma 4.8 that
$1 \leq s \leq n$
, it follows from Lemma 4.8 that
 $$ \begin{align*} \begin{cases} E_1^{(s)} &= E_1^{(s-1)} + x_s \\ E_2^{(s)} &= E_2^{(s-1)} + E_{1}^{(s-1)} x_s + q_{s-1 \, s} \\ E_3^{(s)} &= E_3^{(s-1)} + E_{2}^{(s-1)} x_s + E_{1}^{(s-2)} q_{s-1 \, s} + q_{s-2 \, s} \\ &\vdots \\ E_{s-r+1}^{(s)} &= E_{s-r+1}^{(s-1)} + E_{s-r}^{(s-1)} x_s + E_{s-r-1}^{(s-2)} q_{s-1 \, s} + E_{s-r-2}^{(s-3)} q_{s-2 \, s} + \cdots + E_1^{(r)} q_{r+1 \, s} + q_{rs}. \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} E_1^{(s)} &= E_1^{(s-1)} + x_s \\ E_2^{(s)} &= E_2^{(s-1)} + E_{1}^{(s-1)} x_s + q_{s-1 \, s} \\ E_3^{(s)} &= E_3^{(s-1)} + E_{2}^{(s-1)} x_s + E_{1}^{(s-2)} q_{s-1 \, s} + q_{s-2 \, s} \\ &\vdots \\ E_{s-r+1}^{(s)} &= E_{s-r+1}^{(s-1)} + E_{s-r}^{(s-1)} x_s + E_{s-r-1}^{(s-2)} q_{s-1 \, s} + E_{s-r-2}^{(s-3)} q_{s-2 \, s} + \cdots + E_1^{(r)} q_{r+1 \, s} + q_{rs}. \end{cases} \end{align*} $$
In other words, we have
 $$ \begin{align*} \left( \begin{array}{@{\,}cccccc@{\,}} 1 & & & & & \\ E_1^{(s-1)} & 1 & & & & \\ E_2^{(s-1)} & E_1^{(s-2)} & 1 & & & \\ \vdots & \ddots & \ddots & \ddots & & \\ \vdots & & \ddots & E_1^{(r+1)} & 1 & \\ E_{s-r}^{(s-1)} & \cdots & \cdots & E_2^{(r+1)} & E_1^{(r)} & 1 \end{array} \right) \left( \begin{array}{@{\,}c@{\,}} x_s \\ q_{s-1 \, s} \\ q_{s-2 \, s} \\ \vdots \\ q_{r+1 \, s} \\ q_{rs} \end{array} \right) = \left( \begin{array}{@{\,}c@{\,}} E_1^{(s)}-E_1^{(s-1)} \\ E_2^{(s)}-E_2^{(s-1)} \\ E_3^{(s)}-E_3^{(s-1)} \\ \vdots \\ E_{s-r}^{(s)}-E_{s-r}^{(s-1)} \\ E_{s-r+1}^{(s)}-E_{s-r+1}^{(s-1)} \\ \end{array} \right). \end{align*} $$
$$ \begin{align*} \left( \begin{array}{@{\,}cccccc@{\,}} 1 & & & & & \\ E_1^{(s-1)} & 1 & & & & \\ E_2^{(s-1)} & E_1^{(s-2)} & 1 & & & \\ \vdots & \ddots & \ddots & \ddots & & \\ \vdots & & \ddots & E_1^{(r+1)} & 1 & \\ E_{s-r}^{(s-1)} & \cdots & \cdots & E_2^{(r+1)} & E_1^{(r)} & 1 \end{array} \right) \left( \begin{array}{@{\,}c@{\,}} x_s \\ q_{s-1 \, s} \\ q_{s-2 \, s} \\ \vdots \\ q_{r+1 \, s} \\ q_{rs} \end{array} \right) = \left( \begin{array}{@{\,}c@{\,}} E_1^{(s)}-E_1^{(s-1)} \\ E_2^{(s)}-E_2^{(s-1)} \\ E_3^{(s)}-E_3^{(s-1)} \\ \vdots \\ E_{s-r}^{(s)}-E_{s-r}^{(s-1)} \\ E_{s-r+1}^{(s)}-E_{s-r+1}^{(s-1)} \\ \end{array} \right). \end{align*} $$
By Cramer’s rule, we obtain the desired result.
Set
and define a map
![]() $\varphi $
from
$\varphi $
from
![]() ${\mathbb {C}}[x_{ij} \mid 1 \leq j < i \leq n]$
to the ring
${\mathbb {C}}[x_{ij} \mid 1 \leq j < i \leq n]$
to the ring
![]() $Q_n$
by
$Q_n$
by
Proposition 5.2. The map
![]() $\varphi $
above sends
$\varphi $
above sends
 $$ \begin{align*} \varphi(x_{n-s+1 \, n-s} - x_{n-s+2 \, n-s+1}) &= x_s \ \ \ \text{for} \ s \in [n] \\ \varphi(-F_{n+1-r,n+1-s}) &= q_{rs} \ \ \ \text{for} \ 1 \leq r < s \leq n. \end{align*} $$
$$ \begin{align*} \varphi(x_{n-s+1 \, n-s} - x_{n-s+2 \, n-s+1}) &= x_s \ \ \ \text{for} \ s \in [n] \\ \varphi(-F_{n+1-r,n+1-s}) &= q_{rs} \ \ \ \text{for} \ 1 \leq r < s \leq n. \end{align*} $$
Here, we take the convention that
![]() $x_{n-s+2 \, n-s+1}=0$
whenever
$x_{n-s+2 \, n-s+1}=0$
whenever
![]() $s=1$
and
$s=1$
and
![]() $x_{n-s+1 \, n-s}=0$
whenever
$x_{n-s+1 \, n-s}=0$
whenever
![]() $s=n$
. In particular,
$s=n$
. In particular,
![]() $\varphi $
is surjective.
$\varphi $
is surjective.
Proof. First, one can see from Definition 4.6 that
for any
![]() $s \in [n]$
, which implies that
$s \in [n]$
, which implies that
![]() $x_s=E_1^{(s)} -E_1^{(s-1)}$
. By the definition of
$x_s=E_1^{(s)} -E_1^{(s-1)}$
. By the definition of
![]() $\varphi $
we have
$\varphi $
we have
![]() $\varphi (x_{n-s+1 \, n-s} - x_{n-s+2 \, n-s+1}) = E_1^{(s)} -E_1^{(s-1)} = x_s$
for
$\varphi (x_{n-s+1 \, n-s} - x_{n-s+2 \, n-s+1}) = E_1^{(s)} -E_1^{(s-1)} = x_s$
for
![]() $s \in [n]$
. (Note that if
$s \in [n]$
. (Note that if
![]() $s=n$
, then we used the relation
$s=n$
, then we used the relation
![]() $E_1^{(n)}=0$
in the quotient ring
$E_1^{(n)}=0$
in the quotient ring
![]() $Q_n={\mathbb {C}}[x_1,\ldots ,x_n, q_{rs} \mid 1 \leq r < s \leq n]/(E_1^{(n)}, \ldots , E_n^{(n)})$
.)
$Q_n={\mathbb {C}}[x_1,\ldots ,x_n, q_{rs} \mid 1 \leq r < s \leq n]/(E_1^{(n)}, \ldots , E_n^{(n)})$
.)
Next, it follows from equation (3.3) that
 $$ \begin{align} \varphi(F_{n+1-r,1}) = \left| \begin{array}{@{\,}cccccc@{\,}} 1 & 0 & \cdots & \cdots & 0 & E_1^{(n-1)} \\ E_1^{(n-1)} & 1 & 0 & & \vdots & E_2^{(n-1)} \\ E_2^{(n-1)} & E_1^{(n-2)} & 1 & \ddots & \vdots & \vdots \\ \vdots & \ddots & \ddots & \ddots & 0 & \vdots \\ \vdots & & \ddots & E_1^{(r+1)} & 1 & E_{n-r}^{(n-1)} \\ E_{n-r}^{(n-1)} & \cdots & \cdots & E_2^{(r+1)} & E_1^{(r)} & E_{n-r+1}^{(n-1)} \end{array} \right| \end{align} $$
$$ \begin{align} \varphi(F_{n+1-r,1}) = \left| \begin{array}{@{\,}cccccc@{\,}} 1 & 0 & \cdots & \cdots & 0 & E_1^{(n-1)} \\ E_1^{(n-1)} & 1 & 0 & & \vdots & E_2^{(n-1)} \\ E_2^{(n-1)} & E_1^{(n-2)} & 1 & \ddots & \vdots & \vdots \\ \vdots & \ddots & \ddots & \ddots & 0 & \vdots \\ \vdots & & \ddots & E_1^{(r+1)} & 1 & E_{n-r}^{(n-1)} \\ E_{n-r}^{(n-1)} & \cdots & \cdots & E_2^{(r+1)} & E_1^{(r)} & E_{n-r+1}^{(n-1)} \end{array} \right| \end{align} $$
for
![]() $1 \leq r \leq n-1$
. On the other hand, by Lemma 5.1 we have
$1 \leq r \leq n-1$
. On the other hand, by Lemma 5.1 we have
 $$ \begin{align} q_{rn} = \left| \begin{array}{@{\,}cccccc@{\,}} 1 & 0 & \cdots & \cdots & 0 & -E_{1}^{(n-1)} \\[2pt] E_1^{(n-1)} & 1 & 0 & & \vdots & -E_{2}^{(n-1)} \\ E_2^{(n-1)} & E_1^{(n-2)} & 1 & \ddots & \vdots & -E_{3}^{(n-1)} \\[2pt] \vdots & \ddots & \ddots & \ddots & 0 & \vdots \\[2pt] \vdots & & \ddots & E_1^{(r+1)} & 1 & -E_{n-r}^{(n-1)} \\[2pt] E_{n-r}^{(n-1)} & \cdots & \cdots & E_2^{(r+1)} & E_1^{(r)} & -E_{n-r+1}^{(n-1)} \end{array} \right| \end{align} $$
$$ \begin{align} q_{rn} = \left| \begin{array}{@{\,}cccccc@{\,}} 1 & 0 & \cdots & \cdots & 0 & -E_{1}^{(n-1)} \\[2pt] E_1^{(n-1)} & 1 & 0 & & \vdots & -E_{2}^{(n-1)} \\ E_2^{(n-1)} & E_1^{(n-2)} & 1 & \ddots & \vdots & -E_{3}^{(n-1)} \\[2pt] \vdots & \ddots & \ddots & \ddots & 0 & \vdots \\[2pt] \vdots & & \ddots & E_1^{(r+1)} & 1 & -E_{n-r}^{(n-1)} \\[2pt] E_{n-r}^{(n-1)} & \cdots & \cdots & E_2^{(r+1)} & E_1^{(r)} & -E_{n-r+1}^{(n-1)} \end{array} \right| \end{align} $$
since
![]() $E_1^{(n)}=0, \ldots , E_{n-r+1}^{(n)}=0$
in the quotient ring
$E_1^{(n)}=0, \ldots , E_{n-r+1}^{(n)}=0$
in the quotient ring
![]() $Q_n={\mathbb {C}}[x_1,\ldots ,x_n, q_{rs} \mid 1 \leq r < s \leq n]/(E_1^{(n)}, \ldots , E_n^{(n)})$
. By equations (5.3) and (5.4), we have
$Q_n={\mathbb {C}}[x_1,\ldots ,x_n, q_{rs} \mid 1 \leq r < s \leq n]/(E_1^{(n)}, \ldots , E_n^{(n)})$
. By equations (5.3) and (5.4), we have
![]() $\varphi (F_{n-r+1,1})=-q_{rn}$
for
$\varphi (F_{n-r+1,1})=-q_{rn}$
for
![]() $1 \leq r \leq n-1$
as desired.
$1 \leq r \leq n-1$
as desired.
If
![]() $s <n$
, then by equation (3.4) we have
$s <n$
, then by equation (3.4) we have
 $$ \begin{align*} \varphi(F_{n+1-r,n+1-s}) &= \left| \begin{array}{@{\,}cccccc@{\,}} 1 & 0 & \cdots & \cdots & 0 & 1 \\[2pt] E_1^{(s)} & 1 & 0 & & \vdots & E_1^{(s-1)} \\[2pt] E_2^{(s)} & E_1^{(s-1)} & 1 & \ddots & \vdots & E_2^{(s-1)} \\[2pt] \vdots & E_2^{(s-1)} & \ddots & \ddots & 0 & \vdots \\[2pt] \vdots & \vdots & \ddots & E_1^{(r+1)} & 1 & \vdots \\[2pt] E_{s-r+1}^{(s)} & E_{s-r}^{(s-1)} & \cdots & E_2^{(r+1)} & E_1^{(r)} & E_{s-r+1}^{(s-1)} \end{array} \right| \\[8pt] &= \left| \begin{array}{@{\,}cccccc@{\,}} 0 & 0 & \cdots & \cdots & 0 & 1 \\[2pt] E_1^{(s)}-E_1^{(s-1)} & 1 & 0 & & \vdots & E_1^{(s-1)} \\[2pt] E_2^{(s)}-E_2^{(s-1)} & E_1^{(s-1)} & 1 & \ddots & \vdots & E_2^{(s-1)} \\[2pt] \vdots & E_2^{(s-1)} & \ddots & \ddots & 0 & \vdots \\[2pt] \vdots & \vdots & \ddots & E_1^{(r+1)} & 1 & \vdots \\[2pt] E_{s-r+1}^{(s)}-E_{s-r+1}^{(s-1)} & E_{s-r}^{(s-1)} & \cdots & E_2^{(r+1)} & E_1^{(r)} & E_{s-r+1}^{(s-1)} \end{array} \right| \\[5pt] & \qquad \text{(by subtracting the last column from the first column)} \\[8pt] &= -\left| \begin{array}{@{\,}cccccc@{\,}} 1 & 0 & \cdots & \cdots & 0 & 0 \\[2pt] E_1^{(s-1)} & 1 & 0 & & \vdots & E_1^{(s)}-E_1^{(s-1)} \\[2pt] E_2^{(s-1)} & E_1^{(s-1)} & 1 & \ddots & \vdots & E_2^{(s)}-E_2^{(s-1)} \\[2pt] \vdots & E_2^{(s-1)} & \ddots & \ddots & 0 & \vdots \\[2pt] \vdots & \vdots & \ddots & E_1^{(r+1)} & 1 & \vdots \\[2pt] E_{s-r+1}^{(s-1)} & E_{s-r}^{(s-1)} & \cdots & E_2^{(r+1)} & E_1^{(r)} & E_{s-r+1}^{(s)}-E_{s-r+1}^{(s-1)} \end{array} \right| \\[5pt] & \quad \qquad \text{(by changing the first column and the last column)} \\&= -\left| \begin{array}{@{\,}cccccc@{\,}} 1 & 0 & \cdots & \cdots & 0 & E_{1}^{(s)}-E_{1}^{(s-1)} \\ E_1^{(s-1)} & 1 & 0 & & \vdots & E_{2}^{(s)}-E_{2}^{(s-1)} \\ E_2^{(s-1)} & E_1^{(s-2)} & 1 & \ddots & \vdots & E_{3}^{(s)}-E_{3}^{(s-1)} \\ \vdots & \ddots & \ddots & \ddots & 0 & \vdots \\ \vdots & & \ddots & E_1^{(r+1)} & 1 & E_{s-r}^{(s)}-E_{s-r}^{(s-1)} \\ E_{s-r}^{(s-1)} & \cdots & \cdots & E_2^{(r+1)} & E_1^{(r)} & E_{s-r+1}^{(s)}-E_{s-r+1}^{(s-1)} \end{array} \right| \end{align*} $$
$$ \begin{align*} \varphi(F_{n+1-r,n+1-s}) &= \left| \begin{array}{@{\,}cccccc@{\,}} 1 & 0 & \cdots & \cdots & 0 & 1 \\[2pt] E_1^{(s)} & 1 & 0 & & \vdots & E_1^{(s-1)} \\[2pt] E_2^{(s)} & E_1^{(s-1)} & 1 & \ddots & \vdots & E_2^{(s-1)} \\[2pt] \vdots & E_2^{(s-1)} & \ddots & \ddots & 0 & \vdots \\[2pt] \vdots & \vdots & \ddots & E_1^{(r+1)} & 1 & \vdots \\[2pt] E_{s-r+1}^{(s)} & E_{s-r}^{(s-1)} & \cdots & E_2^{(r+1)} & E_1^{(r)} & E_{s-r+1}^{(s-1)} \end{array} \right| \\[8pt] &= \left| \begin{array}{@{\,}cccccc@{\,}} 0 & 0 & \cdots & \cdots & 0 & 1 \\[2pt] E_1^{(s)}-E_1^{(s-1)} & 1 & 0 & & \vdots & E_1^{(s-1)} \\[2pt] E_2^{(s)}-E_2^{(s-1)} & E_1^{(s-1)} & 1 & \ddots & \vdots & E_2^{(s-1)} \\[2pt] \vdots & E_2^{(s-1)} & \ddots & \ddots & 0 & \vdots \\[2pt] \vdots & \vdots & \ddots & E_1^{(r+1)} & 1 & \vdots \\[2pt] E_{s-r+1}^{(s)}-E_{s-r+1}^{(s-1)} & E_{s-r}^{(s-1)} & \cdots & E_2^{(r+1)} & E_1^{(r)} & E_{s-r+1}^{(s-1)} \end{array} \right| \\[5pt] & \qquad \text{(by subtracting the last column from the first column)} \\[8pt] &= -\left| \begin{array}{@{\,}cccccc@{\,}} 1 & 0 & \cdots & \cdots & 0 & 0 \\[2pt] E_1^{(s-1)} & 1 & 0 & & \vdots & E_1^{(s)}-E_1^{(s-1)} \\[2pt] E_2^{(s-1)} & E_1^{(s-1)} & 1 & \ddots & \vdots & E_2^{(s)}-E_2^{(s-1)} \\[2pt] \vdots & E_2^{(s-1)} & \ddots & \ddots & 0 & \vdots \\[2pt] \vdots & \vdots & \ddots & E_1^{(r+1)} & 1 & \vdots \\[2pt] E_{s-r+1}^{(s-1)} & E_{s-r}^{(s-1)} & \cdots & E_2^{(r+1)} & E_1^{(r)} & E_{s-r+1}^{(s)}-E_{s-r+1}^{(s-1)} \end{array} \right| \\[5pt] & \quad \qquad \text{(by changing the first column and the last column)} \\&= -\left| \begin{array}{@{\,}cccccc@{\,}} 1 & 0 & \cdots & \cdots & 0 & E_{1}^{(s)}-E_{1}^{(s-1)} \\ E_1^{(s-1)} & 1 & 0 & & \vdots & E_{2}^{(s)}-E_{2}^{(s-1)} \\ E_2^{(s-1)} & E_1^{(s-2)} & 1 & \ddots & \vdots & E_{3}^{(s)}-E_{3}^{(s-1)} \\ \vdots & \ddots & \ddots & \ddots & 0 & \vdots \\ \vdots & & \ddots & E_1^{(r+1)} & 1 & E_{s-r}^{(s)}-E_{s-r}^{(s-1)} \\ E_{s-r}^{(s-1)} & \cdots & \cdots & E_2^{(r+1)} & E_1^{(r)} & E_{s-r+1}^{(s)}-E_{s-r+1}^{(s-1)} \end{array} \right| \end{align*} $$
for
![]() $1 \leq r < s < n$
, which is
$1 \leq r < s < n$
, which is
![]() $-q_{rs}$
from Lemma 5.1. This completes the proof.
$-q_{rs}$
from Lemma 5.1. This completes the proof.
It follows from Proposition 5.2 that the image of
![]() $\{-F_{i,j} \mid j \in [n-1] \ \text {and} \ h(j) < i \leq n \}$
under the map
$\{-F_{i,j} \mid j \in [n-1] \ \text {and} \ h(j) < i \leq n \}$
under the map
![]() $\varphi $
in equation (5.2) is
$\varphi $
in equation (5.2) is
![]() $\{q_{rs} \mid 2 \leq s \leq n \ \text {and} \ 1 \leq r \leq n-h(n+1-s) \}$
. Thus, the surjective map
$\{q_{rs} \mid 2 \leq s \leq n \ \text {and} \ 1 \leq r \leq n-h(n+1-s) \}$
. Thus, the surjective map
![]() $\varphi $
induces the surjective homomorphism
$\varphi $
induces the surjective homomorphism
 $$ \begin{align} &\varphi_h: {\mathbb{C}}[x_{ij} \mid 1 \leq j < i \leq n]/(F_{i,j} \mid j \in [n-1] \ \text{and} \ h(j) < i \leq n) \\ & \qquad \twoheadrightarrow Q_n/(q_{rs} \mid 2 \leq s \leq n \ \text{and} \ 1 \leq r \leq n-h(n+1-s)); \ x_{ij} \mapsto \, ^h E_{i-j}^{(n-j)}. \notag \end{align} $$
$$ \begin{align} &\varphi_h: {\mathbb{C}}[x_{ij} \mid 1 \leq j < i \leq n]/(F_{i,j} \mid j \in [n-1] \ \text{and} \ h(j) < i \leq n) \\ & \qquad \twoheadrightarrow Q_n/(q_{rs} \mid 2 \leq s \leq n \ \text{and} \ 1 \leq r \leq n-h(n+1-s)); \ x_{ij} \mapsto \, ^h E_{i-j}^{(n-j)}. \notag \end{align} $$
6 Hilbert series
In order to prove that
![]() $\varphi _h$
in equation (5.5) is an isomorphism, we introduce certain degrees for the variables
$\varphi _h$
in equation (5.5) is an isomorphism, we introduce certain degrees for the variables
![]() $\{x_{ij} \mid 1 \leq j < i \leq n \}$
and
$\{x_{ij} \mid 1 \leq j < i \leq n \}$
and
![]() $\{x_1,\ldots ,x_n, q_{rs} \mid 1 \leq r < s \leq n \}$
so that the two sides of equation (5.5) are graded
$\{x_1,\ldots ,x_n, q_{rs} \mid 1 \leq r < s \leq n \}$
so that the two sides of equation (5.5) are graded
![]() ${\mathbb {C}}$
-algebras. We then show that the two sides have identical Hilbert series.
${\mathbb {C}}$
-algebras. We then show that the two sides have identical Hilbert series.
Let
![]() ${\mathbb {C}}[x_{ij} \mid 1 \leq j < i \leq n]$
and
${\mathbb {C}}[x_{ij} \mid 1 \leq j < i \leq n]$
and
![]() ${\mathbb {C}}[x_1,\ldots ,x_n,q_{rs} \mid 1 \leq r < s \leq n]$
be the polynomial rings equipped with a grading defined by
${\mathbb {C}}[x_1,\ldots ,x_n,q_{rs} \mid 1 \leq r < s \leq n]$
be the polynomial rings equipped with a grading defined by
Remark 6.1. As mentioned in Remark 4.3,
![]() $x_s$
’s are degree
$x_s$
’s are degree
![]() $2$
elements in the cohomology ring of the flag variety by forgetting quantum parameters. Motivated by this fact, our definition for degrees are concentrated in even degrees.
$2$
elements in the cohomology ring of the flag variety by forgetting quantum parameters. Motivated by this fact, our definition for degrees are concentrated in even degrees.
Lemma 6.2. For
![]() $1 \leq r \leq s \leq n$
, the polynomial
$1 \leq r \leq s \leq n$
, the polynomial
![]() $E_r^{(s)}$
is homogeneous of degree
$E_r^{(s)}$
is homogeneous of degree
![]() $2r$
in the polynomial ring
$2r$
in the polynomial ring
![]() ${\mathbb {C}}[x_1,\ldots ,x_n,q_{rs} \mid 1 \leq r < s \leq n]$
.
${\mathbb {C}}[x_1,\ldots ,x_n,q_{rs} \mid 1 \leq r < s \leq n]$
.
Proof. We prove this by induction on s. The base case is
![]() $s=1$
, which is clear since
$s=1$
, which is clear since
![]() $E_1^{(1)}=x_1$
. Now, suppose that
$E_1^{(1)}=x_1$
. Now, suppose that
![]() $s> 1$
and assume by induction that the claim is true for arbitrary
$s> 1$
and assume by induction that the claim is true for arbitrary
![]() $s'$
with
$s'$
with
![]() $s' \leq s-1$
. From Lemma 4.8, we have
$s' \leq s-1$
. From Lemma 4.8, we have
 $$ \begin{align*} E_r^{(s)} = E_r^{(s-1)} + E_{r-1}^{(s-1)} x_s + \sum_{k=1}^{r-1} E_{r-1-k}^{(s-1-k)} q_{s-k \, s}. \end{align*} $$
$$ \begin{align*} E_r^{(s)} = E_r^{(s-1)} + E_{r-1}^{(s-1)} x_s + \sum_{k=1}^{r-1} E_{r-1-k}^{(s-1-k)} q_{s-k \, s}. \end{align*} $$
By the inductive hypothesis with equations (6.2) and (6.3), one can see that
![]() $E_r^{(s)}$
is homogeneous of degree
$E_r^{(s)}$
is homogeneous of degree
![]() $2r$
.
$2r$
.
In order to see that the polynomial
![]() $F_{i,j}$
is homogeneous, we introduce the following polynomials.
$F_{i,j}$
is homogeneous, we introduce the following polynomials.
Definition 6.3. Let
![]() $1 \leq j \leq n-1$
and
$1 \leq j \leq n-1$
and
![]() $j \leq m_j <n$
. For
$j \leq m_j <n$
. For
![]() $i>m_j$
, we define polynomials
$i>m_j$
, we define polynomials
![]() $\tilde F^{\langle m_j\rangle }_{i,j}$
by
$\tilde F^{\langle m_j\rangle }_{i,j}$
by


Here, we take the convention that
![]() $x_{n+1\,j}=0$
for
$x_{n+1\,j}=0$
for
![]() $j \in [n-1]$
.
$j \in [n-1]$
.
By equations (3.3) and (3.4) one has
for
![]() $1 \leq j < i \leq n$
.
$1 \leq j < i \leq n$
.
Lemma 6.4. For
![]() $1 \leq j < i \leq n$
, the polynomial
$1 \leq j < i \leq n$
, the polynomial
![]() $F_{i,j}$
is homogeneous of degree
$F_{i,j}$
is homogeneous of degree
![]() $2(i-j+1)$
in the polynomial ring
$2(i-j+1)$
in the polynomial ring
![]() ${\mathbb {C}}[x_{ij} \mid 1 \leq j < i \leq n]$
.
${\mathbb {C}}[x_{ij} \mid 1 \leq j < i \leq n]$
.
Proof. It suffices to show that
![]() $\tilde F^{\langle m_j\rangle }_{i,j}$
is homogeneous of degree
$\tilde F^{\langle m_j\rangle }_{i,j}$
is homogeneous of degree
![]() $2(i-j+1)$
for
$2(i-j+1)$
for
![]() $j \leq m_j <i$
by equation (6.4). At first, we fix j. We prove this statement by induction on
$j \leq m_j <i$
by equation (6.4). At first, we fix j. We prove this statement by induction on
![]() $m_j$
with this fixed j. The base case is
$m_j$
with this fixed j. The base case is
![]() $m_j =j$
. For arbitrary
$m_j =j$
. For arbitrary
![]() $i> j$
, since we have
$i> j$
, since we have
 $$ \begin{align*} \tilde F^{\langle 1 \rangle}_{i,1}&=\left| \begin{array}{@{\,}cc@{\,}} 1 & x_{21} \\ x_{i1} & x_{i+1 \, 1} \end{array} \right| = x_{i+1 \, 1} - x_{i1}x_{21} \ \text{for} \ j=1; \\ \tilde F^{\langle j \rangle}_{i,j}&=\left| \begin{array}{@{\,}ccc@{\,}} 1 & 0 & 1 \\ x_{j \, j-1} & 1 & x_{j+1 \,j} \\ x_{i \, j-1} & x_{ij} & x_{i+1 \, j} \end{array} \right| = x_{i+1 \, j} + x_{j \, j-1}x_{ij} - x_{i \, j-1} - x_{j+1 \, j}x_{ij} \ \text{for} \ j>1, \end{align*} $$
$$ \begin{align*} \tilde F^{\langle 1 \rangle}_{i,1}&=\left| \begin{array}{@{\,}cc@{\,}} 1 & x_{21} \\ x_{i1} & x_{i+1 \, 1} \end{array} \right| = x_{i+1 \, 1} - x_{i1}x_{21} \ \text{for} \ j=1; \\ \tilde F^{\langle j \rangle}_{i,j}&=\left| \begin{array}{@{\,}ccc@{\,}} 1 & 0 & 1 \\ x_{j \, j-1} & 1 & x_{j+1 \,j} \\ x_{i \, j-1} & x_{ij} & x_{i+1 \, j} \end{array} \right| = x_{i+1 \, j} + x_{j \, j-1}x_{ij} - x_{i \, j-1} - x_{j+1 \, j}x_{ij} \ \text{for} \ j>1, \end{align*} $$
one can easily see from equation (6.1) that
![]() $\tilde F^{\langle j \rangle }_{i,j}$
is homogeneous of degree
$\tilde F^{\langle j \rangle }_{i,j}$
is homogeneous of degree
![]() $2(i-j+1)$
. This shows the base case.
$2(i-j+1)$
. This shows the base case.
We proceed to the inductive step. Suppose now that
![]() $m_j> j$
and that the claim holds for
$m_j> j$
and that the claim holds for
![]() $m_j-1$
with any allowable choices of the first subscript
$m_j-1$
with any allowable choices of the first subscript
![]() $i'$
in
$i'$
in
![]() $\tilde F^{\langle m_j -1\rangle }_{i',j}$
. By the cofactor expansion along the second-to-last column, we have
$\tilde F^{\langle m_j -1\rangle }_{i',j}$
. By the cofactor expansion along the second-to-last column, we have
By the inductive hypothesis and equation (6.1), the right-hand side above is homogeneous of degree
![]() $2(i-j+1)$
, as desired. This completes the proof.
$2(i-j+1)$
, as desired. This completes the proof.
Recall from the end of Section 5 that we constructed the map
![]() $\varphi _h$
in equation (5.5) from
$\varphi _h$
in equation (5.5) from
![]() ${\mathbb {C}}[x_{ij} \mid 1 \leq j < i \leq n]/(F_{i,j} \mid j \in [n-1] \ \text {and} \ h(j) < i \leq n)$
to
${\mathbb {C}}[x_{ij} \mid 1 \leq j < i \leq n]/(F_{i,j} \mid j \in [n-1] \ \text {and} \ h(j) < i \leq n)$
to
![]() $Q_n/(q_{rs} \mid 2 \leq s \leq n \ \text {and} \ 1 \leq r \leq n-h(n+1-s))$
. One can see from Lemmas 6.2 and 6.4 that these are graded
$Q_n/(q_{rs} \mid 2 \leq s \leq n \ \text {and} \ 1 \leq r \leq n-h(n+1-s))$
. One can see from Lemmas 6.2 and 6.4 that these are graded
![]() ${\mathbb {C}}$
-algebras. (Note that
${\mathbb {C}}$
-algebras. (Note that
![]() $Q_n$
is also a graded
$Q_n$
is also a graded
![]() ${\mathbb {C}}$
-algebra.) For the rest of this section, we prove that these graded
${\mathbb {C}}$
-algebra.) For the rest of this section, we prove that these graded
![]() ${\mathbb {C}}$
-algebras have the same Hilbert series.
${\mathbb {C}}$
-algebras have the same Hilbert series.
Definition 6.5. Let
![]() $R=\oplus _{i=0}^\infty R_i$
be a graded
$R=\oplus _{i=0}^\infty R_i$
be a graded
![]() ${\mathbb {C}}$
-algebra where each homogeneous component
${\mathbb {C}}$
-algebra where each homogeneous component
![]() $R_i$
of degree i is a finite-dimensional vector space over
$R_i$
of degree i is a finite-dimensional vector space over
![]() ${\mathbb {C}}$
. Then its Hilbert series is defined to be
${\mathbb {C}}$
. Then its Hilbert series is defined to be

A sequence of homogeneous polynomials
![]() $\theta _1,\ldots ,\theta _p \in R$
of positive degrees is a regular sequence in R if
$\theta _1,\ldots ,\theta _p \in R$
of positive degrees is a regular sequence in R if
![]() $\theta _k$
is a nonzero divisor of
$\theta _k$
is a nonzero divisor of
![]() $R/(\theta _1,\ldots ,\theta _{k-1})$
for all
$R/(\theta _1,\ldots ,\theta _{k-1})$
for all
![]() $1 \leq k \leq p$
.
$1 \leq k \leq p$
.
The following facts are well known in commutative algebra. See [Reference Stanley35, Chapter I, Section 5]. (See also [Reference Fukukawa, Harada and Masuda18, Proposition 5.1].)
Lemma 6.6. Let
![]() $R=\oplus _{i=0}^\infty R_i$
be a graded
$R=\oplus _{i=0}^\infty R_i$
be a graded
![]() ${\mathbb {C}}$
-algebra with
${\mathbb {C}}$
-algebra with
![]() $\dim _{\mathbb {C}} R_i < \infty $
for each i. A sequence of homogeneous polynomials
$\dim _{\mathbb {C}} R_i < \infty $
for each i. A sequence of homogeneous polynomials
![]() $\theta _1,\ldots ,\theta _p \in R$
of positive degrees is a regular sequence in R if and only if the Hilbert series of
$\theta _1,\ldots ,\theta _p \in R$
of positive degrees is a regular sequence in R if and only if the Hilbert series of
![]() $R/(\theta _1,\ldots ,\theta _p)$
is given by
$R/(\theta _1,\ldots ,\theta _p)$
is given by
 $$ \begin{align*} \operatorname{\mathrm{Hilb}}(R/(\theta_1,\ldots,\theta_p),t) = \operatorname{\mathrm{Hilb}}(R,t) \cdot \prod_{k=1}^p (1-t^{\deg \theta_k}). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Hilb}}(R/(\theta_1,\ldots,\theta_p),t) = \operatorname{\mathrm{Hilb}}(R,t) \cdot \prod_{k=1}^p (1-t^{\deg \theta_k}). \end{align*} $$
Lemma 6.7. Let R be a polynomial ring
![]() ${\mathbb {C}}[y_1,\ldots ,y_n]$
. A sequence of homogeneous polynomials
${\mathbb {C}}[y_1,\ldots ,y_n]$
. A sequence of homogeneous polynomials
![]() $\theta _1,\ldots ,\theta _n \in R$
of positive degrees is a regular sequence in R if and only if the solution set of the equations
$\theta _1,\ldots ,\theta _n \in R$
of positive degrees is a regular sequence in R if and only if the solution set of the equations
![]() $\theta _1=0,\ldots ,\theta _n=0$
in
$\theta _1=0,\ldots ,\theta _n=0$
in
![]() ${\mathbb {C}}^n$
consists only of the origin
${\mathbb {C}}^n$
consists only of the origin
![]() $\{0\}$
.
$\{0\}$
.
We remark that the number of the homogeneous polynomials
![]() $\theta _1,\ldots ,\theta _n$
is equal to the number of the variables
$\theta _1,\ldots ,\theta _n$
is equal to the number of the variables
![]() $y_1,\ldots ,y_n$
in the polynomial ring
$y_1,\ldots ,y_n$
in the polynomial ring
![]() ${\mathbb {C}}[y_1,\ldots ,y_n]$
in Lemma 6.7. By using two lemmas above, we compute the Hilbert series of
${\mathbb {C}}[y_1,\ldots ,y_n]$
in Lemma 6.7. By using two lemmas above, we compute the Hilbert series of
![]() ${\mathbb {C}}[x_{ij} \mid 1 \leq j < i \leq n]/(F_{i,j} \mid j \in [n-1] \ \text {and} \ h(j) < i \leq n)$
and
${\mathbb {C}}[x_{ij} \mid 1 \leq j < i \leq n]/(F_{i,j} \mid j \in [n-1] \ \text {and} \ h(j) < i \leq n)$
and
![]() $Q_n/(q_{rs} \mid 2 \leq s \leq n \ \text {and} \ 1 \leq r \leq n-h(n+1-s))$
.
$Q_n/(q_{rs} \mid 2 \leq s \leq n \ \text {and} \ 1 \leq r \leq n-h(n+1-s))$
.
Lemma 6.8. The polynomials
![]() $F_{i,j} \ (1 \leq j < i \leq n)$
form a regular sequence in the polynomial ring
$F_{i,j} \ (1 \leq j < i \leq n)$
form a regular sequence in the polynomial ring
![]() ${\mathbb {C}}[x_{ij} \mid 1 \leq j < i \leq n]$
.
${\mathbb {C}}[x_{ij} \mid 1 \leq j < i \leq n]$
.
Proof. By Lemma 6.7, it is enough to show that the solution set of the equations
![]() $F_{i,j}=0 \ (1 \leq j < i \leq n)$
in
$F_{i,j}=0 \ (1 \leq j < i \leq n)$
in
![]() ${\mathbb {C}}^{\frac {1}{2}n(n-1)}$
(with the variables
${\mathbb {C}}^{\frac {1}{2}n(n-1)}$
(with the variables
![]() $x_{ij} \ (1 \leq j < i \leq n)$
) consists only of the origin
$x_{ij} \ (1 \leq j < i \leq n)$
) consists only of the origin
![]() $\{0\}$
. The intersection of the zero set of
$\{0\}$
. The intersection of the zero set of
![]() $F_{i,j}$
for all
$F_{i,j}$
for all
![]() $1 \leq j < i \leq n$
is
$1 \leq j < i \leq n$
is
![]() $\operatorname {\mathrm {Hess}}(N,id) \cap \Omega _e^\circ $
by Lemma 2.3. However, since
$\operatorname {\mathrm {Hess}}(N,id) \cap \Omega _e^\circ $
by Lemma 2.3. However, since
![]() $\operatorname {\mathrm {Hess}}(N,id)$
consists only of the point
$\operatorname {\mathrm {Hess}}(N,id)$
consists only of the point
![]() $\{eB \}$
, this means that the equations
$\{eB \}$
, this means that the equations
![]() $F_{i,j}=0 \ (1 \leq j<i \leq n)$
implies that
$F_{i,j}=0 \ (1 \leq j<i \leq n)$
implies that
![]() $x_{ij}=0$
for all
$x_{ij}=0$
for all
![]() $1 \leq j < i \leq n$
, as desired.
$1 \leq j < i \leq n$
, as desired.
Proposition 6.9. The Hilbert series of
![]() ${\mathbb {C}}[x_{ij} \mid 1 \leq j < i \leq n]/(F_{i,j} \mid j \in [n-1] \ \text {and} \ h(j) < i \leq n)$
equipped with a grading in equation (6.1) is equal to
${\mathbb {C}}[x_{ij} \mid 1 \leq j < i \leq n]/(F_{i,j} \mid j \in [n-1] \ \text {and} \ h(j) < i \leq n)$
equipped with a grading in equation (6.1) is equal to
 $$ \begin{align*} &\operatorname{\mathrm{Hilb}}({\mathbb{C}}[x_{ij} \mid 1 \leq j < i \leq n]/(F_{i,j} \mid j \in [n-1] \ \text{and} \ h(j) < i \leq n),t) \\ = &\prod_{1 \leq j \leq n-1 \atop j < i \leq h(j)} \frac{1}{1-t^{2(i-j+1)}} \cdot \prod_{k=1}^{n-1} (1+t^2+t^4+\cdots+t^{2k}). \end{align*} $$
$$ \begin{align*} &\operatorname{\mathrm{Hilb}}({\mathbb{C}}[x_{ij} \mid 1 \leq j < i \leq n]/(F_{i,j} \mid j \in [n-1] \ \text{and} \ h(j) < i \leq n),t) \\ = &\prod_{1 \leq j \leq n-1 \atop j < i \leq h(j)} \frac{1}{1-t^{2(i-j+1)}} \cdot \prod_{k=1}^{n-1} (1+t^2+t^4+\cdots+t^{2k}). \end{align*} $$
Proof. Since a subsequence of a regular sequence is also a regular sequence from the definition of a regular sequence, by Lemma 6.8, the polynomials
![]() $F_{i,j} \ (j \in [n-1], h(j) < i \leq n)$
form a regular sequence in the polynomial ring
$F_{i,j} \ (j \in [n-1], h(j) < i \leq n)$
form a regular sequence in the polynomial ring
![]() ${\mathbb {C}}[x_{ij} \mid 1 \leq j < i \leq n]$
. Thus, it follows from Lemma 6.6 that
${\mathbb {C}}[x_{ij} \mid 1 \leq j < i \leq n]$
. Thus, it follows from Lemma 6.6 that
 $$ \begin{align} &\operatorname{\mathrm{Hilb}}({\mathbb{C}}[x_{ij} \mid 1 \leq j < i \leq n]/(F_{i,j} \mid j \in [n-1] \ \text{and} \ h(j) < i \leq n),t) \\[5pt] = &\operatorname{\mathrm{Hilb}}({\mathbb{C}}[x_{ij} \mid 1 \leq j < i \leq n],t) \cdot \prod_{1 \leq j \leq n-1 \atop h(j) < i \leq n} (1-t^{\deg F_{i,j}}) \notag \\ = &\prod_{1 \leq j < i \leq n} \frac{1}{1-t^{2(i-j)}} \cdot \prod_{1 \leq j \leq n-1 \atop h(j) < i \leq n} (1-t^{2(i-j+1)}) \ \ \ \ \ \text{(by Lemma~}6.4). \notag \end{align} $$
$$ \begin{align} &\operatorname{\mathrm{Hilb}}({\mathbb{C}}[x_{ij} \mid 1 \leq j < i \leq n]/(F_{i,j} \mid j \in [n-1] \ \text{and} \ h(j) < i \leq n),t) \\[5pt] = &\operatorname{\mathrm{Hilb}}({\mathbb{C}}[x_{ij} \mid 1 \leq j < i \leq n],t) \cdot \prod_{1 \leq j \leq n-1 \atop h(j) < i \leq n} (1-t^{\deg F_{i,j}}) \notag \\ = &\prod_{1 \leq j < i \leq n} \frac{1}{1-t^{2(i-j)}} \cdot \prod_{1 \leq j \leq n-1 \atop h(j) < i \leq n} (1-t^{2(i-j+1)}) \ \ \ \ \ \text{(by Lemma~}6.4). \notag \end{align} $$
Here, we note that
 $$ \begin{align*} \prod_{1 \leq j < i \leq n} \frac{1}{1-t^{2(i-j)}} \cdot (1-t^2)^{n-1} = \prod_{1 \leq j < i \leq n} \frac{1}{1-t^{2(i-j+1)}} \cdot (1-t^4)(1-t^6) \cdots (1-t^{2n}). \end{align*} $$
$$ \begin{align*} \prod_{1 \leq j < i \leq n} \frac{1}{1-t^{2(i-j)}} \cdot (1-t^2)^{n-1} = \prod_{1 \leq j < i \leq n} \frac{1}{1-t^{2(i-j+1)}} \cdot (1-t^4)(1-t^6) \cdots (1-t^{2n}). \end{align*} $$
In fact, exponents appeared on the left-hand side and exponents on the right-hand side are described as numbers in shaded boxes of the left figure and the right figure in Figure 4, respectively.

Figure 4 The values
![]() $2(i-j)$
and
$2(i-j)$
and
![]() $2(i-j+1)$
for
$2(i-j+1)$
for
![]() $1 \leq j < i \leq n$
$1 \leq j < i \leq n$
This equality leads us to the equality
 $$ \begin{align*} \prod_{1 \leq j < i \leq n} \frac{1}{1-t^{2(i-j)}} = \prod_{1 \leq j < i \leq n} \frac{1}{1-t^{2(i-j+1)}} \cdot \prod_{k=1}^{n-1} (1+t^2+t^4+ \cdots +t^{2k}), \end{align*} $$
$$ \begin{align*} \prod_{1 \leq j < i \leq n} \frac{1}{1-t^{2(i-j)}} = \prod_{1 \leq j < i \leq n} \frac{1}{1-t^{2(i-j+1)}} \cdot \prod_{k=1}^{n-1} (1+t^2+t^4+ \cdots +t^{2k}), \end{align*} $$
so by equation (6.5), one has
 $$ \begin{align*} &\operatorname{\mathrm{Hilb}}({\mathbb{C}}[x_{ij} \mid 1 \leq j < i \leq n]/(F_{i,j} \mid j \in [n-1] \ \text{and} \ h(j) < i \leq n),t) \\[5pt] = &\prod_{1 \leq j < i \leq n} \frac{1}{1-t^{2(i-j+1)}} \cdot \prod_{k=1}^{n-1} (1+t^2+t^4+ \cdots +t^{2k}) \cdot \prod_{1 \leq j \leq n-1 \atop h(j) < i \leq n} (1-t^{2(i-j+1)}) \\[5pt] = &\prod_{1 \leq j \leq n-1 \atop j < i \leq h(j)} \frac{1}{1-t^{2(i-j+1)}} \cdot \prod_{k=1}^{n-1} (1+t^2+t^4+\cdots+t^{2k}), \end{align*} $$
$$ \begin{align*} &\operatorname{\mathrm{Hilb}}({\mathbb{C}}[x_{ij} \mid 1 \leq j < i \leq n]/(F_{i,j} \mid j \in [n-1] \ \text{and} \ h(j) < i \leq n),t) \\[5pt] = &\prod_{1 \leq j < i \leq n} \frac{1}{1-t^{2(i-j+1)}} \cdot \prod_{k=1}^{n-1} (1+t^2+t^4+ \cdots +t^{2k}) \cdot \prod_{1 \leq j \leq n-1 \atop h(j) < i \leq n} (1-t^{2(i-j+1)}) \\[5pt] = &\prod_{1 \leq j \leq n-1 \atop j < i \leq h(j)} \frac{1}{1-t^{2(i-j+1)}} \cdot \prod_{k=1}^{n-1} (1+t^2+t^4+\cdots+t^{2k}), \end{align*} $$
as desired.
Lemma 6.10. The polynomials
![]() $E_1^{(n)},\ldots ,E_n^{(n)}, q_{rs} \ (1 \leq r<s \leq n)$
form a regular sequence in the polynomial ring
$E_1^{(n)},\ldots ,E_n^{(n)}, q_{rs} \ (1 \leq r<s \leq n)$
form a regular sequence in the polynomial ring
![]() ${\mathbb {C}}[x_1,\ldots ,x_n, q_{rs} \mid 1 \leq r < s \leq n]$
.
${\mathbb {C}}[x_1,\ldots ,x_n, q_{rs} \mid 1 \leq r < s \leq n]$
.
Proof. From Lemma 6.7, it suffices to show that the solution set of the equations
![]() $E_1^{(n)}=0,\ldots ,E_n^{(n)}=0, q_{rs}=0 \ (1 \leq r<s \leq n)$
in
$E_1^{(n)}=0,\ldots ,E_n^{(n)}=0, q_{rs}=0 \ (1 \leq r<s \leq n)$
in
![]() ${\mathbb {C}}^{\frac {1}{2}n(n+1)}$
(with the variables
${\mathbb {C}}^{\frac {1}{2}n(n+1)}$
(with the variables
![]() $x_1,\ldots ,x_n, q_{rs} \ (1 \leq r < s \leq n)$
) consists only of the origin
$x_1,\ldots ,x_n, q_{rs} \ (1 \leq r < s \leq n)$
) consists only of the origin
![]() $\{0\}$
. Since
$\{0\}$
. Since
![]() $q_{rs}=0$
for all
$q_{rs}=0$
for all
![]() $1 \leq r<s \leq n$
,
$1 \leq r<s \leq n$
,
![]() $E_1^{(n)}=0,\ldots ,E_n^{(n)}=0$
implies that
$E_1^{(n)}=0,\ldots ,E_n^{(n)}=0$
implies that
![]() $e_1(x_1, \ldots , x_n)=0,\ldots ,e_n(x_1, \ldots , x_n)=0$
, where
$e_1(x_1, \ldots , x_n)=0,\ldots ,e_n(x_1, \ldots , x_n)=0$
, where
![]() $e_i(x_1, \ldots , x_n)$
is the (ordinary) i-th elementary symmetric polynomial in the variables
$e_i(x_1, \ldots , x_n)$
is the (ordinary) i-th elementary symmetric polynomial in the variables
![]() $x_1,\ldots ,x_n$
. Then one can easily see that
$x_1,\ldots ,x_n$
. Then one can easily see that
![]() $x_i=0$
for all
$x_i=0$
for all
![]() $i \in [n]$
. In fact,
$i \in [n]$
. In fact,
![]() $x_1x_2 \cdots x_n = e_n(x_1, \ldots , x_n) = 0$
implies that some
$x_1x_2 \cdots x_n = e_n(x_1, \ldots , x_n) = 0$
implies that some
![]() $x_i$
must be equal to
$x_i$
must be equal to
![]() $0$
. Without loss of generality, we may assume that
$0$
. Without loss of generality, we may assume that
![]() $x_n = 0$
. This implies that
$x_n = 0$
. This implies that
![]() $e_i(x_1, \ldots , x_{n-1}) = 0$
for all
$e_i(x_1, \ldots , x_{n-1}) = 0$
for all
![]() $i \in [n-1]$
. Proceeding in this manner, we conclude that
$i \in [n-1]$
. Proceeding in this manner, we conclude that
![]() $x_i=0$
for all
$x_i=0$
for all
![]() $i \in [n]$
. Thus, the equations
$i \in [n]$
. Thus, the equations
![]() $E_1^{(n)}=0,\ldots ,E_n^{(n)}=0, q_{rs}=0 \ (1 \leq r<s \leq n)$
implies that
$E_1^{(n)}=0,\ldots ,E_n^{(n)}=0, q_{rs}=0 \ (1 \leq r<s \leq n)$
implies that
![]() $x_i=0$
for all
$x_i=0$
for all
![]() $i \in [n]$
and
$i \in [n]$
and
![]() $q_{rs}=0$
for all
$q_{rs}=0$
for all
![]() $1 \leq r<s \leq n$
, as desired.
$1 \leq r<s \leq n$
, as desired.
Proposition 6.11. The Hilbert series of
![]() $Q_n/(q_{rs} \mid 2 \leq s \leq n \ \text {and} \ 1 \leq r \leq n-h(n+1-s))$
equipped with a grading in equations (6.2) and (6.3) is equal to
$Q_n/(q_{rs} \mid 2 \leq s \leq n \ \text {and} \ 1 \leq r \leq n-h(n+1-s))$
equipped with a grading in equations (6.2) and (6.3) is equal to
 $$ \begin{align*} &\operatorname{\mathrm{Hilb}}(Q_n/(q_{rs} \mid 2 \leq s \leq n \ \text{and} \ 1 \leq r \leq n-h(n+1-s)),t) \\[5pt] = &\prod_{1 \leq j \leq n-1 \atop j < i \leq h(j)} \frac{1}{1-t^{2(i-j+1)}} \cdot \prod_{k=1}^{n-1} (1+t^2+t^4+\cdots+t^{2k}). \end{align*} $$
$$ \begin{align*} &\operatorname{\mathrm{Hilb}}(Q_n/(q_{rs} \mid 2 \leq s \leq n \ \text{and} \ 1 \leq r \leq n-h(n+1-s)),t) \\[5pt] = &\prod_{1 \leq j \leq n-1 \atop j < i \leq h(j)} \frac{1}{1-t^{2(i-j+1)}} \cdot \prod_{k=1}^{n-1} (1+t^2+t^4+\cdots+t^{2k}). \end{align*} $$
Proof. Recall from the definition (5.1) that
Lemma 6.10 implies that the monomials
![]() $q_{rs} \ (2 \leq s \leq n, 1 \leq r \leq n-h(n+1-s))$
form a regular sequence in
$q_{rs} \ (2 \leq s \leq n, 1 \leq r \leq n-h(n+1-s))$
form a regular sequence in
![]() $Q_n$
by the definition of a regular sequence. Hence, by Lemma 6.6, we have
$Q_n$
by the definition of a regular sequence. Hence, by Lemma 6.6, we have
 $$ \begin{align} &\operatorname{\mathrm{Hilb}}(Q_n/(q_{rs} \mid 2 \leq s \leq n \ \text{and} \ 1 \leq r \leq n-h(n+1-s)),t) \\[5pt] = &\operatorname{\mathrm{Hilb}}(Q_n,t) \cdot \prod_{2 \leq s \leq n \atop 1 \leq r \leq n-h(n+1-s)} (1-t^{\deg q_{rs}}) \notag \\[5pt] = &\operatorname{\mathrm{Hilb}}(Q_n,t) \cdot \prod_{2 \leq s \leq n \atop 1 \leq r \leq n-h(n+1-s)} (1-t^{2(s-r+1)}). \notag \end{align} $$
$$ \begin{align} &\operatorname{\mathrm{Hilb}}(Q_n/(q_{rs} \mid 2 \leq s \leq n \ \text{and} \ 1 \leq r \leq n-h(n+1-s)),t) \\[5pt] = &\operatorname{\mathrm{Hilb}}(Q_n,t) \cdot \prod_{2 \leq s \leq n \atop 1 \leq r \leq n-h(n+1-s)} (1-t^{\deg q_{rs}}) \notag \\[5pt] = &\operatorname{\mathrm{Hilb}}(Q_n,t) \cdot \prod_{2 \leq s \leq n \atop 1 \leq r \leq n-h(n+1-s)} (1-t^{2(s-r+1)}). \notag \end{align} $$
Since a subsequence of a regular sequence is again a regular sequence from the definition of a regular sequence, the polynomials
![]() $E_1^{(n)},\ldots ,E_n^{(n)}$
form a regular sequence in the polynomial ring
$E_1^{(n)},\ldots ,E_n^{(n)}$
form a regular sequence in the polynomial ring
![]() ${\mathbb {C}}[x_1,\ldots ,x_n, q_{rs} \mid 1 \leq r < s \leq n]$
by Lemma 6.10. By using Lemma 6.6 again, one has
${\mathbb {C}}[x_1,\ldots ,x_n, q_{rs} \mid 1 \leq r < s \leq n]$
by Lemma 6.10. By using Lemma 6.6 again, one has
 $$ \begin{align} \operatorname{\mathrm{Hilb}}(Q_n,t) =& \operatorname{\mathrm{Hilb}}({\mathbb{C}}[x_1,\ldots,x_n, q_{rs} \mid 1 \leq r < s \leq n],t) \cdot \prod_{k=1}^n (1-t^{\deg E_k^{(n)}}) \\[5pt] = &\frac{1}{(1-t^2)^n} \cdot \prod_{1 \leq r < s \leq n} \frac{1}{1-t^{2(s-r+1)}} \cdot \prod_{k=1}^n (1-t^{2k}) \ \ \ \ \ \text{(by Lemma~}6.2) \notag \\[5pt] =& \prod_{1 \leq r < s \leq n} \frac{1}{1-t^{2(s-r+1)}} \cdot \prod_{k=1}^{n-1} (1+t^2+t^4+ \cdots +t^{2k}). \notag \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Hilb}}(Q_n,t) =& \operatorname{\mathrm{Hilb}}({\mathbb{C}}[x_1,\ldots,x_n, q_{rs} \mid 1 \leq r < s \leq n],t) \cdot \prod_{k=1}^n (1-t^{\deg E_k^{(n)}}) \\[5pt] = &\frac{1}{(1-t^2)^n} \cdot \prod_{1 \leq r < s \leq n} \frac{1}{1-t^{2(s-r+1)}} \cdot \prod_{k=1}^n (1-t^{2k}) \ \ \ \ \ \text{(by Lemma~}6.2) \notag \\[5pt] =& \prod_{1 \leq r < s \leq n} \frac{1}{1-t^{2(s-r+1)}} \cdot \prod_{k=1}^{n-1} (1+t^2+t^4+ \cdots +t^{2k}). \notag \end{align} $$
By equations (6.6) and (6.7), we obtain
 $$ \begin{align*} &\operatorname{\mathrm{Hilb}}(Q_n/(q_{rs} \mid 2 \leq s \leq n \ \text{and} \ 1 \leq r \leq n-h(n+1-s)),t) \\ = & \prod_{1 \leq r < s \leq n} \frac{1}{1-t^{2(s-r+1)}} \cdot \prod_{k=1}^{n-1} (1+t^2+t^4+ \cdots +t^{2k}) \cdot \prod_{2 \leq s \leq n \atop 1 \leq r \leq n-h(n+1-s)} (1-t^{2(s-r+1)}) \\ = & \prod_{1 \leq j < i \leq n} \frac{1}{1-t^{2(i-j+1)}} \cdot \prod_{k=1}^{n-1} (1+t^2+t^4+ \cdots +t^{2k}) \cdot \prod_{1 \leq j \leq n-1 \atop h(j)+1 \leq i \leq n} (1-t^{2(i-j+1)}) \\ & \hspace{100pt} (\text{by setting} \ i=n+1-r \ \text{and} \ j=n+1-s \ \text{in the third product}) \\ = &\prod_{1 \leq j \leq n-1 \atop j < i \leq h(j)} \frac{1}{1-t^{2(i-j+1)}} \cdot \prod_{k=1}^{n-1} (1+t^2+t^4+\cdots+t^{2k}), \end{align*} $$
$$ \begin{align*} &\operatorname{\mathrm{Hilb}}(Q_n/(q_{rs} \mid 2 \leq s \leq n \ \text{and} \ 1 \leq r \leq n-h(n+1-s)),t) \\ = & \prod_{1 \leq r < s \leq n} \frac{1}{1-t^{2(s-r+1)}} \cdot \prod_{k=1}^{n-1} (1+t^2+t^4+ \cdots +t^{2k}) \cdot \prod_{2 \leq s \leq n \atop 1 \leq r \leq n-h(n+1-s)} (1-t^{2(s-r+1)}) \\ = & \prod_{1 \leq j < i \leq n} \frac{1}{1-t^{2(i-j+1)}} \cdot \prod_{k=1}^{n-1} (1+t^2+t^4+ \cdots +t^{2k}) \cdot \prod_{1 \leq j \leq n-1 \atop h(j)+1 \leq i \leq n} (1-t^{2(i-j+1)}) \\ & \hspace{100pt} (\text{by setting} \ i=n+1-r \ \text{and} \ j=n+1-s \ \text{in the third product}) \\ = &\prod_{1 \leq j \leq n-1 \atop j < i \leq h(j)} \frac{1}{1-t^{2(i-j+1)}} \cdot \prod_{k=1}^{n-1} (1+t^2+t^4+\cdots+t^{2k}), \end{align*} $$
as desired.
7 Proof of Theorem 4.13
We now prove Theorem 4.13.
Proof of Theorem 4.13.
We first note that there exists a canonical isomorphism
 $$ \begin{align*} &Q_n/(q_{rs} \mid 2 \leq s \leq n \ \text{and} \ 1 \leq r \leq n-h(n+1-s)) \\ \cong & {\mathbb{C}}[x_1,\ldots,x_n, q_{rs} \mid 2 \leq s \leq n, n-h(n+1-s)<r<s]/(^h E_1^{(n)}, \ldots, \, ^h E_n^{(n)}) \end{align*} $$
$$ \begin{align*} &Q_n/(q_{rs} \mid 2 \leq s \leq n \ \text{and} \ 1 \leq r \leq n-h(n+1-s)) \\ \cong & {\mathbb{C}}[x_1,\ldots,x_n, q_{rs} \mid 2 \leq s \leq n, n-h(n+1-s)<r<s]/(^h E_1^{(n)}, \ldots, \, ^h E_n^{(n)}) \end{align*} $$
by Definition 4.10 and equation (5.1). Under the identification above and the presentation in equation (3.7), we can rewrite
![]() $\varphi _h$
in equation (5.5) as
$\varphi _h$
in equation (5.5) as
 $$ \begin{align*} \varphi_h: \Gamma(\mathcal{Z}(N,h)_e, \mathcal{O}_{\mathcal{Z}(N,h)_e}) \twoheadrightarrow \frac{{\mathbb{C}}[x_1,\ldots,x_n, q_{rs} \mid 2 \leq s \leq n, n-h(n+1-s)<r<s]}{(^h E_1^{(n)}, \ldots, \, ^h E_n^{(n)})}, \end{align*} $$
$$ \begin{align*} \varphi_h: \Gamma(\mathcal{Z}(N,h)_e, \mathcal{O}_{\mathcal{Z}(N,h)_e}) \twoheadrightarrow \frac{{\mathbb{C}}[x_1,\ldots,x_n, q_{rs} \mid 2 \leq s \leq n, n-h(n+1-s)<r<s]}{(^h E_1^{(n)}, \ldots, \, ^h E_n^{(n)})}, \end{align*} $$
which is defined by
Here, by slightly abuse of notation we used the same symbol
![]() $\varphi _h$
for the map above. The map
$\varphi _h$
for the map above. The map
![]() $\varphi _h$
is surjective and this preserves the gradings on both graded
$\varphi _h$
is surjective and this preserves the gradings on both graded
![]() ${\mathbb {C}}$
-algebras from equation (6.1) and Lemma 6.2. It follows from Propositions 6.9 and 6.11 that the two sides of
${\mathbb {C}}$
-algebras from equation (6.1) and Lemma 6.2. It follows from Propositions 6.9 and 6.11 that the two sides of
![]() $\varphi _h$
have identical Hilbert series. Therefore, we conclude that
$\varphi _h$
have identical Hilbert series. Therefore, we conclude that
![]() $\varphi _h$
is an isomorphism.
$\varphi _h$
is an isomorphism.
Remark 7.1. Our proof gives an alternative proof of the isomorphism (4.2).
Corollary 7.2. There is an isomorphism of
![]() ${\mathbb {C}}$
-algebras
${\mathbb {C}}$
-algebras
Proof. Applying the isomorphism (4.5) to the case when
![]() $h=id$
, we obtain
$h=id$
, we obtain
where
![]() $e_i(x_1, \ldots , x_n)$
denotes the i-th elementary symmetric polynomial in the variables
$e_i(x_1, \ldots , x_n)$
denotes the i-th elementary symmetric polynomial in the variables
![]() $x_1,\ldots ,x_n$
. As is well known, the right hand side above is a presentation for the cohomology ring
$x_1,\ldots ,x_n$
. As is well known, the right hand side above is a presentation for the cohomology ring
![]() $H^*(Fl({\mathbb {C}}^n))$
(e.g., [Reference Fulton19, Section 10.2, Proposition 3]).
$H^*(Fl({\mathbb {C}}^n))$
(e.g., [Reference Fulton19, Section 10.2, Proposition 3]).
We constructed the isomorphism of graded
![]() ${\mathbb {C}}$
-algebras
${\mathbb {C}}$
-algebras
 $$ \begin{align} \varphi_h: \Gamma(\mathcal{Z}(N,h)_e, \mathcal{O}_{\mathcal{Z}(N,h)_e}) \xrightarrow{\cong} \frac{{\mathbb{C}}[x_1,\ldots,x_n, q_{rs} \mid 2 \leq s \leq n, n-h(n+1-s)<r<s]}{(^h E_1^{(n)}, \ldots, \, ^h E_n^{(n)})}, \end{align} $$
$$ \begin{align} \varphi_h: \Gamma(\mathcal{Z}(N,h)_e, \mathcal{O}_{\mathcal{Z}(N,h)_e}) \xrightarrow{\cong} \frac{{\mathbb{C}}[x_1,\ldots,x_n, q_{rs} \mid 2 \leq s \leq n, n-h(n+1-s)<r<s]}{(^h E_1^{(n)}, \ldots, \, ^h E_n^{(n)})}, \end{align} $$
which sends
![]() $x_{ij}$
to
$x_{ij}$
to
![]() $^h E_{i-j}^{(n-j)}$
for all
$^h E_{i-j}^{(n-j)}$
for all
![]() $1 \leq j < i \leq n$
from the homomorphism
$1 \leq j < i \leq n$
from the homomorphism
![]() $\varphi $
in equation (5.2). The following result follows from Proposition 5.2.
$\varphi $
in equation (5.2). The following result follows from Proposition 5.2.
Proposition 7.3. The inverse map of
![]() $\varphi _h$
in equation (7.1) is given by
$\varphi _h$
in equation (7.1) is given by
 $$ \begin{align*} \varphi_h^{-1}(x_s) &= x_{n-s+1 \, n-s} - x_{n-s+2 \, n-s+1} \ \ \ \text{for} \ s \in [n] \\ \varphi_h^{-1}(q_{rs}) &= -F_{n+1-r,n+1-s} \ \ \ \text{for} \ 2 \leq s \leq n \ \text{and} \ n-h(n+1-s)<r<s \end{align*} $$
$$ \begin{align*} \varphi_h^{-1}(x_s) &= x_{n-s+1 \, n-s} - x_{n-s+2 \, n-s+1} \ \ \ \text{for} \ s \in [n] \\ \varphi_h^{-1}(q_{rs}) &= -F_{n+1-r,n+1-s} \ \ \ \text{for} \ 2 \leq s \leq n \ \text{and} \ n-h(n+1-s)<r<s \end{align*} $$
with the convention that
![]() $x_{n-s+2 \, n-s+1}=0$
whenever
$x_{n-s+2 \, n-s+1}=0$
whenever
![]() $s=1$
and
$s=1$
and
![]() $x_{n-s+1 \, n-s}=0$
whenever
$x_{n-s+1 \, n-s}=0$
whenever
![]() $s=n$
.
$s=n$
.
We conclude the following result from the discussion above.
Corollary 7.4. Let
![]() $h:[n] \rightarrow [n]$
be a Hessenberg function. Then the following commutative diagram holds
$h:[n] \rightarrow [n]$
be a Hessenberg function. Then the following commutative diagram holds

where both vertical arrows denote the canonical surjective maps under the presentation (3.7). In particular, if h is indecomposable, then we obtain the following commutative diagram

where the left vertical arrow is induced from the inclusion
![]() $\operatorname {\mathrm {Hess}}(N,h) \cap \Omega _e^\circ \hookrightarrow Fl({\mathbb {C}}^n) \cap \Omega _e^\circ $
. Note that both vertical arrows are surjective.
$\operatorname {\mathrm {Hess}}(N,h) \cap \Omega _e^\circ \hookrightarrow Fl({\mathbb {C}}^n) \cap \Omega _e^\circ $
. Note that both vertical arrows are surjective.
8 Jacobian matrix
It is an interesting and challenging problem to find an explicit description of the singular locus of (regular nilpotent) Hessenberg varieties
![]() $\operatorname {\mathrm {Hess}}(N,h)$
. There are already partial results for the problem stated above in [Reference Abe and Insko3, Reference Escobar, Precup and Shareshian15, Reference Insko and Yong26]. For the rest of the paper, we will analyze the singular locus of
$\operatorname {\mathrm {Hess}}(N,h)$
. There are already partial results for the problem stated above in [Reference Abe and Insko3, Reference Escobar, Precup and Shareshian15, Reference Insko and Yong26]. For the rest of the paper, we will analyze the singular locus of
![]() $\operatorname {\mathrm {Hess}}(N,h) \cap \Omega _e^\circ $
for some Hessenberg function h as an application of our result. The isomorphism (4.6) in Theorem 4.13 yields that if h is indecomposable, then the singular locus of the open set
$\operatorname {\mathrm {Hess}}(N,h) \cap \Omega _e^\circ $
for some Hessenberg function h as an application of our result. The isomorphism (4.6) in Theorem 4.13 yields that if h is indecomposable, then the singular locus of the open set
![]() $\operatorname {\mathrm {Hess}}(N,h) \cap \Omega _e^\circ $
in
$\operatorname {\mathrm {Hess}}(N,h) \cap \Omega _e^\circ $
in
![]() $\operatorname {\mathrm {Hess}}(N,h)$
is isomorphic to the singular locus of the zero set defined by n polynomials
$\operatorname {\mathrm {Hess}}(N,h)$
is isomorphic to the singular locus of the zero set defined by n polynomials
![]() $^h E_1^{(n)}, \ldots , \, ^h E_n^{(n)}$
in
$^h E_1^{(n)}, \ldots , \, ^h E_n^{(n)}$
in
![]() ${\mathbb {C}}^{n+\sum _{j=1}^n (h(j)-j))}$
with the variables
${\mathbb {C}}^{n+\sum _{j=1}^n (h(j)-j))}$
with the variables
![]() $x_1,\ldots ,x_n, q_{rs} \ (2 \leq s \leq n, n-h(n+1-s)<r<s)$
. In this section, we give an explicit formula for partial derivatives
$x_1,\ldots ,x_n, q_{rs} \ (2 \leq s \leq n, n-h(n+1-s)<r<s)$
. In this section, we give an explicit formula for partial derivatives
![]() $\partial E_i^{(n)}/\partial x_s \ (1 \leq s \leq n)$
and
$\partial E_i^{(n)}/\partial x_s \ (1 \leq s \leq n)$
and
![]() $\partial E_i^{(n)}/\partial q_{rs} \ (1 \leq r < s \leq n)$
for each
$\partial E_i^{(n)}/\partial q_{rs} \ (1 \leq r < s \leq n)$
for each
![]() $i \in [n]$
.
$i \in [n]$
.
For positive integers a and b with
![]() $1 \leq a \leq b \leq n$
, we set
$1 \leq a \leq b \leq n$
, we set
As in Definition 4.6, we introduce the following polynomials.
Definition 8.1. Let
![]() $M_{[a,b]}$
be the matrix of size
$M_{[a,b]}$
be the matrix of size
![]() $(b-a+1) \times (b-a+1)$
defined as
$(b-a+1) \times (b-a+1)$
defined as

We define polynomials
![]() $E_1^{[a,b]}, \ldots , E_{b-a+1}^{[a,b]} \in {\mathbb {C}}[x_a,\ldots ,x_b,q_{rs} \mid a \leq r < s \leq b]$
by
$E_1^{[a,b]}, \ldots , E_{b-a+1}^{[a,b]} \in {\mathbb {C}}[x_a,\ldots ,x_b,q_{rs} \mid a \leq r < s \leq b]$
by
Note that if
![]() $a=1$
, then we obtain
$a=1$
, then we obtain
by the definition. In what follows, we use the symbol
and we take the following convention

for
![]() $b \geq a-1$
. By the same argument for the proof of Lemma 4.8, one can prove the lemma below. We leave the detail to the reader.
$b \geq a-1$
. By the same argument for the proof of Lemma 4.8, one can prove the lemma below. We leave the detail to the reader.
Lemma 8.2. Let
![]() $1 \leq a \leq b \leq n$
. For
$1 \leq a \leq b \leq n$
. For
![]() $1 \leq i \leq b-a+1$
, we have
$1 \leq i \leq b-a+1$
, we have
 $$ \begin{align*} E_i^{[a,b]} = E_i^{[a,b-1]} + E_{i-1}^{[a,b-1]} x_b + \sum_{k=1}^{i-1} E_{i-1-k}^{[a,b-1-k]} q_{b-k \, b} \end{align*} $$
$$ \begin{align*} E_i^{[a,b]} = E_i^{[a,b-1]} + E_{i-1}^{[a,b-1]} x_b + \sum_{k=1}^{i-1} E_{i-1-k}^{[a,b-1-k]} q_{b-k \, b} \end{align*} $$
with the convention that
![]() $\sum _{k=1}^{i-1} E_{i-1-k}^{[a,b-1-k]} q_{b-k \, b}=0$
whenever
$\sum _{k=1}^{i-1} E_{i-1-k}^{[a,b-1-k]} q_{b-k \, b}=0$
whenever
![]() $i=1$
.
$i=1$
.
Lemma 8.3.
-
1. Let
 $s \in [n]$
. For
$s \in [n]$
. For
 $i \in [n]$
, we have
$i \in [n]$
, we have  $$ \begin{align*} \frac{\partial}{\partial x_s} E_i^{(n)} = \sum_{k=0}^{i-1} E_{i-1-k}^{[1,s-1]} E_{k}^{[s+1,n]}. \end{align*} $$
$$ \begin{align*} \frac{\partial}{\partial x_s} E_i^{(n)} = \sum_{k=0}^{i-1} E_{i-1-k}^{[1,s-1]} E_{k}^{[s+1,n]}. \end{align*} $$
-
2. Let
 $1 \leq r < s \leq n$
. Then
$1 \leq r < s \leq n$
. Then  $$ \begin{align*} \frac{\partial}{\partial q_{rs}} E_{i+s-r}^{(n)} = \begin{cases} 0 & \text{if} \ 1-(s-r) \leq i \leq 0, \\ \sum_{k=0}^{i-1} E_{i-1-k}^{[1,r-1]} E_{k}^{[s+1,n]} & \text{if} \ 1 \leq i \leq n-(s-r). \end{cases} \end{align*} $$
$$ \begin{align*} \frac{\partial}{\partial q_{rs}} E_{i+s-r}^{(n)} = \begin{cases} 0 & \text{if} \ 1-(s-r) \leq i \leq 0, \\ \sum_{k=0}^{i-1} E_{i-1-k}^{[1,r-1]} E_{k}^{[s+1,n]} & \text{if} \ 1 \leq i \leq n-(s-r). \end{cases} \end{align*} $$
Proof. (1) By Definition 4.6, one has
We think of
![]() $\lambda $
as a variable in the equality above, and we partial differentiate the both sides with respect to
$\lambda $
as a variable in the equality above, and we partial differentiate the both sides with respect to
![]() $x_s$
. Then
$x_s$
. Then
![]() $\frac {\partial }{\partial x_s} E_i^{(n)}$
is equal to the coefficient of
$\frac {\partial }{\partial x_s} E_i^{(n)}$
is equal to the coefficient of
![]() $\lambda ^{n-i}$
for
$\lambda ^{n-i}$
for
![]() $\frac {\partial }{\partial x_s}\det (\lambda I_n - M_n)$
multiplied by
$\frac {\partial }{\partial x_s}\det (\lambda I_n - M_n)$
multiplied by
![]() $(-1)^{i}$
. Since the variable
$(-1)^{i}$
. Since the variable
![]() $x_s$
appears in only the
$x_s$
appears in only the
![]() $(s,s)$
-th entry of the matrix
$(s,s)$
-th entry of the matrix
![]() $(\lambda I_n - M_n)$
, from the cofactor expansion along the s-th column for
$(\lambda I_n - M_n)$
, from the cofactor expansion along the s-th column for
![]() $\det (\lambda I_n - M_n)$
, we can write
$\det (\lambda I_n - M_n)$
, we can write
for some polynomial
![]() $F \in {\mathbb {C}}[x_1,\ldots ,\widehat {x_s},\ldots ,x_n,q_{ij} \mid 1 \leq i < j \leq n]$
. Here, the caret sign
$F \in {\mathbb {C}}[x_1,\ldots ,\widehat {x_s},\ldots ,x_n,q_{ij} \mid 1 \leq i < j \leq n]$
. Here, the caret sign
![]() $\widehat {}$
over
$\widehat {}$
over
![]() $x_s$
means that the entry is omitted. Hence, we obtain
$x_s$
means that the entry is omitted. Hence, we obtain
 $$ \begin{align*} \frac{\partial}{\partial x_s}\det(\lambda I_n - M_n) &= - \det(\lambda I_{s-1} - M_{[1,s-1]}) \det(\lambda I_{n-s} - M_{[s+1,n]}) \\ &= - \left(\sum_{u=0}^{s-1} (-1)^u E_u^{[1,s-1]} \lambda^{s-1-u} \right) \left( \sum_{v=0}^{n-s} (-1)^v E_v^{[s+1,n]} \lambda^{n-s-v} \right) \\ & \hspace{30pt} \text{(by Definition~}8.1) \\ &= - \sum_{u=0}^{s-1} \sum_{v=0}^{n-s} (-1)^{u+v} E_u^{[1,s-1]}E_v^{[s+1,n]} \lambda^{n-1-(u+v)} \\ &= - \sum_{\ell=0}^{n-1} \left( \sum_{k=0}^{\ell} (-1)^{\ell} E_{\ell-k}^{[1,s-1]}E_k^{[s+1,n]} \right) \lambda^{n-1-\ell}. \end{align*} $$
$$ \begin{align*} \frac{\partial}{\partial x_s}\det(\lambda I_n - M_n) &= - \det(\lambda I_{s-1} - M_{[1,s-1]}) \det(\lambda I_{n-s} - M_{[s+1,n]}) \\ &= - \left(\sum_{u=0}^{s-1} (-1)^u E_u^{[1,s-1]} \lambda^{s-1-u} \right) \left( \sum_{v=0}^{n-s} (-1)^v E_v^{[s+1,n]} \lambda^{n-s-v} \right) \\ & \hspace{30pt} \text{(by Definition~}8.1) \\ &= - \sum_{u=0}^{s-1} \sum_{v=0}^{n-s} (-1)^{u+v} E_u^{[1,s-1]}E_v^{[s+1,n]} \lambda^{n-1-(u+v)} \\ &= - \sum_{\ell=0}^{n-1} \left( \sum_{k=0}^{\ell} (-1)^{\ell} E_{\ell-k}^{[1,s-1]}E_k^{[s+1,n]} \right) \lambda^{n-1-\ell}. \end{align*} $$
Therefore, we conclude that the coefficient of
![]() $\lambda ^{n-i}$
for
$\lambda ^{n-i}$
for
![]() $\frac {\partial }{\partial x_s}\det (\lambda I_n - M_n)$
multiplied by
$\frac {\partial }{\partial x_s}\det (\lambda I_n - M_n)$
multiplied by
![]() $(-1)^{i}$
is equal to
$(-1)^{i}$
is equal to
 $$ \begin{align*} \frac{\partial}{\partial x_s} E_i^{(n)} = \sum_{k=0}^{i-1} E_{i-1-k}^{[1,s-1]}E_k^{[s+1,n]}, \end{align*} $$
$$ \begin{align*} \frac{\partial}{\partial x_s} E_i^{(n)} = \sum_{k=0}^{i-1} E_{i-1-k}^{[1,s-1]}E_k^{[s+1,n]}, \end{align*} $$
as desired.
(2) We partial differentiate the both sides of equation (8.3) with respect to
![]() $q_{rs}$
, then
$q_{rs}$
, then
![]() $\frac {\partial }{\partial q_{rs}} E_j^{(n)}$
is equal to the coefficient of
$\frac {\partial }{\partial q_{rs}} E_j^{(n)}$
is equal to the coefficient of
![]() $\lambda ^{n-j}$
for
$\lambda ^{n-j}$
for
![]() $\frac {\partial }{\partial q_{rs}}\det (\lambda I_n - M_n)$
multiplied by
$\frac {\partial }{\partial q_{rs}}\det (\lambda I_n - M_n)$
multiplied by
![]() $(-1)^{j}$
. Since the variable
$(-1)^{j}$
. Since the variable
![]() $q_{rs}$
appears in only the
$q_{rs}$
appears in only the
![]() $(r,s)$
-th entry of the matrix
$(r,s)$
-th entry of the matrix
![]() $(\lambda I_n - M_n)$
, one can see from similar arguments as in the previous case that
$(\lambda I_n - M_n)$
, one can see from similar arguments as in the previous case that
 $$ \begin{align*} \frac{\partial}{\partial q_{rs}}\det(\lambda I_n - M_n) &= (-1)^{r+s} \frac{\partial}{\partial q_{rs}} (-q_{rs}) \det(\lambda I_{r-1} - M_{[1,r-1]}) \det(\lambda I_{n-s} - M_{[s+1,n]}) \\ &= (-1)^{r+s+1} \left(\sum_{u=0}^{r-1} (-1)^u E_u^{[1,r-1]} \lambda^{r-1-u} \right) \left( \sum_{v=0}^{n-s} (-1)^v E_v^{[s+1,n]} \lambda^{n-s-v} \right) \\ &= (-1)^{r+s+1} \sum_{u=0}^{r-1} \sum_{v=0}^{n-s} (-1)^{u+v} E_u^{[1,r-1]}E_v^{[s+1,n]} \lambda^{n-1-(u+v+s-r)} \\ &= (-1)^{r+s+1} \sum_{\ell=s-r}^{n-1} \left( \sum_{k=0}^{\ell-s+r} (-1)^{\ell-s+r} E_{\ell-s+r-k}^{[1,r-1]}E_k^{[s+1,n]} \right) \lambda^{n-1-\ell}. \end{align*} $$
$$ \begin{align*} \frac{\partial}{\partial q_{rs}}\det(\lambda I_n - M_n) &= (-1)^{r+s} \frac{\partial}{\partial q_{rs}} (-q_{rs}) \det(\lambda I_{r-1} - M_{[1,r-1]}) \det(\lambda I_{n-s} - M_{[s+1,n]}) \\ &= (-1)^{r+s+1} \left(\sum_{u=0}^{r-1} (-1)^u E_u^{[1,r-1]} \lambda^{r-1-u} \right) \left( \sum_{v=0}^{n-s} (-1)^v E_v^{[s+1,n]} \lambda^{n-s-v} \right) \\ &= (-1)^{r+s+1} \sum_{u=0}^{r-1} \sum_{v=0}^{n-s} (-1)^{u+v} E_u^{[1,r-1]}E_v^{[s+1,n]} \lambda^{n-1-(u+v+s-r)} \\ &= (-1)^{r+s+1} \sum_{\ell=s-r}^{n-1} \left( \sum_{k=0}^{\ell-s+r} (-1)^{\ell-s+r} E_{\ell-s+r-k}^{[1,r-1]}E_k^{[s+1,n]} \right) \lambda^{n-1-\ell}. \end{align*} $$
Thus, the coefficient of
![]() $\lambda ^{n-j}$
for
$\lambda ^{n-j}$
for
![]() $\frac {\partial }{\partial q_{rs}}\det (\lambda I_n - M_n)$
multiplied by
$\frac {\partial }{\partial q_{rs}}\det (\lambda I_n - M_n)$
multiplied by
![]() $(-1)^{j}$
is
$(-1)^{j}$
is
 $$ \begin{align*} \frac{\partial}{\partial q_{rs}} E_j^{(n)} = \begin{cases} 0 \ \ \ & \text{if} \ 1 \leq j \leq s-r, \\ \sum_{k=0}^{j-1-s+r} E_{j-1-s+r-k}^{[1,r-1]}E_k^{[s+1,n]} \ \ \ & \text{if} \ s-r+1 \leq j \leq n, \end{cases} \end{align*} $$
$$ \begin{align*} \frac{\partial}{\partial q_{rs}} E_j^{(n)} = \begin{cases} 0 \ \ \ & \text{if} \ 1 \leq j \leq s-r, \\ \sum_{k=0}^{j-1-s+r} E_{j-1-s+r-k}^{[1,r-1]}E_k^{[s+1,n]} \ \ \ & \text{if} \ s-r+1 \leq j \leq n, \end{cases} \end{align*} $$
as desired. This completes the proof.
In what follows, we set
and we see the Jacobian matrix
![]() $\big (\frac {\partial }{\partial q_{rs}} E_{i}^{(n)} \big )_{i,(r,s)}$
below.
$\big (\frac {\partial }{\partial q_{rs}} E_{i}^{(n)} \big )_{i,(r,s)}$
below.
Example 8.4. Let
![]() $n=3$
. Then the Jacobian matrix
$n=3$
. Then the Jacobian matrix
![]() $\big (\frac {\partial }{\partial q_{rs}} E_{i}^{(3)} \big )_{i,(r,s)}$
is described as
$\big (\frac {\partial }{\partial q_{rs}} E_{i}^{(3)} \big )_{i,(r,s)}$
is described as

by Lemma 8.3. Also, the Jacobian matrix
![]() $\big (\frac {\partial }{\partial q_{rs}} E_{i}^{(4)} \big )_{i,(r,s)}$
for
$\big (\frac {\partial }{\partial q_{rs}} E_{i}^{(4)} \big )_{i,(r,s)}$
for
![]() $n=4$
is given by
$n=4$
is given by

The Jacobian matrices above have a full rank. In general, one can verify from Lemma 8.3 that the rank of the Jacobian matrix
![]() $\big (\frac {\partial }{\partial q_{rs}} E_{i}^{(n)} \big )_{i,(r,s)}$
is full for arbitrary n. This fact also follows from the well-known fact that
$\big (\frac {\partial }{\partial q_{rs}} E_{i}^{(n)} \big )_{i,(r,s)}$
is full for arbitrary n. This fact also follows from the well-known fact that
![]() $Fl({\mathbb {C}}^n) \cap \Omega _e^\circ $
is smooth and Theorem 4.13 for the case when
$Fl({\mathbb {C}}^n) \cap \Omega _e^\circ $
is smooth and Theorem 4.13 for the case when
![]() $h=(n,\ldots ,n)$
.
$h=(n,\ldots ,n)$
.
Let
![]() $h: [n] \to [n]$
be a Hessenberg function. As in Definition 4.10, for
$h: [n] \to [n]$
be a Hessenberg function. As in Definition 4.10, for
![]() $0 \leq i \leq n$
and
$0 \leq i \leq n$
and
![]() $a,b$
with
$a,b$
with
![]() $b \geq a-1$
, we define
$b \geq a-1$
, we define
Note that we take the convention in equation (8.2). By the definition (8.5), it is straightforward to see that for arbitrary Hessenberg function
![]() $h: [n] \to [n]$
,
$h: [n] \to [n]$
,
![]() $i \in [n]$
, and
$i \in [n]$
, and
![]() $(r,s)$
with
$(r,s)$
with
![]() $2 \leq s \leq n, n-h(n+1-s)<r \leq s$
,
$2 \leq s \leq n, n-h(n+1-s)<r \leq s$
,
 $$ \begin{align*} \left. \frac{\partial}{\partial q_{rs}} \, ^h E_{i}^{(n)} = \left( \frac{\partial}{\partial q_{rs}} E_{i}^{(n)} \right) \right|_{q_{uv}=0 \ (2 \leq v \leq n \ \text{and} \ 1 \leq u \leq n-h(n+1-v))}. \end{align*} $$
$$ \begin{align*} \left. \frac{\partial}{\partial q_{rs}} \, ^h E_{i}^{(n)} = \left( \frac{\partial}{\partial q_{rs}} E_{i}^{(n)} \right) \right|_{q_{uv}=0 \ (2 \leq v \leq n \ \text{and} \ 1 \leq u \leq n-h(n+1-v))}. \end{align*} $$
Combining this and Lemma 8.3, we have that for
![]() $1 \leq r \leq s \leq n$
,
$1 \leq r \leq s \leq n$
,
 $$ \begin{align} \frac{\partial}{\partial q_{rs}} \, ^h E_{i+s-r}^{(n)} = \begin{cases} 0 & \text{if} \ 1-(s-r) \leq i \leq 0, \\ 1 & \text{if} \ i = 1, \\ \sum_{k=0}^{i-1} \, ^h E_{i-1-k}^{[1,r-1]} \, ^h E_{k}^{[s+1,n]} & \text{if} \ 2 \leq i \leq n-(s-r). \end{cases} \end{align} $$
$$ \begin{align} \frac{\partial}{\partial q_{rs}} \, ^h E_{i+s-r}^{(n)} = \begin{cases} 0 & \text{if} \ 1-(s-r) \leq i \leq 0, \\ 1 & \text{if} \ i = 1, \\ \sum_{k=0}^{i-1} \, ^h E_{i-1-k}^{[1,r-1]} \, ^h E_{k}^{[s+1,n]} & \text{if} \ 2 \leq i \leq n-(s-r). \end{cases} \end{align} $$
For
![]() $2 \leq m \leq n-1$
, we define a Hessenberg function
$2 \leq m \leq n-1$
, we define a Hessenberg function
![]() $h_m:[n] \rightarrow [n]$
by
$h_m:[n] \rightarrow [n]$
by
The zero set of
![]() $\{^{h_m} E_1^{(n)}, \ldots , \, ^{h_m} E_n^{(n)}\}$
in
$\{^{h_m} E_1^{(n)}, \ldots , \, ^{h_m} E_n^{(n)}\}$
in
![]() ${\mathbb {C}}^{\frac {1}{2}n(n+1)-(n-m)}$
with the variables
${\mathbb {C}}^{\frac {1}{2}n(n+1)-(n-m)}$
with the variables
![]() $x_1.\ldots ,x_n,q_{rs} \ (2 \leq s \leq n, n-h_m(n+1-s)<r < s)$
is denoted by
$x_1.\ldots ,x_n,q_{rs} \ (2 \leq s \leq n, n-h_m(n+1-s)<r < s)$
is denoted by
![]() $V\big (\, ^{h_m} E_1^{(n)}, \ldots , \, ^{h_m} E_n^{(n)}\big )$
, that is,
$V\big (\, ^{h_m} E_1^{(n)}, \ldots , \, ^{h_m} E_n^{(n)}\big )$
, that is,
where ![]() .
.
Proposition 8.5. Let
![]() $2 \leq m \leq n-1$
and
$2 \leq m \leq n-1$
and
![]() $h_m$
be the Hessenberg function in equation (8.7). Then, the singular locus of
$h_m$
be the Hessenberg function in equation (8.7). Then, the singular locus of
![]() $V\big (\, ^{h_m} E_1^{(n)}, \ldots , \, ^{h_m} E_n^{(n)}\big )$
in equation (8.8) is given by the solution set of the equations
$V\big (\, ^{h_m} E_1^{(n)}, \ldots , \, ^{h_m} E_n^{(n)}\big )$
in equation (8.8) is given by the solution set of the equations
Here, we recall our convention (8.4) that
![]() $q_{rs}=x_s$
whenever
$q_{rs}=x_s$
whenever
![]() $r=s$
.
$r=s$
.
Before we prove Proposition 8.5, we give an example of the singular locus of the zero set
![]() $V\big (\, ^{h_m} E_1^{(3)}, \, ^{h_m} E_2^{(3)}, \, ^{h_m} E_3^{(3)}\big )$
for
$V\big (\, ^{h_m} E_1^{(3)}, \, ^{h_m} E_2^{(3)}, \, ^{h_m} E_3^{(3)}\big )$
for
![]() $m=2$
by using Proposition 8.5.
$m=2$
by using Proposition 8.5.
Example 8.6. Consider the case when
![]() $h=(2,3,3)$
for
$h=(2,3,3)$
for
![]() $n=3$
. The Jacobian matrix
$n=3$
. The Jacobian matrix
![]() $\big (\frac {\partial }{\partial q_{rs}} \, ^h E_{i}^{(3)} \big )_{i,(r,s) \neq (1,3)}$
is obtained from
$\big (\frac {\partial }{\partial q_{rs}} \, ^h E_{i}^{(3)} \big )_{i,(r,s) \neq (1,3)}$
is obtained from
![]() $\big (\frac {\partial }{\partial q_{rs}} E_{i}^{(3)} \big )_{i,(r,s)}$
by forgetting the quantum parameter
$\big (\frac {\partial }{\partial q_{rs}} E_{i}^{(3)} \big )_{i,(r,s)}$
by forgetting the quantum parameter
![]() $q_{13}$
. As seen in Example 8.4, the Jacobian matrix
$q_{13}$
. As seen in Example 8.4, the Jacobian matrix
![]() $\big (\frac {\partial }{\partial q_{rs}} \, ^h E_{i}^{(3)} \big )_{i,(r,s) \neq (1,3)}$
is shown as
$\big (\frac {\partial }{\partial q_{rs}} \, ^h E_{i}^{(3)} \big )_{i,(r,s) \neq (1,3)}$
is shown as

It follows from Proposition 8.5 that the singular locus of
![]() $V\big (\, ^h E_1^{(3)}, \, ^h E_2^{(3)}, \, ^h E_3^{(3)}\big )$
is given by the solution set of the equations
$V\big (\, ^h E_1^{(3)}, \, ^h E_2^{(3)}, \, ^h E_3^{(3)}\big )$
is given by the solution set of the equations
![]() $^h E_2^{[2,3]}=\, ^h E_1^{[1,1]} \, ^h E_1^{[3,3]}=\, ^h E_2^{[1,2]}=\, ^h E_1^{[3,3]}=\, ^h E_1^{[1,1]}=0$
. The resulting solution is as follows:
$^h E_2^{[2,3]}=\, ^h E_1^{[1,1]} \, ^h E_1^{[3,3]}=\, ^h E_2^{[1,2]}=\, ^h E_1^{[3,3]}=\, ^h E_1^{[1,1]}=0$
. The resulting solution is as follows:
Then it follows from equation (4.6) and Proposition 7.3 that the singular locus of
![]() $\operatorname {\mathrm {Pet}}_3 \cap \Omega _e^\circ $
is given by the solution set of the equations
$\operatorname {\mathrm {Pet}}_3 \cap \Omega _e^\circ $
is given by the solution set of the equations
![]() $x_{32}=0, \ x_{21}=0, \ F_{3,2}=0, \ F_{2,1}=0$
. This is equivalent to
$x_{32}=0, \ x_{21}=0, \ F_{3,2}=0, \ F_{2,1}=0$
. This is equivalent to
Hence, the singular locus of
![]() $\operatorname {\mathrm {Pet}}_3 \cap \Omega _e^\circ $
is
$\operatorname {\mathrm {Pet}}_3 \cap \Omega _e^\circ $
is
![]() $\{eB \}$
. Note that the singular locus of the Peterson variety
$\{eB \}$
. Note that the singular locus of the Peterson variety
![]() $\operatorname {\mathrm {Pet}}_n$
is given by [Reference Insko and Yong26]. We will explain this in Appendix A.
$\operatorname {\mathrm {Pet}}_n$
is given by [Reference Insko and Yong26]. We will explain this in Appendix A.
Proof of Proposition 8.5.
Recall that a point ![]() in
in
![]() ${\mathbb {C}}^{\frac {1}{2}n(n+1)-(n-m)}$
is a singular point of
${\mathbb {C}}^{\frac {1}{2}n(n+1)-(n-m)}$
is a singular point of
![]() $V\big (\, ^{h_m} E_1^{(n)}, \ldots , \, ^{h_m} E_n^{(n)}\big )$
if and only if the rank of the Jacobian matrix
$V\big (\, ^{h_m} E_1^{(n)}, \ldots , \, ^{h_m} E_n^{(n)}\big )$
if and only if the rank of the Jacobian matrix
![]() $\big (\frac {\partial }{\partial q_{rs}} \, ^{h_m} E_{i}^{(n)}(a,p) \big )_{i,(r,s)}$
is not full. It is clear that the Jacobian matrix
$\big (\frac {\partial }{\partial q_{rs}} \, ^{h_m} E_{i}^{(n)}(a,p) \big )_{i,(r,s)}$
is not full. It is clear that the Jacobian matrix
![]() $\big (\frac {\partial }{\partial q_{rs}} \, ^{h_m} E_{i}^{(n)}(a,p) \big )_{i,(r,s)}$
is not full if the n-th row vector is zero. Thus, it is enough to prove that if a point
$\big (\frac {\partial }{\partial q_{rs}} \, ^{h_m} E_{i}^{(n)}(a,p) \big )_{i,(r,s)}$
is not full if the n-th row vector is zero. Thus, it is enough to prove that if a point
![]() $(a,p)$
in
$(a,p)$
in
![]() ${\mathbb {C}}^{\frac {1}{2}n(n+1)-(n-m)}$
is a singular point of
${\mathbb {C}}^{\frac {1}{2}n(n+1)-(n-m)}$
is a singular point of
![]() $V\big (\, ^{h_m} E_1^{(n)}, \ldots , \, ^{h_m} E_n^{(n)}\big )$
, then the n-th row vector
$V\big (\, ^{h_m} E_1^{(n)}, \ldots , \, ^{h_m} E_n^{(n)}\big )$
, then the n-th row vector
![]() $\big ( \frac {\partial }{\partial q_{rs}} \, ^{h_m} E_{n}^{(n)}(a,p) \big )_{(r,s)}$
of the Jacobian matrix is zero.
$\big ( \frac {\partial }{\partial q_{rs}} \, ^{h_m} E_{n}^{(n)}(a,p) \big )_{(r,s)}$
of the Jacobian matrix is zero.
Since the column vector with respect to
![]() $\frac {\partial }{\partial q_{rs}}$
of the Jacobian matrix
$\frac {\partial }{\partial q_{rs}}$
of the Jacobian matrix
![]() $\big (\frac {\partial }{\partial q_{rs}} \, ^{h_m} E_{i}^{(n)}(a,p) \big )_{i,(r,s)}$
is of the form
$\big (\frac {\partial }{\partial q_{rs}} \, ^{h_m} E_{i}^{(n)}(a,p) \big )_{i,(r,s)}$
is of the form
 $(\underbrace {0,\ldots ,0}_{s-r},1,*,\ldots ,*)^t$
by equation (8.6), the first
$(\underbrace {0,\ldots ,0}_{s-r},1,*,\ldots ,*)^t$
by equation (8.6), the first
![]() $n-1$
row vectors of the Jacobian matrix
$n-1$
row vectors of the Jacobian matrix
![]() $\big (\frac {\partial }{\partial q_{rs}} \, ^{h_m} E_{i}^{(n)}(a,p) \big )_{i,(r,s)}$
are linearly independent. By the assumption that
$\big (\frac {\partial }{\partial q_{rs}} \, ^{h_m} E_{i}^{(n)}(a,p) \big )_{i,(r,s)}$
are linearly independent. By the assumption that
![]() $\big (\frac {\partial }{\partial q_{rs}} \, ^{h_m} E_{i}^{(n)}(a,p) \big )_{i,(r,s)}$
does not have full rank, the n-th row vector must be written as a linear combination of the first
$\big (\frac {\partial }{\partial q_{rs}} \, ^{h_m} E_{i}^{(n)}(a,p) \big )_{i,(r,s)}$
does not have full rank, the n-th row vector must be written as a linear combination of the first
![]() $n-1$
row vectors, that is,
$n-1$
row vectors, that is,
 $$ \begin{align} \left(\frac{\partial}{\partial q_{rs}} \, ^{h_m} E_{n}^{(n)}(a,p) \right)_{(r,s)} = \sum_{i=1}^{n-1} c_i \left(\frac{\partial}{\partial q_{rs}} \, ^{h_m} E_{i}^{(n)}(a,p) \right)_{(r,s)} \end{align} $$
$$ \begin{align} \left(\frac{\partial}{\partial q_{rs}} \, ^{h_m} E_{n}^{(n)}(a,p) \right)_{(r,s)} = \sum_{i=1}^{n-1} c_i \left(\frac{\partial}{\partial q_{rs}} \, ^{h_m} E_{i}^{(n)}(a,p) \right)_{(r,s)} \end{align} $$
for some
![]() $c_1,\ldots ,c_{n-1} \in {\mathbb {C}}$
. We note that the pair
$c_1,\ldots ,c_{n-1} \in {\mathbb {C}}$
. We note that the pair
![]() $(r,s)$
can be taken as
$(r,s)$
can be taken as
![]() $2 \leq s \leq n$
and
$2 \leq s \leq n$
and
![]() $n-h_m(n+1-s)<r \leq s$
in the equality above. Recall that we denote the singular point
$n-h_m(n+1-s)<r \leq s$
in the equality above. Recall that we denote the singular point
![]() $(a_1,\ldots ,a_n,p_{rs})_{2 \leq s \leq n, n-h_m(n+1-s)<r < s}$
of
$(a_1,\ldots ,a_n,p_{rs})_{2 \leq s \leq n, n-h_m(n+1-s)<r < s}$
of
![]() $V\big (\, ^{h_m} E_1^{(n)}, \ldots , \, ^{h_m} E_n^{(n)}\big )$
by
$V\big (\, ^{h_m} E_1^{(n)}, \ldots , \, ^{h_m} E_n^{(n)}\big )$
by
![]() $(a,p)$
.
$(a,p)$
.
Claim 1.
The coefficients
![]() $c_i$
of equation (8.9) must be
$c_i$
of equation (8.9) must be
![]() $(-1)^{n-i+1} a_n^{n-i}$
for
$(-1)^{n-i+1} a_n^{n-i}$
for
![]() $i \in [n-1]$
.
$i \in [n-1]$
.
We prove Claim 1 by descending induction on i. The base case is
![]() $i=n-1$
. Comparing the
$i=n-1$
. Comparing the
![]() $(r,s)=(1,n-1)$
-th component of equation (8.9), we have
$(r,s)=(1,n-1)$
-th component of equation (8.9), we have
by equation (8.6). Since
![]() $^{h_m} E_1^{[n,n]}=x_n$
, the equality above implies that
$^{h_m} E_1^{[n,n]}=x_n$
, the equality above implies that
![]() $a_n=c_{n-1}$
. This shows the base case.
$a_n=c_{n-1}$
. This shows the base case.
We now assume that
![]() $i<n-1$
and the assertion of the claim holds for arbitrary k with
$i<n-1$
and the assertion of the claim holds for arbitrary k with
![]() $k \geq i+1$
. It follows from equation (8.6) that the
$k \geq i+1$
. It follows from equation (8.6) that the
![]() $(r,s)=(n-i,n-1)$
-th component of equation (8.9) gives
$(r,s)=(n-i,n-1)$
-th component of equation (8.9) gives
 $$ \begin{align*} &^{h_m} E_{n-i-1}^{[1,n-i-1]}(a,p) \cdot \,^{h_m} E_1^{[n,n]}(a,p) \\=&c_i \cdot 1 + c_{i+1} \cdot \left( ^{h_m} E_1^{[1,n-i-1]}(a,p)+\,^{h_m} E_1^{[n,n]}(a,p) \right) \\&+ c_{i+2} \cdot \left( ^{h_m} E_2^{[1,n-i-1]}(a,p)+\,^{h_m} E_1^{[1,n-i-1]}(a,p)\cdot\,^{h_m} E_1^{[n,n]}(a,p) \right) \\&+ c_{i+3} \cdot \left( ^{h_m} E_3^{[1,n-i-1]}(a,p)+\,^{h_m} E_2^{[1,n-i-1]}(a,p)\cdot\,^{h_m} E_1^{[n,n]}(a,p) \right) \\&+ \cdots + c_{n-1} \cdot \left( ^{h_m} E_{n-i-1}^{[1,n-i-1]}(a,p)+\,^{h_m} E_{n-i-2}^{[1,n-i-1]}(a,p)\cdot\,^{h_m} E_1^{[n,n]}(a,p) \right). \end{align*} $$
$$ \begin{align*} &^{h_m} E_{n-i-1}^{[1,n-i-1]}(a,p) \cdot \,^{h_m} E_1^{[n,n]}(a,p) \\=&c_i \cdot 1 + c_{i+1} \cdot \left( ^{h_m} E_1^{[1,n-i-1]}(a,p)+\,^{h_m} E_1^{[n,n]}(a,p) \right) \\&+ c_{i+2} \cdot \left( ^{h_m} E_2^{[1,n-i-1]}(a,p)+\,^{h_m} E_1^{[1,n-i-1]}(a,p)\cdot\,^{h_m} E_1^{[n,n]}(a,p) \right) \\&+ c_{i+3} \cdot \left( ^{h_m} E_3^{[1,n-i-1]}(a,p)+\,^{h_m} E_2^{[1,n-i-1]}(a,p)\cdot\,^{h_m} E_1^{[n,n]}(a,p) \right) \\&+ \cdots + c_{n-1} \cdot \left( ^{h_m} E_{n-i-1}^{[1,n-i-1]}(a,p)+\,^{h_m} E_{n-i-2}^{[1,n-i-1]}(a,p)\cdot\,^{h_m} E_1^{[n,n]}(a,p) \right). \end{align*} $$
Since
![]() $^{h_m} E_1^{[n,n]}(a,p)=a_n$
and
$^{h_m} E_1^{[n,n]}(a,p)=a_n$
and
![]() $c_k=(-1)^{n-k+1} a_n^{n-k}$
for all
$c_k=(-1)^{n-k+1} a_n^{n-k}$
for all
![]() $i+1 \leq k \leq n-1$
by our inductive assumption,
$i+1 \leq k \leq n-1$
by our inductive assumption,
![]() $^{h_m} E_{n-i-1}^{[1,n-i-1]}(a,p) \cdot a_n$
is equal to
$^{h_m} E_{n-i-1}^{[1,n-i-1]}(a,p) \cdot a_n$
is equal to
 $$ \begin{align*} &c_i + \sum_{k=1}^{n-i-1} (-1)^{n-i-k+1} a_n^{n-i-k} \left( ^{h_m} E_k^{[1,n-i-1]}(a,p)+\,^{h_m} E_{k-1}^{[1,n-i-1]}(a,p)\cdot a_n \right) \\= & c_i + (-1)^{n-i} a_n^{n-i-1} \cdot a_n + a_n \cdot \,^{h_m} E_{n-i-1}^{[1,n-i-1]}(a,p). \end{align*} $$
$$ \begin{align*} &c_i + \sum_{k=1}^{n-i-1} (-1)^{n-i-k+1} a_n^{n-i-k} \left( ^{h_m} E_k^{[1,n-i-1]}(a,p)+\,^{h_m} E_{k-1}^{[1,n-i-1]}(a,p)\cdot a_n \right) \\= & c_i + (-1)^{n-i} a_n^{n-i-1} \cdot a_n + a_n \cdot \,^{h_m} E_{n-i-1}^{[1,n-i-1]}(a,p). \end{align*} $$
This yields that
![]() $c_i=(-1)^{n-i+1} a_n^{n-i}$
and we proved Claim 1.
$c_i=(-1)^{n-i+1} a_n^{n-i}$
and we proved Claim 1.
It follows from Claim 1 and equation (8.9) that
 $$ \begin{align} \left(\frac{\partial}{\partial q_{rs}} \, ^{h_m} E_{n}^{(n)}(a,p) \right)_{(r,s)} = \sum_{i=1}^{n-1} (-1)^{n-i+1} a_n^{n-i} \left(\frac{\partial}{\partial q_{rs}} \, ^{h_m} E_{i}^{(n)}(a,p) \right)_{(r,s)} \end{align} $$
$$ \begin{align} \left(\frac{\partial}{\partial q_{rs}} \, ^{h_m} E_{n}^{(n)}(a,p) \right)_{(r,s)} = \sum_{i=1}^{n-1} (-1)^{n-i+1} a_n^{n-i} \left(\frac{\partial}{\partial q_{rs}} \, ^{h_m} E_{i}^{(n)}(a,p) \right)_{(r,s)} \end{align} $$
for all
![]() $2 \leq s \leq n$
and
$2 \leq s \leq n$
and
![]() $n-h_m(n+1-s)<r \leq s$
.
$n-h_m(n+1-s)<r \leq s$
.
Claim 2.
It holds that
![]() $p_{in}=0$
for all
$p_{in}=0$
for all
![]() $n-m+1 \leq i \leq n-1$
.
$n-m+1 \leq i \leq n-1$
.
We show Claim 2 by descending induction on i. The base case is
![]() $i=n-1$
. The
$i=n-1$
. The
![]() $(r,s)=(1,n-2)$
-th component of equation (8.10) is equal to
$(r,s)=(1,n-2)$
-th component of equation (8.10) is equal to
from equation (8.6). Since
![]() $^{h_m} E_2^{[n-1,n]}(a,p)=a_{n-1}a_n+p_{n-1 \, n}$
and
$^{h_m} E_2^{[n-1,n]}(a,p)=a_{n-1}a_n+p_{n-1 \, n}$
and
![]() $^{h_m} E_1^{[n-1,n]}(a,p)=a_{n-1}+a_n$
, we have
$^{h_m} E_1^{[n-1,n]}(a,p)=a_{n-1}+a_n$
, we have
![]() $p_{n-1 \, n}=0$
, which proves the base case.
$p_{n-1 \, n}=0$
, which proves the base case.
Suppose now that
![]() $i < n-1$
and that the claim holds for any k with
$i < n-1$
and that the claim holds for any k with
![]() $k \geq i+1$
, that is,
$k \geq i+1$
, that is,
![]() $p_{kn}=0$
for all
$p_{kn}=0$
for all
![]() $i+1 \leq k \leq n-1$
. By equation (8.6), the
$i+1 \leq k \leq n-1$
. By equation (8.6), the
![]() $(r,s)=(1,i-1)$
-th component of equation (8.10) is
$(r,s)=(1,i-1)$
-th component of equation (8.10) is
 $$ \begin{align} ^{h_m} E_{n-i+1}^{[i,n]}(a,p) = &(-1)^{n-i+2}a_n^{n-i+1} \cdot 1 + (-1)^{n-i+1}a_n^{n-i} \cdot \, ^{h_m} E_1^{[i,n]}(a,p) \\ &+ (-1)^{n-i}a_n^{n-i-1} \cdot \, ^{h_m} E_2^{[i,n]}(a,p) +\cdots+a_n \cdot \, ^{h_m} E_{n-i}^{[i,n]}(a,p). \notag \end{align} $$
$$ \begin{align} ^{h_m} E_{n-i+1}^{[i,n]}(a,p) = &(-1)^{n-i+2}a_n^{n-i+1} \cdot 1 + (-1)^{n-i+1}a_n^{n-i} \cdot \, ^{h_m} E_1^{[i,n]}(a,p) \\ &+ (-1)^{n-i}a_n^{n-i-1} \cdot \, ^{h_m} E_2^{[i,n]}(a,p) +\cdots+a_n \cdot \, ^{h_m} E_{n-i}^{[i,n]}(a,p). \notag \end{align} $$
Here, we note that
by the cofactor expansion along the last column. The left-hand side is written as
 $$ \begin{align*} \sum_{\ell=0}^{n-i+1} \big( (-1)^\ell E_\ell^{[i,n]}|_{q_{kn}=0 \ (i+1 \leq k \leq n-1)} \big) \lambda^{n-i+1-\ell}, \end{align*} $$
$$ \begin{align*} \sum_{\ell=0}^{n-i+1} \big( (-1)^\ell E_\ell^{[i,n]}|_{q_{kn}=0 \ (i+1 \leq k \leq n-1)} \big) \lambda^{n-i+1-\ell}, \end{align*} $$
and the right-hand side is
 $$ \begin{align*} \lambda^{n-i+1} + \sum_{\ell=1}^{n-i} \big( (-1)^\ell (x_n E_{\ell-1}^{[i,n-1]} + E_\ell^{[i,n-1]}) \big) \lambda^{n-i+1-\ell} + (-1)^{n-i+1} (x_n E_{n-i}^{[i,n-1]} + q_{in}) \end{align*} $$
$$ \begin{align*} \lambda^{n-i+1} + \sum_{\ell=1}^{n-i} \big( (-1)^\ell (x_n E_{\ell-1}^{[i,n-1]} + E_\ell^{[i,n-1]}) \big) \lambda^{n-i+1-\ell} + (-1)^{n-i+1} (x_n E_{n-i}^{[i,n-1]} + q_{in}) \end{align*} $$
by definition. Thus, we obtain that
 $$ \begin{align*} E_\ell^{[i,n]}|_{q_{kn}=0 \ (i+1 \leq k \leq n-1)} &= x_n E_{\ell-1}^{[i,n-1]} + E_\ell^{[i,n-1]} \ \ \ \text{for} \ 1 \leq \ell \leq n-i; \\ E_{n-i+1}^{[i,n]}|_{q_{kn}=0 \ (i+1 \leq k \leq n-1)} &=x_n E_{n-i}^{[i,n-1]} + q_{in}. \end{align*} $$
$$ \begin{align*} E_\ell^{[i,n]}|_{q_{kn}=0 \ (i+1 \leq k \leq n-1)} &= x_n E_{\ell-1}^{[i,n-1]} + E_\ell^{[i,n-1]} \ \ \ \text{for} \ 1 \leq \ell \leq n-i; \\ E_{n-i+1}^{[i,n]}|_{q_{kn}=0 \ (i+1 \leq k \leq n-1)} &=x_n E_{n-i}^{[i,n-1]} + q_{in}. \end{align*} $$
In particular, by our inductive hypothesis
![]() $p_{kn}=0$
for all
$p_{kn}=0$
for all
![]() $i+1 \leq k \leq n-1$
, one has
$i+1 \leq k \leq n-1$
, one has
 $$ \begin{align*} ^{h_m} E_\ell^{[i,n]}(a,p) &= a_n \, ^{h_m} E_{\ell-1}^{[i,n-1]}(a,p) + \, ^{h_m} E_\ell^{[i,n-1]}(a,p) \ \ \ \text{for} \ 1 \leq \ell \leq n-i; \\ ^{h_m} E_{n-i+1}^{[i,n]}(a,p) &=a_n \, ^{h_m} E_{n-i}^{[i,n-1]}(a,p) + p_{in}. \end{align*} $$
$$ \begin{align*} ^{h_m} E_\ell^{[i,n]}(a,p) &= a_n \, ^{h_m} E_{\ell-1}^{[i,n-1]}(a,p) + \, ^{h_m} E_\ell^{[i,n-1]}(a,p) \ \ \ \text{for} \ 1 \leq \ell \leq n-i; \\ ^{h_m} E_{n-i+1}^{[i,n]}(a,p) &=a_n \, ^{h_m} E_{n-i}^{[i,n-1]}(a,p) + p_{in}. \end{align*} $$
Substituting these equalities to equation (8.11), the left-hand side of equation (8.11) is
On the other hand, the right-hand side of equation (8.11) is
 $$ \begin{align*} &(-1)^{n-i+2}a_n^{n-i+1} + \sum_{k=1}^{n-i} (-1)^{n-i-k+2} a_n^{n-i-k+1} \cdot \left(a_n \, ^{h_m} E_{k-1}^{[i,n-1]}(a,p)+\,^{h_m} E_{k}^{[i,n-1]}(a,p) \right) \\ = & a_n \cdot \, ^{h_m} E_{n-i}^{[i,n-1]}(a,p). \end{align*} $$
$$ \begin{align*} &(-1)^{n-i+2}a_n^{n-i+1} + \sum_{k=1}^{n-i} (-1)^{n-i-k+2} a_n^{n-i-k+1} \cdot \left(a_n \, ^{h_m} E_{k-1}^{[i,n-1]}(a,p)+\,^{h_m} E_{k}^{[i,n-1]}(a,p) \right) \\ = & a_n \cdot \, ^{h_m} E_{n-i}^{[i,n-1]}(a,p). \end{align*} $$
Hence, we obtain that
![]() $p_{in}=0$
as desired. This proves Claim 2.
$p_{in}=0$
as desired. This proves Claim 2.
Claim 3.
We have
![]() $a_n=0$
.
$a_n=0$
.
It follows from Theorem 4.13 that
We denote by
![]() $b=(b_{ij})_{1 \leq j < i \leq n} \in \operatorname {\mathrm {Hess}}(N,h_m) \cap \Omega _e^\circ \subset {\mathbb {C}}^{\frac {1}{2}n(n-1)}$
the image of the singular point
$b=(b_{ij})_{1 \leq j < i \leq n} \in \operatorname {\mathrm {Hess}}(N,h_m) \cap \Omega _e^\circ \subset {\mathbb {C}}^{\frac {1}{2}n(n-1)}$
the image of the singular point
![]() $(a,p)$
of
$(a,p)$
of
![]() $V\big (\, ^{h_m} E_1^{(n)}, \ldots , \, ^{h_m} E_n^{(n)}\big )$
under the isomorphism above. One can see from Proposition 7.3 and Claim 2 that
$V\big (\, ^{h_m} E_1^{(n)}, \ldots , \, ^{h_m} E_n^{(n)}\big )$
under the isomorphism above. One can see from Proposition 7.3 and Claim 2 that
Since
![]() $b \in \operatorname {\mathrm {Hess}}(N,h_m) \cap \Omega _e^\circ $
, we also have
$b \in \operatorname {\mathrm {Hess}}(N,h_m) \cap \Omega _e^\circ $
, we also have
by Lemma 2.3. It follows from equations (8.12) and (8.13) and Lemma 2.3 again that the point
![]() ${b=(b_{ij})_{1 \leq j < i \leq n}}$
belongs to
${b=(b_{ij})_{1 \leq j < i \leq n}}$
belongs to
![]() $\operatorname {\mathrm {Hess}}(N,h_1) \cap \Omega _e^\circ $
, where
$\operatorname {\mathrm {Hess}}(N,h_1) \cap \Omega _e^\circ $
, where
![]() $h_1$
is the decomposable Hessenberg function defined by
$h_1$
is the decomposable Hessenberg function defined by ![]() . As seen in Definition 3.2 and surrounding discussion, every flag
. As seen in Definition 3.2 and surrounding discussion, every flag
![]() $V_\bullet \in \operatorname {\mathrm {Hess}}(N,h_1)$
has
$V_\bullet \in \operatorname {\mathrm {Hess}}(N,h_1)$
has
![]() $V_1 = {\mathbb {C}} \cdot (1,0,\ldots ,0)^t$
which implies that
$V_1 = {\mathbb {C}} \cdot (1,0,\ldots ,0)^t$
which implies that
![]() $b_{i1}=0$
for all
$b_{i1}=0$
for all
![]() $2 \leq i \leq n$
. It then follows from Proposition 7.3 that
$2 \leq i \leq n$
. It then follows from Proposition 7.3 that
as desired. We have proven Claim 3.
Combining Claim 3 and equation (8.10), we conclude that the n-th row vector
![]() $\big ( \frac {\partial }{\partial q_{rs}} \, ^{h_m} E_{n}^{(n)}(a,p) \big )_{(r,s)}$
of the Jacobian matrix is zero. This completes the proof.
$\big ( \frac {\partial }{\partial q_{rs}} \, ^{h_m} E_{n}^{(n)}(a,p) \big )_{(r,s)}$
of the Jacobian matrix is zero. This completes the proof.
By using Proposition 8.5, we will explicitly describe the singular locus of
![]() $\operatorname {\mathrm {Hess}}(N,h_m) \cap \Omega _e^\circ $
in Section 10. For this purpose, we will first study the singularity of
$\operatorname {\mathrm {Hess}}(N,h_m) \cap \Omega _e^\circ $
in Section 10. For this purpose, we will first study the singularity of
![]() $\operatorname {\mathrm {Hess}}(N,h_2) \cap \Omega _e^\circ $
in next section.
$\operatorname {\mathrm {Hess}}(N,h_2) \cap \Omega _e^\circ $
in next section.
9 Cyclic quotient singularity
In this section, we analyze the singularity of
![]() $\operatorname {\mathrm {Hess}}(N,h_2) \cap \Omega _e^\circ $
, where
$\operatorname {\mathrm {Hess}}(N,h_2) \cap \Omega _e^\circ $
, where
![]() $h_2=(2,n,\ldots ,n)$
. In fact, we see that the singularity is related with a cyclic quotient singularity. Then we can explicitly describe the singular locus of
$h_2=(2,n,\ldots ,n)$
. In fact, we see that the singularity is related with a cyclic quotient singularity. Then we can explicitly describe the singular locus of
![]() $\operatorname {\mathrm {Hess}}(N,h_2) \cap \Omega _e^\circ $
.
$\operatorname {\mathrm {Hess}}(N,h_2) \cap \Omega _e^\circ $
.
First, we study relations between
![]() $F_{i,j}$
’s and
$F_{i,j}$
’s and
![]() $\tilde F^{\langle m_j\rangle }_{i,j}$
’s, which are defined in equations (3.3) and (3.4), and Definition 6.3, respectively.
$\tilde F^{\langle m_j\rangle }_{i,j}$
’s, which are defined in equations (3.3) and (3.4), and Definition 6.3, respectively.
Lemma 9.1. Let
![]() $1 \leq j \leq n-1$
and
$1 \leq j \leq n-1$
and
![]() $j \leq m_j <n$
. For
$j \leq m_j <n$
. For
![]() $i>m_j$
, we have
$i>m_j$
, we have
 $$ \begin{align*} F_{i,j} = \tilde F^{\langle m_j\rangle}_{i,j} - \sum_{\ell=m_j+1}^{i-1} x_{i\ell} F_{\ell,j}, \end{align*} $$
$$ \begin{align*} F_{i,j} = \tilde F^{\langle m_j\rangle}_{i,j} - \sum_{\ell=m_j+1}^{i-1} x_{i\ell} F_{\ell,j}, \end{align*} $$
where we take the convention that
![]() $\sum _{\ell =m_j+1}^{m_j} x_{i\ell } F_{\ell ,j}=0$
.
$\sum _{\ell =m_j+1}^{m_j} x_{i\ell } F_{\ell ,j}=0$
.
Proof. It suffices to show that
 $$ \begin{align} \tilde F^{\langle i-k \rangle}_{i,j} = \tilde F^{\langle m_j \rangle}_{i,j} - \sum_{\ell=m_j+1}^{i-k} x_{i\ell} F_{\ell,j} \ \ \ \text{for} \ 1 \leq k \leq i-m_j. \end{align} $$
$$ \begin{align} \tilde F^{\langle i-k \rangle}_{i,j} = \tilde F^{\langle m_j \rangle}_{i,j} - \sum_{\ell=m_j+1}^{i-k} x_{i\ell} F_{\ell,j} \ \ \ \text{for} \ 1 \leq k \leq i-m_j. \end{align} $$
Indeed, equation (9.1) for
![]() $k=1$
is the desired equality by equation (6.4). We prove equation (9.1) by descending induction on k. The base case is
$k=1$
is the desired equality by equation (6.4). We prove equation (9.1) by descending induction on k. The base case is
![]() $k=i-m_j$
, which is clear. Now, suppose that
$k=i-m_j$
, which is clear. Now, suppose that
![]() $k < i-m_j$
and assume by induction that the claim is true for
$k < i-m_j$
and assume by induction that the claim is true for
![]() $k+1$
, that is,
$k+1$
, that is,
 $$ \begin{align} \tilde F^{\langle i-k-1 \rangle}_{i,j} = \tilde F^{\langle m_j \rangle}_{i,j} - \sum_{\ell=m_j+1}^{i-k-1} x_{i\ell} F_{\ell,j}. \end{align} $$
$$ \begin{align} \tilde F^{\langle i-k-1 \rangle}_{i,j} = \tilde F^{\langle m_j \rangle}_{i,j} - \sum_{\ell=m_j+1}^{i-k-1} x_{i\ell} F_{\ell,j}. \end{align} $$
Then we show equation (9.1). The left-hand side of equation (9.1) is equal to
by using the cofactor expansion along the second-to-last column. Combining this with the inductive hypothesis (9.2), we have proven equation (9.1).
Proposition 9.2. Let
![]() $1 \leq j \leq n-1$
and
$1 \leq j \leq n-1$
and
![]() $j \leq m_j<n$
. For
$j \leq m_j<n$
. For
![]() $i>m_j$
, the ideal
$i>m_j$
, the ideal
is equal to the ideal
in the polynomial ring
![]() ${\mathbb {C}}[x_{ij} \mid 1 \leq j < i \leq n]$
. In particular, if
${\mathbb {C}}[x_{ij} \mid 1 \leq j < i \leq n]$
. In particular, if
![]() $h:[n] \to [n]$
is an indecomposable Hessenberg function such that
$h:[n] \to [n]$
is an indecomposable Hessenberg function such that
![]() $h \neq (n,\ldots ,n)$
, then we have
$h \neq (n,\ldots ,n)$
, then we have
where ![]() .
.
Proof. We prove the first statement by induction on i. The base case
![]() $i = m_j+1$
is clear since
$i = m_j+1$
is clear since
![]() $F_{m_j+1,j}=\tilde F^{\langle m_j\rangle }_{m_j+1,j}$
by equation (6.4). We proceed to the inductive step. Suppose that
$F_{m_j+1,j}=\tilde F^{\langle m_j\rangle }_{m_j+1,j}$
by equation (6.4). We proceed to the inductive step. Suppose that
![]() $i> m_j+1$
and that the claim holds for
$i> m_j+1$
and that the claim holds for
![]() $i-1$
. Then we have
$i-1$
. Then we have
 $$ \begin{align*} (F_{m_j+1,j},\ldots,F_{i-1,j},F_{i,j}) &=(F_{m_j+1,j},\ldots,F_{i-1,j}, \tilde F^{\langle m_j\rangle}_{i,j}) \ \ \ \text{(from Lemma~}9.1) \\ &=(\tilde F^{\langle m_j\rangle}_{m_j+1,j},\ldots,\tilde F^{\langle m_j\rangle}_{i-1,j},\tilde F^{\langle m_j\rangle}_{i,j}) \ \ \ \text{(by the inductive assumption)} \end{align*} $$
$$ \begin{align*} (F_{m_j+1,j},\ldots,F_{i-1,j},F_{i,j}) &=(F_{m_j+1,j},\ldots,F_{i-1,j}, \tilde F^{\langle m_j\rangle}_{i,j}) \ \ \ \text{(from Lemma~}9.1) \\ &=(\tilde F^{\langle m_j\rangle}_{m_j+1,j},\ldots,\tilde F^{\langle m_j\rangle}_{i-1,j},\tilde F^{\langle m_j\rangle}_{i,j}) \ \ \ \text{(by the inductive assumption)} \end{align*} $$
as desired. The isomorphism (9.3) follows from equation (3.8) and the former statement by setting
![]() $m_j=h(j)$
.
$m_j=h(j)$
.
Example 9.3. Let
![]() $m_j=j+1$
. Then one has
$m_j=j+1$
. Then one has
 $$ \begin{align} &\tilde F^{\langle 2 \rangle}_{i,1}=\left| \begin{array}{@{\,}ccc@{\,}} 1 & 0 & x_{21} \\ x_{21} & 1 & x_{31} \\ x_{i1} & x_{i2} & x_{i+1 \, 1} \end{array} \right| \ \text{for} \ i> 2; \\ &\tilde F^{\langle j+1 \rangle}_{i,j}=\left| \begin{array}{@{\,}cccc@{\,}} 1 & 0 & 0 & 1 \\ x_{j \, j-1} & 1 & 0 & x_{j+1 \, j} \\ x_{j+1 \, j-1} & x_{j+1 \, j} & 1 & x_{j+2 \, j} \\ x_{i \, j-1} & x_{ij} & x_{i \, j+1} & x_{i+1 \, j} \end{array} \right| \ \text{for} \ 2 \leq j \leq n-2 \ \text{and} \ i > j+1. \notag \end{align} $$
$$ \begin{align} &\tilde F^{\langle 2 \rangle}_{i,1}=\left| \begin{array}{@{\,}ccc@{\,}} 1 & 0 & x_{21} \\ x_{21} & 1 & x_{31} \\ x_{i1} & x_{i2} & x_{i+1 \, 1} \end{array} \right| \ \text{for} \ i> 2; \\ &\tilde F^{\langle j+1 \rangle}_{i,j}=\left| \begin{array}{@{\,}cccc@{\,}} 1 & 0 & 0 & 1 \\ x_{j \, j-1} & 1 & 0 & x_{j+1 \, j} \\ x_{j+1 \, j-1} & x_{j+1 \, j} & 1 & x_{j+2 \, j} \\ x_{i \, j-1} & x_{ij} & x_{i \, j+1} & x_{i+1 \, j} \end{array} \right| \ \text{for} \ 2 \leq j \leq n-2 \ \text{and} \ i > j+1. \notag \end{align} $$
By equation (9.3), the coordinate ring
![]() ${\mathbb {C}}[\operatorname {\mathrm {Pet}}_n \cap \Omega _e^\circ ]$
is
${\mathbb {C}}[\operatorname {\mathrm {Pet}}_n \cap \Omega _e^\circ ]$
is
We now explain the cyclic quotient singularity which is also called the type A-singularity. Let
![]() $\zeta $
be a primitive n-th root of unity and
$\zeta $
be a primitive n-th root of unity and
![]() $\mathfrak C_n$
the cyclic group of order n generated by
$\mathfrak C_n$
the cyclic group of order n generated by
![]() $\zeta $
. Consider the action of
$\zeta $
. Consider the action of
![]() $\mathfrak C_n$
on
$\mathfrak C_n$
on
![]() ${\mathbb {C}}^2$
defined by
${\mathbb {C}}^2$
defined by
![]() $\zeta \cdot (x,y)=(\zeta x, \zeta ^{-1} y)$
for
$\zeta \cdot (x,y)=(\zeta x, \zeta ^{-1} y)$
for
![]() $\zeta \in \mathfrak C_n$
and
$\zeta \in \mathfrak C_n$
and
![]() $(x,y) \in {\mathbb {C}}^2$
. This induces the action of
$(x,y) \in {\mathbb {C}}^2$
. This induces the action of
![]() $\mathfrak C_n$
on the polynomial ring
$\mathfrak C_n$
on the polynomial ring
![]() ${\mathbb {C}}[x,y]$
(which is the coordinate ring of
${\mathbb {C}}[x,y]$
(which is the coordinate ring of
![]() ${\mathbb {C}}^2$
), and it is given by
${\mathbb {C}}^2$
), and it is given by
![]() $\zeta \cdot x=\zeta x$
and
$\zeta \cdot x=\zeta x$
and
![]() $\zeta \cdot y=\zeta ^{-1} y$
. As is well known, the
$\zeta \cdot y=\zeta ^{-1} y$
. As is well known, the
![]() $\mathfrak C_n$
-invariants in
$\mathfrak C_n$
-invariants in
![]() ${\mathbb {C}}[x,y]$
is isomorphic to
${\mathbb {C}}[x,y]$
is isomorphic to
which sends X to
![]() $x^n$
, Y to
$x^n$
, Y to
![]() $y^n$
, and Z to
$y^n$
, and Z to
![]() $xy$
. The quotient space
$xy$
. The quotient space
![]() ${\mathbb {C}}^2/\mathfrak C_n$
is called the cyclic quotient singularity or the type
${\mathbb {C}}^2/\mathfrak C_n$
is called the cyclic quotient singularity or the type
![]() $A_{n-1}$
-singularity.
$A_{n-1}$
-singularity.
Example 9.4. Let
![]() $n=3$
. As seen in Example 9.3, the coordinate ring of
$n=3$
. As seen in Example 9.3, the coordinate ring of
![]() $\operatorname {\mathrm {Pet}}_3 \cap \Omega _e^\circ $
is given by
$\operatorname {\mathrm {Pet}}_3 \cap \Omega _e^\circ $
is given by
Here, one can compute
![]() $\tilde F^{\langle 2 \rangle }_{3,1}$
as
$\tilde F^{\langle 2 \rangle }_{3,1}$
as
 $$ \begin{align*} \tilde F^{\langle 2 \rangle}_{3,1} &=\left| \begin{array}{@{\,}ccc@{\,}} 1 & 0 & x_{21} \\ x_{21} & 1 & x_{31} \\ x_{31} & x_{32} & 0 \end{array} \right| =x_{21}^2x_{32}-x_{21}x_{31}-x_{31}x_{32} \\ &=-x_{21}^3+(x_{21}^2-x_{31})(x_{21}+x_{32}). \end{align*} $$
$$ \begin{align*} \tilde F^{\langle 2 \rangle}_{3,1} &=\left| \begin{array}{@{\,}ccc@{\,}} 1 & 0 & x_{21} \\ x_{21} & 1 & x_{31} \\ x_{31} & x_{32} & 0 \end{array} \right| =x_{21}^2x_{32}-x_{21}x_{31}-x_{31}x_{32} \\ &=-x_{21}^3+(x_{21}^2-x_{31})(x_{21}+x_{32}). \end{align*} $$
Thus, we have
which sends X to
![]() $x_{21}^2-x_{31}$
, Y to
$x_{21}^2-x_{31}$
, Y to
![]() $x_{21}+x_{32}$
and Z to
$x_{21}+x_{32}$
and Z to
![]() $x_{21}$
. The ring isomorphism above yields the isomorphism
$x_{21}$
. The ring isomorphism above yields the isomorphism
![]() $\operatorname {\mathrm {Pet}}_3 \cap \Omega _e^\circ \cong {\mathbb {C}}^2/\mathfrak C_3$
.
$\operatorname {\mathrm {Pet}}_3 \cap \Omega _e^\circ \cong {\mathbb {C}}^2/\mathfrak C_3$
.
In Example 9.4, we constructed the polynomial
![]() $XY-Z^n$
from
$XY-Z^n$
from
![]() $\tilde F^{\langle 2 \rangle }_{3,1}$
for
$\tilde F^{\langle 2 \rangle }_{3,1}$
for
![]() $n=3$
. We now generalize this fact to arbitrary n. More specifically, we construct the polynomial
$n=3$
. We now generalize this fact to arbitrary n. More specifically, we construct the polynomial
![]() $XY-Z^n$
from
$XY-Z^n$
from
![]() $\tilde F^{\langle 2 \rangle }_{i,1} \ (2 < i \leq n)$
defined in equation (9.4). By the cofactor expansion along the second column, we have
$\tilde F^{\langle 2 \rangle }_{i,1} \ (2 < i \leq n)$
defined in equation (9.4). By the cofactor expansion along the second column, we have
 $$ \begin{align} &\tilde F^{\langle 2 \rangle}_{i,1}=\left| \begin{array}{@{\,}cc@{\,}} 1 & x_{21} \\ x_{i1} & x_{i+1 \, 1} \end{array} \right| - x_{i2}\left| \begin{array}{@{\,}cc@{\,}} 1 & x_{21} \\ x_{21} & x_{31} \end{array} \right| \ \text{for} \ i> 2. \end{align} $$
$$ \begin{align} &\tilde F^{\langle 2 \rangle}_{i,1}=\left| \begin{array}{@{\,}cc@{\,}} 1 & x_{21} \\ x_{i1} & x_{i+1 \, 1} \end{array} \right| - x_{i2}\left| \begin{array}{@{\,}cc@{\,}} 1 & x_{21} \\ x_{21} & x_{31} \end{array} \right| \ \text{for} \ i> 2. \end{align} $$
Lemma 9.5. For
![]() $2 < i \leq n$
, we have
$2 < i \leq n$
, we have
 $$ \begin{align*} &\tilde F^{\langle 2 \rangle}_{n,1}+x_{21}\tilde F^{\langle 2 \rangle}_{n-1,1}+x_{21}^2\tilde F^{\langle 2 \rangle}_{n-2,1}+\cdots+x_{21}^{n-i} \tilde F^{\langle 2 \rangle}_{i,1} \\ =& \left| \begin{array}{@{\,}cc@{\,}} 1 & x_{21}^{n-i+1} \\ x_{i1} & 0 \end{array} \right| - (x_{n2}+x_{21}x_{n-1 \, 2}+x_{21}^2x_{n-2 \, 2}+\cdots+x_{21}^{n-i}x_{i2})\left| \begin{array}{@{\,}cc@{\,}} 1 & x_{21} \\ x_{21} & x_{31} \end{array} \right|. \end{align*} $$
$$ \begin{align*} &\tilde F^{\langle 2 \rangle}_{n,1}+x_{21}\tilde F^{\langle 2 \rangle}_{n-1,1}+x_{21}^2\tilde F^{\langle 2 \rangle}_{n-2,1}+\cdots+x_{21}^{n-i} \tilde F^{\langle 2 \rangle}_{i,1} \\ =& \left| \begin{array}{@{\,}cc@{\,}} 1 & x_{21}^{n-i+1} \\ x_{i1} & 0 \end{array} \right| - (x_{n2}+x_{21}x_{n-1 \, 2}+x_{21}^2x_{n-2 \, 2}+\cdots+x_{21}^{n-i}x_{i2})\left| \begin{array}{@{\,}cc@{\,}} 1 & x_{21} \\ x_{21} & x_{31} \end{array} \right|. \end{align*} $$
Proof. We prove this by descending induction on i. The base case
![]() $i=n$
is the equality (9.6) for
$i=n$
is the equality (9.6) for
![]() $i=n$
. Suppose now that
$i=n$
. Suppose now that
![]() $i < n$
and that the claim holds for
$i < n$
and that the claim holds for
![]() $i+1$
. Then we have
$i+1$
. Then we have
 $$ \begin{align*} &\tilde F^{\langle 2 \rangle}_{n,1}+x_{21}\tilde F^{\langle 2 \rangle}_{n-1,1}+x_{21}^2\tilde F^{\langle 2 \rangle}_{n-2,1}+\cdots+x_{21}^{n-i-1} \tilde F^{\langle 2 \rangle}_{i+1,1}+x_{21}^{n-i} \tilde F^{\langle 2 \rangle}_{i,1} \\ =& \left| \begin{array}{@{\,}cc@{\,}} 1 & x_{21}^{n-i} \\ x_{i+1 \, 1} & 0 \end{array} \right| - (x_{n2}+x_{21}x_{n-1 \, 2}+x_{21}^2x_{n-2 \, 2}+\cdots+x_{21}^{n-i-1}x_{i+1 \, 2})\left| \begin{array}{@{\,}cc@{\,}} 1 & x_{21} \\ x_{21} & x_{31} \end{array} \right| + x_{21}^{n-i} \tilde F^{\langle 2 \rangle}_{i,1} \\ & \hspace{80pt} \text{(by our descending induction hypothesis)} \\ =& \left| \begin{array}{@{\,}cc@{\,}} 1 & x_{21}^{n-i} \\ x_{i+1 \, 1} & 0 \end{array} \right| - (x_{n2}+x_{21}x_{n-1 \, 2}+x_{21}^2x_{n-2 \, 2}+\cdots+x_{21}^{n-i-1}x_{i+1 \, 2})\left| \begin{array}{@{\,}cc@{\,}} 1 & x_{21} \\ x_{21} & x_{31} \end{array} \right| \\ &+ x_{21}^{n-i} \left| \begin{array}{@{\,}cc@{\,}} 1 & x_{21} \\ x_{i1} & x_{i+1 \, 1} \end{array} \right| - x_{21}^{n-i} x_{i2}\left| \begin{array}{@{\,}cc@{\,}} 1 & x_{21} \\ x_{21} & x_{31} \end{array} \right| \hspace{30pt} \text{(by equation }(9.6)) \\ =& \left| \begin{array}{@{\,}cc@{\,}} 1 & x_{21}^{n-i+1} \\ x_{i1} & 0 \end{array} \right| - (x_{n2}+x_{21}x_{n-1 \, 2}+x_{21}^2x_{n-2 \, 2}+\cdots+x_{21}^{n-i}x_{i2})\left| \begin{array}{@{\,}cc@{\,}} 1 & x_{21} \\ x_{21} & x_{31} \end{array} \right| \end{align*} $$
$$ \begin{align*} &\tilde F^{\langle 2 \rangle}_{n,1}+x_{21}\tilde F^{\langle 2 \rangle}_{n-1,1}+x_{21}^2\tilde F^{\langle 2 \rangle}_{n-2,1}+\cdots+x_{21}^{n-i-1} \tilde F^{\langle 2 \rangle}_{i+1,1}+x_{21}^{n-i} \tilde F^{\langle 2 \rangle}_{i,1} \\ =& \left| \begin{array}{@{\,}cc@{\,}} 1 & x_{21}^{n-i} \\ x_{i+1 \, 1} & 0 \end{array} \right| - (x_{n2}+x_{21}x_{n-1 \, 2}+x_{21}^2x_{n-2 \, 2}+\cdots+x_{21}^{n-i-1}x_{i+1 \, 2})\left| \begin{array}{@{\,}cc@{\,}} 1 & x_{21} \\ x_{21} & x_{31} \end{array} \right| + x_{21}^{n-i} \tilde F^{\langle 2 \rangle}_{i,1} \\ & \hspace{80pt} \text{(by our descending induction hypothesis)} \\ =& \left| \begin{array}{@{\,}cc@{\,}} 1 & x_{21}^{n-i} \\ x_{i+1 \, 1} & 0 \end{array} \right| - (x_{n2}+x_{21}x_{n-1 \, 2}+x_{21}^2x_{n-2 \, 2}+\cdots+x_{21}^{n-i-1}x_{i+1 \, 2})\left| \begin{array}{@{\,}cc@{\,}} 1 & x_{21} \\ x_{21} & x_{31} \end{array} \right| \\ &+ x_{21}^{n-i} \left| \begin{array}{@{\,}cc@{\,}} 1 & x_{21} \\ x_{i1} & x_{i+1 \, 1} \end{array} \right| - x_{21}^{n-i} x_{i2}\left| \begin{array}{@{\,}cc@{\,}} 1 & x_{21} \\ x_{21} & x_{31} \end{array} \right| \hspace{30pt} \text{(by equation }(9.6)) \\ =& \left| \begin{array}{@{\,}cc@{\,}} 1 & x_{21}^{n-i+1} \\ x_{i1} & 0 \end{array} \right| - (x_{n2}+x_{21}x_{n-1 \, 2}+x_{21}^2x_{n-2 \, 2}+\cdots+x_{21}^{n-i}x_{i2})\left| \begin{array}{@{\,}cc@{\,}} 1 & x_{21} \\ x_{21} & x_{31} \end{array} \right| \end{align*} $$
as desired.
Proposition 9.6. We set
 $$ \begin{align*} \begin{cases} X= x_{21}^2-x_{31} \\ Y= x_{21}^{n-2}+x_{32}x_{21}^{n-3}+\cdots+x_{n-1 \, 2}x_{21}+x_{n2} \\ Z= x_{21}. \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} X= x_{21}^2-x_{31} \\ Y= x_{21}^{n-2}+x_{32}x_{21}^{n-3}+\cdots+x_{n-1 \, 2}x_{21}+x_{n2} \\ Z= x_{21}. \end{cases} \end{align*} $$
Then one can write
Proof. By using Lemma 9.5 for
![]() $i=3$
, we obtain
$i=3$
, we obtain
 $$ \begin{align*} &\tilde F^{\langle 2 \rangle}_{n,1}+x_{21}\tilde F^{\langle 2 \rangle}_{n-1,1}+x_{21}^2\tilde F^{\langle 2 \rangle}_{n-2,1}+\cdots+x_{21}^{n-3} \tilde F^{\langle 2 \rangle}_{3,1} \\ =& \left| \begin{array}{@{\,}cc@{\,}} 1 & x_{21}^{n-2} \\ x_{31} & 0 \end{array} \right| - (x_{n2}+x_{21}x_{n-1 \, 2}+x_{21}^2x_{n-2 \, 2}+\cdots+x_{21}^{n-3}x_{32})\left| \begin{array}{@{\,}cc@{\,}} 1 & x_{21} \\ x_{21} & x_{31} \end{array} \right| \\ =& -x_{21}^{n-2}x_{31} - (x_{n2}+x_{21}x_{n-1 \, 2}+x_{21}^2x_{n-2 \, 2}+\cdots+x_{21}^{n-3}x_{32})(x_{31}-x_{21}^2) \\ =& -x_{21}^n+x_{21}^{n-2}(x_{21}^2-x_{31}) + (x_{n2}+x_{21}x_{n-1 \, 2}+x_{21}^2x_{n-2 \, 2}+\cdots+x_{21}^{n-3}x_{32})(x_{21}^2-x_{31})\\ =& -x_{21}^n + (x_{n2}+x_{21}x_{n-1 \, 2}+x_{21}^2x_{n-2 \, 2}+\cdots+x_{21}^{n-3}x_{32}+x_{21}^{n-2})(x_{21}^2-x_{31})\\ =&XY-Z^n.\\[-39pt] \end{align*} $$
$$ \begin{align*} &\tilde F^{\langle 2 \rangle}_{n,1}+x_{21}\tilde F^{\langle 2 \rangle}_{n-1,1}+x_{21}^2\tilde F^{\langle 2 \rangle}_{n-2,1}+\cdots+x_{21}^{n-3} \tilde F^{\langle 2 \rangle}_{3,1} \\ =& \left| \begin{array}{@{\,}cc@{\,}} 1 & x_{21}^{n-2} \\ x_{31} & 0 \end{array} \right| - (x_{n2}+x_{21}x_{n-1 \, 2}+x_{21}^2x_{n-2 \, 2}+\cdots+x_{21}^{n-3}x_{32})\left| \begin{array}{@{\,}cc@{\,}} 1 & x_{21} \\ x_{21} & x_{31} \end{array} \right| \\ =& -x_{21}^{n-2}x_{31} - (x_{n2}+x_{21}x_{n-1 \, 2}+x_{21}^2x_{n-2 \, 2}+\cdots+x_{21}^{n-3}x_{32})(x_{31}-x_{21}^2) \\ =& -x_{21}^n+x_{21}^{n-2}(x_{21}^2-x_{31}) + (x_{n2}+x_{21}x_{n-1 \, 2}+x_{21}^2x_{n-2 \, 2}+\cdots+x_{21}^{n-3}x_{32})(x_{21}^2-x_{31})\\ =& -x_{21}^n + (x_{n2}+x_{21}x_{n-1 \, 2}+x_{21}^2x_{n-2 \, 2}+\cdots+x_{21}^{n-3}x_{32}+x_{21}^{n-2})(x_{21}^2-x_{31})\\ =&XY-Z^n.\\[-39pt] \end{align*} $$
Theorem 9.7. If
![]() $h_2=(2,n,\ldots ,n)$
, then there is an isomorphism of
$h_2=(2,n,\ldots ,n)$
, then there is an isomorphism of
![]() ${\mathbb {C}}$
-algebras
${\mathbb {C}}$
-algebras
which sends
 $$ \begin{align} \begin{array}{l} X \mapsto x_{21}^2-x_{31}; \\ Y \mapsto x_{21}^{n-2}+x_{32}x_{21}^{n-3}+\cdots+x_{n-1 \, 2}x_{21}+x_{n2}; \\ Z \mapsto x_{21}; \\ x_{i2} \mapsto x_{i2} \ \mathrm{for} \ 3 \leq i \leq n-1; \\ x_{ij} \mapsto x_{ij} \ \mathrm{for} \ 3 \leq j < i \leq n. \end{array} \end{align} $$
$$ \begin{align} \begin{array}{l} X \mapsto x_{21}^2-x_{31}; \\ Y \mapsto x_{21}^{n-2}+x_{32}x_{21}^{n-3}+\cdots+x_{n-1 \, 2}x_{21}+x_{n2}; \\ Z \mapsto x_{21}; \\ x_{i2} \mapsto x_{i2} \ \mathrm{for} \ 3 \leq i \leq n-1; \\ x_{ij} \mapsto x_{ij} \ \mathrm{for} \ 3 \leq j < i \leq n. \end{array} \end{align} $$
In other words,
Remark 9.8. We have seen the case when
![]() $n=3$
in Example 9.4.
$n=3$
in Example 9.4.
Proof of Theorem 9.7.
By equation (9.3), we have
Put
It then follows from Proposition 9.6 that
By the definition (9.4),
![]() $\tilde F^{\langle 2 \rangle }_{i,1}=0$
if and only if
$\tilde F^{\langle 2 \rangle }_{i,1}=0$
if and only if
for
![]() $3 \leq i \leq n-1$
. These equalities for
$3 \leq i \leq n-1$
. These equalities for
![]() $i=n-1,n-2,\ldots ,3$
lead us to the isomorphism
$i=n-1,n-2,\ldots ,3$
lead us to the isomorphism
It is straightforward to see that
 $$ \begin{align} & {\mathbb{C}}[x_{21},x_{31},x_{ij} \mid 2 \leq j < i \leq n]/(P_n) \\ \cong &{\mathbb{C}}[X,Y,Z]/(XY-Z^n) \otimes {\mathbb{C}}[x_{32},x_{42},\ldots, x_{n-1 \, 2}] \otimes {\mathbb{C}}[x_{ij} \mid 3 \leq j < i \leq n], \notag \end{align} $$
$$ \begin{align} & {\mathbb{C}}[x_{21},x_{31},x_{ij} \mid 2 \leq j < i \leq n]/(P_n) \\ \cong &{\mathbb{C}}[X,Y,Z]/(XY-Z^n) \otimes {\mathbb{C}}[x_{32},x_{42},\ldots, x_{n-1 \, 2}] \otimes {\mathbb{C}}[x_{ij} \mid 3 \leq j < i \leq n], \notag \end{align} $$
which sends
 $$ \begin{align*} \begin{array}{l} X \mapsto x_{21}^2-x_{31}; \\ Y \mapsto x_{21}^{n-2}+x_{32}x_{21}^{n-3}+\cdots+x_{n-1 \, 2}x_{21}+x_{n2}; \\ Z \mapsto x_{21}; \\ x_{i2} \mapsto x_{i2} \ \mathrm{for} \ 3 \leq i \leq n-1; \\ x_{ij} \mapsto x_{ij} \ \mathrm{for} \ 3 \leq j < i \leq n. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{l} X \mapsto x_{21}^2-x_{31}; \\ Y \mapsto x_{21}^{n-2}+x_{32}x_{21}^{n-3}+\cdots+x_{n-1 \, 2}x_{21}+x_{n2}; \\ Z \mapsto x_{21}; \\ x_{i2} \mapsto x_{i2} \ \mathrm{for} \ 3 \leq i \leq n-1; \\ x_{ij} \mapsto x_{ij} \ \mathrm{for} \ 3 \leq j < i \leq n. \end{array} \end{align*} $$
In fact, the inverse map is given by
 $$ \begin{align*} \begin{array}{l} x_{21} \mapsto Z; \\ x_{31} \mapsto -X+Z^2; \\ x_{n2} \mapsto Y-Z^{n-2}-x_{32}Z^{n-3}-\cdots-x_{n-1 \, 2}Z; \\ x_{i2} \mapsto x_{i2} \ \mathrm{for} \ 3 \leq i \leq n-1; \\ x_{ij} \mapsto x_{ij} \ \mathrm{for} \ 3 \leq j < i \leq n. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{l} x_{21} \mapsto Z; \\ x_{31} \mapsto -X+Z^2; \\ x_{n2} \mapsto Y-Z^{n-2}-x_{32}Z^{n-3}-\cdots-x_{n-1 \, 2}Z; \\ x_{i2} \mapsto x_{i2} \ \mathrm{for} \ 3 \leq i \leq n-1; \\ x_{ij} \mapsto x_{ij} \ \mathrm{for} \ 3 \leq j < i \leq n. \end{array} \end{align*} $$
Combining equations (9.8), (9.9), (9.10) and (9.11), we conclude that
We complete the proof.
For a polynomial
![]() $f \in {\mathbb {C}}[\Omega _e^\circ ] \cong {\mathbb {C}}[x_{ij} \mid 1 \leq j < i \leq n]$
, we denote the zero set of f by
$f \in {\mathbb {C}}[\Omega _e^\circ ] \cong {\mathbb {C}}[x_{ij} \mid 1 \leq j < i \leq n]$
, we denote the zero set of f by
Corollary 9.9. The singular locus of
![]() $\operatorname {\mathrm {Hess}}(N,h_2) \cap \Omega _e^\circ $
is given by
$\operatorname {\mathrm {Hess}}(N,h_2) \cap \Omega _e^\circ $
is given by
 $$ \begin{align*} \operatorname{\mathrm{Sing}}(\operatorname{\mathrm{Hess}}(N,h_2) \cap \Omega_e^\circ) = \bigcap_{i=2}^n V(x_{i1}) \cap V(x_{n2}). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Sing}}(\operatorname{\mathrm{Hess}}(N,h_2) \cap \Omega_e^\circ) = \bigcap_{i=2}^n V(x_{i1}) \cap V(x_{n2}). \end{align*} $$
Proof. By Theorem 9.7, we have
Here,
![]() $V(XY-Z^n)$
denotes the hypersurface defined by the equation
$V(XY-Z^n)$
denotes the hypersurface defined by the equation
![]() $XY-Z^n=0$
in
$XY-Z^n=0$
in
![]() ${\mathbb {C}}^{\frac {1}{2}(n-1)(n-2)+2}$
with the variables
${\mathbb {C}}^{\frac {1}{2}(n-1)(n-2)+2}$
with the variables
![]() $X,Y,Z,x_{32},x_{42},\ldots , x_{n-1 \, 2}, x_{ij} \ (3 \leq j < i \leq n)$
. The singular locus of
$X,Y,Z,x_{32},x_{42},\ldots , x_{n-1 \, 2}, x_{ij} \ (3 \leq j < i \leq n)$
. The singular locus of
![]() $V(XY-Z^n)$
is the solution set of the equations
$V(XY-Z^n)$
is the solution set of the equations
It follows from the correspondence (9.7) that the image of the ideal
![]() $(X,Y,Z)$
under the isomorphism
$(X,Y,Z)$
under the isomorphism
![]() ${\mathbb {C}}[\operatorname {\mathrm {Hess}}(N,h_2) \cap \Omega _e^\circ ] \cong \frac {{\mathbb {C}}[X,Y,Z]}{(XY-Z^n)} \otimes {\mathbb {C}}[x_{32},x_{42},\ldots , x_{n-1 \, 2}] \otimes {\mathbb {C}}[x_{ij} \mid 3 \leq j < i \leq n]$
is
${\mathbb {C}}[\operatorname {\mathrm {Hess}}(N,h_2) \cap \Omega _e^\circ ] \cong \frac {{\mathbb {C}}[X,Y,Z]}{(XY-Z^n)} \otimes {\mathbb {C}}[x_{32},x_{42},\ldots , x_{n-1 \, 2}] \otimes {\mathbb {C}}[x_{ij} \mid 3 \leq j < i \leq n]$
is
in
![]() ${\mathbb {C}}[\operatorname {\mathrm {Hess}}(N,h_2) \cap \Omega _e^\circ ]$
. Hence, by the presentation (9.3), the singular locus of
${\mathbb {C}}[\operatorname {\mathrm {Hess}}(N,h_2) \cap \Omega _e^\circ ]$
. Hence, by the presentation (9.3), the singular locus of
![]() $\operatorname {\mathrm {Hess}}(N,h_2)$
is the solution set of the equations
$\operatorname {\mathrm {Hess}}(N,h_2)$
is the solution set of the equations
 $$ \begin{align} \begin{cases} x_{21}=0 \\ x_{31}=0 \\ x_{n2}=0 \\ \tilde F^{\langle 2 \rangle}_{i,1}=0 \ \ \ \text{for} \ 3 \leq i \leq n-1. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} x_{21}=0 \\ x_{31}=0 \\ x_{n2}=0 \\ \tilde F^{\langle 2 \rangle}_{i,1}=0 \ \ \ \text{for} \ 3 \leq i \leq n-1. \end{cases} \end{align} $$
Note that the equation
![]() $\tilde F^{\langle 2 \rangle }_{n,1}=0$
can be removed above since
$\tilde F^{\langle 2 \rangle }_{n,1}=0$
can be removed above since
![]() $\tilde F^{\langle 2 \rangle }_{n,1}=0$
is derived from the equations (9.13) by Proposition 9.6. It then follows from the equality
$\tilde F^{\langle 2 \rangle }_{n,1}=0$
is derived from the equations (9.13) by Proposition 9.6. It then follows from the equality
![]() $\tilde F^{\langle 2 \rangle }_{i,1} = x_{i+1 \, 1}+x_{21}^2x_{i2}-x_{21}x_{i1}-x_{31}x_{i2}$
for
$\tilde F^{\langle 2 \rangle }_{i,1} = x_{i+1 \, 1}+x_{21}^2x_{i2}-x_{21}x_{i1}-x_{31}x_{i2}$
for
![]() $3 \leq i \leq n-1$
that the solution set of the equations (9.13) is given by
$3 \leq i \leq n-1$
that the solution set of the equations (9.13) is given by
![]() $x_{i1}=x_{n2}=0$
for
$x_{i1}=x_{n2}=0$
for
![]() $2 \leq i \leq n$
, as desired.
$2 \leq i \leq n$
, as desired.
10 Singular locus of
 $\operatorname {\mathrm {Hess}}(N,h_m) \cap \Omega _e^\circ $
$\operatorname {\mathrm {Hess}}(N,h_m) \cap \Omega _e^\circ $
We now give an explicit description for the singular locus of
![]() $\operatorname {\mathrm {Hess}}(N,h_m) \cap \Omega _e^\circ $
where
$\operatorname {\mathrm {Hess}}(N,h_m) \cap \Omega _e^\circ $
where
![]() $h_m$
is defined in equation (8.7).
$h_m$
is defined in equation (8.7).
Theorem 10.1. Let
![]() $2 \leq m \leq n-1$
. Then, the singular locus of
$2 \leq m \leq n-1$
. Then, the singular locus of
![]() $\operatorname {\mathrm {Hess}}(N,h_m) \cap \Omega _e^\circ $
is described as
$\operatorname {\mathrm {Hess}}(N,h_m) \cap \Omega _e^\circ $
is described as
 $$ \begin{align*} \operatorname{\mathrm{Sing}}(\operatorname{\mathrm{Hess}}(N,h_m) \cap \Omega_e^\circ) = \bigcap_{i=2}^n V(x_{i1}) \cap \bigcap_{j=2}^{m} V(x_{nj}), \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Sing}}(\operatorname{\mathrm{Hess}}(N,h_m) \cap \Omega_e^\circ) = \bigcap_{i=2}^n V(x_{i1}) \cap \bigcap_{j=2}^{m} V(x_{nj}), \end{align*} $$
where the notation
![]() $V(f)$
is defined in equation (9.12).
$V(f)$
is defined in equation (9.12).
Proof. We prove this by induction on m. The base case is
![]() $m=2$
, which follows from Corollary 9.9. Suppose now that
$m=2$
, which follows from Corollary 9.9. Suppose now that
![]() $m> 2$
and that the claim holds for
$m> 2$
and that the claim holds for
![]() $m-1$
. It follows from Proposition 8.5 that the singular locus of
$m-1$
. It follows from Proposition 8.5 that the singular locus of
![]() $V\big (\, ^{h_m} E_1^{(n)}, \ldots , \, ^{h_m} E_n^{(n)}\big )$
is given by the solution set of the equations
$V\big (\, ^{h_m} E_1^{(n)}, \ldots , \, ^{h_m} E_n^{(n)}\big )$
is given by the solution set of the equations
By Lemma 8.2, we have
 $$ \begin{align} \begin{cases} E_1^{[n,n]} &= x_n \\ E_2^{[n-1,n]} &= E_{1}^{[n-1,n-1]} x_n + q_{n-1 \, n} \\ E_3^{[n-2,n]} &= E_{2}^{[n-2,n-1]} x_n + E_{1}^{[n-2,n-2]} q_{n-1 \, n} + q_{n-2 \, n} \\ &\vdots \\ E_{m}^{[n-m+1,n]} &= E_{m-1}^{[n-m+1,n-1]} x_n + \cdots + E_1^{[n-m+1,n-m+1]} q_{n-m+2 \, n} + q_{n-m+1 \, n}. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} E_1^{[n,n]} &= x_n \\ E_2^{[n-1,n]} &= E_{1}^{[n-1,n-1]} x_n + q_{n-1 \, n} \\ E_3^{[n-2,n]} &= E_{2}^{[n-2,n-1]} x_n + E_{1}^{[n-2,n-2]} q_{n-1 \, n} + q_{n-2 \, n} \\ &\vdots \\ E_{m}^{[n-m+1,n]} &= E_{m-1}^{[n-m+1,n-1]} x_n + \cdots + E_1^{[n-m+1,n-m+1]} q_{n-m+2 \, n} + q_{n-m+1 \, n}. \end{cases} \end{align} $$
Since it holds that
by equations (8.6) and (10.1), the equalities (10.2) lead us to the following equation

which yields that
![]() $x_n = q_{n-1 \, n} = q_{n-2 \, n} = \cdots = q_{n-m+1 \, n} = 0$
. Since we have
$x_n = q_{n-1 \, n} = q_{n-2 \, n} = \cdots = q_{n-m+1 \, n} = 0$
. Since we have
![]() $q_{n-m+1 \, n} = 0$
and
$q_{n-m+1 \, n} = 0$
and
 $$ \begin{align*} \left. \left( \frac{\partial}{\partial q_{rs}} \, ^{h_m} E_{n}^{(n)} \right) \right|_{q_{n-m+1 \, n}=0} = \frac{\partial}{\partial q_{rs}} \, ^{h_{m-1}}E_{n}^{(n)} \end{align*} $$
$$ \begin{align*} \left. \left( \frac{\partial}{\partial q_{rs}} \, ^{h_m} E_{n}^{(n)} \right) \right|_{q_{n-m+1 \, n}=0} = \frac{\partial}{\partial q_{rs}} \, ^{h_{m-1}}E_{n}^{(n)} \end{align*} $$
for
![]() $2 \leq s \leq n$
and
$2 \leq s \leq n$
and
![]() $n-h_{m-1}(n+1-s)<r \leq s$
, the equations (10.1) imply that
$n-h_{m-1}(n+1-s)<r \leq s$
, the equations (10.1) imply that
 $$ \begin{align} \begin{cases} \frac{\partial}{\partial q_{rs}} \, ^{h_{m-1}}E_{n}^{(n)} &= 0 \ \ \ \text{for all} \ 2 \leq s \leq n \ \text{and} \ n-h_{m-1}(n+1-s)<r \leq s \\ \frac{\partial}{\partial q_{n-m+1 \, n}} \, ^{h_m} E_{n}^{(n)} &= 0 \\ q_{n-m+1 \, n} &= 0. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \frac{\partial}{\partial q_{rs}} \, ^{h_{m-1}}E_{n}^{(n)} &= 0 \ \ \ \text{for all} \ 2 \leq s \leq n \ \text{and} \ n-h_{m-1}(n+1-s)<r \leq s \\ \frac{\partial}{\partial q_{n-m+1 \, n}} \, ^{h_m} E_{n}^{(n)} &= 0 \\ q_{n-m+1 \, n} &= 0. \end{cases} \end{align} $$
Conversely, the equations (10.3) yield equation (10.1). In fact, since one can write
![]() $\, ^{h_{m}}E_{n}^{(n)} = \, ^{h_{m-1}}E_{n}^{(n)}+q_{n-m+1 \, n} \cdot F$
for some polynomial F by Definition 4.10, we have
$\, ^{h_{m}}E_{n}^{(n)} = \, ^{h_{m-1}}E_{n}^{(n)}+q_{n-m+1 \, n} \cdot F$
for some polynomial F by Definition 4.10, we have
![]() $\frac {\partial }{\partial q_{rs}} \, ^{h_{m}}E_{n}^{(n)} = \frac {\partial }{\partial q_{rs}} \, ^{h_{m-1}}E_{n}^{(n)}+q_{n-m+1 \, n} \cdot \frac {\partial }{\partial q_{rs}} F$
for all
$\frac {\partial }{\partial q_{rs}} \, ^{h_{m}}E_{n}^{(n)} = \frac {\partial }{\partial q_{rs}} \, ^{h_{m-1}}E_{n}^{(n)}+q_{n-m+1 \, n} \cdot \frac {\partial }{\partial q_{rs}} F$
for all
![]() $2 \leq s \leq n$
and
$2 \leq s \leq n$
and
![]() $n-h_{m-1}(n+1-s)<r \leq s$
. Hence, equation (10.1) is equivalent to equation (10.3). One has
$n-h_{m-1}(n+1-s)<r \leq s$
. Hence, equation (10.1) is equivalent to equation (10.3). One has
from equations (8.1) and (8.6), so the singular locus of
![]() $V\big (\, ^{h_m} E_1^{(n)}, \ldots , \, ^{h_m} E_n^{(n)}\big )$
is given by the solution set of the equations
$V\big (\, ^{h_m} E_1^{(n)}, \ldots , \, ^{h_m} E_n^{(n)}\big )$
is given by the solution set of the equations
 $$ \begin{align*} \begin{cases}\frac{\partial}{\partial q_{rs}} \, ^{h_{m-1}}E_{n}^{(n)} &= 0 \ \ \ \text{for all} \ 2 \leq s \leq n \ \text{and} \ n-h_{m-1}(n+1-s)<r \leq s \\^{h_m} E_{n-m}^{(n-m)} &= 0 \\q_{n-m+1 \, n} &= 0.\end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases}\frac{\partial}{\partial q_{rs}} \, ^{h_{m-1}}E_{n}^{(n)} &= 0 \ \ \ \text{for all} \ 2 \leq s \leq n \ \text{and} \ n-h_{m-1}(n+1-s)<r \leq s \\^{h_m} E_{n-m}^{(n-m)} &= 0 \\q_{n-m+1 \, n} &= 0.\end{cases} \end{align*} $$
By Corollary 7.4, the following commutative diagram holds

where both vertial arrows are surjective. The ideal defining the singular locus of the zero set
![]() $V\big (\, ^{h_m} E_1^{(n)}, \ldots , \, ^{h_m} E_n^{(n)}\big )$
is
$V\big (\, ^{h_m} E_1^{(n)}, \ldots , \, ^{h_m} E_n^{(n)}\big )$
is
 $$ \begin{align*} \left(\frac{\partial}{\partial q_{rs}} \, ^{h_{m-1}}E_{n}^{(n)} \middle| \ 2 \leq s \leq n, n-h_{m-1}(n+1-s)<r \leq s \right) + (^{h_m} E_{n-m}^{(n-m)})+(q_{n-m+1 \, n}). \end{align*} $$
$$ \begin{align*} \left(\frac{\partial}{\partial q_{rs}} \, ^{h_{m-1}}E_{n}^{(n)} \middle| \ 2 \leq s \leq n, n-h_{m-1}(n+1-s)<r \leq s \right) + (^{h_m} E_{n-m}^{(n-m)})+(q_{n-m+1 \, n}). \end{align*} $$
The image of the ideal above under the isomorphism
![]() $\varphi _{h_m}^{-1}$
in equation (10.4) is equal to
$\varphi _{h_m}^{-1}$
in equation (10.4) is equal to
 $$ \begin{align*} \left(\varphi^{-1}\left(\frac{\partial}{\partial q_{rs}} \, ^{h_{m-1}}E_{n}^{(n)}\right) \middle| \ 2 \leq s \leq n, n-h_{m-1}(n+1-s)<r \leq s \right) + (x_{nm})+(F_{m,1}) \end{align*} $$
$$ \begin{align*} \left(\varphi^{-1}\left(\frac{\partial}{\partial q_{rs}} \, ^{h_{m-1}}E_{n}^{(n)}\right) \middle| \ 2 \leq s \leq n, n-h_{m-1}(n+1-s)<r \leq s \right) + (x_{nm})+(F_{m,1}) \end{align*} $$
in
![]() ${\mathbb {C}}[\operatorname {\mathrm {Hess}}(N,h_m) \cap \Omega _e^\circ ]$
by the definition (7.1) and Proposition 7.3. Hence, the singular locus of
${\mathbb {C}}[\operatorname {\mathrm {Hess}}(N,h_m) \cap \Omega _e^\circ ]$
by the definition (7.1) and Proposition 7.3. Hence, the singular locus of
![]() $\operatorname {\mathrm {Hess}}(N,h_m) \cap \Omega _e^\circ $
is the solution set of the equations
$\operatorname {\mathrm {Hess}}(N,h_m) \cap \Omega _e^\circ $
is the solution set of the equations
 $$ \begin{align} \begin{cases} \varphi^{-1}\left(\frac{\partial}{\partial q_{rs}} \, ^{h_{m-1}}E_{n}^{(n)} \right) = 0 \ \ \ \text{for all} \ 2 \leq s \leq n \ \text{and} \ n-h_{m-1}(n+1-s)<r \leq s \\ F_{m,1} = 0 \\ F_{i,1} = 0 \ \ \ \text{for all} \ m+1 \leq i \leq n \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \varphi^{-1}\left(\frac{\partial}{\partial q_{rs}} \, ^{h_{m-1}}E_{n}^{(n)} \right) = 0 \ \ \ \text{for all} \ 2 \leq s \leq n \ \text{and} \ n-h_{m-1}(n+1-s)<r \leq s \\ F_{m,1} = 0 \\ F_{i,1} = 0 \ \ \ \text{for all} \ m+1 \leq i \leq n \end{cases} \end{align} $$
and
by Lemma 2.3. Since the singular locus of
![]() $\operatorname {\mathrm {Hess}}(N,h_{m-1}) \cap \Omega _e^\circ $
is the solution set of the equations (10.5) from Proposition 8.5, Theorem 4.13 and Lemma 2.3 again, we can describe
$\operatorname {\mathrm {Hess}}(N,h_{m-1}) \cap \Omega _e^\circ $
is the solution set of the equations (10.5) from Proposition 8.5, Theorem 4.13 and Lemma 2.3 again, we can describe
One can see from our inductive assumption that
![]() $\operatorname {\mathrm {Sing}}(\operatorname {\mathrm {Hess}}(N,h_{m-1}) \cap \Omega _e^\circ )= \bigcap _{i=2}^n V(x_{i1}) \cap \bigcap _{j=2}^{m-1} V(x_{nj})$
, so we complete the proof.
$\operatorname {\mathrm {Sing}}(\operatorname {\mathrm {Hess}}(N,h_{m-1}) \cap \Omega _e^\circ )= \bigcap _{i=2}^n V(x_{i1}) \cap \bigcap _{j=2}^{m-1} V(x_{nj})$
, so we complete the proof.
Let
![]() $\mathfrak S_n$
be the permutation group on
$\mathfrak S_n$
be the permutation group on
![]() $[n]$
. For
$[n]$
. For
![]() $w \in \mathfrak S_n$
, the Schubert cell
$w \in \mathfrak S_n$
, the Schubert cell
![]() $X_w^\circ $
is defined to be the B-orbit of the permutation flag
$X_w^\circ $
is defined to be the B-orbit of the permutation flag
![]() $wB$
in the flag variety
$wB$
in the flag variety
![]() $\operatorname {\mathrm {GL}}_n({\mathbb {C}})/B$
. The Schubert variety
$\operatorname {\mathrm {GL}}_n({\mathbb {C}})/B$
. The Schubert variety
![]() $X_w$
is defined by the closure of the Schubert cell
$X_w$
is defined by the closure of the Schubert cell
![]() $X_w^\circ $
, that is,
$X_w^\circ $
, that is,
![]() $X_w=\overline {BwB/B}$
. We put
$X_w=\overline {BwB/B}$
. We put ![]() for
for
![]() $i \in [n]$
, where
$i \in [n]$
, where
![]() $e_1,\ldots , e_n$
are the standard basis for
$e_1,\ldots , e_n$
are the standard basis for
![]() ${\mathbb {C}}^n$
. Under the identification
${\mathbb {C}}^n$
. Under the identification
![]() $Fl({\mathbb {C}}^n) \cong \operatorname {\mathrm {GL}}_n({\mathbb {C}})/B$
, one can describe the Schubert variety
$Fl({\mathbb {C}}^n) \cong \operatorname {\mathrm {GL}}_n({\mathbb {C}})/B$
, one can describe the Schubert variety
![]() $X_w$
as
$X_w$
as
where
![]() $r_w(p,q)=|\{i \in [p] \mid w(i) \leq q \}|$
(e.g., [Reference Fulton19, Section 10.5]). For
$r_w(p,q)=|\{i \in [p] \mid w(i) \leq q \}|$
(e.g., [Reference Fulton19, Section 10.5]). For
![]() $2 \leq m \leq n-1$
, we define the permutation
$2 \leq m \leq n-1$
, we define the permutation
![]() $w_m \in \mathfrak S_n$
as
$w_m \in \mathfrak S_n$
as
 $$ \begin{align} w_m(i)=\begin{cases} 1 \ &\mathrm{if} \ i=1, \\ n+1-i \ &\mathrm{if} \ 2 \leq i \leq m, \\ n \ &\mathrm{if} \ i=m+1, \\ n+2-i \ &\mathrm{if} \ m+2 \leq i \leq n. \end{cases} \end{align} $$
$$ \begin{align} w_m(i)=\begin{cases} 1 \ &\mathrm{if} \ i=1, \\ n+1-i \ &\mathrm{if} \ 2 \leq i \leq m, \\ n \ &\mathrm{if} \ i=m+1, \\ n+2-i \ &\mathrm{if} \ m+2 \leq i \leq n. \end{cases} \end{align} $$
Then one can verify from [Reference Gasharov and Reiner21] that the Schubert variety
![]() $X_{w_m}$
is described as
$X_{w_m}$
is described as
In other words,
![]() $V_\bullet \in X_{w_m}$
if and only if
$V_\bullet \in X_{w_m}$
if and only if
![]() $V_1 = F_1=\operatorname {\mathrm {span}}_{\mathbb {C}} \{e_1 \}$
and
$V_1 = F_1=\operatorname {\mathrm {span}}_{\mathbb {C}} \{e_1 \}$
and
![]() $V_m \subset F_{n-1}=\operatorname {\mathrm {span}}_{\mathbb {C}} \{e_1,\ldots ,e_{n-1} \}$
. In particular, we have
$V_m \subset F_{n-1}=\operatorname {\mathrm {span}}_{\mathbb {C}} \{e_1,\ldots ,e_{n-1} \}$
. In particular, we have
 $$ \begin{align*} X_{w_m} \cap \Omega_e^\circ = \bigcap_{i=2}^n V(x_{i1}) \cap \bigcap_{j=2}^{m} V(x_{nj}). \end{align*} $$
$$ \begin{align*} X_{w_m} \cap \Omega_e^\circ = \bigcap_{i=2}^n V(x_{i1}) \cap \bigcap_{j=2}^{m} V(x_{nj}). \end{align*} $$
Hence, we obtain the following result from Theorem 10.1.
Corollary 10.2. Let
![]() $2 \leq m \leq n-1$
. Then, the singular locus of
$2 \leq m \leq n-1$
. Then, the singular locus of
![]() $\operatorname {\mathrm {Hess}}(N,h_m) \cap \Omega _e^\circ $
is equal to
$\operatorname {\mathrm {Hess}}(N,h_m) \cap \Omega _e^\circ $
is equal to
Remark 10.3. Let A be a nilpotent matrix (not necessarily regular nilpotent). Then it is known from [Reference Escobar, Precup and Shareshian15, Theorem 5] that the singular locus of
![]() $\operatorname {\mathrm {Hess}}(A,h_{n-1})$
is
$\operatorname {\mathrm {Hess}}(A,h_{n-1})$
is
Consider the regular nilpotent case. The Hessenberg function
![]() $h=(1,n-1,\ldots ,n-1,n)$
is decomposable, so every flag
$h=(1,n-1,\ldots ,n-1,n)$
is decomposable, so every flag
![]() $V_\bullet \in \operatorname {\mathrm {Hess}}(N,h)$
has
$V_\bullet \in \operatorname {\mathrm {Hess}}(N,h)$
has
![]() $V_{1} = \operatorname {\mathrm {span}}_{\mathbb {C}} \{e_1\}$
and
$V_{1} = \operatorname {\mathrm {span}}_{\mathbb {C}} \{e_1\}$
and
![]() $V_{n-1} = \operatorname {\mathrm {span}}_{\mathbb {C}} \{e_1,\ldots ,e_{n-1}\}$
(see Definition 3.2 and surrounding discussion). Hence, the result of [Reference Escobar, Precup and Shareshian15, Theorem 5] for
$V_{n-1} = \operatorname {\mathrm {span}}_{\mathbb {C}} \{e_1,\ldots ,e_{n-1}\}$
(see Definition 3.2 and surrounding discussion). Hence, the result of [Reference Escobar, Precup and Shareshian15, Theorem 5] for
![]() $A=N$
gives
$A=N$
gives
A Singular locus of Peterson variety
The singular locus of the Peterson variety
![]() $\operatorname {\mathrm {Pet}}_n$
has been studied in [Reference Insko and Yong26]. Combining the result of [Reference Insko and Yong26] and some result in [Reference Abe, Horiguchi, Kuwata and Zeng2], we describe the decomposition for the singular locus of the Peterson variety into irreducible components.
$\operatorname {\mathrm {Pet}}_n$
has been studied in [Reference Insko and Yong26]. Combining the result of [Reference Insko and Yong26] and some result in [Reference Abe, Horiguchi, Kuwata and Zeng2], we describe the decomposition for the singular locus of the Peterson variety into irreducible components.
It is known that the flag variety
![]() $Fl({\mathbb {C}}^n)$
has a decomposition into Schubert cells
$Fl({\mathbb {C}}^n)$
has a decomposition into Schubert cells
where each
![]() $X_w^\circ $
is isomorphic to
$X_w^\circ $
is isomorphic to
![]() ${\mathbb {C}}^{\ell (w)}$
and
${\mathbb {C}}^{\ell (w)}$
and
![]() $\ell (w)$
denotes the length of w (e.g., [Reference Fulton19]). Tymoczko generalized this fact to the Hessenberg varieties in [Reference Tymoczko36]. In what follows, we explain the work in [Reference Tymoczko36] for the case of the Peterson variety
$\ell (w)$
denotes the length of w (e.g., [Reference Fulton19]). Tymoczko generalized this fact to the Hessenberg varieties in [Reference Tymoczko36]. In what follows, we explain the work in [Reference Tymoczko36] for the case of the Peterson variety
![]() $\operatorname {\mathrm {Pet}}_n$
.
$\operatorname {\mathrm {Pet}}_n$
.
Let I be a subset of
![]() $[n-1]$
. We may regard
$[n-1]$
. We may regard
![]() $[n-1]$
as the set of vertices of the Dynkin diagram in type
$[n-1]$
as the set of vertices of the Dynkin diagram in type
![]() $A_{n-1}$
. Then,
$A_{n-1}$
. Then,
![]() $I \subset [n-1]$
can be decompose into the connected components of the Dynkin diagram of type
$I \subset [n-1]$
can be decompose into the connected components of the Dynkin diagram of type
![]() $A_{n-1}$
:
$A_{n-1}$
:
In other words, each
![]() $I_j \ (1 \leq j \leq m)$
denotes a maximal consecutive subset of
$I_j \ (1 \leq j \leq m)$
denotes a maximal consecutive subset of
![]() $[n-1]$
. To each connected component
$[n-1]$
. To each connected component
![]() $I_j$
, one can assign the longest element
$I_j$
, one can assign the longest element
![]() $w_0^{(I_j)}$
of the permutation subgroup
$w_0^{(I_j)}$
of the permutation subgroup
![]() $\mathfrak S_{I_j}$
on
$\mathfrak S_{I_j}$
on
![]() $I_j$
. Then, we define the permutation
$I_j$
. Then, we define the permutation
![]() $w_I \in \mathfrak S_n$
by
$w_I \in \mathfrak S_n$
by
Example A.1. Let
![]() $n=9$
and
$n=9$
and
![]() $I=\{1,2,3\} \sqcup \{6,7\}$
. Then, the one-line notation of
$I=\{1,2,3\} \sqcup \{6,7\}$
. Then, the one-line notation of
![]() $w_I$
is
$w_I$
is
The Schubert cell
![]() $X_v^\circ $
intersects with the Peterson variety
$X_v^\circ $
intersects with the Peterson variety
![]() $\operatorname {\mathrm {Pet}}_n$
if and only if
$\operatorname {\mathrm {Pet}}_n$
if and only if
![]() $v=w_I$
for some
$v=w_I$
for some
![]() $I \subset [n-1]$
by [Reference Tymoczko36] (see also [Reference Abe, Horiguchi, Kuwata and Zeng2, Lemma 3.5]). We set
$I \subset [n-1]$
by [Reference Tymoczko36] (see also [Reference Abe, Horiguchi, Kuwata and Zeng2, Lemma 3.5]). We set
By intersecting with the Peterson variety
![]() $\operatorname {\mathrm {Pet}}_n$
, the decomposition in equation (A.1) yields that
$\operatorname {\mathrm {Pet}}_n$
, the decomposition in equation (A.1) yields that
It is known from [Reference Tymoczko36] that
![]() $X_J^\circ \cong {\mathbb {C}}^{|J|}$
for any
$X_J^\circ \cong {\mathbb {C}}^{|J|}$
for any
![]() $J \subset [n-1]$
. In general, it follows from [Reference Abe, Horiguchi, Kuwata and Zeng2, Equation (3.7)] that for each
$J \subset [n-1]$
. In general, it follows from [Reference Abe, Horiguchi, Kuwata and Zeng2, Equation (3.7)] that for each
![]() $I \subset [n-1]$
, we have
$I \subset [n-1]$
, we have
It is known that
![]() $X_I$
is a regular nilpotent Hessenberg variety for a certain Hessenberg function
$X_I$
is a regular nilpotent Hessenberg variety for a certain Hessenberg function
![]() $h_I$
as described below. For
$h_I$
as described below. For
![]() $I \subset [n-1]$
, we define a Hessenberg function
$I \subset [n-1]$
, we define a Hessenberg function
![]() $h_I : [n] \rightarrow [n]$
by
$h_I : [n] \rightarrow [n]$
by

Note that if
![]() $I=[n-1]$
, then
$I=[n-1]$
, then
![]() $h_I=(2,3,4,\ldots ,n,n)$
is the Hessenberg function for the Peterson case. Otherwise,
$h_I=(2,3,4,\ldots ,n,n)$
is the Hessenberg function for the Peterson case. Otherwise,
![]() $h_I$
is decomposable (Definition 3.2).
$h_I$
is decomposable (Definition 3.2).
Proposition A.2.
![]() $($
[Reference Abe, Horiguchi, Kuwata and Zeng2, Proposition 3.4]
$($
[Reference Abe, Horiguchi, Kuwata and Zeng2, Proposition 3.4]
![]() $)$
For a subset I of
$)$
For a subset I of
![]() $[n-1]$
, we have
$[n-1]$
, we have
where N is the regular nilpotent element defined in equation (3.1).
It follows from Theorem 3.1 and Proposition A.2 that
![]() $X_I$
is irreducible for any
$X_I$
is irreducible for any
![]() $I \subset [n-1]$
. For positive integers
$I \subset [n-1]$
. For positive integers
![]() $a,b$
with
$a,b$
with
![]() $a \leq b$
, we denote by
$a \leq b$
, we denote by
![]() $[a, b]$
the set
$[a, b]$
the set
![]() $\{a, a + 1, \ldots , b\}$
. The singular locus of the Peterson variety
$\{a, a + 1, \ldots , b\}$
. The singular locus of the Peterson variety
![]() $\operatorname {\mathrm {Pet}}_n$
is described in [Reference Insko and Yong26] as follows.
$\operatorname {\mathrm {Pet}}_n$
is described in [Reference Insko and Yong26] as follows.
Theorem A.3.
![]() $($
[Reference Insko and Yong26, Theorem 4]
$($
[Reference Insko and Yong26, Theorem 4]
![]() $)$
The singular locus of
$)$
The singular locus of
![]() $\operatorname {\mathrm {Pet}}_n$
is given by
$\operatorname {\mathrm {Pet}}_n$
is given by
 $$ \begin{align*} \operatorname{\mathrm{Sing}}(\operatorname{\mathrm{Pet}}_n) = \bigsqcup_{J \subset [n-1] \atop J \neq [n-1], [2,n-1],[1,n-2]} X_J^\circ. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Sing}}(\operatorname{\mathrm{Pet}}_n) = \bigsqcup_{J \subset [n-1] \atop J \neq [n-1], [2,n-1],[1,n-2]} X_J^\circ. \end{align*} $$
Lemma A.4. We have
 $$ \begin{align*} \{J \subset [n-1] \mid J \neq [n-1], [2,n-1],[1,n-2] \} = \bigcup_{j=2}^{n-2} \{ J \subset [n-1] \mid J \not\ni j \} \cup \{J \subset [2,n-2] \}. \end{align*} $$
$$ \begin{align*} \{J \subset [n-1] \mid J \neq [n-1], [2,n-1],[1,n-2] \} = \bigcup_{j=2}^{n-2} \{ J \subset [n-1] \mid J \not\ni j \} \cup \{J \subset [2,n-2] \}. \end{align*} $$
Proof. We first show that the left-hand side is included in the right-hand side. For this, we take a subset J of
![]() $[n-1]$
such that
$[n-1]$
such that
![]() $J \neq [n-1], [2,n-1],[1,n-2]$
. Note that
$J \neq [n-1], [2,n-1],[1,n-2]$
. Note that
![]() $|J| \leq n-2$
.
$|J| \leq n-2$
.
Case (i): Suppose that
![]() $|J| \leq n-3$
. If J contains
$|J| \leq n-3$
. If J contains
![]() $[2,n-2]$
, then
$[2,n-2]$
, then
![]() $J=[2,n-2]$
since
$J=[2,n-2]$
since
![]() $|J| \leq n-3$
. Otherwise, we have
$|J| \leq n-3$
. Otherwise, we have
![]() $J \not \ni j$
for some
$J \not \ni j$
for some
![]() $2 \leq j \leq n-2$
. In both cases, J belongs to the right-hand side.
$2 \leq j \leq n-2$
. In both cases, J belongs to the right-hand side.
Case (ii): Suppose that
![]() $|J| = n-2$
. Since
$|J| = n-2$
. Since
![]() $J \neq [2,n-1],[1,n-2]$
, we see that
$J \neq [2,n-1],[1,n-2]$
, we see that
![]() $J = [n-1] \setminus \{j \}$
for some
$J = [n-1] \setminus \{j \}$
for some
![]() $2 \leq j \leq n-2$
, which belongs to the right-hand side.
$2 \leq j \leq n-2$
, which belongs to the right-hand side.
Hence, we proved that the left-hand side is included in the right-hand side.
Conversely, let J be a subset of
![]() $[n-1]$
appeared in the right-hand side. If
$[n-1]$
appeared in the right-hand side. If
![]() $J \not \ni j$
for some
$J \not \ni j$
for some
![]() ${2 \leq j \leq n-2}$
, then we have that
${2 \leq j \leq n-2}$
, then we have that
![]() $J \neq [n-1], [2,n-1],[1,n-2]$
. If
$J \neq [n-1], [2,n-1],[1,n-2]$
. If
![]() $J \subset [2,n-2]$
, then it is clear that
$J \subset [2,n-2]$
, then it is clear that
![]() ${J \neq [n-1], [2,n-1],[1,n-2]}$
. Thus, the right-hand side is included in the left-hand side, so the equality holds.
${J \neq [n-1], [2,n-1],[1,n-2]}$
. Thus, the right-hand side is included in the left-hand side, so the equality holds.
The following proposition gives the decomposition for the singular locus of the Peterson variety into irreducible components.
Proposition A.5. The singular locus of
![]() $\operatorname {\mathrm {Pet}}_n$
is decomposed into irreducible components as follows:
$\operatorname {\mathrm {Pet}}_n$
is decomposed into irreducible components as follows:
 $$ \begin{align*} \operatorname{\mathrm{Sing}}(\operatorname{\mathrm{Pet}}_n) &= \left( \bigcup_{2 \leq j \leq n-2} X_{[n-1] \setminus \{j\}} \right) \cup X_{[2,n-2]} \\ &=\left( \bigcup_{2 \leq j \leq n-2} \operatorname{\mathrm{Hess}}(N,h_{[n-1] \setminus \{j\}}) \right) \cup \operatorname{\mathrm{Hess}}(N,h_{[2,n-2]}). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Sing}}(\operatorname{\mathrm{Pet}}_n) &= \left( \bigcup_{2 \leq j \leq n-2} X_{[n-1] \setminus \{j\}} \right) \cup X_{[2,n-2]} \\ &=\left( \bigcup_{2 \leq j \leq n-2} \operatorname{\mathrm{Hess}}(N,h_{[n-1] \setminus \{j\}}) \right) \cup \operatorname{\mathrm{Hess}}(N,h_{[2,n-2]}). \end{align*} $$
Proof. By Theorem A.3 and Lemma A.4, we have
 $$ \begin{align*} \operatorname{\mathrm{Sing}}(\operatorname{\mathrm{Pet}}_n) = \left(\bigcup_{2 \leq j \leq n-2} \bigsqcup_{J \subset [n-1] \setminus \{j\}} X_J^\circ \right) \cup \left( \bigsqcup_{J \subset [2,n-2]} X_J^\circ \right). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Sing}}(\operatorname{\mathrm{Pet}}_n) = \left(\bigcup_{2 \leq j \leq n-2} \bigsqcup_{J \subset [n-1] \setminus \{j\}} X_J^\circ \right) \cup \left( \bigsqcup_{J \subset [2,n-2]} X_J^\circ \right). \end{align*} $$
By using the decomposition in equation (A.2), the right-hand side above is equal to
 $$ \begin{align*} \left( \bigcup_{2 \leq j \leq n-2} X_{[n-1] \setminus \{j\}} \right) \cup X_{[2,n-2]}, \end{align*} $$
$$ \begin{align*} \left( \bigcup_{2 \leq j \leq n-2} X_{[n-1] \setminus \{j\}} \right) \cup X_{[2,n-2]}, \end{align*} $$
as desired. Also, this coincides with
![]() $\left ( \bigcup _{2 \leq j \leq n-2} \operatorname {\mathrm {Hess}}(N,h_{[n-1] \setminus \{j\}}) \right ) \cup \operatorname {\mathrm {Hess}}(N,h_{[2,n-2]})$
by Proposition A.2.
$\left ( \bigcup _{2 \leq j \leq n-2} \operatorname {\mathrm {Hess}}(N,h_{[n-1] \setminus \{j\}}) \right ) \cup \operatorname {\mathrm {Hess}}(N,h_{[2,n-2]})$
by Proposition A.2.
Acknowledgements
We are grateful to Hiraku Abe for valuable discussions. We are also grateful to Satoshi Murai for helpful comments on the commutative algebra arguments. We thank the anonymous referee for valuable and perceptive comments.
Funding statement
This research was partly supported by Osaka Central Advanced Mathematical Institute (MEXT Joint Usage/Research Center on Mathematics and Theoretical Physics). The first author is supported in part by JSPS Grant-in-Aid for Young Scientists: 19K14508.
Competing interest
The authors have no competing interest to declare.