A Flow-line Model for Calculating the Surface Profile and the Velocity, Strain-rate, and Stress Fields in an Ice Sheet

Abstract

A flow-line model is presented for calculating the surface profile and the velocity, strain-rate, and stress fields in an ice sheet with given base-elevation profile, ice thickness at the dome (divide), flow-law parameters, mass-balance distribution, and convergence/divergence conditions along the flow line. The model, which is based on a “quasi-similarity” hypothesis as regards the horizontal velocity-depth profiles, accounts for changes along the flow line in the depth distributions of temperature, normal stress deviators, and possible enhanced flow of deep ice of Wisconsin origin. A curvilinear coordinate system is applied with horizontal axes along flow lines and surface-elevation contours, respectively. The flow equations are reduced to two differential equations, one for the surface-elevation profile, and the other for a profile function that determines the depth distributions of velocities and strain-rates. The two equations are coupled through a profile parameter that communicates the influence of velocity-profile changes to the surface-profile equation. It is shown that the variation along the flow line of this parameter should also be considered when deriving flow-law parameters from ice-sheet flow-line data. For a symmetric dome, explicit expressions are derived for the depth distributions of the vertical velocity, strain-rates, and stresses. The strain-rate profiles display an inflection about half-way down the ice sheet, and, in the case of isothermal ice, have surface values 2.2 times their depth-averaged values. The depth distribution of the vertical velocity indicates that a relatively thick layer of almost stagnant ice is present at the ice-sheet base below a dome.

1. Introduction

Palaeo-environmental records obtained from ice cores have stressed the need for ice-sheet models that can provide realistic predictions of age profiles and annual layer-thickness profiles at drill sites. Also, the increasing amount of accurate data collected along flow lines on ice sheets and ice caps stresses the need for realistic flow-line models to which the data can be compared. Since ice sheets and ice caps seldom, if ever, reach a steady state, realistic ice-sheet modelling should in principle always include the time dimension and, in fact, several models have been designed for modelling the evolution of ice sheets in response to a changing environment, e.g. Budd and Smith, 1981; Oerlemanns, 1982; Lingle, 1985. However, in order to keep computation time within reasonable limits, these models are based on simplified ice dynamics, and therefore can account for ice-sheet dynamic behaviour in rather general terms only. Models which disregard the time evolution of the ice mass have been developed to much higher perfection as far as ice dynamics is concerned. There is a significant development from the simple ice-sheet profile models of Vialov (1958), Haefeli (1961), and Weertman (1961) to the flow-line models of Hooke and others (1979), Morland and Johnson (1980), Hutter (1983), Paterson and Waddington (1984), and Reeh and others (1985).

Such time-independent models have contributed a lot to our understanding of ice-sheet dynamics. A strong argument in their favour is that they do not necessarily pre-suppose the ice mass is in a steady state. This is due to the fact that, since inertia does not play any significant role in ice-sheet dynamics, the velocity and strain-rate fields will respond immediately to changing stress configurations caused by changes in: e.g. ice thickness, surface slope, or basal conditions. Therefore, even in the case of an ice sheet which is far from being in a steady state, the velocity and strain-rate fields reflect the actual ice-sheet geometry and ice-flow properties, and hence can in principle be predicted by time-independent modelling, assuming ice-sheet geometry and ice-flow properties are known.

Of course, only quantities that depend solely on the present state of the ice sheet can be determined by this kind of modelling. To calculate quantities such as layer-thickness and age profiles, knowledge of the strain history of the ice sheet is required as far back in time as the profiles are needed and, therefore, in principle, requires modelling including the time dimension. As far as such quantities are concerned, time-independent (steady-state) modelling should rather be considered a means of establishing references to which observations can be compared in order to evaluate to what extent “irregularities” in the data are due to temporal variations.

Recent developments in ice-sheet flow-line modelling seem to follow two different lines:

1. One approach is the “mathematical” approach, represented by the work of, for example, Morland and Johnson (1980), and Hutter (1983), which is based on the rational approximation schemes used in non-Newtonian fluid dynamics. Even though this approach has led to a better understanding of the approximations behind various ice-flow models and also points to a rational manner of improving the models, several aspects known to have a major influence on ice-sheet dynamics are disregarded. Therefore, in their present state of development, the mathematical models, however useful they may be for other reasons and in spite of mathematical perfection, do not yet provide “realistic” solutions to which specific flow-line data can be profitably compared.

2. The other line of development in flow-line modelling applies finite-element methods (e.g. Hooke and others, 1979; Paterson and Waddington, 1984; Fastook, 1985), which are particularly suited for treating differences in ice rheology, i.e. varying flow properties due to variations in, for example, temperature, ice fabric, ice-crystal size, and impurity content. The finite-element models, therefore, have the potential of producing “realistic” solutions and have in fact been successfully applied to explain observed ice-sheet flow-line data (e.g. Hooke and others, 1979).

The flow-line model to be presented here is an alternative to the finite-element models. It is flexible with respect to varying conditions along the flow line, in particular to varying flow properties of the ice. It is based on the fact that, with certain assumptions to be specified later, the integrations of the flow equations horizontally (to determine the surface-elevation profile) and vertically (to determine the velocity, strain-rate, and stress profiles) are coupled through a velocity-profile parameter only, which varies along the flow line, but which can be determined at any location along the flow line from the depth distributions of ice temperature, shear stress, normal-stress deviators, and ice-flow-law parameter. No attempt has been made to apply the approximation schemes of the “mathematical” approach. However, the velocity and stress solutions produced by the model can be checked by substituting the solutions into the flow equations. As long as ice-thickness gradients are moderate, the residuals turn out to be small (see section 3.4 for discussion). For larger ice-thickness gradients, the solution can be used as the intial step in an iteration scheme (see section 3.4).

2. Description of Flow-line Model

The model is developed for calculating the velocity, strain-rate, and stress fields in an ice sheet. It has two versions: (1) with given surface- and base-elevation profiles, estimates of the flow-law parameters n and A can be obtained as well; (2) with given base-elevation profile, ice thickness at the divide (dome), and flow-law parameters, the surface-elevation profile can also be calculated. The model is essentially a generalization of Nye’s simple uniform strain-rate and extending/compressing glacier-flow model (Nye, 1957); all quantities, however, are allowed to vary in the direction of the flow line. Normal strain-rates may also vary with depth, and the flow-law parameter may vary along the flow line and with depth, depending on the temperature field (assumed to be known) and a possible basal layer of soft ice. All these generalizations, however, are introduced at the expense of exact satisfaction of the flow equations; the equation of continuity is strictly satisfied. However, the stress-equilibrium equations and the compatibility conditions are only approximately satisfied. In particular, these equations may be violated close to the base of the ice sheet at places where the ice-thickness gradient is significant and at a possible hard/soft ice transition (see section 3.4).

The model applies the generalized ice-flow law

(1)

Here, έij, σ’ij are strain-rate and stress-deviator components, T_e is effective shear stress defined by is a function of temperature, and A _rand n are constants. E is the enhancement factor for the deformation rate of soft ice relative to hard ice (see section 3.5).

Divergence/convergence of the flow is taken into account both in the calculation of the variation of ice flux along the flow line and by considering the contribution of the transverse normal-stress deviator to the effective shear stress. This means that the model can also be used to describe the slow flow along divides (ridges) with small surface slopes (Reeh and Paterson, 1988). The following capabilities of the model should be emphasized: it takes into account the influence of the depth variations of temperature, effective shear stress, and flow-law parameter A on the depth profiles of velocities and strain-rates, and on the surface profile of the ice sheet, through a coupling between the surface-profile equation and the equations that determine the depth variations of velocities, strain-rates, and stresses. It is flexible with respect to varying conditions along the flow line, in particular, to varying flow properties of the ice. Furthermore, it is possible to introduce into the model a calculation of the temperature field synchronously with the velocity- and stress-field calculations, starting from the divide and moving step-by-step along the flow line. This facility has not yet been implemented.

2.1. Model input

1. Base elevations.

2. Mass-balance distribution along the flow line.

3. Convergence/divergence conditions along the flow line.

4. Temperature field in a vertical section along the flow line.

5. Depth along the flow line of the Holocene/Wisconsinan transition (transition from hard to soft ice).

6. Enhancement factor of soft ice relative to hard ice.

7. Function F(T) for the temperature dependence of the flow-law parameter.

For T ≤ 263.2 K, F(T) is supposed to vary according to the Arrhenius equation with a constant value of the activation energy Q_T = 60 000 J/mol. For 263.2 < T ≤ 273.2 K, a similar relation is applied, however, with a value of the activation energy that increases linearly with T from 60 000 J/mol to 120 000 J/mol. Hence

(2)

Here, A _T and A _r are flow-law parameter values referring to temperatures T (the actual ice temperature) and T _r (a reference temperature), respectively. Q_T and Q_r are activation energies for creep corresponding to temperatures T and T _r T _1O = 263.2 K. Q_T is calculated from the expression:

Q_T = 60 000 J/mol for T≤ 263.2 К,

Q_T = 60 000 (1 + 0.1(T - 263.2)) J/mol for 263.2 K < T≤ 273.2 K,

R = 8.31 J/mol/K is the gas constant.

8. Either (a) surface-elevation profile or (b) ice thickness at the divide and parameters A _r and n of the ice-flow law έ_e = έA _r F(T)T _e, where έ _e, T_e are the effective strain-rate and the effective shear stress.

2.2. Model output

1. Either (a) flow-law parameters n and A _r, or (b) surface-elevation profile.

2. Velocity fields (u and w as functions of x and z). Here, the, x-axis is horizontal, pointing down the flow line, the z-axis is vertical, positive upward, and u, w are the x- and z-components of velocity (see Fig 1).

3. Strain-rate fields (distribution with x and z of longitudinal, tranverse, and vertical strain-rates, and shear strain-rates έ _xz in a vertical plane).

4. Stress fields (normal stress deviators, and shear stresses Τ_xz in a vertical plane).

5. Steady-state particle paths in the vertical section along the flow line and travel times.

6. Steady-state age and annual layer-thickness profiles at any location along the flow line.

2.3 Assumptions

1. Flow lines and surface-elevation contours are orthogonal.

2. The direction of the horizontal flow vector does not change with depth.

3. The shape of the velocity-depth profile varies only slowly with x.

4. The gradient of the longitudinal stress deviator is neglected so that T_xz is given by the standard formula (see section 3.4). All three normal stress deviators, however, are taken into account as regards their contributions to the effective shear stress.

5. 5. Horizontal shear (between the flow line and its neighbours) is neglected.

Assumptions (3) and (4), which are closely related, impose certain restrictions as regards the roughness of the bed topography that can be handled by the model (e.g. Budd, 1970; Hutter, 1981). This problem will be further discussed in section 3.4

Fig.1. a. Shows horizontal, curvilinear coordinate axes χ and y along flow lines and surface-elevation contours, respectively. R and r are radii of curvature of the elevation contour and the flow line at their intersection, b. Shows a vertical section along the flow line. c. Shows transformed vertical section along the flow line (see text for details).

With these assumptions, the integrations in the x-direction (to determine the surface-elevation profile in the case of given n and A _r) and in the z-direction (to determine the velocity, strain-rate, and stress profiles) are coupled through a velocity-profile parameter only, which varies with x and which can be determined at each x from the depth distributions of the temperature, the depth distributions of the shear stress and normal stress deviators, the enhancement factor, and the thickness of a possible soft basal ice layer. Starting from the divide (dome), the calculations can therefore be performed by integrating alternately in the vertical and horizontal directions.

If the surface elevations are used as input, the model will calculate n and the distribution of A _r along the flow line. Experience shows that the A _r distribution calculated in this way displays considerable short-distance variations. These, however, can be eliminated by moderate changes in the basal shear-stress distribution, accomplished, for example, by changing the surface-slope distribution slightly, without violating the surface-input data. This suggests that the calculated A_r variation is not real; in fact, one would not expect such a variation. Therefore, a better procedure is to choose a constant value of A _r, calculate the surface profile, compare this to the observed profile, and then change A _r until a reasonable fit is obtained. The calculated profiles appear to be rather sensitive to changes in A _r so that the modelling gives a specific value for it.

3. Flow Equations

3.1. Coordinate system

A curvilinear, left-handed coordinate system is applied, with a horizontal, curved x-axis following the flow line and oriented in the direction of flow, a horizontal y-axis transverse to the flow line along an elevation contour, and a vertical z-axis, positive upwards (see Fig. 1). The directions of the x- and y-axes vary along the flow line, as indicated by the local unit vectors shown in the map of Figure la. The radii of curvature of the surface-elevation contours and the flow lines at their intersection are denoted R and r, respectively. R and r are considered positive if a movement in the direction of the y-axis, respectively the x-axis, produces an anti-clockwise rotation, when viewed from the respective centers of curvature.

Velocity components in the x- and z-directions are denoted n and w, respectively. Due to the definition of the flow line, and assumption (2) in section 2.3, the y-component of the velocity is zero. However, in general, the transverse strain-rate.

The upper and lower boundary surfaces of the ice mass are denoted S(x,y) and B(x,y), respectively, while H(x,y) = S(x,y) - B(x,y) denotes ice thickness (see Fig. 1b).

3.2. Mass conservation (continuity equations)

Local mass conservation is expressed as

In the coordinate system of Figure 1, the normal strain-rate components are (Jaeger, 1969, p. 45)

where r and R are the radii of curvature of the flow lines and the surface-elevation contours at their points of intersection (see Fig. 1a). Since ν = 0, these expressions reduce to

and the local mass-conservation equation may be re-written

(3)

An equation for the ice-volume flux is determined by integrating this equation vertically:

(4)

where as and a B are net mass balances (positive for accumulation, negative for ablation) at the ice-sheet surface and base, respectively, and is the rate of change of surface elevation. For Equations (3) and (4) to hold, the ice-sheet material must be assumed to be incompressible. In consequence, ice-equivalent thicknesses are used in the model.

It is convenient to define the “flux-effective” mass balance as

If steady state is assumed, , and a = a _S + a _B is simply the net mass balance.

The distribution along the flow line of R, which can be read from a map of surface-elevation contours, determines the convergence/divergence conditions along the flow line. With a and R given, q may be obtained from Equation (4) at any point along the flow line by standard numerical-integration techniques.

3.3. Velocity and strain-rate components

Horizontal velocity

Assumption (3) in section 2.3 allows the horizontal velocity component u to be written:

(5)

where is the depth-averaged velocity, and where ρ is ice density and g is acceleration due to gravity. An approximate solution to these equations is given by

(13)

(14)

(15)

(16)

where is the ratio between the transverse and longitudinal strain-rates, and is basal shear stress. The second member of the expression for σ _y is deduced by means of the stress-strain-rate relations of section 3.5 and the local continuity equation given in section 3.2.

The solution given by Equations (13)–(16) is dependent on the following conditions to be fulfilled:

The first of these conditions is equivalent to requiring , and is satisfied to a very good approximation for most ice-sheet profiles. Also, the second condition is generally very well satisfied. The third condition, however, which is equivalent to requiring the normal stresses to be weak functions of x is a more restrictive condition. There are different ways of dealing with the normal stress-gradient term. Estimates can be made for the minimum smoothing distance for ice thicknesses that will allow the gradient term to be neglected (Budd, 1970). The gradient term can be accounted for by harmonic perturbation theory (e.g. Hutter, 1983; Reeh and others, 1985) or by applying other rational approximation schemes for idealized cases (e.g. McMeeking and Johnson, 1986). In the present model the gradient terms are a priori neglected. Therefore, when the stresses have been calculated, they should be checked by insertion in the stress-gradient condition, and the quality of the solution obtained can then be evaluated as to how well this condition is satisfied. If the agreement is not satisfactory, the x-gradient of σ _x may be calculated from the solution, and a first correction to the vertical shear-stress distribution can be found by integrating this gradient vertically. Also, a first correction to the vertical normal stress can be found by vertical integration of the x-gradient of the shear stress. Corrected velocity and strain-rate distributions compatible with the corrected stresses can then be found by a procedure similar to that described in section 3.6. This iteration process may be repeated until the field equations are satisfied to a desired accuracy.

3.5. Stress-strain-rate relations

The relations between strain-rates and stresses, as given by the ice-flow law in Equation (1), are:

(17)

(18)

where accounts for the depth variation of the flow-law parameter due to temperature variations (F(T), see Equation (2)) and possible enhanced flow . The function used in the model is a step function jumping from the value E below the level to 1 above this level (see Fig. 2). This E-variation is introduced to model the different flow properties of soft ice of Wisconsinan origin and hard ice of Holocene origin (Paterson, 1977; Gundestrup and Hansen, 1984; Dahl-Jensen, 1985), and thus represents the level of the Holocene/ Wisconsinan transition, i.e. the 1O 700 year age horizon (Hammer and others, 1986). Softening of the ice due to the gradual development of a fabric, favorable for shear motion, could also be included in the E actor which in that case should be allowed to vary also in the x-direction. Since T and are allowed to vary with x, so will β. However, it is assumed that the terms are negligible.

Fig.2. Quantities affecting the depth distribution of ice-flow properties, a. Temperature distribution, b. Function (see Equation (2)). c. Enhancement factor . .

The normal stress deviators are obtained by means of Equations (13), (14), and (15):

(19)

where Δσ and α are explained in connection with Equations (13)–(16). The effective shear stress is determined by the expression

(20)

where T _xz is given by Equation (16) and ξ = (1 + α + α²)^1/2/Ɩ1+1/2 α Ɩ.

3.6. Differential equations for the surface-elevation profile and the horizontal velocity-depth profile

Combining Equations (16), (18), and (20) yields

(21)

where the subscript x on β, ξ, and Δσ indicates their weak x-dependence. Another expression for is obtained by means of Equation (11):

The right-hand member of this equation is the product of an x-dependent term u_m(x)/H(x) and a -dependent term Φ’(). Similarly, Equation (21) may be separated into an x-dependent term 2A _r T _B (x) ⁿ and a term that is mainly -dependent, i.e.

(22)

which is the differential equation that determines the surface-elevation profile of the ice sheet, and

(23)

(6)

is a dimensionless vertical coordinate, standardized to the range 0–1. ɸ(), which in the general case varies with x and y, is the shape function of the horizontal velocity/depth profile. It is subject to the condition Furthermore, if the ice sheet does not slide over the base, ɸ(0) = 0.

By means of the coordinate transformation given in Equation (6), the vertical section along the flow line bounded by the irregularly shaped bed and surface curves z = B(x,0) and z = S(x,0) is mapped on to the parallel-sided strip bounded by the straight lines = 0 and = 1 (see Fig. 1c). This transformation, which has been applied by, for example, Philberth and Federer (1971) and Jenssen (1982), implies significant simplifications in the determination of particle paths in a vertical section along the flow line (see section 4), and also simplifies problems involving the heat-transport equation (Jenssen, 1982).

The change of ɸ along the flow line is given by In accordance with assumption (3) of section 2.3, is assumed to be negligible. This quasi-similarity hypothesis for the shape of the horizontal velocity profile, however, does not imply that dɸ /dx can be neglected; by means of Equation (6), we get

(7)

which (unless B and H do not vary with x, i.e. a constant-thickness ice sheet on a horizontal bed, or 3ɸ /9= 0 (i.e. uniform velocity/depth distribution) contributes a non-negligible term to dɸ/dx.

Normal strain-rates

By differentiating Equation (5) with respect to x and applying Equation (7), we get

where ɸ ’ () denotes dɸ/dz. Furthermore, by means of Equation (4), we obtain , and hence the longitudinal strain-rate becomes

(8)

Since έ _y = u/R, the transverse strain-rate is simply

(9)

The vertical strain-rate is obtained by means of Equations (3), (8), and (9):

(10)

It appears from Equations (8) and (10) that the longitudinal and vertical strain-rates are composed of a ɸ -term and а ɸ ’ -term. The ɸ -term is distributed with depth in the same manner as the horizontal velocity, while the ɸ -term is twice the product of the shear strain-rate (see Equation (11)) and a slope term that varies linearly with depth between surface slope ( = 1) and bed slope ( = 0). Where the horizontal velocity changes slowly with depth, i.e. where ɸ’ ~ 0, which is the case in the upper part of an ice sheet, only the φ-term contributes significantly to the strain-rates. However, near the base, where the shear rate is generally large (unless ice motion is mainly due to basal sliding) and the slope term approaches the bed slope, which may also be large, the ɸ ’ -term becomes important, and may even dominate the ɸ -term.

Shear strain-rates

In the coordinate system shown in Figure 1, the shear strain-rates become

Since v = 0 and can be shown to be second-order terms in the surface and base gradients, and therefore are neglected, the shear strain-rates become

For flow along a divide between drainage basins and along the center line of a drainage basin, is zero, since the xy-distribution of the horizontal velocity attains a local minimum and a local maximum along these lines. Moreover, if the divide or center line is a straight line or displays a moderate curvature only, u/r can also be neglected, and the horizontal shear rate έ _xy vanishes. In all other cases, horizontal shear may be important. The importance of horizontal shear in ice-sheet flow will be discussed elsewhere. Here, horizontal shear will be neglected as stated in assumption (5) of section 2.3. Therefore, the only non-vanishing shear strain-rate is έ _xz , which by differentiating Equation (5) is obtained as

(11)

Vertical velocity

Integration of Equation (10) with respect to z yields the vertical velocity-depth distribution

(12)

where , and a_B is the rate of melting or freeze-on of ice at the ice-sheet base. Notice that includes the mass balances at both the surface and the base of the ice sheet, as well as the time rate of change of the surface elevation.

The profile function ψ() is subject to the conditions ψ(0) = 0 and ψ(1) = 1.

Equation (12) shows that the vertical velocity is composed of a ψ term and а ɸ term. The former accounts for the vertical transport of material within the ice sheet, whereas the latter is related to the flow caused by ice-thickness changes. The latter term may be interpreted as the product of the horizontal velocity and the slope term discussed in connection with the normal strain-rates, and may dominate the former term near the base of the ice sheet if the basal gradient is large.

Up till now, the theory has been purely kinematic. It has been based on the quasi-similarity hypothesis for the horizontal velocity profiles and on the principle of mass conservation, and may be considered as an extension of the kinematic ice-sheet models of Dansgaard and Johnsen (1969) and Philberth and Federer (1971) to the case of non-uniform distributions of ice thickness and accumulation rate along the flow line; for any prescribed shape function ɸ () of the horizontal velocity profile, the velocity and strain-rate fields can be determined by the above equations, in the present theory, the velocity-profile function is determined by means of the force-balance equation and the flow law of ice, as shown in the following sections.

3.4. Stress-equilibrium equations

The form of the stress-equilibrium equations valid in the xyz-coordinate system shown in Figure 1 will be discussed elsewhere. It can be shown that for slightly curved flow lines and along symmetric ridges and center lines of drainage basins, the equilibrium equations reduce to those for two-dimensional flow. Moreover, since transverse shear in vertical planes is neglected (assumption (5) in section 2.3), the equations become:

which is the differential equation for the profile function ɸ that determines the depth distributions of velocity components and strain-rates.

The parameter C_x that occurs in both of Equations (22) and (23) is determined by means of the condition

(24)

Since β and ξΔσ/τ_B are weakly dependent on x, so is C as indicated by the subscript x. The C_x parameter is the link between the surface-profile equation and the shape-function equation and, thus, being a function of x, communicates the influence of velocity-profile changes to the surface-profile equation.

It appears from Equation (24) that the value of C_x depends on the depth distribution of the flow-law parameter given by , on the ratio оГ the longitudinal stress deviator to the basal shear stress, and on the degree of basal sliding. Consequently, any change in the E- distribution (for example, due to a change in the relative depth to the Holocene/Wisconsinan transition), any change in the temperature-depth distribution, any change in the ratio of longitudinal stress to basal shear stress, and any change in the ratio of sliding velocity to average velocity, will change the value of C_x . Even though in general the gradient is small, nevertheless large changes in C_x are to be expected along an extended flow line. This has consequences for the established method for deriving ice-flow-law parameters from ice-sheet flow-line studies based on log-log plots of u_m(x)/H(x) against T_B (x)(e.g. Budd and Smith, 1981; Hamley and others, 1985). As indicated by Equation (22), proper derivation of flow-law parameters by this method must consider the magnitude and the variation of C_x along the flow-line section in question. This problem and other consequences of the C_x variation will be discussed in more detail elsewhere.

In the discussion up to now it has been tacitly assumed that Δσ was known as a function of . In fact, this function remains to be determined. This is done by combining Equations (8), (17), (19), and (20) to obtain

(25)

For given x, the depth distributions of Δς _x . and ɸ can be obtained from Equations (23) and (25) by combined numerical integration in the vertical direction starting at the ice-sheet base, and iteration at each step of integration to determine Δσ and α at the corresponding -level. Next, with C_x calculated from Equation (24), the integration of the surface-profile Equation (22) in the horizontal direction can be carried on one step further. In this manner, the depth distributions of velocity components, strain-rates, and stresses, and the surface-elevation profile are determined by integrating alternately in the vertical and horizontal directions.

4. Particle Paths And Travel Times

With the velocity components given by Equations (5) and (12), the particle paths in the vertical section along the flow line are determined by the equations

(26)

and

(27)

As mentioned in the introduction, the expressions for velocity components, strain-rates, and stresses do not presuppose a steady-state assumption. However, for the calculation of particle paths and travel times, steady state must be assumed. It appears that Equation (27) can be replaced by a simpler equation in terms of the transformed coordinate . The time derivative of may be expanded as follows:

Using the identities dz/dz = H ⁻¹, dz/Αt = w, and dx/dt = u, and substituting for dz/dx by means of Equation (7), the above equation may be rewritten

Substituting for и and w by means of Equations (5) and (12), respectively, this equation is simplified to

(28)

Equations (26) and (28) can be solved for x and as functions of time t, by standard numerical integration techniques, to determine travel times and particle paths in the transformed x -coordinate system. In the actual xz-coordinate system, travel times are unchanged, while the particle paths are found by changing into z by means of the transformation z = B(x) + H(x).

5. The Solution for a Symmetrical Dome

At a dome with the xz- and yz-planes as symmetry planes, special conditions prevail, since in that case R = O, u_m = 0, and T_B = 0. Generally, the expressions for velocity components, strain-rates, and stresses are considerably simplified. The expressions for velocities, strain-rates, and stresses can be found by studying the expressions deduced in section 3 at the limit of vanishing R, u_m , and r_B. The components of velocity (Equations (5) and (12)) become

The expressions for the strain-rates are also considerably simplified. Obviously, at the dome έ_xz= 0. Furthermore, from Equations (8), (9), and (10), we get

It is worth noticing that at the dome the depth distributions of all normal strain-rates have the same shape, determined by the profile function ɸ(). Moreover, an explicit expression can be found for this profile function: in the limit of T_b - 0, Equations (23) and (24) yield

(29)

where

Also, for T_b - 0, u_m - 0, and R - 0, Equation (25) is simplified to

This equation can be explicitly solved for Δσ():

(30)

Substituting this solution into Equation (29) yields

(31)

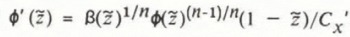
where

The solution of the differential Equation (31) is

(32)

For isothermal, non-enhanced ice, ß(z) = 1. Applying this β distribution and taking n= 3, Equation (32) yields

(33)

from which ¢(1) = 2.1875 and ¢(0.5) = 0.923. Hence, at the dome of an isothermal ice sheet, the surface strain-rates are approximately 2.2 times their depth-averaged values. Halfway down the ice sheet, the strain-rates are 92% their average values, as illustrated in Figure 3a. The strain-rate distribution shown in this figure deviates considerably from the linear distribution suggested by Raymond (1983) as an approximation to the strain-rate variation at the dome. Raymond (1983) pointed out that a linear distribution does not fit the boundary conditions of vanishing shear stress (shear strain) at the base and surface of the ice sheet, i.e. ¢’(0) = 0 and ¢’(1) = 0, and that the true distribution must be concave-up near the surface and concave-down near the base, and thus have an inflection as indicated by Raymond’s precise profile as well as by the present analysis. However, even though there is a qualitative agreement between the profile calculated by Raymond and that of the present analysis, there appears to be a quantitative difference.

One might think of explaining the difference as being due to break-down of the basic assumptions of the present analysis, making this a poor approximation at the divide. However, a more detailed analysis to be given elsewhere shows that this is not the case. Even the gradient of the longitudinal stress deviator vanishes at the divide for reasons of symmetry. The normal-stress distributions are slightly changed by a term that depends on ice thickness and the curvature of the ice-sheet surface in a vertical plane, but strain-rates are essentially unchanged. Raymond (personal communication) has suggested that the spatial resolution in his finite-element model might have smeared out some of the real spatial variations. This might explain the quantitative difference between his calculated profile and the profile of the present analysis.

The depth profile of the vertical velocity ɸ() is found by integrating Equation (33):

(34)

which is shown in Figure 3b. It is evident from this figure that there is a relatively thick layer of almost stagnant ice at the ice-sheet base below a symmetric isothermal dome.

If the dome is supposed to be in a steady state, the annual layer thickness varies with depth in the same manner as the vertical velocity, and so Figure 3b also represents the annual layer-thickness profile.

The age-depth profile at the dome is obtained from the equation

Assuming stready state and zero mass balance at the ice-sheet base (a_B = 0), the time-scale therefore becomes

This time-scale is plotted in Figure 4 together with the Raymond (1983) time-scale and the classical logarithmic Nye (1963) time-scale, which assumes constant vertical strain-rate. The three time-scales show distinctly different assymptotic behaviour for , i.e. , and ln(), respectively. This results in order-of-magnitude different age estimates for the deep ice when applying the different time-scales, the time-scale of this work predicting the oldest ages, and the Nye time-scale the youngest ages. For example, using present-day central Greenland accumulation rate and ice thickness, the age of the ice 300 m above the bottom is predicted as c. 1000 000, 100 000, and 20 000 years by the three models. At a depth of 150 m above the bottom, the differences become even larger, i.e. с. б 500 000, 200 000, and 30 000 years. The ages estimated by the time-scale of this work, are much too old (the Greenland ice sheet is supposed to be of Quaternary age, i.e. at most c. 2.5 Ma old). There are many reasons for the ages to be too old, since several factors tending to decrease the age of the deep ice have been neglected, e.g. the nonuniform temperature-depth profile, enhanced flow of ice-age ice, and, what is probably the main reason, temporal variations of accumulation rate, ice temperature, ice thickness, and dome position. Also, the possibility of basal melting in shorter or longer periods during the glacial/ interglacial cycles must be considered. A more detailed discussion of the influence of these factors on the time-scale at the dome will be given elsewhere.

Fig.3. Depth distribution of strain-rates (a), and vertical velocity (b) at the dome of a symmetrical, isothermal ice sheet consisting of non-enhanced ice throughout.

6. Conclusions

A model study of the flow line from the dome of

Fig.4. Age profile at the dome of a symmetrical, isothermal, steady-state ice sheet (1). The age profiles resulting from Raymond’s (1983) linear strain-rate distribution (2). and Nye’s (1963) uniform strain-rate distribution (3) are also shown for comparison.

Devon Island Ice Cap along a divide (ridge), with low surface slope and through a bore-hole location off the ridge, shows good agreement between observations and the predicted surface-profile and strain-rate variations along the ridge. Also, the observed depth profiles of the horizontal and vertical velocities at the drill site are reasonably well predicted by the model. The details of this study are presented elsewhere (Reeh and Paterson, 1988).

Moreover, there are several “spin-offs” from the model that seem to deserve more detailed investigation:

1. The curvilinear coordinate system with horizontal axes along flow lines and surface-elevation contours, respectively, is very suitable for studying the dynamics of ice flow at domes displaying various degrees of divergence, ranging from the conditions prevailing at a circular dome (έ_y/έ_x = I) to those prevailing at a straight horizontal ice divide (έ_y/έ_x= 0) and, similarly, for studying the dynamics of ice flow near a saddle point with negative έ_y/έ_xratios.

2. Horizontal shear in ice-sheet flow can also be studied profitably by applying the curvilinear coordinate system.

3. The model also provides explicit expressions for the depth distributions of the vertical velocity, the strain-rates, and stresses at the dome with due consideration of the temperature profile and possible enhanced flow. This opens up for study the annual-layer thickness and age profiles at the dome, and even considering the influence of time variations of ice temperature, ice thickness, accumulation rate, and enhancement factor on these profiles.

4. The model indicates how to improve the established method of deriving ice-flow-law parameters from flow-line data by considering the hitherto neglected influence of changing velocity-depth profiles along the flow line.

6. Acknowledgements

A large part of the flow-line model was developed while I was employed at the Department of Glaciology, Geophysical Institute, University of Copenhagen, and was sponsored by the Danish Commission for Scientific Research in Greenland, the Danish Natural Science Research Council, and the Commission of the European Communities under contract CLI-067-DK(G). I wish to thank W.S.B. Paterson for many critical comments on an early version of the manuscript, and C Raymond for his review that resulted in many improvements.