Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-16T07:25:35.219Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE SYMMETRIC SQUARES OF COMPLEX AND QUATERNIONIC PROJECTIVE SPACE

Part of: Fiber spaces and bundles Operations and obstructions

Published online by Cambridge University Press:  13 February 2018

YUMI BOOTE  and
NIGEL RAY
YUMI BOOTE
Affiliation:
School of Mathematics, University of Manchester, Oxford Road, Manchester M13 9PL, England e-mail: [email protected], [email protected]
NIGEL RAY
Affiliation:
School of Mathematics, University of Manchester, Oxford Road, Manchester M13 9PL, England e-mail: [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The problem of computing the integral cohomology ring of the symmetric square of a topological space has long been of interest, but limited progress has been made on the general case until recently. We offer a solution for the complex and quaternionic projective spaces 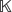$\mathbb{K}$Pn, by utilising their rich geometrical structure. Our description involves generators and relations, and our methods entail ideas from the literature of quantum chemistry, theoretical physics, and combinatorics. We begin with the case 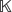$\mathbb{K}$P∞, and then identify the truncation required for passage to finite n. The calculations rely upon a ladder of long exact cohomology sequences, which compares cofibrations associated to the diagonals of the symmetric square and the corresponding Borel construction. These incorporate the one-point compactifications of classic configuration spaces of unordered pairs of points in 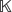$\mathbb{K}$Pn, which are identified as Thom spaces by combining Löwdin's symmetric orthogonalisation (and its quaternionic analogue) with a dash of Pin geometry. The relations in the ensuing cohomology rings are conveniently expressed using generalised Fibonacci polynomials. Our conclusions are compatible with those of Gugnin mod torsion and Nakaoka mod 2, and with homological results of Milgram.

MSC classification

Primary: 55S15: Symmetric products, cyclic products
Secondary: 55R40: Homology of classifying spaces, characteristic classes 55R80: Discriminantal varieties, configuration spaces
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 60 , Issue 3 , September 2018 , pp. 703 - 729
Copyright
Copyright © Glasgow Mathematical Journal Trust 2018 

References

REFERENCES

1. Adem, A., Leida, J. and Ruan, Y., Orbifolds and stringy topology, Cambridge tracts in mathematics, vol. 171 (Cambridge University Press, Cambridge, UK, 2007).Google Scholar
2. Aguilar, M. A. and Prieto, C., A classification of cohomology transfers for ramified covering maps, Fund. Math. 189 (1) (2006), 1–25.Google Scholar
3. Amdeberhan, T., Chen, X., Moll, V. and Sagan, B., Generalized Fibonacci polynomials and Fibonomial coefficients, Ann. Comb. 18 (4) (2014), 541–562.Google Scholar
4. Bakuradze, M., The transfer and symplectic cobordism, Trans. Am. Math. Soc. 349 (11) (1997), 4385–4399.Google Scholar
5. Berg, M., DeWitt-Morette, C., Gwo, S. and Kramer, E., The Pin groups in physics: C, P, and T, Rev. Math. Phys. 13 (08) (2001), 953–1034.Google Scholar
6. Boote, Y., On the symmetric square of quaternionic projective space, PhD Thesis, (University of Manchester, 2016).Google Scholar
7. Boote, Y. and Ray, N., On the symmetric squares of complex and quaternionic projective space, arXiv:1603.02066v2 [math.AT] (2016).Google Scholar
8. Boote, Y. and Ray, N., Compactifications of configuration spaces of pairs; even spaces and the octonionic projective plane, in preparation.Google Scholar
9. Borisov, L., Halpern, M. B. and Schweigert, C., Systematic approach to cyclic orbifolds, Int. J. Modern Phys. A 13 (1998), 125–168.CrossRefGoogle Scholar
10. Bredon, G. E., Introduction to compact transformation groups, Pure and applied mathematics, vol. 46 (Academic Press, New York and London, 1972).Google Scholar
11. Cadek, M., The cohomology of BO(n) with twisted integer coefficients, J. Math. Kyoto Univ. 39 (2) (1999), 277–286.Google Scholar
12. Cartan, H. and Eilenberg, S., Homological algebra, Princeton mathematical series, vol. 19 (Princeton University Press, Princeton, New Jersey, 1956).Google Scholar
13. Dold, A., Lectures on algebraic topology, Classics in mathematics (Springer-Verlag, Berlin, Heidelberg, 1995).CrossRefGoogle Scholar
14. Dold, A. and Thom, R., Quasifaserungen und unendliche symmetrische produkte, Ann. Math. 67 (2) (1958), 239–281.Google Scholar
15. Dominguez, C., Gonzalez, J., and Landweber, P., The integral cohomology of configuration spaces of pairs of points in real projective spaces, Forum Math. 25 (2013), 1217–1248.Google Scholar
16. Feder, S., The reduced symmetric product of projective spaces and the generalized Whitney Theorem, Illinois J. Math. 16 (2) (1972), 323–329.Google Scholar
17. Gould, H. W., A history of the Fibonacci Q-matrix and a higher-dimensional problem, Fibonacci Quart. 19 (3) (1981), 250–257.Google Scholar
18. Gugnin, D. V.. On the integral cohomology ring of symmetric products. arXiv:1502.01862v3 [math.AT] (2015).Google Scholar
19. Hambleton, I., Kreck, M. and Teichner, P., Nonorientable 4-manifolds with fundamental group of order 2, Trans. Am. Math. Soc. 344 (2) (1994), 649–665.Google Scholar
20. Husemoller, D., Fiber bundles, 3rd ed. Graduate texts in mathematics (Springer-Verlag, New York, 1994).Google Scholar
21. Jacobsthal, E., Fibonaccische Polynome und Kreisteilungsgleichungen, Sitzungsberichte Berl. Math. Ges. 17 (1919–1920), 43–57.Google Scholar
22. James, I., Thomas, E., Toda, H. and Whitehead, G. W., The symmetric square of a sphere, J. Math. Mech 12 (5)(1963), 771–776.Google Scholar
23. Kallel, S., Symmetric products, duality and homological dimension of configuration spaces, Geom. Topol. Monogr. 13 (2008), 499–527.CrossRefGoogle Scholar
24. Kallel, S. and Karoui, R., Symmetric joins and weighted barycenters, Adv. Nonlinear Stud. 11 (2011), 117–143.Google Scholar
25. Kallel, S. and Taamallah, W., The geometry and fundamental group of permutation products and fat diagonals, Canad. J. Math. 65 (3) (2013), 575–599.Google Scholar
26. Kirby, R. and Taylor, L., Pin structures on low dimensional manifolds, Geometry of low dimensional manifolds 2 (Durham, 1989), London Mathematical Society lecture note series, vol. 151 (Cambridge University Press, Cambridge, UK, 1990), 177–242.Google Scholar
27. Löwdin, P.-O., On the non-orthogonality problem connected with the use of atomic wave functions in the theory of molecules and crystals, J. Chem. Phys. 18 (3) (1950), 365–375.Google Scholar
28. Milgram, R. J., The homology of symmetric products, Trans. Am. Math. Soc. 138 (1969), 251–265.Google Scholar
29. Mimura, M. and Toda, H., Topology of Lie groups I and II, Translations of mathematical monographs, vol. 91 (American Mathematical Society, Providence, Rhode Island, 1991).Google Scholar
30. Mitchell, S. A., Notes on principal bundles and classifying spaces, http://www.math.washington.edu/mitchell/Notes/prin.pdf (June 2011).Google Scholar
31. Mitchell, S. A. and Priddy, S. B., Symmetric product spectra and splittings of classifying spaces, Am. J. Math. 106 (1) (1984), 219–232.Google Scholar
32. Morse, M., The calculus of variations in the large, American Mathematical Society, vol. 18 (Colloquium Publications, 1934). Current edition, 2012.CrossRefGoogle Scholar
33. Nakaoka, M., Cohomology of the p-fold cyclic products, Proc. Japan Acad. 31 (10) (1955), 665–669.Google Scholar
34. Nakaoka, M., Cohomology theory of a complex with a transformation of prime period and its applications, J. Inst. Poly. Osaka City Univ. Ser. A, Math. 7 (1–2) (1956) 51–102.Google Scholar
35. Nakaoka, M., Decomposition theorem for homology groups of symmetric groups, Ann. Math. 71 (1) (1960), 16–42.Google Scholar
36. Porteous, I. R., Clifford algebras and the classical groups, Cambridge studies in advanced mathematics, volume 50 (Cambridge University Press, Cambridge, UK, 1995).Google Scholar
37. Roush, F. W., On some torsion classes in symplectic cobordism, preprint (1972).Google Scholar
38. Smith, L., Transfer and ramified coverings, Math. Proc. Cambridge Philos. Soc. 93 (1983), 485–493.Google Scholar
39. Steenrod, N. E. and Epstein, D. B. A., Cohomology operations, Annals of Mathematics studies, vol. 50 (Princeton University Press, Princeton, New Jersey, 1962).Google Scholar
40. Totaro, B., The integral cohomology of the Hilbert scheme of two points, Forum Math. Sigma 4 (2016), e8, 22pp.Google Scholar
41. Yasui, T., The reduced symmetric product of a complex projective space and the embedding problem. Hiroshima Math. J. 1 (1971), 27–40.Google Scholar
42. Zhang, F., Quaternions and matrices of quaternions, Linear Algebra Appl. 251 (1997), 21–57.Google Scholar