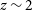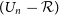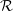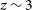1. Introduction
One of the most important and well-studied populations of early star-forming galaxies (SFGs) are the so-called Lyman break galaxies (LBGs) that can be selected based on their rest-frame ultraviolet (UV) colours using as few as three broadband optical filters. The generic Lyman break selection method uses broadband optical photometry sensitive to the discontinuity (‘break’ or ‘drop-out’) in the rest-frame UV spectrum of SFGs blueward of the Lyman limit (912 Å), the decrement in flux in the Lyman-
![]() $\alpha$
forest blueward of the Lyman-
$\alpha$
forest blueward of the Lyman-
![]() $\alpha$
spectral feature (Ly
$\alpha$
spectral feature (Ly
![]() $\alpha$
, 1216 Å), and the relatively flat rest-frame UV continuum redward of Ly
$\alpha$
, 1216 Å), and the relatively flat rest-frame UV continuum redward of Ly
![]() $\alpha$
to efficiently select LBGs in large numbers, on large scales, and across a wide range of redshift pathlengths.
$\alpha$
to efficiently select LBGs in large numbers, on large scales, and across a wide range of redshift pathlengths.
A notable strength of the Lyman break technique is its ability to isolate populations of LBGs at specific redshifts by sampling with different broadband filter combinations. The classic Lyman break technique has been effective at assembling large samples of LBGs in the range
![]() $z\sim3-5$
where the Lyman limit falls at optical wavelengths (e.g., Steidel et al. Reference Steidel2003; Ouchi et al. Reference Ouchi2004; Giavalisco et al. Reference Giavalisco2004; Verma et al. Reference Verma, Lehnert, Förster Schreiber, Bremer and Douglas2007; Iwata et al. Reference Iwata2007; Pentericci et al. Reference Pentericci2010; Bielby et al. Reference Bielby2011; Oteo et al. Reference Oteo2013a; Álvarez-Márquez et al. Reference Álvarez-Márquez2016; Malkan et al. Reference Malkan2017), and the use of space-based observatories has extended the Lyman limit detection window as low as
$z\sim3-5$
where the Lyman limit falls at optical wavelengths (e.g., Steidel et al. Reference Steidel2003; Ouchi et al. Reference Ouchi2004; Giavalisco et al. Reference Giavalisco2004; Verma et al. Reference Verma, Lehnert, Förster Schreiber, Bremer and Douglas2007; Iwata et al. Reference Iwata2007; Pentericci et al. Reference Pentericci2010; Bielby et al. Reference Bielby2011; Oteo et al. Reference Oteo2013a; Álvarez-Márquez et al. Reference Álvarez-Márquez2016; Malkan et al. Reference Malkan2017), and the use of space-based observatories has extended the Lyman limit detection window as low as
![]() $z\sim1$
(e.g., Burgarella et al. Reference Burgarella2006; Ly et al. Reference Ly2009; Basu-Zych et al. Reference Basu-Zych, Hornschemeier, Hoversten, Lehmer and Gronwall2011; Haberzettl et al. Reference Haberzettl, Williger, Lehnert, Nesvadba and Davies2012; Oteo et al. Reference Oteo2013b, Reference Oteo2014; Hathi et al. Reference Hathi2013). Modified selection methods exploiting the Lyman-
$z\sim1$
(e.g., Burgarella et al. Reference Burgarella2006; Ly et al. Reference Ly2009; Basu-Zych et al. Reference Basu-Zych, Hornschemeier, Hoversten, Lehmer and Gronwall2011; Haberzettl et al. Reference Haberzettl, Williger, Lehnert, Nesvadba and Davies2012; Oteo et al. Reference Oteo2013b, Reference Oteo2014; Hathi et al. Reference Hathi2013). Modified selection methods exploiting the Lyman-
![]() $\alpha$
break that dominates the rest-frame UV at redshifts
$\alpha$
break that dominates the rest-frame UV at redshifts
![]() $z\gtrsim5$
have successfully isolated large samples of LBGs at redshifts up to
$z\gtrsim5$
have successfully isolated large samples of LBGs at redshifts up to
![]() $z\sim10$
(e.g., Bouwens et al. Reference Bouwens, Illingworth, Blakeslee and Franx2006, Reference Bouwens2010, Reference Bouwens2015; McLure et al. Reference McLure2011; Ellis et al. Reference Ellis2013; Finkelstein Reference Finkelstein2016; Harikane et al. Reference Harikane2018, Reference Harikane2022b), and the redshift-dependent line blanketing by the Ly
$z\sim10$
(e.g., Bouwens et al. Reference Bouwens, Illingworth, Blakeslee and Franx2006, Reference Bouwens2010, Reference Bouwens2015; McLure et al. Reference McLure2011; Ellis et al. Reference Ellis2013; Finkelstein Reference Finkelstein2016; Harikane et al. Reference Harikane2018, Reference Harikane2022b), and the redshift-dependent line blanketing by the Ly
![]() $\alpha$
forest, in combination with the relatively flat rest-frame UV continuum, has been used to select LBGs in the range
$\alpha$
forest, in combination with the relatively flat rest-frame UV continuum, has been used to select LBGs in the range
![]() $1.4 < z < 2.7$
at which redshifts the Lyman limit is not observable from the ground (Adelberger et al. Reference Adelberger2004; Steidel et al. Reference Steidel2004).
$1.4 < z < 2.7$
at which redshifts the Lyman limit is not observable from the ground (Adelberger et al. Reference Adelberger2004; Steidel et al. Reference Steidel2004).
This feature of the Lyman break selection technique makes it particularly important in terms of the legacy value of the current generation of deep, wide, optical, and near-infrared imaging surveys. Large-area and all-sky optical broadband photometric campaigns such as the Hyper-SuprimeCam Subaru Strategic Program (HSC-SSP: Aihara et al. Reference Aihara2018) and the imminent Vera Rubin Observatory Legacy Survey of Space and Time (LSST: Ivezić et al. Reference Ivezić2019) will exploit the Lyman break technique using 3–6 broadband filters across the rest-frame UV to efficiently and inexpensively select hundreds of millions of galaxies in redshift ranges from
![]() $z\sim2-6$
across many hundreds to thousands of Mpc (e.g., Ono et al. Reference Ono2018; Harikane et al. Reference Harikane2018, Reference Harikane2022b; Wilson & White Reference Wilson and White2019).
$z\sim2-6$
across many hundreds to thousands of Mpc (e.g., Ono et al. Reference Ono2018; Harikane et al. Reference Harikane2018, Reference Harikane2022b; Wilson & White Reference Wilson and White2019).
The Lyman break selection method comes with its own set of selection biases in favour of UV-bright, bluer star-forming galaxies with relatively low dust extinction, resulting in samples that miss a relevant fraction of UV-faint and/or heavily dust-obscured SFGs and passively evolving galaxies, particularly around the peak in cosmic star formation (e.g., Grazian et al. Reference Grazian2007; Ly et al. Reference Ly2011; Shapley Reference Shapley2011; Haberzettl et al. Reference Haberzettl, Williger, Lehnert, Nesvadba and Davies2012; Oteo et al. Reference Oteo2014, Reference Oteo2015). Nevertheless, LBGs are thought to dominate the UV luminosity density, and possibly the global star formation rate (SFR) density, at
![]() $z\sim 2-6$
(e.g., Steidel et al. Reference Steidel, Adelberger, Giavalisco, Dickinson and Pettini1999; Giavalisco et al. Reference Giavalisco2004; Bouwens et al. Reference Bouwens2009; Reddy et al. Reference Reddy2008; Reddy & Steidel Reference Reddy and Steidel2009), and they remain a key target population in recent surveys (e.g., Arrabal Haro et al. Reference Arrabal Haro2018; Ono et al. Reference Ono2018; Toshikawa et al. Reference Toshikawa2018; Harikane et al. 2022a). Moreover, LBGs have been posited as critical populations that meet the demanding requirements of cosmological studies in the era of large-area and all-sky photometric surveys (e.g.,Wilson & White Reference Wilson and White2019; Miyatake et al. Reference Miyatake2022), especially at higher redshifts where only methods based on Ly
$z\sim 2-6$
(e.g., Steidel et al. Reference Steidel, Adelberger, Giavalisco, Dickinson and Pettini1999; Giavalisco et al. Reference Giavalisco2004; Bouwens et al. Reference Bouwens2009; Reddy et al. Reference Reddy2008; Reddy & Steidel Reference Reddy and Steidel2009), and they remain a key target population in recent surveys (e.g., Arrabal Haro et al. Reference Arrabal Haro2018; Ono et al. Reference Ono2018; Toshikawa et al. Reference Toshikawa2018; Harikane et al. 2022a). Moreover, LBGs have been posited as critical populations that meet the demanding requirements of cosmological studies in the era of large-area and all-sky photometric surveys (e.g.,Wilson & White Reference Wilson and White2019; Miyatake et al. Reference Miyatake2022), especially at higher redshifts where only methods based on Ly
![]() $\alpha$
emission or Lyman break detection can be applied in large numbers and over large scales (Finkelstein Reference Finkelstein2016, and references therein).
$\alpha$
emission or Lyman break detection can be applied in large numbers and over large scales (Finkelstein Reference Finkelstein2016, and references therein).
Ly
![]() $\alpha$
has long been pursued as a potential tool to probe the properties of high-redshift SFGs. This endeavour has been motivated by the fact that Ly
$\alpha$
has long been pursued as a potential tool to probe the properties of high-redshift SFGs. This endeavour has been motivated by the fact that Ly
![]() $\alpha$
in absorption and/or emission is the dominant feature in the rest-frame UV spectrum of such galaxies, and is typically much stronger than other diagnostic ISM absorption and emission lines. In addition, there are observational advantages that facilitate deep photometric imaging and spectroscopy in the wavelength range corresponding to Ly
$\alpha$
in absorption and/or emission is the dominant feature in the rest-frame UV spectrum of such galaxies, and is typically much stronger than other diagnostic ISM absorption and emission lines. In addition, there are observational advantages that facilitate deep photometric imaging and spectroscopy in the wavelength range corresponding to Ly
![]() $\alpha$
at
$\alpha$
at
![]() $z\sim2-3$
(Shapley Reference Shapley2011, and references therein)—a cosmologically critical epoch that spans the peak in SFR density (Madau & Dickinson Reference Madau and Dickinson2014, and references therein) and during which more than half of the observable stellar mass of the Universe was assembled (e.g., Ilbert et al. Reference Ilbert2013; Muzzin et al. Reference Muzzin2013). Moreover, Ly
$z\sim2-3$
(Shapley Reference Shapley2011, and references therein)—a cosmologically critical epoch that spans the peak in SFR density (Madau & Dickinson Reference Madau and Dickinson2014, and references therein) and during which more than half of the observable stellar mass of the Universe was assembled (e.g., Ilbert et al. Reference Ilbert2013; Muzzin et al. Reference Muzzin2013). Moreover, Ly
![]() $\alpha$
is the key – and often the only – observable feature in the spectra of Ly
$\alpha$
is the key – and often the only – observable feature in the spectra of Ly
![]() $\alpha$
emitters at the highest redshifts (
$\alpha$
emitters at the highest redshifts (
![]() $z\gtrsim6$
, Finkelstein Reference Finkelstein2016; Ouchi et al. Reference Ouchi, Ono and Shibuya2020, and references therein) and, for this reason, has become critical for our understanding of galaxy populations during the epoch of reionisation, and their contribution to the ionising flux budget of the universe (e.g., Dijkstra Reference Dijkstra2014; Stark et al. Reference Stark2017; Mason et al. Reference Mason2018; Steidel et al. Reference Steidel2018).
$z\gtrsim6$
, Finkelstein Reference Finkelstein2016; Ouchi et al. Reference Ouchi, Ono and Shibuya2020, and references therein) and, for this reason, has become critical for our understanding of galaxy populations during the epoch of reionisation, and their contribution to the ionising flux budget of the universe (e.g., Dijkstra Reference Dijkstra2014; Stark et al. Reference Stark2017; Mason et al. Reference Mason2018; Steidel et al. Reference Steidel2018).
Due to the resonant character of the Ly
![]() $\alpha$
transition, Ly
$\alpha$
transition, Ly
![]() $\alpha$
photons are dispersed in real and frequency space whenever they encounter neutral hydrogen (see Dijkstra Reference Dijkstra2017, for a comprehensive description). The increased scattering and absorption experienced by Ly
$\alpha$
photons are dispersed in real and frequency space whenever they encounter neutral hydrogen (see Dijkstra Reference Dijkstra2017, for a comprehensive description). The increased scattering and absorption experienced by Ly
![]() $\alpha$
photons under the influence of these radiative transfer processes adversely affect the visibility of Ly
$\alpha$
photons under the influence of these radiative transfer processes adversely affect the visibility of Ly
![]() $\alpha$
emission, and complicate its spectroscopic interpretation. However, as a direct result of these same processes, the Ly
$\alpha$
emission, and complicate its spectroscopic interpretation. However, as a direct result of these same processes, the Ly
![]() $\alpha$
signal from the central few kpc of high-redshift galaxies encodes information about the structure, kinematics, and ionisation properties of each galaxy and the interstellar, circumgalactic, and intergalactic media through which it propagates (e.g., Shapley et al. Reference Shapley, Steidel, Pettini and Adelberger2003; Verhamme, Schaerer, & Maselli Reference Verhamme, Schaerer and Maselli2006; Verhamme et al. Reference Verhamme, Schaerer, Atek and Tapken2008; Dijkstra &Wyithe Reference Dijkstra and Wyithe2010; Steidel et al. Reference Steidel2010; Law et al. Reference Law2012a; Hayes Reference Hayes2015; Trainor et al. Reference Trainor, Steidel, Strom and Rudie2015, Reference Trainor2019; Gronke & Dijkstra Reference Gronke and Dijkstra2016; Byrohl & Gronke Reference Byrohl and Gronke2020; Chen et al. Reference Chen2020).
$\alpha$
signal from the central few kpc of high-redshift galaxies encodes information about the structure, kinematics, and ionisation properties of each galaxy and the interstellar, circumgalactic, and intergalactic media through which it propagates (e.g., Shapley et al. Reference Shapley, Steidel, Pettini and Adelberger2003; Verhamme, Schaerer, & Maselli Reference Verhamme, Schaerer and Maselli2006; Verhamme et al. Reference Verhamme, Schaerer, Atek and Tapken2008; Dijkstra &Wyithe Reference Dijkstra and Wyithe2010; Steidel et al. Reference Steidel2010; Law et al. Reference Law2012a; Hayes Reference Hayes2015; Trainor et al. Reference Trainor, Steidel, Strom and Rudie2015, Reference Trainor2019; Gronke & Dijkstra Reference Gronke and Dijkstra2016; Byrohl & Gronke Reference Byrohl and Gronke2020; Chen et al. Reference Chen2020).
Relationships between Ly
![]() $\alpha$
equivalent width (EW) and the spectral and physical properties of early SFGs have been extensively studied in populations of
$\alpha$
equivalent width (EW) and the spectral and physical properties of early SFGs have been extensively studied in populations of
![]() $z=2-4$
LBGs (see for example Shapley et al. Reference Shapley, Steidel, Pettini and Adelberger2003; Reddy et al. Reference Reddy, Steidel, Erb, Shapley and Pettini2006; Erb et al. Reference Erb2006a; Law et al. Reference Law2007; Kornei et al. Reference Kornei2010; Pentericci et al. Reference Pentericci2010; Stark et al. Reference Stark, Ellis, Chiu, Ouchi and Bunker2010; Berry et al. Reference Berry2012; Jones, Stark, & Ellis Reference Jones, Stark and Ellis2012; Law et al. Reference Law2012b,a; Erb et al. Reference Erb2016; Hathi et al. Reference Hathi2016; Trainor et al. Reference Trainor, Strom, Steidel and Rudie2016; Du et al. Reference Du2018; Marchi et al. Reference Marchi2019), and especially recently in samples of the related Lyman-
$z=2-4$
LBGs (see for example Shapley et al. Reference Shapley, Steidel, Pettini and Adelberger2003; Reddy et al. Reference Reddy, Steidel, Erb, Shapley and Pettini2006; Erb et al. Reference Erb2006a; Law et al. Reference Law2007; Kornei et al. Reference Kornei2010; Pentericci et al. Reference Pentericci2010; Stark et al. Reference Stark, Ellis, Chiu, Ouchi and Bunker2010; Berry et al. Reference Berry2012; Jones, Stark, & Ellis Reference Jones, Stark and Ellis2012; Law et al. Reference Law2012b,a; Erb et al. Reference Erb2016; Hathi et al. Reference Hathi2016; Trainor et al. Reference Trainor, Strom, Steidel and Rudie2016; Du et al. Reference Du2018; Marchi et al. Reference Marchi2019), and especially recently in samples of the related Lyman-
![]() $\alpha$
emitters (LAEs) at similar redshifts (e.g., Trainor et al. Reference Trainor, Steidel, Strom and Rudie2015, Reference Trainor2019; Oyarzún et al. Reference Oyarzún, Blanc, González, Mateo and Bailey2017; Guaita et al. Reference Guaita2017; Cullen et al. Reference Cullen2020; Feltre et al. Reference Feltre2020; Santos et al. Reference Santos2020; Matthee et al. Reference Matthee2021). In a systematic study at low redshift (
$\alpha$
emitters (LAEs) at similar redshifts (e.g., Trainor et al. Reference Trainor, Steidel, Strom and Rudie2015, Reference Trainor2019; Oyarzún et al. Reference Oyarzún, Blanc, González, Mateo and Bailey2017; Guaita et al. Reference Guaita2017; Cullen et al. Reference Cullen2020; Feltre et al. Reference Feltre2020; Santos et al. Reference Santos2020; Matthee et al. Reference Matthee2021). In a systematic study at low redshift (
![]() $z\sim0.1$
), the Lyman Alpha Reference Sample collaboration investigated all the quantities thought to be involved in the Ly
$z\sim0.1$
), the Lyman Alpha Reference Sample collaboration investigated all the quantities thought to be involved in the Ly
![]() $\alpha$
transport process (Östlin et al. Reference Östlin2014; Hayes et al. Reference Hayes2014; Pardy et al. Reference Pardy2014; Guaita et al. Reference Guaita2015; Rivera-Thorsen et al. Reference Rivera-Thorsen2015; Duval et al. Reference Duval2016; Herenz et al. Reference Herenz2016; Runnholm et al. Reference Runnholm2020). In both redshift ranges, larger Ly
$\alpha$
transport process (Östlin et al. Reference Östlin2014; Hayes et al. Reference Hayes2014; Pardy et al. Reference Pardy2014; Guaita et al. Reference Guaita2015; Rivera-Thorsen et al. Reference Rivera-Thorsen2015; Duval et al. Reference Duval2016; Herenz et al. Reference Herenz2016; Runnholm et al. Reference Runnholm2020). In both redshift ranges, larger Ly
![]() $\alpha$
emission transmission (or Ly
$\alpha$
emission transmission (or Ly
![]() $\alpha$
EW) was found to be associated with galaxies with bluer UV colours, lower metallicities, lower stellar masses, lower rest-frame UV luminosities, lower star formation rates, harder ionising field strengths, and more compact morphologies. In addition, observed Ly
$\alpha$
EW) was found to be associated with galaxies with bluer UV colours, lower metallicities, lower stellar masses, lower rest-frame UV luminosities, lower star formation rates, harder ionising field strengths, and more compact morphologies. In addition, observed Ly
![]() $\alpha$
emission/absorption strength has been shown to be sensitive to the galactic environment. Not only does Ly
$\alpha$
emission/absorption strength has been shown to be sensitive to the galactic environment. Not only does Ly
![]() $\alpha$
visibility in the early universe reflect the well-established galaxy formation paradigm within which more luminous (massive), older Ly
$\alpha$
visibility in the early universe reflect the well-established galaxy formation paradigm within which more luminous (massive), older Ly
![]() $\alpha$
-absorbing LBGs occupy regions of greater mass overdensity and cluster more strongly than their lower mass, less luminous and younger LAE counterparts (e.g., Ouchi et al. Reference Ouchi2004, Reference Ouchi2010, Reference Ouchi2018; Adelberger et al. Reference Adelberger2005; Jose, Srianand, & Subramanian Reference Jose, Srianand and Subramanian2013; Bielby et al. Reference Bielby2016; Guaita et al. Reference Guaita2017), it is also modulated by the galactic environment on small and large scales (e.g., Cooke et al. Reference Cooke, Berrier, Barton, Bullock and Wolfe2010; Cooke, Omori, & Ryan-Weber Reference Cooke, Omori and Ryan-Weber2013; Díaz et al. 2014; Muldrew, Hatch, & Cooke Reference Muldrew, Hatch and Cooke2015; Toshikawa et al. Reference Toshikawa2016; Lemaux et al. Reference Lemaux2018; Shi et al. Reference Shi2019; Guaita et al. Reference Guaita2020).
$\alpha$
-absorbing LBGs occupy regions of greater mass overdensity and cluster more strongly than their lower mass, less luminous and younger LAE counterparts (e.g., Ouchi et al. Reference Ouchi2004, Reference Ouchi2010, Reference Ouchi2018; Adelberger et al. Reference Adelberger2005; Jose, Srianand, & Subramanian Reference Jose, Srianand and Subramanian2013; Bielby et al. Reference Bielby2016; Guaita et al. Reference Guaita2017), it is also modulated by the galactic environment on small and large scales (e.g., Cooke et al. Reference Cooke, Berrier, Barton, Bullock and Wolfe2010; Cooke, Omori, & Ryan-Weber Reference Cooke, Omori and Ryan-Weber2013; Díaz et al. 2014; Muldrew, Hatch, & Cooke Reference Muldrew, Hatch and Cooke2015; Toshikawa et al. Reference Toshikawa2016; Lemaux et al. Reference Lemaux2018; Shi et al. Reference Shi2019; Guaita et al. Reference Guaita2020).
Such relationships suggest the tantalising prospect of using Ly
![]() $\alpha$
as a multi-purpose tool to elucidate the physical, environmental, and large-scale clustering properties of primordial galaxies. To properly explore these relationships however, large samples that reflect the spectral characteristics of the selected population are necessary and, in most cases, spectroscopic measurement of Ly
$\alpha$
as a multi-purpose tool to elucidate the physical, environmental, and large-scale clustering properties of primordial galaxies. To properly explore these relationships however, large samples that reflect the spectral characteristics of the selected population are necessary and, in most cases, spectroscopic measurement of Ly
![]() $\alpha$
is required in order to extract the physical properties of interest. In an approach that addressed this problem, Cooke (Reference Cooke2009, hereafter C09) reported a method of Ly
$\alpha$
is required in order to extract the physical properties of interest. In an approach that addressed this problem, Cooke (Reference Cooke2009, hereafter C09) reported a method of Ly
![]() $\alpha$
spectral type classification for a population of
$\alpha$
spectral type classification for a population of
![]() $z\sim3$
LBGs by which pure LBG samples displaying either dominant Ly
$z\sim3$
LBGs by which pure LBG samples displaying either dominant Ly
![]() $\alpha$
in absorption (aLBGs) or dominant Ly
$\alpha$
in absorption (aLBGs) or dominant Ly
![]() $\alpha$
in emission (eLBGs) could be isolated using only broadband information. One example of the power of this approach was demonstrated on large scales by Cooke et al. (Reference Cooke, Omori and Ryan-Weber2013, hereafter C13) who performed an auto- and cross-correlation function analysis of pure aLBG and eLBG samples photometrically selected from
$\alpha$
in emission (eLBGs) could be isolated using only broadband information. One example of the power of this approach was demonstrated on large scales by Cooke et al. (Reference Cooke, Omori and Ryan-Weber2013, hereafter C13) who performed an auto- and cross-correlation function analysis of pure aLBG and eLBG samples photometrically selected from
![]() $\sim$
55000
$\sim$
55000
![]() $z\sim3$
LBGs. C13 found that aLBGs preferentially reside in group and cluster environments, eLBGs reside on the outskirts of groups and in the field, the two spectral types avoid each other on small, single halo scales, and that without accounting for the anti-correlation between aLBGs and eLBGs, masses for LBG populations were underestimated.
$z\sim3$
LBGs. C13 found that aLBGs preferentially reside in group and cluster environments, eLBGs reside on the outskirts of groups and in the field, the two spectral types avoid each other on small, single halo scales, and that without accounting for the anti-correlation between aLBGs and eLBGs, masses for LBG populations were underestimated.
One motivation for this paper is to extend the method developed by C09 to other redshifts, especially to
![]() $z\sim2$
, where the availability of a statistical sample of LBGs with consistent multi-band rest-frame UV broadband photometry, uniformly measured net Ly
$z\sim2$
, where the availability of a statistical sample of LBGs with consistent multi-band rest-frame UV broadband photometry, uniformly measured net Ly
![]() $\alpha$
EWs, and kinematic classifications quantitatively determined from IFU-based spectroscopy, prompted the investigation of the relationship between Ly
$\alpha$
EWs, and kinematic classifications quantitatively determined from IFU-based spectroscopy, prompted the investigation of the relationship between Ly
![]() $\alpha$
spectral type and galaxy kinematics described in Paper II in this series (Foran et al. 2023b, submitted).
$\alpha$
spectral type and galaxy kinematics described in Paper II in this series (Foran et al. 2023b, submitted).
More broadly, we aim to develop a method that can be applied to large samples of
![]() $z\sim2-6$
LBGs selected from current and future large-area and all-sky photometric campaigns. The current generation of deep, large-area photometric surveys such as HSC-SSP and LSST will probe cosmic volumes and transverse areas on scales that transcend the cosmic variance of even the largest legacy fields (see e.g., Arcila-Osejo & Sawicki Reference Arcila-Osejo and Sawicki2013). The challenge for spectroscopy and targeted deep multiband/multiwavelength imaging is the huge datasets that will derive from surveys conducted on such scales; in the LSST 10-yr data for example, there will be 20 billion sources that will need to be processed in order to identify hundreds of millions of high-redshift galaxies. Optimising the discovery potential of these investments requires new techniques to statistically characterise the huge datasets they will deliver, and to efficiently select from these the most promising samples for expensive follow-up observations. Here we explore how inexpensive broadband photometric information that is sensitive to the Ly
$z\sim2-6$
LBGs selected from current and future large-area and all-sky photometric campaigns. The current generation of deep, large-area photometric surveys such as HSC-SSP and LSST will probe cosmic volumes and transverse areas on scales that transcend the cosmic variance of even the largest legacy fields (see e.g., Arcila-Osejo & Sawicki Reference Arcila-Osejo and Sawicki2013). The challenge for spectroscopy and targeted deep multiband/multiwavelength imaging is the huge datasets that will derive from surveys conducted on such scales; in the LSST 10-yr data for example, there will be 20 billion sources that will need to be processed in order to identify hundreds of millions of high-redshift galaxies. Optimising the discovery potential of these investments requires new techniques to statistically characterise the huge datasets they will deliver, and to efficiently select from these the most promising samples for expensive follow-up observations. Here we explore how inexpensive broadband photometric information that is sensitive to the Ly
![]() $\alpha$
properties of LBGs might be used to address these challenges, and suggest a means by which the Ly
$\alpha$
properties of LBGs might be used to address these challenges, and suggest a means by which the Ly
![]() $\alpha$
-related physical and spectroscopic properties and environments of
$\alpha$
-related physical and spectroscopic properties and environments of
![]() $z\sim2-3$
LBGs might be explored on the basis of broadband photometric information alone.
$z\sim2-3$
LBGs might be explored on the basis of broadband photometric information alone.
In this paper we demonstrate a statistical relationship between net Ly
![]() $\alpha$
EW and the optical broadband photometric properties of
$\alpha$
EW and the optical broadband photometric properties of
![]() $z\sim2$
LBGs. We characterise the segregation of spectroscopic Ly
$z\sim2$
LBGs. We characterise the segregation of spectroscopic Ly
![]() $\alpha$
-absorbing, and Ly
$\alpha$
-absorbing, and Ly
![]() $\alpha$
-emitting spectral types in colour-magnitude space, and define photometric criteria by which pure sub-samples of LBGs with Ly
$\alpha$
-emitting spectral types in colour-magnitude space, and define photometric criteria by which pure sub-samples of LBGs with Ly
![]() $\alpha$
dominant in absorption (p-aLBGs), and Ly
$\alpha$
dominant in absorption (p-aLBGs), and Ly
![]() $\alpha$
dominant in emission (p-eLBGs), can be selected using only broadband imaging data. As a first step toward the application of our approach to large-area and all-sky surveys, we also present here a set of ugrizy photometric selection criteria by which pure samples of p-aLBGs and p-eLBGs might be isolated from datasets derived from the LSST.
$\alpha$
dominant in emission (p-eLBGs), can be selected using only broadband imaging data. As a first step toward the application of our approach to large-area and all-sky surveys, we also present here a set of ugrizy photometric selection criteria by which pure samples of p-aLBGs and p-eLBGs might be isolated from datasets derived from the LSST.
This paper is structured as follows: in Section 2, we present the photometric and spectroscopic data used in the subsequent sections. Section 3 describes the segregation versus net Ly
![]() $\alpha$
EW of
$\alpha$
EW of
![]() $z\sim2$
LBGs in colour-magnitude space, and the application of this result to determine criteria for the selection of photometric Ly
$z\sim2$
LBGs in colour-magnitude space, and the application of this result to determine criteria for the selection of photometric Ly
![]() $\alpha$
spectral type sub-samples. We summarise the important conclusions and potential applications of this work in Section 4. We assume a
$\alpha$
spectral type sub-samples. We summarise the important conclusions and potential applications of this work in Section 4. We assume a
![]() $\Lambda$
CDM cosmology with
$\Lambda$
CDM cosmology with
![]() $\Omega_{M}$
= 0.3,
$\Omega_{M}$
= 0.3,
![]() $\Omega_{\Lambda}$
= 0.7 and H
$\Omega_{\Lambda}$
= 0.7 and H
![]() $_{0}$
= 70 km s
$_{0}$
= 70 km s
![]() $^{-1}$
Mpc
$^{-1}$
Mpc
![]() $^{-1}$
. All magnitudes are quoted in the AB system of Oke & Gunn (Reference Oke and Gunn1983).
$^{-1}$
. All magnitudes are quoted in the AB system of Oke & Gunn (Reference Oke and Gunn1983).
2. Data
Broadband optical photometry and rest-frame net Ly
![]() $\alpha$
equivalent width (hereafter ‘net Ly
$\alpha$
equivalent width (hereafter ‘net Ly
![]() $\alpha$
EW’) data for a sample of 557 rest-frame UV colour-selected
$\alpha$
EW’) data for a sample of 557 rest-frame UV colour-selected
![]() $z\sim2$
galaxies in the redshift range 1.7
$z\sim2$
galaxies in the redshift range 1.7
![]() $<z<$
2.5 were extracted from the spectroscopic catalog of Steidel et al. (Reference Steidel2004), Reddy et al. (Reference Reddy2008). Similarly, we make use of the rest-frame net Ly
$<z<$
2.5 were extracted from the spectroscopic catalog of Steidel et al. (Reference Steidel2004), Reddy et al. (Reference Reddy2008). Similarly, we make use of the rest-frame net Ly
![]() $\alpha$
EW measurements of Shapley et al. (Reference Shapley, Steidel, Pettini and Adelberger2003) for a sample of 775 LBGs in the redshift range
$\alpha$
EW measurements of Shapley et al. (Reference Shapley, Steidel, Pettini and Adelberger2003) for a sample of 775 LBGs in the redshift range
![]() $2.5 <z< 3.5$
drawn from the catalog of Steidel et al. (Reference Steidel2003). Values for net Ly
$2.5 <z< 3.5$
drawn from the catalog of Steidel et al. (Reference Steidel2003). Values for net Ly
![]() $\alpha$
EW – which incorporate information about Ly
$\alpha$
EW – which incorporate information about Ly
![]() $\alpha$
in both emission and absorption – were measured uniformly across both redshift ranges in their respective source studies using the method described by Kornei et al. (Reference Kornei2010) Typical uncertainties in absolute Ly
$\alpha$
in both emission and absorption – were measured uniformly across both redshift ranges in their respective source studies using the method described by Kornei et al. (Reference Kornei2010) Typical uncertainties in absolute Ly
![]() $\alpha$
EW are
$\alpha$
EW are
![]() $\sim$
25–50% for galaxies with absorption profiles, and
$\sim$
25–50% for galaxies with absorption profiles, and
![]() $\sim$
25% for galaxies with Ly
$\sim$
25% for galaxies with Ly
![]() $\alpha$
dominant in emission (Shapley et al. Reference Shapley, Steidel, Pettini and Adelberger2003).
$\alpha$
dominant in emission (Shapley et al. Reference Shapley, Steidel, Pettini and Adelberger2003).
The parent catalogs of the
![]() $z\sim2$
and
$z\sim2$
and
![]() $z\sim3$
samples derive from an observational campaign that targeted 14 uncorrelated fields with a total survey area of 1 900 arcmin
$z\sim3$
samples derive from an observational campaign that targeted 14 uncorrelated fields with a total survey area of 1 900 arcmin
![]() $^{2}$
, resulting in samples that are minimally affected by systematic biases due to cosmic variance or clustering. The survey used the
$^{2}$
, resulting in samples that are minimally affected by systematic biases due to cosmic variance or clustering. The survey used the
![]() $U_nG\mathcal{R}$
photometric system (Steidel et al. Reference Steidel2003), and the rest-frame UV colour selection criteria of Steidel et al. (Reference Steidel2003) (
$U_nG\mathcal{R}$
photometric system (Steidel et al. Reference Steidel2003), and the rest-frame UV colour selection criteria of Steidel et al. (Reference Steidel2003) (
![]() $z\sim3$
LBGs) and Steidel et al. (Reference Steidel2004) (
$z\sim3$
LBGs) and Steidel et al. (Reference Steidel2004) (
![]() $z\sim2$
BX galaxies). These criteria were designed to recover objects with intrinsic properties, particularly UV luminosity and reddening by dust, that were similar across both redshift ranges. Accordingly, and although the
$z\sim2$
BX galaxies). These criteria were designed to recover objects with intrinsic properties, particularly UV luminosity and reddening by dust, that were similar across both redshift ranges. Accordingly, and although the
![]() $z\sim2$
BX selection method does not probe the Lyman break, we henceforth refer to both samples as ‘LBGs’. These selection criteria result in a net Ly
$z\sim2$
BX selection method does not probe the Lyman break, we henceforth refer to both samples as ‘LBGs’. These selection criteria result in a net Ly
![]() $\alpha$
EW distribution for the
$\alpha$
EW distribution for the
![]() $\mathcal{R}$
$\mathcal{R}$
![]() $<$
25.5 samples that is representative of the intrinsic distribution for the parent population of galaxies (Reddy et al. Reference Reddy2008). The mean redshift of our extracted
$<$
25.5 samples that is representative of the intrinsic distribution for the parent population of galaxies (Reddy et al. Reference Reddy2008). The mean redshift of our extracted
![]() $z\sim2$
sample is z = 2.16
$z\sim2$
sample is z = 2.16
![]() $\pm 0.20$
, corresponding to a mean absolute magnitude sensitivity 0.58 mag fainter in the observed
$\pm 0.20$
, corresponding to a mean absolute magnitude sensitivity 0.58 mag fainter in the observed
![]() $\mathcal{R}$
-band imaging than at z = 2.96, the mean redshift of the
$\mathcal{R}$
-band imaging than at z = 2.96, the mean redshift of the
![]() $z\sim$
3 LBG sample.
$z\sim$
3 LBG sample.
The bulk of galaxies in the
![]() $z\sim2$
LBG sample have stellar masses in the range
$z\sim2$
LBG sample have stellar masses in the range
![]() $9 \lesssim \mathrm{log}({M}_{\star }/{M}_{\odot }) \lesssim 11$
(Shapley et al. Reference Shapley2005; Erb et al. Reference Erb2006b; Reddy et al. Reference Reddy, Steidel, Erb, Shapley and Pettini2006; Reddy & Steidel Reference Reddy and Steidel2009) and star formation rates inferred from rest-frame UV luminosities (uncorrected for extinction) in the range
$9 \lesssim \mathrm{log}({M}_{\star }/{M}_{\odot }) \lesssim 11$
(Shapley et al. Reference Shapley2005; Erb et al. Reference Erb2006b; Reddy et al. Reference Reddy, Steidel, Erb, Shapley and Pettini2006; Reddy & Steidel Reference Reddy and Steidel2009) and star formation rates inferred from rest-frame UV luminosities (uncorrected for extinction) in the range
![]() $3 \lesssim \mathrm{M}_{\odot}$
yr
$3 \lesssim \mathrm{M}_{\odot}$
yr
![]() $^{-1} \lesssim 60$
(Steidel et al. Reference Steidel2004). Accordingly, our
$^{-1} \lesssim 60$
(Steidel et al. Reference Steidel2004). Accordingly, our
![]() $z\sim2$
sample is typical of LBGs/SFGs at these redshifts (Álvarez-Márquez et al. Reference Álvarez-Márquez2016, and references therein) and lies with a range of properties (see Reddy et al. Reference Reddy, Steidel, Erb, Shapley and Pettini2006) on the main sequence of stellar mass and star formation rate for
$z\sim2$
sample is typical of LBGs/SFGs at these redshifts (Álvarez-Márquez et al. Reference Álvarez-Márquez2016, and references therein) and lies with a range of properties (see Reddy et al. Reference Reddy, Steidel, Erb, Shapley and Pettini2006) on the main sequence of stellar mass and star formation rate for
![]() $z\sim2$
SFGs (Daddi et al. Reference Daddi2007).
$z\sim2$
SFGs (Daddi et al. Reference Daddi2007).
The
![]() $z\sim2$
parent sample has
$z\sim2$
parent sample has
![]() $\mathcal{R}$
-band apparent magnitudes in the range
$\mathcal{R}$
-band apparent magnitudes in the range
![]() $22.0 < \mathcal{R}$
$22.0 < \mathcal{R}$
![]() $< 25.5$
, corresponding to rest-frame UV luminosities (absolute magnitudes) of
$< 25.5$
, corresponding to rest-frame UV luminosities (absolute magnitudes) of
![]() $-22.6 < \mathrm{M}_{UV} < -19.1$
. The faint end magnitude cut of
$-22.6 < \mathrm{M}_{UV} < -19.1$
. The faint end magnitude cut of
![]() $\mathcal{R}$
$\mathcal{R}$
![]() $\leq 25.5$
was determined by signal-to-noise requirements of the spectroscopic measurements. Given our need for accurate
$\leq 25.5$
was determined by signal-to-noise requirements of the spectroscopic measurements. Given our need for accurate
![]() $(U_n-\mathcal{R})$
colours, and the different
$(U_n-\mathcal{R})$
colours, and the different
![]() $U_n$
-band depths for the fields targeted by Steidel et al. (Reference Steidel2003, Reference Steidel2004), we applied a further (conservative)
$U_n$
-band depths for the fields targeted by Steidel et al. (Reference Steidel2003, Reference Steidel2004), we applied a further (conservative)
![]() $U_n<26.5$
cut to the
$U_n<26.5$
cut to the
![]() $z\sim2$
,
$z\sim2$
,
![]() $U_n$
-band data to ensure that our sample included only the most reliable photometry. Appendix 1 describes the derivation of indicative photometric uncertainties for our
$U_n$
-band data to ensure that our sample included only the most reliable photometry. Appendix 1 describes the derivation of indicative photometric uncertainties for our
![]() $z\sim2$
and
$z\sim2$
and
![]() $z\sim3$
samples.
$z\sim3$
samples.
3. Analysis and results
3.1. Net Ly
 $\alpha$
EW distribution and spectral type classification
$\alpha$
EW distribution and spectral type classification
The profile of Ly
![]() $\alpha$
in the spectrum of high-redshift LBGs manifests in absorption, emission, or a combination of both. In the
$\alpha$
in the spectrum of high-redshift LBGs manifests in absorption, emission, or a combination of both. In the
![]() $z\sim3$
LBG sample of Shapley et al. (Reference Shapley, Steidel, Pettini and Adelberger2003, hereafter S03), for example, the distribution of net Ly
$z\sim3$
LBG sample of Shapley et al. (Reference Shapley, Steidel, Pettini and Adelberger2003, hereafter S03), for example, the distribution of net Ly
![]() $\alpha$
EWs is centred near zero and varies from
$\alpha$
EWs is centred near zero and varies from
![]() $\lesssim$
$\lesssim$
![]() $-$
50 Å to
$-$
50 Å to
![]() $\gtrsim$
$\gtrsim$
![]() $+$
200 Å. Net Ly
$+$
200 Å. Net Ly
![]() $\alpha$
EW values for our 557
$\alpha$
EW values for our 557
![]() $z\sim2$
LBGs span a similar range (
$z\sim2$
LBGs span a similar range (
![]() $-$
85.0 Å to
$-$
85.0 Å to
![]() $+$
108.7 Å) and, like the S03 sample, are asymmetrically dispersed toward higher net Ly
$+$
108.7 Å) and, like the S03 sample, are asymmetrically dispersed toward higher net Ly
![]() $\alpha$
EWs around a median near zero (
$\alpha$
EWs around a median near zero (
![]() $-$
4.42 Å at
$-$
4.42 Å at
![]() $z\sim2$
and
$z\sim2$
and
![]() $+$
0.56 Å at
$+$
0.56 Å at
![]() $z\sim3$
). These similarities, however, belie a change in the shape of the distribution that is evidenced by a shift in the mean net Ly
$z\sim3$
). These similarities, however, belie a change in the shape of the distribution that is evidenced by a shift in the mean net Ly
![]() $\alpha$
EW for the respective full samples from
$\alpha$
EW for the respective full samples from
![]() $+$
10.3 Å at
$+$
10.3 Å at
![]() $z\sim3$
to
$z\sim3$
to
![]() $-$
2.2 Å at
$-$
2.2 Å at
![]() $z\sim2$
.
$z\sim2$
.

Figure 1. Normalised histograms showing the distribution of net Ly
![]() $\alpha$
EWs for
$\alpha$
EWs for
![]() $z\sim3$
(green) and
$z\sim3$
(green) and
![]() $z\sim2$
(gold) LBG samples. Inset: The same distributions plotted with a logarithmic ordinate axis to accentuate the ’tails’ of the Ly
$z\sim2$
(gold) LBG samples. Inset: The same distributions plotted with a logarithmic ordinate axis to accentuate the ’tails’ of the Ly
![]() $\alpha$
EW distributions. Net Ly
$\alpha$
EW distributions. Net Ly
![]() $\alpha$
EWs less than zero are essentially identical between the two populations, while the
$\alpha$
EWs less than zero are essentially identical between the two populations, while the
![]() $z\sim3$
sample has a significantly larger fraction of net Ly
$z\sim3$
sample has a significantly larger fraction of net Ly
![]() $\alpha$
-emitters (see Table 1).
$\alpha$
-emitters (see Table 1).
The changing shape of the net Ly
![]() $\alpha$
EW distribution with redshift is readily apparent in Fig. 1 that shows normalised histogram plots for the
$\alpha$
EW distribution with redshift is readily apparent in Fig. 1 that shows normalised histogram plots for the
![]() $z\sim2$
and
$z\sim2$
and
![]() $z\sim3$
samples. Consistent with the result of Reddy et al. (Reference Reddy2008), we find that the two distributions are very similar at net Ly
$z\sim3$
samples. Consistent with the result of Reddy et al. (Reference Reddy2008), we find that the two distributions are very similar at net Ly
![]() $\alpha$
EWs
$\alpha$
EWs
![]() $\lesssim$
0 Å, but there is a sharp drop off at
$\lesssim$
0 Å, but there is a sharp drop off at
![]() $z\sim2$
toward higher values of net Ly
$z\sim2$
toward higher values of net Ly
![]() $\alpha$
EW that is largely responsible for the difference in overall mean net Ly
$\alpha$
EW that is largely responsible for the difference in overall mean net Ly
![]() $\alpha$
EW between the two samples.
$\alpha$
EW between the two samples.
Table 1. Statistics for sub-samples of
![]() $z\sim2$
and
$z\sim2$
and
![]() $z\sim3$
LBGs divided on the basis of net Ly
$z\sim3$
LBGs divided on the basis of net Ly
![]() $\alpha$
EW.
$\alpha$
EW.

a
![]() $z\sim3$
LBGs from Shapley et al. (Reference Shapley, Steidel, Pettini and Adelberger2003).
$z\sim3$
LBGs from Shapley et al. (Reference Shapley, Steidel, Pettini and Adelberger2003).
bOur
![]() $z\sim2$
sample divided into numerical quartiles.
$z\sim2$
sample divided into numerical quartiles.
cOur
![]() $z\sim2$
sample divided into aLBG,
$z\sim2$
sample divided into aLBG,
![]() $\rm{G_a}$
,
$\rm{G_a}$
,
![]() $\rm{G_e}$
and eLBG Ly
$\rm{G_e}$
and eLBG Ly
![]() $\alpha$
spectral types as per the definitions given in Section 3.1.
$\alpha$
spectral types as per the definitions given in Section 3.1.
dNumber of galaxies.
eFraction of full sample (
![]() $N_{tot}$
) in sub-sample (N).
$N_{tot}$
) in sub-sample (N).
fMean net Ly
![]() $\alpha$
EW for each (sub)sample.
$\alpha$
EW for each (sub)sample.
The utility of dividing a population of rest-frame UV-colour selected galaxies into sub-samples based on observed net Ly
![]() $\alpha$
EW was first demonstrated by S03, and it continues to be a useful approach in the study of relationships between Ly
$\alpha$
EW was first demonstrated by S03, and it continues to be a useful approach in the study of relationships between Ly
![]() $\alpha$
and the physical and spectral properties of LBGs (e.g., Du et al. Reference Du2018; Pahl et al. Reference Pahl2020). In their discovery of the broadband photometric segregation versus Ly
$\alpha$
and the physical and spectral properties of LBGs (e.g., Du et al. Reference Du2018; Pahl et al. Reference Pahl2020). In their discovery of the broadband photometric segregation versus Ly
![]() $\alpha$
EW in the S03 sample, C09 exploited the same approach to derive the method of photometric Ly
$\alpha$
EW in the S03 sample, C09 exploited the same approach to derive the method of photometric Ly
![]() $\alpha$
spectral-type classification (see Section 3.2).
$\alpha$
spectral-type classification (see Section 3.2).
Table 1 shows a comparison of the statistics for our
![]() $z\sim2$
and
$z\sim2$
and
![]() $z\sim3$
LBG samples divided into numerical quartiles on the basis of net Ly
$z\sim3$
LBG samples divided into numerical quartiles on the basis of net Ly
![]() $\alpha$
EW. There is a shift toward more negative mean net Ly
$\alpha$
EW. There is a shift toward more negative mean net Ly
![]() $\alpha$
EW (
$\alpha$
EW (
![]() $\Delta \sim -5$
Å) of the most absorbing quartile at
$\Delta \sim -5$
Å) of the most absorbing quartile at
![]() $z\sim2$
compared to the same quartile at
$z\sim2$
compared to the same quartile at
![]() $z\sim3$
. The two
$z\sim3$
. The two
![]() $z\sim2$
quartiles that span the more Ly
$z\sim2$
quartiles that span the more Ly
![]() $\alpha$
-emitting end of the distribution show a larger (and increasing) shift to lower average net Ly
$\alpha$
-emitting end of the distribution show a larger (and increasing) shift to lower average net Ly
![]() $\alpha$
EW compared to the analogous quartiles of S03 (
$\alpha$
EW compared to the analogous quartiles of S03 (
![]() $\Delta -9.0$
Å and
$\Delta -9.0$
Å and
![]() $\Delta -32.5$
Å for q3 and q4, respectively).
$\Delta -32.5$
Å for q3 and q4, respectively).
Motivated by these observations, and our results showing a relationship between net Ly
![]() $\alpha$
EW and nebular emission-line kinematics (Foran et al. 2023b, submitted), we applied to our
$\alpha$
EW and nebular emission-line kinematics (Foran et al. 2023b, submitted), we applied to our
![]() $z\sim2$
sample the same net Ly
$z\sim2$
sample the same net Ly
![]() $\alpha$
EW cuts used by S03 to generate numerical quartiles at
$\alpha$
EW cuts used by S03 to generate numerical quartiles at
![]() $z\sim3$
. We define the most absorbing fraction of galaxies with net Ly
$z\sim3$
. We define the most absorbing fraction of galaxies with net Ly
![]() $\alpha$
EW
$\alpha$
EW
![]() $\leq$
$\leq$
![]() $-$
10.0 Å as ‘aLBGs’, and the most strongly emitting fraction with net Ly
$-$
10.0 Å as ‘aLBGs’, and the most strongly emitting fraction with net Ly
![]() $\alpha$
EW
$\alpha$
EW
![]() $\geq$
$\geq$
![]() $+$
20.0 Å as ‘eLBGs’. We further divide the remaining LBGs into
$+$
20.0 Å as ‘eLBGs’. We further divide the remaining LBGs into
![]() $\rm{G_a}$
and
$\rm{G_a}$
and
![]() $\rm{G_e}$
spectral types with net Ly
$\rm{G_e}$
spectral types with net Ly
![]() $\alpha$
EWs
$\alpha$
EWs
![]() $-$
10.0 Å
$-$
10.0 Å
![]() $<$
net Ly
$<$
net Ly
![]() $\alpha$
EW
$\alpha$
EW
![]() $<$
0.0 Å and 0.0 Å
$<$
0.0 Å and 0.0 Å
![]() $<$
net Ly
$<$
net Ly
![]() $\alpha$
EW
$\alpha$
EW
![]() $<$
$<$
![]() $+$
20.0 Å, respectively. Table 1 summarises the population statistics of the
$+$
20.0 Å, respectively. Table 1 summarises the population statistics of the
![]() $z\sim2$
sample and our Ly
$z\sim2$
sample and our Ly
![]() $\alpha$
spectral types compared to the
$\alpha$
spectral types compared to the
![]() $z\sim3$
LBGs of S03.
$z\sim3$
LBGs of S03.
Given that we have defined our spectral types using the same net Ly
![]() $\alpha$
EW cuts as S03, it is not surprising that the central (
$\alpha$
EW cuts as S03, it is not surprising that the central (
![]() $\rm{G_a}$
and
$\rm{G_a}$
and
![]() $\rm{G_e}$
) spectral types have mean net Ly
$\rm{G_e}$
) spectral types have mean net Ly
![]() $\alpha$
EWs similar (
$\alpha$
EWs similar (
![]() $\Delta \sim -1$
Å) to the equivalent quartiles (q2 and q3) in the
$\Delta \sim -1$
Å) to the equivalent quartiles (q2 and q3) in the
![]() $z\sim3$
sample. It is noteworthy, however, that despite the overall shift in mean net Ly
$z\sim3$
sample. It is noteworthy, however, that despite the overall shift in mean net Ly
![]() $\alpha$
EW of
$\alpha$
EW of
![]() $\sim -12.5$
Å between the
$\sim -12.5$
Å between the
![]() $z\sim3$
and
$z\sim3$
and
![]() $z\sim2$
samples, the mean net Ly
$z\sim2$
samples, the mean net Ly
![]() $\alpha$
EW of the
$\alpha$
EW of the
![]() $z\sim2$
aLBGs is similarly only
$z\sim2$
aLBGs is similarly only
![]() $\sim -2$
Å more negative than the equivalent S03 quartile, indicative of a compression of the LBG population toward the Ly
$\sim -2$
Å more negative than the equivalent S03 quartile, indicative of a compression of the LBG population toward the Ly
![]() $\alpha$
-absorbing end of the distribution. This behaviour is likely due to the fact that the measured net Ly
$\alpha$
-absorbing end of the distribution. This behaviour is likely due to the fact that the measured net Ly
![]() $\alpha$
EW becomes insensitive to the total absorption once the Ly
$\alpha$
EW becomes insensitive to the total absorption once the Ly
![]() $\alpha$
absorption feature is saturated. That is, beyond that point, any further decrease in measured EW would reflect only the contribution of the damping wings, and depend weakly on increasing HI column density (see Section 3.2 for manifestation of this effect in the broadband imaging data).
$\alpha$
absorption feature is saturated. That is, beyond that point, any further decrease in measured EW would reflect only the contribution of the damping wings, and depend weakly on increasing HI column density (see Section 3.2 for manifestation of this effect in the broadband imaging data).

Figure 2. Illustration of the origin of the colour separation of Lyman break galaxy (LBG) Ly
![]() $\alpha$
spectral types. Left: Plotted are the G and
$\alpha$
spectral types. Left: Plotted are the G and
![]() $\mathcal{R}$
filter transmission curves (Steidel et al. Reference Steidel2003) in green and orange, respectively, shifted to the
$\mathcal{R}$
filter transmission curves (Steidel et al. Reference Steidel2003) in green and orange, respectively, shifted to the
![]() $z\sim3$
rest-frame. Overlaid are the (smoothed) quartile 1 (red, representative of aLBGs) and quartile 4 (blue, representative of eLBGs) composite spectra of Shapley et al. (Reference Shapley, Steidel, Pettini and Adelberger2003). The composite spectra consist of
$z\sim3$
rest-frame. Overlaid are the (smoothed) quartile 1 (red, representative of aLBGs) and quartile 4 (blue, representative of eLBGs) composite spectra of Shapley et al. (Reference Shapley, Steidel, Pettini and Adelberger2003). The composite spectra consist of
![]() $\sim$
200
$\sim$
200
![]() $z\sim3$
LBG spectra with similar Ly
$z\sim3$
LBG spectra with similar Ly
![]() $\alpha$
EW, with the mean values indicated in the legend. The spectra are shown normalised over the G filter to help illustrate the (
$\alpha$
EW, with the mean values indicated in the legend. The spectra are shown normalised over the G filter to help illustrate the (
![]() $G - \mathcal{R}$
) colour difference in the two spectral types for a given G magnitude. The origin of the Ly
$G - \mathcal{R}$
) colour difference in the two spectral types for a given G magnitude. The origin of the Ly
![]() $\alpha$
spectral type photometric segregation on the
$\alpha$
spectral type photometric segregation on the
![]() $(G-\mathcal{R})$
vs
$(G-\mathcal{R})$
vs
![]() $\mathcal{R}$
CMD results from their colour differences based on the UV continuum slope relationship with spectral type and a small (and inverse) contribution from the Ly
$\mathcal{R}$
CMD results from their colour differences based on the UV continuum slope relationship with spectral type and a small (and inverse) contribution from the Ly
![]() $\alpha$
emission/absorption feature and the magnitude differences in spectral type, in that
$\alpha$
emission/absorption feature and the magnitude differences in spectral type, in that
![]() $z\sim3$
aLBGs are brighter on average than eLBGs. Right: Similar to the left plot, but for LBGs at z
$z\sim3$
aLBGs are brighter on average than eLBGs. Right: Similar to the left plot, but for LBGs at z
![]() $\sim$
2. The composite spectra are shown normalised over the
$\sim$
2. The composite spectra are shown normalised over the
![]() $U_n$
filter (violet, see text). Note: the composite spectra and the normalisation are shown for illustrative purposes and extend to 2000Å, rest-frame. However, the UV continuum slopes of quartiles 1 (red) and 4 (blue) maintain a significant difference in
$U_n$
filter (violet, see text). Note: the composite spectra and the normalisation are shown for illustrative purposes and extend to 2000Å, rest-frame. However, the UV continuum slopes of quartiles 1 (red) and 4 (blue) maintain a significant difference in
![]() $\mathcal{R}$
that is sufficient to separate aLBG and eLBG spectral types in (
$\mathcal{R}$
that is sufficient to separate aLBG and eLBG spectral types in (
![]() $U_n - \mathcal{R}$
) colour and
$U_n - \mathcal{R}$
) colour and
![]() $\mathcal{R}$
magnitude on the CMD. Depending on the redshift of z
$\mathcal{R}$
magnitude on the CMD. Depending on the redshift of z
![]() $\sim$
2 LBGs, the Ly
$\sim$
2 LBGs, the Ly
![]() $\alpha$
feature may fall in or out of the
$\alpha$
feature may fall in or out of the
![]() $U_n$
filter (see Section 3.4).
$U_n$
filter (see Section 3.4).
Conversely, the mean net Ly
![]() $\alpha$
EW of the eLBG spectral type sub-sample at
$\alpha$
EW of the eLBG spectral type sub-sample at
![]() $z\sim2$
is
$z\sim2$
is
![]() $\sim -14$
Å more negative than the analogous (most strongly Ly
$\sim -14$
Å more negative than the analogous (most strongly Ly
![]() $\alpha$
-emitting) S03 quartile, and the relative fraction of eLBGs at
$\alpha$
-emitting) S03 quartile, and the relative fraction of eLBGs at
![]() $z\sim2$
is 0.08 compared to 0.25 at
$z\sim2$
is 0.08 compared to 0.25 at
![]() $z\sim3$
– a clear reflection of the lower relative abundance of net Ly
$z\sim3$
– a clear reflection of the lower relative abundance of net Ly
![]() $\alpha$
emitting LBGs in the universe and/or within the LBG selection function at
$\alpha$
emitting LBGs in the universe and/or within the LBG selection function at
![]() $z\sim2$
compared to
$z\sim2$
compared to
![]() $z\sim3$
.
$z\sim3$
.
3.2. Segregation of
 $z\sim$
2 LBGs in colour-magnitude space
$z\sim$
2 LBGs in colour-magnitude space
C09 discovered that over the redshift path
![]() $z \sim 3.0 \pm 0.3$
, the relationship between rest-frame UV continuum slope and net Ly
$z \sim 3.0 \pm 0.3$
, the relationship between rest-frame UV continuum slope and net Ly
![]() $\alpha$
EW leads to a photometric dispersion of LBGs, and an ability to separate LBG spectral types on a broadband colour-magnitude plane based on their net Ly
$\alpha$
EW leads to a photometric dispersion of LBGs, and an ability to separate LBG spectral types on a broadband colour-magnitude plane based on their net Ly
![]() $\alpha$
EW. At
$\alpha$
EW. At
![]() $z\sim3$
, aLBGs are (on average) brighter in
$z\sim3$
, aLBGs are (on average) brighter in
![]() $\mathcal{R}$
magnitude and redder than eLBGs. They separate in
$\mathcal{R}$
magnitude and redder than eLBGs. They separate in
![]() $(G-\mathcal{R})$
colour as a result of the redder UV continuum slopes of aLBGs, combined with an additional small red enhancement as a result of the Ly
$(G-\mathcal{R})$
colour as a result of the redder UV continuum slopes of aLBGs, combined with an additional small red enhancement as a result of the Ly
![]() $\alpha$
absorption in the G-band, as compared to eLBGs with bluer UV continuum slopes, combined with an additional blue enhancement from the Ly
$\alpha$
absorption in the G-band, as compared to eLBGs with bluer UV continuum slopes, combined with an additional blue enhancement from the Ly
![]() $\alpha$
emission in the G-band. Together, these behaviours enable a statistical segregation of the two populations on a
$\alpha$
emission in the G-band. Together, these behaviours enable a statistical segregation of the two populations on a
![]() $(G-\mathcal{R})$
vs
$(G-\mathcal{R})$
vs
![]() $\mathcal{R}$
colour-magnitude diagram (CMD), with subsets containing pure samples of each spectral type. Fig. 2 illustrates the origin of the
$\mathcal{R}$
colour-magnitude diagram (CMD), with subsets containing pure samples of each spectral type. Fig. 2 illustrates the origin of the
![]() $z\sim3$
broadband imaging segregation of Ly
$z\sim3$
broadband imaging segregation of Ly
![]() $\alpha$
-absorbing and Ly
$\alpha$
-absorbing and Ly
![]() $\alpha$
-emitting LBGs that enables the determination of photometric Ly
$\alpha$
-emitting LBGs that enables the determination of photometric Ly
![]() $\alpha$
spectral types.
$\alpha$
spectral types.
To test whether a similar relationship between broadband photometry and net Ly
![]() $\alpha$
EW might exist at
$\alpha$
EW might exist at
![]() $z\sim2$
, we use
$z\sim2$
, we use
![]() $(U_n-\mathcal{R})$
colours and
$(U_n-\mathcal{R})$
colours and
![]() $\mathcal{R}$
-band magnitudes to construct a CMD for our sample of 557
$\mathcal{R}$
-band magnitudes to construct a CMD for our sample of 557
![]() $z \sim2$
LBGs. We use
$z \sim2$
LBGs. We use
![]() $(U_n-\mathcal{R})$
rather than
$(U_n-\mathcal{R})$
rather than
![]() $(U_n-G)$
, to sample the rest-frame UV continuum farther redward of the Ly
$(U_n-G)$
, to sample the rest-frame UV continuum farther redward of the Ly
![]() $\alpha$
feature so as to increase the segregation between the redder-sloped aLBGs and the bluer-sloped eLBGs, and to avoid any possibility of contamination of our redward filter by Ly
$\alpha$
feature so as to increase the segregation between the redder-sloped aLBGs and the bluer-sloped eLBGs, and to avoid any possibility of contamination of our redward filter by Ly
![]() $\alpha$
emission. The separation in wavelengths probed by the
$\alpha$
emission. The separation in wavelengths probed by the
![]() $U_n$
and G filters at
$U_n$
and G filters at
![]() $z\sim2$
is smaller than the separation of the G and
$z\sim2$
is smaller than the separation of the G and
![]() $\mathcal{R}$
filters at
$\mathcal{R}$
filters at
![]() $z\sim3$
(see Fig. 2).
$z\sim3$
(see Fig. 2).
The left panel of Fig. 3 shows the spectroscopic
![]() $z\sim2$
LBG sample dispersed in colour
$z\sim2$
LBG sample dispersed in colour
![]() $(U_n-\mathcal{R})$
and magnitude
$(U_n-\mathcal{R})$
and magnitude
![]() $\mathcal{R}$
, with symbols colour-coded on a red-to-blue gradient according to their measured net Ly
$\mathcal{R}$
, with symbols colour-coded on a red-to-blue gradient according to their measured net Ly
![]() $\alpha$
EW. For visualisation purposes the colour table is scaled to map the range
$\alpha$
EW. For visualisation purposes the colour table is scaled to map the range
![]() $-$
35.0 Å
$-$
35.0 Å
![]() $<$
net Ly
$<$
net Ly
![]() $\alpha$
EW
$\alpha$
EW
![]() $<$
$<$
![]() $+$
40.0 Å which encompasses
$+$
40.0 Å which encompasses
![]() $\gtrsim$
95% of the galaxies in our sample. Plotting the data in this way (i.e., downplaying the colour effect of the few extreme net Ly
$\gtrsim$
95% of the galaxies in our sample. Plotting the data in this way (i.e., downplaying the colour effect of the few extreme net Ly
![]() $\alpha$
EW cases), the bulk of the LBG sample manifests on the CMD as a visible colour gradient from red to blue moving diagonally from roughly the top left to bottom right. The galaxies in our sample with the most negative net Ly
$\alpha$
EW cases), the bulk of the LBG sample manifests on the CMD as a visible colour gradient from red to blue moving diagonally from roughly the top left to bottom right. The galaxies in our sample with the most negative net Ly
![]() $\alpha$
EW (dark red symbols) do not lie at the extreme end of the colour gradient direction as might be expected for a simple monotonic relationship. While they are certainly well within the ‘absorbing’ half of the CMD, they lie toward the centre of the distribution, and approximately along a line orthogonal to the underlying trend. This apparently anomalous behaviour of the most absorbing galaxies in our sample notwithstanding, the overall trend is confirmed by the points labelled s1 to s6 on the colour gradient plot, that indicate the positions of the magnitude and colour distribution means for the numerical sextiles (of
$\alpha$
EW (dark red symbols) do not lie at the extreme end of the colour gradient direction as might be expected for a simple monotonic relationship. While they are certainly well within the ‘absorbing’ half of the CMD, they lie toward the centre of the distribution, and approximately along a line orthogonal to the underlying trend. This apparently anomalous behaviour of the most absorbing galaxies in our sample notwithstanding, the overall trend is confirmed by the points labelled s1 to s6 on the colour gradient plot, that indicate the positions of the magnitude and colour distribution means for the numerical sextiles (of
![]() $\sim$
93 galaxies each) grouped according to their net Ly
$\sim$
93 galaxies each) grouped according to their net Ly
![]() $\alpha$
EW (see Table 2 for a summary of the sextile statistics). The more positive net Ly
$\alpha$
EW (see Table 2 for a summary of the sextile statistics). The more positive net Ly
![]() $\alpha$
EW LBGs (weaker absorption and more emission) show an overall trend toward fainter
$\alpha$
EW LBGs (weaker absorption and more emission) show an overall trend toward fainter
![]() $\mathcal{R}$
-band magnitudes and bluer (
$\mathcal{R}$
-band magnitudes and bluer (
![]() $U_n-\mathcal{R}$
) colours. Indeed, only the most absorbing sextile (s1 in Fig. 3) does not follow this monotonic trend. That being said, the colours and magnitudes of the
$U_n-\mathcal{R}$
) colours. Indeed, only the most absorbing sextile (s1 in Fig. 3) does not follow this monotonic trend. That being said, the colours and magnitudes of the
![]() $z\sim2$
sextiles converge with increasing Ly
$z\sim2$
sextiles converge with increasing Ly
![]() $\alpha$
absorption strength (i.e., from s6 to s1), unlike at
$\alpha$
absorption strength (i.e., from s6 to s1), unlike at
![]() $z\sim3$
, where the mean colours (magnitudes) continue to redden (brighten) monotonically (cf. C09).
$z\sim3$
, where the mean colours (magnitudes) continue to redden (brighten) monotonically (cf. C09).
Table 2. Statistics for the dispersion of
![]() $z\sim2$
LBGs in colour (
$z\sim2$
LBGs in colour (
![]() $U_n-\mathcal{R}$
)—magnitude (
$U_n-\mathcal{R}$
)—magnitude (
![]() $\mathcal{R}$
) space divided into numerical sextiles based on net Ly
$\mathcal{R}$
) space divided into numerical sextiles based on net Ly
![]() $\alpha$
EW.
$\alpha$
EW.

aFull
![]() $z\sim2$
spectroscopic LBG sample (557 galaxies) divided into sextiles of
$z\sim2$
spectroscopic LBG sample (557 galaxies) divided into sextiles of
![]() $\sim$
93 galaxies each.
$\sim$
93 galaxies each.
We can speculate that the ‘off trend’ positions of the strongest Ly
![]() $\alpha$
absorbers on the CMD is a manifestation of the environmental effect proposed by C13 over their intrinsic net Ly
$\alpha$
absorbers on the CMD is a manifestation of the environmental effect proposed by C13 over their intrinsic net Ly
![]() $\alpha$
EWs. In this scenario, the most negative net Ly
$\alpha$
EWs. In this scenario, the most negative net Ly
![]() $\alpha$
EWs observed, with otherwise typical aLBG colour and magnitude, may be a result of their environment near the cores of groups and proto-clusters and the presence of larger column densities of intra-group/cluster neutral gas at or near the systemic velocity of the LBGs along the line of sight (e.g., Muldrew et al. Reference Muldrew, Hatch and Cooke2015; Toshikawa et al. Reference Toshikawa2016; Lemaux et al. Reference Lemaux2018). More prosaically, it is also plausible that this behaviour, and the grouping of the three most absorbing sextiles (s1–s3) on the CMD, is a reflection of the compression of the
$\alpha$
EWs observed, with otherwise typical aLBG colour and magnitude, may be a result of their environment near the cores of groups and proto-clusters and the presence of larger column densities of intra-group/cluster neutral gas at or near the systemic velocity of the LBGs along the line of sight (e.g., Muldrew et al. Reference Muldrew, Hatch and Cooke2015; Toshikawa et al. Reference Toshikawa2016; Lemaux et al. Reference Lemaux2018). More prosaically, it is also plausible that this behaviour, and the grouping of the three most absorbing sextiles (s1–s3) on the CMD, is a reflection of the compression of the
![]() $z\sim2$
sample towards the more negative end of the net Ly
$z\sim2$
sample towards the more negative end of the net Ly
![]() $\alpha$
EW distribution (as described in Section 3.1), combined with the inherently greater uncertainties (25–50%) associated with the net Ly
$\alpha$
EW distribution (as described in Section 3.1), combined with the inherently greater uncertainties (25–50%) associated with the net Ly
![]() $\alpha$
EW measurements for the most absorbing systems (S03) and the inherent photometric scatter (see Appendix 1).
$\alpha$
EW measurements for the most absorbing systems (S03) and the inherent photometric scatter (see Appendix 1).

Figure 3. Rest-frame UV colour
![]() $(U_n-\mathcal{R})$
–magnitude (
$(U_n-\mathcal{R})$
–magnitude (
![]() $\mathcal{R}$
) diagrams (CMDs) for Lyman break galaxies (LBGs) in the redshift range
$\mathcal{R}$
) diagrams (CMDs) for Lyman break galaxies (LBGs) in the redshift range
![]() $1.7<z<2.5$
, and with magnitude cuts of
$1.7<z<2.5$
, and with magnitude cuts of
![]() $\mathcal{R}$
$\mathcal{R}$
![]() $<$
25.5 and
$<$
25.5 and
![]() $U_n$
$U_n$
![]() $<$
26.5. Left:
$<$
26.5. Left:
![]() $z\sim2$
LBGs dispersed in colour-magnitude space with symbols colour-coded on a red-blue gradient according to their measured net Ly
$z\sim2$
LBGs dispersed in colour-magnitude space with symbols colour-coded on a red-blue gradient according to their measured net Ly
![]() $\alpha$
EW. The colour table maps the range
$\alpha$
EW. The colour table maps the range
![]() $-$
35.0 Å
$-$
35.0 Å
![]() $<$
net Ly
$<$
net Ly
![]() $\alpha$
EW
$\alpha$
EW
![]() $<$
$<$
![]() $+$
40.0 Å, which encompasses
$+$
40.0 Å, which encompasses
![]() $\gtrsim$
95% of the sample. Points labelled s1 to s6 indicate the colour and magnitude distribution means of the numerical sextiles of the LBG sample divided on the basis of net Ly
$\gtrsim$
95% of the sample. Points labelled s1 to s6 indicate the colour and magnitude distribution means of the numerical sextiles of the LBG sample divided on the basis of net Ly
![]() $\alpha$
EW. Right: Grey plus (+) marks denote the 557 galaxies in the
$\alpha$
EW. Right: Grey plus (+) marks denote the 557 galaxies in the
![]() $z\sim2$
spectroscopic sample. Galaxies with net Ly
$z\sim2$
spectroscopic sample. Galaxies with net Ly
![]() $\alpha$
EW
$\alpha$
EW
![]() $\leq -10.0$
Å (aLBGs) are overlaid with red squares, and those with net Ly
$\leq -10.0$
Å (aLBGs) are overlaid with red squares, and those with net Ly
![]() $\alpha$
EW
$\alpha$
EW
![]() $\geq +20.0$
Å (eLBGs) are overlaid with blue triangles. The mean value for each distribution is marked with a black cross (X), with aLBG mean indicated by the upper cross and eLBG mean by the lower. The dotted-dashed blue and dashed red lines indicate a 1.5
$\geq +20.0$
Å (eLBGs) are overlaid with blue triangles. The mean value for each distribution is marked with a black cross (X), with aLBG mean indicated by the upper cross and eLBG mean by the lower. The dotted-dashed blue and dashed red lines indicate a 1.5
![]() $\sigma$
dispersion in colour from the primary cut (green line) that divides the aLBG and eLBG distributions, respectively (see text).
$\sigma$
dispersion in colour from the primary cut (green line) that divides the aLBG and eLBG distributions, respectively (see text).
The association between net Ly
![]() $\alpha$
EW and the photometric properties of
$\alpha$
EW and the photometric properties of
![]() $z\sim2$
LBGs suggested by the trend shown in the left panel of Fig. 3, prompts a statistical examination using the Ly
$z\sim2$
LBGs suggested by the trend shown in the left panel of Fig. 3, prompts a statistical examination using the Ly
![]() $\alpha$
spectral type classification scheme described in Section 3.1 and the method demonstrated by C09. In the right panel of Fig. 3 we plot on the CMD the LBG spectral types as described in Section 3.1, i.e., aLBGs with net Ly
$\alpha$
spectral type classification scheme described in Section 3.1 and the method demonstrated by C09. In the right panel of Fig. 3 we plot on the CMD the LBG spectral types as described in Section 3.1, i.e., aLBGs with net Ly
![]() $\alpha$
EW
$\alpha$
EW
![]() $\le-10$
Å and eLBGs with net Ly
$\le-10$
Å and eLBGs with net Ly
![]() $\alpha$
EW
$\alpha$
EW
![]() $\ge +20$
Å, and show that they segregate into two cohesive, albeit overlapping, distributions.
$\ge +20$
Å, and show that they segregate into two cohesive, albeit overlapping, distributions.
We define a primary cut (solid green line) that passes through the midpoint between the mean colour and magnitude values of the aLBG and eLBG distributions (black crosses), and has slope that maximises the difference in mean net Ly
![]() $\alpha$
EW and spectral-type purity between the sub-samples that lie above and below the broken blue and red lines, respectively. These dashed (red) and dotted-dashed (blue) lines indicate an offset of 1.5
$\alpha$
EW and spectral-type purity between the sub-samples that lie above and below the broken blue and red lines, respectively. These dashed (red) and dotted-dashed (blue) lines indicate an offset of 1.5
![]() $\sigma$
in colour dispersion from the primary cut for the aLBG and eLBG distributions, respectively (see Section 3.3.1). Statistics for the segregation of the aLBG and eLBG spectral types shown in the right panel of Fig. 3 are summarised in Table 3 together with (for comparison) the segregation statistics for the
$\sigma$
in colour dispersion from the primary cut for the aLBG and eLBG distributions, respectively (see Section 3.3.1). Statistics for the segregation of the aLBG and eLBG spectral types shown in the right panel of Fig. 3 are summarised in Table 3 together with (for comparison) the segregation statistics for the
![]() $z\sim3$
sample of C09.
$z\sim3$
sample of C09.
Table 3. Statistics for the photometric segregation of Ly
![]() $\alpha$
-absorbing and Ly
$\alpha$
-absorbing and Ly
![]() $\alpha$
-emitting spectral types in
$\alpha$
-emitting spectral types in
![]() $z\sim$
2 and
$z\sim$
2 and
![]() $z\sim$
3 LBGs.
$z\sim$
3 LBGs.

Although the slope and intercept for the
![]() $z\sim2$
segregation quoted in Table 3 are the values that give the maximum difference in mean net Ly
$z\sim2$
segregation quoted in Table 3 are the values that give the maximum difference in mean net Ly
![]() $\alpha$
EW between the photometrically selected sub-samples, the maximum is shallow, asymmetric, and relatively insensitive to the choice of slope. For example, in the optimal case where
$\alpha$
EW between the photometrically selected sub-samples, the maximum is shallow, asymmetric, and relatively insensitive to the choice of slope. For example, in the optimal case where
![]() $c_{\sigma} = 1.25$
(see Section 3.3.1), the maximum difference in mean net Ly
$c_{\sigma} = 1.25$
(see Section 3.3.1), the maximum difference in mean net Ly
![]() $\alpha$
EW is 17.1 Å at a slope of 0.31. We note, however, that the difference in mean net Ly
$\alpha$
EW is 17.1 Å at a slope of 0.31. We note, however, that the difference in mean net Ly
![]() $\alpha$
EW is greater than 16.0 Å for all slopes between 0.17 and 0.40. Thus we might quote an uncertainty (or ‘range of confidence’) of slope =
$\alpha$
EW is greater than 16.0 Å for all slopes between 0.17 and 0.40. Thus we might quote an uncertainty (or ‘range of confidence’) of slope =
![]() $0.31^{+0.09}_{-0.13}$
. within which any choice of slope would result in photometrically selected sub-samples with a difference in mean net Ly
$0.31^{+0.09}_{-0.13}$
. within which any choice of slope would result in photometrically selected sub-samples with a difference in mean net Ly
![]() $\alpha$
EW that is within
$\alpha$
EW that is within
![]() $\sim$
5% of the maximum. Constraining the primary cut to pass through the mid-point of the aLBG and eLBG distribution means similarly gives intercept values in the range
$\sim$
5% of the maximum. Constraining the primary cut to pass through the mid-point of the aLBG and eLBG distribution means similarly gives intercept values in the range
![]() $-6.62^{+3.43}_{-2.30}$
.
$-6.62^{+3.43}_{-2.30}$
.
3.3. Photometric Ly
 $\alpha$
spectral type selection and sub-sample purity
$\alpha$
spectral type selection and sub-sample purity
3.3.1.
 $z\sim2$
LBGs
$z\sim2$
LBGs
Following the method used by C09 at
![]() $z\sim3$
, we use the parameters of the segregated aLBG and eLBG distributions shown in Fig. 3 to isolate sub-samples with Ly
$z\sim3$
, we use the parameters of the segregated aLBG and eLBG distributions shown in Fig. 3 to isolate sub-samples with Ly
![]() $\alpha$
dominant in absorption (‘photometric’ aLBGs, or p-aLBGs) and with Ly
$\alpha$
dominant in absorption (‘photometric’ aLBGs, or p-aLBGs) and with Ly
![]() $\alpha$
dominant in emission (‘photometric’ eLBGs, or p-eLBGs) from the parent
$\alpha$
dominant in emission (‘photometric’ eLBGs, or p-eLBGs) from the parent
![]() $z\sim2$
LBG sample. Invoking the primary cut slope and intercept values from Table 3, and the supplied broadband photometry, the following relationships can be used to extract sub-samples of the desired photometric Ly
$z\sim2$
LBG sample. Invoking the primary cut slope and intercept values from Table 3, and the supplied broadband photometry, the following relationships can be used to extract sub-samples of the desired photometric Ly
![]() $\alpha$
spectral type.
$\alpha$
spectral type.
For p-aLBGs,
and for p-eLBGs,
where
![]() $c_{\sigma}$
is the coefficient of colour standard deviation by which boundaries used to isolate the photometric spectral type sub-samples are offset from the primary cut on the CMD, and
$c_{\sigma}$
is the coefficient of colour standard deviation by which boundaries used to isolate the photometric spectral type sub-samples are offset from the primary cut on the CMD, and
![]() ${\sigma}_{a}$
(0.3509) and
${\sigma}_{a}$
(0.3509) and
![]() ${\sigma}_{e}$
(0.3558) are the 1
${\sigma}_{e}$
(0.3558) are the 1
![]() $\sigma$
standard deviations of the
$\sigma$
standard deviations of the
![]() $(U_n-\mathcal{R})$
colour distributions for the aLBG and eLBG subsets, respectively.
$(U_n-\mathcal{R})$
colour distributions for the aLBG and eLBG subsets, respectively.
We use
![]() ${\sigma}_a$
and
${\sigma}_a$
and
![]() ${\sigma}_e$
to estimate the density of aLBGs and eLBGs on the CMD. This approach implies that any
${\sigma}_e$
to estimate the density of aLBGs and eLBGs on the CMD. This approach implies that any
![]() $\sigma$
should extend around a distribution mean in some circular (or similar) contour. The primary cut we make between the aLBG and eLBG distribution means (and its use as the basis for estimating photometric spectral type purity) is a line for which our assumptions only formally apply at the point of closest approach (tangent to a circular contour) of our lines to the respective distribution means. Thus, the multiples of
$\sigma$
should extend around a distribution mean in some circular (or similar) contour. The primary cut we make between the aLBG and eLBG distribution means (and its use as the basis for estimating photometric spectral type purity) is a line for which our assumptions only formally apply at the point of closest approach (tangent to a circular contour) of our lines to the respective distribution means. Thus, the multiples of
![]() $c_{\sigma}$
(1.5 in Fig. 3) applied to
$c_{\sigma}$
(1.5 in Fig. 3) applied to
![]() ${\sigma}_a$
and
${\sigma}_a$
and
![]() ${\sigma}_e$
, plus the fraction of
${\sigma}_e$
, plus the fraction of
![]() $\sigma$
by which the primary cut is removed from the respective distribution mean positions (
$\sigma$
by which the primary cut is removed from the respective distribution mean positions (
![]() $\sim 0.5 {\sigma}_a$
and
$\sim 0.5 {\sigma}_a$
and
![]() $\sim 0.5 {\sigma}_e$
), represent a minimum coefficient of
$\sim 0.5 {\sigma}_e$
), represent a minimum coefficient of
![]() $\sigma$
that can be used to estimate the extent and purity of different Ly
$\sigma$
that can be used to estimate the extent and purity of different Ly
![]() $\alpha$
spectral types on the CMD. For example, cuts on the CMD for which
$\alpha$
spectral types on the CMD. For example, cuts on the CMD for which
![]() $c_{\sigma} = 1.5$
along the same slope as the primary cut approximate (for Gaussian distributions) criteria for selecting Ly
$c_{\sigma} = 1.5$
along the same slope as the primary cut approximate (for Gaussian distributions) criteria for selecting Ly
![]() $\alpha$
spectral type sub-samples
$\alpha$
spectral type sub-samples
![]() $\gtrsim$
2
$\gtrsim$
2
![]() $\sigma$
from the mean value of the opposite distribution.
$\sigma$
from the mean value of the opposite distribution.
In theory, the above criteria can be made stricter (or relaxed) by varying the value of
![]() $c_{\sigma}$
, thereby trading sub-sample size for sub-sample purity according to the properties of the parent sample, and the requirements of the intended application. In practice, the range of
$c_{\sigma}$
, thereby trading sub-sample size for sub-sample purity according to the properties of the parent sample, and the requirements of the intended application. In practice, the range of
![]() $c_{\sigma}$
values that can be meaningfully employed is limited by the degree to which the aLBG and eLBG distributions deviate from Gaussian behaviour, and by small-number statistics at higher values of
$c_{\sigma}$
values that can be meaningfully employed is limited by the degree to which the aLBG and eLBG distributions deviate from Gaussian behaviour, and by small-number statistics at higher values of
![]() $c_{\sigma}$
– especially for eLBGs which are
$c_{\sigma}$
– especially for eLBGs which are
![]() $\sim$
4 times less abundant than aLBGs in our
$\sim$
4 times less abundant than aLBGs in our
![]() $z\sim2$
sample. Table 4 summarises the statistics for p-aLBG and p-eLBG Ly
$z\sim2$
sample. Table 4 summarises the statistics for p-aLBG and p-eLBG Ly
![]() $\alpha$
spectral type sub-samples selected from the parent
$\alpha$
spectral type sub-samples selected from the parent
![]() $z\sim2$
LBGs using the selection criteria given in Equations (1) and (2), respectively, and a range of
$z\sim2$
LBGs using the selection criteria given in Equations (1) and (2), respectively, and a range of
![]() $c_{\sigma}$
values.
$c_{\sigma}$
values.
Table 4. Statistics for photometric sub-samples with Ly
![]() $\alpha$
dominant in absorption (p-aLBGs) and Ly
$\alpha$
dominant in absorption (p-aLBGs) and Ly
![]() $\alpha$
dominant in emission (p-eLBGs) selected from the parent
$\alpha$
dominant in emission (p-eLBGs) selected from the parent
![]() $z\sim2$
LBG sample using Equations (1) & (2) and different values of
$z\sim2$
LBG sample using Equations (1) & (2) and different values of
![]() $c_{\sigma}$
.
$c_{\sigma}$
.

aCoefficient of colour standard deviations (
![]() $\sigma_a$
&
$\sigma_a$
&
![]() $\sigma_e$
) by which boundaries used to isolate the photometric spectral type sub-samples are offset from the CMD primary cut.
$\sigma_e$
) by which boundaries used to isolate the photometric spectral type sub-samples are offset from the CMD primary cut.
bNumber of galaxies in the photometric sub-samples.
cFor p-aLBGs: Percent purity with respect to eLBG and (eLBG +
![]() $\rm{G_e}$
) spectral types. For p-eLBGs: Percent purity with respect to aLBG and (aLBG +
$\rm{G_e}$
) spectral types. For p-eLBGs: Percent purity with respect to aLBG and (aLBG +
![]() $\rm{G_a}$
) spectral types.
$\rm{G_a}$
) spectral types.
dMean net Ly
![]() $\alpha$
EW for each sub-sample.
$\alpha$
EW for each sub-sample.
We estimate the purity of each photometric spectral type sub-sample by calculating the degree to which they exclude galaxies with opposite spectral type as determined by their measured net Ly
![]() $\alpha$
EW and our classification scheme described in Section 3.1. That is, for example, for each p-aLBG sub-sample selected using a different value of
$\alpha$
EW and our classification scheme described in Section 3.1. That is, for example, for each p-aLBG sub-sample selected using a different value of
![]() $c_{\sigma}$
, we calculate the contamination fraction of spectroscopic eLBGs and
$c_{\sigma}$
, we calculate the contamination fraction of spectroscopic eLBGs and
![]() $\rm{eLBG} + \rm{G_e}$
spectral types. The purity of the p-aLBG sub-sample thus determined is quoted as a percentage with respect to eLBGs and with respect to
$\rm{eLBG} + \rm{G_e}$
spectral types. The purity of the p-aLBG sub-sample thus determined is quoted as a percentage with respect to eLBGs and with respect to
![]() $\rm{eLBG}$
+
$\rm{eLBG}$
+
![]() $\rm{G_e}$
spectral types (parenthesised) in Table 4. The mean net Ly
$\rm{G_e}$
spectral types (parenthesised) in Table 4. The mean net Ly
![]() $\alpha$
EW of the p-aLBG and p-eLBG sub-samples (also listed in Table 4) is a further measure of the quality of the broadband photometric segregation, and the average properties of the respective sub-samples.
$\alpha$
EW of the p-aLBG and p-eLBG sub-samples (also listed in Table 4) is a further measure of the quality of the broadband photometric segregation, and the average properties of the respective sub-samples.
Across a wide range of
![]() $c_{\sigma}$
values, we select high-purity p-aLBG sub-samples, particularly with respect to contamination by spectroscopic eLBGs. Indeed, even using the primary cut between the aLBG and eLBG spectral types (i.e.,
$c_{\sigma}$
values, we select high-purity p-aLBG sub-samples, particularly with respect to contamination by spectroscopic eLBGs. Indeed, even using the primary cut between the aLBG and eLBG spectral types (i.e.,
![]() $c_{\sigma} = 0.0$
), results in a large sub-sample of 311 p-aLBGs (
$c_{\sigma} = 0.0$
), results in a large sub-sample of 311 p-aLBGs (
![]() $\gtrsim$
55% of total LBGs) that is
$\gtrsim$
55% of total LBGs) that is
![]() $\gtrsim$
97% free of eLBGs and
$\gtrsim$
97% free of eLBGs and
![]() $\gtrsim$
70% pure with respect to galaxies with any detectable net Ly
$\gtrsim$
70% pure with respect to galaxies with any detectable net Ly
![]() $\alpha$
emission. The practical upper limit of
$\alpha$
emission. The practical upper limit of
![]() $c_{\sigma}$
for the selection of p-aLBGs appears to be restricted only by the diminishing return of smaller sub-sample sizes. As a result, large broadband photometric samples can greatly benefit from stricter cuts. The optimal coefficient for the dataset here of
$c_{\sigma}$
for the selection of p-aLBGs appears to be restricted only by the diminishing return of smaller sub-sample sizes. As a result, large broadband photometric samples can greatly benefit from stricter cuts. The optimal coefficient for the dataset here of
![]() $\sigma_e$
(
$\sigma_e$
(
![]() $c_{\sigma} \approx 1.0 -1.25$
) selects
$c_{\sigma} \approx 1.0 -1.25$
) selects
![]() $\sim$
100–140 photometric aLBGs that are
$\sim$
100–140 photometric aLBGs that are
![]() $\gtrsim$
97% and
$\gtrsim$
97% and
![]() $\gtrsim$
79% pure with respect to spectroscopic eLBGs, and
$\gtrsim$
79% pure with respect to spectroscopic eLBGs, and
![]() $\rm{eLBG}$
+
$\rm{eLBG}$
+
![]() $\rm{G_e}$
spectral types respectively, and for which the mean net Ly
$\rm{G_e}$
spectral types respectively, and for which the mean net Ly
![]() $\alpha$
EW is
$\alpha$
EW is
![]() $\sim$
$\sim$
![]() $-$
8 Å.
$-$
8 Å.
With
![]() $c_{\sigma} \approx 1.0 - 1.25$
we select a sample of
$c_{\sigma} \approx 1.0 - 1.25$
we select a sample of
![]() $\sim$
50–70 LBGs with Ly
$\sim$
50–70 LBGs with Ly
![]() $\alpha$
dominant in emission (p-eLBGs) that are
$\alpha$
dominant in emission (p-eLBGs) that are
![]() $\gtrsim$
85% and
$\gtrsim$
85% and
![]() $\gtrsim$
65% pure with respect to spectroscopic aLBGs and
$\gtrsim$
65% pure with respect to spectroscopic aLBGs and
![]() $\rm{aLBG}$
+
$\rm{aLBG}$
+
![]() $\rm{G_a}$
spectral types, respectively, with a mean net Ly
$\rm{G_a}$
spectral types, respectively, with a mean net Ly
![]() $\alpha$
EW of
$\alpha$
EW of
![]() $\sim$
+8 Å. These purities represent a significant enhancement over the native (full sample) abundances of eLBGs (
$\sim$
+8 Å. These purities represent a significant enhancement over the native (full sample) abundances of eLBGs (
![]() $\sim$
8%) and the sum of eLBG and
$\sim$
8%) and the sum of eLBG and
![]() $\rm{G_e}$
spectral types (
$\rm{G_e}$
spectral types (
![]() $\sim$
40%).
$\sim$
40%).
The segregation versus net Ly
![]() $\alpha$
EW of photometrically selected
$\alpha$
EW of photometrically selected
![]() $z\sim2$
p-aLBG and p-eLBG sub-samples with
$z\sim2$
p-aLBG and p-eLBG sub-samples with
![]() $c_{\sigma} = 1.0$
is plotted in the top panel of Fig. 4 compared to the distribution versus net Ly
$c_{\sigma} = 1.0$
is plotted in the top panel of Fig. 4 compared to the distribution versus net Ly
![]() $\alpha$
EW of the parent
$\alpha$
EW of the parent
![]() $z\sim2$
LBG sample. In the optimal case, we select sub-samples with a desired Ly
$z\sim2$
LBG sample. In the optimal case, we select sub-samples with a desired Ly
![]() $\alpha$
spectral type at
$\alpha$
spectral type at
![]() $z\sim2$
that are for p-aLBGs, comparable to, and for p-eLBGs
$z\sim2$
that are for p-aLBGs, comparable to, and for p-eLBGs
![]() $\sim$
10% less pure than, the optimised
$\sim$
10% less pure than, the optimised
![]() $z\sim3$
result of C09 (see Section 3.3.2). The lower optimised purity of p-eLBGs at
$z\sim3$
result of C09 (see Section 3.3.2). The lower optimised purity of p-eLBGs at
![]() $z\sim2$
is attributable to the intrinsic overlap of the aLBG and eLBG distributions, and the relatively lower fraction of Ly
$z\sim2$
is attributable to the intrinsic overlap of the aLBG and eLBG distributions, and the relatively lower fraction of Ly
![]() $\alpha$
-emitting LBGs selected at this redshift. That is, the ratio of aLBGs to eLBGs has increased from around 1:1 at
$\alpha$
-emitting LBGs selected at this redshift. That is, the ratio of aLBGs to eLBGs has increased from around 1:1 at
![]() $z\sim$
3 to more than 4:1 at
$z\sim$
3 to more than 4:1 at
![]() $z\sim$
2 when comparing samples to the same absolute magnitude. This is not specific to our sample. On the contrary, a reduced fraction of Ly
$z\sim$
2 when comparing samples to the same absolute magnitude. This is not specific to our sample. On the contrary, a reduced fraction of Ly
![]() $\alpha$
-emitting galaxies with decreasing redshift is expected from the findings of Stark et al. (Reference Stark, Ellis, Chiu, Ouchi and Bunker2010), Stark, Ellis, & Ouchi (Reference Stark, Ellis and Ouchi2011), Mallery et al. (Reference Mallery2012), Cassata et al. (Reference Cassata2015) who consistently report an evolutionary decrease in the fraction of LBGs with Ly
$\alpha$
-emitting galaxies with decreasing redshift is expected from the findings of Stark et al. (Reference Stark, Ellis, Chiu, Ouchi and Bunker2010), Stark, Ellis, & Ouchi (Reference Stark, Ellis and Ouchi2011), Mallery et al. (Reference Mallery2012), Cassata et al. (Reference Cassata2015) who consistently report an evolutionary decrease in the fraction of LBGs with Ly
![]() $\alpha$
in emission from
$\alpha$
in emission from
![]() $z\sim6$
to
$z\sim6$
to
![]() $z\sim2$
at fixed luminosity.
$z\sim2$
at fixed luminosity.

Figure 4. Histograms of p-aLBGs and p-eLBGs are multiplied by 4 for clarity.
Histograms versus net Ly
![]() $\alpha$
EW of
$\alpha$
EW of
![]() $z\sim2$
and
$z\sim2$
and
![]() $z\sim3$
‘photometric’ aLBG (p-aLBG) and ‘photometric’ eLBG (p-eLBG) spectral type sub-samples overlaid on the distribution versus net Ly
$z\sim3$
‘photometric’ aLBG (p-aLBG) and ‘photometric’ eLBG (p-eLBG) spectral type sub-samples overlaid on the distribution versus net Ly
![]() $\alpha$
EW of their respective parent samples shown in grey. Vertical dashed lines indicate the net Ly
$\alpha$
EW of their respective parent samples shown in grey. Vertical dashed lines indicate the net Ly
![]() $\alpha$
EW thresholds used here to divide the spectroscopic sample into aLBG,
$\alpha$
EW thresholds used here to divide the spectroscopic sample into aLBG,
![]() $\rm{G_a}$
,
$\rm{G_a}$
,
![]() $\rm{G_e}$
and eLBG Ly
$\rm{G_e}$
and eLBG Ly
![]() $\alpha$
spectral types. Red and blue shaded regions indicate aLBGs and eLBGs, respectively. Top:
$\alpha$
spectral types. Red and blue shaded regions indicate aLBGs and eLBGs, respectively. Top:
![]() $z\sim2$
p-aLBGs and p-eLBGs selected from the parent sample of 557
$z\sim2$
p-aLBGs and p-eLBGs selected from the parent sample of 557
![]() $z\sim2$
LBGs using the selection criteria given in Equations (1) & (2) with
$z\sim2$
LBGs using the selection criteria given in Equations (1) & (2) with
![]() $c_{\sigma}=1.0$
. Histograms of p-aLBGs and p-eLBGs are multiplied by 2 for clarity. Bottom:
$c_{\sigma}=1.0$
. Histograms of p-aLBGs and p-eLBGs are multiplied by 2 for clarity. Bottom:
![]() $z\sim3$
p-aLBGs and p-eLBGs selected from the parent sample of 775
$z\sim3$
p-aLBGs and p-eLBGs selected from the parent sample of 775
![]() $z\sim3$
LBGs using the selection criteria given in Equations (3) & (4) with
$z\sim3$
LBGs using the selection criteria given in Equations (3) & (4) with
![]() $c_{\sigma}=1.5$
.
$c_{\sigma}=1.5$
.
3.3.2.
 $z\sim3$
LBGs
$z\sim3$
LBGs
For the purposes of reference and direct comparison, we present here the Ly
![]() $\alpha$
spectral type photometric selection results for
$\alpha$
spectral type photometric selection results for
![]() $z\sim3$
LBGs analysed and presented in the same format as the
$z\sim3$
LBGs analysed and presented in the same format as the
![]() $z\sim2$
result above.
$z\sim2$
result above.
Parameters for the photometric segregation of
![]() $z\sim3$
LBG Ly
$z\sim3$
LBG Ly
![]() $\alpha$
-absorbing and Ly
$\alpha$
-absorbing and Ly
![]() $\alpha$
-emitting spectral types in
$\alpha$
-emitting spectral types in
![]() $(G-\mathcal{R})$
vs
$(G-\mathcal{R})$
vs
![]() $\mathcal{R}$
colour-magnitude space as determined by C09 are listed in Table 3, and we re-produce in Equations (3) & (4) criteria for the photometric selection of p-aLBG and p-eLBG spectral type sub-samples at
$\mathcal{R}$
colour-magnitude space as determined by C09 are listed in Table 3, and we re-produce in Equations (3) & (4) criteria for the photometric selection of p-aLBG and p-eLBG spectral type sub-samples at
![]() $z\sim3$
.
$z\sim3$
.
For p-aLBGs,
and for p-eLBGs,
where for the parent sample of
![]() $z\sim3$
LBGs,
$z\sim3$
LBGs,
![]() $\sigma_a = 0.2392$
and
$\sigma_a = 0.2392$
and
![]() $\sigma_e = 0.3095$
.
$\sigma_e = 0.3095$
.
Table 5 summarises the statistics for p-aLBG and p-eLBG Ly
![]() $\alpha$
spectral type sub-samples selected from a parent sample of 775
$\alpha$
spectral type sub-samples selected from a parent sample of 775
![]() $z\sim3$
LBGs using the above relationships and a range of
$z\sim3$
LBGs using the above relationships and a range of
![]() $c_{\sigma}$
values. The bottom panel of Fig. 4 shows the segregation versus net Ly
$c_{\sigma}$
values. The bottom panel of Fig. 4 shows the segregation versus net Ly
![]() $\alpha$
EW of
$\alpha$
EW of
![]() $z\sim3$
p-aLBG and p-eLBG sub-samples selected with
$z\sim3$
p-aLBG and p-eLBG sub-samples selected with
![]() $c_{\sigma} = 1.5$
compared to the distribution versus net Ly
$c_{\sigma} = 1.5$
compared to the distribution versus net Ly
![]() $\alpha$
EW of the parent
$\alpha$
EW of the parent
![]() $z\sim3$
LBG sample.
$z\sim3$
LBG sample.
Table 5. Statistics for photometric sub-samples with Ly
![]() $\alpha$
dominant in absorption (p-aLBGs) and Ly
$\alpha$
dominant in absorption (p-aLBGs) and Ly
![]() $\alpha$
dominant in emission (p-eLBGs) selected from the parent sample of 775
$\alpha$
dominant in emission (p-eLBGs) selected from the parent sample of 775
![]() $z\sim3$
LBGs using the spectral type criteria of C09a and different values of
$z\sim3$
LBGs using the spectral type criteria of C09a and different values of
![]() $c_{\sigma}$
.
$c_{\sigma}$
.

aFor the purposes of determining photometric segregation criteria, C09 defined aLBGs and eLBGs as having net Ly
![]() $\alpha$
EW
$\alpha$
EW
![]() $\leq -12.0$
and
$\leq -12.0$
and
![]() $\geq +26.5$
Å respectively.
$\geq +26.5$
Å respectively.
bCoefficient of colour standard deviations (
![]() $\sigma_a$
&
$\sigma_a$
&
![]() $\sigma_e$
) by which boundaries used to isolate the photometric spectral type sub-samples are offset from the CMD primary cut.
$\sigma_e$
) by which boundaries used to isolate the photometric spectral type sub-samples are offset from the CMD primary cut.
cNumber of galaxies in the photometric sub-samples.
dFor p-aLBGs: Percent purity with respect to eLBG and (eLBG +
![]() $\rm{G_e}$
) spectral types. For p-eLBGs: Percent purity with respect to aLBG and (aLBG +
$\rm{G_e}$
) spectral types. For p-eLBGs: Percent purity with respect to aLBG and (aLBG +
![]() $\rm{G_a}$
) spectral types. Mean net Ly
$\rm{G_a}$
) spectral types. Mean net Ly
![]() $\alpha$
EW for each sub-sample
$\alpha$
EW for each sub-sample
The optimal coefficient of
![]() $\sigma_e$
(
$\sigma_e$
(
![]() $c_{\sigma} \approx 1.5$
) selects
$c_{\sigma} \approx 1.5$
) selects
![]() $\sim$
120 photometric aLBGs that are
$\sim$
120 photometric aLBGs that are
![]() $\gtrsim$
96% and
$\gtrsim$
96% and
![]() $\gtrsim$
76% pure with respect to spectroscopic eLBGs, and
$\gtrsim$
76% pure with respect to spectroscopic eLBGs, and
![]() $\rm{eLBG}$
+
$\rm{eLBG}$
+
![]() $\rm{G_e}$
spectral types respectively, and for which the mean net Ly
$\rm{G_e}$
spectral types respectively, and for which the mean net Ly
![]() $\alpha$
EW is
$\alpha$
EW is
![]() $\sim$
$\sim$
![]() $-$
5 Å.
$-$
5 Å.
With any coefficient of
![]() $\sigma_a \gtrsim 1.0$
, we select large samples of photometric eLBGs that are
$\sigma_a \gtrsim 1.0$
, we select large samples of photometric eLBGs that are
![]() $\sim$
94–98% pure with respect to spectroscopic aLBGs. Over the range
$\sim$
94–98% pure with respect to spectroscopic aLBGs. Over the range
![]() $c_{\sigma} = 1.0-2.5$
, the purity of the p-eLBG sample with respect to all net Ly
$c_{\sigma} = 1.0-2.5$
, the purity of the p-eLBG sample with respect to all net Ly
![]() $\alpha$
-absorbers (
$\alpha$
-absorbers (
![]() $\rm{aLBG}$
+
$\rm{aLBG}$
+
![]() $\rm{G_a}$
spectral types) increases monotonically from
$\rm{G_a}$
spectral types) increases monotonically from
![]() $\sim$
74% to
$\sim$
74% to
![]() $\sim$
93%, with a commensurate increase in mean net Ly
$\sim$
93%, with a commensurate increase in mean net Ly
![]() $\alpha$
EW from
$\alpha$
EW from
![]() $\sim+27$
to
$\sim+27$
to
![]() $\sim+$
51 Å.
$\sim+$
51 Å.
3.4. The contribution of Ly
 $\alpha$
$\alpha$
The segregation of
![]() $z\sim3$
aLBGs and eLBGs on the CMD is enhanced by the contribution of the Ly
$z\sim3$
aLBGs and eLBGs on the CMD is enhanced by the contribution of the Ly
![]() $\alpha$
feature itself when it falls within the bandpass of the G filter (see Section 3.2 and Fig. 2). The contribution of Ly
$\alpha$
feature itself when it falls within the bandpass of the G filter (see Section 3.2 and Fig. 2). The contribution of Ly
![]() $\alpha$
to the observed luminosities was estimated by C13 to be
$\alpha$
to the observed luminosities was estimated by C13 to be
![]() $\sim$
-0.1 mags for aLBGs,
$\sim$
-0.1 mags for aLBGs,
![]() $\sim$
+0.1 mags for eLBGs, and negligible for LBGs with net Ly
$\sim$
+0.1 mags for eLBGs, and negligible for LBGs with net Ly
![]() $\alpha$
EW near zero. A similar effect might be anticipated at
$\alpha$
EW near zero. A similar effect might be anticipated at
![]() $z\sim2$
when Ly
$z\sim2$
when Ly
![]() $\alpha$
falls within the bandpass of the relevant (
$\alpha$
falls within the bandpass of the relevant (
![]() $U_n$
) filter.
$U_n$
) filter.
Unlike the
![]() $z\sim3$
case where the Ly
$z\sim3$
case where the Ly
![]() $\alpha$
spectral feature lies within the G-band filter across the full redshift range of the sample (
$\alpha$
spectral feature lies within the G-band filter across the full redshift range of the sample (
![]() $2.5<z<3.5$
), about half (
$2.5<z<3.5$
), about half (
![]() $\sim$
52%) of the
$\sim$
52%) of the
![]() $z\sim2$
LBG sample is in the redshift range
$z\sim2$
LBG sample is in the redshift range
![]() $2.17 \leq z \leq 2.50$
, where the Ly
$2.17 \leq z \leq 2.50$
, where the Ly
![]() $\alpha$
feature lies outside the half-power bandpass limits of the
$\alpha$
feature lies outside the half-power bandpass limits of the
![]() $U_n$
filter. Reddy et al. (Reference Reddy2008) showed that the ratio of strong emitters to absorbers for LBGs at redshifts
$U_n$
filter. Reddy et al. (Reference Reddy2008) showed that the ratio of strong emitters to absorbers for LBGs at redshifts
![]() $2.17 \leq z \leq 2.48$
is approximately the same as for those selected by the same set of colour criteria at
$2.17 \leq z \leq 2.48$
is approximately the same as for those selected by the same set of colour criteria at
![]() $z<2.17$
(see the respective population statistics in Table 6). Thus, there is no underlying selection bias of aLBGs versus eLBGs that could affect the segregation properties in the different redshift ranges. This result does not, however, preclude the possibility that the segregation statistics across the full z-range of the sample may be variably affected by the contribution of Ly
$z<2.17$
(see the respective population statistics in Table 6). Thus, there is no underlying selection bias of aLBGs versus eLBGs that could affect the segregation properties in the different redshift ranges. This result does not, however, preclude the possibility that the segregation statistics across the full z-range of the sample may be variably affected by the contribution of Ly
![]() $\alpha$
to the measured
$\alpha$
to the measured
![]() $U_n$
-band photometry. For this reason – and because the measured segregation at
$U_n$
-band photometry. For this reason – and because the measured segregation at
![]() $z\sim2$
is less well resolved than at
$z\sim2$
is less well resolved than at
![]() $z\sim3$
– we look to quantify the effect of Ly
$z\sim3$
– we look to quantify the effect of Ly
![]() $\alpha$
on the observed broadband segregation for galaxies in the
$\alpha$
on the observed broadband segregation for galaxies in the
![]() $z\sim2$
sample in different redshift ranges and with different Ly
$z\sim2$
sample in different redshift ranges and with different Ly
![]() $\alpha$
spectral type.
$\alpha$
spectral type.
Table 6. Statistics for the segregation of
![]() $z\sim2$
LBGs in colour (
$z\sim2$
LBGs in colour (
![]() $U_n-\mathcal{R}$
)—magnitude (
$U_n-\mathcal{R}$
)—magnitude (
![]() $\mathcal{R}$
) space over different redshift ranges.
$\mathcal{R}$
) space over different redshift ranges.

To this end, we divide the
![]() $z\sim2$
LBG sample into two subsets: one containing only galaxies in the range
$z\sim2$
LBG sample into two subsets: one containing only galaxies in the range
![]() $1.7<z<2.17$
where Ly
$1.7<z<2.17$
where Ly
![]() $\alpha$
falls within the bandpass of the
$\alpha$
falls within the bandpass of the
![]() $U_n$
filter (3250–3850 Å), and another comprising galaxies in the
$U_n$
filter (3250–3850 Å), and another comprising galaxies in the
![]() $2.17<z<2.5$
range for which Ly
$2.17<z<2.5$
range for which Ly
![]() $\alpha$
lies beyond the red half-power bandpass limit of the same filter (see Fig. 2). We then optimise the primary cut slope in each redshift bin in the same manner as for the sample as a whole (see Section 3.2), and compare the segregation statistics for the two subsets with each other, and with those for the full z-range sample (see Table 6).
$\alpha$
lies beyond the red half-power bandpass limit of the same filter (see Fig. 2). We then optimise the primary cut slope in each redshift bin in the same manner as for the sample as a whole (see Section 3.2), and compare the segregation statistics for the two subsets with each other, and with those for the full z-range sample (see Table 6).
We find a significantly stronger segregation in the
![]() $2.17<z<2.5$
sample, most apparent in the greater average colour segregation between aLBGs and eLBGs in this redshift range (0.52) compared to that in the lower redshift bin (0.24). This effect is likely due to the larger contribution of the Ly
$2.17<z<2.5$
sample, most apparent in the greater average colour segregation between aLBGs and eLBGs in this redshift range (0.52) compared to that in the lower redshift bin (0.24). This effect is likely due to the larger contribution of the Ly
![]() $\alpha$
forest to the
$\alpha$
forest to the
![]() $U_n$
-band of the
$U_n$
-band of the
![]() $2.17<z<2.5$
sample, leading to redder
$2.17<z<2.5$
sample, leading to redder
![]() $(U_n-\mathcal{R})$
colours on average. There is also a larger colour dispersion of eLBGs (
$(U_n-\mathcal{R})$
colours on average. There is also a larger colour dispersion of eLBGs (
![]() $\sigma = 0.41$
) in the lower redshift range that blurs the photometric segregation.
$\sigma = 0.41$
) in the lower redshift range that blurs the photometric segregation.
This difference in the degree of segregation between aLBGs and eLBGs translates into the purity of p-aLBG and p-eLBG sub-samples that can be selected from the two redshift ranges. Using the same methodology as was applied to the full
![]() $z\sim2$
and
$z\sim2$
and
![]() $z\sim3$
samples in Section 3.3, we determined the purity of p-aLBG and p-eLBG sub-samples selected from each redshift bin using the segregation parameters listed in Table 6, and a range of
$z\sim3$
samples in Section 3.3, we determined the purity of p-aLBG and p-eLBG sub-samples selected from each redshift bin using the segregation parameters listed in Table 6, and a range of
![]() $c_{\sigma}$
values (see Table 7). The optimised purity of the p-aLBGs and p-eLBGs selected from the
$c_{\sigma}$
values (see Table 7). The optimised purity of the p-aLBGs and p-eLBGs selected from the
![]() $2.17<z<2.5$
sample (
$2.17<z<2.5$
sample (
![]() $\sim$
98% and
$\sim$
98% and
![]() $\sim$
94%, respectively) is significantly better than can be achieved from the lower redshift bin (
$\sim$
94%, respectively) is significantly better than can be achieved from the lower redshift bin (
![]() $\sim$
94% for p-aLBGs and
$\sim$
94% for p-aLBGs and
![]() $\sim$
84% for p-eLBGs). In fact, with
$\sim$
84% for p-eLBGs). In fact, with
![]() $c_{\sigma}$
values of 1.0–1.5, the p-aLBG and p-eLBG sub-samples in the
$c_{\sigma}$
values of 1.0–1.5, the p-aLBG and p-eLBG sub-samples in the
![]() $2.17<z<2.5$
range have purities that are essentially indistinguishable from those achievable in the
$2.17<z<2.5$
range have purities that are essentially indistinguishable from those achievable in the
![]() $z\sim3$
sample, and comparably high
$z\sim3$
sample, and comparably high
![]() $\Delta_{Ly\alpha\ EW}$
between them, indicating that any direct contribution of the Ly
$\Delta_{Ly\alpha\ EW}$
between them, indicating that any direct contribution of the Ly
![]() $\alpha$
feature to the segregation properties of aLBGs and eLBGs is dominated by other redshift-dependent spectrophotometric effects such as the one described above.
$\alpha$
feature to the segregation properties of aLBGs and eLBGs is dominated by other redshift-dependent spectrophotometric effects such as the one described above.
Table 7. Statistics for p-aLBG and p-eLBG sub-samples photometrically selected from the parent
![]() $z\sim2$
LBG sample using segregation parameters optimised in different redshift ranges.
$z\sim2$
LBG sample using segregation parameters optimised in different redshift ranges.

aCoefficient of colour standard deviations by which boundaries used to isolate the photometric spectral type sub-samples are offset from the primary cut in each redshift range.
bNumber of galaxies in the photometric sub-samples.
cFor p-aLBGs: Percent purity with respect to eLBG and (eLBG +
![]() $\rm{G_e}$
) spectral types. For p-eLBGs: Percent purity with respect to aLBG and (aLBG +
$\rm{G_e}$
) spectral types. For p-eLBGs: Percent purity with respect to aLBG and (aLBG +
![]() $\rm{G_a}$
) spectral types.
$\rm{G_a}$
) spectral types.
dMean net Ly
![]() $\alpha$
EW for each sub-sample.
$\alpha$
EW for each sub-sample.
eDifference in mean net Ly
![]() $\alpha$
EW between the p-aLBG and p-eLBG sub-samples. In the case of Full
$\alpha$
EW between the p-aLBG and p-eLBG sub-samples. In the case of Full
![]() $_{bins}$
,
$_{bins}$
,
![]() ${\Delta}_{Ly\alpha\ EW}$
is the weighted average of
${\Delta}_{Ly\alpha\ EW}$
is the weighted average of
![]() $\Delta_{Ly\alpha\ EW}$
values for each magnitude bin.
$\Delta_{Ly\alpha\ EW}$
values for each magnitude bin.
3.5. LSST photometric selection criteria for
 $z\sim3$
LBG Ly
$z\sim3$
LBG Ly
 $\alpha$
spectral types
$\alpha$
spectral types
A key objective of this work is to develop a method that can be applied to large samples of
![]() $z\sim2-6$
LBGs identified from current and future large-area and all-sky photometric campaigns. As a first step toward this goal, we adapt the spectrophotometric method of C13 to model photometric selection criteria by which populations of
$z\sim2-6$
LBGs identified from current and future large-area and all-sky photometric campaigns. As a first step toward this goal, we adapt the spectrophotometric method of C13 to model photometric selection criteria by which populations of
![]() $z\sim3$
LBGs with Ly
$z\sim3$
LBGs with Ly
![]() $\alpha$
dominant in absorption and Ly
$\alpha$
dominant in absorption and Ly
![]() $\alpha$
dominant in emission might be selected from the broadband ugri photometric data of the Vera Ruben Observatory Legacy Survey of Space and Time (VRO/LSST).
$\alpha$
dominant in emission might be selected from the broadband ugri photometric data of the Vera Ruben Observatory Legacy Survey of Space and Time (VRO/LSST).
In order to model the segregation statistics for different Ly
![]() $\alpha$
spectral types in the LSST ugri photometric system, it is first necessary to calculate ugri magnitudes for each galaxy in our
$\alpha$
spectral types in the LSST ugri photometric system, it is first necessary to calculate ugri magnitudes for each galaxy in our
![]() $z\sim3$
sample. Our photometric segregation method relies on the fact that LBGs with different net Ly
$z\sim3$
sample. Our photometric segregation method relies on the fact that LBGs with different net Ly
![]() $\alpha$
EW have different spectral properties – in particular rest-frame UV continuum slope – that give rise to different rest-frame UV colours depending on their Ly
$\alpha$
EW have different spectral properties – in particular rest-frame UV continuum slope – that give rise to different rest-frame UV colours depending on their Ly
![]() $\alpha$
absorbing/emitting properties (see Fig. 2). Thus, in order to convert from
$\alpha$
absorbing/emitting properties (see Fig. 2). Thus, in order to convert from
![]() $U_nG\mathcal{R}$
to ugri magnitudes via spectrophotometry, we must be able to assign to each galaxy in our sample, an appropriate spectrum corresponding to its Ly
$U_nG\mathcal{R}$
to ugri magnitudes via spectrophotometry, we must be able to assign to each galaxy in our sample, an appropriate spectrum corresponding to its Ly
![]() $\alpha$
spectral type. For this purpose, we make use of the four composite spectra of Shapley et al. (Reference Shapley, Steidel, Pettini and Adelberger2003), derived from the
$\alpha$
spectral type. For this purpose, we make use of the four composite spectra of Shapley et al. (Reference Shapley, Steidel, Pettini and Adelberger2003), derived from the
![]() $z\sim3$
$z\sim3$
![]() $U_nG\mathcal{R}$
LBGs described in Sections 2 & 3.1 divided into quartiles on the basis of net Ly
$U_nG\mathcal{R}$
LBGs described in Sections 2 & 3.1 divided into quartiles on the basis of net Ly
![]() $\alpha$
EW. C13 showed that spectrophotometry of these composite spectra accurately reproduces the magnitude and colour means and dispersions of each of the four net Ly
$\alpha$
EW. C13 showed that spectrophotometry of these composite spectra accurately reproduces the magnitude and colour means and dispersions of each of the four net Ly
![]() $\alpha$
EW quartile samples, as well as the full distribution of
$\alpha$
EW quartile samples, as well as the full distribution of
![]() $z\sim3$
LBGs on the
$z\sim3$
LBGs on the
![]() $(G-\mathcal{R})$
/G CMD when combined. Thus, although the colours and magnitudes of individual galaxies vary within each quartile, the composite spectra can be used to compute net Ly
$(G-\mathcal{R})$
/G CMD when combined. Thus, although the colours and magnitudes of individual galaxies vary within each quartile, the composite spectra can be used to compute net Ly
![]() $\alpha$
EW means and dispersions on the CMD for our
$\alpha$
EW means and dispersions on the CMD for our
![]() $z\sim3$
LBG sample when viewed through the VRO/LSST ugri filtersFootnote
a
. Fig. 5 shows our
$z\sim3$
LBG sample when viewed through the VRO/LSST ugri filtersFootnote
a
. Fig. 5 shows our
![]() $z\sim3$
$z\sim3$
![]() $U_nG\mathcal{R}$
LBG sample dispersed in VRO/LSST
$U_nG\mathcal{R}$
LBG sample dispersed in VRO/LSST
![]() $(g-r)$
vs r colour-magnitude space with photometry thus derived from spectrophotometry of the net Ly
$(g-r)$
vs r colour-magnitude space with photometry thus derived from spectrophotometry of the net Ly
![]() $\alpha$
EW quartile composite spectra.
$\alpha$
EW quartile composite spectra.
Following the method described in Section 3.3, we use the parameters of the segregated aLBG and eLBG distributions shown in Fig. 5 and tabulated in Table 8 to determine photometric selection criteria by which pure populations of
![]() $z\sim3$
LBGs with Ly
$z\sim3$
LBGs with Ly
![]() $\alpha$
dominant in absorption (p-aLBGs; Equation (5)) and Ly
$\alpha$
dominant in absorption (p-aLBGs; Equation (5)) and Ly
![]() $\alpha$
dominant in emission (p-eLBGs; Equation (6)), might be selected from VRO/LSST LBG data dispersed in
$\alpha$
dominant in emission (p-eLBGs; Equation (6)), might be selected from VRO/LSST LBG data dispersed in
![]() $(g-r)$
vs r space.
$(g-r)$
vs r space.

Figure 5. Rest-frame UV
![]() $(g-r)$
vs r colour-magnitude diagram (CMD) for Steidel et al. (Reference Steidel2003)
$(g-r)$
vs r colour-magnitude diagram (CMD) for Steidel et al. (Reference Steidel2003)
![]() $z\sim3$
LBGs, constructed with VRO/LSST ugri photometry derived from the net Ly
$z\sim3$
LBGs, constructed with VRO/LSST ugri photometry derived from the net Ly
![]() $\alpha$
EW quartile composite spectra of Shapley et al. (Reference Shapley, Steidel, Pettini and Adelberger2003). The CMD shows the segregation with net Ly
$\alpha$
EW quartile composite spectra of Shapley et al. (Reference Shapley, Steidel, Pettini and Adelberger2003). The CMD shows the segregation with net Ly
![]() $\alpha$
EW of galaxies with Ly
$\alpha$
EW of galaxies with Ly
![]() $\alpha$
dominant in absorption (aLBGs, red squares) and Ly
$\alpha$
dominant in absorption (aLBGs, red squares) and Ly
![]() $\alpha$
dominant in emission (eLBGs, blue triangles). Grey plus (+) symbols denote galaxies with intermediate values of net Ly
$\alpha$
dominant in emission (eLBGs, blue triangles). Grey plus (+) symbols denote galaxies with intermediate values of net Ly
![]() $\alpha$
EW. Black crosses mark the mean positions of the aLBG and eLBG distributions. The dashed red and dotted-dashed blue lines indicate a
$\alpha$
EW. Black crosses mark the mean positions of the aLBG and eLBG distributions. The dashed red and dotted-dashed blue lines indicate a
![]() $1.5\sigma$
dispersion in colour from the primary cut (green line) for the aLBG and eLBG distributions, respectively.
$1.5\sigma$
dispersion in colour from the primary cut (green line) for the aLBG and eLBG distributions, respectively.
Table 8. Statistics for the segregation of LSST
![]() $z\sim3$
LBG Ly
$z\sim3$
LBG Ly
![]() $\alpha$
spectral types in
$\alpha$
spectral types in
![]() $(g-r)$
/r colour-magnitude space.
$(g-r)$
/r colour-magnitude space.

aConsistent with C09, we define aLBGs and eLBGs as having net Ly
![]() $\alpha$
EW
$\alpha$
EW
![]() $\leq -12.0$
and
$\leq -12.0$
and
![]() $\geq +26.5$
Å respectively, for the purposes of constructing the CMD and determining photometric segregation criteria.
$\geq +26.5$
Å respectively, for the purposes of constructing the CMD and determining photometric segregation criteria.
Specifically, for p-aLBGs:
and for p-eLBGs:
where
![]() $c_{\sigma}$
,
$c_{\sigma}$
,
![]() ${\sigma}_{a}$
, and
${\sigma}_{a}$
, and
![]() ${\sigma}_{e}$
are the coefficient and respective standard deviations of colour dispersion as described in Section 3.3.1.
${\sigma}_{e}$
are the coefficient and respective standard deviations of colour dispersion as described in Section 3.3.1.
These selection criteria provide a useful starting point for the isolation of p-aLBG and p-eLBG populations from LSST photometry. They will be confirmed and/or refined, and selection criteria in other redshift ranges added – especially at
![]() $z\sim2$
– once LSST data of sufficient depth has been measured in fields within which Ly
$z\sim2$
– once LSST data of sufficient depth has been measured in fields within which Ly
![]() $\alpha$
spectroscopic data are available.
$\alpha$
spectroscopic data are available.
4. Summary and conclusions
The Ly
![]() $\alpha$
observables from a given galaxy are known to be sensitive to a wide range of galactic physical, spectral, and environmental properties. Net Ly
$\alpha$
observables from a given galaxy are known to be sensitive to a wide range of galactic physical, spectral, and environmental properties. Net Ly
![]() $\alpha$
EW in particular has been shown to correlate with, for example, galaxy morphology, rest-frame UV colour, ISM line strengths, gas kinematics, and the large-scale spatial distribution of populations of
$\alpha$
EW in particular has been shown to correlate with, for example, galaxy morphology, rest-frame UV colour, ISM line strengths, gas kinematics, and the large-scale spatial distribution of populations of
![]() $z\gtrsim2$
LAEs and LBGs. Accordingly, the ability to select pure statistical sub-samples of a desired Ly
$z\gtrsim2$
LAEs and LBGs. Accordingly, the ability to select pure statistical sub-samples of a desired Ly
![]() $\alpha$
spectral type from large photometric datasets facilitates the study of a variety of intrinsic and small- to large-scale environmental galactic properties that are related to Ly
$\alpha$
spectral type from large photometric datasets facilitates the study of a variety of intrinsic and small- to large-scale environmental galactic properties that are related to Ly
![]() $\alpha$
, in large numbers and over distance scales for which ancillary multi-wavelength/multi-band photometry and/or spectroscopic information is not usually available (Cooke Reference Cooke2009; Cooke et al. Reference Cooke, Omori and Ryan-Weber2013).
$\alpha$
, in large numbers and over distance scales for which ancillary multi-wavelength/multi-band photometry and/or spectroscopic information is not usually available (Cooke Reference Cooke2009; Cooke et al. Reference Cooke, Omori and Ryan-Weber2013).
In this paper we characterise the broadband imaging segregation of a spectroscopic sample of 557
![]() $z\sim2$
LBGs using sub-samples with Ly
$z\sim2$
LBGs using sub-samples with Ly
![]() $\alpha$
dominant in absorption (aLBGs), and Ly
$\alpha$
dominant in absorption (aLBGs), and Ly
![]() $\alpha$
dominant in emission (eLBGs), and determine photometric criteria by which relatively pure sub-samples with desired Ly
$\alpha$
dominant in emission (eLBGs), and determine photometric criteria by which relatively pure sub-samples with desired Ly
![]() $\alpha$
spectral properties can be selected using imaging data in as few as three optical broadband filters.
$\alpha$
spectral properties can be selected using imaging data in as few as three optical broadband filters.
We draw the following specific conclusions from our study:
-
 $z\sim2$
LBGs segregate according to their net Ly
$z\sim2$
LBGs segregate according to their net Ly
 $\alpha$
EW properties in rest-frame UV colour (
$\alpha$
EW properties in rest-frame UV colour (
 $U_n-\mathcal{R}$
) and magnitude (
$U_n-\mathcal{R}$
) and magnitude (
 $\mathcal{R}$
) space in a manner similar to their
$\mathcal{R}$
) space in a manner similar to their
 $z\sim3$
counterparts in the
$z\sim3$
counterparts in the
 $(G-\mathcal{R})$
/
$(G-\mathcal{R})$
/
 $\mathcal{R}$
plane (see Section 3.2 and cf. Cooke Reference Cooke2009).
$\mathcal{R}$
plane (see Section 3.2 and cf. Cooke Reference Cooke2009). -
Using the segregation statistics for our sample of 557 LBGs in the range
 $1.7<z<2.5$
, we determine photometric criteria for the selection of sub-samples of LBGs with Ly
$1.7<z<2.5$
, we determine photometric criteria for the selection of sub-samples of LBGs with Ly
 $\alpha$
dominant in absorption (p-aLBGs) and Ly
$\alpha$
dominant in absorption (p-aLBGs) and Ly
 $\alpha$
dominant in emission (p-eLBGs). These criteria select sub-samples of p-aLBGs and p-eLBGs that are respectively
$\alpha$
dominant in emission (p-eLBGs). These criteria select sub-samples of p-aLBGs and p-eLBGs that are respectively
 $\gtrsim$
97% and
$\gtrsim$
97% and
 $\sim$
85% pure with respect to contamination by galaxies with the opposite spectral type. The mean net Ly
$\sim$
85% pure with respect to contamination by galaxies with the opposite spectral type. The mean net Ly
 $\alpha$
EW of the optimised p-aLBG and p-eLBG sub-samples selected from the
$\alpha$
EW of the optimised p-aLBG and p-eLBG sub-samples selected from the
 $z\sim2$
$z\sim2$
 $U_nG\mathcal{R}$
LBGs is
$U_nG\mathcal{R}$
LBGs is
 $\sim$
$\sim$
 $-$
8 Å and
$-$
8 Å and
 $\sim$
+8 Å, respectively (Section 3.3.1).
$\sim$
+8 Å, respectively (Section 3.3.1). -
Sub-dividing the
 $z\sim2$
sample into two redshift bins, we find that the degree of photometric segregation in the range
$z\sim2$
sample into two redshift bins, we find that the degree of photometric segregation in the range
 $2.17<z<2.5$
(Ly
$2.17<z<2.5$
(Ly
 $\alpha$
outside the
$\alpha$
outside the
 $U_n$
filter) is significantly greater than in the range
$U_n$
filter) is significantly greater than in the range
 $1.70<z<2.17$
(Ly
$1.70<z<2.17$
(Ly
 $\alpha$
within the
$\alpha$
within the
 $U_n$
filter). We attribute this difference to a larger contribution of the Ly
$U_n$
filter). We attribute this difference to a larger contribution of the Ly
 $\alpha$
forest leading to greater dispersion in
$\alpha$
forest leading to greater dispersion in
 $(U_n-\mathcal{R})$
colour at higher redshifts. In the range
$(U_n-\mathcal{R})$
colour at higher redshifts. In the range
 $2.17<z<2.5$
, we select sub-samples of p-aLBGs and p-eLBGs that are
$2.17<z<2.5$
, we select sub-samples of p-aLBGs and p-eLBGs that are
 $\gtrsim$
95% pure with respect to galaxies of the opposite spectral type, and which segregate in mean net Ly
$\gtrsim$
95% pure with respect to galaxies of the opposite spectral type, and which segregate in mean net Ly
 $\alpha$
EW (
$\alpha$
EW (
 $\Delta_{Ly\alpha\ EW} \approx$
30 Å) on the same order as the
$\Delta_{Ly\alpha\ EW} \approx$
30 Å) on the same order as the
 $z\sim3$
LBGs (Section 3.4).
$z\sim3$
LBGs (Section 3.4). -
Using the result of C09 and spectrophotometry of the composite spectra of
 $z\sim3$
LBGs with different Ly
$z\sim3$
LBGs with different Ly
 $\alpha$
spectral type, we calculate photometric criteria by which populations of p-aLBGs and p-eLBGs can be selected from the ugri broadband imaging of the LSST (Section 3.5).
$\alpha$
spectral type, we calculate photometric criteria by which populations of p-aLBGs and p-eLBGs can be selected from the ugri broadband imaging of the LSST (Section 3.5).
One motivation for this work is to provide the statistical foundation for application of the result described in Paper II in this series (Foran et al. 2023b, submitted) wherein we report a relationship between net Ly
![]() $\alpha$
EW and galaxy kinematics, and demonstrate how the photometric segregation described here can be used to predict the kinematic type (and other properties) of large numbers of
$\alpha$
EW and galaxy kinematics, and demonstrate how the photometric segregation described here can be used to predict the kinematic type (and other properties) of large numbers of
![]() $z\sim2-3$
LBGs without the need for spectroscopic information.
$z\sim2-3$
LBGs without the need for spectroscopic information.
More broadly, we propose that this method has strong potential to expand the legacy value of the current generation of deep, wide, optical and near-infrared, large-area and all-sky photometric campaigns such as the Hyper-SuprimeCam Subaru Strategic Program (HSC-SSP: Aihara et al. Reference Aihara2018) and the upcoming Vera Rubin Observatory Legacy Survey of Space and Time (LSST: Ivezić et al. Reference Ivezić2019) that will exploit the Lyman break technique using 3–5 broadband filters across the rest-frame UV to select hundreds of millions of galaxies in redshift ranges from
![]() $z\sim2-6$
across many hundreds to thousands of Mpc. Optimising the discovery potential of such programs requires new techniques to statistically characterise such huge datasets, and to efficiently select from these the most promising samples for expensive follow-up observations. The techniques and insights presented here and in Paper II, explore how inexpensive broadband photometric information that is sensitive to the Ly
$z\sim2-6$
across many hundreds to thousands of Mpc. Optimising the discovery potential of such programs requires new techniques to statistically characterise such huge datasets, and to efficiently select from these the most promising samples for expensive follow-up observations. The techniques and insights presented here and in Paper II, explore how inexpensive broadband photometric information that is sensitive to the Ly
![]() $\alpha$
properties of LBGs might address this challenge. This approach also provides a statistical framework within which
$\alpha$
properties of LBGs might address this challenge. This approach also provides a statistical framework within which
![]() $z\sim2-3$
LBGs will serve as low-redshift reference samples for the study of galaxy populations at higher redshifts where only selection methods based on Ly
$z\sim2-3$
LBGs will serve as low-redshift reference samples for the study of galaxy populations at higher redshifts where only selection methods based on Ly
![]() $\alpha$
emission or Lyman break detection can be applied in large numbers and over large scales (Finkelstein Reference Finkelstein2016).
$\alpha$
emission or Lyman break detection can be applied in large numbers and over large scales (Finkelstein Reference Finkelstein2016).
Specific applications of this approach might include:
-
study of the environments of Ly
 $\alpha$
absorbers and emitters on small and large scales out to hundreds and thousands of Mpc;
$\alpha$
absorbers and emitters on small and large scales out to hundreds and thousands of Mpc; -
generation of the large samples of Ly
 $\alpha$
absorbers and emitters required for three-point correlation function analysis, whereby the geometry, spatial shape, and distribution of the different spectral types might be mapped relative to the filaments and nodes of the cosmic web;
$\alpha$
absorbers and emitters required for three-point correlation function analysis, whereby the geometry, spatial shape, and distribution of the different spectral types might be mapped relative to the filaments and nodes of the cosmic web; -
investigation of the origins and character of the morphology–density relation at
 $z\sim2$
and beyond;
$z\sim2$
and beyond; -
furnishing of the kinematic properties of large numbers of early galaxies of known Ly
 $\alpha$
spectral-type to aid halo-matching between observations and cosmological simulations; and
$\alpha$
spectral-type to aid halo-matching between observations and cosmological simulations; and -
cosmological studies in which tailored samples of
 $z\sim2-5$
LBGs with varying Ly
$z\sim2-5$
LBGs with varying Ly
 $\alpha$
EW are used in combination with cosmic microwave background lensing cross-correlation analysis, to infer the time evolution of matter-density fluctuations, and to carry out compelling tests of horizon-scale general relativity, neutrino masses, and inflation (e.g., Wilson & White Reference Wilson and White2019).
$\alpha$
EW are used in combination with cosmic microwave background lensing cross-correlation analysis, to infer the time evolution of matter-density fluctuations, and to carry out compelling tests of horizon-scale general relativity, neutrino masses, and inflation (e.g., Wilson & White Reference Wilson and White2019).
As a first step toward these goals, we present here photometric criteria by which populations of
![]() $z\sim3$
LBGs with Ly
$z\sim3$
LBGs with Ly
![]() $\alpha$
dominant in absorption, and Ly
$\alpha$
dominant in absorption, and Ly
![]() $\alpha$
dominant in emission, might be selected from ugri photometric data from the LSST (Section 3.5).
$\alpha$
dominant in emission, might be selected from ugri photometric data from the LSST (Section 3.5).
Appendix 1. Photometric Uncertainties
As part of corrections for photometric incompleteness in their study of the rest-frame UV luminosity function at
![]() $z\sim1.9-3.4$
, Reddy et al. (Reference Reddy2008) applied a Monte Carlo (MC) galaxy population simulation method to joint photometric and spectroscopic samples of
$z\sim1.9-3.4$
, Reddy et al. (Reference Reddy2008) applied a Monte Carlo (MC) galaxy population simulation method to joint photometric and spectroscopic samples of
![]() $z\sim2$
$z\sim2$
![]() $U_nG\mathcal{R}$
LBGs to assess the systematic effects of photometric scatter and the intrinsic variation in colours due to Ly
$U_nG\mathcal{R}$
LBGs to assess the systematic effects of photometric scatter and the intrinsic variation in colours due to Ly
![]() $\alpha$
line emission and absorption. These simulations yielded statistical estimates of the photometric uncertainties for the imaging data used to select the
$\alpha$
line emission and absorption. These simulations yielded statistical estimates of the photometric uncertainties for the imaging data used to select the
![]() $z\sim2$
and
$z\sim2$
and
![]() $z\sim3$
$z\sim3$
![]() $U_nG\mathcal{R}$
LBG samples used in this work. Tables of these uncertainties were supplied (N. Reddy, private communication) in 0.5 mag bins of G and
$U_nG\mathcal{R}$
LBG samples used in this work. Tables of these uncertainties were supplied (N. Reddy, private communication) in 0.5 mag bins of G and
![]() $\mathcal{R}$
magnitude and 0.2 mag bins of
$\mathcal{R}$
magnitude and 0.2 mag bins of
![]() $(U_n-G)$
and
$(U_n-G)$
and
![]() $(G-\mathcal{R})$
colour for all observed fields in the
$(G-\mathcal{R})$
colour for all observed fields in the
![]() $z\sim2$
$z\sim2$
![]() $U_nG\mathcal{R}$
survey. In the absence of source-by-source photometric errors, we calculated from the MC simulation data indicative photometric uncertainties for the
$U_nG\mathcal{R}$
survey. In the absence of source-by-source photometric errors, we calculated from the MC simulation data indicative photometric uncertainties for the
![]() $z\sim2$
and
$z\sim2$
and
![]() $z\sim3$
LBGs dispersed in
$z\sim3$
LBGs dispersed in
![]() $(U_n-\mathcal{R})$
/
$(U_n-\mathcal{R})$
/
![]() $\mathcal{R}$
and
$\mathcal{R}$
and
![]() $(G-\mathcal{R})$
/
$(G-\mathcal{R})$
/
![]() $\mathcal{R}$
colour/magnitude space, respectively.
$\mathcal{R}$
colour/magnitude space, respectively.
For the
![]() $z\sim2$
LBGs,
$z\sim2$
LBGs,
![]() $\mathcal{R}$
-band and
$\mathcal{R}$
-band and
![]() $(G-\mathcal{R})$
uncertainties for each galaxy were extracted from the MC simulation tables for the relevant field according to their observed
$(G-\mathcal{R})$
uncertainties for each galaxy were extracted from the MC simulation tables for the relevant field according to their observed
![]() $\mathcal{R}$
-band luminosity and
$\mathcal{R}$
-band luminosity and
![]() $(G-\mathcal{R})$
colour, and added in quadrature to give calculated estimates of G-band uncertainty. These G-band uncertainties were in turn added in quadrature with the tabulated
$(G-\mathcal{R})$
colour, and added in quadrature to give calculated estimates of G-band uncertainty. These G-band uncertainties were in turn added in quadrature with the tabulated
![]() $(U_n-G)$
uncertainties to give an estimate of the
$(U_n-G)$
uncertainties to give an estimate of the
![]() $U_n$
-band uncertainty for each galaxy. Finally,
$U_n$
-band uncertainty for each galaxy. Finally,
![]() $(U_n-\mathcal{R})$
uncertainties were estimated by subtracting in quadrature the
$(U_n-\mathcal{R})$
uncertainties were estimated by subtracting in quadrature the
![]() $\mathcal{R}$
-band uncertainty from that of the
$\mathcal{R}$
-band uncertainty from that of the
![]() $U_n$
-band.
$U_n$
-band.
For
![]() $z\sim3$
LBGs in the three fields where the
$z\sim3$
LBGs in the three fields where the
![]() $z\sim2$
and
$z\sim2$
and
![]() $z\sim3$
catalogs overlap (i.e., HDF/GOODS-N, Q0933 and Q1422)
$z\sim3$
catalogs overlap (i.e., HDF/GOODS-N, Q0933 and Q1422)
![]() $\mathcal{R}$
-band and
$\mathcal{R}$
-band and
![]() $(G-\mathcal{R})$
uncertainties for each galaxy were extracted similarly to the
$(G-\mathcal{R})$
uncertainties for each galaxy were extracted similarly to the
![]() $z\sim2$
sample. For all other
$z\sim2$
sample. For all other
![]() $z\sim3$
LBGs,
$z\sim3$
LBGs,
![]() $\mathcal{R}$
-band and
$\mathcal{R}$
-band and
![]() $(G-\mathcal{R})$
uncertainties were estimated by averaging values for the HDF/GOODS-N, Q0933 and Q1422 fields at the relevant luminosity and colour.
$(G-\mathcal{R})$
uncertainties were estimated by averaging values for the HDF/GOODS-N, Q0933 and Q1422 fields at the relevant luminosity and colour.
For the purpose of illustrating the representative photometric uncertainties thus calculated, the
![]() $z\sim2$
and
$z\sim2$
and
![]() $z\sim3$
LBG samples were divided into a
$z\sim3$
LBG samples were divided into a
![]() $5\times5$
grid on their respective CMDs. Fig. A.1 shows the mean colour, magnitude, and associated uncertainties, for the galaxies in each grid element overlaid on the full sample for both redshift ranges.
$5\times5$
grid on their respective CMDs. Fig. A.1 shows the mean colour, magnitude, and associated uncertainties, for the galaxies in each grid element overlaid on the full sample for both redshift ranges.

Figure A.1. Indicative photometric uncertainties for
![]() $z\sim2$
(top) and
$z\sim2$
(top) and
![]() $z\sim3$
(bottom)
$z\sim3$
(bottom)
![]() $U_nG\mathcal{R}$
LBGs dispersed in colour-magnitude space and divided into a
$U_nG\mathcal{R}$
LBGs dispersed in colour-magnitude space and divided into a
![]() $5\times5$
grid on the CMD. The green and orange symbols indicate the mean colour, magnitude, and associated uncertainties for the galaxies in each grid element. In each case, the representative symbols are overlaid on their respective full sample (grey symbols).
$5\times5$
grid on the CMD. The green and orange symbols indicate the mean colour, magnitude, and associated uncertainties for the galaxies in each grid element. In each case, the representative symbols are overlaid on their respective full sample (grey symbols).
The estimated typical
![]() $\mathcal{R}$
-band uncertainty of
$\mathcal{R}$
-band uncertainty of
![]() $\lesssim$
$\lesssim$
![]() $0.2$
up to the
$0.2$
up to the
![]() $\mathcal{R}$
$\mathcal{R}$
![]() $= 25.5$
limit, gives confidence for the use of the
$= 25.5$
limit, gives confidence for the use of the
![]() $z\sim2$
$z\sim2$
![]() $U_nG\mathcal{R}$
LBG sample in our analysis. On the other hand, the estimated uncertainties in
$U_nG\mathcal{R}$
LBG sample in our analysis. On the other hand, the estimated uncertainties in
![]() $(U_n-\mathcal{R})$
suggest that
$(U_n-\mathcal{R})$
suggest that
![]() $U_n$
-band magnitudes fainter than
$U_n$
-band magnitudes fainter than
![]() $\sim$
26.0–26.5 introduce photometric errors
$\sim$
26.0–26.5 introduce photometric errors
![]() $\gtrsim$
$\gtrsim$
![]() $0.5$
that are potentially problematic for the colour-magnitude segregation approach investigated here. Given our need for reliable
$0.5$
that are potentially problematic for the colour-magnitude segregation approach investigated here. Given our need for reliable
![]() $(U_n-G)$
and/or
$(U_n-G)$
and/or
![]() $(U_n-\mathcal{R})$
colours, and in the absence of source-by-source photometric uncertainties, the estimates derived from the MC simulations motivated the decision to limit the
$(U_n-\mathcal{R})$
colours, and in the absence of source-by-source photometric uncertainties, the estimates derived from the MC simulations motivated the decision to limit the
![]() $z\sim2$
sample to galaxies with
$z\sim2$
sample to galaxies with
![]() $U_n$
-band magnitudes
$U_n$
-band magnitudes
![]() $\leq$
26.5.
$\leq$
26.5.