1 Introduction
Gradual typing aims to provide a smooth integration between the static and dynamic typing disciplines. In gradual typing, a program with no type annotations usually behaves as a dynamically typed program,Footnote 1 whereas a fully annotated program behaves as a statically typed program. The interesting aspect of gradual typing is that programs can be partially typed in a spectrum ranging from fully dynamically typed into fully statically typed. Several mainstream languages, including TypeScript (Bierman et al., Reference Bierman, Abadi and Torgersen2014), Flow (Chaudhuri et al., Reference Chaudhuri, Vekris, Goldman, Roch and Levi2017), or Dart (Bracha, Reference Bracha2015), enable forms of gradual typing to various degrees. Much research on gradual typing has focused on the pursuit of sound gradual typing (Siek & Taha, Reference Siek and Taha2006, Reference Siek and Taha2007; Wadler & Findler, Reference Wadler and Findler2009), where certain type safety properties, and other properties about the transition between dynamic and static typing, are preserved.
The semantics of gradually typed languages is typically given indirectly via an elaboration into a cast calculus. For instance, the blame calculus (Wadler & Findler, Reference Wadler and Findler2009; Siek et al., Reference Siek, Thiemann and Wadler2015a), the threesome calculus (Siek & Wadler, Reference Siek and Wadler2009), or other cast calculi (Henglein, Reference Henglein1994; Findler & Felleisen, Reference Findler and Felleisen2002; Gray et al., Reference Gray, Findler and Flatt2005; Tobin-Hochstadt & Felleisen, Reference Tobin-Hochstadt and Felleisen2006; Siek et al., Reference Siek, Thiemann and Wadler2015a, 2009) are often used to give the semantics of gradually typed languages. Since a gradual type system can accept programs with unknown types, run-time checks are necessary to ensure type safety. Thus, the job of the (type-directed) elaboration is to insert casts that bridge the gap between known and unknown types. Then the semantics of a cast calculus can be given in a conventional manner.
While elaboration is the most common approach to give the semantics for gradually typed languages, it is also possible to have a direct semantics. In fact, a direct semantics is more conventionally used to provide the meaning to more traditional forms of calculi or programming languages. A direct semantics avoids the extra indirection of a target language and can simplify the understanding of the language. Garcia et al. (Reference Garcia, Clark and Tanter2016), as part of their AGT approach, advocated, and proposed an approach for giving a direct semantics to gradually typed languages. They showed that the cast insertion step provided by elaboration, which was until then seen as essential to gradual typing, could be omitted. Instead, in their approach, they develop the dynamic semantics as proof reductions over source language typing derivations.
We present a different approach to give the semantics of gradually typed languages directly. We use a recently proposed variant of small-step operational semantics (Wright & Felleisen, Reference Wright and Felleisen1994) called type-directed operational semantics (TDOS) (Huang & Oliveira, Reference Huang, Oliveira, Hirschfeld and Pape2020). For the most part, developing a TDOS is similar to developing a standard small step-semantics as advocated by Wright and Felleisen. However, in a TDOS type annotations become operationally relevant and can affect the result of a program. While there have been past formulations of small-step semantics where type annotations are also relevant (Goguen, Reference Goguen1994; Feng & Luo, Reference Feng and Luo2011; Bettini et al., Reference Bettini, Bono, Dezani-Ciancaglini, Giannini and Venneri2018), the distinctive feature of TDOS is the use of a big-step casting relation for casting values under a given type. While typically values are the final result of a program, in TDOS casting can further transform them based on their run-time type. Thus, casting provides an operational interpretation to type conversions in the language, similarly to coercions in coercion-based calculi (Henglein, Reference Henglein1994).
We illustrate how to employ TDOS on gradually typed languages using two calculi. The first calculus, called 
$\lambda B^{g}$, is inspired by the semantics of a variant of the blame calculus (
$\lambda B$) (Wadler & Findler, Reference Wadler and Findler2009) by Siek et al. (Reference Siek, Thiemann and Wadler2015a). However, unlike the blame calculus, 
$\lambda B^{g}$ allows implicit type conversions, enabling it to be used as a gradually typed language. Gradually typed languages can be built on top of 
$\lambda B$ using an elaboration from a source language into 
$\lambda B$. In contrast, 
$\lambda B^{g}$ can already act as a gradual language, without the need for an elaboration process.
The second calculus, called 
$\lambda e$, explores a variant of the eager semantics for gradually typed languages (Herman et al., Reference Herman, Tomb and Flanagan2007, Reference Herman, Tomb and Flanagan2010), inspired by the semantics adopted in AGT (Garcia et al., Reference Garcia, Clark and Tanter2016). In the 
$\lambda B$ calculus, a lambda expression annotated with a chain of types is taken as a value. This means that it accumulates the type annotations and checks if there are errors only when the function is applied to a value. This has some drawbacks. Perhaps most notably, and widely discussed in the literature (Siek & Taha, Reference Siek and Taha2007; Siek et al., Reference Siek, Garcia and Taha2009; Siek & Wadler, Reference Siek and Wadler2009; Herman et al., Reference Herman, Tomb and Flanagan2010; Garcia, Reference Garcia2013), is that the accumulation of annotations affects space efficiency. A nice aspect of the eager semantics is that it avoids the accumulation of type annotations, being more space-efficient. Furthermore, as we shall see, the eager semantics also enables simple proofs for the gradual guarantee (Siek et al., Reference Siek, Vitousek, Cimini and Boyland2015b).
For both calculi, type safety and the gradual guarantee are proved. For 
$\lambda B^{g}$, we also present a variant with blame labels (Wadler & Findler, Reference Wadler and Findler2009). Blame labels are an important feature of gradually typed languages, which enable tracking run-time type errors and pinpointing the origin of the errors. Our variant of 
$\lambda B^{g}$ shows how the TDOS deals with such an important feature of gradually typed languages. This is noteworthy since blame labels can be a significant challenge for some gradual typing approaches. For instance, the AGT approach has yet to provide an account for blame labels. As far as we know, our work provides the first gradually typed calculus without elaboration to an intermediate language but with blame tracking. In addition, we show that blame safety can also be proved directly for 
$\lambda B^{g}$. Finally, we show that 
$\lambda B^{g}$ with blame labels is sound and complete with respect to the blame calculus.
A non-goal of the current paper is to investigate efficient implementations of a TDOS. The three TDOS developed in this paper are directly implementable, but inefficient. We believe that the primary strength of a TDOS is its ability to provide a direct and simple semantics for gradual languages and focus on that in this article. However, it is currently unclear whether a TDOS can also be used to guide efficient implementations of gradually typed languages. While we believe that it is possible to adapt TDOS to account for performance, this would require introducing additional complexity, which would be in conflict with our goals here. We provide some discussion about potential directions to investigate performant TDOS-based implementations, as well as discussing other potential criticisms of the TDOS approach in Section 6.
In summary, the contributions of this work are:
• TDOS for gradual typing: We show that a TDOS can be employed in gradually typed languages. This enables simple and concise specifications of the semantics of gradually typed languages, without resorting to an intermediate cast calculus. A nice aspect of TDOS is that it remains close to the simple and familiar small-step semantics approach by Wright and Felleisen.
-
• The
$\lambda B^{g}$ calculus provides a first concrete illustration of TDOS for gradual typing. It follows closely the semantics of the blame calculus, but it allows implicit type conversions. We show type-safety, determinism, as well as the gradual guarantee. -
• The eager
$\lambda e$ calculus. $\lambda e$ explores a TDOS design with an eager semantics for gradual typing. $\lambda e$ is type-safe and it comes with a gradual guarantee (Siek et al., Reference Siek, Vitousek, Cimini and Boyland2015b), which is quite simple to prove. -
• TDOS with blame labels. We illustrate that the TDOS approach can deal with blame labels. We provide a variant of
$\lambda B^{g}$, called $\lambda B^{g}_{l}$, which supports blame labels and blame tracking. $\lambda B^{g}_{l}$ is type-safe and deterministic, preserves the gradual guarantee and is also blame safe. Two noteworthy results are the soundness and completeness to the blame calculus, and our blame safety proof, which is done directly on $\lambda B^{g}_{l}$ (instead of indirectly via the blame calculus). -
• Coq formalization: All calculi and all associated lemmas and theorems have been formalized in the Coq theorem prover. The Coq formalization can be found in the supplementary materials of this article:
https://github.com/YeWenjia/TypedDirectedGradualTypingWithBlame
This article is an extended, and significantly rewritten, version of a conference paper (Ye et al., Reference Ye, Oliveira and Huang2021). There are three main novelties with respect to the conference version. First, we now cover blame labels and blame tracking and introduce the new 
$\lambda B^{g}_{l}$ calculus, which is a variant of 
$\lambda B^{g}$ with blame labels. The conference work did not account for blame labels at all. Furthermore, this article adds several important results for 
$\lambda B^{g}_{l}$, such as the soundness and completeness to the blame calculus, a novel blame safety theorem and the gradual guarantee for 
$\lambda B^{g}_{l}$. Second, the conference version did not prove the gradual guarantee for 
$\lambda B^{g}$, whereas we now show the gradual guarantee for 
$\lambda B^{g}_{l}$. The gradual guarantee is a nontrivial result for 
$\lambda B^{g}_{l}$, due primarily to the lazy semantics of higher-order casts. Third, the 
$\lambda e$ calculus is also new, and it provides the first TDOS design for a calculus with an eager semantics. In the conference version, we explored a forgetful semantics (Greenberg, Reference Greenberg2015), but we opted to study an eager semantics instead for the journal version since the eager semantics is more widely accepted.
2 Overview
This section provides background on gradual typing and the blame calculus, and then illustrates the key ideas of our work, the 
$\lambda B^{g}$ calculus (with and without blame labels) and the 
$\lambda e$ calculus.
2.1 Background: Gradual typing and the $\boldsymbol\lambda \boldsymbol{B}$ calculus
Traditionally, programming languages can be divided into statically typed languages and dynamically typed languages. In a statically typed language, a type system checks the types of terms before execution or compilation. The language may support type inference, but usually some type annotations are required for type checking. Type annotations bear some extra work for a programmer. However, the benefit of static typing is that type-unsafe programs are rejected before they are executed. On the other hand, in dynamically typed languages terms do not have static types (and no type annotations are needed). This waives the burden of a strict type discipline, making programs more flexible, but at the cost of static type safety.
Gradual typing (Siek & Taha, Reference Siek and Taha2006) is like a bridge connecting the two styles. Gradual typing extends the type system of static languages by allowing terms to have an unknown type 
$ \star $. A term with the unknown type 
$ \star $ is not rejected in any context by the type checker. When all terms in a program have unknown types the type checker does not reject program, similarly to a dynamically typed language. In a gradually typed language, programs can be completely statically typed, or completely dynamically typed, or anything in between.
To cooperate with the very flexible 
$ \star $ type, the common practice in gradual type systems is to define a binary relation called type consistency. Consistency offers a more relaxed notion of type compatibility compared to conventional statically typed languages where equality is used instead. The key feature of consistency is that the unknown type 
$ \star $ is consistent with any other type. Thus, dynamic snippets of code can be embedded into the whole program without breaking type soundness. Of course, the notion of type soundness is relaxed to tolerate some kinds of run-time type errors. Besides type soundness, there are some other criteria for gradual typing systems. One well-recognized standard is the gradual guarantee proposed by Siek et al. (Reference Siek, Vitousek, Cimini and Boyland2015b).
Elaboration Semantics of Gradual Typing and the 
$\boldsymbol\lambda \boldsymbol{B}$ Calculus. The semantics of gradually typed languages is usually given by an elaboration into a cast calculus. This approach has been widely used since the original work on gradual typing by both Siek & Taha (Reference Siek and Taha2006) and Tobin-Hochstadt & Felleisen (Reference Tobin-Hochstadt and Felleisen2006).
One of the most widely used cast calculi for the elaboration of gradually typed languages is the blame calculus (Wadler & Findler, Reference Wadler and Findler2009; Siek et al., Reference Siek, Thiemann and Wadler2015a). Figure 1 shows the definition of the blame calculus. Here we base ourselves in a variant of the blame calculus by Siek et al. (Reference Siek, Thiemann and Wadler2015a). The blame calculus is the simply-typed lambda calculus extended with the unknown type (
$\star$) and the cast expression (
). Meta-variables G and H range over ground types, which include 
$ \mathsf{Int} $ and 
$ \star \rightarrow \star $. The definition of values in the blame calculus contains some interesting forms. In particular, casts (
) and 
are included. Run-time type errors are denoted as 
. The syntactic sort 
represents blame labels. A blame label 
is the complement of label 
and the complement is involutive, which means that 
is the same as 
. Notably, when casting with a label 
, the expression being cast is to blame, while when casting with 
, the context of the cast is to blame. Besides the standard typing rules of the simply typed lambda calculus (STLC), there is an additional typing rule for casts: if term t has type A and A is consistent with B, a cast on t from A to B has type B with blame label 
. The consistency relation for types states that every type is consistent with itself, 
$ \star $ is consistent with all types, and function types are consistent only when input types and output types are consistent with each other. In rule BTyp-c, 
$\rceil c \lceil$ is the dynamic type of the constant c. For example, 
$\rceil$+
$\lceil$ is 
$\mathsf{Int} \rightarrow \mathsf{Int} \rightarrow \mathsf{Int}$. In the premise of rule bstep-dyna, there is a predicate ug which says that type A should be consistent with a ground type G, but it should not be G itself and type 
$ \star $. The definition of ug is
Fig. 1. The 
$\lambda B$ calculus (selected rules).
In rule bstep-c, if 
then 
is returned, while for 
, the result 
is returned.
The bottom of Figure 1 shows a selection of the reduction rules of the blame calculus. The dynamic semantics of the 
$\lambda B$ calculus is standard for most rules. For first-order values, reduction is straightforward: a cast either succeeds or it fails and raises blame. For exampleFootnote 2:
For higher-order values such as functions, the semantics is more complex, since the cast result cannot be immediately obtained. For example, if we cast from 
$ \star \rightarrow \star $ to 
$\mathsf{Int} \rightarrow \mathsf{Int}$, we cannot judge the cast result immediately. So the checking process is deferred until the function is applied to an argument. Rule bstep-abeta shows that process: a function with the cast is a value which does not reduce until it has been applied to a value.
2.2 Motivation for a direct semantics for gradual typing
In this paper, we propose not to use an elaboration semantics into a cast calculus, but to use a direct semantics for gradual typing instead. We are not the first to propose such an approach. For instance, the AGT framework for gradual typing (Garcia et al., Reference Garcia, Clark and Tanter2016) also employs a direct semantics. In that work, the authors state that “developing dynamic semantics for gradually typed languages has typically involved the design of an independent cast calculus that is peripherally related to the source language”. We partly agree with such arguments. In addition, as argued by Huang & Oliveira (Reference Huang, Oliveira, Hirschfeld and Pape2020), there are some other reasons why a direct semantics is beneficial over an elaboration semantics.
A direct semantics enables a simple and direct way for programmers and tools to reason about the behavior of programs. For instance, we can reason directly about source programs by employing the operational semantics rules. With a TDOS, we can easily (and justifiably) employ similar steps to reason about the source language (say GTLC or 
$\lambda B^{g}$). With a semantics defined via elaboration, however, that is not so easy because of the indirect semantics. In essence, with an elaboration semantics, one must first translate a source expression to a target calculus, then reason about the semantics in the target calculus, and finally translate the final result in the target calculus back to the source language. This process is not only more laborious, but it requires knowledge about the target language and its semantics. We refer readers to Huang and Oliveira’s work, which has an extensive discussion about this point. Additionally, some tools, especially some debuggers or tools for demonstrating how programs are computed, require a direct semantics, since those tools need to show transformations that happen after some evaluation of the source program.
Another potential benefit of a direct semantics is simpler and shorter metatheory/implementation. For instance, with a direct semantics we can often save quite a few definitions/proofs, including a second type system, various definitions on well-formedness of terms, substitution operations and lemmas, pretty printers, etc. Though these are not arguably difficult, they do add up. Perhaps more importantly, some proofs can be simpler with a direct semantics. For example, proving the gradual guarantee can often be simpler, since some lemmas that are required with an elaboration semantics (for instance, Lemma 6 in the original work on the refined criteria for gradual typing Siek et al., Reference Siek, Vitousek, Cimini and Boyland2015b) are not needed with a direct operational semantics. Moreover, only the precision relation for the source language is necessary. We shall see some of those benefits in this paper.
Finally, another source of complication in an elaboration semantics, especially in languages with more advanced type systems, is coherence (Reynolds, Reference Reynolds1991). Coherence is a desirable property for an elaboration semantics, where we show that all possible elaborations for a source program have the same semantics in the target language. For simpler languages, coherence is typically not an issue because the elaboration process is deterministic. That is there is always a unique target expression that is generated for the same source program. The elaboration of the GTLC into the blame calculus, for example, is deterministic. Thus, coherence is trivial in that case. However, for more advanced type system features, including implicit polymorphism (Xie et al., Reference Xie, Bi, Oliveira and Schrijvers2019; Bottu et al., Reference Bottu, Xie, Marntirosian and Schrijvers2019) or some systems with subtyping (Huang & Oliveira, Reference Huang, Oliveira, Hirschfeld and Pape2020), coherence becomes nontrivial because the elaboration becomes nondeterministic. That is, for the same source program we may be able to generate multiple distinct target expressions. Then a coherence proof has to show that despite generating different expressions, those expressions have the same meaning. Typically this is done by employing some form of contextual equivalence, and usually requires the use of logical relations (Reynolds, Reference Reynolds1993). In those cases, the coherence proof may become quite nontrivial and involved.
One of the original motivations of the TDOS (Huang & Oliveira, Reference Huang, Oliveira, Hirschfeld and Pape2020) was to avoid the need for coherence proofs. In Huang and Oliveira’s work, the source calculus that they considered had subtyping with intersection types, and during elaboration coercions in the target language were generated by the subtyping relation. Unfortunately, these coercions in a system with intersection types are not unique, requiring an involved proof of coherence using contextual equivalence and logical relations. A TDOS avoids coherence proofs. Instead, we can simply prove that the semantics is deterministic, which can usually be done using standard proof techniques and simple inductions. Similar coherence issues arise with other type systems, such as for instance type systems with type classes. The proof that the elaboration of a language with type classes to a target language without type classes is coherent is highly nontrivial, as shown by the work of Bottu et al. (Reference Bottu, Xie, Marntirosian and Schrijvers2019). Finally, there is also work in gradual typing where coherence issues also arise. For instance, Xie et al. (Reference Xie, Bi, Oliveira and Schrijvers2019) have shown that a source language with gradual typing and higher-ranked type-inference can be elaborated into the polymorphic blame calculus (Ahmed et al., Reference Ahmed, Findler, Siek and Wadler2011). However, coherence was not proved due to its difficulty and was left as an open problem. While in this paper the calculi involved are simple enough that no complications arise from coherence, those complications will arise in more complex settings. Thus, avoiding the complications of coherence is another argument to employ a TDOS.
2.3
$\boldsymbol\lambda \boldsymbol{B}^{\boldsymbol{g}}$: A gradually typed lambda calculus
In this subsection, we introduce some of the key ideas in 
$\lambda B^{g}$, which is a gradually typed lambda calculus that is given a semantics via a TDOS. In Section 3, we provide the full details of 
$\lambda B^{g}$.
Cast Calculi vs Gradually Typed Calculi. Since 
$\lambda B$ requires explicit casts whenever a term’s type is converted, it cannot be considered as a gradually typed calculus. For comparison, the application rule for typing in the Gradually Typed Lambda Calculus (GTLC) (Siek & Taha, Reference Siek and Taha2006, Reference Siek and Taha2007; Siek et al., Reference Siek, Vitousek, Cimini and Boyland2015b):
does not force the input term to have the same type to what the function expects. It just checks the consistency of the two terms’ types and can do implicit type conversions (casts) automatically. Note that the function 
$ T \triangleright T_{{\mathrm{1}}} \rightarrow T_{{\mathrm{2}}} $ allows T to be either a function type or 
$ \star $. When T is a function type, then T itself is returned. Otherwise, if T is 
$ \star $, then 
$ \star \rightarrow \star $ is returned. In a cast calculus, similar flexibility only exists when the term is wrapped with a cast, since the application rule strictly requires the argument type to be the same as the input type of the function type.
Bidirectional Type-Checking for 
$\boldsymbol\lambda \boldsymbol{B}^{\boldsymbol{g}}$. In this paper, a key argument is that we do not need two calculi to formulate the semantics of a gradually typed language. Instead, we can have a single calculus that supports explicit type conversions (like casts in cast calculi) as well as implicit type conversions (like the GTLC). To introduce implicit type conversions, we turn to the bidirectional type checking (Pierce & Turner, Reference Pierce and Turner2000). Unlike in the GTLC or 
$\lambda B$, a bidirectional typing judgment may be in one of the two modes: inference or checking. In the former, a type is synthesized from the term. In the latter, both the type and the term are given as input, and the typing derivation examines whether the term can be used under that type safely. Notably, via the checking mode, the type consistency between a type annotation and a given type is checked. Furthermore, uses of the checking mode in typing essentially denote points where runtime casts need to happen to enforce type-safety.
In a typical bidirectional type system with subtyping, the subsumption rule is only employed in the checking mode, allowing a term to be checked by a supertype of its inferred type. That is to say, the checking mode is more relaxed than the inference mode, which typically infers a unique type. With bidirectional type-checking, the application rule in such a system is not as strict as in the 
$\lambda B$ calculus, as the input term is typed with a checking mode. For example, the rules for applications and subsumption in 
$\lambda B^{g}$ are
Implicit Type Conversion in Function Applications. 
$\lambda B^{g}$ supports annotated lambdas of the form 
$\lambda x . e : A \to B$ with both input and output types for the function. A raw lambda 
$\lambda x.e$ is sugar for a lambda with a function type 
$ \star \rightarrow \star $. Note also that, throughout this article, whenever we have an expression of the form 
$\lambda x . e : A \to B$, this should be interpreted as 
$(\lambda x . e) : A \to B$. In other words, type annotations bind more weakly than lambdas (and other forms of expressions). By using bidirectional type checking, we can type-check programs such as:
In addition bidirectional type checking can also reject ill-typed programs, such as:
\begin{align*} & (\lambda x. not~x : \mathsf{Bool} \rightarrow \mathsf{Bool} )~1 && \text{Rejected!}\end{align*}
In the first two examples, 
$\lambda x.x$ and 
$\lambda x. not~x$ are equivalent to 
$\lambda x.x: \star \rightarrow \star $ and 
$\lambda x. not~x: \star \rightarrow \star $. Thus, in the first example, the argument 1 is type checked with type 
$ \star $. For the 3rd and 4th examples, 1 can be type checked by the function input types 
$ \star $ and 
$ \mathsf{Int} $. However, 1 cannot be checked by type 
$ \mathsf{Bool} $ in the last example, and that program is rejected.
Explicit Type Conversion. Besides implicit conversions, programmers are able to trigger type conversions in an explicit fashion by wrapping the term with a type annotation 
$e : A$, where A denotes the target type. For instance, the two simple examples in 
$\lambda B$ in Section 2.1 can be encoded in 
$\lambda B^{g}$ as
\begin{align*} & 1 : \star : \mathsf{Int} \longmapsto ^{*} 1 \\ & 1 : \star : \mathsf{Bool} \longmapsto ^{*} blame\end{align*}
with similar results to the same programs in the 
$\lambda B$ calculus. Notice that, unlike 
$\lambda B$, there is no cast expression in 
$\lambda B^{g}$. Casts are triggered by type annotations. For instance, in the first expression above (
$1 : \star : \mathsf{Int} $), the first type annotation (
$\star$) triggers a cast from 
$ \mathsf{Int} $ to 
$\star$. The source type 
$ \mathsf{Int} $ is the type of 1, whereas the target type 
$\star$ is specified by the annotation. Then the second annotation 
$ \mathsf{Int} $ will trigger a second cast, but now from 
$\star$ to 
$ \mathsf{Int} $.
2.4 Designing a TDOS for $\boldsymbol\lambda \boldsymbol{B}^{\boldsymbol{g}}$
The most interesting aspect of 
$\lambda B^{g}$ is its dynamic semantics. We discuss the key ideas next.
Background: Type-Directed Operational Semantics. A TDOS is helpful for language features whose semantics is type dependent. TDOS was originally proposed for languages that have intersection types and a merge operator (Huang et al., Reference Huang, Zhao and Oliveira2021). To enable expressive forms of the merge operator, the dynamic semantics has to account for types, just like the semantics of gradually typed languages. In many traditional operational semantics, type annotations are often ignored. In a TDOS that is not the case. Instead, type annotations are used at runtime to determine the result of the reduction. A TDOS has two parts. One part is similar to the traditional reduction rules, modulo some changes on type-related rules, like beta reduction for application, and annotation elimination for values. The second component of a TDOS is the casting relation 
$ v \,\Downarrow_{ A }\, r $.
Casting for 
$\boldsymbol\lambda \boldsymbol{B}^{\boldsymbol{g}}$. Due to consistency, some form of run-time checking is needed in gradual typing. The casting relation 
$ v \,\Downarrow_{ A }\, r $ is used when run-time checks are needed. Casting compares the dynamic type of the input value with the target type. When the type of the input value (v) is not consistent with the target type (A), blame is raised. Otherwise, casting adapts the value to suit the target type. Eventually, terms become more and more precise. Two easy examples to show how casting works are shown next:
\begin{align*} & 1 \,\Downarrow_{ \mathsf{Int} }\, 1 \\ & 1 : \star \,\Downarrow_{ \mathsf{Bool} }\, \mathsf{blame}\end{align*}
If we have an integer value 1 and we want to transform it with type 
$ \mathsf{Int} $, we simply return the original value. In contrast, attempting to transform the value 
$1 : \star $ under type 
$ \mathsf{Bool} $ will result in blame.
Casting takes place in some reduction rules, such as the beta reduction rule and the annotation elimination rule for values. Here we illustrate the beta-reduction rule, and defer the explanation of other reduction rules to Section 3:
Casting is used in beta-reduction to ensure that the argument value 
$v_2$ matches the expected input type of the function (A). Consider another example to illustrate the behavior of casting in beta reduction:
\[(\lambda x.~x: \mathsf{Bool} \to \star )~(1:\star)\]
If we perform substitution directly, as conventionally done in beta-reduction, we would not check if there are run-time errors, for which blame should be raised. Since the typing rule for the argument of the application is in checking mode, we need to check if the type of the argument is consistent with the target type. Therefore, the argument must be further reduced with casting under the expected input type of the function. When we check that the type 
$ \mathsf{Int} $ (the type for the value 1) is not consistent with 
$ \mathsf{Bool} $, blame is raised. However, if we take the example:
then the value 1 (which arises from casting) is substituted in the function body and the result is 2.
2.5
$\boldsymbol\lambda \boldsymbol{e}$: Gradual typing with an eager semantics
To further illustrate the application of a TDOS to gradually typed languages, we also propose a second calculus, called 
$\lambda e$. The 
$\lambda e$ calculus has different design choices in terms of the runtime semantics. In particular, its semantics for casts is a variant of the eager semantics (Herman et al., Reference Herman, Tomb and Flanagan2010) inspired by the approach employeed in AGT (Garcia et al., Reference Garcia, Clark and Tanter2016). Here we overview key ideas in 
$\lambda e$, while the full details of 
$\lambda e$ will be given in Section 5.
Lazy versus Eager. Both the blame calculus and 
$\lambda B^{g}$ employ a lazy semantics for higher-order values, where functions with an arbitrary number of annotations are values. In other words, the checking process for higher-order values is deferred until the function is applied to an argument. Garcia et al. (Reference Garcia, Clark and Tanter2016) proposed the AGT-based methodology, which has been widely applied (Toro et al., Reference Toro, Labrada and Tanter2019; Labrada et al., Reference Labrada, Toro, Tanter and Devriese2022; Ye et al., Reference Ye, Toro and Olmedo2023). In AGT, a variant of the eager semantics is applied for higher-order values. In the following example, we show how higher-order values are reduced in AGT (using our notation):
\begin{align*} & \lambda {x} .\, 1 : \mathsf{Int} \rightarrow \mathsf{Int} : \star \rightarrow \star : \mathsf{Bool} \rightarrow \mathsf{Bool} \longmapsto ^{*} \mathsf{blame}\end{align*}
Unlike the lazy semantics, where a lambda with multiple annotations would be a value, in 
$\lambda e$ the above expression is not a value and it reduces to 
$\mathsf{blame}$. 
$\mathsf{blame}$ is raised directly because, during the reduction process, we attempt to eliminate the intermediate annotation 
$ \star \rightarrow \star $, by checking whether 
$\mathsf{Int} \rightarrow \mathsf{Int}$ and 
$ \mathsf{Bool} \rightarrow \mathsf{Bool} $ are consistent. Since these two types are not consistent 
$\mathsf{blame}$ would be raised in this case.
Meets: Making Sure that no Cast is Forgotten. A complication in the eager semantics is that we should guarantee that possible casts that arise from intermediate annotations are not forgotten. To formalize this behavior, lambda values in 
$\lambda e$ are of the form 
and include three annotations:
• The first annotation (
$A_{{\mathrm{1}}} \rightarrow A_{{\mathrm{2}}}$) is used to type check the lambda body and to cast the argument using the input type before beta-reduction.-
• The second annotation
$B_{{\mathrm{1}}} \rightarrow B_{{\mathrm{2}}}$ is key to the eager semantics: it stores a type, which we call the meet type, that is the greatest lower bound (with respect to precision) of all the intermediate annotations that have been eliminated during reduction of the lambda value. In other words, it is the most imprecise type among the types equivalent to or more precise than the eliminated types. The meet type triggers casts, subsuming the casts needed for the eliminated intermediate annotations. -
• Finally, the outer annotation C is needed for type preservation.
Lets see how meet types are used in the following example:
We first reduce 
$ \lambda {x} .\, {x} : \mathsf{Bool} \rightarrow \star $ to a tagged value 
, which ensures that the intermediate type is more precise than the outer type. The details are explained in Section 5. Then, in the 3rd line, we are safe to remove the outer type and update the intermediate type with the meet result between 
$ \mathsf{Bool} \rightarrow \star $ and 
$ \star \rightarrow \mathsf{Bool} $, which is the more precise type 
$ \mathsf{Bool} \rightarrow \mathsf{Bool} $. Finally, in the 4th line, the meet between 
$ \mathsf{Bool} \rightarrow \mathsf{Bool} $ and 
$ \star \rightarrow \mathsf{Int}$ is undefined and error is raised. Note that, without storing the more precise type 
$ \mathsf{Bool} \rightarrow \mathsf{Bool} $ in the middle, then the type information of the intermediate type annotation 
$ \star \rightarrow \mathsf{Bool} $ would be ignored.
The eager semantics does have some drawbacks compared to the lazy semantics. For instance, New et al. (Reference New, Licata and Ahmed2019) show that the 
$\eta$ principle for the higher-order values is violated. Nevertheless, there are also some nice aspects in an eager semantics. With an eager semantics it is possible to avoid the accumulation of annotations for higher-order values. Another nice aspect of the eager semantics in the AGT approach is that the dynamic gradual guarantee can be formalized in a simple way and proved easily. This is because the number of reduction steps when evaluating a program is not affected by precision (except when runtime errors occur in the less precise version of the program). In a lazy semantics, annotations are sometimes accumulated or added during reduction. So the reduction of more precise and less dynamic programs can take different number of steps in some cases. Here, a more precise program means that the program is more statically typed. For instance, for 
$ \lambda {x} .\, {x} : \mathsf{Int} \rightarrow \mathsf{Int} : \star $ and 
$ \lambda {x} .\, {x} : \star \rightarrow \star : \star $, the more precise program 
$ \lambda {x} .\, {x} : \mathsf{Int} \rightarrow \mathsf{Int} : \star $ should take a step to 
$ \lambda {x} .\, {x} : \mathsf{Int} \rightarrow \mathsf{Int} : \star \rightarrow \star : \star $. In contrast, the less precise one 
$ \lambda {x} .\, {x} : \star \rightarrow \star : \star $ (which is a value) takes zero steps. Since in the eager semantics annotations are not accumulated, the dynamic semantics for more and less precise programs behaves in the same way, satisfying the dynamic gradual guarantee more directly and naturally.
Functions. One interesting aspect in the type system of 
$\lambda e$ is how we deal with lambdas. If the programmer wants to have a function statically type checked, they can write down the full annotations or the annotations can be propagated by bidirectional type checking. For instance, in the term:
The argument to the function (
), which is itself a lambda, has no type annotations. Here bidirectional type-checking propagates the annotations, removing the need for explicit annotations in the lambda. This is in contrast to typical gradual languages, such as the GTLC, where a raw lambda 
$\lambda x.~e$ is syntactic sugar for 
$\lambda (x : \star ).~e$. The key difference is that in GTLC the raw lambda (
) in a similar program to the above would lose type information and be of type 
$ \star \rightarrow \mathsf{Int}$. A consequence of this loss of type precision is that the elaboration of GTLC into a cast calculus would need to insert a few casts here. First, one cast from 
$ \star $ to 
$ \mathsf{Int} $ would be needed to convert the type of the argument. Second, a cast from 
$ \mathsf{Int} $ to 
$ \star $ would be needed to cast x back to an integer. These casts could potentially be avoided if there was no loss of type information. In 
$\lambda e$, the lambda is of type 
$\mathsf{Int} \rightarrow \mathsf{Int}$ and no static information is lost.
To achieve this, our rule for lambda expressions, which is quite standard for bidirectional typing, is:
The premise 
$ A \triangleright A_{{\mathrm{1}}} \rightarrow A_{{\mathrm{2}}} $ in rule TYP-abs ensures that type A can be the unknown type 
$ \star $ or a function type. The unknown type is interpreted as the unknown function 
$ \star \rightarrow \star $. The typing rule TYP-abs is employed to type-check both lambdas above: the first one because the explicit type annotation triggers the checking mode; and the second one because the application rule employs the checking mode to check that arguments conform to the right type.
2.6 Blame tracking
An important feature of gradual typing is blame tracking, which enables pinpointing the source of blame in a program. This is helpful for programmers as they can determine the source of the problem. 
$\lambda B^{g}$ can support blame tracking, showing that the TDOS approach can smoothly deal with such an important feature of gradual typing. Next, we discuss the key ideas of adding blame tracking to 
$\lambda B^{g}$. The full details are discussed in Section 4.
Blame Tracking. For gradually typed lambda calculi, due to the notion of consistency, runtime type errors may arise from type inconsistency. A natural question is what is the cause of the error, and which part of the program is to blame. In the 
$\lambda B$ calculus, blame labels, which are the blue parts in Figure 1, are used to track the source of errors. Blame labels include the positive blame label (
) and the negative blame label (
). Positive blame labels (
) arise when the terms contained in the cast are to blame. Negative blame labels (
) arise when the context which contains the cast is to blame. An example to show the mechanism of blame tracking with different labels in 
$\lambda B$ is:
In this example, when the argument (
) is cast from 
$ \star $ to 
$ \mathsf{Int} $, blame with label 
is raised: the source type 
$ \mathsf{Bool} $ is different from the target type 
$ \mathsf{Int} $ causing blame to be raised.
Blame Tracking for 
$\boldsymbol\lambda \boldsymbol{B}^{\boldsymbol{g}}$. The 
$\lambda B^{g}_{l}$ calculus is a variant of 
$\lambda B^{g}$ with blame tracking. In 
$\lambda B^{g}_{l}$ blame labels are introduced in annotation expressions (
), lambdas 
, application expressions (
), and projections (
). Annotation expressions (
) trigger casts and are similar to cast expressions (
) in 
$\lambda B$. While the label in lambdas is to track the implicit cast in lambda bodies. Notably, there is a blame label for applications since the typing rule for applications is
In this rule, the typing for the argument 
$e_2$ is in checking mode. This means that 
$e_2$ may have a different type, which can be consistent with 
$A_{{\mathrm{1}}}$. However, the cast induced by the application may be the source of blame. For instance, consider the following program:
For this example, the argument (
) is cast under type 
$ \mathsf{Int} $, and the type of 
$\mathsf{True}$ is not consistent with type 
$ \mathsf{Int} $. Blame is raised with the blame label (
). Furthermore, if A is type 
$ \star $, there is an implicit cast to 
$ \star \rightarrow \star $ and label 
is used as well. The label 
in projections 
has the similar behavior. The 
$\lambda B^{g}_{l}$ calculus is proved to be sound and complete with respect to the blame calculus with blame labels. Furthermore, we formalized and proved the gradual guarantee theorem for 
$\lambda B^{g}_{l}$.
Blame Theorem. “Well-typed programs can’t be blamed” is the slogan of Wadler & Findler (Reference Wadler and Findler2009)’s paper. To express this slogan formally, Wadler and Findler proposed the blame theorem, which expresses the idea that we should blame the right part of a program. More specifically, a cast from a more precise type to a less precise type cannot give rise to positive blame, and negative blame cannot be triggered while casting from a less precise type to a more precise type. We have proved the blame theorem for 
$\lambda B^{g}_{l}$, showing that this key result can be proved using a TDOS approach to gradual typing.
3 The $\boldsymbol\lambda \boldsymbol{B}^{\boldsymbol{g}}$ calculus: Syntax, typing, and semantics
In this section, we introduce the gradually typed 
$\lambda B^{g}$ calculus. The semantics of the 
$\lambda B^{g}$ calculus follows closely the semantics of the 
$\lambda B$ cast calculus. It employs a type-directed operational semantics (Huang & Oliveira, Reference Huang, Oliveira, Hirschfeld and Pape2020) to have a direct operational semantics. 
$\lambda B^{g}$ uses bidirectional type-checking (Pierce & Turner, Reference Pierce and Turner2000). We keep the presentation light here to better illustrate the key ideas of our approach. Thus, we mainly focus on presenting the semantics and proving basic results such as determinism and type-soundness. In Section 4, we present an extension of 
$\lambda B^{g}$ with blame labels and develop many more results, such as the gradual guarantee, the blame theorem and the soundness and completeness to the blame calculus.
3.1 Syntax
The syntax of the 
$\lambda B^{g}$ calculus is shown in Figure 2.
Fig. 2. Syntax and well-formed values for the 
$\lambda B^{g}$ calculus.
Types and Ground types. Meta-variables A and B range over types. There is a basic type: the integer type 
$ \mathsf{Int} $. The calculus also has function types 
$A \rightarrow B$, the unknown type 
$\star$, and product types 
$ A \times B $. Compared to 
$\lambda B$ calculus, ground types not only include 
$ \mathsf{Int} $ and 
$\star \to \star$, but also 
$ \star \times \star $. We sometimes use the abbreviation G to denote ground types.
Constants, Expressions, and Results. Meta-variable c ranges over constants. Each constant is assigned a unique type. The constants include integers (i) of type 
$ \mathsf{Int} $ and additions (
, 
). The type of 
is 
$\mathsf{Int} \rightarrow \mathsf{Int} \rightarrow \mathsf{Int}$. The type of 
is 
$\mathsf{Int} \rightarrow \mathsf{Int}$, taking an integer and returning another integer. Meta-variable e ranges over expressions. There are some standard constructs, which include: constants (c); variables (x); annotated expressions (
$e: A$); annotated lambdas (
$ \lambda {x} .\, e : A \rightarrow B$); application expressions (
$e_1~e_2$); products 
$( e_{{\mathrm{1}}} , e_{{\mathrm{2}}} )$; and projections 
$( \pi_{i}~ e )$. Similarly to GTLC, lambdas without type annotations are just sugar for lambdas with the annotation 
$ \star \rightarrow \star $. Results (r) include all expressions and blame, which is used to denote cast-errors at run-time.
Values and Contexts. Typing contexts are standard. 
$\Gamma$ is used to track bound variables x with their type A. The meta-variable v ranges over well-formed values. Values contain constants, annotated values and lambda abstractions (
$ \lambda {x} .\, e : A \rightarrow B$). Similarly to 
$\lambda B$, not all syntactic values are well-formed values. The value predicate, at the bottom of Figure 2, defines well-formed values, which are a subset of syntactic values. Lambda expressions are values (rule value-abs). A syntactic value v with a function type annotation is a well-formed value if the dynamic type of the value is also a function type (rule value-fanno). Note that, for well-typed values, it is guaranteed that the type of v is consistent with the annotation 
$A \rightarrow B$. So, the value predicate only needs to check if the type of the value has an arrow form. The expression 
$v:\star$ is a value only when the type of v is a ground type (rule value-dyn). Products are values if there is a pair of values. Constants are also values. Note that the meta-function 
$ \rceil v \lceil $, defined next, denotes the dynamic type of a value.
Definition 3.1 (Dynamic type) 
$ \rceil v \lceil $ denotes the dynamic type of the value v.
Frame. The meta-variable F ranges over frames (Siek et al., Reference Siek, Thiemann and Wadler2015a), which is a form of evaluation contexts (Felleisen & Hieb, Reference Felleisen and Hieb1992). The frame is mostly standard, though it is perhaps noteworthy that it includes annotated expressions.
3.2 Typing
We use bidirectional typing for our typing rules. The typing judgment is represented as 
$ \Gamma \vdash e \Leftrightarrow A $, which means that the expression e could be inferred (
$\Rightarrow$) or checked (
$\Leftarrow$) by the type A under the typing context 
$\Gamma$. The typing mode (
$\Leftrightarrow$), whose definition is shown at the top of Figure 3, is used to represent the two modes of the bidirectional typing judgment.
Fig. 3. Type system of the 
$\lambda B^{g}$ calculus.
Typing Relation. The typing relation of the 
$\lambda B^{g}$ calculus is shown in Figure 3. Many rules in inference mode follow the 
$\lambda B$ type system. The typing for constants (rule Typ-c) uses the dynamic type definition to infer the type. Rule Typ-var for variables is standard. For lambda expressions, the 
$\lambda B^{g}$ calculus is different from the 
$\lambda B$ calculus: in the 
$\lambda B^{g}$ calculus the function type of a lambda expression is annotated and the function body is checked with the function output type. Lambdas are annotated with full types because at runtime we want to get the type of lambdas without performing type-checking.
For applications 
$e_1~e_2$, the rule is almost standard for bidirectional type-checking: the type of 
$e_1$ is inferred, and the type of 
$e_2$ is checked against the domain type of 
$e_1$. However, there is some additional flexibility in the typing of applications. The expression 
$e_{{\mathrm{1}}}$ can have type 
$ \star $. In that case, 
$ \star $ is interpreted as a dynamic function type 
$ \star \rightarrow \star $, by employing a matching function (shown at the bottom of Figure 3). The rule for annotations (rule Typ-anno) is standard, inferring the annotated type, while checking the expression against the annotated type. Consistency checks happen in the subsumption rule (rule Typ-sim). However, it is important to notice that, since the subsumption rule is in checking mode, all consistency checks can only happen when typing is invoked in the checking mode. This is the case, for instance, for the rule Typ-App, which checks whether the argument is of type 
$A_{{\mathrm{1}}}$. In addition, to type check the product related expressions, we have rule Typ-pro and rule Typ-Pi. A pair 
${(} e_{{\mathrm{1}}} , e_{{\mathrm{2}}} {)}$ is well typed with type 
$ A \times B $, if 
$e_{{\mathrm{1}}}$ is well typed with type A and 
$e_{{\mathrm{2}}}$ is well typed with type B. When performing projections, we should make sure that the projections happen on pairs. Therefore, we use the matching relation 
$ A \blacktriangleright B $ with product types 
$ A_{{\mathrm{1}}} \times A_{{\mathrm{2}}} $. The unknown type 
$ \star $ matches the dynamic product type 
$ \star \times \star $.
Consistency. Consistency plays an important role in a gradually typed lambda calculus, acting as a relaxed equality relation. The consistency relation extends 
$\lambda B$’s consistency, which is already shown in Figure 1, with product types:
In consistency, reflexivity, and symmetry hold. However, it is well known that consistency is not a transitive relation. If consistency were transitive, then every type would be consistent with any other type (Siek & Taha, Reference Siek and Taha2006).
Some important properties of the typing relation are that it computes dynamic types for the inference mode, and the type inference has unique types.
Lemma 3.1 (Dynamic Types for Values). If 
$ \cdot \vdash v \Rightarrow A $ then 
$ \rceil v \lceil = A$.
Lemma 3.2 (Inference is Checkable). If 
$ \Gamma \vdash e \Rightarrow A $ then 
$ \Gamma \vdash e \Leftarrow A $.
Lemma 3.3 (Uniqueness of Inference). If 
$ \Gamma \vdash e \Rightarrow A_{{\mathrm{1}}} $ and 
$ \Gamma \vdash e \Rightarrow A_{{\mathrm{2}}} $ then 
$A_{{\mathrm{1}}}$ = 
$A_{{\mathrm{2}}}$.
3.3 Dynamic semantics
The dynamic semantics of 
$\lambda B^{g}$ employs a TDOS (Huang & Oliveira, Reference Huang, Oliveira, Hirschfeld and Pape2020). In a TDOS, besides the usual reduction relation, there is a special casting relation for values that is used to further reduce values based on the type of the value. Casting is used by the TDOS reduction relation. In a gradually typed calculus with a TDOS, the casting relation plays a role analogous to various cast-related reduction rules in a cast calculus (Siek & Wadler, Reference Siek and Wadler2009;Wadler & Findler, Reference Wadler and Findler2009; Herman et al., Reference Herman, Tomb and Flanagan2007; Siek et al., Reference Siek, Thiemann and Wadler2015a). We first introduce casting and then move on to the definition of reduction.
Casting. We reduce a value under a certain type using the casting relation. The form of the casting relation is 
$ v \,\Downarrow_{ A }\, r $, which means that a value v reduces under type A to a result r. Unlike reduction, casting is defined using a big-step style. Note that the result r produced by casting can only be a value or blame. Blame is raised during casting if we try to reduce the value under a type that is not consistent with the type of the value. For instance, trying to reduce the value 
$1 : \star$ under the type 
$ \mathsf{Bool} $ will raise blame. Thus, it should be clear that casting mimics the behavior of casts in cast calculi such as the 
$\lambda B$ calculus. In the 
$\lambda B$ calculus, 
$ t : B \Rightarrow A $ casts t from source type B into target type A. Using casting in 
$\lambda B^{g}$, the type A is the target type (which arises from a type annotation), whereas the dynamic type of v is the source type.
Figure 4 shows the rules of casting. Rule Cast-abs and rule Cast-v just add a type annotation to the value. In rule Cast-abs, the dynamic type of the value (
$ \rceil v \lceil $) is a function type, thus v annotated with 
$A \rightarrow B$ is a value. Note that several casting rules employ the dynamic type function to compute the type of a value at runtime. However, the type of a value is never computed from scratch, since we use existing type annotations to return the type of a value. In rule Cast-v, 
$v : \star$ is also a value when the dynamic type of v is a ground type. Rule Cast-lit is for integer values: an integer i being reduced under the integer type results in the same integer i. A value 
$v:\star$ cast under 
$\star$ returns the original value as well (rule Cast-dd). In rule Cast-anyd, the premise is that the dynamic type of v should be a ug type which is defined in 
$\lambda B$. It means that the type of v should be any function type 
$A \rightarrow B$ except for 
$ \star \rightarrow \star $ or any product type 
$ A \times B $ except for 
$ \star \times \star $. In the end, v is cast under ground type G and returns the value v’ annotated with 
$ \star $.
Fig. 4. Casting for the 
$\lambda B^{g}$ calculus.
In rule Cast-vany, 
$v : \star $ is cast under the dynamic type of v, returning v and dropping the annotation 
$ \star $. In rule Cast-blame, if the dynamic type of v is not consistent to the type A that we are casting, then blame is raised. Finally, in rule Cast-dyna, a value 
$v : \star $ being cast under type A (where A is a ug type) returns the result of v cast under type A. For products, pairs of values are cast under the corresponding types. Rule Cast-pro models the case when both casts succeeds, while rule Cast-l and rule Cast-r model the cases where at least one of the casts fails.
Properties of Casting. Some properties of casting for the 
$\lambda B^{g}$ calculus are shown next:
Lemma 3.4 (Casting preserves well-formedness of values). If 
$ \textit{value}~ v $ and 
$ v \,\Downarrow_{ A }\, v' $, then 
$ \textit{value}~ v' $.
Lemma 3.5 (Preservation of Casting). If 
$ \cdot \vdash v \Leftarrow A $ and 
$ v \,\Downarrow_{ A }\, v' $, then 
$ \cdot \vdash v' \Rightarrow A $.
Lemma 3.6 (Progress of Casting). If 
$ \cdot \vdash v \Leftarrow A $, then 
$\exists r$, 
$ v \,\Downarrow_{ A }\, r $.
Lemma 3.7 (Determinism of Casting). If 
$ \cdot \vdash v \Leftarrow B $, 
$ v \,\Downarrow_{ A }\, r_{{\mathrm{1}}} $ and 
$ v \,\Downarrow_{ A }\, r_{{\mathrm{2}}} $, then 
$r_1=r_2$.
Lemma 3.8 (Casting Respects Consistency). If 
$ \cdot \vdash v \Rightarrow B $ and 
$ v \,\Downarrow_{ A }\, r $, then 
$ B \sim A $.
According to Lemma 3.4, if the result of a value cast under a type A is a value, then it should be well-formed. Lemma 3.5 shows that the target type A is preserved after casting: if a value v is cast using A, the result type of v’ is of type A. Note that this lemma (and some others) have a premise that ensures that the value under casting must be well typed under some type B. That is, the lemma only holds for well-typed values (which are the only ones that we care about). Lemma 3.6 shows that if a value v is well typed with type A, then casting the value will either return a well-formed value or blame. The casting relation is deterministic for well-typed values (Lemma 3.7): if a well-typed value v is cast by type A, the result will be unique. Finally, if v is cast by A, the dynamic type of v should be consistent with type A (Lemma 3.8). Most of these lemmas are proved by induction on the casting relation.
Reduction. The reduction rules are shown in Figure 5. Rule Step-eval and rule Step-blame are standard rules to reduce subterms under evaluation contexts. A key difference between the reduction rules for 
$\lambda B^{g}$ and the blame calculus lies on the treatment of applications. 
$\lambda B^{g}$ supports flexible applications with implicit type conversions, while the blame calculus does not have such flexibility. To account for the extra flexibility, the semantics of applications needs to be more complex in 
$\lambda B^{g}$.
Fig. 5. Semantics of 
$\lambda B^{g}$.
Rule Step-beta is the beta reduction rule. Importantly, note that casting under type A is needed for 
$v_{{\mathrm{2}}}$: that is we cast value 
$v_{{\mathrm{2}}}$ to 
$v'_{{\mathrm{2}}}$ so that 
$v'_{{\mathrm{2}}}$ has the required input type A. Moreover, the result of the reduction is the substitution 
$e {[} {x} \mapsto v'_{{\mathrm{2}}} {]}$ annotated with type B. In rule Step-abeta, the type of the argument 
$v_{{\mathrm{2}}}$ should also be consistent with the input type (A) of the annotated function value. Furthermore, 
$v_{{\mathrm{1}}} : A \rightarrow B$ is a well-formed value.
From typing, we know that 
$ \star $ matches with a dynamic function type 
$ \star \rightarrow \star $. Therefore, rule step-dyn annotates functional values of the form 
$v_{{\mathrm{1}}} : \star $ with type 
$ \star \rightarrow \star $. Note that, when the value (
$v_{{\mathrm{1}}}$) does not match the required type structure, blame should be raised. For example, program 
${(} 1 : \star {)} \, 2$ raises blame during reduction by first applying rule Step-dyn and then rule Step-annov. Rule Step-pjd follows a similar behavior and it is annotated to product type 
$ \star \times \star $. Rule Step-Annov is used when a value v is annotated with a type A. In that case, the value should have a type consistent with type A. So a cast is performed for the value with target type A and a result (which could be 
$\mathsf{blame}$) is produced by casting.
Rule Step-C shows a rule that deals with primitive operations for 
and 
(we introduced those in Section 2), similarly to those in 
$\lambda B$. The argument value v is cast by the input type of the primitive operations such as 
$ \mathsf{Int} $ for 
. Rule Step-pj projects the values from products.
Determinism. The operational semantics of 
$\lambda B^{g}$ is deterministic: expressions reduce to a unique result. Theorem 3.1 is proved using Lemma 3.7.
Theorem 3.1 (Determinism of 
$\lambda B^{g}$ calculus). If 
$ \cdot \vdash e \Leftrightarrow A $, 
$ e ~ \longmapsto ~ r_{{\mathrm{1}}} $ and 
$ e ~ \longmapsto ~ r_{{\mathrm{2}}} $, then 
$r_1=r_2$.
Type Soundness. The 
$\lambda B^{g}$ calculus is type sound. Theorem 3.2 says that if an expression is well typed with type A, the type will be preserved after the reduction. Progress is given by Theorem 3.3. A well-typed expression e is either a value or it reduces to a result.
Theorem 3.2 (Type Preservation of 
$\lambda B^{g}$ Calculus). If 
$ \cdot \vdash e \Leftrightarrow A $ and 
$ e ~ \longmapsto ~ e' $ then 
$ \cdot \vdash e' \Leftrightarrow A $.
Theorem 3.3 (Progress of 
$\lambda B^{g}$ Calculus). If 
$ \cdot \vdash e \Leftrightarrow A $, then e is a value or 
$\exists r$, 
$ e ~ \longmapsto ~ r $.
4 The $\boldsymbol\lambda \boldsymbol{B}^{\boldsymbol{g}}_{\boldsymbol{l}}$ calculus
In Section 3, we introduced the 
$\lambda B^{g}$ calculus. In this section, we show that the TDOS approach can also support blame labels. We introduce the 
$\lambda B^{g}_{l}$ calculus, which is the 
$\lambda B^{g}$ calculus with blame labels and show that it is sound and complete with respect to 
$\lambda B$ with blame labels. Furthermore, we prove the gradual guarantee and a blame safety theorem for the 
$\lambda B^{g}_{l}$ calculus.
4.1 Static semantics
Syntax. The syntax of the 
$\lambda B^{g}_{l}$ calculus is shown in Figure 6. Most of the syntax is the same as 
$\lambda B^{g}$. One small difference is that for annotations, lambdas, projections, and application expressions, there are labels.
Fig. 6. Static semantics for the 
$\lambda B^{g}_{l}$ calculus.
Typing. The typing rules of 
$\lambda B^{g}_{l}$ are shown at the bottom of Figure 6. The rules follow those of 
$\lambda B^{g}$. Compared to the 
$\lambda B^{g}$ calculus, rule Typ-Abs, Typ-App, Typ-Anno, Typ-pi now deal with blame labels. In particular, for applications 
, the type of the argument (
$e_{{\mathrm{2}}}$) must be consistent with the input type of the function type, which is A. For this reason applications require a label for tracking the implicit cast for the application argument. Furthermore, since the type of 
$e_{{\mathrm{1}}}$ can be 
$ \star $, there can be an implicit cast to type 
$ \star \rightarrow \star $. The label in applications is used to track these possible casts. Similarly, the label for projections 
is used to track the possible cast from 
$ \star $ to 
$ \star \times \star $.
4.2 Dynamic semantics
Casting. The form of the casting relation changes to 
. The new form means that a value v annotated with type A reduces under type A with blame label 
. Blame is raised with a label during casting if we try to reduce a value with unknown type under a type that is not consistent with the type of the value. The label indicates the location in the program to blame. For instance, trying to cast the value 
under the type 
$ \mathsf{Bool} $ with label 
indicates that this cast raises blame and we get the result 
. The same example would be represented in the 
$\lambda B$ calculus as 
, which also raises blame with label 
.
Figure 7 shows the rules of casting. Except for rule cast-blame, the other rules in casting are similar to the 
$\lambda B^{g}$ calculus. For rule cast-blame, we use the blame label tracked by casting to return the blame result. The casting of 
$\lambda B^{g}_{l}$ shares all the same properties in 
$\lambda B^{g}$.
Fig. 7. Casting for the 
$\lambda B^{g}_{l}$ calculus.
Reduction. The reduction rules of 
$\lambda B^{g}_{l}$ are shown in Figure 8. They extend the rules in Figure 5 with blame labels 
. The rule Sstep-beta deals with applications where the functions are annotated: 
. Note that this reduction rule requires casting the arguments before beta-reduction. To type such applications we use:
Fig. 8. Semantics of 
$\lambda B^{g}_{l}$.
Due to the checking mode for the argument of an application, there is an implicit cast, which is tracked by the label 
. For instance, consider 
. In this example, 
needs to be cast to type 
$ \mathsf{Bool} $ with the application label 
and raise 
. The label of applications 
is helpful for two reasons. First, it is used to track blame for casts of the argument. Second, it is also used to track blame when casting 
$e_{{\mathrm{1}}}$ from 
$ \star $ to the dynamic function type 
$ \star \rightarrow \star $ (rule Sstep-dyn). In rule Sstep-abeta, 
is used to track blame in the cast from 
$v_{{\mathrm{1}}}$ to 
$A \rightarrow B$. While removing the annotation 
$A \rightarrow B$, the label of application 
${(} v_{{\mathrm{1}}} \, v'_{{\mathrm{2}}} {)}$ is flipped to 
: if a cast is raised, then the context which contains the cast is to blame.
Let us look at two small examples to illustrate reduction behavior and blame tracking. The first example is the term 
, which reduces to 
.
The second example is a term 
, which reduces to 
. We show the detailed reduction steps below:
Correspondence with 
$\boldsymbol\lambda \boldsymbol{B}^{\boldsymbol{g}}$. We proved that after removing the blame labels in 
$\lambda B^{g}_{l}$, the static and dynamic semantics are the same as in 
$\lambda B^{g}$ (Theorem 4.1). Function 
$\,| \cdot \,|$ removes the blame labels. To distinguish between the typing and reduction relations of 
$\lambda B^{g}$ and 
$\lambda B^{g}_{l}$, we use their name as a superscript in the relation. For example, 
$ \longmapsto ^{ \lambda B^{g}_{l} }$ is the reduction of 
$\lambda B^{g}_{l}$.
Theorem 4.1 (Relation between 
$\lambda B^{g}$and 
$\lambda B^{g}_{l}$). 
$\Gamma$ 
${ \vdash }^{ \lambda B^{g}_{l} }$ e 
$\Leftrightarrow$ A and 
$e \longmapsto ^{ \lambda B^{g}_{l} } r$ iff 
$\Gamma \vdash ^{ \lambda B^{g} } \,| e \,| \Leftrightarrow A$ and 
$ \,| e \,| \longmapsto ^{ \lambda B^{g} } \,| r \,| $.
4.3 A more refined reduction relation for proofs
The reduction relation in the previous section is fine for an implementation. However, for some of our proofs, including the completeness to the blame calculus and the gradual guarantee, it is more convenient to have a more refined reduction relation that introduces some additional reduction steps. Here we present the more refined reduction relation. We proved that this new relation is equivalent to the reduction relation in Section 6.3.
In the new reduction relation (shown in Figure 9), the original rule Sstep-beta, rule Sstep-abeta and rule Sstep-C are divided into two separate steps. While other rules are the same. Figure 10 illustrates the relationship between the original rules and the new rules. Take rule step-beta as an example. There are two steps: (1) cast the argument; and (2) do the substitution. To record that the argument has been cast, we use strict applications 
. In strict applications, the type of the argument matches the input type of function 
$e_{{\mathrm{1}}}$. The typing rule for strict applications is
Fig. 9. New reduction steps.
Fig. 10. Decomposition of reduction steps.
Other rules follow the same principle as rule step-beta. The first step is to cast the argument, and then do the corresponding operations such as substitution and unwrapping type annotations. The bottom-left triangle in Figure 10 regards that 
reduces to 
. Strictly speaking, this does not hold because 
reduces to 
for some C such that 
$ \rceil v_{{\mathrm{1}}} \lceil {=} C \rightarrow D$ by rule step-abeta. However, the result can be regarded as 
because by rule step-app, applications 
convert to strict applications 
, which can also be written as strict applications 
and the casting is then triggered by annotations. We illustrate the new reduction on an earlier example shown in Section 6.3.
4.4 Soundness and completeness to $\boldsymbol\lambda \boldsymbol{B}$
We use an elaboration step in the typing relation to prove the soundness result between the semantics of 
$\lambda B^{g}_{l}$ and 
$\lambda B$. The elaboration from 
$\lambda B^{g}_{l}$ to 
$\lambda B$ is shown at the top of Figure 11. The elaborating typing relation 
shows how to translate expression e in 
$\lambda B^{g}_{l}$ to the term t in 
$\lambda B$. The translation does not include products and projections, since they are not part of 
$\lambda B$. The typing mode 
includes the infer mode 
$ \Rightarrow $ and the checking mode with labels 
. However, in 
$\lambda B^{g}_{l}$, every rule in checking mode induces a cast and we need the label for the elaboration into 
$\lambda B$. Therefore, the blame labels of 
$\lambda B^{g}_{l}$ are transferred to 
$\lambda B$ via the checking mode. In particular, in rule typ-sim, when we produce a 
$\lambda B$ cast expression we need to use the label that was tracked by the checking mode. There are three rules where the blame labels are propagated using the checking mode in the premises (rule typ-abs, rule typ-app and rule typ-anno). Note that the 
$\lambda B^{g}_{l}$ calculus can also act as a source language. An application of expression 
$e_{{\mathrm{1}}}$ can, not only infer a function type, but also infer the unknown type 
$ \star $. Thus, the function 
adds a cast from 
$ \star $ to 
$ \star \rightarrow \star $ to the 
$\lambda B$ term. At the bottom of Figure 11, we show the elaboration from 
$\lambda B$ to 
$\lambda B^{g}_{l}$. The elaboration typing relation 
$ \Gamma \Vdash t : A \leadsto e $ shows the expression t in 
$\lambda B$ to the expression e in 
$\lambda B^{g}_{l}$. The elaboration is straightforward. One thing that needs to be mentioned is that for rule btyp-abs the lambda body (t) is elaborated to an annotated expression, since the body is in checking mode, which triggers an implicit cast. To be aligned between these two calculi, the 
$\lambda B$ calculus adds an identity cast for the lambda body.
Fig. 11. Elaboration between 
$\lambda B^{g}_{l}$ and 
$\lambda B$.
Theorem 4.2 states that both elaborations are type preserving. Theorem 4.3 shows the soundness and completeness property between the dynamic semantics of 
$\lambda B^{g}_{l}$ and 
$\lambda B$. We use 
$\Uparrow$ to represent that a term diverges. The soundness and completeness result are proved using the auxiliary Lemmas 4.1, 4.2, 4.3 and 4.4. In Lemma 4.3, 
$ t \longmapsto ^{j} t'$ means that t takes j steps to evaluate to t’. Lets take an example that shows how can t’ reduce to error. In 
$\lambda B$, we can have a program 
which corresponds to 
in our 
$\lambda B^{g}_{l}$. In 
$\lambda B^{g}_{l}$, error is raised directly but 
$\lambda B$ first reduces to 
and then raises the error.
Theorem 4.2 (Type Preservation of Elaboration).
• If
then $\Gamma \Vdash t : A$.-
• If
$ \Gamma \Vdash t : A \leadsto e $ then $ \Gamma \vdash e \Rightarrow A $.
Lemma 4.1 (Soundness of 
$\lambda B^{g}_{l}$Casting with respect to 
$\lambda B$for Values). If 
and 
then 
$\exists t'$, 
$t \longmapsto ^{*} t'$ and 
$ \cdot \vdash v' \Rightarrow A \leadsto t' $.
Lemma 4.2 (Soundness of 
$\lambda B^{g}_{l}$Casting with respect to 
$\lambda B$for Blame). If 
and 
then 
.
Lemma 4.3 (Completeness of 
$\lambda B^{g}_{l}$Casting with respect to 
$\lambda B$for Values). If 
$ \cdot \Vdash t : B \leadsto v $ and 
then (
$\exists j ~ t'' ~ v'$, 
$0 \leq j \leq 1$, 
$ t' \longmapsto ^{j} t''$, 
and 
$ \cdot \Vdash t'' : A \leadsto v' $) or (
and 
).
Lemma 4.4 (Completeness of 
$\lambda B^{g}_{l}$Casting with respect to 
$\lambda B$for Blame). If 
$ \cdot \Vdash t : B \leadsto v $ and 
then 
.
Theorem 4.3 (Soundness and Completeness between 
$\lambda B^{g}_{l}$and 
$\lambda B$).
(1) if
$ \cdot \vdash e \Rightarrow A \leadsto t $ and $e \longmapsto ^{*} v$ then $\exists v'$, $t \longmapsto ^{*} v'$ and $ \cdot \vdash v \Rightarrow A \leadsto v' $.(2) if
$ \cdot \vdash e \Rightarrow A \leadsto t $ and then .(3) if
$ \cdot \vdash e \Rightarrow A \leadsto t $ and $e \Uparrow$ then $t \Uparrow$.(4) if
$ \cdot \Vdash t : A \leadsto e $ and $t \longmapsto ^{*} v$ then $\exists v'$, $e \longmapsto ^{*} v'$ and $ \cdot \Vdash v : A \leadsto v' $.(5) if
$ \cdot \Vdash t : A \leadsto e $ and then .(6) if
$ \cdot \Vdash t : A \leadsto e $ and $t \Uparrow $ then $e \Uparrow$.
4.5 Gradual guarantee
Siek et al. (Reference Siek, Vitousek, Cimini and Boyland2015b) suggested that a calculus for gradual typing should also enjoy the gradual guarantee, which ensures that programs can smoothly move from being more/less dynamically typed into more/less statically typed. We show how to prove the gradual guarantee for 
$\lambda B^{g}_{l}$ next.
Precision. The top of Figure 12 shows the precision relation on types. 
$A \sqsubseteq B$ means that A is more precise than B. Every type is more precise than type 
$ \star $. A function type 
$A_{{\mathrm{1}}} \rightarrow B_{{\mathrm{1}}}$ is more precise than 
$A_{{\mathrm{2}}} \rightarrow B_{{\mathrm{2}}}$ if type 
$A_1$ is more precise then 
$A_2$ and type 
$B_1$ is more precise than 
$B_2$. A product type 
$ A_{{\mathrm{1}}} \times B_{{\mathrm{1}}} $ is more precise than 
$ A_{{\mathrm{2}}} \times B_{{\mathrm{2}}} $ if type 
$A_1$ is more precise then 
$A_2$ and type 
$B_1$ is more precise than 
$B_2$. The bottom of Figure 12 shows the precision relation for expressions. 
$ \Gamma_{{\mathrm{1}}} ; \Gamma_{{\mathrm{2}}} \vdash e_{{\mathrm{1}}} ~ \sqsubseteq ~ e_{{\mathrm{2}}} $ means that 
$e_1$ is more precise than 
$e_2$ under typing contexts 
$\Gamma_{{\mathrm{1}}}$ and 
$\Gamma_{{\mathrm{2}}}$. The precision relation of expressions is derived from the precision relation of types. Every expression is related to itself. There are contexts 
$\Gamma_{{\mathrm{1}}}$ for 
$e_{{\mathrm{1}}}$ and 
$\Gamma_{{\mathrm{2}}}$ for 
$e_{{\mathrm{2}}}$. The typing contexts are needed because some rules only work for well-typed expressions, and the typing judgment requires typing contexts. We use the following abbreviation 
$ e_{{\mathrm{1}}} ~\sqsubseteq~ e_{{\mathrm{2}}} $ 
$\equiv$ 
$ \cdot ; \cdot \vdash e_{{\mathrm{1}}} ~ \sqsubseteq ~ e_{{\mathrm{2}}} $, when the contexts of the expressions are empty.
Fig. 12. Precision relations.
For annotation expressions, precision is defined as follows: 
$e_{{\mathrm{1}}} : A$ is more precise than 
$e_{{\mathrm{2}}} : B$ if 
$e_{{\mathrm{1}}}$ is more precise than 
$e_{{\mathrm{2}}}$ and A is more precise than B. Similarly, for projections precision holds if the precision between 
$e_{{\mathrm{1}}}$ and 
$e_{{\mathrm{2}}}$ holds. Two lambdas are related when their bodies and annotated types are related. In applications (
and 
) and productions (
${(} e_{{\mathrm{1}}} , e_{{\mathrm{2}}} {)}$), precision holds if the precision between 
$e_{{\mathrm{1}}}$ and 
$e'_{{\mathrm{1}}}$ holds and the precision between 
$e_{{\mathrm{2}}}$ and 
$e'_{{\mathrm{2}}}$ holds.
An important complication arises from the presence of values with an unknown type such as 
$1 : \star $. The term 
$1 : \mathsf{Int}$ is more precise than 
$1 : \star $, but while 
$1 : \star $ is a value, the term 
$1 : \mathsf{Int}$ reduces to 1. Similarly, the term 
${(} \lambda {x} .\, {x} {)} : \mathsf{Int} \rightarrow \mathsf{Int} : \star $ is more precise than 
${(} \lambda {x} .\, {x} {)} : \star \rightarrow \star : \star $, while 
${(} \lambda {x} .\, {x} {)} : \star \rightarrow \star : \star $ is a value and 
${(} \lambda {x} .\, {x} {)} : \mathsf{Int} \rightarrow \mathsf{Int} : \star $ reduces to 
${(} \lambda {x} .\, {x} {)} : \mathsf{Int} \rightarrow \mathsf{Int} : \star \rightarrow \star : \star $. Such examples create the need for the precision relation to deal with unaligned expressions. These unaligned cases are covered by rule epre-annol and rule epre-annor. Rule epre-annol deals with more precise programs with extra annotations, while rule epre-annor is for less precise programs with extra annotations. To ensure that the extra type annotations preserve the type precision relation, the typing judgment is used.
Static Criteria. The dynamic counterpart of expressions (
$\check{e}$) (basically expressions without type annotations) can be encoded in 
$\lambda B^{g}_{l}$ by the translation function 
$(\lceil \check{e} \rceil)$, which annotates dynamic expressions with type 
$ \star $ (Theorem 4.4). The translation function is
Furthermore, if all expressions are static, the type system of 
$\lambda B^{g}_{l}$ is equivalent to a fully static type system (Theorem 4.5). The predicate static on e and A means that the expression and type are fully static. The static type system is represented as 
$\vdash_S$ which is also bidirectional but only type checks the static expressions. Theorem 4.6 shows that the static gradual guarantee holds for the 
$\lambda B^{g}_{l}$ calculus. It says that if e is more precise than e’ and e has type A then e’ has type B and type A is more precise than B.
Theorem 4.4 (Dynamic Embedding). If 
$\check{e}$ is closed then 
$ \cdot $ 
$ \vdash $ 
$\lceil$ 
$\check{e}$ 
$\rceil$ 
$ \Rightarrow $ 
$ \star $.
Theorem 4.5 (Equivalence for Static Type System). 
$For~all~static~\textit{e}~and~\textit{A}, \cdot \vdash _{S} e \Leftrightarrow A$ iff 
$ \cdot \vdash e \Leftrightarrow A $.
Theorem 4.6 (Static Gradual Guarantee of 
$\lambda B^{g}_{l}$ Calculus). If 
$ e \sqsubseteq e' $ and 
$ \cdot \vdash e \Leftrightarrow A $ then 
$\exists B$, 
$ \cdot \vdash e' \Leftrightarrow B $ and 
$ A \sqsubseteq B$.
Dynamic Gradual Guarantee. We formalized and proved the dynamic gradual guarantee for the 
$\lambda B^{g}_{l}$ calculus. Theorems 4.7 and 4.8 show that less precise programs will not change the dynamic semantics of programs. Lemma 4.5 is an important auxiliary lemma for Theorems 4.7 and 4.8. Notably, the dynamic gradual guarantee (Theorem 4.9) is a corollary of Theorems 4.7 and 4.8.
Lemma 4.5 (Dynamic Gradual Guarantee for Casting). If 
$ v_1 \sqsubseteq v_2 $ , 
$ \cdot \vdash v_{{\mathrm{1}}} \Leftarrow A_{{\mathrm{1}}} $, 
$ \cdot \vdash v_{{\mathrm{2}}} \Leftarrow B_{{\mathrm{1}}} $ , 
$ A \sqsubseteq B$ and 
then 
$\exists v_2'$, 
and 
$ v'_{{\mathrm{1}}} \sqsubseteq v'_{{\mathrm{2}}}$.
Theorem 4.7 (Dynamic Gradual Guarantee 
$\sqsubseteq$ ). If 
$e_1 \sqsubseteq e_2$ , 
$ \cdot \vdash e_{{\mathrm{1}}} \Leftrightarrow A $, 
$ \cdot \vdash e_{{\mathrm{2}}} \Leftrightarrow B $ and 
$e_1 \longmapsto e'_{{\mathrm{1}}}$ then 
$\exists e'_{{\mathrm{2}}}$, 
$ e_2 \longmapsto ^{*} e'_{{\mathrm{2}}}$ and 
$e'_{{\mathrm{1}}} \sqsubseteq e'_{{\mathrm{2}}}$.
Theorem 4.8 (Dynamic Gradual Guarantee 
$\sqsupseteq$ ). Suppose 
$e_1 \sqsubseteq e_2$ , 
$ \cdot \vdash e_{{\mathrm{1}}} \Leftrightarrow A $ and 
$ \cdot \vdash e_{{\mathrm{2}}} \Leftrightarrow B $.
• If
$e_2 \longmapsto e'_{{\mathrm{2}}}$ then ($\exists e_{{\mathrm{1}}}$, $ e_{{\mathrm{1}}} \longmapsto ^{*} e'_{{\mathrm{1}}}$ and $e'_{{\mathrm{1}}} \sqsubseteq e'_{{\mathrm{2}}}$) or (, ).-
• If
then , .
Theorem 4.9 (Dynamic Gradual Guarantee). Suppose 
$e_1 \sqsubseteq e_2$ , 
$ \cdot \vdash e_{{\mathrm{1}}} \Leftrightarrow A $ and 
$ \cdot \vdash e_{{\mathrm{2}}} \Leftrightarrow B $.
• If
$e_1 \longmapsto ^{*} v_1$ then $\exists v_2$, $ e_2 \longmapsto ^{*} v_2$ and $v_{{\mathrm{1}}} \sqsubseteq v_{{\mathrm{2}}}$.-
• If
$e_1 \Uparrow$ then $e_2 \Uparrow$. If $e_{{\mathrm{2}}} \longmapsto ^{*} v_{{\mathrm{2}}}$ then $e_{{\mathrm{1}}} \longmapsto ^{*} v_{{\mathrm{1}}}$ and $ v_{{\mathrm{1}}} ~\sqsubseteq~ v_{{\mathrm{2}}} $, or . If $e_{{\mathrm{2}}}$ $\Uparrow$ then $e_{{\mathrm{1}}}$ $\Uparrow$ or .
4.6 Blame theorem
The blame theorem (Wadler & Findler, Reference Wadler and Findler2009) shows that a cast from a more precise type to a less precise type cannot raise positive blame, but negative blame is possible. In addition, a cast from a less precise type to a more precise type cannot raise negative blame, but positive blame is possible. The blame theorem has been proved for the 
$\lambda B$ calculus. From the soundness theorem, which we have shown above, terms in 
$\lambda B^{g}_{l}$ raise blame with label 
, and the corresponding terms in 
$\lambda B$ raise blame with the same label. Thus, the blame theorem also holds in 
$\lambda B^{g}_{l}$. However, this proof of the blame theorem relies on the existence of 
$\lambda B$. While this proof technique works, we cannot easily use it if we extend 
$\lambda B^{g}_{l}$ with new features, because that would require similar extensions to 
$\lambda B$. For instance, we opted to add products and projections in 
$\lambda B^{g}_{l}$, which are not available in 
$\lambda B$. Thus, we cannot obtain the blame theorem for 
$\lambda B^{g}_{l}$ with products via the soundness theorem. Furthermore, having to rely on another calculus makes the proof rather indirect and involved. Therefore, here we show that we can also prove the blame theorem directly on 
$\lambda B^{g}_{l}$.
The top of Figure 13 shows the subtyping, positive subtyping, and negative subtyping relations, which are the same as those for 
$\lambda B$. Note that our type precision is also the same as the naive subtyping relation in 
$\lambda B$. Therefore, Lemmas 4.6 and 4.7 show that subtyping and type precision factor negative and positive subtyping as in 
$\lambda B$.
Fig. 13. Safe expressions of 
$\lambda B^{g}_{l}$.
At the bottom of Figure 13, we have the safe terms for 
$\lambda B^{g}_{l}$. The relation 
denotes that e is safe for label 
under typing context 
$\Gamma$. For safe terms, after the reduction of e, label 
can never be raised. Labels are raised only when casting is performed. Therefore, safe terms require us to consider all the casts (explicit or implicit) in the expressions. In the safe term definition, we are making implicit casts explicit. There are no casts in x and c so they are safe for label 
(rule sf-var and rule sf-c). Lambda abstractions induce a cast from the type of the lambda body to the annotated function output type. Consequently, 
is safe for label 
if 
is safe for label 
(rule sf-abs). Obviously, if one label does not appear in the expression, the expression is safe for that label. So 
is safe for 
if 
is not equal to (
, 
) and e is safe for 
(rule sf-eq). Even when the checking label is the same as the casting label, if the type of the source type is a positive subtype of the target type then the cast is also safe for the checking label (rule sf-neqa).
In the expression 
, the cast from 
$ \mathsf{Int} $ to 
$ \star $, will not raise blame with label 
. In general, 
is safe for 
if e is safe for 
and A (the type of e) is a positive subtype of B. Annotation 
is safe for 
if e is safe for 
and A (the type of e) is a negative subtype of B (rule sf-neqb). For example, 
should be safe for 
since when the argument is applied, which triggers a cast from 
$ \mathsf{Int} $ to 
$ \star $ with 
, blame cannot be raised. For 
, if 
$e_{{\mathrm{1}}}$ has type 
$ \star $, there are two implicit casts: one is for 
$e_{{\mathrm{1}}}$, which casts from 
$ \star $ to 
$ \star \rightarrow \star $, and the other is for 
$e_{{\mathrm{2}}}$ cast from the type of 
$e_{{\mathrm{2}}}$ to the input type of function of 
$e_{{\mathrm{1}}}$. Therefore, if 
$e_{{\mathrm{1}}}$ has type 
$ \star $, 
is safe for label 
if 
is safe for 
and 
is safe for 
. While 
$e_{{\mathrm{1}}}$ has type 
$A \rightarrow B$, 
is safe for label 
if 
$e_{{\mathrm{1}}}$ is safe for 
and 
is safe for 
(rule sf-app). Similarly, for rule sf-pi, if 
$e_{{\mathrm{1}}}$ has type 
$ \star $, there is implicit cast from 
$ \star $ to 
$ \star \times \star $. Thus, if e has type 
$ \star $, 
$ \pi_{i}~ e \, l_{{\mathrm{1}}}$ is safe for label 
if 
is safe for 
. The cast is added via the function 
$ {\langle\!\langle} e , l , A {\rangle\!\rangle} $ at the bottom of figure 11. If e has type 
$ A \times B $, 
is safe for label 
if e is safe for 
. Strict applications 
and productions 
${(} e_{{\mathrm{1}}} , e_{{\mathrm{2}}} {)}$ are safe for 
, if the sub-term 
$e_{{\mathrm{1}}}$ and 
$e_{{\mathrm{2}}}$ are safe for 
(rule sf-appv).
Lemma 4.8 shows the preservation of safe expressions: if e is safe for 
and e reduces to e’ then e’ is safe for 
. Lemma 4.9 says that if e is safe for 
then 
will not be raised. By Lemmas 4.8, 4.9, 4.6 and 4.7, we can derive Corollary 1, showing that if blame is raised, the less precise program is to blame.
Lemma 4.6 (Factoring Subtyping). 
$ A <: B $ if and only if 
$ A <:^{+} B $ and 
$ A <:^{-} B $.
Lemma 4.7 (Factoring Precision). 
$ A \sqsubseteq B $ if and only if 
$ A <:^{+} B $ and 
$ B <:^{-} A $.
Lemma 4.8 (Preservation of Safe Expressions). If 
$ \cdot \vdash e \Leftrightarrow A $, 
and 
$ e ~ \longmapsto ~ e' $ then 
.
Lemma 4.9 (Progress of Safe Expressions). If 
$ \cdot \vdash e \Leftrightarrow A $ and 
then e 
$\not\longmapsto$ 
.
Corollary 4.9.1 (Well-typed programs cannot be blamed). Let e be a well-typed term with a subterm 
where e’ is well typed with type A, containing the only occurrences of 
in e, and 
does not appear in e.
• If
$ A <:^{+} B $ then .-
• If
$ A <:^{-} B $ then . -
• If
$ A <: B $ then and . -
• If
$ A \sqsubseteq B $ then . -
• If
$ B \sqsubseteq A $ then .
5 The $\boldsymbol\lambda \boldsymbol{e}$ calculus
In this section, we will introduce a gradually typed calculus with a variant of the eager semantics (Herman et al., Reference Herman, Tomb and Flanagan2007), inspired by AGT (Garcia et al., Reference Garcia, Clark and Tanter2016). The main idea in this variant of the eager semantics is that if a function value flows through multiple casts, the effect of those casts is preserved in the updated function value. In particular, all types involved in the multiple casts must be checked for consistency.
5.1 Syntax
The syntax of the 
$\lambda e$ calculus is shown in Figure 14.
Fig. 14. Syntax of the 
$\lambda e$ calculus.
Types, Expressions and Results. A type in 
$\lambda e$ is either an integer type 
$ \mathsf{Int} $, a function type 
$A \rightarrow B$, an unknown type 
$ \star $, or a product type 
$ A \times B $. For expressions and results, 
$\lambda e$ is extended with tagged values 
with respect to 
$\lambda B^{g}$.
Values. Metavariable p ranges over raw values. Constants c, annotated lambdas 
${(} \lambda {x} .\, e : A_{{\mathrm{1}}} \rightarrow B_{{\mathrm{1}}} {)} : A_{{\mathrm{2}}} \rightarrow B_{{\mathrm{2}}}$ and products 
${(} p_{{\mathrm{1}}} , p_{{\mathrm{2}}} {)}$ are included in the raw values. Values are tagged raw values. The metavariable v denotes values, which are annotated values (
). Thus 
and 
are examples of values. Notably, in contrast with 
$\lambda B^{g}$, 
$\lambda e$’s notion of (well-formed) values is purely syntactic: no additional constraints (besides syntax) are needed. Moreover, it should be noted that in 
$\lambda e$ values have a bounded number of annotations (up-to three for lambda values), unlike the 
$\lambda B^{g}$ calculus. We should remark that we choose to use tagged values for simplicity. It should be possible to use a more refined notion of values where some values would require no type tag, as in 
$\lambda B^{g}$. Although this would probably require some different rules to distinguish between those different forms of values.
Contexts and Frames. Typing environments are just the same as in the 
$\lambda B^{g}$ calculus. In frames, compared to the 
$\lambda B^{g}$ calculus, the first expression in an application is not a value, but a raw lambda.
5.2. Type system
As the 
$\lambda B^{g}$ calculus, bidirectional typing is used. Before showing the typing rules, we present the dynamic type function.
Dynamic Types for the 
$\boldsymbol\lambda \boldsymbol{e}$ Calculus. As in the 
$\lambda B^{g}$ calculus, dynamic types play an important role in the calculus. 
$ \rceil p \lceil $ denotes the dynamic type of p, and 
$ \rceil v \lceil $ denotes the dynamic type of v. We need both dynamic types for raw values and values, and we can define dynamic types easily.
Definition 5.1 (Dynamic type). 
$ \rceil p \lceil $ returns the dynamic type of the raw values p. 
$ \rceil v \lceil $ returns the dynamic type of the annotated value v.
Typing Rules for the 
$\boldsymbol\lambda \boldsymbol{e}$ Calculus. In 
$\lambda e$, raw lambdas are checked by function types or the unknown type 
$ \star $. Raw lambdas are allowed in applications by using rule TYP-absv. This rule is important to allow beta-reductions to type-check and is essentially a runtime checking rule. That is, rule TYP-absv is used to enable certain intermediate expressions that arise from reduction to type-check. Otherwise, using rule TYP-app, in an application, the function input type is the type of the argument. In rule TYP-value, a well-typed value ensures that the inner raw value p can be checked by the annotated type A. Also the dynamic type of the raw value should be more precise than annotated type A. The bottom of Figure 15 shows the precision relation on types. 
$A \sqsubseteq B$ means that A is more precise than B. Type precision is the same as in 
$\lambda B^{g}_{l}$. Other typing rules are exactly the same as those used by the 
$\lambda B^{g}$ calculus in Figure 3. Lemmas about dynamic types and a typing lemma about the inference mode include:
Fig. 15. Typing rules for 
$\lambda e$.
Lemma 5.1 (Dynamic Types of Raw Values). If 
$ \cdot \vdash p \Rightarrow A $, then 
$ \rceil p \lceil = A$.
Lemma 5.2 (Dynamic Types of Values). If 
$ \cdot \vdash v \Rightarrow A $, then 
$ \rceil v \lceil = A$.
Lemma 5.3 (Inference Uniqueness). If 
$ \Gamma \vdash e \Rightarrow A_{{\mathrm{1}}} $ and 
$ \Gamma \vdash e \Rightarrow A_{{\mathrm{2}}} $, then 
$A_{{\mathrm{1}}}$ = 
$A_{{\mathrm{2}}}$.
5.3 Dynamic semantics
As in the 
$\lambda B^{g}$ calculus, casting is used in the semantics to get a direct operational semantics.
Casting. The casting rules are shown in Figure 16. Compared to 
$\lambda B^{g}$, the rules are simpler. The casting relation casts raw values instead of values. Rule CAST-c returns the constant c. Rule CAST-abs shows that if the type of annotated lambdas 
$A_{{\mathrm{1}}} \rightarrow A_{{\mathrm{2}}}$ is consistent with type C, then type B is replaced by C. Otherwise, if type 
$A_{{\mathrm{1}}} \rightarrow A_{{\mathrm{2}}}$ is not consistent with type C, casting raises blame using rule CAST-absp. In rule CAST-pro, when a product 
${(} p_{{\mathrm{1}}} , p_{{\mathrm{2}}} {)}$ is cast under product type 
$ A_{{\mathrm{1}}} \times A_{{\mathrm{2}}} $, we cast both components under 
$A_{{\mathrm{1}}}$ and 
$A_{{\mathrm{2}}}$, respectively, and return a product of the resulting raw values. Rule CAST-prol and rule CAST-pror cover the case when the casts of 
$p_{{\mathrm{1}}}$ and 
$p_{{\mathrm{2}}}$ raise blame.
Fig. 16. Casting for the 
$\lambda e$ calculus.
Casting Properties. Casting for the 
$\lambda e$ calculus has some interesting properties, similar to those shown in Section 3. In these Lemmas, the meet of two types (
$\sqcap$) is defined at the bottom of Figure 16. The meet of two types is the greatest lower bound between the types in terms of precision. That is, it is the most imprecise type among the types equivalent to or more precise than the given types.
Lemma 5.4 (Preservation of Casting). If 
$ \cdot \vdash p \Leftarrow A $, 
$ \rceil p \lceil \sqcap B = A $ and 
$ p \,\Downarrow_{ A }\, p' $ then 
.
Lemma 5.5 (Progress of Casting). If 
$ \cdot \vdash p \Leftarrow A' $ and 
$ \rceil p \lceil \sqcap A = A' $, then 
$\exists r$, 
$ p \,\Downarrow_{ A' }\, r $.
Lemma 5.6 (Determinism of Casting). If 
$ \cdot \vdash p \Leftarrow B $, 
$ p \,\Downarrow_{ A }\, r_{{\mathrm{1}}} $ and 
$ p \,\Downarrow_{ A }\, r_{{\mathrm{2}}} $, then 
$r_{{\mathrm{1}}} = r_{{\mathrm{2}}}$.
Reduction. Figure 17 shows the reduction rules of the 
$\lambda e$ calculus. Rule STEP-beta is the usual beta reduction rule. For rule STEP-app, the argument 
$e_{{\mathrm{2}}}$ is annotated with the input types, and the annotations with the output types are added in the final expression. As the type system shows, the unknown type 
$ \star $ can be matched as a function type 
$ \star \rightarrow \star $ or a product 
$ \star \times \star $. Because the 
$ \star $ type is consistent with any types, there can be run-time type-errors. For instance 
${(} 1 : \star {)} \, 1$ and 
$ \pi_{i}~ {(} 1 : \star {)} $ raise errors at runtime. Rule STEP-dyn and rule STEP-proip raise blame if the raw values cannot match with function types and product types, respectively. Rule STEP-pro extracts type annotations from a pair of values and rule STEP-proi projects the corresponding value. Rule STEP-abs and rule STEP-i add an extra annotation with the dynamic type to produce a value. For values 
annotated with a type B, we perform consistency checking between the dynamic type of p and B. When consistency checking fails, blame is raised using rule STEP-annop. If consistency checking succeeds, the raw value p is cast by the meet result of A’ and B. If the casting succeeds, the result of casting annotated with type B is returned (rule STEP-annov), otherwise blame is raised using rule STEP-annovp. Note that these two rules and casting are the essence of our variant of the eager semantics: consistency checking happens directly, instead of waiting for the argument to be applied for high-order values. For additions (
$+$ and 
$+_{i}$), if the argument is an integer, then it can be used to do the operation (rule STEP-c) otherwise an error is raised (rule STEP-cf and rule STEP-cfa).
Fig. 17. Semantics of the 
$\lambda e$ calculus.
Example. Let us use an example to explain the behavior of casting with the eager semantics. Suppose that we take a chain of annotations 
$ \lambda {x} .\, {x} : \star \rightarrow \mathsf{Int} : \mathsf{Int} \rightarrow \star : \star : \mathsf{Bool} \rightarrow \mathsf{Bool} $. The reduction (and casting) steps to reduce such an expression are shown next:
First, 
$ \lambda {x} .\, {x} : \star \rightarrow \mathsf{Int}$ reduces to a value 
. Type 
$ \star \rightarrow \mathsf{Int}$ is consistent with type 
$\mathsf{Int} \rightarrow \star $ and the meet of these two types is 
$\mathsf{Int} \rightarrow \mathsf{Int}$. So the intermediate type 
$ \star \rightarrow \mathsf{Int}$ is replaced by 
$\mathsf{Int} \rightarrow \mathsf{Int}$ and the outer type is replaced by 
$ \star \rightarrow \mathsf{Int}$. Similarly, 
$\mathsf{Int} \rightarrow \mathsf{Int}$ is consistent with type 
$ \star $ and the meet of these two types is still 
$\mathsf{Int} \rightarrow \mathsf{Int}$. So only the outer type is replaced by type 
$ \star $. Finally, type 
$\mathsf{Int} \rightarrow \mathsf{Int}$ is not consistent with 
$ \mathsf{Bool} \rightarrow \mathsf{Bool} $ so blame is raised.
One important property is that the reduction relation is deterministic:
Theorem 5.1 (Determinism of the 
$\lambda e$ Calculus). If 
$ \cdot \vdash e \Leftrightarrow A $, 
$ e ~ \longmapsto ~ r_{{\mathrm{1}}} $ and 
$ e ~ \longmapsto ~ r_{{\mathrm{2}}} $, then 
$r_{{\mathrm{1}}} = r_{{\mathrm{2}}}$.
Type Soundess. Another important property is that the 
$\lambda e$ calculus is type sound. Theorems 5.2 and 5.3 for type preservation and progress, respectively, have the same form as in 
$\lambda B^{g}$.
Theorem 5.2 (Type Preservation of the 
$\lambda e$ Calculus). If 
$ \cdot \vdash e \Leftrightarrow A $ and 
$ e ~ \longmapsto ~ e' $, then 
$ \cdot \vdash e' \Leftrightarrow A $.
Theorem 5.3 (Progress of the 
$\lambda e$ Calculus). If 
$ \cdot \vdash e \Rightarrow A $, then e is a value or 
$\exists r$, 
$ e ~ \longmapsto ~ r $.
5.4 Gradual guarantee
Precision. Figure 18 shows the precision relation of expressions for 
$\lambda e$. Compared to Figure 12, lambdas are not annotated with types and rules for pairs and projections are new. For pairs 
${(} e_{{\mathrm{1}}} , e_{{\mathrm{2}}} {)}$ and projections 
${(} \pi_{i}~ e {)}$, precision just employs simple structural rules. For annotated expressions, 
$e_{{\mathrm{1}}} : A$ is more precise than 
$e_{{\mathrm{2}}} : B$ if 
$e_1$ is more precise than 
$e_2$ and A is more precise than B. For two values (rule epre-val), precision holds if the precision of raw values and types hold. To make sure the less precise values 
are well typed, the type of raw values should be more precise than annotated types. Note that there is an implicit assumption that the more precise values are well typed, which ensures that the pre-value is more precise than the type annotation. Thus, no such explicit assumption is needed in rule epre-val for 
$p_1$.
Fig. 18. Precision relations.
One noteworthy point is that the precision relation for expressions in 
$\lambda e$ is significantly simpler than the precision for 
$\lambda B^{g}$. There are a few reasons that contribute to the simpler precision relation:
1. The form of values is similar for both dynamic and static values. Values in
$\lambda e$ have a more consistent form for dynamic and statically typed values. For example, in $\lambda B^{g}$, static integers are represented as i, but dynamic integers are represented as ${i} : \star $. In $\lambda e$ both static and dynamic integers require an annotation ( and ).2. The eager semantics avoids accumulation of annotations. In the eager semantics, we can avoid accumulating annotations for higher-order values. This means that higher-order values always have exactly 3 annotations. Therefore, in combination with the previous point, we can define precision of expressions, while avoiding alignment rules such as those in
$\lambda B^{g}$.3. No need for typing premises and typing contexts. In addition, there are no typing premises. Therefore, typing contexts can also be avoided. The need for inference typing premises in the precision relation of
$\lambda B^{g}_{l}$ follows the blame calculus, which employs similar premises in its precision relation. However, in order to support inference typing premises, lambda expressions need to be annotated. Otherwise, raw lambdas cannot be inferred in the general case, and the precision relation would not be able to deal with raw lambdas. In $\lambda e$, there is no such issue because the precision relation does not include any typing premises. Therefore, raw lambdas can be easily supported in $\lambda e$. We conjecture that it is also possible to support raw lambdas in $\lambda B^{g}_{l}$, but this would require changing the current setup and proof for the dynamic gradual guarantee, which is based on that of the blame calculus. We leave this exploration for future work.4. No need for introducing strict applications. As discussed in Section 4, the proof of the dynamic gradual guarantee for
$\lambda B^{g}_{l}$ requires a second set of reduction rules and the introduction of strict applications. This introduces a significant burden in terms of definitions and proofs compared to $\lambda e$. The need for strict applications for the dynamic gradual guarantee of $\lambda B^{g}_{l}$ is discussed in more detail in Section 6.3.
Static Criteria. The 
$\lambda e$ calculus can also encode the dynamic counterpart of expressions (
$\check{e}$) by the translation function 
$(\lceil \check{e} \rceil_{b})$ (Theorem 5.4). However, unlike in 
$\lambda B^{g}_{l}$, where we need to insert 
$ \star \rightarrow \star $ every time for raw lambdas, in 
$\lambda e$, we can do a simple optimization by exploiting bidirectional type-checking. In essence, when raw lambdas are in checking positions, the types can be inferred from the contextual type information. The translation function 
$(\lceil \check{e} \rceil_{b})$ is shown as follows, and the boolean flag b indicates an unknown type annotation should be inserted or not:
\begin{align*} \lceil {x} \rceil_{b} &= {x} \\ \lceil c \rceil_{\mathsf{true}} &= c : \star \\ \lceil c \rceil_{\mathsf{false}} &= c \\ \lceil \lambda x.\check{e} \rceil_{\mathsf{true}} &= \lambda x. \lceil \check{e} \rceil_{\mathsf{false}} : \star \\ \lceil \lambda x.\check{e} \rceil_{\mathsf{false}} &= \lambda x. \lceil \check{e} \rceil_{\mathsf{false}} \\ \lceil \check{e_{{\mathrm{1}}}}~\check{e_{{\mathrm{2}}}} \rceil_{b} &= \lceil \check{e_{{\mathrm{1}}}} \rceil_{\mathsf{true}} ~ \lceil \check{e_{{\mathrm{2}}}} \rceil_{\mathsf{false}} \end{align*}
For example, the dynamic expression 
${(} \lambda {x} .\, \lambda {y} .\, {x} \, {y} {)} \, {(} \lambda {x} .\, {x} {)} \, 1$ can be translated to 
${(} {(} \lambda {x} .\, \lambda {y} .\, {x} \, {y} {)} : \star {)} \, {(} \lambda {x} .\, {x} {)} \, 1$. Only one unknown type 
$ \star $ is inserted, despite the presence of 3 lambda expressions without annotations in the original expression. We should also remark that, more generally, we can use a similar idea to improve on the syntactic sugar for dynamic lambdas. Instead of blindly adding 
$ \star \rightarrow \star $ annotations to lambdas without type annotations, we only need to add 
$ \star \rightarrow \star $ to lambdas in inference positions.
Theorem 5.5 shows that the static gradual guarantee holds for the 
$\lambda e$ calculus. It says that if e of type A is more precise than e’, then e’ has some type B, and type A is more precise than B.
Theorem 5.4 (Dynamic Embedding). If 
$\check{e}$ is closed then 
$ \cdot $ 
$ \vdash $ 
$\lceil$ 
$\check{e}$ 
$\rceil_{\mathsf{true}}$ 
$ \Rightarrow $ 
$ \star $.
Theorem 5.5 (Static Gradual Guarantee of the 
$\lambda e$ Calculus). If 
$ e \sqsubseteq e' $ and 
$ \cdot \vdash e \Leftrightarrow A $, then 
$\exists B,$ 
$ \cdot \vdash e' \Leftrightarrow B $ and 
$ A \sqsubseteq B$.
Dynamic Gradual Guarantee. The 
$\lambda e$ calculus has a dynamic gradual guarantee. Theorem 5.6 shows that if 
$e_1$ is more precise than 
$e_2$, 
$e_1$, and 
$e_2$ are well typed, and if 
$e_1$ reduces to 
$e'_{{\mathrm{1}}}$, then 
$e_2$ reduces to 
$e'_{{\mathrm{2}}}$. Note that 
$e'_{{\mathrm{1}}}$ is guaranteed to be more precise than 
$e'_{{\mathrm{2}}}$. Theorem 5.6 is similar to the one formalized in the AGT approach Garcia et al., Reference Garcia, Clark and Tanter2016). Theorem 5.7 is derived easily from Theorem 5.6. The auxiliary Lemma 5.7, which shows the property of dynamic gradual guarantee for casting, is helpful to prove Theorem 5.7.
Lemma 5.7 (Dynamic Gradual Guarantee for Casting). If 
$ p_{{\mathrm{1}}} ~\sqsubseteq~ p_{{\mathrm{2}}} $ , 
$ \cdot \vdash p_{{\mathrm{1}}} \Leftarrow A_{{\mathrm{0}}} $, 
$ \cdot \vdash p_{{\mathrm{2}}} \Leftarrow B_{{\mathrm{0}}} $ , 
$ A_{{\mathrm{2}}} \sqsubseteq B_{{\mathrm{2}}} $, 
$ \rceil p_{{\mathrm{1}}} \lceil \sqcap A_{{\mathrm{2}}} = A_{{\mathrm{1}}} $, 
$ \rceil p_{{\mathrm{2}}} \lceil \sqcap B_{{\mathrm{2}}} = B_{{\mathrm{1}}} $ and 
$ p_{{\mathrm{1}}} \,\Downarrow_{ A_{{\mathrm{1}}} }\, p'_{{\mathrm{1}}} $ then 
$\exists p'_{{\mathrm{2}}}$, 
$ p_{{\mathrm{2}}} \,\Downarrow_{ B_{{\mathrm{1}}} }\, p'_{{\mathrm{2}}} $ and 
.
Theorem 5.6 (Dynamic Gradual Guarantee (single-step)). If 
$e_1 \sqsubseteq e_2$ , 
$ \cdot \vdash e_{{\mathrm{1}}} \Leftrightarrow A $, 
$ \cdot \vdash e_{{\mathrm{2}}} \Leftrightarrow B $ and 
$e_1 \longmapsto e'_{{\mathrm{1}}}$ then 
$\exists e'_{{\mathrm{2}}} $, 
$ e_2 \longmapsto e'_{{\mathrm{2}}}$ and 
$e'_{{\mathrm{1}}} \sqsubseteq e'_{{\mathrm{2}}}$.
Theorem 5.7 (Dynamic Gradual Guarantee). Suppose 
$e_1 \sqsubseteq e_2$ , 
$ \cdot \vdash e_{{\mathrm{1}}} \Leftrightarrow A $ and 
$ \cdot \vdash e_{{\mathrm{2}}} \Leftrightarrow B $.
• If
$e_1 \longmapsto ^{*} v_1$ then $\exists v_2$, $ e_2 \longmapsto ^{*} v_2$ and $v_{{\mathrm{1}}} \sqsubseteq v_{{\mathrm{2}}}$.-
• If
$e_1 \Uparrow$ then $e_2 \Uparrow$. If $e_{{\mathrm{2}}} \longmapsto ^{*} v_{{\mathrm{2}}}$ then $e_{{\mathrm{1}}} \longmapsto ^{*} v_{{\mathrm{1}}}$ and $ v_{{\mathrm{1}}} ~\sqsubseteq~ v_{{\mathrm{2}}} $, or $e_{{\mathrm{1}}} \longmapsto ^{*} \mathsf{blame}$. If $e_{{\mathrm{2}}}$ $\Uparrow$ then $e_{{\mathrm{1}}}$ $\Uparrow$ or $e_{{\mathrm{1}}} \longmapsto ^{*} \mathsf{blame}$.
6 Discussion
In this section, we wish to discuss our results and further compare the TDOS-based approach with traditional cast calculi. In particular, we wish to go through some possible criticisms of the TDOS approach and to analyze the results obtained in this work.
To conduct this discussion, we believe that it is useful, at points, to draw an analogy with work on the semantics of object-oriented languages. During the 80s and the 90s, there were at least two schools of thought working on the semantics of OOP languages. One school of thought was on using lambda calculi, such as 
$F_{<:}$ (Curien & Ghelli, Reference Curien and Ghelli1992; Cardelli et al., Reference Cardelli, Martini, Mitchell and Scedrov1994; Pierce, Reference Pierce1994), to give the semantics of OOP languages via an elaboration (Abadi et al., Reference Abadi, Cardelli and Viswanathan1996; Bruce et al., Reference Bruce, Cardelli and Pierce1999). Another school of thought was to give the semantics of OOP languages directly (Abadi & Cardelli, Reference Abadi and Cardelli1996; Igarashi et al., Reference Igarashi, Pierce and Wadler2001). The work on Featherweight Java (FJ) (Igarashi et al., Reference Igarashi, Pierce and Wadler2001) is a highlight of the direct approach. Both lines of work have been highly influential and led to much innovation. We believe that the TDOS can bring some new ideas into the landscape of gradual typing, complementing already established ideas studied with the elaboration approach.
6.1 Comparing TDOS based calculi with traditional cast calculi
The semantics of applications. Perhaps the most notable difference between the TDOS and traditional cast calculi, such as the blame calculus, is on the semantics of applications. In the blame calculus, applications are standard and strict. Here strict means that applications accept only arguments that exactly match the type of the input of the function. Explicit casts, together with strict applications, are then used in the blame calculus to encode flexible applications, where the arguments can have different (but consistent) types and casts bridge the gap between the types.
In a TDOS, we must support flexible applications, because calculi with a TDOS model a gradual typing semantics directly. Since gradual source languages support flexible applications, the semantics of applications in a TDOS needs to be necessarily more complex than that in a cast calculus. This difference can be seen in our work. For instance, in the semantics of 
$\lambda B$ in Figure 1, there are three rules dedicated to the semantics of applications (rule bstep-beta, bstep-abeta, bstep-c). In contrast, for 
$\lambda B^{g}$ (Figure 5), there are five rules for applications (rule Step-betap, Step-beta, Step-abeta, Step-dyn, Step-c). In a TDOS, applications may raise blame due to inconsistent arguments. Thus rule Step-betap is needed in 
$\lambda B^{g}$. In the blame calculus, applications themselves cannot raise blame, since they are strict. So rule Step-betap or similar rules are unnecessary. Furthermore, in 
$\lambda B^{g}$, a function with type 
$ \star $ can be directly applied to an argument, since 
$ \star \sim \star \rightarrow \star $. Thus, we also need rule Step-dyn in 
$\lambda B^{g}$. In the blame calculus, function applications require a function to always have a function type. So rule Step-dyn or similar is also not needed in 
$\lambda B$. In summary, in a TDOS, because applications are more flexible, they can assume less about the functions and the arguments. As a result, to ensure that applications are safe, casting must be used to check that the functions and arguments have adequate value forms at runtime.
There are some important consequences of having flexible applications that are worth noting and are discussed next.
Non-orthogonality of the semantics. A first point is that, from a language design point of view, one may question the non-orthogonality of the semantics of applications in a TDOS. In the blame calculus, applications are strict and no casting is involved. All casting that happens is delegated into a separate cast construct. In a TDOS, applications are not orthogonal to casting, since applications also perform some casting. The non-orthogonality is a direct consequence of the goal to have a direct gradual typing semantics. So, while a TDOS can eliminate the need of a source language, and an elaboration to a cast calculus, a price to pay is some additional complexity on the semantics for applications.
To build on our analogy with the semantics of OOP languages, this is similar to the semantics of method calls versus the semantics of applications in lambda calculi such as 
$F_{<:}$. Method calls in OOP languages have a relatively complex semantics due to dynamic dispatching, where the implementation of the method to be executed may only be determined at runtime. Thus, method calls are analogous to flexible applications and require encodings that involve several constructs, including applications, in conventional lambda calculi. In general, the non-orthogonality of the semantics is one of the trade-offs that we need to make if we want to directly model a semantics similar to the source language. Often, in source languages, constructs are made more flexible to provide programming convenience.
Nonstandard beta-reduction. A more technical point is that beta-reduction in 
$\lambda B^{g}$ is non-standard. It is well established how to efficiently implement standard beta-reduction. But it is unclear whether the form of beta reduction in 
$\lambda B^{g}$ can be efficiently implemented. However, we have shown that, for all calculi presented in this paper, it is possible to recover conventional beta-reduction. For 
$\lambda e$, we already employ a standard beta-reduction rule. For 
$\lambda B^{g}$ and 
$\lambda B^{g}_{l}$, we have seen that it is possible to have an alternative design for the reduction rules (Figure 9). In this alternative design, we introduce a form of strict applications in addition to flexible applications. Then, flexible applications will reduce into strict applications, and the beta-reduction of strict applications is standard. The cost of the alternative design is one extra form of application.
Flexible applications are costly. Another important concern is that flexible applications entail extra runtime costs. Casting must be used in applications to validate the types of arguments and functions being applied. In the elaboration approach, it is possible to detect strict applications, and avoid casts for those applications when doing cast insertion (Siek & Taha, Reference Siek and Taha2006). So, while with the elaboration approach, many applications will be strict and avoid casts, in the TDOS considered in this paper, all applications will require casts. One downside of switching to a TDOS is that it becomes less clear where the dividing line is between static checking and dynamic checking. Therefore, an important question is whether it is possible to optimize TDOS to obtain similar benefits to those of cast insertion. We will discuss this question in more detail next.
6.2 Optimizing a TDOS
We are advocating the TDOS primarily as a more direct way to provide the semantics of gradually typed languages. In doing so, we forfeit some optimization benefits that are well established for the elaboration approach. A question that then arises is whether or not we can recover the same benefits, in terms of optimizations, that we obtain in an elaboration approach. While it is not the goal of this paper to investigate how to optimize the TDOS, here we briefly discuss some possible directions and wish to argue that it is possible to have more efficient TDOS-based implementations.
Simplicity of the semantics versus guiding efficient implementations. A first point that we wish to stress is that the main goal of the TDOS is to express the semantics and metatheory of a gradual language as directly and simply as possible. However, this goal can be in conflict with using the semantics to guide efficient implementations. We believe that this conflict is not specific to the TDOS, but arises in many other formulations of operational semantics. For instance, going back to our OOP analogy, we believe that the semantics of FJ was designed with the primary goal of simplicity in mind. The work on FJ does not provide a direct answer for questions such as how to optimize dynamically dispatched method calls. Although, of course, this is an important concern in the implementation of OOP languages. At the same time, we believe that there is nothing preventing variants of FJ that enable answering such questions directly. For instance, it should be possible to have variants of FJ with multiple kinds of method calls (including dynamic and static), and some pre-processing analysis that detects dynamic calls that can be transformed into static calls. Of course, such an extension to FJ would require more constructs and rules, and thus would have some extra complexity compared to the original calculus. Similarly to FJ, our formulations of the TDOS in this paper express the semantics of all applications with flexible applications, even if many applications can be made strict to achieve better performance.
A point worth mentioning here is that in the elaboration approach for gradual languages, the elaboration itself is, of course, compulsory to give the semantics of the source language. Since the elaboration is compulsory anyway, it makes sense to exploit it and couple some optimizations with this step. In essence, this enables us to exploit static knowledge about the program to generate optimized code in cast calculi. A TDOS does not require an elaboration step. However, we could have an optional step type-checking a TDOS program and attempting to use static type information to generate more efficient code. In such a step, we could do similar optimizations to those performed in the traditional elaboration of gradual languages. For these optimizations to be possible it may be necessary to extend the TDOS with more constructs. We briefly sketch a couple of possible optimizations next.
Optimizing Strict Applications. With the alternative set of reduction rules for 
$\lambda B^{g}_{l}$ in Figure 9, we can avoid casting for arguments if we know that an application is strict. Thus, assuming an optimization pass on a program, before compilation, we could try to optimize some applications. For example, suppose that we would have the application:
With the current set of reduction rules, using flexible applications, we would need to cast the integer argument to an integer. However, we statically know that such a cast is unnecessary. With a preoptimization pass, we could detect this, and then transform the flexible application above into a strict application:
Then the cast of the argument would be avoided at runtime.
Clearly, the alternative syntax and set of rules in Figure 9 does not go far enough into what we could do. For instance, in the example above, although we can avoid the cast of the argument, we still need to cast the result of beta-reduction with the return type of the function. A possible idea here would be to make lambda expressions strict, by ensuring that the return type of the function matches exactly with the type of the body of the function. With such a form of strict lambdas, the expression above could not type check, since 
(the expression in the body) should have type 
$ \mathsf{Int} $, but the return type of the function is 
$ \star $. Strict lambdas do not lose expressiveness compared to the current, more flexible, form of lambdas. This is because we can always insert a cast in the body to encode a flexible lambda. For instance, we could have 
, and now the body would have type 
$ \star $.
We have not fully investigated the optimizations discussed above. For optimizing strict applications, we believe that we could employ techniques similar to existing cast insertion techniques (Siek & Taha, Reference Siek and Taha2006). For the possibility of replacing flexible lambdas by strict lambdas, we have not formalized the idea yet and we may need to pay some attention to the gradual guarantee.
Design Choices in the TDOS. Formulations of the TDOS are relatively new and underexplored. Thus, there could be different design choices with potential advantages over the current design choices. One design choice that we have made is to have lambda values with both input and output annotations. This is in contrast to the blame calculus, where lambda abstractions only include the input type annotation: that is they are of the form 
$ \lambda {x} : A .\, e $. One alternative TDOS design that was explored by Fan et al. (Reference Fan, Huang, Xu, Sun, Oliveira, Ali and Vitek2022) for calculi with the merge operator, models lambda expressions as 
$ \lambda {x} : A .\, e $. However, function values need to be wrapped under an annotation. That is they need to be of the form 
$ \lambda {x} : A .\, e : C$ (where C is the type of the whole function). In a TDOS, output types are needed because casts require the source type of the cast. In the blame calculus, source types are written explicitly. For example, consider the TDOS application:
\[ {(} \lambda {x} .\, {x} : \star \rightarrow \star {)} \, 5 \]
which casts the argument to a dynamic value. In the blame calculus, one possible cast that we could insert to enable the program above would be:
\[ {(} \lambda {x} : \star .\, {x} : \star \rightarrow \star \Rightarrow \mathsf{Int} \rightarrow \star {)} \, 5 \]
Here we cast the function from the source type 
$ \star \rightarrow \star $ to the target type 
$\mathsf{Int} \rightarrow \star $. In the blame calculus, both the source and target types of a cast have to be explicitly written. In a TDOS, we require functions to have output types to ensure that the source type of a cast can be easily computed, and sometimes, the target type can be left implicit. One could wonder if we could compute an imprecise type for 
$ \lambda {x} : A .\, e $ and use that form of lambdas. That is, we could always return 
$ \star $ for the output of function 
$ \rceil \lambda {x} : A .\, e \lceil = A \rightarrow \star $. However, the missing output type information would bring problems in a TDOS. Suppose that we have the following program:
\[ {(} \lambda {x} : \star .\, 1 {)} : \star : \mathsf{Bool} \rightarrow \mathsf{Bool} \]
The dynamic type of the lambda expression 
$ \lambda {x} : \star .\, 1 $ would be 
$ \star \rightarrow \star $, which is a ground type. Thus, the program would reduce to an ill-typed program:
\[ {(} \lambda {x} : \star .\, 1 {)} : \mathsf{Bool} \rightarrow \mathsf{Bool} \]
With our current formulation, the lambda expression takes the form 
$ \lambda {x} .\, 1 : \star \rightarrow \mathsf{Int} $. Then the dynamic type would be the more precise type 
$ \star \rightarrow \mathsf{Int}$, which is not a ground type. Thus the problem with 
${(} \lambda {x} : \star .\, 1 {)} : \star : \mathsf{Bool} \rightarrow \mathsf{Bool} $ would not happen.
6.3 Metatheory and the gradual guarantee
One of our arguments for the TDOS is that it can enable a more direct approach to the semantics of gradual languages, as well as potentially simpler metatheory. For most proofs in the paper, we believe that the proofs are quite simple. This includes proofs of preservation, progress, determinism, and the blame theorem. One proof that deserves more discussion is the (dynamic) gradual guarantee, which we talk about next.
Gradual Guarantee Proofs. Using an elaboration approach to provide the semantics of a source gradual language usually requires two separate precision relations for the source language and the cast calculus. Furthermore, because of the elaboration, properties such as elaboration type preservation are necessary. In contrast, the 
$\lambda e$ calculus leads to a simple proof of the gradual guarantee. Only one set of precision rules is required and no elaboration theorems are needed. For 
$\lambda e$, we believe that the gradual guarantee is simpler than with an elaboration approach.
For 
$\lambda B^{g}_{l}$, however, we faced some issues for the dynamic gradual guarantee. Due to the generalization of the application typing rule, there are some complications in the gradual guarantee for 
$\lambda B^{g}_{l}$. In particular, 
$\lambda B^{g}_{l}$ needs to introduce an alternative set of reduction rules with strict applications 
. So the precision for the dynamic gradual guarantee should account for strict applications, whereas no strict applications are needed for the static gradual guarantee.
It is worthwhile discussing why strict applications are needed. From the precision relation, we know that the following two programs are in a precision relation:
To prove the dynamic gradual guarantee, we need to satisfy Theorem 4.7, which shows that if the more precise expression reduces to a new expression, then the less precise expression, after multiple steps of reduction, must preserve the precision relation. If expression 
takes a reduction step:
Then 
should be in precision with 
after multiple reduction steps. However, if 
takes a step, then beta-reduction is performed, and the result cannot preserve precision. So, the only option is not to reduce. However, the argument 1 is not less precise than 
. The problem is that the argument type is not the same as the function input type. This is due to the generalization of the typing of applications, where there is an implicit cast for the arguments.
To address the issue above, we introduce strict applications to perform the implicit cast earlier. Then, for a strict application, the type of the argument is the same as the function input type. For 
, there is a cast from 1 to function input type 
$ \star $. After we cast 1 to 
$ \star $, the result is 
, which is less precise than 
as expected. Therefore, we use strict applications to label the applications which have performed the implicit cast for arguments, and have the same type as function inputs. Another potential solution would be to use a semantic proof method based on logical relations for proving the dynamic gradual guarantee (New et al., Reference New, Licata and Ahmed2019). With this approach, we believe that the intermediate reduction system with strict applications would not be needed. The key observation is that the final reduction result should be in a precision relation (even if intermediate results may not be in a precision relation). However, a semantic approach introduces its own complexity, so we have not explored this possibility.
In short, for the proof of the dynamic gradual guarantee in 
$\lambda B^{g}_{l}$, while we can avoid some proofs and definitions required by elaboration, we faced other complications. Thus, we cannot claim that the proof of the dynamic gradual guarantee for 
$\lambda B^{g}_{l}$ is simpler than the proof for the blame calculus.
7 Related work
This section discusses related work. We focus on gradual typing criteria, cast calculi, gradually typed calculi, the AGT approach, and typed operational semantics.
Gradual Typing and Criteria. There is a growing number of research work focusing on combining static and dynamic typing (Thatte, Reference Thatte1989; Abadi et al., Reference Abadi, Cardelli, Pierce and Plotkin1991; Meijer & Drayton, Reference Meijer and Drayton2004; Hansen, Reference Hansen2007; Matthews & Findler, Reference Matthews and Findler2009; Wolff et al., Reference Wolff, Garcia, Tanter and Aldrich2011; Rastogi et al., Reference Rastogi, Chaudhuri and Hosmer2012; Strickland et al., Reference Strickland, Tobin-Hochstadt, Findler and Flatt2012; Boyland, Reference Boyland2014; Swamy et al., Reference Swamy, Fournet, Rastogi, Bhargavan, Chen, Strub and Bierman2014). Many mainstream programming languages have some form of integration between static and dynamic typing. These include TypeScript (Bierman et al., Reference Bierman, Abadi and Torgersen2014), Dart (Bracha, Reference Bracha2015), Hack (Verlaguet, Reference Verlaguet2013), Cecil (Chambers, Reference Chambers1992), Bigloo (Serrano &Weis, Reference Serrano and Weis1995), Visual Basic.NET (Meijer & Drayton, Reference Meijer and Drayton2004), ProfessorJ (Gray et al., Reference Gray, Findler and Flatt2005), Lisp (Moon, Reference Moon1989), Dylan (Shalit, 1996), and Typed Racket (Tobin-Hochstadt & Felleisen, Reference Tobin-Hochstadt and Felleisen2008).
A gradually typed lambda calculus (GTLC) should support both fully statically typed and fully dynamically typed programs, as well as partially statically typed or dynamically typed ones. Siek & Taha (Reference Siek and Taha2006) introduced gradual typing with the notion of the unknown type 
$ \star $ and type consistency.
Because run-time checking is needed by a gradually typed language, function type annotations are accumulated at run-time in most of the gradually typed languages. Therefore, the number of accumulated type annotations can be unbound. Herman et al. (Reference Herman, Tomb and Flanagan2007) implemented gradual typing based on coercions and combined adjacent coercions. Thus, space consumption has been limited, and the type system was proved to be type-safe. Addressing the space consumption issues of gradual typing has been an ongoing research effort, with many works on the area (Siek et al., Reference Siek, Garcia and Taha2009; Siek & Wadler, Reference Siek and Wadler2009; Herman et al., Reference Herman, Tomb and Flanagan2010; Garcia, Reference Garcia2013).
Much work in the research literature of gradual typing focuses on the pursuit of sound gradual typing. A language with sound gradual typing should come with a guarantee of type soundness. This often requires some dynamic checks that arise from static type information. Furthermore, gradually typed languages should provide a smooth integration between dynamic and static typing. For instance, one of the criteria for gradual typing is that a program that has static types should behave equivalently to a standard statically typed program (Siek & Taha, Reference Siek and Taha2006). Siek et al. (Reference Siek, Vitousek, Cimini and Boyland2015b) proposed the gradual guarantee to clarify the kinds of guarantees expected in gradually typed languages. The principle of the gradual guarantee is that static and dynamic behavior changes by changing type annotations. For the static (gradual) guarantee, the type of a more precise term should be more precise than the type of a less precise term. For the dynamic (gradual) guarantee, any program that runs without errors should continue to do so with less precise types.
Cast Calculi. The semantics of a gradually typed calculus is normally given indirectly via a translation (or elaboration) into a cast calculus. The process of the translation to cast calculi involves inserting casts whenever type consistency holds between different types. Cast calculi are independent from the GTLC, having their own type systems and operational semantics. In 
$\lambda B^{g}$ and 
$\lambda e$, by using TDOS, the semantics of a GTLC is given directly without translating to any other calculus.
There are several varieties of cast calculi. Findler & Felleisen (Reference Findler and Felleisen2002) introduced assertion-based contracts for higher-order functions. Based on the coercions and checks for higher-order values, which are implemented by an ad-hoc mixture of wrappers, reflection, and dynamic predicates, Gray et al. (Reference Gray, Findler and Flatt2005) provided the following observation. First, the wrapper and reflection operations fit the profile of mirrors. Second, the checks correspond to contracts. Finally, the timing and shape of mirror operations coincide with the timing and shape of contract operations. Consequently, they presented a new model of interoperability that builds on the ideas of mirrors and contracts. Henglein’s dynamically typed 
$\lambda$-calculus (Henglein, Reference Henglein1994) is an extension of the statically typed 
$\lambda$-calculus with a dynamic type and explicit dynamic type coercions. To port portions of programs from scripting languages to sound typed languages, Tobin-Hochstadt & Felleisen (Reference Tobin-Hochstadt and Felleisen2006) presented a framework for expressing this interlanguage migration. They proved that, for a program which consists of modules in the untyped lambda calculus, rewriting one of them in a simply typed lambda calculus can produce an equivalent program and be type safe.
Wadler & Findler (Reference Wadler and Findler2009) introduced the blame calculus. The blame comes from Findler and Felleisen’s contracts and tracks the locations where cast errors happen using blame labels. Siek et al. (Reference Siek, Garcia and Taha2009) explored the design space of higher-order casts. For first-order casts (casts on base types), the semantics is straightforward. But there are issues for higher-order casts (functions): a higher-order cast is not checked immediately. For higher-order casts, checking is deferred until the function is applied to an argument. After application, the cast is checked against the argument and return value. A cast is used as a wrapper and split when the wrapped function is applied to an argument. Wrappers for higher-order casts can lead to unbounded space consumption (Herman et al., Reference Herman, Tomb and Flanagan2010).
There are some different designs for the dynamic semantics for cast calculi in the literature. Wadler & Findler (Reference Wadler and Findler2009) use a lazy error detection strategy, which coerces the arguments of a function to the target type, and checking is only done when the argument is applied. Siek & Taha (Reference Siek and Taha2006) use a different strategy where checking higher-order casts is performed immediately when the source type is the unknown type (
$\star$). Otherwise, the later strategy is the same as lazy error detection.
Siek & Wadler (Reference Siek and Wadler2009) introduced threesomes, where a cast consists of three types instead of two types (twosomes) of the blame calculus. The threesome calculus is proved to be equivalent to a coercion-based calculus (Herman et al., Reference Herman, Tomb and Flanagan2007) without blame labels but with space efficiency. The three types in a threesome contain the source, intermediate, and target types. The intermediate type is computed by the greatest lower bound of all the intermediate types. In 
$\lambda e$, the three annotations in lambda values play a similar role to the three annotations in threesomes. Castagna & Lanvin (Reference Castagna and Lanvin2017) proposed a calculus that discards annotations for higher-order functions, following an eager semantics. The dynamic semantics for higher-order values above can be summarized as two categories. One is the lazy semantics, and the other is the eager semantics which attempts to merge intermediate annotations for higher-order casts. In our work, we study calculi with both variants.
Finally, various cast calculi have been extended with various of features of practical interest. For instance, Ahmed et al. (Reference Ahmed, Findler, Siek and Wadler2011) extended the blame calculus to incorporate polymorphism, based on the dynamic sealing proposed by Matthews & Ahmed (Reference Matthews and Ahmed2008) and Neis et al. (Reference Neis, Dreyer and Rossberg2009).
Cast calculi require explicit casts and cannot be used directly as a gradually typed language. They can be used as the target of source gradual languages via an elaboration that inserts casts where needed. In contrast, the calculi presented in this work support both explicit and implicit casts. Explicit casts are supported via type annotations, which can act as casts at runtime. Implicit casts arise from the use of bidirectional type-checking, where the checking mode denotes points in the program where casts are needed. Because implicit casts are supported in all our calculi (
$\lambda B^{g}$, 
$\lambda B^{g}_{l}$, and 
$\lambda e$), these calculi can all be used directly as gradually typed languages and no elaboration step is necessary.
In the conference version of this work, we introduced the 
$\lambda B^{r}$ calculus (Ye et al., Reference Ye, Oliveira and Huang2021), which uses a forgetful semantics (Greenberg, Reference Greenberg2015) called the blame recovery semantics. The blame recovery semantics ignores intermediate type annotations in a chain of type annotations for higher-order functions. The idea is to only raise blame if the initial source type of the value and final target types are not consistent. Otherwise, even if intermediate annotations trigger type conversions, which would not be consistent, the final result can still be a value provided that the initial source and final target types are themselves consistent. This alternative approach has a bounded number of annotations, which avoids the accumulation of type annotations (upto 2 for higher-order values). In the present work, we opted to present an eager semantics, inspired by the AGT approach, instead. However, the eager semantics in 
$\lambda e$ and traditional AGT (Garcia et al., Reference Garcia, Clark and Tanter2016) is only applied to values. In other work (Siek & Wadler, Reference Siek and Wadler2009; Herman et al., Reference Herman, Tomb and Flanagan2010; Bañados Schwerter et al., Reference Bañados Schwerter, Clark, Jafery and Garcia2021), the eager semantics is applied to all expressions and leads to a space-efficiency GTLC. Furthermore, both AGT and our eager semantics are more eager than the original approach by Herman et al. (Reference Herman, Tomb and Flanagan2010), since, if two types are inconsistent, an error is raised directly. However, in space efficient calculi, error is recorded and raised when arguments are applied. We leave a space-efficient formulation of the eager semantics using TDOS as future work.
Abstracting Gradual Typing (AGT). Garcia et al. (Reference Garcia, Clark and Tanter2016) introduce the abstracting gradual typing (AGT) approach, following an idea by Schwerter et al. ( An externally justified cast calculus is not required in AGT. Instead, runtime checks are deduced by the evidence for the consistency judgment. For the static semantics, AGT uses techniques from abstract interpretation to lift terms of the static system to gradual terms. A concretization function is used to lift gradual types to static type sets. After that, a gradual type system can be derived according to the static type system. The gradual type system retains the type safety of the static type system and enjoys the criteria of Siek et al. (Reference Siek, Vitousek, Cimini and Boyland2015b). The dynamic semantics is given by reasoning about the type derivations obtained from the type safety proof of the static language counterpart. Gradual typing derivations are represented as intrinsically typed terms (Church, Reference Church1940), which correspond to typing derivations directly.
One aspect that the TDOS has in common with the AGT approach is that by using the TDOS for the dynamic semantics and a bidirectional type system, we can design a gradually typed language with a direct semantics. Nevertheless, the two approaches have different and perhaps complementary goals. The goals of TDOS are more modest than those of AGT, which aims at deriving various definitions for gradually typed languages in a systematic manner. In contrast, TDOS and our work have no such goals. Our main aim is to adapt the standard and well-known techniques from small-step semantics into the design of gradually typed languages. We expect that the familiarity and simplicity of the TDOS approach would be a strength, whereas the AGT approach requires some more infrastructure, but the payoff is that many definitions can then be derived. For future work, it would be interesting to see whether it is possible to combine ideas from both approaches. It would be interesting to reuse much of the AGT infrastructure, but with an alternative model for the dynamic semantics based on a TDOS instead. One current limitation of the AGT approach is that it does not offer an account of blame tracking and blame labels. As we have seen in Section 4, the TDOS can model languages with blame tracking and blame labels and be used to prove important theorems such as blame safety.
Typed Operational Semantics. In this paper, we use the TDOS approach (Huang & Oliveira, Reference Huang, Oliveira, Hirschfeld and Pape2020). TDOS was originally used to describe the semantics of languages with intersection types and a merge operator. Like gradual typing, such features require a type-dependent semantics. In a TDOS, type annotations become operationally relevant and can affect the result of a program. Casting is used to provide an operational interpretation to type conversions in the language, similarly to coercions in coercion-based calculi (Henglein, Reference Henglein1994). Our work shows that a TDOS enables a direct semantics for gradual typing. We explored two possible semantics for gradual typing: one following a semantics similar to the blame calculus and another with an eager semantics.
There are other variants of operational semantics that make use of type annotations. Types are used in Goguen’s typed operational semantics (Goguen, Reference Goguen1994), similarly to TDOS. Typed operational semantics has been applied to various calculi, including simply typed lambda calculi (Goguen, Reference Goguen1995) and calculi with dependent types (Feng & Luo, Reference Feng and Luo2011) and higher-order subtyping (Compagnoni & Goguen, Reference Compagnoni and Goguen2003). An extensive overview of related work on type-dependent semantics is given by Huang & Oliveira (Reference Huang, Oliveira, Hirschfeld and Pape2020).
8 Conclusion
In this work, we proposed an alternative approach to give a direct semantics to gradually typed languages without an intermediate cast calculus. Our approach is based on a TDOS (Huang & Oliveira, Reference Huang, Oliveira, Hirschfeld and Pape2020). TDOS is a variant of small-step semantics where type annotations are operationally relevant and a special big-step casting relation gives an interpretation to such type annotations at runtime. We believe that TDOS can be a valuable technique for language designers of gradually typed languages, giving them a simple and direct way to express the semantics of their languages.
We presented two gradually typed lambda calculi: 
$\lambda B^{g}$ and 
$\lambda e$. The 
$\lambda B^{g}$ semantics follows the semantics of 
$\lambda B$. The 
$\lambda e$ calculus explores the use of an eager semantics for gradually typed languages using a TDOS. In addition, the 
$\lambda B^{g}_{l}$ calculus shows that blame labels can be modeled using a TDOS, and results such as the blame theorem and the gradual guarantee can also be proved.
There is much to be done for future work. Although we argued that some benefits of the TDOS include easier and more direct proofs, we have not empirically validated those claims. To do so, we would need to formalize the GTLC and a target cast calculus (such as the blame calculus or a cast calculus with an eager semantics) in Coq together with all the relevant proofs (such as the blame theorem the gradual guarantee and others). Then we could empirically compare the proofs, for instance in terms of size or number of lemmas that are required and/or other metrics. In our work, we have only informally mentioned that some lemmas and definitions would not be needed in a TDOS, but perhaps it could be the case that a TDOS would also require some extra lemmas or extra complexity in the proofs that is not necessary in the conventional approach using an elaboration semantics. One issue that we have identified in the proofs with the TDOS is the dynamic gradual guarantee proof for 
$\lambda B^{g}_{l}$, which we discussed in Section 6. An empirical evaluation would help assessing such benefits (or not) more precisely, and it is one direction for future work.
Obviously, to prove that TDOS is a worthy alternative to existing cast calculi or other approaches for the semantics of gradually typed languages, many more features should be developed with the TDOS. Cast calculi have been shown to support a wide range of features such as polymorphism (Ahmed et al., Reference Ahmed, Findler, Siek and Wadler2011), subtyping (Siek & Taha, Reference Siek and Taha2007) and various other features (Siek & Vachharajani, Reference Siek and Vachharajani2008; Takikawa et al., Reference Takikawa, Strickland, Dimoulas, Tobin-Hochstadt and Felleisen2012). We hope to explore these in the future.
Acknowledgments
We are grateful to anonymous reviewers and our colleagues at the HKU PL group. This work has been sponsored by Hong Kong Research Grants Council projects number 17209520 and 17209821.
Conflicts of interest
None.
Supplementary material
To view supplementary material for this article, please visit https://doi.org/10.1017/S0956796824000078
Open access
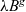
Discussions
No Discussions have been published for this article.