INTRODUCTION
Dengue is an RNA virus in the family Flaviviridae. There are four serotypes of dengue virus, each of which induces a specific antigenic response in humans. Infection with any of the four serotypes can cause disease ranging from dengue fever (DF) to dengue hemorrhagic fever (DHF) and dengue shock syndrome (DSS), in order of increasing severity [Reference Guzmán and Kouri1]. Infection with a serotype provides lifelong immunity to that serotype and an increased risk for the severe forms of disease (DHF and DSS) during subsequent infection with a different serotype [Reference Nagao and Koelle2]. Dengue infection has been recognized in over 100 countries: DF and DHF are important public-health problems, especially in the tropics and subtropics, where nearly 2·5 billion people are at risk of infection [Reference Guzmán and Kouri1]. An estimated 50 million cases of DF occur every year, including 500 000 hospitalizations for DHF [Reference Guzmán3].
Despite the expansion in the geographical range of the virus over past four decades [Reference Beatty4], there is no dengue vaccine licensed for use currently. Dengue vaccine development is an area of active research: significant advances have occurred in recent years and several vaccine candidates are showing promise in clinical studies [Reference Coller and Clements5]. The most advanced vaccine candidate showed efficacy of 30% and protection against three of the four serotypes of dengue [Reference Halstead6]. With several dengue vaccine candidates progressing through clinical trials, a licensed dengue vaccine is expected to be available in less than 10 years [Reference Guzmán3].
Once the vaccine becomes available, policy-makers will have to decide how to best allocate it. As a result, it is imperative to carefully examine the effects of vaccine-allocation policies. Mathematical models of dengue transmission predict complex temporal patterns in prevalence, driven by seasonality in mosquito abundance [Reference Reich7], and may include a transient period immediately after vaccine introduction where prevalence can spike higher than in the pre-vaccination period. An increase in infections, however brief, can raise doubts about the vaccination programme, while the longer-term outcome may be highly favourable. A temporary increase in infections might lead to public doubts and refusal to use the vaccine or even policy-makers ending the vaccination programme altogether. Moreover, these spikes can also pose serious problems by overwhelming resources like available hospital beds. Thus, investigating short- and long-term effects of the vaccination introduction is important.
In the present study, we found that simple dengue transmission models frequently predict large transient spikes in prevalence in the years after vaccination is begun. The presence of these spikes was highly sensitive to the level of vaccination, the efficacy of the vaccine, and the timing of the vaccination programme. Despite the presence or absence of transient spikes, vaccination reduced dengue infections when averaged over the first 15 years after vaccine introduction and when averaged over the very long term.
METHODS AND APPROACH
Here we briefly describe the mathematical models for dengue transmission that we used in this study. See Appendices A–C for detailed descriptions of the models.
We developed standard SIR-type deterministic dengue models to explore the short- and long-term effects of vaccine introduction. In the models, the population was divided into unvaccinated and vaccinated people, and then each of these groups was further divided by infection history (Fig. 1). In the main model, an individual with no prior dengue infection (state S 1) can have a primary infection from any serotype of dengue (I 1), recovery from which provides the individual with lifelong immunity to that serotype (S 2). The individual can then acquire infection from any of the remaining three serotypes, and enter the secondary-infection class (I 2). Third or fourth infections from dengue are very rare [Reference Halstead8], so we assumed that an individual recovering from secondary infection becomes immune to all serotypes (R). Dengue mortality in humans is at most 1–2% [Reference Rajapakse9] and is thus ignored in our model for simplicity. As we are only interested in infections in humans, we did not model mosquito population explicitly [Reference Pandey, Mubayi and Medlock10]. We used model parameters consistent with the literature, along with a small level of seasonal forcing of transmission to capture seasonal oscillations in mosquito population size [Reference Nisalak11].
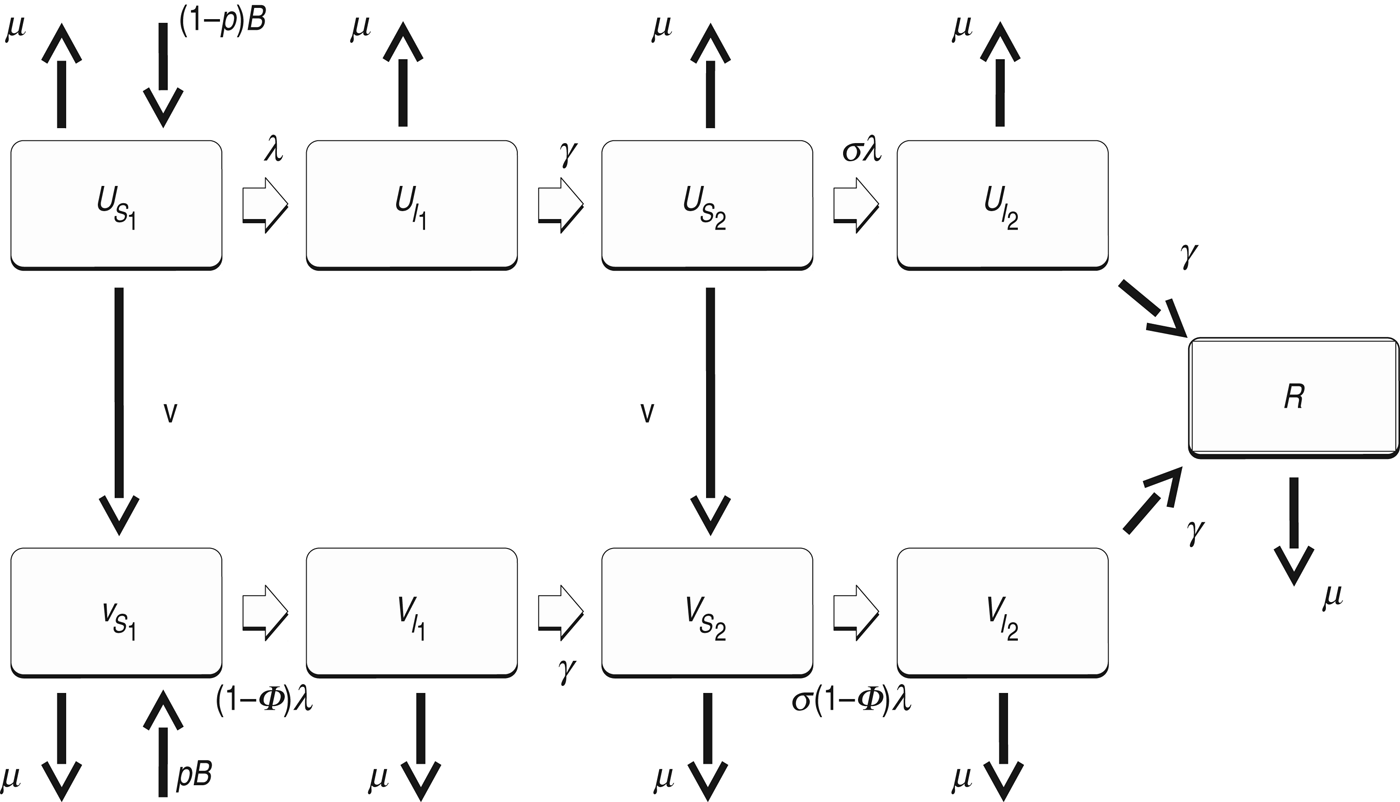
Fig. 1. Diagram of the main model. U denotes unvaccinated individuals, while V denotes vaccinated. S 1 and S 2 are individuals susceptible to primary and secondary dengue infection, respectively. I 1 and I 2 are individuals infected with primary and secondary infections, respectively. R represents individuals recovered from secondary infection and immune to further infections. See Table 1 for definition of the other symbols.
We modelled the vaccine as having efficacy φ at preventing infection. The vaccination programme was modelled as having two possible components: one component vaccinates a proportion p of infants, and the other component vaccinates people in the general population at rate v. For simplicity, for the main results we used only vaccination of infants (v = 0).
To simulate vaccine introduction, we computed a solution to the model with no vaccine (p = 0) from arbitrary initial conditions until it converged to regular periodic oscillations (a stable limit cycle, in mathematical terms [Reference Strogatz12]). From a new initial point on this periodic solution, we then computed the solution to the model with vaccine introduced (p > 0).
RESULTS
The model prevalence converged to regular periodic oscillations, with or without vaccination (e.g. Fig. 2). Without vaccination, prevalence oscillates with a period of 2 years. The perturbation caused by the introduction of vaccine results in a transient period where the prevalence has not yet converged to periodic oscillations. During this transient period, large spikes can occur, to levels above those present before the vaccine was introduced, and this transient period may last many years.

Fig. 2. Simulated dengue prevalence after vaccine introduction. Starting at year t = 0, we assume 78% of infants are vaccinated, i.e. p = 0·78, with a 30% vaccine efficacy; φ = 0·3. The black curves are prevalence after vaccine introduction, while the grey curves are the prevalence had vaccine not been introduced. (a) Shows prevalence for 15 years after vaccine introduction; (b, c) show only the first and last 15 years of this period. See Appendix A for model and parameter definitions.
For example, vaccinating 78% of infants at 30% vaccine efficacy results in an initial period of about 60 years when prevalence can spike more than twice as high as before vaccine introduction (Fig. 2). After the transient period, prevalence converges to annual oscillations with a smaller maximum than in the 2-year oscillations prior to vaccine introduction (Fig. 2 c). By contrast, vaccinating 90% of infants results in a transient period of about 70 years, where prevalence can spike more than three times as high as before vaccine introduction, and prevalence then settles down to 3-year oscillations with a higher maximum than before vaccine introduction (Fig. 3).

Fig. 3. Simulated dengue prevalence after vaccine introduction. The model and parameter values are as in Figure 2, but with 90% of infants vaccinated, i.e. p = 0·9.
These two examples show that the effectiveness of a vaccination programme may differ depending on exactly what is evaluated. Effectiveness may consider individual points in time (e.g. the height of the spikes in prevalence) or periods of time (e.g. total number of infections in a fixed period). In addition, effectiveness may be evaluated over the period just after vaccine introduction or, as is more convenient from a modelling perspective, the period after the prevalence has converged to periodic oscillations. To capture the transient period over many simulations, we considered the transient period to be the first 15 years after vaccine introduction. To quantify the severity of transient spikes at any point in time, we calculated the maximum prevalence during first 15 years after introduction of the vaccine. To examine the effectiveness over a period of time, we also calculated the total number of infections during the first 15 years after vaccine introduction. For the period after prevalence has converged to periodic oscillations, we calculated both the maximum prevalence and the mean prevalence per year.
To explore the transient spikes in prevalence, we varied vaccine coverage (p), for low (φ = 0·3) and high (φ = 0·7) vaccine efficacy (Fig. 4 a). Large transient spikes (i.e. above the pre-vaccine maximum of about 2/1000) were present after vaccine introduction for both levels of vaccine efficacy. Moreover, for the higher vaccine efficacy, large transient spikes appeared at lower vaccine coverage.

Fig. 4. Effectiveness of the vaccination programme at different levels of coverage. (a) Maximum prevalence in the first 15 years after vaccine introduction. (b) Total number of infections over the first 15 years after vaccine introduction. (c) Long-term mean annual incidence.
By varying vaccine efficacy, we found that large transient spikes occur particularly when vaccine efficacy is neither very low nor very high (Fig. 5). For 80% vaccine coverage, when vaccine efficacy is below 30%, the perturbation caused by vaccine introduction is insufficient to generate transient spikes. On the other hand, when vaccine efficacy is higher than 97% at 80% vaccine coverage, vaccination quickly reduces prevalence without large transient spikes. Similarly, with 40% vaccine coverage, there are no large transient spikes below 58% or above 96% vaccine efficacy.

Fig. 5. Maximum prevalence over the 15 years after vaccine introduction for varying vaccine efficacy. Eighty percent (p = 0·8, blue) and 40% (p = 0·4, red) of infants are vaccinated. The dashed grey line is the maximum prevalence prior to vaccine introduction.
Since prevalence oscillates with a period of 2 years without vaccination, we varied the time of vaccine introduction over the 2-year period (Fig. 6). The presence or absence of large transient spikes after vaccine introduction is highly sensitive to the time of vaccine introduction.

Fig. 6. Maximum prevalence over the 15 years after vaccine introduction for varying time of vaccine introduction. Eighty percent of infants are vaccinated (p = 0·8) with a vaccine efficacy of 30% (φ = 0·3, blue) and 70% (φ = 0·7, red). The time that the vaccination programme begins was varied from the beginning (t = 0) to the end (t = 2) of the 2-year cycle in prevalence that exists when there is no vaccine. The dashed grey line is the maximum prevalence prior to vaccine introduction.
Despite the presence of large transient spikes in prevalence, the total number of infections over the first 15 years was lower with vaccine than without in all of the simulations we performed (Fig. 4 b). However, we cannot rule out that the initial burden may be higher in some cases, especially over shorter time spans than 15 years. Moreover, higher vaccine efficacy yields a higher drop in the initial burden at constant vaccine rates. Thus, although the presence of large transient spikes may pose immediate problems by overwhelming the resources, over a 15-year period, vaccination reduces infections.
After the transient period caused by vaccine introduction, prevalence converges again to a regular periodic oscillation, but the oscillation may have a different period and the maximum prevalence may be lower or higher than prior to vaccine introduction (e.g. Figs 2c , 3c ). In all of our simulations, we found that in the long term, the mean annual incidence decreased as vaccine coverage increased (Fig. 4 c). Although some vaccine introductions did lead to long-term prevalance with a higher maximum, their period was longer, so that the mean over many years was always lower than without vaccine. Moreover, as expected, long-term mean annual incidence was lower for higher vaccine efficacy.
The model also showed large transient spikes in prevalence when we modelled vaccination programmes in the whole population rather than just infants (p = 0 and v > 0) and vaccination programmes that combine the two (p > 0 and v > 0). We also tested simpler and more complex dengue models. The simpler model assumed that there are no secondary infections, so that individuals who recover from their first infection move directly to the recovered class (Appendix B). Our more complex model included a period of short-term cross-protection after primary infection [Reference Wearing and Rohani13] (Appendix C). Both models exhibited the potential for large transient spikes (Fig. 7).

Fig. 7. Transient prevalence spikes in (a) simpler and (b) more complex dengue models. (a) Eighty percent of infants are vaccinated (p = 0·8) and the remainder of the population is vaccinated at a per capita rate of ν = 0·6 per year. See Appendix B for model and parameter definitions. (b) Sixty percent of infants are vaccinated (p = 0·6) and the remainder of the population is vaccinated at a per capita rate of ν = 0·9 per year. Vaccine efficacy is 70% in both models, i.e. φ = 0·7. See Appendix C for model and parameter definitions.
DISCUSSION
Using mathematical models of dengue transmission, we found that vaccine introduction may lead to a transient period when infection prevalences spike higher than in the pre-vaccination period. These spikes in infection prevalence may pose serious problems by overwhelming health resources like hospital beds, as well as creating doubt about the efficacy of the vaccination programme. In our models, the presence of large spikes required that vaccine coverage and vaccination efficacy were not both very low or both very high. The occurrence of large transient spikes for lower vaccine coverage and higher vaccine efficacy suggests that a sufficiently large perturbation to the system is required in order for large transient spikes to exist. These perturbations are generated by the combination of vaccine coverage and vaccine efficacy. When vaccine coverage and efficacy are both very high, the vaccination programme reduces prevalence so quickly that no spikes appear.
We also found that the presence or absence of large transient spikes were highly sensitive to the time when the vaccine programme is first begun. Indeed, the results are so sensitive to introduction time, and probably also to changes in parameter values or model structure, that we do not believe that model results can be used to minimize the chance of large transient spikes.
Despite the presence of large transient spikes in prevalence, the total number of infections over the first 15 years after vaccine introduction was always less than in the 15 years prior to vaccine introduction. The decrease in infections was higher for higher efficacy as well as for higher vaccine coverage. Likewise, in the long term, the mean number of infections per year was always smaller than during the pre-vaccination period and decreased with increasing vaccine coverage and vaccine efficacy.
Vaccination reduces the susceptibility of the population, but the short-term interaction of the change in susceptibility with the seasonal forcing of the mosquito population causes complex results, including large transient spikes. When averaged over longer times, the impact is as expected: both the number of infections in the 15 years following vaccine introduction and the long-term annual mean were always found to be lower after vaccine introduction than before.
Large transient spikes after vaccine introduction were frequent for our main model, along with simpler and more complex models that we also tested. In general, we believe that the occurrence of large transient spikes in response to perturbation is a robust phenomenon of seasonally forced epidemic models. We are unaware of any theoretical research on the short-time transient behaviour of seasonally forced epidemic models; however, there is a rich literature on the long-time behaviour of such models [Reference King14–Reference Grenfell, Bjørnstad and Kappey17].
It is possible that interaction between different dengue serotypes may have some impact on the presence or absence of transient spikes after vaccine introduction. Moreover, antibody-dependent enhancement (ADE), increased susceptibility to or increased transmission of secondary infection, has been hypothesized for dengue [Reference Nagao and Koelle2, Reference Wearing and Rohani13, Reference Cummings18]. Using a mathematical model that included ADE, Billings et al. [Reference Billings, Fiorillo and Schwartz19] showed that if a dengue vaccine does not protect against all serotypes, then increased transmission of the strain not covered by vaccine could occur. This increase in dengue transmission could increase the likelihood of large spikes in prevalence after vaccine introduction.
In our models, we have used generic parameter values rather than those for a specific location. In particular, different parameter values may change the period and maximum amplitude of the pre-vaccination oscillation [Reference Nagao and Koelle2, Reference King and Schaffer16]. However, because of the robustness of the appearance of large transient spikes in prevalence, we expect that these spikes would continue to appear for different parameter values. Similarly, we expect large transient spikes would also be present (1) if the vaccination programme were modelled as starting gradually rather than instantaneously, (2) if the human population were growing rather than remaining a constant size and (3) if the vaccine were introduced at a state other than regular periodic oscillation.
Introduction of dengue vaccine reduces the overall prevalence in the long term, but at the risk of large spikes in prevalence immediately after the vaccine introduction. Policy-makers may need to re-evaluate their vaccination programme based on their short- and long-term goals for reduction in total infections. In order to minimize the risk of large spikes in prevalence, it may be necessary to trade a smaller reduction in short-term burden. For example, in Figure 4(a, b) with vaccine efficacy of 70%, vaccinating 25% of infants rather than 40% of infants may be a better strategy to avoid the spikes at the expense of more total infections over 15 years.
We used mathematical models to evaluate the short- and long-term effects of introducing a dengue vaccine. We found that vaccine introduction may lead to a transient period when infection prevalences spike higher than in the pre-vaccination period. We believe such transient spikes are robust to changes in parameters and model structure, and thus must be accounted for in planning vaccination programmes because they may overwhelm health resources. Despite the presence of transient spikes, the vaccination programme is likely to be effective at reducing the total number of infections during the first few years after introduction, as well as decreasing infections in the long term. Policy-makers should be prepared for transient spikes to mitigate their burden and to accurately understand the effectiveness of the vaccine programme.
APPENDIX A. Main model
We developed a simple deterministic model for dengue to explore the short- and long-term effects of vaccine introduction. The model consists of four unvaccinated (U), four vaccinated (V) and one recovered (R) class, the variables for which represent the number of people in that class over time (Fig. 1). An individual with no prior dengue infection (subscript S) can have a primary infection from any serotype of dengue (I 1), recovery from which provides lifelong immunity to that serotype (S 2). The individual can then acquire infection from any of the remaining three serotypes, and enter the secondary-infection class (I 2). Third or fourth infections from dengue is very rare [Reference Halstead8], so we assume that an individual recovering from secondary infection becomes immune to all serotypes (R). Individuals in both primary- and secondary-infection class recover at rate γ = 7/365 yr−1 so that the mean infectious period is 7 days [Reference Gubler20]. The parameters B and μ are natural birth and death rates in humans, respectively, which were chosen to be B = μ = 1/50 yr−1 so that the mean human lifespan is 50 years and the population size is constant. Dengue-induced mortality in humans is around 1–2% [Reference Rajapakse9] and is thus ignored in our model for simplicity. We were only interested in infections in humans, so we did not model mosquito population explicitly [Reference Pandey, Mubayi and Medlock10]. Infection occurs when a susceptible individual comes in contact with individuals from any of the infectious classes through mosquito bites at the rate given by the force of infection
where the total number of people currently infected is
N is the total human population size and β is a composite transmission parameter [Reference Pandey, Mubayi and Medlock10], taken to be β = 400 yr−1 [Reference Cummings18]. Seasonality in the mosquito population was captured by the cosine term in the force of infection, where t is units of years, making transmission most intense at the beginning of a year (i.e. when t is near an integer 0, 1, 2, …) and least intense in the middle of a year (t near 0·5, 1·5, 2·5, …). We used a small amplitude of seasonal forcing, ε = 0·1. The force of infection for secondary infection was reduced by the factor σ = 3/4 since they are only susceptible to three of the four serotypes.
The vaccination programme with two components was modelled: a proportion p of infants are vaccinated and the rest of the susceptible population is vaccinated at rate v. The vaccine efficacy φ was modelled as reducing the force of infection by the factor 1− φ.
The model equations are
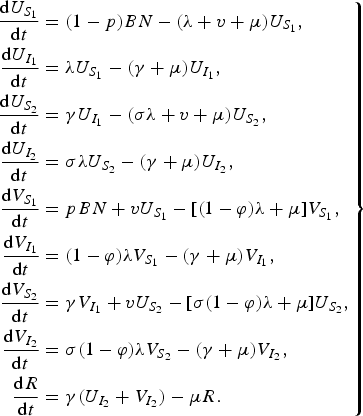 $$\left. \eqalign{\displaystyle{{{\rm d}U_{S_1 } } \over {{\rm d}t}} & = (1 - p)BN - (\lambda + v + \mu )U_{S_1 } , \cr \displaystyle{{{\rm d}U_{I_1 } } \over {{\rm d}t}} & = \lambda U_{S_1 } - (\gamma + \mu )U_{I_1 } , \cr \displaystyle{{{\rm d}U_{S_2 } } \over {{\rm d}t}} & = \gamma U_{I_1 } - (\sigma \lambda + v + \mu )U_{S_2 } , \cr \displaystyle{{{\rm d}U_{I_2 } } \over {{\rm d}t}} & = \sigma \lambda U_{S_2 } - (\gamma + \mu )U_{I_2 } , \cr \displaystyle{{{\rm d}V_{S_1 } } \over {{\rm d}t}} & = pBN + vU_{S_1 } - [(1 - \varphi )\lambda + \mu ]V_{S_1 } , \cr \displaystyle{{{\rm d}V_{I_1 } } \over {{\rm d}t}} & = (1 - \varphi )\lambda V_{S_1 } - (\gamma + \mu )V_{I_1 } , \cr \displaystyle{{{\rm d}V_{S_2 } } \over {{\rm d}t}} & = \gamma V_{I_1 } + vU_{S_2 } - [\sigma (1 - \varphi )\lambda + \mu ]U_{S_2 } , \cr \displaystyle{{{\rm d}V_{I_2 } } \over {{\rm d}t}} & = \sigma (1 - \varphi )\lambda V_{S_2 } - (\gamma + \mu )V_{I_2 } , \cr \displaystyle{{{\rm d}R} \over {{\rm d}t}} & = \gamma (U_{I_2 } + V_{I_2 } ) - \mu R.} \right\}$$
$$\left. \eqalign{\displaystyle{{{\rm d}U_{S_1 } } \over {{\rm d}t}} & = (1 - p)BN - (\lambda + v + \mu )U_{S_1 } , \cr \displaystyle{{{\rm d}U_{I_1 } } \over {{\rm d}t}} & = \lambda U_{S_1 } - (\gamma + \mu )U_{I_1 } , \cr \displaystyle{{{\rm d}U_{S_2 } } \over {{\rm d}t}} & = \gamma U_{I_1 } - (\sigma \lambda + v + \mu )U_{S_2 } , \cr \displaystyle{{{\rm d}U_{I_2 } } \over {{\rm d}t}} & = \sigma \lambda U_{S_2 } - (\gamma + \mu )U_{I_2 } , \cr \displaystyle{{{\rm d}V_{S_1 } } \over {{\rm d}t}} & = pBN + vU_{S_1 } - [(1 - \varphi )\lambda + \mu ]V_{S_1 } , \cr \displaystyle{{{\rm d}V_{I_1 } } \over {{\rm d}t}} & = (1 - \varphi )\lambda V_{S_1 } - (\gamma + \mu )V_{I_1 } , \cr \displaystyle{{{\rm d}V_{S_2 } } \over {{\rm d}t}} & = \gamma V_{I_1 } + vU_{S_2 } - [\sigma (1 - \varphi )\lambda + \mu ]U_{S_2 } , \cr \displaystyle{{{\rm d}V_{I_2 } } \over {{\rm d}t}} & = \sigma (1 - \varphi )\lambda V_{S_2 } - (\gamma + \mu )V_{I_2 } , \cr \displaystyle{{{\rm d}R} \over {{\rm d}t}} & = \gamma (U_{I_2 } + V_{I_2 } ) - \mu R.} \right\}$$
The parameters of the model are also shown in Table 1.
Table 1. Parameters of the dengue models

To minimize the computational rounding error of our simulations, we reformulated our model equations using log-transformed variables [Reference Keeling and Rohani21]. For the pre-vaccination state, using parameter values in Table 1, setting both vaccination rates p and v to 0, and setting the initial conditions for unvaccinated susceptible individuals with no prior infection, unvaccinated infected individuals with no prior infection and permanently recovered individuals to be 0·09, 0·01 and 0·9, respectively, with all other initial conditions to be zero, we simulated the dengue model (3) until it reached a limit cycle, a regular periodic oscillation. With the parameter values used, the model (3) converged to a 2-year cycle (Figs 2 and 3). We defined t = 0 to be just before the year with the larger peak in prevalence (e.g. see Fig. 2 a). In most of the simulations, vaccination was begun at t v = 0, but we also varied the start time t v ∈ [0, 2) (Fig. 6).
To measure effectiveness of the vaccination programme, we used 15-year maximum prevalence
15 year total infections
and long-term annual incidence
where t c is a time after the system has converged to the post-vaccine limit cycle and P is the period of that limit cycle.
APPENDIX B. Simpler model
For our simpler dengue model, we assumed that there is no secondary infection so that an individual after recovering from a dengue infection is immune to all serotypes. This reduces our original dengue model (3) to
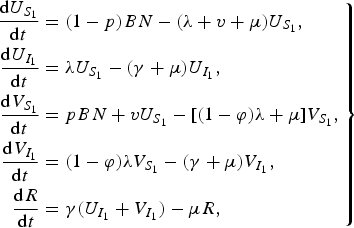 $$\left. \eqalign{\displaystyle{{{\rm d}U_{S_1 } } \over {{\rm d}t}} & = (1 - p)BN - (\lambda + v + \mu )U_{S_1 } , \cr \displaystyle{{{\rm d}U_{I_1 } } \over {{\rm d}t}} & = \lambda U_{S_1 } - (\gamma + \mu )U_{I_1 } , \cr \displaystyle{{{\rm d}V_{S_1 } } \over {{\rm d}t}} & = pBN + vU_{S_1 } - [(1 - \varphi )\lambda + \mu ]V_{S_1 } , \cr \displaystyle{{{\rm d}V_{I_1 } } \over {{\rm d}t}} & = (1 - \varphi )\lambda V_{S_1 } - (\gamma + \mu )V_{I_1 } , \cr \displaystyle{{{\rm d}R} \over {{\rm d}t}} & = \gamma (U_{I_1 } + V_{I_1 } ) - \mu R,} \right\}$$
$$\left. \eqalign{\displaystyle{{{\rm d}U_{S_1 } } \over {{\rm d}t}} & = (1 - p)BN - (\lambda + v + \mu )U_{S_1 } , \cr \displaystyle{{{\rm d}U_{I_1 } } \over {{\rm d}t}} & = \lambda U_{S_1 } - (\gamma + \mu )U_{I_1 } , \cr \displaystyle{{{\rm d}V_{S_1 } } \over {{\rm d}t}} & = pBN + vU_{S_1 } - [(1 - \varphi )\lambda + \mu ]V_{S_1 } , \cr \displaystyle{{{\rm d}V_{I_1 } } \over {{\rm d}t}} & = (1 - \varphi )\lambda V_{S_1 } - (\gamma + \mu )V_{I_1 } , \cr \displaystyle{{{\rm d}R} \over {{\rm d}t}} & = \gamma (U_{I_1 } + V_{I_1 } ) - \mu R,} \right\}$$
with the same force of infection (1), but with total number infected
APPENDIX C. More complex model
A more complex model compared to model (3) was obtained by adding the hypothesis of short-term cross-protection after primary infection. Wearing & Rohani [Reference Wearing and Rohani13] hypothesized that after recovering from primary infection, an individual has short-term cross-protection to the other serotypes for about 9 months, after which he becomes susceptible to the remaining three serotypes. We added two classes of people temporarily immune to all serotypes, one for unvaccinated (U T ) and one for vaccinated (V T ) people, to our existing model. After primary infection, people now enter these temporary immune classes, and before moving on to become susceptible to secondary infection. The model equations for this new model are
 $$\left. \eqalign{\displaystyle{{{\rm d}U_{S_1 } } \over {{\rm d}t}} & = (1 - p)BN - (\lambda + v + \mu )U_{S_1 } , \cr \displaystyle{{{\rm d}U_{I_1 } } \over {{\rm d}t}} & = \lambda U_{S_1 } - (\gamma + \mu )U_{I_1 } , \cr \displaystyle{{{\rm d}U_T } \over {{\rm d}t}} & = \gamma U_{I_1 } - (\rho + \mu )U_T , \cr \displaystyle{{{\rm d}U_{S_2 } } \over {{\rm d}t}} & = \rho U_T - (\sigma \lambda + v + \mu )U_{S_2 } , \cr \displaystyle{{{\rm d}U_{I_2 } } \over {{\rm d}t}} & = \sigma \lambda U_{S_2 } - (\gamma + \mu )U_{I_2 } , \cr \displaystyle{{{\rm d}V_{S_1 } } \over {{\rm d}t}} & = pBN + vU_{S_1 } - [(1 - \varphi )\lambda + \mu ]V_{S_1 } , \cr \displaystyle{{{\rm d}V_{I_1 } } \over {{\rm d}t}} & = (1 - \varphi )\lambda V_{S_1 } - (\gamma + \mu )V_{I_1 } , \cr \displaystyle{{{\rm d}V_T } \over {{\rm d}t}} & = \gamma V_{I_1 } - (\rho + \mu )V_T , \cr \displaystyle{{{\rm d}V_{S_2 } } \over {{\rm d}t}} & = \rho V_T + vU_{S_2 } - [\sigma (1 - \varphi )\lambda + \mu ]U_{S_2 } , \cr \displaystyle{{{\rm d}V_{I_2 } } \over {{\rm d}t}} & = \sigma (1 - \varphi )\lambda V_{S_2 } - (\gamma + \mu )V_{I_2 } , \cr \displaystyle{{{\rm d}R} \over {{\rm d}t}} & = \gamma (U_{I_2 } + V_{I_2 } ) - \mu R,} \right\}$$
$$\left. \eqalign{\displaystyle{{{\rm d}U_{S_1 } } \over {{\rm d}t}} & = (1 - p)BN - (\lambda + v + \mu )U_{S_1 } , \cr \displaystyle{{{\rm d}U_{I_1 } } \over {{\rm d}t}} & = \lambda U_{S_1 } - (\gamma + \mu )U_{I_1 } , \cr \displaystyle{{{\rm d}U_T } \over {{\rm d}t}} & = \gamma U_{I_1 } - (\rho + \mu )U_T , \cr \displaystyle{{{\rm d}U_{S_2 } } \over {{\rm d}t}} & = \rho U_T - (\sigma \lambda + v + \mu )U_{S_2 } , \cr \displaystyle{{{\rm d}U_{I_2 } } \over {{\rm d}t}} & = \sigma \lambda U_{S_2 } - (\gamma + \mu )U_{I_2 } , \cr \displaystyle{{{\rm d}V_{S_1 } } \over {{\rm d}t}} & = pBN + vU_{S_1 } - [(1 - \varphi )\lambda + \mu ]V_{S_1 } , \cr \displaystyle{{{\rm d}V_{I_1 } } \over {{\rm d}t}} & = (1 - \varphi )\lambda V_{S_1 } - (\gamma + \mu )V_{I_1 } , \cr \displaystyle{{{\rm d}V_T } \over {{\rm d}t}} & = \gamma V_{I_1 } - (\rho + \mu )V_T , \cr \displaystyle{{{\rm d}V_{S_2 } } \over {{\rm d}t}} & = \rho V_T + vU_{S_2 } - [\sigma (1 - \varphi )\lambda + \mu ]U_{S_2 } , \cr \displaystyle{{{\rm d}V_{I_2 } } \over {{\rm d}t}} & = \sigma (1 - \varphi )\lambda V_{S_2 } - (\gamma + \mu )V_{I_2 } , \cr \displaystyle{{{\rm d}R} \over {{\rm d}t}} & = \gamma (U_{I_2 } + V_{I_2 } ) - \mu R,} \right\}$$
where 1/ρ = 0·75 yr is the average duration of short-term cross-protection against all serotypes. With the same force of infection and total number infected as before [(1) and (2)].
DECLARATION OF INTEREST
None.











