1. Introduction
Colasante (Reference Colasante2015) communicates an interesting experiment involving a flexible plate that is oscillated along its normal axis by an actuator affixed to its centre. When the plate is brought close to a non-adhesive parallel surface, it becomes subject to an attractive force that allows the exertion of a steady pulling load on the vibrating device, as depicted in figure 1(a). For example, when oscillating near a smooth concrete surface a square aluminium plate (with a thickness of ![]() $1$ mm and a side length of
$1$ mm and a side length of ![]() $61$ cm) at a frequency of
$61$ cm) at a frequency of ![]() $15$ Hz, Colasante (Reference Colasante2023) measures a load capacity of nearly
$15$ Hz, Colasante (Reference Colasante2023) measures a load capacity of nearly ![]() $200$ kgf (kilograms force) with a power consumption of
$200$ kgf (kilograms force) with a power consumption of ![]() ${\approx }200$ W (watts). The device exhibits remarkably low resistance to lateral motion (Colasante Reference Colasante2016), suggesting the presence of a lubricating layer of air that separates the undulating plate from the opposite surface.
${\approx }200$ W (watts). The device exhibits remarkably low resistance to lateral motion (Colasante Reference Colasante2016), suggesting the presence of a lubricating layer of air that separates the undulating plate from the opposite surface.

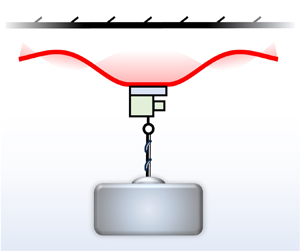
Figure 1. (a) Cartoon and free-body diagram of a load-bearing SFL system enabled by the flexural oscillation of a thin, locally excited disk and (b) a formal schematic of the axisymmetric system geometry used in the problem definition § 2.
In 2021, Weston-Dawkes et al. (Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021) exploited this phenomenon (having arrived at it independently) in the design of a load-carrying robotic device capable of travelling underneath horizontal surfaces and up vertical walls with use of a standard wheel base and a thin, oscillating plastic disk. The device produced an attractive force exceeding ![]() $0.6$ kgf using less than
$0.6$ kgf using less than ![]() $0.3$ W of power (Precision Microdrives 2021), thereby achieving an impressive operating efficiency of over
$0.3$ W of power (Precision Microdrives 2021), thereby achieving an impressive operating efficiency of over ![]() $2$ kgf W
$2$ kgf W![]() $^{-1}$. Subsequently, Jia et al. (Reference Jia, Ramanarayanan, Sánchez and Tolley2023) designed a robot that travelled and rotated controllably beneath a horizontal surface without the use of wheels. Instead, multiple vibration actuators were employed to excite travelling-wave deformations of the plate, the resulting streaming of air within the air layer providing propulsive/rotary shear stresses on the plate (Ramanarayanan & Sánchez Reference Ramanarayanan and Sánchez2023).
$^{-1}$. Subsequently, Jia et al. (Reference Jia, Ramanarayanan, Sánchez and Tolley2023) designed a robot that travelled and rotated controllably beneath a horizontal surface without the use of wheels. Instead, multiple vibration actuators were employed to excite travelling-wave deformations of the plate, the resulting streaming of air within the air layer providing propulsive/rotary shear stresses on the plate (Ramanarayanan & Sánchez Reference Ramanarayanan and Sánchez2023).
The phenomenon described above is commonly referred to as ‘squeeze-film levitation’ (SFL) (Shi et al. Reference Shi, Feng, Hu, Zhu and Cui2019), a method of gaseous lubrication discovered seemingly in the mid 1950s by which the required overpressure inside a wall-bounded gas layer is effectively provided by relative perpendicular oscillation of the walls (Taylor & Saffman Reference Taylor and Saffman1957). In contrast to aerodynamic and aerostatic lubrication, which directly provide quasi-steady overpressures due to relative translational motion of non-parallel walls or external pumping of air, respectively, the oscillating pressure inside a squeeze film exhibits a cycle-averaged value that differs from the ambient value due to the nonlinear effects of gaseous compressibility and convective fluid acceleration (Melikhov et al. Reference Melikhov, Chivilikhin, Amosov and Jeanson2016; Ramanarayanan, Coenen & Sánchez Reference Ramanarayanan, Coenen and Sánchez2022). The resulting pressure difference across the oscillating plate generates a time-averaged normal force that provides a steady load-bearing capacity.
Typical SFL systems involve highly stiff oscillators that are driven by bulky piezoelectric transducers at ultrasonic frequencies, and produce large repulsive forces that render them suitable for conventional bearing lubrication. For example, Zhao (Reference Zhao2010) measured a steady repulsive force of ![]() ${\approx }11.7$ kgf, with an operating efficiency of
${\approx }11.7$ kgf, with an operating efficiency of ![]() ${\approx }0.24\ {\rm kgf}\ {\rm W}^{-1}$, by oscillating a cylindrical oscillator of diameter
${\approx }0.24\ {\rm kgf}\ {\rm W}^{-1}$, by oscillating a cylindrical oscillator of diameter ![]() $5$ cm at a frequency of
$5$ cm at a frequency of ![]() $20\ 000$ Hz. Prior to the experiments by Colasante (Reference Colasante2015), attractive forces had been found to occur only under a limited range of operating conditions – relatively low frequencies or oscillators with small surface area, the corresponding load capacities being thousands of times weaker. For example, a maximal attractive force of just
$20\ 000$ Hz. Prior to the experiments by Colasante (Reference Colasante2015), attractive forces had been found to occur only under a limited range of operating conditions – relatively low frequencies or oscillators with small surface area, the corresponding load capacities being thousands of times weaker. For example, a maximal attractive force of just ![]() ${\approx }0.5$ gf (grams-force) was measured by Sadayuki (Reference Sadayuki2002) using a cylindrical oscillator of diameter
${\approx }0.5$ gf (grams-force) was measured by Sadayuki (Reference Sadayuki2002) using a cylindrical oscillator of diameter ![]() $7$ cm and frequency
$7$ cm and frequency ![]() $200$ Hz. Correspondingly, throughout history, levitation and transportation/rotation systems enabled by repulsive forces have garnered considerable theoretical attention (Zhao Reference Zhao2010; Feng, Liu & Cheng Reference Feng, Liu and Cheng2015; Chen et al. Reference Chen, Gao, Pan and Guo2016; Davis, Gabai & Bucher Reference Davis, Gabai and Bucher2018; Guo & Gao Reference Guo and Gao2018; Shi et al. Reference Shi, Feng, Hu, Zhu and Cui2019), while fewer studies have addressed the emergence of the much weaker attractive forces (Yoshimoto, Shou & Somaya Reference Yoshimoto, Shou and Somaya2013; Andrade et al. Reference Andrade, Ramos, Adamowski and Marzo2020; Ramanarayanan et al. Reference Ramanarayanan, Coenen and Sánchez2022).
$200$ Hz. Correspondingly, throughout history, levitation and transportation/rotation systems enabled by repulsive forces have garnered considerable theoretical attention (Zhao Reference Zhao2010; Feng, Liu & Cheng Reference Feng, Liu and Cheng2015; Chen et al. Reference Chen, Gao, Pan and Guo2016; Davis, Gabai & Bucher Reference Davis, Gabai and Bucher2018; Guo & Gao Reference Guo and Gao2018; Shi et al. Reference Shi, Feng, Hu, Zhu and Cui2019), while fewer studies have addressed the emergence of the much weaker attractive forces (Yoshimoto, Shou & Somaya Reference Yoshimoto, Shou and Somaya2013; Andrade et al. Reference Andrade, Ramos, Adamowski and Marzo2020; Ramanarayanan et al. Reference Ramanarayanan, Coenen and Sánchez2022).
A recent theoretical study (Ramanarayanan & Sánchez Reference Ramanarayanan and Sánchez2022) posited that the impressive magnification of attractive load capacity and energy efficiency observed in the recent experiments by Colasante (Reference Colasante2015) and Weston-Dawkes et al. (Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021), which may conceivably expand the range of practical applications of SFL, can be attributed to the pronounced dynamic bending experienced by the highly flexible oscillators utilized. Through a rigorous analysis of the fluid-flow dynamics in the air layer and its immediate periphery, the authors proved that the attractive force provided by resonant flexural oscillation of a thin circular plate may be thousands of times greater than that provided by rigid-body oscillation under otherwise identical conditions – specifically, the same central displacement amplitude. However, the theoretical predictions of Ramanarayanan & Sánchez (Reference Ramanarayanan and Sánchez2022) and the detailed experimental measurements provided by Weston-Dawkes et al. (Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021) exhibit fundamental disagreements regarding crucial aspects of the underlying physics. For instance, while the experimental data show a gradual rise of the force to a maximal value as the cycle-averaged separation distance between the centre of the oscillating plate and the opposite wall is increased to a value of ![]() ${\approx }1$–
${\approx }1$–![]() $3$ mm, as exemplified in figure 2(a), the theory predicts a rapid growth of comparable magnitude as the distance is increased to values of order
$3$ mm, as exemplified in figure 2(a), the theory predicts a rapid growth of comparable magnitude as the distance is increased to values of order ![]() $50\ \mathrm {\mu }$m. Furthermore, measurements show that the time-averaged gauge pressure in the air layer features a localized region of negative values at its centre, as exemplified in figure 2(b), while the theoretically predicted distribution varies gradually and always features a positive central value.
$50\ \mathrm {\mu }$m. Furthermore, measurements show that the time-averaged gauge pressure in the air layer features a localized region of negative values at its centre, as exemplified in figure 2(b), while the theoretically predicted distribution varies gradually and always features a positive central value.

Figure 2. Approximate reproduction of selected experimental measurements by Weston-Dawkes et al. (Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021): (a) variation of the applied pulling load with the mean central separation distance and (b) time-averaged radial distribution of the gauge pressure in the air layer ![]() $\langle p \rangle (r) - p_a$ (blue) along with the accompanying time-averaged deformation of the oscillating disk in relation to its mean central position
$\langle p \rangle (r) - p_a$ (blue) along with the accompanying time-averaged deformation of the oscillating disk in relation to its mean central position ![]() $\langle w \rangle$(r) (red) (see figure 1 for notation).
$\langle w \rangle$(r) (red) (see figure 1 for notation).
We argue in this paper that these fundamental differences may be attributed to the presence of two-way-coupled fluid–structure interactions in practical systems, whereby the dynamics of the flexible oscillator is affected non-negligibly by the overpressure generated in the air layer due to its motion. The effects of two-way coupling are demonstrably negligible in the case of the highly stiff oscillators used in earlier studies to generate repulsive forces (Li, Liu & Ding Reference Li, Liu and Ding2014). They are, however, palpable in the experiments of Weston-Dawkes et al. (Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021), as evidenced by the observed cycle-averaged deformation of the thin plastic oscillator, exemplified in figure 2(b), which correlates closely with the associated distribution of the time-averaged overpressure pictured in the same panel. Fluid–structure coupling has been explored before in repulsive SFL configurations where a rigid body is levitated above an oscillating plate/piston. The influence of film pressure on the Newtonian dynamics of the levitated body has been studied in the case of rigid oscillators (Brunetière, Blouin & Kastane Reference Brunetière, Blouin and Kastane2018) and those undergoing prescribed standing-wave deformations (Ilssar, Bucher & Flashner Reference Ilssar, Bucher and Flashner2017). Ilssar & Bucher (Reference Ilssar and Bucher2017) additionally explored effects of coupling on the displacement amplitude of a rigid oscillator. Zhang, Xu & Jiang (Reference Zhang, Xu and Jiang2004) and Pandey & Pratap (Reference Pandey and Pratap2007) elucidated the damping effect of viscous flow in the air layer on the resonant dynamic bending of a compliant plate. To the best of our knowledge, a theoretical investigation is yet to be conducted into the effects of two-way coupling on the time-averaged repulsive/attractive load capacity of an SFL system equipped with a flexible oscillator, that being the objective of the present study.
We formulate below in § 2 a reduced mathematical description of the compressible gas flow in a squeeze-film system driven by the flexural oscillation of a compliant plate, by application of the nonlinear theory of elastohydrodynamic lubrication (Sim & Kim Reference Sim and Kim2008; Greenwood Reference Greenwood2020; Wu et al. Reference Wu, Yang, Xu and Wu2020; Poulain et al. Reference Poulain, Carlson, Mandre and Mahadevan2022; Rallabandi Reference Rallabandi2024). The equations governing the fluid–structure dynamics are coupled with a statement of Newton's second law involving the sinusoidal excitation force exerted by the vibration actuator, and the resulting system of equations is solved approximately under the asymptotic limit of small oscillations. The leading-order analysis, presented in § 3, leads to an explicit expression relating the known forcing amplitude of excitation and the consequent displacement amplitude of material points on the oscillating plate. The nonlinear problem that emerges at the following asymptotic order is solved in § 4 to provide a concise analytical expression for the operating efficiency of a flexural SFL system: the ratio of the generated time-averaged force to the supplied excitation amplitude. Simplified forms of these expressions are derived in § 5 to describe centrally forced systems, as a singular limiting case of the general problem. Results of the asymptotic theory are verified in § 6 by comparison with finite-difference computations, and shown in §§ 6 and 7 to provide improved agreement with salient aspects of recently obtained experimental data. Finally, recommendations are provided in § 8 for further theoretical research that may inspire and inform future innovations that exploit this emerging technology.
2. Problem definition
2.1. Modelling approach
Represented in figures 1(a) and 1(b) are simplified schematics of the mechanical configuration involved in recent experiments where strong attractive forces were generated with an SFL system (Colasante Reference Colasante2016; Weston-Dawkes et al. Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021; Omodia, Das & Mahadevan Reference Omodia, Das and Mahadevan2022). A flexible disk of radius ![]() $a$ and uniform thickness
$a$ and uniform thickness ![]() $t_d$ is located near a parallel wall. Glued coaxially to the opposite surface of the disk is a rigid, circular cylinder of radius
$t_d$ is located near a parallel wall. Glued coaxially to the opposite surface of the disk is a rigid, circular cylinder of radius ![]() $r_c < a$, to which a vibration actuator is affixed. The actuator exerts on the cylinder an oscillatory axial force that varies sinusoidally in time with frequency
$r_c < a$, to which a vibration actuator is affixed. The actuator exerts on the cylinder an oscillatory axial force that varies sinusoidally in time with frequency ![]() $\omega /(2{\rm \pi} )$ (where
$\omega /(2{\rm \pi} )$ (where ![]() $\omega$ denotes the associated angular frequency), causing the disk to undergo dynamic bending. The nonlinear dynamics of the oscillatory airflow excited in the air layer separating the disk and the wall (Ramanarayanan et al. Reference Ramanarayanan, Coenen and Sánchez2022), the ‘squeeze film’, gives rise to a cycle-averaged pressure field in the film that provides a steady force attracting the disk toward the wall. This attractive force is able to support an applied pulling load of magnitude
$\omega$ denotes the associated angular frequency), causing the disk to undergo dynamic bending. The nonlinear dynamics of the oscillatory airflow excited in the air layer separating the disk and the wall (Ramanarayanan et al. Reference Ramanarayanan, Coenen and Sánchez2022), the ‘squeeze film’, gives rise to a cycle-averaged pressure field in the film that provides a steady force attracting the disk toward the wall. This attractive force is able to support an applied pulling load of magnitude ![]() ${\mathcal {F}}_\ell$, steadied at the point of application by a vibration damper.
${\mathcal {F}}_\ell$, steadied at the point of application by a vibration damper.
Application of Newton's second law for the rigid central assembly on which the load is exerted and the central portion of the disk to which it is affixed (see the inset in figure 1(a) for clarification) provides
where ![]() $t$ and
$t$ and ![]() $r$ denote, respectively, the time and the radial distance from the axis of symmetry,
$r$ denote, respectively, the time and the radial distance from the axis of symmetry, ![]() ${\mathcal {F}}_m$ denotes the amplitude of the sinusoidal excitation force,
${\mathcal {F}}_m$ denotes the amplitude of the sinusoidal excitation force, ![]() $p(r,t)-p_a$ denotes the distributed gauge pressure acting on the disk surface (with
$p(r,t)-p_a$ denotes the distributed gauge pressure acting on the disk surface (with ![]() $p_a$ denoting the ambient pressure),
$p_a$ denoting the ambient pressure), ![]() $\mathcal {V}_c$ represents the axial structural stress resultant within the disk at the critical radius
$\mathcal {V}_c$ represents the axial structural stress resultant within the disk at the critical radius ![]() $r_c$,
$r_c$, ![]() $m_c$ quantifies the collective mass of the cylinder and other structures involved in the transfer of the vibrational force to the disk,
$m_c$ quantifies the collective mass of the cylinder and other structures involved in the transfer of the vibrational force to the disk, ![]() $\rho _d$ denotes the uniform density of the disk and
$\rho _d$ denotes the uniform density of the disk and ![]() $h_c(t)$ represents the time-varying distance between the wall and the central portion of the disk. The phase shift
$h_c(t)$ represents the time-varying distance between the wall and the central portion of the disk. The phase shift ![]() $\phi$ included in the argument of the excitation force is introduced to facilitate the analysis, and will be discussed later. In writing (2.1), the gravitational acceleration is assumed to be negligibly small in comparison with that induced by the high-frequency excitation, and the weight of the central assembly is assumed to be small relative to the steady pulling load, both assumptions being consistent with the operating conditions used by Weston-Dawkes et al. (Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021).
$\phi$ included in the argument of the excitation force is introduced to facilitate the analysis, and will be discussed later. In writing (2.1), the gravitational acceleration is assumed to be negligibly small in comparison with that induced by the high-frequency excitation, and the weight of the central assembly is assumed to be small relative to the steady pulling load, both assumptions being consistent with the operating conditions used by Weston-Dawkes et al. (Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021).
Experimental data suggest that the central separation distance ![]() $h_c$ fluctuates periodically about a constant mean value
$h_c$ fluctuates periodically about a constant mean value ![]() $h_o$ if the imposed load
$h_o$ if the imposed load ![]() ${\mathcal {F}}_\ell$ is steady. The mean distance
${\mathcal {F}}_\ell$ is steady. The mean distance ![]() $h_o$ grows as the load is quasi-statically increased, until a critical value is reached beyond which the attractive force becomes insufficient and the disk detaches abruptly from the wall, as depicted in figure 2(a) (Weston-Dawkes et al. Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021). It is of great interest to devise a solution of (2.1) that allows prediction of the ‘load capacity’ of an SFL system, the maximal pulling force
$h_o$ grows as the load is quasi-statically increased, until a critical value is reached beyond which the attractive force becomes insufficient and the disk detaches abruptly from the wall, as depicted in figure 2(a) (Weston-Dawkes et al. Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021). It is of great interest to devise a solution of (2.1) that allows prediction of the ‘load capacity’ of an SFL system, the maximal pulling force ![]() $max[{\mathcal {F}}_\ell (h_o)]$ that can be supported without failure. In practical systems, known quantities are typically limited to the structural properties of the disk, the thermodynamic properties of the operating fluid and the amplitude
$max[{\mathcal {F}}_\ell (h_o)]$ that can be supported without failure. In practical systems, known quantities are typically limited to the structural properties of the disk, the thermodynamic properties of the operating fluid and the amplitude ![]() ${\mathcal {F}}_m$ and frequency of the excitation force (Burroughs Reference Burroughs2021). Solution thus requires determining simultaneously the oscillating position
${\mathcal {F}}_m$ and frequency of the excitation force (Burroughs Reference Burroughs2021). Solution thus requires determining simultaneously the oscillating position ![]() $h_c(t)$ of the central assembly and the reactive aerodynamic and structural forces affecting its motion. The nonlinear fluid–structure dynamics involved complicates the solution, in that the periodic cylinder motion may exhibit multiple harmonics in addition to the excitation frequency
$h_c(t)$ of the central assembly and the reactive aerodynamic and structural forces affecting its motion. The nonlinear fluid–structure dynamics involved complicates the solution, in that the periodic cylinder motion may exhibit multiple harmonics in addition to the excitation frequency ![]() $\omega$.
$\omega$.
As shown in the following derivation, the problem simplifies in the case of small axial displacements of the disk relative to the mean separation distance ![]() $h_o$, allowing approximate solution of (2.1) with use of classical perturbation methods. Under the limit of small relative amplitudes, the cylinder may be assumed in the first approximation to oscillate sinusoidally along its axis with a given amplitude
$h_o$, allowing approximate solution of (2.1) with use of classical perturbation methods. Under the limit of small relative amplitudes, the cylinder may be assumed in the first approximation to oscillate sinusoidally along its axis with a given amplitude ![]() $b \ll h_o$ – as indicated in figure 1(b) – and an angular frequency equal to that of the excitation force, so that
$b \ll h_o$ – as indicated in figure 1(b) – and an angular frequency equal to that of the excitation force, so that
Secondary frequencies arising from weak nonlinear dynamics will enter as asymptotic corrections to ![]() $h_c/h_o$ of order
$h_c/h_o$ of order ![]() $(b/h_o)^2 \ll 1$ and smaller, to be discussed later. As indicated in (2.1), the cylinder displacement (2.2) is expected to exhibit a phase lag
$(b/h_o)^2 \ll 1$ and smaller, to be discussed later. As indicated in (2.1), the cylinder displacement (2.2) is expected to exhibit a phase lag ![]() $\phi$ with respect to the excitation force, which is affected non-negligibly by the dissipative effects of viscous stresses in the squeeze film and material friction within the disk (Bettini Reference Bettini2016). In general, the evolving width
$\phi$ with respect to the excitation force, which is affected non-negligibly by the dissipative effects of viscous stresses in the squeeze film and material friction within the disk (Bettini Reference Bettini2016). In general, the evolving width ![]() $h(r,t)$ of the film may be expressed with use of the function
$h(r,t)$ of the film may be expressed with use of the function
which denotes the position of the disk surface bounding the air film. Since the central portion of the disk is glued to the cylinder, it follows from (2.2) that, in the first approximation,
In pursuit of determining simultaneously the central oscillation amplitude ![]() $b$ and the reactive forces modulating its value, we introduce below a reduced theoretical description of the relevant fluid–structure dynamics, which couples the Reynolds equation governing the variation of air pressure
$b$ and the reactive forces modulating its value, we introduce below a reduced theoretical description of the relevant fluid–structure dynamics, which couples the Reynolds equation governing the variation of air pressure ![]() $p$ in the squeeze film with the Kirchhoff–Love equation governing the dynamic displacement
$p$ in the squeeze film with the Kirchhoff–Love equation governing the dynamic displacement ![]() $w$ of the flexible annular portion of the disk
$w$ of the flexible annular portion of the disk ![]() $r_c \le r \le a$. We show that, when
$r_c \le r \le a$. We show that, when ![]() $b/h_o \ll 1$, the coupled equations can be solved with use of (2.4) as the driving kinematic boundary condition to provide analytical expressions for the reactive forces in terms of
$b/h_o \ll 1$, the coupled equations can be solved with use of (2.4) as the driving kinematic boundary condition to provide analytical expressions for the reactive forces in terms of ![]() $b$. Substituting these expressions in (2.1) allows straightforward computation of the value of
$b$. Substituting these expressions in (2.1) allows straightforward computation of the value of ![]() $b$ with relative errors of order
$b$ with relative errors of order ![]() $b/h_o \ll 1$. Solving the nonlinear system of equations that emerges at the following order in the asymptotic description for
$b/h_o \ll 1$. Solving the nonlinear system of equations that emerges at the following order in the asymptotic description for ![]() $b/h_o \ll 1$ allows analytical determination of the levitation force
$b/h_o \ll 1$ allows analytical determination of the levitation force ![]() ${\mathcal {F}}_\ell$ with the same level of accuracy.
${\mathcal {F}}_\ell$ with the same level of accuracy.
The asymptotic formulation will be shown below to provide promising agreement with experimental measurements of the pull-off curve ![]() ${\mathcal {F}}_\ell (h_o)$, the time-averaged overpressure in the squeeze film
${\mathcal {F}}_\ell (h_o)$, the time-averaged overpressure in the squeeze film ![]() $\langle p \rangle (r) - p_a$ and the accompanying steady deformation of the disk
$\langle p \rangle (r) - p_a$ and the accompanying steady deformation of the disk ![]() $\langle w \rangle (r)$ (see figures 1(b) and 2 for clarification). Here, the angled brackets are used to denote the cycle-averaging operator
$\langle w \rangle (r)$ (see figures 1(b) and 2 for clarification). Here, the angled brackets are used to denote the cycle-averaging operator
2.2. Description of the squeeze-film gas dynamics
In modelling the gas flow, it will be assumed that the squeeze film is slender, i.e. ![]() $h_o \ll \lambda$, with the characteristic flexural wavelength
$h_o \ll \lambda$, with the characteristic flexural wavelength ![]() $\lambda$ of the disk being comparable to its radius
$\lambda$ of the disk being comparable to its radius ![]() $a$. Additionally, the viscous time scale
$a$. Additionally, the viscous time scale ![]() $h_o^2/(\mu _a/\rho _a)$, where
$h_o^2/(\mu _a/\rho _a)$, where ![]() $\mu _a$ and
$\mu _a$ and ![]() $\rho _a$ denote respectively the ambient dynamic viscosity and density of the gas, is taken to be much smaller than the oscillation period
$\rho _a$ denote respectively the ambient dynamic viscosity and density of the gas, is taken to be much smaller than the oscillation period ![]() $2{\rm \pi} /\omega$, so that the momentum balance is dominated by viscous forces and the energy balance by transverse heat conduction (since the Prandtl number of air is of order unity (Rohsenow, Hartnett & Cho Reference Rohsenow, Hartnett and Cho1998, p. 2.4)). In this approximation, the gas temperature across the film equals that of the solid boundaries, which is assumed here to equal the ambient gas temperature. In the associated limit of isothermal lubrication theory, the gas flow is determined, with relative errors of order
$2{\rm \pi} /\omega$, so that the momentum balance is dominated by viscous forces and the energy balance by transverse heat conduction (since the Prandtl number of air is of order unity (Rohsenow, Hartnett & Cho Reference Rohsenow, Hartnett and Cho1998, p. 2.4)). In this approximation, the gas temperature across the film equals that of the solid boundaries, which is assumed here to equal the ambient gas temperature. In the associated limit of isothermal lubrication theory, the gas flow is determined, with relative errors of order ![]() $(h_o/a)^2 \!\ll\! 1$ and
$(h_o/a)^2 \!\ll\! 1$ and ![]() $h_o^2\omega /(\mu _a/\rho _a) \!\ll\! 1$, by the familiar equations (Langlois Reference Langlois1962; Ramanarayanan et al. Reference Ramanarayanan, Coenen and Sánchez2022)
$h_o^2\omega /(\mu _a/\rho _a) \!\ll\! 1$, by the familiar equations (Langlois Reference Langlois1962; Ramanarayanan et al. Reference Ramanarayanan, Coenen and Sánchez2022)
where ![]() $y$ is the normal distance to the wall,
$y$ is the normal distance to the wall, ![]() $u$ and
$u$ and ![]() $v$ denote respectively the radial and axial components of the flow velocity and
$v$ denote respectively the radial and axial components of the flow velocity and ![]() $\rho$ and
$\rho$ and ![]() $p$ denote respectively the variable gas density and pressure, the subscript ‘
$p$ denote respectively the variable gas density and pressure, the subscript ‘![]() $a$’ denoting ambient values found in the unperturbed surroundings.
$a$’ denoting ambient values found in the unperturbed surroundings.
The flow velocity in the film must satisfy the no-slip condition ![]() $u=0$ on both bounding surfaces
$u=0$ on both bounding surfaces ![]() $y=0$ and
$y=0$ and ![]() $y=h$ as well as the corresponding no-penetration conditions given by
$y=h$ as well as the corresponding no-penetration conditions given by ![]() $v=0$ at
$v=0$ at ![]() $y=0$ and
$y=0$ and ![]() $v=\partial w/\partial t$ at
$v=\partial w/\partial t$ at ![]() $y=h$. Note that the condition
$y=h$. Note that the condition ![]() $u(y=h)=0$ ignores negligibly small radial displacements of material points on the disk, of the order of
$u(y=h)=0$ ignores negligibly small radial displacements of material points on the disk, of the order of ![]() $(b/h_o)^2(h_o/a)^2a \ll a$. The associated gas pressure must satisfy the conditions of regularity at the central axis of the film and relaxation at its edge
$(b/h_o)^2(h_o/a)^2a \ll a$. The associated gas pressure must satisfy the conditions of regularity at the central axis of the film and relaxation at its edge
respectively, the latter of which neglects variations of pressure existing beyond the edge, which are negligibly small in the lubrication limit, as explained in Appendix A.
The problem defined above affords straightforward reduction to the single equation
the relevant Reynolds lubrication equation for compressible flow (Harrison Reference Harrison1913; Langlois Reference Langlois1962; Ramanarayanan et al. Reference Ramanarayanan, Coenen and Sánchez2022), which relates the disk deformation ![]() $w(r,t)=h-h_o$ with the coupled film pressure
$w(r,t)=h-h_o$ with the coupled film pressure ![]() $p(r,t)$, the latter independent of
$p(r,t)$, the latter independent of ![]() $y$, as follows from (2.6c). The evolving pressure is to be determined by integration of (2.8) subject to the boundary conditions (2.7). Solution requires knowledge of the disk position
$y$, as follows from (2.6c). The evolving pressure is to be determined by integration of (2.8) subject to the boundary conditions (2.7). Solution requires knowledge of the disk position ![]() $w$, whose value for
$w$, whose value for ![]() $0 \le r \le r_c$ is determined in the first approximation by the presumed cylinder motion, as stated in (2.4), while its unknown value in the annular region
$0 \le r \le r_c$ is determined in the first approximation by the presumed cylinder motion, as stated in (2.4), while its unknown value in the annular region ![]() $r_c < r \le a$ must be obtained from an analysis of the disk structural dynamics, as described below.
$r_c < r \le a$ must be obtained from an analysis of the disk structural dynamics, as described below.
2.3. Description of the disk structural dynamics
In analysing the oscillations of the deformable portion of the disk extending for ![]() $r_c \le r \le a$, it will be assumed that the disk is made of a homogeneous, isotropic material, and that its axial deflections, comparable in magnitude to the central amplitude
$r_c \le r \le a$, it will be assumed that the disk is made of a homogeneous, isotropic material, and that its axial deflections, comparable in magnitude to the central amplitude ![]() $b$, are much smaller than its uniform thickness
$b$, are much smaller than its uniform thickness ![]() $t_d$, which in turn is much smaller than its radius
$t_d$, which in turn is much smaller than its radius ![]() $a$, i.e.
$a$, i.e. ![]() $b \ll t_d \ll a$. The excitation frequency is assumed to be sufficiently low for the characteristic flexural wavelength
$b \ll t_d \ll a$. The excitation frequency is assumed to be sufficiently low for the characteristic flexural wavelength ![]() $\lambda$ of the disk to be comparable to the disk radius
$\lambda$ of the disk to be comparable to the disk radius ![]() $a$, consistent with the slender-flow assumption drawn in § 2.2. Under these conditions the disk can be assumed to undergo pure bending (Timoshenko & Woinowsky-Krieger Reference Timoshenko and Woinowsky-Krieger1959, pp. 47–49), whence its dynamic deformations, influenced non-negligibly by the squeeze-film overpressure
$a$, consistent with the slender-flow assumption drawn in § 2.2. Under these conditions the disk can be assumed to undergo pure bending (Timoshenko & Woinowsky-Krieger Reference Timoshenko and Woinowsky-Krieger1959, pp. 47–49), whence its dynamic deformations, influenced non-negligibly by the squeeze-film overpressure ![]() $p(r,t)-p_a$, can be described with use of the Kirchhoff–Love equation (Kelly Reference Kelly2013; Ducceschi Reference Ducceschi2014)
$p(r,t)-p_a$, can be described with use of the Kirchhoff–Love equation (Kelly Reference Kelly2013; Ducceschi Reference Ducceschi2014)
involving the axisymmetric Laplacian operator ![]() $\bar \nabla ^2 = [\partial ^2/\partial r^2 + (1/r)\partial /\partial r]$ and the flexural rigidity
$\bar \nabla ^2 = [\partial ^2/\partial r^2 + (1/r)\partial /\partial r]$ and the flexural rigidity ![]() $\mathcal {D}$ of the disk, the latter defined in terms of the disk Young's modulus
$\mathcal {D}$ of the disk, the latter defined in terms of the disk Young's modulus ![]() $E_d$, mass density
$E_d$, mass density ![]() $\rho _d$ and Poisson's ratio
$\rho _d$ and Poisson's ratio ![]() $\nu _d$. Correspondingly, the axial stress resultant
$\nu _d$. Correspondingly, the axial stress resultant ![]() $\mathcal {V}_c$ affecting the dynamics of the central assembly (2.1) can be expressed as (Yang Reference Yang2005)
$\mathcal {V}_c$ affecting the dynamics of the central assembly (2.1) can be expressed as (Yang Reference Yang2005)
Note that the displacement of the neutral plane of the disk has been substituted in (2.9a) and (2.10) with that of its film-adjacent surface ![]() $w$ (2.3), introducing negligible relative errors of order
$w$ (2.3), introducing negligible relative errors of order ![]() $(b/h_o)(t_d h_o/a^2) \ll 1$. Also, in-plane stresses induced due to fluid shear acting on this surface (Timoshenko & Woinowsky-Krieger Reference Timoshenko and Woinowsky-Krieger1959, pp. 378–380) are smaller than the expected overpressure by a factor of order
$(b/h_o)(t_d h_o/a^2) \ll 1$. Also, in-plane stresses induced due to fluid shear acting on this surface (Timoshenko & Woinowsky-Krieger Reference Timoshenko and Woinowsky-Krieger1959, pp. 378–380) are smaller than the expected overpressure by a factor of order ![]() $(b/h_o)(h_o/a)^2 \ll 1$ (Watanabe & Hara Reference Watanabe and Hara1997; Tulchinsky & Gat Reference Tulchinsky and Gat2016) and, hence, neglected when writing (2.9a).
$(b/h_o)(h_o/a)^2 \ll 1$ (Watanabe & Hara Reference Watanabe and Hara1997; Tulchinsky & Gat Reference Tulchinsky and Gat2016) and, hence, neglected when writing (2.9a).
Equation (2.9a) must be integrated for ![]() $r_c \le r \le a$ with the four boundary conditions
$r_c \le r \le a$ with the four boundary conditions
 \begin{equation} \begin{cases} w - b
\cos(\omega t)={\dfrac{\partial w}{\partial
r}}=0 & {\rm at}\ r = r_c \\ \left(
{\dfrac{\partial ^2}{\partial r^2}} +
\dfrac{\nu_d}{r}{\dfrac{\partial }{\partial r}}
\right) w = {\dfrac{\partial }{\partial r}} (
\bar{\nabla}^2 w) = 0 & {\rm at}\ r = a \end{cases},
\end{equation}
\begin{equation} \begin{cases} w - b
\cos(\omega t)={\dfrac{\partial w}{\partial
r}}=0 & {\rm at}\ r = r_c \\ \left(
{\dfrac{\partial ^2}{\partial r^2}} +
\dfrac{\nu_d}{r}{\dfrac{\partial }{\partial r}}
\right) w = {\dfrac{\partial }{\partial r}} (
\bar{\nabla}^2 w) = 0 & {\rm at}\ r = a \end{cases},
\end{equation}
which state that the annular portion of the disk is clamped at its inner edge ![]() $r=r_c$, where it follows the driving motion of the cylinder (2.4), and that neither bending moments nor axisymmetric axial stresses are supported at its free outer edge
$r=r_c$, where it follows the driving motion of the cylinder (2.4), and that neither bending moments nor axisymmetric axial stresses are supported at its free outer edge ![]() $r=a$ (see Timoshenko & Woinowsky-Krieger Reference Timoshenko and Woinowsky-Krieger1959, pp. 83–84 and Yang Reference Yang2005, pp. 840–841).
$r=a$ (see Timoshenko & Woinowsky-Krieger Reference Timoshenko and Woinowsky-Krieger1959, pp. 83–84 and Yang Reference Yang2005, pp. 840–841).
2.4. Dimensionless formulation and governing parameters
It is useful to reformulate the fluid–structure problem defined in §§ 2.2 and 2.3 in terms of appropriate dimensionless variables, beginning with the temporal and spatial variables ![]() $\tau =\omega t$ and
$\tau =\omega t$ and ![]() $\xi =r/a$. The disk displacement is scaled with the central amplitude
$\xi =r/a$. The disk displacement is scaled with the central amplitude ![]() $b$ to give
$b$ to give ![]() $W(\xi,\tau )=w/b$. We may then use (2.3) to write
$W(\xi,\tau )=w/b$. We may then use (2.3) to write ![]() $h/h_o=1+\varepsilon W$, where
$h/h_o=1+\varepsilon W$, where
defines the relative central oscillation amplitude. It follows from (2.4) that, in the first approximation, ![]() $W=\cos \tau$ for
$W=\cos \tau$ for ![]() $\xi \le {\xi _c}$, where
$\xi \le {\xi _c}$, where ![]() ${\xi _c} = r_c/a$ defines the dimensionless clamping radius. The characteristic scale of film overpressure, deduced readily from (2.6a,b) (see Appendix A), is used to define the variable
${\xi _c} = r_c/a$ defines the dimensionless clamping radius. The characteristic scale of film overpressure, deduced readily from (2.6a,b) (see Appendix A), is used to define the variable ![]() $P=12 (p-p_a)/(\varepsilon \sigma p_a)$, where
$P=12 (p-p_a)/(\varepsilon \sigma p_a)$, where
the classical dimensionless ‘squeeze number’ (Langlois Reference Langlois1962), quantifies the degree of gaseous compressibility in the film induced by viscous retardation of radial airflow.
The Reynolds lubrication equation (2.8) can now be written in the dimensionless form
while the Kirchhoff–Love equation (2.9a) takes the form
where ![]() $\nabla ^2 = [\partial ^2/\partial \xi ^2 + (1/\xi )\partial /\partial \xi ]$. As seen from (2.15), consideration of the disk dynamics introduces two additional dimensionless parameters defined by
$\nabla ^2 = [\partial ^2/\partial \xi ^2 + (1/\xi )\partial /\partial \xi ]$. As seen from (2.15), consideration of the disk dynamics introduces two additional dimensionless parameters defined by
where ![]() $K$ represents the well-known elastic wavenumber characterizing the bending of an isolated disk, i.e. one for which
$K$ represents the well-known elastic wavenumber characterizing the bending of an isolated disk, i.e. one for which ![]() ${\mathcal {C}}=0$ (Warren Reference Warren1930; Yang Reference Yang2005; Ramanarayanan & Sánchez Reference Ramanarayanan and Sánchez2022). In the proceeding analysis, the ratio of the scale of film overpressure to that of disk inertia,
${\mathcal {C}}=0$ (Warren Reference Warren1930; Yang Reference Yang2005; Ramanarayanan & Sánchez Reference Ramanarayanan and Sánchez2022). In the proceeding analysis, the ratio of the scale of film overpressure to that of disk inertia, ![]() ${\mathcal {C}}^6/K^4$, is found to be an important quantity that characterizes the ‘degree’ of flow–structure coupling. Interestingly, in the extreme case of strong coupling
${\mathcal {C}}^6/K^4$, is found to be an important quantity that characterizes the ‘degree’ of flow–structure coupling. Interestingly, in the extreme case of strong coupling ![]() ${\mathcal {C}}^6/K^4 \gg 1$, the parameter
${\mathcal {C}}^6/K^4 \gg 1$, the parameter ![]() $K$ is found to disappear from the formulation and is replaced by
$K$ is found to disappear from the formulation and is replaced by ![]() ${\mathcal {C}}$ as the relevant flexural wavenumber.
${\mathcal {C}}$ as the relevant flexural wavenumber.
As follows from (2.7), (2.14) must be integrated with the boundary conditions
while, based on (2.11), (2.15) must be integrated with
 \begin{equation} \begin{cases} W - \cos
\tau=\partial{W}/\partial{\xi} = 0 & {\rm at}\ \xi =
{\xi_c} \\ \left( {\dfrac{\partial ^2}{\partial
\xi^2}} + \dfrac{\nu_d}{\xi}{\dfrac{\partial
}{\partial \xi}} \right) W = {\dfrac{\partial
}{\partial \xi}} ( \nabla^2 W ) = 0 & {\rm at}\ \xi = 1
\end{cases}. \end{equation}
\begin{equation} \begin{cases} W - \cos
\tau=\partial{W}/\partial{\xi} = 0 & {\rm at}\ \xi =
{\xi_c} \\ \left( {\dfrac{\partial ^2}{\partial
\xi^2}} + \dfrac{\nu_d}{\xi}{\dfrac{\partial
}{\partial \xi}} \right) W = {\dfrac{\partial
}{\partial \xi}} ( \nabla^2 W ) = 0 & {\rm at}\ \xi = 1
\end{cases}. \end{equation}
The problem defined above is to be addressed below for order-unity values of the distinguished dimensionless parameters ![]() $\sigma$,
$\sigma$, ![]() $K$ and
$K$ and ![]() ${\mathcal {C}}$, in order to develop a unifying theoretical description that reconciles the remarkable recent discoveries with the well-understood physics of conventional SFL systems which, together, span a wide parametric range (see, for example, Salbu Reference Salbu1964; Hatanaka et al. Reference Hatanaka, Yoshikazu, Kentaro, Sadayuki and Yoshiki1999; Sadayuki Reference Sadayuki2002; Zhao Reference Zhao2010; Yoshimoto et al. Reference Yoshimoto, Shou and Somaya2013; Colasante Reference Colasante2015; Weston-Dawkes et al. Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021). Analytical progress will be made using classical asymptotic methods that exploit the limit of small relative amplitudes
${\mathcal {C}}$, in order to develop a unifying theoretical description that reconciles the remarkable recent discoveries with the well-understood physics of conventional SFL systems which, together, span a wide parametric range (see, for example, Salbu Reference Salbu1964; Hatanaka et al. Reference Hatanaka, Yoshikazu, Kentaro, Sadayuki and Yoshiki1999; Sadayuki Reference Sadayuki2002; Zhao Reference Zhao2010; Yoshimoto et al. Reference Yoshimoto, Shou and Somaya2013; Colasante Reference Colasante2015; Weston-Dawkes et al. Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021). Analytical progress will be made using classical asymptotic methods that exploit the limit of small relative amplitudes ![]() $\varepsilon = b/h_o \ll 1$, as similar historical approaches have afforded clear insights regarding the simplified physics of SFL configurations that feature extreme values of
$\varepsilon = b/h_o \ll 1$, as similar historical approaches have afforded clear insights regarding the simplified physics of SFL configurations that feature extreme values of ![]() $\sigma$,
$\sigma$, ![]() $K$ and/or
$K$ and/or ![]() ${\mathcal {C}}$ (Taylor & Saffman Reference Taylor and Saffman1957; Langlois Reference Langlois1962; Ramanarayanan et al. Reference Ramanarayanan, Coenen and Sánchez2022).
${\mathcal {C}}$ (Taylor & Saffman Reference Taylor and Saffman1957; Langlois Reference Langlois1962; Ramanarayanan et al. Reference Ramanarayanan, Coenen and Sánchez2022).
3. Leading-order dynamics for small relative amplitudes
We begin by expressing the dimensionless disk displacement and film overpressure as regular perturbation expansions of the forms ![]() $W = W_0 + \varepsilon W_1 + \cdots$ and
$W = W_0 + \varepsilon W_1 + \cdots$ and ![]() $P = P_0 + \varepsilon P_1 + \cdots$, respectively. Substituting these expansions into the governing equations (2.14) and (2.15) and their boundary conditions (2.17) and (2.18), and collecting terms of order unity gives
$P = P_0 + \varepsilon P_1 + \cdots$, respectively. Substituting these expansions into the governing equations (2.14) and (2.15) and their boundary conditions (2.17) and (2.18), and collecting terms of order unity gives
and
 \begin{align} \nabla^4 W_0 + K^4
{\dfrac{\partial ^2 W_0}{\partial \tau^2}} =
{\mathcal{C}}^6 P_0 \left\{\begin{array}{@{}ll} \xi=\xi_c: &
W_0 - \cos \tau=\partial{W_0}/\partial{\xi} = 0 \\ \xi=1 :
& \left( {\dfrac{\partial ^2}{\partial \xi^2}} +
\dfrac{\nu_d}{\xi}{\dfrac{\partial }{\partial
\xi}} \right) W_0 = {\dfrac{\partial }{\partial
\xi}} ( \nabla^2 W_0 ) = 0 \end{array} \right.
.\end{align}
\begin{align} \nabla^4 W_0 + K^4
{\dfrac{\partial ^2 W_0}{\partial \tau^2}} =
{\mathcal{C}}^6 P_0 \left\{\begin{array}{@{}ll} \xi=\xi_c: &
W_0 - \cos \tau=\partial{W_0}/\partial{\xi} = 0 \\ \xi=1 :
& \left( {\dfrac{\partial ^2}{\partial \xi^2}} +
\dfrac{\nu_d}{\xi}{\dfrac{\partial }{\partial
\xi}} \right) W_0 = {\dfrac{\partial }{\partial
\xi}} ( \nabla^2 W_0 ) = 0 \end{array} \right.
.\end{align}
Since the motion of the central portion of the disk is prescribed at leading order by the uniform sinusoidal function ![]() $W_0 =\cos \tau$, as per (2.4), in seeking time-periodic solutions of this linear problem it is convenient to introduce a piecewise-defined ansatz of the form
$W_0 =\cos \tau$, as per (2.4), in seeking time-periodic solutions of this linear problem it is convenient to introduce a piecewise-defined ansatz of the form
 \begin{equation} \left.\begin{array}{c@{}}
P_0 = \mathrm{Re} \{ \bar{\varPi}(\xi)\,
\mathrm{e}^{\mathrm{i}\tau} \} \ {\rm and}\ W_0 =
\mathrm{Re} \{\mathrm{e}^{\mathrm{i}\tau} \} \quad {\rm
for}\ 0 \le \xi \le {\xi_c} \\ P_0 = \mathrm{Re} \{
\varPi(\xi)\, \mathrm{e}^{\mathrm{i}\tau} \} \ {\rm and}\
W_0 = \mathrm{Re} \{\varOmega(\xi)\,
\mathrm{e}^{\mathrm{i}\tau} \} \quad {\rm for}\ {\xi_c} \le
\xi \le 1
\end{array}\right\},\end{equation}
\begin{equation} \left.\begin{array}{c@{}}
P_0 = \mathrm{Re} \{ \bar{\varPi}(\xi)\,
\mathrm{e}^{\mathrm{i}\tau} \} \ {\rm and}\ W_0 =
\mathrm{Re} \{\mathrm{e}^{\mathrm{i}\tau} \} \quad {\rm
for}\ 0 \le \xi \le {\xi_c} \\ P_0 = \mathrm{Re} \{
\varPi(\xi)\, \mathrm{e}^{\mathrm{i}\tau} \} \ {\rm and}\
W_0 = \mathrm{Re} \{\varOmega(\xi)\,
\mathrm{e}^{\mathrm{i}\tau} \} \quad {\rm for}\ {\xi_c} \le
\xi \le 1
\end{array}\right\},\end{equation}
where the complex spatial functions ![]() $\bar {\varPi }$,
$\bar {\varPi }$, ![]() $\varPi$, and
$\varPi$, and ![]() $\varOmega$ are to be determined below.
$\varOmega$ are to be determined below.
In the central portion of the film ![]() $0 \le \xi \le {\xi _c}$, (3.1) reduces to
$0 \le \xi \le {\xi _c}$, (3.1) reduces to ![]() $\bar {\varPi }'' + \bar {\varPi }'/\xi - \sigma \mathrm {i} \bar {\varPi } = 12\,\mathrm {i}$, where a prime superscript denotes the derivative of a spatial function, i.e.
$\bar {\varPi }'' + \bar {\varPi }'/\xi - \sigma \mathrm {i} \bar {\varPi } = 12\,\mathrm {i}$, where a prime superscript denotes the derivative of a spatial function, i.e. ![]() $f'(\xi )= {\rm d} f/ {\rm d} \xi$. Integration with the regularity condition
$f'(\xi )= {\rm d} f/ {\rm d} \xi$. Integration with the regularity condition ![]() $\bar {\varPi }'(0)=0$ gives the reduced pressure
$\bar {\varPi }'(0)=0$ gives the reduced pressure
where ![]() $J_0$ represents the Bessel function of the first kind of zeroth order, and the coefficient
$J_0$ represents the Bessel function of the first kind of zeroth order, and the coefficient ![]() ${\bar A}$ is to be determined by patching the function
${\bar A}$ is to be determined by patching the function ![]() $\bar {\varPi }$ (Bender & Orszag Reference Bender and Orszag1999, pp. 335–336) with the reduced pressure
$\bar {\varPi }$ (Bender & Orszag Reference Bender and Orszag1999, pp. 335–336) with the reduced pressure ![]() $\varPi$ existing in the surrounding annular region
$\varPi$ existing in the surrounding annular region ![]() ${\xi _c} \le \xi \le 1$.
${\xi _c} \le \xi \le 1$.
In the annular region, we use (3.2) and (3.3) to write ![]() $\varPi = {\mathcal {C}}^{-6} ( \nabla ^4 - K^4 ) \varOmega$, substitution of which in (3.1) yields the relevant ‘thin-film’ equation (Poulain et al. Reference Poulain, Carlson, Mandre and Mahadevan2022)
$\varPi = {\mathcal {C}}^{-6} ( \nabla ^4 - K^4 ) \varOmega$, substitution of which in (3.1) yields the relevant ‘thin-film’ equation (Poulain et al. Reference Poulain, Carlson, Mandre and Mahadevan2022)
The general solution to (3.5) can be written in the form
 \begin{equation} \varOmega = \sum_{n=1}^3 [ A_n J_0(\gamma_n \xi) + B_n Y_0(\gamma_n \xi) ] ,\end{equation}
\begin{equation} \varOmega = \sum_{n=1}^3 [ A_n J_0(\gamma_n \xi) + B_n Y_0(\gamma_n \xi) ] ,\end{equation}
whence the reduced pressure ![]() $\varPi$ assumes the form
$\varPi$ assumes the form
 \begin{equation} \varPi = \frac{1}{{\mathcal{C}}^6} \sum_{n=1}^3 (\gamma_n^4-K^4 ) [ A_n J_0(\gamma_n \xi) + B_n Y_0(\gamma_n \xi) ] ,\end{equation}
\begin{equation} \varPi = \frac{1}{{\mathcal{C}}^6} \sum_{n=1}^3 (\gamma_n^4-K^4 ) [ A_n J_0(\gamma_n \xi) + B_n Y_0(\gamma_n \xi) ] ,\end{equation}
both involving the Bessel function of the second kind of zeroth order ![]() $Y_0$, the unknown coefficients
$Y_0$, the unknown coefficients ![]() $A_n$ and
$A_n$ and ![]() $B_n$ (where
$B_n$ (where ![]() $n=1:3$) and the constants
$n=1:3$) and the constants ![]() $\gamma _1,\gamma _2$ and
$\gamma _1,\gamma _2$ and ![]() $\gamma _3$, defined by
$\gamma _3$, defined by
where
The leading-order solution thus involves seven coefficients, ![]() $\bar A$,
$\bar A$, ![]() $A_1$,
$A_1$, ![]() $A_2$,
$A_2$, ![]() $A_3$,
$A_3$, ![]() $B_1$,
$B_1$, ![]() $B_2$ and
$B_2$ and ![]() $B_3$, to be determined by application of the five reduced boundary conditions
$B_3$, to be determined by application of the five reduced boundary conditions
 \begin{equation} \begin{cases} \varOmega - 1 = \varOmega' = 0 & {\rm at}\ \xi = {\xi_c} \\ \varPi = \varOmega'' + \nu_d\varOmega' = \varOmega''' + \varOmega'' - \varOmega' = 0 & {\rm at}\ \xi = 1 \end{cases}, \end{equation}
\begin{equation} \begin{cases} \varOmega - 1 = \varOmega' = 0 & {\rm at}\ \xi = {\xi_c} \\ \varPi = \varOmega'' + \nu_d\varOmega' = \varOmega''' + \varOmega'' - \varOmega' = 0 & {\rm at}\ \xi = 1 \end{cases}, \end{equation}
deduced from (3.1) and (3.2), and the two additional conditions ![]() $\bar {\varPi } = \varPi$ and
$\bar {\varPi } = \varPi$ and ![]() $\bar {\varPi }' = \varPi '$ at
$\bar {\varPi }' = \varPi '$ at ![]() $\xi = {\xi _c}$, which enforce continuity of the pressure and its gradient, respectively, at the interfacial clamp radius. The last condition guarantees continuity of the radial flow speed
$\xi = {\xi _c}$, which enforce continuity of the pressure and its gradient, respectively, at the interfacial clamp radius. The last condition guarantees continuity of the radial flow speed ![]() $u \propto \partial p/\partial r$, evident from the radial momentum balance (2.6b), and involves the reduced pressure gradients in the central and annular regions
$u \propto \partial p/\partial r$, evident from the radial momentum balance (2.6b), and involves the reduced pressure gradients in the central and annular regions
 \begin{align} \bar{\varPi}' ={-}\frac{12\,\mathrm{i}}{\varsigma} {\bar A} J_1(\varsigma \xi) \quad{\rm and}\quad \varPi' = \frac{1}{{\mathcal{C}}^6} \sum_{n=1}^3 \gamma_n ( K^4 - \gamma_n^4 ) [ A_n J_1(\gamma_n \xi) + B_n Y_1(\gamma_n \xi) ], \end{align}
\begin{align} \bar{\varPi}' ={-}\frac{12\,\mathrm{i}}{\varsigma} {\bar A} J_1(\varsigma \xi) \quad{\rm and}\quad \varPi' = \frac{1}{{\mathcal{C}}^6} \sum_{n=1}^3 \gamma_n ( K^4 - \gamma_n^4 ) [ A_n J_1(\gamma_n \xi) + B_n Y_1(\gamma_n \xi) ], \end{align}respectively. Application of these seven conditions with use of (3.6) and (3.7) provides
where ![]() ${\boldsymbol{\mathsf{M}}}^{-1}$ represents the inverse of the square matrix
${\boldsymbol{\mathsf{M}}}^{-1}$ represents the inverse of the square matrix
 \begin{align} {\boldsymbol{\mathsf{M}}}= \small{\begin{bmatrix} 0 & 0 & \dfrac{12{\mathcal{C}}^6 J_0(\varsigma{\xi_c})}{\mathrm{i}\varsigma^2} & \dfrac{12\,\mathrm{i}{\mathcal{C}}^6 J_1(\varsigma{\xi_c})}{\varsigma} & 0 & 0 & 0\\ J_0(\gamma_1{\xi_c}) & \gamma_1J_1(\gamma_1{\xi_c}) & \varPhi_{J}(\gamma_1,{\xi_c}) & \varPsi_{J}(\gamma_1,{\xi_c}) & \varPhi_{J}(\gamma_1,1) & \varTheta_{J}(\gamma_1,1) & \gamma_1^3 J_1(\gamma_1) \\ Y_0(\gamma_1{\xi_c}) & \gamma_1Y_1(\gamma_1{\xi_c}) & \varPhi_{Y}(\gamma_1,{\xi_c}) & \varPsi_{Y}(\gamma_1,{\xi_c}) & \varPhi_{Y}(\gamma_1,1) & \varTheta_{Y}(\gamma_1,1) & \gamma_1^3 Y_1(\gamma_1) \\ J_0(\gamma_2{\xi_c}) & \gamma_2J_1(\gamma_2{\xi_c}) & \varPhi_{J}(\gamma_2,{\xi_c}) & \varPsi_{J}(\gamma_2,{\xi_c}) & \varPhi_{J}(\gamma_2,1) & \varTheta_{J}(\gamma_2,1) & \gamma_2^3 J_1(\gamma_2) \\ Y_0(\gamma_2{\xi_c}) & \gamma_2Y_1(\gamma_2{\xi_c}) & \varPhi_{Y}(\gamma_2,{\xi_c}) & \varPsi_{Y}(\gamma_2,{\xi_c}) & \varPhi_{Y}(\gamma_2,1) & \varTheta_{Y}(\gamma_2,1) & \gamma_2^3 Y_1(\gamma_2) \\ J_0(\gamma_3{\xi_c}) & \gamma_3J_1(\gamma_3{\xi_c}) & \varPhi_{J}(\gamma_3,{\xi_c}) & \varPsi_{J}(\gamma_3,{\xi_c}) & \varPhi_{J}(\gamma_3,1) & \varTheta_{J}(\gamma_3,1) & \gamma_3^3 J_1(\gamma_3) \\ Y_0(\gamma_3{\xi_c}) & \gamma_3Y_1(\gamma_3{\xi_c}) & \varPhi_{Y}(\gamma_3,{\xi_c}) & \varPsi_{Y}(\gamma_3,{\xi_c}) & \varPhi_{Y}(\gamma_3,1) & \varTheta_{Y}(\gamma_3,1) & \gamma_3^3 Y_1(\gamma_3) \end{bmatrix}} , \end{align}
\begin{align} {\boldsymbol{\mathsf{M}}}= \small{\begin{bmatrix} 0 & 0 & \dfrac{12{\mathcal{C}}^6 J_0(\varsigma{\xi_c})}{\mathrm{i}\varsigma^2} & \dfrac{12\,\mathrm{i}{\mathcal{C}}^6 J_1(\varsigma{\xi_c})}{\varsigma} & 0 & 0 & 0\\ J_0(\gamma_1{\xi_c}) & \gamma_1J_1(\gamma_1{\xi_c}) & \varPhi_{J}(\gamma_1,{\xi_c}) & \varPsi_{J}(\gamma_1,{\xi_c}) & \varPhi_{J}(\gamma_1,1) & \varTheta_{J}(\gamma_1,1) & \gamma_1^3 J_1(\gamma_1) \\ Y_0(\gamma_1{\xi_c}) & \gamma_1Y_1(\gamma_1{\xi_c}) & \varPhi_{Y}(\gamma_1,{\xi_c}) & \varPsi_{Y}(\gamma_1,{\xi_c}) & \varPhi_{Y}(\gamma_1,1) & \varTheta_{Y}(\gamma_1,1) & \gamma_1^3 Y_1(\gamma_1) \\ J_0(\gamma_2{\xi_c}) & \gamma_2J_1(\gamma_2{\xi_c}) & \varPhi_{J}(\gamma_2,{\xi_c}) & \varPsi_{J}(\gamma_2,{\xi_c}) & \varPhi_{J}(\gamma_2,1) & \varTheta_{J}(\gamma_2,1) & \gamma_2^3 J_1(\gamma_2) \\ Y_0(\gamma_2{\xi_c}) & \gamma_2Y_1(\gamma_2{\xi_c}) & \varPhi_{Y}(\gamma_2,{\xi_c}) & \varPsi_{Y}(\gamma_2,{\xi_c}) & \varPhi_{Y}(\gamma_2,1) & \varTheta_{Y}(\gamma_2,1) & \gamma_2^3 Y_1(\gamma_2) \\ J_0(\gamma_3{\xi_c}) & \gamma_3J_1(\gamma_3{\xi_c}) & \varPhi_{J}(\gamma_3,{\xi_c}) & \varPsi_{J}(\gamma_3,{\xi_c}) & \varPhi_{J}(\gamma_3,1) & \varTheta_{J}(\gamma_3,1) & \gamma_3^3 J_1(\gamma_3) \\ Y_0(\gamma_3{\xi_c}) & \gamma_3Y_1(\gamma_3{\xi_c}) & \varPhi_{Y}(\gamma_3,{\xi_c}) & \varPsi_{Y}(\gamma_3,{\xi_c}) & \varPhi_{Y}(\gamma_3,1) & \varTheta_{Y}(\gamma_3,1) & \gamma_3^3 Y_1(\gamma_3) \end{bmatrix}} , \end{align}expressed here in terms of the auxiliary functions
 \begin{equation} \left.\begin{array}{c@{}}
\varPhi_{\mathcal{B}}(\gamma_n,\xi) = ( \gamma_n^4 - K^4 )
\mathcal{B}_0(\gamma_n \xi) \\
\varPsi_{\mathcal{B}}(\gamma_n,\xi) = \gamma_n ( K^4 -
\gamma_n^4 ) \mathcal{B}_1(\gamma_n \xi) \\
\varTheta_{\mathcal{B}}(\gamma_n,\xi) = \gamma_n^2 \left[
\mathcal{B}_0(\gamma_n\xi) - \dfrac{1-\nu_d}{\gamma_n\xi}
\mathcal{B}_1(\gamma_n\xi) \right] \end{array}\right\},
\end{equation}
\begin{equation} \left.\begin{array}{c@{}}
\varPhi_{\mathcal{B}}(\gamma_n,\xi) = ( \gamma_n^4 - K^4 )
\mathcal{B}_0(\gamma_n \xi) \\
\varPsi_{\mathcal{B}}(\gamma_n,\xi) = \gamma_n ( K^4 -
\gamma_n^4 ) \mathcal{B}_1(\gamma_n \xi) \\
\varTheta_{\mathcal{B}}(\gamma_n,\xi) = \gamma_n^2 \left[
\mathcal{B}_0(\gamma_n\xi) - \dfrac{1-\nu_d}{\gamma_n\xi}
\mathcal{B}_1(\gamma_n\xi) \right] \end{array}\right\},
\end{equation}
where ![]() $\mathcal {B}_m$ represents a Bessel function of the first/second kind (
$\mathcal {B}_m$ represents a Bessel function of the first/second kind (![]() $J_m$ or
$J_m$ or ![]() $Y_m$) of
$Y_m$) of ![]() $m$th order.
$m$th order.
3.1. Solving for the presumed displacement amplitude  $b$
$b$
The reactive aerodynamic and structural forces affecting the oscillation of the central assembly can now be expressed, with errors of order ![]() $\varepsilon \ll 1$, in the dimensionless forms
$\varepsilon \ll 1$, in the dimensionless forms
 \begin{equation} \frac{\displaystyle \int_0^{r_c} (p-p_a) r\,{\rm d} r}{\varepsilon p_a a^2} ={-}\mathrm{Re}\{ F_c \,\mathrm{e}^{\mathrm{i}\tau} \} , \quad{\rm where}\ F_c = {\xi_c} \left[ \frac{{\xi_c}}{2} + \frac{\bar A}{\varsigma} J_1(\varsigma{\xi_c}) \right] ,\end{equation}
\begin{equation} \frac{\displaystyle \int_0^{r_c} (p-p_a) r\,{\rm d} r}{\varepsilon p_a a^2} ={-}\mathrm{Re}\{ F_c \,\mathrm{e}^{\mathrm{i}\tau} \} , \quad{\rm where}\ F_c = {\xi_c} \left[ \frac{{\xi_c}}{2} + \frac{\bar A}{\varsigma} J_1(\varsigma{\xi_c}) \right] ,\end{equation}and, based on (2.10),
 \begin{equation} \frac{ r_c \mathcal{V}_c }{ \mathcal{D} b/a^2 } ={-}\mathrm{Re}\{ V_c \,\mathrm{e}^{\mathrm{i}\tau} \} , \quad{\rm where}\ V_c = \xi_c \sum_{n=1}^3 \gamma_n^3 [ A_n J_1(\gamma_n\xi_c) + B_n Y_1(\gamma_n\xi_c) ] ,\end{equation}
\begin{equation} \frac{ r_c \mathcal{V}_c }{ \mathcal{D} b/a^2 } ={-}\mathrm{Re}\{ V_c \,\mathrm{e}^{\mathrm{i}\tau} \} , \quad{\rm where}\ V_c = \xi_c \sum_{n=1}^3 \gamma_n^3 [ A_n J_1(\gamma_n\xi_c) + B_n Y_1(\gamma_n\xi_c) ] ,\end{equation}
respectively. Substituting into the governing equation of motion (2.1) the presumed central displacement (2.4), the central pressure force (3.15) and the structural impedance (3.16) reveals a linear relationship between the unknown displacement amplitude ![]() $b$ and the (generally) known excitation amplitude
$b$ and the (generally) known excitation amplitude ![]() ${\mathcal {F}}_m$, given by
${\mathcal {F}}_m$, given by
and an absolute value denotes the modulus of a complex quantity. The associated phase difference ![]() $\phi$ is given simply by
$\phi$ is given simply by ![]() $\phi = {\rm arg}(\mathcal {X})$. Note that this estimate for the value of
$\phi = {\rm arg}(\mathcal {X})$. Note that this estimate for the value of ![]() $b$, accurate with relative errors of order
$b$, accurate with relative errors of order ![]() $\varepsilon =b/h_o \ll 1$, does not require knowledge of the load
$\varepsilon =b/h_o \ll 1$, does not require knowledge of the load ![]() ${\mathcal {F}}_\ell$ which enters in (2.1) as an asymptotic correction of order
${\mathcal {F}}_\ell$ which enters in (2.1) as an asymptotic correction of order ![]() $\varepsilon$.
$\varepsilon$.
4. Time-averaged behaviour at first order
The disk displacement at leading order, ![]() $W_0$, and the associated film overpressure,
$W_0$, and the associated film overpressure, ![]() $P_0$, both vary sinusoidally with time and thus exhibit a zero time average, i.e.
$P_0$, both vary sinusoidally with time and thus exhibit a zero time average, i.e. ![]() $\langle W_0 \rangle =\langle P_0 \rangle =0$, the angled brackets denoting the cycle-averaging operator (2.5). Determining the steady pressure distribution and the steady disk deformation thus requires solving the problem that emerges at the following asymptotic order. Collecting terms of order
$\langle W_0 \rangle =\langle P_0 \rangle =0$, the angled brackets denoting the cycle-averaging operator (2.5). Determining the steady pressure distribution and the steady disk deformation thus requires solving the problem that emerges at the following asymptotic order. Collecting terms of order ![]() $\varepsilon$ in the expanded forms of (2.14) and (2.15) and their boundary conditions (2.17) and (2.18), and computing the cycle average thereof, provides the system of equations
$\varepsilon$ in the expanded forms of (2.14) and (2.15) and their boundary conditions (2.17) and (2.18), and computing the cycle average thereof, provides the system of equations
 \begin{equation}
{\dfrac{\partial }{\partial \xi}} \left[ \xi
\left( 3 \left\langle W_0{\dfrac{\partial
P_0}{\partial \xi}}\right\rangle +
\frac{\sigma}{24}{\dfrac{\partial \langle P^2_0
\rangle}{\partial \xi}} + {\dfrac{\partial
\langle P_1 \rangle}{\partial \xi}} \right) \right] = 0
\left\{\begin{array}{@{}ll} \xi=0: & {\partial \langle P_1
\rangle}/{\partial \xi}=0 \\ \xi=1: & \langle P_1 \rangle=0
\end{array} \right. \end{equation}
\begin{equation}
{\dfrac{\partial }{\partial \xi}} \left[ \xi
\left( 3 \left\langle W_0{\dfrac{\partial
P_0}{\partial \xi}}\right\rangle +
\frac{\sigma}{24}{\dfrac{\partial \langle P^2_0
\rangle}{\partial \xi}} + {\dfrac{\partial
\langle P_1 \rangle}{\partial \xi}} \right) \right] = 0
\left\{\begin{array}{@{}ll} \xi=0: & {\partial \langle P_1
\rangle}/{\partial \xi}=0 \\ \xi=1: & \langle P_1 \rangle=0
\end{array} \right. \end{equation}
and
 \begin{equation} \nabla^4 \langle W_1
\rangle = {\mathcal{C}}^6 \langle P_1 \rangle
\left\{\begin{array}{@{}ll} \xi=\xi_c: & \langle W_1 \rangle =
{\rm d}{\langle W_1 \rangle}/{\rm d}{\xi} = 0 \\ \xi=1 : &
\left( {\dfrac{{\rm d} ^2}{{\rm d} \xi^2}} +
\dfrac{\nu_d}{\xi}{\dfrac{{\rm d} }{{\rm d}
\xi}} \right) \langle W_1 \rangle = {\dfrac{{\rm
d} }{{\rm d} \xi}} \left( \nabla^2 \langle W_1 \rangle
\right) = 0 \end{array} \right.
,\end{equation}
\begin{equation} \nabla^4 \langle W_1
\rangle = {\mathcal{C}}^6 \langle P_1 \rangle
\left\{\begin{array}{@{}ll} \xi=\xi_c: & \langle W_1 \rangle =
{\rm d}{\langle W_1 \rangle}/{\rm d}{\xi} = 0 \\ \xi=1 : &
\left( {\dfrac{{\rm d} ^2}{{\rm d} \xi^2}} +
\dfrac{\nu_d}{\xi}{\dfrac{{\rm d} }{{\rm d}
\xi}} \right) \langle W_1 \rangle = {\dfrac{{\rm
d} }{{\rm d} \xi}} \left( \nabla^2 \langle W_1 \rangle
\right) = 0 \end{array} \right.
,\end{equation}
where the steady overpressure ![]() $\langle P_1 \rangle$ at the film edge
$\langle P_1 \rangle$ at the film edge ![]() $\xi =1$ is negligibly small in the lubrication limit considered here, as explained in Appendix A, and the value of
$\xi =1$ is negligibly small in the lubrication limit considered here, as explained in Appendix A, and the value of ![]() $\langle W_1 \rangle$ vanishes at the clamp radius
$\langle W_1 \rangle$ vanishes at the clamp radius ![]() $\xi =\xi _c$ since the driving cylinder oscillates about a constant mean position, as described below (2.1). In this connection, note from (4.1) and (4.2) that any secondary frequencies exhibited by
$\xi =\xi _c$ since the driving cylinder oscillates about a constant mean position, as described below (2.1). In this connection, note from (4.1) and (4.2) that any secondary frequencies exhibited by ![]() $W_1(\xi,\tau )$ due to nonlinear first-order interactions are irrelevant when solving for the time-averaged quantities of present interest.
$W_1(\xi,\tau )$ due to nonlinear first-order interactions are irrelevant when solving for the time-averaged quantities of present interest.
4.1. Time-averaged squeeze-film overpressure and disk deformation
The steady pressure distribution ![]() $\langle P_1 \rangle (\xi )$, independent of the steady disk deformation
$\langle P_1 \rangle (\xi )$, independent of the steady disk deformation ![]() $\langle W_1 \rangle (\xi )$ under the present perturbative formulation, can be determined by straightforward integration of (4.1) to give
$\langle W_1 \rangle (\xi )$ under the present perturbative formulation, can be determined by straightforward integration of (4.1) to give
where ![]() $x$ serves as a dummy integration variable. Substitution of the expressions given in (3.3) provides
$x$ serves as a dummy integration variable. Substitution of the expressions given in (3.3) provides
 \begin{align} \langle P_1\rangle =
\begin{cases} \displaystyle \frac{1}{2} \mathrm{Re} \left\{
3\left[ \bar{\varPi}({\xi_c}) - \bar{\varPi}(\xi) +
\int_{\xi_c}^1 \varPi'^*({x}) \varOmega({x}) {\rm d}\kern 0.06em {x}
\right] - \dfrac{\sigma}{24} \bar{\varPi}\bar{\varPi}^*
\right\} & 0 \le \xi \le {\xi_c} \\ \displaystyle
\frac{1}{2} \mathrm{Re} \left\{ 3\int_\xi^1 \varPi'^*({x})
\varOmega({x}) {\rm d}\kern 0.06em {x} - \dfrac{\sigma}{24}
\varPi\varPi^* \right\} & {\xi_c} \le \xi \le 1 \end{cases}
,\end{align}
\begin{align} \langle P_1\rangle =
\begin{cases} \displaystyle \frac{1}{2} \mathrm{Re} \left\{
3\left[ \bar{\varPi}({\xi_c}) - \bar{\varPi}(\xi) +
\int_{\xi_c}^1 \varPi'^*({x}) \varOmega({x}) {\rm d}\kern 0.06em {x}
\right] - \dfrac{\sigma}{24} \bar{\varPi}\bar{\varPi}^*
\right\} & 0 \le \xi \le {\xi_c} \\ \displaystyle
\frac{1}{2} \mathrm{Re} \left\{ 3\int_\xi^1 \varPi'^*({x})
\varOmega({x}) {\rm d}\kern 0.06em {x} - \dfrac{\sigma}{24}
\varPi\varPi^* \right\} & {\xi_c} \le \xi \le 1 \end{cases}
,\end{align}
having made use of the identity ![]() $\langle \mathrm {Re}\{ \mathcal {G} \mathrm {e}^{\mathrm {i}\tau }\} \mathrm {Re}\{ \mathcal {H} \mathrm {e}^{\mathrm {i}\tau }\} \rangle = \mathrm {Re} \{ \mathcal {G}^* \mathcal {H} \} / 2$, where
$\langle \mathrm {Re}\{ \mathcal {G} \mathrm {e}^{\mathrm {i}\tau }\} \mathrm {Re}\{ \mathcal {H} \mathrm {e}^{\mathrm {i}\tau }\} \rangle = \mathrm {Re} \{ \mathcal {G}^* \mathcal {H} \} / 2$, where ![]() $\mathcal {G}$ and
$\mathcal {G}$ and ![]() $\mathcal {H}$ are complex spatial functions and an asterisk denotes a complex conjugate.
$\mathcal {H}$ are complex spatial functions and an asterisk denotes a complex conjugate.
Integration of (4.2) provides the accompanying time-averaged deformation of the disk
 \begin{align} \langle W_1 \rangle &=
{\mathcal{C}}^6 \left( {\mathcal{I}}_1({\xi_c}) \ln\left(
\frac{{\xi_c}}{\xi} \right) + \frac{1}{64} \int_{\xi_c}^\xi
x^4 [ 4\ln(x)-5 ] \langle P_1 \rangle ' (x) \, {\rm
d}\kern0.7pt x \right. \nonumber\\ & \quad -
\left.\frac{\ln(\xi)}{16} \int_{\xi_c}^\xi x^4 \langle P_1
\rangle ' (x) \, {\rm d}\kern0.7pt x \ +\ \right|_{\xi_c}^\xi
{\mathcal{I}}_2(\xi) \nonumber\\ & \quad + \left.\frac{
{\xi_c}^2 [ 1+2\ln(\xi/{\xi_c}) ] - \xi^2 }{ 2[ {\xi_c}^2-1
+ 2/(1-\nu_d) ]}\left[ {\mathcal{I}}_1({\xi_c})+
\frac{1}{16} \int_{\xi_c}^1 x^4 \langle P_1 \rangle ' (x)
\, {\rm d}\kern0.7pt x \right] \right)
\end{align}
\begin{align} \langle W_1 \rangle &=
{\mathcal{C}}^6 \left( {\mathcal{I}}_1({\xi_c}) \ln\left(
\frac{{\xi_c}}{\xi} \right) + \frac{1}{64} \int_{\xi_c}^\xi
x^4 [ 4\ln(x)-5 ] \langle P_1 \rangle ' (x) \, {\rm
d}\kern0.7pt x \right. \nonumber\\ & \quad -
\left.\frac{\ln(\xi)}{16} \int_{\xi_c}^\xi x^4 \langle P_1
\rangle ' (x) \, {\rm d}\kern0.7pt x \ +\ \right|_{\xi_c}^\xi
{\mathcal{I}}_2(\xi) \nonumber\\ & \quad + \left.\frac{
{\xi_c}^2 [ 1+2\ln(\xi/{\xi_c}) ] - \xi^2 }{ 2[ {\xi_c}^2-1
+ 2/(1-\nu_d) ]}\left[ {\mathcal{I}}_1({\xi_c})+
\frac{1}{16} \int_{\xi_c}^1 x^4 \langle P_1 \rangle ' (x)
\, {\rm d}\kern0.7pt x \right] \right)
\end{align}
expressed here in terms of the radial pressure gradient
 \begin{equation} \langle P_1 \rangle ' =
{\dfrac{{\rm d} \langle P_1 \rangle }{{\rm d}
\xi}} = \begin{cases} -\dfrac{1}{2} \mathrm{Re} \left\{
\bar{\varPi}'^* \left( 3 + \dfrac{\sigma}{12}\bar{\varPi}
\right) \right\} & 0 \le \xi \le {\xi_c} \\ -\dfrac{1}{2}
\mathrm{Re} \left\{ \varPi'^* \left( 3\varOmega +
\dfrac{\sigma}{12}\varPi \right) \right\} & {\xi_c} \le \xi
\le 1 \end{cases}, \end{equation}
\begin{equation} \langle P_1 \rangle ' =
{\dfrac{{\rm d} \langle P_1 \rangle }{{\rm d}
\xi}} = \begin{cases} -\dfrac{1}{2} \mathrm{Re} \left\{
\bar{\varPi}'^* \left( 3 + \dfrac{\sigma}{12}\bar{\varPi}
\right) \right\} & 0 \le \xi \le {\xi_c} \\ -\dfrac{1}{2}
\mathrm{Re} \left\{ \varPi'^* \left( 3\varOmega +
\dfrac{\sigma}{12}\varPi \right) \right\} & {\xi_c} \le \xi
\le 1 \end{cases}, \end{equation}
and the auxiliary integral functions
 \begin{equation} \left.\begin{array}{c@{}}
\displaystyle {\mathcal{I}}_1(\xi) = \dfrac{\xi^2}{4}
\left[ \dfrac{\xi^2}{4}\langle P_1 \rangle +
\ln(\xi)\int_\xi^1 x^2 \langle P_1 \rangle ' (x) \, {\rm
d}\kern0.7pt x - \int_\xi^1 x^2 \ln(x) \langle P_1 \rangle
' (x) \, {\rm d}\kern0.7pt x \right]\\ \displaystyle
{\mathcal{I}}_2(\xi) = \dfrac{\xi^2}{16} \left[
\dfrac{\xi^2}{4}\langle P_1 \rangle + [2\ln(\xi) - 1]
\int_\xi^1 x^2 \langle P_1 \rangle ' (x) \, {\rm
d}\kern0.7pt x - 2 \int_\xi^1 x^2 \ln(x) \langle P_1
\rangle ' (x) \, {\rm d}\kern0.7pt x \right]
\end{array}\right\}.\end{equation}
\begin{equation} \left.\begin{array}{c@{}}
\displaystyle {\mathcal{I}}_1(\xi) = \dfrac{\xi^2}{4}
\left[ \dfrac{\xi^2}{4}\langle P_1 \rangle +
\ln(\xi)\int_\xi^1 x^2 \langle P_1 \rangle ' (x) \, {\rm
d}\kern0.7pt x - \int_\xi^1 x^2 \ln(x) \langle P_1 \rangle
' (x) \, {\rm d}\kern0.7pt x \right]\\ \displaystyle
{\mathcal{I}}_2(\xi) = \dfrac{\xi^2}{16} \left[
\dfrac{\xi^2}{4}\langle P_1 \rangle + [2\ln(\xi) - 1]
\int_\xi^1 x^2 \langle P_1 \rangle ' (x) \, {\rm
d}\kern0.7pt x - 2 \int_\xi^1 x^2 \ln(x) \langle P_1
\rangle ' (x) \, {\rm d}\kern0.7pt x \right]
\end{array}\right\}.\end{equation}
4.2. An analytical expression for the levitation force
Consistent with the simplified description of gas dynamics presented in § 2.2, the steady, attractive squeeze-film levitation force can be expressed as ![]() ${\mathcal {F}}_\ell = -2{\rm \pi} \int _0^a \langle p-p_a \rangle \, r {\rm d}r$, which follows from a cycle-averaged statement of Newton's second law for the periodically oscillating system cartooned in figure 1(a), comprising both the central assembly and the annular portion of the disk. (This definition for
${\mathcal {F}}_\ell = -2{\rm \pi} \int _0^a \langle p-p_a \rangle \, r {\rm d}r$, which follows from a cycle-averaged statement of Newton's second law for the periodically oscillating system cartooned in figure 1(a), comprising both the central assembly and the annular portion of the disk. (This definition for ![]() ${\mathcal {F}}_\ell$ may be obtained also by integrating the Kirchhoff–Love equation (2.9a) across the annular portion of the disk
${\mathcal {F}}_\ell$ may be obtained also by integrating the Kirchhoff–Love equation (2.9a) across the annular portion of the disk ![]() $r_c \le r \le a$, substituting the resulting expression for the stress resultant
$r_c \le r \le a$, substituting the resulting expression for the stress resultant ![]() $\mathcal {V}_c$ (2.10) into the equation of motion (2.1) and taking the time average thereof.)
$\mathcal {V}_c$ (2.10) into the equation of motion (2.1) and taking the time average thereof.)
Based on the scalings introduced in § 2.4, the force ![]() ${\mathcal {F}}_\ell$ can be normalized with the supplied excitation amplitude
${\mathcal {F}}_\ell$ can be normalized with the supplied excitation amplitude ![]() ${\mathcal {F}}_m$ and the resulting relative oscillation amplitude
${\mathcal {F}}_m$ and the resulting relative oscillation amplitude ![]() $\varepsilon = b/h_o$ to provide a dimensionless expression for the operating efficiency of the system
$\varepsilon = b/h_o$ to provide a dimensionless expression for the operating efficiency of the system
and the complex constant ![]() $\mathcal {X}$ is defined in (3.17). Integration by parts in (4.8b) yields
$\mathcal {X}$ is defined in (3.17). Integration by parts in (4.8b) yields ![]() $\langle F_L \rangle = \int _0^1 \xi ^2 \langle P_1 \rangle ' \, {\rm d} \xi$, wherein substitution of the steady pressure gradient (4.6) provides
$\langle F_L \rangle = \int _0^1 \xi ^2 \langle P_1 \rangle ' \, {\rm d} \xi$, wherein substitution of the steady pressure gradient (4.6) provides
 \begin{align} \langle F_L \rangle &={-} \frac{1}{2}\mathrm{Re}\left\{ \frac{12}{\sigma} {\bar A}^* \left( \frac{2{\xi_c}}{\varsigma^*} [ 2J_1(\varsigma^*{\xi_c}) - \varsigma^*{\xi_c} J_0(\varsigma^*{\xi_c}) ] - \varsigma^*{\bar A} {\mathcal{I}}_{JJ}({\xi_c} ; \varsigma,\varsigma^*) \right) \right. \nonumber\\ & \quad + \left.\left.\sum_{n=1}^3 \sum_{m=1}^3 \frac{ \gamma_n^* ( K^4 - {\gamma_n^*}^4 )}{{\mathcal{C}}^6} \left[ 3 + \frac{\sigma( \gamma_m^4 - K^4 )}{12{\mathcal{C}}^6} \right] \right|_{\xi_c}^1 \mathcal{I}_L(\xi) \right\} , \end{align}
\begin{align} \langle F_L \rangle &={-} \frac{1}{2}\mathrm{Re}\left\{ \frac{12}{\sigma} {\bar A}^* \left( \frac{2{\xi_c}}{\varsigma^*} [ 2J_1(\varsigma^*{\xi_c}) - \varsigma^*{\xi_c} J_0(\varsigma^*{\xi_c}) ] - \varsigma^*{\bar A} {\mathcal{I}}_{JJ}({\xi_c} ; \varsigma,\varsigma^*) \right) \right. \nonumber\\ & \quad + \left.\left.\sum_{n=1}^3 \sum_{m=1}^3 \frac{ \gamma_n^* ( K^4 - {\gamma_n^*}^4 )}{{\mathcal{C}}^6} \left[ 3 + \frac{\sigma( \gamma_m^4 - K^4 )}{12{\mathcal{C}}^6} \right] \right|_{\xi_c}^1 \mathcal{I}_L(\xi) \right\} , \end{align}involving the auxiliary function
and the four operators ![]() ${\mathcal {I}}_{JJ},{\mathcal {I}}_{JY},{\mathcal {I}}_{YJ}$ and
${\mathcal {I}}_{JJ},{\mathcal {I}}_{JY},{\mathcal {I}}_{YJ}$ and ![]() ${\mathcal {I}}_{YY}$, defined collectively by
${\mathcal {I}}_{YY}$, defined collectively by
 \begin{align} {\mathcal{I}}_{FG}(\xi ; \beta_{F},\beta_{G}) &= 2\beta_{G}\xi [ \beta_{G} F_0(\beta_{F}\xi)G_1(\beta_{G}\xi) - \beta_{F} F_1(\beta_{F}\xi)G_0(\beta_{G}\xi) ] / ( \beta_{F}^2-\beta_{G}^2 )^2 \nonumber\\ &\quad + \xi^2 [ \beta_{G} F_0(\beta_{F}\xi)G_0(\beta_{G}\xi) + \beta_{F} F_1(\beta_{F}\xi)G_1(\beta_{G}\xi) ] / (\beta_{F}^2-\beta_{G}^2 ) , \end{align}
\begin{align} {\mathcal{I}}_{FG}(\xi ; \beta_{F},\beta_{G}) &= 2\beta_{G}\xi [ \beta_{G} F_0(\beta_{F}\xi)G_1(\beta_{G}\xi) - \beta_{F} F_1(\beta_{F}\xi)G_0(\beta_{G}\xi) ] / ( \beta_{F}^2-\beta_{G}^2 )^2 \nonumber\\ &\quad + \xi^2 [ \beta_{G} F_0(\beta_{F}\xi)G_0(\beta_{G}\xi) + \beta_{F} F_1(\beta_{F}\xi)G_1(\beta_{G}\xi) ] / (\beta_{F}^2-\beta_{G}^2 ) , \end{align}
where each ![]() $F_m$ and
$F_m$ and ![]() $G_m$ represents a Bessel function of the first or second kind (
$G_m$ represents a Bessel function of the first or second kind (![]() $J_m$ or
$J_m$ or ![]() $Y_m$) of
$Y_m$) of ![]() $m$th order (Rosenheinrich Reference Rosenheinrich2019, p. 301).
$m$th order (Rosenheinrich Reference Rosenheinrich2019, p. 301).
5. Simplified expressions describing centrally forced systems:  $\xi _c \to 0$
$\xi _c \to 0$
Of particular interest in understanding the flow–structure physics of SFL systems is the problem of a disk that is subject to a concentrated load at its centre, experiencing internal structural stresses that grow unboundedly (![]() $\propto r^{-1}$) near its axis
$\propto r^{-1}$) near its axis ![]() $r=0$. Warren (Reference Warren1930) approached this singular problem by analysing the undamped oscillation of an annular disk and considering the limit of a vanishing inner radius. Following this strategy, the general formulation developed in §§ 2–4 is exploited below to derive simplified expressions, independent of
$r=0$. Warren (Reference Warren1930) approached this singular problem by analysing the undamped oscillation of an annular disk and considering the limit of a vanishing inner radius. Following this strategy, the general formulation developed in §§ 2–4 is exploited below to derive simplified expressions, independent of ![]() ${\xi _c}$, that describe the performance of a centrally forced system.
${\xi _c}$, that describe the performance of a centrally forced system.
In the corresponding limit ![]() $\xi _c \to 0$, the regularity condition
$\xi _c \to 0$, the regularity condition ![]() $\partial P/\partial \xi = 0$ for the pressure in the air layer may be applied directly at the clamp radius
$\partial P/\partial \xi = 0$ for the pressure in the air layer may be applied directly at the clamp radius ![]() $\xi = \xi _c$. The constant coefficients that determine at leading order the annular pressure distribution
$\xi = \xi _c$. The constant coefficients that determine at leading order the annular pressure distribution ![]() $P_0$ (3.7) and disk flexure
$P_0$ (3.7) and disk flexure ![]() $W_0$ (3.6) can be expressed as
$W_0$ (3.6) can be expressed as ![]() $\lim _{\xi _c \to 0} [ A_1 \ B_1 \ A_2 \ B_2 \ A_3 \ B_3 ] = [ 1 \ 0 \ 0 \ 0 \ 0 \ 0 ] {\boldsymbol{\mathsf{M}}}_0^{-1}$, in terms of the reduced matrix
$\lim _{\xi _c \to 0} [ A_1 \ B_1 \ A_2 \ B_2 \ A_3 \ B_3 ] = [ 1 \ 0 \ 0 \ 0 \ 0 \ 0 ] {\boldsymbol{\mathsf{M}}}_0^{-1}$, in terms of the reduced matrix ![]() ${\boldsymbol{\mathsf{M}}}_0 = [ {\boldsymbol{\mathsf{U}}}_1 {\boldsymbol{\mathsf{U}}}_2 \ {\boldsymbol{\mathsf{U}}}_3 ]^{\rm T}$, where
${\boldsymbol{\mathsf{M}}}_0 = [ {\boldsymbol{\mathsf{U}}}_1 {\boldsymbol{\mathsf{U}}}_2 \ {\boldsymbol{\mathsf{U}}}_3 ]^{\rm T}$, where
Assuming a massless central assembly (![]() $m_c=0$), the complex constant
$m_c=0$), the complex constant ![]() $\mathcal {X}$ defined in (3.17) reduces here to
$\mathcal {X}$ defined in (3.17) reduces here to ![]() $\lim _{\xi _c \to 0} \mathcal {X} = -4(\mathcal {D}/a^2) (B_1 \gamma _1^2 + B_2 \gamma _2^2 + B_3 \gamma _3^2)$, whence the amplitude of the reactive forces affecting the central dynamics (2.1) can be expressed as
$\lim _{\xi _c \to 0} \mathcal {X} = -4(\mathcal {D}/a^2) (B_1 \gamma _1^2 + B_2 \gamma _2^2 + B_3 \gamma _3^2)$, whence the amplitude of the reactive forces affecting the central dynamics (2.1) can be expressed as
 \begin{equation} \lim_{\xi_c \to 0} |V_c| = \lim_{\xi_c \to 0} \frac{{\mathcal{F}}_m}{ 2{\rm \pi}\mathcal{D}b/a^2 } = \frac{2}{\rm \pi} \left| \sum_{n=1}^3 B_n\gamma_n^2 \right| .\end{equation}
\begin{equation} \lim_{\xi_c \to 0} |V_c| = \lim_{\xi_c \to 0} \frac{{\mathcal{F}}_m}{ 2{\rm \pi}\mathcal{D}b/a^2 } = \frac{2}{\rm \pi} \left| \sum_{n=1}^3 B_n\gamma_n^2 \right| .\end{equation} The time-averaged overpressure ![]() $\langle P_1 \rangle (\xi )$ that emerges as a first-order correction is described by the second branch of the piecewise-defined equation (4.4), while the general expression (4.5) describing the resulting disk deformation
$\langle P_1 \rangle (\xi )$ that emerges as a first-order correction is described by the second branch of the piecewise-defined equation (4.4), while the general expression (4.5) describing the resulting disk deformation ![]() $\langle W_1 \rangle (\xi )$ simplifies here to give
$\langle W_1 \rangle (\xi )$ simplifies here to give
 \begin{align} \lim_{\xi_c \to 0} \langle W_1 \rangle &= {\mathcal{C}}^6 \left( \frac{1}{64} \int_0^\xi x^4 [ 4\ln(x)-5 ] \langle P_1 \rangle ' (x) \, {\rm d}\kern0.7pt x - \frac{ \ln(\xi) }{16} \int_0^\xi x^4 \langle P_1 \rangle ' (x) \, {\rm d}\kern0.7pt x \right.\nonumber\\ &\quad + \left. {\mathcal{I}}_2 (\xi) - \frac{\xi^2(1-\nu_d)}{32(1+\nu_d)} \int_0^1 x^4 \langle P_1 \rangle ' (x) \, {\rm d}\kern0.7pt x \right) , \end{align}
\begin{align} \lim_{\xi_c \to 0} \langle W_1 \rangle &= {\mathcal{C}}^6 \left( \frac{1}{64} \int_0^\xi x^4 [ 4\ln(x)-5 ] \langle P_1 \rangle ' (x) \, {\rm d}\kern0.7pt x - \frac{ \ln(\xi) }{16} \int_0^\xi x^4 \langle P_1 \rangle ' (x) \, {\rm d}\kern0.7pt x \right.\nonumber\\ &\quad + \left. {\mathcal{I}}_2 (\xi) - \frac{\xi^2(1-\nu_d)}{32(1+\nu_d)} \int_0^1 x^4 \langle P_1 \rangle ' (x) \, {\rm d}\kern0.7pt x \right) , \end{align}
both valid only for ![]() $0 < \xi \le 1$. The levitation force (4.9) correspondingly reduces to
$0 < \xi \le 1$. The levitation force (4.9) correspondingly reduces to
 \begin{equation} \lim_{\xi_c \to 0} \langle F_L \rangle ={-} \frac{1}{2}\mathrm{Re}\left\{ \sum_{n=1}^3 \sum_{m=1}^3 \frac{ \gamma_n^* ( K^4 - {\gamma_n^*}^4 )}{{\mathcal{C}}^6} \left[ 3 + \frac{\sigma( \gamma_m^4 - K^4 )}{12{\mathcal{C}}^6} \right] [ \mathcal{I}_L(1) - \mathcal{I}_c ] \right\} ,\end{equation}
\begin{equation} \lim_{\xi_c \to 0} \langle F_L \rangle ={-} \frac{1}{2}\mathrm{Re}\left\{ \sum_{n=1}^3 \sum_{m=1}^3 \frac{ \gamma_n^* ( K^4 - {\gamma_n^*}^4 )}{{\mathcal{C}}^6} \left[ 3 + \frac{\sigma( \gamma_m^4 - K^4 )}{12{\mathcal{C}}^6} \right] [ \mathcal{I}_L(1) - \mathcal{I}_c ] \right\} ,\end{equation}where
Combining (5.4) with (5.2) yields a reduced expression for the levitation efficiency
6. Effects of two-way coupling on the flow–structure dynamics
The fluid–structure problem addressed above is governed by five principal dimensionless parameters as detailed in § 2.4: the perturbation parameter ![]() $\varepsilon = b/h_o \ll 1$, which compares the oscillation amplitude of the disk centre with its mean separation distance from the wall, the relative clamp radius
$\varepsilon = b/h_o \ll 1$, which compares the oscillation amplitude of the disk centre with its mean separation distance from the wall, the relative clamp radius ![]() ${\xi _c}=r_c/a$ beyond which the disk is allowed to bend (see figure 1b), the squeeze number
${\xi _c}=r_c/a$ beyond which the disk is allowed to bend (see figure 1b), the squeeze number ![]() $\sigma$, which quantifies the strength of viscous forces retarding airflow in the film and giving rise to compressibility, the elastic wavenumber
$\sigma$, which quantifies the strength of viscous forces retarding airflow in the film and giving rise to compressibility, the elastic wavenumber ![]() $K$, which correlates inversely with the flexural wavelength of the disk anticipated based on its structural properties, and a coupling parameter
$K$, which correlates inversely with the flexural wavelength of the disk anticipated based on its structural properties, and a coupling parameter ![]() ${\mathcal {C}}$, which measures the influence of pressure variations in the squeeze film on the disk deformations. Of greatest interest here are the final parameters
${\mathcal {C}}$, which measures the influence of pressure variations in the squeeze film on the disk deformations. Of greatest interest here are the final parameters ![]() $\sigma, K$ and
$\sigma, K$ and ![]() ${\mathcal {C}}$ which govern the fundamental fluid–structure dynamics, to be investigated below by focusing mainly on centrally excited configurations, i.e. those involving infinitesimally small values of
${\mathcal {C}}$ which govern the fundamental fluid–structure dynamics, to be investigated below by focusing mainly on centrally excited configurations, i.e. those involving infinitesimally small values of ![]() ${\xi _c}$ (see § 5). In the dimensionless computations presented below, the Poisson's ratio of the disk
${\xi _c}$ (see § 5). In the dimensionless computations presented below, the Poisson's ratio of the disk ![]() $\nu _d$ is assigned a value of
$\nu _d$ is assigned a value of ![]() $0.3$, characteristic approximately of most plastic and metallic materials of relevance here (The Engineering ToolBox 2008; Sonelastic n.d.).
$0.3$, characteristic approximately of most plastic and metallic materials of relevance here (The Engineering ToolBox 2008; Sonelastic n.d.).
6.1. System dynamics under one-way coupling
The general formulation derived above simplifies in the limit ![]() ${\mathcal {C}} \to 0$ to describe one-way-coupled systems, as detailed in Appendix B. It is worth reviewing here the widely studied behaviour of such systems – those for which the oscillations of the disk are unaffected by the squeeze-film overpressure and, hence, the flow–structure physics is governed purely by the parameters
${\mathcal {C}} \to 0$ to describe one-way-coupled systems, as detailed in Appendix B. It is worth reviewing here the widely studied behaviour of such systems – those for which the oscillations of the disk are unaffected by the squeeze-film overpressure and, hence, the flow–structure physics is governed purely by the parameters ![]() $\sigma$ and
$\sigma$ and ![]() $K$. An increase in
$K$. An increase in ![]() $\sigma \propto \omega a^2/h_o^{2}$, realized commonly by reducing the separation distance
$\sigma \propto \omega a^2/h_o^{2}$, realized commonly by reducing the separation distance ![]() $h_o$, is known to result in a magnification of the typically repulsive squeeze-film force
$h_o$, is known to result in a magnification of the typically repulsive squeeze-film force ![]() ${\mathcal {F}}_\ell < 0$ in a manner proportional to the inverse square of
${\mathcal {F}}_\ell < 0$ in a manner proportional to the inverse square of ![]() $h_o$ (Taylor & Saffman Reference Taylor and Saffman1957; Zhao Reference Zhao2010). This magnification is found to occur regardless of the flexibility of the oscillator (Li et al. Reference Li, Liu and Ding2014), the latter quantified by the elastic wavenumber
$h_o$ (Taylor & Saffman Reference Taylor and Saffman1957; Zhao Reference Zhao2010). This magnification is found to occur regardless of the flexibility of the oscillator (Li et al. Reference Li, Liu and Ding2014), the latter quantified by the elastic wavenumber ![]() $K$. A transition to attractive forces
$K$. A transition to attractive forces ![]() ${\mathcal {F}}_\ell >0$ is found to occur for systems with sufficiently low frequency
${\mathcal {F}}_\ell >0$ is found to occur for systems with sufficiently low frequency ![]() $\omega$ (Sadayuki Reference Sadayuki2002) and/or oscillator size
$\omega$ (Sadayuki Reference Sadayuki2002) and/or oscillator size ![]() $a$ (Yoshimoto et al. Reference Yoshimoto, Shou and Somaya2013; Andrade et al. Reference Andrade, Ramos, Adamowski and Marzo2020). For these systems, attraction emerges only beyond a critical separation distance
$a$ (Yoshimoto et al. Reference Yoshimoto, Shou and Somaya2013; Andrade et al. Reference Andrade, Ramos, Adamowski and Marzo2020). For these systems, attraction emerges only beyond a critical separation distance ![]() $h_o$, i.e. below a critical value of
$h_o$, i.e. below a critical value of ![]() $\sigma$.
$\sigma$.
The range of operating conditions ![]() $\omega$ and
$\omega$ and ![]() $a$ for which attraction can be found, as well as the resulting attractive load capacity, are found to depend strongly on the waveform exhibited by the oscillating disk (Ramanarayanan & Sánchez Reference Ramanarayanan and Sánchez2022). In the case of rigid-body oscillation, i.e.
$a$ for which attraction can be found, as well as the resulting attractive load capacity, are found to depend strongly on the waveform exhibited by the oscillating disk (Ramanarayanan & Sánchez Reference Ramanarayanan and Sánchez2022). In the case of rigid-body oscillation, i.e. ![]() $K=0$, repulsive forces exist for nearly all values of
$K=0$, repulsive forces exist for nearly all values of ![]() $\sigma$ (Zhao Reference Zhao2010). Attractive forces can be produced under a very limited range of operating conditions, characterization of which requires modelling the effects of fluid inertia that are neglected in the lubrication approximation drawn in the present study, but the corresponding load capacities are several thousandfold smaller and, thus, of limited practical utility (Yoshimoto et al. Reference Yoshimoto, Shou and Somaya2013; Andrade et al. Reference Andrade, Ramos, Adamowski and Marzo2020). (Analysis of such conditions requires considering separately the contributions of fluid compressibility and inertia with use of the relevant acoustic wavenumber
$\sigma$ (Zhao Reference Zhao2010). Attractive forces can be produced under a very limited range of operating conditions, characterization of which requires modelling the effects of fluid inertia that are neglected in the lubrication approximation drawn in the present study, but the corresponding load capacities are several thousandfold smaller and, thus, of limited practical utility (Yoshimoto et al. Reference Yoshimoto, Shou and Somaya2013; Andrade et al. Reference Andrade, Ramos, Adamowski and Marzo2020). (Analysis of such conditions requires considering separately the contributions of fluid compressibility and inertia with use of the relevant acoustic wavenumber ![]() $K_a = a \omega / \sqrt {p_a/\rho _a}$ and the Womersley number
$K_a = a \omega / \sqrt {p_a/\rho _a}$ and the Womersley number ![]() $\alpha = [h_o^2\omega /(\mu _a/\rho _a)]^{1/2}$, which compare with the oscillation period the time scales of lateral pressure equilibration and transverse viscous diffusion, respectively. These two parameters enter implicitly in the present lubrication limit
$\alpha = [h_o^2\omega /(\mu _a/\rho _a)]^{1/2}$, which compare with the oscillation period the time scales of lateral pressure equilibration and transverse viscous diffusion, respectively. These two parameters enter implicitly in the present lubrication limit ![]() $\alpha ^2 \ll 1$ through the single squeeze number
$\alpha ^2 \ll 1$ through the single squeeze number ![]() $\sigma =12 K_a^2 /\alpha ^2$ (Melikhov et al. Reference Melikhov, Chivilikhin, Amosov and Jeanson2016; Ramanarayanan et al. Reference Ramanarayanan, Coenen and Sánchez2022).) In contrast, for critical values of
$\sigma =12 K_a^2 /\alpha ^2$ (Melikhov et al. Reference Melikhov, Chivilikhin, Amosov and Jeanson2016; Ramanarayanan et al. Reference Ramanarayanan, Coenen and Sánchez2022).) In contrast, for critical values of ![]() $K$ that correspond to the natural frequencies of the disk (see Appendix B), the disk performs resonant standing-wave oscillations, such as those depicted in figure 3(a), and produces powerful attractive forces for a substantial range of values of
$K$ that correspond to the natural frequencies of the disk (see Appendix B), the disk performs resonant standing-wave oscillations, such as those depicted in figure 3(a), and produces powerful attractive forces for a substantial range of values of ![]() $\sigma$ (Ramanarayanan & Sánchez Reference Ramanarayanan and Sánchez2022). Note that excitation of the disk at a non-natural frequency may result in different flexural waveforms that, instead, only magnify the repulsive squeeze-film force. This is often seen in practical systems where the disk is affixed to a Piezoelectric transducer of much greater mass (Da Silva Reference Da Silva1980; Li et al. Reference Li, Liu and Ding2014), yielding a mechanical assembly whose optimal, resonant frequencies presumably differ substantially from the native resonant frequencies of the disk.
$\sigma$ (Ramanarayanan & Sánchez Reference Ramanarayanan and Sánchez2022). Note that excitation of the disk at a non-natural frequency may result in different flexural waveforms that, instead, only magnify the repulsive squeeze-film force. This is often seen in practical systems where the disk is affixed to a Piezoelectric transducer of much greater mass (Da Silva Reference Da Silva1980; Li et al. Reference Li, Liu and Ding2014), yielding a mechanical assembly whose optimal, resonant frequencies presumably differ substantially from the native resonant frequencies of the disk.

Figure 3. Behaviour of an SFL system operating with an elastic wavenumber of ![]() $K=6.2$ and a squeeze number of
$K=6.2$ and a squeeze number of ![]() $\sigma =20$. The flexural disk oscillations that occur under (a) a state of one-way coupling (
$\sigma =20$. The flexural disk oscillations that occur under (a) a state of one-way coupling (![]() ${\mathcal {C}}=0$) are juxtaposed with those that occur for states of (b) moderate two-way coupling (
${\mathcal {C}}=0$) are juxtaposed with those that occur for states of (b) moderate two-way coupling (![]() ${\mathcal {C}}=3$) and (c) strong two-way coupling (
${\mathcal {C}}=3$) and (c) strong two-way coupling (![]() ${\mathcal {C}}>5$). Shown below in (d–f) are the associated radial distributions of time-averaged pressure and disk displacement. Dots and circles in (d–f) represent numerical solutions computed for
${\mathcal {C}}>5$). Shown below in (d–f) are the associated radial distributions of time-averaged pressure and disk displacement. Dots and circles in (d–f) represent numerical solutions computed for ![]() $\varepsilon =0.1$.
$\varepsilon =0.1$.
Motion of a centrally excited disk at its second resonant mode, i.e. ![]() $K \approx 6.2$, is visualized in figure 3(a) for a value of the squeeze number
$K \approx 6.2$, is visualized in figure 3(a) for a value of the squeeze number ![]() $\sigma =20$ that gives rise to an attractive force. As seen from the blue curve in figure 3(d), the distribution of steady pressure generated along the gas layer features two local minima whose radial locations correspond closely with those of the two nodal circles in the standing flexural wave,
$\sigma =20$ that gives rise to an attractive force. As seen from the blue curve in figure 3(d), the distribution of steady pressure generated along the gas layer features two local minima whose radial locations correspond closely with those of the two nodal circles in the standing flexural wave, ![]() $r/a \approx 0.4$ and
$r/a \approx 0.4$ and ![]() $0.8$. In the absence of aerodynamic forcing, the disk oscillates sinusoidally about an undeformed mean position, as indicated by the red line in figure 3(d). While this one-way-coupled description has been shown (Ramanarayanan & Sánchez Reference Ramanarayanan and Sánchez2022) to successfully reproduce the magnification of attractive load capacity found in flexural SFL systems (Colasante Reference Colasante2015; Weston-Dawkes et al. Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021), the predicted distribution of the causal time-averaged overpressure exhibits glaring disagreement with that measured in experiments, the latter exemplified in figure 2(b). Furthermore, setting
$0.8$. In the absence of aerodynamic forcing, the disk oscillates sinusoidally about an undeformed mean position, as indicated by the red line in figure 3(d). While this one-way-coupled description has been shown (Ramanarayanan & Sánchez Reference Ramanarayanan and Sánchez2022) to successfully reproduce the magnification of attractive load capacity found in flexural SFL systems (Colasante Reference Colasante2015; Weston-Dawkes et al. Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021), the predicted distribution of the causal time-averaged overpressure exhibits glaring disagreement with that measured in experiments, the latter exemplified in figure 2(b). Furthermore, setting ![]() ${\mathcal {C}}=0$ precludes characterization of the accompanying time-averaged deformation of the disk, a sample measurement of which is also reproduced in figure 2(b). Accounting for two-way fluid–structure coupling by considering non-zero values of
${\mathcal {C}}=0$ precludes characterization of the accompanying time-averaged deformation of the disk, a sample measurement of which is also reproduced in figure 2(b). Accounting for two-way fluid–structure coupling by considering non-zero values of ![]() ${\mathcal {C}}$ yields greatly improved agreement with these observations, as described below.
${\mathcal {C}}$ yields greatly improved agreement with these observations, as described below.
6.2. System dynamics under two-way coupling
As seen from figures 3(b) and 3(e), increasing the value of the coupling parameter to ![]() ${\mathcal {C}}=3$ yields but minor deviation from the one-way-coupled dynamics depicted in figures 3(a) and 3(d). The two nodal points are slightly disturbed and give way to localized regions of minimal amplitude, symptomatic of a damped oscillator (Geist & McLaughlin Reference Geist and McLaughlin1994). The corresponding steady pressure distribution
${\mathcal {C}}=3$ yields but minor deviation from the one-way-coupled dynamics depicted in figures 3(a) and 3(d). The two nodal points are slightly disturbed and give way to localized regions of minimal amplitude, symptomatic of a damped oscillator (Geist & McLaughlin Reference Geist and McLaughlin1994). The corresponding steady pressure distribution ![]() $\langle P_1 \rangle (\xi )$ is visibly skewed but maintains a similar fundamental shape, and the disk oscillates about an approximately linearly deformed mean shape
$\langle P_1 \rangle (\xi )$ is visibly skewed but maintains a similar fundamental shape, and the disk oscillates about an approximately linearly deformed mean shape ![]() $\langle W_1 \rangle (\xi )$. Much more pronounced changes are observed when the strength of the aerodynamic forcing is further increased by setting
$\langle W_1 \rangle (\xi )$. Much more pronounced changes are observed when the strength of the aerodynamic forcing is further increased by setting ![]() ${\mathcal {C}}=5.25$, for which value the disk exhibits travelling-wave-type oscillations whose amplitude is suppressed severely beyond
${\mathcal {C}}=5.25$, for which value the disk exhibits travelling-wave-type oscillations whose amplitude is suppressed severely beyond ![]() $r/a \approx 0.3$, as shown in figure 3(c). As seen from figure 3(f), the steady gauge pressure then assumes a negative value at the central axis
$r/a \approx 0.3$, as shown in figure 3(c). As seen from figure 3(f), the steady gauge pressure then assumes a negative value at the central axis ![]() $r=0$ and the steady disk deformation varies non-monotonically with radial distance, both in qualitative congruence with the experimental measurements reproduced in figure 2(b) (Weston-Dawkes et al. Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021). The disappearance of the first nodal region indicates that the collection of sand on the disk at
$r=0$ and the steady disk deformation varies non-monotonically with radial distance, both in qualitative congruence with the experimental measurements reproduced in figure 2(b) (Weston-Dawkes et al. Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021). The disappearance of the first nodal region indicates that the collection of sand on the disk at ![]() $r/a \approx 0.3$ observed by Weston-Dawkes et al. (Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021) may not constitute a Chladni pattern, as the authors suggest, and owes instead to gravity-driven transport toward the valley formed by the mean disk deformation. Interestingly, in the limit of strong coupling
$r/a \approx 0.3$ observed by Weston-Dawkes et al. (Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021) may not constitute a Chladni pattern, as the authors suggest, and owes instead to gravity-driven transport toward the valley formed by the mean disk deformation. Interestingly, in the limit of strong coupling ![]() ${\mathcal {C}} \gg 1$, considered separately in Appendix B, the flexural wavenumber of the disk is found to scale with
${\mathcal {C}} \gg 1$, considered separately in Appendix B, the flexural wavenumber of the disk is found to scale with ![]() ${\mathcal {C}}$, in place of the elastic wavenumber
${\mathcal {C}}$, in place of the elastic wavenumber ![]() $K$ that applies for
$K$ that applies for ![]() ${\mathcal {C}} \sim 1$, and the steady gauge pressure is seen to relax sharply from a negative value at the centre of the film toward zero across a small region
${\mathcal {C}} \sim 1$, and the steady gauge pressure is seen to relax sharply from a negative value at the centre of the film toward zero across a small region ![]() $r/a \lesssim 5/{\mathcal {C}}$. For strongly coupled systems, reducing the degree of coupling
$r/a \lesssim 5/{\mathcal {C}}$. For strongly coupled systems, reducing the degree of coupling ![]() ${\mathcal {C}} \propto 1/\sqrt {h_o}$ thus widens this central region, as observed by Weston-Dawkes et al. (Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021) during the pull-off process.
${\mathcal {C}} \propto 1/\sqrt {h_o}$ thus widens this central region, as observed by Weston-Dawkes et al. (Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021) during the pull-off process.
For each of the operating conditions depicted in figure 3, the analytical predictions of the time-averaged pressure distribution and disk deformation are confirmed with use of a finite-difference solution of the governing equations (2.14) and (2.15), results of which are visualized in the form of dots and circles in figures 3(d–f). As can be seen, for the moderately small relative amplitude ![]() $\varepsilon = 0.1$ used in the integration, the numerical solutions display satisfactory agreement with the asymptotic results. The governing equations were discretized with use of second-order central-space finite-difference approximations and marched in time asynchronously, the Reynolds equation with a forward-Euler scheme and the Kirchhoff–Love equation with use of a second-order central-difference scheme (Michael Reference Michael1963; Moin Reference Moin2010). The system was initialized with ambient pressure throughout the film
$\varepsilon = 0.1$ used in the integration, the numerical solutions display satisfactory agreement with the asymptotic results. The governing equations were discretized with use of second-order central-space finite-difference approximations and marched in time asynchronously, the Reynolds equation with a forward-Euler scheme and the Kirchhoff–Love equation with use of a second-order central-difference scheme (Michael Reference Michael1963; Moin Reference Moin2010). The system was initialized with ambient pressure throughout the film ![]() $p(r)=p_a$, a uniform disk displacement
$p(r)=p_a$, a uniform disk displacement ![]() $w(r)=b$ and zero disk velocity
$w(r)=b$ and zero disk velocity ![]() $\partial w/\partial t = 0$. Accurate characterization of the disk motion for
$\partial w/\partial t = 0$. Accurate characterization of the disk motion for ![]() ${\mathcal {C}} \neq 0$ required a sufficiently fine spatial discretization
${\mathcal {C}} \neq 0$ required a sufficiently fine spatial discretization ![]() $\Delta \xi = \Delta r/a$ and, in turn, stable convergence to periodicity of the film pressure required a sufficiently small time step
$\Delta \xi = \Delta r/a$ and, in turn, stable convergence to periodicity of the film pressure required a sufficiently small time step ![]() $\Delta \tau = \omega \Delta t$. For instance, the solution for
$\Delta \tau = \omega \Delta t$. For instance, the solution for ![]() ${\mathcal {C}}=3$ represented in figure 3(e) was obtained using
${\mathcal {C}}=3$ represented in figure 3(e) was obtained using ![]() $\Delta \xi = 0.01$ and
$\Delta \xi = 0.01$ and ![]() $\Delta \tau = 6.3\times 10^{-4}$. The restriction on the time step for numerical stability generally loosened when increasing the degree of damping; for instance, the solution for
$\Delta \tau = 6.3\times 10^{-4}$. The restriction on the time step for numerical stability generally loosened when increasing the degree of damping; for instance, the solution for ![]() ${\mathcal {C}}=5.25$ represented in figure 3(f) was obtained using
${\mathcal {C}}=5.25$ represented in figure 3(f) was obtained using ![]() $\Delta \tau = 8.4\times 10^{-4}$. Note finally that the precise time-averaged shape of the deforming disk
$\Delta \tau = 8.4\times 10^{-4}$. Note finally that the precise time-averaged shape of the deforming disk ![]() $\langle W \rangle$ continued to fluctuate noticeably even after the associated levitation force had converged with a convergence ratio of less than
$\langle W \rangle$ continued to fluctuate noticeably even after the associated levitation force had converged with a convergence ratio of less than ![]() $0.5\,\%$.
$0.5\,\%$.
7. The attractive load capacity
Based on the results outlined above, it is of great interest to explore the influence of two-way fluid–structure coupling on the attractive load capacity ![]() $max({\mathcal {F}}_\ell )$ of a flexural squeeze-film system. The asymptotic formulation developed in this study allows analytical determination of the levitation force
$max({\mathcal {F}}_\ell )$ of a flexural squeeze-film system. The asymptotic formulation developed in this study allows analytical determination of the levitation force ![]() ${\mathcal {F}}_\ell$ in the dimensionless form
${\mathcal {F}}_\ell$ in the dimensionless form ![]() ${\mathcal {F}}_\ell / (\varepsilon {\mathcal {F}}_m)$, a measure of system efficiency that takes into account the amplitude
${\mathcal {F}}_\ell / (\varepsilon {\mathcal {F}}_m)$, a measure of system efficiency that takes into account the amplitude ![]() ${\mathcal {F}}_m$ of the supplied excitation force. In principle, the efficiency will be affected both by structural bending forces within the disk and by the evolving overpressure in the squeeze film (see § 2.1). While it is well known that operating near a resonant frequency maximizes the efficiency for one-way-coupled systems (
${\mathcal {F}}_m$ of the supplied excitation force. In principle, the efficiency will be affected both by structural bending forces within the disk and by the evolving overpressure in the squeeze film (see § 2.1). While it is well known that operating near a resonant frequency maximizes the efficiency for one-way-coupled systems (![]() ${\mathcal {C}}=0$) due to a weakening of structural impedance and a consequent magnification of the displacement amplitude of points on the disk (Li et al. Reference Li, Liu and Ding2014), it is worth exploring here the influence of the additional aerodynamic force that emerges when
${\mathcal {C}}=0$) due to a weakening of structural impedance and a consequent magnification of the displacement amplitude of points on the disk (Li et al. Reference Li, Liu and Ding2014), it is worth exploring here the influence of the additional aerodynamic force that emerges when ![]() ${\mathcal {C}} > 0$. Results are given below in §§ 7.1 and 7.2 for a centrally excited disk (
${\mathcal {C}} > 0$. Results are given below in §§ 7.1 and 7.2 for a centrally excited disk (![]() ${\xi _c} \to 0$), computed using the limiting expressions derived in § 5, and provided in § 7.3 is a sample calculation describing a practical system for which
${\xi _c} \to 0$), computed using the limiting expressions derived in § 5, and provided in § 7.3 is a sample calculation describing a practical system for which ![]() $0 < {\xi _c} < 1$.
$0 < {\xi _c} < 1$.
7.1. Reactive forces that modulate disk oscillation
Exemplified in figures 4(a) and 4(b) is the variation with the governing parameters of the dimensionless amplitude ![]() $|V_c|$ of the oscillatory reactive forces affecting a centrally excited disk, which is evaluated using (5.2). The black dot-dashed curve in each panel, corresponding to a state of one-way coupling
$|V_c|$ of the oscillatory reactive forces affecting a centrally excited disk, which is evaluated using (5.2). The black dot-dashed curve in each panel, corresponding to a state of one-way coupling ![]() ${\mathcal {C}}=0$, exhibits zeros for critical values of the wavenumber
${\mathcal {C}}=0$, exhibits zeros for critical values of the wavenumber ![]() $K \approx 3.0, 6.2, 9.4, \ldots\, $, which represent the resonant modes of the flexurally oscillating disk (Warren Reference Warren1930). As shown in figure 4(a), increasing the strength
$K \approx 3.0, 6.2, 9.4, \ldots\, $, which represent the resonant modes of the flexurally oscillating disk (Warren Reference Warren1930). As shown in figure 4(a), increasing the strength ![]() ${\mathcal {C}}$ of the aerodynamic forcing tends to uniformize
${\mathcal {C}}$ of the aerodynamic forcing tends to uniformize ![]() $|V_c|$ for a range of wavenumbers
$|V_c|$ for a range of wavenumbers ![]() $K$, thereby eliminating the first few resonant modes. The affected range of
$K$, thereby eliminating the first few resonant modes. The affected range of ![]() $K$ and the number of suppressed modes grow as
$K$ and the number of suppressed modes grow as ![]() ${\mathcal {C}}$ is increased. For sufficiently large values of
${\mathcal {C}}$ is increased. For sufficiently large values of ![]() $K$ that satisfy
$K$ that satisfy ![]() $K^4 \sim {\mathcal {C}}^6$, the variation of
$K^4 \sim {\mathcal {C}}^6$, the variation of ![]() $|V_c|$ gradually returns, in accordance with a restored three-term balance in the Kirchhoff–Love equation (2.15). Noting that
$|V_c|$ gradually returns, in accordance with a restored three-term balance in the Kirchhoff–Love equation (2.15). Noting that ![]() $K^4/{\mathcal {C}}^6 \propto \omega$, this result agrees well with the observed decrease of the damping ratio of flexural squeeze-film bearings for increasing near-resonant operating frequencies
$K^4/{\mathcal {C}}^6 \propto \omega$, this result agrees well with the observed decrease of the damping ratio of flexural squeeze-film bearings for increasing near-resonant operating frequencies ![]() $\omega$ (Pandey & Pratap Reference Pandey and Pratap2007). It must be emphasized here that, although
$\omega$ (Pandey & Pratap Reference Pandey and Pratap2007). It must be emphasized here that, although ![]() $|V_c|$ exhibits local minima of decreasing value as
$|V_c|$ exhibits local minima of decreasing value as ![]() $K$ grows, it never vanishes if
$K$ grows, it never vanishes if ![]() ${\mathcal {C}} > 0$ – the dissipative effect of viscous aerodynamic damping precludes idealistic resonance. The curves in figure 4(b) reveal that an increase in the squeeze number
${\mathcal {C}} > 0$ – the dissipative effect of viscous aerodynamic damping precludes idealistic resonance. The curves in figure 4(b) reveal that an increase in the squeeze number ![]() $\sigma$ mitigates modal suppression. The reappearing minima of
$\sigma$ mitigates modal suppression. The reappearing minima of ![]() $|V_c|$ are displaced along the
$|V_c|$ are displaced along the ![]() $K$-axis, with greater displacement occurring for larger values of
$K$-axis, with greater displacement occurring for larger values of ![]() ${\mathcal {C}}$, i.e. the shift of the optimal near-resonant frequency
${\mathcal {C}}$, i.e. the shift of the optimal near-resonant frequency ![]() $\omega \propto K^2$ increases with the degree of damping, as anticipated for a harmonic oscillator (Zhang et al. Reference Zhang, Xu and Jiang2004; Bettini Reference Bettini2016).
$\omega \propto K^2$ increases with the degree of damping, as anticipated for a harmonic oscillator (Zhang et al. Reference Zhang, Xu and Jiang2004; Bettini Reference Bettini2016).

Figure 4. Variation with the elastic wavenumber ![]() $K$ of the dimensionless amplitude of the forces modulating the oscillation of a centrally excited disk, as defined in (5.2). Curves are shown for two distinct values of the squeeze number
$K$ of the dimensionless amplitude of the forces modulating the oscillation of a centrally excited disk, as defined in (5.2). Curves are shown for two distinct values of the squeeze number ![]() $\sigma$ – (a) σ = 1 and (b)
$\sigma$ – (a) σ = 1 and (b) ![]() $\sigma = 500$ – and compared for states of one-way coupling (
$\sigma = 500$ – and compared for states of one-way coupling (![]() ${\mathcal {C}}=0$), moderate two-way coupling (
${\mathcal {C}}=0$), moderate two-way coupling (![]() ${\mathcal {C}}=3$) and strong two-way coupling (
${\mathcal {C}}=3$) and strong two-way coupling (![]() ${\mathcal {C}}>5$).
${\mathcal {C}}>5$).
7.2. Parametric dependences of the operating efficiency
Plotted in figure 5(a) is the variation with the squeeze number ![]() $\sigma$ and the coupling parameter
$\sigma$ and the coupling parameter ![]() ${\mathcal {C}}$ of the levitative efficiency provided by a centrally excited disk that is oscillating near its first natural frequency, i.e.
${\mathcal {C}}$ of the levitative efficiency provided by a centrally excited disk that is oscillating near its first natural frequency, i.e. ![]() $K = 3$. The efficiency is computed in the normalized form
$K = 3$. The efficiency is computed in the normalized form ![]() ${\mathcal {F}}_\ell / (\varepsilon {\mathcal {F}}_m)$, with use of (5.6). In practical systems, the value of the elastic wavenumber
${\mathcal {F}}_\ell / (\varepsilon {\mathcal {F}}_m)$, with use of (5.6). In practical systems, the value of the elastic wavenumber ![]() $K$ is determined by the structural properties of the oscillator and the selected operating frequency, while those of
$K$ is determined by the structural properties of the oscillator and the selected operating frequency, while those of ![]() $\sigma \propto 1/h_o^{2}$ and
$\sigma \propto 1/h_o^{2}$ and ![]() ${\mathcal {C}} \propto 1/\sqrt {h_o}$ vary strongly with the evolving separation distance
${\mathcal {C}} \propto 1/\sqrt {h_o}$ vary strongly with the evolving separation distance ![]() $h_o$ during the pull-off process (see § 2.1 for clarification). Thus, figure 5(a) may be interpreted qualitatively to represent the variation of the normalized efficiency with the inverse of the separation distance.
$h_o$ during the pull-off process (see § 2.1 for clarification). Thus, figure 5(a) may be interpreted qualitatively to represent the variation of the normalized efficiency with the inverse of the separation distance.

Figure 5. (a) Variation with the squeeze number ![]() $\sigma$ and coupling parameter
$\sigma$ and coupling parameter ![]() ${\mathcal {C}}$ of the levitation efficiency (4.8a) for a selected value of the elastic wavenumber
${\mathcal {C}}$ of the levitation efficiency (4.8a) for a selected value of the elastic wavenumber ![]() $K$. (b) Variation with
$K$. (b) Variation with ![]() $K$ of the local maximum in efficiency observed for
$K$ of the local maximum in efficiency observed for ![]() ${\mathcal {C}} \sim 1$, juxtaposed with the universal value approached for
${\mathcal {C}} \sim 1$, juxtaposed with the universal value approached for ![]() ${\mathcal {C}} \gg 1$. Vertical lines in (b) represent resonant wavenumbers of the undamped disk.
${\mathcal {C}} \gg 1$. Vertical lines in (b) represent resonant wavenumbers of the undamped disk.
Note first that the efficiency, which scales with ![]() ${\mathcal {C}}^6$ as per (5.6), vanishes in the limit of one-way coupling
${\mathcal {C}}^6$ as per (5.6), vanishes in the limit of one-way coupling ![]() ${\mathcal {C}} = 0$ for all values of
${\mathcal {C}} = 0$ for all values of ![]() $\sigma$. On the other hand, when
$\sigma$. On the other hand, when ![]() ${\mathcal {C}}=20$, the efficiency is finite and varies weakly with
${\mathcal {C}}=20$, the efficiency is finite and varies weakly with ![]() $\sigma$; further computations reveal that this behaviour is found to occur regardless of the value of
$\sigma$; further computations reveal that this behaviour is found to occur regardless of the value of ![]() $K$, consistent with the observation of modal suppression discussed in § 7.1. In fact, as detailed in Appendix B, in the limit
$K$, consistent with the observation of modal suppression discussed in § 7.1. In fact, as detailed in Appendix B, in the limit ![]() ${\mathcal {C}} \gg 1$, the efficiency is found to converge to a constant value
${\mathcal {C}} \gg 1$, the efficiency is found to converge to a constant value ![]() ${\approx }0.6495$, independent of both
${\approx }0.6495$, independent of both ![]() $\sigma$ and K.
$\sigma$ and K.
It is apparent from figure 5(a) that the efficiency varies non-monotonically with both ![]() $\sigma$ and
$\sigma$ and ![]() ${\mathcal {C}}$, and exhibits a local maximum for a critical combination of the two parameters. Represented in figure 5(b) is the value of this extremum,
${\mathcal {C}}$, and exhibits a local maximum for a critical combination of the two parameters. Represented in figure 5(b) is the value of this extremum, ![]() $max(\varepsilon ^{-1} {\mathcal {F}}_\ell / {\mathcal {F}}_m)$, for various wavenumbers
$max(\varepsilon ^{-1} {\mathcal {F}}_\ell / {\mathcal {F}}_m)$, for various wavenumbers ![]() $K$. The corresponding critical values of
$K$. The corresponding critical values of ![]() $\sigma$ and
$\sigma$ and ![]() ${\mathcal {C}}$, omitted from the figure for clarity, increase nearly monotonically with
${\mathcal {C}}$, omitted from the figure for clarity, increase nearly monotonically with ![]() $K$. For
$K$. For ![]() $K \gtrsim 8.3$, the local maximum exceeds the aforementioned universal value approached in the limit
$K \gtrsim 8.3$, the local maximum exceeds the aforementioned universal value approached in the limit ![]() ${\mathcal {C}} \gg 1$, the latter indicated in the figure by a dashed horizontal line. The curvature of the function
${\mathcal {C}} \gg 1$, the latter indicated in the figure by a dashed horizontal line. The curvature of the function ![]() $[max(\varepsilon ^{-1} {\mathcal {F}}_\ell / {\mathcal {F}}_m)](K)$ diminishes as
$[max(\varepsilon ^{-1} {\mathcal {F}}_\ell / {\mathcal {F}}_m)](K)$ diminishes as ![]() $K$ grows, subsequent peaks which appear for increasing critical values of
$K$ grows, subsequent peaks which appear for increasing critical values of ![]() $K$, marked by dots, being less accentuated. This suggests a favourable reduction in the sensitivity of the load capacity to the precise excitation frequency (Davis et al. Reference Davis, Gabai and Bucher2018) when operating near higher resonant modes. Note, in connection with the concluding discussion in § 7.1, that the critical values of
$K$, marked by dots, being less accentuated. This suggests a favourable reduction in the sensitivity of the load capacity to the precise excitation frequency (Davis et al. Reference Davis, Gabai and Bucher2018) when operating near higher resonant modes. Note, in connection with the concluding discussion in § 7.1, that the critical values of ![]() $K$ corresponding to subsequent peaks are increasingly displaced from the respective ideal resonant wavenumbers, the latter represented in the figure by solid vertical lines.
$K$ corresponding to subsequent peaks are increasingly displaced from the respective ideal resonant wavenumbers, the latter represented in the figure by solid vertical lines.
7.3. Sample calculations for a practical system
While the squeeze number ![]() $\sigma$ and the coupling parameter
$\sigma$ and the coupling parameter ![]() ${\mathcal {C}}$ are formally independent parameters governing the fluid–structure dynamics, during the pull-off process they evolve together as dictated by their respective dependences on the growing separation distance, i.e.
${\mathcal {C}}$ are formally independent parameters governing the fluid–structure dynamics, during the pull-off process they evolve together as dictated by their respective dependences on the growing separation distance, i.e. ![]() $\sigma \propto 1/h_o^{2}$ and
$\sigma \propto 1/h_o^{2}$ and ![]() ${\mathcal {C}} \propto 1/\sqrt {h_o}$. Practical determination of the load capacity
${\mathcal {C}} \propto 1/\sqrt {h_o}$. Practical determination of the load capacity ![]() $max[{\mathcal {F}}_\ell (h_o)]$ thus warrants a system-specific calculation, as exemplified below.
$max[{\mathcal {F}}_\ell (h_o)]$ thus warrants a system-specific calculation, as exemplified below.
Shown in blue in figure 6(a) is the predicted pull-off curve ![]() ${\mathcal {F}}_\ell (h_o)$ for an SFL system operating in standard sea-level air under conditions similar to those used in the recent experiments by Weston-Dawkes et al. (Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021). A vibration actuator with excitation amplitude
${\mathcal {F}}_\ell (h_o)$ for an SFL system operating in standard sea-level air under conditions similar to those used in the recent experiments by Weston-Dawkes et al. (Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021). A vibration actuator with excitation amplitude ![]() ${\mathcal {F}}_m = 74.5$ gf and frequency
${\mathcal {F}}_m = 74.5$ gf and frequency ![]() $\omega /(2{\rm \pi} ) = 200$ Hz is mounted to a cylinder of finite radius
$\omega /(2{\rm \pi} ) = 200$ Hz is mounted to a cylinder of finite radius ![]() $r_c = 10$ mm. The assembly, having an effective mass
$r_c = 10$ mm. The assembly, having an effective mass ![]() $m_c = 10$ g, is affixed concentrically to a polyester plastic disk of radius
$m_c = 10$ g, is affixed concentrically to a polyester plastic disk of radius ![]() $a = 30$ mm and thickness
$a = 30$ mm and thickness ![]() $t_d = 150\ \mathrm {\mu }$m, giving rise to an operating elastic wavenumber of
$t_d = 150\ \mathrm {\mu }$m, giving rise to an operating elastic wavenumber of ![]() $K \approx 3.75$. As
$K \approx 3.75$. As ![]() $h_o$ is increased from approximately
$h_o$ is increased from approximately ![]() $15$ to
$15$ to ![]() $185\ \mathrm {\mu }$m, the squeeze number and coupling parameter vary respectively from
$185\ \mathrm {\mu }$m, the squeeze number and coupling parameter vary respectively from ![]() $[\sigma,{\mathcal {C}}] \approx [10.77,12.43]$ to
$[\sigma,{\mathcal {C}}] \approx [10.77,12.43]$ to ![]() $[0.07,3.54]$. The red curve in the same figure shows the accompanying variation of the central oscillation amplitude
$[0.07,3.54]$. The red curve in the same figure shows the accompanying variation of the central oscillation amplitude ![]() $b(h_o)$.
$b(h_o)$.

Figure 6. Sample calculations for a disk with thickness ![]() $t_d = 150\ \mathrm {\mu }$m made of polyester, for which
$t_d = 150\ \mathrm {\mu }$m made of polyester, for which ![]() $E_d = 3.65$ GPa,
$E_d = 3.65$ GPa, ![]() $\rho _d = 1.38\ {\rm g}\ {\rm cm}^{-3}$ and
$\rho _d = 1.38\ {\rm g}\ {\rm cm}^{-3}$ and ![]() $\nu _d = 0.48$ (Sasmita et al. Reference Sasmita, Candra, Judawisastra and Priambodo2019; MatWeb n.d.), in a gas where
$\nu _d = 0.48$ (Sasmita et al. Reference Sasmita, Candra, Judawisastra and Priambodo2019; MatWeb n.d.), in a gas where ![]() $p_a = 101325$ pa,
$p_a = 101325$ pa, ![]() $\mu _a = 1.81\times 10^{-5}\ {\rm kg}\ ({\rm m}\ {\rm s})^{-1}$ and
$\mu _a = 1.81\times 10^{-5}\ {\rm kg}\ ({\rm m}\ {\rm s})^{-1}$ and ![]() $\rho _a = 1.225\ {\rm kg}\ {\rm m}^{-3}$. (a) Variation with the separation distance
$\rho _a = 1.225\ {\rm kg}\ {\rm m}^{-3}$. (a) Variation with the separation distance ![]() $h_o$ of the attractive force
$h_o$ of the attractive force ![]() ${\mathcal {F}}_\ell$ and the central oscillation amplitude
${\mathcal {F}}_\ell$ and the central oscillation amplitude ![]() $b$, and (b) variation with the disk radius
$b$, and (b) variation with the disk radius ![]() $a$ of the area-normalized load capacity, the latter compared with measurements by Weston-Dawkes et al. (Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021).
$a$ of the area-normalized load capacity, the latter compared with measurements by Weston-Dawkes et al. (Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021).
For small separation distances ![]() $h_o \approx 20\ \mathrm {\mu }$m, the amplitude
$h_o \approx 20\ \mathrm {\mu }$m, the amplitude ![]() $b$ vanishes due to augmented aerodynamic resistance (
$b$ vanishes due to augmented aerodynamic resistance (![]() ${\mathcal {C}} \gtrsim 10$) and the levitation force, which scales with the square of
${\mathcal {C}} \gtrsim 10$) and the levitation force, which scales with the square of ![]() $b$ as seen from (4.8b), also decays. Note that this is in stark contrast with the transition to strong repulsion found in systems where effects of two-way coupling on the oscillator dynamics are negligible (Ramanarayanan & Sánchez Reference Ramanarayanan and Sánchez2022), i.e. those with heavier oscillators driven by powerful actuators (Hatanaka et al. Reference Hatanaka, Yoshikazu, Kentaro, Sadayuki and Yoshiki1999; Sadayuki Reference Sadayuki2002; Andrade et al. Reference Andrade, Ramos, Adamowski and Marzo2020). As the disk is pulled away from the wall, the amplitude rises due to a weakening of aerodynamic resistance and approaches asymptotically a value that is modulated only by structural bending forces within the oscillator. The force
$b$ as seen from (4.8b), also decays. Note that this is in stark contrast with the transition to strong repulsion found in systems where effects of two-way coupling on the oscillator dynamics are negligible (Ramanarayanan & Sánchez Reference Ramanarayanan and Sánchez2022), i.e. those with heavier oscillators driven by powerful actuators (Hatanaka et al. Reference Hatanaka, Yoshikazu, Kentaro, Sadayuki and Yoshiki1999; Sadayuki Reference Sadayuki2002; Andrade et al. Reference Andrade, Ramos, Adamowski and Marzo2020). As the disk is pulled away from the wall, the amplitude rises due to a weakening of aerodynamic resistance and approaches asymptotically a value that is modulated only by structural bending forces within the oscillator. The force ![]() ${\mathcal {F}}_\ell$ also rises and reaches a maximal value
${\mathcal {F}}_\ell$ also rises and reaches a maximal value ![]() $max({\mathcal {F}}_\ell ) \approx 56$ gf at a distance
$max({\mathcal {F}}_\ell ) \approx 56$ gf at a distance ![]() $h_o \approx 82\ \mathrm {\mu }$m, beyond which it decays gradually. In practical systems, displacing the disk beyond the critical distance requires the exertion of a pulling force that exceeds the load capacity
$h_o \approx 82\ \mathrm {\mu }$m, beyond which it decays gradually. In practical systems, displacing the disk beyond the critical distance requires the exertion of a pulling force that exceeds the load capacity ![]() $max({\mathcal {F}}_\ell )$ and yields, instead, an abrupt failure of levitation, as exemplified in figure 2(a). Points on the predicted pull-off curve for distances
$max({\mathcal {F}}_\ell )$ and yields, instead, an abrupt failure of levitation, as exemplified in figure 2(a). Points on the predicted pull-off curve for distances ![]() $h_o \gtrsim 82\ \mathrm {\mu }$m thus represent states of unstable equilibria that occur only in experiments involving artificial control of the separation distance (Sadayuki Reference Sadayuki2002; Yoshimoto et al. Reference Yoshimoto, Shou and Somaya2013; Andrade et al. Reference Andrade, Ramos, Adamowski and Marzo2020).
$h_o \gtrsim 82\ \mathrm {\mu }$m thus represent states of unstable equilibria that occur only in experiments involving artificial control of the separation distance (Sadayuki Reference Sadayuki2002; Yoshimoto et al. Reference Yoshimoto, Shou and Somaya2013; Andrade et al. Reference Andrade, Ramos, Adamowski and Marzo2020).
Furthermore, it is found that the predicted load capacity ![]() $max({\mathcal {F}}_\ell )$ varies strongly and non-monotonically with the disk radius
$max({\mathcal {F}}_\ell )$ varies strongly and non-monotonically with the disk radius ![]() $a$. As
$a$. As ![]() $a$ is increased from an initial value equal to
$a$ is increased from an initial value equal to ![]() $a=r_c=10$ mm,
$a=r_c=10$ mm, ![]() $max({\mathcal {F}}_\ell )$ is seen to grow and reach a value of approximately
$max({\mathcal {F}}_\ell )$ is seen to grow and reach a value of approximately ![]() $81$ gf when
$81$ gf when ![]() $a \approx 18.5$ mm, before declining and approaching oscillatorily a value of approximately
$a \approx 18.5$ mm, before declining and approaching oscillatorily a value of approximately ![]() $45$ gf when
$45$ gf when ![]() $a \gtrsim 50$ mm. The fact that the variation of the load capacity subsides when
$a \gtrsim 50$ mm. The fact that the variation of the load capacity subsides when ![]() $a$ is made sufficiently large is consistent with the aforementioned universal behaviour of the fluid–structure problem in the limit of strong coupling
$a$ is made sufficiently large is consistent with the aforementioned universal behaviour of the fluid–structure problem in the limit of strong coupling ![]() ${\mathcal {C}}^6 \gg K^4 \sim 1$. The value of the area-normalized load capacity
${\mathcal {C}}^6 \gg K^4 \sim 1$. The value of the area-normalized load capacity ![]() $max({\mathcal {F}}_\ell )/({\rm \pi} a^2)$ thus collapses when
$max({\mathcal {F}}_\ell )/({\rm \pi} a^2)$ thus collapses when ![]() $a$ is increased beyond
$a$ is increased beyond ![]() ${\approx }20$ mm, as shown in figure 6(b). As seen from the included inset, this prediction agrees qualitatively with the observations of Weston-Dawkes et al. (Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021), who alluded to the possible benefit of increasing the number of oscillators rather than their size when upscaling an SFL system.
${\approx }20$ mm, as shown in figure 6(b). As seen from the included inset, this prediction agrees qualitatively with the observations of Weston-Dawkes et al. (Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021), who alluded to the possible benefit of increasing the number of oscillators rather than their size when upscaling an SFL system.
In principle, use of the asymptotic formulation introduces relative errors that scale with ![]() $b/h_o$,
$b/h_o$, ![]() $h_o/a$ and
$h_o/a$ and ![]() $h_o^2/(\mu _a/\rho _a/\omega )$, the latter of which is of order unity for this sample SFL system when
$h_o^2/(\mu _a/\rho _a/\omega )$, the latter of which is of order unity for this sample SFL system when ![]() $h_o \gtrsim 75\ \mathrm {\mu }$m. Nevertheless, the scale of forces
$h_o \gtrsim 75\ \mathrm {\mu }$m. Nevertheless, the scale of forces ![]() ${\mathcal {F}}_\ell$ seen in figure 6(a) in the rising portion of the pull-off curve
${\mathcal {F}}_\ell$ seen in figure 6(a) in the rising portion of the pull-off curve ![]() $h_o \lesssim 75\ \mathrm {\mu }$m compares favourably with that reported in the experiment (Weston-Dawkes et al. Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021) for small distances of order
$h_o \lesssim 75\ \mathrm {\mu }$m compares favourably with that reported in the experiment (Weston-Dawkes et al. Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021) for small distances of order ![]() $100\ \mathrm {\mu }$m, as seen from figure 2(a), in stark contrast with the theoretical predictions produced previously with use of a one-way-coupled flow–structure description (Ramanarayanan & Sánchez Reference Ramanarayanan and Sánchez2022). It can be anticipated that accurate description of the observed growth of
$100\ \mathrm {\mu }$m, as seen from figure 2(a), in stark contrast with the theoretical predictions produced previously with use of a one-way-coupled flow–structure description (Ramanarayanan & Sánchez Reference Ramanarayanan and Sánchez2022). It can be anticipated that accurate description of the observed growth of ![]() ${\mathcal {F}}_\ell$ to larger values
${\mathcal {F}}_\ell$ to larger values ![]() ${\approx }500$ gf at greater distances
${\approx }500$ gf at greater distances ![]() $h_o \approx 2500\ \mathrm {\mu }$m, seen in figure 2(a), as well as the associated area-normalized load capacities
$h_o \approx 2500\ \mathrm {\mu }$m, seen in figure 2(a), as well as the associated area-normalized load capacities ![]() $max({\mathcal {F}}_\ell )/({\rm \pi} a^2) > 2$ seen in the inset of figure 6(b), requires generalizing the present formulation to account for effects of fluid inertia that are non-negligible when
$max({\mathcal {F}}_\ell )/({\rm \pi} a^2) > 2$ seen in the inset of figure 6(b), requires generalizing the present formulation to account for effects of fluid inertia that are non-negligible when ![]() $h_o^2 \sim \mu _a/\rho _a/\omega$ (Ramanarayanan et al. Reference Ramanarayanan, Coenen and Sánchez2022).
$h_o^2 \sim \mu _a/\rho _a/\omega$ (Ramanarayanan et al. Reference Ramanarayanan, Coenen and Sánchez2022).
8. Conclusions and recommendations for future work
Developed in this paper is a reduced theoretical description of the oscillatory airflow excited in a slender air layer by the vibration of a compliant bounding surface. This problem of elastohydrodynamic lubrication is relevant to the study of SFL systems that are driven by highly flexible oscillators, which were discovered recently to exhibit attractive load-bearing capacities a thousandfold larger than those driven by stiffer oscillators. Consideration of two-way-coupled fluid–structure interactions is found to provide significantly improved agreement with recent experimental data that revealed (i) a centrally localized distribution of sub-ambient time-averaged pressure within the air layer, (ii) a non-monotonic time-averaged deformation of the disk, (iii) a gradual evolution of the attractive squeeze-film force during the pull-off process and (iv) a non-monotonic variation of the load capacity with oscillator surface area. Summarized below are possible paths for improving the accuracy and utility of the present formulation.
Of primary interest is characterizing the apparent minimum load and the corresponding minimum mean separation distance below which physical contact occurs between the oscillator and the adjacent surface, inducing (i) adverse frictional resistance to lateral motion and (ii) increased noise levels due to the transfer of mechanical vibrations (as noted from personal communication with the authors of Weston-Dawkes et al. Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021; Colasante Reference Colasante2022). (Note that such effects may be tolerable or even desirable in contact-based applications such as suction cups, whose vibration has been shown to increase their load capacity (Zhu et al. Reference Zhu, Liu, Wang and Wang2006; Hong et al. Reference Hong, Liu, Yang and Zhai2009; Wang et al. Reference Wang, Wang, Zong and Li2010).) Accurate description of the flow–structure physics under such small separation distances may require rigorous characterization of intermolecular forces and surface asperities (Hosoi & Mahadevan Reference Hosoi and Mahadevan2004; Poulain et al. Reference Poulain, Carlson, Mandre and Mahadevan2022; Rallabandi Reference Rallabandi2024).
On the other hand, in pursuit of determining accurately the maximum load capacity, the formulation must be generalized to describe (i) nonlinear effects of fluid inertia in the gas layer and its periphery that are no longer negligible under the large separation distances for which the highest attractive forces are measured (Melikhov et al. Reference Melikhov, Chivilikhin, Amosov and Jeanson2016; Ramanarayanan & Sánchez Reference Ramanarayanan and Sánchez2022; Ramanarayanan et al. Reference Ramanarayanan, Coenen and Sánchez2022), (ii) operational stochasticity for highly flexural and larger-scale systems (Weston-Dawkes et al. Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021; Colasante Reference Colasante2023) due possibly in part to hydrodynamic instabilities, (iii) large deformations of the disk that are comparable to its thickness (Timoshenko & Woinowsky-Krieger Reference Timoshenko and Woinowsky-Krieger1959; Soedel & Soedel Reference Soedel and Soedel1994), (iv) dissipative effects of structural damping that may be important in describing near-resonant oscillation (Geist & McLaughlin Reference Geist and McLaughlin1994), (v) adverse effects of surface impurities such as cracks and roughness on the load capacity (Weston-Dawkes et al. Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021; Colasante Reference Colasante2024) and (vi) hysteresis in the pull-off process due to rapid application of the load (Weston-Dawkes et al. Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021). Insights gained by pursuing these avenues of research may also aid the realization and/or improvement of non-axisymmetric SFL configurations, emerging applications of which include low-friction transportation and robotic manipulation (Colasante Reference Colasante2015; Weston-Dawkes et al. Reference Weston-Dawkes, Adibnazari, Hu, Everman, Gravish and Tolley2021; Jia et al. Reference Jia, Ramanarayanan, Sánchez and Tolley2023).
Acknowledgements
We gratefully acknowledge insightful conversations with Mr C. Jia, Dr W. Weston-Dawkes, Mr M. Everman, Professor M. Tolley and Dr D. Colasante regarding practical aspects of SFL, those with Mr I. Frankel and Mr G. Lopez Nozaleda regarding fluid-structure interactions and those with Mr Nozaleda, Dr J. Alaminos Quesada and Dr W. Coenen regarding finite-difference methods. We must also thank Dr W. Coenen as well as the reviewers for suggesting valuable improvements to this paper.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Peripheral pressure variations in the lubrication limit
The presumed relaxation condition ![]() $p(r=a)=p_a$ introduced in (2.7a) implicitly neglects the pressure variations
$p(r=a)=p_a$ introduced in (2.7a) implicitly neglects the pressure variations ![]() $p-p_a$ existing across the small peripheral region of gas flow that extends for distances of order
$p-p_a$ existing across the small peripheral region of gas flow that extends for distances of order ![]() $h_o$ in all directions from the film edge
$h_o$ in all directions from the film edge ![]() $r=a$. These variations, which have been shown to provide a non-negligible contribution to the levitation force for systems with order-unity Womersley number
$r=a$. These variations, which have been shown to provide a non-negligible contribution to the levitation force for systems with order-unity Womersley number ![]() $\alpha = [h_o^2\omega / (\mu _a/\rho _a)]^{1/2}$ (Yoshimoto et al. Reference Yoshimoto, Shou and Somaya2013; Ramanarayanan et al. Reference Ramanarayanan, Coenen and Sánchez2022), can be neglected in the lubrication limit
$\alpha = [h_o^2\omega / (\mu _a/\rho _a)]^{1/2}$ (Yoshimoto et al. Reference Yoshimoto, Shou and Somaya2013; Ramanarayanan et al. Reference Ramanarayanan, Coenen and Sánchez2022), can be neglected in the lubrication limit ![]() $\alpha ^2 \ll 1$ considered in this study. For a proof, we begin by noting that the disk oscillations induce radial airflow of characteristic speed
$\alpha ^2 \ll 1$ considered in this study. For a proof, we begin by noting that the disk oscillations induce radial airflow of characteristic speed ![]() $u \sim u_c= (b/h_o) \omega a$ in the film, as follows from the balance of volumetric dilation rates in the continuity equation (2.6a). A similar analysis of the radial momentum equation (2.6b) then provides
$u \sim u_c= (b/h_o) \omega a$ in the film, as follows from the balance of volumetric dilation rates in the continuity equation (2.6a). A similar analysis of the radial momentum equation (2.6b) then provides ![]() $(p - p_a) \sim (\Delta p)_f= (b/h_o) (\mu _a \omega a^2)/h_o^2$ for the characteristic value of the pressure variations along the film. The nature of the flow induced in the small, non-slender periphery depends on the local Reynolds number
$(p - p_a) \sim (\Delta p)_f= (b/h_o) (\mu _a \omega a^2)/h_o^2$ for the characteristic value of the pressure variations along the film. The nature of the flow induced in the small, non-slender periphery depends on the local Reynolds number ![]() ${\textit {Re}}_p=\rho _a u_c h_o/\mu _a= \alpha ^2 / {\textit {St}}_p$, defined here in terms of the associated local Strouhal number
${\textit {Re}}_p=\rho _a u_c h_o/\mu _a= \alpha ^2 / {\textit {St}}_p$, defined here in terms of the associated local Strouhal number ![]() ${\textit {St}}_p = h_o^2/(ba)$. On the one hand, though the flow in the film is dominated by viscous forces since
${\textit {St}}_p = h_o^2/(ba)$. On the one hand, though the flow in the film is dominated by viscous forces since ![]() $\alpha ^2 \ll 1$ (and the Strouhal number in the film,
$\alpha ^2 \ll 1$ (and the Strouhal number in the film, ![]() $h_o/b$, is necessarily greater than unity), inertial forces can dominate in the periphery if
$h_o/b$, is necessarily greater than unity), inertial forces can dominate in the periphery if ![]() ${\textit {Re}}_p \gg 1$, i.e.
${\textit {Re}}_p \gg 1$, i.e. ![]() ${\textit {St}}_p \ll \alpha ^2$. In that case, the associated pressure drop across the periphery
${\textit {St}}_p \ll \alpha ^2$. In that case, the associated pressure drop across the periphery ![]() $(p - p_a) \sim (\Delta p)_p$ can be expected to scale with the dynamic pressure
$(p - p_a) \sim (\Delta p)_p$ can be expected to scale with the dynamic pressure ![]() $(\Delta p)_p = \rho _a u_c^2$, which is negligibly small compared with the pressure variations along the film, i.e.
$(\Delta p)_p = \rho _a u_c^2$, which is negligibly small compared with the pressure variations along the film, i.e. ![]() $(\Delta p)_p/(\Delta p)_f=\alpha ^2 (b/h_o) \ll 1$. On the other hand, in the opposite limit
$(\Delta p)_p/(\Delta p)_f=\alpha ^2 (b/h_o) \ll 1$. On the other hand, in the opposite limit ![]() ${\textit {Re}}_p \ll 1$, the peripheral flow is also dominated by viscous forces, whence
${\textit {Re}}_p \ll 1$, the peripheral flow is also dominated by viscous forces, whence ![]() $(\Delta p)_p = \mu _a u_c/h_o$, such that
$(\Delta p)_p = \mu _a u_c/h_o$, such that ![]() $(\Delta p)_p/(\Delta p)_f=h_o/a \ll 1$. Thus, regardless of the value of
$(\Delta p)_p/(\Delta p)_f=h_o/a \ll 1$. Thus, regardless of the value of ![]() ${\textit {Re}}_p$, the pressure drop across the periphery can be neglected when analysing the flow in the film.
${\textit {Re}}_p$, the pressure drop across the periphery can be neglected when analysing the flow in the film.
The justification outlined above must be reconsidered carefully in the limit of small relative amplitudes ![]() $\varepsilon =b/h_o \ll 1$. As mentioned above, when
$\varepsilon =b/h_o \ll 1$. As mentioned above, when ![]() ${\textit {Re}}_p \gg 1$,
${\textit {Re}}_p \gg 1$, ![]() $(\Delta p)_p/(\Delta p)_f \sim \varepsilon \alpha ^2$, so that, in the limit
$(\Delta p)_p/(\Delta p)_f \sim \varepsilon \alpha ^2$, so that, in the limit ![]() $\alpha ^2 \ll 1$ considered here, the peripheral pressure variations can be neglected when determining both the leading-order film pressure
$\alpha ^2 \ll 1$ considered here, the peripheral pressure variations can be neglected when determining both the leading-order film pressure ![]() $P_0$ and its first-order correction
$P_0$ and its first-order correction ![]() $P_1$. On the other hand, in the viscous limit
$P_1$. On the other hand, in the viscous limit ![]() ${\textit {Re}}_p \ll 1$,
${\textit {Re}}_p \ll 1$, ![]() $(\Delta p)_p/(\Delta p)_f \sim h_o/a \ll 1$, which can clearly be neglected when determining the leading-order pressure in the film
$(\Delta p)_p/(\Delta p)_f \sim h_o/a \ll 1$, which can clearly be neglected when determining the leading-order pressure in the film ![]() $P_0$, as done in (3.1). However, deducing the value of
$P_0$, as done in (3.1). However, deducing the value of ![]() $P_1(\xi =1,\tau )$ requires, in principle, selecting a distinguished limit relating the magnitudes of
$P_1(\xi =1,\tau )$ requires, in principle, selecting a distinguished limit relating the magnitudes of ![]() $h_o/a \ll 1$ and
$h_o/a \ll 1$ and ![]() $\varepsilon \ll 1$ and carrying out a formal procedure of asymptotic matching with the peripheral-flow solution (Ramanarayanan et al. Reference Ramanarayanan, Coenen and Sánchez2022). Fortunately, this may be avoided in the limit
$\varepsilon \ll 1$ and carrying out a formal procedure of asymptotic matching with the peripheral-flow solution (Ramanarayanan et al. Reference Ramanarayanan, Coenen and Sánchez2022). Fortunately, this may be avoided in the limit ![]() $\alpha ^2 \ll 1$ since we are not interested in determining the time dependence of the first-order film pressure
$\alpha ^2 \ll 1$ since we are not interested in determining the time dependence of the first-order film pressure ![]() $P_1$. Note that the peripheral variations of density are relatively small, i.e.
$P_1$. Note that the peripheral variations of density are relatively small, i.e. ![]() $(\rho - \rho _a)/\rho _a \sim (\Delta p)_p/p_a \sim \varepsilon \sigma (h_o/a)$, such that the nonlinear effects of gaseous compressibility on the peripheral flow are negligible in the first approximation. For
$(\rho - \rho _a)/\rho _a \sim (\Delta p)_p/p_a \sim \varepsilon \sigma (h_o/a)$, such that the nonlinear effects of gaseous compressibility on the peripheral flow are negligible in the first approximation. For ![]() ${\textit {Re}}_p \ll 1$, the problem in either flow region is thus linear at leading order. The time-averaged pressure drop, obtained by considering higher-order corrections, exhibits characteristic values of order
${\textit {Re}}_p \ll 1$, the problem in either flow region is thus linear at leading order. The time-averaged pressure drop, obtained by considering higher-order corrections, exhibits characteristic values of order ![]() $\varepsilon (\Delta p)_f$ and
$\varepsilon (\Delta p)_f$ and ![]() $\varepsilon (\Delta p)_p$ along the film and across the periphery, respectively, their ratio remaining therefore of order
$\varepsilon (\Delta p)_p$ along the film and across the periphery, respectively, their ratio remaining therefore of order ![]() $h_o/a \ll 1$. Thus, regardless of the value of
$h_o/a \ll 1$. Thus, regardless of the value of ![]() $Re_p$, use of the steady relaxation condition
$Re_p$, use of the steady relaxation condition ![]() $\langle P_1 \rangle (\xi =1) = 0$ given in (4.1) introduces asymptotic errors consistent with those involved in the general formulation outlined in § 2.2.
$\langle P_1 \rangle (\xi =1) = 0$ given in (4.1) introduces asymptotic errors consistent with those involved in the general formulation outlined in § 2.2.
Appendix B. Solution for extreme values of the coupling parameter  ${\mathcal {C}}$
${\mathcal {C}}$
B.1. The limit of one-way coupling  ${\mathcal {C}}=0$
${\mathcal {C}}=0$
The limit of one-way coupling where the disk motion is unaffected by aerodynamic damping, considered earlier for the case of central forcing ![]() ${\xi _c}=0$ (Ramanarayanan & Sánchez Reference Ramanarayanan and Sánchez2022), is described here for
${\xi _c}=0$ (Ramanarayanan & Sánchez Reference Ramanarayanan and Sánchez2022), is described here for ![]() $0<{\xi _c}<1$. When
$0<{\xi _c}<1$. When ![]() ${\mathcal {C}}=0$, the Kirchhoff–Love equation (2.15) reduces to
${\mathcal {C}}=0$, the Kirchhoff–Love equation (2.15) reduces to ![]() $\nabla ^4 W + K^4 \partial ^2 W/\partial \tau ^2 = 0$. Straightforward integration with use of the familiar boundary conditions listed in (2.18) provides
$\nabla ^4 W + K^4 \partial ^2 W/\partial \tau ^2 = 0$. Straightforward integration with use of the familiar boundary conditions listed in (2.18) provides ![]() $W = S(\xi )\cos \tau$, with
$W = S(\xi )\cos \tau$, with
 \begin{equation} S = \begin{cases} 1 & 0
\le \xi \le {\xi_c} \\ \dfrac{J_0(K\xi) + C_1 Y_0(K\xi) +
C_2 I_0(K\xi) + C_3 K_0(K\xi)}{J_0(K{\xi_c}) + C_1
Y_0(K{\xi_c}) + C_2 I_0(K{\xi_c}) + C_3 K_0(K{\xi_c})} &
{\xi_c} \le \xi \le 1 \end{cases}
,\end{equation}
\begin{equation} S = \begin{cases} 1 & 0
\le \xi \le {\xi_c} \\ \dfrac{J_0(K\xi) + C_1 Y_0(K\xi) +
C_2 I_0(K\xi) + C_3 K_0(K\xi)}{J_0(K{\xi_c}) + C_1
Y_0(K{\xi_c}) + C_2 I_0(K{\xi_c}) + C_3 K_0(K{\xi_c})} &
{\xi_c} \le \xi \le 1 \end{cases}
,\end{equation}
where ![]() $I_m$ and
$I_m$ and ![]() $K_m$ are the
$K_m$ are the ![]() $m$th-order modified Bessel functions of the first and second kind, respectively. The constant coefficients
$m$th-order modified Bessel functions of the first and second kind, respectively. The constant coefficients ![]() $C_1$,
$C_1$, ![]() $C_2$ and
$C_2$ and ![]() $C_3$ in (B1) are given by
$C_3$ in (B1) are given by
 \begin{equation} \left[ \begin{matrix}
C_1 \\ C_2 \\ C_3 \end{matrix} \right] ={-} \left[
\begin{matrix} Y_1(K{\xi_c}) & - I_1(K{\xi_c}) &
K_1(K{\xi_c}) \\ Y_1(K) & I_1(K) & - K_1(K) \\
\varXi^-_Y(K) & - \varXi^-_I(K) & -\varXi^+_K(K)
\end{matrix} \right] ^ {{-}1} \left[ \begin{matrix}
J_1(K{\xi_c}) \\ J_1(K) \\ \varXi^-_J(K) \end{matrix}
\right], \end{equation}
\begin{equation} \left[ \begin{matrix}
C_1 \\ C_2 \\ C_3 \end{matrix} \right] ={-} \left[
\begin{matrix} Y_1(K{\xi_c}) & - I_1(K{\xi_c}) &
K_1(K{\xi_c}) \\ Y_1(K) & I_1(K) & - K_1(K) \\
\varXi^-_Y(K) & - \varXi^-_I(K) & -\varXi^+_K(K)
\end{matrix} \right] ^ {{-}1} \left[ \begin{matrix}
J_1(K{\xi_c}) \\ J_1(K) \\ \varXi^-_J(K) \end{matrix}
\right], \end{equation}
involving the auxiliary operator ![]() $\varXi ^\pm _{\mathcal {B}}(x) = \mathcal {B}_0(x) \pm [(1-\nu _d)/x] \mathcal {B}_1(x)$, where
$\varXi ^\pm _{\mathcal {B}}(x) = \mathcal {B}_0(x) \pm [(1-\nu _d)/x] \mathcal {B}_1(x)$, where ![]() $\mathcal {B}_m$ represents a Bessel/modified Bessel function of order
$\mathcal {B}_m$ represents a Bessel/modified Bessel function of order ![]() $m$. Integrating the Reynolds equation (2.14) with use of the known function
$m$. Integrating the Reynolds equation (2.14) with use of the known function ![]() $W$ provides the pressure
$W$ provides the pressure ![]() $P$. Expressions for the steady pressure distribution
$P$. Expressions for the steady pressure distribution ![]() $\langle P_1 \rangle (\xi )$ and the levitation force
$\langle P_1 \rangle (\xi )$ and the levitation force ![]() $\langle F_L \rangle$ generated by arbitrary standing-wave oscillations
$\langle F_L \rangle$ generated by arbitrary standing-wave oscillations ![]() $S(\xi )$ are provided by Ramanarayanan & Sánchez (Reference Ramanarayanan and Sánchez2022).
$S(\xi )$ are provided by Ramanarayanan & Sánchez (Reference Ramanarayanan and Sánchez2022).
The resonant wavenumbers ![]() $K$ of the disk, describing states for which the structural impedance
$K$ of the disk, describing states for which the structural impedance ![]() $\mathcal {V}_c$ at the clamp radius
$\mathcal {V}_c$ at the clamp radius ![]() $\xi ={\xi _c}$ vanishes (Warren Reference Warren1930), are found by solving
$\xi ={\xi _c}$ vanishes (Warren Reference Warren1930), are found by solving
 \begin{equation} \det \left( \left[
\begin{matrix} J_1(K{\xi_c}) & Y_1(K{\xi_c}) & -
I_1(K{\xi_c}) & K_1(K{\xi_c}) \\ J_1(K) & Y_1(K) & I_1(K) &
- K_1(K) \\ \varXi^-_J(K) & \varXi^-_Y(K) & - \varXi^-_I(K)
& -\varXi^+_K(K) \\ J_1(K{\xi_c}) & Y_1(K{\xi_c}) &
I_1(K{\xi_c}) & - K_1(K{\xi_c}) \end{matrix} \right]
\right) = 0 .\end{equation}
\begin{equation} \det \left( \left[
\begin{matrix} J_1(K{\xi_c}) & Y_1(K{\xi_c}) & -
I_1(K{\xi_c}) & K_1(K{\xi_c}) \\ J_1(K) & Y_1(K) & I_1(K) &
- K_1(K) \\ \varXi^-_J(K) & \varXi^-_Y(K) & - \varXi^-_I(K)
& -\varXi^+_K(K) \\ J_1(K{\xi_c}) & Y_1(K{\xi_c}) &
I_1(K{\xi_c}) & - K_1(K{\xi_c}) \end{matrix} \right]
\right) = 0 .\end{equation}
For instance, the first four resonant wavenumbers for a centrally forced disk with a Poisson's ratio ![]() $\nu _d = 0.3$ are
$\nu _d = 0.3$ are ![]() $K = 3.0005, 6.2003, 9.3675$ and
$K = 3.0005, 6.2003, 9.3675$ and ![]() $12.5227$. Increasing the clamp radius to
$12.5227$. Increasing the clamp radius to ![]() ${\xi _c} = 0.1$ shifts the first mode to
${\xi _c} = 0.1$ shifts the first mode to ![]() $K=3.0702$, and for
$K=3.0702$, and for ![]() ${\xi _c} = 0.5$, to
${\xi _c} = 0.5$, to ![]() $K=4.8155$. Varying
$K=4.8155$. Varying ![]() $\nu _d$ within the range of interest, i.e.
$\nu _d$ within the range of interest, i.e. ![]() $0.3 \lesssim \nu _d \le 0.5$ (see § 6), has little effect.
$0.3 \lesssim \nu _d \le 0.5$ (see § 6), has little effect.
B.2. The limit of strong coupling  ${\mathcal {C}} \gg 1$
${\mathcal {C}} \gg 1$
Considered here are centrally forced systems (![]() ${\xi _c} \to 0$) subject to strong two-way coupling. In the associated limit
${\xi _c} \to 0$) subject to strong two-way coupling. In the associated limit ![]() ${\xi _c}^{-1} \gg {\mathcal {C}} \gg 1$, the fluid–structure problem is found to be quasi-steady and independent of
${\xi _c}^{-1} \gg {\mathcal {C}} \gg 1$, the fluid–structure problem is found to be quasi-steady and independent of ![]() ${\xi _c}$,
${\xi _c}$, ![]() $\sigma \sim 1$,
$\sigma \sim 1$, ![]() $K \sim 1$ and
$K \sim 1$ and ![]() $\nu _d$. The flexural wavelength of the disk scales with
$\nu _d$. The flexural wavelength of the disk scales with ![]() ${\mathcal {C}}^{-1}$, as follows from (3.5), and the magnitude of the squeeze-film overpressure reduces by a factor
${\mathcal {C}}^{-1}$, as follows from (3.5), and the magnitude of the squeeze-film overpressure reduces by a factor ![]() $O({\mathcal {C}}^2)$, as follows from radial momentum conservation (2.6b). The overpressure may thus be expressed with use of the rescaled expansion
$O({\mathcal {C}}^2)$, as follows from radial momentum conservation (2.6b). The overpressure may thus be expressed with use of the rescaled expansion ![]() ${\mathcal {C}}^2 P = \hat P(X,\tau ) = \hat P_0 + \varepsilon \hat P_1 + \cdots$, where
${\mathcal {C}}^2 P = \hat P(X,\tau ) = \hat P_0 + \varepsilon \hat P_1 + \cdots$, where ![]() $X = {\mathcal {C}} \xi$ is the aptly rescaled radial distance.
$X = {\mathcal {C}} \xi$ is the aptly rescaled radial distance.
The distribution of time-averaged overpressure can then be expressed in the simplified form ![]() $\langle \hat P_1 \rangle (X) = (3/2) \int _X^\infty \mathrm {Re} \{ \hat \varOmega \, {\rm d} \hat \varPi ^* / {\rm d} X \} \, {\rm d} X$, valid for
$\langle \hat P_1 \rangle (X) = (3/2) \int _X^\infty \mathrm {Re} \{ \hat \varOmega \, {\rm d} \hat \varPi ^* / {\rm d} X \} \, {\rm d} X$, valid for ![]() $X > 0$, where
$X > 0$, where
 \begin{align} \hat\varOmega =
\sum_{n=1}^3 [ A_n J_0(\hat\gamma_n X) + B_n
Y_0(\hat\gamma_n X) ] \quad{\rm and}\quad \hat \varPi =
\sum_{n=1}^3 \hat\gamma_n^4 [ A_n J_0(\hat\gamma_n X) + B_n
Y_0(\hat\gamma_n
X)]\end{align}
\begin{align} \hat\varOmega =
\sum_{n=1}^3 [ A_n J_0(\hat\gamma_n X) + B_n
Y_0(\hat\gamma_n X) ] \quad{\rm and}\quad \hat \varPi =
\sum_{n=1}^3 \hat\gamma_n^4 [ A_n J_0(\hat\gamma_n X) + B_n
Y_0(\hat\gamma_n
X)]\end{align}
describe the spatial dependence of the leading-order disk deformation ![]() $W_0(X,\tau ) = \mathrm {Re} \{ \hat \varOmega (X)\, \mathrm {e}^{\mathrm {i}\tau } \}$ and film pressure
$W_0(X,\tau ) = \mathrm {Re} \{ \hat \varOmega (X)\, \mathrm {e}^{\mathrm {i}\tau } \}$ and film pressure ![]() $\hat P_0(X,\tau ) = \mathrm {Re} \{ \hat \varPi (X)\, \mathrm {e}^{\mathrm {i}\tau } \}$, respectively. Both expressions involve the rescaled roots
$\hat P_0(X,\tau ) = \mathrm {Re} \{ \hat \varPi (X)\, \mathrm {e}^{\mathrm {i}\tau } \}$, respectively. Both expressions involve the rescaled roots ![]() $\hat \gamma _n = \lim _{{\mathcal {C}} \gg 1} (\gamma _n / {\mathcal {C}}) = (2^{1/3})(3^{1/6}) \exp [ \mathrm {i} (n{\rm \pi} /3 - {\rm \pi}/12) ]$, for
$\hat \gamma _n = \lim _{{\mathcal {C}} \gg 1} (\gamma _n / {\mathcal {C}}) = (2^{1/3})(3^{1/6}) \exp [ \mathrm {i} (n{\rm \pi} /3 - {\rm \pi}/12) ]$, for ![]() $n = 1:3$, and the coefficients
$n = 1:3$, and the coefficients ![]() $[ A_1 \ B_1 \ A_2 \ B_2 \ A_3 \ B_3] = [ 1 \ 0 \ 0 \ 0 \ 0 \ 0 ] {\boldsymbol{\mathsf{M}}}_\infty ^{-1}$, where
$[ A_1 \ B_1 \ A_2 \ B_2 \ A_3 \ B_3] = [ 1 \ 0 \ 0 \ 0 \ 0 \ 0 ] {\boldsymbol{\mathsf{M}}}_\infty ^{-1}$, where
 \begin{equation}
{\boldsymbol{\mathsf{M}}}_\infty = \begin{bmatrix}
{\boldsymbol{\mathsf{V}}}_1 \\
{\boldsymbol{\mathsf{V}}}_2 \\
{\boldsymbol{\mathsf{V}}}_3 \end{bmatrix} , \quad{\rm
with}\ {\boldsymbol{\mathsf{V}}}_n = \begin{bmatrix} 1 &
0 & 0 & \hat\gamma_n^{3/2} & \hat\gamma_n^{5/2} &
\hat\gamma_n^{7/2} \\ 2\ln(\hat\gamma_n)/{\rm \pi} & 1 &
\hat\gamma_n^4 & \mathrm{i}\hat\gamma_n^{3/2} &
\mathrm{i}\hat\gamma_n^{5/2} & \mathrm{i}\hat\gamma_n^{7/2}
\end{bmatrix} \end{equation}
\begin{equation}
{\boldsymbol{\mathsf{M}}}_\infty = \begin{bmatrix}
{\boldsymbol{\mathsf{V}}}_1 \\
{\boldsymbol{\mathsf{V}}}_2 \\
{\boldsymbol{\mathsf{V}}}_3 \end{bmatrix} , \quad{\rm
with}\ {\boldsymbol{\mathsf{V}}}_n = \begin{bmatrix} 1 &
0 & 0 & \hat\gamma_n^{3/2} & \hat\gamma_n^{5/2} &
\hat\gamma_n^{7/2} \\ 2\ln(\hat\gamma_n)/{\rm \pi} & 1 &
\hat\gamma_n^4 & \mathrm{i}\hat\gamma_n^{3/2} &
\mathrm{i}\hat\gamma_n^{5/2} & \mathrm{i}\hat\gamma_n^{7/2}
\end{bmatrix} \end{equation}
for ![]() $n = 1\,:\,3$. Represented in figures 7(a) and 7(b) are the leading-order disk deformations
$n = 1\,:\,3$. Represented in figures 7(a) and 7(b) are the leading-order disk deformations ![]() $W_0$ and the steady squeeze-film overpressure
$W_0$ and the steady squeeze-film overpressure ![]() $\langle \hat P_1 \rangle$, respectively, for
$\langle \hat P_1 \rangle$, respectively, for ![]() ${\xi _c}^{-1} \gg {\mathcal {C}} \gg 1$.
${\xi _c}^{-1} \gg {\mathcal {C}} \gg 1$.

Figure 7. Universal behaviour in the limit of strong coupling ![]() ${\mathcal {C}}\gg 1$: (a) components of the travelling-wave disk deformations
${\mathcal {C}}\gg 1$: (a) components of the travelling-wave disk deformations ![]() $W_0 = \mathrm {Re}\{ \hat \varOmega (X)\, \mathrm {e}^{\mathrm {i}\tau } \}$ that are in phase and out of phase with the central oscillations and (b) the rescaled time-averaged pressure distribution.
$W_0 = \mathrm {Re}\{ \hat \varOmega (X)\, \mathrm {e}^{\mathrm {i}\tau } \}$ that are in phase and out of phase with the central oscillations and (b) the rescaled time-averaged pressure distribution.
The dimensionless force ![]() $\langle F_L \rangle$ assumes in this limit the simplified form
$\langle F_L \rangle$ assumes in this limit the simplified form ![]() ${\mathcal {C}}^4\langle F_L \rangle \approx 4.919$ and the dimensionless amplitude
${\mathcal {C}}^4\langle F_L \rangle \approx 4.919$ and the dimensionless amplitude ![]() $|V_c|$ of structural impedance at the vanishing clamp radius (
$|V_c|$ of structural impedance at the vanishing clamp radius (![]() $X={\mathcal {C}}{\xi _c} \to 0$) reduces to
$X={\mathcal {C}}{\xi _c} \to 0$) reduces to ![]() ${\mathcal {C}}^{-2} | V_c | \to (2/{\rm \pi} ) | \sum _{n=1}^3 B_n \hat \gamma _n^2 | \approx 3.7867$, whence the operating efficiency (5.6) exhibits a constant value
${\mathcal {C}}^{-2} | V_c | \to (2/{\rm \pi} ) | \sum _{n=1}^3 B_n \hat \gamma _n^2 | \approx 3.7867$, whence the operating efficiency (5.6) exhibits a constant value ![]() ${\mathcal {F}}_\ell /(\varepsilon {\mathcal {F}}_m) \approx 0.6495$.
${\mathcal {F}}_\ell /(\varepsilon {\mathcal {F}}_m) \approx 0.6495$.