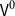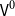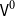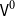1. Introduction
Foundational theories of mathematics are concerned with collections of mathematical objects. Depending on the specific foundation, these collections might be called sets, classes, or types. Among the many schisms of foundational theories, we find the one between material and structural. In a material foundational theory, the objects within a collection have an identity independent of the collection, and it is a sensible question to compare elements of different collections by equality. On the other hand, in a structural theory, the elements of a collection have no identity separate from the collection, and the important aspects of a collection are how its structure interacts with the other collections, for instance through functional relations.
Traditional set theories, such as Zermelo–Fraenkel set theory (ZF), are material foundational theories: there is a global elementhood relation and a global identity relation, meaning that all objects of the theory are possible elements of any set and can be compared to any other elements. This gives each set an inherent structure of membership relations between its elements, the elements of its elements, and so on. On the other hand, intensional Martin-Löf type theory (MLTT) (Martin-Löf Reference Martin-Löf, Rose and Shepherdson1975) is a structural theory where the identity type compares only elements of the same type. Furthermore, in Homotopy Type Theory and Univalent Foundations
Footnote
1
(HoTT/UF) (The Univalent Foundations Program 2013), the Univalence Axiom (UA) (Voevodsky Reference Voevodsky2010) can be seen in structural terms as saying that structural equivalence is identity (Awodey Reference Awodey2013). HoTT/UF also distinguishes its types into h-levels/
![]() $n$
-types: contractible types, h-proposition, h-sets, h-groupoids, and so on (Voevodsky Reference Voevodsky2015). The h-sets correspond to sets as realized by other structural set theories, while types of higher h-levels are (higher dimensional) groupoids which are not primitive objects in other foundational theories.
$n$
-types: contractible types, h-proposition, h-sets, h-groupoids, and so on (Voevodsky Reference Voevodsky2015). The h-sets correspond to sets as realized by other structural set theories, while types of higher h-levels are (higher dimensional) groupoids which are not primitive objects in other foundational theories.
In type theory, the types are organized into universes, and UA is formulated relative to a specific universe. Thus, one can have both univalent and non-univalent universes living side by side. Univalence of a universe is mostly a positive feature: since every definable operation respects equality, structures can be transported along equivalences using univalence. One immediate observation is that in a univalent universe containing at least the booleans, the subuniverse of all h-sets in that universe cannot itself be an h-set. However, there are situations where it would be useful to have a family of h-sets which itself is an h-set. One such situation is when constructing the set model of type theory, as for example a category with families (CwF) (Dybjer Reference Dybjer, Berardi and Coppo1996), within HoTT/UF. The natural way of doing this would be to start with a univalent universe
![]() $\mathcal{U}$
and attempt to equip the corresponding category of h-sets (
$\mathcal{U}$
and attempt to equip the corresponding category of h-sets (
![]() $\mathcal{hSet}_{\mathcal{U}}$
) with a CwF structure. Part of the structure of a CwF is a presheaf
$\mathcal{hSet}_{\mathcal{U}}$
) with a CwF structure. Part of the structure of a CwF is a presheaf
![]() $\mathsf{Ty}$
, which is usually formalized in HoTT/UF as a contravariant functor from the category into h-sets. The objects of the source category are thought of as contexts and the
$\mathsf{Ty}$
, which is usually formalized in HoTT/UF as a contravariant functor from the category into h-sets. The objects of the source category are thought of as contexts and the
![]() $\mathsf{Ty}$
-functor specifies what the types are in a given context. The natural choice when organizing
$\mathsf{Ty}$
-functor specifies what the types are in a given context. The natural choice when organizing
![]() $\mathcal{hSet}_{\mathcal{U}}$
into a CwF would be to let
$\mathcal{hSet}_{\mathcal{U}}$
into a CwF would be to let
![]() $\mathsf{Ty}(\Gamma ) := \Gamma \to \mathsf{hSet}_{\mathcal{U}}$
. Informally, the types in context
$\mathsf{Ty}(\Gamma ) := \Gamma \to \mathsf{hSet}_{\mathcal{U}}$
. Informally, the types in context
![]() $\Gamma$
are simply families of h-sets (in
$\Gamma$
are simply families of h-sets (in
![]() $\mathcal{U}$
) over
$\mathcal{U}$
) over
![]() $\Gamma$
. However, since
$\Gamma$
. However, since
![]() $\mathsf{hSet}_{\mathcal{U}}$
is not an h-set, this is ill-typed.
$\mathsf{hSet}_{\mathcal{U}}$
is not an h-set, this is ill-typed.
The agenda of this paper is to explore how one specific choice of a cumulative hierarchy of h-sets, namely the hierarchy
![]() $\mathsf{V}^0$
as defined by Gylterud (Reference Gylterud2018), can be used as a (non-univalent) universe in HoTT/UF. In particular, we will study the structural and categorical properties of this inherently material structure and use it as the basis for a CwF structure.
$\mathsf{V}^0$
as defined by Gylterud (Reference Gylterud2018), can be used as a (non-univalent) universe in HoTT/UF. In particular, we will study the structural and categorical properties of this inherently material structure and use it as the basis for a CwF structure.
![]() $\mathsf{V}^0$
is a good starting point for our investigation into internal models of type theory since its construction uses only elementary type-formers:
$\mathsf{V}^0$
is a good starting point for our investigation into internal models of type theory since its construction uses only elementary type-formers:
![]() $\prod$
-types,
$\prod$
-types,
![]() $\Sigma$
-types, W-types, and identity types. In particular, neither the type
$\Sigma$
-types, W-types, and identity types. In particular, neither the type
![]() $\mathsf{V}^0$
itself nor the
$\mathsf{V}^0$
itself nor the
![]() $\in$
-relation defined on it require higher-inductive types, truncations, or quotients. Since
$\in$
-relation defined on it require higher-inductive types, truncations, or quotients. Since
![]() $\mathsf{V}^0$
is an h-set, and it is closed under the usual type formers, it assembles into a model of MLTT with uniqueness of identity proofs and function extensionality, constructed within MLTT + UA. In this work, UA plays an essential role. We use it to, for instance, characterize the identity type of
$\mathsf{V}^0$
is an h-set, and it is closed under the usual type formers, it assembles into a model of MLTT with uniqueness of identity proofs and function extensionality, constructed within MLTT + UA. In this work, UA plays an essential role. We use it to, for instance, characterize the identity type of
![]() $\mathsf{V}^0$
. Using UA can sometimes result in constructions which lack the nice computational properties one has in bare MLTT. In our case, however, since
$\mathsf{V}^0$
. Using UA can sometimes result in constructions which lack the nice computational properties one has in bare MLTT. In our case, however, since
![]() $\mathsf{V}^0$
itself is built from elementary type-formers, many of the crucial equations, such as the ones for decoding type formers in
$\mathsf{V}^0$
itself is built from elementary type-formers, many of the crucial equations, such as the ones for decoding type formers in
![]() $\mathsf{V}^0$
, hold definitionally. This makes
$\mathsf{V}^0$
, hold definitionally. This makes
![]() $\mathsf{V}^0$
extremely ergonomic from a formalization perspective.
$\mathsf{V}^0$
extremely ergonomic from a formalization perspective.
Indeed, almost all of this paper has been formalized in the proof assistant
![]() $\texttt{Agda}$
(The Agda Development Team 2023) – a dependently typed programming language where one can construct both programs and proofs using the same syntax. Throughout the paper the
$\texttt{Agda}$
(The Agda Development Team 2023) – a dependently typed programming language where one can construct both programs and proofs using the same syntax. Throughout the paper the
![]() $\texttt{Agda}$
logo,
$\texttt{Agda}$
logo, ![]() , next to a result is a clickable link to the
, next to a result is a clickable link to the
![]() $\texttt{Agda}$
code for that result. For basic results and constructions in HoTT/UF, we have used the
$\texttt{Agda}$
code for that result. For basic results and constructions in HoTT/UF, we have used the
![]() $\texttt{agda}$
-
$\texttt{agda}$
-
![]() $\texttt{unimath}$
library (Rijke et al. Reference Rijke, Stenholm, Prieto-Cubides and Bakke2021) – a large
$\texttt{unimath}$
library (Rijke et al. Reference Rijke, Stenholm, Prieto-Cubides and Bakke2021) – a large
![]() $\texttt{Agda}$
library of formalized mathematics from the univalent point of view. Our formalization is in many places more general than the results presented in this paper as many constructions used here have a generalization to higher h-levels, and it is these generalized constructions that have been formalized. They are used for the univalent material set theory developed by Gylterud and Stenholm (Reference Gylterud and Stenholm2023).
$\texttt{Agda}$
library of formalized mathematics from the univalent point of view. Our formalization is in many places more general than the results presented in this paper as many constructions used here have a generalization to higher h-levels, and it is these generalized constructions that have been formalized. They are used for the univalent material set theory developed by Gylterud and Stenholm (Reference Gylterud and Stenholm2023).
1.1 Formal meta-theory and assumptions
While our formalization has been carried out in
![]() $\texttt{Agda}$
on top of
$\texttt{Agda}$
on top of
![]() $\texttt{agda}$
-
$\texttt{agda}$
-
![]() $\texttt{unimath}$
, the results in this paper can be obtained in a more modest type theory and are modular in the sense that if you strengthen the underlying type theory with more types, such as quotients or more universes, these will be reflected in the internal model. The majority of the results assume that one works in MLTT extended with UA. By “MLTT” we take an intensional version of MLTT with the same types and type formers as in Martin-Löf (Reference Martin-Löf, Cohen, Łoś, Pfeiffer and Podewski1982, Table 2), namely:
$\texttt{unimath}$
, the results in this paper can be obtained in a more modest type theory and are modular in the sense that if you strengthen the underlying type theory with more types, such as quotients or more universes, these will be reflected in the internal model. The majority of the results assume that one works in MLTT extended with UA. By “MLTT” we take an intensional version of MLTT with the same types and type formers as in Martin-Löf (Reference Martin-Löf, Cohen, Łoś, Pfeiffer and Podewski1982, Table 2), namely:
-
•
 $\Pi$
-types, denoted
$\Pi$
-types, denoted
 $\Pi _{x:A}B(x)$
with application denoted by juxtaposition and
$\Pi _{x:A}B(x)$
with application denoted by juxtaposition and
 $\lambda$
-abstraction by
$\lambda$
-abstraction by
 ${\lambda }(x:A).b(x)$
.
${\lambda }(x:A).b(x)$
. -
•
 $\Sigma$
-types, denoted
$\Sigma$
-types, denoted
 ${\Sigma }_{x:A}B(x)$
with projections
${\Sigma }_{x:A}B(x)$
with projections
 $\mathsf{pr}_1$
and
$\mathsf{pr}_1$
and
 $\mathsf{pr}_2$
.
$\mathsf{pr}_2$
. -
• W-types, denoted
 $\mathsf{W}_{x:A}\,B(x)$
with canonical elements
$\mathsf{W}_{x:A}\,B(x)$
with canonical elements
 $\mathsf{sup}\,A\,f$
.
$\mathsf{sup}\,A\,f$
. -
• Identity types, denoted
 $a=a'$
, sometimes subscripted
$a=a'$
, sometimes subscripted
 $a=_Aa'$
for clarity, with reflective elements
$a=_Aa'$
for clarity, with reflective elements
 $\mathsf{refl}_a : a = a$
.
$\mathsf{refl}_a : a = a$
. -
• Binary sum types, denoted
 $A+B$
with injections
$A+B$
with injections
 $\mathsf{inl}$
and
$\mathsf{inl}$
and
 $\mathsf{inr}$
.
$\mathsf{inr}$
. -
• Base types:
 $\mathsf{empty}$
,
$\mathsf{empty}$
,
 $\mathsf{unit}$
,
$\mathsf{unit}$
,
 $\mathsf{bool}$
,
$\mathsf{bool}$
,
 $\mathbb{N}$
, with
$\mathbb{N}$
, with
 $\mathsf{tt}$
being the canonical element of
$\mathsf{tt}$
being the canonical element of
 $\mathsf{unit}$
,
$\mathsf{unit}$
,
 $\mathsf{true}, \mathsf{false}$
the elements of
$\mathsf{true}, \mathsf{false}$
the elements of
 $\mathsf{bool}$
, and elements of
$\mathsf{bool}$
, and elements of
 $\mathbb{N}$
denoted by
$\mathbb{N}$
denoted by
 $\mathsf{0}$
and
$\mathsf{0}$
and
 $\mathsf{s}\,n$
. We also let
$\mathsf{s}\,n$
. We also let
 $\mathsf{Fin}\,n$
denote the type with
$\mathsf{Fin}\,n$
denote the type with
 $n$
elements.
$n$
elements. -
• Universes, denoted
 $\mathcal{U}$
, closed under the aforementioned type formers. For constructions needing more than one universe level, we will subscript them
$\mathcal{U}$
, closed under the aforementioned type formers. For constructions needing more than one universe level, we will subscript them
 ${\mathcal{U}}_0, \mathcal{U}_1, \cdots, \mathcal{U}_\ell, \cdots$
.
${\mathcal{U}}_0, \mathcal{U}_1, \cdots, \mathcal{U}_\ell, \cdots$
.
One important difference to Martin-Löf (Reference Martin-Löf, Cohen, Łoś, Pfeiffer and Podewski1982) though is that we of course do not assume equality reflection and instead have intensional identity types as in Martin-Löf (Reference Martin-Löf, Rose and Shepherdson1975). Another difference is that we, for convenience, assume definitional
![]() $\eta$
for
$\eta$
for
![]() $\Sigma$
-types. Our system is hence very similar to Martín Escardó’s spartan MLTT (Escardó Reference Escardó2019) and the basic system used in
$\Sigma$
-types. Our system is hence very similar to Martín Escardó’s spartan MLTT (Escardó Reference Escardó2019) and the basic system used in
![]() $\texttt{UniMath}$
(Voevodsky et al. Reference Voevodsky, Ahrens and Grayson2020), but with the addition of W-types. The only construction going beyond this is the construction of set quotients in Section 3.3, which assumes that the universe has set quotients. The construction of subuniverses in Section 3.5 also naturally assumes that the starting universe has subuniverses as well. But even with these extensions, the development is completely constructive and predicative, in particular we do not rely on LEM, AC, or any resizing principles (Voevodsky Reference Voevodsky2011).
$\texttt{UniMath}$
(Voevodsky et al. Reference Voevodsky, Ahrens and Grayson2020), but with the addition of W-types. The only construction going beyond this is the construction of set quotients in Section 3.3, which assumes that the universe has set quotients. The construction of subuniverses in Section 3.5 also naturally assumes that the starting universe has subuniverses as well. But even with these extensions, the development is completely constructive and predicative, in particular we do not rely on LEM, AC, or any resizing principles (Voevodsky Reference Voevodsky2011).
For convenience, we also rely on definitions and notational conventions from the HoTT Book. Among these are:
-
• Definitional/judgmental equality is denoted by
 $ \equiv $
.
$ \equiv $
. -
• Homotopy of functions is denoted
 $f \sim g$
, with
$f \sim g$
, with
 $\mathsf{refl\mbox{-}htpy}$
denoting
$\mathsf{refl\mbox{-}htpy}$
denoting
 ${\lambda }a.\mathsf{refl}$
${\lambda }a.\mathsf{refl}$
-
• Type equivalence is denoted
 $A \simeq B$
with identity equivalence
$A \simeq B$
with identity equivalence
 $\mathsf{id\mbox{-}equiv} : A \simeq A$
.
$\mathsf{id\mbox{-}equiv} : A \simeq A$
. -
• h-levels/
 $n$
-types, in this paper we mainly work with types in
$n$
-types, in this paper we mainly work with types in
 $\mathsf{hProp}_{\mathcal{U}}$
and
$\mathsf{hProp}_{\mathcal{U}}$
and
 $\mathsf{hSet}_{\mathcal{U}}$
, that is the h-propositions and h-sets in a given universe.
$\mathsf{hSet}_{\mathcal{U}}$
, that is the h-propositions and h-sets in a given universe. -
• We use pattern-matching freely in definitions and proofs, instead of explicit eliminators.
1.2 Contributions of the paper
While Section 2 sets the stage by recounting the definition of
![]() $\mathsf{V}^0$
, the foundation of this paper’s contributions is built in Section 3: we show that
$\mathsf{V}^0$
, the foundation of this paper’s contributions is built in Section 3: we show that
![]() $\mathsf{V}^0$
forms a Tarski-style universe closed under
$\mathsf{V}^0$
forms a Tarski-style universe closed under
![]() $\prod$
-types,
$\prod$
-types,
![]() $\Sigma$
-types, identity types, coproducts, set quotients, and that it contains basic types like
$\Sigma$
-types, identity types, coproducts, set quotients, and that it contains basic types like
![]() $\mathsf{empty}$
,
$\mathsf{empty}$
,
![]() $\mathsf{unit}$
,
$\mathsf{unit}$
,
![]() $\mathsf{bool}$
,
$\mathsf{bool}$
,
![]() $\mathbb{N}$
and a hierarchy of subuniverses. Proposition 18 is central to this, as it characterizes the small types representable in
$\mathbb{N}$
and a hierarchy of subuniverses. Proposition 18 is central to this, as it characterizes the small types representable in
![]() $\mathsf{V}^0$
as those which can be embedded into it. Since the decoding of all type formers is definitional, this gives an ergonomic universe of h-sets which itself is an h-set, which can be used in HoTT/UF. In Section 4, we shed light on the categorical properties of
$\mathsf{V}^0$
as those which can be embedded into it. Since the decoding of all type formers is definitional, this gives an ergonomic universe of h-sets which itself is an h-set, which can be used in HoTT/UF. In Section 4, we shed light on the categorical properties of
![]() $\mathsf{V}^0$
. In particular, we show that it is a locally cartesian closed category, with finite limits and colimits, and that there is a full and faithful functor back to
$\mathsf{V}^0$
. In particular, we show that it is a locally cartesian closed category, with finite limits and colimits, and that there is a full and faithful functor back to
![]() $\mathcal{hSet}_{\mathcal{U}}$
which preserves this structure. The final technical contribution is the construction of an extensional model of MLTT internal in MLTT + UA, based on
$\mathcal{hSet}_{\mathcal{U}}$
which preserves this structure. The final technical contribution is the construction of an extensional model of MLTT internal in MLTT + UA, based on
![]() $\mathsf{V}^0$
. This is done by giving CwF structure to
$\mathsf{V}^0$
. This is done by giving CwF structure to
![]() $\mathsf{V}^0$
. The formalization of this includes contributions to
$\mathsf{V}^0$
. The formalization of this includes contributions to
![]() $\texttt{agda}$
-
$\texttt{agda}$
-
![]() $\texttt{unimath}$
, in particular the definition of a CwF with associated structure. A bibliographic contribution can be found in Section 6, where we compare our constructions to existing developments on the relationship between set theory and type theory. This relationship has taken many forms over the years and goes back to the 1970s.
$\texttt{unimath}$
, in particular the definition of a CwF with associated structure. A bibliographic contribution can be found in Section 6, where we compare our constructions to existing developments on the relationship between set theory and type theory. This relationship has taken many forms over the years and goes back to the 1970s.
2. Definition of
 $\mathsf{V}^0$
and Its Basic Properties
$\mathsf{V}^0$
and Its Basic Properties
The ideas behind
![]() $\mathsf{V}^0$
trace back to The type theoretic interpretation of constructive set theory by Aczel (Reference Aczel, Macintyre, Pacholski and Paris1978). In op. cit., Aczel constructed a model of set theory in dependent type theory relying upon a non-trivial defined equality relation on the underlying type of the model in order to (hereditarily) force set-extensionality. This underlying type of the model is what we in modern parlance would call a
$\mathsf{V}^0$
trace back to The type theoretic interpretation of constructive set theory by Aczel (Reference Aczel, Macintyre, Pacholski and Paris1978). In op. cit., Aczel constructed a model of set theory in dependent type theory relying upon a non-trivial defined equality relation on the underlying type of the model in order to (hereditarily) force set-extensionality. This underlying type of the model is what we in modern parlance would call a
![]() $\mathsf{W}$
-type. To construct
$\mathsf{W}$
-type. To construct
![]() $\mathsf{V}^0$
, we opt to carve out a subtype of a
$\mathsf{V}^0$
, we opt to carve out a subtype of a
![]() $\mathsf{W}$
-type rather than take such a quotient. Instead of defining an equivalence relation which identifies the elements of the
$\mathsf{W}$
-type rather than take such a quotient. Instead of defining an equivalence relation which identifies the elements of the
![]() $\mathsf{W}$
-type which represent the same set, we shall identify a subtype of the
$\mathsf{W}$
-type which represent the same set, we shall identify a subtype of the
![]() $\mathsf{W}$
-type which contains only the canonical representations of each (iterative) set. Thus, we get a model of set theory in type theory where the equality is interpreted as the identity type and no further non-trivial identifications are required.
$\mathsf{W}$
-type which contains only the canonical representations of each (iterative) set. Thus, we get a model of set theory in type theory where the equality is interpreted as the identity type and no further non-trivial identifications are required.
In this section, we will review the definition of
![]() $\mathsf{V}^0$
and prove some properties about it. In particular, we will show that
$\mathsf{V}^0$
and prove some properties about it. In particular, we will show that
![]() $\mathsf{V}^0$
is an h-set. In order to define
$\mathsf{V}^0$
is an h-set. In order to define
![]() $\mathsf{V}^0$
, we start by recalling the
$\mathsf{V}^0$
, we start by recalling the
![]() $\mathsf{W}$
-type Aczel used: “the unrestricted iterative hierarchy”. It is the type of well-founded trees with branching types chosen freely from a fixed universe
$\mathsf{W}$
-type Aczel used: “the unrestricted iterative hierarchy”. It is the type of well-founded trees with branching types chosen freely from a fixed universe
![]() ${\mathcal{U}}_\ell$
.
${\mathcal{U}}_\ell$
.
Definition 1 (![]() ). Given a universe
). Given a universe
![]() ${\mathcal{U}}_\ell$
, we define the type
${\mathcal{U}}_\ell$
, we define the type
![]() $\mathsf{V}^\infty_\ell$
as
$\mathsf{V}^\infty_\ell$
as
We will usually omit the universe level
![]() $\ell$
for
$\ell$
for
![]() ${\mathcal{U}}_\ell$
and
${\mathcal{U}}_\ell$
and
![]() ${\mathsf{V}}^\infty_\ell$
, and write simply
${\mathsf{V}}^\infty_\ell$
, and write simply
![]() $\mathcal{U}$
and
$\mathcal{U}$
and
![]() $\mathsf{V}^\infty$
. When seeing
$\mathsf{V}^\infty$
. When seeing
![]() $\mathsf{V}^\infty$
as a type of sets, an element
$\mathsf{V}^\infty$
as a type of sets, an element
![]() $\mathsf{sup}\,A\,f :{\mathsf{V}^\infty }$
represents a set whose elements are indexed by the type
$\mathsf{sup}\,A\,f :{\mathsf{V}^\infty }$
represents a set whose elements are indexed by the type
![]() $A : \mathcal{U}$
. The function
$A : \mathcal{U}$
. The function
![]() $f : A\to {\mathsf{V}^\infty }$
picks out the element at each index. Since the function
$f : A\to {\mathsf{V}^\infty }$
picks out the element at each index. Since the function
![]() $f$
need not be injective, the same element can be picked out several times. Indeed, the role of Aczel’s equivalence relation on this type was to erase this multiplicity. If we instead omit this further identification,
$f$
need not be injective, the same element can be picked out several times. Indeed, the role of Aczel’s equivalence relation on this type was to erase this multiplicity. If we instead omit this further identification,
![]() $\mathsf{V}^\infty$
can be seen as a type of multisets (Gylterud Reference Gylterud2020).
$\mathsf{V}^\infty$
can be seen as a type of multisets (Gylterud Reference Gylterud2020).
Notation 2.
Given
![]() $x :{\mathsf{V}^\infty }$
, we follow Aczel (Reference Aczel, Macintyre, Pacholski and Paris1978) and define a pair of operations
$x :{\mathsf{V}^\infty }$
, we follow Aczel (Reference Aczel, Macintyre, Pacholski and Paris1978) and define a pair of operations
![]() $\overline{x} : \mathcal{U}$
and
$\overline{x} : \mathcal{U}$
and
![]() $\widetilde x : \overline x\to {\mathsf{V}^\infty }$
, as follows:
$\widetilde x : \overline x\to {\mathsf{V}^\infty }$
, as follows:
We present two characterizations of equality in
![]() $\mathsf{V}^\infty$
as both are useful in different contexts. We note that both characterizations rely on univalence.
$\mathsf{V}^\infty$
as both are useful in different contexts. We note that both characterizations rely on univalence.
The first is an instance of a more general characterization of equality in
![]() $\mathsf{W}$
-types (Gylterud Reference Gylterud2020, Lemma 1). It states that two elements are equal if they have equivalent underlying indexing types and this equivalence is coherent with respect to the functions picking out the elements.
$\mathsf{W}$
-types (Gylterud Reference Gylterud2020, Lemma 1). It states that two elements are equal if they have equivalent underlying indexing types and this equivalence is coherent with respect to the functions picking out the elements.
Theorem 3 (Gylterud Reference Gylterud2020, Theorem 1, ![]() ). For two elements
). For two elements
![]() $x,y :{\mathsf{V}^\infty }$
the canonical map
$x,y :{\mathsf{V}^\infty }$
the canonical map
 \begin{equation*} \left (x = y\right ) \to \left (\sum _{e :\,\overline {x} \simeq \overline {y}} \widetilde {x} \sim \widetilde {y} \circ e\right ) \end{equation*}
\begin{equation*} \left (x = y\right ) \to \left (\sum _{e :\,\overline {x} \simeq \overline {y}} \widetilde {x} \sim \widetilde {y} \circ e\right ) \end{equation*}
which sends
![]() $\mathsf{refl}$
to
$\mathsf{refl}$
to
![]() $(\mathsf{id\mbox{-}equiv}, \mathsf{refl\mbox{-}htpy})$
, is an equivalence.
$(\mathsf{id\mbox{-}equiv}, \mathsf{refl\mbox{-}htpy})$
, is an equivalence.
The second characterization of equality in
![]() $\mathsf{V}^\infty$
states that two elements in
$\mathsf{V}^\infty$
states that two elements in
![]() $\mathsf{V}^\infty$
are equal when the functions picking out the elements are fiberwise equivalent. Intuitively, this means that they pick out the same elements the same number of times. One can think of this characterization of equality as a higher level generalization of the axiom of extensionality.
$\mathsf{V}^\infty$
are equal when the functions picking out the elements are fiberwise equivalent. Intuitively, this means that they pick out the same elements the same number of times. One can think of this characterization of equality as a higher level generalization of the axiom of extensionality.
Theorem 4 (Gylterud Reference Gylterud2020, Theorem 2, ![]() ). For two elements
). For two elements
![]() $x,y :{\mathsf{V}^\infty }$
the canonical map
$x,y :{\mathsf{V}^\infty }$
the canonical map
which sends
![]() $\mathsf{refl}$
to
$\mathsf{refl}$
to
![]() ${\lambda }z.\mathsf{id\mbox{-}equiv}$
, is an equivalence.
${\lambda }z.\mathsf{id\mbox{-}equiv}$
, is an equivalence.
Proof. We reproduce the proof here for convenience. We have the following chain of equivalences:
 \begin{align*} \left (x = y\right ) \simeq \left (\sum _{e :\,\overline{x}\, \simeq \,\overline{y}} \widetilde{x} \sim \widetilde{y} \circ e\right ) \simeq \left (\prod _{z :{\mathsf{V}^\infty }} \mathsf{fib}\,\widetilde{x}\,z \simeq \mathsf{fib}\,\widetilde{y}\,z\right ) \end{align*}
\begin{align*} \left (x = y\right ) \simeq \left (\sum _{e :\,\overline{x}\, \simeq \,\overline{y}} \widetilde{x} \sim \widetilde{y} \circ e\right ) \simeq \left (\prod _{z :{\mathsf{V}^\infty }} \mathsf{fib}\,\widetilde{x}\,z \simeq \mathsf{fib}\,\widetilde{y}\,z\right ) \end{align*}
The first equivalence is the one constructed in Theorem3. The second equivalence is proven by Gylterud (Reference Gylterud2020, Lemma 5). One directly checks that the constructed equivalence computes as desired for
![]() $\mathsf{refl}$
.
$\mathsf{refl}$
.
We will not dwell much on our structures being models of material set theory, but rather focus on their structural properties in this paper. However, we will define the elementhood relation on
![]() $\mathsf{V}^\infty$
following Gylterud (Reference Gylterud2020). This elementhood relation, and its well-foundedness, will be used in later constructions.
$\mathsf{V}^\infty$
following Gylterud (Reference Gylterud2020). This elementhood relation, and its well-foundedness, will be used in later constructions.
Definition 5 (Elementhood, ![]() ). We define
). We define
![]() $ \in \,:\,{\mathsf{V}^\infty }\to {\mathsf{V}^\infty }\to \mathcal{U}$
by
$ \in \,:\,{\mathsf{V}^\infty }\to {\mathsf{V}^\infty }\to \mathcal{U}$
by
In particular, for canonical elements we get
 \begin{equation*} \left (x \in \mathsf {sup}\,A\,f \right ) \equiv \left (\sum _{a:A}f\,a=x\right ) \end{equation*}
\begin{equation*} \left (x \in \mathsf {sup}\,A\,f \right ) \equiv \left (\sum _{a:A}f\,a=x\right ) \end{equation*}
The exensionality property of Theorem4 can now be reformulated as an equivalence
 \begin{equation*} \left (x = y\right ) \simeq \left (\prod _{z:{\mathsf {V}^\infty }} z \in x \simeq z \in y\right ) \end{equation*}
\begin{equation*} \left (x = y\right ) \simeq \left (\prod _{z:{\mathsf {V}^\infty }} z \in x \simeq z \in y\right ) \end{equation*}
By virtue of univalence, we obtain this extensionality result without taking quotients by set extensionality or bisimulation like Aczel does. In particular, we are able to avoid working with quotients or setoids while still achieving the equivalence above.
Note that
![]() $x \in y$
need not be an h-proposition, that is,
$x \in y$
need not be an h-proposition, that is,
![]() $y$
could contain several instances of
$y$
could contain several instances of
![]() $x$
. This is because, as discussed above, there is no restriction on the function
$x$
. This is because, as discussed above, there is no restriction on the function
![]() $\widetilde{y}$
and its fibers. We will soon focus our attention to a subtype of
$\widetilde{y}$
and its fibers. We will soon focus our attention to a subtype of
![]() $\mathsf{V}^\infty$
where these fibers are h-propositions, that is, where they have at most one inhabitant. But first, we will look at how some familiar sets can be represented in
$\mathsf{V}^\infty$
where these fibers are h-propositions, that is, where they have at most one inhabitant. But first, we will look at how some familiar sets can be represented in
![]() $\mathsf{V}^\infty$
.
$\mathsf{V}^\infty$
.
We define the empty set as follows:
This represents the empty set since for any
![]() $x :{\mathsf{V}^\infty }$
, the type
$x :{\mathsf{V}^\infty }$
, the type
![]() $x \in \emptyset$
is empty.
$x \in \emptyset$
is empty.
Given
![]() $x :{\mathsf{V}^\infty }$
, we can construct the singleton containing
$x :{\mathsf{V}^\infty }$
, we can construct the singleton containing
![]() $x$
as follows:
$x$
as follows:
The type
![]() $x \in \{ x \}$
is inhabited by
$x \in \{ x \}$
is inhabited by
![]() $(\mathsf{tt},\mathsf{refl})$
. Indeed, for any
$(\mathsf{tt},\mathsf{refl})$
. Indeed, for any
![]() $y :{\mathsf{V}^\infty }$
, there is an equivalence
$y :{\mathsf{V}^\infty }$
, there is an equivalence
![]() $\left (y \in \{ x \} \right ) \simeq \left (y = x\right )$
.
$\left (y \in \{ x \} \right ) \simeq \left (y = x\right )$
.
We can also construct the unordered pair of two elements
![]() $x, y :{\mathsf{V}^\infty }$
:
$x, y :{\mathsf{V}^\infty }$
:
For any
![]() $z :{\mathsf{V}^\infty }$
, the type
$z :{\mathsf{V}^\infty }$
, the type
![]() $z \in \{x,y\}$
is equivalent to
$z \in \{x,y\}$
is equivalent to
![]() $(z = x)\,+\,(z = y)$
. Note in particular that the type
$(z = x)\,+\,(z = y)$
. Note in particular that the type
![]() $x \in \{x,x\}$
is equivalent to
$x \in \{x,x\}$
is equivalent to
![]() $(x = x)\,+\,(x = x)$
, which contains at least two distinct elements. Thus,
$(x = x)\,+\,(x = x)$
, which contains at least two distinct elements. Thus,
![]() $\{x,x\}$
is a multiset that contains two copies of
$\{x,x\}$
is a multiset that contains two copies of
![]() $x$
. Using images one can whittle this down to an iterative set, see the forthcoming paper (Gylterud and Stenholm Reference Gylterud and Stenholm2023) for details on the various types of pairing in higher h-levels.
$x$
. Using images one can whittle this down to an iterative set, see the forthcoming paper (Gylterud and Stenholm Reference Gylterud and Stenholm2023) for details on the various types of pairing in higher h-levels.
In order to construct a universe of sets, we need to ensure that the
![]() $\in$
-relation is h-proposition valued, that is, that any element occurs at most once in a set. As the type
$\in$
-relation is h-proposition valued, that is, that any element occurs at most once in a set. As the type
![]() $x \in y$
is the type of homotopy fibers of
$x \in y$
is the type of homotopy fibers of
![]() $\widetilde{y}$
over
$\widetilde{y}$
over
![]() $x$
, this type would be an h-proposition if
$x$
, this type would be an h-proposition if
![]() $\widetilde{y}$
was an embedding:
$\widetilde{y}$
was an embedding:
Definition 6 ((HoTT Book, Definition 4.6.1), ![]() ). A function
). A function
![]() $f : A\to B$
is an embedding if
$f : A\to B$
is an embedding if
![]() $\mathsf{ap}\,f\,x\,y : x = y\to f\,x = f\,y$
is an equivalence for all
$\mathsf{ap}\,f\,x\,y : x = y\to f\,x = f\,y$
is an equivalence for all
![]() $x\,y : A$
.
$x\,y : A$
.
We write
![]() $\mathsf{is\mbox{-}emb}\,f$
for the type of proofs that
$\mathsf{is\mbox{-}emb}\,f$
for the type of proofs that
![]() $f$
is an embedding and
$f$
is an embedding and
![]() $f : A \hookrightarrow B$
for
$f : A \hookrightarrow B$
for
![]() ${\sum }_{f : A\to B}\,\mathsf{is\mbox{-}emb}\,f$
. A key observation about embeddings is
${\sum }_{f : A\to B}\,\mathsf{is\mbox{-}emb}\,f$
. A key observation about embeddings is
Lemma 7 (HoTT Book, Lemma 7.6.2, ![]() ). A function
). A function
![]() $f : A\to B$
is an embedding if and only if it has h-propositional fibers.
$f : A\to B$
is an embedding if and only if it has h-propositional fibers.
This motivates Gylterud’s definition of iterative sets in HoTT/UF (Gylterud Reference Gylterud2018):
Definition 8 (Iterative sets, ![]() ). We define
). We define
![]() $\mathsf{is\mbox{-}iterative\mbox{-}set} :{\mathsf{V}^\infty }\to \mathcal{U}$
as
$\mathsf{is\mbox{-}iterative\mbox{-}set} :{\mathsf{V}^\infty }\to \mathcal{U}$
as
 \begin{equation*} \mathsf {is\mbox {-}iterative\mbox {-}set}\,(\mathsf {sup}\,A\,f) := (\mathsf {is\mbox {-}emb}\,f) \times \left ( \prod _{a : A} \mathsf {is\mbox {-}iterative\mbox {-}set}\,(f\,a) \right ) \end{equation*}
\begin{equation*} \mathsf {is\mbox {-}iterative\mbox {-}set}\,(\mathsf {sup}\,A\,f) := (\mathsf {is\mbox {-}emb}\,f) \times \left ( \prod _{a : A} \mathsf {is\mbox {-}iterative\mbox {-}set}\,(f\,a) \right ) \end{equation*}
The idea is to pick out those elements
![]() $x :{\mathsf{V}^\infty }$
for which the function that selects elements is an embedding and such that the elements of
$x :{\mathsf{V}^\infty }$
for which the function that selects elements is an embedding and such that the elements of
![]() $x$
satisfy the same criterion, recursively. This means that any
$x$
satisfy the same criterion, recursively. This means that any
![]() $y :{\mathsf{V}^\infty }$
element is a member of
$y :{\mathsf{V}^\infty }$
element is a member of
![]() $x$
at most once and, consequently,
$x$
at most once and, consequently,
![]() $x$
encode a set rather than a multiset. For these sets, the
$x$
encode a set rather than a multiset. For these sets, the
![]() $\in$
-relation becomes h-proposition valued by Lemma 7, as desired.
$\in$
-relation becomes h-proposition valued by Lemma 7, as desired.
Not all the elements in
![]() $\mathsf{V}^\infty$
are iterative sets. For example, the unordered pair
$\mathsf{V}^\infty$
are iterative sets. For example, the unordered pair
![]() $\{ \emptyset, \emptyset \}$
from above is not an iterative set as the function in the definition is not an embedding.Footnote
2
On the other hand, the empty set,
$\{ \emptyset, \emptyset \}$
from above is not an iterative set as the function in the definition is not an embedding.Footnote
2
On the other hand, the empty set,
![]() $\emptyset$
, is an iterative set, since
$\emptyset$
, is an iterative set, since
![]() $\mathsf{empty}\mbox{-}\mathsf{elim}$
is always an embedding, regardless of the codomain. Moreover, for any iterative set
$\mathsf{empty}\mbox{-}\mathsf{elim}$
is always an embedding, regardless of the codomain. Moreover, for any iterative set
![]() $x : \mathsf{V}^0$
, the singleton
$x : \mathsf{V}^0$
, the singleton
![]() $\{x\}$
is an iterative set since any map from an h-proposition into an h-set is an embedding (we will see that
$\{x\}$
is an iterative set since any map from an h-proposition into an h-set is an embedding (we will see that
![]() $\mathsf{V}^0$
is an h-set in Theorem12). Furthermore, if
$\mathsf{V}^0$
is an h-set in Theorem12). Furthermore, if
![]() $x$
and
$x$
and
![]() $y$
are distinct iterative sets then
$y$
are distinct iterative sets then
![]() $\{ x, y \}$
is also an iterative set. To see this, it suffices to verify that the below map
$\{ x, y \}$
is also an iterative set. To see this, it suffices to verify that the below map
![]() ${\varphi } : \mathsf{bool}\to \mathsf{V}^0$
is an embedding if it is injective:
${\varphi } : \mathsf{bool}\to \mathsf{V}^0$
is an embedding if it is injective:
Given
![]() $b_1, b_2 : \mathsf{bool}$
, either
$b_1, b_2 : \mathsf{bool}$
, either
![]() $b_1 = b_2$
, in which case we are done, or
$b_1 = b_2$
, in which case we are done, or
![]() $b_1 \neq b_2$
, in which case we get a path between
$b_1 \neq b_2$
, in which case we get a path between
![]() $x$
and
$x$
and
![]() $y$
, from which the result follows by assumption.
$y$
, from which the result follows by assumption.
Definition 9 (Type of iterative sets, ![]() ). We define the type of iterative sets as follows:
). We define the type of iterative sets as follows:
We will extend the previously introduced notation to apply to iterative sets:

Moreover, the elementhood relation
![]() $\in$
defined on
$\in$
defined on
![]() $\mathsf{V}^\infty$
gives rise to an elementhood relation for
$\mathsf{V}^\infty$
gives rise to an elementhood relation for
![]() $\mathsf{V}^0$
given by projecting out the underlying elements in
$\mathsf{V}^0$
given by projecting out the underlying elements in
![]() $\mathsf{V}^\infty$
and applying
$\mathsf{V}^\infty$
and applying
![]() $\in$
: for any
$\in$
: for any
![]() $x,y : \mathsf{V}^0$
we let
$x,y : \mathsf{V}^0$
we let
![]() $x \in y := \mathsf{pr}_1 \, x \in \mathsf{pr}_1 \, y$
. We use the same notation for both relations, as it will be clear from context which one is meant.
$x \in y := \mathsf{pr}_1 \, x \in \mathsf{pr}_1 \, y$
. We use the same notation for both relations, as it will be clear from context which one is meant.
Lemma 10 (![]() ). For all
). For all
![]() $x :{\mathsf{V}^\infty }$
, the type
$x :{\mathsf{V}^\infty }$
, the type
![]() $\mathsf{is\mbox{-}iterative\mbox{-}set}\,x$
is an h-proposition.
$\mathsf{is\mbox{-}iterative\mbox{-}set}\,x$
is an h-proposition.
Proof.
This follows by induction on
![]() $x :{\mathsf{V}^\infty }$
, together with the fact that being an embedding, is an h-proposition.
$x :{\mathsf{V}^\infty }$
, together with the fact that being an embedding, is an h-proposition.
Corollary 11 (![]() ). The projection
). The projection
![]() $\mathsf{pr}_1 : \mathsf{V}^0\to {\mathsf{V}^\infty }$
is an embedding, that is,
$\mathsf{pr}_1 : \mathsf{V}^0\to {\mathsf{V}^\infty }$
is an embedding, that is,
![]() $\mathsf{V}^0$
is a subtype of
$\mathsf{V}^0$
is a subtype of
![]() $\mathsf{V}^\infty$
.
$\mathsf{V}^\infty$
.
Proof.
This is an instance of the fact that for any type
![]() $A$
and family
$A$
and family
![]() $P$
of h-propositions over
$P$
of h-propositions over
![]() $A$
, the first projection
$A$
, the first projection
![]() $\mathsf{pr}_1 : \sum _{a : A} P\,a\to A$
is an embedding.
$\mathsf{pr}_1 : \sum _{a : A} P\,a\to A$
is an embedding.
Having an embedding
![]() $\mathsf{V}^0 \hookrightarrow {\mathsf{V}^\infty }$
means that equality in
$\mathsf{V}^0 \hookrightarrow {\mathsf{V}^\infty }$
means that equality in
![]() $\mathsf{V}^0$
is exactly equality of the corresponding elements in
$\mathsf{V}^0$
is exactly equality of the corresponding elements in
![]() $\mathsf{V}^\infty$
. Since we have already characterized equality in
$\mathsf{V}^\infty$
. Since we have already characterized equality in
![]() $\mathsf{V}^\infty$
, we can use this characterization to show that
$\mathsf{V}^\infty$
, we can use this characterization to show that
![]() $\mathsf{V}^0$
is an h-set.
$\mathsf{V}^0$
is an h-set.
Theorem 12 (![]() ).
).
![]() $\mathsf{V}^0$
is an h-set.
$\mathsf{V}^0$
is an h-set.
Proof.
For
![]() $(x,p), (y,q) : \mathsf{V}^0$
, we have a chain of equivalences:
$(x,p), (y,q) : \mathsf{V}^0$
, we have a chain of equivalences:
 \begin{equation*} \left ((x,p) =_{\mathsf {V}^0} (y,q)\right ) \simeq \left (x =_{{\mathsf {V}^\infty }} y\right ) \simeq \left (\prod _{z : {\mathsf {V}^\infty }} z \in x \simeq z \in y\right ) \end{equation*}
\begin{equation*} \left ((x,p) =_{\mathsf {V}^0} (y,q)\right ) \simeq \left (x =_{{\mathsf {V}^\infty }} y\right ) \simeq \left (\prod _{z : {\mathsf {V}^\infty }} z \in x \simeq z \in y\right ) \end{equation*}
The first equivalence is the characterization of equality in subtypes. The second is Theorem4. Note that
![]() $z \in x \equiv \mathsf{fib}\,\widetilde{x}\,z$
, and
$z \in x \equiv \mathsf{fib}\,\widetilde{x}\,z$
, and
![]() $\widetilde{x}$
is an embedding by
$\widetilde{x}$
is an embedding by
![]() $p$
. Thus
$p$
. Thus
![]() $z \in x$
is an h-proposition. The same holds for
$z \in x$
is an h-proposition. The same holds for
![]() $z \in y$
. Thus, the rightmost type in the chain of equivalences above is a family of equivalences between h-propositions and is thus an h-proposition. It then follows that the type
$z \in y$
. Thus, the rightmost type in the chain of equivalences above is a family of equivalences between h-propositions and is thus an h-proposition. It then follows that the type
![]() $(x,p) =_{\mathsf{V}^0} (y,q)$
is an h-proposition.
$(x,p) =_{\mathsf{V}^0} (y,q)$
is an h-proposition.
Given a type
![]() $A : \mathcal{U}$
and an embedding
$A : \mathcal{U}$
and an embedding
![]() $f : A \hookrightarrow \mathsf{V}^0$
, we can construct an element of
$f : A \hookrightarrow \mathsf{V}^0$
, we can construct an element of
![]() $\mathsf{V}^0$
. This function is the counterpart to
$\mathsf{V}^0$
. This function is the counterpart to
![]() $\mathsf{sup}$
for
$\mathsf{sup}$
for
![]() $\mathsf{V}^\infty$
, and while it is not formally a constructor it behaves like one in that the recursion and elimination principles, with fitting computation rules, are provable for it (Gylterud and Stenholm Reference Gylterud and Stenholm2023).
$\mathsf{V}^\infty$
, and while it is not formally a constructor it behaves like one in that the recursion and elimination principles, with fitting computation rules, are provable for it (Gylterud and Stenholm Reference Gylterud and Stenholm2023).
Remark 13. The underscores in the constructions below denote proof terms for the h-propositions involved. We omit these for readability and refer the interested reader to the formalization.
Definition 14 (![]() ). We define the following function:
). We define the following function:
 \begin{align*} &\mathsf{sup}^0 : \left (\sum _{A : \mathcal{U}} A \hookrightarrow \mathsf{V}^0\right )\to \mathsf{V}^0 \\ &\mathsf{sup}^0\,(A,f) := \left (\mathsf{sup}\,A\,(\pi _0 \circ f), \_\right ) \end{align*}
\begin{align*} &\mathsf{sup}^0 : \left (\sum _{A : \mathcal{U}} A \hookrightarrow \mathsf{V}^0\right )\to \mathsf{V}^0 \\ &\mathsf{sup}^0\,(A,f) := \left (\mathsf{sup}\,A\,(\pi _0 \circ f), \_\right ) \end{align*}
Similarly, given an element of
![]() $\mathsf{V}^0$
, we can extract the underlying type and embedding.
$\mathsf{V}^0$
, we can extract the underlying type and embedding.
Definition 15 (![]() ). We define the following function:
). We define the following function:
 \begin{align*} &\mathsf{desup}^0 : \mathsf{V}^0\to \left (\sum _{A : \mathcal{U}} A \hookrightarrow \mathsf{V}^0\right ) \\ &\mathsf{desup}^0\,(\mathsf{sup}\,A\,f, \_) := (A, (f, \_)) \end{align*}
\begin{align*} &\mathsf{desup}^0 : \mathsf{V}^0\to \left (\sum _{A : \mathcal{U}} A \hookrightarrow \mathsf{V}^0\right ) \\ &\mathsf{desup}^0\,(\mathsf{sup}\,A\,f, \_) := (A, (f, \_)) \end{align*}
By virtue of being a
![]() $\mathsf{W}$
-type,
$\mathsf{W}$
-type,
![]() $\mathsf{V}^\infty$
is the initial algebra to the polynomial functor
$\mathsf{V}^\infty$
is the initial algebra to the polynomial functor
 \begin{equation*} X \mapsto \left (\sum _{A : \mathcal {U}} A \to X\right ) \end{equation*}
\begin{equation*} X \mapsto \left (\sum _{A : \mathcal {U}} A \to X\right ) \end{equation*}
Similarly,
![]() $\mathsf{V}^0$
is the initial algebra for the functor
$\mathsf{V}^0$
is the initial algebra for the functor
![]() $X \mapsto \left (\sum _{A : \mathcal{U}} A \hookrightarrow X\right )$
, even though this functor is not polynomial. The initiality induces an equivalence
$X \mapsto \left (\sum _{A : \mathcal{U}} A \hookrightarrow X\right )$
, even though this functor is not polynomial. The initiality induces an equivalence
![]() $\mathsf{V}^0 \simeq \left (\sum _{A : \mathcal{U}} A \hookrightarrow \mathsf{V}^0\right )$
, realized by the maps
$\mathsf{V}^0 \simeq \left (\sum _{A : \mathcal{U}} A \hookrightarrow \mathsf{V}^0\right )$
, realized by the maps
![]() $\mathsf{sup}^0$
and
$\mathsf{sup}^0$
and
![]() $\mathsf{desup}^0$
above. These results are due to Gylterud and Stenholm (Reference Gylterud and Stenholm2023), who extend this construction to a whole hierarchy of functors
$\mathsf{desup}^0$
above. These results are due to Gylterud and Stenholm (Reference Gylterud and Stenholm2023), who extend this construction to a whole hierarchy of functors
![]() $X \mapsto \left (\sum _{A : \mathcal{U}} A \hookrightarrow _n X\right )$
, for
$X \mapsto \left (\sum _{A : \mathcal{U}} A \hookrightarrow _n X\right )$
, for
![]() $n : \mathbb{N}_{-1}$
. Each of these has an initial algebra, given by a higher level generalization of
$n : \mathbb{N}_{-1}$
. Each of these has an initial algebra, given by a higher level generalization of
![]() $\mathsf{V}^0$
.
$\mathsf{V}^0$
.
3.
 $\mathsf{V}^0$
as a Universe à la Tarski
$\mathsf{V}^0$
as a Universe à la Tarski
The type
![]() $\mathsf{V}^0$
can be thought of as a type of material sets, in the sense that
$\mathsf{V}^0$
can be thought of as a type of material sets, in the sense that
![]() $\mathsf{V}^0$
together with the binary relation
$\mathsf{V}^0$
together with the binary relation
![]() $\in$
is a model of constructive set theory (Gylterud Reference Gylterud2018). This section demonstrates that, more type-theoretically,
$\in$
is a model of constructive set theory (Gylterud Reference Gylterud2018). This section demonstrates that, more type-theoretically,
![]() $\mathsf{V}^0$
can be organized into a universe à la Tarski. In this way,
$\mathsf{V}^0$
can be organized into a universe à la Tarski. In this way,
![]() $\mathsf{V}^0$
becomes a universe of h-sets which is itself an h-set. Furthermore,
$\mathsf{V}^0$
becomes a universe of h-sets which is itself an h-set. Furthermore,
![]() $\mathsf{V}^0$
is a strict universe in the sense that the decoding from codes to types is definitional. For instance, the decoding of the code for the natural numbers is definitionally equal to the type of natural numbers, and the decoding of a
$\mathsf{V}^0$
is a strict universe in the sense that the decoding from codes to types is definitional. For instance, the decoding of the code for the natural numbers is definitionally equal to the type of natural numbers, and the decoding of a
![]() $\Pi$
- or
$\Pi$
- or
![]() $\Sigma$
-type of a family is the actual
$\Sigma$
-type of a family is the actual
![]() $\Pi$
- or
$\Pi$
- or
![]() $\Sigma$
-type of the decoding of the family.
$\Sigma$
-type of the decoding of the family.
We begin by defining the decoding family for our universe,
![]() $\mathsf{V}^0$
, as the underlying index type for each of its elements.
$\mathsf{V}^0$
, as the underlying index type for each of its elements.
Definition 16 (Decoding, ![]() ). We define the decoding function
). We define the decoding function
![]() $\mathsf{El}^0\,: \mathsf{V}^0 \to \mathcal{U}$
by
$\mathsf{El}^0\,: \mathsf{V}^0 \to \mathcal{U}$
by
It is easy to prove that the decoding of each code in
![]() $\mathsf{V}^0$
is also an h-set:
$\mathsf{V}^0$
is also an h-set:
Theorem 17 (![]() ). For every
). For every
![]() $x : \mathsf{V}^0$
the type
$x : \mathsf{V}^0$
the type
![]() $\mathsf{El}^0\,x$
is an h-set.
$\mathsf{El}^0\,x$
is an h-set.
Proof.
Recall that
![]() $\widetilde x$
embeds
$\widetilde x$
embeds
![]() $\mathsf{El}^0\,x$
into
$\mathsf{El}^0\,x$
into
![]() $\mathsf{V}^0$
. By Theorem12
$\mathsf{V}^0$
. By Theorem12
![]() $\mathsf{V}^0$
is an h-set. Since any type which embeds into an h-set is an h-set, it follows that
$\mathsf{V}^0$
is an h-set. Since any type which embeds into an h-set is an h-set, it follows that
![]() $\mathsf{El}^0\,x$
is an h-set.
$\mathsf{El}^0\,x$
is an h-set.
Note that for any
![]() $A : \mathcal{U}$
and embedding
$A : \mathcal{U}$
and embedding
![]() $f : A \hookrightarrow \mathsf{V}^0$
we have the definitional equality
$f : A \hookrightarrow \mathsf{V}^0$
we have the definitional equality
![]() $\mathsf{El}^0\,(\mathsf{sup}^0\,\left (A, \right )f) \equiv A$
. That is, if we construct a code for a type in
$\mathsf{El}^0\,(\mathsf{sup}^0\,\left (A, \right )f) \equiv A$
. That is, if we construct a code for a type in
![]() $\mathcal{U}$
using
$\mathcal{U}$
using
![]() $\mathsf{sup}^0$
(which is what we usually do), then the decoding of this code is definitionally equal to the type we started with. This is very convenient when working with the universe
$\mathsf{sup}^0$
(which is what we usually do), then the decoding of this code is definitionally equal to the type we started with. This is very convenient when working with the universe
![]() $\mathsf{V}^0$
, especially for formalization.
$\mathsf{V}^0$
, especially for formalization.
As a universe,
![]() $\mathsf{V}^0$
contains codes of all the traditional type formers as long as they are present in the underlying universe,
$\mathsf{V}^0$
contains codes of all the traditional type formers as long as they are present in the underlying universe,
![]() $\mathcal{U}$
. Using
$\mathcal{U}$
. Using
![]() $\mathsf{sup}^0$
, one can construct a code for a given type
$\mathsf{sup}^0$
, one can construct a code for a given type
![]() $A : \mathcal{U}$
in
$A : \mathcal{U}$
in
![]() $\mathsf{V}^0$
if there is an embedding
$\mathsf{V}^0$
if there is an embedding
![]() $A \hookrightarrow \mathsf{V}^0$
. In fact, there is a code for
$A \hookrightarrow \mathsf{V}^0$
. In fact, there is a code for
![]() $A$
in
$A$
in
![]() $\mathsf{V}^0$
precisely when it can be embedded into
$\mathsf{V}^0$
precisely when it can be embedded into
![]() $\mathsf{V}^0$
.
$\mathsf{V}^0$
.
Proposition 18 (![]() ). For any
). For any
![]() $A : \mathcal{U}$
there is an equivalence
$A : \mathcal{U}$
there is an equivalence
 \begin{equation*} \left (A \hookrightarrow \mathsf {V}^0\right ) \simeq \left (\sum _{a : \mathsf {V}^0} \mathsf {El}^0\,a = A\right ) \end{equation*}
\begin{equation*} \left (A \hookrightarrow \mathsf {V}^0\right ) \simeq \left (\sum _{a : \mathsf {V}^0} \mathsf {El}^0\,a = A\right ) \end{equation*}
Proof. The maps back and forth are
 \begin{align*} &{\alpha } : \left (A \hookrightarrow \mathsf{V}^0\right )\to \sum _{a : \mathsf{V}^0} \mathsf{El}^0\,a = A \\ &{\alpha }\,f := (\mathsf{sup}^0\,\left (A,f\right ), \mathsf{refl}) \\ \\ &{\beta } : \left (\sum _{a : \mathsf{V}^0} \mathsf{El}^0\,a = A\right )\to (A \hookrightarrow \mathsf{V}^0) \\ &{\beta }\,(a, \mathsf{refl}) := \widetilde{a} \end{align*}
\begin{align*} &{\alpha } : \left (A \hookrightarrow \mathsf{V}^0\right )\to \sum _{a : \mathsf{V}^0} \mathsf{El}^0\,a = A \\ &{\alpha }\,f := (\mathsf{sup}^0\,\left (A,f\right ), \mathsf{refl}) \\ \\ &{\beta } : \left (\sum _{a : \mathsf{V}^0} \mathsf{El}^0\,a = A\right )\to (A \hookrightarrow \mathsf{V}^0) \\ &{\beta }\,(a, \mathsf{refl}) := \widetilde{a} \end{align*}
We compute as follows:
 \begin{gather*}{\alpha }({\beta }(a,\mathsf{refl})) \equiv {\alpha } (\widetilde a) \equiv (\mathsf{sup}^0\,\left (\overline a,\widetilde a\right ),\mathsf{refl}) = (a,\mathsf{refl}) \\ \mathsf{pr}_1 \left ({\beta }({\alpha }\,f)\right ) \equiv \mathsf{pr}_1 \left ({\beta }(\mathsf{sup}^0\,\left (A,f\right ), \mathsf{refl})\right ) \equiv \mathsf{pr}_1 \left (\widetilde{\mathsf{sup}^0\,\left (A,f\right )}\right ) \equiv \mathsf{pr}_1\,f \end{gather*}
\begin{gather*}{\alpha }({\beta }(a,\mathsf{refl})) \equiv {\alpha } (\widetilde a) \equiv (\mathsf{sup}^0\,\left (\overline a,\widetilde a\right ),\mathsf{refl}) = (a,\mathsf{refl}) \\ \mathsf{pr}_1 \left ({\beta }({\alpha }\,f)\right ) \equiv \mathsf{pr}_1 \left ({\beta }(\mathsf{sup}^0\,\left (A,f\right ), \mathsf{refl})\right ) \equiv \mathsf{pr}_1 \left (\widetilde{\mathsf{sup}^0\,\left (A,f\right )}\right ) \equiv \mathsf{pr}_1\,f \end{gather*}
Thus,
![]() $\alpha$
is a quasi-equivalence and therefore an equivalence.
$\alpha$
is a quasi-equivalence and therefore an equivalence.
We emphasize that the definitional equation
![]() $\mathsf{El}^0\,(\mathsf{sup}^0\, (A, f)) \equiv A$
simplifies the definition of
$\mathsf{El}^0\,(\mathsf{sup}^0\, (A, f)) \equiv A$
simplifies the definition of
![]() $\alpha$
as we may then use
$\alpha$
as we may then use
![]() $\mathsf{refl}$
for the second argument. Moreover,
$\mathsf{refl}$
for the second argument. Moreover,
![]() ${\beta } \circ{\alpha }$
definitionally preserves the function underlying the embedding. The same is not true of the witness that this function is an embedding, but such witnesses belong to a contractible type and can safely be ignored.
${\beta } \circ{\alpha }$
definitionally preserves the function underlying the embedding. The same is not true of the witness that this function is an embedding, but such witnesses belong to a contractible type and can safely be ignored.
3.1 Basic types
We now construct codes for some basic types in
![]() $\mathsf{V}^0$
.
$\mathsf{V}^0$
.
Proposition 19 (![]() ).
).
![]() $\mathsf{V}^0$
contains the empty type, unit type and booleans.
$\mathsf{V}^0$
contains the empty type, unit type and booleans.
Proof.
We define the elements
![]() $\mathsf{empty}^0, \mathsf{unit}^0, \mathsf{bool}^0 : \mathsf{V}^0$
as follows:
$\mathsf{empty}^0, \mathsf{unit}^0, \mathsf{bool}^0 : \mathsf{V}^0$
as follows:
 \begin{align*} \mathsf{empty}^0 &:= \emptyset \\ \mathsf{unit}^0 &:= \{\emptyset \} \\ \mathsf{bool}^0 &:= \{ \emptyset, \{\emptyset \} \} \end{align*}
\begin{align*} \mathsf{empty}^0 &:= \emptyset \\ \mathsf{unit}^0 &:= \{\emptyset \} \\ \mathsf{bool}^0 &:= \{ \emptyset, \{\emptyset \} \} \end{align*}
There were all verified to be iterative sets in Section 2.
We note that the expected equations hold up to definitional equality:
Proposition 20 (![]() ).
).
![]() $\mathsf{V}^0$
contains the natural numbers.
$\mathsf{V}^0$
contains the natural numbers.
Proof.
By Proposition 18 it is enough to construct an embedding
![]() $\mathbb{N} \hookrightarrow \mathsf{V}^0$
. Here there is a choice of encoding of the naturals in
$\mathbb{N} \hookrightarrow \mathsf{V}^0$
. Here there is a choice of encoding of the naturals in
![]() $\mathsf{V}^0$
and several encodings are possible. We will use the von Neumann encoding and show that this is an embedding.
$\mathsf{V}^0$
and several encodings are possible. We will use the von Neumann encoding and show that this is an embedding.
First, we define the successor function in
![]() $\mathsf{V}^0$
:
$\mathsf{V}^0$
:
In the above,
![]() $\varphi _{x} : \overline{x}\,+\,\mathsf{unit}\to \mathsf{V}^0$
is defined as follows:
$\varphi _{x} : \overline{x}\,+\,\mathsf{unit}\to \mathsf{V}^0$
is defined as follows:
To see that the map
![]() $\varphi _{x}$
is an embedding, note that for any
$\varphi _{x}$
is an embedding, note that for any
![]() $z : \mathsf{V}^0$
the fiber
$z : \mathsf{V}^0$
the fiber
![]() $\mathsf{fib}\,\varphi _x\,z$
is equivalent to
$\mathsf{fib}\,\varphi _x\,z$
is equivalent to
![]() $(z \in x)\,+\,(x = z)$
. Both summands are h-propositions and they are disjoint: if they were both inhabited we could derive
$(z \in x)\,+\,(x = z)$
. Both summands are h-propositions and they are disjoint: if they were both inhabited we could derive
![]() $x \in x$
which contradicts the well-foundedness of
$x \in x$
which contradicts the well-foundedness of
![]() $\in$
(Gylterud and Stenholm Reference Gylterud and Stenholm2023).
$\in$
(Gylterud and Stenholm Reference Gylterud and Stenholm2023).
The von Neumann encoding of the natural numbers is then the function:
 \begin{align*} &f : \mathbb{N}\to \mathsf{V}^0 \\ &f\,\mathsf{0} := \emptyset \\ &f\,(\mathsf{s}\,n) := \mathsf{suc}^0\,(f\,n) \end{align*}
\begin{align*} &f : \mathbb{N}\to \mathsf{V}^0 \\ &f\,\mathsf{0} := \emptyset \\ &f\,(\mathsf{s}\,n) := \mathsf{suc}^0\,(f\,n) \end{align*}
It remains to show that
![]() $f$
is an embedding. As
$f$
is an embedding. As
![]() $\mathbb{N}$
and
$\mathbb{N}$
and
![]() $\mathsf{V}^0$
are both h-sets it suffices that
$\mathsf{V}^0$
are both h-sets it suffices that
![]() $f$
is injective. Observe that
$f$
is injective. Observe that
![]() $\overline{f\,x} \simeq \mathsf{Fin}\,x$
, so if
$\overline{f\,x} \simeq \mathsf{Fin}\,x$
, so if
![]() $f\,n = f\,m$
then
$f\,n = f\,m$
then
![]() $\mathsf{Fin}\,n \simeq \mathsf{Fin}\,m$
from which
$\mathsf{Fin}\,n \simeq \mathsf{Fin}\,m$
from which
![]() $n = m$
follows.
$n = m$
follows.
Having shown that
![]() $f : \mathbb{N}\to \mathsf{V}^0$
is an embedding, we define the (code for the) natural numbers in
$f : \mathbb{N}\to \mathsf{V}^0$
is an embedding, we define the (code for the) natural numbers in
![]() $\mathsf{V}^0$
as follows:
$\mathsf{V}^0$
as follows:
Note, again, that the decoding holds up to definitional equality:
3.2 Type formers
We now turn to closing
![]() $\mathsf{V}^0$
under the standard type formers. For these constructions we will need ordered pairs.
$\mathsf{V}^0$
under the standard type formers. For these constructions we will need ordered pairs.
Lemma 21 (![]() ). There is an ordered pairing operation
). There is an ordered pairing operation
![]() $\langle \_,\_\rangle : \mathsf{V}^0 \times \mathsf{V}^0 \hookrightarrow \mathsf{V}^0$
.
$\langle \_,\_\rangle : \mathsf{V}^0 \times \mathsf{V}^0 \hookrightarrow \mathsf{V}^0$
.
Proof. Ordered pairs are constructed using the Norbert Wiener encoding. The details of this construction can be found in the proof of Gylterud and Stenholm (Reference Gylterud and Stenholm2023, Theorem 7).
Proposition 22 (![]() ).
).
![]() $\mathsf{V}^0$
is closed under
$\mathsf{V}^0$
is closed under
![]() $\prod$
-types.
$\prod$
-types.
Proof.
Let
![]() $x : \mathsf{V}^0$
and
$x : \mathsf{V}^0$
and
![]() $y : \mathsf{El}^0\,x\to \mathsf{V}^0$
. By Gylterud and Stenholm (Reference Gylterud and Stenholm2023, Lemma 12), there is an embedding:
$y : \mathsf{El}^0\,x\to \mathsf{V}^0$
. By Gylterud and Stenholm (Reference Gylterud and Stenholm2023, Lemma 12), there is an embedding:
 \begin{equation*} \mathsf {graph}_{x,y} : \left (\prod _{a : \mathsf {El}^0\,x} \mathsf {El}^0\,(y\,a)\right ) \hookrightarrow \mathsf {V}^0 \end{equation*}
\begin{equation*} \mathsf {graph}_{x,y} : \left (\prod _{a : \mathsf {El}^0\,x} \mathsf {El}^0\,(y\,a)\right ) \hookrightarrow \mathsf {V}^0 \end{equation*}
This map sends
![]() $\varphi : \prod _{a : \mathsf{El}^0\,x} \mathsf{El}^0\,(y\,a)$
to the element
$\varphi : \prod _{a : \mathsf{El}^0\,x} \mathsf{El}^0\,(y\,a)$
to the element
![]() $\mathsf{sup}^0\,\left (\mathsf{El}^0\,x,{\lambda }a.\langle \widetilde{x}\,a,\widetilde{(y\,a)}\,(\varphi \,a)\rangle \right )$
. The
$\mathsf{sup}^0\,\left (\mathsf{El}^0\,x,{\lambda }a.\langle \widetilde{x}\,a,\widetilde{(y\,a)}\,(\varphi \,a)\rangle \right )$
. The
![]() $\prod$
-type is then defined as follows:
$\prod$
-type is then defined as follows:
 \begin{equation*} \prod ^0\,x\,y := \mathsf {sup}^0\,\left (\prod _{a : \mathsf {El}^0\,x} \mathsf {El}^0\,(y\,a), \mathsf {graph}_{x,y}\right ) \end{equation*}
\begin{equation*} \prod ^0\,x\,y := \mathsf {sup}^0\,\left (\prod _{a : \mathsf {El}^0\,x} \mathsf {El}^0\,(y\,a), \mathsf {graph}_{x,y}\right ) \end{equation*}
The decoding holds up to definitional equality:
 \begin{equation*} \mathsf {El}^0\,\left (\prod ^0\,x\,y\right ) \equiv \mathop\prod\limits_{a : \mathsf {El}^0\,x} \mathsf {El}^0\,(y\,a) \end{equation*}
\begin{equation*} \mathsf {El}^0\,\left (\prod ^0\,x\,y\right ) \equiv \mathop\prod\limits_{a : \mathsf {El}^0\,x} \mathsf {El}^0\,(y\,a) \end{equation*}
Corollary 23 (![]() ).
).
![]() $\mathsf{V}^0$
is closed under (nondependent) function types. Let
$\mathsf{V}^0$
is closed under (nondependent) function types. Let
![]() $x \to ^0 y$
denote the code for the type
$x \to ^0 y$
denote the code for the type
![]() $\mathsf{El}^0\,x\to \mathsf{El}^0\,y$
.
$\mathsf{El}^0\,x\to \mathsf{El}^0\,y$
.
Proposition 24 (![]() ).
).
![]() $\mathsf{V}^0$
is closed under
$\mathsf{V}^0$
is closed under
![]() $\Sigma$
-types.
$\Sigma$
-types.
Proof.
Let
![]() $x : \mathsf{V}^0$
and
$x : \mathsf{V}^0$
and
![]() $y : \mathsf{El}^0\,x\to \mathsf{V}^0$
. Define a putative embedding as follows:
$y : \mathsf{El}^0\,x\to \mathsf{V}^0$
. Define a putative embedding as follows:
 \begin{align*} &f : \left (\sum _{a : \mathsf{El}^0\,x} \mathsf{El}^0\,(y\,a)\right )\to \mathsf{V}^0 \\ &f\,(a,b) := \langle \widetilde{x}\,a,\widetilde{(y\,a)}\,b\rangle \end{align*}
\begin{align*} &f : \left (\sum _{a : \mathsf{El}^0\,x} \mathsf{El}^0\,(y\,a)\right )\to \mathsf{V}^0 \\ &f\,(a,b) := \langle \widetilde{x}\,a,\widetilde{(y\,a)}\,b\rangle \end{align*}
This is the composition of two embeddings:
![]() $\langle \_,\_\rangle$
and
$\langle \_,\_\rangle$
and
![]() ${\lambda }(a,b).(\widetilde{x}\,a,\widetilde{(y\,a)}\,b)$
and therefore an embedding. The last function is an embedding because
${\lambda }(a,b).(\widetilde{x}\,a,\widetilde{(y\,a)}\,b)$
and therefore an embedding. The last function is an embedding because
![]() $\widetilde{x}$
is an embedding and as is
$\widetilde{x}$
is an embedding and as is
![]() $\widetilde{(y\,a)}$
for every
$\widetilde{(y\,a)}$
for every
![]() $a : \mathsf{El}^0\,x$
. We may now define the code for
$a : \mathsf{El}^0\,x$
. We may now define the code for
![]() $\Sigma$
-types:
$\Sigma$
-types:
 \begin{equation*} \Sigma ^0\,x\,y := \mathsf {sup}^0\,\left (\sum _{a : \mathsf {El}^0\,x} \mathsf {El}^0\,(y\,a)\,f\right ) \end{equation*}
\begin{equation*} \Sigma ^0\,x\,y := \mathsf {sup}^0\,\left (\sum _{a : \mathsf {El}^0\,x} \mathsf {El}^0\,(y\,a)\,f\right ) \end{equation*}
The decoding holds up to definitional equality:
Corollary 25 (![]() ).
).
![]() $\mathsf{V}^0$
is closed under cartesian products. Let
$\mathsf{V}^0$
is closed under cartesian products. Let
![]() $x \times ^0 y$
be the code for
$x \times ^0 y$
be the code for
![]() $\mathsf{El}^0\,x \times \mathsf{El}^0\,y$
.
$\mathsf{El}^0\,x \times \mathsf{El}^0\,y$
.
In order to construct coproducts in
![]() $\mathsf{V}^0$
we need two lemmas about embeddings.
$\mathsf{V}^0$
we need two lemmas about embeddings.
Lemma 26 (![]() ). Given types
). Given types
![]() $Y$
,
$Y$
,
![]() $Z$
and h-set
$Z$
and h-set
![]() $X$
with a point
$X$
with a point
![]() $x_0 : X$
, any embedding
$x_0 : X$
, any embedding
![]() $f : X \times Y \hookrightarrow Z$
gives rise to an embedding by fixing the first coordinate:
$f : X \times Y \hookrightarrow Z$
gives rise to an embedding by fixing the first coordinate:
![]() $f\,(x_0,\_) : Y \hookrightarrow Z$
.
$f\,(x_0,\_) : Y \hookrightarrow Z$
.
Proof.
We need to show that for any
![]() $z : Z$
, the fiber of
$z : Z$
, the fiber of
![]() $f\,(x_0,\_)$
over
$f\,(x_0,\_)$
over
![]() $z$
is an h-proposition. But the following chain of equivalences holds:
$z$
is an h-proposition. But the following chain of equivalences holds:
 \begin{equation*} \left (\sum _{y : Y} f\,(x_0,y) = z\right ) \simeq \left (\sum _{y : Y} \sum _{\sum _{x : X} (x = x_0)} f\,(x,y) = z\right ) \simeq \left (\sum _{((x,y),p) : \mathsf {fib}\,f\,z} x = x_0\right ) \end{equation*}
\begin{equation*} \left (\sum _{y : Y} f\,(x_0,y) = z\right ) \simeq \left (\sum _{y : Y} \sum _{\sum _{x : X} (x = x_0)} f\,(x,y) = z\right ) \simeq \left (\sum _{((x,y),p) : \mathsf {fib}\,f\,z} x = x_0\right ) \end{equation*}
The last type is an h-proposition since
![]() $\mathsf{fib}\,f\,z$
is an h-proposition by Lemma 7 and for each
$\mathsf{fib}\,f\,z$
is an h-proposition by Lemma 7 and for each
![]() $((x,y),p) : \mathsf{fib}\,f\,z$
, the type
$((x,y),p) : \mathsf{fib}\,f\,z$
, the type
![]() $x = x_0$
is an h-proposition.
$x = x_0$
is an h-proposition.
Lemma 27 (![]() ). Given types
). Given types
![]() $X$
,
$X$
,
![]() $Y$
, and
$Y$
, and
![]() $Z$
together with embeddings
$Z$
together with embeddings
![]() $f : X \hookrightarrow Z$
and
$f : X \hookrightarrow Z$
and
![]() $g : Y \hookrightarrow Z$
. If
$g : Y \hookrightarrow Z$
. If
![]() $f\,x\,\neq \,g\,y$
for all
$f\,x\,\neq \,g\,y$
for all
![]() $x : X$
and
$x : X$
and
![]() $y : Y$
then the following map is an embedding:
$y : Y$
then the following map is an embedding:
 \begin{align*} &h : X\,+\,Y\to Z \\ &h\,(\mathsf{inl}\,x) := f\,x \\ &h\,(\mathsf{inr}\,y) := g\,y \end{align*}
\begin{align*} &h : X\,+\,Y\to Z \\ &h\,(\mathsf{inl}\,x) := f\,x \\ &h\,(\mathsf{inr}\,y) := g\,y \end{align*}
Proof.
Let
![]() $s,t : X\,+\,Y$
. We need to show that
$s,t : X\,+\,Y$
. We need to show that
![]() $\mathsf{ap}\,h : s = t\to h\,s = h\,t$
is an equivalence. Using induction on coproducts, there are two kinds of cases to consider: when
$\mathsf{ap}\,h : s = t\to h\,s = h\,t$
is an equivalence. Using induction on coproducts, there are two kinds of cases to consider: when
![]() $s$
and
$s$
and
![]() $t$
lie in different summands, and when they lie in the same one.
$t$
lie in different summands, and when they lie in the same one.
First, suppose without loss of generality that
![]() $s \equiv \mathsf{inl}\,x$
and
$s \equiv \mathsf{inl}\,x$
and
![]() $t \equiv \mathsf{inr}\,y$
. In this case, we need to show that
$t \equiv \mathsf{inr}\,y$
. In this case, we need to show that
![]() $\mathsf{ap}\,h : \mathsf{inl}\,x = \mathsf{inr}\,y\to f\,x = g\,y$
is an equivalence. But both types are empty, so any map between them is an equivalence.
$\mathsf{ap}\,h : \mathsf{inl}\,x = \mathsf{inr}\,y\to f\,x = g\,y$
is an equivalence. But both types are empty, so any map between them is an equivalence.
Now, suppose without loss of generality that
![]() $s \equiv \mathsf{inl}\,x$
and
$s \equiv \mathsf{inl}\,x$
and
![]() $t \equiv \mathsf{inl}\,x'$
. We need to show that
$t \equiv \mathsf{inl}\,x'$
. We need to show that
![]() $\mathsf{ap}\,h : \mathsf{inl}\,x = \mathsf{inl}\,x'\to f\,x = f\,x'$
is an equivalence. But note that the following diagram commutes:
$\mathsf{ap}\,h : \mathsf{inl}\,x = \mathsf{inl}\,x'\to f\,x = f\,x'$
is an equivalence. But note that the following diagram commutes:

Since both
![]() $\mathsf{ap}\,f$
and
$\mathsf{ap}\,f$
and
![]() $\mathsf{ap}\,\mathsf{inl}$
are equivalences it follows that
$\mathsf{ap}\,\mathsf{inl}$
are equivalences it follows that
![]() $\mathsf{ap}\,h$
is an equivalence.
$\mathsf{ap}\,h$
is an equivalence.
Proposition 28 (![]() ).
).
![]() $\mathsf{V}^0$
is closed under coproducts.
$\mathsf{V}^0$
is closed under coproducts.
Proof.
Let
![]() $x,y : \mathsf{V}^0$
. Define the map
$x,y : \mathsf{V}^0$
. Define the map
 \begin{align*} &f : \mathsf{El}^0\,x\,+\,\mathsf{El}^0\,y\to \mathsf{V}^0 \\ &f\,(\mathsf{inl}\,a) := \langle \mathsf{empty}^0, \widetilde{x}\,a\rangle \\ &f\,(\mathsf{inr}\,b) := \langle \mathsf{unit}^0, \widetilde{y}\,b\rangle \end{align*}
\begin{align*} &f : \mathsf{El}^0\,x\,+\,\mathsf{El}^0\,y\to \mathsf{V}^0 \\ &f\,(\mathsf{inl}\,a) := \langle \mathsf{empty}^0, \widetilde{x}\,a\rangle \\ &f\,(\mathsf{inr}\,b) := \langle \mathsf{unit}^0, \widetilde{y}\,b\rangle \end{align*}
By Lemma 26 both
![]() ${\lambda }a.\langle \mathsf{empty}^0, \widetilde{x}\,a\rangle$
and
${\lambda }a.\langle \mathsf{empty}^0, \widetilde{x}\,a\rangle$
and
![]() ${\lambda }b.\langle \mathsf{unit}^0, \widetilde{y}\,b\rangle$
are embeddings. Moreover, suppose
${\lambda }b.\langle \mathsf{unit}^0, \widetilde{y}\,b\rangle$
are embeddings. Moreover, suppose
![]() $\langle \mathsf{empty}^0, \widetilde{x}\,a\rangle = \langle \mathsf{unit}^0, \widetilde{y}\,b\rangle$
for some
$\langle \mathsf{empty}^0, \widetilde{x}\,a\rangle = \langle \mathsf{unit}^0, \widetilde{y}\,b\rangle$
for some
![]() $a : \mathsf{El}^0\,x$
and
$a : \mathsf{El}^0\,x$
and
![]() $b : \mathsf{El}^0\,y$
. It then follows that
$b : \mathsf{El}^0\,y$
. It then follows that
![]() $\mathsf{empty}^0 = \mathsf{unit}^0$
, which is a contradiction. Therefore, by Lemma 27 we conclude that
$\mathsf{empty}^0 = \mathsf{unit}^0$
, which is a contradiction. Therefore, by Lemma 27 we conclude that
![]() $f$
is an embedding.
$f$
is an embedding.
We now define the coproduct:
Note that the decoding holds up to definitional equality:
Proposition 29 (![]() ).
).
![]() $\mathsf{V}^0$
is closed under identity types.
$\mathsf{V}^0$
is closed under identity types.
Proof.
Let
![]() $x : \mathsf{V}^0$
and
$x : \mathsf{V}^0$
and
![]() $a,a' : \mathsf{El}^0\,x$
. Define the following map:
$a,a' : \mathsf{El}^0\,x$
. Define the following map:
This is an embedding as it is a map from an h-proposition into an h-set. The identity type in
![]() $\mathsf{V}^0$
is then defined as follows:
$\mathsf{V}^0$
is then defined as follows:
The decoding holds up to definitional equality:
We emphasize that
![]() $\mathsf{El}^0\,x$
is an h-set for any for any
$\mathsf{El}^0\,x$
is an h-set for any for any
![]() $x : \mathsf{V}^0$
. Accordingly,
$x : \mathsf{V}^0$
. Accordingly,
![]() $\mathsf{Id}^0\,x\,a\,a'$
is necessarily a proposition for any
$\mathsf{Id}^0\,x\,a\,a'$
is necessarily a proposition for any
![]() $a,a' : \mathsf{El}^0\,x$
. In particular,
$a,a' : \mathsf{El}^0\,x$
. In particular,
![]() $\mathsf{Id}^0\,x\,a\,a'$
satisfies UIP. As this identity type represents internalizes the ambient identity type, other expected properties of the identity type (such as function extensionality) also hold.
$\mathsf{Id}^0\,x\,a\,a'$
satisfies UIP. As this identity type represents internalizes the ambient identity type, other expected properties of the identity type (such as function extensionality) also hold.
3.3 Set quotients
In order to define set quotients in
![]() $\mathsf{V}^0$
, we must assume that these quotients exist in our starting universe
$\mathsf{V}^0$
, we must assume that these quotients exist in our starting universe
![]() $\mathcal{U}$
. More specifically, we first assume that there is a function of the following type
$\mathcal{U}$
. More specifically, we first assume that there is a function of the following type
We then ensure that
![]() $A / R$
realizes the quotient of
$A / R$
realizes the quotient of
![]() $A$
by the relation
$A$
by the relation
![]() $R$
by requiring a map
$R$
by requiring a map
![]() $[{-}]_R : A\to A / R$
such that
$[{-}]_R : A\to A / R$
such that
![]() $R\,a\,b\to [a]_R = [b]_R$
for all
$R\,a\,b\to [a]_R = [b]_R$
for all
![]() $a,b : A$
. We also assume a suitable elimination principle: given a family of h-sets
$a,b : A$
. We also assume a suitable elimination principle: given a family of h-sets
![]() $P : A / R\to \mathsf{hSet}_{\mathcal{U}}$
, we can construct a function
$P : A / R\to \mathsf{hSet}_{\mathcal{U}}$
, we can construct a function
![]() $\prod _{x : A / R} P\,x$
from a function
$\prod _{x : A / R} P\,x$
from a function
![]() $q : \prod _{x : A / R} P\,[a]_R$
, which coheres with the map
$q : \prod _{x : A / R} P\,[a]_R$
, which coheres with the map
![]() $R\,a\,b\to [a]_R = [b]_R$
. The require that function we get satisfies a coherence condition, and if we precompose it with the quotient map
$R\,a\,b\to [a]_R = [b]_R$
. The require that function we get satisfies a coherence condition, and if we precompose it with the quotient map
![]() $[{-}]_R$
we get back
$[{-}]_R$
we get back
![]() $q$
. (For the exact assumptions, see the formalization
$q$
. (For the exact assumptions, see the formalization ![]() .)
.)
While we do not need to assume that
![]() $R : A\to A\to \mathcal{U}$
is an equivalence relation (h-propositional, symmetric, reflexive, and transitive), the constructions below will use the fact any
$R : A\to A\to \mathcal{U}$
is an equivalence relation (h-propositional, symmetric, reflexive, and transitive), the constructions below will use the fact any
![]() $R$
induces an equivalence relation
$R$
induces an equivalence relation
![]() $|R| : A\to A\to \mathsf{hProp}_{\mathcal{U}}$
defined by
$|R| : A\to A\to \mathsf{hProp}_{\mathcal{U}}$
defined by
![]() $|R|\,a\,b := \left ([a]_R = [b]_R\right )$
.
$|R|\,a\,b := \left ([a]_R = [b]_R\right )$
.
To streamline the process, we will use an interesting formulation of equivalence relations:
Lemma 30.
Given a relation
![]() $R : A\to A\to \mathsf{hProp}_{\mathcal{U}}$
, the following are equivalent:
$R : A\to A\to \mathsf{hProp}_{\mathcal{U}}$
, the following are equivalent:
-
•
 $R$
is an equivalence relation
$R$
is an equivalence relation
-
•
 $R\,a\,b \simeq \prod _{c:A} \left (R\,a\,c \simeq R\,b\,c\right )$
for all
$R\,a\,b \simeq \prod _{c:A} \left (R\,a\,c \simeq R\,b\,c\right )$
for all
 $a,b:A$
$a,b:A$
-
•
 $R\,a\,b \simeq \left (R\,a =_{A\to \mathcal{U}} R\,b\right )$
for all
$R\,a\,b \simeq \left (R\,a =_{A\to \mathcal{U}} R\,b\right )$
for all
 $a,b:A$
$a,b:A$
Proof.
Since
![]() $R$
is an (h-propositional) binary relation, the above statements are all h-propositions. The last two are equivalent by function extensionality and univalence. It thus remains to show that being an equivalence relation is equivalent to one of the last two – we choose the middle one.
$R$
is an (h-propositional) binary relation, the above statements are all h-propositions. The last two are equivalent by function extensionality and univalence. It thus remains to show that being an equivalence relation is equivalent to one of the last two – we choose the middle one.
Assume that
![]() $R$
is an equivalence relation. Everything in sight is an h-proposition, so the equivalences are logical equivalences. Thus, assume that
$R$
is an equivalence relation. Everything in sight is an h-proposition, so the equivalences are logical equivalences. Thus, assume that
![]() $R\,a\,b$
. Then we get a map
$R\,a\,b$
. Then we get a map
![]() $\prod _{c:A} R\,a\,c \leftrightarrow R\,b\,c$
by transitivity and symmetry. In the other direction, if
$\prod _{c:A} R\,a\,c \leftrightarrow R\,b\,c$
by transitivity and symmetry. In the other direction, if
![]() $\prod _{c:A} R\,a\,c \leftrightarrow R\,b\,c$
, choose
$\prod _{c:A} R\,a\,c \leftrightarrow R\,b\,c$
, choose
![]() $c = a$
in order to obtain
$c = a$
in order to obtain
![]() $R\,a\,a \leftrightarrow R\,a\,b$
. Since
$R\,a\,a \leftrightarrow R\,a\,b$
. Since
![]() $R$
is reflexive, we get
$R$
is reflexive, we get
![]() $R\,a\,b$
.
$R\,a\,b$
.
Conversely, assume
![]() $R\,a\,b \simeq \prod _{c:A} \left (R\,a\,c \simeq R\,b\,c\right )$
for all
$R\,a\,b \simeq \prod _{c:A} \left (R\,a\,c \simeq R\,b\,c\right )$
for all
![]() $a,b:A$
. To show reflexivity, let
$a,b:A$
. To show reflexivity, let
![]() $b=a$
and notice that
$b=a$
and notice that
![]() $\prod _{c:A} \left (R\,a\,c \simeq R\,a\,c\right )$
has a canonical element, from which we obtain
$\prod _{c:A} \left (R\,a\,c \simeq R\,a\,c\right )$
has a canonical element, from which we obtain
![]() $R\,a\,a$
. Symmetry is obtained by observing that
$R\,a\,a$
. Symmetry is obtained by observing that
![]() $ \prod _{c:A} \left (R\,a\,c \simeq R\,b\,c\right ) \simeq \prod _{c:A} \left (R\,b\,c \simeq R\,a\,c\right )$
and hence
$ \prod _{c:A} \left (R\,a\,c \simeq R\,b\,c\right ) \simeq \prod _{c:A} \left (R\,b\,c \simeq R\,a\,c\right )$
and hence
![]() $R\,a\,b \simeq R\,b\,a$
. For transitivity, remember that
$R\,a\,b \simeq R\,b\,a$
. For transitivity, remember that
![]() $R\,a\,b$
gives
$R\,a\,b$
gives
![]() $\prod _{c:A} \left (R\,a\,c \simeq R\,b\,c\right )$
, thus if we have
$\prod _{c:A} \left (R\,a\,c \simeq R\,b\,c\right )$
, thus if we have
![]() $R\,b\,c$
we get
$R\,b\,c$
we get
![]() $R\,a\,c$
by following the backwards direction of the equivalence.
$R\,a\,c$
by following the backwards direction of the equivalence.
The property
![]() $R\,a\,b \simeq \prod _{c:A} \left (R\,a\,c \simeq R\,b\,c\right )$
for all
$R\,a\,b \simeq \prod _{c:A} \left (R\,a\,c \simeq R\,b\,c\right )$
for all
![]() $a,b:A$
essentially states that the equivalence classes of
$a,b:A$
essentially states that the equivalence classes of
![]() $R$
behave well. Tangentially, we note that this requirement make sense even when
$R$
behave well. Tangentially, we note that this requirement make sense even when
![]() $R$
is a general binary family, not only of h-propositions. Thus, this property might make for interesting future study.
$R$
is a general binary family, not only of h-propositions. Thus, this property might make for interesting future study.
Proposition 31 (![]() ).
).
![]() $\mathsf{V}^0$
is closed under set quotients. That is, given
$\mathsf{V}^0$
is closed under set quotients. That is, given
![]() $a:\mathsf{V}^0$
and
$a:\mathsf{V}^0$
and
![]() $R : \mathsf{El}^0\,a\to \mathsf{El}^0\,a\to \mathcal{U}$
there is
$R : \mathsf{El}^0\,a\to \mathsf{El}^0\,a\to \mathcal{U}$
there is
![]() $a /^0 R : \mathsf{V}^0$
such that
$a /^0 R : \mathsf{V}^0$
such that
![]() $\mathsf{El}^0\,(a /^0 R ) \equiv (\mathsf{El}^0\,a) / R$
.
$\mathsf{El}^0\,(a /^0 R ) \equiv (\mathsf{El}^0\,a) / R$
.
Proof.
By Proposition 18, it suffices to construct an embedding
![]() $\mathsf{El}^0\,a / R \hookrightarrow \mathsf{V}^0$
. We define
$\mathsf{El}^0\,a / R \hookrightarrow \mathsf{V}^0$
. We define
![]() $f :\,\mathsf{El}^0\,a\to \mathsf{V}^0$
and prove that for any
$f :\,\mathsf{El}^0\,a\to \mathsf{V}^0$
and prove that for any
![]() $x,x':\mathsf{El}^0\,a$
we have
$x,x':\mathsf{El}^0\,a$
we have
![]() $\left ([x]_R = [x']_R\right ) \simeq \left (f\,x = f\,x'\right )$
. By the elimination principle for set quotients, this will induce an embedding
$\left ([x]_R = [x']_R\right ) \simeq \left (f\,x = f\,x'\right )$
. By the elimination principle for set quotients, this will induce an embedding
![]() $\mathsf{El}^0\,a / R \hookrightarrow \mathsf{V}^0$
.
$\mathsf{El}^0\,a / R \hookrightarrow \mathsf{V}^0$
.
Thus, let
![]() $f\,x = \mathsf{sup}^0\,\left (\sum _{y:\mathsf{El}^0\,a}|R|\,x\,y,\widetilde a \circ \mathsf{pr}_1\right )$
, and observe the chain of equivalences:
$f\,x = \mathsf{sup}^0\,\left (\sum _{y:\mathsf{El}^0\,a}|R|\,x\,y,\widetilde a \circ \mathsf{pr}_1\right )$
, and observe the chain of equivalences:
 \begin{align*} \left (f\,x = f\,x'\right ) & \equiv \left (\mathsf{sup}^0\,\left (\sum _{y:\mathsf{El}^0\,a}|R|\,x\,y,\widetilde a \circ \mathsf{pr}_1\right ) = \mathsf{sup}^0\,\left (\sum _{y:\mathsf{El}^0\,a}|R|\,x'\,y,\widetilde a \circ \mathsf{pr}_1\right )\right ) \\ & \simeq \sum _{{\alpha } : \left (\sum _{y:\mathsf{El}^0\,a}|R|\,x\,y\right ) \simeq \left (\sum _{y:\mathsf{El}^0\,a}|R|\,x'\,y\right )} \widetilde a \circ \mathsf{pr}_1 = \widetilde a \circ{\alpha }\circ \mathsf{pr}_1 \\ & \simeq \sum _{{\alpha } : \left (\sum _{y:\mathsf{El}^0\,a}|R|\,x\,y\right ) \simeq \left (\sum _{y:\mathsf{El}^0\,a}|R|\,x'\,y\right )} \mathsf{pr}_1 ={\alpha }\circ \mathsf{pr}_1 \\ & \simeq \prod _{y : \mathsf{El}^0\,a} |R|\,x\,y \simeq |R|\,x'\,y \\ & \simeq |R|\,x\,x' \\ & \equiv \left ([x]_R = [x']_R\right ) \end{align*}
\begin{align*} \left (f\,x = f\,x'\right ) & \equiv \left (\mathsf{sup}^0\,\left (\sum _{y:\mathsf{El}^0\,a}|R|\,x\,y,\widetilde a \circ \mathsf{pr}_1\right ) = \mathsf{sup}^0\,\left (\sum _{y:\mathsf{El}^0\,a}|R|\,x'\,y,\widetilde a \circ \mathsf{pr}_1\right )\right ) \\ & \simeq \sum _{{\alpha } : \left (\sum _{y:\mathsf{El}^0\,a}|R|\,x\,y\right ) \simeq \left (\sum _{y:\mathsf{El}^0\,a}|R|\,x'\,y\right )} \widetilde a \circ \mathsf{pr}_1 = \widetilde a \circ{\alpha }\circ \mathsf{pr}_1 \\ & \simeq \sum _{{\alpha } : \left (\sum _{y:\mathsf{El}^0\,a}|R|\,x\,y\right ) \simeq \left (\sum _{y:\mathsf{El}^0\,a}|R|\,x'\,y\right )} \mathsf{pr}_1 ={\alpha }\circ \mathsf{pr}_1 \\ & \simeq \prod _{y : \mathsf{El}^0\,a} |R|\,x\,y \simeq |R|\,x'\,y \\ & \simeq |R|\,x\,x' \\ & \equiv \left ([x]_R = [x']_R\right ) \end{align*}
Note that we have used the characterization of equivalence relations given by Lemma 30 in the next to last step.
Remark 32.
We note that our choice of embedding to define
![]() $a /^0 R : \mathsf{V}^0$
is similar to the construction of set quotients using type-theoretic replacement due to Rijke (Reference Rijke2017).
$a /^0 R : \mathsf{V}^0$
is similar to the construction of set quotients using type-theoretic replacement due to Rijke (Reference Rijke2017).
3.4 Using the type formers
Using the types and type formers in
![]() $\mathsf{V}^0$
we can construct new types. The decoding of these composite types will then hold up to definitional equality. For example, given elements
$\mathsf{V}^0$
we can construct new types. The decoding of these composite types will then hold up to definitional equality. For example, given elements
![]() $x,y : \mathsf{V}^0$
, a map
$x,y : \mathsf{V}^0$
, a map
![]() $f : \mathsf{El}^0\,x\to \mathsf{El}^0\,y$
and
$f : \mathsf{El}^0\,x\to \mathsf{El}^0\,y$
and
![]() $b : \mathsf{El}^0\,y$
, we can define the code for the fiber of
$b : \mathsf{El}^0\,y$
, we can define the code for the fiber of
![]() $f$
over
$f$
over
![]() $b$
as
$b$
as
After applying the decoding function, we get obtain the following definitional equality:
3.5 Universes
The flexible handling of hierarchies of universes is a key feature of dependent type theory. It makes it easy to formalize higher order concepts and mathematical structures. Our universe construction retains this ability, and in this subsection we demonstrate that by observing that the types
![]() $\mathsf{V}^0_0, \mathsf{V}^0_1, \ldots, \mathsf{V}^0_{\ell }, \ldots$
form a hierarchy of universes, where each universe occurs as a type with a code in the next.
$\mathsf{V}^0_0, \mathsf{V}^0_1, \ldots, \mathsf{V}^0_{\ell }, \ldots$
form a hierarchy of universes, where each universe occurs as a type with a code in the next.
Proposition 33 (![]() ). For any universe level
). For any universe level
![]() $\ell$
there is a code
$\ell$
there is a code
![]() $\mathsf{V}^0_{\ell }\mbox{-}\mathsf{code} : \mathsf{V}^0_{\ell + 1}$
for
$\mathsf{V}^0_{\ell }\mbox{-}\mathsf{code} : \mathsf{V}^0_{\ell + 1}$
for
![]() $\mathsf{V}^0_{\ell }$
with the definitional equality
$\mathsf{V}^0_{\ell }$
with the definitional equality
![]() $\mathsf{El}^0\,\mathsf{V}^0_{\ell }\mbox{-}\mathsf{code} \equiv \mathsf{V}^0_{\ell }$
$\mathsf{El}^0\,\mathsf{V}^0_{\ell }\mbox{-}\mathsf{code} \equiv \mathsf{V}^0_{\ell }$
Proof.
Given a universe level
![]() $\ell$
, we need to construct an embedding
$\ell$
, we need to construct an embedding
![]() $\mathsf{V}^0_{\ell } \hookrightarrow \mathsf{V}^0_{\ell ^+}$
. For this, we start by constructing an embedding
$\mathsf{V}^0_{\ell } \hookrightarrow \mathsf{V}^0_{\ell ^+}$
. For this, we start by constructing an embedding
![]() ${\mathsf{V}^\infty }_{\ell } \hookrightarrow {\mathsf{V}^\infty }_{\ell ^+}$
. Thus define the map
${\mathsf{V}^\infty }_{\ell } \hookrightarrow {\mathsf{V}^\infty }_{\ell ^+}$
. Thus define the map
(Note that we are using cumulative universes in the ambient type theory, so
![]() $A : \mathcal{U}_{\ell ^+}$
whenever
$A : \mathcal{U}_{\ell ^+}$
whenever
![]() $A : \mathcal{U}_{\ell }$
.) To show that
$A : \mathcal{U}_{\ell }$
.) To show that
![]() $\varphi$
is an embedding, let
$\varphi$
is an embedding, let
![]() $\mathsf{sup}\,A\,f, \mathsf{sup}\,B\,g :{\mathsf{V}^\infty }_{\ell }$
be arbitrary elements. We need to show that
$\mathsf{sup}\,A\,f, \mathsf{sup}\,B\,g :{\mathsf{V}^\infty }_{\ell }$
be arbitrary elements. We need to show that
is an equivalence. First, note that the following diagram commutes:

The map
![]() $\mathsf{sup}$
is an equivalence, so
$\mathsf{sup}$
is an equivalence, so
![]() $\varphi$
is an embedding if and only if the top map is an embedding. Thus we need to show the following to be an equivalence:
$\varphi$
is an embedding if and only if the top map is an embedding. Thus we need to show the following to be an equivalence:
While we might hope to argue that this is a fiberwise embedding and therefore the total map is an embedding as well. Unfortunately, our induction hypothesis does not state that
![]() $\varphi$
is an embedding, i.e., that
$\varphi$
is an embedding, i.e., that
![]() $\mathsf{ap}$
is an equivalence for all elements. It only ensures that it is an equivalence for some elements. We must then take a different path and instead note that the diagram below commutes.
$\mathsf{ap}$
is an equivalence for all elements. It only ensures that it is an equivalence for some elements. We must then take a different path and instead note that the diagram below commutes.

The vertical maps are provided by Theorem3. Using 3-for-2, the top map is an equivalence if and only if the bottom one is an equivalence. We now note that it suffices to check this property on fibers, so we need to show that given
![]() $e : A \simeq B$
, the following map is an equivalence:
$e : A \simeq B$
, the following map is an equivalence:
We now recall that postcomposition by a family of maps is an equivalence if it is a family of equivalences. Finally, we must argue that
![]() $\mathsf{ap}\,\varphi : f\,a = g\,(e\,a)\to \varphi \,(f\,a) = \varphi \,(g\,(e\,a))$
is an equivalence for all
$\mathsf{ap}\,\varphi : f\,a = g\,(e\,a)\to \varphi \,(f\,a) = \varphi \,(g\,(e\,a))$
is an equivalence for all
![]() $a : A$
. This follows from the induction hypothesis. Thus, we conclude that
$a : A$
. This follows from the induction hypothesis. Thus, we conclude that
![]() $\varphi :{\mathsf{V}^\infty }_{\ell }\to {\mathsf{V}^\infty }_{\ell ^+}$
is an embedding.
$\varphi :{\mathsf{V}^\infty }_{\ell }\to {\mathsf{V}^\infty }_{\ell ^+}$
is an embedding.
To argue that this equivalence restricts to
![]() $\mathsf{V}^0$
, we must show this equivalence sends iterative sets to iterative sets. Thus, let
$\mathsf{V}^0$
, we must show this equivalence sends iterative sets to iterative sets. Thus, let
![]() $\mathsf{sup}\,A\,f :{\mathsf{V}^\infty }_{\ell }$
be such that
$\mathsf{sup}\,A\,f :{\mathsf{V}^\infty }_{\ell }$
be such that
![]() $f$
is an embedding and
$f$
is an embedding and
![]() $f\,a$
is an iterative set for all
$f\,a$
is an iterative set for all
![]() $a : A$
. We must argue that
$a : A$
. We must argue that
![]() $\mathsf{sup}\,A\,(\varphi \circ f)$
is an iterative set. But the map
$\mathsf{sup}\,A\,(\varphi \circ f)$
is an iterative set. But the map
![]() $\varphi \circ f$
is an embedding as the composition of two embeddings. Moreover, by the induction hypothesis, for any
$\varphi \circ f$
is an embedding as the composition of two embeddings. Moreover, by the induction hypothesis, for any
![]() $a : A$
,
$a : A$
,
![]() $\varphi \,(f\,a)$
is an iterative set since
$\varphi \,(f\,a)$
is an iterative set since
![]() $f\,a$
is an iterative set.
$f\,a$
is an iterative set.
Therefore,
![]() $\varphi$
is an embedding from
$\varphi$
is an embedding from
![]() $\mathsf{V}^0_{\ell }$
into
$\mathsf{V}^0_{\ell }$
into
![]() $\mathsf{V}^0_{\ell ^+}$
. The code for
$\mathsf{V}^0_{\ell ^+}$
. The code for
![]() $\mathsf{V}^0_{\ell }$
in
$\mathsf{V}^0_{\ell }$
in
![]() $\mathsf{V}^0_{\ell ^+}$
is thus defined as
$\mathsf{V}^0_{\ell ^+}$
is thus defined as
Note that the decoding holds up to definitional equality:
Proposition 34.
![]() $\mathsf{V}^0$
is not a univalent universe.
$\mathsf{V}^0$
is not a univalent universe.
Proof.
For
![]() $x, y : \mathsf{V}^0$
,
$x, y : \mathsf{V}^0$
,
![]() $x = y$
is an h-proposition as
$x = y$
is an h-proposition as
![]() $\mathsf{V}^0$
is an h-set, but
$\mathsf{V}^0$
is an h-set, but
![]() $\mathsf{El}^0\,\,x \simeq \mathsf{El}^0\,\,y$
is in general a proper h-set.
$\mathsf{El}^0\,\,x \simeq \mathsf{El}^0\,\,y$
is in general a proper h-set.
4.
 $\mathsf{V}^0$
as a Category
$\mathsf{V}^0$
as a Category
The universe structure on
![]() $\mathsf{V}^0$
induces a category with a full and faithful functor into
$\mathsf{V}^0$
induces a category with a full and faithful functor into
![]() $\mathcal{hSet}_{\mathcal{U}}$
. In this section, we define this category and show that it is closed under many essential constructions (finite limits and colimits, exponentials, and more). This category provides another concrete way for us to measure the adequacy of
$\mathcal{hSet}_{\mathcal{U}}$
. In this section, we define this category and show that it is closed under many essential constructions (finite limits and colimits, exponentials, and more). This category provides another concrete way for us to measure the adequacy of
![]() $\mathsf{V}^0$
as a replacement for
$\mathsf{V}^0$
as a replacement for
![]() $\mathsf{hSet}_{\mathcal{U}}$
; the former induces a closely related category to the latter, sharing many similar properties.
$\mathsf{hSet}_{\mathcal{U}}$
; the former induces a closely related category to the latter, sharing many similar properties.
Definition 35 (![]() ). Let
). Let
![]() $\mathcal{V}$
be the category with
$\mathcal{V}$
be the category with
-
•
 $\mathsf{Ob}\,\mathcal{V} := \mathsf{V}^0$
$\mathsf{Ob}\,\mathcal{V} := \mathsf{V}^0$
-
•
 ${\mathsf{Hom}}_{\mathcal{V}}\,(x,y) := \mathsf{El}^0\,x \to \mathsf{El}^0\,y$
${\mathsf{Hom}}_{\mathcal{V}}\,(x,y) := \mathsf{El}^0\,x \to \mathsf{El}^0\,y$
-
•
 $\mathsf{id}$
and
$\mathsf{id}$
and
 $\circ$
are simply the identity function and function composition.
$\circ$
are simply the identity function and function composition.
All laws hold by
![]() $\mathsf{refl}$
as
$\mathsf{refl}$
as
![]() $\mathsf{id}$
and
$\mathsf{id}$
and
![]() $\circ$
are the identity and composition from the ambient type theory. For
$\circ$
are the identity and composition from the ambient type theory. For
![]() $x,y : \mathsf{V}^0$
, the type
$x,y : \mathsf{V}^0$
, the type
![]() ${\mathsf{Hom}}\,(x,y)$
is an h-set as it consists of functions into an h-set.
${\mathsf{Hom}}\,(x,y)$
is an h-set as it consists of functions into an h-set.
Note that we will take category to denote what the HoTT Book calls “precategory,” univalent category to denote what the book calls “category,” and strict category to denote a category where the objects form an h-set. Hence,
![]() $\mathcal{V}$
is a strict category as
$\mathcal{V}$
is a strict category as
![]() $\mathsf{V}^0$
is an h-set.
$\mathsf{V}^0$
is an h-set.
The following holds more-or-less by construction:
Lemma 36 (![]() ). The map
). The map
![]() $\mathsf{El}^0$
induces a full and faithful functor from
$\mathsf{El}^0$
induces a full and faithful functor from
![]() $\mathcal{V}$
to
$\mathcal{V}$
to
![]() $\mathcal{hSet}_{\mathcal{U}}$
.
$\mathcal{hSet}_{\mathcal{U}}$
.
Clearly,
![]() $\mathcal{V}$
is not a univalent category since it possesses objects with non-trivial automorphisms, but the type of objects in
$\mathcal{V}$
is not a univalent category since it possesses objects with non-trivial automorphisms, but the type of objects in
![]() $\mathcal{V}$
is an h-set. Still, one might ask if
$\mathcal{V}$
is an h-set. Still, one might ask if
![]() $\mathsf{El}^0$
is an equivalence of categories. This does not appear to be true in general, but can be implied by further axioms. For instance, the axiom of choice implies that
$\mathsf{El}^0$
is an equivalence of categories. This does not appear to be true in general, but can be implied by further axioms. For instance, the axiom of choice implies that
![]() $\mathsf{El}^0$
is an equivalence. The core of this is whether every type in
$\mathsf{El}^0$
is an equivalence. The core of this is whether every type in
![]() $\mathcal{U}$
can be equipped with an iterative set-structure – a property known as well-founded materialization. We discuss this further in Section 6.4.
$\mathcal{U}$
can be equipped with an iterative set-structure – a property known as well-founded materialization. We discuss this further in Section 6.4.
Fortunately, even without additional axioms we are able to show that
![]() $\mathcal{V}$
retains much of the essential structure of
$\mathcal{V}$
retains much of the essential structure of
![]() $\mathcal{hSet}_{\mathcal{U}}$
and that
$\mathcal{hSet}_{\mathcal{U}}$
and that
![]() $\mathsf{El}^0$
preserves many important categorical constructions. In order to show that
$\mathsf{El}^0$
preserves many important categorical constructions. In order to show that
![]() $\mathcal{V}$
is closed under some categorical structure, it therefore suffices to break the process into two stages:
$\mathcal{V}$
is closed under some categorical structure, it therefore suffices to break the process into two stages:
-
1. Show that
 $\mathcal{hSet}_{\mathcal{U}}$
is closed under for example, finite limits, exponentials, etc.
$\mathcal{hSet}_{\mathcal{U}}$
is closed under for example, finite limits, exponentials, etc.
-
2. Show that the objects involved land in the image of
 $\mathsf{El}^0$
.
$\mathsf{El}^0$
.
Better still,
![]() $\mathcal{hSet}_{\mathcal{U}}$
is well-studied and known to be closed under all the categorical structures we consider (Rijke and Spitters Reference Rijke and Spitters2015). Our task is therefore reduced only to showing that various objects of
$\mathcal{hSet}_{\mathcal{U}}$
is well-studied and known to be closed under all the categorical structures we consider (Rijke and Spitters Reference Rijke and Spitters2015). Our task is therefore reduced only to showing that various objects of
![]() $\mathcal{hSet}_{\mathcal{U}}$
land in the image of
$\mathcal{hSet}_{\mathcal{U}}$
land in the image of
![]() $\mathsf{El}^0$
. For this, we repeatedly capitalize on the fact that the decoding
$\mathsf{El}^0$
. For this, we repeatedly capitalize on the fact that the decoding
![]() $\mathsf{El}^0$
holds up to definitional equality; it ensures that the final step can be rephrased as follows: show that there exists an iterative structure on the objects involved. This pattern is used repeatedly to prove the following result:
$\mathsf{El}^0$
holds up to definitional equality; it ensures that the final step can be rephrased as follows: show that there exists an iterative structure on the objects involved. This pattern is used repeatedly to prove the following result:
Theorem 37 (![]() ).
).
![]() $\mathcal{V}$
is closed under and
$\mathcal{V}$
is closed under and
![]() $\mathsf{El}^0$
preserves the following:
$\mathsf{El}^0$
preserves the following:
-
1. initial object,
-
2. terminal object,
-
3. finite coproducts,
-
4. pushouts,
-
5. finite products,
-
6. pullbacks, and
-
7. exponentials.
Proof.
As
![]() $\mathcal{hSet}_{\mathcal{U}}$
supports these structures it suffices to show that each of the representing objects land in the image of
$\mathcal{hSet}_{\mathcal{U}}$
supports these structures it suffices to show that each of the representing objects land in the image of
![]() $\mathsf{El}^0\,$
. This clearly follows from the results in Section 3, for instance, the existence of the initial and terminal object follows from Proposition 19, and for example, pullbacks can be constructed through
$\mathsf{El}^0\,$
. This clearly follows from the results in Section 3, for instance, the existence of the initial and terminal object follows from Proposition 19, and for example, pullbacks can be constructed through
![]() $\Sigma ^0\,$
and
$\Sigma ^0\,$
and
![]() $\mathsf{fib}^0$
just like in
$\mathsf{fib}^0$
just like in
![]() $\mathcal{hSet}_{\mathcal{U}}$
.
$\mathcal{hSet}_{\mathcal{U}}$
.
As
![]() $\mathcal{V}$
has pullbacks/pushouts and terminal/initial object we directly get:
$\mathcal{V}$
has pullbacks/pushouts and terminal/initial object we directly get:
Corollary 38.
![]() $\mathcal{V}$
has finite limits and colimits. These are preserved by
$\mathcal{V}$
has finite limits and colimits. These are preserved by
![]() $\mathsf{El}^0$
.
$\mathsf{El}^0$
.
We defer further categorical considerations of
![]() $\mathcal{V}$
to future work and instead turn our attention to slice categories of
$\mathcal{V}$
to future work and instead turn our attention to slice categories of
![]() $\mathcal{V}$
, which play an important role in the study of it as a model of type theory.
$\mathcal{V}$
, which play an important role in the study of it as a model of type theory.
4.1 Slice categories of
 $\mathcal{V}$
$\mathcal{V}$
Similar methods to the ones above also apply when showing that the slice categories
![]() $\mathcal{V}/a$
are well-behaved. In particular,
$\mathcal{V}/a$
are well-behaved. In particular,
![]() $\mathsf{El}^0\,$
induces a full and faithful functor
$\mathsf{El}^0\,$
induces a full and faithful functor
![]() $\mathcal{V}/a \to \mathcal{hSet}_{\mathcal{U}}/\mathsf{El}^0\,a$
. We can use this fact to deduce, for example, that
$\mathcal{V}/a \to \mathcal{hSet}_{\mathcal{U}}/\mathsf{El}^0\,a$
. We can use this fact to deduce, for example, that
![]() $\mathcal{V}/a$
is cartesian closed.
$\mathcal{V}/a$
is cartesian closed.
Proposition 39 (![]() ). For any
). For any
![]() $a : \mathsf{V}^0$
,
$a : \mathsf{V}^0$
,
![]() $\mathcal{V} / a$
has finite limits.
$\mathcal{V} / a$
has finite limits.
Proof.
This can be proved using the standard argument: products in a slice category are realized by pullbacks in the underlying category and connected limits are realized by limits of the underlying diagram. We could also argue by noting that
![]() $\mathcal{hSet}_{\mathcal{U}}/\mathsf{El}^0\,a$
is finitely complete and that limits of diagrams in the image of
$\mathcal{hSet}_{\mathcal{U}}/\mathsf{El}^0\,a$
is finitely complete and that limits of diagrams in the image of
![]() $\mathsf{El}^0\,$
remain in the image of
$\mathsf{El}^0\,$
remain in the image of
![]() $\mathsf{El}^0\,$
.
$\mathsf{El}^0\,$
.
We give a bit more details in the following proof as it showcases the usefulness of being able to encode things directly in
![]() $\mathsf{V}^0$
, combined with the fact that
$\mathsf{V}^0$
, combined with the fact that
![]() $\mathsf{El}^0\,$
strictly decodes to the expected thing in
$\mathsf{El}^0\,$
strictly decodes to the expected thing in
![]() $\mathcal{U}$
.
$\mathcal{U}$
.
Proposition 40 (![]() ). For any
). For any
![]() $a : \mathsf{V}^0$
,
$a : \mathsf{V}^0$
,
![]() $\mathcal{V} / a$
has exponentials.
$\mathcal{V} / a$
has exponentials.
Proof.
Given
![]() $(x,f), (y,g) : \mathsf{Ob}\,(\mathcal{V} / a)$
, define their exponential as the element
$(x,f), (y,g) : \mathsf{Ob}\,(\mathcal{V} / a)$
, define their exponential as the element
Note that we have the following definitional equality:
This is the exponential in
![]() $\mathcal{hSet}_{\mathcal{U}}/\mathsf{El}^0\,a$
, so
$\mathcal{hSet}_{\mathcal{U}}/\mathsf{El}^0\,a$
, so
![]() $\mathsf{exp}\,(x,f)\,(y,g)$
is an exponential object in
$\mathsf{exp}\,(x,f)\,(y,g)$
is an exponential object in
![]() $\mathcal{V}/a$
.
$\mathcal{V}/a$
.
Corollary 41.
![]() $\mathcal{V}$
is locally cartesian closed and
$\mathcal{V}$
is locally cartesian closed and
![]() $\mathsf{El}^0$
is a locally cartesian closed functor.
$\mathsf{El}^0$
is a locally cartesian closed functor.
Finally, the following proposition foreshadows the next section where we build a model of type theory on
![]() $\mathcal{V}$
. In that section, we wish to interpret types in context
$\mathcal{V}$
. In that section, we wish to interpret types in context
![]() $a$
as elements of
$a$
as elements of
![]() $\mathcal{V}/a$
and to realize substitution as pullback. It is well-known, however, that the result is merely pseudofunctorial and therefore insufficient to form a (strict) model of type theory (Curien et al. Reference Curien, Garner and Hofmann2014; Seely Reference Seely1984). In the specific case of
$\mathcal{V}/a$
and to realize substitution as pullback. It is well-known, however, that the result is merely pseudofunctorial and therefore insufficient to form a (strict) model of type theory (Curien et al. Reference Curien, Garner and Hofmann2014; Seely Reference Seely1984). In the specific case of
![]() $\mathcal{hSet}_{\mathcal{U}}$
, there is a well-known pseudo-natural equivalence between the slice category
$\mathcal{hSet}_{\mathcal{U}}$
, there is a well-known pseudo-natural equivalence between the slice category
![]() $\mathcal{hSet}_{\mathcal{U}}/a$
and the functor category
$\mathcal{hSet}_{\mathcal{U}}/a$
and the functor category
![]() $[a,\mathcal{hSet}_{\mathcal{U}}]$
, which remedies the coherence issues. This equivalence restricts to the full subcategory determined by
$[a,\mathcal{hSet}_{\mathcal{U}}]$
, which remedies the coherence issues. This equivalence restricts to the full subcategory determined by
![]() $\mathcal{V}$
:
$\mathcal{V}$
:
Proposition 42 (![]() ). Given
). Given
![]() $a : \mathsf{V}^0$
and writing
$a : \mathsf{V}^0$
and writing
![]() $a$
for the corresponding discrete category associated with
$a$
for the corresponding discrete category associated with
![]() $\mathsf{El}^0\,a$
, there is a canonical equivalence
$\mathsf{El}^0\,a$
, there is a canonical equivalence
![]() $\mathcal{V} / a \simeq [a,\mathcal{V}]$
.
$\mathcal{V} / a \simeq [a,\mathcal{V}]$
.
Proof.
The equivalence is constructed in the standard way. The functor from
![]() $[a,\mathcal{V}]$
to
$[a,\mathcal{V}]$
to
![]() $\mathcal{V} / a$
sends
$\mathcal{V} / a$
sends
![]() $F : \mathsf{Ob}\,[a,\mathcal{V}]$
to the element
$F : \mathsf{Ob}\,[a,\mathcal{V}]$
to the element
![]() $\Sigma ^0\,a\,F$
together with the first projection. In the other direction, an element
$\Sigma ^0\,a\,F$
together with the first projection. In the other direction, an element
![]() $(x,f) : \mathsf{Ob}\,(\mathcal{V} / a)$
is mapped to the functor
$(x,f) : \mathsf{Ob}\,(\mathcal{V} / a)$
is mapped to the functor
![]() $\lambda i. \mathsf{fib}^0\,f\,i$
.
$\lambda i. \mathsf{fib}^0\,f\,i$
.
5.
 $\mathsf{V}^0$
as a Category with Families
$\mathsf{V}^0$
as a Category with Families
Having established that
![]() $\mathsf{V}^0$
organizes into a well-behaved category, we now take this a step further by showing that
$\mathsf{V}^0$
organizes into a well-behaved category, we now take this a step further by showing that
![]() $\mathsf{V}^0$
supports a model of extensional type theory. Since our goal is to do this very formally, our task is threefold: first, we must specify what we mean by a model of type theory. To this end, we have formalized a particular presentation of a CwF (Dybjer Reference Dybjer, Berardi and Coppo1996). This extends a category with the additional structure required to interpret dependent type theory. Next, we show that
$\mathsf{V}^0$
supports a model of extensional type theory. Since our goal is to do this very formally, our task is threefold: first, we must specify what we mean by a model of type theory. To this end, we have formalized a particular presentation of a CwF (Dybjer Reference Dybjer, Berardi and Coppo1996). This extends a category with the additional structure required to interpret dependent type theory. Next, we show that
![]() $\mathcal{V}$
can be equipped with this additional structure. Finally, since our definition of a CwF does not prescribe closure under any connectives, we detail how to extend a CwF with various connectives and show that the CwF structure on
$\mathcal{V}$
can be equipped with this additional structure. Finally, since our definition of a CwF does not prescribe closure under any connectives, we detail how to extend a CwF with various connectives and show that the CwF structure on
![]() $\mathcal{V}$
supports these extensions.
$\mathcal{V}$
supports these extensions.
Remark 43.
Of these three steps, only the first two are fully formalized. The obstruction to formalizing closure under all relevant extensions is, surprisingly, completely independent of
![]() $\mathsf{V}^0$
. Rather, it stems from the fact that the equations governing substitution hold only up to propositional equality, leading to complicated path and transport computations when defining the substitution properties of said structure.
$\mathsf{V}^0$
. Rather, it stems from the fact that the equations governing substitution hold only up to propositional equality, leading to complicated path and transport computations when defining the substitution properties of said structure.
5.1 The definition of categories with families
In the paper and formalization, we rely on the following formulation of categories with families.
Definition 44 (Category with families, ![]() ). A category with families (CwF) consists of:
). A category with families (CwF) consists of:
-
• A category
 $\mathcal{C}$
with a terminal object,
$\mathcal{C}$
with a terminal object,
-
• a presheaf
 $\mathsf{Ty}_{\mathcal{C}} :{{\mathcal{C}}}^{\mathsf{op}}\to \mathcal{hSet}_{\mathcal{U}}$
,
$\mathsf{Ty}_{\mathcal{C}} :{{\mathcal{C}}}^{\mathsf{op}}\to \mathcal{hSet}_{\mathcal{U}}$
, -
• a presheaf
 $\mathsf{Tm}_{\mathcal{C}} :{\left (\int \mkern -3mu \mathsf{Ty}_{\mathcal{C}}\right )}^{\mathsf{op}}\to \mathcal{hSet}_{\mathcal{U}}$
,
$\mathsf{Tm}_{\mathcal{C}} :{\left (\int \mkern -3mu \mathsf{Ty}_{\mathcal{C}}\right )}^{\mathsf{op}}\to \mathcal{hSet}_{\mathcal{U}}$
, -
• a functor
 ${-}.{-} : \int \mkern -3mu \mathsf{Ty}_{\mathcal{C}}\to {\mathcal{C}}$
, and
${-}.{-} : \int \mkern -3mu \mathsf{Ty}_{\mathcal{C}}\to {\mathcal{C}}$
, and
-
• for each
 $\Delta : \mathsf{Ob}\,{\mathcal{C}}$
and
$\Delta : \mathsf{Ob}\,{\mathcal{C}}$
and
 $(\Gamma, A) : \int \mkern -3mu \mathsf{Ty}_{\mathcal{C}}$
a natural equivalence
$(\Gamma, A) : \int \mkern -3mu \mathsf{Ty}_{\mathcal{C}}$
a natural equivalence
 \begin{equation*}{\mathsf {Hom}}\,(\Delta, \Gamma .\,A) \simeq \sum _{\gamma \;: {\mathsf {Hom}}\,(\Delta, \Gamma )} \mathsf {Tm}_{\mathcal {C}}\,(\Delta, A \cdot \gamma )\end{equation*}
\begin{equation*}{\mathsf {Hom}}\,(\Delta, \Gamma .\,A) \simeq \sum _{\gamma \;: {\mathsf {Hom}}\,(\Delta, \Gamma )} \mathsf {Tm}_{\mathcal {C}}\,(\Delta, A \cdot \gamma )\end{equation*}
Here we have written
![]() $A \cdot \gamma$
for
$A \cdot \gamma$
for
![]() $\mathsf{Ty}_{\mathcal{C}}\,(\gamma \,A)$
, and
$\mathsf{Ty}_{\mathcal{C}}\,(\gamma \,A)$
, and
![]() $\int \mkern -3mu \mathsf{Ty}_{\mathcal{C}}$
for the category of elements of
$\int \mkern -3mu \mathsf{Ty}_{\mathcal{C}}$
for the category of elements of
![]() $\mathsf{Ty}_{\mathcal{C}}$
, that is, the total space of the right fibration induced by
$\mathsf{Ty}_{\mathcal{C}}$
, that is, the total space of the right fibration induced by
![]() $\mathsf{Ty}_{\mathcal{C}}$
. Intuitively, objects in
$\mathsf{Ty}_{\mathcal{C}}$
. Intuitively, objects in
![]() $\mathcal{C}$
interpret the contexts of our type theory, while morphisms interpret substitutions. The additional presheaves are used to interpret types and terms. Specifically, the set of semantic types in context
$\mathcal{C}$
interpret the contexts of our type theory, while morphisms interpret substitutions. The additional presheaves are used to interpret types and terms. Specifically, the set of semantic types in context
![]() $\Gamma : \mathsf{Ob}\,{\mathcal{C}}$
is given by
$\Gamma : \mathsf{Ob}\,{\mathcal{C}}$
is given by
![]() $\mathsf{Ty}_{\mathcal{C}}\,\Gamma$
while the set of terms of type
$\mathsf{Ty}_{\mathcal{C}}\,\Gamma$
while the set of terms of type
![]() $A : \mathsf{Ty}_{\mathcal{C}}\,\Gamma$
is given by
$A : \mathsf{Ty}_{\mathcal{C}}\,\Gamma$
is given by
![]() $\mathsf{Tm}_{\mathcal{C}}\,(\Gamma, A)$
. The functoriality of
$\mathsf{Tm}_{\mathcal{C}}\,(\Gamma, A)$
. The functoriality of
![]() $\mathsf{Ty}_{\mathcal{C}}$
and
$\mathsf{Ty}_{\mathcal{C}}$
and
![]() $\mathsf{Tm}_{\mathcal{C}}$
is precisely the structure required to interpret the application of substitutions to types and terms.
$\mathsf{Tm}_{\mathcal{C}}$
is precisely the structure required to interpret the application of substitutions to types and terms.
The terminal object interprets the empty context and the functor from
![]() $\int \mkern -3mu \mathsf{Ty}_{\mathcal{C}}$
to
$\int \mkern -3mu \mathsf{Ty}_{\mathcal{C}}$
to
![]() $\mathcal{C}$
interprets context extension. A context
$\mathcal{C}$
interprets context extension. A context
![]() $\Gamma : \mathsf{Ob}\,{\mathcal{C}}$
can be extended by a type
$\Gamma : \mathsf{Ob}\,{\mathcal{C}}$
can be extended by a type
![]() $A : \mathsf{Ty}_{\mathcal{C}}\,\Gamma$
in that context, to produce a new context
$A : \mathsf{Ty}_{\mathcal{C}}\,\Gamma$
in that context, to produce a new context
![]() $\Gamma .\,A : \mathsf{Ob}\,{\mathcal{C}}$
.
$\Gamma .\,A : \mathsf{Ob}\,{\mathcal{C}}$
.
Finally, the natural equivalence ties together substitutions and elements of
![]() $\mathsf{Tm}_{\mathcal{C}}$
. In particular, the inverse encodes the ability to extend a substitution with a term. Following this last observation, we write
$\mathsf{Tm}_{\mathcal{C}}$
. In particular, the inverse encodes the ability to extend a substitution with a term. Following this last observation, we write
![]() $\Gamma .\,a$
for the element
$\Gamma .\,a$
for the element
![]() ${\mathsf{Hom}}\,(\Delta, \Gamma .\,A)$
induced by the element
${\mathsf{Hom}}\,(\Delta, \Gamma .\,A)$
induced by the element
![]() $(\Gamma, a) : \sum _{\gamma \;:{\mathsf{Hom}}\,(\Delta, \Gamma )} \mathsf{Tm}_{\mathcal{C}}\,(\Delta, A \cdot \,\gamma )$
.
$(\Gamma, a) : \sum _{\gamma \;:{\mathsf{Hom}}\,(\Delta, \Gamma )} \mathsf{Tm}_{\mathcal{C}}\,(\Delta, A \cdot \,\gamma )$
.
5.2 Equipping
 $\mathcal{V}$
with a CwF structure
$\mathcal{V}$
with a CwF structure
We now turn to equipping
![]() $\mathcal{V}$
with a CwF structure. We begin by defining
$\mathcal{V}$
with a CwF structure. We begin by defining
![]() $\mathsf{Ty}_{\mathcal{V}}$
as follows:
$\mathsf{Ty}_{\mathcal{V}}$
as follows:
Intuitively, a type in context
![]() $X$
is precisely an
$X$
is precisely an
![]() $X$
-indexed family of sets. There is, however, a major subtlety in this definition that should be emphasized: the version of the definition where
$X$
-indexed family of sets. There is, however, a major subtlety in this definition that should be emphasized: the version of the definition where
![]() $\mathsf{V}^0$
is replaced by
$\mathsf{V}^0$
is replaced by
![]() $\mathsf{hSet}_{\mathcal{U}}$
would be incorrect. We have required that
$\mathsf{hSet}_{\mathcal{U}}$
would be incorrect. We have required that
![]() $\mathsf{Ty}_{\mathcal{V}}\,X$
always be an h-set as it is assumed to be an
$\mathsf{Ty}_{\mathcal{V}}\,X$
always be an h-set as it is assumed to be an
![]() $\mathsf{hSet}_{\mathcal{U}}$
valued presheaf. Therefore, it is only after finding an adequate “h-set of h-sets” that we can define the set model of type theory in this manner.
$\mathsf{hSet}_{\mathcal{U}}$
valued presheaf. Therefore, it is only after finding an adequate “h-set of h-sets” that we can define the set model of type theory in this manner.
The definition of the presheaf of terms is also reasonably direct:
We now show that, along with
![]() $\mathcal{V}$
, these two definitions assemble into a CwF.
$\mathcal{V}$
, these two definitions assemble into a CwF.
Proposition 45 (![]() ).
).
![]() $\mathcal{V}$
can be equipped with a CwF structure.
$\mathcal{V}$
can be equipped with a CwF structure.
Proof.
We have given the putative definitions of
![]() $\mathsf{Ty}_{\mathcal{V}}$
and
$\mathsf{Ty}_{\mathcal{V}}$
and
![]() $\mathsf{Tm}_{\mathcal{V}}$
. We note that it is straightforward to ensure that both are suitably functorial. The functorial action is given by precomposition and all the required equations hold on-the-nose.
$\mathsf{Tm}_{\mathcal{V}}$
. We note that it is straightforward to ensure that both are suitably functorial. The functorial action is given by precomposition and all the required equations hold on-the-nose.
It remains to show that these three pieces of data satisfy the required properties of a CwF. We have already shown that
![]() $\mathcal{V}$
has a terminal object, so it remains to discuss the interpretation of context extension. Fix
$\mathcal{V}$
has a terminal object, so it remains to discuss the interpretation of context extension. Fix
![]() $X : \mathsf{V}^0$
and
$X : \mathsf{V}^0$
and
![]() $A : \mathsf{Ty}_{\mathcal{V}}\,X$
. We define
$A : \mathsf{Ty}_{\mathcal{V}}\,X$
. We define
![]() $X.\,A : \mathsf{V}^0$
as
$X.\,A : \mathsf{V}^0$
as
![]() $\Sigma ^0\,X\,A$
. The natural equivalence then follows from the
$\Sigma ^0\,X\,A$
. The natural equivalence then follows from the
![]() $\eta$
principle of dependent sums.
$\eta$
principle of dependent sums.
By virtue of Proposition 42, we further note that types
![]() $A$
in context
$A$
in context
![]() $X$
in this model are realized up to equivalence by families
$X$
in this model are realized up to equivalence by families
![]() $\mathsf{El}^0\,A \to \mathsf{El}^0\,X$
and terms are likewise determined by sections. By presenting
$\mathsf{El}^0\,A \to \mathsf{El}^0\,X$
and terms are likewise determined by sections. By presenting
![]() $\mathsf{Ty}_{\mathcal{V}}$
and
$\mathsf{Ty}_{\mathcal{V}}$
and
![]() $\mathsf{Tm}_{\mathcal{V}}$
in terms of (dependent) products rather than families and sections, we are able to equip both with strictly functorial actions.
$\mathsf{Tm}_{\mathcal{V}}$
in terms of (dependent) products rather than families and sections, we are able to equip both with strictly functorial actions.
We emphasize that the accomplishment here is not in the definition itself; it mirrors the naïve definition of the set model of type theory as presented by for example, Hofmann (Reference Hofmann1997). What is crucial is that
![]() $\mathsf{V}^0$
retains enough of the good behavior of
$\mathsf{V}^0$
retains enough of the good behavior of
![]() $\mathsf{hSet}_{\mathcal{U}}$
to support such a straightforward definition of the CwF structure while still managing to be an h-set itself.
$\mathsf{hSet}_{\mathcal{U}}$
to support such a straightforward definition of the CwF structure while still managing to be an h-set itself.
Remark 46.
We note that there are many closely related presentations of models of type theory (categories with attributes (Cartmell Reference Cartmell1986), contextual categories (Cartmell Reference Cartmell1986; Streicher Reference Streicher1991), comprehension categories (Jacobs Reference Jacobs1993, Reference Jacobs1999), natural models (Awodey Reference Awodey2018; Fiore Reference Fiore2012), and so on). We have opted for CwFs because the CwF structure on
![]() $\mathsf{V}^0$
is particularly simple and enjoys an exceptional number of definitional equalities. In particular, as opposed to other models which recover terms indirectly as sections to display maps, CwFs require the presheaf of terms as part of their data. This allows us to choose a particular definitional representative for the type of terms in our model and we are then able to explicitly select dependent functions. We shall see that this makes closing
$\mathsf{V}^0$
is particularly simple and enjoys an exceptional number of definitional equalities. In particular, as opposed to other models which recover terms indirectly as sections to display maps, CwFs require the presheaf of terms as part of their data. This allows us to choose a particular definitional representative for the type of terms in our model and we are then able to explicitly select dependent functions. We shall see that this makes closing
![]() $(\mathcal{V}, \mathsf{Ty}_{\mathcal{V}}, \mathsf{Tm}_{\mathcal{V}})$
under various constructions particularly straightforward, as most naturality conditions hold definitionally.
$(\mathcal{V}, \mathsf{Ty}_{\mathcal{V}}, \mathsf{Tm}_{\mathcal{V}})$
under various constructions particularly straightforward, as most naturality conditions hold definitionally.
5.3 Further structure on
 $\mathsf{V}^0$
as a cwF
$\mathsf{V}^0$
as a cwF
While we have constructed a CwF structure on
![]() $\mathcal{V}$
, we have thus far only shown that the model interprets the basic structural rules of type theory, but not that it is closed under any connectives. The process of extending the model with new connectives is essentially modular: for each connective, we specify the relevant structure on top of a CwF necessary to interpret it and then show that the CwF
$\mathcal{V}$
, we have thus far only shown that the model interprets the basic structural rules of type theory, but not that it is closed under any connectives. The process of extending the model with new connectives is essentially modular: for each connective, we specify the relevant structure on top of a CwF necessary to interpret it and then show that the CwF
![]() $(\mathcal{V},\mathsf{Ty}_{\mathcal{V}},\mathsf{Tm}_{\mathcal{V}})$
supports this additional structure.
$(\mathcal{V},\mathsf{Ty}_{\mathcal{V}},\mathsf{Tm}_{\mathcal{V}})$
supports this additional structure.
We illustrate the process with
![]() $\Pi$
-types. First, we must define a
$\Pi$
-types. First, we must define a
![]() $\Pi$
-structure on a CwF.
$\Pi$
-structure on a CwF.
Definition 47 (
![]() $\prod$
-structure,
$\prod$
-structure, ![]() ). A
). A
![]() $\prod$
-structure on a CwF
$\prod$
-structure on a CwF
![]() $({\mathcal{C}},\mathsf{Ty}_{\mathcal{C}},\mathsf{Tm}_{\mathcal{C}})$
is defined by the following:
$({\mathcal{C}},\mathsf{Ty}_{\mathcal{C}},\mathsf{Tm}_{\mathcal{C}})$
is defined by the following:
-
• An operation
 $\mathsf{pi}_{\mathcal{C}} : \prod _{\Gamma : \mathsf{Ob}\,\mathcal{C}} \mathsf{Ty}_{\mathcal{C}}\,\Gamma\to \mathsf{Ty}_{\mathcal{C}}\,(\Gamma .\,A)\to \mathsf{Ty}_{\mathcal{C}}\,\Gamma$
, natural in
$\mathsf{pi}_{\mathcal{C}} : \prod _{\Gamma : \mathsf{Ob}\,\mathcal{C}} \mathsf{Ty}_{\mathcal{C}}\,\Gamma\to \mathsf{Ty}_{\mathcal{C}}\,(\Gamma .\,A)\to \mathsf{Ty}_{\mathcal{C}}\,\Gamma$
, natural in
 $\Gamma$
.
$\Gamma$
. -
• For any
 $\Gamma : \mathsf{Ob}\,{\mathcal{C}}$
,
$\Gamma : \mathsf{Ob}\,{\mathcal{C}}$
,
 $A : \mathsf{Ty}_{\mathcal{C}}\,\Gamma$
, and
$A : \mathsf{Ty}_{\mathcal{C}}\,\Gamma$
, and
 $B : \mathsf{Ty}_{\mathcal{C}}\,(\Gamma .\,A)$
an isomorphism
$B : \mathsf{Ty}_{\mathcal{C}}\,(\Gamma .\,A)$
an isomorphism
 $\alpha _{\mathsf{pi}_{\mathcal{C}}}$
between
$\alpha _{\mathsf{pi}_{\mathcal{C}}}$
between
 $\mathsf{Tm}_{\mathcal{C}}\,(\Gamma, \mathsf{pi}_{\mathcal{C}}\,\Gamma \,A\,B)$
and
$\mathsf{Tm}_{\mathcal{C}}\,(\Gamma, \mathsf{pi}_{\mathcal{C}}\,\Gamma \,A\,B)$
and
 $\mathsf{Tm}_{\mathcal{C}}\,(\Gamma .A, B)$
, natural in
$\mathsf{Tm}_{\mathcal{C}}\,(\Gamma .A, B)$
, natural in
 $\Gamma$
.
$\Gamma$
.
Remark 48.
One may unpack the content of
![]() $\alpha _{\mathsf{pi}_{\mathcal{C}}}$
to see that it includes the introduction, elimination,
$\alpha _{\mathsf{pi}_{\mathcal{C}}}$
to see that it includes the introduction, elimination,
![]() $\beta$
-, and
$\beta$
-, and
![]() $\eta$
-rules for
$\eta$
-rules for
![]() $\prod$
-types. The additional requirement of naturality enforces the stability of the introduction and elimination rules under substitution.
$\prod$
-types. The additional requirement of naturality enforces the stability of the introduction and elimination rules under substitution.
Lemma 49 (![]() ). The CwF
). The CwF
![]() $(\mathcal{V},\mathsf{Ty}_{\mathcal{V}},\mathsf{Tm}_{\mathcal{V}})$
supports a
$(\mathcal{V},\mathsf{Ty}_{\mathcal{V}},\mathsf{Tm}_{\mathcal{V}})$
supports a
![]() $\prod$
-structure.
$\prod$
-structure.
Proof.
We begin by defining
![]() $\mathsf{pi}_{\mathcal{V}}$
as follows:
$\mathsf{pi}_{\mathcal{V}}$
as follows:
Naturality in
![]() $\Gamma$
is a straightforward computation. The definition of
$\Gamma$
is a straightforward computation. The definition of
![]() $\alpha _{\mathsf{pi}_{\mathcal{V}}}$
, after unfolding, reduces to the manifestly natural equivalence induced by currying:
$\alpha _{\mathsf{pi}_{\mathcal{V}}}$
, after unfolding, reduces to the manifestly natural equivalence induced by currying:
We have formalized both the definition of
![]() $\Pi$
-structures and the particular
$\Pi$
-structures and the particular
![]() $\Pi$
-structure on
$\Pi$
-structure on
![]() $(\mathcal{V},\mathsf{Ty}_{\mathcal{V}},\mathsf{Tm}_{\mathcal{V}})$
in
$(\mathcal{V},\mathsf{Ty}_{\mathcal{V}},\mathsf{Tm}_{\mathcal{V}})$
in
![]() $\texttt{Agda}$
. However, already some small inconveniences emerge. For instance, in the definition of naturality for
$\texttt{Agda}$
. However, already some small inconveniences emerge. For instance, in the definition of naturality for
![]() $\alpha{\mathsf{pi}_{\mathcal{V}}}$
, we must specify an equality dependent on the proof witnessing naturality of
$\alpha{\mathsf{pi}_{\mathcal{V}}}$
, we must specify an equality dependent on the proof witnessing naturality of
![]() $\mathsf{pi}_{\mathcal{V}}$
. The dependence is straightforward in this case, but becomes more complex for the later structures. Accordingly, we present only paper proofs for them.
$\mathsf{pi}_{\mathcal{V}}$
. The dependence is straightforward in this case, but becomes more complex for the later structures. Accordingly, we present only paper proofs for them.
Furthermore,
![]() $(\mathcal{V},\mathsf{Ty}_{\mathcal{V}},\mathsf{Tm}_{\mathcal{C}})$
also supports dependent sums.
$(\mathcal{V},\mathsf{Ty}_{\mathcal{V}},\mathsf{Tm}_{\mathcal{C}})$
also supports dependent sums.
Definition 50 (
![]() $\Sigma$
-structure). A
$\Sigma$
-structure). A
![]() $\Sigma$
-structure on a CwF
$\Sigma$
-structure on a CwF
![]() $({\mathcal{C}},\mathsf{Ty}_{\mathcal{C}},\mathsf{Tm}_{\mathcal{C}})$
consists of the following two pieces of data:
$({\mathcal{C}},\mathsf{Ty}_{\mathcal{C}},\mathsf{Tm}_{\mathcal{C}})$
consists of the following two pieces of data:
-
• An operation
 $\mathsf{sig}_{\mathcal{C}} : \prod _{\Gamma : \mathsf{Ob}\,\mathcal{C}} \mathsf{Ty}_{\mathcal{C}}\,\Gamma\to \mathsf{Ty}_{\mathcal{C}}\,(\Gamma .\,A)\to \mathsf{Ty}_{\mathcal{C}}\,\Gamma$
, natural in
$\mathsf{sig}_{\mathcal{C}} : \prod _{\Gamma : \mathsf{Ob}\,\mathcal{C}} \mathsf{Ty}_{\mathcal{C}}\,\Gamma\to \mathsf{Ty}_{\mathcal{C}}\,(\Gamma .\,A)\to \mathsf{Ty}_{\mathcal{C}}\,\Gamma$
, natural in
 $\Gamma$
.
$\Gamma$
. -
• For any
 $\Gamma : \mathsf{Ob}\,{\mathcal{C}}$
,
$\Gamma : \mathsf{Ob}\,{\mathcal{C}}$
,
 $A : \mathsf{Ty}_{\mathcal{C}}\,\Gamma$
, and
$A : \mathsf{Ty}_{\mathcal{C}}\,\Gamma$
, and
 $B : \mathsf{Ty}_{\mathcal{C}}\,(\Gamma .\,A)$
a natural isomorphism
$B : \mathsf{Ty}_{\mathcal{C}}\,(\Gamma .\,A)$
a natural isomorphism
 $\alpha _{\mathsf{sig}_{\mathcal{C}}}$
between
$\alpha _{\mathsf{sig}_{\mathcal{C}}}$
between
 $\mathsf{Tm}_{\mathcal{C}}\,(\Gamma, \mathsf{sig}_{\mathcal{C}}\,\Gamma \,A\,B)$
and pairs
$\mathsf{Tm}_{\mathcal{C}}\,(\Gamma, \mathsf{sig}_{\mathcal{C}}\,\Gamma \,A\,B)$
and pairs
 $\sum _{a : \mathsf{Tm}_{\mathcal{C}}(\Gamma, A)} \mathsf{Tm}_{\mathcal{C}}\,(\Gamma, B \cdot ({\mathsf{id}}.a))$
.
$\sum _{a : \mathsf{Tm}_{\mathcal{C}}(\Gamma, A)} \mathsf{Tm}_{\mathcal{C}}\,(\Gamma, B \cdot ({\mathsf{id}}.a))$
.
Lemma 51.
The CwF
![]() $(\mathcal{V},\mathsf{Ty}_{\mathcal{V}},\mathsf{Tm}_{\mathcal{V}})$
supports a
$(\mathcal{V},\mathsf{Ty}_{\mathcal{V}},\mathsf{Tm}_{\mathcal{V}})$
supports a
![]() $\Sigma$
-structure.
$\Sigma$
-structure.
Proof.
We define
![]() $\mathsf{sig}_{\mathcal{V}}$
as follows:
$\mathsf{sig}_{\mathcal{V}}$
as follows:
The remaining structure follows directly. In particular, even though the naturality requires complex path algebra to state properly in the specific CwF on
![]() $\mathcal{V}$
all these paths are given by reflexivity.
$\mathcal{V}$
all these paths are given by reflexivity.
We next consider a representative inductive type: booleans.
Definition 52 (
![]() $\mathsf{bool}$
-structure). A
$\mathsf{bool}$
-structure). A
![]() $\mathsf{bool}$
-structure on a CwF
$\mathsf{bool}$
-structure on a CwF
![]() $({\mathcal{C}},\mathsf{Ty}_{\mathcal{C}},\mathsf{Tm}_{\mathcal{C}})$
consists of the following two pieces of data:
$({\mathcal{C}},\mathsf{Ty}_{\mathcal{C}},\mathsf{Tm}_{\mathcal{C}})$
consists of the following two pieces of data:
-
• An operation
 $\mathsf{bool}_{\mathcal{C}} : \prod _{\Gamma : \mathsf{Ob}\,\mathcal{C}} \mathsf{Ty}_{\mathcal{C}}\,\Gamma$
natural in
$\mathsf{bool}_{\mathcal{C}} : \prod _{\Gamma : \mathsf{Ob}\,\mathcal{C}} \mathsf{Ty}_{\mathcal{C}}\,\Gamma$
natural in
 $\Gamma$
.
$\Gamma$
. -
• A pair of operations
 $\mathsf{true}_{\mathcal{C}},\mathsf{false}_{\mathcal{C}} : \prod _{\Gamma : \mathsf{Ob}\,\mathcal{C}} \mathsf{Tm}_{\mathcal{C}}\,(\Gamma, \mathsf{bool}_{\mathcal{C}})$
also natural in
$\mathsf{true}_{\mathcal{C}},\mathsf{false}_{\mathcal{C}} : \prod _{\Gamma : \mathsf{Ob}\,\mathcal{C}} \mathsf{Tm}_{\mathcal{C}}\,(\Gamma, \mathsf{bool}_{\mathcal{C}})$
also natural in
 $\Gamma$
.
$\Gamma$
.
Furthermore, the following canonical map induced by substitution must be an isomorphism for each
![]() $\Gamma : \mathsf{Ob}\,{\mathcal{C}}$
and
$\Gamma : \mathsf{Ob}\,{\mathcal{C}}$
and
![]() $A : \mathsf{Ty}_{\mathcal{C}}\,(\Gamma .\,\mathsf{bool}_{\mathcal{C}})$
:
$A : \mathsf{Ty}_{\mathcal{C}}\,(\Gamma .\,\mathsf{bool}_{\mathcal{C}})$
:
Lemma 53.
The CwF
![]() $(\mathcal{V},\mathsf{Ty}_{\mathcal{V}},\mathsf{Tm}_{\mathcal{V}})$
supports a
$(\mathcal{V},\mathsf{Ty}_{\mathcal{V}},\mathsf{Tm}_{\mathcal{V}})$
supports a
![]() $\mathsf{bool}$
-structure.
$\mathsf{bool}$
-structure.
Proof.
We define
![]() $\mathsf{bool}_{\mathcal{V}}$
as follows:
$\mathsf{bool}_{\mathcal{V}}$
as follows:
By construction,
![]() $\mathsf{Tm}_{\mathcal{V}}\,(\Gamma, \mathsf{bool}_{\mathcal{V}})$
is definitionally equal to
$\mathsf{Tm}_{\mathcal{V}}\,(\Gamma, \mathsf{bool}_{\mathcal{V}})$
is definitionally equal to
![]() $\mathsf{El}^0\,\Gamma \to \mathsf{bool}$
and so we define
$\mathsf{El}^0\,\Gamma \to \mathsf{bool}$
and so we define
![]() $\mathsf{true}_{\mathcal{V}}$
as
$\mathsf{true}_{\mathcal{V}}$
as
![]() $\lambda \gamma .\,\mathsf{true}$
and
$\lambda \gamma .\,\mathsf{true}$
and
![]() $\mathsf{false}_{\mathcal{V}}$
as
$\mathsf{false}_{\mathcal{V}}$
as
![]() $\lambda \gamma .\,\mathsf{false}$
. The calculations that these definitions are natural and that the required map is an isomorphism are routine.
$\lambda \gamma .\,\mathsf{false}$
. The calculations that these definitions are natural and that the required map is an isomorphism are routine.
By similar considerations, we may define and close
![]() $(\mathcal{V},\mathsf{Ty}_{\mathcal{V}},\mathsf{Tm}_{\mathcal{V}})$
under many other connectives already constructed in Section 3: extensional identity types, natural numbers, and universes among others. Putting all of this together, we conclude the following:
$(\mathcal{V},\mathsf{Ty}_{\mathcal{V}},\mathsf{Tm}_{\mathcal{V}})$
under many other connectives already constructed in Section 3: extensional identity types, natural numbers, and universes among others. Putting all of this together, we conclude the following:
Theorem 54.
![]() $\mathcal{V}$
supports a model of extensional type theory with the standard connectives.
$\mathcal{V}$
supports a model of extensional type theory with the standard connectives.
We note that this result, combined with Proposition 42 and the series of results about
![]() $\mathsf{El}^0$
preserving various categorical connectives can be summarized by the informal slogan:
$\mathsf{El}^0$
preserving various categorical connectives can be summarized by the informal slogan:
![]() $\mathcal{V}$
supports a model of type theory which internalizes the set-level fragment of the ambient type theory.
$\mathcal{V}$
supports a model of type theory which internalizes the set-level fragment of the ambient type theory.
6. Relationship to Set Models of Type Theory and Other Set Universes in HoTT/UF
The idea of set theoretic semantics of type theory is of course an old and natural one. An early reference where this is written down more formally is the master thesis of Salvesen (Reference Salvesen1984, Chapter 5). As discussed in the introduction, the work presented in this paper goes back to the model of CZF in type theory of Aczel (Reference Aczel, Macintyre, Pacholski and Paris1978). Aczel also interpreted extensional type theory with universes in an extension of CZF with a hierarchy of inaccessible sets (Aczel, Reference Aczel, Altenkirch, Reus and Naraschewski1999). In fact, Aczel’s V occurs already in the PhD thesis of Leversha (Reference Leversha1976), where it was used to represent ordinals constructively. Various earlier works have also relied on Aczel’s V to model type theory. For instance, Werner (Reference Werner1997) modeled the core system of
![]() $\texttt{Coq}$
in ZFC and vice versa, using Aczel’s encoding of sets. A refinement by Barras (Reference Barras2010, Reference Barras2012) models the core system of
$\texttt{Coq}$
in ZFC and vice versa, using Aczel’s encoding of sets. A refinement by Barras (Reference Barras2010, Reference Barras2012) models the core system of
![]() $\texttt{Coq}$
system in intuitionistic ZF and formalizes the model in
$\texttt{Coq}$
system in intuitionistic ZF and formalizes the model in
![]() $\texttt{Coq}$
(The Coq Development Team 2021). More recently, Palmgren (Reference Palmgren2019) presented an interpretation of extensional MLTT (Martin-Löf Reference Martin-Löf, Cohen, Łoś, Pfeiffer and Podewski1982) into intensional MLTT via setoids, also relying on Aczel’s V. Palmgren’s work was also formalized in
$\texttt{Coq}$
(The Coq Development Team 2021). More recently, Palmgren (Reference Palmgren2019) presented an interpretation of extensional MLTT (Martin-Löf Reference Martin-Löf, Cohen, Łoś, Pfeiffer and Podewski1982) into intensional MLTT via setoids, also relying on Aczel’s V. Palmgren’s work was also formalized in
![]() $\texttt{Agda}$
.
$\texttt{Agda}$
.
Aczel’s V was revisited in HoTT/UF by Gylterud (Reference Gylterud2018, Reference Gylterud2020) who observed that this gives a universe of multisets, but that one can restrict it, as in Definition 9, to get a universe of h-sets. These universes of (multi)sets has recently also been further studied by Escardó and de Jong who has their own
![]() $\texttt{Agda}$
formalization as part of the
$\texttt{Agda}$
formalization as part of the
![]() $\texttt{TypeTopology}$
project (Escardó and de Jong Reference Escardó and de Jong2023). Among many other things, they have two more proofs of Theorem12 formalized. Various HITs for representing finite multisets have also been considered in HoTT/UF (Angiuli et al. Reference Angiuli, Cavallo, Mörtberg and Zeuner2021; Basold et al. Reference Basold, Geuvers and van der Weide2017; Choudhury and Fiore Reference Choudhury and Fiore2019; Frumin et al. Reference Frumin, Geuvers, Gondelman and van der Weide2018; Joram and Veltri Reference Joram, Veltri, Naumowicz and Thiemann2023; Veltri Reference Veltri and Kobayashi2021); however, these are of course not sufficient to model full type theory.
$\texttt{TypeTopology}$
project (Escardó and de Jong Reference Escardó and de Jong2023). Among many other things, they have two more proofs of Theorem12 formalized. Various HITs for representing finite multisets have also been considered in HoTT/UF (Angiuli et al. Reference Angiuli, Cavallo, Mörtberg and Zeuner2021; Basold et al. Reference Basold, Geuvers and van der Weide2017; Choudhury and Fiore Reference Choudhury and Fiore2019; Frumin et al. Reference Frumin, Geuvers, Gondelman and van der Weide2018; Joram and Veltri Reference Joram, Veltri, Naumowicz and Thiemann2023; Veltri Reference Veltri and Kobayashi2021); however, these are of course not sufficient to model full type theory.
We will now discuss other approaches to constructing strict categories of sets in HoTT/UF that could also serve as internal models of type theory. These often require various extensions of the quite minimal univalent type theory that we have relied on in this paper.
6.1 The cumulative hierarchy in the HoTT book
The HoTT book postulates a universe of sets as a higher inductive type called the cumulative hierarchy (HoTT Book, Definition 10.5.1). Gylterud (Reference Gylterud2018, Section 8) establishes an equivalence between the HoTT book
![]() $V$
and
$V$
and
![]() $\mathsf{V}^0$
, which makes it possible to transfer all of our results over to
$\mathsf{V}^0$
, which makes it possible to transfer all of our results over to
![]() $V$
. One remark about the HoTT book
$V$
. One remark about the HoTT book
![]() $V$
is that it is h-set truncated, while
$V$
is that it is h-set truncated, while
![]() $\mathsf{V}^0$
is not. This means that the eliminator one gets for the HoTT book
$\mathsf{V}^0$
is not. This means that the eliminator one gets for the HoTT book
![]() $V$
only lets one directly eliminate into h-sets, while
$V$
only lets one directly eliminate into h-sets, while
![]() $\mathsf{V}^0$
can be directly eliminated into types of arbitrary homotopy level. Similarly many basic constructions, like
$\mathsf{V}^0$
can be directly eliminated into types of arbitrary homotopy level. Similarly many basic constructions, like
![]() $ \in \,:\,V\to V\to \mathcal{U}$
, is a bit more complicated to define for the HoTT book
$ \in \,:\,V\to V\to \mathcal{U}$
, is a bit more complicated to define for the HoTT book
![]() $V$
as it is not sufficient to only define them for point constructors, but one has to check that the definitions are compatible with the higher constructors as well. A practical and appealing aspect of
$V$
as it is not sufficient to only define them for point constructors, but one has to check that the definitions are compatible with the higher constructors as well. A practical and appealing aspect of
![]() $\mathsf{V}^0$
is hence that it is easy to define operations by pattern-matching on it. Another is that it is not postulated, but simply constructed from W-types.
$\mathsf{V}^0$
is hence that it is easy to define operations by pattern-matching on it. Another is that it is not postulated, but simply constructed from W-types.
6.2 Inductive-recursive universes
An alternative approach to modeling type theory in type theory is to rely on quotient inductive-inductive types (QIITs) as considered by Altenkirch and Kaposi (Reference Altenkirch and Kaposi2016). However, they run into the same problem as discussed above when working in HoTT and trying to eliminate their QIIT into
![]() $\mathsf{hSet}_{\mathcal{U}}$
. In particular, as the QIIT representation of type theory is h-set truncated they cannot eliminate directly into
$\mathsf{hSet}_{\mathcal{U}}$
. In particular, as the QIIT representation of type theory is h-set truncated they cannot eliminate directly into
![]() $\mathsf{hSet}_{\mathcal{U}}$
as it is a 1-type (the same issue also applies to the HoTT Book
$\mathsf{hSet}_{\mathcal{U}}$
as it is a 1-type (the same issue also applies to the HoTT Book
![]() $V$
). The authors resolve this by considering an inductive-recursive universe closed under the relevant structure, which can be shown to be a set without any need to set truncate. This enjoys many of the nice properties of
$V$
). The authors resolve this by considering an inductive-recursive universe closed under the relevant structure, which can be shown to be a set without any need to set truncate. This enjoys many of the nice properties of
![]() $\mathsf{V}^0$
, like
$\mathsf{V}^0$
, like
![]() $\mathsf{El}$
decoding type constructors definitionally, but induction-recursion is proof theoretically quite strong, and it is again interesting to emphasize that we can construct
$\mathsf{El}$
decoding type constructors definitionally, but induction-recursion is proof theoretically quite strong, and it is again interesting to emphasize that we can construct
![]() $\mathsf{V}^0$
using only W-types.
$\mathsf{V}^0$
using only W-types.
6.3 Covered marked extensional well-founded orders (MEWOs)
In their recent paper, de Jong et al. (Reference de Jong, Kraus, Forsberg and Xu2023) show that the HoTT Book
![]() $V$
is equivalent to the type of covered marked extensional well-founded orders (
$V$
is equivalent to the type of covered marked extensional well-founded orders (
![]() $\mathsf{MEWO}_{\mathsf{cov}}$
), and hence to
$\mathsf{MEWO}_{\mathsf{cov}}$
), and hence to
![]() $\mathsf{V}^0$
. The results in this paper thus imply that the type
$\mathsf{V}^0$
. The results in this paper thus imply that the type
![]() $\mathsf{MEWO}_{\mathsf{cov}}$
can be equipped with a universe structure. A strength of the universe
$\mathsf{MEWO}_{\mathsf{cov}}$
can be equipped with a universe structure. A strength of the universe
![]() $\mathsf{V}^0$
is the computational aspect of the decoding function
$\mathsf{V}^0$
is the computational aspect of the decoding function
![]() $\mathsf{El}^0\,$
. Unfortunately, the two underlying maps of the equivalence between
$\mathsf{El}^0\,$
. Unfortunately, the two underlying maps of the equivalence between
![]() $\mathsf{V}^0$
and
$\mathsf{V}^0$
and
![]() $\mathsf{MEWO}_{\mathsf{cov}}$
do not compose definitionally to the identity when going from
$\mathsf{MEWO}_{\mathsf{cov}}$
do not compose definitionally to the identity when going from
![]() $\mathsf{V}^0$
to
$\mathsf{V}^0$
to
![]() $\mathsf{MEWO}_{\mathsf{cov}}$
and back again. This means that the induced decoding for
$\mathsf{MEWO}_{\mathsf{cov}}$
and back again. This means that the induced decoding for
![]() $\mathsf{MEWO}_{\mathsf{cov}}$
given by going to
$\mathsf{MEWO}_{\mathsf{cov}}$
given by going to
![]() $\mathsf{V}^0$
and then applying
$\mathsf{V}^0$
and then applying
![]() $\mathsf{El}^0$
is not as computationally well-behaved as
$\mathsf{El}^0$
is not as computationally well-behaved as
![]() $\mathsf{El}^0$
on
$\mathsf{El}^0$
on
![]() $\mathsf{V}^0$
, as the decoding will only hold up to propositional equality.
$\mathsf{V}^0$
, as the decoding will only hold up to propositional equality.
6.4 Relationship to
 $\mathcal{hSet}_{\mathcal{U}}$
$\mathcal{hSet}_{\mathcal{U}}$
One reason to consider the category of iterative sets is to regard it as a replacement for
![]() $\mathcal{hSet}_{\mathcal{U}}$
. As noted in Section 4,
$\mathcal{hSet}_{\mathcal{U}}$
. As noted in Section 4,
![]() $\mathsf{El}^0$
induces a fully faithful functor, but it may fail to be essentially surjective. The statement that
$\mathsf{El}^0$
induces a fully faithful functor, but it may fail to be essentially surjective. The statement that
![]() $\mathsf{El}^0$
is essentially surjective corresponds to Shulman’s axiom of well-founded materialization (Shulman Reference Shulman2010) and which is, in turn, implied by the axiom of choice.
$\mathsf{El}^0$
is essentially surjective corresponds to Shulman’s axiom of well-founded materialization (Shulman Reference Shulman2010) and which is, in turn, implied by the axiom of choice.
If the functor is essentially surjective, it forms a categorical equivalence between
![]() $\mathcal{V}$
and a univalent category and thus describes
$\mathcal{V}$
and a univalent category and thus describes
![]() $\mathcal{hSet}_{\mathcal{U}}$
as the Rezk completion (Ahrens et al. Reference Ahrens, Kapulkin and Shulman2015) of
$\mathcal{hSet}_{\mathcal{U}}$
as the Rezk completion (Ahrens et al. Reference Ahrens, Kapulkin and Shulman2015) of
![]() $\mathcal{V}$
. Informally, this shows, modulo classical axioms, that
$\mathcal{V}$
. Informally, this shows, modulo classical axioms, that
![]() $\mathcal{V}$
is a more rigid presentation of
$\mathcal{V}$
is a more rigid presentation of
![]() $\mathcal{hSet}_{\mathcal{U}}$
. Moreover, even without additional axioms
$\mathcal{hSet}_{\mathcal{U}}$
. Moreover, even without additional axioms
![]() $\mathcal{V}$
and
$\mathcal{V}$
and
![]() $\mathsf{V}^0$
are closed under essentially every construction of interest.
$\mathsf{V}^0$
are closed under essentially every construction of interest.
6.5 Well-ordered sets
Another approach to defining a strict universe of sets, inspired by Voevodsky’s simplicial set model (Kapulkin and Lumsdaine Reference Kapulkin and Lumsdaine2021), is to consider well-ordered sets. By relying heavily on Zermelo’s well-ordering principle, and hence choice, one can obtain a strict category of well-ordered sets with the relevant structure, also as a subcategory of
![]() $\mathcal{hSet}_{\mathcal{U}}$
. This was experimented with in
$\mathcal{hSet}_{\mathcal{U}}$
. This was experimented with in
![]() $\texttt{UniMath}$
(Voevodsky et al. Reference Voevodsky, Ahrens and Grayson2020) by Mörtberg (Reference Mörtberg2018). However, this turned out to be harder to work with formally than expected because of all the propositional truncations and hence not completed. Furthermore, if completed this would only merely give us the existence of an internal model and hence lead to a weaker result than Theorem54.
$\texttt{UniMath}$
(Voevodsky et al. Reference Voevodsky, Ahrens and Grayson2020) by Mörtberg (Reference Mörtberg2018). However, this turned out to be harder to work with formally than expected because of all the propositional truncations and hence not completed. Furthermore, if completed this would only merely give us the existence of an internal model and hence lead to a weaker result than Theorem54.
7. Conclusion and Future Work
We have constructed a universe of h-sets that is itself an h-set and structured it into an internal model of extensional type theory. This main result can perhaps also be proven for other h-set universes of h-sets, such as the ones mentioned in Section 6, but certain properties of our construction make it very convenient to work with, also formally. First and foremost, the definitional decoding of type formers means that one avoids complex transports. Second, the construction is carried out using basic type-formers and has a (provable) elimination principle, which directly allows elimination into general types. This development works in a fairly minimalist univalent type theory, as long as it has W-types. These W-types can be large, and need only be small if one wants to reflect a hierarchy of universes, as in Section 3.5. The results should thus have a broad applicability in models of HoTT/UF.
In the formalization, we stopped short of adding additional structure to the CwF on
![]() $\mathcal{V}$
after
$\mathcal{V}$
after
![]() $\prod$
-types. The obstacles are in fact not in providing the structure for our model, such as
$\prod$
-types. The obstacles are in fact not in providing the structure for our model, such as
![]() $\Sigma$
-structure, but the general formulation of what that extra structure constitutes on CwFs based on categories (see Remark 43 in Section 5). To the best of our knowledge, there are no other formalizations of CwFs with
$\Sigma$
-structure, but the general formulation of what that extra structure constitutes on CwFs based on categories (see Remark 43 in Section 5). To the best of our knowledge, there are no other formalizations of CwFs with
![]() $\Sigma$
-structure out there that do not assume UIP or other axioms and which do not use setoids or a more extensional equality. It would be interesting to attempt formalizing this in cubical type theory (Cohen et al. Reference Cohen, Coquand, Huber, Mörtberg and Uustalu2018) where equality of
$\Sigma$
-structure out there that do not assume UIP or other axioms and which do not use setoids or a more extensional equality. It would be interesting to attempt formalizing this in cubical type theory (Cohen et al. Reference Cohen, Coquand, Huber, Mörtberg and Uustalu2018) where equality of
![]() $\Sigma$
-types is easier to work with because of the primitive path-over types in the form of
$\Sigma$
-types is easier to work with because of the primitive path-over types in the form of
![]() $\mathsf{PathP}$
-types. An experiment along these lines was performed by Vezzosi (Reference Vezzosi2017) in
$\mathsf{PathP}$
-types. An experiment along these lines was performed by Vezzosi (Reference Vezzosi2017) in
![]() $\texttt{Cubical}$
$\texttt{Cubical}$
![]() $\texttt{Agda}$
(Vezzosi et al. Reference Vezzosi, Mörtberg and Abel2021). In this small formalization, Vezzosi considered the CwF structure on h-set valued presheaves. It would of course not have been possible to fully complete this for the same reason as discussed in this paper, but it turned out that some of the constructions and equations that one has to check were easier than in a corresponding formalization in
$\texttt{Agda}$
(Vezzosi et al. Reference Vezzosi, Mörtberg and Abel2021). In this small formalization, Vezzosi considered the CwF structure on h-set valued presheaves. It would of course not have been possible to fully complete this for the same reason as discussed in this paper, but it turned out that some of the constructions and equations that one has to check were easier than in a corresponding formalization in
![]() $\texttt{UniMath}$
by Mörtberg (Reference Mörtberg2017). This also suggests a further direction to explore:
$\texttt{UniMath}$
by Mörtberg (Reference Mörtberg2017). This also suggests a further direction to explore:
![]() $\mathcal{V}$
valued presheaves. These should enjoy the same nice properties as
$\mathcal{V}$
valued presheaves. These should enjoy the same nice properties as
![]() $\mathcal{hSet}_{\mathcal{U}}$
valued presheaves, but it should be possible to organize also them into a model of type theory internally in HoTT/UF.
$\mathcal{hSet}_{\mathcal{U}}$
valued presheaves, but it should be possible to organize also them into a model of type theory internally in HoTT/UF.
Another avenue of further study is to take a closer look at Shulman’s axiom of well-founded materialization. Just like univalence, it makes sense to formulate this axiom relative to a given universe of types. The construction of
![]() $\mathsf{V}^0$
can be carried out on any universe, so a reasonable reformulation of well-founded materialization in type theory could be: a universe
$\mathsf{V}^0$
can be carried out on any universe, so a reasonable reformulation of well-founded materialization in type theory could be: a universe
![]() $\mathcal{U}$
has well-founded materialization if
$\mathcal{U}$
has well-founded materialization if
![]() $\mathsf{El}^0\,: \mathsf{V}^0_{\mathcal{U}}\to \mathcal{hSet}_{\mathcal{U}}$
is essentially surjective. As mentioned, this follows from AC, but does not seem to be inherently nonconstructive. For instance,
$\mathsf{El}^0\,: \mathsf{V}^0_{\mathcal{U}}\to \mathcal{hSet}_{\mathcal{U}}$
is essentially surjective. As mentioned, this follows from AC, but does not seem to be inherently nonconstructive. For instance,
![]() $\mathsf{V}^0$
itself has well-founded materialization for trivial reasons. The most pertinent question is perhaps whether well-founded materialization and univalence can constructively coexist. If we start with a univalent
$\mathsf{V}^0$
itself has well-founded materialization for trivial reasons. The most pertinent question is perhaps whether well-founded materialization and univalence can constructively coexist. If we start with a univalent
![]() $\mathcal{U}$
, one could take the image of
$\mathcal{U}$
, one could take the image of
![]() $\mathsf{El}^0\,$
in
$\mathsf{El}^0\,$
in
![]() $\mathcal{hSet}_{\mathcal{U}}$
to obtain a univalent universe which also somewhat trivially has well-founded materialization. However, it is not immediate that this is closed under
$\mathcal{hSet}_{\mathcal{U}}$
to obtain a univalent universe which also somewhat trivially has well-founded materialization. However, it is not immediate that this is closed under
![]() $\prod$
-types and
$\prod$
-types and
![]() $\Sigma$
-types as a naïve attempt quickly runs into choice problems.
$\Sigma$
-types as a naïve attempt quickly runs into choice problems.
Acknowledgments
Anders would like to thank the late Vladimir Voevodsky for interesting him in the problem of set universes of sets in Univalent Foundations. In the last email Vladimir sent to Anders (on August 17, 2017), he asked about progress on this problem and mentioned that he had had a new idea for its solution. Unfortunately, Vladimir never replied with any details about the solution, but we hope that he would have been pleased with the solution in this paper.
This work is also a testament to influence of the late Peter Aczel, who already in the late 1970s laid the foundations of this work. We are also indebted to the late Erik Palmgren, whose research, teaching, and encouragement shaped the constructions herein.
The authors would like to thank Peter LeFanu Lumsdaine for valuable comments and discussions and for stating our main result before we had done so ourselves. We are also very grateful to Henrik Forssell for helping us get a copy of the relevant chapter of the 1984 master thesis of Salvesen (Reference Salvesen1984), which only seems to exist in hard copy at the University of Oslo library.
Anders Mörtberg has been supported by the Swedish Research Council (Vetenskapsrådet) under Grant No. 2019-04545.
Competing interests
The authors declare no competing interests.