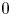1. Introduction
One of the most influential open problems in the study of syzygies over the past ![]() $35$ years, which remains open to this day, is Green's conjecture on canonical curves [Reference GreenGre84, Conjecture 5.1]. It asserts that for a smooth curve
$35$ years, which remains open to this day, is Green's conjecture on canonical curves [Reference GreenGre84, Conjecture 5.1]. It asserts that for a smooth curve ![]() $C$ of genus
$C$ of genus ![]() $g$ in characteristic
$g$ in characteristic ![]() $0$, the (non-)vanishing behavior of the Koszul cohomology groups
$0$, the (non-)vanishing behavior of the Koszul cohomology groups ![]() $K_{p,1}(C,\omega _C)$, where
$K_{p,1}(C,\omega _C)$, where ![]() $\omega _C$ is the canonical bundle, detects the Clifford index of
$\omega _C$ is the canonical bundle, detects the Clifford index of ![]() $C$:
$C$:
The implication ‘![]() $\Longleftarrow$’ was proved by Green and Lazarsfeld in [Reference GreenGre84, Appendix], and the converse amounts by duality to showing that
$\Longleftarrow$’ was proved by Green and Lazarsfeld in [Reference GreenGre84, Appendix], and the converse amounts by duality to showing that
It was soon realized that due to the semi-continuity property of syzygies, one can try to prove generic versions of Green's conjecture by constructing examples of curves that exhibit the vanishing (1.1). Moreover, singular examples of such curves are good enough as long as they are smoothable. Despite some appealing candidates being proposed over the years (such as rational cuspidal curves, nodal curves, ribbons), the vanishing (1.1) for generic curves (where ![]() $\operatorname {Cliff}(C) = \lfloor (g-1)/2\rfloor$) remained open until the tour de force by Voisin [Reference VoisinVoi02, Reference VoisinVoi05] that used cohomology calculations on Hilbert schemes and the geometry of K3 surfaces. Voisin's work shows (1.1) for a generic curve of any gonality
$\operatorname {Cliff}(C) = \lfloor (g-1)/2\rfloor$) remained open until the tour de force by Voisin [Reference VoisinVoi02, Reference VoisinVoi05] that used cohomology calculations on Hilbert schemes and the geometry of K3 surfaces. Voisin's work shows (1.1) for a generic curve of any gonality ![]() $d$ (where
$d$ (where ![]() $\operatorname {Cliff}(C) = d-2$), extending earlier results that were established in large genus:
$\operatorname {Cliff}(C) = d-2$), extending earlier results that were established in large genus: ![]() $g>(d-1)\cdot (d-2)$ in [Reference SchreyerSch89], or
$g>(d-1)\cdot (d-2)$ in [Reference SchreyerSch89], or ![]() $g\geq 3d+2$ in [Reference BigasBig02]. Building on [Reference Hirschowitz and RamananHR98, Reference VoisinVoi05], Aprodu describes, inside each
$g\geq 3d+2$ in [Reference BigasBig02]. Building on [Reference Hirschowitz and RamananHR98, Reference VoisinVoi05], Aprodu describes, inside each ![]() $d$-gonal stratum, explicit loci where Green's conjecture holds [Reference AproduApr05].
$d$-gonal stratum, explicit loci where Green's conjecture holds [Reference AproduApr05].
More recently, a more elementary and algebraic approach using the theory of Koszul modules has been used in [Reference Aprodu, Farkas, Papadima, Raicu and WeymanAFP+19] to prove (1.1) for rational cuspidal curves, fulfilling one of the early proposals [Reference EisenbudEis92, § 3.I] and recovering Green's conjecture for generic curves. The main goal of our paper is to extend the theory of Koszul modules to the bi-graded setting, and verify (1.1) for rational ribbons, proving the canonical ribbon conjecture [Reference Bayer and EisenbudBE95] and recovering Green's conjecture for generic curves in each gonality. We note that a proof of the canonical ribbon conjecture that builds on Voisin's work was obtained recently by Deopurkar [Reference DeopurkarDeo18].
An important advantage of the approach via Koszul modules is that the methods carry over to positive characteristic. As stated, Green's conjecture was known to fail in small characteristic even for generic curves, by work of Schreyer [Reference SchreyerSch86], for instance in genus ![]() $7$ and characteristic
$7$ and characteristic ![]() $2$. It is then natural to try to identify the appropriate characteristic assumptions to ensure that Green's conjecture remains valid (we note that Bopp and Schreyer have proposed a modification of the conjecture that is characteristic-free [Reference Bopp and SchreyerBS21], but we will not pursue this here). Eisenbud and Schreyer investigated this problem further in [Reference Eisenbud and SchreyerES19] and conjectured that (1.1) should hold for generic curves in characteristic
$2$. It is then natural to try to identify the appropriate characteristic assumptions to ensure that Green's conjecture remains valid (we note that Bopp and Schreyer have proposed a modification of the conjecture that is characteristic-free [Reference Bopp and SchreyerBS21], but we will not pursue this here). Eisenbud and Schreyer investigated this problem further in [Reference Eisenbud and SchreyerES19] and conjectured that (1.1) should hold for generic curves in characteristic ![]() $\geq \lfloor (g-1)/2 \rfloor$. Our results confirm this conjecture, and improve on the lower bound
$\geq \lfloor (g-1)/2 \rfloor$. Our results confirm this conjecture, and improve on the lower bound ![]() $\geq (g+2)/2$ from [Reference Aprodu, Farkas, Papadima, Raicu and WeymanAFP+19]. We also note that the restrictions on the characteristic have a clean explanation in our approach, coming from the fact that symmetric and divided powers are not isomorphic as functors in small characteristics.
$\geq (g+2)/2$ from [Reference Aprodu, Farkas, Papadima, Raicu and WeymanAFP+19]. We also note that the restrictions on the characteristic have a clean explanation in our approach, coming from the fact that symmetric and divided powers are not isomorphic as functors in small characteristics.
We now formulate our results more precisely. Throughout this paper we work over an algebraically closed field ![]() ${\mathbf {k}}$. We fix positive integers
${\mathbf {k}}$. We fix positive integers ![]() $a,b$, and let
$a,b$, and let ![]() $\mathcal {S}(a,b)\subset \mathbb {P}^{a+b+1}$ denote the rational normal scroll of type
$\mathcal {S}(a,b)\subset \mathbb {P}^{a+b+1}$ denote the rational normal scroll of type ![]() $(a,b)$. By [Reference Gallego and PurnaprajnaGP97, Theorem 1.3] there is a unique double structure on
$(a,b)$. By [Reference Gallego and PurnaprajnaGP97, Theorem 1.3] there is a unique double structure on ![]() $\mathcal {S}(a,b)$ that is numerically a K3 surface; it is denoted
$\mathcal {S}(a,b)$ that is numerically a K3 surface; it is denoted ![]() $\mathcal {X}(a,b)$ and called a K3 carpet. Our interest in the study of K3 carpets lies in the fact that their hyperplane sections are canonical ribbons of genus
$\mathcal {X}(a,b)$ and called a K3 carpet. Our interest in the study of K3 carpets lies in the fact that their hyperplane sections are canonical ribbons of genus ![]() $g=a+b+1$ and Clifford index
$g=a+b+1$ and Clifford index ![]() $\min (a,b)$, and as such they are degenerations of smooth canonical curves with the same invariants (see [Reference Bayer and EisenbudBE95, Reference FongFon93, Reference Eisenbud and GreenEG95, Reference Eisenbud and SchreyerES19] and § 6). We will prove the following theorem.
$\min (a,b)$, and as such they are degenerations of smooth canonical curves with the same invariants (see [Reference Bayer and EisenbudBE95, Reference FongFon93, Reference Eisenbud and GreenEG95, Reference Eisenbud and SchreyerES19] and § 6). We will prove the following theorem.
Theorem 1.2 Let ![]() $R={\mathbf {k}}[\mathbb {P}^{g}]$ and
$R={\mathbf {k}}[\mathbb {P}^{g}]$ and ![]() $A={\mathbf {k}}[\mathcal {X}(a,b)]$ denote the homogeneous coordinate rings of
$A={\mathbf {k}}[\mathcal {X}(a,b)]$ denote the homogeneous coordinate rings of ![]() $\mathbb {P}^g$ and
$\mathbb {P}^g$ and ![]() $\mathcal {X}(a,b)$, respectively. If
$\mathcal {X}(a,b)$, respectively. If ![]() $p=\operatorname {char}({\mathbf {k}})$ satisfies
$p=\operatorname {char}({\mathbf {k}})$ satisfies ![]() $p=0$ or
$p=0$ or ![]() $p\geq \min (a,b)$ then
$p\geq \min (a,b)$ then
By passing to a hyperplane section (and assuming ![]() $a\leq b$ in the theorem above) we obtain the following results.
$a\leq b$ in the theorem above) we obtain the following results.
Theorem 1.3 (Canonical ribbon conjecture)
Let ![]() $C$ be a rational ribbon of genus
$C$ be a rational ribbon of genus ![]() $g$ and Clifford index
$g$ and Clifford index ![]() $a$. If
$a$. If ![]() $p=\operatorname {char}({\mathbf {k}})$ satisfies
$p=\operatorname {char}({\mathbf {k}})$ satisfies ![]() $p=0$ or
$p=0$ or ![]() $p\geq a$ then
$p\geq a$ then
Corollary 1.4 Over a field ![]() ${\mathbf {k}}$ of characteristic
${\mathbf {k}}$ of characteristic ![]() $p=0$ or
$p=0$ or ![]() $p \ge a$, Green's conjecture is true for a non-empty Zariski open subset inside the locus of genus-
$p \ge a$, Green's conjecture is true for a non-empty Zariski open subset inside the locus of genus-![]() $g$ curves with Clifford index
$g$ curves with Clifford index ![]() $a$.
$a$.
Specializing to the case when the Clifford index is generic, ![]() $a= \lfloor (g-1)/2 \rfloor$, we confirm the following conjecture of Eisenbud and Schreyer [Reference Eisenbud and SchreyerES19, Conjecture 0.1].
$a= \lfloor (g-1)/2 \rfloor$, we confirm the following conjecture of Eisenbud and Schreyer [Reference Eisenbud and SchreyerES19, Conjecture 0.1].
Theorem 1.5 Green's conjecture is true for a general curve of genus ![]() $g$ over a field
$g$ over a field ![]() ${\mathbf {k}}$ of characteristic
${\mathbf {k}}$ of characteristic ![]() $p=0$ or
$p=0$ or ![]() $p\geq \lfloor (g-1)/2 \rfloor$.
$p\geq \lfloor (g-1)/2 \rfloor$.
The main new idea in our paper is the introduction and use of bi-graded Koszul modules, which we explain next. In the singly-graded case, Koszul modules were introduced by Papadima and Suciu in [Reference Papadima and SuciuPS15], and they have been used in [Reference Aprodu, Farkas, Papadima, Raicu and WeymanAFP+19] to prove the generic Green's conjecture via degeneration to cuspidal curves. It is the latter paper that constitutes the inspiration for our work. The motivation of Papadima and Suciu for defining Koszul modules comes from geometric group theory, where various incarnations of these modules have been used to great effect by Sullivan, Dimca, Papadima, Suciu, Hain and many others. In this setting, a more familiar name for Koszul modules is infinitesimal Alexander invariants [Reference Papadima and SuciuPS04, § 1.8]. For new applications in this context and a more extensive survey of the relevant literature, the reader can consult [Reference Aprodu, Farkas, Papadima, Raicu and WeymanAFP+21]. Although we do not pursue this line of thought here, it is reasonable to expect, and worthwhile to pursue, analogous applications in geometric group theory for the algebraic results on bi-graded Koszul modules that we develop here.
To recall the definition of the singly-graded Koszul modules, we consider a vector space ![]() $V$ and form the polynomial ring
$V$ and form the polynomial ring ![]() $S=\operatorname {Sym}(V)$, endowed with the natural grading where the elements of
$S=\operatorname {Sym}(V)$, endowed with the natural grading where the elements of ![]() $V$ have degree
$V$ have degree ![]() $1$. For a subspace
$1$. For a subspace ![]() $K\subset \bigwedge ^2 V$, we form the three-term complex
$K\subset \bigwedge ^2 V$, we form the three-term complex
obtained by replacing ![]() $\bigwedge ^2 V\otimes S$ in the Koszul complex with the submodule
$\bigwedge ^2 V\otimes S$ in the Koszul complex with the submodule ![]() $K\otimes S$. The Koszul module
$K\otimes S$. The Koszul module ![]() $W(V,K)$ is the middle homology of (1.6). It was shown in [Reference Papadima and SuciuPS15] that
$W(V,K)$ is the middle homology of (1.6). It was shown in [Reference Papadima and SuciuPS15] that ![]() $W(V,K)$ is a finite-length module if and only if the orthogonal complement
$W(V,K)$ is a finite-length module if and only if the orthogonal complement ![]() $K^\perp \subset (\bigwedge ^2 V)^\vee$ does not contain any non-zero decomposable tensors
$K^\perp \subset (\bigwedge ^2 V)^\vee$ does not contain any non-zero decomposable tensors ![]() $a\wedge b$, with
$a\wedge b$, with ![]() $a,b\in V^{\vee }$ (equivalently, the projectivization of
$a,b\in V^{\vee }$ (equivalently, the projectivization of ![]() $K^{\perp }$ does not intersect the Grassmannian
$K^{\perp }$ does not intersect the Grassmannian ![]() $\textrm {Gr}(2,V^{\vee })$). Thinking of
$\textrm {Gr}(2,V^{\vee })$). Thinking of ![]() $(\bigwedge ^2 V)^\vee$ as the subspace of skew-symmetric tensors in
$(\bigwedge ^2 V)^\vee$ as the subspace of skew-symmetric tensors in ![]() $V^{\vee }\otimes V^{\vee }$, the decomposable elements
$V^{\vee }\otimes V^{\vee }$, the decomposable elements ![]() $a\wedge b$ precisely correspond to rank-
$a\wedge b$ precisely correspond to rank-![]() $2$ tensors.
$2$ tensors.
For the bi-graded setting, we assume that ![]() $V$ comes with a decomposition
$V$ comes with a decomposition ![]() $V=V_1\oplus V_2$, and endow the polynomial ring
$V=V_1\oplus V_2$, and endow the polynomial ring ![]() $S=\operatorname {Sym}(V)$ with the bi-grading where
$S=\operatorname {Sym}(V)$ with the bi-grading where ![]() $S_{1,0}=V_1$ and
$S_{1,0}=V_1$ and ![]() $S_{0,1}=V_2$. We regard
$S_{0,1}=V_2$. We regard ![]() $V_1\otimes V_2$ as the subspace of bi-degree
$V_1\otimes V_2$ as the subspace of bi-degree ![]() $(1,1)$ elements in
$(1,1)$ elements in ![]() $\bigwedge ^2 V$, and hence we can regard any subspace
$\bigwedge ^2 V$, and hence we can regard any subspace ![]() $K\subset V_1\otimes V_2$ as a subset of
$K\subset V_1\otimes V_2$ as a subset of ![]() $\bigwedge ^2 V$ and form the complex (1.6). The resulting homology group
$\bigwedge ^2 V$ and form the complex (1.6). The resulting homology group ![]() $W(V,K)$ is then naturally bi-graded, and we call it a bi-graded Koszul module.
$W(V,K)$ is then naturally bi-graded, and we call it a bi-graded Koszul module.
We are interested in the case when ![]() $\dim (V_i)\geq 2$, where the aforementioned results of [Reference Papadima and SuciuPS15] imply that
$\dim (V_i)\geq 2$, where the aforementioned results of [Reference Papadima and SuciuPS15] imply that ![]() $W(V,K)$ is never of finite length: indeed, if
$W(V,K)$ is never of finite length: indeed, if ![]() $K \subset V_1 \otimes V_2$ then
$K \subset V_1 \otimes V_2$ then ![]() $\bigwedge ^2 V_i^\vee \subset K^\perp$, hence
$\bigwedge ^2 V_i^\vee \subset K^\perp$, hence ![]() $K^{\perp }$ contains decomposable elements. To generalize the results of [Reference Papadima and SuciuPS15], it is then more convenient to reinterpret the condition that a singly-graded Koszul module
$K^{\perp }$ contains decomposable elements. To generalize the results of [Reference Papadima and SuciuPS15], it is then more convenient to reinterpret the condition that a singly-graded Koszul module ![]() $W(V,K)$ has finite length as saying that the associated coherent sheaf on projective space
$W(V,K)$ has finite length as saying that the associated coherent sheaf on projective space ![]() $\mathbb {P}V$ is
$\mathbb {P}V$ is ![]() $0$. For a bi-graded Koszul module, it is then appropriate to instead consider when the corresponding coherent sheaf on the product of projective spaces
$0$. For a bi-graded Koszul module, it is then appropriate to instead consider when the corresponding coherent sheaf on the product of projective spaces ![]() $\mathbb {P}V_1 \times \mathbb {P}V_2$ is
$\mathbb {P}V_1 \times \mathbb {P}V_2$ is ![]() $0$. Algebraically, this means that
$0$. Algebraically, this means that
Pleasantly, this condition is equivalent to requiring that the orthogonal complement ![]() $K^\perp \subset (V_1 \otimes V_2)^\vee$ contains no non-zero tensors of rank
$K^\perp \subset (V_1 \otimes V_2)^\vee$ contains no non-zero tensors of rank ![]() $\leq 2$ (see Proposition 3.5). By picking bases, elements of
$\leq 2$ (see Proposition 3.5). By picking bases, elements of ![]() $(V_1 \otimes V_2)^\vee$ can be interpreted as matrices, and the rank of an element coincides with the usual rank of a matrix. Geometrically, the projectivization of the locus of rank
$(V_1 \otimes V_2)^\vee$ can be interpreted as matrices, and the rank of an element coincides with the usual rank of a matrix. Geometrically, the projectivization of the locus of rank ![]() $\le 2$ is the secant variety of the Segre embedding of
$\le 2$ is the secant variety of the Segre embedding of ![]() $\mathbb {P}V_1 \times \mathbb {P}V_2$, that is, the Zariski closure of the union of all secant lines through any two points of the Segre embedding. Remarkably, in analogy with [Reference Aprodu, Farkas, Papadima, Raicu and WeymanAFP+19, Theorem 1.3] we can make the vanishing (1.7) effective.
$\mathbb {P}V_1 \times \mathbb {P}V_2$, that is, the Zariski closure of the union of all secant lines through any two points of the Segre embedding. Remarkably, in analogy with [Reference Aprodu, Farkas, Papadima, Raicu and WeymanAFP+19, Theorem 1.3] we can make the vanishing (1.7) effective.
Theorem 1.8 Let ![]() $p=\operatorname {char}({\mathbf {k}})$,
$p=\operatorname {char}({\mathbf {k}})$, ![]() $n_i=\dim (V_i)\geq 2$, and suppose that
$n_i=\dim (V_i)\geq 2$, and suppose that ![]() $p=0$ or
$p=0$ or ![]() $p\geq n_1+n_2-3$. We have that
$p\geq n_1+n_2-3$. We have that
The condition that ![]() $K^{\perp }\subset (V_1 \otimes V_2)^\vee$ contains no non-zero tensors of rank
$K^{\perp }\subset (V_1 \otimes V_2)^\vee$ contains no non-zero tensors of rank ![]() $\leq 2$ can only hold when
$\leq 2$ can only hold when ![]() $\dim (K)\geq 2(n_1+n_2-2)$, which is one more than the dimension of the secant variety of the Segre product
$\dim (K)\geq 2(n_1+n_2-2)$, which is one more than the dimension of the secant variety of the Segre product ![]() $\mathbb {P}V_1\times \mathbb {P}V_2$. In analogy with [Reference Aprodu, Farkas, Papadima, Raicu and WeymanAFP+19, Theorem 1.4], in the borderline case when
$\mathbb {P}V_1\times \mathbb {P}V_2$. In analogy with [Reference Aprodu, Farkas, Papadima, Raicu and WeymanAFP+19, Theorem 1.4], in the borderline case when ![]() $\dim (K)=2(n_1+n_2-2)$, we can determine an exact formula for the Hilbert function in low bi-degrees for a module
$\dim (K)=2(n_1+n_2-2)$, we can determine an exact formula for the Hilbert function in low bi-degrees for a module ![]() $W(V,K)$ satisfying the conditions in Theorem 1.8 (see Theorem 3.3).
$W(V,K)$ satisfying the conditions in Theorem 1.8 (see Theorem 3.3).
We now give a high-level overview of the strategy of proof of Theorem 1.2. If we let ![]() $B$ denote the homogeneous coordinate ring of the scroll
$B$ denote the homogeneous coordinate ring of the scroll ![]() $\mathcal {S}(a,b)$, then we have a short exact sequence
$\mathcal {S}(a,b)$, then we have a short exact sequence
where ![]() $\omega _B$ is the canonical module of
$\omega _B$ is the canonical module of ![]() $B$. The minimal free resolution of
$B$. The minimal free resolution of ![]() $B$ is an Eagon–Northcott complex, while the minimal free resolution of
$B$ is an Eagon–Northcott complex, while the minimal free resolution of ![]() $\omega _B$ is obtained by duality. In particular, we have
$\omega _B$ is obtained by duality. In particular, we have ![]() $\operatorname {Tor}_i(B,{\mathbf {k}})_{i+2}=0$, so to prove the desired vanishing of the Tor groups of
$\operatorname {Tor}_i(B,{\mathbf {k}})_{i+2}=0$, so to prove the desired vanishing of the Tor groups of ![]() $A$, we need to show, for
$A$, we need to show, for ![]() $i<\min (a,b)$, the surjectivity of the connecting homomorphisms
$i<\min (a,b)$, the surjectivity of the connecting homomorphisms
To write everything invariantly, we pick a two-dimensional vector space ![]() $U$ and write
$U$ and write ![]() $\mathbb {P}(U)$ for the corresponding projective line. To keep everything correct in general, we will be careful to distinguish between divided powers
$\mathbb {P}(U)$ for the corresponding projective line. To keep everything correct in general, we will be careful to distinguish between divided powers ![]() $\operatorname {D}$ and symmetric powers
$\operatorname {D}$ and symmetric powers ![]() $\operatorname {Sym}$; if
$\operatorname {Sym}$; if ![]() ${\mathbf {k}}$ has characteristic
${\mathbf {k}}$ has characteristic ![]() $0$, then these are isomorphic to one another, so the reader may replace all instances of divided powers
$0$, then these are isomorphic to one another, so the reader may replace all instances of divided powers ![]() $\operatorname {D}$ with symmetric powers
$\operatorname {D}$ with symmetric powers ![]() $\operatorname {Sym}$ if that is their main scenario of interest. The map above takes the form
$\operatorname {Sym}$ if that is their main scenario of interest. The map above takes the form
where ![]() $\operatorname {D}$ is the divided power,
$\operatorname {D}$ is the divided power, ![]() $\operatorname {Sym}$ is the symmetric power, and
$\operatorname {Sym}$ is the symmetric power, and ![]() $\bigwedge$ is the exterior power. While it is possible to give explicit formulas for this map, proving surjectivity from such a formula is a difficult task (especially since it depends on the characteristic of the field). Instead, we take a roundabout method that begins with Hermite reciprocity, which is an
$\bigwedge$ is the exterior power. While it is possible to give explicit formulas for this map, proving surjectivity from such a formula is a difficult task (especially since it depends on the characteristic of the field). Instead, we take a roundabout method that begins with Hermite reciprocity, which is an ![]() $\operatorname {SL}(U)$-equivariant isomorphism
$\operatorname {SL}(U)$-equivariant isomorphism
described in [Reference Aprodu, Farkas, Papadima, Raicu and WeymanAFP+19, § 3.4]. If we decompose both sides of (1.9) using the identity
 \begin{equation} \bigwedge^d(E \oplus F) = \bigoplus_{u+v=d} \bigwedge^u E \otimes \bigwedge^v F, \end{equation}
\begin{equation} \bigwedge^d(E \oplus F) = \bigoplus_{u+v=d} \bigwedge^u E \otimes \bigwedge^v F, \end{equation}then via Hermite reciprocity, the connecting homomorphism takes the form

If we focus on a particular bi-degree ![]() $(u,v)$ and sum over all
$(u,v)$ and sum over all ![]() $a \ge u$ and
$a \ge u$ and ![]() $b \ge v$, then the domain becomes
$b \ge v$, then the domain becomes ![]() $\operatorname {D}^i U \otimes \operatorname {Sym}(\operatorname {D}^{u+1} U \oplus \operatorname {D}^{v+1} U)$, a free module over the bi-graded polynomial ring
$\operatorname {D}^i U \otimes \operatorname {Sym}(\operatorname {D}^{u+1} U \oplus \operatorname {D}^{v+1} U)$, a free module over the bi-graded polynomial ring
Miraculously, the target can be given the structure of a finitely generated ![]() $S$-module, so that this map is a module homomorphism, namely, it is the middle homology of a complex
$S$-module, so that this map is a module homomorphism, namely, it is the middle homology of a complex
This identification is subtle and occupies a great deal of the paper! Since ![]() $i=u+v$, this leads to a three-term complex of free
$i=u+v$, this leads to a three-term complex of free ![]() $S$-modules
$S$-modules
where ![]() $K$ is some extension of
$K$ is some extension of ![]() $\operatorname {D}^{u+v}U$ by
$\operatorname {D}^{u+v}U$ by ![]() $\operatorname {D}^{u+v+2}U$ (which is split if the characteristic of
$\operatorname {D}^{u+v+2}U$ (which is split if the characteristic of ![]() ${\mathbf {k}}$ is zero or large). We denote the middle homology by
${\mathbf {k}}$ is zero or large). We denote the middle homology by ![]() $W^{(u+1,v+1)}$ and call it a bi-graded Weyman module (see § 4, and [Reference Aprodu, Farkas, Papadima, Raicu and WeymanAFP+19, § 5.1] for the singly-graded case). In fact, this is an instance of a bi-graded Koszul module with
$W^{(u+1,v+1)}$ and call it a bi-graded Weyman module (see § 4, and [Reference Aprodu, Farkas, Papadima, Raicu and WeymanAFP+19, § 5.1] for the singly-graded case). In fact, this is an instance of a bi-graded Koszul module with ![]() $V_1=\operatorname {D}^{u+1} U$ and
$V_1=\operatorname {D}^{u+1} U$ and ![]() $V_2=\operatorname {D}^{v+1} U$. Specializing Theorem 1.8 to this situation gives the following theorem, which itself implies Theorem 1.2.
$V_2=\operatorname {D}^{v+1} U$. Specializing Theorem 1.8 to this situation gives the following theorem, which itself implies Theorem 1.2.
Theorem 1.11 If ![]() $p=\operatorname {char}({\mathbf {k}})$ satisfies
$p=\operatorname {char}({\mathbf {k}})$ satisfies ![]() $p=0$ or
$p=0$ or ![]() $p>u+v$ then
$p>u+v$ then
Finally, we note that in this situation, we have ![]() $\dim (K) = 2(\dim (V_1)+\dim (V_2)-2)$; from the previous discussion, we have a formula for the Hilbert function of
$\dim (K) = 2(\dim (V_1)+\dim (V_2)-2)$; from the previous discussion, we have a formula for the Hilbert function of ![]() $W^{(u,v)}$. Based on this, the reader can deduce formulas for certain bi-graded components of the
$W^{(u,v)}$. Based on this, the reader can deduce formulas for certain bi-graded components of the ![]() $\operatorname {Tor}$-modules of
$\operatorname {Tor}$-modules of ![]() $A$.
$A$.
Organization
In § 2 we recall basic constructions in multilinear algebra, and discuss Hermite reciprocity. Section 3 is concerned with the basic theory of bi-graded Koszul modules, and contains the proof of the vanishing Theorem 1.8. In § 4 we discuss Weyman modules, showing that they satisfy the hypothesis of the vanishing theorem and deriving Theorem 1.11. The relationship between the syzygies of K3 carpets and Weyman modules is presented in § 5, while the geometric applications are summarized in § 6.
2. Preliminaries
In this section we collect some basic facts and notation regarding multilinear algebra, and recall some useful aspects of Hermite reciprocity following [Reference Aprodu, Farkas, Papadima, Raicu and WeymanAFP+19].
2.1 Multilinear algebra
Let ![]() $E$ be a vector space. The tensor power
$E$ be a vector space. The tensor power ![]() $E^{\otimes d}$ has an action of the symmetric group
$E^{\otimes d}$ has an action of the symmetric group ![]() $\mathfrak {S}_d$ via permuting tensor factors. The divided power
$\mathfrak {S}_d$ via permuting tensor factors. The divided power ![]() $\operatorname {D}^d E$ is the invariant subspace and the symmetric power
$\operatorname {D}^d E$ is the invariant subspace and the symmetric power ![]() $\operatorname {Sym}^d E$ is the space of coinvariants. In formulas:
$\operatorname {Sym}^d E$ is the space of coinvariants. In formulas:
 \begin{align*} \operatorname{D}^d E &= \{x \in E^{{\otimes} d} \mid \sigma(x) = x\ \text{for all }\sigma \in \mathfrak{S}_d\},\\ \operatorname{Sym}^d E &= E^{{\otimes} d} / \{x - \sigma(x) \mid \sigma \in \mathfrak{S}_d, \ x \in U^{{\otimes} d}\}. \end{align*}
\begin{align*} \operatorname{D}^d E &= \{x \in E^{{\otimes} d} \mid \sigma(x) = x\ \text{for all }\sigma \in \mathfrak{S}_d\},\\ \operatorname{Sym}^d E &= E^{{\otimes} d} / \{x - \sigma(x) \mid \sigma \in \mathfrak{S}_d, \ x \in U^{{\otimes} d}\}. \end{align*}There is a natural isomorphism
If ![]() $d!$ is non-zero in
$d!$ is non-zero in ![]() ${\mathbf {k}}$, and in particular if
${\mathbf {k}}$, and in particular if ![]() $\operatorname {char}({\mathbf {k}})=0$, then the composition
$\operatorname {char}({\mathbf {k}})=0$, then the composition ![]() $\operatorname {D}^d E \to E^{\otimes d} \to \operatorname {Sym}^d E$ is an isomorphism with inverse
$\operatorname {D}^d E \to E^{\otimes d} \to \operatorname {Sym}^d E$ is an isomorphism with inverse ![]() $\operatorname {Sym}^d E \cong \operatorname {D}^d E$ given by
$\operatorname {Sym}^d E \cong \operatorname {D}^d E$ given by ![]() $x \mapsto ({1}/{d!}) \sum _{\sigma \in \mathfrak {S}_d} \sigma (x)$.
$x \mapsto ({1}/{d!}) \sum _{\sigma \in \mathfrak {S}_d} \sigma (x)$.
The exterior powers ![]() $\bigwedge ^d E$ are the skew-invariants of
$\bigwedge ^d E$ are the skew-invariants of ![]() $E^{\otimes d}$, that is,
$E^{\otimes d}$, that is,
For ![]() $e_1,\ldots,e_d \in E$, we use the notation
$e_1,\ldots,e_d \in E$, we use the notation
 \[ e_1 \wedge \cdots \wedge e_d = \sum_{\sigma \in \mathfrak{S}_d} \mathrm{sgn}(\sigma) e_{\sigma(1)} \otimes \cdots \otimes e_{\sigma(d)} \in \bigwedge^d E \]
\[ e_1 \wedge \cdots \wedge e_d = \sum_{\sigma \in \mathfrak{S}_d} \mathrm{sgn}(\sigma) e_{\sigma(1)} \otimes \cdots \otimes e_{\sigma(d)} \in \bigwedge^d E \]
and ![]() $e_1\cdots e_d$ to denote the image of
$e_1\cdots e_d$ to denote the image of ![]() $e_1 \otimes \cdots \otimes e_d$ in
$e_1 \otimes \cdots \otimes e_d$ in ![]() $\operatorname {Sym}^d E$.
$\operatorname {Sym}^d E$.
For ![]() $\operatorname {D}^d E$, and
$\operatorname {D}^d E$, and ![]() $d_1+\cdots +d_r=d$, we use
$d_1+\cdots +d_r=d$, we use ![]() $e_1^{(d_1)} \cdots e_r^{(d_r)}$ to denote the sum over the orbit of
$e_1^{(d_1)} \cdots e_r^{(d_r)}$ to denote the sum over the orbit of ![]() $e_1^{\otimes d_1} \otimes \cdots \otimes e_r^{\otimes d_r}$ in
$e_1^{\otimes d_1} \otimes \cdots \otimes e_r^{\otimes d_r}$ in ![]() $E^{\otimes d}$. For
$E^{\otimes d}$. For ![]() $u,v \ge 0$, we define comultiplication maps
$u,v \ge 0$, we define comultiplication maps
which are the linear duals of the multiplication maps
Since multiplication is associative, comultiplication is coassociative, that is, we have ![]() $(1 \otimes \Delta _{v,w}) \circ \Delta _{u,v+w} = (\Delta _{u,v} \otimes 1) \circ \Delta _{u+v,w}$ as maps
$(1 \otimes \Delta _{v,w}) \circ \Delta _{u,v+w} = (\Delta _{u,v} \otimes 1) \circ \Delta _{u+v,w}$ as maps ![]() $\operatorname {D}^{u+v+w} E \to \operatorname {D}^u E \otimes \operatorname {D}^v E \otimes \operatorname {D}^w E$.
$\operatorname {D}^{u+v+w} E \to \operatorname {D}^u E \otimes \operatorname {D}^v E \otimes \operatorname {D}^w E$.
Similarly, we also define comultiplication maps
as the linear duals of the multiplication maps
Again, this comultiplication is coassociative.
2.2 Hermite reciprocity
We let ![]() $U$ be a two-dimensional
$U$ be a two-dimensional ![]() ${\mathbf {k}}$-vector space, and use
${\mathbf {k}}$-vector space, and use ![]() $\operatorname {SL}(U)$ to denote the group of linear operators on
$\operatorname {SL}(U)$ to denote the group of linear operators on ![]() $U$ with determinant 1. We fix a basis
$U$ with determinant 1. We fix a basis ![]() $\{1,x\}$ for
$\{1,x\}$ for ![]() $U$ which gives an identification
$U$ which gives an identification ![]() $\bigwedge ^2 U \simeq {\mathbf {k}}$ via
$\bigwedge ^2 U \simeq {\mathbf {k}}$ via ![]() $1 \wedge x \mapsto 1$, and we use this to identify
$1 \wedge x \mapsto 1$, and we use this to identify ![]() $U\simeq U^{\vee }$. Hermite reciprocity is an
$U\simeq U^{\vee }$. Hermite reciprocity is an ![]() $\operatorname {SL}(U)$-equivariant isomorphism
$\operatorname {SL}(U)$-equivariant isomorphism
We will not make use of the explicit form of this isomorphism, but the reader can see [Reference Aprodu, Farkas, Papadima, Raicu and WeymanAFP+19, § 3.4] for details. Under Hermite reciprocity, the multiplication map
takes the form
See [Reference Aprodu, Farkas, Papadima, Raicu and WeymanAFP+19, Eq. (43) and Proof of Lemma 3.3] for a formula for ![]() $\nu$.
$\nu$.
Proposition 2.1 The following square commutes:

where the left map is comultiplication on both factors followed by multiplication, and the right map is exterior comultiplication.
Proof. See [Reference Aprodu, Farkas, Papadima, Raicu and WeymanAFP+19, Proposition 5.9].
3. Bi-graded Koszul modules
In this section we generalize the notion of Koszul modules to the bi-graded setting, and study the natural analogue of finite-length modules (see [Reference Papadima and SuciuPS15, Reference Aprodu, Farkas, Papadima, Raicu and WeymanAFP+21]). We show that these modules satisfy a strong vanishing theorem, and we give a sharp upper bound for their bi-graded Hilbert function (our results parallel [Reference Aprodu, Farkas, Papadima, Raicu and WeymanAFP+19, Theorems 1.3 and 1.4]). We let ![]() $V_1,V_2$ denote finite-dimensional
$V_1,V_2$ denote finite-dimensional ![]() ${\mathbf {k}}$-vector spaces, and let
${\mathbf {k}}$-vector spaces, and let ![]() $V = V_1\oplus V_2$. We write
$V = V_1\oplus V_2$. We write ![]() $n_i=\dim (V_i)$, assume that
$n_i=\dim (V_i)$, assume that ![]() $n_i\geq 2$, and let
$n_i\geq 2$, and let ![]() $n=n_1+n_2$. We consider a subspace
$n=n_1+n_2$. We consider a subspace ![]() $K\subseteq V_1\otimes V_2$ and let
$K\subseteq V_1\otimes V_2$ and let ![]() $m=\dim (K)$. We have a decomposition
$m=\dim (K)$. We have a decomposition
which allows us to think of ![]() $K$ as a subspace of
$K$ as a subspace of ![]() $\bigwedge ^2 V$. We consider the symmetric algebra
$\bigwedge ^2 V$. We consider the symmetric algebra ![]() $S=\operatorname {Sym}(V)$ and define the Koszul module
$S=\operatorname {Sym}(V)$ and define the Koszul module ![]() $W(V,K)$ to be the middle homology of the three-term complex
$W(V,K)$ to be the middle homology of the three-term complex
where ![]() $\delta _1,\delta _2$ are Koszul differentials.
$\delta _1,\delta _2$ are Koszul differentials.
We consider ![]() $S$ as a bi-graded polynomial ring where the elements of
$S$ as a bi-graded polynomial ring where the elements of ![]() $V_1$ have degree
$V_1$ have degree ![]() $(1,0)$, and those of
$(1,0)$, and those of ![]() $V_2$ have degree
$V_2$ have degree ![]() $(0,1)$. The bi-degree
$(0,1)$. The bi-degree ![]() $(d,e)$ component is
$(d,e)$ component is
The Koszul module ![]() $W(V,K)$ inherits a natural bi-grading, where the bi-degree
$W(V,K)$ inherits a natural bi-grading, where the bi-degree ![]() $(d,e)$ component is the homology of
$(d,e)$ component is the homology of
We are interested in understanding the vanishing behavior of ![]() $W_{d,e}(V,K)$. We note that
$W_{d,e}(V,K)$. We note that ![]() $W(V,K)$ is generated in bi-degree
$W(V,K)$ is generated in bi-degree ![]() $(0,0)$, so if
$(0,0)$, so if ![]() $W_{d_0,e_0}(V,K)=0$ for some
$W_{d_0,e_0}(V,K)=0$ for some ![]() $(d_0,e_0)$ then
$(d_0,e_0)$ then ![]() $W_{d,e}(V,K)=0$ for all
$W_{d,e}(V,K)=0$ for all ![]() $(d,e)$ with
$(d,e)$ with ![]() $d\geq d_0$,
$d\geq d_0$, ![]() $e\geq e_0$.
$e\geq e_0$.
Theorem 3.2 Let ![]() $p=\operatorname {char}({\mathbf {k}})$ and suppose that
$p=\operatorname {char}({\mathbf {k}})$ and suppose that ![]() $p=0$ or
$p=0$ or ![]() $p\geq n-3$. We have that
$p\geq n-3$. We have that
As explained in Remark 3.6 below, the equivalent conditions in Theorem 3.2 can only be true when ![]() $m\geq 2n-4$. If we further assume that
$m\geq 2n-4$. If we further assume that ![]() $m=2n-4$ then we get an exact formula for the Hilbert function of
$m=2n-4$ then we get an exact formula for the Hilbert function of ![]() $W(V,K)$ in low bi-degrees, as follows (compare with [Reference Aprodu, Farkas, Papadima, Raicu and WeymanAFP+19, Theorem 1.4]).
$W(V,K)$ in low bi-degrees, as follows (compare with [Reference Aprodu, Farkas, Papadima, Raicu and WeymanAFP+19, Theorem 1.4]).
Theorem 3.3 With the assumptions in Theorem 3.2, suppose that ![]() $W_{n_2-2,n_1-2}(V,K)=0$. If we let
$W_{n_2-2,n_1-2}(V,K)=0$. If we let ![]() $\Delta _1 = n_1-2-e$ and
$\Delta _1 = n_1-2-e$ and ![]() $\Delta _2=n_2-2-d$, then we have for all
$\Delta _2=n_2-2-d$, then we have for all ![]() $d\leq n_2-2$ and
$d\leq n_2-2$ and ![]() $e\leq n_1-2$ that
$e\leq n_1-2$ that
 \begin{align*} &\dim(W_{d,e}(V,K))\\ &\quad\leq 2 \cdot {d+n_1-1 \choose d}\cdot{e+n_2-1\choose e} \cdot \frac{{n_1-1\choose 2}\cdot \Delta_2 + {n_2-1\choose 2}\cdot \Delta_1 - (n-3)\cdot\Delta_1\cdot\Delta_2}{(d+1)\cdot(e+1)}. \end{align*}
\begin{align*} &\dim(W_{d,e}(V,K))\\ &\quad\leq 2 \cdot {d+n_1-1 \choose d}\cdot{e+n_2-1\choose e} \cdot \frac{{n_1-1\choose 2}\cdot \Delta_2 + {n_2-1\choose 2}\cdot \Delta_1 - (n-3)\cdot\Delta_1\cdot\Delta_2}{(d+1)\cdot(e+1)}. \end{align*}
Moreover, equality holds when ![]() $m=2n-4$.
$m=2n-4$.
To understand geometrically the asymptotic vanishing property of the bi-graded components of ![]() $W(V,K)$, we consider the associated Koszul sheaf on
$W(V,K)$, we consider the associated Koszul sheaf on ![]() ${\textbf P} = \mathbb {P}V_1 \times \mathbb {P}V_2$, denoted by
${\textbf P} = \mathbb {P}V_1 \times \mathbb {P}V_2$, denoted by ![]() $\mathcal {W}(V,K)$, and defined as the middle homology of
$\mathcal {W}(V,K)$, and defined as the middle homology of
In what follows, we let ![]() $\mathcal {G} = \ker (\beta )$, so it fits into the short exact sequence
$\mathcal {G} = \ker (\beta )$, so it fits into the short exact sequence
Note that ![]() $\mathcal {G}$ is locally free since
$\mathcal {G}$ is locally free since ![]() $\beta$ is surjective.
$\beta$ is surjective.
We have that ![]() $W_{d,e}(V,K) = \mathrm {H}^0({\textbf P}, \mathcal {W}(V,K) \otimes \mathcal {O}_{{\textbf P}}(d,e))$ for
$W_{d,e}(V,K) = \mathrm {H}^0({\textbf P}, \mathcal {W}(V,K) \otimes \mathcal {O}_{{\textbf P}}(d,e))$ for ![]() $d,e\gg 0$, and in particular the vanishing holds asymptotically if and only if
$d,e\gg 0$, and in particular the vanishing holds asymptotically if and only if ![]() $\mathcal {W}(V,K)$ is the zero sheaf. To characterize this condition, we define the orthogonal complement of
$\mathcal {W}(V,K)$ is the zero sheaf. To characterize this condition, we define the orthogonal complement of ![]() $K$ to be
$K$ to be
and prove the following proposition.
Proposition 3.5 We have that ![]() $\mathcal {W}(V,K)=0$ if and only if
$\mathcal {W}(V,K)=0$ if and only if ![]() $K^{\perp }$ contains no non-zero tensors of rank at most
$K^{\perp }$ contains no non-zero tensors of rank at most ![]() $2$.
$2$.
Proof. The condition ![]() $\mathcal {W}(V,K)=0$ is equivalent to the exactness of (3.4a) in the middle, which in turn is equivalent to the surjectivity of the induced map
$\mathcal {W}(V,K)=0$ is equivalent to the exactness of (3.4a) in the middle, which in turn is equivalent to the surjectivity of the induced map ![]() $\alpha \colon K \otimes \mathcal {O}_{{\textbf P}} \longrightarrow \mathcal {G}$. This can be checked fiber by fiber, and since
$\alpha \colon K \otimes \mathcal {O}_{{\textbf P}} \longrightarrow \mathcal {G}$. This can be checked fiber by fiber, and since ![]() $\mathcal {G}$ is locally free, the middle exactness of (3.4a) can also be checked fiber by fiber. Fix a
$\mathcal {G}$ is locally free, the middle exactness of (3.4a) can also be checked fiber by fiber. Fix a ![]() ${\mathbf {k}}$-point
${\mathbf {k}}$-point ![]() $p=([f_1],[f_2]) \in {\textbf P}$, with
$p=([f_1],[f_2]) \in {\textbf P}$, with ![]() $f_i\in V_i^{\vee }$, and restrict (3.4a). We get a complex of vector spaces
$f_i\in V_i^{\vee }$, and restrict (3.4a). We get a complex of vector spaces
which is exact if and only if the dual complex
is exact. Writing ![]() $V^{\vee } = V_1^{\vee } \oplus V_2^{\vee }$ and
$V^{\vee } = V_1^{\vee } \oplus V_2^{\vee }$ and ![]() $f=(f_1,f_2)$, we observe that the map
$f=(f_1,f_2)$, we observe that the map ![]() $\alpha _p^{\vee }$ is obtained as the composition
$\alpha _p^{\vee }$ is obtained as the composition
where the second map is the dual projection to the inclusion ![]() $K\subset \bigwedge ^2 V$, and therefore has kernel equal to
$K\subset \bigwedge ^2 V$, and therefore has kernel equal to ![]() $\bigwedge ^2 V_1^{\vee } \oplus K^{\perp } \oplus \bigwedge ^2 V_2^{\vee }$. It follows that (3.5a) fails to be exact if and only if one can find
$\bigwedge ^2 V_1^{\vee } \oplus K^{\perp } \oplus \bigwedge ^2 V_2^{\vee }$. It follows that (3.5a) fails to be exact if and only if one can find ![]() $g=(g_1,g_2)\in V^{\vee }$ which is not a multiple of
$g=(g_1,g_2)\in V^{\vee }$ which is not a multiple of ![]() $f$ and such that
$f$ and such that ![]() $f\wedge g\in \bigwedge ^2 V_1^{\vee } \oplus K^{\perp } \oplus \bigwedge ^2 V_2^{\vee }$. Since
$f\wedge g\in \bigwedge ^2 V_1^{\vee } \oplus K^{\perp } \oplus \bigwedge ^2 V_2^{\vee }$. Since
we get that (3.5a) fails to be exact if and only if ![]() $K^{\perp }$ contains a non-zero tensor
$K^{\perp }$ contains a non-zero tensor ![]() $f_1\otimes g_2 - g_1 \otimes f_2$ of rank at most
$f_1\otimes g_2 - g_1 \otimes f_2$ of rank at most ![]() $2$.
$2$.
Remark 3.6 Note that ![]() $K^{\perp }$ defines a linear space
$K^{\perp }$ defines a linear space ![]() $H$ of codimension
$H$ of codimension ![]() $m$ in
$m$ in ![]() $\mathbb {P}(V_1\otimes V_2)$, which in turn is the ambient space of the Segre embedding
$\mathbb {P}(V_1\otimes V_2)$, which in turn is the ambient space of the Segre embedding ![]() $X$ of
$X$ of ![]() $\mathbb {P}V_1 \times \mathbb {P}V_2$. The condition in Proposition 3.5 is then equivalent to the fact that
$\mathbb {P}V_1 \times \mathbb {P}V_2$. The condition in Proposition 3.5 is then equivalent to the fact that ![]() $H$ is disjoint from
$H$ is disjoint from ![]() $\operatorname {Sec}(X)$, the variety of secant lines to
$\operatorname {Sec}(X)$, the variety of secant lines to ![]() $X$. Since
$X$. Since ![]() $\dim (\operatorname {Sec}(X))=2n-5$, this is only possible when
$\dim (\operatorname {Sec}(X))=2n-5$, this is only possible when ![]() $m\geq 2n-4$. Moreover, if
$m\geq 2n-4$. Moreover, if ![]() $H$ is generic of codimension
$H$ is generic of codimension ![]() $m=2n-4$ then
$m=2n-4$ then ![]() $H\cap \operatorname {Sec}(X) = \emptyset$.
$H\cap \operatorname {Sec}(X) = \emptyset$.
Lemma 3.7 For ![]() $r=0,\ldots,n-4$ we have that
$r=0,\ldots,n-4$ we have that ![]() $\operatorname {Sym}^r(\mathcal {G}^{\vee }) \otimes \mathcal {O}_{\bf P}(-1,-1)$ has no non-zero cohomology groups.
$\operatorname {Sym}^r(\mathcal {G}^{\vee }) \otimes \mathcal {O}_{\bf P}(-1,-1)$ has no non-zero cohomology groups.
Proof. Dualizing (3.4b) and taking symmetric powers, we get a short exact sequence
where
It is then enough to check that the sheaves ![]() $\operatorname {Sym}^r(\mathcal {V}) \otimes \mathcal {O}_{{\textbf P}}(-1,-1)$ and
$\operatorname {Sym}^r(\mathcal {V}) \otimes \mathcal {O}_{{\textbf P}}(-1,-1)$ and ![]() $\operatorname {Sym}^{r-1}(\mathcal {V}) \otimes \mathcal {O}_{{\textbf P}}(-2,-2)$ have no non-zero cohomology groups.
$\operatorname {Sym}^{r-1}(\mathcal {V}) \otimes \mathcal {O}_{{\textbf P}}(-2,-2)$ have no non-zero cohomology groups.
First note that ![]() $\operatorname {Sym}^r(\mathcal {V}) \otimes \mathcal {O}_{{\textbf P}}(-1,-1)$ decomposes as a direct sum of
$\operatorname {Sym}^r(\mathcal {V}) \otimes \mathcal {O}_{{\textbf P}}(-1,-1)$ decomposes as a direct sum of ![]() $\mathcal {O}_{{\textbf P}}(i,j)$ with
$\mathcal {O}_{{\textbf P}}(i,j)$ with ![]() $i,j<0$ and
$i,j<0$ and ![]() $i+j = -r-2 \geq -n+2$, while
$i+j = -r-2 \geq -n+2$, while ![]() $\operatorname {Sym}^{r-1}(\mathcal {V}) \otimes \mathcal {O}_{{\textbf P}}(-2,-2)$ decomposes as a direct sum of
$\operatorname {Sym}^{r-1}(\mathcal {V}) \otimes \mathcal {O}_{{\textbf P}}(-2,-2)$ decomposes as a direct sum of ![]() $\mathcal {O}_{{\textbf P}}(i,j)$ with
$\mathcal {O}_{{\textbf P}}(i,j)$ with ![]() $i,j<0$ and
$i,j<0$ and ![]() $i+j = (-r+1)-4 \geq -n+1$.
$i+j = (-r+1)-4 \geq -n+1$.
Next, the condition ![]() $i+j\geq -n+1$ implies that either
$i+j\geq -n+1$ implies that either ![]() $i\geq -n_1+1$ or
$i\geq -n_1+1$ or ![]() $j\geq -n_2+1$, so at least one of
$j\geq -n_2+1$, so at least one of ![]() $\mathcal {O}_{\mathbb {P}V_1}(i)$ or
$\mathcal {O}_{\mathbb {P}V_1}(i)$ or ![]() $\mathcal {O}_{\mathbb {P}V_2}(j)$ has no non-zero cohomology groups and so
$\mathcal {O}_{\mathbb {P}V_2}(j)$ has no non-zero cohomology groups and so ![]() $\mathcal {O}_{{\textbf P}}(i,j)$ has no non-zero cohomology groups by Künneth's formula.
$\mathcal {O}_{{\textbf P}}(i,j)$ has no non-zero cohomology groups by Künneth's formula.
In the next proof we will need the Buchsbaum–Rim complex, for which we now recall the important details. Let ![]() $X$ be a scheme and
$X$ be a scheme and ![]() $\alpha \colon E \to F$ be a morphism of locally free sheaves on
$\alpha \colon E \to F$ be a morphism of locally free sheaves on ![]() $X$ with
$X$ with ![]() $\textrm {rank}(E)=e$ and
$\textrm {rank}(E)=e$ and ![]() $\textrm {rank}(F)=f$ (and
$\textrm {rank}(F)=f$ (and ![]() $e \ge f$). The Buchsbaum–Rim complex
$e \ge f$). The Buchsbaum–Rim complex ![]() $B(\alpha )_\bullet$ of
$B(\alpha )_\bullet$ of ![]() $\alpha$ has terms
$\alpha$ has terms
 \begin{align*} B(\alpha)_0 &= F,\\ B(\alpha)_1 &= E,\\ B(\alpha)_r &= \bigwedge^{r+f-1} E \otimes \textrm{det} (F^\vee) \otimes \operatorname{D}^{r-2} (F^\vee) \quad\text{for }r=2,\ldots,e-f+1, \end{align*}
\begin{align*} B(\alpha)_0 &= F,\\ B(\alpha)_1 &= E,\\ B(\alpha)_r &= \bigwedge^{r+f-1} E \otimes \textrm{det} (F^\vee) \otimes \operatorname{D}^{r-2} (F^\vee) \quad\text{for }r=2,\ldots,e-f+1, \end{align*}
and the differential ![]() $B(\alpha )_1 \to B(\alpha )_0$ is
$B(\alpha )_1 \to B(\alpha )_0$ is ![]() $\alpha$ (this is the complex
$\alpha$ (this is the complex ![]() $\mathcal {C}^1$ in [Reference EisenbudEis95, § A2.6] where it is treated in the local setting – the terms
$\mathcal {C}^1$ in [Reference EisenbudEis95, § A2.6] where it is treated in the local setting – the terms ![]() $\textrm {det}(F^\vee )$, which are omitted there, are necessary to globalize this construction). This is exact in positive degrees if the ideal sheaf of maximal minors of
$\textrm {det}(F^\vee )$, which are omitted there, are necessary to globalize this construction). This is exact in positive degrees if the ideal sheaf of maximal minors of ![]() $\alpha$ has depth
$\alpha$ has depth ![]() $\ge e-f+1$, with the convention that the unit ideal has infinite depth (exactness can be checked locally, in which case it follows from [Reference EisenbudEis95, Theorem A2.10]). In our application below,
$\ge e-f+1$, with the convention that the unit ideal has infinite depth (exactness can be checked locally, in which case it follows from [Reference EisenbudEis95, Theorem A2.10]). In our application below, ![]() $X = {\textbf P}$ and
$X = {\textbf P}$ and ![]() $\alpha$ is surjective, and hence the ideal sheaf of maximal minors is the unit ideal.
$\alpha$ is surjective, and hence the ideal sheaf of maximal minors is the unit ideal.
Proof of Theorem 3.2 The implication ‘![]() $\Leftarrow$’ follows from the fact that
$\Leftarrow$’ follows from the fact that ![]() $W(V,K)$ is generated in bi-degree
$W(V,K)$ is generated in bi-degree ![]() $(0,0)$. To prove ‘
$(0,0)$. To prove ‘![]() $\Rightarrow$’, we first reduce to the case
$\Rightarrow$’, we first reduce to the case ![]() $m=2n-4$. As remarked earlier, the vanishing
$m=2n-4$. As remarked earlier, the vanishing ![]() $W_{d,e}(V,K)=0$ for
$W_{d,e}(V,K)=0$ for ![]() $d,e\gg 0$ is equivalent to
$d,e\gg 0$ is equivalent to ![]() $\mathcal {W}(V,K) = 0$, which is further equivalent to the fact that the linear space
$\mathcal {W}(V,K) = 0$, which is further equivalent to the fact that the linear space ![]() $H\subseteq \mathbb {P}(V_1\otimes V_2)$ corresponding to
$H\subseteq \mathbb {P}(V_1\otimes V_2)$ corresponding to ![]() $K^{\perp }$ is disjoint from
$K^{\perp }$ is disjoint from ![]() $\operatorname {Sec}(X)$. Assuming that this condition is satisfied, a generic choice of a linear space
$\operatorname {Sec}(X)$. Assuming that this condition is satisfied, a generic choice of a linear space ![]() $H'\supseteq H$ of codimension
$H'\supseteq H$ of codimension ![]() $2n-4$ will still have the property that
$2n-4$ will still have the property that ![]() $H'\cap \operatorname {Sec}(X) = \emptyset$, so it gives a bi-graded Koszul module
$H'\cap \operatorname {Sec}(X) = \emptyset$, so it gives a bi-graded Koszul module ![]() $W(V,K')$ with
$W(V,K')$ with ![]() $K'\subseteq K$ and
$K'\subseteq K$ and ![]() $\dim (K')=2n-4$. The inclusion
$\dim (K')=2n-4$. The inclusion ![]() $K'\subseteq K$ induces a natural surjection
$K'\subseteq K$ induces a natural surjection ![]() $W(V,K') \twoheadrightarrow W(V,K)$, so a vanishing for
$W(V,K') \twoheadrightarrow W(V,K)$, so a vanishing for ![]() $W(V,K')$ will imply the corresponding vanishing for
$W(V,K')$ will imply the corresponding vanishing for ![]() $W(V,K)$.
$W(V,K)$.
We assume that ![]() $m=2n-4$ and let
$m=2n-4$ and let ![]() $\mathcal {G} = \ker (\beta )$ as in the proof of Proposition 3.5. Since
$\mathcal {G} = \ker (\beta )$ as in the proof of Proposition 3.5. Since ![]() $\mathcal {W}(V,K)=0$, we have that the map
$\mathcal {W}(V,K)=0$, we have that the map ![]() $\alpha \colon K\otimes \mathcal {O}_{{\textbf P}}\longrightarrow \mathcal {G}$ is surjective, so it gives an exact Buchsbaum–Rim complex
$\alpha \colon K\otimes \mathcal {O}_{{\textbf P}}\longrightarrow \mathcal {G}$ is surjective, so it gives an exact Buchsbaum–Rim complex ![]() $\mathcal {B}_{\bullet }$ with
$\mathcal {B}_{\bullet }$ with
 \begin{align*} \mathcal{B}_0&=\mathcal{G},\\ \mathcal{B}_1 &= K\otimes\mathcal{O}_{{\textbf P}},\\ \mathcal{B}_r &= \bigwedge^{n+r-2}K \otimes \textrm{det}\big(\mathcal{G}^{{\vee}}\big) \otimes \operatorname{D}^{r-2}\big(\mathcal{G}^{{\vee}}\big)\quad\text{for }r=2,\ldots,n-2. \end{align*}
\begin{align*} \mathcal{B}_0&=\mathcal{G},\\ \mathcal{B}_1 &= K\otimes\mathcal{O}_{{\textbf P}},\\ \mathcal{B}_r &= \bigwedge^{n+r-2}K \otimes \textrm{det}\big(\mathcal{G}^{{\vee}}\big) \otimes \operatorname{D}^{r-2}\big(\mathcal{G}^{{\vee}}\big)\quad\text{for }r=2,\ldots,n-2. \end{align*}
The condition ![]() $W_{n_2-2,n_1-2}(V,K)=0$ is equivalent to the fact that after twisting by
$W_{n_2-2,n_1-2}(V,K)=0$ is equivalent to the fact that after twisting by ![]() $\mathcal {O}_{{\textbf P}}(n_2-2, n_1-2)$, the induced map on global sections
$\mathcal {O}_{{\textbf P}}(n_2-2, n_1-2)$, the induced map on global sections
is surjective. Since ![]() $\mathcal {B}_{\bullet }(n_2-2,n_1-2)$ is an exact complex, its hypercohomology groups are all zero. Using the hypercohomology spectral sequence, in order to prove the surjectivity of (3.8) it suffices to check that the sheaves
$\mathcal {B}_{\bullet }(n_2-2,n_1-2)$ is an exact complex, its hypercohomology groups are all zero. Using the hypercohomology spectral sequence, in order to prove the surjectivity of (3.8) it suffices to check that the sheaves ![]() $\mathcal {B}_{r}(n_2-2,n_1-2)$ have no cohomology (in fact, it is enough that
$\mathcal {B}_{r}(n_2-2,n_1-2)$ have no cohomology (in fact, it is enough that ![]() $\mathrm {H}^{r-1}({\textbf P},\mathcal {B}_{r}(n_2-2,n_1-2))=0$) for
$\mathrm {H}^{r-1}({\textbf P},\mathcal {B}_{r}(n_2-2,n_1-2))=0$) for ![]() $r=2,\ldots,n-2$.
$r=2,\ldots,n-2$.
Since ![]() $0\leq r-2\leq n-4$, it follows from our hypothesis that
$0\leq r-2\leq n-4$, it follows from our hypothesis that ![]() $p=0$ or
$p=0$ or ![]() $p>r-2$, thus
$p>r-2$, thus ![]() $\operatorname {D}^{r-2}(\mathcal {G}^{\vee }) = \operatorname {Sym}^{r-2}(\mathcal {G}^{\vee })$. Moreover, we have that
$\operatorname {D}^{r-2}(\mathcal {G}^{\vee }) = \operatorname {Sym}^{r-2}(\mathcal {G}^{\vee })$. Moreover, we have that ![]() $\textrm {det}(\mathcal {G}^{\vee }) = \mathcal {O}_{{\textbf P}}(-n_2+1,-n_1+1)$, so
$\textrm {det}(\mathcal {G}^{\vee }) = \mathcal {O}_{{\textbf P}}(-n_2+1,-n_1+1)$, so
The desired vanishing now follows from Lemma 3.7.
Proof of Theorem 3.3 Using the projection argument from the proof of Theorem 3.2, it suffices to consider the case when ![]() $m=2n-4$ and show that we get an exact formula for
$m=2n-4$ and show that we get an exact formula for ![]() $\dim (W_{d,e}(V,K))$ in the given range. Restricting (3.1) to bi-degree
$\dim (W_{d,e}(V,K))$ in the given range. Restricting (3.1) to bi-degree ![]() $(d,e)$, we get a complex
$(d,e)$, we get a complex
whose middle homology is ![]() $W_{d,e}(V,K)$. We get that
$W_{d,e}(V,K)$. We get that ![]() $\dim (W_{d,e}(V,K)) \geq \chi _{d,e}$, where
$\dim (W_{d,e}(V,K)) \geq \chi _{d,e}$, where
is the Euler characteristic of the above complex. Moreover, since ![]() $\beta _{d,e}$ is surjective, we have that
$\beta _{d,e}$ is surjective, we have that ![]() $\dim (W_{d,e}(V,K)) = \chi _{d,e}$ if and only if
$\dim (W_{d,e}(V,K)) = \chi _{d,e}$ if and only if ![]() $\alpha _{d,e}$ is injective. A direct calculation shows that
$\alpha _{d,e}$ is injective. A direct calculation shows that
so to prove Theorem 3.3 it suffices to show that ![]() $\alpha _{d,e}$ is injective for
$\alpha _{d,e}$ is injective for ![]() $d\leq n_2-2$,
$d\leq n_2-2$, ![]() $e\leq n_1-2$. Since
$e\leq n_1-2$. Since ![]() $\alpha _{d,e}$ is a homogeneous component of a map of free modules, we have that if
$\alpha _{d,e}$ is a homogeneous component of a map of free modules, we have that if ![]() $\alpha _{d_0,e_0}$ is injective then
$\alpha _{d_0,e_0}$ is injective then ![]() $\alpha _{d,e}$ is also injective for all
$\alpha _{d,e}$ is also injective for all ![]() $d\leq d_0$ and
$d\leq d_0$ and ![]() $e\leq e_0$. It is then enough to prove that
$e\leq e_0$. It is then enough to prove that ![]() $\alpha _{n_2-2,n_1-2}$ is injective. Notice that for
$\alpha _{n_2-2,n_1-2}$ is injective. Notice that for ![]() $d=n_2-2$ and
$d=n_2-2$ and ![]() $e=n_1-2$, we have
$e=n_1-2$, we have ![]() $\Delta _1=\Delta _2=0$, so
$\Delta _1=\Delta _2=0$, so ![]() $\chi _{n_2-2,n_1-2}=0$. Moreover, we know by Theorem 3.2 that
$\chi _{n_2-2,n_1-2}=0$. Moreover, we know by Theorem 3.2 that ![]() $W_{n_2-2,n_1-2}(V,K)=0$, so
$W_{n_2-2,n_1-2}(V,K)=0$, so ![]() $\alpha _{n_2-2,n_1-2}$ is injective.
$\alpha _{n_2-2,n_1-2}$ is injective.
4. Bi-graded Weyman modules
The fundamental connection described in [Reference Aprodu, Farkas, Papadima, Raicu and WeymanAFP+19] between (standard graded) Koszul modules and syzygies goes through Weyman modules. We define their analogues in the bi-graded setting, and show that they satisfy (in most characteristics) the hypothesis of Theorem 3.2.
For ![]() $i,j\geq 0$ we consider the surjective multiplication map
$i,j\geq 0$ we consider the surjective multiplication map
The kernel of ![]() $\mu _{u,v}$ is naturally identified with
$\mu _{u,v}$ is naturally identified with ![]() $\operatorname {Sym}^{u-1} U \otimes \operatorname {Sym}^{v-1} U$ via the inclusion
$\operatorname {Sym}^{u-1} U \otimes \operatorname {Sym}^{v-1} U$ via the inclusion
More generally, for ![]() $t\leq u,v$ the composition
$t\leq u,v$ the composition ![]() $\iota ^t_{u,v} = \iota _{u,v} \circ \iota _{u-1,v-1} \circ \cdots \circ \iota _{u-t+1,v-t+1}$ is given by
$\iota ^t_{u,v} = \iota _{u,v} \circ \iota _{u-1,v-1} \circ \cdots \circ \iota _{u-t+1,v-t+1}$ is given by
 \[ f\otimes g \mapsto \sum_{i=0}^t ({-}1)^i{t\choose i} \cdot x^if\otimes x^{t-i}g. \]
\[ f\otimes g \mapsto \sum_{i=0}^t ({-}1)^i{t\choose i} \cdot x^if\otimes x^{t-i}g. \]We let
which gives a short exact sequence
In characteristic ![]() $0$ (or sufficiently large characteristic), one has an
$0$ (or sufficiently large characteristic), one has an ![]() $\operatorname {SL}(U)$-equivariant decomposition
$\operatorname {SL}(U)$-equivariant decomposition ![]() $Q_{u,v} \simeq \operatorname {Sym}^{u+v}U \oplus \operatorname {Sym}^{u+v-2}U$, but in general we only have an extension
$Q_{u,v} \simeq \operatorname {Sym}^{u+v}U \oplus \operatorname {Sym}^{u+v-2}U$, but in general we only have an extension
Remark 4.2 If ![]() $\operatorname {char}({\mathbf {k}})=p>0$ then
$\operatorname {char}({\mathbf {k}})=p>0$ then ![]() ${p \choose i}=0$ in
${p \choose i}=0$ in ![]() ${\mathbf {k}}$ for
${\mathbf {k}}$ for ![]() $0< i< p$, and thus for
$0< i< p$, and thus for ![]() $u,v\geq p$ we have
$u,v\geq p$ we have
Since ![]() $\operatorname {Im}(\iota ^p_{u,v}) \subset \operatorname {Im}(\iota ^2_{u,v}) = \ker (\Psi _{u,v})$, this shows that
$\operatorname {Im}(\iota ^p_{u,v}) \subset \operatorname {Im}(\iota ^2_{u,v}) = \ker (\Psi _{u,v})$, this shows that ![]() $\ker (\Psi _{u,v})$ contains rank-
$\ker (\Psi _{u,v})$ contains rank-![]() $2$ tensors. We will show that this is no longer the case when
$2$ tensors. We will show that this is no longer the case when ![]() $p>\min (u,v)$.
$p>\min (u,v)$.
We let ![]() $V_i = (\operatorname {Sym}^{n_i-1}U)^{\vee } = \operatorname {D}^{n_i-1}U$, and let
$V_i = (\operatorname {Sym}^{n_i-1}U)^{\vee } = \operatorname {D}^{n_i-1}U$, and let ![]() $K = Q_{n_1-1,n_2-1}^{\vee }$, considered as a subspace of
$K = Q_{n_1-1,n_2-1}^{\vee }$, considered as a subspace of ![]() $V_1\otimes V_2$ via the inclusion
$V_1\otimes V_2$ via the inclusion ![]() $\Psi _{n_1-1,n_2-1}^{\vee }$. We note that
$\Psi _{n_1-1,n_2-1}^{\vee }$. We note that
We define the bi-graded Weyman module ![]() $W^{(n_1-1,n_2-1)}:= W(V,K)$.
$W^{(n_1-1,n_2-1)}:= W(V,K)$.
Proposition 4.3 Let ![]() $p=\operatorname {char}({\mathbf {k}})$ and suppose that
$p=\operatorname {char}({\mathbf {k}})$ and suppose that ![]() $p=0$ or that
$p=0$ or that ![]() $p>\min (u,v)$. Then
$p>\min (u,v)$. Then ![]() $\ker (\Psi _{u,v})$ contains no non-zero tensors of rank at most
$\ker (\Psi _{u,v})$ contains no non-zero tensors of rank at most ![]() $2$.
$2$.
Proof. We assume without loss of generality that ![]() $u \le v$, identify as usual
$u \le v$, identify as usual ![]() $\operatorname {Sym}^d U$ with polynomials of degree
$\operatorname {Sym}^d U$ with polynomials of degree ![]() $\leq d$ in
$\leq d$ in ![]() $x$, and consider the derivation
$x$, and consider the derivation ![]() $\partial = {\partial }/{\partial x} \colon {\mathbf {k}}(x)\longrightarrow {\mathbf {k}}(x)$. We note that
$\partial = {\partial }/{\partial x} \colon {\mathbf {k}}(x)\longrightarrow {\mathbf {k}}(x)$. We note that ![]() $\ker (\Psi _{u,v}) = \operatorname {Im}(\iota ^2_{u,v})$ is generated by elements of the form
$\ker (\Psi _{u,v}) = \operatorname {Im}(\iota ^2_{u,v})$ is generated by elements of the form
which are both in ![]() $\ker (\mu _{u,v})$ and in the kernel of the composition
$\ker (\mu _{u,v})$ and in the kernel of the composition

Suppose now that ![]() $T\in \ker (\Psi _{u,v})$ is a non-zero tensor of rank at most
$T\in \ker (\Psi _{u,v})$ is a non-zero tensor of rank at most ![]() $2$. If
$2$. If ![]() $T=f \otimes g$, then
$T=f \otimes g$, then ![]() $0=\mu _{u,v}(T)=fg$, which forces either
$0=\mu _{u,v}(T)=fg$, which forces either ![]() $f=0$ or
$f=0$ or ![]() $g=0$, contradicting the fact that
$g=0$, contradicting the fact that ![]() $T\neq 0$. We may therefore assume that
$T\neq 0$. We may therefore assume that
Using the fact that ![]() $0 = \mu _{u,v}(T) = f_1g_1+f_2g_2$, we get
$0 = \mu _{u,v}(T) = f_1g_1+f_2g_2$, we get
Since ![]() $\ker (\partial )={\mathbf {k}}(x^p)$, we conclude that
$\ker (\partial )={\mathbf {k}}(x^p)$, we conclude that ![]() ${f_1}/{f_2}\in {\mathbf {k}}(x^p)$. By our hypothesis, we have that
${f_1}/{f_2}\in {\mathbf {k}}(x^p)$. By our hypothesis, we have that ![]() $p=0$ or
$p=0$ or ![]() $p>u$, which in turn forces
$p>u$, which in turn forces ![]() ${f_1}/{f_2}\in {\mathbf {k}}$, contradicting the fact that
${f_1}/{f_2}\in {\mathbf {k}}$, contradicting the fact that ![]() $f_1,f_2$ were not proportional.
$f_1,f_2$ were not proportional.
It follows from Proposition 4.3 that if ![]() $p=0$ or
$p=0$ or ![]() $p\geq \min (n_1,n_2)$ then Proposition 3.5 applies to the bi-graded Weyman module
$p\geq \min (n_1,n_2)$ then Proposition 3.5 applies to the bi-graded Weyman module ![]() $W^{(n_1-1,n_2-1)}$. Using Theorem 3.2, we obtain the following corollary.
$W^{(n_1-1,n_2-1)}$. Using Theorem 3.2, we obtain the following corollary.
Corollary 4.4 If ![]() $n_1,n_2\geq 2$ and
$n_1,n_2\geq 2$ and ![]() $p=\operatorname {char}({\mathbf {k}})$ satisfies
$p=\operatorname {char}({\mathbf {k}})$ satisfies ![]() $p=0$ or
$p=0$ or ![]() $p\geq n_1+n_2-3$ then
$p\geq n_1+n_2-3$ then
5. Syzygies of K3 carpets
Fix positive integers ![]() $a,b$. In this section we study the syzygies of the K3 carpet
$a,b$. In this section we study the syzygies of the K3 carpet ![]() $\mathcal {X}(a,b)$, obtained as a double structure on a rational normal scroll of type
$\mathcal {X}(a,b)$, obtained as a double structure on a rational normal scroll of type ![]() $(a,b)$. We show that via Hermite reciprocity, these syzygies can be built from components of bi-graded Weyman modules. Using Corollary 4.4, this yields a vanishing result for syzygies of K3 carpets that was conjectured by Eisenbud and Schreyer in [Reference Eisenbud and SchreyerES19].
$(a,b)$. We show that via Hermite reciprocity, these syzygies can be built from components of bi-graded Weyman modules. Using Corollary 4.4, this yields a vanishing result for syzygies of K3 carpets that was conjectured by Eisenbud and Schreyer in [Reference Eisenbud and SchreyerES19].
5.1 Rational normal scrolls
Let
denote the rational normal scroll of type ![]() $(a,b)$. It is abstractly isomorphic to the projective bundle
$(a,b)$. It is abstractly isomorphic to the projective bundle ![]() $\mathbb {P}_{\mathbb {P}U}(\mathcal {E})$, where
$\mathbb {P}_{\mathbb {P}U}(\mathcal {E})$, where ![]() $\mathcal {E} = \mathcal {E}_1 \oplus \mathcal {E}_2$,
$\mathcal {E} = \mathcal {E}_1 \oplus \mathcal {E}_2$, ![]() $\mathcal {E}_1=\mathcal {O}_{\mathbb {P}U}(a)$,
$\mathcal {E}_1=\mathcal {O}_{\mathbb {P}U}(a)$, ![]() $\mathcal {E}_2=\mathcal {O}_{\mathbb {P}U}(b)$. Let
$\mathcal {E}_2=\mathcal {O}_{\mathbb {P}U}(b)$. Let ![]() $B$ denote the homogeneous coordinate ring of the scroll, which is naturally bi-graded with
$B$ denote the homogeneous coordinate ring of the scroll, which is naturally bi-graded with
We let
denote the homogeneous coordinate ring of the ambient projective space, with its natural bi-grading. We have that ![]() $B=R/I$, where
$B=R/I$, where ![]() $I$ is the ideal of the scroll, generated by
$I$ is the ideal of the scroll, generated by
More explicitly, the multiplication map
can be represented as a ![]() $2 \times (a+b)$ matrix whose entries are the linear forms in
$2 \times (a+b)$ matrix whose entries are the linear forms in ![]() $R$, and
$R$, and ![]() $I$ is generated by the
$I$ is generated by the ![]() $2 \times 2$ minors of this matrix. In particular, it is resolved by an Eagon–Northcott complex and so
$2 \times 2$ minors of this matrix. In particular, it is resolved by an Eagon–Northcott complex and so
The canonical module ![]() $\omega _B$ of
$\omega _B$ of ![]() $B$ is identified with
$B$ is identified with ![]() $\mathrm {H}^0(\mathbb {P}U,\omega _{\mathbb {P}U} \otimes \textrm {det}(\mathcal {E}) \otimes \operatorname {Sym}(\mathcal {E}))$, with bi-grading
$\mathrm {H}^0(\mathbb {P}U,\omega _{\mathbb {P}U} \otimes \textrm {det}(\mathcal {E}) \otimes \operatorname {Sym}(\mathcal {E}))$, with bi-grading
and in particular it is generated in bi-degree ![]() $(1,1)$ by
$(1,1)$ by ![]() $(\omega _B)_{1,1} = \operatorname {Sym}^{a+b-2}U$. Dualizing (5.1) and taking into account the bi-grading gives (with
$(\omega _B)_{1,1} = \operatorname {Sym}^{a+b-2}U$. Dualizing (5.1) and taking into account the bi-grading gives (with ![]() $u+v=i$)
$u+v=i$)
We have a surjective map ![]() $\phi \colon I \longrightarrow \omega _B$, which at the level of generators is given by a map
$\phi \colon I \longrightarrow \omega _B$, which at the level of generators is given by a map

where ![]() $\phi _{1,1}$ sends
$\phi _{1,1}$ sends ![]() $\bigwedge ^2(\operatorname {Sym}^{a-1}U)$ and
$\bigwedge ^2(\operatorname {Sym}^{a-1}U)$ and ![]() $\bigwedge ^2(\operatorname {Sym}^{b-1}U)$ to zero, and it is described on
$\bigwedge ^2(\operatorname {Sym}^{b-1}U)$ to zero, and it is described on ![]() $\operatorname {Sym}^{a-1}U\otimes \operatorname {Sym}^{b-1}U$ by the natural multiplication map. We let
$\operatorname {Sym}^{a-1}U\otimes \operatorname {Sym}^{b-1}U$ by the natural multiplication map. We let ![]() $A$ denote the coordinate ring of the associated K3 carpet
$A$ denote the coordinate ring of the associated K3 carpet ![]() $\mathcal {X}(a,b)$, which is obtained as an
$\mathcal {X}(a,b)$, which is obtained as an ![]() $R$-module extension
$R$-module extension
induced by ![]() $\phi \in \operatorname {Hom}_R(I,\omega _B) = \operatorname {Ext}^1_R(B,\omega _B)$.
$\phi \in \operatorname {Hom}_R(I,\omega _B) = \operatorname {Ext}^1_R(B,\omega _B)$.
For the next result, we collapse the bi-grading on ![]() $A$ to a single grading by
$A$ to a single grading by ![]() $A_n = \bigoplus _{i+j=n} A_{i,j}$.
$A_n = \bigoplus _{i+j=n} A_{i,j}$.
Proposition 5.4 The Hilbert series of ![]() $A$ is
$A$ is
 \[ \sum_{n \ge 0} (\dim A_n) t^n = \frac{1 + (a+b-1)t + (a+b-1)t^2 + t^3}{(1-t)^3}. \]
\[ \sum_{n \ge 0} (\dim A_n) t^n = \frac{1 + (a+b-1)t + (a+b-1)t^2 + t^3}{(1-t)^3}. \]Proof. The Hilbert series of ![]() $A$ is a sum of the Hilbert series of
$A$ is a sum of the Hilbert series of ![]() $B$ and
$B$ and ![]() $\omega _B$, so we calculate each separately. We have
$\omega _B$, so we calculate each separately. We have ![]() $B_{i,j} = \operatorname {Sym}^{ia+jb} U$, so
$B_{i,j} = \operatorname {Sym}^{ia+jb} U$, so ![]() $\dim B_{i,j} = ia+jb+1$, and hence
$\dim B_{i,j} = ia+jb+1$, and hence
 \[ \dim B_n = \sum_{i=0}^n (ia+(n-i)b+1) = \frac{n(n+1)}{2}(a+b) + n+1. \]
\[ \dim B_n = \sum_{i=0}^n (ia+(n-i)b+1) = \frac{n(n+1)}{2}(a+b) + n+1. \]
Next, we have ![]() $(\omega _B)_{i,j} = \operatorname {Sym}^{ia+jb-2} U$ for
$(\omega _B)_{i,j} = \operatorname {Sym}^{ia+jb-2} U$ for ![]() $i,j \ge 1$ and 0 otherwise, and in particular,
$i,j \ge 1$ and 0 otherwise, and in particular,
 \[ \dim (\omega_B)_n = \sum_{i=1}^{n-1} (ia+(n-i)b-1) = \frac{n(n-1)}{2}(a+b) - n+1 \quad (n \ge 1). \]
\[ \dim (\omega_B)_n = \sum_{i=1}^{n-1} (ia+(n-i)b-1) = \frac{n(n-1)}{2}(a+b) - n+1 \quad (n \ge 1). \]So
and
 \[ \sum_{n \ge 0} (\dim A_n) t^n = \frac{(a+b)t(t+1)}{(1-t)^3} + \frac{2}{1-t} - 1 = \frac{1+(a+b-1)t + (a+b-1)t^2 + t^3}{(1-t)^3}. \]
\[ \sum_{n \ge 0} (\dim A_n) t^n = \frac{(a+b)t(t+1)}{(1-t)^3} + \frac{2}{1-t} - 1 = \frac{1+(a+b-1)t + (a+b-1)t^2 + t^3}{(1-t)^3}. \]5.2 The main result
One has that ![]() $A$ is Gorenstein with Castelnuovo–Mumford regularity
$A$ is Gorenstein with Castelnuovo–Mumford regularity ![]() $3$, and it is conjectured in [Reference Eisenbud and SchreyerES19] that
$3$, and it is conjectured in [Reference Eisenbud and SchreyerES19] that
provided that ![]() $p=\operatorname {char}({\mathbf {k}})$ satisfies
$p=\operatorname {char}({\mathbf {k}})$ satisfies ![]() $p=0$ or
$p=0$ or ![]() $p\geq \min (a,b)$. We prove this conjecture as a consequence of our basic results on bi-graded Koszul modules. More precisely, we show the following theorem.
$p\geq \min (a,b)$. We prove this conjecture as a consequence of our basic results on bi-graded Koszul modules. More precisely, we show the following theorem.
Theorem 5.5 Consider non-negative integers ![]() $u,v\geq 0$ with
$u,v\geq 0$ with ![]() $u+v=i$. We have that
$u+v=i$. We have that
In particular, if ![]() $p=\operatorname {char}({\mathbf {k}})$ satisfies
$p=\operatorname {char}({\mathbf {k}})$ satisfies ![]() $p=0$ or
$p=0$ or ![]() $p\geq \min (a,b)$ and if
$p\geq \min (a,b)$ and if ![]() $i<\min (a,b)$ then
$i<\min (a,b)$ then
To prove the first part of the theorem, we note that (5.3) induces an exact sequence
Since ![]() $\operatorname {Tor}_i^R(B,{\mathbf {k}})_{i+2}=0$ for all
$\operatorname {Tor}_i^R(B,{\mathbf {k}})_{i+2}=0$ for all ![]() $i$, and
$i$, and ![]() $\operatorname {Tor}_{i+1}^R(B,{\mathbf {k}})_{i+2}=\operatorname {Tor}_i^R(I,{\mathbf {k}})_{i+2}$, it follows that
$\operatorname {Tor}_{i+1}^R(B,{\mathbf {k}})_{i+2}=\operatorname {Tor}_i^R(I,{\mathbf {k}})_{i+2}$, it follows that
where the maps are induced by the surjection ![]() $I\twoheadrightarrow \omega _B$ described earlier.
$I\twoheadrightarrow \omega _B$ described earlier.
Proposition 5.6 We have
Proof. Using (5.1), we have
so the identification follows abstractly from Hermite reciprocity.
Define
 \begin{align*} \mathscr{S}(u,v) &= \operatorname{Sym}(\operatorname{D}^{u+1} U \oplus \operatorname{D}^{v+1} U),\\ \mathscr{M}(u,v) &= \bigoplus_{d+e \ge 2} \operatorname{Sym}^{d+e-2} U \otimes \operatorname{Sym}^d (\operatorname{D}^uU) \otimes \operatorname{Sym}^e(\operatorname{D}^vU). \end{align*}
\begin{align*} \mathscr{S}(u,v) &= \operatorname{Sym}(\operatorname{D}^{u+1} U \oplus \operatorname{D}^{v+1} U),\\ \mathscr{M}(u,v) &= \bigoplus_{d+e \ge 2} \operatorname{Sym}^{d+e-2} U \otimes \operatorname{Sym}^d (\operatorname{D}^uU) \otimes \operatorname{Sym}^e(\operatorname{D}^vU). \end{align*}
For simplicity, we will also write ![]() $S$ for
$S$ for ![]() $\mathscr {S}(u,v)$. Both have bi-gradings via
$\mathscr {S}(u,v)$. Both have bi-gradings via
 \begin{align*} S_{d,e} &= \operatorname{Sym}^d(\operatorname{D}^{u+1} U) \otimes \operatorname{Sym}^e(\operatorname{D}^{v+1} U),\\ \mathscr{M}(u,v)_{d,e} &= \operatorname{Sym}^{d+e-2} U \otimes \operatorname{Sym}^d(\operatorname{D}^uU) \otimes \operatorname{Sym}^e(\operatorname{D}^vU). \end{align*}
\begin{align*} S_{d,e} &= \operatorname{Sym}^d(\operatorname{D}^{u+1} U) \otimes \operatorname{Sym}^e(\operatorname{D}^{v+1} U),\\ \mathscr{M}(u,v)_{d,e} &= \operatorname{Sym}^{d+e-2} U \otimes \operatorname{Sym}^d(\operatorname{D}^uU) \otimes \operatorname{Sym}^e(\operatorname{D}^vU). \end{align*}
We will see in the proof of the next result that ![]() $\mathscr {M}(u,v)$ can be given the structure of a finitely generated
$\mathscr {M}(u,v)$ can be given the structure of a finitely generated ![]() $S$-module.
$S$-module.
Proposition 5.7 ![]() $\operatorname {Tor}_i^R(\omega _B,{\mathbf {k}})_{u+1,v+1} = W_{a-1-u,b-1-v}(V,K)$, where
$\operatorname {Tor}_i^R(\omega _B,{\mathbf {k}})_{u+1,v+1} = W_{a-1-u,b-1-v}(V,K)$, where ![]() $V = \operatorname {D}^{u+1}U\oplus \operatorname {D}^{v+1}U$ and
$V = \operatorname {D}^{u+1}U\oplus \operatorname {D}^{v+1}U$ and ![]() $K=\operatorname {D}^{u+v+2}U$.
$K=\operatorname {D}^{u+v+2}U$.
Proof. Apply Hermite reciprocity to (5.2) to get
We have a short exact sequence of vector bundles over ![]() $\mathbb {P}(U)$:
$\mathbb {P}(U)$:
Using [Reference WeymanWey03, § 5], we have a minimal complex ![]() ${\bf F}_\bullet$ with terms
${\bf F}_\bullet$ with terms
 \[ {\bf F}_i = \bigoplus_{j \ge 0} \mathrm{H}^j\left(\mathbb{P}U, \bigwedge^{i+j}( \mathcal{O}({-}u-1) \oplus \mathcal{O}({-}v-1)) \otimes \mathcal{O}({-}2)\right) \otimes S({-}i-j) \]
\[ {\bf F}_i = \bigoplus_{j \ge 0} \mathrm{H}^j\left(\mathbb{P}U, \bigwedge^{i+j}( \mathcal{O}({-}u-1) \oplus \mathcal{O}({-}v-1)) \otimes \mathcal{O}({-}2)\right) \otimes S({-}i-j) \]whose homology is
 \begin{align*} \mathrm{H}_0({\bf F}_\bullet) &= \mathrm{H}^0(\mathbb{P}(U); \operatorname{Sym}((\operatorname{D}^u U)(1) \oplus (\operatorname{D}^v U)(1)) \otimes \mathcal{O}({-}2)) = \mathscr{M}(u,v),\\ \mathrm{H}_{{-}1}({\bf F}_\bullet) &= \mathrm{H}^1(\mathbb{P}(U); \operatorname{Sym}((\operatorname{D}^u U)(1) \oplus (\operatorname{D}^v U)(1)) \otimes \mathcal{O}({-}2)) = {\mathbf{k}}. \end{align*}
\begin{align*} \mathrm{H}_0({\bf F}_\bullet) &= \mathrm{H}^0(\mathbb{P}(U); \operatorname{Sym}((\operatorname{D}^u U)(1) \oplus (\operatorname{D}^v U)(1)) \otimes \mathcal{O}({-}2)) = \mathscr{M}(u,v),\\ \mathrm{H}_{{-}1}({\bf F}_\bullet) &= \mathrm{H}^1(\mathbb{P}(U); \operatorname{Sym}((\operatorname{D}^u U)(1) \oplus (\operatorname{D}^v U)(1)) \otimes \mathcal{O}({-}2)) = {\mathbf{k}}. \end{align*}
Here we treat the terms as singly-graded modules, though they can be made bi-graded by setting ![]() $\deg (\operatorname {D}^{u+1}U)=(1,0)$ and
$\deg (\operatorname {D}^{u+1}U)=(1,0)$ and ![]() $\deg (\operatorname {D}^{v+1}U)=(0,1)$. Explicitly, the terms are
$\deg (\operatorname {D}^{v+1}U)=(0,1)$. Explicitly, the terms are
 \begin{align*} {\bf F}_{{-}1} &= S,\\ {\bf F}_0 &= (\operatorname{D}^{u+1} U \otimes S({-}1,0)) \oplus (\operatorname{D}^{v+1} U \otimes S(0,-1)),\\ {\bf F}_1 &= \operatorname{D}^{u+v+2} U \otimes S({-}1,-1). \end{align*}
\begin{align*} {\bf F}_{{-}1} &= S,\\ {\bf F}_0 &= (\operatorname{D}^{u+1} U \otimes S({-}1,0)) \oplus (\operatorname{D}^{v+1} U \otimes S(0,-1)),\\ {\bf F}_1 &= \operatorname{D}^{u+v+2} U \otimes S({-}1,-1). \end{align*}
Hence ![]() $\mathscr {M}(u,v)$ is realized as a bi-graded Koszul module with
$\mathscr {M}(u,v)$ is realized as a bi-graded Koszul module with ![]() $K = \operatorname {D}^{u+v+2} U$,
$K = \operatorname {D}^{u+v+2} U$, ![]() $V_1 = \operatorname {D}^{u+1} U$, and
$V_1 = \operatorname {D}^{u+1} U$, and ![]() $V_2= \operatorname {D}^{v+1} U$, and so
$V_2= \operatorname {D}^{v+1} U$, and so
Using the dual of (4.1), we can form the Weyman module ![]() $W^{(u+1,v+1)} = W(V,Q_{u+1,v+1}^{\vee })$ in two steps. We first use the subspace
$W^{(u+1,v+1)} = W(V,Q_{u+1,v+1}^{\vee })$ in two steps. We first use the subspace ![]() $K=\operatorname {D}^{u+v+2}U \subset Q_{u+1,v+1}^{\vee }$ and form the Koszul module
$K=\operatorname {D}^{u+v+2}U \subset Q_{u+1,v+1}^{\vee }$ and form the Koszul module ![]() $W(V,K)$ in part (2). Then there is a natural map
$W(V,K)$ in part (2). Then there is a natural map
induced by the identification ![]() $\operatorname {D}^{u+v}U \simeq Q_{u+1,v+1}^{\vee } / K$, and the cokernel of this map is by definition
$\operatorname {D}^{u+v}U \simeq Q_{u+1,v+1}^{\vee } / K$, and the cokernel of this map is by definition ![]() $W(V,Q_{u+1,v+1}^{\vee }) = W^{(u+1,v+1)}$.
$W(V,Q_{u+1,v+1}^{\vee }) = W^{(u+1,v+1)}$.
5.3 Some complexes
Make the following definitions:
 \begin{align*} \mathscr{A}(u,v) &= \operatorname{D}^{u+v+2} U \otimes S({-}1,-1) & (u,v \ge -1),\\ \mathscr{B}(u,v) &= \operatorname{D}^{u+1} U \otimes \operatorname{D}^{v+1} U \otimes S({-}1,-1) & (u,v \ge -1),\\ \mathscr{C}'(u,v) &= \operatorname{D}^u U \otimes \operatorname{D}^v U \otimes S({-}1,-1) & (u,v \ge 0),\\ \mathscr{C}(u,v) &= \operatorname{D}^{u-1} U \otimes \operatorname{D}^{v-1} U \otimes S({-}1,-1) & (u,v \ge 1),\\ \mathscr{D}_1(u,v) &= \operatorname{D}^{u+1} U \otimes S({-}1,0) & (u \ge -1),\\ \mathscr{D}_2(u,v) &= \operatorname{D}^{v+1} U \otimes S(0,-1) & (v \ge -1),\\ \mathscr{D}(u,v) &= \mathscr{D}_1(u,v) \oplus \mathscr{D}_2(u,v) & (u,v \ge -1),\\ \mathscr{N}(u,v) &= \operatorname{D}^{u+v} U \otimes S({-}1,-1) & (u,v \ge 0). \end{align*}
\begin{align*} \mathscr{A}(u,v) &= \operatorname{D}^{u+v+2} U \otimes S({-}1,-1) & (u,v \ge -1),\\ \mathscr{B}(u,v) &= \operatorname{D}^{u+1} U \otimes \operatorname{D}^{v+1} U \otimes S({-}1,-1) & (u,v \ge -1),\\ \mathscr{C}'(u,v) &= \operatorname{D}^u U \otimes \operatorname{D}^v U \otimes S({-}1,-1) & (u,v \ge 0),\\ \mathscr{C}(u,v) &= \operatorname{D}^{u-1} U \otimes \operatorname{D}^{v-1} U \otimes S({-}1,-1) & (u,v \ge 1),\\ \mathscr{D}_1(u,v) &= \operatorname{D}^{u+1} U \otimes S({-}1,0) & (u \ge -1),\\ \mathscr{D}_2(u,v) &= \operatorname{D}^{v+1} U \otimes S(0,-1) & (v \ge -1),\\ \mathscr{D}(u,v) &= \mathscr{D}_1(u,v) \oplus \mathscr{D}_2(u,v) & (u,v \ge -1),\\ \mathscr{N}(u,v) &= \operatorname{D}^{u+v} U \otimes S({-}1,-1) & (u,v \ge 0). \end{align*}The map (5.8) is the middle homology of the following map between three-term complexes.

The right-hand side is just the complex computing ![]() $W(V,K)$, and the middle horizontal map comes from the inclusion
$W(V,K)$, and the middle horizontal map comes from the inclusion
Let ![]() $Z$ be one of the symbols
$Z$ be one of the symbols ![]() $\mathscr {A}, \mathscr {B}, \mathscr {C}', \mathscr {C}, \mathscr {D}, \mathscr {S}$. We construct a double complexFootnote 1
$\mathscr {A}, \mathscr {B}, \mathscr {C}', \mathscr {C}, \mathscr {D}, \mathscr {S}$. We construct a double complexFootnote 1 ![]() $\Phi (Z)$ of free
$\Phi (Z)$ of free ![]() $R$-modules with terms
$R$-modules with terms
We will now describe the differentials, which on generators take the form
 \begin{align*} Z(u,v)_{a-u,b-v} &\to Z(u-1,v)_{a-u+1,b-v} \otimes \operatorname{Sym}^a U,\\ Z(u,v)_{a-u,b-v} &\to Z(u,v-1)_{a-u,b-v+1} \otimes \operatorname{Sym}^b U. \end{align*}
\begin{align*} Z(u,v)_{a-u,b-v} &\to Z(u-1,v)_{a-u+1,b-v} \otimes \operatorname{Sym}^a U,\\ Z(u,v)_{a-u,b-v} &\to Z(u,v-1)_{a-u,b-v+1} \otimes \operatorname{Sym}^b U. \end{align*}
We call the first map the ‘![]() $u$-component’ and the second map the ‘
$u$-component’ and the second map the ‘![]() $v$-component’.
$v$-component’.
For the cases ![]() $Z \in \{\mathscr {A}, \mathscr {B}, \mathscr {C}', \mathscr {C}\}$, we can write
$Z \in \{\mathscr {A}, \mathscr {B}, \mathscr {C}', \mathscr {C}\}$, we can write ![]() $Z(u,v)$ as
$Z(u,v)$ as ![]() $G_Z(u,v) \otimes S(-1,-1)$. In each of these cases, we have two maps
$G_Z(u,v) \otimes S(-1,-1)$. In each of these cases, we have two maps
via comultiplication. We will describe the differentials in terms of these maps for these cases.
The ![]() $u$-component takes the form
$u$-component takes the form

Applying Hermite reciprocity, this becomes

To define this map, we use the comultiplication maps
 \begin{align*} G_Z(u,v) &\to G_Z(u-1,v) \otimes U,\\ \bigwedge^{u+1}(\operatorname{Sym}^{a-1} U) &\to \bigwedge^u(\operatorname{Sym}^{a-1} U) \otimes \operatorname{Sym}^{a-1} U \end{align*}
\begin{align*} G_Z(u,v) &\to G_Z(u-1,v) \otimes U,\\ \bigwedge^{u+1}(\operatorname{Sym}^{a-1} U) &\to \bigwedge^u(\operatorname{Sym}^{a-1} U) \otimes \operatorname{Sym}^{a-1} U \end{align*}
and then apply multiplication on the last two factors to get the factor ![]() $\operatorname {Sym}^a U$. The
$\operatorname {Sym}^a U$. The ![]() $v$-component is defined in a completely analogous way.
$v$-component is defined in a completely analogous way.
Now consider ![]() $Z = \mathscr {D}_1$. The
$Z = \mathscr {D}_1$. The ![]() $u$-component takes the form
$u$-component takes the form

Applying Hermite reciprocity, this maps takes the form

This is defined as before: we use the comultiplication maps
 \begin{align*} \operatorname{D}^{u+1} U &\to \operatorname{D}^u U \otimes U\\ \bigwedge^{u+1} (\operatorname{Sym}^{a-1} U) &\to \bigwedge^u(\operatorname{Sym}^{a-1} U) \otimes \operatorname{Sym}^{a-1} U \end{align*}
\begin{align*} \operatorname{D}^{u+1} U &\to \operatorname{D}^u U \otimes U\\ \bigwedge^{u+1} (\operatorname{Sym}^{a-1} U) &\to \bigwedge^u(\operatorname{Sym}^{a-1} U) \otimes \operatorname{Sym}^{a-1} U \end{align*}
and multiply the last factors together. Under Hermite reciprocity, the ![]() $v$-component takes the form
$v$-component takes the form

This is obtained by simply using the comultiplication map on the last exterior power factor. The definitions for ![]() $\mathscr {D}_2$ are completely analogous, so we will omit the details.
$\mathscr {D}_2$ are completely analogous, so we will omit the details.
Now consider ![]() $Z=\mathscr {S}$. The
$Z=\mathscr {S}$. The ![]() $u$-component takes the form (the horizontal equalities are Hermite reciprocity)
$u$-component takes the form (the horizontal equalities are Hermite reciprocity)

The right vertical map is defined using exterior comultiplication.
5.4 Maps between the complexes
Applying ![]() $\Phi$ to (5.9), we get the following diagram.
$\Phi$ to (5.9), we get the following diagram.

Proposition 5.10 All of the maps above are morphisms of double complexes.
Proof. For the map ![]() $\Phi (\mathscr {A}) \to \Phi (\mathscr {B})$, compatibility in the
$\Phi (\mathscr {A}) \to \Phi (\mathscr {B})$, compatibility in the ![]() $u$-direction amounts to the commutativity of the following diagram, which follows from coassociativity of the divided power comultiplication:
$u$-direction amounts to the commutativity of the following diagram, which follows from coassociativity of the divided power comultiplication:

Compatibility in the ![]() $v$-direction is analogous. The map
$v$-direction is analogous. The map ![]() $\Phi (\mathscr {A}) \to \Phi (\mathscr {D})$ is analogous.
$\Phi (\mathscr {A}) \to \Phi (\mathscr {D})$ is analogous.
Now consider ![]() $\Phi (\mathscr {B}) \to \Phi (\mathscr {C})$. We can factor it into two pieces:
$\Phi (\mathscr {B}) \to \Phi (\mathscr {C})$. We can factor it into two pieces: ![]() $\Phi (\mathscr {B}) \to \Phi (\mathscr {C}') \to \Phi (\mathscr {C})$. First, we have the formula
$\Phi (\mathscr {B}) \to \Phi (\mathscr {C}') \to \Phi (\mathscr {C})$. First, we have the formula
 \begin{align*} \iota_{u+1,v+1}^* \colon \operatorname{D}^{u+1} U \otimes \operatorname{D}^{v+1} U &\to \operatorname{D}^{u} U \otimes \operatorname{D}^{v} U\\ x^{(i)} \otimes x^{(j)} &\mapsto x^{(i-1)} \otimes x^{(j)} - x^{(i)} \otimes x^{(j-1)}. \end{align*}
\begin{align*} \iota_{u+1,v+1}^* \colon \operatorname{D}^{u+1} U \otimes \operatorname{D}^{v+1} U &\to \operatorname{D}^{u} U \otimes \operatorname{D}^{v} U\\ x^{(i)} \otimes x^{(j)} &\mapsto x^{(i-1)} \otimes x^{(j)} - x^{(i)} \otimes x^{(j-1)}. \end{align*}It follows from this explicit formula that the following diagram commutes, where the vertical maps are comultiplication:

This implies compatibility of ![]() $\Phi (\mathscr {B}) \to \Phi (\mathscr {C}')$ in the
$\Phi (\mathscr {B}) \to \Phi (\mathscr {C}')$ in the ![]() $u$-direction, and the
$u$-direction, and the ![]() $v$-direction is similar. Also similarly, this can be used to prove compatibility of the map
$v$-direction is similar. Also similarly, this can be used to prove compatibility of the map ![]() $\Phi (\mathscr {C}') \to \Phi (\mathscr {C})$.
$\Phi (\mathscr {C}') \to \Phi (\mathscr {C})$.
Compatibility of ![]() $\Phi (\mathscr {D}) \to \Phi (\mathscr {S})$ reduces to Proposition 2.1.
$\Phi (\mathscr {D}) \to \Phi (\mathscr {S})$ reduces to Proposition 2.1.
Finally, we prove compatibility of ![]() $\Phi (\mathscr {B}) \to \Phi (\mathscr {D})$. This map is a sum of two components, and the check is similar for both of them, so we will just explain the map
$\Phi (\mathscr {B}) \to \Phi (\mathscr {D})$. This map is a sum of two components, and the check is similar for both of them, so we will just explain the map ![]() $\Phi (\mathscr {B}) \to \Phi (\mathscr {D}_1)$. Compatibility in the
$\Phi (\mathscr {B}) \to \Phi (\mathscr {D}_1)$. Compatibility in the ![]() $u$-direction is formal: the differential acts on different factors from the map
$u$-direction is formal: the differential acts on different factors from the map ![]() $\Phi (\mathscr {B}) \to \Phi (\mathscr {D})$. Compatibility in the
$\Phi (\mathscr {B}) \to \Phi (\mathscr {D})$. Compatibility in the ![]() $v$-direction follows from Proposition 2.1.
$v$-direction follows from Proposition 2.1.
5.5 Homology of these complexes
Consider the following data:

In each case, we have a short exact sequence ![]() $0 \to E \to \operatorname {Sym}^a U \oplus \operatorname {Sym}^b U \to F \to 0$ of vector bundles over the projective variety
$0 \to E \to \operatorname {Sym}^a U \oplus \operatorname {Sym}^b U \to F \to 0$ of vector bundles over the projective variety ![]() $\mathbb {P}U$ such that
$\mathbb {P}U$ such that
 \[ \mathrm{tot}(\Phi(Z))_{i-1} = \bigoplus_{j \ge 0} \mathrm{H}^j(\mathbb{P}U, \mathcal{O}({-}2) \otimes \bigwedge^{i+j} E) \otimes R. \]
\[ \mathrm{tot}(\Phi(Z))_{i-1} = \bigoplus_{j \ge 0} \mathrm{H}^j(\mathbb{P}U, \mathcal{O}({-}2) \otimes \bigwedge^{i+j} E) \otimes R. \]
Following [Reference WeymanWey03, § 5], the terms on the right-hand side have the structure of a minimal complex over ![]() $R$ by taking the derived pushforward of the Koszul complex on
$R$ by taking the derived pushforward of the Koszul complex on ![]() $E$. This describes the differentials that we have defined on the terms on the left-hand side, so we conclude that the homology is
$E$. This describes the differentials that we have defined on the terms on the left-hand side, so we conclude that the homology is
Explicitly, we get
 \begin{align*} \mathrm{H}_{{-}2}(\Phi(\mathscr{A})) &= {\mathbf{k}},\\ \mathrm{H}_{{-}1}(\Phi(\mathscr{A})) &= \bigoplus_{d,e \ge 0} \operatorname{Sym}^{da+eb-2} U,\\ \mathrm{H}_{{-}2}(\Phi(\mathscr{D}_1)) &= {\mathbf{k}},\\ \mathrm{H}_{{-}1}(\Phi(\mathscr{D}_1)) &= \bigoplus_{d \ge 0} \operatorname{Sym}^{da-2} U,\\ \mathrm{H}_{{-}2}(\Phi(\mathscr{D}_2)) &= {\mathbf{k}},\\ \mathrm{H}_{{-}1}(\Phi(\mathscr{D}_2)) &= \bigoplus_{e \ge 0} \operatorname{Sym}^{eb-2} U. \end{align*}
\begin{align*} \mathrm{H}_{{-}2}(\Phi(\mathscr{A})) &= {\mathbf{k}},\\ \mathrm{H}_{{-}1}(\Phi(\mathscr{A})) &= \bigoplus_{d,e \ge 0} \operatorname{Sym}^{da+eb-2} U,\\ \mathrm{H}_{{-}2}(\Phi(\mathscr{D}_1)) &= {\mathbf{k}},\\ \mathrm{H}_{{-}1}(\Phi(\mathscr{D}_1)) &= \bigoplus_{d \ge 0} \operatorname{Sym}^{da-2} U,\\ \mathrm{H}_{{-}2}(\Phi(\mathscr{D}_2)) &= {\mathbf{k}},\\ \mathrm{H}_{{-}1}(\Phi(\mathscr{D}_2)) &= \bigoplus_{e \ge 0} \operatorname{Sym}^{eb-2} U. \end{align*} Next, ![]() $\Phi (\mathscr {N})$ and
$\Phi (\mathscr {N})$ and ![]() $\Phi (\mathscr {M})$ are respectively the homology of
$\Phi (\mathscr {M})$ are respectively the homology of ![]() $\Phi (\mathscr {A}) \to \Phi (\mathscr {B}) \to \Phi (\mathscr {C})$ and
$\Phi (\mathscr {A}) \to \Phi (\mathscr {B}) \to \Phi (\mathscr {C})$ and ![]() $\Phi (\mathscr {A}) \to \Phi (\mathscr {D}) \to \Phi (\mathscr {S})$, and hence they inherit the structure of double complex. We now identify the corresponding total complexes.
$\Phi (\mathscr {A}) \to \Phi (\mathscr {D}) \to \Phi (\mathscr {S})$, and hence they inherit the structure of double complex. We now identify the corresponding total complexes.
Proposition 5.11 ![]() $\Phi (\mathscr {N})$ is the quotient complex of the minimal free resolution of the ideal
$\Phi (\mathscr {N})$ is the quotient complex of the minimal free resolution of the ideal ![]() $I$ of the rational normal scroll by the terms
$I$ of the rational normal scroll by the terms ![]() $\operatorname {D}^i U \otimes \bigwedge ^{i+2}(\operatorname {Sym}^{a-1} U) \otimes R$ and
$\operatorname {D}^i U \otimes \bigwedge ^{i+2}(\operatorname {Sym}^{a-1} U) \otimes R$ and ![]() $\operatorname {D}^i U \otimes \bigwedge ^{i+2}(\operatorname {Sym}^{b-1} U) \otimes R$.
$\operatorname {D}^i U \otimes \bigwedge ^{i+2}(\operatorname {Sym}^{b-1} U) \otimes R$.
Proof. First, we have a short exact sequence of double complexes
as shown in the proof of Proposition 5.10. Next, we have a short exact sequence
where the last map is a morphism of double complexes, and hence ![]() $\Phi (\mathscr {N})$ inherits a double complex structure from being the kernel of this map.
$\Phi (\mathscr {N})$ inherits a double complex structure from being the kernel of this map.
By coassociativity of comultiplication, the following diagram commutes.

commutes, where in the bottom map the ![]() $U$ factor is not being used in
$U$ factor is not being used in ![]() $\mu _{u-1,v}^*$.
$\mu _{u-1,v}^*$.
This implies that for the ![]() $u$-component of
$u$-component of ![]() $\Phi (\mathscr {N})$, we use the comultiplication maps
$\Phi (\mathscr {N})$, we use the comultiplication maps
 \begin{align*} \operatorname{D}^{u+v} U &\to \operatorname{D}^{u+v-1} U \otimes U,\\ \bigwedge^{u+1}(\operatorname{Sym}^{a-1} U) &\to \bigwedge^u(\operatorname{Sym}^{a-1} U) \otimes \operatorname{Sym}^{a-1} U \end{align*}
\begin{align*} \operatorname{D}^{u+v} U &\to \operatorname{D}^{u+v-1} U \otimes U,\\ \bigwedge^{u+1}(\operatorname{Sym}^{a-1} U) &\to \bigwedge^u(\operatorname{Sym}^{a-1} U) \otimes \operatorname{Sym}^{a-1} U \end{align*}
together with the multiplication ![]() $U\otimes \operatorname {Sym}^{a-1} U \to \operatorname {Sym}^a U$. The
$U\otimes \operatorname {Sym}^{a-1} U \to \operatorname {Sym}^a U$. The ![]() $v$-component is defined similarly. This agrees with the quotient complex of the minimal free resolution of the ideal
$v$-component is defined similarly. This agrees with the quotient complex of the minimal free resolution of the ideal ![]() $I$ of the rational normal scroll.
$I$ of the rational normal scroll.
Proposition 5.12 ![]() $\Phi (\mathscr {M})$ is the first linear strand of the minimal free resolution of
$\Phi (\mathscr {M})$ is the first linear strand of the minimal free resolution of ![]() $\omega _B$.
$\omega _B$.
Proof. First, the total complex of ![]() $\Phi (\mathscr {S})$ is a Koszul complex on
$\Phi (\mathscr {S})$ is a Koszul complex on ![]() $\operatorname {Sym}^a U \oplus \operatorname {Sym}^b U$ shifted by 2, so
$\operatorname {Sym}^a U \oplus \operatorname {Sym}^b U$ shifted by 2, so ![]() $\mathrm {H}_{-2}(\Phi (\mathscr {S})) = {\mathbf {k}}$ and any other homology vanishes.
$\mathrm {H}_{-2}(\Phi (\mathscr {S})) = {\mathbf {k}}$ and any other homology vanishes.
From the proof of Proposition 5.7, we have a complex
whose middle homology is ![]() $\Phi (\mathscr {M})$. From the exact sequence
$\Phi (\mathscr {M})$. From the exact sequence
and the calculations earlier, we conclude that
Next, from the short exact sequence ![]() $0 \to \Phi (\mathscr {A}) \to \ker f \to \Phi (\mathscr {M}) \to 0$, we get an exact sequence
$0 \to \Phi (\mathscr {A}) \to \ker f \to \Phi (\mathscr {M}) \to 0$, we get an exact sequence
and ![]() $\mathrm {H}_{a+b-2}(\Phi (\mathscr {M}))=R$. Since
$\mathrm {H}_{a+b-2}(\Phi (\mathscr {M}))=R$. Since ![]() $\Phi (\mathscr {M})$ is concentrated in non-negative homological degrees, we conclude that
$\Phi (\mathscr {M})$ is concentrated in non-negative homological degrees, we conclude that
Next, ![]() $\Phi (\mathscr {M})_0 = \operatorname {Sym}^{a+b-2} U \otimes R$, so
$\Phi (\mathscr {M})_0 = \operatorname {Sym}^{a+b-2} U \otimes R$, so ![]() $\mathrm {H}_0(\Phi (\mathscr {M}))$ is generated by its lowest-degree term. We conclude that
$\mathrm {H}_0(\Phi (\mathscr {M}))$ is generated by its lowest-degree term. We conclude that ![]() $\Phi (\mathscr {M})$ is the first linear strand of the minimal free resolution of
$\Phi (\mathscr {M})$ is the first linear strand of the minimal free resolution of ![]() $\omega _B$.
$\omega _B$.
Proof of Theorem 5.5 Proposition 5.10 implies that we get a map of complexes
On components of degree 0 this takes the form
This is the standard multiplication map, which follows from the explicit description of the map ![]() $\Phi (\mathscr {B}) \to \Phi (\mathscr {D})$. In particular,
$\Phi (\mathscr {B}) \to \Phi (\mathscr {D})$. In particular, ![]() $F$ lifts the surjection
$F$ lifts the surjection ![]() $I \to \omega _B$, so that we can identify its maps with the induced maps on Tor.
$I \to \omega _B$, so that we can identify its maps with the induced maps on Tor.
To prove the last vanishing statement, we fix a bi-degree ![]() $(u+1,v+1)$, with
$(u+1,v+1)$, with ![]() $u+v=i$. We use Corollary 4.4, with
$u+v=i$. We use Corollary 4.4, with ![]() $n_1=u+2$ and
$n_1=u+2$ and ![]() $n_2=v+2$. We have that
$n_2=v+2$. We have that ![]() $n_1+n_2-3 = u+v+1=i+1\leq \min (a,b)$, so the assumptions on the characteristic in the corollary are satisfied. We have, moreover, that
$n_1+n_2-3 = u+v+1=i+1\leq \min (a,b)$, so the assumptions on the characteristic in the corollary are satisfied. We have, moreover, that ![]() $a-1-u\geq i-u=n_2-2$, and
$a-1-u\geq i-u=n_2-2$, and ![]() $b-1-v\geq i-v=n_1-2$, so
$b-1-v\geq i-v=n_1-2$, so ![]() $W^{(u+1,v+1)}_{a-1-u,b-1-v} =0$.
$W^{(u+1,v+1)}_{a-1-u,b-1-v} =0$.
6. Green's conjecture
A canonical ribbon is a scheme which is a double structure on a rational normal curve. A hyperplane section of ![]() $\mathcal {X}(a,g-1-a)$ corresponds to a choice of polynomials
$\mathcal {X}(a,g-1-a)$ corresponds to a choice of polynomials ![]() $(f_1,f_2) \in \operatorname {Sym}^a U \oplus \operatorname {Sym}^{g-1-a} U$ and is a canonical ribbon if and only if
$(f_1,f_2) \in \operatorname {Sym}^a U \oplus \operatorname {Sym}^{g-1-a} U$ and is a canonical ribbon if and only if ![]() $f_1,f_2$ is a regular sequence [Reference Bayer and EisenbudBE95, § 2]. These ribbons have Clifford index
$f_1,f_2$ is a regular sequence [Reference Bayer and EisenbudBE95, § 2]. These ribbons have Clifford index ![]() $a$ in the sense of [Reference Bayer and EisenbudBE95, § 2]. Since the homogeneous coordinate ring of
$a$ in the sense of [Reference Bayer and EisenbudBE95, § 2]. Since the homogeneous coordinate ring of ![]() $\mathcal {X}(a,g-1-a)$ is Cohen–Macaulay, it has the same graded Betti numbers as any canonical ribbon of Clifford index
$\mathcal {X}(a,g-1-a)$ is Cohen–Macaulay, it has the same graded Betti numbers as any canonical ribbon of Clifford index ![]() $a$ in
$a$ in ![]() ${\textbf P}^{g-1}$. Theorem 5.5 then implies that the graded Betti numbers
${\textbf P}^{g-1}$. Theorem 5.5 then implies that the graded Betti numbers ![]() $\beta _{i,i+2}$ of canonical ribbons of Clifford index
$\beta _{i,i+2}$ of canonical ribbons of Clifford index ![]() $a$ are 0 for
$a$ are 0 for ![]() $i< a$.
$i< a$.
Proposition 6.1 Assume that the characteristic is not ![]() $2$. The canonical ribbons realized above can be smoothed out to a curve of gonality
$2$. The canonical ribbons realized above can be smoothed out to a curve of gonality ![]() $a+2$ and Clifford index
$a+2$ and Clifford index ![]() $a$.
$a$.
Proof. In characteristic ![]() $0$, this follows from the proof of [Reference FongFon93, Theorem 2]. The two key inputs for the proof are:
$0$, this follows from the proof of [Reference FongFon93, Theorem 2]. The two key inputs for the proof are:
• [Reference FongFon93, Theorem 1], which identifies ribbon structures with lines in the normal space to the hyperelliptic locus in the versal deformation space at some fixed hyperelliptic curve; and
• [Reference Eisenbud and GreenEG95, Theorem 2.1], which states that if a family of smooth curves of Clifford index
 $e$ degenerates to a ribbon, then the resulting Clifford index is
$e$ degenerates to a ribbon, then the resulting Clifford index is  $\le e$.
$\le e$.
The proof of the first result goes through verbatim if we assume that 2 is invertible in ![]() ${\mathbf {k}}$. To replace the latter result, it suffices to prove the following: if
${\mathbf {k}}$. To replace the latter result, it suffices to prove the following: if ![]() $C$ is the generic fiber of a flat family of smooth curves degenerating to one of the canonical ribbons above, then the Clifford index of
$C$ is the generic fiber of a flat family of smooth curves degenerating to one of the canonical ribbons above, then the Clifford index of ![]() $C$ is
$C$ is ![]() $\ge a$. To see this, we note first that the Hilbert series for a canonical ribbon is the same as the Hilbert series of a canonical curve of genus
$\ge a$. To see this, we note first that the Hilbert series for a canonical ribbon is the same as the Hilbert series of a canonical curve of genus ![]() $a+b+1$, namely,
$a+b+1$, namely,
which follows by passing to a hyperplane section in Proposition 5.4 (and using that ![]() $A$ is Cohen–Macaulay). Using [Reference Boratyński and GrecoBG85, Proposition 2.15], it follows that the Betti numbers in our family are upper semicontinuous. From the discussion above, we know that for the canonical ribbon
$A$ is Cohen–Macaulay). Using [Reference Boratyński and GrecoBG85, Proposition 2.15], it follows that the Betti numbers in our family are upper semicontinuous. From the discussion above, we know that for the canonical ribbon ![]() $\beta _{i,i+2}=0$ for
$\beta _{i,i+2}=0$ for ![]() $i< a$, so we must also have that
$i< a$, so we must also have that ![]() $\beta _{i,i+2}(C)=0$ for
$\beta _{i,i+2}(C)=0$ for ![]() $i< a$. Using [Reference EisenbudEis05, Corollary 9.7], this implies that the Clifford index of
$i< a$. Using [Reference EisenbudEis05, Corollary 9.7], this implies that the Clifford index of ![]() $C$ is
$C$ is ![]() $\ge a$.
$\ge a$.
We are now ready to deduce the generic Green's conjecture in each gonality.
Theorem 6.2 Pick integers ![]() $a \ge 1$ and
$a \ge 1$ and ![]() $g \ge 2a+1$. If the characteristic of
$g \ge 2a+1$. If the characteristic of ![]() ${\mathbf {k}}$ is either
${\mathbf {k}}$ is either ![]() $0$ or
$0$ or ![]() $p \ge a$, then there is a non-empty Zariski open subset of curves of gonality
$p \ge a$, then there is a non-empty Zariski open subset of curves of gonality ![]() $a+2$ and Clifford index
$a+2$ and Clifford index ![]() $a$ which satisfy Green's conjecture, that is,
$a$ which satisfy Green's conjecture, that is, ![]() $\beta _{i,i+2}=0$ for
$\beta _{i,i+2}=0$ for ![]() $i< a$ under the canonical embedding.
$i< a$ under the canonical embedding.
Proof. If ![]() $p=2$, then
$p=2$, then ![]() $a$ is 1 or 2. If
$a$ is 1 or 2. If ![]() $a \ge 1$, then
$a \ge 1$, then ![]() $\beta _{0,2}=0$ for non-hyperelliptic curves by Noether's theorem. If
$\beta _{0,2}=0$ for non-hyperelliptic curves by Noether's theorem. If ![]() $a=2$, then
$a=2$, then ![]() $\beta _{1,3}=0$ for non-trigonal curves by Petri's theorem. So for the remainder of the proof, we may assume that the characteristic is different from 2.
$\beta _{1,3}=0$ for non-trigonal curves by Petri's theorem. So for the remainder of the proof, we may assume that the characteristic is different from 2.
The condition ![]() $\beta _{i,i+2}=0$ for
$\beta _{i,i+2}=0$ for ![]() $i< a$ is open in the locus of curves of gonality
$i< a$ is open in the locus of curves of gonality ![]() $a+2$ in the moduli of curves of genus
$a+2$ in the moduli of curves of genus ![]() $g$. The condition that a curve of gonality
$g$. The condition that a curve of gonality ![]() $a+2$ has Clifford index
$a+2$ has Clifford index ![]() $a$ is also open. Their intersection is non-empty by Proposition 6.1.
$a$ is also open. Their intersection is non-empty by Proposition 6.1.
As a consequence, we solve [Reference Eisenbud and SchreyerES19, Conjecture 0.1].
Corollary 6.3 Let ![]() ${\mathbf {k}}$ be a field of characteristic
${\mathbf {k}}$ be a field of characteristic ![]() $p$ where either
$p$ where either ![]() $p=0$ or
$p=0$ or ![]() $\,p \ge \lfloor (g-1)/2 \rfloor$. Then a general curve of genus
$\,p \ge \lfloor (g-1)/2 \rfloor$. Then a general curve of genus ![]() $g$ satisfies Green's conjecture, that is,
$g$ satisfies Green's conjecture, that is, ![]() $\beta _{i,i+2}=0$ for
$\beta _{i,i+2}=0$ for ![]() $i<\lfloor (g-1)/2 \rfloor$.
$i<\lfloor (g-1)/2 \rfloor$.
Proof. A curve of genus ![]() $g$ has Clifford index
$g$ has Clifford index ![]() $\le \lfloor ({g-1})/{2} \rfloor$ and for a general curve, this is the value of the Clifford index [Reference EisenbudEis05, Theorem 8.16]. Hence the result follows from Theorem 6.2.
$\le \lfloor ({g-1})/{2} \rfloor$ and for a general curve, this is the value of the Clifford index [Reference EisenbudEis05, Theorem 8.16]. Hence the result follows from Theorem 6.2.
Acknowledgements
The authors would like to thank Marian Aprodu, David Eisenbud, Gabi Farkas, Eric Riedl, Frank Schreyer, Claire Voisin, Jerzy Weyman, and Mengyuan Zhang for interesting discussions related to this project, for helpful suggestions, and for clarifications regarding the literature. We would also like to thank the anonymous referee for helping us improve the presentation of the paper. Experiments with the computer algebra software Macaulay2 [Reference Grayson and StillmanGS] have provided many valuable insights.