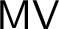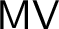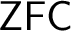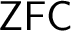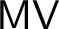1 Introduction
1.1 Steel’s Programme
In Reference Steel and Kennedy[25], John Steel presented a version of the set-theoretic multiverse consisting of ‘worlds’ (set-generic extensions of V and their grounds), and a collection of axioms for it,
![]() $\mathsf {MV}$
, and also made the hypothesis that such a multiverse might contain a core, that is, a world included in all other worlds, which would act as ‘preferred universe’, as the ‘real V’.Footnote
1
A few years after the appearance of Steel Reference Steel and Kennedy[25], in the context of research on set-theoretic geology,Footnote
2
it was proved by Usuba (in Reference Usuba[28]) that, if there exists an extendible cardinal, then V has a smallest ground, and that such smallest ground is the
$\mathsf {MV}$
, and also made the hypothesis that such a multiverse might contain a core, that is, a world included in all other worlds, which would act as ‘preferred universe’, as the ‘real V’.Footnote
1
A few years after the appearance of Steel Reference Steel and Kennedy[25], in the context of research on set-theoretic geology,Footnote
2
it was proved by Usuba (in Reference Usuba[28]) that, if there exists an extendible cardinal, then V has a smallest ground, and that such smallest ground is the
![]() $\kappa $
-mantle of V itself, where
$\kappa $
-mantle of V itself, where
![]() $\kappa $
is the least extendible cardinal. A noticeable consequence of Usuba’s result is that the multiverse of the theory
$\kappa $
is the least extendible cardinal. A noticeable consequence of Usuba’s result is that the multiverse of the theory
![]() $\mathsf {MV}_T$
, where
$\mathsf {MV}_T$
, where
![]() $T=\mathsf {ZFC}+$
‘there exists a proper class of extendible cardinals’ has a core. Now, given the presuppositions of
$T=\mathsf {ZFC}+$
‘there exists a proper class of extendible cardinals’ has a core. Now, given the presuppositions of
![]() $\mathsf {MV}$
, in particular, its reliance upon the whole hierarchy of Large Cardinals (LCs), it makes full sense to investigate the features of the multiverse of
$\mathsf {MV}$
, in particular, its reliance upon the whole hierarchy of Large Cardinals (LCs), it makes full sense to investigate the features of the multiverse of
![]() $\mathsf {MV}_T$
, in particular, the features of its core.
$\mathsf {MV}_T$
, in particular, the features of its core.
Steel’s ‘core hypothesis’ also has connections with another, recently arisen, fundamental set-theoretic hypothesis, that is, Woodin’s ‘Ultimate-L Conjecture’.Footnote
3
The inner model programme has progressively unveiled the existence of ‘canonical’ inner models of
![]() $\mathsf {ZFC}$
+LCs; Woodin’s Ultimate-L Conjecture asserts that
$\mathsf {ZFC}$
+LCs; Woodin’s Ultimate-L Conjecture asserts that
![]() $\mathsf {ZFC}$
+LCs also proves the existence of a weak extender model for a cardinal
$\mathsf {ZFC}$
+LCs also proves the existence of a weak extender model for a cardinal
![]() $\delta $
being supercompact which also satisfies V=Ultimate-L.Footnote
4
In turn, Steel has made the hypothesis that Ultimate-L might be the most ‘suitable’ candidate as the core of
$\delta $
being supercompact which also satisfies V=Ultimate-L.Footnote
4
In turn, Steel has made the hypothesis that Ultimate-L might be the most ‘suitable’ candidate as the core of
![]() $\mathsf {MV}$
.Footnote
5
$\mathsf {MV}$
.Footnote
5
Now, given
![]() $\mathsf {MV}_T$
, where, again,
$\mathsf {MV}_T$
, where, again,
![]() $T=\mathsf {ZFC}$
+‘there exists a proper class of extendible cardinals’, Steel’s Programme, as we will call it, may be formulated as follows:
$T=\mathsf {ZFC}$
+‘there exists a proper class of extendible cardinals’, Steel’s Programme, as we will call it, may be formulated as follows:
Steel’s Programme. Use facts about the core of
![]() $\mathsf {MV}_T$
as evidence for the following claims:
$\mathsf {MV}_T$
as evidence for the following claims:
-
1. V is the core.
-
2. The core is Ultimate-L.
-
3.
 $\mathsf {ZFC}$
+LCs+V=Ultimate-L has a better claim than any other theory to be seen as the best (ultimate) extension of
$\mathsf {ZFC}$
+LCs+V=Ultimate-L has a better claim than any other theory to be seen as the best (ultimate) extension of
 $\mathsf {ZFC}$
.Footnote
6
$\mathsf {ZFC}$
.Footnote
6
As we shall see in more detail later on, the execution (and meaningfulness) of Steel’s Programme crucially depends on the relationship between
![]() $\mathcal {L}_{\mathsf {MV}}$
, the multiverse language, and
$\mathcal {L}_{\mathsf {MV}}$
, the multiverse language, and
![]() $\mathcal {L}_{\mathsf {\in }}$
, the language of set theory, as expressed by a ‘translation function’, which, in turn, shows that
$\mathcal {L}_{\mathsf {\in }}$
, the language of set theory, as expressed by a ‘translation function’, which, in turn, shows that
![]() $\mathcal {L}_{\mathsf {MV}}$
is a sublanguage of
$\mathcal {L}_{\mathsf {MV}}$
is a sublanguage of
![]() $\mathcal {L}_{\mathsf {\in }}$
. As a consequence of this, the existence of the core of the multiverse of
$\mathcal {L}_{\mathsf {\in }}$
. As a consequence of this, the existence of the core of the multiverse of
![]() $\mathsf {MV}$
has bearings on set theory, as ‘standardly’ construed as the theory of V, thus, Steel’s Programme makes full sense. In broader philosophical terms, the interaction between the two ‘languages’ may be construed as a way to provide set-theorists with a strategy to respond to the following question:
$\mathsf {MV}$
has bearings on set theory, as ‘standardly’ construed as the theory of V, thus, Steel’s Programme makes full sense. In broader philosophical terms, the interaction between the two ‘languages’ may be construed as a way to provide set-theorists with a strategy to respond to the following question:
Question 1.1. Is there a ‘preferred’ universe of sets?
Clearly, if the Programme is successful, then the response to this question is in the positive, a fact which would have a considerable impact on our understanding of set theory, in particular, of its foundations.
The main purpose of the paper is to provide a comprehensive assessment of the Programme, by focussing on three main topics: (1) its ‘evidential framework’: in particular, the use of LCs and of forcing extensions of V as ‘worlds’ in the
![]() $\mathsf {MV}$
axiomatic set-up (Section 2); (2) the core: the assumptions needed for its existence, and its level of (in)determinacy over
$\mathsf {MV}$
axiomatic set-up (Section 2); (2) the core: the assumptions needed for its existence, and its level of (in)determinacy over
![]() $\mathsf {MV}$
(Sections 3 and 4); and (3) the hypothesis that Ultimate-L is the core, and the justification for this claim (Section 5).
$\mathsf {MV}$
(Sections 3 and 4); and (3) the hypothesis that Ultimate-L is the core, and the justification for this claim (Section 5).
But first, we would like to introduce very briefly the general features of the broader philosophical context in which Steel’s Programme may be discussed.
1.2 Two kinds of universism
![]() $\mathsf {MV}$
locates itself in the current universe/multiverse debate, and, consequently, in the debate on pluralism, that is, on the issue of whether mathematical truth splits into many, mutually incompatible, truths.Footnote
7
Pluralism is very often taken to correspond to ‘ontological’ pluralism, that is, to the view that:
$\mathsf {MV}$
locates itself in the current universe/multiverse debate, and, consequently, in the debate on pluralism, that is, on the issue of whether mathematical truth splits into many, mutually incompatible, truths.Footnote
7
Pluralism is very often taken to correspond to ‘ontological’ pluralism, that is, to the view that:
(Ontological) Pluralism. There are many, alternative universes of set theory (there is a set-theoretic multiverse).Footnote 8
But note that some pluralists would just commit themselves to semantic pluralism, that is, to the view that the truth-value of all set-theoretic statements undecidable from the
![]() $\mathsf {ZFC}$
axioms is indeterminate (neither true nor false). The opposite camp is represented by:
$\mathsf {ZFC}$
axioms is indeterminate (neither true nor false). The opposite camp is represented by:
(Ontological) Non-pluralism. There is just one universe of set theory.Footnote 9
In what follows, we will mostly refer to the position above as:
Classic Universism. Set theory is the theory of a single universe, V, whose features are pinned down by the
![]() $\mathsf {ZFC}$
axioms (and, potentially, by other axioms extending
$\mathsf {ZFC}$
axioms (and, potentially, by other axioms extending
![]() $\mathsf {ZFC}$
).Footnote
10
$\mathsf {ZFC}$
).Footnote
10
Steel himself introduces and considers several theses, of different nature and strength, concerning set-theoretic ontology and truth. The philosophical thesis which postulates the existence of the core of
![]() $\mathsf {MV}$
’s multiverse is what Steel calls Weak Absolutism:
$\mathsf {MV}$
’s multiverse is what Steel calls Weak Absolutism:
Weak Absolutism. The multiverse has a core.Footnote 11
Crucially for our purposes, Weak Absolutism quite naturally leads to the following stronger view:
Core Universism. Set theory is the theory of multiple (set-theoretic) universes, that is, of a multiverse, which also contains a core universe. Such a universe has a better claim to be seen as the ‘ultimate universe of sets’ than any other universe.
We believe that this position makes sense, especially in view of Steel’s programme, insofar as, if the core of the multiverse of
![]() $\mathsf {MV}$
exists, then it makes sense to claim that V is the core of such multiverse.
$\mathsf {MV}$
exists, then it makes sense to claim that V is the core of such multiverse.
To state very quickly the main differences between Classic and Core Universism: the Classic Universist may be standardly characterised as someone believing that our intuition of sets, or the ‘concept of set’ itself, will provide us with a unique, consistent extension of the
![]() $\mathsf {ZFC}$
axioms which will uniquely fix the truth-value of the undecidable statements.Footnote
12
By contrast, the Core Universist may be characterised as someone who takes all alternative ‘universes’ to be equally legitimate; however, such a Universist will also hold that each universe (or, if you wish, theory) contains ‘traces’ of a single, ‘preferred’ universe, and much of the value of the position consists in showing that the claim is true, that is, that a core universe is really detectable within the multiverse itself. Of course, the Core Universist also expects to be able to describe the properties of the core in a satisfactory way.
$\mathsf {ZFC}$
axioms which will uniquely fix the truth-value of the undecidable statements.Footnote
12
By contrast, the Core Universist may be characterised as someone who takes all alternative ‘universes’ to be equally legitimate; however, such a Universist will also hold that each universe (or, if you wish, theory) contains ‘traces’ of a single, ‘preferred’ universe, and much of the value of the position consists in showing that the claim is true, that is, that a core universe is really detectable within the multiverse itself. Of course, the Core Universist also expects to be able to describe the properties of the core in a satisfactory way.
In order to attain a reduction of set-theoretic incompleteness, the Classic Universist will suggest further exploration of our intuitions about sets, or sharpening of the concept of set, whereas the Core Universist will suggest further exploration of the properties of the core through the multiverse axioms.
Now, it is clear that Steel’s Programme advocates the Core Universist’s standpoint, and, therefore, has deep implications on the preferability of Core over Classic Universism: as already said, the Programme, if successful, would lend support to Core Universism. Indeed, the Core Universist’s construal of the Programme’s goals and results could be condensed as follows: ‘Non-pluralism about set-theoretic ontology cannot be correct, as we are aware of the existence of many alternative universes (as well as of alternative theories extending
![]() $\mathsf {ZFC}$
). However, given a suitable version of the multiverse, one resting upon significant bits of current set-theoretic practice (upon the ‘evidential framework’ addressed in the next section), we may identify a ‘preferred’ universe within the multiverse itself. But then, for all our foundational purposes, such a universe might be seen as a fully adequate instantiation of our pre-theoretic notion of ‘single universe’, perhaps not exactly the Classic Universist’s one, indeed, a more ‘pragmatic’, but equally justified, version of it.’
$\mathsf {ZFC}$
). However, given a suitable version of the multiverse, one resting upon significant bits of current set-theoretic practice (upon the ‘evidential framework’ addressed in the next section), we may identify a ‘preferred’ universe within the multiverse itself. But then, for all our foundational purposes, such a universe might be seen as a fully adequate instantiation of our pre-theoretic notion of ‘single universe’, perhaps not exactly the Classic Universist’s one, indeed, a more ‘pragmatic’, but equally justified, version of it.’
The Weak Absolutist’s position has already been vindicated by Usuba’s result: if there are sufficiently strong LCs, then
![]() $\mathsf {MV}$
has a core. However, whether, and in what sense, the core could be seen as the ‘ultimate’ (‘preferred’) universe of sets, as claimed by the Core Universist, namely as the equivalent of the Classic Universist’s V, is still open to debate, as we shall see in the next sections.
$\mathsf {MV}$
has a core. However, whether, and in what sense, the core could be seen as the ‘ultimate’ (‘preferred’) universe of sets, as claimed by the Core Universist, namely as the equivalent of the Classic Universist’s V, is still open to debate, as we shall see in the next sections.
2 The evidential framework of
 $\mathsf {MV}$
$\mathsf {MV}$
In the preliminaries of Reference Steel and Kennedy[25], Steel introduces and advocates a few distinctive positions, which he takes to be the main motivation for, and underlying conceptual framework of, his multiverse conception, as embodied by the
![]() $\mathsf {MV}$
axioms. We summarise them below:
$\mathsf {MV}$
axioms. We summarise them below:
-
1. Large Cardinals are ‘practically’ necessary to extend
 $\mathsf {ZFC}$
, mostly as a consequence of the following two phenomena:
$\mathsf {ZFC}$
, mostly as a consequence of the following two phenomena:-
(a) LCs ‘calibrate’ the consistency of extensions of
 $\mathsf {ZFC}$
, and of most undecidable set-theoretic statements;
$\mathsf {ZFC}$
, and of most undecidable set-theoretic statements; -
(b) LCs maximise interpretative power, insofar as the hierarchy of consistency strengths of Large Cardinal Axioms (LCAs) is very aptly matched by the hierarchy of proof-theoretic strengths of extensions of
 $\mathsf {ZFC}$
.Footnote
13
$\mathsf {ZFC}$
.Footnote
13
-
-
2. Set theory should fundamentally be seen as the theory of the forcing extensions and inner models of models of the theory:
 $\mathsf {ZFC}+$
LCAs. This position, in turn, rests upon the fact that independence proofs are practically carried out in the model theory of (fragments of)
$\mathsf {ZFC}+$
LCAs. This position, in turn, rests upon the fact that independence proofs are practically carried out in the model theory of (fragments of)
 $\mathsf {ZFC}+$
LCAs and, most crucially for Steel’s purposes, also upon the fact that all ‘natural’ theories extending
$\mathsf {ZFC}+$
LCAs and, most crucially for Steel’s purposes, also upon the fact that all ‘natural’ theories extending
 $\mathsf {ZFC}$
may be mutually connected through using models with LCs.Footnote
14
$\mathsf {ZFC}$
may be mutually connected through using models with LCs.Footnote
14
-
3. Set theory, as currently practised and interpreted, splits into several ‘natural’ theories, all of which extend
 $\mathsf {ZFC}$
. Part of the rationale for adopting set theory as a foundation of mathematics, thus, consists in describing all such theories and their connections through exploiting, in turn, connections between LCs and models containing them.Footnote
15
$\mathsf {ZFC}$
. Part of the rationale for adopting set theory as a foundation of mathematics, thus, consists in describing all such theories and their connections through exploiting, in turn, connections between LCs and models containing them.Footnote
15
-
4. In order to describe all such theories, one should make use of forcing. To be sure, models obtained through forcing have become an essential tool to produce a wide range of set-theoretic ‘universes’ upholding or violating set-theoretic principles, and, in particular, models obtained through forcing are used to prove the equiconsistency of theories with LCs. So, in practice, forcing extensions of the universe should be taken to stand for different universes (Steel’s worlds).Footnote 16
In the next subsections, we wish to discuss at length salient aspects of the points above and, through this, provide an assessment of the evidence for the
![]() $\mathsf {MV}$
axioms.
$\mathsf {MV}$
axioms.
2.1 Natural theories, large cardinals, and worlds
As stated in bullet point (3.), one of the purposes of Steel’s multiverse conception is precisely that of ‘representing’ all ‘natural’ theories extending
![]() $\mathsf {ZFC}$
within a unified axiomatic framework, without explicitly and directly having to deal with ‘universes’.
$\mathsf {ZFC}$
within a unified axiomatic framework, without explicitly and directly having to deal with ‘universes’.
However, in order to show that the axioms are not semantically vacuous, there will have to be objects fixing their interpretation, and such objects are, on the one hand, sets and, on the other, worlds.Footnote
17
But notice the peculiar use of worlds in
![]() $\mathsf {MV}$
: the latter are introduced, and described, to account for the representability of different theories.Footnote
18
The strategy is, crucially, facilitated by both proof-theoretic and model-theoretic facts concerning LCs, in particular, by the following conjecture:
$\mathsf {MV}$
: the latter are introduced, and described, to account for the representability of different theories.Footnote
18
The strategy is, crucially, facilitated by both proof-theoretic and model-theoretic facts concerning LCs, in particular, by the following conjecture:
Conjecture 2.1. Any ‘natural’ extension of
![]() $\mathsf {ZFC}$
is either equiconsistent with
$\mathsf {ZFC}$
is either equiconsistent with
![]() $\mathsf {ZFC}$
or equiconsistent with
$\mathsf {ZFC}$
or equiconsistent with
![]() $\mathsf {ZFC}+A$
, where A is a LCA. Moreover, the consistency strengths of ‘natural’ extensions of
$\mathsf {ZFC}+A$
, where A is a LCA. Moreover, the consistency strengths of ‘natural’ extensions of
![]() $\mathsf {ZFC}$
are well-ordered.Footnote
19
$\mathsf {ZFC}$
are well-ordered.Footnote
19
The main upshot of Conjecture 2.1 is that, since all theories
![]() $\mathsf {ZFC}$
+LCA considered so far are arranged in a well-ordered scale of consistency strengths,Footnote
20
then also all natural theories are. Thus, the ‘invisible web’ binding together all natural theories is, finally, cast into sharp relief by the proof-theoretic connections among all LCAs.
$\mathsf {ZFC}$
+LCA considered so far are arranged in a well-ordered scale of consistency strengths,Footnote
20
then also all natural theories are. Thus, the ‘invisible web’ binding together all natural theories is, finally, cast into sharp relief by the proof-theoretic connections among all LCAs.
The next step is to exploit the fact that, using LCs, one is able to construct models, in particular set-forcing extensions and inner models, which satisfy any natural theory. Using this fact, and Conjecture 2.1, Steel is, therefore, able to formulate, in full, the main meta-theoretic constraint presiding over his ‘multiverse’ (bullet point (2.)):
Meta-theoretic constraint.
![]() $\mathsf {MV}$
’s worlds are just those models of
$\mathsf {MV}$
’s worlds are just those models of
![]() $\mathsf {ZFC}$
+LCA which are needed to incorporate all natural theories extending
$\mathsf {ZFC}$
+LCA which are needed to incorporate all natural theories extending
![]() $\mathsf {ZFC}$
.
$\mathsf {ZFC}$
.
Finally, since inner models may well be defined inside forcing extensions, what we just need to characterise worlds are LCs and forcing: the
![]() $\mathsf {MV}$
axioms reflect this state of affairs, by quantifying over set-forcing extensions (and their grounds) with LCs.
$\mathsf {MV}$
axioms reflect this state of affairs, by quantifying over set-forcing extensions (and their grounds) with LCs.
We will deal with the models of
![]() $\mathsf {MV}$
later on, but, first, we wish to express several concerns about Steel’s use of, and primary reliance upon, LCs, and about the notion of ‘naturalness’.
$\mathsf {MV}$
later on, but, first, we wish to express several concerns about Steel’s use of, and primary reliance upon, LCs, and about the notion of ‘naturalness’.
The first qualm refers to Conjecture 2.1, that all ‘natural’ extensions of
![]() $\mathsf {ZFC}$
are equiconsistent with either
$\mathsf {ZFC}$
are equiconsistent with either
![]() $\mathsf {ZFC}$
or some LCA. While no evidence against it has been found thus far, the conjecture is far from being settled, and things are compounded by the fact that we lack a general definition of ‘large cardinal’. Now, it would certainly be unfair to have the unsharpness of the notion count against Steel’s project; however, the absence of ultimate evidence that any undecidable statement will turn out to be equiconsistent with a LCA is a fact, which casts some doubts on the tenability of the conjecture.
$\mathsf {ZFC}$
or some LCA. While no evidence against it has been found thus far, the conjecture is far from being settled, and things are compounded by the fact that we lack a general definition of ‘large cardinal’. Now, it would certainly be unfair to have the unsharpness of the notion count against Steel’s project; however, the absence of ultimate evidence that any undecidable statement will turn out to be equiconsistent with a LCA is a fact, which casts some doubts on the tenability of the conjecture.
A second, possibly more malignant, issue is that the notion of ‘natural theory’ is unclear. What we are told by Steel, at the very outset, is that a set-theoretic statement does qualify as ‘natural’ if it is consistent with
![]() $\mathsf {ZFC}$
, asserts some ‘facts’ about sets, and is not of a metamathematical or proof-theoretic nature, but this is really not much.Footnote
21
Moreover,
$\mathsf {ZFC}$
, asserts some ‘facts’ about sets, and is not of a metamathematical or proof-theoretic nature, but this is really not much.Footnote
21
Moreover,
![]() $\mathsf {MV}$
’s scope for ‘naturalness’ is too restrictive from the beginning, as it leaves out theories, such as
$\mathsf {MV}$
’s scope for ‘naturalness’ is too restrictive from the beginning, as it leaves out theories, such as
![]() $\mathsf {ZF}+$
AD, which unquestionably express deep set-theoretic facts.
$\mathsf {ZF}+$
AD, which unquestionably express deep set-theoretic facts.
As an interpretative option, one could define a set-theoretic statement
![]() $\varphi $
to be ‘natural’ if
$\varphi $
to be ‘natural’ if
![]() $\mathsf {ZFC}$
plus some LCA proves that
$\mathsf {ZFC}$
plus some LCA proves that
![]() $\varphi $
holds in a forcing extension of V, or in some definable (allowing for set parameters) inner model of
$\varphi $
holds in a forcing extension of V, or in some definable (allowing for set parameters) inner model of
![]() $\mathsf {ZFC}$
of a forcing extension of V (including definable, with set parameters, class forcing extensions that preserve
$\mathsf {ZFC}$
of a forcing extension of V (including definable, with set parameters, class forcing extensions that preserve
![]() $\mathsf {ZFC}$
). By this interpretation, all
$\mathsf {ZFC}$
). By this interpretation, all
![]() $\mathsf {ZFC}$
axioms as well as all LCAs are natural, and so are CH, V=L, V=HOD, SCH, as well as their negations (in fact, all genuinely set-theoretic statements known to be consistent with
$\mathsf {ZFC}$
axioms as well as all LCAs are natural, and so are CH, V=L, V=HOD, SCH, as well as their negations (in fact, all genuinely set-theoretic statements known to be consistent with
![]() $\mathsf {ZFC}$
and asserting some facts about sets). Moreover, in this case, even theories contradicting Choice, like
$\mathsf {ZFC}$
and asserting some facts about sets). Moreover, in this case, even theories contradicting Choice, like
![]() $\mathsf {ZF}$
+AD, would now be seen as ‘natural’, as they are also equiconsistent with
$\mathsf {ZF}$
+AD, would now be seen as ‘natural’, as they are also equiconsistent with
![]() $\mathsf {ZFC}$
+LCAs.Footnote
22
$\mathsf {ZFC}$
+LCAs.Footnote
22
This interpretation seems to fit Steel’s goals, but, surely, ‘equiconsistency with
![]() $\mathsf {ZFC}$
or
$\mathsf {ZFC}$
or
![]() $\mathsf {ZFC}$
+LCAs’ does not seem to square very well with the common-sense, intuitive meaning of ‘naturalness’. Moreover, one could easily reverse this approach, consider a theory natural if it can be expressed in models of
$\mathsf {ZFC}$
+LCAs’ does not seem to square very well with the common-sense, intuitive meaning of ‘naturalness’. Moreover, one could easily reverse this approach, consider a theory natural if it can be expressed in models of
![]() $\mathsf {ZF}$
+LCAs, which also allow for the existence of even stronger LCs, such as Reinhardt and Berkeley Cardinals, and ‘incorporate’ theories with Choice in models of
$\mathsf {ZF}$
+LCAs, which also allow for the existence of even stronger LCs, such as Reinhardt and Berkeley Cardinals, and ‘incorporate’ theories with Choice in models of
![]() $\mathsf {ZF}$
+LCAs.Footnote
23
$\mathsf {ZF}$
+LCAs.Footnote
23
2.2 Large cardinals as maximality principles
Steel’s preference for LCs is also motivated by another principle, that he calls ‘maximise interpretative power’, which might be seen as consisting of two parts:
Maximise Interpretative Power [MIP]. (A.) The
![]() $\mathsf {MV}$
axioms should be able to ‘represent’ as many theories (‘natural extensions of
$\mathsf {MV}$
axioms should be able to ‘represent’ as many theories (‘natural extensions of
![]() $\mathsf {ZFC}$
’) as possible; (B.) all the theories represented by the
$\mathsf {ZFC}$
’) as possible; (B.) all the theories represented by the
![]() $\mathsf {MV}$
axioms should be such that, for any two of them, T and S, if
$\mathsf {MV}$
axioms should be such that, for any two of them, T and S, if
![]() $Con(T) \rightarrow Con(S)$
, then
$Con(T) \rightarrow Con(S)$
, then
![]() $\Gamma _S \subseteq \Gamma _T$
(where, given a theory T,
$\Gamma _S \subseteq \Gamma _T$
(where, given a theory T,
![]() $\Gamma _T=\{\phi : T \vdash \phi \}$
).Footnote
24
$\Gamma _T=\{\phi : T \vdash \phi \}$
).Footnote
24
LCAs constitute a paradigmatic case study with respect to MIP. As far as (A.) is concerned, we have seen that each ‘natural’ theory T is satisfied in a forcing extension or inner model of another ‘natural’ theory S, provided both T and S are equiconsistent with LCAs; as regards (B.), we know that the amount of mutual interpretability of natural theories rises in proportion with their consistency strength. Thus, in the end, it would be legitimate to expect that:
(*) As natural theories proceed up the large cardinal hierarchy in consistency strength, they agree on an ever-increasing class of mathematical statements.Footnote 25
A few observations are in order. The first one, concerning (B.), is that, so far, MIP has been shown to be satisfied by LCAs only partially, that is, for specific kinds of sentences in the Lévy hierarchy of arithmetical sentences. The following is the most one can hope to prove so far:
Empirical fact. For any two natural theories
![]() $T, S$
whose consistency strength is at least that of the theory:
$T, S$
whose consistency strength is at least that of the theory:
![]() $\mathsf {ZFC}$
+‘there exist infinitely many Woodin cardinals’, such that
$\mathsf {ZFC}$
+‘there exist infinitely many Woodin cardinals’, such that
![]() $Con(T) \rightarrow Con(S)$
, we have that
$Con(T) \rightarrow Con(S)$
, we have that
![]() $({\Pi ^{1}_\omega })_S \subseteq ({\Pi ^{1}_\omega })_T$
(where, given a theory T,
$({\Pi ^{1}_\omega })_S \subseteq ({\Pi ^{1}_\omega })_T$
(where, given a theory T,
![]() $({\Pi ^{1}_\omega })_T$
is the set of
$({\Pi ^{1}_\omega })_T$
is the set of
![]() $\Pi ^{1}_{\omega }$
sentences provable in T).
$\Pi ^{1}_{\omega }$
sentences provable in T).
As a consequence, the applicability of MIP to LCAs has only been verified up to the level of second-order arithmetic.
The second observation is as follows. Steel’s purpose is that of representing a multiplicity of theories, all of which extend
![]() $\mathsf {ZFC}$
+LCs, and we wonder whether MIP is really compatible with this goal. For suppose (B.) were applicable to all sentences in the Lévy hierarchy; then, clearly, all the theories targeted by (A.), would not, just, be represented, but, for all practical purposes, they would rather be amalgamated into just one theory.Footnote
26
One way out of this difficulty would be to see (A.) as being sanctioned by the presently limited range of applicability of (B.), but this wouldn’t help fully ease the tension between (A.) and (B.).
$\mathsf {ZFC}$
+LCs, and we wonder whether MIP is really compatible with this goal. For suppose (B.) were applicable to all sentences in the Lévy hierarchy; then, clearly, all the theories targeted by (A.), would not, just, be represented, but, for all practical purposes, they would rather be amalgamated into just one theory.Footnote
26
One way out of this difficulty would be to see (A.) as being sanctioned by the presently limited range of applicability of (B.), but this wouldn’t help fully ease the tension between (A.) and (B.).
Finally, although this is very speculative, the hierarchy of LCs contradicting Choice might, potentially, be more successful at instantiating MIP than the hierarchy of LCs with Choice, but, as we have seen, none of these theories features among those targeted by
![]() $\mathsf {MV}$
.Footnote
27
$\mathsf {MV}$
.Footnote
27
2.3 Models for
 $\mathsf {MV}$
$\mathsf {MV}$
A major asset of
![]() $\mathsf {MV}$
is that this theory is complete with respect to a specific class of models
$\mathsf {MV}$
is that this theory is complete with respect to a specific class of models
![]() $M^{G}$
, with which we will deal in a moment, that is, one has that:
$M^{G}$
, with which we will deal in a moment, that is, one has that:
We will not delve into the philosophical reasons for preferring a complete axiomatisation of the multiverse over one which is not, as this task has already been carried out satisfactorily.Footnote
28
In this subsection, we would rather like to focus on the semantics of
![]() $\mathsf {MV}$
, in particular, on its ‘natural’ models,
$\mathsf {MV}$
, in particular, on its ‘natural’ models,
![]() $M^G$
,Footnote
29
and bring to light a slightly different mathematical approach to it (Proposition 2.2).
$M^G$
,Footnote
29
and bring to light a slightly different mathematical approach to it (Proposition 2.2).
We start with reviewing, very quickly, the axioms. The language of
![]() $\mathsf {MV}$
is the first-order language of set theory with two sorts, namely Set and World. We introduce a minor tweak to Steel’s original formulation of the axioms. As we already know,
$\mathsf {MV}$
is the first-order language of set theory with two sorts, namely Set and World. We introduce a minor tweak to Steel’s original formulation of the axioms. As we already know,
![]() $\mathsf {MV}$
has, as its own base, the axioms of
$\mathsf {MV}$
has, as its own base, the axioms of
![]() $\mathsf {ZFC}$
plus LCs (we shall mostly refer to the base theory as T). Now, let a T-theory be a theory extending
$\mathsf {ZFC}$
plus LCs (we shall mostly refer to the base theory as T). Now, let a T-theory be a theory extending
![]() $\mathsf {ZFC}$
which is preserved by set-forcing extensions, and by going to set-forcing grounds: it turns out that any theory of the form
$\mathsf {ZFC}$
which is preserved by set-forcing extensions, and by going to set-forcing grounds: it turns out that any theory of the form
![]() $\mathsf {ZFC}$
+‘there exists a proper class of some kind of LCs’ is a T-theory. Then, the
$\mathsf {ZFC}$
+‘there exists a proper class of some kind of LCs’ is a T-theory. Then, the
![]() $\mathsf {MV}$
axioms for
$\mathsf {MV}$
axioms for
![]() $T (\mathsf {MV}_T)$
, which we will be mostly referring to and using throughout the paper, are the following ones:
$T (\mathsf {MV}_T)$
, which we will be mostly referring to and using throughout the paper, are the following ones:
-
1. (Extensionality for Worlds) If two worlds have the same sets, then they are equal.
-
2. Every world is a model of T.
-
3. Every world is a transitive proper class. An object is a set if and only if it belongs to some world. All worlds have the same ordinals.
-
4. If W is a world and
 ${\mathbb P} \in W$
is a poset, then there is a world of the form
${\mathbb P} \in W$
is a poset, then there is a world of the form
 $W[G]$
, where G is
$W[G]$
, where G is
 ${\mathbb P}$
-generic over W.
${\mathbb P}$
-generic over W. -
5. If U is a world and
 $U=W[G]$
, where G is
$U=W[G]$
, where G is
 ${\mathbb P}$
-generic over W, then W is also a world.
${\mathbb P}$
-generic over W, then W is also a world. -
6. (Amalgamation) If U and W are worlds, then there are posets
 ${\mathbb P}\in U$
and
${\mathbb P}\in U$
and
 ${\mathbb Q}\in W$
, and sets G and
${\mathbb Q}\in W$
, and sets G and
 $H\ {\mathbb P}$
-generic and
$H\ {\mathbb P}$
-generic and
 ${\mathbb Q}$
-generic over U and W, respectively, such that
${\mathbb Q}$
-generic over U and W, respectively, such that
 $U[G]=W[H]$
.
$U[G]=W[H]$
.
If M is a countable model of T and G is
![]() $Coll(\omega , <Ord)^M$
-generic over M, let
$Coll(\omega , <Ord)^M$
-generic over M, let
![]() $M^G$
be the model whose sets are those in
$M^G$
be the model whose sets are those in
![]() $M[G]$
(in the case M is ill-founded, then
$M[G]$
(in the case M is ill-founded, then
![]() $M[G]$
is defined accordingly) and whose worlds are the grounds of models of the form
$M[G]$
is defined accordingly) and whose worlds are the grounds of models of the form
![]() $M[G\restriction \alpha ]$
, for some
$M[G\restriction \alpha ]$
, for some
![]() $\alpha \in Ord^M$
. It can be easily shown that
$\alpha \in Ord^M$
. It can be easily shown that
![]() $M^G$
is a model of
$M^G$
is a model of
![]() $\mathsf {MV}_{T}$
, when
$\mathsf {MV}_{T}$
, when
![]() $T=\mathsf {ZFC}$
.Footnote
30
Moreover, if T is obtained by adding to
$T=\mathsf {ZFC}$
.Footnote
30
Moreover, if T is obtained by adding to
![]() $\mathsf {ZFC}$
axioms such as ‘There is a proper class of P-cardinals’, where P stands for any of the usual large-cardinal properties, then it can also be proved that
$\mathsf {ZFC}$
axioms such as ‘There is a proper class of P-cardinals’, where P stands for any of the usual large-cardinal properties, then it can also be proved that
![]() $M^G$
is a model of
$M^G$
is a model of
![]() $\mathsf {MV}_{T}$
.
$\mathsf {MV}_{T}$
.
The collection of all models
![]() $M^G$
provides a complete semantics, and the axiom which guarantees the completeness of
$M^G$
provides a complete semantics, and the axiom which guarantees the completeness of
![]() $\mathsf {MV}_T$
is, as has been shown by Maddy and Meadows [Reference Maddy and Meadows21, p. 134], Amalgamation. But, as stressed by the authors, a consequence of this fact is that, in any model of the form
$\mathsf {MV}_T$
is, as has been shown by Maddy and Meadows [Reference Maddy and Meadows21, p. 134], Amalgamation. But, as stressed by the authors, a consequence of this fact is that, in any model of the form
![]() $M^G$
, not all generic filters for posets in M may be taken into account to produce forcing extensions which act, as required by the Meta-Theoretic Constraint of Section 2.1, as the ‘worlds’ of
$M^G$
, not all generic filters for posets in M may be taken into account to produce forcing extensions which act, as required by the Meta-Theoretic Constraint of Section 2.1, as the ‘worlds’ of
![]() $\mathsf {MV}$
, but only those which are produced by the
$\mathsf {MV}$
, but only those which are produced by the
![]() $Coll(\omega , Ord^M)$
-generic filter G over M.
$Coll(\omega , Ord^M)$
-generic filter G over M.
We now proceed to prove the following:
Proposition 2.2. The
![]() $\mathsf {MV}_T$
axioms imply that the multiverse is a homogeneous class-forcing extension of each of its worlds.
$\mathsf {MV}_T$
axioms imply that the multiverse is a homogeneous class-forcing extension of each of its worlds.
Proof. Since the models
![]() $M^G$
give a complete semantics for
$M^G$
give a complete semantics for
![]() $\mathsf {MV}_T$
, we may assume that every model of
$\mathsf {MV}_T$
, we may assume that every model of
![]() $\mathsf {MV}_T$
is of this form. Now, working in a model
$\mathsf {MV}_T$
is of this form. Now, working in a model
![]() $M^G$
as above, let W be a world. So W is a ground of a model of the form
$M^G$
as above, let W be a world. So W is a ground of a model of the form
![]() $M[G\restriction \alpha ]$
, for some
$M[G\restriction \alpha ]$
, for some
![]() $\alpha \in Ord^M$
.
$\alpha \in Ord^M$
.
Let
![]() ${\mathbb P}\in W$
be a poset such that for some
${\mathbb P}\in W$
be a poset such that for some
![]() $H_0\ {\mathbb P}$
-generic over W,
$H_0\ {\mathbb P}$
-generic over W,
![]() $W[H_0]=M[G\restriction \alpha ]$
, and let
$W[H_0]=M[G\restriction \alpha ]$
, and let
![]() $\kappa \geq \alpha $
be an uncountable
$\kappa \geq \alpha $
be an uncountable
![]() $W[H_0]$
-cardinal such that the cardinality of
$W[H_0]$
-cardinal such that the cardinality of
![]() ${\mathbb P}$
, as computed in W, is less than
${\mathbb P}$
, as computed in W, is less than
![]() $\kappa $
. Let
$\kappa $
. Let
![]() $H_1$
be
$H_1$
be
![]() $Coll(\omega , <\kappa +1) /G\restriction \alpha $
-generic over
$Coll(\omega , <\kappa +1) /G\restriction \alpha $
-generic over
![]() $M[G\restriction \alpha ]$
so that
$M[G\restriction \alpha ]$
so that
![]() $M[G\restriction \alpha ][H_1]=M[G\restriction \kappa +1]$
. Thus,
$M[G\restriction \alpha ][H_1]=M[G\restriction \kappa +1]$
. Thus,
![]() $W[H_0][H_1]=M[G\restriction \kappa +1]$
is a generic extension of W by a poset of cardinality
$W[H_0][H_1]=M[G\restriction \kappa +1]$
is a generic extension of W by a poset of cardinality
![]() $\kappa $
that collapses
$\kappa $
that collapses
![]() $\kappa $
to
$\kappa $
to
![]() $\omega $
, hence by Kripke’s theorem [Reference Jech13, Lemma 26.7] equivalent to
$\omega $
, hence by Kripke’s theorem [Reference Jech13, Lemma 26.7] equivalent to
![]() $Coll(\omega , \kappa )$
. Since
$Coll(\omega , \kappa )$
. Since
![]() $Coll(\omega , \kappa )$
is homogeneous, the proposition follows. □
$Coll(\omega , \kappa )$
is homogeneous, the proposition follows. □
The following straightforward consequence of the
![]() $\mathsf {MV}_T$
axioms asserts that every set-forcing generic extension of a world is also a world.
$\mathsf {MV}_T$
axioms asserts that every set-forcing generic extension of a world is also a world.
Proposition 2.3. The
![]() $\mathsf {MV}_T$
axioms imply that if W is a world and G is
$\mathsf {MV}_T$
axioms imply that if W is a world and G is
![]() ${\mathbb P}$
-generic over W for some poset
${\mathbb P}$
-generic over W for some poset
![]() ${\mathbb P} \in W$
, then
${\mathbb P} \in W$
, then
![]() $W[G]$
is also a world.
$W[G]$
is also a world.
Proof. Suppose W is a world and G is
![]() $\mathbb {P}$
-generic over W, for some poset
$\mathbb {P}$
-generic over W, for some poset
![]() $\mathbb {P}\in W$
. By Axiom 3, let
$\mathbb {P}\in W$
. By Axiom 3, let
![]() $W'$
be a world such that
$W'$
be a world such that
![]() $G\in W'$
. By Amalgamation (Axiom 6), let
$G\in W'$
. By Amalgamation (Axiom 6), let
![]() $W''$
be a world such that both W and
$W''$
be a world such that both W and
![]() $W'$
are grounds of
$W'$
are grounds of
![]() $W''$
. As
$W''$
. As
![]() $W\subseteq W[G]\subseteq W''$
, and W is a ground of
$W\subseteq W[G]\subseteq W''$
, and W is a ground of
![]() $W''$
, the forcing extension
$W''$
, the forcing extension
![]() $W[G]$
of W is also a ground of
$W[G]$
of W is also a ground of
![]() $W''$
. Hence, since every ground of a world is also a world (Axiom 5),
$W''$
. Hence, since every ground of a world is also a world (Axiom 5),
![]() $W[G]$
is a world, as wanted. □
$W[G]$
is a world, as wanted. □
2.4
 $M^{G}$
and the translation function
$M^{G}$
and the translation function
As already anticipated in Section 1.1, Steel’s conception rests upon the crucial fact that the language of
![]() $\mathsf {MV}$
,
$\mathsf {MV}$
,
![]() $\mathcal {L}_{\mathsf {MV}}$
, may be seen as a sublanguage of
$\mathcal {L}_{\mathsf {MV}}$
, may be seen as a sublanguage of
![]() $\mathcal {L}_{\mathsf {\in }}$
. In order to show this, Steel defines a recursive translation function t from
$\mathcal {L}_{\mathsf {\in }}$
. In order to show this, Steel defines a recursive translation function t from
![]() $\mathcal {L}_{\mathsf {MV}}$
into
$\mathcal {L}_{\mathsf {MV}}$
into
![]() $\mathcal {L}_{\in }$
, such that:
$\mathcal {L}_{\in }$
, such that:
where T, as said, is
![]() $\mathsf {ZFC}$
+LCs. The translation function may be rendered more transparently in terms of the semantics of
$\mathsf {ZFC}$
+LCs. The translation function may be rendered more transparently in terms of the semantics of
![]() $\mathsf {MV}$
as follows:
$\mathsf {MV}$
as follows:
Theorem 2.4 (Translation function).
For any sentence
![]() $\varphi $
of
$\varphi $
of
![]() $\mathcal {L}_{\mathsf {MV}}$
, every countable model M of
$\mathcal {L}_{\mathsf {MV}}$
, every countable model M of
![]() $\mathsf {ZFC}$
and every
$\mathsf {ZFC}$
and every
![]() $G \ Coll(\omega , <Ord^M)$
-generic over M
$G \ Coll(\omega , <Ord^M)$
-generic over M
It should be noted that, in the presence of the specified semantics of
![]() $\mathsf {MV}$
, the sentence
$\mathsf {MV}$
, the sentence
![]() $t(\varphi )$
asserts ‘
$t(\varphi )$
asserts ‘
![]() $\varphi $
is true in all multiverses obtained from me’.Footnote
31
Equivalently, ‘
$\varphi $
is true in all multiverses obtained from me’.Footnote
31
Equivalently, ‘
![]() $\varphi $
is true in some multiverse obtained from me’. Now, as said (section 2.3), Amalgamation is needed to show that the models
$\varphi $
is true in some multiverse obtained from me’. Now, as said (section 2.3), Amalgamation is needed to show that the models
![]() $M^G$
provide a complete semantics for
$M^G$
provide a complete semantics for
![]() $\mathsf {MV}_T$
.
$\mathsf {MV}_T$
.
3 The core of
 $\mathsf {MV}$
$\mathsf {MV}$
In this section, we will, on the one hand, show how the ‘core hypothesis’ arises in the context of the
![]() $\mathsf {MV}$
axioms, in particular, how it is mathematically justified; this will help us provide an answer to the following question:
$\mathsf {MV}$
axioms, in particular, how it is mathematically justified; this will help us provide an answer to the following question:
Question 3.1. Under what circumstances is the core definable, and how?
On the other hand, we will show why Usuba’s result (Theorem 3.5) implies that
![]() $\mathsf {MV}_T$
, where
$\mathsf {MV}_T$
, where
![]() $T=\mathsf {ZFC}$
+‘there exists a proper class of extendible cardinals’, proves that there exists a core universe.
$T=\mathsf {ZFC}$
+‘there exists a proper class of extendible cardinals’, proves that there exists a core universe.
However, before proceeding to review all such results, we address the ‘core hypothesis’ in the context of just
![]() $\mathsf {ZFC}$
, and recall relevant set-theoretic geological concepts and theorems which make sense of the hypothesis, and which will be instrumental to present our own results in Section 4.
$\mathsf {ZFC}$
, and recall relevant set-theoretic geological concepts and theorems which make sense of the hypothesis, and which will be instrumental to present our own results in Section 4.
3.1 Prelude: the (outer) core of
 $\mathsf {ZFC}$
$\mathsf {ZFC}$
Initiated by Reitz and Hamkins a few years ago, set-theoretic geology has brought forward a very innovative approach to ‘universes of set theory’ producible using forcing.Footnote 32 Here follows a very brief review of its fundamental concepts.
Take V to be a model of the axioms
![]() $\mathsf {ZFC}$
. Hypothetically, it might be that V is a forcing extension of a ground model W, that is, that there exists a W-generic filter
$\mathsf {ZFC}$
. Hypothetically, it might be that V is a forcing extension of a ground model W, that is, that there exists a W-generic filter
![]() $G \subseteq \mathbb {P} \in W$
such that
$G \subseteq \mathbb {P} \in W$
such that
![]() $V=W[G]$
. If this is the case, then it makes sense to explore the ‘geology’ of V, that is, the collection of grounds, the generic extensions of grounds and their grounds, and so on, which V might contain, where a ground of a model M is a model N of
$V=W[G]$
. If this is the case, then it makes sense to explore the ‘geology’ of V, that is, the collection of grounds, the generic extensions of grounds and their grounds, and so on, which V might contain, where a ground of a model M is a model N of
![]() $\mathsf {ZFC}$
such that M has been obtained through forcing over N, that is, as an extension
$\mathsf {ZFC}$
such that M has been obtained through forcing over N, that is, as an extension
![]() $M=N[G]$
, where G is a generic filter of a partial order
$M=N[G]$
, where G is a generic filter of a partial order
![]() $\mathbb {P} \in N$
. Further ‘geological’ notions will then crop up, which can be spelt out as follows.
$\mathbb {P} \in N$
. Further ‘geological’ notions will then crop up, which can be spelt out as follows.
The mantle
![]() $\mathbb {M}$
is the intersection of all the grounds of a model M of
$\mathbb {M}$
is the intersection of all the grounds of a model M of
![]() $\mathsf {ZFC}$
, and the bedrock is a class W which is a minimal ground of V. By results of Usuba Reference Usuba[27], the mantle is a model of
$\mathsf {ZFC}$
, and the bedrock is a class W which is a minimal ground of V. By results of Usuba Reference Usuba[27], the mantle is a model of
![]() $\mathsf {ZFC}$
. Since Reitz Reference Reitz[23], the following axiom has proved to be central to all geological investigations:
$\mathsf {ZFC}$
. Since Reitz Reference Reitz[23], the following axiom has proved to be central to all geological investigations:
Axiom 3.2 (Ground Axiom (GA)).
V has no proper grounds.
Now, if the mantle itself satisfies GA, then the mantle is a bedrock, in particular, a minimum bedrock contained in all other grounds, and the latter could legitimately be seen as the core universe of the set-generic multiverse (generated over it) that we’ll be describing in full detail in the next subsection.Footnote
33
A fuller mathematical characterisation of the core may, thus, be attempted. However, already at this point, it emerges that the features of the core may be (over
![]() $\mathsf {ZFC}$
) indeterminate. This is shown by the following, fundamental theorem:
$\mathsf {ZFC}$
) indeterminate. This is shown by the following, fundamental theorem:
Theorem 3.3 (Fuchs et al.).
Every countable model of
![]() $\mathsf {ZFC}$
can be the mantle of another model of
$\mathsf {ZFC}$
can be the mantle of another model of
![]() $\mathsf {ZFC}$
.Footnote
34
$\mathsf {ZFC}$
.Footnote
34
In an attempt to both attain a more determinate core, and further investigate its nature, set-theoretic geologists have taken into account a different hypothesis, which can be expounded as follows. If the mantle does not satisfy GA, then it makes sense to take into account the ‘mantle of the mantle’,
![]() $\mathbb {M}^1=\mathbb {M}^{\mathbb {M}}$
, and then, always under the assumption that GA is not satisfied, the ‘mantle of the mantle of the mantle’ and so on. In other terms, it makes sense to take into account the iteration of the ‘mantle operation’. Now, iterating the mantle is not a trivial task, as there are technical aspects involved which may prevent one from even defining the nth iterates of the mantle.Footnote
35
Assuming these difficulties may be overcome, one might ask whether, for an
$\mathbb {M}^1=\mathbb {M}^{\mathbb {M}}$
, and then, always under the assumption that GA is not satisfied, the ‘mantle of the mantle of the mantle’ and so on. In other terms, it makes sense to take into account the iteration of the ‘mantle operation’. Now, iterating the mantle is not a trivial task, as there are technical aspects involved which may prevent one from even defining the nth iterates of the mantle.Footnote
35
Assuming these difficulties may be overcome, one might ask whether, for an
![]() $\alpha \in Ord$
iterate of the mantle, one has that
$\alpha \in Ord$
iterate of the mantle, one has that
![]() $\mathbb {M}^{\alpha }=\mathbb {M}^{\beta }$
, for all
$\mathbb {M}^{\alpha }=\mathbb {M}^{\beta }$
, for all
![]() $\beta>\alpha $
, that is, whether there is a minimal
$\beta>\alpha $
, that is, whether there is a minimal
![]() $\alpha $
such that
$\alpha $
such that
![]() $\mathbb {M}^{\alpha } \models $
GA. If there is one, then
$\mathbb {M}^{\alpha } \models $
GA. If there is one, then
![]() $\mathbb {M}^{\alpha }$
is said to be the outer core of the initial model (of V, if V was such model). However, in this case, as in the previous one where
$\mathbb {M}^{\alpha }$
is said to be the outer core of the initial model (of V, if V was such model). However, in this case, as in the previous one where
![]() $\mathbb {M} \models $
GA, Theorem 3.3 will imply that also the outer core does not have determinate features, namely, that it might satisfy a wide range of mutually incompatible properties.
$\mathbb {M} \models $
GA, Theorem 3.3 will imply that also the outer core does not have determinate features, namely, that it might satisfy a wide range of mutually incompatible properties.
Moreover, it has been shown that the outer core cannot be uniquely pinned down in the iteration process, as a recent result by Reitz and Williams has confirmed Fuchs et al. Reference Fuchs, Hamkins and Reitz[9]’s Conjecture 74,Footnote
36
and shown that, for any
![]() $\alpha \in Ord$
, the outer core of a model M could be any
$\alpha \in Ord$
, the outer core of a model M could be any
![]() $\mathbb {M}^{\alpha }$
, that is, any
$\mathbb {M}^{\alpha }$
, that is, any
![]() $\alpha $
th iterate of the mantle of M (possibly also including including
$\alpha $
th iterate of the mantle of M (possibly also including including
![]() $\mathbb {M}^{Ord}$
, although no proof is currently available for this specific case).Footnote
37
$\mathbb {M}^{Ord}$
, although no proof is currently available for this specific case).Footnote
37
To sum up,
![]() $\mathsf {ZFC}$
alone does not, in itself, guarantee the existence of a ‘core universe’ and, moreover, over
$\mathsf {ZFC}$
alone does not, in itself, guarantee the existence of a ‘core universe’ and, moreover, over
![]() $\mathsf {ZFC}$
, no full-fledged, definite mathematical characterisation of the core may arise. As we shall see, a slightly different scenario comes to light, if one takes onboard LCs.
$\mathsf {ZFC}$
, no full-fledged, definite mathematical characterisation of the core may arise. As we shall see, a slightly different scenario comes to light, if one takes onboard LCs.
3.2 The proof of the existence
Steel [Reference Steel and Kennedy25, p. 168] credits Woodin for observing that ‘if the multiverse has a definable world, then it has a unique definable world, and this world is included in all the others’.Footnote 38 We give next a proof of this fact.Footnote 39
Theorem 3.4. If the multiverse has a definable world, then it has a unique definable world. More precisely, suppose
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
are formulas in the language of the multiverse with only one free variable for sets. Then,
$\psi $
are formulas in the language of the multiverse with only one free variable for sets. Then,
Proof. Working in a model
![]() $M^G$
of
$M^G$
of
![]() $\mathsf {MV}_T$
(see Section 2.3), let U and W be worlds defined by
$\mathsf {MV}_T$
(see Section 2.3), let U and W be worlds defined by
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
, respectively. Since U and W are transitive and contain the same ordinals, it will be sufficient to show that
$\psi $
, respectively. Since U and W are transitive and contain the same ordinals, it will be sufficient to show that
![]() $U\subseteq W$
by showing
$U\subseteq W$
by showing
![]() $V_\alpha ^U\subseteq W$
by induction on
$V_\alpha ^U\subseteq W$
by induction on
![]() $\alpha $
. This is clear for
$\alpha $
. This is clear for
![]() $\alpha =0$
, and also clear for
$\alpha =0$
, and also clear for
![]() $\alpha $
a limit ordinal provided it holds for all ordinals less than
$\alpha $
a limit ordinal provided it holds for all ordinals less than
![]() $\alpha $
. So suppose
$\alpha $
. So suppose
![]() $V_\alpha ^U \subseteq W$
and let us show
$V_\alpha ^U \subseteq W$
and let us show
 $V_{\alpha +1}^U\subseteq W$
. Note that
$V_{\alpha +1}^U\subseteq W$
. Note that
![]() $V_\alpha ^U\subseteq W$
implies
$V_\alpha ^U\subseteq W$
implies
![]() $V_\alpha ^U \in W$
. This is because
$V_\alpha ^U \in W$
. This is because
Hence,
![]() $V_\alpha ^U$
is definable in W with parameter
$V_\alpha ^U$
is definable in W with parameter
![]() $\alpha $
.
$\alpha $
.
Now let
![]() $Y\subseteq V_{\alpha }^U$
,
$Y\subseteq V_{\alpha }^U$
,
![]() $Y\in U$
. We must check that
$Y\in U$
. We must check that
![]() $Y\in W$
. As in Proposition 2.2, we can find
$Y\in W$
. As in Proposition 2.2, we can find
![]() $\gamma $
large enough so that
$\gamma $
large enough so that
 $$ \begin{align*}W^{Coll(\omega,\gamma)}\models '\mbox{I am a forcing extension of}\ X,\ \mbox{for some world}\ X\ \mbox{which } \\[-24pt] \end{align*} $$
$$ \begin{align*}W^{Coll(\omega,\gamma)}\models '\mbox{I am a forcing extension of}\ X,\ \mbox{for some world}\ X\ \mbox{which } \\[-24pt] \end{align*} $$
It follows that
![]() $U\subset W[H]$
for all
$U\subset W[H]$
for all
![]() $H\ Coll(\omega ,\gamma )$
-generic over W. So
$H\ Coll(\omega ,\gamma )$
-generic over W. So
![]() $Y\in W[H]$
for all such H. Letting
$Y\in W[H]$
for all such H. Letting
![]() $\dot {Y}\in W$
be a
$\dot {Y}\in W$
be a
![]() $Coll(\omega ,\gamma )$
-name for Y, we have that Y is definable in W as the set of all
$Coll(\omega ,\gamma )$
-name for Y, we have that Y is definable in W as the set of all
![]() $x\in V_\alpha ^U$
which are forced by
$x\in V_\alpha ^U$
which are forced by
![]() $Coll(\omega , \gamma )$
to belong to
$Coll(\omega , \gamma )$
to belong to
![]() $\dot {Y}$
. Hence,
$\dot {Y}$
. Hence,
![]() $Y\in W$
. □
$Y\in W$
. □
It follows that if there is a definable world U in the multiverse, then it is unique and, by Proposition 2.2, is contained in all of
![]() $\mathsf {MV}$
’s worlds.Footnote
40
Clearly, since the core, if it exists, is definable, the core exists if and only if there is a definable world.
$\mathsf {MV}$
’s worlds.Footnote
40
Clearly, since the core, if it exists, is definable, the core exists if and only if there is a definable world.
3.3 The core is the mantle of V
We proceed to introduce the fundamental result, due to Toshimichi Usuba, which shows that, under the assumption of sufficiently strong LCs, V has a smallest ground.
Theorem 3.5 (Usuba [Reference Usuba28, p. 72]).
Suppose there exists an extendible cardinal. Then the mantle is a ground of V. In fact if
![]() $\kappa $
is extendible, the
$\kappa $
is extendible, the
![]() $\kappa $
-mantle of V is its smallest ground.Footnote
41
$\kappa $
-mantle of V is its smallest ground.Footnote
41
Now, since all grounds are downwards-directed,Footnote 42 by using Theorem 3.5, we can now prove the following:
Proposition 3.6 (Existence of the core of the multiverse of
 $\mathsf {MV}_T$
).
$\mathsf {MV}_T$
).
Let T be
![]() $\mathsf {ZFC}$
+‘there exists a proper class of extendible cardinals’. Then the
$\mathsf {ZFC}$
+‘there exists a proper class of extendible cardinals’. Then the
![]() $\mathsf {MV}_T$
axioms imply that the multiverse has a core, which is the mantle (and a ground) of every world in the multiverse.Footnote
43
$\mathsf {MV}_T$
axioms imply that the multiverse has a core, which is the mantle (and a ground) of every world in the multiverse.Footnote
43
Proof. By Theorem 3.5, the mantle
![]() $\mathbb {M}_W$
of every world W of the multiverse is a ground, hence by Axiom 5 of
$\mathbb {M}_W$
of every world W of the multiverse is a ground, hence by Axiom 5 of
![]() $\mathsf {MV}$
, it is also a world. Now suppose
$\mathsf {MV}$
, it is also a world. Now suppose
![]() $U_0$
and
$U_0$
and
![]() $U_1$
are worlds. By Amalgamation, they are also grounds of some world W containing them. Hence, since the grounds are downwards-directed,
$U_1$
are worlds. By Amalgamation, they are also grounds of some world W containing them. Hence, since the grounds are downwards-directed,
![]() $\mathbb {M}_{U_0}=\mathbb {M}_{U_1}$
. It follows that all the worlds of the multiverse have the same mantle
$\mathbb {M}_{U_0}=\mathbb {M}_{U_1}$
. It follows that all the worlds of the multiverse have the same mantle
![]() $\mathbb {M}$
, which is the intersection of all the worlds. Thus,
$\mathbb {M}$
, which is the intersection of all the worlds. Thus,
![]() $\mathbb {M}$
is definable by the formula
$\mathbb {M}$
is definable by the formula
Hence by Theorem 3.4 the mantle
![]() $\mathbb {M}$
is the core of the multiverse. □
$\mathbb {M}$
is the core of the multiverse. □
3.4 The strength of the large-cardinal assumptions
By Proposition 3.6, if M satisfies that there exists an extendible cardinal, then
![]() $M^G$
has a core. It is legitimate to ask whether the large-cardinal assumption in Theorem 3.5 might be weakened to the level of a LC lower in the consistency strength hierarchy; more generally:
$M^G$
has a core. It is legitimate to ask whether the large-cardinal assumption in Theorem 3.5 might be weakened to the level of a LC lower in the consistency strength hierarchy; more generally:
Question 3.7. For what choices of T does
![]() $\mathsf {MV}_T$
prove the existence of the core of its multiverse?
$\mathsf {MV}_T$
prove the existence of the core of its multiverse?
The following theorem shows that the existence of a proper class of supercompact cardinals is not sufficient to prove the existence of the core, thus suggesting a potential threshold for the choice of T mentioned by Question 3.7.
Theorem 3.8. Assume there is a proper class of supercompact cardinals. Then there is a class forcing notion which forces that there exists a proper class of supercompact cardinals and there is no core.
Proof. First, force with a class-forcing iteration with Easton support in order to make every supercompact
![]() $\kappa $
indestructible by
$\kappa $
indestructible by
![]() $<\!\!\kappa $
-directed-closed forcing (see Reference Apter[2]), followed by the Jensen’s class-forcing iteration that forces the GCH. Standard arguments show that all the supercompact cardinals are preserved and no new supercompact cardinals are created. Over the generic extension, make again all supercompact cardinals
$<\!\!\kappa $
-directed-closed forcing (see Reference Apter[2]), followed by the Jensen’s class-forcing iteration that forces the GCH. Standard arguments show that all the supercompact cardinals are preserved and no new supercompact cardinals are created. Over the generic extension, make again all supercompact cardinals
![]() $\kappa $
indestructible by
$\kappa $
indestructible by
![]() $<\kappa $
-directed-closed forcing (which preserves the GCH and does not create new supercompact cardinals) and call the resulting model
$<\kappa $
-directed-closed forcing (which preserves the GCH and does not create new supercompact cardinals) and call the resulting model
![]() $V[G]$
. Now force with a class-forcing iteration
$V[G]$
. Now force with a class-forcing iteration
![]() $\mathbb {P}$
with Easton support that forces a version of the Continuous Coding Axiom (CCA), similarly as in Reference Reitz[23], which codes every set of ordinals proper-class-many times into the power-set function on the class S of supercompact cardinals that are not limit of supercompact cardinals. Again, standard arguments show that all supercompact cardinals in S are preserved and no new supercompact cardinals are created. Let
$\mathbb {P}$
with Easton support that forces a version of the Continuous Coding Axiom (CCA), similarly as in Reference Reitz[23], which codes every set of ordinals proper-class-many times into the power-set function on the class S of supercompact cardinals that are not limit of supercompact cardinals. Again, standard arguments show that all supercompact cardinals in S are preserved and no new supercompact cardinals are created. Let
![]() $V[G][H_0]$
be this model. Finally, force over
$V[G][H_0]$
be this model. Finally, force over
![]() $V[G][H_0]$
with the class-forcing product
$V[G][H_0]$
with the class-forcing product
 $$ \begin{align*}\mathbb{Q}=\prod_{\kappa \in ORD}\mathbb{Q}(\kappa),\end{align*} $$
$$ \begin{align*}\mathbb{Q}=\prod_{\kappa \in ORD}\mathbb{Q}(\kappa),\end{align*} $$
where
![]() $\mathbb {Q}(\kappa )$
is the forcing for adding a Cohen subset of
$\mathbb {Q}(\kappa )$
is the forcing for adding a Cohen subset of
![]() $\kappa $
, if
$\kappa $
, if
![]() $\kappa $
is in S, and is the trivial forcing otherwise. Let the resulting model be
$\kappa $
is in S, and is the trivial forcing otherwise. Let the resulting model be
![]() $V[G][H_0][H_1]$
. We claim that supercompact cardinals in S are preserved. So let
$V[G][H_0][H_1]$
. We claim that supercompact cardinals in S are preserved. So let
![]() $\kappa \in S$
. Working in
$\kappa \in S$
. Working in
![]() $V[G][H_0]$
, note first that
$V[G][H_0]$
, note first that
![]() $\mathbb {Q}$
factors as
$\mathbb {Q}$
factors as
![]() $\mathbb {Q}_{\kappa } \times \mathbb {Q}_{[\kappa +1 , Ord)}$
. Also note that, since
$\mathbb {Q}_{\kappa } \times \mathbb {Q}_{[\kappa +1 , Ord)}$
. Also note that, since
![]() $\kappa $
is not a limit of supercompact cardinals,
$\kappa $
is not a limit of supercompact cardinals,
![]() ${\textrm {{sup}}}(S\cap \kappa )<\kappa $
. So,
${\textrm {{sup}}}(S\cap \kappa )<\kappa $
. So,
![]() $\mathbb {Q}_{\kappa }$
factors as
$\mathbb {Q}_{\kappa }$
factors as
 $\mathbb {Q}_{{\textrm {{sup}}}(S\cap \kappa )}\times \mathbb {Q}(\kappa )$
, where
$\mathbb {Q}_{{\textrm {{sup}}}(S\cap \kappa )}\times \mathbb {Q}(\kappa )$
, where
![]() $\mathbb {Q}(\kappa )$
is the forcing that adds a Cohen subset of
$\mathbb {Q}(\kappa )$
is the forcing that adds a Cohen subset of
![]() $\kappa $
. The product
$\kappa $
. The product
 $\mathbb {Q}_{{\textrm {{sup}}}(S\cap \kappa )}\times \mathbb {Q}(\kappa )$
is equivalent, as a forcing notion, to
$\mathbb {Q}_{{\textrm {{sup}}}(S\cap \kappa )}\times \mathbb {Q}(\kappa )$
is equivalent, as a forcing notion, to
 $\mathbb {Q}(\kappa )\times \mathbb {Q}_{{\textrm {{sup}}}(S\cap \kappa )}$
. Also, since
$\mathbb {Q}(\kappa )\times \mathbb {Q}_{{\textrm {{sup}}}(S\cap \kappa )}$
. Also, since
![]() $\mathbb {Q}_{{\textrm {{sup}}}(S\cap \kappa )}$
has cardinality less than
$\mathbb {Q}_{{\textrm {{sup}}}(S\cap \kappa )}$
has cardinality less than
![]() $\kappa $
and
$\kappa $
and
![]() $\mathbb {Q}(\kappa )$
does not add new bounded subsets of
$\mathbb {Q}(\kappa )$
does not add new bounded subsets of
![]() $\kappa $
,
$\kappa $
,
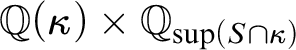 $\mathbb {Q}(\kappa )\times \mathbb {Q}_{{\textrm {{sup}}}(S\cap \kappa )}$
is equivalent to
$\mathbb {Q}(\kappa )\times \mathbb {Q}_{{\textrm {{sup}}}(S\cap \kappa )}$
is equivalent to
 $\mathbb {Q}(\kappa )\ast \mathbb {Q}_{{\textrm {{sup}}}(S\cap \kappa )}$
. Now, since
$\mathbb {Q}(\kappa )\ast \mathbb {Q}_{{\textrm {{sup}}}(S\cap \kappa )}$
. Now, since
![]() $\mathbb {Q}(\kappa )$
is
$\mathbb {Q}(\kappa )$
is
![]() $<\kappa $
-directed closed it preserves the supercompactness of
$<\kappa $
-directed closed it preserves the supercompactness of
![]() $\kappa $
, and then so does
$\kappa $
, and then so does
![]() $\mathbb {Q}_{{\textrm {{sup}}}(S\cap \kappa )}$
subsequently, since it has cardinality less than
$\mathbb {Q}_{{\textrm {{sup}}}(S\cap \kappa )}$
subsequently, since it has cardinality less than
![]() $\kappa $
. Moreover,
$\kappa $
. Moreover,
![]() $\mathbb {Q}_\kappa $
forces that
$\mathbb {Q}_\kappa $
forces that
![]() $\mathbb {Q}_{[\kappa +1 , Ord)}$
is
$\mathbb {Q}_{[\kappa +1 , Ord)}$
is
![]() $<\kappa $
-directed-closed, and therefore it also preserves the supercompactness of
$<\kappa $
-directed-closed, and therefore it also preserves the supercompactness of
![]() $\kappa $
. Since
$\kappa $
. Since
![]() $\kappa ^{<\kappa }=\kappa $
for every
$\kappa ^{<\kappa }=\kappa $
for every
![]() $\kappa \in S$
, the forcing
$\kappa \in S$
, the forcing
![]() $\mathbb {Q}$
preserves cardinals and the power-set function. Now we may argue similarly as in Reference Reitz[23] to show that every ground of
$\mathbb {Q}$
preserves cardinals and the power-set function. Now we may argue similarly as in Reference Reitz[23] to show that every ground of
![]() $V[G][H_0][H_1]$
has a proper subground, hence there is no core.Footnote
44
For suppose W is a ground of
$V[G][H_0][H_1]$
has a proper subground, hence there is no core.Footnote
44
For suppose W is a ground of
![]() $V[G][H_0][H_1]$
. Let
$V[G][H_0][H_1]$
. Let
![]() $\mathbb {P}$
be a poset in W and g a
$\mathbb {P}$
be a poset in W and g a
![]() $\mathbb {P}$
-generic filter over W such that
$\mathbb {P}$
-generic filter over W such that
![]() $V[G][H_0][H_1]=W[g]$
. Since the two models
$V[G][H_0][H_1]=W[g]$
. Since the two models
![]() $V[G][H_0][H_1]$
and W agree on the values of the power-set function for a tail of elements of S, as well as on statements of the form “
$V[G][H_0][H_1]$
and W agree on the values of the power-set function for a tail of elements of S, as well as on statements of the form “
![]() $\kappa $
is the
$\kappa $
is the
![]() $\alpha $
th element of S” for a tail of cardinals
$\alpha $
th element of S” for a tail of cardinals
![]() $\kappa $
in S, every element of
$\kappa $
in S, every element of
![]() $V[G][H_0]$
is coded into the power-set function of W on S, hence
$V[G][H_0]$
is coded into the power-set function of W on S, hence
![]() $V[G][H_0]\subseteq W$
. Now let
$V[G][H_0]\subseteq W$
. Now let
![]() $\kappa $
in S be greater than
$\kappa $
in S be greater than
![]() $|\mathbb {P}|$
, and let
$|\mathbb {P}|$
, and let
![]() $h_\kappa $
be the Cohen generic subset of
$h_\kappa $
be the Cohen generic subset of
![]() $\kappa $
added by H. Since
$\kappa $
added by H. Since
![]() $V[G][H_0]\subseteq W$
, every condition of the forcing
$V[G][H_0]\subseteq W$
, every condition of the forcing
![]() $\mathbb {Q}(\kappa )$
, therefore every bounded subset of
$\mathbb {Q}(\kappa )$
, therefore every bounded subset of
![]() $h_\kappa $
, belongs to W. Hence, since the pair
$h_\kappa $
, belongs to W. Hence, since the pair
![]() $\langle W, W[h]\rangle $
satisfies the
$\langle W, W[h]\rangle $
satisfies the
![]() $\kappa $
-approximation property,
$\kappa $
-approximation property,
![]() $h_\kappa \in W$
. Thus, writing
$h_\kappa \in W$
. Thus, writing
![]() $H_1$
as the product
$H_1$
as the product
 $H_1^{\leq \kappa }\times H_1^{>\kappa }$
, we have that
$H_1^{\leq \kappa }\times H_1^{>\kappa }$
, we have that
![]() $V[G][H_0][H^{>\kappa }]\subseteq W$
, and
$V[G][H_0][H^{>\kappa }]\subseteq W$
, and
![]() $V[G][H_0][H^{>\kappa }]$
is a ground of W. Now, if
$V[G][H_0][H^{>\kappa }]$
is a ground of W. Now, if
![]() $\kappa _0 <\kappa _1$
are the first two members of S greater than
$\kappa _0 <\kappa _1$
are the first two members of S greater than
![]() $|\mathbb {P}|$
, then
$|\mathbb {P}|$
, then
 $V[G][H_0][H^{>\kappa _1}_1]$
is a proper ground of
$V[G][H_0][H^{>\kappa _1}_1]$
is a proper ground of
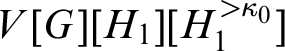 $V[G][H_1][H_1^{>\kappa _0}]$
, hance also a proper ground of W. □
$V[G][H_1][H_1^{>\kappa _0}]$
, hance also a proper ground of W. □
Therefore, although no formal evidence may currently be provided, it is reasonable to conjecture, that, as a consequence of Theorem 3.8, no LCA of consistency strength lower than that of ‘there exists an extendible cardinal’ will be sufficient to prove the existence of the core. However, more work is needed to shed further light on the issue.
4 The core: CH and forcing axioms
4.1 The core and CH
We know that, under certain assumptions on T, the core of the multiverse of
![]() $\mathsf {MV}_T$
exists, so it makes sense to find out what features it has and, based on these, what it may reveal to us about such undecidable statements as CH. In particular, we would like to address the following question:
$\mathsf {MV}_T$
exists, so it makes sense to find out what features it has and, based on these, what it may reveal to us about such undecidable statements as CH. In particular, we would like to address the following question:
Question 4.1. Does
![]() $\mathsf {MV}_T$
prove that the core satisfies the CH, where
$\mathsf {MV}_T$
prove that the core satisfies the CH, where
![]() $T=\mathsf {ZFC}+$
‘there exists a class of extendible cardinals’?
$T=\mathsf {ZFC}+$
‘there exists a class of extendible cardinals’?
The question may, in fact, extend to any other statement
![]() $\varphi $
which is not decided by
$\varphi $
which is not decided by
![]() $\mathsf {ZFC}$
. In particular, for each such
$\mathsf {ZFC}$
. In particular, for each such
![]() $\varphi $
, one may ask whether the core implies the truth or falsity of
$\varphi $
, one may ask whether the core implies the truth or falsity of
![]() $\varphi $
.
$\varphi $
.
The results which follow provide answers to such questions, and, overall, starkly expose the indeterminacy of the core. We, first, outline the mathematical strategy for CH.
If the core exists, then it satisfies GA, namely, it does not have any proper grounds. Reitz Reference Reitz[23] proved that every model of
![]() $\mathsf {ZFC}$
has a class-forcing extension which preserves any desired
$\mathsf {ZFC}$
has a class-forcing extension which preserves any desired
![]() $V_\alpha $
, satisfies V=HOD, and is a model of
$V_\alpha $
, satisfies V=HOD, and is a model of
![]() $\mathsf {ZFC}$
+GA.Footnote
45
By results in Reference Bagaria and Poveda[5], the class-forcing used to obtain the model preserves extendible cardinals. So, starting with a model M satisfying
$\mathsf {ZFC}$
+GA.Footnote
45
By results in Reference Bagaria and Poveda[5], the class-forcing used to obtain the model preserves extendible cardinals. So, starting with a model M satisfying
![]() $T=\mathsf {ZFC}+$
‘There is a proper class of extendible cardinals’ we may class-force over it to obtain a model
$T=\mathsf {ZFC}+$
‘There is a proper class of extendible cardinals’ we may class-force over it to obtain a model
![]() $M[H]$
of T satisfying GA and, e.g.,
$M[H]$
of T satisfying GA and, e.g.,
![]() $\neg $
CH. And then by forcing with
$\neg $
CH. And then by forcing with
![]() $Coll(\omega , <Ord)^{M[H]}$
over
$Coll(\omega , <Ord)^{M[H]}$
over
![]() $M[H]$
we obtain a model of
$M[H]$
we obtain a model of
![]() $\mathsf {MV}_T$
whose core is
$\mathsf {MV}_T$
whose core is
![]() $M[H]$
and satisfies
$M[H]$
and satisfies
![]() $\neg $
CH.
$\neg $
CH.
Now we show how this strategy can be extended to all
![]() $\Sigma _2$
set-forceable statements
$\Sigma _2$
set-forceable statements
![]() $\varphi $
:
$\varphi $
:
Theorem 4.2. Let
![]() $\varphi $
be a
$\varphi $
be a
![]() $\Sigma _2$
statement (with parameters) that can be forced by set forcing. Assume there is a proper class of extendible cardinals. Then in some class-forcing extension of V that preserves extendible cardinals the statement
$\Sigma _2$
statement (with parameters) that can be forced by set forcing. Assume there is a proper class of extendible cardinals. Then in some class-forcing extension of V that preserves extendible cardinals the statement
![]() $\varphi $
holds in the core of
$\varphi $
holds in the core of
![]() $\mathsf {MV}$
’s multiverse built around the extension itself.
$\mathsf {MV}$
’s multiverse built around the extension itself.
Proof. First force
![]() $\varphi $
by set forcing. In the forcing extension let
$\varphi $
by set forcing. In the forcing extension let
![]() $\kappa \in C^{(1)}$
be such that
$\kappa \in C^{(1)}$
be such that
![]() $V_\kappa \models \varphi $
. Then force the GCH above
$V_\kappa \models \varphi $
. Then force the GCH above
![]() $\kappa $
, in the usual way using class forcing, so that
$\kappa $
, in the usual way using class forcing, so that
![]() $V_\kappa $
is not changed. As in [Reference Reitz23], we may further class-force to get a model of GA, so that
$V_\kappa $
is not changed. As in [Reference Reitz23], we may further class-force to get a model of GA, so that
![]() $V_\kappa $
is still unchanged. By results contained in [Reference Bagaria and Poveda5, Reference Tsaprounis26], both class-forcing notions preserve extendible cardinals.Footnote
46
Hence, since the final extension M satisfies the GA, if G is
$V_\kappa $
is still unchanged. By results contained in [Reference Bagaria and Poveda5, Reference Tsaprounis26], both class-forcing notions preserve extendible cardinals.Footnote
46
Hence, since the final extension M satisfies the GA, if G is
![]() $Coll(\omega , <Ord)^M$
-generic over M, then the core of the
$Coll(\omega , <Ord)^M$
-generic over M, then the core of the
![]() $\mathsf {MV}$
multiverse given by
$\mathsf {MV}$
multiverse given by
![]() $M^G$
, which exists because in M there exists a proper class of extendible cardinals, is M itself. Also, since
$M^G$
, which exists because in M there exists a proper class of extendible cardinals, is M itself. Also, since
![]() $V_\kappa $
has not been changed and satisfies
$V_\kappa $
has not been changed and satisfies
![]() $\varphi $
, in M we have that
$\varphi $
, in M we have that
![]() $V_\kappa \models \varphi $
and, moreover,
$V_\kappa \models \varphi $
and, moreover,
![]() $\kappa \in C^{(1)}$
, because being in
$\kappa \in C^{(1)}$
, because being in
![]() $C^{(1)}$
is characterized by being uncountable and satisfying
$C^{(1)}$
is characterized by being uncountable and satisfying
![]() $V_\kappa =H_\kappa $
. Hence,
$V_\kappa =H_\kappa $
. Hence,
![]() $M\models \varphi $
. □
$M\models \varphi $
. □
Corollary 4.3. If
![]() $T=\mathsf {ZFC}+$
‘There exists a proper class of extendible cardinals’ is consistent, then so is
$T=\mathsf {ZFC}+$
‘There exists a proper class of extendible cardinals’ is consistent, then so is
![]() $\mathsf {MV}_T$
plus that the core satisfies the CH, or
$\mathsf {MV}_T$
plus that the core satisfies the CH, or
![]() $\neg $
CH, with any possible value of the size of the continuum.
$\neg $
CH, with any possible value of the size of the continuum.
Besides the CH and
![]() $\neg $
CH there are many other relevant
$\neg $
CH there are many other relevant
![]() $\Sigma _2$
statements that are set-forceable, and therefore consistently hold in the core of the
$\Sigma _2$
statements that are set-forceable, and therefore consistently hold in the core of the
![]() $\mathsf {MV}_T$
multiverse. We give next a couple more examples.
$\mathsf {MV}_T$
multiverse. We give next a couple more examples.
Corollary 4.4. If T as above is consistent, then so is
![]() $\mathsf {MV}_T$
plus that the core satisfies
$\mathsf {MV}_T$
plus that the core satisfies
![]() $\square _{\omega _2}$
, or its negation.
$\square _{\omega _2}$
, or its negation.
Proof.
![]() $\square _{\omega _2}$
is a forcible, by countably-directed and
$\square _{\omega _2}$
is a forcible, by countably-directed and
![]() $\omega _1$
-strategically closed forcing,
$\omega _1$
-strategically closed forcing,
![]() $\Sigma _1$
statement, with
$\Sigma _1$
statement, with
![]() $\omega _1$
and
$\omega _1$
and
![]() $\omega _2$
as parameters. Also, its negation is forced by
$\omega _2$
as parameters. Also, its negation is forced by
![]() $Coll(\omega _1, <\kappa )$
, with
$Coll(\omega _1, <\kappa )$
, with
![]() $\kappa $
a Mahlo cardinal. □
$\kappa $
a Mahlo cardinal. □
The well-known forcing axiom
![]() $\mathrm {MA}_{\aleph _1}$
is also equivalent to a
$\mathrm {MA}_{\aleph _1}$
is also equivalent to a
![]() $\Sigma _2$
statement, with
$\Sigma _2$
statement, with
![]() $\aleph _1$
as a parameter. Thus, Theorem 4.2 yields the following:
$\aleph _1$
as a parameter. Thus, Theorem 4.2 yields the following:
Corollary 4.5. If T as above is consistent, then so is
![]() $\mathsf {MV}_T$
plus that the core satisfies
$\mathsf {MV}_T$
plus that the core satisfies
![]() $\mathrm {MA}_{\aleph _1}$
.
$\mathrm {MA}_{\aleph _1}$
.
4.2 The core and strong forcing axioms
Corollary 4.5 helps us to introduce, in fuller generality, the examination of the behaviour of the core with respect to forcing axioms. Now, what has neatly come to surface is that the core of
![]() $\mathsf {MV}_T$
, where T may, and even may not, have extendible cardinals, is also consistent with strong forcing axioms. Corollary 3.8 of Reference Reitz[23] already proves that the Proper Forcing Axiom (PFA) is consistent with the GA.Footnote
47
We extend this result also to MM, MM
$\mathsf {MV}_T$
, where T may, and even may not, have extendible cardinals, is also consistent with strong forcing axioms. Corollary 3.8 of Reference Reitz[23] already proves that the Proper Forcing Axiom (PFA) is consistent with the GA.Footnote
47
We extend this result also to MM, MM
![]() $^{++}$
, etc.
$^{++}$
, etc.
Recall that MM
![]() $^{++}$
states that for every poset
$^{++}$
states that for every poset
![]() ${\mathbb P}$
that preserves stationary subsets of
${\mathbb P}$
that preserves stationary subsets of
![]() $\omega _1$
, every collection
$\omega _1$
, every collection
![]() $\{ D_\alpha :\alpha <\omega _1\}$
of dense open subsets of
$\{ D_\alpha :\alpha <\omega _1\}$
of dense open subsets of
![]() ${\mathbb P}$
, and every collection
${\mathbb P}$
, and every collection
![]() $\{ \sigma _\alpha :\alpha <\omega _1\}$
of
$\{ \sigma _\alpha :\alpha <\omega _1\}$
of
![]() ${\mathbb P}$
-names for stationary subsets of
${\mathbb P}$
-names for stationary subsets of
![]() $\omega _1$
, there exists a filter
$\omega _1$
, there exists a filter
![]() $G\subseteq {\mathbb P}$
that is generic for
$G\subseteq {\mathbb P}$
that is generic for
![]() $\{ D_\alpha :\alpha <\omega _1\}$
(i.e.,
$\{ D_\alpha :\alpha <\omega _1\}$
(i.e.,
![]() $G\cap D_\alpha \ne \varnothing $
, all
$G\cap D_\alpha \ne \varnothing $
, all
![]() $\alpha $
), and such that
$\alpha $
), and such that
![]() $\sigma _\alpha [G]$
is a stationary subset of
$\sigma _\alpha [G]$
is a stationary subset of
![]() $\omega _1$
, all
$\omega _1$
, all
![]() $\alpha $
. It is well-known that MM
$\alpha $
. It is well-known that MM
![]() $^{++}$
can be forced, assuming the existence of a supercompact cardinal.
$^{++}$
can be forced, assuming the existence of a supercompact cardinal.
Theorem 4.6. If
![]() $\mathsf {ZFC}$
plus the existence of a supercompact cardinal is consistent, then so is MM
$\mathsf {ZFC}$
plus the existence of a supercompact cardinal is consistent, then so is MM
![]() $^{++}$
plus GA.
$^{++}$
plus GA.
Proof. Let V satisfy
![]() $\mathsf {ZFC}$
plus the existence of a supercompact cardinal. Force over V to obtain a model of
$\mathsf {ZFC}$
plus the existence of a supercompact cardinal. Force over V to obtain a model of
![]() $\mathsf {ZFC}$
plus MM
$\mathsf {ZFC}$
plus MM
![]() $^{++}$
. Call this model
$^{++}$
. Call this model
![]() $V[G]$
. Then force with an
$V[G]$
. Then force with an
![]() $\omega _2$
-directed-closed
$\omega _2$
-directed-closed
![]() $ORD$
-length iteration
$ORD$
-length iteration
![]() ${\mathbb P}$
over
${\mathbb P}$
over
![]() $V[G]$
to obtain a model
$V[G]$
to obtain a model
![]() $V[G][H]$
of GA (as in Reference Reitz[23]). We claim that MM
$V[G][H]$
of GA (as in Reference Reitz[23]). We claim that MM
![]() $^{++}$
holds in
$^{++}$
holds in
![]() $V[G][H]$
. For suppose
$V[G][H]$
. For suppose
![]() $\tau $
is a
$\tau $
is a
![]() ${\mathbb P}$
-name for a poset that preserves stationary subsets of
${\mathbb P}$
-name for a poset that preserves stationary subsets of
![]() $\omega _1$
,
$\omega _1$
,
![]() $\{ \dot {D}_\alpha : \alpha <\omega _1 \}$
is a
$\{ \dot {D}_\alpha : \alpha <\omega _1 \}$
is a
![]() ${\mathbb P}$
-name for a collection of dense open subsets of
${\mathbb P}$
-name for a collection of dense open subsets of
![]() $\tau $
, and
$\tau $
, and
![]() $\{ \dot {\sigma }_\alpha :\alpha <\omega _1\}$
is a
$\{ \dot {\sigma }_\alpha :\alpha <\omega _1\}$
is a
![]() ${\mathbb P}$
-name for a collection of
${\mathbb P}$
-name for a collection of
![]() $\tau $
-names for stationary subsets of
$\tau $
-names for stationary subsets of
![]() $\omega _1$
. Let
$\omega _1$
. Let
![]() $\lambda $
be a large enough cardinal such that
$\lambda $
be a large enough cardinal such that
![]() $\tau $
and
$\tau $
and
![]() $\langle \dot {D}_\alpha : \alpha <\omega _1 \rangle $
and
$\langle \dot {D}_\alpha : \alpha <\omega _1 \rangle $
and
![]() $\{ \dot {\sigma }_\alpha :\alpha <\omega _1\}$
are
$\{ \dot {\sigma }_\alpha :\alpha <\omega _1\}$
are
![]() ${\mathbb P}_\lambda $
-names. Since
${\mathbb P}_\lambda $
-names. Since
![]() ${\mathbb P}_\lambda $
is
${\mathbb P}_\lambda $
is
![]() $\omega _2$
-directed-closed, arguing similarly as in Reference Larson[18], we can show that
$\omega _2$
-directed-closed, arguing similarly as in Reference Larson[18], we can show that
![]() ${\mathbb P}_\lambda $
preserves MM
${\mathbb P}_\lambda $
preserves MM
![]() $^{++}$
.
$^{++}$
.
We claim that in
![]() $V[G][H_\lambda ]$
, the poset
$V[G][H_\lambda ]$
, the poset
![]() $\tau [H_\lambda ]$
preserves stationary subsets of
$\tau [H_\lambda ]$
preserves stationary subsets of
![]() $\omega _1$
: For suppose
$\omega _1$
: For suppose
![]() $S\subseteq \omega _1$
is stationary and
$S\subseteq \omega _1$
is stationary and
![]() $\dot {C}$
is a
$\dot {C}$
is a
![]() $\tau [H_\lambda ]$
-name for a club subset of
$\tau [H_\lambda ]$
-name for a club subset of
![]() $\omega _1$
. Since the remaining part of the iteration does not add any new subsets of
$\omega _1$
. Since the remaining part of the iteration does not add any new subsets of
![]() $\omega _1$
, S is also stationary in
$\omega _1$
, S is also stationary in
![]() $V[G][H]$
. Moreover, since being a club is absolute for transitive models, and every
$V[G][H]$
. Moreover, since being a club is absolute for transitive models, and every
![]() $\tau [H_\lambda ]$
-generic filter over
$\tau [H_\lambda ]$
-generic filter over
![]() $V[G][H]$
is also
$V[G][H]$
is also
![]() $\tau [H_\lambda ]$
-generic over
$\tau [H_\lambda ]$
-generic over
![]() $V[G][H_\lambda ]$
, we have that in
$V[G][H_\lambda ]$
, we have that in
![]() $V[G][H]$
,
$V[G][H]$
,
![]() $\dot {C}$
is a
$\dot {C}$
is a
![]() $\tau [H_\lambda ]$
-name for a club subset of
$\tau [H_\lambda ]$
-name for a club subset of
![]() $\omega _1$
. Hence, since in
$\omega _1$
. Hence, since in
![]() $V[G][H]$
the poset
$V[G][H]$
the poset
![]() $\tau [H_\lambda ]$
preserves stationary subsets of
$\tau [H_\lambda ]$
preserves stationary subsets of
![]() $\omega _1$
, we have that
$\omega _1$
, we have that
 $\Vdash _{\tau [H]}``\check {S}\cap \dot {C}\ne \varnothing "$
. But the latter is absolute for transitive models, and so it holds in
$\Vdash _{\tau [H]}``\check {S}\cap \dot {C}\ne \varnothing "$
. But the latter is absolute for transitive models, and so it holds in
![]() $V[G][H_\lambda ]$
.
$V[G][H_\lambda ]$
.
Moreover, in
![]() $V[G][H_\lambda ]$
,
$V[G][H_\lambda ]$
,
![]() $\{\dot {\sigma }_\alpha [H_\lambda ] :\alpha <\omega _1\}$
is a collection of
$\{\dot {\sigma }_\alpha [H_\lambda ] :\alpha <\omega _1\}$
is a collection of
![]() $\tau $
-names for stationary subsets of
$\tau $
-names for stationary subsets of
![]() $\omega _1$
. Since MM
$\omega _1$
. Since MM
![]() $^{++}$
holds in
$^{++}$
holds in
![]() $V[G][H_\lambda ]$
, there exists a filter
$V[G][H_\lambda ]$
, there exists a filter
![]() $F\subseteq \tau [H_\lambda ]$
that is generic for the collection
$F\subseteq \tau [H_\lambda ]$
that is generic for the collection
![]() $\{ \dot {D}_\alpha [H_\lambda ]:\alpha <\omega _1\}$
, and such that
$\{ \dot {D}_\alpha [H_\lambda ]:\alpha <\omega _1\}$
, and such that
![]() $\dot {\sigma }_\alpha [H_\lambda ][F]$
is stationary. By absoluteness this is also true in
$\dot {\sigma }_\alpha [H_\lambda ][F]$
is stationary. By absoluteness this is also true in
![]() $V[G][H]$
. This shows that MM
$V[G][H]$
. This shows that MM
![]() $^{++}$
holds in
$^{++}$
holds in
![]() $V[G][H]$
. □
$V[G][H]$
. □
It follows from the theorem above that if
![]() $T=\mathsf {ZFC}$
+‘there exists a supercompact cardinal’ is consistent, then so is that the core of
$T=\mathsf {ZFC}$
+‘there exists a supercompact cardinal’ is consistent, then so is that the core of
![]() $\mathsf {MV}_T$
satisfies MM
$\mathsf {MV}_T$
satisfies MM
![]() $^{++}$
. Also, since the class-iteration
$^{++}$
. Also, since the class-iteration
![]() ${\mathbb P}$
that forces the GA preserves extendible cardinals,Footnote
48
if the theory
${\mathbb P}$
that forces the GA preserves extendible cardinals,Footnote
48
if the theory
![]() $T=\mathsf {ZFC}+$
‘there exists a proper class of extendible cardinals’ is consistent, then so is
$T=\mathsf {ZFC}+$
‘there exists a proper class of extendible cardinals’ is consistent, then so is
![]() $\mathsf {MV}_T$
plus that the core satisfies MM
$\mathsf {MV}_T$
plus that the core satisfies MM
![]() $^{++}$
. Moreover, in both cases, by results in Reference Asperó and Schindler[3], the core also satisfies Woodin’s
$^{++}$
. Moreover, in both cases, by results in Reference Asperó and Schindler[3], the core also satisfies Woodin’s
![]() $(\ast )$
axiom.
$(\ast )$
axiom.
5 Probing Steel’s programme: the core as Ultimate-L
Let’s take stock. All the results illustrated in Sections 3 and 4 show that, assuming a proper class of extendible cardinals, the core of the multiverse of
![]() $\mathsf {MV}$
exists, but is still a highly indeterminate object. In particular, we have seen that the core may satisfy any of the strongest known forcing axioms, all of which imply that the continuum has size
$\mathsf {MV}$
exists, but is still a highly indeterminate object. In particular, we have seen that the core may satisfy any of the strongest known forcing axioms, all of which imply that the continuum has size
![]() $\aleph _2$
, and it may also satisfy CH, and, for that matter, any other
$\aleph _2$
, and it may also satisfy CH, and, for that matter, any other
![]() $\Sigma _2$
set-forceable statement, with parameters (Theorem 4.2).
$\Sigma _2$
set-forceable statement, with parameters (Theorem 4.2).
Two immediate considerations are in order. The first is that, based on the provable, under certain assumptions, existence of the core of the multiverse of
![]() $\mathsf {MV}$
, the Universist may now be licensed to shift to the Core Universist view that V is the core, by settling on a theory, in
$\mathsf {MV}$
, the Universist may now be licensed to shift to the Core Universist view that V is the core, by settling on a theory, in
![]() $\mathcal {L}_{\in }$
, which states this explicitly, that is, a theory which contains
$\mathcal {L}_{\in }$
, which states this explicitly, that is, a theory which contains
![]() $V=\mathcal {C}$
as an axiom (henceforth,
$V=\mathcal {C}$
as an axiom (henceforth,
![]() $\mathcal {C}$
will be our designated symbol for the core); in the next section we will examine this possibility in more detail.Footnote
49
The second one is that, as a consequence of the persistent indeterminacy of the core also in the presence of LCs, even if the Core Universist decided to settle on
$\mathcal {C}$
will be our designated symbol for the core); in the next section we will examine this possibility in more detail.Footnote
49
The second one is that, as a consequence of the persistent indeterminacy of the core also in the presence of LCs, even if the Core Universist decided to settle on
![]() $V=\mathcal {C}$
as the correct extension of
$V=\mathcal {C}$
as the correct extension of
![]() $\mathsf {ZFC}$
+LCs, he wouldn’t still be able to fix the features of the core, and thus, the truth-value, in
$\mathsf {ZFC}$
+LCs, he wouldn’t still be able to fix the features of the core, and thus, the truth-value, in
![]() $\mathcal {L}_{\in }$
, of the undecidable statements.
$\mathcal {L}_{\in }$
, of the undecidable statements.
So, it is time for Steel’s Programme to kick in, and, in the next subsections, we will examine its execution and assess its prospects.
5.1 Ultimate-L and
 $\mathsf {MV}$
$\mathsf {MV}$
In recent years, as a consequence of the far-reaching developments of the inner model programme, the possibility of the existence of a canonical inner model for a supercompact cardinal is emerging. Woodin has called such a model Ultimate-L, insofar as this model would incorporate all features of an L-like inner model, as well as all LCs, thus leading to the completion of the inner model programme itself.Footnote
50
If such a model exists, then one could say that it represents an ‘optimal’ approximation of V, something which would justify viewing the axiom V=Ultimate-L as the most natural extension of
![]() $\mathsf {ZFC}$
, and Steel Reference Steel and Kennedy[25] has precisely taken into account such a possibility.Footnote
51
$\mathsf {ZFC}$
, and Steel Reference Steel and Kennedy[25] has precisely taken into account such a possibility.Footnote
51
In this subsection, we will first be concerned with mathematical results about Ultimate-L and the core and, in the next one, we will articulate the Core Universist position based on these results. We start with Woodin’s definition of the axiom V=Ultimate-L.
Definition 5.1 (V=Ultimate-L). The axiom V=Ultimate-L asserts:
-
1. There is a proper class of Woodin cardinals, and
-
2. For each
 $\Sigma _2$
sentence
$\Sigma _2$
sentence
 $\varphi $
, if
$\varphi $
, if
 $\varphi $
holds in V, then there is a universally-Baire set
$\varphi $
holds in V, then there is a universally-Baire set
 $A\subseteq \mathbb {R}$
such that
$A\subseteq \mathbb {R}$
such that  $$ \begin{align*}HOD^{L(A,\mathbb{R})}\models \varphi.\end{align*} $$
$$ \begin{align*}HOD^{L(A,\mathbb{R})}\models \varphi.\end{align*} $$
Woodin has shown that V=Ultimate-L implies the CH.Footnote 52 It also implies the Ground Axiom, i.e., that V is not a set-generic extension of any inner model, and that V=HOD.
Woodin has made the following conjecture. First, recall that an inner model N is a weak extender model for the supercompactness of
![]() $\delta $
if for every
$\delta $
if for every
![]() $\lambda \geq \delta $
there is a normal fine measure
$\lambda \geq \delta $
there is a normal fine measure
![]() $\mathcal {U}$
on
$\mathcal {U}$
on
![]() $\mathcal {P}_\delta \lambda $
such that:
$\mathcal {P}_\delta \lambda $
such that:
-
1.
 $\mathcal {U}\cap N\in N.$
$\mathcal {U}\cap N\in N.$
-
2.
 $\mathcal {P}_\delta \lambda \cap N \in \mathcal {U}$
.
$\mathcal {P}_\delta \lambda \cap N \in \mathcal {U}$
.
Conjecture 5.2 (Woodin’s Ultimate-L Conjecture).
Suppose that
![]() $\delta $
is an extendible cardinal. Then there is an inner model
$\delta $
is an extendible cardinal. Then there is an inner model
![]() $N\subseteq HOD$
such that:
$N\subseteq HOD$
such that:
-
1. N is a weak extender model for the supercompactness of
 $\delta $
.
$\delta $
. -
2.
 $N\models $
‘V=Ultimate-L’.
$N\models $
‘V=Ultimate-L’.
Now, crucially for our purposes, if the Ultimate-L Conjecture holds, then letting T be the theory
![]() $\mathsf {ZFC}+$
‘There exists a proper class of extendible cardinals’ we have that
$\mathsf {ZFC}+$
‘There exists a proper class of extendible cardinals’ we have that
![]() $\mathsf {MV}_T$
proves that the core has an inner model
$\mathsf {MV}_T$
proves that the core has an inner model
![]() $\mathcal {V}$
which is contained in HOD, and satisfies V=Ultimate-L. Moreover, by Woodin’s Universality Theorem,Footnote
53
$\mathcal {V}$
which is contained in HOD, and satisfies V=Ultimate-L. Moreover, by Woodin’s Universality Theorem,Footnote
53
![]() $\mathcal {V}$
satisfies that there exists a proper class of extendible cardinals. However,
$\mathcal {V}$
satisfies that there exists a proper class of extendible cardinals. However,
![]() $\mathcal {V}$
need not be a world itself, but, if it is so, then
$\mathcal {V}$
need not be a world itself, but, if it is so, then
![]() $\mathcal {V}$
is the core. So, here follows the first result of this subsection:
$\mathcal {V}$
is the core. So, here follows the first result of this subsection:
Proposition 5.3. Let T be
![]() $\mathsf {ZFC}+$
‘There exists a proper class of extendible cardinals’. Then
$\mathsf {ZFC}+$
‘There exists a proper class of extendible cardinals’. Then
![]() $\mathsf {MV}_T$
proves that the following are equivalent:
$\mathsf {MV}_T$
proves that the following are equivalent:
-
1. There exists a world satisfying ‘V=Ultimate-L’.
-
2.
 $\mathcal {C}\models $
‘V=Ultimate-L’.
$\mathcal {C}\models $
‘V=Ultimate-L’.
Proof. Let
![]() $M^G$
be a model of
$M^G$
be a model of
![]() $\mathsf {MV}_T$
, and let
$\mathsf {MV}_T$
, and let
![]() $\mathcal {W}$
be a world in
$\mathcal {W}$
be a world in
![]() $M^G$
that satisfies V=Ultimate-L. Then
$M^G$
that satisfies V=Ultimate-L. Then
![]() $\mathcal {W}$
is a ground of some world. But
$\mathcal {W}$
is a ground of some world. But
![]() $\mathcal {W}$
has no proper grounds, hence since
$\mathcal {W}$
has no proper grounds, hence since
![]() $MV_T$
implies that the core exists and is the mantle,
$MV_T$
implies that the core exists and is the mantle,
![]() $\mathcal {W}$
must be contained in the core, and therefore it must be the core. □
$\mathcal {W}$
must be contained in the core, and therefore it must be the core. □
The following two propositions nail down the consistency of V=Ultimate-L with
![]() $\mathsf {MV}_T$
(where
$\mathsf {MV}_T$
(where
![]() $T=\mathsf {ZFC}$
+‘there exists a class of extendible cardinals’), assuming V=Ultimate-L’s own consistency.
$T=\mathsf {ZFC}$
+‘there exists a class of extendible cardinals’), assuming V=Ultimate-L’s own consistency.
Proposition 5.4. Let T be
![]() $\mathsf {ZFC}+$
‘There exists a proper class of extendible cardinals’. If
$\mathsf {ZFC}+$
‘There exists a proper class of extendible cardinals’. If
![]() $T+$
‘
$T+$
‘
![]() $V=\mbox {Ultimate}$
-L’ is consistent, then so is
$V=\mbox {Ultimate}$
-L’ is consistent, then so is
![]() $\mathsf {MV}_T$
plus ‘
$\mathsf {MV}_T$
plus ‘
![]() $\mathcal {C}\models $
T+V=Ultimate-L’.
$\mathcal {C}\models $
T+V=Ultimate-L’.
Proof. Let M be a model of
![]() $T+$
‘
$T+$
‘
![]() $V=\mbox {Ultimate}$
-L’. Then for every
$V=\mbox {Ultimate}$
-L’. Then for every
![]() $G\subseteq Coll(\omega , <Ord)^M$
-generic filter over M,
$G\subseteq Coll(\omega , <Ord)^M$
-generic filter over M,
![]() $M^G$
satisfies ‘
$M^G$
satisfies ‘
![]() $\mathcal {C}\models V=$
Ultimate-L’, by the last Proposition. □
$\mathcal {C}\models V=$
Ultimate-L’, by the last Proposition. □
Proposition 5.5. Assume the Ultimate-L Conjecture. If
![]() $T=\mathsf {ZFC}+$
‘There exists a proper class of extendible cardinals’ is consistent, then so is
$T=\mathsf {ZFC}+$
‘There exists a proper class of extendible cardinals’ is consistent, then so is
![]() $\mathsf {MV}_T+$
‘
$\mathsf {MV}_T+$
‘
![]() $\mathcal {C}\models V$
=Ultimate-L’.
$\mathcal {C}\models V$
=Ultimate-L’.
Proof. Let M be a model of T. Let
![]() $\delta $
be the least extendible cardinal in M. By the Ultimate-L Conjecture, M has an inner model N satisfying
$\delta $
be the least extendible cardinal in M. By the Ultimate-L Conjecture, M has an inner model N satisfying
![]() $V=$
Ultimate-L and which is a weak extender model for the supercompactness of
$V=$
Ultimate-L and which is a weak extender model for the supercompactness of
![]() $\delta $
. By the Universality Theorem, in N there is a proper class of extendible cardinals. Now let
$\delta $
. By the Universality Theorem, in N there is a proper class of extendible cardinals. Now let
![]() $G\subseteq Coll(\omega , <Ord)^N$
be generic over N. Then
$G\subseteq Coll(\omega , <Ord)^N$
be generic over N. Then
![]() $N^G$
is a model of
$N^G$
is a model of
![]() $\mathsf {MV}_T$
plus
$\mathsf {MV}_T$
plus
![]() $\mathcal {C}\models ``V=$
Ultimate-
$\mathcal {C}\models ``V=$
Ultimate-
![]() $L."$
□
$L."$
□
However, also the negation of V=Ultimate-L, as shown by the following proposition, is consistent with
![]() $\mathsf {MV}_T$
:
$\mathsf {MV}_T$
:
Proposition 5.6. If the theory
![]() $T=\mathsf {ZFC}+$
‘There exists a proper class of extendible cardinals’+‘V=Ultimate-L’ is consistent, then so is
$T=\mathsf {ZFC}+$
‘There exists a proper class of extendible cardinals’+‘V=Ultimate-L’ is consistent, then so is
![]() $\mathsf {ZFC}+$
‘There exists a proper class of extendible cardinals’+‘
$\mathsf {ZFC}+$
‘There exists a proper class of extendible cardinals’+‘
![]() $\, {\mathcal C} \not \models V$
=Ultimate-L’.
$\, {\mathcal C} \not \models V$
=Ultimate-L’.
Proof. Let M be a model of T. Force GA by class forcing, as in Reference Reitz[23], so that (by Reference Bagaria and Poveda[5]) in the resulting model N there is a proper class of extendible cardinals. If
![]() $G\subseteq Coll(\omega , <Ord)^N$
is generic over N, then
$G\subseteq Coll(\omega , <Ord)^N$
is generic over N, then
![]() $N^G$
is a model of
$N^G$
is a model of
![]() $\mathsf {MV}_T$
plus
$\mathsf {MV}_T$
plus
![]() $\mathcal {C}=N\not \models `V$
=Ultimate-L’. □
$\mathcal {C}=N\not \models `V$
=Ultimate-L’. □
5.2 The role of Ultimate-L within
 $\mathsf {MV}$
$\mathsf {MV}$
From what Steel says in Reference Steel and Kennedy[25], it seems reasonable to assume that he would encourage the adoption of
![]() $\mathsf {ZFC}$
+LCs+V=Ultimate-L as the Core Universist’s ultimate theory. It is crucial to make clear how this could possibly happen.
$\mathsf {ZFC}$
+LCs+V=Ultimate-L as the Core Universist’s ultimate theory. It is crucial to make clear how this could possibly happen.
Steel declares V=Ultimate-L to be the right axiom for the core for the following reasonsFootnote
54
: (1.) it implies
![]() $V=\mathcal {C}$
; (2.) it implies the existence of a ‘fine structure theory’ for the core; (3.) it is consistent with all LCs.Footnote
55
But, as we know, in view of
$V=\mathcal {C}$
; (2.) it implies the existence of a ‘fine structure theory’ for the core; (3.) it is consistent with all LCs.Footnote
55
But, as we know, in view of
![]() $\mathsf {MV}$
’s own machinery and goals, these motivations may just be seen as auxiliary arguments for the acceptance of V=Ultimate-L, as our prospects to settle on V=Ultimate-L as the right extension of
$\mathsf {MV}$
’s own machinery and goals, these motivations may just be seen as auxiliary arguments for the acceptance of V=Ultimate-L, as our prospects to settle on V=Ultimate-L as the right extension of
![]() $\mathsf {ZFC}$
entirely depend, by
$\mathsf {ZFC}$
entirely depend, by
![]() $\mathsf {MV}$
’s own lights, on detecting its presence in
$\mathsf {MV}$
’s own lights, on detecting its presence in
![]() $\mathcal {L}_{\mathsf {MV}}$
.
$\mathcal {L}_{\mathsf {MV}}$
.
So we proceed to assess these prospects by resuming the narrative about the Core Universist’s possible choices laid out at the beginning of section 5.Footnote 56
As said there, the Universist might tentatively interpret the
![]() $\mathcal {L}_{\in }$
-translate of the
$\mathcal {L}_{\in }$
-translate of the
![]() $\mathcal {L}_{\mathsf {MV}}$
-sentence ‘the core exists’ as suggesting (‘practically implying’) the view that V is the core. Syntactically, this would correspond to adopting the theory
$\mathcal {L}_{\mathsf {MV}}$
-sentence ‘the core exists’ as suggesting (‘practically implying’) the view that V is the core. Syntactically, this would correspond to adopting the theory
![]() $\mathsf {ZFC}+$
LCs+
$\mathsf {ZFC}+$
LCs+
![]() $V=\mathcal {C}$
. So, our Universist could, provisionally, settle on such a theory as the ultimate extension of
$V=\mathcal {C}$
. So, our Universist could, provisionally, settle on such a theory as the ultimate extension of
![]() $\mathsf {ZFC}$
. However, as we know, the core is a highly indeterminate object, so
$\mathsf {ZFC}$
. However, as we know, the core is a highly indeterminate object, so
![]() $V=\mathcal {C}$
wouldn’t be very informative. By contrast, if our Universist interpreted the
$V=\mathcal {C}$
wouldn’t be very informative. By contrast, if our Universist interpreted the
![]() $\mathcal {L}_{\in }$
-translate of ‘the core exists’ as suggesting that V=Ultimate-L, then he would be able to determinately fix the features of the core, and would get
$\mathcal {L}_{\in }$
-translate of ‘the core exists’ as suggesting that V=Ultimate-L, then he would be able to determinately fix the features of the core, and would get
![]() $V=\mathcal {C}$
as a bonus. To be more precise, in the presence of such an interpretation,
$V=\mathcal {C}$
as a bonus. To be more precise, in the presence of such an interpretation,
![]() $\mathsf {ZFC}+$
LCs+V=Ultimate-L would prove that CH, as expressed in
$\mathsf {ZFC}+$
LCs+V=Ultimate-L would prove that CH, as expressed in
![]() $\mathcal {L}_{\mathsf {\in }}$
, is equivalent to
$\mathcal {L}_{\mathsf {\in }}$
, is equivalent to
![]() $t($
‘CH holds in the core’), and this strategy may be extended to all
$t($
‘CH holds in the core’), and this strategy may be extended to all
![]() $\varphi $
’s in
$\varphi $
’s in
![]() $\mathcal {L}_{\mathsf {\in }}$
which aren’t decided by
$\mathcal {L}_{\mathsf {\in }}$
which aren’t decided by
![]() $T= \mathsf {ZFC}+$
LCs.
$T= \mathsf {ZFC}+$
LCs.
So far so good, but is this strategy really workable? In fact, as we would like to point out, there may be severe hindrances in the way of its execution. First of all, if one looks at the functioning of (Transl), the
![]() $\mathcal {L}_{\mathsf {MV}}$
-sentence ‘the core exists’, doesn’t literally translate to the
$\mathcal {L}_{\mathsf {MV}}$
-sentence ‘the core exists’, doesn’t literally translate to the
![]() $\mathcal {L}_{\in }$
-sentence ‘V is the core’, let alone to ‘V=Ultimate-L’ (see Definition 2.4). Therefore, some less quick, and more subtle kind of reasoning might underlie the adoption of
$\mathcal {L}_{\in }$
-sentence ‘V is the core’, let alone to ‘V=Ultimate-L’ (see Definition 2.4). Therefore, some less quick, and more subtle kind of reasoning might underlie the adoption of
![]() $V=\mathcal {C}$
on the Universist’s part, and this may have to do with the definability of the core in
$V=\mathcal {C}$
on the Universist’s part, and this may have to do with the definability of the core in
![]() $\mathsf {MV}$
. As we know, if
$\mathsf {MV}$
. As we know, if
![]() $\mathsf {MV}$
has a definable world, then it has a unique definable world (cf. Theorem 3.4). Now, we know that the core is definable, and since there is just one such object in
$\mathsf {MV}$
has a definable world, then it has a unique definable world (cf. Theorem 3.4). Now, we know that the core is definable, and since there is just one such object in
![]() $\mathsf {MV}$
,
$\mathsf {MV}$
,
![]() $\mathsf {MV}$
’s unique definable world is the core itself. Therefore, the Core Universist might thrive on considerations about the definability of the core within
$\mathsf {MV}$
’s unique definable world is the core itself. Therefore, the Core Universist might thrive on considerations about the definability of the core within
![]() $\mathsf {MV}$
, and see these as strongly suggesting that
$\mathsf {MV}$
, and see these as strongly suggesting that
![]() $V=\mathcal {C}$
. But even if this argument ultimately persuaded us to adopt
$V=\mathcal {C}$
. But even if this argument ultimately persuaded us to adopt
![]() $V=\mathcal {C}$
, it wouldn’t be sufficient to persuade us to adopt V=Ultimate-L, anyway.
$V=\mathcal {C}$
, it wouldn’t be sufficient to persuade us to adopt V=Ultimate-L, anyway.
For a different strategy, we could think that what we would need here to make the
![]() $\mathcal {L}_{\mathsf {\in }}$
-translate of the
$\mathcal {L}_{\mathsf {\in }}$
-translate of the
![]() $\mathcal {L}_{\mathsf {MV}}$
-sentence ‘the core exists’ suggest that ‘V=Ultimate-L’, would be some strengthening of T in the theory
$\mathcal {L}_{\mathsf {MV}}$
-sentence ‘the core exists’ suggest that ‘V=Ultimate-L’, would be some strengthening of T in the theory
![]() $\mathsf {MV}_T$
. As we shall see, unfortunately, all such strengthenings will produce results which are not fully satisfactory.
$\mathsf {MV}_T$
. As we shall see, unfortunately, all such strengthenings will produce results which are not fully satisfactory.
Two main cases are possible. First, take T to be the theory
![]() $\mathsf {ZFC}$
+LCs+V= Ultima-te-L, and consider
$\mathsf {ZFC}$
+LCs+V= Ultima-te-L, and consider
![]() $\mathsf {MV}_T$
. The theory could, potentially, do the required job, but it is inconsistent. The reason is, any model of such theory would violate the Axiom 4 of
$\mathsf {MV}_T$
. The theory could, potentially, do the required job, but it is inconsistent. The reason is, any model of such theory would violate the Axiom 4 of
![]() $\mathsf {MV}$
, as no forcing extension of
$\mathsf {MV}$
, as no forcing extension of
![]() ${V}$
could be a world satisfying T. A more modest strengthening of T, on the other hand, might suit our purposes. Take T to be:
${V}$
could be a world satisfying T. A more modest strengthening of T, on the other hand, might suit our purposes. Take T to be:
![]() $\mathsf {ZFC}$
+LCs+‘
$\mathsf {ZFC}$
+LCs+‘
![]() $\mathcal {C}\models V$
=Ultimate-L’, then the
$\mathcal {C}\models V$
=Ultimate-L’, then the
![]() $\mathcal {L}_{\mathsf {\in }}$
-translate of ‘the core is Ultimate-L’ would be a lot closer to what we would need to have at hand, but, still, the translation wouldn’t automatically imply ‘V is the core’. But there’s also another trouble with this choice of T: the axiom ‘
$\mathcal {L}_{\mathsf {\in }}$
-translate of ‘the core is Ultimate-L’ would be a lot closer to what we would need to have at hand, but, still, the translation wouldn’t automatically imply ‘V is the core’. But there’s also another trouble with this choice of T: the axiom ‘
![]() $\mathcal {C}\models V$
=Ultimate-L’ wouldn’t, prima facie, seem to be justified on the grounds of
$\mathcal {C}\models V$
=Ultimate-L’ wouldn’t, prima facie, seem to be justified on the grounds of
![]() $\mathsf {MV}$
’s very evidential framework, so the only reason why one would add it to T in
$\mathsf {MV}$
’s very evidential framework, so the only reason why one would add it to T in
![]() $\mathsf {MV}_T$
would have to do with other, ‘external’, reasons, such as, (1.)–(3.) above, or our prior belief in the correctness of V=Ultimate-L, but now relying on such reasons, somehow, would beg the question of why the Core Universist should adopt V=Ultimate-L.
$\mathsf {MV}_T$
would have to do with other, ‘external’, reasons, such as, (1.)–(3.) above, or our prior belief in the correctness of V=Ultimate-L, but now relying on such reasons, somehow, would beg the question of why the Core Universist should adopt V=Ultimate-L.
But maybe there are ways to make ‘
![]() $\mathcal {C}\models $
V=Ultimate-L’ justified on the grounds of
$\mathcal {C}\models $
V=Ultimate-L’ justified on the grounds of
![]() $\mathsf {MV}$
’s very evidential framework. We proceed to examine arguments potentially to that effect in the next subsections.
$\mathsf {MV}$
’s very evidential framework. We proceed to examine arguments potentially to that effect in the next subsections.
5.3 Woodin’s argument for Ultimate-L
The first argument derives from Woodin’s own reflections on the philosophical aspects of Conjecture 5.2 (Ultimate-L exists).
In Reference Woodin, Baaz, Papadimitriou, Scott and Putnam[29], Woodin has proposed to construe the Inner Model Programme as the expression of the fundamentally non-formalistic character of set theory. Woodin’s Argument, as we shall call it, first introduces two different positions about set-theoretic truth, the Skeptic’s and the Set-Theorist’s.
-
• Skeptic: set-theoretic theorems are truths about finitary objects (proofs).
-
• Set-theorist: set-theoretic theorems are truths about an existing realm of mathematical objects.
Now, Woodin argues that the dialectic between the Skeptic and the Set-Theorist reaches its climax on the issue of the consistency of LCs: the Skeptic holds that the consistency of LCs is a purely finitistic fact (Skeptic’s Retreat), whereas the Set-Theorist believes that it depends on intuitions about universes which contain them, in particular, canonical inner models. In order to further articulate the Set-Theorist’s position, Woodin formulates the following principle:
Set-Theorist’s Cosmological Principle (SCP). A Large Cardinal Axiom is consistent if and only if there is an inner model which satisfies it; the prediction of its consistency is correct, because LCAs are true.
Woodin also indicates concrete ways in which SCP might be disconfirmed and the Skeptic’s Retreat be validated, but we shall leave aside the issue here, and exclusively focus on the potential usefulness of Woodin’s Argument for our Core Universist.Footnote 57
The argument revolves around the idea that our belief in the correctness of all LCs is based on the belief that they are consistent, in turn, via SCP, that they have inner models. Thus, it could suggest that, if one sees LCs as the ‘right’ extensions of
![]() $\mathsf {ZFC}$
, it is because one views them as consistent via inner models. So, the reasoning goes, once one commits oneself to all LCs, as the
$\mathsf {ZFC}$
, it is because one views them as consistent via inner models. So, the reasoning goes, once one commits oneself to all LCs, as the
![]() $\mathsf {MV}$
supporter does, then, there is a sense in which one also commits oneself to Ultimate-L, that is, to Conjecture 5.2.Footnote
58
But then, if Ultimate-L exists, it should be a definable world and, thus, based on Theorem 3.4, it would be the core; the correctness of ‘
$\mathsf {MV}$
supporter does, then, there is a sense in which one also commits oneself to Ultimate-L, that is, to Conjecture 5.2.Footnote
58
But then, if Ultimate-L exists, it should be a definable world and, thus, based on Theorem 3.4, it would be the core; the correctness of ‘
![]() $\mathcal {C} \models $
V=Ultimate-L’ would thus finally be vindicated, seemingly, on
$\mathcal {C} \models $
V=Ultimate-L’ would thus finally be vindicated, seemingly, on
![]() $\mathsf {MV}$
’s own evidential grounds.
$\mathsf {MV}$
’s own evidential grounds.
However, the argument has two main problems for our
![]() $\mathsf {MV}$
-based Core Universist.
$\mathsf {MV}$
-based Core Universist.
The first one is that the evidential resources it invokes (truth, consistency predictions, etc.) are not, in fact, available to him. Steel’s conception prides itself on not being dependent on any ‘metaphysics’ of universes. Therefore, intuitions about the structure of models with LCs, which underlie Woodin’s Argument and SCP, if argumentatively efficacious, may not bear on our Core Universist’s acceptance of ‘
![]() $\mathcal {C}\models $
Ultimate-L’.
$\mathcal {C}\models $
Ultimate-L’.
The other one is that, by using Woodin’s Argument in the present context, then the Core Universist would become practically indistinguishable from the Classic Universist who supports V=Ultimate-L: even coming from slightly different backgrounds, both would, indeed, agree on the fact that there is one universe of set theory (Ultimate-L) which is preferable to all others from the beginning, and it does not seem that the
![]() $\mathsf {MV}$
supporter’s evidential framework would commit him to such a view.
$\mathsf {MV}$
supporter’s evidential framework would commit him to such a view.
Let us now move on to explore another potential justificatory strategy.
5.4 An extrinsic argument
A different argument is based on resuming Steel’s reasons to adopt V=Ultimate-L (1.)–(3.) stated in Section 5.2: these, overall, suggest to the Core Universist that V=Ultimate-L is a very successful axiom, which could be seen as being already justified ‘extrinsically’ – insofar as practically all undecidable statements are settled by it.
More precisely, the Core Universist might use a form of ‘regressive’ reasoning here: he will require
![]() $\mathsf {MV}_T$
to incorporate ‘
$\mathsf {MV}_T$
to incorporate ‘
![]() $\mathcal {C} \models $
V=Ultimate-L’ in T, because he takes ‘V=Ultimate-L’ to be an already independently justified axiom.
$\mathcal {C} \models $
V=Ultimate-L’ in T, because he takes ‘V=Ultimate-L’ to be an already independently justified axiom.
However, in Section 5.2, we have already hinted at the inherent limitations of this strategy:
![]() $\mathsf {MV}$
would no longer be used as a means to indicate what bits of
$\mathsf {MV}$
would no longer be used as a means to indicate what bits of
![]() $\mathcal {L}_{\in }$
ought to be believed to be ‘meaningful’ (to legitimately hold); on the contrary, it would be
$\mathcal {L}_{\in }$
ought to be believed to be ‘meaningful’ (to legitimately hold); on the contrary, it would be
![]() $\mathcal {L}_{\in }$
to provide us information about what specific T should be chosen in
$\mathcal {L}_{\in }$
to provide us information about what specific T should be chosen in
![]() $\mathsf {MV}_T$
. In other terms, the Core Universist wanting to use this ‘extrinsic’ argument would, ultimately, violate his own unbiasedness about all different theories expressed by
$\mathsf {MV}_T$
. In other terms, the Core Universist wanting to use this ‘extrinsic’ argument would, ultimately, violate his own unbiasedness about all different theories expressed by
![]() $\mathsf {MV}$
.
$\mathsf {MV}$
.
Another, more general, concern is that V=Ultimate-L isn’t the only successful axiom he has at hand. In particular, since he knows that the core need not be Ultimate-L, and that T in
![]() $\mathsf {MV}_T$
is consistent with ‘
$\mathsf {MV}_T$
is consistent with ‘
![]() $\mathcal {C} \not \models $
V=Ultimate-L’ (Theorem 5.6), the Core Universist could ultimately settle on other, equally successful, axioms for the core. For instance, he might want to adopt ‘
$\mathcal {C} \not \models $
V=Ultimate-L’ (Theorem 5.6), the Core Universist could ultimately settle on other, equally successful, axioms for the core. For instance, he might want to adopt ‘
![]() $\mathcal {C} \models $
MM
$\mathcal {C} \models $
MM
![]() $^{++}$
’, as MM
$^{++}$
’, as MM
![]() $^{++}$
implies that
$^{++}$
implies that
![]() $c=\aleph _2$
, and is clearly able to settle many other undecidable statements.
$c=\aleph _2$
, and is clearly able to settle many other undecidable statements.
One final worry about the argument, which is worth mentioning, is that ‘success’ wasn’t really part of Steel’s narrative concerning
![]() $\mathsf {MV}$
from the beginning, although, clearly, LCs may be interpreted as being very ‘successful’ axioms. We do not want to delve into the full intricacies of the topic, but ‘success’ may really be a very volatile criterion, which, although helpful, may not lead the Core Universist to make ultimate choices about the nature of
$\mathsf {MV}$
from the beginning, although, clearly, LCs may be interpreted as being very ‘successful’ axioms. We do not want to delve into the full intricacies of the topic, but ‘success’ may really be a very volatile criterion, which, although helpful, may not lead the Core Universist to make ultimate choices about the nature of
![]() $\mathsf {MV}$
.
$\mathsf {MV}$
.
5.5 Summary
Let’s take stock. The progression from
![]() $\mathsf {ZFC}$
to
$\mathsf {ZFC}$
to
![]() $T=\mathsf {ZFC}$
+LCs+‘
$T=\mathsf {ZFC}$
+LCs+‘
![]() $\mathcal {C} \models $
V=Ultimate-L’, summarised in Table 1, shows that ascending through interpretative power (and consistency strength) of theories, is, presently, insufficient to suggest to the Core Universist that V is the core, or that V is any specific ‘world’, for instance, Ultimate-L. As we have seen, on the one hand, by adding further hypotheses to T in
$\mathcal {C} \models $
V=Ultimate-L’, summarised in Table 1, shows that ascending through interpretative power (and consistency strength) of theories, is, presently, insufficient to suggest to the Core Universist that V is the core, or that V is any specific ‘world’, for instance, Ultimate-L. As we have seen, on the one hand, by adding further hypotheses to T in
![]() $\mathsf {MV}_T$
, one may get an inconsistent theory; on the other, one could make choices, such as the addition of ‘
$\mathsf {MV}_T$
, one may get an inconsistent theory; on the other, one could make choices, such as the addition of ‘
![]() $\mathcal {C} \models $
V=Ultimate-L’, which, however, on
$\mathcal {C} \models $
V=Ultimate-L’, which, however, on
![]() $\mathsf {MV}$
’s own evidential grounds, do not seem to be much justified. This, overall, leaves us with the following, somewhat unpalatable, dilemma: either to stay with
$\mathsf {MV}$
’s own evidential grounds, do not seem to be much justified. This, overall, leaves us with the following, somewhat unpalatable, dilemma: either to stay with
![]() $T=\mathsf {ZFC}$
+LCs in
$T=\mathsf {ZFC}$
+LCs in
![]() $\mathsf {MV}_T$
, and thus view the core as fundamentally indeterminate, or move to a, globally, less justified strengthening of T, but finally get a determinate core.
$\mathsf {MV}_T$
, and thus view the core as fundamentally indeterminate, or move to a, globally, less justified strengthening of T, but finally get a determinate core.
Table 1 Behaviour of
![]() $\mathsf {MV}_T$
with respect to the core for different choices of T.
$\mathsf {MV}_T$
with respect to the core for different choices of T.

6 Concluding remarks and ways forward
Based on what one can prove in the theory
![]() $\mathsf {MV}_T$
, where
$\mathsf {MV}_T$
, where
![]() $T=\mathsf {ZFC}$
+‘there exists a proper class of extendible cardinals’, and further potential strengthenings, we have assessed the prospects of what we have called Steel’s Programme, and of the corresponding philosophical position that we have called Core Universism.
$T=\mathsf {ZFC}$
+‘there exists a proper class of extendible cardinals’, and further potential strengthenings, we have assessed the prospects of what we have called Steel’s Programme, and of the corresponding philosophical position that we have called Core Universism.
Our tentative conclusion is that there might still be a long way to go before the view that the core is Ultimate-L and, consequently, that V=Ultimate-L is the ultimate axiom for the Core Universist, gets fully validated; meanwhile, as is clear, V=Ultimate-L might ultimately be accepted on entirely different grounds.
We conclude the paper with suggesting some possible future scenarios for the investigation of the ‘core hypothesis’ within
![]() $\mathsf {MV}$
:
$\mathsf {MV}$
:
First Scenario. Stronger, hitherto unknown, LCs will, ‘more determinately’, settle the features of the core.
The idea, here, is that further ascending through consistency strength in an ideally ‘richer’ large-cardinal hierarchy will help settle the features of the core. Clearly, at present, nobody could possibly foresee whether there will be concrete developments in this direction, but note that Usuba’s key theorem (Theorem 3.5) has set an interesting precedent for results in this area which were widely unexpected.Footnote 59
Second Scenario. The ‘core hypothesis’ will ultimately be taken to just be a theoretical tool to foster and study the interplay between multiverse and universe thinking while dealing with set-theoretic incompleteness.
The scenario above construes Steel’s efforts as going in the direction of clarifying, not prescribing solutions for, the issues of whether there is a core universe and of what the core should be like. In this scenario, the core hypothesis would not, per se, suggest a unique course of action for Universists, yet may be taken to be informative on what resources and additional hypotheses are needed if one wants to settle the undecidable statements.Footnote 60
Third Scenario. The issue of the existence of a ‘preferred universe’ will be declared to be insoluble on purely proof-theoretic grounds (that is, by just focussing on the relationship between multiverse language and language of set theory), whilst further conceptual resources will ultimately be seen as fundamental to solve it.
As we have seen, Woodin’s Argument, for instance, provides us with alternative resources to solve the issue of what counts as a ‘preferred’ universe. Now, one could conjecture that it will turn out to be inevitable to resort to this kind of arguments to meet the Core Universist’s requirements.
In the paper, we have also addressed and, by our lights, made more transparent, several features, both mathematical and philosophical, of
![]() $\mathsf {MV}$
: in particular, the proof of the existence of the core, its persistent indeterminacy over different choices of T for
$\mathsf {MV}$
: in particular, the proof of the existence of the core, its persistent indeterminacy over different choices of T for
![]() $\mathsf {MV}_T$
, the connections between Ultimate-L and
$\mathsf {MV}_T$
, the connections between Ultimate-L and
![]() $\mathsf {MV}$
, the justifiability and role of LCs. Now, further mathematical work is, already at this stage, needed in order to further assess
$\mathsf {MV}$
, the justifiability and role of LCs. Now, further mathematical work is, already at this stage, needed in order to further assess
![]() $\mathsf {MV}$
’s hypotheses. In particular, ideally, much more should be known about:
$\mathsf {MV}$
’s hypotheses. In particular, ideally, much more should be known about:
-
• The status of the Ultimate-L Conjecture
-
• The prospects of a unified account of LCs
-
• A better understanding of the notion of ‘canonicity’ with respect to (alternative) models of set theory
We expect that further enlightenment on these issues will also carry with itself a more detailed understanding of what the Core Universist may legitimately claim, based on the structure of the multiverse. But, as we have seen, definite answers to many issues concerning
![]() $\mathsf {MV}$
, some confirming, others disconfirming, the Core Universist’s expectations, can already be provided.
$\mathsf {MV}$
, some confirming, others disconfirming, the Core Universist’s expectations, can already be provided.