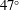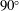1 Introduction
Superhydrophobic surfaces are a special class of patterned surfaces on which the presence of free surface menisci spanning surface protrusions in the microstructure of the surface is presumed to supply close to no-shear regions that can enhance slip (Rothstein Reference Rothstein2010). Over the last decade, there has been huge research effort in trying to understand the slip properties of such surfaces. However, the historical development of these endeavours has been characterized by contradictory observations with large discrepancies among the slippage levels reported across the literature. A useful recent review with many of the relevant references has been given by Lee, Choi & Kim (Reference Lee, Choi and Kim2016).
There is now mounting evidence that contamination by surfactants, even in trace amounts (Peaudecerf et al. Reference Peaudecerf, Landel, Goldstein and Luzzatto-Fegiz2017), can immobilize superhydrophobic surfaces, rendering them, essentially, no-slip surfaces. Kim & Hidrovo (Reference Kim and Hidrovo2012) performed experiments in a rectangular microchannel with regular sidewall patterning to visualize the location of the air–water interface within the roughness elements. One of their principal conclusions from this study of Poiseuille flow through the microchannel was that the air–water interface more closely resembles a no-slip boundary than a shear-free one, and that a Wenzel state can have better friction reducing properties than the Cassie state. In a joint experimental and numerical study of a longitudinal flow scenario, Bolognesi, Cottin-Bizonne & Pirat (Reference Bolognesi, Cottin-Bizonne and Pirat2014) tracked the effects of the meniscus shape, and the liquid–air interfacial friction properties, to examine the surface drag reduction properties. In this way, they were able to test the no-shear assumption on the menisci. These authors also suggested that their observed results were more consistent with immobilized no-slip free surfaces than those exhibiting zero shear. Bolognesi et al. (Reference Bolognesi, Cottin-Bizonne and Pirat2014) suggested surfactants or other surface contaminants as possible causes for this surface immobilization. In a very recent study, Peaudecerf et al. (Reference Peaudecerf, Landel, Goldstein and Luzzatto-Fegiz2017) focused on examining the effect of surfactants on hydrodynamic slip in longitudinal flows along unidirectionally patterned surfaces. Careful pressure control was used to maintain flat menisci, with the conclusion that even trace amounts of surfactants can cause a dramatic reduction in the expected slip enhancement properties of the surfaces, again, by causing an immobilization of these surfaces into effective no-slip zones.
The purpose of this paper is to offer complementary theoretical insights into the question of which surface condition is active on curved menisci in unidirectional superhydrophobic surfaces: an explicit comparison of the effective slip lengths for both no-shear and no-slip boundary conditions in longitudinal and transverse shear flows is performed. To elucidate further, an important class of superhydrophobic surfaces consists of those with a periodic unidirectional patterning of no-slip pillars separated by grooves that, in the Cassie state, are spanned by free surface menisci that trap a second fluid (e.g. air) in the subphase grooves (here, we ignore subphase fluid effects). Often, due to high pressures in the working fluid, the menisci will bow down into the grooves. Assuming, in the zero-capillary-number limit, that the menisci are shear-free, then they will be circular arcs with curvature determined by a Laplace–Young force balance. For steady longitudinal semi-infinite shear flow
![]() $(u,v,w)=(0,0,w(x,y))$
with shear rate
$(u,v,w)=(0,0,w(x,y))$
with shear rate
![]() $\dot{\unicode[STIX]{x1D6FE}}$
over such surfaces, the longitudinal effective slip length
$\dot{\unicode[STIX]{x1D6FE}}$
over such surfaces, the longitudinal effective slip length
![]() $\unicode[STIX]{x1D706}^{||}$
is defined as the quantity such that, as
$\unicode[STIX]{x1D706}^{||}$
is defined as the quantity such that, as
![]() $y\rightarrow \infty$
,
$y\rightarrow \infty$
,
For a steady transverse shear flow
![]() $(u,v,0)$
, the effective transverse slip length
$(u,v,0)$
, the effective transverse slip length
![]() $\unicode[STIX]{x1D706}^{\bot }$
is such that, as
$\unicode[STIX]{x1D706}^{\bot }$
is such that, as
![]() $y\rightarrow \infty$
, the velocity has the form
$y\rightarrow \infty$
, the velocity has the form
It is important to note that these two effective slip lengths can be defined whatever the nature of the boundary condition imposed on the curved meniscus. If a curved meniscus happens to be a no-slip surface – that is, it has been immobilized by some means – then we are equivalently dealing with a corrugated no-slip wall with circular-arc ‘riblets’, and it is more common then to refer to these effective slip lengths as protrusion heights (Bechert & Bartenwerfer Reference Bechert and Bartenwerfer1989; Luchini, Manzo & Pozzi Reference Luchini, Manzo and Pozzi1991). In the latter context, since the choice of the
![]() $y$
-origin is arbitrary, the only physically significant quantity is the difference
$y$
-origin is arbitrary, the only physically significant quantity is the difference
![]() $\unicode[STIX]{x1D706}^{||}-\unicode[STIX]{x1D706}^{\bot }$
, which is independent of the choice of
$\unicode[STIX]{x1D706}^{||}-\unicode[STIX]{x1D706}^{\bot }$
, which is independent of the choice of
![]() $y$
-origin, and quantifies how much a corrugated no-slip wall impedes a transverse shear relative to a longitudinal shear.
$y$
-origin, and quantifies how much a corrugated no-slip wall impedes a transverse shear relative to a longitudinal shear.

Figure 1. Downward protruding circular meniscus in a period-
![]() $L$
superhydrophobic surface. This paper compares effective slip lengths when the meniscus is both no-shear and no-slip.
$L$
superhydrophobic surface. This paper compares effective slip lengths when the meniscus is both no-shear and no-slip.
We now summarize our results. Consider the unidirectional superhydrophobic surface whose period window of length
![]() $L$
is shown in figure 1: a meniscus, of width
$L$
is shown in figure 1: a meniscus, of width
![]() $2c$
, protrudes into the groove by angle
$2c$
, protrudes into the groove by angle
![]() $\unicode[STIX]{x1D719}$
(here, we will not consider menisci protruding above
$\unicode[STIX]{x1D719}$
(here, we will not consider menisci protruding above
![]() $y=0$
). On introducing the usual complex variable
$y=0$
). On introducing the usual complex variable
![]() $z=x+\text{i}y$
, we introduce a family of approximating surfaces described by the image of a unit
$z=x+\text{i}y$
, we introduce a family of approximating surfaces described by the image of a unit
![]() $\unicode[STIX]{x1D701}$
-circle in a parametric
$\unicode[STIX]{x1D701}$
-circle in a parametric
![]() $\unicode[STIX]{x1D701}$
-plane under the conformal map
$\unicode[STIX]{x1D701}$
-plane under the conformal map
with parameters
![]() $a$
and
$a$
and
![]() $\unicode[STIX]{x1D701}_{0}$
given in terms of
$\unicode[STIX]{x1D701}_{0}$
given in terms of
![]() $c,L$
and
$c,L$
and
![]() $\unicode[STIX]{x1D719}$
as
$\unicode[STIX]{x1D719}$
as
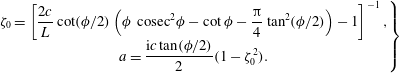 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D701}_{0}=\left[\frac{2c}{L}\cot (\unicode[STIX]{x1D719}/2)\left(\unicode[STIX]{x1D719}~\text{cosec}^{2}\unicode[STIX]{x1D719}-\cot \unicode[STIX]{x1D719}-\frac{\unicode[STIX]{x03C0}}{4}\tan ^{2}(\unicode[STIX]{x1D719}/2)\right)-1\right]^{-1},\\ \displaystyle a=\frac{\text{i}c\tan (\unicode[STIX]{x1D719}/2)}{2}(1-\unicode[STIX]{x1D701}_{0}^{2}).\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D701}_{0}=\left[\frac{2c}{L}\cot (\unicode[STIX]{x1D719}/2)\left(\unicode[STIX]{x1D719}~\text{cosec}^{2}\unicode[STIX]{x1D719}-\cot \unicode[STIX]{x1D719}-\frac{\unicode[STIX]{x03C0}}{4}\tan ^{2}(\unicode[STIX]{x1D719}/2)\right)-1\right]^{-1},\\ \displaystyle a=\frac{\text{i}c\tan (\unicode[STIX]{x1D719}/2)}{2}(1-\unicode[STIX]{x1D701}_{0}^{2}).\end{array}\right\}\end{eqnarray}$$
Clearly,
![]() $\unicode[STIX]{x1D701}_{0}$
is real and
$\unicode[STIX]{x1D701}_{0}$
is real and
![]() $a$
is purely imaginary. This class of mappings is found to give images of the unit
$a$
is purely imaginary. This class of mappings is found to give images of the unit
![]() $\unicode[STIX]{x1D701}$
-disc that are very close to the semi-infinite period window with the same values of
$\unicode[STIX]{x1D701}$
-disc that are very close to the semi-infinite period window with the same values of
![]() $c,L$
and
$c,L$
and
![]() $\unicode[STIX]{x1D719}$
as shown in figure 1. Figure 2 shows the image of the map (1.3) for
$\unicode[STIX]{x1D719}$
as shown in figure 1. Figure 2 shows the image of the map (1.3) for
![]() $\unicode[STIX]{x1D719}=90^{\circ }$
and the values
$\unicode[STIX]{x1D719}=90^{\circ }$
and the values
![]() $c=d=0.1,0.3,0.5$
together with superpositions of actual semicircular arcs separated by straight lines along
$c=d=0.1,0.3,0.5$
together with superpositions of actual semicircular arcs separated by straight lines along
![]() $y=0$
characterized by the same geometry. The domains are almost indistinguishable in all cases, with just mild smoothing out of the corner points. This is found to be the case for all choices of the parameters
$y=0$
characterized by the same geometry. The domains are almost indistinguishable in all cases, with just mild smoothing out of the corner points. This is found to be the case for all choices of the parameters
![]() $c,L$
and
$c,L$
and
![]() $\unicode[STIX]{x1D719}$
.
$\unicode[STIX]{x1D719}$
.

Figure 2. Surface shapes with period
![]() $L=1$
described by (1.3) and (1.4) for
$L=1$
described by (1.3) and (1.4) for
![]() $c=d=0.5,0.3$
and
$c=d=0.5,0.3$
and
![]() $0.1$
(this is the case
$0.1$
(this is the case
![]() $\unicode[STIX]{x1D719}=90^{\circ }$
; other protrusion angle choices with
$\unicode[STIX]{x1D719}=90^{\circ }$
; other protrusion angle choices with
![]() $c\neq d$
can be taken). The menisci are very close to being semicircular with near-flat inter-groove spacing of length approximately
$c\neq d$
can be taken). The menisci are very close to being semicircular with near-flat inter-groove spacing of length approximately
![]() $L-2d$
. The broken lines show exactly semicircular menisci of radius
$L-2d$
. The broken lines show exactly semicircular menisci of radius
![]() $d$
separated by straight lines along
$d$
separated by straight lines along
![]() $y=0$
; these broken lines are barely visible except near mildly smoothed-out corners, indicating the accuracy of the approximation.
$y=0$
; these broken lines are barely visible except near mildly smoothed-out corners, indicating the accuracy of the approximation.
The significance of this observation is that, for the special class of surfaces (1.3) approximating the superhydrophobic surface geometry, we are able to solve explicitly for both longitudinal and transverse shear flow over these surfaces if the menisci are taken to be no-slip surfaces. Consequently, we derive the following analytical slip length formulae:
with
![]() $\unicode[STIX]{x1D701}_{0}$
given in terms of the geometrical parameters
$\unicode[STIX]{x1D701}_{0}$
given in terms of the geometrical parameters
![]() $c,L$
and
$c,L$
and
![]() $\unicode[STIX]{x1D719}$
by (1.4). We expect (1.5) and (1.6) – which are the exact effective slip lengths for the approximating surfaces – to give excellent approximations to the effective slip lengths for shear flow over the no-slip circular-arc geometries of figure 1. On a physical note, it is by no means clear that the actual shape of a steady immobilized meniscus will be a circular arc – this will be a function of precisely what physical mechanism is immobilizing it (e.g. surfactant or thermally induced Marangoni stresses, transition to a Wenzel state) – but, for purposes of comparing effective slip lengths with the zero-capillary-number limit of a no-shear meniscus, we proceed under this assumption.
$\unicode[STIX]{x1D719}$
by (1.4). We expect (1.5) and (1.6) – which are the exact effective slip lengths for the approximating surfaces – to give excellent approximations to the effective slip lengths for shear flow over the no-slip circular-arc geometries of figure 1. On a physical note, it is by no means clear that the actual shape of a steady immobilized meniscus will be a circular arc – this will be a function of precisely what physical mechanism is immobilizing it (e.g. surfactant or thermally induced Marangoni stresses, transition to a Wenzel state) – but, for purposes of comparing effective slip lengths with the zero-capillary-number limit of a no-shear meniscus, we proceed under this assumption.
With formulae (1.5) and (1.6) to hand, we then compare them with analogous results for longitudinal and transverse shear flows over the same surfaces but where the menisci are now shear-free; the required results already exist in the literature. (Concerning the arbitrary choice of
![]() $y$
-origin just discussed, since we compare the quantities
$y$
-origin just discussed, since we compare the quantities
![]() $\unicode[STIX]{x1D706}^{||}$
and
$\unicode[STIX]{x1D706}^{||}$
and
![]() $\unicode[STIX]{x1D706}^{\bot }$
for the same surface geometry but two different choices of boundary condition, the results have physical significance in quantifying the difference between the effective slip properties for shear flow over surfaces with these two boundary condition choices.) The implications of these new results for possible immobilization of superhydrophobic surfaces by impurities or surfactant contamination are examined in § 5.
$\unicode[STIX]{x1D706}^{\bot }$
for the same surface geometry but two different choices of boundary condition, the results have physical significance in quantifying the difference between the effective slip properties for shear flow over surfaces with these two boundary condition choices.) The implications of these new results for possible immobilization of superhydrophobic surfaces by impurities or surfactant contamination are examined in § 5.

Figure 3. Conformal mapping from the unit
![]() $\unicode[STIX]{x1D701}$
-disc with logarithmic branch cut to a single period of the surface. Points labelled by the same letter correspond under the mapping (1.3). The area
$\unicode[STIX]{x1D701}$
-disc with logarithmic branch cut to a single period of the surface. Points labelled by the same letter correspond under the mapping (1.3). The area
![]() $A_{g}$
beneath
$A_{g}$
beneath
![]() $y=0$
is also indicated. Point
$y=0$
is also indicated. Point
![]() $A$
in the physical plane is at
$A$
in the physical plane is at
![]() $z=0$
.
$z=0$
.
2 A special class of surfaces
The class of surfaces to be studied will be described mathematically by conformal mappings (1.3) from the cut unit disc in a complex parametric
![]() $\unicode[STIX]{x1D701}$
-plane to a single period window of the flow pattern over the
$\unicode[STIX]{x1D701}$
-plane to a single period window of the flow pattern over the
![]() $L$
-periodic surface (figure 3). We need
$L$
-periodic surface (figure 3). We need
![]() $|\unicode[STIX]{x1D701}_{0}|>1$
so that the mapping avoids a simple pole inside the unit
$|\unicode[STIX]{x1D701}_{0}|>1$
so that the mapping avoids a simple pole inside the unit
![]() $\unicode[STIX]{x1D701}$
-disc. Other constraints on
$\unicode[STIX]{x1D701}$
-disc. Other constraints on
![]() $a$
and
$a$
and
![]() $\unicode[STIX]{x1D701}_{0}$
arise from the need to ensure univalency of the mapping. The branch of the logarithm (the two sides of the branch cut represent the two period window edges) is chosen to be along the positive real
$\unicode[STIX]{x1D701}_{0}$
arise from the need to ensure univalency of the mapping. The branch of the logarithm (the two sides of the branch cut represent the two period window edges) is chosen to be along the positive real
![]() $\unicode[STIX]{x1D701}$
-axis. The preimage of infinity is
$\unicode[STIX]{x1D701}$
-axis. The preimage of infinity is
![]() $\unicode[STIX]{x1D701}=0$
. The constant term in (1.3) ensures that
$\unicode[STIX]{x1D701}=0$
. The constant term in (1.3) ensures that
![]() $z(1)=0$
. It should be noted that
$z(1)=0$
. It should be noted that
![]() $A_{g}$
, defined as the fluid area below
$A_{g}$
, defined as the fluid area below
![]() $y=0$
, is
$y=0$
, is
Suppose now that we seek maps within this class that are ‘close’ to a circular-arc groove of length
![]() $2c$
with protrusion angle downwards
$2c$
with protrusion angle downwards
![]() $\unicode[STIX]{x1D719}$
. The geometry is clearly parametrized by
$\unicode[STIX]{x1D719}$
. The geometry is clearly parametrized by
![]() $c$
and
$c$
and
![]() $\unicode[STIX]{x1D719}$
, but we now seek the corresponding mapping parameters
$\unicode[STIX]{x1D719}$
, but we now seek the corresponding mapping parameters
![]() $a$
and
$a$
and
![]() $\unicode[STIX]{x1D701}_{0}$
. From simple geometrical considerations, it can be shown that
$\unicode[STIX]{x1D701}_{0}$
. From simple geometrical considerations, it can be shown that
To construct the class of mappings (1.3)–(1.4), we now insist that the image of
![]() $\unicode[STIX]{x1D701}=\text{e}^{\text{i}\unicode[STIX]{x03C0}}=-1$
under (1.3) is at
$\unicode[STIX]{x1D701}=\text{e}^{\text{i}\unicode[STIX]{x03C0}}=-1$
under (1.3) is at
![]() $L/2-\text{i}d$
, with
$L/2-\text{i}d$
, with
![]() $d$
given as in (2.2), and that the area
$d$
given as in (2.2), and that the area
![]() $A_{g}$
beneath the surface is given by the formula in (2.2). This leads, on use of (2.1) and (2.3), to
$A_{g}$
beneath the surface is given by the formula in (2.2). This leads, on use of (2.1) and (2.3), to
On substituting for
![]() $A_{g}$
and
$A_{g}$
and
![]() $d$
from (2.2), where they are given as functions of
$d$
from (2.2), where they are given as functions of
![]() $c$
and
$c$
and
![]() $\unicode[STIX]{x1D719}$
, we arrive after some algebra at (1.4). While the boundary shapes encoded in the class of conformal mappings (1.3)–(1.4) are approximations to the circular-arc boundaries in figure 1, by construction, the area
$\unicode[STIX]{x1D719}$
, we arrive after some algebra at (1.4). While the boundary shapes encoded in the class of conformal mappings (1.3)–(1.4) are approximations to the circular-arc boundaries in figure 1, by construction, the area
![]() $A_{g}$
beneath the
$A_{g}$
beneath the
![]() $y=0$
surface is exactly the same for both – an important fact given that, for longitudinal flow with a no-slip boundary condition, any effective slip is intuitively associated with changes in the cross-sectional area of the flow. Figure 2 gives evidence of how closely these mappings approximate downward protruding circular arcs. One should note the serendipity of this: we have no right to expect, a priori, that the fitting of just two parameters will produce conformal mappings with images that are uniformly close to the desired target curve. That it happens to be successful is pure mathematical luck.
$y=0$
surface is exactly the same for both – an important fact given that, for longitudinal flow with a no-slip boundary condition, any effective slip is intuitively associated with changes in the cross-sectional area of the flow. Figure 2 gives evidence of how closely these mappings approximate downward protruding circular arcs. One should note the serendipity of this: we have no right to expect, a priori, that the fitting of just two parameters will produce conformal mappings with images that are uniformly close to the desired target curve. That it happens to be successful is pure mathematical luck.
3 Longitudinal flow
Assuming no driving pressure gradient, the longitudinal flow
![]() $w(x,y)$
satisfies
$w(x,y)$
satisfies
in the fluid region above the surface, so it is natural to introduce the complex potential (Crowdy Reference Crowdy2011b
)
![]() $h(z)=\unicode[STIX]{x1D712}+\text{i}w$
. Since
$h(z)=\unicode[STIX]{x1D712}+\text{i}w$
. Since
![]() $w\rightarrow \dot{\unicode[STIX]{x1D6FE}}y$
as
$w\rightarrow \dot{\unicode[STIX]{x1D6FE}}y$
as
![]() $|z|\rightarrow \infty$
, then we require
$|z|\rightarrow \infty$
, then we require
as
![]() $z\rightarrow \infty$
with the no-slip condition
$z\rightarrow \infty$
with the no-slip condition
Now, consider the function
It can be directly verified that this function satisfies all requirements. Since, from (1.3), we can write
then, on comparison with (1.1), the slip length
![]() $\unicode[STIX]{x1D706}^{||}$
can be determined as
$\unicode[STIX]{x1D706}^{||}$
can be determined as
On use of (1.4) and (2.2) to substitute for
![]() $d$
and
$d$
and
![]() $\unicode[STIX]{x1D701}_{0}$
in terms of
$\unicode[STIX]{x1D701}_{0}$
in terms of
![]() $c$
and
$c$
and
![]() $\unicode[STIX]{x1D719}$
, we arrive at (1.5).
$\unicode[STIX]{x1D719}$
, we arrive at (1.5).
4 Transverse flow
The transverse flow problem is more difficult, not least because it is not conformally invariant, but, remarkably, it is exactly solvable for domains described by conformal mappings of the form (1.3), as we now show. Our mathematical derivation of the transverse flow solution is similar in spirit to that of Richardson (Reference Richardson1973), but we have eschewed his approach based on Taylor series, since, for our class of solutions (1.3), it would require an infinite number of terms. We adopt a more function theoretic approach.
The streamfunction
![]() $\unicode[STIX]{x1D713}(x,y)$
associated with a two-dimensional Stokes flow of a fluid of viscosity
$\unicode[STIX]{x1D713}(x,y)$
associated with a two-dimensional Stokes flow of a fluid of viscosity
![]() $\unicode[STIX]{x1D707}$
satisfies the biharmonic equation (Langlois Reference Langlois1964; Crowdy Reference Crowdy2011a
)
$\unicode[STIX]{x1D707}$
satisfies the biharmonic equation (Langlois Reference Langlois1964; Crowdy Reference Crowdy2011a
)
With
![]() $z=x+\text{i}y$
, the general solution to (4.1) is available in the form
$z=x+\text{i}y$
, the general solution to (4.1) is available in the form
where
![]() $f(z)$
and
$f(z)$
and
![]() $g(z)$
are two analytic functions in the fluid region. Let
$g(z)$
are two analytic functions in the fluid region. Let
denote the components of the fluid speed and let
![]() $p$
denote the fluid pressure. It can be shown (Langlois Reference Langlois1964; Crowdy Reference Crowdy2011a
) that
$p$
denote the fluid pressure. It can be shown (Langlois Reference Langlois1964; Crowdy Reference Crowdy2011a
) that
where primes denote differentiation with respect to the argument of the function. For the required shear flow as
![]() $y\rightarrow \infty$
, we need
$y\rightarrow \infty$
, we need
Henceforth, we take
![]() $\dot{\unicode[STIX]{x1D6FE}}=1$
. It is convenient to define the Schwarz function (Davis Reference Davis1974)
$\dot{\unicode[STIX]{x1D6FE}}=1$
. It is convenient to define the Schwarz function (Davis Reference Davis1974)
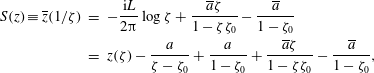 $$\begin{eqnarray}\displaystyle S(z)\equiv \overline{z}(1/\unicode[STIX]{x1D701}) & = & \displaystyle -\frac{\text{i}L}{2\unicode[STIX]{x03C0}}\log \unicode[STIX]{x1D701}+\frac{\overline{a}\unicode[STIX]{x1D701}}{1-\unicode[STIX]{x1D701}\unicode[STIX]{x1D701}_{0}}-\frac{\overline{a}}{1-\unicode[STIX]{x1D701}_{0}}\nonumber\\ \displaystyle & = & \displaystyle z(\unicode[STIX]{x1D701})-\frac{a}{\unicode[STIX]{x1D701}-\unicode[STIX]{x1D701}_{0}}+\frac{a}{1-\unicode[STIX]{x1D701}_{0}}+\frac{\overline{a}\unicode[STIX]{x1D701}}{1-\unicode[STIX]{x1D701}\unicode[STIX]{x1D701}_{0}}-\frac{\overline{a}}{1-\unicode[STIX]{x1D701}_{0}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S(z)\equiv \overline{z}(1/\unicode[STIX]{x1D701}) & = & \displaystyle -\frac{\text{i}L}{2\unicode[STIX]{x03C0}}\log \unicode[STIX]{x1D701}+\frac{\overline{a}\unicode[STIX]{x1D701}}{1-\unicode[STIX]{x1D701}\unicode[STIX]{x1D701}_{0}}-\frac{\overline{a}}{1-\unicode[STIX]{x1D701}_{0}}\nonumber\\ \displaystyle & = & \displaystyle z(\unicode[STIX]{x1D701})-\frac{a}{\unicode[STIX]{x1D701}-\unicode[STIX]{x1D701}_{0}}+\frac{a}{1-\unicode[STIX]{x1D701}_{0}}+\frac{\overline{a}\unicode[STIX]{x1D701}}{1-\unicode[STIX]{x1D701}\unicode[STIX]{x1D701}_{0}}-\frac{\overline{a}}{1-\unicode[STIX]{x1D701}_{0}},\end{eqnarray}$$
where we have used (1.3); hence,
![]() $S(z)=\overline{z}$
on the meniscus. Now, we define
$S(z)=\overline{z}$
on the meniscus. Now, we define
It will be shown that a class of explicit solutions is given by
where
![]() $F_{1},G_{0},G_{1}$
and
$F_{1},G_{0},G_{1}$
and
![]() $G_{-1}$
are constants to be determined. Two of these are related by
$G_{-1}$
are constants to be determined. Two of these are related by
To understand why (4.7) is the required solution, it should be noted first that the function
![]() $S(z)f^{\prime }(z)$
appearing in
$S(z)f^{\prime }(z)$
appearing in
![]() $G(\unicode[STIX]{x1D701})$
can be written as a function of
$G(\unicode[STIX]{x1D701})$
can be written as a function of
![]() $\unicode[STIX]{x1D701}$
on use of (4.6) and the chain rule
$\unicode[STIX]{x1D701}$
on use of (4.6) and the chain rule
![]() $f^{\prime }(z)=F^{\prime }(\unicode[STIX]{x1D701})/z^{\prime }(\unicode[STIX]{x1D701})$
. Condition (4.9) removes the simple pole of
$f^{\prime }(z)=F^{\prime }(\unicode[STIX]{x1D701})/z^{\prime }(\unicode[STIX]{x1D701})$
. Condition (4.9) removes the simple pole of
![]() $G(\unicode[STIX]{x1D701})$
due to the term
$G(\unicode[STIX]{x1D701})$
due to the term
![]() $-S(z)f^{\prime }(z)$
at
$-S(z)f^{\prime }(z)$
at
![]() $\unicode[STIX]{x1D701}=1/\unicode[STIX]{x1D701}_{0}$
, which is inside the unit disc. Both
$\unicode[STIX]{x1D701}=1/\unicode[STIX]{x1D701}_{0}$
, which is inside the unit disc. Both
![]() $F(\unicode[STIX]{x1D701})$
and
$F(\unicode[STIX]{x1D701})$
and
![]() $G(\unicode[STIX]{x1D701})$
are then analytic in the unit
$G(\unicode[STIX]{x1D701})$
are then analytic in the unit
![]() $\unicode[STIX]{x1D701}$
-disc except for singularities at
$\unicode[STIX]{x1D701}$
-disc except for singularities at
![]() $\unicode[STIX]{x1D701}=0$
which are chosen to ensure that the far-field conditions (4.5) are satisfied. Since, from (4.6),
$\unicode[STIX]{x1D701}=0$
which are chosen to ensure that the far-field conditions (4.5) are satisfied. Since, from (4.6),
![]() $S(z)\rightarrow z+\text{const.}$
as
$S(z)\rightarrow z+\text{const.}$
as
![]() $|z|\rightarrow \infty$
, then it is easy to check that
$|z|\rightarrow \infty$
, then it is easy to check that
![]() $F(\unicode[STIX]{x1D701})$
and
$F(\unicode[STIX]{x1D701})$
and
![]() $G(\unicode[STIX]{x1D701})$
satisfy (4.5) as
$G(\unicode[STIX]{x1D701})$
satisfy (4.5) as
![]() $\unicode[STIX]{x1D701}\rightarrow 0$
. The corresponding (complex) velocity field is
$\unicode[STIX]{x1D701}\rightarrow 0$
. The corresponding (complex) velocity field is
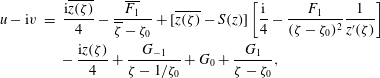 $$\begin{eqnarray}\displaystyle u-\text{i}v & = & \displaystyle \frac{\text{i}\overline{z(\unicode[STIX]{x1D701})}}{4}-\frac{\overline{F_{1}}}{\overline{\unicode[STIX]{x1D701}}-\unicode[STIX]{x1D701}_{0}}+[\overline{z(\unicode[STIX]{x1D701})}-S(z)]\left[\frac{\text{i}}{4}-\frac{F_{1}}{(\unicode[STIX]{x1D701}-\unicode[STIX]{x1D701}_{0})^{2}}\frac{1}{z^{\prime }(\unicode[STIX]{x1D701})}\right]\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\text{i}z(\unicode[STIX]{x1D701})}{4}+\frac{G_{-1}}{\unicode[STIX]{x1D701}-1/\unicode[STIX]{x1D701}_{0}}+G_{0}+\frac{G_{1}}{\unicode[STIX]{x1D701}-\unicode[STIX]{x1D701}_{0}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u-\text{i}v & = & \displaystyle \frac{\text{i}\overline{z(\unicode[STIX]{x1D701})}}{4}-\frac{\overline{F_{1}}}{\overline{\unicode[STIX]{x1D701}}-\unicode[STIX]{x1D701}_{0}}+[\overline{z(\unicode[STIX]{x1D701})}-S(z)]\left[\frac{\text{i}}{4}-\frac{F_{1}}{(\unicode[STIX]{x1D701}-\unicode[STIX]{x1D701}_{0})^{2}}\frac{1}{z^{\prime }(\unicode[STIX]{x1D701})}\right]\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\text{i}z(\unicode[STIX]{x1D701})}{4}+\frac{G_{-1}}{\unicode[STIX]{x1D701}-1/\unicode[STIX]{x1D701}_{0}}+G_{0}+\frac{G_{1}}{\unicode[STIX]{x1D701}-\unicode[STIX]{x1D701}_{0}},\end{eqnarray}$$
which can be shown to be
![]() $L$
-periodic. On the surface where
$L$
-periodic. On the surface where
![]() $|\unicode[STIX]{x1D701}|=1$
, and on use of (4.6), this becomes
$|\unicode[STIX]{x1D701}|=1$
, and on use of (4.6), this becomes
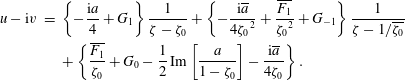 $$\begin{eqnarray}\displaystyle u-\text{i}v & = & \displaystyle \left\{-\frac{\text{i}a}{4}+G_{1}\right\}\frac{1}{\unicode[STIX]{x1D701}-\unicode[STIX]{x1D701}_{0}}+\left\{-\frac{\text{i}\overline{a}}{4{\unicode[STIX]{x1D701}_{0}}^{2}}+\frac{\overline{F_{1}}}{{\unicode[STIX]{x1D701}_{0}}^{2}}+G_{-1}\right\}\frac{1}{\unicode[STIX]{x1D701}-1/\overline{\unicode[STIX]{x1D701}_{0}}}\nonumber\\ \displaystyle & & \displaystyle +\left\{\frac{\overline{F_{1}}}{\unicode[STIX]{x1D701}_{0}}+G_{0}-\frac{1}{2}\,\text{Im}\left[\frac{a}{1-\unicode[STIX]{x1D701}_{0}}\right]-\frac{\text{i}\overline{a}}{4\unicode[STIX]{x1D701}_{0}}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u-\text{i}v & = & \displaystyle \left\{-\frac{\text{i}a}{4}+G_{1}\right\}\frac{1}{\unicode[STIX]{x1D701}-\unicode[STIX]{x1D701}_{0}}+\left\{-\frac{\text{i}\overline{a}}{4{\unicode[STIX]{x1D701}_{0}}^{2}}+\frac{\overline{F_{1}}}{{\unicode[STIX]{x1D701}_{0}}^{2}}+G_{-1}\right\}\frac{1}{\unicode[STIX]{x1D701}-1/\overline{\unicode[STIX]{x1D701}_{0}}}\nonumber\\ \displaystyle & & \displaystyle +\left\{\frac{\overline{F_{1}}}{\unicode[STIX]{x1D701}_{0}}+G_{0}-\frac{1}{2}\,\text{Im}\left[\frac{a}{1-\unicode[STIX]{x1D701}_{0}}\right]-\frac{\text{i}\overline{a}}{4\unicode[STIX]{x1D701}_{0}}\right\}.\end{eqnarray}$$
We can therefore satisfy the no-slip condition everywhere on the surface if we make all of the curly-bracketed terms vanish. This implies the conditions
These three equations, together with (4.9), determine the four constants
![]() $F_{1},G_{-1},G_{0}$
and
$F_{1},G_{-1},G_{0}$
and
![]() $G_{1}$
. On elimination of
$G_{1}$
. On elimination of
![]() $G_{-1}$
between (4.9) and (4.12b
), we find
$G_{-1}$
between (4.9) and (4.12b
), we find
With
![]() $F_{1}$
thus determined, the parameters
$F_{1}$
thus determined, the parameters
![]() $G_{-1},G_{0}$
and
$G_{-1},G_{0}$
and
![]() $G_{1}$
follow explicitly from (4.9) and (4.12). Finally, the slip length is obtained by analysis of expression (4.10) as
$G_{1}$
follow explicitly from (4.9) and (4.12). Finally, the slip length is obtained by analysis of expression (4.10) as
![]() $\unicode[STIX]{x1D701}\rightarrow 0$
and comparison with (1.2):
$\unicode[STIX]{x1D701}\rightarrow 0$
and comparison with (1.2):
After some algebra, on use of expression (4.13) for
![]() $F_{1}$
, we arrive at (1.6).
$F_{1}$
, we arrive at (1.6).

Figure 4. Normalized longitudinal slip length for grooves of aspect ratio
![]() $2c/L=0.5$
as a function of downward protrusion angle
$2c/L=0.5$
as a function of downward protrusion angle
![]() $\unicode[STIX]{x1D719}$
. The no-shear results are based on a slip length formula of Crowdy (Reference Crowdy2016); the no-slip results are from (1.5). Data points for
$\unicode[STIX]{x1D719}$
. The no-shear results are based on a slip length formula of Crowdy (Reference Crowdy2016); the no-slip results are from (1.5). Data points for
![]() $\unicode[STIX]{x1D719}=0.1870$
and
$\unicode[STIX]{x1D719}=0.1870$
and
![]() $\unicode[STIX]{x1D719}=0.1$
corresponding to estimates of the meniscus geometries of experiments M1 and M2 of Bolognesi et al. (Reference Bolognesi, Cottin-Bizonne and Pirat2014) are shown. The no-slip results show behaviour consistent with the experiments.
$\unicode[STIX]{x1D719}=0.1$
corresponding to estimates of the meniscus geometries of experiments M1 and M2 of Bolognesi et al. (Reference Bolognesi, Cottin-Bizonne and Pirat2014) are shown. The no-slip results show behaviour consistent with the experiments.
5 Comparison of no-slip and no-shear assumptions
Since the consensus in much previous work has been that the menisci in superhydrophobic surfaces are close to shear-free, there has been great effort in seeking to quantify the effective slip properties under a shear-free assumption. Those prior results, coupled with the complementary results derived here for the same class of superhydrophobic surface geometries, allow us to test this assumption. For longitudinal flow, Crowdy (Reference Crowdy2016) has derived a formula for the effective slip length for exactly circular no-shear menisci. The effective slip length in (1.4) of Crowdy (Reference Crowdy2016) is plotted as a function of
![]() $\unicode[STIX]{x1D719}$
in figure 4 along with the new slip length result (1.5) for a no-slip surface with the same fixed value of
$\unicode[STIX]{x1D719}$
in figure 4 along with the new slip length result (1.5) for a no-slip surface with the same fixed value of
![]() $2c/L=0.5$
, corresponding to the no-shear fraction used in the experiments of Bolognesi et al. (Reference Bolognesi, Cottin-Bizonne and Pirat2014). (Formula (1.4) of Crowdy (Reference Crowdy2016) is known to be accurate to within 1 %–2 % for this normalized groove width.) An immediate observation is that, as
$2c/L=0.5$
, corresponding to the no-shear fraction used in the experiments of Bolognesi et al. (Reference Bolognesi, Cottin-Bizonne and Pirat2014). (Formula (1.4) of Crowdy (Reference Crowdy2016) is known to be accurate to within 1 %–2 % for this normalized groove width.) An immediate observation is that, as
![]() $\unicode[STIX]{x1D719}$
increases, the slip associated with a no-shear surface decreases while the slip associated with a no-slip surface increases. In two experiments, referred to as M1 and M2, Bolognesi et al. (Reference Bolognesi, Cottin-Bizonne and Pirat2014) observed that a more depressed groove associated with experiment M1 is associated with a larger slip length than experiment M2, where the interface invaded the groove to a lesser degree. As those authors pointed out, this is precisely not what is expected if the meniscus is a no-shear surface. Bolognesi et al. (Reference Bolognesi, Cottin-Bizonne and Pirat2014) went on to suggest that the observed behaviour is more consistent with the meniscus being a no-slip surface. Figure 4 provides theoretical evidence to support this.
$\unicode[STIX]{x1D719}$
increases, the slip associated with a no-shear surface decreases while the slip associated with a no-slip surface increases. In two experiments, referred to as M1 and M2, Bolognesi et al. (Reference Bolognesi, Cottin-Bizonne and Pirat2014) observed that a more depressed groove associated with experiment M1 is associated with a larger slip length than experiment M2, where the interface invaded the groove to a lesser degree. As those authors pointed out, this is precisely not what is expected if the meniscus is a no-shear surface. Bolognesi et al. (Reference Bolognesi, Cottin-Bizonne and Pirat2014) went on to suggest that the observed behaviour is more consistent with the meniscus being a no-slip surface. Figure 4 provides theoretical evidence to support this.
From figure 3 of Bolognesi et al. (Reference Bolognesi, Cottin-Bizonne and Pirat2014), we fitted our theoretical profiles to the experimental meniscus profiles by visually estimating the geometrical parameters
![]() $d/c=1.5~\unicode[STIX]{x03BC}\text{m}/16~\unicode[STIX]{x03BC}\text{m}$
for experiment M1 and
$d/c=1.5~\unicode[STIX]{x03BC}\text{m}/16~\unicode[STIX]{x03BC}\text{m}$
for experiment M1 and
![]() $d/c=0.8~\unicode[STIX]{x03BC}\text{m}/16~\unicode[STIX]{x03BC}\text{m}$
for experiment M2. On use of (2.2), the associated downward protrusion angles
$d/c=0.8~\unicode[STIX]{x03BC}\text{m}/16~\unicode[STIX]{x03BC}\text{m}$
for experiment M2. On use of (2.2), the associated downward protrusion angles
![]() $\unicode[STIX]{x1D719}$
can be calculated, and these are indicated by the two dotted ordinates shown in figure 4. It is found that the slip associated with M1 is approximately 80 % greater than that associated with M2. Bolognesi et al. (Reference Bolognesi, Cottin-Bizonne and Pirat2014) reported an increase of 40 %, but full quantitative agreement cannot be expected since the experiments were carried out in a closed geometry, while our formula (1.5) does not take a no-slip upper wall into account. Moreover, the experimentally observed menisci display flattened bottoms, while the results here are for near-circular arcs – a fact that reminds us of the comment made earlier that it is not clear what the true shape of any immobilized meniscus will actually be. Nevertheless, the results here are in corroborative qualitative agreement with the experimental observations. Bolognesi et al. (Reference Bolognesi, Cottin-Bizonne and Pirat2014) compared their observed global slip length against the prediction of a flat-meniscus no-shear result due to Philip (Reference Philip1972) and noticed that the former is approximately a tenth of that predicted by the no-shear model. It is clear from the ordinates drawn on figure 4 that the slip length according to the no-slip model is close to 10 % of that predicted by a no-shear model, in broad agreement with the experiments (Bolognesi et al.
Reference Bolognesi, Cottin-Bizonne and Pirat2014).
$\unicode[STIX]{x1D719}$
can be calculated, and these are indicated by the two dotted ordinates shown in figure 4. It is found that the slip associated with M1 is approximately 80 % greater than that associated with M2. Bolognesi et al. (Reference Bolognesi, Cottin-Bizonne and Pirat2014) reported an increase of 40 %, but full quantitative agreement cannot be expected since the experiments were carried out in a closed geometry, while our formula (1.5) does not take a no-slip upper wall into account. Moreover, the experimentally observed menisci display flattened bottoms, while the results here are for near-circular arcs – a fact that reminds us of the comment made earlier that it is not clear what the true shape of any immobilized meniscus will actually be. Nevertheless, the results here are in corroborative qualitative agreement with the experimental observations. Bolognesi et al. (Reference Bolognesi, Cottin-Bizonne and Pirat2014) compared their observed global slip length against the prediction of a flat-meniscus no-shear result due to Philip (Reference Philip1972) and noticed that the former is approximately a tenth of that predicted by the no-shear model. It is clear from the ordinates drawn on figure 4 that the slip length according to the no-slip model is close to 10 % of that predicted by a no-shear model, in broad agreement with the experiments (Bolognesi et al.
Reference Bolognesi, Cottin-Bizonne and Pirat2014).

Figure 5. Normalized transverse slip length for grooves of aspect ratio
![]() $2c/L=0.2$
as a function of downward protrusion angle
$2c/L=0.2$
as a function of downward protrusion angle
![]() $\unicode[STIX]{x1D719}$
. The no-shear results are based on the slip length formula of Davis & Lauga (Reference Davis and Lauga2009); the no-slip results are from (1.6). Cross-over occurs at a critical angle of
$\unicode[STIX]{x1D719}$
. The no-shear results are based on the slip length formula of Davis & Lauga (Reference Davis and Lauga2009); the no-slip results are from (1.6). Cross-over occurs at a critical angle of
![]() $\unicode[STIX]{x1D719}\approx 46.8^{\circ }$
$\unicode[STIX]{x1D719}\approx 46.8^{\circ }$
The results for the transverse flow case are also revealing. Figure 5 shows results for
![]() $2c/L=0.2$
, which has been deliberately chosen to be sufficiently small that we can make use of the dilute limit slip length formula found by Davis & Lauga (Reference Davis and Lauga2009). Figure 5 shows the predictions of this no-shear model for an exactly circular arc together with the results from the new formula (1.6) for no-slip surfaces of very nearly the same shape. Once again, we find that the slip length for a no-slip surface increases with the downward protrusion angle
$2c/L=0.2$
, which has been deliberately chosen to be sufficiently small that we can make use of the dilute limit slip length formula found by Davis & Lauga (Reference Davis and Lauga2009). Figure 5 shows the predictions of this no-shear model for an exactly circular arc together with the results from the new formula (1.6) for no-slip surfaces of very nearly the same shape. Once again, we find that the slip length for a no-slip surface increases with the downward protrusion angle
![]() $\unicode[STIX]{x1D719}$
, in contrast to the decrease in slip length under the assumption that the menisci are shear-free. A new feature, not observed for longitudinal flow, is that we find a critical downward protrusion angle
$\unicode[STIX]{x1D719}$
, in contrast to the decrease in slip length under the assumption that the menisci are shear-free. A new feature, not observed for longitudinal flow, is that we find a critical downward protrusion angle
![]() $\unicode[STIX]{x1D719}\approx 0.816\approx 46.8^{\circ }$
at which the effective slip length associated with a no-shear surface exactly coincides with that associated with a no-slip surface. This means that, for this critical surface geometry, it is impossible to tell the nature of the boundary condition on the surface by looking at the effective slip length. Expressed differently, close to such critical meniscus geometries, one might believe that a no-shear boundary condition is active on the interface, and is thus responsible for enhanced slip, but really the enhanced slip is caused by the downward deformation of an immobilized no-slip meniscus. Indeed, albeit with respect to longitudinal flows, Bolognesi et al. (Reference Bolognesi, Cottin-Bizonne and Pirat2014) made the comment ‘Discriminating between the effects of a deformed meniscus, on one side, and the interfacial friction at the liquid–air interface, on the other side, is not an easy task as this requires measuring the flow nearby the meniscus while simultaneously determining its shape and position’. Our theoretical results here underline this concern: the crossing of graphs in figure 5 provides evidence of a source of possible error in interpreting experimental results based purely on effective slip data. Figure 5 shows that for angles well above critical, a no-slip meniscus can be significantly more slippery than a no-shear surface. Indeed, by changing the normalized groove width
$\unicode[STIX]{x1D719}\approx 0.816\approx 46.8^{\circ }$
at which the effective slip length associated with a no-shear surface exactly coincides with that associated with a no-slip surface. This means that, for this critical surface geometry, it is impossible to tell the nature of the boundary condition on the surface by looking at the effective slip length. Expressed differently, close to such critical meniscus geometries, one might believe that a no-shear boundary condition is active on the interface, and is thus responsible for enhanced slip, but really the enhanced slip is caused by the downward deformation of an immobilized no-slip meniscus. Indeed, albeit with respect to longitudinal flows, Bolognesi et al. (Reference Bolognesi, Cottin-Bizonne and Pirat2014) made the comment ‘Discriminating between the effects of a deformed meniscus, on one side, and the interfacial friction at the liquid–air interface, on the other side, is not an easy task as this requires measuring the flow nearby the meniscus while simultaneously determining its shape and position’. Our theoretical results here underline this concern: the crossing of graphs in figure 5 provides evidence of a source of possible error in interpreting experimental results based purely on effective slip data. Figure 5 shows that for angles well above critical, a no-slip meniscus can be significantly more slippery than a no-shear surface. Indeed, by changing the normalized groove width
![]() $2c/L$
in the interval [0, 0.47] (where Teo & Khoo (Reference Teo and Khoo2016) have shown the formula of Davis & Lauga (Reference Davis and Lauga2009) to be 10 % accurate), we find that for downward protrusion angles around
$2c/L$
in the interval [0, 0.47] (where Teo & Khoo (Reference Teo and Khoo2016) have shown the formula of Davis & Lauga (Reference Davis and Lauga2009) to be 10 % accurate), we find that for downward protrusion angles around
![]() $80^{\circ }$
, the surface can be almost twice as slippery if immobilized as if it is free of shear (cf. Kim & Hidrovo Reference Kim and Hidrovo2012).
$80^{\circ }$
, the surface can be almost twice as slippery if immobilized as if it is free of shear (cf. Kim & Hidrovo Reference Kim and Hidrovo2012).
In confined longitudinal microchannel flows with a lower superhydrophobic wall, say, the effective slip length is usually defined by equating the pressure-driven flux through the channel with that in a channel having a Navier slip condition,
![]() $\unicode[STIX]{x1D706}_{NS}\,\text{d}w/\text{d}y=w$
, imposed on the lower wall; the value of
$\unicode[STIX]{x1D706}_{NS}\,\text{d}w/\text{d}y=w$
, imposed on the lower wall; the value of
![]() $\unicode[STIX]{x1D706}_{NS}$
for which these fluxes are equal (for the same driving pressure gradient) is the effective slip length. It is easy to show that for channels whose height is large compared with the pitch of the surface, this effective slip length
$\unicode[STIX]{x1D706}_{NS}$
for which these fluxes are equal (for the same driving pressure gradient) is the effective slip length. It is easy to show that for channels whose height is large compared with the pitch of the surface, this effective slip length
![]() $\unicode[STIX]{x1D706}_{NS}$
coincides, at leading order in an aspect ratio expansion, with the effective slip lengths found here.
$\unicode[STIX]{x1D706}_{NS}$
coincides, at leading order in an aspect ratio expansion, with the effective slip lengths found here.
Finally, a different interpretation of our results is that we have found new analytical solutions for simple shear over a periodic array of near-circular surface notches (or ‘riblets’) in the Wenzel state with fully penetrated grooves and no free surfaces (Bechert & Bartenwerfer Reference Bechert and Bartenwerfer1989; Luchini et al. Reference Luchini, Manzo and Pozzi1991).
Acknowledgements
The author is supported by an EPSRC Established Career Fellowship (EP/K019430/10), EPSRC Grant EP/K041134/1 and a Royal Society Wolfson Research Merit Award.