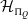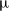1. Introduction
Given a quiver Q, in [Reference Kontsevich and Soibelman26] Kontsevich and Soibelman define the cohomological Hall algebra
which has as underlying vector space the singular cohomology of the stack of finite-dimensional complex representations of Q, shifted in cohomological degree by the Euler form (see (2.1) for the definition). As indicated by (1.1), this algebra is graded by the dimension vectors of representations of Q. The multiplication is defined by taking push-forward and pull-back of cohomology in the usual correspondence diagram
In the diagram (1.2),
![]() $\mathfrak{M}(Q)=\coprod_{\textbf{d}\in \mathbb{N}^{Q_0}}\mathfrak{M}_{\textbf{d}}(Q)$
is the stack of finite-dimensional Q-representations,
$\mathfrak{M}(Q)=\coprod_{\textbf{d}\in \mathbb{N}^{Q_0}}\mathfrak{M}_{\textbf{d}}(Q)$
is the stack of finite-dimensional Q-representations,
![]() $\mathfrak{E}\textrm{xact}(Q)$
is the stack of short exact sequences of Q-representations, and
$\mathfrak{E}\textrm{xact}(Q)$
is the stack of short exact sequences of Q-representations, and
![]() $\unicode{x03C0}_i$
is the morphism taking a short exact sequence to its ith entry.
$\unicode{x03C0}_i$
is the morphism taking a short exact sequence to its ith entry.
If Q is moreover symmetric (i.e. for every pair of vertices i,j, there are as many arrows from i to j as from j to i), then the multiplication respects the cohomological degree, and a theorem of Efimov [Reference Efimov15] states that (a slight modification of)
![]() $\mathcal{A}_Q$
is a free supercommutative algebra; the ‘super’ here means that elements in odd cohomological degrees anti-commute with each other.
$\mathcal{A}_Q$
is a free supercommutative algebra; the ‘super’ here means that elements in odd cohomological degrees anti-commute with each other.
There are a couple of instances in which this result is possible to check by hand; indeed, it was observed in [Reference Kontsevich and Soibelman26, Section 2.5] that if
![]() $Q^{(l)}$
denotes the quiver with one vertex and l loops, then
$Q^{(l)}$
denotes the quiver with one vertex and l loops, then
where
![]() $[{-}1]$
denotes a cohomological shift, and
$[{-}1]$
denotes a cohomological shift, and
![]() $u^i$
is placed in cohomological degree 2i. Both algebras are free supercommutative algebras generated by a countable set of symbols
$u^i$
is placed in cohomological degree 2i. Both algebras are free supercommutative algebras generated by a countable set of symbols
![]() $\unicode{x03B1}_i$
for
$\unicode{x03B1}_i$
for
![]() $i\geq 0$
, with
$i\geq 0$
, with
![]() $\unicode{x03B1}_i$
placed in cohomological degree
$\unicode{x03B1}_i$
placed in cohomological degree
![]() $1+2i$
in the zero-loop case, and in cohomological degree 2i in the one-loop case. In other words, (1.3) states that
$1+2i$
in the zero-loop case, and in cohomological degree 2i in the one-loop case. In other words, (1.3) states that
![]() $\mathcal{A}_{Q^{(0)}}$
is a free exterior algebra with countably many generators, while (1.4) states that
$\mathcal{A}_{Q^{(0)}}$
is a free exterior algebra with countably many generators, while (1.4) states that
![]() $\mathcal{A}_{Q^{(1)}}$
is a free commutative algebra with the same generators. As observed in [Reference Kontsevich and Soibelman26], the fact that the underlying vector spaces of the two algebras are the same (since
$\mathcal{A}_{Q^{(1)}}$
is a free commutative algebra with the same generators. As observed in [Reference Kontsevich and Soibelman26], the fact that the underlying vector spaces of the two algebras are the same (since
![]() $\mathfrak{M}_n(Q^{(l)})$
is homotopic to
$\mathfrak{M}_n(Q^{(l)})$
is homotopic to
![]() $\textrm{BGl}_n$
, regardless of l) can be seen as a consequence of the boson-fermion correspondence in representation theory.
$\textrm{BGl}_n$
, regardless of l) can be seen as a consequence of the boson-fermion correspondence in representation theory.
Now let Q be an arbitrary finite quiver. We form the tripled quiver
![]() $\tilde{Q}$
, by adjoining to the quiver Q an arrow
$\tilde{Q}$
, by adjoining to the quiver Q an arrow
![]() $a^*$
with the opposite orientation to a, for each a an arrow of Q, and also adjoining a loop
$a^*$
with the opposite orientation to a, for each a an arrow of Q, and also adjoining a loop
![]() $\omega_i$
at each vertex i of Q. So for instance,
$\omega_i$
at each vertex i of Q. So for instance,
![]() $\widetilde{Q^{(1)}}\cong Q^{(3)}$
. The quiver
$\widetilde{Q^{(1)}}\cong Q^{(3)}$
. The quiver
![]() $\tilde{Q}$
carries a canonical cubic potential
$\tilde{Q}$
carries a canonical cubic potential
and one may define (again as in [Reference Kontsevich and Soibelman26]) the critical cohomological Hall algebra
![]() $\mathcal{A}_{\tilde{Q},\tilde{W}}$
. Again, the multiplication respects cohomological degree. The underlying vector space of this algebra is the vanishing cycle cohomology of the function
$\mathcal{A}_{\tilde{Q},\tilde{W}}$
. Again, the multiplication respects cohomological degree. The underlying vector space of this algebra is the vanishing cycle cohomology of the function
![]() $\text{Tr}(\tilde{W})$
on the stack
$\text{Tr}(\tilde{W})$
on the stack
![]() $\mathfrak{M}\!\left(\tilde{Q}\right)$
. The multiplication is defined via pull-back and push-forward of vanishing cycle cohomology along the same correspondence diagram (1.2). Via dimensional reduction [Reference Davison8] the algebra
$\mathfrak{M}\!\left(\tilde{Q}\right)$
. The multiplication is defined via pull-back and push-forward of vanishing cycle cohomology along the same correspondence diagram (1.2). Via dimensional reduction [Reference Davison8] the algebra
![]() $\mathcal{A}_{\tilde{Q},\tilde{W}}$
is isomorphic [Reference Ren and Soibelman38, Reference Yang and Zhao45] to the cohomological Hall algebra structure on the Borel–Moore homology of the stack of representations of the preprojective algebra
$\mathcal{A}_{\tilde{Q},\tilde{W}}$
is isomorphic [Reference Ren and Soibelman38, Reference Yang and Zhao45] to the cohomological Hall algebra structure on the Borel–Moore homology of the stack of representations of the preprojective algebra
![]() $\Pi_Q$
constructed by Schiffmann and Vasserot in [Reference Schiffmann and Vasserot40] and studied in [Reference Yang and Zhao46].
$\Pi_Q$
constructed by Schiffmann and Vasserot in [Reference Schiffmann and Vasserot40] and studied in [Reference Yang and Zhao46].
In general, the algebra
![]() $\mathcal{A}_{\tilde{Q},\tilde{W}}$
is not supercommutative; for example,
$\mathcal{A}_{\tilde{Q},\tilde{W}}$
is not supercommutative; for example,
![]() $\mathcal{A}_{\tilde{Q},\tilde{W}}$
contains the universal enveloping algebra of the Kac–Moody Lie algebra associated with the quiver Q
′ obtained by removing all vertices from Q that support 1-cycles [Reference Davison10]. On the other hand, via the cohomological integrality theorem [Reference Davison and Meinhardt11], the entire algebra
$\mathcal{A}_{\tilde{Q},\tilde{W}}$
contains the universal enveloping algebra of the Kac–Moody Lie algebra associated with the quiver Q
′ obtained by removing all vertices from Q that support 1-cycles [Reference Davison10]. On the other hand, via the cohomological integrality theorem [Reference Davison and Meinhardt11], the entire algebra
![]() $\mathcal{A}_{\tilde{Q},\tilde{W}}$
satisfies a Poincaré–Birkhoff–Witt theorem, meaning that we have an
$\mathcal{A}_{\tilde{Q},\tilde{W}}$
satisfies a Poincaré–Birkhoff–Witt theorem, meaning that we have an
![]() $\mathbb{N}^{Q_0}$
-graded isomorphism of cohomologically graded vector spaces (but not of algebras):
$\mathbb{N}^{Q_0}$
-graded isomorphism of cohomologically graded vector spaces (but not of algebras):
 \begin{align}\mathcal{A}_{\tilde{Q},\tilde{W}}\cong \textbf{Sym}\!\left(\bigoplus_{\textbf{d}\in\mathbb{N}^{Q_0}}\Big(\textrm{BPS}_{\tilde{Q},\tilde{W},\textbf{d}}\otimes \mathbb{Q}[u]\Big)[{-}1]\right).\end{align}
\begin{align}\mathcal{A}_{\tilde{Q},\tilde{W}}\cong \textbf{Sym}\!\left(\bigoplus_{\textbf{d}\in\mathbb{N}^{Q_0}}\Big(\textrm{BPS}_{\tilde{Q},\tilde{W},\textbf{d}}\otimes \mathbb{Q}[u]\Big)[{-}1]\right).\end{align}
In the isomorphism (1.6),
![]() $\textrm{BPS}_{\tilde{Q},\tilde{W},\textbf{d}}$
is a cohomologically graded vector space, the whole of
$\textrm{BPS}_{\tilde{Q},\tilde{W},\textbf{d}}$
is a cohomologically graded vector space, the whole of
![]() $\textrm{BPS}_{\tilde{Q},\tilde{W},\textbf{d}}\otimes \mathbb{Q}[u]$
is placed in
$\textrm{BPS}_{\tilde{Q},\tilde{W},\textbf{d}}\otimes \mathbb{Q}[u]$
is placed in
![]() $\mathbb{N}^{Q_0}$
-degree
$\mathbb{N}^{Q_0}$
-degree
![]() $\textbf{d}$
,
$\textbf{d}$
,
![]() $u^i$
has cohomological degree 2i, and the symbol
$u^i$
has cohomological degree 2i, and the symbol
![]() $[{-}1]$
denotes the cohomological shift as before. Moreover by [Reference Davison9], the Poincaré polynomial of the cohomologically graded vector space
$[{-}1]$
denotes the cohomological shift as before. Moreover by [Reference Davison9], the Poincaré polynomial of the cohomologically graded vector space
![]() $\textrm{BPS}_{\tilde{Q},\tilde{W},\textbf{d}}$
satisfies the relation
$\textrm{BPS}_{\tilde{Q},\tilde{W},\textbf{d}}$
satisfies the relation
where
![]() $\texttt{a}_{Q,\textbf{d}}(q)$
is the Kac polynomial [Reference Kac20], counting absolutely indecomposable
$\texttt{a}_{Q,\textbf{d}}(q)$
is the Kac polynomial [Reference Kac20], counting absolutely indecomposable
![]() $\textbf{d}$
-dimensional Q-representations over a field of order q. For example, we observe that
$\textbf{d}$
-dimensional Q-representations over a field of order q. For example, we observe that
![]() $Q^{(1)}\cong\widetilde{Q^{(0)}}$
and calculate
$Q^{(1)}\cong\widetilde{Q^{(0)}}$
and calculate
 \begin{align*}\texttt{a}_{Q^{(0)},\textbf{d}}(q)=\begin{cases} 1&\textrm{if }\textbf{d}=1\\0&\textrm{if }\textbf{d}\geq 2\end{cases}\end{align*}
\begin{align*}\texttt{a}_{Q^{(0)},\textbf{d}}(q)=\begin{cases} 1&\textrm{if }\textbf{d}=1\\0&\textrm{if }\textbf{d}\geq 2\end{cases}\end{align*}
recovering (1.4) from (1.6) and (1.7).
In particular, we see that for arbitrary finite Q, the algebra
![]() $\mathcal{A}_{\tilde{Q},\tilde{W}}$
is bosonic, in the sense that it is situated entirely in even cohomological degree. Having observed that
$\mathcal{A}_{\tilde{Q},\tilde{W}}$
is bosonic, in the sense that it is situated entirely in even cohomological degree. Having observed that
![]() $\mathcal{A}_{Q^{(1)}}=\mathcal{A}_{\widetilde{Q^{(0)}},\tilde{W}}$
has a fermionic counterpart
$\mathcal{A}_{Q^{(1)}}=\mathcal{A}_{\widetilde{Q^{(0)}},\tilde{W}}$
has a fermionic counterpart
![]() $\mathcal{A}_{Q^{(0)}}$
, we may ask the following
$\mathcal{A}_{Q^{(0)}}$
, we may ask the following
Question 1.1. For a finite quiver Q, is there a ‘fermionic’ version of
![]() $\mathcal{A}_{\tilde{Q},\tilde{W}}$
?
$\mathcal{A}_{\tilde{Q},\tilde{W}}$
?
It is a consequence of the purity of the cohomological BPS invariants for the quiver with potential
![]() $\left(\tilde{Q},\tilde{W}\right)$
(again, see [Reference Davison9]) that there is an equality
$\left(\tilde{Q},\tilde{W}\right)$
(again, see [Reference Davison9]) that there is an equality
between the Poincaré polynomial and the virtual Poincaré polynomialFootnote 1 of
![]() $\textrm{BPS}_{\tilde{Q},\tilde{W},\textbf{d}}$
. The polynomials
$\textrm{BPS}_{\tilde{Q},\tilde{W},\textbf{d}}$
. The polynomials
![]() $\unicode{x03C7}_{q^{1/2}}(\textrm{BPS}_{\tilde{Q},\tilde{W},\textbf{d}})$
are essentially by definition the refined BPS invariants for the quiver
$\unicode{x03C7}_{q^{1/2}}(\textrm{BPS}_{\tilde{Q},\tilde{W},\textbf{d}})$
are essentially by definition the refined BPS invariants for the quiver
![]() $\tilde{Q}$
with potential
$\tilde{Q}$
with potential
![]() $\tilde{W}$
. Expressed in the language of refined Donaldson–Thomas theory, the analogue of Question 1.1 is
$\tilde{W}$
. Expressed in the language of refined Donaldson–Thomas theory, the analogue of Question 1.1 is
Question 1.2. Is there quiver Q ′ with potential W ′ such that the refined BPS invariants satisfy
In this paper, we will answer these two questions in the affirmative.
1.1 Counting rational curves
At least in the case in which Q is an affine Dynkin quiver, there are strong hints from the McKay correspondence that the answer to Question 1.2 should be at least a partial ‘yes’. We recall some geometric background; see [Reference Bryan, Katz and Leung3, Reference Katz and Morrison24] for more details.
Fix a finite subgroup
![]() $G\subset SL_2(\mathbb{C})$
and denote by
$G\subset SL_2(\mathbb{C})$
and denote by
![]() $X_0=\mathbb{C}^2/G$
the associated Kleinian singularity. We denote by
$X_0=\mathbb{C}^2/G$
the associated Kleinian singularity. We denote by
![]() $\Gamma$
the McKay graph of G, and by
$\Gamma$
the McKay graph of G, and by
![]() $\Gamma^{\prime}$
the full ADE type sub-graph of
$\Gamma^{\prime}$
the full ADE type sub-graph of
![]() $\Gamma$
obtained by removing the vertex corresponding to the trivial representation. We denote by
$\Gamma$
obtained by removing the vertex corresponding to the trivial representation. We denote by
![]() $p\,:\, Y_0\rightarrow X_0$
the minimal resolution of
$p\,:\, Y_0\rightarrow X_0$
the minimal resolution of
![]() $X_0$
. The surface
$X_0$
. The surface
![]() $X_0$
contains an isolated singularity x, and the exceptional fibre
$X_0$
contains an isolated singularity x, and the exceptional fibre
![]() $p^{-1}(x)$
consists of a chain of rational curves, with incidence graph
$p^{-1}(x)$
consists of a chain of rational curves, with incidence graph
![]() $\Gamma^{\prime}$
. The space
$\Gamma^{\prime}$
. The space
![]() $Y_0$
has a universal deformation Y parametrised by
$Y_0$
has a universal deformation Y parametrised by
![]() $\mathfrak{h}$
, the Cartan subalgebra of the simple Lie algebra corresponding to
$\mathfrak{h}$
, the Cartan subalgebra of the simple Lie algebra corresponding to
![]() $\Gamma^{\prime}$
, so that we have a Cartesian diagram
$\Gamma^{\prime}$
, so that we have a Cartesian diagram

The generic fibre of
![]() $\unicode{x03C0}$
contains no rational curves, while if
$\unicode{x03C0}$
contains no rational curves, while if
![]() $h\in\mathfrak{h}$
lies in a root hyperplane corresponding to a vertex i of
$h\in\mathfrak{h}$
lies in a root hyperplane corresponding to a vertex i of
![]() $\Gamma^{\prime}$
, the rational curve
$\Gamma^{\prime}$
, the rational curve
![]() $C_i$
corresponding to i deforms along the line
$C_i$
corresponding to i deforms along the line
![]() $t\cdot h$
for
$t\cdot h$
for
![]() $t\in\mathbb{C}$
[Reference Bryan, Katz and Leung3, Prop.2.2]. We pick
$t\in\mathbb{C}$
[Reference Bryan, Katz and Leung3, Prop.2.2]. We pick
![]() $h\in\mathfrak{h}$
and form the Cartesian diagram
$h\in\mathfrak{h}$
and form the Cartesian diagram

For
![]() $\unicode{x03B2}\in \textbf{H}_2(Y^h,\mathbb{Z})$
and
$\unicode{x03B2}\in \textbf{H}_2(Y^h,\mathbb{Z})$
and
![]() $n\in\mathbb{N}$
, let
$n\in\mathbb{N}$
, let
![]() $\mathcal{M}_{\unicode{x03B2},n}\left(Y^h\right)$
denote the moduli space of semistable coherent sheaves
$\mathcal{M}_{\unicode{x03B2},n}\left(Y^h\right)$
denote the moduli space of semistable coherent sheaves
![]() $\mathcal{F}$
on Y
′, with fundamental class of the support of
$\mathcal{F}$
on Y
′, with fundamental class of the support of
![]() $\mathcal{F}$
equal to
$\mathcal{F}$
equal to
![]() $\unicode{x03B2}$
, and with
$\unicode{x03B2}$
, and with
![]() $\unicode{x03C7}(\mathcal{F})=n$
.
$\unicode{x03C7}(\mathcal{F})=n$
.
Consider the case in which
![]() $\unicode{x03B2}=[C_i]$
for some
$\unicode{x03B2}=[C_i]$
for some
![]() $i\in Q_0$
, so that stability is equivalent to semistability. Since a stable coherent sheaf
$i\in Q_0$
, so that stability is equivalent to semistability. Since a stable coherent sheaf
![]() $\mathcal{F}$
cannot split as a direct sum, it is supported on a single fibre of the morphism
$\mathcal{F}$
cannot split as a direct sum, it is supported on a single fibre of the morphism
![]() $\unicode{x03C0}^{\prime}$
. If
$\unicode{x03C0}^{\prime}$
. If
![]() $C_i$
deforms along
$C_i$
deforms along
![]() $\mathbb{A}^1$
, with curve over
$\mathbb{A}^1$
, with curve over
![]() $t\in\mathbb{A}_1$
labelled
$t\in\mathbb{A}_1$
labelled
![]() $C_{i,t}$
, then in each fibre
$C_{i,t}$
, then in each fibre
![]() $\unicode{x03C0}^{\prime}(t)$
there is a unique semistable coherent sheaf
$\unicode{x03C0}^{\prime}(t)$
there is a unique semistable coherent sheaf
![]() $\mathscr{O}_{C_{i,t}}(n-1)$
with Euler characteristic n and
$\mathscr{O}_{C_{i,t}}(n-1)$
with Euler characteristic n and
![]() $\left[\mathscr{O}_{C_{i,t}}(n-1)\right]=\unicode{x03B2}$
. If
$\left[\mathscr{O}_{C_{i,t}}(n-1)\right]=\unicode{x03B2}$
. If
![]() $C_i$
does not deform, then there is a unique semistable coherent sheaf on the whole of
$C_i$
does not deform, then there is a unique semistable coherent sheaf on the whole of
![]() $Y^h$
of class
$Y^h$
of class
![]() $(\unicode{x03B2},n)$
, supported above
$(\unicode{x03B2},n)$
, supported above
![]() $0\in \mathbb{A}^1$
. So
$0\in \mathbb{A}^1$
. So
 \begin{align*}\mathcal{M}_{[C_i],n}\left(Y^h\right)=\begin{cases} {\text{pt}} &\textrm{if }h\notin i^{\perp}\\[4pt]\mathbb{A}^1&\textrm{if }h\in i^{\perp}.\end{cases}\end{align*}
\begin{align*}\mathcal{M}_{[C_i],n}\left(Y^h\right)=\begin{cases} {\text{pt}} &\textrm{if }h\notin i^{\perp}\\[4pt]\mathbb{A}^1&\textrm{if }h\in i^{\perp}.\end{cases}\end{align*}
The cohomological BPS invariants
![]() $\textrm{BPS}_{\unicode{x03B2},n}$
of the 3-fold
$\textrm{BPS}_{\unicode{x03B2},n}$
of the 3-fold
![]() $Y^h$
are in general hard to define rigorously, involving vanishing cycle cohomology, d-critical structures [Reference Joyce19], orientation data, perverse filtrations, etc. However, for simple classes like the ones we are considering here, the definition/calculation boils down to something more straightforward:
$Y^h$
are in general hard to define rigorously, involving vanishing cycle cohomology, d-critical structures [Reference Joyce19], orientation data, perverse filtrations, etc. However, for simple classes like the ones we are considering here, the definition/calculation boils down to something more straightforward:
 \begin{align*}\textrm{BPS}_{[C_i],n}\left(Y^h\right) &= \textbf{H}\!\left(\mathcal{M}_{[C_i],n}\!\left(Y^h\right),\mathbb{Q}\right)_{\text{vir}}\\[4pt]&\cong\begin{cases}\mathbb{Q}&\textrm{if }h\notin i^{\perp}\\[4pt]\mathbb{Q}[1]&\textrm{if }h\in i^{\perp}.\end{cases}\end{align*}
\begin{align*}\textrm{BPS}_{[C_i],n}\left(Y^h\right) &= \textbf{H}\!\left(\mathcal{M}_{[C_i],n}\!\left(Y^h\right),\mathbb{Q}\right)_{\text{vir}}\\[4pt]&\cong\begin{cases}\mathbb{Q}&\textrm{if }h\notin i^{\perp}\\[4pt]\mathbb{Q}[1]&\textrm{if }h\in i^{\perp}.\end{cases}\end{align*}
The subscript vir denotes the cohomological shift
![]() $[{\dim}(\mathcal{M}_{[C_i],n})]$
by the dimension of the space we are taking the singular cohomology of and accounts for the shift in the
$[{\dim}(\mathcal{M}_{[C_i],n})]$
by the dimension of the space we are taking the singular cohomology of and accounts for the shift in the
![]() $h\in i^{\perp}$
case. So in both cases, the cohomological BPS invariants for simple curve classes are one-dimensional vector spaces and are concentrated in even or odd cohomological degree, depending on whether the choice of h means that
$h\in i^{\perp}$
case. So in both cases, the cohomological BPS invariants for simple curve classes are one-dimensional vector spaces and are concentrated in even or odd cohomological degree, depending on whether the choice of h means that
![]() $C_i$
is rigid or not.
$C_i$
is rigid or not.
Similarly, the definition and calculation of the simplest degree zero cohomological BPS invariant
![]() $\textrm{BPS}_{0,1}\!\left(Y^h\right)$
is much easier than the general case, and we have
$\textrm{BPS}_{0,1}\!\left(Y^h\right)$
is much easier than the general case, and we have
It is easy to verify that the singular cohomology of
![]() $Y^h$
does not depend on the choice of h at all. In general, one expects
$Y^h$
does not depend on the choice of h at all. In general, one expects
![]() $\textrm{BPS}_{0,n}\cong \textrm{BPS}_{0,1}$
(compare with [Reference Behrend, Byan and Szendröi2]), so it turns out that the degree zeroFootnote 2 cohomological DT theory of
$\textrm{BPS}_{0,n}\cong \textrm{BPS}_{0,1}$
(compare with [Reference Behrend, Byan and Szendröi2]), so it turns out that the degree zeroFootnote 2 cohomological DT theory of
![]() $Y^h$
does not depend on h.
$Y^h$
does not depend on h.
To put this geometric discussion in very leading language: for the most degenerate case
![]() $h=0$
, all of the cohomological DT theory is bosonic, since the vanishing cycle cohomology ends up living in even cohomological degree (taking into account the shift
$h=0$
, all of the cohomological DT theory is bosonic, since the vanishing cycle cohomology ends up living in even cohomological degree (taking into account the shift
![]() $[{-}1]$
in (1.6)). On the other hand, modifying the deforming family defined by
$[{-}1]$
in (1.6)). On the other hand, modifying the deforming family defined by
![]() $h\in\mathfrak{h}$
to be more generic, a portion of the cohomological DT theory is fermionised, depending on which root hyperplanes h avoids.
$h\in\mathfrak{h}$
to be more generic, a portion of the cohomological DT theory is fermionised, depending on which root hyperplanes h avoids.
1.2 The noncommutative conifold and central extensions of the preprojective algebra
Let Q
′ be the
![]() $A_1$
quiver, and let Q be its affine extension, which we label as follows:
$A_1$
quiver, and let Q be its affine extension, which we label as follows:

Then as a special case of [Reference Kapranov and Vasserot21], there is a derived equivalence between the category of finitely generated modules for the preprojective algebra
![]() $\Pi_Q$
of Q, and the category of coherent sheaves on
$\Pi_Q$
of Q, and the category of coherent sheaves on
![]() $Y_0$
, the minimal resolution of the type
$Y_0$
, the minimal resolution of the type
![]() $A_1$
singularity defined by the equation
$A_1$
singularity defined by the equation
![]() $x^2+y^2=z^2$
:
$x^2+y^2=z^2$
:
We have that

The Kac polynomials of Q are possible to calculate by hand, so that we can calculate the cohomological BPS invariants for
![]() $\text{Jac}\!\left(\tilde{Q},\tilde{W}\right)$
via (1.7)
$\text{Jac}\!\left(\tilde{Q},\tilde{W}\right)$
via (1.7)
 \begin{equation}\textrm{BPS}_{\tilde{Q},\tilde{W},(m,n)}\cong\begin{cases} \mathbb{Q}[3]\oplus\mathbb{Q}[1]&\textrm{if }m=n\\[4pt]\mathbb{Q}[1] &\textrm{if }m=n\pm 1\\[4pt]0&\textrm{otherwise.}\end{cases}\end{equation}
\begin{equation}\textrm{BPS}_{\tilde{Q},\tilde{W},(m,n)}\cong\begin{cases} \mathbb{Q}[3]\oplus\mathbb{Q}[1]&\textrm{if }m=n\\[4pt]\mathbb{Q}[1] &\textrm{if }m=n\pm 1\\[4pt]0&\textrm{otherwise.}\end{cases}\end{equation}
There is an isomorphism
![]() $\text{Jac}\!\left(\tilde{Q},\tilde{W}\right)\cong \Pi_Q[\omega]=\Pi_Q\otimes \mathbb{C}[\omega]$
, so that we have in addition a derived equivalence (see e.g. [Reference Szendröi42])
$\text{Jac}\!\left(\tilde{Q},\tilde{W}\right)\cong \Pi_Q[\omega]=\Pi_Q\otimes \mathbb{C}[\omega]$
, so that we have in addition a derived equivalence (see e.g. [Reference Szendröi42])
where
![]() $Y^0$
is defined via the construction in the previous subsection by setting
$Y^0$
is defined via the construction in the previous subsection by setting
![]() $h=0\in\mathfrak{h}$
, i.e.
$h=0\in\mathfrak{h}$
, i.e.
![]() $Y^0=Y_0\times \mathbb{A}^1$
.
$Y^0=Y_0\times \mathbb{A}^1$
.
For the
![]() $A_1$
-singularity, the Cartan subalgebra
$A_1$
-singularity, the Cartan subalgebra
![]() $\mathfrak{h}$
is one-dimensional, so aside from 0 there is an essentially unique choice of
$\mathfrak{h}$
is one-dimensional, so aside from 0 there is an essentially unique choice of
![]() $h\in\mathfrak{h}$
. Defining
$h\in\mathfrak{h}$
. Defining
![]() $Y_{\text{con}}=Y^h$
for a nonzero choice of
$Y_{\text{con}}=Y^h$
for a nonzero choice of
![]() $h\in\mathfrak{h}$
in diagram (1.9), we obtain the resolved conifold. As noted in the previous section, instead of having an
$h\in\mathfrak{h}$
in diagram (1.9), we obtain the resolved conifold. As noted in the previous section, instead of having an
![]() $\mathbb{A}^1$
-family of rational curves giving rise to cohomological BPS invariants in odd degrees, the resolved conifold contains a unique rigid curve. It follows that the cohomological BPS invariants corresponding to sheaves supported on the curve flip parity and are supported in even cohomological degrees, so that they contribute to the fermionic part of the cohomological DT theory of the resolved conifold (as ever, taking into account the shift defined as in (1.6))
$\mathbb{A}^1$
-family of rational curves giving rise to cohomological BPS invariants in odd degrees, the resolved conifold contains a unique rigid curve. It follows that the cohomological BPS invariants corresponding to sheaves supported on the curve flip parity and are supported in even cohomological degrees, so that they contribute to the fermionic part of the cohomological DT theory of the resolved conifold (as ever, taking into account the shift defined as in (1.6))
The resolved conifold also has a noncommutative model, studied in this context by Szendröi, which we recall (see [Reference Szendröi41] for details on the noncommutative Donaldson–Thomas theory of the conifold, and also [Reference Galakhov and Yamazaki17, Reference Li and Yamazaki27, Reference Rapcak, Soibelman, Yang and Zhao37] for more recent work on CoHAs related to toric 3-folds). We consider the double

Set
![]() $W_{\texttt{KW}}=aa^*bb^*-a^*ab^*b$
to be the Klebanov–Witten potential [Reference Klebanov and Witten25]. Then (e.g. as a special case of a result due to Van den Bergh [Reference van den Bergh43]), there is a derived equivalence
$W_{\texttt{KW}}=aa^*bb^*-a^*ab^*b$
to be the Klebanov–Witten potential [Reference Klebanov and Witten25]. Then (e.g. as a special case of a result due to Van den Bergh [Reference van den Bergh43]), there is a derived equivalence
To interpolate between the two cases (
![]() $h=0,h\neq 0$
), it turns out to be more instructive to consider the quiver
$h=0,h\neq 0$
), it turns out to be more instructive to consider the quiver
![]() $\tilde {Q}$
with the potential
$\tilde {Q}$
with the potential
As we recall in Section 2.1, the resulting Jacobi algebra has already been studied: it is a special case of the central extensions of
![]() $\Pi_Q$
introduced by Etingof and Rains in [Reference Etingof and Rains16]. There is an isomorphism (see Example 2.2)
$\Pi_Q$
introduced by Etingof and Rains in [Reference Etingof and Rains16]. There is an isomorphism (see Example 2.2)
and the cohomological DT theory of the Jacobi algebras in (1.12) turns out to be the same. The cohomological BPS invariants for the noncommutative conifold can be deduced from [Reference Morrison, Mozgovoy, Nagao and Szendröi30] and purity (proved as in [Reference Davison, Ongaro and Szendröi12, Thm.4.7]):
 \begin{equation}\textrm{BPS}_{\tilde{Q},\tilde{W}^{(1,-1)},m,n}\cong\begin{cases} \textbf{H}(Y_{\text{con}},\mathbb{Q})[3]\cong \mathbb{Q}[3]\oplus \mathbb{Q}[1] &\textrm{if }m=n\\[4pt]\mathbb{Q}&\textrm{if }m=n\pm 1\\[4pt]0&\textrm{otherwise.}\end{cases}\end{equation}
\begin{equation}\textrm{BPS}_{\tilde{Q},\tilde{W}^{(1,-1)},m,n}\cong\begin{cases} \textbf{H}(Y_{\text{con}},\mathbb{Q})[3]\cong \mathbb{Q}[3]\oplus \mathbb{Q}[1] &\textrm{if }m=n\\[4pt]\mathbb{Q}&\textrm{if }m=n\pm 1\\[4pt]0&\textrm{otherwise.}\end{cases}\end{equation}
Comparing (1.11) with (1.13), we see exactly the same pattern as in the commutative case of Section 1.1, with the passage from trivial
![]() $\mathbb{A}^1$
-deformations of
$\mathbb{A}^1$
-deformations of
![]() $Y_0$
to nontrivial ones replaced in the context of noncommutative algebraic geometry by the passage from the trivial central extension of the algebra
$Y_0$
to nontrivial ones replaced in the context of noncommutative algebraic geometry by the passage from the trivial central extension of the algebra
![]() $\Pi_Q$
to the nontrivial ones constructed by Etingof and Rains; this change provokes a flip in the parity of some, but not all, of the cohomological BPS invariants.
$\Pi_Q$
to the nontrivial ones constructed by Etingof and Rains; this change provokes a flip in the parity of some, but not all, of the cohomological BPS invariants.
1.3 Main results
In the rest of the paper, we prove that the above discussion regarding the (noncommutative) conifold forms part of a general procedure for (selectively) ‘fermionising’ the cohomological Hall algebras of preprojective algebras. This culminates in the following theorem:
Theorem A. Let
![]() $\unicode{x03BC}\in\mathbb{C}^{Q_0}$
. Set
$\unicode{x03BC}\in\mathbb{C}^{Q_0}$
. Set
![]() $\tilde{W}^{\unicode{x03BC}}=\sum_{a\in Q_1}[a,a^*]\sum_{i\in Q_0}\omega_i+\frac{1}{2}\sum_{i\in Q_0} \unicode{x03BC}_i\omega_i^2$
. Then the cohomological BPS invariants for the quiver
$\tilde{W}^{\unicode{x03BC}}=\sum_{a\in Q_1}[a,a^*]\sum_{i\in Q_0}\omega_i+\frac{1}{2}\sum_{i\in Q_0} \unicode{x03BC}_i\omega_i^2$
. Then the cohomological BPS invariants for the quiver
![]() $\tilde{Q}$
with potential
$\tilde{Q}$
with potential
![]() $\tilde{W}^{\unicode{x03BC}}$
satisfy
$\tilde{W}^{\unicode{x03BC}}$
satisfy
 \begin{equation}\texttt{p}\!\left(\textrm{BPS}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}},\textbf{d}},q^{1/2}\right)=\begin{cases}\texttt{a}_{Q,\textbf{d}}\!\left(q^{-1}\right) & \textrm{if } \textbf{d}\cdot \unicode{x03BC}\neq 0\\[5pt]q^{-1/2}\texttt{a}_{Q,\textbf{d}}\!\left(q^{-1}\right) &\textrm{if }\textbf{d}\cdot \unicode{x03BC}=0,\end{cases}\end{equation}
\begin{equation}\texttt{p}\!\left(\textrm{BPS}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}},\textbf{d}},q^{1/2}\right)=\begin{cases}\texttt{a}_{Q,\textbf{d}}\!\left(q^{-1}\right) & \textrm{if } \textbf{d}\cdot \unicode{x03BC}\neq 0\\[5pt]q^{-1/2}\texttt{a}_{Q,\textbf{d}}\!\left(q^{-1}\right) &\textrm{if }\textbf{d}\cdot \unicode{x03BC}=0,\end{cases}\end{equation}
where
![]() $\texttt{a}_{Q,\textbf{d}}(q)$
are the Kac polynomials for Q. In addition, the natural mixed Hodge structure on the cohomological BPS invariants
$\texttt{a}_{Q,\textbf{d}}(q)$
are the Kac polynomials for Q. In addition, the natural mixed Hodge structure on the cohomological BPS invariants
![]() $\textrm{BPS}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}},\textbf{d}}$
is pure, of Tate type, so that we have isomorphisms of Hodge theoretic BPS invariants
$\textrm{BPS}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}},\textbf{d}}$
is pure, of Tate type, so that we have isomorphisms of Hodge theoretic BPS invariants
 \begin{equation}\textrm{BPS}^{\text{hdg}}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}},\textbf{d}}\cong\begin{cases}\bigoplus_{i\in\mathbb{Z}}(\mathscr{L}^{\,\,i})^{\oplus \texttt{a}_{Q,\textbf{d},-i}}&\textrm{if } \textbf{d}\cdot\unicode{x03BC}\neq 0\\[5pt]\bigoplus_{i\in\mathbb{Z}}\!\left(\mathscr{L}^{\,\,i-1/2}\right)^{\oplus \texttt{a}_{Q,\textbf{d},-i}}&\textrm{if } \textbf{d}\cdot \unicode{x03BC}= 0,\end{cases}\end{equation}
\begin{equation}\textrm{BPS}^{\text{hdg}}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}},\textbf{d}}\cong\begin{cases}\bigoplus_{i\in\mathbb{Z}}(\mathscr{L}^{\,\,i})^{\oplus \texttt{a}_{Q,\textbf{d},-i}}&\textrm{if } \textbf{d}\cdot\unicode{x03BC}\neq 0\\[5pt]\bigoplus_{i\in\mathbb{Z}}\!\left(\mathscr{L}^{\,\,i-1/2}\right)^{\oplus \texttt{a}_{Q,\textbf{d},-i}}&\textrm{if } \textbf{d}\cdot \unicode{x03BC}= 0,\end{cases}\end{equation}
where
![]() $\mathscr{L}\,:\!=\, \textbf{H}_c(\mathbb{A}^1,\mathbb{Q})$
. By purity, the virtual Poincaré polynomials of the cohomological BPS invariants agree with the above Poincaré polynomials, so that we have equalities for the refined BPS invariants
$\mathscr{L}\,:\!=\, \textbf{H}_c(\mathbb{A}^1,\mathbb{Q})$
. By purity, the virtual Poincaré polynomials of the cohomological BPS invariants agree with the above Poincaré polynomials, so that we have equalities for the refined BPS invariants
 \begin{equation}\unicode{x03C7}_{q^{1/2}}\!\left(\textrm{BPS}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}},\textbf{d}}\right)=\begin{cases}\texttt{a}_{Q,\textbf{d}}\!\left(q^{-1}\right) & \textrm{if } \textbf{d}\cdot \unicode{x03BC}\neq 0\\[5pt]q^{-1/2}\texttt{a}_{Q,\textbf{d}}\!\left(q^{-1}\right) &\textrm{if }\textbf{d}\cdot \unicode{x03BC}=0.\end{cases}\end{equation}
\begin{equation}\unicode{x03C7}_{q^{1/2}}\!\left(\textrm{BPS}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}},\textbf{d}}\right)=\begin{cases}\texttt{a}_{Q,\textbf{d}}\!\left(q^{-1}\right) & \textrm{if } \textbf{d}\cdot \unicode{x03BC}\neq 0\\[5pt]q^{-1/2}\texttt{a}_{Q,\textbf{d}}\!\left(q^{-1}\right) &\textrm{if }\textbf{d}\cdot \unicode{x03BC}=0.\end{cases}\end{equation}
Comparing with (1.7), we see that for dimension vectors
![]() $\textbf{d}$
satisfying
$\textbf{d}$
satisfying
![]() $\textbf{d}\cdot \unicode{x03BC}\neq 0$
the cohomological BPS invariants have switched parity. In particular, for generic choices of
$\textbf{d}\cdot \unicode{x03BC}\neq 0$
the cohomological BPS invariants have switched parity. In particular, for generic choices of
![]() $\unicode{x03BC}$
, the algebra
$\unicode{x03BC}$
, the algebra
![]() $\mathcal{A}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}}}$
is a fermionised version of
$\mathcal{A}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}}}$
is a fermionised version of
![]() $\mathcal{A}_{\tilde{Q},\tilde{W}}$
, so (1.15) and (1.16) answer Questions 1.1 and (1.2) respectively in the affirmative.
$\mathcal{A}_{\tilde{Q},\tilde{W}}$
, so (1.15) and (1.16) answer Questions 1.1 and (1.2) respectively in the affirmative.
Still fixing
![]() $\unicode{x03BC}\in \mathbb{C}^{Q_0}$
the deformed preprojective algebra, introduced by Crawley–Boevey and Holland in [Reference Crawley-Boevey and Holland6], is defined by
$\unicode{x03BC}\in \mathbb{C}^{Q_0}$
the deformed preprojective algebra, introduced by Crawley–Boevey and Holland in [Reference Crawley-Boevey and Holland6], is defined by
 \begin{align*}\Pi_{Q,\unicode{x03BC}}\,:\!=\,\mathbb{C}\overline{Q}/\left\langle \sum_{a\in Q_1}[a,a^*]+\sum_{i\in Q_0} \unicode{x03BC}_i e_i\right\rangle,\end{align*}
\begin{align*}\Pi_{Q,\unicode{x03BC}}\,:\!=\,\mathbb{C}\overline{Q}/\left\langle \sum_{a\in Q_1}[a,a^*]+\sum_{i\in Q_0} \unicode{x03BC}_i e_i\right\rangle,\end{align*}
where
![]() $e_i$
is the path of length zero beginning and ending at the vertex i. Via the methods used to prove Theorem A, we are able to calculate the Borel–Moore homology (along with its mixed Hodge structure) of all stacks of representations of deformed preprojective algebras, simultaneously generalising a result of Crawley–Boevey and Van den Bergh [Reference Crawley-Boevey and Van den Bergh7] from the case of generic
$e_i$
is the path of length zero beginning and ending at the vertex i. Via the methods used to prove Theorem A, we are able to calculate the Borel–Moore homology (along with its mixed Hodge structure) of all stacks of representations of deformed preprojective algebras, simultaneously generalising a result of Crawley–Boevey and Van den Bergh [Reference Crawley-Boevey and Van den Bergh7] from the case of generic
![]() $\unicode{x03BC}$
and indivisible dimension vector
$\unicode{x03BC}$
and indivisible dimension vector
![]() $\textbf{d}$
, and the result from [Reference Davison9] which deals with the case
$\textbf{d}$
, and the result from [Reference Davison9] which deals with the case
![]() $\unicode{x03BC}=0$
and arbitrary
$\unicode{x03BC}=0$
and arbitrary
![]() $\textbf{d}$
:
$\textbf{d}$
:
Theorem B. For arbitrary
![]() $\unicode{x03BC}\in R$
and
$\unicode{x03BC}\in R$
and
![]() $\textbf{d}\in\mathbb{N}^{Q_0}$
there is an isomorphism of
$\textbf{d}\in\mathbb{N}^{Q_0}$
there is an isomorphism of
![]() $\mathbb{N}^{Q_0}$
-graded mixed Hodge structures
$\mathbb{N}^{Q_0}$
-graded mixed Hodge structures
 \begin{equation}\bigoplus_{\textbf{d}\in \mathbb{N}^{Q_0}}\textbf{H}_c\!\left(\mathfrak{M}_{\textbf{d}}(\Pi_{Q,\unicode{x03BC}}),\mathbb{Q}\right)\otimes \mathscr{L}^{\,\,\unicode{x03C7}_Q(\textbf{d},\textbf{d})}\cong \textbf{Sym}\!\left(\bigoplus_{\substack{0\neq \textbf{d}\in\mathbb{N}^{Q_0}\\ \textbf{d}\cdot\unicode{x03BC}=0}}\textrm{BPS}_{\tilde{Q},\tilde{W},\textbf{d}}^{\text{hdg},\vee}\otimes\textbf{H}_c({\text{pt}}/\mathbb{C}^*,\mathbb{Q})_{\text{vir}}\right),\end{equation}
\begin{equation}\bigoplus_{\textbf{d}\in \mathbb{N}^{Q_0}}\textbf{H}_c\!\left(\mathfrak{M}_{\textbf{d}}(\Pi_{Q,\unicode{x03BC}}),\mathbb{Q}\right)\otimes \mathscr{L}^{\,\,\unicode{x03C7}_Q(\textbf{d},\textbf{d})}\cong \textbf{Sym}\!\left(\bigoplus_{\substack{0\neq \textbf{d}\in\mathbb{N}^{Q_0}\\ \textbf{d}\cdot\unicode{x03BC}=0}}\textrm{BPS}_{\tilde{Q},\tilde{W},\textbf{d}}^{\text{hdg},\vee}\otimes\textbf{H}_c({\text{pt}}/\mathbb{C}^*,\mathbb{Q})_{\text{vir}}\right),\end{equation}
where
and
In particular, the compactly supported cohomology of
![]() $\mathfrak{M}(\Pi_{Q,\unicode{x03BC}})$
, the stack of representations of the deformed preprojective algebra, is pure, of Tate type.
$\mathfrak{M}(\Pi_{Q,\unicode{x03BC}})$
, the stack of representations of the deformed preprojective algebra, is pure, of Tate type.
2. Cohomological DT theory for quivers with potential
2.1 Some algebras from quivers
A quiver is determined by a set of vertices
![]() $Q_0$
, a set of edges
$Q_0$
, a set of edges
![]() $Q_1$
, and two morphisms
$Q_1$
, and two morphisms
![]() $s,t\,:\, Q_1\rightarrow Q_0$
taking an arrow to its source and target respectively. We always assume that
$s,t\,:\, Q_1\rightarrow Q_0$
taking an arrow to its source and target respectively. We always assume that
![]() $Q_0$
and
$Q_0$
and
![]() $Q_1$
are finite. We define the Euler form
$Q_1$
are finite. We define the Euler form
Where there is no possibility of confusion, we drop the quiver Q from the notation and just write
![]() $\unicode{x03C7}(\cdot,\cdot)$
. We denote by
$\unicode{x03C7}(\cdot,\cdot)$
. We denote by
![]() $\overline{Q}$
the doubled quiver of Q, obtained by adding an arrow
$\overline{Q}$
the doubled quiver of Q, obtained by adding an arrow
![]() $a^*$
for every arrow
$a^*$
for every arrow
![]() $a\in Q_1$
, where
$a\in Q_1$
, where
![]() $a^*$
has the opposite orientation to a. We denote by
$a^*$
has the opposite orientation to a. We denote by
![]() $\tilde{Q}$
the tripled quiver, obtained from
$\tilde{Q}$
the tripled quiver, obtained from
![]() $\overline{Q}$
by adding a loop
$\overline{Q}$
by adding a loop
![]() $\omega_i$
at each vertex
$\omega_i$
at each vertex
![]() $i\in Q_0$
.
$i\in Q_0$
.
Given a ring A and a quiver Q, we denote by AQ the free path algebra of Q with coefficients in A. We denote by
![]() $R\subset \mathbb{C}Q$
the semisimple subalgebra spanned by length zero paths, so we may identify
$R\subset \mathbb{C}Q$
the semisimple subalgebra spanned by length zero paths, so we may identify
![]() $R= \mathbb{C}^{Q_0}$
. We denote by
$R= \mathbb{C}^{Q_0}$
. We denote by
![]() $\Pi_Q$
the preprojective algebra for Q, defined to be the quotient of the free path algebra
$\Pi_Q$
the preprojective algebra for Q, defined to be the quotient of the free path algebra
![]() $\mathbb{C}\overline{Q}$
by the two-sided ideal generated by the element
$\mathbb{C}\overline{Q}$
by the two-sided ideal generated by the element
![]() $\sum_{a\in Q_1}[a,a^*]$
. As in the introduction, we denote by
$\sum_{a\in Q_1}[a,a^*]$
. As in the introduction, we denote by
![]() $\Pi_Q[\omega]$
the trivial extension obtained by adjoining a central element
$\Pi_Q[\omega]$
the trivial extension obtained by adjoining a central element
![]() $\omega$
to the algebra
$\omega$
to the algebra
![]() $\Pi_Q$
, i.e.
$\Pi_Q$
, i.e.
![]() $\Pi_Q[\omega]=\Pi_Q\otimes \mathbb{C}[\omega]$
.
$\Pi_Q[\omega]=\Pi_Q\otimes \mathbb{C}[\omega]$
.
Let
![]() $\unicode{x03BC}\in R$
. We recall the central extension of
$\unicode{x03BC}\in R$
. We recall the central extension of
![]() $\Pi_Q$
introduced by Etingof and Rains [Reference Etingof and Rains16]:
$\Pi_Q$
introduced by Etingof and Rains [Reference Etingof and Rains16]:
 \begin{align*}\Pi_Q^{\unicode{x03BC}}=\mathbb{C}[\omega]\overline{Q}/\left\langle \sum_{a\in Q_1}[a,a^*]+\unicode{x03BC} \omega\right\rangle.\end{align*}
\begin{align*}\Pi_Q^{\unicode{x03BC}}=\mathbb{C}[\omega]\overline{Q}/\left\langle \sum_{a\in Q_1}[a,a^*]+\unicode{x03BC} \omega\right\rangle.\end{align*}
There is an obvious isomorphism
and natural isomorphisms
 \begin{align*}\Pi_{Q,\unicode{x03BC}}\cong\ &\Pi_Q^{\unicode{x03BC}}/\langle \omega-1\rangle\\[4pt]\Pi_{Q}\cong\ &\Pi_Q^{\unicode{x03BC}}/\langle \omega\rangle,\end{align*}
\begin{align*}\Pi_{Q,\unicode{x03BC}}\cong\ &\Pi_Q^{\unicode{x03BC}}/\langle \omega-1\rangle\\[4pt]\Pi_{Q}\cong\ &\Pi_Q^{\unicode{x03BC}}/\langle \omega\rangle,\end{align*}
where
![]() $\Pi_{Q,\unicode{x03BC}}$
is the deformed preprojective algebra recalled in the introduction. The algebra
$\Pi_{Q,\unicode{x03BC}}$
is the deformed preprojective algebra recalled in the introduction. The algebra
![]() $\Pi_Q^{\unicode{x03BC}}$
provides an
$\Pi_Q^{\unicode{x03BC}}$
provides an
![]() $\mathbb{A}^1$
-family of algebras interpolating between the preprojective algebra
$\mathbb{A}^1$
-family of algebras interpolating between the preprojective algebra
![]() $\Pi_Q$
and the deformed preprojective algebra
$\Pi_Q$
and the deformed preprojective algebra
![]() $\Pi_{Q,\unicode{x03BC}}$
.
$\Pi_{Q,\unicode{x03BC}}$
.
Let Q be a quiver and let
![]() $W\in\mathbb{C}Q/[\mathbb{C} Q,\mathbb{C} Q]$
be a potential, i.e. a linear combination of cyclic words, where cyclic words are considered to be equivalent if they can be cyclically permuted to each other. We will call the data of a quiver with potential (Q,W) a QP. Given
$W\in\mathbb{C}Q/[\mathbb{C} Q,\mathbb{C} Q]$
be a potential, i.e. a linear combination of cyclic words, where cyclic words are considered to be equivalent if they can be cyclically permuted to each other. We will call the data of a quiver with potential (Q,W) a QP. Given
![]() $a\in Q_1$
, if
$a\in Q_1$
, if
![]() $W=a_1\ldots a_n$
is a single cyclic word we define
$W=a_1\ldots a_n$
is a single cyclic word we define
and define
![]() $\partial W/\partial a$
for general W by extending linearly. We define
$\partial W/\partial a$
for general W by extending linearly. We define
In this paper, we will study Jacobi algebras obtained from the tripled QP
![]() $\left(\tilde{Q},\tilde{W}\right)$
defined in (1.5) by adding polynomials in the extra loops
$\left(\tilde{Q},\tilde{W}\right)$
defined in (1.5) by adding polynomials in the extra loops
![]() $\omega_i$
; we refer the reader to [Reference Ginzburg18, Sect. 4] for general background on this construction, [Reference Quintero Vélez and Boer36, Reference Szendröi42] for the noncommutative geometry background in type ADE, and [Reference Cachazo, Katz and Vafa4] for the physics perspective.
$\omega_i$
; we refer the reader to [Reference Ginzburg18, Sect. 4] for general background on this construction, [Reference Quintero Vélez and Boer36, Reference Szendröi42] for the noncommutative geometry background in type ADE, and [Reference Cachazo, Katz and Vafa4] for the physics perspective.
Proposition 2.1. [Reference Ginzburg18, Ex. 4.3.5] Let
![]() $\unicode{x03BC}=\sum_i \unicode{x03BC}_ie_i$
. Set
$\unicode{x03BC}=\sum_i \unicode{x03BC}_ie_i$
. Set
![]() $\tilde{W}^{\unicode{x03BC}}=\tilde{W}+\frac{1}{2}\sum_{i\in Q_0} \unicode{x03BC}_i\omega_i^2$
. Then there is an isomorphism
$\tilde{W}^{\unicode{x03BC}}=\tilde{W}+\frac{1}{2}\sum_{i\in Q_0} \unicode{x03BC}_i\omega_i^2$
. Then there is an isomorphism
In particular, there is a natural isomorphism
Proof. This follows more or less from the definitions. The noncommutative derivatives of
![]() $\tilde{W}^{\unicode{x03BC}}$
with respect to the arrows a impose the relation that
$\tilde{W}^{\unicode{x03BC}}$
with respect to the arrows a impose the relation that
![]() $\omega$
commutes with the arrows
$\omega$
commutes with the arrows
![]() $a^*$
, and vice versa, while the noncommutative derivatives with respect to the loops
$a^*$
, and vice versa, while the noncommutative derivatives with respect to the loops
![]() $\omega_i$
impose the defining relations of
$\omega_i$
impose the defining relations of
![]() $\Pi^{\unicode{x03BC}}_Q$
as a quotient of
$\Pi^{\unicode{x03BC}}_Q$
as a quotient of
![]() $\mathbb{C}[\omega]\overline{Q}$
.
$\mathbb{C}[\omega]\overline{Q}$
.
Example 2.2. Let Q be defined as in (1.10), and set
![]() $\unicode{x03BC}=e_0-e_1$
. Then
$\unicode{x03BC}=e_0-e_1$
. Then
After the noncommutative change of variables
the potential transforms to
Now the relations
![]() $\partial W/\partial \omega_i=\pm\omega_i$
mean that in the Jacobi algebra we may simply remove the loops
$\partial W/\partial \omega_i=\pm\omega_i$
mean that in the Jacobi algebra we may simply remove the loops
![]() $\omega_i$
. Thus, there is a natural isomorphism
$\omega_i$
. Thus, there is a natural isomorphism
giving the isomorphism (1.12). In particular, the noncommutative conifold is isomorphic to one of the central extensions of
![]() $\Pi_Q$
considered above, for Q as in (1.10).
$\Pi_Q$
considered above, for Q as in (1.10).
Later we will use the following elementary result.
Proposition 2.3. Let
![]() $\rho$
be a
$\rho$
be a
![]() $\textbf{d}$
-dimensional simple
$\textbf{d}$
-dimensional simple
![]() $\text{Jac}\!\left(\tilde{Q},\tilde{W}^{\unicode{x03BC}}\right)$
-module. Then, the operator
$\text{Jac}\!\left(\tilde{Q},\tilde{W}^{\unicode{x03BC}}\right)$
-module. Then, the operator
![]() $\rho(\omega)$
acts on the underlying vector space of
$\rho(\omega)$
acts on the underlying vector space of
![]() $\rho$
by multiplication by some scalar
$\rho$
by multiplication by some scalar
![]() $\lambda\in \mathbb{C}$
, and if
$\lambda\in \mathbb{C}$
, and if
![]() $\unicode{x03BC}\cdot\textbf{d}\neq 0$
then
$\unicode{x03BC}\cdot\textbf{d}\neq 0$
then
![]() $\lambda=0$
.
$\lambda=0$
.
Proof. The first part follows from the fact that
![]() $\omega=\sum_{i\in Q_0}\omega_i$
is central in
$\omega=\sum_{i\in Q_0}\omega_i$
is central in
![]() $\text{Jac}\!\left(\tilde{Q},\tilde{W}^{\unicode{x03BC}}\right)$
, so each eigenspace of
$\text{Jac}\!\left(\tilde{Q},\tilde{W}^{\unicode{x03BC}}\right)$
, so each eigenspace of
![]() $\rho(\omega)$
is preserved by the action of
$\rho(\omega)$
is preserved by the action of
![]() $\text{Jac}\!\left(\tilde{Q},\tilde{W}^{\unicode{x03BC}}\right)$
. For the second part, consider the relation in
$\text{Jac}\!\left(\tilde{Q},\tilde{W}^{\unicode{x03BC}}\right)$
. For the second part, consider the relation in
![]() $\text{Jac}\!\left(\tilde{Q},\tilde{W}^{\unicode{x03BC}}\right)$
$\text{Jac}\!\left(\tilde{Q},\tilde{W}^{\unicode{x03BC}}\right)$
Applying
![]() $\rho$
and taking the trace, the final sum vanishes, and we find
$\rho$
and taking the trace, the final sum vanishes, and we find
 \begin{align*}0& = \sum_{i\in Q_0} \unicode{x03BC}_i \lambda \text{Tr}\!\left(\text{Id}_{\textbf{d}_i\times\textbf{d}_i}\right)\\& = \lambda \unicode{x03BC}\cdot \textbf{d}\end{align*}
\begin{align*}0& = \sum_{i\in Q_0} \unicode{x03BC}_i \lambda \text{Tr}\!\left(\text{Id}_{\textbf{d}_i\times\textbf{d}_i}\right)\\& = \lambda \unicode{x03BC}\cdot \textbf{d}\end{align*}
as required.
2.2 Moduli spaces of quiver representations
Given a quiver Q and a dimension vector
![]() $\textbf{d}\in\mathbb{N}^{Q_0}$
we set
$\textbf{d}\in\mathbb{N}^{Q_0}$
we set
 \begin{align*}\mathbb{A}_{\textbf{d}}(Q)\,:\!=\, &\prod_{a\in Q_1}\text{Hom}\!\left(\mathbb{C}^{\textbf{d}_{s(a)}},\mathbb{C}^{\textbf{d}_{t(a)}}\right)\\\text{GL}_{\textbf{d}}\,:\!=\, & \prod_{i\in Q_0}\text{GL}_{\textbf{d}_i}(\mathbb{C}).\end{align*}
\begin{align*}\mathbb{A}_{\textbf{d}}(Q)\,:\!=\, &\prod_{a\in Q_1}\text{Hom}\!\left(\mathbb{C}^{\textbf{d}_{s(a)}},\mathbb{C}^{\textbf{d}_{t(a)}}\right)\\\text{GL}_{\textbf{d}}\,:\!=\, & \prod_{i\in Q_0}\text{GL}_{\textbf{d}_i}(\mathbb{C}).\end{align*}
The group
![]() $\text{GL}_{\textbf{d}}$
acts on
$\text{GL}_{\textbf{d}}$
acts on
![]() $\mathbb{A}_{\textbf{d}}(Q)$
via change of basis. We denote by
$\mathbb{A}_{\textbf{d}}(Q)$
via change of basis. We denote by
![]() $\mathfrak{M}_{\textbf{d}}(Q)$
the stack of
$\mathfrak{M}_{\textbf{d}}(Q)$
the stack of
![]() $\textbf{d}$
-dimensional
$\textbf{d}$
-dimensional
![]() $\mathbb{C} Q$
-modules. There is an isomorphism of stacks
$\mathbb{C} Q$
-modules. There is an isomorphism of stacks
We denote by
![]() $\mathcal{M}_{\textbf{d}}(Q)$
the coarse moduli space of
$\mathcal{M}_{\textbf{d}}(Q)$
the coarse moduli space of
![]() $\textbf{d}$
-dimensional
$\textbf{d}$
-dimensional
![]() $\mathbb{C} Q$
-modules. Geometric K-points of
$\mathbb{C} Q$
-modules. Geometric K-points of
![]() $\mathcal{M}_{\textbf{d}}(Q)$
are in natural bijection with semisimple KQ-modules. There is an isomorphism
$\mathcal{M}_{\textbf{d}}(Q)$
are in natural bijection with semisimple KQ-modules. There is an isomorphism
We denote by
![]() $\texttt{JH}_{\textbf{d}}\,:\, \mathfrak{M}_{\textbf{d}}(Q)\rightarrow \mathcal{M}_{\textbf{d}}(Q)$
the affinisation morphism. Although this morphism is not projective, it is approximated by projective maps in the sense of [Reference Davison and Meinhardt11], meaning that
$\texttt{JH}_{\textbf{d}}\,:\, \mathfrak{M}_{\textbf{d}}(Q)\rightarrow \mathcal{M}_{\textbf{d}}(Q)$
the affinisation morphism. Although this morphism is not projective, it is approximated by projective maps in the sense of [Reference Davison and Meinhardt11], meaning that
![]() $\texttt{JH}_*$
and
$\texttt{JH}_*$
and
![]() $\texttt{JH}_!$
commute with vanishing cycle functors (introduced in the next section).
$\texttt{JH}_!$
commute with vanishing cycle functors (introduced in the next section).
For spaces and morphisms involving a subscript
![]() $\textbf{d}$
, if we omit the subscript, the union over all dimension vectors is intended.
$\textbf{d}$
, if we omit the subscript, the union over all dimension vectors is intended.
There is a finite morphism [Reference Meinhardt and Reineke33]
which at the level of geometric points takes a pair of KQ-modules to their direct sum. Since this morphism is invariant under swapping the two factors of
![]() $\mathcal{M}(Q)$
in the domain, and finite morphisms are exact with respect to the perverse t structure, we obtain an induced symmetric monoidal product on
$\mathcal{M}(Q)$
in the domain, and finite morphisms are exact with respect to the perverse t structure, we obtain an induced symmetric monoidal product on
![]() $\textbf{Perv}(\mathcal{M}(Q))$
, defined by
$\textbf{Perv}(\mathcal{M}(Q))$
, defined by
Given a potential
![]() $W\in \mathbb{C}Q/[\mathbb{C} Q,\mathbb{C} Q],$
we form the function
$W\in \mathbb{C}Q/[\mathbb{C} Q,\mathbb{C} Q],$
we form the function
![]() $\text{Tr}(W)_{\textbf{d}}$
on
$\text{Tr}(W)_{\textbf{d}}$
on
![]() $\mathbb{A}_{\textbf{d}}(Q)$
. This is well defined and
$\mathbb{A}_{\textbf{d}}(Q)$
. This is well defined and
![]() $\text{GL}_{\textbf{d}}$
-invariant by cyclic invariance of trace. As such,
$\text{GL}_{\textbf{d}}$
-invariant by cyclic invariance of trace. As such,
![]() $\text{Tr}(W)_{\textbf{d}}$
induces functions on
$\text{Tr}(W)_{\textbf{d}}$
induces functions on
![]() $\mathfrak{M}_{\textbf{d}}(Q)$
and
$\mathfrak{M}_{\textbf{d}}(Q)$
and
![]() $\mathcal{M}_{\textbf{d}}(Q)$
, which we continue to denote by
$\mathcal{M}_{\textbf{d}}(Q)$
, which we continue to denote by
![]() $\text{Tr}(W)_{\textbf{d}}$
, or just Tr(W) if there is no risk of ambiguity.
$\text{Tr}(W)_{\textbf{d}}$
, or just Tr(W) if there is no risk of ambiguity.
2.3 Cohomological Donaldson–Thomas theory of quivers with potential
Given a function f on a smooth complex variety X, we define
![]() $X_0=f^{-1}(0)$
and consider the diagram
$X_0=f^{-1}(0)$
and consider the diagram

in which the square is Cartesian. Then, we define the nearby cycles functor
![]() $\psi_f\,:\, \mathcal{D}^{\textrm{b}}(\textbf{Perv}(X))\rightarrow \mathcal{D}^{\textrm{b}}(\textbf{Perv}(X))$
via
$\psi_f\,:\, \mathcal{D}^{\textrm{b}}(\textbf{Perv}(X))\rightarrow \mathcal{D}^{\textrm{b}}(\textbf{Perv}(X))$
via
The vanishing cycles functor
![]() $\unicode{x03D5}_f$
is defined so that for
$\unicode{x03D5}_f$
is defined so that for
![]() $\mathcal{F}\in \text{Ob}\!\left(\mathcal{D}^{\textrm{b}}\!\left(\textbf{Perv}(X)\right)\right)$
there is a distinguished triangle
$\mathcal{F}\in \text{Ob}\!\left(\mathcal{D}^{\textrm{b}}\!\left(\textbf{Perv}(X)\right)\right)$
there is a distinguished triangle
Both
![]() ${{}^{\mathfrak{p}}\!}\psi_{f}\,:\!=\, \psi_f[{-}1]$
and
${{}^{\mathfrak{p}}\!}\psi_{f}\,:\!=\, \psi_f[{-}1]$
and
![]() ${{}^{\mathfrak{p}}\!}\unicode{x03D5}_{f}\,:\!=\,\unicode{x03D5}_f[{-}1]$
send perverse sheaves to perverse sheaves [Reference Kashiwara and Schapira23, Cor. 10.3.13] and (naturally) commute with Verdier duality [Reference Massey29].
${{}^{\mathfrak{p}}\!}\unicode{x03D5}_{f}\,:\!=\,\unicode{x03D5}_f[{-}1]$
send perverse sheaves to perverse sheaves [Reference Kashiwara and Schapira23, Cor. 10.3.13] and (naturally) commute with Verdier duality [Reference Massey29].
We give a lightning account of the critical cohomological Hall algebra associated with a quiver with potential. More details can be found in [Reference Davison and Meinhardt11, Reference Kontsevich and Soibelman26]. For a stack
![]() $\mathfrak{M}$
for which each connected component is irreducible and generically smooth, we define the intersection complex
$\mathfrak{M}$
for which each connected component is irreducible and generically smooth, we define the intersection complex
i.e. it is the intermediate extension of the constant perverse sheaf from the smooth locus. We define
The morphism
![]() $\unicode{x03C0}_2$
from (1.2) is proper, so that there is a natural integration map
$\unicode{x03C0}_2$
from (1.2) is proper, so that there is a natural integration map
(the shift is given by the relative dimension of
![]() $\unicode{x03C0}_2$
). Composing appropriate shifts of the morphisms
$\unicode{x03C0}_2$
). Composing appropriate shifts of the morphisms
and the sum of
![]() $\texttt{JH}_*{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}(W)}\unicode{x03B1}_{\textbf{d}^{\prime},\textbf{d}^{\prime\prime}}$
over pairs
$\texttt{JH}_*{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}(W)}\unicode{x03B1}_{\textbf{d}^{\prime},\textbf{d}^{\prime\prime}}$
over pairs
![]() $(\textbf{d}^{\prime},\textbf{d}^{\prime\prime})$
, and using commutativity of vanishing cycle functors with proper and with smooth morphisms, we obtain the morphism
$(\textbf{d}^{\prime},\textbf{d}^{\prime\prime})$
, and using commutativity of vanishing cycle functors with proper and with smooth morphisms, we obtain the morphism
Finally, composing
![]() $\unicode{x03B2}$
with
$\unicode{x03B2}$
with
![]() $\oplus_*(\texttt{JH}\times\texttt{JH})_*\texttt{TS}$
, where
$\oplus_*(\texttt{JH}\times\texttt{JH})_*\texttt{TS}$
, where
![]() $\texttt{TS}$
is (a shift of) the Thom–Sebastiani isomorphism [Reference Massey28]
$\texttt{TS}$
is (a shift of) the Thom–Sebastiani isomorphism [Reference Massey28]
we define the (relative) Hall algebra multiplication
The cohomology
 \begin{align*}\mathcal{A}_{Q,W} & \,:\!=\, \textbf{H}\!\left(\mathfrak{M}(Q),{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}(W)}\mathcal{IC}_{\mathfrak{M}(Q)}\right)\\[2pt]& \cong\textbf{H}\!\left(\mathcal{M}(Q),\mathcal{RA}_{Q,W}\right)\end{align*}
\begin{align*}\mathcal{A}_{Q,W} & \,:\!=\, \textbf{H}\!\left(\mathfrak{M}(Q),{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}(W)}\mathcal{IC}_{\mathfrak{M}(Q)}\right)\\[2pt]& \cong\textbf{H}\!\left(\mathcal{M}(Q),\mathcal{RA}_{Q,W}\right)\end{align*}
has a
![]() $\mathbb{N}^{Q_0}$
-grading by dimension vectors induced by the decomposition
$\mathbb{N}^{Q_0}$
-grading by dimension vectors induced by the decomposition
![]() $\mathcal{M}(Q)=\coprod_{\textbf{d}\in\mathbb{N}^{Q_0}}\mathcal{M}_{\textbf{d}}(Q)$
, and the associative product induced by taking derived global sections of the morphism (2.2) respects this grading.
$\mathcal{M}(Q)=\coprod_{\textbf{d}\in\mathbb{N}^{Q_0}}\mathcal{M}_{\textbf{d}}(Q)$
, and the associative product induced by taking derived global sections of the morphism (2.2) respects this grading.
Assume that Q is symmetricFootnote 3. For
![]() $\textbf{d}\in \mathbb{N}^{Q_0},$
we define
$\textbf{d}\in \mathbb{N}^{Q_0},$
we define
 \begin{equation}\mathcal{BPS}_{Q,W,\textbf{d}}\,:\!=\, \begin{cases}{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}(W)}\mathcal{IC}_{\mathcal{M}_{\textbf{d}}(Q)}& \textrm{if there is a $\textbf{d}$-dimensional simple $\mathbb{C}Q$-module}\\ 0&\textrm{otherwise.}\end{cases}\end{equation}
\begin{equation}\mathcal{BPS}_{Q,W,\textbf{d}}\,:\!=\, \begin{cases}{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}(W)}\mathcal{IC}_{\mathcal{M}_{\textbf{d}}(Q)}& \textrm{if there is a $\textbf{d}$-dimensional simple $\mathbb{C}Q$-module}\\ 0&\textrm{otherwise.}\end{cases}\end{equation}
According to our conventions,
![]() $\mathcal{IC}_{\mathcal{M}_{\textbf{d}}(Q)}$
is the intermediate extension of the constant perverse sheaf
$\mathcal{IC}_{\mathcal{M}_{\textbf{d}}(Q)}$
is the intermediate extension of the constant perverse sheaf
![]() $\mathbb{Q}_{\mathcal{M}^{simp}_{\textbf{d}}(Q)}[1-\unicode{x03C7}(\textbf{d},\textbf{d})]$
on the (open, dense) subscheme of
$\mathbb{Q}_{\mathcal{M}^{simp}_{\textbf{d}}(Q)}[1-\unicode{x03C7}(\textbf{d},\textbf{d})]$
on the (open, dense) subscheme of
![]() $\mathcal{M}_{\textbf{d}}(Q)$
corresponding to simple modules. Since
$\mathcal{M}_{\textbf{d}}(Q)$
corresponding to simple modules. Since
![]() $\mathcal{IC}_{\mathcal{M}_{\textbf{d}}(Q)}$
is Verdier self-dual, and vanishing cycle functors commute with Verdier duality [Reference Massey29], there are natural isomorphisms
$\mathcal{IC}_{\mathcal{M}_{\textbf{d}}(Q)}$
is Verdier self-dual, and vanishing cycle functors commute with Verdier duality [Reference Massey29], there are natural isomorphisms
We recall the following version of the cohomological integrality theorem from [Reference Davison and Meinhardt11]
Theorem 2.4. There is an isomorphism of bounded above complexes of perverse sheaves
 \begin{align*}\texttt{JH}_!{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}(W)}\mathcal{IC}_{\mathfrak{M}(Q)}\cong\textbf{Sym}_{\boxtimes_{\oplus}}\!\left(\bigoplus_{\mathbb{N}^{Q_0}\ni\textbf{d}\neq 0}\mathcal{BPS}_{Q,W,\textbf{d}}\otimes\textbf{H}_c\!\left({\text{pt}}/\mathbb{C}^*\right)_{\text{vir}}\right),\end{align*}
\begin{align*}\texttt{JH}_!{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}(W)}\mathcal{IC}_{\mathfrak{M}(Q)}\cong\textbf{Sym}_{\boxtimes_{\oplus}}\!\left(\bigoplus_{\mathbb{N}^{Q_0}\ni\textbf{d}\neq 0}\mathcal{BPS}_{Q,W,\textbf{d}}\otimes\textbf{H}_c\!\left({\text{pt}}/\mathbb{C}^*\right)_{\text{vir}}\right),\end{align*}
where
We define the cohomological BPS invariants
Applying the compactly supported cohomology functor to Theorem 2.4, and using self-Verdier duality (2.4) of
![]() $\mathcal{BPS}_{Q,W,\textbf{d}}$
, yields
$\mathcal{BPS}_{Q,W,\textbf{d}}$
, yields
 \begin{align*}\bigoplus_{\textbf{d}\in\mathbb{N}^{Q_0}}\textbf{H}_c(\mathfrak{M}_{\textbf{d}}(Q),{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}(W)}\mathcal{IC}_{\mathfrak{M}_{\textbf{d}}(Q)})\cong \textbf{Sym}\!\left(\bigoplus_{\mathbb{N}^{Q_0}\ni\textbf{d}\neq 0}\textrm{BPS}^{\vee}_{Q,W,\textbf{d}}\otimes\textbf{H}_c\!\left({\text{pt}}/\mathbb{C}^*\right)_{\text{vir}}\right).\end{align*}
\begin{align*}\bigoplus_{\textbf{d}\in\mathbb{N}^{Q_0}}\textbf{H}_c(\mathfrak{M}_{\textbf{d}}(Q),{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}(W)}\mathcal{IC}_{\mathfrak{M}_{\textbf{d}}(Q)})\cong \textbf{Sym}\!\left(\bigoplus_{\mathbb{N}^{Q_0}\ni\textbf{d}\neq 0}\textrm{BPS}^{\vee}_{Q,W,\textbf{d}}\otimes\textbf{H}_c\!\left({\text{pt}}/\mathbb{C}^*\right)_{\text{vir}}\right).\end{align*}
The BPS invariants of the Jacobi algebra Jac(Q,W) are defined via
 \begin{align*}\omega_{Q,W,\textbf{d}}& = \unicode{x03C7}\!\left(\textbf{H}\!\left(\mathcal{M}_{\textbf{d}}(Q),\mathcal{BPS}_{Q,W,\textbf{d}}\right)\right)\\&\,:\!=\, \sum_{i\in\mathbb{Z}}(-1)^i\dim\!\left( \textbf{H}^i\!\left(\mathcal{M}_{\textbf{d}}(Q),\mathcal{BPS}_{Q,W,\textbf{d}}\right)\right)\\& = \unicode{x03C7}\!\left(\textbf{H}_c\!\left(\mathcal{M}_{\textbf{d}}(Q),\mathcal{BPS}_{Q,W,\textbf{d}}\right)\right),\end{align*}
\begin{align*}\omega_{Q,W,\textbf{d}}& = \unicode{x03C7}\!\left(\textbf{H}\!\left(\mathcal{M}_{\textbf{d}}(Q),\mathcal{BPS}_{Q,W,\textbf{d}}\right)\right)\\&\,:\!=\, \sum_{i\in\mathbb{Z}}(-1)^i\dim\!\left( \textbf{H}^i\!\left(\mathcal{M}_{\textbf{d}}(Q),\mathcal{BPS}_{Q,W,\textbf{d}}\right)\right)\\& = \unicode{x03C7}\!\left(\textbf{H}_c\!\left(\mathcal{M}_{\textbf{d}}(Q),\mathcal{BPS}_{Q,W,\textbf{d}}\right)\right),\end{align*}
where the final identity again follows from Verdier self-duality of the BPS sheaf. Turning to Verdier duals, we have instead
Theorem 2.5. [Reference Davison and Meinhardt11] There is an isomorphism of unbounded complexes of perverse sheaves
 \begin{align*}\mathcal{RA}_{Q,W}\cong\textbf{Sym}_{\boxtimes_{\oplus}}\!\left(\bigoplus_{\mathbb{N}^{Q_0}\ni\textbf{d}\neq 0}\mathcal{BPS}_{Q,W,\textbf{d}}\otimes\textbf{H}\!\left({\text{pt}}/\mathbb{C}^*\right)_{\text{vir}}\right),\end{align*}
\begin{align*}\mathcal{RA}_{Q,W}\cong\textbf{Sym}_{\boxtimes_{\oplus}}\!\left(\bigoplus_{\mathbb{N}^{Q_0}\ni\textbf{d}\neq 0}\mathcal{BPS}_{Q,W,\textbf{d}}\otimes\textbf{H}\!\left({\text{pt}}/\mathbb{C}^*\right)_{\text{vir}}\right),\end{align*}
where
so that
Applying the natural transformation
![]() ${}^{\mathfrak{p}}\unicode{x03C4}^{\leq 1}\rightarrow \text{id}$
to
${}^{\mathfrak{p}}\unicode{x03C4}^{\leq 1}\rightarrow \text{id}$
to
![]() $\mathcal{RA}_{Q,W}$
and taking hypercohomology, there is a natural inclusion
$\mathcal{RA}_{Q,W}$
and taking hypercohomology, there is a natural inclusion
The image of this inclusion is closed under the commutatorFootnote 4 Lie bracket induced by the associative algebra structure on
![]() $\mathcal{A}_{Q,W}$
.
$\mathcal{A}_{Q,W}$
.
The resulting Lie algebra
![]() $\mathfrak{g}_{Q,W}$
is called the BPS Lie algebra for the pair (Q,W), see [Reference Davison and Meinhardt11] for more details.
$\mathfrak{g}_{Q,W}$
is called the BPS Lie algebra for the pair (Q,W), see [Reference Davison and Meinhardt11] for more details.
2.4 Hodge theoretic BPS invariants
We give another lightning introduction, this time to Hodge theoretic DT theory, via monodromic mixed Hodge modules. For more details, we refer the reader to [Reference Davison and Meinhardt11, Reference Kontsevich and Soibelman26], and for a comparison with the treatment of monodromic mixed Hodge modules in [Reference Saito39], we refer the reader to [Reference Davison and Meinhardt11, Sec. 2]. Mixed Hodge structures are important in the subject of refined DT theory, since the extra q-variable appearing in refined DT theory keeps track of the weight filtration on certain mixed Hodge structures. On the other hand, our main result states that all mixed Hodge structures appearing in this paper are pure, so that weight polynomials can be replaced by Poincaré polynomials. The takeaway is that this section can be skimmed by the reader that is happy to use the purity part of Theorem A to identify the refined BPS invariants of
![]() $\text{Jac}\!\left(\tilde{Q},\tilde{W}^{\unicode{x03BC}}\right)$
with the Poincaré polynomials of the BPS cohomology.
$\text{Jac}\!\left(\tilde{Q},\tilde{W}^{\unicode{x03BC}}\right)$
with the Poincaré polynomials of the BPS cohomology.
For X a variety we denote by
![]() $\textbf{MHM}(X)$
the category of mixed Hodge modules on X. There is an equivalence of categories between
$\textbf{MHM}(X)$
the category of mixed Hodge modules on X. There is an equivalence of categories between
![]() $\textbf{MHM}({\text{pt}})$
and the category of graded-polarisable mixed Hodge structures. Let
$\textbf{MHM}({\text{pt}})$
and the category of graded-polarisable mixed Hodge structures. Let
![]() $\mathcal{B}_X$
denote the full subcategory of
$\mathcal{B}_X$
denote the full subcategory of
![]() $\textbf{MHM}(X\times\mathbb{A}^1)$
containing those mixed Hodge modules
$\textbf{MHM}(X\times\mathbb{A}^1)$
containing those mixed Hodge modules
![]() $\mathcal{F}$
such that for each
$\mathcal{F}$
such that for each
![]() $x\in X$
and
$x\in X$
and
![]() $i\in\mathbb{Z}$
the mixed Hodge modules
$i\in\mathbb{Z}$
the mixed Hodge modules
are locally constant away from
![]() $x\times \{0\}$
. We denote by
$x\times \{0\}$
. We denote by
![]() $\mathcal{C}_X$
the full subcategory of
$\mathcal{C}_X$
the full subcategory of
![]() $\mathcal{B}_X$
containing those
$\mathcal{B}_X$
containing those
![]() $\mathcal{F}$
such that each (2.5) is constant. Equivalently, we may define
$\mathcal{F}$
such that each (2.5) is constant. Equivalently, we may define
![]() $\mathcal{C}_X$
as the essential image of
$\mathcal{C}_X$
as the essential image of
![]() $\unicode{x03C0}_X^*[1]$
, for
$\unicode{x03C0}_X^*[1]$
, for
![]() $\unicode{x03C0}_X\,:\, X\times\mathbb{A}^1\rightarrow X$
the projection. We denote by
$\unicode{x03C0}_X\,:\, X\times\mathbb{A}^1\rightarrow X$
the projection. We denote by
![]() $\textbf{MMHM}(X)$
the Serre quotient
$\textbf{MMHM}(X)$
the Serre quotient
![]() $\mathcal{B}_X/\mathcal{C}_X$
. There is an embedding of categories
$\mathcal{B}_X/\mathcal{C}_X$
. There is an embedding of categories
![]() $\textbf{MHM}(X)\hookrightarrow \textbf{MMHM}(X)$
defined via
$\textbf{MHM}(X)\hookrightarrow \textbf{MMHM}(X)$
defined via
The direct image functor
induces an equivalence of categories between the category of mixed Hodge modules on
![]() $X\times \mathbb{C}^*$
with locally constant cohomology sheaves after restriction to each
$X\times \mathbb{C}^*$
with locally constant cohomology sheaves after restriction to each
![]() $\{x\}\times \mathbb{C}^*$
and the category of monodromic mixed Hodge modules on X. Denoting by
$\{x\}\times \mathbb{C}^*$
and the category of monodromic mixed Hodge modules on X. Denoting by
![]() $\Theta^{-1}$
an inverse equivalence, there is a faithful forgetful functor
$\Theta^{-1}$
an inverse equivalence, there is a faithful forgetful functor
taking a monodromic mixed Hodge module to its underlying perverse sheaf on X. We abuse notation by denoting this functor also by
![]() $\textbf{rat}$
. For X a variety, we denote by
$\textbf{rat}$
. For X a variety, we denote by
![]() $\underline{\mathbb{Q}}_X$
the lift of the constant sheaf
$\underline{\mathbb{Q}}_X$
the lift of the constant sheaf
![]() $\mathbb{Q}_X$
to a complex of mixed Hodge modules on X. For f a regular function on X, we define the vanishing cycles functor
$\mathbb{Q}_X$
to a complex of mixed Hodge modules on X. For f a regular function on X, we define the vanishing cycles functor
 \begin{align*}\unicode{x03D5}^{\text{mon}}_{f}\,:\,&\textbf{MHM}(X)\rightarrow \textbf{MMHM}(X)\\&\mathcal{F}\mapsto \Theta \underline{\unicode{x03D5}}_{u\cdot f}\!\left(\mathcal{F}\boxtimes\underline{\mathbb{Q}}_{\mathbb{C}^*}\right)[1],\end{align*}
\begin{align*}\unicode{x03D5}^{\text{mon}}_{f}\,:\,&\textbf{MHM}(X)\rightarrow \textbf{MMHM}(X)\\&\mathcal{F}\mapsto \Theta \underline{\unicode{x03D5}}_{u\cdot f}\!\left(\mathcal{F}\boxtimes\underline{\mathbb{Q}}_{\mathbb{C}^*}\right)[1],\end{align*}
where u is the coordinate on
![]() $\mathbb{C}^*$
and
$\mathbb{C}^*$
and
![]() $\underline{\unicode{x03D5}}_{u\cdot f}$
is the lift of
$\underline{\unicode{x03D5}}_{u\cdot f}$
is the lift of
![]() ${{}^{\mathfrak{p}}\!}\unicode{x03D5}_{u\cdot f}$
to the categories of mixed Hodge modules. There is a natural isomorphism
${{}^{\mathfrak{p}}\!}\unicode{x03D5}_{u\cdot f}$
to the categories of mixed Hodge modules. There is a natural isomorphism
![]() $\textbf{rat} \unicode{x03D5}^{\text{mon}}_{f}\cong {{}^{\mathfrak{p}}\!}\unicode{x03D5}_{f}\textbf{rat}$
.
$\textbf{rat} \unicode{x03D5}^{\text{mon}}_{f}\cong {{}^{\mathfrak{p}}\!}\unicode{x03D5}_{f}\textbf{rat}$
.
An object
![]() $\mathcal{F}\in \text{Ob}(\textbf{MMHM}(X))$
inherits a weight filtration from the weight filtration on objects of
$\mathcal{F}\in \text{Ob}(\textbf{MMHM}(X))$
inherits a weight filtration from the weight filtration on objects of
![]() $\textbf{MHM}(X\times\mathbb{A}^1)$
. We say that
$\textbf{MHM}(X\times\mathbb{A}^1)$
. We say that
![]() $\mathcal{F}$
is pure of weight n if the associated graded object with respect to this filtration is concentrated in degree n. We say that an object
$\mathcal{F}$
is pure of weight n if the associated graded object with respect to this filtration is concentrated in degree n. We say that an object
![]() $\mathcal{F}\in \text{Ob}\!\left(\mathcal{D}^{\textrm{b}}(\textbf{MMHM}(X))\right)$
is pure if each
$\mathcal{F}\in \text{Ob}\!\left(\mathcal{D}^{\textrm{b}}(\textbf{MMHM}(X))\right)$
is pure if each
![]() $\mathcal{H}^i(\mathcal{F})$
is pure of weight i.
$\mathcal{H}^i(\mathcal{F})$
is pure of weight i.
The cohomologically graded mixed Hodge structure
![]() $\mathscr{L}=\textbf{H}_c\!\left(\mathbb{A}^1,\mathbb{Q}\right)$
is pure: it is concentrated in cohomological degree two and is pure of weight two. This object has a tensor square root in
$\mathscr{L}=\textbf{H}_c\!\left(\mathbb{A}^1,\mathbb{Q}\right)$
is pure: it is concentrated in cohomological degree two and is pure of weight two. This object has a tensor square root in
![]() $\mathcal{D}^{\textrm{b}}(\textbf{MMHM}(\text{pt}))$
provided by
$\mathcal{D}^{\textrm{b}}(\textbf{MMHM}(\text{pt}))$
provided by
where
![]() $d\,:\, \mathbb{A}^1\rightarrow \mathbb{A}^1$
is the morphism
$d\,:\, \mathbb{A}^1\rightarrow \mathbb{A}^1$
is the morphism
![]() $z\mapsto z^2$
. We say a monodromic mixed Hodge structure is of Tate type if it is a direct sum of (possibly negative) tensor powers of the monodromic mixed Hodge structure
$z\mapsto z^2$
. We say a monodromic mixed Hodge structure is of Tate type if it is a direct sum of (possibly negative) tensor powers of the monodromic mixed Hodge structure
![]() $\mathscr{L}^{\,\,1/2}[1]$
.
$\mathscr{L}^{\,\,1/2}[1]$
.
For X an irreducible variety, we denote by
the natural lift of
![]() $\mathcal{IC}_X$
to a pure weight zero monodromic mixed Hodge module.
$\mathcal{IC}_X$
to a pure weight zero monodromic mixed Hodge module.
We define
 \begin{equation}\mathcal{BPS}^{\text{hdg}}_{Q,W,\textbf{d}}\,:\!=\, \begin{cases}\unicode{x03D5}^{\text{mon}}_{\text{Tr}(W)}\mathcal{IC}^{\text{hdg}}_{\mathcal{M}_{\textbf{d}}(Q)}& \textrm{if there is a $\textbf{d}$-dimensional simple $\mathbb{C}Q$-module}\\[4pt] 0&\textrm{otherwise.}\end{cases}\end{equation}
\begin{equation}\mathcal{BPS}^{\text{hdg}}_{Q,W,\textbf{d}}\,:\!=\, \begin{cases}\unicode{x03D5}^{\text{mon}}_{\text{Tr}(W)}\mathcal{IC}^{\text{hdg}}_{\mathcal{M}_{\textbf{d}}(Q)}& \textrm{if there is a $\textbf{d}$-dimensional simple $\mathbb{C}Q$-module}\\[4pt] 0&\textrm{otherwise.}\end{cases}\end{equation}
This is the natural lift of the BPS sheaf to a monodromic mixed Hodge module, i.e.
![]() $\textbf{rat}\!\left(\mathcal{BPS}^{\text{hdg}}_{Q,W,\textbf{d}}\right)\cong\mathcal{BPS}_{Q,W,\textbf{d}}$
. Similarly, we define the monodromic mixed Hodge structure
$\textbf{rat}\!\left(\mathcal{BPS}^{\text{hdg}}_{Q,W,\textbf{d}}\right)\cong\mathcal{BPS}_{Q,W,\textbf{d}}$
. Similarly, we define the monodromic mixed Hodge structure
satisfying
![]() $\textbf{rat}\!\left(\textrm{BPS}^{\text{hdg}}_{Q,W,\textbf{d}}\right)\cong \textrm{BPS}_{Q,W,\textbf{d}}$
. We defineFootnote 5
$\textbf{rat}\!\left(\textrm{BPS}^{\text{hdg}}_{Q,W,\textbf{d}}\right)\cong \textrm{BPS}_{Q,W,\textbf{d}}$
. We defineFootnote 5
Since all of the natural transformations defining the multiplication on the Hall algebra
![]() $\mathcal{A}_{Q,W}$
lift to categories of monodromic mixed Hodge modules [Reference Davison8, Reference Davison and Meinhardt11, Reference Kontsevich and Soibelman26], as does the Thom–Sebastiani theorem [Reference Saito39], we may define a multiplication on
$\mathcal{A}_{Q,W}$
lift to categories of monodromic mixed Hodge modules [Reference Davison8, Reference Davison and Meinhardt11, Reference Kontsevich and Soibelman26], as does the Thom–Sebastiani theorem [Reference Saito39], we may define a multiplication on
![]() $\mathcal{RA}_{Q,W}^{\text{hdg}}$
that recovers the multiplication on
$\mathcal{RA}_{Q,W}^{\text{hdg}}$
that recovers the multiplication on
![]() $\mathcal{RA}_{Q,W}$
after applying the functor
$\mathcal{RA}_{Q,W}$
after applying the functor
![]() $\textbf{rat}$
. Likewise, taking derived direct image to a point we obtain the algebra object
$\textbf{rat}$
. Likewise, taking derived direct image to a point we obtain the algebra object
![]() $\mathcal{A}^{\text{hdg}}_{Q,W}$
in monodromic mixed Hodge structures. Then by [Reference Davison and Meinhardt11], Theorems 2.3 and 2.4 lift to the categories of monodromic mixed Hodge modules and monodromic mixed Hodge structures. In particular, the BPS Lie algebra
$\mathcal{A}^{\text{hdg}}_{Q,W}$
in monodromic mixed Hodge structures. Then by [Reference Davison and Meinhardt11], Theorems 2.3 and 2.4 lift to the categories of monodromic mixed Hodge modules and monodromic mixed Hodge structures. In particular, the BPS Lie algebra
![]() $\mathfrak{g}_{Q,W}=\textrm{BPS}_{Q,W}[{-}1]$
lifts to a Lie algebra object
$\mathfrak{g}_{Q,W}=\textrm{BPS}_{Q,W}[{-}1]$
lifts to a Lie algebra object
inside
![]() $\mathcal{D}^{\textrm{b}}(\textbf{MMHM}(\text{pt}))$
. This is a Lie subalgebra of
$\mathcal{D}^{\textrm{b}}(\textbf{MMHM}(\text{pt}))$
. This is a Lie subalgebra of
![]() $\mathcal{A}_{Q,W}^{\text{hdg}}$
, considered as a Lie algebra in the category of
$\mathcal{A}_{Q,W}^{\text{hdg}}$
, considered as a Lie algebra in the category of
![]() $\mathbb{N}^{Q_0}$
-graded, cohomologically graded monodromic mixed Hodge structures, via the commutator Lie bracket. See [Reference Davison8, Reference Davison and Meinhardt11] for full details.
$\mathbb{N}^{Q_0}$
-graded, cohomologically graded monodromic mixed Hodge structures, via the commutator Lie bracket. See [Reference Davison8, Reference Davison and Meinhardt11] for full details.
2.5 Cohomological Donaldson–Thomas theory for preprojective algebras
In this section, we restrict our attention to ‘tripled’ QPs of the form
![]() $\left(\tilde{Q},\tilde{W}\right)$
, as in the introduction. Firstly, we recall the following purity result on the BPS cohomology of the Jacobi algebra
$\left(\tilde{Q},\tilde{W}\right)$
, as in the introduction. Firstly, we recall the following purity result on the BPS cohomology of the Jacobi algebra
![]() $\text{Jac}\!\left(\tilde{Q},\tilde{W}\right)$
:
$\text{Jac}\!\left(\tilde{Q},\tilde{W}\right)$
:
Theorem 2.6. [Reference Davison9] For an arbitrary quiver Q and dimension vector
![]() $\textbf{d}\in\mathbb{N}^{Q_0}$
, the mixed Hodge structure
$\textbf{d}\in\mathbb{N}^{Q_0}$
, the mixed Hodge structure
![]() $\textrm{BPS}^{\text{hdg}}_{\tilde{Q},\tilde{W},\textbf{d}}$
is pure, of Tate type. In addition (or as a consequence of the cohomological integrality theorem), the mixed Hodge structure on
$\textrm{BPS}^{\text{hdg}}_{\tilde{Q},\tilde{W},\textbf{d}}$
is pure, of Tate type. In addition (or as a consequence of the cohomological integrality theorem), the mixed Hodge structure on
is pure, of Tate type.
We denote by
the closed embedding that sends a pair
![]() $(\rho,t)$
to the
$(\rho,t)$
to the
![]() $\mathbb{C}\tilde{Q}$
-module
$\mathbb{C}\tilde{Q}$
-module
![]() $\rho^{\prime}$
for which the action of the arrows
$\rho^{\prime}$
for which the action of the arrows
![]() $a,a^*\in\overline{Q}$
are the same as for
$a,a^*\in\overline{Q}$
are the same as for
![]() $\rho$
, and the action of each
$\rho$
, and the action of each
![]() $\rho^{\prime}(\omega_i)$
is given by multiplication by t.
$\rho^{\prime}(\omega_i)$
is given by multiplication by t.
We will need the following result on the support and equivariance of the BPS sheaf itself:
Lemma 2.7. [Reference Davison9] For a quiver Q and dimension vector
![]() $\textbf{d}\in\mathbb{N}^{Q_0},$
there is a perverse sheaf
$\textbf{d}\in\mathbb{N}^{Q_0},$
there is a perverse sheaf
such that there is an isomorphism
The same result holds at the level of monodromic mixed Hodge modules.
In words, the theorem says that the BPS sheaf is supported on the subspace of
![]() $\mathbb{C} \tilde{Q}$
-modules for which all of the generalised eigenvalues of the operators
$\mathbb{C} \tilde{Q}$
-modules for which all of the generalised eigenvalues of the operators
![]() $\rho(\omega_i)$
are the same, and the sheaf is moreover equivariant for the
$\rho(\omega_i)$
are the same, and the sheaf is moreover equivariant for the
![]() $\mathbb{A}^1$
-action that acts by adding scalar multiples of the identity to all of the operators
$\mathbb{A}^1$
-action that acts by adding scalar multiples of the identity to all of the operators
![]() $\rho(\omega_i)$
simultaneously.
$\rho(\omega_i)$
simultaneously.
We recall from [Reference Davison9] the description of the BPS cohomology of the Jacobi algebra
![]() $\text{Jac}\!\left(\tilde{Q},\tilde{W}\right)$
in terms of Kac polynomials:
$\text{Jac}\!\left(\tilde{Q},\tilde{W}\right)$
in terms of Kac polynomials:
Theorem 2.8. The Poincaré polynomials of the cohomological BPS invariants for the QP
![]() $\left(\tilde{Q},\tilde{W}\right)$
satisfy
$\left(\tilde{Q},\tilde{W}\right)$
satisfy
where
is the Kac polynomial, counting the number of isomorphism classes of absolutelyFootnote 6 indecomposable
![]() $\mathbb{F}_qQ$
-modules for
$\mathbb{F}_qQ$
-modules for
![]() $\mathbb{F}_q$
a field of order q. Furthermore, the natural mixed Hodge structure on
$\mathbb{F}_q$
a field of order q. Furthermore, the natural mixed Hodge structure on
![]() $\textrm{BPS}_{\tilde{Q},\tilde{W},\textbf{d}}$
is pure, of Tate type, so that we can write
$\textrm{BPS}_{\tilde{Q},\tilde{W},\textbf{d}}$
is pure, of Tate type, so that we can write
and so
3. Deformed dimensional reduction and proofs of main results
3.1 Deformed dimensional reduction
The main tool in proving Theorem A will be deformed dimensional reduction, as introduced in joint work with Tudor Pădurariu [Reference Davison and Pădurariu13]. This is a geometric result about vanishing cycle functors for functions satisfying certain
![]() $\mathbb{C}^*$
-equivariance properties. We state the version that we need below.
$\mathbb{C}^*$
-equivariance properties. We state the version that we need below.
Theorem 3.1. [Reference Davison and Pădurariu13, Thm. 1.3] Let the algebraic group G act on a variety X and affine space
![]() $\mathbb{A}^n$
. Assume that
$\mathbb{A}^n$
. Assume that
![]() $\mathbb{A}^n$
is also given a
$\mathbb{A}^n$
is also given a
![]() $\mathbb{C}^*$
-action, with non-negative weights, which commutes with the G-action. Let
$\mathbb{C}^*$
-action, with non-negative weights, which commutes with the G-action. Let
![]() $\mathbb{C}^*$
act on
$\mathbb{C}^*$
act on
![]() $\overline{X}=X\times\mathbb{A}^n$
via the product of the given action on
$\overline{X}=X\times\mathbb{A}^n$
via the product of the given action on
![]() $\mathbb{A}^n$
with the trivial action on X. Let g be a function on
$\mathbb{A}^n$
with the trivial action on X. Let g be a function on
![]() $\overline{X}$
that is G-invariant and
$\overline{X}$
that is G-invariant and
![]() $\mathbb{C}^*$
-semi-invariant, with strictly positive weight. Assume that we are given a
$\mathbb{C}^*$
-semi-invariant, with strictly positive weight. Assume that we are given a
![]() $G\times\mathbb{C}^*$
-equivariant decomposition
$G\times\mathbb{C}^*$
-equivariant decomposition
![]() $\mathbb{A}^n=\mathbb{A}^m\times \mathbb{A}^{n-m}$
and that we can write
$\mathbb{A}^n=\mathbb{A}^m\times \mathbb{A}^{n-m}$
and that we can write
where the functions
![]() $g_0,\ldots g_m$
are pulled back from
$g_0,\ldots g_m$
are pulled back from
![]() $X\times \mathbb{A}^{n-m}$
and
$X\times \mathbb{A}^{n-m}$
and
![]() $t_1,\ldots,t_m$
are a system of coordinates for
$t_1,\ldots,t_m$
are a system of coordinates for
![]() $\mathbb{A}^m$
. Let
$\mathbb{A}^m$
. Let
![]() $Z\subset X\times \mathbb{A}^{n-m}$
be the vanishing locus of the functions
$Z\subset X\times \mathbb{A}^{n-m}$
be the vanishing locus of the functions
![]() $g_1,\ldots,g_m$
. Then, Z is G-invariant. Set
$g_1,\ldots,g_m$
. Then, Z is G-invariant. Set
![]() $\overline{Z}=Z\times\mathbb{A}^{m}\subset \overline{X}$
. We denote by
$\overline{Z}=Z\times\mathbb{A}^{m}\subset \overline{X}$
. We denote by
the natural projections. Then, the natural transformation
is an isomorphism.
Since the functor
![]() $\textbf{rat}$
is faithful, the same statement is true at the level of (monodromic) mixed Hodge modules: the natural transformation
$\textbf{rat}$
is faithful, the same statement is true at the level of (monodromic) mixed Hodge modules: the natural transformation
is an isomorphism inFootnote 7
![]() $\mathcal{D}^{\textrm{b}}(\textbf{MMHM}(X/G))$
.
$\mathcal{D}^{\textrm{b}}(\textbf{MMHM}(X/G))$
.
3.2 Proof of Theorem A
We proceed by applying deformed dimensional reduction to the function
![]() $\text{Tr}\!\left(\tilde{W}^{\unicode{x03BC}}\right)$
.
$\text{Tr}\!\left(\tilde{W}^{\unicode{x03BC}}\right)$
.
Proof of Theorem A. Given a quiver Q, we denote by
![]() $Q^+$
the quiver obtained by adding a loop
$Q^+$
the quiver obtained by adding a loop
![]() $\omega_i$
at each vertex
$\omega_i$
at each vertex
![]() $i\in Q_0$
, or equivalently the quiver obtained by removing all of the arrows
$i\in Q_0$
, or equivalently the quiver obtained by removing all of the arrows
![]() $a^*$
from
$a^*$
from
![]() $\tilde{Q}$
. We denote by
$\tilde{Q}$
. We denote by
![]() $\mathfrak{I}(Q)$
the stack of pairs
$\mathfrak{I}(Q)$
the stack of pairs
![]() $(\rho,f)$
, consisting of a
$(\rho,f)$
, consisting of a
![]() $\mathbb{C} Q$
-module
$\mathbb{C} Q$
-module
![]() $\rho$
and an endomorphism
$\rho$
and an endomorphism
![]() $f\in {\text{Hom}}_{\mathbb{C} Q}(\rho,\rho)$
. Then, we consider the commutative diagram
$f\in {\text{Hom}}_{\mathbb{C} Q}(\rho,\rho)$
. Then, we consider the commutative diagram

In the above diagram, i is the natural embedding of stacks, sending a pair
![]() $(\rho,f)$
to the
$(\rho,f)$
to the
![]() $\mathbb{C} Q^+$
-module
$\mathbb{C} Q^+$
-module
![]() $\rho^{\prime}$
for which the underlying
$\rho^{\prime}$
for which the underlying
![]() $\mathbb{C} Q$
-module is
$\mathbb{C} Q$
-module is
![]() $\rho$
, and the action of the loops
$\rho$
, and the action of the loops
![]() $\omega_i$
is given by f. All of the horizontal arrows are the natural forgetful maps. We set
$\omega_i$
is given by f. All of the horizontal arrows are the natural forgetful maps. We set
We denote by
![]() $\Omega$
the quiver containing the same vertices as Q and for which the only arrows are the loops
$\Omega$
the quiver containing the same vertices as Q and for which the only arrows are the loops
![]() $\omega_i$
. We denote by
$\omega_i$
. We denote by
![]() $Q^{\text{op}}$
the quiver containing the same vertices as Q, and only the arrows
$Q^{\text{op}}$
the quiver containing the same vertices as Q, and only the arrows
![]() $a^*$
for
$a^*$
for
![]() $a\in Q_1$
, i.e.
$a\in Q_1$
, i.e.
![]() $Q^{\text{op}}$
is the opposite quiver to Q. In the notation of Theorem 3.1, we set
$Q^{\text{op}}$
is the opposite quiver to Q. In the notation of Theorem 3.1, we set
 \begin{align}X&=\mathbb{A}_{\textbf{d}}(Q)\\[2pt]\mathbb{A}^m&=\mathbb{A}_{\textbf{d}}\!\left(Q^{\text{op}}\right)\nonumber\\[2pt]\nonumber \mathbb{A}^{n-m}&=\mathbb{A}_{\textbf{d}}(\Omega)\\[2pt] \nonumber G&= \text{GL}_{\textbf{d}}.\end{align}
\begin{align}X&=\mathbb{A}_{\textbf{d}}(Q)\\[2pt]\mathbb{A}^m&=\mathbb{A}_{\textbf{d}}\!\left(Q^{\text{op}}\right)\nonumber\\[2pt]\nonumber \mathbb{A}^{n-m}&=\mathbb{A}_{\textbf{d}}(\Omega)\\[2pt] \nonumber G&= \text{GL}_{\textbf{d}}.\end{align}
We let
![]() $\mathbb{C}^*$
act on
$\mathbb{C}^*$
act on
![]() $\mathbb{A}^m$
and
$\mathbb{A}^m$
and
![]() $\mathbb{A}^{n-m}$
with weight one.
$\mathbb{A}^{n-m}$
with weight one.
We set
so
![]() $\tilde{W}^{\unicode{x03BC}}=\tilde{W}+L_{\unicode{x03BC}}$
. Then
$\tilde{W}^{\unicode{x03BC}}=\tilde{W}+L_{\unicode{x03BC}}$
. Then
![]() $\text{Tr}\!\left(\tilde{W}+L_{\unicode{x03BC}}\right)$
satisfies the conditions of Theorem 3.1; for example, it is
$\text{Tr}\!\left(\tilde{W}+L_{\unicode{x03BC}}\right)$
satisfies the conditions of Theorem 3.1; for example, it is
![]() $\mathbb{C}^*$
semi-invariant with weight two. In the notation of that theorem
$\mathbb{C}^*$
semi-invariant with weight two. In the notation of that theorem
![]() $Z\subset X\times \mathbb{A}^{n-m}=\mathbb{A}_{\textbf{d}}(Q^+)$
is the locus containing those
$Z\subset X\times \mathbb{A}^{n-m}=\mathbb{A}_{\textbf{d}}(Q^+)$
is the locus containing those
![]() $\mathbb{C} Q^+$
-modules
$\mathbb{C} Q^+$
-modules
![]() $\rho$
such that the endomorphisms
$\rho$
such that the endomorphisms
![]() $\rho(\omega_i)$
determine an endomorphism of the underlying
$\rho(\omega_i)$
determine an endomorphism of the underlying
![]() $\mathbb{C} Q$
-module of
$\mathbb{C} Q$
-module of
![]() $\rho$
. It follows that
$\rho$
. It follows that
![]() $Z/G=\mathfrak{Z}(G)$
. By Theorem 3.1, there is an isomorphismFootnote 8
$Z/G=\mathfrak{Z}(G)$
. By Theorem 3.1, there is an isomorphismFootnote 8
If instead we set
set
![]() $n=m$
, and again let
$n=m$
, and again let
![]() $\mathbb{C}^*$
act on
$\mathbb{C}^*$
act on
![]() $\mathbb{A}^m$
with weight one, then the function
$\mathbb{A}^m$
with weight one, then the function
![]() $\text{Tr}(\tilde{W})$
still satisfies the conditions of Theorem 3.1 (now it is semi-invariant with weight one). So instead we arrive at the isomorphism
$\text{Tr}(\tilde{W})$
still satisfies the conditions of Theorem 3.1 (now it is semi-invariant with weight one). So instead we arrive at the isomorphism
Since
![]() $\texttt{JH}^+$
is approximated by proper maps, there is a natural isomorphism (see [Reference Davison and Meinhardt11, Sec. 4.1])
$\texttt{JH}^+$
is approximated by proper maps, there is a natural isomorphism (see [Reference Davison and Meinhardt11, Sec. 4.1])
Combining all of the above, we can writeFootnote 9
 \begin{align*}\unicode{x03C0}^{\prime}_!\tilde{\texttt{JH}}_!{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}(\tilde{W}^{\unicode{x03BC}})}\mathcal{IC}_{\mathfrak{M}\!\left(\tilde{Q}\right)} & \cong \texttt{JH}_!\unicode{x03C0}_!{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}(\tilde{W}^{\unicode{x03BC}})}\mathcal{IC}_{\mathfrak{M}\!\left(\tilde{Q}\right)}&\\&\cong \texttt{JH}_!q_!{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}\!\left(L_{\unicode{x03BC}}\right)}\mathbb{Q}_{\mathfrak{I}(Q)} &\textrm{by }(3.3)\\&\cong \texttt{JH}_!q_!{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}\!\left(L_{\unicode{x03BC}}\right)}p_!{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}(\tilde{W})}\mathcal{IC}_{\mathfrak{M}\!\left(\tilde{Q}\right)}&\textrm{by }(3.4)\\&\cong q^{\prime}_!\texttt{JH}^+_!{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}\!\left(L_{\unicode{x03BC}}\right)}p_!{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}(\tilde{W})}\mathcal{IC}_{\mathfrak{M}\!\left(\tilde{Q}\right)}\\&\cong q^{\prime}_!{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}\!\left(L_{\unicode{x03BC}}\right)}\texttt{JH}^+_!p_!{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}(\tilde{W})}\mathcal{IC}_{\mathfrak{M}\!\left(\tilde{Q}\right)}&\textrm{by } (3.5)\\&\cong q^{\prime}_!{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}\!\left(L_{\unicode{x03BC}}\right)}p^{\prime}_!\tilde{\texttt{JH}}_!{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}(\tilde{W})}\mathcal{IC}_{\mathfrak{M}\!\left(\tilde{Q}\right)}\\&\cong q^{\prime}_!{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}\!\left(L_{\unicode{x03BC}}\right)}p^{\prime}_!\textbf{Sym}_{\oplus}\!\left(\bigoplus_{\textbf{d}\in\mathbb{N}^{Q_0}\setminus 0} \mathcal{BPS}_{\tilde{Q},\tilde{W},\textbf{d}}\otimes\textbf{H}_c\!\left({\text{pt}}/\mathbb{C}^*\right)_{\text{vir}}\right)&\textrm{by Theorem }(2.4)\\&\cong q^{\prime}_!{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}\!\left(L_{\unicode{x03BC}}\right)}\textbf{Sym}_{\oplus}\!\left(\bigoplus_{\textbf{d}\in\mathbb{N}^{Q_0}\setminus 0} p^{\prime}_!\mathcal{BPS}_{\tilde{Q},\tilde{W},\textbf{d}}\otimes\textbf{H}_c\!\left({\text{pt}}/\mathbb{C}^*\right)_{\text{vir}}\right)&\textrm{since }p^{\prime}\textrm{ is a monoid map}\\&\cong q^{\prime}_!\textbf{Sym}_{\oplus}\!\left(\bigoplus_{\textbf{d}\in\mathbb{N}^{Q_0}\setminus 0} {{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}\!\left(L_{\unicode{x03BC}}\right)}p^{\prime}_!\mathcal{BPS}_{\tilde{Q},\tilde{W},\textbf{d}}\otimes\textbf{H}_c\!\left({\text{pt}}/\mathbb{C}^*\right)_{\text{vir}}\right)&\textrm{by Thom\unicode{x2015}Sebastiani.}\end{align*}
\begin{align*}\unicode{x03C0}^{\prime}_!\tilde{\texttt{JH}}_!{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}(\tilde{W}^{\unicode{x03BC}})}\mathcal{IC}_{\mathfrak{M}\!\left(\tilde{Q}\right)} & \cong \texttt{JH}_!\unicode{x03C0}_!{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}(\tilde{W}^{\unicode{x03BC}})}\mathcal{IC}_{\mathfrak{M}\!\left(\tilde{Q}\right)}&\\&\cong \texttt{JH}_!q_!{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}\!\left(L_{\unicode{x03BC}}\right)}\mathbb{Q}_{\mathfrak{I}(Q)} &\textrm{by }(3.3)\\&\cong \texttt{JH}_!q_!{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}\!\left(L_{\unicode{x03BC}}\right)}p_!{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}(\tilde{W})}\mathcal{IC}_{\mathfrak{M}\!\left(\tilde{Q}\right)}&\textrm{by }(3.4)\\&\cong q^{\prime}_!\texttt{JH}^+_!{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}\!\left(L_{\unicode{x03BC}}\right)}p_!{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}(\tilde{W})}\mathcal{IC}_{\mathfrak{M}\!\left(\tilde{Q}\right)}\\&\cong q^{\prime}_!{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}\!\left(L_{\unicode{x03BC}}\right)}\texttt{JH}^+_!p_!{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}(\tilde{W})}\mathcal{IC}_{\mathfrak{M}\!\left(\tilde{Q}\right)}&\textrm{by } (3.5)\\&\cong q^{\prime}_!{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}\!\left(L_{\unicode{x03BC}}\right)}p^{\prime}_!\tilde{\texttt{JH}}_!{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}(\tilde{W})}\mathcal{IC}_{\mathfrak{M}\!\left(\tilde{Q}\right)}\\&\cong q^{\prime}_!{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}\!\left(L_{\unicode{x03BC}}\right)}p^{\prime}_!\textbf{Sym}_{\oplus}\!\left(\bigoplus_{\textbf{d}\in\mathbb{N}^{Q_0}\setminus 0} \mathcal{BPS}_{\tilde{Q},\tilde{W},\textbf{d}}\otimes\textbf{H}_c\!\left({\text{pt}}/\mathbb{C}^*\right)_{\text{vir}}\right)&\textrm{by Theorem }(2.4)\\&\cong q^{\prime}_!{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}\!\left(L_{\unicode{x03BC}}\right)}\textbf{Sym}_{\oplus}\!\left(\bigoplus_{\textbf{d}\in\mathbb{N}^{Q_0}\setminus 0} p^{\prime}_!\mathcal{BPS}_{\tilde{Q},\tilde{W},\textbf{d}}\otimes\textbf{H}_c\!\left({\text{pt}}/\mathbb{C}^*\right)_{\text{vir}}\right)&\textrm{since }p^{\prime}\textrm{ is a monoid map}\\&\cong q^{\prime}_!\textbf{Sym}_{\oplus}\!\left(\bigoplus_{\textbf{d}\in\mathbb{N}^{Q_0}\setminus 0} {{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}\!\left(L_{\unicode{x03BC}}\right)}p^{\prime}_!\mathcal{BPS}_{\tilde{Q},\tilde{W},\textbf{d}}\otimes\textbf{H}_c\!\left({\text{pt}}/\mathbb{C}^*\right)_{\text{vir}}\right)&\textrm{by Thom\unicode{x2015}Sebastiani.}\end{align*}
By Lemma 2.7, we can write
where
Writing
![]() $f=\text{Tr}\!\left(L_{\unicode{x03BC}}\right)\lvert_{\mathcal{M}_{\textbf{d}}(Q)\times\mathbb{A}^1}$
, we have
$f=\text{Tr}\!\left(L_{\unicode{x03BC}}\right)\lvert_{\mathcal{M}_{\textbf{d}}(Q)\times\mathbb{A}^1}$
, we have
 \begin{align*}f\,:\, &\mathcal{M}_{\textbf{d}}(Q)\times\mathbb{A}^1\rightarrow\mathbb{C}\\&(\rho,t)\mapsto \frac{1}{2}(\unicode{x03BC}\cdot \textbf{d})t^2.\end{align*}
\begin{align*}f\,:\, &\mathcal{M}_{\textbf{d}}(Q)\times\mathbb{A}^1\rightarrow\mathbb{C}\\&(\rho,t)\mapsto \frac{1}{2}(\unicode{x03BC}\cdot \textbf{d})t^2.\end{align*}
It follows from (3.6) that
 \begin{align*}{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}\!\left(L_{\unicode{x03BC}}\right)}p^{\prime}_!\mathcal{BPS}_{\tilde{Q},\tilde{W},\textbf{d}}\cong\begin{cases}e_!(\mathcal{F}\boxtimes \mathbb{Q}_0)&\textrm{if }\unicode{x03BC}\cdot \textbf{d}\neq 0\\[5pt] e_!\left(\mathcal{F}\boxtimes \mathcal{IC}_{\mathbb{A}^1}\right)&\textrm{if }\unicode{x03BC}\cdot \textbf{d}= 0,\end{cases}\end{align*}
\begin{align*}{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}\!\left(L_{\unicode{x03BC}}\right)}p^{\prime}_!\mathcal{BPS}_{\tilde{Q},\tilde{W},\textbf{d}}\cong\begin{cases}e_!(\mathcal{F}\boxtimes \mathbb{Q}_0)&\textrm{if }\unicode{x03BC}\cdot \textbf{d}\neq 0\\[5pt] e_!\left(\mathcal{F}\boxtimes \mathcal{IC}_{\mathbb{A}^1}\right)&\textrm{if }\unicode{x03BC}\cdot \textbf{d}= 0,\end{cases}\end{align*}
so that
where we define
 \begin{align*}g(\textbf{d})=\begin{cases} 1&\textrm{if }\unicode{x03BC}\cdot\textbf{d}=0\\[5pt]0&\textrm{if }\unicode{x03BC}\cdot \textbf{d}\neq 0.\end{cases}\end{align*}
\begin{align*}g(\textbf{d})=\begin{cases} 1&\textrm{if }\unicode{x03BC}\cdot\textbf{d}=0\\[5pt]0&\textrm{if }\unicode{x03BC}\cdot \textbf{d}\neq 0.\end{cases}\end{align*}
Finally, we deduce that
 \begin{align}\textbf{H}_c\!\left(\mathfrak{M}\!\left(\tilde{Q}\right),{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}(\tilde{W}^{\unicode{x03BC}})}\mathcal{IC}_{\mathfrak{M}\!\left(\tilde{Q}\right)}\right)& = \unicode{x03C4}_!\unicode{x03C0}^{\prime}_!\tilde{\texttt{JH}}_!{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}(\tilde{W}^{\unicode{x03BC}})}\mathcal{IC}_{\mathfrak{M}\!\left(\tilde{Q}\right)}\nonumber \\& \cong \textbf{Sym}\!\left(\bigoplus_{\textbf{d}\in\mathbb{N}^{Q_0}\setminus 0}\left(\textbf{H}_c(\mathcal{M}_{\textbf{d}}(\Pi_Q),\mathcal{BPS}_{\Pi_Q,\textbf{d}})\otimes \textbf{H}_c\!\left({\text{pt}}/\mathbb{C}^*\right)_{\text{vir}} \right)[{-}g(\textbf{d})]\right).\end{align}
\begin{align}\textbf{H}_c\!\left(\mathfrak{M}\!\left(\tilde{Q}\right),{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}(\tilde{W}^{\unicode{x03BC}})}\mathcal{IC}_{\mathfrak{M}\!\left(\tilde{Q}\right)}\right)& = \unicode{x03C4}_!\unicode{x03C0}^{\prime}_!\tilde{\texttt{JH}}_!{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}(\tilde{W}^{\unicode{x03BC}})}\mathcal{IC}_{\mathfrak{M}\!\left(\tilde{Q}\right)}\nonumber \\& \cong \textbf{Sym}\!\left(\bigoplus_{\textbf{d}\in\mathbb{N}^{Q_0}\setminus 0}\left(\textbf{H}_c(\mathcal{M}_{\textbf{d}}(\Pi_Q),\mathcal{BPS}_{\Pi_Q,\textbf{d}})\otimes \textbf{H}_c\!\left({\text{pt}}/\mathbb{C}^*\right)_{\text{vir}} \right)[{-}g(\textbf{d})]\right).\end{align}
On the other hand, by Theorem 2.4 again, we have
 \begin{equation}\textbf{H}_c(\mathfrak{M}\!\left(\tilde{Q}\right),{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}(\tilde{W}^{\unicode{x03BC}})}\mathcal{IC}_{\mathfrak{M}\!\left(\tilde{Q}\right)})\cong \textbf{Sym}\!\left(\bigoplus_{\textbf{d}\in\mathbb{N}^{Q_0}\setminus 0}\textrm{BPS}^{\vee}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}},\textbf{d}}\otimes \textbf{H}_c\!\left({\text{pt}}/\mathbb{C}^*\right)_{\text{vir}}\right).\end{equation}
\begin{equation}\textbf{H}_c(\mathfrak{M}\!\left(\tilde{Q}\right),{{}^{\mathfrak{p}}\!}\unicode{x03D5}_{\text{Tr}(\tilde{W}^{\unicode{x03BC}})}\mathcal{IC}_{\mathfrak{M}\!\left(\tilde{Q}\right)})\cong \textbf{Sym}\!\left(\bigoplus_{\textbf{d}\in\mathbb{N}^{Q_0}\setminus 0}\textrm{BPS}^{\vee}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}},\textbf{d}}\otimes \textbf{H}_c\!\left({\text{pt}}/\mathbb{C}^*\right)_{\text{vir}}\right).\end{equation}
Comparing (3.7) and (3.8), we find
 \begin{align*}\textrm{BPS}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}},\textbf{d}}\cong\ &\left(\textbf{H}_c\!\left(\mathcal{M}_{\textbf{d}}\!\left(\Pi_Q\right),\mathcal{BPS}_{\Pi_Q,\textbf{d}}\right)\right)^{\vee}[g(\textbf{d})]\\\cong\ &\left(\textbf{H}_c\!\left(\mathcal{M}_{\textbf{d}}\!\left(\tilde{Q}\right),\mathcal{BPS}_{\tilde{Q},\tilde{W},\textbf{d}}\right)[1]\right)^{\vee}[g(\textbf{d})]& \textrm{by Theorem 2.7}\\\cong\ &\textbf{H}_c\!\left(\mathcal{M}_{\textbf{d}}\!\left(\tilde{Q}\right),\mathcal{BPS}_{\tilde{Q},\tilde{W},\textbf{d}}\right)^{\vee}[g(\textbf{d})-1]\\\cong\ &\textrm{BPS}_{\tilde{Q},\tilde{W},\textbf{d}}[g(\textbf{d})-1]\end{align*}
\begin{align*}\textrm{BPS}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}},\textbf{d}}\cong\ &\left(\textbf{H}_c\!\left(\mathcal{M}_{\textbf{d}}\!\left(\Pi_Q\right),\mathcal{BPS}_{\Pi_Q,\textbf{d}}\right)\right)^{\vee}[g(\textbf{d})]\\\cong\ &\left(\textbf{H}_c\!\left(\mathcal{M}_{\textbf{d}}\!\left(\tilde{Q}\right),\mathcal{BPS}_{\tilde{Q},\tilde{W},\textbf{d}}\right)[1]\right)^{\vee}[g(\textbf{d})]& \textrm{by Theorem 2.7}\\\cong\ &\textbf{H}_c\!\left(\mathcal{M}_{\textbf{d}}\!\left(\tilde{Q}\right),\mathcal{BPS}_{\tilde{Q},\tilde{W},\textbf{d}}\right)^{\vee}[g(\textbf{d})-1]\\\cong\ &\textrm{BPS}_{\tilde{Q},\tilde{W},\textbf{d}}[g(\textbf{d})-1]\end{align*}
and now (2.8) follows from Theorem 2.8.
Performing the same calculations in the category of monodromic mixed Hodge structures, isomorphisms (3.7) and (3.8) yield the isomorphism of
![]() $\mathbb{N}^{Q_0}$
-graded complexes of monodromic mixed Hodge structures
$\mathbb{N}^{Q_0}$
-graded complexes of monodromic mixed Hodge structures
 \begin{equation}\textbf{Sym}\!\left(\bigoplus_{\textbf{d}\in\mathbb{N}^{Q_0}\setminus 0}\textrm{BPS}^{\text{hdg},\vee}_{\tilde{Q},\tilde{W},\textbf{d}}\otimes \mathscr{L}^{\,\,(g(\textbf{d})-1)/2}\otimes \textbf{H}_c\!\left({\text{pt}}/\mathbb{C}^*\right)_{\text{vir}} \right)\cong \textbf{Sym}\!\left(\bigoplus_{\textbf{d}\in\mathbb{N}^{Q_0}\setminus 0}\textrm{BPS}^{\text{hdg},\vee}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}},\textbf{d}}\otimes \textbf{H}_c\!\left({\text{pt}}/\mathbb{C}^*\right)_{\text{vir}}\right),\end{equation}
\begin{equation}\textbf{Sym}\!\left(\bigoplus_{\textbf{d}\in\mathbb{N}^{Q_0}\setminus 0}\textrm{BPS}^{\text{hdg},\vee}_{\tilde{Q},\tilde{W},\textbf{d}}\otimes \mathscr{L}^{\,\,(g(\textbf{d})-1)/2}\otimes \textbf{H}_c\!\left({\text{pt}}/\mathbb{C}^*\right)_{\text{vir}} \right)\cong \textbf{Sym}\!\left(\bigoplus_{\textbf{d}\in\mathbb{N}^{Q_0}\setminus 0}\textrm{BPS}^{\text{hdg},\vee}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}},\textbf{d}}\otimes \textbf{H}_c\!\left({\text{pt}}/\mathbb{C}^*\right)_{\text{vir}}\right),\end{equation}
where
On the other hand, by Theorem 2.6 the mixed Hodge structure
![]() $\textrm{BPS}^{\text{hdg}}_{\Pi_Q,\textbf{d}}$
is pure, so that
$\textrm{BPS}^{\text{hdg}}_{\Pi_Q,\textbf{d}}$
is pure, so that
![]() $\textrm{BPS}^{\text{hdg},\vee}_{\Pi_Q,\textbf{d}}\otimes\mathscr{L}^{\,n/2}$
is pure for all
$\textrm{BPS}^{\text{hdg},\vee}_{\Pi_Q,\textbf{d}}\otimes\mathscr{L}^{\,n/2}$
is pure for all
![]() $n\in\mathbb{Z}$
. It follows that both sides of (3.9) are pure. The isomorphism
$n\in\mathbb{Z}$
. It follows that both sides of (3.9) are pure. The isomorphism
then follows from (3.9) and semisimplicity of the category of pure monodromic mixed Hodge structures as in [Reference Davison and Pădurariu13, Cor. 7.1].
Example 3.2. To recover the example that we started the paper with, consider the quiver
![]() $Q^{(0)}$
with one vertex and no arrows. We label the unique arrow of the one-loop quiver
$Q^{(0)}$
with one vertex and no arrows. We label the unique arrow of the one-loop quiver
![]() $Q^{(1)}=\widetilde{Q^{(0)}}$
by
$Q^{(1)}=\widetilde{Q^{(0)}}$
by
![]() $\omega_0$
. For
$\omega_0$
. For
![]() $\unicode{x03BC}=\unicode{x03BC}_0e_0$
to be generic, we just have to pick
$\unicode{x03BC}=\unicode{x03BC}_0e_0$
to be generic, we just have to pick
![]() $\unicode{x03BC}_0\neq 0$
. Then, we find
$\unicode{x03BC}_0\neq 0$
. Then, we find
and so the fermionic version of
![]() $\mathcal{A}_{\widetilde{Q^{(0)}},\tilde{W}}=\mathcal{A}_{Q^{(1)}}$
is indeed
$\mathcal{A}_{\widetilde{Q^{(0)}},\tilde{W}}=\mathcal{A}_{Q^{(1)}}$
is indeed
![]() $\mathcal{A}_{Q^{(0)}}$
.
$\mathcal{A}_{Q^{(0)}}$
.
Example 3.3. We return once more to the noncommutative conifold. As observed in Example 2.2, this algebra is obtained by setting
![]() $\unicode{x03BC}=(1,-1)$
for the quiver (1.10) and considering
$\unicode{x03BC}=(1,-1)$
for the quiver (1.10) and considering
![]() $\text{Jac}\!\left(\tilde{Q},\tilde{W}^{\unicode{x03BC}}\right)$
. The cohomological BPS invariants of the QP
$\text{Jac}\!\left(\tilde{Q},\tilde{W}^{\unicode{x03BC}}\right)$
. The cohomological BPS invariants of the QP
![]() $\left(\tilde{Q},\tilde{W}\right)$
are given in (1.11), while the cohomological BPS invariants of the noncommutative conifold are given in (1.13). Comparing the two, there is a cohomological shift between the respective (m,n)th cohomological BPS invariants precisely if
$\left(\tilde{Q},\tilde{W}\right)$
are given in (1.11), while the cohomological BPS invariants of the noncommutative conifold are given in (1.13). Comparing the two, there is a cohomological shift between the respective (m,n)th cohomological BPS invariants precisely if
![]() $m\neq n$
, i.e. precisely if
$m\neq n$
, i.e. precisely if
![]() $\unicode{x03BC}\cdot(m,n)\neq 0$
.
$\unicode{x03BC}\cdot(m,n)\neq 0$
.
Recall from the introduction that the BPS invariants for the resolved conifold are only a partially fermionised version of the BPS invariants of
![]() $Y_0\times\mathbb{A}^1$
. In view of the main result, we see that the generic deformation in the commutative algebraic geometry context corresponds to the deformation
$Y_0\times\mathbb{A}^1$
. In view of the main result, we see that the generic deformation in the commutative algebraic geometry context corresponds to the deformation
![]() $\unicode{x03BC}=(1,-1)$
. To fully fermionise the DT theory, we are obliged to work in the fully noncommutativeFootnote 10 context provided by generic
$\unicode{x03BC}=(1,-1)$
. To fully fermionise the DT theory, we are obliged to work in the fully noncommutativeFootnote 10 context provided by generic
![]() $\unicode{x03BC}$
. Note that deformations within algebraic geometry of the Kleinian singularity were parameterised by
$\unicode{x03BC}$
. Note that deformations within algebraic geometry of the Kleinian singularity were parameterised by
![]() $\mathfrak{h}$
, the Cartan subalgebra of the (reduced) McKay graph
$\mathfrak{h}$
, the Cartan subalgebra of the (reduced) McKay graph
![]() $\Gamma^{\prime}$
, whereas noncommutative deformations are parameterised by the Cartan subalgebra of the full McKay graph.
$\Gamma^{\prime}$
, whereas noncommutative deformations are parameterised by the Cartan subalgebra of the full McKay graph.
Remark 3.4. Along the course of the proof of Theorem A, we have shown that
 \begin{align*}\unicode{x03C0}^{\prime}_*\mathcal{BPS}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}},\textbf{d}}\cong \begin{cases} \unicode{x03C0}^{\prime}_*\mathcal{BPS}_{\tilde{Q},\tilde{W}}[{-}1] &\textrm{if }\unicode{x03BC}\cdot \textbf{d}\neq 0\\[4pt]\unicode{x03C0}^{\prime}_*\mathcal{BPS}_{\tilde{Q},\tilde{W}}&\textrm{otherwise.}\end{cases}\end{align*}
\begin{align*}\unicode{x03C0}^{\prime}_*\mathcal{BPS}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}},\textbf{d}}\cong \begin{cases} \unicode{x03C0}^{\prime}_*\mathcal{BPS}_{\tilde{Q},\tilde{W}}[{-}1] &\textrm{if }\unicode{x03BC}\cdot \textbf{d}\neq 0\\[4pt]\unicode{x03C0}^{\prime}_*\mathcal{BPS}_{\tilde{Q},\tilde{W}}&\textrm{otherwise.}\end{cases}\end{align*}
With a little effort, one may lift this statement to the level of monodromic mixed Hodge module complexes.
3.3 Proof of Theorem B
Given a quiver Q, an element
![]() $\unicode{x03BC}\in R$
, and a number
$\unicode{x03BC}\in R$
, and a number
![]() $n\in\mathbb{Z}_{\geq 1}$
, define
$n\in\mathbb{Z}_{\geq 1}$
, define
Then in the decomposition (3.2), we let
![]() $\mathbb{C}^*$
act with weight 1 on
$\mathbb{C}^*$
act with weight 1 on
![]() $\mathbb{A}_{\textbf{d}}(\Omega)$
, weight
$\mathbb{A}_{\textbf{d}}(\Omega)$
, weight
![]() $n-1$
on
$n-1$
on
![]() $\mathbb{A}_{\textbf{d}}\!\left(Q^{\text{op}}\right)$
, and trivially on
$\mathbb{A}_{\textbf{d}}\!\left(Q^{\text{op}}\right)$
, and trivially on
![]() $\mathbb{A}_{\textbf{d}}(Q)$
, so
$\mathbb{A}_{\textbf{d}}(Q)$
, so
![]() $\text{Tr}(\tilde{W}^{\unicode{x03BC}}_{\textbf{d}})$
satisfies the conditions of Theorem 3.1 (now it is a weight n function). Then, the argument of Section 3.2 gives that
$\text{Tr}(\tilde{W}^{\unicode{x03BC}}_{\textbf{d}})$
satisfies the conditions of Theorem 3.1 (now it is a weight n function). Then, the argument of Section 3.2 gives that
Theorem A follows from the special case
![]() $n=2$
and Theorem 2.8, observing that
$n=2$
and Theorem 2.8, observing that
![]() $\textbf{H}\!\left(\mathbb{A}^1,\unicode{x03D5}^{\text{mon}}_{x^2}\underline{\mathbb{Q}}_{\mathbb{A}^1}\right)=\mathscr{L}^{\,\,1/2}$
.
$\textbf{H}\!\left(\mathbb{A}^1,\unicode{x03D5}^{\text{mon}}_{x^2}\underline{\mathbb{Q}}_{\mathbb{A}^1}\right)=\mathscr{L}^{\,\,1/2}$
.
In this section, we consider instead the special case
![]() $n=1;$
, i.e., we consider the quiver
$n=1;$
, i.e., we consider the quiver
![]() $\tilde{Q}$
with the potential
$\tilde{Q}$
with the potential
This potential is linear in the loops
![]() $\omega_i$
, so that the following proposition is a straightforward application of (undeformed) dimensional reduction:
$\omega_i$
, so that the following proposition is a straightforward application of (undeformed) dimensional reduction:
Proposition 3.5. There is an isomorphism in the derived category of complexes of mixed Hodge modules
Proof. In the setup of Theorem 3.1, we put
![]() $X=\mathbb{A}_{\textbf{d}}(\overline{Q})$
,
$X=\mathbb{A}_{\textbf{d}}(\overline{Q})$
,
![]() $n=m$
,
$n=m$
,
![]() $\mathbb{A}^m=\mathbb{A}_{\textbf{d}}(\Omega)$
and
$\mathbb{A}^m=\mathbb{A}_{\textbf{d}}(\Omega)$
and
![]() $G=\text{GL}_{\textbf{d}}$
. Then,
$G=\text{GL}_{\textbf{d}}$
. Then,
![]() $g_0$
is the zero function, so that there is a natural isomorphism
$g_0$
is the zero function, so that there is a natural isomorphism
![]() $\unicode{x03D5}^{\text{mon}}_{g_0}\rightarrow \text{id}$
, and the result follows from Theorem 3.1 and
$\unicode{x03D5}^{\text{mon}}_{g_0}\rightarrow \text{id}$
, and the result follows from Theorem 3.1 and
![]() $\dim(\mathbb{A}_{\textbf{d}}(\Omega))=\textbf{d}\cdot\textbf{d}$
.
$\dim(\mathbb{A}_{\textbf{d}}(\Omega))=\textbf{d}\cdot\textbf{d}$
.
Proof of Theorem B. We have isomorphisms of
![]() $\mathbb{N}^{Q_0}$
-graded mixed Hodge structures
$\mathbb{N}^{Q_0}$
-graded mixed Hodge structures
 \begin{align*}\bigoplus_{\textbf{d}\in \mathbb{N}^{Q_0}}\textbf{H}_c\!\left(\mathfrak{M}_{\textbf{d}}(\Pi_{Q,\unicode{x03BC}}),\mathbb{Q}\right)\otimes \mathscr{L}^{\,\,\unicode{x03C7}_Q(\textbf{d},\textbf{d})}\cong &\bigoplus_{\textbf{d}\in\mathbb{N}^{Q_0}}\textbf{H}_c\!\left(\mathfrak{M}_{\textbf{d}}\!\left(\tilde{Q}\right),\unicode{x03D5}^{\text{mon}}_{\text{Tr}(W_1^{\unicode{x03BC}})}\mathcal{IC}_{\mathfrak{M}_{\textbf{d}}\!\left(\tilde{Q}\right)}\right)\\\cong&\textbf{Sym}\!\left(\bigoplus_{\mathbb{N}^{Q_0}\ni \textbf{d}\neq 0}\textrm{BPS}^{\text{hdg},\vee}_{\tilde{Q},W_1^{\unicode{x03BC}},\textbf{d}}\otimes\textbf{H}_c\!\left({\text{pt}}/\mathbb{C}^*\right)_{\text{vir}}\right),\end{align*}
\begin{align*}\bigoplus_{\textbf{d}\in \mathbb{N}^{Q_0}}\textbf{H}_c\!\left(\mathfrak{M}_{\textbf{d}}(\Pi_{Q,\unicode{x03BC}}),\mathbb{Q}\right)\otimes \mathscr{L}^{\,\,\unicode{x03C7}_Q(\textbf{d},\textbf{d})}\cong &\bigoplus_{\textbf{d}\in\mathbb{N}^{Q_0}}\textbf{H}_c\!\left(\mathfrak{M}_{\textbf{d}}\!\left(\tilde{Q}\right),\unicode{x03D5}^{\text{mon}}_{\text{Tr}(W_1^{\unicode{x03BC}})}\mathcal{IC}_{\mathfrak{M}_{\textbf{d}}\!\left(\tilde{Q}\right)}\right)\\\cong&\textbf{Sym}\!\left(\bigoplus_{\mathbb{N}^{Q_0}\ni \textbf{d}\neq 0}\textrm{BPS}^{\text{hdg},\vee}_{\tilde{Q},W_1^{\unicode{x03BC}},\textbf{d}}\otimes\textbf{H}_c\!\left({\text{pt}}/\mathbb{C}^*\right)_{\text{vir}}\right),\end{align*}
where the first isomorphism is dimensional reduction (as in Proposition 3.5) and the second is the cohomological integrality theorem. So the theorem follows from (2.9) and the claim that
 \begin{align*}\textrm{BPS}^{\text{hdg}}_{\tilde{Q},W_1^{\unicode{x03BC}},\textbf{d}}\cong\begin{cases} \textrm{BPS}^{\text{hdg}}_{\tilde{Q},\tilde{W},\textbf{d}} &\textrm{if }\textbf{d}\cdot\unicode{x03BC}=0\\0& \textrm{otherwise.}\end{cases}\end{align*}
\begin{align*}\textrm{BPS}^{\text{hdg}}_{\tilde{Q},W_1^{\unicode{x03BC}},\textbf{d}}\cong\begin{cases} \textrm{BPS}^{\text{hdg}}_{\tilde{Q},\tilde{W},\textbf{d}} &\textrm{if }\textbf{d}\cdot\unicode{x03BC}=0\\0& \textrm{otherwise.}\end{cases}\end{align*}
This follows from (3.10) and the observation that for
![]() $\lambda\in\mathbb{C}$
$\lambda\in\mathbb{C}$
 \begin{align*}\textbf{H}\!\left(\mathbb{A}^1,\unicode{x03D5}^{\text{mon}}_{\lambda x}\mathcal{IC}_{\mathbb{A}^1}\right)\cong\begin{cases} \mathscr{L}^{\,-1/2}& \textrm{if }\lambda=0\\0&\textrm{if }\lambda\neq 0.\end{cases}\tag*{$\square$}\end{align*}
\begin{align*}\textbf{H}\!\left(\mathbb{A}^1,\unicode{x03D5}^{\text{mon}}_{\lambda x}\mathcal{IC}_{\mathbb{A}^1}\right)\cong\begin{cases} \mathscr{L}^{\,-1/2}& \textrm{if }\lambda=0\\0&\textrm{if }\lambda\neq 0.\end{cases}\tag*{$\square$}\end{align*}
Assume that the dimension vector
![]() $\textbf{d}$
is indivisible, meaning that there is no
$\textbf{d}$
is indivisible, meaning that there is no
![]() $n\in \mathbb{Z}_{\geq 2}$
such that
$n\in \mathbb{Z}_{\geq 2}$
such that
![]() $\frac{1}{n}\textbf{d}\in\mathbb{N}^{Q_0}$
. Assume also that
$\frac{1}{n}\textbf{d}\in\mathbb{N}^{Q_0}$
. Assume also that
![]() $\unicode{x03BC}$
is chosen to be generic, subject to the constraint that
$\unicode{x03BC}$
is chosen to be generic, subject to the constraint that
![]() $\textbf{d}\cdot\unicode{x03BC}=0$
. Equivalently,
$\textbf{d}\cdot\unicode{x03BC}=0$
. Equivalently,
![]() $\textbf{d}$
and
$\textbf{d}$
and
![]() $\unicode{x03BC}$
are chosen so that
$\unicode{x03BC}$
are chosen so that
![]() $\textbf{d}^{\prime}\cdot \unicode{x03BC}=0$
implies that
$\textbf{d}^{\prime}\cdot \unicode{x03BC}=0$
implies that
![]() $\textbf{d}^{\prime}$
is an integer multiple of
$\textbf{d}^{\prime}$
is an integer multiple of
![]() $\textbf{d}$
. Then (1.17) simplifies to
$\textbf{d}$
. Then (1.17) simplifies to
 \begin{equation}\bigoplus_{n\in\mathbb{Z}_{\geq 0}}\textbf{H}_c\!\left(\mathfrak{M}_{n \textbf{d}}(\Pi_{Q,\unicode{x03BC}}),\mathbb{Q}\right)\otimes \mathscr{L}^{\,n^2\unicode{x03C7}_Q(\textbf{d},\textbf{d})}\cong \textbf{Sym}\!\left(\bigoplus_{n\in\mathbb{Z}_{>0}}\textrm{BPS}_{\tilde{Q},\tilde{W},n\textbf{d}}^{\text{hdg},\vee}\otimes\textbf{H}_c({\text{pt}}/\mathbb{C}^*,\mathbb{Q})_{\text{vir}}\right).\end{equation}
\begin{equation}\bigoplus_{n\in\mathbb{Z}_{\geq 0}}\textbf{H}_c\!\left(\mathfrak{M}_{n \textbf{d}}(\Pi_{Q,\unicode{x03BC}}),\mathbb{Q}\right)\otimes \mathscr{L}^{\,n^2\unicode{x03C7}_Q(\textbf{d},\textbf{d})}\cong \textbf{Sym}\!\left(\bigoplus_{n\in\mathbb{Z}_{>0}}\textrm{BPS}_{\tilde{Q},\tilde{W},n\textbf{d}}^{\text{hdg},\vee}\otimes\textbf{H}_c({\text{pt}}/\mathbb{C}^*,\mathbb{Q})_{\text{vir}}\right).\end{equation}
Our assumptions imply that
![]() $\mathcal{M}_{\textbf{d}}(\Pi_Q)$
is a fine moduli scheme, and
$\mathcal{M}_{\textbf{d}}(\Pi_Q)$
is a fine moduli scheme, and
![]() $\mathfrak{M}_{\textbf{d}}(\Pi_Q)$
is a trivial
$\mathfrak{M}_{\textbf{d}}(\Pi_Q)$
is a trivial
![]() $\textrm{B}\mathbb{C}^*$
-gerbe over it, meaning that
$\textrm{B}\mathbb{C}^*$
-gerbe over it, meaning that
Recall that there is an isomorphism
From the
![]() $n=1$
piece of (3.11), we deduce the following slightly stronger version of a result of Crawley–Boevey and Van den Bergh [Reference Crawley-Boevey and Van den Bergh7]:
$n=1$
piece of (3.11), we deduce the following slightly stronger version of a result of Crawley–Boevey and Van den Bergh [Reference Crawley-Boevey and Van den Bergh7]:
Corollary 3.6. Let
![]() $\textbf{d}$
be indivisible, and
$\textbf{d}$
be indivisible, and
![]() $\unicode{x03BC}$
be generic. Then, there is an isomorphism of mixed Hodge structures
$\unicode{x03BC}$
be generic. Then, there is an isomorphism of mixed Hodge structures
In particular,
![]() $\textbf{H}_c(\mathcal{M}_{\textbf{d}}(\Pi_{Q,\unicode{x03BC}}),\mathbb{Q})$
is pure of Tate type.
$\textbf{H}_c(\mathcal{M}_{\textbf{d}}(\Pi_{Q,\unicode{x03BC}}),\mathbb{Q})$
is pure of Tate type.
4. Further directions
4.1 Calculating the BPS sheaves
While our main theorem gives a way to calculate the BPS cohomology
![]() $\textrm{BPS}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}},\textbf{d}}$
for arbitrary Q,
$\textrm{BPS}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}},\textbf{d}}$
for arbitrary Q,
![]() $\textbf{d}\in \mathbb{N}^{Q_0}$
and
$\textbf{d}\in \mathbb{N}^{Q_0}$
and
![]() $\unicode{x03BC}\in R$
, the actual BPS sheaf
$\unicode{x03BC}\in R$
, the actual BPS sheaf
![]() $\mathcal{BPS}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}},\textbf{d}}$
remains a little mysterious. We can at least generalise (part of) the support lemma (Lemma 2.7) from the case
$\mathcal{BPS}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}},\textbf{d}}$
remains a little mysterious. We can at least generalise (part of) the support lemma (Lemma 2.7) from the case
![]() $\unicode{x03BC}=0$
.
$\unicode{x03BC}=0$
.
Lemma 4.1. For a quiver Q, and dimension vector
![]() $\textbf{d}\in\mathbb{N}^{Q_0}$
, we have
$\textbf{d}\in\mathbb{N}^{Q_0}$
, we have
 \begin{align*}\text{supp}(\mathcal{BPS}_{\Pi^{\unicode{x03BC}}_Q,\textbf{d}})\subset\begin{cases}\tilde{e}(\mathcal{M}_{\textbf{d}}(\Pi_Q)\times\mathbb{A}^1)& \textrm{if } \unicode{x03BC}\cdot \textbf{d}=0\\[5pt]\tilde{e}(\mathcal{M}_{\textbf{d}}(\Pi_Q)\times\{0\})&\textrm{if }\unicode{x03BC}\cdot\textbf{d}\neq 0,\end{cases}\end{align*}
\begin{align*}\text{supp}(\mathcal{BPS}_{\Pi^{\unicode{x03BC}}_Q,\textbf{d}})\subset\begin{cases}\tilde{e}(\mathcal{M}_{\textbf{d}}(\Pi_Q)\times\mathbb{A}^1)& \textrm{if } \unicode{x03BC}\cdot \textbf{d}=0\\[5pt]\tilde{e}(\mathcal{M}_{\textbf{d}}(\Pi_Q)\times\{0\})&\textrm{if }\unicode{x03BC}\cdot\textbf{d}\neq 0,\end{cases}\end{align*}
where
![]() $\tilde{e}$
is defined in (2.7).
$\tilde{e}$
is defined in (2.7).
Proof. The proof is very similar to [Reference Davison9, Lem. 4.1]. Let
![]() $\rho$
be a
$\rho$
be a
![]() $\text{Jac}\!\left(\tilde{Q},\tilde{W}^{\unicode{x03BC}}\right)$
-module lying in the support of
$\text{Jac}\!\left(\tilde{Q},\tilde{W}^{\unicode{x03BC}}\right)$
-module lying in the support of
![]() $\mathcal{BPS}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}},\textbf{d}}$
. By definition,
$\mathcal{BPS}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}},\textbf{d}}$
. By definition,
![]() $\rho$
is semisimple, and so since
$\rho$
is semisimple, and so since
![]() $\rho\!\left(\sum_{i\in Q_0}\omega_i\right)$
is central, it acts via a diagonal matrix. Arguing as in [Reference Davison9, Lem. 4.1] and using centrality of
$\rho\!\left(\sum_{i\in Q_0}\omega_i\right)$
is central, it acts via a diagonal matrix. Arguing as in [Reference Davison9, Lem. 4.1] and using centrality of
![]() $\rho\!\left(\sum_{i\in Q_0}\omega_i\right)$
along with the cohomological integrality theorem, we deduce that the generalised eigenvalues of
$\rho\!\left(\sum_{i\in Q_0}\omega_i\right)$
along with the cohomological integrality theorem, we deduce that the generalised eigenvalues of
![]() $\rho(\omega)$
are all the same, i.e.
$\rho(\omega)$
are all the same, i.e.
![]() $\rho(\omega)$
acts via scalar multiplication, establishing the lemma in the case
$\rho(\omega)$
acts via scalar multiplication, establishing the lemma in the case
![]() $\unicode{x03BC}\cdot\textbf{d}\neq 0$
. Arguing as in Proposition 2.3, if
$\unicode{x03BC}\cdot\textbf{d}\neq 0$
. Arguing as in Proposition 2.3, if
![]() $\unicode{x03BC}\cdot\textbf{d}\neq 0$
, we must have
$\unicode{x03BC}\cdot\textbf{d}\neq 0$
, we must have
![]() $\lambda=0$
. This establishes the lemma in the case
$\lambda=0$
. This establishes the lemma in the case
![]() $\unicode{x03BC}\cdot\textbf{d}\neq 0$
.
$\unicode{x03BC}\cdot\textbf{d}\neq 0$
.
Even in the case
![]() $\unicode{x03BC}\cdot \textbf{d}=0,$
this is a slightly weaker statement than Lemma 2.7; it is harder to show that
$\unicode{x03BC}\cdot \textbf{d}=0,$
this is a slightly weaker statement than Lemma 2.7; it is harder to show that
![]() $\mathcal{BPS}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}},\textbf{d}}$
is
$\mathcal{BPS}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}},\textbf{d}}$
is
![]() $\mathbb{A}^1$
-equivariant (where
$\mathbb{A}^1$
-equivariant (where
![]() $\mathbb{A}^1$
acts by adding a scalar multiple of the identity matrix to
$\mathbb{A}^1$
acts by adding a scalar multiple of the identity matrix to
![]() $\rho(\omega)$
) since the function
$\rho(\omega)$
) since the function
![]() $\text{Tr}(\tilde{W}^{\unicode{x03BC}})$
is not
$\text{Tr}(\tilde{W}^{\unicode{x03BC}})$
is not
![]() $\mathbb{A}^1$
-invariant unless
$\mathbb{A}^1$
-invariant unless
![]() $\unicode{x03BC}=0$
.
$\unicode{x03BC}=0$
.
It would be interesting to compare
![]() $\mathcal{BPS}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}},\textbf{d}}$
with
$\mathcal{BPS}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}},\textbf{d}}$
with
![]() $\mathcal{BPS}_{\tilde{Q},\tilde{W},\textbf{d}}\cong \tilde{e}_!\left(\mathcal{BPS}_{\Pi_Q,\textbf{d}}\boxtimes \mathcal{IC}_{\mathbb{A}^1}\right)$
in the case
$\mathcal{BPS}_{\tilde{Q},\tilde{W},\textbf{d}}\cong \tilde{e}_!\left(\mathcal{BPS}_{\Pi_Q,\textbf{d}}\boxtimes \mathcal{IC}_{\mathbb{A}^1}\right)$
in the case
![]() $\unicode{x03BC}\cdot\textbf{d}=0$
, and with
$\unicode{x03BC}\cdot\textbf{d}=0$
, and with
![]() $\tilde{e}_!\left(\mathcal{BPS}_{\Pi_Q,\textbf{d}}\boxtimes \mathbb{Q}_0\right)$
in the case
$\tilde{e}_!\left(\mathcal{BPS}_{\Pi_Q,\textbf{d}}\boxtimes \mathbb{Q}_0\right)$
in the case
![]() $\unicode{x03BC}\cdot \textbf{d}\neq 0$
. In particular, we may ask the following question:
$\unicode{x03BC}\cdot \textbf{d}\neq 0$
. In particular, we may ask the following question:
Question 4.2. Is the monodromic mixed Hodge module
![]() $\mathcal{BPS}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}},\textbf{d}}$
pure?
$\mathcal{BPS}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}},\textbf{d}}$
pure?
By [Reference Davison10, Thm. A], we know that
![]() $\mathcal{BPS}_{\tilde{Q},\tilde{W},\textbf{d}}$
is a pure monodromic mixed Hodge module, i.e. we know that for
$\mathcal{BPS}_{\tilde{Q},\tilde{W},\textbf{d}}$
is a pure monodromic mixed Hodge module, i.e. we know that for
![]() $\unicode{x03BC}=0$
the answer to Question 4.2 is yes.
$\unicode{x03BC}=0$
the answer to Question 4.2 is yes.
4.2 The BPS algebra
Identifying the BPS cohomology of the Jacobi algebra
![]() $\mathbb{C}\!\left(\tilde{Q},\tilde{W}^{\unicode{x03BC}}\right)$
is only part of understanding its cohomological DT theory; it tells us the size of the graded pieces of
$\mathbb{C}\!\left(\tilde{Q},\tilde{W}^{\unicode{x03BC}}\right)$
is only part of understanding its cohomological DT theory; it tells us the size of the graded pieces of
![]() $\mathcal{A}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}}}$
, but nothing about the algebra structure above what we already know from [Reference Davison and Meinhardt11] regarding general quivers with potential (e.g. the PBW theorem). At least for
$\mathcal{A}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}}}$
, but nothing about the algebra structure above what we already know from [Reference Davison and Meinhardt11] regarding general quivers with potential (e.g. the PBW theorem). At least for
![]() $\unicode{x03BC}=0$
, the algebra
$\unicode{x03BC}=0$
, the algebra
![]() $\mathcal{A}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}}}$
has been studied from various points of view (see e.g. [Reference Diaconescu, Porta and Sala14, Reference Kapranov and Vasserot22, Reference Maulik and Okounkov31, Reference Nakajima35, Reference Varagnolo44]) while for the
$\mathcal{A}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}}}$
has been studied from various points of view (see e.g. [Reference Diaconescu, Porta and Sala14, Reference Kapranov and Vasserot22, Reference Maulik and Okounkov31, Reference Nakajima35, Reference Varagnolo44]) while for the
![]() $\unicode{x03BC}\neq 0$
case, it would be interesting (at least for noncommutative resolutions of toric CY3s) to relate these algebras to the Yangians defined in terms of (generalised) McMahon modules and crystal melting in [Reference Galakhov and Yamazaki17, Reference Li and Yamazaki27].
$\unicode{x03BC}\neq 0$
case, it would be interesting (at least for noncommutative resolutions of toric CY3s) to relate these algebras to the Yangians defined in terms of (generalised) McMahon modules and crystal melting in [Reference Galakhov and Yamazaki17, Reference Li and Yamazaki27].
For general Q and
![]() $\unicode{x03BC}$
, the shifted BPS cohomology
$\unicode{x03BC}$
, the shifted BPS cohomology
![]() $\mathfrak{g}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}}}\,:\!=\, \textrm{BPS}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}}}[{-}1]$
carries a Lie algebra structure (by Theorem 2.5). Even in the case
$\mathfrak{g}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}}}\,:\!=\, \textrm{BPS}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}}}[{-}1]$
carries a Lie algebra structure (by Theorem 2.5). Even in the case
![]() $\unicode{x03BC}=0,$
we do not yet fully understand this Lie algebra for general Q. We can at least try to relate the case of general
$\unicode{x03BC}=0,$
we do not yet fully understand this Lie algebra for general Q. We can at least try to relate the case of general
![]() $\unicode{x03BC}$
to the case
$\unicode{x03BC}$
to the case
![]() $\unicode{x03BC}=0$
, via the following construction: Fix Q and
$\unicode{x03BC}=0$
, via the following construction: Fix Q and
![]() $\unicode{x03BC}$
, and define
$\unicode{x03BC}$
, and define
 \begin{align*}\mathfrak{g}_{\text{even}}\,:\!=\, &\bigoplus_{\textbf{d}\in\mathbb{N}^{Q_0} \;\lvert\; \textbf{d}\cdot\unicode{x03BC}=0}\mathfrak{g}_{\tilde{Q},\tilde{W},\textbf{d}}\\\mathfrak{g}_{\text{odd}}\,:\!=\, &\bigoplus_{\textbf{d}\in\mathbb{N}^{Q_0} \;\lvert\; \textbf{d}\cdot\unicode{x03BC}\neq 0}\mathfrak{g}_{\tilde{Q},\tilde{W},\textbf{d}}.\end{align*}
\begin{align*}\mathfrak{g}_{\text{even}}\,:\!=\, &\bigoplus_{\textbf{d}\in\mathbb{N}^{Q_0} \;\lvert\; \textbf{d}\cdot\unicode{x03BC}=0}\mathfrak{g}_{\tilde{Q},\tilde{W},\textbf{d}}\\\mathfrak{g}_{\text{odd}}\,:\!=\, &\bigoplus_{\textbf{d}\in\mathbb{N}^{Q_0} \;\lvert\; \textbf{d}\cdot\unicode{x03BC}\neq 0}\mathfrak{g}_{\tilde{Q},\tilde{W},\textbf{d}}.\end{align*}
Then,
![]() $\mathfrak{g}_{\text{even}}$
is a Lie subalgebra of
$\mathfrak{g}_{\text{even}}$
is a Lie subalgebra of
![]() $\mathfrak{g}_{\tilde{Q},\tilde{W}}$
, and
$\mathfrak{g}_{\tilde{Q},\tilde{W}}$
, and
![]() $\mathfrak{g}_{\text{odd}}$
is a Lie module for it, and we consider the extension
$\mathfrak{g}_{\text{odd}}$
is a Lie module for it, and we consider the extension
with the Lie bracket
Question 4.3. Is there is an isomorphism of Lie algebras
Proposition 4.4. The answer to Question 4.3 is yes in the case
![]() $\unicode{x03BC}=0$
, and for generic
$\unicode{x03BC}=0$
, and for generic
![]() $\unicode{x03BC}$
.
$\unicode{x03BC}$
.
Proof. The case
![]() $\unicode{x03BC}=0$
is trivial, since then
$\unicode{x03BC}=0$
is trivial, since then
and
![]() $\tilde{W}^{\unicode{x03BC}}=\tilde{W}$
. In the case of generic
$\tilde{W}^{\unicode{x03BC}}=\tilde{W}$
. In the case of generic
![]() $\unicode{x03BC}$
, Theorem A tells us that there is an isomorphism
$\unicode{x03BC}$
, Theorem A tells us that there is an isomorphism
as cohomologically graded vector spaces, and so it is sufficient to show that the Lie bracket on
![]() $\mathfrak{g}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}}}$
vanishes, since the Lie bracket on
$\mathfrak{g}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}}}$
vanishes, since the Lie bracket on
![]() $\mathfrak{g}^{\unicode{x03BC}}\,:\!=\, \mathfrak{g}_{\textrm{odd}}[{-}1]$
does by definition. Combining (4.1) and (2.10), we deduce that
$\mathfrak{g}^{\unicode{x03BC}}\,:\!=\, \mathfrak{g}_{\textrm{odd}}[{-}1]$
does by definition. Combining (4.1) and (2.10), we deduce that
![]() $\mathfrak{g}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}}}$
lies entirely in odd cohomological degree. Since the Hall algebra multiplication, and hence the commutator Lie bracket, preserves cohomological degree, the Lie bracket vanishes as required.
$\mathfrak{g}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}}}$
lies entirely in odd cohomological degree. Since the Hall algebra multiplication, and hence the commutator Lie bracket, preserves cohomological degree, the Lie bracket vanishes as required.
In this paper, we have ignored completely the question of whether there is a natural double to the Lie algebra
![]() $\mathfrak{g}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}}}$
. Despite Proposition 4.4 the expected answer to Question 4.3, once extended to the double of
$\mathfrak{g}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}}}$
. Despite Proposition 4.4 the expected answer to Question 4.3, once extended to the double of
![]() $\mathfrak{g}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}}}$
is no; one of the motivations for this paper is work of Kevin Costello [Reference Costello5], in which he conjectures that in the case of, for example, the resolved conifold, the Lie bracket does not vanish on the fermionic part of the (doubled) BPS Lie algebra. As we saw in Section 1.2, and Example 3.3 the (noncommutative) resolved conifold is a partial fermionisation of the QP
$\mathfrak{g}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}}}$
is no; one of the motivations for this paper is work of Kevin Costello [Reference Costello5], in which he conjectures that in the case of, for example, the resolved conifold, the Lie bracket does not vanish on the fermionic part of the (doubled) BPS Lie algebra. As we saw in Section 1.2, and Example 3.3 the (noncommutative) resolved conifold is a partial fermionisation of the QP
![]() $\left(\tilde{Q},\tilde{W}\right)$
where
$\left(\tilde{Q},\tilde{W}\right)$
where
![]() $\tilde{Q}$
is the affine
$\tilde{Q}$
is the affine
![]() $A_1$
quiver; so the conifold is precisely the kind of case that Proposition 4.4 does not cover.
$A_1$
quiver; so the conifold is precisely the kind of case that Proposition 4.4 does not cover.
4.3 Representation theory
The boson-fermion correspondence is typically considered (by mathematicians) to be a part of representation theory, and so it would be remiss to finish the paper without saying anything about representations of
![]() $\mathcal{A}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}}}$
.
$\mathcal{A}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}}}$
.
Fix a quiver Q, and a framing dimension vector
![]() $\textbf{f}\in \mathbb{N}^{Q_0}$
. We form the quiver
$\textbf{f}\in \mathbb{N}^{Q_0}$
. We form the quiver
![]() $Q_{\textbf{f}}$
by adding one extra vertex (labelled
$Q_{\textbf{f}}$
by adding one extra vertex (labelled
![]() $\infty$
) to
$\infty$
) to
![]() $Q_0$
, and
$Q_0$
, and
![]() $\textbf{f}_i$
arrows from
$\textbf{f}_i$
arrows from
![]() $\infty$
to i for each
$\infty$
to i for each
![]() $i\in Q_0$
. Set
$i\in Q_0$
. Set
![]() $\mathscr{Q}=\widetilde{Q_{\textbf{f}}}$
. In other words, this is the usual doubled framed quiver that one uses to define Nakajima quiver varieties, but with an extra loop at every vertex (including a loop
$\mathscr{Q}=\widetilde{Q_{\textbf{f}}}$
. In other words, this is the usual doubled framed quiver that one uses to define Nakajima quiver varieties, but with an extra loop at every vertex (including a loop
![]() $\omega_{\infty}$
at the framing vertex).
$\omega_{\infty}$
at the framing vertex).
For
![]() $\unicode{x03BC}=\sum_{i\in Q_0} \unicode{x03BC}_i e_i$
we define
$\unicode{x03BC}=\sum_{i\in Q_0} \unicode{x03BC}_i e_i$
we define
 \begin{align*}\tilde{W}_{\textbf{f}}^{\unicode{x03BC}}=\left(\sum_{i\in \mathscr{Q}_0}\omega_i\right) \left(\sum_{a\in(Q_{\textbf{f}})_{1}}[a,a^*]\right)+\sum_{i\in Q_0}\unicode{x03BC}_i\omega_i^2.\end{align*}
\begin{align*}\tilde{W}_{\textbf{f}}^{\unicode{x03BC}}=\left(\sum_{i\in \mathscr{Q}_0}\omega_i\right) \left(\sum_{a\in(Q_{\textbf{f}})_{1}}[a,a^*]\right)+\sum_{i\in Q_0}\unicode{x03BC}_i\omega_i^2.\end{align*}
We write dimension vectors for
![]() $\mathscr{Q}$
as
$\mathscr{Q}$
as
![]() $\textrm{e}=(\textbf{d},n)$
where
$\textrm{e}=(\textbf{d},n)$
where
![]() $\textbf{d}\in\mathbb{N}^{Q_0}$
and
$\textbf{d}\in\mathbb{N}^{Q_0}$
and
![]() $n=\textrm{e}_{\infty}\in\mathbb{N}$
. We define
$n=\textrm{e}_{\infty}\in\mathbb{N}$
. We define
to be the subvariety containing those
![]() $\rho$
such that
$\rho$
such that
![]() $\rho_{\infty}$
generates
$\rho_{\infty}$
generates
![]() $\rho$
as a
$\rho$
as a
![]() $\mathbb{C}\mathscr{Q}$
-module. We call such
$\mathbb{C}\mathscr{Q}$
-module. We call such
![]() $\mathbb{C}\mathscr{Q}$
-modules stable. Then, we define
$\mathbb{C}\mathscr{Q}$
-modules stable. Then, we define
This is a smooth variety and is naturally isomorphic to the stack of stable
![]() $(\textbf{d},1)$
-dimensional
$(\textbf{d},1)$
-dimensional
![]() $\mathbb{C}\mathscr{Q}$
-modules along with a trivialisation
$\mathbb{C}\mathscr{Q}$
-modules along with a trivialisation
![]() $\rho_{\infty}\cong\mathbb{C}$
. We define
$\rho_{\infty}\cong\mathbb{C}$
. We define
to be the stack of pairs of a stable
![]() $(\textbf{d},1)$
-dimensional
$(\textbf{d},1)$
-dimensional
![]() $\mathbb{C} \mathscr{Q}$
-module
$\mathbb{C} \mathscr{Q}$
-module
![]() $\rho$
, along with a
$\rho$
, along with a
![]() $(\textbf{d}^{\prime},0)$
-dimensional submodule
$(\textbf{d}^{\prime},0)$
-dimensional submodule
![]() $\rho^{\prime}\subset \rho$
and a trivialisation
$\rho^{\prime}\subset \rho$
and a trivialisation
![]() $\rho_{\infty}\cong\mathbb{C}$
. Set
$\rho_{\infty}\cong\mathbb{C}$
. Set
![]() $\textbf{d}^{\prime\prime}=\textbf{d}-\textbf{d}^{\prime}$
. In the correspondence diagram,
$\textbf{d}^{\prime\prime}=\textbf{d}-\textbf{d}^{\prime}$
. In the correspondence diagram,
![]()
the morphism
![]() $\unicode{x03C0}_2$
is proper, and so via push-forward and pull-back in vanishing cycle cohomology, we obtain an action of
$\unicode{x03C0}_2$
is proper, and so via push-forward and pull-back in vanishing cycle cohomology, we obtain an action of
![]() $\mathcal{A}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}}}$
on
$\mathcal{A}_{\tilde{Q},\tilde{W}^{\unicode{x03BC}}}$
on
Given a quiver Q, we denote by
 \begin{align*}\unicode{x03BC}_{Q,\textbf{d}}\,:\, \mathbb{A}_{\textbf{d}}(\overline{Q})&\rightarrow \mathfrak{{gl}}_{\textbf{d}}\\\rho&\mapsto \sum_{a\in Q_1}[\rho(a),\rho(a^*)].\end{align*}
\begin{align*}\unicode{x03BC}_{Q,\textbf{d}}\,:\, \mathbb{A}_{\textbf{d}}(\overline{Q})&\rightarrow \mathfrak{{gl}}_{\textbf{d}}\\\rho&\mapsto \sum_{a\in Q_1}[\rho(a),\rho(a^*)].\end{align*}
the usual moment map. We define
the vanishing locus of the composition of
![]() $\unicode{x03BC}_{Q_{\textbf{f}},(\textbf{d},1)}$
with the natural projection
$\unicode{x03BC}_{Q_{\textbf{f}},(\textbf{d},1)}$
with the natural projection
![]() $\mathfrak{{gl}}_{(\textbf{d},1)}\rightarrow \mathfrak{{gl}}_{\textbf{d}}$
. Here, the stability condition is the same as above: we restrict to the open locus of those
$\mathfrak{{gl}}_{(\textbf{d},1)}\rightarrow \mathfrak{{gl}}_{\textbf{d}}$
. Here, the stability condition is the same as above: we restrict to the open locus of those
![]() $\rho$
such that
$\rho$
such that
![]() $\rho_{\infty}$
generates. Then, the Nakajima quiver variety is defined to be the smooth variety
$\rho_{\infty}$
generates. Then, the Nakajima quiver variety is defined to be the smooth variety
Proposition 4.5. Denote by g the restriction of the function
![]() $\text{Tr}\!\left(\tilde{W}_{\textbf{f}}^{\unicode{x03BC}}\right)$
to
$\text{Tr}\!\left(\tilde{W}_{\textbf{f}}^{\unicode{x03BC}}\right)$
to
![]() $\mathscr{N}_{\textbf{f},\textbf{d}}(Q)$
, then
$\mathscr{N}_{\textbf{f},\textbf{d}}(Q)$
, then
 \begin{align*}\text{crit}(g)\cong \begin{cases}X(\textbf{f},\textbf{d})&\textrm{if }\unicode{x03BC}\cdot\textbf{d}\neq 0\\X(\textbf{f},\textbf{d})\times\mathbb{A}^1&\textrm{if }\unicode{x03BC}\cdot\textbf{d}=0.\end{cases}\end{align*}
\begin{align*}\text{crit}(g)\cong \begin{cases}X(\textbf{f},\textbf{d})&\textrm{if }\unicode{x03BC}\cdot\textbf{d}\neq 0\\X(\textbf{f},\textbf{d})\times\mathbb{A}^1&\textrm{if }\unicode{x03BC}\cdot\textbf{d}=0.\end{cases}\end{align*}
Moreover, the monodromic mixed Hodge module
is analytically locally isomorphic to the constant mixed Hodge module on the critical locus of g.
Proof. The second part follows from the first: the holomorphic Bott–Morse lemma tells us that since the critical locus of g is scheme-theoretically smooth, g can be written analytically locally around crit(g) in the form
where c is the codimension of crit(g) inside
![]() $\mathcal{N}_{\textbf{f},\textbf{d}}(Q)$
. The first part follows by the same argument as Proposition 2.3.
$\mathcal{N}_{\textbf{f},\textbf{d}}(Q)$
. The first part follows by the same argument as Proposition 2.3.
In the special case
![]() $\unicode{x03BC}=0,$
it is possible to show that the monodromy of the rank one local system
$\unicode{x03BC}=0,$
it is possible to show that the monodromy of the rank one local system
![]() ${{}^{\mathfrak{p}}\!}\unicode{x03D5}_{g}\underline{\mathbb{Q}}_{\mathscr{N}_{\textbf{f},\textbf{d}^{\prime\prime}}(Q)}$
is trivial [Reference Davison10, Prop. 6.3], and we conjecture that this is always true. Assuming the conjecture, Proposition 4.5 implies that there are isomorphisms
${{}^{\mathfrak{p}}\!}\unicode{x03D5}_{g}\underline{\mathbb{Q}}_{\mathscr{N}_{\textbf{f},\textbf{d}^{\prime\prime}}(Q)}$
is trivial [Reference Davison10, Prop. 6.3], and we conjecture that this is always true. Assuming the conjecture, Proposition 4.5 implies that there are isomorphisms
 \begin{equation}\textbf{M}^{\unicode{x03BC}}_{\textbf{f}}(Q)\cong \!\left(\bigoplus_{\substack{\textbf{d}\in\mathbb{N}^{Q_0}\\ \unicode{x03BC}\cdot\textbf{d}\neq 0}}\textbf{H}(X(\textbf{f},\textbf{d}),\mathbb{Q})_{\text{vir}}\right)\oplus \!\left(\bigoplus_{\substack{\textbf{d}\in\mathbb{N}^{Q_0}\\ \unicode{x03BC}\cdot\textbf{d}= 0}}\textbf{H}(X(\textbf{f},\textbf{d}),\mathbb{Q})_{\text{vir}}\otimes \mathscr{L}^{\,-1/2}\right).\end{equation}
\begin{equation}\textbf{M}^{\unicode{x03BC}}_{\textbf{f}}(Q)\cong \!\left(\bigoplus_{\substack{\textbf{d}\in\mathbb{N}^{Q_0}\\ \unicode{x03BC}\cdot\textbf{d}\neq 0}}\textbf{H}(X(\textbf{f},\textbf{d}),\mathbb{Q})_{\text{vir}}\right)\oplus \!\left(\bigoplus_{\substack{\textbf{d}\in\mathbb{N}^{Q_0}\\ \unicode{x03BC}\cdot\textbf{d}= 0}}\textbf{H}(X(\textbf{f},\textbf{d}),\mathbb{Q})_{\text{vir}}\otimes \mathscr{L}^{\,-1/2}\right).\end{equation}
Note that the vacuum vector, spanning
![]() $\textbf{H}(X(\textbf{f},0),\mathbb{Q})$
, lies in the second summand.
$\textbf{H}(X(\textbf{f},0),\mathbb{Q})$
, lies in the second summand.
Let Q
′ be the full subquiver of Q obtained by removing all vertices that support loops, as well as arrows to or from them, and let
![]() $\mathfrak{n}^-_{Q^{\prime}}$
be the negative piece of the Kac–Moody Lie algebra associated with Q
′. By [Reference Davison10, Thm. 6.6], there is an inclusion of Lie algebras
$\mathfrak{n}^-_{Q^{\prime}}$
be the negative piece of the Kac–Moody Lie algebra associated with Q
′. By [Reference Davison10, Thm. 6.6], there is an inclusion of Lie algebras
as the part of the BPS Lie algebra lying in cohomological degree zero, so that (4.2) in case
![]() $\unicode{x03BC}=0$
allows us to reconstruct (one half of) Nakajima’s action of
$\unicode{x03BC}=0$
allows us to reconstruct (one half of) Nakajima’s action of
![]() $\mathfrak{g}_{Q^{\prime}}$
on the cohomology of quiver varieties [Reference Nakajima34]. The conjecture suggests that the cohomology of Nakajima quiver varieties should be as crucial to the representation theory of partially fermionised BPS Lie algebras as they are to the representation theory of their bosonic counterparts.
$\mathfrak{g}_{Q^{\prime}}$
on the cohomology of quiver varieties [Reference Nakajima34]. The conjecture suggests that the cohomology of Nakajima quiver varieties should be as crucial to the representation theory of partially fermionised BPS Lie algebras as they are to the representation theory of their bosonic counterparts.
Acknowledgments
The suggestion that partial fermionisation of BPS Lie algebras should be modelled by the passage from
![]() $\text{Tot}(\mathcal{O}_{\mathbb{P}^1}(-2)\oplus \mathcal{O}_{\mathbb{P}^1})$
to
$\text{Tot}(\mathcal{O}_{\mathbb{P}^1}(-2)\oplus \mathcal{O}_{\mathbb{P}^1})$
to
![]() $\text{Tot}(\mathcal{O}_{\mathbb{P}^1}(-1)\oplus\mathcal{O}_{\mathbb{P}^1}(-1))$
is based on conversations with, and unpublished work of Kevin Costello. I am very grateful to him for being so generous with his time and ideas. I learnt about connections between the various Jacobi algebras appearing in this paper from Victor Ginzburg, and I am similarly grateful to him. Thanks also to Hans Franzen, Tudor Pădurariu and Markus Reineke for stimulating conversations about DT theory. My thanks also go to Tommaso Scognamiglio for questions that led to the addition of Section 3.3 to an earlier draft. This paper was written for the British Mathematical Colloquium, held (virtually) in Glasgow in 2021. Many thanks are due to the organisers for managing to run such an engaging online event. During the writing of the paper, I was supported by the starter grant ‘Categorified Donaldson–Thomas theory’ No. 759967 of the European Research Council and also supported by a Royal Society university research fellowship.
$\text{Tot}(\mathcal{O}_{\mathbb{P}^1}(-1)\oplus\mathcal{O}_{\mathbb{P}^1}(-1))$
is based on conversations with, and unpublished work of Kevin Costello. I am very grateful to him for being so generous with his time and ideas. I learnt about connections between the various Jacobi algebras appearing in this paper from Victor Ginzburg, and I am similarly grateful to him. Thanks also to Hans Franzen, Tudor Pădurariu and Markus Reineke for stimulating conversations about DT theory. My thanks also go to Tommaso Scognamiglio for questions that led to the addition of Section 3.3 to an earlier draft. This paper was written for the British Mathematical Colloquium, held (virtually) in Glasgow in 2021. Many thanks are due to the organisers for managing to run such an engaging online event. During the writing of the paper, I was supported by the starter grant ‘Categorified Donaldson–Thomas theory’ No. 759967 of the European Research Council and also supported by a Royal Society university research fellowship.