Hostname: page-component-669899f699-vbsjw Total loading time: 0 Render date: 2025-04-25T01:34:19.422Z Has data issue: false hasContentIssue false
  • English
  • Français

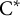$\mathrm{C}^{*}$-algebras hereditarily containing nonzero, square-zero elements

Part of: Topological algebras, normed rings and algebras, Banach algebras Selfadjoint operator algebras

Published online by Cambridge University Press:  04 November 2024

Massoud Amini Open the ORCID record for Massoud Amini [Opens in a new window] ,
George A. Elliott  and
Mohammad Rouzbehani Open the ORCID record for Mohammad Rouzbehani [Opens in a new window]
Massoud Amini
Affiliation:
Department of Mathematics, Faculty of Mathematical Sciences, Tarbiat Modares University, Tehran, 14115-134, Iran e-mail: [email protected] [email protected].
George A. Elliott
Affiliation:
Department of Mathematics, University of Toronto, Toronto, ON, M5S 2E4, Canada e-mail: [email protected]
Mohammad Rouzbehani*
Affiliation:
School of Mathematics, Statistics and Computer Science, College of Science, University of Tehran, Tehran, 1417614411, Iran
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce and study the weak Glimm property for 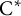$\mathrm{C}^{*}$-algebras, and also a property we shall call (HS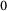$_0$). We show that the properties of being nowhere scattered and residual (HS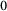$_0$) are equivalent for any $\mathrm{C}^{*}$-algebra. Also, for a 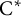$\mathrm{C}^{*}$-algebra with the weak Glimm property, the properties of being purely infinite and weakly purely infinite are equivalent. It follows that for a 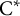$\mathrm{C}^{*}$-algebra with the weak Glimm property such that the absolute value of every nonzero, square-zero, element is properly infinite, the properties of being (weakly, locally) purely infinite, nowhere scattered, residual (HS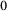$_0$), residual (HS$_{\text {t}}$), and residual (HI) are all equivalent, and are equivalent to the global Glimm property. This gives a partial affirmative answer to the global Glimm problem, as well as certain open questions raised by Kirchberg and Rørdam.

Keywords

C*-algebrasquare-zero elementsfiniteness properties

MSC classification

Primary: 46L05: General theory of $C^*$-algebras
Secondary: 46L85: Noncommutative topology 46H10: Ideals and subalgebras
Type
Article
Information
Canadian Mathematical Bulletin , Volume 67 , Issue 4 , December 2024 , pp. 1081 - 1091
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The first author was partly supported by a grant from the Institute for Research in Fundamental Sciences (IPM) (Grant No. 4027151). The second author was supported by a grant from the Natural Sciences and Engineering Research Council of Canada (NSERC).

References

Blackadar, B., Operator algebras. Theory of C*-algebras and von Neumann algebras, Encyclopaedia of Mathematical Sciences, 122, Springer, Berlin, 2006.Google Scholar
Blanchard, E. and Kirchberg, E., Non-simple purely infinite C*-algebras: The Hausdorff case . J. Funct. Anal. 207(2004), no. 2, 461–513.CrossRefGoogle Scholar
Elliott, G. A. and Rouzbehani, M., Weakly purely infinite C*-algebras with topological dimension zero are purely infinite . C. R. Math. Acad. Sci. Soc. R. Can. 45(2023), no. 4, 87–91.Google Scholar
Enders, D. and Shulman, T., Commutativity of central sequence algebras . Adv. Math. 401(2022), Article no. 108262.CrossRefGoogle Scholar
Gardella, E. and Thiel, H., Rings and C*-algebras generated by commutators, J. Algebra 662(2025), 214–241.CrossRefGoogle Scholar
Kirchberg, E. and Rørdam, M., Non-simple purely infinite C*-algebras . Amer. J. Math. 122(2000), no. 3, 637–666.CrossRefGoogle Scholar
Kirchberg, E. and Rørdam, M., Infinite non-simple C*-algebras: Absorbing the Cuntz algebra $\mathcal {O}_{\infty }$ . Adv. Math. 167(2002), no. 2, 195–264.CrossRefGoogle Scholar
Ortega, E., Perera, F., and Rørdam, M., The corona factorization property, stability, and the Cuntz semigroup of a C*-algebra . Int. Math. Res. Not. IMRN 2012(2012), no. 1, 34–66.CrossRefGoogle Scholar
Pasnicu, C. and Phillips, N. C., Crossed products by spectrally free actions . J. Funct. Anal. 269(2015), no. 4, 915–967.CrossRefGoogle Scholar
Pasnicu, C. and Rouzbehani, M., Topological dimension zero and some related properties, Publ. Mat., to appear.Google Scholar
Pedersen, G. K., C*-algebras and their automorphism groups, Academic Press, London, 1979.Google Scholar
Robert, L., On the Lie ideals of C*-algebras . J. Operator Theory 75(2016), 387–408.CrossRefGoogle Scholar
Rouzbehani, M., Amini, M., and Asadi, M. B., Goldie dimension for C*-algebras . Proc. Edinburgh Math. Soc. 67(2024), no. 1, 200–223.CrossRefGoogle Scholar
Rørdam, M., The stable and the real rank of $\mathcal{Z}$ -absorbing C*-algebras . Internat. J. Math. 15(2004), no. 10, 1065–1085.CrossRefGoogle Scholar
Thiel, H. and Vilalta, E., The global Glimm property . Trans. Amer. Math. Soc. 376(2023), no. 7, 4713–4744.CrossRefGoogle Scholar
Thiel, H. and Vilalta, E., Nowhere scattered C*-algebras . J. Noncommut. Geom. 18(2024), 231–263.CrossRefGoogle Scholar