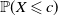1. Introduction
A remarkable result by Scarf [Reference Scarf11] provides an explicit solution to the problem of minimizing
![]() ${\mathbb{E}}(X \wedge c)$
, with c a positive constant, over the set of all positive random variables X with given mean and variance (see Theorem 4.1 below). The infimum is shown to have two different expressions depending on whether the parameter c is above or below a certain threshold and to be attained by a random variable taking only two values. About thirty years after the publication of [Reference Scarf11], Lo [Reference Lo7] noticed that Scarf’s result immediately implies an upper bound for
${\mathbb{E}}(X \wedge c)$
, with c a positive constant, over the set of all positive random variables X with given mean and variance (see Theorem 4.1 below). The infimum is shown to have two different expressions depending on whether the parameter c is above or below a certain threshold and to be attained by a random variable taking only two values. About thirty years after the publication of [Reference Scarf11], Lo [Reference Lo7] noticed that Scarf’s result immediately implies an upper bound for
![]() ${\mathbb{E}}(X-c)^+$
, with X and c as before. This has an obvious financial interpretation as an upper bound for the price at time zero of a European call option with strike c on an asset with value at maturity equal to X (in discounted terms, assuming that expectation is meant with respect to a pricing measure). More recently, de la Peña, Ibragimov, and Jordan [Reference de la Peña, Ibragimov and Jordan5] obtained, among other things, a sharp upper bound for
${\mathbb{E}}(X-c)^+$
, with X and c as before. This has an obvious financial interpretation as an upper bound for the price at time zero of a European call option with strike c on an asset with value at maturity equal to X (in discounted terms, assuming that expectation is meant with respect to a pricing measure). More recently, de la Peña, Ibragimov, and Jordan [Reference de la Peña, Ibragimov and Jordan5] obtained, among other things, a sharp upper bound for
![]() ${\mathbb{E}}(X-c)^+$
over the set of random variables X for which mean and variance as well as the probability
${\mathbb{E}}(X-c)^+$
over the set of random variables X for which mean and variance as well as the probability
![]() $\mathbb{P}(X \leqslant c)$
are known (see Theorem 3.1 below).
$\mathbb{P}(X \leqslant c)$
are known (see Theorem 3.1 below).
Our goal is to prove that the estimate by de la Peña, Ibragimov, and Jordan is stronger than Scarf’s in the sense that the former implies the latter. This may appear somewhat counterintuitive, as the former estimate requires the extra input
![]() $\mathbb{P}(X \leqslant c)$
, while the latter has an extra positivity constraint.
$\mathbb{P}(X \leqslant c)$
, while the latter has an extra positivity constraint.
The proof by Scarf, while relatively elementary, is quite ingenious. A different proof, also covering substantial generalizations, has been obtained in [Reference Bertsimas and Popescu2] using duality methods in semi-definite optimization. The arguments used in [Reference de la Peña, Ibragimov and Jordan5] are instead based on classical probabilistic inequalities and a ‘toy’ version of decoupling. The proof of Scarf’s estimate given here is entirely elementary and self-contained. Starting from an alternative proof of the relevant estimates in [Reference de la Peña, Ibragimov and Jordan5], another proof of Scarf’s result is obtained that is certainly not as deft as the original, but that would hopefully seem more natural to anyone who, like the author, would hardly ever come up with the ingenious idea used in [Reference Scarf11]. Our proof is based, roughly speaking, on a representation of the set of random variables with given mean and variance as a union of subsets of equivalent random variables, where two random variables
![]() $X_1$
and
$X_1$
and
![]() $X_2$
are equivalent if
$X_2$
are equivalent if
![]() $\mathbb{P}(X_1 \leqslant c) = \mathbb{P}(X_2 \leqslant c)$
. This allows to establish a link between the two inequalities and to reduce the problem of proving a version of Scarf’s result without the positivity constraint to the minimization of a function of one real variable. Finally, the positivity constraint is taken into account, thus establishing the full version of Scarf’s result. Moreover, the fact that optimizers exist and are given by two-point distributed random variables appears in a natural way and plays an important role in the proof.
$\mathbb{P}(X_1 \leqslant c) = \mathbb{P}(X_2 \leqslant c)$
. This allows to establish a link between the two inequalities and to reduce the problem of proving a version of Scarf’s result without the positivity constraint to the minimization of a function of one real variable. Finally, the positivity constraint is taken into account, thus establishing the full version of Scarf’s result. Moreover, the fact that optimizers exist and are given by two-point distributed random variables appears in a natural way and plays an important role in the proof.
The result proved in this article may also clarify, or at least complement, several qualitative remarks made in [Reference de la Peña, Ibragimov and Jordan5] about the relation between the two abovementioned inequalities. For instance, the authors note that their inequality is simpler than Lo’s in the sense that the right-hand side does not depend on the value of c. Here we show that this is only due to the positivity constraint in [Reference Scarf11], with very explicit calculations showing how the threshold value for c arises. Moreover, the sharpness of their inequality is proved in a much more natural way, i.e. showing that a two-point distributed random variable always attains the bound.
Apart from the application to bounds for option prices, estimates of (functions of)
![]() $X \wedge c$
, sometimes called the Winsorization of X, are important in several areas of applied probability and statistics (see, e.g., [Reference Pinelis and Molzon10]). For results in this direction, as well as for an informative discussion with references to the literature, we refer to [Reference Pinelis9].
$X \wedge c$
, sometimes called the Winsorization of X, are important in several areas of applied probability and statistics (see, e.g., [Reference Pinelis and Molzon10]). For results in this direction, as well as for an informative discussion with references to the literature, we refer to [Reference Pinelis9].
2. Preliminaries
Let
![]() $(\Omega,\mathscr{F},\mathbb{P})$
be a probability space, on which all random elements will be defined. We shall write, for simplicity,
$(\Omega,\mathscr{F},\mathbb{P})$
be a probability space, on which all random elements will be defined. We shall write, for simplicity,
![]() $L^2$
to denote
$L^2$
to denote
![]() $L^2(\Omega,\mathscr{F},\mathbb{P})$
, and
$L^2(\Omega,\mathscr{F},\mathbb{P})$
, and
![]() ${\lVert{\cdot}\rVert}_2$
for its norm. For any
${\lVert{\cdot}\rVert}_2$
for its norm. For any
![]() $m \in \mathbb{R}$
and
$m \in \mathbb{R}$
and
![]() $\sigma \in \mathbb{R}_+$
, the sphere of
$\sigma \in \mathbb{R}_+$
, the sphere of
![]() $L^2$
of radius
$L^2$
of radius
![]() $\sigma$
centered in m will be denoted by
$\sigma$
centered in m will be denoted by
![]() $\mathscr{X}_{m,\sigma}$
, and just by
$\mathscr{X}_{m,\sigma}$
, and just by
![]() $\mathscr{X}$
if
$\mathscr{X}$
if
![]() $m=0$
and
$m=0$
and
![]() $\sigma=1$
. In other words,
$\sigma=1$
. In other words,
![]() $\mathscr{X}_{m,\sigma}$
stands for the set of random variables X such that
$\mathscr{X}_{m,\sigma}$
stands for the set of random variables X such that
![]() ${\mathbb{E}} X=m$
and
${\mathbb{E}} X=m$
and
![]() $\operatorname{Var}(X) = {\mathbb{E}}(X-m)^2 = \sigma^2$
. It is clear that
$\operatorname{Var}(X) = {\mathbb{E}}(X-m)^2 = \sigma^2$
. It is clear that
![]() $\mathscr{X}_{m,\sigma} = m + \sigma \mathscr{X}$
. The intersection of
$\mathscr{X}_{m,\sigma} = m + \sigma \mathscr{X}$
. The intersection of
![]() $\mathscr{X}_{m,\sigma}$
with the cone of random variables bounded below by
$\mathscr{X}_{m,\sigma}$
with the cone of random variables bounded below by
![]() $\alpha \in \mathbb{R}$
will be denoted by
$\alpha \in \mathbb{R}$
will be denoted by
![]() $\mathscr{X}_{m,\sigma}^\alpha$
. It is easily verified that, for any
$\mathscr{X}_{m,\sigma}^\alpha$
. It is easily verified that, for any
![]() $m \in \mathbb{R}$
and
$m \in \mathbb{R}$
and
![]() $\sigma \in \mathbb{R}_+$
,
$\sigma \in \mathbb{R}_+$
,
Recall that a random variable is said to be two-point distributed if it takes only two (distinct) values. The set of two-point distributed random variables belonging to
![]() $\mathscr{X}$
can be parametrized by the open interval
$\mathscr{X}$
can be parametrized by the open interval
![]() $\mathopen]0,1\mathclose[$
: let X take the values
$\mathopen]0,1\mathclose[$
: let X take the values
![]() $x,y \in \mathbb{R}$
,
$x,y \in \mathbb{R}$
,
![]() $x < y$
, and set
$x < y$
, and set
![]() $p \,:\!=\, \mathbb{P}(X=x)$
,
$p \,:\!=\, \mathbb{P}(X=x)$
,
![]() $1-p = \mathbb{P}(X=y)$
. Then
$1-p = \mathbb{P}(X=y)$
. Then
![]() $X \in \mathscr{X}$
if and only if
$X \in \mathscr{X}$
if and only if
![]() $px + (1-p)y = 0$
and
$px + (1-p)y = 0$
and
![]() $px^2 + (1-p)y^2 = 1$
, which implies
$px^2 + (1-p)y^2 = 1$
, which implies
Note that
![]() $p=0$
and
$p=0$
and
![]() $p=1$
are not allowed, and hence
$p=1$
are not allowed, and hence
![]() $p \in \mathopen]0,1\mathclose[$
. This is also obvious a priori, as there is no degenerate random variable with mean zero and variance one. The following simple observations, the proofs of which are immediate consequences of (2.2) and elementary algebra, will be useful.
$p \in \mathopen]0,1\mathclose[$
. This is also obvious a priori, as there is no degenerate random variable with mean zero and variance one. The following simple observations, the proofs of which are immediate consequences of (2.2) and elementary algebra, will be useful.
Lemma 2.1. Let
![]() $X \in \mathscr{X}$
be the
$X \in \mathscr{X}$
be the
![]() $\{x,y\}$
-valued random variable identified by the parameter
$\{x,y\}$
-valued random variable identified by the parameter
![]() $p \in \mathopen]0,1\mathclose[$
, and
$p \in \mathopen]0,1\mathclose[$
, and
![]() $c \in \mathbb{R}$
.
$c \in \mathbb{R}$
.
-
(i) If
 $c \geqslant 0$
, then
$c \geqslant 0$
, then
 $x < c \leqslant y$
if and only if
$x < c \leqslant y$
if and only if
 $p \geqslant {c^2}/({1+c^2})$
.
$p \geqslant {c^2}/({1+c^2})$
. -
(ii) If
 $c < 0$
, then
$c < 0$
, then
 $x \leqslant c < y$
if and only if
$x \leqslant c < y$
if and only if
 $p \leqslant {1}/({1+c^2})$
.
$p \leqslant {1}/({1+c^2})$
.
We shall also need the following elementary lattice identities.
Lemma 2.2. Let
![]() $a,b,c \in \mathbb{R}$
. The following hold:
$a,b,c \in \mathbb{R}$
. The following hold:
-
(i)
 $a + (b \wedge c) = (a+b) \wedge (a+c)$
;
$a + (b \wedge c) = (a+b) \wedge (a+c)$
; -
(ii) if
 $a \geqslant 0$
, then
$a \geqslant 0$
, then
 $a (b \wedge c) = (ab) \wedge (ac)$
;
$a (b \wedge c) = (ab) \wedge (ac)$
; -
(iii)
 $(a-b)^+ = a - (a \wedge b)$
.
$(a-b)^+ = a - (a \wedge b)$
.
Proof. The identities in (i) and (ii) are clear. The identity in (iii) can be verified ‘case by case’, but it can also be deduced from the identity
![]() $(a-b)^+ = (a-b) + (a-b)^-$
, where, using (i),
$(a-b)^+ = (a-b) + (a-b)^-$
, where, using (i),
from which the claim follows immediately.
3. de la Peña–Ibragimov–Jordan bound
The following sharp estimates are proved in [Reference de la Peña, Ibragimov and Jordan5].
Theorem 3.1. (de la Peña, Ibragimov, and Jordan) Let
![]() $X \in \mathscr{X}_{m,\sigma}$
and
$X \in \mathscr{X}_{m,\sigma}$
and
![]() $c \in \mathbb{R}$
. Setting
$c \in \mathbb{R}$
. Setting
![]() $p_0 \,:\!=\, \mathbb{P}(X>c)$
, we have
$p_0 \,:\!=\, \mathbb{P}(X>c)$
, we have
The proof of (3.1) in [Reference de la Peña, Ibragimov and Jordan5] is very elegant, the main idea being the introduction of an independent copy of the random variable X. Here we give an alternative, entirely elementary, proof.
Proof. Let us start with the lower bound. We can assume, without loss of generality, that
![]() $m \geqslant c$
, otherwise there is nothing to prove. Since
$m \geqslant c$
, otherwise there is nothing to prove. Since
it suffices to show that
![]() ${\mathbb{E}} X \mathbf{1}_{\{X>c\}} \geqslant m \mathbb{P}(X>c)$
. To this purpose, note that
${\mathbb{E}} X \mathbf{1}_{\{X>c\}} \geqslant m \mathbb{P}(X>c)$
. To this purpose, note that
where, thanks to the assumption
![]() $m \geqslant c$
,
$m \geqslant c$
,
and hence
![]() $ {\mathbb{E}} X \mathbf{1}_{\{X>c\}} \geqslant m - m\mathbb{P}(X \leqslant c) = m \mathbb{P}(X>c) $
.
$ {\mathbb{E}} X \mathbf{1}_{\{X>c\}} \geqslant m - m\mathbb{P}(X \leqslant c) = m \mathbb{P}(X>c) $
.
To prove the upper bound, note that
hence, adding and subtracting
![]() ${\mathbb{E}} Xp_0 = mp_0$
on the right-hand side, the Cauchy–Schwarz inequality yields
${\mathbb{E}} Xp_0 = mp_0$
on the right-hand side, the Cauchy–Schwarz inequality yields
thus completing the proof.
Remark 3.1. Even if
![]() $m < c$
, the inequality
$m < c$
, the inequality
![]() ${\mathbb{E}} X \mathbf{1}_{\{X>c\}} \geqslant m \mathbb{P}(X>c)$
is still true. In fact,
${\mathbb{E}} X \mathbf{1}_{\{X>c\}} \geqslant m \mathbb{P}(X>c)$
is still true. In fact,
![]() $ m \mathbb{P}(X>c) \leqslant c \mathbb{P}(X>c) = {\mathbb{E}} c \mathbf{1}_{\{X>c\}} \leqslant {\mathbb{E}} X \mathbf{1}_{\{X>c\}} $
.
$ m \mathbb{P}(X>c) \leqslant c \mathbb{P}(X>c) = {\mathbb{E}} c \mathbf{1}_{\{X>c\}} \leqslant {\mathbb{E}} X \mathbf{1}_{\{X>c\}} $
.
Theorem 3.1 implies useful one-sided Chebyshev-like bounds.
Corollary 3.1. Let
![]() $X \in \mathscr{X}$
and
$X \in \mathscr{X}$
and
![]() $c \in \mathbb{R}$
. The following hold:
$c \in \mathbb{R}$
. The following hold:
-
(i) if
 $c \geqslant 0$
, then
$c \geqslant 0$
, then
 $\mathbb{P}(X \leqslant c) \geqslant \mathbb{P}(X < c) \geqslant {c^2}/({1+c^2})$
;
$\mathbb{P}(X \leqslant c) \geqslant \mathbb{P}(X < c) \geqslant {c^2}/({1+c^2})$
; -
(ii). if
 $c<0$
, then
$c<0$
, then
 $\mathbb{P}(X \leqslant c) \leqslant {1}/({1+c^2})$
.
$\mathbb{P}(X \leqslant c) \leqslant {1}/({1+c^2})$
.
Proof. The proof of Theorem 3.1 remains valid with
![]() $p_1 \,:\!=\, \mathbb{P}(X \geqslant c)$
in place of
$p_1 \,:\!=\, \mathbb{P}(X \geqslant c)$
in place of
![]() $p_0$
; hence, as the right-hand side of (3.1) must be positive,
$p_0$
; hence, as the right-hand side of (3.1) must be positive,
![]() $ \sqrt{p_1(1-p_1)} \geqslant cp_1 $
. If
$ \sqrt{p_1(1-p_1)} \geqslant cp_1 $
. If
![]() $c \geqslant 0$
, squaring both sides yields a linear inequality that is satisfied if and only if
$c \geqslant 0$
, squaring both sides yields a linear inequality that is satisfied if and only if
![]() $p_1 \leqslant 1/(1+c^2)$
. This proves (i).
$p_1 \leqslant 1/(1+c^2)$
. This proves (i).
For (ii), if
![]() $c<0$
,
$c<0$
,
![]() $ \mathbb{P}(X \leqslant c) = \mathbb{P}({-}X \geqslant -c) = 1 - \mathbb{P}({-}X < -c) $
. Since
$ \mathbb{P}(X \leqslant c) = \mathbb{P}({-}X \geqslant -c) = 1 - \mathbb{P}({-}X < -c) $
. Since
![]() $-X \in \mathscr{X}$
and
$-X \in \mathscr{X}$
and
![]() $-c>0$
, (i) implies that
$-c>0$
, (i) implies that
![]() $ \mathbb{P}({-}X < -c) \geqslant {c^2}/({1+c^2}) $
, and hence
$ \mathbb{P}({-}X < -c) \geqslant {c^2}/({1+c^2}) $
, and hence
Remark 3.2. Let
![]() $X \in \mathscr{X}$
and
$X \in \mathscr{X}$
and
![]() $c \in \mathbb{R}_+$
. By reasoning entirely analogous to the proof of Corollary 3.1(ii), both
$c \in \mathbb{R}_+$
. By reasoning entirely analogous to the proof of Corollary 3.1(ii), both
![]() $\mathbb{P}(X > c)$
and
$\mathbb{P}(X > c)$
and
![]() $\mathbb{P}(X < -c)$
are bounded above by
$\mathbb{P}(X < -c)$
are bounded above by
![]() $1/(1+c^2)$
; hence
$1/(1+c^2)$
; hence
![]() $\mathbb{P}(|{X}|>c) \leqslant 2/(1+c^2)$
, which is sharper than Chebyshev’s inequality
$\mathbb{P}(|{X}|>c) \leqslant 2/(1+c^2)$
, which is sharper than Chebyshev’s inequality
![]() $\mathbb{P}(|{X}|>c) \leqslant 1/c^2$
if
$\mathbb{P}(|{X}|>c) \leqslant 1/c^2$
if
![]() $c<1$
.
$c<1$
.
4. Scarf–Lo bound
The following estimate is obtained in [Reference Scarf11].
Theorem 4.1. (Scarf) Let
![]() $c,m,\sigma$
be strictly positive real numbers. The infimum of the function
$c,m,\sigma$
be strictly positive real numbers. The infimum of the function
![]() $X \mapsto {\mathbb{E}}(X \wedge c)$
on the set
$X \mapsto {\mathbb{E}}(X \wedge c)$
on the set
![]() $\mathscr{X}_{m,\sigma}^0$
is attained, i.e. it is a minimum, and is given by
$\mathscr{X}_{m,\sigma}^0$
is attained, i.e. it is a minimum, and is given by
 \begin{equation*} \min_{X \in \mathscr{X}_{m,\sigma}^0} {\mathbb{E}}(X \wedge c) = \begin{cases} \displaystyle \frac{m^2}{m^2+\sigma^2}c & \text{if } \displaystyle c \leqslant \frac{m^2+\sigma^2}{2m},\\[12pt] \displaystyle \frac{c+m}{2} - \frac12 \bigl( (c-m)^2 + \sigma^2 \bigr)^{1/2} & \text{if } \displaystyle c \geqslant \frac{m^2+\sigma^2}{2m}. \end{cases} \end{equation*}
\begin{equation*} \min_{X \in \mathscr{X}_{m,\sigma}^0} {\mathbb{E}}(X \wedge c) = \begin{cases} \displaystyle \frac{m^2}{m^2+\sigma^2}c & \text{if } \displaystyle c \leqslant \frac{m^2+\sigma^2}{2m},\\[12pt] \displaystyle \frac{c+m}{2} - \frac12 \bigl( (c-m)^2 + \sigma^2 \bigr)^{1/2} & \text{if } \displaystyle c \geqslant \frac{m^2+\sigma^2}{2m}. \end{cases} \end{equation*}
Note that the constraint
![]() $X \geqslant 0$
is dictated by the structure of the practical inventory problem considered by Scarf. It is not needed, however, to avoid the infimum being minus infinity. In fact,
$X \geqslant 0$
is dictated by the structure of the practical inventory problem considered by Scarf. It is not needed, however, to avoid the infimum being minus infinity. In fact,
where
![]() $ \bigl({\mathbb{E}} X^2 \bigr)^{1/2} = \lVert{X}\rVert_2 = \lVert{X-m+m}\rVert_2 \leqslant \sigma + |{m}|$
, which implies
$ \bigl({\mathbb{E}} X^2 \bigr)^{1/2} = \lVert{X}\rVert_2 = \lVert{X-m+m}\rVert_2 \leqslant \sigma + |{m}|$
, which implies
As observed in [Reference Lo7], Lemma 2.2(iii) immediately yields the following result.
Corollary 4.1. (Lo) Let
![]() $c,m,\sigma$
be strictly positive real numbers. The supremum of the function
$c,m,\sigma$
be strictly positive real numbers. The supremum of the function
![]() $X \mapsto {\mathbb{E}}(X - c)^+$
on the set
$X \mapsto {\mathbb{E}}(X - c)^+$
on the set
![]() $\mathscr{X}_{m,\sigma}^0$
is attained, i.e. it is a maximum, and is given by
$\mathscr{X}_{m,\sigma}^0$
is attained, i.e. it is a maximum, and is given by
 \begin{equation*} \max_{X \in \mathscr{X}_{m,\sigma}^0} {\mathbb{E}}(X - c)^+ = \begin{cases} \displaystyle m - \frac{m^2}{m^2+\sigma^2}c & \text{if } \displaystyle c \leqslant \frac{m^2+\sigma^2}{2m},\\[10pt] \displaystyle \frac{m-c}{2} + \frac12 \bigl( (m-c)^2 + \sigma^2 \bigr)^{1/2} & \text{if } \displaystyle c \geqslant \frac{m^2+\sigma^2}{2m}. \end{cases} \end{equation*}
\begin{equation*} \max_{X \in \mathscr{X}_{m,\sigma}^0} {\mathbb{E}}(X - c)^+ = \begin{cases} \displaystyle m - \frac{m^2}{m^2+\sigma^2}c & \text{if } \displaystyle c \leqslant \frac{m^2+\sigma^2}{2m},\\[10pt] \displaystyle \frac{m-c}{2} + \frac12 \bigl( (m-c)^2 + \sigma^2 \bigr)^{1/2} & \text{if } \displaystyle c \geqslant \frac{m^2+\sigma^2}{2m}. \end{cases} \end{equation*}
The remainder of this section is dedicated to showing that Theorem 4.1, and hence also its corollary, are consequences of Theorem 3.1. We shall argue by a sequence of elementary lemmas and propositions. The first is a reduction step that, in spite of its simplicity, considerably reduces the burden of symbolic calculations. Throughout the section we assume that
![]() $c,m,\sigma \in \mathbb{R}$
, with
$c,m,\sigma \in \mathbb{R}$
, with
![]() $\sigma>0$
. Further constraints (that do not imply any loss of generality) will be introduced as needed.
$\sigma>0$
. Further constraints (that do not imply any loss of generality) will be introduced as needed.
Lemma 4.1. Let
![]() $ \widetilde{c} \,:\!=\, ({c-m})/{\sigma} $
. Then
$ \widetilde{c} \,:\!=\, ({c-m})/{\sigma} $
. Then
Proof. Since
![]() $\mathscr{X}^0_{m,\sigma} = m + \sigma \mathscr{X}^{-m/\sigma}$
by (2.1), we have
$\mathscr{X}^0_{m,\sigma} = m + \sigma \mathscr{X}^{-m/\sigma}$
by (2.1), we have
where, by Lemma 2.2,
which immediately yields the conclusion.
The lemma implies that it suffices to study the problem of minimizing the function
![]() $X \mapsto {\mathbb{E}}(X \wedge c)$
over the set
$X \mapsto {\mathbb{E}}(X \wedge c)$
over the set
![]() $\mathscr{X}^{-m}$
. We shall first study the minimization problem without the lower-boundedness constraint, i.e. on
$\mathscr{X}^{-m}$
. We shall first study the minimization problem without the lower-boundedness constraint, i.e. on
![]() $\mathscr{X}$
rather than on
$\mathscr{X}$
rather than on
![]() $\mathscr{X}^{-m}$
. We shall need some more notation: the subset of
$\mathscr{X}^{-m}$
. We shall need some more notation: the subset of
![]() $\mathscr{X}_{m,\sigma}$
such that
$\mathscr{X}_{m,\sigma}$
such that
![]() $\mathbb{P}(X \leqslant c) = p$
is denoted by
$\mathbb{P}(X \leqslant c) = p$
is denoted by
![]() $\mathscr{X}_{m,\sigma}(p;c)$
. Note that, in view of Corollary 3.1, these sets are nonempty only for certain combinations of the parameters p and c. Let
$\mathscr{X}_{m,\sigma}(p;c)$
. Note that, in view of Corollary 3.1, these sets are nonempty only for certain combinations of the parameters p and c. Let
![]() $L_c \colon \mathopen]0,1\mathclose[ \mapsto \mathbb{R}$
be the function defined by
$L_c \colon \mathopen]0,1\mathclose[ \mapsto \mathbb{R}$
be the function defined by
![]() $ L_c\colon p \longmapsto - (p-p^2)^{1/2} + c(1-p)$
.
$ L_c\colon p \longmapsto - (p-p^2)^{1/2} + c(1-p)$
.
Lemma 4.2.
![]() $ \inf_{X \in \mathscr{X}(c;p)} {\mathbb{E}}(X \wedge c) \geqslant L_c(p) $
.
$ \inf_{X \in \mathscr{X}(c;p)} {\mathbb{E}}(X \wedge c) \geqslant L_c(p) $
.
Proof. Lemma 2.2 (iii) implies
![]() $ {\mathbb{E}} (X-c)^+ = -{\mathbb{E}}(X \wedge c) $
for any X with mean zero; hence, by Theorem 3.1,
$ {\mathbb{E}} (X-c)^+ = -{\mathbb{E}}(X \wedge c) $
for any X with mean zero; hence, by Theorem 3.1,
We are now going to show that the infimum in Lemma 4.2 is achieved, and that the minimizer is a two-point distributed random variable. We shall only consider, without loss of generality, those values of p such that
![]() $\mathscr{X}(p;c)$
is nonempty, that is, by Corollary 3.1, setting
$\mathscr{X}(p;c)$
is nonempty, that is, by Corollary 3.1, setting
 \begin{equation*}\Pi_c \,:\!=\,\begin{cases} \displaystyle \biggl] 0 , \frac{1}{1+c^2} \biggr] &\quad \text{if } c<0,\\[17pt] \displaystyle \biggl[ \frac{c^2}{1+c^2} , 1 \biggr[ &\quad \text{if } c \geqslant 0,\end{cases}\end{equation*}
\begin{equation*}\Pi_c \,:\!=\,\begin{cases} \displaystyle \biggl] 0 , \frac{1}{1+c^2} \biggr] &\quad \text{if } c<0,\\[17pt] \displaystyle \biggl[ \frac{c^2}{1+c^2} , 1 \biggr[ &\quad \text{if } c \geqslant 0,\end{cases}\end{equation*}
to
![]() $p \in \Pi_c$
.
$p \in \Pi_c$
.
Lemma 4.3. Let
![]() $p \in \Pi_c$
, and
$p \in \Pi_c$
, and
![]() $X_0 \in \mathscr{X}$
be the two-point distributed random variable with parameter p. Then
$X_0 \in \mathscr{X}$
be the two-point distributed random variable with parameter p. Then
![]() $ {\mathbb{E}}(X_0 \wedge c) = L_c(p) $
, and hence
$ {\mathbb{E}}(X_0 \wedge c) = L_c(p) $
, and hence
Proof. Since
![]() $p \in \Pi_c$
, Lemma 2.1 implies that the random variable
$p \in \Pi_c$
, Lemma 2.1 implies that the random variable
![]() $X_0$
, taking the values x and y as defined in (2.2), is such that
$X_0$
, taking the values x and y as defined in (2.2), is such that
![]() $x \leqslant c \leqslant y$
. In particular,
$x \leqslant c \leqslant y$
. In particular,
![]() $\mathbb{P}(X_0 \leqslant c) = p$
, that is,
$\mathbb{P}(X_0 \leqslant c) = p$
, that is,
![]() $X_0 \in \mathscr{X}(p;c)$
, and an elementary computation finally shows that
$X_0 \in \mathscr{X}(p;c)$
, and an elementary computation finally shows that
![]() ${\mathbb{E}}(X_0 \wedge c) = L_c(p)$
.
${\mathbb{E}}(X_0 \wedge c) = L_c(p)$
.
The following result essentially shows that Theorem 3.1 implies Theorem 4.1 in the unconstrained case (i.e. without assuming that the minimizer should be bounded from below).
Proposition 4.1.
![]() $ \inf_{X \in \mathscr{X}} {\mathbb{E}}(X \wedge c) = \inf_{p \in \Pi_c} L_c(p) $
.
$ \inf_{X \in \mathscr{X}} {\mathbb{E}}(X \wedge c) = \inf_{p \in \Pi_c} L_c(p) $
.
Proof. The decomposition
![]() $ \mathscr{X} = \bigcup_{p \in \Pi_c} \mathscr{X}(p;c) $
implies (see, e.g., [Reference Bourbaki3, p. III.11])
$ \mathscr{X} = \bigcup_{p \in \Pi_c} \mathscr{X}(p;c) $
implies (see, e.g., [Reference Bourbaki3, p. III.11])
so that Lemma 4.3 implies the claim.
This clearly indicates that the next step should be to find the minimum of the function
![]() $L_c$
.
$L_c$
.
Lemma 4.4. The function
![]() $L_c$
satisfies the following properties:
$L_c$
satisfies the following properties:
-
(i) it is decreasing on the interval
 $ \biggl] 0, \dfrac12 + \dfrac12 \dfrac{c}{(1+c^2)^{1/2}}\biggr] $
;
$ \biggl] 0, \dfrac12 + \dfrac12 \dfrac{c}{(1+c^2)^{1/2}}\biggr] $
; -
(ii) it is increasing on the interval
 $ \biggl[ \dfrac12 + \dfrac12 \dfrac{c}{(1+c^2)^{1/2}}, 1 \biggr[ $
;
$ \biggl[ \dfrac12 + \dfrac12 \dfrac{c}{(1+c^2)^{1/2}}, 1 \biggr[ $
; -
(iii) it admits a unique minimum point
 $p_\ast$
defined by
$p_\ast$
defined by
 $ p_\ast \,:\!=\, \dfrac12 + \dfrac12 \dfrac{c}{(1+c^2)^{1/2}} $
.
$ p_\ast \,:\!=\, \dfrac12 + \dfrac12 \dfrac{c}{(1+c^2)^{1/2}} $
.
Moreover,
![]() $p_\ast$
belongs to
$p_\ast$
belongs to
![]() $\Pi_c$
and
$\Pi_c$
and
![]() $ L_c(p_\ast) = \frac12 c - \frac12 (1+c^2)^{1/2} $
.
$ L_c(p_\ast) = \frac12 c - \frac12 (1+c^2)^{1/2} $
.
Proof. The argument is elementary, so it will be sketched only (the details can be found in [Reference Marinelli8]). The function
![]() $L_c$
is smooth and its derivative is the function
$L_c$
is smooth and its derivative is the function
hence, standard calculus yields the claims (i)–(iii). It only remains to show that
![]() $p_\ast \in \Pi_c$
; if
$p_\ast \in \Pi_c$
; if
![]() $c \geqslant 0$
, this is equivalent to
$c \geqslant 0$
, this is equivalent to
Setting
![]() $x \,:\!=\, c/(1+c^2)^{1/2} \in [0,1\mathclose[$
, this reduces to
$x \,:\!=\, c/(1+c^2)^{1/2} \in [0,1\mathclose[$
, this reduces to
![]() $1+x \geqslant 2x^2$
, which is satisfied if
$1+x \geqslant 2x^2$
, which is satisfied if
![]() $x \in [0,1]$
. If
$x \in [0,1]$
. If
![]() $c<0$
,
$c<0$
,
![]() $p_\ast$
belongs to
$p_\ast$
belongs to
![]() $\Pi_c$
if and only if
$\Pi_c$
if and only if
that is, setting
![]() $\langle c \rangle \,:\!=\, (1+c^2)^{1/2}$
for convenience, if and only if
$\langle c \rangle \,:\!=\, (1+c^2)^{1/2}$
for convenience, if and only if
![]() $\langle c \rangle \lvert{c}\rvert \geqslant \langle c \rangle^2 - 2$
. This inequality is easily seen to be satisfied for every
$\langle c \rangle \lvert{c}\rvert \geqslant \langle c \rangle^2 - 2$
. This inequality is easily seen to be satisfied for every
![]() $c \in [-1,0]$
. If
$c \in [-1,0]$
. If
![]() $c \leqslant -1$
, the inequality is equivalent to
$c \leqslant -1$
, the inequality is equivalent to
![]() $ \langle c \rangle^2 c^2 \geqslant (c^2-1)^2 $
, which simplifies to
$ \langle c \rangle^2 c^2 \geqslant (c^2-1)^2 $
, which simplifies to
![]() $3c^2 \geqslant 1$
, i.e. it is verified for every
$3c^2 \geqslant 1$
, i.e. it is verified for every
![]() $\lvert{c}\rvert \geqslant 1/\sqrt{3} \vee 1$
, that is for every
$\lvert{c}\rvert \geqslant 1/\sqrt{3} \vee 1$
, that is for every
![]() $c \leqslant -1$
. Finally, the expression for
$c \leqslant -1$
. Finally, the expression for
![]() $L_c(p_\ast)$
follows by elementary algebra.
$L_c(p_\ast)$
follows by elementary algebra.
We have thus solved the problem of of minimizing the function
![]() $X \mapsto {\mathbb{E}}(X \wedge c)$
on
$X \mapsto {\mathbb{E}}(X \wedge c)$
on
![]() $\mathscr{X}$
.
$\mathscr{X}$
.
Proposition 4.2. Let
![]() $p_\ast$
be defined as in Lemma 4.4, and
$p_\ast$
be defined as in Lemma 4.4, and
The two-point distributed random variable
![]() $X_0$
with
$X_0$
with
![]() $\mathbb{P}(X_0 = x_\ast) = p_\ast$
,
$\mathbb{P}(X_0 = x_\ast) = p_\ast$
,
![]() $\mathbb{P}(X_0 = y_\ast) = 1-p_\ast$
is a minimizer of
$\mathbb{P}(X_0 = y_\ast) = 1-p_\ast$
is a minimizer of
![]() $\inf_{X \in \mathscr{X}} {\mathbb{E}}(X \wedge c)$
, i.e.
$\inf_{X \in \mathscr{X}} {\mathbb{E}}(X \wedge c)$
, i.e.
If the parameters of the problem are such that
![]() $X_0$
, as defined in Proposition 4.2, is bounded below by
$X_0$
, as defined in Proposition 4.2, is bounded below by
![]() $-m$
, the original minimization problem is clearly solved. We shall assume, until further notice, that
$-m$
, the original minimization problem is clearly solved. We shall assume, until further notice, that
![]() $m\geqslant 0$
and
$m\geqslant 0$
and
![]() $c>-m$
. This comes at no loss of generality, as
$c>-m$
. This comes at no loss of generality, as
![]() $\mathscr{X}^{-m}$
is empty if
$\mathscr{X}^{-m}$
is empty if
![]() $m<0$
, and the problem degenerates if
$m<0$
, and the problem degenerates if
![]() $c \leqslant -m$
, in the sense that
$c \leqslant -m$
, in the sense that
![]() ${\mathbb{E}}(X \wedge c) = c$
for every
${\mathbb{E}}(X \wedge c) = c$
for every
![]() $X \geqslant -m$
.
$X \geqslant -m$
.
Corollary 4.2. Let
![]() $X_0$
be defined as in Proposition 4.2. Then
$X_0$
be defined as in Proposition 4.2. Then
if and only if
![]() $ c \geqslant ({1-m^2})/{2m} $
.
$ c \geqslant ({1-m^2})/{2m} $
.
Proof. By definition of
![]() $X_0$
, the lower bound
$X_0$
, the lower bound
![]() $X_0 \geqslant -m $
holds if and only if
$X_0 \geqslant -m $
holds if and only if
![]() $p_\ast \geqslant 1/(1+m^2)$
, i.e. if and only if
$p_\ast \geqslant 1/(1+m^2)$
, i.e. if and only if
or, equivalently,
where the left-hand side takes values in the interval
![]() $\mathopen]-1,1\mathclose]$
. Elementary algebra shows that the inequality
$\mathopen]-1,1\mathclose]$
. Elementary algebra shows that the inequality
is verified if and only if
Replacing
![]() $\beta$
by
$\beta$
by
![]() $2/(1+m^2)-1$
finally implies that
$2/(1+m^2)-1$
finally implies that
![]() $X_0 \geqslant -m$
if and only if
$X_0 \geqslant -m$
if and only if
from which the claim follows immediately.
In view of the corollary, we only need to consider the problem under the condition
Note that this implies
![]() $c < 1/m$
.
$c < 1/m$
.
Let us start by observing that, for any
![]() $X \geqslant -m$
,
$X \geqslant -m$
,
 \begin{align} {\mathbb{E}}(X \wedge c) &= {\mathbb{E}}\bigl( X \mathbf{1}_{\{X \leqslant c\}} + c\mathbf{1}_{\{X>c\}} \bigr)\nonumber\\ &\geqslant -m \mathbb{P}(X \leqslant c) + c\mathbb{P}(X>c)\\ &= {\mathbb{E}}(Y \wedge c), \nonumber\end{align}
\begin{align} {\mathbb{E}}(X \wedge c) &= {\mathbb{E}}\bigl( X \mathbf{1}_{\{X \leqslant c\}} + c\mathbf{1}_{\{X>c\}} \bigr)\nonumber\\ &\geqslant -m \mathbb{P}(X \leqslant c) + c\mathbb{P}(X>c)\\ &= {\mathbb{E}}(Y \wedge c), \nonumber\end{align}
where Y is a random variable taking values in
![]() $\{-m,y\}$
,
$\{-m,y\}$
,
![]() $y \geqslant c$
, with
$y \geqslant c$
, with
In order for the random variable Y to belong to
![]() $\mathscr{X}$
, it is sufficient and necessary, in view of (2.2) and Lemma 2.1, that
$\mathscr{X}$
, it is sufficient and necessary, in view of (2.2) and Lemma 2.1, that
and either
![]() $c \leqslant 0$
or
$c \leqslant 0$
or
![]() $c \geqslant 0$
and
$c \geqslant 0$
and
In other words, Y belongs to
![]() $\mathscr{X}$
and takes values in
$\mathscr{X}$
and takes values in
![]() $\{-m,y\}$
with
$\{-m,y\}$
with
![]() $y \geqslant c$
if and only if
$y \geqslant c$
if and only if
![]() $c \leqslant 0$
or
$c \leqslant 0$
or
![]() $c>0$
and
$c>0$
and
As this inequality is satisfied if and only if
![]() $cm \leqslant 1$
, which holds by assumption, Y satisfies the abovementioned conditions if and only if
$cm \leqslant 1$
, which holds by assumption, Y satisfies the abovementioned conditions if and only if
![]() $\mathbb{P}(X \leqslant c) = 1/(1+m^2)$
. Let us then define the random variable
$\mathbb{P}(X \leqslant c) = 1/(1+m^2)$
. Let us then define the random variable
![]() $Y_0 \in \mathscr{X}^{-m}$
as the (unique) random variable in
$Y_0 \in \mathscr{X}^{-m}$
as the (unique) random variable in
![]() $\mathscr{X}$
identified by the parameter
$\mathscr{X}$
identified by the parameter
![]() $p_m = {1}/({1+m^2})$
. We are going to show that
$p_m = {1}/({1+m^2})$
. We are going to show that
![]() $Y_0$
is in fact the minimizer of the problem.
$Y_0$
is in fact the minimizer of the problem.
Proposition 4.3. If
![]() $c < (1-m^2)/(2m)$
, then
$c < (1-m^2)/(2m)$
, then
Proof. Let us rewrite (4.1) as
![]() $ {\mathbb{E}}(X \wedge c) \geqslant -c + (m+c) \mathbb{P}(X \leqslant c) $
, which holds for every
$ {\mathbb{E}}(X \wedge c) \geqslant -c + (m+c) \mathbb{P}(X \leqslant c) $
, which holds for every
![]() $X \in \mathscr{X}^{-m}$
. Since
$X \in \mathscr{X}^{-m}$
. Since
![]() $m+c>0$
by assumption, the function
$m+c>0$
by assumption, the function
![]() $p \mapsto -c + (m+c)p$
is decreasing. Therefore, for every
$p \mapsto -c + (m+c)p$
is decreasing. Therefore, for every
![]() $X \in \mathscr{X}^{-m}$
such that
$X \in \mathscr{X}^{-m}$
such that
![]() $\mathbb{P}(X \leqslant c) \leqslant p_m$
, we have
$\mathbb{P}(X \leqslant c) \leqslant p_m$
, we have
Let
![]() $X \in \mathscr{X}^{-m}$
be such that
$X \in \mathscr{X}^{-m}$
be such that
![]() $p\,:\!=\,\mathbb{P}(X \leqslant c)>p_m$
. Then Lemma 4.2 yields
$p\,:\!=\,\mathbb{P}(X \leqslant c)>p_m$
. Then Lemma 4.2 yields
Since
![]() $p_* < p_m$
by assumption and the function
$p_* < p_m$
by assumption and the function
![]() $L_c$
is increasing on
$L_c$
is increasing on
![]() $\mathopen]p_*,1\mathclose[$
by Lemma 4.4, it follows that
$\mathopen]p_*,1\mathclose[$
by Lemma 4.4, it follows that
![]() $ {\mathbb{E}}(X \wedge c) \geqslant L_c(p) \geqslant L_c(p_m) = {\mathbb{E}}(X_0 \wedge c) $
, which concludes the proof.
$ {\mathbb{E}}(X \wedge c) \geqslant L_c(p) \geqslant L_c(p_m) = {\mathbb{E}}(X_0 \wedge c) $
, which concludes the proof.
We have therefore proved the main result, which reads as follows.
Theorem 4.2. Let
![]() $c,m,\sigma \in \mathbb{R}$
with
$c,m,\sigma \in \mathbb{R}$
with
![]() $m \geqslant 0$
,
$m \geqslant 0$
,
![]() $\sigma>0$
, and
$\sigma>0$
, and
![]() $c>-m$
. Then
$c>-m$
. Then
 \begin{equation*} \inf_{X \in \mathscr{X}^{-m}} {\mathbb{E}}(X \wedge c) = \begin{cases} \displaystyle {\mathbb{E}}(Y_0 \wedge c) = L_c(p_m) = c - (m+c)\frac{1}{1+m^2} &\quad \displaystyle \text{if } c \leqslant \frac{1-m^2}{2m}, \\[10pt] \displaystyle {\mathbb{E}}(X_0 \wedge c) = L_c(p_*) = \frac12 c - \frac12 (1+c^2)^{1/2} &\quad \displaystyle \text{if } c \geqslant \frac{1-m^2}{2m}. \end{cases} \end{equation*}
\begin{equation*} \inf_{X \in \mathscr{X}^{-m}} {\mathbb{E}}(X \wedge c) = \begin{cases} \displaystyle {\mathbb{E}}(Y_0 \wedge c) = L_c(p_m) = c - (m+c)\frac{1}{1+m^2} &\quad \displaystyle \text{if } c \leqslant \frac{1-m^2}{2m}, \\[10pt] \displaystyle {\mathbb{E}}(X_0 \wedge c) = L_c(p_*) = \frac12 c - \frac12 (1+c^2)^{1/2} &\quad \displaystyle \text{if } c \geqslant \frac{1-m^2}{2m}. \end{cases} \end{equation*}
Using the notation X(p) to denote a two-point distributed random variable in
![]() $\mathscr{X}$
with parameter p, we could write, more concisely,
$\mathscr{X}$
with parameter p, we could write, more concisely,
The bound by Scarf, and hence the one by Lo, i.e. Theorem 4.1 and its corollary, follow immediately by the previous theorem and Lemma 4.1.
5. Applications to option prices
In order to also consider bounds for put options, we record an easy consequence of Theorem 3.1.
Corollary 5.1. Under the hypotheses of Theorem 3.1, let
![]() $p \,:\!=\, \mathbb{P}(X \leqslant c)$
. Then
$p \,:\!=\, \mathbb{P}(X \leqslant c)$
. Then
Proof. It immediately follows from the identities
![]() ${\mathbb{E}}(c-X)^+ = {\mathbb{E}}(X-c)^+ - (m - c)$
and
${\mathbb{E}}(c-X)^+ = {\mathbb{E}}(X-c)^+ - (m - c)$
and
![]() $p-p^2=p(1-p)=(1-p_0)p_0=p_0-p_0^2$
.
$p-p^2=p(1-p)=(1-p_0)p_0=p_0-p_0^2$
.
Let us also note that a simple but useful sharpening of the lower bound in Theorem 3.1 can be given: Jensen’s inequality implies that
as well as
![]() ${\mathbb{E}}(c-X)^+ \geqslant (c-m)^+$
.
${\mathbb{E}}(c-X)^+ \geqslant (c-m)^+$
.
Assume that the probability space
![]() $(\Omega,\mathscr{F},\mathbb{P})$
is equipped with a filtration
$(\Omega,\mathscr{F},\mathbb{P})$
is equipped with a filtration
![]() $(\mathscr{F}_t)_{t\in[0,T]}$
satisfying the so-called usual conditions. Let
$(\mathscr{F}_t)_{t\in[0,T]}$
satisfying the so-called usual conditions. Let
![]() $\widehat{S}$
and
$\widehat{S}$
and
![]() $\beta$
be the price processes of two traded assets, the latter of which is strictly positive and is used as numéraire, so that
$\beta$
be the price processes of two traded assets, the latter of which is strictly positive and is used as numéraire, so that
![]() $S\,:\!=\,\beta^{-1}\widehat{S}$
is the discounted price process of the former asset. We assume that no asset pays dividends. A classical result [Reference Delbaen and Schachermayer6] asserts that a suitable version of no-arbitrage holds (precisely, no free lunch with vanishing risk) if and only if there exists a probability measure
$S\,:\!=\,\beta^{-1}\widehat{S}$
is the discounted price process of the former asset. We assume that no asset pays dividends. A classical result [Reference Delbaen and Schachermayer6] asserts that a suitable version of no-arbitrage holds (precisely, no free lunch with vanishing risk) if and only if there exists a probability measure
![]() $\mathbb{Q}$
equivalent to
$\mathbb{Q}$
equivalent to
![]() $\mathbb{P}$
such that S is a
$\mathbb{P}$
such that S is a
![]() $\sigma$
-martingale with respect to
$\sigma$
-martingale with respect to
![]() $\mathbb{Q}$
. For simplicity of notation, let us assume that
$\mathbb{Q}$
. For simplicity of notation, let us assume that
![]() $\mathbb{P}$
is already an equivalent
$\mathbb{P}$
is already an equivalent
![]() $\sigma$
-martingale measure that is used for pricing. We are then interested in upper and lower bounds for
$\sigma$
-martingale measure that is used for pricing. We are then interested in upper and lower bounds for
We first establish an easy consequence of the
![]() $\sigma$
-martingale property of S.
$\sigma$
-martingale property of S.
Lemma 5.1.
-
(i) If S is a supermartingale (in particular, if S is bounded from below), then
 $ \pi_p \geqslant \bigl( K {\mathbb{E}}\beta_T^{-1} - S_0 \bigr)^+ $
.
$ \pi_p \geqslant \bigl( K {\mathbb{E}}\beta_T^{-1} - S_0 \bigr)^+ $
. -
(ii) If S is a martingale, then
 $ \pi_c \geqslant \bigl( S_0 - K {\mathbb{E}}\beta_T^{-1} \bigr)^+ $
.
$ \pi_c \geqslant \bigl( S_0 - K {\mathbb{E}}\beta_T^{-1} \bigr)^+ $
.
Proof. Recall first that a
![]() $\sigma$
-martingale bounded from below is a local martingale thanks to the Ansel–Stricker lemma [Reference Ansel and Stricker1, p. 309], thus also a supermartingale by an application of Fatou’s lemma. This implies that
$\sigma$
-martingale bounded from below is a local martingale thanks to the Ansel–Stricker lemma [Reference Ansel and Stricker1, p. 309], thus also a supermartingale by an application of Fatou’s lemma. This implies that
![]() ${\mathbb{E}} S_T \leqslant S_0$
, and hence, by Jensen’s inequality,
${\mathbb{E}} S_T \leqslant S_0$
, and hence, by Jensen’s inequality,
which proves (i). The proof of (ii) is entirely analogous.
Remark 5.1. The lower bound for
![]() $\pi_c$
is in general not true without the hypothesis that S is a martingale. This is essentially equivalent to the failure of put–call parity for asset prices with so-called bubbles (cf., e.g., [Reference Cox and Hobson4]).
$\pi_c$
is in general not true without the hypothesis that S is a martingale. This is essentially equivalent to the failure of put–call parity for asset prices with so-called bubbles (cf., e.g., [Reference Cox and Hobson4]).
It is clear that the estimates of Theorem 3.1 and Corollary 4.1 cannot be directly applied, as
![]() $\beta_T$
is a random variable. In some cases, however, this is indeed possible. For instance, apart from the trivial case where the price process
$\beta_T$
is a random variable. In some cases, however, this is indeed possible. For instance, apart from the trivial case where the price process
![]() $\beta$
of the numéraire is non-random, if the random variables
$\beta$
of the numéraire is non-random, if the random variables
![]() $\beta_T^{-1}$
and
$\beta_T^{-1}$
and
![]() $\widehat{S}_T^+$
belong to
$\widehat{S}_T^+$
belong to
![]() $L^2$
, and
$L^2$
, and
![]() $\beta_T^{-1}$
and
$\beta_T^{-1}$
and
![]() $(S_T-K)^+$
are uncorrelated, so that
$(S_T-K)^+$
are uncorrelated, so that
estimates on
![]() $\pi_c$
can be obtained by Corollary 4.1 in terms of the mean of
$\pi_c$
can be obtained by Corollary 4.1 in terms of the mean of
![]() $\beta_T^{-1}$
and the mean and variance of
$\beta_T^{-1}$
and the mean and variance of
![]() $\widehat{S}_T$
. In order to apply Theorem 3.1, the value of the distribution function of
$\widehat{S}_T$
. In order to apply Theorem 3.1, the value of the distribution function of
![]() $\widehat{S}_T$
at K is also needed. In the following we make the stronger assumption that the random variables
$\widehat{S}_T$
at K is also needed. In the following we make the stronger assumption that the random variables
![]() $\beta_T$
and
$\beta_T$
and
![]() $\widehat{S}_T$
are independent. Furthermore, we assume that S is a supermartingale. By independence,
$\widehat{S}_T$
are independent. Furthermore, we assume that S is a supermartingale. By independence,
and hence
![]() ${\mathbb{E}}\widehat{S}_T \leqslant S_0 / {\mathbb{E}}\beta_T^{-1}$
. Setting
${\mathbb{E}}\widehat{S}_T \leqslant S_0 / {\mathbb{E}}\beta_T^{-1}$
. Setting
![]() $k \,:\!=\, K {\mathbb{E}}\beta_T^{-1}$
and
$k \,:\!=\, K {\mathbb{E}}\beta_T^{-1}$
and
![]() $\widehat{\sigma} \,:\!=\, \lVert{\widehat{S}_T - {\mathbb{E}}\widehat{S}_T}\rVert_2$
, we thus have the bounds
$\widehat{\sigma} \,:\!=\, \lVert{\widehat{S}_T - {\mathbb{E}}\widehat{S}_T}\rVert_2$
, we thus have the bounds
If S is a martingale, then
![]() ${\mathbb{E}} S_T=S_0$
, so the bounds for
${\mathbb{E}} S_T=S_0$
, so the bounds for
![]() $\pi_p$
and
$\pi_p$
and
![]() $\pi_c$
assume a more symmetric form.
$\pi_c$
assume a more symmetric form.
Adapting Lo’s estimate to option prices can be done along the same lines. It does not seem possible, though, to exploit the supermartingale property of S to obtain bounds involving
![]() $S_0$
rather than
$S_0$
rather than
![]() ${\mathbb{E}} S_T$
. On the other hand, if S is a martingale, and if the constraint
${\mathbb{E}} S_T$
. On the other hand, if S is a martingale, and if the constraint
![]() $\widehat{S}_T \geqslant 0$
is not enforced, it follows from the proofs in Section 4 and elementary computations that
$\widehat{S}_T \geqslant 0$
is not enforced, it follows from the proofs in Section 4 and elementary computations that
from which a corresponding upper bound for put options can be obtained by put–call parity.