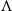Nomenclature
-
 ${\rm{\Lambda }}$
${\rm{\Lambda }}$
-
sweep angle, deg
-
 ${U_\infty }$
${U_\infty }$
-
free stream velocity, m/s
-
 $\alpha \;$
$\alpha \;$
-
angle-of-attack, deg
-
 ${q_\infty }$
${q_\infty }$
-
dynamic pressure (=
 $\rho U_\infty ^2/2$
)
$\rho U_\infty ^2/2$
) -
 $X,Y,Z\;$
$X,Y,Z\;$
-
coordinate measured along the streamwise, spanwise direction and normal to surface, respectively, mm, with respect to the origin located at the apex
-
 $C,b,S$
$C,b,S$
-
root chord, maximum wing span and planform area
-
 ${b^2}/S,X/C$
${b^2}/S,X/C$
-
aspect ratio, and non-dimensional chordwise location along streamwise direction
- Re
-
Reynolds number based on the root chord
-
 ${C_L}$
${C_L}$
-
lift coefficient (=
 $L/\left( {{q_\infty }S} \right)$
)
$L/\left( {{q_\infty }S} \right)$
) -
 ${C_D}$
${C_D}$
-
drag coefficient (=
 $D/\left( {{q_\infty }S} \right)$
)
$D/\left( {{q_\infty }S} \right)$
) -
 ${C_{PM}}$
${C_{PM}}$
-
pitching moment coefficient (=
 $PM/\left( {{q_\infty }SC} \right)$
) (pitching moment positive for nose up)
$PM/\left( {{q_\infty }SC} \right)$
) (pitching moment positive for nose up) -
 ${X_{cg}}$
${X_{cg}}$
-
non-dimensional distance of centre of gravity from apex of model
-
 ${X_{cp}}$
${X_{cp}}$
-
non-dimensional distance of centre of pressure from apex of model
-
 ${C_p}$
${C_p}$
-
coefficient of mean pressure (=
 $p - {p_\infty }/\left( {\rho U_\infty ^2/2} \right))$
$p - {p_\infty }/\left( {\rho U_\infty ^2/2} \right))$
-
 ${C_{p,{\rm{\;\;}}RMS}}$
${C_{p,{\rm{\;\;}}RMS}}$
-
coefficient of root-mean-squared pressure
-
 ${Y_{max}}$
${Y_{max}}$
-
maximum spanwise distance from root chord
-
 $\eta = Y/{Y_{max}}$
$\eta = Y/{Y_{max}}$
-
normalised spanwise distance
-
 $dt$
$dt$
-
time step
-
 ${X_{VB}}$
${X_{VB}}$
-
vortex breakdown location normalised with root-chord of the flying wing, along streamwise direction
-
 ${X_{f,{\rm{\;\;}}RMS}}$
${X_{f,{\rm{\;\;}}RMS}}$
-
root-mean-squared of the fluctuation of the Vortex breakdown location, normalised with root-chord of the flying wing, along streamwise direction
-
 ${X_{vc}}$
${X_{vc}}$
-
coordinate along the longitudinal plane passing through the trajectory of vortex core
-
 ${\omega _X},{\rm{\;\;}}{\omega _{vc}}$
${\omega _X},{\rm{\;\;}}{\omega _{vc}}$
-
ensemble-averaged axial vorticity and azimuthal vorticity
-
 ${\bar u_{vc}},u'_{\!\!vc},{u_I},{u_{RMS}}$
${\bar u_{vc}},u'_{\!\!vc},{u_I},{u_{RMS}}$
-
mean velocity, velocity fluctuation and instantaneous velocity, m/s along vortex core and Root mean squared velocity
Abbreviation and Subscripts
- vc
-
vortex core
- VB
-
vortex breakdown
- MRP
-
moment reference point from apex of the flying wing
- LEV
-
leading-edge vortex
- PIV
-
proper image velocitimetry
- POD
-
proper orthogonal decomposition
-
 $\infty $
$\infty $
-
freestream conditions
- RMS
-
root-mean-squared
- UCAV
-
unmanned combat aerial vehicle
1.0 Introduction
In the past decades, aerodynamic characteristics and leading-edge vortical flow field have been a field of interest over non-slender flying wing [Reference Visbal and Gaitonde1–Reference Gursul, Gordnier and Visbal5]. A slender/non-slender flying wing is defined based on the leading-edge sweep angle [Reference Gursul, Gordnier and Visbal5, Reference Gursul, Allan and Badcock6]; if the sweep angle (
![]() ${\rm{\Lambda }}$
) is greater than 55°, the wing is called a slender wing; otherwise, it is termed as a non-slender wing (
${\rm{\Lambda }}$
) is greater than 55°, the wing is called a slender wing; otherwise, it is termed as a non-slender wing (
![]() ${\rm{\Lambda }} \le $
55°), as can be seen in Fig. 1. A flying wing is a type of aircraft that has no tail, and its wings make up most of the structure. The wings are connected to the fuselage. This design allows the aircraft to generate most of its aerodynamic forces and moments from the wings alone [Reference Bishop7, Reference Maddock8]. At high angles of attack, the leading-edge primary vortex (LEV) of a flying wing experiences a phenomenon called vortex breakdown. This is characterised by sudden expansion of the vortex core, presence of a stagnation point on the vortex axis and an increase in adverse pressure gradient and turbulence levels [Reference Lambourne and Bryer9–Reference Gordnier and Visbal13]. Vortex breakdown can affect both the steady and unsteady aerodynamics of the flying wing, which in turn can cause a loss of lift [Reference Hall10, Reference Payne, Ng, Nelson and Schiff11, Reference Menke, Yang and Gursul14, Reference Kumar, Mandal and Poddar15]. It is, therefore, critical to study the behaviour of the leading-edge vortices and understand the vortex breakdown phenomenon in order to develop safe and effective flying wing designs.
${\rm{\Lambda }} \le $
55°), as can be seen in Fig. 1. A flying wing is a type of aircraft that has no tail, and its wings make up most of the structure. The wings are connected to the fuselage. This design allows the aircraft to generate most of its aerodynamic forces and moments from the wings alone [Reference Bishop7, Reference Maddock8]. At high angles of attack, the leading-edge primary vortex (LEV) of a flying wing experiences a phenomenon called vortex breakdown. This is characterised by sudden expansion of the vortex core, presence of a stagnation point on the vortex axis and an increase in adverse pressure gradient and turbulence levels [Reference Lambourne and Bryer9–Reference Gordnier and Visbal13]. Vortex breakdown can affect both the steady and unsteady aerodynamics of the flying wing, which in turn can cause a loss of lift [Reference Hall10, Reference Payne, Ng, Nelson and Schiff11, Reference Menke, Yang and Gursul14, Reference Kumar, Mandal and Poddar15]. It is, therefore, critical to study the behaviour of the leading-edge vortices and understand the vortex breakdown phenomenon in order to develop safe and effective flying wing designs.
Peckham and Atkinson [Reference Peckham and Atkinson16] found the existence of a vortex breakdown at the trailing edge of a Gothic wing, whereas Werlé [Reference Werlé17, Reference Werlé18] was the first to point out the sudden bursting of the leading-edge vortex using the flow visualisation technique on a slender delta wing. Following that, various theoretical and experimental aspects of vortex breakdown are explained based on instability, wave propagation and flow stagnation over cylindrical tubes and slender delta wings (Harvey [Reference Harvey19]; Lambourne [Reference Lambourne and Bryer9]; Benjamin [Reference Benjamin20]; Sarpkaya [Reference Sarpkaya21]; Hall [Reference Hall10]; Leibovich [Reference Leibovich22]; Escudier [Reference Escudier23]; Brown and Lopez [Reference Brown and Lopez24]; Lopez and Perry [Reference Lopez and Perry25]; Delery [Reference Delery26]). Over a delta wing, there exist two primary forms of vortex breakdown: a bubble type, which has an axisymmetric shape, and a spiral type, which has a non-axisymmetric spiral/corkscrew type shape [Reference Lambourne and Bryer9, Reference Payne, Ng, Nelson and Schiff11]. The vortex breakdown also causes buffeting, unsteadiness and poor control of flying vehicles [Reference Peake and Tobak27]. Subsequently, experimental investigations were focused on the characteristics and unsteady nature of the vortex breakdown, as well as its onset criterion [Reference Özgören, Sahin and Rockwell12, Reference Menke, Yang and Gursul14, Reference Lin and Rockwell28–Reference Menke and Gursul30]. Some studies reported that the bubble type and the spiral type can interchange each other from time to time. Additionally, the spiral type occurs more frequently than the bubble type over a slender delta wing [Reference Lucca-Negro and O’doherty31, Reference Gursul32].

Figure 1. The schematic shows the (a) Isometric view, (b) Side view, (c) Front view, and (d) Top view of the Catia design of the non-slender flying wing model for the present investigation.
Recently, the NATO RTO/AVT-113 Task group [Reference Hummel33] investigated various aspects of flow topology, including the formation of vortical flow at different angles of attack, the influence of Reynolds and Mach numbers, transition behaviour on vortex dynamics, vortex breakdown and boundary layer flow over a delta wing with a round leading edge. These extensive tests served to validate numerical findings based on inviscid CFD simulations of a delta wing (
![]() ${\rm{\Lambda }}$
= 65°) with a sharp leading edge.
${\rm{\Lambda }}$
= 65°) with a sharp leading edge.
These studies indicate that vortex structure and vortex breakdown phenomena were extensively studied in the past for a slender delta wing configuration. However, it is equally important to investigate the flow field over a non-slender delta wing for the next-generation micro-air vehicles and unmanned combat air vehicles [Reference Gursul, Gordnier and Visbal5]. The three-dimensional complex flow field resulting from the vortex breakdown and its associated flow structures at the pre-stall, near-stall and post-stall over a non-slender flying wing configuration are not fully understood. Also, as compared to the slender delta wing, there is a limited amount of literature available on the vortical flow and vortex breakdown phenomena over a non-slender delta wing [Reference Ol and Gharib3–Reference Gursul, Gordnier and Visbal5, Reference Gursul32, Reference Yaniktepe and Rockwell34–Reference Wang, Gao, Wei, Li and Wang36].
However, some studies have recently been performed on an actual non-slender flying wing with variable leading-edge geometries using UCAV 1303 [Reference Chandrasekhara and McLain37] and UCAV stability and control configuration (SACCON) [Reference Schütte, Hummel and Hitzel38–Reference Konrath, Roosenboom, Schröder, Pallek and Otter40] to explain the aerodynamic behaviour and vortex dynamics. However, the leading-edge radius varies along the longitudinal direction for the SACCON configuration, with a sharp LE around the nose, a decreasing LE radius at mid-section, and a decreasing radius along with thickness up to the wingtip. A twist (0–5°) on the leading edge of the wings is also present in this case. Both the experimental and numerical approaches were used to understand the vortical flow physics in connection with the non-linear aerodynamic behaviour over the SACCON (
![]() ${\rm{\Lambda }}$
= 53°) configuration. Similarly, Kumar et al. [Reference Kumar, Mandal and Poddar15] considered a non-slender flying wing and found that the lift curve is non-linear and the slope of the lift curve is gradual at higher angles of attack, as compared to the slender delta wing. Their experiments also indicate presence of a vortical flow without and with vortex breakdown. But the type of the vortex breakdown, and the associated flow physics, as well as its effects on the aerodynamic characteristics for the non-slender flying wing configurations are hardly available in the literature. Therefore, the flow field associated with vortex breakdown over a non-slender flying wing is worth studying.
${\rm{\Lambda }}$
= 53°) configuration. Similarly, Kumar et al. [Reference Kumar, Mandal and Poddar15] considered a non-slender flying wing and found that the lift curve is non-linear and the slope of the lift curve is gradual at higher angles of attack, as compared to the slender delta wing. Their experiments also indicate presence of a vortical flow without and with vortex breakdown. But the type of the vortex breakdown, and the associated flow physics, as well as its effects on the aerodynamic characteristics for the non-slender flying wing configurations are hardly available in the literature. Therefore, the flow field associated with vortex breakdown over a non-slender flying wing is worth studying.
Specifically, we make an effort here to address the following questions: What is the relation between the surface flow topology over the flying wing and the pitching moment characteristics? How does a vortex breakdown manifest in the surface flow visualisation? How do its location and size change with Reynolds number and angle-of-attack? What is the type of vortex breakdown for a flying wing?
To investigate these aspects, surface oil flow visualisations, surface pressure measurements and the entire flow field measurements using the particle image velocimetry (PIV) technique are carried out at different angles of attack and Reynolds numbers. The PIV measurements were carried out at different cross-flow planes as well as in a longitudinal plane. The present article has been organised as follows: the experimental details and methodology are described in Section 2, results and discussions are presented in Section 3, followed by the summary and concluding remarks in Section 4.
2.0 Experimental setup and methodology
2.1 Wind tunnel and flying wing model
The present experimental work was carried out in a low-speed tunnel. It is a closed-circuit tunnel with a test section size of 1.68 m
![]() $ \times $
0.9 m
$ \times $
0.9 m
![]() $ \times $
0.6 m (length
$ \times $
0.6 m (length
![]() $ \times $
width
$ \times $
width
![]() $ \times $
height), and the ratio of its contraction cone is 6.5. It is equipped with a speed controller made by Siemens to control the wind speed in the test section. The maximum speed of the tunnel is 35 m/s, and the turbulence level in the test section was measured to be 0.3% of the freestream velocity.
$ \times $
height), and the ratio of its contraction cone is 6.5. It is equipped with a speed controller made by Siemens to control the wind speed in the test section. The maximum speed of the tunnel is 35 m/s, and the turbulence level in the test section was measured to be 0.3% of the freestream velocity.
A flying wing configuration with a complex geometrical profile was used for the present investigation. The Trust for Applied Aerodynamics in India (TAAI) proposed this configuration at the event of the Symposium for Promotion of Indigenous CFD Process in Engineering Sciences (SPICES-2013). The geometrical profile of this flying wing that blends delta and lambda wing shapes has a rounded leading edge with decreasing thickness and radius along the chordwise direction from its apex to the wingtip without control surfaces, as shown in Fig. 1. A sting was used to mount the model inside the tunnel test section. The sting was attached with a pitching mechanism, which was used to change the angle-of-attack. In the current study, apex of the flying wing model is considered as the origin of the axis system, as shown in Fig. 1; here,
![]() $X$
and
$X$
and
![]() $Y$
denote the streamwise direction and the spanwise direction, respectively, whereas
$Y$
denote the streamwise direction and the spanwise direction, respectively, whereas
![]() $Z$
indicates the normal to the surface. The selective laser sintering process was used to manufacture the flying wing model with the help of micron-sized polymer powder (PA 2200), as this provides a smooth surface finish to the wing model. The polymer, which is thermoplastic in nature, has a high tensile strength (
$Z$
indicates the normal to the surface. The selective laser sintering process was used to manufacture the flying wing model with the help of micron-sized polymer powder (PA 2200), as this provides a smooth surface finish to the wing model. The polymer, which is thermoplastic in nature, has a high tensile strength (
![]() $ \approx $
48 MPa), high melting point (
$ \approx $
48 MPa), high melting point (
![]() $ \approx $
172–180°C), good chemical resistance, lightweight (bulk density
$ \approx $
172–180°C), good chemical resistance, lightweight (bulk density
![]() $ \approx $
0.45 g/cm
$ \approx $
0.45 g/cm
![]() $^3$
) and excellent long-term constant behaviour. This ensures that the fabricated model considered in the present study is rigid enough with a smooth surface finish.
$^3$
) and excellent long-term constant behaviour. This ensures that the fabricated model considered in the present study is rigid enough with a smooth surface finish.
The fabricated flying wing model has a leading-edge sweep angle,
![]() ${\rm{\Lambda }} = 53$
°; it can be considered as a non-slender flying wing [Reference Gursul, Gordnier and Visbal5]. The model has a root chord (
${\rm{\Lambda }} = 53$
°; it can be considered as a non-slender flying wing [Reference Gursul, Gordnier and Visbal5]. The model has a root chord (
![]() $C$
) of 0.39 m and a maximum span (
$C$
) of 0.39 m and a maximum span (
![]() $b$
) of 0.551 m. The planform area (
$b$
) of 0.551 m. The planform area (
![]() $S$
) is defined as the area of the geometric shape seen in the top view (Fig. 1(d)), and it is found to be 0.1074 m
$S$
) is defined as the area of the geometric shape seen in the top view (Fig. 1(d)), and it is found to be 0.1074 m
![]() $^2$
. The aspect ratio of the model is defined as
$^2$
. The aspect ratio of the model is defined as
![]() ${b^2}/S$
, and it is found to be 2.84. The blockage ratio is defined as the ratio of the frontal area of the flying wing model at a particular angle-of-attack to the area of the test section, and it is found to be 9.65
${b^2}/S$
, and it is found to be 2.84. The blockage ratio is defined as the ratio of the frontal area of the flying wing model at a particular angle-of-attack to the area of the test section, and it is found to be 9.65
![]() ${\rm{\% }}$
at
${\rm{\% }}$
at
![]() $\alpha $
= 30° (Barlow et al. [Reference Barlow, Rae and Pope41]).
$\alpha $
= 30° (Barlow et al. [Reference Barlow, Rae and Pope41]).
2.2 Force measurement and oil flow visualisation technique
A six-component strain-gauge balance was used to measure the aerodynamic forces and moment coefficients. This balance was first calibrated in a calibration rig. However, the voltage signals from the force balance were acquired at a rate of 300 samples per second. These signals were then converted to the force and moment data using the calibration matrix. These force and moment data were acquired for 10 seconds duration to calculate an average of these quantities. It should also be noted that the force balance data were corrected for the tunnel blockage effect using the simple tunnel correction approach, as reported by Shindo [Reference Shindo42]. This force balance was used in many of our previous works e.g. Kumar et al. [Reference Kumar, Mandal and Poddar15].
Surface oil flow visualisation is often used to depict the surface flow pattern, as it is easy and inexpensive (Lu [Reference Lu43]; Bisgood [Reference Bisgood44]). This qualitative technique was used here for surface flow patterns over the flying wing. For oil flow visualisation, surface of the model was painted using a mixture of titanium dioxide powder, transformer oil and oleic acid. A halogen lamp was used to illuminate the painted surface for imaging purposes. A streaky deposit of the mixture marked the direction of the flow while air flowed over the surface. Further, using a DSLR camera (Nikon, D750, in monochromatic mode) with a lens (Nikkor, 24–120 mm focal range), the surface oil pattern was imaged at different angles of attack, as shown in Fig. 2.

Figure 2. Schematic view showing the arrangement of the flying wing model and DSLR cameras in the test section for oil flow visualisation.
2.3 Pressure measurement technique
In order to measure pressure on the surface of the model, various static pressure ports were made on the surface of the model along the spanwise direction (i.e.
![]() $Y$
direction) at various chordwise locations (
$Y$
direction) at various chordwise locations (
![]() $X/C$
), as shown in Fig. 3; here,
$X/C$
), as shown in Fig. 3; here,
![]() $X$
denotes the chordwise distance from the apex of the flying wing model along the streamwise direction. Measurements were carried out at different spanwise locations,
$X$
denotes the chordwise distance from the apex of the flying wing model along the streamwise direction. Measurements were carried out at different spanwise locations,
![]() $Y/{Y_{max}}$
(see Fig. 3); here
$Y/{Y_{max}}$
(see Fig. 3); here
![]() $Y$
is the spanwise distance from the root chord of the flying wing model, and
$Y$
is the spanwise distance from the root chord of the flying wing model, and
![]() ${Y_{max}}$
is the local semi-span of the flying wing model. A total of 109 pressure ports on the upper surface of the flying wing model were utilised. It may be noted that the pressure ports/taps on the port side of the flying wing model at
${Y_{max}}$
is the local semi-span of the flying wing model. A total of 109 pressure ports on the upper surface of the flying wing model were utilised. It may be noted that the pressure ports/taps on the port side of the flying wing model at
![]() $X/C$
= 0.6 were used to ensure the symmetric nature of the pressure distribution. Many pressure ports were made between the leading edge and 75%
$X/C$
= 0.6 were used to ensure the symmetric nature of the pressure distribution. Many pressure ports were made between the leading edge and 75%
![]() ${Y_{max}}$
line, and the number of ports was made coarser beyond 75%
${Y_{max}}$
line, and the number of ports was made coarser beyond 75%
![]() ${Y_{max}}$
, as shown in Fig. 3. This pressure port distribution was chosen to capture the steep pressure gradient near the leading edge of the flying wing.
${Y_{max}}$
, as shown in Fig. 3. This pressure port distribution was chosen to capture the steep pressure gradient near the leading edge of the flying wing.

Figure 3. A diagrammatic representation of pressure port distribution on the flying wing.
For surface pressure measurement, electronically scanned pressure (ESP) scanners were used. Measurements at 32 ports can be carried out using a single ESP, which is a differential pressure scanner. Other than the ESP, the pressure measurement system consists of a multiplexer unit, a high-speed 14-bit DAQ module (PXI-6133) with a PXI system and a workstation with an interface board (PCI-8336). A total of four scanners were used: three scanners with a 20-inch water column range and one scanner with a 10-inch water column. While conducting the measurements, these scanners were kept inside the flying wing. Reference pressure was measured using a Pitot-static tube, which was mounted on the wall of the test section. Applying the unique binary address to the multiplexers, the output of each ESP was selectively routed to the DAQ module (PXI- 6133). These multiplexers can switch between ports at maximum rates of up to 20,000 ports/s. However, in the present measurements, the pressure was scanned at the rate of 19,520 ports/s, yielding a sampling rate of 610 samples/s/port. The voltage output from the pressure scanners was converted to pressure data using the calibration coefficients with the help of Labview-based virtual instrumentation.
2.4 Particle image velocimetry (PIV) technique
Two-dimensional PIV measurements (2D-PIV) were carried out in both the crossflow plane and the longitudinal plane. Two CCD cameras were used for simultaneous PIV measurements on the starboard side and the port side of the flying wing, as shown in Fig. 4(a); here, the light sheet, which was perpendicular to the surface, was aligned in crossflow plane. The measurements in the longitudinal plane were carried out along the trajectory of vortex core around the before and after vortex breakdown region and perpendicular to the surface of the flying wing model, as shown in Fig. 4(b); here, the trajectory of vortex core was identified using surface oil flow visualisation. In this case, only one CCD camera was used, as shown in Fig. 4(b). Illumination of the measurement plane was achieved using a dual-head Nd-YAG laser (Quantel Evergreen, 200 mJ/pulse, 15 Hz) with an acquisition rate of 10 Hz. The laser pulses were controlled by a synchroniser (IDTvision) with a suitable time delay. A commercial fog generator (Antari Z1500II-R) was used for seeding particles in the flow. It was placed near the diffuser section of the closed-circuit wind tunnel to allow better mixing of the seeding particles (dia.
![]() $\sim $
1–2
$\sim $
1–2
![]() $\mu $
m) before entering the test section.
$\mu $
m) before entering the test section.

Figure 4. Schematic diagram of the experimental setups for particle image velocimetry (PIV) measurements in (a) the crossflow plane, and (b) the longitudinal plane passing through the trajectory of vortex core.
Images of the seeding particles were acquired using the MicroVec software (Vision Asia, Singapore) with a CCD camera (8 MP resolution, pixel array 3,312
![]() $ \times $
2,488, 8 bit, Imprex), which was equipped with a suitable lens (50 mm/85 mm focal length). At each measurement location, 1,000 pairs of images were acquired for data analysis. Using the Provision XS package (IDTvision, USA), these images were then processed with a correlation window size of 32
$ \times $
2,488, 8 bit, Imprex), which was equipped with a suitable lens (50 mm/85 mm focal length). At each measurement location, 1,000 pairs of images were acquired for data analysis. Using the Provision XS package (IDTvision, USA), these images were then processed with a correlation window size of 32
![]() $ \times $
32 pixels. It should be noted that this PIV processing package includes a mesh-free second-order algorithm and a high spatial resolution feature (Lourenco and Krothapalli [Reference Lourenco and Krothapalli45]). This package was also used in previous works (Kumar et al. [Reference Kumar, Mandal and Poddar15]).
$ \times $
32 pixels. It should be noted that this PIV processing package includes a mesh-free second-order algorithm and a high spatial resolution feature (Lourenco and Krothapalli [Reference Lourenco and Krothapalli45]). This package was also used in previous works (Kumar et al. [Reference Kumar, Mandal and Poddar15]).
In addition, the time-resolved PIV (TR-PIV) technique was also used in the longitudinal plane to measure the time sequence of the flow field along the trajectory of vortex core. Raw images were acquired using a CMOS camera (PCO Dimax HS4 camera, 4 MP resolution, pixel array 2,000
![]() $ \times $
2,000) equipped with 85 mm lens. The flow field was illuminated using a Nd-YLF dual-head laser (Photonic Industries, USA), which can provide 40 mJ/pulse at 1 kHz. Motion-Pro timing hub (IDTvision, USA) was used to synchronise both the laser and the camera. In the case of TR-PIV measurements, Safex fog generator (procured through Dantec Dynamics) was used to seed the flow. PIV images were acquired at 1 kHz (i.e. 1,000 image pairs per second) on the starboard side of the flying wing, as shown in Fig. 4(b). In one experimental run, 6,000 image pairs were acquired. These images were then processed using the PIVlab software with a correlation window of 32
$ \times $
2,000) equipped with 85 mm lens. The flow field was illuminated using a Nd-YLF dual-head laser (Photonic Industries, USA), which can provide 40 mJ/pulse at 1 kHz. Motion-Pro timing hub (IDTvision, USA) was used to synchronise both the laser and the camera. In the case of TR-PIV measurements, Safex fog generator (procured through Dantec Dynamics) was used to seed the flow. PIV images were acquired at 1 kHz (i.e. 1,000 image pairs per second) on the starboard side of the flying wing, as shown in Fig. 4(b). In one experimental run, 6,000 image pairs were acquired. These images were then processed using the PIVlab software with a correlation window of 32
![]() $\; \times {\rm{\;}}$
32 pixels and an overlap of 50% (Thielicke [Reference Thielicke46]; Thielicke and Sonntag [Reference Thielicke and Sonntag76]).
$\; \times {\rm{\;}}$
32 pixels and an overlap of 50% (Thielicke [Reference Thielicke46]; Thielicke and Sonntag [Reference Thielicke and Sonntag76]).
Based on the above PIV processing parameters, the effective region of interest, number of vectors, vector spacing, etc., are given in Table 1. In the crossflow plane, these quantities are given for the maximum and minimum regions of interest. It should be noted here that the effective region of interest means the area of the acquired image that was processed for velocity fields.
Table 1. PIV processing parameters for various cases

2.5 Uncertainty analysis
Uncertainty analyses were carried out to estimate the uncertainties of various measured quantities reported here. The maximum uncertainty values for the lift coefficient (
![]() ${C_L}$
), drag coefficient (
${C_L}$
), drag coefficient (
![]() ${C_D}$
) and the pitching moment coefficient (
${C_D}$
) and the pitching moment coefficient (
![]() ${C_{PM}}$
) are found to be
${C_{PM}}$
) are found to be
![]() $ \approx $
1
$ \approx $
1
![]() ${\rm{\% }}$
,
${\rm{\% }}$
,
![]() $ \approx $
2
$ \approx $
2
![]() ${\rm{\% }}$
, and
${\rm{\% }}$
, and
![]() $ \approx $
1.5
$ \approx $
1.5
![]() ${\rm{\% }}$
, respectively. The uncertainty of the pressure measurements mainly depends on the maximum errors of the ESP scanner and the manometer. The maximum uncertainties of both the ESP scanners and the manometer used in this experimental work are 0.05% of the full-scale pressure range. Based on these factors, uncertainty in the pressure coefficient is found to be 0.07%. Uncertainty in the PIV measurements mainly depends on the seeding particles, optical setup, calibration, image acquisition, image processing software and timing error (Gui and Wereley [Reference Gui and Wereley47]; Raffel et al. [Reference Raffel, Willert, Scarano and Kähler48]; Sciacchitano [Reference Sciacchitano49]; Balamurugan and Mandal [Reference Balamurugan and Mandal50]). The maximum uncertainty in the velocity measurements reported here is found to be
${\rm{\% }}$
, respectively. The uncertainty of the pressure measurements mainly depends on the maximum errors of the ESP scanner and the manometer. The maximum uncertainties of both the ESP scanners and the manometer used in this experimental work are 0.05% of the full-scale pressure range. Based on these factors, uncertainty in the pressure coefficient is found to be 0.07%. Uncertainty in the PIV measurements mainly depends on the seeding particles, optical setup, calibration, image acquisition, image processing software and timing error (Gui and Wereley [Reference Gui and Wereley47]; Raffel et al. [Reference Raffel, Willert, Scarano and Kähler48]; Sciacchitano [Reference Sciacchitano49]; Balamurugan and Mandal [Reference Balamurugan and Mandal50]). The maximum uncertainty in the velocity measurements reported here is found to be
![]() $ \approx $
2.5% of the freestream velocity.
$ \approx $
2.5% of the freestream velocity.
3.0 Results and discussion
Here, we present the results based on our force measurements, surface flow visualisations, surface pressure measurements and PIV measurements at different angles of attack. Measurements were carried out at different Reynolds numbers based on the root chord of the flying wing.
3.1 Aerodynamic characteristics and surface flow features
Characteristics of the pitching moment coefficient (
![]() ${C_{PM}}$
) along with the lift (
${C_{PM}}$
) along with the lift (
![]() ${C_L}$
) and drag (
${C_L}$
) and drag (
![]() ${C_D}$
) coefficients are shown in Fig. 5, for different Reynolds numbers. Peaks and valleys in the pitching moment curve clearly appear to be associated with the change of slope of the lift curve; we may note that
${C_D}$
) coefficients are shown in Fig. 5, for different Reynolds numbers. Peaks and valleys in the pitching moment curve clearly appear to be associated with the change of slope of the lift curve; we may note that
![]() ${C_L}$
and
${C_L}$
and
![]() ${C_D}$
data for Re = 7.5
${C_D}$
data for Re = 7.5
![]() $\; \times \;$
10
$\; \times \;$
10
![]() $^5$
are reproduced from Kumar et al. [Reference Kumar, Mandal and Poddar15], for comparison purpose. However, using the surface flow visualisation and the lift curve, we make an effort to explain the variation of the pitching moment coefficient. While doing so, we utilise the leading-edge suction analogy (Polhamus [Reference Polhamus51, Reference Polhamus52]; Traub [Reference Traub53]). The total lift of the flying wing can be considered as a summation of the potential lift that is generated due to the pressure distribution over the surface of the wing in the absence of the leading-edge vortex and the vortex-assisted lift, which is generated due to the leading-edge vortex assisted pressure distribution. However, considering the normal force (
$^5$
are reproduced from Kumar et al. [Reference Kumar, Mandal and Poddar15], for comparison purpose. However, using the surface flow visualisation and the lift curve, we make an effort to explain the variation of the pitching moment coefficient. While doing so, we utilise the leading-edge suction analogy (Polhamus [Reference Polhamus51, Reference Polhamus52]; Traub [Reference Traub53]). The total lift of the flying wing can be considered as a summation of the potential lift that is generated due to the pressure distribution over the surface of the wing in the absence of the leading-edge vortex and the vortex-assisted lift, which is generated due to the leading-edge vortex assisted pressure distribution. However, considering the normal force (
![]() $N$
) is approximately equal to the lift force (
$N$
) is approximately equal to the lift force (
![]() $L$
), the pitching moment about the centre of gravity or equivalently the pitching moment coefficient (
$L$
), the pitching moment about the centre of gravity or equivalently the pitching moment coefficient (
![]() ${C_{PM}}$
) about the centre of gravity can approximately be written as
${C_{PM}}$
) about the centre of gravity can approximately be written as
![]() ${C_{PM}} \approx A{C_L}\!\left( {{X_{cg}} - {X_{cp}}} \right)$
; here,
${C_{PM}} \approx A{C_L}\!\left( {{X_{cg}} - {X_{cp}}} \right)$
; here,
![]() $A$
is a constant,
$A$
is a constant,
![]() ${X_{cg}}$
and
${X_{cg}}$
and
![]() ${X_{cp}}$
denote the distances of the centre of gravity and the centre of pressure from the nose of the model, respectively. Negative values of
${X_{cp}}$
denote the distances of the centre of gravity and the centre of pressure from the nose of the model, respectively. Negative values of
![]() ${C_{PM}}$
about
${C_{PM}}$
about
![]() ${X_{cg}}$
(i.e. nose down moment) for
${X_{cg}}$
(i.e. nose down moment) for
![]() $\alpha \gt $
0°, as seen in Fig. 5, indicates that
$\alpha \gt $
0°, as seen in Fig. 5, indicates that
![]() ${X_{cp}}$
is always behind
${X_{cp}}$
is always behind
![]() ${X_{cg}}$
.
${X_{cg}}$
.

Figure 5. Aerodynamic coefficients of the flying wing for Re = 3.5
![]() $ \times {\rm{\;}}$
10
$ \times {\rm{\;}}$
10
![]() $^5$
, 4.3
$^5$
, 4.3
![]() $\; \times {\rm{\;}}$
10
$\; \times {\rm{\;}}$
10
![]() $^5$
and 7.5
$^5$
and 7.5
![]() $\; \times {\rm{\;}}$
10
$\; \times {\rm{\;}}$
10
![]() $^5$
; lift,
$^5$
; lift,
![]() ${C_L}$
, and drag,
${C_L}$
, and drag,
![]() ${C_D}$
, coefficients at Re = 7.5
${C_D}$
, coefficients at Re = 7.5
![]() $ \times {\rm{\;}}$
10
$ \times {\rm{\;}}$
10
![]() $^5$
are reproduced from Kumar et al. [Reference Kumar, Mandal and Poddar15].
$^5$
are reproduced from Kumar et al. [Reference Kumar, Mandal and Poddar15].

Figure 6. Surface oil flow visualisation on the upper surface of the flying wing at (a)
![]() $\alpha $
= 6°, (b)
$\alpha $
= 6°, (b)
![]() $\alpha $
= 8°, (c)
$\alpha $
= 8°, (c)
![]() $\alpha $
= 12°, and (d)
$\alpha $
= 12°, and (d)
![]() $\alpha $
= 17° for Re = 7.5
$\alpha $
= 17° for Re = 7.5
![]() $ \times $
10
$ \times $
10
![]() $^5$
.
$^5$
.
Figure 5 shows that the pitching moment coefficient decreases almost linearly for 0°
![]() $ \le \alpha \le $
6°, while the lift and the lift curve slope increase. Enhancement of lift is certainly due to the enhanced pressure difference between the upper and the lower surface. The lift in this range of
$ \le \alpha \le $
6°, while the lift and the lift curve slope increase. Enhancement of lift is certainly due to the enhanced pressure difference between the upper and the lower surface. The lift in this range of
![]() $\alpha $
consists of both potential lift, as indicated by surface flow visualisation showing mostly attached flow over the surface of the flying wing, and lift (loss) resulting from flow separation at the rear portion of the flying wing, as observed at rear portion in Fig. 6(a). The small change in the lift coefficient within the range of 0°
$\alpha $
consists of both potential lift, as indicated by surface flow visualisation showing mostly attached flow over the surface of the flying wing, and lift (loss) resulting from flow separation at the rear portion of the flying wing, as observed at rear portion in Fig. 6(a). The small change in the lift coefficient within the range of 0°
![]() $ \le \alpha \le $
6° is attributed to these small separated regions, which, as expected, are found to reduce with increasing Reynolds numbers. Therefore, the rapid decrease of the moment coefficient,
$ \le \alpha \le $
6° is attributed to these small separated regions, which, as expected, are found to reduce with increasing Reynolds numbers. Therefore, the rapid decrease of the moment coefficient,
![]() ${C_{PM}}$
, about the centre of gravity can mainly be attributed to a rapid increase of
${C_{PM}}$
, about the centre of gravity can mainly be attributed to a rapid increase of
![]() ${C_L}$
, as compared to the expected decrease of the moment arm
${C_L}$
, as compared to the expected decrease of the moment arm
![]() $\left( {\left| {{X_{cg}} - {X_{cp}}} \right|} \right)$
. Though the lift coefficient continues to increase, the lift curve slope starts to reduce at
$\left( {\left| {{X_{cg}} - {X_{cp}}} \right|} \right)$
. Though the lift coefficient continues to increase, the lift curve slope starts to reduce at
![]() $\alpha \approx $
6° and continues to do so until
$\alpha \approx $
6° and continues to do so until
![]() $\alpha \approx $
10°. Interestingly, the pitching moment coefficient starts to increase within 6°
$\alpha \approx $
10°. Interestingly, the pitching moment coefficient starts to increase within 6°
![]() $ \le \alpha \le $
10°, before it starts to reduce at about
$ \le \alpha \le $
10°, before it starts to reduce at about
![]() $\alpha \approx $
10°. This may be associated with a possible rapid decrease of the moment arm, as compared to the slower increase of
$\alpha \approx $
10°. This may be associated with a possible rapid decrease of the moment arm, as compared to the slower increase of
![]() ${C_L}$
. The flow visualisation indicates that the decrease of lift curve slop (for 6°
${C_L}$
. The flow visualisation indicates that the decrease of lift curve slop (for 6°
![]() $ \le \alpha \le $
10°) is due to the presence of a small separated flow region along the leading edge before a fully developed leading-edge vortex (primary vortex) originates along the leading edge (see Fig. 6(b)). Further, an increase of the lift curve slope can clearly be noticed for 10°
$ \le \alpha \le $
10°) is due to the presence of a small separated flow region along the leading edge before a fully developed leading-edge vortex (primary vortex) originates along the leading edge (see Fig. 6(b)). Further, an increase of the lift curve slope can clearly be noticed for 10°
![]() $ \le \alpha \le $
14° in Fig. 5. This increase can be attributed to the generation of the fully developed leading-edge vortex (primary vortex) that produces the vortex-generated lift. The flow visualisation in Fig. 6(c) shows the presence of a leading-edge vortex. The reduction in the pitching moment coefficient within this
$ \le \alpha \le $
14° in Fig. 5. This increase can be attributed to the generation of the fully developed leading-edge vortex (primary vortex) that produces the vortex-generated lift. The flow visualisation in Fig. 6(c) shows the presence of a leading-edge vortex. The reduction in the pitching moment coefficient within this
![]() $\alpha $
range may again be attributed to the rapid increase of
$\alpha $
range may again be attributed to the rapid increase of
![]() ${C_L}$
. Further reduction of the lift curve slope and an increase of the pitching moment coefficient for 14°
${C_L}$
. Further reduction of the lift curve slope and an increase of the pitching moment coefficient for 14°
![]() $ \le \alpha \le $
24° may again be attributed to the reduction of lift curve slope, mainly due to the flow separation and the vortex breakdown over the wing (Figs. 6(d) and 7), and the expected decrease of the moment arm, respectively. A similar drop in the pitching moment curve was also reported for the SACCON geometry for Re = 1.6
$ \le \alpha \le $
24° may again be attributed to the reduction of lift curve slope, mainly due to the flow separation and the vortex breakdown over the wing (Figs. 6(d) and 7), and the expected decrease of the moment arm, respectively. A similar drop in the pitching moment curve was also reported for the SACCON geometry for Re = 1.6
![]() $\; \times {\rm{\;}}$
10
$\; \times {\rm{\;}}$
10
![]() $^6$
[Reference Zimper and Hummel39, Reference Schütte, Hummel and Hitzel54].
$^6$
[Reference Zimper and Hummel39, Reference Schütte, Hummel and Hitzel54].

Figure 7. Surface oil flow visualisation on the upper surface of the flying wing at pre-stall angle,
![]() $\alpha $
= 20° for (a) Re = 2.5
$\alpha $
= 20° for (a) Re = 2.5
![]() $ \times $
10
$ \times $
10
![]() $^5$
, and (b) for Re = 7.5
$^5$
, and (b) for Re = 7.5
![]() $ \times $
10
$ \times $
10
![]() $^5$
.
$^5$
.

Figure 8. Mean velocity vectors over the contours of the normalised ensemble averaged axial vorticity,
![]() ${\omega _X}C/{U_\infty }$
at
${\omega _X}C/{U_\infty }$
at
![]() $X/C$
= 0.45, 0.5, 0.6, 0.8 and 1.0 at
$X/C$
= 0.45, 0.5, 0.6, 0.8 and 1.0 at
![]() $\alpha $
= 20° (pre-stall flow field) for both the (a) starboard, (b) port sides of the flying wing, respectively. Additionally, (c) shows the perspective view at
$\alpha $
= 20° (pre-stall flow field) for both the (a) starboard, (b) port sides of the flying wing, respectively. Additionally, (c) shows the perspective view at
![]() $X/C$
= 1 for the starboard side of the flying wing.
$X/C$
= 1 for the starboard side of the flying wing.
For a better understanding of the leading-edge vortex and its eventual breakdown at different Reynolds numbers, the surface flow visualisations at
![]() $\alpha $
= 20°, for Re = 2.5
$\alpha $
= 20°, for Re = 2.5
![]() $ \times {\rm{\;}}$
10
$ \times {\rm{\;}}$
10
![]() $^5$
and 7.5
$^5$
and 7.5
![]() $\; \times {\rm{\;}}$
10
$\; \times {\rm{\;}}$
10
![]() $^5$
, are shown in Fig. 7(a) and (b), respectively. The signature of the leading-edge vortex, which is often mentioned as the leading-edge primary vortex in the literature, can clearly be identified from these surface flow visualisations. This leading-edge vortex is the result of the primary separation of the shear layer emanating from the leading edge and its roll-up. The separated shear layer finally reattaches with the upper surface of the flying wing. However, Fig. 7(a) also shows two wave-like surface patterns near the leading edge followed by a kink within the chordwise distance, 0.3
$^5$
, are shown in Fig. 7(a) and (b), respectively. The signature of the leading-edge vortex, which is often mentioned as the leading-edge primary vortex in the literature, can clearly be identified from these surface flow visualisations. This leading-edge vortex is the result of the primary separation of the shear layer emanating from the leading edge and its roll-up. The separated shear layer finally reattaches with the upper surface of the flying wing. However, Fig. 7(a) also shows two wave-like surface patterns near the leading edge followed by a kink within the chordwise distance, 0.3
![]() $ \le X/C \le $
0.6 on the starboard and port sides of the flying wing, respectively. In the range of chordwise distance, 0.4
$ \le X/C \le $
0.6 on the starboard and port sides of the flying wing, respectively. In the range of chordwise distance, 0.4
![]() $ \le X/C \le $
0.5, a sudden expansion of the skin friction lines on the flying wing appears to indicate the onset of the vortex breakdown, which is adjacent to the wave-like surface pattern over the upper surface of the flying wing configuration, as shown in Fig. 7(a). The white lines over the starboard side of the flying wing in Fig. 7(a) indicate the centreline or trajectory of the primary vortex. Along the vortex centreline,
$ \le X/C \le $
0.5, a sudden expansion of the skin friction lines on the flying wing appears to indicate the onset of the vortex breakdown, which is adjacent to the wave-like surface pattern over the upper surface of the flying wing configuration, as shown in Fig. 7(a). The white lines over the starboard side of the flying wing in Fig. 7(a) indicate the centreline or trajectory of the primary vortex. Along the vortex centreline,
![]() $X1$
,
$X1$
,
![]() ${X_{vb}}$
, and
${X_{vb}}$
, and
![]() $X3$
in the enlarged view in Fig. 7(a), denotes the starting of the wave-like surface pattern and the onset of vortex breakdown location and the ending of the wave-like surface pattern, respectively. These wave-like patterns move upstream with increasing angle-of-attack, as shown in Figs. 6(d) and 7(b) for
$X3$
in the enlarged view in Fig. 7(a), denotes the starting of the wave-like surface pattern and the onset of vortex breakdown location and the ending of the wave-like surface pattern, respectively. These wave-like patterns move upstream with increasing angle-of-attack, as shown in Figs. 6(d) and 7(b) for
![]() $\alpha $
= 17° and 20°, respectively, at Re = 7.5
$\alpha $
= 17° and 20°, respectively, at Re = 7.5
![]() $\; \times $
10
$\; \times $
10
![]() $^5$
. The size of the wave-like surface flow pattern reduces as the Reynolds number increases (from Re = 2.5
$^5$
. The size of the wave-like surface flow pattern reduces as the Reynolds number increases (from Re = 2.5
![]() $ \times $
10
$ \times $
10
![]() $^5$
to 7.5
$^5$
to 7.5
![]() $ \times $
10
$ \times $
10
![]() $^5$
) at pre-stall flow region (
$^5$
) at pre-stall flow region (
![]() $\alpha $
= 20°), as seen in Fig. 7. Further quantitative assessments of these flow features are discussed in the following.
$\alpha $
= 20°), as seen in Fig. 7. Further quantitative assessments of these flow features are discussed in the following.
3.2 Mean vortical flow field in the crossflow plane
For further investigation, the two-dimensional (2D) PIV measurements were carried out at different crossflow planes, which are perpendicular to the vortex axis. The measurements were carried out at five different chordwise locations (
![]() $X/C$
) for both the starboard and the port sides of the flying wing model for Re = 2.5
$X/C$
) for both the starboard and the port sides of the flying wing model for Re = 2.5
![]() $ \times {\rm{\;}}$
10
$ \times {\rm{\;}}$
10
![]() $^5$
at angles of attack,
$^5$
at angles of attack,
![]() $\alpha $
= 20°, 25° and 30°, as shown in Figs. 8, 9 and 10, respectively.
$\alpha $
= 20°, 25° and 30°, as shown in Figs. 8, 9 and 10, respectively.

Figure 9. Mean velocity vectors over the contours of the normalised ensemble averaged axial vorticity,
![]() ${\omega _X}C/{U_\infty }$
at
${\omega _X}C/{U_\infty }$
at
![]() $X/C$
= 0.2, 0.3, 0.4, 0.8 and 1.0 at
$X/C$
= 0.2, 0.3, 0.4, 0.8 and 1.0 at
![]() $\alpha $
= 25° (near-stall flow field) for both the (a) starboard and (b) port sides of the flying wing, respectively.
$\alpha $
= 25° (near-stall flow field) for both the (a) starboard and (b) port sides of the flying wing, respectively.

Figure 10. Mean velocity vectors over the contours of the normalised ensemble averaged axial vorticity,
![]() ${\omega _X}C/{U_\infty }$
at
${\omega _X}C/{U_\infty }$
at
![]() $X/C$
= 0.1, 0.2, 0.3, 0.8 and 1.0 at
$X/C$
= 0.1, 0.2, 0.3, 0.8 and 1.0 at
![]() $\alpha $
= 30° (post-stall flow field) for both the (a) starboard and (b) port sides of the flying wing, respectively.
$\alpha $
= 30° (post-stall flow field) for both the (a) starboard and (b) port sides of the flying wing, respectively.
For the pre-stall flow regime at
![]() $\alpha $
= 20°, Fig. 8 shows the mean velocity vectors over the normalised contours of the mean axial vorticity,
$\alpha $
= 20°, Fig. 8 shows the mean velocity vectors over the normalised contours of the mean axial vorticity,
![]() ${\omega _X}C/{U_\infty }$
at chordwise locations,
${\omega _X}C/{U_\infty }$
at chordwise locations,
![]() $X/C$
= 0.45, 0.5, 0.6, 0.8 and 1.0 for starboard and port sides of the flying model; here
$X/C$
= 0.45, 0.5, 0.6, 0.8 and 1.0 for starboard and port sides of the flying model; here
![]() ${\omega _X}$
is the ensemble-averaged axial vorticity and
${\omega _X}$
is the ensemble-averaged axial vorticity and
![]() ${U_\infty }$
is freestream velocity. Figure 8 shows that the averaged vorticity values are concentrated in a smaller area and higher at
${U_\infty }$
is freestream velocity. Figure 8 shows that the averaged vorticity values are concentrated in a smaller area and higher at
![]() $X/C$
= 0.45, as compared to the locations,
$X/C$
= 0.45, as compared to the locations,
![]() $X/C \geq $
0.45. The velocity vectors, normalised with their respective magnitude for clarity and overlaid with the vorticity contours, reveal the vortical structure over the flying wing. A symmetric nature of the leading-edge vortices can clearly be noticed in this figure. The leading-edge vortices are found to be oval shaped over the flying wing. Moreover, the vortical structure is found to be associated with diffused vorticity in the vortex core, and its size appears to increase rather gradually in the chordwise distance, 0.45
$X/C \geq $
0.45. The velocity vectors, normalised with their respective magnitude for clarity and overlaid with the vorticity contours, reveal the vortical structure over the flying wing. A symmetric nature of the leading-edge vortices can clearly be noticed in this figure. The leading-edge vortices are found to be oval shaped over the flying wing. Moreover, the vortical structure is found to be associated with diffused vorticity in the vortex core, and its size appears to increase rather gradually in the chordwise distance, 0.45
![]() $ \le X/C \le $
0.5, as compared to the sudden increase in vortex size for the case of a slender delta wing [Reference Gursul, Gordnier and Visbal5, Reference Payne, Ng, Nelson and Schiff11, Reference Breitsamter55–Reference Chen, Wang, Zuo and Feng57]. At downstream locations, i.e. at
$ \le X/C \le $
0.5, as compared to the sudden increase in vortex size for the case of a slender delta wing [Reference Gursul, Gordnier and Visbal5, Reference Payne, Ng, Nelson and Schiff11, Reference Breitsamter55–Reference Chen, Wang, Zuo and Feng57]. At downstream locations, i.e. at
![]() $X/C$
= 0.8 and 1.0, the vorticity is found to be diffused within the vortex core in both sides of the flying wing. Interestingly, two counter-rotating vortices are observed at
$X/C$
= 0.8 and 1.0, the vorticity is found to be diffused within the vortex core in both sides of the flying wing. Interestingly, two counter-rotating vortices are observed at
![]() $X/C$
= 1.0, an elongated one in size as the leading-edge vortex and another one small in size as the trailing-edge vortex on either side of the flying wing. Various authors reported presence of multiple vortices on the surface of a delta/double delta wing [Reference Konrath, Klein and Schröder58–Reference Karasu and Durhasan61]. However, these works on a delta/double delta wing indicate that the trailing edge does not play any role in the generation of these multiple vortices. But the present flying wing configuration has two swept wing-like portions near
$X/C$
= 1.0, an elongated one in size as the leading-edge vortex and another one small in size as the trailing-edge vortex on either side of the flying wing. Various authors reported presence of multiple vortices on the surface of a delta/double delta wing [Reference Konrath, Klein and Schröder58–Reference Karasu and Durhasan61]. However, these works on a delta/double delta wing indicate that the trailing edge does not play any role in the generation of these multiple vortices. But the present flying wing configuration has two swept wing-like portions near
![]() $X/C$
= 1 (see Fig. 1). Due to the pressure difference between the upper and lower surfaces, the shear layers from both the surfaces of the wing roll up to generate two counter-rotating vortices, as clearly seen in the perspective view in Fig. 8(c). Therefore, the present counter rotating vortices at
$X/C$
= 1 (see Fig. 1). Due to the pressure difference between the upper and lower surfaces, the shear layers from both the surfaces of the wing roll up to generate two counter-rotating vortices, as clearly seen in the perspective view in Fig. 8(c). Therefore, the present counter rotating vortices at
![]() $X/C$
= 1 are actually generated due to the leading and trailing edges of the flying wing (see Fig. 8(c)).
$X/C$
= 1 are actually generated due to the leading and trailing edges of the flying wing (see Fig. 8(c)).
For the near-stall flow regime at
![]() $\alpha $
= 25°, Fig. 9 shows the mean velocity vectors over the normalised contours of the mean axial vorticity,
$\alpha $
= 25°, Fig. 9 shows the mean velocity vectors over the normalised contours of the mean axial vorticity,
![]() ${\omega _X}C/{U_\infty }$
, at chordwise locations
${\omega _X}C/{U_\infty }$
, at chordwise locations
![]() $X/C$
= 0.2, 0.3, 0.4, 0.8 and 1.0, for the starboard and the port sides of the flying wing. At this higher angle-of-attack,
$X/C$
= 0.2, 0.3, 0.4, 0.8 and 1.0, for the starboard and the port sides of the flying wing. At this higher angle-of-attack,
![]() $\alpha $
= 25°, the normalised vorticity values are seen to be higher up to the chordwise location,
$\alpha $
= 25°, the normalised vorticity values are seen to be higher up to the chordwise location,
![]() $X/C$
= 0.3, for both sides of the flying wing. Similar to the pre-stall flow regime, the symmetric nature of the oval-shaped leading-edge vortices can be seen even at a near-stall angle-of-attack over the flying wing. However, the vortices are found to be comparatively larger in size at the corresponding
$X/C$
= 0.3, for both sides of the flying wing. Similar to the pre-stall flow regime, the symmetric nature of the oval-shaped leading-edge vortices can be seen even at a near-stall angle-of-attack over the flying wing. However, the vortices are found to be comparatively larger in size at the corresponding
![]() $X/C$
locations. Similar to the pre-stall case, two counter-rotating vorticities are observed on either side of the flying wing at the chordwise location at
$X/C$
locations. Similar to the pre-stall case, two counter-rotating vorticities are observed on either side of the flying wing at the chordwise location at
![]() $X/C$
= 1.0, and the trailing-edge vortices also increase in size.
$X/C$
= 1.0, and the trailing-edge vortices also increase in size.
Furthermore, for the post-stall flow regime at
![]() $\alpha $
= 30°, Fig. 10 shows that the mean velocity vectors and axial vorticity patterns still exist at chordwise locations,
$\alpha $
= 30°, Fig. 10 shows that the mean velocity vectors and axial vorticity patterns still exist at chordwise locations,
![]() $X/C$
= 0.1, 0.2, 0.3, 0.8 and 1.0 for both sides of the flying wing. The normalised vorticity values are seen to be higher till the chordwise location,
$X/C$
= 0.1, 0.2, 0.3, 0.8 and 1.0 for both sides of the flying wing. The normalised vorticity values are seen to be higher till the chordwise location,
![]() $X/C$
= 0.2, beyond which the vorticity values are found to be highly diffused within the increasing sizes of the vortices.
$X/C$
= 0.2, beyond which the vorticity values are found to be highly diffused within the increasing sizes of the vortices.
Sudden changes from the concentrated vorticity values to the diffused vorticity along the vortex core, as seen in the above PIV measurements (Figs. 8, 9 and 10), indicate the presence of the vortex breakdown phenomena in the range of the chordwise distance, 0.45
![]() $ \le X/C \le $
0.5, 0.3
$ \le X/C \le $
0.5, 0.3
![]() $ \le X/C \le $
0.4 and 0.2
$ \le X/C \le $
0.4 and 0.2
![]() $ \le X/C \le $
0.3 over the flying wing, for
$ \le X/C \le $
0.3 over the flying wing, for
![]() $\alpha $
= 20°, 25° and 30°, respectively. The concentrated vorticity in the primary vortex core, which diffuses while moving downstream, is found to be similar to the observation of Ol and Gharib [Reference Ol and Gharib3] on a non-slender delta wing. However, the present observation also indicates that the onset of vortex breakdown moves towards the apex with increasing angle-of-attack, and it has not reached the apex even at the post-stall angle-of-attack,
$\alpha $
= 20°, 25° and 30°, respectively. The concentrated vorticity in the primary vortex core, which diffuses while moving downstream, is found to be similar to the observation of Ol and Gharib [Reference Ol and Gharib3] on a non-slender delta wing. However, the present observation also indicates that the onset of vortex breakdown moves towards the apex with increasing angle-of-attack, and it has not reached the apex even at the post-stall angle-of-attack,
![]() $\alpha $
= 30°. Vortices are also found to be larger in size with increasing angle-of-attack.
$\alpha $
= 30°. Vortices are also found to be larger in size with increasing angle-of-attack.
3.3 Surface pressure measurements
For further analysis, the surface pressure measurements at various chordwise locations were carried out on the starboard side of the flying wing configuration at
![]() $\alpha $
= 20°, 25° and 30°, for Re = 2.5
$\alpha $
= 20°, 25° and 30°, for Re = 2.5
![]() $ \times $
10
$ \times $
10
![]() $^5$
. The coefficient of mean pressure variations along the normalised spanwise distance,
$^5$
. The coefficient of mean pressure variations along the normalised spanwise distance,
![]() $\eta $
=
$\eta $
=
![]() $Y/{Y_{max}}$
, are displayed in Fig. 11; here
$Y/{Y_{max}}$
, are displayed in Fig. 11; here
![]() $Y$
is the spanwise distance and
$Y$
is the spanwise distance and
![]() ${Y_{max}}$
is the maximum local half-span from the root chord of the flying wing, as mentioned earlier. Therefore, the locations of the root chord and the leading edge are given by
${Y_{max}}$
is the maximum local half-span from the root chord of the flying wing, as mentioned earlier. Therefore, the locations of the root chord and the leading edge are given by
![]() $\eta \left( { = Y/{Y_{max}}} \right)$
= 0 and 1, respectively.
$\eta \left( { = Y/{Y_{max}}} \right)$
= 0 and 1, respectively.

Figure 11. Surface pressure distribution (
![]() ${C_p}$
) at cross-sections,
${C_p}$
) at cross-sections,
![]() $X/C$
= 0.2, 0.3, 0.4, 0.5, 0.6, 0.7 and 0.8 on the starboard side of the flying wing along the span-wise distance at
$X/C$
= 0.2, 0.3, 0.4, 0.5, 0.6, 0.7 and 0.8 on the starboard side of the flying wing along the span-wise distance at
![]() $\alpha $
= 20°, 25° and 30°. The grey color shaded region in the first panel shows a representative front view of the starboard side of the flying wing.
$\alpha $
= 20°, 25° and 30°. The grey color shaded region in the first panel shows a representative front view of the starboard side of the flying wing.
Figure 11 shows that there exists a strong suction in the range of 0.2
![]() $ \le X/C \le $
0.4 at
$ \le X/C \le $
0.4 at
![]() $\alpha $
= 20°, that is, for the pre-stall flow regime. This, in turn, indicates that the leading-edge primary vortex is strong up to
$\alpha $
= 20°, that is, for the pre-stall flow regime. This, in turn, indicates that the leading-edge primary vortex is strong up to
![]() $X/C$
= 0.4. Beyond
$X/C$
= 0.4. Beyond
![]() $X/C$
= 0.4, a gradual decrease in suction can be noticed in Fig. 11, which clearly indicates the onset of vortex breakdown in between the chordwise locations 0.4
$X/C$
= 0.4, a gradual decrease in suction can be noticed in Fig. 11, which clearly indicates the onset of vortex breakdown in between the chordwise locations 0.4
![]() $ \le X/C \le $
0.5. The suction peak in between 0.2
$ \le X/C \le $
0.5. The suction peak in between 0.2
![]() $ \le X/C \le $
0.5 is seen to move toward the root chord of the flying wing. However, at
$ \le X/C \le $
0.5 is seen to move toward the root chord of the flying wing. However, at
![]() $\alpha $
= 25°, that is, in the near-stall regime, the suction is seen to be strong within 0.2
$\alpha $
= 25°, that is, in the near-stall regime, the suction is seen to be strong within 0.2
![]() $ \le X/C \le $
0.3, and beyond
$ \le X/C \le $
0.3, and beyond
![]() $X/C$
= 0.3, a gradual decrease in suction can be noticed indicating the onset of vortex breakdown, which has moved upstream (0.3
$X/C$
= 0.3, a gradual decrease in suction can be noticed indicating the onset of vortex breakdown, which has moved upstream (0.3
![]() $ \le X/C \le $
0.4), as compared to the one at
$ \le X/C \le $
0.4), as compared to the one at
![]() $\alpha $
= 20°. It can be noticed that the vortex breakdown is yet to reach the apex of the flying wing, even at this near-stall flow regime. This observation is consistent with the PIV data shown in Fig. 9. At
$\alpha $
= 20°. It can be noticed that the vortex breakdown is yet to reach the apex of the flying wing, even at this near-stall flow regime. This observation is consistent with the PIV data shown in Fig. 9. At
![]() $\alpha $
= 30°, that is, at the post-stall flow regime, the pressure distribution indicates that the primary vortex is strong till
$\alpha $
= 30°, that is, at the post-stall flow regime, the pressure distribution indicates that the primary vortex is strong till
![]() $X/C$
= 0.2. After this, a gradual decrease in suction is observed within the chordwise location, 0.2
$X/C$
= 0.2. After this, a gradual decrease in suction is observed within the chordwise location, 0.2
![]() $ \le X/C \le $
0.3. This, in turn, indicates that the onset of vortex breakdown is further shifted upstream, as compared to the previous two cases. It is also interesting to note that the leading-edge primary vortex still exists even after the stall has occurred on the flying wing. This is also consistent with the cross-plane PIV measurements for this case, as shown in Fig. 10.
$ \le X/C \le $
0.3. This, in turn, indicates that the onset of vortex breakdown is further shifted upstream, as compared to the previous two cases. It is also interesting to note that the leading-edge primary vortex still exists even after the stall has occurred on the flying wing. This is also consistent with the cross-plane PIV measurements for this case, as shown in Fig. 10.
Figure 12 shows the coefficient of root-mean-squared (RMS) values of pressure fluctuation,
![]() ${C_{p,{\rm{\;\;}}RMS}}$
, along the spanwise direction,
${C_{p,{\rm{\;\;}}RMS}}$
, along the spanwise direction,
![]() $\eta $
, at angles of attack,
$\eta $
, at angles of attack,
![]() $\alpha $
= 20°, 25° and 30°, for the various chordwise locations. The peak in
$\alpha $
= 20°, 25° and 30°, for the various chordwise locations. The peak in
![]() ${C_{p,{\rm{\;\;}}RMS}}$
starts to appear nearly at the onset of the wave-like pattern, as shown in Fig. 7(a), and then it continues to be present in all the downstream locations presented here. Further, it is observed that the peak in
${C_{p,{\rm{\;\;}}RMS}}$
starts to appear nearly at the onset of the wave-like pattern, as shown in Fig. 7(a), and then it continues to be present in all the downstream locations presented here. Further, it is observed that the peak in
![]() ${C_{p,{\rm{\;\;}}RMS}}$
moves towards the root chord while moving downstream. After carefully checking the crossflow PIV data, we found that the vortex core region over the surface of the flying wing is associated with the maximum RMS pressure peaks for all
${C_{p,{\rm{\;\;}}RMS}}$
moves towards the root chord while moving downstream. After carefully checking the crossflow PIV data, we found that the vortex core region over the surface of the flying wing is associated with the maximum RMS pressure peaks for all
![]() $\alpha $
. This aspect along with PIV and pressure data (Fig. 13) has further been elaborated in the following paragraph. Therefore, shifting of maximum
$\alpha $
. This aspect along with PIV and pressure data (Fig. 13) has further been elaborated in the following paragraph. Therefore, shifting of maximum
![]() ${C_{p,{\rm{\;\;}}RMS}}$
towards the root chord can be attributed to the shifting of the vortex core towards the root chord. Gursul et al. [Reference Gursul, Gordnier and Visbal5] reported a similar observation based on the
${C_{p,{\rm{\;\;}}RMS}}$
towards the root chord can be attributed to the shifting of the vortex core towards the root chord. Gursul et al. [Reference Gursul, Gordnier and Visbal5] reported a similar observation based on the
![]() ${u_{RMS}}$
for a delta wing. However, the pressure (fluctuation is also seen to be maximum in the range of chordwise location, 0.3
${u_{RMS}}$
for a delta wing. However, the pressure (fluctuation is also seen to be maximum in the range of chordwise location, 0.3
![]() $ \le X/C \le $
0.6, 0.3
$ \le X/C \le $
0.6, 0.3
![]() $ \le X/C \le $
0.4 and 0.2
$ \le X/C \le $
0.4 and 0.2
![]() $ \le X/C \le $
0.3, for
$ \le X/C \le $
0.3, for
![]() $\alpha $
= 20°, 25°, 30°, respectively. Interestingly, the wave-like pattern is also seen to be present in these chordwise locations for respective
$\alpha $
= 20°, 25°, 30°, respectively. Interestingly, the wave-like pattern is also seen to be present in these chordwise locations for respective
![]() $\alpha $
, as can be seen in Fig. 7(a) for
$\alpha $
, as can be seen in Fig. 7(a) for
![]() $\alpha $
= 20°. This indicates that the leading-edge vortex is highly unsteady around the wave-like pattern. Also, the maximum RMS pressure fluctuation is found at the near-stall flow regime, at
$\alpha $
= 20°. This indicates that the leading-edge vortex is highly unsteady around the wave-like pattern. Also, the maximum RMS pressure fluctuation is found at the near-stall flow regime, at
![]() $\alpha $
= 25°, as compared to the pre-stall and the post-stall flow regimes.
$\alpha $
= 25°, as compared to the pre-stall and the post-stall flow regimes.

Figure 12. Surface pressure fluctuation intensities (
![]() ${C_{p,{\rm{\;\;}}RMS}}$
) at cross-sections
${C_{p,{\rm{\;\;}}RMS}}$
) at cross-sections
![]() $X/C$
= 0.2, 0.3, 0.4, 0.5, 0.6, 0.7 and 0.8 on the starboard side of the flying wing along the spanwise distance at
$X/C$
= 0.2, 0.3, 0.4, 0.5, 0.6, 0.7 and 0.8 on the starboard side of the flying wing along the spanwise distance at
![]() $\alpha $
= 20°, 25° and 30°. The grey color shaded region in the first panel shows a representative front view of the starboard side of the flying wing.
$\alpha $
= 20°, 25° and 30°. The grey color shaded region in the first panel shows a representative front view of the starboard side of the flying wing.

Figure 13. Effect of Reynolds number on the surface mean pressure (
![]() ${C_p}$
) and RMS pressure (
${C_p}$
) and RMS pressure (
![]() ${C_{p,{\rm{\;\;}}RMS}}$
) distributions at
${C_{p,{\rm{\;\;}}RMS}}$
) distributions at
![]() $\alpha $
= 20° (Panels
$\alpha $
= 20° (Panels
![]() $a,b,c,d$
) and
$a,b,c,d$
) and
![]() $\alpha $
= 30° (Panels
$\alpha $
= 30° (Panels
![]() $b,c,d,e$
). Color contours of the averaged axial vorticity (
$b,c,d,e$
). Color contours of the averaged axial vorticity (
![]() ${\omega _X}C/{U_\infty }$
) and the velocity vectors obtained from the PIV measurements at the corresponding locations are shown for Re = 2.5
${\omega _X}C/{U_\infty }$
) and the velocity vectors obtained from the PIV measurements at the corresponding locations are shown for Re = 2.5
![]() $ \times $
10
$ \times $
10
![]() $^5$
. For
$^5$
. For
![]() $\alpha $
= 20°,
$\alpha $
= 20°,
![]() $X/C$
= 0.4 corresponds to the location before the breakdown and
$X/C$
= 0.4 corresponds to the location before the breakdown and
![]() $X/C$
= 0.5 corresponds to the location after the breakdown. Similarly, for
$X/C$
= 0.5 corresponds to the location after the breakdown. Similarly, for
![]() $\alpha $
= 20°,
$\alpha $
= 20°,
![]() $X/C$
= 0.2 corresponds to the location before the breakdown and
$X/C$
= 0.2 corresponds to the location before the breakdown and
![]() $X/C$
= 0.3 corresponds to the location after the breakdown.
$X/C$
= 0.3 corresponds to the location after the breakdown.
To find the effect of Reynolds number on the peak suction pressure and the RMS (
![]() ${C_{p,RMS}}$
) pressure, we have plotted the pressure distributions in Fig. 13 at the locations just before and after the vortex breakdown, for three different Reynolds number, named as Re = 2.5
${C_{p,RMS}}$
) pressure, we have plotted the pressure distributions in Fig. 13 at the locations just before and after the vortex breakdown, for three different Reynolds number, named as Re = 2.5
![]() $\; \times {\rm{\;}}$
10
$\; \times {\rm{\;}}$
10
![]() $^5$
, 5.0
$^5$
, 5.0
![]() $ \times {\rm{\;}}$
10
$ \times {\rm{\;}}$
10
![]() $^5$
and 6.2
$^5$
and 6.2
![]() $\; \times {\rm{\;}}$
10
$\; \times {\rm{\;}}$
10
![]() $^5$
. For better understanding, the pressure distributions have been displayed over the vorticity contours and velocity vectors at the corresponding location for Re = 2.5
$^5$
. For better understanding, the pressure distributions have been displayed over the vorticity contours and velocity vectors at the corresponding location for Re = 2.5
![]() $\; \times \;$
10
$\; \times \;$
10
![]() $^5$
. The panels in the left column in Fig. 13 refer to
$^5$
. The panels in the left column in Fig. 13 refer to
![]() $\alpha = 20$
°, and those in the right column refer to
$\alpha = 20$
°, and those in the right column refer to
![]() $\alpha = 30$
°. The first two panels (one mean pressure and one RMS pressure) in the left column correspond to the location just before the vortex breakdown, and the next two panels (one mean pressure and one RMS pressure) in the left column correspond to the location after the vortex breakdown. Similarly, the panels in the right column correspond to the locations before and after the vortex breakdown at
$\alpha = 30$
°. The first two panels (one mean pressure and one RMS pressure) in the left column correspond to the location just before the vortex breakdown, and the next two panels (one mean pressure and one RMS pressure) in the left column correspond to the location after the vortex breakdown. Similarly, the panels in the right column correspond to the locations before and after the vortex breakdown at
![]() $\alpha = $
30°. Figure 13(a, e, c, and g) shows that the minimum suction pressure, i.e. minimum mean
$\alpha = $
30°. Figure 13(a, e, c, and g) shows that the minimum suction pressure, i.e. minimum mean
![]() $ - {C_p}$
values, occurs near the reattachment location, as indicated by the velocity vectors of the flow field, similar to a swept delta wing [Reference Zharfa, Ozturk and Yavuz62], whereas the peak suction pressure (mean
$ - {C_p}$
values, occurs near the reattachment location, as indicated by the velocity vectors of the flow field, similar to a swept delta wing [Reference Zharfa, Ozturk and Yavuz62], whereas the peak suction pressure (mean
![]() $-{C_p}$
) occurs near the vortex core, albeit with slight offset towards the leading edge. On the other hand, Fig. 13(b, f, d and h) shows that the peak RMS (
$-{C_p}$
) occurs near the vortex core, albeit with slight offset towards the leading edge. On the other hand, Fig. 13(b, f, d and h) shows that the peak RMS (
![]() ${C_{p,RMS}}$
) pressure occurs in-between the vortex core and the reattachment around the vortex breakdown region for both the pre-stall and post-stall angles of attack. Further, the peak RMS pressure appears to move toward the leading edge with increasing Reynolds number.
${C_{p,RMS}}$
) pressure occurs in-between the vortex core and the reattachment around the vortex breakdown region for both the pre-stall and post-stall angles of attack. Further, the peak RMS pressure appears to move toward the leading edge with increasing Reynolds number.
3.4 Mean flow field in the longitudinal plane along the vortex core
For further investigation of the above unsteadiness, the 2D-PIV measurements were carried out in a longitudinal plane, perpendicular to the surface along the trajectory of vortex core, i.e. along the white line, as shown in Fig. 7(a); it may be noted that
![]() ${X_{vc}}$
denotes the coordinate along this plane. The PIV measurements were performed at
${X_{vc}}$
denotes the coordinate along this plane. The PIV measurements were performed at
![]() $\alpha $
= 20°, 25° and 30° for Re = 2.5
$\alpha $
= 20°, 25° and 30° for Re = 2.5
![]() $ \times {\rm{\;}}$
10
$ \times {\rm{\;}}$
10
![]() $^5$
. The mean velocity contours and the associated streamlines are shown in Fig. 14(a), (b) and (c), respectively. It should be noted that the mean quantities are obtained based on an ensemble average of 1,000 PIV realisations. The mean velocity along the vortex core is denoted by
$^5$
. The mean velocity contours and the associated streamlines are shown in Fig. 14(a), (b) and (c), respectively. It should be noted that the mean quantities are obtained based on an ensemble average of 1,000 PIV realisations. The mean velocity along the vortex core is denoted by
![]() $\overline {{u_{vc}}} $
and the corresponding fluctuating velocity is
$\overline {{u_{vc}}} $
and the corresponding fluctuating velocity is
![]() $u'_{\!\!vc}\!\left( { = {u_I} - \overline {{u_{vc}}} } \right)$
; here,
$u'_{\!\!vc}\!\left( { = {u_I} - \overline {{u_{vc}}} } \right)$
; here,
![]() ${u_I}$
is the instantaneous velocity along the vortex core.
${u_I}$
is the instantaneous velocity along the vortex core.

Figure 14. Contours of normalised ensemble averaged axial velocity,
![]() $\overline {{u_{vc}}} /{U_\infty }$
and the associated streamlines pattern with critical points; sectional streamlines are multicolored by normalised ensemble averaged axial velocity,
$\overline {{u_{vc}}} /{U_\infty }$
and the associated streamlines pattern with critical points; sectional streamlines are multicolored by normalised ensemble averaged axial velocity,
![]() $\overline {{u_{vc}}} /{U_\infty }$
at (a)
$\overline {{u_{vc}}} /{U_\infty }$
at (a)
![]() $\alpha $
= 20°, (b)
$\alpha $
= 20°, (b)
![]() $\alpha $
= 25°, (c)
$\alpha $
= 25°, (c)
![]() $\alpha $
= 30°.
$\alpha $
= 30°.
The normalised mean velocity contours,
![]() $\overline {{u_{vc}}} /{U_\infty }$
, in Fig. 14, show that the value of the mean velocity reduces gradually followed by a reverse flow regime,
$\overline {{u_{vc}}} /{U_\infty }$
, in Fig. 14, show that the value of the mean velocity reduces gradually followed by a reverse flow regime,
![]() $\overline {{u_{vc}}} /{U_\infty }$
$\overline {{u_{vc}}} /{U_\infty }$
![]() $ \le $
0. The corresponding streamline patterns, which are also shown in these figures, clearly reveal the existence of a stagnation point (
$ \le $
0. The corresponding streamline patterns, which are also shown in these figures, clearly reveal the existence of a stagnation point (
![]() $\overline {{u_{vc}}} /{U_\infty }$
= 0) along the vortex core. Since existence of a stagnation point along the vortex core indicates the onset of vortex breakdown [Reference Escudier23, Reference Wang, Gao, Wei, Li and Wang36, Reference Oberleithner, Paschereit, Seele and Wygnanski63]
$\overline {{u_{vc}}} /{U_\infty }$
= 0) along the vortex core. Since existence of a stagnation point along the vortex core indicates the onset of vortex breakdown [Reference Escudier23, Reference Wang, Gao, Wei, Li and Wang36, Reference Oberleithner, Paschereit, Seele and Wygnanski63]
![]() $\overline {{u_{vc}}} /{U_\infty }$
= 0 is considered here as the criterion for vortex breakdown. It should be noted that, similar to a non-slender delta wing [Reference Gordnier and Visbal13, Reference Taylor and Gursul64], a jet-like profile before the vortex breakdown and a wake-like profile after the breakdown are found even in the present study, but not shown for brevity.
$\overline {{u_{vc}}} /{U_\infty }$
= 0 is considered here as the criterion for vortex breakdown. It should be noted that, similar to a non-slender delta wing [Reference Gordnier and Visbal13, Reference Taylor and Gursul64], a jet-like profile before the vortex breakdown and a wake-like profile after the breakdown are found even in the present study, but not shown for brevity.
However, based on the above breakdown criterion, the onset of vortex breakdown is found to start at chordwise locations,
![]() $X/C \approx $
0.48, 0.35 and 0.23 for
$X/C \approx $
0.48, 0.35 and 0.23 for
![]() $\alpha $
= 20°, 25° and 30°, respectively. These exact values of the breakdown location corroborate well with the ranges estimated from the coefficient of pressure distribution (see Fig. 11). Interestingly, the onset of vortex breakdown is found to be associated with the wave-like structures, as seen in flow visualisations for the corresponding angle-of-attack.
$\alpha $
= 20°, 25° and 30°, respectively. These exact values of the breakdown location corroborate well with the ranges estimated from the coefficient of pressure distribution (see Fig. 11). Interestingly, the onset of vortex breakdown is found to be associated with the wave-like structures, as seen in flow visualisations for the corresponding angle-of-attack.
For a better understanding of the flow field downstream of the onset of vortex breakdown, the selected regions of the mean flow streamlines are shown in enlarged views in Fig. 14(a), (b) and (c), for
![]() $\alpha $
= 20°, 25° and 30°, respectively. Following the work of Perry and Chong [Reference Perry and Chong65], Chong et al. [Reference Chong, Perry and Cantwell66] and Rockwell [Reference Goruney and Rockwell67], we find that there exist three unstable foci (denoted by F
$\alpha $
= 20°, 25° and 30°, respectively. Following the work of Perry and Chong [Reference Perry and Chong65], Chong et al. [Reference Chong, Perry and Cantwell66] and Rockwell [Reference Goruney and Rockwell67], we find that there exist three unstable foci (denoted by F
![]() ${\rm{\;}}_1^ - $
, F
${\rm{\;}}_1^ - $
, F
![]() ${\rm{\;}}_2^ - $
and F
${\rm{\;}}_2^ - $
and F
![]() ${\rm{\;}}_3^ - $
), as the streamlines are seen to spiral out from the centre, and two saddle nodes (S
${\rm{\;}}_3^ - $
), as the streamlines are seen to spiral out from the centre, and two saddle nodes (S
![]() ${\rm{\;}}_1^ + $
and S
${\rm{\;}}_1^ + $
and S
![]() ${\rm{\;}}_2^ + $
), as there exist incoming and outgoing streamlines at those nodes, for
${\rm{\;}}_2^ + $
), as there exist incoming and outgoing streamlines at those nodes, for
![]() $\alpha $
= 20°. On the other hand, only one unstable focus is found to exist for
$\alpha $
= 20°. On the other hand, only one unstable focus is found to exist for
![]() $\alpha $
= 25° and 30°. Further, these unstable nodes and foci indicate that the nature of the vortex breakdown may be spiral-type, as the streamlines are asymmetric about the vortex core after the onset of vortex breakdown.
$\alpha $
= 25° and 30°. Further, these unstable nodes and foci indicate that the nature of the vortex breakdown may be spiral-type, as the streamlines are asymmetric about the vortex core after the onset of vortex breakdown.
Another interesting phenomenon that has been observed is the oscillation of the vortex breakdown location in the streamwise direction over the surface of the flying wing, similar to those seen on a delta wing [Reference Menke, Yang and Gursul14, Reference Gursul and Yang68]. Here, we investigate this oscillating phenomenon at different Reynolds numbers and angles of attack. Mean and root-mean-squared values of the vortex breakdown location (
![]() ${X_{VB}}$
) have been estimated from the acquired PIV realisations in the longitudinal plane. Remarkably, our findings, as shown in Fig. 15(a), reveal a compelling trend. In particular, for the pre-stall angle-of-attack (
${X_{VB}}$
) have been estimated from the acquired PIV realisations in the longitudinal plane. Remarkably, our findings, as shown in Fig. 15(a), reveal a compelling trend. In particular, for the pre-stall angle-of-attack (
![]() $\alpha $
= 20°), our quantitative measurements show a downstream shift in the mean breakdown location as the Reynolds number increases, whereas no significant changes in the breakdown location can be noticed for the near-stall (
$\alpha $
= 20°), our quantitative measurements show a downstream shift in the mean breakdown location as the Reynolds number increases, whereas no significant changes in the breakdown location can be noticed for the near-stall (
![]() $\alpha $
= 25°) and post-stall (
$\alpha $
= 25°) and post-stall (
![]() $\alpha $
= 30°) angles of attack. To find out the unsteady nature of the breakdown location, we have also estimated the RMS values of the breakdown location (
$\alpha $
= 30°) angles of attack. To find out the unsteady nature of the breakdown location, we have also estimated the RMS values of the breakdown location (
![]() ${X_{f,{\rm{\;\;}}RMS}}$
), as shown in Fig. 15(b). One may notice that
${X_{f,{\rm{\;\;}}RMS}}$
), as shown in Fig. 15(b). One may notice that
![]() ${X_{f,{\rm{\;\;}}RMS}}$
values increase with Reynolds number for the pre-stall
${X_{f,{\rm{\;\;}}RMS}}$
values increase with Reynolds number for the pre-stall
![]() $\alpha $
= 20°, whereas the values for the near stall and post-stall angles of attack seem to arrive at some constant magnitudes after an initial drop. This result suggests that the breakdown location is more unsteady for the pre-stall angle-of-attack than the near-stall and post-stall angles of attack. Further, the unsteadiness increases with the Reynolds number for the pre-stall angle-of-attack, whereas it does not significantly change with the Reynolds number for the near-stall and post-stall angles of attack.
$\alpha $
= 20°, whereas the values for the near stall and post-stall angles of attack seem to arrive at some constant magnitudes after an initial drop. This result suggests that the breakdown location is more unsteady for the pre-stall angle-of-attack than the near-stall and post-stall angles of attack. Further, the unsteadiness increases with the Reynolds number for the pre-stall angle-of-attack, whereas it does not significantly change with the Reynolds number for the near-stall and post-stall angles of attack.

Figure 15. Reynolds number effects on variations of (a) the mean vortex breakdown location (
![]() ${X_{VB}}$
) and (b) the root-mean-squared (RMS) of fluctuation of the breakdown location (
${X_{VB}}$
) and (b) the root-mean-squared (RMS) of fluctuation of the breakdown location (
![]() ${X_{f,{\rm{\;\;}}RMS}}$
) for
${X_{f,{\rm{\;\;}}RMS}}$
) for
![]() $\alpha $
= 20°, 25° and 30°.
$\alpha $
= 20°, 25° and 30°.
3.5 Proper orthogonal decomposition of the flow field
Proper orthogonal decomposition (POD) analysis along the longitudinal plane has been performed to investigate the low-dimensional nature of the vortical flows over the flying wing. Since its introduction to fluid mechanics by Lumley [Reference Lumley69], this decomposition technique is often used to extract the coherent structures from an unsteady flow field [Reference Sirovich70]. The PIV measurements in a flow field provide a large volume of data, and therefore, it is useful to use such a tool to extract the dominant flow structures. The method of snapshot, proposed by Sirovich [Reference Sirovich70], has been used here to calculate the POD modes and the associated energy. The present POD methodology is adapted from the work of Mandal et al. [Reference Mandal, Venkatakrishnan and Dey71], as briefly discussed below.
The fluctuating velocity field (
![]() ${\bf{u}}{\rm{'}} = {{\bf{u}}_{\bf{I}}} - \bar{\bf{u}}$
) has been obtained by subtracting the ensemble mean (
${\bf{u}}{\rm{'}} = {{\bf{u}}_{\bf{I}}} - \bar{\bf{u}}$
) has been obtained by subtracting the ensemble mean (
![]() $\bar{\bf{u}}$
) from each instantaneous PIV realisation (
$\bar{\bf{u}}$
) from each instantaneous PIV realisation (
![]() ${\bf{u}}$
). The covariance matrix is then obtained as
${\bf{u}}$
). The covariance matrix is then obtained as
![]() ${R_{ij}} = \left( {{\bf{u}}{{\rm{'}}_{\!\!i}},{\bf{u}}{{\rm{'}}_{\!\!j}}} \right)$
, where
${R_{ij}} = \left( {{\bf{u}}{{\rm{'}}_{\!\!i}},{\bf{u}}{{\rm{'}}_{\!\!j}}} \right)$
, where
![]() $i = 1,2, \ldots ,M$
and
$i = 1,2, \ldots ,M$
and
![]() $j = 1,2, \ldots ,M$
. Here,
$j = 1,2, \ldots ,M$
. Here,
![]() $M$
is the total number of PIV realisations. The covariance matrix
$M$
is the total number of PIV realisations. The covariance matrix
![]() ${R_{ij}}$
is symmetric and its non-negative eigenvalues,
${R_{ij}}$
is symmetric and its non-negative eigenvalues,
![]() ${\lambda _i}$
, indicate the relative importance of each POD mode. The summation of all the eigenvalues can be considered as the total energy,
${\lambda _i}$
, indicate the relative importance of each POD mode. The summation of all the eigenvalues can be considered as the total energy,
![]() ${\rm{E}}\left( { = \mathop \sum \nolimits_{i = 1}^M {\lambda _i}} \right)$
, and the relative energy of each POD mode can be defined as
${\rm{E}}\left( { = \mathop \sum \nolimits_{i = 1}^M {\lambda _i}} \right)$
, and the relative energy of each POD mode can be defined as
![]() ${{\rm{E}}_k} = {\lambda _k}/{\rm{E}}$
[Reference Mandal, Venkatakrishnan and Dey71]. The eigenfunctions or POD modes are defined as
${{\rm{E}}_k} = {\lambda _k}/{\rm{E}}$
[Reference Mandal, Venkatakrishnan and Dey71]. The eigenfunctions or POD modes are defined as
where
![]() ${\phi ^k}$
are orthogonal eigenvectors, which form a complete set, and
${\phi ^k}$
are orthogonal eigenvectors, which form a complete set, and
![]() $\phi _i^k$
indicates the
$\phi _i^k$
indicates the
![]() ${i^{th}}$
component of the
${i^{th}}$
component of the
![]() ${k^{th}}$
eigenvector. The eigenfunctions,
${k^{th}}$
eigenvector. The eigenfunctions,
![]() ${{\rm{\Phi }}^k}$
, are normalised such that
${{\rm{\Phi }}^k}$
, are normalised such that
3.5.1 POD analysis in the longitudinal plane
The POD analysis has been performed on time-resolved PIV data, which were acquired in the longitudinal plane of the leading-edge vortex on the starboard side of the flying wing. For this analysis, 6,000 TR-PIV realisations were used. The relative and cumulative energy distributions of the first 30 POD modes are shown in Fig. 16(a) and (b), for
![]() $\alpha $
= 20° and
$\alpha $
= 20° and
![]() $\alpha $
= 30°, respectively. A rapid decrease of the relative energy and rapid increase of the cumulative energy with mode numbers can be noticed for both
$\alpha $
= 30°, respectively. A rapid decrease of the relative energy and rapid increase of the cumulative energy with mode numbers can be noticed for both
![]() $\alpha $
= 20° and 30°. Four dominant POD modes are also shown in Fig. 16(a) and (b), for
$\alpha $
= 20° and 30°. Four dominant POD modes are also shown in Fig. 16(a) and (b), for
![]() $\alpha $
= 20° and 30°, respectively. The first mode contains 4.67% of total energy at
$\alpha $
= 20° and 30°, respectively. The first mode contains 4.67% of total energy at
![]() $\alpha $
= 20°, whereas the next three modes carry approximately 1.9%, 1.53% and 1.3%, respectively. Similarly, the first dominant mode contains 2.5% of total energy at
$\alpha $
= 20°, whereas the next three modes carry approximately 1.9%, 1.53% and 1.3%, respectively. Similarly, the first dominant mode contains 2.5% of total energy at
![]() $\alpha $
= 30°, and the following three modes contain approximately 1.21%, 1.03% and 0.85%, respectively. The cumulative energy distribution, in Fig. 16(a), shows that the first 30 POD modes contain 21.76% energy, whereas 378 POD modes are required to capture 50.03% energy at
$\alpha $
= 30°, and the following three modes contain approximately 1.21%, 1.03% and 0.85%, respectively. The cumulative energy distribution, in Fig. 16(a), shows that the first 30 POD modes contain 21.76% energy, whereas 378 POD modes are required to capture 50.03% energy at
![]() $\alpha $
= 20°. Similarly, the first 30 POD modes carry 14.1% energy, and one needs 563 POD modes to capture 50.03% energy at
$\alpha $
= 20°. Similarly, the first 30 POD modes carry 14.1% energy, and one needs 563 POD modes to capture 50.03% energy at
![]() $\alpha $
= 30°. This indicates that the small scales are generated as we increase the angle-of-attack.
$\alpha $
= 30°. This indicates that the small scales are generated as we increase the angle-of-attack.

Figure 16. Relative and cumulative energies along with four POD modes in a plane passing through the trajectory of vortex core. (a)
![]() $\alpha $
= 20°, and (b)
$\alpha $
= 20°, and (b)
![]() $\alpha $
= 30°.
$\alpha $
= 30°.
Figure 16(a) and (b) also show the first four dominant POD modes at
![]() $\alpha $
= 20° (pre-stall regime) and
$\alpha $
= 20° (pre-stall regime) and
![]() $\alpha $
= 30° (post-stall regime). At both angles of attack, the first mode shows large velocity fluctuations around the vortex breakdown location, indicating highly unsteady flow phenomena around that location. In fact, fluctuation of the breakdown location about the mean location is also estimated from the entire PIV realisations. The RMS values of these fluctuations about the mean locations, for
$\alpha $
= 30° (post-stall regime). At both angles of attack, the first mode shows large velocity fluctuations around the vortex breakdown location, indicating highly unsteady flow phenomena around that location. In fact, fluctuation of the breakdown location about the mean location is also estimated from the entire PIV realisations. The RMS values of these fluctuations about the mean locations, for
![]() $\alpha $
= 20° and 30°, are found to be 1.62% and 1.68% of the root chord, respectively.
$\alpha $
= 20° and 30°, are found to be 1.62% and 1.68% of the root chord, respectively.
Further, Fig. 16 shows that the first POD mode in the longitudinal plane is involved either with negative or positive
![]() $u$
fluctuations. A non-axisymmetric nature of these velocity fluctuations with considerable magnitude along the vortex core can also be noticed. Higher modes (i.e. from mode 2 onward) represent smaller flow structures with similar non-axisymmetric velocity fluctuations. A POD mode itself can be different from a coherent structure; that is, it does not necessarily represent a structure that needs to evolve coherently in the flow field [Reference Towne, Schmidt and Colonius72, Reference Podvin, Pellerin, Fraigneau, Evrard and Cadot73]. A coherent structure may be composed of a few POD modes confined in some spatial domain [Reference Podvin, Pellerin, Fraigneau, Evrard and Cadot73]. Since a POD mode itself does not clearly reveal whether the vortex breakdown is associated with spiral-type breakdown or bubble-type breakdown, we have reconstructed the instantaneous flow fields using the first ten dominant POD modes for a clear understanding of the type of vortex breakdown. Figure 17 shows the reconstructed time sequence of the flow fields. We can clearly see in Fig. 17 that all the reconstructed velocity fields are associated with some counter-rotating vortex pairs along the axis of the leading-edge vortex, together with some patches of positive and negative
$u$
fluctuations. A non-axisymmetric nature of these velocity fluctuations with considerable magnitude along the vortex core can also be noticed. Higher modes (i.e. from mode 2 onward) represent smaller flow structures with similar non-axisymmetric velocity fluctuations. A POD mode itself can be different from a coherent structure; that is, it does not necessarily represent a structure that needs to evolve coherently in the flow field [Reference Towne, Schmidt and Colonius72, Reference Podvin, Pellerin, Fraigneau, Evrard and Cadot73]. A coherent structure may be composed of a few POD modes confined in some spatial domain [Reference Podvin, Pellerin, Fraigneau, Evrard and Cadot73]. Since a POD mode itself does not clearly reveal whether the vortex breakdown is associated with spiral-type breakdown or bubble-type breakdown, we have reconstructed the instantaneous flow fields using the first ten dominant POD modes for a clear understanding of the type of vortex breakdown. Figure 17 shows the reconstructed time sequence of the flow fields. We can clearly see in Fig. 17 that all the reconstructed velocity fields are associated with some counter-rotating vortex pairs along the axis of the leading-edge vortex, together with some patches of positive and negative
![]() $u$
fluctuations. These flow features indicate a spiral-type flow breakdown, as schematically detailed in the following.
$u$
fluctuations. These flow features indicate a spiral-type flow breakdown, as schematically detailed in the following.

Figure 17. Time sequence of the reconstructed fluctuating velocity field over the contours of
![]() $u{{\rm{'}}_{vc}}$
. Ten POD modes are used for reconstruction at
$u{{\rm{'}}_{vc}}$
. Ten POD modes are used for reconstruction at
![]() $\alpha $
= 20°.
$\alpha $
= 20°.
Flow field inside a bubble type breakdown is often seen to be symmetric about the mid-plane of the vortex axis, as compared to the spiral breakdown, which is highly asymmetric about the midplane of the vortex axis [Reference Brücker and Althaus74, Reference Brücker and Althaus75]. A simple sketch of a spiral-type vortex breakdown is shown in Fig. 18(a). During a PIV measurement in the midplane of the vortex axis, a laser sheet can cut a spiral vortex at some specific locations, for example, at locations L1, L2, L3, L4 and L5, as schematically shown in Fig. 18(b), which will appear as counter-rotating vortex pairs in the laser plane (i.e. in the measurement plane). This is exactly what we can observe in Figure 18. Therefore, the POD analysis clearly indicates that there exists a spiral-type vortex breakdown.

Figure 18. (a) A simple schematic depicting spiral vortex breakdown and (b) The PIV measurement plane along the midplane of the leading-edge vortex core.
4.0 Summary and concluding remarks
An experimental study at some pre-stall, near-stall and post-stall angles of attack has been carried out to understand better some non-linear aerodynamic characteristics of a non-slender flying wing configuration. To achieve this, various measurements, i.e. force, surface pressure and whole flow field measurements, including surface flow visualisation, were conducted in both the cross-flow and longitudinal planes. The findings of this study are summarised as follows.
-
1. The present study clearly reveals that changes in flow patterns at particular angles of attack over the surface of the flying wing lead to highly non-linear lift curve behaviour and associated peaks and valleys in the pitching moment coefficient. Additionally, surface flow visualisation showed a wave-like surface pattern followed by a kink, symmetric about the root chord at
 $\alpha $
= 20° for Re
$\alpha $
= 20° for Re
 $ = $
2.5
$ = $
2.5
 $\; \times {\rm{\;}}$
10
$\; \times {\rm{\;}}$
10
 $^5$
. The wave-like pattern is found to move upstream with an increasing angle-of-attack, and its size is reduced with increasing Reynolds number.
$^5$
. The wave-like pattern is found to move upstream with an increasing angle-of-attack, and its size is reduced with increasing Reynolds number. -
2. The PIV measurements in the crossflow plane reveal symmetrical vortices about the root chord, which increase in size after the wave-like pattern. A sudden enlargement of the vortex size after the wave-like pattern, accompanied by diffused axial vorticity, indicates vortex breakdown over the flying wing. Additionally, our measurements at
 $X/C = $
0.1 demonstrate two counter-rotating vortices, one primary leading-edge vortex, and another trailing-edge vortex. Interestingly, we also observe that a primary leading-edge vortex can persist even at a post-stall angle-of-attack (
$X/C = $
0.1 demonstrate two counter-rotating vortices, one primary leading-edge vortex, and another trailing-edge vortex. Interestingly, we also observe that a primary leading-edge vortex can persist even at a post-stall angle-of-attack (
 $\alpha = $
30°), and the vortex breakdown can still occur at some downstream location of the apex of the wing.
$\alpha = $
30°), and the vortex breakdown can still occur at some downstream location of the apex of the wing. -
3. The PIV measurements in the longitudinal plane clearly reveal the existence of a stagnation point (
 ${\bar u_{vc}}/{U_\infty } = $
0) followed by a reverse flow region (
${\bar u_{vc}}/{U_\infty } = $
0) followed by a reverse flow region (
 ${\bar u_{vc}}/{U_\infty }$
${\bar u_{vc}}/{U_\infty }$
 $ \le $
0). The stagnation point shifts towards the upstream with an increasing angle-of-attack. However, the PIV measurements, along with the pressure distribution, confirm that the wave-like surface flow pattern is associated with the vortex breakdown, as the location of the stagnation point is found to correspond to the wave-like structure, as seen in the flow visualisation image. This is further supported by the fact that
$ \le $
0). The stagnation point shifts towards the upstream with an increasing angle-of-attack. However, the PIV measurements, along with the pressure distribution, confirm that the wave-like surface flow pattern is associated with the vortex breakdown, as the location of the stagnation point is found to correspond to the wave-like structure, as seen in the flow visualisation image. This is further supported by the fact that
 ${C_{p,{\rm{\;\;}}RMS}}$
increases on the onset of a wave-like pattern, as one can expect a highly unsteady flow field after the vortex breakdown. The maximum unsteadiness (
${C_{p,{\rm{\;\;}}RMS}}$
increases on the onset of a wave-like pattern, as one can expect a highly unsteady flow field after the vortex breakdown. The maximum unsteadiness (
 ${C_{p,{\rm{\;\;}}RMS}}$
) is found near-stall angle-of-attack. The mean location of the vortex breakdown moves in the downstream direction with increasing Reynolds number at a pre-stall (
${C_{p,{\rm{\;\;}}RMS}}$
) is found near-stall angle-of-attack. The mean location of the vortex breakdown moves in the downstream direction with increasing Reynolds number at a pre-stall (
 $\alpha = $
20°) angle-of-attack, whereas it does not change significantly with Reynolds number for the near-stall (
$\alpha = $
20°) angle-of-attack, whereas it does not change significantly with Reynolds number for the near-stall (
 $\alpha = $
25°) and the post-stall (
$\alpha = $
25°) and the post-stall (
 $\alpha = $
30°) angles of attack.
$\alpha = $
30°) angles of attack. -
4. Existence of unstable nodes and foci in the streamline topology indicates a spiral-type vortex breakdown. To confirm this, the velocity fields obtained from the TR-PIV measurements in the longitudinal plane are reconstructed using the first 10 POD modes to remove the high-frequency noise from the data. A time sequence of the reconstructed velocity fields reveals the wiggling nature of the velocity fluctuations with considerable magnitude along the vortex core. These results suggest that the vortex breakdown is a spiral-type breakdown.
On the whole, the present investigation clearly reveals that a spiral-type vortex breakdown on a flying wing configuration manifests as a wave-like surface pattern, which moves upstream with an increasing angle-of-attack. This pattern moves downstream and shrinks in size with an increasing Reynolds number.
Acknowledgements
The authors are grateful for the assistance provided by the technical staff at Low-Speed Lab, Department of Aerospace Engineering, IIT Kanpur, during the experiments.
Competing interests
The authors report no competing interests.
Funding
This research received no external funding.