Hostname: page-component-669899f699-7xsfk Total loading time: 0 Render date: 2025-04-25T14:42:40.748Z Has data issue: false hasContentIssue false
  • English
  • Français

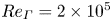Turbulent vortex pair at equilibrium and its interaction with the ground at $Re_{\varGamma } = 2 \times 10^5$

Published online by Cambridge University Press:  23 May 2024

Grégoire Winckelmans Open the ORCID record for Grégoire Winckelmans [Opens in a new window] ,
Matthieu Duponcheel Open the ORCID record for Matthieu Duponcheel [Opens in a new window] ,
Laurent Bricteux Open the ORCID record for Laurent Bricteux [Opens in a new window] ,
Ivan De Visscher Open the ORCID record for Ivan De Visscher [Opens in a new window]  and
Olivier Thiry
Grégoire Winckelmans*
Affiliation:
Université catholique de Louvain (UCLouvain), Institute of Mechanics, Materials and Civil Engineering (iMMC), 1348 Louvain-la-Neuve, Belgium
Matthieu Duponcheel
Affiliation:
Université catholique de Louvain (UCLouvain), Institute of Mechanics, Materials and Civil Engineering (iMMC), 1348 Louvain-la-Neuve, Belgium
Laurent Bricteux
Affiliation:
Fluids and Machines Department, Université de Mons (UMONS), 7000 Mons, Belgium
Ivan De Visscher
Affiliation:
Wake Prediction Technologies (WaPT), 1348 Louvain-la-Neuve, Belgium
Olivier Thiry
Affiliation:
Cadence Design Systems, 1170 Brussels, Belgium
*
†Email address for correspondence: gregoire.winckelmans@uclouvain.be
Get access Rights & Permissions [Opens in a new window]

Abstract

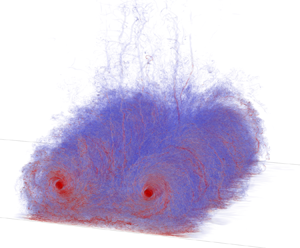
A turbulent two-vortex system (T-2VS) is obtained by inserting analytical model wake vortices into very weak homogeneous isotropic turbulence (HIT) and by evolving them in time using large-eddy simulation until a turbulent state at statistical equilibrium is reached. The T-2VS is characterised as follows: circulation distribution of the vortices; energy of the mean and fluctuating fields; energy dissipation rate. It is also verified that essentially the same T-2VS is obtained when varying the initial model or initial HIT perturbation. A wall-resolved simulation of the T-2VS further interacting with a smooth ground is then performed at $Re_\varGamma = 2 \times 10^5$; this is $10 \times$ higher than in previous works, which allows us to better capture the high Reynolds number behaviour. The high release height of the T-2VS also ensures a physically correct approach to the ground. The results are compared with the literature and also to what is obtained for the case of non-turbulent vortices interacting with the same ground at the same Reynolds number. The flow topologies are discussed, and significant differences are highlighted regarding the separation of the boundary layer generated at the ground, and the way this secondary vorticity interacts with the primary vortices and makes them decay. The vortex trajectories are also measured, together with their circulation distribution and global circulation evolution, and the differences are discussed.

JFM classification

Vortex Flows: Vortex dynamics Turbulent Flows: Turbulence simulation Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 987 , 25 May 2024 , A34
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

‡

Past affiliation: UCLouvain/iMMC.

§

Past affiliation: UCLouvain/iMMC.

References

Bricteux, L., Duponcheel, M., De Visscher, I. & Winckelmans, G. 2016 LES investigation of the transport and decay of various-strengths wake vortices in ground effect and subjected to a turbulent crosswind. Phys. Fluids 28 (6), 065105.CrossRefGoogle Scholar
Bricteux, L., Duponcheel, M. & Winckelmans, G. 2009 A multiscale subgrid model for both free vortex flows and wall-bounded flows. Phys. Fluids 21 (10), 105102.CrossRefGoogle Scholar
de Bruin, A. & Winckelmans, G. 2005 Cross-flow kinetic energy and core size growth of analytically defined wake vortex pairs. Tech. Rep. NLR-CR-2005-412. Netherlands Aerospace Center.Google Scholar
Burnham, D.C. & Hallock, J.N. 1982 Wake vortex decay. In Chicago Monostatic Acoustic Vortex Sensing System. Tech. Rep. DOT/FAA/RD-79-103, IV, U.S. Department of Transportation, Federal Aviation Administration.Google Scholar
Canuto, C., Yousuff Hussaini, M., Quarteroni, A. & Zang, T.A. 2006 Spectral Methods: Fundamentals in Single Domains. Springer.CrossRefGoogle Scholar
Corjon, A. & Poinsot, T. 1997 Behavior of wake vortices near ground. AIAA J. 35 (5), 849–855.CrossRefGoogle Scholar
Coustols, E., Jacquin, L. & Schrauf, G. 2006 Status of wake vortex alleviation in the framework of European collaboration: validation using tests and CFD results. In ECCOMAS CFD 2006: Proceedings of the European Conference on Computational Fluid Dynamics, Egmond aan Zee, The Netherlands (ed. J. Périaux, P. Wesseling & E. Oñate). Delft University of Technology.Google Scholar
Crow, S.C. 1970 Stabilities theory for a pair of trailing vortices. AIAA J. 8, 2172–2179.CrossRefGoogle Scholar
De Visscher, I., Bricteux, L. & Winckelmans, G. 2013 a Aircraft vortices in stably stratified and weakly turbulent atmospheres: simulation and modeling. AIAA J. 51 (3), 551–566.CrossRefGoogle Scholar
De Visscher, I., Lonfils, T. & Winckelmans, G. 2013 b Fast-time modeling of ground effects on wake vortex transport and decay. J. Aircraft 50 (5), 1514–1525.CrossRefGoogle Scholar
De Visscher, I., Winckelmans, G., Lonfils, T., Bricteux, L., Duponcheel, M. & Bourgeois, N. 2010 The WAKE4D simulation platform for predicting aircraft wake vortex transport and decay: description and examples of application. In AIAA Atmospheric and Space Environments Conference. AIAA.CrossRefGoogle Scholar
De Visscher, I., Winckelmans, G. & Treve, V. 2016 Characterization of aircraft wake vortex circulation decay in reasonable worst case conditions. In 54th AIAA Aerospace Sciences Meeting (AIAA SciTech), 4–8 January 2016, San Diego, California, USA. AIAA.CrossRefGoogle Scholar
Doligalski, T.L., Smith, C.R. & Walker, J.D.A. 1994 Vortex interactions with walls. Annu. Rev. Fluid Mech. 26 (1), 573–616.CrossRefGoogle Scholar
Fabre, D. & Jacquin, L. 2004 Short-wave cooperative instabilities in representative aircraft vortices. Phys. Fluids 16 (5), 1366–1378.CrossRefGoogle Scholar
Gerz, T., Holzäpfel, F. & Darracq, D. 2002 Commercial aircraft wake vortices. Prog. Aerosp. Sci. 38 (3), 181–208.CrossRefGoogle Scholar
Harris, D.M. & Williamson, C.H.K. 2012 Instability of secondary vortices generated by a vortex pair in ground effect. J. Fluid Mech. 700, 148–186.CrossRefGoogle Scholar
Harvey, J.K. & Perry, F.J. 1971 Flowfield produced by trailing vortices in the vicinity of the ground. AIAA J. 9 (8), 1659–1660.CrossRefGoogle Scholar
Holzäpfel, F. & Steen, M. 2007 Aircraft wake-vortex evolution in ground proximity: analysis and parameterization. AIAA J. 45 (1), 218–227.CrossRefGoogle Scholar
Holzäpfel, F., Tchipev, N. & Stephan, A. 2016 Wind impact on single vortices and counterrotating vortex pairs in ground proximity. Flow Turbul. Combust. 97 (3), 829–848.CrossRefGoogle Scholar
Lamb, H. 1932 Hydrodynamics, 6th edn. Cambridge University Press.Google Scholar
Leweke, T., Le Dizès, S. & Williamson, C.H.K. 2016 Dynamics and instabilities of vortex pairs. Annu. Rev. Fluid Mech. 48 (1), 507–541.CrossRefGoogle Scholar
Luton, J.A. & Ragab, S.A. 1997 Three-dimensional interaction of a vortex pair with a wall. Phys. Fluids 9 (10), 2967–2980.CrossRefGoogle Scholar
Misaka, T., Holzäpfel, F. & Gerz, T. 2015 Large-eddy simulation of aircraft wake evolution from roll-up until vortex decay. AIAA J. 53 (9), 2646–2670.CrossRefGoogle Scholar
Morinishi, Y., Lund, T.S., Vasilyev, O.V. & Moin, P. 1998 Fully conservative higher order finite difference schemes for incompressible flow. J. Comput. Phys. 143 (1), 90–124.CrossRefGoogle Scholar
Nicoud, F. & Ducros, F. 1999 Subgrid-scale stress modelling based on the square of the velocity gradient tensor. Flow Turbul. Combust. 62 (3), 183–200.CrossRefGoogle Scholar
Proctor, F.H. 1998 The NASA-Langley wake vortex modelling effort in support of an operational aircraft spacing system. In 36th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA. AIAA.CrossRefGoogle Scholar
Proctor, F.H., Ahmad, N., Switzer, G. & Duparcmeur, F.L. 2010 Three-phased wake vortex decay. In AIAA Atmospheric and Space Environments Conference, Toronto, Ontario, Canada. AIAA.CrossRefGoogle Scholar
Proctor, F.H. & Han, J. 1999 Numerical study of wake vortex interaction with the ground using the terminal area simulation system. In 37th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA. AIAA.CrossRefGoogle Scholar
Proctor, F.H., Hinton, D.A., Han, J., Schowalter, D.G & Lin, Y.-L. 1997 Two dimensional wake vortex simulations in the atmosphere : preliminary sensitivity studies. In 35th AIAA Aerosp. Sci. Meet. & Exhib., Reno, NV. AIAA Paper 97–0056. AIAA.CrossRefGoogle Scholar
Proctor, F.H., Hamilton, D.W. & Han, H. 2000 Wake vortex transport and decay in ground effect: vortex linking with the ground. In 38th AIAA Aerospace Sciences Meeting and Exhibition, Reno, NV, USA. p. 0757. AIAA.CrossRefGoogle Scholar
Rooseleer, F., Treve, V., De Visscher, I. & Graham, R. 2016 Wake turbulence re-categorisation on approach and departure for safe and more efficient air traffic management. In 30th Congress of the International Council of the Aeronautical Sciences (ICAS 2016), Daejeon, Korea, September 25–30. International Council of the Aeronautical Sciences.Google Scholar
Sagaut, P. 2006 Large-Eddy Simulation for Incompressible Flows: An Introduction, 3rd edn. Springer.Google Scholar
Spalart, P.R. 1998 Airplane trailing vortices. Annu. Rev. Fluid Mech. 30 (1), 107.CrossRefGoogle Scholar
Stephan, A., Holzäpfel, F. & Misaka, T. 2013 Aircraft wake-vortex decay in ground proximity – physical mechanisms and artificial enhancement. J. Aircraft 50 (4), 1250–1260.CrossRefGoogle Scholar
Stephan, A., Holzäpfel, F. & Misaka, T. 2014 Hybrid simulation of wake-vortex evolution during landing on flat terrain and with plate line. Intl J. Heat Fluid Flow 49, 18–27.CrossRefGoogle Scholar
Stephan, A., Rohlmann, D., Holzäpfel, F. & Rudnik, R. 2019 Effects of detailed aircraft geometry on wake vortex dynamics during landing. J. Aircraft 56 (3), 974–989.CrossRefGoogle Scholar
Türk, L., Coors, D. & Jacob, D. 1999 Behavior of wake vortices near the ground over a large range of Reynolds numbers. Aerosp. Sci. Technol. 3 (2), 71–81.CrossRefGoogle Scholar
Vasilyev, O.V. 2000 High order finite difference schemes on non-uniform meshes with good conservation properties. J. Comput. Phys. 157, 746–761.CrossRefGoogle Scholar
Widnall, S.E., Bliss, D.B. & Tsai, C.Y. 1974 The instability of short waves on a vortex ring. J. Fluid Mech. 66, 35–47.CrossRefGoogle Scholar
Zheng, Z.C. & Ash, R.L. 1996 Study of aircraft wake vortex behavior near the ground. AIAA J. 34 (3), 580–589.CrossRefGoogle Scholar