Published online by Cambridge University Press: 23 October 2023
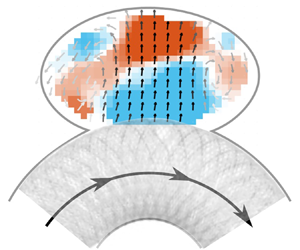
Characterizing the haemodynamics in intracranial aneurysms is of high interest as it impacts aneurysm growth, rupture and treatment, especially with flow-diverting stents (FDS). Flow in these geometries is known to depend on the Dean, Reynolds and Womersley numbers,  $De$,
$De$,  $Re$,
$Re$,  $Wo$, but is also influenced by geometrical parameters such as the sac shape or the size of the opening. Via particle image velocimetry, this parametric study aimed at evaluating the combined effects of
$Wo$, but is also influenced by geometrical parameters such as the sac shape or the size of the opening. Via particle image velocimetry, this parametric study aimed at evaluating the combined effects of  $Re$,
$Re$,  $De$,
$De$,  $Wo$ and the geometry of the aneurysmal sac on the haemodynamics before and after treatment with FDS. Eight ellipsoidal idealized aneurysm models were created with two curvatures of the parent vessel, two aspect ratios of the sac and two neck sizes. Before treatment, a single counter-rotating vortex, whose strength increases with
$Wo$ and the geometry of the aneurysmal sac on the haemodynamics before and after treatment with FDS. Eight ellipsoidal idealized aneurysm models were created with two curvatures of the parent vessel, two aspect ratios of the sac and two neck sizes. Before treatment, a single counter-rotating vortex, whose strength increases with  $Re$ and
$Re$ and  $De$, as well as with the neck size and the aspect ratio, was observed in the sac for all but one geometry. After treatment with FDS, four different flow topologies were observed, depending on the geometry: no separation, separation for part of the cycle, two opposing vortices or a single counter-rotating vortex. A linear model with interaction revealed the predominant effect of
$De$, as well as with the neck size and the aspect ratio, was observed in the sac for all but one geometry. After treatment with FDS, four different flow topologies were observed, depending on the geometry: no separation, separation for part of the cycle, two opposing vortices or a single counter-rotating vortex. A linear model with interaction revealed the predominant effect of  $De$ and the curvature of the parent vessel on the haemodynamics before and after treatment. This work once more demonstrated the primary role of haemodynamics in the treatment of intracranial aneurysms with FDS. Future work will consider the complexity of patient-specific geometries, and their effects on both the haemodynamics in the sac and the porosity of the FDS.
$De$ and the curvature of the parent vessel on the haemodynamics before and after treatment. This work once more demonstrated the primary role of haemodynamics in the treatment of intracranial aneurysms with FDS. Future work will consider the complexity of patient-specific geometries, and their effects on both the haemodynamics in the sac and the porosity of the FDS.