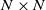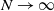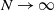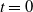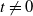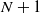1. Introduction
The characteristic polynomials of random matrices have received considerable attention over the past 20 years. One of the principal motivations stems from their connections to the statistical properties of the Riemann zeta-function and other families of L-functions [Reference Keating and Snaith37, Reference Keating and Snaith36, Reference Hughes, Keating and O’Connell33, Reference Conrey and Gonek15, Reference Conrey, Farmer, Keating, Rubinstein and Snaith13, Reference Conrey, Farmer, Keating, Rubinstein and Snaith14, Reference Keating and Snaith35, Reference Fyodorov, Hiary and Keating25, Reference Fyodorov and Keating27]. In this context, the value distributions of the characteristic polynomials of random unitary, orthogonal and symplectic matrices have been calculated using a variety of approaches. For example, the moments have been computed in all three cases and the results used to develop conjectures for the moments of the Riemann zeta-function
![]() $\zeta(s)$
on its critical line and for the moments of families of L-functions at the centre of the critical strip. Specifically, if A is an
$\zeta(s)$
on its critical line and for the moments of families of L-functions at the centre of the critical strip. Specifically, if A is an
![]() $N\times N$
unitary matrix, drawn at random uniformly with respect to Haar measure on the unitary group U(N), then for
$N\times N$
unitary matrix, drawn at random uniformly with respect to Haar measure on the unitary group U(N), then for
![]() $\textrm{Re}\beta>-1/2$
$\textrm{Re}\beta>-1/2$
from which one can deduce that as
![]() $N\to\infty$
$N\to\infty$
where G(s) is the Barnes G-function, and for
![]() $k\in\mathbb{N}$
$k\in\mathbb{N}$
 \begin{equation}\mathbb{E}_{A\in U(N)}\big[|\det(I-Ae^{-i\theta})|^{2k}\big]\sim\left(\prod_{m=0}^{k-1}\frac{m!}{(m+k)!}\right)N^{k^2}.\end{equation}
\begin{equation}\mathbb{E}_{A\in U(N)}\big[|\det(I-Ae^{-i\theta})|^{2k}\big]\sim\left(\prod_{m=0}^{k-1}\frac{m!}{(m+k)!}\right)N^{k^2}.\end{equation}
These formulae lead to the conjectures [Reference Keating and Snaith37] that for
![]() $\textrm{Re}\beta>-1/2$
, as
$\textrm{Re}\beta>-1/2$
, as
![]() $T\rightarrow\infty$
$T\rightarrow\infty$
and for
![]() $k\in\mathbb{N}$
, as
$k\in\mathbb{N}$
, as
![]() $T\rightarrow\infty$
$T\rightarrow\infty$
where
 \begin{equation}a(s)=\prod_p\left[\left(1-\frac{1}{p^s}\right)^{s^2}\sum_{m=0}^\infty\left(\frac{\Gamma(m+s)}{m!\Gamma(s)}\right)^2p^{-m}\right]\end{equation}
\begin{equation}a(s)=\prod_p\left[\left(1-\frac{1}{p^s}\right)^{s^2}\sum_{m=0}^\infty\left(\frac{\Gamma(m+s)}{m!\Gamma(s)}\right)^2p^{-m}\right]\end{equation}
with the product running over primes p.
Our focus here will primarily be on the Gaussian Unitary Ensemble (GUE) of random complex Hermitian matrices. For an
![]() $N\times N$
matrix M drawn from the GUE, the joint eigenvalue density function is
$N\times N$
matrix M drawn from the GUE, the joint eigenvalue density function is
where
![]() ${\mathscr{Z}_N^{\,(H)}}$
is a normalisation constant. When t is fixed, Brezin and Hikami [Reference Brézin and Hikami9] calculated the
${\mathscr{Z}_N^{\,(H)}}$
is a normalisation constant. When t is fixed, Brezin and Hikami [Reference Brézin and Hikami9] calculated the
![]() $N\to\infty$
asymptotics of the moments of the associated characteristic polynomials to be
$N\to\infty$
asymptotics of the moments of the associated characteristic polynomials to be
 \begin{equation}\mathbb{E}^{(H)}_N\left[\det(t-M)^{2k}\right] \sim e^{-Nk}e^{Nk\frac{t^2}{2}}(2\pi N\rho_{sc}(t))^{k^2}\prod_{j=0}^{k-1}\frac{j!}{(k+j)!},\quad k\in\mathbb{N},\end{equation}
\begin{equation}\mathbb{E}^{(H)}_N\left[\det(t-M)^{2k}\right] \sim e^{-Nk}e^{Nk\frac{t^2}{2}}(2\pi N\rho_{sc}(t))^{k^2}\prod_{j=0}^{k-1}\frac{j!}{(k+j)!},\quad k\in\mathbb{N},\end{equation}
where the asymptotic eigenvalue density is given by the Wigner semi-circle law
This corresponds precisely to (1.3), where the mean density is constant.
Our purpose is to investigate the series expansion in powers of t for the moments of the characteristic polynomials of GUE matrices, and of matrices drawn from other unitarily invariant ensembles, when appropriately scaled. We obtain a general formula for the coefficients, which are polynomials in N. They depend strongly on whether N is odd or even and diverge when N grows, meaning that the series expansion has a radius of convergence which shrinks. This is related to increasingly rapid oscillations in t when N grows. When
![]() $t=0$
, as
$t=0$
, as
![]() $N\to\infty$
we recover the asymptotic formula predicted by (1.8). When
$N\to\infty$
we recover the asymptotic formula predicted by (1.8). When
![]() $t\ne0$
, the series expansion cannot be used straightforwardly to compute the asymptotics of the moments, because of the non-uniform convergence. However, we observe a surprising cancellation when we average formally over consecutive values of N: this procedure leads to an exact cancellation in the parts of the expansion coefficients that diverge when
$t\ne0$
, the series expansion cannot be used straightforwardly to compute the asymptotics of the moments, because of the non-uniform convergence. However, we observe a surprising cancellation when we average formally over consecutive values of N: this procedure leads to an exact cancellation in the parts of the expansion coefficients that diverge when
![]() $N\to\infty$
, leaving precisely the values consistent with (1.8). Drawing attention to this observation is our main purpose.
$N\to\infty$
, leaving precisely the values consistent with (1.8). Drawing attention to this observation is our main purpose.
Brezin and Hikami [Reference Brézin and Hikami9] used orthogonal polynomial techniques to arrive at (1.8). Other studies to-date relating to the asymptotics of the moments of characteristic polynomials have relied mainly on the orthogonal polynomial method and saddle point techniques [Reference Brézin and Hikami9, Reference Brézin and Hikami10, Reference Baik, Deift and Strahov3], the Riemann–Hilbert method [Reference Strahov and Fyodorov44], Hankel determinants with Fisher–Hartwig symbols [Reference Krasovsky38, Reference Forrester and Frankel18, Reference Garoni32] and supersymmetric representations [Reference Andreev and Simons2, Reference Fyodorov and Strahov30, Reference Fyodorov23, Reference Szabo45]. In the present study, we take a different approach: we express the moments in terms of certain multivariate orthogonal polynomials and take a combinatorial approach to compute the asymptotics of the moments using the properties of these polynomials. By doing so, we discover that even and odd dimensional GUE matrices give different contributions in the large N limit, and that only a formal average gives formulae consistent with (1.8). In Section 3.2.1, this phenomenon is discussed in detail for the second moment of the characteristic polynomial.
In addition to connections with number theory, characteristic polynomials have found numerous applications in quantum chaos [Reference Andreev and Simons2], mesoscopic systems [Reference Fyodorov and Quantum Physics22], quantum chromodynamics [Reference Damgaard and Nishigaki16], and in a variety of combinatorial problems [Reference Strahov43, Reference Diaconis and Gamburd17]. The asymptotic study of negative moments and ratios of characteristic polynomials is another active area of research, see for example [Reference Berry and Keating6, Reference Fyodorov and Keating26, Reference Fyodorov and Strahov31, Reference Baik, Deift and Strahov3, Reference Strahov and Fyodorov44, Reference Forrester and Keating19, Reference Borodin and Strahov7, Reference Breuer and Strahov8, Reference Fyodorov, Grela and Strahov24, Reference Akemann, Strahov and Würfel1]. More recently, the statistics of the maximum of the characteristic polynomial are being extensively studied, motivated by the relations to logarithmically correlated Gaussian processes. For example, see [Reference Fyodorov, Hiary and Keating25, Reference Fyodorov and Keating27, Reference Fyodorov and Le Doussal28, Reference Fyodorov and Simm29] and references therein. We expect that the techniques developed here will have applications to those calculations as well.
This paper is structured as follows. In Section 2, we review the background results we shall need and discuss exact formulae for the moments of characteristic polynomials. In Section 3, we investigate these formulae fin the GUE case asymptotically, when the matrix size tends to infinity. In the last section, Section 4, as an application of our results, we compute the correlations of secular coefficients, which are the coefficients of a characteristic polynomial when expanded as a function of the spectral variable.
2. Background
A partition
![]() $\mu$
is a sequence of integers
$\mu$
is a sequence of integers
![]() $(\mu_1,\dots,\mu_l)$
such that
$(\mu_1,\dots,\mu_l)$
such that
![]() $\mu_1\geq\dots\geq\mu_l>0$
. Here l is the length of the partition and we denote
$\mu_1\geq\dots\geq\mu_l>0$
. Here l is the length of the partition and we denote
![]() $|\mu|=\mu_1+\dots+\mu_l$
to be the weight of the partition. We do not distinguish partitions that only differ by a sequence of zeros at the end. A partition can be represented with a Young diagram which is a left adjusted table of
$|\mu|=\mu_1+\dots+\mu_l$
to be the weight of the partition. We do not distinguish partitions that only differ by a sequence of zeros at the end. A partition can be represented with a Young diagram which is a left adjusted table of
![]() $|\mu|$
boxes and
$|\mu|$
boxes and
![]() $l(\mu)$
rows such that the first row contains
$l(\mu)$
rows such that the first row contains
![]() $\mu_1$
boxes, the second row contains
$\mu_1$
boxes, the second row contains
![]() $\mu_2$
boxes and so on. The conjugate partition
$\mu_2$
boxes and so on. The conjugate partition
![]() $\mu^\prime$
is defined by transposing the Young diagram of
$\mu^\prime$
is defined by transposing the Young diagram of
![]() $\mu$
along the main diagonal.
$\mu$
along the main diagonal.
For a partition
![]() $\mu$
, let
$\mu$
, let
![]() $\varPhi_\mu$
be the multivariate symmetric polynomial, with leading coefficient equal to 1, that obey the orthogonality relation
$\varPhi_\mu$
be the multivariate symmetric polynomial, with leading coefficient equal to 1, that obey the orthogonality relation
for a weight function w(x). Here, the lengths of the partitions
![]() $\mu$
and
$\mu$
and
![]() $\nu$
are less than or equal to the number of variables n, and
$\nu$
are less than or equal to the number of variables n, and
![]() $C_\mu$
is a constant which depends on n. Polynomial
$C_\mu$
is a constant which depends on n. Polynomial
![]() $\varPhi_\mu$
can be expressed as a ratio of determinants, as given in [Reference Sergeev and Veselov42],
$\varPhi_\mu$
can be expressed as a ratio of determinants, as given in [Reference Sergeev and Veselov42],
where
![]() $\varphi_j(x)$
is a monic polynomial of degree j orthogonal with respect to w(x). We focus in particular to the case when w(x) in (2.1) is one of the following weights
$\varphi_j(x)$
is a monic polynomial of degree j orthogonal with respect to w(x). We focus in particular to the case when w(x) in (2.1) is one of the following weights
 \begin{equation}w(x) =\left\{\begin{array}{l@{\quad}l@{\quad}l@{\quad}l}e^{-\dfrac{N x^2}{2}}, & x\in \mathbb{R}, & \text{Gaussian},\\ \\[-7pt]x^\gamma e^{-2Nx}, & x\in \mathbb{R}_+,& \gamma>-1, &\text{Laguerre},\\ \\[-7pt]x^{\gamma_1}(1-x)^{\gamma_2}, & x\in[0,1], & \gamma_1,\gamma_2>-1, & \text{Jacobi}.\end{array}\right.\end{equation}
\begin{equation}w(x) =\left\{\begin{array}{l@{\quad}l@{\quad}l@{\quad}l}e^{-\dfrac{N x^2}{2}}, & x\in \mathbb{R}, & \text{Gaussian},\\ \\[-7pt]x^\gamma e^{-2Nx}, & x\in \mathbb{R}_+,& \gamma>-1, &\text{Laguerre},\\ \\[-7pt]x^{\gamma_1}(1-x)^{\gamma_2}, & x\in[0,1], & \gamma_1,\gamma_2>-1, & \text{Jacobi}.\end{array}\right.\end{equation}
Note that the Gaussian and Laguerre weights are rescaled with a parameter N which we later take to infinity.
When
![]() $\varphi_n(x)$
in (2.2) is chosen to be one of the monic Hermite, Laguerre and Jacobi polynomials of degree n, we get their multivariable analogues denoted by
$\varphi_n(x)$
in (2.2) is chosen to be one of the monic Hermite, Laguerre and Jacobi polynomials of degree n, we get their multivariable analogues denoted by
![]() $\mathscr{H}_\mu$
,
$\mathscr{H}_\mu$
,
![]() $\mathscr{L}^{(\gamma)}_\mu$
and
$\mathscr{L}^{(\gamma)}_\mu$
and
![]() $\mathscr{J}^{(\gamma_1,\gamma_2)}_\mu$
. These multivariate generalisations are the eigenfunctions of differential equations called Calogero–Sutherland Hamiltonians. Several properties such as recursive relations and integration formulas extend to the multivariate case [Reference Baker and Forrester4, Reference Baker and Forrester5].
$\mathscr{J}^{(\gamma_1,\gamma_2)}_\mu$
. These multivariate generalisations are the eigenfunctions of differential equations called Calogero–Sutherland Hamiltonians. Several properties such as recursive relations and integration formulas extend to the multivariate case [Reference Baker and Forrester4, Reference Baker and Forrester5].
The Schur polynomials
![]() $S_\lambda$
, indexed by a partition
$S_\lambda$
, indexed by a partition
![]() $\lambda$
, are defined as
$\lambda$
, are defined as
for
![]() $l(\lambda)\leq n$
, and
$l(\lambda)\leq n$
, and
![]() $S_\lambda=0$
for
$S_\lambda=0$
for
![]() $l(\lambda)>n$
. The polynomials
$l(\lambda)>n$
. The polynomials
![]() $\mathscr{H}_\mu$
,
$\mathscr{H}_\mu$
,
![]() $\mathscr{L}^{\,(\gamma)}_\mu$
and
$\mathscr{L}^{\,(\gamma)}_\mu$
and
![]() $\mathscr{J}^{\,(\gamma_1,\gamma_2)}_\mu$
form a basis for symmetric polynomials of degree
$\mathscr{J}^{\,(\gamma_1,\gamma_2)}_\mu$
form a basis for symmetric polynomials of degree
![]() $|\mu|$
. Therefore, Schur polynomials can be expanded as [Reference Jonnadula, Keating and Mezzadri34]
$|\mu|$
. Therefore, Schur polynomials can be expanded as [Reference Jonnadula, Keating and Mezzadri34]
where
![]() $\varPhi_\nu(\textbf{x})$
can be either
$\varPhi_\nu(\textbf{x})$
can be either
![]() $\mathscr{H}_\nu$
,
$\mathscr{H}_\nu$
,
![]() $\mathscr{L}^{\,(\gamma)}_\nu$
, or
$\mathscr{L}^{\,(\gamma)}_\nu$
, or
![]() $\mathscr{J}^{\,(\gamma_1,\gamma_2)}_\nu$
. In the following the superscripts (H), (L) and (J) indicate Hermite, Laguerre and Jacobi, respectively. The coefficients in (2.5) are
$\mathscr{J}^{\,(\gamma_1,\gamma_2)}_\nu$
. In the following the superscripts (H), (L) and (J) indicate Hermite, Laguerre and Jacobi, respectively. The coefficients in (2.5) are
 \begin{align}\Psi_{\lambda\nu}^{(J)} &= \frac{G_\lambda(n,\gamma_1)G_\lambda(n,0)}{G_\nu(n,\gamma_1)G_\nu(n,0)}\left(\prod_{j=1}^n\Gamma(2\nu_j+2n-2j+\gamma_1+\gamma_2+2)\right)\mathcal{D}^{(J)}_{\lambda\nu},\end{align}
\begin{align}\Psi_{\lambda\nu}^{(J)} &= \frac{G_\lambda(n,\gamma_1)G_\lambda(n,0)}{G_\nu(n,\gamma_1)G_\nu(n,0)}\left(\prod_{j=1}^n\Gamma(2\nu_j+2n-2j+\gamma_1+\gamma_2+2)\right)\mathcal{D}^{(J)}_{\lambda\nu},\end{align}
where
 \begin{align}C_\lambda(N) &= \prod_{j=1}^N\frac{(\lambda_j+N-j)!}{(N-j)!}, \nonumber\\[3pt] G_\lambda(N,\gamma) &= \prod_{j=1}^N\Gamma(\lambda_j+N-j+\gamma +1),\end{align}
\begin{align}C_\lambda(N) &= \prod_{j=1}^N\frac{(\lambda_j+N-j)!}{(N-j)!}, \nonumber\\[3pt] G_\lambda(N,\gamma) &= \prod_{j=1}^N\Gamma(\lambda_j+N-j+\gamma +1),\end{align}
and
 \begin{align}&D_{\lambda\nu}^{(H)} = \det\left[\unicode{x1D7D9}_{\lambda_j-\nu_k-j+k= \text{0 mod 2}}\,\dfrac{1}{\left(\frac{\lambda_j-\nu_k-j+k}{2}\right)!}\right]_{1\leq j,k\leq l(\lambda)},\end{align}
\begin{align}&D_{\lambda\nu}^{(H)} = \det\left[\unicode{x1D7D9}_{\lambda_j-\nu_k-j+k= \text{0 mod 2}}\,\dfrac{1}{\left(\frac{\lambda_j-\nu_k-j+k}{2}\right)!}\right]_{1\leq j,k\leq l(\lambda)},\end{align}
 \begin{align}&D^{(L)}_{\lambda\nu}= \text{det}\left[\unicode{x1D7D9}_{\lambda_j-\nu_k-j+k\geq 0\dfrac{1}{(\lambda_j-\nu_k-j+k)!}}\right]_{1\leq j,k\leq l(\lambda)},\end{align}
\begin{align}&D^{(L)}_{\lambda\nu}= \text{det}\left[\unicode{x1D7D9}_{\lambda_j-\nu_k-j+k\geq 0\dfrac{1}{(\lambda_j-\nu_k-j+k)!}}\right]_{1\leq j,k\leq l(\lambda)},\end{align}
Similarly, when
![]() $\varPhi_\lambda$
is one of the
$\varPhi_\lambda$
is one of the
![]() $\mathscr{H}_\lambda$
,
$\mathscr{H}_\lambda$
,
![]() $\mathscr{L}^{\,(\gamma)}_\lambda$
,
$\mathscr{L}^{\,(\gamma)}_\lambda$
,
![]() $\mathscr{J}^{\,(\gamma_1,\gamma_2)}_\lambda$
, the Schur expansion is
$\mathscr{J}^{\,(\gamma_1,\gamma_2)}_\lambda$
, the Schur expansion is
with
 \begin{align}\Upsilon_{\lambda\mu}^{(J)}&=(\!-1)^{|\lambda|+|\mu|}\left(\prod_{j=1}^n\frac{1}{\Gamma(2\lambda_j+2n-2j+\gamma_1+\gamma_2+1)}\right)\frac{G_\lambda(n,\gamma_1)G_\lambda(n,0)}{G_\mu(n,\gamma_1)G_\mu(n,0)}\tilde{\mathcal{D}}^{(J)}_{\lambda\mu},\end{align}
\begin{align}\Upsilon_{\lambda\mu}^{(J)}&=(\!-1)^{|\lambda|+|\mu|}\left(\prod_{j=1}^n\frac{1}{\Gamma(2\lambda_j+2n-2j+\gamma_1+\gamma_2+1)}\right)\frac{G_\lambda(n,\gamma_1)G_\lambda(n,0)}{G_\mu(n,\gamma_1)G_\mu(n,0)}\tilde{\mathcal{D}}^{(J)}_{\lambda\mu},\end{align}
and
The coefficients
![]() $\Psi_{\lambda\mu}$
and
$\Psi_{\lambda\mu}$
and
![]() $\Upsilon_{\lambda\mu}$
are nothing but the determinants
$\Upsilon_{\lambda\mu}$
are nothing but the determinants
![]() $\det(a_{\lambda_j+n-j,\mu_k+n-k})$
and
$\det(a_{\lambda_j+n-j,\mu_k+n-k})$
and
![]() $\det(b_{\lambda_j+n-j,\mu_k+n-k})$
where
$\det(b_{\lambda_j+n-j,\mu_k+n-k})$
where
![]() $a_{j,k}$
and
$a_{j,k}$
and
![]() $b_{j,k}$
are the coefficients that appear when the monomial is expanded in the univariate polynomial basis and vice-versa, respectively. Coefficients
$b_{j,k}$
are the coefficients that appear when the monomial is expanded in the univariate polynomial basis and vice-versa, respectively. Coefficients
![]() $\Psi_{\lambda\mu}$
and
$\Psi_{\lambda\mu}$
and
![]() $\Phi_{\lambda\mu}$
differ slightly from [Reference Jonnadula, Keating and Mezzadri34] since we used monic polynomials in the definition (2.2). In this paper, the above results play an important role in studying the correlations of characteristic polynomials and secular coefficients.
$\Phi_{\lambda\mu}$
differ slightly from [Reference Jonnadula, Keating and Mezzadri34] since we used monic polynomials in the definition (2.2). In this paper, the above results play an important role in studying the correlations of characteristic polynomials and secular coefficients.
2.1 Moments of characteristic polynomials
Analogous to the Dual Cauchy identity satisfied by the Schur polynomials, which plays a crucial role in computing the correlations of characteristic polynomials of the unitary group, the multivariate polynomials satisfy the following identity.
Lemma 2.1 (Generalised dual Cauchy identity). Let
![]() $k,N\in\mathbb{N}$
. For
$k,N\in\mathbb{N}$
. For
![]() $\lambda\subseteq (N^k)\equiv (\underbrace{N,\dots,N}_{k})$
, let
$\lambda\subseteq (N^k)\equiv (\underbrace{N,\dots,N}_{k})$
, let
![]() $\tilde{\lambda}=(k-\lambda_N^\prime,\dots,k-\lambda_1^\prime)$
. Then
$\tilde{\lambda}=(k-\lambda_N^\prime,\dots,k-\lambda_1^\prime)$
. Then
 \begin{equation}\prod_{i=1}^k\prod_{j=1}^N(t_i-x_j) = \sum_{\lambda\subseteq (N^k)} (\!-1)^{|\tilde{\lambda}|}\varPhi_\lambda(t_1,\dots,t_k)\varPhi_{\tilde{\lambda}}(x_1,\dots ,x_N).\end{equation}
\begin{equation}\prod_{i=1}^k\prod_{j=1}^N(t_i-x_j) = \sum_{\lambda\subseteq (N^k)} (\!-1)^{|\tilde{\lambda}|}\varPhi_\lambda(t_1,\dots,t_k)\varPhi_{\tilde{\lambda}}(x_1,\dots ,x_N).\end{equation}
Here
![]() $\lambda=(\lambda_1,\dots,\lambda_k)$
is a sub-partition of
$\lambda=(\lambda_1,\dots,\lambda_k)$
is a sub-partition of
![]() $(N^k)$
indicated by
$(N^k)$
indicated by
![]() $\lambda\subseteq (N^k)$
(each
$\lambda\subseteq (N^k)$
(each
![]() $\lambda_j\leq N$
for
$\lambda_j\leq N$
for
![]() $j=1,\dots, k$
) and
$j=1,\dots, k$
) and
![]() $\lambda^\prime$
is the conjugate partition of
$\lambda^\prime$
is the conjugate partition of
![]() $\lambda$
. As the polynomials
$\lambda$
. As the polynomials
![]() $\varPhi_\lambda$
are orthogonal with respect to the joint eigenvalue density of Hermitian ensembles,
$\varPhi_\lambda$
are orthogonal with respect to the joint eigenvalue density of Hermitian ensembles,
(2.18) gives a compact way to calculate the correlation functions and moments of characteristic polynomials of unitary invariant Hermitian ensembles.
Proposition 2.1 Let M be an
![]() $N\times N$
GUE, LUE or JUE matrix and
$N\times N$
GUE, LUE or JUE matrix and
![]() $t_1,\dots, t_k\in\mathbb{C}$
. Then, using the generalised dual Cauchy identity [Reference Jonnadula, Keating and Mezzadri34],
$t_1,\dots, t_k\in\mathbb{C}$
. Then, using the generalised dual Cauchy identity [Reference Jonnadula, Keating and Mezzadri34],
 \begin{align}(a)\quad\mathbb{E}^{(H)}_N\left[\prod_{j=1}^k\det(t_j - M)\right] &=\mathscr{H}_{(N^k)}(t_1,\dots, t_k)\end{align}
\begin{align}(a)\quad\mathbb{E}^{(H)}_N\left[\prod_{j=1}^k\det(t_j - M)\right] &=\mathscr{H}_{(N^k)}(t_1,\dots, t_k)\end{align}
 \begin{align}(b)\quad\mathbb{E}^{(L)}_N\left[\prod_{j=1}^k\det(t_j-M)\right] &= \mathscr{L}^{(\gamma)}_{(N^k)}(t_1,\dots,t_k)\end{align}
\begin{align}(b)\quad\mathbb{E}^{(L)}_N\left[\prod_{j=1}^k\det(t_j-M)\right] &= \mathscr{L}^{(\gamma)}_{(N^k)}(t_1,\dots,t_k)\end{align}
 \begin{align}(c)\quad\mathbb{E}^{(J)}_N\left[\prod_{j=1}^k\det(t_j-M)\right] &= \mathscr{J}^{(\gamma_1,\gamma_2)}_{(N^k)}(t_1,\dots,t_k).\end{align}
\begin{align}(c)\quad\mathbb{E}^{(J)}_N\left[\prod_{j=1}^k\det(t_j-M)\right] &= \mathscr{J}^{(\gamma_1,\gamma_2)}_{(N^k)}(t_1,\dots,t_k).\end{align}
The moments can be readily computed from the above formulae by taking the limit
![]() $t_j\rightarrow t$
for
$t_j\rightarrow t$
for
![]() $j=1,\dots ,k$
. This leads to a determinantal formula for the moments involving the derivatives of orthogonal polynomials. Alternatively, using the expansions equations (2.14), (2.15), (2.16) and the relations
$j=1,\dots ,k$
. This leads to a determinantal formula for the moments involving the derivatives of orthogonal polynomials. Alternatively, using the expansions equations (2.14), (2.15), (2.16) and the relations
 \begin{equation}\begin{split}S_\lambda(t,\dots,t)&=t^{|\lambda|}S_\lambda(1,\dots,1),\\S_\lambda(\underbrace{1,\dots,1}_{k})& =\frac{1}{|\lambda|!}C_\lambda(k)\,{\text{dim $V_\lambda$}},\end{split}\end{equation}
\begin{equation}\begin{split}S_\lambda(t,\dots,t)&=t^{|\lambda|}S_\lambda(1,\dots,1),\\S_\lambda(\underbrace{1,\dots,1}_{k})& =\frac{1}{|\lambda|!}C_\lambda(k)\,{\text{dim $V_\lambda$}},\end{split}\end{equation}
where the dimension of the irreducible representation of the symmetric group is
one can compute the moments of the characteristic polynomials.
Proposition 2.2. Let
![]() $\lambda=(N^{k})$
. The moments of characteristic polynomial are given by [Reference Jonnadula, Keating and Mezzadri34]
$\lambda=(N^{k})$
. The moments of characteristic polynomial are given by [Reference Jonnadula, Keating and Mezzadri34]
 \begin{align} \mathbb{E}^{(H)}_N\left[\det(t-M)^k\right] &= C_\lambda(k)\sum_{\nu\subseteq \lambda}\left(\frac{-1}{2N}\right)^{\frac{|\lambda|-|\nu|}{2}}\frac{\dim V_\nu}{|\nu|!} D^{(H)}_{\lambda\nu}t^{|\nu|}\end{align}
\begin{align} \mathbb{E}^{(H)}_N\left[\det(t-M)^k\right] &= C_\lambda(k)\sum_{\nu\subseteq \lambda}\left(\frac{-1}{2N}\right)^{\frac{|\lambda|-|\nu|}{2}}\frac{\dim V_\nu}{|\nu|!} D^{(H)}_{\lambda\nu}t^{|\nu|}\end{align}
 \begin{align}\mathbb{E}^{(J)}_N\left[\det(t-M)^k\right] &= \left(\prod_{j=N}^{N+k-1}\frac{1}{\Gamma(2j+\gamma_1+\gamma_2+1)}\right)(\!-1)^{Nk}\frac{G_\lambda(k,\gamma_1)G_\lambda(k,0)}{G_0(k,0)}\nonumber\\&\quad\times \sum_{\nu\subseteq\lambda}\frac{(\!-1)^{|\nu|}}{|\nu|!\,G_\nu(k,\gamma_1)}\dim V_\nu \tilde{\mathcal{D}}^{(J)}_{\lambda\nu}t^{|\nu|}.\end{align}
\begin{align}\mathbb{E}^{(J)}_N\left[\det(t-M)^k\right] &= \left(\prod_{j=N}^{N+k-1}\frac{1}{\Gamma(2j+\gamma_1+\gamma_2+1)}\right)(\!-1)^{Nk}\frac{G_\lambda(k,\gamma_1)G_\lambda(k,0)}{G_0(k,0)}\nonumber\\&\quad\times \sum_{\nu\subseteq\lambda}\frac{(\!-1)^{|\nu|}}{|\nu|!\,G_\nu(k,\gamma_1)}\dim V_\nu \tilde{\mathcal{D}}^{(J)}_{\lambda\nu}t^{|\nu|}.\end{align}
These results give an expansion in powers of the spectral parameter t for a fixed N. Equations (2.25), (2.26), (2.27) can also be interpreted as a formal power series in the variable t for small t. In the next section, we perform explicit calculations to investigate the N-dependence of the coefficients and the convergence properties of the sum.
3. Asymptotics
In this section, we consider the asymptotics of the moments of characteristic polynomials, appropriately scaled, for the GUE. By exploiting the integral representation of the classical Hermite polynomials, Brezin and Hikami [Reference Brézin and Hikami9] showed that the moments of characteristic polynomials satisfy
 \begin{equation}\mathbb{E}^{(H)}_N\left[\det(t-M)^{2k}\right] \sim e^{-Nk}e^{Nk\frac{t^2}{2}}(2\pi N\rho_{sc}(t))^{k^2}\prod_{j=0}^{k-1}\frac{j!}{(k+j)!},\end{equation}
\begin{equation}\mathbb{E}^{(H)}_N\left[\det(t-M)^{2k}\right] \sim e^{-Nk}e^{Nk\frac{t^2}{2}}(2\pi N\rho_{sc}(t))^{k^2}\prod_{j=0}^{k-1}\frac{j!}{(k+j)!},\end{equation}
as
![]() $N\to\infty$
with t fixed, where the asymptotic eigenvalue density is
$N\to\infty$
with t fixed, where the asymptotic eigenvalue density is
Using (2.25), we show in Section 3.1 that
 \begin{equation}\mathbb{E}^{(H)}_N\left[\det M^{2k}\right] \sim e^{-Nk}(2N)^{k^2}\prod_{j=0}^{k-1}\frac{j!}{(k+j)!},\end{equation}
\begin{equation}\mathbb{E}^{(H)}_N\left[\det M^{2k}\right] \sim e^{-Nk}(2N)^{k^2}\prod_{j=0}^{k-1}\frac{j!}{(k+j)!},\end{equation}
which coincides with (3.1) for
![]() $t=0$
. For
$t=0$
. For
![]() $t\neq 0$
, the radius of convergence of the series expansion of the moments, scaled to compare with (3.1) shrinks when
$t\neq 0$
, the radius of convergence of the series expansion of the moments, scaled to compare with (3.1) shrinks when
![]() $N\to\infty$
and the expansion cannot be used straightforwardly to compute the asymptotics. Moreover, the formula is different for even and odd dimensional GUE matrices. However, we observe that when one averages over consecutive even and odd dimensions, the divergent N-dependence of the coefficients cancels, leaving terms that do coincide with the expansion of
$N\to\infty$
and the expansion cannot be used straightforwardly to compute the asymptotics. Moreover, the formula is different for even and odd dimensional GUE matrices. However, we observe that when one averages over consecutive even and odd dimensions, the divergent N-dependence of the coefficients cancels, leaving terms that do coincide with the expansion of
![]() $\rho_{sc}(x)$
. These cases are discussed in Sections 3.1 and 3.2 in more detail.
$\rho_{sc}(x)$
. These cases are discussed in Sections 3.1 and 3.2 in more detail.
3.1 Centre of the semi-circle
Let
![]() $\lambda=(N^{2k})$
. For any finite N, we have
$\lambda=(N^{2k})$
. For any finite N, we have
Proposition 3.1.
 \begin{equation}\begin{split}D^{(H)}_{\lambda 0} &= \prod_{j=0}^{k-1} \frac{j!^2}{(m+j)!^2}, \quad N=2m,\,\, m\in\mathbb{N},\\D^{(H)}_{\lambda 0} &= (\!-1)^k\frac{m!}{(m+k)!}\prod_{j=0}^{k-1} \frac{j!^2}{(m+j)!^2}, \quad N=2m+1,\quad m\in\mathbb{N}.\end{split}\end{equation}
\begin{equation}\begin{split}D^{(H)}_{\lambda 0} &= \prod_{j=0}^{k-1} \frac{j!^2}{(m+j)!^2}, \quad N=2m,\,\, m\in\mathbb{N},\\D^{(H)}_{\lambda 0} &= (\!-1)^k\frac{m!}{(m+k)!}\prod_{j=0}^{k-1} \frac{j!^2}{(m+j)!^2}, \quad N=2m+1,\quad m\in\mathbb{N}.\end{split}\end{equation}
Proof. The determinant
![]() $D^{(H)}_{\lambda 0}$
can be evaluated as follows. Let
$D^{(H)}_{\lambda 0}$
can be evaluated as follows. Let
![]() $N=2m$
, then
$N=2m$
, then
 \begin{align}D^{(H)}_{\lambda 0}&=\det\left[\unicode{x1D7D9}_{i-j=\text{0 mod 2}}\left(\left(m+\frac{i-j}{2}\right)!\right)^{-1}\right]_{1\leq i,j\leq k} \nonumber\\&= \prod_{j=0}^{k-1}\frac{1}{(m+j)!^2}\left|\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c}1 & 0 & m & 0 &\dots &\dfrac{m!}{(m-k+1)!} & 0\\0 & 1 & 0 & m &\dots & 0 & \dfrac{m!}{(m-k+1)!}\\ \\[-8pt]1 & 0 & m+1 & 0 &\dots & \dfrac{(m+1)!}{(m-k+2)!} &0\\ \\[-8pt]0 & 1 & 0 & m+1 &\dots &0 &\dfrac{(m+1)!}{(m-k+2)!}\\ \\[-8pt] & & & &\vdots & & \\ \\[-8pt]1 & 0 &m+k-1 & 0 &\dots &\dfrac{(m+k-1)!}{m!} &0\\ \\[-8pt]0 & 1 & 0 &m+k-1 &\dots &0 &\dfrac{(m+k-1)!}{m!}\end{array}\right|.\end{align}
\begin{align}D^{(H)}_{\lambda 0}&=\det\left[\unicode{x1D7D9}_{i-j=\text{0 mod 2}}\left(\left(m+\frac{i-j}{2}\right)!\right)^{-1}\right]_{1\leq i,j\leq k} \nonumber\\&= \prod_{j=0}^{k-1}\frac{1}{(m+j)!^2}\left|\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c}1 & 0 & m & 0 &\dots &\dfrac{m!}{(m-k+1)!} & 0\\0 & 1 & 0 & m &\dots & 0 & \dfrac{m!}{(m-k+1)!}\\ \\[-8pt]1 & 0 & m+1 & 0 &\dots & \dfrac{(m+1)!}{(m-k+2)!} &0\\ \\[-8pt]0 & 1 & 0 & m+1 &\dots &0 &\dfrac{(m+1)!}{(m-k+2)!}\\ \\[-8pt] & & & &\vdots & & \\ \\[-8pt]1 & 0 &m+k-1 & 0 &\dots &\dfrac{(m+k-1)!}{m!} &0\\ \\[-8pt]0 & 1 & 0 &m+k-1 &\dots &0 &\dfrac{(m+k-1)!}{m!}\end{array}\right|.\end{align}
Perform the row operations
![]() $R_{2j}=R_{2j}-R_{2j-2}$
,
$R_{2j}=R_{2j}-R_{2j-2}$
,
![]() $R_{2j-1}=R_{2j-1}-R_{2j-3}$
with j running from
$R_{2j-1}=R_{2j-1}-R_{2j-3}$
with j running from
![]() $k,k-1,\dots,2$
in that order. Using the Pascal’s rule for binomial coefficients, we get
$k,k-1,\dots,2$
in that order. Using the Pascal’s rule for binomial coefficients, we get
 \begin{equation}D^{(H)}_{\lambda 0} = (k-1)!^2\prod_{j=0}^{k-1}\frac{1}{(m+j)!^2}\left|\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c}1 & 0 & m & 0 &\dots &\dfrac{m!}{(m-k+1)!} & 0\\ \\[-9pt]0 & 1 & 0 & m &\dots & 0 & \dfrac{m!}{(m-k+1)!}\\ \\[-9pt]0 & 0 & 1 & 0 &\dots & \dfrac{m!}{(m-k+2)!} & 0\\ \\[-9pt]0 & 0 & 0 & 1 &\dots & 0 & \dfrac{m!}{(m-k+2)!} \\ \\[-9pt]& & & &\vdots & & \\ \\[-9pt]0 & 0 & 1 & 0 &\dots & \dfrac{(m+k-2)!}{m!} & 0\\ \\[-9pt]0 & 0 & 0 & 1 &\dots & 0 & \dfrac{(m+k-2)!}{m!}\end{array}\right|.\end{equation}
\begin{equation}D^{(H)}_{\lambda 0} = (k-1)!^2\prod_{j=0}^{k-1}\frac{1}{(m+j)!^2}\left|\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c}1 & 0 & m & 0 &\dots &\dfrac{m!}{(m-k+1)!} & 0\\ \\[-9pt]0 & 1 & 0 & m &\dots & 0 & \dfrac{m!}{(m-k+1)!}\\ \\[-9pt]0 & 0 & 1 & 0 &\dots & \dfrac{m!}{(m-k+2)!} & 0\\ \\[-9pt]0 & 0 & 0 & 1 &\dots & 0 & \dfrac{m!}{(m-k+2)!} \\ \\[-9pt]& & & &\vdots & & \\ \\[-9pt]0 & 0 & 1 & 0 &\dots & \dfrac{(m+k-2)!}{m!} & 0\\ \\[-9pt]0 & 0 & 0 & 1 &\dots & 0 & \dfrac{(m+k-2)!}{m!}\end{array}\right|.\end{equation}
Next perform
![]() $R_{2j}=R_{2j}-R_{2j-2}$
,
$R_{2j}=R_{2j}-R_{2j-2}$
,
![]() $R_{2j-1}=R_{2j-1}-R_{2j-3}$
with j running from
$R_{2j-1}=R_{2j-1}-R_{2j-3}$
with j running from
![]() $k,k-1,\dots,3$
in that order. Repeat this process
$k,k-1,\dots,3$
in that order. Repeat this process
![]() $k-2$
more times to reach an upper triangular matrix with determinant given in (3.5). Similarly,
$k-2$
more times to reach an upper triangular matrix with determinant given in (3.5). Similarly,
![]() $D^{(H)}_{\lambda 0} $
can be calculated for N odd.
$D^{(H)}_{\lambda 0} $
can be calculated for N odd.
Define
 \begin{equation}\begin{split}&D_e(N)= \prod_{j=0}^{k-1}\frac{j!^2}{(m+j)!^2},\quad N=2m,\\&D_o(N) = (\!-1)^k\frac{m!}{(m+k)!}\prod_{j=0}^{k-1}\frac{j!^2}{(m+j)!^2},\quad N=2m+1.\end{split}\end{equation}
\begin{equation}\begin{split}&D_e(N)= \prod_{j=0}^{k-1}\frac{j!^2}{(m+j)!^2},\quad N=2m,\\&D_o(N) = (\!-1)^k\frac{m!}{(m+k)!}\prod_{j=0}^{k-1}\frac{j!^2}{(m+j)!^2},\quad N=2m+1.\end{split}\end{equation}
Using this notation, (3.4) reads
 \begin{equation} \mathbb{E}^{(H)}_N\left[\det M^{2k}\right] = \left(\!-\frac{1}{2N}\right)^{Nk}\times \begin{cases} C_\lambda(2k) D_e(N),\quad \text{N even},\\ \\[-8pt] C_\lambda(2k)D_o(N),\quad \text{N odd}. \end{cases} \end{equation}
\begin{equation} \mathbb{E}^{(H)}_N\left[\det M^{2k}\right] = \left(\!-\frac{1}{2N}\right)^{Nk}\times \begin{cases} C_\lambda(2k) D_e(N),\quad \text{N even},\\ \\[-8pt] C_\lambda(2k)D_o(N),\quad \text{N odd}. \end{cases} \end{equation}
The functions
![]() $C_\lambda(2k) D_e(N)$
and
$C_\lambda(2k) D_e(N)$
and
![]() $C_\lambda(2k) D_o(N)$
,
$C_\lambda(2k) D_o(N)$
,
![]() $\lambda=(N^{2k})$
, can be expressed in terms of the ratios of factorials,
$\lambda=(N^{2k})$
, can be expressed in terms of the ratios of factorials,
 \begin{equation}\begin{split}C_{(N^{2k})}(2k) D_e(N) &= \prod_{j=0}^{k-1}\frac{(2m+j)!(2m+k+j)!}{\left(m+j\right)!^2}\frac{j!}{(k+j)!},\quad N=2m,\\C_{(N^{2k})}(2k) D_o(N) &= (\!-1)^k\frac{m!}{(m+k)!}\prod_{j=0}^{k-1}\frac{(2m+1+j)!(2m+1+k+j)!}{\left(m+j\right)!^2}\frac{j!}{(k+j)!},\quad N=2m+1.\end{split}\end{equation}
\begin{equation}\begin{split}C_{(N^{2k})}(2k) D_e(N) &= \prod_{j=0}^{k-1}\frac{(2m+j)!(2m+k+j)!}{\left(m+j\right)!^2}\frac{j!}{(k+j)!},\quad N=2m,\\C_{(N^{2k})}(2k) D_o(N) &= (\!-1)^k\frac{m!}{(m+k)!}\prod_{j=0}^{k-1}\frac{(2m+1+j)!(2m+1+k+j)!}{\left(m+j\right)!^2}\frac{j!}{(k+j)!},\quad N=2m+1.\end{split}\end{equation}
Denote
 \begin{equation}\gamma_k = \prod_{j=0}^{k-1}\frac{j!}{(k+j)!}.\end{equation}
\begin{equation}\gamma_k = \prod_{j=0}^{k-1}\frac{j!}{(k+j)!}.\end{equation}
The universal constant
![]() $\gamma_k$
is present in the moments for any finite N. To compute the large N limit, we require the asymptotic expansion of (3.10). In Appendix A, we compute the first few terms in this expansion. As
$\gamma_k$
is present in the moments for any finite N. To compute the large N limit, we require the asymptotic expansion of (3.10). In Appendix A, we compute the first few terms in this expansion. As
![]() $N\rightarrow\infty$
,
$N\rightarrow\infty$
,
 \begin{equation}\begin{split}&C_{(N^{2k})}(2k)D_e(N) = e^{-Nk}(2N)^{Nk+k^2}\gamma_k\left[1+\frac{k}{6N}(4k^2+1) + O(N^{-2})\right], \quad N\,\, \text{even},\\ \\[-8pt] &C_{(N^{2k})}(2k)D_o(N) = (\!-1)^ke^{-Nk}(2N)^{Nk+k^2}\gamma_k\left[1 + \frac{k}{3N}(2k^2-1) + O(N^{-2})\right], \, N\,\, \text{odd}.\end{split}\end{equation}
\begin{equation}\begin{split}&C_{(N^{2k})}(2k)D_e(N) = e^{-Nk}(2N)^{Nk+k^2}\gamma_k\left[1+\frac{k}{6N}(4k^2+1) + O(N^{-2})\right], \quad N\,\, \text{even},\\ \\[-8pt] &C_{(N^{2k})}(2k)D_o(N) = (\!-1)^ke^{-Nk}(2N)^{Nk+k^2}\gamma_k\left[1 + \frac{k}{3N}(2k^2-1) + O(N^{-2})\right], \, N\,\, \text{odd}.\end{split}\end{equation}
Plugging (3.12) in (3.9), the leading order behaviour of the moments for N even and N odd is
which coincides with (3.1) for
![]() $t=0$
. On the other hand, the sub-leading behaviour depends on the parity of N.
$t=0$
. On the other hand, the sub-leading behaviour depends on the parity of N.
3.2 Away from the centre of the semi-circle
Recall that
 \begin{equation}\begin{split} \mathbb{E}^{(H)}_N\left[\det(t-M)^{2k}\right] &= C_\lambda(2k)\sum_{\nu\subseteq\lambda}\left(\!-\frac{1}{2N}\right)^{\frac{|\lambda|-|\nu|}{2}}\frac{\text{dim}\, V_\nu}{|\nu|!} D^{(H)}_{\lambda\nu}t^{|\nu|}. \end{split} \end{equation}
\begin{equation}\begin{split} \mathbb{E}^{(H)}_N\left[\det(t-M)^{2k}\right] &= C_\lambda(2k)\sum_{\nu\subseteq\lambda}\left(\!-\frac{1}{2N}\right)^{\frac{|\lambda|-|\nu|}{2}}\frac{\text{dim}\, V_\nu}{|\nu|!} D^{(H)}_{\lambda\nu}t^{|\nu|}. \end{split} \end{equation}
To compute the asymptotics near the centre of the semi-circle,
![]() $t\neq 0$
, we need to evaluate
$t\neq 0$
, we need to evaluate
![]() $D^{(H)}_{\lambda\nu}$
for a non-empty partition
$D^{(H)}_{\lambda\nu}$
for a non-empty partition
![]() $\nu$
. In Table. 1, we give the values of
$\nu$
. In Table. 1, we give the values of
![]() $D^{(H)}_{\lambda\nu}$
when
$D^{(H)}_{\lambda\nu}$
when
![]() $\nu$
is a partition of 2 and 4.
$\nu$
is a partition of 2 and 4.
Table 1. The values of determinant
![]() $D^{(H)}_{\lambda\nu}$
for
$D^{(H)}_{\lambda\nu}$
for
![]() $\lambda=(N^{2k})$
. Determinants
$\lambda=(N^{2k})$
. Determinants
![]() $D_e$
and
$D_e$
and
![]() $D_o$
are given in (3.8).
$D_o$
are given in (3.8).
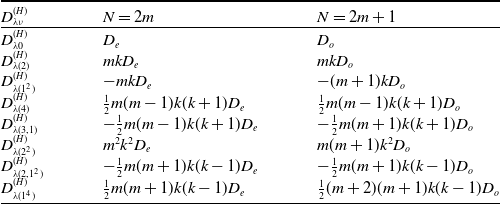
Therefore,
 \begin{equation} \begin{split} \mathbb{E}^{(H)}_N\left[\det(t-M)^{2k}\right] =& \sum_{\nu\subseteq\lambda}\left(\!-\frac{1}{2N}\right)^{\frac{|\lambda|-|\nu|}{2}}\frac{\text{dim}\, V_\nu}{|\nu|!}t^{|\nu|}\,\text{poly}_{\frac{|\nu|}{2}}(N,k)\\ &\times \begin{cases} C_\lambda(2k) D_e,\quad \text{N even},\\ \\[-8pt] C_\lambda(2k)D_o,\quad \text{N odd}, \end{cases} \end{split} \end{equation}
\begin{equation} \begin{split} \mathbb{E}^{(H)}_N\left[\det(t-M)^{2k}\right] =& \sum_{\nu\subseteq\lambda}\left(\!-\frac{1}{2N}\right)^{\frac{|\lambda|-|\nu|}{2}}\frac{\text{dim}\, V_\nu}{|\nu|!}t^{|\nu|}\,\text{poly}_{\frac{|\nu|}{2}}(N,k)\\ &\times \begin{cases} C_\lambda(2k) D_e,\quad \text{N even},\\ \\[-8pt] C_\lambda(2k)D_o,\quad \text{N odd}, \end{cases} \end{split} \end{equation}
where
![]() $\text{poly}_{j}(N,k)$
denotes a polynomial of degree j in the variables N, k, and the explicit expressions are given in Table 1 for
$\text{poly}_{j}(N,k)$
denotes a polynomial of degree j in the variables N, k, and the explicit expressions are given in Table 1 for
![]() $j\leq 4$
. By referring to (3.10), it is interesting to see that the universal constant
$j\leq 4$
. By referring to (3.10), it is interesting to see that the universal constant
![]() $\gamma_k$
is a factor of the moments for any finite N. The first few terms in the moments of characteristic polynomials are
$\gamma_k$
is a factor of the moments for any finite N. The first few terms in the moments of characteristic polynomials are
 \begin{equation}\begin{split}\mathbb{E}^{(H)}_N[\det(t-M)^{2k}]&=\left(\!-\frac{1}{2N}\right)^{Nk}C_\lambda(2k)D_e\\ \\[-8pt]&\quad\times \left[1 + \left(\frac{2^2N^2}{4!}\right)Nk\,t^4 + \left(\frac{2^3N^3}{6!}\right)2Nk(2k-N)t^6 \right.\\ \\[-8pt]&\qquad\left. +\left(\frac{2^4N^4}{8!}\right)Nk (4 N^2 - 17 Nk + 16 k^2+2)t^8 \right.\\ \\[-8pt]&\qquad\left.+ O(t^{10}) \right],\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \text{N even},\\ \\[-8pt]\mathbb{E}^{(H)}_N[\det(t-M)^{2k}]&=\left(\!-\frac{1}{2N}\right)^{Nk}C_\lambda(2k)D_o\left[1 +\left(\frac{2N}{2!}\right)kt^2 +\left(\frac{2^2N^2}{4!}\right)(k^2-Nk)\,t^4\right.\\ \\[-8pt]&\quad\left. + \left(\frac{2^3N^3}{6!}\right)k(2N^2-3Nk+k^2)t^6 \right.\\ \\[-8pt]&\quad\left. +\left(\frac{2^4N^4}{8!}\right)k (\!- 4 N^3+ 15 N^2k - 6 N k^2 -2N+ k^3-4k)t^8\right.\\ \\[-8pt]&\quad\left. +\,\, O(t^{10}) \right],\quad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \text{N odd}.\end{split}\end{equation}
\begin{equation}\begin{split}\mathbb{E}^{(H)}_N[\det(t-M)^{2k}]&=\left(\!-\frac{1}{2N}\right)^{Nk}C_\lambda(2k)D_e\\ \\[-8pt]&\quad\times \left[1 + \left(\frac{2^2N^2}{4!}\right)Nk\,t^4 + \left(\frac{2^3N^3}{6!}\right)2Nk(2k-N)t^6 \right.\\ \\[-8pt]&\qquad\left. +\left(\frac{2^4N^4}{8!}\right)Nk (4 N^2 - 17 Nk + 16 k^2+2)t^8 \right.\\ \\[-8pt]&\qquad\left.+ O(t^{10}) \right],\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \text{N even},\\ \\[-8pt]\mathbb{E}^{(H)}_N[\det(t-M)^{2k}]&=\left(\!-\frac{1}{2N}\right)^{Nk}C_\lambda(2k)D_o\left[1 +\left(\frac{2N}{2!}\right)kt^2 +\left(\frac{2^2N^2}{4!}\right)(k^2-Nk)\,t^4\right.\\ \\[-8pt]&\quad\left. + \left(\frac{2^3N^3}{6!}\right)k(2N^2-3Nk+k^2)t^6 \right.\\ \\[-8pt]&\quad\left. +\left(\frac{2^4N^4}{8!}\right)k (\!- 4 N^3+ 15 N^2k - 6 N k^2 -2N+ k^3-4k)t^8\right.\\ \\[-8pt]&\quad\left. +\,\, O(t^{10}) \right],\quad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \text{N odd}.\end{split}\end{equation}
Up to a factor of
![]() $(\!-1)^k$
, both
$(\!-1)^k$
, both
![]() $C_\lambda D_e$
and
$C_\lambda D_e$
and
![]() $C_\lambda D_o$
have the same leading term,
$C_\lambda D_o$
have the same leading term,
but they differ at sub-leading order as shown in (3.12). In Appendix A, we give the expansion of
![]() $C_\lambda(N)D_e$
and
$C_\lambda(N)D_e$
and
![]() $C_\lambda(N)D_o$
up to
$C_\lambda(N)D_o$
up to
![]() $O(N^{-6})$
. Note that the fact that the coefficients are polynomial functions of N means that the radius of convergence of the expansion shrinks as
$O(N^{-6})$
. Note that the fact that the coefficients are polynomial functions of N means that the radius of convergence of the expansion shrinks as
![]() $N\to\infty$
. This means that for
$N\to\infty$
. This means that for
![]() $t\ne 0$
we cannot use this expansion straightforwardly to determine the large-N asymptotics.
$t\ne 0$
we cannot use this expansion straightforwardly to determine the large-N asymptotics.
3.2.1 Second moment
The correlations of characteristic polynomials are connected to the correlation functions of random matrices [Reference Mehta40, Reference Forrester20, Reference Mezzadri, Snaith and Hitchin41]. In particular,
where
![]() $R^{(N)}_1$
is the one-point density of eigenvalues of matrix size N. As the second moment of the characteristic polynomial is related to the density of states, it is natural to expect the semi-circle law in the limit
$R^{(N)}_1$
is the one-point density of eigenvalues of matrix size N. As the second moment of the characteristic polynomial is related to the density of states, it is natural to expect the semi-circle law in the limit
![]() $N\rightarrow\infty$
as given in (3.1) for a fixed t inside the support of the spectrum. Re-writing (3.1) for
$N\rightarrow\infty$
as given in (3.1) for a fixed t inside the support of the spectrum. Re-writing (3.1) for
![]() $k=1$
,
$k=1$
,
which as an expansion in t reads
We now make an observation that we consider surprising: for
![]() $k=1$
, starting with (3.14) there is a formal procedure that leads to (3.20). Inserting the asymptotics of
$k=1$
, starting with (3.14) there is a formal procedure that leads to (3.20). Inserting the asymptotics of
![]() $C_\lambda D_e$
and
$C_\lambda D_e$
and
![]() $C_\lambda D_o$
in (3.16), one obtains
$C_\lambda D_o$
in (3.16), one obtains
 \begin{align}&e^{-\frac{N t^2}{2}}\mathbb{E}^{(H)}_{N}\left[\det(t-M)^{2}\right] \nonumber\\&= 2Ne^{-N}\bigg[1+\left(\!-\frac{1}{2}N-\frac{5}{12}+O(N^{-1})\right)t^2+\left(\frac{1}{6}N^3 +\frac{19}{72}N^2+\frac{17}{216}N-\frac{811}{77,760}+O(N^{-1})\right)t^4 \nonumber\\&\qquad+\left(\!-\frac{1}{45}N^5-\frac{31}{540}N^4-\frac{323}{6480}N^3-\frac{3667}{291,600}N^2+\frac{799}{1,749,600}N-\frac{640,879}{587,865,600}+ O(N^{-1})\right)t^6 \nonumber\\&\qquad +O(N^{7})O(t^8)\bigg],\quad\text{N even}, \nonumber\\&e^{-\frac{N t^2}{2}}\mathbb{E}^{(H)}_{N}\left[\det(t-M)^{2}\right] \nonumber\\&= 2Ne^{-N}\bigg[1+\left(\frac{1}{2}N+\frac{1}{6}+O(N^{-1})\right)t^2+\left(\!-\frac{1}{6}N^3-\frac{19}{72}N^2-\frac{17}{216}N-\frac{101}{19,440}+O(N^{-1})\right)t^4 \nonumber\\&\quad +\left(\frac{1}{45}N^5+\frac{31}{540}N^4+\frac{323}{6480}N^3+\frac{3667}{291,600}N^2-\frac{799}{1,749,600}N-\frac{15,853}{18,370,800}+O(N^{-1})\right)t^6 \nonumber\\&\qquad +O(N^{7})O(t^8)\bigg],\quad\text{N odd}.\end{align}
\begin{align}&e^{-\frac{N t^2}{2}}\mathbb{E}^{(H)}_{N}\left[\det(t-M)^{2}\right] \nonumber\\&= 2Ne^{-N}\bigg[1+\left(\!-\frac{1}{2}N-\frac{5}{12}+O(N^{-1})\right)t^2+\left(\frac{1}{6}N^3 +\frac{19}{72}N^2+\frac{17}{216}N-\frac{811}{77,760}+O(N^{-1})\right)t^4 \nonumber\\&\qquad+\left(\!-\frac{1}{45}N^5-\frac{31}{540}N^4-\frac{323}{6480}N^3-\frac{3667}{291,600}N^2+\frac{799}{1,749,600}N-\frac{640,879}{587,865,600}+ O(N^{-1})\right)t^6 \nonumber\\&\qquad +O(N^{7})O(t^8)\bigg],\quad\text{N even}, \nonumber\\&e^{-\frac{N t^2}{2}}\mathbb{E}^{(H)}_{N}\left[\det(t-M)^{2}\right] \nonumber\\&= 2Ne^{-N}\bigg[1+\left(\frac{1}{2}N+\frac{1}{6}+O(N^{-1})\right)t^2+\left(\!-\frac{1}{6}N^3-\frac{19}{72}N^2-\frac{17}{216}N-\frac{101}{19,440}+O(N^{-1})\right)t^4 \nonumber\\&\quad +\left(\frac{1}{45}N^5+\frac{31}{540}N^4+\frac{323}{6480}N^3+\frac{3667}{291,600}N^2-\frac{799}{1,749,600}N-\frac{15,853}{18,370,800}+O(N^{-1})\right)t^6 \nonumber\\&\qquad +O(N^{7})O(t^8)\bigg],\quad\text{N odd}.\end{align}
Treating the above expansions as a formal series in N and taking their average gives (3.20). In Appendix B, it is shown that the average over even and odd N coincides with the semi-circle law up to
![]() $O(t^{10})$
. Also, a general expression for the coefficient of
$O(t^{10})$
. Also, a general expression for the coefficient of
![]() $t^{2j}$
in (3.14) is given for
$t^{2j}$
in (3.14) is given for
![]() $k=1$
.
$k=1$
.
Remark 1. For a fixed j, notice that the leading order terms in the coefficients of
![]() $t^{2j}$
, which depend on N, differ only by a sign for N even and odd. Therefore, after a formal average of both the series in (3.21), the coefficient of
$t^{2j}$
, which depend on N, differ only by a sign for N even and odd. Therefore, after a formal average of both the series in (3.21), the coefficient of
![]() $t^{2j}$
is equal to
$t^{2j}$
is equal to
![]() $c_{2j}+O(N^{-1})$
. The constant
$c_{2j}+O(N^{-1})$
. The constant
![]() $c_{2j}$
turns out to be the appropriate coefficient of
$c_{2j}$
turns out to be the appropriate coefficient of
![]() $t^{2j}$
in the semi-circle law.
$t^{2j}$
in the semi-circle law.
Remark 2. The behaviour exhibited by (3.21) can be understood by considering Figure 1. For a fixed N, the plot shows the behaviour of
as a function of t. The function f(N,t) is oscillatory. The magnitude of the oscillations decreases as N increases, but their length-scale decreases. Moreover, the peaks and troughs of f(N,t) for N even coincides with the troughs and peaks of N odd, respectively. For a fixed j, this explains the divergent polynomial part of N in the coefficients of
![]() $t^{2j}$
and the sign change of leading order terms in the N even and odd cases. Formally averaging the two series of f(N,t) when N is even and odd cancels out these oscillations and leaves a result that converges to the semi-circle law.
$t^{2j}$
and the sign change of leading order terms in the N even and odd cases. Formally averaging the two series of f(N,t) when N is even and odd cancels out these oscillations and leaves a result that converges to the semi-circle law.

Figure 1. We plot in (a) f(N,t), defined in (3.22), as a function of t when t is close to the origin for
![]() $N=50,\, 51$
; (b) denotes the same for
$N=50,\, 51$
; (b) denotes the same for
![]() $N=150,\, 151$
.
$N=150,\, 151$
.
Remark 3. As discussed, the size of oscillations in f(N,t) decreases as N increases. Therefore, f(N,t) converges to the semi-circle law as
![]() $N\to\infty$
independent of whether N is even or odd. But, at finite but large N, the average of f(N,t) between two consecutive integers is a significantly smoother approximation to the semi-circle law.
$N\to\infty$
independent of whether N is even or odd. But, at finite but large N, the average of f(N,t) between two consecutive integers is a significantly smoother approximation to the semi-circle law.
3.2.2 Higher moments
For higher moments, the correlations of characteristic polynomials are related to the correlation functions of eigenvalues as
 \begin{equation}R^{(N)}_k(t_1,\dots,t_k) = \frac{N!}{(N-k)!}\frac{\mathscr{Z}^{(H)}_{N-k}}{\mathscr{Z}^{(H)}_N}\exp\left(\!-\frac{N}{2}\sum_{j=1}^k t_j^2\right)\Delta^2(t_1,\dots,t_k)\mathbb{E}^{(H)}_{N-k}\left[\prod_{j=1}^k\det(t_j-M)^{2}\right],\end{equation}
\begin{equation}R^{(N)}_k(t_1,\dots,t_k) = \frac{N!}{(N-k)!}\frac{\mathscr{Z}^{(H)}_{N-k}}{\mathscr{Z}^{(H)}_N}\exp\left(\!-\frac{N}{2}\sum_{j=1}^k t_j^2\right)\Delta^2(t_1,\dots,t_k)\mathbb{E}^{(H)}_{N-k}\left[\prod_{j=1}^k\det(t_j-M)^{2}\right],\end{equation}
where
![]() $R^{(N)}_k(t_1,\dots,t_k)$
denotes a
$R^{(N)}_k(t_1,\dots,t_k)$
denotes a
![]() $k-$
point correlation function of a GUE matrix of size N. The correlations of characteristic polynomials of matrices of size
$k-$
point correlation function of a GUE matrix of size N. The correlations of characteristic polynomials of matrices of size
![]() $N-k$
are related to the correlation functions of eigenvalues of matrices of size N. The Dyson sine-kernel for the
$N-k$
are related to the correlation functions of eigenvalues of matrices of size N. The Dyson sine-kernel for the
![]() $k-$
point correlation function and (3.1) for the moments of characteristic polynomials are recovered in the Dyson limit:
$k-$
point correlation function and (3.1) for the moments of characteristic polynomials are recovered in the Dyson limit:
![]() $t_i-t_j\rightarrow 0$
,
$t_i-t_j\rightarrow 0$
,
![]() $N\rightarrow\infty$
and
$N\rightarrow\infty$
and
![]() $N(t_i-t_j)$
is kept finite when
$N(t_i-t_j)$
is kept finite when
![]() $|t_j|<2$
,
$|t_j|<2$
,
![]() $j=1,\dots,k$
.
$j=1,\dots,k$
.
In terms of the Schur polynomials,
![]() $\lambda=(N^{2k})$
,
$\lambda=(N^{2k})$
,
 \begin{equation}\mathbb{E}^{(H)}_N\left[\prod_{j=1}^{2k}\det(t_j-M)\right]=C_{\lambda}(2k) \sum_{\nu\subseteq\lambda}\left(\!-\frac{1}{2N}\right)^{\frac{|\lambda|-|\nu|}{2}}\frac{1}{C_\nu(2k)}D^{(H)}_{\lambda \nu}S_\nu(t_1,\dots,t_{2k}).\end{equation}
\begin{equation}\mathbb{E}^{(H)}_N\left[\prod_{j=1}^{2k}\det(t_j-M)\right]=C_{\lambda}(2k) \sum_{\nu\subseteq\lambda}\left(\!-\frac{1}{2N}\right)^{\frac{|\lambda|-|\nu|}{2}}\frac{1}{C_\nu(2k)}D^{(H)}_{\lambda \nu}S_\nu(t_1,\dots,t_{2k}).\end{equation}
Computing the asymptotics of moments of characteristic polynomials in the Dyson limit using (3.24) is highly non-trivial. Instead, we fix
![]() $t_j=t$
,
$t_j=t$
,
![]() $j=1,\dots, 2k$
, and give an expansion of the moments as a function of t in the large N limit.
$j=1,\dots, 2k$
, and give an expansion of the moments as a function of t in the large N limit.
As
![]() $N\rightarrow\infty$
, up to
$N\rightarrow\infty$
, up to
![]() $O(t^2)$
,
$O(t^2)$
,
 \begin{equation}\begin{split}&\mathbb{E}^{(H)}_N\left[\det(t-M)^{2k}\right] = (2N)^{k^2}e^{-Nk}\gamma_k\left[1 + O(N^3)O(t^4)\right],\qquad\qquad\qquad\qquad\qquad\quad\,\, N\,\,\text{even}\\&\mathbb{E}^{(H)}_N\left[\det(t-M)^{2k}\right] = (2N)^{k^2}e^{-Nk}\gamma_k\\&\qquad\qquad\qquad\qquad\quad\times \left[1 + t^2\left(Nk+\frac{k^2}{3}(2k^2-1) + O(N^{-1})\right) + O(N^3)O(t^4)\right],\quad N\,\,\text{odd}.\end{split}\end{equation}
\begin{equation}\begin{split}&\mathbb{E}^{(H)}_N\left[\det(t-M)^{2k}\right] = (2N)^{k^2}e^{-Nk}\gamma_k\left[1 + O(N^3)O(t^4)\right],\qquad\qquad\qquad\qquad\qquad\quad\,\, N\,\,\text{even}\\&\mathbb{E}^{(H)}_N\left[\det(t-M)^{2k}\right] = (2N)^{k^2}e^{-Nk}\gamma_k\\&\qquad\qquad\qquad\qquad\quad\times \left[1 + t^2\left(Nk+\frac{k^2}{3}(2k^2-1) + O(N^{-1})\right) + O(N^3)O(t^4)\right],\quad N\,\,\text{odd}.\end{split}\end{equation}
Note that the coefficient of
![]() $t^2$
is identically zero for even N, where as for odd N it is a polynomial in N and k. Treating the above expansions as a formal series in N and t and taking their average gives
$t^2$
is identically zero for even N, where as for odd N it is a polynomial in N and k. Treating the above expansions as a formal series in N and t and taking their average gives
By comparing with (3.1), the terms in the first and second parenthesis of (3.26) are the expansions of
![]() $e^{\frac{Nkt^2}{2}}$
and
$e^{\frac{Nkt^2}{2}}$
and
![]() $\pi\rho_{sc}(t)$
up to
$\pi\rho_{sc}(t)$
up to
![]() $O(t^2)$
, respectively.
$O(t^2)$
, respectively.
Similarly, as
![]() $N\rightarrow\infty$
, up to
$N\rightarrow\infty$
, up to
![]() $O(t^4)$
,
$O(t^4)$
,
 \begin{equation}\begin{split}\mathbb{E}^{(H)}_N\left[\det(t-M)^{2k}\right] &= (2N)^{k^2}e^{-Nk}\gamma_k\left[1 + t^4\frac{N^3k}{6}\Big(1+\frac{k}{6N}(4k^2+1) \right.\\[3pt]&\qquad \left. + \frac{k^2}{72N^2}(16k^4-16k^2-11)+\frac{k}{6480N^3}(320k^8-1200k^6 \right.\\[3pt]&\qquad \left. +708k^4+1265k^2-756)+O(N^{-4})\Big) + O(N^{5}) O(t^{6})\right],\qquad\qquad\qquad\,\, \text{N even},\\[3pt]\mathbb{E}^{(H)}_N\left[\det(t-M)^{2k}\right] &= (2N)^{k^2}e^{-Nk}\gamma_k\left[1 + t^2\left(Nk+\frac{k^2}{3}(2k^2-1) +O(N^{-1})\right)\right.\\&\qquad\left. + t^4\frac{N^3k}{6}\Big(\!-1 - \frac{2k}{3N}(k^2-2) -\frac{k^2}{18N^2}(4k^4-22k^2+13)\right.\\&\qquad\left. -\frac{k}{405N^3}(20k^8-210k^6+483k^4-385k^2+54)+O(N^{-4})\Big) \right.\\&\qquad\left. +O(N^{5})O(t^6)\right],\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad N\,\,\text{odd}.\end{split}\end{equation}
\begin{equation}\begin{split}\mathbb{E}^{(H)}_N\left[\det(t-M)^{2k}\right] &= (2N)^{k^2}e^{-Nk}\gamma_k\left[1 + t^4\frac{N^3k}{6}\Big(1+\frac{k}{6N}(4k^2+1) \right.\\[3pt]&\qquad \left. + \frac{k^2}{72N^2}(16k^4-16k^2-11)+\frac{k}{6480N^3}(320k^8-1200k^6 \right.\\[3pt]&\qquad \left. +708k^4+1265k^2-756)+O(N^{-4})\Big) + O(N^{5}) O(t^{6})\right],\qquad\qquad\qquad\,\, \text{N even},\\[3pt]\mathbb{E}^{(H)}_N\left[\det(t-M)^{2k}\right] &= (2N)^{k^2}e^{-Nk}\gamma_k\left[1 + t^2\left(Nk+\frac{k^2}{3}(2k^2-1) +O(N^{-1})\right)\right.\\&\qquad\left. + t^4\frac{N^3k}{6}\Big(\!-1 - \frac{2k}{3N}(k^2-2) -\frac{k^2}{18N^2}(4k^4-22k^2+13)\right.\\&\qquad\left. -\frac{k}{405N^3}(20k^8-210k^6+483k^4-385k^2+54)+O(N^{-4})\Big) \right.\\&\qquad\left. +O(N^{5})O(t^6)\right],\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad N\,\,\text{odd}.\end{split}\end{equation}
Taking average of the above series and factorising gives
 \begin{equation}\begin{split}&(2N)^{k^2}e^{-Nk}\gamma_k\left(1 + \frac{Nkt^2}{2} + \frac{N^2k^2t^4}{8} + O(N^{3})O(t^6)\right)\left(1 - \frac{k^2t^2}{8} + \frac{t^4}{128}k^2(k^2-2) + O(t^6)\right)\\&\times\left[1 + \frac{1}{N}\left(\frac{k}{12}(8k^2-1) + \frac{kt^2}{96}(13k^2-1)+O(t^4)\right) + \frac{1}{N^2}\left(\frac{k^2}{144}(32k^4 - 56k^2 + 17) + O(t^2)\right)\right.\\&\left. +O(N^{-3})\right],\end{split}\end{equation}
\begin{equation}\begin{split}&(2N)^{k^2}e^{-Nk}\gamma_k\left(1 + \frac{Nkt^2}{2} + \frac{N^2k^2t^4}{8} + O(N^{3})O(t^6)\right)\left(1 - \frac{k^2t^2}{8} + \frac{t^4}{128}k^2(k^2-2) + O(t^6)\right)\\&\times\left[1 + \frac{1}{N}\left(\frac{k}{12}(8k^2-1) + \frac{kt^2}{96}(13k^2-1)+O(t^4)\right) + \frac{1}{N^2}\left(\frac{k^2}{144}(32k^4 - 56k^2 + 17) + O(t^2)\right)\right.\\&\left. +O(N^{-3})\right],\end{split}\end{equation}
where the first two brackets correspond to the expansion of
![]() $e^{\frac{Nkt^2}{2}}$
and
$e^{\frac{Nkt^2}{2}}$
and
![]() $\pi\rho_{sc}(t)$
, respectively, up to
$\pi\rho_{sc}(t)$
, respectively, up to
![]() $O(t^4)$
, and the last factor is sub-leading.
$O(t^4)$
, and the last factor is sub-leading.
4. Secular coefficients
Consider a matrix M of size N. Its characteristic polynomial can be expanded as
where
![]() $\textrm{Sc}_j$
is the
$\textrm{Sc}_j$
is the
![]() $j\textrm{th}$
secular coefficient of the characteristic polynomial. We have
$j\textrm{th}$
secular coefficient of the characteristic polynomial. We have
These secular coefficients are nothing but the elementary symmetric polynomials
![]() $e_j$
defined as
$e_j$
defined as
for
![]() $j\leq N$
and
$j\leq N$
and
![]() $e_j=0$
for
$e_j=0$
for
![]() $j>N$
.
$j>N$
.
The correlations of secular coefficients and their connections to combinatorics have been studied previously [Reference Forrester and Gamburd21, Reference Diaconis and Gamburd17]. For example, the joint moments of secular coefficients of the unitary group are connected to the enumeration of magic squares: matrices with positive entries with prescribed row and column sum. In a similar way, the joint moments of secular coefficients of Hermitian ensembles, such as the GUE, are connected to matching polynomials of closed graphs. In this section, we compute these correlations and indicate their combinatorial properties.
Gaussian ensemble: Elementary symmetric polynomials can be expanded in terms of multivariate Hermite polynomials as
 \begin{equation}e_r = \sum_{j=0}^{\lfloor\frac{r}{2}\rfloor}\Psi^{(H)}_{(1^r)(1^{r-2j})}\mathscr{H}_{(1^{r-2j})},\end{equation}
\begin{equation}e_r = \sum_{j=0}^{\lfloor\frac{r}{2}\rfloor}\Psi^{(H)}_{(1^r)(1^{r-2j})}\mathscr{H}_{(1^{r-2j})},\end{equation}
where
Equivalently, we have
with
 \begin{equation}\begin{split}\Psi^{(H)}_{(1^{2r})(1^{2j})} &= (\!-1)^{r-j}\frac{1}{(2N)^{r-j}(r-j)!}\frac{(N-2j)!}{(N-2r)!},\\ \\[-8pt]\Psi^{(H)}_{(1^{2r+1})(1^{2j+1})} &= (\!-1)^{r-j}\frac{1}{(2N)^{r-j}(r-j)!}\frac{(N-2j-1)!}{(N-2r-1)!}.\end{split}\end{equation}
\begin{equation}\begin{split}\Psi^{(H)}_{(1^{2r})(1^{2j})} &= (\!-1)^{r-j}\frac{1}{(2N)^{r-j}(r-j)!}\frac{(N-2j)!}{(N-2r)!},\\ \\[-8pt]\Psi^{(H)}_{(1^{2r+1})(1^{2j+1})} &= (\!-1)^{r-j}\frac{1}{(2N)^{r-j}(r-j)!}\frac{(N-2j-1)!}{(N-2r-1)!}.\end{split}\end{equation}
Because of the orthogonality of the
![]() $\mathcal{H}_\mu$
,
$\mathcal{H}_\mu$
,
 \begin{equation}\mathbb{E}^{(H)}_N[\textrm{Sc}_r] = \mathbb{E}^{(H)}_N[e_r] =\begin{cases}(\!-1)^{\dfrac{r}{2}}\frac{1}{(2N)^{\frac{r}{2}}\frac{r}{2}!}\frac{N!}{(N-r)!},& \text{if r is even},\\ \\[-8pt]0,& \text{if r is odd}.\end{cases}\end{equation}
\begin{equation}\mathbb{E}^{(H)}_N[\textrm{Sc}_r] = \mathbb{E}^{(H)}_N[e_r] =\begin{cases}(\!-1)^{\dfrac{r}{2}}\frac{1}{(2N)^{\frac{r}{2}}\frac{r}{2}!}\frac{N!}{(N-r)!},& \text{if r is even},\\ \\[-8pt]0,& \text{if r is odd}.\end{cases}\end{equation}
These expectations are nothing but the coefficients of Hermite polynomial of degree N. Thus,
 \begin{equation}\begin{split}\mathbb{E}^{(H)}_N[\det(t-M)] &= \sum_{j=0}^{\lfloor\frac{N}{2}\rfloor}\mathbb{E}^{(H)}_N[\textrm{Sc}_{2j}(M)]t^{N-2j}=h_N(t),\end{split}\end{equation}
\begin{equation}\begin{split}\mathbb{E}^{(H)}_N[\det(t-M)] &= \sum_{j=0}^{\lfloor\frac{N}{2}\rfloor}\mathbb{E}^{(H)}_N[\textrm{Sc}_{2j}(M)]t^{N-2j}=h_N(t),\end{split}\end{equation}
which coincides with (2.20) for
![]() $p=1$
. The expectation
$p=1$
. The expectation
![]() $|N^j\mathbb{E}^{(H)}_N[\textrm{Sc}_{2j}(M)]|$
is equal to the number of 2j matchings in the complete graph [Reference Diaconis and Gamburd17, Reference Forrester and Gamburd21].
$|N^j\mathbb{E}^{(H)}_N[\textrm{Sc}_{2j}(M)]|$
is equal to the number of 2j matchings in the complete graph [Reference Diaconis and Gamburd17, Reference Forrester and Gamburd21].
By using (4.4), the second moment of the secular coefficient can also be computed. Similar to the univariate case, multivariate Hermite polynomials
![]() $\mathscr{H}_\lambda$
corresponding to even and odd
$\mathscr{H}_\lambda$
corresponding to even and odd
![]() $|\lambda|$
do not mix. Hence, we obtain
$|\lambda|$
do not mix. Hence, we obtain
and
 \begin{equation}\begin{split}\mathbb{E}^{(H)}_N[\textrm{Sc}_{2r}(M)\textrm{Sc}_{2s}(M)] &= \sum_{j=0}^r\sum_{k=0}^s\Psi^{(H)}_{(1^{2r})(1^{2j})}\Psi^{(H)}_{(1^{2s})(1^{2k})}\mathbb{E}^{(H)}_N[\mathscr{H}_{(1^{2j})}\mathscr{H}_{(1^{2k})}]\\&= \sum_{j=0}^{\min(r,s)}\frac{1}{N^{2j}}\Psi^{(H)}_{(1^{2r})(1^{2j})}\Psi^{(H)}_{(1^{2s})(1^{2j})}C_{(1^{2j})}(N)\\&=\left(\!-\frac{1}{2N}\right)^{r+s}\, \sum_{j=0}^{\min(r,s)}\frac{2^{2j}}{(r-j)!(s-j)!}\frac{N!(N-2j)!}{(N-2r)!(N-2s)!}.\end{split}\end{equation}
\begin{equation}\begin{split}\mathbb{E}^{(H)}_N[\textrm{Sc}_{2r}(M)\textrm{Sc}_{2s}(M)] &= \sum_{j=0}^r\sum_{k=0}^s\Psi^{(H)}_{(1^{2r})(1^{2j})}\Psi^{(H)}_{(1^{2s})(1^{2k})}\mathbb{E}^{(H)}_N[\mathscr{H}_{(1^{2j})}\mathscr{H}_{(1^{2k})}]\\&= \sum_{j=0}^{\min(r,s)}\frac{1}{N^{2j}}\Psi^{(H)}_{(1^{2r})(1^{2j})}\Psi^{(H)}_{(1^{2s})(1^{2j})}C_{(1^{2j})}(N)\\&=\left(\!-\frac{1}{2N}\right)^{r+s}\, \sum_{j=0}^{\min(r,s)}\frac{2^{2j}}{(r-j)!(s-j)!}\frac{N!(N-2j)!}{(N-2r)!(N-2s)!}.\end{split}\end{equation}
Similarly, we write
 \begin{equation}\mathbb{E}^{(H)}_N[\textrm{Sc}_{2r+1}(M)\textrm{Sc}_{2s+1}(M)] = \left(\!-\frac{1}{2N}\right)^{r+s}\,\sum_{j=0}^{\min(r,s)}\frac{2^{2j}}{(r-j)!(s-j)!}\frac{(N-1)!(N-2j-1)!}{(N-2r-1)!(N-2s-1)!}.\end{equation}
\begin{equation}\mathbb{E}^{(H)}_N[\textrm{Sc}_{2r+1}(M)\textrm{Sc}_{2s+1}(M)] = \left(\!-\frac{1}{2N}\right)^{r+s}\,\sum_{j=0}^{\min(r,s)}\frac{2^{2j}}{(r-j)!(s-j)!}\frac{(N-1)!(N-2j-1)!}{(N-2r-1)!(N-2s-1)!}.\end{equation}
Computing higher order correlations requires evaluating integrals involving a sequence of multivariate Hermite polynomials. Busbridge [Reference Busbridge11, Reference Busbridge12] calculated these integrals for the univariate case, but the results are still unknown for the multivariate generalisation. Instead, we take a different approach by first expressing the product
![]() $\prod_j\textrm{Sc}_j(M))^{b_j}$
in terms of the
$\prod_j\textrm{Sc}_j(M))^{b_j}$
in terms of the
![]() $\mathscr{H}_\mu$
and then using orthogonality for the
$\mathscr{H}_\mu$
and then using orthogonality for the
![]() $\mathscr{H}_\mu$
.
$\mathscr{H}_\mu$
.
Proposition 4.1. Consider a partition
![]() $\lambda = (\lambda_1,\dots ,\lambda_l)$
. We have
$\lambda = (\lambda_1,\dots ,\lambda_l)$
. We have
 \begin{equation}\mathbb{E}^{(H)}_N\big[\prod_{j=1}^l\textrm{Sc}_{\lambda_j}(M)\big] =\begin{cases}\sum_\mu \dfrac{1}{(2N)^{\frac{\mu}{2}}\frac{|\mu|}{2}!}K_{\lambda^\prime\mu}\chi^{\mu}_{(2^{|\mu|/2})}C_\mu(N),&\quad \text{if $|\lambda|$ is even},\\ \\[-9pt] 0, &\quad \text{otherwise}.\end{cases}\end{equation}
\begin{equation}\mathbb{E}^{(H)}_N\big[\prod_{j=1}^l\textrm{Sc}_{\lambda_j}(M)\big] =\begin{cases}\sum_\mu \dfrac{1}{(2N)^{\frac{\mu}{2}}\frac{|\mu|}{2}!}K_{\lambda^\prime\mu}\chi^{\mu}_{(2^{|\mu|/2})}C_\mu(N),&\quad \text{if $|\lambda|$ is even},\\ \\[-9pt] 0, &\quad \text{otherwise}.\end{cases}\end{equation}
Here
![]() $K_{\lambda\mu}$
are Kostka numbersFootnote 1 and
$K_{\lambda\mu}$
are Kostka numbersFootnote 1 and
![]() $\chi^\mu_\nu$
is the character of the symmetric group.
$\chi^\mu_\nu$
is the character of the symmetric group.
Proof. For a partition
![]() $\lambda$
, denote
$\lambda$
, denote
Elementary symmetric polynomials
![]() $e_\lambda$
can be expanded in Schur basis as follows:
$e_\lambda$
can be expanded in Schur basis as follows:
where
![]() $K_{\lambda\mu}$
are the Kostka numbers [Reference Macdonald39] and
$K_{\lambda\mu}$
are the Kostka numbers [Reference Macdonald39] and
![]() $\mu$
is a partition of
$\mu$
is a partition of
![]() $|\lambda|$
. Using (2.5),
$|\lambda|$
. Using (2.5),
When
![]() $|\lambda|$
is odd,
$|\lambda|$
is odd,
![]() $\mathbb{E}^{(H)}_N[e_\lambda]=0$
due to the orthogonality of multivariate Hermite polynomials. When
$\mathbb{E}^{(H)}_N[e_\lambda]=0$
due to the orthogonality of multivariate Hermite polynomials. When
![]() $|\lambda|$
is even,
$|\lambda|$
is even,
 \begin{equation}\begin{split}\mathbb{E}^{(H)}_N[e_\lambda] &= \mathbb{E}^{(H)}_N\big[\prod_{j=1}^l\textrm{Sc}_{\lambda_j}(M)\big]\\ &= \mathbb{E}^{(H)}_N\big[\sum_{\mu}\sum_\nu K_{\lambda^\prime\mu}\Psi^{(H)}_{\mu \nu}\mathscr{H}_\nu\big]\\ &=K_{\lambda^\prime\mu}\Psi^{(H)}_{\mu 0}.\end{split}\end{equation}
\begin{equation}\begin{split}\mathbb{E}^{(H)}_N[e_\lambda] &= \mathbb{E}^{(H)}_N\big[\prod_{j=1}^l\textrm{Sc}_{\lambda_j}(M)\big]\\ &= \mathbb{E}^{(H)}_N\big[\sum_{\mu}\sum_\nu K_{\lambda^\prime\mu}\Psi^{(H)}_{\mu \nu}\mathscr{H}_\nu\big]\\ &=K_{\lambda^\prime\mu}\Psi^{(H)}_{\mu 0}.\end{split}\end{equation}
It can be shown that [Reference Jonnadula, Keating and Mezzadri34]
Putting everything together completes the proof.
Laguerre ensemble: All the calculations discussed for the Gaussian ensemble can be extended to the Laguerre and the Jacobi ensembles.
The polynomials
![]() $e_r$
can be expanded as
$e_r$
can be expanded as
where
By using the orthogonality of the multivariate Laguerre polynomials we arrive at
which are the absolute values of the coefficients of the Laguerre polynomial of degree N. For the characteristic polynomial, we have
The correlations of secular coefficients can be computed similar to the Gaussian case.
Proposition 4.2. Let
![]() $\lambda = (\lambda_1,\dots ,\lambda_l)$
, we have
$\lambda = (\lambda_1,\dots ,\lambda_l)$
, we have
 \begin{equation}\mathbb{E}^{(L)}_N\big[\prod_{j=1}^l\textrm{Sc}_{\lambda_j}(M)\big] =\sum_{\mu\vdash |\lambda|}\frac{1}{(2N)^{|\lambda|}}\frac{G_\mu(N,\gamma)G_\mu(N,0)}{G_0(N,\gamma)G_0(N,0)}\frac{\chi^\mu_{(1^{|\mu|})}}{|\lambda|!} K_{\lambda^\prime\mu}.\end{equation}
\begin{equation}\mathbb{E}^{(L)}_N\big[\prod_{j=1}^l\textrm{Sc}_{\lambda_j}(M)\big] =\sum_{\mu\vdash |\lambda|}\frac{1}{(2N)^{|\lambda|}}\frac{G_\mu(N,\gamma)G_\mu(N,0)}{G_0(N,\gamma)G_0(N,0)}\frac{\chi^\mu_{(1^{|\mu|})}}{|\lambda|!} K_{\lambda^\prime\mu}.\end{equation}
Proof. The proof is similar to the Gaussian case. By writing
and using the orthogonality of the multivariate Laguerre polynomials along with the result [Reference Jonnadula, Keating and Mezzadri34]
proves the proposition.
Jacobi ensemble. The
![]() $e_r$
can be expanded as
$e_r$
can be expanded as
where
![]() $\Psi^{(J)}_{\lambda\nu}$
is given in (2.8). The expected values of the
$\Psi^{(J)}_{\lambda\nu}$
is given in (2.8). The expected values of the
![]() $e_r$
are related to the coefficients of the Jacobi polynomial of degree N.
$e_r$
are related to the coefficients of the Jacobi polynomial of degree N.
Acknowledgements
FM is grateful for support from the University Research Fellowship of the University of Bristol. JPK is pleased to acknowledge support from a Royal Society Wolfson Research Merit Award and ERC Advanced Grant 740900 (LogCorRM).
Appendix
A. Asymptotics of ratio of factorials
The asymptotics of the ratio of factorials can be computed as follows. First we look at
![]() $C_\lambda(2k)D_{e}$
with
$C_\lambda(2k)D_{e}$
with
![]() $\lambda=(2m,\dots,2m)$
. Consider
$\lambda=(2m,\dots,2m)$
. Consider
Now, one can see that
Using the duplication formula for the Gamma functions
and Stirling’s series
the asymptotic expansion for the ratio of Gamma functions can be found. Here
![]() $B_j$
is the Bernoulli polynomial of degree j. Combining all the formulae, up to first order correction,
$B_j$
is the Bernoulli polynomial of degree j. Combining all the formulae, up to first order correction,
 \begin{equation}C_{((2m)^{2k})}(2k) D_e = e^{-2mk}2^{4mk+2k^2}m^{2mk+k^2}\left(\prod_{j=0}^{k-1}\frac{j!}{(k+j)!}\right)\left[1 + \frac{k}{12m}(4k^2+1)+O(m^{-2})\right].\end{equation}
\begin{equation}C_{((2m)^{2k})}(2k) D_e = e^{-2mk}2^{4mk+2k^2}m^{2mk+k^2}\left(\prod_{j=0}^{k-1}\frac{j!}{(k+j)!}\right)\left[1 + \frac{k}{12m}(4k^2+1)+O(m^{-2})\right].\end{equation}
Similarly for the case
![]() $C_\lambda(2k)D_o$
, we obtain
$C_\lambda(2k)D_o$
, we obtain
Let
![]() $z=m+\frac{1}{2}$
, then
$z=m+\frac{1}{2}$
, then
and
Combining the above formulae and using (A.3) and (A.4),
 \begin{equation}\begin{split}C_{((2m+1)^{2k})}D_o\equiv C_{((2z)^{2k})}D_o= & (\!-1)^ke^{-2zk}z^{k^2+2kz}2^{2k^2+4kz}\left(\prod_{j=0}^{k-1}\frac{j!}{(k+j)!}\right)\\&\quad\times \left[1 + \frac{k}{6z}(2k^2-1)+O(z^{-2})\right].\end{split}\end{equation}
\begin{equation}\begin{split}C_{((2m+1)^{2k})}D_o\equiv C_{((2z)^{2k})}D_o= & (\!-1)^ke^{-2zk}z^{k^2+2kz}2^{2k^2+4kz}\left(\prod_{j=0}^{k-1}\frac{j!}{(k+j)!}\right)\\&\quad\times \left[1 + \frac{k}{6z}(2k^2-1)+O(z^{-2})\right].\end{split}\end{equation}
Higher order corrections can also be calculated with some effort or using any commercial software like Mathematica. Writing in terms of the matrix size N, as
![]() $N\rightarrow\infty$
, we have
$N\rightarrow\infty$
, we have
 \begin{equation}\begin{split}&C_{(N^{2k})}D_e = e^{-Nk}(2N)^{Nk+k^2}\left(\prod_{j=0}^{k-1}\frac{j!}{(k+j)!}\right)\left[1+\frac{k}{6N}(4k^2+1) + \frac{k^2}{72N^2}(16k^4-16k^2-11) \right.\\&\qquad\qquad\qquad\left. +\frac{k}{6480N^3}(320k^8-1200k^6+708k^4+1265k^2-756) \right.\\&\qquad\qquad\qquad\left. +\frac{k^2}{155,520N^4} ( 1280 k^{10}- 10,240 k^8+ 25,248 k^6 - 6400 k^4- 56,371 k^2 +51,408)\right.\\&\qquad\qquad\qquad \left. +\frac{k}{6,531,840N^5}\Big(7168 k^{14}- 98,560 k^{12} +499,072 k^{10} - 982,688 k^8 - 399,844 k^6\right.\\&\qquad\qquad\qquad\qquad\left. + 4,606,735 k^4- 5,598,936 k^2 +1,607,040 \Big)\right.\\&\qquad\qquad\qquad\left. + \frac{k^2}{1,175,731,200N^6}\Big(143,360 k^{16} -3,010,560 k^{14} + 25,294,080 k^{12} - 103,093,760 k^{10} \right.\\&\qquad\qquad\qquad\qquad\left.+ 158,864,016 k^8 +298,943,760 k^6- 1,697,420,809 k^4 + 2,663,679,600 k^2 \right.\\&\qquad\qquad\qquad\left. -1,390,123,296\Big)+O\left(\frac{1}{N^{7}}\right)\right], \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad N\,\, \text{even}.\end{split}\end{equation}
\begin{equation}\begin{split}&C_{(N^{2k})}D_e = e^{-Nk}(2N)^{Nk+k^2}\left(\prod_{j=0}^{k-1}\frac{j!}{(k+j)!}\right)\left[1+\frac{k}{6N}(4k^2+1) + \frac{k^2}{72N^2}(16k^4-16k^2-11) \right.\\&\qquad\qquad\qquad\left. +\frac{k}{6480N^3}(320k^8-1200k^6+708k^4+1265k^2-756) \right.\\&\qquad\qquad\qquad\left. +\frac{k^2}{155,520N^4} ( 1280 k^{10}- 10,240 k^8+ 25,248 k^6 - 6400 k^4- 56,371 k^2 +51,408)\right.\\&\qquad\qquad\qquad \left. +\frac{k}{6,531,840N^5}\Big(7168 k^{14}- 98,560 k^{12} +499,072 k^{10} - 982,688 k^8 - 399,844 k^6\right.\\&\qquad\qquad\qquad\qquad\left. + 4,606,735 k^4- 5,598,936 k^2 +1,607,040 \Big)\right.\\&\qquad\qquad\qquad\left. + \frac{k^2}{1,175,731,200N^6}\Big(143,360 k^{16} -3,010,560 k^{14} + 25,294,080 k^{12} - 103,093,760 k^{10} \right.\\&\qquad\qquad\qquad\qquad\left.+ 158,864,016 k^8 +298,943,760 k^6- 1,697,420,809 k^4 + 2,663,679,600 k^2 \right.\\&\qquad\qquad\qquad\left. -1,390,123,296\Big)+O\left(\frac{1}{N^{7}}\right)\right], \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad N\,\, \text{even}.\end{split}\end{equation}
 \begin{equation}\begin{split}&C_{(N^{2k})}D_o= (\!-1)^ke^{-Nk}(2N)^{Nk+k^2}\left(\prod_{j=0}^{k-1}\frac{j!}{(k+j)!}\right)\left[1 + \frac{k}{3N}(2k^2-1) + \frac{k^2}{18N^2}(4k^4-10k^2+7)\right.\\&\left. \qquad\qquad \qquad + \frac{k}{810N^3}(40k^8-240k^6+516k^4-455k^2+108)\right.\\&\qquad\qquad\qquad\left.+\frac{k^2}{9720N^4}(80 k^{10}- 880 k^8+ 3828 k^6 - 8356 k^4 + 9509 k^2-4320)\right.\\&\qquad\qquad\qquad \left. + \frac{k}{204,120N^5}\Big(224\,k^{14} - 3920\, k^{12} +28,616\,k^{10} - 113,428\,k^8 + 266,818\,k^6\right.\\&\qquad\qquad\qquad\qquad\left. - 372,127\,k^4 + 255,528\,k^2 -51,840 \Big)\right.\\&\qquad\qquad\qquad\left. +\frac{k^2}{18,370,800N^6}\Big(2240\,k^{16} - 57,120\,k^{14}+ 628,320\,k^{12} - 3,919,160\,k^{10} \right.\\&\qquad\qquad\quad\qquad\left. + 15,363,624\,k^8 - 39,481,170\,k^6 + 65,605,589\,k^4 - 62,864,640\,k^2 +25,046,496 \Big)\right.\\ &\qquad\qquad\qquad\left. + O\left(\frac{1}{N^7}\right)\right], \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad N\,\, \text{odd}.\end{split}\end{equation}
\begin{equation}\begin{split}&C_{(N^{2k})}D_o= (\!-1)^ke^{-Nk}(2N)^{Nk+k^2}\left(\prod_{j=0}^{k-1}\frac{j!}{(k+j)!}\right)\left[1 + \frac{k}{3N}(2k^2-1) + \frac{k^2}{18N^2}(4k^4-10k^2+7)\right.\\&\left. \qquad\qquad \qquad + \frac{k}{810N^3}(40k^8-240k^6+516k^4-455k^2+108)\right.\\&\qquad\qquad\qquad\left.+\frac{k^2}{9720N^4}(80 k^{10}- 880 k^8+ 3828 k^6 - 8356 k^4 + 9509 k^2-4320)\right.\\&\qquad\qquad\qquad \left. + \frac{k}{204,120N^5}\Big(224\,k^{14} - 3920\, k^{12} +28,616\,k^{10} - 113,428\,k^8 + 266,818\,k^6\right.\\&\qquad\qquad\qquad\qquad\left. - 372,127\,k^4 + 255,528\,k^2 -51,840 \Big)\right.\\&\qquad\qquad\qquad\left. +\frac{k^2}{18,370,800N^6}\Big(2240\,k^{16} - 57,120\,k^{14}+ 628,320\,k^{12} - 3,919,160\,k^{10} \right.\\&\qquad\qquad\quad\qquad\left. + 15,363,624\,k^8 - 39,481,170\,k^6 + 65,605,589\,k^4 - 62,864,640\,k^2 +25,046,496 \Big)\right.\\ &\qquad\qquad\qquad\left. + O\left(\frac{1}{N^7}\right)\right], \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad N\,\, \text{odd}.\end{split}\end{equation}
B. More on the second moment
Fix
![]() $\lambda=(N,N)$
. The second moment of the characteristic polynomial is given by
$\lambda=(N,N)$
. The second moment of the characteristic polynomial is given by
Let
![]() $\nu=(\nu_1,\nu_2)\subseteq \lambda$
. Since
$\nu=(\nu_1,\nu_2)\subseteq \lambda$
. Since
![]() $|\nu|$
is even, either both
$|\nu|$
is even, either both
![]() $\nu_1$
,
$\nu_1$
,
![]() $\nu_2$
are even or both of them are odd. For
$\nu_2$
are even or both of them are odd. For
![]() $N=2m$
,
$N=2m$
,
![]() $m\in\mathbb{N}$
,
$m\in\mathbb{N}$
,
 \begin{equation}D^{(H)}_{\lambda\nu} =\begin{cases}\dfrac{1}{\left(m-\frac{\nu_1}{2}\right)!\left(m-\frac{\nu_2}{2}\right)!},\qquad\qquad\,\, \text{$\nu_1$, $\nu_2$ are even},\\ \\[-9pt] -\dfrac{1}{\left(m-\frac{\nu_1+1}{2}\right)!\left(m-\frac{\nu_2-1}{2}\right)!},\quad\quad\text{$\nu_1$, $\nu_2$ are odd}.\end{cases}\end{equation}
\begin{equation}D^{(H)}_{\lambda\nu} =\begin{cases}\dfrac{1}{\left(m-\frac{\nu_1}{2}\right)!\left(m-\frac{\nu_2}{2}\right)!},\qquad\qquad\,\, \text{$\nu_1$, $\nu_2$ are even},\\ \\[-9pt] -\dfrac{1}{\left(m-\frac{\nu_1+1}{2}\right)!\left(m-\frac{\nu_2-1}{2}\right)!},\quad\quad\text{$\nu_1$, $\nu_2$ are odd}.\end{cases}\end{equation}
Therefore,
 \begin{equation}C_\lambda(2)D^{(H)}_{\lambda\nu} =(2m)!(2m+1)!\begin{cases}\frac{1}{\left(m-\frac{\nu_1}{2}\right)!}\frac{1}{\left(m-\frac{\nu_2}{2}\right)!},\qquad\quad\,\, \text{$\nu_1$, $\nu_2$ are even},\\ \\[-8pt]-\dfrac{1}{\left(m-\frac{\nu_1+1}{2}\right)!}\frac{1}{\left(m-\frac{\nu_2-1}{2}\right)!},\quad\,\text{$\nu_1$, $\nu_2$ are odd}.\end{cases}\end{equation}
\begin{equation}C_\lambda(2)D^{(H)}_{\lambda\nu} =(2m)!(2m+1)!\begin{cases}\frac{1}{\left(m-\frac{\nu_1}{2}\right)!}\frac{1}{\left(m-\frac{\nu_2}{2}\right)!},\qquad\quad\,\, \text{$\nu_1$, $\nu_2$ are even},\\ \\[-8pt]-\dfrac{1}{\left(m-\frac{\nu_1+1}{2}\right)!}\frac{1}{\left(m-\frac{\nu_2-1}{2}\right)!},\quad\,\text{$\nu_1$, $\nu_2$ are odd}.\end{cases}\end{equation}
Similarly, for
![]() $N=2m+1$
,
$N=2m+1$
,
![]() $m\in\mathbb{N}$
, we have
$m\in\mathbb{N}$
, we have
 \begin{equation}D^{(H)}_{\lambda\nu} =\begin{cases}-\dfrac{1}{\left(m-\frac{\nu_1}{2}\right)!\left(m-\frac{\nu_2-2}{2}\right)!},\qquad\quad \text{$\nu_1$, $\nu_2$ are even},\\ \\[-8pt]\dfrac{1}{\left(m-\frac{\nu_1-1}{2}\right)!\left(m-\frac{\nu_2-1}{2}\right)!},\qquad\quad\text{$\nu_1$, $\nu_2$ are odd},\end{cases}\end{equation}
\begin{equation}D^{(H)}_{\lambda\nu} =\begin{cases}-\dfrac{1}{\left(m-\frac{\nu_1}{2}\right)!\left(m-\frac{\nu_2-2}{2}\right)!},\qquad\quad \text{$\nu_1$, $\nu_2$ are even},\\ \\[-8pt]\dfrac{1}{\left(m-\frac{\nu_1-1}{2}\right)!\left(m-\frac{\nu_2-1}{2}\right)!},\qquad\quad\text{$\nu_1$, $\nu_2$ are odd},\end{cases}\end{equation}
and
 \begin{equation}C_\lambda(2)D^{(H)}_{\lambda\nu} =(2m+1)!(2m+2)!\begin{cases}-\dfrac{1}{\left(m-\frac{\nu_1}{2}\right)!}\frac{1}{\left(m-\frac{\nu_2-2}{2}\right)!},\quad \text{$\nu_1$, $\nu_2$ are even},\\ \\[-8pt]\dfrac{1}{\left(m-\frac{\nu_1-1}{2}\right)!}\frac{1}{\left(m-\frac{\nu_2-1}{2}\right)!},\quad\text{$\nu_1$, $\nu_2$ are odd}.\end{cases}\end{equation}
\begin{equation}C_\lambda(2)D^{(H)}_{\lambda\nu} =(2m+1)!(2m+2)!\begin{cases}-\dfrac{1}{\left(m-\frac{\nu_1}{2}\right)!}\frac{1}{\left(m-\frac{\nu_2-2}{2}\right)!},\quad \text{$\nu_1$, $\nu_2$ are even},\\ \\[-8pt]\dfrac{1}{\left(m-\frac{\nu_1-1}{2}\right)!}\frac{1}{\left(m-\frac{\nu_2-1}{2}\right)!},\quad\text{$\nu_1$, $\nu_2$ are odd}.\end{cases}\end{equation}
For a partition of length 2,
![]() $\nu=(\nu_1,\nu_2)$
,
$\nu=(\nu_1,\nu_2)$
,
Inserting (B.3), (B.5), (B.6) in (B.1), and observing that
![]() $\nu$
runs over all partitions such that
$\nu$
runs over all partitions such that
![]() $0\leq|\nu|\leq 2N$
gives
$0\leq|\nu|\leq 2N$
gives
 \begin{equation}\begin{split}\mathbb{E}^{(H)}_{N}\left[\det(t-M)^{2}\right] & = \left(\!-\frac{1}{2N}\right)^NC_\lambda(2)D^{(H)}_{\lambda 0}\sum_{k=0}^N(\!-2N)^kt^{2k}\\&\quad\times\Big[\sum_{j=0}^{\lfloor{\frac{k-1}{2}}\rfloor}\left(\frac{2k+1-4j}{(2k+1-2j)!(2j)!}-\frac{2k-1-4j}{(2k-2j)!(2j+1)!}\right)\frac{\left(\frac{N}{2}\right)!^2}{(\frac{N}{2}-k+j)!(\frac{N}{2}-j)!}\\&\qquad\qquad\quad + \frac{1}{k!(k+1)!}\frac{\left(\frac{N}{2}\right)!^2}{\left(\frac{N}{2}-\frac{k}{2}\right)!^2}\unicode{x1D7D9}_{k= 0\,\text{mod}\,2}\Big].\end{split}\end{equation}
\begin{equation}\begin{split}\mathbb{E}^{(H)}_{N}\left[\det(t-M)^{2}\right] & = \left(\!-\frac{1}{2N}\right)^NC_\lambda(2)D^{(H)}_{\lambda 0}\sum_{k=0}^N(\!-2N)^kt^{2k}\\&\quad\times\Big[\sum_{j=0}^{\lfloor{\frac{k-1}{2}}\rfloor}\left(\frac{2k+1-4j}{(2k+1-2j)!(2j)!}-\frac{2k-1-4j}{(2k-2j)!(2j+1)!}\right)\frac{\left(\frac{N}{2}\right)!^2}{(\frac{N}{2}-k+j)!(\frac{N}{2}-j)!}\\&\qquad\qquad\quad + \frac{1}{k!(k+1)!}\frac{\left(\frac{N}{2}\right)!^2}{\left(\frac{N}{2}-\frac{k}{2}\right)!^2}\unicode{x1D7D9}_{k= 0\,\text{mod}\,2}\Big].\end{split}\end{equation}
for N even. Similarly, for N odd, one gets
 \begin{equation}\begin{split}&\mathbb{E}^{(H)}_{N}\left[\det(t-M)^{2}\right]\ \\ & = \left(\!-\frac{1}{2N}\right)^NC_\lambda(2)D^{(H)}_{\lambda 0}\sum_{k=0}^N(\!-2N)^kt^{2k}\\&\times\bigg[\sum_{j=0}^{\lfloor{\frac{k-2}{2}}\rfloor}\left(\!-\frac{2k-1-4j}{(2k-2j)!(2j+1)!}+\frac{2k-3-4j}{(2k-2j-1)!(2j+2)!}\right)\frac{\left(\frac{N-1}{2}\right)!\,\left(\frac{N+1}{2}\right)!}{\left(\left(\frac{N+1}{2}\right)-k+j\right)!\left(\left(\frac{N-1}{2}\right)-j\right)!}\\&\qquad\qquad\quad +\frac{1}{(2k)!}\frac{\left(\frac{N-1}{2}\right)!}{\left(\left(\frac{N-1}{2}\right)-k\right)!}- \frac{1}{k!(k+1)!}\frac{\left(\frac{N-1}{2}\right)!\,\left(\frac{N+1}{2}\right)!}{\left(\left(\frac{N-1}{2}\right)-\frac{k-1}{2}\right)!^2}\unicode{x1D7D9}_{k= 1\,\text{mod}\,2}\bigg].\end{split}\end{equation}
\begin{equation}\begin{split}&\mathbb{E}^{(H)}_{N}\left[\det(t-M)^{2}\right]\ \\ & = \left(\!-\frac{1}{2N}\right)^NC_\lambda(2)D^{(H)}_{\lambda 0}\sum_{k=0}^N(\!-2N)^kt^{2k}\\&\times\bigg[\sum_{j=0}^{\lfloor{\frac{k-2}{2}}\rfloor}\left(\!-\frac{2k-1-4j}{(2k-2j)!(2j+1)!}+\frac{2k-3-4j}{(2k-2j-1)!(2j+2)!}\right)\frac{\left(\frac{N-1}{2}\right)!\,\left(\frac{N+1}{2}\right)!}{\left(\left(\frac{N+1}{2}\right)-k+j\right)!\left(\left(\frac{N-1}{2}\right)-j\right)!}\\&\qquad\qquad\quad +\frac{1}{(2k)!}\frac{\left(\frac{N-1}{2}\right)!}{\left(\left(\frac{N-1}{2}\right)-k\right)!}- \frac{1}{k!(k+1)!}\frac{\left(\frac{N-1}{2}\right)!\,\left(\frac{N+1}{2}\right)!}{\left(\left(\frac{N-1}{2}\right)-\frac{k-1}{2}\right)!^2}\unicode{x1D7D9}_{k= 1\,\text{mod}\,2}\bigg].\end{split}\end{equation}
We have
 \begin{equation}C_\lambda(2)D^{(H)}_{\lambda 0} =\begin{cases}\dfrac{N!(N+1)!}{\left(\frac{N}{2}\right)!^2},\qquad\quad\,\,\,\, \text{N even},\\ \\[-9pt]-\dfrac{N!(N+1)!}{\left(\frac{N-1}{2}\right)!\left(\frac{N+1}{2}\right)!},\quad \text{N odd}.\end{cases}\end{equation}
\begin{equation}C_\lambda(2)D^{(H)}_{\lambda 0} =\begin{cases}\dfrac{N!(N+1)!}{\left(\frac{N}{2}\right)!^2},\qquad\quad\,\,\,\, \text{N even},\\ \\[-9pt]-\dfrac{N!(N+1)!}{\left(\frac{N-1}{2}\right)!\left(\frac{N+1}{2}\right)!},\quad \text{N odd}.\end{cases}\end{equation}
The asymptotics of the ratio of the factorials are already discussed in Appendix A. For the special case in (B.9),
 \begin{equation}\begin{split} \frac{N!(N+1)!}{\left(\frac{N}{2}\right)!^2}&\sim e^{-N}(2N)^{N+1}\prod_{j=1}^\infty \exp\left(\frac{(\!-1)^j(2^{j+1}-2)B_{j+1}}{j(j+1)N^{j}}\right),\\ \\[-8pt] \frac{N!(N+1)!}{\left(\frac{N-1}{2}\right)!\left(\frac{N+1}{2}\right)!}&\sim e^{-N}(2N)^{N+1}\prod_{j=1}^\infty \exp\left(\frac{(\!-1)^{j+1}2^{j+1}B_{j+1}}{j(j+1)N^{j}}\right),\end{split}\end{equation}
\begin{equation}\begin{split} \frac{N!(N+1)!}{\left(\frac{N}{2}\right)!^2}&\sim e^{-N}(2N)^{N+1}\prod_{j=1}^\infty \exp\left(\frac{(\!-1)^j(2^{j+1}-2)B_{j+1}}{j(j+1)N^{j}}\right),\\ \\[-8pt] \frac{N!(N+1)!}{\left(\frac{N-1}{2}\right)!\left(\frac{N+1}{2}\right)!}&\sim e^{-N}(2N)^{N+1}\prod_{j=1}^\infty \exp\left(\frac{(\!-1)^{j+1}2^{j+1}B_{j+1}}{j(j+1)N^{j}}\right),\end{split}\end{equation}
where
![]() $B_n$
are Bernoulli numbers. The explicit asymptotic expansion is
$B_n$
are Bernoulli numbers. The explicit asymptotic expansion is
 \begin{align}C_\lambda(2)D^{(H)}_{\lambda 0}&= e^{-N}(2N)^{N+1}\left[1+\frac{5}{6\,N}-\frac{11}{72\,N^2}+\frac{337}{6480\,N^3}+\frac{985}{31,104\,N^4}-\frac{360,013}{6,531,840\,N^5}\right. \nonumber\\[3pt]&\left.\qquad\qquad\qquad-\frac{46,723,609}{1,175,731,200\,N^6} +\frac{224,766,221}{1,410,877,440\,N^7}+\frac{41,757,020,981}{338,610,585,600\,N^8}\right. \nonumber\\[3pt]&\left.\qquad\qquad\qquad-\frac{889,926,952,101,377}{1,005,673,439,232,000\,N^9}+O(N^{-10})\right],\, \text{N even}, \nonumber\\[3pt]C_\lambda(2)D^{(H)}_{\lambda 0}&= -e^{-N}(2N)^{N+1}\left[1+\frac{1}{3\,N}+\frac{1}{18\,N^2}-\frac{31}{810\,N^3}-\frac{139}{9720\,N^4}+\frac{9871}{204,120\,N^5}\right. \nonumber\\[3pt]&\left.\qquad\qquad\qquad+\frac{324,179}{18,370,800\,N^6} -\frac{8,225,671}{55,112,400\,N^7}-\frac{69,685,339}{1,322,697,600\,N^8}\right. \nonumber\\[3pt]&\left.\qquad\qquad\qquad+\frac{1,674,981,058,019}{1,964,205,936,000\,N^9}+O(N^{-10})\right],\quad \text{N odd}.\end{align}
\begin{align}C_\lambda(2)D^{(H)}_{\lambda 0}&= e^{-N}(2N)^{N+1}\left[1+\frac{5}{6\,N}-\frac{11}{72\,N^2}+\frac{337}{6480\,N^3}+\frac{985}{31,104\,N^4}-\frac{360,013}{6,531,840\,N^5}\right. \nonumber\\[3pt]&\left.\qquad\qquad\qquad-\frac{46,723,609}{1,175,731,200\,N^6} +\frac{224,766,221}{1,410,877,440\,N^7}+\frac{41,757,020,981}{338,610,585,600\,N^8}\right. \nonumber\\[3pt]&\left.\qquad\qquad\qquad-\frac{889,926,952,101,377}{1,005,673,439,232,000\,N^9}+O(N^{-10})\right],\, \text{N even}, \nonumber\\[3pt]C_\lambda(2)D^{(H)}_{\lambda 0}&= -e^{-N}(2N)^{N+1}\left[1+\frac{1}{3\,N}+\frac{1}{18\,N^2}-\frac{31}{810\,N^3}-\frac{139}{9720\,N^4}+\frac{9871}{204,120\,N^5}\right. \nonumber\\[3pt]&\left.\qquad\qquad\qquad+\frac{324,179}{18,370,800\,N^6} -\frac{8,225,671}{55,112,400\,N^7}-\frac{69,685,339}{1,322,697,600\,N^8}\right. \nonumber\\[3pt]&\left.\qquad\qquad\qquad+\frac{1,674,981,058,019}{1,964,205,936,000\,N^9}+O(N^{-10})\right],\quad \text{N odd}.\end{align}
Substituting the above asymptotic series in
and taking the average over N even and odd gives
 \begin{equation}\begin{split}&\lim_{N\rightarrow\infty}\frac{1}{2N}e^{N}\exp\left(\!-\frac{N t^2}{2}\right)\mathbb{E}^{(H)}_{N}\left[\det(t-M)^{2}\right] \\=& 1 - \frac{1}{8}t^2 - \frac{1}{128}t^4 - \frac{1}{1024}t^6-\frac{5}{32768}t^8-\frac{7}{262144}t^{10} + O(t^{12}).\end{split}\end{equation}
\begin{equation}\begin{split}&\lim_{N\rightarrow\infty}\frac{1}{2N}e^{N}\exp\left(\!-\frac{N t^2}{2}\right)\mathbb{E}^{(H)}_{N}\left[\det(t-M)^{2}\right] \\=& 1 - \frac{1}{8}t^2 - \frac{1}{128}t^4 - \frac{1}{1024}t^6-\frac{5}{32768}t^8-\frac{7}{262144}t^{10} + O(t^{12}).\end{split}\end{equation}
The R.H.S. in (B.13) coincides with
![]() $\pi\rho_{sc}(t)$
up to
$\pi\rho_{sc}(t)$
up to
![]() $O(t^{10})$
.
$O(t^{10})$
.